Navigation and Acquisition of Spatial
Knowledge in a Virtual Maze
Sabine Gillner and Hanspeter A. Mallot
Max-Planck-Institut für biologische Kybernetik
Abstract
n Spatial behavior in humans and animals includes a wide
variety of behavioral competences and makes use of a large
number of sensory cues. Here we studied the ability of human
subjects to search locations, to ªnd shortcuts and novel paths,
to estimate distances between remembered places, and to draw
sketch maps of the explored environment; these competences
are related to goal-independent memory of space, or cognitive
maps. Information on spatial relations was restricted to two
types: a visual motion sequence generated by simulated move-
ments in a virtual maze and the subject’s own movement
decisions deªning the path through the maze. Visual informa-
tion was local (i.e., no global landmarks or compass informa-
tion was provided). Other position and movement information
(vestibular or proprioceptive) was excluded. The amount of
visual information provided was varied over four experimental
conditions. The results indicate that human subjects are able
to learn a virtual maze from sequences of local views and
movements. The information acquired is local, consisting of
recognized positions and movement decisions associated to
them. Although simple associations of this type can be shown
to be present in some subjects, more complete conªgurational
knowledge is acquired as well. The results are discussed in a
view-based framework of navigation and the representation of
spatial knowledge by means of a view graph. n
INTRODUCTION
Spatial Memory and Cognitive Maps
All organisms capable of locomotion have to deal with
space and spatial relations within their environment.
Simple tasks like efªcient grazing and foraging, path
integration, or systematic search can be achieved with-
out a mental representation of space, whereas more
advanced competences require the recognition of places
as well as knowledge of spatial relations, such as the
distance and bearing of a goal, routes, or conªgurations
of places. In this paper, we address the problem of
exploration, path planning, and navigation in a virtual
maze (i.e., in an environment composed of streets and
junctions and with goals that are not generally visible
from the starting position). The knowledge or mental
representation required for this task is studied by be-
havioral experiments with human subjects navigating
in a virtual environment simulated on a computer
screen.
Mental representations of space are often called cog-
nitive maps. More speciªcally, there seem to be at least
three more or less independent ideas related to the
concept of a cognitive map:
1. Cognitive map as a spatial reasoning stage. Tol-
man’s original notion (Tolman, 1948) considers the abil-
ity to ªnd (or infer) novel shortcuts as crucial for the
presence of a cognitive map.
2. Cognitive map as a cue integration stage. Spatial
behavior rests on a fair number of different information
sources that are not easily combined. At the stage where
the integration occurs, all information has to be present
in a compatible way. This interaction stage may be called
a cognitive map (see Gallistel, 1990).
3. Cognitive map as goal-independent memory of
space. Information about spatial relations can be ac-
quired in neutral (unrewarded) situations and can be
used for goal-directed behaviors later (latent learning). In
contrast, routes are always headed toward a goal. See
O’Keefe and Nadel (1978) for a detailed discussion.
Clearly, the above deªnitions are not mutually exclusive
but simply highlight different aspects of cognitive maps.
In terms of the underlying mechanisms, the third notion
seems to allow the most clear-cut distinctions: If spatial
learning is achieved by a mere modiªcation of the
mechanism generating the behavior, it will be stereo-
typed, and we will not call this a cognitive map. If,
however, a separate storage is involved that does not
itself produce behavior but is “loaded” into ºexible
mechanisms or referred to during planning, the term
appears to be appropriate. This distinction is akin to the
procedural versus declarative memory dichotomy as dis-
cussed by Squire (1987).
© 1998 Massachusetts Institute of Technology
Journal of Cognitive Neuroscience 10:4, pp. 445–463
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
n
t
p
o
a
:
d
/
e
/
d
m
i
f
r
t
o
p
m
r
h
c
.
p
s
i
l
d
v
i
r
e
e
c
r
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
c
m
n
/
j
a
o
r
t
c
i
c
n
e
/
–
a
p
d
r
t
1
i
0
c
l
4
e
4
–
4
p
5
d
1
f
9
/
3
1
1
0
8
/
3
4
9
/
0
4
8
4
9
5
8
/
9
1
2
7
9
5
9
8
8
3
5
8
6
2
1
8
/
6
0
1
8
9
p
8
d
9
b
2
y
9
9
g
8
u
e
5
s
6
t
2
o
8
n
6
0
1
7
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
o
n
f
/
t
.
1
8
M
a
y
2
0
2
1
Types of Spatial Memory
What types of spatial behavior can be achieved without
a cognitive map, and which ones cannot? We will split
the discussion of this question into three parts, related
to three basic navigational mechanisms: (1) path integra-
tion, (2) approaching recognized views (e.g., “homing”),
and (3) route and graph memory.
Path Integration
In insect navigation, it has been shown that many impor-
tant tasks can be achieved by some kind of working
memory such as a continuously updated “home vector”
holding the egocentric coordinates of the starting posi-
tion of the current excursion (Wehner & Menzel, 1990).
The current position of some starting point in egocen-
tric coordinates can easily be computed by triangulation
(see Maurer & Séguinot, 1995, for review). Path integra-
tion has been studied in blind and blindfolded human
subjects by Loomis et al. (1993) and in sighted subjects
using virtual reality by May, Wartenberg, and Péruch
(1997). The representation required for path integration
is a simple buffer storing the two vector components
(Mittelstaedt & Mittelstaedt, 1972/73; see also Touretzky,
Redish, & Wan, 1993). Recently, McNaughton et al. (1996)
have proposed an alternative mechanism based on hip-
pocampal place cells. In all models, storage is achieved
by neuronal activity (rather than synaptic plasticity), that
is, by some kind of working or short-term memory.
The memory involved in repetitions of a previously
traveled distance can be based on more elaborate
mechanisms as well. Recent results by Berthoz, Israël,
Georges-François, Grasso, and Tsuzuku (1995) indicate
that, in humans, the repetition of short distances involves
not just a continuously updated vector buffer but uses a
stored velocity proªle. It is not clear, however, how this
result extends to longer routes.
An intriguing property of path integration is its close
relation to metric information. Although it is sometimes
assumed that the access to metric information requires
highly sophisticated cognitive maps, it appears that met-
ric is in fact one of the most basic properties of spatial
short-term memory.
Approaching Recognized Views
Recognizing and approaching views (local landmarks)
requires a long-term memory of the view or some of its
features. A strictly associative mechanism for this task has
been proposed by Barto and Sutton (1981). It actually
stores the required approach direction for every position
identiªed by its local position information. A more gen-
eral mechanism for homing that computes the approach
direction from the comparison of current and stored
views has been proposed by Cartwright and Collett
(1982). This scheme involves long-term memory of the
approached view, but not of the required movements,
which are computed. If only one view is to be ap-
proached (homing in a strict sense), memory can be
realized in a procedural and stereotyped way (e.g., by
some sort of matched ªlter for the home view). If, how-
ever, the same machinery is to be used for many different
approach tasks, the appropriate target views would have
to be “loaded” into a comparison stage as needed. In the
meantime, they must be kept in some long-term memory.
The same argument applies to the somewhat more pow-
erful model by Benhamou, Bouvet, and Poucet (1995)
describing homing behavior in mammals. (See also Franz,
Schölkopf, Mallot & Bülthoff, 1998, for an alternative
implementation of this approach mechanism.)
Routes and Conªgurations
As the basic element of route memory and conªguration
memory, we consider an association of the form
(current view, (movement direction,
expected next view))
(1)
which is illustrated in Figure 1d. Associations between
views and movement decisions have been demonstrated,
for example, in bees (Collett & Baron, 1995) and have
been used in the associative schemes of Barto and Sutton
(1981) and McNaughton and Morris (1987). When going
from one view to the next, navigation can initially follow
the movement direction associated with the present
view. A scheme for robot navigation based on recognized
landmarks and movement behaviors associated with
them has been suggested by Kuipers and Byun (1991).
The additional information on what view to expect next
is required in order to switch to the appropriate ap-
proach behavior when arriving in the neighborhood
(“catchment area”) of that view. Alternatively, stereotyped
approach behaviors for all known views could be active
in parallel. In this case, they would need to produce a
conªdence measure allowing the selection of the cor-
rect one.
Chains of such association structures implement a
route memory. If different routes are to be learned that
share some common section, the decision at the cross-
roads requires more complicated memory. One way to
think of this memory is to store all possible connections
(current view, (movement direction 1,
expected next view)
.
.
.
(movement direction n,
expected next view))
(2)
and have a separate planning device select one of the
possible movements. A neural network theory for storing
the required information in the form of a labeled graph
has been presented by Schölkopf and Mallot (1995). For
446 Journal of Cognitive Neuroscience
Volume 10, Number 4
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
n
t
p
o
a
:
d
/
e
/
d
m
i
f
r
t
o
p
m
r
h
c
.
p
s
i
l
d
v
i
r
e
e
c
r
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
c
m
n
/
j
a
o
r
t
c
i
c
n
e
/
–
a
p
d
r
t
1
i
0
c
l
4
e
4
–
4
p
5
d
1
f
9
/
3
1
1
0
8
/
3
4
9
/
0
4
8
4
9
5
8
/
9
1
2
7
9
5
9
8
8
3
5
8
6
2
1
8
/
6
0
1
8
9
p
8
d
9
b
2
y
9
9
g
8
u
e
5
s
6
t
2
o
8
n
6
0
1
7
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
o
n
f
t
.
/
1
8
M
a
y
2
0
2
1
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
n
t
p
o
a
:
d
/
e
/
d
m
i
f
r
t
o
p
m
r
h
c
.
p
s
i
l
d
v
i
r
e
e
c
r
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
c
m
n
/
j
a
o
r
t
c
i
c
n
e
/
–
a
p
d
r
t
1
i
0
c
l
4
e
4
–
4
p
5
d
1
f
9
/
3
1
1
0
8
/
3
4
9
/
0
4
8
4
9
5
8
/
9
1
2
7
9
5
9
8
8
3
5
8
6
2
1
8
/
6
0
1
8
9
p
8
d
9
b
2
y
9
9
g
8
u
e
5
s
6
t
2
o
8
n
6
0
1
7
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
o
n
f
/
.
t
1
8
M
a
y
2
0
2
1
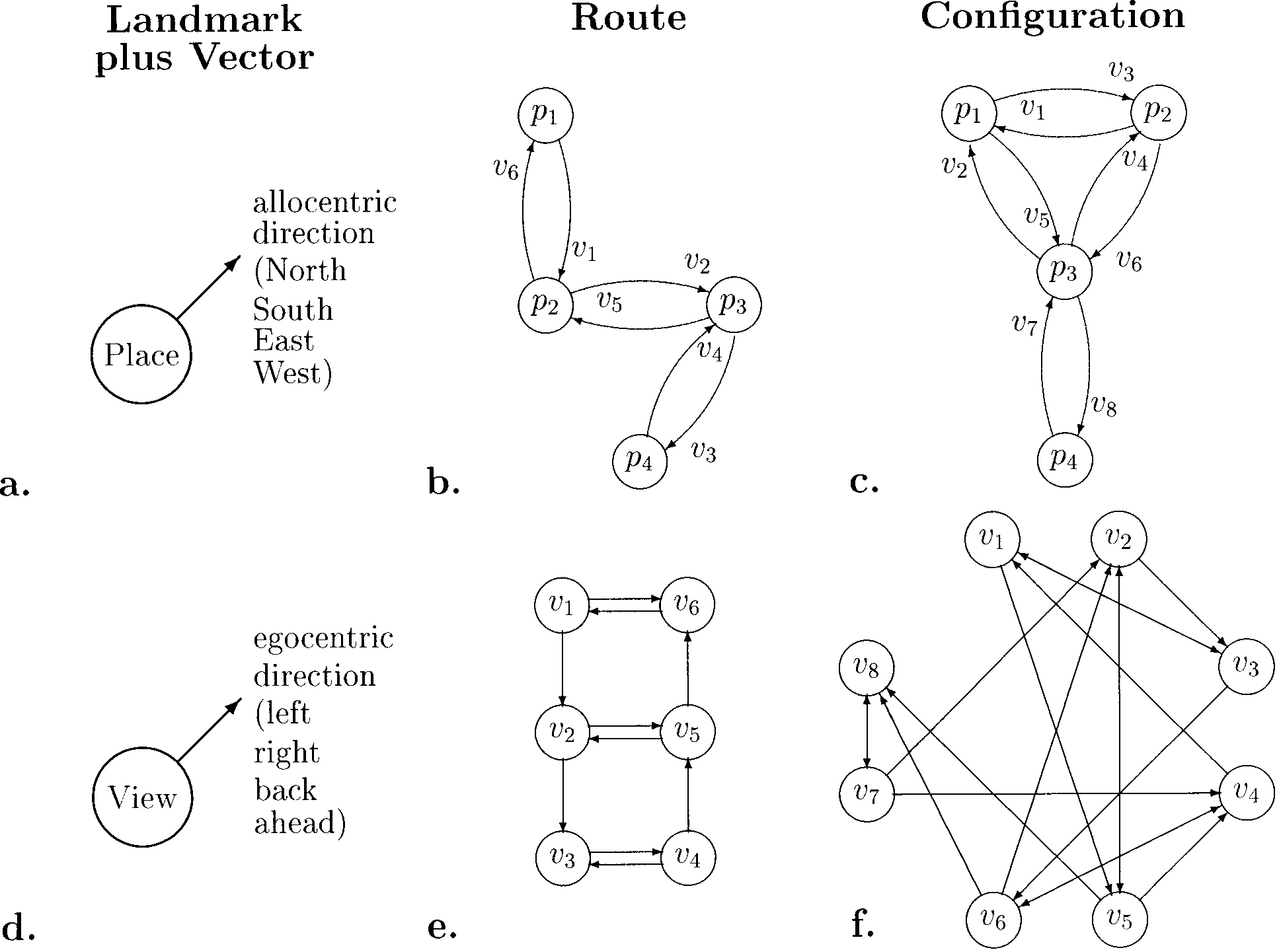
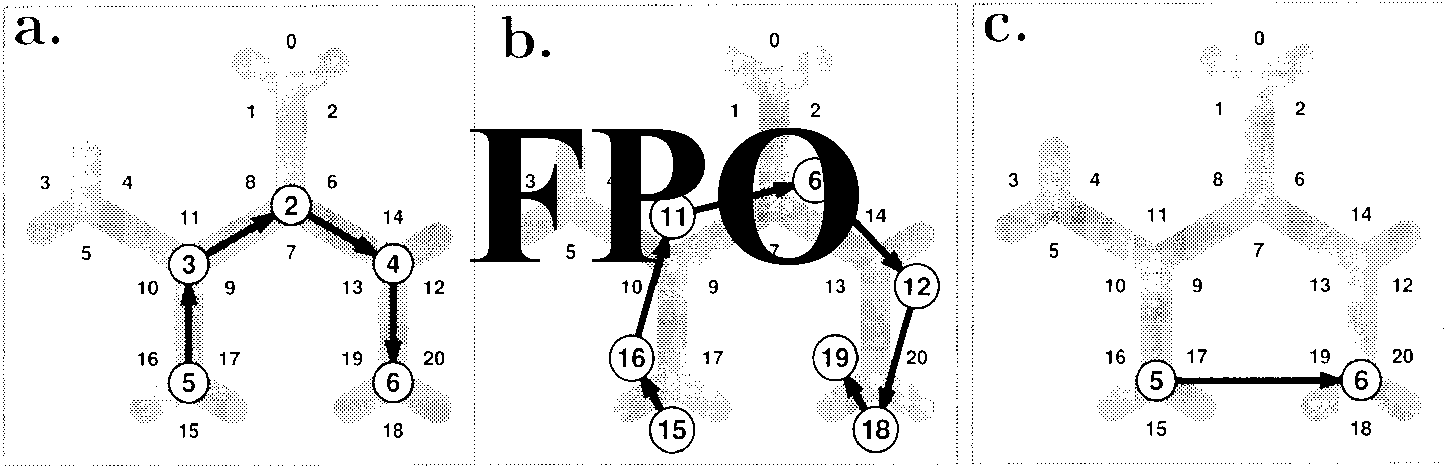
Figure 1. The graph approach to space representation. Top row (a–c): Place graphs. The nodes are places recognized irrespective of body ori-
entation, the links (arrows) between them carry allocentric direction information. Bottom row (d–f): View graphs. The nodes are recognizable
views or other positional information (i.e., depend on the observer’s viewing direction), and the arrows carry directional information relative
to gaze. Each view vi in parts e and f corresponds to a directed connection in parts b and c. From left to right, increasingly more complicated
spatial layouts are shown.
related approaches including hippocampal modeling,
see Muller, Stead, and Pach (1996), Prescott (1996) and
Touretzky and Redish (1996).
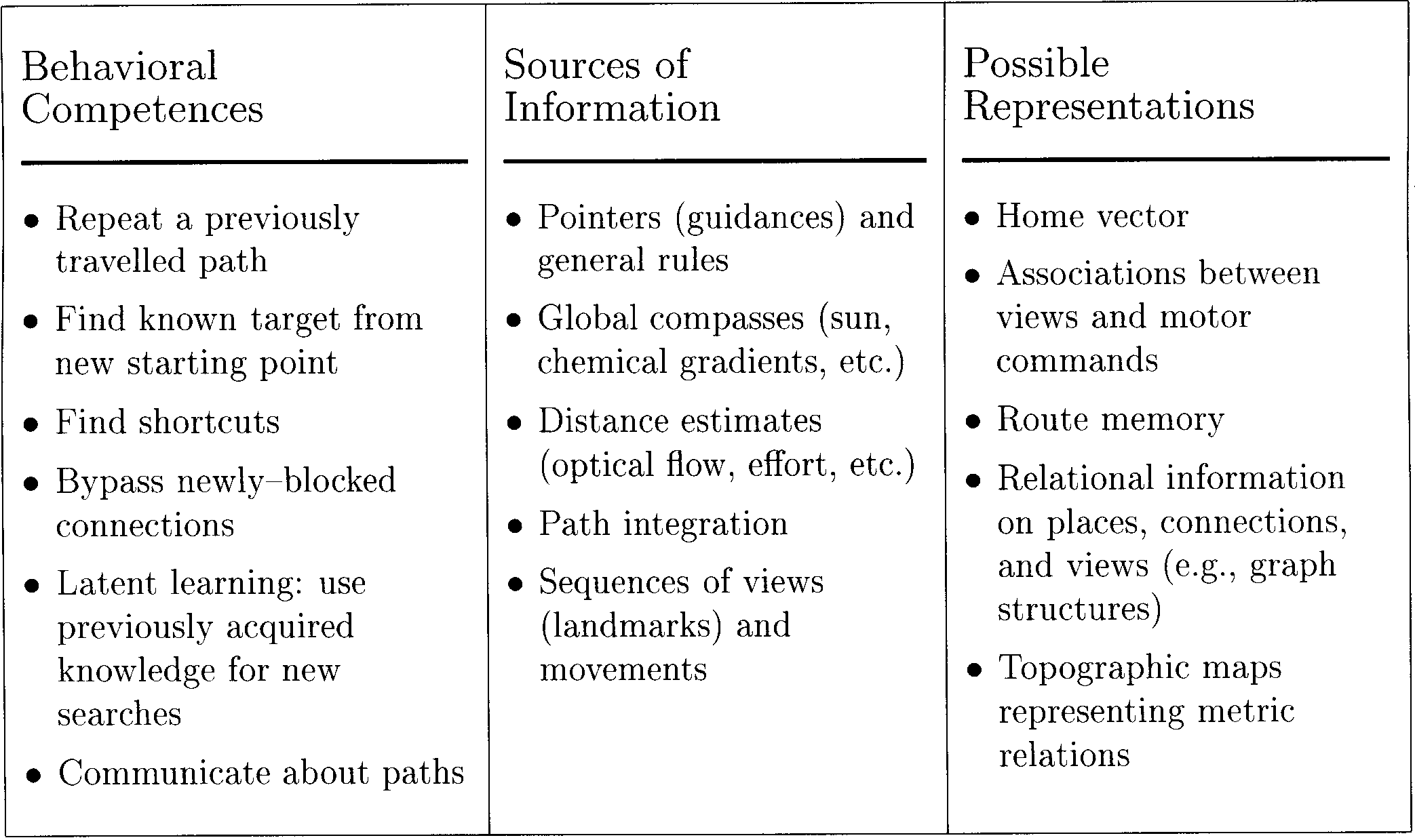
An Ecological View of Spatial Memory
In this paper, we will deal mostly with memory of routes
and conªgurations (i.e., relational knowledge of position
and the movements leading from one position to an-
other). A further breakdown of this problem is given in
Table 1. The behavioral competences have been ar-
ranged in order of increasing complexity. Cognitive maps
may be unnecessary for the ªrst two but become in-
creasingly more relevant for the more complex tasks.
The list of sources of information usable in navigation
tasks is probably not complete. Again, there are trivial
cases like pointers, which do not require any spatial
knowledge or map, as well as more complicated cues
that can only be interpreted correctly if map information
is available. Note that we have included “path integra-
tion” as a source of information. Simple path integration
does not require a cognitive map and can thus be con-
sidered a separate mechanism feeding into the map
module. Possible representations acquired by spatial
learning are listed in the third column of Table 1. As was
discussed earlier, the home vector is a form of working
memory. Associations and simple (nonbifurcating) chains
of associations can be learned in a stereotyped or pro-
cedural way. If the same knowledge is to be used in the
pursuit of different goals, a goal-independent, graphlike
memory is required. Finally, a topographic map with
coordinates and distances is the richest but rather un-
likely representation.
The View-Based Approach to Navigation
The problem, then, is to ªnd the minimum repre-
sentation required to explain an animal’s or human’s
Gillner and Mallot 447
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
n
t
p
o
a
:
d
/
e
/
d
m
i
f
r
t
o
p
m
r
h
c
.
p
s
i
l
d
v
i
r
e
e
c
r
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
c
m
n
/
j
a
o
r
t
c
i
c
n
e
/
–
a
p
d
r
t
1
i
0
c
l
4
e
4
–
4
p
5
d
1
f
9
/
3
1
1
0
8
/
3
4
9
/
0
4
8
4
9
5
8
/
9
1
2
7
9
5
9
8
8
3
5
8
6
2
1
8
/
6
0
1
8
9
p
8
d
9
b
2
y
9
9
g
8
u
e
5
s
6
t
2
o
8
n
6
0
1
7
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
o
n
.
f
/
t
1
8
M
a
y
2
0
2
1
Table 1. An ecological view of cognitive maps. For explanation, see text.
behavioral competences in the presence of a certain
type of environmental information. This idea of eco-
nomic or parsimonious explanations of spatial behavior
is especially well developed for insect navigation.1 For
the type of knowledge studied here (i.e., the expectation
of the next snapshot generated from the current snap-
shot and the intended movement), the most simple ele-
ment is shown in Figure 1a and d and Equation 1. In
Figure 1a it is assumed that places are recognized irre-
spective of the observer’s direction of gaze. Intended
movements are then represented in a global coordinate
system (i.e., in relation to an additional system such as
global landmarks or path integration). These elements
can be combined into chains (Figure 1b) or graphs
(Figure 1c). In contrast to this “place-based” approach,
the view-based approach (lower row of Figure 1) as-
sumes that views, rather than places, are recognized and
movements are represented in egocentric coordinates
(i.e., without reference to an independent compass sys-
tem). This approach can be extended to chains and
graphs just like the place-based approach. For a mathe-
matical analysis of the resulting view graphs, see Schöl-
kopf and Mallot (1995).
Both the place- and the view-graph approaches are
local in the sense that bits and pieces of spatial informa-
tion can be accumulated without checking for global
consistency. They focus on topological properties (con-
nectivity); metric relations can be added as labels to the
links. The main differences between the two approaches
are (1) that metric labels of the place graph have to be
allocentric (world-centered), whereas those of the view
graph are egocentric (observer-centered) and (2) that
the place graph is planar and symmetric (knowledge of
a connection implies how to return), whereas the view
graph is not.
It should be noted that the view-based approach to
navigation is closely related to view-based mechanisms
in direction-invariant object recognition (see Bülthoff,
Edelman, & Tarr, 1995). Places and objects can be repre-
sented by their respective views in quite similar ways.
The graph structure resulting for a maze with many
places is generally not planar (cf. Figure 1f), whereas the
view graphs for object recognition are.
Behavioral Experiments in Virtual Reality
In the work reported in this paper, we chose interactive
computer graphics, or virtual reality (VR), as our experi-
mental method. Previous studies using virtual reality
have focussed on the transfer of knowledge between
different media used for acquisition and testing. May,
Péruch, and Savoyant (1995) and Tlauka and Wilson
(1996), for example, have tested map-acquired knowl-
edge in a pointing task performed in virtual reality. Tong,
Marlin, and Frost (1995), using a VR bicycle, showed that
active exploration leads to better spatial knowledge than
passive stimulus presentation. Sketch maps produced
after exploration of various virtual environments have
448 Journal of Cognitive Neuroscience
Volume 10, Number 4
been studied by Billinghurst and Weghorst (1995). De-
sign principles for constructing easy-to-navigate virtual
environments have been studied by Darken and Sibert
(1996). In the present paper, we use virtual reality to
isolate the various cues used for the build-up of spatial
knowledge and to study the underlying mechanisms. The
advantages of virtual reality for this application are (1)
the high controllability of computer graphics stimuli and
(2) the easy access to behavioral data, such as the sub-
ject’s movement decisions.
Measuring Behavior
Navigation performance can be accessed most directly
by the paths or trajectories that the subjects take during
the exploration. In virtual reality experiments, egomo-
tion is very simple to record, because it is equivalent to
the course of the view port used for rendering the
computer graphics. In this paper, we present a number
of novel techniques for data evaluation that are par-
ticularly suited for the virtual reality experiments de-
scribed.
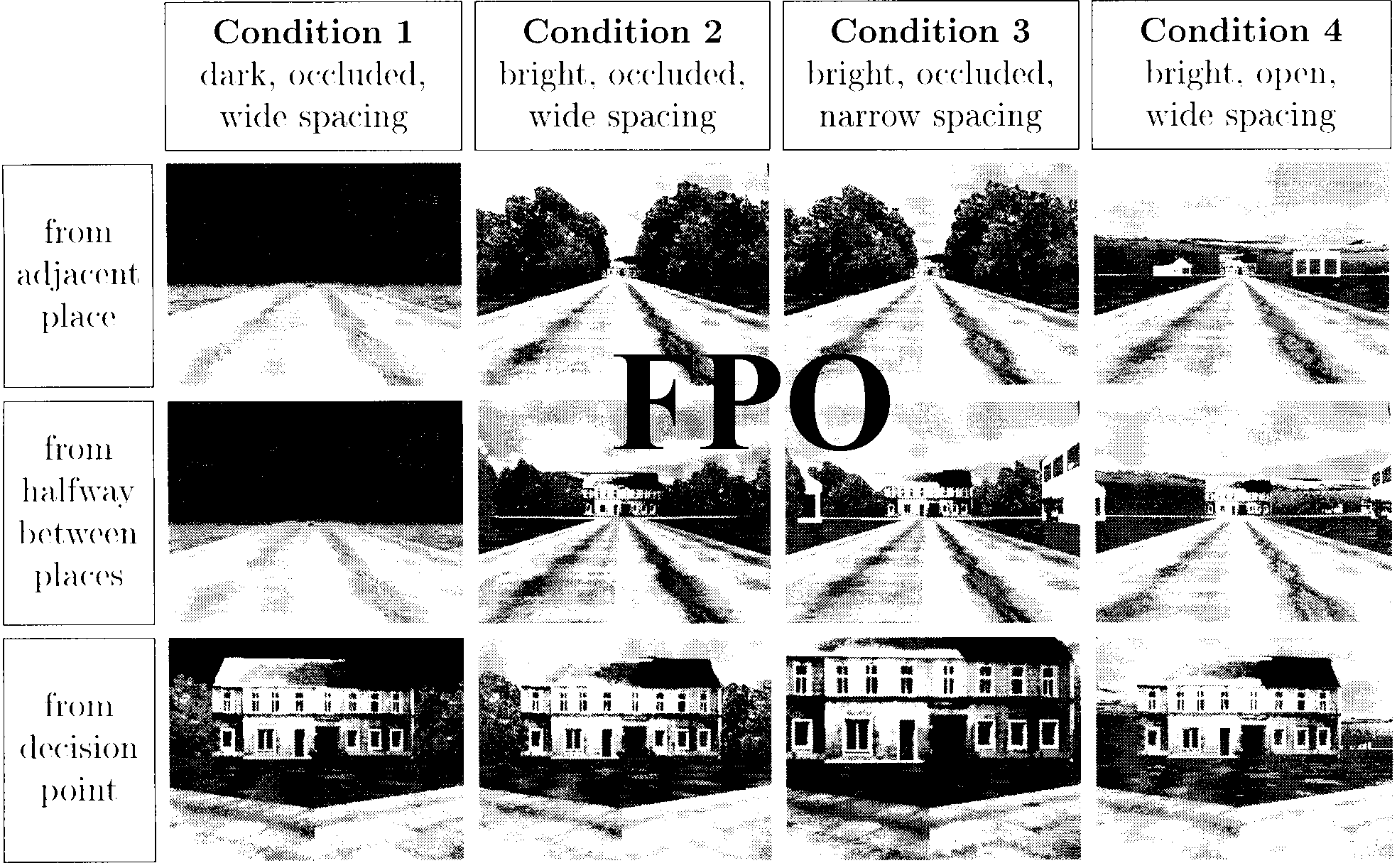
Stimulus Control
Plan of the Paper
When investigating the information sources used in navi-
gation, it is advantageous to be aware of the exact move-
ment trajectories of the subjects and the visual
information available along these trajectories. This can
easily be achieved with interactive computer graphic
(see “Methods” section). The various parameters of the
sensory input can be easily separated. For instance, in
our experiments, we varied the number of buildings
visible simultaneously in one view without changing the
illumination, etc. In real-world experiments, such sepa-
rate stimulus conditions are much harder to realize.
Another
is the
interesting experimental paradigm
modiªcation or exchange of various features of the en-
vironment after learning. Aginsky, Harris, Rensink, and
Beusmans (1996) exchanged landmarks after training in
a route-learning task. The effects of landmark exchange
on navigation have been addressed by Gillner and Mallot
(1996).
The method also allows complete control over ves-
tibular and proprioceptive feedback. In our experiments,
both were completely absent, allowing the effects of
visual input to be studied in isolation.
The virtual reality setup and the procedure used in the
experiments are described in the “Methods” section at
the end of the paper. In the “Results” section, we present
subjects’ trajectories obtained during a search task, as
well as two derived measures for transfer of knowl-
edge between routes and for persistent associations of
views to particular movements. In addition, distance es-
timates collected from the subjects after exploration are
compared to theoretical distances from various candi-
date representations. Finally, some examples of subjects’
sketch maps will be presented.
RESULTS
Exploration and Search
Performance
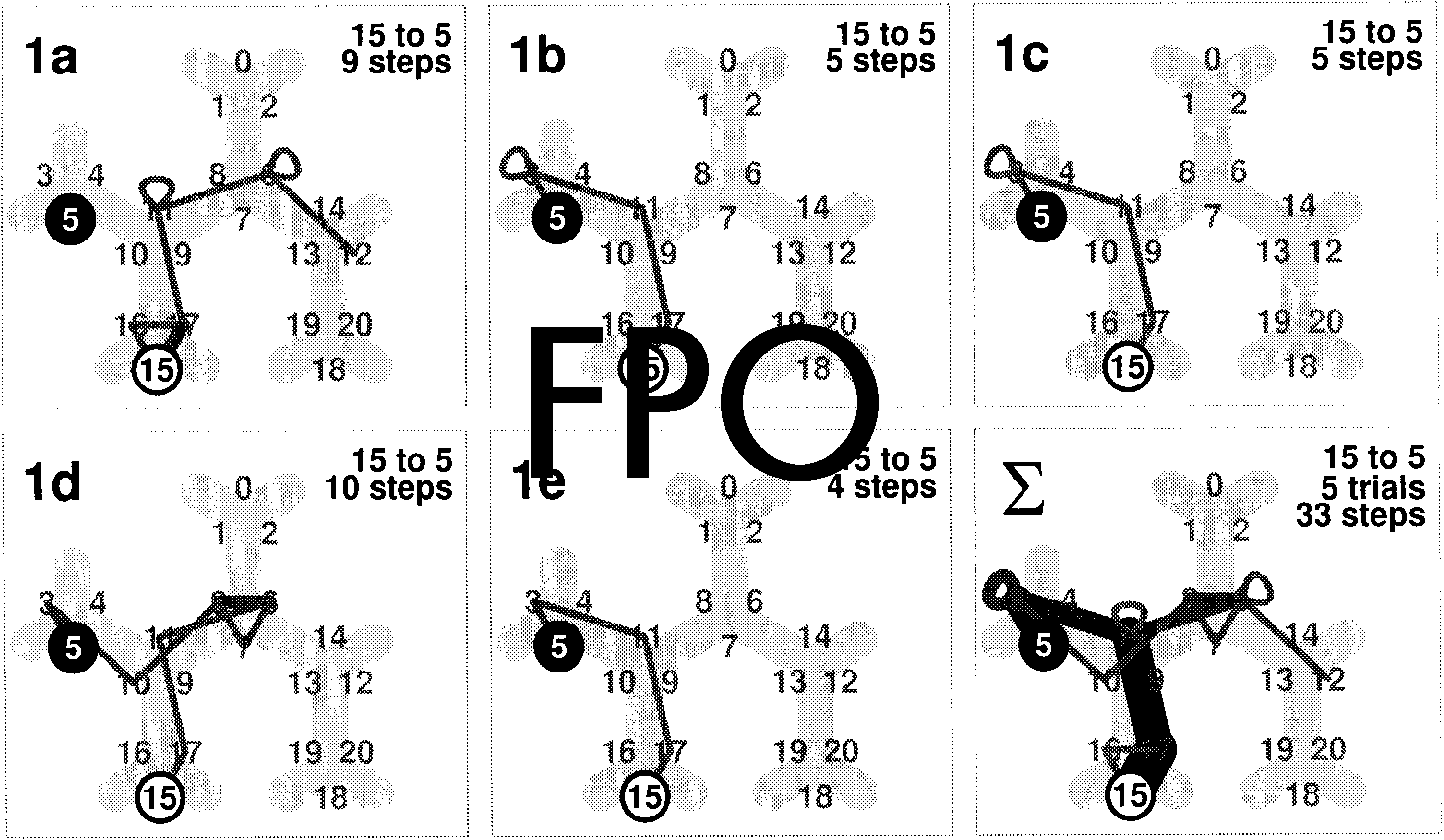
Figure 2 shows an example for the trajectory taken by a
single subject when searching view number 5 from start
view 15. In the ªrst trial, the subject made a complete
turn in the starting position and then started the explo-
ration via view 17. At view 11, he performed a loop,
Figure 2. Sample trajectories
for subject GPK (condition:
dark) searching the way from
view 15 (start) to view 5.
1a–1e: Search trials. In part 1e
the shortest path is found for
the first time completing the
task 15 fi
: Accumulated
trajectory from all five trials.
This plot appears again in
part 1 of Figure 3.
5. (cid:229)
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
n
t
p
o
a
:
d
/
e
/
d
m
i
f
r
t
o
p
m
r
h
c
.
p
s
i
l
d
v
i
r
e
e
c
r
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
c
m
n
/
j
a
o
r
t
c
i
c
n
e
/
–
a
p
d
r
t
1
i
0
c
l
4
e
4
–
4
p
5
d
1
f
9
/
3
1
1
0
8
/
3
4
9
/
0
4
8
4
9
5
8
/
9
1
2
7
9
5
9
8
8
3
5
8
6
2
1
8
/
6
0
1
8
9
p
8
d
9
b
2
y
9
9
g
8
u
e
5
s
6
t
2
o
8
n
6
0
1
7
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
o
n
t
.
/
f
1
8
M
a
y
2
0
2
1
Gillner and Mallot 449
turning 60(cid:176) to face a street and back again. He then
proceeded to view 6, where he performed the same
search behavior. At view 12, the trial was stopped be-
cause the subject deviated from the shortest path by
more than one segment. In the second trial (part 1b in
Figure 2), he ªnds the goal, though not the shortest
possible path. Interestingly, the third trial is an exact
replication of the second one. The ªrst time he ªnds the
shortest way is trial 5 (part 1e), which thus terminates
the exploration of that route.
The cumulative trajectory shown in the lower right
panel of Figure 2 appears again in the upper left panel
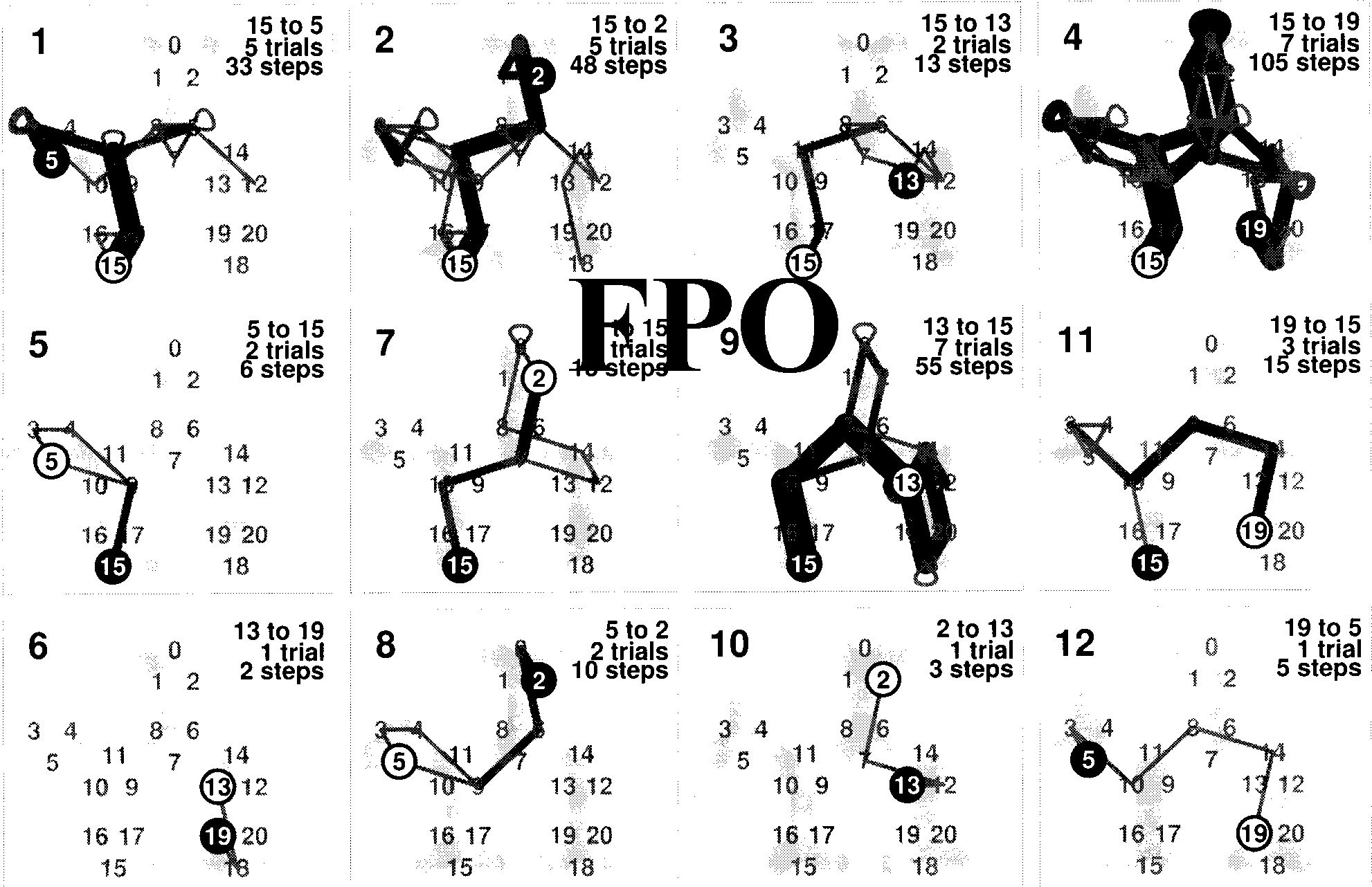
of Figure 3. The other panels in this ªgure show the
cumulative trajectories for the other routes performed
subsequently in the sequence indicated by the number
in the upper left of each panel. Paths 1 through 4 are
excursions, 5, 7, 9, and 11 are returns, and 6, 8, 10, and
12 are novel routes. Overall, there is a tendency for lower
error rates in the search tasks performed later. That is to
say, there is a transfer of knowledge obtained in earlier
searches to the later searches. The decrease of errors is
not monotonic, though. Note, however, that the three last
routes were found in just ªve trials. In some subjects, no
such decrease of the error rate is found.
Error Rates
Errors were deªned locally as decisions that do not
reduce the distance of the goal. Each movement decision
equals clicking the mouse buttons twice (cf. Figure 12
in the “Methods” section). Distance to the goal is meas-
ured as the minimum number of decisions needed to
reach it (“decision distance”). Thus, if a subject enters a
street leading away from the goal, the return from that
street will be counted as a correct decision even though
the current position is not part of the shortest path. In
cases where the correct decision is a 60(cid:176) turn left fol-
lowed by a “go,” the 120(cid:176) turn left would leave the
decision distance to the goal unchanged. This decision
(and the mirror-symmetric case) is also counted as an
error.
Average error rates for each path type are shown in
Figure 4. For each viewing condition (1 through 4; see
“Methods” section), the excursions, returns, and novel
paths were lumped into groups of four. As mentioned
above, the excursions were preformed ªrst, and the
novel and return paths were performed alternatingly,
starting with a return in one group of subjects and
starting with a novel route in a second group. The data
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
n
t
p
o
a
:
d
/
e
/
d
m
i
f
r
t
o
p
m
r
h
c
.
p
s
i
l
d
v
i
r
e
e
c
r
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
c
m
n
/
j
a
o
r
t
c
i
c
n
e
/
–
a
p
d
r
t
1
i
0
c
l
4
e
4
–
4
p
5
d
1
f
9
/
3
1
1
0
8
/
3
4
9
/
0
4
8
4
9
5
8
/
9
1
2
7
9
5
9
8
8
3
5
8
6
2
1
8
/
6
0
1
8
9
p
8
d
9
b
2
y
9
9
g
8
u
e
5
s
6
t
2
o
8
n
6
0
1
7
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
o
n
/
.
f
t
1
8
M
a
y
2
0
2
1
Figure 3. Traveling frequencies for each view transition for the 12 paths, subject GPK (viewing condition: 1; sequence condition: returns first).
Top row: excursions, middle row: returns, bottom row: novel paths. The overall number of errors decreases at later stages of exploration.
450 Journal of Cognitive Neuroscience
Volume 10, Number 4
transfer occurs, the route explored ªrst should have
higher error rates in both cases. We deªne
ER,1 –
t =
ER,2 + EN,1 –
ER,1 + EN,1
EN,2
(3)
If error rates do not depend on position, t will be zero;
if everything is learned already when exploring the ªrst
route, ER,2 and EN,2 will be zero and t evaluates to 1.
Statistical signiªcance of transfer is tested by comparing
the various error rates with the t test.
4 routes ·
For this evaluation, the subjects from viewing condi-
tions 1 and 2 were pooled because there were no sig-
niªcant differences between the respective error rates
(three-way ANOVA 2 conditions ·
2 gender,
F(1, 36) = 0.014, p = 0.9075). If we take the average over
all 40 subjects, no signiªcant effect of transfer is found.
If, however, only the 20 subjects with the lowest overall
error rate are considered, a transfer effect with t = 0.4
is found (see Figure 5). In this case, 11 subjects were
from the returns-ªrst condition and 9 subjects from the
novel-ªrst condition. The result indicates that the good
navigators show signiªcant transfer learning even from
one route to the next. Transfer across more steps of the
exploration procedure is not visible in this evaluation,
which does not mean that we exclude such a transfer.
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
n
t
p
o
a
:
d
/
e
/
d
m
i
f
r
t
o
p
m
r
h
c
.
p
s
i
l
d
v
i
r
e
e
c
r
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
c
m
n
/
j
a
o
r
t
c
i
c
n
e
/
–
a
p
d
r
t
1
i
0
c
l
4
e
4
–
4
p
5
d
1
f
9
/
3
1
1
0
8
/
3
4
9
/
0
4
8
4
9
5
8
/
9
1
2
7
9
5
9
8
8
3
5
8
6
2
1
8
/
6
0
1
8
9
p
8
d
9
b
2
y
9
9
g
8
u
e
5
s
6
t
2
o
8
n
6
0
1
7
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
o
n
/
f
.
t
1
8
M
a
y
2
0
2
1
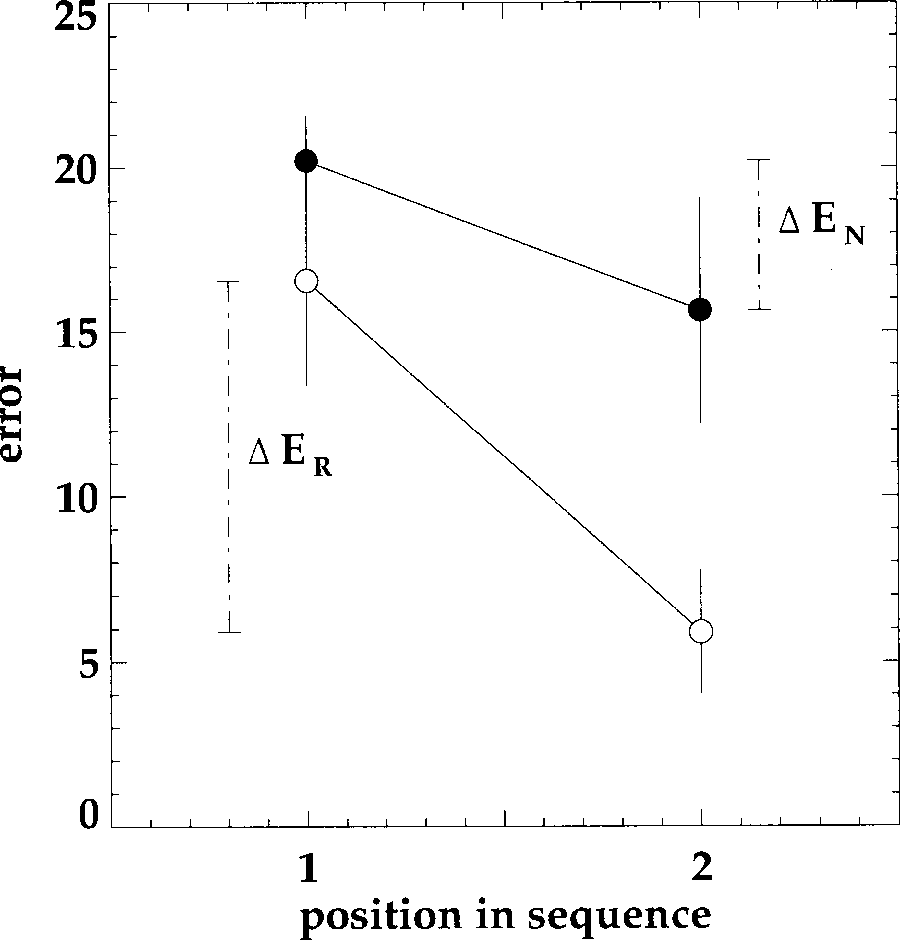
Figure 5. Average error rates for novel paths and returns in the
novel-first and returns-first sequence conditions. All subjects from
viewing conditions 1 and 2 with an overall error rate below the me-
dian were included in this plot. • novel routes; + returns. For both
returns and novel routes, error rate drops when other routes are ex-
plored before. The transfer coefficient (Equation 3) is t = 0.4.
Gillner and Mallot 451
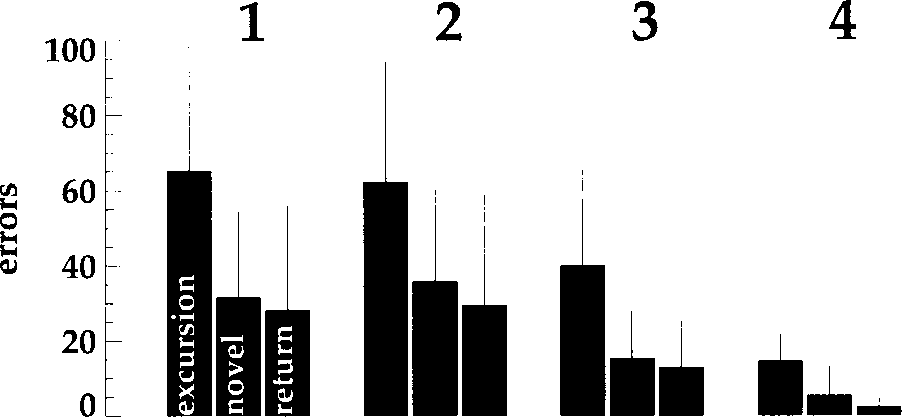
Figure 4. Total number of wrong movements performed in the dif-
ferent path types (excursion, novel, return). Numbers are averaged
over 20 subjects, error bars are standard deviations. 1 through 4:
viewing conditions.
show a learning effect in the sense that excursions take
more errors than the later paths. They also show a clear
effect of condition: Higher visibility results in lower error
rates. This general relation does not hold for the com-
parison of conditions 1 and 2, however, which differ in
the visibility of the neighboring places.
3 path types ·
A three-way analysis of variance (ANOVA, 4 condi-
tions ·
2 genders) of error rate as the
dependent variable reveals signiªcant effects of condi-
tion (F(3, 72) = 17.31, p < 10-4) and path type (F(2,
144) = 60.65, p < 10-4) but not of gender (F(1, 72) =
0.22, n.s.). Additionally we found an interaction of con-
dition and path type (F(6, 144) = 2.66, p = 0.018). The
error rates of novel paths are slightly higher than those
of the returns (see Figure 4). This effect is not signiªcant,
however.
Transfer
In our procedure, learning occurs on two time scales.
During each of the 12 tasks, a route is learned as illus-
trated in the example in Figure 2. When switching from
one route to the next, part of the knowledge acquired
in the earlier routes might be transferred to the new
ones. To test this, we deªne a transfer coefªcient t in the
following way:
Let R and N denote two routes, for instance the ªrst
return and novel path, respectively. Our group of sub-
jects is divided into two subgroups, one of which ex-
plores R ªrst and N second, whereas the second group
explores N and then R. As can be seen from Figure 15,
four such pairs of routes have been tested. We accumu-
late the data from these four tested pairs of returns and
novel paths:
ER,1 Errors in returns in the returns-ªrst condition
EN,1 Errors in novel paths in the novel-ªrst condition
ER,2 Errors in returns in the novel-ªrst condition
EN,2 Errors in novel paths in the returns-ªrst condition
Thus, ER,1 and EN,2 refer to the ªrst group of subjects
(returns-ªrst condition) and EN,1, ER,2 to the second. If
The transfer-coefªcient t averages the transfer in both
directions. In order to look at direction-speciªc transfer
effects, let us consider the two subject groups separately.
In Figure 5, this would amount to connecting the left
open dot with right ªlled dot, etc. It turns out that there
is a much stronger improvement in the novel-ªrst con-
dition (t test: t = 6.13, FG = 16, p < 0.001) but no
improvement in the returns-ªrst condition (t = 0.19,
FG = 20, n.s.).
Persistence
An inspection of Figure 2 shows that the subject re-
peated the ªrst route that led to the goal (trial 2) exactly
in the following trial. Similarly, it can be seen from Fig-
ure 3 that in almost all cases where the subject started
from view 15, the ªrst movement decision was LL even
though RR would have been just as good. These and
similar observations from other subjects lead to the
conjecture that at least some movement decisions reºect
simple, ªxed associations between the current view and
some motion that is performed whenever the view oc-
curs. In order to test this in more detail, we analyzed the
return statistics of the decision sequences.
˛
Let mh,u
{LL, LG, LR, RL, RG, RR} denote the move-
ment decision taken at the h th encounter of view u
(see
Figure 12 for possible movement decisions). We are in-
terested in cases where the movement chosen at the h th
encounter of view u
is the same as that taken at the
1th encounter. More generally, we count the cases
1 and move-
{LL, LG, LR, RL, RG, RR}):
-
where movement j is taken at encounter h -
ment i at encounter h
Fi,j:= #{(h, u
1,u = j}.
= i, mh
(i,j ˛
)|mh,u
(4)
-
-1,u ˛
It is important to note two points: First, the two encoun-
ters h
and h
1 do not occur in subsequent time steps
{RL, LR}). Rather, long sequences of other
(unless mh
views may occur in between. Second, the frequency Fi,j
is accumulated over all views. Thus we are looking for
an average persistence rate rather than for a view-
speciªc one.
In the experiments, each search task is repeated until
the subject ªnds the shortest possible path. This proce-
dure can in itself produce repetition rates above chance
if parts of the path are created correctly several times.
To exclude this type of error, we restrict our analysis to
repetitions where both decisions were false in the sense
that they did not lead to an approach to the goal (local
deªnition of errors). Finally, we dropped the cases involv-
ing the decisions LR and RL because these are quite rare.
Example data from individual subjects are shown in
Figure 6. The numbers on the diagonal correspond to
cases where the same decision was chosen in two sub-
sequent encounters even though the decision was false
in both cases. From these matrices, we can estimate
average movement transition probabilities pij := P(mh, . =
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
n
t
p
o
a
:
d
/
e
/
d
m
i
f
r
t
o
p
m
r
h
c
.
p
s
i
l
d
v
i
r
e
e
c
r
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
c
m
n
/
j
a
o
r
t
c
i
c
n
e
/
-
a
p
d
r
t
1
i
0
c
l
4
e
4
-
4
p
5
d
1
f
9
/
3
1
1
0
8
/
3
4
9
/
0
4
8
4
9
5
8
/
9
1
2
7
9
5
9
8
8
3
5
8
6
2
1
8
/
6
0
1
8
9
p
8
d
9
b
2
y
9
9
g
8
u
e
5
s
6
t
2
o
8
n
6
0
1
7
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
o
n
t
.
f
/
Figure 6. Examples of return statistics for selected subjects for the
four viewing conditions. In the subjects shown for the first three
conditions, hypothesis 1 could be rejected in all cases (i.e., persist-
ence rate l
was significantly different from zero). For condition 4,
where error rates were generally very low, hypothesis 1 could not
be rejected for any subject.
i | mh
,. = j ); averaging is performed with respect to the
-1
different views involved. A simple statistical model for
these transition probabilities is
1
8
M
a
y
2
0
2
1
pij =
l + pi
pi
if i = j
if i „ j
(5)
,0 £ l £
1 and l
where l
pi = 1. It states that there
is a bias l
for the repetition of the movement chosen at
the previous encounter. Other than that, the decisions at
+ S
4
i =1
452 Journal of Cognitive Neuroscience
Volume 10, Number 4
h
-
(cid:236)
(cid:237)
(cid:238)
= 0, true
Judged Distances
subsequent encounters are independent. If l
independence is obtained.
This model was ªtted to the data by a maximum
likelihood procedure, that is, by minimizing
4
c 2 := (cid:229)
i = 1
4
(cid:229)
j = 1
(Fij -
pijFi(cid:215))2
pijFi(cid:215)
(6)
where Fi(cid:215) denotes the marginal frequencies S
4 Fij. If
j=1
Fi(cid:215) = 0 (empty columns in the matrices of Figure 6), the
corresponding terms were deleted from the above sum.
The analysis could be applied to data from 67 out of
80 subjects. For the remaining 13 subjects, the number
of total errors was too low to ªt the model. Ten of these
had been tested in viewing condition 4, where the error
rates were lowest. Goodness of ªt was tested with the
c 2 test; choosing a signiªcance level of 5%, the best-
ªtting model could not be rejected in any of the 67
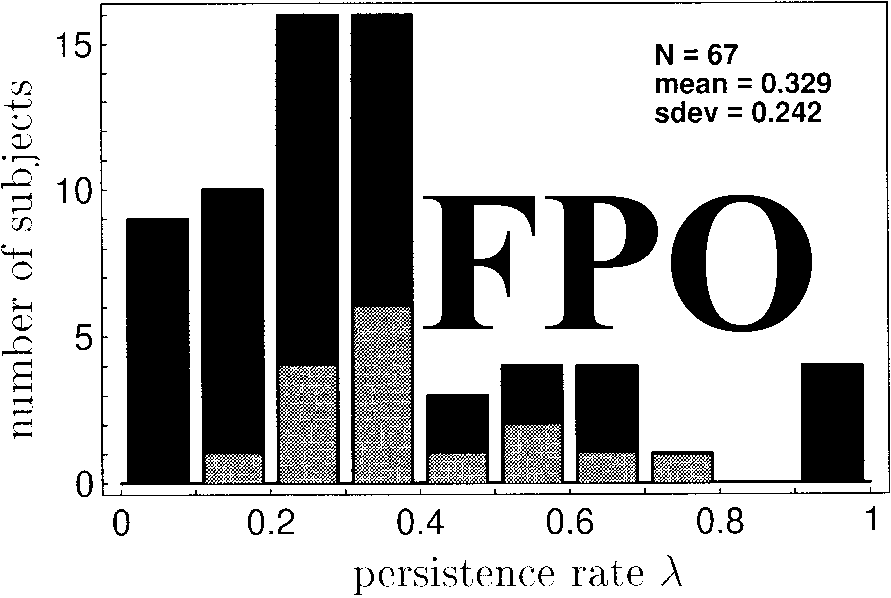
subjects. Figure 7 shows the histogram for the best-ªtting
persisting rates.
In order to get an impression of the conªdence inter-
vals for l
, we repeated the analysis with ªxed l
= 0 in
Equation 5. By testing goodness of ªt for this model with
the c 2 test, 18 cases could be rejected on the 10% level,
9 of which could be rejected on the 1% level as well.
The 18 cases are highlighted in Figure 7. Here, persist-
ence rate is signiªcantly different from zero.
Average persistence rate over all subjects was 0.33,
indicating that about one-third of the decisions were
based on persistence. A regression analysis of persistence
rate l
with the overall number of errors for each subject
did not reveal a signiªcant correlation.
Figure 7. Histogram of best-fitting persistence values l
. Dark col-
umns: Data from n = 67 subjects where the analysis could be ap-
plied (mean = 0.329, s
= 0.242). Light columns: Data from n = 18
subjects where l
was significantly different from zero. Data are cu-
mulated from viewing conditions 1 through 4.
Analysis of Variance
Following the exploration phase, subjects were asked to
rate the distances between 20 pairs of views (see Table
6) on an ordinal scale from 0 to 4. A 20 · 4 ·
2 ANOVA
on ranks as dependent variable and view pair, viewing
condition, and instruction as independent variables re-
veals a signiªcant effect of view pair (F(19, 1368) = 38.7,
p < 10-4) but no effect of viewing condition (F(3, 72) =
1.63, p = 0.19) or instruction (F(1, 72) = 1.39, p = 0.24).
In addition, a signiªcant interaction of view pair and
viewing condition was found (F(57, 1368) = 1.74, p =
0.0007). Thus, the instruction (“distance” versus “airline
distance”) did not inºuence the result.
In the following, we discuss the two signiªcant effects
separately.
Judged and True Distance
Depending on the type of representation acquired, dif-
ferent distance estimates could be expected (Figure 8):
1. Walking distance. This is the length of the mini-
mum path connecting the two views. Because all seg-
ments have the same length in our model, it is equivalent
to the number of streets traveled or the number of
“Go”-decisions taken, that is, to the graph distance in the
place graphs (top row of Figure 1).
2. Decision distance. This is the minimum number of
decisions (mouse clicks) required to travel from one
view to the other. It is also the number of views encoun-
tered and thus the length of a chain of view-movement
associations or the graph distance in the view graph.
Using the conventions of Figure 12, we take the unit to
be a view-to-view transition (i.e., two subsequent mouse
clicks).
3. Metric or euclidian distance. Metric distance can
be measured in meters in the three-dimensional model
underlying the simulation.
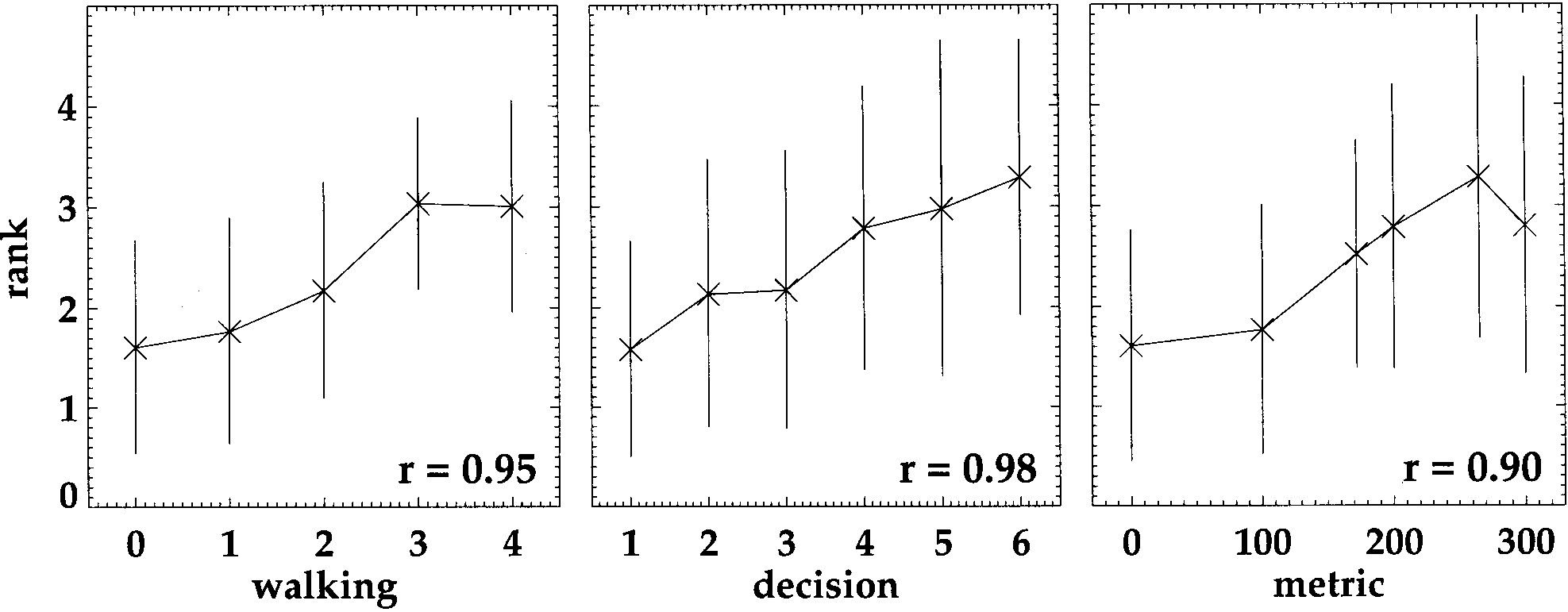
Figure 9 shows the average distance ratings from all 80
subjects as functions of each of the three possible dis-
tance measures. Judged distance increases with true dis-
tance, indicating that subjects have in fact learned some
of the distance relations. This dependence of the ratings
on the actual distance between the views of the pair
accounts at least in part for the effect of view pair found
in the ANOVA. However, it is not obvious from the data
presented in Figure 9 which of the three theoretical
measures is closer to the subject’s sense of distance.
Correlation with the data is highest for decision distance,
whereas standard deviations are smallest for walking
distance. One reason for this poor discrimination lies in
the fact that all three theoretical measures are closely
correlated to each other.
Clearer distinctions between the three theoretical dis-
Gillner and Mallot 453
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
n
t
p
o
a
:
d
/
e
/
d
m
i
f
r
t
o
p
m
r
h
c
.
p
s
i
l
d
v
i
r
e
e
c
r
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
c
m
n
/
j
a
o
r
t
c
i
c
n
e
/
-
a
p
d
r
t
1
i
0
c
l
4
e
4
-
4
p
5
d
1
f
9
/
3
1
1
0
8
/
3
4
9
/
0
4
8
4
9
5
8
/
9
1
2
7
9
5
9
8
8
3
5
8
6
2
1
8
/
6
0
1
8
9
p
8
d
9
b
2
y
9
9
g
8
u
e
5
s
6
t
2
o
8
n
6
0
1
7
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
o
n
/
t
f
.
1
8
M
a
y
2
0
2
1
Figure 8. Possible distance
measures. a. Walking distance,
b. Decision distance, c. Metric
distance. For further explana-
tion see text.
D
o
w
n
l
o
a
d
e
d
b and b fi
tance measures can be achieved by selecting discriminat-
ing view pairs. For example, the decision distance of
view pairs a fi
a is often different, whereas
walking and metric distances of both directions are of
course the same. Table 2 shows the results for the four
such cases tested in our experiments. The ratings do not
depend on direction (i.e., they do not reºect the deci-
sion distance). This result was also obtained when sepa-
rately comparing the ratings from the different viewing
conditions.
For the comparison of metric and walking distance,
we pooled the ratings from both directions of each view
pair, which were shown to be equal in Table 2. The
results from discriminating cases are shown in Table 3.
The ªrst two rows compare view pairs with equal metric
distance and different walking distance. Here, the ratings
differ signiªcantly and are in agreement with walking
distance. The next two rows of Table 3 show the reverse
case (i.e., equal walking distance but different metric
distance). Here again, a signiªcant difference is found,
which, however, does not agree with metric distance:
pair 5 «
19 is rated closer than pair 15 «
19, in
contradiction to the metric distances. Thus, the differ-
ence between these two ratings does not indicate an
inºuence of metric distance. In the last row of the table,
a possible alternative explanation is illustrated. Here, a
signiªcant difference between two pairs with equal
walking and metric distance is found. The pair involving
view 15 (“home”) is rated further apart. This might indi-
cate a perceptive expansion of the area around view 15,
which would also explain the ratings found in rows 3
and 4 of Table 3. However, further experiments are
needed to clarify this point.
The effects illustrated in Table 3 do not depend on
viewing condition, even though the signiªcances are
weaker when analyzing the four groups separately.
Interaction of View Pair and Condition
In the ANOVA including all ratings (Analysis of Variance
section), no effect of viewing condition was found, indi-
cating that average ratings were the same in all condi-
l
l
/
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
n
t
p
o
a
:
d
/
e
/
d
m
i
f
r
t
o
p
m
r
h
c
.
p
s
i
l
d
v
i
r
e
e
c
r
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
c
m
n
/
j
a
o
r
t
c
i
c
n
e
/
-
a
p
d
r
t
1
i
0
c
l
4
e
4
-
4
p
5
d
1
f
9
/
3
1
1
0
8
/
3
4
9
/
0
4
8
4
9
5
8
/
9
1
2
7
9
5
9
8
8
3
5
8
6
2
1
8
/
6
0
1
8
9
p
8
d
9
b
2
y
9
9
g
8
u
e
5
s
6
t
2
o
8
n
6
0
1
7
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
o
n
f
t
/
.
1
8
M
a
y
2
0
2
1
Figure 9. Average distance ratings from all subjects and all viewing conditions (n = 80) plotted as a function of a. walking distance, b. deci-
sion distance, and c. metric distance. r: Pearson correlation (ranks treated as numbers). Error bars are standard deviations.
454 Journal of Cognitive Neuroscience
Volume 10, Number 4
Table 2. Distance rating in view pairs with different
decision distance and equal walking and metric distance
(different directions on the same path). dw: walking distance
(number of segments). dd: decision distance (number of
double mouse clicks required). p significance of difference
as obtained from the Mann-Whitney U-test (n = 80). Errors
are standard deviations. No significant differences are found.
Pair
7fi 10
10fi 7
5fi 15
15fi 5
2fi 15
15fi 2
19fi 15
15fi 19
dw
dd
1
1
2
2
3
3
4
4
1
3
2
4
3
5
4
6
Rating
1.48– 1.36
1.51– 1.09
2.33– 1.01
2.43– 0.98
3.24– 0.72
3.33– 0.73
3.14– 0.96
3.29– 0.83
p
0.39
0.31
0.22
0.22
tions. More interestingly, however, a signiªcant interac-
tion between viewing condition and view pair could be
demonstrated. One possible explanation of this interac-
tion is that in one viewing condition, ratings correlate
more strongly with true distance than in another view-
ing condition. To test this possibility, we calculated Pear-
son (product moment) correlations individually for each
viewing condition (Table 4). The correlation is smallest
Table 3. Distance rating in view pairs discriminating for
walking and metric distance. dw: walking distance (number
of segments). dm: metric distance (meters). p significance of
difference as obtained from the Mann-Whitney U-test (n =
160). Errors are standard deviations. For explanation see text.
Pair
dw
dm(m)
2 «
15 «
5 «
15 «
2 «
2 «
15 «
5 «
2 «
5 «
13
19
15
19
5
15
19
19
13
15
2
4
2
4
3
3
4
4
2
2
173
173
173
173
200
265
173
300
173
173
Rating
1.96– 1.12
3.21– 0.90
2.38– 1.00
3.21– 0.90
2.74– 0.91
3.28– 0.72
3.21– 0.90
2.80– 1.15
1.96– 1.12
2.38– 1.00
p
<10–5
<10–5
<10–5
0.001
0.0005
Table 4. Pearson correlation r of distance ratings with
walking distance in the four viewing conditions.
Condition
Correlation, r
1
0.99
2
0.92
3
0.94
4
0.89
in condition 4 (open environment) and highest in con-
dition 1 (dark). Additionally, the interaction might be due
to condition-dependent rating differences of view pairs
with equal true distances; such dependencies have not
been found, however (see Judged and True Distance
section).
Sketch Maps
As a ªnal part of the experiments, subjects were asked
to draw a map of the explored maze. Three subjects
refused to draw a map (i.e., 77 maps have been col-
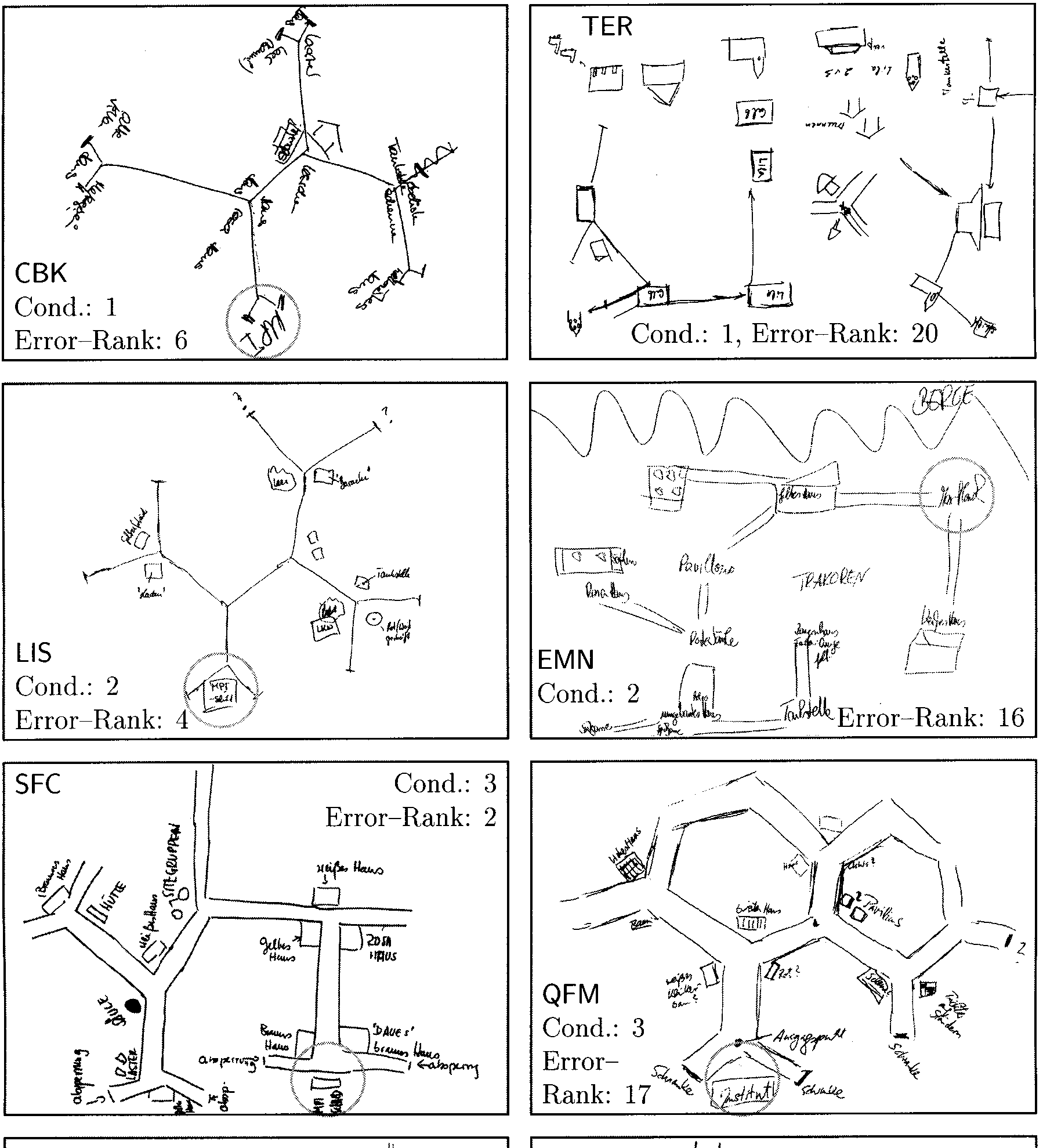
lected). Each row of Figure 10 shows examples from one
viewing condition, a good navigator (few errors in ex-
ploration phase) on the left side and a poor navigator
(many errors in exploration phase) on the right side. In
each viewing condition, subjects were ranked according
to the number of errors that occurred during the explo-
ration phase. The best navigator is ranked 1, the poorest
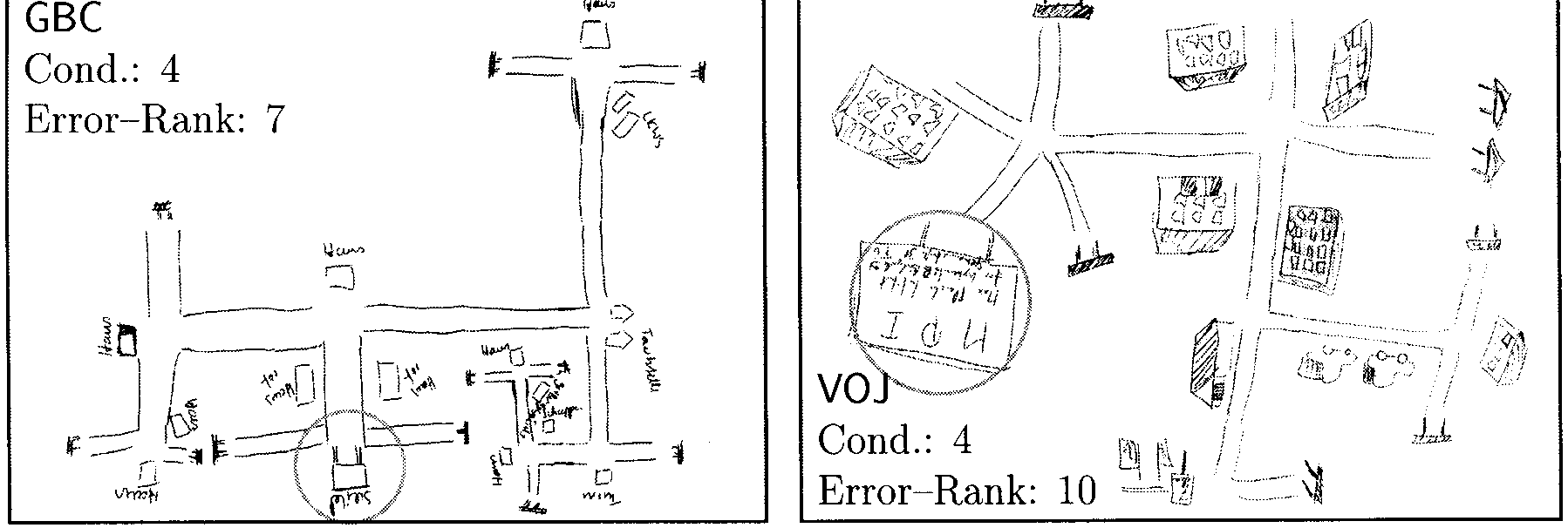
is ranked 20. The position of view 15 (often labeled “MP,”
“Institut,” or “Schild” by the subjects) is marked with a
circle. It has been chosen as the start of the drawing by
74 out of 77 subjects. In Figure 10 all maps have been
oriented in roughly the same way.
Good navigators often produce sketch maps that are
topologically or even metrically correct and contain
identiªable objects. Subject CBK, for example, drew a
perfectly correct map except for four missing objects
whose locations are included. An equally good map had
been drawn by two other subjects, whose maps are not
included in the ªgure.
A frequent deªcit of maps are omissions or additions
of places. For example, subject LIS drew a good map
with the rightmost place missing. Subject GBC, on the
other hand, included two nonexisting places in a map
with otherwise correct connectivity: one in the lower
left and one in the spiral part on the right side. This map
(GBC) also shows another interesting feature: The regu-
lar Y junctions (120(cid:176) ) are represented as T junctions. This
locally feasible assumption leads to global problems such
as nonexistent intersections. In her drawing, GBC solved
this problem by rolling the right branch to a spiral. T
junctions were found in 11 out of the 77 sketch maps.
In most maps (43 out of 77) three streets meet at each
place. Examples of four- and ªve-way junctions appear
in the map of VOJ.
The number of structurally correct places Np (i.e.,
junctions meeting nonortho-
identiªable three-way
gonally) has been determined for each sketch map. The
Gillner and Mallot 455
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
n
t
p
o
a
:
d
/
e
/
d
m
i
f
r
t
o
p
m
r
h
c
.
p
s
i
l
d
v
i
r
e
e
c
r
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
c
m
n
/
j
a
o
r
t
c
i
c
n
e
/
-
a
p
d
r
t
1
i
0
c
l
4
e
4
-
4
p
5
d
1
f
9
/
3
1
1
0
8
/
3
4
9
/
0
4
8
4
9
5
8
/
9
1
2
7
9
5
9
8
8
3
5
8
6
2
1
8
/
6
0
1
8
9
p
8
d
9
b
2
y
9
9
g
8
u
e
5
s
6
t
2
o
8
n
6
0
1
7
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
o
n
t
f
/
.
1
8
M
a
y
2
0
2
1
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
n
t
p
o
a
:
d
/
e
/
d
m
i
f
r
t
o
p
m
r
h
c
.
p
s
i
l
d
v
i
r
e
e
c
r
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
c
m
n
/
j
a
o
r
t
c
i
c
n
e
/
-
a
p
d
r
t
1
i
0
c
l
4
e
4
-
4
p
5
d
1
f
9
/
3
1
1
0
8
/
3
4
9
/
0
4
8
4
9
5
8
/
9
1
2
7
9
5
9
8
8
3
5
8
6
2
1
8
/
6
0
1
8
9
p
8
d
9
b
2
y
9
9
g
8
u
e
5
s
6
t
2
o
8
n
6
0
1
7
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
o
n
t
.
/
f
1
8
M
a
y
2
0
2
1
Figure 10. Sample sketch maps from eight subjects. Cond: viewing condition. Error-rank: subject’s rank in terms of navigation errors during
the exploration phase. Rank 1 indicates lowest number of errors in the respective condition group, and rank 20 indicates highest error num-
ber. For further explanation see text.
456 Journal of Cognitive Neuroscience
Volume 10, Number 4
“place error,” |Np -
7|, is taken as a measure of map
quality. It correlates moderately with the navigation er-
rors in the exploration phase (Table 5), indicating that
good navigators tend to include the correct number of
places in their sketch maps. An ANOVA over the viewing
conditions revealed a signiªcant dependence of Np on
condition (F(3, 76) = 3.18, p = 0.029). As can be seen
from Table 5, this relation is not monotonic. Place error
is high in conditions 2 and 4 and low in conditions 1 and
3.
Figure 10 also illustrates two kinds of global errors.
Subject SFC drew a map with largely correct connectiv-
ity that is basically a mirror image of the correct map.
The lower left place (with two trucks, identiªed by the
word “Laster”), however, has been replaced from its cor-
rect position at the upper end of the drawing without
any changes to its local structure. Altogether, three mir-
ror-inverted maps were drawn. Another example of
global errors is the map of subject QFM, who invented
closed hexagonal loops.
Most maps distinguish places and objects (67 out of
77). In the remaining cases, each junction or place is
identiªed by just one object, resulting in a structure
resembling a view graph (EMN). Subject TER has a re-
duced number of connections, so that the map consists
mainly of isolated objects.
DISCUSSION
Navigation in Virtual Environments
The results presented in this paper clearly show that
spatial relations can be learned from exploration in a
virtual environment even under rather restricted view-
ing conditions. Here, we brieºy summarize the most
important ªndings:
conditions. Bringing the objects closer to the places in
condition 3 and removing the occluding hedges in con-
dition 4 are reminiscent of zooming out the whole scene
with a wide-ªeld lens. May et al. (1997) showed that this
zooming does not improve path-integration performance
in a triangle-completion task. This discrepancy may char-
acterize a difference between path integration and land-
mark navigation. Alternatively, it may be due to the
marked errors in perspective associated with zooming.
The comparison between conditions 1 and 2 (night
and day) does not show an improvement in error rates.
This is surprising because more information is available
in condition 2 (objects at the far end of the streets
become visible). This ªnding may be related to the fact
that the local structure of the maze becomes more
complicated in condition 2, where six objects are visible
from each place.
The correlation of distance estimates with walking
distance in the maze decreases from viewing condition
1 to viewing condition 4 (Interaction of View Pair and
Condition section). We take this as evidence that less
information is stored in the open environment where
navigation need not rely on memory as strongly as in the
other conditions. This interpretation is also in line with
the observation that sketch maps from condition 4 are
not better than those from condition 1. In conclusion, it
appears that the amount of knowledge acquired is de-
termined not by its availability but by the different needs
in the four conditions.
Irrespective of this difference of correlation between
the viewing conditions, the analysis of discriminating
view pairs shows that walking distance is the theoretical
distance measure closest to the subject’s ratings. This
may indicate that the structure of the representation
acquired from all four conditions is the same.
Effect of Viewing Condition
Transfer and Latent Learning
The four viewing conditions differ in the amount of
information available to the subjects. Not surprisingly,
the number of errors during the search phase decreases
as more information is provided. This is in spite of the
fact that the ªeld of view was the same in all four
Table 5. Average number of structurally correct places Np
in the sketch maps and the correlation of |Np -
number of errors made in the exploration phase. r coefª-
cient of correlation. n = 20.
7| with the
Condition
1
2
3
4
Np – s
6.05– 3.70
3.10– 3.24
5.75– 3.21
3.95– 3.45
r
0.61
0.48
0.47
0.35
The overall number of errors was smaller for the later
search tasks. For the 50% best subjects, this effect was
already clearly visible for the comparison of one search
task with the next (Figure 5). If subjects simply learned
a set of independent routes (e.g., by reinforcement learn-
ing), each search would be a new task and no such
transfer would be expected. The knowledge being trans-
ferred from one route to the next is not just a route
memory but involves the recombination of route seg-
ments; this is to say, it is of the conªguration type. Its
acquisition is akin to latent learning, because knowledge
obtained during one search can be employed later in
other, unrelated search tasks.
As can be seen from Figure 5, transfer was strong from
the novel to the return paths but not the other way
around. One possible explanation of this ªnding is that
the novel paths are more difªcult than the returns. When
considering the shortest possible paths, the novel paths
involve 14 different views, 8 of which also occur in the
Gillner and Mallot 457
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
n
t
p
o
a
:
d
/
e
/
d
m
i
f
r
t
o
p
m
r
h
c
.
p
s
i
l
d
v
i
r
e
e
c
r
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
c
m
n
/
j
a
o
r
t
c
i
c
n
e
/
-
a
p
d
r
t
1
i
0
c
l
4
e
4
-
4
p
5
d
1
f
9
/
3
1
1
0
8
/
3
4
9
/
0
4
8
4
9
5
8
/
9
1
2
7
9
5
9
8
8
3
5
8
6
2
1
8
/
6
0
1
8
9
p
8
d
9
b
2
y
9
9
g
8
u
e
5
s
6
t
2
o
8
n
6
0
1
7
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
o
n
.
/
f
t
1
8
M
a
y
2
0
2
1
returns. The returns involve only 9 different views (i.e.,
almost all of their views are already known from the
novel paths). The only view not occurring in the novel
paths is the ªnal goal of the returns, view 15. The transfer
asymmetry may thus be due to the fact that the novel
routes contained more information about the returns
than vice versa.
The occurrence of transfer from one route to another
is also evidence for the presence of goal-independent
memory of space (i.e., a cognitive map).
Persistence
Along with these arguments for conªguration knowl-
edge, evidence for simpler types of spatial learning was
also found. The persistence rates presented in Figure 7
indicate that at least some of the subjects based a con-
siderable part of their movement decisions on simple
associations of views with movements. This strategy is
efªcient for learning nonintersecting routes but will lead
to errors for views at a crossroads where the correct
motion decision depends on the current goal. We specu-
late that the persistence rate will decrease if longer
training sequences are used.
Distance Measures
Judged distance agrees best with the walking distance in
the maze, rather than with metric or decision distance.
This result is based on the rather small number of “dis-
criminating view pairs” where the theoretical measures
disagree. It holds irrespective of the instruction (“dis-
tance” versus “airline distance”). The analysis of distance
ratings presented here rests on the assumption that dis-
tances in different parts of the maze can be compared.
As was discussed with respect to Table 3, this need not
be the case. Rather, the perceived distances in the vicin-
ity of well-known places (home) might be increased.
Subject Differences
Subjects differed strongly in terms of the number of
errors made when searching a goal as well as in the
quality of their distance estimates. However, no cluster-
ing in different groups can be obtained from our data. In
particular, no signiªcant gender differences were found.
View-Based Navigation
In viewing conditions 1 and 2, subjects had to rely on
local views as their only position information. Their per-
formance and the transfer learning is therefore view-
based in an obvious sense. However, this result does not
exclude the possibility that some more complicated rep-
resentation of space is constructed from the local view
information. Here we summarize the evidence against
such a representation (i.e., evidence for a view-based
mechanism of navigation).
Returns Aren’t Easy
After having learned the four excursions, the returns to
the starting point along the very same paths are almost
as difªcult as novel paths (Figure 4). The advantage on
the order of just one error per search task is not sig-
niªcant (F(1, 76) = 2.860, p = 0.095). If the subjects
acquired a place-based representation of space, it would
be the same for excursions and returns, because the
corresponding place graphs are symmetric (see Figure
1). In this case, we would therefore expect that returns
should be much easier and more reliable than novel
paths. The weak difference between the number of er-
rors occurring in returns and novel paths seems to indi-
cate that this is not the case. It is rather more in line with
a view-based mechanism. because the views occurring
along the return path are as different from the original
views as are any other views in the maze.
Recognition and Action
The average persistence rate of 32.9% (Figure 7) indi-
cates that direct associations of views to movement
decisions can be learned. As was pointed out in the
introduction, the association pair of view and motion
decision is the basic element of a view-based memory of
space.
Local Information Combined to a Graph?
If the representation is in fact view-based, a graph struc-
ture is the only representation we can think of that
would account for the transfer and planning behavior
observed. Independent evidence for a graphlike repre-
sentation comes mainly from the sketch maps: as was
point out in the Sketch Maps section, maps are often
locally correct but globally inconsistent. Also, places with
correct local connectivity have been translocated to er-
roneous positions. Connectivity can be correct even
though metric properties of the sketch maps, such as
angles and lengths, are grossly mistaken.
The distance estimates do not reºect the decision
distance, which is the graph distance of the view graph,
but correlate better with walking distance (i.e., the graph
distance of the place graph). It therefore appears that we
cannot decide between the view- and place-graph repre-
sentations at this point. In ongoing work (Mallot & Gill-
ner, 1997), this question is addressed with additional
experiments.
CONCLUSION
In our view, the most important result of this study is
the fact that conªguration knowledge can be acquired
458 Journal of Cognitive Neuroscience
Volume 10, Number 4
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
n
t
p
o
a
:
d
/
e
/
d
m
i
f
r
t
o
p
m
r
h
c
.
p
s
i
l
d
v
i
r
e
e
c
r
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
c
m
n
/
j
a
o
r
t
c
i
c
n
e
/
-
a
p
d
r
t
1
i
0
c
l
4
e
4
-
4
p
5
d
1
f
9
/
3
1
1
0
8
/
3
4
9
/
0
4
8
4
9
5
8
/
9
1
2
7
9
5
9
8
8
3
5
8
6
2
1
8
/
6
0
1
8
9
p
8
d
9
b
2
y
9
9
g
8
u
e
5
s
6
t
2
o
8
n
6
0
1
7
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
o
n
.
f
/
t
1
8
M
a
y
2
0
2
1
in virtual environments. This is in spite of the fact that
the subjects did not actually move but were interacting
with a computer graphics simulation. With respect to the
high controllability of visual input, this result may well
make virtual reality a valuable addition to more realistic
ªeld studies, where stimulus control is often a problem.
As a novel experimental opportunity, we are presently
using object transpositions after learning, which could
be done in real environment only with great difªculties
(Gillner & Mallot, 1996).
With respect to our starting point (i.e., view-based
navigation), we think that three conclusions can be
drawn:
1. Views sufªce. Map learning is possible if only local
(i.e., view information) is provided. In this sense, naviga-
tion can be view-based.
2. Graph versus view from above. The representation
contains local elements (i.e., a place or view with one or
several movement decisions and the respective outcome
associated with it). These local elements need not be
globally consistent, and they need not combine into a
metric survey map. Rather, a graphlike representation is
sufªcient to account for our results.
3. Places versus views. It is not clear from our data
whether the nodes of this graph are places or views. We
have not found evidence that the local views are com-
bined into a representation of space independent of the
orientation of the viewer. So, a view-based representation
seems more likely at this point.
METHODS
The Virtual Maze (Hexatown)
The virtual town was constructed using Medit software
and animated with a frame rate of 36 Hz on a SGI Onyx
RealityEngine2 using IRIX Performer software. A sche-
matic map of the town appears in Figure 11. It is built
on a hexagonal raster with a distance between two
places of 100 m. At each junction, one object, normally
a building, was located in each of the 120(cid:176) angles be-
tween the streets; so each place consisted of three ob-
jects. In the places with less than three incoming streets,
dead ends were added instead, ending with a barrier at
about 50 m. The hexagonal layout was chosen to make
all junctions look alike. In contrast, in Cartesian grids
(city-block raster), long corridors are visible at all times
and the possible decisions at a junction are highly un-
equal: going straight to a visible target or turning to
something not presently visible. The whole town was
surrounded by a distant circular mountain ridge that
showed no salient features. The mountains were con-
structed from a small model that was repeated peri-
odically every 20(cid:176) .
Subjects could move about the town using a com-
puter mouse. In order to have controlled visual input
and not to distract subject’s attention too much, move-
ments were restricted in the following way. Subjects
could move along the street on an invisible rail right in
the middle of each street. This movement was initiated
by hitting the middle mouse button and was then car-
ried out with a predeªned velocity proªle without fur-
interact. The
ther possibilities for the subject to
translation took 8.4 sec with a fast acceleration to the
maximum speed of 17 m/sec and a slow deceleration.
The movement ended at the next junction, in front of
the object facing the incoming street. Sixty-degree turns
could be performed similarly by pressing the left or right
mouse button. Again, the simulated movement was “bal-
listic” (i.e., following a predeªned velocity proªle). Turns
took 1.7 sec with a maximum speed of 70(cid:176) /sec and
symmetric acceleration and deceleration.
Figure 12 shows the movement decisions that subjects
could choose from. Each transition between two views
is mediated by two movement decisions. When facing an
object (e.g., the one marked “a” in Figure 12), 60(cid:176) turns
left or right (marked “L”, “R”) can be performed; they will
lead to a view down a street. If this is not a dead end,
three decisions are possible: the middle mouse button
triggers a translation down the street (marked “G” for
go), whereas the left and right buttons lead to 60(cid:176) turns.
If the street is a dead end, turns are the only possible
decision. In any case, the second movement will end in
front of another object.
An aerial view of Hexatown is shown in Figure 13. It
gives an impression of the objects used. The spacing and
position of the trees correspond to viewing conditions
1 and 2 (see below).
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
n
t
p
o
a
:
d
/
e
/
d
m
i
f
r
t
o
p
m
r
h
c
.
p
s
i
l
d
v
i
r
e
e
c
r
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
c
m
n
/
j
a
o
r
t
c
i
c
n
e
/
-
a
p
d
r
t
1
i
0
c
l
4
e
4
-
4
p
5
d
1
f
9
/
3
1
1
0
8
/
3
4
9
/
0
4
8
4
9
5
8
/
9
1
2
7
9
5
9
8
8
3
5
8
6
2
1
8
/
6
0
1
8
9
p
8
d
9
b
2
y
9
9
g
8
u
e
5
s
6
t
2
o
8
n
6
0
1
7
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
o
n
/
t
f
.
1
8
M
a
y
2
0
2
1
Figure 11. Street map of the virtual maze with 7 places num-
bered 0 through 6 and 21 views numbered 0 through 20. The ring
around each place indicates the hedges used in viewing conditions
1 through 3 to occlude distant places.
Gillner and Mallot 459
arrangement was such that when entering the circular
hedge in conditions 1 and 2, the buildings to the left and
right were already outside the observer’s ªeld of view
(60(cid:176) ). Thus, the three buildings at one junction could
never be seen together in these conditions. In condition
3, the buildings were at a distance of only 15 m from the
junction. In this case, all three buildings were seen at
once when entering the place. The town was illuminated
from the bright sky, except in condition 1, where an
exploration at night was simulated. Here, illumination
was as with a torch or the headlights of a car and
reached about 60 m. Thus, the building at the far end of
a street was not visible in this condition. A summary of
the viewing conditions and variants of Hexatown is
given in Figure 14.
Procedure
Figure 12. Possible movement decisions when facing the view
marked a. L: turn left 60(cid:176) . R: turn right 60(cid:176) . G: go ahead to next
place.
We used four stimulus conditions with varying de-
grees of visibility of the environment. In conditions 1, 2,
and 3, a circular hedge or row of trees was placed
around each junction with an opening for each of the
three streets (or dead ends) connected to that junction.
This hedge looked the same for all junctions and pre-
vented subjects from seeing the objects at more distant
junctions. In conditions 1, 2, and 4, the objects were
placed 22 m away from the center of the junction. The
Experiments were performed using a standard 19-in SGI
monitor. Subjects were seated comfortably in front of the
screen and no chin rest was used. They moved their
heads in a range of about 40 to 60 cm in front of the
screen, which results in a viewing angle of about 35 to
50(cid:176) .
The experiment was performed in three phases. In the
exploration phase, subjects found themselves facing
some view v1. They were then presented with a target
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
n
t
p
o
a
:
d
/
e
/
d
m
i
f
r
t
o
p
m
r
h
c
.
p
s
i
l
d
v
i
r
e
e
c
r
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
c
m
n
/
j
a
o
r
t
c
i
c
n
e
/
-
a
p
d
r
t
1
i
0
c
l
4
e
4
-
4
p
5
d
1
f
9
/
3
1
1
0
8
/
3
4
9
/
0
4
8
4
9
5
8
/
9
1
2
7
9
5
9
8
8
3
5
8
6
2
1
8
/
6
0
1
8
9
p
8
d
9
b
2
y
9
9
g
8
u
e
5
s
6
t
2
o
8
n
6
0
1
7
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
o
n
f
t
/
.
1
8
M
a
y
2
0
2
1
Figure 13. Aerial view of Hexatown. Orientation as in Figure 11. The white rectangle in the left foreground is view 15, used as “home” posi-
tion in our experiments. The aerial view was not available to the subjects. Object models are courtesy of Silicon Graphics, Inc., and Prof.
F. Leberl, Graz.
460 Journal of Cognitive Neuroscience
Volume 10, Number 4
view v2 printed out on a sheet of paper and asked to
ªnd this view in the virtual town (task v1 fi
v2). When
they found the view, feedback was given in the form of
a little sign appearing on the screen. If they got lost in
the maze (i.e., if they deviated from the shortest possible
path by more than one segment), the trial was stopped
and another sign announced the failure. This feature of
the procedure was included in order not to discourage
subjects by long unsuccessful searches. In pilot experi-
ments with free exploration (no goals speciªed), learn-
ing was much harder. The number of terminations varied
from 9.9 times per subject in viewing condition 1 to 1.5
in viewing condition 4; terminations occurred almost
exclusively during the excursion phase (see below). If a
trial was terminated, or if the way found was not the
shortest possible way, the subject was relocated to the
starting point and a new trial for the same goal started.
The sequence was terminated when the shortest possi-
ble way, that is, the way involving the minimal number
of decisions (mouse clicks), was found. The whole explo-
ration phase contained 12 such search tasks, or ways to
be found. The ªrst four ways were excursions from view
15, which served as a “home” position. View 15 showed
a poster wall saying “Max-Planck-Institut für biologische
Kybernetik.” The following eight searches were either
returns to home or novel paths not touching on view
15. The return and novel path tasks were presented
alternatingly in two sequence conditions: in the returns-
ªrst condition, the ªrst task was a return, whereas in the
novel-ªrst condition, the sequence started with a novel
path. In both conditions, the four excursions were per-
formed prior to both returns and novel paths (Figure
15).
In the distance estimation phase, following immedi-
ately after the exploration, subjects were presented with
pairs of views on the screen. The ªrst view was shown
without time limit; after hitting the spacebar, the second
view was presented again without time limit. Subjects
were asked to rate the distance between the two views
on an integer scale ranging from 0 to 4, where 0 meant
“very close” and 4 “very far apart.” One of two instruc-
tions was used: In the ªrst, subjects were asked to rate
according to distance (“Abstand”); in the second, they
were told to estimate the airline (metric) distance
(“Luftlinie”). After hitting the appropriate number button,
the next view pair was presented. Ranking data from a
total of 20 view pairs was collected from each subject
(Table 6).
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
n
t
p
o
a
:
d
/
e
/
d
m
i
f
r
t
o
p
m
r
h
c
.
p
s
i
l
d
v
i
r
e
e
c
r
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
c
m
n
/
j
a
o
r
t
c
i
c
n
e
/
-
a
p
d
r
t
1
i
0
c
l
4
e
4
-
4
p
5
d
1
f
9
/
3
1
1
0
8
/
3
4
9
/
0
4
8
4
9
5
8
/
9
1
2
7
9
5
9
8
8
3
5
8
6
2
1
8
/
6
0
1
8
9
p
8
d
9
b
2
y
9
9
g
8
u
e
5
s
6
t
2
o
8
n
6
0
1
7
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
o
n
t
/
.
f
1
8
M
a
y
2
0
2
1
Figure 14. Viewing conditions used in the experiments. For each condition, three views ar shown. The views in the top row occur when look-
ing from a place (no. 5) into a street. The views in the middle row can be seen during the motion along a street, in this example from place 5
to place 3. The views in the bottom row show an object (view 11) as seen from the corresponding junction (place 3). Object models are cour-
tesy of Silicon Graphics, Inc., and Prof. F. Leberl, Graz.
Gillner and Mallot 461
In the sketching phase, subjects were asked to draw a
sketch map of the virtual town on a sheet of paper.
The experiment was run on 80 paid volunteers, 40
male and 40 female, aged 15 to 38. Twenty subjects (10
male, 10 female) took part in each of the four viewing
conditions (Figure 14). Within each viewing condition,
the group of subjects was split equally (10 to 10) be-
tween the two sequence conditions (returns ªrst and
novel ªrst, Figure 15), as well as the two instructions for
the distance estimation (“distance” and “airline dis-
tance”).
Acknowledgment
This work was supported by the Deutsche Forschungsgemein-
schaft, Schwerpunktprogramm Raumkognition. We are grateful
to Silicon Graphics Inc. and Prof. F. Leberl (University of Graz)
for providing VR-models used in the experiments. We are also
grateful to Tordis Philipps for help with the experiments and
to Heinrich H. Bülthoff, Bernhard Schölkopf, and Hendrik-Jan
van Veen for comments on prior versions of the manuscript.
The writing of the ªnal text was supported by a fellowship
from the Institute of Advanced Study Berlin to HAM.
Reprint requests should be sent to H. A. Mallot, Max-Planck-
Institut für biologische Kybernetik, Spemannstr. 38, D-72076
Tübingen, Germany, or via e-mail: hanspeter.mallot@
tuebingen.mpg.de.
Notes
1. Bennett (1996) has driven the minimalistic view to the
point of denying the very existence of declarative memory of
spatial relations. Although this may be true for insects (Wehner
& Menzel, 1990), we argue that such memory does exist in
humans. The view-graph model is a simple model of declarative
memory of spatial conªgurations that builds on features of
insect spatial memory.
2. Additional material on Hexatown
is available
http://www.kyb.tuebingen.mpg.de/links/hexatown.html.
from
REFERENCES
Aginsky, V., Harris, C., Rensink, R., & Beusmans, J. (1996). Two
strategies for learning a route in a driving simulator. Techni-
cal Report CBR TR 96-6, Cambridge Basic Research, 4 Cam-
bridge Center, Cambridge, Massachusetts 02142 U.S.A.
Barto, A. G., & Sutton, R. S. (1981). Landmark learning: An illus-
tration of associative search. Biological Cybernetics, 42, 1–
8.
Benhamou, S., Bovet, P., & Poucet, B. (1995). A model for
place navigation in mammals. Journal of Theoretical Biol-
ogy, 173, 163–178.
Bennett, A. T. D. (1996). Do animals have cognitive maps? The
Journal of Experimental Biology, 199, 219–224.
Berthoz, A., Israël, I., Georges-François, P., Grasso, R., &
Tsuzuku, T. (1995). Spatial memory of body linear displace-
ment: What is being stored? Science, 269, 95–98.
Billinghurst, M., & Weghorst, S. J. (1995). The use of sketch
maps to measure cognitive maps of virtual environments.
Proc. IEEE 1995 Virtual Reality Annual International
Symposium, 40–47.
Bülthoff, H. H., Edelman, S. Y., & Tarr, M. J. (1995). How are
Figure 15. Sequence of search tasks identified by the numbers of
start and goal view. Left: Returns-first condition. Right: Novel-first
condition.
Table 6. View pairs tested in the distance estimation phase.
dw, dd, and dm are theoretical distance measures; see Judged
and True Distance section.
Pair
6 fi 8
8 fi
10 fi
11 fi
7 fi
10 fi
13 fi
19 fi
2 fi
13 fi
5 fi
15 fi
2 fi
6
11
10
10
7
19
13
13
2
15
5
5
5 fi 2
2 fi
15 fi
15 fi
19 fi
5 fi
19 fi
15
2
19
15
19
5
dw
0
0
0
0
1
1
1
1
2
2
2
2
3
3
3
3
4
4
4
4
dd
2
2
2
2
2
6
4
4
6
6
4
8
8
8
6
10
12
8
10
10
dm
0
0
0
0
100
100
100
100
173
173
173
173
200
200
265
265
173
173
300
300
462 Journal of Cognitive Neuroscience
Volume 10, Number 4
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
n
t
p
o
a
:
d
/
e
/
d
m
i
f
r
t
o
p
m
r
h
c
.
p
s
i
l
d
v
i
r
e
e
c
r
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
c
m
n
/
j
a
o
r
t
c
i
c
n
e
/
-
a
p
d
r
t
1
i
0
c
l
4
e
4
-
4
p
5
d
1
f
9
/
3
1
1
0
8
/
3
4
9
/
0
4
8
4
9
5
8
/
9
1
2
7
9
5
9
8
8
3
5
8
6
2
1
8
/
6
0
1
8
9
p
8
d
9
b
2
y
9
9
g
8
u
e
5
s
6
t
2
o
8
n
6
0
1
7
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
o
n
f
.
/
t
1
8
M
a
y
2
0
2
1
three-dimensional objects represented in the brain? Cere-
bral Cortex, 5, 247–260.
Cartwright, B. A., & Collett, T. S. (1982). How honey bees use
landmarks to guide their return to a food source. Nature,
295, 560–564.
Collett, T. S., & Baron, J. (1995). Learnt sensori-motor map-
pings in honeybees: Interpolation and its possible rele-
vance to navigation. Journal of Comparative Physiology
A, 177, 287–298.
Darken, R. P., & Sibert, J. L. (1996). Navigating large virtual
spaces. International Journal of Human-Computer Inter-
action, 8, 49–71.
Franz, M. O., Schölkopf, B., Mallot, H. A., & Bülthoff, H. H.
(1998). Learning view graphs for robot navigation. Autono-
mous Robots, 5, 111–125.
Gallistel, C. R. (1990). The organization of learning. Cam-
bridge, MA: MIT Press.
Jung, M. W., Knierim, J. J., Kudrimoti, H., Qin, Y., Skaggs,
W. E., Suster, M., & Weaver, K. L. (1996). Deciphering the
hippocampal polyglot: The hippocampus as a path integra-
tion system. The Journal of Experimental Biology, 199,
173–185.
McNaughton, B. L., & Morris, R. G. M. (1987). Hippocampal sy-
naptic enhancement and information storage within a dis-
tributed memory system. Trends in Neurosciences, 10,
408–415.
Mittelstaedt, H., & Mittelstaedt, M.-L. (1972/73). Mechanismen
der orientierung ohne richtende außenreize [Mechanisms
of orientation without orienting external stimuli]. Fort-
schritte der Zoologie, 21, 46–58.
Muller, R. U., Stead, M., & Pach, J. (1996). The hippocampus
as a cognitive graph. Journal of General Physiology, 107,
663–694.
O’Keefe, J., & Nadel, L. (1978). The hippocampus as a cogni-
Gillner, S., & Mallot, H. A. (1996). Place-based versus view-
tive map. Oxford: Clarendon.
based navigation: Experiments in changing virtual environ-
ments. Perception, 25, 93.
Prescott, T. (1996). Spatial representation for navigation in ani-
mals. Adaptive Behavior, 4, 85–123.
Kuipers, B. J., & Byun, Y.-T. (1991). A robust exploration and
Schölkopf, B., & Mallot, H. A. (1995). View-based cognitive
mapping strategy based on a semantic hierarchy of spatial
representations. Journal of Robotics and Autonomous Sys-
tems, 8, 47–63.
mapping and path planning. Adaptive Behavior, 3, 311–
348.
Squire, L. R. (1987). Memory and brain. New York: Oxford
Loomis, J. M., Klatzky, R. L., Golledge, R. G., Cicinelli, J. G.,
University Press.
Pellegrino, J. W., & Fry, P. A. (1993). Nonvisual navigation by
blind and sighted: Assessment of path integration ability.
Journal of Experimental Psychology: General, 122, 73–91.
Mallot, H. A., & Gillner, S. (1997). Psychophysical support for
a view-based strategy in navigation. Investigative Ophthal-
mology and Visual Science, 38, S1007.
Maurer, R., & Séguinot, V. (1995). What is modelling for? A
critical review of the models of path integration. Journal
of Theoretical Biology, 175, 457–475.
May, M., Péruch, P., & Savoyant, A. (1995). Navigating in a vir-
tual environment with map-acquired knowledge: Encoding
and alignment effects. Ecological Psychology, 7, 21–36.
May, M., Wartenberg, F., & Péruch, P. (1997). Raumorien-
tierung in virtuellen Umgebungen. [Spatial orientation in
virtual environments]. In R. H. Kluwe, (Ed.), Kognitionswis-
senschaft: Strukturen und prozesse intelligenter systeme.
Wiesbaden: Deutscher Universitätsverlag.
McNaughton, B. L., Barnes, C. A., Gerrard, J. L., Gothard, K.,
Tlauka, M., & Wilson, P. N. (1996). Orientation-free repre-
sentations from navigation through a computer-simulated
environment. Environment and Behavior, 28, 647–664.
Tolman, E. C. (1948). Cognitive maps in rats and man. Psycho-
logical Review, 55, 189–208.
Tong, F. H., Marlin, S. G., & Frost, B. J. (1995). Visual-motor inte-
gration and spatial representation in a visual virtual envi-
ronment. Investigative Ophthalmology and Visual
Science, 36, S1679.
Touretzky, D. S., & Redish, A. D. (1996). Theory of rodent navi-
gation based on interacting representations of space. Hip-
pocampus, 6, 247–270.
Touretzky, D. S., Redish, A. D., & Wan, H. S. (1993). Neural rep-
resentation of space using sinusoidal arrays. Neural Com-
putation, 5, 869–884.
Wehner, R., & Menzel, R. (1990). Do insects have cognitive
maps? Annual Review of Neuroscience, 13, 403–414.
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
n
t
p
o
a
:
d
/
e
/
d
m
i
f
r
t
o
p
m
r
h
c
.
p
s
i
l
d
v
i
r
e
e
c
r
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
c
m
n
/
j
a
o
r
t
c
i
c
n
e
/
-
a
p
d
r
t
1
i
0
c
l
4
e
4
-
4
p
5
d
1
f
9
/
3
1
1
0
8
/
3
4
9
/
0
4
8
4
9
5
8
/
9
1
2
7
9
5
9
8
8
3
5
8
6
2
1
8
/
6
0
1
8
9
p
8
d
9
b
2
y
9
9
g
8
u
e
5
s
6
t
2
o
8
n
6
0
1
7
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
o
n
t
.
/
f
1
8
M
a
y
2
0
2
1
Gillner and Mallot 463