Modeling Global and Local Node Contexts
for Text Generation from Knowledge Graphs
Leonardo F. R. Ribeiro†, Yue Zhang‡, Claire Gardent§ and Iryna Gurevych†
†Research Training Group AIPHES and UKP Lab, Technische Universit¨at Darmstadt
‡School of Engineering, Westlake University, §CNRS/LORIA, Nancy, France
ribeiro@aiphes.tu-darmstadt.de, yue.zhang@wias.org.cn
claire.gardent@loria.fr, gurevych@ukp.informatik.tu-darmstadt.de
Abstract
Recent graph-to-text models generate text
from graph-based data using either global or
local aggregation to learn node representa-
tions. Global node encoding allows explicit
communication between two distant nodes,
thereby neglecting graph topology as all nodes
are directly connected. In contrast, local node
encoding considers the relations between neigh-
bor nodes capturing the graph structure, but it
can fail to capture long-range relations. In this
work, we gather both encoding strategies, pro-
posing novel neural models that encode an
input graph combining both global and local
node contexts, in order to learn better contextu-
alized node embeddings. In our experiments,
we demonstrate that our approaches lead to
significant
improvements on two graph-to-
text datasets achieving BLEU scores of 18.01
on the AGENDA dataset, and 63.69 on the
WebNLG dataset for seen categories, outper-
forming state-of-the-art models by 3.7 and 3.1
points, respectively.1
1 Introduction
Graph-to-text generation refers to the task of gen-
erating natural language text from input graph
structures, which can be semantic representations
(Konstas et al., 2017) or knowledge graphs (KGs)
(Gardent et al., 2017; Koncel-Kedziorski et al.,
2019). Whereas most recent work (Song et al.,
2018; Ribeiro et al., 2019; Guo et al., 2019) fo-
cuses on generating sentences, a more challenging
and interesting scenario emerges when the goal is
to generate multisentence texts. In this context, in
addition to sentence generation, document plan-
ning needs to be handled: The input needs to be
mapped into several sentences; sentences need to
1Code is available at https://github.com/UKPLab/
kg2text.
589
be ordered and connected using appropriate dis-
course markers; and inter-sentential anaphora and
ellipsis may need to be generated to avoid repeti-
tion. In this paper, we focus on generating texts
rather than sentences where the output are short
texts (Gardent et al., 2017) or paragraphs (Koncel-
Kedziorski et al., 2019).
A key issue in neural graph-to-text generation is
how to encode the input graphs. The basic idea is
to incrementally compute node representations by
aggregating structural context information. To this
end, two main approaches have been proposed: (i)
models based on local node aggregation, usually
built upon Graph Neural Networks (GNNs) (Kipf
and Welling, 2017; Hamilton et al., 2017) and
(ii) models that leverage global node aggregation.
Systems that adopt global encoding strategies are
typically based on Transformers (Vaswani et al.
2017), using self-attention to compute a node
representation based on all nodes in the graph. This
approach enjoys the advantage of a large node con-
text range, but neglects the graph topology by
effectively treating every node as being connected
to all the others in the graph. In contrast, models
based on local aggregation learn the representation
of each node based on its adjacent nodes as
defined in the input graph. This approach effect-
ively exploits the graph topology, and the graph
structure has a strong impact on the node repre-
sentation (Xu et al., 2018). However, encoding
relations between distant nodes can be challenging
by requiring more graph encoding layers, which
can also propagate noise (Li et al., 2018).
For example, Figure 1a presents a KG, for
which a corresponding text is shown in Figure 1b.
Note that there is a mismatch between how enti-
ties are connected in the graph and how their nat-
ural language descriptions are related in the text.
Some entities syntactically related in the text are
not connected in the graph. For instance, in the
Transactions of the Association for Computational Linguistics, vol. 8, pp. 589–604, 2020. https://doi.org/10.1162/tacl a 00332
Action Editor: Alessandro Moschitti. Submission batch: 2/2019; Revision batch: 5/2020; Published 9/2020.
c(cid:13) 2020 Association for Computational Linguistics. Distributed under a CC-BY 4.0 license.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
3
2
1
9
2
3
1
9
0
/
/
t
l
a
c
_
a
_
0
0
3
3
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
from KG triples. For example, in Figure 1a, GAT
reaches node embeddings through the GNN. This
transitive relation can be captured by a local
encoder, as shown in Figure 1d. Capturing this
form of relationship also can support text gene-
ration at the sentence level.
In this paper, we investigate novel graph-to-
text architectures that combine both global and
local node aggregations, gathering the benefits
from both strategies. In particular, we propose a
unified graph-to-text framework based on Graph
Attention Networks (GATs) (Veliˇckovi´c et al.,
2018). As part of this framework, we empirically
compare two main architectures: a cascaded archi-
tecture that performs global node aggregation
before performing local node aggregation, and a
parallel architecture that performs global and
local aggregations simultaneously. The cascaded
architecture allows the local encoder to leverage
global encoding features, and the parallel architec-
ture allows more independent features to comple-
ment each other. To further consider fine-grained
integration, we additionally consider layer-wise
integration of the global and local encoders.
Extensive experiments show that our ap-
proaches consistently outperform recent models
on two benchmarks for text generation from KGs.
To the best of our knowledge, we are the first to
consider integrating global and local context ag-
gregation in graph-to-text generation, and the first
to propose a unified GAT structure for combining
global and local node contexts.
2 Related Work
(Flanigan et
Early efforts for graph-to-text generation used
statistical methods
al., 2016;
Pourdamghani et al., 2016; Song et al., 2017).
Recently, several neural graph-to-text models
have exhibited success by leveraging encoder
mechanisms based on LSTMs, GNNs, and
Transformers.
AMR-to-Text Generation. Various neural mo-
dels have been proposed to generate sentences
from Abstract Meaning Representation (AMR)
graphs. Konstas et al. (2017) provide the first neu-
ral approach for this task, by linearizing the input
graph as a sequence of nodes and edges. Song et al.
(2018) propose the graph recurrent network to di-
rectly encode the AMR nodes, whereas Beck et al.
(2018) develop a model based on gated GNNs.
Figure 1: A graphical representation (a) of a scientific
text (b). (c) A global encoder directly captures longer
dependencies between any pair of nodes (blue and red
arrows), but fails in capturing the graph structure. (d) A
local encoder explicitly accesses information from the
adjacent nodes (blue arrows) and implicitly captures
distant information (dashed red arrows).
sentence ‘‘For the link prediction task, first we
learn node embeddings using DistMult method.’’,
although the entity mentions are dependent of the
same verb, in the graph, the node embeddings node
has no explicit connection with link prediction
and DistMult nodes, which are in a different
connected component. This example illustrates
the importance of encoding distant information in
the input graph. As shown in Figure 1c, a global
encoder is able to learn a node representation
for node embeddings which captures information
from non-connected entities such as DistMult. By
modeling distant connections between all nodes,
we allow for these missing links to be captured,
as KGs are known to be highly incomplete (Dong
et al., 2014; Schlichtkrull et al., 2018).
In contrast, the local strategy refines the node
representation with richer neighborhood informa-
tion, as nodes that share the same neighborhood
exhibit a strong homophily: Two similar entities
are much more likely to be connected than at
random. Consequently, the local context enriches
the node representation with local information
590
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
3
2
1
9
2
3
1
9
0
/
/
t
l
a
c
_
a
_
0
0
3
3
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
However, both approaches only use local node
aggregation strategies. Damonte and Cohen
(2019) combine graph convolutional networks
and LSTMs in order to learn complementary node
contexts. However, differently from Transformers
and GNNs, LSTMs generate node representations
that are influenced by the node order. Ribeiro et al.
(2019) develop a model based on different GNNs
that learns node representations which simulta-
neously encode a top–down and a bottom–up
views of the AMR graphs, whereas Guo et al.
(2019) leverage dense connectivity in GNNs. Re-
cently, Wang et al. (2020) propose a local graph
encoder based on Transformers using separated
attentions for incoming and outgoing neighbors.
Recent methods (Zhu et al., 2019; Cai and Lam,
2020) also use Transformers, but learn globalized
node representations, modeling graph paths in
order to capture structural relations.
KG-to-Text Generation.
In this work, we focus
on generating text from KGs. In comparison to
AMRs, which are rooted and connected graphs,
KGs do not have a defined topology, which may
vary widely among different datasets, making
the generation process more demanding. KGs are
sparse structures that potentially contain a large
number of relations. Moreover, we are typically
interested in generating multisentence texts from
KGs, and this involves solving document planning
issues (Konstas and Lapata, 2013).
Recent neural approaches for KG-to-text gener-
ation simply linearize the KG triples, thereby
loosing graph structure information. For instance,
Colin and Gardent (2018), Moryossef et al. (2019),
and Adapt (Gardent et al., 2017) utilize LSTM/
GRU to encode WebNLG graphs. Castro Ferreira
et al. (2019) systematically compare pipeline and
text generation from
end-to-end models for
WebNLG graphs. Trisedya et al. (2018) develop
a graph encoder based on LSTMs that captures
relationships within and between triples. Previous
work has also studied how to explicitly encode
the graph structure using GNNs or Transformers.
Marcheggiani and Perez Beltrachini (2018) pro-
pose an encoder based on graph convolutional net-
works, that consider explicitly local node contexts,
and show superior performance compared with
LSTMs. Recently, Koncel-Kedziorski et al. (2019)
proposed a Transformer-based approach that com-
putes the node representations by attending over
node neighborhoods following a self-attention
strategy. In contrast, our models focus on distinct
global and local message passing mechanisms,
capturing complementary graph contexts.
Integrating Global Information. There has
been recent work that attempts to integrate global
context in order to learn better node representa-
tions in graph-to-text generation. To this end,
existing methods use an artificial global node for
message exchange with the other nodes. This
strategy can be regarded as extending the graph
structure but using similar message passing mech-
anisms. In particular, Koncel-Kedziorski et al.
(2019) add a global node to the graph and use
its representation to initialize the decoder. Re-
cently, Guo et al. (2019) and Cai and Lam (2020)
also utilized an artificial global node with direct
edges to all other nodes to allow global message
exchange for AMR-to-text generation. Similarly,
Zhang et al. (2018) use a global node to a graph
recurrent network model for sentence represen-
tation. Different from the above methods, we
consider integrating global and local contexts at
the node level, rather than the graph level, by
investigating model alternatives rather than graph
structure changes. In addition, we integrate GAT
and Transformer architectures into a unified
global-local model.
3 Graph-to-Text Model
This section first describes (i) the graph transfor-
mation adopted to create a relational graph from
the input (Section 3.1), and (ii) the graph encoders
of our framework based on GAT (Veliˇckovi´c et al.,
2018), for dealing with both global (Section 3.3)
and local (Section 3.4) node contexts. We adopt
GAT because it is closely related to the Trans-
former architecture (Vaswani et al., 2017), which
provides a convenient prototype for modeling
global node context. Then, (iii) we proposed stra-
tegies to combined the global and local graph en-
oders (Section 3.5). Finally, (iv) we describe the
decoding and training procedures (Section 3.6).
3.1 Graph Preparation
We represent a KG as a multi-relational graph2
Ge = (Ve, Ee, R) with entity nodes e ∈ Ve and
labeled edges (eh, r, et) ∈ Ee, where r ∈ R
2In this paper, multi-relational graphs refer to directed
graphs with labeled edges.
591
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
3
2
1
9
2
3
1
9
0
/
/
t
l
a
c
_
a
_
0
0
3
3
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
denotes the relation existing from the entity eh
to et.3
Unlike other current approaches (Koncel-
Kedziorski et al., 2019; Moryossef et al., 2019), we
represent an entity as a set of nodes. For instance,
the KG node “node embedding” in Figure 1 will
be represented by two nodes, one for the token
“node” and the other for the token “embedding”.
Formally, we transform each Ge into a new graph
G = (V, E, R), where each token of an entity
e ∈ Ve becomes a node v ∈ V. We convert each
edge (eh, r, et) ∈ Ee into a set of edges (with the
same relation r) and connect every token of eh
to every token of et. That is, an edge (u, r, v)
will belong to E if and only if there exists an edge
(eh, r, et) ∈ Ee such that u ∈ eh and v ∈ et, where
eh and et are seen as sets of tokens. We represent
v ∈ Rdv ,
each node v ∈ V with an embedding h0
generated from its corresponding token.
The new graph G increases the representational
power of the models because it allows learning
node embeddings at a token level, instead of
entity level. This is particularly important for text
generation as it permits the model to be more
flexible, capturing richer relationships between
entity tokens. This also allows the model to learn
relations and attention functions between source
and target tokens. However, it has the side effect
of removing the natural sequential order of multi-
word entities. To preserve this information, we
use position embeddings (Vaswani et al., 2017),
that is, h0
v becomes the sum of the corresponding
token embedding and the positional embedding
for v.
3.2 Graph Neural Networks (GNN)
Multilayer GNNs work by iteratively learning a
representation vector hv of a node v based on
both its context node neighbors and edge features,
through an information propagation scheme. More
formally, the l-th layer aggregates the representa-
tions of v’s context nodes:
h(l)
N (v) = AGGR(l)
(cid:16)n(cid:16)h(l−1)
u
, ruv(cid:17) : u ∈ N (v)o(cid:17),
where AGGR(l)(.) is an aggregation function,
shared by all nodes on the l-th layer. ruv represents
the relation between u and v. N (v) is a set
3R contains relations both in canonical direction (e.g.,
used-for) and in inverse direction (e.g., used-for-inv), so that
the models consider the differences in the incoming and
outgoing relations.
592
of context nodes for v. In most GNNs,
the
context nodes are those adjacent to v. h(l)
N (v) is
the aggregated context representation of N (v) at
layer l. h(l)
N (v) is used to update the representation
of v:
v = COMBINE(l)
h(l)
(cid:16)h(l−1)
v
, h(l)
N (v)(cid:17) .
After L iterations, a node’s representation
encodes the structural information within its L-
hop neighborhood. The choices of AGGR(l)(.)
and COMBINE(l)(.) differ by the specific GNN
model. An example of AGGR(l)(.) is the sum
of the representations of N (v). An example
of COMBINE(l)(.) is a concatenation after the
feature transformation.
3.3 Global Graph Encoder
A global graph encoder aggregates the global
context for updating each node based on all
nodes of the graph (see Figure 1c). We use
the attention mechanism as the message passing
scheme, extending the self-attention network
structure of Transformer to a GAT structure.
In particular, we compute a layer of the global
convolution for a node v ∈ V, which takes the
input feature representations hv as input, adopting
AGGR(l)(.) as:
hN (v) =
Xu∈V
αvuWg hu,
(1)
where Wg ∈ Rdv ×dz is a model parameter. The
attention weight αvu is calculated as:
αvu =
exp(evu)
Pk∈V exp(evk)
,
where
evu = (cid:16)(Wqhv)⊤ (Wkhu)(cid:17) /dz
(2)
(3)
is the attention function which measures the
global importance of node u’s features to node
v. Wq, Wk ∈ Rdv ×dz are model parameters
and dz is a scaling factor. To capture distinct
relations between nodes, K independent global
convolutions are calculated and concatenated:
ˆhN (v) =
(cid:13)
(cid:13)
K
k=1h(k)
N (v).
(4)
Finally, we define COMBINE(l)(.) using layer
normalization (LayerNorm) and a fully connected
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
3
2
1
9
2
3
1
9
0
/
/
t
l
a
c
_
a
_
0
0
3
3
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
feed-forward network (FFN), in a similar way as
the transformer architecture:
generating ˆhN (v). Finally, we define COMBINE(l)
(.) as:
ˆhv = LayerNorm(ˆhN (v) + hv),
= FFN(ˆhv) + ˆhN (v) + hv.
hglobal
v
(5)
(6)
Note that the global encoder creates an artificial
complete graph with O(n2) edges and does not
consider the edge relations. In particular, if the
labeled edges were considered, the self-attention
space complexity would increase to Θ(|R|n2).
v
3.4 Local Graph Encoder
The representation hglobal
captures macro relation-
ships from v to all other nodes in the graph.
However, this representation lacks both structural
information regarding the local neighborhood of v
and the graph topology. Also, it does not capture
labeled edges (relations) between nodes (see
Equations 1 and 3). In order to capture these
crucial graph properties and impose a strong
inductive bias, we build a graph
relational
encoder to aggregate the local context by utilizing
a modified version of GAT augmented with
relational weights. In particular, we compute a
layer of the local convolution for a node v ∈ V,
adopting AGGR(l)(.) as:
hN (v) =
Xu∈N (v)
αvuWrhu,
(7)
where Wr ∈ Rdv×dz encodes the relation r ∈ R
between u and v. N (v) is a set of nodes adjacent
to v and v itself. The attention coefficient αvu is
computed as:
αvu =
exp(evu)
Pk ∈ N (v) exp(evk)
,
where
evu = σ
a⊤[Wvhv k Wrhu]
(cid:1)
(cid:0)
(8)
(9)
is the attention function which calculates the local
importance of adjacent nodes, considering the
edge labels. σ is an activation function, k denotes
concatenation and Wv ∈ Rdv×dz and a ∈ R2dz are
model parameters.
We use multihead attentions to learn local re-
lations in different perspectives, as in Equation 4,
v = RNN(hv, ˆhN (v)),
hlocal
(10)
where we use as RNN a Gated Recurrent Unit
(GRU) (Cho et al., 2014). GRU facilitates infor-
mation propagation between local layers. This
choice is motivated by recent work (Xu et al.,
2018; Dehmamy et al., 2019) that theoretically
demonstrates that sharing information between
layers helps the structural signals propagate. In a
similar direction, AMR-to-text generation models
use LSTMs (Song et al., 2017) and dense connec-
tions (Guo et al., 2019) between GNN layers.
3.5 Combining Global and Local Encodings
Our goal is to implement a graph encoder capable
of encoding global and local aspects of the input
graph. We hypothesize that these two sources of
information are complementary, and a combina-
tion of both enriches node representations for text
generation. In order to test this hypothesis, we
investigate different combined architectures.
Intuitively, there are two general methods for
integrating two types of representation. The first
is to concatenate vectors of global and local
contexts, which we call a parallel representation.
The second is to form a pipeline, where a global
representation is first obtained, which is then used
as a input for calculating refined representations
based on the local node context. We call this
approach a cascaded representation.
Parallel and cascaded integration can be per-
formed at the model level, considering the global
and local graph encoders as two representation
learning units disregarding internal structures.
However, because our model takes a multilayer
architecture, where each layer makes a level of
abstraction in representation, we can alternatively
consider integration on the layer level, so that
more interaction between global and local contexts
may be captured. As a result, we present four
architectures for integration, as shown in Figure 2.
All models serve the same purpose, and their
relative strengths should be evaluated empirically.
Parallel Graph Encoding (PGE).
In this setup,
we compose global and local graph encoders in
a fully parallel structure (Figure 2a). Note that
each graph encoder can have different numbers
of layers and attention heads. The final node
593
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
3
2
1
9
2
3
1
9
0
/
/
t
l
a
c
_
a
_
0
0
3
3
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 2: Overview of the proposed encoder architectures. (a) Parallel Graph Encoder (PGE) with separated parallel
global and local node encoders. (b) Cascaded Graph Encoder (CGE) with separated cascaded encoders. (c) PGE-
LW: global and local node representations are concatenated layer-wise. (d) CGE-LW: Both node representations
are cascaded layer-wise.
representation is the concatenation of the local
and global node representations of the last layers
of both graph encoders:
Layer-wise Cascaded Graph Encoding. We
also propose cascading the graph encoders layer-
wise (CGE-LW, Figure 2d). In particular, we
compute each encoder layer as follows:
hglobal
= GE(h0
v
hlocal
v = LE(h0
hv = [ hglobal
v
v, {h0
v, {h0
u : u ∈ V})
u : u ∈ N (v)})
k hlocal
v
] ,
(11)
hglobal
= GEl(hl−1
v
v = LEl(hglobal
hl
v
v
, {hl−1
u
: u ∈ V})
, {hglobal
u
: u ∈ N (v)}).
(14)
where GE and LE denote the global and local
graph encoders, respectively. h0
v is the initial node
embedding used in the first layer of both encoders.
(CGE). We
Cascaded Graph Encoding
cascade local and global graph encoders as
shown in Figure 2b. We first compute a globally
contextualized node embedding, and then refine it
with the local node context. h0
v is the initial input
for the global encoder and hglobal
is the initial
v
input for the local encoder. In particular, the final
node representation is calculated as follows:
hglobal
v
v, {h0
= GE(h0
hv = LE(hglobal
u : u ∈ V})
,{hglobal
u
v
: u ∈ N (v)}). (12)
Layer-wise Parallel Graph Encoding. To
allow fine-grained interaction between the two
types of graph contextual information, we also
combine the encoders in a layer-wise (LW)
fashion. As shown in Figure 2c, for each graph
layer, we use both global and local encoders in a
parallel structure (PGE-LW). More precisely, each
encoder layer is calculates as follows:
hglobal
= GEl(hl−1
v
v
v = LEl(hl−1
hlocal
v
v = [ hglobal
hl
v
, {hl−1
u
, {hl−1
u
k hlocal
v
] ,
: u ∈ V})
: u ∈ N (v)})
(13)
where GEl and LEl refer to the l-th layers of the
global and local graph encoders, respectively.
594
3.6 Decoder and Training
Our decoder follows the core architecture of a
Transformer decoder (Vaswani et al., 2017). Each
time step t is updated by performing multihead
attentions over the output of the encoder (node
embeddings hv) and over previously generated
tokens (token embeddings). An additional chal-
lenge in our setup is to generate multisentence
outputs. In order to encourage the model to gen-
erate longer texts, we implement a length penalty
(Wu et al., 2016) to refine the pure max-probability
beam search.
The model is trained to optimize the negative
log-likelihood of each gold-standard output text.
We use label smoothing regularization to prevent
the model from predicting the tokens too confi-
dently during training and generalizing poorly.
4 Data and Preprocessing
We attest the effectiveness of our models on
two datasets: AGENDA (Koncel-Kedziorski et al.,
2019) and WebNLG (Gardent et al., 2017). Table 1
shows the statistics for both datasets.
AGENDA.
In this dataset, KGs are paired with
scientific abstracts extracted from proceedings of
12 top AI conferences. Each instance consists
of the paper title, a KG, and the paper abstract.
Entities correspond to scientific terms that are
often multiword expressions (co-referential enti-
ties are merged). We treat each token in the title as
a node, creating a unique graph with title and KG
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
3
2
1
9
2
3
1
9
0
/
/
t
l
a
c
_
a
_
0
0
3
3
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
#train
#dev
#test
#relations
avg #entities
avg #nodes
avg #edges
avg #CC avg length
AGENDA 38,720
18,102
WebNLG
1,000
872
1,000
971
7
373
12.4
4.0
44.3
34.9
68.6
101.0
19.1
1.5
140.3
24.2
Table 1: Data statistics. Nodes, edges, and CC values are calculated after the graph transformation.
The average values are calculated for all splits (training, dev, and test sets). CC refers to the number of
connected components.
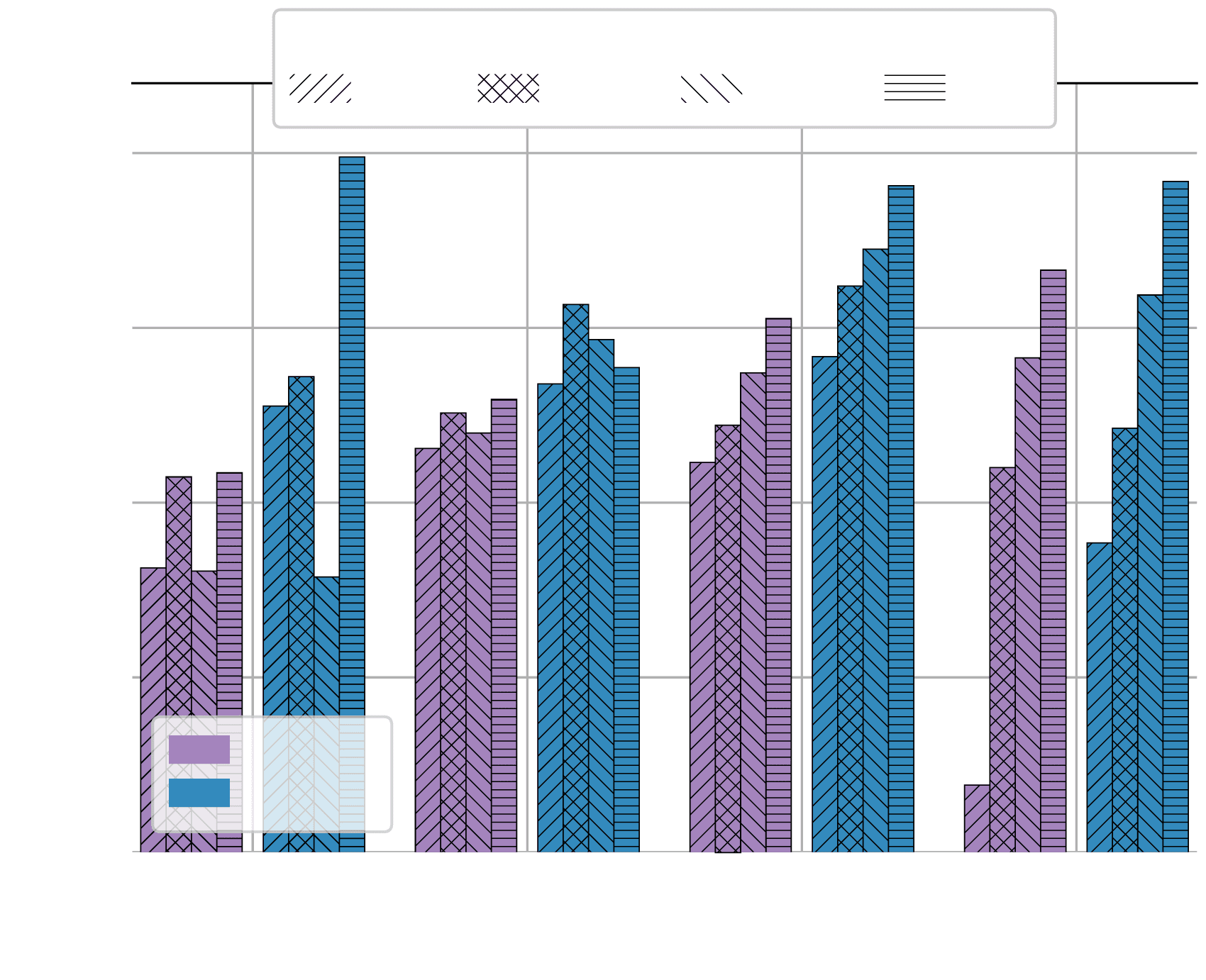
Figure 3: BLEU scores for the AGENDA dev set, with respect to (a) the encoder layers, (b) the encoder hidden
dimensions, and (c) the number of parameters.
tokens as nodes. As shown in Table 1, the average
output length is considerably large, as the target
outputs are multisentence abstracts.
WebNLG.
In this dataset, each instance con-
tains a KG extracted from DBPedia. The target
text consists of sentences that verbalize the graph.
We evaluate the models on the test set with seen
categories. Note that this dataset has a conside-
rable number of edge relations (see Table 1).
In order to avoid parameter explosion, we use
regularization based on the basis function decom-
position to define the model relation weights
(Schlichtkrull et al., 2018). Also, as an alternative,
we use the Levi Transformation to create nodes
from relational edges between entities (Beck et al.,
2018). That is, we create a new relation node for
each edge relation between two nodes. The new
relation node is connected to the subject and object
token entities by two binary relations, respectively.
seeds, for the test sets, we report the averages over
4 training runs along with their standard deviation.
We use byte pair encoding (Sennrich et al., 2016)
to split entity words into smaller more frequent
pieces. Therefore some nodes in the graph can
be sub-words. We also obtain sub-words on the
target side. Following previous works, we evaluate
the results with BLEU (Papineni et al., 2002),
METEOR (Denkowski and Lavie, 2014), and
CHRF++ (Popovi´c, 2015) automatic metrics and
also perform a human evaluation (Section 5.6).
For layer-wise models, the number of encoder
layers are chosen from {2, 4, 6}, and for PGE
and CGE, the global and local layers are chosen
from and {2, 4, 6} and {1, 2, 3}, respectively.
The hidden encoder dimensions are chosen from
{256, 384, 448} (see Figure 3). Hyperparameters
are tuned on the development set of both datasets.
We report the test results when the BLEU score
on dev set is optimal.
5 Experiments
5.1 Results on AGENDA
We implemented all our models using PyTorch
Geometric (PyG) (Fey and Lenssen, 2019) and
OpenNMT-py (Klein et al., 2017). We use the
Adam optimizer with β1 = 0.9 and β2 = 0.98.
Our learning rate schedule follows Vaswani et al.
(2017), with 8,000 and 16,000 warming-up steps
for WebNLG and AGENDA, respectively. The
vocabulary is shared between the node and target
tokens. In order to mitigate the effects of random
Table 2 shows the results, where we report the
number of layers and attention heads utilized. We
train models with only global or local encoders as
baselines. Each model has the respective parame-
ter size that gives the best results on the dev set.
First, the local encoder, which requires fewer
encoder layers and parameters, has a better per-
formance compared with the global encoder. This
shows that explicitly encoding the graph structure
595
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
3
2
1
9
2
3
1
9
0
/
/
t
l
a
c
_
a
_
0
0
3
3
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Model
#L
#H
BLEU
METEOR
CHRF++
Koncel-Kedziorski et al. (2019)
6
Global Encoder
Local Encoder
PGE
CGE
PGE-LW
CGE-LW
6
3
6, 3
6, 3
6
6
8
8
8
8, 8
8, 8
8, 8
8, 8
14.30 ± 1.01
18.80 ± 0.28
–
15.44 ± 0.25
16.03 ± 0.19
17.55 ± 0.154
17.82 ± 0.134
17.42 ± 0.25
18.01 ± 0.14
20.76 ± 0.194
21.12 ± 0.32
22.02 ± 0.07
22.23 ± 0.09
21.78 ± 0.20
22.34 ± 0.07
43.95 ± 0.40
44.70 ± 0.29
46.41 ± 0.07
46.47 ± 0.10
45.79 ± 0.32
46.69 ± 0.17
#P
–
54.4
54.0
56.1
61.5
69.0
69.8
Table 2: Results on the AGENDA test set. #L and #H are the numbers of layers and the attention heads
in each layer, respectively. When more than one, the values are for the global and local encoders,
respectively. #P stands for the number of parameters in millions (node embeddings included).
Model
BLEU
METEOR
CHRF++
UPF-FORGe (Gardent et al., 2017)
Melbourne (Gardent et al., 2017)
Adapt (Gardent et al., 2017)
Marcheggiani and Perez Beltrachini (2018)
Trisedya et al. (2018)
Castro Ferreira et al. (2019)
40.88
54.52
60.59
55.90
58.60
57.20
40.00
41.00
44.00
39.00
40.60
41.00
–
70.72
76.01
–
–
–
#P
–
–
–
4.9
–
–
CGE
CGE (Levi Graph)
CGE-LW
CGE-LW (Levi Graph)
62.30 ± 0.27
63.10 ± 0.13
62.85 ± 0.07
63.69 ± 0.10
43.51 ± 0.18
44.11 ± 0.09
43.75 ± 0.21
44.47 ± 0.12
75.49 ± 0.34
76.33 ± 0.10
75.73 ± 0.31
76.66 ± 0.10
13.9
12.8
11.2
10.4
Table 3: Results on the WebNLG test set with seen categories.
is important to improve the node representations.
Second, our approaches substantially outperform
both baselines. CGE-LW outperforms Koncel-
Kedziorski et al. (2019), a transformer model that
focuses on the relations between adjacent nodes,
by a large margin, achieving the new state-of-the-
art BLEU score of 18.01, 25.9% higher. We also
note that KGs are highly incomplete in this dataset,
with an average number of connected components
of 19.1 (see Table 1). For this reason, the global
encoder plays an important role in our models as it
enables learning node representations based on all
connected components. The results indicate that
combining the local node context, leveraging the
graph topology, and the global node context, cap-
turing macro-level node relations, leads to better
performance. We find that, even though CGE has
a small number of parameters compared to CGE-
LW, it achieves comparable performance. PGE-LW
has the worse performance among the proposed
models. Finally, note that cascaded architec-
tures are more effective according to different
metrics.
5.2 Results on WebNLG
We compare the performance of our more
effective models (CGE, CGE-LW) with six state-
of-the-art results reported on this dataset. Three
systems are the best competitors in the WebNLG
challenge for
seen categories: UPF-FORGe,
Melbourne, and Adapt. UPF-FORGe follows a
rule-based approach, whereas the others use neural
encoder-decoder models with linearized triple sets
as input.
Table 3 presents the results. CGE achieves a
BLEU score of 62.30, 8.9% better than the best
model of Castro Ferreira et al. (2019), who use
an end-to-end architecture based on GRUs. CGE
using Levi graphs outperforms Trisedya et al.
(2018), an approach that encodes both intra-
triple and inter-triple relationships, by 4.5 BLEU
points. Interestingly, their intra-triple and inter-
triple mechanisms are closely related with the
local and global encodings. However, they rely on
encoding entities based on sequences generated by
traversal graph algorithms, whereas we explicitly
596
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
3
2
1
9
2
3
1
9
0
/
/
t
l
a
c
_
a
_
0
0
3
3
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
exploit the graph structure, throughout the local
neighborhood aggregation.
CGE-LW with Levi graphs as inputs has the
best performance, achieving 63.69 BLEU points,
even thought it uses fewer parameters. Note that
this approach allows the model to handle new
relations, as they are treated as nodes. Moreover,
the relations become part of the shared vocabulary,
making this information directly usable during the
decoding phase. We outperform an approach based
on GNNs (Marcheggiani and Perez Beltrachini,
2018) by a large margin of 7.7 BLEU points, show-
ing that our combined graph encoding strategies
lead to better text generation. We also outperform
Adapt, a strong competitor that utilizes subword
encodings, by 3.1 BLEU points.
5.3 Development Experiments
We report several development experiments in
Figure 3. Figure 3a shows the effect of the number
of encoder layers in the four encoding methods.4
In general, the performance increases when we
gradually enlarge the number of layers, achieving
the best performance with 6 encoder layers.
Figure 3b shows the choices of hidden sizes for the
encoders. The best performances for global and
PGE are achieved with 384 dimensions, whereas
the other models have the better performance with
448 dimensions. In Figure 3c, we evaluate the per-
formance employing different number of parame-
ters.5 When the models are smaller, parallel
encoders obtain better results than the cascaded
ones. When the models are larger, cascaded
models perform better. We speculate that for some
models, the performance can be further improved
with more parameters and layers. However, we do
not attempt this owing to hardware limitations.
5.4 Ablation Study
In Table 4, we report an ablation study on the
impact of each module used in CGE model on the
dev set of AGENDA. We also report the number
of parameters used in each configuration.
Global Graph Encoder. We start by an ablation
on the global encoder. After removing the global
attention coefficients,
the performance of the
model drops by 1.79 BLEU and 1.97 CHRF++
4For CGE and PGE the values refer to the global layers
and the number of local layers is fixed to 3.
5It was not possible to execute the local model with larger
number of parameters because of memory limitations.
Model
CGE
BLEU CHRF++
#P
17.38
45.68
61.5
Global Encoder
-Global Attention
-FFN
-Global Encoder
Local Encoder
-Local Attention
-Weight Relations
-GRU
-Local Encoder
-Shared Vocab.
Decoder
–Length Penalty
15.59
16.33
15.17
16.92
16.88
16.38
14.68
16.92
43.71
44.86
43.30
45.97
45.61
44.71
42.98
46.16
59.0
50.4
45.6
61.5
53.6
60.2
51.8
81.8
16.68
44.68
61.5
Table 4: Ablation study for modules used in the
encoder and decoder of the CGE model.
scores. Results also show that using FFN in the
global COMBINE(.) function is important to the
model but less effective than the global attention.
However, when we remove FNN, the number of
parameters drops considerably (around 18%) from
61.5 to 50.4 million. Finally, without the entire
global encoder, the result drops substantially by
2.21 BLEU points. This indicates that enriching
node embeddings with a global context allows
learning more expressive graph representations.
Local Graph Encoder. We first remove the
local graph attention and the BLEU score drops
to 16.92, showing that the neighborhood attention
improves the performance. After removing the
relation types, encoded as model weights, the
performance drops by 0.5 BLEU points. However,
the number of parameters is reduced by around
7.9 million. This indicates that we can have a
more efficient model, in terms of the number of
parameters, with a slight drop in performance.
Removing the GRU used on the COMBINE(.)
function decreases the performance considerably.
The worse performance occurs if we remove
the entire local encoder, with a BLEU score of
14.68, essentially making the encoder similar to
the global baseline.
Finally, we find that vocabulary sharing
improves the performance, and the length penalty
is beneficial as we generate multisentence outputs.
597
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
3
2
1
9
2
3
1
9
0
/
/
t
l
a
c
_
a
_
0
0
3
3
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4: CHRF++ scores for the AGENDA test set, with respect to (a) the number of nodes, and (b) the graph
diameter. (c) Distribution of length of the gold references and models’ outputs for the AGENDA test set.
5.5 Impact of the Graph Structure and
Output Length
The overall performance on both datasets suggests
the strength of combining global and local node
representations. However, we are also interested
in estimating the models’ performance concerning
different data properties.
Graph Size. Figure 4a shows the effect of the
graph size, measured in number of nodes, on the
performance, measured using CHRF++ scores,6
for the AGENDA. We evaluate global and local
graph encoders, PGE-LW and CGE-LW. We find
that the score increases as the graph size increases.
Interestingly, the gap between the local and global
encoders increases when the graph size increases.
This suggests that, because larger graphs may
have very different topologies, modeling the rela-
tions between nodes based on the graph structure
is more beneficial than allowing direct communi-
cation between nodes, overlooking the graph
structure. Also note that the the cascaded model
(CGE-LW) is consistently better than the parallel
model (PGE-LW) over all graph sizes.
Table 5 shows the effect of the graph size,
measured in number of triples, on the performance
for the WebNLG. Our model obtains better scores
over all partitions. In contrast to AGENDA, the
performance decreases as the graph size increases.
This behavior highlights a crucial difference
between AGENDA and AMR and WebNLG
datasets, in which the models’ general perfor-
mance decreases as the graph size increases
(Gardent et al., 2017; Cai and Lam, 2020).
In WebNLG, the graph and sentence sizes are
correlated, and longer sentences are more chal-
lenging to generate than the smaller ones. Differ-
6CHRF++ score is used as it is a sentence-level metric.
ently, AGENDA contains similar text lengths7
and when the input is a larger graph, the model
has more information to be leveraged during the
generation.
Graph Diameter. Figure 4b shows the impact
of the graph diameter8 on the performance for the
AGENDA. Similarly to the graph size, the score
increases as the diameter increases. As the global
encoder is not aware of the graph structure, this
module has the worst scores, even though it
enables direct node communication over long
the local encoder can
distance.
propagate precise node information throughout
the graph structure for k-hop distances, making
the relative performance better. Table 5 shows the
models’ performances with respect to the graph
diameter for WebNLG. Similarly to the graph size,
the score decreases as the diameter increases.
In contrast,
Output Length. One interesting phenomenon
to analyze is the length distribution (in number of
words) of the generated outputs. We expect that
our models generate texts with similar output
lengths as the reference texts. As shown in
Figure 4c, the references usually are bigger than
the texts generated by all models for AGENDA.
The texts generated by CGE-no-pl, a CGE model
without length penalty, are consistently shorter
than the texts from the global and CGE models.
We increase the length of the texts when we use the
length penalty (see Section 3.6). However, there is
still a gap between the reference and the generated
text lengths. We leave further investigation of this
aspect for future work.
7As shown on Figure 4c, 82% of the reference abstracts
have more than 100 words.
8The diameter of a graph is defined as the length of the
longest shortest path between two nodes. We convert the
graphs into undirected graphs to calculate the diameters.
598
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
3
2
1
9
2
3
1
9
0
/
/
t
l
a
c
_
a
_
0
0
3
3
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
#T
1-2
3-4
5-7
#DP Melbourne Adapt CGE-LW
396
386
189
78.74
66.84
61.85
83.10
72.02
69.28
84.35
72.27
70.25
#D #DP Melbourne Adapt CGE-LW
1
2
≥ 3
#S
1
2
3
4
≥ 5
222
469
280
82.27
69.94
62.87
87.54
74.54
69.30
88.04
75.90
69.41
#DP Melbourne Adapt CGE-LW
388
306
151
66
60
77.19
67.29
66.30
66.73
61.93
81.66
73.29
72.46
71.26
67.57
82.03
73.78
73.21
75.16
69.20
Table 5: CHRF++ scores with respect to the
number of triples (#T), graph diameters (#D),
and number of sentences (#S) on the WebNLG
test set. #DP refers to the number of datapoints.
Table 5 shows the models’ performances with
respect to the number of sentences for WebNLG.
In general, increasing the number of sentences
reduces the performance of all models. Note
that when the number of sentences increases, the
gap between CGE-LW and the baselines becomes
larger. This suggests that our approach is able to
better handle complex graph inputs in order to
generate multisentence texts.
Effect of the Number of Nodes on the Output
Length. Figure 5 shows the effect of the size of
a graph, defined as the number of nodes, on the
quality (measured in CHRF++ scores) and length
of the generated text (in number of words) in the
AGENDA dev set. We bin both the graph size and
the output length in 4 classes. CGE consistently
outperforms the global model, in some cases by
a large margin. When handling smaller graphs
(with ≤ 35 nodes), both models have difficulties
generating good summaries. However, for these
smaller graphs, our model achieves a score 12.2%
better when generating texts with length ≤ 75.
Interestingly, when generating longer texts (>140)
from smaller graphs, our model outperforms the
global encoder by an impressive 21.7%, indicating
that our model is more effective in capturing
semantic signals from graphs with scarce infor-
mation. Our approach also performs better when
Figure 5: Relation between the number of nodes and
the length of the generated text, in number of words.
the graph size is large (> 55) but the generation
output is small (≤ 75), beating the global encoder
by 9 points.
5.6 Human Evaluation
To further assess the quality of the generated text,
we conduct a human evaluation on the WebNLG
dataset.9 Following previous work (Gardent et al.,
2017; Castro Ferreira et al., 2019), we assess two
quality criteria: (i) Fluency (i.e., does the text flow
in a natural, easy to read manner?) and (ii) Ade-
quacy (i.e., does the text clearly express the data?).
We divide the datapoints into seven different
sets by the number of triples. For each set, we
randomly select 20 texts generated by Adapt,
CGE with Levi graphs, and their corresponding
human reference (420 texts in total). Because the
number of datapoints for each set is not balanced
(see Table 5), this sampling strategy ensures that
we have the same number of samples for the
different triple sets. Moreover, having human
references may serve as an indicator of the sanity
of the human evaluation experiment. We recruited
human workers from Amazon Mechanical Turk
to rate the text outputs on a 1–5 Likert scale. For
each text, we collect scores from 4 workers and
average them. Table 6 shows the results. We first
note a similar trend as in the automatic evaluation,
with CGE outperforming Adapt on both fluency
and adequacy. In sets with the number of triples
smaller than 5, CGE was the highest rated system
in fluency. Similarly to the automatic evaluation,
both systems are better in generating text from
9Because AGENDA is scientific in nature, we choose to
crowd-source human evaluations only for WebNLG.
599
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
3
2
1
9
2
3
1
9
0
/
/
t
l
a
c
_
a
_
0
0
3
3
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
#T
Adapt
CGE
Reference
AGENDA
F
A
F
A
F
A
Model
BLEU CHRF++
All
1–2
3–4
5–7
#D
3.96C 4.44C 4.12B 4.54B 4.24A 4.63A
3.94C 4.59B 4.18B 4.72A 4.30A 4.69A
3.79C 4.45B 3.96B 4.50AB 4.14A 4.66A
4.08B 4.35B 4.18B 4.45B 4.28A 4.59A
Adapt
CGE
Reference
F
A
F
A
F
A
1–2
≥ 3
3.98C 4.50B 4.16B 4.61A 4.28A 4.66A
3.91C 4.33B 4.03B 4.43B 4.17A 4.60A
Table 6: Fluency (F) and Adequacy (A) obtained
in the human evaluation. #T refers to the number
of input triples and #D to graph diameters. The
ranking was determined by pair-wise Mann-
Whitney tests with p < 0.05, and the difference
between systems that have a letter in common is
not statistically significant.
graphs with smaller diameters. Note that bigger
diameters pose difficulties to the models, which
achieve their worst performance for diameters
≥ 3.
5.7 Additional Experiments
Impact of the Vocabulary Sharing and Length
Penalty. During the ablation studies, we note
that the vocabulary sharing and length penalty are
beneficial for the performance. To better estimate
their impact, we evaluate CGE-LW model with
its variations without using vocabulary sharing,
length penalty and without both mechanisms,
on the test set of both datasets. Table 7 shows
the results. We observe that sharing vocabulary
is more important to WebNLG than AGENDA.
This suggests that sharing vocabulary is beneficial
when the training data is small, as in WebNLG. On
the other hand, length penalty is more effective for
AGENDA, as it has longer texts than WebNLG,10
improving the BLEU score by 0.71 points.
How Far Does the Global Attention Look?
Following previous work (Voita et al., 2019;
Cai and Lam, 2020), we investigate the attention
distribution of each graph encoder global layer of
CGE-LW on the AGENDA dev set. In particular,
for each node, we verify its global neighbor that
CGE-LW
-Shared Vocab
-Length Penalty
-Both
18.17
17.88
17.46
17.24
46.80
47.12
45.76
46.14
WebNLG
Model
BLEU CHRF++
CGE-LW
-Shared Vocab
-Length Penalty
-Both
63.86
63.07
63.28
62.60
76.80
76.17
76.51
75.80
Table 7: Effects of
the vocabulary
sharing and length penalty on the test
sets of AGENDA and WebNLG.
receives the maximum attention weight and record
the distance between them.11 Figure 7 shows the
averaged distances for each global
layer. We
observe that the global encoder mainly focuses
on distant nodes, instead of the neighbors and
closest nodes. This is very interesting and agrees
with our intuition: Whereas the local encoder
is concerned about the local neighborhood, the
global encoder focuses on the information from
long-distance nodes.
Case Study. Figure 6 shows examples of gen-
erated texts when the WebNLG graph is complex
(7 triples). While CGE generates a factually correct
text (it correctly verbalises all triples), the Adapt’s
output is repetitive. The example also illustrates
how the text generated by CGE closely follows
the graph structure whereby the first sentence ver-
balises the right-most subgraph, the second the
left-most one and the linking node Turkey makes
the transition (using hyperonymy and a definite
description, i.e., The country). The text created
by CGE is also more coherent than the reference.
As noted above, the input graph includes two
subgraphs linked by Turkey. In natural language,
such a meaning representation corresponds to a
topic shift with the first part of the text describing
an entity from one subgraph, the second part an
entity from the other subgraph, and the linking
entity (Turkey) marking the topic shift. Typically,
10As shown in Table 1, AGENDA has texts 5.8 times
11The distance between two nodes is defined as the number
longer than WebNLG on average.
of edges in a shortest path connecting them.
600
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
3
2
1
9
2
3
1
9
0
/
/
t
l
a
c
_
a
_
0
0
3
3
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6: (a) A WebNLG input graph and the outputs for (b) Adapt and (c) CGE. The colored text indicates
repetition.
We point out some directions for future work.
First, it is interesting to study different fusion
strategies to assemble the global and local
encodings. Second, a promising direction is
incorporating pre-trained contextualized word
embeddings in graphs. Third, as discussed in
Section 5.5, it is worth studying ways to diminish
the gap between the reference and the generated
text lengths.
Acknowledgments
We would like to thank Pedro Savarese, Markus
Zopf, Mohsen Mesgar, Prasetya Ajie Utama,
Ji-Ung Lee, and Kevin Stowe for their feedback on
this work, as well as the anonymous reviewers for
detailed comments that improved this paper. This
work has been supported by the German Research
Foundation as part of the Research Training
Group Adaptive Preparation of Information from
Heterogeneous Sources (AIPHES) under grant
No. GRK 1994/1.
References
Daniel Beck, Gholamreza Haffari, and Trevor
Cohn. 2018. Graph-to-sequence learning using
gated graph neural networks. In Proceedings
of the 56th Annual Meeting of the Association
for Computational Linguistics (Volume 1: Long
Papers), pages 273–283, Melbourne, Australia.
Association for Computational Linguistics.
Deng Cai and Wai Lam. 2020. Graph transformer
for graph-to-sequence learning. In Proceedings
of The Thirty-Fourth AAAI Conference on
Artificial Intelligence (AAAI).
Figure 7: The average distance between nodes for the
maximum attention for each head. ∞ indicates no path
between two nodes, that is, they belong to distinct
connected components.
in English, a topic shift is marked by a definite
noun phrase in the subject position. Although this
is precisely the discourse structure generated by
CGE (Turkey is realized in the second sentence by
the definite description The country in the subject
position), the reference fails to mark the topic
shift, resulting in a text with weaker discourse
coherence.
6 Conclusion
In this work, we introduced a unified graph atten-
tion network structure for investigating graph-to-
text models that combines global and local graph
encoders in order to improve text generation. An
extensive evaluation of our models demonstrated
that the global and local contexts are empirically
complementary, and a combination can achieve
In
state-of-the-art
addition, cascaded architectures give better results
compared with parallel ones.
results on two datasets.
601
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
3
2
1
9
2
3
1
9
0
/
/
t
l
a
c
_
a
_
0
0
3
3
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Thiago Castro Ferreira, Chris van der Lee, Emiel
van Miltenburg, and Emiel Krahmer. 2019.
Neural data-to-text generation: A comparison
between pipeline and end-to-end architectures.
In Proceedings of
the 2019 Conference on
in Natural Language
Empirical Methods
Processing and the 9th International Joint
Conference on Natural Language Processing
(EMNLP-IJCNLP),
552–562. Hong
pages
Kong, China. Association for Computational
Linguistics.
Kyunghyun Cho, Bart van Merrienboer, Caglar
Gulcehre, Dzmitry Bahdanau, Fethi Bougares,
Holger Schwenk, and Yoshua Bengio. 2014.
Learning phrase representations using RNN
encoder–decoder for statistical machine trans-
lation. In Proceedings of the 2014 Conference
on Empirical Methods in Natural Language
Processing (EMNLP), pages 1724–1734. Doha,
Qatar. Association for Computational Linguis-
tics.
Emilie Colin and Claire Gardent. 2018. Generat-
ing syntactic paraphrases. In Proceedings of the
2018 Conference on Empirical Methods in
Natural Language Processing, pages 937–943,
Brussels, Belgium. Association for Computa-
tional Linguistics.
Marco Damonte and Shay B. Cohen. 2019.
Structural neural encoders for AMR-to-text
generation. In Proceedings of the 2019 Confer-
ence of the North American Chapter of the
Association for Computational Linguistics:
Human Language Technologies, Volume 1
(Long and Short Papers), pages 3649–3658.
Minneapolis, Minnesota. Association for Com-
putational Linguistics.
Nima Dehmamy, Albert-Laszlo Barabasi, and
Rose Yu. 2019. Understanding the representa-
ion power of graph neural networks in learning
graph topology, In H. Wallach, H. Larochelle,
A. Beygelzimer, F. Alch´e-Buc, E. Fox, and R.
Garnett, editors, Advances in Neural Informa-
tion Processing Systems 32, pages 15387–15397.
Curran Associates, Inc.
Michael Denkowski and Alon Lavie. 2014. Meteor
universal: Language specific translation evalu-
ation for any target language. In Proceedings
of the Ninth Workshop on Statistical Machine
Translation, pages 376–380, Baltimore, Mary-
land, USA. Association for Computational
Linguistics.
Xin Luna Dong, Evgeniy Gabrilovich, Geremy
Heitz, Wilko Horn, Ni Lao, Kevin Murphy,
Thomas Strohmann, Shaohua Sun, and Wei
Zhang. 2014. Knowledge vault: A web-scale
approach to probabilistic knowledge fusion. In
The 20th ACM SIGKDD International Confer-
ence on Knowledge Discovery and Data Min-
ing,z KDD ’14, New York, NY, USA - August
24 - 27, 2014, pages 601–610.
Matthias Fey and Jan E. Lenssen. 2019. Fast
graph representation learning with PyTorch
Geometric. In ICLR Workshop on Represen-
tation Learning on Graphs and Manifolds.
Jeffrey Flanigan, Chris Dyer, Noah A. Smith,
and Jaime Carbonell. 2016. Generation from
abstract meaning representation using tree
transducers. In Proceedings of the 2016 Con-
ference of the North American Chapter of the
Association for Computational Linguistics:
Human Language Technologies, pages 731–739,
San Diego, California. Association for Compu-
tational Linguistics.
Claire Gardent, Anastasia Shimorina, Shashi
Narayan, and Laura Perez-Beltrachini. 2017.
The WebNLG challenge: Generating text from
RDF data. In Proceedings of the 10th Inter-
national Conference on Natural Language
Generation, pages 124–133, Santiago de Com-
postela, Spain. Association for Computational
Linguistics.
Zhijiang Guo, Yan Zhang, Zhiyang Teng, and
Wei Lu. 2019. Densely connected graph convo-
lutional networks for graph-to-sequence learn-
ing. Transactions of the Association for Compu-
tational Linguistics, 7:297–312.
Will Hamilton, Zhitao Ying, and Jure Leskovec.
2017. Inductive representation learning on large
graphs, In I. Guyon, U. V. Luxburg, S. Bengio,
H. Wallach, R. Fergus, S. Vishwanathan, and R.
Garnett, editors, Advances in Neural Informa-
tion Processing Systems 30, pages 1024–1034.
Curran Associates, Inc.
Thomas N. Kipf and Max Welling. 2017. Semi-
Supervised Classification with Graph Convo-
lutional Networks. In Proceedings of the 5th
602
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
3
2
1
9
2
3
1
9
0
/
/
t
l
a
c
_
a
_
0
0
3
3
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
International Conference on Learning Repre-
sentations, ICLR ’17.
Guillaume Klein, Yoon Kim, Yuntian Deng,
Jean Senellart, and Alexander Rush. 2017.
for neural
OpenNMT: Open-source toolkit
machine translation. In Proceedings of ACL
2017, System Demonstrations, pages 67–72.
Vancouver, Canada. Association for Computa-
tional Linguistics.
Rik Koncel-Kedziorski, Dhanush Bekal, Yi Luan,
Mirella Lapata, and Hannaneh Hajishirzi. 2019.
Text Generation from Knowledge Graphs with
Graph Transformers. In Proceedings of
the
2019 Conference of the North American Chap-
ter of the Association for Computational Linguis-
tics: Human Language Technologies, Volume 1
(Long and Short Papers), pages 2284–2293,
Minneapolis, Minnesota. Association for Com-
putational Linguistics.
Ioannis Konstas, Srinivasan Iyer, Mark Yatskar,
Yejin Choi, and Luke Zettlemoyer. 2017.
Neural amr: Sequence-to-sequence models for
parsing and generation. In Proceedings of the
55th Annual Meeting of the Association for
Computational Linguistics (Volume 1: Long
Papers), pages 146–157, Vancouver, Canada.
Association for Computational Linguistics.
Ioannis Konstas and Mirella Lapata. 2013. Induc-
ing document plans for concept-to-text genera-
tion. In Proceedings of the 2013 Conference on
Empirical Methods in Natural Language Pro-
cessing, pages 1503–1514, Seattle, Washington,
USA. Association for Computational Linguis-
tics.
Q. Li, Z. Han, and X.-M. Wu. 2018. Deeper
Insights into Graph Convolutional Networks
for Semi-Supervised Learning. In The Thirty-
Second AAAI Conference on Artificial Intelli-
gence. AAAI.
Diego Marcheggiani and Laura Perez Beltrachini.
2018. Deep graph convolutional encoders for
structured data to text generation. In Procee-
the 11th International Conference
dings of
on Natural Language Generation, pages 1–9,
Tilburg University, The Netherlands. Associa-
tion for Computational Linguistics.
Amit Moryossef, Yoav Goldberg, and Ido Dagan.
2019. Step-by-step: Separating planning from
realization in neural data-to-text generation. In
Proceedings of the 2019 Conference of the
North American Chapter of the Association for
Computational Linguistics: Human Language
Technologies, Volume 1 (Long and Short
Papers),
2267–2277, Minneapolis,
Minnesota. Association for Computational
Linguistics.
pages
Kishore Papineni, Salim Roukos, Todd Ward,
and Wei-Jing Zhu. 2002. Bleu: A method for
automatic evaluation of machine translation.
In Proceedings of the 40th Annual Meeting
on Association for Computational Linguistics,
ACL ’02, pages 311–318. Stroudsburg, PA,
USA. Association for Computational Linguistics.
Maja Popovi´c. 2015. chrF: character n-gram
f-score for automatic MT evaluation. In Pro-
ceedings of the Tenth Workshop on Statistical
Machine Translation, pages 392–395, Lisbon,
Portugal. Association
for Computational
Linguistics.
Nima Pourdamghani, Kevin Knight, and Ulf
Hermjakob. 2016. Generating English from
abstract meaning representations. In Proceed-
ings of
the 9th International Natural Lan-
guage Generation conference, pages 21–25,
Edinburgh, UK. Association for Computational
Linguistics.
Leonardo F. R. Ribeiro, Claire Gardent, and
Iryna Gurevych. 2019. Enhancing AMR-to-
text generation with dual graph representations.
In Proceedings of
the 2019 Conference on
in Natural Language
Empirical Methods
Processing and the 9th International Joint
Conference on Natural Language Processing
(EMNLP-IJCNLP), pages 3181–3192, Hong
Kong, China. Association for Computational
Linguistics.
Michael Sejr Schlichtkrull, Thomas N. Kipf, Peter
Bloem, Rianne van den Berg, Ivan Titov, and
Max Welling. 2018. Modeling relational data
with graph convolutional networks. In The
Semantic Web - 15th International Conference,
ESWC 2018, Heraklion, Crete, Greece, June
3-7, 2018, Proceedings, pages 593–607.
Rico Sennrich, Barry Haddow, and Alexandra
Birch. 2016. Neural machine translation of rare
words with subword units. In Proceedings of
603
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
3
2
1
9
2
3
1
9
0
/
/
t
l
a
c
_
a
_
0
0
3
3
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
the 54th Annual Meeting of the Association
for Computational Linguistics (Volume 1: Long
Papers), pages 1715–1725, Berlin, Germany.
Association for Computational Linguistics.
Linfeng Song, Xiaochang Peng, Yue Zhang,
Zhiguo Wang, and Daniel Gildea. 2017.
AMR-to-text generation with synchronous node
replacement grammar. In Proceedings of the
55th Annual Meeting of the Association for
Computational Linguistics (Volume 2: Short
Papers), pages 7–13, Vancouver, Canada.
Association for Computational Linguistics.
Linfeng Song, Yue Zhang, Zhiguo Wang, and
Daniel Gildea. 2018. A graph-to-sequence
model for AMR-to-text generation. In Proceed-
ings of the 56th Annual Meeting of the Associa-
tion for Computational Linguistics (Volume 1:
Long Papers), pages 1616–1626, Melbourne,
for Computational
Australia. Association
Linguistics.
Bayu Distiawan Trisedya, Jianzhong Qi, Rui
Zhang, and Wei Wang. 2018. GTR-LSTM: A
triple encoder for sentence generation from
RDF data. In Proceedings of the 56th Annual
the Association for Computa-
Meeting of
tional Linguistics (Volume 1: Long Papers),
pages 1627–1637, Melbourne, Australia. Assoc-
iation for Computational Linguistics.
Ashish Vaswani, Noam Shazeer, Niki Parmar,
Jakob Uszkoreit, Llion Jones, Aidan N. Gomez,
Łukasz Kaiser, and Illia Polosukhin. 2017.
Attention is all you need. In I. Guyon, U. V.
Luxburg, S. Bengio, H. Wallach, R. Fergus,
S. Vishwanathan, and R. Garnett, editors,
Advances in Neural Information Processing
Systems 30, pages 5998–6008. Curran Assoc-
iates, Inc.
Petar Veliˇckovi´c, Guillem Cucurull, Arantxa
Casanova, Adriana Romero, Pietro Li`o, and
Yoshua Bengio. 2018. Graph Attention Net-
works. In International Conference on Learning
Representations. Vancouver, Canada.
Elena Voita, David Talbot, Fedor Moiseev, Rico
Sennrich, and Ivan Titov. 2019. Analyzing
multi-head self-attention: Specialized heads do
the heavy lifting, the rest can be pruned. In
Proceedings of the 57th Annual Meeting of
the Association for Computational Linguistics,
pages 5797–5808, Florence, Italy. Association
for Computational Linguistics.
Tianming Wang, Xiaojun Wan, and Hanqi Jin.
2020. AMR-to-text generation with graph
transformer. Transactions of the Association
for Computational Linguistics, 8:19–33.
Yonghui Wu, Mike Schuster, Zhifeng Chen,
Quoc V. Le, Mohammad Norouzi, Wolfgang
Macherey, Maxim Krikun, Yuan Cao, Qin
Gao, Klaus Macherey, Jeff Klingner, Apurva
Shah, Melvin Johnson, Xiaobing Liu, Lukasz
Kaiser, Stephan Gouws, Yoshikiyo Kato, Taku
Kudo, Hideto Kazawa, Keith Stevens, George
Kurian, Nishant Patil, Wei Wang, Cliff Young,
Jason Smith, Jason Riesa, Alex Rudnick,
Oriol Vinyals, Greg Corrado, Macduff Hughes,
and Jeffrey Dean. 2016. Google’s neural
machine translation system: Bridging the gap
between human and machine translation. CoRR,
abs/1609.08144.
Keyulu Xu, Chengtao Li, Yonglong Tian,
Tomohiro Sonobe, Ken ichi Kawarabayashi,
and Stefanie Jegelka. 2018. Representation
learning on graphs with jumping knowledge
networks. In ICML.
Yue Zhang, Qi Liu, and Linfeng Song. 2018.
Sentence-state LSTM for text representation.
In Proceedings of the 56th Annual Meeting of
the Association for Computational Linguis-
tics (Volume 1: Long Papers), pages 317–327,
Melbourne, Australia. Association for Compu-
tational Linguistics.
Jie Zhu, Junhui Li, Muhua Zhu, Longhua Qian,
Min Zhang, and Guodong Zhou. 2019. Model-
ing graph structure in transformer for better
AMR-to-text generation. In Proceedings of
the 2019 Conference on Empirical Methods
in Natural Language Processing and the 9th
International Joint Conference on Natural
Language
(EMNLP-IJCNLP),
pages
5458–5467, Hong Kong, China.
Association for Computational Linguistics.
Processing
604
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
3
2
1
9
2
3
1
9
0
/
/
t
l
a
c
_
a
_
0
0
3
3
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3