METHODS - Specialized Research AI at MIT

METHODS

Consensus clustering approach to group brain
connectivity matrices

Javier Rasero

1,2,3

, Mario Pellicoro
6
Daniele Marinazzo

, Leonardo Angelini
, and Sebastiano Stramaglia

2,3,4

, Jesus M. Cortes

2,3,4

1,5

1Biocruces Health Research Institute. Hospital Universitario de Cruces, Barakaldo, Spain
2Dipartimento di Fisica, Università degli Studi Aldo Moro, Bari, Italy
3Istituto Nazionale di Fisica Nucleare, Sezione di Bari, Italy
4TIRES-Center of Innovative Technologies for Signal Detection and Processing, Università degli Studi Aldo Moro Bari, Italy
Ikerbasque, the Basque Foundation for Science, Bilbao, Spain
6Faculty of Psychology and Educational Sciences, Department of Data Analysis, Ghent University, Ghent, Belgium

a n o p e n a c c e s s

j o u r n a l

Keywords: Unsupervised learning, Consensus clustering, Resting fMRI, Structural DTI

ABSTRACT

A novel approach rooted on the notion of consensus clustering, a strategy developed for
community detection in complex networks, is proposed to cope with the heterogeneity
that characterizes connectivity matrices in health and disease. The method can be
summarized as follows: (a) deﬁne, for each node, a distance matrix for the set of subjects
by comparing the connectivity pattern of that node in all pairs of subjects; (b) cluster the
distance matrix for each node; (c) build the consensus network from the corresponding
partitions; and (d) extract groups of subjects by ﬁnding the communities of the consensus
network thus obtained. Different from the previous implementations of consensus clustering,
we thus propose to use the consensus strategy to combine the information arising from the
connectivity patterns of each node. The proposed approach may be seen either as an
exploratory technique or as an unsupervised pretraining step to help the subsequent
construction of a supervised classiﬁer. Applications on a toy model and two real datasets
show the effectiveness of the proposed methodology, which represents heterogeneity of a
set of subjects in terms of a weighted network, the consensus matrix.

INTRODUCTION

In the supervised analysis of human connectome data (Craddock et al., 2013; Sporns, 2010),
subjects are usually grouped under a common umbrella corresponding to high-level clini-
cal categories (e.g., patients and controls), and typical approaches aim at deducing a deci-
sion function from the labeled training data (see Fornito & Bullmore, 2010). However, the
populations of subjects (healthy as well as patients) are usually highly heterogeneous: clus-
tering algorithms ﬁnd natural groupings in the data, and therefore constitute a promising
technique for disentangling the heterogeneity that is inherent to many conditions, and to
the cohort of controls. Such an unsupervised classiﬁcation may also be used as a prepro-
cessing stage, so that the subsequent supervised analysis might exploit the knowledge of the
structure of data. Some studies dealt with similar issues: semisupervised clustering of imag-
ing data was considered in Filipovych, Resnick, and Davatzikos (2011, 2012); other recent
approaches cope with the heterogeneity of subjects using multiplex biomarkers techniques
(Steiner, Guest, Rahmoune, & Martins-de-Souza, 2017) and combinations of imaging and
genetic patterns (Varol, Sotiras, Davatzikos, & Alzheimer’s Disease Neuroimaging Initiative,
2017), while a strategy to overcome intersubject variability while predicting behavioral

Citation: Rasero, J., Pellicoro, M.,
Angelini, L., Cortes, J. M., Marinazzo,
D., & Stramaglia, S. (2017). Consensus
clustering approach to group brain
connectivity matrices. Network
Neuroscience, 1(3), 242–253.
https://doi.org/10.1162/netn_a_00017

DOI:
https://doi.org/10.1162/netn_a_00017

Supporting Information:
https://github.com/jrasero/consensus
https://github.com/CPernet/Robust_
Statistical_Toolbox/

Competing Interests: The authors have
declared that no competing interests
exist.

Corresponding Author:
Sebastiano Stramaglia
sebastiano.stramaglia@ba.infn.it

Handling Editor:
Olaf Sporns

Copyright: © 2017
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license

The MIT Press

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
3
2
4
2
1
0
9
2
0
7
2
n
e
n
_
a
_
0
0
0
1
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Consensus clustering approach to group brain connectivity matrices

Brain connectivity network
(connectome):
A network in which the nodes
are brain regions and the links
are anatomical connections
(“anatomical/structural
connectivity”), or statistical
dependencies (“functional
connectivity”).

Consensus matrix:
Given several partitions of a given
set of nodes, for each pair of nodes
the consensus matrix provides the
fraction of partitions in which the
two nodes belong to the same subset.

Distance matrix:
For each node, a distance matrix for
the set of subjects is constructed
based on the Spearman correlation
between the nodal connectivity
patterns of the given node in the
two subjects.

K-medoids:
Clustering algorithm similar to
k-means, which in contrast chooses
data points as center (so-called
medoids), making it more robust to
outliers.

Network Neuroscience

variables from imaging data has been proposed in Takerkart, Auzias, Thirion, and Ralaivola
(2014). Connectivity features have been used in data-driven approaches for analysis and
classiﬁcation of MRI data in Amico et al. (2017) and Iraji et al. (2016). The purpose of this
work is to introduce a novel approach that is rooted on the notion of consensus clustering
(Lancichinetti & Fortunato, 2012), a strategy developed for community detection in complex
networks (Barabási, 2003).

To introduce our method, let us assume that a connectivity matrix is associated with each
item to be classiﬁed (usually a subject, but also individual scans for the same subject as in the
example illustrated below). The goal of supervised analysis is to mine those features of matrices
that provide the best prediction of available environmental and phenotypic factors, such as task
performance, psychological traits, and disease states. When it comes to using unsupervised
analysis of matrices to ﬁnd groups of subjects, the most straightforward approach would be to
extract a vector of features from each connectivity matrix, and to cluster these vectors using
one of the commonly used clustering algorithms. The purpose of the present work is to propose
a new strategy for unsupervised clustering of connectivity matrices. In the proposed approach
the different features, extracted from connectivity matrices, are not combined in a single vector
to feed the clustering algorithm; rather, the information coming from the various features are
combined by constructing a consensus network (Lancichinetti & Fortunato, 2012). Consensus
clustering is commonly used to generate stable results out of a set of partitions delivered by
different clustering algorithms (and/or parameters) applied to the same data (Strehl & Ghosh,
2002); here, instead, we use the consensus strategy to combine the information about the data
structure arising from different features so as to summarize them in a single consensus matrix.

The unsupervised strategy that we propose here to group subjects, without using phenotypic
measures, can be summarized as follows, and as depicted in Figure 1: (a) deﬁne, for each node,
a distance matrix for the set of subjects; (b) cluster the distance matrix for each node; (c) build
the consensus network from the corresponding partitions; and (d) extract groups of subjects by
ﬁnding the communities of the consensus network thus obtained. We remark that the proposed
approach provides not only a partition of subjects in communities, but also the consensus
In the next section we
matrix, which is a geometrical representation of the set of subjects.
describe in detail the method and apply it to a toy model, then we show the application on
two real MRI datasets. Finally, some conclusions are drawn.

METHODS
(structural) N × N connectivity matrix
Let us consider m subjects whose functional
(Rubinov & Sporns, 2010), where N is the number of nodes, will be denoted by {A(i, j)α},
α = 1, . . . , m and i, j = 1, . . . , N. For each node i, we build a distance matrix for the set
of subjects as follows. Consider a pair of subjects α and β, and consider the corresponding
nodal connectivity patterns {A(i, :)α} and {A(i, :)β}; let r be their Spearman correlation. As
the distance between the two subjects, for the node i, we take dαβ = 1 − r; other choices for
2(1 − r), where r is the Pearson corre-
the distance can be used, like, for example dαβ =
lation. The m × m distance matrix dαβ corresponding to node i will be denoted by Di, with
i = 1, . . . , N. The set of D matrices may be seen as corresponding to layers of a multilayer
network (Boccaletti et al., 2014), each brain node providing a layer.

(cid:2)

Each distance matrix Di is then partitioned into k groups of subjects using k-medoids method
(Brito, Bertrand, Cucumel, & Carvalho, 2007). Subsequently, an m × m consensus matrix C is
evaluated: its entry Cαβ indicates the number of partitions in which subjects α and β are as-
signed to the same group, divided by the number of partitions N. The number of clusters k may

243

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
3
2
4
2
1
0
9
2
0
7
2
n
e
n
_
a
_
0
0
0
1
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Consensus clustering approach to group brain connectivity matrices

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
3
2
4
2
1
0
9
2
0
7
2
n
e
n
_
a
_
0
0
0
1
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 1. Flowchart of the proposed methodology.

be kept ﬁxed, thus rendering the consensus matrix depending on k; a better strategy, however,
is to average the consensus matrix over k ranging in an interval, so as to fuse, in the consensus
matrix, information about structures at different resolutions.

The consensus matrix, obtained as explained before, is eventually partitioned in commu-
nities by modularity maximization, with the consensus matrix C being compared against the
ensemble of all consensus matrices one may obtain randomly and independently permuting
the cluster labels obtained after applying the k-medoids algorithm to each of the set of distance
matrices. More precisely, a modularity matrix is evaluated as

B = C − P,

where P is the expected coassignment matrix, uniform as a consequence of the null ensemble
chosen here, obtained by repeating many times the permutation of labels; the modularity
matrix B is eventually submitted to a modularity optimization algorithm to obtain the output
partition by the proposed approach. We used the community Louvain routine in the Brain
Connectivity Toolbox (Rubinov & Sporns, 2010), which admits modularity matrices instead of
connectivity matrices as input.

Network Neuroscience

244

Consensus clustering approach to group brain connectivity matrices

We remark that the proposed approach has similarities with the one adopted in Shehzad
et al. (2014), where techniques from genome-wide association studies coping with the prob-
lem of a huge number of comparisons were applied to connectomes, thus identifying nodes
whose whole-brain connectivity patterns vary signiﬁcantly with a phenotypic variable. The ap-
proach in Shehzad et al. (2014) consists of two steps. First, for each node in the connectome, a
whole-brain functional connectivity map is evaluated, and then the similarity between the con-
nectivity maps of all possible pairings of participants, using spatial correlation, is calculated.
Then, in the second stage, a statistic is evaluated for each node, indicating the strength of the
relationship between a phenotypic measure and variations in its connectivity patterns across
subjects. The main similarity with the proposed approach is that in both methods, for each
node in the connectome, the comparison between the connectivity maps yields a distance
matrix in the space of subjects.

A TOY MODEL

As a toy model to describe the application of our method, we simulate a set of 100 subjects,
divided in four groups of 25 each. The subjects are supposed to be described by 30 nodes.
We will compare our proposed approach with a standard procedure such as averaging the dis-
tance matrices and then applying the clustering algorithm to the average distance
matrix.

The distance matrices corresponding to the ﬁrst 10 nodes are constructed in the following
way: the distance for pairs belonging to the same group is sampled uniformly in the interval
[0.1, 0.4], while the distance for pairs belonging to different groups is sampled uniformly in
the interval [0.2, 0.4]. The distance matrices corresponding to the 20 remaining nodes have
all the entries sampled uniformly in the interval [0.2, 0.4]. It follows that in our toy model only
10 nodes, out of 30, carry information about the presence of the four groups.

First of all, we evaluate the distance matrix among subjects, averaged over the 30 nodes,
and apply the k-medoids algorithm to this matrix , searching for k = 4 clusters (thus exploiting
the knowledge of the number of classes present in data); this procedure leads to an accuracy
of 0.89, measured as follows. Let us call {Gα}, α = 1, . . . , 4 the four groups in the model and
let M be the minimum between 4 and the number of clusters found by modularity maximiza-
tion clustering; we denote {Ci}, i = 1, . . . , M the largest M clusters found by clustering. The
accuracy is then given by

1
m

M
∑
i=1

maxα|Gα ∩ Ci|,

where |Gα ∩ Ci| is the cardinality of the intersection of the two sets, and m = 100 is the total
number of subjects.

Subsequently, we run the proposed approach by applying separately to each distance
matrix for each of the 30 nodes the k-medoids algorithm with varying k. We then build the
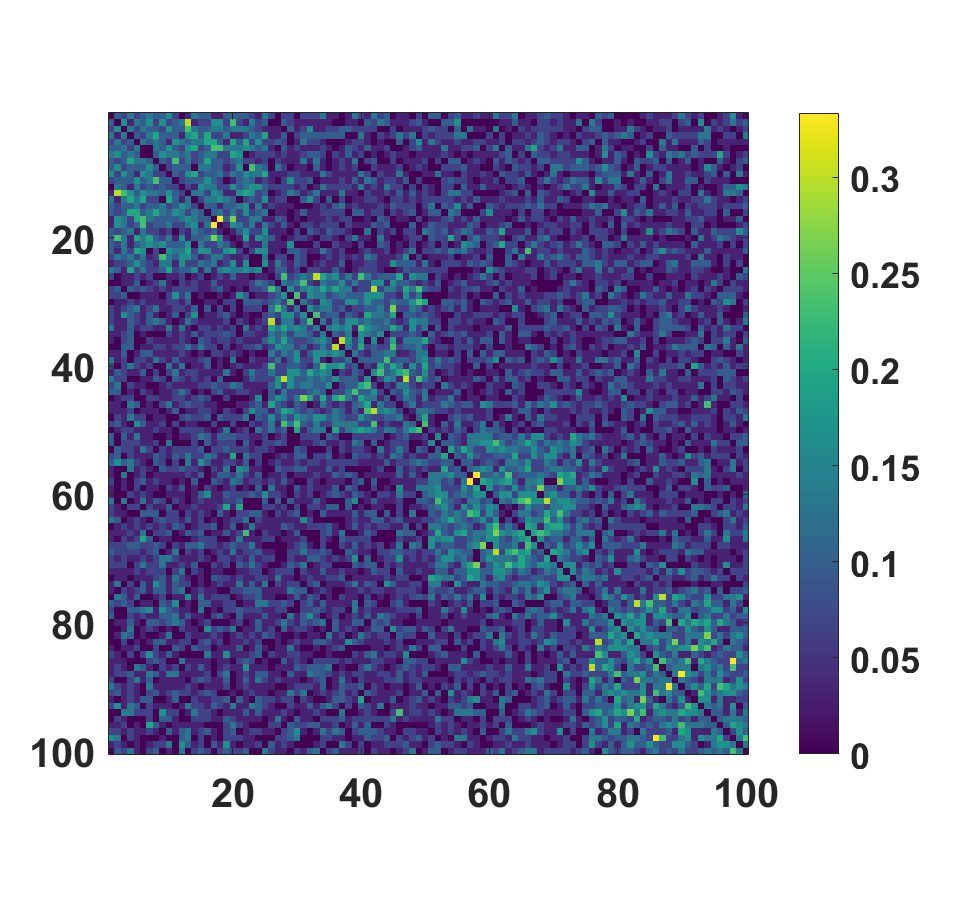
corresponding consensus matrix. For example, in Figure 2 the consensus matrix among sub-
jects is depicted as obtained by applying k-medoids with k = 10 separately to each of the
30 layers. Then, the communities of the consensus matrices have been estimated as described
in the previous section.

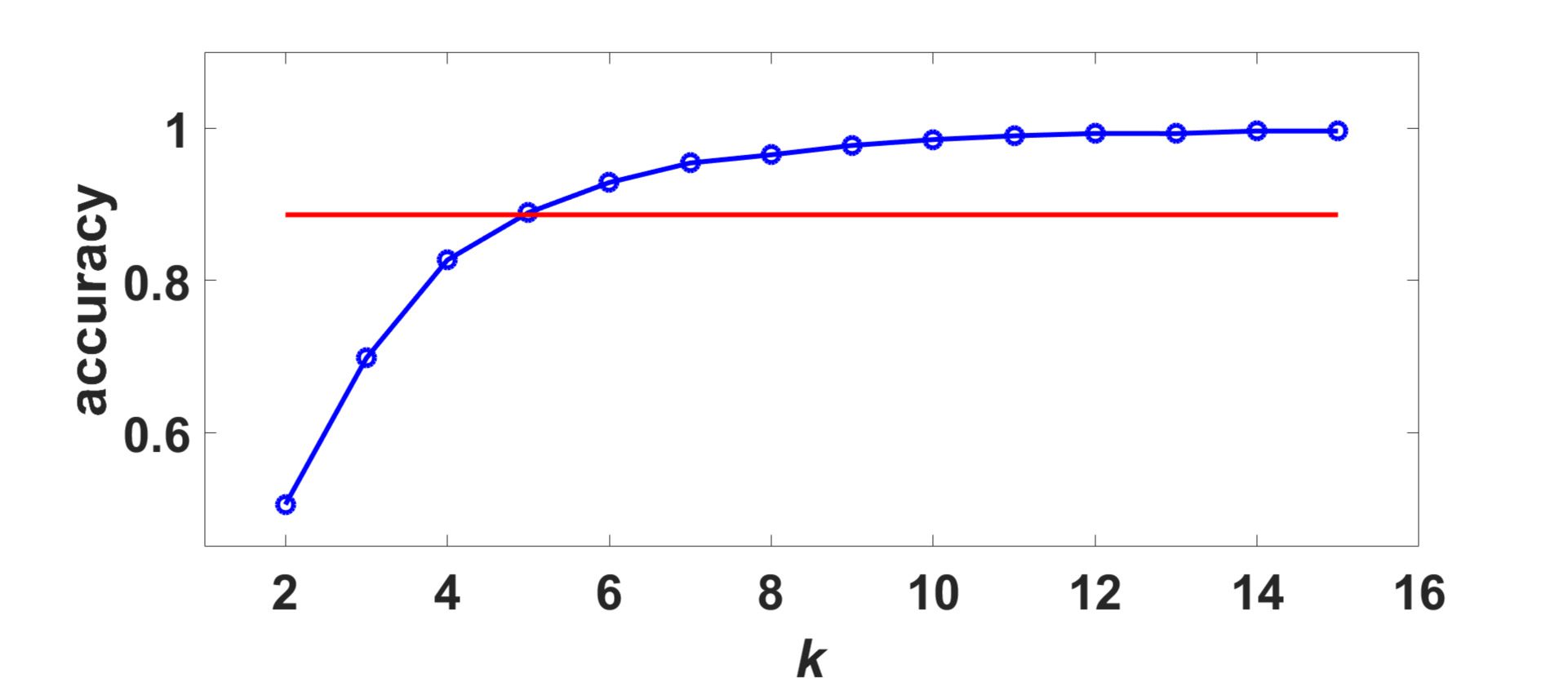
In Figure 3 the accuracy of the partition, provided by modularity maximization on the
consensus matrix, is depicted versus k, in order to show how it varies with k: it shows that
the proposed method performs better than the partition of the average distance matrix on
this example, for large k; we remark that the accuracy 0.89 is reached by k-medoids on the

Network Neuroscience

245

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
3
2
4
2
1
0
9
2
0
7
2
n
e
n
_
a
_
0
0
0
1
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Consensus clustering approach to group brain connectivity matrices

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
3
2
4
2
1
0
9
2
0
7
2
n
e
n
_
a
_
0
0
0
1
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

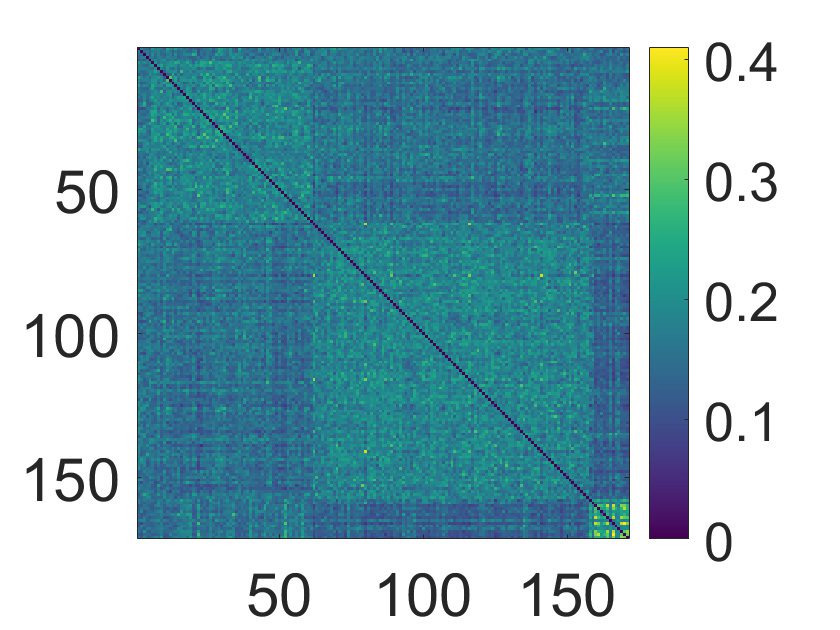
Figure 2. Consensus matrix among subjects in the toy model, obtained by applying k-medoids
with k = 10 separately to each of the 30 layers. Each entry Cαβ of the matrix represents the number
of partitions in which subjects α and β were assigned to the same group, divided by the number of
partitions N.

average distance using k = 4, that is exploiting the knowledge of the number of groups
present in the dataset, while the proposed algorithm determines both the number of clus-
ters and the partition. Intuitively, the proposed approach works better in this example for large
k, because in the distance matrix corresponding to an informative node, due to chance, the
block corresponding to a group is seen as fragmented in smaller pieces; those pieces can
be retrieved using k-medoids with large k. On the other hand, when the consensus is made
across the different informative nodes, all those pieces merge in the consensus matrix and
build the block corresponding to the four groups.

It is also worth noting that the accuracy by clustering the averaged consensus matrix
(over the values of k) is one, that is, perfect group reconstruction. Averaging over the values
of k appears then to be a convenient strategy. Moreover, averaging over values of parame-
ters is a common strategy for consensus clustering, hence building the consensus matrix
while joining several values of k is in line with the philosophy of consensus clustering
(Lancichinetti & Fortunato, 2012).

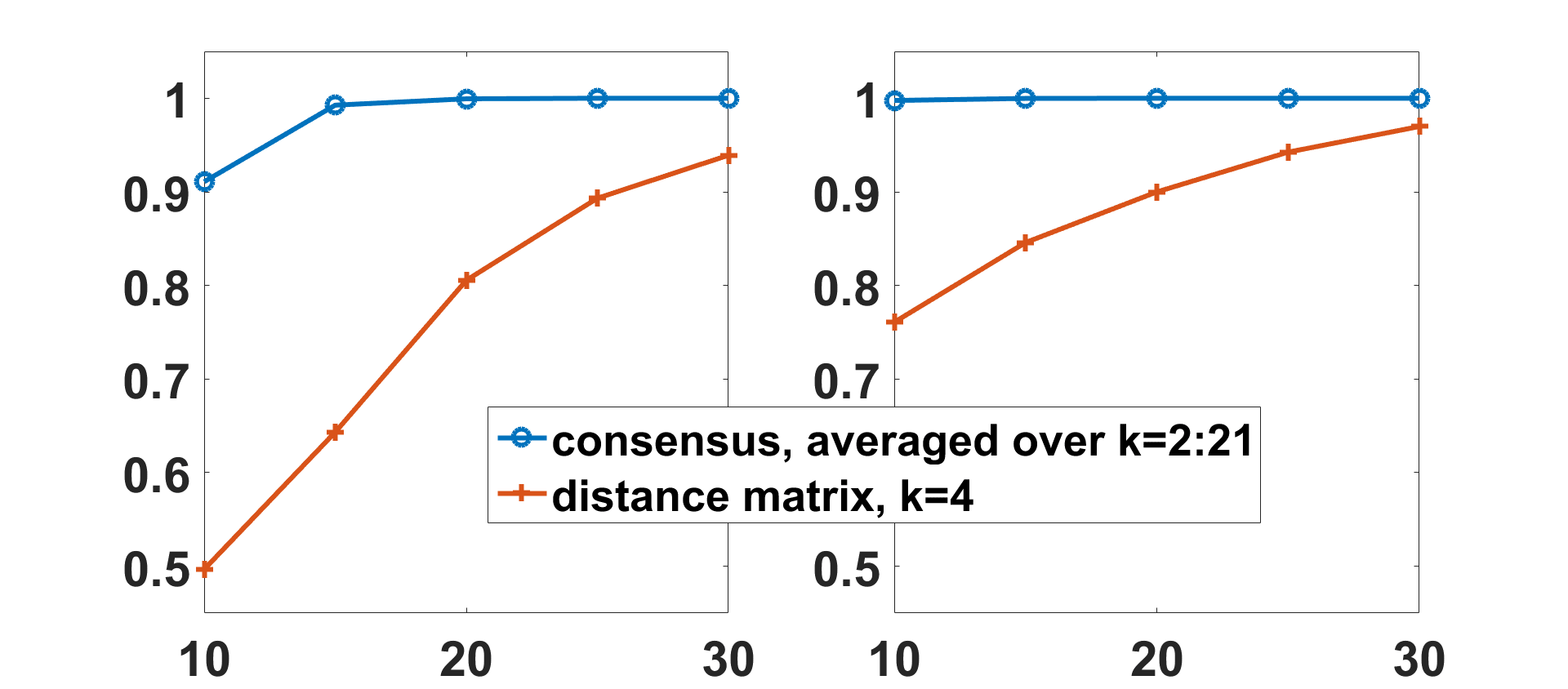
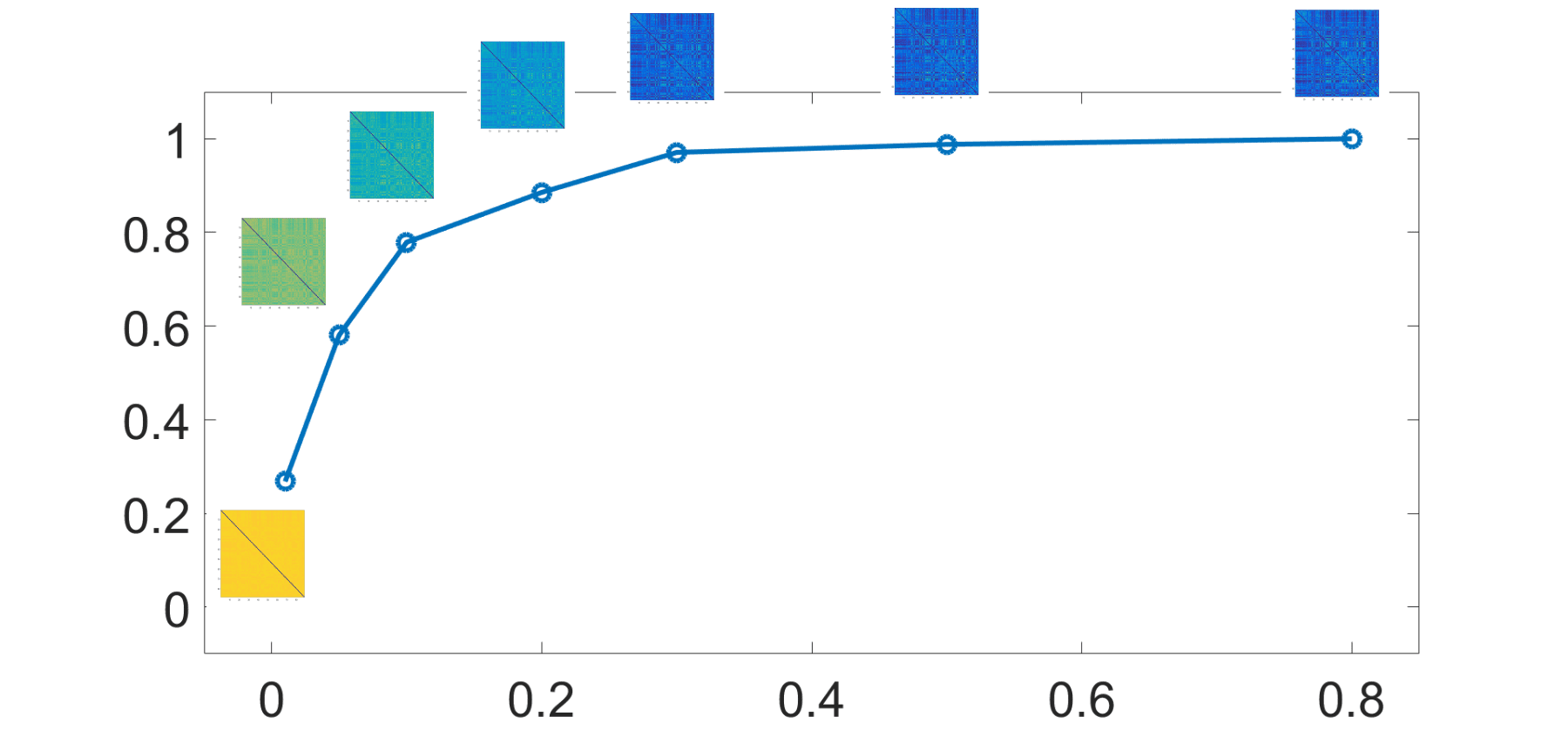
In order to show the effectiveness of the proposed approach under different conditions, we
change the toy model by varying the number of informative nodes and the number of groups.
We also use different parameters with reference to the previous simulations; the distance for

Network Neuroscience

246

Consensus clustering approach to group brain connectivity matrices

Figure 3. The accuracy of the partition, provided by modularity maximization on the consensus
matrix, is depicted versus k. The horizontal line represents the accuracy obtained by clustering the
average distance matrix using k-medoids and k = 4.

pairs belonging to the same group are still sampled uniformly in the interval [0.1, 0.4], while the
distance for pairs belonging to different groups is sampled uniformly in the interval [0.15, 0.4].
The results, displayed in Figure 4, show that the proposed approach works better than the
application of k-medoids to the average distance matrix.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
3
2
4
2
1
0
9
2
0
7
2
n
e
n
_
a
_
0
0
0
1
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 4. The accuracy of the partition, provided by modularity maximization on the consensus
matrix averaged over 20 values of k, is depicted versus the number of informative nodes (when
it is 30, all the nodes are informative).
In the left panel, the plots correspond to four groups of
25 subjects; the blue curve is the accuracy by the proposed method and the red line is the accuracy
obtained by clustering the average distance matrix using k-medoids and k = 4. In the right panel, the
case of two groups, each of 50 subjects, is considered; the blue line is the accuracy by the proposed
method and the red line is the accuracy obtained by clustering the average distance matrix using
k-medoids and k = 2. In all cases the consensus approach gives better results.

Network Neuroscience

247

Consensus clustering approach to group brain connectivity matrices

Resting-state fMRI:
Functional magnetic resonance
imaging acquired while the subject is
simply instructed to stay awake.

APPLICATION TO REAL DATASETS

Longitudinal dataset

Growing interest is devoted to longitudinal phenotyping in cognitive neuroscience: accord-
ingly we consider here data from the MyConnectome project
(Laumann et al., 2015;
Poldrack et al., 2015), where fMRI scans from a single subject were recorded over 18 months.
In Shine, Koyejo, & Poldrack (2016), the presence of two distinct temporal states has been
identiﬁed, which ﬂuctuated over the course of time. These temporal states were associated
with distinct patterns of time-resolved blood oxygen level dependent (BOLD) connectivity
within individual scanning sessions and also related to signiﬁcant alterations in global ef-
ﬁciency of brain connectivity as well as differences in self-reported attention. These data
Its accession number is ds000031. The func-
were obtained from the OpenfMRI database.
tional MRI (fMRI) data were preprocessed with FSL (FMRIB Software Library v5.0). The ﬁrst
10 volumes were discarded for correction of the magnetic saturation effect. The remaining
volumes were corrected for motion, after which slice timing correction was applied to correct
for temporal alignment. All voxels were spatially smoothed with a 6 mm FWHM (full width at
half maximum) isotropic Gaussian kernel and after intensity normalization, a band pass ﬁlter
was applied between 0.01 and 0.08 Hz. In addition, linear and quadratic trends were removed.
We next regressed out the motion time courses, the average cerebrospinal ﬂuid (CSF) signal,
and the average white matter signal. Global signal regression was not performed. Data were
transformed to the MNI152 template, such that a given voxel had a volume of 3 mm × 3 mm ×
3 mm. Finally, we obtained 268 time series, each corresponding to an anatomical region of
interest (ROI), by averaging the voxel signals according to the functional atlas described in
Shen, Tokoglu, Papademetris, & Constable (2013).

CONSENSUS MATRIX

DISTANCE MATRIX

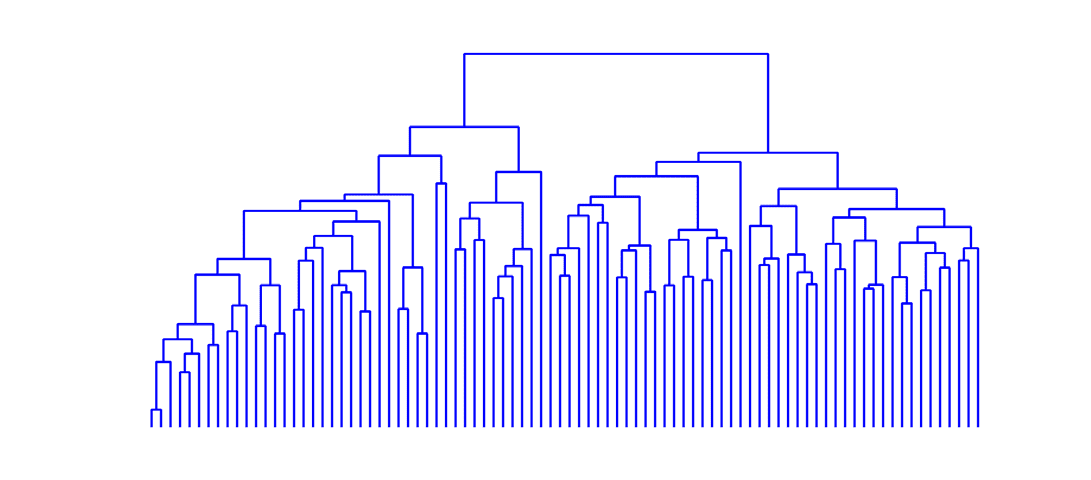
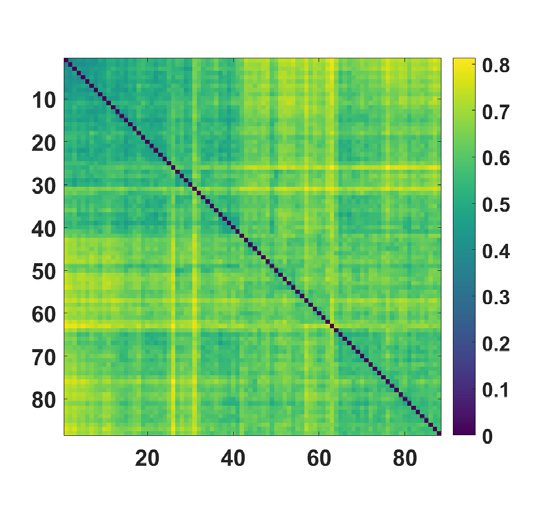
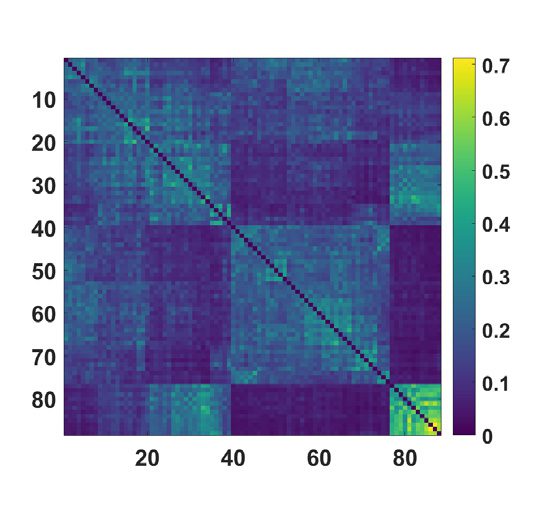
Figure 5.
(Top) Concerning the MyConnectome dataset, the consensus matrix, obtained averag-
ing over k, by the proposed approach is displayed with nodes ordered according to hierarchical
clustering, with the corresponding dendrogram. (Bottom) The average distance matrix, among the
different sessions of the same subject, and the corresponding dendrogram.

Network Neuroscience

248

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
3
2
4
2
1
0
9
2
0
7
2
n
e
n
_
a
_
0
0
0
1
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Consensus clustering approach to group brain connectivity matrices

PANAS (Positive and Negative
Affect Schedule):
The PANAS comprises two mood
scales, one that measures positive
affect and one that measures negative
affect. Participants in the PANAS are
required to respond to a 20-item test.

Each of the 89 sessions resulted in a 268 × 268 matrix of Pearson correlation coefﬁcients.
We treated the sessions as if they were connectivity matrices of different subjects, and applied
the proposed methodology.
In Figure 5 we depict the distance matrix, among the different
sessions of the same subject, and the consensus matrix, obtained averaging over 10 values of
k. Sessions are ordered, in both cases, according to hierarchical clustering; the corresponding
dendrograms are also shown in the ﬁgure. It is clear that the consensus matrix shows a hier-
archical structure. Maximization of the modularity provides two communities with modular-
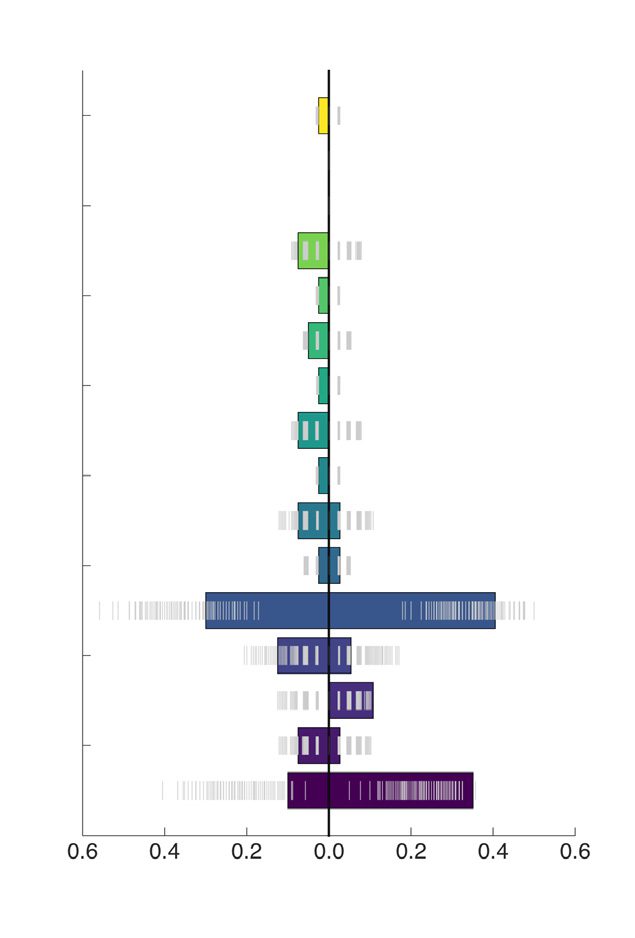
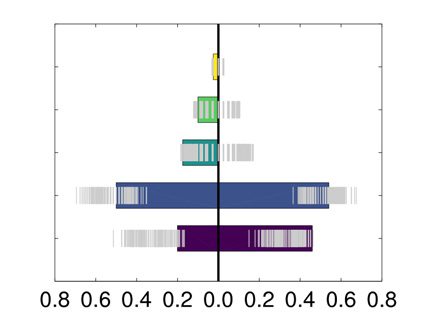
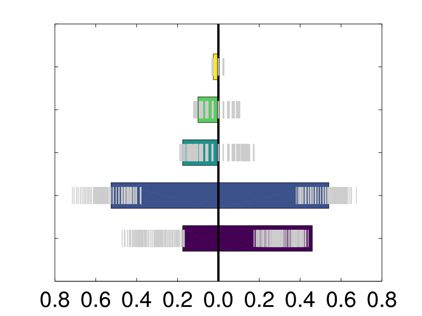
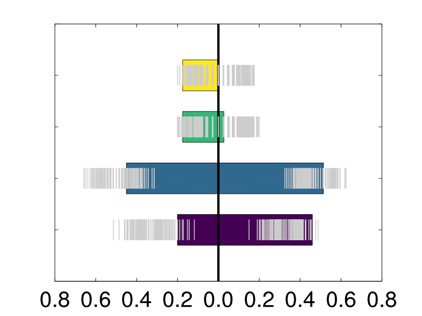
ity equal to 0.175. As depicted in Figure 6, the two communities are signiﬁcantly different
for several PANAS scores, all associated with tiredness. This is assessed visually using a null
distribution obtained by shufﬂing 500 times the pairing between behavioral variable and con-
nectome matrix and with a nonparametric Wilcoxon rank sum test: drowsy (Bonferroni cor-
rected p value = 0.028), tired (Bonferroni corrected p value = 0.041), sluggish (Bonferroni
corrected p value = 0.026), sleepy (Bonferroni corrected p value = 0.012), fatigue (Bonferroni
corrected p value = 0.022). This conﬁrms the presence of two distinct temporal states. How-
ever, the hierarchical structure of the consensus matrix that we obtained suggests that longer
longitudinal recordings are needed to further evidence the richness of distinct functional states
for single subjects.

It
the proposed algorithm:

is also worth considering the effects of network thresholding on the performance
of
thresholding is a relevant problem in brain connectivity
(Fallani, Latora, & Chavez, 2017; Van Wijk, Stam, & Daffertshofer, 2010). The functional net-
works in this dataset are thresholded so as to retain a varying fraction (density) of the largest
In Figure 7 we plot the similarity between the consensus matrices obtained by the
entries.
proposed algorithm after thresholding and the corresponding consensus matrix in the absence
of thresholding, as a function of the density. The similarity between the consensus matrices is
evaluated as the Pearson correlation between the entries of the two matrices. On one side the
results show the robustness of the proposed approach to moderate thresholding; indeed, up to

E
U
G
I
T
A
F

–

D
E
R
I
T

–

+
H
S
I
G
G
U
L
S
–

Y
P
E
E
L
S

–

Y
S
W
O
R
D

–

Figure 6. MyConnectome dataset: distributions of the values of the PANAS scores that are sig-
niﬁcantly different among the two communities found by modularity optimization on the consen-
sus matrix provided by the proposed approach. An expected null distribution, whose quantiles are
reported in gray, was obtained by shufﬂing the association between the PANAS score and connec-
tome matrix.

Network Neuroscience

249

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
3
2
4
2
1
0
9
2
0
7
2
n
e
n
_
a
_
0
0
0
1
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Consensus clustering approach to group brain connectivity matrices

H
T
I
W
N
O
I
T
A
L
E
R
R
O
C

X
I
R
T
A
M
L
L
U
F

DENSITY

Figure 7. The consensus matrix evaluated by the proposed approach, on the brain connectivity
matrices of the MyConnectome dataset, is compared with the consensus matrix from the proposed
method on thresholded matrices. The linkwise similarity between the two consensus matrices is
evaluated as the Pearson correlation of the corresponding entries in the two matrices, and is plotted
versus the density of retained largest entries.

20% thresholding, the consensus matrix is very close to what is obtained using the full matrices.
On the other hand, the consensus matrix by the proposed approach is substantially different for
sparser networks. This might speak to the fact that the correlation value is a debatable choice
of a thresholding criterion for correlation matrices, and that the proposed approach is suited
for weighted networks.

Resting healthy subjects, functional and structural connectivity

In this case the networks have 118 nodes.

We consider 171 healthy subjects from the NKI Rockland dataset (Nooner et al., 2012); for
each subject we use both the structural diffusion tensor imaging (DTI) network and the func-
tional network, already obtained from processed data as described in Brown, Rudie,
In
Bandrowski, VanHorn, & Bookheimer, 2012.
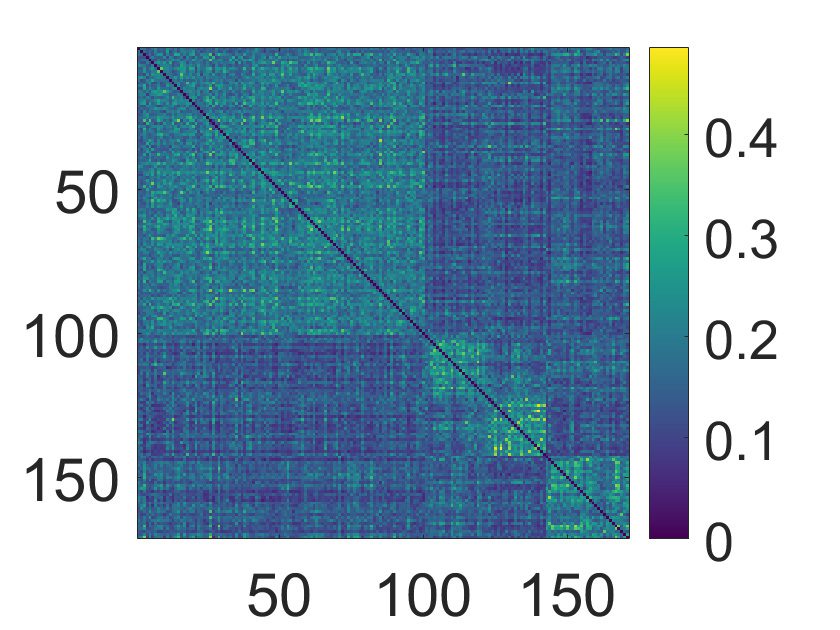
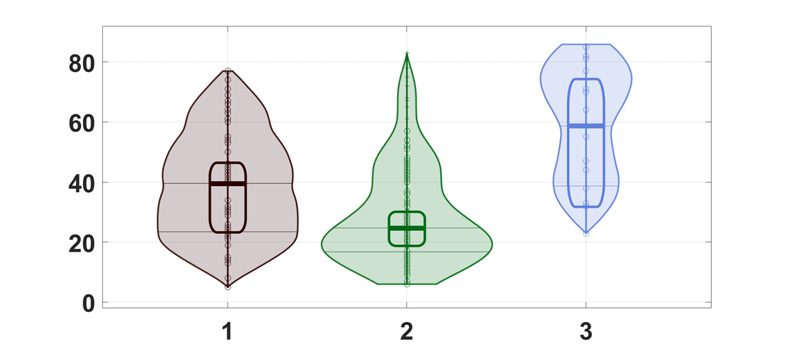
Figure 8 we depict the consensus matrix for both DTI and fMRI networks; modularity max-
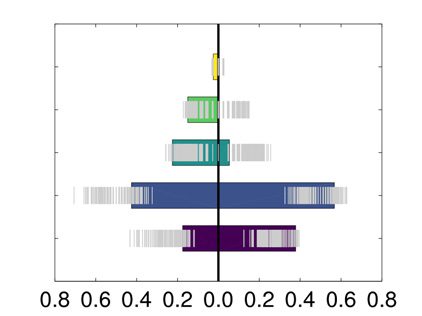
imization yields three communities for DTI networks and four communities for fMRI. Con-
cerning DTI, the three communities are signiﬁcantly characterized by different ages, with
p values equal to 9 × 10−4
, and 0.003 for the group comparisons 1-2, 2-3, and
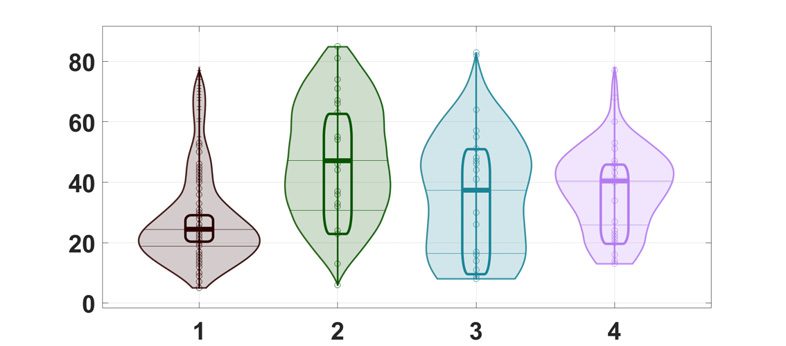
1-3 respectively (see Figure 8). Considering fMRI data, the ﬁrst group by the proposed algo-
rithm has a different age than the second, the third, and the fourth ones (taken as a whole) with
probability 7 × 10−4
. P values reported here refer to a nonparametric rank sum test; similar
signiﬁcance was found using parametric tests. We remark that our method performs different
from k-medoids over the average distance, where we obtain two groups with different ages,
t test with probability 10−3
using the functional distance, while no signiﬁcant difference in age
using the structural connectivity.

, 2 × 10−5

Inspired by the results found by our method, we also performed a multivariate distance
regression (Shehzad et al., 2014), that allowed us to build a pseudo F statistic to test whether
age correlates with the differences observed in the distance matrix for each node. We have

Network Neuroscience

250

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
3
2
4
2
1
0
9
2
0
7
2
n
e
n
_
a
_
0
0
0
1
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Consensus clustering approach to group brain connectivity matrices

STRUCTURAL

FUNCTIONAL

E
G
A

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
3
2
4
2
1
0
9
2
0
7
2
n
e
n
_
a
_
0
0
0
1
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

COMMUNITY

Figure 8.
(Top) Concerning the NKI dataset, the consensus matrices found by the proposed ap-
proach are shown for structural (top left) and functional (top right) connectivity. (Bottom) The dis-
tribution of age values (in years) in the resulting communities are reported. The rectangles indicate
the estimator with 95% high density interval, calculated by Bayesian bootstrap. The shaded areas
indicate random average shifted histograms, with a kernel density estimate. The code for these plots
is available at Pernet (2017).

achieved this by comparing the observed F statistic with the pseudo F distribution (that is, not
normal) after 105
data permutations. As expected, for both structural and functional data, we
found 124 and 76 nodes statistically related with age respectively, thus suggesting that age is
one of the variables responsible for the community structure found by our method.

CONCLUSIONS

An important issue such as dealing with the heterogeneity that characterizes healthy condi-
tions, as well as diseases, requires the development of effective methods capable of highlight-
ing the structure of sets of subjects at varying resolutions. The approach that we propose here
is applied to sets of subjects, each described by a connectivity matrix. We propose a strategy,
rooted in complex networks theory, to obtain a consensus matrix that describes the geometry
of the dataset, providing at different resolutions groups of similar subjects. While the straight-
forward application of consensus clustering to a given data set combines the output from dif-
ferent clustering, our proposal is to apply a clustering algorithm separately to the connectivity
map of each node. Hence the consensus strategy is exploited to combine the information aris-
ing from the different nodes. Obviously, the choice of k-medoids as the clustering algorithm
for the individual layers is not mandatory; other algorithms can be used, as well as the deﬁ-
nition of the distance among subjects to be used by this algorithm. Moreover, in the present
work the features that we considered are the connectivity maps resulting from the whole-brain
connectivity pattern of each node; however, other subsets of entries of matrices can be taken as
well, and the same strategy can be applied to fuse the different layers and produce a consensus
matrix. Likewise, our framework is not limited to considering the whole brain, and therefore it

Network Neuroscience

251

Consensus clustering approach to group brain connectivity matrices

can be applied to analyze speciﬁc regions relevant to the problem at hand so as to exploit the
beneﬁts of our method. To summarize, our approach aims to disentangle the heterogeneity
of groups corresponding to high-level categories, like healthy and diseased, ﬁnding natural
groups within the cohort of patients (and within the cohort of controls). While dealing with
data with both healthy and controls, it can be seen as a preprocessing step, which helps the
subsequent construction of a supervised classiﬁer healthy/subject.

ACKNOWLEDGMENTS

The authors are grateful to Richard Betzel (University of Pennsylvania) and an anonymous
referee for valuable suggestions. They also thank Guillaume Rousselet for valuable suggestions
on data representation.

SUPPORTING INFORMATION

The code for the construction of the consensus matrix, out of the set of connectivity matrices,
is available at Rasero (2017).

AUTHOR CONTRIBUTIONS

Javier Rasero: Data curation; Methodology; Software; Writing – review & editing. Mario
Pellicoro:
Investigation; Software; Writing – review & editing. Leonardo Angelini: Investi-
gation; Writing – review & editing. Jesus M. Cortes: Investigation; Writing – review & edit-
ing. Daniele Marinazzo: Conceptualization; Data curation; Investigation; Writing – review &
editing. Sebastiano Stramaglia: Conceptualization; Investigation; Methodology; Supervision;
Writing – original draft.

FUNDING INFORMATION

JR acknowledges ﬁnancial support from the Minister of Education, Language Policy and Culture
(Basque government) under the Doctoral Research Staff Improvement Programme.

REFERENCES

Amico, E., Marinazzo, D., Di Perri, C., Heine, L., Annen, J., Martial,
(2017). Mapping the functional connectome

C., . . . Goñi, J.
traits of levels of consciousness. NeuroImage, 148, 201–211.

Barabási, A.-L.

(2003).

Linked: The new science of networks.

Cambridge, MA: Perseus.

Boccaletti, S., Bianconi, G., Criado, R., Del Genio, C. I., Gómez-
Gardenes, J., Romance, M., . . . Zanin, M. (2014). The structure
and dynamics of multilayer networks. Physics Reports, 544(1),
1–122.

Brito, P., Bertrand, P., Cucumel, G., & Carvalho, F. D.

(2007).
Clustering by means of medoids. Selected contributions in data
analysis and classiﬁcation. Berlin/Heidelberg: Springer Science
& Business Media.

Brown, J. A., Rudie, J. D., Bandrowski, A., Van Horn, J. D., &
(2012). The UCLA multimodal connectivity
Bookheimer, S. Y.
database: A web-based platform for brain connectivity matrix
sharing and analysis. Frontiers in Neuroinformatics, 6, 28.

Craddock, R. C.,

Jbabdi, S., Yan, C.-G., Vogelstein,

Castellanos, F. X., Di Martino, A., . . . Milham, M. P.

J. T.,
(2013).

Imaging human connectomes at the macroscale. Nature Meth-
ods, 10(6), 524–539.

Fallani, F. D. V., Latora, V., & Chavez, M.

(2017). A topological
criterion for ﬁltering information in complex brain networks.
PLoS Computational Biology, 13(1), e1005305.
Filipovych, R., Resnick, S. M., & Davatzikos, C.

(2011). Semi-
supervised cluster analysis of imaging data. NeuroImage, 54(3),
2185–2197.

Filipovych, R., Resnick, S. M., & Davatzikos, C.

Joint-
MMCC: Joint maximum-margin classiﬁcation and clustering of
IEEE Transactions on Medical Imaging, 31(5),
imaging data.
1124–1140.

(2012).

Fornito, A., & Bullmore, E. T.

(2010). What can spontaneous
ﬂuctuations of the blood oxygenation-level-dependent signal tell
us about psychiatric disorders? Current Opinion in Psychiatry,
23(3), 239–249.

Iraji, A., Calhoun, V. D., Wiseman, N. M., Davoodi-Bojd, E.,
Avanaki, M. R., Haacke, E. M., & Kou, Z.
The
connectivity domain: Analyzing resting state fmri data using

(2016).

Network Neuroscience

252

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
3
2
4
2
1
0
9
2
0
7
2
n
e
n
_
a
_
0
0
0
1
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Consensus clustering approach to group brain connectivity matrices

feature-based data-driven and model-based methods. Neuro-
Image, 134, 494–507.

Lancichinetti, A., & Fortunato, S. (2012). Consensus clustering in

complex networks. Scientiﬁc reports, 2.

Laumann, T. O., Gordon, E. M., Adeyemo, B., Snyder, A. Z., Joo,
S. J., Chen, M.-Y., . . . Petersen, S. E.
(2015). Functional sys-
tem and areal organization of a highly sampled individual human
brain. Neuron, 87(3), 657–670.

Nooner, K. B., Colcombe, S., Tobe, R., Mennes, M., Benedict, M.,
Moreno, A., . . . Milham, M. P.
(2012). The NKI-Rockland
sample: A model for accelerating the pace of discovery science
in psychiatry. Frontiers in Neuroscience, 6, 152.

Pernet, C. (2017). Robust statistical toolbox, GitHub, https://github.

com/CPernet/Robust_Statistical_Toolbox/

Poldrack, R. A., Laumann, T. O., Koyejo, O., Gregory, B., Hover,
A., Chen, M.-Y., . . . Mumford, J. A.
(2015). Long-term neural
and physiological phenotyping of a single human. Nature Com-
munications, 6.

Rasero, J. (2017). Code to calculate a consensus matrix from a set of
distance matrices using k-medoids, GitHub, https://github.com/
jrasero/consensus

Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52(3),
1059–1069.

Shehzad, Z., Kelly, C., Reiss, P. T., Craddock, R. C., Emerson,
J. W., McMahon, K., . . . Milham, M. P. (2014). A multivariate
distance-based analytic framework for connectome-wide asso-
ciation studies. NeuroImage, 93, 74–94.

Shen, X., Tokoglu, F., Papademetris, X., & Constable, R. T. (2013).
Groupwise whole-brain parcellation from resting-state fMRI
data for network node identiﬁcation. NeuroImage, 82, 403–415.
Shine, J. M., Koyejo, O., & Poldrack, R. A. (2016). Temporal meta-
states are associated with differential patterns of time-resolved
connectivity, network topology, and attention. Proceedings of
the National Academy of Sciences, 201604898.

(2010). Networks of the brain. Cambridge, MA: MIT

Sporns, O.
Press.
J., Guest, P. C., Rahmoune, H., & Martins-de-Souza,
Steiner,
(2017). The application of multiplex biomarker techniques
D.
for
improved stratiﬁcation and treatment of schizophrenia
patients. Multiplex Biomarker Techniques: Methods and Appli-
cations, 19–35.
Strehl, A., & Ghosh, J.

(2002). Cluster ensembles: A knowledge
In AAAI/IAAI

reuse framework for combining partitionings.
(pp. 93–99).

Takerkart, S., Auzias, G., Thirion, B., & Ralaivola, L. (2014). Graph-
based inter-subject pattern analysis of fMRI data. PloS ONE, 9(8),
e104586.

Van Wijk, B. C., Stam, C. J., & Daffertshofer, A. (2010). Comparing
brain networks of different size and connectivity density using
graph theory. PloS ONE, 5(10), e13701.

Varol, E., Sotiras, A., Davatzikos, C., & Alzheimer’s Disease
(2017). HYDRA: Revealing hetero-
Neuroimaging Initiative.
imaging and genetic patterns through a multiple
geneity of
max-margin discriminative analysis framework. NeuroImage,
145, 346–364.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

1
3
2
4
2
1
0
9
2
0
7
2
n
e
n
_
a
_
0
0
0
1
7
p
d