METHODS
Temporal Mapper: Transition networks in
simulated and real neural dynamics
Mengsen Zhang1,2*, Samir Chowdhury1*, and Manish Saggar1
1Department of Psychiatry and Behavioral Sciences, Stanford University, Stanford, CA, USA
2Department of Psychiatry, University of North Carolina at Chapel Hill, NC, USA
*These authors contributed equally to this work.
Keywords: TDA, Mapper, Dynamical systems, Attractors, Networks, Nonlinear dynamics,
Multistability, Optimal transport
a n o p e n a c c e s s
j o u r n a l
ABSTRACT
Characterizing large-scale dynamic organization of the brain relies on both data-driven and
mechanistic modeling, which demands a low versus high level of prior knowledge and
assumptions about how constituents of the brain interact. However, the conceptual translation
between the two is not straightforward. The present work aims to provide a bridge between
data-driven and mechanistic modeling. We conceptualize brain dynamics as a complex
landscape that is continuously modulated by internal and external changes. The modulation can
induce transitions between one stable brain state (attractor) to another. Here, we provide a novel
method—Temporal Mapper—built upon established tools from the field of topological data
analysis to retrieve the network of attractor transitions from time series data alone. For theoretical
validation, we use a biophysical network model to induce transitions in a controlled manner,
which provides simulated time series equipped with a ground-truth attractor transition network.
Our approach reconstructs the ground-truth transition network from simulated time series
data better than existing time-varying approaches. For empirical relevance, we apply our
approach to fMRI data gathered during a continuous multitask experiment. We found that
occupancy of the high-degree nodes and cycles of the transition network was significantly
associated with subjects’ behavioral performance. Taken together, we provide an important
first step toward integrating data-driven and mechanistic modeling of brain dynamics.
AUTHOR SUMMARY
Brain dynamics are often described by data-driven models or mechanistic dynamical systems
models to understand how specific brain states persist or change (transition). However, there
lacks a computational framework that explicitly connects states/transitions discovered by data-
driven methods to those of mechanistic models, leading to a disconnection between data
analysis and theoretical modeling. To begin bridging this gap, we develop a data-driven
method, the Temporal Mapper, to extract dynamical systems features from time series and
represent them as attractor transition networks. The Temporal Mapper can reconstruct ground-
truth transition networks of mechanistic models. When applied to human fMRI data, the
method helps predict behavioral performance from the topology of transition networks.
Potential applications include characterizing brain dynamic organization in health and
diseases and designing brain stimulation protocols.
Citation: Zhang, M., Chowdhury, S., &
Saggar, M. (2023). Temporal Mapper:
Transition networks in simulated
and real neural dynamics. Network
Neuroscience, 7(2), 431–460. https://
doi.org/10.1162/netn_a_00301
DOI:
https://doi.org/10.1162/netn_a_00301
Supporting Information:
https://doi.org/10.1162/netn_a_00301
Received: 29 July 2022
Accepted: 7 December 2022
Competing Interests: The authors have
declared that no competing interests
exist.
Corresponding Authors:
Mengsen Zhang
mengsen_zhang@med.unc.edu
Manish Saggar
saggar@stanford.edu
Handling Editor:
Christopher Honey
Copyright: © 2023
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license
The MIT Press
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal Mapper
Nonlinear dynamics:
The study of a type of dynamical
systems, where dynamics of the
whole system differs from that of
independent parts.
Attractors:
States and a set of states that attract
nearby trajectories of the dynamical
system. They are stable as the system
returns to an attractor when slightly
perturbed.
Phase transitions:
Change in state of a dynamical
system from the regime of one
attractor to that of another either due
to noise or underlying changes in
the parameter of the system leading
to destabilization of the current
attractor.
Multistability:
A feature of some nonlinear
dynamical systems, where multiple
attractors coexist in the state space.
Metastability:
A type of dynamics in some
nonlinear dynamical systems, where
the system slows down (dwell) at
specific preferred states and then
escapes from it.
INTRODUCTION
The brain exhibits complex dynamics (Buzsaki, 2006; Kelso, 1995). Characterizing its overall
dynamic organization is a fundamental step in assessing brain functions and brain fingerprint-
ing for healthy individuals and patients with psychiatric disorders (Saggar & Uddin, 2019).
One common approach is to infer dominant “brain states” and the transitions between them
from neuroimaging time series data (e.g., Cavanna et al., 2018; Li et al., 2017; Meer et al.,
2020; Saggar et al., 2018; Taghia et al., 2018; Tang et al., 2012; Zalesky et al., 2014). Such
“states” and transitions can be defined by a diverse array of data-driven methods. Here we
categorized a model as data driven if it does not require additional knowledge of the brain
other than the time series data recorded from it. On the other side of the spectrum, brain
dynamics are often modeled by large-scale nonlinear dynamical systems models with various
levels of biophysical details (Breakspear, 2017; Deco et al., 2011). Here we categorize this
type of model as mechanistic, as they aim to describe the dynamical mechanism of interaction
between constituents of the brain, which requires prior knowledge or assumptions about the
biophysical and anatomical features of the brain in addition to the time series data measured.
States and transitions discovered using data-driven methods often share conceptual appeal to
nonlinear dynamics concepts such as attractors (stable states) and phase transitions. Yet, a
direct link between data-driven and mechanistic modeling of the brain remains missing. In this
work, we develop a data analysis method to represent time series data as a directed graph, whose
nodes and edges could reasonably map directly to the underlying attractors and phase transitions
in a nonlinear dynamic model of the brain. We first validate our method by using simulated
transitions and then apply the method to human fMRI data to demonstrate its empirical relevance
in assessing transitions associated with cognitive task switching. This work helps build the missing
link between data-driven and mechanistic modeling of complex brain dynamics. With a direct
link to mechanistic models, data-driven models may better inform experimenters and clinicians
of the network effect of causal perturbation (e.g., transcranial magnetic stimulation) in basic
neuroscience and in the treatment of psychiatric disorders.
A signature of nonlinear brain dynamics is multistability, that is, the coexistence of multiple
stable brain activity patterns (Kelso, 2012), which may be referred to as attractors in technical
terms or persistent brain states colloquially. Transitions between these brain states may occur
either driven by external influences or internal dynamics. Intermittent visits to different brain
states are often referred to as metastability (Tognoli & Kelso, 2014). Multistability and
metastability—the existence of and the transitions between different brain states—are key ele-
ments in the mechanistic modeling of brain dynamics and functional connectivity (FC) (van den
Heuvel & Hulshoff Pol, 2010). Typically, such modeling approaches use large-scale biophysi-
cal network models that also incorporate biologically informed parameters and the human
structural connectome (Deco et al., 2011, 2013, 2014; Deco & Jirsa, 2012; Golos et al.,
2015; Hansen et al., 2015; Zhang et al., 2022).
The mechanistic modeling of state transitions in large-scale brain dynamics was motivated
by, among other things, the observations of how large-scale FC patterns vary as a function of
time, that is, the dynamic functional connectivity (dFC) (Hutchison et al., 2013; Preti et al.,
2017). dFC patterns are primarily computed as correlation coefficients between time series
within a sliding window. More recently, single time-frame methods (e.g., Faskowitz et al.,
2020; Esfahlani et al., 2020) have been developed to tackle FC analysis at the finest temporal
resolution and reduce the amount of data needed for stably estimating dFC patterns (Laumann
et al., 2017; Leonardi & Van De Ville, 2015). Altogether, (d)FC analyses play a central role in the
empirical understanding of brain dynamic organization. Abnormal FC and abnormal transitions
between dFC patterns have been linked to a wide spectrum of psychiatric and neurological
Network Neuroscience
432
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal Mapper
Repellers:
States and a set of states that repel
nearby trajectories of the dynamical
system. They are unstable as the
system moves further away from
these states when slightly perturbed.
Topological data analysis (TDA):
A field of applied mathematics that
uses algebraic and computational
techniques to represent data as
topological objects and to compute
global topological features of such
objects.
Mapper:
A TDA-based technique for
generating graph representations that
identify meaningful subgroups of
high-dimensional data.
Hysteresis:
A feature of multistable dynamical
systems, where the system ends up in
a different attractor than the one it
started with as the control parameter
changes continuously and returns to
the same value.
Network Neuroscience
disorders (Barber et al., 2018; Díez-Cirarda et al., 2018; Du et al., 2021; Fox & Greicius, 2010;
Garrity et al., 2007; Lui et al., 2011; Rabany et al., 2019; Saggar & Uddin, 2019).
What remains unclear is to what extent dFC patterns can be mapped to dynamical systems
concepts such as attractors or stable states. With a data-driven approach, dFC patterns that
repeat in time can be assigned to a relatively small number of “FC states” using, for example,
clustering methods (Allen et al., 2014) or hidden Markov models (Quinn et al., 2018; Rabiner,
1989; Vidaurre et al., 2017). However, directly conceptualizing FC states as dynamical system
states or attractors is not easy, especially when one needs to write down the differential equa-
tions governing the state evolution. Thus, mechanistic models of large-scale brain dynamics
typically use mean-field neural activity (Cabral et al., 2017) (e.g., population firing rate, the
fraction of open synaptic channels) or its derived BOLD signal (Friston et al., 2003), rather than
vectorized dFC patterns, as state variables. FC states can be derived post hoc from simulated
neural dynamics (Golos et al., 2015; Hansen et al., 2015), but a direct correspondence
between such post hoc FC states and dynamical system attractors is yet to be demonstrated.
Our recent modeling work suggests that FC patterns may be signatures of phase transitions
between stable states rather than the states themselves (Zhang et al., 2022). All the above point
to the need for a data-driven method to quantify stable brain states and transitions directly from
time series data and allow mapping of such states/transitions to underlying attractors and
phase transitions derived from mechanistic modeling.
In the present work, we leverage existing methods of computational topology/geometry and
large-scale biophysical network modeling to bridge this gap. Topological and geometrical
analysis of dynamical systems traces back to the time of Poincaré (Poincaré, 1967). However,
efficient computational infrastructure for generalizing such methods to higher dimensional
dynamics was not in place until recently. Morse decomposition has been used in the rigorous
analysis of nonlinear dynamical systems, for example, to represent a dynamical system as a
directed graph whose nodes map to attractors (and repellers) and edges to transitions (connect-
ing orbits) (Cummins et al., 2016; Kalies et al., 2005). However, neuroimaging data live in a
very high dimensional space sparsely covered by samples, which renders many rigorous
methods inapplicable. With a data-driven approach, combinatorial representations (e.g.,
graphs or simplicial complexes) of neural time series or FC patterns can be generated using
existing topological data analysis (TDA) tools such as Mapper (Carlsson, 2009; Geniesse et al.,
2019, 2022; Saggar et al., 2018, 2022; Singh et al., 2007) and persistent homology (Billings
et al., 2021; Carlsson, 2009; Chazal & Michel, 2021; Edelsbrunner & Morozov, 2013; Giusti
et al., 2015; Petri et al., 2014). In between, there are emerging efforts to develop dynamical
system-oriented TDA methods (Garland et al., 2016; Kim & Mémoli, 2021; Munch, 2013;
Myers et al., 2019; Perea, 2019; Tymochko et al., 2020), some specifically supported by mech-
anistic models of biological dynamics (Gameiro et al., 2004; Topaz et al., 2015; Ulmer et al.,
2019; Zhang et al., 2020). The present work falls under this in-between category, building on
our previous work on the TDA (Geniesse et al., 2019, 2022; Saggar et al., 2018) and biophys-
ical network modeling of large-scale brain dynamics (Zhang et al., 2022).
In the current work, our contribution is threefold. First, we introduce a novel method to
extract features associated with dynamical systems (i.e., attractors and their directed transi-
tions) from the observed time series data alone. Second, to validate our approach, we develop
a method to simulate a complex sequence of phase transitions in a large-scale neural dynamic
model in a controlled manner. This simulated data not only provides a ground truth of the
coexisting attractors in the model and their respective transitions, but also allows examination
of intricate but relevant nonlinear dynamic concepts such as hysteresis. Third, we apply our
method to a real-world human fMRI dataset to examine the efficacy of our method in capturing
433
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal Mapper
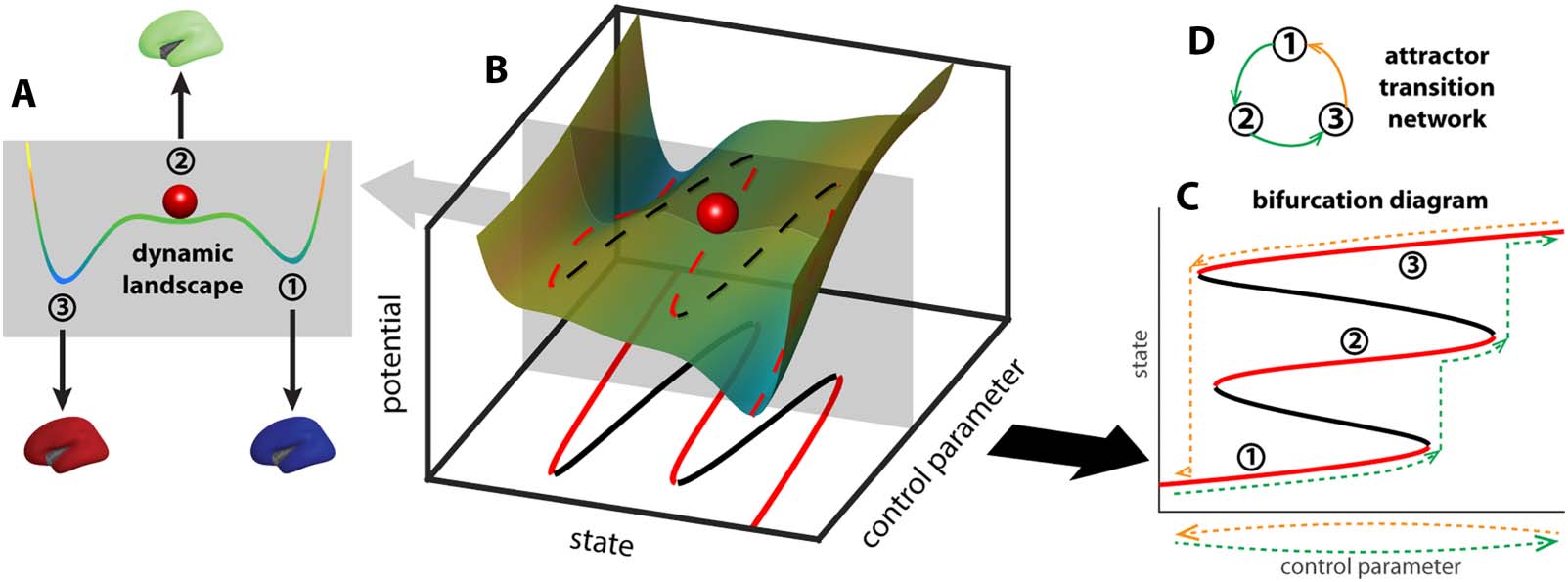
Figure 1. Deformation of the brain dynamic landscape induces transitions between stable brain states. A toy example of a dynamic land-
scape is shown as a colored curve in (A). The horizontal axis represents all possible brain states, that is, the state space, whereas the position of
the red ball represents the current brain state. States at the local minima of the landscape (A, 1–3) are attractors—slight perturbation of the
current state (e.g., red ball) leads to relaxation back to the same state. States at the local maxima of the landscape are repellers (to the left and
right of state 2, unlabeled)—slight perturbation of the state pushes the system into the basin of one of the attractors. The landscape may be
deformed by continuous changes in the brain structure, physiology, or the external environment, here represented abstractly as a control
parameter (B). As the landscape deforms (sliding the gray plane in B), the attractors and repellers shift continuously with it, for the most part,
marked by dashed lines in red and black, respectively. At critical points where an attractor and a repeller collide, there is a sudden change in
the repertoire of attractors, potentially leading to a transition between attractors. The change of the landscape is commonly visualized as a
bifurcation diagram (C), which keeps track of the change of attractors (red lines, 1–3) and repellers (black lines). Here “attractor” is used in a
general sense, referring to both the points in the state space (the intersections between red lines and the gray plane in the bottom plane in B)
and the connected components resulting from the continuous deformation of these points in the product between the state space and the
parameter space (red lines in C). Due to multistability and hysteresis, the system may take different paths in the bifurcation diagram as the
control parameter moves back and forth along the same line (dashed lines in C; green indicates forward paths, yellow indicates backward
paths). In an even simpler form, this path dependency can be represented as a directed graph (D), denoting the sequence in which attractors
are visited (color indicates forward and backward paths in C).
states and their transitions associated with cognitive task switching from time series data alone.
Taken together, we provide a critical methodological step toward bridging the mechanistic and
data-driven modeling of large-scale brain dynamics.
RESULTS
In this section, for larger accessibility of our results, we first provide a brief introduction to the
key nonlinear dynamics concepts and intuitions. We then introduce the framework to simulate
a complex sequence of phase transitions using a large-scale neural dynamic model. Finally,
we present an introduction to our Temporal Mapper approach and its application to simulated
as well as real-world fMRI datasets.
Nonlinear Dynamics and the Brain
Brain activities can be thought of as dynamics unfolding on a nonlinear landscape (Figure 1A).
Each state in this landscape represents a pattern of activation over the whole brain. Some states
are stable, which are termed attractors (Figure 1A, 1–3) since they attract nearby states to evolve
toward them. The coexistence of multiple attractors—multistability—is a signature of the brain’s
dynamic complexity (Kelso, 2012). The landscape can be shaped by a variety of intrinsic and
extrinsic factors, such as external input, synaptic conductance, and structural connectivity (Zhang
et al., 2022). Theoretically, these factors are often considered control parameters (Figure 1B).
As the control parameter changes, the landscape deforms with it. For illustration, sliding the
gray plane in Figure 1B up and down the control parameter axis changes the landscape within
the plane. With sufficient multistability, changing a control parameter back and forth along the
Control parameter:
A parameter of a dynamical system
that is controlled or varied externally,
which is not a state variable.
Network Neuroscience
434
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal Mapper
Bifurcation:
A qualitative change in a dynamical
system, where an attractor (repeller)
is created, destroyed, or substantially
modified by continuous changes in
control parameter(s).
Attractor transition network:
A directed graph represents the path
of phase transitions in a dynamical
system, whose nodes represent
attractors visited and edges represent
transitions occurred.
same path (Figure 1C, dashed lines below the horizontal axis) can lead to distinct paths of transi-
tions between attractors (Figure 1C, dashed lines in the bifurcation diagram above the horizontal
axis)—a feature known as hysteresis. Due to the asymmetry in the path of transitions, directed
graphs are better suited to minimally represent the transition network (Figure 1D), where the nodes
map to the attractors visited (nodes 1–3) and edges map to the transitions between attractors.
The topological complexity of this attractor transition network reflects the brain’s intrinsic
complexity through its interaction with the internal or external environment. In the present
work, we develop a method to retrieve such transition networks from simulated neural dynam-
ics and human fMRI data. In the following sections, we demonstrate that the networks recon-
structed from simulated data are reasonable approximations of the theoretical ground truth,
and those constructed from fMRI data help predict human behavioral performance.
Computational Framework to Simulate Complex Sequences of Phase Transitions and Represent Them as
an Attractor Transition Network
In this subsection, we introduce the computational framework used to simulate neural dynamics.
Simulations convey several advantages: (a) we can parametrically control and induce transitions
between attractors, (b) we can compute the ground-truth transition network given the exact equa-
tions, and (c) we can directly compare the reconstructed network (from simulated time series
alone without knowing the equations or any parameters) to the ground truth to assess the quality
of reconstruction.
(i ), SI
For simulations and computing the ground-truth transition network, we choose a biophysi-
cally informed model of human brain dynamics (Figure 2A; for details, see section Biophysical
Network Model of the Human Brain in Methods). The model describes the dynamics of a net-
work of 66 brain regions, shown to capture FC patterns in human resting fMRI (Zhang et al.,
2022) (the cartoon in Figure 2A includes six regions only for illustrative purposes). The model is
an adaptation of the reduced Wong–Wang model (Deco et al., 2014; Wong & Wang, 2006) in
the form of the Wilson–Cowan model (Wilson & Cowan, 1972, 1973) with improved multi-
stability (Zhang et al., 2022). Each region i consists of an excitatory population (E) and an inhib-
(i )). Long-range connections between
itory population (I), with associated state variables (SE
regions (Cij in Figure 2A) are defined by the human connectome using data from the Human
Connectome Project (Civier et al., 2019; Van Essen et al., 2013) (see Methods for details). The
overall strength of global interaction is modulated by an additional global coupling parameter
G. We define G as the control parameter, whose dynamics (Figure 2B) modulate the shape of
the underlying dynamic landscape and induce transitions between attractors through bifurca-
tion (see bifurcation diagram Figure 2D). The simulated neural dynamics in this time-varying
landscape are shown in Figure 2C. It is important to note that here we assume the control
parameter G, and consequently the shape of the underlying landscape itself, is changing much
slower than the state dynamics occurring within the landscape (the ball in Figure 1A can roll
quickly into the valley when the landscape has barely deformed). In other words, the present
conceptual framework assumes a separation of time scale between the dynamics of the control
parameter (e.g., G) and intrinsic state dynamics (e.g., defined in Equations 1 and 2 by the time
constants τE and τI for the excitatory and inhibitory neuronal population, respectively). Physi-
ologically, the changes in global coupling G can be interpreted as changes in the arousal level
due to, for example, task demands. Recent work of Munn and colleagues (2021) suggests that
cortical dynamic landscapes are modulated by ascending subcortical arousal systems mediated
by the locus coeruleus (adrenergic) and the basal nucleus of Meynert (cholinergic). In partic-
ular, the locus coeruleus-mediated system promotes global integration across the cortex and
reduces the energy barrier for state transitions.
Network Neuroscience
435
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal Mapper
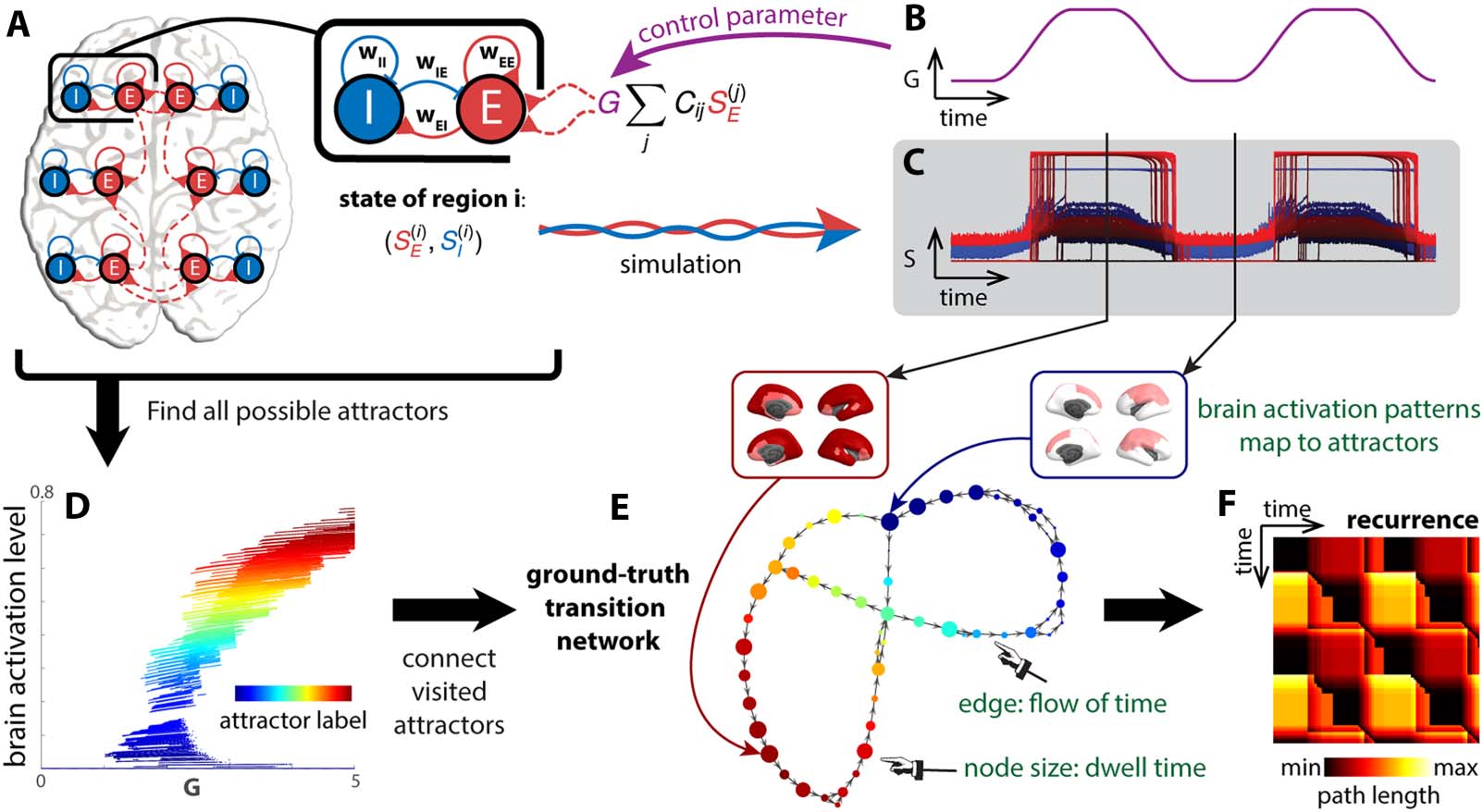
Figure 2. Attractor transition network for simulated neural dynamics. A biophysical network model (Zhang et al., 2022) is used to describe the
dynamics of the brain (A). Each brain region is modeled as a pair of excitatory (E) and inhibitory (I) populations, connected by local excitatory (wEE,
wEI) and inhibitory (wIE, wII) synapses. Each region is also connected to others through long-range connections (red dashed lines). The overall
strength of long-range interaction is scaled by a parameter G, the global coupling. To simulate neural dynamics in a changing landscape (C), G is
varied in time (B), mimicking the rise and fall of arousal during rest and tasks. The duration of the simulation is 20 min. To construct a ground-truth
transition network between attractors (E), fixed points of the differential equations (Equations 4 and 5) are computed for different levels of G and
classified by local linear stability analysis. Fixed points classified as attractors are shown in a bifurcation diagram (D). Each attractor traces out a
continuous line in a high-dimensional space—the direct product of the state space S and the parameter space G. These lines or attractors can be
identified as clusters in S × G. Each time point in (B, C) is classified as the regime of one attractor in the high-dimensional space S × G. All visited
attractors constitute the nodes of the ground-truth transition network (E), colored accordingly. A directed edge links one attractor to another if there
is a transition from the former to the latter in time. To examine how dynamics unfold in time in this attractor transition network (E), we construct a
recurrence plot (F) that indicates the shortest path length between any two time points (the attractors visited) in the network.
Recurrence plot:
A N-by-N matrix for a time series of
N samples, where element (i, j )
describes the dissimilarity between
the state of system at time i and at
time j.
Our methodological goal is to recover the cross-attractor transitions from the simulated
(i )) and the BOLD signals derived from them (down-
neural dynamics (the gating variables SE
sampled to TR = 720 ms as in the Human Connectome Project (Van Essen et al., 2013)). The
transitions can be encapsulated as a transition network (Figure 2E) and unfolded in time as a
recurrence plot (Figure 2F). The recurrence plot depicts how far away the attractor occupied at
each time point is from that of every other time point. Here, “how far away” is measured by the
shortest path length from one node to another in the attractor transition network instead of the
Euclidean distance between states in the original state space. The path length takes into
account the underlying dynamics: two states can be far away in the state space but closely
connected by transitions in the dynamical system, and conversely, two states can be close
in the state space, but it could be costly to transition between each other against the under-
lying dynamics. The theoretical ground truth (Figure 2E and F) is constructed by assigning each
time point to an attractor (Figure 2D and E) precomputed from Equations 4 and 5 (see section
Computation of the Attractor Repertoire and Ground-Truth Transition Network in Methods).
Computation of the ground truth requires all model parameters, including the state variables
(i ), and the control parameter G, for example. As depicted, the transition network is
SE
directed to capture the “flow” of time. Further, the size of the node in the transition network
represents how many sequential time points map onto that attractor, that is, the dwell time.
(i ), SI
We assess the efficacy of our and others’ methods by comparing the reconstructed networks
(Figure 3Bi and Bii) and recurrence plots (Figure 3Ci and Cii) to the ground truth (Figure 2E and F).
Network Neuroscience
436
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal Mapper
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
t
.
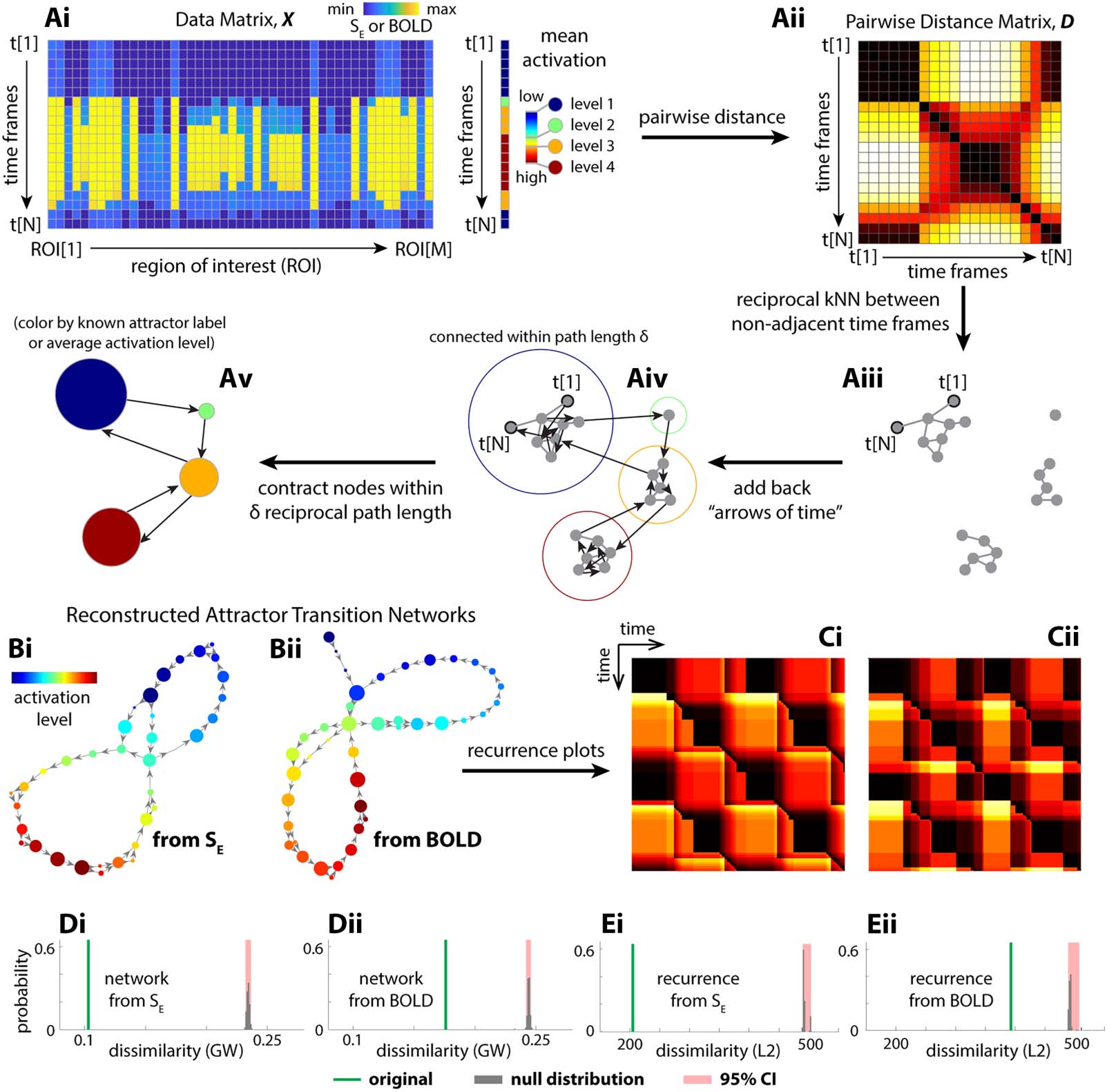
Figure 3. Reconstructed transition network using the Temporal Mapper approach captures theoretical ground truth. (A) The basic procedures
of the Temporal Mapper in reconstructing attractor transition networks from time series data. Neural time series is treated as a point cloud of N
points (N time points) in an M-dimensional space (M ROIs). As the system moves between different attractors, the activation level changes
discretely. The mean activation level can be used to label each discrete state or attractor, as in Figure 2D. Pairwise distance (Aii) between data
points that are not temporally adjacent was used to construct the spatial k nearest neighbor (kNN) graph (Aiii). The temporal connectivity, that
is, the “arrows of time,” is then added to the graph as directed edges (Aiv). To further compress the graph, nodes within a path length δ to each
other are contracted to a single node in the final attractor transition network (Av). Each node of the attractor transition network can be colored
to reflect the properties of the time points associated with it (e.g., ground-truth attractor labels or, when ground truth is unknown, the average
brain activation level for time points associated with the node). (Bi) The attractor transition network reconstructed from simulated neural
dynamics SE (the fraction of open synaptic channels; cf. Figure 2C) with k = 16 and δ = 10. (Bii) The attractor transition network reconstructed
from the SE-derived BOLD signals with k = 14 and δ = 10, and further parameter perturbation analysis is provided in Figure S2. The node color
in panel B reflects the rank of the average brain activation level for sample points associated with each node. (Ci and Cii) The recurrence plots
defined for (Bi) and (Bii), respectively. Comparing Bi and Bii to Figure 2E and Ci, Cii to Figure 2F, we see that the reconstructions are rea-
sonable approximations of the ground truth. Quantitatively, we evaluate the error of approximation as the dissimilarity between the recon-
structed attractor transition networks and the ground-truth transition network (Gromov–Wasserstein distance, GW; green lines in Di and Dii)
and the dissimilarity between their respective recurrence plots (L2 distance; green lines in Ei and Eii). The reconstruction error from the orig-
inal time series is significantly lower than that of randomly permuted time series (gray bars, null distribution; red areaits 95% confidence
interval).
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
437
Temporal Mapper
Gromov–Wasserstein (GW) distance:
A measure of dissimilarity between
two (possibly directed) graphs of
possibly different sizes that optimizes
over correspondences between the
node sets of the two graphs.
K nearest neighbor (kNN) graph:
A graph built on point cloud data
where nodes correspond to data
points, and edges connect a node to
its k (a positive integer) closest data
points.
Temporal Mapper to Reconstruct Attractor Transition Network From Time Series Alone
To reconstruct the attractor transition network, using only time series data, our Temporal Map-
per approach first constructs a temporal version of the k nearest neighbor (kNN) graph from
samples in the time series (Figure 3Ai–iv). The time series data from multiple brain regions
(Figure 3Ai) are first used to compute the pairwise distance between time points in Euclidean
space (Figure 3Aii). This distance matrix is used to determine the k-nearest neighbors for each
time point. Time points that are reciprocal k-nearest neighbors (excluding temporal neighbors)
are connected by edges, forming the spatial kNN graph (Figure 3Aiii). Reciprocal edges in the
neighborhood graph (Figure 3Aiii) connect spatial neighbors, while directed edges connect
temporal neighbors, indicating the “arrow of time” (Figure 3Aiv). Nodes that are close to each
other in the neighborhood graph are contracted to a single node in its compressed version
(Figure 3Av). We consider the compressed graphs (Figure 3Av) as reconstructed attractor transition
networks. Further details of this construction are provided in section Temporal Mapper–
Construction of Transition Networks in Methods. Visually, the reconstructions (Figure 3Bi
and Ci) are reasonable approximations of the ground truth (Figure 2E and F). This result is con-
firmed by quantitative comparisons against permuted time series (Figure 3D and E) and phase-
randomized time series (Figure S1). The reconstruction remains robust at lower sampling rates
(e.g., TR = 2 s; see Supporting Information Figures S11 and S12 for reconstruction accuracy
drop-off rate under down-sampling) and across different realizations and integration time steps
(Figure S14). See section Gromov–Wasserstein Distance Between Transition Networks in
Methods for details of the graph dissimilarity measures used in these comparisons.
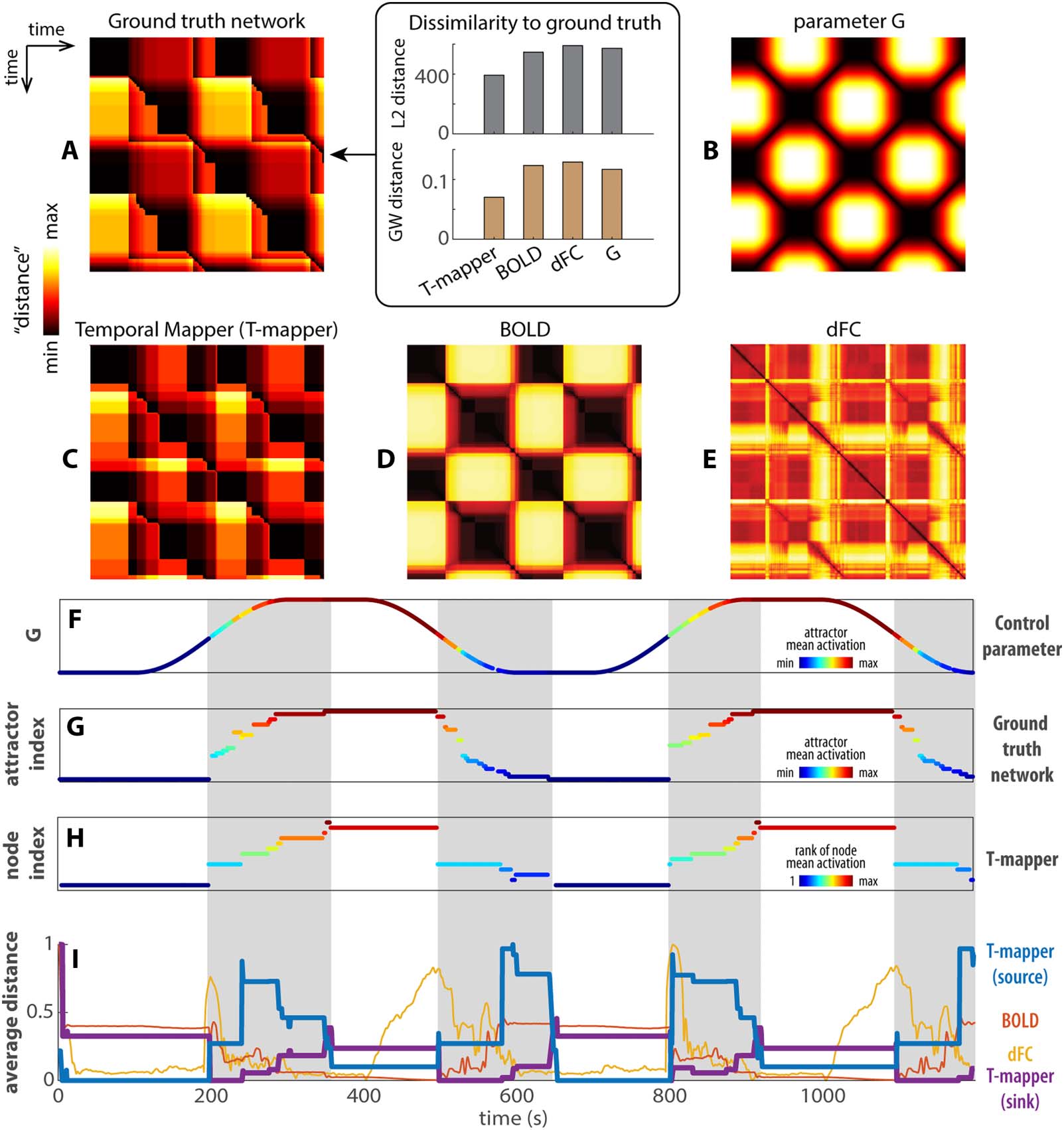
The transition network, BOLD signals, and dFC reveal different facets of brain dynamics. Next, we
use the simulated data to compare the dynamics in the reconstructed transition networks to its
associated BOLD dynamics (from which the network is reconstructed) and dFC. Given the a
priori knowledge of the ground truth, we are able to examine how different representations of
the simulated time series capture different aspects of the model brain dynamics.
Dynamics in different spaces of representation (e.g., transition network, BOLD, dFC) can be
compared in terms of the recurrence plots—a distance matrix that describes how far away the
states at any two time points are from each other. The recurrence plot of the ground-truth tran-
sition network (Figure 4A, reproduced from Figure 2G) and that of the control parameter G
(Figure 4B) provide an a priori reference for comparing the reconstructed network (Figure 4C),
BOLD (Figure 4D), and dFC (Figure 4E). In the networks (Figure 4A and C), the interstate dis-
tance used to compute the recurrence plots is the shortest path length from one node to
another. For the control parameter G and BOLD (Figure 4B and D), the distance is simply
the Euclidean distance between states. For dFC (Figure 4E), the distance is the Euclidean dis-
tance between vectorized dFC matrices (Fisher-z transformed elements in the lower triangle)
computed in a 30-TR sliding window. fMRI data in 20–30 TR windows have been shown to
generate stable correlations (Allen et al., 2014; Hutchison et al., 2013).
Dynamics in the ground truth and the reconstructed transition networks can also be repre-
sented as the state (attractor) dynamics shown in Figure 4G and H, respectively. In this represen-
tation, we can visualize which attractors are visited during the course of time. Here, we sorted
(and colored) the attractors based on their SE values (i.e., higher values mean more excitation).
As evident, the dynamics extracted using the reconstructed transition network (from the Tempo-
ral Mapper approach) closely follow the dynamics of the ground-truth network, indicating the
nodes of the Temporal Mapper network map onto underlying dynamical attractors reasonably
well. A similar visualization for BOLD and dFC can be constructed using traditional community
detection approaches on the recurrence matrix (see Figure S3 for more details).
Network Neuroscience
438
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal Mapper
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4. Comparisons between reconstructed transition networks, BOLD, and dFC. (A and B) The recurrence plots of the ground-truth tran-
sition network (A-left, reproduced from Figure 2F) and the control parameter G (B), respectively. They provide a basis for comparing the
reconstructed transition network using the Temporal Mapper (T-mapper) (C), the corresponding BOLD signal (D), and dFC (E). The difference
between the ground-truth network (A) and the parameter G (B) reflects the organization of the underlying dynamic landscape. The greatest
distinction is that the recurrence plot A is highly asymmetric compared to B. The lack of symmetry in A reflects the path dependency and
hysteresis of the underlying dynamical system. From visual inspection, the reconstructed transition network (C) is the best approximation of the
ground-truth network (A), especially for the asymmetric features. In contrast, the raw BOLD (D) clearly follows G (B) though some transitions
are also visible. dFC (computed from BOLD in 30-TR windows) is neither an obvious representation of the ground-truth network nor that of the
parameter G. Quantitatively, we computed the L2 and GW distance between each recurrent plot (C, D, E, B) to the ground truth (box in A). For
both measures, Temporal Mapper produces the most similar recurrence plot to ground truth, while dFC produces the most dissimilar recur-
rence plot. (F–H) compare the reconstructed network (H) more directly to the ground-truth network (G) and the parameter G (F) in terms of the
attractors visited at each point in time (only attractors that persisted greater than 5 TRs are shown). Colors in F and G reflect the attractor indices
of the ground truth (y-axis of G) ordered by the global average brain activity (i.e., mean SE ) associated with each attractor, as shown in
Figure 2D. Similarly, state dynamics in the T-mapper reconstructed network (H) are ordered and colored by the global average of the simulated
BOLD (rank) associated with each node. Gray areas highlight the sequence of state transitions that distinguishes nonlinear brain dynamics (G,
H) from the continuous change of the control parameter (F). (I) Comparison of the T-mapper reconstructed transition network, BOLD, and dFC
by the row/column averages of the corresponding recurrence plots (C–E). Since BOLD and dFC recurrence plots are symmetrical, their row and
column averages are identical (red trace for BOLD, yellow trace for dFC in I). For T-mapper reconstructed transition network, the row average
is the source distance (average distance from the current state to all other states; blue trace), and the column average is the sink distance
(average distance from all other states to the current state; purple trace). See text for details.
Network Neuroscience
439
Temporal Mapper
The recurrence plot for the ground-truth transition network is more complex than that of the
control parameter G (Figure 4A vs. B)—this added complexity reflects that of the underlying
dynamic landscape, which is what we aim to examine. In terms of the state dynamics, the model
brain passed through a sequence of attractors and transitions in a path-dependent manner (gray
areas, Figure 4G), while the control parameter undergoes continuous and reversible changes
(Figure 4F, color coded by attractor index to show the model brain can visit distinct attractors
given the same level of G). Such path dependency in the ground-truth transition network is
indicative of multistability and hysteresis of the underlying dynamic landscape (cf. Figure 1C).
Thus, the discrete sequence of attractor transitions (gray areas, Figure 4G) is the signature of the
model brain dynamics. The reconstructed transition network (Figure 4C) reasonably approxi-
mates the ground truths (Figure 4A) both in terms of the recurrence plot (Figure 4C) and the state
dynamics (Figure 4H). Though some detailed transitions in the ground truth are not resolved by
the reconstructed network, it is not surprising due to the low-pass filtering effect of the hemody-
namic response—faster neural activity may not be recoverable from BOLD signals in principle.
The recurrence plot of the simulated BOLD (Figure 4D) to a large extent follows the control
parameter G, though some transitions are already visible without further state detection. Inter-
estingly, the recurrence plot of dFC (Figure 4E) approximates neither that of the ground-truth
transition network nor that of the parameter G. dFC does not differentiate distinct attractors
and exhibits a mixed reaction to transitions and parameter changes (see Figure S3D for how
dFC states differ from attractors states in Figure S3B and BOLD states in Figure S3C).
A further comparison between the reconstructed transition network, BOLD, and dFC is
shown in Figure 4I as the row (or column) averages of the corresponding recurrence plots, that
is, the average distance from the state/attractor at each time point to all other time points. This
simplified representation helps us visualize the difference between dynamics in different spaces.
This method was used by Saggar et al. (2018) to examine transitions between tasks in the afore-
mentioned continuous multitask experiment (Gonzalez-Castillo et al., 2015). To understand
what information each representation captures, we separate the dynamics into two different
regimes: one with a single highly persistent attractor (white areas in Figure 4G), and one with
a sequence of transitions between less persistent attractors (gray area). The average distance in
the reconstructed network (blue, purple curves in Figure 4I) and BOLD (red) change little in the
single-attractor regime (white areas). In the same single-attractor regime, the average distance of
dFC (yellow curve in Figure 4I) appears to track the time derivative of the control parameter G
only when G is decreasing (2nd and 4th white areas). Clearly, dFC states are not equivalent to
persistent attractors. The distinction between the single-attractor and the transition regimes
(white vs. gray areas in Figure 4I) is best indicated by the average distance in the reconstructed
network (blue, purple curve). Specifically, the persistent attractors are more source-like (high
sink distance, low source distance—purple above blue curve in the white areas of Figure 4I)
while the sequence of transitions between less persistent attractors are more sink like (high
source distance, low sink distance—purple below blue curve in the gray areas of Figure 4I).
In contrast, the average distance of BOLD (Figure 4I, red) best mirrors the value of G (Figure 4F
high G is associated with low average BOLD distance and vice versa). In short, the dynamics in
the reconstructed transition network most effectively separate the regimes of attractor persis-
tence and transitions in the model brain, compared to BOLD and dFC.
Application of Temporal Mapper to Real Human fMRI Dataset
Following the above theoretical analysis, we now apply the method to real human fMRI data
to characterize the dynamic landscape of the human brain. We examine what features of the
reconstructed transition networks are relevant to cognitive performance to demonstrate how
Network Neuroscience
440
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal Mapper
the method developed above can be used in empirical settings. Data from 18 subjects were
acquired from a continuous multitask experiment (Gonzalez-Castillo et al., 2015). Each sub-
ject performed eight blocks (color coded in Figure 5G) of tasks (memory, video, math) or rest in
a single 25.4-min scan. The theoretical model used in the previous sections was designed to
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
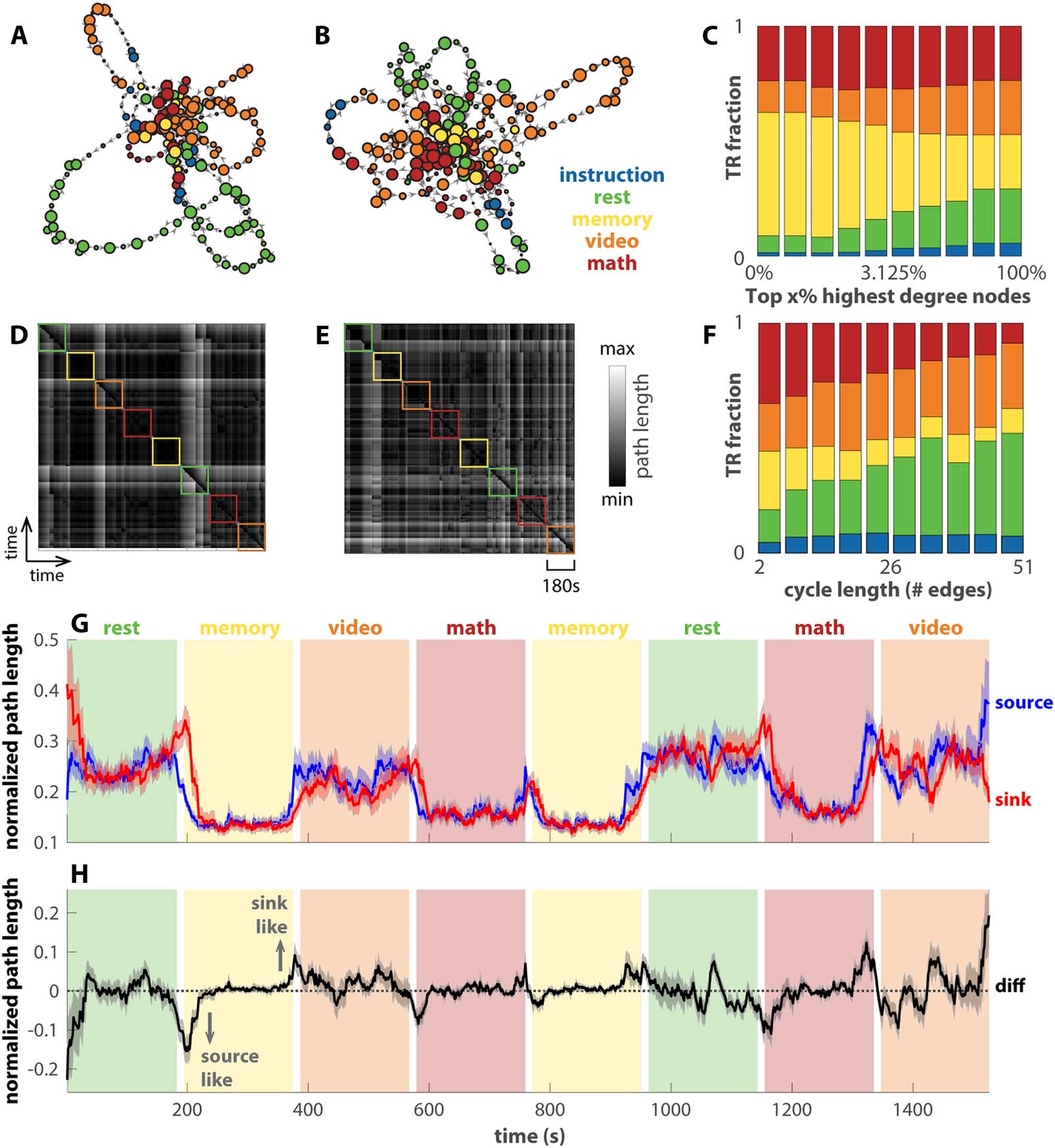
Figure 5. Transition networks of human fMRI data differentiate tasks and reveal transitions. (A and B) The transition networks constructed
from two subjects’ fMRI data in a continuous multitask experiment as examples (Gonzalez-Castillo et al., 2015). Panel A is for subject-17,
among the best task performers, and panel B for subject-12, among the worst task performers. The color of each node denotes the dominant
task label of the associated time points. The corresponding recurrence plots are shown in panels D and E. Panel C shows how tasks TR are
distributed in the top x% highest degree nodes of the networks across all subjects (x-axis in log scale). Memory and math clearly dominate the
highest degree nodes. In addition, panel F shows how task TRs are distributed over cycles of various lengths that pass through the top 2% of
highest degree nodes, excluding the TRs in the high-degree nodes themselves. Rest and video dominate longer cycles. Panel G shows the
average path length from each TR as a source to all other TRs (blue) or to each TR as a sink from all other TRs (red). The path length is
normalized by the maximal distance for each subject. Solid lines show the averages across subjects; shaded areas show the corresponding
standard errors. A smaller average distance indicates that the node being occupied is a better source (sink) for other nodes. The difference
between the source distance and the sink distance is shown in H. A negative (positive) number indicates that the node occupied at the time is
more of a source (sink) to other nodes.
Network Neuroscience
441
Temporal Mapper
reflect this type of block design using the time-varying parameter G. During construction of the
transition networks, we set the parameters to k = 5 and δ = 2. Justification for this choice as
well as further parameter perturbation analysis is reported in Figures S9 and S10.
Figure 5A and D show the reconstructed transition network and the corresponding recurrence
plot for a subject with good behavioral performance (top four in accuracy and reaction time),
and Figure 5B and E for a subject with bad behavioral performance (bottom four in accuracy and
reaction time). For both subjects, the central nodes are occupied mainly during the memory and
math tasks (yellow, red nodes in Figure 5A and B) and go on excursions during the video task
and rest (orange, green nodes). In aggregate across all subjects (Figure 5C), the memory task clearly
dominates the highest degree nodes (yellow bars on the left end). In contrast, rest and the video
task dominate the long excursions through the highest degree nodes (green and orange bars on
the right end in Figure 5F). Later, we use this separation between the more cognitively
demanding tasks (memory and math) and the relatively less demanding tasks (video and rest)
over different types of nodes to predict subjects’ behavior performance (Figure 6).
Similar to Figure 4I for the theoretical model, here we examine the dynamics in the transition
networks constructed from human fMRI data in Figure 5G as the row average (source distance,
blue) and column average (sink distance, red) of the recurrence plots. Both the source and sink
distance clearly track the transitions between blocks. Interestingly, both math and memory are
associated with a low average distance in contrast to video and rest, which suggests brain states
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
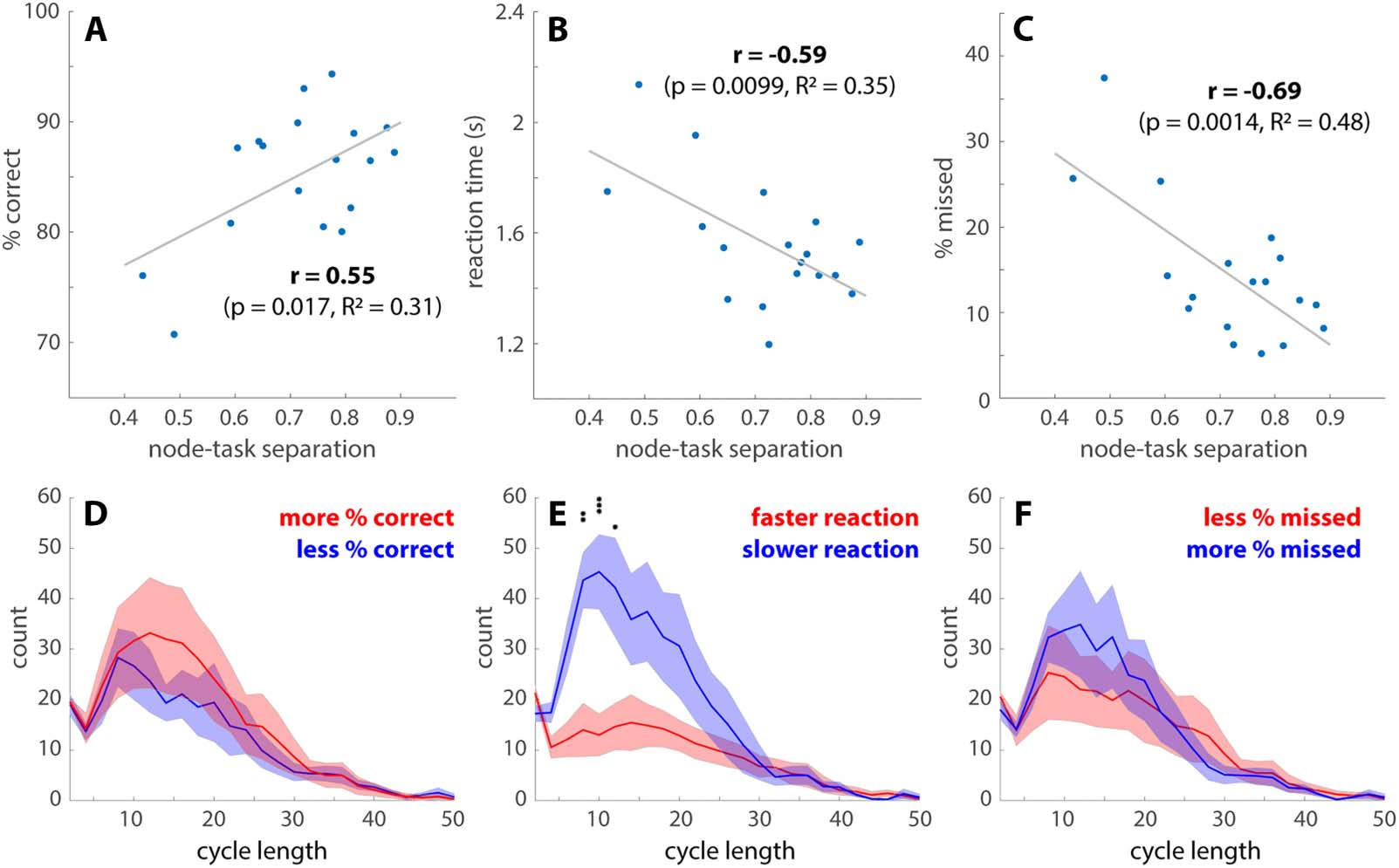
Features of transition networks predict behavioral performance. (A–C) The overall task performance is associated with separations
Figure 6.
between the high-cognitive demand tasks (math and memory) and low-cognitive demand tasks (video and rest) over the transition network.
The node-task separation is measured by the fraction of memory and math TRs in the top 2% highest degree nodes of the transition networks,
which also measures the preference of video and rest for low-degree nodes (cf. Figure 5C). Subjects with a greater node-task separation have a
greater percentage of correct responses (A), a faster reaction time (B), and fewer missed trials (C) across all tasks. (D–F) The length distributions
of the cycles passing through the high-degree nodes. Solid lines indicate the number of cycles at each length averaged across subjects, who are
split into two groups (red vs. blue) by the median of the percentage of correct responses (D), reaction time (E), or the percentage of missed trials
(F). Shaded areas indicate the corresponding standard errors. An abundance of intermediate-length cycles is associated with slower reaction
time (E). There are no length-specific effects on the percentage of correct responses (D) or missed trials (F). See text for related main effects (*p <
0.05, **p < 0.01, ***p < 0.001, with Tukey-HSD for multiple comparisons).
Network Neuroscience
442
Temporal Mapper
associated with math and memory are in the more central part of the transition network. The
observation is consistent with our previous findings using related methods, Mapper (Saggar
et al., 2018) and NeuMapper (Geniesse et al., 2022), where the task-positive brain activation
patterns were found concentrated at the core of the graph with a clear core-periphery structure.
Figure 5H shows the difference between the source and sink distance. When this sink-source
difference deviates from zero (black dashed line), the brain occupies a node that is either more
of a source to other nodes (source-like, negative values) or more of a sink to other nodes (sink-
like, positive values; see Figure S6 for example networks). The source-like or sink-like deviation
is visibly more prominent near the transitions between tasks, for example, block 2 in Figure 5H.
This observation is verified statistically in Figure S7A. The source-like or sink-like deviation is
also more prominent during rest and the video task than during the memory and math tasks
(cf. Figure S7B). A closer examination of the dynamics in Figure 5H reveals that the brain tends
to enter the memory and math tasks through source-like nodes (downward arrow in Figure 5H)
and exit the block through sink-like nodes (upward arrow in Figure 5H). This is not the case
for rest and the video task. The corresponding statistical verification is shown in Figure S8.
This may be due to the fact that math and memory tasks are more structured such that the
brain enters the task via specific source states, while the brain can enter the resting state, for
example, from any state. In short, the transition networks and recurrence plots exhibit mul-
tiple features that keep track of the task and block structure.
Figure 6 shows how features of the transition networks relate to subjects’ behavioral
performance. Greater separation between cognitively demanding tasks (memory and math)
and less demanding tasks (video and rest) over the highest degree nodes predicts a higher per-
centage of correct responses (Figure 6A), a faster reaction time (Figure 6B), and fewer missed trials
(Figure 6C). The statistical significance of the correlation coefficients is further validated against
1,000 random permutations of the subject-performance correspondence (95% confidence inter-
vals: −0.4697, 0.5163; −0.5123, 0.4302; and −0.5340, 0.4342 for Figure 6A, B, and C, respec-
tively). The number of cycles connecting each high-degree node back to itself also exhibits
behavioral relevance (Figure 6D–F). On average, a greater number of cycles is strongly associated
with slower reaction time (F(1, 400) = 46.63, p < 10−10; Figure 6E). There is also a scale-specific
effect—cycles around length 10 are especially predictive of slower reactions. Here the cycle
length can be roughly interpreted as the number of TRs required to leave and return to a
high-degree node. To a lesser extent, a greater total number of cycles is also associated with a
greater percentage of correct responses (F(1, 400) = 4.17, p = 0.014). There is no statistically sig-
nificant relation between the number of cycles and the percentage of missed trials. In short, high-
degree nodes and the excursions from them, that is, cycles, are key behavioral relevant features.
DISCUSSION
In the present work, we propose a computational method for reconstructing attractor transition
networks from neural time series, named the Temporal Mapper. The method represents a time
series as a directed graph whose nodes and edges map to attractors and phase transitions in the
underlying dynamical system. In particular, the method addresses the scenario where the
underlying system is nonstationary or nonautonomous, as, for example, when the brain is
under continuously varying task demand, environmental changes, arousal levels. Using sim-
ulated brain dynamics, we demonstrate that the method provides a good approximation of the
theoretical ground truth of cross-attractor transitions. Applying the method to human fMRI
data, we show that the dynamics in the reconstructed networks clearly track the transitions
between tasks. High-degree nodes and cycles of the network are key features that help predict
human behavioral performance. Together, the theoretical and empirical analyses provide a
Network Neuroscience
443
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal Mapper
basic theoretical and computational framework for bridging the data-driven and mechanistic
modeling of brain states and transitions.
The present method builds on our previous works on characterizing neural dynamic
landscape using TDA. In particular, it belongs to a family of neural time series analysis tools
(Geniesse et al., 2019, 2022; Saggar et al., 2018, 2022) based on Mapper (Singh et al., 2007).
NeuMapper (Geniesse et al., 2022) is the closest methodological match to Temporal Mapper in
that it uses a reciprocal kNN graph construction without using local low-dimensional embed-
dings as an intermediate step. In another variant of Mapper approach, used in Saggar et al.
(2022), an embedding step is typically utilized to examine the latent space, with any chosen
dimension reduction techniques. Across the family of Mapper-based tools and related topolog-
ical methods (Carlsson, 2009; Munch, 2013), time series are commonly treated as distributions
of sample points in the state space. Constructing a topological representation, for example, a
graph, from such a distribution often concerns only the spatial distance between points in the
state space or that of their lower dimensional projections. The fact that these sample points are
part of a time series—that there is an explicit sequential relation between sample points—is
unutilized. Specifically, within the realm of fMRI data, which has been traditionally studied using
time series techniques, previous applications of Mapper (Geniesse et al., 2022; Saggar et al.,
2018, 2022) have focused on the geometric distribution of sample points and discarded the tem-
poral information in the sequence of sample points. The present method is designed precisely to
take advantage of this sequential information, that is, the arrow of time. Incorporating the arrow
of time better reflects the fact that the system that generates the time series, for example, the
brain, is a dynamical system. That is, the subsequent states of the system depend on the current
state, and the exact nature of this dependency is the nature of the dynamical system. Restoring
this temporal dependency in the construction has several consequences that we describe next.
First, the arrow of time restores the connectivity between sample points that could be far
apart in the state space but tightly linked dynamically. The implication is most significant during
a phase transition (vertical dashed lines in Figure 1C). At a transition, the dynamical system
jumps suddenly from one attractor to another at a time scale much faster than the state dynam-
ics within the same attractor. The combination of high velocity and even sampling in time
makes consecutive sample points far apart in the state space, despite the direct dynamic depen-
dency between them. Without the arrow of time, the increase of velocity during transitions is
unaccounted for. The spatial information alone cannot determine the dynamic linkage between
states of the system during the transitions, which happen to be key moments of interest.
Second, path lengths in the transition networks carry dynamical rather than purely geomet-
rical information. The arrow of time introduces directedness into the networks. Thus, the short-
est path lengths between two nodes are no longer symmetric and thus cannot be interpreted as
geometric distance. The arrow of time attaches information about the underlying dynamic
landscape to the state space. At an intuitive level, the shortest path from node x to node y
can be considered the path of least time, or least action, within the landscape. In other words,
paths in the transition networks could putatively encode actions in the state space.
Lastly, incorporating the arrow of time distinguishes the present method from common point
cloud–based TDA techniques. Point cloud data—sets of disconnected points—are fundamental
substrates of topological or geometrical analysis and learning. Such analysis includes nonlinear
dimension reduction techniques such as Isomap (Tenenbaum et al., 2000) or Laplacian Eigen-
maps (Belkin & Niyogi, 2003), TDA methodologies such as persistent homology (Carlsson,
2009; Edelsbrunner & Morozov, 2013), and deep learning (Qi et al., 2017). With the points first
connected to their temporal neighbors, the present method operates on, in essence, a discretized
Network Neuroscience
444
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal Mapper
version of a curve with a direction defined on it—naturally depicting a trajectory of an auton-
omous, deterministic dynamical system. Constructing a spatiotemporal neighborhood graph
(Figure 3B) is thus folding a directed curve rather than “connecting dots.” An exposition of
the mathematical consequences of the construction is beyond the scope of the present work
but worthy of further study, especially with regard to its behavior as the sampling rate of the time
series approaches infinity and when multiple trajectories are included in the construction.
One may find the transition networks in the present work reminiscent of hidden Markov
models (HMM) for detecting discrete states in brain dynamics and transition probabilities
between states (Baker et al., 2014; Meer et al., 2020; Ou et al., 2013; Rezek & Roberts,
2005; Vidaurre et al., 2017). A key distinction is that the number of discrete states in an
HMM is set a priori, while its analog in the present method—the number of attractors
visited—is data driven. The dynamic landscape of the human brain can be highly complex
and sensitive to the organization of the large-scale structural connectome (Zhang et al.,
2022). There is no a priori way to determine how many attractors may be visited during tasks
and rest. Moreover, the dynamic landscape of each subject is shaped by the structural con-
nectivity in each subject’s own brain. It cannot be assumed that the same number of attractors
would be visited across subjects. Thus, the present method presents a flexible framework that
requires fewer assumptions about the underlying dynamical system. For example, the Markov
property for HMM (dependency on present state only) may not be satisfied in nonautonomous
dynamical systems as conceptualized in the present work (see Figure S13 for an application of
HMM on the simulated data), while the Temporal Mapper does not require the Markov prop-
erty. Apart from statistical inference methods such as the HMM, topological representations of
attractor networks also figure in differential equation-oriented state space decomposition
methods, for example, based on the Conley Index Theory (Ban & Kalies, 2006; Kalies et al.,
2005). In comparison to such mathematically rigorous approaches, the present method better
accommodates empirical applications where the state space is often sparsely covered by data
and the underlying dynamical system is changing with time. Conceptually, the attractor tran-
sition networks in the present study should be thought of not as representing the structure of an
autonomous dynamical system, but rather the complex interaction between the environment
and the brain dynamic landscape.
Our flexible, individualized construction of transition networks comes with a cost—there
lacks a direct correspondence between different networks. An advantage of an HMM con-
structed from data concatenated across subjects (cf. Meer et al., 2020) is that the model
comes with a fixed number of states across all subjects, with direct one-to-one correspon-
dence. In contrast, the correspondence problem for the present method is data driven and
needs to be solved separately. For example, attractor transition networks for different subjects
(Figure 5A and B) contain different numbers of nodes (attractors) and edges (transitions). How
nodes and edges in Figure 5A map to those in Figure 5B is not obvious. Even when compar-
ing attractor transition networks with the same number of nodes, obtaining a correspondence
is equivalent to solving an instance of the Graph Matching problem, which is a hard, funda-
mental challenge in graph processing (Umeyama, 1988; Zaslavskiy et al., 2009). In the pres-
ent work, the correspondence between networks is made using techniques from optimal
transport theory, specifically the use of Gromov–Wasserstein (GW) matchings between net-
works (Figure 3E and G) which can provide approximate graph matching solutions even for
graphs with different numbers of nodes. GW matching does not require a temporal corre-
spondence or any a priori knowledge of how the networks are constructed and can thus
be used in a broad context. For example, for resting-state fMRI, there is no a priori way to
map the transition network constructed from one recording session to that of another. GW
Network Neuroscience
445
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal Mapper
matchings provide a solution to compare a subject’s resting transition networks in different
sessions to examine the stability of the brain dynamic landscape, or to compare transition
networks of healthy subjects to that of the psychiatric patients to examine the dynamic basis
of the disorder. We therefore introduce this tool to the neuroimaging community with broader
future applications in mind.
The present work also brings attention to the interpretation of dFC states. It is shown in
Figure 4E and I and Figure S3D that dFC states are not equivalent to attractors in the brain
dynamics: dFC is in part sensitive to the transitions (Figure 4I gray areas) and in part to the
change in the control parameter without inducing any phase transition (Figure 4E white areas).
It has been proposed that resting-state FC reflects cross-attractor transitions (Zhang et al.,
2022). While dFC-based clustering can differentiate tasks very well (Gonzalez-Castillo
et al., 2019), this differentiation may not be interpreted as the brain occupying distinct attrac-
tors during different tasks, but rather, these tasks involve different transitions and environment-
driven correlations. Complementing existing dFC-based approaches, the attractor transition
networks incorporate information of the underlying dynamical system and provide a channel
to connect data-driven representations to dynamical systems concepts. Future work may fur-
ther explore the relation between attractor transition networks and dFC by using single-frame
techniques for FC quantification (Esfahlani et al., 2020; Faskowitz et al., 2020).
In application to the human fMRI data, we provide a series of analyses comparable to those
of an earlier work (Saggar et al., 2018), where undirected networks were constructed using
Mapper (Singh et al., 2007) from the same dataset (Gonzalez-Castillo et al., 2015). Saggar
et al. (2018) observed that the core of the networks was dominated by cognitively demanding
tasks, such as memory, math, and to a lesser extent, video tasks, while the peripheries were
dominated by rest. In the same vein, we observe that the highest degree nodes are dominated
by memory and math (Figure 5C), and that the level of dominance predicts behavioral per-
formance (Figure 6A–C). Note that due to the compression step in the present construction
(Figure 3B–C), tightly connected nodes in the neighborhood graph (Figure 3B) are contracted
to a single node in the final attractor transition network (Figure 3C). It is reasonable to
assume that tightly connected nodes that serve as the core for periphery nodes in the neigh-
borhood graph would become a high-degree node in the compressed graph. Thus, the high-
degree nodes in the present work may be thought of as a loose counterpart to the core of the
Mapper-based construction (Saggar et al., 2018).
The periphery structures of interest in the present construction are the cycles that connect
the high-degree nodes back to themselves. For the human fMRI data, long cycles are domi-
nated by rest and the video task (Figure 5F), analogous to the Mapper-based result (Saggar
et al., 2018) that periphery nodes are dominated by rest. Importantly, the present cycle-based
analysis of the periphery structure allows us to examine recurrent dynamics of different
duration (reflected as cycle length, Figure 5F) and identify the behavioral relevant time scales
(Figure 6D–F). Interestingly, slower reaction time during tasks is associated with an excess of
intermediate but not long cycles (Figure 6E). This suggests that intermediate cycles putatively
represent the stray path that the brain took, resulting in slower reaction times. Interestingly, a
greater number of cycles predicts higher accuracy, which, combined with the reaction time
results, may reflect a speed-accuracy trade-off. It provides an example of process-based anal-
ysis of brain dynamics afforded by the present, dynamics-minded, construction. From a more
technical viewpoint, the spectrum of cycle length (Figure 6D–F) is tightly connected to the
multiscale nature of the attractor transition network. The Temporal Mapper naturally admits
multiscale construction via the compression distance δ (Figure 3Aiv). That is, one can consider
the attractor transition network as a sequence of networks at different scales δ (see Figure S9,
Network Neuroscience
446
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal Mapper
Network Neuroscience
for example) instead of a single graph. At a specific scale, any smaller recurrent processes, that
is, smaller cycles formed by a few recurring attractors, will be contracted into a single node.
Thus, the spectrum of cycle length indicates at which scales the graph can be further
compressed. Further method development and empirical testing are required to better take
advantage of the multiscale information in the Temporal Mapper. In addition, unfolding the
dynamics in time as the average distance in the transition network tracks the transition
between tasks (Figure 5G), comparable to Mapper-based results (Saggar et al., 2018). In the
present work, the directed nature of the attractor transition networks introduces additional
information—the direction of least action between states. Some nodes have a characteristic
direction as a sink or a source (positive or negative deviation in Figure 5H), serving as entry
and exit for the cognitively demanding tasks (Figure S8). Note that the sink-/source-ness of the
associated brain activity patterns may not be absolute, as it is possible for the sink-/source-ness
to depend on the specific design of the experiment (e.g., what types of tasks are included in the
session and the time allocation for each task). Further studies are necessary to elucidate
the interpretation of sink/sourceness in a more general context, which will require applying
the Temporal Mapper to a wider range of datasets. Nevertheless, the present study demon-
strates that the directedness introduced by the arrow time is task specific. Future work may
further explore the cognitive correlates of different directed features of the graph, including
the sink/sourceness of the nodes. Moreover, this directedness may be useful for designing
neural stimulation protocols to more effectively perturb the brain into desirable states.
In conclusion, we propose a computational method for constructing attractor transition net-
works from simulated and empirical time series of brain dynamics. Complementing existing
geometrical and statistical approaches to characterizing brain dynamics, the present work
aims to provide a channel of correspondence between data-driven topological modeling
and mechanistic modeling. Incorporating time in the construction of spatiotemporal neighbor-
hoods, paths in the attractor transition networks encode the action of the underlying dynam-
ical systems. The method is both validated using a biophysical network model of the brain and
shown to reveal behavioral and cognitive relevant features in human fMRI data. The present
work serves as a starting point for dynamical theory-driven topological analysis of brain
dynamics. Future work will compare the present state and transition detection methods more
extensively to existing community detection methods and further validate the method using
consortium-sized data (Gordon et al., 2017; Saggar et al., 2022; Smith et al., 2013).
MATERIALS AND METHODS
Biophysical Network Model of the Human Brain
The theoretical components of the present work are based on a biophysical network model of
large-scale brain dynamics (Zhang et al., 2022), which is an variant of the reduced Wong–
Wang model (Deco et al., 2013, 2014; Wong & Wang, 2006). The model is a Wilson–Cowan
type model (Wilson & Cowan, 1972, 1973). The whole brain is modeled in terms of the
mean-field activity of neuronal populations in each brain region (Figure 2A). Each model
region contains a pair of excitatory (E) and inhibitory (I) populations, whose activity is
described by the local model (Figure 2A, right box) in terms of the state variables SE and SI:
dSE
dt
¼ − SE
τE
dSI
dt
¼ − SI
τI
þ 1 − SE
ð
Þγ
E HE wEE SE − wIE SI þ IE
ð
Þ
ð
þ 1 − SI
Þγ
IHI wEISE − wIISI þ II
ð
Þ
(1)
(2)
447
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal Mapper
SE and SI indicate the fraction of open synaptic channels in their respective populations,
referred to as the gating variables. Through local connections (w’s), the excitatory population
excites itself with strength wEE and the inhibitory population with strength wEI, while the inhib-
itory population inhibits itself with strength wII and the excitatory population with strength wIE.
Each population can also receive input from outside of this region, denoted as IE and II. The
activity of each population has a natural decay time of τE and τI respectively. Each population’s
activity tends to increase with the fraction of closed channels (1 − Sp) and the population firing
rate (Hp), scaled by a factor γp for p 2 {E, I}. HE and HI are transfer functions that map synaptic
current input to population firing rate of the excitatory and the inhibitory population, respec-
tively. In particular, they are sigmoidal functions of the form
Hp xð Þ ¼
rmax þ apx − bp − rmax
ð
1 − edp apx−bp−rmax
ð
1 − e−dp apx−bp
Þ
Þ
(3)
whose output increases with input monotonically and saturates at rmax—the maximal firing
rate limited by the absolute refractory period of neurons. The specific shape of each transfer
function is determined by three additional parameters ap, bp, and dp (ap and bp determine the
location and slope of the near-linear segment in the middle; dp determines the smoothness of
the corners bordering the said near-linear segment). This transfer function is converted from
Wong and Wang’s original formulation (Abbott & Chance, 2005; Wong & Wang, 2006) (a soft
rectifier function, adopted into large-scale biophysical network models of the brain by Deco
et al., 2013, 2014) into a sigmoidal form, while retaining the original value of parameters ap,
bp, and dp (shown in Table 1). The parameters were chosen to approximate the average
response of a population of spiking pyramidal cells (p = E ) and interneurons (p = I ), respec-
tively, incorporating physiologically plausible parameters (Wang, 2002; Wong & Wang,
2006).
Connecting the local models into a global network (Figure 2A, left, dashed lines) gives us
the global model:
ið Þ
dSE
dt
ið Þ
¼ − SE
τE
(cid:1)
þ 1 − SE
(cid:3)
(cid:1)
E HE wEE
γ
ið Þ
ið ÞSE
ið Þ − wIE
ið ÞSI
ið Þ þ IG
(cid:3)
→(cid:1) (cid:3)
ið Þ SE
þ σξ
E
ið Þ tð Þ
(4)
ið Þ
dSI
dt
ið Þ
¼ − SI
τI
(cid:1)
þ 1 − SI
(cid:3)
γ
(cid:1)
IHI wEI
ið Þ
ið ÞSE
ið Þ − wII
ið ÞSI
ið Þ þ II
(cid:3)
þ σξ
I
ið Þ tð Þ;
(5)
(i ) and SI
(i ) are the synaptic gating variable of the excitatory and the inhibitory popu-
where SE
lation of the i-th brain region, respectively, and ξ·
(i ) is a noise term scaled to an amplitude σ. For
computing the fixed points, σ = 0; for numeric simulations, σ = 0.01 following Zhang et al.
→
(2022). The state of all excitatory populations is denoted as a vector SE
which is SE
and the ongoing state of, other brain regions,
, the i-th element of
(i ). The global input to the i-th brain region depends on both its connectivity with,
→(cid:1) (cid:3)
ið Þ SE
IG
¼ G
X
N
j¼1;j≠i
jð Þ
CijSE
(6)
where N denotes the total number of brain areas, Cij ≥ 0 the long-range structural connectivity
from the j-th to the i-th brain region and G is a global coupling parameter that controls the
Network Neuroscience
448
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal Mapper
Parameter
τE
τI
γE
γl
aE
bE
dE
aI
bI
dI
rmax
wEE
wEI
wIE
wII
II
G
Cij
σ
Table 1.
The interpretation and value of model parameters
Interpretation
Decay time of NMDA receptor
Decay time of GABA receptor
Kinetic parameter of excitatory population
Kinetic parameter of inhibitory population
Parameter of HE
Parameter of HE
Parameter of HE
Parameter of HI
Parameter of HI
Parameter of HI
Maximal firing rate
Excitatory-to-excitatory coupling
Excitatory-to-inhibitory coupling
Inhibitory-to-excitatory coupling
Inhibitory-to-inhibitory coupling
External input to inhibitory population
Global coupling
Structural connectivity between brain regions
Value
0.1 (s)
0.01 (s)
0.641
1
310 (nC −1)
125 (Hz)
0.16 (s)
615 (nC −1)
177 (Hz)
0.087 (s)
500 (Hz)
2.8 (nA)
1 (nA)
2.8 (nA)
0.05 (nA)
0.1 (nA)
1.1–5 (nA)
Human structural connectome
(Civier et al., 2019;
Van Essen et al., 2013)
Noise amplitude
0.01
Note. Here we summarize the parameters used in the global model (Equation 4 and 5). Critical parameters are inherited from Wong and Wang (2006) to
maintain biological plausibility.
overall level of interaction across brain regions. Since Cij is only intended to represent long-
range connectivity, we let Cij = 0 for any i = j to preclude recurrent connections. For the effects
of G and Cij to be independently comparable, here we impose a normalization condition on
the matrix norm:
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Ck k∞ ¼ max
i
(cid:1)
X
N
j¼1
(cid:3)
jCij j
¼ 1
(7)
In the present work, nodes of the global network correspond to anatomical regions in the
human brain based on a 66-region parcellation used in Deco et al. (2013) and Hagmann
et al. (2008) (Table S1); the weight of edges reflects the strength of long-range structural con-
nectivity between brain regions, estimated using structural data from the Human Connectome
Project (Civier et al., 2019; Van Essen et al., 2013). Specific parameter values are given in
Table 1.
Network Neuroscience
449
Temporal Mapper
Network Neuroscience
Computation of the Attractor Repertoire and Ground-Truth Transition Network
Fixed points of the global model (Equations 4–6) are computed using fsolve in MATLAB for
each parameter G (in 0.01 increments). A subset of the fixed points is further classified as
attractors based on local stability analysis using the Jacobian matrix and simulated perturba-
tion. These attractors are visualized in Figure 2D as a bifurcation diagram (for further compu-
tational details, see Zhang et al., 2022). Attractors that continuously map to each other under
the variation of parameter G are considered qualitatively equivalent. Thus, in the present
work, the term “attractor” is used in a broad sense, referring to the connected components
of (narrow sense) attractors in the product of the state space and the parameter space. Com-
putationally, single-linkage clustering is used to obtain these connected components. The set
of all connected components or clusters constitutes the attractor repertoire, providing a com-
pact description of the model dynamic landscape (Zhang et al., 2022).
The attractor repertoire further provides a skeleton to convert any simulated times series of
the state variables (within the appropriate parameter range) into the corresponding symbolic
dynamics. Here symbolic dynamics refers to a sequence of symbols, where each symbol rep-
resents an attractor, and the sequence represents the order in which the attractors are visited in
time. Computationally, each time point in the simulated time series is assigned to an attractor
using nearest neighbor classification in the product of the state space and the parameter space,
given the precomputed attractor repertoire. The resulting symbolic dynamics is used to con-
struct the ground-truth attractor transition network (Figure 2F). Nodes of the network are
unique symbols appearing in the sequence. There is a link from node i to node j if the corre-
sponding symbol i appears immediately before symbol j in the sequence. Each node is
equipped with a probability measure proportional to the dwell time at the corresponding
attractor (i.e., node size in Figure 2F).
Simulated Brain Activities and BOLD Signals
We simulate time series of brain activities and the derived BOLD signals as substrates for
data-driven construction of attractor transition networks (see section Temporal Mapper—
Construction of Transition Networks in Methods). The neural activity of each model brain
(i ) (Equations 4–6), simu-
region i is represented by the local excitatory population activity SE
lated using the Heun stochastic integration scheme with a 0.001 s time step.
The derived BOLD activities are computed using the Balloon–Windkessel model (Buxton
et al., 1998; Friston et al., 2000, 2003; Mandeville et al., 1999):
_si ¼ SE
ið Þ − κisi − γ
ð
i fi − 1
Þ
_
f i ¼ si
τi _v i ¼ fi − vi
1=α
h
τi _qi ¼ fi
ρi
ð
1 − 1 − ρi
Þ1=fi
i
− vi
1=α−1qi
BOLDi ¼ V0 k1 1 − qi
ð
½
ð
Þ þ k2 1 − qi=vi
ð
Þ þ k3 1 − vi
(cid:2);
Þ
(8)
(9)
(10)
(11)
(12)
where the interpretation and values of the parameters are given in Table 2. The initial condi-
tion is:
½
si 0ð Þ; fi 0ð Þ; vi 0ð Þ; qi 0ð Þ
(cid:2) ¼ 0; 1; 1; 1
½
(cid:2);
(13)
450
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal Mapper
Table 2.
et al. (2003)
Parameters of the Balloon–Windkessel model of BOLD activity, obtained from Friston
Parameter
si
Interpretation
Vasodilatory signal
fi
vi
qi
κi
γi
τi
α
ρ
V0
k1
k2
k3
Blood inflow
Blood volume
Deoxyhemoglobin content
Rate of signal decay
Rate of flow-dependent elimination
Hemodynamic transit time
Grubb’s exponent
Resting oxygen extraction fraction
Resting blood volume fraction
BOLD weight parameter
BOLD weight parameter
BOLD weight parameter
Value
Variable
Variable
Variable
Variable
0.65 (s−1)
0.41 (s−1)
0.98 (s)
0.32
0.34
0.02
7ρi
2
2ρi − 0.2
which is a hemodynamic equilibrium state without neural activity. The BOLD dynamics are
(i ), simulated using the Euler method with an integration
passively driven by neural activity SE
time step of 0.001 s.
Temporal Mapper—Construction of Transition Networks
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
t
.
The fundamental backbones of our transition networks are the k nearest-neighbor graphs
(kNNG) that often appear in dimension reduction techniques (van der Maaten et al., 2009).
Before introducing this construction, we first set up some preliminaries.
Given a d-dimensional vector v and p ≥ 1, the p-norm of v is defined by writing ‖v ‖p :=
P
d
jp)1/p. Unless specified otherwise, we will use p = 2 throughout this work, that is, the
i¼1 vij
(
Euclidean norm. Next, given a dataset X as an n × d matrix, we will typically interpret X as a
collection of n points {x1, x2, …, xn} in d-dimensional space. Finally, for any positive integer
k ≥ 1, the collection of top-k nearest neighbors for any point xi, denoted top(k, xi), is the col-
lection of the k points closest to xi in the sense of the Euclidean norm. The standard kNNG on
X is defined to be the graph with node set {x1, x2, …, xn} and edge set:
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
(cid:5)
(cid:6)
(cid:4)
xi; xj
(cid:4)
: xi 2 top k; xj
(cid:5)
or xj 2 top k; xi
ð
Þ
(cid:7)
:
A related construction is the reciprocal k-nearest neighbor graph (rkNNG) construction. Here
the nodes are given as before, but a stricter convention is followed for the edge set:
(cid:4)
(cid:6)
(cid:4)
(cid:7)
(cid:5)
(cid:5)
xi; xj
: xi 2 top k; xj
and xj 2 top k; xi
ð
Þ
:
The reciprocal construction takes more information about local densities into account than the
standard kNNG, and is occasionally more useful in practice (Qin et al., 2011).
Network Neuroscience
451
Temporal Mapper
Reciprocal clustering of digraphs:
An agglomerative clustering
technique that takes asymmetric
edge weights into account when
producing clusters.
With this setup in place, we are ready to describe our construction. In our setting, data
points that are close in time also have a tendency to be close in space, as the states change
continuously (i.e., without sharp jumps) within an attractor. Keeping this tendency in mind, we
carry out the following procedure:
1. Construct a standard kNNG
2. Remove edges of the form (xi, xi+1) (these will be added back in)
3. Remove all nonreciprocal connections, that is, only retain edges (xi, xj) if xi 2 top(k, xj)
and xj 2 top(k, xi)
4. Add directed temporal links (xi, xi+1); existing undirected edges (xi, xj) are viewed as
double edges (xi, xj), (xj, xi). This final digraph is denoted eG.
The initial pruning of temporal neighbors is carried out to help recover directionality in the
data (see Figure S5). Other strategies may be possible, but the current method worked suffi-
ciently well for our purposes. The intermediate step of removing nonreciprocal connections
is a strategy for disambiguating between points that have differing local densities (Qin et al.,
2011). The final addition of the temporal links injects the “arrow of time” back into the
graphical representation. Note that this final step is not typical, but is possible in our setting
because we work with time series data and know an explicit ordering of our data points. An
important feature of the networks that we constructed was that they tended to be strongly
connected as digraphs, meaning that it was possible to take a directed path between any two
vertices. Our construction also accommodates multiple time series or time series with missing
frames (frame censoring is common in fMRI time series to remove motion artifacts): the arrow of
time is only removed and reintroduced between consecutive time points in the same time series
or epoch in step 2 and 4 above. When the data constitute a single uninterrupted time series, the
digraph will always have one connected component by virtue of the arrows of time that connect
every pair of consecutive time points. When the data contain multiple disjoint time series, it is
possible for the digraph to have multiple connected components for certain parameter k as the
connectivity across time series depends solely on the existence of reciprocal spatial neighbors. If
it is desirable for the digraph to have a single connected component, one can choose to (a)
increase k until reciprocal kNN exists between any pair of time series, or (b) pre-align the
time series to increase the spatial proximity between them.
The final step in the construction of the transition network achieves compression and
follows the notion of reciprocal clustering of digraphs introduced by Carlsson et al. (2013).
For a fixed parameter δ > 0 (specifically, δ = 2 in this work), we construct an auxiliary undi-
(cid:4)
: dGe xi; xj
: The connected com-
rected graph U on X with edges
ponents of U partition the vertex set of eG into blocks B1, B2, …, Bm. The final compressed
transition network G is now constructed with vertex set V(G) = {B1, B2, …, Bm} and edge set
(cid:4)
≤ δ; dGe xj; xi
xi; xj
≤ δ
(cid:7)
(cid:6)
(cid:5)
(cid:5)
(cid:4)
(cid:5)
n
(cid:4)
Þ≔ Bi; Bj
E Gð
(cid:5)
: there exists v; v 0
ð
(cid:1) (cid:3)
Þ 2 E eG
for some v 2 Bi; v 0 2 Bj
:
o
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Note that if v and v0 belongs to the same connected component of the kNNG eG, there exists
some edge between the partitions of the said connected component. Thus, the number of
connected components does not change due to compression.
Gromov–Wasserstein Distance Between Transition Networks
Temporal Mapper produces directed graphs where arrows display temporal structure. In gen-
eral, comparing such graphs directly requires solving a correspondence problem as different
Network Neuroscience
452
Temporal Mapper
graphs may have different numbers of nodes. To solve this correspondence problem, we use
the Gromov–Wasserstein (GW) distance (Mémoli, 2007). While originally formulated for
metric spaces, the GW formulation was shown to admit a bona fide distance between directed
graphs with arbitrary edge weights in Chowdhury and Mémoli (2019) and has recently enjoyed
significant attention from the machine learning community (Flamary et al., 2021; Peyré et al.,
2016; Peyré & Cuturi, 2019; Solomon et al., 2016; Titouan et al., 2019; Xu et al., 2019). In the
(di)graph setting, the GW distance allows one to compare the full structure of two (di)graphs
without reducing to summary statistics such as degree distributions or centrality.
The GW distance formulation for graphs proceeds as follows. Let G = (V, E ), H = (W, F ) be
two graphs (possibly directed and/or weighted) on vertex sets V, W of possibly different sizes.
For Temporal Mapper, E and F are the (asymmetric) geodesic distance matrices—note that
these matrices are well-defined because the underlying digraphs are strongly connected.
Additionally, let p, q be two probability distributions on V, W, respectively, denoting the
significance of each node. In the Temporal Mapper setting, this is just the number of data
points in each node, appropriately normalized, and thus reflects the compression at each
node. In matrix-vector notation, we have:
E a jV j (cid:3) jV j matrix; p a jV j (cid:3) 1 vector such that pi > 0 for all 1 ≤ i ≤ jV j and
F a jW j (cid:3) jW j matrix; q a jW j (cid:3) 1 vector such that qi > 0 for all 1 ≤ i ≤ jW j and
XjV j
i¼1 pi ¼ 1:
XjW j
i¼1 qi ¼ 1:
The correspondence between nodes is represented as a joint probability distribution matrix C
of size jV j × jW j satisfying nonnegativity and summation constraints Cij ≥ 0, (cid:2)i,j Cij = 1 as
well as marginal constraints such that the rows and columns of C correspond to p and q,
respectively. Such a joint distribution is typically referred to as a coupling matrix, and the col-
lection of coupling matrices is denoted C (p, q). Intuitively, a coupling describes “how much
each node in V corresponds to a given node in W ” (Peyré & Cuturi, 2019).
Finally, the GW distance between the two graphs is a given as the result of the following
optimization problem:
ð
dGW E; pð
Þ; F; qð
Þ
Þ2 ¼ min
C 2C p;qð
Þ
X
(cid:8)
(cid:8)
ijkl Eik − Fjl
(cid:8)
(cid:8)2
CklCij:
This is a nonconvex quadratic optimization problem (nonconvex because symmetries in the
graphs may lead to different correspondences achieving the same minimum, quadratic
because the C appears twice) and is generally difficult to solve. Intuitively, this distance
measures the expected distortion that the edges of G would necessarily undergo upon being
transformed into the graph H. While significant progress has been made in obtaining local
minimizers of the underlying optimization through regularization or gradient descent (Flamary
et al., 2021; Peyré & Cuturi, 2019), it is in general difficult to assess the quality of these local
minimizers except in certain domain areas such as computer vision where the output can be
directly inspected in two or three dimensions.
Instead, we opt to solve a lower bound for the GW problem that can be formulated as a
linear program with an exact solution. This lower bound, which was referred to as the third
lower bound (TLB) in Chowdhury and Mémoli (2019), arises by decoupling the quadratic opti-
mization problem and instead solving:
ð
TLB E; pð
Þ; F; qð
Þ2 ¼ min
Þ
B;C2C p;qð
Þ
X
(cid:8)
(cid:8)
ijkl Eik − Fjl
(cid:8)
(cid:8)2
(cid:9)
BklCij ¼ min
C 2C p;qð
Þ
min
B2C p;qð
Þ
(cid:8)
(cid:8)
Eik − Fjl
(cid:8)
(cid:8)2
(cid:10)
Bkl
Cij :
Network Neuroscience
453
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal Mapper
It can be shown (Schmitzer & Schnörr, 2013) that the inner infimization problem has a closed
form solution. In other words, the preceding problem amounts to solving the following linear
program:
X
ij
Jij Cij ;
min
C 2C p;qð
Þ
where Jij ¼ min
B2C p;qð
Þ
X
(cid:8)
(cid:8)
kl
Eik − Fjl
(cid:8)
(cid:8)2
Bkl;
and each Jij can be individually solved in closed form.
Because there are jV j × jW j individual entries making up jJj, and the entries can all be
computed independently, this problem is perfectly suited for GPU computations. Our GPU
implementation of the TLB computes each coefficient Jij in a separate thread block so that
all coefficients are computed in parallel. The final linear program can be solved easily using
standard linear solvers, for example, using the network simplex algorithm (Bonneel et al.,
2011). For applications in the present work, the GPU-infused version accelerates the original
implementation (Chowdhury & Mémoli, 2019) by roughly 200 times.
Cycles of Transition Networks
Enumerating all cycles in a graph can be computationally expensive (Giscard et al., 2019).
However, the transition networks that appear in our setting are small enough that we can enu-
merate all cycles and carry out further postprocessing in reasonable time. Given a transition
network G with vertices indexed as {v1, v2, …, vd }, we proceed via the following heuristic
approach. First we loop over all pairs of vertices (vi, vj) and use MATLAB’s native shortest path
algorithm (i.e., a breadth-first search of complexity O(|V | + |E |)) to find the shortest paths from
vi to vj and from vj to vi, respectively. These paths are then concatenated (avoiding trivial rep-
etition at endpoints) to obtain a cycle. If a cycle has repeated nodes, that is, is not a simple
cycle, then it is discarded. Finally, after the loop terminates, there may be multiple copies of
the same cycle with different starting points. For each of these cases, we retain the copy start-
ing at the smallest index and discard the others.
The Continuous Multitask Experiment
In this study, we utilized an fMRI dataset comprising 18 participants collected by Gonzalez-
Castillo et al. (2015) by using a continuous multitask paradigm (CMP). We retrieved the data
from the XNAT Central public repository (https://central.xnat.org; Project ID: FCStateClassif ).
Informed consent was obtained from all participants, and the local Institutional Review Board
of the National Institute of Mental Health in Bethesda, MD, reviewed and approved the CMP
data collection. We briefly describe the experiment structure and preprocessing below.
Participants were scanned continuously for 25 min and 24 s while performing four different
cognitive tasks. Each task was presented for two separate 180-s blocks, and each task block
was preceded by a 12-s instruction period. These four tasks were (a) Rest (R), where partici-
pants were instructed to fixate on a crosshair in the center of the screen and let their mind
wander; (b) 2-back Working Memory (M), where participants were presented with a continu-
ous sequence of individual geometric shapes and were instructed to press a button whenever
the current shape was the same as the shape that appeared two shapes before; (c)
Math/arithmetic (A), where participants were presented with simple arithmetic operations,
involving three numbers between 1 and 10 and two operands (either addition or subtraction);
and (d) Video ( V), where participants watched a video of a fish tank from a single point of view
with different types of fish swimming into an out of the frame, and were instructed to press a
button when a red crosshair appeared on a clown fish and another when it appeared on any
other type of fish. For arithmetic, the operations remained on the screen for 4 s, and successive
Network Neuroscience
454
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal Mapper
trials were separated by a blank screen that appeared for 1 s, yielding a total of 36 operations
per each 180-s block. For video, the targets appeared for 200 ms with a total of 16 targets
during each of the 180-s blocks. The order of task blocks was randomized such that the same
task did not appear in two consecutive blocks, and the same ordering of tasks was used for all
participants. The randomized task order was R-M-V-A-M-R-A-V.
The fMRI data were acquired on a Siemens 7 Tesla MRI scanner equipped with a
32-channel head coil using a whole-brain echo planar imaging (EPI) sequence (repetition time
[TR] = 1.5 s, echo time [TE] = 25 ms, and voxel size = 2 mm isotropic). A total of 1,017
volumes were acquired while participants performed the CMP.
Functional and anatomical MR images were preprocessed using the Configurable Pipeline
for the Analysis of Connectomes (C-PAC version 0.3.4; https://fcp-indi.github.io/docs/user
/index.html). We used the preprocessing utilized in a previous study (Saggar et al., 2018).
Briefly, the fMRI data preprocessing steps included ANTS registration into MNI152 space, slice
timing correction, motion correction, skull stripping, grand mean scaling, spatial smoothing
(FWHM of 4 mm), and temporal band-pass filtering (0.009 Hz < f < 0.08 Hz). For each ROI,
nuisance signal correction was performed by regressing out linear and quadratic trends, phys-
iological noise (white matter and cerebrospinal fluid), motion-related noise (three translational
and three rotational head-motion parameters) using the Volterra expansion (Friston et al.,
1996) (i.e., six parameters, their temporal derivatives, and each of these values squared),
and residual signal unrelated to neural activity extracted using the CompCor algorithm
(Behzadi et al., 2007) (i.e., five principal components derived from noise regions in which
the time series data were unlikely to be modulated by neural activity). The resulting data were
brought to 3-mm MNI space, and the mean time series was extracted from 375 predefined
regions of interest (ROIs) using the Shine et al. (2016) atlas. The atlas includes 333 cortical
regions from the Gordon et al. (2016) atlas, 14 subcortical regions from the Harvard–Oxford
subcortical atlas, and 28 cerebellar regions from the SUIT atlas (Diedrichsen et al., 2009).
Individual ROIs with zero variance were excluded prior to computing attractor transition
networks.
The behavioral data included both responses and reaction times for Working Memory,
Math, and Video tasks. Participants were instructed to respond as quickly and accurately as
possible with only one response per question. Behavior scores including the percent correct,
percent missed, and response times for Working Memory (M), Math (A), and Video ( V) tasks
were computed for each participant.
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00301.
Custom MATLAB scripts used to generate simulated data and the implementation of Temporal
Mapper is available at https://github.com/braindynamicslab/tmapper. The human fMRI data
was originally collected by Gonzalez-Castillo et al. (2015) and is available for download from
the XNAT Central public repository (https://central.xnat.org; Project ID: FCStateClassif ).
AUTHOR CONTRIBUTIONS
Mengsen Zhang: Conceptualization; Formal analysis; Investigation; Methodology; Software;
Visualization; Writing – original draft; Writing – review & editing. Samir Chowdhury: Concep-
tualization; Formal analysis; Methodology; Software; Validation; Visualization; Writing –
original draft; Writing – review & editing. Manish Saggar: Conceptualization; Funding
Network Neuroscience
455
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal Mapper
acquisition; Investigation; Methodology; Project administration; Supervision; Validation;
Writing – review & editing.
FUNDING INFORMATION
Manish Saggar, National Institute of Mental Health (https://dx.doi.org/10.13039/100000025),
Award ID: MH119735. Manish Saggar, Stanford Maternal and Child Health Research Institute
(https://dx.doi.org/10.13039/100015521), Award ID: Faculty Scholar.
REFERENCES
Abbott, L. F., & Chance, F. S. (2005). Drivers and modulators from
push-pull and balanced synaptic input. Progress in Brain
Research, 149, 147–155. https://doi.org/10.1016/S0079-6123
(05)49011-1, PubMed: 16226582
Allen, E. A., Damaraju, E., Plis, S. M., Erhardt, E. B., Eichele, T., &
Calhoun, V. D. (2014). Tracking whole-brain connectivity
dynamics in the resting state. Cerebral Cortex, 24(3), 663–676.
https://doi.org/10.1093/cercor/bhs352, PubMed: 23146964
Baker, A. P., Brookes, M. J., Rezek, I. A., Smith, S. M., Behrens, T.,
Probert Smith, P. J., & Woolrich, M. (2014). Fast transient net-
works in spontaneous human brain activity. eLife, 3, e01867.
https://doi.org/10.7554/eLife.01867, PubMed: 24668169
Ban, H., & Kalies, W. D. (2006). A computational approach to Conley’s
decomposition theorem. Journal of Computational and Nonlinear
Dynamics, 1(4), 312–319. https://doi.org/10.1115/1.2338651
Barber, A. D., Lindquist, M. A., DeRosse, P., & Karlsgodt, K. H.
(2018). Dynamic functional connectivity states reflecting
psychotic-like experiences. Biological Psychiatry: Cognitive Neu-
roscience and Neuroimaging, 3(5), 443–453. https://doi.org/10
.1016/j.bpsc.2017.09.008, PubMed: 29735154
Behzadi, Y., Restom, K., Liau, J., & Liu, T. T. (2007). A component
based noise correction method (CompCor) for BOLD and perfu-
sion based fMRI. NeuroImage, 37(1), 90–101. https://doi.org/10
.1016/j.neuroimage.2007.04.042, PubMed: 17560126
Belkin, M., & Niyogi, P. (2003). Laplacian eigenmaps for dimension-
ality reduction and data representation. Neural Computation,
15(6), 1373–1396. https://doi.org/10.1162/089976603321780317
Billings, J., Saggar, M., Hlinka, J., Keilholz, S., & Petri, G. (2021).
Simplicial and topological descriptions of human brain dynamics.
Network Neuroscience, 5(2), 549–568. https://doi.org/10.1162
/netn_a_00190, PubMed: 34189377
Bonneel, N., van de Panne, M., Paris, S., & Heidrich, W. (2011).
Displacement interpolation using Lagrangian mass transport. In
Proceedings of the 2011 SIGGRAPH Asia Conference (pp. 1–12,
Article 158). Association for Computing Machinery. https://doi
.org/10.1145/2024156.2024192
Breakspear, M. (2017). Dynamic models of large-scale brain activity.
Nature Neuroscience, 20(3), 340–352. https://doi.org/10.1038/nn
.4497, PubMed: 28230845
Buxton, R. B., Wong, E. C., & Frank, L. R. (1998). Dynamics of
blood flow and oxygenation changes during brain activation:
The balloon model. Magnetic Resonance in Medicine, 39(6),
855–864. https://doi.org/10.1002/mrm.1910390602, PubMed:
9621908
Buzsaki, G. (2006). Rhythms of the brain. Oxford, UK: Oxford Uni-
versity Press. https://doi.org/10.1093/acprof:oso/9780195301069
.001.0001
Cabral, J., Kringelbach, M. L., & Deco, G. (2017). Functional con-
nectivity dynamically evolves on multiple time-scales over a
static structural connectome: Models and mechanisms. Neuro-
Image, 160, 84–96. https://doi.org/10.1016/j.neuroimage.2017
.03.045, PubMed: 28343985
Carlsson, G. (2009). Topology and data. Bulletin of the American
Mathematical Society, 46(2), 255–308. https://doi.org/10.1090
/S0273-0979-09-01249-X
Carlsson, G., Mémoli, F., Ribeiro, A., & Segarra, S. (2013). Axiom-
atic construction of hierarchical clustering in asymmetric net-
works. In 2013 IEEE International Conference on Acoustics,
Speech and Signal Processing (pp. 5219–5223). IEEE. https://doi
.org/10.1109/ICASSP.2013.6638658
Cavanna, F., Vilas, M. G., Palmucci, M., & Tagliazucchi, E. (2018).
Dynamic functional connectivity and brain metastability during altered
states of consciousness. NeuroImage, 180(Pt B), 383–395. https://doi
.org/10.1016/j.neuroimage.2017.09.065, PubMed: 28986208
Chazal, F., & Michel, B. (2021). An introduction to topological data
analysis: Fundamental and practical aspects for data scientists.
Frontiers in Artificial Intelligence, 4, 667963. https://doi.org/10
.3389/frai.2021.667963, PubMed: 34661095
Chowdhury, S., & Mémoli, F. (2019). The Gromov–Wasserstein dis-
tance between networks and stable network invariants. Informa-
tion and Inference: A Journal of the IMA, 8(4), 757–787. https://
doi.org/10.1093/imaiai/iaz026
Civier, O., Smith, R. E., Yeh, C.-H., Connelly, A., & Calamante, F.
(2019). Is removal of weak connections necessary for graph-
theoretical analysis of dense weighted structural connectomes
from diffusion MRI? NeuroImage, 194, 68–81. https://doi.org/10
.1016/j.neuroimage.2019.02.039, PubMed: 30844506
Cummins, B., Gedeon, T., Harker, S., Mischaikow, K., & Mok, K.
(2016). Combinatorial representation of parameter space for
switching networks. SIAM Journal on Applied Dynamical Sys-
tems, 15(4), 2176–2212. https://doi.org/10.1137/15M1052743,
PubMed: 30774565
Deco, G., & Jirsa, V. K. (2012). Ongoing cortical activity at rest: Crit-
icality, multistability, and ghost attractors. Journal of Neurosci-
ence, 32(10), 3366–3375. https://doi.org/10.1523/JNEUROSCI
.2523-11.2012, PubMed: 22399758
Deco, G., Jirsa, V. K., & McIntosh, A. R. (2011). Emerging concepts
for the dynamical organization of resting-state activity in the
Network Neuroscience
456
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal Mapper
brain. Nature Reviews Neuroscience, 12(1), 43–56. https://doi
.org/10.1038/nrn2961, PubMed: 21170073
Deco, G., Ponce-Alvarez, A., Hagmann, P., Romani, G. L., Mantini,
D., & Corbetta, M. (2014). How local excitation–inhibition ratio
impacts the whole brain dynamics. Journal of Neuroscience,
34(23), 7886–7898. https://doi.org/10.1523/ JNEUROSCI.5068
-13.2014, PubMed: 24899711
Deco, G., Ponce-Alvarez, A., Mantini, D., Romani, G. L.,
Hagmann, P., & Corbetta, M. (2013). Resting-state functional
connectivity emerges from structurally and dynamically shaped
slow linear fluctuations. Journal of Neuroscience, 33(27),
11239–11252. https://doi.org/10.1523/ JNEUROSCI.1091-13
.2013, PubMed: 23825427
Diedrichsen, J., Balsters, J. H., Flavell, J., Cussans, E., & Ramnani,
N. (2009). A probabilistic MR atlas of the human cerebellum.
N e u ro I m a g e , 4 6 ( 1 ) , 3 9 – 4 6 . h t t p s : / / d o i . o rg / 1 0 . 1 0 1 6 / j
.neuroimage.2009.01.045, PubMed: 19457380
Díez-Cirarda, M., Strafella, A. P., Kim, J., Peña, J., Ojeda, N.,
Cabrera-Zubizarreta, A., & Ibarretxe-Bilbao, N. (2018). Dynamic
functional connectivity in Parkinson’s disease patients with mild
cognitive impairment and normal cognition. NeuroImage:
Clinical, 17, 847–855. https://doi.org/10.1016/j.nicl.2017.12
.013, PubMed: 29527489
Du, M., Zhang, L., Li, L., Ji, E., Han, X., Huang, G., Liang, Z., Shi,
L., Yang, H., & Zhang, Z. (2021). Abnormal transitions of
dynamic functional connectivity states in bipolar disorder: A
whole-brain resting-state fMRI study. Journal of Affective Disor-
ders, 289, 7–15. https://doi.org/10.1016/j.jad.2021.04.005,
PubMed: 33906006
Edelsbrunner, H., & Morozov, D. (2013). Persistent homology:
Theory and practice. In European Congress of Mathematics,
Kraków, 2–7 July, 2012 (pp. 31–50). European Mathematical
Society. https://doi.org/10.4171/120-1/3
Esfahlani, F. Z., Jo, Y., Faskowitz, J., Byrge, L., Kennedy, D. P.,
Sporns, O., & Betzel, R. F. (2020). High-amplitude cofluctuations
in cortical activity drive functional connectivity. Proceedings of
the National Academy of Sciences, 117(45), 28393–28401.
https://doi.org/10.1073/pnas.2005531117, PubMed: 33093200
Faskowitz, J., Esfahlani, F. Z., Jo, Y., Sporns, O., & Betzel, R. F.
(2020). Edge-centric functional network representations of
human cerebral cortex reveal overlapping system-level architec-
ture. Nature Neuroscience, 23(12), 1644–1654. https://doi.org/10
.1038/s41593-020-00719-y, PubMed: 33077948
Flamary, R., Courty, N., Gramfort, A., Alaya, M. Z., Boisbunon, A,
Chambon, S., Chapel, L., Corenflos, A., Fatras, K., Fournier, N.,
Gautheron, L., Gayraud, N. T. H., Janati, H., Rakotomamonjy, A.,
Redko, I., Rolet, A., Schutz, A., Seguy, V., Sutherland, D. J., …
Vayer, T. (2021). POT: Python optimal transport. Journal of
Machine Learning Research, 22(78), 1–8. https://www.jmlr.org
/papers/volume22/20-451/20-451.pdf?ref=https://githubhelp
.com
Fox, M. D., & Greicius, M. (2010). Clinical applications of resting
state functional connectivity. Frontiers in Systems Neuroscience,
4, 19. https://doi.org/10.3389/fnsys.2010.00019, PubMed:
20592951
Friston, K. J., Harrison, L., & Penny, W. (2003). Dynamic causal
modelling. NeuroImage, 19(4), 1273–1302. https://doi.org/10
.1016/S1053-8119(03)00202-7, PubMed: 12948688
Friston, K. J., Mechelli, A., Turner, R., & Price, C. J. (2000). Nonlin-
ear responses in fMRI: The Balloon model, Volterra kernels, and
other hemodynamics. NeuroImage, 12(4), 466–477. https://doi
.org/10.1006/nimg.2000.0630, PubMed: 10988040
Friston, K. J., Williams, S., Howard, R., Frackowiak, R. S., & Turner,
R. (1996). Movement-related effects in fMRI time-series. Mag-
netic Resonance in Medicine, 35(3), 346–355. https://doi.org
/10.1002/mrm.1910350312, PubMed: 8699946
Gameiro, M., Mischaikow, K., & Kalies, W. (2004). Topological
characterization of spatial-temporal chaos. Physical Review E,
70(3 Pt 2), 035203. https://doi.org/10.1103/ PhysRevE.70
.035203, PubMed: 15524574
Garland, J., Bradley, E., & Meiss, J. D. (2016). Exploring the topol-
ogy of dynamical reconstructions. Physica D, 334, 49–59. https://
doi.org/10.1016/j.physd.2016.03.006
Garrity, A. G., Pearlson, G. D., McKiernan, K., Lloyd, D., Kiehl,
K. A., & Calhoun, V. D. (2007). Aberrant “default mode” func-
tional connectivity in schizophrenia. American Journal of Psychi-
atry, 164(3), 450–457. https://doi.org/10.1176/ajp.2007.164.3
.450, PubMed: 17329470
Geniesse, C., Chowdhury, S., & Saggar, M. (2022). NeuMapper: A
scalable computational framework for multiscale exploration of
the brain’s dynamical organization. Network Neuroscience, 6(2),
467–498. https://doi.org/10.1162/netn_a_00229, PubMed:
35733428
Geniesse, C., Sporns, O., Petri, G., & Saggar, M. (2019). Generating
dynamical neuroimaging spatiotemporal representations
(DyNeuSR) using topological data analysis. Network Neurosci-
ence, 3(3), 763–778. https://doi.org/10.1162/netn_a_00093,
PubMed: 31410378
Giscard, P.-L., Kriege, N., & Wilson, R. C. (2019). A general pur-
pose algorithm for counting simple cycles and simple paths of
any length. Algorithmica, 81(7), 2716–2737. https://doi.org/10
.1007/s00453-019-00552-1
Giusti, C., Pastalkova, E., Curto, C., & Itskov, V. (2015). Clique
topology reveals intrinsic geometric structure in neural correla-
tions. Proceedings of the National Academy of Sciences, 112(44),
13455–13460. https://doi.org/10.1073/pnas.1506407112,
PubMed: 26487684
Golos, M., Jirsa, V., & Daucé, E. (2015). Multistability in large scale
models of brain activity. PLoS Computational Biology, 11(12),
e1004644. https://doi.org/10.1371/journal.pcbi.1004644,
PubMed: 26709852
Gonzalez-Castillo, J., Caballero-Gaudes, C., Topolski, N.,
Handwerker, D. A., Pereira, F., & Bandettini, P. A. (2019). Imaging
the spontaneous flow of thought: Distinct periods of cognition
contribute to dynamic functional connectivity during rest. Neuro-
Image, 202, 116129. https://doi.org/10.1016/j.neuroimage.2019
.116129, PubMed: 31461679
Gonzalez-Castillo, J., Hoy, C. W., Handwerker, D. A., Robinson,
M. E., Buchanan, L. C., Saad, Z. S., & Bandettini, P. A. (2015).
Tracking ongoing cognition in individuals using brief,
whole-brain functional connectivity patterns. Proceedings of
the National Academy of Sciences, 112(28), 8762–8767.
https://doi.org/10.1073/pnas.1501242112, PubMed: 26124112
Gordon, E. M., Laumann, T. O., Adeyemo, B., Huckins, J. F., Kelley,
W. M., & Petersen, S. E. (2016). Generation and evaluation of a
cortical area parcellation from resting-state correlations. Cerebral
Network Neuroscience
457
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal Mapper
Cortex, 26(1), 288–303. https://doi.org/10.1093/cercor/bhu239,
PubMed: 25316338
Gordon, E. M., Laumann, T. O., Gilmore, A. W., Newbold, D. J.,
Greene, D. J., Berg, J. J., Ortega, M., Hoyt-Drazen, C., Gratton,
C., Sun, H., Hampton, J. M., Coalson, R. S., Nguyen, A. L.,
McDermott, K. B., Shimony, J. S., Snyder, A. Z., Schlaggar,
B. L., Petersen, S. E., Nelson, S. M., & Dosenbach, N. U. F.
(2017). Precision functional mapping of individual human
brains. Neuron, 95(4), 791–807. https://doi.org/10.1016/j
.neuron.2017.07.011, PubMed: 28757305
Hagmann, P., Cammoun, L., Gigandet, X., Meuli, R., Honey, C. J.,
Wedeen, V. J., & Sporns, O. (2008). Mapping the structural core
of human cerebral cortex. PLoS Biology, 6(7), e159. https://doi
.org/10.1371/journal.pbio.0060159, PubMed: 18597554
Hansen, E. C. A., Battaglia, D., Spiegler, A., Deco, G., & Jirsa, V. K.
(2015). Functional connectivity dynamics: Modeling the switching
behavior of the resting state. NeuroImage, 105, 525–535. https://
doi.org/10.1016/j.neuroimage.2014.11.001, PubMed: 25462790
Hutchison, R. M., Womelsdorf, T., Allen, E. A., Bandettini, P. A.,
Calhoun, V. D., Corbetta, M., Della Penna, S., Duyn, J. H.,
Glover, G. H., Gonzalez-Castillo, J., Handwerker, D. A.,
Keilholz, S., Kiviniemi, V., Leopold, D. A., de Pasquale, F.,
Sporns, O., Walter, M., & Chang, C. (2013). Dynamic functional
connectivity: promise, issues, and interpretations. NeuroImage,
80, 360–378. https://doi.org/10.1016/j.neuroimage.2013.05
.079, PubMed: 23707587
Kalies, W. D., Mischaikow, K., & VanderVorst, R. C. A. M. (2005).
An algorithmic approach to chain recurrence. Foundations of
Computational Mathematics, 5(4), 409–449. https://doi.org/10
.1007/s10208-004-0163-9
Kelso, J. A. S. (1995). Dynamic patterns: The self-organization of
brain and behavior. Cambridge, MA: MIT Press.
Kelso, J. A. S. (2012). Multistability and metastability: Understand-
ing dynamic coordination in the brain. Philosophical Transac-
tions of the Royal Society of London. Series B, Biological
Sciences, 367(1591), 906–918. https://doi.org/10.1098/rstb
.2011.0351, PubMed: 22371613
Kim, W., & Mémoli, F. (2021). Spatiotemporal persistent homology
for dynamic metric spaces. Discrete & Computational Geometry,
66(3), 831–875. https://doi.org/10.1007/s00454-019-00168-w
Laumann, T. O., Snyder, A. Z., Mitra, A., Gordon, E. M., Gratton,
C., Adeyemo, B., Gilmore, A. W., Nelson, S. M., Berg, J. J.,
Greene, D. J., McCarthy, J. E., Tagliazucchi, E., Laufs, H.,
Schlaggar, B. L., Dosenbach, N. U. F., & Petersen, S. E. (2017).
On the stability of BOLD fMRI correlations. Cerebral Cortex,
27(10), 4719–4732. https://doi.org/10.1093/cercor/ bhw265,
PubMed: 27591147
Leonardi, N., & Van De Ville, D. (2015). On spurious and real fluc-
tuations of dynamic functional connectivity during rest. Neuro-
Image, 104, 430–436. https://doi.org/10.1016/j.neuroimage
.2014.09.007, PubMed: 25234118
Li, J., Zhang, D., Liang, A., Liang, B., Wang, Z., Cai, Y., Gao, M.,
Gao, Z., Chang, S., Jiao, B., Huang, R., & Liu, M. (2017). High
transition frequencies of dynamic functional connectivity states
in the creative brain. Scientific Reports, 7, 46072. https://doi
.org/10.1038/srep46072, PubMed: 28383052
Lui, S., Wu, Q., Qiu, L., Yang, X., Kuang, W., Chan, R. C. K., Huang,
X., Kemp, G. J., Mechelli, A., & Gong, Q. (2011). Resting-state
functional connectivity in treatment-resistant depression. Ameri-
can Journal of Psychiatry, 168(6), 642–648. https://doi.org/10
.1176/appi.ajp.2010.10101419, PubMed: 21362744
Mandeville, J. B., Marota, J. J., Ayata, C., Zaharchuk, G.,
Moskowitz, M. A., Rosen, B. R., & Weisskoff, R. M. (1999).
Evidence of a cerebrovascular postarteriole Windkessel with
delayed compliance. Journal of Cerebral Blood Flow and Metab-
olism, 19(6), 679–689. https://doi.org/10.1097/00004647
-199906000-00012, PubMed: 10366199
Meer, J. N. van der, Breakspear, M., Chang, L. J., Sonkusare, S., &
Cocchi, L. (2020). Movie viewing elicits rich and reliable brain
state dynamics. Nature Communications, 11(1), 5004. https://doi
.org/10.1038/s41467-020-18717-w, PubMed: 33020473
Mémoli, F. (2007). On the use of Gromov-Hausdorff distances for
shape comparison. In M. Botsch, R. Pajarola, B. Chen, & M.
Zwicker (Eds.), Eurographics symposium on point-based graphics
(pp. 81–90). The Eurographics Association. https://doi.org/10
.2312/spbg/spbg07/081-090
Munch, E. (2013). Applications of persistent homology to time varying
systems (Publication No. 3557917) [Doctoral Dissertation, Duke
University]. ProQuest Dissertations Publishing. https://search
.proquest.com/openview/5e127805020f33cd8fd1d126ac40fc2e
/1?pq-origsite=gscholar&cbl=18750
Munn, B. R., Müller, E. J., Wainstein, G., & Shine, J. M. (2021). The
ascending arousal system shapes neural dynamics to mediate
awareness of cognitive states. Nature Communications, 12(1),
6016. https://doi.org/10.1038/s41467-021-26268-x, PubMed:
34650039
Myers, A., Munch, E., & Khasawneh, F. A. (2019). Persistent homol-
ogy of complex networks for dynamic state detection. Physical
Review E, 100(2-1), 022314. https://doi.org/10.1103/PhysRevE
.100.022314, PubMed: 31574743
Ou, J., Xie, L., Wang, P., Li, X., Zhu, D., Jiang, R., Wang, Y., Chen,
Y., Zhang, J., & Liu, T. (2013). Modeling brain functional
dynamics via hidden Markov models. In 2013 6th International
IEEE/EMBS Conference on Neural Engineering (NER) (pp. 569–572).
IEEE. https://doi.org/10.1109/NER.2013.6695998
Perea, J. A. (2019). Topological time series analysis. Notices of the
American Mathematical Society, 66(5), 686–694. https://www
.ams.org/journals/notices/201905/rnoti-p686.pdf. https://doi.org
/10.1090/noti1869
Petri, G., Expert, P., Turkheimer, F., Carhart-Harris, R., Nutt, D.,
Hellyer, P. J., & Vaccarino, F. (2014). Homological scaffolds of
brain functional networks. Journal of the Royal Society: Interface,
11(101), 20140873. https://doi.org/10.1098/rsif.2014.0873,
PubMed: 25401177
Peyré, G., & Cuturi, M. (2019). Computational optimal transport:
With applications to data science. Boston, MA: Now Publishers.
https://doi.org/10.1561/9781680835519
Peyré, G., Cuturi, M., & Solomon, J. (2016). Gromov-Wasserstein
averaging of kernel and distance matrices. In M. F. Balcan &
K. Q. Weinberger (Eds.), Proceedings of the 33rd International
Conference on Machine Learning (Vol. 48, pp. 2664–2672).
PMLR. https://proceedings.mlr.press/v48/peyre16.html
Poincaré, H. (1967). New methods of celestial mechanics. Wash-
ington, DC: National Aeronautics and Space Administration.
Preti, M. G., Bolton, T. A., & Van De Ville, D. (2017). The dynamic
functional connectome: State-of-the-art and perspectives.
Network Neuroscience
458
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal Mapper
NeuroImage, 160, 41–54. https://doi.org/10.1016/j.neuroimage
.2016.12.061, PubMed: 28034766
Qi, C. R., Su, H., Mo, K., & Guibas, L. J. (2017). PointNet: Deep
learning on point sets for 3D classification and segmentation.
In Proceedings of the IEEE Conference on Computer Vision and
Pattern Recognition (CVPR) (pp. 652–660). IEEE. https://
openaccess.thecvf.com/content_cvpr_2017/ html/Qi_PointNet
_Deep_Learning_CVPR_2017_paper.html. https://doi.org/10
.1109/CVPR.2017.16
Qin, D., Gammeter, S., Bossard, L., Quack, T., & van Gool, L. (2011).
Hello neighbor: Accurate object retrieval with k-reciprocal nearest
neighbors. In CVPR 2011 (pp. 777–784). IEEE. https://doi.org/10
.1109/CVPR.2011.5995373
Quinn, A. J., Vidaurre, D., Abeysuriya, R., Becker, R., Nobre, A. C., &
Woolrich, M. W. (2018). Task-evoked dynamic network analysis
through hidden Markov modeling. Frontiers in Neuroscience, 12,
603. https://doi.org/10.3389/fnins.2018.00603, PubMed: 30210284
Rabany, L., Brocke, S., Calhoun, V. D., Pittman, B., Corbera, S.,
Wexler, B. E., Bell, M. D., Pelphrey, K., Pearlson, G. D., & Assaf,
M. (2019). Dynamic functional connectivity in schizophrenia
and autism spectrum disorder: Convergence, divergence and
classification. NeuroImage: Clinical, 24, 101966. https://doi.org
/10.1016/j.nicl.2019.101966, PubMed: 31401405
Rabiner, L. R. (1989). A tutorial on hidden Markov models and
selected applications in speech recognition. Proceedings of the
IEEE, 77(2), 257–286. https://doi.org/10.1109/5.18626
Rezek, I., & Roberts, S. (2005). Ensemble hidden Markov models
with extended observation densities for biosignal analysis. In D.
Husmeier, R. Dybowski, & S. Roberts (Eds.), Probabilistic modeling
in bioinformatics and medical informatics (pp. 419–450). London,
UK: Springer. https://doi.org/10.1007/1-84628-119-9_14
Saggar, M., Shine, J. M., Liégeois, R., Dosenbach, N. U. F., & Fair, D.
(2022). Precision dynamical mapping using topological data
analysis reveals a unique hub-like transition state at rest. Nature
Communications, 13(1), 4791. https://doi.org/10.1038/s41467
-022-32381-2, PubMed: 35970984
Saggar, M., Sporns, O., Gonzalez-Castillo, J., Bandettini, P. A.,
Carlsson, G., Glover, G., & Reiss, A. L. (2018). Towards a new
approach to reveal dynamical organization of the brain using topo-
logical data analysis. Nature Communications, 9(1), 1399. https://
doi.org/10.1038/s41467-018-03664-4, PubMed: 29643350
Saggar, M., & Uddin, L. Q. (2019). Pushing the boundaries of
psychiatric neuroimaging to ground diagnosis in biology.
eNeuro, 6(6), ENEURO.0384-19.2019. https://doi.org/10.1523
/ENEURO.0384-19.2019, PubMed: 31685674
Schmitzer, B., & Schnörr, C. (2013). Modelling convex shape priors
and matching based on the Gromov-Wasserstein distance. Jour-
nal of Mathematical Imaging and Vision, 46(1), 143–159. https://
doi.org/10.1007/s10851-012-0375-6
Shine, J. M., Bissett, P. G., Bell, P. T., Koyejo, O., Balsters, J. H.,
Gorgolewski, K. J., Moodie, C. A., & Poldrack, R. A. (2016).
The dynamics of functional brain networks: Integrated network
states during cognitive task performance. Neuron, 92(2),
544–554. https://doi.org/10.1016/j.neuron.2016.09.018,
PubMed: 27693256
Singh, G., Mémoli, F., & Carlsson, G. E. (2007). Topological
methods for the analysis of high dimensional data sets and 3D
object recognition. In M. Botsch, R. Pajarola, B. Chen, & M.
Zwicker (Eds.), Eurographics symposium on point-based graphics
(pp. 91–100). The Eurographics Association. https://doi.org/10
.2312/spbg/spbg07/091-100
Smith, S. M., Beckmann, C. F., Andersson, J., Auerbach, E. J.,
Bijsterbosch, J., Douaud, G., Duff, E., Feinberg, D. A., Griffanti,
L., Harms, M. P., Kelly, M., Laumann, T., Miller, K. L., Moeller, S.,
Petersen, S., Power, J., Salimi-Khorshidi, G., Snyder, A. Z., Vu,
A. T., … WU-Minn HCP Consortium. (2013). Resting-state fMRI
in the Human Connectome Project. NeuroImage, 80, 144–168.
https://doi.org/10.1016/j.neuroimage.2013.05.039, PubMed:
23702415
Solomon, J., Peyré, G., Kim, V. G., & Sra, S. (2016). Entropic metric
alignment for correspondence problems. ACM Transactions on
Graphics, 35(4), 1–13. https://doi.org/10.1145/2897824.2925903
Taghia, J., Cai, W., Ryali, S., Kochalka, J., Nicholas, J., Chen, T., &
Menon, V. (2018). Uncovering hidden brain state dynamics that
regulate performance and decision-making during cognition.
Nature Communications, 9(1), 2505. https://doi.org/10.1038
/s41467-018-04723-6, PubMed: 29950686
Tang, Y.-Y., Rothbart, M. K., & Posner, M. I. (2012). Neural corre-
lates of establishing, maintaining, and switching brain states.
Trends in Cognitive Sciences, 16(6), 330–337. https://doi.org/10
.1016/j.tics.2012.05.001, PubMed: 22613871
Tenenbaum, J. B., de Silva, V., & Langford, J. C. (2000). A global
geometric framework for nonlinear dimensionality reduction.
Science, 290(5500), 2319–2323. https://doi.org/10.1126
/science.290.5500.2319, PubMed: 11125149
Titouan, V., Courty, N., Tavenard, R., Laetitia, C., & Flamary, R.
(2019). Optimal transport for structured data with application
on graphs. In K. Chaudhuri & R. Salakhutdinov (Eds.), Proceed-
ings of the 36th International Conference on Machine Learning
(Vol. 97, pp. 6275–6284). PMLR. https://proceedings.mlr.press
/v97/titouan19a.html
Tognoli, E., & Kelso, J. A. S. (2014). The metastable brain. Neuron,
81(1), 35–48. https://doi.org/10.1016/j.neuron.2013.12.022,
PubMed: 24411730
Topaz, C. M., Ziegelmeier, L., & Halverson, T. (2015). Topological
data analysis of biological aggregation models. PLoS One, 10(5),
e0126383. https://doi.org/10.1371/journal.pone.0126383,
PubMed: 25970184
Tymochko, S., Munch, E., & Khasawneh, F. A. (2020). Using zigzag
persistent homology to detect Hopf bifurcations in dynamical sys-
tems. Algorithms, 13(11), 278. https://doi.org/10.3390/a13110278
Ulmer, M., Ziegelmeier, L., & Topaz, C. M. (2019). A topological
approach to selecting models of biological experiments. PLoS
One, 14(3), e0213679. https://doi.org/10.1371/journal.pone
.0213679, PubMed: 30875410
Umeyama, S. (1988). An eigendecomposition approach to
weighted graph matching problems. IEEE Transactions on Pattern
Analysis and Machine Intelligence, 10(5), 695–703. https://doi
.org/10.1109/34.6778
van den Heuvel, M. P., & Hulshoff Pol, H. E. (2010). Exploring the
brain network: A review on resting-state fMRI functional connec-
tivity. European Neuropsychopharmacology, 20(8), 519–534.
https://doi.org/10.1016/j.euroneuro.2010.03.008, PubMed:
20471808
van der Maaten, L., Postma, E., & van den Herik, J. (2009). Dimen-
sionality reduction: A comparative review. Journal of Machine
Network Neuroscience
459
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal Mapper
Learning Research, 10, 66–71. https://members.loria.fr/moberger
/Enseignement/AVR/Exposes/TR_Dimensiereductie.pdf
Van Essen, D. C., Smith, S. M., Barch, D. M., Behrens, T. E. J.,
Yacoub, E., Ugurbil, K., & WU-Minn HCP Consortium. (2013).
The WU-Minn Human Connectome Project: An overview. Neu-
roImage, 80, 62–79. https://doi.org/10.1016/j.neuroimage.2013
.05.041, PubMed: 23684880
Vidaurre, D., Smith, S. M., & Woolrich, M. W. (2017). Brain network
dynamics are hierarchically organized in time. Proceedings of the
National Academy of Sciences, 114(48), 12827–12832. https://
doi.org/10.1073/pnas.1705120114, PubMed: 29087305
Wang, X.-J. (2002). Probabilistic decision making by slow rever-
beration in cortical circuits. Neuron, 36(5), 955–968. https://
doi.org/10.1016/S0896-6273(02)01092-9, PubMed: 12467598
Wilson, H. R., & Cowan, J. D., (1972). Excitatory and inhibitory
interactions in localized populations of model neurons. Biophys-
ical Journal, 12(1), 1–24. https://doi.org/10.1016/S0006-3495(72)
86068-5, PubMed: 4332108
Wilson, H. R., & Cowan, J. D. (1973). A mathematical theory of the
functional dynamics of cortical and thalamic nervous tissue.
Kybernetik, 13(2), 55–80. https://doi.org/10.1007/BF00288786,
PubMed: 4767470
Wong, K.-F., & Wang, X.-J. (2006). A recurrent network mechanism of
time integration in perceptual decisions. Journal of Neuroscience,
26(4), 1314–1328. https://doi.org/10.1523/JNEUROSCI.3733-05
.2006, PubMed: 16436619
Xu, H., Luo, D., & Carin, L. (2019). Scalable Gromov-Wasserstein
learning for graph partitioning and matching. In Proceedings of the
33rd International Conference on Neural Information Processing
Systems (pp. 3052–3062, Article 274). Curran Associates Inc.
h t t p s : / / p r o c e e d i n g s . n e u r i p s . c c / p a p e r / 2 0 1 9 / h a s h
/6e62a992c676f611616097dbea8ea030-Abstract.html
Zalesky, A., Fornito, A., Cocchi, L., Gollo, L. L., & Breakspear, M.
(2014). Time-resolved resting-state brain networks. Proceedings
of the National Academy of Sciences, 111(28), 10341–10346.
https://doi.org/10.1073/pnas.1400181111, PubMed: 24982140
Zaslavskiy, M., Bach, F., & Vert, J.-P. (2009). A path following
algorithm for the graph matching problem. IEEE Transactions on
Pattern Analysis and Machine Intelligence, 31(12), 2227–2242.
https://doi.org/10.1109/TPAMI.2008.245, PubMed: 19834143
Zhang, M., Kalies, W. D., Kelso, J. A. S., & Tognoli, E. (2020). Topo-
logical portraits of multiscale coordination dynamics. Journal of
Neuroscience Methods, 339, 108672. https://doi.org/10.1016/j
.jneumeth.2020.108672, PubMed: 32151601
Zhang, M., Sun, Y., & Saggar, M. (2022). Cross-attractor repertoire
provides new perspective on structure-function relationship in
the brain. Neuroimage, 259, 119401. https://doi.org/10.1016/j
.neuroimage.2022.119401, PubMed: 35732244
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
4
3
1
2
1
1
8
4
0
0
n
e
n
_
a
_
0
0
3
0
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
460