METHODS
Structural connectome constrained graphical
lasso for MEG partial coherence
Anirudh Wodeyar1,2,3,4 and Ramesh Srinivasan2
1Department of Cognitive Sciences, University of California, Irvine, California, USA
2Department of Statistics, University of California, Irvine, California, USA
3Department of Biomedical Engineering, University of California, Irvine, California, USA
4Department of Mathematics and Statistics, Boston University, Boston, Massachusetts, USA
Keywords: MEG, Gaussian graphical model, Coherence, Structural connectivity, Functional
connectivity
a n o p e n a c c e s s
j o u r n a l
ABSTRACT
Structural connectivity provides the backbone for communication between neural populations.
Since axonal transmission occurs on a millisecond time scale, measures of M/EEG functional
connectivity sensitive to phase synchronization, such as coherence, are expected to reflect
structural connectivity. We develop a model of MEG functional connectivity whose edges are
constrained by the structural connectome. The edge strengths are defined by partial coherence,
a measure of conditional dependence. We build a new method—the adaptive graphical lasso
(AGL)—to fit the partial coherence to perform inference on the hypothesis that the structural
connectome is reflected in MEG functional connectivity. In simulations, we demonstrate that
the structural connectivity’s influence on the partial coherence can be inferred using the AGL.
Further, we show that fitting the partial coherence is superior to alternative methods at
recovering the structural connectome, even after the source localization estimates required to
map MEG from sensors to the cortex. Finally, we show how partial coherence can be used
to explore how distinct parts of the structural connectome contribute to MEG functional
connectivity in different frequency bands. Partial coherence offers better estimates of the
strength of direct functional connections and consequently a potentially better estimate of
network structure.
INTRODUCTION
Electrophysiological signals are sampled on a millisecond time scale capturing aggregate syn-
aptic activity from populations of neurons. These neuro-physiological signals have intrinsic
time scales, organized in frequency bands; and intrinsic spatial organization, organized by
functional localization and integrated by the anatomical connectivity (Nunez & Srinivasan,
2006). Functional connectivity (FC) (Friston, 2011) refers to statistical dependence between
signals recorded from two different areas of the brain, usually measured in a predefined
frequency band. This broad definition encompasses different preprocessing methods
and statistical models that emphasize different temporal and spatial scales of the underlying
brain activity.
Coherence is a widely used measure of electroencephalography and magnetoencephalog-
raphy (M/EEG) functional connectivity (Nunez & Srinivasan, 2006). Coherence is modulated
Citation: Wodeyar, A., & Srinivasan, R.
(2022). Structural connectome
constrained graphical lasso for
MEG partial coherence. Network
Neuroscience, 6(4), 1219–1242.
https://doi.org/10.1162/netn_a_00267
DOI:
https://doi.org/10.1162/netn_a_00267
Supporting Information:
https://github.com/wodeyara
/AdaptiveGraphicalLassoforParCoh
Received: 13 April 2022
Accepted: 6 July 2022
Competing Interests: The authors have
declared that no competing interests
exist.
Corresponding Author:
Anirudh Wodeyar
wodeyar@bu.edu
Handling Editor:
Vince Calhoun
Copyright: © 2022
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license
The MIT Press
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
2
1
9
2
0
5
9
8
0
7
n
e
n
_
a
_
0
0
2
6
7
p
d
t
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
SC constrained graphical lasso for MEG partial coherence
across different cognitive tasks and clinical disease states (Baillet, 2017; Gross et al., 2013;
Rouhinen, Panula, Palva, & Palva, 2013; Roux & Uhlhaas, 2014; Siebenhühner, Wang, Palva,
& Palva, 2016; Stam, 2014). Coherence is expected to reflect delayed signal transmission
along white-matter tracts, that is, structural connections (Abdelnour, Voss, & Raj, 2014; Chu
et al., 2015; Meier et al., 2016; Nunez & Srinivasan, 2006; Schneider, Dann, Sheshadri,
Scherberger, & Vinck, 2020; Srinivasan, Winter, Ding, & Nunez, 2007) and is thus used to
characterize network structure.
However, mapping coherence to the anatomy is difficult due to its susceptibility to inflation
from leakage effects. Leakage effects are the shared activity across brain sources caused by the
limited resolution of source localization methods (Baillet, Mosher, & Leahy, 2001; Brookes
et al., 2011; Gross et al., 2001; Hämäläinen & Ilmoniemi, 1994; Wipf & Nagarajan, 2009)
to spatially separate source activity mixed by EEG volume conduction and MEG field spread
(Nunez & Srinivasan, 2006; Srinivasan et al., 2007). Leakage effects result in common signals
with zero phase difference between sources. One approach suggested to reduce leakage
effects, the imaginary coherence (Nolte et al., 2004), is based on using only the projection
of signals onto a phase difference of +/−90 degrees. However, this distorts the interpretation
of the strength of functional connectivity, by weighting toward signals with preselected phase
differences. Moreover, this approach is still susceptible to spurious connections when genuine
long-range connections exist at a delay and this activity is leaked to neighboring regions (Palva
et al., 2018).
We can use coherence or imaginary coherence to define the network edge weights, a crit-
ical first step for analyzing network structure, for example, using graph theoretical methods
(De Vico Fallani, Richiardi, Chavez, & Achard, 2014; Maldjian, Davenport, & Whitlow,
2014; Niso et al., 2015; Schoonheim et al., 2013). However, both coherence and imaginary
coherence reflect activity over single and multistep structural connectivity (Abdelnour et al.,
2014; Chu et al., 2015; Meier et al., 2016). This distorts the definition of a path (Avena-
Koenigsberger, Misic, & Sporns, 2018; Blinowska & Kaminski, 2013; Kaminski & Blinowska,
2018) over an undirected network and thus raises questions about the validity of network
structure analyses using networks defined by the strength of coherence.
In contrast to the coherence or imaginary coherence, partial coherence accounts for both
instantaneous and lagged shared information across multiple areas (Dahlhaus, 2000; Reid
et al., 2019; Sanchez-Romero & Cole, 2021). Partial coherence has a long history in neuro-
science: initially applied to spike trains (Rosenberg, Halliday, Breeze, & Conway, 1998) and
generalized in Baccalá and Sameshima (2001) to the partial directed coherence. The real-
valued analogue, partial correlation, has been applied to fMRI data across many studies
(Hinne, Janssen, Heskes, & van Gerven, 2015; Huang et al., 2010; Ng, Varoquaux, Poline,
& Thirion, 2012; Ryali, Chen, Supekar, & Menon, 2012; Smith et al., 2011; Varoquaux,
Gramfort, Poline, & Thirion, 2010; Wodeyar, Cassidy, Cramer, & Srinivasan, 2020). Partial
coherence represents the strength of linear relationships between a pair of brain areas when
accounting for their relationships with all other brain areas (Dahlhaus, 2000; Epskamp & Fried,
2018; Whittaker, 2009). It reduces false positive detection of direct connections resulting from
activity over indirect connections, as would result from leakage effects and multistep paths.
Thus, we can better interpret partial coherence as connection strength to define a functional
network. However, partial coherence estimation can be challenging. Most previous studies
using partial coherence have focused on cases where there are only a few nodes in the net-
work or used the L2-norm penalization for regularization (Baccalá & Sameshima, 2001;
Colclough et al., 2016; Dahlhaus, 2000; Medkour, Walden, & Burgess, 2009; Ter Wal
et al., 2018), without obvious justification. The use of the L2-norm is counterintuitive, as
Leakage effects:
Artifactual shared activity across
brain regions after M/EEG source
localization.
Partial coherence:
Transformation of the cross-spectral
density that allows inference of
conditional dependencies.
L2-norm penalization:
Penalizing the sum of squares of
precision weights, which we
normalize to get the partial
coherence.
Penalization structure:
The L1-norm penalties chosen for the
edges and non-edges of the network
constraint provided to the adaptive
graphical lasso.
Network Neuroscience
1220
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
2
1
9
2
0
5
9
8
0
7
n
e
n
_
a
_
0
0
2
6
7
p
d
.
/
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
SC constrained graphical lasso for MEG partial coherence
L1-norm penalization:
Estimating the precision while
penalizing the sum of the absolute
values of the precision.
Adaptive graphical lasso:
Extension of Ll-norm penalization
that permits different penalties to be
applied to different edges of the
precision.
the structural connectivity of the brain is known to be sparse, and there is little reason to
minimize the edge strengths. In the fMRI literature, when estimating partial correlation, several
studies have experimented with alternative regularization approaches: L1-norm (Huang et al.,
2010), elastic net (Ryali et al., 2012), group-based penalization approaches (Varoquaux et al.,
2010), edge-specific penalization (Ng et al., 2012), as well as Bayesian approaches to estima-
tion (Hinne et al., 2015). However, these alternative regularization approaches have not been
attempted in partial coherence estimation, in part because of the difficulty in implementing them.
We expect that functional connectivity is constrained by the structural connectome. In this
article, we make explicit use of the structural connectome to facilitate regularization of partial
coherence estimates. We use a graphical lasso technique modified to use the structural
connectome to guide the L1 penalization, a method we call the adaptive graphical lasso
(AGL). To our knowledge, this is the first time that the graphical lasso (L1-norm), and further
the graphical lasso using a constraint-based penalization, has been used to estimate partial
coherence for neural signals (Colclough et al., 2016; Ter Wal et al., 2018). We select the lasso
penalization through a novel cross-validation technique that separately identifies the optimal
penalization on and off the structural connectome. If the penalization is lower for edges in the
structural connectome, we have clearly identified that the pattern of connectivity is influenced
by the structural connectome. Note that the entire structural connectome need not be esti-
mated in the partial coherence, a subset may be estimated as a function of the data. Through
simulations, we aim to demonstrate that (1) the partial coherence can be estimated accurately
using the AGL, (2) we can directly test whether the structural connectome is a useful constraint
in network identification, and (3) the partial coherence serves as a better functional connec-
tivity metric than the coherence or imaginary coherence. Finally, we use the AGL-estimated
partial coherence to demonstrate distinct contributions of the structural connectome to MEG
signals in different frequency bands.
METHODS
Overview
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
2
1
9
2
0
5
9
8
0
7
n
e
n
_
a
_
0
0
2
6
7
p
d
t
.
/
This work is guided by the intuition that the statistics of neural activity data collected at
the mesoscale (intracranial electrocorticography – ECoG) and macroscale (M/ EEG) are
constrained by structural connectivity of the axon fiber systems of the cortex. As such, we have
built a minimal generative computational model, representing the partial coherence, that is
derived from estimates of structural connectivity and we have developed a method to infer
model parameters. We allowed the structural connectivity to potentially guide the estimation
of the partial coherence and developed new simulations to link this work with M/EEG and
ECoG data.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Structural Connectome
We built a template of the structural connectome (SC) from a probabilistic atlas. We used
streamlines generated with deterministic tractography by Yeh et al. (2018) using the
HCP842 dataset (Van Essen et al., 2013) transformed to the MNI152 template brain obtained
from the FMRIB Software Library (FSL). In this dataset experts vet the streamlines to remove
potentially noisy estimates of axonal fibers. We applied the Lausanne parcellation (Cammoun
et al., 2012) of 114 cortical and 15 subcortical regions of interest (ROIs) to the MNI152
template brain and generated a volumetric representation for each region of interest using
the easy_lausanne toolbox (Cieslak, 2015). Each streamline was approximated by a single
100-point cubic spline using code adapted from the along-tract-stats toolbox (Colby et al.,
Network Neuroscience
1221
SC constrained graphical lasso for MEG partial coherence
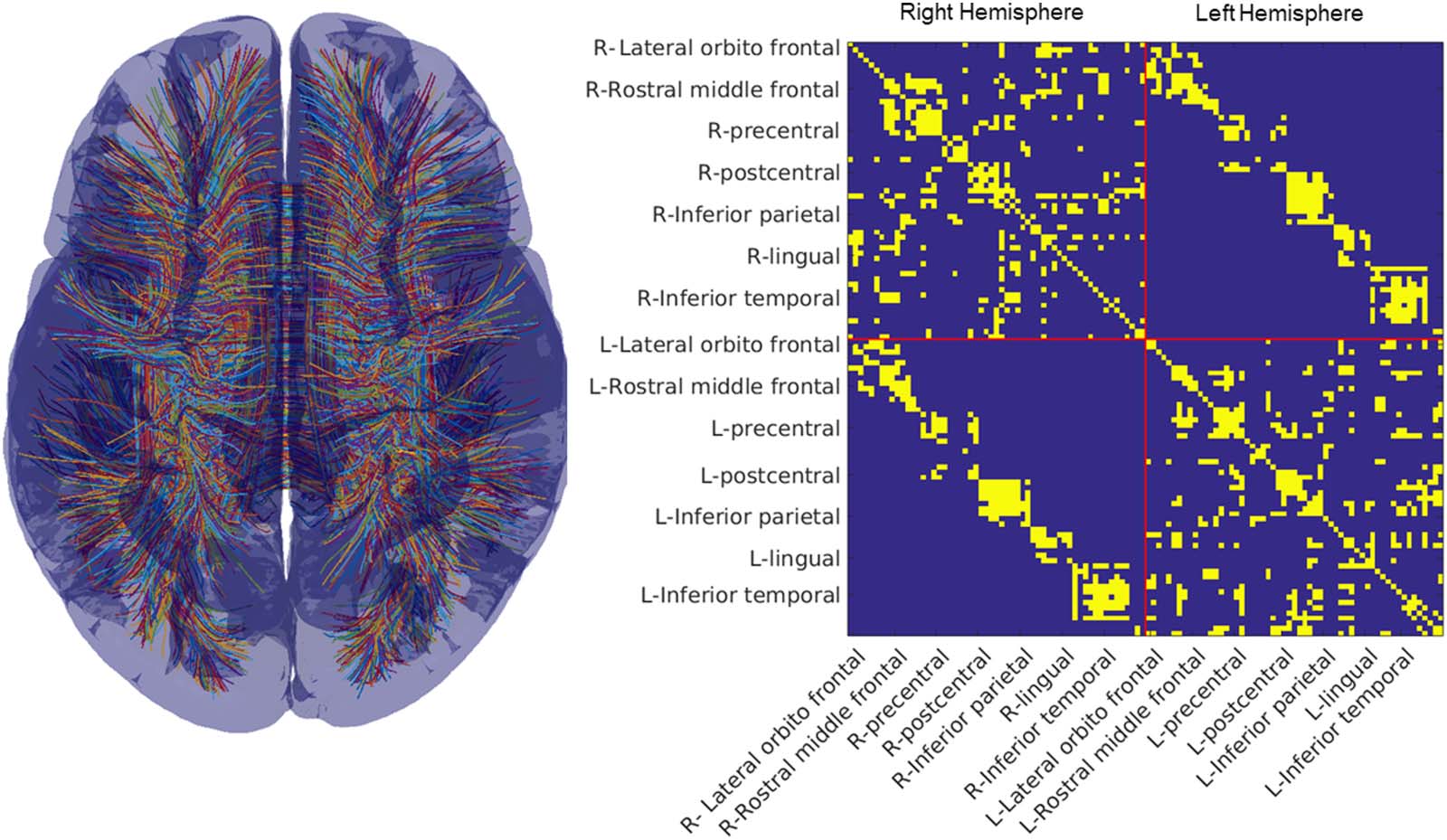
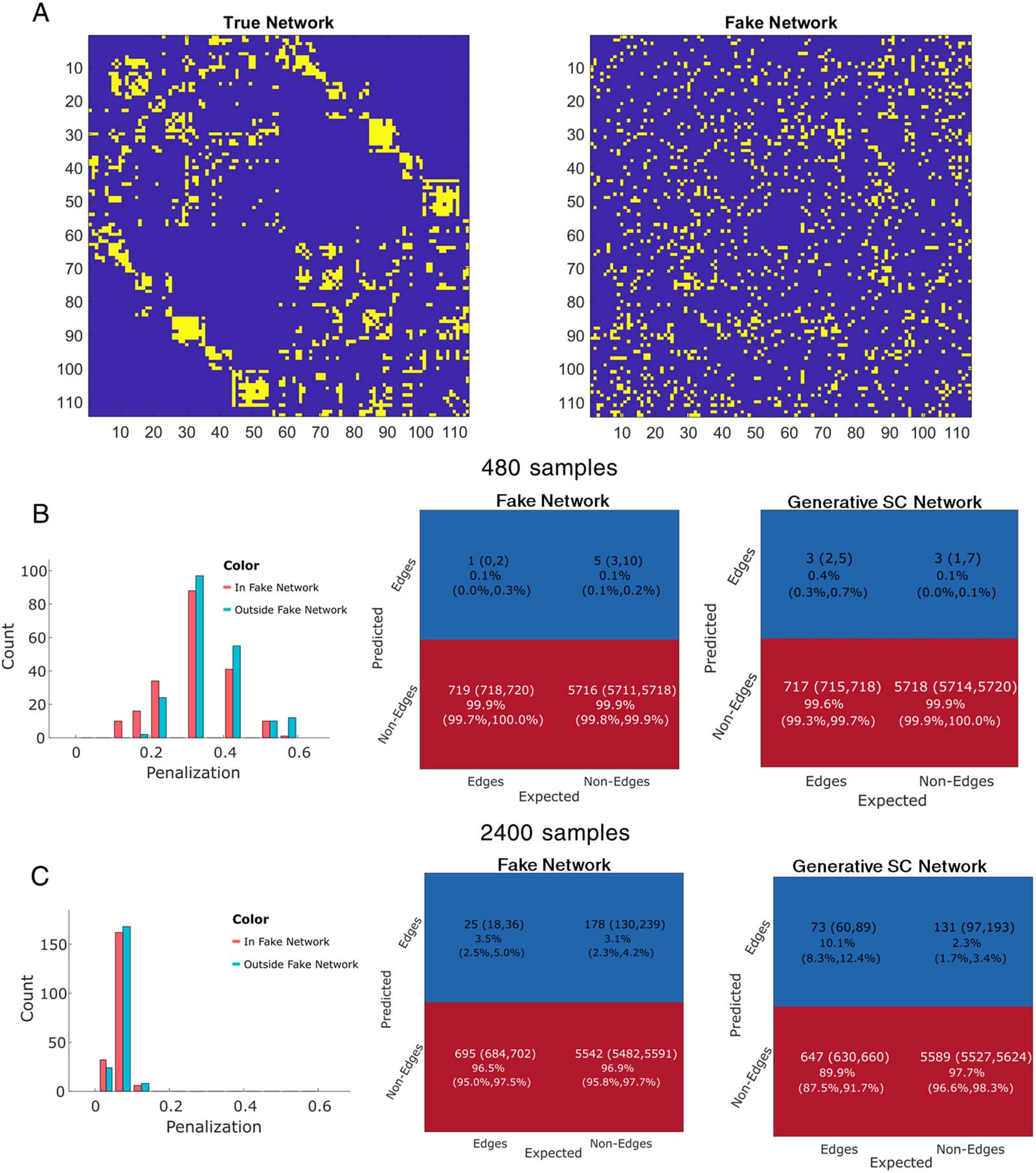
Structural connectome. (Left) We show streamlines derived from the work of Yeh et al. (2018) using the HCP-842 dataset. (Right)
Figure 1.
The structural connectome for the 114 areas of the Lausanne parcellation. We have labeled a subset of areas each with one to three subdi-
visions (see Cammoun et al., 2012, for all subdivisions of the Lausanne parcellation). We show the undirected and unweighted SC, with any
nonzero edge being shown in yellow.
2012). By identifying the streamlines which terminated in a pair of ROIs, we were able to
create the SC for the Lausanne parcellation. Each streamline only connected a single pair
of ROIs. An edge Wij for ROIs i and j existed if there was a streamline connecting the pair.
From this process, we built the 129 × 129 undirected and unweighted structural connec-
tome with 1,132 edges. We reduced this matrix to 114 × 114 with 720 edges (see Figure 1)
after removing all the subcortical structures and limiting interhemispheric connections to
homologous white-matter tracts. This latter step helped remove potentially noisy estimates
of connections (while potentially increasing false negatives) where streamlines intersected
and passed outside the cortical surface before reaching the terminal point in a brain region.
The resulting template of structural connectivity shown in Figure 1 is referred to as the struc-
tural connectome (SC). This template is incomplete in that it does not include subcortical to
cortical projections. Thus, functional connectivity resulting from structural connections not
captured by this template may exist in the data. Our estimation procedure for the graphical
models of functional connectivity described in the next section allows for such connections, if
needed, to account for the statistical structure in the data.
Generative Model
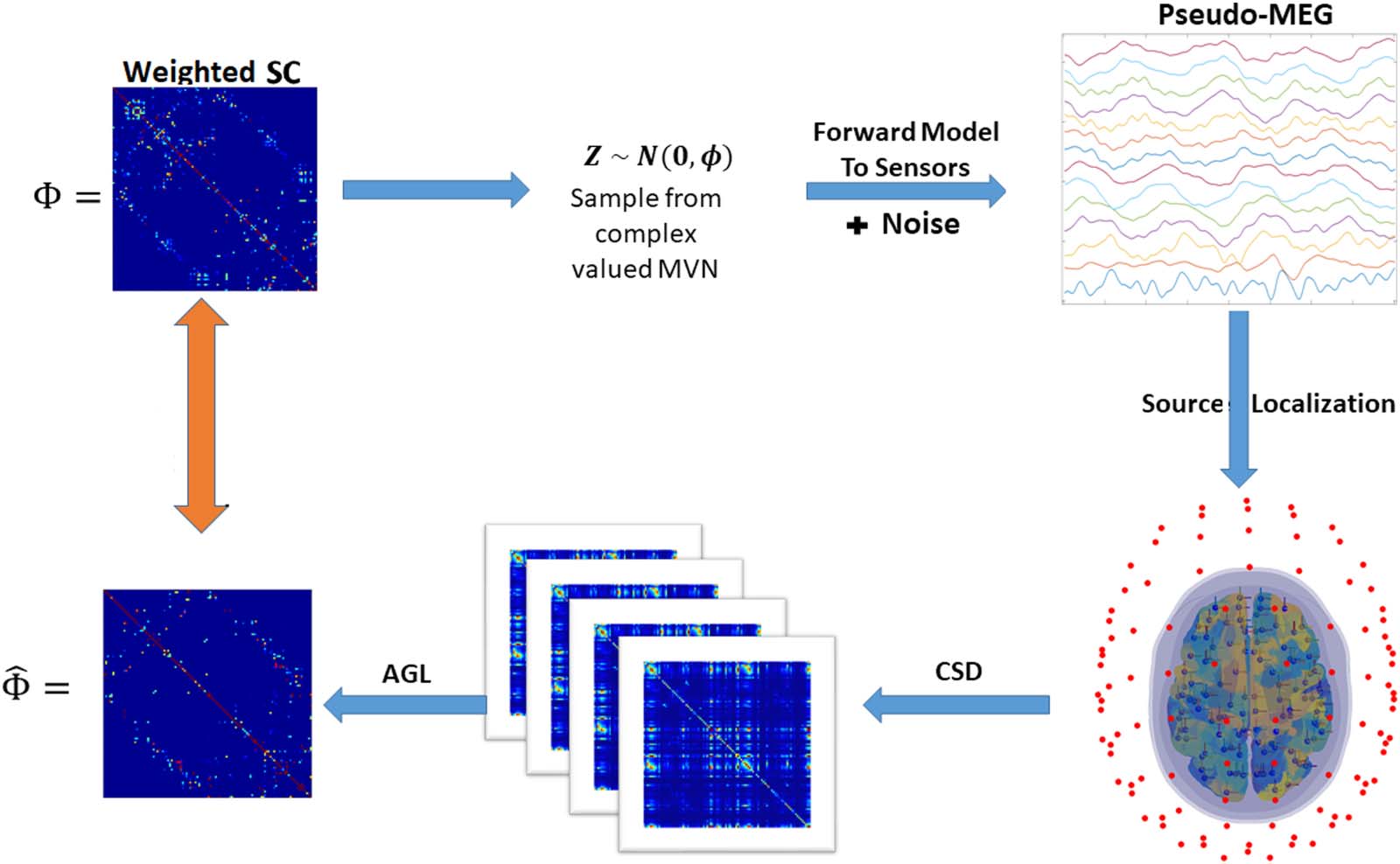
Complex-valued Gaussian graphical model. We assume that a vector of activity (Z) in one fre-
quency band is a sample drawn from a complex-valued multivariate Gaussian. Here Φ is
the precision—the unnormalized partial coherence—and is determined by the SC:
Z ∼ N 0; Φð
Þ
(1)
In the frequency domain, a signal can be characterized by samples of amplitude and phase, or
equivalently, by complex-valued coefficients with real and imaginary parts corresponding to
sine and cosine components of the signal.
Network Neuroscience
1222
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
2
1
9
2
0
5
9
8
0
7
n
e
n
_
a
_
0
0
2
6
7
p
d
/
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
SC constrained graphical lasso for MEG partial coherence
The complex-valued multivariate Gaussian for a zero-mean (where E(Z) = 0 + 0i) process
(Schreier & Scharf, 2010) is defined as:
where
and
ρ Zð Þ ¼
1
πn det
1
2 Σð Þ
(cid:1)
exp − 1
2
(cid:3)
ZΣ−1ZH
(cid:4)
Σ ¼
(cid:5)
Rzz
eRH
eRzz
zz Rzz
H
(cid:6)
Rzz ¼ E zzH
(cid:7)
(cid:6)
; eRzz ¼ E zzT
(cid:7)
(2)
(3)
(4)
The key parameter in this model is the covariance matrix Θ and its inverse, the precision
matrix Φ = Θ−1. As defined in Equations 3 and 4, the covariance matrix for complex-valued
data is composed of the familiar cross-spectrum Rzz and the complementary cross-spectrum
eR
zz. Most spectral analysis methods only make use of Rzz and implicitly assume circular sym-
metry, that is, eR
zz = 0 (Schreier & Scharf, 2010). In this case, the complex-valued data is
labeled as proper. With the assumption of circular symmetry, we can parameterize the
complex-valued Gaussian using the precision as:
Φ ¼ Rzz
−1
(5)
Each value in the precision matrix Φ is the conditional covariance between any two variables
(here, sources representing two ROIs) given the other variables (all other ROIs). The precision
represents a model of functional connectivity—the conditional dependence between sources.
The strength of the conditional dependence represents the linear relationship between any
pair of sources when linear effects from all other sources are removed (see Section 2.2.2 of
Pourahmadi, 2011 for an intuitive explanation in terms of multivariate linear regression). For
any pair of sources, if the precision is zero, there is no need for a relationship between the
sources to account for observed coherence. Such apparent coherences arise from
connections mediated via other sources in the model. Note that the precision directly
represents a complex-valued Gaussian graphical model (Whittaker, 2009).
In the generative model, we choose to set up the precision matrix Φ to have a nonzero entry
only at edges that have a connection in the SC. We are assuming that in each frequency band,
coherence represents the result of joint random fluctuations of a set of oscillators whose con-
nections are determined by the SC. The precision vales are estimated using the graphical lasso
in a cross-validated procedure that allows potentially using the SC as a guide for the L1 penal-
ization. In this way the nonzero locations and values of the precision are determined by
the data.
Adaptive graphical lasso. The graphical lasso (Friedman, Hastie, & Tibshirani, 2008) is a
method that has been applied in multiple fields in the past decade, from genomics (Menéndez,
Kourmpetis, ter Braak, & van Eeuwijk, 2010) to fMRI functional connectivity (Ng et al., 2012;
Ryali et al., 2012; Varoquaux et al., 2010; Wodeyar et al., 2020) and climate models (Zerenner,
Friederichs, Lehnertz, & Hense, 2014). It is used to identify a sparse approximation to the
regularized precision matrix while solving problems arising from rank deficiency and small
numbers of samples. To apply the lasso, we optimize the penalized likelihood function for a
Network Neuroscience
1223
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
2
1
9
2
0
5
9
8
0
7
n
e
n
_
a
_
0
0
2
6
7
p
d
.
t
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
SC constrained graphical lasso for MEG partial coherence
multivariate Gaussian (Meinshausen & Bühlmann, 2006) to estimate the precision—where Θ
(Rzz in Equation 4) is the cross-spectral density (CSD):
^Φ ¼ arg minΦ≻0 − log detΦð
Þ þ tr ΘΦð
X
(cid:8)
(cid:8)
Þ þ λ
(cid:8)
(cid:8)
Φjk
j
ð
− log detΦ
ð
ð
ð
Þ þ tr Θ þ δ * I
Þ
ÞΦ
Þ
(8)
Since Θ (covariance) is usually rank deficient, we add a small value (δ) along the diagonal to
make it full rank. We fixed δ as 0.001 times the maximum value along the upper triangle of the
covariance.
Cross-validation. We test whether the AGL produced estimates of the precision that show
reduced error relative to applying the graphical lasso using cross-validation. Note that applying
the graphical lasso would be equivalent to having the penalization inside and outside the SC be
equal, that is, λ1 = λ2. We estimated the appropriate value for λ1 and λ2 using cross-validation.
We split data into four ensembles, and repeated the following analysis with each ensemble.
We estimated the precision eΦi on one ensemble of the data (i) and estimated the deviance
when using this precision as the inverse for the covariance Θj for all the other ensembles j
of the data (and vice versa). Deviance was estimated as:
Dev ¼
X
X
i¼1:4
j¼1:4;j≠i
(cid:9)
(cid:9)
− log deteΦi
(cid:10)
(cid:9)
þ tr Θj
eΦi
(cid:10)
(cid:10)
(9)
In every frequency band, or for each iteration of our simulation, we esti-
Partial coherence.
mated the precision for complex-valued data incorporating amplitude and phase for a
Deviance:
Estimate of the goodness-of-fit
between the estimated precision and
out-of-sample estimated cross-
spectral density.
Network Neuroscience
1224
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
6
4
1
2
1
9
2
0
5
9
8
0
7
n
e
n
_
a
_
0
0
2
6
7
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
SC constrained graphical lasso for MEG partial coherence
frequency band. The normalization of the precision (Φ) yields the partial coherence (PC )
(Dahlhaus, 2000), estimated using:
PCz1z2
¼
(cid:8)
(cid:8)
(cid:8)
(cid:8)
p
Φz1z2
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
Φz1z1 * Φz2z2
2
(cid:8)
(cid:8)
(cid:8)
(cid:8)
(10)
Contemporary Methods for Functional Connectivity
We considered three alternative methods to compare the partial coherence model estimated
from AGL: coherence, imaginary coherence, and the partial coherence estimated when regu-
larizing using the L2 norm. We estimate coherence C from the cross-spectral density Θ, where
z1, z2 are the amplitude and phase information in one frequency band from two sources, as:
Cz1z2
¼
(cid:8)
(cid:8)
(cid:8)
(cid:8)
p
(cid:8)
(cid:8)
Θz1z2
(cid:8)
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
(cid:8)
Θz1z1 * Θz2z2
2
(11)
Imaginary coherence is believed to reduce the influence of volume conduction and zero
phase lag connectivity (such as would exist from source leakage). The idea is to minimize this
effect by estimating the consistency of the imaginary part of the cross-spectral density between
two sources. We measure it using (where imag refers to the imaginary component of the com-
plex value from the cross-spectral density):
(cid:8)
(cid:8)
(cid:8)
(cid:8)
(12)
ICz1z2
(cid:8)
(cid:8)
(cid:8)
(cid:8)
p
2
Þ
ð
¼ imag Θz1z2
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
Θz1z1 * Θz2z2
Coherence and imaginary coherence networks are defined using a threshold derived using
bootstrapping (Zoubir & Boashash, 1998). We define a population distribution by resampling
1,000 times with replacement. We kept C or IC edges with distributions that did not cover 0 at
an alpha value of 0.05.
Finally, we consider an alternative regularization to estimate the partial coherence—an
L2-norm penalization. This style of regularization does not force precision values to zero
but instead minimizes them to optimize the likelihood. The penalized likelihood for the L2
norm inverse is:
^Φ ¼ arg minΦ≻0 − log detΦð
Þ þ tr ΘΦð
Þ þ η *
X
(cid:8)
(cid:8)
(cid:8)
(cid:8)2
Φjk
j