METHODS

Toward an information theoretical description of
communication in brain networks

Enrico Amico1,2, Kausar Abbas3,4, Duy Anh Duong-Tran4, Uttara Tipnis3,4, Meenusree
Rajapandian4, Evgeny Chumin5, Mario Ventresca4, Jaroslaw Harezlak6, and Joaquín Goñi3,4,7

1Institute of Bioengineering, Center for Neuroprosthetics, EPFL, Geneva, Switzerland
2Department of Radiology and Medical Informatics, University of Geneva (UNIGE), Geneva, Switzerland
3Purdue Institute for Integrative Neuroscience, Purdue University, West Lafayette, IN, USA
4School of Industrial Engineering, Purdue University, West Lafayette, IN, USA
5Psychological and Brain Sciences, Indiana University, Bloomington, IN, USA
6Department of Epidemiology and Biostatistics, Indiana University, Bloomington, IN, USA
7Weldon School of Biomedical Engineering, Purdue University, West Lafayette, IN, USA

Keywords: Human connectome, Communication regimes, Brain connectomics, Information theory,
Brain networks

ABSTRACT

Modeling communication dynamics in the brain is a key challenge in network neuroscience.
We present here a framework that combines two measurements for any system where different
communication processes are taking place on top of a fixed structural topology: path
processing score (PPS) estimates how much the brain signal has changed or has been
transformed between any two brain regions (source and target); path broadcasting strength
(PBS) estimates the propagation of the signal through edges adjacent to the path being
assessed. We use PPS and PBS to explore communication dynamics in large-scale brain
networks. We show that brain communication dynamics can be divided into three main
“communication regimes” of information transfer: absent communication (no communication
happening); relay communication (information is being transferred almost intact); and
transducted communication (the information is being transformed). We use PBS to categorize
brain regions based on the way they broadcast information. Subcortical regions are mainly
direct broadcasters to multiple receivers; Temporal and frontal nodes mainly operate as
broadcast relay brain stations; visual and somatomotor cortices act as multichannel
transducted broadcasters. This work paves the way toward the field of brain network
information theory by providing a principled methodology to explore communication
dynamics in large-scale brain networks.

INTRODUCTION

Deciphering communication dynamics in the human brain is one of the biggest open chal-
lenges in modern neuroscience (Avena-Koenigsberger et al., 2018). Communication in the
brain can be measured and modeled at different spatial scales: starting from the fine-grained
microscale exploration of information transfer between neuronal spikes (Quian Quiroga &
Panzeri, 2009; Timme & Lapish, 2018), to inferring communication at mesoscale from

a n o p e n a c c e s s

j o u r n a l

Citation: Amico, E., Abbas, K., Duong-
Tran, D. A., Tipnis, U., Rajapandian, M.,
Chumin, E., Ventresca, M., Harezlak, J.,
& Goñi, J. (2021). Toward an
information theoretical description of
communication in brain networks.
Network Neuroscience, 5(3), 646–665.
https://doi.org/10.1162/netn_a_00185

DOI:
https://doi.org/10.1162/netn_a_00185

Supporting Information:
https://doi.org/10.1162/netn_a_00185

Received: 06 November 2019
Accepted: 18 January 2021

Corresponding Author:
Joaquín Goñi
jgonicor@purdue.edu

Handling Editor:
Daniel Graham

Copyright: © 2021
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license

The MIT Press

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

t

/

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
3
6
4
6
1
9
6
0
4
9
0
n
e
n
_
a
_
0
0
1
8
5
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Toward an information theoretical description of the human connectome

Graph:
An ordered pair formed by a set of
nodes and a set of edges (which
represent connections between pairs
of nodes). Nodes are usually
represented by circles, whereas
edges are represented by lines or arcs
connecting pairs of nodes.

Connectome or structural
connectivity (SC) matrix:
A network representation of the
physical connections in the brain.
Nodes represent brain regions,
whereas edges represent physical
connections of pairs of brain regions
through the white matter. Weights
typically denote the density or also
the integrity of the connections.

Functional magnetic resonance
imaging (fMRI):
A noninvasive technique that
estimates brain activity by detecting
changes associated with blood flow.
The rationale of this technique relies
on the fact that there is a positive
association between cerebral blood
flow and neuronal activation.

Functional connectome/connectivity
(FC) matrix:
A network representation of the
functional coupling between brain
regions. Such coupling is usually
measured by quantifying the
statistical dependencies between
time series of brain regions (e.g.,
pairwise Pearson’s correlation,
mutual information) as obtained by
functional magnetic resonance
imaging (fMRI).

Search information:
measurement that quantifies the
accessibility or hiddenness of the
shortest path between a source node
and a target node within the network
by measuring the amount of
knowledge or information (expressed
in bits) needed to access that exact
path.

electrical activity of cortical populations (Laughlin & Sejnowski, 2003; Nigam et al., 2016), up
to macroscale brain networks estimated from in vivo magnetic resonance imaging (MRI) data;
the latter being the focus of this work.

Particularly, in large-scale (MRI-based) brain networks, many hurdles have made the inves-
tigation of brain communication challenging. One issue arises from data acquisition, which
outputs noisy and indirect measurements of neuronal activity (and subsequent connectivity
or information transfer). Another issue is the difficulty of validating in silico brain communi-
cation models, although meaningful progress has been made (see Aerts et al., 2018; Cabral
et al., 2017; Glomb et al., 2017; Ritter et al., 2013; Sanz Leon et al., 2013). Additionally, sev-
eral methodological factors such as selection of temporal scales, frequency ranges, time win-
dows, and time-varying or lagged dependencies can have significant impact on assessment of
brain communication dynamics (Avena-Koenigsberger et al., 2018).

Nonetheless, in the last two decades, improvements in MRI hardware and development of
new data acquisition sequences have allowed for application of methodologies from graph
theory and dynamical systems, giving rise to the field of network neuroscience or brain con-
nectomics (Bassett & Sporns, 2017; Fornito et al., 2016). In brain connectomics, the investi-
gation of functional and structural connections in the human brain is modeled using tools and
methods from network science (Fornito et al., 2016; Sporns, 2010). Structural connections be-
tween brain region pairs are modeled from diffusion-weighted imaging data, denominated as
structural connectome or structural connectivity (SC). Functional connections are modeled
from functional magnetic resonance imaging data (fMRI), by measuring temporal statistical
dependences between brain region pairs, usually defined as functional connectivity or func-
tional connectome (FC). Examining human brain connectivity data offers new insights on how
the integration and segregation of information in the brain relates to human behavior (Deco
et al., 2015; Sporns, 2013), and how network organization may be altered in neurological
diseases and disorders (Bassett & Bullmore, 2009; Fornito et al., 2015; Rosazza & Minati,
2011; Stam, 2014).

Brain connectomics has provided a proper mathematical framework upon which network
neuroscientists have begun to layout several alternative models to capture and explain the
complex patterns of brain communication dynamics stemming from large-scale brain net-
works. Pioneering work started by assessing the link between network topology and commu-
nication, from routing-based models with full knowledge of the topology of the brain network
(i.e., signaling along shortest paths, de Pasquale et al., 2016; Graham, 2014), to diffusion
models “uninformed” of the topology of the network (Abdelnour et al., 2014; Raj et al.,
2012). Hybrid models exploring a spectrum of communication dynamics, including search
information (Goñi et al., 2013, 2014), navigation (Seguin et al., 2018), or k-shortest path en-
sembles (Avena-Koenigsberger et al., 2017), have also been investigated. Recent studies have
also looked into alternative network communication measures such as Markovian queuing
networks (Mišić et al., 2014b), linear transmission models of spreading dynamics (Mišić
et al., 2015; Worrell et al., 2017), cooperative learning (Tipnis et al., 2018), and diffusion pro-
cesses based on memory-biased random walks (Masuda et al., 2017), as well as studying
asymmetries of communication in large-scale brain networks (Seguin et al., 2019).

Despite all these efforts in the development of communication models that explain human
brain dynamics (Hahn et al., 2019; Joglekar et al., 2018), there is a lack of a principled theory
of brain network communication, which aims to address the following question: how can one
characterize the multifold communication regimes originating in the brain, on top of a fixed
physical constrain represented by its structural connections?

Network Neuroscience

647

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

t

/

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
3
6
4
6
1
9
6
0
4
9
0
n
e
n
_
a
_
0
0
1
8
5
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Toward an information theoretical description of the human connectome

Path processing score (PPS):
Estimates how much a brain signal
has changed or transformed on a
specific path between a source and a
target brain region. A negative score
is indicative of a path that is not
being used for communication;
a PPS around zero indicates that
information is passed almost intact
along a path from the source to the
target, whereas a high PPS indicates
that the signal has gone through
considerable transformation. Units
are bits.

Path broadcasting strength (PBS):
Estimates the propagation of the
signal through the edges adjacent to
a path being assessed (in this study
we specifically assessed shortest
paths). A low PBS indicates a routing-
based communication along a path,
whereas a high PBS indicates that the
communication is not specific to that
path, but is also being broadcast or
propagated through neighboring
edges. Units are bits/mm when using
fiber length (mm) derived structural
connectomes to establish the paths.

As a matter of fact, human brain connectivity can be modeled by a multilayered complex
network that contains one slowly evolving structural topology (its structural connectome) and
one rapidly evolving task-dependent functional architecture (its FC) (Amico et al., 2019; Cole
et al., 2014). In this context, there is a lack of a well-grounded mathematical framework that
can associate structural and functional patterns and quantify the many facets of communication
dynamics.

Here, we introduce a framework that combines two information-theoretical measurements
for any system where different communication processes are taking place over a fixed struc-
tural topology. The first measurement, path processing score (PPS), estimates how much the
brain signal has changed or transformed on a path between a source and a target brain region.
A negative score is indicative of a path that is not being used for communication, a PPS
around zero indicates that information is passed almost intact along a path from the source
to the target, whereas a high PPS indicates that the signal has gone through considerable trans-
formation. The second measurement, path broadcasting strength (PBS), estimates the propa-
gation of the signal through the edges adjacent to the path being assessed. A low PBS indicates
a routing-based communication along a path, whereas a high PBS indicates that the commu-
nication is not specific to that path, but is also being broadcast or propagated through neigh-
boring edges.

We apply these two measurements to investigate the communication dynamics in resting-
state and task functional MRI (fMRI) of 100 unrelated subjects from the Human Connectome
Project (HCP). By assessing PPS, we show that routing communication dynamics in large-scale
brain networks can be separated into three main “regimes”: absent communication, where no
communication is happening along that path; relay communication, where communication is
specific to that path (i.e., unchanged or minimally changed brain signal); and transducted
communication, where communication is not path specific (i.e., transformed; modified brain
signal). In addition to these three regimes, we show that our second metric, PBS, can quantify
the spread of information transfer around the path (i.e., routing or diffused communication/
broadcasting).

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

t

/

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
3
6
4
6
1
9
6
0
4
9
0
n
e
n
_
a
_
0
0
1
8
5
p
d

t

.

The information theoretical framework presented here allows for the joint assessment of
structural and functional connectivity and has revealed different communication regimes
across brain regions and different cognitive tasks. Furthermore, it also revealed a regional
specificity in the way the brain broadcasts information, by categorizing brain regions into three
main “communication modalities”: direct broadcasters to multiple receivers (predominantly
subcortical regions); broadcast relay brain stations (mainly limbic system); and, finally, multi-
channel transducted broadcasters (mainly visual and somatomotor cortices).

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

This investigation was motivated by a need to better understand communication dynamics
in large-scale brain networks, and it was partly inspired by the seminal masterpiece by Claude
Shannon (Shannon, 1948). Several studies have shown functional connectivity changes across
fMRI conditions (Amico et al., 2019, 2020; Cole et al., 2014; Gonzalez-Castillo & Bandettini,
2018; Mohr et al., 2016; Schultz & Cole, 2016). In other words, there is an adaptation or func-
tional reconfiguration that occurs as subjects perform different tasks and/or switch between
different cognitive modes (Gilson et al., 2018; Gonzalez-Castillo & Bandettini, 2018; Shine
et al., 2016; Shine & Poldrack, 2018). In this paper, we further investigate how those changes
can be reflected by communication regimes tracked on underlaying SC paths. With this work,
we introduce a new framework based on information theoretical principles to infer the basic
units of information transfer in large-scale human brain networks, as well as to assess how they
change and evolve between subjects or across cognitive tasks.

Network Neuroscience

648

Toward an information theoretical description of the human connectome

Diffusion-weighted imaging (DWI):
A form of magnetic resonance
imaging (MRI) technique based on
measuring the random Brownian
motion of water molecules within
a voxel based on sampling 3D
directions. This technique allows for
estimating white matter streamlines
and fiber bundles connecting brain
regions.

METHODS

Dataset

The dataset of functional and structural neuroimaging data used in this work came from the
Human Connectome Project (HCP, https://www.humanconnectome.org/), Release Q3. Per
HCP protocol, all subjects gave written informed consent to the HCP consortium. These data
contained fMRI and diffusion-weighted imaging (DWI) acquisitions from 100 unrelated sub-
jects of the HCP 900 data release (Van Essen et al., 2012, 2013). All HCP scanning protocols
were approved by the local Institutional Review Board at Washington University in St. Louis.

HCP: fMRI Acquisition

We used fMRI runs from the 100 unrelated subjects of the HCP 900 subjects data release (Van
Essen et al., 2012, 2013). The fMRI resting-state runs (HCP filenames: rfMRI_REST1 and
rfMRI_REST2) were acquired in separate sessions on two different days, with two different acqui-
sitions (left to right or LR and right to left or RL) per day (Glasser et al., 2013; Van Essen et al.,
2012, 2013). The seven fMRI tasks were the following: gambling (tfMRI_GAMBLING), relational
(tfMRI_RELATIONAL), social (tfMRI_SOCIAL), working memory (tfMRI_WM), motor
(tfMRI_MOTOR), language (tfMRI_LANGUAGE, including both a story-listening and arithmetic
task), and emotion (tfMRI_EMOTION). The working memory, gambling, and motor tasks were
acquired on the first day; all other tasks were acquired on the second day (Barch et al., 2013;
Glasser et al., 2013). For all sessions, data from both the LR and RL phase-encoding runs were
used to calculate connectivity matrices and averaged together. Full details on the HCP dataset
have been published previously (Barch et al., 2013; Glasser et al., 2013; S. M. Smith et al., 2013).

HCP: DWI Acquisition

We used DWI data from the same 100 unrelated subjects of the HCP 900 subjects data release
(Van Essen et al., 2012, 2013). The diffusion-weighted (DW) acquisition protocol is covered in
detail elsewhere (Glasser et al., 2013; Sotiropoulos et al., 2013). Below we mention the main
characteristics. Very high resolution acquisitions (1.25 mm isotropic) were obtained by using a
Stejskal–Tanner (monopolar) (Stejskal & Tanner, 1965) diffusion-encoding scheme. Sampling in
q-space was performed by including three shells at b = 1,000, 2,000 and 3,000 s/mm2. For
each shell, a corresponding 90 diffusion gradient directions and 5 b0 volumes were acquired
twice, with the phase-encoding (PE) direction reversed for each pair (i.e., LR and RL pairs).
Directions were optimized within and across shells (i.e., staggered) to maximize angular cov-
erage using the approach of Caruyer et al. (2011) (https://www-sop.inria.fr/members/Emmanuel
.Caruyer/q-space-sampling.php) and form a total of 270 noncollinear directions for each PE
direction. Correction for echo planar acquisition and eddy-current-induced distortions in the
diffusion data was based on manipulation of the acquisitions so that a given distortion manifests
itself differently in different images (Andersson et al., 2003). To ensure better correspondence
between the PE reversed pairs, the whole set of DW volumes was acquired in six separate se-
ries. These series were grouped into three pairs, and within each pair the two series contained
the same DW directions but with reversed phase encoding (i.e., a series of DW volumes with
RL phase encoding is followed by a series of volumes with LR phase encoding).

Brain Parcellation

We employed a cortical parcellation of 360 brain regions, as recently proposed by Glasser
et al. (2016) for definition of brain network nodes. For completeness, 14 subcortical regions
were added, as provided by the HCP release (filename “Atlas_ROI2.nii.gz”), as analogously

Network Neuroscience

649

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

t

/

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
3
6
4
6
1
9
6
0
4
9
0
n
e
n
_
a
_
0
0
1
8
5
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Toward an information theoretical description of the human connectome

done in previous papers (Amico et al., 2019; Amico & Goñi, 2018a, 2018b). To do so, this file
was converted from NIFTI to CIFTI format by using the HCP workbench software (Glasser et al.,
2013; Marcus et al., 2011) (command -cifti-create-label https://www.humanconnectome.org
/software/connectome-workbench.html).

HCP: fMRI Preprocessing

Data were processed following the HCP functional preprocessing guidelines (Glasser et al.,
2013; S. M. Smith et al., 2013). Briefly, processing steps included artifact removal, motion
correction, and registration to standard Montreal Neurological Institute space in both volumet-
ric and grayordinate formats (i.e., where brain locations are stored as surface vertices; S. M.
Smith et al., 2013), with weak highpass temporal filtering (>2,000s full width at half maximum)
applied to both formats, for slow drift removal. MELODIC ICA (Jenkinson et al., 2012) was
applied to volumetric data, and artifact components were subsequently identified using FSL-
FIX (Salimi-Khorshidi et al., 2014). Artifacts and motion-related time courses (i.e., the six rigid-
body parameter time series, their backward-looking temporal derivatives, plus all 12 resulting
regressors squared) were then regressed out of both volumetric and grayordinate data (S. M.
Smith et al., 2013).

For the resting-state fMRI data, we also added the following steps (Amico et al., 2019;
Amico & Goñi, 2018a, 2018b): global gray matter signal was regressed out of the voxel time
courses (Power et al., 2014); a bandpass first-order Butterworth filter in forward and reverse
directions [0.001 Hz, 0.08 Hz] was applied (Matlab functions butter and filtfilt); voxel time
courses were z-scored and then averaged per brain region, excluding outlier time points out-
side of 3 standard deviation from the mean, using the workbench software (Marcus et al.,
2011) (workbench command -cifti-parcellate). For task fMRI data, we applied the same steps,
with exception of a less restrictive range for the bandpass filter [0.001 Hz, 0.25 Hz].

Functional connectivity network edge weights were defined as mutual information (Cover
& Thomas, 2012; Shannon, 1948) between all node pairs, calculated by uniform binning of
the z-scored BOLD time courses (bin widths = 0.5 standard deviation, spanning range = [−3.5
3.5] z-scored BOLD activation). This resulted in a positive symmetric connectivity matrix for
each fMRI session of each subject. On top of using MI-bin equal to 0.5, we have also explored
three additional z-score bin widths (0.75, 1, and 2) within the z-score range [−3.5 to 3.5]. This
binning procedure was applied to the z-scored BOLD time series before computing mutual
information. Results shown in the Supporting Information Table S1 indicate that MI pairwise
measurements are stable across different bin sizes. Functional connectivity matrices from the
LR and RL phase-encoding runs were averaged to improve signal-to-noise ratio (as done in
Finn et al., 2015). The functional connectomes were kept in its weighted form (as measured
by mutual information), hence neither thresholded nor binarized.

Finally, the resulting individual functional connectivity matrices were ordered (rows and
columns) according to seven resting-state cortical networks, as proposed by Yeo et al. (2011).
For completeness, an eighth subnetwork including the 14 HCP subcortical regions was added
(as analogously done in recent papers: Amico et al., 2019; Amico & Goñi, 2018a, 2018b).

HCP: DWI Preprocessing

The HCP DWI data were processed following the MRtrix3 (Tournier, Calamante, & Connelly,
2012) guidelines (for the full documentation see https://mrtrix.readthedocs.io/en/latest/tutorials
/hcp_connectome.html). The following were carried out: (a) generation of a tissue-type seg-
mented image appropriate for anatomically constrained tractography (MRtrix command 5ttgen;

650

Tractography:
Computational reconstruction
procedure that may be used to
obtain, from DWI data, white matter
streamlines or fiber tracts connecting
different brain regions.

Network Neuroscience

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
3
6
4
6
1
9
6
0
4
9
0
n
e
n
_
a
_
0
0
1
8
5
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Toward an information theoretical description of the human connectome

R. E. Smith et al., 2012); (b) estimation of the multishell multitissue response function (MRtrix com-
mand dwi2response msmt_5tt; Christiaens et al., 2015); (c) multishell, multitissue constrained
spherical deconvolution (MRtrix dwi2fod msmt_csd; Jeurissen et al., 2014); (d) generation of the
initial tractogram (MRtrix command tckgen, 10 million streamlines, maximum tract length = 250,
FA cutoff = 0.06); and (e) application of the second version of Spherical-deconvolution Informed
Filtering of Tractograms (SIFT2; R. E. Smith et al., 2015) methodology (MRtrix command tcksift2).
Both SIFT (R. E. Smith et al., 2013) and SIFT2 (R. E. Smith et al., 2015, p. 2) methods provide more
biologically meaningful estimates of structural connection density. However, SIFT2 allows for a
more logically direct and computationally efficient solution to the streamlines connectivity
quantification problem: by determining an appropriate cross-sectional area multiplier for each
streamline rather than removing streamlines altogether, biologically accurate measures of white
matter fiber connectivity are obtained while making use of the complete streamlines recon-
struction (R. E. Smith et al., 2015). SIFT2 obtained streamlines were then mapped onto the
374 chosen brain regions (see Brain Parcellation Atlas section for details), and the average
streamline length (millimeters) was calculated for all brain regions pairs (MRtrix command
tck2connectome). Henceforth, what we will refer to as “structural connectome” represents
the physical distance (in millimeters) between brain regions pairs. Here we opted for the
streamline length in this case, because we wanted to link information transfer in brain networks
with the sender-channel-receiver schematics proposed in electronic communication by
Shannon (1948). Therefore, we approximated the concept of communication channels to
shortest paths based on structural fiber length in brain networks (Bullmore & Sporns, 2012).

Mathematical Foundations of Communication in Large-Scale Brain Structural-Functional Networks

There are two main fundamental assumptions behind the framework we are proposing here.
First, in order to transfer (send or receive) information directly, two brain nodes must be struc-
turally connected through white matter fibers (or streamlines, as obtained through tractogra-
phy); second, the amount of communication taking place between two structurally connected
nodes can be estimated as the functional coupling between them, here measured as the mu-
tual information (Cover & Thomas, 2012) between the corresponding BOLD time series.

In summary, we define two brain regions as “communicating” when they are structurally
connected and their correspondent time series show statistical dependence, with the amount
of “communication” being measured through pairwise mutual information. Please note that
we are using the word communication here in Shannon’s sense, that is, we are trying to char-
acterize the amount of information shared between sent and received fMRI BOLD signals, as
measured through mutual information.

Starting from these two assumptions, we here lay the basis for an information-theoretical
evaluation of communication following (structural) shortest paths in human large-scale brain
networks. Note, however, that although this work focused on communication along shortest
paths, the proposed framework can be generalized to any existing path.

Assessment of Well-Behaved Communication Along Shortest Paths

Part of the conceptualization of this framework was strongly inspired by seminal work by
Claude Shannon, “A Mathematical Theory of Communication,” particularly one main concept
stemming from that work: the concept of data processing inequality (DPI; Cover & Thomas,
2012). In brief, the DPI theorem states that in a Markov chain of three random variables X, Y,
Z, where X!Y!Z, then MI(X;Y) ≥ MI(X; Z), where MI(X; Y) and MI(X; Z) denote the mutual
information between X and Y and between X and Z, respectively. Note that this theorem can
be easily extended to chains larger than N = 3 (Cover & Thomas, 2012).

Network Neuroscience

651

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
3
6
4
6
1
9
6
0
4
9
0
n
e
n
_
a
_
0
0
1
8
5
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Toward an information theoretical description of the human connectome

In other words, processing Y cannot add new information about X. This theorem has a rea-
sonable analogy. Think of the children’s “telephone game”. Briefly, players form a line, and the
first player comes up with a message and whispers it to the second player in line. The second
player repeats the message to the third player, and so on. In those conditions, the message sent
to player Z through “middle player” Y can never be more intact than the original version
sent by the first player X, at most equal or worse (i.e., player Y might mishear player X and
alter the message).

Inspired by the concept of DPI on a chain, we defined a novel brain network measure, the PPS.
Let Πtask
s!t be the shortest path between a brain region source (S) and a brain region target (T) for a
specific fMRI task (e.g., resting state, language, etc.). We defined such shortest path as a sequence
of nodes Ωs!t = {S, K1, K2, …, Km, T }, starting at the source S and ending at the target T, with m
intermediate nodes in between. Let us define also Ω
s→t* = {S, K1,
K2, …, Km} as the sequences of shortest path nodes without the source and the target on the
structural connectome (SC), respectively. The SC reference model used in this study is based
on fiber length. Please note that such SC was not binarized or thresholded. The shortest path
computation is entirely based on the group-averaged positive-weighted matrix defined by pairwise
fiber lengths.

s*!t = {K1, K2, …, Km, T } and Ω

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

t

/

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
3
6
4
6
1
9
6
0
4
9
0
n
e
n
_
a
_
0
0
1
8
5
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Note also that Πtask

s!t is a structural shortest path (i.e., obtained from the structural connec-
tome), where weights {S ! K1
! T } along the path are substituted by the
mutual information values calculated on the FC, that is, {MI(S; K1), MI(K1; K2) … MI(Km−1; Km),
MI(Km; T )}. Each term represents the mutual information between the fMRI time series of brain
regions along the structurally connected shortest path for a specific task.

! … ! Km

! K2

The PPS of a structural shortest path associated with a specific functional task is then defined as:

(cid:1)
PPS Πtask
s!t

(cid:3)

¼

X

i2Ω

(cid:2)!t
s

ð

ð
MI S; K1

Þ − MI S; i

ð

Þ
Þ

In a nutshell, PPS estimates how much the signal has changed or been transformed between
any source and target in the brain network. In a sense, it is a relaxation of the DPI, a more
qualitative measurement than the Shannon’s “strict” data processing theorem. This choice is
based on the idea that in human MRI brain networks, it is extremely likely that communication
between two brain regions can happen on nonshortest paths (Avena-Koenigsberger et al.,
2017; Goñi et al., 2014; Tipnis et al., 2018). Therefore, a score such as PPS allows for a more
flexible exploration of the communication dynamics underlying the fixed structural topology.
Note that PPS is not defined for pairs of brain regions with a shortest path that consists of one
edge. Also note that PPS is a nonsymmetric measurement, that is, PPS(s!t) 6¼ PPS(t!s).

As a simple example, let us assume a shortest path defined as a simple chain of three nodes
(source S, intermediate node X, target T). PPS in this case is simply defined as: PPS(Π
s!t) = MI
(S; X ) − MI(S; T ). If this difference is positive, it means that the mutual information along the
path has decreased, which then can be understood as an attenuation of the signal (or increase
in noise). However, if the difference is negative, that would mean that the DPI is not satisfied.
In that case, it adds evidence that the communication between S and T might not be traveling
along that path (e.g., that communication path is unlikely to be in use for regions S and T).

The evaluation of PPS for a shortest path can tell us a lot about the communication regime
taking place between source region S and target region T (see Figure 1B). For instance, a low (or
close to zero) PPS indicates that information is passed almost intact from the source to the target:
hence, we are in presence of a relay communication regime. Conversely, a high-processing load

Network Neuroscience

652

Toward an information theoretical description of the human connectome

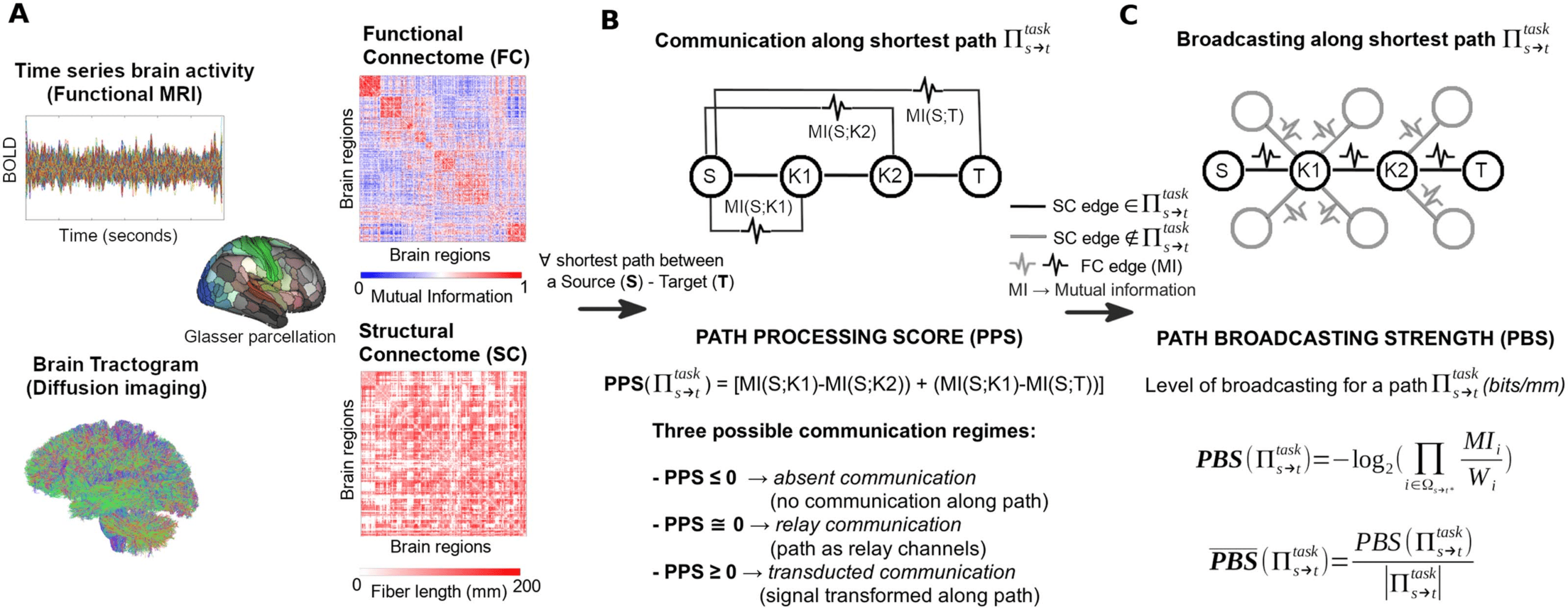
Figure 1. Toward a mathematical theory of communication for the human connectome. (A) Functional and structural connectomes are ex-
tracted from brain data for a multimodal brain parcellation (Glasser et al., 2016). (B) For every shortest path between a source-target pair of
brain regions, path processing score (PPS) is computed and the path is assigned to its correspondent communication regime. (C) For each
communication regime, path broadcasting strength (PBS) is evaluated to determine the spread of information across the shortest path.

indicates that the signal has gone through considerable transformations (due to either internal or
external inputs): the shortest path is then operating in a transducted communication regime.
Finally, if the PPS is negative, it means that, despite the relaxation of the DPI theorem, commu-
nication along the shortest path is absent, that is, the mutual information along the path increases
with respect to the mutual information of the original message.

Assessment of Information Broadcasting Along Shortest Paths

Search information (SI) quantifies the hiddenness of the shortest path between a source node
and a target node within the network by measuring the amount of knowledge or information in
bits needed to access the path (Goñi et al., 2014; Rosvall et al., 2005; Sneppen et al., 2005).
The more nested the shortest path between two brain regions, the higher its SI value. Conversely,
the less hidden or integrated the path, the lower its SI value.

Inspired by this concept, we defined a measure of PBS. Similarly to the PPS defined earlier,
PBS is measured as the SI (Goñi et al., 2014) along the structural shortest path Πtask
s!t, but super-
imposing the functional weights corresponding to pairwise mutual information between the
brain regions along the structural path. Hence, let MIs!t = {MI(S; K1), MI(K1; K2), …, MI(Km−1;
Km), MI(Km; T )} be the set of mutual information values along the shortest path and W = {wS, wK1,
… wKm, wT} be the set of the nodal strength along the shortest path (again, note that the nodal
wK2
strength is calculated from the mutual information values where a structural edge is present).
Nodal strength of a brain region i is defined as Wi = (cid:2)
j MIij, for all j 6¼ i, which sums all functional
connectivity values in which brain region i participates.

We can then define the PBS as:

(cid:1)
PBS Πtask
s!t

(cid:3)

¼ − log2

!

Y

i2Ω

(cid:2)

s!t

s!t

MIi
Wi

Nodal strength:
In a weighted graph (i.e., where
edges have assigned numerical
values), it represents the total sum of
the edge weights attached to a node.

Network Neuroscience

653

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
3
6
4
6
1
9
6
0
4
9
0
n
e
n
_
a
_
0
0
1
8
5
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Toward an information theoretical description of the human connectome

s→t. Analogously, MIi

where Wi refers to the i-th element of the ordered sequence of nodal strengths along the path
Πtask
s→t refers to the i-th element of the MIs→t ordered sequence along the
path Πtask
s→t. This equation does not take into account the bias arising from different path lengths.
That is, longer shortest paths will have a tendency to yield higher PBS values. To account for
this, we therefore normalize PBS:

(cid:1)
(cid:3)
PBS Πtask
s→t

(cid:3)

(cid:3)

(cid:1)
¼ PBS Πtask
s→t
(cid:4)
(cid:4)
(cid:4)
(cid:4)
Πtask
s→t

where |Πtask
s→t| is the total sum of the shortest path length (in millimeters, in this case). Henceforth,
what we will refer to as PBS is its normalized version. PBS is essentially the SI (Goñi et al., 2014)
computed on the functional values superimposed on a fixed structural topology (Figure 1C).
However, conceptually the interpretation differs. In fact, measuring SI on functional edges allow
us to investigate how communication propagates along shortest paths. For instance, when PBS is
low, the signal is flowing primarily along the shortest path, hence communication between
source and target regions takes place through a routing mode. Conversely, when PBS is high,
the communication between a regions pair is being propagated through edges adjacent to the
shortest path as well, hence operating in a broadcasting mode.

Therefore, we can associate to each of the two communication regimes defined through PPS
(i.e., relay and transducted ), as well as for (structurally) directly connected nodes (i.e., direct
communication), its corresponding communication mode (routing or broadcasting), for any
shortest path between a brain region source S and a target T (Table 1; see also Figure 1). Note
that, by defining edge weights as mean streamline length (in millimeters), the resultant units of
PBS are bits/mm.

Note that PBS is a 374 × 374 nonsymmetric matrix, since every source-target pair in the
brain network has a PBS score. Hence, based on PBS, we define two different nodal broad-
casting strengths, differentiating when a brain region k is a sender (WBSsender(k)) or a receiver
(WBSreceiver(k)):

WBSsender kð Þ ¼

XN

PBSik

i

; WBSreceiver kð Þ ¼

XN

PBSki

i

Table 1.
the spread of information (communication mode) along the shortest path, as assessed through path broadcasting strength (PBS)

Schematic of the different communication regimes based on the path processing score (PPS) measurement, and their associations to

Communication regime (PPS)

Broadcasting level (PBS)

Communication mode

Direct communication

(single-edge shortest path, PPS not defined)

Low broadcasting → Single-edge routing

High broadcasting → Multi-edge routing

Absent communication (PPS < 0) No broadcasting No communication along shortest path along shortest path Relay communication (PPS ffiffiffiffiffiffiffi 0) Low broadcasting → Routing relay path Transducted communication (PPS > 0)

Low broadcasting → Routing transduction

High broadcasting → Broadcasting relay path

High broadcasting → Broadcasting transduction

Network Neuroscience

654

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
3
6
4
6
1
9
6
0
4
9
0
n
e
n
_
a
_
0
0
1
8
5
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Toward an information theoretical description of the human connectome

Nodal broadcasting strength ( WBS):
The average of WBSsender and
WBSreceiver. WBSsender is the sum
(strength) all PBS values when a brain
region is a sender (source of a path).
WBSreceiver is the sum (strength) all
PBS values when a brain region is a
receiver (target of a path).

where N = 374 (number of brain regions). Finally, we define the (symmetric) nodal
broadcasting strength ( WBS) as the average, per brain region k, of both measurements:

WBS kð Þ ¼ WBSsender kð Þ þ WBSreceiver kð Þ

2

DMN-Based Model for Identification of Communication Regimes

We defined the boundaries of the relay communication regime based on the PPS distribution
obtained by considering only all pairwise within default mode network (DMN) interactions.
The DMN at rest is a highly coherent integrated functional network. Hence we used DMN at
rest for setting the boundaries of relay communication with respect to broken and transducted
communication. Therefore, for each subject, we obtained the DMN-based shortest paths and
their corresponding PPS for resting state. Finally, the boundaries for a PPS to be considered
“close to zero” or in relay communication were set to the [5, 95] percentiles of the DMN-based
distribution, specifically to the PPS range [−0.04 0.07] (see Supporting Information Figure S1).

Here we used PPS and PBS to investigate, respectively, the communication regimes and
communication modes of large-scale brain networks in 100 HCP subjects, for resting state
and seven different cognitive tasks (see HCP: fMRI Acquisition section for details). The scheme
depicted in Figure 1 provides a summary of these two information-theoretical measurements of
brain communication.

RESULTS

We evaluated communication dynamics in large-scale human brain networks obtained from the
MRI dataset of 100 unrelated subjects (Van Essen et al., 2013) under resting-state and task con-
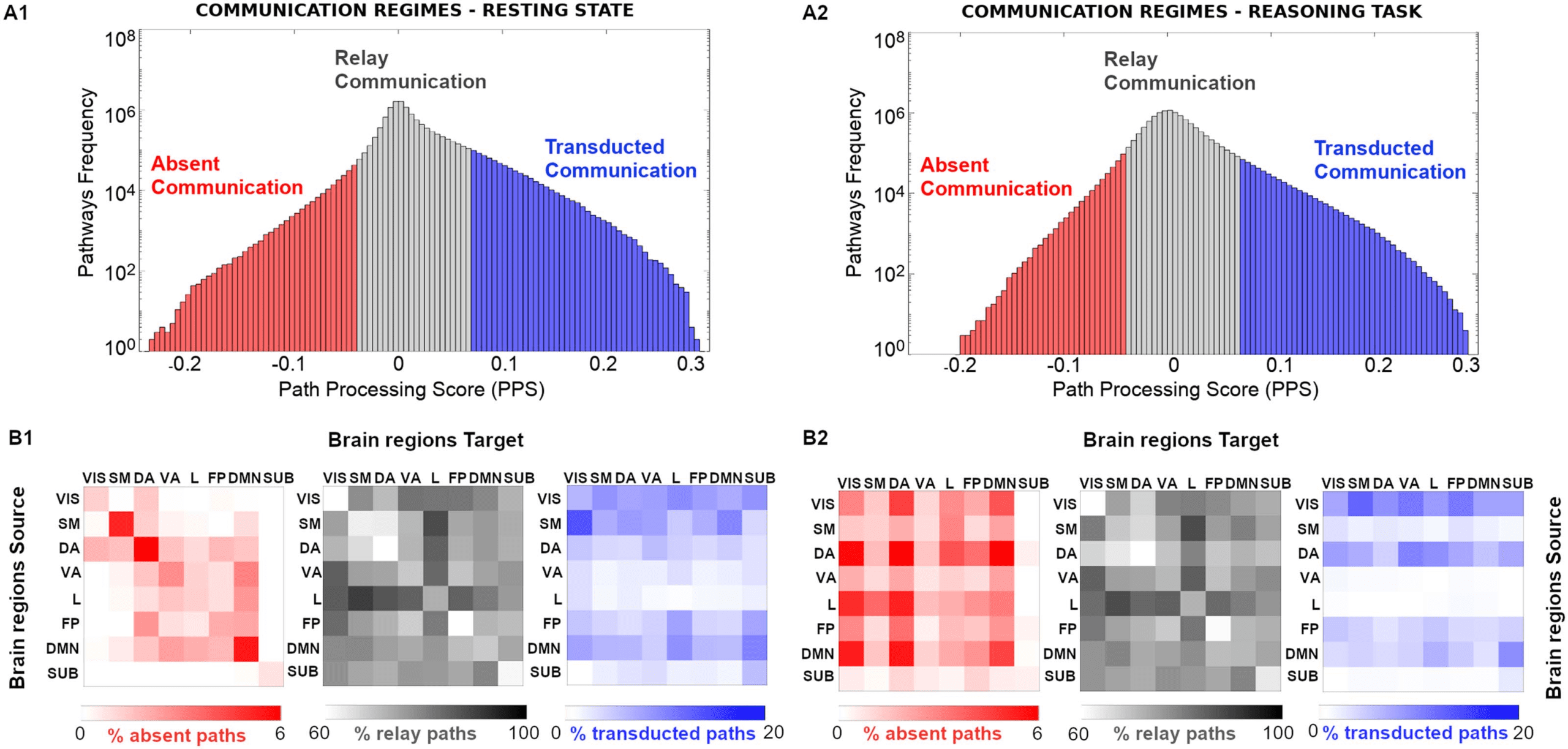
ditions. Task results presented in Figure 2A2 and 2B2 refer to the reasoning task (see Supporting
Information Figure S2 for the other 6 fMRI tasks). First, we used the PPS measurement (see
Methods section) to characterize the shortest paths based on the three different communication
regimes (absent, relay, and transducted; Figure 2A1 and A2). Note that the boundaries for the
communication regimes were calculated from a DMN-based PPS distribution obtained from
resting-state data (for details see Methods: DMN-Based Model section for communication re-
gimes; Supporting Information Figure S1 shows the distribution obtained with dashed vertical
lines indicating 5 and 95 percentiles). Also note that even though we decided in this work to
focus on the group-averaged connectomes (and trials), PBS and PPS are very stable when com-
pared across subjects and source-target pair (see Supporting Information Table S2).

For each of the three different communication regimes, we stratified shortest paths into the
seven functional networks as defined by Yeo et al. (2011) (adding the subcortical set as in Amico
et al., 2017b) to investigate whether communication regimes were functional networks specific.
We observed interesting structure in the distribution of communication pathways per functional
network (Figure 2): the limbic system seems to be a hub for the relay communication regime for
both task and resting-state connectomes, while the streams toward visual and DMN modules are
mostly present at the transducted communication regime for both resting-state and reasoning
task (Figure 2B1 and B2, gray and blue patterns; the same applies to the other tasks, see
Supporting Information Figure S2). Notably, for absent paths, differential patterns emerged for
the resting-state and reasoning task, where absent paths predominantly appeared within net-
work at rest and between networks during the reasoning task (Figure 2B1 and B2, red patterns).
A similar pattern was observed for the other task conditions (Supporting Information Figure S2).

Network Neuroscience

655

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
3
6
4
6
1
9
6
0
4
9
0
n
e
n
_
a
_
0
0
1
8
5
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Toward an information theoretical description of the human connectome

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
3
6
4
6
1
9
6
0
4
9
0
n
e
n
_
a
_
0
0
1
8
5
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Figure 2. Communication regimes in large-scale brain networks. (A1 and A2) Path processing score (PPS) on indirect pathways allows to
separate brain network communication in three different regimes: absent, relay communication, and transducted communication). Note that a
common SC reference (group average) was used to estimate shortest paths based on fiber length (see more details in Methods section). (B1 and
B2) The percentage of paths, for the three different communication regimes, corresponding to the within and between seven functional
networks source-target pairs, as specified by Yeo et al. (2011). An eighth subcortical set was added for completeness.

This might be related to the tendency of going out of the optimal “routing” strategy (preferential
in resting) when switching to a cognitive task.

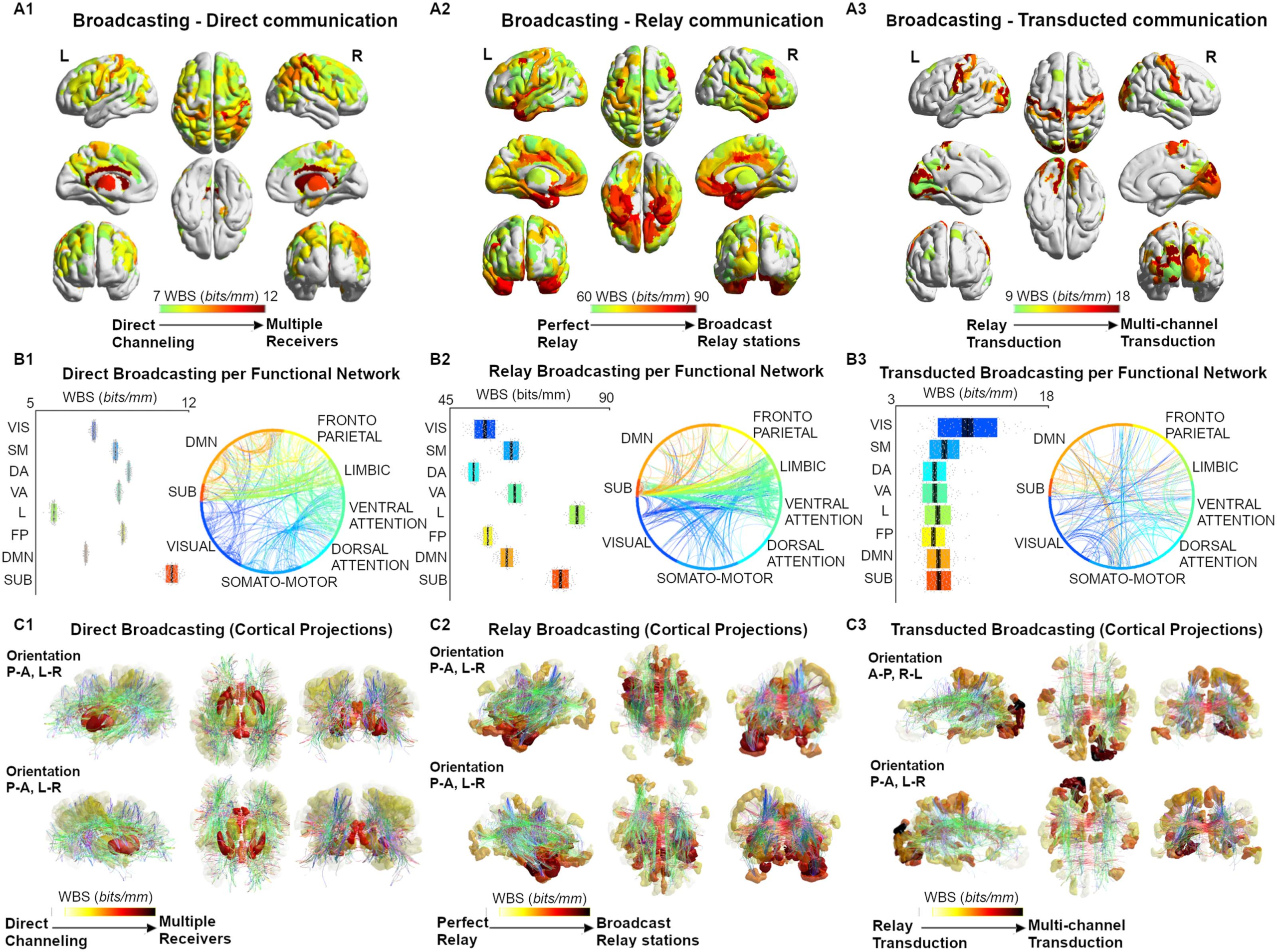
We further characterized shortest path communication regimes into two communication
modes (routing or broadcasting) based on our second proposed metric, the PBS (see Methods
and Table 1 for details). PBS quantifies the degree to which information would propagate solely
along the shortest path (routing) or spread out to nodes branching from the shortest path (broad-
casting). In addition to the relay and transducted regimes, which constitute paths of at least two
hops, PBS was also evaluated on direct (one hop) paths (here referred to as the Direct
Communication regime, Table 1). Notably, regional specificity emerged at each level of broad-
casting (computed as nodal broadcasting strength or WBS; see Methods) (Figure 3A1–3A3).
Specifically, within the direct communication regime, paths that involved subcortical nodes
(as source/target) displayed the highest degree of broadcasting (Figure 3A1, 3B1, and 3C1;
average nodal PBS of 12 bits/mm). For the relay communication regime, paths from/to the
limbic and subcortical regions had the highest PBS (~90 bits/mm), operating as broadcast relay
stations (Figure 3A2, 3B2, and 3C2) while, in the transducted regime pathways, visual and
somatomotor cortices were the hubs of broadcasting transduction (Figure 3A3, 3B3, 3C3;
PBS ~ 15 bits/mm).

To further investigate the top regions involved in different broadcasting scenarios, we outlined
the sender-receiver broadcasting changes (using WBSsender and WBSreceiver; see Methods section)
for the top 10 brain regions in the three different communication regimes depicted in Figure 3.

Network Neuroscience

656

Toward an information theoretical description of the human connectome

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
3
6
4
6
1
9
6
0
4
9
0
n
e
n
_
a
_
0
0
1
8
5
p
d

.

t

Figure 3. Broadcasting in large-scale brain networks during rest. (A1–A3) Nodal broadcasting strength ( WBS, measured in bits/mm; see
Methods section for details) shown for the top 100 brain regions for the three different communication regimes (direct communication, relay
communication, transducted communication). (B1–B3) Broadcasting properties evaluated for each of the seven functional networks specified
by Yeo et al. (2011). An eighth subcortical community was added for completeness. (C1–C3) The broadcasting matrices are projected onto brain
renders, where tracts (color coded by direction; red: left-right; green: anterior-posterior; blue: superior-inferior) represent nonzero edges in the
masks, and nodal strength (A1–A3) is mapped onto the cortical meshes from low WBS (white, transparent) to high WBS (opaque, bright red).

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Overall, these regions corroborate the hypothesis of a regional specificity in the communication
dynamics in large-scale human brain networks (Figure 4). Specifically, significant source-target
asymmetries were found when brain regions were broadcasting in the transducted regime
−16 when testing
(Wilcoxon rank-sum test, p = 8.7 × 10
across all 374 brain nodes); tendency toward asymmetry was found for the nodal broadcasting
−04 for the top 10 regions, p = 0.67 when testing
strength in the relay regime (Wilcoxon p = 1.8 × 10
across all 374 brain nodes); finally, no significant source-target skewness in broadcasting was
found in direct communication (Wilcoxon p = 0.66 for the top 10 regions, p = 0.91 when testing
across all 374 brain nodes).

−05 for the top 10 regions, p = 7.9 × 10

Network Neuroscience

657

Toward an information theoretical description of the human connectome

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
3
6
4
6
1
9
6
0
4
9
0
n
e
n
_
a
_
0
0
1
8
5
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

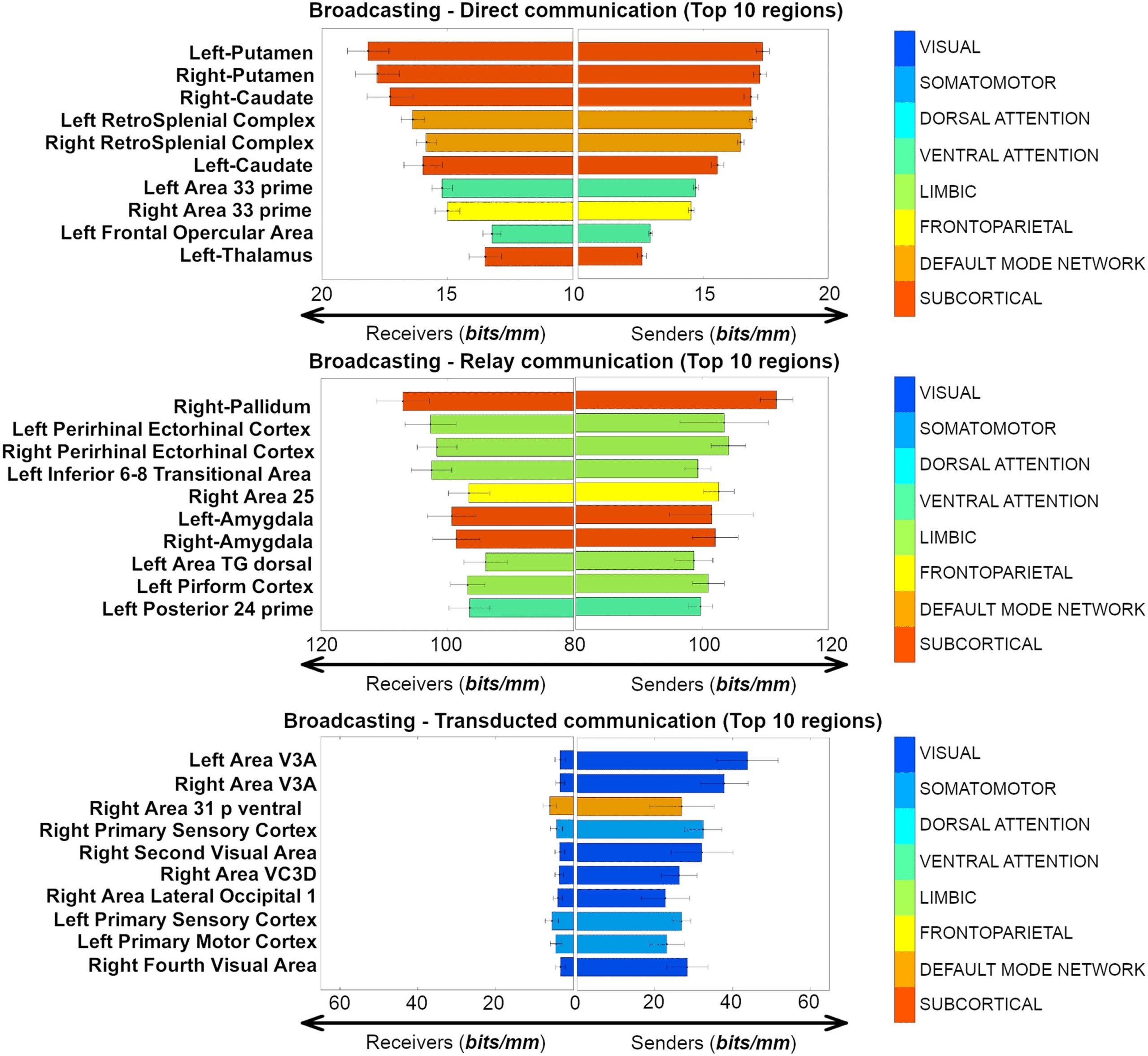
Figure 4. Anatomical sender-receiver list of the top 10 brain regions involved in each of the three different broadcasting regimes (direct, relay,
transducted) expressed as sender and receiver nodal broadcasting strengths ( WBSsender and WBSreceiver respectively, both measured in bits/mm).

DISCUSSION

Understanding how the brain processes information is one of the major challenges facing the
neuroscientific community in the next decade. Nonetheless, the investigation advances across
different temporal and spatial scales, from neuronal population (Quian Quiroga & Panzeri, 2009)
to MRI-based connectomes (Avena-Koenigsberger et al., 2018; Marinazzo et al., 2014; Mišic(cid:4)

Network Neuroscience

658

Toward an information theoretical description of the human connectome

et al., 2015). Information theory provides a well-established mathematic framework to explore
the statistical dependencies present in brain data (Wibral, Lizier, & Priesemann, 2015; Wibral,
Vicente, & Lizier, 2014).

What is still lacking, in our opinion, is a theory that would allow us to investigate the infor-
mation carrying capacity of a brain network. MRI-based connectomes can indeed be modeled
as a system of multiple dynamically interacting senders and receivers (Mišic(cid:4) et al., 2014a,
2014b, 2015; Tipnis et al., 2018). Exploration of the presence of different communication
regimes in brain networks will introduce new elements and insights in brain communication
problems, such as interference and cooperation and feedback between brain regions.
Extending the communication problem to a brain network level can help our understanding
of how communication dynamics relate to cognitive transitions and, ultimately, behavior.

In our investigation, we aim to contribute to the field by using information-theoretical tools for
assessing communication dynamics in brain networks, based on their functional and structural
topology. Here we introduced two information-theoretical measurements to account for commu-
nication transferred on top of a structural topology in human brain networks, specifically along the
shortest paths connecting pairs of brain regions. Taking inspiration from Shannon’s seminal papers
on communication, we defined PPS to serve as a quality index of how likely a shortest path is to
take part in communication dynamics between a pair of regions. Using this score, we defined and
explored three different regimes of communication in an MRI-based brain network: absent, relay,
and transducted (Figure 2). Qualitative comparisons of communication regimes of resting-state
and task (reasoning task) derived functional connectomes showed similar patterns emerging for
the relay and transduction regimes, but not for absent paths (Figure 2B). This corroborates the idea
of a relationship between communication dynamics and brain functional reconfigurations
(Schultz & Cole, 2016). That is, depending on the “cognitive state” in which the brain operates,
communication might diffuse along many diverse paths, not necessarily the shortest.

Additionally, we define a second measurement that is complementary to PPS, termed the path
broadcasting strength (PBS), which is a measurement of the likelihood that communication along a
path is being transferred or spread around to the neighboring nodes. Within each of the defined
PPS regimes, with the addition of direct (single-edge) paths, we explored the broadcasting capacity
of the resting-state connectome in the HCP dataset. Notably, we found subcortical regions (cau-
date, thalamus, and cingulum areas) to be broadcaster hubs in the direct communication regimes;
the limbic system (amygdala and insula cortices) to be major broadcast relay stations; finally, the
visual and ventral cortices to be primary centers of broadcasting transduction streams (Figure 3).

Inspired by a recent work (Seguin et al., 2019), we further explored this regional specificity
by evaluating the asymmetry of broadcasting, for each communication regime, on the brain
regions with highest nodal broadcasting strength. To do so, we distinguished those brain regions
when being a target (receiver) or a source (sender). Interestingly, direct broadcasting showed
greatest symmetry in paths originating/terminating primarily in subcortical nodes. Sender-
receiver asymmetry becomes more pronounced in regions with a high broadcasting strength
in relay, followed by transducted regime paths (Figure 4).

As a matter of fact, in the case of communication of directly connected nodes, top PBS regions
were those of the subcortical and attention/default networks, and showed a similar PBS magni-
tude when serving as either a sender or a receive node. Striatal regions are known to receive
direct inputs from brainstem and cortical regions, serving to integrate information related to
motor function and reward (Haber, 2016). Attention related areas (retrosplenial cortex) have
been demonstrated to be involved in learning and navigation, working in concert with thalamic
and hippocampal regions (Vann et al., 2009), a function that is complementary to the striatal role

Network Neuroscience

659

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
3
6
4
6
1
9
6
0
4
9
0
n
e
n
_
a
_
0
0
1
8
5
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Toward an information theoretical description of the human connectome

in motor control. Therefore, based on the findings presented here, it is likely that the direct
communication regime captures activity of nodes that receive several inputs, integrate the
information, and send widespread outputs to higher order cortical regions with little augmen-
tation of the signal (Choi et al., 2012).

For the relay transduction regime (i.e., paths where the signal is not or minimally transformed
on its way from source to target), half of the top 10 regions belonged to the limbic network, 3 to
subcortical, and 1 to each fronto-parietal and ventral attention network. These nodes were pri-
marily in the temporal lobe (perirhinal ectorhinal, amygdala, piriform) and frontal lobe (inferior
68 transitional [approximately dorsolateral prefrontal] and area 25 [subcallosal]; Figure 4), with
the remaining relay nodes belonging to left posterior insula and right pallidum. In this regime,
PBS values are higher when they serve as the receiver in shortest paths, as compared to being a
sender. This suggests that under the relay regime, arriving information has a greater specificity to
the path traveled, compared to departing (sent out) information, which has greater tendency to
spread out to neighboring nodes on the path. The default mode system is commonly thought of
as being active at rest, or during passive tasks, where its temporal and frontal subsystems provide
information for construction and flexible use of mental simulations, respectively (Buckner et al.,
2008; Yeo et al., 2011). Interpretation of our results in the context of previous work on the DMN
may hinge on the association between function and communication regime. In particular, a
routing-like mode during retrieval of information from memory, and a broadcasting mode for
construction and output of mental simulations (e.g., thinking about the future).

Transducted communication pathways, where signal undergoes modification on its path
from source to target, showed greater broadcasting on paths where they were the source (as com-
pared to target). Among the top regions in this regime were areas of the visual and default mode
networks that were in some cases bilateral (Area V3A [visual]) or adjacent (left second and third
visual areas [visual]; left area 31p ventral and area ventral 23a+b [limbic]; right fourth and eighth
visual areas [visual]; Figure 4). Areas of the visual network receive highly specific visual input
from their receptive visual field via the lateral geniculate nuclei of the thalamus. Upon reaching
the visual cortex information is propagated out to other regions via processing streams that are
involved in object recognition, motion, and representation in space, among others. In this
regard, the information captured by PBS, from the joint structure/function connectomes, agrees
with our neuroanatomical understanding of the visual system.

This study has some limitations. The impact of the brain parcellation on the definition of the
communication regimes needs to be explored, as well as the choice of the soft boundaries
between them (here defined on a resting-state DMN-based PPS distribution; see Methods for
details); the effect of the uniform binning on the mutual information-derived connectomes
should be further investigated, as well as the use of other information-based measurement of
entropy between brain time series (e.g., transfer entropy or multivariate mutual information;
Amico et al., 2017a; Schreiber, 2000). The use of resting state as a “null” condition or baseline
for the tasks depends on several assumptions about neural activity during “rest” (Cole et al.,
2014; Schultz & Cole, 2016). The effect of using different null conditions needs to be further
investigated in terms of communication characteristics. Our study has focused on static func-
tional connectomes as estimated by using the entire scanning length of each fMRI condition.
Further studies should cover changes in communication and communication regimes within
fMRI conditions by using the framework provided in this paper on dynamical functional connec-
tivity (Hutchison et al., 2013; Preti et al., 2017; Shine et al., 2016). Finally, the choice of a ref-
erence baseline model to define the boundaries between the communication regimes (broken,
relay, and transducted) is somewhat arbitrary. We introduced the use of DMN at rest as the
functional subcircuit in which most of the communication should be identified as relay and

Network Neuroscience

660

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

t

/

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
3
6
4
6
1
9
6
0
4
9
0
n
e
n
_
a
_
0
0
1
8
5
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Toward an information theoretical description of the human connectome

hence establish relative associations of communication regimes with respect to the resulting PPS
distribution (see Supporting Information Figure S1). However, other null models attending to a
different rationale or also imposing different topological invariants might identify different PPS
communication boundaries.

There are many possible extensions of this initial work on brain network information theory.
For instance, the framework can be used on connectivity based on other modalities of brain data
(as obtained via MEG, EEG, etc.) and can be extended to brain networks at different spatial scales
(i.e., neuronal networks, mesoscopic brain networks). The utility of PPS and PBS for predicting
behavioral, demographics, and/or clinical scores should also be further investigated. Finally,
one might want to consider PPS and PBS along multiple paths or path ensembles, thus not re-
stricting to the shortest ones (Avena-Koenigsberger et al., 2017), or even select the “best com-
munication pathway” based on PPS (or a variation of it). In the context of this framework,
concepts such as interference or cooperation and feedback (Mišic(cid:4) et al., 2015) may additionally
be included in the model. Finally, while we used fiber length, structural contribution of stream-
line count or a combination of the two, might be considered as well.

In conclusion, we proposed a novel methodology, rooted in information theory, to inves-
tigate communication regimes and communication modes in large-scale brain networks (i.e.,
brain network information theory). This framework sets the ground for a better characterization
of brain communication regimes and how they change as subjects perform different tasks.

ACKNOWLEDGMENTS

Data were provided (in part) by the Human Connectome Project, WU-Minn Consortium
(Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by the
16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research, and by
the McDonnell Center for Systems Neuroscience at Washington University. Joaquín Goñi ac-
knowledges financial support Purdue Discovery Park Data Science Award “Fingerprints of the
Human Brain: A Data Science Perspective.” Enrico Amico acknowledges financial support from
the SNSF Ambizione project “Fingeprinting the Brain: Network Science to Extract Features of
Cognition, Behavior and Dysfunction” (grant number: PZ00P2_185716).

SUPPORTING INFORMATION

Supporting information for this article is available at https://doi.org/10.1162/netn_a_00185.
The code used for computing PPS and PBS will be made available on the CONNplexity lab
website (https://engineering.purdue.edu/ConnplexityLab).

AUTHOR CONTRIBUTIONS

Enrico Amico: Conceptualization; Data curation; Formal analysis; Methodology; Writing – original
draft; Writing – review & editing. Kausar Abbas: Methodology; Writing – original draft; Writing –
review & editing. Duy Anh Duong-Tran: Formal analysis; Methodology; Writing – original draft.
Uttara Tipnis: Methodology; Writing – original draft. Meenusree Rajapandian: Formal analysis;
Writing – original draft. Evgeny Chumin: Formal analysis; Writing – original draft. Mario
Ventresca: Conceptualization; Methodology; Writing – original draft. Jaroslaw Harezlak:
Conceptualization; Funding acquisition; Writing – original draft. Joaquín Goñi: Conceptualization;
Formal analysis; Funding acquisition; Investigation; Methodology; Supervision; Validation; Writing –
original draft; Writing – review & editing.

Network Neuroscience

661

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
3
6
4
6
1
9
6
0
4
9
0
n
e
n
_
a
_
0
0
1
8
5
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Toward an information theoretical description of the human connectome

FUNDING INFORMATION

Joaquín Goñi, National Institutes of Health (https://dx.doi.org/10.13039/100000002), Award
ID: R01EB022574. Jaroslaw Harezlak, National Institutes of Health (https://dx.doi.org/10
.13039/100000002), Award ID: R01MH108467. Joaquín Goñi, National Institutes of Health
(https://dx.doi.org/10.13039/100000002), Award ID: P60AA07611.

REFERENCES

Abdelnour, F., Voss, H. U., & Raj, A. (2014). Network diffusion ac-
curately models the relationship between structural and functional
brain connectivity networks. NeuroImage, 90, 335–347. https://
doi.org/10.1016/j.neuroimage.2013.12.039, PubMed: 24384152
Aerts, H., Schirner, M., Jeurissen, B., Van Roost, D., Achten, E.,
Ritter, P., & Marinazzo, D. (2018). Modeling brain dynamics in
brain tumor patients using the virtual brain. ENeuro, 5(3). https://
doi.org/10.1523/ENEURO.0083-18.2018, PubMed: 29911173
Amico, E., Arenas, A., & Goñi, J. (2019). Centralized and distributed
cognitive task processing in the human connectome. Network
Neuroscience, 3(2), 455–474. https://doi.org/10.1162/netn_a
_00072, PubMed: 30793091

Amico, E., Bodart, O., Rosanova, M., Gosseries, O., Heine, L., Van
Mierlo, P., Martial, C., Massimini, M., Marinazzo, D., & Laureys,
S. (2017a). Tracking dynamic interactions between structural and
functional connectivity: A TMS/ EEG-dMRI study. Brain
Connectivity, 7(2), 84–97. https://doi.org/10.1089/ brain.2016
.0462, PubMed: 28092972

Amico, E., Dzemidzic, M., Oberlin, B. G., Carron, C. R., Harezlak,
J., Goñi, J., & Kareken, D. A. (2020). The disengaging brain:
Dynamic transitions from cognitive engagement and alcoholism
risk. NeuroImage, 209, 116515. https://doi.org/10.1016/j
.neuroimage.2020.116515, PubMed: 31904492

Amico, E., & Goñi, J. (2018a). Mapping hybrid functional-structural con-
nectivity traits in the human connectome. Network Neuroscience,
2(3), 306. https://doi.org/10.1162/netn_a_00049, PubMed:
30259007

Amico, E., & Goñi, J. (2018b). The quest for identifiability in human
functional connectomes. Scientific Reports, 8(1), 1–14. https://
doi.org/10.1038/s41598-018-25089-1, PubMed: 29844466

Amico, E., Marinazzo, D., Di Perri, C., Heine, L., Annen, J., Martial,
C., Dzemidzic, M., Kirsch, M., Bonhomme, V., Laureys, S., &
Goñi, J. (2017b). Mapping the functional connectome traits of
levels of consciousness. NeuroImage, 148, 201–211. https://doi
.org/10.1016/j.neuroimage.2017.01.020, PubMed: 28093358
Andersson, J. L. R., Skare, S., & Ashburner, J. (2003). How to correct sus-
ceptibility distortions in spin-echo echo-planar images: Application to
diffusion tensor imaging. NeuroImage, 20(2), 870–888. https://doi.org
/10.1016/S1053-8119(03)00336-7, PubMed: 14568458

Avena-Koenigsberger, A., Mišic(cid:4), B., Hawkins, R. X. D., Griffa, A.,
Hagmann, P., Goñi, J., & Sporns, O. (2017). Path ensembles
and a tradeoff between communication efficiency and resilience
in the human connectome. Brain Structure and Function, 222(1),
603–618. https://doi.org/10.1007/s00429-016-1238-5, PubMed:
27334341

Avena-Koenigsberger, A., Misic, B., & Sporns, O. (2018).
Communication dynamics in complex brain networks. Nature

Reviews Neuroscience, 19(1), 17–33. https://doi.org/10.1038/nrn
.2017.149, PubMed: 29238085

Barch, D. M., Burgess, G. C., Harms, M. P., Petersen, S. E., Schlaggar,
B. L., Corbetta, M., Glasser, M. F., Curtiss, S., Dixit, S., Feldt, C.,
Nolan, D., Bryant, E., Hartley, T., Footer, O., Bjork, J. M., Poldrack,
R., Smith, S., Johansen-Berg, H., Snyder, A. Z., & Van Essen, D. C.
(2013). Function in the human connectome: Task-fMRI and indi-
vidual differences in behavior. NeuroImage, 80, 169–189. https://
doi.org/10.1016/j.neuroimage.2013.05.033, PubMed: 23684877
Bassett, D. S., & Bullmore, E. T. (2009). Human brain networks in
health and disease. Current Opinion in Neurology, 22(4), 340–347.
https://doi.org/10.1097/ WCO.0b013e32832d93dd, PubMed:
19494774

Bassett, D. S., & Sporns, O. (2017). Network neuroscience. Nature
Neuroscience, 20(3), 353–364. https://doi.org/10.1038/nn.4502,
PubMed: 28230844

Buckner, R. L., Andrews-Hanna, J. R., & Schacter, D. L. (2008). The
brain’s default network. Annals of the New York Academy of
Sciences, 1124(1), 1–38. https://doi.org/10.1196/annals.1440
.011, PubMed: 18400922

Bullmore, E., & Sporns, O. (2012). The economy of brain network
organization. Nature Reviews Neuroscience, 13(5), 336–349.
https://doi.org/10.1038/nrn3214, PubMed: 22498897

Cabral, J., Kringelbach, M. L., & Deco, G. (2017). Functional con-
nectivity dynamically evolves on multiple time-scales over a
static structural connectome: Models and mechanisms.
NeuroImage, 160, 84–96. https://doi.org/10.1016/j.neuroimage
.2017.03.045, PubMed: 28343985

Caruyer, E., Cheng, J., Lenglet, C., Sapiro, G., Jiang, T., & Deriche, R.
(2011). Optimal Design of Multiple Q-shells experiments for
Diffusion MRI. MICCAI Workshop on Computational Diffusion
MRI – CDMRI’11. https://hal.inria.fr/inria-00617663/document
Choi, E. Y., Yeo, B. T. T., & Buckner, R. L. (2012). The organization
of the human striatum estimated by intrinsic functional connec-
tivity. Journal of Neurophysiology, 108(8), 2242–2263. https://
doi.org/10.1152/jn.00270.2012, PubMed: 22832566

Christiaens, D., Reisert, M., Dhollander, T., Sunaert, S., Suetens, P.,
& Maes, F. (2015). Global tractography of multi-shell diffusion-
weighted imaging data using a multi-tissue model. NeuroImage,
123, 89–101. https://doi.org/10.1016/j.neuroimage.2015.08
.008, PubMed: 26272729

Cole, M. W., Bassett, D. S., Power, J. D., Braver, T. S., & Petersen,
S. E. (2014). Intrinsic and task-evoked network architectures of
the human brain. Neuron, 83(1), 238–251. https://doi.org/10
.1016/j.neuron.2014.05.014, PubMed: 24991964

Cover, T. M., & Thomas, J. A. (2012). Elements of information theory.

John Wiley & Sons.

Network Neuroscience

662

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

t

/

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
3
6
4
6
1
9
6
0
4
9
0
n
e
n
_
a
_
0
0
1
8
5
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Toward an information theoretical description of the human connectome

de Pasquale, F., Della Penna, S., Sporns, O., Romani, G. L., &
Corbetta, M. (2016). A dynamic core network and global efficiency
in the resting human brain. Cerebral Cortex, 26(10), 4015–4033.
https://doi.org/10.1093/cercor/bhv185, PubMed: 26347485

Deco, G., Tononi, G., Boly, M., & Kringelbach, M. L. (2015).
Rethinking segregation and integration: Contributions of whole-
brain modelling. Nature Reviews Neuroscience, 16(7), 430–439.
https://doi.org/10.1038/nrn3963, PubMed: 26081790

Finn, E. S., Shen, X., Scheinost, D., Rosenberg, M. D., Huang, J., Chun,
M. M., Papademetris, X., & Constable, R. T. (2015). Functional
connectome fingerprinting: Identifying individuals using patterns
of brain connectivity. Nature Neuroscience, 18(11), 1664–1671.
https://doi.org/10.1038/nn.4135, PubMed: 26457551

Fornito, A., Zalesky, A., & Breakspear, M. (2015). The connec-
tomics of brain disorders. Nature Reviews Neuroscience, 16(3),
159–172. https://doi.org/10.1038/nrn3901, PubMed: 25697159
Fornito, A., Zalesky, A., & Bullmore, E. (2016). Fundamentals of

brain network analysis. Academic Press.

Gilson, M., Deco, G., Friston, K. J., Hagmann, P., Mantini, D., Betti, V.,
Romani, G. L., & Corbetta, M. (2018). Effective connectivity inferred
from fMRI transition dynamics during movie viewing points to a
balanced reconfiguration of cortical interactions. NeuroImage,
180, 534–546. https://doi.org/10.1016/j.neuroimage.2017.09
.061, PubMed: 29024792

Glasser, M. F., Coalson, T. S., Robinson, E. C., Hacker, C. D.,
Harwell, J., Yacoub, E., Ugurbil, K., Andersson, J., Beckmann,
C. F., Jenkinson, M., Smith, S. M., & Van Essen, D. C. (2016).
A multi-modal parcellation of human cerebral cortex. Nature,
536(7615), 171–178. https://doi.org/10.1038/nature18933,
PubMed: 27437579

Glasser, M. F., Sotiropoulos, S. N., Wilson, J. A., Coalson, T. S.,
Fischl, B., Andersson, J. L., Xu, J., Jbabdi, S., Webster, M.,
Polimeni, J. R., Van Essen, D. C., & Jenkinson, M. (2013). The
minimal preprocessing pipelines for the Human Connectome
Project. NeuroImage, 80, 105–124. https://doi.org/10.1016/j
.neuroimage.2013.04.127, PubMed: 23668970

Glomb, K., Ponce-Alvarez, A., Gilson, M., Ritter, P., & Deco, G.
(2017). Resting state networks in empirical and simulated dy-
namic functional connectivity. NeuroImage, 159, 388–402.
https://doi.org/10.1016/j.neuroimage.2017.07.065, PubMed:
28782678

Goñi, J., Avena-Koenigsberger, A., Mendizabal, N. V. de, Heuvel,
M. P van den, Betzel, R. F., & Sporns, O. (2013). Exploring the
morphospace of communication efficiency in complex networks.
PLoS ONE, 8(3), e58070. https://doi.org/10.1371/journal.pone
.0058070, PubMed: 23505455

Goñi, J., Heuvel, M. P. van den, Avena-Koenigsberger, A.,
Mendizabal, N. V. de, Betzel, R. F., Griffa, A., Hagmann, P.,
Corominas-Murtra, B., Thiran, J.-P., & Sporns, O. (2014).
Resting-brain functional connectivity predicted by analytic mea-
sures of network communication. Proceedings of the National
Academy of Sciences of the United States of America, 111(2),
833–838. https://doi.org/10.1073/pnas.1315529111, PubMed:
24379387

Gonzalez-Castillo, J., & Bandettini, P. A. (2018). Task-based dy-
namic functional connectivity: Recent findings and open ques-
tions. NeuroImage, 180, 526–533. https://doi.org/10.1016/j
.neuroimage.2017.08.006, PubMed: 28780401

Graham, D. J. (2014). Routing in the brain. Frontiers in
Computational Neuroscience, 8. https://doi.org/10.3389/fncom
.2014.00044, PubMed: 24782752

Haber, S. N. (2016). Corticostriatal circuitry. Dialogues in Clinical
Neuroscience, 18(1), 7–21. https://doi.org/10.31887/ DCNS
.2016.18.1/shaber, PubMed: 27069376

Hahn, G., Ponce-Alvarez, A., Deco, G., Aertsen, A., & Kumar, A.
(2019). Portraits of communication in neuronal networks. Nature
Reviews Neuroscience, 20(2), 117–127. https://doi.org/10.1038
/s41583-018-0094-0, PubMed: 30552403

Hutchison, R. M., Womelsdorf, T., Allen, E. A., Bandettini, P. A.,
Calhoun, V. D., Corbetta, M., Della Penna, S., Duyn, J. H.,
Glover, G. H., Gonzalez-Castillo, J., Handwerker, D. A.,
Keilholz, S., Kiviniemi, V., Leopold, D. A., de Pasquale, F.,
Sporns, O., Walter, M., & Chang, C. (2013). Dynamic functional
connectivity: Promise, issues, and interpretations. NeuroImage,
80, 360–378. https://doi.org/10.1016/j.neuroimage.2013.05
.079, PubMed: 23707587

Jenkinson, M., Beckmann, C. F., Behrens, T. E. J., Woolrich, M. W., &
Smith, S. M. (2012). FSL. NeuroImage, 62(2), 782–790. https://doi
.org/10.1016/j.neuroimage.2011.09.015, PubMed: 21979382
Jeurissen, B., Tournier, J.-D., Dhollander, T., Connelly, A., & Sijbers, J.
(2014). Multi-tissue constrained spherical deconvolution for
improved analysis of multi-shell diffusion MRI data. NeuroImage,
103, 411–426. https://doi.org/10.1016/j.neuroimage.2014.07
.061, PubMed: 25109526

Joglekar, M. R., Mejias, J. F., Yang, G. R., & Wang, X.-J. (2018).
Inter-areal balanced amplification enhances signal propagation
in a large-scale circuit model of the primate cortex. Neuron,
98(1), 222–234. https://doi.org/10.1016/j.neuron.2018.02.031,
PubMed: 29576389

Laughlin, S. B., & Sejnowski, T. J. (2003). Communication in neu-
ronal networks. Science, 301(5641), 1870–1874. https://doi.org
/10.1126/science.1089662, PubMed: 14512617

Marcus, D., Harwell, J., Olsen, T., Hodge, M., Glasser, M., Prior, F.,
Jenkinson, M., Laumann, T., Curtiss, S., & Van Essen, D. (2011).
Informatics and data mining tools and strategies for the Human
Connectome Project. Frontiers in Neuroinformatics, 5. https://doi
.org/10.3389/fninf.2011.00004, PubMed: 21743807

Marinazzo, D., Pellicoro, M., Wu, G., Angelini, L., Cortés, J. M., &
Stramaglia, S. (2014). Information transfer and criticality in the
Ising model on the human Connectome. PLoS ONE, 9(4),
e93616. https://doi.org/10.1371/journal.pone.0093616,
PubMed: 24705627

Masuda, N., Porter, M. A., & Lambiotte, R. (2017). Random walks
and diffusion on networks. Physics Reports, 716–717, 1–58.
https://doi.org/10.1016/j.physrep.2017.07.007

Mišic(cid:4), B., Betzel, R. F., Nematzadeh, A., Goñi, J., Griffa, A.,
Hagmann, P., Flammini, A., Ahn, Y.-Y., & Sporns, O. (2015).
Cooperative and competitive spreading dynamics on the human
connectome. Neuron, 86(6), 1518–1529. https://doi.org/10.1016
/j.neuron.2015.05.035, PubMed: 26087168

Mišic(cid:4), B., Goñi, J., Betzel, R. F., Sporns, O., & McIntosh, A. R.
(2014a). A network convergence zone in the hippocampus.
PLoS Computational Biology, 10(12), e1003982. https://doi.org
/10.1371/journal.pcbi.1003982, PubMed: 25474350

Mišic(cid:4), B., Sporns, O., & McIntosh, A. R. (2014b). Communication
efficiency and congestion of signal traffic in large-scale brain

Network Neuroscience

663

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
3
6
4
6
1
9
6
0
4
9
0
n
e
n
_
a
_
0
0
1
8
5
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Toward an information theoretical description of the human connectome

networks. PLoS Computational Biology, 10(1), e1003427. https://
doi.org/10.1371/journal.pcbi.1003427, PubMed: 24415931
Mohr, H., Wolfensteller, U., Betzel, R. F., Mišic(cid:4), B., Sporns, O.,
Richiardi, J., & Ruge, H. (2016). Integration and segregation of
large-scale brain networks during short-term task automatization.
Nature Communications, 7(1), 13217. https://doi.org/10.1038
/ncomms13217, PubMed: 27808095

Nigam, S., Shimono, M., Ito, S., Yeh, F.-C., Timme, N.,
Myroshnychenko, M., Lapish, C. C., Tosi, Z., Hottowy, P., Smith,
W. C., Masmanidis, S. C., Litke, A. M., Sporns, O., & Beggs, J. M.
(2016). Rich-club organization in effective connectivity among
cortical neurons. Journal of Neuroscience, 36(3), 670–684. https://
doi.org/10.1523/JNEUROSCI.2177-15.2016, PubMed: 26791200
Power, J. D., Mitra, A., Laumann, T. O., Snyder, A. Z., Schlaggar,
B. L., & Petersen, S. E. (2014). Methods to detect, characterize,
and remove motion artifact in resting state fMRI. NeuroImage,
84, 320–341. https://doi.org/10.1016/j.neuroimage.2013.08
.048, PubMed: 23994314

Preti, M. G., Bolton, T. A., & Van De Ville, D. (2017). The dynamic
functional connectome: State-of-the-art and perspectives.
NeuroImage, 160, 41–54. https://doi.org/10.1016/j.neuroimage
.2016.12.061, PubMed: 28034766

Quian Quiroga, R., & Panzeri, S. (2009). Extracting information
from neuronal populations: Information theory and decoding ap-
proaches. Nature Reviews Neuroscience, 10(3), 173–185. https://
doi.org/10.1038/nrn2578, PubMed: 19229240

Raj, A., Kuceyeski, A., & Weiner, M. (2012). A network diffusion
model of disease progression in dementia. Neuron, 73(6),
1204–1215. https://doi.org/10.1016/j.neuron.2011.12.040,
PubMed: 22445347

Ritter, P., Schirner, M., McIntosh, A. R., & Jirsa, V. K. (2013). The
virtual brain integrates computational modeling and multimodal
neuroimaging. Brain Connectivity, 3(2), 121–145. https://doi.org
/10.1089/brain.2012.0120, PubMed: 23442172

Rosazza, C., & Minati, L. (2011). Resting-state brain networks:
Literature review and clinical applications. Neurological
Sciences, 32(5), 773–785. https://doi.org/10.1007/s10072-011
-0636-y, PubMed: 21667095

Rosvall, M., Trusina, A., Minnhagen, P., & Sneppen, K. (2005).
Networks and cities: An information perspective. Physical Review
Letters, 94(2), 028701. https://doi.org/10.1103/ PhysRevLett.94
.028701, PubMed: 15698238

Salimi-Khorshidi, G., Douaud, G., Beckmann, C. F., Glasser, M. F.,
Griffanti, L., & Smith, S. M. (2014). Automatic denoising of func-
tional MRI data: Combining independent component analysis
and hierarchical fusion of classifiers. NeuroImage, 90, 449–468.
https://doi.org/10.1016/j.neuroimage.2013.11.046, PubMed:
24389422

Sanz Leon, P., Knock, S. A., Woodman, M. M., Domide, L.,
Mersmann, J., McIntosh, A. R., & Jirsa, V. (2013). The Virtual
Brain: A simulator of primate brain network dynamics. Frontiers
in Neuroinformatics, 7. https://doi.org/10.3389/fninf.2013
.00010, PubMed: 23781198

Schreiber, T. (2000). Measuring information transfer. Physical
Review Letters, 85(2), 461–464. https://doi.org/10.1103
/PhysRevLett.85.461, PubMed: 10991308

Schultz, D. H., & Cole, M. W. (2016). Higher intelligence is asso-
ciated with less task-related brain network reconfiguration.

Journal of Neuroscience, 36(33), 8551–8561. https://doi.org/10
.1523/JNEUROSCI.0358-16.2016, PubMed: 27535904

Seguin, C., Heuvel, M. P. van den, & Zalesky, A. (2018).
Navigation of brain networks. Proceedings of the National
Academy of Sciences of the United States of America, 115(24),
6297–6302. https://doi.org/10.1073/pnas.1801351115,
PubMed: 29848631

Seguin, C., Razi, A., & Zalesky, A. (2019). Send-receive communi-
cation asymmetry in brain networks: Inferring directionality of
neural signalling from undirected structural connectomes.
BioRxiv, 573071. https://doi.org/10.1101/573071

Shannon, C. E. (1948). A mathematical theory of communication.
Bell System Technical Journal, 27(3), 379–423. https://doi.org/10
.1002/j.1538-7305.1948.tb01338.x

Shine, J. M., Bissett, P. G., Bell, P. T., Koyejo, O., Balsters, J. H.,
Gorgolewski, K. J., Moodie, C. A., & Poldrack, R. A. (2016).
The dynamics of functional brain networks: Integrated network
states during cognitive task performance. Neuron, 92(2), 544–554.
https://doi.org/10.1016/j.neuron.2016.09.018, PubMed: 27693256
Shine, J. M., & Poldrack, R. A. (2018). Principles of dynamic net-
work reconfiguration across diverse brain states. NeuroImage,
180, 396–405. https://doi.org/10.1016/j.neuroimage.2017.08
.010, PubMed: 28782684

Smith, R. E., Tournier, J.-D., Calamante, F., & Connelly, A. (2012).
Anatomically-constrained tractography: Improved diffusion MRI
streamlines tractography through effective use of anatomical in-
formation. NeuroImage, 62(3), 1924–1938. https://doi.org/10
.1016/j.neuroimage.2012.06.005, PubMed: 22705374

Smith, R. E., Tournier, J.-D., Calamante, F., & Connelly, A. (2013).
SIFT: Spherical-deconvolution informed filtering of tractograms.
NeuroImage, 67, 298–312. https://doi.org/10.1016/j.neuroimage
.2012.11.049, PubMed: 23238430

Smith, R. E., Tournier, J.-D., Calamante, F., & Connelly, A. (2015).
SIFT2: Enabling dense quantitative assessment of brain white
matter connectivity using streamlines tractography. NeuroImage,
119, 338–351. https://doi.org/10.1016/j.neuroimage.2015.06
.092, PubMed: 26163802

Smith, S. M., Beckmann, C. F., Andersson, J., Auerbach, E. J.,
Bijsterbosch, J., Douaud, G., Duff, E., Feinberg, D. A., Griffanti,
L., Harms, M. P., Kelly, M., Laumann, T., Miller, K. L., Moeller,
S., Petersen, S., Power, J., Salimi-Khorshidi, G., Snyder, A. Z., Vu,
A. T., … Glasser, M. F. (2013). Resting-state fMRI in the Human
Connectome Project. NeuroImage, 80, 144–168. https://doi.org
/10.1016/j.neuroimage.2013.05.039, PubMed: 23702415

Sneppen, K., Trusina, A., & Rosvall, M. (2005). Hide-and-seek on
complex networks. EPL (Europhysics Letters), 69(5), 853. https://
doi.org/10.1209/epl/i2004-10422-0

Sotiropoulos, S. N., Jbabdi, S., Xu, J., Andersson, J. L., Moeller, S.,
Auerbach, E. J., Glasser, M. F., Hernandez, M., Sapiro, G.,
Jenkinson, M., Feinberg, D. A., Yacoub, E., Lenglet, C., Van
Essen, D. C., Ugurbil, K., & Behrens, T. E. J. (2013). Advances
in diffusion MRI acquisition and processing in the Human
Connectome Project. NeuroImage, 80, 125–143. https://doi.org
/10.1016/j.neuroimage.2013.05.057, PubMed: 23702418

Sporns, O. (2010). Networks of the brain. MIT Press. https://doi.org

/10.7551/mitpress/8476.001.0001

Sporns, O. (2013). Network attributes for segregation and integra-
tion in the human brain. Current Opinion in Neurobiology, 23(2),

Network Neuroscience

664

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
3
6
4
6
1
9
6
0
4
9
0
n
e
n
_
a
_
0
0
1
8
5
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Toward an information theoretical description of the human connectome

162–171. https://doi.org/10.1016/j.conb.2012.11.015, PubMed:
23294553

Stam, C. J. (2014). Modern network science of neurological disor-
ders. Nature Reviews Neuroscience, 15(10), 683–695. https://doi
.org/10.1038/nrn3801, PubMed: 25186238

Stejskal, E. O., & Tanner, J. E. (1965). Spin diffusion measurements:
Spin echoes in the presence of a time-dependent field gradient.
The Journal of Chemical Physics, 42(1), 288–292. https://doi.org
/10.1063/1.1695690

Timme, N. M., & Lapish, C. (2018). A tutorial for information theory
in neuroscience. ENeuro, 5(3. https://doi.org/10.1523/ENEURO
.0052-18.2018, PubMed: 30211307

Tipnis, U., Amico, E., Ventresca, M., & Goñi, J. (2018). Modeling
communication processes in the human connectome through
cooperative learning. IEEE Transactions on Network Science
and Engineering, 7, 476–488. https://doi.org/10.1109/ TNSE
.2018.2878487

Tournier, J.-D., Calamante, F., & Connelly, A. (2012). MRtrix:
Diffusion tractography in crossing fiber regions. International
Journal of Imaging Systems and Technology, 22(1), 53–66.
https://doi.org/10.1002/ima.22005

Van Essen, D. C., Ugurbil, K., Auerbach, E., Barch, D., Behrens, T. E. J.,
Bucholz, R., Chang, A., Chen, L., Corbetta, M., Curtiss, S. W., Della
Penna, S., Feinberg, D., Glasser, M. F., Harel, N., Heath, A. C.,
Larson-Prior, L., Marcus, D., Michalareas, G., Moeller, S., …
WU-Minn HCP Consortium. (2012). The Human Connectome

Project: A data acquisition perspective. NeuroImage, 62(4),
2222–2231. https://doi.org/10.1016/j.neuroimage.2012.02.018,
PubMed: 22366334

Van Essen, D. C., Smith, S. M., Barch, D. M., Behrens, T. E. J., Yacoub,
E., & Ugurbil, K. (2013). The WU-Minn Human Connectome
Project: An overview. NeuroImage, 80, 62–79. https://doi.org/10
.1016/j.neuroimage.2013.05.041, PubMed: 23684880

Vann, S. D., Aggleton, J. P., & Maguire, E. A. (2009). What does the
retrosplenial cortex do? Nature Reviews Neuroscience, 10(11),
792–802. https://doi.org/10.1038/nrn2733, PubMed: 19812579
Wibral, M., Lizier, J. T., & Priesemann, V. (2015). Bits from brains
for biologically inspired computing. Frontiers in Robotics and AI, 2.
https://doi.org/10.3389/frobt.2015.00005

Wibral, M., Vicente, R., & Lizier, J. T. (2014). Directed information
measures in neuroscience. Springer. https://doi.org/10.1007/978
-3-642-54474-3

Worrell, J. C., Rumschlag, J., Betzel, R. F., Sporns, O., & Mišic(cid:4), B.
(2017). Optimized connectome architecture for sensory-motor
integration. Network Neuroscience, 1(4), 415–430. https://doi
.org/10.1162/NETN_a_00022, PubMed: 30090872

Yeo, B. T. T., Krienen, F. M., Sepulcre, J., Sabuncu, M. R., Lashkari, D.,
Hollinshead, M., Roffman, J. L., Smoller, J. W., Zöllei, L., Polimeni,
J. R., Fischl, B., Liu, H., & Buckner, R. L. (2011). The organization of
the human cerebral cortex estimated by intrinsic functional con-
nectivity. Journal of Neurophysiology, 106(3), 1125–1165.
https://doi.org/10.1152/jn.00338.2011, PubMed: 21653723

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

t

/

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
3
6
4
6
1
9
6
0
4
9
0
n
e
n
_
a
_
0
0
1
8
5
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Network Neuroscience

665

Download pdf