METHODS

Exploratory factor analysis with structured
residuals for brain network data

Erik-Jan van Kesteren 1 and Rogier A. Kievit

2

1Utrecht University, Department of Methodology and Statistics, Utrecht, the Netherlands
2University of Cambridge, MRC Cognition and Brain Sciences Unit, Cambridge, UK

Keywords: Dimension reduction, Exploratory Factor analysis, Structural covariance, Functional
connectivity, Symmetry, Structural equation model

a n o p e n a c c e s s

j o u r n a l

ABSTRACT

Dimension reduction is widely used and often necessary to make network analyses and their
interpretation tractable by reducing high-dimensional data to a small number of underlying
variables. Techniques such as exploratory factor analysis (EFA) are used by neuroscientists to
reduce measurements from a large number of brain regions to a tractable number of factors.
However, dimension reduction often ignores relevant a priori knowledge about the structure
of the data. For example, it is well established that the brain is highly symmetric. In this
paper, we (a) show the adverse consequences of ignoring a priori structure in factor analysis,
(b) propose a technique to accommodate structure in EFA by using structured residuals
(EFAST), and (c) apply this technique to three large and varied brain-imaging network
datasets, demonstrating the superior fit and interpretability of our approach. We provide
an R software package to enable researchers to apply EFAST to other suitable datasets.

INTRODUCTION

Using modern imaging techniques, it is possible to investigate brain networks involving many
regions, across different modalities such as grey matter volume, white matter tracts, and func-
tional connectivity. To examine the relation of these networks with external variables of interest,
it is often necessary to summarize them, using a small number of dimensions, often called
factors or components. These low-dimensional components representing the networks can be
tracked over the lifespan (de Mooij, Henson, Waldorp, & Kievit, 2018; DuPre & Spreng, 2017),
compared to behavioural measures (Colibazzi et al., 2008), or related to phenotypes such as
intelligence (Ferguson, Anderson, & Spreng, 2017). In the fields of statistics and mathematics,
such methods for making analyses tractable and interpretable are collectively called dimension
reduction.

Many popular dimension reduction techniques make use of covariance. For example, prin-
cipal components analysis (PCA) can be estimated using only a decomposition of the covari-
ance matrix. Covariance underlies many brain imaging and network analysis approaches, too:
in analysis of structural connectivity, regions of grey matter volume or white matter tractog-
raphy which covary across individuals may constitute connected networks (Alexander-Bloch,
Giedd, & Bullmore, 2013; Mechelli, Friston, Frackowiak, & Price, 2005), and in resting-state
fMRI analysis, regions which covary within an individual over time are considered to have a
functional connection (Van Den Heuvel & Pol, 2010). Thus, dimension reduction on the basis
of covariance matrices is directly applicable to the field of network neuroscience.

Citation: van Kesteren, E.-J., & Kievit,
R. A. (2021). Exploratory factor
analysis with structured residuals
for brain network data. Network
Neuroscience, 5(1), 1–27. https://
doi.org/10.1162/netn_a_00162

DOI:
https://doi.org/10.1162/netn_a_00162

Supporting Information:
https://doi.org/10.1162/netn_a_00162
https://doi.org/10.5281/zenodo.3779927
https://doi.org/10.5281/zenodo.3779908

Received: 9 June 2020
Accepted: 28 July 2020

Competing Interests: The authors have
declared that no competing interests
exist.

Corresponding Author:
Erik-Jan van Kesteren
e.vankesteren1@uu.nl

Handling Editor:
Alex Fornito

Copyright: © 2020
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license

The MIT Press

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
1
1
1
8
8
9
7
4
7
n
e
n
_
a
_
0
0
1
6
2
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Exploratory factor analysis with structure for brain network data

Dimension reduction:
Summarizing a set of variables by
using a smaller set of components
or factors.

Structural equation model:
Method for estimating latent
variables and their relations by
using observed covariances,
assuming linearity and normally
distributed residuals.

Confirmatory factor analysis:
Factor model where the factor
loading structure is predefined based
on theory; typically, each factor only
predicts a subset of the observed
variables.

Multitrait-multimethod model:
Factor model which also assumes
there is residual covariance between
some variables because they are
measured using the same method.

Network Neuroscience

Exploratory factor analysis (EFA) is one such method for dimension reduction based on
covariance. EFA models the observed covariance matrix of a set of P variables by assuming
there are M < P factors, which predict the values on the observed variables. Although other techniques such as PCA and independent component analysis (ICA) are more common in neu- roimaging analysis, EFA has been used since the early days of MRI (see McIntosh & Protzner, 2012, for a review and Machado, Gee, & Campos, 2004 for an early methodological investi- gation). For instance, Tien et al. (1996) performed an EFA on 60 controls and 44 schizophrenia patients for a selection of regions of interest, explicitly noting the high degree of left/right sym- metry and a disruption of this symmetry in patients. Similarly early studies used EFA to model morphology (Stievenart et al., 1997) and width (Denenberg, Kertesz, & Cowell, 1991) of the corpus callosum. Some approaches combined structural equation modeling (SEM) and PCA to model latent factors of grey matter structure in clinical populations (Yeh et al., 2010). These approaches have also been used to study typical population of children and adults (Colibazzi et al., 2008). More recently, EFA has been used to reduce individual differences in white matter microstructure in clinical populations (Herbert et al., 2018), as well as (extremely) large-scale population studies (Cox et al., 2016). Hybrid approaches have combined exploratory and confirmatory factor analysis approaches (Baskin-Sommers, Neumann, Cope, & Kiehl, 2016; de Mooij et al., 2018) and used EFA in multimodal structural acquisitions (Mancini et al., 2016). EFA has also been used for functional imaging, including both fMRI (e.g., James et al., 2009) and EEG (Scharf & Nestler, 2018; Tucker & Roth, 1984). Most excitingly, recent work has used EFA to compare and contrast patterns of individual differences in brain structure at base- line with individual differences in developmental change over time, noting striking differences in dimensionality of change versus cross-sectional differences (Cox et al., 2020). Although the above is not intended to be a comprehensive review, it shows that EFA has been used widely in the imaging literature since early days. Many related dimension reduction techniques exist beyond EFA, including partial least squares (PLS), ICA, spectral decomposition, and many more beyond our current scope (see Roweis & Ghahramani, 1999; Sorzano, Vargas, & Montano, 2014). All of these tech- niques aim to approximate the observed data by means of a lower dimensional representation. These techniques, although powerful, share a particular limitation, at least in their canonical implementations, namely that they cannot easily integrate prior knowledge of (additional) co- variance structure present in the data. In other words, all observed covariation is modeled by the underlying factor structure. This limitation is relevant in the context of structural and functional brain connectivity data because of symmetry: Much like other body parts, contralateral (left/right) brain regions are highly correlated due to developmental and genetic mechanisms which govern the gross mor- phology of the brain. Ignoring this prior information will adversely affect the dimension re- duction step, leading to worse representation of the high-dimensional data by the extracted factors. Simple workarounds, such as averaging left and right into a single index per region, have other drawbacks: they throw away information, preclude the discovery of (predominantly) lateralized factors, and prevent the study of (a)symmetry as a topic of interest in and of itself. Other classes of techniques, developed largely within psychometrics, can naturally ac- commodate additional covariance structure such as symmetry. These techniques started with multitrait-multimethod (MTMM) matrices (Campbell & Fiske, 1959) and later confirmatory fac- tor analysis (CFA) with residual covariances (e.g., Kenny, 1976). MTMM is designed to extract factors when these factors are measured in different ways: when measuring personality through a self-report questionnaire and behaviour ratings, there are factors that explain correlation 2 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 5 1 1 1 8 8 9 7 4 7 n e n _ a _ 0 0 1 6 2 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Exploratory factor analysis with structure for brain network data Residual covariance: Covariance among unexplained parts of variables, after taking into account the model (in this case the factors). Factor loadings: Weights matrix indicating the strength of the association between each latent factor and each observed variable. Network Neuroscience among items corresponding to a specific trait such as “extraversion,” and there are factors that explain additional correlation between items because they are gathered using the same methods (self-report and behavioural ratings). Thus MTMM techniques separate the correlation matrix into two distinct, summative parts: correlation due to the underlying traits (factors) of central interest, and correlation due residual structure in the measurements. However, MTMM requires a priori knowledge of the trait structure (e.g., the OCEAN model of personality) for estimation. In this paper, we combine dimension reduction (e.g., across many brain regions) and prior structure knowledge (e.g., symmetry) by introducing EFA with structured residuals (EFAST). EFAST builds on standard implementations of EFA, CFA, and MTMM, but goes beyond these techniques by simultaneously allowing for exploration and the incorporation of residual struc- ture. We show that EFAST outperforms EFA in empirically plausible scenarios, and that ignoring the problem of structured residuals in these scenarios adversely affects inferences. This paper is structured as follows. First, we explain why using standard EFA or CFA for brain imaging data may lead to undesirable results, and we develop EFAST based on novel techniques from SEM. Then, we show that EFAST performs well in simulations, demonstrating superior performance compared to EFA in terms of factor recovery, factor covariance estima- tion, and the number of extracted factors when dealing with symmetry. Third, we illustrate EFAST in a large neuroimaging cohort (Cam-CAN; Shafto et al., 2014). We illustrate EFAST for three distinct datasets: grey matter volume, white matter microstructure, and within-subject fMRI functional connectivity. We show how EFAST outperforms EFA both conceptually and statistically in all three datasets, showing the generality of our technique. We conclude with an overview and suggestions for further research. Accompanying this paper, we provide tools for researchers to use and expand upon with their own datasets. These tools take the form of (a) an R package called EFAST and a tutorial with example code (van Kesteren & Kievit, 2020a), and (b) synthetic data and code to reproduce the empirical examples and simulations (van Kesteren & Kievit, 2020b). FACTOR ANALYSIS WITH STRUCTURED RESIDUALS In this section, we compare and contrast existing approaches in their ability to perform factor analysis in an exploratory way while at the same time accounting for residual structure. We discuss new developments in the field of exploratory structural equation modeling (ESEM) that enable simultaneous estimation of exploratory factors and structured residuals, after which we develop the EFAST model as an ESEM with a single exploratory block. We will use brain morphology data with bilateral symmetry as our working example throughout, although the principles here can be generalized to datasets with similar properties. EFA, as implemented in software programs such as SPSS, R, and Mplus, models the observed correlation matrix through two summative components: the factor loading matrix Λ, relating the predefined number M of factors to the observed variables, and a diagonal residual variance matrix Θ, signifying the variance in the observed variables unexplained by the factors. Using maximum likelihood, principal axis factoring, or least squares (Harman & Jones, 1966), the factor loadings and residual variances are estimated such that the implied correlation matrix Σ = ΛΛT + Θ best approximates the observed correlation matrix S. After estimation, the factor loadings are rotated to their final interpretable solution by using objectives such as oblimin, varimax, or geomin (Bernaards & Jennrich, 2005). 3 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 5 1 1 1 8 8 9 7 4 7 n e n _ a _ 0 0 1 6 2 p d . 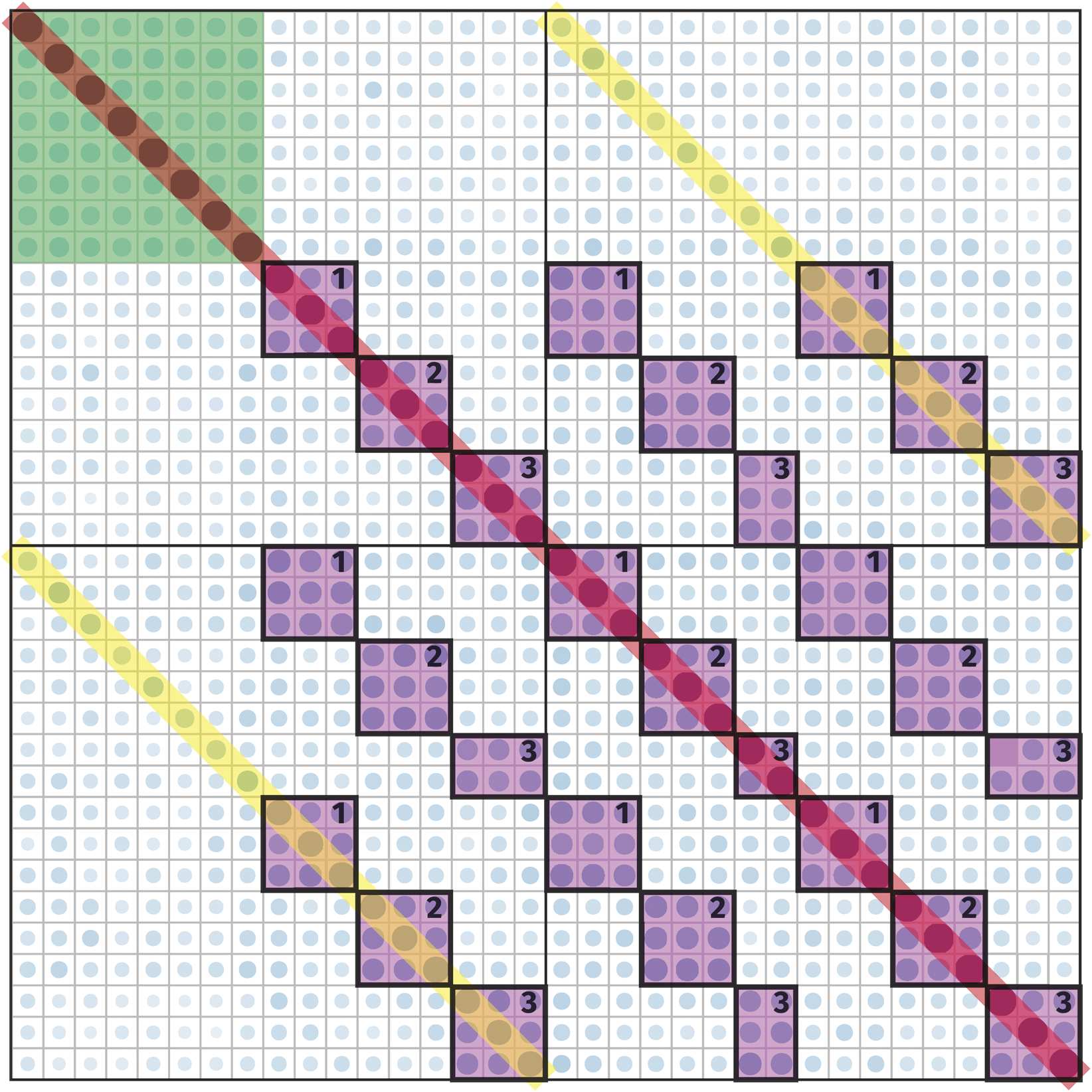t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Exploratory factor analysis with structure for brain network data Figure 1. Example observed correlation matrix and its associated decomposition according to EFA (top) and according to CFA (bottom) into a factor-implied correlation component (ΛΨΛT), residual variance component Θ, and—in CFA with residual structure only—residual structure component. We illustrate the challenge and the rationale behind our approach in Figure 1. The true correlation matrix is highlighted on the left, with correlations due to three factors shown as diagonal blocks. However, there is also considerable off-diagonal structure: the secondary diagonals show a symmetry pattern similar to that observed in real-world brain structure data (Taylor et al., 2017). The top panel of Figure 1 shows that a traditional EFA approach will separate this data matrix into two components: (a) covariance due to the hypothesized factor structure and (b) the diagonal residual matrix. The key challenge is that EFA will attempt to approximate all the off-diagonal elements of the correlation matrix through the factors, even if this adversely affects the recovery of the true factor structure. Performing EFA with such a symmetry pattern may affect the factor solution in a variety of ways. For instance, in this toy example, the EFA model requires more than 12 factors to represent the data, instead of the 3 factors specified (see Supporting Information Figure S1). In other words, in such cases it is essential to incorporate the known residual structure via a set of additional assumptions. As an alternative to EFA, we may implement a CFA instead. In contrast to EFA, CFA im- poses a priori constraints on the Λ matrix: some observed variables do not load on some factors. Moreover, in contrast to standard EFA approaches, residual structure can be easily im- plemented in CFA by using standard SEM software such as lavaan (Rosseel, 2012). In other words, CFA would allow us to tackle the problem in Figure 1: We can allow for the residual structure known a priori to be present in the data. By allowing for the residual structure in the data, a CFA yields the implied matrices shown in the bottom panel of Figure 1, retrieving the correct factor loadings, residual variance, and residual structure. However, this is only possible because in this toy example we know the factor structure. In many empirical situations this is precisely what we wish to discover. In the absence of theory about the underlying factors, it is thus not possible to benefit from these features of CFA. As such, we need an approach that can combine the strengths of EFA (estimating the fac- tor structure in the absence of strong a priori theory) with those from CFA (the potential to Network Neuroscience 4 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 5 1 1 1 8 8 9 7 4 7 n e n _ a _ 0 0 1 6 2 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Exploratory factor analysis with structure for brain network data allow for a priori residual structure). Here, we propose a hybrid between the two, which we call exploratory factor analysis with structured residuals, or EFAST. In order to implement and estimate these models, we make use of recent developments in the field of SEM. In the next section, we explain how these developments make EFAST estimation possible. Exploratory SEM Exploratory SEM (ESEM) is an extension to SEM which allows for blocks of exploratory fac- tor analysis within the framework of confirmatory SEM (Asparouhov & Muthén, 2009; Brown, 2006; Guàrdia-Olmos, Peró-Cebollero, Benítez-Borrego, & Fox, 2009; Jöreskog, 1969; Marsh, Morin, Parker, & Kaur, 2014; Rosseel, 2019). ESEM is a two-step procedure. In the first step, a regular SEM model is estimated, where each of the EFA blocks have a diagonal latent co- variance matrix Ψ and the Λ matrix of each block is of transposed echelon form, meaning all elements above the diagonal are constrained to 0. For a nine-variable, three-factor EFA block b the matrices would then be: Ψ b = 1 0 0    0 1 0 0 0 1    , Λ b =                   0 0 0 λ11 λ21 λ22 λ31 λ32 λ33 λ41 λ42 λ43 λ51 λ52 λ53 λ61 λ62 λ63 λ71 λ72 λ73 λ81 λ82 λ83 λ91 λ92 λ93                   This means there are M2 b constraints for each EFA block b. This is the same number of constraints as conventional EFA (Asparouhov & Muthén, 2009). The second step in ESEM is to rotate the solution by using a rotation matrix H. Just as in regular EFA, this rotation matrix is constructed using objectives such as geomin or oblimin. In ESEM, the rotation affects the factor loadings and latent covariances of the EFA blocks, but also almost all other parameters in the model (Asparouhov & Muthén, 2009) provide an overview of how rotation changes these parameter estimates). Despite these changes, a key property of ESEM is that different rotation solutions lead to the same overall model fit. ESEM has long been available only in Mplus (Asparouhov & Muthén, 2009; Muthén & Muthén, 1998). More recently, it has become available in open sourced R packages psych (for specific models, Revelle, 2018) as well as lavaan (since version 0.6-4, Rosseel, 2019)—a comprehensive package for structural equation modeling. An example of a basic EFA model using lavaan syntax with three latent variables and nine observed variables is the following: efa(‘‘block1’’)*F1 =~ x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 efa(‘‘block1’’)*F2 =~ x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 efa(‘‘block1’’)*F3 =~ x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 In effect, this model specifies three latent variables (F1, F2, and F3) which are each indi- cated by all nine observed variables (x1 to x9). The efa(‘‘block1’’) part is a modifier for this model which imposes the constraints on Ψ and Λ mentioned above. For a more detailed explanation of the lavaan syntax, see Rosseel (2012). Figure 2 shows a comparison of the factor loadings obtained using conventional factor analysis (factanal() in R) and lavaan’s Network Neuroscience 5 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 5 1 1 1 8 8 9 7 4 7 n e n _ a _ 0 0 1 6 2 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Exploratory factor analysis with structure for brain network data Figure 2. Exploratory factor analysis of nine variables in the Holzinger and Swineford (1939) dataset. On the y-axis are the estimated factor loadings using the oblimin rotation functionality in lavaan version 0.6-4, and the loadings on the x-axis are derived from factanal with oblimin rotation from the GPArotation package (Bernaards & Jennrich, 2005). The loadings are all on the diagonal with a correlation of 1, meaning the solutions obtained from these different methods are equal. efa() modifier. As shown, the solution obtained is exactly the same, with perfect correlation among the loadings for each of the factors. With this tool as the basis for model estimation, the next section provides a detailed devel- opment of the construction of EFAST models. EFAST Models We propose using EFA with corrections for contralateral covariance within the ESEM frame- work. The corrections we propose are the same as in MTMM models or CFA with residual co- variance. In EFAST the method factors use CFA, and the remaining correlations are explained by EFA. Thus, unlike standard MTMM methods, EFAST contains exploratory factor analysis on the trait side, as the factor structure of the traits is unknown beforehand: the goal of the analysis is to extract an underlying low-dimensional set of features which explain the observed corre- lations as well as possible. For our running example of brain imaging data with contralateral symmetry, we consider each region of interest (ROI) a “method” factor, loading on only two regions. Note that in the context of brain imaging, Lövdén et al. (2013, Figure 1, model A) have had similar ideas, but their factor analysis operates on the level of left-right combined ROIs rather than individual ROIs. The EFAST model has M exploratory factors in a single EFA block, and one method factor per homologous ROI pair, each with loadings constrained to 1 and its own variance estimated. The estimated variance of the method factors then represents the amount of covariance due to symmetry, over and above the covariance represented by the traits. In Figure 3, the model is displayed graphically for a simplified example with six ROIs in each hemisphere. An alternative parametrization for this model is also available. Specifically, we can use the correlations between the residuals of the observed variables instead of method factors with freely estimated variances. In the SEM framework, this would amount to moving the symmetry structure from the factor-explained matrix (ΛΨΛT) to the residual covariance matrix Θ. This model is exactly equivalent, meaning the same correlation matrix decomposition, the same factor structure, and the same model fit will be obtained. However, we favour the method factor parametrization as it is closer to MTMM-style models, it is easier to extract potentially relevant Network Neuroscience 6 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 5 1 1 1 8 8 9 7 4 7 n e n _ a _ 0 0 1 6 2 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Exploratory factor analysis with structure for brain network data Figure 3. EFAST model with morphology of six regions of interest measured in the left hemisphere (LH) and right hemisphere (RH). The dashed lines indicate fixed loadings, and the two-headed ar- rows indicate variance/covariance parameters. The method factors are constrained to be orthogonal, and the loadings of the M traits are estimated in an exploratory way. metrics such as a “lateralisation coefficient,” and easier to extend to other data situations where multiple indicators load on each method factor. To implement the EFAST model we use the package lavaan, which allows for easy scaling of the input data, different estimation methods, missing data handling through full informa- tion maximum likelihood, and more. Estimation of the model in Figure 3 can be done with a variety of methods. Here we use the default maximum likelihood estimation method as im- plemented in lavaan. Accompanying this paper, we are making available a convenient R package called efast that can fit EFAST models for datasets with residual structure due to symmetry. For more implementation details, the package and its documentation can be found at https://github.com/vankesteren/efast. In the next section, we show how our implementation of EFAST compares to regular EFA in terms of factor loading estimation, factor covariance estimation, as well as the estimated number of factors. SIMULATIONS In this section, we use simulated data to examine different properties of EFAST models when compared to regular EFA in controlled conditions. The purpose of this simulation is not an exhaustive investigation, but rather a pragmatically focused study of data properties (neuro) scientists wishing to use this technique are likely to encounter. First, we explain how data were simulated to follow a specific correlation structure, approximating the general structure of empirical data such as that in the Cam-CAN study (see Empirical Examples section). Then, we investigate the effects of structured residuals on the extracted factors from EFA and EFAST: in several different conditions, we investigate how the estimation of factor loadings, the co- variances between factors, and the number of factors changes with increasing symmetry. Network Neuroscience 7 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 5 1 1 1 8 8 9 7 4 7 n e n _ a _ 0 0 1 6 2 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Exploratory factor analysis with structure for brain network data Data Generation Data were generated following a controlled population correlation matrix Σtrue. This matrix represents the true correlation between measurements of brain structure in 17 left-hemisphere and 17 right-hemisphere ROIs. An example correlation matrix from our data-generating mech- anism is shown in Figure 4. Σtrue was constructed through the summation of three separate matrices, as in the lower panel of Figure 1: 1. The factor component Σ f actor is constructed as ΛΨΛT, where the underlying factor co- variance matrix Ψ can be either an identity matrix (orthogonal factors) or a matrix with nonzero off-diagonal elements (oblique factors). There are four true underlying factors in this simulation. One of the factors is completely lateralized (top left, highlighted in green), meaning that it loads only on ROIs in the left hemisphere. An additional illustra- tion of this left-hemisphere factor is shown in Figure 5. The remaining three factors have both left- and right-hemisphere indicators. 2. The structure component matrix is a matrix with all 0 elements except on the second- ary diagonal, that is, the diagonal elements of the bottom left and top right quadrant are nonzero. The values of these secondary diagonals determine the strength of the symmetry. 3. The residual variance component matrix is a diagonal matrix where the elements are chosen such that the diagonal of Σtrue is 1. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 5 1 1 1 8 8 9 7 4 7 n e n _ a _ 0 0 1 6 2 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 4. Example covariance matrix of the data-generating mechanism used in the simulations. This matrix results from simulated data of 650 brain images, with a factor loading of .595 for the lateralized factor, a loading of .7 for the remaining factors, a factor correlation of .5, and a symmetry correlation of .2. The first 17 variables indicate regions of interest (ROIs) in the left hemisphere, and the remaining variables indicate their contralateral homologues. Note the secondary diagonals, indicating contralateral symmetry, and the block of eight variables in the top left resulting from the lateralized factor. Network Neuroscience 8 Exploratory factor analysis with structure for brain network data l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 5 1 1 1 8 8 9 7 4 7 n e n _ a _ 0 0 1 6 2 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 5. Example lateralized factor (the first factor in the simulation). Grey matter volume in eight left-hemisphere regions of interest are predicted by the value on this factor. For the following sections, data were generated with a sample size of 650, 130, or 65, a latent correlation of either 0 or 0.5, bilateral factor loadings of 0.5 or 0.7, lateral factor loadings of .425 or .595, and contralateral homology correlations of either 0 (pure EFA), 0.2 (minor symmetry), or 0.4 (major symmetry). These conditions were chosen to be plausible scenarios, similar to the observed data from our empirical examples. In each condition, 120 datasets were generated on which EFA and EFAST models with four factors were estimated. Thus, in each analysis the true number of factors is correctly specified before estimation. In the last simulation we then explore different criteria for the choice of number of factors in the case of contralateral symmetry. Effect of Structured Residuals on Factor Loadings In this section, we compare estimated factor loadings from EFA and EFAST to the true factor loadings from the simulation’s data-generating process. For each condition, 120 datasets were generated, to which both EFA and EFAST models were fit. The factor loading matrix for each model was then extracted, the columns reordered to best fit the true matrix, and the mean absolute error of the factor loadings per factor was calculated. As hypothesized, allowing structured residuals affects how well the factor loadings are es- timated from the datasets. Notably, as shown in Figure 6 when performing regular EFA, the estimation error of the factor loadings increases when the symmetry becomes stronger, whereas the factor loading estimation error for the EFAST model remains at the level of regular EFA when there is no symmetry. Looking at the lateralized factor in particular, the adverse effect of omit- ting symmetry in dimension reduction becomes even stronger: in EFA, the lateralized factor becomes bilateral, leading to a larger error and an incorrect inference regarding the nature of the thus estimated factor. Although Figure 6 shows only the condition with a sample size of 650, factor loadings of 0.5, and factor covariance of 0.5, the pattern is similar for different Mean absolute error: In a simulation study, the absolute difference between the estimated and the true parameter values. Network Neuroscience 9 Exploratory factor analysis with structure for brain network data l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 5 1 1 1 8 8 9 7 4 7 n e n _ a _ 0 0 1 6 2 p d t . 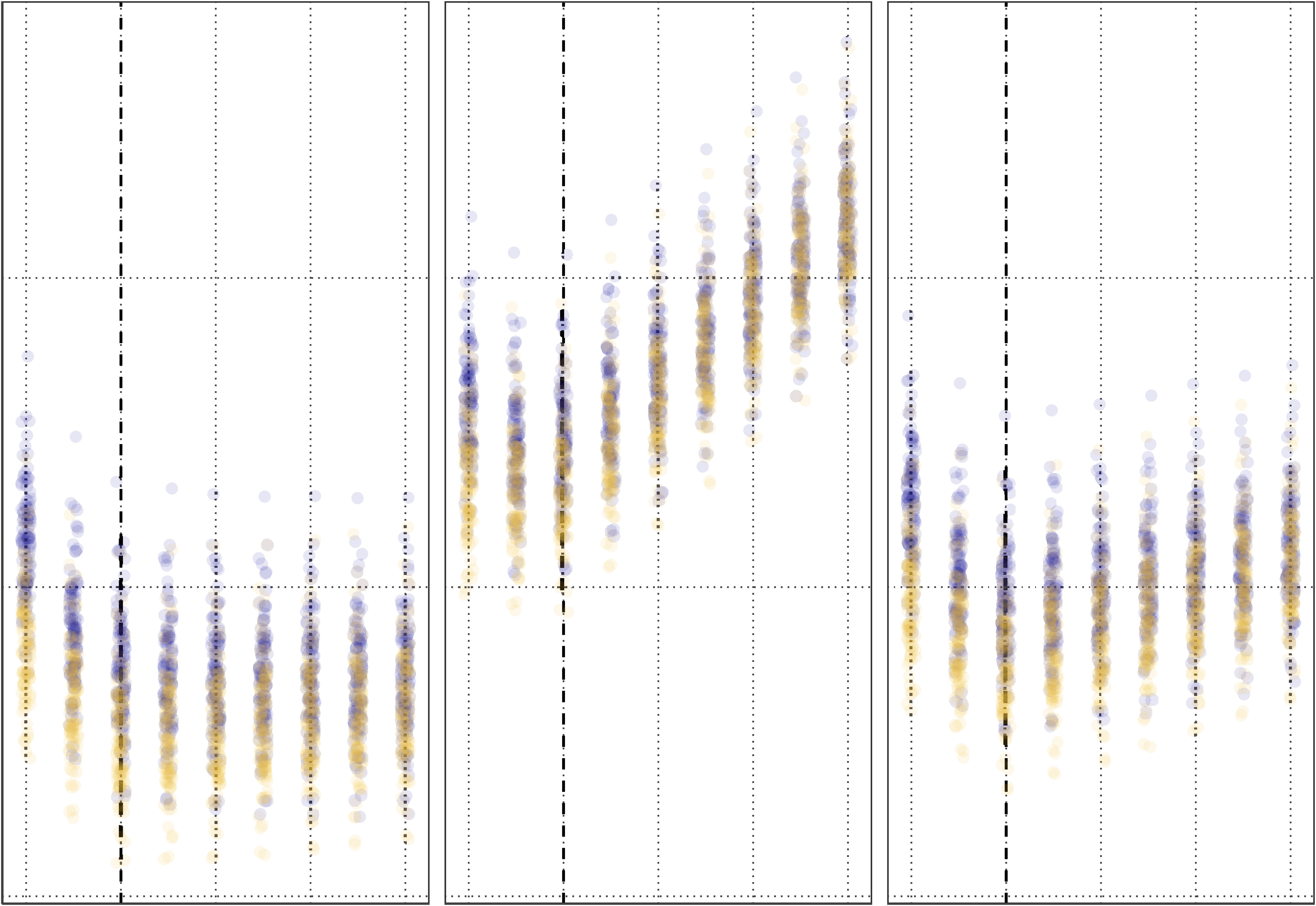f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 6. Mean absolute error for factor loadings of EFA versus EFAST models with increasing amounts of contralateral symmetry correlation. This plot comes from the condition where the sam- ple size is 650, the covariance of the latent variables is 0.5, and the factor loadings are 0.5. The plot shows that for both bilateral and lateralised factors, EFA starts to exhibit more error as sym- metry increases, more so for the lateral factor, whereas EFAST performance is nominal over these conditions. Error bars indicate 95% Wald-type confidence intervals. sample sizes, different factor loading strengths, and with no factor covariance (see Supporting Information Figures S2 and S3). In addition, sample size analysis shows that EFAST and EFA show moderate to high con- vergence rates for small (65) to moderate (130) sample sizes (see Supporting Information Figure S4). Although other drawbacks of smaller sample sizes remain (e.g., imprecise esti- mates, favouring of insufficiently complex models), this shows the feasibility, in principle, of using such analyses in commonly available sample sizes. To assess whether a particular com- bination of sample size, atlas dimensionality (i.e., number of regions) and strength of factor loadings is feasible for analysis using EFAST, we recommend a simulation approach. Software packages such as lavaan offer versatile tools to generate data under various specifications, al- lowing researchers to see whether a particular analysis is in principle feasible under certain idealized conditions before proceeding with real data. Results from this section suggest that for the purpose of factor loading estimation, EFA and EFAST perform equally well in the case where a model without residual structure is the true underlying model, but EFAST outperforms EFA when residual structure in the observed data becomes stronger. In other words, implementing EFAST in the absence of residual structure does not seem to have negative consequences for estimation error, suggesting it may also be a useful default if a specific residual structure is thought, but not known, to exist. This is in line with Cole, Ciesla, and Steiger (2007), who argue that in many situations including correlated residuals does not have adverse effects, but omitting them does. Network Neuroscience 10 Exploratory factor analysis with structure for brain network data Effect of Structured Residuals on Factor Covariances Here, we compare how well EFA and EFAST retrieve the true factor covariance values. For both methods, we used geomin rotation with an epsilon value of 0.01 as implemented in lavaan 0.6.4 (Rosseel, 2019). The matrix product of the obtained rotation matrix H then represents the estimated factor covariance structure of the EFA factors: Ψ EFA = H T H (Asparouhov & Muthén, 2009, eq. 22). The mean of the off-diagonal elements of the Ψ EFA matrix were then compared to the true value of 0.5 for increasing symmetry strength. The results are shown graphically in Figure 7. Here, it can be seen that with this rotation method the latent covariance is underestimated in all cases, although less so with stronger factor loadings. Furthermore, EFA performs worse as the symmetry increases, whereas the performance of EFAST remains stable regardless of the degree of contralateral homology, again suggesting no adverse effects to implementing EFAST in the absence of contralateral correlations. In the case of uncorrelated factors (not shown), the two methods perform similarly well. The results from this section show that in addition to better factor recovery for EFAST, the recovery of factor covariance is also improved relative to EFA. Again, even when the data- generating mechanism does not contain symmetry, EFAST performs at least at the level of the EFA model. Note that in this case the overall model fit in terms of AIC and BIC is slightly better for the EFA model, as it has fewer parameters: for factor loadings of .5 and no symmetry, the mean AIC is 60148 (EFA) versus 60164 (EFAST), and BIC is 60882 (EFA) versus 60974 (EFAST). This, together with the comparable convergence rates for most conditions (Supporting Information Figure S4), suggests that it is viable to use EFAST as a “keep it maximal” strategy l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 5 1 1 1 8 8 9 7 4 7 n e n _ a _ 0 0 1 6 2 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 7. Latent covariance estimates for different levels of contralateral homology correlation. The true underlying latent covariance is 0.5; both methods underestimate the latent covariance but EFA becomes more biased as symmetry increases. Error bars indicate 95% Wald-type confidence intervals. Network Neuroscience 11 Exploratory factor analysis with structure for brain network data Information criterion: An indicator weighing model fit (likelihood) and model complexity (number of parameters); lower values indicate better models. (Barr, Levy, Scheepers, & Tily, 2013), where EFAST can be used initially with no drawbacks, but one can use model evidence to favour classical EFA instead. Effect of Structured Residuals on Model Fit In the above analyses, the number of factors was specified correctly for each model estimation (using either EFA or EFAST). However, in empirical applications the number of factors will rarely be known beforehand, so has to be decided on the basis of some criterion. A common approach to extracting the number of factors, aside from computationally expensive strategies such as parallel analysis (Horn, 1965), is model comparison through information criteria such as the AIC or BIC (e.g., Vrieze, 2012). In this procedure, models with increasing numbers of factors are estimated, and the best fitting model in terms of these criteria is chosen. In this simulation, we generated 100 datasets as in Figure 4, i.e., strong loadings and medium symmetry, and we fit EFA and EFAST models with 2 to 10 factors. Across these solutions we then compute the information criteria of interest. Here we choose the two most common infor- mation criteria (the AIC and BIC) as well as the sample size adjusted–BIC (SSABIC), as this is the default in the ESEM function of the psych package (Revelle, 2018). The results of this proce- dure are shown in Figure 8. Each point indicates a fitted model. The means of the information criteria are indicated by the solid lines. The plot in Figure 8 shows that across all factor solutions, EFAST shows better fit than EFA, suggesting the improvement in model fit outweighs the additionally estimated parameters. As the number of requested factors increases beyond optimality, this model fit improvement diminishes as EFA explains more of the symmetry structure through the additional factors. In general, the Akaike information criterion (AIC) tends to overextract factors, the Bayesian information criterion (BIC) slightly underextracts, and the SSABIC shows the best extraction l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 5 1 1 1 8 8 9 7 4 7 n e n _ a _ 0 0 1 6 2 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 8. AIC and BIC values for increasing number of factors with EFA and EFAST models. Lines indicate expectations: the vertices are at the mean values for these criteria. The true number of factors is 4 (dashed vertical line). Network Neuroscience 12 Exploratory factor analysis with structure for brain network data performance (see also Supporting Information Figure S5). In practice, therefore, we suggest us- ing SSABIC for determining the number of factors when model fit is of primary concern. Note that a researcher may also wish to determine the number of factors based on other considera- tions, such as usability in further analysis, estimation tractability, or theory. EFAST IN PRACTICE: MODELING BRAIN IMAGING DATA In the field of cognitive neuroscience, a large body of work has demonstrated close ties be- tween individual differences in brain structure and concurrent individual differences in cogni- tive performance such as intelligence tasks (e.g., Basten, Hilger, & Fiebach, 2015). Moreover, different aspects of brain structure can be sensitive to clinical and preclinical conditions such as grey matter for multiple sclerosis (Eshaghi et al., 2018), white matter hyperintensities for cardiovascular factors (Fuhrmann et al., 2019), and white matter microstructure for conditions such as ALS (Bede et al., 2015), Huntingtons (Rosas et al., 2010), and many other conditions. However, one perennial challenge in imaging is how to deal with the dimensionality of imaging data. Depending on the spatial resolution, a brain image can be divided into as many as 100,000 individual regions, or voxels, rendering mass univariate approaches vulnerable to issues of multiple comparison. An alternative approach is to focus on sections called regions of interest (ROIs) defined either anatomically (e.g., Desikan et al., 2006) or functionally (e.g., Schaefer et al., 2018). However, this only solves the challenge of dimensionality in part, by grouping adjacent voxels into meaningful regions. An emerging approach is therefore to study how neural measures covary across populations or time, either in these ROIs (Sripada et al., 2019) or at the voxel level (DuPre & Spreng, 2017). This offers a promising strategy to reduce the high-dimensional differences in brain structure into a tractable number of components, or factors, not limited by spatial adjacency. However, standard techniques such as EFA or PCA do not easily allow for the integration of a fundamental biological fact: that there exists strong contralateral symmetry between brain regions, such that any given region (e.g., the left lingual gyrus) is generally most similar to the same region on the other side of the brain. Here, we show how we can combine the strengths of exploratory data reduction with the integration of a priori knowledge about the brain into a more sensible, anatomically plausible factor structure which can either be pursued as an object of intrinsic interest or used as the basis for further investigations (e.g., which brain factors are most strongly associated with phenotypic outcomes). Empirical Example: Grey Matter Volume The data we use is drawn from the Cambridge Centre for Ageing and Neu- Data Description roscience (Shafto et al., 2014; Taylor et al., 2017). Cam-CAN is a community derived lifespan sample (ages 18–88) of healthy individuals. Notably, the raw data from the Cam-CAN cohort is freely available through our data portal https://camcan-archive.mrc-cbu.cam.ac.uk/dataaccess/. The sample we discuss here is based on 647 individuals. For the purposes of this project we use morphometric brain measures derived from the T1 scans. Specifically, we used the Mindboggle pipeline (Klein et al., 2017) to estimate region-based grey matter volume, using the underlying freesurfer processing pipeline. To delineate the regions, we here use the Desikan–Killiany– Tourville atlas for determining the ROIs (Klein & Tourville, 2012) as illustrated in Figure 9. Network Neuroscience 13 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 5 1 1 1 8 8 9 7 4 7 n e n _ a _ 0 0 1 6 2 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Exploratory factor analysis with structure for brain network data Figure 9. Desika–Killiany–Tourville atlas used in the empirical illustration, as included in the ggseg package (Mowinckel & Vidal-Piñeiro, 2019). l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 5 1 1 1 8 8 9 7 4 7 n e n _ a _ 0 0 1 6 2 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 10. Correlation plot of cortical grey matter volume in 647 T1 weighted images of the Cam- CAN sample, estimated through Mindboggle in 34 brain regions in each hemisphere according to DKT segmentation. Numbers on the colour scale indicate the strength of the estimated correla- tion, with darker blue indicating stronger positive correlations. Secondary diagonal lines are visible indicating correlation due to contralateral homology. Network Neuroscience 14 Exploratory factor analysis with structure for brain network data We focus only on grey matter (not white matter) and only on cortical regions (not subcor- tical or miscellaneous regions such as ventricles) with the above atlas, for a total of 68 brain regions. The correlation matrix of regional volume metrics is shown in Figure 10, where the first 34 variables are ROIs in the left hemisphere, and the last 34 variables are ROIs in the right hemisphere. The presence of higher covariance due to contralateral homology is clearly visible in the darker secondary diagonal ‘stripes’ which show the higher covariance between the left/right version of each anatomical region. Our goal is to reduce this high-dimensional matrix into a tractable set of ‘brain factors,’ which we may then use in further analyses, such as differences in age sensitivity, in a way that respects known anatomical constraints. The default estimation using EFA will attempt to account for the strong covariance among homologous regions seen in this data, meaning it is unlikely for, say, the left insula and the right insula to load on different factors, and/or for a factor to be characterized only/mostly by regions in one hemisphere. To illustrate this phenomenon, we first run a six-factor, geomin- rotated EFA for the above data (the BIC suggests six factors for this data using the EFAST model). The factor loadings for each ROI in the left and right hemispheres are plotted in Figure 11. A strong factor loading for a ROI in the left hemisphere is likely to have a strong factor loading in the right hemisphere due to the homologous correlation, as shown by the strong correlations for each of the factors. In EFA, the resulting factors thus inevitably capture correlation due to contralateral symme- try, inflating or deflating factor loadings due to these contralateral residual correlations. Most problematically from a substantive neuroscientific standpoint, this distortion means it is effec- tively impossible to discover lateralized factors, that is, patterns of covariance among regions expressed only, or dominantly, in one hemisphere. This is undesirable, as there is both sugges- tive and conclusive evidence that some neuroscientific mechanisms may display asymmetry. For instance, typical language ability is associated with an asymmetry in focal brain regions l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 5 1 1 1 8 8 9 7 4 7 n e n _ a _ 0 0 1 6 2 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 11. Left-right hemisphere factor loading correlations. The correlations between the load- ings are high, indicating a strong similarity between the loadings in the left and right hemispheres. Network Neuroscience 15 Exploratory factor analysis with structure for brain network data (e.g., Bishop, 2013; Gauger, Lombardino, & Leonard, 1997), whereas structural differences in the right hemisphere may be more strongly associated with face perception mechanisms (Frässle et al., 2016). Developmentally, there is evidence that the degree of asymmetry changes across the lifespan (e.g., Plessen, Hugdahl, Bansal, Hao, & Peterson, 2014; Roe et al., 2020). Within a SEM context, recent work shows that model fit of a hypothesized covariance struc- ture may differ substantially between the right and left hemispheres despite focusing on the same brain regions (Meyer, Garzón, Lövdén, & Hildebrandt, 2019). The ignorance of tradi- tional techniques for the residual structure may cause lateralized covariance factors to appear symmetrical instead, or to not be observed at all. In this section, we compare the model fit and factor solutions of EFA and EFAST for Results the Cam-CAN data, and we show how EFAST decomposes the correlation matrix in Figure 10 into factor, structure, and residual variance components. The full annotated analysis script to reproduce these results is available as Supporting Information to this manuscript. Overall, the EFAST model performs considerably better than standard EFA using common information criteria (Figure 12). The BIC criterion, combined with the convergence of the mod- els to an admissible solution, suggests that six factors is optimal for this dataset. While both AIC and SSABIC show that more factors may be needed to properly represent the data, we see that this quickly leads to nonconvergence. We here consider six factors to be a tractable number for further analysis. First and foremost, this six-factor solution shows a much better model solution under EFAST (BIC ≈ 87, 500) than under EFA (BIC ≈ 90, 000), emphasizing the empirical benefits of appropriately modeling known biological constraints. Additionally, statistical model comparison through a likelihood ratio test shows that the EFAST model fits significantly better (see Table 1). Other fit measures such as CFI, root-mean-square error of ap- proximation (RMSEA), and standardized root mean residual (SRMR) paint a similar story. The full factor loading matrix for both EFAST and EFA are shown in Supporting Information Table S1. RMSEA: Root-mean-square error of approximation, a popular model fit index based on the log- likelihood and the degrees of freedom of a structural equation model. Values closer to 0 indicate better fit. SRMR: Standardized root mean residual, a value indicating how well a predicted correlation matrix approximates the observed correlation matrix. Values closer to 0 indicate better fit. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 5 1 1 1 8 8 9 7 4 7 n e n _ a _ 0 0 1 6 2 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 12. AIC and BIC for the increasing numbers of EFA factors. Semitransparent points indicate models which are inadmissible either due to nonconvergence or convergence to a solution with problems (e.g., Heywood cases). In these cases we plot the information criteria based on the log- likelihood computed at the time the estimation terminated. Network Neuroscience 16 Exploratory factor analysis with structure for brain network data Table 1. Comparing the fit of the EFAST and EFA models with six factors, using a likelihood ratio test and several fit criteria EFAST EFA CFI 0.912 0.843 RMSEA 0.057 0.075 SRMR 0.209 0.342 χ2 5762.676 8818.146 Df 1851 1885 ∆χ2 ∆Df Pr(> χ2)

3055.471

34

< .001 Figure 13. Extracted correlation matrix components using a six-factor EFAST model with uncon- strained correlations. Darker blue indicates stronger positive correlation. From left to right: factor- implied correlations, residual variance, and structure matrix. The EFAST model decomposes the observed correlation matrix from Figure 10 into the three components displayed in Figure 13. The most notable observation here is the separation of sym- metry structure (last panel) and latent factor-implied structure (first panel): the factor solution (first panel) does not attempt to explain the symmetry structure seen in the data (i.e., the char- acteristic diagonal streaks are no longer present). This indicates that the EFAST model correctly separates symmetry covariance from underlying trait covariance in real-world data. We also extracted the estimated factor covariance, shown as a network plot in Figure 14. For EFA, some latent variables show very strong covariance, clustering them together due to the contralateral symmetry. This effect is not visible in the EFAST model, which shows a more Figure 14. Network plots of the latent covariance for EFA (A) and EFAST (B). Network Neuroscience 17 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 5 1 1 1 8 8 9 7 4 7 n e n _ a _ 0 0 1 6 2 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Exploratory factor analysis with structure for brain network data l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 5 1 1 1 8 8 9 7 4 7 n e n _ a _ 0 0 1 6 2 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 15. Correlation matrix for Cam-CAN white matter tractography data (fractional anisotropy). Numbers on the colour scale indicate the strength of the estimated correlation, with darker blue indicating stronger positive correlations. Secondary diagonal lines are visible indicating correlation due to contralateral homology. well-separated latent covariance structure. This suggests that one consequence of a poorly specified EFA can be the considerable overestimation of factor covariance, which in turn ad- versely affects the opportunities to understand distinct causes or consequences of individual differences in these factors. Empirical Example: White Matter Microstructure Data Description Our second empirical example uses white matter structural covariance net- works. We use 42 tracts from the ICBM-DTI-81 atlas (Mori et al., 2008), including only those tracts with atlas-separated left/right tracts (i.e., excluding divisions of the corpus callosum). As anatomical metric we use tract-based mean fractional anisotropy, a summary metric sen- sitive (but not specific) to several microstructural properties (Jones, Knösche, & Turner, 2013). The resulting correlation matrix is shown in Figure 15. For more details regarding the anal- ysis pipeline, see Kievit et al. (2016). The same tracts and data were previously analysed in Jacobucci, Branmaier, and Kievit (2019). Results We chose 6 factors for the EFAST and EFA models based on the SSABIC in combi- nation with the convergence limitations. In Table 2, the two models are compared on various Network Neuroscience 18 Exploratory factor analysis with structure for brain network data Table 2. Comparing the fit of the EFAST and EFA models with six factors for the white matter data, using a likelihood ratio test and several fit criteria EFAST EFA CFI 0.899 0.756 RMSEA 0.081 0.123 SRMR 0.205 0.198 Df 603 624 χ2 3137.462 6770.048 ∆χ2 ∆Df Pr(> χ2)

3632.586

21

< .001 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 5 1 1 1 8 8 9 7 4 7 n e n _ a _ 0 0 1 6 2 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 16. Visual representation of the root square residual (observed, implied) correlations, which form the basis of the SRMR fit index. Numbers on the colour scale indicate root square residual correlation, darker blue indicates larger residual. characteristics. From the likelihood ratio test, we can see that the EFAST model represents the white matter data significantly better (χ2(21) = 3632.586, p < .001), and inspecting the SSABIC values (EFA = 59,120, EFAST = 55,727) leads to the same conclusion. In addition, the CFI, RMSEA, indicate better fit for the EFAST model, too. The only index which indicates slightly poorer fit is the SRMR. The difference is very small in this case, but nonetheless it is relevant to show where these differences lie. A visual repre- sentation of the root square residual (observed, implied) correlations, which form the basis of the SRMR fit index, can be found in Figure 16. The figure shows that EFAST is able to represent the symmetry better: it has almost no residuals on the secondary diagonals. The remaining residuals are very similar, though slightly higher, leading to a higher SRMR. Empirical Example: Resting-State Functional Connectivity Data Description Our previous examples deal with correlation matrices capturing between- individual similarities across regions. However, the same techniques can be implemented at the within-subject level given suitable data. One such measure is functional connectivity which reflects the temporal connectivity between regions during rest or a given task, and captures the purported strength of interactions, or communications, between regions (Van Den Heuvel & Pol, 2010). Here we use functional connectivity matrices from five participants in the Cam- CAN study measured during an eyes-closed resting-state block. We focus on 90 cortical and subcortical regions from the AAL atlas (Tzourio-Mazoyer et al., 2002). The methodology to compute the connectivity metrics is outlined in (Geerligs, Tsvetanov, & Henson, 2017), and the data reported here have been used in Lehmann et al. (2019). The correlation matrix for the first participant is shown in Figure 17. Network Neuroscience 19 Exploratory factor analysis with structure for brain network data l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 5 1 1 1 8 8 9 7 4 7 n e n _ a _ 0 0 1 6 2 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 17. Correlation matrix for the first participant in the Cam-CAN resting-state functional connectivity dataset. Numbers on the colour scale indicate the strength of the estimated correla- tion, with darker blue indicating stronger positive correlations. Secondary diagonal lines are visible indicating correlation due to contralateral homology. For this example, data from the first participant was used to perform the model fit Results assessments. We performed a similar routine as with the previous empirical datasets for deter- mining the number of factors: we fit the EFAST and EFA models for 2–16 factors and compare their information criteria. All of the models converged, and the optimal model based on the BIC is a 13-factor EFAST model. BIC was chosen as a criterion for the number of factors in order to keep the analysis tractable; the other criteria indicated an optimum beyond 16 factors. The 13-factor EFAST model was then compared to the 13-factor EFA model on various fit indices. The results of this comparison can be found in Table 3. Across the board, the EFAST model has better fit, as the EFAST CFI, RMSEA, SRMR, and χ2 fit indices outperform those for the EFA model, demonstrating that accounting for the bilateral symmetry in dimension reduction through factor analysis leads to better fitting model of the data. This approach also allows for comparing the factor loadings for the different participants. For illustration, the plot in Figure 18 shows the profile of factor loadings for the first three factors (columns) across the five participants (rows). These profile plots can be a starting point for com- parison of the connectivity structure across participants, where higher correlation among par- ticipants means a more similar connectivity structure, while taking into account the symmetry Network Neuroscience 20 Exploratory factor analysis with structure for brain network data Table 3. Comparing the fit of the EFAST and EFA models with 13 factors for the functional resting- state data, using a likelihood ratio test and several fit criteria CFI 0.836 0.774 RMSEA 0.093 0.108 SRMR 0.253 0.272 Df 2868 2913 EFAST EFA χ2 9350.278 11828.126 ∆χ2 ∆Df Pr(> χ2)

2477.848

45

0.000

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
1
1
1
8
8
9
7
4
7
n
e
n
_
a
_
0
0
1
6
2
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 18. Comparison of factor loading profiles for the first three factors (columns) across five
participants (rows). The left side of each subplot corresponds to the left hemisphere, and the right
side corresponds to the right hemisphere.

in the brain. For example, for Factor 1, participant 3 has a quite different functional connectivity
factor loading profile than the other participants.

MODEL-BASED LATERALIZATION INDEX

In the simulations, we showed how the EFAST approach yields a more veridical representation
of the factor structure than EFA. However, using EFAST yields an additional benefit: our model
allows for estimating the extent of symmetry in each ROI, while taking into account the over-
all factor structure. This enables researchers to use this component of the analysis for further
study. The (lack of) symmetry may be of intrinsic interest, such as in language development
research (Schuler et al., 2018), intelligence in elderly (Moodie et al., 2019), and age-related
changes in cortical thickness asymmetry (Plessen et al., 2014). In the EFAST package, we have
implemented a specific form of lateralization which is based on a variance decomposition in
the ROIs. Our lateralization index (LI) is a dissimilarity measure representing the proportion of
residual variance (given the trait factors) in an ROI that cannot be explained by symmetry. The

Network Neuroscience

21

Exploratory factor analysis with structure for brain network data

index value is 0 if the bilateral ROIs are fully symmetric (conditional on the trait factors), and
1 if there is no symmetry:

i and urh

LIi = 1 − cor(ulh

i , urh
i )
i are residuals given the trait factors of interest of the ith ROI in the left and
where ulh
right hemisphere, respectively. The correlation cor(· , ·) between these residuals represents the
amount of symmetry, so the LIi represents the residual dissimilarity of the ith ROI in the two
hemispheres after taking into account the factor structure in the data. When LIi is 0, the ROIs

(1)

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

Figure 19. Amount of grey matter volume asymmetry per ROI. Dark blue areas are highly symmet-
ric given the previously estimated 6-factor solution, and bright yellow areas are highly asymmetric.
Such plots can be made and compared for different groups and statistically investigated for differ-
ences in symmetry for a common factor solution. A lateralization index (LI) of 0 means that the
regions are fully symmetric conditional on the trait factors.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
1
1
1
8
8
9
7
4
7
n
e
n
_
a
_
0
0
1
6
2
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 20. White matter lateralization index for a selected set of regions given the previously
estimated 6-factor solution. Lower values mean that bilateral ROIs are more symmetric conditional
on the trait factors, higher values that they are less so. The line ranges indicate 95% confidence
intervals, computed as LI ± 1.96 × SELI, where the standard error SELI is computed using the delta
method.

Network Neuroscience

22

Exploratory factor analysis with structure for brain network data

are fully symmetric given the traits, and a LIi of 1 indicates no symmetry. Note that LIi can be
larger than 1 if the residuals are negatively correlated.

The LI for each ROI in the grey matter volume example is shown in Figure 19. Here, we can
see that there is high lateralization in the superior temporal sulcus and medial orbitofrontal
cortex, but high symmetry in the lateral orbitofrontal cortex and the insula. In Figure 20, we
additionally show in the white matter example that LI can naturally be supplemented by stan-
dard errors and confidence intervals. Thus, the EFAST procedure not only improves the factor
solution under plausible circumstances for such datasets, but in doing so yields an intrinsically
interesting metric of symmetry.

SUMMARY AND DISCUSSION

In this paper, we have developed and implemented EFAST, a method for performing dimension
reduction with residual structure. We show how this new method outperforms standard EFA
across three separate datasets, by taking into account hemispheric symmetry in brain covari-
ance data. We have argued through both simulations and real-world data analysis that our
method is an improvement in the dimension reduction step of such high-dimensional, struc-
tured data, yielding a more veridical factor solution. Such a factor solution can be the basis for
further analysis, such as an extension of the factor model to prediction of continuous pheno-
type variables such as intelligence scores, or the comparison among different age groups. These
extensions will be improved by building on a factor solution which appropriately takes into
account the symmetry of the brain. Furthermore, we believe that many data reduction prob-
lems in social, cognitive, and behavioural sciences have a similar structure: residual structure is
known, but precise theory about the underlying factor structure is not (Asparouhov & Muthén,
2009). As such, although we focus on brain imaging data, our approach is likely more widely
applicable.

Care is needed in the interpretation of the factor solution as underlying dimensions, as
the empirical application has shown that the absolute level of fit for both the EFA and EFAST
models is not optimal. In addition, estimation of more complex factor models may lead to non-
convergence or inadmissible solutions. Such problems would need to be further investigated,
potentially leading to more stable estimation, for example, through a form of principal axis
factoring, or potentially through penalization of SEM (Jacobucci et al., 2019; van Kesteren &
Oberski, 2019). However, these limitations hold equally for EFA, and when comparing both
methods it is clear from the results in this paper that the inclusion of structured residuals greatly
improves the representation of the high-dimensional raw data by the low-dimensional factors.
In summary, this relatively simple but versatile extension of classical EFA may be of consid-
erable value to applied researchers with data that possess similar qualities to those outlined
above. We hope our tool will allow those researchers to easily and flexibly specify and fit such
models.

Note that we are not the first to suggest using structured residuals in EFA to take into ac-
count prior knowledge about structure in the observed variables. Adding covariances among
residuals is a common method to take into account features of the data-generating process
(e.g., Cole et al., 2007), and this has been possible in the context of EFA since the release of
the ESEM capability in MPlus (Asparouhov & Muthén, 2009) and in lavaan (Rosseel, 2019).
In the context of neuroscientific data, similar methods in accounting for structure in dimension
reduction have been researched by De Munck, Huizenga, Waldorp, and Heethaar (2002) in
source localization for EEG/MEG. Our goal for this paper has been to provide a compelling

Network Neuroscience

23

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
1
1
1
8
8
9
7
4
7
n
e
n
_
a
_
0
0
1
6
2
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Exploratory factor analysis with structure for brain network data

argument for the use of such structured residuals from the point of view of neuroscience, as
well as a user-friendly, open-source implementation of this method for dimension reduction
in real-world datasets.

ACKNOWLEDGMENTS

We would like to thank Yves Rosseel for valuable input and the development of key tools,
Linda Geerligs for providing the functional connectivity data, and Jonathan Helm and Øystein
Sørensen for their helpful comments on an earlier version of this manuscript.

SUPPORTING INFORMATION

Supporting information for this article is available at https://www.doi.org/10.1162/00157,
https://doi.org/10.5281/zenodo.3779927 (van Kesteren & Kievit, 2020a), and https://doi.org/10
.5281/zenodo.3779908 (van Kesteren & Kievit, 2020b).

AUTHOR CONTRIBUTIONS

Erik-Jan van Kesteren: Conceptualization; Formal analysis; Investigation; Methodology; Soft-
ware; Visualization; Writing – Original Draft; Writing – Review & Editing. Rogier A. Kievit: Con-
ceptualization; Data curation; Investigation; Methodology; Project administration; Resources;
Supervision; Writing – Review & Editing.

FUNDING INFORMATION

Erik-Jan van Kesteren, Nederlandse Organisatie voor Wetenschappelijk Onderzoek (http://dx
.doi.org/10.13039/501100003246), Award ID: 406.17.057. Rogier A. Kievit, Medical Research
Council (http://dx.doi.org/10.13039/501100000265), Award ID: SUAG/047 G101400. Rogier
A. Kievit, Horizon 2020 (http://dx.doi.org/10.13039/501100007601), Award ID: 732592.

REFERENCES

Alexander-Bloch, A., Giedd, J. N., & Bullmore, E. (2013). Imaging
structural co-variance between human brain regions. Nature Re-
views Neuroscience, 14(5), 322. DOI: https://doi.org/10.1038
/nrn3465, PMID: 23531697, PMCID: PMC4043276

Asparouhov, T., & Muthén, B. (2009). Exploratory structural equa-
tion modeling. Structural Equation Modeling: A Multidisciplinary
Journal, 16(3), 397–438. DOI: https://doi.org/10.1080/1070551
0903008204

Barr, D. J., Levy, R., Scheepers, C., & Tily, H. J. (2013). Random ef-
fects structure for confirmatory hypothesis testing: Keep it maximal.
Journal of Memory and Language, 68(3), 255–278. DOI: https://
doi.org/10.1016/j.jml.2012.11.001, PMID: 24403724, PMCID:
PMC3881361

Baskin-Sommers, A. R., Neumann, C. S., Cope, L. M., & Kiehl,
K. A. (2016). Latent-variable modeling of brain gray-matter vol-
ume and psychopathy in incarcerated offenders. Journal of Ab-
normal Psychology, 125(6), 811. DOI: https://doi.org/10.1037
/abn0000175, PMID: 27269123, PMCID: PMC4980206

Basten, U., Hilger, K., & Fiebach, C. J. (2015). Where smart brains are
different: A quantitative meta-analysis of functional and structural
brain imaging studies on intelligence. Intelligence, 51, 10–27.
DOI: https://doi.org/10.1016/j.intell.2015.04.009

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Bede, P., Elamin, M., Byrne, S., McLaughlin, R., Kenna, K., Vajda,
A., . . . Hardiman, O. (2015). Patterns of cerebral and cerebellar
white matter degeneration in ALS. Journal of Neurology Neuro-
surgery and Psychiatry, 86(4), 468–470. DOI: https://doi.org/10
.1136/jnnp-2014-308172, PMID: 25053771, PMCID: PMC4392231
Bernaards, C. A., & Jennrich, R. I. (2005). Gradient projection algo-
rithms and software for arbitrary rotation criteria in factor anal-
ysis. Educational and Psychological Measurement, 65, 676–696.
DOI: https://doi.org/10.1177/0013164404272507

Bishop, D. V. (2013). Cerebral asymmetry and language develop-
ment: Cause, correlate, or consequence? Science, 340(6138),
1230531. DOI: https://doi.org/10.1126/science.1230531, PMID:
23766329, PMCID: PMC4031634

Brown, T. A.

(2006). Confirmatory factor analysis for applied re-

search. Guilford Publications.

Campbell, D. T., & Fiske, D. W. (1959). Convergent and discrimi-
nant validation by the multitrait-multimethod matrix. Psycholog-
ical Bulletin, 56(2), 81. DOI: https://doi.org/10.1037/h0046016,
PMID: 13634291

Cole, D. A., Ciesla, J. A., & Steiger, J. H. (2007). The insidious effects
of failing to include design-driven correlated residuals in latent-
variable covariance structure analysis. Psychological Methods,

Network Neuroscience

24

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

t

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
1
1
1
8
8
9
7
4
7
n
e
n
_
a
_
0
0
1
6
2
p
d

.

t

Exploratory factor analysis with structure for brain network data

12(4), 381. DOI: https://doi.org/10.1037/1082-989X.12.4.381,
PMID: 18179350

Colibazzi, T., Zhu, H., Bansal, R., Schultz, R. T., Wang, Z., &
Peterson, B. S. (2008). Latent volumetric structure of the human
brain: Exploratory factor analysis and structural equation model-
ing of gray matter volumes in healthy children and adults. Human
Brain Mapping, 29(11), 1302–1312. DOI: https://doi.org/10.1002
/hbm.20466, PMID: 17935179, PMCID: PMC2656433

Cox, S. R., Harris, M. A., Ritchie, S. J., Buchanan, C. R., Hernández,
M. d. C. V., Corley, J., . . . others. (2020). Three major dimensions
of human brain cortical ageing in relation to cognitive decline
across the 8th decade of life. BioRxiv.

Cox, S. R., Ritchie, S. J., Tucker-Drob, E. M., Liewald, D. C.,
Hagenaars, S. P., Davies, G., . . . Deary, I. J. (2016). Ageing and
brain white matter structure in3,513 UK Biobank participants. Nat-
ure Communications, 7(1), 1–13. DOI: https://doi.org/10.1038
/ncomms13629, PMID: 27976682, PMCID: PMC5172385

de Mooij, S. M., Henson, R. N., Waldorp, L. J., & Kievit, R. A.
(2018). Age differentiation within gray matter, white matter, and
between memory and white matter in an adult life span co-
hort. Journal of Neuroscience, 38(25), 5826–5836. DOI: https://
doi.org/10.1523/JNEUROSCI.1627-17.2018, PMID: 29848485,
PMCID: PMC6010564

De Munck, J. C., Huizenga, H. M., Waldorp, L. J., & Heethaar, R.
(2002). Estimating stationary dipoles from MEG/EEG data con-
taminated with spatially and temporally correlated background
noise. IEEE Transactions on Signal Processing, 50(7), 1565–1572.
DOI: https://doi.org/10.1109/TSP.2002.1011197

Denenberg, V. H., Kertesz, A., & Cowell, P. E. (1991). A factor anal-
ysis of the human’s corpus callosum. Brain Research, 548(1–2),
126–132. DOI: https://doi.org/10.1016/0006-8993(91)91113-F
Desikan, R. S., Ségonne, F., Fischl, B., Quinn, B. T., Dickerson, B. C.,
Blacker, D., . . . others. (2006). An automated labeling system for
subdividing the human cerebral cortex on MRI scans into gyral
based regions of interest. Neuroimage, 31(3), 968–980. DOI:
https://doi.org/10.1016/j.neuroimage.2006.01.021, PMID:
16530430

DuPre, E., & Spreng, R. N. (2017). Structural covariance networks
across the life span, from 6 to 94 years of age. Network Neu-
roscience, 1(3), 302–323. DOI: https://doi.org/10.1162/NETN_a
_00016, PMID: 29855624, PMCID: PMC5874135

Eshaghi, A., Marinescu, R. V., Young, A. L., Firth, N. C., Prados, F.,
Jorge Cardoso, M., . . . others.
(2018). Progression of regional
grey matter atrophy in multiple sclerosis. Brain, 141(6), 1665–1677.
DOI: https://doi.org/10.1093/brain/awy088, PMID: 29741648,
PMCID: PMC5995197

Ferguson, M. A., Anderson, J. S., & Spreng, R. N. (2017). Fluid and
flexible minds: Intelligence reflects synchrony in the brain’s in-
trinsic network architecture. Network Neuroscience, 1(2), 192–207.
DOI: https://doi.org/10.1162/NETN_a_00010, PMID: 29911673,
PMCID: PMC5988392

Frässle, S., Paulus, F. M., Krach, S., Schweinberger, S. R., Stephan,
K. E., & Jansen, A. (2016). Mechanisms of hemispheric laterali-
zation: Asymmetric interhemispheric recruitment in the face per-
ception network. NeuroImage, 124, 977–988. DOI: https://doi
.org/10.1016/j.neuroimage.2015.09.055, PMID: 26439515

Fuhrmann, D., Nesbitt, D., Shafto, M., Rowe, J. B., Price, D., Gadie,
A., . . . Kievit, R. A. (2019). Strong and specific associations be-
tween cardiovascular risk factors and white matter micro-and
macrostructure in healthy aging. Neurobiology of Aging, 74,
46–55. DOI: https://doi.org/10.1016/j.neurobiolaging.2018.10
.005, PMID: 30415127, PMCID: PMC6338676

Gauger, L. M., Lombardino, L. J., & Leonard, C. M.

(1997).
Brain morphology in children with specific language impairment.
Journal of Speech, Language, and Hearing Research, 40(6),
1272–1284. DOI: https://doi.org/10.1044/jslhr.4006.1272, PMID:
9430748

Geerligs, L., Tsvetanov, K. A., & Henson, R. N. (2017). Challenges in
measuring individual differences in functional connectivity using
fMRI: The case of healthy aging. Human Brain Mapping, 38(8),
4125–4156. DOI: https://doi.org/10.1002/hbm.23653, PMID:
28544076, PMCID: PMC5518296

Guàrdia-Olmos, J., Peró-Cebollero, M., Benítez-Borrego, S., & Fox,
J. (2009). Using SEM library in R software to analyze exploratory
structural equation models. In 59th ISI World Statistics Congress.
(1966). Factor analysis by mini-
mizing residuals (minres). Psychometrika, 31(3), 351–368. DOI:
https://doi.org/10.1007/BF02289468, PMID: 5221131

Harman, H. H., & Jones, W. H.

Herbert, E., Engel-Hills, P., Hattingh, C., Fouche, J.-P., Kidd, M.,
Lochner, C., . . . van Rensburg, S. J. (2018). Fractional anisotropy
of white matter, disability and blood iron parameters in multiple
sclerosis. Metabolic Brain Disease, 33(2), 545–557. DOI: https://
doi.org/10.1007/s11011-017-0171-5, PMID: 29396631

Holzinger, K. J., & Swineford, F. (1939). A study in factor analysis:
The stability of a bi-factor solution. Supplementary Educational
Monographs. Chicago, IL: University of Chicago Press.

Horn, J.

(1965). A rationale and test for the number of factors in
factor analysis. Psychometrika, 30(2), 179–185. DOI: https://doi
.org/10.1007/BF02289447, PMID: 14306381

Jacobucci, R., Brandmaier, A. M., & Kievit, R. A. (2019). A practical
guide to variable selection in structural equation modeling by
using regularized multiple-indicators, multiple-causes models.
Advances in Methods and Practices in Psychological Science,
2(1), 55–76. DOI: https://doi.org/10.1177/2515245919826527,
PMID: 31463424, PMCID: PMC6713564

James, G. A., Kelley, M. E., Craddock, R. C., Holtzheimer, P. E.,
Dunlop, B. W., Nemeroff, C. B., . . . Hu, X. P.
(2009). Explor-
atory structural equation modeling of resting-state fMRI: Appli-
cability of group models to individual subjects. NeuroImage, 45(3),
778–787. DOI: https://doi.org/10.1016/j.neuroimage.2008.12.049,
PMID: 19162206, PMCID: PMC2653594

Jones, D. K., Knösche, T. R., & Turner, R. (2013). White matter in-
tegrity, fiber count, and other fallacies: The do’s and don’ts of diffu-
sion MRI. NeuroImage, 73, 239–254. DOI: https://doi.org/10.1016
/j.neuroimage.2012.06.081, PMID: 22846632

Jöreskog, K. G. (1969). A general approach to confirmatory maxi-
mum likelihood factor analysis. Psychometrika, 34(2), 183–202.
DOI: https://doi.org/10.1007/BF02289343

Kenny, D. A. (1976). An empirical application of confirmatory fac-
tor analysis to the multitrait-multimethod matrix. Journal of Exper-
imental Social Psychology, 12(3), 247–252. DOI: https://doi.org
/10.1016/0022-1031(76)90055-X

Network Neuroscience

25

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

/

/

t

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
1
1
1
8
8
9
7
4
7
n
e
n
_
a
_
0
0
1
6
2
p
d

.

t

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Exploratory factor analysis with structure for brain network data

Kievit, R. A., Davis, S. W., Griffiths, J., Correia, M. M., Henson,
R. N., et al. (2016). A watershed model of individual differences
in fluid intelligence. Neuropsychologia, 91, 186–198. DOI: https://
doi.org/10.1016/j.neuropsychologia.2016.08.008,PMID: 27520470,
PMCID: PMC5081064

DOI: https://doi.org/10.1016/j.neuroimage.2007.12.035, PMID:
18255316, PMCID: PMC2478641

Mowinckel, A. M., & Vidal-Piñeiro, D. (2019). Visualisation of brain
statistics with R-packages ggseg and ggseg3d. arXiv:1912.08200.
Muthén, L. K., & Muthén, B. O. (1998). Mplus user’s guide (version

Klein, A., & Tourville, J.

(2012). 101 labeled brain images and a
consistent human cortical labeling protocol. Frontiers in Neuro-
science, 6, 171. DOI: https://doi.org/10.3389/fnins.2012.00171,
PMID: 23227001, PMCID: PMC3514540

Klein, A., Ghosh, S. S., Bao, F. S., Giard, J., Häme, Y., Stavsky, E.,
. . . & Keshavan, A.
(2017). Mindboggling morphometry of hu-
man brains. PLoS computational biology, 12(2), e1005350. DOI:
https://doi.org/10.1371/journal.pcbi.1005350

Lehmann, B. C., Henson, R. N., Geerligs, L., White, S. R., et al.
(2019). Characterising group-level brain connectivity: A frame-
work using bayesian exponential random graph models. bioRxiv,
665398. DOI: https://doi.org/10.1101/665398

Lövdén, M., Laukka, E. J., Rieckmann, A., Kalpouzos, G., Li, T.-Q.,
Jonsson, T., . . . Bäckman, L.
(2013). The dimensionality of
between-person differences in white matter microstructure in old
age. Human Brain Mapping, 34(6), 1386–1398. DOI: https://doi
.org/10.1002/hbm.21518, PMID: 22331619, PMCID: PMC6870246
(2004). Structural
shape characterization via exploratory factor analysis. Artificial
Intelligence in Medicine, 30(2), 97–118. DOI: https://doi.org/10
.1016/S0933-3657(03)00039-3

Machado, A. M., Gee, J. C., & Campos, M. F.

Mancini, M., Giulietti, G., Spanò, B., Bozzali, M., Cercignani, M.,
& Conforto, S. (2016). Estimating multimodal brain connectiv-
ity in multiple sclerosis: An exploratory factor analysis. In 2016
38th Annual International Conference of the IEEE Engineering in
Medicine and Biology Society (EMBC) (pp. 1131–1134). DOI:
https://doi.org/10.1109/EMBC.2016.7590903, PMID: 28268525

Marsh, H. W., Morin, A. J., Parker, P. D., & Kaur, G.

(2014). Ex-
ploratory structural equation modeling: An integration of the best
features of exploratory and confirmatory factor analysis. Annual
Review of Clinical Psychology, 10, 85–110. DOI: https://doi.org
/10.1146/annurev-clinpsy-032813-153700, PMID: 24313568
McIntosh, A. R., & Protzner, A. B. (2012). Handbook of structural
In R. H. Hoyle (Ed.), (pp. 636–649). New

equation modeling.
York, NY: The Guilford Press.

Mechelli, A., Friston, K.

J., Frackowiak, R. S., & Price, C.

J.
Journal of
(2005). Structural covariance in the human cortex.
Neuroscience, 25(36), 8303–8310. DOI: https://doi.org/10.1523
/JNEUROSCI.0357-05.2005, PMID: 16148238, PMCID:
PMC6725541

Meyer, K., Garzón, B., Lövdén, M., & Hildebrandt, A. (2019). Are
global and specific interindividual differences in cortical thick-
ness associated with facets of cognitive abilities, including face
cognition? Royal Society Open Science, 6(7), 180857. DOI:
https://doi.org/10.1098/rsos.180857, PMID: 31417686, PMCID:
PMC6689650

Moodie, J., Ritchie, S. J., Cox, S. R., Harris, M. A., Maniega, S. M.,
Hernández, M. C. V., . . . others. (2019). Structural brain asym-
metry and general intelligence in 73-year-olds. PsyArXiv.

Mori, S., Oishi, K., Jiang, H., Jiang, L., Li, X., Akhter, K., . . . Woods,
R. (2008). Stereotaxic white matter atlas based on diffusion ten-
sor imaging in an ICBM template. NeuroImage, 40(2), 570–582.

7). Los Angeles, CA: Muthén & Muthén. 2004.

Plessen, K.

J., Hugdahl, K., Bansal, R., Hao, X., & Peterson,
B. S. (2014). Sex, age, and cognitive correlates of asymmetries
Journal
in thickness of the cortical mantle across the life span.
of Neuroscience, 34(18), 6294–6302. DOI: https://doi.org/10
.1523/JNEUROSCI.3692-13.2014, PMID: 24790200, PMCID:
PMC4004815

Revelle, W. (2018). psych: Procedures for psychological, psycho-
metric, and personality research [Computer software manual].
Evanston, Illinois. Retrieved from https://CRAN.R-project.org
/package=psych (R package version 1.8.12)

Roe, J. M., Vidal-Piñeiro, D., Sørensen, Ø., Brandmaier, A. M.,
Düzel, S., Gonzalez, H. A., . . . others. (2020). Asymmetric thin-
ning of the cerebral cortex across the adult lifespan is accel-
erated in Alzheimer’s disease. bioRxiv. DOI: https://doi.org/10
.1101/2020.06.18.158980

Rosas, H. D., Lee, S. Y., Bender, A. C., Zaleta, A. K., Vangel, M.,
Yu, P., . . . others.
(2010). Altered white matter microstructure
in the corpus callosum in Huntington’s disease: implications
for cortical “disconnection”. NeuroImage, 49(4), 2995–3004.
DOI: https://doi.org/10.1016/j.neuroimage.2009.10.015, PMID:
19850138, PMCID: PMC3725957

Rosseel, Y.

(2012).

lavaan: An R package for structural equa-
tion modeling. Journal of Statistical Software, 48(2), 1–36. DOI:
https://doi.org/10.18637/jss.v048.i02

Rosseel, Y. (2019). lavaan version 0.6-4 [Computer software man-

ual]. (R package version 0.6-4).

Roweis, S., & Ghahramani, Z. (1999). A unifying review of linear
gaussian models. Neural Computation, 11(2), 305–345. DOI:
https://doi.org/10.1162/089976699300016674, PMID: 9950734
Schaefer, A., Kong, R., Gordon, E. M., Laumann, T. O., Zuo, X.-N.,
Holmes, A. J., . . . Yeo, B. T.
Local-global parcel-
lation of the human cerebral cortex from intrinsic functional con-
nectivity MRI. Cerebral Cortex, 28(9), 3095–3114. DOI: https://
doi.org/10.1093/cercor/bhx179, PMID: 28981612, PMCID:
PMC6095216

(2018).

Scharf, F., & Nestler, S.

(2018). Principles behind variance mis-
allocation in temporal exploratory factor analysis for ERP data:
Insights from an inter-factor covariance decomposition. Interna-
tional Journal of Psychophysiology, 128, 119–136. DOI: https://
doi.org/10.1016/j.ijpsycho.2018.03.019, PMID: 29621554
Schuler, A.-L., Bartha-Doering, L., Jakab, A., Schwartz, E., Seidl, R.,
Kienast, P., . . . Kasprian, G. (2018). Tracing the structural origins
of atypical language representation: Consequences of prenatal
mirror-imaged brain asymmetries in a dizygotic twin couple.
Brain Structure and Function, 223(8), 3757–3767. DOI: https://
doi.org/10.1007/s00429-018-1717-y, PMID: 30062562

Shafto, M. A., Tyler, L. K., Dixon, M., Taylor, J. R., Rowe, J. B.,
Cusack, R., . . . others. (2014). The Cambridge Centre for Ageing
and Neuroscience (Cam-CAN) Study Protocol: A cross-sectional,
lifespan, multidisciplinary examination of healthy cognitive

Network Neuroscience

26

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

t

/

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
1
1
1
8
8
9
7
4
7
n
e
n
_
a
_
0
0
1
6
2
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Exploratory factor analysis with structure for brain network data

ageing. BMC Neurology, 14(1), 204. DOI: https://doi.org/10.1186
/s12883-014-0204-1, PMID: 25412575, PMCID: PMC4219118
Sorzano, C. O. S., Vargas, J., & Montano, A. P. (2014). A survey of
dimensionality reduction techniques. ARXIV preprint arXiv:1403.
2877.

Sripada, C., Angstadt, M., Rutherford, S., Kessler, D., Kim, Y., Yee,
M., & Levina, E. (2019). Basic units of inter-individual variation
in resting state connectomes. Scientific Reports, 9(1), 1–12. DOI:
https://doi.org/10.1038/s41598-018-38406-5, PMID: 30760808,
PMCID: PMC6374507

Stievenart, J.-L., Iba-Zizen, M.-T., Tourbah, A., Lopez, A., Thibierge,
M., Abanou, A., & Cabanis, E. (1997). Minimal surface: A useful
paradigm to describe the deeper part of the corpus callosum?
Brain Research Bulletin, 44(2), 117–124. DOI: https://doi.org/10
.1016/S0361-9230(97)00113-5

Taylor, J. R., Williams, N., Cusack, R., Auer, T., Shafto, M. A., Dixon,
M., . . . others.
(2017). The Cambridge Centre for Ageing
and Neuroscience (Cam-CAN) data repository: Structural and
functional MRI, MEG, and cognitive data from a cross-sectional
adult lifespan sample. NeuroImage, 144, 262–269. DOI: https://
doi.org/10.1016/j.neuroimage.2015.09.018, PMID: 26375206,
PMCID: PMC5182075

Tien, A. Y., Eaton, W. W., Schlaepfer, T. E., McGilchrist, I. K.,
Menon, R., Richard, P., . . . Peralson, G. D. (1996). Exploratory
factor analysis of MRI brain structure measures in schizophre-
nia. Schizophrenia Research, 19(2–3), 93–101. DOI: https://doi
.org/10.1016/0920-9964(96)88520-3

Tucker, D. M., & Roth, D. L. (1984). Factoring the coherence ma-
trix: Patterning of the frequency-specific covariance in a multi-
channel EEG. Psychophysiology, 21(2), 228–236. DOI: https://
doi.org/10.1111/j.1469-8986.1984.tb00211.x, PMID: 6728989

Tzourio-Mazoyer, N., Landeau, B., Papathanassiou, D., Crivello,
F., Etard, O., Delcroix, N., . . . Joliot, M.
(2002). Automated
anatomical labeling of activations in SPM using a macroscopic
anatomical parcellation of the MNI MRI single-subject brain.
NeuroImage, 15(1), 273–289. DOI: https://doi.org/10.1006
/nimg.2001.0978, PMID: 11771995

Van Den Heuvel, M. P., & Pol, H. E. H. (2010). Exploring the brain
network: A review on resting-state fMRI functional connectivity.
European Neuropsychopharmacology, 20(8), 519–534. DOI:
https://doi.org/10.1016/j.euroneuro.2010.03.008, PMID: 20471808
(2020a). efast, GitHub. DOI:

van Kesteren, E.-J., & Kievit, R. A.

https://doi.org/10.5281/zenodo.3779927

van Kesteren, E.-J., & Kievit, R. A.

(2020b). efast, GitHub. DOI:

https://doi.org/10.5281/zenodo.3779908

van Kesteren, E.-J., & Oberski, D. L. (2019). Structural equation mod-
els as computation graphs. ARXIV preprint arXiv:1905.04492.
DOI: https://doi.org/10.1016/j.euroneuro.2010.03.008, PMID:
20471808
Vrieze, S. I.

(2012). Model selection and psychological theory:
A discussion of the differences between the akaike information
criterion (AIC) and the Bayesian information criterion (BIC). Psy-
chological Methods, 17(2), 228. DOI: https://doi.org/10.1037
/a0027127, PMID: 22309957, PMCID: PMC3366160

Yeh, P.-H., Zhu, H., Nicoletti, M. A., Hatch, J. P., Brambilla, P., &
Soares, J. C. (2010). Structural equation modeling and principal
component analysis of gray matter volumes in major depressive
and bipolar disorders: Differences in latent volumetric structure.
Psychiatry Research: Neuroimaging, 184(3), 177–185. DOI:
https://doi.org/10.1016/j.pscychresns.2010.07.007, PMID:
21051206, PMCID: PMC3001135

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

t

/

/

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

/

5
1
1
1
8
8
9
7
4
7
n
e
n
_
a
_
0
0
1
6
2
p
d

t

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Network Neuroscience

27

Download pdf