Maximizing the Adjacent Possible - Specialized Research AI at MIT

Maximizing the Adjacent Possible
in Automata Chemistries

Abstract Automata chemistries are good vehicles for experimentation
in open-ended evolution, but they are by necessity complex systems
whose low-level properties require careful design. To aid the process
of designing automata chemistries, we develop an abstract model that
classifies the features of a chemistry from a physical (bottom up)
perspective and from a biological (top down) perspective. There are
two levels: things that can evolve, and things that cannot. We equate the
evolving level with biology and the non-evolving level with physics. We
design our initial organisms in the biology, so they can evolve. We design
the physics to facilitate evolvable biologies. This architecture leads to a
set of design principles that should be observed when creating an
instantiation of the architecture. These principles are Everything Evolves,
Everything ʼs Soft, and Everything Dies. To evaluate these ideas, we present
experiments in the recently developed Stringmol automata chemistry.
We examine the properties of Stringmol with respect to the principles,
and so demonstrate the usefulness of the principles in designing
automata chemistries.

Simon Hickinbotham*,**
Edward Clark**
Adam Nellis**
Susan Stepney**
Tim Clarke
Peter Young
University of York

‡

†

Keywords
Artificial chemistries, automata
chemistries, evolutionary computation,
open-ended evolution

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
2
1
4
9
1
6
6
5
2
8
4
a
r
t
l

_
a
_
0
0
1
8
0
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

1 Introduction

The field of artificial life (ALife) has twin goals of understanding and designing living systems [4]. A
key property of such systems is that their evolutionary pathways are open-ended, by which we mean
here: capable of producing new forms with a generally increasing level of complexity. A coevolu-
tionary system steps through a sequence of adjacent possible [27] states, the viable states that are a
single evolutionary step away from the systemʼs current state. It is the adjacent possible of the entire
state space of the ecosystem—and that adjacency might include a change to the state space (e.g., new
dimensions due to new species, niches); that is, a move out of, not merely movement through, the
current state space. To realize the stated goals, we require an ALife experimental platform to have
rich behavior that maximizes its adjacent possible, enabling a diverse set of open-ended evolutionary
paths.

Here we define and investigate three design principles for such a platform: (1) Everything Evolves;
(2) Everythingʼs Soft ; and (3) Everything Dies. The principles are intended to help in the design of sys-
tems that have the open-endedness property. In order to study these ideas, we develop a definition
of open-endedness and present a measure for it in Section 2. We provide some background on

* Contact author.
** Department of Computer Science, University of York, Heslington, York, YO10 5GH, United Kingdom. E-mail: sjh518@york.ac.uk (S.H.)
† Department of Electronics, University of York, Heslington, York, YO10 5GH, United Kingdom.
‡ Department of Biology, University of York, Heslington, York, YO10 5GH, United Kingdom.

S. Hickinbotham et al.

Maximizing the Adjacent Possible in Automata Chemistries

artificial chemistries (aChems) and automata chemistries (autChems) in Section 3. We use the def-
initions to develop a new metaphor for autChems in Section 4. This gives rise to a set of design
principles detailed in Section 5, following which we describe an implementation in Section 6. Finally
we describe a series of experiments that test them, in Section 7.

2 Open-Endedness, Complexity, and Evolutionary Activity

2.1 Definition of Open-Endedness
The field of ALife lacks precise definitions of many of its core concepts. A full survey of important
work towards this goal is beyond the scope of this article. We refer the interested reader to [35] for
an overview of the issues. Below we give definitions of the important terms in our experiments.
Note that the definitions are intended only to be applicable to ALife simulations, but they may
be applied more loosely to other synthetic and biological evolutionary systems.

We stated in the introduction that a key property of ALife systems is that their evolutionary
pathways are open-ended: capable of producing new forms with a generally increasing level of com-
plexity. Here we develop this rather loose description of open-endedness into a set of definitions,
and then map the definitions into a quantitative measure, which we apply to the experiments de-
scribed below.

An evolving system exists in a state space, which changes over time, and is capable of growing. At
any one time, the evolving system occupies a position in this state space. Evolution is the movement
of the system through the state space. Some evolutionary moves will change (and grow) the state
space. Open-ended evolution is the continual exploration of states not previously visited within this
space.

It is obvious that an evolutionary system cannot be classified as truly open-ended if the state
space that it occupies is finite. However, if the number of states visited through evolution is vastly
less than the number of states in the state space, we can say that the evolutionary process has been
effectively open-ended. Since we cannot guarantee that the evolving system will never move to a previ-
ously occupied state, a system can only be classified as effectively open-ended on a per-trial basis.
It is intuitive to think of biological evolution as “open,” in the sense that it is never possible to
identify a time from which no new novel forms are produced. This is clearly the case in biological
evolution, but less clear-cut in synthetic systems. These latter systems exist within computers, and so
are guaranteed to have finite (but large) state spaces. For example, in Tierra [33] and Avida [26], an
individual is represented as a sequence of opcodes. In these systems, the number o of distinct op-
codes and the maximum length L of an opcode sequence can be used to calculate N, the total
number of possible different species in the system: N =
L ol. (In real biological systems, L
l = 1
cannot be known, but the lower bound on its estimated value is sufficiently large to illustrate the
point being made here.)

0
For any cohort of species S, there exists a relatively limited range of potential new species S
.
These are adjacent in sequence space—they are the set of species that can be created in a small number
of viable mutations from the current state. In the study of open-ended evolution, a system meets the
0 ≪ N. In biology and in appropriate ALife simulations, the
requirement for new forms as long as S
0 ≈ 1,000
vast majority of species are never created. For example, in Stringmol, typical runs give S
P
species, and N =
2000 33l. Finally, we note that the state space of a system involves more than one
l = 1
species, so the number of states is vastly larger than N. In this sense then, many ALife systems can
be said to be effectively open-ended.

Given the observations above, this component of open-endedness is simply stated as:

Definition 1: Novelty generation is the perpetual production of previously unseen forms, where S

0 ≪ N.

This definition alone is insufficient for our notion of open-endedness. Consider the following: If
there is no replicating program in the system, we see a collapse to a primitive state, akin to a reactive

Artificial Life Volume 22, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
2
1
4
9
1
6
6
5
2
8
4
a
r
t
l

_
a
_
0
0
1
8
0
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

S. Hickinbotham et al.

Maximizing the Adjacent Possible in Automata Chemistries

chemical “soup.” Reactions would continue and new forms could appear—for example, in the form
of simple polymers of constituent materials—but the absence of evolutionary pressure means that
selection does not force the system into new states.

The second component of open-endedness is the idea that an open-ended evolutionary system must
generally increase its complexity. This is a more difficult concept to give a definition, for there is no
generally agreed definition of complexity [35]. Here we adopt the following as a working definition:

Definition 2: Complexity is a term generally used to characterize something with many parts that
interact with each other in multiple ways.

Given this definition, increasing complexity is:

Definition 3:
number of parts, or whose parts interact with each other in an increasing number of ways, or both.

Increasing complexity is a term generally used to characterize a system either with an increasing

We can now combine Definition 1 and Definition 3 to give our definition of open-endedness:

Definition 4: Open-endedness is a term generally used to characterize a system such that:

1. It exhibits the perpetual production of previously unseen forms.

2. S

0 ≪ N.

3. Those forms interact with each other in an increasing number of ways.

2.2 Measuring Open-Endedness
We now turn to the problem of measuring open-endedness, given Definition 4 above. We have two
practical problems to deal with. The first concerns obtaining sufficient detail about the interactions
in a single system. The second concerns how to carry out comparisons between systems.

Automata chemistries exist in software, so it is always possible to know in intimate detail how
reactions proceed. However, given that we are looking for new species that interact in new ways,
it is not generally practical to devise a comprehensive means of measuring all possible new interac-
tions. In addition, even if one could do this, one could not guarantee that the measurement of inter-
action would not be biased in some way, distorting comparisons between systems. For these reasons,
we believe that the process of measuring open-endedness should not examine interactions directly.
There currently exists no generally accepted measure of the complexity of these interactions, and the
measures that do exist tend to be more concerned with stability than with open-endedness [2, 17, 29].
An alternative approach, with a long history in ALife [6, 7], is to measure the evolutionary activity of
a system, and compare measures. Evolutionary activity measures analyze the population dynamics of
an evolving system as new species emerge, but are not concerned with directly measuring complex-
ity. They are generally applied to systems that are claimed to exhibit open-ended evolution. Note
however that while the concept of evolutionary activity is directly applicable to Definition 1, it has
no explicit measure of increasing complexity as specified by Definition 3. To use an evolutionary
activity measure as a proxy for the measurement of open-endedness, we need to explore the link
between increasing complexity and population dynamics. Fortunately, this link is straightforward to
make: Any innovation (mutation) that confers selective advantage on one or more components of a
system will be reflected by a rapid increase in the numbers of instances of that component. In ad-
dition, we posit that a system with more interactions is likely to show more fluctuations in the pop-
ulations of its individual components. By measuring these changes, we can infer the relative levels of
open-endedness in two or more systems, and thus conclude which is more evolvable.

The longer established techniques of investigating evolutionary activity involved visual inspection
of plots of changes in a measure of activity over time. While this remains a useful technique, it has

Artificial Life Volume 22, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
2
1
4
9
1
6
6
5
2
8
4
a
r
t
l

_
a
_
0
0
1
8
0
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

S. Hickinbotham et al.

Maximizing the Adjacent Possible in Automata Chemistries

two drawbacks: It is subjective and it is impractical for large data sets. Recent work has focused on
developing a numerical measure that can be applied to a range of simulations and can deliver useful
comparative statistics. This is called the quantitative non-neutral (QNN) measure of evolutionary activ-
ity [11]. We use this measure to compare results in all experiments in this article. We will now
describe the technique.

2.3 QNN Measure of Evolutionary Activity
We are setting out to test the hypothesis that our design principles have a positive influence on the
evolutionary activity in a system. Here we recap the measure of evolutionary activity presented in
[11], which gives a numerical summary of evolutionary activity and thus allows different configura-
tions to be compared.

The reasoning behind the measure is as follows. In a complex system, a component type can be
assigned a unique label. There can be many instances of a component type in a system. Thus in
biology, a species is a component, and an organism is an instance of a species. Firstly, it is assumed
that a component demonstrating some new adaptation will exhibit a rapidly increasing population.
By contrast, a new component with no selective advantage will not show a rapid increase in pop-
ulation size—the population will exhibit neutral drift. Therefore, by creating a measure of popula-
tions that are rapidly increasing, we can detect evolutionary activity. Rather than look for specific
levels of increase, the measure downweights small changes in population size over time; hence the
name non-neutral evolutionary activity.

To distill this approach into a quantitative measure, we study changes in population sizes of all
I components ci at each discrete time step t. We first calculate the total population Ct as follows:

Ct ¼

i 2 I

ci; t

and use this to calculate the species proportions pi at t :

pi; t ¼ ci; t =Ct

(1)

(2)

The expected proportion ei of a component is simply the proportion observed in the previous time
step:

(cid:2)
ei; t ¼ pi; t − 1
0

if t > 0
if t ¼ 0

(3)

The new activity measure for component i at time t is the square of positive values of p − e scaled by
the total population at t :

Di; t ¼

(cid:4)

pi; t − ei; t

(cid:2)

(cid:3)

if pi; t > ei; t
otherwise

(4)

This measure of activity of each species at each time step is summed together to give the total non-
neutral activity A of the whole simulation:

A ¼

i 2 I

t ¼ 0

Di; t

(5)

Note that the value of A is not scaled by T. It is important to compare the same time frames
between runs, even if the system goes extinct before T. This measure is applicable to any systems

Artificial Life Volume 22, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
2
1
4
9
1
6
6
5
2
8
4
a
r
t
l

_
a
_
0
0
1
8
0
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

S. Hickinbotham et al.

Maximizing the Adjacent Possible in Automata Chemistries

where changes in population over time can be measured. An implementation of the measure in the R
programming language is available from the authorʼs website.1

3 Artificial Chemistries and Automata Chemistries

Many researchers have developed different platforms (computer programs) to try to achieve open-
endedness. Some of these systems are artificial chemistries (AChems) [10]. The AChem model is suf-
ficiently broad that it encompasses most of ALife, which is useful because it gives the research
community one language in which a range of systems that aim to generate open-ended evolution
can be described.

Evolution in AChems implies the generation of novel structures, called by convention molecules or
molecular species. This means that closed systems (in which the complete set of molecular species is
explicitly specified during the initialization of the system) are not a good fit for experimentation.
Following the classification in [10], we find that most types of AChems are not particularly suitable
for experimenting in open-endedness for any but the most abstract of analyses. Rewriting systems [14],
while not closed by the previous definition, are also not sufficiently open, since they operate using a
fixed set of rules. Chemistries based on arithmetic operations [3], and autocatalytic polymer chemistries [42],
have the potential to be sufficiently rich to be open-ended for practical purposes, but the properties
of the reaction of each molecule in the chemistry exists only in terms of its sequence; each monomer in
the chemistry (for example, monomers A, B, C, D) has exactly the same property. A similar frame-
work is defined in lattice molecular systems [23]. Here, the chemistries are similar to cellular automata in
that each cell in a regular lattice is occupied by an atom of a molecule. The whole molecule is defined
by a series of bonds across the cells in the lattice. While each cell has certain low-level reactions avail-
able to it, other, high-level reaction pathways arise by the formation of patterns at the higher level.
By contrast, automata chemistries (AutChems) [33, 26] have an explicit encoding of different prop-
erties in different tokens. The sequences of tokens can then be thought of as constituting a highly
specialized programming language, in which the reaction between sequences is the result of execu-
tion of the program in a (sub)sequence. This means that mutating the tokens in the sequence changes
the behavior of the molecule, raising the potential for open-ended evolution.

If we require automata to solve a particular problem, then it is possible to use evolutionary search
to find a suitable specification. This was demonstrated by Jefferson and coworkers [25], who
evolved solutions to a maze problem using finite state automata and artificial neural networks.
The main relevance to the work presented here is that properties of a programming paradigm ame-
nable to evolution were set out. In particular, the idea of a simple model of computation, realized on
a small interpreter and combined with a computationally complete set of operators, has echoes in
the principles set out below. These ideas are particularly important if we are trying to evolve self-
replicating systems.

The issue of composability has a long history in AutChems, going back at least as far as the

1940s, when John von Neumann was working on his self-replicating automata [40]:

There is no rigorous description of what choice is reasonable and what choice is not.
First of all, one may define parts in such numbers, and each of them so large and
involved, that one has defined the whole problem away. If you choose to define as
elementary objects things which are analogous to whole living organisms, then you
obviously have killed the problem, because you would have to attribute to these parts
just those functions of the living organism which you would like to describe or
understand. So, by choosing the parts too large, by attributing too many and too
complex functions to them, you lose the problem at the moment of defining it.

1 See http://www-users.cs.york.ac.uk/∼sjh/software.

Artificial Life Volume 22, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
2
1
4
9
1
6
6
5
2
8
4
a
r
t
l

_
a
_
0
0
1
8
0
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

S. Hickinbotham et al.

Maximizing the Adjacent Possible in Automata Chemistries

One also loses the problem by defining the parts too small, for instance, by insisting that

nothing larger than a single molecule, single atom, or single elementary particle will rate
as a part. In this case, one would probably get completely bogged down in questions
which, while very important and interesting are entirely anterior to our problem. . . . Even
if one chooses the parts in the right order of magnitude, there are many ways of
choosing them, none of which is intrinsically much better than any other. . . . So, while
the choice of the . . . elements is enormously important and absolutely basic for any
application this choice is neither rigorously justifiable nor humanly unambiguously
justifiable. All one can do is try to submit a system which will stand up under common
sense criteria.

The fewer operator types there are in the system, the higher the chance of spontaneous assembly
into a functioning whole. This was demonstrated in Pargellisʼ Amoeba system [32], where sponta-
neous emergence of self-replicators happened when the number of operators, o, was small. How-
ever, as we have seen above, systems like this are less likely to be considered to be open-ended.

3.1 Automata Chemistries Are the Best Choice for Open Systems
String- or tape-based evolutionary simulations have been reported frequently in the literature, and
there are many parallels between biology and computer science in the area. Turing machines make
use of a tape and read-write heads [37]. They preceded von Neumannʼs self-reproducing automata
[40]. Universal Turing machines and von Neumannʼs architecture both have interdependence of
data and program, and use universality (of computation, of copying) as key demonstrators of the
function of the system. Also, both architectures specify that the genome should be a tape, but there is
no such restriction on the other components in the system.

A less well-known but related theme is that of expressing the organism as a container for a large
set of strings, each of which contribute to the metabolism (and hence fitness) of the organism. Ex-
amples include Laingʼs kinematic machines from the 1970s [28], Hofstaderʼs typogenetics [22, 38],
and Suzukiʼs string rewriting system [36]. In these systems, all the evolving components are strings,
but the strings are only part of the whole system.

If these systems are interpreted as chemistries, then the individuals within the systems are very
simple state machines, with only a loose analogy to the concept of the molecule (or organism). More
recently, Rayʼs Tierra [33] and the Avida architecture [26] have expanded on the paradigm of organ-
ism as tape, with interesting emergent phenomena that mirror biology. The concept of mutation is
also realized in Tierra and Avida. These two systems have a single tape per individual, mirroring the
function of DNA in the organism.

The symbolic set of atomic operations (opcodes) that form the strings tend to have more con-
sistent definition across these systems. These opcodes have their roots in computer science rather
than biology, and have similar mechanisms to primitive programming languages such as BF [5]. An
example of a very simple instruction set in an ALife setting is Nanopond [24].

The strings in these systems are frequently described as the “genome” of the simulation, and the
remaining components as the “phenotype.” In the next section we challenge this stance, and argue
that a different view is needed to create open-ended ALife systems.

3.2 An Abstract Architecture of Automata Chemistries is Needed to Navigate the

Design Space

AutChem models and implementations offer a complete environment in which individual programs
compete to maintain their populations. In particular, they demonstrate that low-probability events
can trigger cascades of reactions that lead to a tipping point in the overall state of the system [1, 19],
in a manner akin to that observed in natural systems. However, this flexibility comes at a cost: The
simulations tend to require myriad parameters, each of which requires careful selection and tuning.
That is, these models are highly parameterized, and even if the range of parameters in each model is

Artificial Life Volume 22, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
2
1
4
9
1
6
6
5
2
8
4
a
r
t
l

_
a
_
0
0
1
8
0
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

S. Hickinbotham et al.

Maximizing the Adjacent Possible in Automata Chemistries

sampled appropriately, they can only ever be tiny samples of the design space of automata chem-
istries. Dittrich et al.ʼs definition [10] of an artificial chemistry encompasses this space: Chemicals C
meet via some mixing function M and react following reaction rules R. But the definition of the
space does not show where the fruitful designs might lie.

Most automata chemistries draw a direct analogy between the sequence of the individual agent
and the concept of the genotype: Each “organism” contains a sequence of operations. There is a
loose analogy with the RNA world [15], where each agent is both phenotype (“executing machine”)
and genotype (“template”), and most agents are self-replicators. However, the complete phenotype of
the individual contains all of the components of a virtual computer, such as pointers, registers,
stacks, and I/O. It uses these, along with the operational semantics of the opcode symbols, to pro-
vide the semantics of the phenotypeʼs “execution” (behavior ). Importantly, none of these structures
except the sequence (order and composition of the symbols) is subject to heritable change. The as-
sociated structures that allow the sequence to be interpreted as an executing machine are fixed by a
predetermined specification (which we later call the physics of the AutChem). The non-evolvability of
this physics potentially places severe restriction on the open-endedness of AutChems.

If we are to make headway in this huge design space, we need to define as clearly as possible what
our goals are. In the next section we attempt to do so, by taking a fresh look at the architecture for
automata chemistries, which has been driven by a mixture of inspiration from ecology, computer
science, and RNA world models.

3.3 The Architecture Leads to Three Design Principles
In this article, we test some of the ideas behind the design decisions made during the development
of the AutChem Stringmol, and link this thinking to ideas about living systems. We first present, in
Section 4, an abstract architecture for automata chemistries that defines the scope of evolutionary
pressures in these systems. With the architecture to hand, Section 5 motivates the original design
decisions. There are three motivating principles in this design/test cycle:

(cid:129) Everything Evolves considers molecular representation;
(cid:129) Everythingʼs Soft considers the need for soft (i.e., non-Boolean and nondeterministic)

activation functions both in forming an interaction between chemicals (binding) and in
program execution;

(cid:129) Everything Dies considers the link between the energy economy and the durability and decay

of molecules.

We describe the motivation for promoting these principles in the next section.

4 A New Metaphor for Open-Ended Automata Chemistries

In AutChems, a molecule is represented by a sequence of opcodes. A collection of molecules forms
the program, and the execution behavior of each sequence in the collection provides a portion of the
overall behavior program. The idea of sequences of codes running programs—sometimes on them-
selves, sometimes on each other—is an attractive model for open-ended evolutionary experiments,
because it appears to raise the possibility that the programs might configure the sequences (via evo-
lution) to exploit the expressiveness of the codes. In order to realize this goal, a virtual universe
needs to be constructed to contain the sequences and allow them to operate on each other. How-
ever, we must also bear in mind that in AutChems (as in real biology), selection acts on only one
aspect of the universe, namely the composition (e.g., sequence) of the molecules that exist within it.
The operation of each code in the system forms the underlying physics, so evolutionary selection can
only manipulate the composition of these physical operations. This is illustrated in Figure 1, where
the physico-chemical world provides the universe in which evolutionary feedback mechanisms are

Artificial Life Volume 22, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
2
1
4
9
1
6
6
5
2
8
4
a
r
t
l

_
a
_
0
0
1
8
0
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

S. Hickinbotham et al.

Maximizing the Adjacent Possible in Automata Chemistries

Figure 1. Evolution as feedback in a chemical world. A fixed, designed physics P imposes reaction rules on a collection of
chemical entities. A subset of these entities forms a viable biological cohort. Chemicals can be destroyed (checked box in
physics layer ), or take part in reactions to create different chemicals (black box in the physics layer ). The nature of the
reaction is determined in the physics of the system. Evolution is the change in the self-maintaining biological cohort,
caused by selection.

an emergent property of the interactions between complex chemicals. The challenge is to make the
evolving code sequences of AutChems as expressive as possible, with the goal of generating com-
plex behaviors as the system evolves. In this section, we develop an abstract architecture for the
design of artificial chemistries for open-ended evolution, which places emphasis on the structures
that can be (re)constructed and optimized by evolutionary mechanisms.

4.1 Biological Evolution Cannot Change the Laws of Physics
We can model an evolving complex system as the physical universe P, an abstract set of forces and
operations within which approximately repeating phenotypic constructs B can be observed. Biology
is an example of such a system. The physical forces between matter and energy, and the resulting
structures that emerge, are governed by physical laws. Under certain conditions (e.g., constant flux
of organic molecules and energy through micropores), a local community of structures emerges that
possesses the facility to construct a functional approximation of itself.

Genetic systems are specified by a sequence of codes (DNA). Importantly, the sequence is em-
bodied within the system, thus allowing the enzymes that the sequence encodes to act on the em-
bodiment of the sequence itself and thus modify it, as shown in Figure 1. An artificial chemistry can
be thought of as the interface between processes that are operating on different scales. The sequence
specifies structures at the biological level, upon which selection can act, but the sequence itself is also
encoded by its physical representation [21]. The evolutionary feedback loop places the sequence man-
agement apparatus under control of the sequence itself, eventually exploiting the available possibil-
ities that the physico-chemical properties provide to the embodied system. This phenomenon is the
basis of biological evolutionary systems, where the embodiment of a genetic code in a carrier mol-
ecule allows the encoded proteins to “curate” the genome.

The challenge we begin to address in this article is how to approach the simulation of such a

model in a computationally efficient manner.

4.2 Automata Chemistries Should Aim to Build Function at the Composite Level
Although we are designing a single AutChem system, it must operate on two distinct levels: P, the
physical level of fixed atomic properties and execution meanings; and B, the biological level of evolvable
molecular properties and their consequent emergent execution meanings.

Artificial Life Volume 22, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
2
1
4
9
1
6
6
5
2
8
4
a
r
t
l

_
a
_
0
0
1
8
0
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

S. Hickinbotham et al.

Maximizing the Adjacent Possible in Automata Chemistries

The overall design of the system works at these two levels simultaneously, but in distinct ways.
The AutChem design brief is to create an environment in P that allows a language to emerge in B
within which it is tractable to design a self-replicating entity without direct reference to P. In other
words, the design is completed via the embodiment of both the physico-chemical properties and the
sequence of codes in a physical world. The physico-chemical properties of the system are immuta-
ble, but they can be arranged into an unboundedly large number of patterns or sequences of oper-
ations. The biological aspect of the system lies in the composition of these patterns, and focuses on
the patterns that have a facility to get themselves copied. Initial experiments [19, 18] into implement-
ing such a system have resulted in the Stringmol AutChem.

We illustrate the distinction between these two design spaces by example of an opcode in an
artificial chemistry. Consider the copy operation in Stringmol, denoted by the symbol ‘=’. The op-
eration has a function specified in P: It accesses two sequence locations, given by the read and write
pointers, and copies the symbol at one to the other. The program in P must accommodate all pos-
sible eventualities in this operation, no matter where the read and write pointers are located: The
action of ‘=’ must never “crash the universe.”

Now consider the same operator from the point of view of B. The operation is available to B
only if it forms part of a sequence, even if it is a sequence of length 1 containing only ‘=’. In
addition, precisely what symbol gets copied and where it is copied to depends on the state of the
reaction (the positions of the pointers) at the time the operation is executed. It is impossible for
B to copy the symbol anywhere other than the location of the write pointer. However, since this
location is determined during execution by the sequence, it can be manipulated by evolutionary
selection.

AutChem simulations tend to be seeded with sequences that embody some behavior; commonly
this is to copy other sequences in the system. The important point is: The mere fact that an
operation appears in a sequence does not mean that evolutionary selection can change its indi-
vidual behavior; all evolutionary selection can do is change the sequence, and thereby change the
overall behavior. The design goal then is to define opcodes that are: (1) expressive, (2) safe (all op-
erations are valid), and (3) most likely to form some behavior when placed in a sequence with other
opcodes.

Seen in this light, we can observe that many automata chemistries make some behaviors inacces-
sible to evolutionary selection, since they are represented by a single atomic opcode. Furthermore,
many structures in AutChems (registers, stacks, etc.) are in the physics of the system, and cannot be
manipulated by the biology. We need to make these structures available as much as possible to be
evolved, by somehow specifying them on the string.

4.3 Summary
Stringmol attempts to place more of the functionality of the AutChem P under control of B, where
selection can act upon it. We focus on three aspects of this approach in the following section, and
give details of experiments to test the ideas in the remainder of the article.

5 Design Principles of Automata Chemistries

We now consider how the architecture we have described above can be implemented in computer
code (while also building on the work done with previous automata chemistries). In this section, we
identify three areas of investigation that we argue are needed in order to build open-ended AutChems.
Recall that our driving theme is that evolution in AutChems can only be done by re-composition
of sequences in B, and the implementation of functionality in P is immutable. The architecture
described in this section comprises several features that we evaluate experimentally, each of which
allows elements of P to be manipulated by sequence composition in B.

Artificial Life Volume 22, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
2
1
4
9
1
6
6
5
2
8
4
a
r
t
l

_
a
_
0
0
1
8
0
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

S. Hickinbotham et al.

Maximizing the Adjacent Possible in Automata Chemistries

5.1 Everything Evolves: Emphasis on Sequence Manipulation Semantics
Structures such as registers, and atomic operations like the copy opcode, are specified in P. Evo-
lutionary selection cannot manipulate these structures and primitive operations; it can determine
only how they are used, via the molecular sequences.

In order to maximize the open-endedness of a system, it is necessary to maximize the expressive
power of B—the range of functionality that can be engendered by changing the composition of each
molecule in the automata chemistry. Accordingly, our first design principle is to move as much of
the behavior from fixed P into evolvable B. Structures extraneous to the sequence, including the
function of the opcodes, should be minimized. This principle also emphasizes the composability of the
operators as much as the individual function.

It may be practical for some structures and operations to persist in P in future AutChem designs,
but the physical operations encapsulated in atomic opcodes should be broken up as much as pos-
sible into sequences of simpler opcodes, in order to allow evolution to work upon those sequences.
The state of the reaction (i.e., the program in B ) becomes more fine-grained, giving more oppor-
tunity for incremental mutations in evolutionary space, while preserving the possibility of large or
neutral mutations. Our first step in achieving this goal is to reduce the “virtual CPU” of our mo-
lecular design to the bare minimum. In Section 7.1 we demonstrate that such a system is capable of
innovation in B.

5.2 Everythingʼs Soft: Reactions Follow More than One Pathway
A commonly observed feature of molecular evolution is that of duplication and divergence of
reaction pathways. Firstly a functional collection of genes, called an operon, is duplicated on the
genome. The duplicated operon will either evolve to function outside of the original network (diver-
gence), or share a common function with the original across many speciation events [41]. This latter is
known as degeneracy and is one of the means by which evolutionary pressures gain purchase on a
physical system: They enlarge the range of the adjacent possible. The advantage is that degenerate
proteins can act as a cohort of functions, sharing optimality in different conditions. We believe that it
is important to emulate these observations in open-ended systems.

In AutChems, the reaction between molecules is run as a computer program. Traditional pro-
gramming languages are designed to be deterministic. Work is required to build degeneracy into the
programs when we wish to emulate real biochemistry. There is little facility in existing languages for
the sort of evolved changes observed in the phylogeny of proteins.

Our second design principle is that reaction pathways that are executed in P should include an
element of stochastic branching, where the probability of following a particular branch is somehow
encoded in the sequence. This encoding is then part of B, allowing the probabilities to be evolvable.
We detail experiments with this approach in Section 7.2.

5.3 Everything Dies: The Way Molecules Are Destroyed Should Be a Function of

the Moleculeʼs Sequence

Given our arguments regarding the segregation of events in P and B, we now turn to one of the
most important aspects of AutChems, namely the method by which molecules are selected for de-
struction. Earlier AutChems have also wrestled with this problem. In both Tierra and Avida, mol-
ecules are removed from the system only when the creation of a new molecule demands space in the
container. Avida selects the molecule to be destroyed randomly; in Tierra, the stochastic element is
augmented by a ranking of each molecule in terms of its age and its success in copying. When mol-
ecules are continuously destroyed, the cohort of molecules has to replicate itself in order to be sus-
tained. This is a key feature of biology [12].

In order to make the likelihood of molecular decay a function of properties in B and hence
evolvable, we first remove any container-level influence on molecular decay. This has two influences
on the design of our container. Firstly, it can never be full (although it can get overcrowded, leading
to intractable computational overheads). Secondly, it is possible for all molecules in the system to

Artificial Life Volume 22, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
2
1
4
9
1
6
6
5
2
8
4
a
r
t
l

_
a
_
0
0
1
8
0
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

S. Hickinbotham et al.

Maximizing the Adjacent Possible in Automata Chemistries

decay, and the system become empty. The system must be allowed to become empty of molecules,
the equivalent of extinction or death, in order to provide evolutionary pressure to replicate. In ad-
dition to the container-level issues, there are two further aspects to our Everything Dies principle:
Firstly, there should be no state of the molecule that forbids decay; secondly, the rate of decay should
be a function of the properties of the sequence itself (in the spirit of the Everything Evolves prin-
ciple). We demonstrate the effects of this in Section 7.4.

6 Implementing the Design: Stringmol

We give here a brief overview of Stringmol, the experimental AutChem used to test our architecture,
described fully in [20, 18]. A summary of the chemistry is presented below, followed by a description
and discussion of molecular structure.

6.1 “Physical” Architecture: The Non-evolvable Components of the System
The architecture for our physical environment P has been designed to be as simple as possible. We
assume that raw materials are available in saturation, so our molecular system has no need to con-
serve mass. Instead, we limit the supply of energy to the system as a means of controlling the rates
of program execution—each instruction in the chemistry requires a unit of energy to execute. Mol-
ecules have no facility to store energy, so the energy availability in the container is a rate-limiting
factor. Future work will investigate the merits of this design and alternatives.

6.1.1 Container Design
A Stringmol simulation is a set of reacting molecules whose movements inside a container are gov-
erned by a stochastic mixing function. The system has a discrete-time clock. At each time step, the
state of all the molecules in the system is updated. Changes in state occur only if energy is available.
Energy is consumed either by binding, or by executing an instruction in a reaction; these events each
consume one unit of energy, loosely analogous to the activation energy in chemical reactions. At
each time step, energy is injected into the system. If energy is not used in one time step, the con-
tainer holds it in reserve for consumption in subsequent time steps. The selection of which mole-
cules consume the available energy is stochastic. When a container is fully populated, only a fraction
of the molecules in the container are able to execute an instruction.

The system also sets a stochastic decay rate on molecules, which specifies the probability of the
molecule being removed from the system at each time step. The balance between energy availability
and the decay rate of the molecule maintains a steady population of molecules. We currently specify
that only two molecules can ever participate in a single reaction, and that raw materials for the as-
sembly of new molecules are available in saturation.

6.1.2 Molecular Design
Should molecules come sufficiently close to one another, then they may bind and, should they bind
successfully, react. The reaction may proceed in such a way that one or more new molecules are
created, countering the effects of decay. The system uses a simple stochastic mixing function, which
emulates changes in adjacency of the elements within the container. For a randomly selected agent in
a bimolecular reaction, the chance of the second randomly selected agent in the reaction being close
enough to react is

ð
P Bvc ; va; n

ð
Þ ¼ 1 − 1 − va=vc

Þn

(6)

= 2500 is the volume of the container, va

where vc
number of molecules of the type of the second agent in the system.

= 10 is the volume of each molecule, and n is the

In Stringmol, a molecule is a sequence of opcodes together with pointers to positions on the
sequence. The opcodes represent both the structure of the molecule and a series of instructions.

Artificial Life Volume 22, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
2
1
4
9
1
6
6
5
2
8
4
a
r
t
l

_
a
_
0
0
1
8
0
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

S. Hickinbotham et al.

Maximizing the Adjacent Possible in Automata Chemistries

The pointers are moved around by the program and mark positions along the sequence where pro-
grammed events occur. There are four pointer types: the instruction pointer I, the read pointer R,
the write pointer W, and the flow pointer F. There are two pointers of each type, one for each
molecule in the reaction. Each pair has a flag indicating which pointer in the pair is currently ref-
erenced by the reaction. Apart from these structures, a molecule has no stacks or registers, or access
to any global controllers. The opcodes in the molecular sequence are instructions that manipulate the
pointers, thereby implementing the moleculeʼs function.

Molecules bind at loci along sequences if there is a match between the sequences at that point.
Binding is a complementary sequence alignment process, using the ROT13 substitution cypher to
generate and test complementarity [20]. The match can be inexact, and the match similarity can be
mapped to the probability of a bind occurring. The basis of the soft alignment scoring function is
based on the scoring method of [34] and is defined in [20].

In Stringmol, binding and reaction are chronologically and conceptually separate. Once a bind is
effected, it remains in place for the duration of the reaction. Another bind cannot interrupt a reac-
tion; a third molecule cannot bind to a reaction in progress. This is a simpler state of affairs than the
biology that Stringmol attempts to emulate.

Once bound, molecules execute the program specified by one of their strings of instructions, and
have the potential both to create further molecules and to change their own composition, thus form-
ing new molecules. This is the reaction component of the system.

The entry point for the program that is executed is determined when a reaction starts, intrinsically
via the positions of the alignments on the molecular strings. For any binding alignment, the reaction
program starts on the molecule whose alignment is furthest from the start of the string. (If the
alignments start at the same relative position, each molecule has an equal chance of becoming
the program.) The program starts where the alignment starts. This allows multiple reaction programs
to be encoded on a single molecular string. The different programs can be triggered by different
molecules binding to different regions with different affinities. In accordance with our architecture,
the selection of which program is run is part of B, and is therefore available to evolve. The function
of a molecule is thus context-dependent, the context being the sequence of the partner molecule in
any reaction.

All molecules are subject to decay (spontaneous destruction). The probability of decay is con-

trolled by a stochastic rate function.

6.1.3 Opcodes
Stringmol has seven functional opcodes, represented as non-alphabetical characters ‘$’, ‘>’, ‘^’, ‘?’, ‘=’, ‘%’, and ‘}’. Stringmol uses these functional opcodes to manipulate the pointers that indicate positions on the molecule, and the opcodes that the pointers index. During a reaction, alignments are used to specify program flow, commonly acting as place markers and analogues of “goto” state- ments. A detailed description of our microcode implementation can be found in [20]. Table 1 pro- vides a summary of these codes, which manipulate the pointers and control the execution pathways of the molecular microprograms. One of the functional symbols that merits special attention is the copy operation ‘=’. This op- eration reads the symbol at the read pointer R, and writes a copy of that symbol at the write pointer W. To implement mutation-on-copy, we specify that a copy operation writes a different symbol from that being read, with a small probability ps = 0.00001. Insertion of an extra random symbol, or deletion of the symbol being read, takes place with a smaller probability pi = ps/10n, where n is the number of different opcodes. In addition to these functional opcodes, we include 26 nonfunctional, or template, opcodes in the instruction set. These correspond to the three n-op codes in Avida and Tierra, but ours do not specify particular registers. Instead they can be used as variable nonfunctional regions to aid prob- abilistic matching during the binding and reaction phases. 60 Artificial Life Volume 22, Number 1 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u a r t l / / l a r t i c e – p d f / / / / 2 2 1 4 9 1 6 6 5 2 8 4 a r t l / _ a _ 0 0 1 8 0 p d . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 S. Hickinbotham et al. Maximizing the Adjacent Possible in Automata Chemistries Table 1. Symbols and actions used in the current implementation of molecular microprograms. For a detailed description see [20]. Opcode(s) A–Z $

}

Name

n-op

move

toggle

copy

cleave

end

Description

Inactive template code and instruction modifier

Shift *F to a matching template

Shift pointers to the flow pointer

Switch pointer to molecular bind partner

Conditional increment of instruction pointer

Insert at *W a copy of the symbol at *R

Split a sequence and generate a new molecule

Terminate execution and break the bond between molecules

6.2 “Biological” Architecture: Evolvable Sequences of Opcodes
Having described the components of P in Stringmol, we now turn to the components that evolu-
tionary selection can affect: the sequence of codes in the molecules. In the presence of molecular
decay, a cohort of molecules must create new copies of itself sufficiently quickly to survive. The
simplest of these cohorts consists of multiple copies of an identical molecular species, which we call
a replicase, since it autocatalyzes the synthesis of copies of itself. This hand-designed molecule per-
forms the core function of previous AutChems [33, 26], and it forms the basic design of the exper-
iments we report in subsequent sections.

6.2.1 Core Design of a Stringmol Replicase Molecule
The molecule we describe here (Figure 2) is one of many possible replicases. There are several
regions:

1. Two binding regions, to allow a replicase to bind to a copy of itself; recall that binding is
complementary. The two binding sites in our seed molecule do not align perfectly, which
enables us to evaluate the evolutionary pressure on binding.

2. A junk region: In the context of the design, mutations here have no effect on the binding
or the reaction program, allowing us to explore the effects of neutral mutation drift.
Note that mutations in the junk region can never be guaranteed to be neutral.

Figure 2. The seed replicase. The top line indicates the regions of the sequence. The sequence itself is shown in the center
box. Complementary alignments are indicated by black connecting lines at the bottom of the figure.

Artificial Life Volume 22, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
2
1
4
9
1
6
6
5
2
8
4
a
r
t
l

_
a
_
0
0
1
8
0
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

S. Hickinbotham et al.

Maximizing the Adjacent Possible in Automata Chemistries

3. A reaction region: In a replicase, the reaction creates a copy of the partner molecule.

Alignments in the reaction region control program flow.

This seed replicase is 65 opcodes long. The reaction takes 240 time steps to construct a new

replicase molecule.

6.3 Summary
The design of the Stringmol AutChem follows the architecture specified in Section 4: The biological
architecture B is in essence the sequence of each species in the cohort of molecules; if the opcodes
forming the sequence access the functions in P appropriately, then the expressive power of the
language in B can be exploited by evolutionary processes. The likelihood and locus of binding
between two molecules, the nature of the reaction between them, and the molecular decay rate
are all embodied in the sequence of each molecule in the container.

7 Experimental Evaluation

The experiments detailed below all follow a similar configuration. Firstly, a cohort of molecules is
designed to initialize the experimental trial. Unless otherwise stated, the molecules are similar to the
replicase molecules detailed in Section 6.2. Each trial runs until no molecules remain in the container.
A number of trials (at least 100) for each configuration are run. The figures in the experiments
detailed below illustrate the dynamics that were observed in these trials.

7.1 Everything Evolves I—Hypercycles in Stringmol
As a result of observing the principles derived from our architecture, Stringmol has only four
address registers, which point to positions on the sequence of a molecule. This is important for
two reasons:

1. Stringmol demonstrates that we can still get just as much emergent complexity as systems
that use more complicated computational apparatus. We can measure this using the
QNN value for different configurations. So if we are interested in evolution in ALife
systems, complicated constructs existing only in P and that cannot be manipulated in B
are a diversion.

2. We can do computing on the molecule: It can be embodied, and referenced in different ways.

We can illustrate these points by reference to a previously published experiment [19], summarized
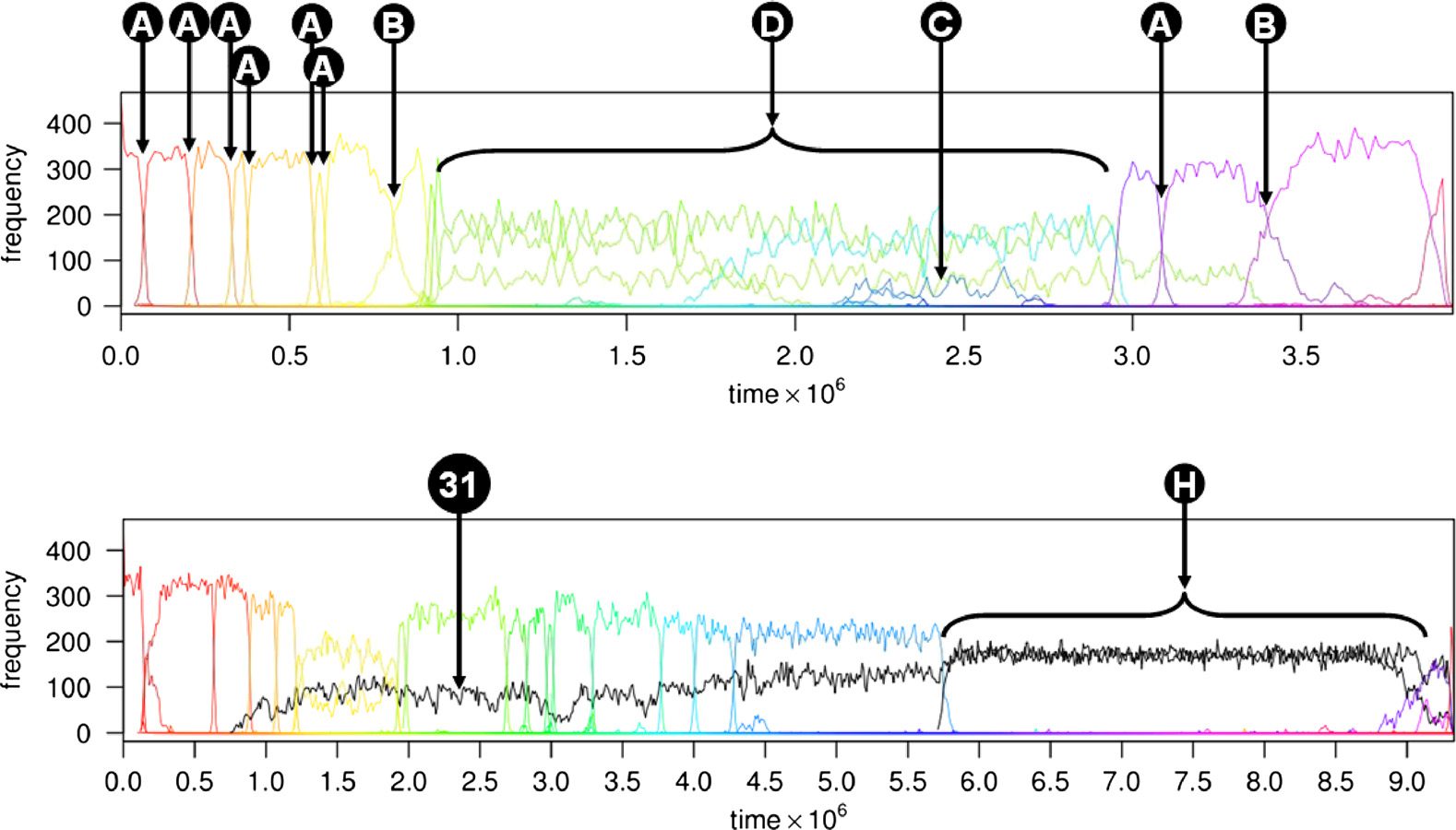
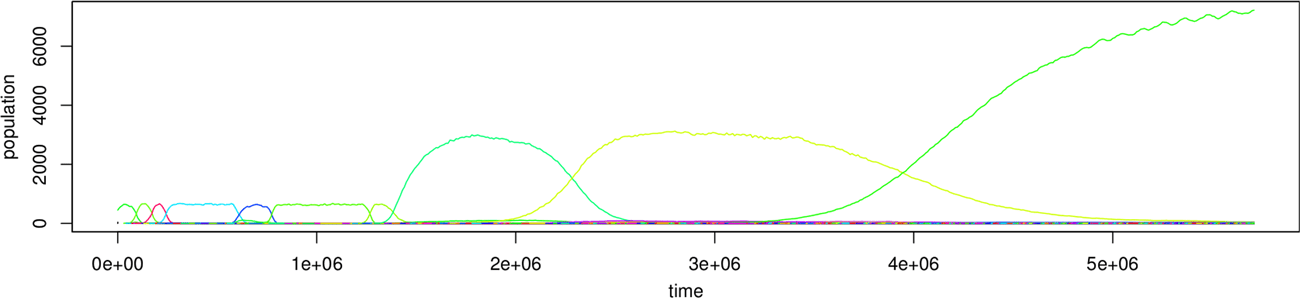
in Figure 3. The first experiment is an evaluation of the key phenomena we observed in 1,000 trials
seeded with the replicase molecule described in Section 6.2. These phenomena were identified by
visual inspection of the plots of changes in the populations of molecular species, as shown in Figure 3,
which shows two runs of a replicase trial. In these experiments, the observed phenomena were:
lethal and benign parasitism; sweeps, where an incumbent dominant species is driven to extinction
by a new dominant species; rapid sweep sequences; subpopulations; neutral drift. For details of these
see [19]. Here we focus on the most innovative mutation sequence we observed: the formation of
hypercycles.

Emergent hypercycles occur as follows. An enduring subpopulation increases in number until it
becomes codominant with a dominant species. The species forming the enduring subpopulation
is not self-maintaining. It is copied by the dominant species and acts as a copier for the dominant
species. A succession of dominant species ensues, each of which has less self-self affinity than
the previous one, until a dominant species arises that has lost the ability to self-maintain alto-
gether. The hypercycle occurs when the ability of the dominant population to self-maintain is

Artificial Life Volume 22, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
2
1
4
9
1
6
6
5
2
8
4
a
r
t
l

_
a
_
0
0
1
8
0
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

S. Hickinbotham et al.

Maximizing the Adjacent Possible in Automata Chemistries

Figure 3. Complex interactions in Stringmol. The top plot shows (A) characteristic sweeps, (B) slow sweeps, (C) subpop-
ulations, and (D) multi-species hypercycles. The bottom plot shows a short replicase (species 31), which emerges at
t = 0.75 × 106 and forms a hypercycle (H) at t = 5.75 × 106.

lost, and the two species become codependent. We discovered this emergent behavior in 8 of the
1,000 trials. Hypercycles end with a sweep, but occasionally one of the partner molecules is still
able to maintain a subpopulation. A series of sweeps ensues, in which the subpopulation declines
slightly following each sweep. This occurred in six of the eight trials that exhibited emergent
hypercycles.

Spontaneous hypercycles are emergent hypercycles that form from species that both arise in the im-

mediately preceding epoch. The mechanism is under investigation. These occur in 15 trials.

Multi-species hypercycles occur in 14 trials, when there appears to be a mutual dependence among
more than two species (Figure 3). For details of the mechanisms of the emergence of hypercycles,
see [19].

While observing these properties confirms that rich behavior is not dependent on computational
structures in P, it does not give a statistical framework to test the hypothesis. This is presented in the
following section.

7.2 Everything Evolves II—Opcode Granularity in Stringmol
While the previous section illustrated that emergent behavior can still arise in an AutChem with
minimal computational structures, it does not demonstrate the selective advantage that composability
can endow on a system. Our Everything Evolves principle suggests that evolution occurs via re-
composition of relatively constant units. In biology, these units can be amino acids in proteins,
or nucleotides in xNA. In AutChems, the units are the symbols in the strings, each of which can
be interpreted as an operator in a programming language. The problem for ALife is determining the
constitution of each unit—the opcodes that form the strings in Stringmol. If the Everything Evolves
principle holds, then a more granular representation of a program in a Stringmol sequence should
yield more evolutionary activity, which can be detected using the QNN measure.

We devised a simple experiment to test this claim by changing the formulation of the copying
process in Stringmol. This was achieved by decomposing the function of the copy opcode (denoted

Artificial Life Volume 22, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
2
1
4
9
1
6
6
5
2
8
4
a
r
t
l

_
a
_
0
0
1
8
0
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

S. Hickinbotham et al.

Maximizing the Adjacent Possible in Automata Chemistries

by ‘=’) into two opcodes that could be combined to carry out the same function. The copy function
can be summarized as follows (for details see [20]):

1. Copy the opcode in the location that the read pointer is pointing at to the location that the

write pointer is pointing at.

2. Increment the read and write pointers.

To decompose this operation, we made a new version of Stringmol, hereinafter called Granular
Stringmol, in which the copy operator only performed step 1 of these operations. The second oper-
ation was encoded in a new operator, called increment and denoted by the symbol ‘+’. As in other
Stringmol operators, ‘+’ has modifier codes associated with it, namely the n-ops ‘A’, ‘B’, and ‘C’. This
strategy allowed us to bestow the following behavior on the opcode:

case ‘+A’:

increment read pointer

case ‘+B’:

increment write pointer

case ‘+C’:

increment flow pointer

default:

increment instruction pointer

As a result, the operator ‘=’ in Stringmol was the exact equivalent of the string ‘=+A+B’ in Granular
Stringmol.

Having defined a more granular representation of the copy operator, we were then able to define
a replicase molecule in the Granular Stringmol opcode language. One effect of increasing the gran-
ularity was that the core processing loop that iteratively called the ‘=’ opcode took four more time
steps to process a single iteration. The copy loop ‘$=?>’ in Stringmol is the equivalent operation to ‘$=+A+B?>’ in Granular Stringmol. It was necessary to reduce the decay rate of the simulations in
order for the replicase molecule to maintain a cohort of reasonable size (around 200 molecules).
Once we had selected an appropriate decay rate, we used the same rate in the standard Stringmol
language, and used the same sequence for the replicase molecule in both Stringmol and Granular
Stringmol, simply making ‘+’ act as a n-op in Stringmol.

We ran 1,000 simulations of both Stringmol and Granular Stringmol in the configurations defined
above. We then applied the QNN measure to each run in the simulation. A boxplot of the QNN scores
for each run of the two configurations is shown in Figure 4. The Mann-Whitney U-test on the distribution
−65 (***) for these, and the A-test [39]
of QNN scores for the two simulation types gave a p-value of 10
effect size measure was 0.72 (large) for the distributions of QNN measures for the two configurations. It
is thus clear that the Granular Stringmol configuration yields more evolutionary activity, providing evi-
dence for our claim that putting more composability into the strings yields more evolutionary activity.

7.3 Everythingʼs Soft—Probabilistic Binding Protects against Parasitism
In nature, reactions between chemicals are the basis of complex networks of interactions that chan-
nel energy into the process of survival. In the molecular interaction networks of living systems,
binding is highly specific (A binds to B but not to C ) but not completely deterministic (A doesnʼt
always bind to B). However, ALife systems designed to emulate these natural systems often imple-
ment a deterministic binding scheme, in which a pair of molecules either always bind to each other,
or never bind to each other [13, 9]. There is no option for setting binding rates between the species
in a reaction, and there is no option for binding in different regions of the molecule with different

Artificial Life Volume 22, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
2
1
4
9
1
6
6
5
2
8
4
a
r
t
l

_
a
_
0
0
1
8
0
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

S. Hickinbotham et al.

Maximizing the Adjacent Possible in Automata Chemistries

Figure 4. Comparison of QNN scores for 1,000 runs of Stringmol and Granular Stringmol.

likelihoods. We suggest that these features make the chance appearance of innovative behavior more
likely than in systems that use deterministic binding.

To investigate the effects of the binding scheme on system dynamics, we compare two Stringmol
configurations that are identical but for the binding scheme, and compare how the systems respond
as they mutate to create new molecular sequences. This work is described in detail in [8]. The two
binding schemes we used were the standard Stringmol binding scheme based on the strength of
Smith-Waterman sequence alignments, and sticky Stringmol, in which any selected pair of molecules
is obliged to bind regardless of any matching sequence, the selection of the executing molecule in
the reaction is stochastic, and program execution commences at the beginning of the molecule. This
was the simplest alternative binding scheme that we could conceive that allowed us to test the Ev-
erythingʼs Soft principle. Alternative approaches, such as having an exact match requirement as in
[9], for example, will be the subject of future work.

One of the challenges to an evolving system is the emergence of parasitism. A parasite molecule is
replicated by other molecular species, but does not replicate other molecules in return. Parasite evasion
is when the cohort of molecules survives the introduction of a parasite, which becomes extinct. We
carried out experiments to determine the relationship between the emergence of parasitism and ob-
ligate (sticky Stringmol) or probabilistic (Stringmol) binding. We consider the system to have evaded
the parasite when no parasitic molecules (of that strain) remain, while a replicating cohort persists.
Figure 5 shows the functional region of the original replicase R and the parasitic mutant M,
which can appear via a single-point mutation. The mutation changes the reaction so that the parasite
does not implement the copy loop in the microprogram that allows characters on the bound mol-
ecule to be iteratively copied. Instead, only the first character of the string is copied into a new
molecule. When the parasite M is the executing microprogram, the product of the reaction is species
O, whose sequence is a string of length one consisting of the single character ‘O’.

We examined how the Stringmol container survives this type of parasite in the original trials [19].
We found that a new strain of replicase S arose via a mutation in the binding region of R. This new

Figure 5. The functional regions of the replicase R (upper ) and mutant M (lower ). The location of the mutation is indicated
by |. The mutation has the effect of breaking the copy loop.

Artificial Life Volume 22, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
2
1
4
9
1
6
6
5
2
8
4
a
r
t
l

_
a
_
0
0
1
8
0
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

S. Hickinbotham et al.

Maximizing the Adjacent Possible in Automata Chemistries

Table 2. Interactions of: the replicase R; parasitic mutant M; product of the mutant, O; new strain of replicase that is
immune to the parasite, S. The body of the table shows the product of the reaction for each possible combination of
active and passive molecules. The symbol ‘-’ indicates that no product is formed in the reaction.

e
v
i
t
c
A

–

Passive

–

strain is never the executing molecule in reactions with R or M and is thus immune to the parasite.
The set of products of reactions between these molecules are shown in Table 2. Note that the new
strain S that averts the death of the container would take over the container via a sweep even in the
absence of a parasitic mutant, as it is always passive when reacting with R. In the original trial, both
R and M die out relatively quickly and the new strain S becomes dominant. Figure 6 shows results
of this scenario, depicting typical dynamics of cases where this parasite is fatal and where the system
evolves a resistant strain of replicase. The population can sometimes mutate to evade what is a
potentially fatal parasite.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
2
1
4
9
1
6
6
5
2
8
4
a
r
t
l

_
a
_
0
0
1
8
0
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Figure 6. Stringmol (with mutation) in the parasite evasion trial. In both the upper and lower graphs the seed replicase, R,
starts at the top at t = 0. The upper graph shows a typical example of the dynamics when the parasite M is lethal to the
container. The yellow peak in towards the end of the run is the product of the parasite O. The parasite M peaks at the
same time as O, but to a population size of 200. The lower graph is an example where mutation gives rise to a new strain
of replicase that is immune to the parasite and takes over the container. The spike is again the product of the parasite O.
The parasite M is fatal to the seed replicase R, but at the same time as that parasite and O are spiking, a new replicase
molecule S1 emerges. Typical Stringmol behavior can be seen for the remainder of the run, with two sweeps (where the
dominant replicase is replaced by mutations S2 and S3) occurring.

Artificial Life Volume 22, Number 1

S. Hickinbotham et al.

Maximizing the Adjacent Possible in Automata Chemistries

To test these observations experimentally, we initiated a number of trials with two string types in
the container: a replicase R and a parasitic mutant M, which were initialized to population sizes of
300 and 10 respectively at the start of each trial. Each trial continues until either no molecules remain
or 500,000 time steps are processed. In each case we recorded whether the container survived the
parasite. We ran 100 trials for two binding schemes: Stringmol and sticky Stringmol.

Upon analysis of the results, we found no examples of parasite evasion in sticky Stringmol. By
contrast, we observed 32 evasions out of 100 experiments in Stringmol. The probabilistic binding
scheme allows the system to be more successful at evading the parasite. There are two mechanisms
by which the Stringmol container can evade a (potentially fatal) parasite. One is by having a suffi-
ciently low probability of binding, making it hard for new strains to establish themselves in the con-
tainer. The second mechanism is the potential to mutate to a resistant strain of replicase, S, which
the parasite cannot bind to.

Sticky Stringmol appears unable to escape this parasite scenario. The deterministic binding

scheme causes the parasite to dominate the container every time.

These results demonstrate the importance of nontrivial binding. It is not only which molecules
bind to which that is important. The probability of binding also plays a role in determining the
system-level properties. Reducing the probability of binding from 1 to 0.66 does more than simply
cause the same outcome to happen more slowly; binding is only one rate among many rates in
the system. The reduction in binding rate allows some of the replicase cohort to be held in reserve
by the system. An evolvable binding rate confers further advantages, allowing the system to move
away from unfortunate bindings.

The distribution of QNN measurements for the configurations described above is shown in Figure 7.
Some Stringmol runs produced lower QNN scores than any sticky Stringmol trials, but the median
QNN was higher. The Mann-Whitney U-test on the distribution of QNN scores shows that Stringmol
is significantly different from sticky Stringmol at the *** level ( p = 5.34e−05). The A-measure of the
effect size, 0.638, is classified as a medium value. It is striking that the significance of the p-value is not
reflected in the effect size, but this is because the medians are so similar for the two configurations even
though the distributions are so different. In conclusion, following the Everythingʼs Soft principle, it is
clear that the inexact string matching that is used for binding molecules in Stringmol raises the possibility
for mutation to create a new molecular species that cannot be bound to by a parasite.

7.4 Everything Dies—Selection at the Molecular Level
In biological cells, molecules do not tend to exist in the cell for any long period of time, unless the
system acts to maintain them. In our simulations, we refer to this process as decay. In simulation, it is

Figure 7. Comparison of QNN scores for 100 runs of Stringmol and sticky Stringmol.

Artificial Life Volume 22, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
2
1
4
9
1
6
6
5
2
8
4
a
r
t
l

_
a
_
0
0
1
8
0
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

S. Hickinbotham et al.

Maximizing the Adjacent Possible in Automata Chemistries

necessary to implement decay explicitly, or our artificial molecules will persist indefinitely. The stan-
dard implementation of Stringmol uses a very simple scheme for molecular decay: Decay is stochas-
tic, and occurs at a fixed rate for all molecules. This approach guarantees that no molecules can
persist forever without new instances being constantly created. However, since there is no reference
to the sequence of the molecule, the process is external to B, and so different decay rates cannot
evolve. Moreover, the process of decay is clearly a key part of selection at the molecular level, which
will contribute to the emergence of selection at the level of the container.

In this section, we compare four methods of removing molecules from the container and dem-

onstrate how they influence the evolution of the system.

To carry out experiments with decay, we selected two ways that the properties of a Stringmol
molecule can be used to influence the rate of decay of the molecule: whether the molecule is bound
to another molecule, and the length of the sequence of the molecule. Both of these properties are
variable, depending on the sequence of the molecule, and so should lead to different evolutionary
selection pressures on the composition of the sequence.

If only unbound agents decay, there is selection pressure towards reaction complexes forming
infinite processing loops, which donʼt decay, but do nothing for the system. If we allow decay in
reactions, we have to deal with the bound partner, which may be in an intermediate state, halfway
through a reaction. We could just allow the bound partner to “float off,” leaving lots of incomplete
fragments in the container, which would introduce new dynamics into the system. For a clearer
comparison, we decided to stipulate that if one bound partner was selected for decay, then the other
would decay also. The small effective increase in decay rate was thought to have negligible effects
within the experimental framework.

We also examined the effect of making the rate of decay a function of the length of the molecular
sequence, compared with a fixed rate. We ran experiments where the decay rate is inversely propor-
tional to the length of the molecule: The longer the molecule, the less likely it is to decay. We have
no way of knowing in advance what the median length of useful sequences might be; longer se-
quences tend to take longer to be constructed than shorter sequences; hence there is a natural bias
towards shorter molecules. Choosing a decay rate biased to the survival of longer molecules can
balance this. Also, we want long DNA-like molecules to be preserved in the system. While this
pressure may be useful once emergent systems are produced, the main consideration was to create
a platform upon which emergent behavior can happen at all.

A problem with this experiment was that one of the configurations resulted in very large numbers
of molecular species being generated, slowing down the processing. We made the problem tractable
by limiting the number of time steps to one million, and running 100 trials.

We ran four replicase trials (as detailed in Section 7) with the following decay configurations:

1. Decay rate inversely proportional to length, on unbound molecules only.

2. Fixed decay rate, on unbound molecules only.

3. Decay rate inversely proportional to length, on all molecules.

4. Fixed decay rate, on all molecules.

Typical results for these trials are shown in Figure 8. We can observe that the system dynamics for
the four configurations are very different. If decay occurs only to molecules that are unbound, and at a
rate inversely proportional to the length of the sequence (Figure 8a), we observe successive periods
dominated by ever larger populations of molecules. By looking up the sequences of the dominant mo-
lecular species, we see that the increase in population size corresponds to sequence length. Molecules
with long sequences tend not to be destroyed, since they tend to run longer programs, and so be bound
together for longer. While this scenario is not problematic from a theoretical standpoint, the processing
time increases quadratically with the population size, making the study of these systems intractable.

A different problem emerges if decay only applies to unbound molecules at a fixed rate. In such
systems, any pair of molecules that bind together and run a reaction with an infinite execution loop

Artificial Life Volume 22, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
2
1
4
9
1
6
6
5
2
8
4
a
r
t
l

_
a
_
0
0
1
8
0
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

S. Hickinbotham et al.

Maximizing the Adjacent Possible in Automata Chemistries

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
2
1
4
9
1
6
6
5
2
8
4
a
r
t
l

_
a
_
0
0
1
8
0
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Figure 8. Sample trials for different decay regimes.

in them perpetuate forever in the system. Figure 8b shows a situation where a new dominant mol-
ecule binds to copies of itself and runs an infinite loop. The cohort converges to a constant com-
position, as these loops consume all available energy in the system and never decay. Where decay is a
function of length, ever longer molecules are bound together for ever longer periods, and exist at
ever higher population sizes, as in Figure 8a, where dominant molecular lengths of 65, 130, and 195
opcodes show stable population sizes of approximately 620, 2800, and 7000 respectively. This con-
figuration yields different dynamics from that of molecules stuck in infinite loops, which persist
forever but do not increase in number, as in Figure 8b.

It is clear then that the decay function must apply to all molecules regardless of their state. The
bottom two rows of Figure 8 show examples of trials with this protocol. The first of these, Figure 8c,
shows a typical trial from a protocol where the decay rate is inversely proportional to the length of the
molecule. Again there is selection pressure that favors longer molecules, but a different effect arises:
Since the mutation rate is set on a per-character basis, longer molecules tend to have more mutations,
leading to an increase in the diversity of the cohort.

Figure 8d shows the default configuration of Stringmol, where a fixed decay rate applies to
all molecules in the system. While the dynamics show emergent behavior and are computationally

Artificial Life Volume 22, Number 1

S. Hickinbotham et al.

Maximizing the Adjacent Possible in Automata Chemistries

Figure 9. Comparison of QNN scores for 100 runs of Stringmol with four different molecular decay functions.

tractable to run and to analyze, it is nevertheless the case that this decay regime exists only in P,
which violates our proposed architecture. In fact, any decay regime that was independent of the
symbols in the strings exists only in P, because it cannot evolve. If decay is a fixed function of
string length, then the only strategy for enhanced survival is to make a longer string, but the content
of the string is irrelevant and the system cannot evolve an altered relationship between length and
decay, because you have fixed this in P. If decay were affected by the arrangement of symbols, a
“DNA” could evolve to have a different composition and longevity from that of a “protein,” even
with the same alphabet.

The QNN values for these experiments are shown in Figure 9. A statistical evaluation of the
distributions of QNN scores for these configurations is shown in Table 3. The biggest difference
in the configurations appears to be when decay is a function of length, and the comparison is be-
tween allowing all molecules to decay and only allowing unbound molecules to decay. Perhaps coun-
terintuitively, the configuration where all molecules decay gives higher QNN. A similar scenario is
observed where decay is not a function of length, but random. However, here the difference be-
tween allowing all molecules to decay and allowing only unbound molecules to decay is not signif-
icant. We suggest that there is no significant difference in this case, because populations of bound
molecules that do not decay will not generate any evolutionary activity, and will (rightly) not con-
tribute any value to the QNN measurement.

Seen from the perspective of the Everything Dies principle, the QNN scoring of these experi-
ments make sense—the highest-scoring formulation is when the chance of decay is fully stochastic,

Table 3. p-values and effect size (A-value) for decay experiments.

p-value

A-value

Any Unb

Long All

Long Unb

Any Unb

Long All

Long Unb

Any

All

* (1.78e−01)

ns (7.70e−01)

** (4.97e−03) None (0.555) None (0.512)

Small (0.615)

Any Unb

Long All

** (8.13e−02)

* (1.66e−01)

Small (0.571) None (0.556)

*** (5.78e−04)

Medium (0.641)

Artificial Life Volume 22, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
2
1
4
9
1
6
6
5
2
8
4
a
r
t
l

_
a
_
0
0
1
8
0
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

S. Hickinbotham et al.

Maximizing the Adjacent Possible in Automata Chemistries

not a function of the length or reaction state of the molecule. If only unbound molecules can be
selected for decay, the system evolves towards a state where a small number of molecules are bound
in perpetuity, effectively running infinite loops and squandering resources. Where decay happens
more often to shorter molecules than longer ones, we see that the system evolves to a state where
the dominant molecules are very long. Because these molecules are longer, there is an increased
likelihood that a mutation will occur when an individual molecule is copied. We see an explosion
in diversity, but this causes a lower QNN because there are no sweeps as a new species becomes
dominant in the system.

We must note a conflict here in the Everything Dies and Everything Evolves principles. It is arguable
that using the length of the molecule as the basis of a decay function follows the Everything Evolves
principle, yet the QNN measure shows the opposite. More work is needed here, but from these exper-
iments it appears that Everything Dies takes precedence over Everything Evolves. In addition, if we
want open-ended systems, it is difficult to design a reaper function that is better than random.

The selection of the decay function is of critical importance, as it is an implicit measure of fitness.
It is so far the only way we have found of driving selection at the molecular level. Earlier AutChem
designs have similar decay functions. Tierra uses a reaper queue to order the destruction of the mol-
ecules in the system, which is partly stochastic, and partly based on the recorded success of the
molecule at copying itself. Our analysis of the literature [16] and source code of Tierra version
6.02 suggests that Tierraʼs reaper function is much more of a straightforward fitness function than
is generally realized. It is biased to select organisms that are older, and that have not created new
offspring. There is clear pressure towards making lots of new Tierrans, which may be why parasites
emerge so frequently. There is an important principle here: survival determines fitness—not the other
way around, as encoded in Tierra, where the fitness of the individual determines its place in the
reaper queue. In nature, fitness is implicit, and the survival and reproduction of the individual are
the only indicators of its fitness (kin or group selection leads to a broader notion of “inclusive fit-
ness,” but this is not considered in our study). Avida is fully stochastic, once the array of available
organism cells is full. Neither of these systems has decay encoded in B, and both make reference to
container-level properties of the system in selecting molecules for decay. Although we have not
formulated a decay regime that can be manipulated in B in Stringmol, we have removed the need
to make reference to container-level measurements.

We have developed a Stringmol system in which molecules are randomly selected for deletion.
Yet there are problems with maintaining a dynamic system in this environment. For example, if our
goal is to create a system that contains a DNA analogue, we must ensure that the DNA is not
destroyed for most of the lifetime of the cell, whereas the analogues of other molecules are con-
stantly destroyed and created in response to prevailing conditions.

To summarize:

(cid:129) If long molecules decay more rarely, the system quickly comes to be composed of

long molecules.

(cid:129) If decay happens only when unbound, the system evolves to lock replicases in an infinite

loop.

(cid:129) A combination of basing the rate of decay on the length of molecules and permitting

decay regardless of the binding state results in a multi-species set of very long
molecules.

(cid:129) In the Any configuration, differences between All and Unb are masked because there

is zero QNN when the population is static.

(cid:129) In the Long configuration, the All configuration has higher QNN than the Unb. This

fits the Everything Dies principle.

(cid:129) However, the Long configuration is associated with large computational overheads, and is

impractical to analyze at present.

Artificial Life Volume 22, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
2
1
4
9
1
6
6
5
2
8
4
a
r
t
l

_
a
_
0
0
1
8
0
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

S. Hickinbotham et al.

Maximizing the Adjacent Possible in Automata Chemistries

8 Discussion

8.1 Summary of This Contribution
This contribution has set out new design principles for AutChems. Key to this new approach is the
separation of the design of components of the system into a physical world P with a fixed set of
rules, and a biological world B that can change via evolutionary processes. By moving much of the
system out of the domain of P and into the domain of B, we approach a system where “Everything
Evolves.” By increasing the stochasticity of binding and program execution, we approach a system
where “Everythingʼs Soft.” Finally, we have explored the concept of “Everything Dies,” as de-
scribed in Section 7.4.

We have demonstrated in Section 7.1 that this architecture maintains and develops the capabil-
ities of AutChems for open-ended evolution, despite having a simpler implementation, so demonstrat-
ing the principle that Everything Evolves. Experiments with stochasticity in binding in Section 7.3
show that Stringmol has the Everythingʼs Soft property. The principle that Everything Dies was im-
plemented in several different ways in Section 7.4. The experiments show that this principle is very
powerful, since sequences rapidly evolved to exploit the decay function and become the most resis-
tant to destruction wherever possible.

8.2 Next Steps: Designing AutChems in the Adjacent Possible of Stringmol
While the experiments we have presented here demonstrate that Stringmol is a loose but effective
emulation of the design principles, we recognize that there is much to be done before a computa-
tional implementation of the principles can be achieved. We list here three simple changes to the
Stringmol language that would emphasize the concept of molecular embodiment and make infor-
mation processing easier to implement on a sequence.

8.2.1 Improving the Implementation of Everything Evolves
The Stringmol instruction set is broadly similar to the instruction sets in Avida and Tierra, but with-
out opcodes for manipulating stacks and registers. In the course of designing the sequences for the
experiments above, it has become apparent that there is scope for improvement of these opcodes
that could make them more powerful manipulators of B by promoting the development of novel
combinations of simple operations in P.

There are seven operators in Stringmol, which use four pointers to reference other regions of the
sequence and apply different actions to them. We demonstrated in Section 7.2 that the copy operator
could be decomposed into simpler operators. We suggest that this method could be applied to the other
operators in Stringmol. For example, the move operator ‘>’ carries out the following series of actions:

1. Get the position of the flow pointer.

2. Select which pointer should be moved to it (read, write, or instruction pointer ).

3. Move the selected pointer to the flow pointer.
4. Increment the instruction pointer if it hasnʼt been moved.

This sequence of operations is encoded in a single operator, and is therefore part of P. If we
decomposed the operator into four smaller operators, we would have made it part of B, and hence
evolvable. While it is unlikely that the move operation could be further optimized, decomposing the
action into a sequence of components allows evolutionary selection to explore the adjacent possible
of the move operator and so build new functions in B. A richer set of efficient higher-level oper-
ations could be built from combinations of these simpler codes.

In tandem with the suggestion of a more fine-grained instruction set, we also argue for a further
review of the non-sequence structures that make up a molecule in Stringmol. These structures

Artificial Life Volume 22, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
2
1
4
9
1
6
6
5
2
8
4
a
r
t
l

_
a
_
0
0
1
8
0
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

S. Hickinbotham et al.

Maximizing the Adjacent Possible in Automata Chemistries

comprise two sets of four pointers (one set for each molecule in the reaction) and an array of flags
indicating which pointer in each set is active. There are two obvious alternatives to this approach.
One is to allow any pointers and associated flags to be specified as part of the string. A more am-
bitious implementation would have no pointers, but allow the strings to move across each other as
the reaction proceeds [31], emulating a ribosome. While the latter approach is a full implementation
of the Everything Evolves principle, it may either be computationally intractable, or make it infea-
sible to design or initialize molecules with a specified function by hand.

8.2.2 Improving the Implementation of Everythingʼs Soft
We have given an example of the implementation of Everythingʼs Soft in Section 7.3. There are two
areas of research needed to develop this concept further, one in the domain of P and one in the
domain of B.

The physical domain of Stringmol is subject to hard energy constraints: If energy is available, then
an instruction is executed, and if energy is absent, then the execution hangs until such time as it is
available again. Unfortunately, this simple model precludes the possibility of constructing switching
behaviors based on the availability of energy. We envisage a straightforward operator similar to the
‘?’ operator that increments the instruction pointer a number of times dependent upon the availabil-
ity of energy in the system. This would allow regulation of energy use to occur and give rise to
selection at the molecular level that is not currently possible: Energetically expensive actions such
as the creation of a new molecule could be regulated so that they only occur when there is sufficient
energy available to make successful completion of the task sufficiently likely.

Regulation of some behavior could occur if promoter regions could be made possible. We need
further experimentation in this area before we can conclude that systems that only permit bimolec-
ular interaction cannot achieve some of the regulatory properties observed in biological systems.
We have attempted elsewhere [30] to construct these in the B of Stringmol; an input signal re-
programmed the replicator molecule so that it made an output signal. This was the only way to
achieve switching on of a receptor site that is normally modeled as a trimolecular reaction.

8.2.3 Improving the Implementation of Everything Dies
Our default model for destruction of molecules is based purely in P. There are two areas of research
needed to develop this further, and once again, one is in the domain of P and one is in the domain
of B.

One approach to making the decay model more tractable might be to apply the Everythingʼs Soft
principle. To achieve this, we could specify that the molecules can break apart, rather than be
completely removed from the system. This has the desirable effect of introducing some complexity
in the system “for free,” but may be computationally intractable, as the number of species would
increase much more rapidly than we have observed.

A more viable approach would be to implement a curator molecule in B. This would bind to
molecules with a low (but variable) probability, and proceed to disassemble them into small chunks.
This would be more manageable than implementing the decay in P, and it affords the possibility of
some molecules (such as a DNA analogue) surviving longer than others. This would allow us to
build more sophisticated cohorts of molecular machines, and so begin to design selection at the
container level, rather than the cellular level.

8.3 Closing Remarks
Our goal in this article is to create an AutChem in which evolutionary pathways are open-ended: ca-
pable of producing new forms with a generally increasing level of complexity. This is the grand
challenge of ALife. The architecture we describe in this article aims to give principles for the design
of systems that approach this challenge. It has the following merits: It can be used to design new
systems; it can be used to interpret existing systems; finally, it can be applied to the biology of the
real world. Stringmol, our current implementation of the architecture, has demonstrated the use of

Artificial Life Volume 22, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
2
1
4
9
1
6
6
5
2
8
4
a
r
t
l

_
a
_
0
0
1
8
0
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

S. Hickinbotham et al.

Maximizing the Adjacent Possible in Automata Chemistries

the architecture in both design and evaluation of novel ALife systems. Our intention is both to
improve the implementation of the architecture in new versions of Stringmol, and to further develop
the architecture itself.

References
1. Adami, C., Ofria, C., & Collier, T. (2000). Evolution of biological complexity. Proceedings of the National

Academy of Sciences of the U.S.A., 97(9), 4463–4468.

2. Allesina, S., & Tang, S. (2012). Stability criteria for complex ecosystems. Nature, 483(7388), 205–208.

3. Banzhaf, W., Dittrich, P., & Eller, B. (1999). Self-organization in a system of binary strings with

topological interactions. Physica D, 125(1–2), 85–104.

4. Bedau, M. A. (2007). Artificial life. In M. Matthen & C. Stephens (Eds.), Handbook of the philosophy of

biology (pp. 585–603). Amsterdam: Elsevier.

5. Bobrik, M., Kvasnicka, V., & Pospichal, J. (2008). Artificial chemistry and molecular Darwinian evolution
of DNA/RNA-like systems I—typogenetics and chemostat. In A. Kelemen, A. Abraham, & Y. Liang
(Eds.), Computational intelligence in medical informatics (pp. 295–336). Berlin: Springer.

6. Bullock, S., & Bedau, M. A. (2006). Exploring the dynamics of adaptation with evolutionary activity

plots. Artificial Life, 12(2), 193–197.

7. Channon, A. (2006). Unbounded evolutionary dynamics in a system of agents that actively process and

transform their environment. Genetic Programming and Evolvable Machines, 7(3), 253–281.

8. Clark, E., Nellis, A., Hickinbotham, S., Stepney, S., Clarke, T., Pay, M., & Young, P. (2011). Degeneracy

enriches artificial chemistry binding systems. In Advances in artificial life, 11th European Conference on
Artificial Life (pp. 133–140). Cambridge, MA: MIT Press.

9. Decraene, J., Mitchell, G. G., & McMullin, B. (2008). Unexpected evolutionary dynamics in a string

based artificial chemistry. In Artificial life XI: Proceedings of the Tenth International Conference on the Synthesis
and Simulation of Living Systems (pp. 158–165). Cambridge, MA: MIT Press.

10. Dittrich, P., Ziegler, J., & Banzhaf, W. (2001). Artificial chemistries—a review. Artificial Life, 7(3), 225–275.

11. Droop, A., & Hickinbotham, S. (2012). A quantitative measure of non-neutral evolutionary activity
for systems that exhibit intrinsic fitness. In Artificial life 13, the Thirteenth International Conference on the
Simulation and Synthesis of Living Systems (pp. 45–52). Cambridge, MA: MIT Press.

12. Ehrenfeucht, A., & Rozenberg, G. (2004). Basic notions of reaction systems. In Developments in Language

Theory, 8th International Conference (pp. 27–29). Berlin: Springer.

13. Fontana, W. (1991). Algorithmic chemistry: A model for functional self-organization. In Artificial life II,

The Second Interdisciplinary Workshop on the Synthesis and Simulation of Living Systems (pp. 159–209).
Boston: Addison-Wesley.

14. Fontana, W., & Buss, L. W. (1994). “The arrival of the fittest”: Toward a theory of biological organization.

Bulletin of Mathematical Biology, 56(1), 1–64.

15. Gilbert, W. (1986). Origin of life: The RNA world. Nature, 319(6055), 618.

16. Harada, T., & Takadama, K. (2013). Asynchronous evaluation based genetic programming: Comparison
of asynchronous and synchronous evaluation and its analysis. In K. Krawiec, A. Moraglio, T. Hu,
A. S. Etaner-Uyar, & B. Hu (Eds.), Proceedings of the 16th European Conference on Genetic Programming
(pp. 241–252). Berlin: Springer.

17. Harvey, I. (2011). Opening stable doors: Complexity and stability in nonlinear systems. In Advances in
artificial life, 11th European Conference on Artificial Life (pp. 318–325). Cambridge, MA: MIT Press.

18. Hickinbotham, S., Clark, E., Stepney, S., Clarke, T., Nellis, A., Pay, M., & Young, P. (2009). Molecular
microprograms. In Advances in artificial life, 10th European Conference on Artificial Life (pp. 297–304).
Berlin: Springer.

19. Hickinbotham, S., Clark, E., Stepney, S., Clarke, T., Nellis, A., Pay, M., & Young, P. (2010). Diversity

from a monoculture: Effects of mutation-on-copy in a string-based artificial chemistry. In Artificial life XII:
The Twelfth International Conference on the Synthesis and Simulation of Living Systems (pp. 24–31). Cambridge,
MA: MIT Press.

Artificial Life Volume 22, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
2
1
4
9
1
6
6
5
2
8
4
a
r
t
l

_
a
_
0
0
1
8
0
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

S. Hickinbotham et al.

Maximizing the Adjacent Possible in Automata Chemistries

20. Hickinbotham, S., Clark, E., Stepney, S., Clarke, T., Nellis, A., Pay, M., & Young, P. (2010). Specification
of the Stringmol chemical programming language version 0.2 (Technical report YCS-2010-458). York: Department
of Computer Science, University of York.

21. Hickinbotham, S., Stepney, S., Nellis, A., Clarke, T., Clark, E., Pay, M., & Young, P. (2011). Embodied
genomes and metaprogramming. In Advances in artificial life, 11th European Conference on Artificial Life
(pp. 334–341). Cambridge, MA: MIT Press.

22. Hofstadter, D. R. (1979). Gödel, Escher, Bach: An eternal golden braid. New York: Basic Books.

23. Holland, J. (1976). Studies of the spontaneous emergence of self-replicating systems using cellular
automata and formal grammars. In A. Lindenmayer & G. Rozenberg (Eds.), Automata, languages,
development (pp. 385–404). Amsterdam: North-Holland.

24. Ierymenko, A. (2010). Nanopond: A very tiny artificial life virtual machine. Available at http://adam.ierymenko.

name/nanopond.shtml (accessed May 2015).

25. Jefferson, D., Collins, R., Cooper, C., Dyer, M., Flowers, M., Korf, R., Taylor, C., & Wang, A.

(1991). Evolution as a theme in artificial life: The genesys/tracker system. In C. Lanton, C. Taylor,
J. Farmer, & S. Rasmussen (Eds.), Artificial life II: The 2nd Interdisciplinary Workshop on the Synthesis
and Simulation of Living Systems (pp. 549–578). Boston: Addison-Wesley.

26. Johnson, T. J., & Wilke, C. O. (2004). Evolution of resource competition between mutually dependent

digital organisms. Artificial Life, 10(2), 145–156.

27. Kauffman, S. A. (2000). Investigations. Oxford, UK: Oxford University Press.

28. Laing, R. (1977). Automaton models of reproduction by self-inspection. Journal of Theoretical Biology, 66(3),

437–456.

29. May, R. M. (1973). Stability and complexity in model ecosystems. Princeton: Princeton University Press.

30. Nagle, F., & Hickinbotham, S. (2011). Embodied reaction logic in a simulated chemical computer.
In Advances in artificial life, 11th European Conference on Artificial Life (pp. 573–580). Cambridge,
MA: MIT Press.

31. Nellis, A., & Stepney, S. (2011). Embodied copying for richer evolution. In Advances in artificial life,

11th European Conference on Artificial Life (pp. 597–604). Cambridge, MA: MIT Press.

32. Pargellis, A. N. (2001). Digital life behavior in the Amoeba world. Artificial Life, 7(1), 63–75.

33. Ray, T. (1991). An approach to the synthesis of life. In Artificial life II: The 2nd Interdisciplinary Workshop

on the Synthesis and Simulation of Living Systems (pp. 371–408). Boston: Addison-Wesley.

34. Smith, T. F., & Waterman, M. S. (1981). Identification of common molecular subsequences. Journal of

Molecular Biology, 147(1), 195–197.

35. Standish, R. K. (2001). On complexity and emergence. Complexity International, 9, 1–6.

36. Suzuki, H., & Ono, N. (2002). Universal replication in a string-based artificial chemistry system.

Journal of Three Dimensional Images, 16(4), 154–159.

37. Turing, A. M. (1937). On computable numbers, with an application to the Entscheidungsproblem.

Proceedings of the London Mathematical Society, 2(1), 230–265.

38. Varetto, L. (1998). Studying artificial life with a molecular automaton. Journal of Theoretical Biology, 193(2),

257–285.

39. Vargha, A., & Delaney, H. (2000). A critique and improvement of the CL common language effect
size statistics of McGraw and Wong. Journal of Educational and Behavioral Statistics, 25(2), 101–132.

40. von Neumann, J. (1966). Theory of self-reproducing automata. Champaign: University of Illinois Press.

41. Wagner, A. (2000). The role of population size, pleiotropy and fitness effects of mutations in the

evolution of overlapping gene functions. Genetics, 154(3), 1389–1401.

42. Yamamoto, L. (2008). Plasmidpl: A plasmid-inspired language for genetic programming. In M. OʼNeill,
L. Vanneschi, S. M. Gustafson, A. Esparcia-Alcázar, I. D. Falco, A. D. Cioppa, & E. Tarantino (Eds.),
Genetic Programming, 11th European Conference, EuroGP (pp. 337–349). Berlin: Springer.

Artificial Life Volume 22, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
2
1
4
9
1
6
6
5
2
8
4
a
r
t
l