LETTER
Communicated by Ian Robertson
Deeply Felt Affect: The Emergence of Valence
in Deep Active Inference
Casper Hesp*
c.hesp@uva.nl
Department of Psychology and Amsterdam Brain and Cognition Centre, University
of Amsterdam, 1098 XH Amsterdam, Netherlands; Institute for Advanced Study,
University of Amsterdam, 1012 GC Amsterdam, Netherlands; and Wellcome Centre
for Human Neuroimaging, University College London, London WC1N 3BG, U.K.
Ryan Smith*
RSmith@laureateinstitute.org
Laureate Institute for Brain Research, Tulsa, OK 74136, U.S.A.
Thomas Parr
thomas.parr.12@ucl.ac.uk
Wellcome Centre for Human Neuroimaging, University College London,
London WC1N 3BG, U.K.
Micah Allen
micah.allen@medschl.cam.ac.uk
Aarhus Institute of Advanced Studies, Aarhus University, Aarhus 8000, Denmark;
Centre of Functionally Integrative Neuroscience, Aarhus University Hospital,
Aarhus 8200, Denmark; and Cambridge Psychiatry, Cambridge University,
Cambridge CB2 8AH. U.K.
Karl J. Friston
k.friston@ucl.ac.uk
Wellcome Centre for Human Neuroimaging, University College London,
London WC1N 3BG, U.K.
Maxwell J. D. Ramstead
maxwell.d.ramstead@gmail.com
Wellcome Centre for Human Neuroimaging, University College London, London
WC1N 3BG, U.K.; Division of Social and Transcultural Psychiatry, Department
of Psychiatry and Culture, Mind, and Brain Program, McGill University,
Montreal H3A 0G4, QC, Canada
*C.H. and R.S. made equal contributions and are designated co–first authors.
Neural Computation 33, 398–446 (2021)
https://doi.org/10.1162/neco_a_01341
© 2020 Massachusetts Institute of Technology.
Published under a Creative Commons
Attribution 4.0 International (CC BY 4.0) license.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Deeply Felt Affect
399
The positive-negative axis of emotional valence has long been recognized
as fundamental to adaptive behavior, but its origin and underlying func-
tion have largely eluded formal theorizing and computational modeling.
Using deep active inference, a hierarchical inference scheme that rests
on inverting a model of how sensory data are generated, we develop a
principled Bayesian model of emotional valence. This formulation as-
serts that agents infer their valence state based on the expected precision
of their action model—an internal estimate of overall model fitness (“sub-
jective fitness”). This index of subjective fitness can be estimated within
any environment and exploits the domain generality of second-order be-
liefs (beliefs about beliefs). We show how maintaining internal valence
representations allows the ensuing affective agent to optimize confidence
in action selection preemptively. Valence representations can in turn be
optimized by leveraging the (Bayes-optimal) updating term for subjec-
tive fitness, which we label affective charge (AC). AC tracks changes in
fitness estimates and lends a sign to otherwise unsigned divergences be-
tween predictions and outcomes. We simulate the resulting affective in-
ference by subjecting an in silico affective agent to a T-maze paradigm
requiring context learning, followed by context reversal. This formula-
tion of affective inference offers a principled account of the link between
affect, (mental) action, and implicit metacognition. It characterizes how a
deep biological system can infer its affective state and reduce uncertainty
about such inferences through internal action (i.e., top-down modulation
of priors that underwrite confidence). Thus, we demonstrate the potential
of active inference to provide a formal and computationally tractable ac-
count of affect. Our demonstration of the face validity and potential util-
ity of this formulation represents the first step within a larger research
program. Next, this model can be leveraged to test the hypothesized role
of valence by fitting the model to behavioral and neuronal responses.
1 Introduction
We naturally aspire to attain and maintain aspects of our lives that make us
feel “good.” On the flip side, we strive to avoid environmental exchanges
that make us feel “bad.” Feeling good or bad—emotional valence—is a cru-
cial component of affect and plays a critical role in the struggle for existence
in a world that is ever-changing yet also substantially predictable (Johnston,
2003). Across all domains of our lives, affective responses emerge in context-
dependent yet systematic ways to ensure survival and procreation (i.e., to
maximize fitness).
In healthy individuals, positive affect tends to signal prospects of in-
creased fitness, such as the satisfaction and anticipatory excitement of
eating. In contrast, negative affect tends to signal prospects of decreased
fitness—such as the pain and anticipatory anxiety associated with physical
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
400
Hesp et al.
harm. Such valenced states can be induced by any sensory modality, and
even by simply remembering or imagining scenarios unrelated to one’s cur-
rent situation, allowing for a domain-general adaptive function. However,
that very same domain-generality has posed difficulties when attempting
to capture such good and bad feelings in formal or normative treatments.
This kind of formal treatment is necessary to render valence quantifiable,
via mathematical or numerical analysis (i.e., computational modeling). In
this letter, we propose a computational model of valence to help meet this
need.
In formulating our model, we build on both classic and contemporary
work on understanding emotional valence at psychological, neuronal, be-
havioral, and computational levels of description. At the psychological
level, a classic perspective has been that valence represents a single dimen-
sion (from negative to positive) within a two-dimensional space of “core
affect” (Russell, 1980; Barrett & Russell, 1999), with the other dimension
being physiological arousal (or subjective intensity); further dimensions
beyond these two have also been considered (e.g., control, predictability;
Fontaine, Scherer, Roesch, & Ellsworth, 2007). Alternatively, others have
suggested that valence is itself a two-dimensional construct (Cacioppo &
Berntson, 1994; Briesemeister, Kuchinke, & Jacobs, 2012), with the inten-
sity of negative and positive valence each represented by its own axis (i.e.,
where high negative and positive valence can coexist to some extent during
ambivalence).
At a neurobiological level, there have been partially corresponding re-
sults and proposals regarding the dimensionality of valence. Some brain
regions (e.g., ventromedial prefrontal (VMPFC) regions) show activation
patterns consistent with a one-dimensional view (reviewed in Lindquist,
Satpute, Wager, Weber, & Barrett, 2016). In contrast, single neurons have
been found that respond preferentially to positive or negative stimuli
(Paton, Belova, Morrison, & Salzman, 2006; Morrison & Salzman, 2009),
and separable brain systems for behavioral activation and inhibition (of-
ten linked to positive and negative valence, respectively) have been pro-
posed (Gray, 1994), based on work highlighting brain regions that show
stronger associations with reward and/or approach behavior (e.g., nu-
cleus accumbens, left frontal cortex, dopamine systems; Rutledge, Skan-
dali, Dayan, & Dolan, 2015) or punishment and/or avoidance behavior
(e.g., amygdala, right frontal cortex; Davidson, 2004). However, large meta-
analyses (e.g., Lindquist et al., 2016) have not found strong support for these
views (with the exception of one-dimensional activation in VMPFC), in-
stead finding that the majority of brain regions are activated by increases in
both negative and positive valence, suggesting a more integrative, domain-
general use of valence information, which has been labeled an “affective
workspace” model (Lindquist et al., 2016). Note that the associated domain-
general (“constructivist”) account of emotions (Barrett, 2017)—as opposed
to just valence—contrasts with older views suggesting domain-specific
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Deeply Felt Affect
401
subcortical neuronal circuits and associated “affect programs” for differ-
ent emotion categories (e.g., distinct circuits for generating the feelings and
visceral/behavioral expressions of anger, fear, or happiness; Ekman, 1992;
Panksepp, Lane, Solms, & Smith, 2017). However, this debate between con-
structivist and “basic emotions” views goes beyond the scope of our pro-
posal. Questions about the underlying basis of valence treated here are
much narrower than (and partially orthogonal to) debates about the nature
of specific emotions, which further encompasses appraisal processes, facial
expression patterns, visceral control, cognitive biases, and conceptualiza-
tion processes, among others (Smith & Lane, 2015; Smith, Killgore, Alkozei,
& Lane, 2018; Smith, Killgore, & Lane, 2020).
At a computational level of description, prior work related to valence
has primarily arisen out of reinforcement learning (RL) models—with for-
mal models of links between reward/punishment (with close ties to pos-
itive/negative valence), learning, and action selection (Sutton & Barto,
2018). More recently, models of related emotional phenomena (mood) have
arisen as extensions of RL (Eldar, Rutledge, Dolan, & Niv, 2016; Eldar &
Niv, 2015). These models operationalize mood as reflecting a recent history
in unexpected rewards or punishments (positive or negative reward pre-
diction errors (RPEs)), where many recent better-than-expected outcomes
lead to positive mood and repeated worse-than-expected outcomes lead to
negative mood. The formal mood parameter in these models functions to
bias the perception of subsequent rewards and punishments with the sub-
jective perception of rewards and punishments being amplified by positive
and negative mood, respectively. Interestingly, in the extreme, this can lead
to instabilities (reminiscent of bipolar or cyclothymic dynamics) in the con-
text of stable reward values. However, these modeling efforts have had a
somewhat targeted scope and have not aimed to account for the broader
domain-general role of valence associated with findings supporting the af-
fective workspace view mentioned above.
In this letter, we demonstrate that hierarchical (i.e., deep) Bayesian net-
works, solved using active inference (Friston, Parr, & de Vries, 2018), af-
ford a principled formulation of emotional valence—building on both the
work mentioned above as well as prior work on other emotional phenom-
ena within the active inference framework (Smith, Parr, & Friston, 2019;
Smith, Lane, Parr, & Friston, 2019); Smith, Lane, Nadel, L., & Moutoussis,
2020; Joffily & Coricelli, 2013; Clark, Watson, & Friston, 2016; Seth & Friston,
2016). Our hypothesis is that emotional valence can be formalized as a state
of self that is inferred on the basis of fluctuations in the estimated confidence
(or precision) an agent has in her generative model of the world that in-
forms her decisions. This is implemented as a hierarchically superordinate
state representation that takes the aforementioned confidence estimates at
the lower level as data for further self-related inference. After motivating
our approach on theoretical and observational grounds, we demonstrate
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
402
Hesp et al.
affective inference by simulating a synthetic animal that “feels” its way
forward during successive explorations of a T-maze. We use unexpected
context changes to elicit affective responses, motivated in part by the fact
that affective disorders are associated with deficiencies in performing this
kind of task (Adlerman et al., 2011; Dickstein et al., 2010).
2 A Bayesian View on Life: Survival of the Fittest Model
Every living thing from bachelors to bacteria seeks glucose proactively—
and does so long before internal stocks run out. As adaptive creatures, we
seek outcomes that tend to promote our long-term functional and structural
integrity (i.e., the well-bounded set of states that characterize our pheno-
types). That adaptive and anticipatory nature of biological life is the focus
of the formal Bayesian framework called active inference. This framework
revolves around the notion that all living systems embody statistical mod-
els of their worlds (Friston, 2010; Gallagher & Allen, 2018). In this way,
beliefs about the consequences of different possible actions can be evalu-
ated against preferred (typically phenotype-congruent) consequences to in-
form action selection. In active inference, every organism enacts an implicit
phenotype-congruent model of its embodied existence (Ramstead, Kirch-
hoff, Constant, & Friston, 2019; Hesp et al., 2019), which has been referred
to as self-evidencing (Hohwy, 2016). Active inference has been used to de-
velop neural process theories and explain the acquisition of epistemic habits
(Friston, FitzGerald et al. 2016; Friston, FitzGerald, Rigoli, Schwartenbeck,
& Pezzulo, 2017). This framework provides a formal account of the balance
between seeking informative outcomes (that optimize future expectations)
versus preferred outcomes (based on current expectations; Schwartenbeck,
FitzGerald, Mathys, Dolan, & Friston, 2015).
Active inference formalizes our survival and procreation in terms of a
single imperative: to minimize the divergence between observed outcomes
and phenotypically expected (i.e., preferred) outcomes under a (generative)
model that is fine-tuned over phylogeny and ontogeny (Badcock, 2012; Bad-
cock, Davey, Whittle, Allen, & Friston, 2017; Badcock, Friston, & Ramstead,
2019). This discrepancy can be quantified using an information-theoretic
quantity called variational free energy (denoted F; see appendix A1; Friston,
2010). To minimize free energy is mathematically equivalent to maximizing
(a lower bound on) Bayesian model evidence, which quantifies model fit
or subjective fitness; this contrasts with biological fitness, which is defined
as actual reproductive success (Constant, Ramstead, Veissière, Campbell,
& Friston, 2018). Subjective fitness more specifically pertains to the per-
ceived (i.e., internally estimated) efficacy of an organism’s action model
in realizing phenotype-congruent (i.e., preferred) outcomes. Through nat-
ural selection, organisms that can realize phenotype-congruent outcomes
more efficiently than their conspecifics will (on average) tend to experience
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Deeply Felt Affect
403
a fitness benefit. This type of natural (model) selection will favor a strong
correspondence between subjective fitness and biological fitness by select-
ing for phenotype-congruent preferences and the means of achieving them.
This Bayesian perspective casts groups of organisms and entire species
as families of viable models that vary in their fit to a particular niche.
On this higher level of description, evolution can be cast as a process of
Bayesian model selection (Campbell, 2016; Constant et al., 2018; Hesp et al.,
2019), in which biological fitness now becomes the evidence (also known
as marginal likelihood) that drives model (i.e., natural) selection across
generations. In the balance of this letter, we exploit the correspondence be-
tween subjective fitness and model evidence to characterize affective va-
lence. Section 3 begins by reviewing the formalism that underlies active
inference. In brief, active inference offers a generic approach to planning
as inference (Attias, 2003; Botvinick & Toussaint, 2012; Kaplan & Friston,
2018) under the free energy principle (Friston, 2010). It provides an account
of belief updating and behavior as the inversion of a generative model. In
this section we emphasize the hierarchical and nested nature of generative
models and describe the successive steps of increasing model complexity
that enable an agent to navigate increasingly complicated environments.
Of the lowest complexity is a simple, single-time-point model of percep-
tion. Somewhat more complex perceptual models can include anticipation
of future observations. Complexity increases when a model incorporates ac-
tion selection and must therefore anticipate the observed consequences of
different possible plans or policies. As we explain, one key aspect of adap-
tive planning is the need to afford the right level of precision or confidence
in one’s own action model. This constitutes an even higher level of model
complexity, which can be regarded as an implicit (i.e., subpersonal) form of
metacognition—a (typically) unconscious process estimating the reliability
of one’s own model. This section concludes by describing the setup we use
to illustrate affective inference and the key role of an update term within
our model that we refer to as “affective charge.”
In section 3, we also introduce the highest level of model complexity we
consider, which affords a model the ability to perform affective inference. In
brief, we add a representation of confidence, in terms of “good” and “bad”
(i.e., valenced) states that endow our affective agent with explicit (i.e., po-
tentially self-reportable) beliefs about valence and enable her to optimize
her confidence in expected (epistemic and pragmatic) consequences.
Having defined a deep generative model (with two hierarchical levels
of state representation) that is apt for representing and leveraging valence
representations, section 4 uses numerical analyses (i.e., simulations) to illus-
trate the associated belief updating and behavior. We conclude in section
5 with a discussion of the implications of this work, such as the relation-
ship between implicit metacognition and affect, connections to reinforce-
ment learning, and future empirical directions.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
404
Hesp et al.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
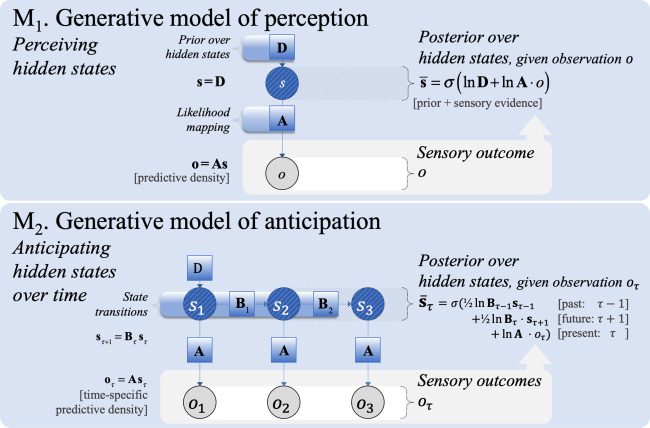
Figure 1: The first (M1, top panel) and second steps (M2, bottom panel) of a
generative model of increasing complexity. M1: A minimal generative model
of perception can infer hidden states s from an observation o, based on prior
beliefs (D) and a likelihood mapping (A). M2: A generative model of anticipation
extends perception (as in M1) forward into the future (and backward into the
past) using a transition matrix (Bτ ) for hidden states.
3 Methods
3.1 An Incremental Primer on Active Inference. At the core of active
inference lie generative models that operate with—and only with—local
information (i.e., without external supervision, which maintains biologi-
cal plausibility). We focus on partially observable Markov decision pro-
cesses (MDPs), a common generative model for Bayesian inference over
discretized states, where beliefs take the form of categorical probability dis-
tributions. MDPs can be used to update beliefs about hidden states of the
world “out there” (denoted s), based on sensory inputs (referred to as out-
comes or observations, denoted o). Given the importance of the temporally
deep and hierarchical structure afforded by MDPs in our formulation, we
introduce several steps of increasing model complexity on which our for-
mulation will build, following the sequence in Figure 1.
3.1.1 Step 1: Perception. At the lowest complexity, we consider a gen-
erative model of perception (see Table 1) at a single point in time: M1 in
Deeply Felt Affect
405
Table 1: A Generative Model of Perception.
Prior Beliefs (Generative Model) (P) Approximate Posterior Beliefs (Q)
Q(s) = Cat(¯s)
(cid:2) (cid:3)(cid:4) (cid:5)
state posterior
¯s = σ ( ln D(cid:2)(cid:3)(cid:4)(cid:5)
prior
beliefs
+ ln A · o
)
(cid:2) (cid:3)(cid:4) (cid:5)
sensory
evidence
P(s) = Cat(D)
(cid:2) (cid:3)(cid:4) (cid:5)
state prior
P(o|s) = Cat(A)
(cid:2) (cid:3)(cid:4) (cid:5)
likelihood
= D
= As
s(cid:2)(cid:3)(cid:4)(cid:5)
state
expectations
o(cid:2)(cid:3)(cid:4)(cid:5)
outcome
expectations
Notes: The generative model is defined in terms of prior beliefs about hid-
den states P(s) = Cat(D) (where D is a vector encoding the prior probabil-
ity of each state) and a likelihood mapping P(o|s) = Cat(A) (where A is a
matrix encoding the probability of each outcome given a particular state).
Cat(X) denotes a categorical probability distribution (see also the supple-
mentary information A3). Through variational inference, the beliefs about
hidden states s are updated given an observed sensory outcome o, thus ar-
riving at an approximate posterior Q(s) = Cat(¯s) (see also supplementary
information in appendix A1), where ¯s = σ (ln D + ln A · o). Here, the dot
notation indicates backward matrix multiplication (in the case of a normal-
ized set of probabilities and a likelihood mapping): for a given outcome,
A · o returns the (renormalized) probability or likelihood of each hidden
state s (see also the supplementary information in appendix A2).
Figure 1 (top panel). It entails prior beliefs about hidden states (prior ex-
pectation D), as well as beliefs about how hidden states generate sensory
outcomes (via a likelihood mapping A). Perception here corresponds to a pro-
cess of inferring which hidden states (posterior expectations ¯s) provide the
best explanation for observed outcomes (see also appendix A2). However,
this model of perception is too simple for modeling most agents, because
it fails to account for the transitions between hidden states over time that
lend the world—and subsequent inference—dynamics or narratives. This
takes us to the next level of model complexity.
3.1.2 Step 2: Anticipation. The next increase in complexity involves a gen-
erative model that specifies how hidden states evolve from one point in
time to the next (according to state transition probabilities Bτ ). As shown in
Table 2 (M2 in Figure 1, top panel), updating posterior beliefs about hidden
states (¯sτ ) now involves the integration of beliefs about past states (¯sτ −1),
sensory evidence (oτ ), and beliefs about future states (¯sτ +1). From here, the
natural third step is to consider how dynamics depend on the choices of the
creature in question.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
406
Hesp et al.
Table 2: A Generative Model of Anticipation (M2 in Figure 1, Bottom Panel).
Generative Model (P)
Approximate Posterior Beliefs (Q)
P(s1 ) = Cat(D)
(cid:2) (cid:3)(cid:4) (cid:5)
Q(sτ ) = Cat(¯sτ )
(cid:2) (cid:3)(cid:4) (cid:5)
initial state prior
state posterior
¯s1
¯s2
¯s3
P(sτ |sτ +1 ) = Cat(Bτ )
(cid:2) (cid:3)(cid:4) (cid:5)
state transitions
s1
= D
= Bτ sτ
sτ +1
(cid:2)(cid:3)(cid:4)(cid:5)
state expectations
oτ(cid:2)(cid:3)(cid:4)(cid:5)
= Asτ
outcome expectations
= σ (1/
= σ (1/
= σ (ln B2 ¯s2
(cid:2) (cid:3)(cid:4) (cid:5)
2 ln B1 ¯s1
2 ln D + ln A · o1
+ ln A · o2
+ ln A · o3
(cid:2) (cid:3)(cid:4) (cid:5)
sensory
evidence
forward
messages
+ 1/
2 ln B1
+ 1/
2 ln B2
· ¯s2 )
· ¯s3 )
)
(cid:2)
(cid:3)(cid:4)
(cid:5)
backward
messages
Notes: The generative model is defined in terms of prior beliefs about initial
|sτ ) = Cat(Bτ ),
hidden states P(s1 ) = Cat(D), hidden state transitions P(sτ +1
and a likelihood mapping P(o|s) = Cat(A). Note the factor of 1/
2 in posterior
state beliefs ¯sτ results from the marginal message-passing approximation in-
troduced by Parr et al. (2019).
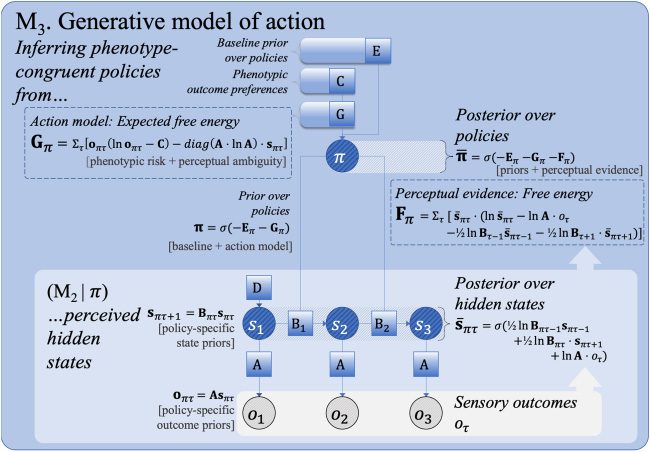
3.1.3 Step 3: Action. The temporally extended generative model already
discussed can be extended to model planning (M3 in Figure 2; see Table 3)
by conditioning transition probabilities (Bτ ) on action. Policy selection (i.e.,
planning) can now be cast as a form of Bayesian model selection, in which
each policy (a sequence of Bπ τ -matrices, subscripted by π for policy) rep-
resents a possible version of the future. A priori, the agent’s beliefs about
policies (π) depend on a baseline prior expectation about the most likely
policies (which can often be thought of as habits, denoted Eπ ) and an esti-
mate of the negative log evidence it expects to obtain for each policy—the
expected free energy (denoted Gπ ). The latter is biased toward phenotype-
congruence in the sense that any given behavioral phenotype is associated
with a range of species—typical (i.e., preferred) sensory outcomes. For ex-
ample, within their respective ecological niches, different creatures will be
more or less likely to sense different temperatures through their thermore-
ceptors (i.e., those consistent with their survival). These phenotypic priors
(“prior preferences”) are cast in terms of a probability over observed future
outcomes. Together, the baseline and action model priors (Eπ + Gπ ) are sup-
plemented by the evidence that each new observation provides for a partic-
ular policy—leading to a posterior distribution over policies with the form
− ln ¯π = Eπ + Gπ + Fπ , which is equivalent to ¯π = σ (−Eπ − Gπ − Fπ ).
Expected free energy can be decomposed into two terms, referred to
as the risk and ambiguity for each policy. The risk of a policy is the ex-
pected divergence between anticipated and preferred outcomes (denoted
by C), where the latter is a prior that encodes phenotype-congruent out-
comes (e.g., reward or reinforcement in behavioral paradigms). Risk can
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Deeply Felt Affect
407
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
Figure 2: The third step (M3) of an incremental summary of active inference. In a
generative model of action, state transitions are conditioned on policies π . Prior
policy beliefs π are informed by the baseline prior over policies (“model free,”
denoted Eπ ) and the expected free energy (Gπ ), which evaluates each policy-
specific perception model (as in M2) in terms of the expected risk and ambiguity.
Risk biases the action model toward phenotype-congruent preferences (C). Pos-
terior policy beliefs are informed by the fit between anticipated (policy-specific)
and preferred outcomes, while at the same time minimizing their ambiguity.
therefore be thought of as similar to a reward probability estimate for each
policy. The ambiguity of a policy corresponds to the perceptual uncer-
tainty associated with different states (e.g., searching under a streetlight
versus searching in the dark). Policies with lower ambiguity (i.e., those ex-
pected to provide the most informative observations) will have a higher
probability, providing the agent with an information-seeking drive. The
resulting generative model provides a principled account of the subjec-
tive relevance of behavioral policies and their expected outcomes, in which
an agent trades off between seeking reward and seeking new information
(Friston, FitzGerald, Rigoli, Schwartenbeck, & Pezzulo, 2017. Furthermore,
it generalizes many established formulations of optimal behavior (Itti &
Baldi, 2009; Schmidhuber, 2010; Mirza, Adams, Mathys, & Friston, 2016;
Veale, Hafed, & Yoshida, 2017) and provides a formal description of the
motivated and self-preserving behavior of living systems (Friston, Levin,
Sengupta, & Pezzulo, 2015).
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
408
Hesp et al.
Table 3: A Generative Model of Action (M3 in Figure 2).
Prior Beliefs (Generative Model) (P)
Posterior Beliefs (Q) and Expectations
P(π ) = Cat(π)
(cid:2) (cid:3)(cid:4) (cid:5)
policy prior
π
policy
expectations
Gπ
expected
free energy
= σ ( −Eπ
− Gπ
)
baseline prior
action model
(cid:6)
=
τ oπ τ · (ln oπ τ − C)
(cid:5)
(cid:3)(cid:4)
(cid:2)
expected phenotypic risk
− diag(A · ln A) · sπ τ
(cid:5)
(cid:3)(cid:4)
(cid:2)
expected perceptual ambiguity
= ln P(oτ )
C(cid:2)(cid:3)(cid:4)(cid:5)
phenotypic
preferences
P(sτ +1
|sτ , π ) = Cat(Bπ τ )
(cid:5)
(cid:2)
(cid:3)(cid:4)
Q(π ) = Cat( ¯π)
(cid:2) (cid:3)(cid:4) (cid:5)
policy posterior
¯π = σ (ln Eπ − Gπ −
Fπ(cid:2)(cid:3)(cid:4)(cid:5)
)
perceptual evidence
(cid:2)
Fπ =
τ ¯sπ τ · (ln ¯sπ τ − ln A · oτ
−1/
(cid:2)
2 ln Bπ τ −1 ¯sπ τ −1
− 1/
2 ln Bπ τ · ¯sπ τ +1
)
(cid:5)
(cid:3)(cid:4)
policy-specific prediction error
Q(sτ |π ) = Cat(¯sπ τ )
(cid:5)
(cid:3)(cid:4)
(cid:2)
policy-specific
state transitions
policy-specific
state posterior
s1
sπ τ +1
oπ τ(cid:2)(cid:3)(cid:4)(cid:5)
= D
= Bπ τ sπ τ
= Asπ τ
policy-specific
expectations
¯sπ τ = σ (1/
+ 1/
2 ln Bπ τ −1 ¯sπ τ −1
2 ln Bπ τ · ¯sπ τ +1 )
+ ln A · oτ
Note: Posterior policies ¯π inferred from (policy-specific) posterior beliefs about hidden
states sπ τ , based on (policy-specific) state transitions Bπ τ , the baseline policy prior Eπ ,
the expected free energy Gπ (action model), and prior preferences over outcomes C.
3.1.4 Step 4: Implicit Metacognition. The three steps of increasing com-
plexity are jointly sufficient for the vast majority of (current) active infer-
ence applications. However, a fourth level is required to enable an agent
to estimate its own success, which could be thought of as a minimal form
of (implicit, non-reportable) metacognition (M4 in Figure 3; see Table 4).
Estimation of an agent’s own success specifically depends on an expected
precision term (denoted γ) that reflects prior confidence in the expected free
energy over policies (Gπ ). This expected precision term modulates the influ-
ence of expected free energy on policy selection, relative to the fixed-form
policy prior (Eπ ): higher γ values afford a greater influence of the expected
free energies of each policy entailed by one’s current action model. Formu-
lated in this way, we can think of γ as an internal estimate of model fitness
(subjective fitness), because it represents an estimate of confidence (M4) in
a phenotype-congruent model of actions (M3), given inferred hidden states
of the environment (M2).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Deeply Felt Affect
409
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3: The fourth step (M4) of our incremental description of active infer-
ence in terms of the nested processes of perception (M1−2 in Figure 1), action
(M3 in Figure 2), and implicit metacognition (M4 in this figure), emphasizing
the inherently hierarchical, recurrent nature of these generative models. This
generative model infers confidence in its own action model in terms of the ex-
pected precision (γ), which modulates reliance on Gπ for policy selection (as in
M3), based on perceptual inferences (as in M2). Expected precision (γ) changes
when inferred policies differ from expected policies. This term increases when
posterior (policy-averaged) expected free energy is lower than when averaged
under the policy prior (AC = (π − ¯π) · Gπ < 0), and decreases when it is higher
AC > 0).
In turn, estimates for this precision term (γ) are informed by a (gamma)
prior that is usually parameterized by a rate parameter β, with which it has
an inverse relation. When expected model evidence is greater under poste-
rior beliefs compared to prior beliefs (i.e., when (π − ¯π) · Gπ > 0), γ values
increase. That is, confidence in the success of one’s model rises. In the oppo-
site case (when (π − ¯π) · Gπ < 0), γ values decrease. That is, confidence in
the success of one’s model falls. Note that while related, γ values are not re-
dundant with the precision of the distribution over policies (π). High values
of the latter (which correspond to high confidence in the best policy or ac-
tion) need not always correspond to high confidence in the success of one’s
model (high γ). To emphasize its relation to valence in our formulation, go-
ing forward we refer to γ updates using the term affective charge (AC):
AC = −(cid:6) ¯β = (π − ¯π) · Gπ .
(3.1)
410
Hesp et al.
Table 4: A Generative Model of Minimal (Implicit) Metacognition—(M4 in Fig-
ure 3): Inferring Expected Precision γ from Posterior Policies π, Based on a
Gamma Distribution with Temperature β.
Prior Beliefs (Generative Model) (P)
Posterior Beliefs (Q) and Expectations
P(γ ) = (cid:8)(1,
β
(cid:2)(cid:3)(cid:4)(cid:5)
)
temperature
parameter
≡ EP(γ )[γ ] = 1/β
γ
(cid:2)(cid:3)(cid:4)(cid:5)
expected
precision
Q(γ ) = (cid:8)(1, ¯β)
¯γ
(cid:2)(cid:3)(cid:4)(cid:5)
≡ EQ(γ )[γ ] = 1/ ¯β
posterior
precision
¯β = β − AC
AC(cid:2)(cid:3)(cid:4)(cid:5)
affective
charge
= (π − ¯π) · Gπ
(cid:5)
(cid:3)(cid:4)
(cid:2)
phenotypic progress
π = σ (−Eπ −
γGπ
(cid:2) (cid:3)(cid:4) (cid:5)
)
¯π = σ (−Eπ − γGπ − Fπ )
precision-weighted
action model
Note: Bayes-optimal updates of β differ only in sign from the term we label
affective charge (AC = −(cid:6) ¯β; see also M4 in Figure 3).
This shows that the timescale over which beliefs about policies are updated
sets of the relevant timescale for AC, such that valence is linked inextrica-
bly to action. AC can only be nonzero when inferred policies differ from
expected policies π (cid:3)= ¯π. It is positive when perceptual evidence favors
an agent’s action model and negative otherwise. In other words, positive
and negative AC corresponds, respectively, to increased and decreased
confidence in one’s action model. Accordingly, because Gπ is a function of
achieving preferred outcomes, AC can be construed as a reward prediction
error, where reward is inversely proportional to Gπ (Friston et al., 2014). For
example, a predator may be confidently pleased with itself after spotting a
prey (positive AC) and frustrated when it escapes (negative AC). However,
having precise beliefs about policies should not be confused with having
confidence in one’s action model. For instance, consider prey animals that
are nibbling happily on food and suddenly find themselves being pursued
by a voracious predator. While fleeing was initially an unlikely policy, this
dramatically changes upon encountering the predator. Now these animals
have a very precise belief that they should flee, but this dramatic change in
their expected course of action suggests that their action model has become
unreliable. Thus, while they have precise beliefs about action, AC would
be highly negative (i.e., a case of negative valence but confident action
selection).
This completes our formal description of active inference under Markov
decision process models. This description emphasizes the recursive and hi-
erarchical composition of such models that equip a simple likelihood map-
ping between unobservable (hidden) states and observable outcomes with
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Deeply Felt Affect
411
dynamics. These dynamics (i.e., state transitions) are then cast in terms of
policies, where the policies themselves have to be inferred. Finally, the ensu-
ing planning as inference is augmented with metacognitive beliefs in order
to optimize the reliance on expected free energy (i.e., based on one’s current
model) during policy selection. This model calls for Bayesian belief updat-
ing that can be framed in terms of affective charge (AC).
AC is formally related to reward prediction error within reinforcement
learning models (Friston et al., 2014; Schultz, Dayan, & Montague, 1997;
Stauffer, Lak, & Schultz, 2014). Accordingly, it may be reported or encoded
by neuromodulators like dopamine in the brain (Friston, Rigoli et al., 2015;
Schwartenbeck et al., 2015), a view that has been empirically supported us-
ing functional magnetic resonance imaging of decision making under un-
certainty (Schwartenbeck et al., 2015). The formal relationship between AC
(across each time step) and the neuronal dynamics that may optimize it
within each time step can be obtained (in the usual way) through a gradi-
ent descent on free energy (as derived in Friston, FitzGerald et al., 2017).
Through substitution of AC, we find that posterior beliefs about expected
precision ( ¯γ = 1/ ¯β) satisfy the following equality:
˙¯β(t) = β − AC − ¯β(t),
(3.2)
where t denotes the passage of time within a trial time step and thus sets
the timescale of convergence (here the bar notation indicates posterior be-
liefs; dot notation indicates rate of change). The corresponding analytical
solution shows that the magnitude of fluctuations in expected precision is
proportional to AC:
¯β(t) = β − AC(1 − e
˙¯β(t) = −ACe
−t.
−t )
(3.3)
We discuss the potential neural basis of AC further below. In the next sec-
tion, we describe the simulation setup that we will use to quantitatively
illustrate the proposed role of AC in affective behavior.
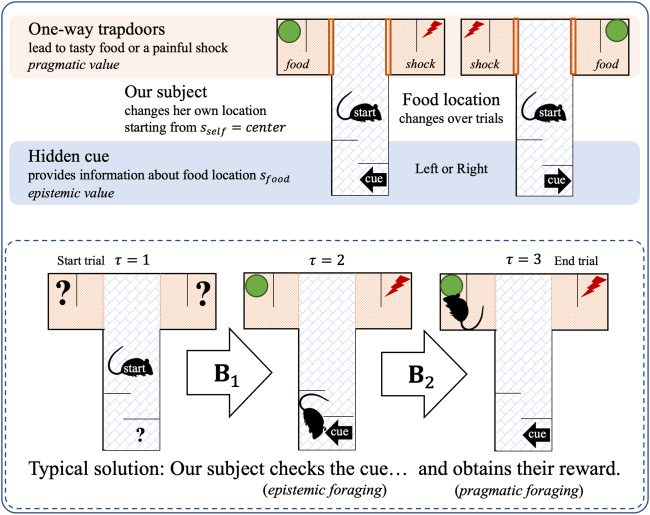
3.1.5 The T-Maze Paradigm. The generative model we have described has
been formulated in a generic way (reflecting the domain-generality of our
formulation). The particular implementation of active (affective) inference
we use in this letter is based on a T-maze paradigm (see Figure 4), for which
an active-inference MDP has been validated previously (Pezzulo, Rigoli, &
Friston, 2015). Here we describe this implementation and subsequently use
it to show simulations demonstrating affective inference in a synthetic ani-
mal. Simulated behavior in this paradigm is consistent with that observed
in real rats within such contexts.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
412
Hesp et al.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4: The setup of the T-maze task (top panel) and its typical solution (bot-
tom panel). The synthetic agent (here, a rat) starts in the middle of the T-maze.
If it moves up, it will encounter two one-way doors, left and right, which lead to
either a rewarding food source or a painful shock (high versus low pragmatic
value, respectively). If it moves downward, it will encounter an informative
cue (high epistemic value) that indicates whether the food is in the left or right
arm.
For the sake of simplicity, the agent is equipped with (previously gath-
ered) prior knowledge about the workings of the T-maze in her generative
model. Starting near the central intersection, the agent can either stay put
or move in three different directions: left, right, or down in the T-maze. She
knows that a tasty reward is located in either the left or right arm of the
T-maze, and a painful shock is in the opposite arm. She is also aware that
the left and right arms are one-way streets (i.e., absorbing states): once en-
tered, she must remain there until the end of the trial. She knows that an
informative cue at the downward location provides reliable contextual in-
formation about whether the reward is located in the left or right arm in the
current trial. The key probability distributions for the generative model are
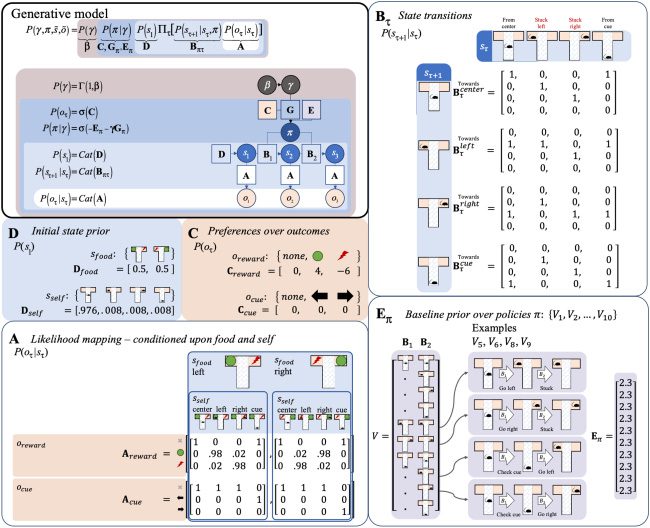
provided in Figure 5.
Although this generative model is relatively simple, it has most of
the ingredients needed to illustrate fairly sophisticated behavior. Because
Deeply Felt Affect
413
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5: A generative model for the T-maze setup of Figure 4, with the pri-
ors (top-left panel) as in Figure 3, now specified as vectors or matrices. Here,
the probabilities reflect a set of simple assumptions embedded in the agent’s
generative model, each of which could itself be optimized by fitting to empiri-
cal data. Middle-left panel: Prior expectations D for initial states are defined as
uniform, given the rat has been trained in a series of random left and right trials.
Middle panel: The vector C encoding preferences is defined such that reward
outcomes are strongly preferred (green circles): odds e4:1 compared to “none”
outcomes labeled “none” (gray crosses), and punishments are extremely non-
preferred (red): odds e−6:1 compared to outcomes labeled “none.” Bottom-left
panel: The matrix A for the likelihood mapping reflects two assumptions about
the agent’s beliefs given each particular context (which could be trained through
prior trials). First, the location-reward mappings always have some minimal
amount of uncertainty (.02 probability). Second, the cue is a completely reliable
context indicator. Top-right panel: The matrix B for the state transitions reflects
the fact that changing location is either very easy (100% efficacious) or impos-
sible when stuck in one of the one-way arms. Bottom-right panel: The vector V
for the policies reflects possible combinations of actions over the two time steps
and associated baseline prior over policies E, which starts at an initial, uniformly
distributed level of evidence for each policy, which can be seen as reflecting an
initial period of free exploration of the maze structure (here the value of 2.3 reg-
ulates the impact of subsequently observed policies, where the value for each
policy increments by 1 each time it is subsequently chosen).
414
Hesp et al.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
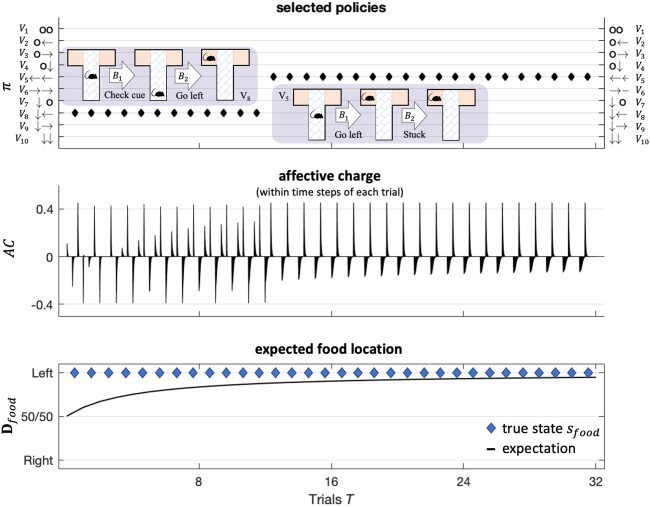
Figure 6: Simulated responses over 32 trials with food located on the left side of
the T-maze. This figure reports the behavioral and (simulated) affective charge
responses during successive trials. The top panel shows, for each trial, the se-
lected policy (in image format) over the policies considered (arrows indicate
moving to each respective arm; circles indicate staying in, or returning to, the
center position). The policy selected in the first 12 trials corresponds to an ex-
ploratory policy, which involves examining the cue in the lower arm and then
going to the left or right arm to secure the reward (i.e., depending on the cue,
which here always indicates that reward is on the left). After the agent be-
comes sufficiently confident that the context does not change (after trial 12),
she indulges in pragmatic behavior, moving immediately to the reward without
checking the cue. The middle panel shows the associated fluctuations in affec-
tive charge. The bottom panel shows the accumulated posterior beliefs about
the initial state.
actions can lead to epistemic or informative outcomes, which change be-
liefs, it naturally accommodates situations or paradigms that involve both
exploration and exploitation under uncertainty. Our primary focus here is
on the expected precision term and its updates (i.e., AC), that we have al-
ready described.
Figure 6 illustrates typical behavior under this particular generative
model. These results were modeled after Friston, FitzGerald et al. (2017)
Deeply Felt Affect
415
and show a characteristic transition from exploratory behavior to exploita-
tive behavior as the rat becomes more confident about the context in which
she is operating—here, learning that the reward is always on the left. This
increase in confidence is mediated by changes in prior beliefs about the con-
text state (the location of the reward) that are accumulated by repeated ex-
posure to the paradigm over 32 trials (this accumulation is here modeled
using a Dirichlet parameterization of posterior beliefs about initial states).
These changes mean that the rat becomes increasingly confident about what
she will do, with concomitant increases or updates to the expected precision
term. These increases are reflected by fluctuations in affective charge (mid-
dle panel). We will use this kind of paradigm later to see what happens
when the reward contingencies reverse.
3.2 Affective Valence as an Estimate of Model Fitness in Deep Tem-
poral Models. Within various modeling paradigms, a few researchers have
recognized and aimed to formalize the relation between subjective fitness
and valence. For example, Phaf and Rotteveel (2012) used a connection-
ist approach to argue that valence corresponds broadly to match-mismatch
processes in neural networks, thus monitoring the fit between a neural ar-
chitecture and its input. As another example, Joffily and Coricelli (2013) pro-
posed an interpretation of emotional valence in terms of rates of change in
variational free energy. However, this proposal did not include formal con-
nection to action.
The notion of affective charge that we describe might be seen as build-
ing on such previous work by linking changes in free energy (and the cor-
responding match-mismatch between a model and sensory input) to an
explicit model of action selection. In this case, an agent can gauge sub-
jective fitness by evaluating its phenotype-congruent action model (Gπ )
against perceptual evidence deduced from actual outcomes (Fπ ). Such a
comparison, and a metric for its computation, is exactly what is provided
by affective charge, which specifies changes in the expected precision of
(i.e., confidence in) one’s action model (see M4 in Figure 3). Along these
lines, various researchers have developed conceptual models of valence
based on the expected precision of beliefs about behavior (Seth & Friston,
2016; Badcock et al., 2017; Clark et al., 2018). Crucially, negatively valenced
states lead to behavior suggesting a reduced reliance on prior expectations
(Bodenhausen, Sheppard, & Kramer, 1994; Gasper & Clore, 2002), while
positively valenced states appear to increase reliance on prior expectations
(Bodenhausen, Kramer, & Süsser, 1994; Park & Banaji, 2000)—both consis-
tent with the idea that valence relates to confidence in one’s internal model
of the world.
One might correspondingly ask whether an agent should rely to a greater
or lesser extent on the expected free energy of policies when deciding how
to act. In effect, the highest level of the generative model shown in Figure 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
416
Hesp et al.
(M4, also outlined in Table 4) provides an uninformative prior over expected
precision that may or may not be apt in a given world. If the environment
is sufficiently predictable to support a highly reliable model of the world,
then high confidence should be afforded to expected free energy in forming
(posterior) plans. In economic terms, this would correspond to increasing
risk sensitivity, where risk-minimizing policies are selected. Conversely, in
an unpredictable environment, it may be impossible to predict risk, and
expected precision should, a priori, be attenuated, thereby paying more at-
tention to sensory evidence.
This suggests that in a capricious environment, behavior would benefit
from prior beliefs about expected precision that reflect the prevailing envi-
ronmental volatility—in other words, beliefs that reflect how well a model
of that environment can account for patterns in its own action-dependent
observations. In what follows, we equip the generative model with an ad-
ditional (hierarchically and temporally deeper) level of state representation
that allows an agent to represent and accumulate evidence for such beliefs,
and we show how this leads naturally to a computational account of va-
lence from first principles.
Deep temporal models of this kind (with two levels of state representation)
have been used in previous research on active inference (Friston, Rosch,
Parr, Price, & Bowman, 2017). In these models, posterior state representa-
tions at the lower level are treated as observations at the higher level. State
representations at the higher level in turn provide prior expectations over
subsequent states at the lower level (see section 3.3). This means that higher-
level state representations evolve more slowly, as they must accumulate
evidence from sequences of state inferences at the lower level. Previous re-
search has shown, for example, how this type of deep hierarchical structure
can allow an agent to hold information in working memory (Parr & Friston,
2017) and to infer the meaning of sentences based on recognizing a sequence
of words (Friston, Rosch et al., 2017).
Here we extend this previous work by allowing an agent to infer higher-
level states not just from lower-level states, but also from changes in lower-
level expected precision (AC). This entails a novel form of parametric depth,
in which higher-level states are now informed by lower-level model pa-
rameter estimates. As we will show, this then allows for explicit higher-
level state representations of valence (i.e., more slowly evolving estimates
of model fitness), based on the integration of patterns in affective charge
over time. In anthropomorphic terms, the agent is now equipped to explic-
itly represent whether her model is doing “good” or “bad” at a timescale
that spans many decisions and observed outcomes. Hence, something with
similar properties as valence (i.e., with intrinsically good/bad qualities)
emerges naturally out of a deep temporal model that tracks its own success
to inform future action. Note that “good” and “bad” are inherently domain-
general here, and yet—as we will now show—they can provide empirical
priors on specific courses of action.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Deeply Felt Affect
417
3.3 Affective Inference. This letter characterizes the valence compo-
nent of affective processing with respect to inference about domain-general
valence states—those inferred from patterns in expected precision updates
over time. In particular, we focus on how valence emerges from an internal
monitoring of subjective fitness by an agent. To do so, we specify how affec-
tive states participate in the generative model and what kind of outcomes
they generate. Since deep models involve the use of empirical priors—from
higher levels of state representation—to predict representations at subordi-
nate levels (Friston, Parr, & Zeidman 2018), we can apply such top-down
predictions to supply an empirical prior for expected precision (γ ). For-
mally, we associate alternative discrete outcomes from a higher-level model
with different values of the rate parameter (β) for the gamma prior on ex-
pected precision.
Note that we are not associating the affective charge term to emotional
valence directly. The affective charge term tracks fluctuations in subjective
fitness. To model emotional valence, we introduce a new layer of state infer-
ence that takes fluctuations in the value of γ (i.e., AC-driven updates) over
a slower timescale as evidence favoring one valence state versus another.
By implementing this hierarchical step in an MDP scheme, we effec-
tively formulate affective inference as a parametrically deep form of active
inference. Parametric depth means that higher-order affective processes
generate priors that parameterize lower-order (context-specific) inferences,
which in turn provide evidence for those higher-order affective states.
3.3.1 Simulating the Affective Ups and Downs of a Synthetic Rat. As a con-
crete example, we implement a minimal model of valence in which a syn-
thetic rat infers whether her own affective state is positive or negative
within the T-maze paradigm. Our hierarchical model of the T-maze task
comprises a lower-level MDP for context-specific active inference (M4 in
Figure 3) and a higher-level MDP for affective inference (see Figure 7). Note,
however, that this is simply an example; the lowerlevel model in princi-
ple could generalize to any other type of task that is relevant to the agent
in question. The hidden states at the higher level provide empirical priors
over any variable at the lower level that does not change over the timescale
associated with that level. These variables include the initial state, priors
over expected precision, fixed priors over policies, and so on (see the MDP
model descriptions in section 3.1). Here, we consider higher-level priors on
the initial state and the rate parameter of the priors over expected precision.
By construction, state transitions at the higher (affective) level are over tri-
als endowing the model with a deep temporal structure. This enables it to
keep track of slow changes over multiple trials, such as the location of the
reward. In other words, belief updating at the second level from trial to trial
enables the agent to accumulate evidence and remember contingencies that
are conserved over trials.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
418
Hesp et al.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7: A generative model for affective inference in terms of its key equa-
tions and probabilistic graphical model (top left panel) and the associated ma-
trices, again reflecting a number of relatively minimal assumptions about the
agent’s beliefs concerning the experimental setup—where each of these param-
eters could itself be optimized by fitting to empirical data. Bottom left: Prior
expectations D(2) for initial states at the second level are distributed uniformly.
(Bottom middle) The likelihood matrix A(A) reflects some degree of uncertainty
in the affective predictions (.03), which, when multiplied by β(+,−), sets the
lower-level prior on expected precision, allowing it to vary between 0.5 and 2.0.
Bottom right: The matrix A(C) for the likelihood mapping from context states to
the lower level reflects that the agent is always certain which context she ob-
served after each trial is over. Top right: The matrix B(2) for the state transitions
at the second level reflects two assumptions for cross-trial changes: (1) Both af-
fective and contextual states vary strongly but have some stability across trials
(.2–.3 probability of changing) and (2) the agent has a positivity bias in the sense
that she is more likely to switch from a negative to a positive state than vice versa
(.3 versus .2 probability). The lower-level model is the same as in Figure 5.
In our example, we use two distinct sets of hidden states (i.e., hidden
state factors) at the second level, each with two states. The first state factor
corresponded to the location of the reward (food on the left or right, de-
noted L and R), and the second state factor corresponded to valence (posi-
tive or negative, denoted + and −). We will refer to these as Contexts (sC) and
Affective states (sA), respectively—that is, s(2)
T ). This means the
T
rat could contextualize her behavior in terms of a prior over second-level
= (s(C)
T
, s(A)
Deeply Felt Affect
419
states (D(2)) and their state transitions from trial to trial (B(2)), in terms of
both where she believes the reward is most likely to be (Context) and how
confident she should be in her action model (Valence).
In short, our synthetic subject was armed with high-level beliefs about
context and affective states that fluctuate slowly over trials. In what follows,
we consider the belief updating in terms of messages that descend from the
affective level to the lower level and ascend from the lower level to the af-
fective level. Descending messages provide empirical priors that optimize
policy selection. This optimization can be regarded as a form of covert ac-
tion or attention that allows the impact of one’s generative model on action
selection to vary in a state-dependent manner. Ascending messages can be
interpreted as mediating belief updates about the current context and affec-
tive state: affective inference reflecting belief updates about model fitness.
3.3.2 Descending Messages: Contextual and Affective Priors. On each trial,
discrete prior beliefs about the reward being on the left (L, R) are encoded
in empirical priors or posterior beliefs at the second level, which inherit
from the previous posterior and enable belief updating from trial to trial.
Similarly, beliefs over discrete valence beliefs (+, −) are equipped with an
initial prior at the affective level and are updated from trial to trial based
on a second-level probability transition matrix. From the perspective of the
generative model, the initial context states at the lower level are conditioned
on the context states at the higher level, while the rate parameter β, (which
constitutes prior beliefs about expected precision) is conditioned on affec-
tive states.
Because affective states are discrete and the rate parameter is continu-
ous, message passing between these random variables calls for the mixed
or hybrid scheme (described in Friston, Parr, & de Vries, 2018). In these
simulations, the affective states (i.e., valence) were associated with two
values of the rate parameter β(+,−) = (0.5, 2.0), where the corresponding
precisions provide evidence for positive valence (γ+ = 2.0) and negative
valence (γ− = 0.5). Effectively, γ+ and γ− are upper and lower bounds on
the expected precision under the two levels of the affective state. The de-
scending messages correspond to Bayesian model averages, a mixture of
the priors under each level of the context and affective states:
(cid:8)
(cid:8)
(cid:7)
s(1)
1
P
s(C)
T
(cid:9)
(cid:7)
= Cat
(cid:9)
A(C)
(cid:10)
(cid:7)
γ
(cid:8)
(cid:8)
P
P(γ ) = EQ(s(2)
T )
β = β(+,−) · A(A)s(A)
T
s(A)
T
= (cid:8)(1, β)
(cid:9)(cid:11)
.
In short, the empirical priors over the initial state at the lower level (and
expected precision) now depend on hidden (valence) states at the second
level.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
420
Hesp et al.
3.3.3 Ascending Messages: Contextual and Affective Evidence. During each
trial, exogenous (reward location) and endogenous (affective charge) sig-
nals induce belief updating at the second level of hidden states. They do so
in such a way that fluctuations in context and affective beliefs (across trials)
are slower than fluctuations in lower-level beliefs concerning states, poli-
cies, and expected precision. These belief updates following each trial are
mediated by ascending messages that are gathered from posterior beliefs
about the initial food location at the end of each trial (¯s(1)
1 ), which serves as
Bayesian model evidence for the appropriate context state:
(cid:7)
¯s(C)
T
= σ
ln B(C) ¯s(C)
T−1
+ ln A(C) · ¯s(1)
1
(cid:9)
(context evidence).
As with inference at the first level, this second-level expectation comprises
empirical priors from the previous trial and evidence based on the posterior
expectation of the initial (context) state at the lower level.
For the ascending messages from the (continuous) expected precision
to the (discrete) affective states, we use Bayesian model reduction (for the
derivation, see Friston, Parr, and Zeidman, 2018) to evaluate the marginal
likelihood under the priors associated with each affective state:
(cid:12)
¯s(A)
T
= σ
ln B(A) ¯s(A)
T−1
− ln
(cid:13)
β(+,−) − AC
β(+,−)
β
β − AC
(affective evidence).
Again, this contains empirical priors based on previous affective expec-
tations and evidence for changes in affective state based on affective charge,
AC = ( ¯π − π) · Gπ , evaluated at the end of each trial time step. Notice that
when the affective charge is zero, the affective expectations on the current
trial are determined completely by the expectations at the previous trial (as
the logarithm of one is zero). See Figure 7 for a graphical description of this
deep generative model.
We used this generative model to simulate affective inference of a syn-
thetic rat that experiences 64 T-maze trials, in which the food location
switches after 32 trials from the left arm to the right arm. When our syn-
thetic subject becomes more confident that her actions will realize preferred
outcomes (C), increased (subpersonal) confidence in her action model (Gπ )
should provide evidence for a positively valenced state (through AC). Con-
versely, when she is less confident about whether her actions will realize
preferred outcomes, there will be evidence for a negatively valenced state.
In that case, our affective agent will fall back on her baseline prior over
policies (Eπ ), a quick and dirty heuristic that tends to be useful in situations
that require urgent action to survive (i.e., in the absence of opportunity to
resolve uncertainty via epistemic foraging).
In this setting, our synthetic subject can receive either a tasty reward or a
painful shock, based on whether she chooses left or right. Of course, she has
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Deeply Felt Affect
421
a high degree of control over the outcome, provided she forages for context
information and then chooses left or right, accordingly. However, her gen-
erative model includes a small amount of uncertainty about these divergent
outcomes, which corresponds to a negatively valenced (anxious) affective
state at the initial time point. Starting from that negative state, we expected
that our synthetic rat would become more confident over time, as she grew
to rely increasingly on her context beliefs about the reward location. We
hoped to show that at some point, our rat would infer a state of positive
valence and be sufficiently confident to take her reward directly. Skipping
the information-foraging step would allow her to enjoy more of the reward
before the end of each trial (comprising two moves). The second set of 32
trials involved a somewhat cruel twist (introduced by Friston, FitzGerald
et al., 2016): we reversed the context by placing the reward on the opposite
(right) arm. This type of context reversal betrays our agent’s newly found
confidence that T-mazes contain their prize on the left. Given enough tri-
als with a consistent reward location, our synthetic rat should ultimately be
able to regain her confidence.
4 Results
Figure 8 shows the simulation outcomes for the setup we have described.
The dynamics of this simulation can be roughly divided into four quarters:
two periods within each of the 32 trials before and after the context reversal.
These periods show an initial phase of negative valence (quarters 1 and 3),
followed by a phase of purposeful confidence (positive valence; quarters
2 and 4). As stipulated in terms of priors, our subject started in a negative
anxious state. Because it takes time to accumulate evidence, her affective
beliefs lagged somewhat behind the affective evidence at hand (patterns in
affective charge). As our rat kept finding food on the left, her expected pre-
cision increased until she entered a robustly positive state around trial 12.
Later, around trial 16, she became sufficiently confident to take the short-
cut to the food—without checking the informative cue. After we reversed
the context at trial 33, our rat realized that her approach had ceased to bear
fruit. Unsure of what to do, she lapsed into an affective state of negative
valence—and returned to her information-foraging strategy. More slowly
than before (about 15 trials after the context reversal, as opposed to 12 trials
after the first trial), our subject returned to her positive feeling state as she
figured out the new contingency: food is now always on the right. It took
her about 22 trials following context reversal to gather enough courage (i.e.,
confidence) to take the shortcut to the food source on the right. The fact that
it took more trials (22 instead of 16) before taking the shortcut suggests that
she had become more skeptical about consistent contingencies in her envi-
ronment (and rightly so).
Roughly speaking, our agent experienced (i.e., inferred) a negatively va-
lenced state during quarters 1 and 3 and a positively valenced state during
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
422
Hesp et al.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Deeply Felt Affect
423
quarters 2 and 4 of the 64 trials. A closer look at these temporal dynamics re-
veals a dissociation between positive valence and confident risky behaviors:
a robust positive state (Figure 8d) preceded the agent’s pragmatic choice of
taking the shortcut to the food (Figure 8b).
To illustrate the importance of higher-level beliefs in this kind of setting,
we repeated the simulations in the absence of higher-level contextual and
affective states. After removing the higher level, the resulting (less sophisti-
cated) agent, which could be thought of as an agent with a “lesion” to higher
levels of neural processing, updated expectations about food location by
simply accumulating evidence in terms of the number of times a particu-
lar outcome was encountered. Figure 9 provides a summary of differences
in belief updating and behavior between this simpler model and an affec-
tive inference model. In the top panel of Figure 9, we see that higher-level
context states can quickly adjust lower-level expectations based on recent
observations (recency effects), while the less sophisticated rat is unable to
forget about past observations (after observing 32 times left and right, its ex-
pected food location is again 50/50). The effect of removing affective states
is subtler. This effect becomes apparent when we inspect the difference
Figure 8: A summary of belief updating and behavior of our simulated affective
agent over 64 trials. Probabilistic beliefs are plotted using a blue-yellow gradient
(corresponding with high-low certainty). As shown in the graphic that connects
panels c and d, the dynamics of this simulation can be divided into four quar-
ters: two periods within each of the 32 trials before and after the context reversal,
each comprising an initial phase of negative valence (anxiety; quarters 1 and 3),
followed by a phase of positive valence (confidence; quarters 2 and 4). (a) The
context changed midway through the experiment (indicated in all panels with
a vertical green line): food was on the left for the first 32 trials (L) and on the
right for the subsequent 32 trials (R). (b, c) These density plots show the sub-
ject’s beliefs about the best course of action, both before (panel b) and after the
trial (panel c). Prior beliefs were based purely on baseline priors and her action
model, which entailed high ambiguity (yellow) during quarters 1 and 3 of the
trial series (corresponding with cue-checking policies V8−9) and high certainty
(blue) during quarters 2 and 4 (corresponding to shortcut policies V5−6). After
perceptual evidence was accumulated (after the trial), posterior beliefs about
policies always converged to the best policy, except in the first trial after context
reversal (trial 33, when the rat receives a highly unexpected shock), which ex-
plains her initial confusion. Whenever prior certainty about policies was high,
expectations agreed with posterior beliefs about policies (again, except for trial
33). (d) This density plot illustrates affective inference in terms of beliefs about
her valence state (confident positive or anxious negative states s(A)). Roughly
speaking, our rat experienced a negatively valenced state during quarters 1 and
3 and a positively valenced state during quarters 2 and 4. (e) We plot lower-level
expected precision (γ), overlaid on a density plot of valence beliefs (grayscale
version of panel d).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
424
Hesp et al.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
between the strongest prior beliefs about policies with and without affec-
tive states in play (second panel). As expected, we see that affective states
and associated fluctuations in expected precision (as in Figures 8d and 8e)
are associated with much larger variation in the strength of prior beliefs
about policies at the start of the trial (when our rat is still in the centre of the
maze). Furthermore, a comparison in terms of the AC elicited within trials
(third versus fourth panel of Figure 9) demonstrates how higher-level mod-
ulation of expected precision tends to attenuate the generation of AC within
trials. Conversely, the simpler agent cannot habituate to its own successes
and failures: after every trial, expected precision is reset and AC is elicited
again and again. Finally, the combined effects of lesioning the higher level
neatly explain the observed behavioral outcomes (bottom panel of Figure
9). Before context reversal, both agents end up selecting the same policies.
The absence of the higher-level affective state beliefs particularly disrupts
the capacity to deal with the change in context. First, she persisted in prag-
matic foraging for three trials despite receiving several painful shocks—as
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Deeply Felt Affect
425
opposed to the affective inference rat, which switched after a single unex-
pected observation. Second, the affective inference rat switched back to her
default strategy right away (checking the cue, then getting the food), but
the less sophisticated rat (with a “lesion” to the higher-level model) started
avoiding both left and right arms altogether. For eight consecutive trials,
she checked the informative cue but either stayed with the cue or returned
to the center. Only after she had gathered enough evidence about the re-
liability of the new food location did she dare to move to the right arm
(reminiscent of drift diffusion models of decision making). She kept using
that strategy until the end of the experiment, while our affective inference
rat moved directly to the right arm for the last quarter of the series of trials.
Figure 9: A comparison of belief updating (four top rows) and behavior (bottom
row) over 64 trials in our affective agent (plotted in orange) and an agent with-
out higher-level contextual and affective states (plotted in gray). Context was
changed midway through (vertical green line): food was on the left for the first
32 trials and on the right for the subsequent 32 trials. (First panel) The top panel
shows differences in temporal dynamics of food location expectations. Thanks
to her higher-level context states (which decayed over time due to uncertainty
about cross-trial state transitions as defined in Figure 8), our affective agent
(orange) weighed recent evidence more heavily, allowing her to shift context
beliefs. In contrast, the agent without the higher affective level (gray) counted
events only over time. While her expectations developed similarly to the affec-
tive agent for the first 32 trials, she was much slower in adjusting to the change
in context (her beliefs return to 50/50 only after observing 32 trials for both left
and right). (Second panel) This panel displays the strongest prior belief about
policies for each agent (pretrial), tracking the product of the expected precision
and the maximum of model evidence (negative Gπ ). The affective agent varied
(pretrial) her expected precision dynamically with context reliability. The nonaf-
fective agent instead obtained (initial) certainty about the best course of action
much more slowly, only as a function of her action model (as initial expected
precision was constant). (Third and fourth panels) A comparison of within-trial
AC responses (fluctuations in expected precision) between the affective agent
(third panel, orange) and the nonaffective agent (fourth panel, gray). Our affec-
tive agent exhibited large fluctuations in expected precision within trials only
when she was switching between affective states: she attenuated AC responses
by integrating them across trials, adjusting expected precision preemptively. In
contrast, the nonaffective agent exhibited large fluctuations throughout the se-
ries of trials, being surprised repeatedly because she was unable to integrate
affective charge. (Fifth panel) The bottom panel shows the behavioral outcomes
for both agents. Before context reversal, their behaviors were indistinguishable.
After context reversal, the nonaffective agent only foraged for information and
exhibited avoidance behaviors, either staying down (policy 10) or moving back
to the center (policy 7).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
426
Hesp et al.
Clearly, one can imagine many other variants of the generative model we
used to illustrate affective inference; we will explore these in future work.
For example, it is not necessary to have separate contextual and affective
states on the higher level. One set of higher-level states could stand in for
both, providing empirical priors for beliefs about contingencies between
particular contexts and valence states. Nevertheless, our simulations pro-
vide a sufficient vehicle to discuss a number of key insights offered by af-
fective inference.
5 Discussion
In this letter, we have constructed and simulated a formal model of emo-
tional valence using deep active inference. We provided a computational
proof of principle of affective inference in which a synthetic rat was able to
infer not only the states of the world but also her own affective (valence)
states. Crucially, her generative model inferred valence based on patterns
in the expected precision of her phenotype-congruent action model. To be
clear, we do not equate this notion of expected precision (or confidence)
with valence directly; rather, we suggest that AC signals (updates in ex-
pected precision) are an important source of evidence for valence states.
Aside from AC, valence estimates could also be informed by other types of
evidence (e.g., exteroceptive affective cues). Our formulation thus provides
a way to characterize valenced signals across domains of experience. We
showed the face validity of this formulation of a simple form of affect, in
that sudden changes in environmental contingencies resulted in negative
valence and low confidence in one’s action model.
Extending nested active inference models of perception, action, and im-
plicit metacognition (M4; see Figure 3), our deep formulation of affective
inference can be seen as a logical next step. It required us to specify mu-
tual (i.e., top-down and bottom-up) constraints between higher-level con-
textual and affective inferences (across contexts) and lower-level inferences
(within contexts) about states, policies, and expected precision. In Figure 10,
we emphasize the inherent hierarchical and nested structure of the compu-
tational architecture of our affective agent. It evinces a metacognitive (i.e.,
implicitly self-reflective) capacity, where creatures hold alternative hy-
potheses about their own affective state, reflecting internal estimates of
model fitness. This affords a type of mental action (Limanowski & Fris-
ton, 2018; Metzinger, 2017) in the sense that the precision ascribed to low-
level policies is influenced by higher levels in the hierarchy. Concurrently,
at each level (top-down constrained), prior beliefs follow a gradient ascent
on an upper bound on model evidence, thus providing mutual constraints
between levels in forming posterior beliefs.
5.1 Implicit Metacognition and Affect: “I Think, Therefore I Feel.”
Our affective agent evinces a type of implicit metacognitive capacity that
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Deeply Felt Affect
427
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
Figure 10: A schematic breakdown of the nested processes of Bayesian in-
ference in terms of the affective agent presented in this letter. At each level,
top-down prior beliefs change along a gradient ascent on bottom-up model ev-
idence (negative F), moving the entire hierarchy toward mutually constrained
posteriors. Perception (light blue; M2 in Figure 1 and Table 2) provides evidence
for beliefs over policies (blue; M3 in Figure 2 and Table 3) and higher-level con-
textual states. Action outcomes inform subjective fitness estimates through af-
fective charge (brown; M4 in Figure 3 and Table 4), which provides evidence to
inform valence beliefs (orange). These nested processes of inference unfold con-
tinuously in each individual phenotype throughout development and learning
(e.g., neural Darwinism, natural selection; see Campbell, 2016; Constant et al.,
2018). In turn, the reproductive success of each phenotype provides model evi-
dence that shapes the evolution of a species.
is more sophisticated than that of the generative model presented in our
primer on active inference (M1−4 in Figures 1–3). Beliefs about her own af-
fective state are informed by signals conveying the phenotype congruence
of what she did or is going to do; put another way, they are informed by
the degree to which actions did, or are expected to, bring about preferred
outcomes. This echoes other work on Bayesian approaches to metacogni-
tion (Stephan et al., 2016). The emergence of this metacognitive capacity
rests on having a parametrically deep generative model, which can in-
corporate other types of signals from within and from without. Beyond
internal fluctuations in subjective fitness (AC, as in our formulation),
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
428
Hesp et al.
affective inference is also plausibly informed by exteroceptive cues as well
as interoceptive signals (e.g., heart rate variability; Allen, Levy, Parr, & Fris-
ton, 2019; Smith, Thayer, Khalsa, & Lane, 2017). The link to exogenous sig-
nals or stimuli is crucial: equipped with affective inference, our affective
agent can associate affective states with particular contexts (through D(2)
and B(2)). Such associations can be used to inform decisions on how to re-
spond in a given context (given a higher-level set of policies π (2)) or how to
forage for information within a given niche (via π (1)). If our synthetic subject
can forage efficiently for affective information, she will be able to modulate
her confidence in a context-sensitive manner, as a form of mental action.
Furthermore, levels deeper in the cortical hierarchy (e.g., in prefrontal cor-
tex) might regulate such affective responses by inferring or enacting the
policies that would produce observations leading to positive AC. Such pro-
cesses could correspond to several widely studied automatic and voluntary
emotion regulation mechanisms (Buhle et al., 2014; Phillips, Ladouceur, &
Drevets, 2008; Gyurak, Gross, & Etkin, 2011; Smith, Alkozei, Lane, & Kill-
gore, 2016; Smith, Alkozei, Bao, & Killgore, 2018), as well as capacities for
emotional awareness (Smith, Steklis, Steklis, Weihs, & Lane, 2020; Smith,
Bajaj et al., 2018; Smith, Weihs, Alkozei, Killgore, & Lane, 2019; Smith, Kill-
gore, & Lane, 2020), each of them central to current evidence-based psy-
chotherapies (Barlow, Allen, & Choate, 2016; Hayes, 2016).
5.2 Reinforcement Learning and the Bayesian Brain. It is useful to con-
trast the view of motivated behavior on offer here with existing normative
models of behavior and associated neural theories. In studies on reinforce-
ment learning (De Loof et al., 2018; Sutton & Barto, 2018), signed reward
prediction error (RPE) has been introduced as a measure of the difference
between expected and obtained reward, which is used to update beliefs
about the values of actions. Positive versus negative RPEs are often also
(at least implicitly) assumed to correspond to unexpected pleasant and un-
pleasant experiences, respectively. Note, however, that reinforcement learn-
ing can occur in the absence of changes in conscious affect, and pleasant or
unpleasant experiences need not always be surprising (Smith & Lane, 2016;
Smith, Kaszniak et al., 2019; Panksepp et al., 2017; Winkielman, Berridge,
& Wilbarger, 2005; Pessiglione et al., 2008; Lane, Weihs, Herring, Hishaw, &
Smith, 2015; Lane, Solms, Weihs, Hishaw, & Smith, 2020). The term we have
labeled affective charge can similarly attain both positive and negative val-
ues that are of affective significance. However, unlike reinforcement learn-
ing, our formulation focuses on positively and negatively valenced states
and the role of AC in updating beliefs about these affective states (i.e., as
opposed to directly mediating reward learning). While similar in spirit to
RPE, the concept of AC has a principled definition and a well-defined role
in terms of belief updating, and it is consistent with the neuronal process
theories that accompany active inference.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Deeply Felt Affect
429
Specifically, affective charge scores differences between expected and
obtained results as the agent strives to minimize risk and ambiguity (Gπ ;
see Table 3). In cases where expected ambiguity is negligible, AC becomes
equivalent to RPE, as both score differences in utility between expected
and obtained outcomes (see Rao, 2010; Colombo, 2014; FitzGerald, Dolan,
& Friston, 2015). However, expected ambiguity becomes important when
one’s generative model entails uncertainty (e.g., driving exploratory behav-
iors such as those typical of young children). This component of affective in-
ference allows us to link valenced states to ambiguity reduction, while also
accounting for the delicate balance between exploitation and exploration.
In traditional RL models (as described by Sutton & Barton, 2018), the
primary candidates for valence appear to be reward and punishment or ap-
proach and avoidance tendencies. In contrast to our model, RL models tend
to be task specific and do not traditionally involve any internal representa-
tion of valence (e.g., reward is simply defined as an input signal that mod-
ifies the probability of future actions). More recent models have suggested
that mood reflects the recent history of reward prediction errors, which
serves the function of biasing perception of future reward (Eldar et al.,
2016; Eldar & Niv, 2015). This contrasts with our approach, which identi-
fies valence with a domain-general signal that emerges naturally within a
Bayesian model of decision making and can be used to inform represen-
tations of valence that track the success of one’s internal model and adap-
tively modify behavior in a manner that could not be accomplished without
hierarchical depth. Presumably this type of explicit valence representation
is also a necessary condition for self-reportable experience of valence. The
adaptive benefits of this type of representation are illustrated in Figure 9.
Only with this higher-order valence representation was the agent able to
arbitrate the balance between behavior driven by expected free energy (i.e.,
explicit goals and beliefs) and behavior driven by a baseline prior over poli-
cies (i.e., habits). More generally, the agent endowed with the capacity for
affective inference could more flexibly adapt to a changing situation than
an agent without the capacity for valence representation, since it was able to
evaluate how well it was doing and modulate reliance on its action model
accordingly. Thus, unlike other modeling approaches, valence is here re-
lated to, but distinct from, both reward and punishment and approach and
avoidance behavior (i.e., consistent with empirically observed dissociations
between self-reported valence and these other constructs; see Smith & Lane,
2016; Panksepp et al., 2017; Winkielman et al., 2005) and serves a unique and
adaptive domain-general function.
Prior work has suggested that expected precision updates (i.e., AC) may
be encoded by phasic dopamine responses (e.g., see Schwartenbeck, 2015).
If so, our model would suggest a link between dopamine and valence.
When considering this biological interpretation, however, it is important
to contrast and dissociate AC from a number of related constructs. This
includes the notion of RPEs discussed above, as well as that of salience,
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
430
Hesp et al.
wanting, pleasure, and motivation, each of which has been related to
dopamine in previous literature and appears distinct from AC (Berridge
& Robinson, 2016). In reward learning tasks, phasic dopamine responses
have been linked to RPEs, which play a central role in learning within sev-
eral RL algorithms (Sutton & Barto, 2018); however, dopamine activity also
increases in response to salient events independent of reward (Berridge &
Robinson, 2016). Further, there are contexts in which dopamine appears
to motivate energetic approach behaviors aimed at “wanting” something,
which can be dissociated from the hedonic pleasure upon receiving it (e.g.,
amphetamine addicts gaining no pleasure from drug use despite continued
drives to use; Berridge & Robinson, 2016). Thus, if AC is linked to valence, it
is not obvious a priori that its tentative link to dopamine is consistent with,
or can account for, these previous findings.
While these considerations may point to the need for future extensions of
our model, many can be partially addressed. First, there are alternative in-
terpretations of the role of dopamine proposed within the active inference
field (FitzGerald et al., 2015; Friston et al., 2014)—namely, that it encodes
expected precision as opposed to RPEs. Mathematically, it can be demon-
strated that changes in the expected precision term (gamma) will always
look like RPEs in the context of reward tasks (i.e., because reward cues up-
date beliefs about future action and relate closely to changes in expected
free energy). However, since salient (but nonrewarding) cues also carry
action-relevant information (i.e., they change confidence in policy selec-
tion), gamma also changes in response to salient events. Thus, this alterna-
tive interpretation can actually account for both salience and RPE aspects of
dopaminergic responses. Furthermore, reward learning is not in fact com-
promised by attenuated dopamine responses and therefore does not play a
necessary role in this process (Fitzgerald et al., 2015). The active inference
interpretation can thus explain dissociations between learning and appar-
ent RPEs.
Arguably, the strongest and most important challenge for claiming a re-
lation of dopamine, AC, and valence arises from previous studies linking
dopamine more closely to “wanting” than pleasure (i.e., which is closely
related to positive valence; Berridge & Robinson, 2016). On the one hand,
some studies have linked dopamine to the magnitude of “liking” in re-
sponse to reward (Rutledge et al., 2015), and some effective antidepres-
sants are dopaminergic agonists (Pytka et al., 2016); thus, there is evidence
supporting an (at least indirect) link to pleasure. However, pleasure is also
associated with other neural signals (e.g., within the opioid system). A lim-
itation of our model is that it does not currently have the resources to ac-
count for these other valence-related signals. It is also worth considering
that because only one study to date has directly tested and found support
for a link between AC and dopamine (Schwartenbeck et al., 2015), future re-
search will be necessary to establish whether AC might better correspond to
other nondopaminergic signals. We point out, however, that our model only
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Deeply Felt Affect
431
entails that AC provides one source of evidence for higher-level valence rep-
resentations and that pleasure is only one source of positive valence. Thus,
it does not rule out the additional influence of other signals on valence,
which would allow the possibility that AC contributes to, but is also disso-
ciable from, hedonic pleasure (for additional considerations of functional
neuroanatomy in relation to affective inference, see appendix A4).
5.3 Affective Charge Lies in the Mind of the Beholder. Given that
our formulation of affective inference is decidedly action oriented, we owe
readers an explanation of how valence is elicited within aspects of our
mental lives that appear to be somewhat distant from action. For exam-
ple, we all tend to experience a rush of satisfaction when we solve a puzzle
or understand the punchline of a joke (an “aha!” moment). Our explana-
tion is straightforward: in active inference, biologically plausible forms of
cognition inevitably involve policy selection, whether internal (e.g., direct-
ing one’s attention to affective stimuli and manipulating affective informa-
tion within working memory; Smith, Lane et al., 2017; Smith, Lane, Alkozei
et al., 2018; Smith, Lane, Sanova et al., 2018) or external (e.g., saccade selec-
tion to affective cues; Adolphs et al., 2005; Moriuchi, Klin, & Jones, 2017).
Therefore, AC is also elicited by mental action, typically in the form of
top-down modulation of (lower-level) priors. Across domains of experi-
ence, positive versus negative valence has been linked to cognitive matches
versus mismatches (e.g., Williams & Gordon, 2007), coherence versus inco-
herence (e.g., Topolinski, Likowski, Weyers, & Strack, 2009), resonance ver-
sus dissonance (e.g., Sohal, Zhang, Yizhar, & Deisseroth, 2009), and fluency
versus disfluency (e.g., Willems & Van der Linden, 2006). Affective infer-
ence can account for all of these different findings in terms of reductions of
ambiguity resulting from attentional policy selection. This provides a for-
mal way to relate changes in processing fluency across different domains to
particular affective states, formalizing previous conceptual models (Phaf &
Rotteveel, 2012; Joffily & Coricelli, 2013; Van de Cruys, 2017).
In this context, we remind readers that expected precision (γ ) and its dy-
namics (directed by AC) reflect the agent’s confidence in the use of expected
free energy to inform action selection. Expected free energy can be inter-
preted as an evaluation of how well one’s model is doing on the whole (i.e.,
it scores departures from preferred outcomes), such that the expected pre-
cision (gamma) term represents confidence in the entirety of one’s action
model. This is distinct from confidence in any particular course of action
and thus distinguishes AC from the related notions of agency and control.
While AC reflects an evaluation of how one’s generative model is doing
in general, notions of agency and control are somewhat narrower and, al-
though related to AC, they would in fact map to distinct model elements.
Specifically, these constructs are likely best captured in relation to the preci-
sion of expected transitions given each allowable policy (i.e., the precision of
the transition matrices B in the model). When policy-dependent transitions
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
432
Hesp et al.
have high precision, the agent will be confident in the outcomes of her
actions—and hence her ability to control the environment as desired. How-
ever, this will not always co-vary with AC. Generally, high B precision is
necessary but not sufficient for positive AC (e.g., one can have precise ex-
pectations about state transitions associated with nonpreferred outcomes).
In other contexts, it has been suggested that action model precision up-
dates (what we have labeled AC) could be used to inform selective atten-
tion (e.g., Clark et al., 2018; Palacios, Razi, Parr, Kirchhoff, & Friston, 2019).
When compared to a particular baseline of subjective fitness, any signifi-
cant departure, whether positive or negative, will tend to signify a fork in
the road: an opportunity or threat that requires (internal and external) ac-
tion. As one possible extension of our model, extreme values of AC could
therefore be used to inform arousal states, accompanied by an affect-driven
orienting process. In this scheme, the automatic (bottom-up) capture of at-
tention by affective stimuli can then emerge spontaneously, as such stimuli
provide reliable information about the agent’s affective state. In turn, this
could be used to model the types of tunnel vision experiences that occur in
mammals when they are highly aroused.
We pursue this line of reasoning in a forthcoming sequel to this letter,
which builds naturally on prior work in active inference (Parr & Friston,
2017) showing how the salience of a stimulus can be formally related to the
potential reduction of uncertainty afforded by selecting a policy pertaining
to that stimulus (e.g., a visual saccade). For example, for our affective agent,
the perceptual salience of a stimulus is proportional to her expectation
of reducing perceptual uncertainty (about lower-level perceptual states).
Affective salience could thus be framed similarly as an agent’s expecta-
tion of reducing affective ambiguity (about higher-level affective states).
Interestingly, the implied hierarchical (and temporal) dissociation is corrob-
orated by Niu, Todd, and Anderson (2012), who synthesize findings that
suggest a dissociation between perceptual salience and affective salience.
5.4 On the Dimensionality of Valence. Because we have posited a close
relationship between AC and valence, a number of questions may arise. For
example, in our model simulations, AC corresponds to a one-dimensional
signal, taking on either negative or positive values, that is used to up-
date higher-level valence representations. However, one might question
whether valence has this unidimensional structure. Indeed, there are many
competing perspectives on this issue (for a review, see Lindquist et al., 2016).
Some perspectives in emotion research and associated neuroscience re-
search posit that valence is unidimensional (Russell, 1980; Barrett & Russell,
1999) and assume (for example) that a single neural system should increase
(or decrease) in activity as valence changes along this dimension. Other
perspectives posit two dimensions (Fontaine et al., 2007), potentially cor-
responding to two independent neural systems activated by negative and
positive valence, respectively. Finally, affective workspace views (Lindquist
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Deeply Felt Affect
433
et al., 2016) posit that there are no distinct “valence systems” and that a
range of domain-general neural systems use, and are thus activated by, in-
formation regarding both negative and positive valence information in a
context-specific and flexible manner. In addition to the dimensionality of
valence in particular, a related question corresponds to whether our model
can account for granular, multidimensional aspects of emotional experience
more broadly.
While these considerations certainly highlight the oversimplified nature
of the formal simulations we have presented, they also point to a potential
strength of our formulation. Specifically, our formulation offers a few dif-
ferent conceptual resources to begin to address these issues. First, although
AC is a unidimensional signal, it is important to stress that the generation
of this signal does not imply that it is used in the same manner by all down-
stream systems that receive it (i.e., it need not simply provide evidence for
a single higher-level state as in our simulations). Indeed, some downstream
systems could selectively use negative or positive AC information (as in a
two-dimensional model), or multiple systems could use bivalent informa-
tion for a diverse set of functions (as in affective workspace views; Lindquist
et al., 2016). Second, each level in a hierarchical system could in principle
generate its own AC signal and pass this signal forward, which opens up
the possibility that affective charge could be positive at one level (or in one
neural subsystem) and negative at another level (or in another subsystem),
potentially allowing for more nuanced mixtures of valenced experience.
That said, it is unclear how affective charge could be integrated across levels
or systems to inform experience. Furthermore, not all levels in a represen-
tational hierarchy plausibly contribute to conscious experience (Dehaene,
Charles, King, & Marti, 2014; Whyte & Smith, in press; Smith & Lane, 2015),
and it is an open question which level or subset of levels may be privileged
with respect to its contribution to affective phenomenology). Finally, it is
important to stress that our claim is specific to valence and does not aim
to address more complex experiential components of emotion. There are
several further experiential aspects of emotion (e.g., interoceptive/somatic
sensations, approach/avoidance drives, changes in attention/vigilance)
that go beyond valence and would need to be incorporated into a future
model.
5.5 Addressing Potential Counterexamples: Negative Valence with
Confident Action. Here, we carefully consider potential counterexamples
and explain how these do not threaten the face validity of our formulation.
One class of potential counterexamples involves situations with seemingly
inevitable nonpreferred outcomes (i.e., in which there is little uncertainty
about future outcomes that will be highly unpleasant). For example, some-
one falling out of a plane without a parachute may feel very unpleasant
despite near certainty that he or she will hit the ground and die. Here, it
is important to emphasize that negative AC is generated whenever there
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
434
Hesp et al.
is an increase in the divergence between preferred outcomes and the
outcomes expected under a policy that one could choose. Thus, under the
assumption that smashing into the ground is not consistent with one’s pref-
erences, falling from a plane without a parachute would be a case in which
all policies available to an individual would be expected to lead to outcomes
that diverge strongly from those preferences (e.g., no particular action will
prevent crashing into the ground). As such, the agent will have high uncer-
tainty about how to act to fulfill her preferences (high expected free energy),
despite accurately predicting the future outcomes themselves, and would
thus experience negative valence on our account.
A second class of potential counterexamples involves cases in which con-
fidence in actions is seemingly high and yet valence is negative, most no-
tably in situations associated with fear and anger. In fear, one can feel very
confident one should be running away from a predator. In anger, one can
feel very confident in wanting to hurt someone. A short response that ap-
plies to most counterexamples of this kind is that AC signals indicate rel-
ative changes in one’s current affective state; it serves a modulatory role
in such scenarios. While for simplicity we have included only binary cate-
gories of negative and positive valence in our formal model, it is important
to keep in mind that, experimentally, valence is measured on a continuous
scale„ from very negative to very positive. Thus, even in scenarios that are
categorically negative, the intensity of negative valence can vary in a way
that correlates negatively with AC. For example, while one would be ex-
pected to experience negative affect when running away from a predator,
this feeling would likely be even more intense if one were trapped and had
no idea how to escape (this would involve more negative AC values). Fur-
thermore, the more confident one was that running away would succeed,
the better one would be expected to feel. Therefore, negative AC signals will
still be expected to track the intensity of negative affect in cases of fear.
Despite initial appearances, our formulation of valence can also account
for the example of anger mentioned above, in which one yet remains very
confident in how to act (e.g., having a strong drive to hurt someone). First,
negatively valenced anger experience can be accounted for by the increased
divergence from preferred outcomes associated with anger-inducing events
(e.g., being unexpectedly insulted by a friend). Second, confidently acting
on anger can be associated with positive valence (e.g., punching someone
who insulted you can feel good), whereas conflicting drives during anger
are associated with more negative valence (e.g., wanting to punch someone
but also not wanting to compromise a valued relationship). Thus, each of
these aspects of anger remains consistent with our formulation, as the de-
gree of negative and positive valence during such episodes of anger would
still map onto AC values.
Next, there are some interesting cases where expected free energy will in-
crease, despite induction of a highly precise posterior distribution over poli-
cies. These cases occur when an agent is highly confident in one policy and
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Deeply Felt Affect
435
then observes an outcome that unexpectedly leads to very high confidence
in a different policy, which can be seen as evidence that confidence in one’s
action model should decrease. This may actually be a common occurrence
within the cases just mentioned—for example, if one started out highly con-
fident in the “calmly walk around in the woods” policy and, upon seeing a
predator, unexpectedly became highly confident in the “run away” policy
or if one started out highly confident in the “act friendly” policy and, upon
being insulted by a friend, unexpectedly became highly confident in the
“respond sternly to my friend” policy. Thus, while AC often covaries with
uncertainty in action selection due to its relation to preferred outcomes and
its nonlinear relationship with posterior precision over policies, these other
types of cases can be accommodated naturally.
Finally, we should also consider cases where people report a highly pos-
itive experience but their current fit to the environment is not good in any
measurable way. Such divergences between subjective fitness and external
measures of fitness (e.g., reproductive success) can naturally occur in af-
fective inference, highlighting an important strength of our formulation.
Because internal estimates of fitness can be inaccurate, our formulation pro-
vides resources for modeling maladaptive affective phenomena, such as
delusions of grandeur in mania (exaggerated subjective fitness) or learned
helplessness in depression (virtually zero subjective fitness). This notion
of Bayes-optimal inference within suboptimal models has been used to
study psychiatric disorders in computational psychiatry (Schwartenbeck
et al., 2015). Furthermore, due to the role of natural selection in sculpt-
ing prior preferences, one can also describe phenomena in our framework
that appear at odds with individual biological fitness (e.g., a bee sacrific-
ing itself for the hive). This thus makes contact with other evolved human
behaviors with affective components, such as altruistic and self-sacrificial
behaviors (e.g., associated with kin selection mechanisms and reciprocal al-
truism within evolutionary psychology; Buss, 2015).
5.6 Deep Feelings and Temporal Depth: Toward Emotive Artificial
Intelligence. It is an open question how deep a computational hierarchy
should be in order to account for the experience of valence. While our two-
level model seems to be complex, it is actually quite minimal in attempt-
ing to account for any type of subjective phenomenology. Although any
decision-making organism can be equipped with sensory and motor rep-
resentations in a one-level model and be equipped with tendencies to ap-
proach some situations and avoid others, we have shown that a higher
level is necessary to represent estimates about oneself. We assume, based
on what is known about conscious versus unconscious neural processes
(e.g., Dehaene et al., 2014; Whyte & Smith, in press), that explicit state rep-
resentation is a necessary condition for self-reportable experience, and thus
that higher-level valence representation (as in our model) will be neces-
sary for conscious experience of valence. Under this plausible assumption,
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
436
Hesp et al.
while very simple organisms can exhibit approach and avoidance tenden-
cies, only more complex organisms equipped with hierarchical models that
can integrate internal evidence for different internal states will be capable
of experiencing valence.
We deemed affective inference (as opposed to mere valence inference) an
appropriate label for our model because deep, active inference can be di-
rectly applied to model other affective state components (e.g., arousal) and
affect-related phenomena (e.g., affective salience). This is an important fu-
ture direction for our framework. Enriched affective state representations of
this type (e.g., with high and low arousal states) can serve as higher-level
explanations for conditional dependencies between hyperparameters and
related effects on behavior. In future work, we will move beyond AC and
characterize the richness of core affective states in the (hyper)parameters of
a generative model that applies to a wide range of lower-level generative
models (i.e., of many different shapes and settings). Another important di-
rection will be to connect our model to other active inference models used
to simulate approach/avoidance behavior and emotion-cognition (Linson,
Parr, & Friston, 2020; Smith, Parr, & Friston, 2019; Smith, Lane, Parr, & Fris-
ton, 2019; Smith, Kirlic et al., in press).
A longer-term aim of extending our model in these directions is to build
toward a generalizable form of emotive artificial intelligence. An emotional
artificial agent of this kind would be able to infer which groups of hyperpa-
rameters (e.g., characterizing “go” versus “no go” responses; fight, flight,
or freeze; tend or befriend) tend to provide the best fit for particular stimuli
and contexts. For example, by adding a term that parameterizes the pre-
cision of the baseline prior over policies (Eπ ), an affective agent can in-
crease and decrease her general tendency to rely on automatic responses
in a context-sensitive manner. The model of valence we have proposed,
and its natural extension to core affective states involving arousal, could
also be seamlessly integrated into active inference models of emotion con-
cept learning and emotional awareness (Smith, Parr, & Friston, 2019; Smith,
Lane, Parr et al., 2019). In these models, an agent can use combinations of
lower-level affective, interoceptive, exteroceptive, and cognitive represen-
tations (treated as observations) to infer and learn about emotion concepts
(e.g., sadness, anger) and to reflect on those emotional states in working
memory. Here, emotion concepts correspond to regularities in and across
those lower-level states. Because valence is treated as an observation in
these models, our formulation of AC would provide an important compo-
nent that is currently missing in this previous work.
5.7 Future Empirical Directions. This letter has taken the first step in
a larger research program aimed at characterizing the neurocomputational
basis of emotion. We have demonstrated the face validity of the affective
dynamics emerging from an active inference model that incorporates ex-
plicit representations of valence. The next step will be to link our model
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Deeply Felt Affect
437
to specific neuroimaging or behavioral paradigms (or both) and compare
it with alternative modeling frameworks such as reinforcement learning.
In doing so, empirical data can be fit to these models, and Bayesian model
comparison can be used to identify the model (and model parameters) that
best accounts for neuronal and behavioral responses at both the individ-
ual and group level—an approach called computational phenotyping (as
in Schwartenbeck et al., 2015; Smith, Kirlic et al., in press); Smith, Kuplicki,
Feinstein et al., 2020; Smith, Schwartenbeck, Stewart et al., 2020; Smith, Ku-
plicki, Teed, Upshaw, & Khalsa, 2020). Our affective inference model would
be supported if it best accounts for empirical data when compared to other
models. A further step will be to develop computational phenotypes that
best explain typical and atypical socioemotional functioning in humans and
how these can devolve into stable attractors that we associate with psychi-
atric conditions (see Hesp, Tschantz, Millidge, Ramstead, Friston, & Smith,
forthcoming). A final and more distant goal may be that by fitting affec-
tive model parameters to patients with symptoms of emotional disorders,
psychiatrists might eventually be able to derive additional diagnostic and
prognostic information about their patients that could inform treatment
selection, an approach called computational nosology (Friston, Redish, &
Gordon, 2017).
In terms of empirical predictions, our formulation of affective inference
suggests that in the majority of circumstances, standard measures of va-
lence (e.g., self-report scales of pleasant or unpleasant subjective experi-
ence, potentiated startle responses; Watson, Clark, & Tellegen, 1988; Bradley
& Lang, 1994; Bublatzky, Guerra, Pastor, Schupp, & Vila, 2013) should
be correlated with experimental inductions of uncertainty about the ac-
tions that will lead to preferred outcomes. Furthermore, when fitting an
affective-inference model to experimental data on an individual level dur-
ing and across a task, trial-by-trial changes in AC would be predicted to
correlate with those same valence measures (i.e., when also assessed on a
trial-by-trial basis). as well as with established neuroimaging correlates of
valence (Fouragnan, Retzler, & Philiastides, 2018; Lindquist et al., 2016).
A future research direction will be to test for patterns of human or non-
human animal behavior that can be better explained by our affective infer-
ence model than by other models. Recent work has begun to compare active
inference models with common reinforcement learning models, often sup-
porting the claim that active inference offers added explanatory power in
accounting for human behavior (Schwartenbeck et al., 2015). Comparisons
between reinforcement learning and active inference also tend to provide
evidence for the claim that the latter tends to have comparable performance
to, or can outperform, the latter, especially in environments with changing
contingencies and sparse rewards (Sajid, Ball, & Friston, 2020). Similar com-
parative approaches will need to be taken to determine empirically whether
affective inference can offer further explanatory resources. Qualitatively,
our model appears capable of accounting for previously observed effects
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
438
Hesp et al.
of valence on behavior (see especially the comparison to a non-affective ac-
tive inference agent in Figure 9), but future work will be necessary to test
its potentially unique explanatory power.
6 Conclusion
In this letter, we presented a Bayesian model of emotional valence, based
on deep active inference, that integrates previous theoretical and empirical
work. Accordingly, we provided a computational proof of principle of the
ensuing affective inference in a synthetic rat. Our deep formulation allows
for inference about one’s own valence state based on one’s confidence in
a phenotype-congruent action model (i.e., subjective fitness) and the corre-
sponding belief-updating term that tracks its progress and regress: affective
charge (AC). The domain generality of this formulation underwrites a view
of evolved life as exploiting the flexibility of second-order beliefs—those
about how to form beliefs. Our work provides a principled account of the
inextricable link between affect, implicit metacognition, and (mental) ac-
tion. The intriguing result is a view of deep biological systems that infer
their own affective state (using evidence gathered from lower-level posteri-
ors) and reducing uncertainty about such inferences through internal action
(through top-down modulation of lower-level priors). We look forward to
theoretical extensions and empirical applications of this novel formulation.
Acknowledgments
This research was undertaken thanks in part to funding from an NWO Re-
search Talent Grant of the Dutch government (C.H.; no. 406.18.535), the
Canada First Research Excellence Fund, awarded to McGill University for
the Healthy Brains for Healthy Lives initiative (M.R.), the Social Sciences
and Humanities Research Council of Canada (M.R.), and by a Wellcome
Trust Principal Research Fellowship (K.F.—088130/Z/09/Z). T.P. is sup-
ported by the Rosetrees Trust (award 173346). R.S. is funded by the William
K. Warren Foundation. M.A. is supported by a Lundbeckfonden Fellowship
(R272-2017-4345), the AIAS-COFUND II fellowship program that is sup-
ported by the Marie Skłodowska-Curie actions under the European Union’s
Horizon 2020 (grant agreement 754513), and the Aarhus University Re-
search Foundation. We are grateful to Paul Badcock, Axel Constant, and
Samuel Veissière for helpful comments on earlier versions of this letter.
Author Contributions
C.H. implemented the formalism of affective inference, conducted the sim-
ulations, and made the figures. C.H. and M.R. wrote the first draft of
the manuscript. R.S. played a primary role in editing and extending the
manuscript and linking its conceptual interpretation with prior work in the
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Deeply Felt Affect
439
affective sciences. All other authors also worked on the manuscript, the lit-
erature review components, and the theoretical background. C.H., T.P., K.F.,
and M.R. developed the formalism for affective inference and worked on its
conceptual interpretation. M.A. also worked on the conceptual interpreta-
tion of affective inference.
Additional Information
There are four appendixes in the supplementary information. We have
uploaded the simulation code to a public folder on GitHub (see https://
github.com/CasperHesp/deeplyfeltaffect). These scripts were adapted
from the Matlab scripts for Markov decision processes in active inference
that are included in SPM12 (freely available here: https://www.fil.ion.ucl.
ac.uk/spm/software/download/), which also contains a few functions
called within our code. We declare no competing interests.
References
Adlerman, N. E., Kayser, R., Dickstein, D., Blair, R. J. R., Pine, D., & Leibenluft, E.
(2011). Neural correlates of reversal learning in severe mood dysregulation and
pediatric bipolar disorder. Journal of the American Academy of Child and Adolescent
Psychiatry, 50(11), 1173–1185, e1172. https://doi.org/10.1016/j.jaac.2011.07.011
Adolphs, R., Gosselin, F., Buchanan, T. W., Tranel, D., Schyns, P., & Damasio, A. R.
(2005). A mechanism for impaired fear recognition after amygdala damage. Na-
ture, 433(7021), 68–72.
Allen, M., Levy, A., Parr, T., & Friston, K. J. (2019). In the body’s eye: The computational
anatomy of interoceptive inference. bioRxiv. https://doi.org/10.1101/603928
Attias, H. (2003). Planning by probabilistic inference. In Proceedings of the 9th Inter-
national Workshop on Artificial Intelligence and Statistics. https://doi.org/10.1.1.13.
9135
Badcock, P. B. (2012). Evolutionary systems theory: A unifying meta-theory of psy-
chological science. Review of General Psychology, 16(1), 1023. https://doi.org/10.
1037/a0026381
Badcock, P. B., Davey, C. G., Whittle, S., Allen, N. B., & Friston, K. J. (2017). The de-
pressed brain: An evolutionary systems theory. Trends in Cognitive Sciences, 21(3),
182194. https://doi.org/10.1016/j.tics.2017.01.005
Badcock, P. B., Friston, K. J., & Ramstead, M. J. D. (2019). The hierarchically mechanis-
tic mind: A free-energy formulation of the human psyche. Physics of Life Reviews,
31, 104–121. https://doi.org/10.1016/J
Barlow, D. H., Allen, L. B., & Choate, M. L. (2016). Toward a unified treatment for
emotional disorders. Behavior Therapy, 47(6), 838–853.
Barrett, L. F. (2017). How emotions are made: The secret life of the brain. Boston: Houghton
Mifflin.
Barrett, L. F., & Russell, J. A. (1999). The structure of current affect: Controver-
sies and emerging consensus. Current Directions in Psychological Science, 8(1), 10–
14.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
440
Hesp et al.
Berridge, K. C., & Robinson, T. E. (2016). Liking, wanting, and the incentive-
sensitization theory of addiction. American Psychologist, 71(8), 670.
Bodenhausen, G. V., Kramer, G. P., & Süsser, K. (1994). Happiness and stereotypic
thinking in social judgment. Journal of Personality and Social Psychology, 66(4), 621–
632. https://doi.org/10.1037/0022-3514.66.4.621
Bodenhausen, G. V., Sheppard, L. A., & Kramer, G. P. (1994). Negative affect and
social judgment: The differential impact of anger and sadness. European Journal
of Social Psychology, 24(1), 4562. https://doi.org/10.1002/ejsp.2420240104
Botvinick, M., & Toussaint, M. (2012). Planning as inference. Trends Cogn. Sci., 16,
485–488.
Bradley, M. M., & Lang, P. J. (1994). Measuring emotion: The self–assessment
manikin and the semantic differential. Journal of Behavior Therapy and Experimental
Psychiatry, 25(1), 49–59.
Briesemeister, B. B., Kuchinke, L., & Jacobs, A. M. (2012). Emotional valence:
A bipolar continuum or two independent dimensions? Sage Open, 1(4),
2158244012466558.
Bublatzky, F., Guerra, P. M., Pastor, M. C., Schupp, H. T., & Vila, J. (2013). Additive
effects of threat-of-shock and picture valence on startle reflex modulation. PLOS
One, 8(1), e54003.
Buhle, J. T., Silvers, J. A., Wager, T. D., Lopez, R., Onyemekwu, C., Kober, H., &
Ochsner, K. N. (2014). Cognitive reappraisal of emotion: A meta-analysis of hu-
man neuroimaging studies. Cerebral Cortex, 24(11), 2981–2990.
Buss, D. (2015). Evolutionary psychology: The new science of the mind. Hove, UK: Psy-
chology Press.
Cacioppo, J. T., & Berntson, G. G. (1994). Relationship between attitudes and evalu-
ative space: A critical review, with emphasis on the separability of positive and
negative substrates. Psychological Bulletin, 115, 401–423.
Campbell, J. O. (2016). Universal Darwinism as a process of Bayesian inference. Fron-
tiers in Systems Neuroscience, 10, 49. https://doi.org/10.3389/fnsys.2016.00049
Clark, J. E., Watson, S., & Friston, K. J. (2018). What is mood? A computational
perspective. Psychological Medicine, 48(14), 22772284. https://doi.org/10.1017/
S0033291718000430
Constant, A., Ramstead, M. J. D., Veissière, S. P. L., Campbell, J. O., & Friston, K. J.
(2018). A variational approach to niche construction. Journal of the Royal Society
Interface, 15, 2017.0685. https://doi.org/10.1098/rsif.2017.0685
Colombo, M. (2014). Deep and beautiful. The reward prediction error hypothesis
of dopamine. Studies in History and Philosophy of Science Part C?, 45(1), 5767.
https://doi.org/10.1016/j.shpsc.2013.10.006
Davidson, R. J. (2004). What does the prefrontal cortex “do” in affect? Perspectives
on frontal EEG asymmetry research. Biological Psychology, 67(1–2), 219–234.
Dehaene, S., Charles, L., King, J. R., & Marti, S. (2014). Toward a computational the-
ory of conscious processing. Current Opinion in Neurobiology, 25, 76–84.
De Loof, E., Ergo, K., Naert, L., Janssens, C., Talsma, D., van Opstal, F., & Verguts,
T. (2018). Signed reward prediction errors drive declarative learning. PLOS One,
13(1).
Dickstein, D. P., Finger, E. C., Brotman, M. A., Rich, B. A., Pine, D. S., Blair, J. R.,
& Leibenluft, E. (2010). Impaired probabilistic reversal learning in youths with
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Deeply Felt Affect
441
mood and anxiety disorders. Psychological Medicine, 40(7), 1089–1100. https://doi.
org/10.1017/S0033291709991462
Ekman, P. (1992). Are there basic emotions? Psychological Review, 99(3), 550553.
Eldar, E., & Niv, Y. (2015). Interaction between emotional state and learning under-
lies mood instability. Nature Communications, 6(1), 1–10.
Eldar, E., Rutledge, R. B., Dolan, R. J., & Niv, Y. (2016). Mood as representation of
momentum. Trends in Cognitive Sciences, 20(1), 15–24. https://doi.org/10.1016/j.
tics.2015.07.010
FitzGerald, T. H., Dolan, R. J., & Friston, K. (2015). Dopamine, reward learning, and
active inference. Front. Comput. Neurosci., 9, 136.
Fontaine, J. R., Scherer, K. R., Roesch, E. B., & Ellsworth, P. C. (2007). The world of
emotions is not two-dimensional. Psychological Science, 18(12), 1050–1057.
Fouragnan, E., Retzler, C., & Philiastides, M. G. (2018). Separate neural represen-
tations of prediction error valence and surprize: Evidence from an fMRI meta-
analysis. Human Brain Mapping, 39(7), 2887–2906.
Friston, K. (2010). The free-energy principle: A unified brain theory? Nature Reviews
Neuroscience, 11(2), 127–138. https://doi.org/10.1038/nrn2787
Friston, K., FitzGerald, T., Rigoli, F., Schwartenbeck, P., O’Doherty, J., & Pezzulo, G.
(2016). Active inference and learning. Neurosci. Biobehav. Rev., 68, 862–879.
Friston, K., FitzGerald, T., Rigoli, F., Schwartenbeck, P., & Pezzulo, G. (2017). Active
inference: A process theory. Neural Computation, 29(1), 1–49.
Friston, K., Levin, M., Sengupta, B., & Pezzulo, G. (2015). Knowing one’s place: A
free–energy approach to pattern regulation. J.R. Soc. Interface, 12, 20141383.
Friston, K. J., Parr, T., & de Vries, B. (2018). The graphical brain: Belief propaga-
tion and active inference. Network Neuroscience, 1(4), 381414. https://doi.org/10.
1162/NETN_a_00018
Friston, K., Parr, T., & Zeidman, P. (2018). Bayesian model reduction. arXiv:1805.07092.
Friston, K. J., Redish, A. D., & Gordon, J. A. (2017). Computational nosology and
precision psychiatry. Computational Psychiatry, 1, 2–23. https://doi.org/10.1162/
CPSY_a_00001
Friston, K., Rigoli, F., Ognibene, D., Mathys, C., Fitzgerald, T., & Pezzulo, G. (2015).
Active inference and epistemic value. Cogn. Neurosci., 6(4), 187–214.
Friston, K. J., Rosch, R., Parr, T., Price, C., & Bowman, H. (2017). Deep temporal
models and active inference. Neuroscience and Biobehavioral Reviews, 77, 388402.
https://doi.org/10.1016/J.NEUBIOREV.2017.04.009
Friston, K., Schwartenbeck, P., FitzGerald, T., Moutoussis, M., Behrens, T., & Dolan,
R. J. (2014). The anatomy of choice: Dopamine and decision–making. Philos. Trans.
R. Soc. Lond. B. Biol. Sci., 369(1655).
Gallagher, S., & Allen, M. (2018). Active inference, enactivism and the hermeneu-
tics of social cognition. Synthese, 195(6), 26272648. https://doi.org/10.1007/
s11229-016-1269-8
Gasper, K., & Clore, G. L. (2002). Attending to the big picture: Mood and global
versus local processing of visual information. Psychological Science, 13(1), 3440.
https://doi.org/10.1111/1467-9280.00406
Gray, J. A. (1994). Three fundamental emotion systems. In P. Ekman & R. J. David-
son (Eds.), The nature of emotion (pp. 243–247). New York: Oxford University
Press.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
442
Hesp et al.
Gyurak, A., Gross, J. J., & Etkin, A. (2011). Explicit and implicit emotion regulation:
A dual-process framework. Cognition and Emotion, 25(3), 400–412.
Hayes, S. C. (2016). Acceptance and commitment therapy, relational frame theory,
and the third wave of behavioral and cognitive therapies. Behavior Therapy, 47(6),
869–885.
Hesp, C., Tschantz, A., Millidge, B., Ramstead, M. J. D., Friston, K. J., & Smith,
R. (Forthcoming). Sophisticated affective inference: Simulating anticipatory af-
fective dynamics of imagining future events. In Proceedings of the First Interna-
tional Workshop on Active Inference—Communications in Computer and Information
Science.
Hesp, C., Ramstead, M., Constant, A., Badcock, P., Kirchhoff, M., & Friston, K. (2019).
A multi-scale view of the emergent complexity of life: A free-energy proposal. In
Springer Proceedings in Complexity (pp. 195–227). Berlin: Springer.
Hohwy, J. (2016). The self-evidencing brain. Nous, 50(2), 259285. https://doi.org/10.
1111/nous.12062
Itti, L., & Baldi, P. (2009). Bayesian surprise attracts human attention. Vision Research,
49(10), 12951306. https://doi.org/10.1016/j.visres.2008.09.007
Joffily, M., & Coricelli, G. (2013). Emotional valence and the free–energy principle.
PLOS Computational Biology, 9(6), e1003094. https://doi.org/10.1371/journal.
pcbi.1003094
Johnston, V. S. (2003). The origin and function of pleasure. Cognition and Emotion, 17,
167–179.
Kaplan, R., & Friston, K. J. (2018). Planning and navigation as active inference. Bio-
logical Cybernetics, 112, 323–343.
Lane, R., Solms, M., Weihs, K., Hishaw, A., & Smith, R. (2020). Affective agnosia:
A core affective processing deficit in the alexithymia spectrum. BioPsychoSocial
Medicine, 14, 20. https://doi.org/10.1186/s13030-020-00184-w
Lane, R. D., Weihs, K. L., Herring, A., Hishaw, A., & Smith, R. (2015). Affective
agnosia: Expansion of the alexithymia construct and a new opportunity to in-
tegrate and extend Freud’s legacy. Neurosci. Biobehav. Rev., 55, 594–611. https:
//doi.org/10.1016/j.neubiorev.2015.06.007
Limanowski, J., & Friston, K. (2018). “Seeing the dark”: Grounding phenomenal
transparency and opacity in precision estimation for active inference. Frontiers
in Psychology, 9, 643. https://doi.org/10.3389/fpsyg.2018.00643
Lindquist, K. A., Satpute, A. B., Wager, T. D., Weber, J., & Barrett, L. F. (2016). The
brain basis of positive and negative affect: Evidence from a meta-analysis of the
human neuroimaging literature. Cerebral Cortex, 26(5), 1910–1922.
Linson, A., Parr, T., & Friston, K. J. (2020). Active inference, stressors, and psychologi-
cal trauma: A neuroethological model of (mal)adaptive explore–exploit dynamics
in ecological context. Behavioral Brain Research, 380, 112421.
Metzinger, T. (2017). The problem of mental action. In T. Metzinger & W. Wiese (Eds.),
Philosophy and predictive processing. Frankfurt am Main: MIND Group.
Mirza, M. B., Adams, R. A., Mathys, C. D., & Friston, K. J. (2016). Scene construction,
visual foraging, and active inference. Frontiers in Computational Neuroscience, 10,
56. https://doi.org/10.3389/fncom.2016.00056
Moriuchi, J. M., Klin, A., & Jones, W. (2017). Mechanisms of diminished attention to
eyes in autism. American Journal of Psychiatry, 174(1), 26–35.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Deeply Felt Affect
443
Morrison, S. E., & Salzman, C. D. (2009). The convergence of information about re-
warding and aversive stimuli in single neurons. J. Neurosci., 29, 11471–11483.
Niu, Y., Todd, R. M., & Anderson, A. K. (2012). Affective salience can reverse the
effects of stimulus-driven salience on eye movements in complex scenes. Frontiers
in Psychology, 3, 336. https://doi.org/10.3389/fpsyg.2012.00336
Palacios, E. R., Razi, A., Parr, T., Kirchhoff, M., & Friston, K. (2019). On Markov
blankets and hierarchical self-organisation. Journal of Theoretical Biology, 486.
https://doi.org/10.1016/j.jtbi.2019.110089
Panksepp, J., Lane, R. D., Solms, M., & Smith, R. (2017). Reconciling cognitive and
affective neuroscience perspectives on the brain basis of emotional experience.
Neuroscience and Biobehavioral Reviews, 76, 187–215.
Park, J., & Banaji, M. R. (2000). Mood and heuristics: The influence of happy and
sad states on sensitivity and bias in stereotyping. Journal of Personality and Social
Psychology, 78(6), 10051023. https://doi.org/10.1037/0022-3514.78.6.1005
Parr, T., & Friston, K.
(2017). Working memory, attention, and salience
in active inference. Scientific Reports, 7(1), 14678. https://doi.org/10.1038/
s41598-017-15249-0
J.
Parr, T., Markovic, D., Kiebel, S. J., & Friston, K. J. (2019). Neuronal message passing
using mean-field, Bethe, and marginal approximations. Scientific Reports, 9, 1889.
https://doi.org/10.1038/s41598-018-38246-3
Paton, J. J., Belova, M. A., Morrison, S. E., & Salzman, C. D. (2006). The primate amyg-
dala represents the positive and negative value of visual stimuli during learning.
Nature, 439, 865870.
Pessiglione, M., Petrovic, P., Daunizeau, J., Palminteri, S., Dolan, R. J., & Frith, C. D.
(2008). Subliminal instrumental conditioning demonstrated in the human brain.
Neuron, 59(4), 561–567.
Pezzulo, G., Rigoli, F., & Friston, K. (2015). Active inference, homeostatic regulation
and adaptive behavioural control. Progress in Neurobiology, 134, 17–35. https://
doi.org/10.1016/j.pneurobio.2015.09.001
Phaf, R. H., & Rotteveel, M. (2012). Affective monitoring: A generic mechanism for af-
fect elicitation. Frontiers in Psychology, 3, 47. https://doi.org/10.3389/fpsyg.2012.
00047
Phillips, M. L., Ladouceur, C. D., & Drevets, W. C. (2008). A neural model of vol-
untary and automatic emotion regulation: Implications for understanding the
pathophysiology and neurodevelopment of bipolar disorder. Molecular Psychi-
atry, 13(9), 833–857.
Pytka, K., Podkowa, K., Rapacz, A., Podkowa, A., Zmudzka, E., Olczyk, A., & Fil-
ipek, B. (2016). The role of serotonergic, adrenergic and dopaminergic receptors
in antidepressantlike effect. Pharmacological Reports, 68(2), 263–274.
Ramstead, M. J. D., Kirchhoff, M. D., Constant, A., & Friston, K. J. (2019). Multiscale
integration: Beyond internalism and externalism. Synthese, 130. https://doi.org/
10.1007/s11229-019-02115-x
Rao, R. P. N. (2010). Decision making under uncertainty: A neural model based on
partially observable Markov decision processes. Frontiers in Computational Neu-
roscience, 4, 146. https://doi.org/10.3389/fncom.2010.00146
Russell, J. A. (1980). A circumplex model of affect. Journal of Personality and Social
Psychology, 39(6), 1161.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
444
Hesp et al.
Rutledge, R. B., Skandali, N., Dayan, P., & Dolan, R. J. (2015). Dopaminergic modula-
tion of decision making and subjective well-being. Journal of Neuroscience, 35(27),
9811–9822.
Sajid, N., Ball, P. J., & Friston, K. J. (2020). Active inference: Demystified and compared.
http://arxiv.org/abs/1909.10863
Schmidhuber, J. (2010). Formal theory of creativity, fun, and intrinsic motivation
(1990–2010). IEEE Transactions on Autonomous Mental Development, 2(3), 230247.
https://doi.org/10.1109/TAMD.2010.2056368
Schultz, W., Dayan, P., & Montague, P. R. (1997). A neural substrate of prediction and
reward. Science, 275, 1593–1599.
Schwartenbeck, P., FitzGerald, T. H. B., Mathys, C., Dolan, R., & Friston, K.
(2015). The dopaminergic midbrain encodes the expected certainty about desired
outcomes. Cerebral Cortex, 25(10), 3434–3445. https://doi.org/10.1093/cercor/
bhu159
Seth, A. K., & Friston, K. J. (2016). Active interoceptive inference and the emotional
brain. Philosophical Transactions of the Royal Society B: Biological Sciences, 371(1708),
20160007. https://doi.org/10.1098/rstb.2016.0007
Smith, R., Alkozei, A., Bao, J., & Killgore, W. D. S. (2018). Successful goal-directed
memory suppression is associated with increased inter-hemispheric coordina-
tion between right and left frontoparietal control networks. Psychological Reports,
121(1), 93111. https://doi.org/10.1177/0033294117723018
Smith, R., Alkozei, A., Lane, R. D., & Killgore, W. D. S. (2016). Unwanted reminders:
The effects of emotional memory suppression on subsequent neuro-cognitive
processing. Consciousness and Cognition, 44, 103–113. https://doi.org/10.1016/j.
concog.2016.07.008
Smith, R., Bajaj, S., Dailey, N. S., Alkozei, A., Smith, C., Sanova, A., . . . Killgore, W.
D. S. (2018). Greater cortical thickness within the limbic visceromotor network
predicts higher levels of trait emotional awareness. Consciousness and Cognition,
57, 5461. https://doi.org/10.1016/j.concog.2017.11.004
Smith, R., Kaszniak, A. W., Katsanis, J., Lane, R. D., & Nielsen, L. (2019). The impor-
tance of identifying underlying process abnormalities in alexithymia: Implica-
tions of the three-process model and a single case study illustration. Consciousness
and Cognition, 68, 33–46. https://doi.org/10.1016/j.concog.2018.12.004
Smith, R., Killgore, W. D. S., Alkozei, A., & Lane, R. D. (2018). A neuro-cognitive
process model of emotional intelligence. Biol. Psychol., 139, 131–151. https://doi.
org/10.1016/j.biopsycho.2018.10.012
Smith, R., Killgore, W. D., & Lane, R. D. (2020). The structure of emotional experience
and its relation to trait emotional awareness: A theoretical review. Emotion, 18(5),
670.
Smith, R., Kirlic, N., Stewart, J. L., Touthang, J., Kuplicki, R., Khalsa, S. S., . . . Aup-
perle, R. (in press). Greater decision uncertainty characterizes a transdiagnostic
patient sample during approach-avoidance conflict: A computational modeling
approach. Journal of Psychiatry and Neuroscience.
Smith, R., Kuplicki, R., Feinstein, J., Forthman, K. L., Stewart, J. L., Paulus, M. P., . . .
Kalsa, S. S. (2020). A Bayesian computational model reveals a failure to adapt interocep-
tive precision estimates across depression, anxiety, eating, and substance use disorders.
medRxiv:2020.06.03.20121343.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Deeply Felt Affect
445
Smith, R., Kuplicki, R., Teed, A., Upshaw, V., & Khalsa, S. S. (2020). Confirmatory evi-
dence that healthy individuals can adaptively adjust prior expectations and interoceptive
precision estimates. Paper presented at the First International Workshop on Ac-
tive Inference. https://www.biorxiv.org/content/biorxiv/early/2020/09/01/
2020.08.31.275594.full.pdf
Smith, R., & Lane, R. D. (2015). The neural basis of one’s own conscious and uncon-
scious emotional states. Neuroscience and Biobehavioral Reviews, 57, 1–29.
Smith, R., & Lane, R. D. (2016). Unconscious emotion: A cognitive neuroscientific
perspective. Neuroscience and Biobehavioral Reviews, 69, 216–238.
Smith, R., Lane, R. D., Alkozei, A., Bao, J., Smith, C., Sanova, A., . . . Killgore, W.
D. S. (2017). Maintaining the feelings of others in working memory is associated
with activation of the left anterior insula and left frontal–parietal control network.
Social Cognitive and Affective Neuroscience, 12(5), 848860. https://doi.org/10.1093/
scan/nsx011
Smith, R., Lane, R., Alkozei, A., Bao, J., Smith, C., Sanova, A., . . . Killgore, W. (2018).
The role of medial prefrontal cortex in the working memory maintenance of one’s
own emotional responses. Scientific Reports, 8.
Smith, R., Lane, R., Nadel, L., & Moutoussis, M. (2020). A computational neuro-
science perspective on the change process in psychotherapy. In R. Lane & L.
Nadel (Eds.), Neuroscience of enduring change: Implications for psychotherapy. New
York: Oxford University press.
Smith, R., Lane, R. D., Parr, T., & Friston, K. J. (2019). Neurocomputational mecha-
nisms underlying emotional awareness: Insights afforded by deep active infer-
ence and their potential clinical relevance. Neuroscience and Biobehavioral Reviews,
107, 473–491.
Smith, R., Lane, R., Sanova, A., Alkozei, A., Smith, C., & Killgore, W. W. D. (2018).
Common and unique neural systems underlying the working memory main-
tenance of emotional vs. bodily reactions to affective stimuli: The moderat-
ing role of trait emotional awareness. Frontiers in Human Neuroscience, 12, 370.
https://doi.org/10.3389/fnhum.2018.00370
Smith, R., Parr, T., & Friston, K. J. (2019). Simulating emotions: An active inference
model of emotional state inference and emotion concept learning. Front. Psychol.,
10, 2844. https://doi.org/10.3389/fpsyg.2019.02844
Smith, R., Schwartenbeck, P., Stewart, J. L., Kuplicki, R., Ekhtiari, H., Paulus, M., &
Tulsa 1000 Investigators (2020). Imprecise action selection in substance use disor-
der: Evidence for active learning impairments when solving the explore–exploit
dilemma. Drug and Alcohol Dependence, 2015, 108208.
Smith, R., Steklis, H. D., Steklis, N. G., Weihs, K. L., & Lane, R. D. (2020). The evolu-
tion and development of the uniquely human capacity for emotional awareness:
A synthesis of comparative anatomical, cognitive, neurocomputational, and evo-
lutionary psychological perspectives. Biological Psychology, 154, 107925.
Smith, R., Thayer, J. F., Khalsa, S. S., & Lane, R. D. (2017). The hierarchical basis of
neurovisceral integration. Neuroscience and Biobehavioral Reviews, 75, 274–296.
Smith, R., Weihs, K. L., Alkozei, A., Killgore, W. D. S., & Lane, R. D. (2019). An
embodied neurocomputational framework for organically integrating biopsy-
chosocial processes: An application to the role of social support in health
and disease. Psychosomatic Medicine, 81, 125–145. https://doi.org/10.1097/
PSY.0000000000000661
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
446
Hesp et al.
Sohal, V. S., Zhang, F., Yizhar, O., and Deisseroth, K. (2009). Parvalbumin neurons
and gamma rhythms synergistically enhance cortical circuit performance. Nature,
459, 698702.
Stauffer, W. R., Lak, A., & Schultz, W. (2014). Dopamine reward prediction error re-
sponses reflect marginal utility. Current Biology, 24, 2491–2500.
Stephan, K. E., Manjaly, Z. M., Mathys, C. D., Weber, L. A. E., Paliwal, S., Gard, T.,
. . . Petzschner, F. H. (2016). Allostatic self–efficacy: A metacognitive theory of
dyshomeostasis-induced fatigue and depression. Frontiers in Human Neuroscience,
10, 550. https://doi.org/10.3389/fnhum.2016.00550
Sutton, R. S., & Barto, A. G. (2018). Reinforcement learning: An introduction. Cam-
bridge, MA: MIT Press.
Topolinski, S., Likowski, K. U., Weyers, P., & Strack, F. (2009). The face of fluency:
Semantic coherence automatically elicits a specific pattern of facial muscle reac-
tions. Cogn. Emot., 23, 260271.
Van de Cruys, S. (2017). Affective value in the predictive mind. Open Mind.
https://doi.org/10.15502/9783958573253
Veale, R., Hafed, Z. M., & Yoshida, M. (2017). How is visual salience computed
in the brain? Insights from behavior, neurobiology and modeling. Philosoph-
ical Transactions of the Royal Society B: Biological Sciences, 372(1714), 20160113.
https://doi.org/10.1098/rstb.2016.0113
Watson, D., Clark, L. A., & Tellegen, A. (1988). Development and validation of brief
measures of positive and negative affect: The PANAS scales. Journal of Personality
and Social Psychology, 54(6), 1063.
Whyte, C. J., & Smith, R. (in press). The predictive global neuronal workspace: A
formal active inference model of visual consciousness. Progress in Neurobiology.
Willems, S., & Van der Linden, M. (2006). Mere exposure effect: A consequence of di-
rect and indirect fluency-preference links. Consciousness and Cognition, 15, 323341.
Williams, L. M., & Gordon, E. (2007). Dynamic organization of the emotional brain:
Responsivity, stability, and instability. Neuroscientist, 13, 349370
Winkielman, P., Berridge, K. C., & Wilbarger, J. L. (2005). Unconscious affective reac-
tions to masked happy versus angry faces influence consumption behavior and
judgments of value. Personality and Social Psychology Bulletin, 31(1), 121–135.
Received March 3, 2020; accepted August 17, 2020.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
2
3
9
8
1
8
9
6
8
4
9
n
e
c
o
_
a
_
0
1
3
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3