LETTER
Communicated by Frederic Crevecoeur
Model-Free Robust Optimal Feedback Mechanisms
of Biological Motor Control
Tao Bian
tbian@nyu.edu
Control and Networks Lab, Department of Electrical and Computer Engineering,
Tandon School of Engineering, New York University, Brooklyn, NY 11201, U.S.A.
Daniel M. Wolpert
wolpert@columbia.edu
Zuckerman Mind Brain Behavior Institute, Department of Neuroscience, Columbia
University, New York, NY 10027, U.S.A., and Department of Engineering,
University of Cambridge, Cambridge CB2 1PZ, U.K.
Zhong-Ping Jiang
zjiang@nyu.edu
Control and Networks Lab, Department of Electrical and Computer Engineering,
Tandon School of Engineering, New York University, Brooklyn, NY 11201, U.S.A.
Sensorimotor tasks that humans perform are often affected by different
sources of uncertainty. Nevertheless, the central nervous system (CNS)
can gracefully coordinate our movements. Most learning frameworks
rely on the internal model principle, which requires a precise inter-
nal representation in the CNS to predict the outcomes of our motor
commands. However, learning a perfect internal model in a complex
environment over a short period of time is a nontrivial problem. Indeed,
achieving proficient motor skills may require years of training for some
difficult tasks. Internal models alone may not be adequate to explain
the motor adaptation behavior during the early phase of learning. Re-
cent studies investigating the active regulation of motor variability, the
presence of suboptimal inference, and model-free learning have chal-
lenged some of the traditional viewpoints on the sensorimotor learning
mechanism. As a result, it may be necessary to develop a computational
framework that can account for these new phenomena. Here, we de-
velop a novel theory of motor learning, based on model-free adaptive
optimal control, which can bypass some of the difficulties in existing
theories. This new theory is based on our recently developed adaptive
dynamic programming (ADP) and robust ADP (RADP) methods and is
especially useful for accounting for motor learning behavior when an
internal model is inaccurate or unavailable. Our preliminary computa-
tional results are in line with experimental observations reported in the
Neural Computation 32, 562–595 (2020)
https://doi.org/10.1162/neco_a_01260
© 2020 Massachusetts Institute of Technology
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Model-Free Robust Optimal Motor Control
563
literature and can account for some phenomena that are inexplicable
using existing models.
1 Introduction
Humans develop coordinated movements that allow efficient interaction
with the environment. Despite extensive research on the topic, the underly-
ing computational mechanism of sensorimotor control and learning is still
largely an open problem (Flash & Hogan, 1985; Uno, Kawato, & Suzuki,
1989; Harris & Wolpert, 1998; Haruno & Wolpert, 2005; Todorov & Jordan,
2002; Todorov, 2004, 2005; Bhushan & Shadmehr, 1999; Shadmehr & Mussa-
Ivaldi, 1994; Wolpert & Ghahramani, 2000). Indeed, recent research find-
ings, including model-free learning (Huang, Haith, Mazzoni, & Krakauer,
2011; Haith & Krakauer, 2013), the active regulation of motor variability
(Renart & Machens, 2014; Wu, Miyamoto, Castro, Olveczky, & Smith, 2014;
Cashaback, McGregor, & Gribble, 2015; Lisberger & Medina, 2015; Pekny,
Izawa, & Shadmehr, 2015; Vaswani et al., 2015), and the presence of subop-
timal inference (Beck, Ma, Pitkow, Latham, & Pouget, 2012; Bach & Dolan,
2012; Renart & Machens, 2014; Acerbi, Vijayakumar, & Wolpert, 2014), have
challenged some of the traditional models of sensorimotor learning, poten-
tially requiring the development of a new computational framework.
Several computational theories have been proposed to account for senso-
rimotor control and learning (Shadmehr & Mussa-Ivaldi, 2012). One widely
accepted conjecture is that the central nervous system (CNS) selects trajec-
tories so as to minimize a cost function (Flash & Hogan, 1985; Uno et al.,
1989; Harris & Wolpert, 1998; Haruno & Wolpert, 2005; Todorov & Jordan,
2002; Qian, Jiang, Jiang, & Mazzoni, 2012). This perspective has inspired
a number of optimization-based models of motor control over the past
three decades. In early work, Flash and Hogan (1985) and Uno et al. (1989)
proposed that the CNS coordinates movements by minimizing the time in-
tegral of the jerk or torque change. Although simulations under these theo-
ries are consistent with experimental results, it is not clear why and how the
CNS would minimize these specific types of costs. Being aware of this diffi-
culty, Wolpert and his coworkers (Harris & Wolpert, 1998; van Beers, Bara-
duc, & Wolpert, 2002; Haruno & Wolpert, 2005) suggested an alternative
theory that the goal of the motor system is to minimize the end-point vari-
ance caused by signal-dependent noise. Later, Todorov and his colleagues
(Todorov & Jordan, 2002; Todorov, 2004, 2005) considered sensorimotor con-
trol within the framework of linear quadratic regulator (LQR) and linear
quadratic gaussian (LQG) theories and conjectured that the CNS aims to
minimize a mixed cost function with components that specify both accuracy
and energy costs. Despite the different interpretations of the cost, a com-
mon assumption in these frameworks is that the CNS first identifies the sys-
tem dynamics and then solves the optimization or optimal control problem
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
564
T. Bian, D. Wolpert, and Z.-P. Jiang
based on the identified model (Shadmehr & Mussa-Ivaldi, 1994; Wolpert,
Ghahramani, & Jordan, 1995; Kawato, 1999; Todorov & Jordan, 2002; Liu
& Todorov, 2007; Zhou et al., 2016). Indeed, this identification-based idea
has been used extensively to study motor adaptation under external force
field perturbations (Shadmehr & Mussa-Ivaldi, 1994; Bhushan & Shadmehr,
1999; Burdet, Osu, Franklin, Milner, & Kawato, 2001; Franklin, Burdet, Osu,
Kawato, & Milner, 2003). Although these models can explain many charac-
teristics of motor control, such as approximately straight movement trajec-
tories and bell-shape velocity curves (Morasso, 1981), there is no compelling
experimental evidence as to how the CNS manages to generate a perfect in-
ternal representation of the environment in a short period of time, especially
for complex environments.
Huang et al. (2011) and Haith and Krakauer (2013) proposed a different
learning mechanism, known as model-free learning, to explain sensorimo-
tor learning behavior. Some well-known experimentally validated phenom-
ena, such as savings, could be attributed to this learning mechanism. Huang
et al. (2011), Huberdeau, Krakauer, and Haith (2015), and Vaswani et al.
(2015) studied these experimental results via reinforcement learning (RL)
(Sutton & Barto, 2018), a theory in machine learning that studies how an
agent iteratively improves its actions based on the observed responses from
its interacting environment. The study on RL was originally inspired by
the decision-making process in animals and humans (Minsky, 1954). Doya
(2000) discussed that certain brain areas can realize the RL and suggested a
learning scheme for the neurons based on temporal difference (TD) learning
(Sutton, 1988). Izawa, Rane, Donchin, and Shadmehr (2008) used an actor-
critic-based optimal learner in which an RL scheme was proposed to di-
rectly update the motor command. A possible shortcoming of traditional
RL is that discretization and sampling techniques are needed to transform
a continuous-time problem into the setting of discrete-time systems with
discrete-state-action space, which may be computationally intensive. More-
over, rigorous convergence proofs and stability analysis are usually missing
in the related literature.
Another discovery that has challenged the traditional motor learning
framework is that the CNS can regulate, and even amplify, motor variabil-
ity instead of minimizing its effects (Renart & Machens, 2014; Wu et al.,
2014; Cashaback et al., 2015; Lisberger & Medina, 2015; Pekny et al., 2015;
Vaswani et al., 2015). Wu et al. (2014) and Cashaback et al. (2015) conjectured
that this puzzling phenomenon is related to the use of RL in sensorimotor
learning. Motor variability facilitates the exploration phase in RL and, as a
result, promotes motor learning. The importance of motor variability was
also illustrated in Pekny et al. (2015) by showing that the ability to increase
motor variability is impaired in patients with Parkinson’s disease. Despite
these experimental results, there still lacks a convincing theoretical analysis
that can justify the need to regulate motor variability.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Model-Free Robust Optimal Motor Control
565
Finally, it has been reported recently (Beck et al., 2012; Bach & Dolan,
2012; Renart & Machens, 2014; Acerbi et al., 2014) that motor variability,
traditionally thought of as a consequence of the internal noise character-
ized by neural variation in the sensorimotor circuit (Harris & Wolpert, 1998;
van Beers, 2007; Faisal, Selen, & Wolpert, 2008; Chaisanguanthum, Shen, &
Sabes, 2014; Herzfeld, Vaswani, Marko, & Shadmehr, 2014), can also arise
through suboptimal inference. Beck et al. (2012) argued that suboptimal
inference, usually caused by modeling errors of the real-world environ-
ment, should be the dominant factor in motor variation with factors such
as signal-dependent noise having only a limited influence. The presence of
such suboptimal inference has also been studied by Acerbi et al. (2014) us-
ing Bayesian decision theory. Regardless of these new results, it is still an
open problem how to integrate the presence of suboptimal inference into
the existing optimal control-based motor learning framework.
In light of the above challenges, here we propose a new sensorimotor
learning theory based on adaptive dynamic programming (ADP) (Lewis,
Vrabie, & Vamvoudakis, 2012; Vrabie et al., 2013; Lewis & Liu, 2013; Bian,
Jiang, & Jiang, 2014, 2016; Bertsekas, 2017; He & Zhong, 2018) and its ro-
bust variant (RADP) (Jiang & Jiang, 2013, 2017; Wang, He, & Liu, 2017).
ADP and RADP combine ideas from RL and (robust) optimal control the-
ory and have several advantages over existing motor control theories. First,
sharing some essential features with RL, ADP, and RADP are data-driven,
non-model-based approaches that directly update the control policy with-
out the need to identify the dynamical system. Fundamentally different
from traditional RL, ADP aims at developing a stabilizing optimal control
policy for discrete-time and continuous-time dynamical systems via online
learning and thus is an ideal candidate for studying the model-free learning
mechanism in the human sensorimotor system. Second, under our theory,
motor variability plays an important role in the sensorimotor learning pro-
cess. Similar to the exploration noise in RL, the active regulation of motor
variability promotes the search for better control strategies in each learn-
ing cycle and, as a result, improves the learning performance in terms of
accuracy and convergence speed. Moreover, both signal-dependent noise
and suboptimal inference (also known as dynamic uncertainty in the
nonlinear control literature; see Liu, Jiang, & Hill, 2014; Jiang & Liu, 2018)
are taken into account in our model. Hence, our model of learning resolves
the apparent inconsistency between existing motor control theories and the
experimental observation of the positive impact of motor variability. Third,
in contrast to our prior results (Jiang & Jiang, 2014, 2015), the proposed mo-
tor learning framework is based on our recently developed continuous-time
value iteration (VI) approach (Bian & Jiang, 2016), in which the knowledge
of an initial stabilizing control input is no longer required. As a result, the
proposed ADP and RADP learning mechanisms can resolve both stabil-
ity and optimality issues during online learning. Consequently, this new
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
566
T. Bian, D. Wolpert, and Z.-P. Jiang
learning theory is more suitable for explaining, for example, model-free
learning in unstable environments (Burdet et al., 2001, 2006).
During the writing of this letter, we noticed that Crevecoeur, Scott, and
Cluff (2019) have also studied the model-free control mechanism in human
sensorimotor systems from the perspective of H∞
control, where model-
ing uncertainty and signal-dependent noise are modeled as an unknown
disturbance.
2 Human Arm Movement Model
We focus on the sensorimotor learning tasks that Harris and Wolpert (1998)
and Burdet et al. (2001) considered, in which human subjects make point-
to-point reaching movements in the horizontal plane.
In our computer experiment, the dynamics of the arm are simplified to
a point-mass model as follows:
˙p = v,
m ˙v = a − bv + f,
τ ˙a = u − a + G1uξ
+ G2uξ
2
,
1
(2.1)
(2.2)
(2.3)
x
v
y]T , a = [ax ay]T , and u = [ux uy]T denote the
where p = [px py]T , v = [v
two-dimensional hand position, velocity, actuator state, and control input,
respectively; m denotes the mass of the hand; b is the viscosity constant;
τ is the time constant; ξ
2 are gaussian white noises (Arnold, 1974);
and
1 and ξ
(cid:2)
(cid:3)
c1
c2
0
0
=
G1
and G2
=
(cid:3)
(cid:2)
0 −c2
c1
0
are gain matrices of the signal-dependent noise (Harris & Wolpert, 1998;
Liu & Todorov, 2007).
We use f to model possible external disturbances (Liu & Todorov, 2007).
For example, setting f = β px with β > 0 produces the divergent force field
(DF) generated by the parallel-link direct drive air-magnet floating manip-
ulandum (PFM) used in Burdet et al. (2001).
To fit this model into the standard optimal control framework, we rewrite
system 2.1 to 2.3 with f = 0 in the form of a stochastic dynamical system
(Arnold, 1974),
dx = Axdt + B(udt + G1udw
1
+ G2udw
2),
(2.4)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Model-Free Robust Optimal Motor Control
567
Table 1: Parameters of the Arm Movement Model.
Parameters
Description
Value
m
b
τ
c1
c2
Hand mass
Viscosity constant
Time constant
Noise magnitude
Noise magnitude
1.3 kg
10 N·s/m
0.05 s
0.075
0.025
where w
1 and w
2 are standard Brownian motions, and
⎤
⎡
⎤
⎥
⎦ , A =
⎡
⎢
⎣
p
v
a
x =
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
0
0
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0 − b
1
0
m
m
0 − b
1
0
m
m
0 − 1
0
τ
0 − 1
τ
0
0
0
0
0
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
, B =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
0
0
0
0
1
τ
0
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
.
0
0
0
0
0
1
τ
The model parameters used in our simulations throughout this letter are
given in Table 1.
Following Todorov and Jordan (2002) and Liu and Todorov (2007), the
optimal control problem is formulated as one of finding an optimal con-
troller to minimize the following cost with respect to the nominal system of
equation 2.4 without the signal-dependent noise,
J (x(0); u) =
(cid:10) ∞
(cid:11)
0
xT Qx + uT Ru
(cid:12)
dt,
(2.5)
where Q = QT > 0 and R = RT > 0 are constant weighting matrices.
It is well known that J is minimized under the optimal controller u∗ =
−K∗x, where K∗ = R−1BT P∗, with P∗ = P∗T > 0 the unique solution to the
following algebraic Riccati equation:
AT P + PA − PBR
−1BT P + Q = 0.
(2.6)
Moreover, infu J (x; u) = xT P∗x.
Note that Q and R represent the trade-off between movement accuracy
(Q) and the effort exerted by the human subject to accomplish the task (R).
Generally, choosing R with small eigenvalues leads to a high-gain optimal
controller. This improves the transient performance, yet the price to be paid
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
568
T. Bian, D. Wolpert, and Z.-P. Jiang
is a large control input and higher energy consumption. For illustration, we
define R = I2 and Q as
xT Qx = 0.3xT
x Qxxx
+ 0.7xT
y Qyxy
,
(2.7)
where xx and xy are the components in x- and y-coordinates of the system
state, respectively, and
Qx
= Qy
=
⎡
⎢
⎣
1 × 104
0
0
⎤
⎥
⎦ .
0
1 × 102
0
0
0
1 × 10
−3
In this letter, in contrast to Liu and Todorov (2007), we develop an itera-
tive algorithm known as VI (Bian & Jiang, 2016, algorithm 1) to approximate
P∗
. On the basis of this algorithm, we then give a novel model-free
method to learn the optimal control policy without knowing model param-
eters. First, we give the VI algorithm:
and K∗
1. Start with a P0
2. Repeat the following two steps until convergence:
> 0. Set k = 0.
= PT
0
Pk+1
= Pk
+ (cid:5)
k
(cid:11)
AT Pk
+ PkA − PkBR
−1BT Pk
(cid:12)
+ Q
,
Kk+1
= R
−1BT Pk
,
where the step size (cid:5)
(cid:5)
k
= ∞.
k
> 0 decreases monotonically to 0 and
(2.8)
(2.9)
(cid:13)∞
k=0
Theorem 1 guarantees the convergence of the algorithm. The proof of
theorem 1 is omitted since it is a direct extension of the proof of Bian and
Jiang (2016, theorem 3.3).
Theorem 1. For sufficiently small (cid:5)
limk→∞Kk
= K∗.
0
> 0, we have limk→∞Pk
= P∗, and
3 Model-Free Learning in Human Sensorimotor Systems
In section 2, we briefly reviewed the model-based optimal motor control
problem. We have not yet touched on the topic of how the human subject
learns the optimal controller when the model parameters are not precisely
known.
In this section, we extend the ADP algorithm from Bian and Jiang
(2019) to study human biological learning behavior. The learning process
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Model-Free Robust Optimal Motor Control
569
considered in this section consists of multiple trials. In each trial, the hu-
man subject performs a reaching movement from the starting point to the
target. We say a learning trial is successful if the human subject can reach a
predefined small neighborhood of the target state successfully. If the human
subject hits the boundary of the experimental environment before reaching
the target area, this learning trial is terminated and the next learning trial
starts.
< · · · < tl−1
3.1 ADP-Based Model-Free Learning. Before giving our online ADP
<
learning algorithm, we introduce an increasing time sequence t j, 0 ≤ t0
< tl in one learning trial, where the movement starts at time 0
t1
and tl is the time when the human subject reaches the target area or hits the
, t j+1], we introduce
boundary of the experimental environment. Over [t j
the following feature vectors,1
ψ
j
=
(cid:10)
t j
t j+1
(cid:11)
q
[xT v T
k ]T
(cid:12)
dt,
φ
j
=
(cid:2)
(cid:14)
(cid:14)t j+1
qT (x)
t j
(cid:10)
t j+1
−
t j
qT (dx)
(cid:3)
rkdt
T
,
(cid:10)
t j+1
t j
where rk(t) = xT (t)Qx(t) + uT
k (t)Ruk(t) and v
k
= uk
+ G1uk
ξ
1
+ G2uk
ξ
2.
Now we are ready to give our ADP algorithm (algorithm 1).2 Note that
Fk in algorithm 1 is the advantage matrix, which contains the information
of the model parameters:
(cid:2)
=
Fk
PkA + AT Pk
BT Pk
+ Q PkB
R
(cid:3)
(cid:2)
:=
(cid:3)
.
Fk,11 Fk,12
FT
k,12 Fk,22
Algorithm 1 is a direct extension of Bian and Jiang (2019, algorithm 2) to the
stochastic environment. The convergence of algorithm 1 is guaranteed in
the following theorem. It is straightforward to deduce the proof of theorem
2 from Bian and Jiang (2019).
(cid:13)
Theorem 2. If the conditions in theorem 1 hold and there exist l0
ψ
such that 1
j
l
1 converge to P∗ and u∗, respectively.
> 0 and α > 0
> αI for all l > l0, then Pk and uk obtained from algorithm
ψ T
j
l
j=1
The initial input u0 in algorithm 1 represents the a priori belief on the op-
timal control policy. In particular, u0 corresponds to an initial control policy
obtained from our daily experience, which may be stabilizing or optimal in
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
1
2
For any x ∈ Rn, denote q(x) = [x2
1
For any A = AT ∈ Rn×n, denote vech(A) = [a11
∈ R is the (i, j)th element of matrix A.
, 2x1x2
, . . . , 2x1xn, x2
, 2x2x3
2
, . . . , a1n
, a12
where ai j
, . . . , 2xn−1xn, x2
, . . . , an−1n
, a22
, a23
n]T .
, ann]T ,
570
T. Bian, D. Wolpert, and Z.-P. Jiang
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
the absence of external disturbance (such as the divergent force field, DF).
However, in the presence of DF, u0 may no longer be stabilizing. In this case,
the human sensorimotor system will require some form of motor learning.
In the end, a new stabilizing optimal control policy with respect to this new
environment will be obtained.
Algorithm 1 is an off-policy method (Sutton & Barto, 2018) in the sense
that the controller updated by the algorithm—the estimation policy in RL
literature (Sutton & Barto, 2018)—is different from the system input used
to generate the online data (also known as behavior policy in RL literature).
Indeed, the control policy learned from the kth iteration in our algorithm is
uk, while v
k is used to generate the online data. An advantage of this differ-
ence is that the behavior policy can generate a system trajectory satisfying
the persistent excitation (PE) condition on ψ
j in theorem 2 by including the
exploration noise (ξ
1 and ξ
2 in our case); at the same time, we can still accu-
rately estimate and update the estimation policy.
Note that {(cid:5)
} relates to the learning rate of the human subject. Espe-
cially, (cid:5)
k is large at the beginning of the learning phase, meaning the learning
mechanism is aggressive and greedy; as the number of learning iterations
increases, the learning process slows down, and the human subject tends to
k
Model-Free Robust Optimal Motor Control
571
be more conservative. Discussions on how the step size affects the learning
rate and the savings behavior are given in section 5.
It is interesting to note that our ADP learning algorithm shares some
> 0 is sufficiently small, we
similarities with TD learning. Indeed, when (cid:5)
k
have
(cid:5)xT (t)(Fk,11
− Fk,12F
−1
22 FT
k,12)x(t)
+ Pk(Ax(t) + Bu) + xT (t)Qx(t) + uT Ru}
(cid:10)
{(Ax(t) + Bu)T Pk
= (cid:5) inf
u
(cid:15)
xT (t + (cid:5))Pkx(t + (cid:5)) − xT (t)Pkx(t) +
≈ inf
u
t
t+(cid:5)
(cid:16)
(xT Qx + uT Ru)ds
,
(3.1)
which is consistent with the definition of TD error (Sutton, 1988). Note that
this error term represents the difference between P∗
and Pk, since equation
3.1 reduces to zero when Pk
= P∗
.
The online learning framework proposed in this section has two unique
features that make it an ideal candidate to study human sensorimotor
learning behavior. First, different from traditional motor learning models
based on RL and optimal control, our learning framework is based on the
continuous-time ADP. Similar to other RL methods, ADP is a model-free
approach that directly updates the control policy with online data with-
out the need to identify the dynamic model. However, unlike RL, which is
mainly devised for discrete environments, ADP can tackle a large number
of continuous-time dynamical systems with continuous-state-action space.
Moreover, the stability and the robustness of the closed-loop dynamical
system can be guaranteed under the ADP framework. Second, the pro-
posed VI-driven learning scheme is also fundamentally different from the
PI-based stochastic ADP methods in the literature (Jiang & Jiang, 2014, 2015;
Bian et al., 2016). A significant improvement of using VI is that an initial
stabilizing control policy is no longer required. This learning framework
provides a theoretical justification for the human sensorimotor system to
regain both stability and optimality from unstable environments.
3.2 Simulation Validation.
3.2.1 Divergence Force Field. First, we simulate the motor learning exper-
iment in the divergence force field (DF). In this case, we choose f = β px in
equation 2.1 with β > 0 to represent the DF generated by the PFM. Here we
pick β = 150. Since before conducting the experiment, the human subjects
are asked to practice in the NF for a long period, we assume that the hu-
man subject has already adapted to this NF; that is, an optimal controller
with respect to the NF has been obtained. We denote the control gain matrix
with respect to this optimal controller in the NF as K0 and the corresponding
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
572
T. Bian, D. Wolpert, and Z.-P. Jiang
Figure 1: ADP learning in the DF. Five hand paths are shown in the DF at differ-
ent stages of the experiment. (a) First five trials on exposure to the DF. (b) Five
trials after ADP learning in the DF is complete. (c) Five sequential trials in the
postexposure phase when the NF is reapplied.
performance matrix as P0:
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
(cid:2)
=
P0
=
K0
1039.23
0.00
87.60
0.00
2.74
0.00
0.00
1949.88
0.00
144.70
0.00
4.18
87.60
0.00
10.44
0.00
0.33
0.00
⎤
⎥
⎥
⎥
⎥
⎥
,
⎥
⎥
⎥
⎥
⎦
0.00
2.74 0.00
144.70 0.00 4.18
0.33 0.00
0.00
0.00 0.50
16.86
0.01 0.00
0.00
0.00 0.02
0.50
(cid:3)
54.77
0.00
6.67
0.00
0.23
83.67 0.00 10.00 0.00
0.00
0.00
0.33
.
Once the adaptation to the NF is achieved (i.e., the human subjects have
achieved a number of successful trials), the DF is activated. At this stage,
subjects practice in the DF. No information is given to the human subjects
as to when the force field trials will begin. The trajectories in the first five
trials in DF are shown in Figures 1a and 2a. We can easily see that when the
human subject is first exposed to the DF, due to the presence of the force field
( f = β px), the variations are amplified by the divergence force, and thus the
movement is no longer stable under u = −K0x. Indeed, after inspecting the
mathematical model of the motor system in the DF, we see that A − BK0 has
positive eigenvalues.
Note from the movement profile of px in Figure 2a that the divergence in
x-direction is dependent on the initial moving direction. This initial moving
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Model-Free Robust Optimal Motor Control
573
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Figure 2: ADP learning in the DF. Plots show time series of position, velocity,
and acceleration in the x- and y-dimension for a reaching movement to a target
displayed only in y from the start location. Five sequential trials are shown in
the DF at different stages of the experiment. (a) First five trials on exposure to the
DF. (b) Five trials after ADP learning in the DF is complete. (c) Five sequential
trials in the postexposure phase when the NF is reapplied.
574
T. Bian, D. Wolpert, and Z.-P. Jiang
direction is caused by the stochastic disturbance in ax at the starting point of
the movement. In other words, if there was no signal-dependent noise in the
model, the movement would have always been in the y-direction, and hence
no divergence in the x-direction. Moreover, we observe that compared with
Figures 2b and 2c, it takes longer to correct ax from negative to positive, or
vice versa. Thus, we can conclude that the signal-dependent noise causes
bias in the starting movement direction and eventually leads to the unstable
motor behavior.
Denote the optimal gain matrix in the DF as K∗
. Starting from K0 and P0,
the control gain matrix obtained after 50 learning trials is already very close
to K∗
:
(cid:2)
=
K50
(cid:2)
∗ =
K
426.43
0.00
426.48
0.00
0.00
83.67
0.00
83.67
28.11
0.00
28.12
0.00
0.00
0.78
10.00 0.00
0.00
0.33
0.00
0.78 0.00
10.00 0.00 0.33
(cid:3)
,
.
(cid:3)
The simulation results of the sensorimotor system under this new control
policy are given in Figures 1b and 2b. Comparing Figure 1b with Figure 1a,
we can see that after learning, the human subject has regained stability in
the DF. Indeed, compared with K0, some elements in the first row of K50 are
much larger, indicating a higher gain in the x-direction (i.e., the direction of
the divergence force). To further illustrate the effect of high-gain feedback,
the stiffness adaptation is shown in Figure 3. During the learning process,
stiffness increased significantly in the x-direction. Moreover, we see from
Figure 2b that at the beginning of the movement, the magnitude of ax due
to noise is not negligible compared with Figure 2a. However, the control
input derived from the motor learning restrains ax from diverging to infin-
ity and, as a result, achieves stability. An important conclusion drawn from
our learning theory and simulation result is that the target of sensorimotor
learning is not to simply minimize the effects of sensorimotor noise. In fact,
the noise effect is not necessarily small even after ADP learning. Remov-
ing the motor variation completely requires a control input with extremely
high gain, which is both impractical and unnecessary for the human motor
system. Instead, the aim here is to regulate the effects of signal-dependent
noise properly, so that the motor system can remain stable and achieve ac-
ceptable transient performance.
To test the after-effect, we suddenly remove the DF. The after-effect trials
are shown in Figures 1c and 2c. Obviously the trajectories are much closer
to the y-axis. This is due to the high-gain controller learned in the DF. Here,
different from Burdet et al. (2001) and Franklin et al. (2003), we conjecture
that during the (at least early phase of) learning process, the CNS, instead of
relying on the internal model completely, simply updates the control strat-
egy through online model-free learning. This is because conducting model
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Model-Free Robust Optimal Motor Control
575
Figure 3: Adaptation of stiffness ellipse to the DF. Stiffness ellipse before (green)
and after (red) adaptation to the DF.
identification is slow and computationally expensive (Shadmehr & Mussa-
Ivaldi, 2012) and thus can provide only limited information to guide motor
adaptation in the early phase of learning. On the other hand, visual and
motor sensory feedbacks are extremely active during this phase in the mo-
tor learning, which in turn provide a large amount of online data to conduct
ADP learning. During the later phase of motor learning, a complete internal
model has been established, and predictions drawn from the internal model
can be incorporated with the visual feedback to provide better estimates of
the state.
3.2.2 Velocity-Dependent Force Field. Next, we simulate the experiment in
the velocity-dependent force field (VF). Different from DF, here we have
(Franklin et al., 2003)
f = χ
(cid:2)
13 −18
13
18
(cid:3) (cid:2)
(cid:3)
vx
vy
in equation 2.2, where χ ∈ [2/3, 1] is a constant that can be adjusted to the
subject’s strength. In our simulation, we set χ = 0.7.
The simulation results are summarized in Figures 4 and 5. Different from
the case in DF, the human subject maintains stability throughout the experi-
ment. However, we see from Figures 4a and 5a that the trajectory of the hand
is not a straight line and exhibits a large bias to the left-hand side. This bias
is caused by the presence of VF. After 50 learning trials, the human subject
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
576
T. Bian, D. Wolpert, and Z.-P. Jiang
Figure 4: ADP learning in the VF. Five hand paths are shown in the VF at differ-
ent stages of the experiment. (a) First five trials on exposure to the VF. (b) Five
trials after ADP learning in the VF is complete. (c) Five sequential trials in the
postexposure phase when the NF is reapplied.
regains optimality, as the trajectory is approximately a straight line and vy
is a bell-shaped curve. The reaching time is also within 0.7 seconds, which
is consistent with experimental data (Franklin et al., 2003). This implies that
model-free learning also appears in the motor adaptation in VF. Finally, the
after-effect is shown in Figures 5c and 4c. Our simulation clearly shows the
after-effect in VF, as the hand movement is biased to the opposite side of
the VF.
Finally, note that our simulation results in this section are overall con-
sistent with the experimental results provided by different research groups
(Burdet et al., 2001; Franklin et al., 2003; Zhou et al., 2016).
4 Robustness to Dynamic Uncertainties
In this section, we depart from the classical optimal control framework
(Todorov & Jordan, 2002; Liu & Todorov, 2007) and study the sensorimotor
control mechanism from a robust and adaptive optimal control perspec-
tive. As we discussed in section 1, motor variability is usually caused by
different factors. However, system 2.1 to 2.3 only models the motor varia-
tion caused by the signal-dependent noise. As another important source of
motor variation, the dynamic uncertainty has not been fully considered.
The dynamic uncertainty could be attributed to the uncertainties in the
internal model, especially during the early phase of learning, when the in-
ternal model may still be under construction. Dynamic uncertainty is an
ideal mathematical representation of this modeling error. Moreover, dy-
namic uncertainty covers the the fixed model error (Crevecoeur et al., 2019)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Model-Free Robust Optimal Motor Control
577
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5: ADP learning in the VF. Five sequential trials are shown in the VF
at different stages of the experiment. (a) First five trials on exposure to the VF.
(b) Five trials after ADP learning in the VF is complete. (c) Five sequential trials
in the postexposure phase when the NF is reapplied. Format as in Figure 2.
578
T. Bian, D. Wolpert, and Z.-P. Jiang
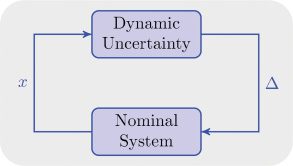
Figure 6: Structure of the sensorimotor system subject to dynamic uncertainty.
as a special case. Dynamic uncertainty may also come from model reduc-
tion (Scarciotti & Astolfi, 2017). Given that the motor system could be a
multidimensional, highly nonlinear system, it is too computationally ex-
pensive for the CNS to solve the optimal control policy directly. Finding the
optimal control policy for a general control system requires solving a non-
linear partial differential equation known as the Hamilton-Jacobi-Bellman
(HJB) equation. Due to the curse of dimensionality (Bellman, 1957), solving
the HJB equation for high-order systems is hard, if not impossible. Due to
this difficulty, we conjecture that the CNS aims only at finding the optimal
control policy for a simplified model, which in turn guarantees robustness
to the mismatch between this simplified model and the original nonlinear
system. As we show below, the presence of dynamic uncertainty does not
compromise the stability of the closed-loop system, provided that a certain
small-gain condition (Jiang & Liu, 2018; Liu et al., 2014) is satisfied. More-
over, the optimal controller obtained based on the simplified linear model
provides similar transient behavior compared with the experimental data,
even in the presence of dynamic uncertainty.
4.1 Robust Optimal Control Framework. To take into account the effect
of dynamic uncertainty, we rewrite equation 2.3 as
τ da = (u − a + (cid:10))dt + G1(u + (cid:10))dw
1
+ G2(u + (cid:10))dw
2
, (cid:10) := (cid:10)(ς, x).
(4.1)
Here (cid:10) and ς are the output and state of the dynamic uncertainty. In gen-
eral, the dynamic uncertainty is a dynamical system interconnected with
the nominal system, equations 2.1 to 2.3 (see Figure 6). In particular, ς is
unobservable to the CNS.
For simplicity, we assume that (cid:10) enters the sensorimotor control model
through the same input channel as signal-dependent noise. The analysis
here can be easily extended to the more general case with unmatched dis-
turbance input (see Jiang & Jiang, 2015, and Bian & Jiang, 2018, for more
details).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Model-Free Robust Optimal Motor Control
579
The challenge we face here is that due to the presence of (cid:10), the optimal
controller derived in previous sections may no longer stabilize this inter-
connected system. In addition, given that ς is unobservable, learning an
optimal sensorimotor controller for the full interconnected system is unre-
alistic. To overcome these challenges, we introduce a new concept of motor
learning: robust optimal learning.
First, to account for the disturbance passed from dynamic uncertainty to
the CNS, we introduce an extra term in the quadratic cost (2.5)3,
J (x(0); u, (cid:10)) =
(cid:10) ∞
(cid:11)
0
xT Qx + uT Ru − γ 2|(cid:10)|2
(cid:12)
dt,
(4.2)
where γ is a real number satisfying R < γ 2I2. γ is called the “gain” of the nominal system in the sense that it models the disturbance (cid:10) on motor sys- tem performance. The concept of gain has already been investigated in the sensorimotor control literature (see Prochazka, 1989, for instance). γ , (cid:10)∗ Here the objective of u and (cid:10) is to minimize and maximize J , respec- tively. It is clear that equation 4.2, together with system 2.1, 2.2, and 4.1 forms a zero-sum differential game problem. Denote by (u∗ ) the pair of the optimal controller and the worst-case disturbance with respect to the performance index, equation 4.2. We say u∗ γ is robust optimal if it not only solves the zero-sum game presented above, but also is robustly stabilizing (with probability one) when the disturbance (cid:10) is presented. To ensure the stability of the motor system, we conjecture that the CNS aims at developing a robust optimal controller by assigning the sensorimotor gain γ properly. Following the same technique in section 3.1, we can directly adopt algo- rithm 1 in our robust optimal controller design, except that the input sig- nal now becomes v 2, and an extra term γ −2Fk,12FT k,12 is added in the updating equation of Pk in algorithm 1. + (cid:10) + G1(uk + G2(uk + (cid:10))ξ 1 + (cid:10))ξ = uk Besides the computational efficiency, an additional benefit of consider- ing a robust optimal controller is that the signal-dependent noise and the disturbance input from the dynamic uncertainty can facilitate motor explo- ration during the learning phase. Note that if (cid:10) and the signal-dependent noise do not exist, then x and v k become linearly dependent. As a result, the condition on ψ j in theorem 3 is no longer satisfied. In fact, these distur- bances play a role similar to that of the exploration noise in RL. k 4.2 Robust Stability Analysis. In this section, we analyze the stabil- ity of the closed-loop system in the presence of signal-dependent noise and dynamic uncertainty. Before giving the robust stability analysis, we first im- pose the following assumption on the dynamic uncertainty: 3 | · | denotes the Euclidean norm for vectors or the induced matrix norm for matrices. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 2 3 5 6 2 1 8 6 4 6 5 7 n e c o _ a _ 0 1 2 6 0 p d . / f b y g u e s t t o n 0 9 S e p e m b e r 2 0 2 3 580 T. Bian, D. Wolpert, and Z.-P. Jiang Assumption 1. The dynamic uncertainty is stochastic input-to-state stable (SISS) (Tang & Ba¸sar, 2001), and admits a proper4 stochastic Lyapunov func- tion V0, such that AV0(ς ) ≤ γ 2 0 |x|2 − |(cid:10)|2, where γ 0 ≥ 0, and A is the infinitesimal generator (Kushner, 1967). Assumption 1 essentially assumes that dynamic uncertainty admits a stochastic linear L2 gain less than or equal to γ 0, with x as input and (cid:10) as output. Using a small-gain type of theorem, we have the following result: Theorem 3. For sufficiently small |G1 | and |G2 1. System 2.4 with u = u∗ is globally asymptotically stable with probability |, we have one. 2. There exists γ > 0, such that u∗
γ is robust optimal under assumption 1.
The proof of theorem 3 is provided in the appendix. Although theorem
3 requires small |G1
|, this does not necessarily imply that the vari-
ance of the signal-dependent noise is small, since the stochastic noise is also
dependent on the system input.
| and |G2
Finally, note that the proposed RADP framework also improves our re-
cent results (Bian & Jiang, 2016, 2018, 2019) by considering both signal-
dependent noise and dynamic uncertainty in the synthesis of our learning
algorithm. This improvement increases the usability of our learning algo-
rithm in practical applications.
4.3 Simulation Validation. For illustration, we choose the following
model to represent dynamic uncertainty,
Tdς = A0
ςdt + D3adw
3
+ D4adw
4
, (cid:10) = γ
ς,
0
(4.3)
∈ R, ς (0) = [0 0]T , w
3 and w
0
4 are independent Brownian
=
A0
−1 −10.8
−1
10.8
(cid:3)
(cid:2)
, D3
=
−0.5
1
1
0.5
(cid:3)
(cid:2)
, D4
=
(cid:3)
.
0.5
1
1
−0.5
In the simulation, we set T = 1 and γ
0
related to the SISS gain of the above dynamic uncertainty.
= 0.1. Note that T and γ
0 are directly
We first simulate the same sensorimotor learning experiment in DF as
in section 3.2, with the same parameters. Note that equations 4.2 and 4.3
are considered here. Simulation results under the RADP design are pre-
sented in Figures 7 and 8. To reveal the impacts of dynamic uncertainty and
4
A function f : Rn → R+ is called proper, if lim|x|→∞ f (x) = ∞.
where T > 0, γ
motions, and
(cid:2)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Model-Free Robust Optimal Motor Control
581
Figure 7: RADP learning in the DF. Five hand paths are shown in the DF at
different stages of the experiment. (a) First five trials on exposure to the DF. (b)
Five trials after RADP learning in the DF is complete. (c) Five sequential trials
in the postexposure phase when the NF is reapplied.
compare with the results in section 3.2, we choose a large γ = 10 here. Note
that even under dynamic uncertainty, both stability and optimality can be
achieved under RADP learning. The after-effect is also clearly illustrated. In
fact, Figures 7 and 8 are quite similar to the results in section 3.2. However,
one noticeable difference in Figure 8 is that the system state has larger varia-
tion. Furthermore, the end-point variance is much larger compared with the
trajectories in Figure 2, clearly due to the disturbance from dynamic uncer-
tainty. This observation confirms our theoretical analysis that the presence
of dynamic uncertainties indeed compromises the stability and robustness
of the closed-loop system.
To further illustrate the impact of sensorimotor gains, we plot system
trajectories after RADP learning under different values of γ and γ
0 in Figure
9. Comparing Figures 9a and 9b (and also Figures 9c and 9d), we observe
that for a fixed γ
0, the smaller γ is, the more stable the motor system is. In
other words, the robustness of the motor system can be tuned by including
the term γ 2|(cid:10)|2 in equation 4.2. By symmetry, for a fixed γ , a smaller γ
0
leads to a more stable trajectory, and when γ
0 becomes sufficiently large, the
dynamic uncertainty has a large input-output gain, thereby giving rise to
instability in the closed-loop system (see Figures 9a, 9c, and 9e). When both
γ and γ
0 are large enough, the motor system may exhibit instability (see
Figure 9f). These phenomena are in line with the small-gain theory (Jiang
& Liu, 2018).
Nevertheless, the increase of state variation promotes the exploration ef-
j in theorem 2 can be easily satis-
(cid:13)
j under
fect, in the sense that the condition on ψ
fied. In Table 2, we calculate the conditional number of 1
l
l
j=1
ψ T
ψ
j
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
582
T. Bian, D. Wolpert, and Z.-P. Jiang
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Figure 8: RADP learning in the DF. Five sequential trials are shown in the DF
at different stages of the experiment. (a) First five trials on exposure to the
DF. (b) Five trials after RADP learning in the DF is complete. (c) Five sequen-
tial trials in the postexposure phase when the NF is reapplied. Format as in
Figure 2.
Model-Free Robust Optimal Motor Control
583
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Figure 9: Five hand paths after RADP learning in the DF under different L2
gains, γ and γ
0.
Table 2: Conditional Number of 1
l
(cid:13)
l
j=1
ψ
ψ T
j .
j
γ
0
0.001
0.1
1
λ
M
/λm
1.04 × 1017
4.45 × 1016
2.07 × 1014
j
ψ T
l
j=1
different γ
0. Denote λm and λM as the minimum and maximum eigenvalues
(cid:13)
ψ
of 1
j , respectively. We simulate the first learning trial in DF for
l
0.7 s and calculate the conditional number λM/λm for different choices of
γ
0. Note that the exploration noise should be chosen so that the closed-loop
ψ T
system is stable and that 1
j does not exhibit singularity—that is,
l
the conditional number λM/λm should be small. This way, the control policy
l
j=1
(cid:13)
ψ
j
584
T. Bian, D. Wolpert, and Z.-P. Jiang
can be updated using algorithm 1 with high accuracy. We see from Table 2
that by increasing γ
0, the conditional number of matrix 1
is re-
l
duced. This, together with Figure 9, illustrates that the motor variability
should be properly regulated to promote motor learning.
ψ T
j
l
j=1
(cid:13)
ψ
j
5 Model-Free Learning and Savings
Huang et al. (2011) and Haith and Krakauer (2013) have claimed that
model-free learning is a key factor behind the savings. In this section,
we investigate the relationship between our adaptive (robust) optimal
control approach and the learning algorithms developed in the literature
(Smith, Ghazizadeh, & Shadmehr, 2006; Zarahn, Weston, Liang, Mazzoni,
& Krakauer, 2008; Vaswani et al., 2015) to explain savings.
5.1 Learning Rate and Error Sensitivity. A key requirement in our
learning algorithm is that (cid:5)
0 (step size) should not be too large, that is,
the learning process cannot be arbitrarily fast. This assumption matches the
common sense that the human subject usually cannot dramatically improve
her motor performance in a single learning trial. As we illustrated in equa-
tion 3.1, our learning algorithm is essentially driven by the TD error. Step
size is related to sensitivity to the TD error. Since step size is decreasing in
our algorithm, error sensitivity is also decreasing. This is because at the ini-
tial phase of learning, P0, which represents our prior estimate on P∗
, is far
from P∗
. Hence, we have to rely more on the TD error feedback from the
environment to adjust our estimate on P∗
. As the trial number increases, Pk
becomes closer to P∗
, and the TD error has less contribution to the learn-
ing: the human subject is unwilling to adjust the control policy because the
motor outcome is already quite satisfactory.
To further investigate the relationship between motor learning perfor-
mance and the updating of step sizes, we test the ADP-based sensorimotor
learning behavior under different step size. Denote
(cid:5)
k
= a
kc + b
,
where a, b, and c are three positive scalars.
To illustrate the influence of step size, we simulate the first 50 learning
trials in the DF. For simplicity, we fix a = 1 in the simulation. The degree of
− K∗| at the kth trial, which represents
motor adaptation is measured as |Kk
the difference between the optimal controller and the controller learned
from ADP algorithm. Our simulation result is given in Figure 10. Note that
when the step size is small, the learning rate is also small. In this case, motor
learning is steady yet slow. Especially, the adaptation curve is smooth, and
no oscillation is observed. As we increase the step size, the learning rate
starts to increase. However, when the step size is too large, the adaptation
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Model-Free Robust Optimal Motor Control
585
Figure 10: ADP learning under different step sizes. Adaptation (norm of the
difference between the actual and optimal control gain matrices) as a function
of trial number on the introduction of the DF. The decrease in the cost depends
on the step size, which is controlled through parameters b and c.
curve is no longer smooth and monotone. The adaptation error increases
during a short period of time and, as a result, leads to a slower convergence
speed. This implies that a large step size may compromise learning speed
and accuracy. In fact, when the step size is too large, the learning algorithm
becomes unstable, and learning fails.
5.2 Multirate Model. Smith et al. (2006), Zarahn et al. (2008), and
Vaswani et al. (2015) have suggested that savings is a combined effect of
two different states (multirate model): the fast state and the slow state. Both
states follow linear updating equations in the following form (Smith et al.,
2006; Vaswani et al., 2015):
f z f (n) + β
z f (n + 1) = α
f e(n),
zs(n + 1) = αszs(n) + βse(n),
z(n + 1) = zs(n + 1) + z f (n + 1),
β
f
> βs,
f and αs
where n is the trial number, z f and zs are the fast and slow states, α
are retention factors, β
f and βs are the learning rates, and e is the error signal.
It has been conjectured that in a washout phase, due to the small learning
rate, the slow state may not return to zero, while the fast state can quickly
deadapt and show an overshoot such that the net adaptation is zero. As
a result, readpatation shows savings due to the nonzero state of the slow
learner. Despite vast supporting experimental evidence, the convergence
of the above model is still an open problem, and it is still unclear if the
human motor system adopts the linear structure in this format. Moreover,
the relationship between the above learning model and the kinetic model
of human body remains an open issue.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
586
T. Bian, D. Wolpert, and Z.-P. Jiang
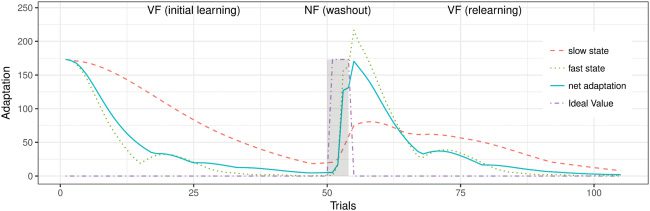
Figure 11: Adaptation as a multirate model based on ADP learning in VF. Adap-
tation over trials in a sequence of trials in VF followed by NF (gray shading) and
reexposure to VF. The net adaptation (blue) shows savings, which is due to the
slow process (red) retaining memory of the initial exposure.
Here, we propose a multirate model based on our ADP learning method.
To be specific, in the updating equation of Pk in algorithm 1, we define two
states, P f (fast state) and Ps (slow state), via
P f
k
Ps
k
← P f
k
← Ps
k
+ (cid:5) f
j (F f
k,11
j (Fs
k,11
− F f
k,22)
k,12(F f
k,12(Fs
k,22)
− Fs
−1(F f
k,12)T ),
k,12)T ),
−1(Fs
+ (cid:5)s
Pk
= α
f P f
k
+ αsPs
k
, Kk
= α
f K f
k
+ αsKs
k
,
f
≥ (cid:5)s
∈ (0, 1); αs + α
where (cid:5) f
j are step sizes; αs, α
k are
j
solved from algorithm 1, with Pk replaced by P f
k , respectively. Note
that our model, after a simple mathematical manipulation, is consistent
with the formulation of the multirate model in the literature. It is easy to
see that both P f
. As a result, the convergence of Pk
and Kk in the above learning model is guaranteed.
k converge to P∗
= 1; and F f
k and Fs
k and Ps
k and Ps
f
Next, we simulate the motor adaptation and savings behaviors in VF.
The measurement criterion of motor adaptation is still chosen as the one
− K∗|. The
in section 5.1: the adaption error at the kth trial is defined as |Kk
simulation result is given in Figure 11. First, the human subject conducts
50 trials of motor movement in the VF. Figure 11 shows that Kk gradually
converges to the optimal control gain. Next, we simulate 5 washout trials
in NF. Then the human subject is reexposed to the VF and conducts another
50 learning trials. Note that the adaptation in the second learning phase is
faster than in the first learning phase. During the washout trials, the slow
state is not fully reset, and the fast state shows a clear overshoot. Moreover,
we see that the fast state curve is not smooth due to the large step size.
A similar phenomenon appears in the experimental results in Smith et al.
(2006) and Zarahn et al. (2008).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Model-Free Robust Optimal Motor Control
587
Figure 12: Adaptation as a multirate model based on ADP learning in DF.
Adaptation over trials in a sequence of trials in DF followed by NF (gray shad-
ing) and reexposure to DF. The net adaptation (blue) shows savings, which is
due to the slow process (red) retaining memory of the initial exposure.
Similar to the case in VF, we also study the motor adaptation and savings
behaviors in DF. We can see from Figure 12 that the multirate ADP model
also recreates savings behavior in DF.
Compared with the existing literature, the proposed framework has a
solid theoretical background, as a detailed convergence analysis can be
drawn from our ADP theory. Moreover, our model incorporates the kinetic
model of the human motor system into the sensorimotor learning algo-
rithm. As a result, our ADP-based learning algorithm provides a unified
framework for the human motor learning system.
6 Discussion
6.1 Summary of the Main Results. In this letter, we have investigated
human sensorimotor learning from an adaptive optimal control perspec-
tive. In particular, the model we have developed shares several similar
features with existing results, such as the presence of model-free learning
(Huang et al., 2011; Haith & Krakauer, 2013), an alternative source of mo-
tor variability (Beck et al., 2012; Bach & Dolan, 2012; Renart & Machens,
2014; Acerbi et al., 2014), and the fact that actively regulated motor vari-
ability promotes sensorimotor learning (Renart & Machens, 2014; Wu et al.,
2014; Cashaback et al., 2015; Lisberger & Medina, 2015; Pekny et al., 2015;
Vaswani et al., 2015). The key idea behind our learning theory is that a spe-
cific model is not required, and the motor control strategy can be iteratively
improved directly using data from sensory feedback. This learning scheme
is especially useful in the early stage of sensorimotor learning, since during
this period, the internal model is still under development and the CNS re-
lies more on sensory feedback to fine-tune the motor commands. We have
used the proposed learning framework to study the motor learning exper-
iment in both a divergent force field and a velocity-dependent force field.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
588
T. Bian, D. Wolpert, and Z.-P. Jiang
Our model successfully reproduces the experimental phenomena reported
in the work of others (Burdet et al., 2001; Franklin et al., 2003; Zhou et al.,
2016). In particular, the model, like human subjects, can regain stability and
optimality through ADP learning even in an unstable environment with
external perturbation. In addition, we have extended our adaptive optimal
controller design to tackle the robust optimal control problem caused by
the presence of dynamic uncertainties. Dynamic uncertainties may appear
in the human motor system as modeling uncertainties (Beck et al., 2012;
Renart & Machens, 2014) and dynamic external disturbance (Jiang & Jiang,
2015). Using the robust optimal controller allows us to analyze the influence
of dynamic uncertainties on the stability of human motor systems. As we
have shown in the simulation, the motor system can still achieve stability in
the presence of dynamic uncertainties, provided that a small sensorimotor
gain is assigned by the CNS. Moreover, a larger motor variation has been
observed as a result of the disturbance input from dynamic uncertainties.
Our model shows that this motor variability can contribute to ADP learning
and, as a result, promote the sensorimotor learning. Finally, our simulation
suggests that the model-free learning may indeed be linked to the savings
phenomenon.
6.2 Reinforcement Learning and Adaptive Dynamic Programming.
The idea of RL can be traced back to Minsky’s PhD dissertation (Minsky,
1954). An essential characteristic of RL is that it provides an efficient way
to solve dynamic programming problems without using any modeling in-
formation of the underlying system. Due to this advantage, RL has become
an ideal candidate to model human decision making and learning behavior
(Doya, Samejima, Katagiri, & Kawato, 2002; Dayan & Balleine, 2002; Rangel,
Camerer, & Montague, 2008; Glimcher, 2011; Bernacchia, Seo, Lee, & Wang,
2011; Taylor & Ivry, 2014).
Despite the appealing features of RL, it is difficult to show the conver-
gence of the learning scheme or analyze the stability and robustness of the
motor system. Moreover, since both the time and the state-action-space are
continuous in motor systems, it is not trivial to extend traditional RL tech-
niques to study a sensorimotor control mechanism. Similar to other RL
methods, ADP is a non-model-based approach that directly updates the
control policy without the need to identify the dynamic model. Different
from traditional RL, ADP aims at developing a stabilizing optimal con-
trol policy for dynamical systems via online learning. ADP-based optimal
control designs for dynamical systems have been investigated by several
research groups over the past few years. Compared with the extensive re-
sults on RL, the research on ADP, especially for continuous-time dynam-
ical systems, is still underdeveloped. In this letter, we have introduced a
novel sensorimotor learning framework built on top of our recent results on
continuous-time ADP and RADP methods (Bian & Jiang, 2016, 2018, 2019).
These results bypass several obstacles in existing learning algorithms by
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Model-Free Robust Optimal Motor Control
589
relaxing the requirement on the initial condition, reducing the computa-
tional complexity, and covering a broader class of disturbances.
6.3 Sensorimotor Noise Enhances Motor Exploration. It has been con-
jectured (Harris & Wolpert, 1998; van Beers et al., 2002; Haruno & Wolpert,
2005) over the past decade that the goal of the motor system is to minimize
end-point variance caused by signal-dependent noise. Later, Todorov and
Jordan (2002) and Todorov (2004, 2005) further explored this idea by using
linear optimal control theory based on the LQR or LQG methods. However,
several recent experimental results (Wu et al., 2014; Cashaback et al., 2015)
suggest that motor variability facilitates motor exploration and, as a result,
can increase learning speed. These surprising results have challenged the
optimal control viewpoint in the sense that motor variability is not purely
an unwanted consequence of sensorimotor noise whose effects should be
minimized.
In this letter, we have justified the contribution of motor variability from
a robust/adaptive optimal control perspective based on ADP and RADP
theory. Indeed, motor variability serves a similar role as exploration noise,
which has been proved essential to ADP and RADP learning. To be specific,
if motor variability is regulated properly, we can show mathematically that
the system will keep improving motor behavior until convergence. Hence,
our model can resolve the inconsistency between existing motor control
theories and recent experimental discoveries on motor variability. More-
over, our model also shows that the existence of exploration noise does
not destabilize the motor system even for learning tasks in an unstable
environment.
6.4 System Decomposition, Small-Gain Theorem, and Quantification
of the Robustness-Optimality Trade-Off. A novel feature of the proposed
motor learning theory is the viewpoint of system decomposition. Building
an exact mathematical model for biological systems is usually difficult. Fur-
thermore, even if the system model is precisely known, it may be highly
nonlinear, and it is generally impossible to solve the DP equation to ob-
tain the optimal controller. In this case, simplified models (nominal motor
system) are often preferable (Beck et al., 2012). The mismatch between the
simplified model and the original motor system is referred to as dynamic
uncertainty. Generally dynamic uncertainty involves unmeasurable state
variables and unknown system order. After decomposing the system into
an interconnection of the nominal model and dynamic uncertainty, we only
need to design a robust optimal control policy using partial-state feedback.
To handle the dynamic interaction between two subsystems, the robust gain
assignment and small-gain techniques (Jiang & Liu, 2018; Liu et al., 2014)
in modern nonlinear control theory are employed in the control design. In
this way, we can preserve the near-optimality for the motor system, as well
as guarantee the robustness of stability for the overall system.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
590
T. Bian, D. Wolpert, and Z.-P. Jiang
6.5 Comparisons with Other Learning Methods. We note several ap-
proaches that also aim at explaining sensorimotor learning mechanisms
from a model-free perspective.
Zhou et al. (2016) studied the human motor learning problem using
model reference iterative learning control (MRILC). In this framework, a
reference model is learned from the data during the initial phase of learning.
Then the motor command is updated through the iterative learning algo-
rithm by comparing the different outputs between the reference model and
the real-world model. Fundamentally different from the model-free learn-
ing presented in this letter, MRILC relies heavily on the knowledge of a
reference model, which plays the same role as an internal model. However,
it is not clear how the CNS conducts motor learning before establishing the
reference model. In addition, the effect of different types of motor varia-
tions is still not considered in the MRILC learning scheme. Note that these
difficulties do not occur in our learning theory.
An alternative way is to update the motor command directly using er-
ror feedback (Herzfeld, Vaswani, Marko, & Shadmehr, 2014; Vaswani et al.,
2015; Albert & Shadmehr, 2016). In this model, a difference equation is used
to generate the motor prediction. Then, by comparing the predicted mo-
tor output with the sensory feedback data, a prediction error is obtained
and used to modify the prediction in the next learning trial. By consider-
ing different error sensitivities (Herzfeld et al., 2014) and structures (Smith
et al., 2006), it is possible to reproduce some experimental phenomena, such
as savings, using this model. This model represents the relationship be-
tween motor command and prediction error as a static function, and the dy-
namical system of the kinetic model is ignored. This missing link between
optimal control theory (Todorov & Jordan, 2002) and the error-updating
model (Herzfeld et al., 2014) raises several open questions, including the
convergence problem of the algorithm and the stability issue of the kinetic
model. On the other hand, the framework we propose in our letter incor-
porates the numerical optimization framework into the optimal control de-
sign for motor systems. Instead of using the prediction error, our learning
model is driven by the TD error, and rigorous convergence analysis has been
provided.
Appendix: Proof of Theorem 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Denote V (x) = xT P∗x. Following the definitions of K∗
the squares, we have
(cid:17)
Q + K
AV (x) = −xT
x + xT K
∗T (cid:14)(P
∗T RK
)K
(cid:18)
∗
∗
∗
x,
and P∗
, by completing
where (cid:14)(P) = GT
K∗
are fixed. If |G1
1 BT PBG1
| and |G2
+ GT
2 BT PBG2. For fixed Q and R matrices, P∗
and
| are sufficiently small, the second term on the
Model-Free Robust Optimal Motor Control
591
right-hand side of the above equality is dominated by the first term. Then x
converges to the origin asymptotically with probability one (Kushner, 1967).
To show uγ is robust optimal, we rewrite equation 2.4 as
dx = Axdt + B((u + (cid:10))dt + G1(u + (cid:10))dw
1
+ G2(u + (cid:10))dw
2).
Then from the zero-sum game theory, (u∗
γ , (cid:10)∗
) is solved as
∗
γ = −R
−1BT P
∗
γ x ≡ −K
γ x, (cid:10)∗ = γ −2BT P
∗
∗
γ x,
u
where P∗
γ = P∗
γ
T > 0 is the solution to
0 = AT P + PA − PB
(cid:11)
−1 − γ −2I
R
(cid:12)
BT P + Q.
Note that since R < γ 2I, P∗
Following the definitions of K∗
γ indeed uniquely exists. Denote Vγ (x) = xT P∗
γ x.
γ , by completing the squares, we have
γ and P∗
AVγ (x) = −xT
(cid:17)
∗
Q + K
γ
T (R − (cid:14)(P
∗
∗
γ ))K
γ
(cid:18)
x − γ −2xT P
∗
γ BBT P
∗
γ x
+ 2(cid:10)T (BT P
(cid:17)
∗
Q + K
γ
≤ −xT
∗
γ − (cid:14)(P
∗
γ )K
∗
)x + (cid:10)T (cid:14)(P
(cid:18)
∗
γ )(cid:10)
T (R − 2(cid:14)(P
∗
∗
γ ))K
γ
x + (cid:10)T (γ 2I + 2(cid:14)(P
∗
γ ))(cid:10)
≤ −α
1
|x|2 + (γ 2 + α
2)|(cid:10)|2,
1 and α
where α
we can choose γ 2 < α
1
/γ 2
0
− α
2 such that
2 are real constants. Then, for sufficiently small |G1
| and |G2
|,
AV (x, ς ) ≤ −δ|x|2 − δ|(cid:10)|2
for some δ > 0, where V (x, ς ) := γ
1V0(ς ). Thus, both x and (cid:10) con-
0Vγ (x) + α
verge to the origin asymptotically with probability one (Kushner, 1967).
Then, since the dynamic uncertainty is SISS, ς also converges to the origin
asymptotically with probability one.
Acknowledgments
This work was partially supported by the U.S. National Science Foundation
under grants ECCS-1230040, ECCS-1501044, and EPCN-1903781 to Z.P.J.;
and the Wellcome Trust and the Royal Society Noreen Murray Professor-
ship in Neurobiology (to D.M.W.).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
592
References
T. Bian, D. Wolpert, and Z.-P. Jiang
Acerbi, L., Vijayakumar, S., & Wolpert, D. M. (2014). On the origins of suboptimality
in human probabilistic inference. PLOS Computational Biology, 10(6), e1003661EP.
Albert, S. T., & Shadmehr, R. (2016). The neural feedback response to error as a teach-
ing signal for the motor learning system. Journal of Neuroscience, 36(17), 4832–4845.
Arnold, L. (1974). Stochastic differential equations: Theory and applications. New York:
Wiley.
Bach, D. R., & Dolan, R. J. (2012). Knowing how much you don’t know: A neural
organization of uncertainty estimates. Nature Reviews Neuroscience, 13(8), 572–586.
Beck, J. M., Ma, W. J., Pitkow, X., Latham, P. E., & Pouget, A. (2012). Not noisy, just
wrong: The role of suboptimal inference in behavioral variability. Neuron, 74(1),
30–39.
Bellman, R. E. (1957). Dynamic programming. Princeton, NJ: Princeton University
Press.
Bernacchia, A., Seo, H., Lee, D., & Wang, X.-J. (2011). A reservoir of time constants
for memory traces in cortical neurons. Nature Neuroscience, 14(3), 366–372.
Bertsekas, D. P. (2017). Value and policy iterations in optimal control and adaptive
dynamic programming. IEEE Transactions on Neural Networks and Learning Sys-
tems, 28(3), 500–509.
Bhushan, N., & Shadmehr, R. (1999). Computational nature of human adaptive con-
trol during learning of reaching movements in force fields. Biological Cybernetics,
81(1), 39–60.
Bian, T., & Jiang, Z. P. (2016). Value iteration and adaptive dynamic programming
for data-driven adaptive optimal control design. Automatica, 71, 348–360.
Bian, T., & Jiang, Z. P. (2018). Stochastic and adaptive optimal control of uncertain in-
terconnected systems: A data-driven approach. Systems and Control Letters, 115(5),
48–54.
Bian, T., & Jiang, Z. P. (2019). Reinforcement learning for linear continuous-time sys-
tems: An incremental learning approach. IEEE/CAA Journal of Automatica Sinica,
6(2), 433–440.
Bian, T., Jiang, Y., & Jiang, Z. P. (2014). Adaptive dynamic programming and optimal
control of nonlinear nonaffine systems. Automatica, 50(10), 2624–2632.
Bian, T., Jiang, Y., & Jiang, Z. P. (2016). Adaptive dynamic programming for stochastic
systems with state and control dependent noise. IEEE Transactions on Automatic
Control, 61(12), 4170–4175.
Burdet, E., Osu, R., Franklin, D. W., Milner, T. E., & Kawato, M. (2001). The central
nervous system stabilizes unstable dynamics by learning optimal impedance. Na-
ture, 414(6862), 446–449.
Burdet, E., Tee, K. P., Mareels, I. M. Y., Milner, T. E., Chew, C.-M., Franklin, D. W.,
. . . Kawato, M. (2006). Stability and motor adaptation in human arm movements.
Biological Cybernetics, 94(1), 20–32.
Cashaback, J. G. A., McGregor, H. R., & Gribble, P. L. (2015). The human motor sys-
tem alters its reaching movement plan for task-irrelevant, positional forces. Jour-
nal of Neurophysiology, 113(7), 2137–2149.
Chaisanguanthum, K. S., Shen, H. H., & Sabes, P. N. (2014). Motor variability arises
from a slow random walk in neural state. Journal of Neuroscience, 34(36), 12071–
12080.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Model-Free Robust Optimal Motor Control
593
Crevecoeur, F., Scott, S. H., & Cluff, T. (2019). Robust control in human reaching
movements: A model-free strategy to compensate for unpredictable disturbances.
Journal of Neuroscience, 39(41), 8135–8148.
Dayan, P., & Balleine, B. W. (2002). Reward, motivation, and reinforcement learning.
Neuron, 36(2), 285–298.
Doya, K. (2000). Reinforcement learning in continuous time and space. Neural Com-
putation, 12(1), 219–245.
Doya, K., Samejima, K., Katagiri, K.-i., & Kawato, M. (2002). Multiple model-based
reinforcement learning. Neural Computation, 14(6), 1347–1369.
Faisal, A. A., Selen, L. P. J., & Wolpert, D. M. (2008). Noise in the nervous system.
Nature Reviews Neuroscience, 9(4), 292–303.
Flash, T., & Hogan, N. (1985). The coordination of arm movements: An experimen-
tally confirmed mathematical model. Journal of Neuroscience, 5(7), 1688–1703.
Franklin, D. W., Burdet, E., Osu, R., Kawato, M., & Milner, T. (2003). Functional sig-
nificance of stiffness in adaptation of multijoint arm movements to stable and
unstable dynamics. Experimental Brain Research, 151(2), 145–157.
Glimcher, P. W. (2011). Understanding dopamine and reinforcement learning: The
dopamine reward prediction error hypothesis. Proceedings of the National Academy
of Sciences, 108(Suppl. 3), 15647–15654.
Haith, A. M., & Krakauer, J. W. (2013). Model-based and model-free mechanisms of
human motor learning. In M. J. Richardson, M. A. Riley, & K. Shockley (Eds.),
Progress in motor control (pp. 1–21). New York: Springer.
Harris, C. M., & Wolpert, D. M. (1998). Signal-dependent noise determines motor
planning. Nature, 394(6695), 780–784.
Haruno, M., & Wolpert, D. M. (2005). Optimal control of redundant muscles in step-
tracking wrist movements. Journal of Neurophysiology, 94(6), 4244–4255.
He, H., & Zhong, X. (2018). Learning without external reward [research frontier].
IEEE Computational Intelligence Magazine, 13(3), 48–54.
Herzfeld, D. J., Vaswani, P. A., Marko, M. K., & Shadmehr, R. (2014). A memory of
errors in sensorimotor learning. Science, 345(6202), 1349–1353.
Huang, V. S., Haith, A., Mazzoni, P., & Krakauer, J. W. (2011). Rethinking motor learn-
ing and savings in adaptation paradigms: Model-free memory for successful ac-
tions combines with internal models. Neuron, 70(4), 787–801.
Huberdeau, D. M., Krakauer, J. W., & Haith, A. M. (2015). Dual-process decomposi-
tion in human sensorimotor adaptation. Current Opinion in Neurobiology, 33, 71–
77.
Izawa, J., Rane, T., Donchin, O., & Shadmehr, R. (2008). Motor adaptation as a process
of reoptimization. Journal of Neuroscience, 28(11), 2883–2891.
Jiang, Y., & Jiang, Z. P. (2014). Adaptive dynamic programming as a theory of senso-
rimotor control. Biological Cybernetics, 108(4), 459–473.
Jiang, Y., & Jiang, Z. P. (2015). A robust adaptive dynamic programming principle
for sensorimotor control with signal-dependent noise. Journal of Systems Science
and Complexity, 28(2), 261–288.
Jiang, Y., & Jiang, Z. P. (2017). Robust Adaptive Dynamic Programming. Hoboken, NJ:
Wiley-IEEE Press.
Jiang, Z. P., & Jiang, Y. (2013). Robust adaptive dynamic programming for linear and
nonlinear systems: An overview. European Journal of Control, 19(5), 417–425.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
594
T. Bian, D. Wolpert, and Z.-P. Jiang
Jiang, Z. P., & Liu, T. (2018). Small-gain theory for stability and control of dynamical
networks: A survey. Annual Reviews in Control, 46, 58–79.
Kawato, M. (1999). Internal models for motor control and trajectory planning. Cur-
rent Opinion in Neurobiology, 9(6), 718–727.
Kushner, H. J. (1967). Stochastic stability and control. London: Academic Press.
Lewis, F. L., & Liu, D. (2013). Reinforcement learning and approximate dynamic program-
ming for feedback control. Hoboken, NJ: Wiley.
Lewis, F. L., Vrabie, D., & Vamvoudakis, K. G. (2012). Reinforcement learning and
feedback control: Using natural decision methods to design optimal adaptive
controllers. IEEE Control Systems, 32(6), 76–105.
Lisberger, S. G., & Medina, J. F. (2015). How and why neural and motor variation are
related. Current Opinion in Neurobiology, 33, 110–116.
Liu, D., & Todorov, E. (2007). Evidence for the flexible sensorimotor strategies
predicted by optimal feedback control. Journal of Neuroscience, 27(35), 9354–
9368.
Liu, T., Jiang, Z. P., & Hill, D. J. (2014). Nonlinear control of dynamic networks. Boca
Raton, FL: CRC Press.
Minsky, M. L. (1954). Theory of neural-analog reinforcement systems and its application
to the brain model problem. PhD diss., Princeton University.
Morasso, P. (1981). Spatial control of arm movements. Experimental Brain Research,
42(2), 223–227.
Pekny, S. E., Izawa, J., & Shadmehr, R. (2015). Reward-dependent modulation of
movement variability. Journal of Neuroscience, 35(9), 4015–4024.
Prochazka, A. (1989). Sensorimotor gain control: A basic strategy of motor systems?
Progress in Neurobiology, 33(4), 281–307.
Qian, N., Jiang, Y., Jiang, Z. P., & Mazzoni, P. (2012). Movement duration, Fitts’s law,
and an infinite-horizon optimal feedback control model for biological motor sys-
tems. Neural Computation, 25(3), 697–724.
Rangel, A., Camerer, C., & Montague, P. R. (2008). A framework for studying the
neurobiology of value-based decision making. Nature Reviews Neuroscience, 9(7),
545–556.
Renart, A., & Machens, C. K. (2014). Variability in neural activity and behavior. Cur-
rent Opinion in Neurobiology, 25, 211–220.
Scarciotti, G., & Astolfi, A. (2017). Data-driven model reduction by moment match-
ing for linear and nonlinear systems. Automatica, 79, 340–351.
Shadmehr, R., & Mussa-Ivaldi, F. A. (1994). Adaptive representation of dynamics
during learning of a motor task. Journal of Neuroscience, 14(5), 3208–3224.
Shadmehr, R., & Mussa-Ivaldi, S. (2012). Biological learning and control: How the brain
builds representations, predicts events, and makes decisions. Cambridge, MA: MIT
Press.
Smith, M. A., Ghazizadeh, A., & Shadmehr, R. (2006). Interacting adaptive processes
with different timescales underlie short-term motor learning. PLOS Biology, 4(6),
e179.
Sutton, R. S. (1988). Learning to predict by the methods of temporal differences. Ma-
chine Learning, 3(1), 9–44.
Sutton, R. S., & Barto, A. G. (2018). Reinforcement learning: An introduction (2nd ed.).
Cambridge, MA: MIT Press.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Model-Free Robust Optimal Motor Control
595
Tang, C., & Ba¸sar, T. (2001). Stochastic stability of singularly perturbed nonlinear
systems. In Proceedings of the 40th IEEE Conference on Decision and Control (vol. 1,
pp. 399–404). Piscataway, NJ: IEEE.
Taylor, J. A., & Ivry, R. B. (2014). Cerebellar and prefrontal cortex contributions to
adaptation, strategies, and reinforcement learning. Progress in Brain Research, 210,
217–253.
Todorov, E. (2004). Optimality principles in sensorimotor control. Nature Neuro-
science, 7(9), 907–915.
Todorov, E. (2005). Stochastic optimal control and estimation methods adapted to
the noise characteristics of the sensorimotor system. Neural Computation, 17(5),
1084–1108.
Todorov, E., & Jordan, M. I. (2002). Optimal feedback control as a theory of motor
coordination. Nature Neuroscience, 5(11), 1226–1235.
Uno, Y., Kawato, M., & Suzuki, R. (1989). Formation and control of optimal trajectory
in human multijoint arm movement. Biological Cybernetics, 61(2), 89–101.
van Beers, R. J. (2007). The sources of variability in saccadic eye movements. Journal
of Neuroscience, 27(33), 8757–8770.
van Beers, R. J., Baraduc, P., & Wolpert, D. M. (2002). Role of uncertainty in sensori-
motor control. Philosophical Transactions of the Royal Society of London B: Biological
Sciences, 357(1424), 1137–1145.
Vaswani, P. A., Shmuelof, L., Haith, A. M., Delnicki, R. J., Huang, V. S., Mazzoni, P.,
. . . Krakauer, J. W. (2015). Persistent residual errors in motor adaptation tasks: Re-
version to baseline and exploratory escape. Journal of Neuroscience, 35(17), 6969–
6977.
Vrabie, D., Vamvoudakis, K. G., & Lewis, F. L. (2013). Optimal adaptive control and
differential games by reinforcement learning principles. London: Institution of Engi-
neering and Technology.
Wang, D., He, H., & Liu, D. (2017). Adaptive critic nonlinear robust control: A survey.
IEEE Transactions on Cybernetics, 47(10), 3429–3451.
Wolpert, D. M., & Ghahramani, Z. (2000). Computational principles of movement
neuroscience. Nature Neuroscience, 3, 1212–1217.
Wolpert, D. M., Ghahramani, Z., & Jordan, M. I. (1995). An internal model for sen-
sorimotor integration. Science, 269(29), 1880–1882.
Wu, H. G., Miyamoto, Y. R., Castro, L. N. G., Olveczky, B. P., & Smith, M. A. (2014).
Temporal structure of motor variability is dynamically regulated and predicts
motor learning ability. Nature Neuroscience, 17(2), 312–321.
Zarahn, E., Weston, G. D., Liang, J., Mazzoni, P., & Krakauer, J. W. (2008). Explaining
savings for visuomotor adaptation: Linear time-invariant state-space models are
not sufficient. Journal of Neurophysiology, 100(5), 2537–2548.
Zhou, S.-H., Fong, J., Crocher, V., Tan, Y., Oetomo, D., & Mareels, I. M. Y. (2016).
Learning control in robot-assisted rehabilitation of motor skills—A review. Jour-
nal of Control and Decision, 3(1), 19–43.
Received November 10, 2018; accepted October 11, 2019.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
3
5
6
2
1
8
6
4
6
5
7
n
e
c
o
_
a
_
0
1
2
6
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3