Let’s Play Mono-Poly: BERT Can Reveal Words’ Polysemy Level
and Partitionability into Senses
Aina Gar´ı Soler
Universit´e Paris-Saclay
CNRS, LISN
91400, Orsay, France
aina.gari@limsi.fr
Marianna Apidianaki
Department of Digital Humanities
University of Helsinki
Helsinki, Finland
marianna.apidianaki@helsinki.fi
Abstract
Pre-trained language models (LMs) encode
rich information about
linguistic structure
but their knowledge about lexical polysemy
remains unclear. We propose a novel exper-
imental setup for analyzing this knowledge
in LMs specifically trained for different lan-
guages (English, French, Spanish, and Greek)
and in multilingual BERT. We perform
our analysis on datasets carefully designed
to reflect different sense distributions, and
control for parameters that are highly cor-
related with polysemy such as frequency and
grammatical category. We demonstrate that
BERT-derived representations reflect words’
polysemy level and their partitionability into
senses. Polysemy-related information is more
clearly present in English BERT embeddings,
but models in other languages also man-
age to establish relevant distinctions between
words at different polysemy levels. Our results
contribute to a better understanding of the
knowledge encoded in contextualized rep-
resentations and open up new avenues for
multilingual lexical semantics research.
1
Introduction
Pre-trained contextual language models have ad-
vanced the state of the art in numerous natural
language understanding tasks (Devlin et al., 2019;
Peters et al., 2018). Their success has motivated
a large number of studies exploring what these
models actually learn about language (Voita et al.,
2019a; Clark et al., 2019; Voita et al., 2019b;
Tenney et al., 2019). The bulk of this interpreta-
tion work relies on probing tasks that serve to
predict linguistic properties from the represen-
tations generated by the models (Linzen, 2018;
Rogers et al., 2020). The focus was initially put
825
on linguistic aspects pertaining to grammar and
syntax (Linzen et al., 2016; Hewitt and Manning,
2019; Hewitt and Liang, 2019). The first prob-
ing tasks addressing semantic knowledge explored
phenomena in the syntax-semantics interface, such
as semantic role labeling and coreference (Tenney
et al., 2019; Kovaleva et al., 2019), and the sym-
bolic reasoning potential of LM representations
(Talmor et al., 2020).
Lexical meaning was largely overlooked in
early interpretation work, but is now attracting
increasing attention. Pre-trained LMs have been
shown to successfully leverage sense annotated
data for disambiguation (Wiedemann et al., 2019;
Reif et al., 2019). The interplay between word
type and token-level information in the hidden
representations of LSTM LMs has also been
explored (Aina et al., 2019), as well as the
similarity estimates that can be drawn from
contextualized representations without directly
addressing word meaning (Ethayarajh, 2019). In
recent work, Vuli´c et al. (2020) probe BERT
representations for lexical semantics, addressing
out-of-context word similarity. Whether these
models encode knowledge about lexical polysemy
and sense distinctions is, however, still an open
question. Our work aims to fill this gap.
We propose methodology for exploring the
knowledge about word senses in contextualized
representations. Our approach follows a rigorous
experimental protocol proper to lexical semantic
analysis, which involves the use of datasets
carefully designed to reflect different sense
distributions. This allows us to investigate the
knowledge models acquire during training, and
the influence of context variation on token
representations. We account
the strong
correlation between word frequency and number
of senses (Zipf, 1945), and for the relationship
between grammatical category and polysemy,
by balancing the frequency and part of speech
for
Transactions of the Association for Computational Linguistics, vol. 9, pp. 825–844, 2021. https://doi.org/10.1162/tacl a 00400
Action Editor: Walter Daelemans. Submission batch: 11/2020; Revision batch: 3/2021; Published 8/2021.
c(cid:2) 2021 Association for Computational Linguistics. Distributed under a CC-BY 4.0 license.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
0
0
1
9
5
5
2
0
4
/
/
t
l
a
c
_
a
_
0
0
4
0
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Camacho-Collados, 2020); determine the needs
in terms of context size for disambiguation (e.g.,
in queries, chatbots); help lexicographers define
the number of entries for a word to be present in
a resource, and plan the time and effort needed
in semantic annotation tasks (McCarthy et al.,
2016). It could also guide cross-lingual transfer,
serving to identify polysemous words for which
transfer might be harder. Finally, analyzing words’
semantic space can be highly useful for the study
of lexical semantic change (Rosenfeld and Erk,
2018; Dubossarsky et al., 2019; Giulianelli et al.,
2020; Schlechtweg et al., 2020). We make our
code and datasets available to enable comparison
across studies and to promote further research in
these directions.1
2 Related Work
The knowledge pre-trained contextual LMs
encode about lexical semantics has only recently
started being explored. Works by Reif et al. (2019)
and Wiedemann et al. (2019) propose experiments
using representations built from Wikipedia and
the SemCor corpus (Miller et al., 1993), and
show that BERT can organize word usages in
the semantic space in a way that reflects the
meaning distinctions present in the data. It is
also shown that BERT can perform well
in
the word sense disambiguation (WSD) task by
leveraging the sense-related information available
in these resources. These works address the
disambiguation capabilities of the model but do
not show what BERT actually knows about words’
polysemy, which is the main axis of our work.
In our experiments, sense annotations are not
used to guide the models into establishing sense
distinctions, but rather for creating controlled
conditions that allow us to analyze BERT’s
inherent knowledge of lexical polysemy.
Probing has also been proposed for lexical
semantics analysis, but addressing different
questions than the ones posed in our work. Aina
et al., (2019) probe the hidden representations of
a bidirectional (bi-LSTM) LM for lexical (type-
level) and contextual (token-level) information.
They specifically train diagnostic classifiers on
the tasks of retrieving the input embedding of
a word and a representation of its contextual
1Our code and data are available at https://github
.com/ainagari/monopoly.
(poly) words
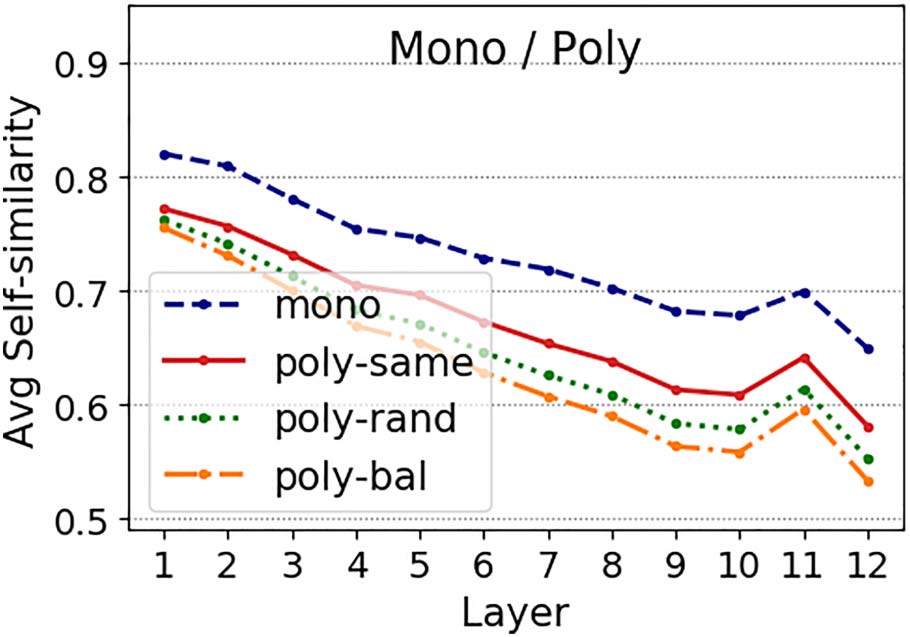
Figure 1: BERT distinguishes monosemous (mono)
from polysemous
layers.
Representations for a poly word are obtained from
sentences reflecting up to ten different senses (poly-
the same sense (poly-same), or natural
bal),
occurrence in a corpus (poly-rand).
in all
(PoS) distributions in our datasets and applying a
frequency-based model to polysemy prediction.
Importantly, our
investigation encompasses
monolingual models in different languages (En-
glish, French, Spanish, and Greek) and multi-
lingual BERT (mBERT). We demonstrate that
BERT contextualized representations encode an
impressive amount of knowledge about poly-
semy, and are able to distinguish monosemous
(mono) from polysemous (poly) words in a vari-
ety of settings and configurations (cf. Figure 1).
Importantly, we demonstrate that representations
derived from contextual LMs encode knowl-
edge about words’ polysemy acquired through
pre-training which is combined with informa-
tion from new contexts of use (Sections 3–6).
Additionally, we show that BERT representa-
tions can serve to determine how easy it is to
partition a word’s semantic space into senses
(Section 7).
Our methodology can serve for the analy-
sis of words and datasets from different topics,
domains and languages. Knowledge about words’
polysemy and sense partitionability has numerous
practical
implications: It can guide decisions
towards a sense clustering or a per-instance
approach in applications (Reisinger and Mooney,
2010; Neelakantan et al., 2014; Camacho-
Collados and Pilehvar, 2018); point
to words
with stable semantics which can be safe cues
for disambiguation in running text (Leacock et al.,
1998; Agirre and Martinez, 2004; Loureiro and
826
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
0
0
1
9
5
5
2
0
4
/
/
t
l
a
c
_
a
_
0
0
4
0
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
it
is given a central
meaning (as reflected in its lexical substitutes).
The results show that the information about the
input word that is present in LSTM representations
is not
lost after contextualization; however,
the quality of the information available for a
word is assessed through the model’s ability
to identify the corresponding embedding, as in
Adi et al. (2017) and Conneau et al. (2018).
Also, lexical ambiguity is only viewed through
In our work,
the lens of contextualization.
on the contrary,
role:
We explicitly address the knowledge BERT
encodes about words’ degree of polysemy and
partitionability into senses. Vuli´c et al. (2020) also
propose to probe contextualized models for lexical
semantics, but they do so using ‘‘static’’ word
embeddings obtained through pooling over several
contexts, or extracting representations for words
in isolation and from BERT’s embedding layer,
before contextualization. These representations
are evaluated on tasks traditionally used for
assessing the quality of static embeddings, such as
out-of-context similarity and word analogy, which
are not tailored for addressing lexical polysemy.
Other contemporaneous work explores lexical
polysemy in static embeddings
(Jakubowski
et al., 2020), and the relation of ambiguity
and context uncertainty as approximated in the
space constructed by mBERT using information-
theoretic measures (Pimentel et al., 2020). Finally,
work by Ethayarajh (2019) provides useful
observations regarding the impact of context on
the representations, without explicitly addressing
the semantic knowledge encoded by the models.
Through an exploration of BERT, ELMo, and
GPT-2 (Radford et al., 2019), the author highlights
the highly distorted similarity of the obtained
contextualized representations which is due to
the vector space built by
the anisotropy of
each model.2 The question of meaning is not
addressed in this work, making it hard to draw any
conclusions about lexical polysemy.
Our proposed experimental setup is aimed at
investigating the polysemy information encoded
in the representations built at different layers of
deep pre-trained LMs. Our approach basically
relies on the similarity of contextualized repre-
sentations, which amounts to word usage similar-
ity (Usim) estimation, a classical task in lexical
semantics (Erk et al., 2009; Huang et al., 2012;
Erk et al., 2013). The Usim task precisely involves
predicting the similarity of word instances in con-
text without use of sense annotations. BERT has
been shown to be particularly good at this task
(Gar´ı Soler et al., 2019; Pilehvar and Camacho-
Collados, 2019). Our experiments allow us to
explore and understand what this ability is due to.
3 Lexical Polysemy Detection
3.1 Dataset Creation
is important
We build our English dataset using SemCor
3.0 (Miller et al., 1993), a corpus manually
annotated with WordNet senses (Fellbaum, 1998).
to note that we do not use
It
the annotations for training or evaluating any
of the models. These only serve to control the
composition of the sentence pools that are used
for generating contextualized representations, and
to analyze the results. We form sentence pools
for monosemous (mono) and polysemous (poly)
words that occur at least ten times in SemCor.3
For each mono word, we randomly sample ten of
its instances in the corpus. For each poly word,
we form three sentence pools of size ten reflecting
different sense distributions:
• Balanced (poly-bal). We sample a
sentence for each sense of
the word in
SemCor until a pool of ten sentences is
formed.
• Random (poly-rand). We randomly
sample ten poly word instances from
SemCor. We expect this pool to be highly
biased towards a specific sense due to the
skewed frequency distribution of word senses
(Kilgarriff, 2004; McCarthy et al., 2004).
This configuration is closer to the expected
natural occurrence of senses in a corpus, it
thus serves to estimate the behaviour of the
models in a real-world setting.
• Same sense (poly-same). We sample ten
sentences illustrating only one sense of the
poly word. Although the composition of this
pool is similar to that of the mono pool (i.e. all
instances describe the same sense) we call it
2This issue affects all tested models and is particularly
present in the last layers of GPT-2, resulting in highly similar
representations even for random words.
3We find the number of senses for a word of a specific part
of speech (PoS) in WordNet 3.0, which we access through
the NLTK interface (Bird et al., 2009).
827
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
0
0
1
9
5
5
2
0
4
/
/
t
l
a
c
_
a
_
0
0
4
0
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Setting
Word
Sense
Sentences
mono
hotel.n
poly-same room.n
poly-bal
room.n
INN
INN
CHAMBER
CHAMBER
CHAMBER
The walk ended, inevitably, right in front of his hotel building.
Maybe he’s at the hotel.
The room vibrated as if a giant hand had rocked it.
(. . .) Tell her to come to Adam’s room (. . .)
(. . .) he left the room, walked down the hall (. . .)
It gives them room to play and plenty of fresh air.
SPACE
OPPORTUNITY Even here there is room for some variation, for metal surfaces vary (. . .)
Table 1: Example sentences for the monosemous noun hotel and the polysemous noun room.
poly-same because it describes one sense
of a polysemous word.4 Specifically, we want
to explore whether BERT representations
derived from these instances can serve to
distinguish mono from poly words.
The controlled composition of the poly sentence
pools allows us to investigate the behavior of
the models when they are exposed to instances
of polysemous words describing the same or
different senses. There are 1,765 poly words
in SemCor with at least 10 sentences available.5
We randomly subsample 418 from these in or-
der to balance the mono and poly classes. Our
English dataset is composed of 836 mono and
poly words, and their instances in 8,195 unique
sentences. Table 1 shows a sample of the sentences
in different pools. For French, Spanish, and Greek,
we retrieve sentences from the Eurosense corpus
(Delli Bovi et al., 2017) which contains texts from
Europarl automatically annotated with BabelNet
word senses (Navigli and Ponzetto, 2012).6 We
extract sentences from the high-precision version7
of Eurosense, and create sentence pools in the
same way as in English, balancing the number of
monosemous and polysemous words (418). We
determine the number of senses for a word as the
number of its Babelnet senses that are mapped to
a WordNet sense.8
4The polysemous words are the same as in poly-bal
and poly-rand.
5We use sentences of up to 100 words.
6BabelNet is a multilingual semantic network built from
multiple lexicographic and encyclopedic resources, such as
WordNet and Wikipedia.
7The high coverage version of Eurosense is larger than
the high-precision one, but disambiguation is less accurate.
8This filtering serves to exclude BabelNet senses that
correspond to named entities and are not useful for our
purposes (such as movie or album titles), and to run these
experiments under similar conditions across languages.
3.2 Contextualized Word Representations
We experiment with representations generated by
three English models: BERT (Devlin et al., 2019),9
ELMo (Peters et al., 2018), and context2vec
(Melamud et al., 2016). BERT is a Transformer
architecture (Vaswani et al., 2017) that is jointly
trained for a masked LM and a next sentence
prediction task. Masked LM inolves a Cloze-style
task, where the model needs to guess randomly
masked words by jointly conditioning on their
left and right context. We use the bert-base-
uncased and bert-base-cased models,
pre-trained on the BooksCorpus (Zhu et al., 2015)
and English Wikipedia. ELMo is a bi-LSTM LM
trained on Wikipedia and news crawl data from
WMT 2008-2012. We use 1024-d representations
from the 5.5B model.10 Context2vec is a neural
model based on word2vec’s CBOW architecture
(Mikolov et al., 2013) which learns embeddings
of wide sentential contexts using a bi-LSTM. The
model produces representations for words and
their context. We use the context representations
from a 600-d context2vec model pre-trained on
the ukWaC corpus (Baroni et al., 2009).11
For French, Spanish, and Greek, we use BERT
models specifically trained for each language:
Flaubert (flaubert base uncased) (Le et al.,
2020), BETO (bert-base-spanish-wwm-
uncased) (Cañete et al., 2020), and Greek
BERT (bert-base-greek-uncased-v1)
(Koutsikakis et al., 2020). We also use the bert-
base-multilingual-cased model for each
of the four languages. mBERT was trained on
9We use Huggingface transformers (Wolf et al.,
2020).
10https://allennlp.org/elmo.
11https://github.com/orenmel/context2vec.
828
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
0
0
1
9
5
5
2
0
4
/
/
t
l
a
c
_
a
_
0
0
4
0
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Wikipedia data of 104 languages.12 All BERT
models generate 768-d representations.
presented in the next section provide additional
evidence in this respect.
3.3 The Self-Similarity Metric
All models produce representations that describe
word meaning in specific contexts of use. For each
instance i of a target word w in a sentence, we
extract its representation from: (i) each of the 12
layers of a BERT model;13 (ii) each of the three
ELMo layers; and (iii) context2vec. We calculate
self-similarity (Self Sim) (Ethayarajh, 2019) for
w in a sentence pool p and a layer l, by taking the
average of the pairwise cosine similarities of the
representations of its instances in l:
(cid:2)
(cid:2)
SelfSiml(w) =
1
|I|2 − |I|
cos(xwli, xwlj)
i∈I
j∈I
j(cid:4)=i
(1)
In formula 1, |I| is the number of instances for
w (ten in our experiments); xwli and xwlj are the
representations for instances i and j of w in layer
l. The Self Sim score is in the range [−1, 1]. We
report the average Self Sim for all w’s in a pool p.
We expect it to be higher for monosemous words
and words with low polysemy than for highly
polysemous words. We also expect the poly-
same pool to have a higher average Self Sim
score than the other poly pools which contain
instances of different senses.
Contextualization has a strong impact on
Self Sim since it
introduces variation in the
token-level representations, making them more
dissimilar. The Self Sim value for a word
would be 1 with non-contextualized (or static)
embeddings, as all its instances would be assigned
the same vector. In contextual models, Self Sim
is lower in layers where the impact of the context
is stronger (Ethayarajh, 2019). It is, however,
important to note that contextualization in BERT
models is not monotonic, as shown by previous
studies of the models’ internal workings (Voita
et al., 2019a; Ethayarajh, 2019). Our experiments
12The mBERT model developers recommend using the
cased version of the model rather than the uncased one,
especially for languages with non-Latin alphabets, because
it fixes normalization issues. More details about this model
can be found here: https://github.com/google
-research/bert/blob/master/multilingual
.md.
13We also tried different combinations of the last four lay-
ers, but this did not improve the results. When a word is split
into multiple wordpieces (WPs), we obtain its representation
by averaging the WPs.
829
3.4 Results and Discussion
3.4.1 Mono-Poly in English
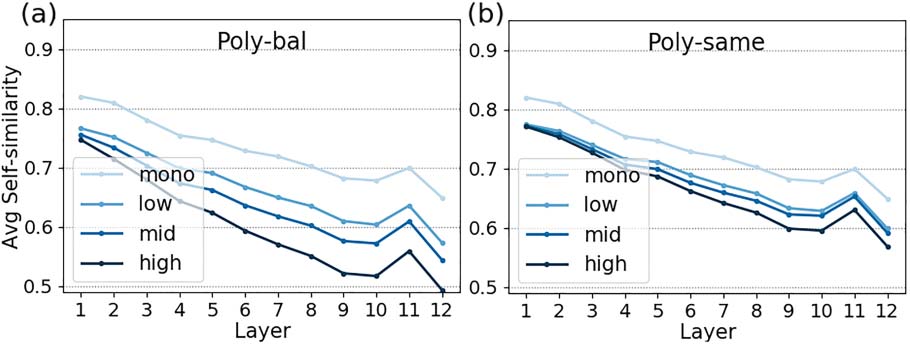
Figure 2 shows the average Self Sim value
obtained for each sentence pool with representa-
tions produced by BERT models. The thin lines in
the first plot illustrate the average Self Sim score
calculated for mono and poly words using repre-
sentations from each layer of the uncased English
BERT model. We observe a clear distinction of
words according to their polysemy: Self Sim is
higher for mono than for poly words across
all layers and sentence pools. BERT establishes
a clear distinction even between the mono and
poly-same pools, which contain instances of
only one sense. This distinction is important; it
suggests that BERT encodes information about
a word’s monosemous or polysemous nature
regardless of the sentences that are used to derive
the contextualized representations. Specifically,
BERT produces less similar representations for
word instances in the poly-same pool com-
pared to mono, reflecting that poly words can
have different meanings.
We also observe a clear ordering of the three
poly sentence pools: Average Self Sim is higher
in poly-same, which only contains instances
of one sense, followed by mid-range values in
poly-rand, and gets its lowest values in the
balanced setting (poly-bal). This is noteworthy
given that poly-rand contains a mix of senses
but with a stronger representation of w’s most
frequent sense than poly-bal (71% vs. 47%).14
Our results demonstrate that BERT represen-
tations encode two types of lexical semantic
the polysemous
knowledge:
nature of words acquired through pre-training
(as reflected in the distinction between mono
and poly-same), and information from the par-
ticular instances of a word used to create the
contextualized representations (as shown by the
finer-grained distinctions between different poly
settings). BERT’s knowledge about polysemy can
be due to differences in the types of context where
words of different polysemy levels occur. We
expect poly words to be seen in more varied
contexts than mono words, reflecting their differ-
ent senses. BERT encodes this variation with the
information about
14Numbers are macro-averages for words in the pools.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
0
0
1
9
5
5
2
0
4
/
/
t
l
a
c
_
a
_
0
0
4
0
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
0
0
1
9
5
5
2
0
4
/
/
t
l
a
c
_
a
_
0
0
4
0
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
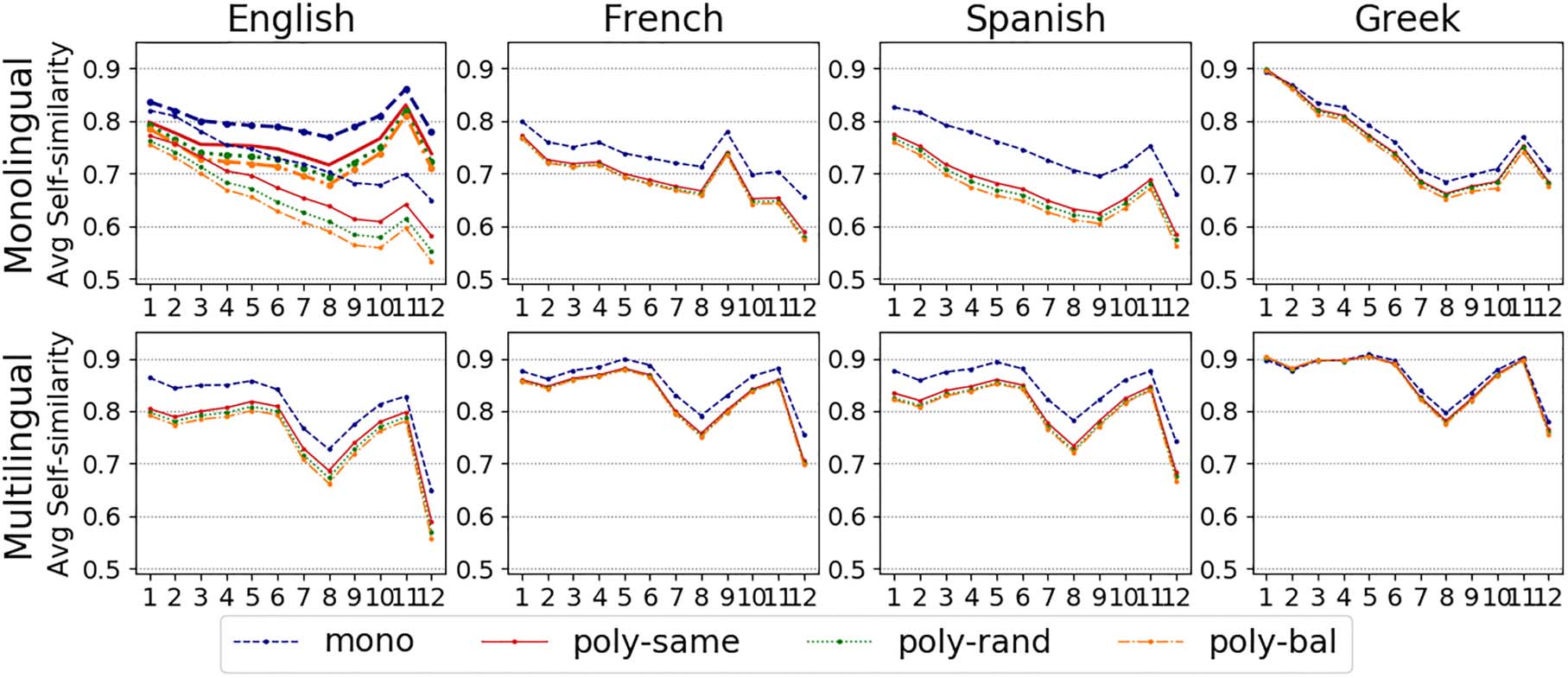
Figure 2: Average Self Sim obtained with monolingual BERT models (top row) and mBERT (bottom row) across
all layers (horizontal axis). In the first plot, thick lines correspond to the cased model.
LM objective through exposure to large amounts
of data, and this is reflected in the represen-
tations. The same ordering pattern is observed
with mBERT (lower part of Figure 2) and with
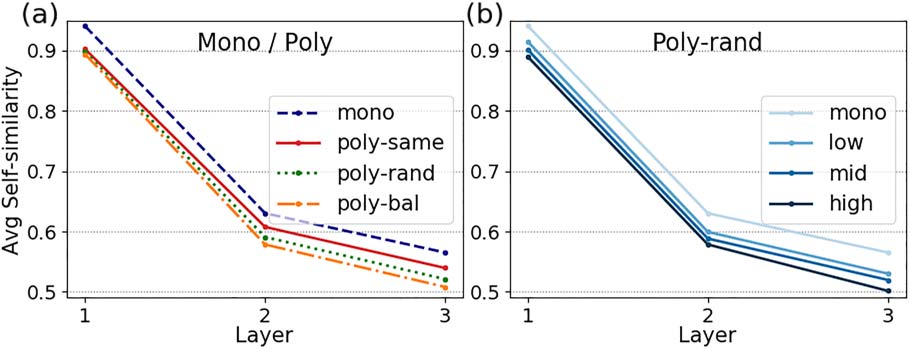
ELMo (Figure 3(a)). With context2vec, average
Self Sim in mono is 0.40, 0.38 in poly-same,
0.37 in poly-rand, and 0.35 in poly-bal.
This suggests that these models also have some
inherent knowledge about lexical polysemy, but
differences are less clearly marked than in BERT.
Using the cased model leads to an overall
increase in Self Sim and to smaller differences
between bands, as shown by the thick lines in the
first plot of Figure 2. Our explanation for the lower
distinction ability of the bert-base-cased
model is that it encodes sparser information about
words than the uncased model. It was trained
on a more diverse set of strings, so many WPs
are present in both their capitalized and non-
capitalized form in the vocabulary. In spite of
that, it has a smaller vocabulary size (29K WPs)
than the uncased model (30.5K). Also, a higher
number of WPs correspond to word parts than in
the uncased model (6,478 vs 5,829).
the
We test
t-tests when
the statistical significance of
the
mono/poly-rand distinction using unpaired
two-samples
normality
assumption is met (as determined with Shapiro
Wilk’s tests). Otherwise, we run a Mann Whitney
U test, the non-parametrical alternative of this
t-test. In order to lower the probability of type
increases when
I errors (false positives) that
performing multiple tests, we correct p-values
using the Benjamini–Hochberg False Discovery
Figure 3: Comparison of average Self Sim obtained
for mono and poly words using ELMo representations
(a), and for words in different polysemy bands in the
poly-rand sentence pool (b).
Rate (FDR) adjustment (Benjamini and Hochberg,
1995). Our results show that differences are
significant across all embedding types and layers
(α = 0.01).
The decreasing trend in Self Sim observed for
BERT in Figure 2, and the peak in layer 11,
confirm the phases of context encoding and token
reconstruction observed by Voita et al. (2019a).15
In earlier layers, context variation makes re-
presentations more dissimilar and Self Sim
decreases. In the last layers, information about the
input token is recovered for LM prediction and
similarity scores are boosted. Our results show
clear distinctions across all BERT and ELMo
layers. This suggests that lexical information is
spread throughout the layers of the models, and
contributes new evidence to the discussion on the
localization of semantic information inside the
models (Rogers et al., 2020; Vuli´c et al., 2020).
15They study the information flow in the Transformer
estimating the MI between representations at different layers.
830
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
0
0
1
9
5
5
2
0
4
/
/
t
l
a
c
_
a
_
0
0
4
0
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4: Average Self Sim obtained with monolingual BERT models (top row) and mBERT (bottom row)
for mono and poly words in different polysemy bands. Representations are derived from sentences in the
poly-rand pool.
3.4.2 Mono-Poly in Other Languages
The top row of Figure 2 shows the average
Self Sim obtained for French, Spanish, and
Greek words using monolingual models. Flaubert,
BETO, and Greek BERT representations clearly
distinguish mono and poly words, but average
Self Sim values for different poly pools are
much closer than in English. BETO seems to
capture these fine-grained distinctions slightly
better than the French and Greek models. The
second row of the figure shows results obtained
with mBERT representations. We observe the
highly similar average Self Sim values assigned
to different poly pools, which show that
distinction is harder than in monolingual models.
Statistical tests show that the difference between
Self Sim values in mono and poly-rand is
significant in all layers of BETO, Flaubert, Greek
BERT, and mBERT for Spanish and French.16
The magnitude of the difference in Greek BERT
is, however, smaller compared to the other models
(0.03 vs. 0.09 in BETO at the layers with the
biggest difference in average Self Sim).
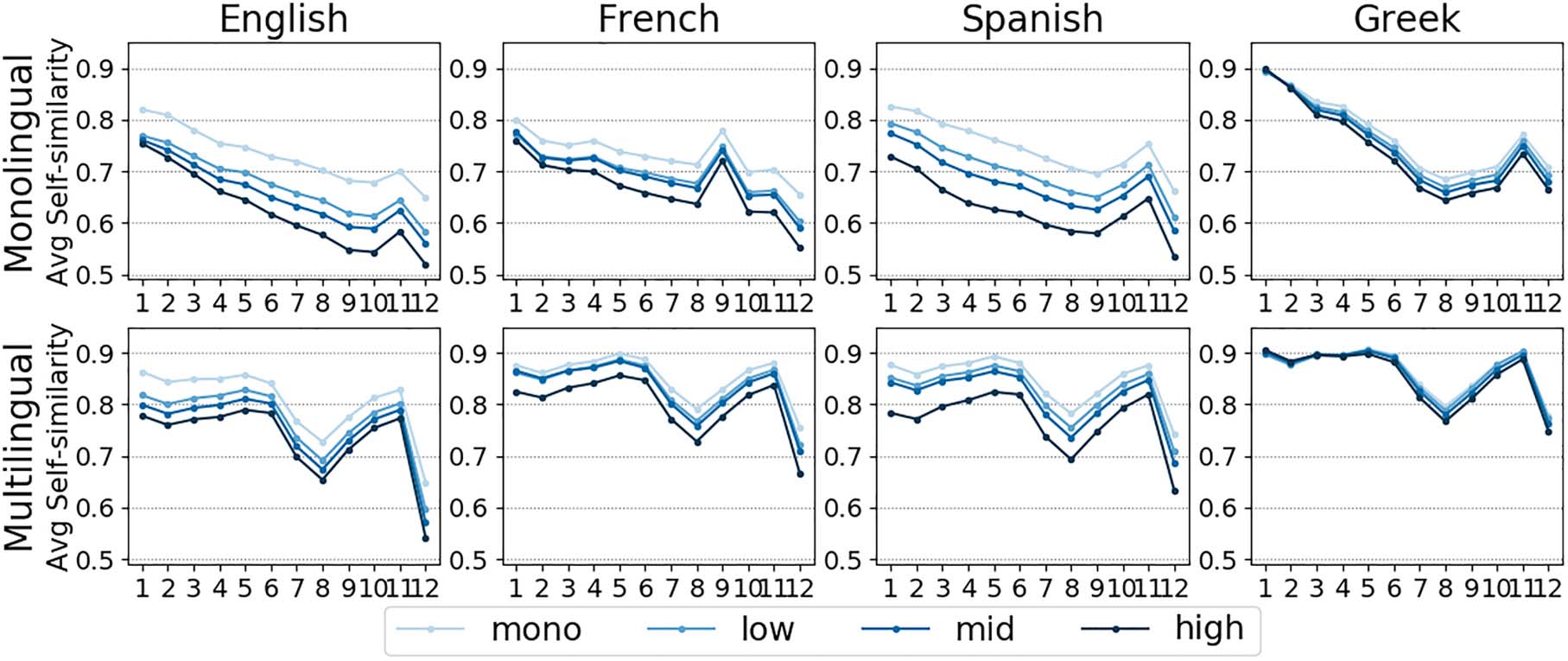
4 Polysemy Level Prediction
4.1 SelfSim-based Ranking
In this set of experiments, we explore the impact of
words’ degree of polysemy on the representations.
We control for this factor by grouping words into
three polysemy bands as in McCarthy et al. (2016),
Figure 5: Comparison of BERT average Self Sim for
mono and poly words in different polysemy bands in
the poly-bal and poly-same sentence pools.
which correspond to a specific number of senses
(k): low: 2 ≤ k ≤ 3, mid: 4 ≤ k ≤ 6, high:
k > 6. For English, the three bands are popu-
lated with a different number of words: low: 551,
mid: 663, high: 551. In the other languages,
we form bands containing 300 words each.17 In
Figure 4, we compare mono words with words
in each polysemy band in terms of their average
Self Sim. Values for mono words are taken from
Section 3. For poly words, we use representations
from the poly-rand sentence pool, which better
approximates natural occurrence in a corpus. For
comparison, we report in Figure 5 results obtained
in English using sentences from the poly-same
and poly-bal pools.18
In English, the pattern is clear in all plots:
Self Sim is higher for mono than for poly
words in any band, confirming that BERT is
17We only used 418 of these poly words in Section 3 in
order to have balanced mono and poly pools.
16In mBERT for Greek, the difference is significant in ten
18We omit the plots for poly-bal and poly-same for
layers.
the other models due to space constraints.
831
able to distinguish mono from poly words at
different polysemy levels. The range of Self Sim
values for a band is inversely proportional to its
k: Words in low get higher values than words
in high. The results denote that the meaning
of highly polysemous words is more variable
(lower Self Sim) than the meaning of words with
fewer senses. As expected, scores are higher and
inter-band similarities are closer in poly-same
(cf. Figure 5(b)) compared with poly-rand
and poly-bal, where distinctions are clearer.
The observed differences confirm that BERT can
predict the polysemy level of words, even from
instances describing the same sense.
We observe similar patterns with ELMo (cf.
Figure 3(b)) and context2vec representations
in poly-rand,19 but smaller absolute inter-
band differences. In poly-same, both models
fail to correctly order the bands. Overall, our
that BERT encodes higher
results highlight
quality knowledge about polysemy. We test the
significance of the inter-band differences detected
in poly-rand using the same approach as in
Section 3.4.1. These are significant in all but a
few20 layers of the models.
The bands are also correctly ranked in the
other three languages but with smaller inter-band
differences than in English, especially in Greek
where clear distinctions are only made in a few
middle layers. This variation across languages can
be explained to some extent by the quality of
the automatic EuroSense annotations, which has
a direct impact on the quality of the sentence
pools. Results of a manual evaluation conducted
by Delli Bovi et al. (2017) showed that WSD
precision is ten points higher in English (81.5)
and Spanish (82.5) than in French (71.8). The
Greek portion, however, has not been evaluated.
Plots in the second row of Figure 4 show
results obtained using mBERT. Similarly to
the previous experiment (Section 3.4), mBERT
overall makes less clear distinctions than the
monolingual models. The low and mid bands
often get similar Self Sim values, which are
close to mono in French and Greek. Still, inter-
band differences are significant in most layers of
Figure 6: The left plots show the similarity between
random words in models for each language. Plots on the
right side show the difference between the similarity of
random words and Self Sim in poly-rand.
mBERT and the monolingual French, Spanish,
and Greek models.21
4.2 Anisotropy Analysis
In order to better understand the reasons behind
the smaller inter-band differences observed with
mBERT, we conduct an additional analysis of
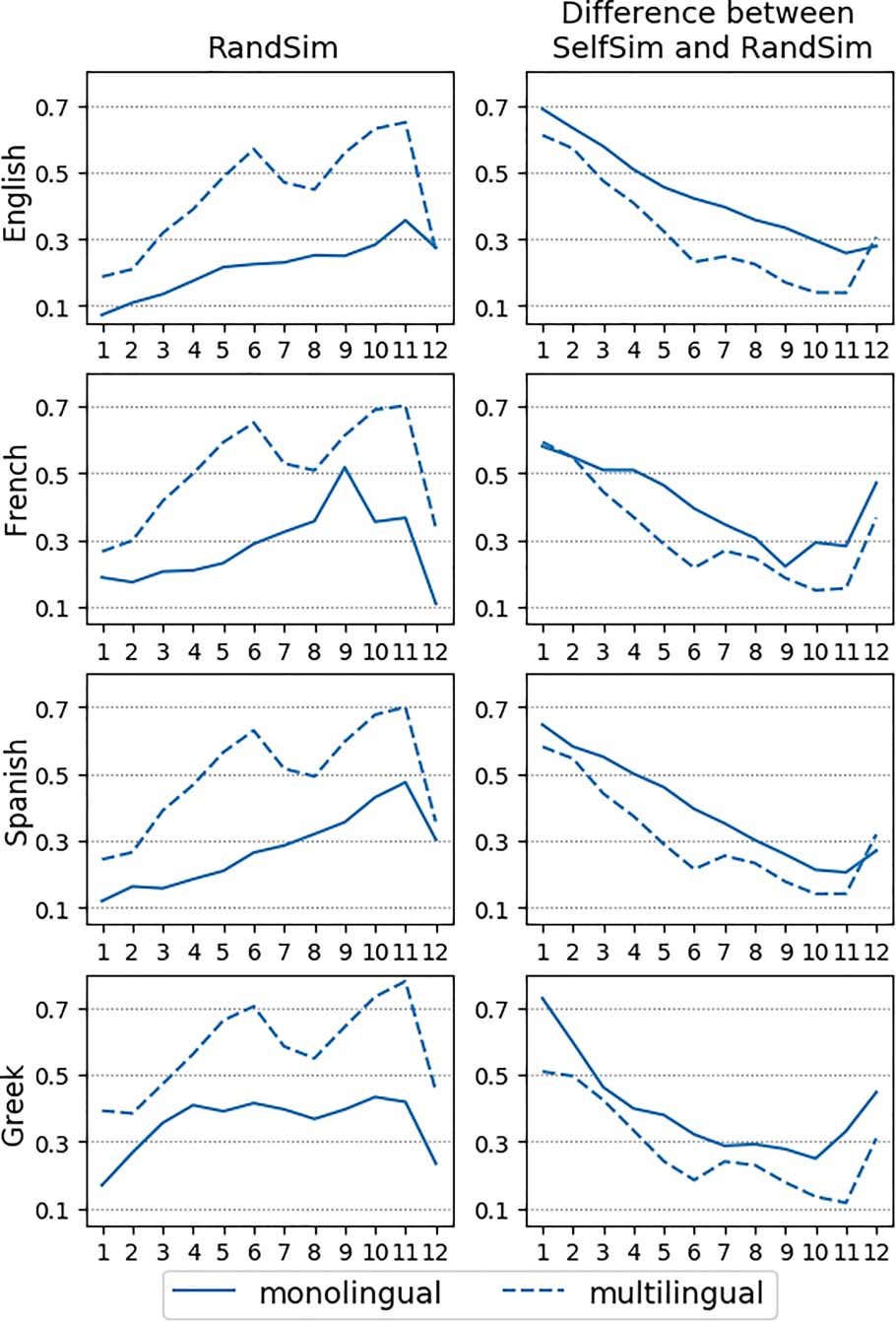
the models’ anisotropy. We create 2,183 random
word pairs from the English mono, low, mid
and high bands, and 1,318 pairs in each of
the other languages.22 We calculate the cosine
similarity between two random instances of the
words in each pair and take the average over all
pairs (RandSim). The plots in the left column
of Figure 6 show the results. We observe a clear
difference in the scores obtained by monolingual
models (solid lines) and mBERT (dashed lines).
Clearly, mBERT assigns higher similarities to
19Average Self Sim values for context2vec in the
poly-rand setting: low: 0.37, mid: 0.36, high: 0.36.
20low→ mid in ELMo’s third layer, and mid→high in
21With the exception of mono→ low in mBERT for
Greek, and low→mid in Flaubert and in mBERT for French.
221,318 is the total number of words across bands in
context2vec and in BERT’s first layer.
French, Spanish, and Greek.
832
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
0
0
1
9
5
5
2
0
4
/
/
t
l
a
c
_
a
_
0
0
4
0
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
random words, an indication that its semantic
space is more anisotropic than the one built by
monolingual models. High anisotropy means that
representations occupy a narrow cone in the vector
space, which results in lower quality similarity
estimates and in the model’s limited potential to
establish clear semantic distinctions.
We also compare RandSim to the average
Self Sim obtained for poly words in the poly-
rand sentence pool (cf. Section 3.1). In a quality
semantic space, we would expect Self Sim
(between same word instances) to be much higher
than RandSim. The right column of Figure 6
shows the difference between these two scores.
diff in a layer l is calculated as in Equation (2):
diffl = AvgSelfSiml(poly-rand)−RandSiml
(2)
We observe that the difference is smaller in the
space built by mBERT, which is more anisotropic
than the space built by monolingual models.
This is particularly obvious in the upper layers
of the model. This result confirms the lower
quality of mBERT’s semantic space compared
to monolingual models.
Finally, we believe that another factor behind
the worse mBERT performance is that
the
multilingual WP vocabulary is mostly English-
driven,
resulting in arbitrary partitionings of
words in the other languages. This word splitting
procedure must have an impact on the quality of
the lexical information in mBERT representations.
5 Analysis by Frequency and PoS
Given the strong correlation between word
frequency and number of senses (Zipf, 1945),
we explore the impact of frequency on BERT
representations. Our goal is to determine the extent
to which it influences the good mono/poly
detection results obtained in Sections 3.4 and 4.1.
5.1 Dataset Composition
We perform this analysis in English using
frequency information from Google Ngrams
(Brants and Franz, 2006). For French, Spanish,
and Greek, we use frequency counts gathered
from the OSCAR corpus (Su´arez et al., 2019). We
split the words into four ranges (F ) corresponding
to the quartiles of frequencies in each dataset.
Each range f in F contains the same number of
words. We provide detailed information about the
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
0
0
1
9
5
5
2
0
4
/
/
t
l
a
c
_
a
_
0
0
4
0
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
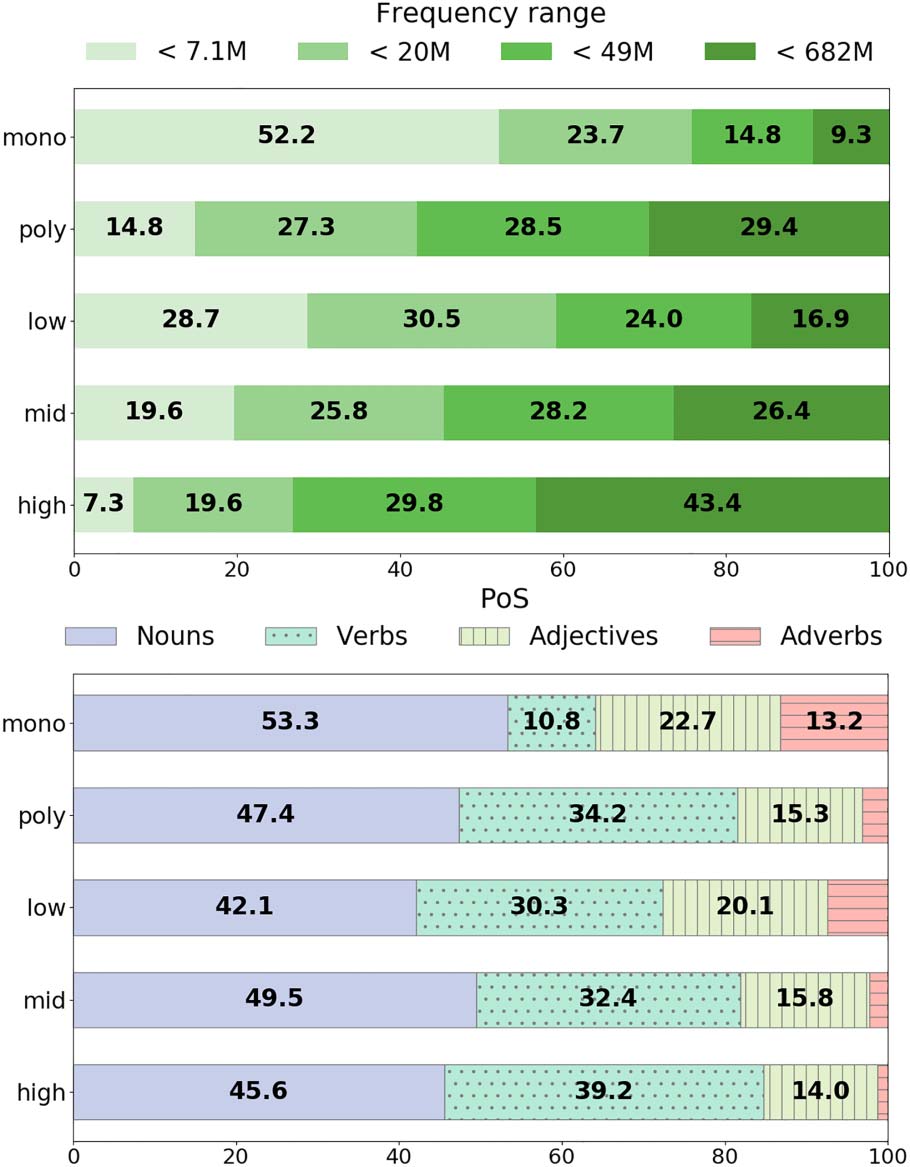
Figure 7: Composition of the English word bands in
terms of frequency (a) and grammatical category (b).
composition of the English dataset in Figure 7.23
Figure 7(a) shows that mono words are much less
frequent than poly words. Figure 7(b) shows the
distribution of different PoS categories in each
band. Nouns are the prevalent category in all
bands and verbs are less present among mono
words (10.8%), as expected. Finally, adverbs are
hardly represented in the high polysemy band
(1.2% of all words).
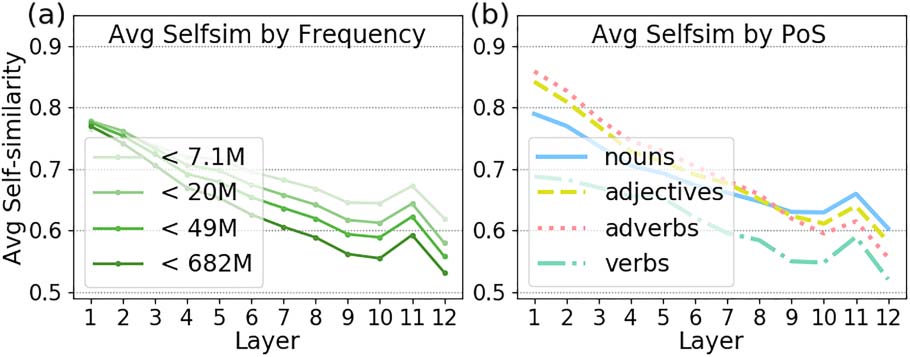
5.2 Self-Sim by Frequency Range and PoS
We examine the average BERT Self Sim per
frequency range in poly-rand. Due to space
constraints, we only report detailed results for the
English BERT model in Figure 8 (plot (a)). The
clear ordering by range suggests that BERT can
successfully distinguish words by their frequency,
especially in the last layers. Plot (b) in Figure 8
shows the average Self Sim for words of each
PoS category. Verbs have the lowest Self Sim
which is not surprising given that they are highly
polysemous (as shown in Figure 7(b)). We observe
the same trend for monolingual models in the other
three languages.
23The composition of each band is the same as in Sections 3
and 4.
833
Figure 8: Average Self Sim for English words of
different frequencies and part of speech categories
with BERT representations.
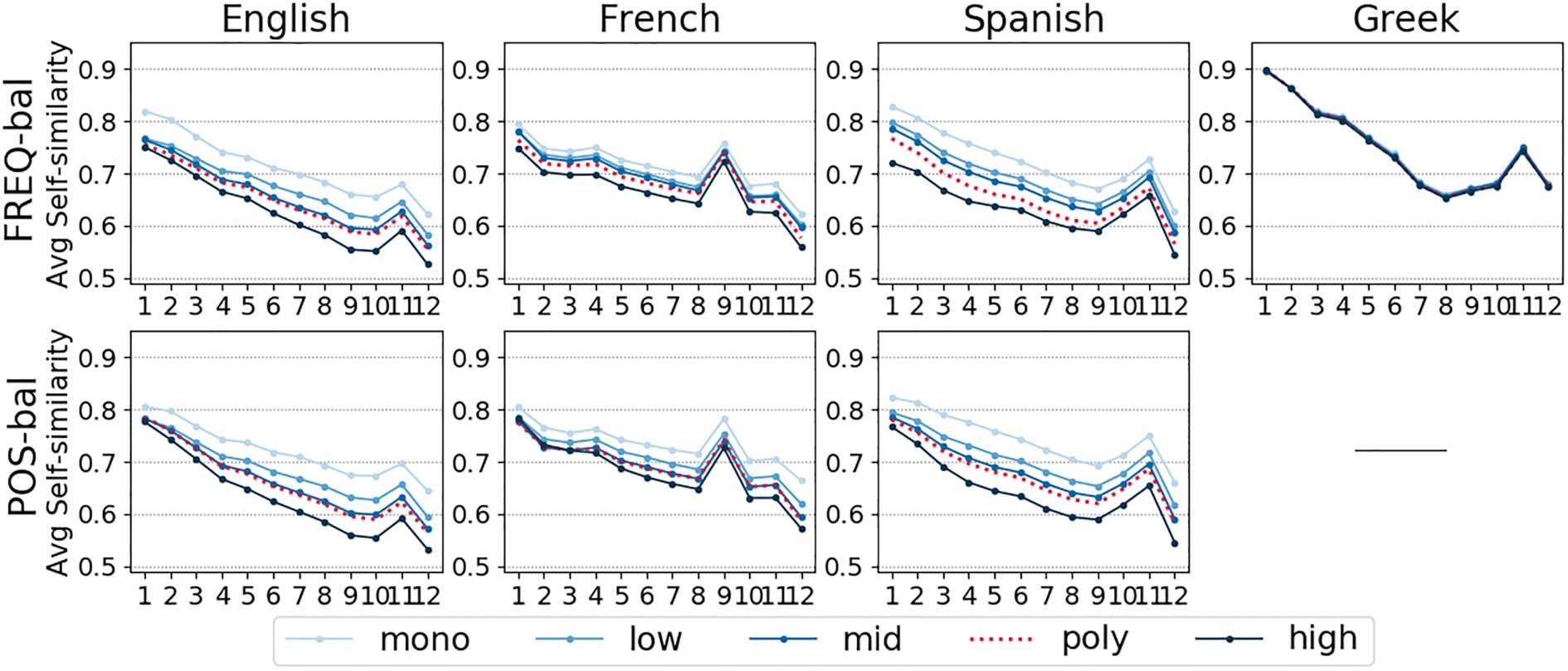
5.3 Controlling for Frequency and PoS
We conduct an additional experiment where we
control for the composition of the poly bands
in terms of grammatical category and word
frequency. We call these two settings POS-bal and
FREQ-bal. We define npos, the smallest number of
words of a specific PoS that can be found in a band.
We form the POS-bal bands by subsampling from
each band the same number of words (npos) of that
PoS. For example, all POS-bal bands have nn nouns
and nv verbs. We follow a similar procedure to
balance the bands by frequency in the FREQ-bal
setting. In this case, nf is the minimum number
of words of a specific frequency range f that can
be found in a band. We form the FREQ-bal dataset
by subsampling from each band the same number
of words (nf ) of a given range f in F .
Table 2 shows the distribution of words per
PoS and frequency range in the POS-bal and FREQ-
bal settings for each language. The table reads as
follows: The English POS-bal bands contain 198
nouns, 45 verbs, 64 adjectives, and 7 adverbs;
similarly for the other two languages. Greek is
not included in this POS-based analysis because
all sense-annotated Greek words in EuroSense are
nouns. In FREQ-bal, each English band contains 40
words that occur less than 7.1M times in Google
Ngrams, and so on and so forth.
We examine the average Self Sim values
obtained for words in each band in poly-
rand. Figure 9 shows the results for monolingual
models. We observe that the mono and poly
words in the POS-bal and FREQ-bal bands are ranked
similarly to Figure 4. This shows that BERT’s
polysemy predictions do not rely on frequency
or part of speech. The only exception is Greek
BERT, which cannot establish correct inter-band
distinctions when the influence of frequency is
neutralized in the FREQ-bal setting. A general
observation that applies to all models is that
POS-bal
Nouns Verbs Adjectives Adverbs
198
171
167
64
29
40
45
32
22
7
9
0
FREQ-bal
99
70m
43
7.1M 20M
40
23m
17
64m 233m
12
14m
13
39
40m
41
49M
62
210m
67
793m
58
111m
70
682M
39
41M
38
59M
48
1.9M
42
en
fr
es
en
fr
es
el
Table 2: Content of the polysemy bands in the
POS-bal and FREQ-bal settings. All bands for a
language contain the same number of words of a
specific grammatical category or frequency range.
M stands for a million and m for a thousand
occurrences of a word in a corpus.
although inter-band distinctions become less clear,
the ordering of the bands is preserved. We observe
the same trend with ELMo and context2vec.
tests
Statistical
show that all
inter-band
distinctions established by English BERT are still
significant in most layers of the model.24 This is
not the case for ELMo and context2vec, which can
distinguish between mono and poly words but
fail to establish significant distinctions between
polysemy bands in the balanced settings. For
French and Spanish, the statistical analysis shows
that all distinctions in POS-bal are significant in at
least one layer of the models. The same applies
to the mono→poly distinction in FREQ-bal but
finer-grained distinctions disappear.25
6 Classification by Polysemy Level
Our finding that word instance similarity differs
across polysemy bands suggests that this feature
can be useful for classification. In this section,
we probe the representations for polysemy using
a classification experiment where we test their
ability to guess whether a word is polysemous,
and which poly band it
falls in. We use
24Note that the sample size in this analysis is smaller
compared to that used in Sections 3.4 and 4.1.
25With a few exceptions: mono→low and mid→ high
are significant in all BETO layers.
834
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
0
0
1
9
5
5
2
0
4
/
/
t
l
a
c
_
a
_
0
0
4
0
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
0
0
1
9
5
5
2
0
4
/
/
t
l
a
c
_
a
_
0
0
4
0
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 9: Average Self Sim inside the poly bands balanced for frequency (FREQ-bal) and part of speech (POS-bal).
Self Sim is calculated using representations generated by monolingual BERT models from sentences in each
language-specific pool. We do not balance the Greek dataset for PoS because it only contains nouns.
the poly-rand sentence pools and a standard
train/dev/test split (70%/15%/15%) of the data.
For the mono/poly distinction (i.e., the data
used in Section 3), this results in 584/126/126
words per set in each language. To guarantee a
fair evaluation, we make sure there is no overlap
between the lemmas in the three sets. We use two
types of features: (i) the average Self Sim for
a word; and (ii) all pairwise cosine similarities
collected for its instances, which results in 45
features per word (pairCos). We train a binary
logistic regression classifier for each type of
representation and feature.
As explained in Section 4, the three poly
bands (low, mid, and high) and mono contain
a different number of words. For classification
into polysemy bands, we balance each class by
randomly subsampling words from each band.
In total, we use 1,168 words for training, 252 for
development, and 252 for testing (70%/15%/15%)
in English. In the other languages, we use a
split of 840/180/180 words. We train multi-class
logistic regression classifiers with the two types
of features, Self Sim and pairCos. We compare
the results of the classifiers to a baseline that
predicts always the same class, and to a frequency-
based classifier which only uses the words’ log
frequency in Google Ngrams, or in the OSCAR
corpus, as a feature.
Table 3 presents classification accuracy on the
test set. We report results obtained with the best
layer for each representation type and feature as
mono/poly
poly bands
Self Sim pairCos Self Sim pairCos
0.7610
0.778
0.692
0.61
0.587
0.669
Model
BERT
mBERT
ELMo
context2vec
Frequency
Flaubert
mBERT
Frequency
BETO
mBERT
Frequency
GreekBERT 0.704
0.607
mBERT
Frequency
Baseline
0.709
0.6911
N
E
R
F
S
E
L
E
0.77
0.61
0.67
0.63
0.50
0.798
0.758
0.633
0.61
0.556
0.649
0.667
0.647
0.644
0.657
0.4910
0.4612
0.372
0.34
0.4610
0.4312
0.343
0.31
0.298
0.387
0.426
0.389
0.41
0.37
0.279
0.388
0.485
0.437
0.41
0.344
0.3211
0.386
0.349
0.35
0.25
Table 3: Accuracy of binary (mono/poly)
and multi-class (poly bands) classifiers using
Self Sim and pairCos features on the test sets.
Comparison to a baseline that predicts always the
same class and a classifier that only uses log fre-
quency as feature. Subscripts denote the layers
used.
determined on the development sets. In English,
best accuracy is obtained by BERT in both
the binary (0.79) and multiclass settings (0.49),
followed by mBERT (0.77 and 0.46). Despite its
simplicity, the frequency-based classifier obtains
better results than context2vec and ELMo, and
performs on par with mBERT in the binary
setting. This shows that frequency information
835
is highly relevant for the mono-poly distinction.
All classifiers outperform the same class baseline.
These results are very encouraging, showing that
BERT embeddings can be used to determine
whether a word has multiple meanings, and
provide a rough indication of its polysemy level.
Results in the other three languages are not as high
as those obtained in English, but most models
results than the frequency-based
give higher
classifier.26
instances, on the contrary, share a different number
of substitutes depending on their proximity. The
need for manual annotations, however, constrains
the method’s applicability to specific datasets.
We propose to extend and scale up the
McCarthy et al. (2016) clusterability approach
using contextualized representations, in order to
make it applicable to a larger vocabulary. These
experiments are carried out in English due to the
lack of evaluation data in other languages.
7 Word Sense Clusterability
7.2 Data
We have shown that representations from pre-
trained LMs encode rich information about
words’ degree of polysemy. They can successfully
distinguish mono from poly lemmas, and predict
the polysemy level of words. Our previous
experiments involved a set of controlled settings
representing different sense distributions and
polysemy levels. In this section, we explore
whether these representations can also point to the
clusterability of poly words in an uncontrolled
setting.
7.1 Task Definition
Instances of some poly words are easier to group
into interpretable clusters than others. This is, for
example, a simple task for the ambiguous noun
rock which can express two clearly separate senses
(STONE and MUSIC), but harder for book, which
might refer to the CONTENT or OBJECT senses of the
word (e.g., I read a book vs. I bought a book). In
what follows, we test the ability of contextualized
representations to estimate how easy this task is
for a specific word, that is, its partitionability into
senses.
Following McCarthy et al. (2016), we use
the clusterability metrics proposed by Ackerman
and Ben-David (2009) to measure the ease of
clustering word instances into senses. McCarthy
et al. base their clustering on the similarity of
manual meaning-preserving annotations (lexical
substitutes and translations). Instances of different
senses, such as: Put granola bars in a bowl
vs. That’s not a very high bar, present no
overlap in their in-context substitutes: {snack,
biscuit, block, slab} vs. {pole, marker, hurdle,
barrier, level, obstruction}. Semantically related
26Only exceptions are Greek mBERT in the multi-class
setting, and Flaubert in both settings.
We run our experiments on the usage similarity
(Usim) dataset (Erk et al., 2013) for comparison
with previous work. Usim contains ten instances
for 56 target words of different PoS from the
SemEval Lexical Substitution dataset (McCarthy
and Navigli, 2007). Word instances are manually
annotated with pairwise similarity scores on a
scale from 1 (completely different) to 5 (same
meaning).
We represent target word instances in Usim
in two ways: using contextualized represen-
tations generated by BERT, context2vec, and
ELMo (BERT-REP, c2v-REP, ELMo-REP);27 using
substitute-based representations with automat-
ically generated substitutes. The substitute-based
approach allows for a direct comparison with the
method of McCarthy et al. (2016). They represent
each instance i of a word w in Usim as a vector(cid:3)i,
where each substitute s assigned to w over all its
instances (i ∈ I) becomes a dimension (ds). For
a given i, the value for each ds is the number of
annotators who proposed substitute s. ds contains
a zero entry if s was not proposed for i. We
refer to this type of representation as Gold-SUB.
We generate our substitute-based representations
with BERT using the simple ‘‘word similarity’’
approach in Zhou et al. (2019). For an instance i
of word w in context C, we rank a set of candidate
substitutes S = {s1, s2, . . . , sn} based on the
cosine similarity of the BERT representations for
i and for each substitute sj ∈ S in the same con-
text C. We use representations from the last layer
of the model. As candidate substitutes, we use
the unigram paraphrases of w in the Paraphrase
27We do not use the first layer of ELMo in this experiment.
It is character-based, so most representations of a lemma are
identical and we cannot obtain meaningful clusters.
836
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
0
0
1
9
5
5
2
0
4
/
/
t
l
a
c
_
a
_
0
0
4
0
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Database (PPDB) XXL package (Ganitkevitch
et al., 2013; Pavlick et al., 2015).28
For each instance i of w, we obtain a ranking
R of all substitutes in S. We remove low-quality
substitutes (i.e., noisy paraphrases or substitutes
referring to a different sense of w) using the
filtering approach proposed by Gar´ı Soler et al.
(2019). We check each pair of substitutes in
subsequent positions in R, starting from the top;
if a pair is unrelated in PPDB, all substitutes from
that position onwards are discarded. The idea is
that good quality substitutes should be both high-
ranked and semantically related. We build vectors
as in McCarthy et al. (2016), using the cosine
similarity assigned by BERT to each substitute as
a value. We call this representation BERT-SUB.
7.3 Sense Clustering
The clusterability metrics that we use are metrics
initially proposed for estimating the quality of the
optimal clustering that can be obtained from a
dataset; the better the quality of this clustering,
the higher the clusterability of the dataset it is
derived from (Ackerman and Ben-David, 2009).
In order to estimate the clusterability of a word
w, we thus need to first cluster its instances in
the data. We use the k-means algorithm which
requires the number of senses for a lemma.
This is, of course, different for every lemma in
our dataset. We define the optimal number of
clusters k for a lemma in a data-driven manner
using the Silhouette coefficient (SIL) (Rousseeuw,
1987), without recourse to external resources.29
For a data point i, SIL compares the intra-cluster
the average distance from i to
distance (i.e.,
every other data point in the same cluster) with
the average distance of i to all points in its
nearest cluster. The SIL value for a clustering is
obtained by averaging SIL for all data points, and
it ranges from −1 to 1. We cluster each type of
representation for w using k-means with a range
of k values (2 ≤ k ≤ 10), and retain the k of the
clustering with the highest mean SIL. Additionally,
since BERT representations’ cosine similarity
correlates well with usage similarity (Gar´ı Soler
et al., 2019), we experiment with Agglomerative
Clustering with average linkage directly on the
28We use PPDB (http://www.paraphrase.org) to
reduce variability in our substitute sets, compared to the ones
that would be proposed by looking at the whole vocabulary.
29We do not use McCarthy et al.’s graph-based approach
because it is not compatible with all our representation types.
cosine distance matrix obtained with BERT
representations (BERT-AGG). For comparison,
we also use Agglomerative Clustering on the gold
usage similarity scores from Usim, transformed
into distances (Gold-AGG).
7.4 Clusterability Metrics
We use in our experiments the two best performing
metrics from McCarthy et al. (2016): Variance
Ratio (VR) (Zhang, 2001) and Separability (SEP)
(Ostrovsky et al., 2012). VR calculates the ratio
of the within- and between-cluster variance for
a given clustering solution. SEP measures the
difference in loss between two clusterings with
k − 1 and k clusters and its range is [0,1). We use
k-means’ sum of squared distances of data points
to their closest cluster center as the loss. Details
about these two metrics are given in Appendix A.30
We also experiment with SIL as a clusterability
metric, as it can assess cluster validity. For VR and
SIL, a higher value indicates higher clusterability.
The inverse applies to SEP.
We calculate Spearman’s ρ correlation between
the results of each clusterability metric and two
gold standard measures derived from Usim: Uiaa
and Umid. Uiaa is the inter-annotator agreement
for a lemma in terms of average pairwise
correlation between annotators’
Spearman’s
judgments. Higher Uiaa values indicate higher
clusterability, meaning that sense partitions are
clearer and easier to agree upon. Umid is the
proportion of mid-range judgments (between 2
and 4) assigned by annotators to all instances of
a target word. It indicates how often usages do
not have identical (5) or completely different (1)
meaning. Therefore, higher Umid values indicate
lower clusterability.
7.5 Results and Discussion
The clusterability results are given in Table 4.
Agglomerative Clustering on the gold Usim
similarity scores (Gold-AGG) gives best results
on the Uiaa evaluation in combination with
the SIL clusterability metric (ρ = 0.80). This
is unsurprising,
since Uiaa and Umid are
derived from the same Usim scores. From
our automatically generated representations, the
strongest correlation with Uiaa (0.69) is obtained
30Note that the VR and SEP metrics are not compatible with
Gold-AGG which relies on Usim similarity scores, because
we need vectors for their calculation. For BERT-AGG, we
calculate VR and SEP using BERT embeddings.
837
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
0
0
1
9
5
5
2
0
4
/
/
t
l
a
c
_
a
_
0
0
4
0
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Gold Metric
Uiaa
Umid
BERT-REP
SEP (cid:7) −0.48*10
VR (cid:8)
0.1712
SIL (cid:8)
0.61*11
SEP (cid:8)
0.43*9
VR (cid:7) −0.249
SIL (cid:7) −0.46*10
c2v-REP ELMo-REP BERT-SUB Gold-SUB BERT-AGG Gold-AGG
−0.12
0.14
0.06
−0.01
−0.08
0.05
−0.48*11
0.33*12
0.69*10
0.43*9
−0.32*5
−0.44*8
−0.20
0.34*
0.32*
0.16
−0.24
−0.38*
–
–
0.80*
–
–
−0.48*
−0.242
0.192
0.212
0.083
−0.153
−0.062
−0.03
0.09
0.10
0.05
−0.15
−0.11
Table 4: Spearman’s ρ correlation between automatic metrics and gold standard clusterability
estimates. Significant correlations (where the null hypothesis ρ = 0 is rejected with α < 0.05) are
marked with *. The arrows indicate the expected direction of correlation for each metric. Subscripts
indicate the layer that achieved best performance. The two strongest correlations obtained with each
gold standard measure are in boldface.
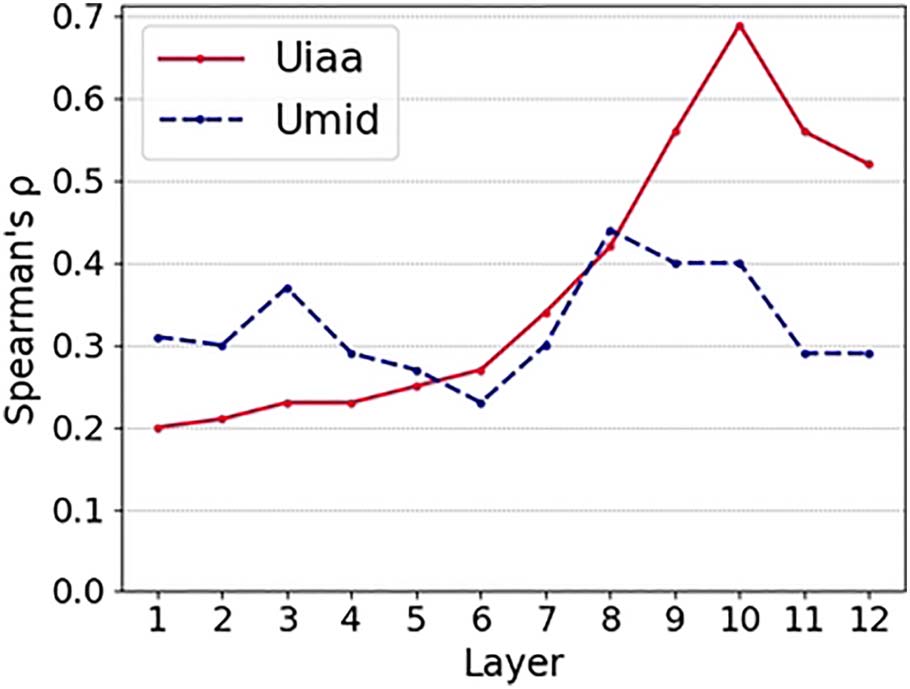
layer analysis of
We present a per
the
correlations obtained with the best performing
BERT representations (BERT-AGG) and the SIL
the absolute
metric in Figure 10. We report
values of the correlation coefficient for a more
straightforward comparison. For Uiaa, the higher
layers of the model make the best predictions:
Correlations increase monotonically up to layer
10, and then they show a slight decrease. Umid
prediction shows a more irregular pattern: It peaks
at layers 3 and 8, and decreases again in the last
layers.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
0
0
1
9
5
5
2
0
4
/
/
t
l
a
c
_
a
_
0
0
4
0
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 10: Spearman’s ρ correlations between the gold
standard Uiaa and Umid scores, and clusterability
estimates obtained using Agglomerative Clustering on
a cosine distance matrix of BERT representations.
with BERT-AGG and the SIL clusterability metric.
The SIL metric also works well with BERT-REP
achieving the strongest correlation with Umid
(−0.46). It constitutes, thus, a good alternative to
the SEP and VR metrics used in previous studies
when combined with BERT representations.
Interestingly, the correlations obtained using
raw BERT contextualized representations are
much higher
than the ones observed with
McCarthy et al. (2016)’s representations that
rely on manual substitutes (Gold-SUB). These
were in the range of 0.20–0.34 for Uiaa and
0.16–0.38 for Umid (in absolute value). The
results demonstrate that BERT representations
offer good estimates of the partitionability of
words into senses,
improving over substitute
annotations. As expected, the substitution-based
approach performs better with clean manual
substitutes (Gold-SUB) than with automatically
generated ones (BERT-SUB).
8 Conclusion
We have shown that contextualized BERT repre-
sentations encode rich information about lexical
polysemy. Our experimental results suggest that
this high quality knowledge about words, which
allows BERT to detect polysemy in different
configurations and across all layers, is acquired
during pre-training. Our findings hold for the
English BERT as well as for BERT models in
other languages, as shown by our experiments on
French, Spanish, and Greek, and to a lesser extent
for multilingual BERT. Moreover, English BERT
representations can be used to obtain a good
estimation of a word’s partitionability into senses.
These results open up new avenues for research in
multilingual semantic analysis, and we can con-
sider various theoretical and application-related
extensions for this work.
The polysemy and sense-related knowledge
revealed by the models can serve to develop
novel methodologies for improved cross-lingual
alignment of embedding spaces and cross-lingual
transfer, pointing to more polysemous (or less
clusterable) words for which transfer might be
838
harder. Predicting the polysemy level of words can
also be useful for determining the context needed
for acquiring representations that properly reflect
the meaning of word instances in running text.
From a more theoretical standpoint, we expect this
work to be useful for studies on the organization
of the semantic space in different languages and
on lexical semantic change.
Acknowledgments
This work has been supported by the French Na-
tional Research Agency under project ANR-16-
CE33-0013. The work is also part of the FoTran
project, funded by the European Research Council
(ERC) under
the European Union’s Horizon
2020 research and innovation programme (grant
agreement No 771113). We thank the anonymous
reviewers and the TACL Action Editor for their
careful reading of our paper,
their thorough
reviews, and their helpful suggestions.
References
Margareta Ackerman and Shai Ben-David. 2009.
Clusterability: A Theoretical Study. Journal of
Machine Learning Research, 5:1–8.
Yossi Adi, Einat Kermany, Yonatan Belinkov,
Ofer Lavi, and Yoav Goldberg. 2017. Fine-
grained analysis of sentence embeddings using
auxiliary prediction tasks. In Proceedings of
ICLR. Toulon, France.
Eneko Agirre
and David Martinez. 2004.
Unsupervised WSD based on automatically
retrieved examples: The importance of bias.
the 2004 Conference on
In Proceedings of
Empirical Methods
in Natural Language
Processing, pages 25–32, Barcelona, Spain.
Association for Computational Linguistics.
Laura Aina, Kristina Gulordava, and Gemma
Boleda. 2019. Putting words in context: LSTM
language models and lexical ambiguity. In
Proceedings of the 57th Annual Meeting of
the Association for Computational Linguistics,
pages 3342–3348, Florence, Italy. Association
for Computational Linguistics.
Marco Baroni, Silvia Bernardini, Adriano
Ferraresi, and Eros Zanchetta. 2009. The
WaCky Wide Web: A collection of very
large linguistically processed web-crawled
corpora. Journal of Language Resources and
Evaluation, 43(3):209–226. https://doi
.org/10.1007/s10579-009-9081-4
Yoav Benjamini and Yosef Hochberg. 1995. Con-
trolling the false discovery rate: A practical and
powerful approach to multiple testing. Journal
of
the Royal Statistical Society: Series B
(Methodological), 57(1):289–300. https://
doi.org/10.1111/j.2517-6161.1995
.tb02031.x
Steven Bird, Ewan Klein, and Edward Loper.
2009. Natural Language Processing with
Python: Analyzing Text with the Natural
Language Toolkit. O’Reilly Media,
Inc.,
Beijing.
Thorsten Brants and Alex Franz. 2006. Web 1T 5-
gram Version 1. In LDC2006T13. Philadelphia,
Pennsylvania. Linguistic Data Consortium.
Jos´e Camacho-Collados and Mohammad Taher
Pilehvar. 2018. From word to sense embed-
dings: A survey on vector representations of
meaning. Journal of Artificial Intelligence Re-
search, 63:743–788. https://doi.org/10
.1613/jair.1.11259
José Cañete, Gabriel Chaperon, Rodrigo Fuentes,
and Jorge Pérez. 2020. Spanish pre-trained
BERT model and evaluation data. In Proceed-
ings of the ICLR 2020 Workshop on Practi-
cal ML for Developing Countries (PML4DC).
Addis Ababa, Ethiopia.
Kevin Clark, Urvashi Khandelwal, Omer Levy,
and Christopher D. Manning. 2019. What does
BERT look at? An analysis of BERT’s atten-
tion. In Proceedings of the ACL 2019 Work-
shop BlackboxNLP: Analyzing and Interpreting
Neural Networks for NLP, pages 276–286,
Italy. Association for Computa-
Florence,
tional Linguistics. https://doi.org/10
.18653/v1/W19-4828
Alexis Conneau, German Kruszewski, Guillaume
Lample, Lo¨ıc Barrault, and Marco Baroni.
2018. What you can cram into a single
$&!#* vector: Probing sentence embeddings
for linguistic properties. In Proceedings of the
56th Annual Meeting of the Association for
Computational Linguistics (Volume 1: Long
839
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
0
0
1
9
5
5
2
0
4
/
/
t
l
a
c
_
a
_
0
0
4
0
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
pages
Papers),
2126–2136, Melbourne,
Australia. Association for Computational Lin-
guistics. https://doi.org/10.18653
/v1/P18-1198
Claudio Delli Bovi, Jose Camacho-Collados,
Alessandro Raganato, and Roberto Navigli.
2017. EuroSense: Automatic harvesting of
multilingual sense annotations from paral-
lel text. In Proceedings of the 55th Annual
Meeting of
the Association for Computa-
tional Linguistics (Volume 2: Short Papers),
pages 594–600, Vancouver, Canada. Associa-
tion for Computational Linguistics. https://
doi.org/10.18653/v1/P17-2094
Jacob Devlin, Ming-Wei Chang, Kenton Lee, and
Kristina Toutanova. 2019. BERT: Pre-training
of deep bidirectional transformers for language
the 2019
understanding. In Proceedings of
Conference of the North American Chapter
of the Association for Computational Linguis-
tics: Human Language Technologies, Volume 1
(Long and Short Papers), pages 4171–4186,
Minneapolis, Minnesota. Association
for
Computational Linguistics.
lexical
Haim Dubossarsky, Simon Hengchen, Nina
Tahmasebi, and Dominik Schlechtweg. 2019.
Time-Out: Temporal referencing for robust
In
modeling of
Proceedings of the 57th Annual Meeting of
the Association for Computational Linguistics,
pages 457–470, Florence, Italy. Association
for Computational Linguistics. https://
doi.org/10.18653/v1/P19-1044
semantic change.
Katrin Erk, Diana McCarthy, and Nicholas
Gaylord. 2009. Investigations on word senses
and word usages. In Proceedings of the Joint
Conference of the 47th Annual Meeting of the
ACL and the 4th International Joint Conference
on Natural Language Processing of the AFNLP,
pages 10–18, Suntec, Singapore. Association
for Computational Linguistics.
Katrin Erk, Diana McCarthy, and Nicholas
Gaylord. 2013. Measuring word meaning in con-
text. Computational Linguistics, 39(3):511–554.
https://doi.org/10.1162/COLI a
00142
840
Kawin Ethayarajh. 2019. How contextual are
contextualized word representations? Com-
paring the geometry of BERT, ELMo, and
GPT-2 embeddings. In Proceedings of
the
2019 Conference on Empirical Methods in
Natural Language Processing and the 9th
International
Joint Conference on Natu-
ral Language Processing (EMNLP-IJCNLP),
pages 55–65, Hong Kong, China. Associa-
tion for Computational Linguistics. https://
doi.org/10.18653/v1/D19-1006
Christiane Fellbaum.
1998. WordNet: An
Lexical Database. Language,
Electronic
Speech,
and Communication. Cambridge,
MA. MIT Press. https://doi.org/10
.7551/mitpress/7287.001.0001
Juri Ganitkevitch, Benjamin Van Durme, and
Chris Callison-Burch. 2013. PPDB: The para
phrase database. In Proceedings of the 2013
the North American Chap-
Conference of
ter of
the Association for Computational
Linguistics: Human Language Technologies,
pages 758–764, Atlanta, Georgia. Association
for Computational Linguistics.
Aina Gar´ı Soler, Marianna Apidianaki, and
Alexandre Allauzen. 2019. Word usage simi-
larity estimation with sentence representations
In Proceedings
and automatic substitutes.
the Eighth Joint Conference on Lexi-
of
(*SEM
cal and Computational Semantics
2019), pages 9–21, Minneapolis, Minnesota.
Association for Computational Linguistics.
https://doi.org/10.18653/v1/S19
-1002
Mario Giulianelli, Marco Del Tredici, and
Raquel Fern´andez. 2020. Analysing lexical
semantic change with contextualized word
representations. In Proceedings of
the 58th
Annual Meeting of the Association for Compu-
tational Linguistics, pages 3960–3973, Online.
Association for Computational Linguistics.
https://doi.org/10.18653/v1/2020
.acl-main.365
John Hewitt and Percy Liang. 2019. Designing and
interpreting probes with control tasks. In Pro-
ceedings of the 2019 Conference on Empirical
Methods in Natural Language Processing and
the 9th International Joint Conference on Nat-
ural Language Processing (EMNLP-IJCNLP),
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
0
0
1
9
5
5
2
0
4
/
/
t
l
a
c
_
a
_
0
0
4
0
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
pages 2733–2743, Hong Kong, China. Associa-
tion for Computational Linguistics. https://
doi.org/10.18653/v1/D19-1275
John Hewitt and Christopher D. Manning. 2019.
A structural probe for finding syntax in word
representations. In Proceedings of the 2019
Conference of the North American Chapter
of the Association for Computational Linguis-
tics: Human Language Technologies, Volume 1
(Long and Short Papers), pages 4129–4138,
Minneapolis, Minnesota. Association
for
Computational Linguistics.
Eric Huang, Richard Socher, Christopher
Manning, and Andrew Ng. 2012. Improving
word representations via global context and
multiple word prototypes. In Proceedings of
the 50th Annual Meeting of the Association
for Computational Linguistics (Volume 1: Long
Papers), pages 873–882, Jeju Island, Korea.
Association for Computational Linguistics.
Alexander
Jakubowski, Milica Gasic,
and
Marcus Zibrowius. 2020. Topology of word
embeddings: Singularities reflect polysemy. In
Proceedings of
the Ninth Joint Conference
on Lexical and Computational Semantics,
pages 103–113, Barcelona, Spain (Online).
Association for Computational Linguistics.
Adam Kilgarriff. 2004. How dominant
is the
commonest sense of a word? In Lecture Notes
in Computer Science (vol. 3206), Text, Speech
and Dialogue, Sojka Petr, Kopeˇcek Ivan, Pala
Karel (eds.), pages 103–112, Springer. Berlin,
Heidelberg. https://doi.org/10.1007
/978-3-540-30120-2_14
John Koutsikakis,
Ilias Chalkidis, Prodromos
Malakasiotis, and Ion Androutsopoulos. 2020.
GREEK-BERT: The Greeks visiting Sesame
Street. In Proceedings of the 11th Hellenic
Conference on Artificial Intelligence (SETN
2020),
110–117, Athens, Greece.
https://doi.org/10.1145/3411408
.3411440
pages
Olga Kovaleva, Alexey Romanov, Anna Rogers,
and Anna Rumshisky. 2019. Revealing the
dark secrets of BERT. In Proceedings of the
2019 Conference on Empirical Methods in
Natural Language Processing and the 9th
International Joint Conference on Natural
841
Processing
(EMNLP-IJCNLP),
Language
4365–4374, Hong Kong, China.
pages
Association for Computational Linguistics.
https://doi.org/10.18653/v1/D19
-1445
Hang Le, Lo¨ıc Vial, Jibril Frej, Vincent Segonne,
Maximin Coavoux, Benjamin Lecouteux,
Alexandre Allauzen, Benoˆıt Crabb´e, Laurent
Besacier, and Didier Schwab. 2020. FlauBERT:
Unsupervised language model Pre-training for
In Proceedings of The 12th Lan-
French.
guage Resources and Evaluation Conference,
pages 2479–2490, Marseille, France. European
Language Resources Association.
Claudia Leacock, Martin Chodorow, and George
A. Miller. 1998. Using corpus statistics and
WordNet
relations for sense identification.
Computational Linguistics, 24(1):147–165.
Tal Linzen. 2018. What can linguistics and deep
learning contribute to each other? arXiv pre-
print:1809.04179v2. https://doi.org/10
.1162/tacl a 00115
Tal Linzen, Emmanuel Dupoux, and Yoav
Goldberg. 2016. Assessing the ability of
LSTMs to learn syntax-sensitive dependencies.
Transactions of the Association for Compu-
tational Linguistics, 4:521–535.
Daniel Loureiro and Jose Camacho-Collados.
2020. Don’t neglect the obvious: On the role of
unambiguous words in word sense disambigua-
tion. In Proceedings of the 2020 Conference on
Empirical Methods in Natural Language Pro-
cessing (EMNLP), pages 3514–3520, Online.
Association for Computational Linguistics.
https://doi.org/10.18653/v1/2020
.emnlp-main.283
Diana McCarthy, Marianna Apidianaki, and
Katrin Erk. 2016. Word sense clustering
and clusterability. Computational Linguistics,
42(2):245–275. https://doi.org/10.1162
/COLI a 00247
Diana McCarthy, Rob Koeling, Julie Weeds,
and John Carroll. 2004. Finding predominant
word senses in untagged text. In Proceedings
of the 42nd Annual Meeting of the Associa-
tion for Computational Linguistics (ACL-04),
pages 279–286. Barcelona, Spain. https://
doi.org/10.3115/1218955.1218991
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
0
0
1
9
5
5
2
0
4
/
/
t
l
a
c
_
a
_
0
0
4
0
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
In Proceedings of
Diana McCarthy and Roberto Navigli. 2007.
SemEval-2007 Task 10: English lexical
the
substitution task.
Fourth International Workshop on Semantic
Evaluations (SemEval-2007), pages 48–53,
Prague, Czech Republic. Association for
Computational Linguistics. https://doi
.org/10.3115/1621474.1621483
Oren Melamud,
Jacob Goldberger, and Ido
Dagan. 2016. context2vec: Learning generic
context embedding with bidirectional LSTM.
In Proceedings of the 20th SIGNLL Confer-
ence on Computational Natural Language
Learning, pages 51–61, Berlin, Germany.
Association for Computational Linguistics.
https://doi.org/10.18653/v1/K16
-1006
Tomas Mikolov, Kai Chen, Greg Corrado, and
Jeffrey Dean. 2013. Efficient estimation of
word representations in vector space. arXiv
preprint:1301.3781v3.
George A. Miller, Claudia Leacock, Randee
Tengi, and Ross T. Bunker. 1993. A semantic
concordance. In Human Language Technology:
Proceedings of a Workshop Held at Plains-
boro. New Jersey. https://doi.org/10
.3115/1075671.1075742
Roberto Navigli and Simone Paolo Ponzetto.
2012. BabelNet: The automatic construction,
evaluation and application of a wide-coverage
multilingual semantic network. Artificial Intel-
ligence, 193:217–250. https://doi.org
/10.1016/j.artint.2012.07.001
Arvind Neelakantan, Jeevan Shankar, Alexandre
Passos, and Andrew McCallum. 2014. Efficient
non-parametric estimation of multiple embed-
dings per word in vector space. In Proceedings
of the 2014 Conference on Empirical Meth-
ods in Natural Language Processing (EMNLP),
pages 1059–1069, Doha, Qatar. Association for
Computational Linguistics. https://doi
.org/10.3115/v1/D14-1113
Rafail Ostrovsky, Yuval Rabani, Leonard J.
Schulman, and Chaitanya Swamy. 2012. The
effectiveness of Lloyd-type methods for the
the ACM
k-means problem.
(JACM), 59(6):28. https://doi.org/10
.1145/2395116.2395117
Journal of
Ellie Pavlick, Pushpendre Rastogi, Juri Gan-
itkevitch, Benjamin Van Durme, and Chris
Callison-Burch. 2015. PPDB 2.0: Better
paraphrase ranking,
fine-grained entailment
relations, word embeddings, and style classi-
fication. In Proceedings of the 53rd Annual
Meeting of the Association for Computational
Linguistics and the 7th International Joint
Conference on Natural Language Processing
(Volume 2: Short Papers), pages 425–430,
Beijing, China. Association for Computational
Linguistics. https://doi.org/10.3115
/v1/P15-2070
the 2018 Conference of
Matthew Peters, Mark Neumann, Mohit Iyyer,
Matt Gardner, Christopher Clark, Kenton Lee,
and Luke Zettlemoyer. 2018. Deep contex-
In Proceed-
tualized word representations.
ings of
the North
American Chapter of
the Association for
Computational Linguistics: Human Language
Technologies, Volume 1 (Long Papers),
pages 2227–2237, New Orleans, Louisiana.
Association for Computational Linguistics.
https://doi.org/10.18653/v1/N18
-1202
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
0
0
1
9
5
5
2
0
4
/
/
t
l
a
c
_
a
_
0
0
4
0
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
for
evaluating
Mohammad Taher Pilehvar and Jose Camacho-
Collados. 2019. WiC: The Word-in-Context
dataset
context-sensitive
meaning representations. In Proceedings of
the 2019 Conference of the North American
Chapter of the Association for Computational
Linguistics: Human Language Technologies,
Short Papers),
Volume
pages 1267–1273, Minneapolis, Minnesota.
Association for Computational Linguistics.
(Long
and
1
Tiago Pimentel, Rowan Hall Maudslay, Damian
Blasi, and Ryan Cotterell. 2020. Speakers
lexical semantic gaps with context. In
fill
Proceedings of
the 2020 Conference on
Empirical Methods in Natural Language Pro-
cessing (EMNLP), pages 4004–4015, Online.
Association for Computational Linguistics.
https://doi.org/10.18653/v1/2020
.emnlp-main.328
Alec Radford, Jeffrey Wu, Rewon Child, David
Luan, Dario Amodei, and Ilya Sutskever. 2019.
Language models are unsupervised multitask
learners. OpenAI Blog, 1(8):9.
842
Emily Reif, Ann Yuan, Martin Wattenberg,
Fernanda B. Viegas, Andy Coenen, Adam
Pearce, and Been Kim. 2019. Visualizing and
measuring the geometry of BERT. In Advances
in Neural Information Processing Systems,
pages 8592–8600, Vancouver, Canada.
Joseph Reisinger and Raymond J. Mooney.
2010. Multi-prototype vector-space models of
word meaning. In Human Language Tech-
nologies: The 2010 Annual Conference of the
North American Chapter of the Association for
Computational Linguistics, pages 109–117,
Los Angeles, California. Association for
Computational Linguistics.
Anna Rogers, Olga Kovaleva,
and Anna
Rumshisky. 2020. A primer in BERTology:
What we know about how BERT works. Trans-
actions of the Association for Computational
Linguistics, 8:842–866.
Alex Rosenfeld and Katrin Erk. 2018. Deep neural
models of semantic shift. In Proceedings of
the 2018 Conference of the North American
Chapter of the Association for Computational
Linguistics: Human Language Technologies,
Volume 1 (Long Papers), pages 474–484,
New Orleans, Louisiana. Association for
Computational Linguistics. https://doi
.org/10.1162/tacl_a_00349
Peter J. Rousseeuw. 1987. Silhouettes: A graphical
aid to the interpretation and validation of cluster
analysis. Journal of Computational and Applied
Mathematics, 20:53–65.
Dominik Schlechtweg, Barbara McGillivray,
Simon Hengchen, Haim Dubossarsky, and Nina
Tahmasebi. 2020. SemEval-2020 Task 1: Unsu-
pervised lexical semantic change detection. In
Proceedings of the Fourteenth Workshop on
Semantic Evaluation, pages 1–23, Barcelona
(online). International Committee for Compu-
tational Linguistics. https://doi.org/10
.1016/0377-0427(87)90125-7
Pedro Javier Ortiz Su´arez, Benoˆıt Sagot, and
Laurent Romary. 2019. Asynchronous pipeline
for processing huge corpora on medium to
low resource infrastructures. In Proceedings
of
the 7th Workshop on the Challenges in
the Management of Large Corpora (CMLC-7).
Cardiff, UK. Leibniz-Institut
Sprache.
f¨ur Deutsche
Alon Talmor, Yanai Elazar, Yoav Goldberg, and
Jonathan Berant. 2020. oLMpics—On what
language model pre-training captures. Trans-
actions of the Association for Computational
Linguistics, 8:743–758. https://doi.org
/10.1162/tacl_a_00342
Ian Tenney, Dipanjan Das, and Ellie Pavlick.
2019. BERT rediscovers the classical NLP
pipeline. In Proceedings of the 57th Annual
Meeting of the Association for Computational
Linguistics, pages 4593–4601, Florence, Italy.
Association for Computational Linguistics.
https://doi.org/10.18653/v1/P19
-1452
Ashish Vaswani, Noam Shazeer, Niki Parmar,
Jakob Uszkoreit, Llion Jones, Aidan N. Gomez,
Łukasz Kaiser, and Illia Polosukhin. 2017.
In Advances
Attention is all you need.
in Neural Information Processing Systems,
pages 5998–6008. Long Beach, California,
USA.
Elena Voita, Rico Sennrich, and Ivan Titov.
repre-
2019a. The bottom-up evolution of
sentations in the transformer: A study with
machine translation and language modeling
objectives. In Proceedings of the 2019 Con-
ference on Empirical Methods in Natural Lan-
guage Processing and the 9th International
Joint Conference on Natural Language Pro-
cessing (EMNLP-IJCNLP), pages 4396–4406,
Hong Kong, China. Association for Com-
putational Linguistics. https://doi.org
/10.18653/v1/D19-1448
Elena Voita, David Talbot, Fedor Moiseev, Rico
Sennrich, and Ivan Titov. 2019b. Analyzing
multi-head self-attention: Specialized heads
do the heavy lifting, the rest can be pruned.
In Proceedings of the 57th Annual Meeting
the Association for Computational Lin-
of
guistics, pages 5797–5808, Florence,
Italy.
Association for Computational Linguistics.
https://doi.org/10.18653/v1/P19
-1580
Ivan Vuli´c, Edoardo Maria Ponti, Robert Litschko,
Goran Glavaˇs, and Anna Korhonen. 2020. Prob-
ing pretrained language models for lexical
843
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
0
0
1
9
5
5
2
0
4
/
/
t
l
a
c
_
a
_
0
0
4
0
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
semantics. In Proceedings of the 2020 Con-
ference on Empirical Methods in Natural Lan-
guage Processing (EMNLP), pages 7222–7240,
Online. Association for Computational Linguis-
tics. https://doi.org/10.18653/v1
/2020.emnlp-main.586
Gregor Wiedemann, Steffen Remus, Avi Chawla,
and Chris Biemann. 2019. Does BERT make
any sense? Interpretable word sense disam-
biguation with contextualized embeddings. In
Proceedings of the 15th Conference on Natural
Language Processing (KONVENS 2019): Long
Papers, pages 161–170, Erlangen, Germany.
German Society for Computational Linguistics
& Language Technology.
Thomas Wolf, Lysandre Debut, Victor Sanh,
Julien Chaumond, Clement Delangue, Anthony
Moi, Pierric Cistac, Tim Rault, Remi Louf,
Morgan Funtowicz, Joe Davison, Sam Shleifer,
Patrick von Platen, Clara Ma, Yacine Jernite,
Julien Plu, Canwen Xu, Teven Le Scao, Sylvain
Gugger, Mariama Drame, Quentin Lhoest,
and Alexander Rush. 2020. Transformers:
State-of-the-art natural language processing. In
Proceedings of the 2020 Conference on Empir-
ical Methods in Natural Language Processing:
System Demonstrations, pages 38–45, Online.
Association for Computational Linguistics.
https://doi.org/10.18653/v1/2020
.emnlp-demos.6
Bin Zhang. 2001. Dependence of clustering
algorithm performance on clustered-ness of
data. HP Labs Technical Report HPL-2001-91.
Wangchunshu Zhou, Tao Ge, Ke Xu, Furu Wei,
and Ming Zhou. 2019. BERT-based lexical
substitution. In Proceedings of the 57th Annual
Meeting of the Association for Computational
Linguistics, pages 3368–3373, Florence, Italy.
Association for Computational Linguistics.
Yukun Zhu, Ryan Kiros, Rich Zemel, Ruslan
Salakhutdinov, Raquel Urtasun, Antonio
Torralba, and Sanja Fidler. 2015. Aligning
In Proceedings of
books and movies: Towards story-like visual
explanations by watching movies and reading
the 2015 IEEE
books.
International Conference on Computer Vision
(ICCV’15), pages 19–27, Santiago, Chile. IEEE
Computer Society. https://doi.org/10
.1109/ICCV.2015.11
George Kingsley Zipf. 1945. The meaning-
frequency relationship of words. Journal of
General Psychology, 33(2):251–256. https://
doi.org/10.1080/00221309.1945
.10544509
A Clusterability Metrics
Variance Ratio. First, the variance of a cluster y
is calculated:
σ2(Y ) =
1
|y|
(cid:2)
i(cid:2)y
(yi − ¯y)2
(3)
where ¯y denotes the centroid of cluster y. Then the
within-cluster variance W and the between-cluster
variance B of a clustering solution C are
calculated in the following way:
W (C) =
B(C) =
k(cid:2)
j=1
k(cid:2)
j=1
pjσ2(xj)
pj(¯xj − ¯x)2
(4)
(5)
|xj |
where x is the set of all data points and pj =
|x| .
xj are the data points in cluster j. Finally, the VR
of a clustering C is obtained as the ratio between
B(C) and W (C):
V R =
B(C)
W (C)
(6)
Separability (SEP). In an optimal clustering Ck
of the dataset x with k clusters, SEP is defined as
follows:
SEP (x, k) =
loss(Ck)
loss(Ck−1)
(7)
844
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
0
0
1
9
5
5
2
0
4
/
/
t
l
a
c
_
a
_
0
0
4
0
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3