Learning Typed Entailment Graphs with Global Soft Constraints
Mohammad Javad Hosseini(cid:63)§ Nathanael Chambers(cid:63)(cid:63) Siva Reddy† Xavier R. Holt‡
Shay B. Cohen(cid:63) Mark Johnson‡ and Mark Steedman(cid:63)
(cid:63)University of Edinburgh
§The Alan Turing Institute, UK
(cid:63)(cid:63)United States Naval Academy
†Stanford University
‡Macquarie University
javad.hosseini@ed.ac.uk, nchamber@usna.edu, sivar@stanford.edu
{xavier.ricketts-holt,mark.johnson}@mq.edu.au
{scohen,steedman}@inf.ed.ac.uk
Abstract
This paper presents a new method for learn-
ing typed entailment graphs from text. We
extract predicate-argument structures from
multiple-source news corpora, and compute
local distributional similarity scores to learn
entailments between predicates with typed
arguments (e.g., person contracted disease).
Previous work has used transitivity con-
straints to improve local decisions, but these
constraints are intractable on large graphs.
We instead propose a scalable method
that
learns globally consistent similarity
scores based on new soft constraints that
consider both the structures across typed
entailment graphs and inside each graph.
Learning takes only a few hours to run over
100K predicates, and our results show large
improvements over local similarity scores
on two entailment data sets. We further
show improvements over paraphrases and
entailments from the Paraphrase Database
and prior state-of-the-art entailment graphs.
We show that the entailment graphs improve
performance in a downstream task.
1
Introduction
Recognizing textual entailment and paraphrasing
is critical to many core natural language process-
ing applications such as question answering and
semantic parsing. The surface form of a sentence
that answers a question such as “Does Verizon
own Yahoo?” frequently does not directly corre-
spond to the form of the question, but is rather
a paraphrase or an expression such as “Verizon
bought Yahoo,” that entails the answer. The lack
of a well-established form-independent semantic
representation for natural language is the most im-
portant single obstacle to bridging the gap between
queries and text resources.
This paper seeks to learn meaning postulates
(e.g., buying entails owning) that can be used to
703
augment the standard form-dependent semantics.
Our immediate goal is to learn entailment rules be-
tween typed predicates with two arguments, where
the type of each predicate is determined by the
types of its arguments. We construct typed entail-
ment graphs, with typed predicates as nodes and
entailment rules as edges. Figure 1 shows simple
examples of such graphs with arguments of types
company,company and person,location.
Entailment relations are detected computing
a similarity score between the typed predicates
based on the distributional inclusion hypothesis,
which states that a word (predicate) u entails
another word (predicate) v if in any context that u
can be used, v can be used in its place (Dagan
et al., 1999; Geffet and Dagan, 2005; Herbelot and
Ganesalingam, 2013; Kartsaklis and Sadrzadeh,
2016). Most previous work has taken a “local
learning” approach (Lin, 1998; Weeds and Weir,
2003; Szpektor and Dagan, 2008; Schoenmackers
et al., 2010), namely, learning entailment rules in-
dependently from each other.
One problem facing local learning approaches
is that many correct edges are not identified be-
cause of data sparsity and many wrong edges
are spuriously identified as valid entailments. A
“global learning” approach, where dependencies
between entailment rules are taken into account,
can improve the local decisions significantly.
Berant et al. (2011) imposed transitivity con-
straints on the entailments, such that the inclusion
of rules i→j and j→k implies that of i→k. Al-
though they showed transitivity constraints to be
effective in learning entailment graphs, the Inte-
ger Linear Programming (ILP) solution of Berant
et al. is not scalable beyond a few hundred nodes.
In fact,
the problem of finding a maximally
weighted transitive subgraph of a graph with arbi-
trary edge weights is NP-hard (Berant et al., 2011).
This paper instead proposes a scalable solu-
tion that does not rely on transitivity closure, but
Transactions of the Association for Computational Linguistics, vol. 6, pp. 703–718, 2018. Action Editor: Katrin Erk.
Submission batch: 4/2018; Revision batch: 8/2018; Published 12/2018.
c(cid:13) 2018 Association for Computational Linguistics. Distributed under a CC-BY 4.0 license.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
0
1
5
6
7
6
7
0
/
/
t
l
a
c
_
a
_
0
0
2
5
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 1: Examples of typed entailment graphs for
arguments of types company,company and person,
location.
instead uses two global soft constraints that main-
tain structural similarity both across and within
each typed entailment graph (Figure 2). We intro-
duce an unsupervised framework to learn globally
consistent similarity scores given local similarity
scores (§4). Our method is highly parallelizable
and takes only a few hours to apply to more than
100K predicates.1,2
Our experiments (§6) show that
the global
scores improve significantly over local scores and
outperform state-of-the-art entailment graphs on
two standard entailment rule data sets (Berant
et al., 2011; Holt, 2018). We ultimately intend
the typed entailment graphs to provide a resource
for entailment and paraphrase rules for use in se-
mantic parsing and open domain question answer-
ing, as has been done for similar resources such
as the Paraphrase Database (PPDB; Ganitkevitch
et al., 2013; Pavlick et al., 2015) in Wang et al.
(2015) and Dong et al. (2017).3 With that end in
view, we have included a comparison with PPDB
in our evaluation on the entailment data sets. We
also show that the learned entailment rules im-
prove performance on a question-answering task
(§7) with no tuning or prior knowledge of the task.
2 Related Work
Our work is closely related to Berant et al. (2011),
where entailment graphs are learned by impos-
ing transitivity constraints on the entailment rela-
tions. However, the exact solution to the problem
is not scalable beyond a few hundred predicates,
whereas the number of predicates that we capture
is two orders of magnitude larger (§5). Hence, it is
necessary to resort to approximate methods based
1We performed our experiments on a 32-core 2.3 GHz
machine with 256GB of RAM.
2Our code, extracted binary relations, and the learned en-
tailment graphs are available at https://github.com/
mjhosseini/entGraph.
3Predicates inside each clique in the entailment graphs
are considered to be paraphrases.
704
Figure 2: Learning entailments that are consistent (A)
across different but related typed entailment graphs and
(B) within each graph. 0 ≤ β ≤ 1 determines how
much different graphs are related. The dotted edges are
missing, but will be recovered by considering relation-
ships shown by across-graph (red) and within-graph
(light blue) connections.
on assumptions concerning the graph structure.
Berant et al. (2012, 2015) propose Tree-Node-Fix
(TNF), an approximation method that scales bet-
ter by additionally assuming the entailment graphs
are “forest reducible,” where a predicate cannot
entail two (or more) predicates j and k such that
neither j→k nor k→j (FRG assumption). How-
ever, the FRG assumption is not correct for many
real-world domains. For example, a person visit-
ing a place entails both arriving at that place and
leaving that place, although the latter do not neces-
sarily entail each other. Our work injects two other
types of prior knowledge about the structure of the
graph that are less expensive to incorporate and
yield better results on entailment rule data sets.
Abend et al. (2014) learn entailment relations
over multi-word predicates with different levels of
compositionality. Pavlick et al. (2015) add variety
of relations, including entailment, to phrase pairs
in PPDB. This includes a broader range of entail-
ment relations such as lexical entailment. In con-
trast to our method, these works rely on supervised
data and take a local learning approach.
Another
related strand of
research is link
prediction (Bordes et al., 2013; Riedel et al.,
2013; Socher et al., 2013; Yang et al., 2015;
Trouillon et al., 2016; Dettmers et al., 2018),
where the source data are extractions from text,
facts in knowledge bases, or both. Unlike our
work, which directly learns entailment relations
between predicates, these methods aim at predict-
ing the source data—that is, whether two enti-
ties have a particular relationship. The common
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
0
1
5
6
7
6
7
0
/
/
t
l
a
c
_
a
_
0
0
2
5
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
t3=person,t4=locationvisitarrive inleaveLeave fort1=company,t2=companyown’s acquisition ofbuyt3=living_thing,t4=diseaset1=government_agency,t2=event!(trigger,(t1,t2),(t3,t4))t5=medicine,t6=disease(B)treatcausecureuseful fortriggercausetrigger(A)
wisdom is that entailment relations are a by-
product of these methods (Riedel et al., 2013).
However, this assumption has not usually been
explicitly evaluated. Explicit entailment rules pro-
vide explainable resources that can be used in
downstream tasks. Our experiments show that our
method significantly outperforms a state-of-the-art
link prediction method.
3 Computing Local Similarity Scores
We first extract binary relations as predicate-
argument pairs using a combinatory categorial
grammar (CCG; Steedman, 2000) semantic parser
(§3.1). We map the arguments to their Wikipedia
URLs using a named entity linker (§3.2). We ex-
tract types such as person and disease for each
argument (§3.2). We then compute local similarity
scores between predicate pairs (§3.3).
3.1 Relation Extraction
The semantic parser of Reddy et al. (2014),
GraphParser,
is run on the NewsSpike corpus
(Zhang and Weld, 2013) to extract binary re-
lations between a predicate and its arguments
from sentences. GraphParser uses CCG syntac-
tic derivations and λ-calculus to convert sen-
tences to neo-Davisonian semantics, a first-order
logic that uses event identifiers (Parsons, 1990).
For example, for the sentence, Obama visited
Hawaii in 2012, GraphParser produces the logi-
cal form ∃e.visit1(e, Obama) ∧ visit2(e, Hawaii)∧
visitin(e, 2012), where e denotes an event. We
will consider a relation for each pair of argu-
ments, hence, there will be three relations for the
given sentence: visit1,2 with arguments (Obama,
Hawaii), visit1,in with arguments (Obama,2012),
and visit2,in with arguments (Hawaii,2012). We cur-
rently only use extracted relations that involve two
named entities or one named entity and a noun. We
constrain the relations to have at least one named
entity to reduce ambiguity in finding entailments.
We perform a few automatic post-processing
steps on the output of the parser. First, we normal-
ize the predicates by lemmatization of their head
words. Passive predicates are mapped to active
ones and we extract negations and particle verb
predicates. Next, we discard unary relations and
relations involving coordination of arguments. Fi-
nally, whenever we see a relation between a sub-
ject and an object, and a relation between object
and a third argument connected by a preposi-
tional phrase, we add a new relation between
the subject and the third argument by concate-
nating the relation name with the object. For ex-
ample, for the sentence China has a border with
India, we extract a relation have border1,with
between China and India. We perform a simi-
lar process for prepositional phrases attached to
verb phrases. Most of the light verbs and multi-
word predicates will be extracted by the above
post-processing (e.g., take care1,of ), which will
recover many salient ternary relations.
Although entailments and paraphrasing can
benefit from n-ary relations—for example, person
visits a location in a time—we currently follow
previous work (Lewis and Steedman, 2013a);
(Berant et al., 2015) in confining our attention to
binary relations, leaving the construction of n-ary
graphs to future work.
3.2 Linking and Typing Arguments
Entailment and paraphrasing depend on context.
Although using exact context is impractical in
forming entailment graphs, many authors have
used the type of the arguments to disambiguate
polysemous predicates (Berant et al., 2011, 2015;
Lewis and Steedman, 2013a; Lewis, 2014). Typ-
ing also reduces the size of the entailment graphs.
Because named entities can be referred to in
many different ways, we use a named entity link-
ing tool to normalize the named entities. In the fol-
lowing experiments, we use AIDALight (Nguyen
et al., 2014), a fast and accurate named entity
linker, to link named entities to their Wikipedia
URLs (if any). We thus type all entities that
can be grounded in Wikipedia. We first map
the Wikipedia URL of the entities to Freebase
(Bollacker et al., 2008). We select the most no-
table type of the entity from Freebase and map it to
FIGER types (Ling and Weld, 2012) such as build-
ing, disease, person, and location, using only the
first level of the FIGER type hierarchy.4 For exam-
ple, instead of event/sports_event, we use event as
type. If an entity cannot be grounded in Wikipedia
or its Freebase type does not have a mapping to
FIGER, we assign the default type thing to it.
3.3 Local Distributional Similarities
For each typed predicate (e.g., visit1,2 with types
person,location), we extract a feature vector. We
use as feature types the set of argument pair strings
449 types out of 113 FIGER types.
705
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
0
1
5
6
7
6
7
0
/
/
t
l
a
c
_
a
_
0
0
2
5
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
(e.g., Obama-Hawaii) that instantiate the binary
relations of the predicates. The value of each
feature is the pointwise mutual information be-
tween the predicate and the feature. We use the
feature vectors to compute three local similarity
scores (both symmetric and directional) between
typed predicates: Weeds (Weeds and Weir, 2003),
Lin (Lin, 1998), and Balanced Inclusion (BInc;
Szpektor and Dagan, 2008) similarities.
4 Learning Globally Consistent
Entailment Graphs
We learn globally consistent similarity scores
based on local similarity scores. The global scores
will be used to form typed entailment graphs.
4.1 Problem Formulation
Let T be a set of types and P be a set of predicates.
We denote by ¯V (t1, t2) the set of typed predicates
p(:t1, :t2), where t1, t2 ∈ T and p ∈ P . Each
p(:t1, :t2) ∈ ¯V (t1, t2) takes as input arguments of
types t1 and t2. An example of a typed predicate is
win1,2(:team,:event) that can be instantiated with
win1,2(Seahawks:team,Super Bowl:event).
We define V (t1, t2) = ¯V (t1, t2) ∪ ¯V (t2, t1).
We often denote elements of V (t1, t2) by i, j,
and k, where each element is a typed predicate as
above. For an i=p(:t1, :t2) ∈ V (t1, t2), we de-
note by π(i)=p, τ1(i)=t1 and τ2(i)=t2. We com-
pute distributional similarities between predicates
with the same argument types. We denote by
W0(t1, t2) ∈ [0, 1]|V (t1,t2)|×|V (t1,t2)| the (sparse)
matrix containing all local similarity scores w0
ij
between predicates i and j with types t1 and t2,
where |V (t1, t2)| is the size of V (t1, t2).5
Predicates can entail each other with the
same argument order (direct) or in the reverse
order—that is, p(:t1, :t2) might entail q(:t1, :t2)
or q(:t2, :t1). For
the graphs with the same
types (e.g., t1=t2=person), we keep two copies
of the predicates, one for each of
the pos-
sible orderings. This allows us to model en-
tailments with reverse argument orders (e.g.,
is son of1,2(:person1,:person2) → is parent
of1,2(:person2,:person1)).
We define V = (cid:83)
the set
t1,t2
typed predicates, and W0 as a block-
of all
diagonal matrix consisting of all the local sim-
V (t1, t2),
5For each similarity measure, we define one separate ma-
trix and run the learning algorithm separately, but for simplic-
ity of notation, we do not show the similarity measure names.
706
ilarity matrices W0(t1, t2). Similarly, we de-
fine W(t1, t2) and W as the matrices consisting
of globally consistent similarity scores wij we
wish to learn. The global similarity scores are
used to form entailment graphs by thresholding
W. For a δ > 0, we define typed entailment
graphs as Gδ(t1, t2) = (cid:0)V (t1, t2), Eδ(t1, t2)(cid:1),
where V (t1, t2) are the nodes and E(t1, t2) =
{(i, j)|i, j ∈ V (t1, t2), wij ≥ δ} are the edges
of the entailment graphs.
4.2 Learning Algorithm
Existing approaches to learn entailment graphs
from text miss many correct edges because of data
sparsity—namely, the lack of explicit evidence in
the corpus that a predicate i entails another predi-
cate j. The goal of our method is to use evidence
from the existing edges that have been assigned
high confidence to predict missing ones and re-
move spurious edges. We propose two global soft
constraints that maintain structural similarity both
across and within each typed entailment graph.
The constraints are based on the following two
observations.
First, it is standard to learn a separate typed
entailment graph for each (plausible) type-pair be-
cause arguments provide necessary disambigua-
tion for predicate meaning (Berant et al., 2011,
2012, 2015; Lewis and Steedman, 2013a,b). How-
ever, many entailment relations for which we have
direct evidence only in a few subgraphs may in fact
apply over many others (Figure 2A). For exam-
ple, we may not have found direct evidence that
mentions of a living_thing (e.g., a virus) trigger-
ing a disease are accompanied by mentions of the
living_thing causing that disease (because of data
sparsity), whereas we have found that mentions of
a government_agency triggering an event are re-
liably accompanied by mentions of causing that
event. While we show that typing is necessary to
learning entailments (§6), we propose to learn all
typed entailment graphs jointly.
Second, we encourage paraphrase predicates
(where i→j and j→i) to have the same patterns
of entailment (Figure 2B), that is, to entail and
be entailed by the same predicates, global soft
constraints that we call paraphrase resolution.
Using these soft constraints, a missing entailment
(e.g., medicine treats disease → medicine is use-
ful for disease) can be identified by considering
the entailments of a paraphrase predicate (e.g.,
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
0
1
5
6
7
6
7
0
/
/
t
l
a
c
_
a
_
0
0
2
5
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J(W ≥ 0, (cid:126)β ≥ 0) = LwithinGraph + LcrossGraph + LpResolution + λ1(cid:107)W(cid:107)1
LwithinGraph =
(wij − w0
(cid:88)
ij)2
(1)
(2)
LcrossGraph =
i,j∈V
1
(cid:88)
2
i,j∈V
(cid:88)
β
(i(cid:48),j(cid:48))∈
N (i,j)
(cid:16)
π(i), (cid:0)τ1(i), τ2(i)(cid:1), (cid:0)τ1(i(cid:48)), τ2(i(cid:48))(cid:1)(cid:17)
(wij − wi(cid:48)j(cid:48))2 +
λ2
2
(cid:107)(cid:126)1 − (cid:126)β(cid:107)2
2
(3)
LpResolution =
1
2
(cid:88)
(cid:88)
Iε(wij)Iε(wji)(cid:2)(wik − wjk)2 + (wki − wkj)2(cid:3)
(4)
t1,t2∈T
i,j,k∈V (t1,t2)
k(cid:54)=i,k(cid:54)=j
Figure 3: The objective function to jointly learn global scores W and the compatibility function β, given local
scores W0. LwithinGraph encourages global and local scores to be close; LcrossGraph encourages similarities to be
consistent between different typed entailment graphs; LpResolution encourages paraphrase predicates to have the
same pattern of entailment. We use an (cid:96)1 regularization penalty to remove entailments with low confidence.
medicine cures disease → medicine is useful for
disease).
Sharing entailments across different typed en-
tailment graphs is only semantically correct for
some predicates and types. In order to learn when
we can generalize an entailment from one graph
to another, we define a compatibility function
β : P × (T ×T ) × (T ×T ) → [0, 1]. The func-
tion is defined for a predicate and two type pairs
(Figure 2A). It specifies the extent of compat-
ibility for a single predicate between different
typed entailment graphs, with 1 being completely
compatible and 0 being irrelevant. In particu-
2)(cid:1) determines how much
lar, β(cid:0)p, (t1, t2), (t(cid:48)
we expect the outgoing edges of p(:t1, :t2) and
p(:t(cid:48)
2) to be similar. We constrain β to be sym-
metric between t1, t2 and t(cid:48)
1, t(cid:48)
2 as compatibility of
1, :t(cid:48)
outgoing edges of p(:t1, :t2) with p(:t(cid:48)
2) should
be the same as p(:t(cid:48)
2) with p(:t1, :t2). We de-
note by (cid:126)β a vectorization consisting of the values
of β for all possible input predicates and types.
1, :t(cid:48)
1, :t(cid:48)
1, t(cid:48)
Note that the global similarity scores W and
the compatibility function (cid:126)β are not known in ad-
vance. Given local similarity scores W0, we learn
W and (cid:126)β jointly. We minimize the loss function
defined in Equation (1), which consists of three
soft constraints defined below and an (cid:96)1 regular-
ization term (Figure 3).
LwithinGraph. Equation (2) encourages global
scores wij to be close to local scores w0
ij, so that
the global scores will not stray too far from the
original scores.
LcrossGraph. Equation (3) encourages each pred-
icate’s entailments to be similar across typed en-
tailment graphs (Figure 2A) if the predicates have
707
similar neighbors. We penalize the difference of
entailments in two different graphs when the com-
patibility function is high. For each pair of typed
predicates (i, j) ∈ V (t1, t2), we define a set of
neighbors (predicates with different types):
N (i, j) =
(cid:110)
(i(cid:48), j(cid:48)) ∈ V (t(cid:48)
1, t(cid:48)
2 ∈ T,
(i(cid:48), j(cid:48)) (cid:54)= (i, j), π(i) = π(i(cid:48)),
2)|t(cid:48)
1, t(cid:48)
π(j) = π(j(cid:48)), a(i, j) = a(i(cid:48), j(cid:48))
(cid:111)
(5)
where a(i, j) is true if the argument orders of i and
j match, and false otherwise. For each (i(cid:48), j(cid:48)) ∈
N (i, j), we penalize the difference of entailments
by adding the term β(·)(wij − wi(cid:48)j(cid:48))2. We add a
prior term on (cid:126)β as λ2(cid:107)(cid:126)1 − (cid:126)β(cid:107)2
2, where (cid:126)1 is a vector
of the same size as (cid:126)β with all 1s. Without the prior
term (i.e., λ2=0), all the elements of (cid:126)β will be-
come zero. Increasing λ2 will keep (some of the)
elements of (cid:126)β non-zero and encourages communi-
cations between related graphs.
LpResolution. Equation (4) denotes the para-
phrase resolution global soft constraints that en-
courage paraphrase predicates to have the same
patterns of entailments (Figure 2B). The function
Iε(x) equals x if x > ε and zero, otherwise.6
Unlike LcrossGraph in Equation (3), Equation (4)
operates on the edges within each graph. If both
wij and wji are high, their incoming and out-
going edges from/to nodes k are encouraged to
be similar. We name this global constraint para-
phrase resolution, because it might add missing
6In our experiments, we set ε = .3. Smaller values of ε
yield similar results, but learning is slower.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
0
1
5
6
7
6
7
0
/
/
t
l
a
c
_
a
_
0
0
2
5
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
links (e.g., i→k) if i and j are paraphrases of
each other and j→k, or break the paraphrase rela-
tion, if the incoming and outgoing edges are very
different.
We impose an (cid:96)1 penalty on the elements of
W as λ1(cid:107)W(cid:107)1, where λ1 is a nonnegative tuning
hyperparameter that controls the strength of the
penalty applied to the elements of W. This term
removes entailments with low confidence from the
entailment graphs. Note that Equation (1) has W0
and average of W0 across different typed entail-
ment graphs (§5.4) as its special cases. The for-
mer is achieved by setting λ1=λ2=0 and ε=1
and the latter by λ1=0, λ2=∞ and ε=1. We
do not explicitly weight the different components
of the loss function, as the effect of LcrossGraph
and LpResolution can be controlled by λ2 and ε,
respectively.
1, t(cid:48)
Equation (1) can be interpreted as an infer-
ence problem in a Markov random field (MRF)
(Kindermann and Snell, 1980), where the nodes of
the MRF are the global scores wij and the param-
2)(cid:1). The MRF will have
eters β(cid:0)p, (t1, t2), (t(cid:48)
five log-linear factor types: one unary factor type
for LwithinGraph, one three-variable factor type for
the first term of LcrossGraph, a unary factor type
for the prior on (cid:126)β, one four-variable factor type
for LpResolution, and a unary factor type for the
(cid:96)1 regularization term. Figure 2 shows an exam-
ple factor graph (unary factors are not shown for
simplicity).
We learn W and (cid:126)β jointly using a message
passing approach based on the Block Coordinate
Descent method (Xu and Yin, 2013). We initial-
ize W = W0. Assuming that we know the
global similarity scores W, we learn how much
the entailments are compatible between different
types ((cid:126)β) and vice versa. Given W fixed, each
wij sends messages to the corresponding β(·)
elements, which will be used to update (cid:126)β. Given
(cid:126)β fixed, we do one iteration of learning for each
wij. Each β(·) and wij elements send messages to
the related elements in W, which will be in turn
updated. Based on the update rules (Appendix A),
we always have wij ≤ 1 and (cid:126)β ≤ (cid:126)1.
Each iteration of the learning method takes
O(cid:0)(cid:107)W(cid:107)0|T |2 + (cid:80)
i∈V ((cid:107)wi:(cid:107)0+(cid:107)w:i(cid:107)0)2(cid:1) time,
where (cid:107)W (cid:107)0 is the number of nonzero elements
of W (number of edges in the current graph), |T |
is the number of types, and (cid:107)wi:(cid:107)0 ((cid:107)w:i(cid:107)0) is the
number of nonzero elements of the ith row (col-
umn) of the matrix (out-degree and in-degree of
the node i).7 In practice, learning converges af-
ter five iterations of full updates. The method is
highly parallelizable, and our efficient implemen-
tation does the learning in only a few hours.
5 Experimental Set-up
We extract binary relations from a multiple-source
news corpus (§5.1) and compute local and global
scores. We form entailment graphs based on the
similarity scores and test our model on two entail-
ment rules data sets (§5.2). We then discuss pa-
rameter tuning (§5.3) and baseline systems (§5.4).
5.1 Training Corpus: Multiple-Source News
We use the multiple-source NewsSpike corpus of
Zhang and Weld (2013). NewsSpike was deliber-
ately built to include different articles from differ-
ent sources describing identical news stories. They
scraped RSS news feeds from January–February
2013 and linked them to full stories collected
through a Web search of the RSS titles. The corpus
contains 550K news articles (20M sentences). Be-
cause this corpus contains multiple sources cover-
ing the same events, it is well suited to our purpose
of learning entailment and paraphrase relations.
We extracted 29M binary relations using the
procedure in §3.1.
In our experiments, we used
two cut-offs within each typed subgraph to re-
(1) re-
duce the effect of noise in the corpus:
move any argument-pair that is observed with
fewer than C1=3 unique predicates; (2) remove
any predicate that is observed with fewer than
C2=3 unique argument-pairs. This leaves us with
|P |=101K unique predicates in 346 entailment
graphs. The maximum graph size is 53K nodes,8
and the total number of non-zero local scores in
all graphs is 66M. In the future, we plan to test
our method on an even larger corpus, but prelim-
inary experiments suggest that data sparsity will
persist regardless of the corpus size, because of
the power law distribution of the terms. We com-
pared our extractions qualitatively with Stanford
Open IE (Etzioni et al., 2011; Angeli et al., 2015).
Our CCG-based extraction generated noticeably
7In our experiments,
the total number of edges is
≈ .01|V |2 and most of predicate pairs are seen in less than
20 subgraphs, rather than |T |2.
8There are 4 graphs with more than 20K nodes, 3 graphs
with 10K to 20K nodes, and 16 graphs with 1K to 10K nodes.
708
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
0
1
5
6
7
6
7
0
/
/
t
l
a
c
_
a
_
0
0
2
5
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
better relations for longer sentences with long-
range dependencies such as those involving coor-
dination.
5.2 Evaluation Entailment Data Sets
Levy/Holt’s Entailment Data Set Levy and
Dagan (2016) proposed a new annotation method
(and a new data set) for collecting relational in-
ference data in context. Their method removes a
major bias in other inference data sets such as
Zeichner’s (Zeichner et al., 2012), where candi-
date entailments were selected using a directional
similarity measure. Levy and Dagan form ques-
tions of the type which city (qtype), is located near
(qrel), mountains (qarg)? and provide possible
is sur-
answers of the form Kyoto (aanswer),
rounded by (arel), mountains (aarg). Annotators
are shown a question with multiple possible an-
swers, where aanswer is masked by qtype to reduce
the bias towards world knowledge. If the annota-
tor indicates the answer as True (False), it is in-
terpreted that the predicate in the answer entails
(does not entail) the predicate in the question.
Whereas the Levy and Dagan entailment data
set removes bias, a recent evaluation identified a
high labeling error rate for entailments that hold
only in one direction (Holt, 2018). Holt analyzed
150 positive examples and showed that 33% of
the claimed entailments are correct only in the
opposite direction, and 15% do not entail in any
direction. Holt (2018) designed a task to crowd-
annotate the data set by a) adding the reverse
entailment (q→a) for each original positive en-
tailment (a→q) in Levy and Dagan’s data set;
and b) directly asking the annotators if a posi-
tive example (or its reverse) is an entailment or
not (as opposed to relying on a factoid question).
We test our method on this re-annotated data set of
18,407 examples (3,916 positive and 14,491 neg-
ative), which we refer to as Levy/Holt.9 We run
our CCG-based binary relation extraction on the
examples and perform our typing procedure (§3.2)
on aanswer (e.g., Kyoto) and aarg (e.g., mountains)
to find the types of the arguments. We split the re-
annotated data set into dev (30%) and test (70%)
such that all the examples with the same qtype and
qrel are assigned to only one of the sets.
Berant’s Entailment Data Set Berant et al.
(2011) annotated all the edges of 10 typed entail-
ment graphs based on the predicates in their cor-
pus. The data set contains 3,427 edges (positive),
and 35,585 non-edges (negative). We evaluate our
method on all the examples of Berant’s entailment
data set. The types of this data set do not match
with FIGER types, but we perform a simple hand-
mapping between their types and FIGER types.10
5.3 Parameter Tuning
We selected λ1=.01 and ε=.3 based on prelim-
inary experiments on the dev set of Levy/Holt’s
data set. The hyperparameter λ2 is selected from
{0, 0.01, 0.1, 0.5, 1, 1.5, 2, 10, ∞}.11 We do not
tune λ2 for Berant’s data set. We instead use the
selected value based on the Levy/Holt dev set. In
all our experiments, we remove any local score
w0
ij < .01. We show precision–recall curves by
changing the threshold δ on the similarity scores.
5.4 Comparison
We test our model by ablation of the global soft
constraints LcrossGraph and LpResolution, testing
simple baselines to resolve sparsity and compar-
ing to the state-of-the-art resources. We also com-
pare with two distributional approaches that can
be used to predict predicate similarity. We com-
pare the following models and resources.
CG_PR is our novel model with both global
soft constraints LcrossGraph and LpResolution. CG
is our model without LpResolution. Local is the lo-
cal distributional similarities without any change.
AVG is the average of local scores across all the
entailment graphs that contain both predicates in
an entailment of interest. We set λ2 = ∞, which
forces all the values of (cid:126)β to be 1, hence resulting in
a uniform average of local scores. Untyped scores
are local scores learned without types. We set the
cut-offs C1=20 and C2=20 to have a graph with
total number of edges similar to the typed entail-
ment graphs.
ConvE scores are cosine similarities of low-
dimensional predicate representations learned by
ConvE (Dettmers et al., 2018), a state-of-the-
art model for link prediction. ConvE is a multi-
layer convolutional network model that is highly
parameter efficient. We learn 200-dimensional
vectors for each predicate (and argument) by
applying ConvE to the set of extractions of the
above untyped graph. We learned embeddings
9www.github.com/xavi-ai/relational-
implication-dataset.
1010 mappings in total (e.g., animal to living_thing).
11The selected value was usually around 1.5.
709
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
0
1
5
6
7
6
7
0
/
/
t
l
a
c
_
a
_
0
0
2
5
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
for each predicate and its reverse to handle exam-
ples where the argument order of the two predi-
cates are different. Additionally, we tried TransE
(Bordes et al., 2013), another link prediction
method that, despite its simplicity, produces very
competitive results in knowledge base completion.
However, we do not present its full results, as they
were worse than ConvE.12
PPDB is based on the Paraphrase Database
(PPDB) of Pavlick et al. (2015). We accept an
example as entailment if it is labeled as a para-
phrase or entailment in the PPDB XL lexical or
phrasal collections.13 Berant_ILP is based on the
entailment graphs of Berant et al. (2011).14 For
Berant’s data set, we directly compared our results
to the ones reported in Berant et al. (2011). For
Levy/Holt’s data set, we used publicly available
entailment rules derived from Berant et al. (2011)
that give us one point of precision and recall in the
plots. Although the rules are typed and can be ap-
plied in a context-sensitive manner, ignoring the
types and applying the rules out of context yields
much better results (Levy and Dagan, 2016). This
is attributable to both the non-standard types used
by Berant et al. (2011) and also the general data
sparsity issue.
In all our experiments, we first test a set of
rule-based constraints introduced by Berant et al.
(2011) on the examples before the prediction by
our methods. In the experiments on Levy/Holt’s
data set, in order to maintain compatibility with
Levy and Dagan (2016), we also run the lemma-
based heuristic process used by them before
applying our methods.We do not apply the lemma-
based process on Berant’s data set in order to
compare with Berant et al’s (2011) reported results
directly. In experiments with CG_PR and CG, if
the typed entailment graph corresponding to an
example does not have one or both predicates, we
resort to the average score between all typed en-
tailment graphs.
6 Results and Discussion
To test the efficacy of our globally consistent
entailment graphs, we compare them with the
12We also tried the average of GloVe embeddings
(Pennington et al., 2014) of the words in each predicate, but
the results were worse than ConvE.
13We also tested the largest collection (XXXL), but the
precision was very low on Berant’s data set (below 30%).
baseline systems in Section 6.1. We test the ef-
fect of approximating transitivity constraints in
Section 6.2. Section 6.3 concerns error analysis.
6.1 Globally Consistent Entailment Graphs
We test our method using three distributional sim-
ilarity measures: Weeds similarity (Weeds and
Weir, 2003), Lin similarity (Lin, 1998), and
Balanced Inclusion (BInc; Szpektor and Dagan,
2008). The first two similarity measures are sym-
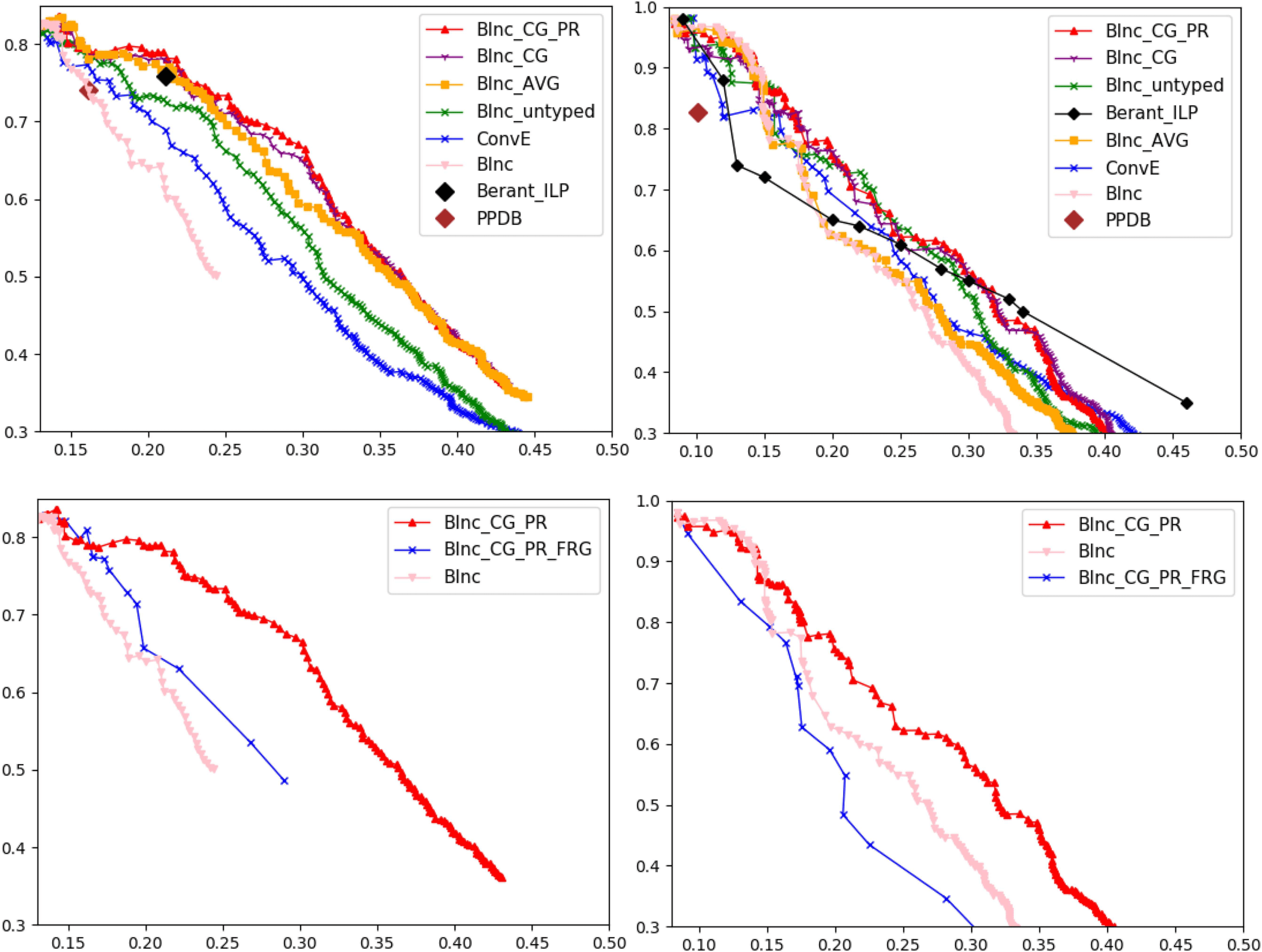
metric,15 and BInc is directional. Figures 4A and
4B show precision-recall curves of the different
methods on Levy/Holt’s and Berant’s data sets, re-
spectively, using BInc. We show the full curve for
BInc; as it is directional and on the development
portion of Levy/Holt’s data set, it yields better re-
sults than Weeds and Lin.
In addition, Table 1 shows the area under the
precision-recall curve (AUC) for all variants of the
three similarity measures. Note that each method
covers a different range of precisions and recalls.
We compute AUC for precisions in the range
[0.5, 1], because predictions with precision better
than random guess are more important for end
applications such as question answering and se-
mantic parsing. For each similarity measure, we
tested statistical significance between the methods
using bootstrap resampling with 10K experiments
(Efron and Tibshirani, 1985; Koehn, 2004). In
Table 1, the best result for each data set and sim-
ilarity measure is boldfaced. If the difference of
another model with the best result is not signifi-
cantly different with p-value < 0.05, the second
model is also boldfaced.
Among the distributional similarities based on
BInc, BInc_CG_PR outperforms all
the other
models in both data sets. In comparison with
BInc score’s AUC, we observe more than 100%
improvement on Levy/Holt’s data set and about
30% improvement on Berant’s. Given the con-
sistent gains, our proposed model appears to al-
leviate the data sparsity and the noise inherent
to local scores. Our method also outperforms
PPDB and Berant_ILP on both data sets. The
second-best performing model is BInc_CG, which
improves the results significantly, especially on
Berant’s data set, over the BInc_AVG (AUC of
.177 vs. .144). This confirms that learning what
14We also tested Berant et al. (2015), but do not report
15Weeds similarity is the harmonic average of Weeds pre-
the results as they are very similar.
cision and Weeds recall, hence a symmetric measure.
710
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
0
1
5
6
7
6
7
0
/
/
t
l
a
c
_
a
_
0
0
2
5
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
0
1
5
6
7
6
7
0
/
/
t
l
a
c
_
a
_
0
0
2
5
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4: Comparison of globally consistent entailment graphs to the baselines on Levy/Holt’s (A) and Berant’s
(B) data sets. The results are compared to graphs learned by Forest Reducible Graph Assumption on Levy/Holts’s
(C) and Berant’s (D) data sets.
subset of entailments should be generalized across
different typed entailment graphs ((cid:126)β) is effective.
The untyped models yield a single large entail-
ment graph. It contains (noisy) edges that are not
found in smaller typed entailment graphs. Despite
the noise, untyped models for all three similarity
measures still perform better than the typed ones
in terms of AUC. However, they do worse in the
high-precision range. For example, BInc_untyped
is worse than BInc for precision > 0.85. The AVG
models do surprisingly well (only about 0.5 to 3.5
below CG_PR in terms of AUC), but note that only
a subset of the typed entailment graphs might have
(untyped) predicates p and q of interest (usually
not more than 10 typed entailment graphs out of
367 graphs). Therefore, the AVG models are gen-
erally expected to outperform the untyped ones
(with only one exception in our experiments), as
typing has refined the entailments and averaging
just improves the recall. Comparison of CG_PR
with CG models confirms that explicitly encour-
aging paraphrase predicates to have the same pat-
It improves the
terns of entailment is effective.
results for BInc score, which is a directional sim-
ilarity measure. We also tested applying the para-
phrase resolution soft constraints alone, but the
differences with the local scores were not statis-
tically significant. This suggests that the para-
phrase resolution is more helpful when similarities
are transferred between graphs, as this can cause
inconsistencies around the predicates with trans-
ferred similarities, which are then resolved by the
paraphrase resolution constraints.
The results of the distributional representations
learned by ConvE are worse than most other meth-
ods. We attribute this outcome to the fact that a)
while entailment relations are directional, these
methods are symmetric; b) the learned embed-
dings are optimized for tasks other than entailment
or paraphrase detection; and c) the embeddings
711
local
untyped AVG CG CG_PR
Error type
Example
BInc
Lin
Weed
ConvE
BInc
Lin
Weed
ConvE
.076
.074
.073
–
.138
.147
.146
–
LEVY/HOLT’S data set
.162
.157
.127
.151
.146
.120
.149
.143
.115
–
–
.112
BERANT’S data set
.177
.144
.186
.172
.184
.171
–
–
.167
.158
.154
.144
.165
.149
.147
–
.179
.189
.187
–
Table 1: Area under the precision–recall curve (for
precision > 0.5) for different variants of similarity
measures: local, untyped, AVG, crossGraph (CG) and
crossGraph + pResolution (CG_PR). We report results
on two data sets. Bold indicates statistical significance
(see text).
Spurious
correlation
(57%)
Relation
normalization
(31%)
Lemma based
process &
parsing (12%)
Sparsity
(93%)
Wrong label
& parsing
(7%)
False positive
Microsoft released Internet Ex-
plorer → Internet Explorer was
developed by Microsoft
The pain may be relieved by as-
pirin → The pain can be treated
with aspirin
President Kennedy came to Texas
→ President Kennedy came from
Texas
False negative
Cape town lies at the foot of
mountains → Cape town is lo-
cated near mountains
Horses are imported from Aus-
tralia → Horses are native to Aus-
tralia
are learned regardless of argument types. How-
ever, even the BInc_untyped baseline outperforms
ConvE, showing that it is important to use a di-
rectional measure that directly models entailment.
We hypothesize that learning predicate represen-
tations based on the distributional inclusion hy-
potheses which do not have the above limitations
might yield better results.
6.2 Effect of Transitivity Constraints
Our largest graph has 53K nodes; we thus tested
approximate methods instead of the ILP to close
entailment relations under transitivity (§2). The
approximate TNF method of Berant et al. (2011)
did not scale to the size of our graphs with moder-
ate sparsity parameters. Berant et al. (2015) also
present a heuristic method, High-To-Low Forest
Reducible Graph (HTL-FRG), which gets slightly
better results than TNF on their data set, and which
scales to graphs of the size we work with.16
We applied the HTL-FRG method to the
globally consistent similarity scores (BInc_CG_
PR_HTL) and changed the threshold on the scores
to get a precision-recall curve. Figures 4C and 4D
show the results of this method on Levy/Holt’s and
Berant’s data sets. Our experiments show, in con-
trast to the results of Berant et al. (2015), that the
HTL-FRG method leads to worse results when ap-
plied to our global scores. This result is caused
both by the use of heuristic methods in place of
16TNF did not converge after two weeks for threshold δ =
.04. For δ = .12 (precisions higher than 80%), it converged,
but with results slightly worse than HTL-FRG on both data
sets.
Table 2: Examples of different error categories and
relative frequencies. The cause of errors is boldfaced.
globally optimizing via ILP, and by the removal
of many valid edges arising from the fact that
the FRG assumption is not correct for many real-
world domains.
6.3 Error Analysis
We analyzed 100 false positive (FP) and 100 false
negative (FN) randomly selected examples (using
BInc_CG_ST results on Levy/Holt’s data set and
at the precision level of Berant_ILP, i.e. 0.76). We
present our findings in Table 2. Most of the FN
errors are due to data sparsity, but a few errors are
due to wrong labeling of the data and parsing er-
rors. More than half of the FP errors are because
of spurious correlations in the data that are cap-
tured by the similarity scores, but are not judged to
constitute entailment by the human judges. About
one-third of the FP errors are because of the
normalization we currently perform on the rela-
tions (e.g., we remove modals and auxiliaries).
The remaining errors are mostly due to parsing
and our use of Levy and Dagan’s (2016) lemma-
based heuristic process.
7 Extrinsic Evaluation
To further test the utility of explicit entailment
rules, we evaluate the learned rules on an ex-
trinsic task: answer selection for machine read-
ing comprehension on NewsQA, a data set that
712
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
0
1
5
6
7
6
7
0
/
/
t
l
a
c
_
a
_
0
0
2
5
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
The board hailed Romney for his solid credentials.
Researchers announced this week that they’ve found a new
gene, ALS6, which is responsible for . . .
One out of every 17 children under 3 years old in America
has a food allergy, and some will outgrow their sensitivities.
The reported compromise could itself run afoul of European
labor law, opening the way for foreign workers . . .
. . . Barnes & Noble CEO William Lynch said as he unveiled
his company’s Nook Tablet on Monday.
The report said opium has accounted for more than half of
Afghanistan’s gross domestic product in 2007.
Who praised Mitt Romney’s credentials?
Which gene did the ALS association dis-
cover ?
How many Americans suffer from food
allergies?
What law might the deal break?
Who launched the Nook Tablet?
What makes up half of Afghanistans
GDP ?
Table 3: Examples where explicit entailment relations improve the rankings. The related words are boldfaced.
contains questions about CNN articles (Trischler
et al., 2017). Machine reading comprehension is
usually evaluated by posing questions about a
text passage and then assessing the answers of
a system (Trischler et al., 2017). The data sets
that are used for this task are often in the form
of (document,question,answer) triples, where an-
swer is a short span of the document. Answer
selection is an important task, where the goal is
to select the sentence(s) that contain the answer.
We show improvements by adding knowledge
from our learned entailments without changing the
graphs or tuning them to this task in any way.
Inverse sentence frequency (ISF) is a strong
baseline for answer selection (Trischler et al.,
2017). The ISF score between a sentence Si
and a question Q is defined as ISF(Si, Q) =
(cid:80)
w∈Si∩Q IDF(w), where IDF(w) is the inverse
document frequency of the word w by considering
each sentence in the whole corpus as one docu-
ment. The state-of-the-art methods for answer se-
lection use ISF, and by itself it already does quite
well (Trischler et al., 2017; Narayan et al., 2018).
We propose to extend the ISF score with entail-
ment rules. We define a new score,
ISFEnt(Si, Q) = αISF(Si, Q)
+ (1 − α)|{r1 ∈ Si, r2 ∈ Q : r1 → r2}|
where α ∈ [0, 1] is a hyper-parameter and r1
and r2 denote relations in the sentence and the
question, respectively. The intuition is that if a
sentence such as “Luka Modric sustained a frac-
ture to his right fibula” is a paraphrase of or en-
tails the answer of a question such as “What does
Luka Modric suffer from?”, it will contain the an-
swer span. We consider an entailment decision
ISF
ISFEnt
ACC MRR MAP
48.57
48.99
36.18
49.63
50.06
37.61
Table 4: Results (in percentage) for answer selection
on the NewsQA data set.
between two typed predicates if their global simi-
larity BInc_CG_PR is higher than a threshold δ.
We also considered entailments between unary
relations (one argument) by leveraging our learned
binary entailments. We split each binary entail-
ment into two potential unary entailments. For
example, the entailment visit1,2(:person,:location)
→ arrive1,in(:person,:location),
into
visit1(:person) → arrive1(:person) and visit2
(:location) → arrivein(:location). We computed
unary similarity scores by averaging over all re-
lated binary scores. This is particularly helpful
when one argument is not present (e.g., adjuncts or
Wh questions) or does not exactly match between
the question and the answer.
split
is
We test the proposed answer selection score on
NewsQA, a data set that contains questions about
CNN articles (Trischler et al., 2017). The data set
is collected in a way that encourages lexical and
syntactic divergence between questions and doc-
uments. The crowdworkers who wrote questions
saw only a news article headline and its summary
points, but not the full article. This process en-
courages curiosity about the contents of the full
article and prevents questions that are simple re-
formulations of article sentences (Trischler et al.,
2017). This is a more realistic and suitable setting
to test paraphrasing and entailment capabilities.
We use the development set of the data set
(5,165 samples) to tune α and δ and report re-
sults on the test set (5,124 examples) in Table 4.
713
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
0
1
5
6
7
6
7
0
/
/
t
l
a
c
_
a
_
0
0
2
5
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
wij = 1(cij > λ1)(cij − λ1)/τij
cij = w0
(cid:88)
ij +
β(·)wi(cid:48)j(cid:48) − 1(wij > ε)Iε(wji)
(cid:88)
(cid:2)(wik − wjk)2 + (wki − wkj)2(cid:3)
(i(cid:48),j(cid:48))∈N (i,j)
k∈V (τ1(i),τ2(i))
+ 2
(cid:88)
Iε(wjk)Iε(wkj)wik + Iε(wik)Iε(wki)wkj
k∈V (τ1(i),τ2(i))
(cid:88)
τij = 1 +
β(·) + 2
(cid:88)
Iε(wjk)Iε(wkj) + Iε(wik)Iε(wki)
(i(cid:48),j(cid:48))∈N (i,j)
(cid:16)
1 − (cid:0) (cid:88)
β(·) = I0
k∈V (τ1(i),τ2(i))
(cid:88)
(wij − wi(cid:48)j(cid:48))2(cid:1)/λ2
(cid:17)
.
j∈V (τ1(i),τ2(i))
(i(cid:48),j(cid:48))∈N (i,j)
Figure 5: The update rules for wij and β(·).
(6)
(7)
(8)
(9)
We observe about 1.4% improvement in accuracy
(ACC) and 1% improvement in mean reciprocal
rank (MRR) and mean average precision (MAP),
confirming that entailment rules are helpful for an-
swer selection.17 Table 3 shows some of the ex-
amples where ISFEnt ranks the correct sentences
higher than ISF. These examples are very chal-
lenging for methods that do not have entailment
and paraphrasing knowledge, and illustrate the se-
mantic interpretability of the entailment graphs.
We also performed a similar evaluation on
the Stanford Natural Language Inference data set
(SNLI; Bowman et al., 2015) and obtained 1%
improvement over a basic neural network archi-
tecture that models sentences with an n-layered
LSTM (Conneau et al., 2017). However, we did
not obtain improvements over the state-of-the-
art results, because only a few of the SNLI ex-
amples require external knowledge of predicate
entailments. Most examples require reasoning ca-
pabilities such as A ∧ B → B and simple lexical
entailments such as boy → person, which are often
present in the training set.
8 Conclusions and Future Work
We have introduced a scalable framework to learn
typed entailment graphs directly from text. We
use global soft constraints to learn globally con-
sistent entailment scores for entailment relations.
Our experiments show that generalizing in this
way across different but related typed entail-
ment graphs significantly improves performance
over local similarity scores on two standard text-
entailment data sets. We show around 100% in-
crease in AUC on Levy/Holt’s data set and 30%
on Berant’s data set. The method also outper-
forms PPDB and the prior state-of-the-art entail-
ment graph-building approach due to Berant et al.
(2011). Paraphrase resolution further improves the
results. We have in addition showed the utility of
entailment rules on answer selection for machine
reading comprehension.
In the future, we plan to show that the global
soft constraints developed in this paper can be
extended to other structural properties of entail-
ment graphs such as transitivity. Future work
might also look at entailment relation learning
and link prediction tasks jointly. The entailment
graphs can be used to improve relation extrac-
tion, similar to Eichler et al. (2017), but cov-
ering more relations. In addition, we intend to
collapse cliques in the entailment graphs to para-
phrase clusters with a single relation identifier, to
replace the form-dependent lexical semantics of
the CCG parser with these form-independent rela-
tions (Lewis and Steedman, 2013a), and to use the
entailment graphs to derive meaning postulates for
use in tasks such as question-answering and con-
struction of knowledge-graphs from text (Lewis
and Steedman, 2014).
Appendix A
17The accuracy results of Narayan et al. (2018) are not
consistent with their own MRR and MAP (ACC>MRR in
come cases), as they break ties between ISF scores differ-
ently when computing ACC compared to MRR and MAP. See
also http://homepages.inf.ed.ac.uk/scohen/
acl18external-errata.pdf.
Figure 5 shows the update rules of the learning
algorithm. The global similarity scores wij are up-
dated using Equation (6), where cij and τij are
defined in Equation (7) and Equation (8), respec-
tively. 1(x) equals 1 if the condition x is satisfied
714
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
0
1
5
6
7
6
7
0
/
/
t
l
a
c
_
a
_
0
0
2
5
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
and zero, otherwise. The compatibility functions
β(·) are updated using Equation (9).
the Association for Computational Linguistics,
pages 117–125.
Acknowledgments
We thank Thomas Kober and Li Dong for
helpful comments and feedback on the work,
Reggie Long for preliminary experiments on
openIE extractions, and Ronald Cardenas for pro-
viding baseline code for the NewsQA experi-
ments. The authors would also like to thank
Katrin Erk and the three anonymous reviewers
for their valuable feedback. This work was sup-
ported in part by the Alan Turing Institute un-
der EPSRC grant EP/N510129/1. The experiments
were made possible by Microsoft’s donation of
Azure credits to The Alan Turing Institute. The re-
search was supported in part by ERC Advanced
Fellowship GA 742137 SEMANTAX, a Google
faculty award, a Bloomberg L. P. Gift award, and
a University of Edinburgh/Huawei Technologies
award to Steedman. Chambers was supported in
part by the National Science Foundation under
grant IIS-1617952. Steedman and Johnson were
supported by the Australian Research Council’s
Discovery Projects funding scheme (project num-
ber DP160102156).
References
Omri Abend, Shay B. Cohen,
and Mark
Steedman. 2014. Lexical Inference over Multi-
Word Predicates: A Distributional Approach.
In Proceedings of the 52nd Annual Meeting of
the Association for Computational Linguistics,
pages 644–654.
Gabor Angeli, Melvin Johnson Premkumar, and
Christopher D. Manning. 2015. Leveraging Lin-
guistic Structure for Open Domain Information
Extraction. In Proceedings of the 53rd Annual
Meeting of the Association for Computational
Linguistics, pages 344–354.
Jonathan Berant, Noga Alon, Ido Dagan, and
Jacob Goldberger. 2015. Efficient Global
Learning of Entailment Graphs. Computational
Linguistics, 42:221–263.
Jonathan Berant, Ido Dagan, Meni Adler, and
Jacob Goldberger. 2012. Efficient Tree-Based
Approximation for Entailment Graph Learning.
In Proceedings of the 50th Annual Meeting of
Jonathan Berant,
Jacob Goldberger, and Ido
Dagan. 2011. Global Learning of Typed Entail-
ment Rules. In Proceedings of the 49th Annual
Meeting of the Association for Computational
Linguistics, pages 610–619.
Kurt Bollacker, Colin Evans, Praveen Paritosh,
Tim Sturge, and Jamie Taylor. 2008. Freebase:
A Collaboratively Created Graph Database for
Structuring Human Knowledge. In Proceedings
of the ACM SIGMOD international conference
on Management of data, pages 1247–1250.
Antoine Bordes, Nicolas Usunier, Alberto
Garcia-Duran,
and Oksana
Jason Weston,
Yakhnenko. 2013. Translating Embeddings for
Modeling Multi-Relational Data. In Advances
information processing systems,
in neural
pages 2787–2795.
Samuel R. Bowman, Gabor Angeli, Christopher
Potts, and Christopher D. Manning. 2015. A
Large Annotated Corpus for Learning Natu-
ral Language Inference. In Proceedings of the
Conference on Empirical Methods in Natural
Language Processing, pages 632–642.
Alexis Conneau, Douwe Kiela, Holger Schwenk,
Loïc Barrault, and Antoine Bordes. 2017. Su-
pervised Learning of Universal Sentence Rep-
resentations from Natural Language Inference
Data. In Proceedings of the Conference on Em-
pirical Methods in Natural Language Process-
ing, pages 670–680.
Ido Dagan, Lillian Lee, and Fernando C.N.
Pereira. 1999. Similarity-Based Models of
Word Cooccurrence Probabilities. Machine
learning, 34(1-3):43–69.
Tim Dettmers, Minervini Pasquale, Stenetorp
Pontus, and Sebastian Riedel. 2018. Convo-
lutional 2D Knowledge Graph Embeddings. In
Proceedings of the 32th AAAI Conference on
Artificial Intelligence, pages 1811–1818.
Li Dong, Jonathan Mallinson, Siva Reddy, and
Mirella Lapata. 2017. Learning to Paraphrase
for Question Answering. In Proceedings of the
Conference on Empirical Methods in Natural
Language Processing, pages 875–886.
715
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
0
1
5
6
7
6
7
0
/
/
t
l
a
c
_
a
_
0
0
2
5
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Bradley Efron and Robert Tibshirani. 1985. The
Bootstrap Method for Assessing Statistical
Accuracy. Behaviormetrika, 12(17):1–35.
Kathrin Eichler, Feiyu Xu, Hans Uszkoreit, and
Sebastian Krause. 2017. Generating Pattern-
Based Entailment Graphs for Relation Ex-
the 6th Joint
traction.
Conference on Lexical and Computational
Semantics (* SEM 2017), pages 220–229.
In Proceedings of
Oren Etzioni, Anthony Fader, Janara Christensen,
Stephen Soderland, and Mausam Mausam.
2011. Open Information Extraction: The Sec-
ond Generation. In Proceedings of the 22nd
International Joint Conference on Artificial
Intelligence, pages 3–10.
Juri Ganitkevitch, Benjamin Van Durme, and
Chris Callison-Burch. 2013. PPDB: The Para-
In Proceedings of the 2013
phrase Database.
Conference of the North American Chapter of
the Association for Computational Linguistics:
Human Language Technologies, pages 758–764.
Maayan Geffet and Ido Dagan. 2005. The Dis-
tributional Inclusion Hypotheses and Lexical
Entailment. In Proceedings of the 43rd Annual
Meeting on Association for Computational Lin-
guistics, pages 107–114.
Aurélie Herbelot and Mohan Ganesalingam. 2013.
Measuring Semantic Content in Distributional
Vectors. In Proceedings of
the 51st Annual
Meeting of the Association for Computational
Linguistics, pages 440–445.
Xavier R. Holt. 2018. Probabilistic Models of
Relational Implication. Master’s thesis, Mac-
quarie University.
Dimitri Kartsaklis and Mehrnoosh Sadrzadeh.
2016. Distributional Inclusion Hypothesis for
In Proceedings
Tensor-based Composition.
the 26th International Conference on
of
Computational Linguistics: Technical Papers,
pages 2849–2860.
Ross Kindermann and J Laurie Snell. 1980.
Markov Random Fields and their Applications,
volume 1. American Mathematical Society.
Philipp Koehn. 2004. Statistical Significance
Tests for Machine Translation Evaluation. In
Proceedings of the Conference on Empirical
Methods in Natural Language Processing,
pages 388–395.
Omer Levy and Ido Dagan. 2016. Annotating Re-
lation Inference in Context via Question An-
swering. In Proceedings of the 54th Annual
Meeting of the Association for Computational
Linguistics, pages 249–255.
Mike Lewis. 2014. Combined Distributional and
Logical Semantics. Ph.D. thesis, University of
Edinburgh.
Mike Lewis and Mark Steedman. 2013a. Com-
bined Distributional and Logical Semantics.
Transactions of the Association for Computa-
tional Linguistics, 1:179–192.
Mike Lewis and Mark Steedman. 2013b. Unsu-
pervised Induction of Cross-Lingual Semantic
Relations. In Proceedings of the Conference on
Empirical Methods in Natural Language Pro-
cessing, pages 681–692.
Mike Lewis and Mark Steedman. 2014. Com-
bining Formal and Distributional Models of
In Pro-
Temporal and Intensional Semantics.
ceedings of the ACL Workshop on Semantic
Parsing, pages 28–32.
Dekang Lin. 1998. Automatic Retrieval and Clus-
tering of Similar Words. In Proceedings of the
36th Annual Meeting of the Association for
Computational Linguistics, pages 768–774.
Xiao Ling and Daniel S. Weld. 2012. Fine-
Grained Entity Recognition. In Proceedings
of
the Associa-
tion for Advancement of Artificial Intelligence,
pages 94–100.
the National Conference of
Shashi Narayan, Ronald Cardenas, Nikos
Papasarantopoulos, Shay B. Cohen, Mirella
Lapata, Jiangsheng Yu, and Yi Chang. 2018.
Document Modeling with External Attention
For Sentence Extraction. In Proceedings of the
56th Annual Meeting of the Association for
Computational Linguistics, pages 2020–2030.
Dat Ba Nguyen,
Johannes Hoffart, Martin
Theobald, and Gerhard Weikum. 2014. AIDA-
light: High-Throughput Named-Entity Dis-
ambiguation. In Workshop on Linked Data on
the Web, pages 1–10.
716
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
0
1
5
6
7
6
7
0
/
/
t
l
a
c
_
a
_
0
0
2
5
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Terence Parsons. 1990. Events in the Semantics of
English: A Study in Subatomic Semantics. MIT
Press, Cambridge, MA.
Ellie
Pavlick,
Pushpendre Rastogi,
Juri
Ganitkevitch, Benjamin Van Durme,
and
Chris Callison-Burch. 2015. PPDB 2.0: Better
Paraphrase Ranking, Fine-Grained Entailment
Relations, Word Embeddings, and Style Clas-
In Proceedings of the 53rd Annual
sification.
Meeting of the Association for Computational
Linguistics, pages 425–430.
Jeffrey Pennington, Richard Socher,
and
Christopher D. Manning.
2014. GloVe:
Global Vectors for Word Representation. In
Proceedings of the Conference on Empirical
Methods in Natural Language Processing,
pages 1532–1543.
Siva Reddy, Mirella Lapata, and Mark Steedman.
2014. Large-Scale Semantic Parsing with-
out Question-Answer Pairs. Transactions of
the Association for Computational Linguistics,
2:377–392.
Sebastian Riedel, Limin Yao, Andrew McCallum,
and Benjamin M. Marlin. 2013. Relation Ex-
traction with Matrix Factorization and Univer-
sal Schemas. In Proceedings of the Conference
of the North American Chapter of the Associ-
ation for Computational Linguistics: Human
Language Technologies, pages 74–84.
Stefan Schoenmackers, Oren Etzioni, Daniel S.
Weld, and Jesse Davis. 2010. Learning First-
Order Horn Clauses From Web Text.
In
Proceedings of
the Conference on Empiri-
cal Methods in Natural Language Processing,
pages 1088–1098.
Richard Socher, Danqi Chen, Christopher D.
Manning, and Andrew Ng. 2013. Reasoning
with Neural Tensor Networks for Knowledge
Base Completion. In Advances in neural infor-
mation processing systems, pages 926–934.
Mark Steedman. 2000. The Syntactic Process.
MIT Press, Cambridge, MA.
Idan Szpektor and Ido Dagan. 2008. Learning
Entailment Rules for Unary Templates. In Pro-
717
ceedings of the 22nd International Conference
on Computational Linguistics, pages 849–856.
Adam Trischler, Tong Wang, Xingdi Yuan, Justin
Harris, Alessandro Sordoni, Philip Bachman,
and Kaheer Suleman. 2017. NewsQA: A Ma-
chine Comprehension Dataset. In Proceedings
of the 2nd Workshop on Representation Learn-
ing for NLP, pages 191–200.
Théo Trouillon, Johannes Welbl, Sebastian Riedel,
Éric Gaussier, and Guillaume Bouchard. 2016.
Complex Embeddings for Simple Link Pre-
diction. In Proceedings of the 33rd Interna-
tional Conference on International Conference
on Machine Learning, pages 2071–2080.
Yushi Wang, Jonathan Berant, and Percy Liang.
2015. Building a Semantic Parser Overnight.
In Proceedings of the 53rd Annual Meeting of
the Association for Computational Linguistics,
pages 1332–1342.
Julie Weeds and David Weir. 2003. A Gen-
eral Framework for Distributional Similarity.
In Proceedings of the Conference on Empiri-
cal Methods in Natural Language Processing,
pages 81–88.
Yangyang Xu and Wotao Yin. 2013. A Block
Coordinate Descent Method for Regularized
Multiconvex Optimization with Applications to
Nonnegative Tensor Factorization and Com-
pletion. SIAM Journal on imaging sciences,
6(3):1758–1789.
Bishan Yang, Wen-tau Yih, Xiaodong He,
Jianfeng Gao, and Li Deng. 2015. Embedding
Entities and Relations for Learning and Infer-
In Proceedings of
ence in Knowledge Bases.
the International Conference on Learning Rep-
resentations.
Naomi Zeichner, Jonathan Berant, and Ido Dagan.
2012. Crowdsourcing Inference-Rule Evalu-
the 50th Annual
ation.
Meeting of the Association for Computational
Linguistics, pages 156–160.
In Proceedings of
Congle Zhang and Daniel S. Weld. 2013. Harvest-
ing Parallel News Streams to Generate Para-
phrases of Event Relations. In Proceedings of
the Conference on Empirical Methods in Natu-
ral Language Processing, pages 1776–1786.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
0
1
5
6
7
6
7
0
/
/
t
l
a
c
_
a
_
0
0
2
5
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
0
1
5
6
7
6
7
0
/
/
t
l
a
c
_
a
_
0
0
2
5
0
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3