Learning Fair Representations via Rate-Distortion Maximization
Somnath Basu Roy Chowdhury and Snigdha Chaturvedi
UNC Chapel Hill, USA
{somnath, snigdha}@cs.unc.edu
Abstract
representations
Text
learned by machine
learning models often encode undesirable de-
mographic information of the user. Predictive
models based on these representations can rely
on such information, resulting in biased deci-
sions. We present a novel debiasing technique,
Fairness-aware Rate Maximization (FaRM),
that removes protected information by making
representations of instances belonging to the
same protected attribute class uncorrelated, us-
ing the rate-distortion function. FaRM is able
to debias representations with or without a tar-
get task at hand. FaRM can also be adapted to
remove information about multiple protected
attributes simultaneously. Empirical evalua-
tions show that FaRM achieves state-of-the-art
performance on several datasets, and learned
representations leak significantly less pro-
tected attribute information against an attack
by a non-linear probing network.
1
Introduction
Democratization of machine learning has led to
deployment of predictive models for critical appli-
cations like credit approval (Ghailan et al., 2016)
and college application reviewing (Basu et al.,
2019). Therefore, it is important to ensure that
decisions made by these models are fair towards
different demographic groups (Mehrabi et al.,
2021). Fairness can be achieved by ensuring that
the demographic information does not get en-
coded in the representations used by these mod-
els (Blodgett et al., 2016; Elazar and Goldberg,
2018; Elazar et al., 2021).
However,
controlling demographic informa-
tion encoded in a model’s representations is a
challenging task for textual data. This is because
natural language text is highly indicative of an au-
thor’s demographic attributes even when it is not
explicitly mentioned (Koppel et al., 2002; Burger
et al., 2011; Nguyen et al., 2013; Verhoeven and
Daelemans, 2014; Weren et al., 2014; Rangel
et al., 2016; Verhoeven et al., 2016; Blodgett
et al., 2016).
In this work, we debias information about a
protected attribute (e.g., gender, race) from textual
data representations. Previous debiasing methods
(Bolukbasi et al., 2016; Ravfogel et al., 2020)
project representations in a subspace that does
not reveal protected attribute information. These
methods are only able to guard protected attributes
against an attack by a linear function (Ravfogel
et al., 2020). Other methods (Xie et al., 2017; Basu
Roy Chowdhury et al., 2021) adversarially remove
protected information while retaining information
about a target attribute. However, they are difficult
to train (Elazar and Goldberg, 2018) and require a
target task at hand.
We present a novel debiasing technique,
Fairness-aware Rate Maximization (FaRM), that
removes demographic information by control-
ling the rate-distortion function of the learned
representations. Intuitively, in order to remove
information about a protected attribute from a
set of representations, we want the representa-
tions from the same protected attribute class to
be uncorrelated to each other. We achieve this by
maximizing the number of bits (rate-distortion)
required to encode representations with the same
protected attribute. Figure 1 illustrates the pro-
cess. The representations are shown as points in
a two-dimensional feature space, color-coded ac-
cording to their protected attribute class. FaRM
learns a function φ(x) such that representations
of the same protected class become uncorre-
lated and similar to other representations, thereby
making it difficult
the information
about the protected attribute from the learned
representations.
to extract
We perform rate-distortion maximization based
(a) un-
debiasing in the following setups:
constrained debiasing—we remove information
about a protected attribute g while retain-
ing remaining information as much as possible
(e.g., debiasing gender information from word
1159
Transactions of the Association for Computational Linguistics, vol. 10, pp. 1159–1174, 2022. https://doi.org/10.1162/tacl a 00512
Action Editor: Christopher Potts. Submission batch: 2/2022; Revision batch: 6/2022; Published 10/2022.
c(cid:2) 2022 Association for Computational Linguistics. Distributed under a CC-BY 4.0 license.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
5
1
2
2
0
5
4
6
9
7
/
/
t
l
a
c
_
a
_
0
0
5
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
• We empirically show FaRM leaks signif-
icantly less protected information against
a non-linear probing attack, outperforming
prior approaches.
• We present
two variations of FaRM for
debiasing multiple protected attributes simul-
taneously, which is also effective against an
attack for intersectional group biases.
2 Related Work
Removing sensitive attributes from data rep-
resentations for fair classification was initially
introduced as an optimization task (Zemel et al.,
2013). Subsequent works have used adversarial
frameworks (Goodfellow et al., 2014) for this task
(Zhang et al., 2018; Li et al., 2018; Xie et al., 2017;
Elazar and Goldberg, 2018; Basu Roy Chowdhury
et al., 2021). However, adversarial networks are
difficult to train (Elazar and Goldberg, 2018) and
cannot function without a target task at hand.
Unconstrained debiasing frameworks focus on
removing a protected attribute from representa-
tions, without relying on a target task. Bolukbasi
et al. (2016) demonstrated that GloVe embeddings
encode gender information, and proposed an un-
constrained debiasing framework for identifying
gender direction and neutralizing vectors along
that direction. Building on this approach, Ravfogel
et al. (2020) proposed INLP, a robust framework
to debias representations by iteratively identifying
protected attribute subspaces and projecting rep-
resentations onto the corresponding nullspaces.
However, these approaches fail to guard protected
information against an attack by a non-linear prob-
ing network. Dev et al. (2021) showcased that
nullspace projection approaches can be extended
for debiasing in a constrained setup as well.
In contrast to prior works, we present a novel
debiasing framework based on the principle of
rate-distortion maximization. Coding rate maxi-
mization was introduced as an objective function
by Ma et al. (2007) for image segmentation. It
has also been used in explaining feature selec-
tion by deep networks (Macdonald et al., 2019).
Recently, Yu et al. (2020) proposed maximal cod-
ing rate (MCR2) based on rate-distortion theory,
a representation-level objective function that can
serve as an alternative to empirical risk minimiza-
tion methods. Our work is similar to MCR2 as
we learn representations using a rate-distortion
Figure 1: Illustration of unconstrained debiasing using
FaRM. Representations are color-coded (in blue, red
and green) according to their protected attribute class.
Before debiasing (left), representations within each
class are similar to each other (intra-class information
content is low). Debiasing enforces the within class
representations to be uncorrelated by increasing their
information content.
embeddings), and (b) constrained debiasing—we
retain information about a target attribute y while
removing information pertaining to g (e.g., re-
moving racial information from representations
during text classification). In the unconstrained
setup, debiased representations can be used for
different downstream tasks, whereas for con-
strained debiasing the user is interested only in
the target task. For unconstrained debiasing, we
evaluate FaRM for removing gender information
from word embeddings and demographic infor-
mation from text representations that can then be
used for a downstream NLP task (we show their
utility for biography and sentiment classification
in our experiments). Our empirical evaluations
show that representations learned using FaRM in
an unconstrained setup leak significantly less pro-
tected attribute information compared to prior
approaches against an attack by a non-linear
probing network.
For constrained debiasing, FaRM achieves
state-of-the-art debiasing performance on 3 data-
sets, and representations are able to guard pro-
tected attribute information significantly better
than previous approaches. We also perform ex-
periments to show that FaRM is able to remove
multiple protected attributes simultaneously while
guarding against
intersectional group biases
(Subramanian et al., 2021). To summarize, our
main contributions are:
• We present Fairness-aware Rate Maximi-
zation (FaRM) for debiasing of textual data
representations in unconstrained and con-
strained setups, by controlling their rate-
distortion functions.
1160
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
5
1
2
2
0
5
4
6
9
7
/
/
t
l
a
c
_
a
_
0
0
5
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
framework, but instead of tuning representations
for classification we remove protected attribute
information from them.
3 Preliminaries
Our
framework performs debiasing by mak-
ing representations of the same protected at-
tribute class uncorrelated. To achieve this, we
leverage a principled objective function called
rate-distortion, to measure the compactness of a
set of representations. In this section, we introduce
the fundamentals of rate-distortion theory.1
Rate-Distortion.
In lossy data compression
(Cover, 1999),
the compactness of a random
distribution is measured by the minimal num-
ber of binary bits required to encode it. A lossy
coding scheme encodes a finite set of vectors
Z = {z1, . . . , zn} ∈ Rn×d from a distribution
P (Z), such that the decoded vectors {ˆzi}n
i=1 can be
recovered up to a precision (cid:3)2. The rate-distortion
function R(Z, (cid:3)) measures the minimal number of
bits per vector required to encode the sequence Z.
i=1 are i.i.d. samples
from a zero-mean multi-dimensional Gaussian
distribution N (0, Σ), the optimal rate-distortion
function is given as:
In case the vectors {zi}n
R(Z, (cid:3)) =
1
2
(cid:2)
log2 det
I +
(cid:3)
d
n(cid:3)2 ZZT
(1)
n ZZT = ˆΣ is the estimate of covariance
where 1
matrix Σ for the Gaussian distribution. As the
eigenvalues of the matrices ZZT and ZT Z are
equal, the rate-distortion function R(Z, (cid:3)) is the
same for both of them (Ma et al., 2007). In most se-
tups d (cid:4) n, therefore, we use ZT Z for efficiently
computing R(Z, (cid:3)).
In rate-distortion theory, we need nR(Z, (cid:3)) bits
to encode n vectors of Z. The optimal codebook
also depends on data dimension (d) and requires
dR(Z, (cid:3)) bits to encode. Therefore, a total of
(n + d)R(Z, (cid:3)) is bits required to encode the
sequence Z. Ma et al. (2007) showed that this
provides a tight bound even in cases where the
underlying distribution P (Z) is degenerate. This
enables the use of this loss function for real-world
data, where the underlying distribution may not
be well defined.
In general, a set of compact vectors (low infor-
mation content) would require a small number of
bits to encode, which would correspond to a small
value of R(Z, (cid:3)) and vice versa.
Rate Distortion for a Mixed Distribution.
In
the set of vectors Z can be from a
general,
mixture distribution (e.g., feature representations
for multi-class data). The rate-distortion func-
tion can be computed by splitting the data into
multiple subsets: Z = Z 1 ∪ Z 2 . . . ∪ Zk, based
on their distribution. For each subset, we can
compute the R(Zi, (cid:3)) (Equation 1). To facili-
tate the computation, we define a membership
matrix Π = {Πj}k
j=1 as a set of k matrices to
encode membership information in each subset
Zj. The membership matrix Πj for each subset is
a diagonal matrix defined as:
Πj = diag(π1j, π2j, . . . , πnj) ∈ Rn×n
(2)
where πij ∈ [0, 1] denotes the probability of a
vector zi belonging to the j-th subset and n is the
number of vectors in the sequence Z. The matri-
j Πj =
ces satisfy the constraints:
In×n, Πj (cid:6) 0. The expected number of vectors
in the j-th subset Zj is tr(Πj) and the correspond-
1
tr(Πj ) ZΠjZT . The overall
ing covariance matrix:
rate-distortion function is given as:
j πij = 1,
(cid:4)
(cid:4)
Rc(Z, (cid:3)|Π) =
k(cid:5)
tr(Πj)
2n
(cid:2)
log2 det
I +
(cid:3)
d
tr(Πj)(cid:3)2 ZΠjZT
j=1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
5
1
2
2
0
5
4
6
9
7
/
/
t
l
a
c
_
a
_
0
0
5
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
For multi-class data, where a vector zi can
only be a member of a single class, we restrict
πij = {0, 1}, and therefore the covariance matrix
for the j-th subset is ZjZj T
. In general, if the rep-
resentations within each subset Zj are similar to
each other, they will have low intra-class variance,
and it would correspond to a small Rc(Z, (cid:3)|Π) and
vice versa.
4 Fairness-Aware Rate Maximization
In this section, we describe FaRM to debias
representations in unconstrained and constrained
setups.
4.1 Unconstrained Debiasing using FaRM
1We borrow some notations from Yu et al. (2020) to
explain concepts of rate-distortion theory.
In this setup, we aim to remove information about
a protected attribute g from data representations
1161
4:
5:
Algorithm 1 Unconstrained Debiasing Routine
1: Input: (X, G) input data set with protected
attribute labels. Number of training epochs
N .
2: for i = 1, . . . , N do
3:
Z = LayerNorm(φ(X))
Πg = ConstructMatrix(G)
(cid:5) retrieve
membership matrix using G
Update φ using gradients ∇
φ
Ju(Z, Πg)
6: end for
7: Zdebiased = φ(X) (cid:5) debiased representations
8: return φ
(cid:5) debiasing network
X while retaining the remaining information. To
achieve this, the debiased representations Z should
have the following properties:
(a) Intra-class Incoherence: Representations be-
longing to the same protected attribute class
should be highly uncorrelated. This would
make it difficult for a classifier to extract any
information about g from the representations.
(b) Maximal Informativeness: Representations
should be maximally informative about the
remaining information.
there are k protected attribute
Assuming that
classes, we can write Z = Z 1 ∪ . . . ∪ Zk. To
achieve (a), we need to ensure that the represen-
tations in a subset Zj belonging to the same
protected class are dissimilar and have large
intra-class variance. An increased intra-class vari-
ance would correspond to an increase in the
number of bits to encode samples within each
class and the rate-distortion function Rc(Z, (cid:3)|Πg)
would be large. For (b), we want the represen-
tations Z to retain maximal possible information
from the input X. Increasing information content
in Z, would require a larger number of bits to en-
code it. This means that the rate-distortion R(Z, (cid:3))
should also be large.
FaRM achieves (a) and (b) simultaneously by
maximizing the following objective function:
Ju(Z, Πg) = Rc(Z, (cid:3)|Πg) + R(Z, (cid:3))
(3)
Figure 2: Visualization for regularization loss in Jc for
constrained debiasing. The red and blue circles rep-
resent 2D representations from two different protected
class. The gray arrows are induced by Rc(Z, (cid:3)|Πg)
term and the green ones are induced by R(Z, (cid:3)) term.
The unconstrained debiasing routine is de-
scribed in Algorithm 1. We use a deep neural
network φ as our feature map to obtain debiased
representations z = φ(x). The objective function
Ju is sensitive to the scale of the representations.
Therefore, we normalize the Frobenius norm of
the representations to ensure individual input sam-
ples have an equal impact on the loss. We use layer
normalization (Ba et al., 2016) to ensure that all
representations have the same magnitude and lie
on a sphere zi ∈ Sd−1(r) of radius r. The feature
encoder φ is updated using gradients from the ob-
jective function Ju. The debiased representations
are retrieved by feeding input data X through the
trained network φ. An illustration of the debiasing
process in the unconstrained setup is shown in
Figure 1.
4.2 Constrained Debiasing using FaRM
In this setup, we aim to remove information about
a protected attribute g from data representations X
while retaining information about a specific target
attribute y. The learned representations should
have the following properties:
(a) Target-Class Informativeness: Representa-
tions should be maximally informative about
the target task attribute y.
(b) Inter-class Coherence: Representations from
different protected attribute classes should
be similar to each other. This would make
it difficult to extract information about g
from Z.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
5
1
2
2
0
5
4
6
9
7
/
/
t
l
a
c
_
a
_
0
0
5
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
where the membership matrix Πg, is constructed
using the protected attribute g (see Equation 2).
Our constrained debiasing setup is shown in
Figure 3, where representations are retrieved from
1162
where ˆy is the target prediction label, y is the
ground-truth label and λ is a hyperparameter.2 We
select the hyperparameters using grid search and
discuss the hyperparameter sensitivity of FaRM
in Section 8. We follow a similar routine to obtain
debiased representations in the constrained setup
as shown in Algorithm 1.
5 Experimental Setup
In this section, we discuss the datasets, experimen-
tal setup, and metrics used for evaluating FaRM.
The implementation of FaRM is publicly available
at https://github.com/brcsomnath/FaRM.
5.1 Datasets
We evaluate FaRM using several datasets. Among
these, the DIAL and Biographies datasets are used
for evaluating both constrained and unconstrained
debiasing. PAN16 and GloVe embeddings are used
only for constrained and unconstrained debiasing,
respectively. We use the same train-test split as
prior works for all datasets.
(a) DIAL (Blodgett et al., 2016) is a Twitter-based
sentiment classification dataset. Each tweet
is
associated with sentiment and mention labels
(treated as the target attribute in constrained
evaluation) and ‘‘race’’ information (protected
attribute) of the author. The sentiment
labels
are ‘‘happy’’ or
‘‘sad’’ and the race cate-
gories are ‘‘African-American English’’ (AAE)
or ‘‘Standard American English’’ (SAE).
(b) Biography classification dataset (De-Arteaga
et al., 2019) contains biographies that are associ-
ated with a profession (target attribute) and gender
label (protected attribute). There are 28 distinct
profession categories and 2 gender classes.
(c) PAN16 (Rangel et al., 2016) is also a Tweet-
classification dataset where each Tweet is anno-
tated with the author’s age and gender information,
both of which are binary protected attributes. The
target task is mention detection.
(d) GloVe embeddings: We follow the setup of
Ravfogel et al. (2020) to debias the most com-
mon 150,000 GloVe word embeddings (Zhao
2Note, we cannot use the same regularization term
(Equation 4) for unconstrained debiasing, as minimizing
R(Z, (cid:2)) without the supervision of target loss CE(ˆy, y) re-
sults in all representations converging to a compact space,
thereby losing most of the information.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
5
1
2
2
0
5
4
6
9
7
/
/
t
l
a
c
_
a
_
0
0
5
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3: Constrained debiasing setup using FaRM.
Representation z retrieved from the feature map φ
is used to predict the target label and control the
rate-distortion objective function.
a feature map φ followed by a target task classifier
f . In this setup, we achieve (a) by training f to
predict the target class ˆy = f (z) and minimize
the cross-entropy loss CE(ˆy, y), where y is the
ground-truth target label. For (b), we need to en-
sure that representations from different protected
classes are similar and overlap in the represen-
tation space. This is achieved by maximizing
the rate Rc(Z, (cid:3)|Πg) while minimizing R(Z, (cid:3)).
Maximizing Rc(Z, (cid:3)|Πg) ensures samples in the
same protected class are dissimilar and have large
intra-class variance. However, simply increasing
intra-class variance does not guarantee the overlap
of different protected class representations—as
the overall feature space can expand and rep-
resentations can still be discriminative w.r.t. g.
Therefore, we also minimize R(Z, (cid:3)) ensuring a
lower number of bits are required to encode all rep-
resentations Z, thereby making the representation
space compact. This process is illustrated visually
in Figure 2. The blue and red circles correspond
to representations from two protected classes. The
gray arrows are induced by the term Rc(Z, (cid:3)|Πg)
that encourages the representations to be dissim-
ilar to samples in the same protected class. The
green arrows induced by R(Z, (cid:3)) try to make the
representation space more compact. To achieve
this objective, FaRM adds a rate-distortion based
regularization constraint to the target classifica-
tion loss. Overall, FaRM achieves (a) and (b)
simultaneously by maximizing the following
objective function:
Jc(Z, Y, Πg) = −CE(ˆy, y)
(cid:6)
+ λ
Rc(Z, (cid:3)|Πg) − R(Z, (cid:3))
(cid:7) (4)
1163
et al., 2018). For training, we use the 7500 most
male-biased, female-biased, and neutral words
(determined by the magnitude of the word vec-
tor’s projection onto the gender direction, which
is the largest principal component of the space
of vectors formed using the difference gendered
word vector pairs).
5.2 Implementation Details
We use a multi-layer neural network with ReLU
non-linearity as our feature map φ in the un-
constrained setup. This setup is optimized using
stochastic gradient descent with a learning rate
of 0.001 and momentum of 0.9. For constrained
debiasing, we used BERTbase as φ, and a 2-layer
neural network as f . Constrained setup is opti-
mized using the AdamW (Loshchilov and Hutter,
2019) optimizer with a learning rate of 2×10−5.
We set λ = 0.01 for all experiments. Hyperpa-
rameters were tuned on the development set of the
respective datasets. Our models were trained on a
single Nvidia Quadro RTX 5000 GPU.
5.3 Probing Metrics
Following previous work (Elazar and Goldberg,
2018; Ravfogel et al., 2020; Basu Roy Chowdhury
et al., 2021), we evaluate the quality of our debias-
ing by probing the learned representations for the
protected attribute g and target attribute y. In our
experiments, we probe all representations using
a non-linear classifier. We use an MLP Classi-
fier from the scikit-learn library (Pedregosa et al.,
2011). We report the Accuracy and Minimum De-
scription Length (MDL) (Voita and Titov, 2020)
for predicting g and y. A large MDL signifies
that more effort is needed by a probing network to
achieve a certain performance. Hence, we expect
debiased representations to have a large MDL for
protected attribute g and a small MDL for pre-
dicting target attribute y. Also, we expect a high
accuracy for y and low accuracy for g.
5.4 Group Fairness Metrics
TPR-GAP. Based on the notion of equal-
ized odds, De-Arteaga et al. (2019) introduced
TPR-GAP, which measures the true positive rate
(TPR) difference of a classifier between two
protected groups.
TPR-GAP for a target attribute label y is:
TPRg,y = p(ˆy = y|g = g, y = y)
Gapg,y = TPRg,y − TPR¯g,y
where y is the target attribute, g is a binary
protected attribute with possible values g, ¯g, and
ˆy denotes the predicted target attribute. Romanov
et al. (2019) proposed a single bias score for the
classifier called GapRMS
g
(cid:8)
, which is defined as:
GapRMS
g =
1
|Y|
(cid:5)
(Gapg,y)2
(5)
y∈Y
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
5
1
2
2
0
5
4
6
9
7
/
/
t
l
a
c
_
a
_
0
0
5
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
where is Y is the set of target attribute labels.
Demographic Parity (DP). DP measures the dif-
ference in prediction w.r.t. to protected attribute g.
DP =
(cid:5)
y∈Y
|p(ˆy = y|g = g) − p(ˆy = y|g = ¯g)|
where g, ¯g are possible values of the binary pro-
tected attribute g and Y is the set of possible target
attribute labels.
Bickel et al. (1975) illustrated that notions
of demographic parity and equalized odds can
strongly differ in a real-world scenario. For rep-
resentation learning, Zhao and Gordon (2019)
demonstrated an inherent tradeoff between the
utility and fairness of representations. TPR-GAP
described above is not a good indicator of fair-
ness if y and g are correlated, as debiasing would
lead to a drop in target task performance as well.
For our experiments, we compare models using
both metrics for completeness. However, like prior
work, in some cases we observe conflicting results
due to the tradeoff.
6 Results: Unconstrained Debiasing
We evaluate FaRM for unconstrained debiasing in
three different setups: word embedding debiasing,
and debiasing text representations for biographies
and sentiment classification. For the classifica-
tion tasks, we retrieve text representations from
a pre-trained encoder, debias them using FaRM
(without taking the target task into account) and
evaluate the debiased representations by probing
for y and g. In all settings, we train the feature en-
coder φ, and evaluate the retrieved representations
Zdebiased = φ(X). All tables mention the expected
trend of a metric using ↑ (higher) or ↓ (lower).
6.1 Word Embedding Debiasing
We revisit the problem of debiasing gender in-
formation from word embeddings introduced by
Bolukbasi et al. (2016).
1164
Method Accuracy (↓) MDL (↑) Rank (↑)
Metric
Method
FastText BERT
GloVe
INLP
FaRM
100.0
86.3
53.9
0.1
8.6
24.6
300
210
247
Profession
Acc.
(↑)
Table 1: Debiasing performance on GloVe word
embeddings. FaRM significantly outperforms
INLP (Ravfogel et al., 2020) in guarding gender
information. Best debiasing results are in bold.
Gender
Acc.
(↓)
DP (↓)
GapRMS
g
(↓)
Original
INLP
FaRM
Original
INLP
FaRM
Original
INLP
FaRM
Original
INLP
FaRM
79.9
76.3
54.8
98.9
67.4
57.6
1.65
1.51
0.12
0.185
0.089
0.006
80.9
77.8
55.8
99.6
94.9
55.6
1.68
1.50
0.14
0.171
0.096
0.079
Figure 4: Projections of GloVe embeddings before
(left) and after (right) debiasing. Intial female and
male biased representations are shown in red and blue,
respectively.
Setup. We debias gender
information from
GloVe embeddings using a 4-layer neural net-
work with ReLU non-linearity as the feature map
φ(x). We discuss the choice of the feature map φ
in Section 8.
Results. Table 1 presents the result of debiasing
word embeddings for baseline INLP (Ravfogel
et al., 2020) and FaRM. We observe that when
compared with INLP, FaRM reduces the accuracy
of the network by an absolute margin of 32.4% and
achieves a steep increase in MDL. FaRM is able to
guard the protected attribute against an attack by
a non-linear probing network (near-random accu-
racy). We also report the rank of the resulting word
embedding matrix. The information content of a
matrix is captured by its rank (maximal number
of linearly independent columns). An increase in
rank of the resultant embedding matrix indicates
that FaRM is able to retain more information in
the representations, in general, compared to INLP.
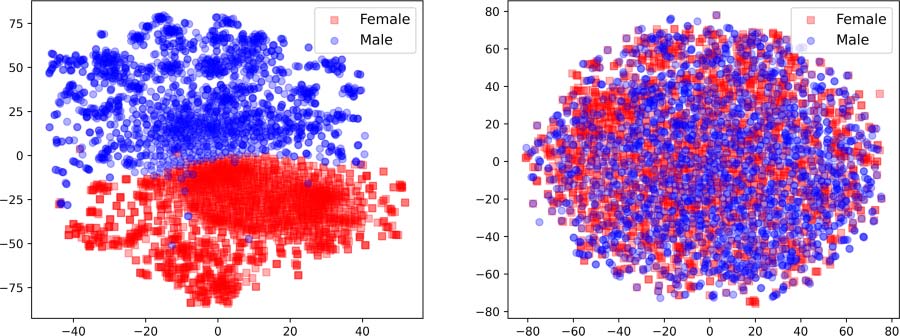
Visualization. We visualize the t-SNE (Van
der Maaten and Hinton, 2008) projections of
GloVe embeddings before and after debiasing
in Figures 4a and 4b, respectively. Female and
male-biased word vectors are represented by red
and blue dots, respectively. The figures clearly
Table 2: Evaluation results of FaRM on the Biogra-
phies dataset. Compared to INLP (Ravfogel et al.,
2020), representations from FaRM leak significantly
less gender information and achieve better fairness
scores.
demonstrate that the gendered vectors are not
separable after debiasing. In order to quantify
the improvement, we perform k-means clustering
with K = 2 (one for each gender label). We com-
pute the V-measure (Rosenberg and Hirschberg,
2007)—a measure to quantify the overlap between
clusters. V-measure in the original space drops
from 99.9% to 0.006% using FaRM (compared to
0.31% using INLP). This indicates that debiased
representations from FaRM are more difficult to
disentangle. We further analyze the quality of the
debiased word embeddings in Section 8.
6.2 Biography Classification
Next, we evaluate FaRM by debiasing text repre-
sentations in an unconstrained setup and using the
representations for fair biography classification.
Setup. We obtain the text representations using
two methods: FastText (Joulin et al., 2017) and
BERT (Devlin et al., 2019). For FastText, we
sum the individual token representations in each
biography. For BERT, by retrieving the final layer
hidden representation above the [CLS] token
from a pre-trained BERTbase model. We choose
the feature map φ(x) as a 4-layer neural network
with ReLU non-linearity.
Results. Table 2 presents the unconstrained de-
biasing results of FaRM on this dataset. ‘Original’
in the table refers to the pre-trained embeddings
1165
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
5
1
2
2
0
5
4
6
9
7
/
/
t
l
a
c
_
a
_
0
0
5
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
g
from BERTbase or FastText. We observe that
FaRM significantly outperforms INLP in fairness
metrics—DP (improvement of 92% for FastText
and 91% for BERT) and GapRMS
(improvement
of 93% for FastText and 18% for BERT). We
observe that FaRM achieves near-random gen-
der classification performance (majority baseline:
53.9%) against a non-linear probing attack. FaRM
improves upon INLP’s gender leakage by an ab-
solute margin of 9.8% and 39.4% for FastText
and BERT respectively. However, we observe a
substantial drop in the accuracy for identifying
professions (target attribute) using the debiased
embeddings.3 This is possibly because in this da-
taset, gender is highly correlated with the profes-
sion and removing gender information results in
loss of profession information. Zhao and Gordon
(2019) identified this phenomenon by noting the
tradeoff between learning fair representations and
performing well on target task, when protected and
target attributes are correlated. The results in this
setup (Table 2) demonstrate this phenomenon. In
unconstrained debiasing, we remove information
about protected attributes from the representations
without taking into account the target task. As a
result target task performance suffers from more
debiasing.4 This calls for constrained debiasing for
such datasets. In Section 7, we show that FaRM is
able to retain target performance while debiasing
for this dataset in the constrained setup.
6.3 Controlled Sentiment Classification
Lastly, for the DIAL dataset, we perform un-
constrained debiasing in a controlled setting.
Setup. Following the setup of Barrett et al.
(2019) and Ravfogel et al. (2020), we control the
proportion of protected attributes within a target
task class. For example, if target class split = 80%
that means ‘‘happy’’ sentiment (target) class con-
tains 80% AAE / 20% SAE, while the ‘‘sad’’ class
contains 20% AAE / 80% SAE (AAE and SAE are
protected class labels mentioned in Section 5.1).
We train DeepMoji (Felbo et al., 2017) followed
by a 1-layer MLP for sentiment classification.
We retrieve representations from the DeepMoji
encoder and debias them using FaRM. For debi-
asing, we choose the feature map φ(x) to be a
3Majority baseline for profession classification ≈29%.
4In our experiments, we found profession accuracy to be
high with a shallow feature map or training for earlier epochs,
but the gender leakage was significant in these scenarios.
Metric
Method
Split
Sentiment
Acc.
(↑)
Race
Acc. (↓)
DP (↓)
GapRMS
g
(↓)
50% 60% 70% 80%
Original 75.5
75.1
INLP
FaRM 74.8
Original 87.7
INLP
69.5
FaRM 54.2
Original
INLP
FaRM
Original
INLP
FaRM
0.26
0.16
0.09
0.15
0.12
0.09
75.5
73.1
73.2
87.8
82.2
69.9
0.44
0.33
0.10
0.24
0.18
0.10
74.4
69.2
67.3
87.3
80.3
69.0
0.63
0.30
0.17
0.33
0.16
0.12
71.9
64.5
63.5
87.4
69.9
52.1
0.81
0.28
0.22
0.41
0.16
0.14
the DeepMoji
Table 3: Evaluation results of unconstrained de-
biasing on the DIAL dataset. We report the per-
formance of
INLP
(Ravfogel et al., 2020), and FaRM representations.
We observe that FaRM achieves the best fair-
ness scores in all setups, while maintaining similar
performance on sentiment classification task.
(Original),
7-layer neural network with ReLU non-linearity.
After debiasing, we train a non-linear MLP to
investigate the quality of debiasing. We evaluate
the debiasing performance of FaRM in various
stages of label imbalance.
g
Results. The results of this experiment are re-
ported in Table 3. We see that FaRM is able to
achieve the best fairness scores—an improvement
(≥12.5%) and DP (≥21%) across all
in GapRMS
setups. Considering the accuracy of identifying
the protected attribute (race) we can see that
FaRM significantly reduces leakage of race in-
formation by an absolute margin of 11%–17%
across different target class splits. FaRM also
achieves similar performance to INLP in senti-
ment (target attribute) classification. We observe
that the fairness score for FaRM deteriorates with
an increasing correlation between the protected
attribute and the target attribute. In cases where
the target and the protected attributes are highly
correlated (split = 70% and 80%), we observe
a low sentiment classification accuracy (for both
INLP and FaRM) compared to the original clas-
sifier. This is similar to the observation made
for the Biographies dataset and shows that it is
difficult to debias information about protected at-
tribute while retaining overall information about
1166
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
5
1
2
2
0
5
4
6
9
7
/
/
t
l
a
c
_
a
_
0
0
5
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
DIAL
Method
Sentiment (y)
Race (g)
Fairness
Mention (y)
Race (g)
Fairness
F1↑ MDL↓ ΔF1↓ MDL↑ DP↓ GapRMS
g
↓ F1↑ MDL↓ ΔF1↓ MDL↑ DP↓ GapRMS
g
↓
BERTbase (pre-trained) 63.9
76.9
BERTbase (fine-tuned)
72.9
AdS
73.2
FaRM
300.7
99.0
56.9
17.9
10.9
18.4
5.2
0.2
242.6
176.2
290.6
296.5
0.41
0.30
0.43
0.26
0.20
0.14
0.21
0.14
66.1
81.7
81.1
78.8
290.1
49.1
7.6
3.1
24.6
28.7
21.7
0.3
258.8
199.2
270.3
324.8
0.20
0.06
0.06
0.06
0.10
0.03
0.03
0.03
PAN16
Method
Mention (y)
Gender (g)
Fairness
Mention (y)
Age (g)
Fairness
F1↑ MDL↓ ΔF1↓ MDL↑ DP↓ GapRMS
g
↓ F1↑ MDL↓ ΔF1↓ MDL↑ DP↓ GapRMS
g
↓
BERTbase (pre-trained) 72.3
89.7
BERTbase (fine-tuned)
89.7
AdS
88.7
FaRM
259.7
4.0
7.6
1.7
7.4
15.1
4.9
0.0
300.5
267.6
313.9
312.4
0.11
0.04
0.04
0.04
0.056
0.007
0.007
0.007
72.8
89.3
89.2
88.6
262.6
4.8
6.0
0.8
6.1
7.4
1.1
0.0
302.0
295.4
315.1
312.6
0.14
0.04
0.04
0.03
0.078
0.006
0.004
0.008
Method
BIOGRAPHIES
Profession (y)
Gender (g)
Fairness
F1↑ MDL↓ ΔF1↓ MDL↑ DP↓ GapRMS
g
↓
BERTbase (pre-trained) 74.3
99.9
BERTbase (fine-tuned)
99.9
AdS
99.9
FaRM
499.9
2.2
3.3
7.6
45.2
8.3
3.1
7.4
27.6
448.9
449.5
460.3
0.43
0.46
0.45
0.42
0.169
0.001
0.003
0.002
Table 4: Evaluation results for constrained debiasing on DIAL, PAN16, and Biographies. For DIAL and PAN16,
we evaluate the approaches for two different configurations of target and proteccted variables, and report the
performances in each setting. FaRM outperforms AdS (Basu Roy Chowdhury et al., 2021) in DP metric in all
setups, while achieving comparable target task performance.
the target task when the protected attribute is
highly correlated with the target attribute. In the
constrained setup, we observe FaRM is able to
retain target performance (Section 7).
7 Results: Constrained Debiasing
In this section, we present the results of con-
strained debiasing using FaRM. For all exper-
iments, we use a BERTbase model as φ and a
2-layer neural network with ReLU non-linearity
as f (Figure 3).
7.1 Single Attribute Debiasing
In this setup, we focus on debiasing a single
protected attribute g while retaining information
about the target attribute y.
Setup. We conduct experiments on 3 datasets:
DIAL (Blodgett et al., 2016), PAN16 (Rangel et al.,
2016), and Biographies (De-Arteaga et al., 2019).
target and pro-
We experiment with different
tected attribute configurations in DIAL (y: Sen-
timent/Mention, g: Race) and PAN16 (y: Mention,
g: Gender/Age). For Biographies, we use the
same setup as described in Section 6.2. For the
protected attribute g, we report ΔF1—the differ-
ence between F1-score and the majority baseline.
We also report fairness metrics: GapRMS
and De-
mographic Parity (DP) of the learned classifier.
We compare FaRM with the state-of-the-art AdS
(Basu Roy Chowdhury et al., 2021), BERTbase
sequence classifier, and pre-trained BERTbase
representations.
g
In particular,
Results. Table 4 presents the results of this
experiment. We observe that in general, FaRM
achieves good fairness performance while main-
it
taining target performance.
achieves the best DP scores across all setups. In
PAN16, FaRM achieves perfect fairness in terms
of protected attribute probing accuracy ΔF1 = 0
with comparable performance to AdS in terms
of MDL of g. In the Biographies dataset, the
task accuracy of FaRM is the same as AdS but
FaRM outperforms AdS in fairness metrics. We
also observe that for this dataset, some baselines
performed very well on one (but not both) of the
1167
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
5
1
2
2
0
5
4
6
9
7
/
/
t
l
a
c
_
a
_
0
0
5
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
PAN16
SETUP
Fairness (g1)
Age (g1)
Mention (y)
F1↑ MDL↓ ΔF1↓ MDL↑ DP↓ GapRMS
g
Gender (g2)
Fairness (g2)
↓ ΔF1↓ MDL↑ DP↓ GapRMS
g
Inter. Groups (g1, g2)
↓ ΔF1↓
MDL↑
BERTbase (fine-tuned) 88.6
88.6
ADS
FaRM (N -partition)
87.0
FaRM (1-partition)
86.4
6.8
5.5
13.4
15.6
14.9
2.2
0.0
0.0
196.4
231.5
234.3
234.6
0.06
0.05
0.03
0.05
0.009
0.006
0.003
0.006
16.5
1.6
0.0
0.0
192.0
230.9
234.2
234.2
0.04
0.04
0.06
0.02
0.014
0.017
0.025
0.009
20.7
9.1
0.7
0.0
117.2
118.5
468.0
467.7
Table 5: Evaluation results for debiasing multiple protected attributes using FaRM. Both configura-
tions of FaRM outperform AdS (Basu Roy Chowdhury et al., 2021) in guarding protected attribute
and intersectional group biases.
two fairness metrics, which can be attributed to the
inherent tradeoff between them (see Section 5.4).
However, FaRM achieves a good balance between
the two metrics. Overall, this shows that FaRM
is able to robustly remove sensitive information
about the protected attribute while achieving good
target task performance.
7.2 Multiple Attribute Debiasing
In this setup, we focus on debiasing multiple pro-
tected attributes gi simultaneously, while retaining
information about target attribute y. We evaluate
FaRM on the PAN16 dataset with y as Men-
tion, g1 as Gender, and g2 as Age. Subramanian
et al. (2021) showed that debiasing a categor-
ical attribute can still reveal information about
intersectional groups (e.g., if age (young/old) and
gender (male/female) are two categorical pro-
tected attributes, then (age = old, gender = male)
is an intersectional group). We report the ΔF1/
MDL scores for probing intersectional groups.
Approach. We present two variations of FaRM
to remove multiple attributes simultaneously in a
constrained setup. Assuming there are N protected
attributes, the variations are discussed below:
(a) N -partition: In this variation, we compute
a membership matrix Πgi
for each protected
attribute gi. We modify Equation 4 as follows:
stance, we can represent the ith protected attribute
as a one-hot vector gi ∈ R|gi| (where |gi| is
the dimension of protected attribute gi). Then
the combined vector G ∈ R(|g1|+…+|gN |) can be
obtained by concatenating individual vectors gi.
Since G is a concatenation of multiple vectors,
we normalize G such that all of its elements
sum to 1. Therefore each element of G is either
N . We use G to construct the partition
0 or
function ΠG, which captures information about
N attributes simultaneously. Each component of
ΠG satisfies:
}.
The resultant objective function takes the same
form as in Equation 4 with the modified parition
function Jc(Z, Y, ΠG).
j = In×n and πij ∈ {0, 1
N
j=1 ΠG
(cid:4)
N
1
Results. We present the results of debiasing
multiple attributes in Table 5. We observe that
FaRM improves upon AdS’ ΔF1-score of age and
gender, with N -partition and 1-partition setups
performing equally well. The performance on the
target task is comparable with AdS, although there
is a slight rise in MDL. It is important to note that
even though AdS performs decently well in pre-
venting leakage about g1 and g2, it still leaks a
significant amount of information about the in-
tersectional groups. In both of its configurations,
FaRM is able to prevent leakage of intersectional
biases while considering the protected attributes
independently. This shows that robustly remov-
ing information about multiple attributes helps
in preventing leakage about intersectional groups
as well.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
5
1
2
2
0
5
4
6
9
7
/
/
t
l
a
c
_
a
_
0
0
5
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Jc(Z, y,Πg1, . . . , ΠgN ) = −CE(ˆy, y)
(cid:6)
N(cid:5)
R(Z, (cid:3)|Πgi) − R(Z, (cid:3))
+ λ
i=1
(cid:7)
8 Model Analysis
(b) 1-partition: Unlike the previous setup, we
can consider each protected attribute gi as an
independent variable and combine them to form
a single protected attribute G. For each input in-
In this section, we present several analysis
experiments to evaluate the functioning of FaRM.
Robustness to Label Corruption. We eval-
uate the robustness of FaRM by randomly
1168
Method SimLex-999 WordSim-353 MTurk-771
GloVe
FaRM
0.374
0.242
0.695
0.503
0.684
0.456
Table 6: Word similarity scores before and after
debiasing GloVe embeddings using FaRM.
large, showcasing that the model does not con-
verge on the target task. This is expected as the
regularization term (Equation 4) is much larger
than CE(ˆy, y) term, and boosting it further with
λ = 10 makes it difficult for the target task
loss to converge. Similarly, when λ ≤ 10−5, the
regularization term is much smaller compared to
CE(ˆy, y), and there is a substantial drop in MDL
for g. However, we show that FaRM achieves
good performance over a broad spectrum of λ.
Therefore, reproducing the desired results does
not require extensive hyperparameter tuning.
Probing Word Embeddings. A limitation of
using FaRM for debiasing word embeddings is that
distances in the original embedding space are not
preserved. The Mazur–Ulam theorem (Fleming
and Jamison, 2003) states that isometry for a
mapping φ : V → W is preserved only if the
function φ is affine. FaRM uses a non-linear
feature map φ(x). Therefore, distances cannot be
preserved. A linear map φ(x) is also not ideal
because it does not guard protected attributes
against an attack by a non-linear probing network.
We investigate the utility of debiased embeddings
by performing the following experiments:
(a) Word Similarity Evaluation: In this experi-
ment, we evaluate the debiased embeddings on
the following datasets: SimLex-999 (Hill et al.,
2015), WordSim-353 (Agirre et al., 2009), and
MTurk-771 (Halawi et al., 2012). In Table 6, we
report the Spearman correlation between the gold
similarity scores of word pairs and the cosine sim-
ilarity scores obtained before (top row) and after
(bottom row) debiasing GloVe embeddings. We
observe a significant drop in correlation with gold
scores, which is expected since debiasing is re-
moving some information from the embeddings.
In spite of the drop, there is a reasonable corre-
lation with the gold scores indicating that FaRM
is able to retain a significant degree of semantic
information.
(b) Part-of-speech Tagging: We evaluate debi-
ased embeddings for detecting POS tags in a
Figure 5: Performance of FaRM with varying fraction
of corrupted training set labels in (a) unconstrained and
(b) constrained debiasing setups.
Figure 6: MDL of target (y) and protected (g) attributes
with different λ for DIAL and PAN16 datasets.
sub-sampling instances from the dataset and mod-
ifying the protected attribute label. In Figure 5a,
we report the protected attribute leakage (ΔF1
score) from the debiased word embeddings with
varying fractions of training set label corruption.
We observe that FaRM’s performance degrades
with an increase in label corruption. This is ex-
pected as, at high corruption ratios, most of the
protected attribute labels are wrong, resulting in
poor performance.
In the constrained setup (Figure 5b), we observe
that FaRM is able to debias protected attribute in-
formation (y-axis scale in Figure 5b and 5a are
different) even at high corruption ratios. We be-
lieve this enhanced performance (compared to
unconstrained setup) is due to the additional su-
pervision in the form of target loss, which enables
FaRM to learn robust representations even with
corrupted protected attribute labels.
Sensitivity to λ. We measure the sensitivity
of FaRM’s performance w.r.t. λ (Equation 4) in
the constrained setup. In Figure 6, we show the
MDL of the target attribute y (in blue) and pro-
tected attribute g (in red) for DIAL and PAN16
for different λ. We observe that when 10−4 ≤
λ ≤ 1,
the performance of FaRM does not
change much. For λ = 10, MDL for y is quite
1169
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
5
1
2
2
0
5
4
6
9
7
/
/
t
l
a
c
_
a
_
0
0
5
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Limitations. A limitation of FaRM is that we
lack a principled feature map φ(x) selection ap-
proach. In the unconstrained setup, we relied on
empirical observations and found that a 4-layer
ReLU network sufficed for GloVe and Biogra-
phies, while a 7-layer network was required for
DIAL. For the constrained setup, BERTbase proved
to be expressive enough to perform debiasing
in all setups. Future works can explore white-
box network architectures (Chan et al., 2022)
for debiasing.
9 Conclusion
We proposed Fairness-aware Rate Maximization
(FaRM), a novel debiasing technique based on the
principle of rate-distortion maximization. FaRM
is effective in removing protected information
from representations in both unconstrained and
constrained debiasing setups. Empirical evalua-
tions show that FaRM outperforms prior works
in debiasing representations by a large margin
on several datasets. Extensive analysis showcase
that FaRM is sample efficient, and robust to label
corruptions and minor hyperparameter changes.
Future works can focus on leveraging FaRM for
achieving fairness in complex tasks like language
generation.
10 Ethical Considerations
In this work, we present FaRM—a robust rep-
resentation learning framework to selectively
remove protected information. FaRM is developed
with an intent to enable development of fair learn-
ing systems. However, FaRM can be misused to
remove salient features from representations and
perform classification by leveraging demographic
information. Debiasing using FaRM is only eval-
uated on datasets with binary protected attribute
variables. This may not be ideal while removing
protected information about gender, which can ex-
tend beyond binary categories. Currently, we lack
datasets with fine-grained gender annotation. It is
important to collect data and develop techniques,
that would benefit everyone in our community.
References
Eneko Agirre, Enrique Alfonseca, Keith Hall, Jana
Kravalova, Marius Pas¸ca, and Aitor Soroa.
2009. A study on similarity and relatedness
Figure 7: Loss evolution in the unconstained setup (left)
where both terms – R(Z, (cid:3)) (red) and Rc(Z, (cid:3)|Πg)
(black) start increasing simultaneously. In the con-
strained setup (right) with λ = 0.01 – bias loss (black)
starts converging earlier than the target loss (red).
sentence using the Universal tagset (Petrov et al.,
2012). GloVe embeddings achieve an F1-score
of 95.2% and FaRM achieves an F1-score of
93.0% on this task. This shows FaRM’s debiased
embeddings still possess a significant amount of
morphological information about the language.
(c) Sentiment Classification: We perform senti-
ment classification using word embeddings on
the IMDb movies dataset (Maas et al., 2011).
GloVe embeddings achieve an accuracy of 80.9%,
while debiased embeddings achieve an accu-
racy of 74.6%. The drop in this task is slightly
more compared to POS tagging, but FaRM is
still able to achieve reasonable performance on
this task.
These experiments showcase that even though
exact distances aren’t preserved using FaRM,
the debiased embeddings still retain relevant
information useful in downstream tasks.
Evolution of Loss Components. We evalu-
ate how FaRM’s loss components evolve during
training. In the unconstrained setup for GloVe
debiasing, we evaluate how the evolution of
components—R(Z, (cid:3)) (in red) and Rc(Z, (cid:3)|Πg)
(in black). In Figure 7a, we observe that both
loss terms start increasing simultaneously, with
their difference remaining constant in the final
iterations. Next
the
evolution of target loss CE(ˆy, y) and bias loss
R(Z, (cid:3)) − Rc(Z, (cid:3)|Πg) for DIAL dataset are shown
in Figure 7b. We observe that the bias term con-
verges first followed by the target loss. This is
expected as the magnitude of rate-distortion loss
is larger than target loss, which forces the model
to minimize it first.
in the constrained setup,
1170
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
5
1
2
2
0
5
4
6
9
7
/
/
t
l
a
c
_
a
_
0
0
5
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
using distributional and WordNet-based ap-
proaches. In Proceedings of Human Language
Technologies: The 2009 Annual Conference of
the North American Chapter of the Association
for Computational Linguistics, pages 19–27,
Boulder, Colorado. Association for Computa-
tional Linguistics. https://doi.org/10
.3115/1620754.1620758
Jimmy Lei Ba, Jamie Ryan Kiros, and Geoffrey
E. Hinton. 2016. Layer normalization. arXiv
preprint arXiv:1607.06450
Maria Barrett, Yova Kementchedjhieva, Yanai
Elazar, Desmond Elliott, and Anders Søgaard.
2019. Adversarial removal of demographic at-
tributes revisited. In Proceedings of the 2019
Conference on Empirical Methods in Natural
Language Processing and the 9th International
Joint Conference on Natural Language Pro-
cessing (EMNLP-IJCNLP), pages 6330–6335,
Hong Kong, China. Association for Computa-
tional Linguistics. https://doi.org/10
.18653/v1/D19-1662
In Proceed-
of African-American English.
the 2016 Conference on Empirical
ings of
Methods in Natural Language Processing,
pages 1119–1130, Austin, Texas. Associa-
tion for Computational Linguistics. https://
doi.org/10.18653/v1/D16-1120
Tolga Bolukbasi, Kai-Wei Chang, James Y.
Zou, Venkatesh Saligrama, and Adam Tauman
Kalai. 2016. Man is to computer programmer
as woman is to homemaker? debiasing word
embeddings. In Advances in Neural Informa-
tion Processing Systems 29: Annual Conference
Information Processing Systems
on Neural
2016, December 5–10, 2016, Barcelona, Spain,
pages 4349–4357.
John D. Burger, John Henderson, George Kim,
and Guido Zarrella. 2011. Discriminating gen-
der on Twitter. In Proceedings of the 2011
Conference on Empirical Methods in Natu-
ral Language Processing, pages 1301–1309.
Edinburgh, Scotland, UK. Association for
Computational Linguistics.
Kanadpriya Basu, Treena Basu, Ron Buckmire,
and Nishu Lal. 2019. Predictive models of
student college commitment decisions using
machine learning. Data, 4(2):65. https://
doi.org/10.3390/data4020065
Kwan Ho Ryan Chan, Yaodong Yu, Chong You,
Haozhi Qi, John Wright, and Yi Ma. 2022.
Redunet: A white-box deep network from the
principle of maximizing rate reduction. Journal
of Machine Learning Research, 23(114):1–103.
In Proceedings of
Somnath Basu Roy Chowdhury, Sayan Ghosh,
Yiyuan Li, Junier Oliva, Shashank Srivastava,
and Snigdha Chaturvedi. 2021. Adversarial
scrubbing of demographic information for text
the 2021
classification.
Conference on Empirical Methods in Nat-
ural Language Processing, pages 550–562,
Online and Punta Cana, Dominican Repub-
lic. Association for Computational Linguis-
tics. https://doi.org/10.18653/v1
/2021.emnlp-main.43
Peter J. Bickel, Eugene A. Hammel, and J. William
O’Connell. 1975. Sex bias in graduate admis-
sions: Data from berkeley: Measuring bias is
harder than is usually assumed, and the evidence
is sometimes contrary to expectation. Science,
187(4175):398–404. https://doi.org/10
.1126/science.187.4175.398, PubMed:
17835295
Su Lin Blodgett, Lisa Green, and Brendan
O’Connor. 2016. Demographic dialectal vari-
study
ation
social media: A case
in
Thomas M. Cover. 1999. Elements of Informa-
tion Theory. John Wiley & Sons.
Maria De-Arteaga, Alexey Romanov, Hanna
Wallach, Jennifer Chayes, Christian Borgs,
Alexandra Chouldechova,
Sahin Geyik,
Krishnaram Kenthapadi, and Adam Tauman
Kalai. 2019. Bias in bios: A case study of
semantic representation bias in a high-stakes
setting. In proceedings of the Conference on
Fairness, Accountability, and Transparency,
120–128. https://doi.org/10
pages
.1145/3287560.3287572
Sunipa Dev, Tao Li, Jeff M. Phillips, and
Vivek Srikumar. 2021. OSCaR: Orthogo-
nal subspace correction and rectification of
In Proceed-
biases
in word embeddings.
the 2021 Conference on Empirical
ings of
Methods in Natural Language Processing,
pages 5034–5050, Online and Punta Cana,
Dominican Republic. Association for Compu-
tational Linguistics. https://doi.org/10
.18653/v1/2021.emnlp-main.411
1171
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
5
1
2
2
0
5
4
6
9
7
/
/
t
l
a
c
_
a
_
0
0
5
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Jacob Devlin, Ming-Wei Chang, Kenton Lee, and
Kristina Toutanova. 2019. BERT: Pre-training
of deep bidirectional transformers for language
understanding. In Proceedings of
the 2019
Conference of the North American Chapter
of the Association for Computational Linguis-
tics: Human Language Technologies, Volume
1 (Long and Short Papers), pages 4171–4186,
Minneapolis, Minnesota. Association for Com-
putational Linguistics.
Yanai Elazar and Yoav Goldberg. 2018. Ad-
versarial removal of demographic attributes
from text data. In Proceedings of the 2018
Conference on Empirical Methods in Nat-
ural Language Processing, pages 11–21,
Brussels, Belgium. Association for Computa-
tional Linguistics. https://doi.org/10
.18653/v1/D18-1002
Yanai Elazar, Shauli Ravfogel, Alon Jacovi,
and Yoav Goldberg. 2021. Amnesic probing:
Behavioral explanation with amnesic coun-
terfactuals. Transactions of
the Association
for Computational Linguistics, 9:160–175.
https://doi.org/10.1162/tacl a 00359
Bjarke Felbo, Alan Mislove, Anders Søgaard, Iyad
Rahwan, and Sune Lehmann. 2017. Using mil-
lions of emoji occurrences to learn any-domain
representations for detecting sentiment, emo-
tion and sarcasm. In Proceedings of the 2017
Conference on Empirical Methods in Natu-
ral Language Processing, pages 1615–1625,
Copenhagen, Denmark. Association for Com-
putational Linguistics. https://doi.org
/10.18653/v1/D17-1169
Richard J. Fleming and James E. Jamison. 2003.
Function Spaces. Chapman & Hall/CRC.
Omar Ghailan, Hoda MO Mokhtar, and Osman
Hegazy. 2016. Improving credit scorecard mod-
eling through applying text analysis. Institu-
tions, 7(4). https://doi.org/10.14569
/IJACSA.2016.070467
Ian Goodfellow, Jean Pouget-Abadie, Mehdi
Mirza, Bing Xu, David Warde-Farley, Sherjil
Ozair, Aaron Courville, and Yoshua Bengio.
2014. Generative adversarial nets. In Advances
in Neural Information Processing Systems,
volume 27. Curran Associates, Inc.
Guy Halawi, Gideon Dror, Evgeniy Gabrilovich,
and Yehuda Koren. 2012. Large-scale learning
of word relatedness with constraints. In The
18th ACM SIGKDD International Conference
on Knowledge Discovery and Data Mining,
KDD ’12, Beijing, China, August 12–16, 2012,
pages 1406–1414. ACM. https://doi
.org/10.1145/2339530.2339751
Felix Hill, Roi Reichart, and Anna Korhonen.
2015. SimLex-999: Evaluating semantic mod-
similarity estimation.
els with (genuine)
Computational Linguistics,
41(4):665–695.
https://doi.org/10.1162/COLI a 00237
Armand Joulin, Edouard Grave, Piotr Bojanowski,
and Tomas Mikolov. 2017. Bag of tricks for
efficient text classification. In Proceedings of
the 15th Conference of the European Chapter
of the Association for Computational Linguis-
tics: Volume 2, Short Papers, pages 427–431,
Valencia, Spain. Association for Computa-
tional Linguistics. https://doi.org/10
.18653/v1/E17-2068
Moshe Koppel, Shlomo Argamon, and Anat
Rachel Shimoni. 2002. Automatically catego-
rizing written texts by author gender. Liter-
ary and Linguistic Computing, 17(4):401–412.
https://doi.org/10.1093/llc/17.4.401
Yitong Li, Timothy Baldwin, and Trevor Cohn.
2018. Towards robust and privacy-preserving
text representations. In Proceedings of
the
56th Annual Meeting of the Association for
Computational Linguistics (Volume 2: Short
Papers), pages 25–30, Melbourne, Australia.
Association for Computational Linguistics.
Ilya Loshchilov and Frank Hutter. 2019. De-
coupled weight decay regularization. In 7th
International Conference on Learning Repre-
sentations, ICLR 2019, New Orleans, LA, USA,
May 6–9, 2019. OpenReview.net.
Yi Ma, Harm Derksen, Wei Hong, and John
Wright. 2007. Segmentation of multivariate
mixed data via lossy data coding and compres-
sion. IEEE Transactions on Pattern Analysis
and Machine Intelligence, 29(9):1546–1562.
https://doi.org/10.1109/TPAMI.2007
.1085, PubMed: 17627043
Andrew L. Maas, Raymond E. Daly, Peter T.
Pham, Dan Huang, Andrew Y. Ng, and
Christopher Potts. 2011. Learning word vec-
tors for sentiment analysis. In Proceedings of
1172
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
5
1
2
2
0
5
4
6
9
7
/
/
t
l
a
c
_
a
_
0
0
5
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
the 49th Annual Meeting of the Association
for Computational Linguistics: Human Lan-
guage Technologies, pages 142–150, Portland,
Oregon, USA. Association for Computational
Linguistics.
Laurens Van der Maaten and Geoffrey Hinton.
2008. Visualizing data using t-sne. Journal of
Machine Learning Research, 9(11).
Jan Macdonald, Stephan W¨aldchen, Sascha
Hauch, and Gitta Kutyniok. 2019. A rate-
distortion framework for explaining neu-
preprint,
ral
abs/1905.11092.
decisions. ArXiv
network
Ninareh Mehrabi, Fred Morstatter, Nripsuta
Saxena, Kristina Lerman, and Aram Galstyan.
2021. A survey on bias and fairness in ma-
chine learning. ACM Computing Surveys, 54(6).
https://doi.org/10.1145/3457607
Dong Nguyen, Rilana Gravel, Dolf Trieschnigg,
and Theo Meder. 2013. ‘‘How old do you
think i am?’’ A study of language and age
in Twitter. In Proceedings of the International
AAAI Conference on Web and Social Media,
volume 7.
Fabian Pedregosa, Ga¨el Varoquaux, Alexandre
Gramfort, Vincent Michel, Bertrand Thirion,
Olivier Grisel, Mathieu Blondel,
Peter
Prettenhofer, Ron Weiss, Vincent Dubourg,
and Jake Vanderplas, Alexandre Passos, David
Cournapeau, Matthieu Brucher, Matthieu
Perrot, and ´Edouard Duchesnay. 2011. Scikit-
learn: Machine learning in Python. Journal of
Machine Learning Research, 12:2825–2830.
Slav Petrov, Dipanjan Das, and Ryan McDonald.
2012. A universal part-of-speech tagset. In
Proceedings of the Eighth International Con-
ference on Language Resources and Evalu-
ation (LREC’12), pages 2089–2096, Istanbul,
Turkey. European Language Resources Asso-
ciation (ELRA).
Francisco Rangel, Paolo Rosso, Ben Verhoeven,
Walter Daelemans, Martin Potthast, and Benno
the 4th author
Stein. 2016. Overview of
profiling task at pan 2016: Cross-genre eval-
uations. Working Notes Papers of the CLEF,
2016:750–784.
Shauli Ravfogel, Yanai Elazar, Hila Gonen,
Michael Twiton, and Yoav Goldberg. 2020.
Null it out: Guarding protected attributes by it-
erative nullspace projection. In Proceedings of
the 58th Annual Meeting of the Association for
Computational Linguistics, pages 7237–7256,
Online. Association for Computational Linguis-
tics. https://doi.org/10.18653/v1
/2020.acl-main.647
Alexey Romanov, Maria De-Arteaga, Hanna
Wallach, Jennifer Chayes, Christian Borgs,
Alexandra Chouldechova,
Sahin Geyik,
Krishnaram Kenthapadi, Anna Rumshisky, and
Adam Kalai. 2019. What’s in a name? Reduc-
ing bias in bios without access to protected
attributes. In Proceedings of the 2019 Con-
ference of
the North American Chapter of
the Association for Computational Linguis-
tics: Human Language Technologies, Volume
1 (Long and Short Papers), pages 4187–4195,
Minneapolis, Minnesota. Association for Com-
putational Linguistics. https://doi.org
/10.18653/v1/N19-1424
Andrew Rosenberg and Julia Hirschberg. 2007.
V-measure: A conditional entropy-based exter-
nal cluster evaluation measure. In Proceedings
of
the 2007 Joint Conference on Empiri-
cal Methods in Natural Language Processing
and Computational Natural Language Learn-
ing (EMNLP-CoNLL), pages 410–420, Prague,
Czech Republic. Association for Computational
Linguistics.
Shivashankar
Subramanian, Xudong Han,
Timothy Baldwin, Trevor Cohn, and Lea
Frermann. 2021. Evaluating debiasing tech-
niques for intersectional biases. In Proceed-
ings of
the 2021 Conference on Empirical
Methods in Natural Language Processing,
pages 2492–2498, Online and Punta Cana,
Dominican Republic. Association for Compu-
tational Linguistics. https://doi.org/10
.18653/v1/2021.emnlp-main.193
Ben Verhoeven and Walter Daelemans. 2014.
CLiPS stylometry investigation (CSI) corpus:
A Dutch corpus for the detection of age, gen-
der, personality, sentiment and deception in
text. In Proceedings of the Ninth International
Conference on Language Resources and Evalu-
ation (LREC’14), pages 3081–3085, Reykjavik,
Iceland. European Language Resources Asso-
ciation (ELRA).
1173
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
5
1
2
2
0
5
4
6
9
7
/
/
t
l
a
c
_
a
_
0
0
5
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Ben Verhoeven, Walter Daelemans, and Barbara
Plank. 2016. TwiSty: A multilingual Twitter
stylometry corpus for gender and personality
profiling. In Proceedings of the Tenth Interna-
tional Conference on Language Resources and
Evaluation (LREC’16), pages 1632–1637, Por-
toroˇz, Slovenia. European Language Resources
Association (ELRA).
Elena
and
Ivan
Voita
Titov.
In Proceedings of
2020.
Information-theoretic probing with minimum
the
description length.
2020 Conference on Empirical Methods
in Natural Language Processing (EMNLP),
pages 183–196, Online. Association for Com-
putational Linguistics. https://doi.org
/10.18653/v1/2020.emnlp-main.14
Edson R. D. Weren, Anderson U. Kauer, Lucas
Mizusaki, Viviane P. Moreira, J. Palazzo, M.
de Oliveira, and Leandro K. Wives. 2014. Ex-
amining multiple features for author profiling.
Journal of Information and Data Management,
5(3):266–266.
Qizhe Xie, Zihang Dai, Yulun Du, Eduard H.
Hovy, and Graham Neubig. 2017. Control-
lable invariance through adversarial feature
learning. In Advances in Neural Information
Processing Systems 30: Annual Conference on
Neural Information Processing Systems 2017,
December 4–9, 2017, Long Beach, CA, USA,
pages 585–596.
Yaodong Yu, Kwan Ho Ryan Chan, Chong You,
Chaobing Song, and Yi Ma. 2020. Learning
diverse and discriminative representations via
the principle of maximal coding rate reduction.
In Advances in Neural Information Processing
Systems, volume 33, pages 9422–9434. Curran
Associates, Inc.
Richard S. Zemel, Yu Wu, Kevin Swersky,
Toniann Pitassi, and Cynthia Dwork. 2013.
Learning fair representations. In Proceedings of
the 30th International Conference on Machine
Learning, ICML 2013, Atlanta, GA, USA, 16–21
June 2013, volume 28 of JMLR Workshop
and Conference Proceedings, pages 325–333.
JMLR.org.
Brian Hu Zhang, Blake Lemoine, and Margaret
Mitchell. 2018. Mitigating unwanted biases
with adversarial learning. In Proceedings of
the 2018 AAAI/ACM Conference on AI, Ethics,
and Society, pages 335–340. https://doi
.org/10.1145/3278721.3278779
Han Zhao and Geoffrey J. Gordon. 2019. Inher-
ent tradeoffs in learning fair representations.
In Advances in Neural Information Processing
Systems 32: Annual Conference on Neural In-
formation Processing Systems 2019, NeurIPS
2019, December 8–14, 2019, Vancouver, BC,
Canada, pages 15649–15659.
Jieyu Zhao, Yichao Zhou, Zeyu Li, Wei Wang, and
Kai-Wei Chang. 2018. Learning gender-neutral
word embeddings. In Proceedings of the 2018
Conference on Empirical Methods in Natu-
ral Language Processing, pages 4847–4853,
Brussels, Belgium. Association for Computa-
tional Linguistics. https://doi.org/10
.18653/v1/D18-1521
1174
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
5
1
2
2
0
5
4
6
9
7
/
/
t
l
a
c
_
a
_
0
0
5
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3