Israel Neuman
University of Iowa
Department of Computer Science
14 MacLean Hall
Iowa City, Iowa 52242-1419, USA
isneuman@gmail.com
Generative Tools for
Interactive Composition:
Real-Time Musical
Structures Based on
Schaeffer’s TARTYP and on
Klumpenhouwer Networks
Abstract: Interactive computer music is comparable to improvisation because it includes elements of real-time
composition performed by the computer. This process of real-time composition often incorporates stochastic
techniques that remap a predetermined fundamental structure to a surface of sound processing. The hierarchical
structure is used to pose restrictions on the stochastic processes, but, in most cases, the hierarchical structure in
itself is not created in real time. This article describes how existing musical analysis methods can be converted
into generative compositional tools that allow composers to generate musical structures in real time. It proposes
a compositional method based on generative grammars derived from Pierre Schaeffer’s TARTYP, and describes the
development of a compositional tool for real-time generation of Klumpenhouwer networks. The approach is based
on the intersection of musical ideas with fundamental concepts in computer science including generative grammars,
predicate logic, concepts of structural representation, and various methods of categorization.
Music is a time-based sequence of audible events
that emerge from an underlying structure. Such
a fundamental structure is more often than not
multi-layered and hierarchical in nature. Although
hierarchical structures are commonly conceptu-
alized as predetermined compositional elements,
analysis of jazz performances highlights their ex-
istence in improvised music, where performers
use their knowledge of the musical language and
performance practices to compose in real time. For
example, Steven Block has shown sophisticated
pitch organizations in free jazz compositions by
Ornette Coleman, John Coltrane, Cecil Taylor, and
Anthony Braxton. In the conclusion of his study,
Block (1990, p. 202) calls for greater analytical at-
tention to “the complexities of the musical fabric
in free jazz” and more innovative interpretation of
the “hybrid language of many free compositions.”
Jazz groups, such as the Art Ensemble of Chicago,
collectively create complex musical “fabrics” that
are unified by hierarchical structures. In many cases,
the only pre-composed elements in these compo-
sitions are a chord progression or a melody, and in
Computer Music Journal, 38:2, pp. 63–77, Summer 2014
doi:10.1162/COMJ a 00240
c(cid:2) 2014 Massachusetts Institute of Technology.
free improvisation the entire musical structure is
composed in real time.
Interactive computer music is comparable to
improvisation because it includes elements of real-
time composition performed by the computer. Arne
Eigenfeldt (2011, p. 13) maintains that “composers
of real-time computer music have most often
relied upon constrained random procedures to
make musical decisions.” Hence, the process of
real-time composition often incorporates stochastic
techniques that remap a predetermined fundamental
structure to a surface of sound processing. The
hierarchical structure is used to pose restrictions on
the stochastic processes and maintain the unity of
the piece. Yet, unlike in free jazz improvisation, the
hierarchical structure in itself is not created in real
time, but only fleshed out by stochastic means.
The eventual goal of my research is to develop
software that would allow composers to regener-
ate musical structures in real time in the same
manner as an improviser. In this article, I describe
how existing methods used in musical analysis can
be converted into generative compositional tools.
My approach is based on the intersection of musi-
cal ideas with fundamental concepts in computer
science, including generative grammars, predicate
logic, concepts of structural representation, and
Neuman
63
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
8
2
6
3
1
8
5
6
0
0
4
/
c
o
m
_
a
_
0
0
2
4
0
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
various methods of categorization. The relevancy of
such methods to music is rooted in their effective-
ness as language definers and structure generators.
Since these are fairly simple and commonly used
methods, they can also be readily embedded in inter-
active tools. Because of the central role occupied by
the Max language in interactive composition, I re-
strict my software development to tools that can be
embedded and used in Max/MSP and Pure Data (Pd).
The bulk of this article is a revision of a conference
paper (Neuman 2013) that proposed a compositional
method using an interactive compositional tool
based on generative grammars derived from Pierre
Schaeffer’s Tableau R ´ecapitulatif de la Typologie
(TARTYP, “Summary Table of Typology [of sound
objects],” cf. Schaeffer 1966). These grammars
enable the creation of new hierarchical musical
structures that are, in turn, derived from the hierar-
chical structure of Schaeffer’s table. These complex
structures are brought to life at the surface of the
composition in a versatile way, utilizing the spectral
signatures of sound objects from Schaeffer’s audio
examples.
The following background section presents the
motivation for creating a TARTYP-based interactive
compositional tool, as well as presenting related
work. The third section of this article presents the
reading of TARTYP that formed the foundation
for the generative grammars presented in the
fourth section. The following two sections describe
the design and implementation of the software.
In the seventh section, I describe my current
research, which is focused on the development of
a compositional tool for real-time generation of
Klumpenhouwer networks (Lewin 1990, 1994). In
the final section, I voice a call for the development
of an extensible tool that gives the composer the
freedom to incorporate a broader collection of
musical theories, classifications, languages, and
generative methods for interactive composition.
Background
In 1957, Noam Chomsky introduced phrase
structure (PS) grammars, a form of generation
systems denoted [
, F], where
is a set of initial
(cid:2)
(cid:2)
symbols and F is a set of rewrite rules. Such rewrite
rules have proven to be a suitable tool for musical
analysis and composition, where a phrase is often
expanded or contracted to define the different
hierarchical levels of musical structures. Hence,
if a set of rewrite rules defines and produces a
“legal” musical phrase it can also produce musical
structures that are more complex. Steven R.
Holtzman (1981) demonstrated the use of the
Generative Grammar Definition Language to
describe the micro-components of musical objects,
as well as complete sections of a composition. Fred
Lerdahl and Ray Jackendoff (1993) compare their use
of PS grammars for defining hierarchical structures
of temporal organization to the processes known in
Schenkerian theory as prolongation and reduction.
Both Chomsky’s theory and contemporary music
in general have strong ties to set theory. Chomsky
was interested in classes of derivations and sets
of rules that would generate the same terminal
language (Chomsky 1966; Lasnik, Depiante, and
Stepanov 2000). Yet PS grammars are effective
in describing musical language because they can
be used to create multiple legal variants of the
same sentence. Consider Chomsky’s example “the
man hit the ball” (Chomsky 1966). In the grammar
describing this sentence, the terminals are the words
(the, man, hit, the, ball): variants of this sentence can
be formed, e.g., by replacing nouns with placeholder
variables, yielding “the X hit the Y,” where X =
[man |woman |boy] and Y = [ball |table |wall]. By
replacing each terminal by typed variables denoting
classes of words, the same set of rewrite rules would
produce legal variants of the original sentence.
The recent focus on classification in musical
research corresponds to the introduction of musi-
cal set theory, where terms such as “pitch class”
and “interval class” are commonly used. Serialism
expands the use of classifications to compositional
elements other than pitch, such as rhythm, dy-
namics, articulation, orchestration, and timbre. A
well-formed classification method of compositional
material, however, is not always sufficient for defin-
ing ways for composing out this material. Pierre
Boulez’s system for multiplication of pitch-class
sets produces domains or collections of pitch-class
sets that are structurally tied to the twelve-tone
64
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
8
2
6
3
1
8
5
6
0
0
4
/
c
o
m
_
a
_
0
0
2
4
0
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
series from which they originate. Although it is
known that Boulez used this classification in Le
marteau sans maˆıtre (1955), the order by which the
collections are used in the composition is a matter
of some debate among researchers (Koblyakov 1990;
Heinemann 1998).
Schaeffer introduced TARTYP in 1966 as part
of his typology of sound objects (Schaeffer 1966).
The table is a classification of sound objects based
on their properties in the time and frequency
domains, and it introduces an alphanumeric no-
tation for sound objects. Its structure alludes to
inter-relationships between subcollections of sound
objects. Nevertheless, Schaeffer provides limited di-
rection for how to use the classification in a compo-
sitional process, focusing mainly on using the table’s
notation to construct sequences of symbols describ-
ing sounds that are more complex (Thoresen 2007).
Most studies of TARTYP offer a translation,
adaptation, or revision of this classification of sound
objects. Lasse Thoresen (2007), in his adaptation,
removes some of the elements defining the time-
domain axis of the table. Robert Normandeau (2010),
in his revision to the table, interprets its main pairs
of sound characteristics: mass-facture, duration-
variation, and balance-originality. John Dack (2001)
discusses the Excentric sound objects, a group
of sound objects that were defined by Schaeffer
as unsuitable for music, yet according to Dack
these objects are commonly used in electroacoustic
compositions. These studies, like many others (such
as the work described in this article) rely on Michel
Chion’s Guide to Sound Objects ([1983] 2009) for
a lexical collection of many terms in Schaefferian
theory, including the terms defining TARTYP.
The work of Bernard Bel (1992, 1998; Bel and
Kippen 1992) combines the Schaefferian approach to
sound objects and generative grammars in a creative
environment that he calls the Bol Processor. This
environment supports composition and improvisa-
tion, using a system of rewrite rules. The grammars
of the Bol Processor are derived from the metaphoric
language for drumming in Asia and Africa called
Qa’idas. The focus here is on the mapping of the
objects to a structural organization in physical time,
hence, the consideration is of the time domain
properties of sound objects (i.e., it does not take into
Figure 1. Pierre Schaeffer’s
TARTYP (after Chion
[1983] 2009). The time-
domain terms along the up-
per row of the table and the
frequency-domain terms
along the leftmost column
are highlighted in gray.
account classifications and defining features). The
output of the Bol Processor is a list of MIDI messages
or a CSound score. Although it has some real-time
capabilities, the Bol Processor relies on an external
sound processor to produce real-time output.
In contrast, the TARTYP-based compositional
tools presented in the following sections utilize
existing interactive real-time environments; as
extensions of the Java-based MaxObject class, these
tools are embedded in Max/MSP or Pd and directly
engage the sound-processing capabilities of these
environments. The grammars of these tools are
based on Schaeffer’s classification of sound objects
as presented in TARTYP and as interpreted by
Chion ([1983] 2009) and Normandeau (2010). These
grammars, as well as the compositional process
suggested in this article, take into account the
characteristics of sound objects in both the time and
frequency domain as presented in the TARTYP table
and demonstrated by Schaeffer’s sound examples
(Schaeffer 2012).
TARTYP Sound-Object Classification
Sound-object characteristics are specified in TAR-
TYP at the margins of the table, with time-
domain characteristics along the upper row and
the frequency-domain characteristics along the left-
most column (see Figure 1). The frequency-domain
Neuman
65
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
8
2
6
3
1
8
5
6
0
0
4
/
c
o
m
_
a
_
0
0
2
4
0
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 2. The division of
the body of TARTYP into
subcollections of
sound-object classes.
terms that correspond to rows in the table describe
the frequency content of sound objects by their
variability on a scale between fixed sound (mass)
and unpredictable noise. Hence, fixed mass can be
of definite pitch (harmonic sound) or of complex
pitch (with some inharmonicity and noise). In addi-
tion, the not very variable mass is a glissando-like
sound and the unpredictable variation of mass is
a non-periodic noise sound. Variation in this table
refers to internal variation in the frequency domain,
i.e., sounds such that their endings differ from their
beginnings (Chion [1983] 2009).
The seven terms that describe the time domain
characteristics correspond to columns in the table.
The central column is labeled impulse, referring
to a very short sound. To the right of this column
appear terms describing the characteristics or gain
envelopes of iterative sounds, including formed
iteration, (iterative) nonexistent facture, and (itera-
tive) unpredictable facture. To the left appear terms
describing the characteristics of held sounds includ-
ing formed sustain, (held) nonexistent facture, and
(held) unpredictable facture. The term facture refers
to the way a sound evolves over time (Normandeau
2010). Nonexistent factures are sounds that are too
redundant to exhibit change over time. Similarly,
unpredictable factures exhibit too much instabil-
ity to be “formed.” A formed sound is a sound
of medium duration with a “closed” facture, very
similar to a traditional musical note (Chion [1983]
2009).
Combinations of time-domain characteristics
(i.e., the table’s column headings) with frequency-
domain characteristics (i.e., the row headings) result
in the sound objects notated in the body of the
table. Hence, the combination of an impulse-type
envelope and a definite pitch points to the sound
object notated as N(cid:2). Similarly, sound object X(cid:2)(cid:2)
is defined by a formed-iteration type of envelope
and a complex pitch. This notation provides an
abstraction of the different types of sound objects.
Clearly, there are multiple sound objects that fit
the defining characteristics of N(cid:2) or X(cid:2)(cid:2): thus, in
Schaeffer’s sound examples, most of the nota-
tion symbols are demonstrated by more than one
sample (Schaeffer 2012). Each symbol therefore
represents a sound-object class, a collection of
S
E
L
P
M
A
S
(En)
Hn
(Ex)
Hx
D
L
E
H
_
H
R
(Ey)
E
Tn
Tx
T
N
X
Y
N’
X’
BALANCED
N”
Zn
(An)
X”
Zx
R
E
T
I
_
H
R
S
N
O
I
T
A
L
U
M
U
C
C
A
(Ax)
(Ay)
Y’
Y”
Zy
W
EXCENTRIC
ϕ
K
P
A
sound objects that share the same TARTYP defining
characteristics.
As indicated by Chion ([1983] 2009), TARTYP
is subdivided into subcollections of sound-object
classes that are not explicitly notated in the table
(see Figure 2). The center of the table is a collection of
nine sound-object classes (N, N(cid:2), N(cid:2)(cid:2), X, X(cid:2), X(cid:2)(cid:2), Y, Y(cid:2),
Y(cid:2)(cid:2)). These sound-object classes are called Balanced
sound objects. The columns to the right and left
of the Balanced sound objects (three rows from
the top) define the Redundant and Homogeneous
(RH) subcollection, which is further subdivided
into RH Held (Hn, Hx, Tn, Tx) and RH Iter (Zn,
Zx, Zy). The entire bottom row of the table and
the far-right and far-left columns constitute the
subcollection of Excentric objects, some of which
are further subdivided into Sample objects (in the
far-left column: En, Ex, Ey, E) and Accumulation
objects (in the far-right column: An, Ax, Ay, A).
Note that the sound-object classes in the bottom
row of table (E, T, W, (cid:2), K, P, A) are simply referred
to as Excentric objects. Hence, the term “Excentric”
is applied to two layers of subcollections: a larger
subcollection of Excentric objects that includes the
smaller subcollections of Sample and Accumulation
objects; and the smaller, second layer, subcollection
of Excentric objects. The sound-object class E is a
member of both the Sample objects and the smaller
subcollection of Excentric objects, and the sound-
object class A is a member of both the Accumulation
objects and the smaller subcollection of Excentric
objects.
66
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
8
2
6
3
1
8
5
6
0
0
4
/
c
o
m
_
a
_
0
0
2
4
0
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
TARTYP-Derived Grammars
In this section, I present generative grammars
derived from TARTYP classifications of sound
objects and its defining elements as well as from the
structure of the table and its subcollections. The
rewrite rules of these grammars use the time and
frequency properties specified at the margins of the
table as terminals. For each of the subcollections
of the table, I define a grammar in which each
terminal equals a subset of the notated sound-object
classes. A set of rewrite rules in such a grammar
yields a large number of paths, each of which can
be composed out as a sequence of sound objects. In
addition, I present a table grammar that unifies all
the subcollection-based grammars and initiates a
hierarchical structure of sound object sequences.
To explain and exemplify a subcollection-based
grammar, the following discussion will focus on the
grammar of the Balanced object subcollection. As
stated previously, this collection includes the nine
sound-object classes at the center of the table (N,
N(cid:2), N(cid:2)(cid:2), X, X(cid:2), X(cid:2)(cid:2), Y, Y(cid:2), Y(cid:2)(cid:2)). The grammar for this
subcollection uses the set of terminals specified in
Equations 1.1 through 1.6. The right-hand side of
these definitions also specifies the subsets of the
Balanced object subcollection that are equivalent to
each one of these terminals.
DEFINITE = {[N | N(cid:2) | N(cid:2)(cid:2) |]+}
COMPLEX = {[X | X(cid:2) | X(cid:2)(cid:2) |]+}
VARIABLE = {[Y | Y(cid:2) | Y(cid:2)(cid:2) |]+}
IMPULSE = {[N(cid:2) | X(cid:2) | Y(cid:2) |]+}
FORMED ITER = {[N(cid:2)(cid:2) | X(cid:2)(cid:2) | Y(cid:2)(cid:2) |]+}
FORMED SUS = {[N | X | Y |]+}
The general structure of a rewrite rule in a
(1.1)
(1.2)
(1.3)
(1.4)
(1.5)
(1.6)
generative grammar is:
head -> body
(2)
denoting that the head of the rule can be rewritten
as the body. More specifically, the structure of rules
in the subcollection-based grammars discussed in
this section is:
head -> [terminal] terminal [non-terminal]
where the items in [] are optional, yielding four
different legal instantiations:
(3)
head -> terminal
head -> terminal terminal
head -> terminal non-terminal
head -> terminal terminal non-terminal
(4.1)
(4.2)
(4.3)
(4.4)
A terminal corresponds to subsets of sound-
object classes, and a non-terminal may be any other
symbol. The head is always selected from the set of
non-terminal symbols plus a special start symbol.
An example of a legal set of rewrite rules for
the Balanced grammar having special start symbol
“balanced” is:
bal expre v -> VARIABLE
(5.1)
bal expre fs -> FORMED SUS
(5.2)
bal expre fi -> FORMED ITER COMPLEX (5.3)
bal expre fs -> FORMED SUS IMPULSE
(5.4)
bal expre i -> IMPULSE FORMED SUS
bal expre fs
bal expre v -> VARIABLE FORMED ITER
bal expre fi
bal expre fi -> FORMED ITER IMPULSE
bal expre i
bal expre fi -> FORMED ITER VARIABLE
bal expre v
bal expre v -> VARIABLE FORMED SUS
bal expre fs
(5.6)
(5.5)
(5.9)
(5.8)
(5.7)
bal expre fs -> FORM SUS FORM SUS
bal expre fs
bal expre fs -> FORMED SUS IMPULSE
bal expre i
(5.10)
(5.11)
bal expre i -> IMPULSE IMPULSE bal expre i
bal expre v -> VARIABLE IMPULSE bal expre i
(5.12)
(5.13)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
8
2
6
3
1
8
5
6
0
0
4
/
c
o
m
_
a
_
0
0
2
4
0
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
(5.14)
bal expre c -> COMPLEX FORMED SUS
bal expre fs
bal expre fs -> FORMED SUS COMPLEX
bal expre c
bal expre d -> DEFINITE FORMED SUS
bal expre fs
bal expre c -> COMPLEX FORMED ITER
bal expre fi
(5.17)
bal expre v -> VARIABLE VARIABLE bal expre v
(5.18)
(5.19)
(5.20)
balanced -> FORMED SUS bal expre fs
balanced -> IMPULSE bal expre i
(5.16)
(5.15)
Neuman
67
Figure 3. A path generated
from the sample rule set of
Equations 5.1–5.20. This is
one of many alternative le-
gal paths through the space
defined by these rules.
Figure 4. Grammar-based
hierarchical structure
enabled by the Table and
Sub-Table grammars. This
tree-like hierarchy unifies
all the types of grammar.
Here, all caps indicate terminals, and lower case
indicates non-terminals. A rule set is legal when:
(1) it contains at least one rule with a start head, (2) it
contains no duplicate rules, and (3) all non-terminal
symbols that appear in the body of a rule have at
least one other corresponding rule where they appear
only in the head.
The rewrite rules are used to construct a path,
that is, a sequence of terminal symbols selected
according to the grammar expressed in the rewrite
rules. To construct a path, set it initially to the
special start symbol (e.g., “balanced” in rules 5.19
and 5.20). While the path contains non-terminals
symbols, select at random a rule having that non-
terminal as the head, and replace the non-terminal
with the body of the rule. Figure 3 shows an
example of a path constructed by the set of rules
from Equations 5.1–5.20, consisting of a sequence
of terminals derived from rules 5.20, 5.12, 5.5,
and 5.2.
The structure of a rewrite rule and a rule-set in
the other grammars—RH Held, RH Iter, Excentric,
Sample, and Accumulation—is similar to that
of Balanced grammar. The differences between
these grammars lie in the set of terminal symbols
of each grammar and in the equivalent subsets
of sound-object classes. The following example
specifies the set of terminals and the equivalent
subsets of sound-object classes for the Sample
grammar:
DEFINITE = {[ En ]+}
COMPLEX = {[ Ex ]+}
VARIABLE = {[ Ey]+}
UNPREDICTABLE = {[ E ]+}
(6.1)
(6.2)
(6.3)
(6.4)
HELD UF = {[En | Ex | Ey | E ]+} (6.5)
To combine these six grammars into a single
process, I add collections of rules whose terminals
correspond to the six different special start symbols
of the six different grammars. Thus, generating a
path in this Table grammar consists of sequencing
invocations of the other six grammars accordingly,
starting from the new global special start symbol
“start.” Note that the new grammar reflects the
structure of TARTYP subcollections; thus, I can
implement the Sub-Table grammar as shown in
Figure 4. The latter represents the larger subcollec-
tion of Excentric objects. The title “Sub-Table” is
used to prevent duplication. Hence, in the gram-
mars, the name “Excentric” represents only the
smaller subcollection of Excentric objects in the
bottom row of the TARTYP table.
Rule Generation
I implemented a generate-and-test algorithm de-
signed to produce a set of rewrite rules that con-
forms to the three legality criteria discussed in
the previous section. The input to this generation
algorithm consists of a set of parameters indicating
how many rules are in the rule set, how many
of these rules are required for each special start
symbol, and how many rules have bodies consisting
solely of terminal nodes. The algorithm selects the
next rule to generate in accordance with the rule
set parameters (e.g., having a special start symbol
as head, or having only terminals in the body). The
terminals in the rule body are randomly selected
from the terminal symbols and then, optionally, a
non-terminal symbol is included in accordance with
the terminal symbols used. The head of the rule
is either a special start symbol or one of the other
non-terminal symbols. Duplicate rules are rejected,
and a new rule is generated to replace it. Once the
rule set is complete, it is checked for consistency,
ensuring that every non-terminal in a rule body has
at least one matching head in some other rule in the
rule set. If a rule with no such match exists, it is
68
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
8
2
6
3
1
8
5
6
0
0
4
/
c
o
m
_
a
_
0
0
2
4
0
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5. Formal speci-
fication of an algorithm
for generating legal rule
sets as described in text.
Figure 6. A Max/MSP
patch using a coll object
for storing and accessing a
path as a list.
eliminated, and a new rule is generated to replace it
(see Figure 5).
Once a legal rule set is produced, a second
algorithm can be used to repeatedly extract a
path or a sequence of terminals. First, a rule is
randomly selected from among all the rules whose
head matches the start symbol. Next, a rule is
randomly selected from among all the rules whose
head matches the non-terminal ending of the rule
previously selected. Finally, if the rule selected in
the second step has a non-terminal, the second step
is repeated.
Interactive Interface and Composition
These algorithms were implemented as four Java
classes. The four classes are embedded in the
Max/MSP or the Pd environments as extensions of
the MaxObject class. They are combined to create an
mxj type object (or pdj object in Pd) that creates, in
real time, a legal set of rules in one of the grammars
and then constructs (again, in real time) multiple
legal paths from the same set of rules. The process
repeats, generating new sets of rules and extracting
additional paths. There are mxj objects available
for all grammars—Balanced, RH Held, RH Iter,
Excentric, Sample, and Accumulation, as well as for
the structural grammars Table and Sub-Table. These
grammar objects function in a simple way. They
receive a list of integers in the left inlet. This list is
interpreted by the object as the number of rules of
each type to be generated. The set of rules is posted
in the Max window. Following the generation of the
rule set, with each bang received in the left inlet the
object outputs a path or a sequence of terminals as a
symbol list from its outlet.
I now present a way to create an interactive
interface with the mxj grammar objects, as well as a
method to compose with this interactive interface.
Because an mxj grammar object produces a path as a
symbol list, this list can be stored in a coll object to
allow access to items on this list. The list is entered
into the coll object and read from it using the patch
shown in Figure 6. The list is read, in this case, using
an arbitrary timing based on the bangs generated by
a metro object; however, a similar patch can be used
to reflect a structural time organization instead.
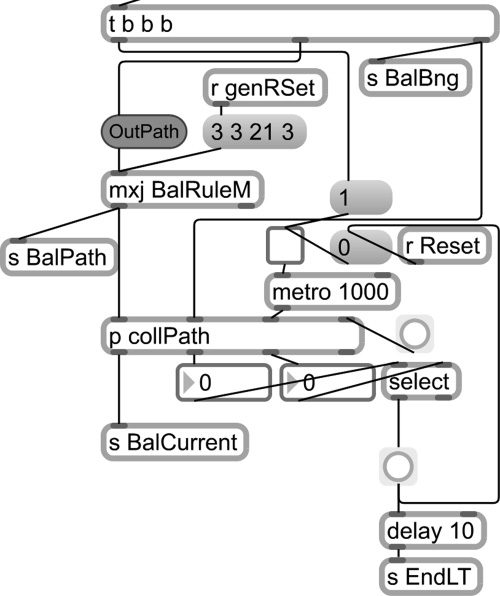
The patch in Figure 6 is embedded in the patch
in Figure 7. The latter includes the grammar object
mxj BalRuleM. As shown in the figure, a message
box sends a list to the inlet of this object that
specifies the number of rules to be generated. The
live.text object bangs the mxj BalRuleM object
to output a path. The patch in Figure 7 is part of a
larger patch that simulates the tree-like hierarchy
Neuman
69
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
8
2
6
3
1
8
5
6
0
0
4
/
c
o
m
_
a
_
0
0
2
4
0
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7. A Max/MSP
patch using a grammar
object to generate rule sets
and paths.
second terminal will be read only when the path
in the Balanced grammar has ended. Therefore, the
middle-ground grammars are a defining element in
the time organization of the hierarchical structure
generated by this patch.
There are many ways to connect such a structure
to a foreground of sound generation and processing.
One possible way is to map the terminals through
select objects to bang messages that activate the
playback of sound files. An alternative method uses
spectral signatures derived from Pierre Schaeffer’s
sound recordings that exemplified TARTYP and
its defining characteristics (Schaeffer 2012). From
each one of the sound objects in these examples
of Schaeffer’s, I extracted 64-bin frames from a fast
Fourier transform (FFT) to create a spectral signature.
These frames were saved as lists of values in simple
text files. In a Pd patch like the one shown in
Figure 9, the FFT frames are used to filter a live sound
and apply the spectral signature of a Schaefferian
sound object on the live sound. Similarly, the
waveform of a Schaefferian sound object, stored in
an array object, is used to generate the amplitude
envelope of the processed signal.
The sub-patch [pd Paths] in the upper-right
corner of Figure 9 uses the grammar objects to
generate rule-sets and sequences of terminals in
the way exemplified in Figures 6 and 7. The patch
then selects FFT frames and waveforms originating
from sound objects that are members of the subsets
equivalent to terminals in the sequence. The data of
these FFT frames and waveforms are entered into the
arrays FFTframe and AmpEnv. For example, if the
terminal DEFINITE is part of a path extracted from
the Balanced grammar it will cause the selection
of FFT frames and waveforms extracted from the
sound objects exemplifying the sound-object classes
N, N(cid:2), or N(cid:2)(cid:2).
This sound-processing system is combined with
the hierarchical structure generated by the gram-
mars discussed in previous sections. As discussed
before, the subcollection grammars define the time
organization at the middle ground of this compo-
sitional process. At the foreground, the temporal
organization is derived from the amplitude en-
velopes generated by the waveforms selected from
Schaefferian sound objects. For example, if the
represented in Figure 4. The upper part of this larger
patch includes the grammar object mxj TabRuleM
that generates a rule set in the Table grammar. When
a path is output by this object, the list of terminals
is compared in a select object that activates the
grammars Balanced, RH Held, or RH Iter, or the
Sub-Table grammar that, in turn, would activate the
grammars Excentric, Sample, and Accumulation.
The activity in this tree-like patch is monitored in
an interface such as the one shown in Figure 8.
In the tree-like hierarchy shown in Figure 4,
the Table and Sub-Table grammars provide the
background level of the structural organization
while the other grammars are the middle ground
of this organization. A path extracted in the Table
or Sub-Table grammars would be advanced in
relation to the paths extracted in the middle-ground
grammars. If, for example, the path [BALANCED,
RH HELD, BALANCED, RH ITER] is extracted in
the Table grammar, when the first terminal is read
it activates a path in the Balanced grammar. The
70
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
8
2
6
3
1
8
5
6
0
0
4
/
c
o
m
_
a
_
0
0
2
4
0
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 8. A sample
interface used to monitor
the activity in the tree-like
Max/MSP patch described
in the text. In this
interface, for each
grammar the extracted
path is shown in a large
box, and the terminal
currently playing is shown
in the message box under
the title of the grammar.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
8
2
6
3
1
8
5
6
0
0
4
/
c
o
m
_
a
_
0
0
2
4
0
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
DEFINITE terminal of the previous paragraph is
followed by an IMPULSE terminal, the latter will be
read once the envelope generated for the DEFINITE
terminal ends.
Interactive Klumpenhouwer Networks
The discussion so far has focused on using Scha-
effer’s taxonomy of sound objects, as expressed in
TARTYP, to create a generative compositional tool.
In this section, I will describe the development of an
interactive tool for real-time generation of Klumpen-
houwer networks (K-networks) that provides the
composer more flexibility in defining underlying
structures and the context of application. Henry
Klumpenhouwer and David Lewin introduced the
K-networks in 1990 (Lewin 1994) to describe the
pitch organization of post-tonal compositions based
on transformational relationships. Although K-
networks are traditionally an analytical tool used
to identify structural pitch-class relationships in a
composition, I have applied a generative approach
to this method for incorporating such networks
as structural elements in real-time composition.
In the following paragraphs, I present a very basic
introduction to the K-network analytical method
and the generative compositional tool that is based
on this method.
The basic element of the network is the graph
describing transformational relationships within a
pitch-class set. The nodes of this graph represent
pitch classes and the edges represent the transfor-
mations between these pitch classes. There are two
types of edges: unidirectional edges for transposi-
tion (marked Tn where n is an integer mod 12) and
bidirectional edges for inversion (marked In where n
is an integer mod 12). A K-network is expanded to
include multiple pitch-class sets by isomorphism.
Two networks are considered isographic if they have
the same configuration of nodes and arrows and
there exists a function that maps the transformation
system used to label the arrows of one network into
the transformation system used to label the arrows
of the other. Hence, if the transformation X labels an
arrow of the one network, then the transformation
F (X) labels the corresponding arrow of the other
(Lewin 1990).
Neuman
71
Figure 9. A sample
sound-processing Pd
patch applying the spectral
signature of a Schaefferian
sound object on live sound.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
8
2
6
3
1
8
5
6
0
0
4
/
c
o
m
_
a
_
0
0
2
4
0
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Five rules for isomorphism apply to Klumpen-
houwer networks (Lewin 1990). The first four rules
are summarized in the following equations:
F (cid:3)1, j(cid:4)(Tn) = Tn;
F (cid:3)11, j(cid:4)(Tn) = T11n;
F (cid:3)5, j(cid:4)(Tn) = T5n;
F (cid:3)7, j(cid:4)(Tn) = T7n;
F (cid:3)1, j(cid:4)(In) = In+ j
F (cid:3)11, j(cid:4)(In) = I11n+ j
F (cid:3)5, j(cid:4)(In) = I5n+ j
F (cid:3)7, j(cid:4)(In) = I7n+ j
(7.1)
(7.2)
(7.3)
(7.4)
The fifth and last rule simply states that two
K-networks will be isographic only if one of the
rules expressed in Equations 7.1–7.4 holds.
Positively isographic networks are networks that
share the same configuration of nodes and arrows,
where the transposition levels of corresponding
arrows are equal and the inversion indices of corre-
sponding arrows differ by some constant j mod 12.
Negatively isographic networks are networks that
share the same configuration of nodes and arrows,
where the transposition levels of corresponding
arrows are complements and the inversion indices
of corresponding arrows differ by some constant j
mod 12 (Lewin 1990). The transformation between
two pitch-class set networks is often referred to
72
Computer Music Journal
Figure 10. Prolog code
generating a K-network.
as hyper-transformation (Lambert 2002). Based on
Equations 7.1–7.4, the hyper-transformation be-
tween two isographic K-networks is marked F (cid:3)u, j(cid:4)
where u ∈ {1, 5, 7, 11} and j is some constant mod 12.
The hyper-transformation between two K-networks,
which are both isographic to a given third K-
network, can be calculated by Lewin’s formula 1
(Lewin 1990):
F (cid:3)u, j(cid:4)F (cid:3)v, k(cid:4) = F (cid:3)uv, uk + j(cid:4)
F (cid:3)u, j(cid:4)F (cid:3)v, k(cid:4)(Tn) = F (cid:3)u, j(cid:4)(Tvn) = Tuvn
F (cid:3)u, j(cid:4)F (cid:3)v, k(cid:4)(In) = F (cid:3)u, j(cid:4)(Ivn+k) = Iuvn+uk+ j
(8.1)
(8.2)
(8.3)
In positive and negative isographs, two types
of hyper-transformations are considered: hyperT
for positive isographs and hyperI for negative
isographs, with u ∈ {1, 11}, respectively. Hence, the
relationships expressed in Equations 8.1–8.3 yield
four possible cases specified by Lewin’s formula 2
(Lewin 1990):
(cid:3)1, j(cid:4)(cid:3)1, k(cid:4) = (cid:3)1, j + k(cid:4)
hyper Tj+k
(cid:3)1, j(cid:4)(cid:3)11, k(cid:4) = (cid:3)11, j + k(cid:4) hyper Ij+k
(cid:3)11, j(cid:4)(cid:3)1, k(cid:4) = (cid:3)11, j − k(cid:4) hyper Ij−k
(cid:3)11, j(cid:4)(cid:3)11, k(cid:4) = (cid:3)1, j − k(cid:4) hyper Tj−k
(9.1)
(9.2)
(9.3)
(9.4)
Using predicate logic and the Prolog program-
ming language, I have designed a tool that generates
a K-network and subsequently extracts random
paths from within the network. A path is a se-
quence of pitch-class sets that can be incorporated
in the pitch organization of a composition or that
can be mapped to other compositional elements.
The Prolog program that implements the tool thus
necessarily has two modes, one to generate the
K-network and one to extract paths from an existing
network. In the first mode, the program receives
a set of user-defined parameters and generates the
K-network accordingly. These parameters include
an initial pitch-class set, a set of u values (such
that u ∈ {1,11}+) specifying positive and negative
isographs, a set of constant j values and a set of trans-
position levels specifying the “bass note” of each
newly generated pitch-class set. The program ana-
lyzes the initial set, generates isographs according
to the specified parameters, and returns the gener-
ated network as well as all its hyperT and hyperI
relations.
The Prolog code in Figure 10 generates a K-
network that includes multiple pitch-class sets.
The genAndAssert() statement is the top-level call
invoked to generate a network. It returns an aKNet()
statement that specifies the pitch-class sets of a
K-network and a new unique label L assigned to this
K-network. Furthermore, genAndAssert() inserts
aKNet() statements into a database, which then
can be used to derive the hyperI() and hyperT()
statements that define the internal structure of the
network.
For example, consider the following query:
genAndAssert([3,10,4],[11,11,11,11,1],
[2,1,8,2,6],[4,10,5,10,6], ).
which inserts the following K-network description
in the database:
aKNet([[3,10,4],[4,9,3],[10,2,9],
[5,2,4],[10,3,9],[6,1,7]],aknet0).
The unique newly generated label for this network
is “aknet0.” The query also inserts the following
Neuman
73
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
8
2
6
3
1
8
5
6
0
0
4
/
c
o
m
_
a
_
0
0
2
4
0
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 11. Prolog code
generating a path from a
known K-network.
associated set of hyper-transformations into the
database:
hyperT([3,10,4],[6,1,7],6,aknet0).
hyperT([5,2,4],[10,3,9],6,aknet0).
hyperT([10,2,9],[5,2,4],5,aknet0).
hyperT([10,2,9],[10,3,9],11,aknet0).
hyperT([4,9,3],[10,2,9],1,aknet0).
hyperT([4,9,3],[5,2,4],6,aknet0).
hyperT([4,9,3],[10,3,9],0,aknet0).
hyperI([3,10,4],[4,9,3],2,aknet0).
hyperI([3,10,4],[10,2,9],1,aknet0).
hyperI([3,10,4],[5,2,4],8,aknet0).
hyperI([3,10,4],[10,3,9],2,aknet0).
hyperI([10,3,9],[6,1,7],8,aknet0).
hyperI([5,2,4],[6,1,7],2,aknet0).
hyperI([10,2,9],[6,1,7],7,aknet0).
hyperI([4,9,3],[6,1,7],8,aknet0).
Once the network has been generated, the
program, operating in the second mode, can perform
a random-walk search to extract paths from this
network on demand. Although the search tree of
any K-network can potentially grow exponentially
as the size of the network increases, the user can
specify the start and end nodes (pitch-class sets), the
maximum depth of the search, and a limit to the
number of repetitions (cycles) in the generated path
when issuing the appropriate chain() statements,
as shown in Figure 11. A chain() statement is the
Prolog query that generates a path from a known
network with optional start and destination sets.
The search tree is rooted in the hyperI() and hyperT()
statements. The program looks for a random path in
this tree, meaning it picks a random branch at each
choice point as well as a random instantiation from
among the legal instantiations at the root hyperI()
and hyperT() statements. Recall that hyperT() is
a unidirectional edge in the network graph, and
hyperI() is a bidirectional edge; hence, there are three
possible mapping functions between two sets in the
network. These mapping are represented explicitly
by the following three statements.
related(X,Y,T,L,0) :- hyperT(X,Y,T,L).
related(X,Y,I,L,1) :- hyperI(X,Y,I,L).
related(X,Y,I,L,2) :- hyperI(Y,X,I,L).
Using a random number generator (that has been
seeded randomly) to elect which of the three legal
paths to take at each call to a related() statement, the
modrelated() statements shown here step through
all three related clauses in some randomly chosen
but deterministic order determined by the input
random “seed,” S:
modrelated(X,Y,T,L,S) :-
N is mod(S,3),related(X,Y,T,L,N).
modrelated(X,Y,T,L,S) :-
N is mod(S+1,3),related(X,Y,T,L,N).
modrelated(X,Y,T,L,S) :-
N is mod(S+2,3),related(X,Y,T,L,N).
The chain() statement in Figure 11 uses the
modrelated() statements to build a path. The user
can impose a fixed horizon by specifying a value for
the parameter H. For example, if H = 4 the program
will execute four recursive steps and return a path
of length five or less. The user can also limit the
maximum number of repetitions (or cycles) in the
path by specifying a value for D. For example, to
find a path from source set [3,10,4] to destination
set [6,1,7] with a length of no more than four steps,
and with no more than two copies of any set in the
network labeled aknet0, the query is:
findPath([3,10,4],[6,1,7],
Path, aknet0,4,2).
74
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
8
2
6
3
1
8
5
6
0
0
4
/
c
o
m
_
a
_
0
0
2
4
0
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
The program may return, depending on the initial
random seed, for example:
Path = [[3,10,4],[6,1,7],[5,2,4],
[10,3,9],[6,1,7]]
Future Work
The latest research in musical artificial intelligence
has followed trends and computational models de-
rived from biological evolution, cultural evolution,
and social interaction (Miranda 2011). A great deal
of attention has been given to the development
of compositional tools for interactive music and
computer improvisation. For example, Eigenfeldt
(2011) uses multi-agent social interaction software
and evolutionary systems to model the spontaneity
of improvisation and the musical interaction be-
tween improvisers. David Plans and Davide Morelli
(2011) attribute the success of free improvisers to
experience-based acquisition of listening skill and
“thin-slicing” intuition. They have used machine
learning, genetic coevolution algorithms, and fast-
and-frugal heuristics to develop software to mimic
these skills. Free improvisers, however, as noted in
the beginning of this article, define their own “hy-
brid language.” Their listening skill and thin-slicing
intuition emerge, by and large, from mastering
this musical language. Although machine-learning
techniques generally require a great deal of sample
data and can be cumbersome to apply in a real-time
context, tools for defining musical languages and
generating musical structures are inexpensive and
can be embedded in interactive environments such
as Max/MSP.
It is straightforward to implement the tools
that were presented in this preliminary research
as real-time musical structure generators for the
Max/MSP and Pd environments. The implementa-
tion’s limitations emerge from what Miller Puckette
defines as the Max paradigm. The latter, according
to Puckette (2002, p. 31), is “a way of combining
predesigned building blocks into configurations
useful for real-time computer music performance.”
These predesigned building blocks insulate the user
from basic programming elements such as data
structures, Boolean functions, logic operation, and
type definitions, all of which are common constructs
in conventional programming languages, including
C, the underlying language of Max/MSP. This limits
the user’s ability to implement complex algorithms
and manipulate more elaborate data structures such
as multi-dimensional arrays. In order to create the
tools described in this article, I have written new
Max externals. My implementation entails making
contextual choices that limit the flexibility available
to the composer. Hence, the composer can use my
TARTYP-based grammar object to regenerate differ-
ent sets of rewrite rules, but cannot, for example,
change the set of terminal symbols in order to refer
to a different sound taxonomy or compositional clas-
sification. Similarly, the composer cannot change
the functions in the K-network code to generate a
new type of network, because such changes would
require rewriting the externals’ code.
In future work I propose to develop software to
allow composers of interactive music to generate
musical structures in real time in the manner of
a free improviser. My goal is to design a tool that
enables the composer to define a musical language
and specify a generative method without resorting
to writing his or her own Max externals. The main
challenge in developing such a tool will be to ac-
commodate the largest possible array of creative
ideas. My plan is to follow the model of the FTM
shared library developed by the Real-Time Musi-
cal Interactions research team at the Institut de
Recherche et de Coordination Acoustique/Musique
(IRCAM). This model emerged from the idea that
the integration and manipulation of data structures
in Max/MSP that are more complex will “open
new possibilities to the user for powerful and ef-
ficient data representations and modularization
of applications” (Schnell et al. 2005). FTM has
been used as the foundation for the design of ap-
plications for score following, sound analysis and
re-synthesis, statistical modeling, database access,
advanced signal processing, and gestural analysis. It
includes data structures, editors and visualization
tools, expression evaluation, and file import and
export. It allows the static and dynamic instanti-
ation of FTM classes and the dynamic creation of
objects.
Neuman
75
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
8
2
6
3
1
8
5
6
0
0
4
/
c
o
m
_
a
_
0
0
2
4
0
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Conclusion
This article has presented two generative compo-
sitional tools that generate and re-compose unified
musical structures in real time. The first tool is
based on generative grammars that reflect the struc-
ture of Schaeffer’s classification of sound objects
as presented in his TARTYP, while the grammars
preserve the terminology and meaningful interclass
relationships which are an essential part of this
table. The article presents a compositional method
that utilizes this tool and maintains contextual ties
to the same resource. The second tool continues this
same generative approach with Klumpenhouwer
networks. The level of structural relationships
generated by these tools is achieved partly by pre-
determined programming elements, as well as by a
predetermined choice of context and resources. In
future work, I hope to develop tools that will allow
the user to define musical languages and specify
generative methods according to the composer’s
choices of context and resources, while maintaining
the same level of structural relationships.
Acknowledgment
I would like to thank Professor Alberto M. Segre
from the University of Iowa Department of Com-
puter Science for his guidance and insight, and for
collaborating with me in the development of the
software discussed in this article.
References
Bel, B. 1992. “Symbolic and Sonic Representations of
Sound-Object Structures.” In K. Ebcioglu, O. Laske,
and M. Balaban, eds. Understanding Music with
AI: Perspectives on Music Cognition. Cambridge,
Massachusetts: MIT Press, pp. 65–109.
Bel, B. 1998. “Migrating Musical Concepts: An Overview
of the Bol Processor.” Computer Music Journal 22(2):56–
64.
Bel, B., and J. Kippen. 1992. “Bol Processor Grammars.” In
K. Ebcioglu, O. Laske, and M. Balaban, eds. Understand-
ing Music with AI: Perspectives on Music Cognition.
Cambridge, Massachusetts: MIT Press, pp. 366–400.
Block, S. 1990. “Pitch-Class Transformation in Free Jazz.”
Music Theory Spectrum 12(2):181–202.
Chion, M. (1983) 2009. Guide to Sound Objects: Pierre
Schaeffer and Musical Research. J. Dack and C. North,
trans. Paris: Buchet/Chastel. Available online at
www.ears.dmu.ac.uk/IMG/pdf/Chion-guide. Accessed
9 January 2013.
Chomsky, N. 1966. Syntactic Structures. The Hague:
Mouton.
Dack, J. 2001.“At the Limits of Schaeffer’s TARTYP.” In
Proceedings of the International Conference “Music
without Walls? Music without Instruments?” Available
online at www.dmu.ac.uk/ documents/art-design-and
-humanities-documents/research/mtirc/nowalls/mww
-dack.pdf. Accessed 23 October 2013.
Eigenfeldt, A. 2011. “A-Life Multi-Agent Modeling for
Real-Time Complex Rhythmic Interaction.” In E. R.
Miranda, ed. A-Life for Music: Music and Computer
Models of Living System. Middleton, Wisconsin: A-R
Editions, pp. 13–35.
Heinemann, S. 1998. “Pitch-Class Set Multiplication
in Theory and Practice.” Music Theory Spectrum
20(1):72–96.
Holtzman, S. R. 1981. “Using Generative Grammars
for Music Composition.” Computer Music Journal
5(1):51–64.
Koblyakov, L. 1990. Pierre Boulez: A World of Harmony.
New York: Harwood.
Lambert, P. 2002. “Isographies and Some Klumpenhouwer
Networks They Involve.” Music Theory Spectrum
24(2):165–195.
Lasnik, H., M. Depiante, and A. Stepanov. 2000. Syn-
tactic Structures Revisited: Contemporary Lectures
on Classic Transformational Theory. Cambridge,
Massachusetts: MIT Press.
Lerdahl, F., and R. Jackendoff. 1993. “An Overview of
Hierarchical Structure in Music.” In S. M. Schwanauer
and D. A. Levitt, eds. Machine Models of Music.
Cambridge, Massachusetts: MIT Press, pp. 289–312.
Lewin, D. 1990. “Klumpenhouwer Networks and Some
Isographies That Involve Them.” Music Theory Spec-
trum 12(1):83–120.
Lewin, D. 1994. “A Tutorial on Klumpenhouwer Net-
works, Using the Chorale in Schoenberg’s Opus 11, No.
2.” Journal of Music Theory 38(1):79–101.
Miranda, E. R. 2011. “Preface.” In E. R. Miranda, ed.
A-Life for Music: Music and Computer Models of
Living System. Middleton, Wisconsin: A-R Editions,
pp. xix–xxiv.
Neuman, I. 2013. “Generative Grammars for Interac-
tive Composition Based on Schaeffer’s TARTYP.” In
76
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
8
2
6
3
1
8
5
6
0
0
4
/
c
o
m
_
a
_
0
0
2
4
0
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Proceedings of the International Computer Music
Conference, pp. 132–139.
Normandeau, R. 2010. “A Revision of the TARTYP
Published by Pierre Schaeffer.” In Proceedings of
the Seventh Electroacoustic Music Studies Net-
work Conference. Available at www.ems-network
.Org/IMG/pdf EMS10 Normandeau.pdf. Accessed 10
July 2012.
Plans, D., and D. Morelli. 2011. “Using Coevolution in
Music Improvisation.” In E. R. Miranda, ed. A-Life for
Music: Music and Computer Models of Living System.
Middleton, Wisconsin: A-R Editions, pp. 37–52.
Puckette, M. 2002. “Max at Seventeen.” Computer Music
Journal 26(4):31–43.
Schaeffer, P. 1966. Trait ´e des objets musicaux. Paris:
´Editions du Seuil.
Schaeffer, P. 2012. “Schaeffer’s Typology of Sound
Objects.” In Cinema for the Ear: A History and
Aesthetics of Electroacoustic Music. Available
at www.dmu.uem.br/aulas/tecnologia/SolObjSon/
HTMLs/Schaeffer.html. Accessed 10 July 2012.
Schnell, N., et al. 2005. “FTM: Complex Data Structures
for Max.” In Proceedings of the International Computer
Music Conference, pp. 9–12.
Thoresen, L. 2007. “Spectromorphological Analysis
of Sound Objects: An Adaptation of Pierre Scha-
effer’s Typomorphology.” Organised Sound 12(2):
129–141.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
3
8
2
6
3
1
8
5
6
0
0
4
/
c
o
m
_
a
_
0
0
2
4
0
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Neuman
77