Identity-Based Patterns in Deep Convolutional Networks: Generative
Adversarial Phonology and Reduplication
Gaˇsper Beguˇs
University of California, Berkeley, USA
begus@berkeley.edu
Abstract
This paper models unsupervised learning of an
identity-based pattern (or copying) in speech
called reduplication from raw continuous data
with deep convolutional neural networks. We
use the ciwGAN architecture (Beguˇs, 2021a)
in which learning of meaningful representa-
tions in speech emerges from a requirement
that the CNNs generate informative data. We
propose a technique to wug-test CNNs trained
on speech and, based on four generative tests,
argue that the network learns to represent an
identity-based pattern in its latent space. By
manipulating only two categorical variables
in the latent space, we can actively turn an
unreduplicated form into a reduplicated form
with no other substantial changes to the output
in the majority of cases. We also argue that the
network extends the identity-based pattern to
unobserved data. Exploration of how meaning-
ful representations of identity-based patterns
emerge in CNNs and how the latent space
variables outside of the training range corre-
late with identity-based patterns in the output
has general implications for neural network
interpretability.
1 Introduction
The relationship between symbolic representa-
to
tions and connectionism has been subject
ongoing discussions in computational cognitive
science. Phonology offers a unique testing ground
in this debate as it is concerned with the first
discretization that human language users per-
form: from continuous phonetic data to discretized
mental representations of meaning-distinguishing
sounds called phonemes.
Identity-based patterns, repetition, or copying
have been at the center of this debate (Marcus
et al., 1999). Reduplication is a morphophonolo-
gical process where phonological content (pho-
nemes) get copied from a word (also called the
base) with some added meaning (Inkelas and Zoll,
2005; Urbanczyk, 2017). It can be total, which
means that all phonemes in a word get copied (e.g.,
/pula/ → [pula-pula]), or partial, where only a
subset of segments gets copied (e.g., /pula/ →
[pu-pula]).
Reduplication is indeed unique among pro-
cesses in natural language because combining
learned entities based on training data distributions
does not yield the desired outputs. For example,
a learner can be presented with pairs of bare and
reduplicated words, such as /pala/ ∼ /papala/ and
/tala/ ∼ /tatala/. The learner can then be tested on
providing a reduplicated variant of a novel unob-
served item with an initial sound /k/ that they have
not been exposed to (e.g., /kala/). If the learner
learns the reduplication pattern, they will output
[kakala]. If the learner simply learns that /pa/ and
/ta/ are optional constituents that can be attached
to words based on data distribution, they will out-
put [pakala] or [takala]. Reduplication is thus an
identity-based pattern (similar to copying), which
is computationally more challenging to learn
(Gasser, 1993), both in connectionist (Brugiapaglia
et al., 2020) and non-connectionist frameworks
(Savitch, 1989; Dolatian and Heinz, 2020). In
/kiajkiajla/, the two sounds in the reduplicative
morpheme, /ki/ and /aj/, need to be in an identity
relationship with the first two segments of the base,
/ki/ and /aj/, and the learner needs to copy rather
than recombine learned elements.
Marcus et al. (1999) argue that connectionist
models such as simple neural networks are un-
able to learn a simple reduplication pattern that
7-month old human infants are able to learn (see
also Gasser, 1993). According to Marcus et al.
(1999), the behavioral outcomes of their exper-
iments cannot be modeled by simple counting,
attention to statistical trends in the input, attention
to repetition, or connectionist (simple neural net-
work) computational models. Instead, they argue,
the results support the claim that human infants use
1180
Transactions of the Association for Computational Linguistics, vol. 9, pp. 1180–1196, 2021. https://doi.org/10.1162/tacl a 00421
Action Editor: Micha Elsner. Submission batch: 3/2021; Revision batch: 7/2021; Published 10/2021.
c(cid:4) 2021 Association for Computational Linguistics. Distributed under a CC-BY 4.0 license.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
2
1
1
9
7
1
8
1
4
/
/
t
l
a
c
_
a
_
0
0
4
2
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
‘‘algebraic rules’’ (Marcus et al., 1999; Marcus,
2001; Berent, 2013) to learn reduplication patterns
(for a discussion, see, among others, McClelland
and Plaut 1999; Endress et al., 2007).
With the development of neural network archi-
tectures, several studies revisited the claim that
neural networks are unable to learn reduplicative
patterns (Alhama and Zuidema, 2018; Prickett
et al., 2018; Nelson et al., 2020; Brugiapaglia
et al., 2020), arguing that identity-based patterns
can indeed be learned with more complex architec-
tures.1 All these computational experiments, how-
ever, operate on an already discretized level and
most of these experiments model reduplication
with supervised learning.
Examples like [pu-pula] and [pula-pula] are
discretized representations of reduplication, using
characters to represent continuous sounds. Most,
if not all, computational models of reduplication,
to the author’s knowledge, model reduplication as
character or feature manipulation (the inputs to the
models are either characters representing phones
or phonemes or discrete binary featural repre-
sentations of phonemes). For example, a seq2seq
model treats reduplication as a pairing between
the input unreduplicated sequence of ‘‘characters’’
(such as /tala/) and an output—a reduplicated se-
quence (such as /tatala/). Already abstracted and
discretized phonemes or ‘‘characters’’, however,
are not the primary input to language-learning in-
fants. The primary linguistic data of most hearing
infants is raw continuous speech. Hearing infant
learners need to acquire reduplication from contin-
uous speech data that is substantially more com-
plex than already discretized characters or binary
features.
Furthermore, most of the existing models of
reduplication are also supervised. Seq2seq mod-
els, for example, are fully supervised: The training
consists of pairs of unreduplicated (input) and
reduplicated strings of characters or binary fea-
tures (output). While the performance can be
tested on unobserved data or even on unobserved
segments, the training is nevertheless supervised.
Human language learners do not have access to
input-output pairings: They are only presented
with positive, surface, and continuous acoustic
data. While equivalents of copying/identity-based
1Wilson (2018, 2020) proposes another approach that
allows modeling reduplication. For a non-connectionist com-
putational model of reduplication, see Dolatian and Heinz
(2018, 2020).
patterns can be constructed in the visual domain,
we are not aware of studies that test identity-based
visual patterns with deep convolutional neural
networks.
In this paper, we model reduplication, one of
the computationally most challenging processes,
from raw unlabeled acoustic data with deep con-
volutional networks in the GAN framework. The
advantage of the GAN framework for cognitive
modeling is that the network has to learn to output
raw acoustic data from a latent noise distribution
without directly accessing the training data. We
argue that CNNs discretize continuous phonetic
data and encode linguistically meaningful units
into individual latent variables. The emergence of
a discretized representation of an identity-based
pattern (reduplication) is induced by a model that
forces the Generator network to output informative
data (ciwGAN; Section 4). Additionally, we add
inductive bias towards symbolic-like representa-
tions by binarizing code variables with which the
Generator encodes meaningful representations.
We also test whether a deep convolutional network
learns reduplication without the two inductive bi-
ases (without the requirement on the Generator
to output informative data and without binariza-
tion of the latent space) in the bare WaveGAN
architecture (Section 5).
The experiments bear implications for
the
discussion between symbolic and connectionist
approaches to language modelling by testing the
emergence of rule-like symbolic representations
within the connectionist framework from raw
speech in an unsupervised manner. Results of the
experiments suggest that both models, ciwGAN
and WaveGAN learn the identity-based patterns,
but inductive biases for informative representation
and binarization facilitate learning and yield better
results. We discuss properties of symbolic-like rep-
resentations and how they emerge in the models:
discretization, causality (in the sense that manipu-
lation of individual elements results in desired out-
come), and categoricity (for discussions on these
and other aspects of the debate, see Rumelhart et al.,
1986; McClelland et al., 1986; Fodor and Pylyshyn,
1988; Minsky, 1991; Dyer, 1991; Marcus et al.,
1999; Marcus, 2001; Manning, 2003; Berent,
2013; and Maruyama, 2021).
How can we test learning of reduplication in
a deep convolutional network that is trained only
on raw positive data? We propose a technique to
test the ability of the Generator to produce forms
1181
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
2
1
1
9
7
1
8
1
4
/
/
t
l
a
c
_
a
_
0
0
4
2
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
absent from the training data set. For example, we
train the networks on acoustic data of items such as
/pala/ ∼ /papala/ and /tala/ ∼ /tatala/, but test redu-
plication on acoustic forms of items such as /sala/,
which is never reduplicated in the training data.
Using the technique proposed in Beguˇs (2020),
we can identify latent variables that correspond
to some phonetic or phonological representation
such as reduplication. By manipulating and inter-
polating a single latent variable, we can actively
generate data with and without reduplication. In
fact, we can observe a direct relationship between
a single latent variable (out of 100) and reduplica-
tion that with interpolation gradually disappears
from the output. Additionally, we can identify
latent variables that correspond to [s] in the out-
put. By forcing both reduplication and [s] in the
output through latent space manipulation, we can
‘‘wug-test’’ the network’s learning of reduplica-
tion on unobserved data. In other words, we can
observe what the network will output if we force
it to output reduplication and an [s] at the same
time. A comparison of generated outputs with
human outputs that were withheld from training
reveals a high degree of similarity. We perform
an additional computational experiment to repli-
cate the results from the first experiment (from
Section 4). In the replication experiment, evi-
dence for learning of the reduplicative pattern also
emerges. To the author’s knowledge, this is the
first attempt to model reduplication with neu-
ral network architectures trained on raw acoustic
speech data.
The computational experiments reveal another
property about representation learning in deep
neural networks: We argue that
the network
extracts information in the training data and repre-
sents a continuous acoustic identity-based pattern
with discretized representation. Out of 100 vari-
ables, the network encodes reduplication with one
or two variables, which is suggested by the fact
that a small subset of variables are substantially
more strongly correlated with presence of redupli-
cation. In other words, there is a near categorical
drop in regression estimates between one vari-
able and the rest of the latent space. Setting the
identified variables to values well beyond the
training range results in near categorical presence
of a desired variable in the output. This tech-
nique (proposed for non-identity-based patterns
in Beguˇs, 2020) allows us to directly explore
how the networks encode dependencies in data,
their underlying values, and interactions between
variables, and thus get a better understanding of
how exactly deep convolutional networks encode
meaningful representations.
Recent developments in zero-resource speech
modeling (Dunbar et al., 2017, 2019, 2020) enable
modeling of speech processes in an unsupervised
manner from raw acoustic data. Several proposals
exist for modeling unsupervised lexical learning
(Kamper et al., 2014; Lee et al., 2015; Chung et al.,
2016) that include generative models such as vari-
ational autoencoders (Chung et al., 2016; Baevski
et al., 2020; Niekerk et al., 2020) and GANs
(Beguˇs, 2021a). This framework allows not only
unsupervised lexical
term discovery, but also
phone-level identification (Eloff et al., 2019; Shain
and Elsner, 2019; Chung et al., 2016; Chorowski
et al., 2019). While zero-resource speech modeling
has yielded promising results in unsupervised la-
beling, the proposals generally do not model pho-
nological or morphophonological processes. This
paper thus also tests applicability of the unsuper-
vised speech processing framework for cognitive
modeling and network interpretability.
2 Model
GenerativeAdversarialNetworks(GANs; Goodfellow
et al., 2014) are a neural network architecture with
two main components: the Generator network
and the Discriminator network. The Generator is
trained on generating data from some latent space
that is randomly distributed. The Discriminator
takes real training data and the Generator’s outputs
and estimates which inputs are real and which are
generated. The minimax training, where the Gen-
erator is trained on maximizing the Discrimina-
tor’s error rate and the Discriminator is trained on
minimizing its own error rate, results in the Gen-
erator network outputting data such that the Dis-
criminator’s success in distinguishing them from
real data is low. It has been shown that GANs not
only learn to produce innovative data that resem-
ble speech, but also learn to encode phonetic and
phonological representations in the latent space
(Beguˇs, 2020). The major advantage of the GAN
architecture for modeling speech is that the Gen-
erator network does not have direct access to the
training data and is not trained on replicating data
(unlike in the autoencoder architecture; R¨as¨anen
et al., 2016; Eloff et al., 2019; Shain and Elsner,
2019). Instead, the network has to learn to generate
1182
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
2
1
1
9
7
1
8
1
4
/
/
t
l
a
c
_
a
_
0
0
4
2
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
2
1
1
9
7
1
8
1
4
/
/
t
l
a
c
_
a
_
0
0
4
2
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 1: (Left) The ciwGAN architecture as proposed in Beguˇs (2021a) and used in this paper with training data
as described in Section 3. (Right) The structure of the Generator in the ciwGAN architecture as proposed in Beguˇs
(2021a) (based on Donahue et al., 2019).
data from noise in a completely unsupervised
manner—without ever directly accessing the train-
ing data.
In the first experiment, we use the ciwGAN
(Categorical InfoWaveGAN) model proposed in
Beguˇs (2021a). The ciwGAN model combines the
WaveGAN and InfoGAN architectures. Wave-
GAN, proposed by Donahue et al. (2019), is a
Deep Convolutional Generative Adversarial Net-
work (DCGAN; proposed by Radford et al., 2016)
adapted for time-series audio data. The basic ar-
chitecture is the same as in DCGAN, the main
difference being that
in the WaveGAN pro-
posal, the deep convolutional networks take one-
dimensional time-series data as inputs or outputs.
The structure of the Generator and the Discrim-
inator networks in the ciwGAN architecture are
taken from Donahue et al. (2019). InfoGAN (Chen
et al., 2016) is an extension of the GAN architec-
ture that aims to maximize mutual information be-
tween the latent space and generated outputs. The
Discriminator/Q-network learns to retrieve the
Generator’s latent categorical or continuous codes
(Chen et al., 2016) in addition to estimating real-
ness of generated outputs and real training data.
Beguˇs (2021a) proposes a model that combines
these two proposals and introduces a new latent
space structure (in the fiwGAN architecture). Be-
cause we are primarily interested in simple bi-
nary classification between bare and reduplicated
forms, we use the ciwGAN variant of the proposal.
The model introduces a separate deep convolu-
tional Q-network that learns to retrieve the Gen-
erator’s internal representations. Separating the
Discriminator and the Q-network into two net-
works is advantageous from the cognitive model-
ing perspective: the architecture features a separate
network that models speech production (the Gen-
erator) and a separate network that models speech
categorization (the Q-network). The latter intro-
duces an inductive bias that forces the Generator to
output informative data and encode linguistically
meaningful properties into its code variables. The
network learns to generate data such that by ma-
nipulating these code variables, we can force the
desired linguistic property in the output (Beguˇs,
2021a).
The architecture involves three networks: the
Generator that takes latent codes (a one-hot vector)
and uniformly distributed z-variables and gener-
ates waveforms, a Discriminator that distinguishes
real from generated outputs, and a Q-network that
takes generated outputs and estimates the latent
code (one-hot vector) used by the Generator. More
specifically, the Generator network is a deep con-
volutional network that takes as its input 100 latent
variables (see Figure 1).2 Two of the 100 variables
are code variables (c1 and c2) that constitute a
one-hot vector. The remaining 98 z-variables are
uniformly distributed on the interval (−1, 1). The
Generator learns to take as the input the 2 code
variables and the 98 latent variables and output
16,384 samples that constitute just over one sec-
ond of audio file sampled at 16 kHz through five
convolutional layers. The Discriminator network
takes real and generated data (again in the form
2The number of latent variables were adopted from
Radford et al. (2016) and Donahue et al. (2019). Probing
how the number of z-variables affects learning of speech
representations is left for future work.
1183
of 16,384 samples that constitute just over one
second of audio file) and learns to estimate the
Wasserstein distance between generated and real
data (according to the proposal in Arjovsky et al.,
2017) through five convolutional layers. In the
majority of InfoGAN proposals, the Discrimina-
tor and the Q-network share convolutions. Beguˇs
(2021a) introduces a separate Q-network (also in
Rodionov 2018).3
The Q-network is in its structure identical to the
Discriminator network, but the final layer is fully
connected to nodes that correspond to the number
of categorical variables (Beguˇs, 2021a). In the ciw-
GAN architecture, the Q-network is trained on
estimating the latent code variables with a soft-
max function (Beguˇs, 2021a). In other words, the
Q-network takes the Generator’s outputs (wave-
forms) and estimates the Generator’s latent code
variables c1 and c2. Weights of both the Generator
network and the Q-network are updated according
to the Q-network’s loss function: to minimize the
distance between the actual one-hot vector (c1 and
c2) used by the Generator and the one-hot vec-
tor estimated with a softmax in the Q-network’s
final layer using cross-entropy. This forces the
Generator to output informative data.
The advantage of the ciwGAN architecture is
that the network not only learns to output innova-
tive data that resemble speech in the input, but also
provides meaningful representations about data in
an unsupervised manner. For example, as will be
argued in Section 4, the ciwGAN network encodes
reduplication as a meaningful category: it learns
to assign a unique code for bare and reduplicated
items. This encoding emerges in an unsupervised
fashion from the requirement that the Generator
output data such that unique information is retriev-
able from its acoustic outputs. Given the structure
of the training data, the Generator is most infor-
mative if it encodes presence of reduplication in
the code variables.
To replicate the results and to test learning
of an identity-based pattern without binarization
and without the requirement on the Generator to
output informative data, we run an independent
experiment on a bare WaveGAN (Donahue et al.,
2019) architecture using the same training data.
The difference between the two architectures is
that the bare GAN architecture does not involve
a Q-network and the latent space only includes
3For all details about the architecture, see Beguˇs (2021a).
voiceless C1
voiced C1
C1 = [m, n, v]
C1 = [s]
C1V2C3V4
C1V2C1V2C3V4
C1V2C3V4
C1V2C1V2C3V4
C1V2C3V4
C1V2C1V2C3V4
C1V2C3V4
C1V2C1V2C3V4 —
“phAli
p2″phAli
“bAli
b2″bAli
“mAli
m2″mAli
“sAli
Table 1: A schematic illustration of the training
data in the International Phonetic Alphabet.
latent variables uniformly distributed on the in-
terval (−1, 1).
Beguˇs (2020) and Beguˇs (2021a) also propose
a technique for latent space interpretability in
GANs: Manipulating individual variables to val-
ues well beyond the training range can reveal
underlying representations of different parts of
the latent space. We use this technique throughout
the paper to evaluate learning of reduplication.
3 Reduplication in Training Data
The training data was constructed to test a sim-
ple reduplication pattern, common in human
languages: partial CV reduplication found in lan-
guages such as Paamese, Roviana, Tawala, among
others (Inkelas and Zoll, 2005). Base items are of
the shape C1V2C3V4 (C = consonant; V = vowel;
e.g., /tala/). Reduplicated forms are of the shape
C1V2C1V2C3V4, where the first syllable (C1V2)
is repeated. The items were constructed so that C1
contains a voiceless stop /p, t, k/, a voiced stop
/b, d, g/, a labiodental voiced fricative /v/, and
nasals /m, n/. The vowels V2 and V4 consist of
/A (@), i, u/. C3 consists of /l, ô, j/. All permutations
of these elements were created. The stress was
always placed on V2 in the base forms and on the
same syllable in reduplicated forms ([“phAl@] ∼
[p@”phAl@]). Because the reader of the training data
was a speaker of American English, the training
data is phonetically even more complex. The ma-
jor phonetic effects in the training data include (i)
reduction of the vowel in the unstressed redupli-
cated forms and in the final syllable (e.g., from [A]
to [2/@]) and (ii) deaspiration of voiceless stops
in the unstressed reduplication syllable (e.g., from
[ph] to [p]). The training data includes two unique
repetitions of each item and two repetitions of
the corresponding reduplicated forms. Table 1
illustrates the training data.
1184
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
2
1
1
9
7
1
8
1
4
/
/
t
l
a
c
_
a
_
0
0
4
2
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
The training data also includes base forms
C1V2C3V4 with the initial consonant C1 being a
fricative [s]. These items, however, always appear
unreduplicated in the training data—the purpose
of [s]-initial item is to test how the network extends
the reduplicative pattern to novel unobserved data.
All 27 permutations of sV2C3V4 were included.
To increase representation of [s]-initial words,
four or five repetitions of each unique [s]-initial
base were used in training.4 Altogether, 132 repe-
titions of the 27 unique unreduplicated words with
an initial [s] were used in training.
Sibilant fricative [s] was chosen as C1 for test-
ing learning of reduplication because its frication
noise is acoustically prominent and sufficiently
different from C1s in the training data both
acoustically and phonologically. This satisfies the
requirement that a model learns to generalize to
novel segments and feature values (Berent, 2013;
Prickett et al., 2018).5 In phonological terms, the
model is tested on a novel feature (sibilant fricative
or [±strident]; Hayes 2009)—the training data did
not consist of any bare or reduplicated forms with
other sibilant fricatives. To make the learning even
more complex, voiceless fricatives ([f, T, S]) are al-
together absent from the training data. All voiced
fricatives except for [v] are absent too. Spectral
properties of the voiced non-sibilant fricative [v]
in the training data (and in Standardized American
English in general) are so substantially different
from a voiceless sibilant fricative [s] that we kept
them in the training data. We excluded all items
with initial sequences /ti/, /tu/, and /ki/ from the
training data, because acoustic properties of these
sequences, especially frication of the aspiration of
/t/ and /k/, are similar to those of frication noise
in /s/. Altogether 996 unique sliced items used
in training were recorded in a sound attenuated
booth by a female speaker of American English
with a MixPre 6 (SoundDevices) preamp/recorder
and the AKG C544L head-mounted microphone.
4Items [“sala], [“suru], and [“suju] each miss one repetition
(four altogether).
5For an ‘‘across the board’’ generalization, Berent (2013)
requires that generalization occur to segments fully absent
from the inventory. It is challenging to elicit reduplication of
segments that are fully absent from the training data in the
proposed models. Even in human subject experiments testing
the ‘‘across the board’’ generalization, subjects need to be
exposed to the novel segment at least as a prompt. In our
case, the novel segment needs to be part of the training data,
but only in unreduplicated forms.
4 CiwGAN (Beguˇs, 2021a)
The Generator features two latent code variables,
c1 and c2, and 98 uniformly distributed variables
z (Figure 1). In the training phase, the two code
variables (c1 and c2) compose the one-hot vector
with two levels: [0, 1] and [1, 0]. This means
that the network can encode two categories in
its latent space structure that correspond to some
meaningful feature about the data. The Q-network
forces the Generator to encode information in its
latent space. In other words, the loss function of
the Q-network forces the Generator to output data
such that the Q-network is effective in retrieving
the latent code c1 and c2 from the Generator’s
acoustic outputs only. Nothing in the training
data pairs base and reduplicated forms. There is
no overt connection between the bases and their
reduplicated correspondents. Yet, the structure of
the data is such that given two categories, the
most informative way for the Generator to encode
unique information in its acoustic outputs is to
associate one unique code with base forms and
another with reduplicated forms. The Generator
would thus have a meaningful unique representa-
tion of reduplication that arises in an unsupervised
manner exclusively from the requirement on the
Generator to output informative data.
To test whether the Generator encodes redu-
plication in latent codes, we train the network
for 15,920 steps (or approximately 5,114 epochs)
with the data described in Section 3. The choice
of the number of steps is based on two objectives;
first, the output data should approximate speech
to the degree that allows acoustic analysis. Sec-
ond, the Generator network should not be trained
to the degree that it replicates data completely.
As such, overfitting rarely occurs in the GAN
architecture (Adlam et al., 2019; Donahue et al.,
2019). The best evidence against overfitting in
the ciwGAN architecture comes from the fact that
the Generator outputs data that violate training
distributions substantially (see Section 4.2 below)
(Beguˇs, 2021a,b). Despite these guidelines, the
choice of number of steps is somewhat arbitrary
(for discussion, see Beguˇs, 2020).
We generate 100 outputs for each latent code
[0, 1] and [1, 0] (200 total) and annotate them for
presence or absence of reduplication. All annota-
tions here and in other sections are performed by
the author in Praat (Boersma and Weenink, 2015).
Distinguishing unreduplicated from reduplicated
1185
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
2
1
1
9
7
1
8
1
4
/
/
t
l
a
c
_
a
_
0
0
4
2
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Code
[1, 0]
[0, 1]
[5, 0]
[0, 5]
Bare
Redup.
% Redup.
78
40
98
13
22
60
2
87
22%
60%
2%
87%
Table 2: Counts of bare and reduplicated (redup.)
outputs when the latent codes c1 and c2 are set to
[1, 0], [0, 1], [5, 0], and [0, 5].
is very salient; for less salient annotations, we pro-
vide waveforms and spectrograms (e.g., Figure 4
and 6).6
There is a significant correlation between the
two levels of latent code and presence of redu-
plication. Counts are given in Table 2. When the
code is set to [1, 0], 78% of the generated outputs
are base forms; when set to [0, 1], 60% of outputs
are reduplicated (odds ratio = 5.27, p < 0.0001,
Fisher Exact Test). When the latent codes are set
to [0, 5] and [5, 0], we get a near categorical
distribution of bare and reduplicated forms. For
[5, 0], the Generator outputs an unreduplicated
bare form in 98% samples. For [0, 5], it outputs
a reduplicated form in 87% outputs (odds ratio =
308.3, p < 0.0001, Fisher Exact Test). These out-
comes suggest that the Generator encodes redu-
plication in its latent codes and again confirm that
manipulating latent variables well beyond training
range reveals the underlying learning representa-
tions in deep convolutional networks (as proposed
in Beguˇs, 2020; Beguˇs, 2021a).
4.1 Interpolation
That the Generator uses latent codes to encode
reduplication is further suggested by another gen-
erative test performed on interpolated values of
the latent code. To test how exactly the relation-
ship between the latent codes (c1 and c2) works,
we created sets of generated outputs based on
interpolated values of the code c1 and c2. We ma-
nipulate c1 and c2 from the value 1.5 towards 0 in
increments of 0.125. For example, we start with
[1.5, 0] and interpolated first to [0, 0] ([1.375, 0],
[1.25, 0], etc.). From [0, 0] we further interpolate
in increments of 0.125 to [0, 1.5] (e.g., [0, 0.125],
[0, 0.25]). All other variables in the latent space
6The code is available at https://github.com
/gbegus/fiwGAN-ciwGAN. The generated data and
checkpoints are available at https://doi.org/10
.17605/osf.io/zbjcp.
are kept constant across all interpolated values.
Each such set thus contains 25 generated samples.
We generate 100 such sets (altogether 2500 out-
puts) and analyze each output. Out of the 100 sets,
the output was either bare or reduplicated through-
out the interpolated values and did not change in
55 sets. As suggested by Section 4 and Table 2,
the number of bare and reduplicated forms for
each level rises to near categorical values as the
variables approach values of 5.
In the 45/100 sets, the output changes from
the base form to a reduplicated form at some
point as the codes are interpolated. If the network
only learned to randomly associate base and redu-
plicated forms with each endpoint of the latent
code, we would expect base forms to be unrelated
to reduplicated forms. For example, a base form
["khulu] could turn into reduplicated [d@"dAl@]. An
acoustic analysis of the generated sets, however,
suggests that the latent code directly corresponds
to reduplication. In approximately 25 out of 45
sets (55.6%) of generated outputs that undergo
the change from base to a reduplicated form (or
25% of the total sets), the base form is identi-
cal to the reduplicated form with the only major
difference between the two being the presence
of reduplication (waveforms and spectrograms of
the 25 outputs are in Figure 6). This propor-
tion would likely be even higher with a higher
interpolation resolution (higher than 0.125) and
because we do not count cases in which major
changes of sounds occur besides the addition of
the reduplication syllable (e.g., if ["nAôi] changes to
[nU"nuôi], we count the output as unsuccessful). In
the remaining 20 outputs, several outputs undergo
changes, where several segments or their features
are kept constant, but the degree to which they
differ can vary (e.g., ["phil@] ∼ [p@"phiôi], ["thiju] ∼
["phiô@] ∼
["nAô@] ∼ [d@"dAôi], or
[d@"dAji],
[t@"thAli]).
Under the null hypothesis, if the Generator
learns to pair the base and reduplicated forms
randomly, each base form could be associated
with any of the unique 243 reduplicated forms
at the probability of 1/243 (0.004). Even if we
assume very conservatively that each base form
could be associated with only each subgroup of
reduplicated consonant (C1; e.g., voiceless stops,
voiced stops, [m], [n], [v]) disregarding the vowel
and disregarding changes in the base, the prob-
ability of both forms being identical would still
be at only 0.2 (for each of the five subgroups). In
1186
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
2
1
1
9
7
1
8
1
4
/
/
t
l
a
c
_
a
_
0
0
4
2
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
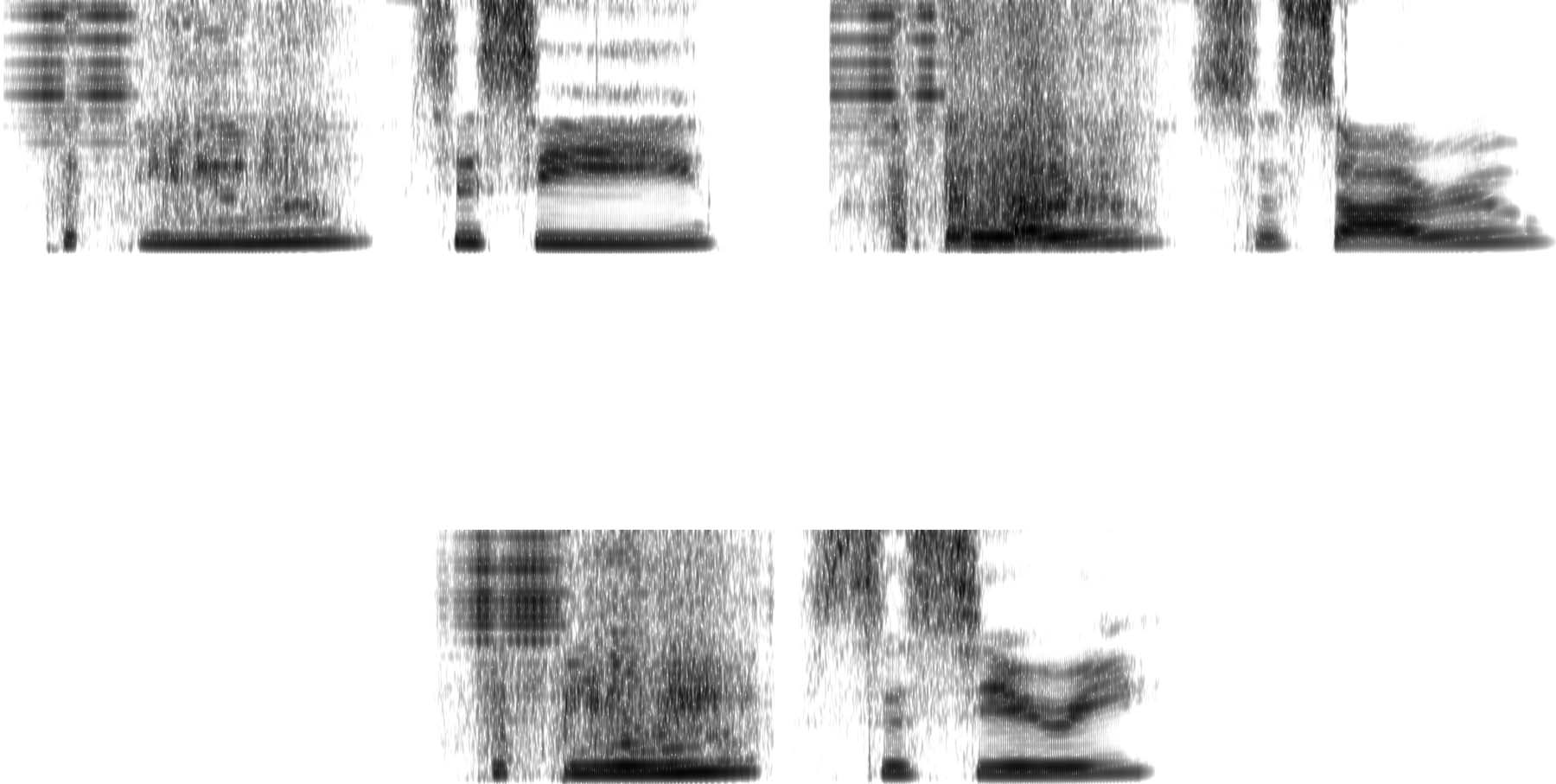
Figure 2: Waveforms showing how interpolation of
latent codes c1 and c2 has a direct effect on presence
of reduplicattion: As the values are interpolated from
[1.5, 0] to [0, 1.5], the reduplication gradually ap-
pears/disappears from the output. Waveforms on the
left represent reduplication of ["phiôu] to [p@"phiôu];
waveforms on the right represent reduplication of
["dAji] to [d@"dAji].
both cases, the ratio of identical base-reduplication
pairs, although not categorical, is highly signifi-
cant (CI = [0.4, 0.7], p < 0.0001 for both cases
according to Exact Binomial Test).
Figure 2 illustrates how, keeping the la-
tent space constant except for the manipulation
of the latent code with which the Generator
represents reduplication, the generated outputs
gradually transition from the base forms ["phiôu]
and ["dAji] to the reduplicated forms [p@"phiôu] and
[d@"dAji].7 Other major properties of the output are
unchanged.
This interpolative generative test again suggests
that the network learns reduplication and encodes
the process in the latent codes. By interpolating the
codes we can actively force reduplication in the
output with no other substantial changes in the ma-
jority of cases.
4.2 Reduplication of Unobserved Data
To test whether the ciwGAN network learns to
generalize the reduplicative pattern on unobserved
data, we use latent space manipulation to force
reduplication at the same time as presence of [s]
in the output. Items with a [s] as the initial conso-
nants (e.g., ["siju]) appear only in bare forms in the
training data. In Sections 4 and 4.1, we established
that the network uses the latent code (c1 and c2) to
represent reduplication. Following Beguˇs (2020)
and Beguˇs (2021a), we can force any phonetic
property in the output by manipulating the latent
variables well beyond the training range. Redupli-
cation is forced by setting the latent code to values
7The exact vowel quality estimation in the generated
outputs is challenging, especially in short vocalic elements of
reduced vowels in the reduplicative syllables. For this reason,
we default transcriptions to a [@].
Figure 3: Absolute Lasso regression estimates (sorted
from highest on the right-hand side) for a ciwGAN
model identifying presence of [s] after 1000 transcribed
outputs, 500 for each latent code (with the same latent
variable structure of the remaining 98 variables across
the two conditions). Variable z90 is identified as the
variable corresponding to presence of [s] (the variable
with the highest regression estimates).
higher than [0, 1]. We can simultaneously force
[s] in the output to test the network’s performance
on reduplication in unseen data.
To identify latent variables with which the Gen-
erator encodes the sound [s] in the output, we
generate 1000 samples with randomly sampled
latent variables, but with the latent code variables
(c1 and c2) set at [0, 1] and [1, 0] (500 samples
each with the same latent variable structure of the
remaining 98 variables across the two conditions).
We annotate outputs for presence of [s] for the
two sets and fit the data to a Lasso logistic regres-
sion model in the glmnet package (Simon et al.,
2011). Presence of [s] is the dependent variable
coded as a success; the independent variables
are the 98 latent variables uniformly distributed
on the interval (−1, 1) (for the technique, see
Beguˇs, 2020). Lambda is computed with 10-fold
cross validation. Estimates of the Lasso regres-
sion model (Figure 3) suggest that z90 with the
highest regression estimates is one of the vari-
ables with which the Generator encodes presence
of [s] in the output. For a generative test providing
evidence that Lasso regression estimates correlate
with network’s internal representations, see Beguˇs
(2020).
We can thus set z90 to marginal levels well
beyond the training range and the latent code
(c1, c2) to levels well beyond [0, 1] in order to
force reduplication and [s] in the output simulta-
neously. For example, when the latent code is set
to [0, 3] (which forces reduplication in the output)
1187
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
2
1
1
9
7
1
8
1
4
/
/
t
l
a
c
_
a
_
0
0
4
2
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
2
1
1
9
7
1
8
1
4
/
/
t
l
a
c
_
a
_
0
0
4
2
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4: Waveforms and spectrograms (0–8000 Hz) of reduplicated forms containing an [s] which were absent
from the training data. The generated forms on the left are paired with recordings of a female speaker reading
reduplicated forms that were absent from the training data. (left) When the latent code is set to [0, 3] and z90 to 4,
the network outputs a reduplicated [s@"siji]. (right) When the latent code is set to [0, 7.5] and z4 to 9.5, we obtain
[s@"sAôu]. (bottom) In the bare GAN architecture, when z5 (forcing reduplication) is set to −9.25 and z17 (forcing
[s] in the output) to −9.0, the Generator outputs a reduplicated [s@"siôi].
and z90 to 4 (forcing [s] in the output),
the
network outputs a reduplicated [s@"siji] (among
other outputs) even though items containing an
[s] are never reduplicated in the training data.
When the code is set to even higher number,
[0, 7.25], and z90 to 7,
the network outputs
[s@"siru] in a different output. The spectrograms in
Figure 4 show a clear period of frication noise char-
acteristic of a sibilant fricative [s], interrupted by
a reduplicative vowel and followed by a repeated
period of frication noise characteristic of [s].
In fact, at the values [0, 7.25], and z90 = 7,
the network generates approximately 33 (out of
100 tested or 33%) outputs that can be reliably
analyzed as reduplicated forms with initial sV-
reduplication unseen in the training data. The other
67 outputs are reduplicated forms containing other
C1s or unreduplicated [s]-forms. No outputs were
observed in which C1 of the reduplication syllable
and C1 of the base would be substantially differ-
ent. While all the cases when z90 is manipulated
involve a front vowel [i] in the base item, we
can also elicit reduplication for other vowels. For
example, we identify variable z4 as corresponding
to an [s] and a low vowel [A] in the output (with
the same technique as described for z90 above but
with presence of [sA] as the dependent variable in
the Lasso regression model). By manipulating z4
to 9.5 (forcing [sA] in the output) and setting the
latent codes to [0, 7.5], we obtain [s@"sAôu] in the
output (Figure 4).
For comparison, the same L1 speaker of English
who read the words in the training data read the
reduplicated [s@"siji] and [s@"sAôu] that were not
included in the training data. Figure 4 parallels
the generated reduplicated forms based on unob-
served data (which were elicited by forcing [s]
and reduplication in the output) and the recording
of the same reduplicated form read by a human
speaker. The spectrograms show clear acoustic
parallels between the Generated outputs and the
recording read by a human speaker (who read the
words prior to computational experiments and did
not hear or analyze the generated outputs).
1188
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
2
1
1
9
7
1
8
1
4
/
/
t
l
a
c
_
a
_
0
0
4
2
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5: Absolute Lasso regression estimates (sorted from highest on the right-hand side) for two models
identifying (a) presence of reduplication and (b) presence of [s] in the generated outputs of the bare GAN model
(Section 5).
5 Replication: Bare WaveGAN
(Donahue et al., 2019)
To test whether the learning of reduplicative pat-
terns in GANs is a robust or idiosyncratic property
of the model presented in Section 4, we conduct
a replication experiment. We introduce two cru-
cial differences in the replication experiment: We
train the Generator without the requirement to pro-
duce informative data and without binary latent
codes. We use the model in Donahue et al. (2019),
which features a ‘‘bare’’ GAN architecture for
audio data: only the Generator and Discriminator
networks without the Q-network. This architecture
has the potential to inform us how GANs represent
reduplicative patterns without an explicit require-
ment to learn informative data, that is, without
an explicit requirement to encode some salient
feature of the training data in the latent space. The
data used for training is the same as in the experi-
ment in Section 3. We train the network for 15,930
steps or approximately 5,118 epochs, which is al-
most identical to the number of steps/epochs in
the ciwGAN experiment (Section 4).
5.1
Identifying Variables
Testing the learning of reduplication in the bare
GAN architecture requires that we force redu-
plication and presence of
in the output
simultaneously. To identify which latent variables
correspond to the two properties, we use the same
technique as described in Section 4. We generate
and annotate 500 outputs of the Generator net-
work with randomly sampled latent variables. We
[s]
annotate the presence of [s] and the presence of
reduplication. The annotations are fit to a Lasso
logistic regression (as in Section 4.2): Presence
of reduplication or [s] are the dependent vari-
ables and each of the 100 latent z-variables are the
independent predictors. Lambda values were com-
puted with 10-fold cross validation. Regression
estimates are given in Figure 5.
The plots illustrate a steep drop in regression
estimates between the few latent variables with the
highest estimates and the rest of the latent space.
In fact, in both models, one or two variables per
model emerge with substantially higher regression
estimates: z91 and z5 when the dependent variable
is PRESENCE OF REDUPLICATION and z17 when the
dependent variable is PRESENCE OF [s] in the output.
We can assume the Generator network uses these
two variables to encode presence of reduplication
and [s], respectively.
It has been argued in Beguˇs (2020) that GANs
learn to encode phonetic and phonological repre-
sentations with a subset of latent variables. The
discretized representation of continuous phonetic
properties in the latent space appears even more
radical in the present case. For example, in Beguˇs
(2020), presence of [s] as a sound in the output
is represented by at least seven latent variables,
each of which likely controls different spectral
properties of the frication noise. In the present
experiment, the Generator appears to learn to en-
code presence of [s] with a single latent variable,
as is suggested by a steep drop of regression
estimates after the first variables with the high-
est estimates. For a generative test showing that
1189
regression estimates correlate to actual rates of
a given property in generated data, see Beguˇs
(2020). Such near-categorical cutoff is likely a
consequence of the training data in the present
case being considerably less variable compared to
TIMIT (used for training in Beguˇs, 2020). The
network also represents an identity-based pro-
cess, reduplication, with only two latent variables
and features a substantial drop in regression esti-
mates after these two variables. This discretized
representation thus emerges even without the re-
quirement of the Generator to output informative
data.
In the replication experiment too, the Generator
network outputs reduplicated forms for unob-
served data when both reduplication and [s] are
forced in the output via latent space manipula-
tion, but significantly less so than in the ciwGAN
architecture. When z91 (forcing reduplication) and
z17 (forcing [s] in the output) are set to value −8.5,
a higher level compared to the generated samples
in the ciwGAN architecture (7 and 7.25), the net-
work outputs only one reduplicated form with
[s]-reduplication out of 100 generated outputs. By
comparison, the proportion of the [s]-reduplication
in the ciwGAN architecture is 33/100 – a sig-
nificantly higher ratio (odds ratio = 48.1, p <
0.0001; Fisher Exact Test). When z5 (forcing
reduplication) is set to −9.25 and z17 (forcing [s]
in the output) to −9.0, the proportion of redu-
plicated [s]-items is slightly higher (4/100), but
still significantly lower than in the ciwGAN ar-
chitecture (odds ratio = 11.7, p < 0.0001; Fisher
Exact Test). Despite these lower proportions of
reduplicated [s] in the output, the bare GAN net-
work nevertheless extends reduplication on novel
unobserved data. Figure 4 illustrates an exam-
ple of a reduplicated [s]-item from the Generator
network trained in the bare GAN architecture:
[s@"siôi]. The spectrogram reveals a clear period of
frication noise characteristic of an [s], followed by
a reduplicative vowel period, followed by another
period of frication.
6 Discussion
We perform four generative tests to model learning
of reduplication in deep convolutional networks:
(i) a test of proportion of outputs when latent
codes are manipulated to marginal values, (ii) a
test of interpolating latent variables, (iii) a test of
reduplication on unobserved data in the ciwGAN
architecture, and (iv) a replication test of redupli-
cation on unobserved data in the bare WaveGAN
architecture. All four tests suggest that deep con-
volutional networks learn a simple identity-based
pattern in speech called reduplication, that is, a
process that copies some phonological material
to express new meaning. The ciwGAN network
learns to encode a meaningful representation—
presence of reduplication into its latent codes.
There is a near one-to-one correspondence be-
tween the two latent codes c1 and c2 and redupli-
cation. By interpolating latent codes, we cause the
bare form to gradually turn into a reduplicated
form with no other major changes in the output
in the majority of cases. These results are close to
what would be considered appearance of symbolic
computation or algebraic rules.
Additional evidence that an approximation of
symbolic computation emerges comes from the
bare GAN experiment: There is a substantial drop
in regression estimates after the first one or two
latent variables with highest regression estimates,
suggesting that even without the requirement to
produce informative data, the network discretizes
the continuous and highly variable phonetic fea-
ture (presence of reduplication) and uses a small
subset of the latent space to represent this morpho-
phonological property.
Finally, we can force the Generator to output
reduplication at nearly categorical levels. When
latent codes are set to marginal levels outside of
training range (e.g., to [5, 0] or [0, 5]), the outputs
are almost categorically unreduplicated or redu-
plicated (at 98% for [5, 0]). Beguˇs (2021a) shows
that even higher values (e.g., 15) result in perfor-
mance at 100% for a subset of variables. Not all
aspects of the models in this paper are categorical
(e.g., interpolation of latent codes does not always
change an unreduplicated to a reduplicated form
without other major changes). Improving perfor-
mance on this particular task is left for future
work. Inability to derive categorical processes has
long been an argument against the connectionist
approaches to language modeling. The results of
this experiments add to the work suggesting that
manipulating variables to extreme marginal values
results in near categorical or categorical outputs
(depending on the value) of a desired property
(Beguˇs, 2020; Beguˇs, 2021a).
In sum, three properties of rule-like symbolic rep-
resentations emerge in deep convolutional net-
work tested here: discretized representations, the
1190
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
2
1
1
9
7
1
8
1
4
/
/
t
l
a
c
_
a
_
0
0
4
2
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
ability to generate desired property by manip-
ulating a small number of variables, and near
categoricity for a subset of representations. These
symbolic-like outcomes are facilitated by two in-
ductive biases: the binary nature of latent codes
and the requirement on the Generator to output
informative data (forced by the Q-network). At
least a subset of these properties also emerges in
the bare WaveGAN architecture that lacks these
biases, but at a reduced performance.
Encoding an identity-based pattern as a mean-
ingful representation in the latent space emerges in
a completely unsupervised manner in the ciwGAN
architecture—only from the requirement that the
Generator output informative data. Reduplicated
and unreduplicated forms are never paired in the
training data. The network is fed bare and redupli-
cated forms randomly. This unsupervised training
approximates conditions in language acquisition
(for hearing learners): The human language learner
needs to represent reduplication and to pair bare
and reduplicated forms from raw unlabeled acous-
tic data. The ciwGAN learns to group reduplicated
and unreduplicated forms and assign a unique rep-
resentation to the process of reduplication. In fact,
the one-hot vector (c1 and c2) that the Generator
learns to associate with reduplication in training
can be modeled as a representation of the unique
meaning/function that reduplication adds, in line
with an approach to represent unique semantics
with one-hot vectors (e.g., in Steinert-Threlkeld
and Szymanik, 2020).
The paper also argues that deep convolutional
networks can learn a simple identity-based pattern
(copying) from raw continuous data and extend
the pattern to novel unobserved data. While the
network was not trained on reduplicated items that
start with an [s], we were able to elicit reduplica-
tion in the output following a technique proposed
in Beguˇs (2020). First, we identify variables that
correspond to some phonetic/phonological repre-
sentation such as presence of [s]. We argue that
setting single variables well above training range
can reveal the underlying value for each latent
variable and force the desired property in the
output. We can thus force both [s] and redupli-
cation in the output simultaneously. For example,
the network outputs [s@siju] if we force both
reduplication and [s] in the output; however,
it never sees [s@siju] in the training data—only
[siju] and other reduplicated forms, none of which
included an [s].
Thus, these experiments again confirm that the
network uses individual latent variables to rep-
resent linguistically meaningful representations
(Beguˇs, 2020; Beguˇs, 2021a). Setting these indi-
vidual variables to values well above the training
interval reveals their underlying values. By manip-
ulating these individual variables, we can explore
how the representations are learned as well as how
interactions between different variables work (for
example, between the representation of redupli-
cation and presence of [s]). The results of this
study suggest that the deep convolutional network
is not only capable of encoding different phonetic
properties in individual latent variables, but also
processes as abstract as copying or reduplication.
One of the advantages of probing learning in
deep convolutional neural networks on speech
data trained with GANs is that the innovative out-
puts violate training data in structured and highly
informative ways. The innovative outputs with
reduplication of [s]-initial forms such as [s@siju]
can be directly paralleled to acoustic outputs read
by L1 speaker of American English that were
absent from the training data. Acoustic analysis
shows a high degree of similarity between the
generated reduplicated forms and human record-
ings, meaning that the network learns to output
novel data that are linguistically interpretable and
resemble human speech processes even though
they are absent from the training data. Thus, the
results of the experiments have implications for
cognitive models of speech acquisition. It appears
that one of the processes that has long been held as
a hallmark of symbolic computation in language,
reduplication, can emerge in deep convolutional
network without language-specific components in
the model even when they are trained on raw
acoustic inputs.
The present paper tests a simple partial redu-
plicative pattern where only CV is copied and
appears before the base item. This is perhaps
computationally the simplest reduplicative pat-
tern. The training data are also highly controlled
and recorded by a single speaker. We can use
the well-understood identity-based patterns in
speech with various degrees of complexity (longer
reduplication, embedding into non-reduplicative
patterns) to further test how inductive biases and
hyperparameter/architecture choices interact with
learning in deep convolutional networks. Finally,
learning biases in the ciwGAN model can be (su-
perficially) compared to learning biases in human
1191
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
2
1
1
9
7
1
8
1
4
/
/
t
l
a
c
_
a
_
0
0
4
2
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
subjects in future work. This paper suggests that
the Generator provides informative outputs even
if trained on comparatively small data sets (for
a similar conclusion for other processes, see
Beguˇs, 2021b). This means we can use the same
training data to probe learning in CNNs and in
human artificial grammar learning experiments
(for a methodology, see Beguˇs, 2021b). Although
these comparisons are necessarily superficial at
this point, they can provide insights into com-
mon learning biases between human learners and
computational models.
Acknowledgments
This work was supported by a grant to new fac-
ulty at the University of Washington. I would like
to thank Ella Deaton for recording and prepar-
ing stimuli as well as anonymous reviewers and
the Action Editor for useful comments on earlier
versions of this paper.
References
Ben Adlam, Charles Weill, and Amol Kapoor.
2019. Investigating under and overfitting in
Wasserstein Generative Adversarial Networks.
In ICML Understanding and Improving Gener-
alization in Deep Learning Workshop (2019).
arXiv 1910.14137v1.
Raquel G. Alhama and Willem H. Zuidema.
2018. Pre-wiring and pre-training: What does
a neural network need to learn truly general
identity rules? Journal of Artificial Intelligence
Research, 61:927–946. https://doi.org
/10.1613/jair.1.11197
Martin Arjovsky, Soumith Chintala, and L´eon
Bottou. 2017. Wasserstein Generative Adver-
sarial Networks. In Proceedings of the 34th
International Conference on Machine Learn-
ing, volume 70 of Proceedings of Machine
Learning Research, pages 214–223, Interna-
tional Convention Centre, Sydney, Australia.
PMLR.
Alexei Baevski, Steffen Schneider, and Michael
Auli. 2020. vq-wav2vec: Self-supervised learn-
In
ing of discrete speech representations.
International Conference on Learning Repre-
sentations, pages 1–12.
Gaˇsper Beguˇs. 2021a. Ciwgan and fiwgan: Encod-
ing information in acoustic data to model lexi-
cal learning with Generative Adversarial Networks.
Neural Networks, 139:305–325. https://doi
.org/10.1016/j.neunet.2021.03.017
Gaˇsper Beguˇs. 2021b. Local and non-local de-
pendency learning and emergence of rule-like
representations in speech data by Deep Con-
volutional Generative Adversarial Networks.
Computer Speech & Language, page 101244.
https://doi.org/10.1016/j.csl.2021
.101244
Gaˇsper Beguˇs. 2020. Generative adversarial pho-
nology: Modeling unsupervised phonetic and
learning with neural networks.
phonological
Frontiers
Intelligence, 3:44.
https://doi.org/10.3389/frai.2020
.00044
in Artificial
Iris Berent. 2013. The phonological mind. Trends
in Cognitive Sciences, 17(7):319–327. https://
doi.org/10.1016/j.tics.2013.05.004
Paul Boersma and David Weenink. 2015. Praat:
Doing phonetics by computer [computer pro-
gram]. version 5.4.06. Retrieved 21 February
2015 from http://www.praat.org/.
Simone Brugiapaglia, Matthew Liu, and Paul
Tupper. 2020. Generalizing outside the training
set: When can neural networks learn identity ef-
fects? ArXiv preprint https://arxiv.org
/abs/2005.04330.
Xi Chen, Yan Duan, Rein Houthooft, John
Schulman, Ilya Sutskever, and Pieter Abbeel.
2016. InfoGAN: Interpretable representation
learning by information maximizing Genera-
tive Adversarial Nets. Daniel D. Lee, Masashi
Sugiyama, Ulrike von Luxburg, Isabelle Guyon,
and Roman Garnett, editors, Advances in
Neural Information Processing Systems 29,
pages 2172–2180. Curran Associates, Inc.
Jan Chorowski, Ron J. Weiss, Samy Bengio,
and A¨aron van den Oord. 2019. Unsupervised
speech representation learning using WaveNet
IEEE/ACM Transactions on
autoencoders.
Audio, Speech, and Language Processing,
27(12):2041–2053. https://doi.org/10
.1109/TASLP.2019.2938863
1192
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
2
1
1
9
7
1
8
1
4
/
/
t
l
a
c
_
a
_
0
0
4
2
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Yu-An Chung, Chao-Chung Wu, Chia-Hao Shen,
Hung-Yi Lee, and Lin-Shan Lee. 2016. Audio
word2vec: Unsupervised learning of audio
segment
representations using sequence-to-
sequence autoencoder. In Interspeech 2016,
pages 765–769. https://doi.org/10
.21437/Interspeech.2016-82
Hossep Dolatian and Jeffrey Heinz. 2018. Modeling
reduplication with 2-way finite-state transduc-
ers. In Proceedings of
the Fifteenth Work-
shop on Computational Research in Phonetics,
Phonology, and Morphology, pages 66–77,
Brussels, Belgium. Association for Computa-
tional Linguistics. https://doi.org/10
.18653/v1/W18-5807
Hossep Dolatian and Jeffrey Heinz. 2020. Com-
puting and classifying reduplication with 2-way
finite-state transducers. Journal of Language
8(1):179–250. https://doi
Modelling,
.org/10.15398/jlm.v8i1.245
Chris Donahue, Julian J. McAuley, and Miller S.
Puckette. 2019. Adversarial audio synthesis.
In 7th International Conference on Learning
Representations, ICLR 2019, New Orleans,
LA, USA, May 6-9, 2019. OpenReview.net,
https://openreview.net/forum?id
=ByMVTsR5KQ
Ewan Dunbar, Robin Algayres, Julien Karadayi,
Mathieu Bernard, Juan Benjumea, Xuan-Nga
Cao, Lucie Miskic, Charlotte Dugrain, Lucas
Ondel, Alan W. Black, Laurent Besacier,
Sakriani Sakti, and Emmanuel Dupoux. 2019.
The zero resource speech challenge 2019: TTS
without T. In Proceedings of Interspeech 2019,
pages 1088–1092.
Ewan Dunbar, Xuan Nga Cao, Juan Benjumea,
Julien Karadayi, Mathieu Bernard, Laurent
Besacier, Xavier Anguera, and Emmanuel
Dupoux. 2017. The zero resource speech
In 2017 IEEE Automatic
challenge 2017.
Speech Recognition and Understanding Work-
shop (ASRU), pages 323–330. https://doi
.org/10.1109/ASRU.2017.8268953
Ewan Dunbar, Julien Karadayi, Mathieu Bernard,
Xuan-Nga Cao, Robin Algayres, Lucas
Ondel, Laurent Besacier, Sakriani Sakti, and
Emmanuel Dupoux. 2020. The zero resource
speech challenge 2020: Discovering discrete
subword and word units. Interspeech 2020.
https://doi.org/10.21437/Interspeech
.2020-2743
Michael G. Dyer. 1991. Connectionism versus sym-
In Terence
bolism in high-level cognition.
Horgan and John Tienson, editors, Connection-
ism and the Philosophy of Mind, pages 382–416.
Springer Netherlands, Dordrecht. https://
doi.org/10.1007/978-94-011-3524-5 17
Ryan Eloff, Andr´e Nortje, Benjamin van Niekerk,
Avashna Govender, Leanne Nortje, Arnu
der
Pretorius, Elan Biljon, Ewald
Westhuizen, Lisa Staden, and Herman Kamper.
2019. Unsupervised acoustic unit discovery for
speech synthesis using discrete latent-variable
neural networks. In Proceedings of Interspeech
2019, pages 1103–1107. https://doi.org
/10.21437/Interspeech.2019-1518
van
Ansgar D. Endress, Ghislaine Dehaene-Lambertz,
and Jacques Mehler. 2007. Perceptual con-
straints and the learnability of simple grammars.
105(3):577–614. https://doi
Cognition,
.org/10.1016/j.cognition.2006.12
.014
Jerry A. Fodor and Zenon W. Pylyshyn. 1988.
Connectionism and cognitive architecture: A
critical analysis. Cognition, 28(1):3–71. https://
doi.org/10.1016/0010-0277(88)90031-5
Michael Gasser. 1993. Learning words in time:
Towards a modular connectionist account of the
acquisition of receptive morphology. Indiana
University, Bloomington.
Ian Goodfellow, Jean Pouget-Abadie, Mehdi
Mirza, Bing Xu, David Warde-Farley, Sherjil
Ozair, Aaron Courville, and Yoshua Bengio.
2014. Generative adversarial nets. Zoubin
Ghahramani, Max Welling, Corinna Cortes,
Neil D. Lawrence, and Kilian Q. Weinberger,
editors, Advances in Neural Information Pro-
cessing Systems 27, pages 2672–2680. Curran
Associates, Inc.
Bruce Hayes. 2009.
Introductory Phonology.
Wiley-Blackwell, Malden, MA.
Sharon Inkelas and Cheryl Zoll. 2005. Redupli-
cation: Doubling in Morphology. Cambridge
Studies in Linguistics. Cambridge University
Press.
1193
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
2
1
1
9
7
1
8
1
4
/
/
t
l
a
c
_
a
_
0
0
4
2
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Herman Kamper, Aren Jansen, Simon King,
and Sharon Goldwater. 2014. Unsupervised
lexical clustering of
speech segments us-
ing fixed-dimensional acoustic embeddings. In
2014 IEEE Spoken Language Technology Work-
shop (SLT), pages 100–105. https://doi
.org/10.1109/SLT.2014.7078557
Chia-ying Lee, Timothy J. O’Donnell, and
James Glass. 2015. Unsupervised lexicon dis-
covery from acoustic input. Transactions of
the Association for Computational Linguistics,
3:389–403.
Christopher D. Manning. 2003. Probabilistic syn-
tax, Rens Bod, Jennifer Hay, and Stefanie
Jannedy, editors, Probabilistic Linguistics,
pages 289–342. MIT Press, Cambridge, MA.
Gary F. Marcus. 2001. The Algebraic Mind: Inte-
grating Connectionism and Cognitive Science.
MIT Press. https://doi.org/10.1126
/science.283.5398.77
Gary F. Marcus, Sujith Vijayan, Shoba Bandi
Rao, and Peter M. Vishton. 1999. Rule
learning by seven-month-old infants. Science,
283(5398):77–80.
Yoshihiro Maruyama. 2021. Symbolic and statis-
tical theories of cognition: Towards integrated
artificial intelligence. In Software Engineering
and Formal Methods. SEFM 2020 Collocated
Workshops, pages 129–146, Cham, Springer In-
ternational Publishing. https://doi.org
/10.1007/978-3-030-67220-1_11
James L. McClelland and David C. Plaut. 1999.
Does generalization in infant learning implicate
abstract algebra-like rules? Trends in Cognitive
Sciences, 3(5):166–168. https://doi.org
/10.1016/S1364-6613(99)01320-0
James L. McClelland, David E. Rumelhart,
and PDP Research Group. 1986. Parallel
Distributed Processing: Explorations in the Mi-
crostructure of Cognition, volume 2. MIT Press,
Cambridge, MA.
Marvin L. Minsky. 1991. Logical versus analog-
ical or symbolic versus connectionist or neat
versus scruffy. AI Magazine, 12(2):34.
Max Nelson, Hossep Dolatian, Jonathan Rawski,
and Brandon Prickett. 2020. Probing RNN
encoder-decoder generalization of subregular
functions using reduplication. Proceedings of
the Society for Computation in Linguistics,
3(1):31–42.
Benjamin van Niekerk, Leanne Nortje, and
Herman Kamper. 2020. Vector-quantized neu-
ral networks for acoustic unit discovery in the
ZeroSpeech 2020 challenge. Interspeech 2020.
https://doi.org/10.21437/Interspeech
.2020-1693
Brandon Prickett, Aaron Traylor, and Joe Pater.
2018. Seq2Seq models with dropout can learn
In Proceedings
generalizable reduplication.
of the Fifteenth Workshop on Computational
Research in Phonetics, Phonology, and Mor-
phology, pages 93–100, Brussels, Belgium.
Association for Computational Linguistics.
https://doi.org/10.18653/v1/W18-5810
Alec Radford, Luke Metz, and Soumith Chintala.
2016. Unsupervised representation learning
with deep convolutional generative adversar-
ial networks. In 4th International Conference
on Learning Representations, ICLR 2016, San
Juan, Puerto Rico, May 2-4, 2016. arXiv
1511.06434v2.
Okko R¨as¨anen, Tasha Nagamine, and Nima
Mesgarani. 2016. Analyzing distributional
learning of phonemic categories in unsuper-
vised deep neural networks. CogSci 2016,
2016:1757–1762.
Sergey Rodionov. 2018. info-wgan-gp. GitHub
repository. https://github.com/singnet
/semantic-vision/tree/master/experiments
/concept learning/gans/info-wgan-gp. Last
accessed on July 16, 2021.
David E. Rumelhart,
James L. McClelland,
and PDP Research Group. 1986. Parallel
Distributed Processing: Explorations in the
Microstructure of Cognition, volume 1. MIT
Press, Cambridge, MA. https://doi.org
/10.7551/mitpress/5236.001.0001
Walter
J. Savitch. 1989. A formal model
for context-free languages augmented with
Linguistics,
reduplication.
15(4):250–261.
Computational
Cory Shain and Micha Elsner. 2019. Measuring
the perceptual availability of phonological
features during language acquisition using
1194
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
2
1
1
9
7
1
8
1
4
/
/
t
l
a
c
_
a
_
0
0
4
2
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
unsupervised binary stochastic autoencoders.
In Proceedings of the 2019 Conference of the
North American Chapter of the Association for
Computational Linguistics: Human Language
Technologies, Volume 1 (Long and Short Pa-
pers), pages 69–85, Minneapolis, Minnesota.
Association for Computational Linguistics.
https://doi.org/10.18653/v1/N19
-1007
Noah Simon, Jerome Friedman, Trevor Hastie,
and Rob Tibshirani. 2011. Regularization paths
for Cox’s proportional hazards model via
coordinate descent. Journal of Statistical Soft-
ware, 39(5):1–13. https://doi.org/10
.18637/jss.v039.i05
Shane Steinert-Threlkeld and Jakub Szymanik.
learning explains semantic
2020. Ease of
universals. Cognition, 195:104076. https://
doi.org/10.1016/j.cognition.2019.104076
Suzanne Urbanczyk. 2017. Phonological and mor-
phological aspects of reduplication. In Oxford
Research Encyclopedia of Linguistics. Oxford
University Press. https://doi.org/10.1093
/acrefore/9780199384655.013.80
Colin Wilson. 2018. Modeling morphological af-
fixation with interpretable recurrent networks:
Sequential rebinding controlled by hierarchical
attention. In CogSci 2018, pages 2693–2698.
Colin Wilson. 2020. Re(current) reduplication:
Interpretable neural network models of morpho-
logical copying. In Proceedings of the Society
for Computation in Linguistics (SCiL) 2020,
volume 2, pages 379–380.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
2
1
1
9
7
1
8
1
4
/
/
t
l
a
c
_
a
_
0
0
4
2
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1195
A Appendix
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
2
1
1
9
7
1
8
1
4
/
/
t
l
a
c
_
a
_
0
0
4
2
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6: Waveforms and spectrgrograms (0-5000 Hz) of the 25 reduplicated-unreduplicated form pairs annotated
as involving no other major changes than the presence of the reduplicative syllable. Reduplicated outputs are
on the left; unreduplicated outputs on the right. Values of the latent code are listed below each output; all other
98 z-variables are kept constant across the two pairs. In two cases involving a nasal C1, it is challenging to
distinguish between very short remnants of the vocalic period of reduplication and periodic vibration of the nasal
(the difference between reduplicated and unreduplicated form), but there is a clear contrast between the two forms
of the pair.
1196