Identifying Patterns from
One-Rule-Firing Cellular Automata
Jae Kyun Shin*
Yeungnam University
Keywords
Cellular automata, one-rule firing, flower
patterns, complexity
Abstract A new firing scheme for cellular automata in which only one
rule is fired at a time produces myriad patterns. In addition to geometric
patterns, natural patterns such as flowers and snow crystals were also
generated. This study proposes an efficient method identifying the
patterns using a minimal number of digits. Complexity of the generated
patterns is discussed in terms of the shapes and colors of the patterns.
1 Introduction
Since its introduction by von Neumann [11], the cellular automaton (CA) has been applied to various
fields, including physics and computer science. Wolframʼs work on complexity classification [17] and
Conwayʼs game of Life [1] are examples of famous works involving the CA. In the present study,
the CA is considered a generic mechanism for a class of symmetric patterns in the 2D plane. In particular,
a new rule-firing scheme that causes the emergence of diverse patterns, which are unprecedented in
previous CA literature, is proposed.
In most CAs, the rules are applied synchronously on all cells in the system. However, several asyn-
chronous updating schemes have been reported in previous literature.
The simplest such scheme is the one-cell updating scheme, in which only one cell is updated at a time
[7]. This is comparable to blockwise asynchronous updating in which the whole system is divided into
several blocks and different firing schemes are applied from block to block, such that inter-block up-
dating is asynchronous and intra-block updating is synchronous [15, 16]. Because updating within the
block is synchronous, blockwise updating could not be considered genuinely asynchronous.
The probabilistic CA also involves a kind of asynchronous updating, in which the rules fire with some
probability [8]. In some cases, asynchronous updating generated natural patterns, such as the color
patterns of mollusks. Accordingly, a proposal followed that asynchrony is intrinsic to living systems
[6]. However, natural patterns resulting from such CAs are limited to a few types. One such type is
the snow crystal pattern [2, 9, 12]. Packardʼs snowflake is the simplest pattern within the snow crystal
category [9], for which an integer-valued hexagonal cell is used. Real-valued CAs, also known as fuzzy
CAs, demonstrated the power of the CA as a means to generate more diverse and complex snow crystal
patterns [2, 12]. However, the patterns were limited to snow crystals.
The present article suggests a method of partial firing of CA rules on 2D hexagonal cells. The firing
scheme is similar to that of the blockwise asynchronous CA. The key difference is how the updating block
is defined. In the present study, the block is defined in terms of the neighborhood conditions rather
than the spatial location of the cells. In addition, an efficient method of identifying patterns is proposed,
so that any pattern generated has its own identification number, which can be decoded later to restore
the pattern.
* School of Mechanical Engineering, Yeungnam University, Kyongsan, 712-749, South Korea. E-mail: jkshin@yu.ac.kr
© 2011 Massachusetts Institute of Technology
Artificial Life 17: 21–32 (2011)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
1
2
1
1
6
6
2
7
5
6
a
r
t
l
/
_
a
_
0
0
0
1
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
J. K. Shin
2 Model
Identifying Patterns from One-Rule-Firing Cellular Automata
The CA system in the present study is composed of a hexagonal array of cells in the 2D plane. An
occupied cell possesses values, or color codes, ranging from 1 to m. Each occupied cell is called an
element. For convenience, an empty cell is assigned a color code value of 0. Thus, a cell can be in any
of the M = m + 1 possible cell states. Once defined, an element does not change its value or return to
being an empty cell. A cell has a set of neighborhood cells composed of its six nearest cells. The six
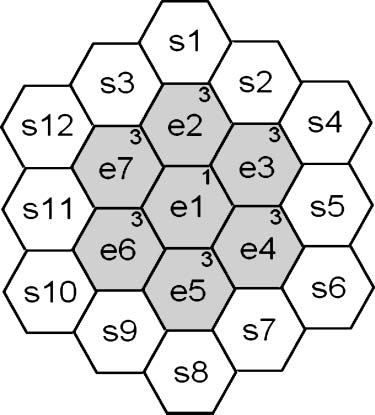
neighborhood cells are designated as b1, b2, … , b6, as shown in Figure 1. The neighborhood cells are
always numbered clockwise starting from the top center cell. An empty cell is called a surface cell if it has
at least one element in its neighborhood. The numbering of the elements and of the surface cells is
important for the present study and will be discussed in further detail later.
The CA rule is applied in a synchronous manner to only a few of the surface cells. A rule determines
the value (or color code) of a surface cell at the next time step as a function of the states of the neighbor-
ing cells at the present time step. In general, the number of possible states for the six neighboring cells
will be M6. A rule set has M6 rules, each of them mapping the states of the neighboring cells to a value.
Because the number of rules in a rule set increases vary fast with M, it is not easy to express the rules in
compact form, even for small values of M. For example, when M = 7, a rule set has 76 = 117,649 rules. In
order to describe each rule set, we need 117,649 digits, where each digit represents a rule value. This study
investigates a manner in which we can overcome this difficulty and conveniently specify a rule set.
Starting from a single element at time step 0, the system evolves into a complex pattern, applying the
rules repeatedly to the surface cells. One of the main purposes of the present article to observe the
patterns that emerge with the application of the rules.
3 One-Rule-Firing Scheme
The six-color problem in which m = 6 and M = 7 is the only problem considered in the present study,
unless stated otherwise. Because of the very large number of possible rule sets, the present study will be
limited to a certain category of rules. In particular, symmetry-preserving rule sets are considered. The
key idea of the present study is to fire the rules selectively. In typical CAs with synchronous updating,
the rules are applied to all of the candidate cells at a given time step. In the present article, only one rule is
fired in a time step. Accordingly, the process of choosing the single rule that is to be fired should be
clearly defined.
Rules are defined in terms of the states of the six neighboring cells. A state of the six neighbors will
be represented with a six-digit number such as 335012, where each digit represents the state (color code)
of the neighboring elements and/or empty cells. In general, a different rule can be specified for each of
the different neighborhood states. However, rotational symmetry is assumed in the present study: Any
Figure 1. Six neighbors of an element.
22
Artificial Life Volume 17, Number 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
1
2
1
1
6
6
2
7
5
6
a
r
t
l
/
_
a
_
0
0
0
1
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
J. K. Shin
Identifying Patterns from One-Rule-Firing Cellular Automata
cyclic rotation of a given set of six represents the same state. With rotational symmetry implied, the
number of rules in a rule set is reduced to 19,684. In this case, a rule set can be represented with
19,684 digits. An example of it might look like 110346…6001 (19,684 digits), keeping in mind that
the first digit is for the rule value of the first rule, and so on. For convenience, the neighborhood states
will be used to denote the rule number. If the neighborhood state of a surface cell is 001234 or 234001,
for example, then the rule number to be applied will be 1234.
A single seed element at time step 0 will be used as an example to demonstrate the key concepts of this
present study. At time step 0, only one element, e1, exists in the system. Throughout the present study,
assume that the seed element e1 possesses a color code of 1. This will be represented as e1 = 1. The
element e1 has six neighbors. Each of the six neighbor cells is currently a surface cell and has the same
neighborhood state, equivalent to 000001. The rule number to be applied will simply be 1. Assume, for
example, the rule value for rule 1 is 3, or rule(1) = 3. Applying the rule to the six surface cells will end
iteration 1. Regardless of the synchronous updating scheme, the order of the updating should be carefully
monitored, solely for the purpose of determining the order of the newly generated elements. The updating
should start from surface cell 1 in this case, or from the lowest numbered surface cells in general. After
iteration 1, Figure 2 is obtained. Elements are denoted by shaded cells in which the identifying numbers
are marked at the centers of the cells. They are numbered according to birth order. The small number in
each element cell represents the color of the element. The color (designated as 3) of e2 through e7 was
determined from the application of rule(1) = 3. After the first iteration, the system contained a total of
12 surface cells, as shown in Figure 2. The surface cells are numbered elementwise first, and then neigh-
borhoodwise. In other words, the surface cells contacting the lowest-numbered elements should be
numbered first. In Figure 2, the three surface cells S1, S2, and S3 neighbor e2, possessing lower surface
cell numbers than the other surface cells. Each of these three surface cells is located on the b1, b2, and b6
neighborhood positions of element e2, as defined in Figure 1. Assigning a lower surface cell number to a
lower neighborhood position, we get S1, S2, and S3, exactly as shown in Figure 2. S3 is observed again
when handling the surface cells contacting element e7. However, since S3 was previously numbered, it is
skipped when approaching element e7. Surface cell numbering is scratched after each iteration, and restarts
in every iteration. Once an element number is chosen, it is maintained throughout later time steps.
In the subsequent process, the CA rules are applied to the 12 surface cells of the present time step.
Table 1 illustrates the details. The rules are applied to the surface cells depending on their neighborhood
status. For example, surface cells S1, S4, S6, S8, S10, and S12 each possess a neighborhood status
Figure 2. Numbering of elements and surface cells.
Artificial Life Volume 17, Number 1
23
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
1
2
1
1
6
6
2
7
5
6
a
r
t
l
/
_
a
_
0
0
0
1
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
J. K. Shin
Identifying Patterns from One-Rule-Firing Cellular Automata
Table 1. Application of rules, assuming r(1) = 3, r(3) = 4, r(33) = 6.
Iteration
Surface cell
Neighborhood code
Valuea
Fired
1
2
S1
S2
.
..
S6
S1
S2
S3
S4
.
..
S9
S10
S11
S12
1
1
.
..
1
3
33
33
3
.
..
33
3
33
3
Y
Y
.
..
Y
Y
Y
.
..
Y
Y
.
..
3
.
..
(6)b
4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
1
2
1
1
6
6
2
7
5
6
a
r
t
l
/
_
a
_
0
0
0
1
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
aMarked only when the rule first appears with backward counting of sur-
face cells.
bRule value is defined, but not fired, at least in present iteration.
equivalent to 000003, indicating that rule 3 should be applied to these cells. The neighborhood status for
the other cells, including S2, S3, …, S11, is equivalent to 000033, and rule 33 should be applied, if ever,
to these cells. The rule number and rule value that correspond to each of the surface cells are shown in
Table 1, columns 2 and 3. Two new rule values are assumed: rule(3) = 4 and rule(33) = 6. In a con-
ventional CA, the two rules 3 and 33 will be fired at time step 2, resulting in the potential generation of
twelve new elements.
However, the present study proposes a new variation, in which only one rule is fired in a given time
step. Among several easily conceived possible one-rule firing schemes, last-nonzero-rule firing is the
main scheme utilized here. Among the rules to be fired in a given time step, the last rule not possessing
a value of 0 was chosen. Here, the last refers to the surface cell number. For example, at iteration 2,
rules 3 and 33 were waiting to be fired. Of the two rules, rule 3 is the last rule of the time step, as it
is combined with the last surface element of the time step. Because the value (equal to 4) of rule 3 is not
zero, rule 3 was chosen to be fired at iteration 2. Rule 3 is the last nonzero rule in time step 2. Rule 33
is not fired in this time step, and the six surface cells S2, S3, S5, S7, S9, and S11 remain as empty cells
even after iteration 2. By applying rule 3, six new elements of color code 4 are generated at iteration 2.
The fired surface cells are marked in the last column of Table 1. The same process was already applied
in iteration 1. If a rule is ever fired, it proceeds from the lowest-numbered surface cells that could
be applied. The order of firing is important, as it determines the numbering of the newly generated
24
Artificial Life Volume 17, Number 1
J. K. Shin
Identifying Patterns from One-Rule-Firing Cellular Automata
elements, which, in turn, determines the numbering of the surface cells in the next time step. In the
fourth column of Table 1, the rule values are given when the rule is first considered to be fired through-
out an entire iteration. As seen before, some of those rules do not fire at the time step in which they first
appear. In actuality, rule 33 does not contribute to the system up to time step 2.
Continuing on with the process, we can easily imagine that different rule sets generate different pat-
terns. With 719,684 ≈ 9 × 1016,634 rule sets, we can predict that to be the number of patterns in the 2D
space of CA. On the other hand, every pattern that appears will have its own rule set, composed of
19,684 rules. Theoretically speaking, a pattern can be identified with its rule set. This means that we need
19,684 characters in order to identify a pattern, in which each character represents a rule value. When
the size of a rule set is sufficiently small, we can directly represent the rules with a manageable number of
characters. For example, in a one-dimensional space for a CA, a rule set can be identified by only three
digits [18]. But when the number of rules increases, it will be inconvenient to use a long sequence of
codes in order to identify a pattern. The present study demonstrates an efficient method that compen-
sates for this difficulty.
In conclusion, we can only list the rule values that were fired, as shown in the fourth column of Table 1.
For example, the sequence of rule values 34 and so forth can identify the pattern. It is unnecessary to
memorize the rule number for each rule value fired. The rule number is embedded in the pattern itself. The
sequence of the rule values will be called the F-code (for “code of fired rules”) for convenience.
However, one problem remains to be solved: How do we address the situation where the value of
the last rule is zero? For example, assume rule(3) = 0 in the example case given in Table 1. The case
is explained in Table 2. The first iteration is the same as before. But for the second iteration, because
Table 2. Application of rules, assuming r(1) = 3, r(3) = 0, r(33) = 6.
Iteration
Surface cell
Neighborhood code
Value
Fired
1
2
S1
S2
.
..
S6
S1
S2
S3
S4
.
..
S9
S10
S11
S12
1
1
.
..
1
3
33
33
3
.
..
33
3
33
3
Y
Y
.
..
Y
Y
Y
.
..
Y
Y
.
..
3
.
..
6
0
Artificial Life Volume 17, Number 1
25
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
1
2
1
1
6
6
2
7
5
6
a
r
t
l
/
_
a
_
0
0
0
1
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
J. K. Shin
Identifying Patterns from One-Rule-Firing Cellular Automata
the value for last rule is 0, we cannot fire it. Firing a rule possessing the value 0 does not alter the
patterns, and it is the same as doing nothing. So we skip the rule of value 0. For the case shown in
Table 2 at iteration 2, rule(33) = 6 is the last nonzero rule, which is then chosen as the rule to be
fired. In such a case, we can include the code 0 in the F-code so as to remember that the rule is not
fired on the last surface cell. As a result, the F-code will be 306 instead of 36, for the case shown in
Table 2. It should be noted that a rule already contributed to the F-code in an earlier time step does
not enter again in an F-code, even if it fires again in later time steps. In general, the length of the F-
code can increase with the time step. But the length should be far shorter than 19,684 in most cases.
We can identify a pattern with F-codes a few to a few hundred characters in length.
4 Example Patterns
Generating F-codes using the previous procedure is not difficult. For example, start with generating
a rule set at random. For clarity, a procedure for generating a pattern, or equivalently an F code, is
listed as follows:
Step 1. Choose a rule set composed of 19,684 rules.
Step 2. Choose a seed element.
Step 3.
Identify surface elements of the present time step, and order them elementwise first
and then neighborhoodwise.
Step 4. Apply the last nonzero rule to all the corresponding surface cells. Application of a rule
is simultaneous, but the ordering of newly added elements depends on the order of the
surface cell on which the element is generated.
Step 5.
If the last nonzero rule in step 4 is a new rule that has never been fired up to this time step,
update the F-code by concatenating the rule value (code) at the end of the present F-code.
Step 6. To continue the process, go to step 3.
As generalizations, we may consider different possibilities of rule sets for step 1. Step 2 can also
be generalized. In principle, any set of initial conditions is welcome. The initial conditions should
specify the spatial position(s) and color code(s) of the initial element(s), including their numbering.
It should be noted that the F-codes for two different initial conditions should not be compared
directly. We can consider different firing schemes for step 4. A different firing scheme indicates a
separate F-code system. The F-code scheme is quite general; however, the conditions under which
the F-code is generated must be thoroughly understood.
Because of the rotational symmetry imposed on the rules, all the patterns generated in this study
have a sixfold rotational symmetry about the center cell. Figure 3 illustrates the simplest forms found
during the present study. In particular, the shape shown in Figure 3a is the simplest pattern in which
the F-code retains the value 1, or F = 1. Only one rule, rule 1, with rule(1) = 1, is necessary to
generate this pattern. This pattern is well known as Packardʼs snowflake [9]. It is surprising that such
a complex shape can be generated with a single rule. But in actuality, this pattern is known to be
obtained when an element is added whenever a cell has only one neighborhood. This is implied by
F = 1. For convenience, we call this pattern F1.
For later discussion, consider the validity of an F-code. When we consider, for example, a ran-
domly generated code such as F = 120314, we soon find that the codes, except for the first appear-
ance of 1, are meaningless. When the first value of an F-code is 1, the pattern can grow infinitely
without consuming any other rules. Thus the code F = 1 is the only code that can start with color
code 1. In general, an arbitrary sequence of rule values is not worth its full length. From now on,
only the F-codes that are valid through their full length will be considered.
26
Artificial Life Volume 17, Number 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
1
2
1
1
6
6
2
7
5
6
a
r
t
l
/
_
a
_
0
0
0
1
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
J. K. Shin
Identifying Patterns from One-Rule-Firing Cellular Automata
Figure 3. Simple patterns: (a) F = 1, (b) F = 201, (c) F = 20222.
We can categorize the valid F-codes into two groups: finished and unfinished. A finished F code
signifies that additional codes are unnecessary in the continuation of the iteration to an arbitrary time
step. Finished F-codes can be further distinguished into two subgroups. In some, like the case in
which F is equivalent to 1 and 21, the patterns can grow infinitely with the given codes. On the other
hand, certain F-codes reach completion, because the patterns discontinue growth after some itera-
tion. This happens when all surface cells at a given time step are assigned to a rule (or rules) of value 0.
For example, for F = 200 and F = 320110132021010133031003122312101123103023 the pattern dies
at iterations 3 and 80, respectively.
Unfinished F-codes require more explanation. For example, F = 2032 is an unfinished F-code. If we
decode F = 2032, a new rule will be necessary after firing the last given code. If we supply a next code of
1, for example, then the F-code grows to F = 20321. This sequence may continue excessively. Un-
finished F-codes exist because the iterations are not continued infinitely. Theoretically, an unfinished
F-code cannot exist if the iteration is continued infinitely. This is because the maximum length of the
F-code is 19,684. If we consider all F-codes up to that maximum length, all F-codes should be finished.
However, it is more realistic to state that an F-code is unfinished up to a specified time step. In addition,
if an F code is not proven to be finished at the specified time step, it will also be taken as unfinished. The
finished and the unfinished codes will be distinguished in the following manner: A lowercase f signifies
an unfinished F-code, while an uppercase F designates a finished code. Thus, F = 2342 represents a
finished F-code, and f = 2032 represents an unfinished one.
A relatively small number of patterns were observed with short F-codes. We have already seen that
F = 1 is the only F-code of length one. Additionally, only one group of patterns exists for an F-code of
length 2: F = 22, 33, 44, 55, and 66 generates similar patterns to F1, but possesses two colors, indicating
different cell values. The number of colors used in the pattern can be counted simply by observing an
F-code. For example, F = 201 is generated using two rules, whose values are 2 and 1. This means that
F = 201 uses two colors. When counting the number of colors used, we should remember the initial
seed element, which has color code 1. Thus F = 22 is a two-color pattern, including the initial element.
Figure 3b shows the third simplest pattern, which has an F-code of length 3. The branches in Figure 3b
grow endlessly with the time step. Each of F = 201, 301, 401, 501, and 601 generates the same pattern
as shown in Figure 3b. The main observable difference among the aforementioned codes is the color
retained by each. Figure 3c shows a pattern with F = 20222.
All possible F-codes cannot be listed, but sample patterns can be easily generated using the afore-
mentioned method. The single-rule-firing scheme produces many interesting patterns. Figure 4 shows
a few examples. The patterns are shown according to increasing lengths of the F-codes (or f-codes).
Figure 4a illustrates a similar shape to F1, differing only in color. If we neglect the colors, we observe that
the shape of F1 repeatedly occurs whenever F-codes do not include 0. For example, F = 1, 22, 323,
2344, 32541, and 325462 result in the shape of F1. From an exhaustive simulation for all F-codes up
to length 7, the conclusion followed that the maximum length of F-codes not containing 0 is six. In
Artificial Life Volume 17, Number 1
27
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
1
2
1
1
6
6
2
7
5
6
a
r
t
l
/
_
a
_
0
0
0
1
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
J. K. Shin
Identifying Patterns from One-Rule-Firing Cellular Automata
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
1
2
1
1
6
6
2
7
5
6
a
r
t
l
/
_
a
_
0
0
0
1
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4. Miscellaneous patterns: (a) Multicolored F1, F = 264531, Iter = 91. (b) A snow crystal, F = 20212020, Iter = 61. (c)
A flower pattern, f = 530220402410633633421424631012641254064350520610000 (51 digits), Iter = 421. (d) Palm tree,
f = 6203203210253346253045601315350161554520132566153342200260605623524521546616555235110616445151-
60365425413323 (108 digits), Iter = 1221.
general, the maximum length of F-codes without 0 corresponds to the number of colors used in the
rule set. If an F-code contains a 0, the shape deviates from the F1 pattern, as observed in the patterns
of F = 201 and 20222 listed in Figure 3.
More diverse shapes are shown in Figure 4b–d. The length of an F-code can exceed 6 only when the
F-code includes a 0. The following is a brief explanation as to why F-codes not containing a 0 result in
the same shape: For codes not containing a 0, the rule always fires on the last surface cell in each time
step. But when a zero is assigned to the last surface cell, the rule is fired on a cell other than the last
surface cell. Subsequently, altering the firing location gives birth to diverse shapes. Thus, a necessary
condition for the shape deviation from the basic pattern of F1 is that the F-code should contain at least
one zero. However, the converse does not generally hold true. That is, instances are found in which the
F-code contained at least one 0 and still resulted in a shape the same as, or at least similar to, F1. The
pattern in Figure 4b has an F-code of length 8. This pattern resembles a snow crystal. Only two colors are
used in this case. The snow crystal patterns were observed frequently when only two colors were used
in the F-code. All three patterns shown in Figure 3 and the pattern in Figure 4b are generated with only
two colors. However, this does not mean that snow crystals cannot be obtained with multiple colors.
The length of an F-code measures the complexity of the corresponding patterns, indicating the num-
ber of rules used to generate the pattern. Conceptually, it is similar to Birkhoffʼs measure of the complex-
ity of an image, which is defined as the number of elements composing the image [5]. Because F-codes
of different lengths can yield the same shapes, we can conclude that color is one origin of the complexity.
28
Artificial Life Volume 17, Number 1
J. K. Shin
Identifying Patterns from One-Rule-Firing Cellular Automata
For example, the shape F1 is found to have a complexity of up to the number of colors used. On the
other hand, because long F-codes can be generated using only two colors, especially when 0 is included
in the F-code, we find that shape is another source of the complexity. With the combined contribution
of shape and color, a wide variety of complex patterns emerge. In Figure 4c,d, two patterns with long
f-codes are shown. For these two patterns, the length continually grows up to time steps 421 and 1221,
respectively. If we increase the time step, new rules will appear and commence to be fired. The last two
patterns shown in Figure 4 interestingly resemble flowers and plants, respectively. Purely geometric pat-
terns, such as snow crystals, and lifelike patterns can emerge under the same algorithm.
The aforementioned patterns sufficiently illustrate the effects of the one-rule firing scheme. If we use
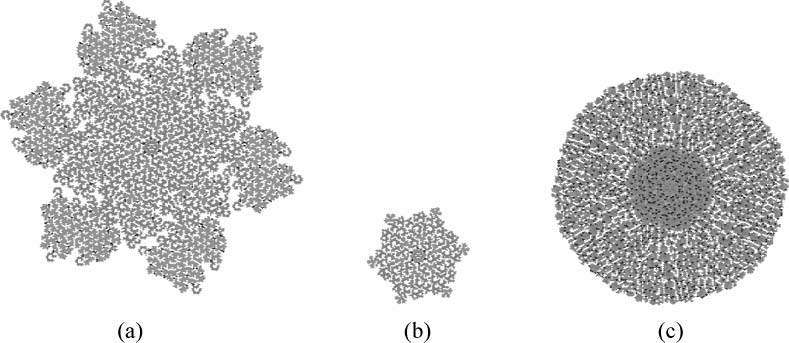
a conventional all-rule-firing scheme, the resulting patterns are quite different. In Figure 5, a comparison
is made between the patterns generated from the one-rule-firing and an all-rule-firing scheme. For this
comparison, a full set of 19,684 rules were generated first, and the iteration is processed as explained in
the present study. Figure 5a shows the resulting pattern from one-rule firing up to iteration 301. The
pattern in Figure 5b is the same up to iteration 91. Figure 5c is a pattern generated by firing all the rules
up to time step 91. In every time step, all the surface cells with nonzero rule values are fired. When all
the rules are fired, the pattern grows very rapidly. Roughly the same scale is maintained for these three
patterns in Figure 5. In most cases, the shape generated under the all-rule-firing scheme has one of the
two shapes. The shape of F1 appears most frequently under all-rule firing, but a circular shape as shown
in Figure 5c appears at times. This example clearly shows the magic of the one-rule firing strategy. By one-
rule firing, we can dig buried flowers out of a mud ball.
Among the patterns generated in the present study, flowerlike patterns are the most interesting, in
view of the clearly distinguishable characteristics that separate them from geometric patterns found in
the previous literature. The F-codes are reminiscent of genetic codes in biological systems. For example,
we can mutate F-codes to find variations of the original flower patterns. Figure 6 shows three flowers
in which the f-codes are the same except at a single location, differing only at the 20th location, which is
represented as X. The three patterns with X = 0, 1, and 5 possess similar shapes near the center. How-
ever, differences emerge as the pattern expands outward from the center. Additionally, two F-codes
could be crossed in order to find daughter flowers.
5 Discussion
The one-rule-firing scheme first provides a new dimension, shape, to the patterns that depended only on
the color of the all-rule firing scheme. It was a startling speculation that diverse shapes can result from
Figure 5. One-rule firing and all-rule firing: (a) f = 652040430032650204605024105 (27 digits), Iter = 301. (b) f =
6520404300326502046050 (22 digits), Iter = 91. (c) All-rule firing, Iter = 91.
Artificial Life Volume 17, Number 1
29
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
1
2
1
1
6
6
2
7
5
6
a
r
t
l
/
_
a
_
0
0
0
1
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
J. K. Shin
Identifying Patterns from One-Rule-Firing Cellular Automata
Figure 6. Cloning the flowers: f = 4501430233150000020X006500620055, Iter = 211: (a) X = 0, (b) X = 1, (c) X = 5.
differential growth along different directions. The partial rule-firing scheme realizes the concept of
differential growth, and (not surprisingly) numerous patterns were discovered, including geometric pat-
terns (snow crystals) and flowerlike patterns. Without resorting to the complex rules of the fuzzy cellular
automaton [2, 11], the one-rule-firing scheme successfully generated snow crystals with a conventional
discrete CA. The natural patterns generated in the present study are reminiscent of the L-system as a
classic rule-based system to represent natural patterns [10, 14]. One interesting aspect of the one-rule-
firing CA is in its diversity: Both natural and non-natural patterns can be represented under the same
scheme. Another notable CA system comparable to the present one-rule CA may be the mobile cellular
automaton [18], in which the rule is updated only in one active cell. It is called mobile because the location
of the active cell moves from iteration to iteration. In the mobile CA, an additional rule is necessary to
describe which one is the active cell for each of the time steps. On the contrary, both the evolution rules
and the active cells are included in a single F-code.
Although an F-code can efficiently identify a pattern, it should be stressed that it is valid only
within a specified boundary. An F-code should be defined under a given set of conditions, including
(i) the color of the initial seed element, (ii) the numbering schemes of the neighborhoods, the ele-
ments, and the surface cells, (iii) the firing strategy, and (iv) the equivalence relation between the
states of the surface cells (in addition to the basics of the CA, such as cell shapes). If at least one of
the above definitions is different for two F-codes, they cannot be compared directly.
In actuality, the last-nonzero-rule firing is only one of the many possible partial firing schemes. For
example, Figure 7 shows two flower patterns that were obtained by firing all the rules that have the same
rule value with the last nonzero rule at a given time step. The F-codes are not given in these cases, as it
Figure 7. Flowers generated with another rule-firing scheme.
30
Artificial Life Volume 17, Number 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
1
2
1
1
6
6
2
7
5
6
a
r
t
l
/
_
a
_
0
0
0
1
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
J. K. Shin
Identifying Patterns from One-Rule-Firing Cellular Automata
is meaningless to directly compare the F-codes of two different firing schemes. If we focused on a
simpler coding system, we could think of a rule-firing scheme that works without numbering the surface
cells and the elements. For example, if we choose to fire the rule with the smallest rule number in the
present time step, we do not need to keep track of the numberings of the surface cells and the elements.
This simplifies the process, allowing for pattern growth to easily occur. When implemented during the
present study, the patterns generated under this minimum-rule-firing scheme were found to be less
diverse than those from the last-rule-firing scheme.
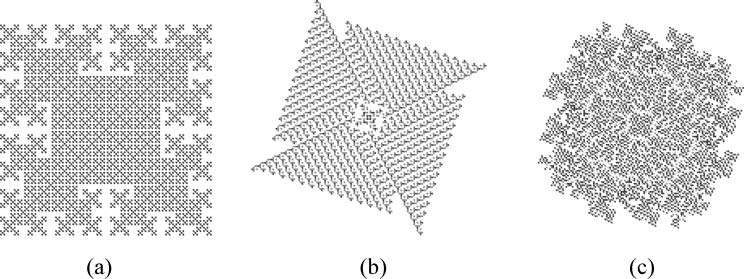
The present firing scheme can also be applied to systems based on different types of cells. For ex-
ample, Figure 8 shows patterns generated on 2D square cells. Four colors (m = 4) are used for these
examples. Although the cell type and the number of colors used are changed, the patterns generated can
be similarly classified. Figure 8a shows the F1 pattern under the new category. It consumes only one code
and can grow infinitely. This pattern is already known in the literature as code 942 [18]. The other two
figures in Figure 8 show a geometric pattern and a flowerlike one, respectively. Some complex patterns on
2D square cells were also reported in a special type of sandpile system in which grains are added to only
one site of the system [13]. It is not presently clear whether such sandpile patterns can be represented
in terms of the F-code, just as the Packard-type snow crystal is identified as F = 1. In general, it is of
theoretical interest whether a pattern can be represented by an F-code or not. In addition, one may ques-
tion the uniqueness of the F-code. It is clear that an F-code can define a pattern uniquely. It seems that the
reverse is not always true. For example, each of the F-codes 201, 301, 401, 501, and 601 generates the
monochrome pattern shown in Figure 3b. These five patterns differ only in color. Because these patterns
are monochrome, they are essentially the same. But it is not known whether two different codes can
result in exactly the same pattern, both in color and in shape. The solution of this problem is not a main
focus of the present study and is left as a topic for future study.
In addition to the uniqueness question, the present study elicits several interesting questions. Firstly,
how many possible finished F-codes can be generated at a given length? Up to iteration 60, totals of 1,
10, 70, 305, 875, 3780, and 19765 F-codes were identified from length 1 to length 7, respectively. Ex-
tending the numbers to longer F-codes is challenging. The second question at hand is whether we can
classify the rules, or equivalently the patterns, as in the cases of Wolfram [17] and other researchers
[3, 4]. Finally, do the flowerlike patterns possess any relation to real flowers? In addition to these the-
oretical questions, finding interesting patterns using different partial-firing schemes (together with, e.g.,
an application of a genetic algorithm) will be an exciting game.
6 Conclusion
The partial firing of rules on a growing cellular automaton generated myriad patterns, ranging from
natural shapes, such as flowers, to the well-known snow crystals and simple geometric patterns. A list
Figure 8. Patterns from square cell system with m = 4: (a) F1 on square cell, Iter = 61. (b) Geometric pattern, f =
(16 digits), Iter = 151. (c) Flower-like pattern, f = (31 digits), Iter = 241.
Artificial Life Volume 17, Number 1
31
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
1
2
1
1
6
6
2
7
5
6
a
r
t
l
/
_
a
_
0
0
0
1
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
J. K. Shin
Identifying Patterns from One-Rule-Firing Cellular Automata
of all the fired-rule values (F-codes) to generate a pattern is suggested as an efficient identifier of the
pattern. The Packard type of snowflake, which is the only shape resulting from a single-digit F-code, was
identified as the simplest of all the shapes under the assumed category of patterns defined in the present
study. Some complex shapes were found having F-codes with more than one hundred digits. A large
number of F-codes containing up to seven digits were identified through exhaustive numerical search.
A method of obtaining new patterns by mutating the F-codes was demonstrated through an example.
Also, the length of an F-code is suggested as a natural measure of the complexity of the given pattern,
indicating the number of different rules necessary to generate the pattern. The complexity of patterns is
believed to originate from two distinct sources: color and shape. In particular, the existence of code 0
in the F-codes was found to be a necessary condition for generating diverse shapes. Finally, a number of
topics for future research were discussed.
Acknowledgments
This research was supported by Yeungnam University research grants in 2010.
References
1. Guy, R., Conway, J., & Berlekamp, E. (1982). Winning ways: For your mathematical plays: Vol. 2. San Diego, CA:
Academic Press.
2. Coxe, A., & Reiter, C. (2003). Fuzzy hexagonal automata and snowflakes. Computers and Graphics, 27, 447–454.
3. Emmert-Streib, F. (2010). Exploratory analysis of spatiotemporal patterns of cellular automata by clustering
compressibility. Physical Review E, 81, 026103.
4. Gerling, R. (1990). Classification of triangular and honeycomb cellular automata. Physica A: Statistical and
Theoretical Physics, 162(2), 196–209.
5. Rigau, J., Feixas, M., & Sbert, M. (2007). Conceptualizing Birkhoffʼs aesthetic measure using Shannon
entropy and Kolmogorov complexity. In D. W. Cunningham, G. Meyer, & L. Neumann (Eds.),
Computational Aesthetics, 2007, Eurographics Workshop on Computational Aesthetics in Graphics, Visualization,
and Imaging. Boca Raton, FL: CRC Press.
6. Gunji, Y. (1990). Pigment color patterns of mollusks as an autonomous process generated by asynchronous
automata. Biosystems, 23(4), 317–334.
7. Ingerson, T., & Buvel, R. (1984). Structure in asynchronous cellular automata. Physica D, 10, 59–68.
8. Lee, J., Adachi, S., & Peper, F. (2007). Reliable self-replicating machines in asynchronous cellular automata.
Artificial Life, 13, 397–413.
9. Levy, S. (1992). Artificial life. New York: Vintage Books.
10. Lindenmayer, A. (1968). Mathematical models for cellular interaction in development. Journal of Theoretical
Biology, 18, 280–315.
11. von Neumann, J. (1966). The theory of self-reproducing automata, A. W. Burks (Ed.). Champaign-Urbana, IL:
University of Illinois Press.
12. Ning, C., & Reiter, C. (2007). A cellular model for three-dimensional snow crystallization. Computers and
Graphics, 31, 668–677.
13. Ostojic, S. (2003). Patterns formed by addition of grains to only one site of an abelian sandpile. Physica A,
318, 187–199.
14. Prusinkiewicz, P., & Lindenmayer, A. (1991). The algorithmic beauty of plants. Berlin: Springer-Verlag.
15. Schoenfisch, B., & Roos, A. (1999). Synchronous and asynchronous updating in cellular automata.
Biosystems, 51, 123–143.
16. Suzudo, T. (2004). Spatial pattern formation in asynchronous cellular automata with mass conservation.
Physica A, 343, 185–200.
17. Wolfram, S. (1984). Universality and complexity in cellular automata. Physica D, 10, 1–35.
18. Wolfram, S. (2002). A new kind of science. Champaign-Urbana, IL: Wolfram Media.
32
Artificial Life Volume 17, Number 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
1
2
1
1
6
6
2
7
5
6
a
r
t
l
/
_
a
_
0
0
0
1
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3