HOLD BACK TO MOVE FORWARD?
EARLY GRADE RETENTION AND
STUDENT MISBEHAVIOR
Umut ¨Ozek
American Institutes for
Research
1000 Thomas Jefferson St. NW
Washington, DC 20007
uozek@air.org
Abstract
Test-based accountability has become the new norm in
public education over the last decade. In many states
and school districts nationwide, student performance on
standardized tests plays an important role in high-stakes
decisions, such as grade retention. This study examines
the effects of grade retention on student misbehavior
in Florida, which requires students with reading skills
below grade level to be retained in the third grade. The
regression discontinuity estimates suggest that grade re-
tention increases the likelihood of disciplinary incidents
and suspensions in the short run, yet these effects dis-
sipate over time. The findings also suggest that these
short-term adverse effects are concentrated among eco-
nomically disadvantaged and male students.
350
doi:10.1162/EDFP_a_00166
© 2015 Association for Education Finance and Policy
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
0
3
3
5
0
1
6
8
9
9
1
0
e
d
p
_
a
_
0
0
1
6
6
p
d
f
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Umut ¨Ozek
1. INTRODUCTION
Accountability remains at the forefront of the education policy debate more
than a decade after the No Child Left Behind Act of 2001 was signed into
law. The last decade has witnessed the nationwide implementation of an
educational system where student test performance plays an important role
in high-stakes decisions, such as school closures and teacher retention and
compensation. All states have established test-based performance benchmarks
for students and meeting these standards is a prerequisite for high school
graduation and grade promotion in many states.
Grade retention has been a long-standing and highly debated intervention
for low-performing students. The biggest point of contention is the academic
benefits of grade retention—that is, whether holding back students who are not
ready for more challenging course content translates into higher achievement
in the following years.1 The overarching conclusion of the earlier literature is
that retained students perform significantly worse than their promoted peers
in the years that follow. On the other hand, more recent studies, which better
address the identification challenges by using the nonlinearities in retention
policies, show that grade retention, especially in early grades, has a positive
impact on test scores in the short term.2
Equally contentious are the possible adverse effects of grade retention
policies. Critics of these policies commonly argue that grade retention imposes
significant emotional burdens on students because they are stigmatized as
failing and they face the challenges of adjusting to new peers, which might in
turn lead to student disengagement from schooling. In fact, two recent studies
have found evidence that grade retention in eighth grade reduces the likelihood
of high school graduation under some conditions (Jacob and Lefgren 2009),
whereas early grade retention has no significant impact on student attendance
in the following years (Schwerdt and West 2012).
This study explores another way this emotional burden might manifest
itself, by examining the possible adverse effects of early grade retention on
student disruptive behavior in the years that follow. Using the test-based third-
grade promotion policy in Florida, regression discontinuity estimates suggest
that “just-retained” students are significantly more likely to have disciplinary
problems and receive suspensions in the two years that follow, yet these ef-
fects vanish in the long run. Further, subgroup analyses reveal this adverse
effect is mostly concentrated among economically-disadvantaged and male
students. These findings might help better assess the costs and benefits of
1. Holmes (1989) and Jimerson (1999) provide excellent meta-analysis of the earlier grade retention
research.
2. Some examples are Jacob and Lefgren (2004, 2009), Greene and Winters (2007, 2012), and Schwerdt
and West (2012).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
0
3
3
5
0
1
6
8
9
9
1
0
e
d
p
_
a
_
0
0
1
6
6
p
d
.
f
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
351
GRADE RETENTION AND STUDENT MISBEHAVIOR
grade retention in an era where test-based accountability is becoming the new
norm.
The remainder of the paper is organized as follows. Section 2 provides
background on the Florida early grade retention policy. Section 3 describes the
data and details the empirical strategy, section 4 presents the findings, and
section 5 concludes.
2. POLICY BACKGROUND
The Just Read, Florida! Initiative, enacted in 2001, uses frequent progress
monitoring, intensive instructional assistance, and grade retention to ensure
all students meet the reading benchmarks described in Florida’s Sunshine
States Standards before they reach the fourth grade, when students tradition-
ally begin to “read to learn” rather than “learn to read.” Since 2002, all third
graders in Florida are categorized into “achievement levels” based on their
reading performance in the curriculum standards-based Florida Curriculum
Assessment Test (FCAT-SSS). If a student fails to perform at achievement
level 2 or higher, the law requires that they should not be promoted to the
fourth grade. This discontinuity in grade promotion is the key element of my
identification strategy described subsequently.
The legislation requires that schools provide development strategies for
retained students. These include proven effective teaching strategies, assign-
ing retained students to high-performing teachers, participation in summer
reading camps, and at least ninety minutes of reading instruction each day.
If the retained student can demonstrate the required reading level before the
beginning of the following school year or during the school year, they might
be eligible for mid-year grade promotion.
There are several “good cause exemptions” under which students can be
promoted to fourth grade even though they fail the high-stakes reading test.
For instance, if a student can demonstrate an acceptable level of performance
on an alternative standardized test approved by the State Board of Education,
the student is promoted to the next grade. Further, limited English proficiency
(LEP) students with less than two years in the English for Speakers of Other
Languages program, special education students with certain disabilities, stu-
dents who show through a teacher-developed portfolio that they can read at
grade level, and students who have received intensive reading remediation for
two years and who have already been retained twice between kindergarten and
third grade are granted the good cause exemption.3
3. For more information, see www.justreadflorida.com/docs/read_to_learn.pdf.
352
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
0
3
3
5
0
1
6
8
9
9
1
0
e
d
p
_
a
_
0
0
1
6
6
p
d
.
/
f
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Umut ¨Ozek
3. DATA AND EMPIRICAL STRATEGY
Data
To examine the consequences of grade retention, I utilize student-level ad-
ministrative data and track seven cohorts of students in Florida entering third
grade for the first time between 2003–04 and 2009–10. The data set includes
demographic information on students such as race, gender, free or reduced-
price lunch (FRPL) eligibility, LEP status, LEP program entry and exit dates,
exceptional student education status, and FCAT-SSS scores in reading and
math.
More importantly for the purposes of this study, the data set contains de-
tailed information about student disciplinary incidents. In particular, for each
incident, I observe the type of disciplinary/referral action taken and the dura-
tion of the suspension (if applicable) for at least two years after the students in
the sample first enter third grade. These incidents can be triggered by a wide
array of student misbehavior, ranging from disruptive behavior in the class-
room to gang involvement.4 Based on the severity of the incident, teachers and
principals have full discretion over the type of action taken, which may include
corporal punishment, in-school or out-of-school suspension, placement in a
different program, and expulsion.
Table 1 breaks down by grade the incident rates, types of disciplinary action,
and days suspended. There are several findings worth highlighting. First, inci-
dent rates increase monotonically as grade increases, with a significant jump
between elementary and middle school, which might be driven by differences
in teacher and principal tolerance toward student misbehavior between grade
levels. This trend is also observed in the average suspension days. Second,
punishment types differ considerably across grade levels, with more frequent
use of corporal punishment and out-of-school suspensions in earlier grades.
Finally, suspension is the most frequent form of student punishment, with
almost all students involved in disciplinary incidents (80 to 90 percent) receiv-
ing in-school or out-of-school suspensions. In the analyses that follow, I am
interested in the likelihood of student misbehavior (as measured by the inci-
dent indicator), and the severity of the misbehavior (as measured by whether
the student received an in-school or out-of-school suspension), noting that the
results are similar when the number of suspended days is used as an indicator
of severity.
Table 2 presents the descriptive statistics for the entire sample (first col-
umn) along with the promoted students with scores below cutoff (second
4. The data also contain indicators for severe misbehaviors, such as use of alcohol, drugs, or weapons,
involvement in a hate crime, and involvement in a gang. Because the prevalence of these incidents
is very low at the grade levels in which I am interested in this study, I do not use these indicators as
outcomes in the analysis that follows.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
0
3
3
5
0
1
6
8
9
9
1
0
e
d
p
_
a
_
0
0
1
6
6
p
d
/
f
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
353
GRADE RETENTION AND STUDENT MISBEHAVIOR
Table 1. Disciplinary Incidents and Punishment Types by Grade
All Students
Students Involved in Disciplinary Incidents
Incident
Rate
Corporal
Punishment
In-School
Suspension
Out-of-School
Suspension
Days
Suspended
0.024
(0.152)
0.033
(0.177)
0.040
(0.196)
0.053
(0.223)
0.062
(0.242)
0.076
(0.265)
0.217
(0.412)
0.253
(0.435)
0.256
(0.436)
0.271
(0.445)
0.260
(0.439)
0.174
(0.379)
0.151
(0.358)
0.065
(0.246)
0.042
(0.201)
0.032
(0.177)
0.027
(0.161)
0.024
(0.153)
0.020
(0.139)
0.007
(0.085)
0.007
(0.082)
0.006
(0.077)
0.003
(0.058)
0.004
(0.065)
0.005
(0.071)
0.006
(0.078)
0.236
(0.424)
0.289
(0.454)
0.306
(0.461)
0.306
(0.461)
0.320
(0.467)
0.326
(0.469)
0.493
(0.500)
0.497
(0.500)
0.495
(0.500)
0.543
(0.498)
0.552
(0.497)
0.549
(0.498)
0.540
(0.498)
0.570
(0.495)
0.526
(0.499)
0.521
(0.500)
0.527
(0.499)
0.524
(0.499)
0.526
(0.499)
0.385
(0.487)
0.386
(0.487)
0.389
(0.487)
0.360
(0.480)
0.339
(0.473)
0.337
(0.473)
0.338
(0.473)
1.524
(2.497)
1.591
(2.473)
1.663
(3.051)
1.746
(3.185)
1.826
(4.005)
1.959
(4.301)
2.696
(6.774)
2.908
(8.234)
3.103
(9.151)
3.131
(10.33)
3.035
(10.15)
2.963
(9.992)
2.816
(9.269)
Grade
K
1
2
3
4
5
6
7
8
9
10
11
12
Notes: Standard deviations are given in parentheses.
column) and retained students below cutoff (third column). During this time
frame, roughly 16 percent of all third graders scored below the retention cutoff
and 8 percent were retained, with significantly higher retention rates in the
earlier cohorts (roughly 11 percent in the first cohort versus 6 percent in the
last). Compared with their promoted peers, retained students are significantly
more likely to have disciplinary issues during the third grade, more likely to
come from economically disadvantaged families, more likely to belong to a
racial/ethnic minority group (other than Asian), less likely to have English
as their native language, and more likely to be first generation immigrants.
Conditional on low performance on the high-stakes reading test in the third
354
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
0
3
3
5
0
1
6
8
9
9
1
0
e
d
p
_
a
_
0
0
1
6
6
p
d
.
/
f
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Umut ¨Ozek
Table 2. Descriptive Statistics
Below Cutoff: Below Cutoff:
All
Promoted
Retained
Third grade
Retained
Disciplinary incident
In-school suspension
Out-of-school suspension
FCAT math score
Age (in months)
Limited English proficiency
Special education
FRPL eligible
Male
White
Black
Hispanic
Asian
Foreign born
English not native
0.081
(0.273)
0.051
(0.22)
0.021
(0.143)
0.032
(0.175)
0.035
(1.002)
104.718
(6.039)
0.087
(0.282)
0.150
(0.357)
0.552
(0.497)
0.510
(0.5)
0.460
(0.498)
0.223
(0.416)
0.249
(0.432)
0.023
(0.151)
0.079
(0.27)
0.261
(0.439)
0.107
(0.309)
0.041
(0.198)
0.074
(0.262)
−1.079
(0.934)
109.169
(8.056)
0.238
(0.426)
0.450
(0.497)
0.782
(0.413)
0.591
(0.492)
0.284
(0.451)
0.337
(0.473)
0.331
(0.471)
0.013
(0.115)
0.139
(0.346)
0.363
(0.481)
0.117
(0.322)
0.045
(0.206)
0.081
(0.273)
−1.276
(0.88)
105.699
(6.621)
0.188
(0.39)
0.301
(0.459)
0.802
(0.398)
0.588
(0.492)
0.247
(0.431)
0.409
(0.492)
0.302
(0.459)
0.010
(0.1)
0.086
(0.281)
0.333
(0.471)
N
1,298,460
110,373
98,746
Note: Standard deviations are given in parentheses.
grade, these differences seem to subside considerably, yet the promoted low
performers are significantly more likely to be LEP and/or special education
students because of the exemption clauses in the policy.
The biggest challenge in revealing the causal impact of grade retention is
that the retention decisions are typically made by teachers and principals based
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
0
3
3
5
0
1
6
8
9
9
1
0
e
d
p
_
a
_
0
0
1
6
6
p
d
.
/
f
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
355
GRADE RETENTION AND STUDENT MISBEHAVIOR
on student attributes that are not necessarily observable to the researcher,
such as parental involvement and student motivation, which in turn affect
future student outcomes. Therefore, regression-adjusted differences based
on observable student attributes between promoted and retained students are
likely to yield biased inferences. In this study, I utilize the non-linearity created
by the retention policy and compare students who scored right below and right
above the promotion cutoff in a regression discontinuity framework. In what
follows, I detail this empirical approach.
Empirical Framework
Let Si denote the difference between the third-grade reading score of student
i and the retention cutoff, with negative values indicating scores below cutoff.
Defining treatment, Ri , as being retained at the end of third grade, a common
regression model representation of this evaluation problem would become:
Di = α + β Ri + εi ,
(1)
where Di is the disciplinary outcome of student i. Because students on both
sides of the retention cutoff can be promoted or retained under the Florida
policy, I utilize a fuzzy regression discontinuity (RD) design where the causal
impact of retention on disciplinary problems is given by:
β =
lim
S↑0
lim
S↑0
E [D|S] − lim
S↓0
E [R|S] − lim
S↓0
E [D|S]
E [R|S]
.
(2)
β will yield an unbiased estimate of the causal impact of retention provided
that there is a significant jump in retentions at the cutoff (large denominator
in equation 2) and that
lim
S↑0
lim
S↑0
E [ε|S] − lim
S↓0
E [R|S] − lim
S↓0
E [ε|S]
E [R|S]
= 0.
(3)
There are several ways to estimate β in this context. First is to estimate equa-
tion 2 nonparametrically using kernel-weighted local polynomial smoothing
initially as proposed by Hahn, Todd, and van der Klaauw (2001) and later de-
veloped by Porter (2003) to include higher-order polynomial estimators. This
method reduces the possibility of misspecification bias in parametric models
and achieves the optimal rate of convergence. When the selection variable is
discrete, however, as in this case, a nonparametric estimator might lead to bi-
ased estimates as it is not feasible to compare averages within arbitrarily small
neighborhoods around the cutoff (Lee and Card 2008). Therefore, following
356
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
0
3
3
5
0
1
6
8
9
9
1
0
e
d
p
_
a
_
0
0
1
6
6
p
d
.
f
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Umut ¨Ozek
Figure 1. Retention and Third-Grade Reading Scores. Notes: The figure presents the local linear
smoothing of the retention indicator on relative reading score of the student separately for the left
of the cutoff date and the right. The triangle kernel and a bandwidth of 5 points are used in the
estimation. The solid circles represent raw cell means.
Lee and Card (2008), I estimate equation 2 parametrically using the following
two-stage least squares framework:
Ri = φ + δ Bi + k(Si ) + k(Si ) ∗ Bi + υi ,
Yi = α + β ˆRi + k(Si ) + k(Si ) ∗ Bi + εi ,
(4a)
(4b)
where k(Si ) is a polynomial function of the relative reading score and Bi is an
indicator for students below the cutoff. In the preferred specification, I limit
the analysis to students within a bandwidth of 5 points, because increasing
bandwidth is expected to produce biased estimates in situations such as the
case examined here, where the selection variable is correlated with the outcome
conditional on treatment status. I check the robustness of this specification
using different bandwidths (1, 10, 15, and 20) and polynomial orders (0, 1, 2,
3, and 4), and cluster the standard errors at the relative reading score level as
suggested by Lee and Card (2008).
4. RESULTS
I first check to make sure there is a significant discontinuity in the treatment
variable at the cutoff. Figure 1 presents the local linear smoothing of the
retention indicator on the relative reading score, calculated separately for each
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
0
3
3
5
0
1
6
8
9
9
1
0
e
d
p
_
a
_
0
0
1
6
6
p
d
f
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
357
GRADE RETENTION AND STUDENT MISBEHAVIOR
side of the cutoff using the triangle kernel and the bandwidth of 5 points, with
the solid circles representing the retention rate for each test score. This figure
shows that students who score just below the retention cutoff are approximately
30 percentage points more likely to be retained compared with their peers who
scored right at the cutoff. This is true for each cohort with slightly larger
discontinuities observed for the third graders in the earlier cohorts.
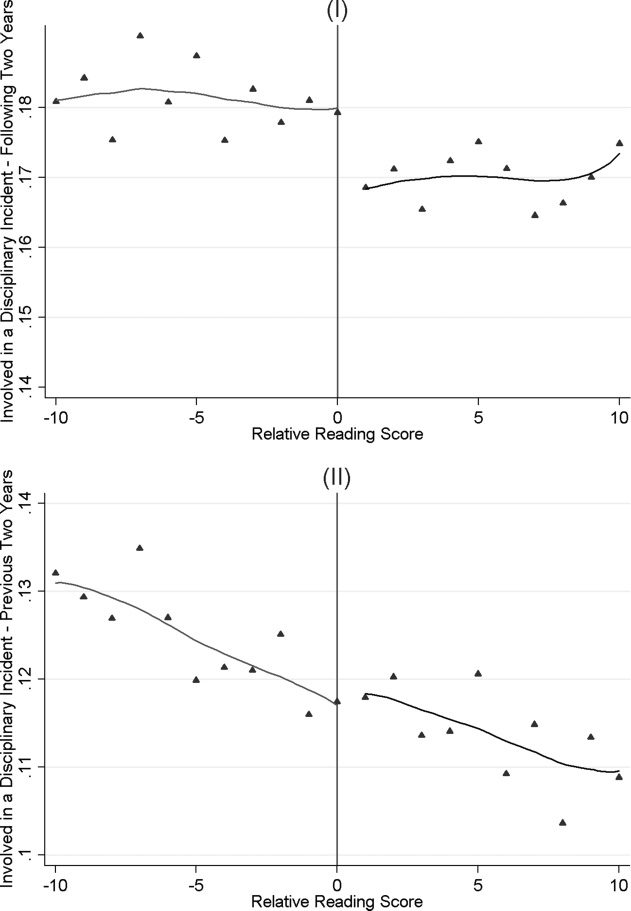
Figure 2 presents a graphical inspection of the effects of retention on
student discipline, replacing the retention indicator in figure 1 with whether
the student was involved in a disciplinary incident in the next two years (in
the upper panel) or in the past two years (lower panel). Whereas the third
graders who scored right below the promotion cutoff were no more likely to
have disciplinary issues during the previous two school years than their peers
on the other side, they are significantly more likely to be involved in incidents
in the following two years. Using the jump in the retention rate at the cutoff
displayed in figure 1, the simple Wald estimator given in equation 2 indicates
the magnitude of this difference is roughly 4–5 percentage points. This gap
approximately corresponds to one fourth of the control mean at the cutoff.
Table 3 presents the short-term effects of grade retention on disciplinary
incidents and suspensions in the years following the retention. In the first two
columns, I estimate equations 4a and 4b using a bandwidth of 5 points and a
linear k(Si ), and the last two columns use 20 points and a quartic polynomial.
In all specifications, I include cohort fixed-effects to take differences between
cohorts into account, although the results are robust to the exclusion of these
fixed effects.
The estimated effects reported in columns labeled as (I) align well with
the earlier graphical analysis. Grade retention increases the likelihood of dis-
ciplinary incidents by about 3 to 5 percentage points (30 to 50 percent of the
control mean of 0.107 at the cutoff) in the following year, and roughly by 5 to 6
percentage points (40 to 50 percent of the control mean of 0.132 at the cutoff)
in the second year that follows. Just-retained students are also significantly
more likely to receive suspensions in the following two years. The estimated
effects are positive for both in-school and out-of-school suspensions, but the
point estimates are only statistically significant for out-of-school suspensions
in the first year and in-school suspensions in the second year. One possible
explanation behind this discrepancy is that the retained students are involved
in more severe incidents in the first year after they are retained, and thus
receive out-of-school suspensions, compared with the second year.
Table 4 explores the effects of grade retention beyond the first two years. In
this analysis, I restrict the sample to earlier cohorts (first-time third graders be-
tween 2003 and 2006) that are observed for at least six years after third grade.
The estimates presented in columns (I) indicate that there are no significant
358
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
0
3
3
5
0
1
6
8
9
9
1
0
e
d
p
_
a
_
0
0
1
6
6
p
d
/
f
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Umut ¨Ozek
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
0
3
3
5
0
1
6
8
9
9
1
0
e
d
p
_
a
_
0
0
1
6
6
p
d
/
.
f
Figure 2. Retention and Disciplinary Incidents. Notes: The two panels examine the disciplinary
incidents in the two years following (upper panel), and in the two years prior to (lower panel), the
first time students enter the third grade. Both panels present the local linear smoothing of the
corresponding incident indicator on relative reading score of the student, separately for the left and
the right of the retention cutoff score.
discontinuities at the retention cutoff in the long-run, except for the signifi-
cant negative discontinuity during the third year after retention. Important to
note here, however, is that during that year the majority of the just-promoted
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
359
GRADE RETENTION AND STUDENT MISBEHAVIOR
Table 3.
Early Grade Retention and Misbehavior Same Age Comparisons, Short-Term Effects
Score Range
1 year later
Disciplinary incident
In-school suspension
Out-of-school suspension
2 years later
Disciplinary incident
In-school suspension
Out-of-school suspension
First-stage discontinuity
Linear
Quartic
(I)
5
(II)
5
(I)
20
(II)
20
0.031∗∗∗
(0.008)
0.009
(0.009)
0.037∗∗∗
(0.012)
0.050∗∗∗
(0.010)
0.034∗∗∗
(0.003)
0.025∗∗
(0.007)
0.313∗∗∗
(0.007)
0.039∗∗∗
(0.009)
0.009
(0.009)
0.045∗∗∗
(0.013)
0.055∗∗∗
(0.011)
0.033∗∗∗
(0.004)
0.028
(0.009)
0.319∗∗∗
(0.006)
0.046∗∗∗
(0.014)
0.013
(0.011)
0.046∗∗∗
(0.016)
0.048∗∗∗
(0.017)
0.040∗∗∗
(0.009)
0.018
(0.012)
0.314∗∗∗
(0.008)
0.064∗∗∗
(0.012)
0.016
(0.011)
0.062∗∗∗
(0.016)
0.054∗∗
(0.020)
0.040∗∗∗
(0.009)
0.025∗
(0.014)
0.322∗∗∗
(0.007)
N
Cohort FE
Student covariates
Within-school peer average
43,793
43,793
178,248
178,248
Yes
No
No
Yes
Yes
Yes
Yes
No
No
Yes
Yes
Yes
Notes: Robust standard errors, clustered at the relative reading score level, are given
in parentheses. Discontinuity estimates are obtained parametrically using the specified
polynomial order and the score range. Columns labeled as (I) present the estimates
from the base specification in equations 4a and 4b, with the addition of cohort fixed
effects, and the columns labeled as (II) add student covariates and within-school peer
averages to the estimation.
∗Statistical significance at 10%; ∗∗statistical significance at 5%; ∗∗∗statistical signifi-
cance at 1%.
students attend middle school whereas their just-retained peers are in ele-
mentary school. It is possible, therefore, that the observed discontinuities are
reflections of the aforementioned jump in the incident and suspension rates
between elementary and middle grades.
The estimates presented so far have relied on the same-age comparisons be-
tween retained and promoted students. The primary concern in this approach
is that the estimated differences in disciplinary incidents might be caused by
the differences in incident rates across grades. Note, however, that the incident
rates increase with grade, as reported in table 1. Further, table 5 presents the
same-grade comparisons between retained and promoted students around the
360
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
0
3
3
5
0
1
6
8
9
9
1
0
e
d
p
_
a
_
0
0
1
6
6
p
d
/
f
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Umut ¨Ozek
Table 4.
Early Grade Retention and Misbehavior Same Age Comparisons, Long-Term Effects
Score Range
3 years later
Disciplinary incident
In-school suspension
Out-of-school suspension
4 years later
Disciplinary incident
In-school suspension
Out-of-school suspension
5 years later
Disciplinary incident
In-school suspension
Out-of-school suspension
First-stage discontinuity
N
Cohorts
Cohort FE
Student covariates
Within-school peer average
Linear
Quartic
(I)
5
(II)
5
(I)
20
(II)
20
−0.092∗∗
(0.045)
−0.108∗∗∗
(0.020)
−0.042
(0.028)
0.016
(0.028)
0.007
(0.018)
0.020
(0.030)
−0.009
(0.013)
0.006
(0.013)
−0.017
(0.012)
0.012
(0.036)
−0.012
(0.014)
−0.042
(0.028)
0.028
(0.027)
0.021
(0.015)
0.020
(0.030)
−0.008
(0.018)
0.0001
(0.012)
−0.017
(0.012)
−0.122∗∗∗
(0.051)
−0.137∗∗∗
(0.021)
−0.047
(0.033)
0.033
(0.036)
0.027
(0.026)
0.021
(0.037)
−0.007
(0.026)
−0.005
(0.019)
−0.004
(0.020)
−0.021
(0.039)
−0.037∗∗
(0.018)
−0.047
(0.032)
0.042
(0.036)
0.035
(0.026)
0.021
(0.037)
−0.011
(0.028)
−0.018
(0.016)
−0.004
(0.020)
0.347∗∗∗
(0.009)
0.356∗∗∗
(0.010)
0.345∗∗∗
(0.009)
0.356∗∗∗
(0.010)
21,712
21,712
87,924
87,924
2003–2006
2003–2006
2003–2006
2003–2006
Yes
No
No
Yes
Yes
Yes
Yes
No
No
Yes
Yes
Yes
Notes: Robust standard errors, clustered at the relative reading score level, are given in
parentheses. Discontinuity estimates are obtained parametrically using the specified polyno-
mial order and the score range. Columns labeled as (I) present the estimates from the base
specification in equations 4a and 4b, with the addition of cohort fixed effects, and the columns
labeled as (II) add student covariates and within-school peer averages to the estimation.
∗∗Statistical significance at 5%; ∗∗∗statistical significance at 1%.
cutoff. That is, I compare promoted students with their retained peers around
the cutoff when they reach the same grade level. Once again, I restrict the
sample to the 2003–06 cohorts who are old enough to reach eighth grade by
the end of my sample. The findings reinforce the conclusion that the retained
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
0
3
3
5
0
1
6
8
9
9
1
0
e
d
p
_
a
_
0
0
1
6
6
p
d
.
/
f
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
361
GRADE RETENTION AND STUDENT MISBEHAVIOR
Table 5.
Early Grade Retention and Misbehavior Same Grade Comparisons
Score Range
4th grade
Disciplinary incident
In-school suspension
Out-of-school suspension
5th grade
Disciplinary incident
In-school suspension
Out-of-school suspension
6th grade
Disciplinary incident
In-school suspension
Out-of-school suspension
7th grade
Disciplinary incident
In-school suspension
Out-of-school suspension
8th grade
Disciplinary incident
In-school suspension
Out-of-school suspension
First-stage discontinuity
N
Cohorts
Linear
Quartic
(I)
5
(II)
5
(I)
20
(II)
20
0.045∗∗∗
(0.016)
0.009
(0.008)
0.044∗∗
(0.020)
0.055∗∗∗
(0.021)
0.046∗∗∗
(0.014)
0.023∗∗
(0.011)
0.051
(0.042)
0.008
(0.020)
0.055∗∗
(0.025)
−0.004
(0.022)
−0.002
(0.012)
−0.008
(0.024)
0.005
(0.023)
0.004
(0.026)
−0.0003
(0.013)
0.329∗∗∗
(0.002)
0.046∗∗∗
(0.009)
0.005
(0.007)
0.046∗∗∗
(0.015)
0.056∗∗∗
(0.016)
0.047∗∗∗
(0.013)
0.026∗∗∗
(0.008)
0.059∗∗
(0.030)
0.016
(0.020)
0.060∗∗∗
(0.016)
0.013
(0.024)
0.005
(0.011)
0.004
(0.028)
0.024∗
(0.013)
0.022
(0.019)
0.012
(0.018)
0.046∗∗
(0.021)
0.004
(0.012)
0.050∗∗
(0.022)
0.065∗∗∗
(0.026)
0.053∗∗∗
(0.020)
0.018
(0.016)
0.025
(0.046)
−0.027
(0.019)
0.056∗∗
(0.027)
0.017
(0.033)
0.014
(0.020)
0.009
(0.031)
0.017
(0.029)
−0.016
(0.022)
0.035
(0.026)
0.319∗∗∗
(0.006)
0.314∗∗∗
(0.008)
21,712
21,712
87,924
0.050∗∗∗
(0.014)
0.002
(0.010)
0.054∗∗∗
(0.016)
0.063∗∗∗
(0.020)
0.053∗∗∗
(0.018)
0.021∗
(0.012)
0.031
(0.034)
−0.019∗
(0.011)
0.062∗∗∗
(0.019)
0.037
(0.033)
0.022
(0.020)
0.028
(0.034)
0.032
(0.020)
0.003
(0.019)
0.044∗
(0.024)
0.322∗∗∗
(0.007)
87,924
2003–2006
2003–2006
2003–2006
2003–2006
362
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
0
3
3
5
0
1
6
8
9
9
1
0
e
d
p
_
a
_
0
0
1
6
6
p
d
.
f
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Umut ¨Ozek
Table 5. Continued.
Score Range
Cohort FE
Student covariates
Within-school peer average
Linear
Quartic
(I)
5
Yes
No
No
(II)
5
Yes
Yes
Yes
(I)
20
Yes
No
No
(II)
20
Yes
Yes
Yes
Notes: Robust standard errors, clustered at the relative reading score level, are given in paren-
theses. Discontinuity estimates are obtained parametrically using the specified polynomial order
and the score range. Columns labeled as (I) present the estimates from the base specification
in equations 4a and 4b, with the addition of cohort fixed effects, and the columns labeled as (II)
add student covariates and within-school peer averages to the estimation.
∗Statistical significance at 10%; ∗∗statistical significance at 5%; ∗∗∗statistical significance at 1%.
students are significantly more likely to have disciplinary problems in the short
run, yet these differences dissipate in middle school.
Identification Checks
Other than the causal effect of retention, there are several alternative scenarios
that might explain the observed discontinuities in disciplinary problems. One
of these explanations is the differences in student attributes (e.g., prior dis-
ciplinary problems, achievement, demographics, family characteristics, and
other observed and unobserved traits) between retained and promoted stu-
dents around the cutoff. I investigate this possibility by replacing the disci-
plinary outcomes in equation 4b with student characteristics and check for
possible discontinuities. The findings presented in table 6 reject this explana-
tion and show that the students on the two sides of the retention cutoff are
comparable along these observed traits. To further examine whether differ-
ences in student attributes explain the gaps in disciplinary outcomes at the
cutoff, columns labeled as (II) in tables 3, 4, and 5 present the parametric esti-
mates controlling for observed student attributes listed in table 6, along with
cohort fixed-effects and within-school average peer outcomes. Tables A.1 and
A.2 in the Appendix present the full first- and second-stage results for column
II in table 2. The inclusion of these covariates does not seem to significantly
change the estimated impact of retention, except for the discontinuities in the
third year after retention.
Unlike test scores, disciplinary outcomes are not standardized measures
across educational settings. That is, given two identical student behaviors,
different disciplinary outcomes might emerge based on factors such as the
principal attitude or the school environment. To see whether such differences
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
0
3
3
5
0
1
6
8
9
9
1
0
e
d
p
_
a
_
0
0
1
6
6
p
d
/
.
f
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
363
GRADE RETENTION AND STUDENT MISBEHAVIOR
Table 6.
Early Grade Retention and Student Characteristics
Score Range/Bandwidth
Current year
Disciplinary incident
In-school suspension
Out-of-school suspension
Prior year
Disciplinary incident
In-school suspension
Out-of-school suspension
Limited English proficiency
Special education
FRPL eligible
Male
Age in 3rd grade (in months)
FCAT Math score: 3rd grade
White
Black
Hispanic
Asian
Foreign born
English not native
Peer incident rate
1 year later
Linear
5
Quartic
20
−0.012
(0.023)
0.002
(0.011)
−0.011
(0.015)
−0.005
(0.007)
−0.015∗
(0.009)
−0.004
(0.005)
0.019
(0.012)
0.002
(0.012)
0.003
(0.017)
−0.050∗∗∗
(0.013)
0.572∗∗∗
(0.220)
0.006
(0.022)
−0.020
(0.029)
−0.009
(0.009)
0.033
(0.030)
−0.034
(0.023)
−0.006
(0.011)
−0.021
(0.018)
−0.007
(0.010)
−0.019
(0.016)
−0.005
(0.006)
0.025
(0.015)
−0.014
(0.021)
−0.004
(0.018)
−0.043∗∗∗
(0.015)
0.392
(0.282)
0.070
(0.045)
0.001
(0.035)
−0.020
(0.020)
0.022
(0.042)
−0.016∗∗∗
(0.004)
−0.023∗∗∗
(0.005)
0.027
(0.021)
0.035
(0.022)
0.004
(0.021)
0.027
(0.027)
−0.0003
(0.002)
0.0009
(0.003)
364
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
0
3
3
5
0
1
6
8
9
9
1
0
e
d
p
_
a
_
0
0
1
6
6
p
d
/
f
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Umut ¨Ozek
Table 6. Continued.
Score Range/Bandwidth
2 years later
3 years later
4 years later
5 years later
Linear
5
−0.0002
(0.003)
−0.110∗∗∗
(0.007)
−0.007
(0.005)
0.001
(0.008)
Quartic
20
0.0005
(0.003)
−0.101∗∗∗
(0.006)
−0.008
(0.006)
−0.004
(0.009)
Notes: Robust standard errors, clustered relative reading score
level, are given in parentheses. Discontinuity estimates are ob-
tained parametrically using the specified polynomial order and
the score range. Both specifications include the cohort fixed ef-
fects.
∗Statistical significance at 10%; ∗∗∗statistical significance at 1%.
explain the differences between retained and promoted students, I calculate
the percentage of peers involved in disciplinary incidents at the school-year
level for each student. If, for instance, retained students are attending schools
with stricter principals, one would expect to observe higher peer incident
rates for these students. The last five rows of table 5 present the discontinuity
estimates along this dimension and show that students on the two sides of the
cutoff are attending similar schools. This is not the case for the third year after
retention, however, which presents evidence justifying the earlier explanation
for the third-year discontinuity in disciplinary problems. In fact, when peer
differences are accounted for in column II of table 4, the estimated differences
at the cutoff in the third year are no longer statistically significant.
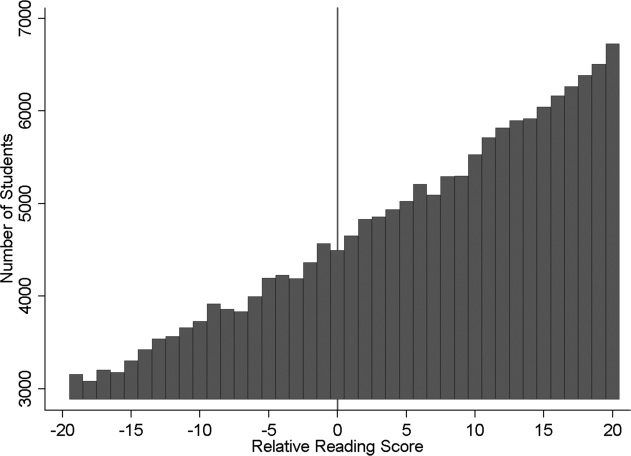
Another concern regarding identification in the RD design in this context,
as noted in McCrary (2008), is the possibility of selection variable manipulation
(i.e., the reading scores in this case) by teachers and/or principals. Under this
scenario, one would expect to see an unusual discontinuity in the test score
distribution around the promotion cutoff. It is important to note here that
this is very unlikely, because FCAT scores are assessed without any teacher
or principal involvement. Regardless, I present graphical evidence to dismiss
this possibility, because the formal test developed by McCrary (2008) is not
appropriate in this case as it relies on local linear regressions, which might
lead to incorrect inferences when the running variable is discrete (Card and
Lee 2008). Figure 3 provides the reading score distribution around the cutoff.
The number of students in each bin seems to be increasing as the retention
cutoff falls on the left tail of the normally distributed reading scores, but the
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
0
3
3
5
0
1
6
8
9
9
1
0
e
d
p
_
a
_
0
0
1
6
6
p
d
.
/
f
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
365
GRADE RETENTION AND STUDENT MISBEHAVIOR
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
0
3
3
5
0
1
6
8
9
9
1
0
e
d
p
_
a
_
0
0
1
6
6
p
d
f
/
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3. Selection Into/Out of Treatment. Notes: The figure presents the number of students in
each reading score bin between 20 points below and above the retention cutoff, which is shown by
the vertical line.
results present no unusual discontinuity at the cutoff and hence no evidence
of strategic sorting around the cutoff.
Finally, differential attrition might lead to biased estimates if retained
students leave the sample at higher rates than their promoted peers or if
retained stayers differ from the promoted stayers in the following years. I
first check the attrition rates around the cutoff. The discontinuity estimates
presented in table 7 suggest retained students are equally likely to leave the
Florida public school system as the promoted students around the cutoff.
Second, I compare the just-retained stayers with just-promoted stayers along
observable student characteristics. Conditional on staying in the sample during
the following two years, comparisons reported in table 8, combined with the
results in table 6, suggest the retained leavers are quite similar to promoted
students who left the sample in the years that follow.
Robustness Checks
To check the robustness of these findings, table 9 repeats the main analysis
using various bandwidths and polynomial orders, ranging from a bandwidth
of 1 and order zero, under which the RD design is equivalent to the traditional
instrumental variable framework, to a bandwidth of 15 points and quartic poly-
nomial. In all specifications, I include the aforementioned student covariates,
average peer outcome at the school-level, and cohort fixed-effects to improve
366
Umut ¨Ozek
Table 7.
Early Grade Retention and Attrition
Score Range/Bandwidth
Left at the end of the
Current year
First year after
Second year after
Third year after
Linear
5
Quartic
20
0.0006
(0.005)
0.009
(0.008)
0.008
(0.013)
0.009
(0.008)
−0.006
(0.005)
0.011
(0.009)
0.011
(0.012)
0.021∗∗∗
(0.007)
Notes: Robust standard errors, clustered at the relative reading
score level, are given in parentheses. Discontinuity estimates
are obtained parametrically using the specified polynomial or-
der and the score range. Both specifications include the cohort
fixed effects.
∗∗∗Statistical significance at 1%.
the precision of the estimates. The estimated discontinuities are positive and
statistically different from zero in all but two specifications. The impact sizes
are comparable to the ones in the original specifications, ranging from 3 to 7
percent in the first year and 4 to 10 percent in the second year.
I also conduct additional robustness checks using different covariates in
the model. Table A.3 presents estimates from regression models where (1) I
also control for special education and limited English proficiency indicators
interacted with being below the cutoff to account for the exemption clauses in
the policy (in column I); and (2) I use school fixed-effects to eliminate time-
invariant across-school differences in disciplinary outcomes. The findings are
almost identical to the estimates presented in table 3, reinforcing the previous
conclusions.
Subgroup Analysis
Having provided evidence that grade retention, on average, leads to disruptive
behavior, I now check to see whether the estimated effects of grade reten-
tion are heterogeneous by observed student characteristics. Table 10 presents
the estimated discontinuities in whether the student was involved in a disci-
plinary incident in the following two years by socioeconomic status in the first
panel, by race/ethnicity in the second panel, and by gender in the third panel.
All regressions include student covariates, cohort fixed effects, and within-
school average peer outcome. The most striking result is that the adverse ef-
fect of retention is primarily concentrated among economically disadvantaged
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
0
3
3
5
0
1
6
8
9
9
1
0
e
d
p
_
a
_
0
0
1
6
6
p
d
f
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
367
GRADE RETENTION AND STUDENT MISBEHAVIOR
Table 8.
Attrition and Student Characteristics
Score Range/Bandwidth
Current year
Disciplinary incident
In-school suspension
Out-of-school suspension
Prior year
Disciplinary incident
In-school suspension
Out-of-school suspension
Limited English proficiency
Special education
FRPL eligible
Male
Age in 3rd grade (in months)
FCAT Math score: 3rd grade
White
Black
Hispanic
Asian
Foreign born
English not native
In Sample – Following
Year
In Sample – Two Years
Later
Linear
5
Quartic
20
Linear
5
Quartic
20
−0.017
(0.023)
0.002
(0.011)
−0.013
(0.015)
−0.006
(0.006)
−0.016∗∗∗
(0.002)
−0.005
(0.006)
0.018
(0.011)
0.005
(0.012)
0.001
(0.015)
−0.051∗∗∗
(0.014)
0.585∗∗∗
(0.215)
0.020
(0.018)
−0.025
(0.028)
−0.011
(0.010)
0.038
(0.029)
−0.040∗
(0.022)
−0.006
(0.010)
−0.025
(0.018)
−0.008
(0.010)
−0.020∗∗∗
(0.007)
−0.006
(0.007)
0.026
(0.016)
−0.011
(0.021)
−0.006
(0.017)
−0.043∗∗
(0.016)
0.369
(0.274)
0.084∗∗
(0.040)
−0.004
(0.034)
−0.023
(0.019)
0.028
(0.041)
−0.019
(0.025)
0.002
(0.012)
−0.016
(0.016)
−0.005
(0.006)
−0.014∗∗∗
(0.003)
−0.006
(0.005)
0.010
(0.013)
0.004
(0.012)
−0.003
(0.013)
−0.061∗∗∗
(0.013)
0.596∗∗
(0.276)
0.016
(0.015)
−0.031
(0.027)
−0.004
(0.010)
0.036
(0.030)
−0.016∗∗∗
(0.004)
−0.023∗∗∗
(0.005)
−0.016∗∗∗
(0.004)
0.025
(0.021)
0.037∗
(0.021)
0.002
(0.021)
0.029
(0.027)
0.023
(0.020)
0.032
(0.022)
−0.046∗
(0.024)
−0.007
(0.012)
−0.029
(0.018)
−0.007
(0.009)
−0.017∗
(0.007)
−0.007
(0.006)
0.012
(0.017)
−0.007
(0.019)
−0.016
(0.018)
−0.053∗∗∗
(0.015)
0.321
(0.307)
0.094∗∗∗
(0.033)
−0.011
(0.032)
−0.011
(0.019)
0.021
(0.040)
−0.023∗∗∗
(0.005)
−0.001
(0.021)
0.016
(0.025)
Notes: Robust standard errors, clustered relative reading score level, are given in parentheses.
Discontinuity estimates are obtained parametrically using the specified polynomial order and the
score range. Both specifications include the cohort fixed effects.
∗Statistical significance at 10%; ∗∗statistical significance at 5%; ∗∗∗statistical significance at 1%.
368
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
0
3
3
5
0
1
6
8
9
9
1
0
e
d
p
_
a
_
0
0
1
6
6
p
d
f
/
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Umut ¨Ozek
Table 9. Robustness Checks Using Different Bandwidths and Poly-
nomial Orders
Score
Range
Polynomial
Order
Incident
Following Year
Incident Two
Years Later
1
5
10
10
10
15
15
15
20
0
2
1
2
3
1
3
4
1
0.035∗∗
(0.018)
[8,643]
0.049∗∗∗
(0.019)
[43,793]
0.028∗∗
(0.012)
0.035∗∗
(0.017)
0.074∗∗∗
(0.018)
[84,914]
0.013
(0.011)
0.043∗∗∗
(0.016)
0.071∗∗∗
(0.018)
[128,441]
0.008
(0.010)
[172,584]
0.051∗∗∗
(0.021)
[8,643]
0.089∗∗∗
(0.012)
[43,793]
0.042∗∗∗
(0.011)
0.038∗
(0.020)
0.106∗∗∗
(0.010)
[84,914]
0.026∗∗
(0.011)
0.050∗∗∗
(0.019)
0.085∗∗∗
(0.018)
[128,441]
0.021∗∗∗
(0.009)
[172,584]
Notes: Robust standard errors, clustered at the relative reading
score level, are given in parentheses. Discontinuity estimates
are obtained parametrically using the specified polynomial order
and the score range. All regressions control for the student co-
variates listed above, cohort fixed effects, and within-school peer
averages. Sample sizes are given in square brackets.
∗Statistical significance at 10%; ∗∗statistical significance at 5%;
∗∗∗statistical significance at 1%.
students as measured by their FRPL eligibility. Grade retention leads to a 7 to 9
percentage point increase in disciplinary incidents for economically disadvan-
taged students, whereas it has no statistically significant effect on more affluent
students. The estimated discontinuities are positive for all major racial/ethnic
groups in Florida, but the largest effect seems to be on African American
students. Similarly, grade retention affects students of both genders, but the
point estimates are larger for boys.5
5.
Important to note here is that subgroup effects are not statistically different from each other, mainly
because of smaller sample size and less precise estimates.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
0
3
3
5
0
1
6
8
9
9
1
0
e
d
p
_
a
_
0
0
1
6
6
p
d
f
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
369
GRADE RETENTION AND STUDENT MISBEHAVIOR
Table 10.
Early Grade Retention and Misbehavior Subgroup Analysis
Score Range/Bandwidth
Incident within two years
All
First-stage discontinuity
N
Socioeconomic status
FRPL Eligible
First-stage discontinuity
N
FRPL Ineligible
First-stage discontinuity
N
Race/Ethnicity
White
First-stage discontinuity
N
Black
First-stage discontinuity
N
Hispanic
First-stage discontinuity
N
Gender
Male
First-stage discontinuity
N
Female
Linear
5
Quartic
20
0.053∗∗∗
(0.011)
0.320∗∗∗
(0.007)
44,247
0.062∗∗∗
(0.013)
0.329∗∗∗
(0.008)
32,991
0.026
(0.021)
0.295∗∗∗
(0.006)
11,256
0.048∗∗
(0.021)
0.288∗∗∗
(0.009)
13,250
0.076∗∗∗
(0.020)
0.353∗∗∗
(0.007)
15,718
0.027∗
(0.015)
0.322∗∗∗
(0.009)
13,007
0.065∗∗
(0.032)
0.328∗∗∗
(0.007)
23,891
0.039
(0.024)
0.071∗∗∗
(0.015)
0.322∗∗∗
(0.008)
180,066
0.081∗∗∗
(0.019)
0.329∗∗∗
(0.010)
132,875
0.044∗
(0.023)
0.303∗∗∗
(0.005)
47,191
0.079∗∗
(0.026)
0.290∗∗∗
(0.009)
54,858
0.101∗∗∗
(0.027)
0.352∗∗∗
(0.009)
62,613
0.031
(0.023)
0.328∗∗∗
(0.011)
53,135
0.100∗∗∗
(0.033)
0.331∗∗∗
(0.010)
96,815
0.037
(0.028)
370
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
0
3
3
5
0
1
6
8
9
9
1
0
e
d
p
_
a
_
0
0
1
6
6
p
d
f
/
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Umut ¨Ozek
Table 10. Continued.
Score Range/Bandwidth
First-stage discontinuity
N
Time spent in current school
Different school in 2nd grade
First-stage discontinuity
N
Same school in 2nd grade
First-stage discontinuity
Linear
5
0.310∗∗∗
(0.007)
20,356
0.051
(0.032)
0.334∗∗∗
(0.010)
10,722
0.053∗∗∗
(0.020)
0.315∗∗∗
(0.009)
Quartic
20
0.312∗∗∗
(0.008)
83,251
0.035
(0.037)
0.343∗∗∗
(0.005)
43,227
0.083∗∗∗
(0.021)
0.315∗∗∗
(0.009)
N
33,525
136,839
Number of retained peers in school
Fewer than 5 peers
First-stage discontinuity
N
More than 10 peers
First-stage discontinuity
N
0.097∗∗∗
(0.013)
0.177∗∗∗
(0.007)
13,737
0.021∗∗∗
(0.008)
0.433∗∗∗
(0.010)
20,129
0.164∗∗∗
(0.051)
0.173∗∗∗
(0.007)
56,741
0.036∗∗
(0.023)
0.443∗∗∗
(0.011)
80,361
Notes: Robust standard errors, clustered at the relative reading
score level, are given in parentheses. Discontinuity estimates are
obtained parametrically using the specified polynomial order and
the score range. All regressions control for the student covariates
listed above, cohort fixed effects, and within-school average peer
outcomes.
∗∗Statistical significance at 5%; ∗∗∗statistical significance at 1%.
Understanding the Mechanisms behind the Retention Effect
There are several mechanisms that might explain the adverse effect of grade
retention on student behavior. For instance, the observed discontinuity at the
retention cutoff might arise if the students who are old for their grade are
more likely to misbehave. Controlling for relative age, however, would lead
to misleading inferences in the framework outlined herein, because retention
is highly correlated with relative age in the years following retention. There-
fore, to see if relative age is associated with student misbehavior, I conduct an
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
0
3
3
5
0
1
6
8
9
9
1
0
e
d
p
_
a
_
0
0
1
6
6
p
d
/
f
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
371
GRADE RETENTION AND STUDENT MISBEHAVIOR
exploratory analysis where I restrict the sample to all fourth and fifth graders
in the sample, the grades during which the negative effects of retention are
observed. To account for the possibility that relative age is correlated with un-
observed student characteristics, I also restrict the sample to students born in
August and September and use the “September-born” indicator as an instru-
ment for relative age (in months), taking advantage of Florida’s school starting
age policy.6 Hence, I exploit the variation in relative age created by the policy,
which is presumably exogenous to unobserved student attributes.
The results, which are available upon request, suggest a strong first-stage
(students born in September, on average, are six months older than their peers
in the same grade), and a second stage estimate of 0.0008, which is statistically
significant at the 1 percent level. This indicates that a twelve-month increase
in relative age, such as the one created by grade retention, would increase
the likelihood of disciplinary incident by 1 percentage point. Although not
necessarily conclusive, these findings provide evidence that the increase in
relative age caused by retention might be playing a role in the retention effect.
Another possible explanation is the emotional distress associated with loss
of friends and stigma caused by being left behind. Although it is not possible to
directly test for these hypotheses using administrative data, I present indirect
evidence using subgroup analysis. First, I break down the regression disconti-
nuity estimation by how much time the student has spent in the same school
before the third grade. The idea here is that the longer the student has spent in
the same school, the larger the emotional burden of loss of friends will be. The
estimates provided in the second-to-last panel in table 10 somewhat support
this hypothesis. For students who entered the school during the third grade,
the effect of retention is not statistically different from zero, whereas for the
“stable” students, the effects are negative and statistically significant.
I also check to see whether retention effects are larger for students in
schools with fewer retained students. The idea in this exercise is that the
stigma associated with being held back is presumably less severe for students
if most of their peers are also retained. The last panel in table 10 presents the
discontinuity estimates using schools with fewer than five retained students
in a given year and schools with more than ten retained third graders. The
estimated effects seem to support this hypothesis, with larger effect sizes for
the former subgroup of schools. For instance, for schools with fewer than
five retained students, the retained students are 10 to 16 percentage points
more likely to be involved in a disciplinary incident, whereas that number is 2
6. In Florida, children who have attained the age of five years on or before 1 September of the school
year are eligible for admission to public kindergarten. In the regressions, I also control for student
covariates such as FRPL eligibility, race/ethnicity, special education status, measures of English
proficiency, and school, year, and grade fixed effects.
372
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
0
3
3
5
0
1
6
8
9
9
1
0
e
d
p
_
a
_
0
0
1
6
6
p
d
/
f
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Umut ¨Ozek
to 4 percentage points for schools with high retention rates. Overall, all three
explanations seem to be playing a role on the adverse effects of grade retention.
5. CONCLUDING REMARKS
Test-based accountability has become the new norm in public education over
the last decade, with demands for greater accountability intensifying in the
wake of recent initiatives such as the Race to the Top. In many states and school
districts nationwide, not only schools and teachers are held accountable for
the performance of their students but low performance in standardized tests
also carries significant implications for students. One of these implications is
grade retention for low performers.
In this study, I examine the effects of grade retention on student mis-
behavior using the non-linearity created by the Just Read, Florida! program,
a reading initiative that requires students with reading skills below grade
level to be retained in the third grade. The regression discontinuity estimates
suggest grade retention increases the likelihood of disciplinary incidents and
suspensions among just-retained students who are otherwise comparable to
their peers on the other side of the retention cutoff. The findings also suggest
these adverse effects are concentrated among the economically disadvantaged,
African Americans, and boys.
The overarching conclusion in the recent literature is that grade retention,
especially in early grades, leads to significant achievement gains in the short
run. The findings presented in this study reveal that these short-run benefits
come with the burden of higher rates of student misbehavior. If, however,
early grade retention policies gradually lead to improved learning in grades
before the third grade, and hence lower retention rates (as retention policies
typically intend to accomplish), then these adverse effects might become less
significant in the long run. That is, despite the fact that the adverse effects of
grade retention on misbehavior persist, these effects might become less
concerning over time if reading achievement improves and fewer students are
retained. In fact, this seems to be the trend in Florida, with significantly more
students scoring above grade level in third grade and fewer students being
retained (12 percent retention rate in 2003 compared with 7 percent in 2011).
Finally, it is important to note that the estimated effects in this study reflect
the combined effects of the grade retention and the instructional support com-
ponents of the Florida policy. Therefore, the findings presented here might
not be generalizable to other grade retention policies. Nevertheless, this study
might help better assess the costs and benefits associated with increasingly
popular test-based retention policies that are commonly tied to support mech-
anisms for the retained students.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
0
3
3
5
0
1
6
8
9
9
1
0
e
d
p
_
a
_
0
0
1
6
6
p
d
f
/
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
373
GRADE RETENTION AND STUDENT MISBEHAVIOR
This research was supported by the National Center for the Analysis of Longitudinal
Data in Education Research (CALDER) funded through grant R305A060018 to the
American Institutes for Research from the Institute of Education Sciences, U.S. De-
partment of Education. The opinions expressed are those of the author and do not
represent views of the Institute or the U.S. Department of Education. I would like to
thank Tiffany Chu and Kennan Cepa for excellent research assistance. All errors are
mine.
REFERENCES
Greene, Jay P., and Marcus A. Winters. 2007. Revisiting grade retention: An evaluation
of Florida’s test-based promotion policy. Education Finance and Policy 2(4):319–340.
doi:10.1162/edfp.2007.2.4.319
Jay P., and Marcus A. Winters. 2012. The medium-run effects of
Greene,
Florida’s test-based promotion policy. Education Finance and Policy 7(3):305–330.
doi:10.1162/EDFP_a_00069
Hahn, Jinyong, Petra Todd, and Wilbert van der Klaauw. 2001. Identification and
estimation of treatment effects with a regression-discontinuity design. Econometrica
69(1):201–209.
Holmes, Thomas C. 1989. Grade level retention effects: A meta-analysis of research
studies. In Flunking grades: Research and policies on retention, edited by Lorrie A. Shepard
and Mary Lee Smith, pp. 16–33. New York: The Falmer Press.
Jacob, Brian A., and Lars Lefgren. 2004. Remedial education and student achievement:
A regression-discontinuity analysis. Review of Economics and Statistics 86(1):226–244.
doi:10.1162/003465304323023778
Jacob, Brian A., and Lars Lefgren. 2009. The effect of grade retention on
high school completion. American Economic Journal: Applied Economics 1(3):33–58.
doi:10.1257/app.1.3.33
Jimerson, Shane R. 1999. On the failure of failure: Examining the association between
early grade retention and education and employment outcomes during late adolescence.
Journal of School Psychology 37(3):243–272. doi:10.1016/S0022-4405(99)00005-9
Lee, David S., and David Card. 2008. Regression discontinuity inference with specifica-
tion error. Journal of Econometrics 142(2):655–674. doi:10.1016/j.jeconom.2007.05.003
McCrary, Justin. 2008. Manipulation of
the running variable in the regres-
sion discontinuity design: A density test. Journal of Econometrics 142(2):698–714.
doi:10.1016/j.jeconom.2007.05.005
Porter, Jack. 2003. Estimation in the regression discontinuity model. Unpublished
paper, Harvard University.
Schwerdt, Guido, and Martin R. West. 2012. The effects of early grade retention on
student outcomes over time: Regression discontinuity evidence from Florida. Harvard
University, Program on Education Policy and Governance Working Paper Series No.
PEPG 12–09.
374
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
0
3
3
5
0
1
6
8
9
9
1
0
e
d
p
_
a
_
0
0
1
6
6
p
d
.
/
f
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Umut ¨Ozek
APPENDIX
Table A.1.
Early Grade Retention and Misbehavior First Stage Estimates
Score Range
Below cutoff
Incident one year before
Incident current year
LEP
Special education
FRPL eligible
Male
Age in 3rd grade
3rd grade FCAT Math score
White
Black
Hispanic
Asian
Foreign born
English not native
Cohort FE
Student covariates
N
Linear
5
0.319∗∗∗
(0.006)
0.012
(0.008)
0.012∗
(0.007)
−0.016∗∗∗
(0.006)
−0.057∗∗∗
(0.004)
0.017∗∗∗
(0.004)
0.024∗∗∗
(0.003)
−0.004∗∗∗
(0.0001)
−0.067∗∗∗
(0.002)
0.0001
(0.009)
0.001
(0.009)
−0.007
(0.01)
−0.018
(0.016)
−0.026∗∗∗
(0.007)
0.002
(0.006)
Yes
Yes
Quartic
20
0.322∗∗∗
(0.007)
0.009∗∗
(0.004)
0.016∗∗∗
(0.003)
−0.021∗∗∗
(0.003)
−0.061∗∗∗
(0.002)
0.013∗∗∗
(0.002)
0.022∗∗∗
(0.002)
−0.005∗∗∗
(0.0001)
−0.061∗∗∗
(0.001)
0.01∗∗
(0.004)
0.007
(0.004)
0.002
(0.004)
0.002
(0.007)
−0.025∗∗∗
(0.003)
0.0001
(0.003)
Yes
Yes
42,393
178,248
Notes: Robust standard errors, clustered at the relative reading score
level, are given in parentheses. The results present the full first stage
estimates for columns labeled (II) in table 3.
∗Statistical significance at 10%; ∗∗statistical significance at 5%;
∗∗∗statistical significance at 1%.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
0
3
3
5
0
1
6
8
9
9
1
0
e
d
p
_
a
_
0
0
1
6
6
p
d
/
f
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
375
GRADE RETENTION AND STUDENT MISBEHAVIOR
Table A.2.
Early Grade Retention and Misbehavior Second Stage Estimates
Incident One Year Later
Incident Two Years Later
Score Range
Retained
Incident one year before
Incident current year
LEP
Special education
FRPL eligible
Male
Age in 3rd grade
3rd grade FCAT Math score
White
Black
Hispanic
Asian
Foreign born
English not native
Cohort FE
Student covariates
Within-school peer average
Linear
5
0.039∗∗∗
(0.009)
0.219∗∗∗
(0.01)
0.262∗∗∗
(0.006)
−0.004
(0.003)
−0.004
(0.004)
0.031∗∗∗
(0.003)
0.055∗∗∗
(0.003)
0.002∗∗∗
(0.0003)
−0.005∗∗
(0.002)
−0.019∗∗∗
(0.006)
0.033∗∗∗
(0.005)
−0.021∗∗∗
(0.006)
−0.028∗∗∗
(0.008)
−0.014∗∗∗
(0.005)
−0.019∗∗∗
(0.004)
Yes
Yes
Yes
Quartic
20
0.064∗∗∗
(0.012)
0.201∗∗∗
(0.005)
0.264∗∗∗
(0.003)
−0.003
(0.002)
−0.001
(0.002)
0.029∗∗∗
(0.002)
0.056∗∗∗
(0.001)
0.003∗∗∗
(0.0001)
−0.003∗∗
(0.001)
−0.009∗∗∗
(0.003)
0.042∗∗∗
(0.003)
−0.011∗∗∗
(0.004)
−0.024∗∗∗
(0.004)
−0.011∗∗∗
(0.002)
−0.018∗∗∗
(0.002)
Yes
Yes
Yes
Linear
5
0.055∗∗∗
(0.011)
0.181∗∗∗
(0.01)
0.234∗∗∗
(0.011)
0.0001
(0.005)
−0.006
(0.004)
0.044∗∗∗
(0.004)
0.074∗∗∗
(0.004)
0.003∗∗∗
(0.0002)
−0.007∗∗∗
(0.001)
−0.01
(0.008)
0.043∗∗∗
(0.007)
−0.018∗∗
(0.008)
−0.032∗∗∗
(0.011)
−0.013∗∗
(0.005)
−0.031∗∗∗
(0.003)
Yes
Yes
Yes
Quartic
20
0.054∗∗∗
(0.022)
0.191∗∗∗
(0.005)
0.24∗∗∗
(0.004)
0.002
(0.002)
−0.01∗∗∗
(0.002)
0.04∗∗∗
(0.002)
0.067∗∗∗
(0.002)
0.003∗∗∗
(0.0001)
−0.007∗∗∗
(0.002)
−0.013∗∗∗
(0.004)
0.042∗∗∗
(0.004)
−0.023∗∗∗
(0.004)
−0.034∗∗∗
(0.006)
−0.019∗∗∗
(0.002)
−0.026∗∗∗
(0.002)
Yes
Yes
Yes
N
43,793
178,248
43,793
178,248
Notes: Robust standard errors, clustered at the relative reading score level, are given in parenthe-
ses. The results present the full second stage estimates for columns labeled (II) in table 3.
∗∗Statistical significance at 5%; ∗∗∗statistical significance at 1%.
376
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
0
3
3
5
0
1
6
8
9
9
1
0
e
d
p
_
a
_
0
0
1
6
6
p
d
f
/
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Umut ¨Ozek
Table A.3.
Early Grade Retention and Misbehavior: Alternative Specifications
Score Range
1 year later
Disciplinary incident
In-school suspension
Out-of-school suspension
2 years later
Disciplinary incident
In-school suspension
Out-of-school suspension
First-stage discontinuity
Linear
Quartic
(I)
5
(II)
5
(I)
20
(II)
20
0.036∗∗∗
(0.010)
0.013
(0.010)
0.040∗∗∗
(0.014)
0.050∗∗∗
(0.013)
0.030∗∗∗
(0.005)
0.025∗∗∗
(0.009)
0.347∗∗∗
(0.008)
0.039∗∗∗
(0.009)
0.009
(0.007)
0.037∗∗∗
(0.011)
0.054∗∗∗
(0.013)
0.032∗∗∗
(0.004)
0.027∗∗∗
(0.005)
0.319∗∗∗
(0.006)
0.058∗∗∗
(0.013)
0.017
(0.010)
0.056∗∗∗
(0.015)
0.054∗∗∗
(0.018)
0.039∗∗∗
(0.008)
0.024∗∗
(0.012)
0.358∗∗∗
(0.008)
0.062∗∗∗
(0.013)
0.017
(0.011)
0.044∗∗∗
(0.015)
0.052∗∗∗
(0.022)
0.037∗∗∗
(0.010)
0.017
(0.011)
0.323∗∗∗
(0.007)
N
Cohort FE
Student covariates
Peer incident rate at school
School FE
Includes LEP and SPED interacted
with the below-cutoff indicator
43,793
43,793
178,248
178,248
Yes
Yes
Yes
No
Yes
Yes
Yes
No
Yes
No
Yes
Yes
Yes
No
Yes
Yes
Yes
No
Yes
No
Notes: Robust standard errors, clustered at the relative reading score level, are given in paren-
theses. Discontinuity estimates are obtained parametrically using the specified polynomial
order and the score range. All regressions control for the student covariates listed above,
cohort fixed effects, and within-school average peer outcomes.
∗∗Statistical significance at 5%; ∗∗∗statistical significance at 1%.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
0
3
3
5
0
1
6
8
9
9
1
0
e
d
p
_
a
_
0
0
1
6
6
p
d
f
/
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
377