Harmonic Amplitude Summation for
Frequency-tagging Analysis
Talia L. Retter1
, Bruno Rossion2,3
, and Christine Schiltz1
Abstract
■ In the approach of frequency tagging, stimuli that are pre-
sented periodically generate periodic responses of the brain.
Following a transformation into the frequency domain, the
brain’s response is often evident at the frequency of stimula-
tion, F, and its higher harmonics (2F, 3F, etc.). This approach
is increasingly used in neuroscience, as it affords objective mea-
sures to characterize brain function. However, whether these
specific harmonic frequency responses should be combined
for analysis—and if so, how—remains an outstanding issue. In
most studies, higher harmonic responses have not been
described or were described only individually; in other studies,
harmonics have been combined with various approaches, for
example, averaging and root-mean-square summation. A rationale
for these approaches in the context of frequency-based analysis
principles and an understanding of how they relate to the brain’s
response amplitudes in the time domain have been missing.
Here, with these elements addressed, the summation of (baseline-
corrected) harmonic amplitude is recommended. ■
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
3
3
1
1
2
3
7
2
1
9
6
7
7
8
4
/
/
j
o
c
n
_
a
_
0
1
7
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
INTRODUCTION
Frequency Tagging
It has long been known that a stimulus presented at a
periodic rate elicits a response from an observer’s brain
at exactly that rate. For example, a light flickering on and
off at a periodic rate, 14 times a second, elicits a measur-
able response in the EEG of a human observer 14 times a
second (Adrian & Mathews, 1934). In the time domain, a
response is evident as periodic changes in the brain’s re-
sponse amplitude across time. Following Fourier trans-
formation into a frequency domain representation
(Danielson & Lanczos, 1942; Fourier, 1822), the response
is evident as a high amplitude “peak” at exactly the funda-
mental stimulus presentation rate (frequency = F ) and/or
its higher harmonics, that is, at frequencies that are integer
multiples of F (2F, 3F, etc.; Regan, 1966, 1989).
The approach of presenting stimuli and analyzing
neural responses at the frequency of stimulation is referred
to by many names: “Frequency tagging” (Srinivasan,
Russell, Edelman, & Tononi, 1999; Tononi, Srinivasan,
Russell, & Edelman, 1998) is the one that will be used
here. Other names for this approach differ mainly on their
point of reference: to the responses that appear consis-
tently periodic to stimuli presented at high rates, that is,
“steady-state” responses, for example, “steady-state
visual-evoked potentials” (Norcia, Appelbaum, Ales,
Cottereau, & Rossion, 2015; Heinrich, 2010; Di Russo,
Teder-Salajarvi, & Hillyard, 2002; Regan, 1966, 1989)
1University of Luxembourg, 2Université de Lorraine, Nancy,
France, 3Université de Lorraine, CHRU-Nancy
and “auditory steady state potentials/responses” (Watkin,
2008; Geisler, 1960) or “traveling wave” responses (Engel,
Glover, & Wandell, 1997); to the “stimulation” mode itself
(“fast periodic visual stimulation”; Rossion, 2014; Rossion,
Retter, & Liu-Shuang, 2020); or the “analysis” occurring in the
frequency domain (“Fourier analysis/synthesis”; Zhou,
Melloni, Poeppel, & Ding, 2016; Bach & Meigen, 1999;
Movshon, Thompson, & Tolhurst, 1978; or simply “frequency
(domain) analysis,” for example, as in McKeefry, Russell,
Murray, & Kulikowski, 1996). Despite the varying terminolo-
gies, the principles of the approach are the same. In a similar
vein, various types of stimulation modalities (visual, auditory,
somatosensory, cross-modal) and recording methods (EEG,
electroretinogram, fMRI, single-cell recordings, etc.) may
be applied with various participant groups (human adults,
children, infants, nonhuman primates, cats, rodents, frogs,
insects, etc.), resulting in some practical differences, but
the same fundamentals, of the approach.
In (cognitive) neuroscience research, the frequency-
tagging approach is associated with undeniable advan-
tages. As noted early on, this approach is well suited
for specifically relating brain processes to external events:
“This gives a method of tracing the visual messages in the
brain, for by means of the flicker rhythm they can be
made easy to recognize” (Adrian, 1944, p. 361). More
recently, its objectivity and sensitivity (i.e., high signal-
to-noise ratio) have been highlighted, and the use of
the paradigm is undoubtedly on the rise, having been
extended from the study of basic sensory processes and
their modulation by spatial/selective attention to the direct
measurement of higher levels of cognition in recent years
(see Norcia et al., 2015, for a review). However, frequency
© 2021 by the Massachusetts Institute of Technology. Published under
a Creative Commons Attribution 4.0 International (CC BY 4.0) license.
Journal of Cognitive Neuroscience 33:11, pp. 2372–2393
https://doi.org/10.1162/jocn_a_01763
tagging is still fundamentally limited by outstanding con-
ceptual and methodological ambiguities in dealing with
responses occurring across harmonics.
Higher Harmonics
Another way of describing frequency tagging is the fol-
lowing: Given a periodic stimulus, responses of the brain
periodic to that stimulus are investigated. In this formu-
lation, it is evident that the brain’s responses may occur
at the rate of stimulation, F, but also at the other rates
periodic to the stimulation: the higher harmonics (2F,
3F, etc.). For example, a stimulus modulated 8 times a
second, at 8 Hz, may generate responses that are evident
as amplitude peaks in the frequency domain representa-
tion of the brain recording at 8 Hz (F, the first harmonic,
corresponding to the fundamental frequency1), but also
at 16 Hz (2F, the second harmonic) and 24 Hz (3F, the
third harmonic). Because only responses at higher har-
monics are periodic to the fundamental frequency, it is
uniquely at the higher harmonics, rather than at a diffuse
band, that higher frequency constituents of frequency-
tagged brain responses are present.
Although responses of the brain are not always generated
at the higher harmonics, they often do occur (Rossion et al.,
2020; Zhou et al., 2016; Norcia et al., 2015; Rossion, 2014;
Heinrich, 2010; Vialatte, Maurice, Dauwels, & Cichocki,
2010; Bach & Meigen, 1999; Regan, 1966). Note that
responses are not always generated at F either; for a classic
example, in the case of alternating symmetrical stimulus
inputs (e.g., pattern-reversing checkerboards), the brain
responds only at 2F and higher even harmonics (Cobb,
Morton, & Ettlinger, 1967; reviewed in Norcia et al., 2015;
for different examples, Zhou et al., 2016; Heinrich, 2010;
Movshon et al., 1978). Furthermore, note that, throughout
this article, only harmonics that are specific to their funda-
mental frequency are addressed, which is always the case
when a single stimulus presentation frequency is used
(but for an extension to other cases, with more complex
stimulation paradigms, please see the Which Harmonics
to Consider? section).
At present, although higher harmonic responses are
an integral part of brain responses, they are not system-
atically addressed in frequency-tagging research. In
many studies, higher harmonic responses are not even
reported (e.g., Bekhtereva, Pritschmann, Keil, & Müller,
2018; Min, Dähne, Ahn, Noh, & Müller, 2016; Paulk,
Kirszenblat, Zhou, & van Swinderen, 2015; Coia, Jones,
Duncan, & Crognale, 2014; Kuś et al., 2013; Cottereau
et al., 2011; Wattam-Bell et al., 2010; Di Russo et al.,
2007; Müller et al., 2006; Braddick, Birtles, Wattam-Bell,
& Atkinson, 2005; Chen, Seth, Gally, & Edelman, 2003;
Heinrich & Bach, 2001; Regan & Regan, 1988a; Tononi
et al., 1998; Peterzell & Norcia, 1997; Müller, Teder, &
Hillyard, 1997; Morgan, Hansen, & Hillyard, 1996, or are
extirpated by narrow [band-pass, Gabor, etc.] filtering,
e.g., Davidson, Mithen, Hogendoorn, van Boxtel, &
Tsuchiya, 2020; Miskociv & Keil, 2013; Anderson &
Müller, 2010; Regan, 1975). Does it matter? Yes, at least
when there is considerable amplitude at the higher har-
monics, relative to F. In this case, higher harmonics do
contribute significantly to the response measurement
(for a dramatic illustration to this effect, see Figure 1).
How often is there considerable amplitude at the higher
harmonics? Can the cost of omitting higher harmonics in
published studies be evaluated? Unfortunately, most stud-
ies do not report whether or not there were responses at
higher harmonics, as mentioned above. Moreover, when
higher harmonic responses were reported to be present,
they were often not described, for example, “Peaks were
also present at the harmonics of the stimulus frequency
but were not analyzed in this study” (Srinivasan et al.,
1999, p. 5438); “Higher harmonics may play a role, espe-
cially at lower temporal frequencies (see, for example, the
double peaks in the 12-Hz data in Figure 1), but these
are not considered here” (Kremers, Rodrigues, Silveira,
& da Silva Filho, 2010, p. 579); “Note however that 2 Hz
is a harmonic of 1 Hz and may actually be a relevant
spectral region to consider (albeit outside the scope of
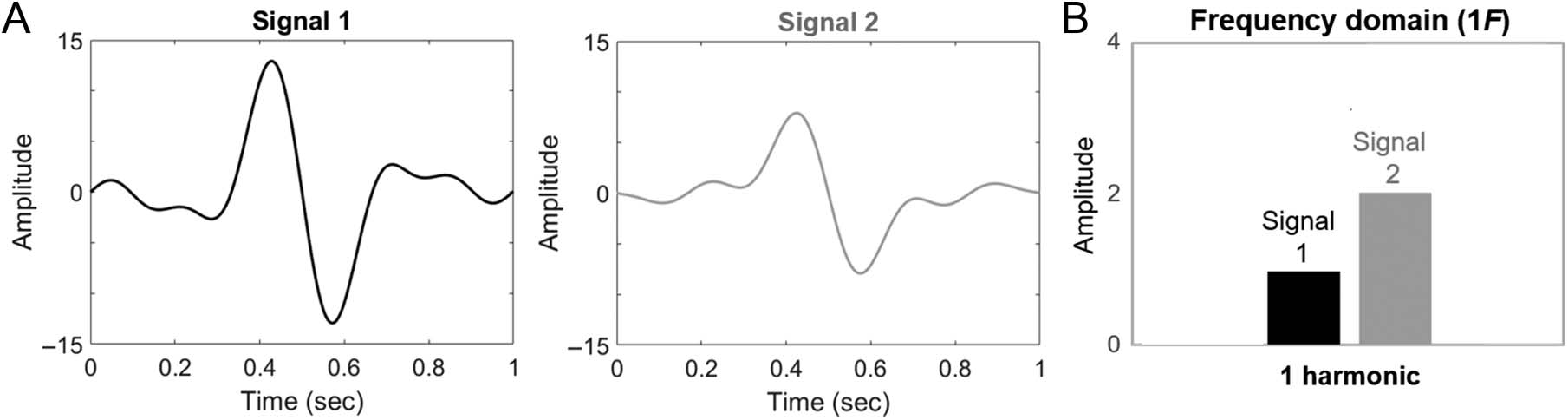
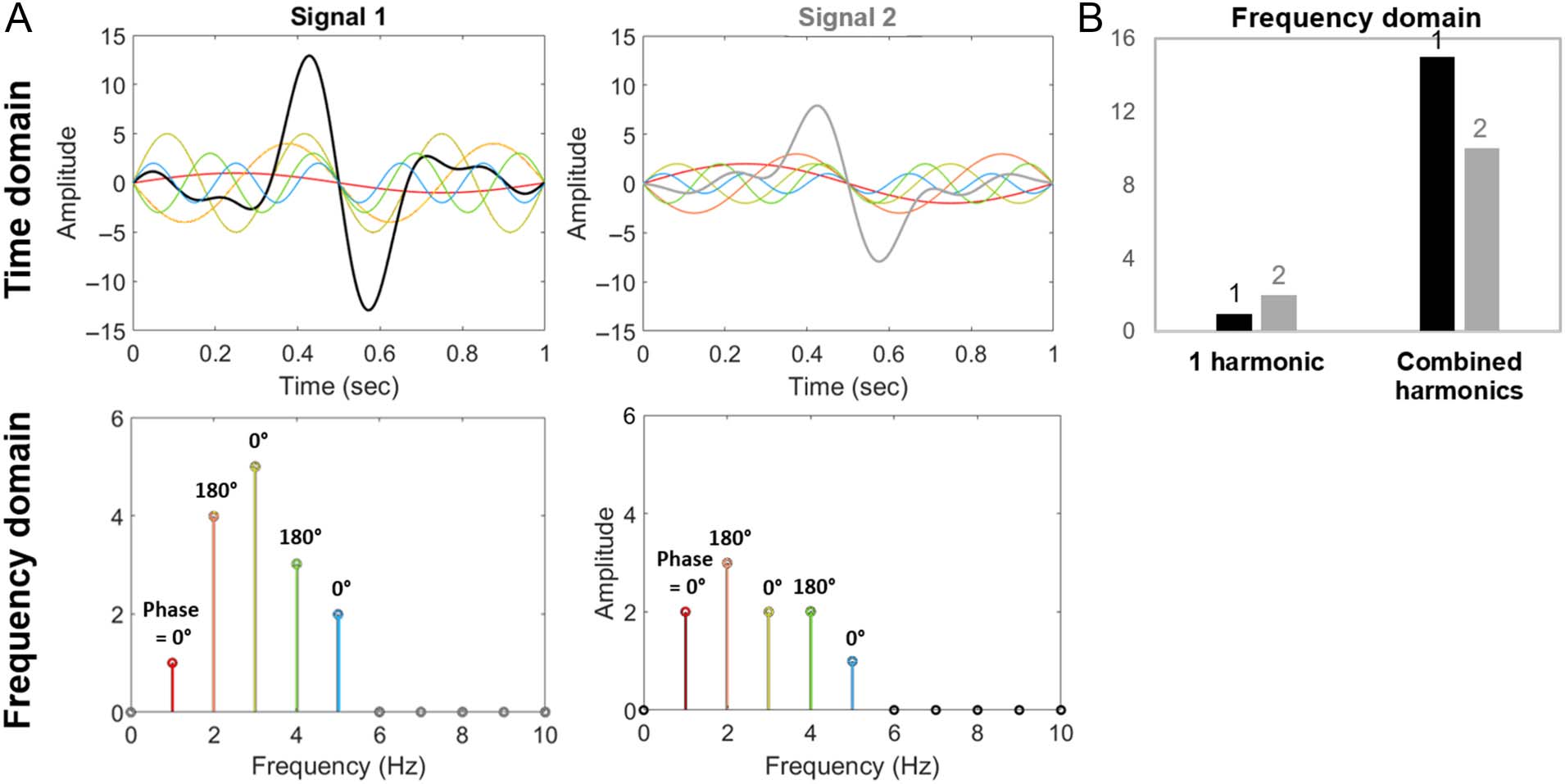
Figure 1. A demonstration of the importance of considering higher harmonics in frequency-tagged response analyses. (A) Two synthetic periodic
signals, each composed of five harmonic frequencies. (B) In the frequency domain, a consideration of only one harmonic (at the fundamental
frequency) describes Signal 2 as larger than Signal 1. This description is not in agreement with typical time domain response analyses (e.g., peak
amplitudes) to compare these signals. Note that this figure will be revisited (expanded) in the Interpreting Harmonics section.
Retter, Rossion, and Schiltz
2373
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
3
3
1
1
2
3
7
2
1
9
6
7
7
8
4
/
/
j
o
c
n
_
a
_
0
1
7
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
this report)” (Kosem, Gramfort, & Van Wassenhove, 2014,
Figure S2; evident in figures but not discussed or included
in analyses: Schettino, Porcu, Gundlach, Keitel, & Müller,
2020; Eidelman-Rothman et al., 2019; Chadnova et al.,
2018; Winawer et al., 2013; Hönegger et al., 2011; Katzner
et al., 2009; Pastor, Artieda, Arbizu, Valencia, & Masdeu,
2003; Pastor et al., 2002; Kaspar, Hassler, Martens,
Trujillo-Barreto, & Gruber, 2001; Müller et al., 1998), pre-
venting a wide-scale review.
From some studies that have described the presence or
absence of higher harmonics, there appear to be a couple,
specific cases in which their amplitude was not consider-
able and may be neglected with little cost. The most
well-documented case is that in which high stimulus pre-
sentation rates are used (as will be demonstrated in the
following section; with electrophysiology: Retter &
Rossion, 2016a; Heinrich, Groten, & Bach, 2015; Alonso-
Prieto, Van Belle, Liu-Shuang, Norcia, & Rossion, 2013;
Capilla, Pazo-Alvarez, Darriba, Campo, & Gross, 2011;
Tlumak, Durrant, Delgado, & Robert Boston, 2011;
Vialatte, Maurice, Dauwels, & Cichocki, 2009; Luck,
2005; Kremers & Scholl, 2001; Ross, Borgmann,
Draganova, Roberts, & Pantev, 2000; Regan, 1989; Van
der Tweel & Verduyn Lunel, 1965; with neuroimaging:
Retter, Webster, & Jiang, 2019; Gao, Gentile, & Rossion,
2018; Puce, Allison, Gore, & McCarthy, 1995). However,
the case of high stimulus presentation rates cannot be
readily identified across studies. This is because “high” is
dependent on the relationship of the stimulus presenta-
tion rate to the duration of the brain responses being
measured, by the recording technique, in the assessed
population (Retter, Jiang, Webster, & Rossion, 2020;
Keysers & Perrett, 2002; see also Heinrich, 2010).
A second case is that in which low-amplitude first har-
monic responses were reported, such as responses elicited
with subtle stimuli (e.g., with no higher harmonic ampli-
tude above noise: Lochy, Schiltz, & Rossion, 2020; Park,
2018; Retter & Rossion, 2017; Brazier, 1964; with very
low higher harmonic amplitudes: Moungou, Thonnard, &
Mouraux, 2016; McFadden et al., 2014; Ales, Farzin, Rossion,
& Norcia, 2012). However, this case also does not allow
general inferences: low first harmonic amplitudes may still
coincide with large higher harmonic amplitudes (see the
Frequency-tagged Responses in the Frequency Domain
section; also, e.g., Gaume, Vialatte, & Dreyfus, 2014;
Alonso-Prieto et al., 2013; Capilla et al., 2011; Vialatte
et al., 2009), such that the amplitude of the first harmonic
itself is not diagnostic.
On the other hand, considerable amplitude at higher
harmonics has been reported in a wide array of studies.
For example, higher harmonics often exceed the funda-
mental in studies on the brain’s responses for an extensive
range of processes (with F usually below 8 Hz, recorded to
visual stimuli with EEG/MEG): from luminance (patterns:
Gaume et al., 2014; Capilla et al., 2011; Vialatte et al., 2009;
Davila, Srebro, & Ghaleb, 1998; electrocorticography:
Winawer et al., 2013; electroretinogram: Baker & Hess,
1984) to color and motion (McKeefry et al., 1999; Tyler
& Kaitz, 1977) to face perception (Liu-Shuang, Norcia, &
Rossion, 2014; Alonso-Prieto et al., 2013; below about
40 Hz to auditory stimuli: Ross et al., 2000; see also
Tlumak et al., 2011). Higher harmonics may also be pres-
ent, each with a lower amplitude than the fundamental,
but with their amplitude distributed across a large range
of harmonic frequencies (e.g., Cunningham, Baker, &
Pierce, 2017; Retter & Rossion, 2016a; Gaume et al.,
2014; Painter, Dux, Travis, & Mattingley, 2014; Alonso-
Prieto et al., 2013; Capilla et al., 2011; Vialatte et al.,
2009). Considerable higher harmonics have also been
demonstrated with low-temporal resolution techniques,
including fMRI, given appropriately slow stimulus presen-
tation frequencies (e.g., with F well below 0.1 Hz; motor
activity: Bandettini, Jesmanowicz, Wong, & Hyde, 1993;
luminance patterns: Engel et al., 1997).
In some cases, the conclusions of studies considering
and not considering higher harmonics can be compared.
For example, in frequency-tuning studies, without consid-
ering higher harmonics, maximal visual responses were
reported to stimuli modulated at about 10–15 Hz with
EEG (e.g., Ding, Sperling, & Srinivasan, 2006; Pastor
et al., 2003; Regan, 1966; see also Vialatte et al., 2009).
However, when higher harmonics were considered, the
lowest stimulation frequency tested (3 Hz) yielded the
maximal visual EEG responses, being over 3 times higher
than the responses to 12 Hz stimulation with natural
images (Retter et al., 2020, Figure S3). Similarly, maximal
auditory responses were reported to stimuli modulated at
about 40 Hz with EEG (e.g., Pastor et al., 2002; Ross et al.,
2000; Galambos, Makeig, & Talmachoff, 1981), but a
consideration of higher harmonics produced the maximal
auditory EEG responses at the lowest stimulation fre-
quency tested (0.75 Hz; Tlumak et al., 2011, Figure 4).
Overall, although it is thus impossible to ascertain what
the impact of unreported or uncharacterized higher har-
monic responses in most studies may have been, it is
likely that it was often considerable.
Should Higher Harmonic Responses Be Combined,
and If So, How?
At present, harmonics are surrounded by many ques-
tions: Why do they occur? What do they represent?
Which, or how many, harmonics should be considered?
Should they be taken into account for response identifi-
cation and measurement, and if so, how? Indeed, the lack
of understanding and standard practice regarding higher
harmonics has limited the ease (i.e., objectivity) of
frequency-tagged response identification and measure-
ment. This is particularly significant because objectivity
is given as a primary advantage of the frequency-tagging
technique, contributing to its increasing application in
(cognitive) neuroscience research and clinical applica-
tions (e.g., see Rossion et al., 2020; Norcia et al., 2015).
2374
Journal of Cognitive Neuroscience
Volume 33, Number 11
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
3
3
1
1
2
3
7
2
1
9
6
7
7
8
4
/
/
j
o
c
n
_
a
_
0
1
7
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
In previous studies that reported harmonic responses,
most often these responses have been described individ-
ually (e.g., at F, 2F, 3F) and have not been taken into ac-
count for response measurement (e.g., Cunningham
et al., 2017; Moungou et al., 2016; Painter et al., 2014;
Alonso-Prieto et al., 2013; Ales et al., 2012; Capilla et al.,
2011; Rossion & Boremanse, 2011; Vialatte et al., 2009;
Herrmann, 2001; Ross et al., 2000; Srinivasan et al., 1999;
Bandettini et al., 1993; Tyler & Kaitz, 1977). Although con-
sidering harmonic responses separately is considerably
better than not at all, individual harmonic responses do
not represent independent aspects of a time domain
response (e.g., see Tang & Norcia, 1995; for dependent
harmonic amplitude examples: Retter & Rossion, 2016a;
Zhou et al., 2016; for qualitatively similar neighboring
harmonic examples: Rossion et al., 2020; Zemon & Gordon,
2018; Jacques, Retter, & Rossion, 2016; Rossion, 2014; see
the Interpreting Harmonics section).
In practice, considering higher harmonic responses
improves response detection, measurement, and classifi-
cation (e.g., Zemon & Gordon, 2018; Retter & Rossion,
2016a; Tlumak et al., 2011; Cebulla, Stürzebecher, &
Elberling, 2006; Davila et al., 1998; for brain–computer/
machine interfaces: Cetin, Ozekes, & Varol, 2020; Chen
et al., 2015; Muller-Putz, Scherer, Brauneis, & Pfurtscheller,
2005). Combining harmonics is particularly useful for
comparing response amplitudes across experimental
conditions. Otherwise, if one input produces a response
with larger amplitudes than another input at some har-
monics but not others, how could these responses be
evaluated overall? Or, how could the relative change
(e.g., percent increase) of one response relative to
another be calculated overall? In some previous studies,
harmonic responses have been combined with various
approaches, such as root-mean-square summation (that
is, the square root of the summed squared amplitudes,
also known as the “root sum square”, or “summation in
quadrature”; e.g., Tlumak et al., 2011; Appelbaum, Ales,
Cottereau, & Norcia, 2010; Appelbaum, Wade, Vildavski,
Pettet, & Norcia, 2006; Hou, Pettet, Sampath, Candy, &
Norcia, 2003), (weighted) summation (e.g., Zhang,
Jamison, Engel, He, & He, 2011; Wang, Gao, Hong, Jia,
& Gao, 2008; Cheng, Gao, Gao, & Xu, 2002), or averaging
(e.g., Milton et al., 2020; Lochy, Van Belle, & Rossion, 2015;
Liu-Shuang et al., 2014). However, these approaches
have not been justified and have not been related to
approaches analyzing the brain’s response amplitudes in
the time domain (or physiologically: see Heinrich, 2010).
In the following, a validated methodology for combining
(baseline-corrected) harmonic amplitudes through simple
summation will be provided. This approach derives from a
theoretical basis of how signals over time are represented
through mathematical transformations into the frequency
domain (see the Frequency Domain Representations sec-
tion), extended to experimental responses in practice
(see the Frequency-tagged Responses in the Frequency
Domain section). This approach was indicated empirically
by Retter and Rossion (2016a), and it has since been
applied in a number of studies, however, primarily by
those authors or associated research groups (e.g., van de
Walle de Ghelcke, Rossion, Schiltz, & Lochy, 2021;
Damon, Leleu, Rekow, Foncet, & Baudouin, 2020;
Fisher, Towler, Rossion, & Eimer, 2020; Gwinn & Jiang,
2019; Dwyer, Xu, & Tanaka, 2019; Van der Donck et al.,
2019; Beck, Rossion, & Samson, 2018; Chemin, Huang,
Mulders, & Mouraux, 2018; De Keyser, Mouraux, Quek,
Torta, & Legrain, 2018; Guillaume, Mejias, Rossion,
Dzhelyova, & Schiltz, 2018; Gwinn, Matera, O’Neil, &
Webster, 2018; Leleu et al., 2018; Xu, Liu-Shuang, Rossion,
& Tanaka, 2017). To be of further use to the scientific
community, the approach requires deeper methodological
evaluation and, especially, evaluation in a theoretical
context, which is the goal throughout this article. From
this, some practical guidelines are offered (see the
Combining Harmonic Responses section) and implications
are drawn for the interpretation of harmonic responses
more generally (see the Interpreting Harmonics section).
FREQUENCY DOMAIN REPRESENTATIONS
Sine Waves
When a signal is transformed into the frequency domain
(by means of a Fourier transform), it becomes represented
through a combination of sine waves, which are the funda-
mental units of the frequency domain. Although there
are many texts on the mathematics of frequency transfor-
mations and representations (e.g., Gonzalez & Woods,
2018; Forinash & Christian, 2016; Patel, 2012; Strang,
2007; Smith, 1997; Press, Falnnery, & Teukolsky, 1993),
a basic understanding of sine waves and their combina-
tion is a sufficient foundation for the interpretation of
multiharmonic responses of the brain (Regan, 1989).
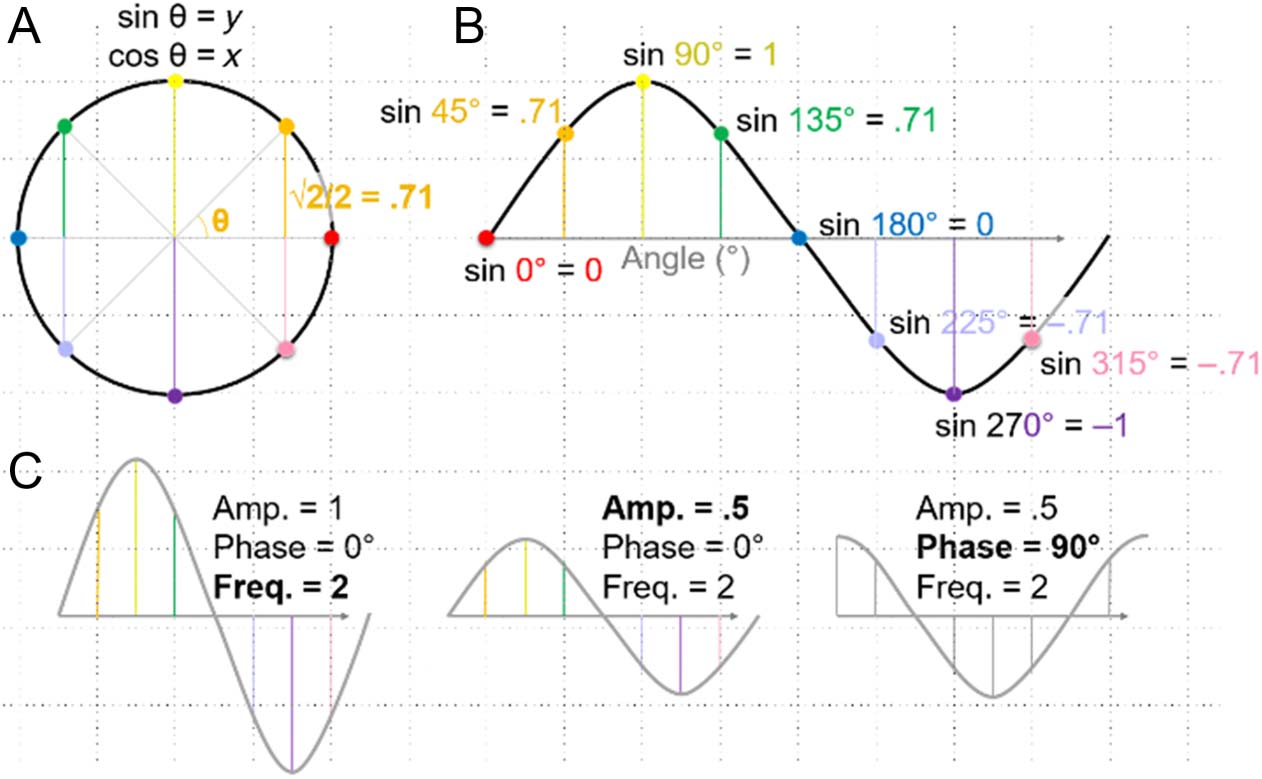
Briefly, sine waves are trigonometric functions that
describe periodic signals in terms of frequency, amplitude,
and phase (Figure 2). The frequency of a sine wave
describes the number of cycles (of 360°; equivalent to 2π
radians) per unit of time or space (time is typically given
in units of cycles/sec = sec−1 = Hertz = Hz). Note that
the cycles of sine waves are periodic and could repeat their
pattern infinitely, as a circle could be endlessly traced (the
sine wave, as in Figure 2B, derives from the y-axis values of a
unit circle, as shown in Figure 2A). The amplitude of a sine
wave is defined along the y-axis (e.g., in Figure 2B, the sine
wave, spanning from −1 to 1, has an amplitude of 1; its unit
in EEG recordings is typically microvolts). The phase of a
sine wave is a measure of its starting angle (indicated by theta
in Figure 2A), with an arbitrary beginning at zero (in units of
degrees or radians), as is shown in Figure 2B. Changes in
frequency, amplitude, and phase, which help demonstrate
these properties, are illustrated in Figure 2C. For those
whom it helps to see it mathematically, the expression of
a sine wave, as a function of x, is: y(x) = asin(2πfx + ϕ),
where a = amplitude (scaling on the y-axis), f = frequency
(by cycles), and ϕ = phase (x-axis shifts).
Retter, Rossion, and Schiltz
2375
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
3
3
1
1
2
3
7
2
1
9
6
7
7
8
4
/
/
j
o
c
n
_
a
_
0
1
7
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 2. The sine wave.
(A) A unit circle, with a radius
of 1, illustrates the underlying
trigonometry of sine (and
cosine) functions. (B) A
sine wave derives from
the y-axis values of points
on the unit circle as a
function of angle (here,
this is emphasized with
corresponding angle colors).
A complete cycle of
a sine wave contains 360°.
(Note that a cosine wave,
which derives from the
x-axis values, has the same
shape but with a 90° phase
shift.) (C) Sine waves are
described in terms of frequency
(cycles per unit), amplitude
( y-axis scale), and phase (x-axis
shift). The given examples exhibit sequential changes in these properties (beginning in reference to B, then from left to right;
the changed property is indicated in bold). Amp. = amplitude; Freq. = frequency.
A Lot of Sine Waves
A frequency domain representation of a signal is essen-
tially a lot of sine waves. That is, when a signal is trans-
formed into the frequency domain, the resultant x-axis
describes the frequency of its constituent sine waves.
The other descriptors of sine waves, amplitude, and
phase are described in the transformed, complex-valued
y-axis at each frequency, which is typically plotted as sep-
arate amplitude and/or phase frequency spectra.2 The
resolution (x-axis sampling) of the frequency domain
spectrum is the inverse of the signal recording length
and the range spans from zero to half of the signal sam-
pling rate (note that these properties have practical im-
plications for frequency-tagging experimental design,
e.g., as addressed in Bach & Meigen, 1999). The combi-
nation, through summation, of these sine waves de-
scribed in the frequency domain reconstructs the
original signal in the time domain. Here, the focus will
be on periodic signals over time, but note that frequency
domain analyses can be applied in many settings (e.g.,
signals over space or over two dimensions).
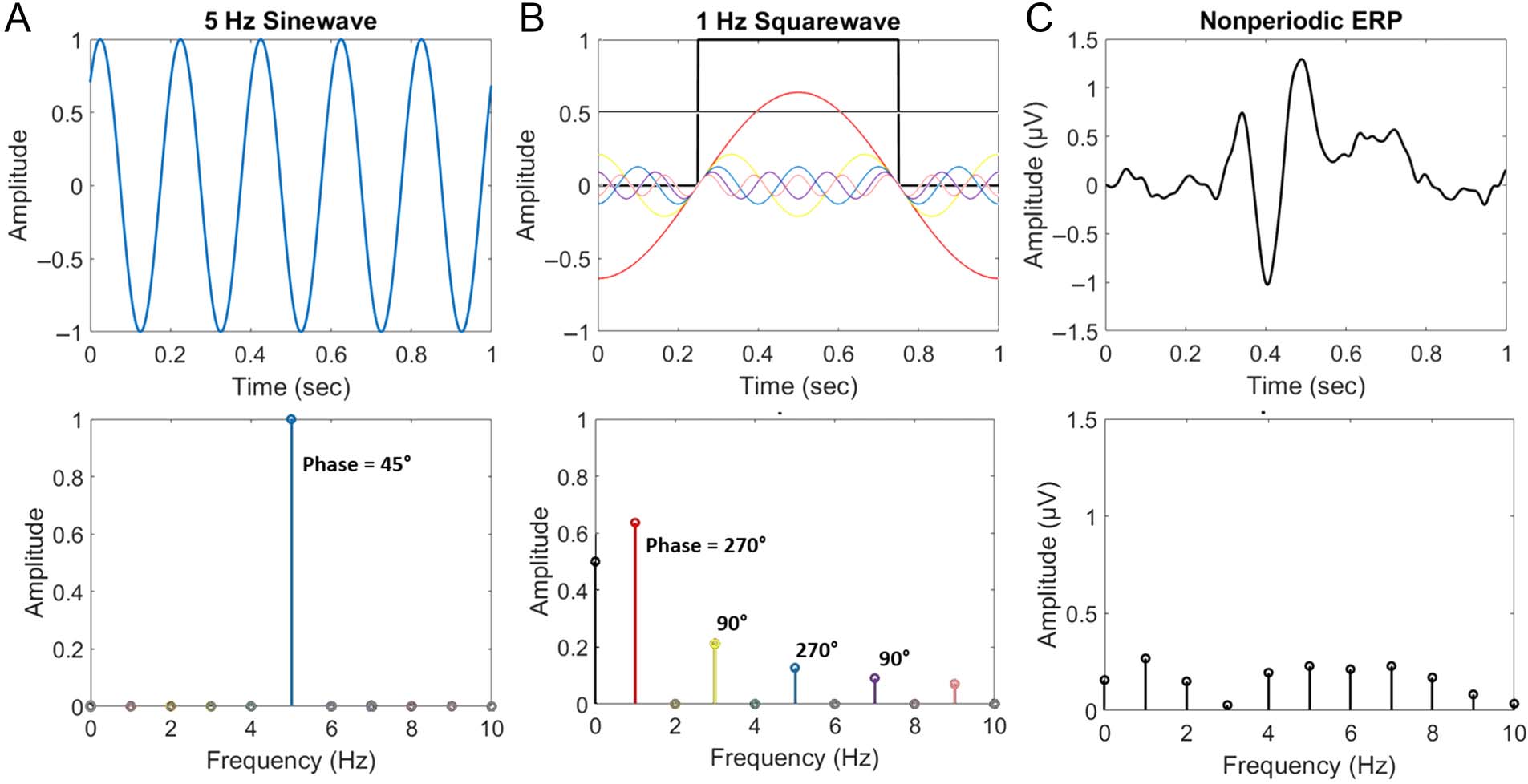
In the simplest case, a periodic signal that is a perfect
sine wave is represented in the frequency domain by a sin-
gle frequency, representing a single sine wave (Figure 3A).
Another way to understand this is to observe that, in this
case, the frequency, amplitude, and phase of a single sine
wave in the frequency domain are sufficient to reconstruct
the original signal in the time domain. In most cases, sig-
nals are more complex (i.e., nonsinusoidal), but this does
not pose a problem: A combination of sine waves at
different frequencies can sum to model any signal. In a
classic example, a periodic squarewave signal is shown
to be represented with a sum of sine waves specific to its
periodicity (Figure 3B). Nonperiodic signals, for example,
ERPs to temporally jittered stimuli, can also be repre-
sented in the frequency domain, but because they are
not specific to limited frequencies, their interpretation
does not correspond to that of frequency-tagged signals
(Figure 3C). Although frequency-based analyses of non-
periodic signals may be applied (e.g., see Herrmann,
Rach, Vosskuhl, & Strüber, 2014; Başar & Schürmann,
1994; Regan, 1989; see also Chemin et al., 2018), these
are outside the present focus on frequency tagging.
It may be observed that a simple sine wave ranging from
−1 to 1 in the time domain has an amplitude of 1 in the
frequency domain, but that the relationship between the
time domain and frequency domain amplitudes for
multiharmonic signals is more complex (compare
Figure 3A and B). However, there is a direct relationship
between these dimensions: Because energy is conserved
from the time to the frequency domain, the sum of the
root-mean-square amplitudes of the time domain signal
equals the sum of the squared root mean amplitudes of
the frequency domain signal (Parseval’s relation; Parseval
des Chênes, 1806; e.g., see Smith, 1997).3 For example,
the sum of the squared amplitudes per cycle of the time
domain signal in Figure 3A is equal to 0.5, and the sum
of the squared root-mean-square amplitudes of its discrete
frequency domain signal is equal to 0.5. Multiharmonic
signals also preserve this relationship, although their time
domain amplitude range does not directly relate to their
frequency domain amplitude (being affected by phase;
see the What About Phase? section).
FREQUENCY-TAGGED RESPONSES IN THE
FREQUENCY DOMAIN
One Harmonic; A Lot of Harmonics
Frequency tagging is an approach in which stimuli are pre-
sented periodically to generate periodic responses of the
brain that can thus be identified in the frequency domain
at specific frequencies harmonic to the stimulation (i.e.,
2376
Journal of Cognitive Neuroscience
Volume 33, Number 11
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
3
3
1
1
2
3
7
2
1
9
6
7
7
8
4
/
/
j
o
c
n
_
a
_
0
1
7
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
the fundamental and the higher harmonic frequencies). In
the following, examples will be taken only for harmonics
that are specific to a single tagged frequency: Again, for de-
termining specific harmonics in the context of multiple
tagged frequencies, see the Which Harmonics to
Consider? section).
According to the principles of frequency analyses, a
simple, sinusoidal brain response would be represented
only at the fundamental frequency F, whereas more com-
plex brain responses would be represented with a com-
bination of F and its higher harmonics, 2F, 3F, and so
on. Generally, this is evidenced with experimental brain
responses. In the event that the brain responses are
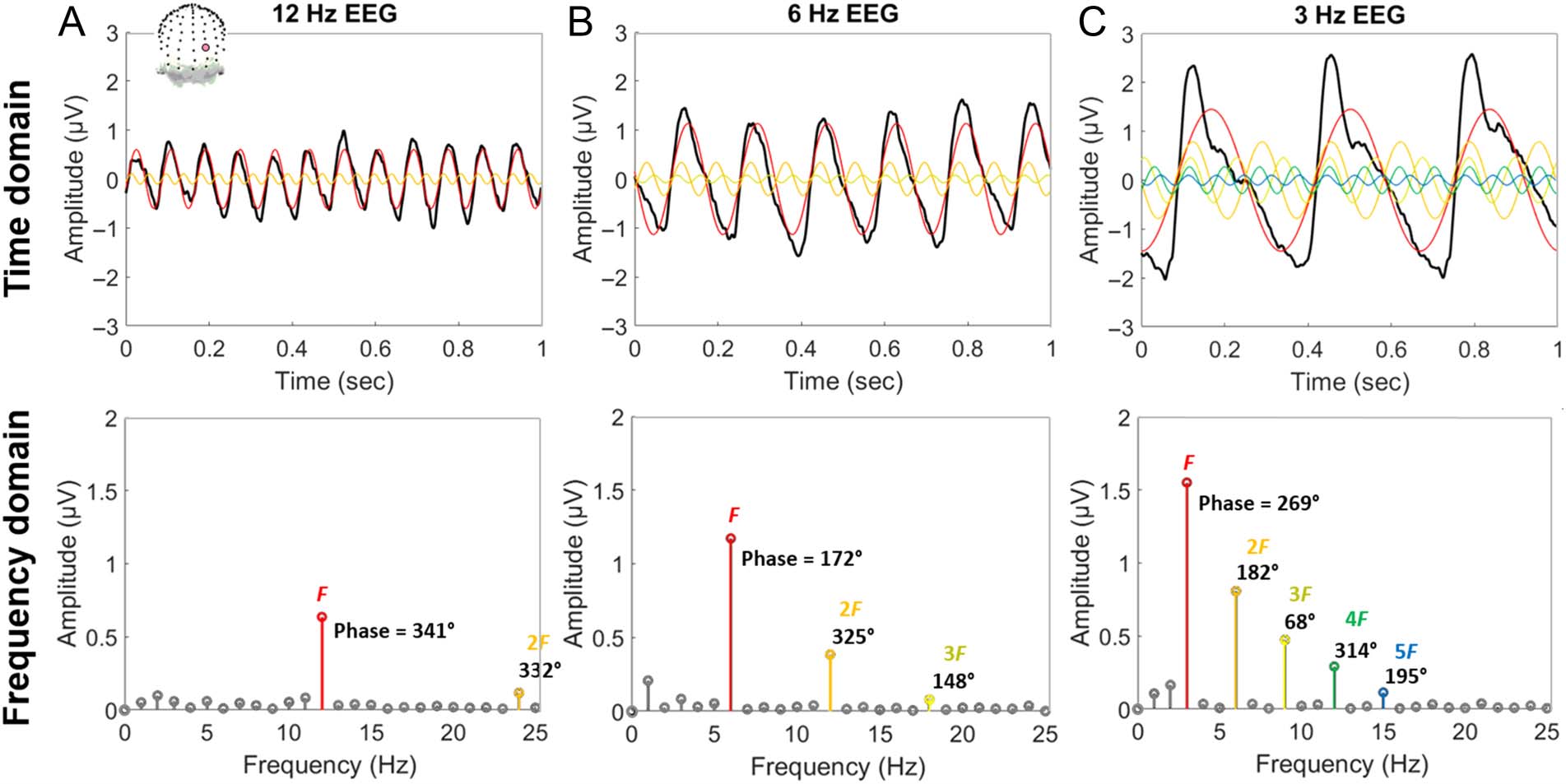
nearly sinusoidal, the response is dominated by ampli-
tude at F (e.g., at a high stimulus presentation rate:
Figure 4A); in the event that the responses of the brain
are complex, a combination of sine waves at different fre-
quencies (i.e., the higher harmonics) can sum to model
any signal (Figure 4C). In many studies, complex, nonsi-
nusoidal responses of the brain evoked over time are
represented in the frequency domain not only at F, but
with considerable amplitude at its higher harmonics (as
addressed in the Introduction, e.g., Rossion et al., 2020;
Retter & Rossion, 2016a; Zhou et al., 2016; Norcia et al.,
2015; Alonso-Prieto et al., 2013; Tlumak et al., 2011;
Heinrich, 2010; Vialatte et al., 2009, 2010; Kremers &
Scholl, 2001; Ross et al., 2000; Bach & Meigen, 1999;
Sieving, Arnold, Jamison, Liepa, & Coats, 1998; Regan,
1966, 1989; Donker, 1975; Van der Tweel & Verduyn
Lunel, 1965; Brazier, 1964).
Indeed, higher harmonic responses may be accounted
for in relation to the complex (i.e., nonsinusoidal) re-
sponses of the brain, in accordance with the principles
of frequency domain analysis of periodic signals (as in
Rossion et al., 2020; Zhou et al., 2016; Norcia et al.,
2015; Heinrich, 2010; Regan, 1989). This account ex-
plains that higher harmonics are present when complex
brain responses are present, but does not implicate a
specific source of complex brain responses (see
Heinrich, 2010). However, it is important to note that
complex brain responses are not a product of frequency
tagging and may equivalently occur with nonperiodic
(event-related) stimulus presentation modes.4
The harmonics do not represent new information, spe-
cific to the frequency domain: They are merely highlighted
in an alternative, frequency domain representation of
the original time domain signal (certain variations may
be represented more or less clearly in each domain).
These domains are interchangeable: As time domain data
can be transformed into the frequency domain, frequency
domain data can also be inversely transformed back
into the time domain; indeed, time domain responses
can be reconstructed from frequency domain harmonic
amplitudes and phases (e.g., Ruhnau, Keitel, Lithari,
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
3
3
1
1
2
3
7
2
1
9
6
7
7
8
4
/
/
j
o
c
n
_
a
_
0
1
7
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3. Lots of sine waves build frequency domain representations of signals. Top row: time domain signals. Bottom row: these signals
transformed into the frequency domain. (A) A periodic sine wave is represented with a single frequency in the frequency domain. (B) A periodic
squarewave (thick, black line) is represented with a combination of many specific harmonic frequencies (lines colored correspondingly across top
and bottom panels). Literally, the sum of these (and higher, not illustrated) colored lines’ amplitude at each time point reconstructs the original
signal. (C) A nonperiodic, ERP signal is represented with a combination of many nonspecific frequencies (data from Retter et al., 2020). Note several
properties of the frequency domain signal: (1) the 0 frequency bin reflects the mean amplitude (DC offset) of the signal; (2) the x-axis resolution is
the inverse of the signal recording duration; (3) although the frequency domain is plotted only until 10 Hz here, its range spans further (up to half of
the signal sampling rate); and (4) although only the phase of tagged frequencies is indicated on the lower row here, each frequency in the spectrum
has a corresponding phase value.
Retter, Rossion, and Schiltz
2377
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
3
3
1
1
2
3
7
2
1
9
6
7
7
8
4
/
/
j
o
c
n
_
a
_
0
1
7
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4. The higher the stimulus presentation rate (F ), generally the lower the amplitude of higher harmonic responses (2F, 3F, etc.) relative to
the fundamental (F ). Top row: Example brain responses, recorded with EEG (channel POO6 displayed here), were elicited from periodic visual
stimulation of natural object images at various presentation frequencies (thick black lines; data from Retter et al., 2020). Harmonic sine waves from
the frequency domain analysis, as represented below, are superimposed in color, to illustrate their relationship with the original signal. Bottom row:
Frequency domain representations of these signals. The amplitude of harmonic responses above 5% of that of the fundamental are plotted in color,
corresponding with the top row. (A) 12-Hz stimulation elicits nearly sinusoidal brain responses. (B) Intermediate, 6-Hz stimulation. (C) 3-Hz
stimulation elicits more complex brain responses in the time domain, represented with frequency domain amplitude more distributed across higher
harmonics.
Weisz, & Neuling, 2016; Sieving et al., 1998). The next
section focuses on the combination of harmonic re-
sponses; however, individual harmonics will be further
addressed in the Interpreting Harmonics section.
Imperfect Signals: Accounting for Baseline Noise
In theoretical examples of signal transformation into the
frequency domain (as in the Frequency Domain
Representations section), the signal is pure signal. In fre-
quency tagging, as in all brain recordings, the signal
(here, i.e., the responses of the brain at the tagged fre-
quencies) also carries “noise,” a term that refers to both
non-event-related brain activity and artifacts (e.g., Luck,
2005; Regan, 1989). Note that there are many methods
for correcting for noise (i.e.,
isolating signal) in
frequency-tagging research, although a discussion of
these is more general than the scope of this article (see
instead, e.g., Meigen & Bach, 2000; Appendix 2 of Norcia
et al., 2015). In the examples given here, a simple correc-
tion for noise will be applied that subtracts a local base-
line from the amplitude of the frequencies of interest
(e.g., Retter & Rossion, 2016a).5 The baseline is defined
as the mean amplitude of a symmetrical range of neigh-
boring (i.e., continuously adjacent6) frequency bins (for
theoretical justification, see Norcia et al., 2015; Regan,
1989; e.g., Boremanse, Norcia, & Rossion, 2013; Meigen
& Bach, 2000; Peterzell & Norcia, 1997; with power rather
than amplitude: Mouraux et al., 2011; Vialatte et al., 2009;
Srinivasan et al., 1999). This method is used to provide a
measure of signal amplitude in the frequency domain
that is relatable (i.e., both in the same unit) to amplitude
in the time domain and with a noise level at zero, while
compensating for local variations of noise inherent to
brain recordings across the frequency spectrum.
COMBINING HARMONIC RESPONSES
Combining Harmonic Response Amplitude
The combination of sine waves is simple: Sine waves sum
linearly to reconstruct a signal. However, with the goal of
identifying and measuring overall response amplitude in
the frequency domain, because sine waves carry both am-
plitude and phase information, their sum is not intuitive
to interpret in terms of amplitude only (or phase only).
Note that there are alternative approaches for combining
harmonics that incorporate both amplitude and phase;
however, these approaches make use of phase as an
indicator of reliability (coherence), typically across short
stimulation durations (e.g., Delorme & Makeig, 2004;
Strasburger, 1987; Jervis, Nichols, Johnson, Allen, &
Hudson, 1983). Furthermore, although the amplitude of
a single sine wave in the frequency domain directly relates
to its time domain peak amplitude, that is, half its positive
to negative peak range (e.g., Figure 3A; similarly, see
Figure 4A), the frequency domain amplitude of complex
2378
Journal of Cognitive Neuroscience
Volume 33, Number 11
time domain signals (summed sine waves) is not as easily
visualized from the time domain. Perhaps for these rea-
sons, various approaches have been taken for the combi-
nation of frequency-tagged multiharmonic brain response
amplitude in the frequency domain (e.g., as mentioned
previously, averaging or root-mean-square summing, re-
spectively, Liu-Shuang et al., 2014; Hou et al., 2003).
The summation of harmonic amplitudes is recom-
mended here for identifying and measuring the overall
brain response (based on Retter & Rossion, 2016a; see
also Heinrich, 2009). In the study of Retter and Rossion
(2016a), this approach was validated empirically by qual-
itative comparison of time and frequency domain re-
sponses, in the situation where several equivalent time
domain EEG responses were produced by several slow
target stimulus presentation frequencies. There, it was
observed that despite different distributions of harmonic
amplitudes stemming from the different fundamental tar-
get stimulus presentation frequencies (1.1–2.5 Hz), the
summation of baseline-subtracted harmonic amplitude
across a common frequency range led to equivalent over-
all amplitudes that related to approximately equivalent
response amplitude peaks in the time domain by visual
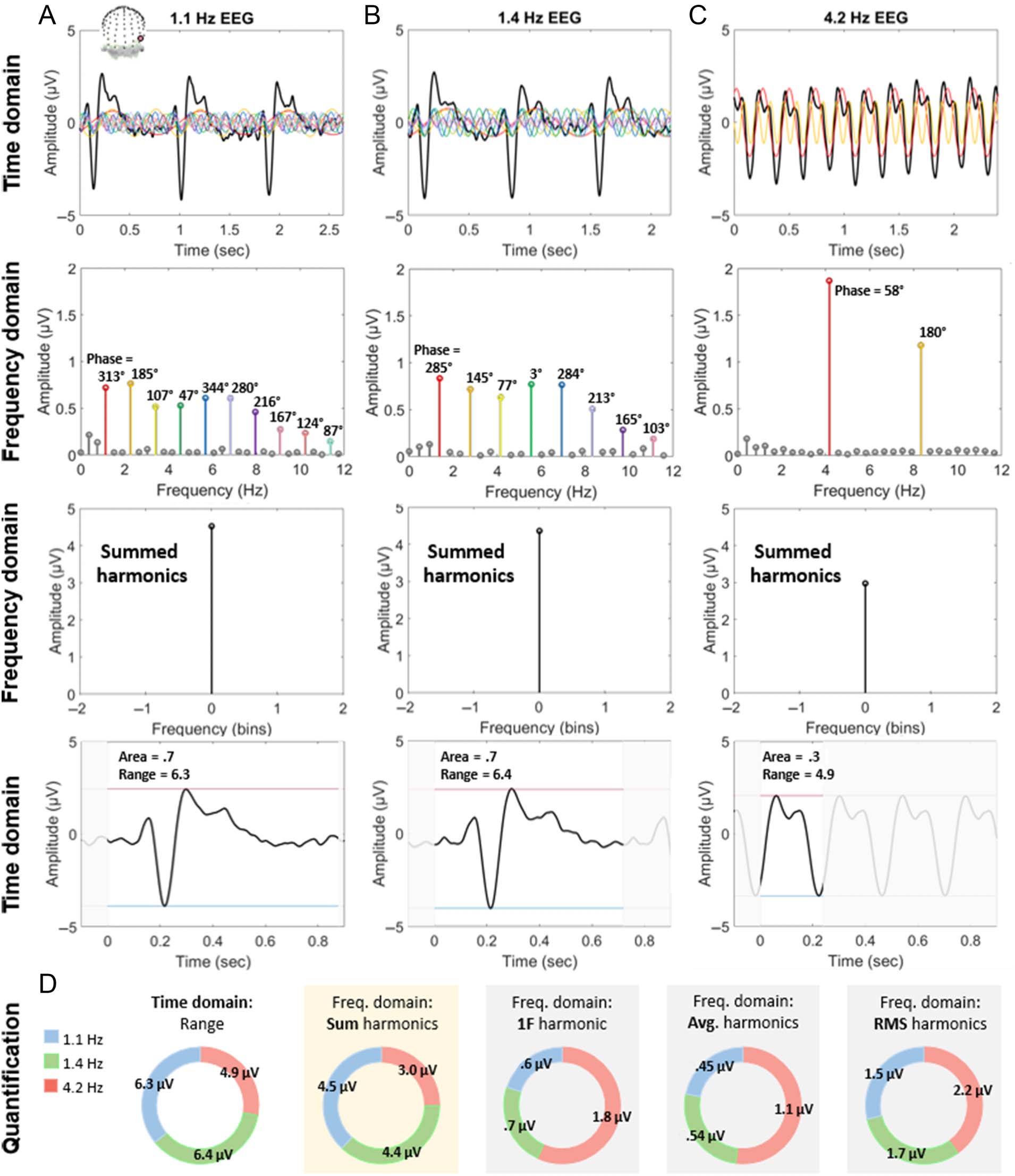
inspection (see Figure 5A and B, Row 1, here, for exam-
ples of reprocessing of that data in combination with the
underlying harmonic distributions). Moreover, a faster
stimulus presentation rate (4.2 Hz), which produced visu-
ally lower amplitude deflections in the time domain
(Figure 5C, Row 1), also produced a lower summed har-
monic response amplitude.
Here, these data are revisited quantitatively, with typical
time domain interpretations of response amplitudes:
peak-to-peak amplitude of the largest deflections and the
area under the curve of the response deflections (Figure 5,
Row 4). Note that an exact comparison of specific deflec-
tions, as is more commonly done in relating brain re-
sponses, is possible for the conditions at 1.1 and 1.4 Hz,
but that a different response pattern is observed for the
condition at 4.2 Hz, preventing such a direct comparison.
The summed harmonic response amplitude is shown
to be congruent with these measures (Figure 5D).
Critically, other approaches for harmonic combination
would not have led to these conclusions when compar-
ing conditions. Here, in the frequency domain, a large
fundamental harmonic amplitude relates to a smaller
number of harmonic responses (with an amplitude above
0.1 μV). Therefore, for example, averaging the harmonic
responses would have generated lower amplitude re-
sponses the slower the stimulus presentation frequency
(1.1 Hz < 1.4 Hz < 4.2 Hz; Figure 5D). For another ex-
ample, the root-mean-square harmonic amplitude would
have generated the highest amplitude for the highest
stimulus presentation rate (4.2 Hz; Figure 5D). For a last
example, using non-baseline-corrected amplitudes would
have produced a larger response at 1.1 Hz than 1.4 Hz,
because “noise” would have been included at more and
lower frequency (noisier) harmonics at 1.1 Hz.
Thus, summing baseline-subtracted harmonic ampli-
tudes is advantageous for a correspondence with interpre-
tations of time domain brain responses. This approach has
been used to quantify and compare overall response
amplitude in a number of studies following Retter and
Rossion (2016a), as mentioned previously (e.g., including
time domain correspondences: De Keyser et al., 2018;
Leleu et al., 2018; frequency domain analyses only:
Damon et al., 2020; Dwyer et al., 2019; Gwinn & Jiang,
2019; Beck et al., 2018; Chemin et al., 2018; Guillaume
et al., 2018; Gwinn et al., 2018; Xu et al., 2017).7
If measures other than amplitude are desired (e.g.,
signal-to-noise ratio, z scores, or another statistic), the
harmonic amplitudes can be extracted with an inclusion
of a baseline frequency range (i.e., as a “chunk” of X Hz,
centered around each frequency of interest), and then
summed before these baseline-relative computations
(Retter & Rossion, 2016a; see also Appendix 2 of Norcia
et al., 2015; Box 2 of Rossion et al., 2020). In this way, a
single statistical measure can be applied to the combined
harmonic amplitude relative to its combined baseline
amplitude (i.e., “noise”). Note that different approaches
for combining harmonics may serve different ends, in
that they describe different aspects of the signal, for
example, the root-mean-square amplitude relates to the
equivalent power of a flat (nonsinusoidal) signal; how-
ever, these aspects must be justified in relation to their
physiological meaning.
What About Phase?
As addressed previously, there is a direct relationship
between signal amplitude in the time and frequency
domains. As a reminder, this relationship is given by
Parseval’s relation, which states that energy is conserved
across the time domain (where energy equals the sum of
the squared amplitudes) and frequency domain (where
energy equals the sum of the squared root-mean-square
amplitudes). In light of this, the amplitude across the har-
monics relates to the overall amplitude of the signal in the
time domain, regardless of phase.
However, to fully relate signals across the time and fre-
quency domains, both the amplitude and phase of the
representative frequency domain sine waves need to be
taken into account. Without phase information, the fluc-
tuation of amplitude across time (e.g., affecting local am-
plitude peaks) cannot be determined. Therefore, there is
a cost toward relating time and frequency domain signals
when excluding phase information. However, this cost is
reasonably minor, for example, as relative phase changes
across harmonics, it is possible that the latency of signal
peaks varies, but that their amplitude does not (Figure 6A
and B). When relative phase does affect peak amplitudes,
this influence is limited (e.g., compare Figure 6B and C).
Moreover, despite relative phase changes, the area under
the curve of the time domain signal may remain approx-
imately constant (Figure 6A–C; see also Heinrich, 2010).8
Retter, Rossion, and Schiltz
2379
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
3
1
1
2
3
7
2
1
9
6
7
7
8
4
/
/
j
o
c
n
_
a
_
0
1
7
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
3
1
1
2
3
7
2
1
9
6
7
7
8
4
/
/
j
o
c
n
_
a
_
0
1
7
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5. The combination of harmonic amplitude. For A–C: Row 1: example brain responses, recorded with EEG (channel PO10 displayed here),
were elicited from periodic visual stimulation of natural face (vs. object) images at various frequencies (data from Retter & Rossion, 2016a). Row 2:
Frequency domain representations of these responses. The amplitude of harmonic responses above 0.1 μV are plotted in color, and these harmonic
sine waves are superimposed in the corresponding color in Row 1. Row 3: The colored harmonic responses above are summed (set at Bin 0),
following a baseline subtraction of “noise,” defined as the average amplitude of the two adjacent frequency bins. Row 4: Similar response amplitudes
are demonstrated in the time domain in Panels A and B, consistent with Row 3. Time outside one cycle duration is shadowed in gray, and the
response amplitude range is emphasized between the horizontal red and blue lines. (A) 1.1 Hz target (face) stimulation elicits complex brain
responses. (B) 1.4 Hz target stimulation elicits a similar response to 1.1 Hz stimulation in the time domain and the amplitude of summed,
baseline-subtracted harmonics in the frequency domain, despite a different distribution of harmonic frequency amplitudes. (C) 4.2 Hz target
stimulation elicits more simple and lower amplitude neural responses in both the time and frequency domains. (D) Quantification in the time
domain (amplitude range) is compared with different methods of harmonic assessment in the frequency domain, with baseline-subtracted
amplitudes. The sum of harmonics provides a better correspondence with the time domain, across conditions, than the fundamental harmonic
(F ) only, average of harmonics, or root-mean-square (RMS) of harmonics.
2380
Journal of Cognitive Neuroscience
Volume 33, Number 11
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
3
1
1
2
3
7
2
1
9
6
7
7
8
4
/
/
j
o
c
n
_
a
_
0
1
7
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
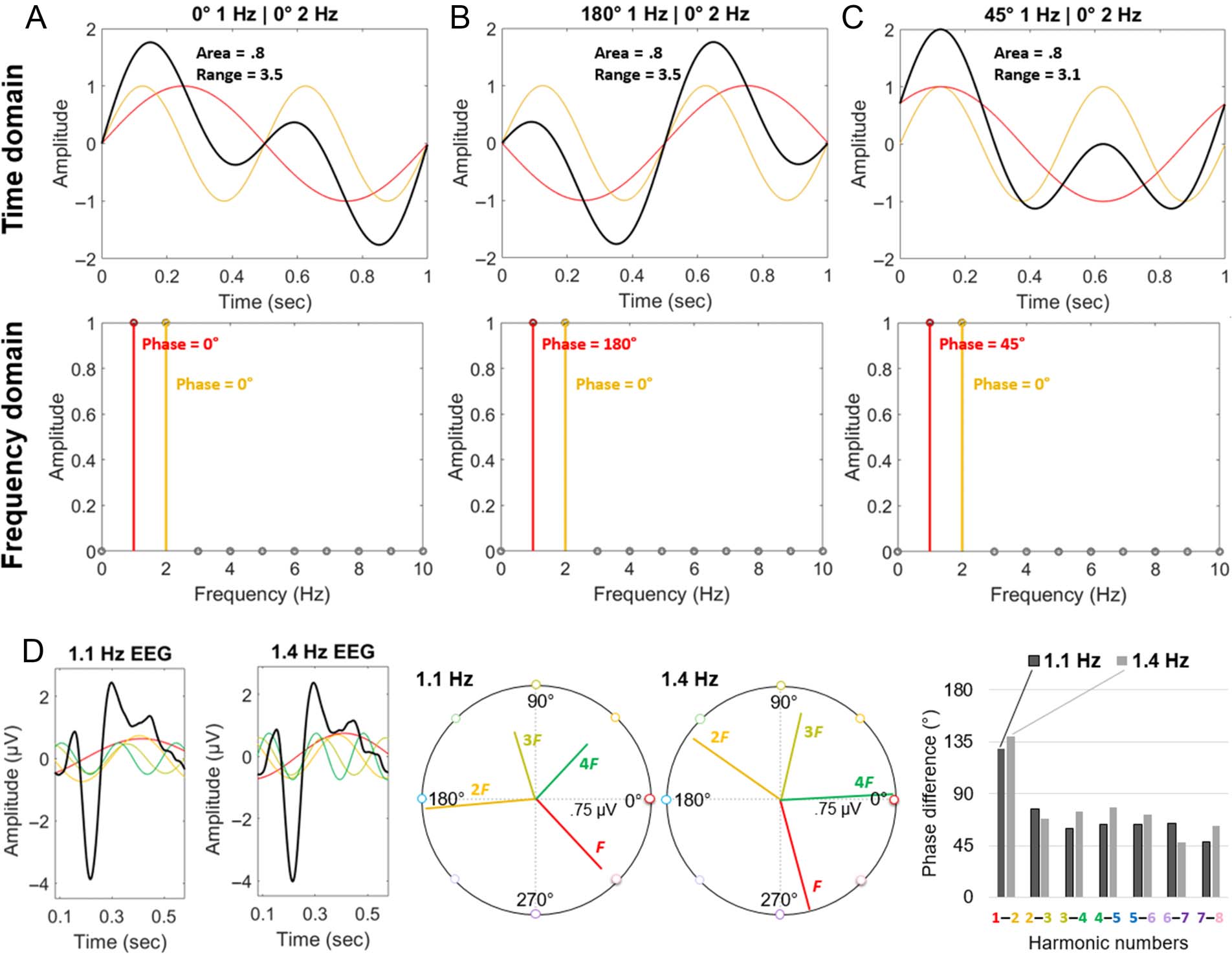
Figure 6. The influence of harmonic phase on the combination of harmonic amplitude. Synthetic time domain signals (in thick black lines; Row 1)
are the sum of two harmonic sine waves: a 1-Hz sine wave with varying phase (A: 0°; B: 180°; C: 45°; plotted in red) and a 2-Hz sine wave with
constant phase (0°; plotted in orange). Each sine wave has an amplitude of 1. Row 2: Frequency domain representations of these signals show the
consistent 1-Hz amplitude at 1 and 2 Hz across the panels. In the time domain, the area under the curve (absolute value) also remains approximately
constant, although the amplitude peaks (positive and negative) and range may be influenced by the relative harmonic phase. (D) 1.1-Hz and 1.4-Hz
EEG responses (data from Figure 5). Left: Time domain responses, highlighting the phase of the first four harmonics. Middle: Polar plots, in which
each of these four harmonic frequency domain responses is represented with a vector: angle = phase; length = amplitude. Right: Despite the
different fundamental frequencies, the difference across sequential harmonics’ phase is similar.
Moreover, in frequency tagging, it is worth remembering
that the phase is not arbitrary: The phase of each relevant
harmonic is determined relative to the time domain signal.
In other words, the aligning positive and negative peaks of
the sine waves across harmonic frequencies correspond to
the time of the positive and negative peaks of the signal
in the time domain (see again Figure 3B, for an example
of deconstructive [when the signal is 0] and constructive
[when the signal is 1], phase-locked harmonic sine wave
superpositioning). This leads to phase differences across
harmonics that are similar to describe time domain signals
with similar temporal dynamics, despite the use of different
stimulation frequencies (Figure 6D; see also Strasburger,
1987). Thus, the influence of phase on combined har-
monics is largely invariant of the stimulus presentation
frequency, given consistent temporal dynamics of the re-
sponse (as hinted at empirically, e.g., Retter & Rossion,
2016a; Appelbaum et al., 2006). Finally, it is worth noting
a couple of helpful restrictions in the context of frequency
tagging for combining harmonic responses: Only one sine
wave is represented at each frequency bin, and nonhar-
monic frequencies are not considered, such that the re-
sponse is fully periodic at the cycle duration of the
fundamental frequency, F.9
Which Harmonics to Consider?
Before combining harmonics, a decision of which har-
monics to consider is required. To this extent, harmonics
of interest (similarly to a ROI) must be defined. The first
criterion for determining harmonics of interest is whether
a higher harmonic is specific to its fundamental fre-
quency. As mentioned previously, in frequency-tagging
paradigms using a single-stimulation frequency, the
higher harmonics are always specific to the fundamental
frequency. However, in paradigms deploying multiple
Retter, Rossion, and Schiltz
2381
stimulation frequencies, unspecific harmonics may occur,
which are often excluded from the analyses (for a
paradigm-focused review, see Norcia et al., 2015). For ex-
ample, two stimuli may be simultaneously presented at
different spatial locations, one at 8 Hz (F1) and the other
at 6 Hz (F2). If a response occurred at 24 Hz, it would not
be specific to either stimulus, being the third harmonic of
8 Hz (3F1) and the fourth harmonic of 6 Hz (4F2), and would
therefore be excluded from the analyses of responses to
each stimulus (for further examples, see Table 1).
A second consideration for determining harmonics of
interest aims to exclude extreme harmonic frequencies
(e.g., the 30th harmonic of 8 Hz, at 240 Hz) at which no
signal is expected or found. A limited selection of har-
monics has been made based on various types of criteria:
(1) amplitude, power, signal-to-noise ratio, or significance
thresholds (e.g., Rossion, Torfs, Jacques, & Liu-Shuang,
2015; Hou, Pettet, & Norcia, 2008; Donker, 1975); (2)
frequency range (e.g., Leleu et al., 2018; Zemon &
Gordon, 2018; Jacques et al., 2016; Sieving et al., 1998);
(3) harmonic series number (e.g., Wittevrongel et al.,
2018; Appelbaum et al., 2006; Donker, 1975); (4) in relation
to other stimulation frequencies (e.g., Milton et al., 2020;
Heinrich, Mell, & Bach, 2009); and (5) correlation with
the time domain response (e.g., Engel et al., 1997;
Bandettini et al., 1993).
The use of a limiting frequency range is recommended
here, either as determined a priori or from an assessment
of the highest harmonic meeting a threshold (in terms of
amplitude, signal-to-noise ratio, or significance). This is rec-
ommended because the upper frequency limit of harmonic
responses, although affected by the overall strength of the
signal, generally relates to the highest frequency that is
strongly represented in the signal (see the Interpreting
Harmonics section). The upper frequency limit of har-
monic responses is thus often conserved across funda-
mental stimulation frequencies (see Figure 2 of Retter
& Rossion, 2016a).
Note that the highest harmonic of interest can be
determined either at the group level across conditions
or as presented by any participant for any condition,
but that typically a common range of frequencies of in-
terest should be used across participants and conditions
(e.g., Jacques et al., 2016). In this approach, there may
be harmonic frequencies included for consideration at
which there is no signal (e.g., in some participants, con-
ditions, or regions of interest); however, including a
small number of such frequencies is likely less detrimental
(given that an appropriate baseline noise correction is
applied, e.g., so that approximately zero amplitude values
are added) than missing some frequencies containing a
weak signal. Similarly, although responses are typically
expected to occur consecutively across harmonic frequen-
cies, in the event that a small number of within-range
harmonic frequencies do not contain signal (above
threshold), including them is typically tolerable (e.g.,
Rossion et al., 2020; Liu-Shuang et al., 2014).
Finally, in some cases, harmonic responses appear to be
qualitatively different from one another. This may occa-
sionally be related to physiological sources: for example,
different harmonic response patterns are generated from
the recordings of frequency-tagged responses from single-
versus double-opponent cortical cells (Movshon et al.,
1978). However, more often, physiological sources may
only be tentatively inferred, for example, when different
EEG scalp topographies are observed at different har-
monic frequency ranges (e.g., Rossion, 2014; see the
What Do Higher Harmonic Responses Represent? section).
In this case, is it appropriate to select subranges of quali-
tatively homogeneous harmonics to consider and/or com-
bine? Perhaps, although it should be remembered that
harmonic responses are not independent of one another
(e.g., Retter & Rossion, 2016a; Zhou et al., 2016) and there-
fore should also be described individually and/or summed
all together (see the Should Higher Harmonic Responses
Be Combined, and If So, How? (Reprise) section).
It is not advised to select or subgroup harmonics a priori
in accordance to only their number, unless this is explicitly
derived from the stimulation paradigm (see Table 1). For
example, there is a persistent history of considering the
first versus second harmonic response (Saupe, Schröger,
Andersen, & Müller, 2009; Pastor, Valencia, Artieda,
Alegre, & Masdeu, 2007; Kremers & Scholl, 2001; Falsini
et al., 1999; Burns, Elsner, & Kreitz, 1992; Baker & Hess,
1984; the first vs. second harmonic, rather than odd vs.
even harmonics: Kim, Grabowecky, Paller, & Suzuki,
2011; Kim, Grabowecky, Paller, Muthu, & Suzuki, 2007).
This relates to early interpretations of the first harmonic
reflecting asymmetries in responses following on and off
stimulation cycles (e.g., Clynes, Kohn, & Lifshitz, 1964)
and the second harmonic being typically dominant with
pattern reversal stimulation (see the following section).
However, the presence of third, fourth, and further higher
harmonics—and their interdependence—is indicative of
the limits of such an oversimplification in most cases.
INTERPRETING HARMONICS
Why Are There Higher Harmonics?
Nonsinusoidal Brain Responses
Higher harmonic responses represent complex neural
responses in the time domain. At a fundamental level,
these harmonic responses are like any other frequency
domain representations: They are sine waves described
by frequency, amplitude, and phase (Figure 2). Although
only one sine wave is required to describe a sinusoidal
signal in the time domain, a combination of (a lot of ) sine
waves is required to describe complex signals in the time
domain (Figure 3). Frequency-tagged brain responses are
periodic in the time domain, and thus, only sine waves
periodic to their fundamental frequency (i.e., the har-
monics) are mathematically available to describe them.
Simple brain responses require few harmonics, whereas
2382
Journal of Cognitive Neuroscience
Volume 33, Number 11
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
3
1
1
2
3
7
2
1
9
6
7
7
8
4
/
/
j
o
c
n
_
a
_
0
1
7
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Table 1. Identifying Specific Harmonics for Consideration in Response Analysis, According to Different Frequency-tagging Stimulation Paradigms
Paradigm
Frequency 1
Frequency 2
Overlap
Analysis
References
Single frequency
A-A-A-A-A-A-A-…
F
Multiple frequencies
(F1: A-A-A-A-A-A…)
(F2: B-B-B-B-B-B…)
Symmetry/asymmetry
(A-B-A-B-A-B-A-B…)
F1 (e.g., 8 Hz)
F2 (e.g., 6 Hz)
—
—
F and its harmonics
Adrian and Matthews (1934),
Any coinciding harmonics
of F1 and F2 (e.g., 24 Hz)
Exclude overlapping harmonics
from analysis of both F1
and F2
Regan (1989)
Regan and Heron (1969),
Regan (1989)
2F = stimulus
presentation
(symmetry response)
F = stimulus alternation
(asymmetry response)
F harmonics coinciding with
2F and its harmonics
Exclude 2F (even) harmonics
from the analysis of the
F (odd) harmonics
Tyler and Kaitz (1977),
Victor and Zemon (1985)
Oddball
(A-A-A-B-A-A-A-B…)
F = stimulus
presentation
F/n = oddball B presentation,
with oddballs occurring as
every nth stimulus
F/n harmonics coinciding
with F and its harmonics
Exclude F and its harmonics
from the analysis of F/n
Heinrich et al. (2009),
Liu-Shuang et al. (2014)
In the paradigm example sequence illustrations: A = one stimulus or stimulus type; B = another stimulus or stimulus type. Special cases: In the case that A and B stimuli in a symmetry/asymmetry paradigm
lead to symmetrical brain responses (e.g., if representing pattern reversals), only even harmonics are observed (Norcia et al., 2015; Hou et al., 2003; Cobb et al., 1967); in a combined symmetry/asymmetry
and oddball design (Braddick et al., 2005), the odd harmonic analysis is unaffected. In the case that multiple frequencies lead to intermodulation (i.e., additive and subtractive interaction frequencies and
their harmonics), the analysis of the intermodulation harmonics should exclude the overlapping harmonics of F1 and F2 (e.g., Gordon et al., 2019; Boremanse et al., 2013; Applebaum et al., 2009; Hou et al.,
2003; Burns et al., 1992; Zemon & Ratliff, 1984). In the case that a stepwise sweep design is applied to a symmetry/asymmetry paradigm, this does not affect the harmonic analysis (see Norcia et al., 2015).
R
e
t
t
e
r
,
R
o
s
s
i
o
n
,
a
n
d
S
c
h
i
l
t
z
2
3
8
3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
3
1
1
2
3
7
2
1
9
6
7
7
8
4
/
/
j
o
c
n
_
a
_
0
1
7
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
complex responses require more harmonics (Figure 4). For
example, lower stimulation frequency responses often
have more harmonics, because there are relatively more
harmonic frequencies available within a relevant fre-
quency range ceiling (Figure 5).
Limitations of a nonlinearity account. Higher har-
monic responses have often been interpreted as being
caused by nonlinearities in the stimulus presentation
and/or brain responses (e.g., Gordon, Hohwy, Davidson,
van Boxtel, & Tsuchiya, 2019; Norcia et al., 2015; Burns
et al., 1992; Regan, 1966, 1989; Troelstra, 1971; Spekreijse,
1969; Van der Tweel & Verduyn Lunel, 1964, 1965; see also
Shapley, 2009). This relates to early attempts to present
stimuli perfectly sinusoidally (e.g., a uniform field being
modulated sinusoidally in luminance; since van der Tweel
et al., 1958). The rationale was that if the brain’s response
to a sinusoidal stimulus was linear at the level of recording,
it too would be perfectly sinusoidal in following this
stimulus and would be represented in the frequency
domain by a response only at the fundamental frequency,
that is, without higher harmonics (see the Frequency
Domain Representations section). Contrarily, higher
harmonic brain responses were produced in most cases
and were attributed to nonlinearities in the brain’s
responses themselves (e.g., nonlinear action potential
firing, neural population response dynamics; Shapley,
2009; Skottun et al., 1991; Movshon et al., 1978).10
However, more recent studies suggest that the amount
of nonlinearity, or complex temporal frequency content,
in stimulus presentation may not correspond with the
amount of nonlinearity in the brain’s response at the
population level: There was little to no difference in
the higher harmonic amplitude distributions in response
to (imperfect) sinusoidal versus squarewave (i.e., abrupt
on/off ) complex stimulus presentation (Dzhelyova,
Jacques, & Rossion, 2017; Retter, 2016; Fawcett, Barnes,
Hillebrand, & Singh, 2004; Burns et al., 1992). Moreover,
although the inherent nonlinearity of the brain’s
responses could account for higher harmonics, in prac-
tice, the amplitude of the higher harmonics is not always
above noise level (as addressed in the Introduction) or is
very low, suggesting only a modest contribution of this
factor (see the Frequency-tagged Responses In The
Frequency Domain section). That being said, one source
of complexity in the brain’s responses (even those under-
lying the first harmonic) may be these nonlinearities.
What Do Higher Harmonic Responses Represent?
Higher harmonic responses represent the relevant
frequency characteristics of the response in the time
domain (e.g., Rossion et al., 2020; Zemon & Gordon,
2018; Retter & Rossion, 2016a; Zhou et al., 2016; Gaume
et al., 2014; Heinrich, 2010; Norcia, Sato, Shinn, & Mertus,
1986; Baker & Hess, 1984; Galambos et al., 1981). That is,
dynamics of the time domain response best represented at
different frequency ranges will produce more amplitude in
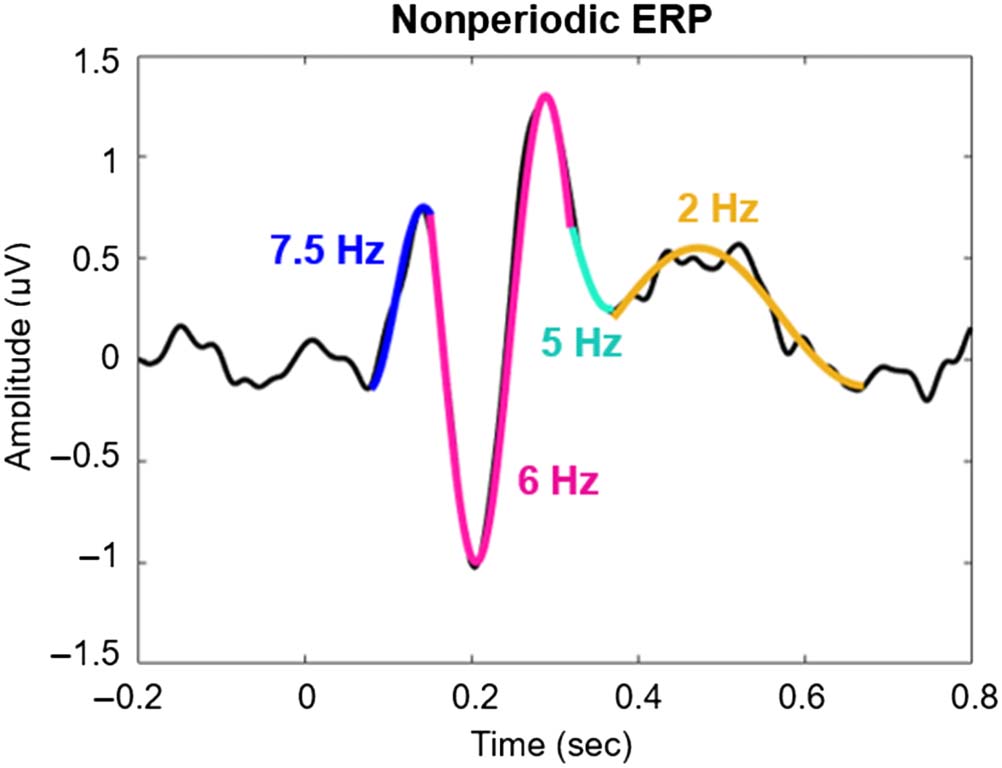
those frequency ranges in the frequency domain (Figure 7;
compare with the frequency domain representation in
Figure 3C; for another example of frequency representa-
tions over time, see Makeig et al., 2002). To visualize the
impact of (a range of ) individual harmonics, partial har-
monic time domain reconstructions have been plotted
(Sieving et al., 1998; Baker & Hess, 1984). Note that the
amplitude distribution of harmonics across frequencies
is, however, affected by the fundamental stimulation
frequency and the overall amplitude of the signal.
Moreover, individual harmonics do not represent indepen-
dent or temporally separated aspects of a time domain re-
sponse (e.g., Retter & Rossion, 2016a; Zhou et al., 2016).
In line with the above interpretation, harmonic re-
sponses may be (gradually) influenced, quantitatively
and/or qualitatively, by the frequency at which they fall.
For example, Retter and Rossion (2016a, Figure 2C)
described harmonic EEG responses that were gradually
characterized by frequency, in terms of amplitude and scalp
lateralization, commonly across conditions with different,
Figure 7. A time domain signal
can be fit with segments of sine
waves of different frequencies.
Although this is not analogous
to a frequency transformation,
it hints at the range of
frequencies that may be
optimal for representing this
signal (over time).
2384
Journal of Cognitive Neuroscience
Volume 33, Number 11
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
3
1
1
2
3
7
2
1
9
6
7
7
8
4
/
/
j
o
c
n
_
a
_
0
1
7
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
3
1
1
2
3
7
2
1
9
6
7
7
8
4
/
/
j
o
c
n
_
a
_
0
1
7
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 8. Combining higher harmonics in frequency domain analyses, expanded from Figure 1. (A) Row 1: Two periodic signals (thick lines), with
their five constituent harmonic frequencies (in thin lines, with colors corresponding to the frequencies below). Row 2: Frequency domain
representations of these signals. (B) In the frequency domain, a consideration of only the fundamental harmonic describes Signal 2 as (two times)
larger than Signal 1. A summation of the five harmonic amplitudes more appropriately describes Signal 1 as (50%) larger than Signal 2.
low stimulation frequencies. Harmonic responses may also
appear to group into somewhat distinct frequency ranges,
for example, visually evoked EEG responses above about
10 Hz having a more medial-occipital (“low-level”) scalp to-
pography ( Jacques et al., 2016; Rossion, 2014; see also
Zemon & Gordon, 2018). In general, higher harmonics
may be more associated with earlier response dynamics,
as the onset slopes of (ERP) responses are typically steeper
than the offsets (Norcia et al., 1986; as in Figure 7). In some
cases, different experimental effects may be pronounced at
some harmonic frequencies and not others (e.g., an in-
creased response because of attention: Saupe et al., 2009;
Pei, Pettet, & Norcia, 2002; opposing effects following
current stimulation: Ruhnau et al., 2016). Indeed, limited
frequency ranges may be appropriate for measuring certain
properties (e.g., a lower frequency range for chromatic than
luminance signals; see Parry et al., 2012; Burns et al., 1992).
Thus, in addition to combining harmonics, investigating
individual (ranges of ) harmonics may provide insight into
the functional dynamics of the neural processes that occur
at their respective frequencies.
Differing harmonic response distributions may stem
from the same fundamental stimulation frequency, such
as are observed across conditions (along with time domain
response dynamic differences: e.g., Dzhelyova et al., 2017;
Jacques et al., 2016), populations (e.g., clinical: Van der
Donck et al., 2019; Falsini et al., 1999; age/grade levels:
van de Walle de Ghelcke et al., 2021; Hou et al., 2003),
and individuals (as observed in Heinrich et al., 2015;
Tlumak et al., 2011; Heinrich & Bach, 2001; used in classi-
fying individuals across testing sessions: Dzhelyova et al.,
2019). In past studies, individual harmonic amplitudes
have been displayed with frequency domain spectra or ta-
bles, sometimes with additional descriptors, such as func-
tional images or topographies (e.g., Jacques et al., 2016;
Liu-Shuang et al., 2014; Bandettini et al., 1993). In more
global visualizations, colored/shaded matrices of harmonic
responses by ROIs or participant have been plotted (Liu-
Shuang et al., 2014, Figure 3; Rossion et al., 2015, Figure 3),
as well as close-shaped “fingerprint” plots, using connected
vectors of which the angle is determined by harmonic
frequency and length by amplitude (van de Walle de
Ghelcke et al., 2021, Figure 6).
It is not recommended to display harmonics indepen-
dently by their sequential number (e.g., across different
fundamental stimulation frequencies: Herrmann, 2001;
Ross et al., 2000; Troelstra, 1971). Indeed, because har-
monic responses are characterized by their frequency,
they are generally not well characterized by sequential
number, irrespective of frequency, unless differentially
tagged in the stimulation paradigm (see the Which
Harmonics to Consider? section). However, one case in
which harmonic frequency does not characterize re-
sponses well is at high stimulus presentation frequencies,
for which the first harmonic is dominant. At high frequen-
cies, overlapping responses interfere with one another,
decreasing the measured response’s complexity and
amplitude and therefore harmonic contents (see the
Frequency-tagged Responses in the Frequency Domain
section). Thus, a dominant exponential decrease of har-
monic amplitude may be observed across sequential har-
monics (compare Figure 4B and C; Retter et al., 2020,
Retter, Rossion, and Schiltz
2385
Figure S2). However, this must not be taken as evidence of
distinct brain responses being evidenced at the first versus
second (vs. third, etc.) harmonic (e.g., see the discussion
of Saupe et al., 2009).
Finally, it may be noted that consecutive response inter-
ference is not only dependent upon the duration of the
brain response being measured but is also influenced by
the spatiotemporal dynamics of the interfering response
components. In models of consecutive responses,
destructive superpositioning of overlapping (ERP)
response components may reduce or even eliminate
(selective harmonic) responses (constructive superposi-
tioning is also possible; see Heinrich, 2010, Figures 1
and 2; see also Footnote 4). In practice, overlapping brain
responses do not occur independently of one another
(see Retter et al., 2020; Keysers & Perrett, 2002).
However, particularly when distinct response sources
are implicated (e.g., light- and dark-preferring neural
populations or across sensory modalities), differential
interactions of stimulation frequency and selective
harmonic amplitudes could also provide insights into
the underlying dynamics of the brain responses.
Should Higher Harmonic Responses be Combined,
and If So, How? (Reprise)
Limiting the analysis of frequency-tagged responses to a
(nonpredominant) fundamental harmonic is not recom-
mended: Taking harmonic responses into account leads
to substantially improved response quantification and
classification (Figure 8; Cetin et al., 2020; Zemon &
Gordon, 2018; Retter & Rossion, 2016a; Chen et al.,
2015; Tlumak et al., 2011; Cebulla et al., 2006; Muller-
Putz et al., 2005; Davila et al., 1998). The combination
of harmonic amplitudes through summation is justified
through the principles of frequency-based analyses, and
it leads to a combined response measurement that re-
lates to typical time domain amplitude measurements.
It is useful for comparing brain response amplitudes
overall, especially those with different temporal dynamics
or following different stimulus presentation rates. Note
that it is does not preclude, but rather is complementary,
to the description of harmonic responses individually.
CONCLUSION
Stimuli that are presented periodically generate periodic
responses of the brain that are often complex (i.e., non-
sinusoidal). To capture and describe these complex brain
responses overall, (baseline-corrected) frequency-tagged
harmonic response amplitude can be combined through
simple summation.
Acknowledgments
The authors thank those who gave feedback on earlier drafts of
this article: Carrie Georges, Aliette Lochy, Milena Dzhelyova,
Fang Jiang, Michael Webster, Anthony Norcia, three anonymous
reviewers, and journal editors. Synthetic signals were generated
in MATLAB, R2019b (The Mathworks).
Reprint requests should be sent to Talia L. Retter, University of
Luxembourg, Maison des Science Humaines, 11 Porte des
Sciences, 4366 Esch-sur-Alzette, Luxembourg, or via e-mail:
talia.retter@uni.lu.
Author Contibutions
Talia L. Retter: Conceptualization; Data curation; Formal
analysis; Investigation; Methodology; Project administration;
Software; Visualization; Writing—original draft; Writing—
review & editing. Bruno Rossion: Conceptualization;
Funding acquisition; Methodology; Writing—review &
editing. Christine Schiltz: Conceptualization; Funding
acquisition; Resources; Supervision; Writing—review &
editing.
Funding Information
This work was supported by the Face Perception INTER
project (INTER/FNRS/15/11015111 to C. S.), funded by
the Luxembourgish Fund for Scientific Research (https://
dx.doi.org/10.13039/501100001866) and the Belgian
National Foundation for Scientific Research (https://dx
.doi.org/10.13039/501100002661), grant number PDR
T.0207.16 FNRS to B. R.
Diversity in Citation Practices
A retrospective analysis of the citations in every article
published in this journal from 2010 to 2020 has revealed a
persistent pattern of gender imbalance: Although the pro-
portions of authorship teams (categorized by estimated
gender identification of first author/last author) publishing
in the Journal of Cognitive Neuroscience ( JoCN) during
this period were M(an)/M = .408, W(oman)/M = .335,
M/ W = .108, and W/ W = .149, the comparable proportions
for the articles that these authorship teams cited were
M/M = .579, W/M = .243, M/ W = .102, and W/ W = .076
(Fulvio et al., JoCN, 33:1, pp. 3–7). Consequently, JoCN
encourages all authors to consider gender balance explicitly
when selecting which articles to cite and gives them the
opportunity to report their article’s gender citation balance.
Notes
1. A note on nomenclature: Here, the “first” harmonic is the
fundamental stimulation frequency. In another existent conven-
tion, the “first” harmonic is the double of the fundamental stim-
ulation frequency.
2. Note that in frequency domain transformations, technically,
a complex-valued combination of sine waves and cosine waves
is used to represent the signal. In many discrete, fast Fourier
transforms, the sine component carries only the amplitude in-
formation, and the cosine component carries only the phase in-
formation. Here, “sine waves” are referred to as complex
entities themselves, combining both amplitude and phase infor-
mation. Additionally, note that phase spectra are rarely plotted
2386
Journal of Cognitive Neuroscience
Volume 33, Number 11
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
3
1
1
2
3
7
2
1
9
6
7
7
8
4
/
/
j
o
c
n
_
a
_
0
1
7
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
in the same format as amplitude spectra, because (1) their
values are circular (e.g., with equivalent distance from 0° to
359° and from 0° to 1°; see an alternative plotting example in
Figure 6D) and (2) the phase at non-frequency-tagged signal
frequencies is random (i.e., full-range noise).
3.
In the time domain, energy is equal to power over time, which
is equal to the sum of the squared amplitudes. In the frequency
domain, energy is equal to the sum of the squared root-mean-
square amplitudes (root-mean-square amplitude of a sine wave =
amplitude/√2; see Smith, 1997).
4. Although largely beyond the scope here, note that it is exten-
sively debated whether frequency-tagged EEG responses reflect the
(linear) superposition of ERPs or whether they reflect an interaction
with endogenous oscillations in the brain (see Zoefel, Oever, &
Sack, 2018; Retter & Rossion, 2016a; Heinrich et al., 2015; Norcia
et al., 2015; Keitel, Quigley, & Ruhnau, 2014; Gruss, Wieser,
Schweinberger, & Keil, 2012; Capilla et al., 2011; Heinrich, 2010;
Makeig et al., 2002; Herrmann, 2001; Galambos, Makeig &
Talmachoff, 1981; Donker, 1975).
5. Note that, further, the signal and noise may interact nonli-
nearly (supra-additively), but when the signal is much (e.g., 3 or
4 times) greater than noise, this modest contribution is negligible
(Norcia, Tyler, Hamer, & Wesemann, 1989; Peli, McCormack, &
Sokol, 1988; Strasburger, 1987; see Bach & Meigen, 1999).
Particularly for weaker signals, a more conservative baseline
correction could be computed as the square root of the signal-
power-minus-noise-power (see Appendix 1 of Norcia et al., 1989).
6. Please note an exception: Sometimes, the first adjacent bin,
on either side of the frequency bin of interest, is excluded, so as
to avoid overspill, that is, signal leakage, in the noise estimate at
high-frequency resolutions (e.g., Rossion, Alonso-Prieto,
Boremanse, Kuefner, & Van Belle, 2012).
See also publications motivated by the as yet unpublished
7.
findings of Retter and Rossion (2016a) from the Face
Categorization Lab (https://face-categorization-lab.webnode.com/;
Jacques, Retter & Rossion, 2016; Jonas et al., 2016; Liu-Shuang,
Torfts & Rossion, 2016; Lochy, Van Reybroeck, & Rossion, 2016;
Retter & Rossion, 2016b; Dzhelyova & Rossion, 2014a, 2014b).
8.
In any case, it remains unclear at present how phase could be
combined meaningfully across harmonics, beyond time domain
latency, to relate to functional, physiological processes (see
Strasburger, 1987).
In frequency tagging with a single-stimulation frequency,
9.
there are not multiple sine waves of the same frequency that inter-
fere with each other, for example, sine waves with a 180° phase
difference that produce complete interference (zero amplitude
sum). Furthermore, when a complete F cycle is considered, the
amplitude is representative of the complete signal (which is not
the case for multiple [nonharmonic] frequencies that may sum dif-
ferentially across short time segments of evaluation). Note that
these conditions are not always met in other contexts in which
frequency-based analyses are performed.
10. Higher (intermodulation) harmonic responses have then
been used to characterize the nonlinearities of brain responses,
leading to the exclusion of some potential nonlinear models in
specific cases (e.g., Baker & Wade, 2017; Hou et al., 2003; Victor
& Conte, 2000; Regan & Regan, 1988b).
REFERENCES
Adrian, E. D. (1944). Brain rhythms. Nature, 153, 360–362.
https://doi.org/10.1038/153360a0
Adrian, E. D., & Matthews, B. H. C. (1934). The Berger rhythm:
Potential changes from the occipital lobes in man. Brain, 4,
355–385. https://doi.org/10.1093/brain/57.4.355
Ales, J., Farzin, F., Rossion, B., & Norcia, A. M. (2012). An objective
method for measuring face detection thresholds using the
sweep steady-state evoked response. Journal of Vision, 12,
18. https://doi.org/10.1167/12.10.18, PubMed: 23024355
Alonso-Prieto, E. A., Van Belle, G., Liu-Shuang, J., Norcia, A. M.,
& Rossion, B. (2013). The 6Hz fundamental frequency rate
for individual face discrimination in the right occipito-
temporal cortex. Neuropsychologia, 51, 2863–2975. https://
doi.org/10.1016/j.neuropsychologia.2013.08.018, PubMed:
24007879
Anderson, S. K., & Müller, M. M. (2010). Behavioral performance
follows the time course of neural facilitation and suppression
during cued shifts of feature-selective attention. Proceedings
of the National Academy of Sciences, 107, 13878–13882.
https://doi.org/10.1073/pnas.1002436107, PubMed: 20643918
Appelbaum, L. G., Ales, J. M., Cottereau, B., & Norcia, A. M.
(2010). Configural specificity of the lateral occipital cortex.
Neuropsychologia, 48, 3323–3328. https://doi.org/10.1016/j
.neuropsychologia.2010.07.016, PubMed: 20638395
Appelbaum, L. G., Wade, A. R., Vildavski, V. Y., Pettet, M. W., &
Norcia, A. M. (2006). Cue-invariant networks for figure and
background processing in human visual cortex. Journal of
Neuroscience, 26, 11695–11708. https://doi.org/10.1523
/JNEUROSCI.2741-06.2006, PubMed: 17093091
Bach, M., & Meigen, T. (1999). Do’s and don’ts in Fourier analysis
of steady-state potentials. Documenta Ophthalmologica, 99,
69–82. https://doi.org/10.1023/A:1002648202420, PubMed:
10947010
Baker, C. L., Jr., & Hess, R. F. (1984). Linear and nonlinear
components of human electroretinogram. Journal of
Neurophysiology, 51, 952–967. https://doi.org/10.1152/jn
.1984.51.5.952, PubMed: 6726320
Baker, D. H., & Wade, A. R. (2017). Evidence for an optimal
algorithm underlying signal combination in human visual
cortex. Cerebral Cortex, 27, 254–264. https://doi.org/10.1093
/cercor/bhw395
Bandettini, P. A., Jesmanowicz, A., Wong, E. C., & Hyde, J. S.
(1993). Processing strategies for time-course data set in
functional MRI of the human brain. Magnetic Resonance in
Medicine, 30, 161–173. https://doi.org/10.1002/mrm
.1910300204, PubMed: 8366797
Başar, E., & Schürmann, M. (1994). Functional aspects of
evoked alpha and theta responses in humans and cats.
Biological Cybernetics, 72, 175–183. https://doi.org/10.1007
/BF00205981, PubMed: 7880921
Beck, A. A., Rossion, B., & Samson, D. (2018). An objective
neural signature of rapid perspective taking. Social Cognitive
and Affective Neuroscience, 13, 72–79. https://doi.org/10
.1093/scan/nsx135, PubMed: 29186550
Bekhtereva, V., Pritschmann, R., Keil, A., & Müller, M. M. (2018).
The neural signature of extracting emotional content from
rapid visual streams at multiple presentation rates: A cross-
laboratory study. Psychophysiology, 55, e13222. https://doi
.org/10.1111/psyp.13222, PubMed: 30112759
Boremanse, A., Norcia, A. M., & Rossion, B. (2013). An objective
signature for visual binding of face parts in the human brain.
Journal of Vision, 13, 6. https://doi.org/10.1167/13.11.6,
PubMed: 24023273
Braddick, O., Birtles, D., Wattam-Bell, J., & Atkinson, J. (2005).
Motion- and orientation-specific cortical responses in infancy.
Vision Research, 45, 3169–3179. https://doi.org/10.1016/j
.visres.2005.07.021, PubMed: 16137739
Brazier, M. A. B. (1964). A study of the variability of response to
flicker: The influence of other sensory stimuli. Documenta
Ophthalmologica, 18, 221–237. https://doi.org/10.1007
/BF00160575, PubMed: 14214270
Burns, S. A., Elsner, A. E., & Kreitz, M. R. (1992). Analysis of
nonlinearities in the flicker ERG. Optometry and Vision
Science, 69, 95–105. https://doi.org/10.1097/00006324
-199202000-00002, PubMed: 1584559
Retter, Rossion, and Schiltz
2387
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
3
1
1
2
3
7
2
1
9
6
7
7
8
4
/
/
j
o
c
n
_
a
_
0
1
7
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Capilla, A., Pazo-Alvarez, P., Darriba, A., Campo, P., & Gross, J.
Danielson, G. C., & Lanczos, C. (1942). Some improvements in
(2011). Steady-state visual evoked potentials can be
explained by temporal superposition of transient event-
related responses. PLoS One, 6, e14543. https://doi.org/10
.1371/journal.pone.0014543, PubMed: 21267081
Cebulla, M., Stürzebecher, E., & Elberling, C. (2006). Objective
detection of auditory steady-state responses: Comparison
of one-sample and q-sample tests. Journal of the American
Academy of Audiology, 17, 93–103. https://doi.org/10.3766
/jaaa.17.2.3, PubMed: 16640063
Cetin, V., Ozekes, S., & Varol, H. S. (2020). Harmonic analysis
of steady-state visual evoked potentials in brain computer
interfaces. Biomedical Signal Processing and Control, 60,
101999. https://doi.org/10.1016/j.bspc.2020.101999
Chadnova, E., Reynaud, A., Clavagnier, S., Baker, D. H., Baillet, S.,
& Hess, R. F. (2018). Interocular interaction of contrast and
luminance signals in human primary visual cortex. Neuroimage,
167, 23–30. https://doi.org/10.1016/j.neuroimage.2017.10.035,
PubMed: 29122719
Chemin, B., Huang, G., Mulders, D., & Mouraux, A. (2018). EEG
time-warping to study non-strictly-periodic EEG signals
related to the production of rhythmic movements. Journal
of Neuroscience Methods, 308, 106–115. https://doi.org/10
.1016/j.jneumeth.2018.07.016, PubMed: 30053483
Chen, X., Wang, Y., Nakanishi, M., Gao, X., Jung, T.-P., & Gao, S.
(2015). High-speed spelling with a noninvasive brain–
computer interface. Proceedings of the National Academy of
Sciences, U.S.A., 112, E6058–E6067. https://doi.org/10.1073
/pnas.1508080112, PubMed: 26483479
Chen, Y., Seth, A. K., Gally, J. A., & Edelman, G. M. (2003). The
power of human brain magnetoencephalographic signals can
be modulated up or down by changes in an attentive visual
task. Proceedings of the National Academy of Sciences, U.S.A.,
100, 3501–3506. https://doi.org/10.1073/pnas.0337630100,
PubMed: 12626756
Cheng, M., Gao, X., Gao, S., & Xu, D. (2002). Design and
implementation of a brain–computer interface with high
transfer rates. IEEE Transactions on Biomedical Engineering,
49, 1181–1186. https://doi.org/10.1109/TBME.2002.803536,
PubMed: 12374343
Clynes, M., Kohn, M., & Lifshitz, K. (1964). Dynamics and spatial
behavior of light evoked potentials, their modification under
hypnosis, and on-line correlation in relation to rhythmic
components. Annals of the New York Academy of Sciences,
112, 468–509. https://doig.org/10.1111/j.1749-6632.1964
.tb26764.x, PubMed: 14188111
Cobb, W. A., Morton, H. B., & Ettlinger, G. (1967). Cerebral
potentials evoked by pattern reversal and their suppression
in visual rivalry. Nature, 216, 1123–1125. https://doi.org/10
.1038/2161123b0, PubMed: 6075260
Coia, A., Jones, C., Duncan, C., & Crognale, M. (2014).
Physiological correlates of watercolor effect. Journal of the
Optical Society of America. A, Optics, Image Science, and
Vision, 31, A15–A22. https://doi.org/10.1364/JOSAA.31
.000A15, PubMed: 24695164
Cottereau, B., Lorenceau, J., Gramfort, A., Clerc, M., Thirion, B.,
& Baillet, S. (2011). Phase delays within visual cortex shape
the response to steady-state visual stimulation. Neuroimage,
54, 1919–1929. https://doi.org/10.1016/j.neuroimage.2010.10
.004, PubMed: 20937397
Cunningham, D. G. M., Baker, D. H., & Pierce, J. W. (2017).
Measuring nonlinear signal combination using EEG. Journal
of Vision, 17, 10. https://doi.org/10.1167/17.5.10, PubMed:
28538990
Damon, F., Leleu, A., Rekow, D., Foncet, F., & Baudouin, J.-Y.
(2020). Expertise for conspecific face individuation in the
human brain. Neuroimage, 204, 116218. https://doi.org/10
.1016/j.neuroimage.2019.116218, PubMed: 31550510
practical Fourier analysis and their application to X-ray
scattering from liquids. Journal of the Franklin Institute,
233, 365–380. https://doi.org/10.1016/S0016-0032(42)90767-1
Davidson, M. J., Mithen, W., Hogendoorn, H., van Boxtel, J. J.-A.,
& Tsuchiya, N. (2020). The SSVEP tracks attention, not
consciousness, during perceptual filling-in. eLife, e60031.
https://doi.org/10.7554/eLife.60031, PubMed: 33170121
Davila, C. E., Srebro, R., & Ghaleb, I. A. (1998). Optimal detection
of visual evoked potentials. IEEE Transactions on Bio-Medical
Engineering, 45, 800–803. https://doi.org/10.1109/10.678615,
PubMed: 9609945
De Keyser, R., Mouraux, A., Quek, G. L., Torta, D. M., & Legrain,
V. (2018). Fast periodic visual stimulation to study tool-
selective processing in the human brain. Experimental Brain
Research, 236, 2751–2763. https://doi.org/10.1007/s00221
-018-5331-2, PubMed: 30019235
Delorme, A., & Makeig, S. (2004). EEGLAB: An open source
toolbox for analysis of single-trial EEG dynamics including
independent component analysis. Journal of Neuroscience
Methods, 134, 9–21. https://doi.org/10.1016/j.jneumeth.2003
.10.009, PubMed: 15102499
Di Russo, F., Pitzalis, S., Aprile, T., Spitoni, G., Patria, F., Stella,
A., et al. (2007). Spatiotemporal analysis of the cortical
sources of the steady-state visual evoked potential. Human
Brain Mapping, 28, 323–334. https://doi.org/10.1002/hbm
.20276, PubMed: 16779799
Di Russo, F., Teder-Salajarvi, W. A., & Hillyard, S. A. (2002).
Steady-state VEP and attentional visual processing. In A. Zani
& A. Proberbio (Eds.), The cognitive electrophysiology of
mind and brain (pp. 257–272). New York: Academic Press.
Ding, J., Sperling, G., & Srinivasan, R. (2006). Attentional
modulation of SSVEP power depends on the network tagged
by the flicker frequency. Cerebral Cortex, 16, 1016–1029.
https://doi.org/10.1093/cercor/bhj044, PubMed: 16221931
Donker, D. N. J. (1975). Harmonic composition and topographic
distribution of responses to sine wave modulated light (SML),
their reproducibility and their interhemispheric relationship.
Electroencephalography and Clinical Neurophysiology,
39, 561–574. https://doi.org/10.1016/0013-4694(75)90069-3,
PubMed: 53136
Dwyer, P., Xu, B., & Tanaka, J. W. (2019). Investigating the
perception of face identity in adults on the autism spectrum
using behavioural and electrophysiological measures. Vision
Research, 157, 132–141. https://doi.org/10.1016/j.visres.2018
.02.013, PubMed: 30012353
Dzhelyova, M., Jacques, C., Dormal, G., Michel, C., Schiltz, C., &
Rossion, B. (2019). High test–retest reliability of a neural
index of rapid automatic discrimination of unfamiliar
individual faces. Visual Cognition, 27, 127–141. https://doi
.org/10.1080/13506285.2019.1616639
Dzhelyova, M., Jacques, C., & Rossion, B. (2017). At a single
glance: Fast periodic visual stimulation uncovers the spatio-
temporal dynamics of brief facial expression changes in the
human brain. Cerebral Cortex, 27, 4106–4123. https://doi.org
/10.1093/cercor/bhw223
Dzhelyova, M., & Rossion, B. (2014a). Supra-additive
contribution of shape and surface information to individual
face discrimination as revealed by fast periodic visual
stimulation. Journal of Vision, 14, 15. https://doi.org/10.1167
/14.14.15, PubMed: 25540264
Dzhelyova, M., & Rossion, B. (2014b). The effect of parametric
stimulus size variation on individual face discrimination
indexed by fast periodic visual stimuliation. BMC
Neuroscience, 15, 87. https://doi.org/10.1186/1471-2202-15
-87, PubMed: 25038784
Eidelman-Rothman, M., Ben-Simon, E., Freche, D., Keil, A.,
Hendler, T., & Levit-Binnun, N. (2019). Sleepless and
2388
Journal of Cognitive Neuroscience
Volume 33, Number 11
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
3
1
1
2
3
7
2
1
9
6
7
7
8
4
/
/
j
o
c
n
_
a
_
0
1
7
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
desynchronized: Impaired inter trial phase coherence of
steady-state potentials following sleep deprivation.
Neuroimage, 202, 116055. https://doi.org/10.1016/j.neuroimage
.2019.116055, PubMed: 31351165
Engel, S. A., Glover, G. H., & Wandell, B. A. (1997). Retinotopic
organization in human visual cortex and the spatial precision
of functional MRI. Cerebral Cortex, 7, 181–192. https://doi
.org/10.1093/cercor/7.2.181, PubMed: 9087826
Falsini, B., Iarossi, G., Fadda, A., Porrello, G., Valentini, P.,
Piccardi, M., et al. (1999). The fundamental and second
harmonic of the photopic flicker electroretinogram:
Temporal frequency-dependent abnormalities in retinitis
pigmentosa. Clinical Neurophysiology, 110, 1554–1562.
https://doi.org/10.1016/S1388-2457(99)00106-6, PubMed:
10479022
Fawcett, I. P., Barnes, G. R., Hillebrand, A., & Singh, K. D.
(2004). The temporal frequency tuning of human visual
cortex investigated using synthetic aperture magnetometry.
Neuroimage, 21, 1542–1553. https://doi.org/10.1016/j
.neuroimage.2003.10.045, PubMed: 15050578
Fisher, K., Towler, J., Rossion, B., & Eimer, M. (2020). Neural
responses in a fast periodic visual stimulation paradigm
reveal domain-general visual discrimination deficits in
developmental prosopagnosia. Cortex, 133, 76–102. https://
doi.org/10.1016/j.cortex.2020.09.008, PubMed: 33099077
Forinash, K., & Christian, W. (2016). Sound: An interactive
ebook. https://www.compadre.org/books/SoundBook
Fourier, J. (1822). Théorie analytique de la chaleur.
Paris: F. Didot.
Galambos, R., Makeig, S., & Talmachoff, P. J. (1981). A 40-Hz
auditory potential recorded from the human scalp. Proceedings
of the National Academy of Sciences, U.S.A., 78, 2643–2647.
https://doi.org/10.1073/pnas.78.4.2643, PubMed: 6941317
Gao, X., Gentile, F., & Rossion, B. (2018). Fast periodic
stimulation: A highly effective approach in fMRI brain
mapping. Brain Structure and Function, 223, 2433–2454.
https://doi.org/10.1007/s00429-018-1630-4, PubMed: 29502144
Gaume, A., Vialatte, F., & Dreyfus, G. (2014). Transient brain
activity explains the spectral content of steady-state visual
evoked potentials. Proceedings of the 2014 36th Annual
International Conference of the IEEE Engineering in
Medicine and Biology Society, 688–692. https://doi.org/10
.1109/EMBC.2014.6943684
Geisler, C. D. (1960). Average responses to clicks in man
recorded by scalp electrodes (Technical Report 380).
Cambridge, MA: MIT Research Laboratory of Electronics.
Gonzalez, R., & Woods, R. (2018). Digital image processing
(4th ed.). Essex, UK: Pearson.
Gordon, N., Hohwy, J., Davidson, M. J., van Boxtel, J., &
Tsuchiya, N. (2019). From intermodulation components to
visual perception and cognition—A review. Neuroimage,
199, 480–494. https://doi.org/10.1016/j.neuroimage.2019.06
.008, PubMed: 31173903
Gruss, L. F., Wieser, M. J., Schweinberger, S. R., & Keil, A.
(2012). Face-evoked steady-state visual potentials: Effects of
presentation rate and face inversion. Frontiers of Human
Neuroscience, 6, 316. https://doi.org/10.3389/fnhum.2012
.00316, PubMed: 23205009
Guillaume, M., Mejias, S., Rossion, B., Dzhelyova, M., & Schiltz,
C. (2018). A rapid, objective and implicit measure of visual
quantity discrimination. Neuropsychologia, 111, 180–189.
https://doi.org/10.1016/j.neuropsychologia.2018.01.044,
PubMed: 29408421
Gwinn, O. S., & Jiang, F. (2019). Hemispheric asymmetries
in deaf and hearing during sustained peripheral selective
attention. Journal of Deaf Studies and Deaf Education,
25, 1–9. https://doi.org/10.1093/deafed/enz030, PubMed:
31407782
Gwinn, O. S., Matera, C. N., O’Neil, S. F., & Webster, M. A.
(2018). Asymmetric neural responses for facial expressions
and anti-expressions. Neuropsychologia, 119, 405–416.
https://doi.org/10.1016/j.neuropsychologia.2018.09.001,
PubMed: 30193846
Heinrich, S. P. (2009). Permutation-based significance tests
for multiharmonic steady-state evoked potentials. IEEE
Transactions on Biomedical Engineering, 56, 534–537.
https://doi.org/10.1109/TBME.2008.2006021, PubMed:
19272910
Heinrich, S. P. (2010). Some thoughts on the interpretation of
steady-state evoked potentials. Documenta Ophthalmologica,
120, 205–214. https://doi.org/10.1007/s10633-010-9212-7,
PubMed: 20101435
Heinrich, S. P., & Bach, M. (2001). Adaptation dynamics in
pattern-reversal visual evoked potentials. Documenta
Ophthalmologica, 102, 141–156. https://doi.org/10.1023
/A:1017509717071, PubMed: 11518457
Heinrich, S. P., Groten, M., & Bach, M. (2015). Relating the
steady-state visual evoked potential to single-stimulus
responses derived from m-sequence stimulation.
Documenta Opthalmologica, 131, 13–24. https://doi.org/10
.1007/s10633-015-9492-z, PubMed: 25743033
Heinrich, S. P., Mell, D., & Bach, M. (2009). Frequency-domain
analysis of fast oddball responses to visual stimuli: A
feasibility study. International Journal of Psychophysiology,
73, 287–293. https://doi.org/10.1016/j.ijpsycho.2009.04.011,
PubMed: 19426768
Herrmann, C. (2001). Human EEG responses to 1–100 Hz
flicker: Resonance phenomena in visual cortex and their
potential correlation to cognitive phenomena. Experimental
Brain Research, 137, 346–353. https://doi.org/10.1007
/s002210100682, PubMed: 11355381
Herrmann, C. S., Rach, S., Vosskuhl, J., & Strüber, D. (2014).
Time-frequency analysis of event-related potentials: A brief
tutorial. Brain Topography, 27, 438–450. https://doi.org/10
.1007/s10548-013-0327-5, PubMed: 24194116
Hönegger, C., Atteneder, C., Griesmayr, B., Holz, E., Weber, E.,
& Sauseng, P. (2011). Neural correlates of visuo-spatial
working memory encoding—An EEG study. Neuroscience
Letters, 500, 118–122. https://doi.org/10.1016/j.neulet.2011.06
.017, PubMed: 21704123
Hou, C., Pettet, M. W., & Norcia, A. M. (2008). Abnormalities of
coherent motion processing in strabismic amblyopia: Visual-
evoked potential measurements. Journal of Vision, 8, 2–212.
https://doi.org/10.1167/8.4.2, PubMed: 18484841
Hou, C., Pettet, M. W., Sampath, V., Candy, T. R., & Norcia, A. M.
(2003). Development of the spatial organization and
dynamics of lateral interactions in the human visual system.
Journal of Neuroscience, 23, 8630–8640. https://doi.org/10
.1523/JNEUROSCI.23-25-08630.2003, PubMed: 14507962
Jacques, C., Retter, T. L., & Rossion, B. (2016). A single glance at
a face generates larger and qualitatively different category-
selective spatio-temporal signatures than other ecologically-
relevant categories in the human brain. Neuroimage, 137,
21–33. https://doi.org/10.1016/j.neuroimage.2016.04.045,
PubMed: 27138205
Jervis, B. W., Nichols, M. J., Johnson, T. E., Allen, E., & Hudson,
N. R. (1983). A fundamental investigation of the composition
of auditory evoked potentials. IEEE Transactions on
Biomedical Engineering, 30, 43–50. https://doi.org/10.1109
/TBME.1983.325165, PubMed: 6826185
Jonas, J., Jacques, C., Liu-Shuang, J., Brissart, H., Colnat-Coulbois,
S., Maillard, L., et al. (2016). A face-selective ventral occipito-
temporal map of the human brain with intracerebral
potentials. Proceeding of the National Academy of Sciences,
U.S.A., 113, E4088–E4097. https://doi.org/10.1073/pnas
.1522033113, PubMed: 27354526
Retter, Rossion, and Schiltz
2389
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
3
1
1
2
3
7
2
1
9
6
7
7
8
4
/
/
j
o
c
n
_
a
_
0
1
7
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Kaspar, K., Hassler, U., Martens, U., Trujillo-Barreto, N., &
Gruber, T. (2001). Steady-state visually evoked potential
correlates of object recognition. Brain Research, 1343,
112–121. https://doi.org/10.1016/j.brainres.2010.04.072,
PubMed: 20450897
Katzner, S., Nauhaus, I., Benucci, A., Bonin, V., Ringach, D. L., &
Carandini, M. (2009). Local origin of field potentials in visual
cortex. Neuron, 61, 35–41. https://doi.org/10.1016/j.neuron
.2008.11.016, PubMed: 19146811
Keitel, C., Quigley, C., & Ruhnau, P. (2014). Stimulus-driven
brain oscillations in the alpha range: Entrainment of intrinsic
rhythms or frequency-following response? Journal of
Neuroscience, 34, 10137–10140. https://doi.org/10.1523
/JNEUROSCI.1904-14.2014, PubMed: 25080577
Keysers, C., & Perrett, D. I. (2002). Visual masking and RSVP
reveal neural competition. Trends in Cognitive Sciences, 6,
120–125. https://doi.org/10.1016/S1364-6613(00)01852-0,
PubMed: 11861189
Kim, Y.-J., Grabowecky, M., Paller, K. A., & Suzuki, S. (2011).
Differential roles of frequency-following and frequency-
doubling visual responses revealed by evoked neural
harmonics. Journal of Cognitive Neuroscience, 23,
1875–1886. https://doi.org/10.1162/jocn.2010.21536,
PubMed: 20684661
Kim, Y.-J., Grabowecky, M., Paller, K., Muthu, K., & Suzuki, S.
(2007). Attention induces synchronization-based response
gain in steady-state visual evoked potentials. Nature
Neuroscience, 10, 117–125. https://doi.org/10.1038/nn1821,
PubMed: 17173045
Kosem, A., Gramfort, A., & Van Wassenhove, V. (2014).
Encoding of event timing in the phase of neural oscillations.
Neuroimage, 92, 274–284. https://doi.org/10.1016/j
.neuroimage.2014.02.010, PubMed: 24531044
Kremers, J., Rodrigues, A. R., Silveira, L. C., & da Silva Filho, M.
(2010). Flicker ERGs representing chromaticity and
luminance signals. Investigative Ophthalmology & Visual
Science, 51, 577–587. https://doi.org/10.1167/iovs.09-3899,
PubMed: 19737882
Kremers, J., & Scholl, H. (2001). Rod-/L-cone and rod-/M-cone
interactions in electroretinograms at different temporal
frequencies. Visual Neuroscience, 18, 339–351. https://doi
.org/10.1017/S095252380118301X, PubMed: 11497411
Kuś, R., Duszyk, A., Milanowski, P., Łabęcki, M., Bierzyńska, M.,
Radzikowska, Z., et al. (2013). On the quantification of SSVEP
frequency responses in human EEG in realistic BCI
conditions. PLoS One, 8, e77536. https://doi.org/10.1371
/journal.pone.0077536, PubMed: 24204862
Leleu, A., Dzhelyova, D., Rossion, B., Brochrd, R., Durand, K.,
Schaal, B., et al. (2018). Tuning functions for automatic
detection of brief changes of facial expression in the human
brain. Neuroimage, 179, 245–251. https://doi.org/10.1016/j
.neuroimage.2018.06.048, PubMed: 29913283
Leleu, A., Rekow, D., Poncet, F., Schaal, B., Durand, K., Rossion,
B., et al. (2020). Maternal odor shapes rapid face
categorization in the infant brain. Developmental Science,
23, e12877. https://doi.org/10.1111/desc.12877, PubMed:
31175678
Liu-Shuang, J., Norcia, A. M., & Rossion, B. (2014). An objective
index of individual face discrimination in the right occipito-
temporal cortex by means of fast periodic visual stimulation.
Neuropsychologia, 52, 57–72. https://doi.org/10.1016/j
.neuropsychologia.2013.10.022, PubMed: 24200921
Liu-Shuang, J., Torfs, K., & Rossion, B. (2016). An objective
electrophysiological marker of face individualisation
impairment in acquired prosopagnosia with fast periodic
visual stimulation. Neuropsychologia, 83, 100–113. https://
doi.org/10.1016/j.neuropsychologia.2015.08.023, PubMed:
26318239
Lochy, A., Schiltz, C., & Rossion, B. (2020). The right hemispheric
dominance for face perception in preschool children depends
on visual discrimination level. Developmental Science,
23, e12914. https://doi.org/10.1111/desc.12914, PubMed:
31618490
Lochy, A., Van Belle, G., & Rossion, B. (2015). A robust index of
lexical representation in the left occipito-temporal cortex
as evidenced by EEG responses to fast periodic visual
stimulation. Neuropsychologia, 66, 18–31. https://doi.org/10
.1016/j.neuropsychologia.2014.11.007, PubMed: 25448857
Lochy, A., Van Reybroeck, M., & Rossion, B. (2016). Left cortical
specialization for visual letter strings predicts rudimentary
knowledge of letter-sound association in preschoolers.
Proceedings of the National Academy of Sciences, U.S.A.,
113, 8544–8549. https://doi.org/10.1073/pnas.1520366113,
PubMed: 27402739
Luck, S. J. (2005). An Introduction to the event-related
potential technique. Cambridge, MA: MIT Press.
Makeig, S., Westerfield, M., Jung, T. P., Enghoff, S., Townsend,
J., Courchesne, E., et al. (2002). Dynamic brain sources of
visual evoked responses. Science, 295, 690–694. https://doi
.org/10.1126/science.1066168, PubMed: 11809976
McFadden, K. L., Steinmetz, S. E., Carroll, A. M., Simon, S. T.,
Wallace, A., & Rojas, D. C. (2014). Test–retest reliability of the
40 Hz EEG auditory steady-state response. PLoS One, 9,
e85748. https://doi.org/10.1371/journal.pone.0085748,
PubMed: 24465679
McKeefry, D. J., Russell, M. H., Murray, I. J., & Kulikowski, J. J.
(1996). Amplitude and phase variations of harmonic
components in human achromatic and chromatic visual
evoked potentials. Visual Neuroscience, 13, 639–653. https://
doi.org/10.1017/s0952523800008543, PubMed: 8870222
Meigen, T., & Bach, M. (2000). On the statistical significance
of electrophysiological steady-state responses. Documenta
Ophthalmologica, 98, 207–232. https://doi.org/10.1023
/A:1002097208337, PubMed: 10945442
Milton, A., Rowland, A., Stothart, G., Clatworthy, P., Pennington,
C. M., & Kazanina, N. (2020). Fast periodic visual stimulation
indexes preserved semantic memory in healthy ageing.
Scientific Reports, 10, 13159. https://doi.org/10.1038/s41598
-020-69929-5, PubMed: 32753662
Min, B. K., Dähne, S., Ahn, M. H., Noh, Y.-K., & Müller, K.-R.
(2016). Decoding of top–down cognitive processing for
SSVEP-controlled BMI. Scientific Reports, 6, 36267. https://doi
.org/10.1038/srep36267, PubMed: 27808125
Miskociv, V., & Keil, A. (2013). Perceiving threat in the face of
safety: Excitation and inhibition of conditioned fear in human
visual cortex. Journal of Neuroscience, 33, 72–78. https://doi
.org/10.1523/JNEUROSCI.3692-12.2013, PubMed: 23283323
Morgan, S. T., Hansen, J. C., & Hillyard, S. A. (1996). Selective
attention to stimulus location modulates the steady-state
visual evoked potential. Proceedings of the National
Academy of Sciences, U.S.A., 93, 4770–4774. https://doi.org
/10.1073/pnas.93.10.4770, PubMed: 8643478
Moungou, A., Thonnard, J.-L., & Mouraux, A. (2016). EEG
frequency tagging to explore the cortical activity related to
the tactile exploration of natural textures. Scientific Reports,
6, 20738. https://doi.org/10.1038/srep20738, PubMed:
26853820
Mouraux, A., Iannetti, G. D., Colon, E., Nozaradan, S., Legrain,
V., & Plaghki, L. (2011). Nociceptive steady-state evoked
potentials elicited by rapid periodic thermal stimulation of
cutaneous nociceptors. Journal of Neuroscience, 31,
6079–6087. https://doi.org/10.1523/JNEUROSCI.3977-10
.2011, PubMed: 21508233
Movshon, J. A., Thompson, I. D., & Tolhurst, D. J. (1978).
Receptive field organization of complex cells in the cat’s
striate cortex. The Journal of Physiology, 283, 79–99.
2390
Journal of Cognitive Neuroscience
Volume 33, Number 11
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
3
1
1
2
3
7
2
1
9
6
7
7
8
4
/
/
j
o
c
n
_
a
_
0
1
7
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
https://doig.org/10.1113/jphysiol.1978.sp012489, PubMed:
722592
Müller, M. M., Andersen, S., Trujillo, N. J., ValdesSosa, P.,
Malinowski, P., & Hillyard, S. A. (2006). Feature-selective
attention enhances color signals in early visual areas of the
human brain. Proceedings of the National Academy of
Sciences, U.S.A., 103, 14250–14254. https://doi.org/10.1073
/pnas.0606668103, PubMed: 16956975
Müller, M. M., Picton, T. W., Valdes-Sosa, P., Riera, J., Teder-
Sälejärvi, W. A., & Hillyard, S. A. (1998). Effects of spatial
selective attention on the steady-state visual evoked potential
in the 20–28 Hz range. Cognitive Brain Research, 6, 249–261.
https://doi.org/10.1016/S0926-6410(97)00036-0, PubMed:
9593922
Müller, M. M., Teder, W., & Hillyard, S. A. (1997).
Magnetoencephalographic recording of steadystate visual
evoked cortical activity. Brain Topography, 9, 163–168.
https://doi.org/10.1007/BF01190385, PubMed: 9104827
Muller-Putz, G. R., Scherer, R., Brauneis, C., & Pfurtscheller, G.
(2005). Steady-state visual evoked potential (SSVEP)-based
communication: Impact of harmonic frequency components.
Journal of Neural Engineering, 2, 123–130. https://doi.org
/10.1088/1741-2560/2/4/008, PubMed: 16317236
Norcia, A. M., Appelbaum, L. G., Ales, J. M., Cottereau, B., &
Rossion, B. (2015). The steady-state visual evoked potential
in vision research: A review. Journal of Vision, 15, 4. https://
doi.org/10.1167/15.6.4, PubMed: 26024451
Norcia, A. M., Sato, T., Shinn, P., & Mertus, J. (1986). Methods
for the identification of evoked response components in the
frequency and combined time/frequency domains.
Electoencephalography and Clinical Neurophysiology, 65,
212–226. https://doi.org/10.1016/0168-5597(86)90056-0
Norcia, A. M., Tyler, C. W., Hamer, R. D., & Wesemann, W.
(1989). Measurement of spatial contrast sensitivity with the
swept contrast VEP. Vision Research, 29, 627–637. https://doi
.org/10.1016/0042-6989(89)90048-5, PubMed: 2603399
Painter, D. R., Dux, P. E., Travis, S. L., & Mattingley, J. B.
(2014). Neural responses to target features outside a search
array are enhanced during conjunction but not unique-
feature search. Journal of Neuroscience, 34, 3390–3401.
https://doi.org/10.1523/JNEUROSCI.3630-13.2014, PubMed:
24573295
Park, J. (2018). A neural basis for the visual sense of number
and its development: A steady-state visual evoked potential
study in children and adults. Developmental Cognitive
Neuroscience, 30, 333–343. https://doi.org/10.1016/j.dcn
.2017.02.011, PubMed: 28342780
Parry, N. R., Murray, I. J., Panorgias, A., McKeefry, D. J., Lee, B. B.,
& Kremers, J. (2012). Simultaneous chromatic and luminance
human electroretinogram responses. Journal of Physiology,
590, 3141–3154. https://doi.org/10.1113/jphysiol.2011.226951,
PubMed: 22586211
Parseval des Chênes, M.-A. (1806). Mémoire sur les séries et
sur l’intégration complète d’une équation aux différences
partielles linéaire du second ordre, à coefficients constants.
Mémoires présentés à l’Institut des Sciences, Lettres et Arts,
par divers savants, et lus dans ses assemblées: Sciences,
Mathématiques et Physiques, 1, 638–648.
Pastor, M. A., Artieda, J., Arbizu, J., Marti-Climent, J. M., Peñuelas,
I., & Masdeu, J. C. (2002). Activation of human cerebral and
cerebellar cortex by auditory stimulation at 40 Hz. Journal
of Neuroscience, 22, 10501–10506. https://doi.org/10.1523
/JNEUROSCI.22-23-10501.2002, PubMed: 12451150
Pastor, M. A., Artieda, J., Arbizu, J., Valencia, M., & Masdeu, J. C.
(2003). Human cerebral activation during steady-state
visual-evoked responses. Journal of Neuroscience, 23,
11621–11627. https://doi.org/10.1523/JNEUROSCI.23-37
-11621.2003, PubMed: 14684864
Pastor, M. A., Valencia, M., Artieda, J., Alegre, M., & Masdeu, J. C.
(2007). Topography of cortical activation differs for
fundamental and harmonic frequencies of the steady-state
15O study.
visual-evoked responses. An EEG and PET H2
Cerebral Cortex, 17, 1899–1905. https://doi.org/10.1093
/cercor/bhl098, PubMed: 17060366
Patel, M. R. (2012). Introduction to electrical power and power
electronics. Boca Raton, FL: CRC Press.
Paulk, A. C., Kirszenblat, L., Zhou, Y., & van Swinderen, B. (2015).
Closed-loop behavioral control increases coherence in the fly
brain. Journal of Neuroscience, 35, 10304–10315. https://doi
.org/10.1523/JNEUROSCI.0691-15.2015, PubMed: 26180205
Pei, F., Pettet, M. W., & Norcia, A. M. (2002). Neural correlates
of object-based attention. Journal of Vision, 2, 588–596.
https://doi.org/10.1167/2.9.1, PubMed: 12678630
Peli, E., McCormack, G., & Sokol, S. (1988). Signal to noise ratio
considerations in the analysis of sweep visual-evoked
potentials. Applied Optics, 27, 1094–1098. https://doi.org/10
.1364/AO.27.001094, PubMed: 20531523
Peterzell, D. H., & Norcia, A. M. (1997). Spatial frequency
masking with the sweep-VEP. Vision Research, 37, 2349–2359.
https://doi.org/10.1016/s0042-6989(97)00046-1, PubMed:
9381671
Press, W. H., Falnnery, B. P., & Teukolsky, S. A. (1993). Numerical
recipes in fortran 77: The art of scientific computing (2nd ed.).
Cambridge, United Kingdom: Cambridge University Press.
Puce, A., Allison, T., Gore, J. C., & McCarthy, G. (1995). Face-
sensitive regions in human extrastriate cortex studied by
functional MRI. Journal of Neurophysiology, 74,
1192–1199. https://doi.org/10.1152/jn.1995.74.3.1192,
PubMed: 7500143
Regan, D. (1966). Some characteristics of average steady-state
and transient responses evoked by modulated light.
Electroencephalography and Clinical Neurophysiology,
20, 238–248. https://doi.org/10.1016/0013-4694(66)90088-5,
PubMed: 4160391
Regan, D. (1975). Colour coding of pattern responses in man
investigated by evoked potential feedback and direct plot
techniques. Vision Research, 15, 175–183. https://doi.org/10
.1016/0042-6989(75)90205-9, PubMed: 1129975
Regan, D. (1989). Human brain electrophysiology: Evoked
potentials and evoked magnetic fields in science and
medicine. New York: Elsevier.
Regan, D., & Heron, J. R. (1969). Clinical investigation of lesions
of the visual pathway: A new objective technique. Journal of
Neurology, Neurosurgery & Psychiatry, 32, 479–483. https://
doi.org/10.1136/jnnp.32.5.479, PubMed: 5360055
Regan, D., & Regan, M. P. (1988a). Nonlinearity in human visual
responses to two-dimensional patterns, and a limitation of
Fourier methods. Vision Research, 27, 2181–2183. https://doi
.org/10.1016/0042-6989(87)90132-5, PubMed: 3447366
Regan, M. P., & Regan, D. (1988b). A frequency domain
technique for characterizing nonlinearities in biological
systems. Journal of Theoretical Biology, 133, 293–317.
https://doi.org/10.1016/S0022-5193(88)80323-0
Retter, T. L., Jiang, F., Webster, M. A., & Rossion, B. (2020).
All-or-none visual categorization in the human brain.
Neuroimage, 213, 116685. https://doi.org/10.1016/j
.neuroimage.2020.116685, PubMed: 32119982
Retter, T. L., & Rossion, B. (2016a). Uncovering the neural
magnitude and spatio-temporal dynamics of natural image
categorization in a fast visual stream. Neuropsychologia,
91, 9–28. https://doi.org/10.1016/j.neuropsychologia.2016.07
.028, PubMed: 27461075
Retter, T. L., & Rossion, B. (2016b). Visual adaptation provides
objective electrophysiological evidence of facial identity
discrimination. Cortex, 80, 35–50. https://doi.org/10.1016/j
.cortex.2015.11.025, PubMed: 26875725
Retter, Rossion, and Schiltz
2391
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
3
1
1
2
3
7
2
1
9
6
7
7
8
4
/
/
j
o
c
n
_
a
_
0
1
7
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Retter, T. L., & Rossion, B. (2017). Visual adaptation reveals
an objective electrophysiological measure of high-level
individual face discrimination. Scientific Reports, 7, 3269.
https://doi.org/10.1038/s41598-017-03348-x, PubMed: 28607389
Retter, T. L., Webster, M. A., & Jiang, F. (2019). Directional
visual motion is represented in the auditory and association
cortices of early deaf individuals. Journal of Cognitive
Neuroscience, 31, 1126–1140. https://doi.org/10.1162/jocn_a
_01378, PubMed: 30726181
Ross, B., Borgmann, C., Draganova, R., Roberts, L. E., & Pantev, C.
(2000). A high-precision magnetoencephalographic study
of human auditory steady-state responses to amplitude-
modulated tones. Journal of the Acoustical Society of
America, 108, 679–691. https://doi.org/10.1121/1.429600,
PubMed: 10955634
Rossion, B. (2014). Understanding individual face discrimination
by means of fast periodic visual stimulation. Experimental
Brain Research, 232, 1599–1621. https://doi.org/10.1007
/s00221-014-3934-9
Rossion, B., Alonso-Prieto, E., Boremanse, A., Kuefner, D., &
Van Belle, G. (2012). A steady-state visual evoked potential
approach to individual face perception: Effect of inversion,
contrast-reversal and temporal dynamics. Neuroimage, 63,
1585–1600. https://doi.org/10.1016/j.neuroimage.2012.08
.033, PubMed: 22917988
Rossion, B., & Boremanse, A. (2011). Robust sensitivity to facial
identity in the right human occipito-temporal cortex as
revealed by steady-state visual-evoked potentials. Journal of
Vision, 11, 16. https://doi.org/10.1167/11.2.16, PubMed:
21346000
Rossion, B., Retter, T. L., & Liu-Shuang, J. (2020). Understanding
human individuation of unfamiliar faces with oddball fast
periodic visual stimulation and electroencephalography.
European Journal of Neuroscience, 52, 4283–4344. https://
doi.org/10.1111/ejn.14865, PubMed: 32542962
Rossion, B., Torfs, K., Jacques, C., & Liu-Shuang, J. (2015). Fast
periodic presentation of natural face images reveals a robust
face-selective electophysiological response in the human
brain. Journal of Vision, 15, 18. https://doi.org/10.1167/15.1
.18, PubMed: 25597037
Ruhnau, P., Keitel, C., Lithari, C., Weisz, N., & Neuling, T. (2016).
Flicker-driven responses in visual cortex change during
matched-frequency transcranial alternating current stimulation.
Frontiers in Human Neuroscience, 10, 184. https://doi.org/10
.3389/fnhum.2016.00184, PubMed: 27199707
Saupe, K., Schröger, E., Andersen, S. K., & Müller, M. M. (2009).
Neural mechanisms of intermodal sustained selective
attention with concurrently presented auditory and visual
stimuli. Frontiers in Human Neuroscience, 3, 58. https://doi
.org/10.3389/neuro.09.058.2009, PubMed: 20011221
Schettino, A., Porcu, E., Gundlach, C., Keitel, C., & Müller, M. M.
(2020). Rapid processing of neutral and angry expressions
within ongoing facial stimulus streams: Is it all about isolated
facial features? PLoS One, 15, e0231982. https://doi.org/10
.1371/journal.pone.0231982, PubMed: 32330160
Shapley, R. (2009). Linear and nonlinear systems analysis of the
visual system: Why does it seem so linear? A review dedicated
to the memory of Henk Spekreijse. Vision Research, 49,
907–921. https://doi.org/10.1016/j.visres.2008.09.026,
PubMed: 18940193
Sieving, P. A., Arnold, E. B., Jamison, J., Liepa, A., & Coats, C.
(1998). Submicrovolt flicker electroretinogram: Cycle-by-cycle
recording of multiple harmonics with statistical estimation
of measurement uncertainty. Investigative Ophthalmology &
Visual Science, 39, 1462–1469. PubMed: 9660495
Skottun, B. C., De Valois, R. L., Grosof, D. H., Movshon, A.,
Albrecht, D. G., & Bonds, A. B. (1991). Classifying simple and
complex cells on the basis of response modulation. Vision
Research, 31, 1079–1086. https://doi.org/10.1016/0042-6989
(91)90033-2
Smith, S. W. (1997). The scientist and engineer’s guide to
digital signal processing (2nd ed.). San Diego: California
Technical Publishing.
Spekreijse, H. (1969). Rectification in the goldfish retina:
Analysis by sinusoidal and auxiliary stimulation. Vision
Research, 9, 1461–1472. https://doi.org/10.1016/0042-6989
(69)90062-5, PubMed: 5367436
Srinivasan, R., Russell, D. P., Edelman, G. M., & Tononi, G.
(1999). Increased synchronization of neuromagnetic
responses during conscious perception. Journal of
Neuroscience, 19, 5435–5448. https://doi.org/10.1523
/JNEUROSCI.19-13-05435.1999, PubMed: 10377353
Strang, G. (2007). Computational science and engineering.
Wellesley-Cambridge Press.
Strasburger, H. (1987). The analysis of steady state evoked
potentials revisited. Clinical Vision Science, 1, 245–256.
Tang, Y., & Norcia, A. M. (1995). An adaptive filter for steady-
state evoked responses. Electroencephalography and
Clinical Neurophysiology, 96, 268–277. https://doi.org/10
.1016/0168-5597(94)00309-3
Tlumak, A. I., Durrant, J. D., Delgado, R. E., & Robert Boston, J.
(2011). Steady-state analysis of auditory evoked potentials
over a wide range of stimulus repetition rates: Profile in
adults. International Journal of Audiology, 50, 448–458.
https://doi.org/10.3109/14992027.2011.560903, PubMed:
21434788
Tononi, G., Srinivasan, R., Russell, D. P., & Edelman, G. M. (1998).
Investigating neural correlates of conscious perception by
frequency-tagged neuromagnetic responses. Proceedings of the
National Academy of Sciences, U.S.A., 95, 3198–3203. https://
doi.org/10.1073/pnas.95.6.3198, PubMed: 9501240
Troelstra, A. (1971). Harmonic distortion in the frog’s ERG and
its possible relation to differences in latencies. Vision
Research, 11, 393–403. https://doi.org/10.1016/0042-6989(71)
90082-4, PubMed: 5558924
Tyler, C. W., & Kaitz, M. (1977). Movement adaptation in the
visual evoked response. Experimental Brain Research, 27,
203–209. https://doi.org/10.1007/BF00237698, PubMed:
838009
van de Walle de Ghelcke, A., Rossion, B., Schiltz, C., & Lochy, A.
(2021). Developmental changes in letter-selective neural
sensitivity: A one-year follow-up of beginning readers.
Developmental Science, 24, e12999. https://doi.org/10.1111
/desc.12999, PubMed: 32452594
Van der Donck, S., Dzhelyova, M., Vettori, S., Thielen, H.,
Steyaert, J., Rossion, B., et al. (2019). Fast periodic visual
stiulation EEG reveals reduced neural sensitivity to fearful
faces in children with Autism. Journal of Autism and
Developmental Disorders, 49, 4658–4673. https://doi.org/10
.1007/s10803-019-04172-0, PubMed: 31468275
van der Tweel, L. H. (1964). Relation between psychophysics
and electrophysiology of flicker. Documenta
Ophthalmologica, 18, 287–304. https://doi.org/10.1007
/BF00160581, PubMed: 14214273
van der Tweel, L. H., Sem-Jacobson, C. W., Kamp, A., Storm van
Leeuwen, W., & Veringa, F. T. H. (1958). Objective
determination of response to modulated light. Acta
Physiologica et Pharmacologica Neerlandica, 7, 528–529.
Van der Tweel, L. H., & Verduyn Lunel, H. F. E. V. (1965).
Human visual responses to sinusoidally modulated light.
Electroencephalography and Clinical Neurophysiology, 18,
587–598. https://doi.org/10.1016/0013-4694(65)90076-3
Vialatte, F.-B., Maurice, M., Dauwels, J., & Cichocki, A. (2009).
Steady state visual evoked potentials in the delta range
(0.5–5 Hz). In M. Köppen, N. Kasabov, & G. Coghill (Eds.),
Advances in neuro-information processing (pp. 399–406).
2392
Journal of Cognitive Neuroscience
Volume 33, Number 11
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
3
1
1
2
3
7
2
1
9
6
7
7
8
4
/
/
j
o
c
n
_
a
_
0
1
7
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Berlin, Heidelberg: Springer. https://doi.org/10.1007/978-3
-642-02490-0_49
Vialatte, F. B., Maurice, M., Dauwels, J., & Cichocki, A. (2010).
Steady-state visually evoked potentials: Focus on essential
paradigms and future perspectives. Progress in Neurobiology,
90, 418–438. https://doi.org/10.1016/j.pneurobio.2009.11.005,
PubMed: 19963032
Victor, J. D., & Conte, M. M. (2000). Two-frequency analysis of
interactions elicited by Vernier stimuli. Visual Neuroscience,
17, 959–973. https://doi.org/10.1017/s0952523800176151,
PubMed: 11193112
Victor, J. D., & Zemon, V. (1985). The human visual evoked
potential: Analysis of components due to elementary and
complex aspects of form. Vision Research, 25, 1829–1842.
https://doi.org/10.1016/0042-6989(85)90006-9, PubMed:
3832607
Wang, B. Y., Gao, X., Hong, B., Jia, C., & Gao, S. (2008). Brain–
computer interfaces based on visual evoked potentials. IEEE
Engineering in Medicine and Biology Magazine, 27, 64–71.
https://doi.org/10.1109/MEMB.2008.923958, PubMed:
18799392
Watkin, P. (2008). In G. Rance (Ed.), Auditory steady-state
response: Generation, recording, and clinical applications.
San Diego, CA: Plural.
Wattam-Bell, J., Birtles, D., Nystrom, P., von Hofsten, C.,
Rosander, K., Anker, S., et al. (2010). Reorganization of global
form and motion processing during human visual
development. Current Biology, 20, 411–415. https://doi.org
/10.1016/j.cub.2009.12.020, PubMed: 20171101
Winawer, J., Kay, K. N., Foster, B. L., Rauschecker, A. M., Parvizi,
J., & Wandell, B. A. (2013). Asynchronous broadband signals
are the principal source of the BOLD response in human
visual cortex. Current Biology, 23, 1145–1153. https://doi.org
/10.1016/j.cub.2013.05.001, PubMed: 23770184
Wittevrongel, B., Khachatryan, E., Hnazaee, M. F., Camarrone, F.,
Carrette, E., De Taeye, L., et al. (2018). Decoding steady-state
visual evoked potentials from electrocorticography. Frontiers
in Neuroinformatics, 12, 1–14. https://doi.org/10.3389/fninf
.2018.00065, PubMed: 30319386
Xu, B., Liu-Shuang, J., Rossion, B., & Tanaka, J. W. (2017).
Individual differences in face identity processing with fast
periodic visual stimulation. Journal of Cognitive
Neuroscience, 29, 1368–1377. https://doi.org/10.1162/jocn_a
_01126, PubMed: 28358660
Zemon, V. M., & Gordon, J. (2018). Quantification and statistical
analysis of the transient visual evoked potential to a contrast-
reversing pattern: A frequency-domain approach. European
Journal of Neuroscience, 48, 1765–1788. https://doi.org/10
.1111/ejn.14049, PubMed: 6487677
Zemon, V., & Ratliff, F. (1984). Intermodulation components of
the visual evoked potential: Responses to lateral and
superimposed stimuli. Biological Cybernetics, 50, 401–408.
https://doi.org/10.1007/BF00335197, PubMed: 6487677
Zhang, P., Jamison, K., Engel, S., He, B., & He, S. (2011).
Binocular rivalry requires visual attention. Neuron, 71,
362–369. https://doi.org/10.1016/j.neuron.2011.05.035,
PubMed: 21791293
Zhou, H., Melloni, L., Poeppel, D., & Ding, N. (2016).
Interpretations of frequency domain analyses of neural
entrainment: Periodicity, fundamental frequency, and
harmonics. Frontiers in Human Neuroscience, 10, 274.
https://doi.org/10.3389/fnhum.2016.00274
Zoefel, B., Oever, S. T., & Sack, A. T. (2018). The
involvement of endogenous neural oscillations in the
processing of rhythmic input: More than a regular
repetition of evoked neural responses. Frontiers in
Neuroscience, 12, 95. https://doi.org/10.3389/fnins.2018
.00095, PubMed: 29563860
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
3
1
1
2
3
7
2
1
9
6
7
7
8
4
/
/
j
o
c
n
_
a
_
0
1
7
6
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Retter, Rossion, and Schiltz
2393