Global Adaptation in
Networks of Selfish
Components: Emergent
Associative Memory
at the System Scale
In some circumstances complex adaptive systems
Abstract
composed of numerous self-interested agents can self-organize into
structures that enhance global adaptation, efficiency, or function.
However, the general conditions for such an outcome are poorly
understood and present a fundamental open question for domains
as varied as ecology, sociology, economics, organismic biology,
and technological infrastructure design. In contrast, sufficient
conditions for artificial neural networks to form structures that
perform collective computational processes such as associative
memory/recall, classification, generalization, and optimization
are well understood. Such global functions within a single agent
or organism are not wholly surprising, since the mechanisms
(e.g., Hebbian learning) that create these neural organizations may
be selected for this purpose; but agents in a multi-agent system
have no obvious reason to adhere to such a structuring protocol
or produce such global behaviors when acting from individual
self-interest. However, Hebbian learning is actually a very simple
and fully distributed habituation or positive feedback principle.
Here we show that when self-interested agents can modify how
they are affected by other agents (e.g., when they can influence
which other agents they interact with), then, in adapting these
inter-agent relationships to maximize their own utility, they will
necessarily alter them in a manner homologous with Hebbian
learning. Multi-agent systems with adaptable relationships will
thereby exhibit the same system-level behaviors as neural networks
under Hebbian learning. For example, improved global efficiency
in multi-agent systems can be explained by the inherent ability
of associative memory to generalize by idealizing stored patterns
and/or creating new combinations of subpatterns. Thus distributed
multi-agent systems can spontaneously exhibit adaptive global
behaviors in the same sense, and by the same mechanism, as
the organizational principles familiar in connectionist models of
organismic learning.
Richard A. Watson*,**
University of Southampton
Rob Mills**
University of Southampton
†
C. L. Buckley
Sussex University
Keywords
Self-organization, adaptive networks,
Hebbian learning, multi-agent systems,
social networks, emergent computation,
games on networks
A version of this paper with color figures is
available online at http://dx.doi.org/10.1162/
artl_a_00029. Subscription required.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
3
1
4
7
1
6
6
2
7
7
9
a
r
t
l
/
_
a
_
0
0
0
2
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
* Contact author. E-mail: raw@ecs.soton.ac.uk
** Natural Systems Group, Electronics and Computer Science, University of Southampton, SO17 1BJ, UK.
† Informatics, Sussex University, BN1 9RH, UK.
© 2011 Massachusetts Institute of Technology
Artificial Life 17: 147–166 (2011)
R. A. Watson et al.
Global Adaptation in Networks of Selfish Components
1 Selfish Changes to Connections and Global Adaptation
One of the key open questions in the field of artificial life and adaptive systems is how, if at all, it is
possible that a complex system that is not evolved can exhibit adaptation or increased functionality
without design. Self-organization [33] has the potential to play a role in the formation of prebiotic
organizations, or in moving from one level of biological organization to another [42], for example,
but theory to understand exactly what this means or how it might work is limited. In contrast, theory
to understand distributed adaptive processes in neural networks is well developed, but generally
assumed to be relevant only to brains and nervous systems “programmed” to exhibit such adapta-
tion. Here we show that organizational principles familiar in learning neural networks emerge spon-
taneously in distributed networks of self-interested agents. This enables us to utilize the theoretical
framework of neural networks to understand how self-organization produces global adaptation in
complex adaptive systems.
The behavior that is rational for a self-interested agent (e.g., a person in a social network, or a species
in an ecosystem) is generally sensitive to its environment or context—that is, the best response for an
agent often depends on the strategy adopted by the other agents it interacts with [41]. How the strategy
of one agent affects another, and then feeds back to influence the first, can be significantly affected
by the topology of a network, and different interaction structures can create conditions that are more
or less conducive to high levels of cooperation or system efficiency in a multi-agent system [51, 52, 69,
72, 86]. Often, although an agent may not be able to control the strategy of others, it may have some
influence over which agents it interacts with [2, 15, 75], and by altering this set an agent can produce
contexts that subsequently change its own social behavior or function [54, 55, 59, 62]. Accordingly,
many types of agents do not merely change their own behaviors in response to context, but in fact
engineer their context by changing which agents they interact with, how frequently they interact with
them, and how much they depend on one agent or another. Network models where agents can alter
the topology of the network on which they interact therefore provide a flexible way to model the
self-organization of interaction structure [29, 30, 31, 33, 55, 56, 73, 74, 75] and have been used to
illustrate examples where this enhances cooperation [55, 72]. More generally, the conditions where
multi-agent systems can produce a self-organized structure that enhances system-level or holistic func-
tion are not well understood. In this article we wish to better understand the relationship between self-
organization in interaction networks among selfish agents and the potential for enhanced global
adaptation [17, 33, 55, 62, 72, 91, 92].
Although both the structure of the network and the behaviors on the network are dynamic vari-
ables, a conceptual separation between agent behaviors that affect the structure of interactions from
other, “ordinary” agent behaviors (e.g., whether an agent plays a defecting or a cooperating strategy)
is natural in many types of systems where there is a separation of timescales. In adaptive networks
[12] it is common to conceptually separate the dynamical behavior of agents in a network from
the structure of the network even though agents can often (slowly) alter the network structure.
For example, ecological population dynamics are controlled by a slow-changing network of evolved
interspecies relationships [60, 65], selection of individual genetic traits is altered by a slow-changing
network of evolved pleiotropic and epistatic interactions [57, 76], and social behaviors are affected
by a slow-changing network of social connections [55, 56, 74]. Understanding how behaviors in
networks promote changes in the structure of the network and, in turn, how the modified structure
of the network affects global function and efficiency [51, 52] is important for domains as varied
as social networks [86, 87], the evolution of evolvability [76], the evolution of altruism [88], tech-
nological infrastructures [67], epidemiology [34, 50, 88], and ecosystem complexity [20, 70, 90].
However, the strategy with which agents alter network structure may be domain specific; which
makes a general theory to understand the coupling between behaviors on networks and changes
to network structure problematic.
In this article we adopt a simple and general assumption: that agents modify relationships with
one another (i.e., connections in a network) selfishly. That is, the changes to network structure are
148
Artificial Life Volume 17, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
3
1
4
7
1
6
6
2
7
7
9
a
r
t
l
/
_
a
_
0
0
0
2
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
R. A. Watson et al.
Global Adaptation in Networks of Selfish Components
carried out by the agents on the network rationally with respect to their individual utility [30, 31, 50,
75]. By this we simply mean that behaviors of agents on a network and behaviors of agents that
alter that network should have the same motivations—that is, be controlled by maximization of the
same individual utility function. Specifically, we assume, as is conventional, that the individual utility
of an agent is a function of its behavior and its connection to other agents, and that agents can adopt
a behavior to maximize their individual utility given the current network structure and the behaviors
of others (a best-response strategy). But we also assume that they have the ability to change their
network connections and will do so in a manner that increases the utility of their current behavior
(a best-response strategy applied to restructuring behaviors). Hence, we refer to these as selfish
changes to network structure. (In this article we address continuous changes to network structure,
i.e., changes in the strength and sign of connections, rather than a topological rewiring of the net-
work [29, 30, 31, 55, 75].)
This is a very general assumption. For example, social agents that seek to minimize conflict or
maximize consensus with friends may change their behavior to be compatible with the behaviors of
friends, but logically they may also change friends to strengthen relationships with others who are
already compatible (and weaken connections with friends who conflict) [69]. Similarly, evolving species
in an ecosystem will evolve traits that maximize their fitness given the other species they interact with in
their biotic context, but natural selection also demands that, where possible, they will evolve behaviors
that alter the set of species they interact with so as to maximize their fitness given their current traits.
In an economic market, businesses may adopt pricing plans that maximize profit given the other
businesses they currently trade with, but a profit-seeking business may also change the network of
businesses it trades with to maximize the profit from its current pricing plan [69]. In all cases, we do
not need to adopt an arbitrary mapping between behaviors on the network and behaviors that change
the network; instead we are simply assuming that agents will change the network structure in a manner
that is consistent with the same factors that govern their behaviors on the network—be it minimizing
conflict, or maximizing fitness, profit, or productivity. All such scenarios can be modeled abstractly as
maximization of utility.
We will assess how selfish changes to interagent relationships change the dynamics of the system,
and specifically, whether they cause self-interested agents given these new relationships to subsequently
adopt more cooperative behaviors, or conversely, result in more interagent conflict and lower levels of
cooperation. The fundamental question of cooperation is whether agents that are acting to maximize
individual utility have the result of increasing the utility of others. This is assessed by measuring total
welfare or total utility, which is simply the sum of individual utilities (see Section 3). Using a sum of
individual utilities in this manner in no way assumes that individual and global utilities are aligned,
nor that individual utilities are not conflicted—an increase in utility of one individual may cause a
decrease in utility of another. Indeed, these constraints are what make total utility a quantity worth
measuring. For example, the prisonerʼs dilemma [41, 72] is interesting precisely because individuals
seeking to maximize individual utility will arrive at an equilibrium that does not maximize the sum of
individual utilities. Likewise, in systems where agents can benefit from a public good without contribut-
ing to it, a tragedy of the commons can result, where individual (relative) gains result in global (absolute)
losses [41]. However, preoccupation with the prisonerʼs dilemma—where the only Nash equilibrium
of individual strategies minimizes the sum of individual utilities—may lead one to assume that individual
and global interests must be completely opposed in this sense in every two-player game in order for
cooperation to be meaningful. But this is not the case. Even in two-player games, cooperation can be
meaningful without the prisonerʼs dilemma [61, 64, 69], and more generally, even if the underlying
two-player games present no obvious conflict of interest, games of multiple players can present un-
resolvable conflicts. In particular, multi-player non-zero-sum games may have many equilibria, and dif-
ferent equilibria may have different total utilities. Consequently, whereas all equilibria locally maximize
the individual utility of all agents (by definition), different equilibria vary in the extent to which they are
successful in maximizing total utility. As the system approaches a given local equilibrium, it may well be
the case that total utility also increases, that is, individual and total utility are not completely opposed.
But a given local equilibrium will not in general globally maximize total utility, so neither are individual
Artificial Life Volume 17, Number 3
149
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
3
1
4
7
1
6
6
2
7
7
9
a
r
t
l
/
_
a
_
0
0
0
2
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
R. A. Watson et al.
Global Adaptation in Networks of Selfish Components
and total utility completely aligned. Such partial alignment between individual and total utility arises
naturally given that individuals have conflicting or constrained interests (unless they are specifically
contrived to have completely opposed interests, as in the prisonerʼs dilemma). Conflicts of interest
between agents are created in our model by a network of random pairwise constraints (coordination
and anticoordination games [73]) that cannot be simultaneously satisfied. This representation cannot
represent all possible games, but it does represent tensions between individual and global utility, creating
a system that exhibits multiple Nash equilibria, some of which have higher total utility than others. We
show that the problem of maximizing total utility is equivalent to a combinatorial optimization problem
that is difficult in a formal sense.
In any model where the game is static, however, the degree to which individually selfish actions align
with global welfare is simply an outcome intrinsic to the setup of the game employed. But when agents
have the ability to alter the set of agents they play with, or the relative strength of their relationships with
other agents, this is equivalent to changing the underlying game [72] (or changing how individuals per-
ceive or experience the game [7, 72]). Our question is not, therefore, whether individual interests are
aligned with global interests in the initial game we define, but rather whether the selfish restructuring of
the interactions in the system leads, in effect, to agents that (because they are playing a modification of
the underlying game) exhibit better alignment with total utility over time. We thus define global adapta-
tion as an increase in the ability of the system to maximize total utility.
In summary, we examine systems under the following conditions: (1) Changes to agent behaviors
and to connections between agents are carried out selfishly by the agents in the system to maximize
individual utility. (2) A separation of timescales exists between fast changes to behaviors and slow
changes to connections. (3) The initial dynamics of the agent behaviors (given the initial connections
between them) exhibits multiple point attractors (Nash equilibria [49]). (4) The agent behaviors are
subject to external perturbations such that they sample many different attractors (on a timescale where
connections change slowly).
The first two conditions are straightforward, and the third, although restrictive, is a useful simplify-
ing assumption (we will show that if this condition is true of the original system, it will remain true of
the system as relationships change, and we will briefly discuss relaxation of this assumption later). But
it is easy to see that these three assumptions alone do not necessarily produce any interesting con-
sequences for global adaptation. That is, if the behavioral states change much more rapidly than con-
nections, then almost all changes to connections will occur after the system has reached whatever
behavioral attractor it is going to reach. Selfish changes to connections (as we will show) have the
effect of reinforcing the current state configuration (because they simply favor exploitation of local
utility gradients)—making it more stable in that the agents involved are less inclined to change their
behaviors. Thus, the long term dynamical consequences of such changes for global adaptation are
degenerate [60]: Whichever local equilibrium happens to be found first becomes essentially canalized
by changes to connections.
But we will show that under the fourth assumption (the condition of external perturbations), selfish
changes to connections have a much more interesting outcome. Under this condition, the initial struc-
ture does not dictate a single attractor state, but a distribution of attractor states, and this distribution
changes as the connections of the system are modified. Specifically, we find that selfish agents change
the structure of interactions in the system so that the equilibria of the new system are a special subset of
those in the original system, specifically those that have high total utility. We can therefore view this
restructuring as effecting equilibrium selection [5, 14] that enhances the global level of adaptation (rather
than merely finding an arbitrary local equilibrium). Accordingly, under these conditions, individually
selfish changes to relationships have the effect of increasing global adaptation.
2 Selfish Changes to Connections and Hebbian Learning
Our objective in this article is not merely to show that selfish changes to connections can increase
global adaptation under certain conditions, but to provide a formal framework to understand why.
150
Artificial Life Volume 17, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
3
1
4
7
1
6
6
2
7
7
9
a
r
t
l
/
_
a
_
0
0
0
2
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
R. A. Watson et al.
Global Adaptation in Networks of Selfish Components
Specifically, the key to understanding this result is that selfish agents necessarily modify connections
in a manner consistent with Hebbʼs rule [16]—a simple learning rule familiar in computational
neuroscience (Section 3). This means that a system of selfish agents, each modifying its connections
with other agents selfishly and in a completely distributed manner, will produce dynamical con-
sequences for the system as a whole that are functionally identical to a learning neural network. This
result seems initially surprising—there is no a priori reason why selfish agents should change con-
nections with other agents in a Hebbian manner. In a cognitive system, in contrast, we suppose that
natural selection is responsible for creating a Hebbian learning mechanism—but here we claim that
in an ecosystem or a multi-agent system of selfish agents, Hebbian learning at the system level arises
spontaneously as a result of rational agent choices at the individual level. In fact, Hebbʼs rule is a
very simple positive feedback principle, and in light of this, it is not so surprising that selfish com-
ponents in a complex adaptive system will naturally adhere to such a principle, as we will discuss
(Section 3). Having shown this equivalence, we can then employ concepts and theory from com-
putational neuroscience to help us understand what consequences this will have for global behavior
and how global adaptation is enhanced [1, 6, 10, 19, 22, 23, 25, 36, 66].
In particular, recent work of our own [78, 81] provides a foundation for the current article by in-
tegrating two well-known behaviors of the Hopfield network [22] in a novel combination. Specifically,
the ability of the Hopfield network with Hebbian learning to learn a set of training patterns and recall
them from noisy or partial samples is well known [22]. And in previously unrelated work, it is shown
that the Hopfield network can also be used as an optimization method; here the weights of the net-
work are not learned, but preprogrammed to represent the constraints of an optimization problem,
and running the network then provides locally optimal solutions to the optimization problem [23,
24]. Our work shows that these two behaviors can be combined in the same network at different
timescales to improve optimization. Specifically, a networkʼs initial weights are programmed to repre-
sent an optimization problem as before, but the system is repeatedly perturbed, causing it to visit many
different locally optimal solutions. While this is happening, the weights of the network are slowly
updated by Hebbian learning. If the system spends most of its time at local optima (i.e., the system
perturbations are infrequent and dynamical transients are relatively short), then Hebbian learning will
tend to enlarge the basin of attraction for existing local attractors in proportion to how often they are
visited. In effect, the network is overlaying an associative memory [22] of its behavioral experience onto
its own original dynamics, or self-modeling [78].
Since the enlargement of one attractor must result in the decrease of another, attractors compete
with one another during this process, and the system tends to enlarge the attractors that it visits most
often at the expense of those that are visited less often. As its behavior becomes dominated by learned
connections rather than the original connections, positive feedback accelerates this competition be-
tween incompatible attractor patterns. The surprising finding is that this competition results in the
enlargement of basins of attraction that lead to especially high-total-utility attractors at the expense
of low-utility attractors. This is explained in part by the fact that in systems built out of the superposi-
tion of many low-order constraints, low-energy (high-utility) attractors necessarily have large basins of
attraction [10, 37, 38, 39]. So, the better the attractor, the more it is visited, thus the more it is enlarged
by learning, and the more it is visited in the future, and so on. Thus, if the learning rate is sufficiently low,
the system will with high likelihood enlarge the attractor of the globally optimal system configuration.
More interestingly, generalization inherent in associative memory [6, 36] causes the system to generate
new combinations of common features from past configurations, enlarging the basin of attraction
for high-utility attractors that have not yet been experienced. Thus the system does not merely recall
good configurations that have already been visited, but can find good configurations more quickly even
for the first time [78, 81].
The novel contribution of the current article is to show that these behaviors, shown straightforwardly
in a neural network where we may assume Hebbian learning, also occur spontaneously in a complex
adaptive system of self-interested components that alter connections selfishly (without assuming or
mandating Hebbian learning). We argue that these behaviors are natural for any complex adaptive sys-
tem with plastic connections that are altered by selfish agents, because selfish agents in such systems will
Artificial Life Volume 17, Number 3
151
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
3
1
4
7
1
6
6
2
7
7
9
a
r
t
l
/
_
a
_
0
0
0
2
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
R. A. Watson et al.
Global Adaptation in Networks of Selfish Components
necessarily alter connections in a Hebbian manner. We discuss the implications of this finding for various
types of complex adaptive systems, thus transferring the optimization result from neural networks into
the domain of multi-agent systems of selfish components. Thus, the principles of associative memory and
distributed learning usually reserved for organismic neural networks (i.e., brains and nervous systems)
apply directly to self-organized complex adaptive systems and multi-agent systems. This associative induction
does not in any way require that the system as a whole have any motivations to adapt holistically, nor does it
require that the network have been holistically evolved to produce such an adaptation. The behaviors that
we observe are the spontaneous, self-organized result of many essentially uncoordinated agents acting
selfishly. Nonetheless, we show that their independent motivation to optimize individual utility causes
them to selectively strengthen or weaken connections with other agents so that the system as a whole
becomes more likely to find combinations of behaviors that resolve conflicts and result in higher total
utility in a nontrivial and quantifiable sense.
3 Methods
3.1 Behaviors, Connections, and Total Utility
Each agent in a network adopts one of two discrete behaviors or states, si = ±1 (e.g., tall/short, a/A,
trade-x/trade-y, vote-A/vote-B), so as to maximize an individual payoff, fitness, or utility, ui, which is a
weighted sum of interactions between the state it adopts and the states of other agents in the network,
ui ¼
XN
j
Nij si sj ;
ð1Þ
where Nij = (−1,1) is the current interaction coefficient or connection strength between agent i and
agent j. In principle, an agent may have interactions with all other agents, but nonconnected agents
may be represented by Nij = 0. A behavioral dynamics of this form provides a general model for a dy-
namical system in many domains, from neural networks to spin-glass models to ecosystems. Since an
agentʼs utility depends on many connections, not all connections can be satisfied simultaneously in all
cases. An agent will thus adopt the behavior that is the best compromise for it, given the states of other
agents. For each connection we can say that the behavioral constraint that the connection imposes is satis-
fied if Nijsisj > 0; otherwise it remains unsatisfied, or in tension.
In some scenarios (e.g., social networks) an agent may be free to modify interactions directly (i.e.,
make or break friendships). In other scenarios the network of interactions that are alterable by an
agent will augment or supplement a network of interactions that are immutable, or external to the
system. For example, epistasis between alleles is partly the result of external selective dependences
and partly the result of evolvable developmental details, and fitness dependences between species in
an ecosystem are likewise partly external and partly the result of evolvable characteristics of each
species. We thus suppose that Nij is composed of two components, Nij(t ) = Nij
L (t ), where
Nij
O represents the original dependences between components of the system that are external and
unalterable by the agents themselves, and Nij
L represents the component of agent interactions that
are learnable or evolvable via agent adaptation [81]. For simplicity we may suppose that the original
L (t = 0) = 0. As the agents in the
behavior of the system is determined entirely by Nij
network modify Nij
O with Nij
L, this will alter the dynamics of the system.
O + Nij
As each agent chooses the state that maximizes its own utility, this may increase or decrease the
utility of other agents in the network. We are interested in how this affects the total system utility, or
global payoff of the system, which is simply the sum of individual utilities, measured using Nij
O :
U ¼
XN
XN
i
j
ij si sj :
NO
152
ð2Þ
Artificial Life Volume 17, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
3
1
4
7
1
6
6
2
7
7
9
a
r
t
l
/
_
a
_
0
0
0
2
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
R. A. Watson et al.
Global Adaptation in Networks of Selfish Components
This quantifies the degree to which this combination of behaviors satisfies the original behavioral
constraints among all agents. In general, the collective effect of many independently maximizing
agents will not produce combinations of states that find the maximum possible total utility, but
merely locally optimal equilibria.
3.2 Selfish Changes to Connections
When an agent modifies its connections with other agents selfishly, this simply means that it does so
in a manner that maximizes its own utility. Formally, given Equation 1,
ui′ > ui ⇒
XN
j
Nij′si sj >
XN
j
Nij si sj
(cid:1)
⇒
Nij′ > Nij
Nij′ < Nij
if si sj > 0;
if si sj < 0:
ð3Þ
Intuitively, this means that an agent strengthens connections that are currently satisfied and weakens
connections that are currently in tension. Note that although the change in the magnitude or
strength of a connection is dependent on the product Nijsisj, the sign of the absolute change in
the connection, DNij = Nij′ − Nij, is not sensitive to the sign of Nij, but only to the signs of the agentsʼ
behaviors. This means that the effect of selfish changes to connections is to reinforce the current
combination of behaviors, regardless of whether that combination satisfies the constraint between
them. A general form of Hebbʼs rule [16] is often stated as DNij = ysisj, with y > 0 for Hebbian
learning, and y < 0 for anti-Hebbian learning [1, 25], where y is a constant controlling the learning
rate. It is easy to see from the above that each and every change to connections that increases indi-
vidual utility (for a given behavioral configuration) will necessarily change connections in a Hebbian
direction, regardless of the properties of the existing connection matrix. Accordingly, changes to con-
nections will be determined by whether states are more often correlated or anticorrelated, not by the
existing interaction coefficient between them. Although there is positive feedback between a connec-
tion and the correlation of states it connects, any one connection only partially controls the correlation
of these states, since each agent also has many other connections to satisfy. Importantly, this means
that the sign of a connection may thus be inverted by selfish modifications if the agentsʼ behaviors
often disagree with the sign of the connection.
3.3 Connection Dynamics
For a deterministic model of connection dynamics as considered here (e.g., a rational-agent model),
we may suppose that both DNij = +r and DNij = −r, where r is a constant controlling the rate with
which weights are changed, are systematically considered, and whichever case increases individual
utility is applied. In other cases it may be natural to assume that the probability of accepting or
rejecting a particular change in N (generated from a distribution of DN values with mean zero) is
proportional to the increase in utility, Du > 0, that it confers, that is, P[Nij ← Nij + DNij] = yDu =
y(DNijsisj). For example, if each agent is evolving by natural selection given random variation and
nondeterministic selection in its connections to others, then the probability of a beneficial change
fixing in the population when it arises is proportional to the fitness benefit it confers [13]. Thus
both the magnitude and sign of DNij under selfish changes will have an expected value proportional
to sisj, that is, E[DNij] = ysisj, as per Hebbʼs rule.
The magnitude of a weight change under Hebbian learning, |ysisj|, will be a constant in the discrete-
state system; hence |DNij| = r, as above, matches Hebbian magnitudes and signs in the deterministic
system as well as in the probabilistic. In the following experiments all weights are also capped at a
Artificial Life Volume 17, Number 3
153
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
3
1
4
7
1
6
6
2
7
7
9
a
r
t
l
/
_
a
_
0
0
0
2
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
R. A. Watson et al.
Global Adaptation in Networks of Selfish Components
magnitude of 1 by a linear threshold function u, that is, if x > 1 then u(x) = 1; if x < −1 then u(x) = −1;
else u(x) = x. Thus,
h
i
Nij ðtÞ ¼ u NO
ij
þ NL
ij
ðtÞ
;
where
NL
ij
ðt þ 1Þ ¼ NL
ij
ðtÞ þ rsi ðtÞsj ðtÞ:
Note that for a given state configuration the pressures on changes to connections are symmetric (i.e.,
DNij = DNji), even if the original connections are asymmetric or of different signs. This implies that over
time, given the positive feedback on state configurations created by changes to connections, Nij and Nji
will eventually take the same sign even if their initial values do not. This ensures that this type of mod-
ification to connections will tend to simplify the dynamics of systems over time (i.e., make fixed-point
attractors more likely) rather than cause them to become chaotic.
3.4 Perturbations and Relaxations
The state of the system takes a random state configuration, R = {−1|1}N, every H time steps, where
H is sufficiently large to ensure that the system has spent most of its time at an attractor, but suffi-
ciently small compared to r that many attractors are visited in the time that significant modifications
to connections take place. We refer to each period of H time steps as a relaxation of the system. For
(cid:4)
the following experiments we use 3
as a heuristic to allow sufficient time for the network
to relax (derived from [48]). These perturbations show that no inheritance of system configurations
is required (as one might have expected from either a stochastic local search process or simulated
annealing [35, 48] or a group selection model [92]); the only values inherited from one relaxation to
the next are the connection values. Smaller perturbations will not fully explore the space of system
configurations, but will still provide opportunities to learn new associations so long as different
attractors are visited. In evolutionary scenarios, changes in environmental conditions [57], for exam-
ple, by migration to different spatial localities [83], may preclude the need for such perturbations by,
in effect, enabling different attractors to be sampled in parallel rather than in series.
4 eN ln N
(cid:5)
Given sufficiently short transients compared to the length of each relaxation, the cumulative effect
of modifications to connections over a single relaxation of the network will be approximately equal to
updating the connections (with a larger r ) only at the attractor. We use this end-of-relaxation update
method in the following experiments, but a continuous update model may be more natural in some
systems—for example, when attractors are not point attractors.
3.5 Initial Connection Matrices
We examine two simple test cases that are at opposite extremes of a structure dimension: (1) a net-
work with initially unstructured connections, and (2) a network with initially modular consistent con-
nections. To ensure contractive dynamics, and to utilize formal treatments [78, 81], we restrict our
attention to symmetric connections, that is, Nij = Nji [22] (this ensures that the total system is a
potential game). Note that the results presented above (i.e., that DNij will be Hebbian, and DNij = DNji)
do not depend on this symmetry. Symmetric interactions are not suitable to represent all types of
interactions1 (e.g., predator-prey interactions, which will generally create cyclic or sometimes chaotic
1 Making Nij = Nji means that with respect to the reciprocal connection between two agents, a strategy change that increases the contribution to
utility from this one connection to agent i also increases the contribution to utility from this one connection to agent j. But the significance of
this should not be overinterpreted. In particular, since the balance of constraints on each agent depends on its connections with all its neigh-
bors, it does not mean that “what is good for agent i is good for agent j”—that is, a strategy that increases the utility of agent i may decrease the
utility of agent j (because i forgoes mutual benefit with j in order to receive benefit from some other agent k). More specifically, circuits of
constraints among multiple agents cannot be simultaneously satisfied when they contain an odd number of negative weights [28] (e.g., Nij = Nji =
1, Njk = Nkj = 1, Nki = Nik = −1 creates a condition where j needs to coordinate with both i and k, but i needs to anticoordinate with k).
154
Artificial Life Volume 17, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
7
3
1
4
7
1
6
6
2
7
7
9
a
r
t
l
/
_
a
_
0
0
0
2
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
R. A. Watson et al.
Global Adaptation in Networks of Selfish Components
attractors). But positive symmetric weights create a balanced coordination game (see also the stag hunt
[69]), and negative weights define an anticoordination game, so we address example systems where
mixed constraints (S1) or differently weighted constraints (S2) make maximization of total utility for-
mally difficult; namely, Nij
O creates numerous local optima in total utility such that selfish maximization
of individual utilities arrives at suboptimal equilibria (see Section 4). Our setup is thereby formally
equivalent to scenarios where an energy function [71] is used to represent an optimization problem
[23, 24], in which case the system necessarily has only fixed-point attractors (corresponding to local
minima of the energy function and thus local optima of the optimization problem) but may nonetheless
represent a difficult optimization problem [81] (see the problem of finding the ground state of a spin-
glass system [28]). We also know that (nonassociative) local search processes or (nonassociative) evolution
cannot scale well on the modular problem (S2) even though it is consistent (i.e., in consistent problems,
configurations exist that satisfy all constraints simultaneously, but many configurations that fail to satisfy
all constraints are local equilibria) [80].
S1. Random sparse symmetric matrices. A connection matrix of N variables with Nk nonzero
connections (i.e., the density of nonzero connections is Nk/N2 = k/N, or k dependences
per node on average). Nonzero connections take the value −1 or 1 with equal probability.
O = {−1,0,1}. N = 120, k = 8.
Nij
S2. Modular consistent connectivity matrix. Intramodule connections are set to 1, all intermodule
connections are set to p ( p > 0); that is,2
(cid:6) (cid:7)
NO
ij
¼ 1
if
;
NO
ij
¼ p;
otherwise;
(cid:6) (cid:7)
i
k
¼ j
k
where k is the size of modules. N = 100, k = 5, p = 0.01.
In the modular function the connections within the block diagonal regions are stronger than the
intermodule connections [68, 79]. Intermediate p, as used here, where intermodule dependences are
weak but nontrivial, creates 2N/k local equilibria (corresponding to local optima in total utility), only
two of which are globally optimal [81].
4 Results
In overview, the experiments are as follows. A network of agents is created with either an initially
random or an initially modular connection structure. Both systems have a very large number of local
equilibria, which exhibit various total-utility values. The behaviors of the agents on the network are
repeatedly perturbed to different initial conditions and allowed to relax again to an attractor. The total
utility of the state configuration found at that attractor is recorded. We also allow agents to alter their
connections with other agents (by a fixed-magnitude increment, r ) in whichever direction increases their
individual utility. We assess how these selfish changes to the connection structure, accumulated slowly
as the system visits many local equilibria, alters the distribution of attractors that the system visits.
Note that the total utility is measured using the original connection values, so that we can assess
how the new/augmented connections of the network affect the likelihood of finding state configura-
tions that resolve the tensions imposed by the original constraints of the network.
Figure 1 shows that selfish modification of connections results in enlargement of high-utility attrac-
tors at the expense of low-utility attractors, such that the total utility of equilibria found by the network
with the modified connections is higher on average than the total utility of equilibria found by the
2 ⌊x⌋ is the integer part of x (x ≥ 0).
Artificial Life Volume 17, Number 3
155
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
3
1
4
7
1
6
6
2
7
7
9
a
r
t
l
/
_
a
_
0
0
0
2
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
R. A. Watson et al.
Global Adaptation in Networks of Selfish Components
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
3
1
4
7
1
6
6
2
7
7
9
a
r
t
l
/
_
a
_
0
0
0
2
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 1. Histograms of the total utility (U ) at end-of-relaxation state configurations before and after modification of the
network connections: (a) initially random structure (S1, learning rate r = 0.0002), (b) initially modular structure (S2,
r = 0.002). (Here “after” means after 500 and 150 relaxations with restructuring for S1 and S2, respectively. Data are
averaged from 100 independent runs in each case, and distributions are generated from 100 sample relaxations per run
for S1, and 25 sample relaxations per run for S2.) These show that the probability of finding configurations that are of
high total utility is significantly increased by selfish modifications to the connections. In the unstructured (S1) case,
99.56% of the attractors found before restructuring have lower total utility than the modal attractor found after restruc-
turing. The effect is even more pronounced in the modular system, S2, where the modal attractor after restructuring
is the attractor with globally maximal total utility, and whereas only 0.08% of relaxations hit this configuration before
restructuring, 95.8% of relaxations do so after restructuring.
network with the original connections. In the modular system, the attractors of the system are known,
and we can estimate how the size of the basin of attraction for each attractor class (grouped by total
utility) changes over time. There are many more low-utility attractors than high-utility attractors in
this system, and the global optimum is rarely visited initially (Figure 2). With unmodified connections,
the time to first hit of the global optimum is 1009.8 ± 92.00 relaxations (s.e.m.) on average (over
100 independent experiments). In contrast, with slowly modified connections the time to first hit is
156
Artificial Life Volume 17, Number 3
R. A. Watson et al.
Global Adaptation in Networks of Selfish Components
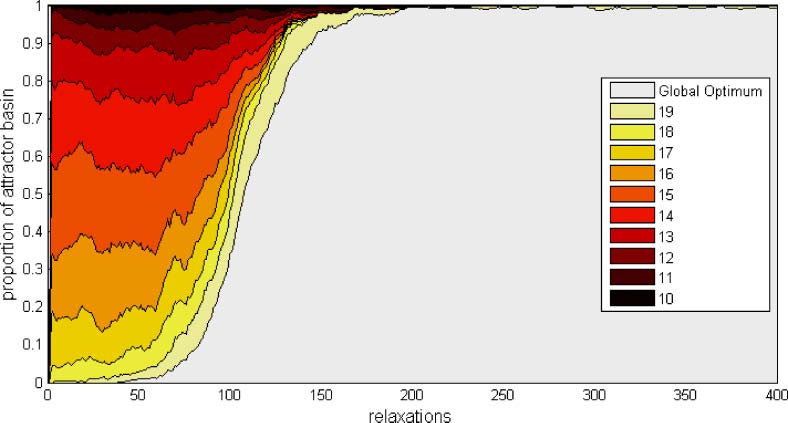
Figure 2. The change in the size of the attractor basins in the (initially) modular system over time (stacked plot). Shading
indicates membership in the 11 possible U-value classes (for 20 modules). The attractor of the globally optimal configura-
tion (lightest shade) is initially very small, but becomes the only significant attractor of the system. (The attractor basin size
is averaged using a sliding window of 20 relaxations and averaged over 100 independent runs.)
75.9 ± 2.51 (s.e.m.) (the mean time to first hit of the global optimum is different with confidence
p-value < 10-5). Indeed, after 200 relaxations with slowly modified connections the global optimum
has become practically the only attractor of the system (Figure 2). This means that selfish modifica-
tions to connections are not merely enlarging the basin of attraction for high-utility attractors that
have already been visited, but are enlarging the basin of attraction for such attractors before they are
visited for the first time. In the modular system the original multimodal optimization problem posed
by the original connections has been transformed into an easy single-optimum problem (see Figure 3,
discussed in Section 5.2).
Naively, it might seem obvious that selfish agents will modify the malleable dependences in the
problem structure to make the problem they face easier for themselves. But recall that we are mea-
suring total utility using only the original, unchanged connections and constraints. How does altering
the malleable constraints improve satisfaction of the unaltered constraints? Although the total utility
of any given behavioral configuration after connections are altered is the same as it was before con-
nections were altered (i.e., alterations affect Nij
O ), the average total utility of configura-
tions that are visited can change. This occurs not because the utility of any configuration has increased,
but because the distribution of configurations that are visited has been altered so that higher-utility
configurations are visited more often. Specifically, the easy-to-find local optimum of the new system
dynamics is in fact the hard-to-find maximally optimal local attractor of the original system dynam-
ics. The malleable constraints of the system thus induce dynamical behavior that solves the con-
straints imposed by the original and unmodifiable connections (Section 5).
L but not Nij
5 Discussion
5.1 Are Selfish Changes to Connections Necessarily Hebbian?
The suggestion that theory from neural networks might be directly relevant to other types of com-
plex adaptive systems is not unique [9, 10, 43, 53, 60]. But the utility of this transfer depends on
whether the manner in which selfish agents alter connections is homologous with the learning rules
familiar in neural networks.
Artificial Life Volume 17, Number 3
157
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
7
3
1
4
7
1
6
6
2
7
7
9
a
r
t
l
/
_
a
_
0
0
0
2
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
R. A. Watson et al.
Global Adaptation in Networks of Selfish Components
When an agent modifies connections to maximize individual utility, it necessarily strengthens con-
nections that support the current state of the agent and weakens those that oppose it (see Section 3).
It therefore strengthens connections that are currently satisfied and weakens connections that are
currently in tension. Changes of this form are preferred because only these will increase the immediate
payoff that the agent receives—increasing its preference for the current combination of behavioral
states. Since connections change slowly, the pair of behaviors experienced when the modification
took place will also be preferred more in future (as well as immediately). The consequence for the
dynamics of the system as a whole is to increase the basin of attraction for state configurations that
have been previously experienced. Although it might not be immediately apparent, the fact that self-
ish changes to connections will necessarily be Hebbian should not be too much of a surprise, given
what we know about Hebbian learning. Specifically, Hebbian learning creates an associative memory
by increasing the basin of attraction for the presented pattern, and to do that it must increase the
preference (or decrease the energy) for the combinations of states in that pattern, and in order to do
that it must (just as a selfish agent would) increase the strength of connections that agree with the
pattern and weaken those that would disrupt it. The Appendix discusses how this result holds re-
gardless of the form of utility function used.
To be clear, agents do not modify connections in a Hebbian manner in order to alter the dynamics of
the system, nor to create an associative memory, nor to increase the utility of others or their own future
utility (although the modifications do all these things), but purely for immediate individual benefit.
Nonetheless, the result of these changes produces the same dynamical consequences that are well
known for Hebbian learning in neural dynamics, such as the potential to form an associative memory,
to “recall” past patterns of activation from similar initial conditions, and in some cases to generalize
patterns of activation to create new combinations of features observed in past state configurations [22].
5.2 Memory, Optimization, and Generalization
Although the energy minimization behavior of the Hopfield network and its interpretation as an opti-
mization process (Figure 3a) are well known [23, 24, 71], and similarly, the ability of Hebbian learning
Figure 3. Schematic of well-known behaviors of the Hopfield network (a, b), and comparison with their combination in
our model, where network connections are adapted in response to the systemʼs own dynamical attractors (c) [78, 81].
158
Artificial Life Volume 17, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
7
3
1
4
7
1
6
6
2
7
7
9
a
r
t
l
/
_
a
_
0
0
0
2
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
R. A. Watson et al.
Global Adaptation in Networks of Selfish Components
to implement an associative memory of a set of training patterns and “recall” them or “recognize” them
from noisy or partial examples (Figure 3b) is also well known [22], in contrast, the result of combining
these two behaviors in the same network is novel (Figure 3c) [78, 81]. Given that good attractors are
large attractors [10, 37, 38, 39], the results above can then be partly explained by the development of
an associative memory that simply “recalls” the best configurations previously visited, since these are
the configurations that are most frequently visited.
However, the results we observe cannot be entirely explained this way, because the network modi-
fication enlarges the basin of attraction for the global optimum before it is visited for the first time (see
Section 4). In other words, the system is “predicting” the location of high-utility attractors, not merely
“recalling” them. This behavior can be understood via the inherent ability of associative learning to
generalize training patterns (Figure 4). Thus the enlargement of attractors depends not only on the
frequency with which different behavioral patterns are visited, but also on the commonality of features
between those patterns.
The potential for Hebbian learning to generate new combinations of features by generalizing over
observed patterns, including the phenomenon known as spurious attractors [32], is particularly important
in this respect. Spurious attractors are attractors in an associative memory and that are distant from any
training pattern (Figure 4c). These are created when many training patterns have large components in
common and the new attractors correspond to novel combinations of these features [32]. In an asso-
ciative memory this is naturally considered to be a nuisance (e.g., [11]), but in optimization the ability to
produce new combinations of successful features is highly desirable [21, 77, 80, 81]. Mills [44, 47, 48]
shows that the automatic discovery and utilization of modular structure in an optimization problem, as
facilitated by learned associations, can be used to provide significant optimization performance (see also
[26, 27, 84, 93]). This result thereby shows that a distributed optimization process, based on nothing
more than repeated relaxation of state configurations plus local selfish reinforcement of connections,
has the effect not only of creating an associative memory of its past local optimization behavior, but also
of generalizing its past behavior and enabling superior optimization and, in the context of a multi-agent
system, global adaptation.
The equivalence between an explicit global optimization process and spontaneous global adaptation
in multi-agent systems, shown here, is made exact by the use of an agent system whose dynamics can
be described with an energy or potential function (increasing total utility) [71], and this is possible be-
cause we assumed symmetric constraints [22, 24]. In more general systems, actions that increase in-
dividual utility will not necessarily increase total utility even locally (i.e., total utility will not provide a
Figure 4. Schematic of mechanisms involved in finding high-utility attractors: (a) “recall,” (b) generalization in unstructured
problems, (c) generalization in modular problem structures. The last is made possible by the fact that the landscape must be
a superposition of many independent components. In high-dimensional structured spaces (unlike the two-dimensional illus-
tration shown here), the original system dynamics may be very unlikely to visit the global optimum, but nonetheless very
likely to visit a set of points that together contain all the components of the global optimum (hence providing the necessary
data for successful generalization).
Artificial Life Volume 17, Number 3
159
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
7
3
1
4
7
1
6
6
2
7
7
9
a
r
t
l
/
_
a
_
0
0
0
2
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
R. A. Watson et al.
Global Adaptation in Networks of Selfish Components
potential function for agent behaviors), and in this case the attractor states that the system spends most
time in (and are thereby enlarged the most by changes to connections) will not necessarily correspond to
local optima in total utility. In particular, the configuration that is globally optimal in total utility may not
be an equilibrium, and in that case it cannot be enlarged by selfish changes to connections. This does
not mean that selfish changes to connections will not produce an increase in global adaptation, however.
That is, in the subset of configurations that are local equilibria, some will have higher total utility than
others. If it is still true that local equilibria with higher total utility tend to have larger basins of attraction,
then those attractors (and generalizations thereof ) will be enlarged at the expense of lower-utility at-
tractors. We conjecture that, in systems built out of the superposition of many low-order interactions,
this must be true on average [11, 38, 37, 39]. But of course, it will not be true in every instance—and in
systems that have only one equilibrium (e.g., as in a single two-player prisonerʼs dilemma), the enlarge-
ment of this attractor will have neither a positive nor a detrimental effect on total utility.
5.3 How Can Selfish Behaviors Be Cooperative?
All the changes in our system, both in the agentsʼ basic behaviors and in their network restructuring
behaviors, are entirely explicable in terms of selfish motives. Finding the joint equilibrium of these
two types of selfish behaviors thus explains the observations in our results [61, 62, 69]. Moreover,
in a deep sense, this must be the case if we seek a mechanistic explanation of the results, avoiding
mystical sources of spontaneous cooperation. So if individual selfishness motivates and explains the
results, in what sense then is it necessary or even meaningful to suggest that the resulting system
is holistically adapted?3 Indeed, the very idea that selfish behaviors can create increased cooperation
seems contradictory. But the idea that selfish changes to relationships can create cooperative behaviors
is not a contradiction. That is, a perspective that maintains a conceptual separation of the ordinary
behaviors and the restructuring behaviors resolves this paradox by viewing the structure of the sys-
tem at any given time as a parameter of the ordinary behaviors. It will necessarily be the case that
the ordinary behaviors given the current structure at any point in time are selfish, but selfish behaviors in
one structure yield higher total utility than selfish behaviors in another structure. Without this con-
ceptual separation between ordinary and restructuring behaviors, questions about how the system
adapts over time have no meaning—we cannot say that the systemʼs behavior is better or worse
than it used to be; it is simply the same system in a new state.4 This separation of population struc-
ture and social behavior [61, 69] is also exploited in related work examining the concurrent evolu-
tion of non-network-based population structuring traits and cooperative traits, both changing under
natural selection [63, 64].
5.4 Related Work
In the social network domain we have also shown [7] that habituating agents, acting as “creatures of
habit” due to a tendency to increase their preference for the status quo, are also formally equivalent to
Hebbian learning at the system level and produce global adaptation in the same manner as that shown
here. This work frames the utility function as a weighted multi-player coordination game [41, 69, 73],
and the system dynamics as repeated episodes of attempting to reach consensus given constraints
among players. This work separates the component of a constraint that can be changed and the
O, respectively) into the “perception” of a game
L and Nij
component that cannot be changed (here, Nij
and the “actual” game (or its true utility). Since agentsʼ behaviors are selected based on their distorted
perceptions, they will sometimes select behaviors that decrease their true utility (which must be the
case if the attractors of the system are to be different). But the different attractors that are consequently
3 We note that the same tension causes detailed group selection models to “explain away” the phenomenon they sought to capture
[61, 89, 91].
4 This can be described as a metadynamical system [4]—that is, a dynamical system of ordinary behaviors, S, with parameters that include
the connection topology—but these parameters are actually slowly changing variables in a larger dynamical system, S′. We then ask
how the dynamics of S′ reorganize the structure of, and hence change the dynamics of, S.
160
Artificial Life Volume 17, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
7
3
1
4
7
1
6
6
2
7
7
9
a
r
t
l
/
_
a
_
0
0
0
2
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
R. A. Watson et al.
Global Adaptation in Networks of Selfish Components
reached have higher total true utility (and accordingly, higher individual utility on average) than the
attractors reached by immediate maximization of true utility. This work also discusses the close re-
lationship between actions that amplify the immediate preference for the status quo averaged over long
timescales (i.e., given a slow-changing preference) and actions that actually maximize the long-term utility
of an individual. This is closely related to a simple form of reinforcement learning where agents play
the strategy that maximizes their utility given the expected strategies adopted by other agents based on
past behavior [40]. But given the separation of timescales (i.e., rapid relaxations and slowly changing
associations) adopted in the self-modeling framework [78], a simple “habituation” of correlations
observed at equilibria (i.e., preferring the status quo) achieves the same outcome as a preferential re-
inforcement of “good” correlations.
In an evolutionary scenario, an individual-based simulation [83, 85] supports the conclusion that
individuals will evolve associations that reinforce locally stable equilibria as shown here. More exactly,
this work shows that associations canalize common components of locally stable equilibria—in other
words, they create groups that reflect the commonly occurring subpatterns of configurations that are
visited, not the entire configuration patterns. Whereas the present work implements a subtle form
of social niche construction [59, 62, 63], altering interaction coefficients that affect the attractors of the
behavioral dynamics [59, 63], this related work shows how similar principles determine how evolving
agents create new vehicles [8] in the sense of strongly correlated codispersal probabilities (cf. “macro
variation” [44, 47]). The grouping of evolved species or symbioses produced can be understood as a
decomposition of the problem variables into subsets that are approximately independent from one
another but strongly interdependent internally. The scalability of an associative optimization process
based on these principles is also shown to be algorithmically superior to nonassociative evolution in
a formal sense [46, 84, 85]. The associative memory principles discussed here may therefore help us
better understand the mechanisms of major evolutionary transitions [42] (developed elsewhere [83, 84]).
Recent results on the evolution of evolvability suggest intriguing parallels between the evolution of
gene expression networks and other complex adaptive systems discussed here. Specifically, Parter et al.
[57] investigated how the evolvability of a population changes over time when it is subjected to a fluc-
tuating environment (we achieve the same conditions using repeated perturbation in a static environ-
ment [82]). They find that organisms develop a “memory” of their evolutionary history and observe that
evolved networks “generalise to future environments, exhibiting high adaptability to novel goals.”
Wagner et al. [76] explain part of the mechanism that might be involved by referring to genetic loci
that affect the correlation of phenotypic traits [58] as follows: “natural selection can act on [variation
in the strength of the pleiotropic effects between genes] to either increase the correlation among traits
or decrease it depending on whether the traits are simultaneously under directional selection or not …
[resulting in] a reinforcement of pleiotropic effects among co-selected traits and suppression of
pleiotropic effects that are not selected together” [76]. This clearly describes a Hebbian modification
of gene interactions. Recent work of our own [82] has unified Wagner and Parterʼs observations with
the findings of the current article to provide a mechanism that explains the increase in evolvability that
Parter et al. observe. The interesting finding of these evolutionary scenarios is that changes to connec-
tions within a network will be Hebbian regardless of whether the unit being evolved is the individual
node in the network or the whole network, thus explaining equally well both global adaptation (e.g., in
an ecosystem) and increased evolvability (e.g., in a gene expression network).
We note that the interplay of rapid behavioral change and simultaneous but slower changes to
connections offers a close analogy with the Baldwin effect [3, 18, 45, 77] that warrants further
investigation. In the Baldwin effect a relatively slow learning mechanism canalizes the results of fast
phenotypic exploration. But by canalizing associations between behaviors, rather than fixing indi-
vidual behaviors, the effects of Hebbian learning on adaptation are made more flexible, creating
what we might term a second-order canalization, that is, a canalization that can bias which combinations
of behaviors occur without precluding any individual behavioral values.
Relaxation of the symmetry conditions (adopted here in the initial connections) and the cyclic or
chaotic attractors that may result should also be investigated. The two extremes of initial structure
studied here (viz., totally random structure and neat modularity) suggest we should also explore the
Artificial Life Volume 17, Number 3
161
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
7
3
1
4
7
1
6
6
2
7
7
9
a
r
t
l
/
_
a
_
0
0
0
2
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
R. A. Watson et al.
Global Adaptation in Networks of Selfish Components
effect of semi-modular or “nearly decomposable” systems [68, 79, 77]. The simplification we have
employed by studying fully connected weighted networks rather than sparsely connected topologies
also warrants further investigation. When connections are all-or-nothing, as they often are in social
network models, a connection creates either correlation or anticorrelation in the states that it con-
nects and cannot represent an average of state correlations observed over time as modeled here.
However, on average an ensemble of all-or-nothing connections may represent past state correlation
in a probabilistic or aggregate sense.
6 Conclusions
We have shown that organizational principles familiar in or association induction organismic learning
occur implicitly in distributed complex adaptive systems. System-level “learning” or association
induction happens as a direct consequence of the fact that selfish modifications to relationships
between components are equivalent to Hebbʼs rule. Such changes are motivated by purely local
and immediate benefits, but have the side effect of enlarging the basin of attraction for behavior
combinations in future state dynamics. Thus networks of selfish agents self-organize the connection
structure of a network in a manner that creates an associative memory of state configurations that
the system experiences.
Given this, when the state of the system is sufficiently perturbed and the changes to connections are
sufficiently slow, agents will modify connections in a manner that enhances total utility. More exactly,
agents find connections that coordinate their behaviors with other agentsʼ more effectively, so that the
system as a whole finds better solutions to the original constraints between agents (even though these
constraints cannot be altered). The improved global efficiency that results can be understood via the
inherent ability of associative learning to generalize by idealizing stored patterns and/or creating new
combinations of learned subpatterns. These findings suggest that distributed complex adaptive systems
of self-interested components, such as individuals in a social network or species in an ecosystem, may
exhibit organizational principles in common with those familiar in organismic learning, developing an
associative memory of their past behavior that enhances system-level efficiency in future. In the case of
species in an ecosystem, although each species may adapt its relationships with other species via natural
selection, the global adaptation of the network does not require that the ecosystem as a whole be
reproduced with inheritance, variation, and selection. This work thereby demonstrates a completely
distributed adaptive process that we view as a natural extension to the “emergent collective computa-
tional abilities” that come “for free” in physical systems [22].
Acknowledgments
We thank Simon Powers, Alex Penn, Adam Davies, Chrisantha Fernando, Jason Noble, Seth Bullock,
Hod Lipson, Archie Chapman, and Nic Palmius for helpful discussion.
References
1. Ackley, D. H., Hinton, G. E., & Sejnowski, T. J. (1985). A learning algorithm for Boltzmann machines.
Cognitive Science, 9, 147–169.
2. Aktipis, C. A. (2004). Know when to walk away: Contingent movement and the evolution of cooperation.
Journal of Theoretical Biology, 231(2), 249–260.
3. Baldwin, J. M. (1896). A new factor in evolution. American Naturalist, 30, 441–451.
4. Bourgine, P., & Varela, F. J. (1992). Toward a practice of autonomous systems. In F. J. Varela & P. Bourgine
(Eds.), Toward a Practice of Autonomous Systems: Proceedings of the First European Conference on Artificial Life
(pp. xi–xvii). Cambridge, MA: MIT Press.
5. Boyd, R., & Richerson, P. J. (1990). Group selection among alternative evolutionarily stable strategies.
Journal of Theoretical Biology, 145, 331–342.
6. Branchtein, M. C., & Arenzon, J. J. (1992). Categorization and generalization in the Hopfield model.
Journal de Physique (Paris) I, 2(11), 2019–2024.
162
Artificial Life Volume 17, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
7
3
1
4
7
1
6
6
2
7
7
9
a
r
t
l
/
_
a
_
0
0
0
2
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
R. A. Watson et al.
Global Adaptation in Networks of Selfish Components
7. Davies, A. P., Watson, R. A., Mills, R., Buckley, C. L., & Noble, J. (2011). “If you canʼt be with the one
you love, love the one youʼre with”: How individual habituation of agent interactions improves global
utility. Artificial Life, 17(3), 167–181.
8. Dawkins, R. (1976). The selfish gene. Oxford, UK: Oxford University Press.
9. Fernando, C., & Szathmary, S. (2010). Natural selection in the brain. In B. Glatzeder, V. Goel, &
A. von Müller (Eds.), Towards a theory of thinking Vol. 2 (Chap. 20, pp. 292–322). Berlin: Springer-Verlag.
10. Fernando, C., Liekens, A. M. L., Bingle, L. E. H., Beck, C., Lenser, T., Stekel, D. J., & Rowe, J. E.
(2008). Molecular circuits for associative learning in single-celled organisms. Journal of the Royal Society
Interface, 6(34), 463–469.
11. Gascuel, J.-D., Moobed, B., & Weinfeld, M. (1994). An internal mechanism for detecting parasite attractors
in a Hopfield network. Neural Computation, 6, 902–915.
12. Gross, T., & Sayama, H. (Eds.). (2009). Adaptive networks: Theory, models and applications. Berlin:
Springer-Verlag.
13. Haldane, J. B. S. (1927). A mathematical theory of natural and artificial selection. V. Selection and
mutation. Proceedings of the Cambridge Philosophical Society, 23, 838–844.
14. Harsany, J. C., & Selten, R. (1988). A general theory of equilibrium selection in games. Cambridge, MA: MIT Press.
15. Hauert, C., De Monte, S., Hofbauer, J., & Sigmund, K. (2002). Volunteering as Red Queen mechanism
for cooperators in public goods games. Science, 296, 1129–1132.
16. Hebb, D. O. (1949). The organization of behavior. New York: Wiley.
17. Heylighen, F., Gershenson, C., Staab, S., Flake, G. W., Pennock, D. M., Fain, D. C., De Roure, D.,
Aberer, K., Shen, W.-M., Dousse, O., & Thiran, P. (2003). Neurons, viscose fluids, freshwater polyp
hydra—And self-organizing information systems. Intelligent Systems, 18(4), 72–86.
18. Hinton, G. E., & Nowlan, S. J. (1987). How learning can guide evolution. Complex Systems, 1, 495–502.
19. Hinton, G. E., & Sejnowski, T. J. (1985). Learning in Boltzmann machines. Cognitiva (Paris), 85,
599–604.
20. Hogeweg, P. (2007). From population dynamics to ecoinformatics: Ecosystems as multilevel information
processing systems. Ecological Informatics, 2, 103–111.
21. Holland, J. H. (1975). Adaptation in natural and artificial systems. Ann Arbor: University of Michigan Press.
22. Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective computational
abilities. Proceedings of the National Academy of Sciences of the USA, 79(8), 2554–2558.
23. Hopfield, J. J., & Tank, D. W. (1985). “Neural” computation of decisions in optimization problems.
Biological Cybernetics, 52, 141–152.
24. Hopfield, J. J., & Tank, D. W. (1986). Computing with neural circuits: A model. Science, 233, 625–633.
25. Hopfield, J. J., Feinstein, D., & Palmer, R. (1983). “Unlearning” has a stabilizing effect in collective
memories. Nature, 304, 158–159.
26. Iclanzan, D., & Dumitrescu, D. (2007). Overcoming hierarchical difficulty by hill-climbing the
building block structure. In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO 2007)
(pp. 1256–1263).
27. Iclanzan, D., & Dumitrescu, D. (2008). How can artificial neural networks help making the intractable
search spaces tractable. In IEEE Congress on Evolutionary Computation (CEC 2008) (pp. 4015–4022).
28. Istrail, S. (2000). Statistical mechanics, three-dimensionality and NP-completeness: I. Universality of
intractability of the partition functions of the Ising model across non-planar lattices. In Proceedings of the
32nd ACM Symposium on the Theory of Computing (STOC00) (pp. 87–96).
29. Jackson, M. O., & Watts, A. (2002). On the formation of interaction networks in social coordination
games. Games and Economic Behavior, 41(2), 265–291.
30. Jackson, M. O., & Watts, A. (2002). The evolution of social and economic networks. Journal of Economic
Theory, 106(2), 265–295.
31. Jackson, M. O., & Wolinsky, A. (1996). A strategic model of social and economic networks. Journal of
Economic Theory, 71, 44–74.
Artificial Life Volume 17, Number 3
163
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
7
3
1
4
7
1
6
6
2
7
7
9
a
r
t
l
/
_
a
_
0
0
0
2
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
R. A. Watson et al.
Global Adaptation in Networks of Selfish Components
32. Jang, J.-S., Kim, M. W., & Lee, Y. (1992). A conceptual interpretation of spurious memories in the Hopfield-
type neural network. In International Joint Conference on Neural Networks, 1992 (IJCNN) Vol. 1 (pp. 21–26).
33. Kauffman, S. (1993). The origins of order: Self-organization and selection in evolution. Oxford, UK: Oxford
University Press.
34. Keeling, M. J. (2005). The implications of network structure for epidemic dynamics. Theoretical Population
Biology, 67, 1–8.
35. Kirkpatrick, S., Gelatt, C. D., & Vecchi M. P. (1983). Optimization by simulated annealing. Science,
New Series, 220(4598), 671–680.
36. Krebs, P. R., & Theumann, W. K. (1993). Generalization in a Hopfield network with noise. Journal of
Physics A: Mathematical and General, 26, 3983.
37. Kryzhanovsky, B., Magomedov, B. M., & Fonarev, A. B. (2006). On the probability of finding local
minima in optimization problems. In IJCNN 2006 (pp. 3243–3248).
38. Kryzhanovsky, B., & Kryzhanovsky, V. (2008). Binary optimization: On the probability of a local
minimum detection in random search. In ICAISC 2008 (pp. 89–100).
39. Kryzhanovsky, B., Kryzhanovsky, V., & Mikaelian, A. L. (2007). Binary optimization: A relation between
the depth of a local minimum and the probability of its detection. In ICINCO-ICSO 2007 (pp. 5–10).
40. Leslie, D. S., & Collins, E. J. (2006). Generalised weakened fictitious play. Games and Economic Behavior,
56(2), 285–298.
41. Maynard Smith, J. (1982). Evolution and the theory of games. Cambridge, UK: Cambridge University Press.
42. Maynard Smith, J., & Szathmary, E. (1995). The major transitions in evolution. Oxford, UK: Oxford
University Press.
43. Mikhailova, A. S., Mitʼkov, I. V., & Sveshnikov, N. A. (1990). Molecular associative memory. Biosystems,
23(4), 291–295.
44. Mills, R. (2010). How micro-evolution can guide macro-evolution: Multi-scale search via evolved modular variation.
Doctoral dissertation, University of Southampton, Southampton, UK.
45. Mills, R., & Watson, R. A. (2006). On crossing fitness valleys with the Baldwin effect. In Proceedings of
the Tenth International Conference on the Simulation and Synthesis of Living Systems (pp. 493–499).
46. Mills, R., & Watson, R. A. (2009). Symbiosis enables the evolution of rare complexes in structured
environments. In G. Kampis, I. Karsai, & E. Szathmary (Eds.), Proceedings of European Conference on
Artificial Life 2009, Part II (pp. 106–113).
47. Mills, R., & Watson, R. A. (in prep.). Multi-scale search, modular variation, and adaptive neighbourhoods.
48. Muehlenbein, H. (1992). How genetic algorithms really work: Mutation and hill climbing. In Proceedings
of Parallel Problem Solving from Nature 2 (pp. 15–26).
49. Nash, J. (1951). Non-cooperative games. The Annals of Mathematics, 54(2), 286–295.
50. Newman, M. E. J. (2002). Spread of epidemic disease on networks. Physical Review E, 66, 016128.
51. Newman, M. E. J. (2003). The structure and function of complex networks. SIAM Review, 45(2), 167–256.
52. Newman, M. E. J., Barabasi, A. L., & Watts, D. J. (Eds.). (2006). The structure and dynamics of networks.
Princeton, NJ: Princeton University Press.
53. Noonburg, V. W. (1989). A neural network modeled by an adaptive Lotka-Volterra system. SIAM Journal
on Applied Mathematics, 49(6), 1779–1792.
54. Odling-Smee, F. J., Laland, K. N., & Feldman, M. W. (2003). Niche construction. The neglected process in
evolution. Monographs in Population Biology, 37. Princeton, NJ: Princeton University Press.
55. Pacheco, J. M., Lenaerts, T., & Santos, F. C. (2007). Evolution of cooperation in a population of
selfish adaptive agents. In Advances in Artificial Life 2007 (pp. 535–544). Berlin: Springer.
56. Pacheco, J. M., Traulsen, A., & Nowak, M. A. (2006). Coevolution of strategy and structure in
complex networks with dynamical linking. Physical Review Letters, 97, 258103.
57. Parter, M., Kashtan, N., & Alon, U. (2008). Facilitated variation: How evolution learns from past
environments to generalize to new environments. PLoS Computational Biology, 4(11), e1000206.
164
Artificial Life Volume 17, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
7
3
1
4
7
1
6
6
2
7
7
9
a
r
t
l
/
_
a
_
0
0
0
2
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
R. A. Watson et al.
Global Adaptation in Networks of Selfish Components
58. Pavlicev, M., Kenney-Hunt, J. P., Norgard, E. A., Roseman, C. C., Wolf, J. B., & Cheverud, J. M.
(2008). Genetic variation in pleiotropy: Differential epistasis as a source of variation in the allometric
relationship between long bone lengths and body weight. Evolution, 62(1), 199–213.
59. Penn, A. S. (2006). Ecosystem selection: Simulation, experiment and theory. Doctoral dissertation, University
of Sussex, Falmer, UK.
60. Poderoso, F. C., & Fontanari, J. F. (2007). Model ecosystem with variable interspecies interactions.
Journal of Physics A: Mathematical and Theoretical, 40, 8723–8738.
61. Powers, S. T. (2010). Social niche construction: Evolutionary explanations for cooperative group formation. Doctoral
dissertation, ECS Southampton University, Southampton.
62. Powers, S. T., Mills, R., Penn, A. S., & Watson, R. A. (2009). Social niche construction provides an
adaptive explanation for new levels of individuality (Abstract). In Proceedings of Workshop on Levels of
Selection and Individuality in Evolution. European Conference on Artificial Life.
63. Powers, S. T., Penn, A. S., & Watson, R. A. (2007). Individual selection for cooperative group formation.
In Proceedings of European Conference on Artificial Life 2007 (pp. 585–594).
64. Powers, S. T., Penn, A. S., & Watson, R. A. (in press). The concurrent evolution of social traits and
the population structures that support them. Evolution.
65. Roughgarden, J. (1979). Theory of population genetics and evolutionary ecology: An introduction. New York:
Macmillan Publishing Company.
66. Rumelhart, D. E., & McClelland, J. M. (1986). Parallel distributed processing—Explorations in the microstructure
of cognition. Volume 1: Foundations. Cambridge, MA: MIT Press.
67. Sachtjen, M. L., Carreras, B. A., & Lynch, V. E. (2000). Disturbances in a power transmission system.
Physical Review E, 61, 4877.
68. Simon, H. A. (1969). The sciences of the artificial. Cambridge, MA: MIT Press.
69. Skyrms, B. (2004). The stag hunt and evolution of social structure. Cambridge, UK: Cambridge University Press.
70. Solé, R. V., Alonso, D., & McKane, A. (2000). Scaling in a network model of a multispecies ecosystem.
Physica A, 286, 337–344.
71. Strogatz, S. H. (1994). Nonlinear dynamics and chaos. Reading, MA: Addison-Wesley.
72. Taylor, C., & Nowak, M. A. (2007). Transforming the dilemma. Evolution, 61(10), 2281–2292.
73. Tomassini, M., & Pestelacci, E. (2010). Coordination games on dynamical networks. Games, 1(3), 242–261.
74. Traulsen, A., Santos, F. C., & Pacheco, J. M. (2008). Evolutionary games in self-organizing populations.
In T. Gross & H. Sayama (Eds.), Adaptive networks: Theory, models and applications. New York: Springer.
75. Van Segbroeck, S., Santos, F. C., Pacheco, J. M., & Lenaerts, T. (2010). Coevolution of cooperation,
response to adverse social ties and network structure. Games, 1(3), 317–337.
76. Wagner, G. P., Pavlicev, M., & Cheverud, J. M. (2007). The road to modularity. Nature Reviews Genetics, 8, 921–931.
77. Watson, R. A. (2006). Compositional evolution: The impact of sex, symbiosis and modularity on the gradualist
framework of evolution. Cambridge, MA: MIT Press.
78. Watson, R. A., Buckley, C. L., & Mills, R. (2011). Optimization in “self-modeling” complex adaptive
systems. Complexity, http://onlinelibrary.wiley.com/doi/10.1002/cplx.20346/pdf.
79. Watson, R. A., & Pollack, J. B. (2005). Modular interdependency in complex dynamical systems. Artificial
Life, 11(4), 445–457.
80. Watson, R. A., & Jansen, T. (2007). A building-block royal road where crossover is provably essential.
In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO 2007) (pp. 1452–1459).
81. Watson, R. A., Buckley, C. L., & Mills, R. (2009). The effect of Hebbian learning on optimisation in Hopfield
networks (Technical report). Southampton, UK: ECS University of Southampton.
82. Watson, R. A., Buckley, C. L., Mills, R., & Davies, A. (2010). Associative memory in gene regulation
networks. In Proceedings of Artificial Life 2010 (pp. 194–202).
83. Watson, R. A., Jackson, A., Palmius, N., Mills, R., Powers, S. T., & Penn, A. S. (in prep.). The origin of
group selection via individual selection.
Artificial Life Volume 17, Number 3
165
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
7
3
1
4
7
1
6
6
2
7
7
9
a
r
t
l
/
_
a
_
0
0
0
2
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
R. A. Watson et al.
Global Adaptation in Networks of Selfish Components
84. Watson, R. A., Mills, R., & Buckley, C. L. (in press). Transformations in the scale of behaviour
and the global optimisation of constraints in adaptive networks. Adaptive Behaviour.
85. Watson, R. A., Palmius, N., Mills, R., Powers, S. T., & Penn, A. S. (2009). Can selfish symbioses effect
higher-level selection? In G. Kampis, I. Karsai, & E. Szathmary (Eds.), European Conference on Artificial
Life 2009, Part II (pp. 26–33).
86. Watts, D. J., & Dodds, P. S. (2007). Influentials, networks, and public opinion formation. Journal of Consumer
Research, 34, 441.
87. Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of small-world networks. Nature, 393, 440–442.
88. Werfel, J., & Bar-Yam, Y. (2004). The evolution of reproductive restraint through social communication.
Proceedings of the National Academy of Sciences of the USA, 101(30), 11019–11024.
89. Wild, G., Gardner, A., & West, S. A. (2009). Adaptation and the evolution of parasite virulence in a
connected world. Nature, 459, 983–986.
90. Wilmers, C. C. (2007). Understanding ecosystem robustness. Trends in Ecology & Evolution, 22(10), 504–506.
91. Wilson, D. S., & Wilson, E. O. (2007). Rethinking the theoretical foundation of socio-biology. The
Quarterly Review of Biology, 82(4), 327–348.
92. Wilson, D. S. (1980). The natural selection of populations and communities. San Francisco: Benjamin/Cummings.
93. Yu, T.-L., Goldberg, D. E., Yassine, A., & Chen, Y.-P. (2003). Genetic algorithm design inspired by
organizational theory: Pilot study of a dependency structure matrix driven genetic algorithm. In Proceedings
of Artificial Neural Networks in Engineering 2003 (ANNIE 2003) (pp. 327–332).
Appendix
Syntactically, the result that selfish changes to connections are Hebbian is sensitive to the form of the
original utility function we assumed5 (Equation 1). For example, if instead we had assumed maximiza-
tion of Equation 4
ui ¼ −
XN
j
Nij si sj ;
ð4Þ
then selfish changes to connections would (syntactically) be anti-Hebbian (i.e., y < 0), not Hebbian.
However, this is merely a labeling error with respect to the semantics of a connection. Specifically,
Hebbʼs rule assumes that positive weights increase the correlation between connected states, rather than
decrease it (i.e., an excitatory connection causes the activation of one neuron to excite another, not
depress it). Under Equation 4 a connectionʼs sign has the opposite meaning, and likewise the syntax
of Hebbʼs rule must be reversed in order to maintain the intended effect of Hebbian learning. Speci-
fically, the general rule is that Hebbian learning must increase the basin of attraction for the current
configuration—otherwise it would not create a memory for the current configuration in the systemʼs
dynamics. Under Equation 4, Hebbian learning must be reversed to achieve this (i.e., y < 0). The syntactic
definition of Hebbian learning is therefore unfortunately misleading in this respect. But the important
observation for our purposes is that selfish changes to connections will always increase the utility of the
current state configuration (by definition of a selfish change), and will therefore increase the basin of
attraction for this configuration, regardless of the form of utility function used. This is the dynamic con-
sequence that matters for the intended semantics of Hebbian learning. That is, by definition, a selfish
change to a connection amplifies the benefit of the current states—and this will always increase the
likelihood that this configuration of behaviors will be visited again. Intuitively, this just means that selfish
changes to connections “exploit” the current configuration of behaviors by amplifying their benefit,
rather than “exploring” or inducing new and different state configurations.
5 We thank Hywell Williams for this observation.
166
Artificial Life Volume 17, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
7
3
1
4
7
1
6
6
2
7
7
9
a
r
t
l
/
_
a
_
0
0
0
2
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3