GILE: A Generalized Input-Label Embedding for Text Classification
Nikolaos Pappas
James Henderson
Idiap Research Institute, Martigny 1920, Switzerland
{nikolaos.pappas,james.henderson@idiap.ch}
Abstract
Neural
text classification models typically
treat output labels as categorical variables that
lack description and semantics. This forces
their parametrization to be dependent on the
label set size, and, hence, they are unable
to scale to large label sets and generalize to
unseen ones. Existing joint input-label text
models overcome these issues by exploiting
label descriptions, but
they are unable to
capture complex label relationships, have rigid
parametrization, and their gains on unseen
labels happen often at the expense of weak
performance on the labels seen during training.
In this paper, we propose a new input-label
model
that generalizes over previous such
models, addresses their limitations, and does
not compromise performance on seen labels.
The model consists of a joint nonlinear input-
label embedding with controllable capacity
and a joint-space-dependent classification unit
that is trained with cross-entropy loss to opti-
mize classification performance. We evaluate
models on full-resource and low- or zero-
resource text classification of multilingual
news and biomedical text with a large label
set. Our model outperforms monolingual and
multilingual models that do not leverage label
semantics and previous joint input-label space
models in both scenarios.
1
Introduction
Text classification is a fundamental NLP task
with numerous real-world applications such as
topic recognition (Tang et al., 2015; Yang et al.,
2016), sentiment analysis (Pang and Lee, 2005;
Yang et al., 2016), and question answering (Chen
et al., 2015; Kumar et al., 2015). Classification
139
also appears as a sub-task for sequence prediction
tasks such as neural machine translation (Cho
et al., 2014; Luong et al., 2015) and summarization
(Rush et al., 2015). Despite numerous studies,
existing models are trained on a fixed label set
using k-hot vectors, and therefore treat target
labels as mere atomic symbols without any
particular structure to the space of labels, ignoring
potential linguistic knowledge about the words
used to describe the output labels. Given that
semantic representations of words have been
shown to be useful for representing the input,
it is reasonable to expect that they are going to be
useful for representing the labels as well.
Previous work has leveraged knowledge from
the label texts through a joint input-label space,
initially for image classification (Weston et al.,
2011; Mensink et al., 2012; Frome et al., 2013;
Socher et al., 2013). Such models generalize to
labels both seen and unseen during training, and
scale well on very large label sets. However,
as we explain in Section 2, existing input-label
models for text (Yazdani and Henderson, 2015;
Nam et al., 2016) have the following limitations:
(i) their embedding does not capture complex
label relationships due to its bilinear form, (ii)
their output layer parametrization is rigid because
it depends on the dimensionality of the encoded
text and labels, and (iii) they are outperformed on
seen labels by classification baselines trained with
cross-entropy loss (Frome et al., 2013; Socher
et al., 2013).
In this paper, we propose a new joint input-
label model that generalizes over previous such
models, addresses their limitations, and does
not compromise performance on seen labels
(see Figure 1). The proposed model is composed
input-label embedding
of a joint nonlinear
with controllable capacity and a joint-space-
dependent classification unit which is trained
Transactions of the Association for Computational Linguistics, vol. 7, pp. 139–155, 2019. Action Editor: Eneko Agirre.
Submission batch: 9/2018; Revision batch: 1/2019; Published 4/2019.
c(cid:13) 2019 Association for Computational Linguistics. Distributed under a CC-BY 4.0 license.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
9
1
9
2
3
3
6
8
/
/
t
l
a
c
_
a
_
0
0
2
5
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
with cross-entropy loss to optimize classification
performance.1 The need for capturing complex
label relationships is addressed by two nonlinear
transformations that have the same target joint
space dimensionality. The parametrization of the
output layer is not constrained by the dimen-
sionality of the input or label encoding, but is
instead flexible with a capacity that can be easily
controlled by choosing the dimensionality of the
joint space. Training is performed with cross-
entropy loss, which is a suitable surrogate loss for
classification problems, as opposed to a ranking
loss such as WARP loss (Weston et al., 2010),
which is more suitable for ranking problems.
Evaluation is performed on full-resource and
low- or zero-resource scenarios of two text clas-
sification tasks, namely, on biomedical semantic
indexing (Nam et al., 2016) and on multilingual
news classification (Pappas and Popescu-Belis,
2017), against several competitive baselines. In
both scenarios, we provide a comprehensive abla-
tion analysis that highlights the importance of
each model component and the difference with
previous embedding formulations when using the
same type of architecture and loss function.
Our main contributions are the following:
(i) We identify key theoretical and practical lim-
itations of existing joint input-label models.
(ii) We propose a novel joint input-label embed-
ding with flexible parametrization that gen-
eralizes over the previous such models and
addresses their limitations.
(iii) We provide empirical evidence of the supe-
riority of our model over monolingual and
multilingual models that
ignore label se-
mantics, and over previous joint input-label
models on both seen and unseen labels.
The remainder of this paper is organized as
follows. Section 2 provides background knowl-
edge and explains limitations of existing models.
Section 3 describes the model components, train-
ing, and relation to previous formulations. Sec-
tion 4 describes our evaluation results and
analysis, while Section 5 provides an overview
of previous work and Section 6 concludes the
paper and provides future research directions.
1Our code is available at: github.com/idiap/gile.
2 Background: Neural Text
Classification
We are given a collection D = {(xi, yi), i =
1, . . . , N } made of N documents, where each
is associated with labels yi =
document xi
{yij ∈ {0, 1} | j = 1, . . . , k}, and k is the
total number of labels. Each document xi =
{w11, w12, . . . , wKiTKi
} is a sequence of words
grouped into sentences, with Ki being the number
of sentences in document i and Tj being the
number of words in sentence j. Each label j has
a textual description composed of multiple words,
cj = {cj1, cj2, . . . , cjLj | j = 1, . . . , k} with Lj
being the number of words in each description.
Given the input texts and their associated labels
seen during the training portion of D, our goal
is to learn a text classifier that is able to predict
labels both in the seen, Ys, or unseen, Yu, label
sets, defined as the sets of unique labels that have
been seen or not during training, respectively, and,
hence, Y ∩ Yu = ∅ and Y = Ys ∪ Yu.2
2.1
Input Text Representation
To encode the input text, we focus on hierar-
chical attention networks (HANs), which are
competitive for monolingual (Yang et al., 2016)
and multilingual text classification (Pappas and
Popescu-Belis, 2017). The model takes as input
a document x and outputs a document vector h.
The input words and label words are represented
by vectors in IRd from the same3 embeddings
E ∈ IR|V|×d, where V is the vocabulary and d is
the embedding dimension; E can be pre-trained
or learned jointly with the rest of the model. The
model has two levels of abstraction, word and
sentence. The word level is made of an encoder
network gw and an attention network aw, while
the sentence level similarly includes an encoder
and an attention network.
Encoders. The function gw encodes the se-
quence of input words {wit | t = 1, . . . , Ti} for
each sentence i of the document, noted as:
h(it)
w = gw(wit), t ∈ [1, Ti]
(1)
2Note that depending on the number of labels per docu-
ment the problem can be a multi-label or multi-class problem.
3This statement holds true for multilingual classifica-
tion problems, too, if the embeddings are aligned across
languages.
140
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
9
1
9
2
3
3
6
8
/
/
t
l
a
c
_
a
_
0
0
2
5
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
and at the sentence level, after combining the
intermediate word vectors {h(it)
w | t = 1, . . . , Ti}
to a sentence vector si ∈ IRdw (see below), where
dw is the dimension of the word encoder, the
function gs encodes the sequence of sentence
vectors {si | i = 1, . . . , K}, noted as h(i)
s . The gw
and gs functions can be any feed-forward (DENSE)
or recurrent networks, for example, GRU (Cho
et al., 2014).
Attention. The αw and αs attention mechanisms,
which estimate the importance of each hidden
state vector, are used to obtain the sentence si
and document representation h, respectively. The
sentence vector is thus calculated as follows:
si =
Ti(cid:88)
t=1
w h(it)
α(it)
w =
Ti(cid:88)
t=1
ituw)
exp(v(cid:62)
j exp(v(cid:62)
ijuw)
(cid:80)
h(it)
w
(2)
where vit = fw(h(it)
w ) is a fully connected net-
work with Ww parameters. The document vector
h ∈ IRdh, where dh is the dimension of the sen-
tence encoder, is calculated similarly, by replacing
uit with vi = fs(h(i)
s ) which is a fully connected
network with Ws parameters, and uw with us,
which are parameters of the attention functions.
2.2 Label Text Representation
To encode the label
text we use an encoder
function that takes as input a label description
cj and outputs a label vector ej ∈ IRdc ∀j =
1, . . . , k. For efficiency reasons, we use a simple,
parameter-free function to compute ej, namely,
the average of word vectors which describe label
j, namely, ej = 1
t=1 cjt, and hence dc = d
Lj
in this case. By stacking all these label vectors
into a matrix, we obtain the label embedding
E ∈ IR|Y|×d. In principle, we could also use the
same encoder functions as the ones for input
text, but
this would increase the computation
significantly; hence, we keep this direction as
future work.
(cid:80)Lj
2.3 Output Layer Parametrizations
2.3.1 Typical Linear Unit
The most typical output layer consists of a linear
unit with a weight matrix W ∈ IRdh×|Y| and a
bias vector b ∈ IR|Y| followed by a softmax or
sigmoid activation function. Given the encoder’s
hidden representation h with dimension size dh,
141
the probability distribution of output y given input
x is proportional to the following quantity:
p(y|x) ∝ exp(W (cid:62)h + b)
(3)
The parameters in W can be learned separately or
be tied with the parameters of the embedding E
by setting W = ET if the input dimension of W is
restricted to be the same as that of the embedding
E (d = dh) and each label is represented by a
single word description (i.e., when Y corresponds
to V and E = E). In the latter case, Equation (3)
becomes:
p(y|x) ∝ exp(Eh + b)
(4)
Either way, the parameters of such models are
typically learned with cross-entropy loss, which
is suitable for classification problems. However,
in both cases they cannot be applied to labels that
are not seen during training, because each label
has learned parameters which are specific to that
label, so the parameters for unseen labels cannot
be learned. We now turn our focus to a class of
models that can handle unseen labels.
2.3.2 Bilinear Input-Label Unit
Joint input–output embedding models can gen-
eralize from seen to unseen labels because the
parameters of the label encoder are shared. The
previously proposed joint input–output embed-
ding models by Yazdani and Henderson (2015)
and Nam et al. (2016) are based on the following
bilinear ranking function f (·):
f (x, y) = EWh
(5)
where E ∈ IR|Y|×d is the label embedding and
W ∈ IRd×dh
is the bilinear embedding. This
function allows one to define the rank of a given
label y with respect to x and is trained using hinge
loss to rank positive labels higher than negative
ones. But note that the use of this ranking loss
means that they do not model the conditional
probability, as do the traditional models above.
Limitations. Firstly, Equation (5) can only cap-
ture linear relationships between encoded text
(h) and label embedding (E) through W. We
argue that
the relationships between different
labels are nonlinear because of the complex
interactions of the semantic relations across labels
but also between labels and different encoded
inputs. A more appropriate form for this purpose
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
9
1
9
2
3
3
6
8
/
/
t
l
a
c
_
a
_
0
0
2
5
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
would include a nonlinear transformation σ(·), for
example, with either:
(a) σ(EW)
(cid:124) (cid:123)(cid:122) (cid:125)
Label structure
h or
(b) E σ(Wh)
(cid:124) (cid:123)(cid:122) (cid:125)
Input structure
(6)
Secondly, it is hard to control their output layer
capacity because of their bilinear form, which
uses a matrix of parameters (W) whose size is
bounded by the dimensionalities of the label
embedding and the text encoding. Thirdly, their
loss function optimizes ranking instead of clas-
sification performance and thus treats the ground-
truth as a ranked list when in reality it consists of
one or more independent labels.
Summary. We hypothesize that these are the
reasons why these models do not yet perform well
on seen labels compared to models that make use
of the typical linear unit, and they do not take full
advantage of the structure of the problem when
tested on unseen labels. Ideally, we would like to
have a model that will address these issues and
will combine the benefits from both the typical
linear unit and the joint input-label models.
3 The Proposed Output Layer
Parametrization for Text
Classification
We propose a new output layer parametrization
for neural text classification which is composed of
a generalized input-label embedding that captures
the structure of the labels, the structure of the
encoded texts and the interactions between the
two, followed by a classification unit which is
independent of the label set size. The resulting
model has the following properties: (i) it is able
to capture complex output structure, (ii) it has a
flexible parametrization that allows its capacity
to be controlled, and (iii) it is trained with a
classification surrogate loss such as cross-entropy.
The model is depicted in Figure 1. In this section,
we describe the model in detail, showing how it
can be trained efficiently for arbitrarily large label
sets and how it is related to previous models.
Figure 1: Each encoded text and label are projected
to a joint input-label multiplicative space, the output
of which is processed by a classification unit with
label-set-size independent parametrization.
row vector from the label embedding matrix E,
which have the following form:
e(cid:48)
j = gout(ej) = σ(ejU + bu)
h(cid:48) = gin(h) = σ(V h + bv)
(7)
(8)
where σ(·) is a nonlinear activation function such
as ReLU or Tanh, the matrix U ∈ IRd×dj and bias
bu ∈ IRdj are the linear projection of the labels,
and the matrix V ∈ IRdj×dh and bias bv ∈ IRdj are
the linear projection of the encoded input. Note
j could be
that
high-rank or low-rank depending on their initial
dimensions and the target joint space dimension.
Also let E (cid:48) ∈ IR|Y|×dj be the matrix resulting from
projecting all the outputs ej to the joint space, that
is, gout(E).
the projections for h(cid:48) and e(cid:48)
The conditional output probability distribution
can now be rewritten as:
p(y|x) ∝ exp(cid:0)E (cid:48)h(cid:48)(cid:1)
∝ exp(cid:0)gout(E)gin(h)(cid:1)
∝ exp(cid:0) σ(EU + bu)
(cid:124)
(cid:125)
(cid:123)(cid:122)
Label Structure
σ(V h + bv)
(cid:124)
(cid:125)
(cid:123)(cid:122)
Input Structure
(cid:1)
(9)
this function has no label-set-size
Crucially,
dependent parameters, unlike W and b in Equa-
tion (3). In principle, this parametrization can be
used for both multi-class and multi-label problems
by defining the exponential in terms of a softmax
and sigmoid functions, respectively. However, in
this paper we will focus on the latter.
3.2 Classification Unit
3.1 A Generalized Input-Label Embedding
Let gin(h) and gout(ej) be two nonlinear projec-
tions of the encoded input, namely, the document
h, and any encoded label ej, where ej is the jth
We require that our classification unit parameters
depend only on the joint input-label space above.
To represent the compatibility between any en-
coded input text hi and any encoded label ej
for this task, we define their joint representation
142
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
9
1
9
2
3
3
6
8
/
/
t
l
a
c
_
a
_
0
0
2
5
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
h’ e2UV∧h’ e1Classification unitwy1∧y2…Joint spaceh’ ekyk∧…LabelEncodercj1cj2cjLj…eiInputEncoderw11w12wKiTKi…h Encodersdh x djd x dj Word embeddings”’T
based on multiplicative interactions in the joint
space:
g(ij)
joint = gin(hi) (cid:12) gout(ej)
(10)
where (cid:12) is component-wise multiplication.
The probability for hi to belong to one of the
k known labels is modeled by a linear unit that
maps any point in the joint space into a score
which indicates the validity of the combination:
val = g(ij)
p(ij)
jointw + b
(11)
where w ∈ IRdj and b are a scalar variables. We
compute the output of this linear unit for each
known label which we would like to predict for a
given document i, namely:
P (i)
val =
p(i1)
val
p(i2)
val
. . .
p(ik)
val
=
g(i1)
jointw + b
g(i2)
jointw + b
. . .
g(ik)
jointw + b
3.3 Training Objectives
The training objective for the multi-label classifi-
cation task is based on binary cross-entropy loss.
Assuming θ contains all the parameters of the
model, the training loss is computed as follows:
L(θ) = −
1
N k
N
(cid:88)
k
(cid:88)
i=1
j=1
H(yij, ˆyij)
(15)
where H is the binary cross-entropy between the
gold label yij and predicted label ˆyij for a docu-
ment i and a candidate label j.
We handle multiple languages according to
Firat et al. (2016) and Pappas and Popescu-Belis
(2017). Assuming that Θ = {θ1, θ2, …, θM } are
all the parameters required for each of the M
languages, we use a joint multilingual objective
based on the sum of cross-entropy losses:
(12)
L(Θ) = −
1
Z
Ne(cid:88)
M
(cid:88)
k
(cid:88)
i
l
j=1
H(y(l)
ij , ˆy(l)
ij )
(16)
For each row, the higher the value the more likely
the label is to be assigned to the document. To
obtain valid probability estimates and be able to
train with binary cross-entropy loss for multi-
label classification, we apply a sigmoid function
as follows:
ˆyi = ˆp(yi|xi) =
1
1 + e−P (i)
val
(13)
Summary. By adding the above changes to
the general form of Equation (9) the conditional
probability p(yi|xi) is now proportional to the
following quantity:
exp(cid:0)σ(EU + bu)(σ(V h + bv) (cid:12) w) + b(cid:1) (14)
Note that the number of parameters in this equation
is independent of the size of the label set, given
that U , V , w, and b depend only on dj, and k can
vary arbitrarily. This allows the model to scale up
to large label sets and generalize to unseen labels.
Lastly, the proposed output layer addresses all the
limitations of the previous models, as follows:
(i) it is able to capture complex structure in the
joint input–output space, (ii) it provides a means
to easily control its capacity dj, and (iii) it is
trainable with cross-entropy loss.
where Z = NeM k with Ne being the number
of examples per epoch. At each iteration, a
document-label pair for each language is sampled.
In addition, multilingual models share a certain
subset of the encoder parameters during train-
ing while the output layer parameters are kept
language-specific, as described by Pappas and
Popescu-Belis (2017). In this paper, we share
most of the output layer parameters, namely, the
ones from the input-label space (U, V, bv, bu), and
we keep only the classification unit parameters
(w, b) language-specific.
3.4 Scaling Up to Large Label Sets
For a very large number dj of joint-space di-
mensions in our parametrization, the computa-
tional complexity increases prohibitively because
our projection requires a large matrix multiplica-
tion between U and E, which depends on |Y|. In
such cases, we resort to sampling-based training
by adopting the commonly used negative sampling
method proposed by Mikolov et al. (2013). Let
xi ∈ IRd and yik ∈ {0, 1} be an input-label pair
and ˆyik the output probabilities from our model
(Equation (14)). By introducing the sets kp
i and
kn
i , which contain the indices of the positive and
negative labels respectively for the i-th input, the
143
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
9
1
9
2
3
3
6
8
/
/
t
l
a
c
_
a
_
0
0
2
5
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
loss L(θ) in Equation (15) can be re-written as
follows:
Data set
abbrev.
Documents
# count # words
¯wd # count
= −
= −
1
Z
1
Z
N
(cid:88)
k
(cid:88)
(cid:104)
yij log ˆyij + ¯yij log (1 − ˆyij)
(cid:105)
i=1
j=1
N
(cid:88)
(cid:104)
kp
i(cid:88)
i=1
j=1
log ˆyij +
kn
i(cid:88)
j=1
log (1 − ˆyij)
(cid:105)
(17)
i | to create the set kn
where Z = N k and ¯yij is (1 − yij). To reduce
the computational cost needed to evaluate ˆyij
for all the negative label set kn
i , we sample k∗
labels from the negative label set with probability
p = 1
i . This enables training
|kn
on arbitrarily large label sets without increasing
the computation required. By controlling the
number of samples we can drastically speed up
the training time, as we demonstrate empirically
in Section 4.2.2. Exploring more informative
sampling methods (e.g.,
importance sampling)
would be an interesting direction of future work.
3.5 Relation to Previous Parametrizations
The proposed embedding form can be seen as
a generalization over the input-label embeddings
with a bilinear form, because its degenerate form
is equivalent to the bilinear form of Equation (5).
In particular, this can be simply derived if we set
one of the two nonlinear projection functions in
the second line of Equation (9) to be the identity
function (e.g., gout(·) = I), set all biases to zero,
and make the σ(.) activation function linear, as
follows:
σ(EU + bu)σ(V h + bv) = (EI) (V h)
= EV h
(18)
where V by consequence has the same number
of dimensions as W ∈ IRd×dh from the bilinear
input-label embedding model of Equation (5).
(cid:3)
4 Experiments
The evaluation is performed on large-scale
biomedical semantic indexing using the BioASQ
data set, obtained by Nam et al. (2016), and on
multilingual news classification using the DW
corpus, which consists of eight language data sets
obtained by Pappas and Popescu-Belis (2017). The
statistics of these data sets are listed in Table 1.
BioASQ 11,705,534 528,156 214
598,304 884,272 436
112,816 110,971 516
132,709 261,280 424
75,827 130,661 412
39,474
58,849 571
35,423 105,240 342
108,076 123,493 330
58,922 357
57,697
34,856 538
36,282
DW
– en
– de
– es
– pt
– uk
– ru
– ar
– fa
Labels
¯wl
26,104 35.0
2.3
5,637
2.1
1,385
1.8
1,176
4.7
843
1.8
396
1.7
288
1.8
916
2.4
435
2.5
198
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
9
1
9
2
3
3
6
8
/
/
t
l
a
c
_
a
_
0
0
2
5
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Table 1: Data set statistics. #count is the number of
documents, #words are the number of unique words in
the vocabulary V, ¯wd and ¯wl are the average number
of words per document and label, respectively.
4.1 Biomedical Text Classification
We evaluate on biomedical
text classification
to demonstrate that our generalized input-label
model scales to very large label sets and performs
better than previous joint input-label models on
both seen and unseen label prediction scenarios.
4.1.1 Settings
We follow the exact evaluation protocol, data,
and settings of Nam et al. (2016), as described
below. We use the BioASQ Task 3a data set,
which is a collection of scientific publications in
biomedical research. The data set contains about
12M documents labeled with around 11 labels
out of 27,455, which are defined according to
the Medical Subject Headings (MESH) hierarchy.
The data were minimally pre-processed with
tokenization, number replacements (NUM), rare
word replacements (UNK), and split with the
provided script by year so that the training set
includes all documents until 2004 and the ones
from 2005 to 2015 were kept for the test set; this
corresponded to 6,692,815 documents for training
and 4,912,719 for testing. For validation, a set of
100,000 documents were randomly sampled from
the training set. We report the same ranking-based
evaluation metrics as Nam et al. (2016), namely,
rank loss (RL), average precision (AvgPr), and
one-error loss (OneErr).
Our hyper-parameters were selected on valida-
tion data based on average precision as follows:
100-dimensional word embeddings, encoder, at-
tention (same dimensions as the baselines), joint
input-label embedding of 500, batch size of 64,
144
Model
abbrev.
] WSABIE+
6
1
N
[
AiTextML avg
AiTextML inf
s WAN
e
n
i
l
e
s
a
B
BIL-WAN [YH15]
BIL-WAN [N16]
GILE-WAN
− constrained dj
− only label (Eq. 6a)
− only input (Eq. 6b)
s
r
u
O
Layer form
output
EWht
EWht
EWht
W (cid:62)ht
σ(EW)Wht
EWht
σ(EU )σ(V ht)
σ(EW)σ(Wht)
σ(EW)ht
Eσ(Wht)
Dim
#count RL AvgPr OneErr RL AvgPr OneErr
Unseen labels
Seen labels
100
100
100
–
100
100
500
100
100
100
5.21 36.64
3.54 32.78
3.54 32.78
1.53 42.37
1.21 40.68
1.12 41.91
0.78 44.39
1.01 37.71
1.06 40.81
1.07 39.78
41.72
25.99
25.99
11.23
17.52
16.94
11.60
16.16
13.77
15.67
0.37
48.81
0.39
52.89
2.66
21.62
–
–
18.72
9.50
16.26 10.55
12.95
9.06
10.34 11.21
14.71
9.77
7.18
19.28
99.94
99.94
98.61
–
93.89
93.23
91.90
93.38
90.56
95.91
Params
#count
722.10M
724.47M
724.47M
55.60M
52.85M
52.84M
52.93M
52.85M
52.84M
52.84M
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
9
1
9
2
3
3
6
8
/
/
t
l
a
c
_
a
_
0
0
2
5
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Table 2: Biomedical semantic indexing results computed over labels seen and unseen during training, i.e., the
full-resource versus zero-resource settings. Best scores among the competing models are marked in bold.
maximum number of 300 words per document
and 50 words per label, ReLU activation, 0.3%
negative label sampling, and optimization with
ADAM until convergence. The word embeddings
were learned end-to-end on the task.4
The baselines are the joint input-label models
from Nam et al. (2016), noted as [N16], namely:
• WSABIE+: This model is an extension of
the original WSABIE model by Weston et al.
(2011), which, instead of learning a ranking
model with fixed document features, jointly
learns features for documents and words, and
is trained with the WARP ranking loss.
• AiTextML: This model is the one proposed
by Nam et al. (2016) with the purpose of
learning joint representations of documents,
labels, and words, along with a joint input-
label space that is trained with the WARP
ranking loss.
The scores of the WSABIE+ and AiTextML
baselines in Table 2 are the ones reported by
Nam et al. (2016). In addition, we report scores
of a word-level attention neural network (WAN)
with DENSE encoder and attention followed by a
sigmoid output layer, trained with binary cross-
entropy loss.5 Our model replaces WAN’s output
4Here, the word embeddings are included in the parameter
statistics because they are variables of the network.
5In our preliminary experiments, we also trained the
neural model with a hinge loss as WSABIE+ and AiTextML,
but it performed similarly to them and much worse than
WAN, so we did not further experiment with it.
layer with a generalized input-label embedding
layer and its variations, noted GILE-WAN. For
comparison, we also compare to bilinear input-
label embedding versions of WAN for the model
by Yazdani and Henderson (2015), noted as
BIL-WAN [YH16], and the one by Nam et al.
(2016), noted as BIL-WAN [N16]. Note that the
AiTextML parameter space is huge and makes
learning difficult for our models (linear with
respect to labels and documents). Instead, we
make sure that our models have far fewer pa-
rameters than the baselines (Table 2).
4.1.2 Results
The results on biomedical semantic indexing on
seen and unseen labels are shown in Table 2.
We observe that the neural baseline, WAN, out-
performs WSABIE+ and AiTextML on the seen
labels, by +5.73 and +9.59 points in terms of
AvgPr, respectively. The differences are even
more pronounced when considering the ranking
loss and one error metrics. This result is com-
patible with previous findings that existing joint
input-label models are not able to outperform
strong supervised baselines on seen labels. How-
ever, WAN is not able to generalize at all to unseen
labels, hence the WSABIE+ and AiTextML have
a clear advantage in the zero-resource setting.
In contrast, our generalized input-label model,
GILE-WAN, outperforms WAN even on seen
labels, where our model has higher average
precision by +2.02 points, better ranking loss
by +43% and comparable OneErr (−3%). And
this gain is not at the expense of performance
145
on unseen labels. GILE-WAN outperforms
WSABIE+ and AiTextML variants6 by a large
margin in both cases—for example, by +7.75,
+11.61 points on seen labels and by +12.58,
+10.29 points in terms of average precision on
unseen labels, respectively. Interestingly, our GILE-
WAN model also outperforms the two previous
bilinear input-label embedding formulations of
Yazdani and Henderson (2015) and Nam et al.
(2016), namely, BIL-WAN [YH15] and BIL-WAN
[N16], by +3.71, +2.48 points on seen labels
and +3.45 and +2.39 points on unseen labels,
respectively, even when they are trained with the
same encoders and loss as ours. These models are
not able to outperform the WAN baseline when
evaluated on the seen labels, that is they have
−1.68 and −0.46 points lower average precision
than WAN, but they outperform WSABIE+ and
AiTextML on both seen and unseen labels.
Overall, the results show a clear advantage of our
generalized input-label embedding model against
previous models on both seen and unseen labels.
4.1.3 Ablation Analysis
To evaluate the effectiveness of individual com-
ponents of our model, we performed an ablation
study (last three rows in Table 2). Note that when
we use only the label or only the input embedding
in our generalized input-label formulation, the
dimensionality of the joint space is constrained
to be the dimensionality of the encoded labels
and inputs respectively (i.e., dj=100 in our
experiments).
All three variants of our model outperform
previous embedding formulations of Nam et al.
(2016) and Yazdani and Henderson (2015) in all
metrics except for AvgPr on seen labels, where
they score slightly lower. The decrease in AvgPrec
for our model variants with dj=100 compared
with the neural baselines could be attributed
to the difficulty in learning the parameters of
a highly nonlinear space with only a few hid-
den dimensions. Indeed, when we increase the
number of dimensions (dj=500), our full model
outperforms them by a large margin. Recall that
this increase in capacity is only possible with our
full model definition in Equation (9) and none
of the other variants allow us to do this without
interfering with the original dimensionality of the
encoded labels (E) and input (ht). In addition, our
model variants with dj=100 exhibit consistently
higher scores than baselines in terms of most
metrics on both seen and unseen labels, which
they are able to capture more
suggests that
complex relationships across labels and between
encoded inputs and labels.
Overall, the best performance among our model
variants is achieved when using only the label
embedding and, hence, it is the most significant
component of our model. Surprisingly, our model
with only the label embedding achieves higher
performance than our full model on unseen labels
but it is far behind our full model when we
consider performance on both seen and unseen
labels. When we constrain our full model to have
the same dimensionality with the other variants
(i.e., dj=100), it outperforms the one that uses
only the input embedding in most metrics and it is
outperformed by the one that uses only the label
embedding.
4.2 Multilingual News Text Classification
We evaluate on multilingual news text clas-
sification to demonstrate that our output layer
based on the generalized input-label embedding
outperforms previous models with a typical output
layer in a wide variety of settings, even for labels
that have been seen during training.
4.2.1 Settings
We follow the exact evaluation protocol, data, and
settings of Pappas and Popescu-Belis (2017), as
described below. The data set is split per language
into 80% for training, 10% for validation, and
10% for testing. We evaluate on both types of
labels (general Yg, and specific Ys) in a full-
resource scenario, and we evaluate only on the
general labels (Yg) in a low-resource scenario.
Accuracy is measured with the micro-averaged
F1 percentage scores.
The word embeddings for this task are the
aligned pre-trained 40-dimensional multi-CCA
multilingual word embeddings by Ammar et al.
(2016) and are kept fixed during training.7 The
sentences are already truncated at a length of
30 words and the documents at a length of 30
sentences. The hyper-parameters were selected
6Namely, avg when using the average of word vectors
and inf when using inferred label vectors to make predictions.
7The word embeddings are not included in the parameters
statistics because they are not variables of the network.
146
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
9
1
9
2
3
3
6
8
/
/
t
l
a
c
_
a
_
0
0
2
5
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
ar
pt
pt
ru
ru
Yg
Models
abbrev.
o NN (Avg)
n
o
] M
7
1
B
P
[
HNN (Avg)
HAN (Att)
i MHAN-Enc
t
l
MHAN-Att
u
M
MHAN-Both
o GILE-NN (Avg)
n
o
s M
r
u
O
Languages (en + aux → aux)
Languages (en + aux → en)
de
fa
uk
es
de
fa
ar
uk
es
53.1 70.0 57.2 80.9 59.3 64.4 66.6
50.7 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
67.9 82.5 70.5 86.8 77.4 79.0 76.6
70.0 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
71.2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
71.8 82.8 71.3 85.3 79.8 80.5 76.6
71.0 69.9 69.2 70.8 71.5 70.0 71.3 69.7 82.9 69.7 86.8 80.3 79.0 76.0
74.0 74.2 74.1 72.9 73.9 73.8 73.3 72.5 82.5 70.8 87.7 80.5 82.1 76.3
72.8 71.2 70.5 65.6 71.1 68.9 69.2 70.4 82.8 71.6 87.5 80.8 79.1 77.1
60.3 76.6 62.1 82.0 65.7 77.4 68.6
60.1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
71.3 83.3 72.6 88.3 81.5 81.9 77.1
74.8 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
GILE-HNN (Avg)
76.5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
74.2 83.4 71.9 86.1 82.7 81.0 77.2
GILE-HAN (Att)
75.1 74.0 72.7 70.7 74.4 73.5 73.2 72.7 83.4 73.0 88.7 82.8 83.3 77.4
i GILE-MHAN-Enc
t
l
76.5 76.5 76.3 75.3 76.1 75.6 75.2 74.5 83.5 72.7 88.0 83.4 82.1 76.7
GILE-MHAN-Att
u
M
GILE-MHAN-Both 75.3 73.7 72.1 67.2 72.5 73.8 69.7 72.6 84.0 73.5 89.0 81.9 82.0 77.7
de
Models
fa
uk
de
fa
uk
21.8 22.1 24.3 33.0 26.0 24.1 32.1
o NN (Avg)
24.4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
n
39.6 37.9 33.6 42.2 39.3 34.6 43.1
39.3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
o
] M
7
43.4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
44.8 46.3 41.9 46.4 45.8 41.2 49.4
1
B
45.4 45.9 44.3 41.1 42.1 44.9 41.0 43.9 46.2 39.3 47.4 45.0 37.9 48.6
P
[
46.3 46.0 45.9 45.6 46.4 46.4 46.1 46.5 46.7 43.3 47.9 45.8 41.3 48.0
45.7 45.6 41.5 41.2 45.6 44.6 43.0 45.9 46.4 40.3 46.3 46.1 40.7 50.3
27.5 28.4 29.2 36.8 31.6 32.1 35.6
27.5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
43.4 42.0 37.7 43.0 42.9 36.6 44.1
43.1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
GILE-HNN (Avg)
45.9 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
47.3 47.4 42.6 46.6 46.9 41.9 48.6
GILE-HAN (Att)
46.0 46.6 41.2 42.5 46.4 43.4 41.8 47.2 47.7 41.5 49.5 46.6 41.4 50.7
i GILE-MHAN-Enc
47.3 47.0 45.8 45.5 46.2 46.5 45.5 47.6 47.9 43.5 49.1 46.5 42.2 50.3
GILE-MHAN-Att
u
M
GILE-MHAN-Both 47.0 46.7 42.8 42.0 45.6 42.8 39.3 48.0 47.6 43.1 48.5 46.0 42.1 49.0
HNN (Avg)
HAN (Att)
i MHAN-Enc
MHAN-Att
u
M
MHAN-Both
o GILE-NN (Avg)
n
o
s M
r
u
O
Ys
ru
es
ru
es
pt
pt
ar
ar
t
l
t
l
Stat.
avg
57.6
73.6
74.7
74.1
76.3
74.2
65.2
77.1
78.0
76.7
78.0
76.0
avg
25.3
38.9
44.2
43.8
45.8
44.5
29.5
42.2
45.9
45.1
46.5
45.0
Table 3: Full-resource classification results on general (upper half) and specific (lower half) labels using
monolingual and bilingual models with DENSE encoders on English as target (left) and the auxiliary language as
target (right). The average bilingual F1-score (%) is noted avg and the top ones per block are underlined. The
monolingual scores on the left come from a single model, hence a single score is repeated multiple times; the
repetition is marked with consecutive dots.
on validation data as follows: 100-dimensional
encoder and attention, ReLU activation, batch
size 16, epoch size 25k, no negative sampling (all
labels are used), and optimization with ADAM
until convergence. To ensure equal capacity to
baselines, we use approximately the same number
of parameters ntot with the baseline classification
layers, by setting:
dj (cid:39)
dh ∗ |k(i)|
dh + d
, i = 1, . . . , M
(19)
in the monolingual case, and similarly, dj (cid:39)
(dh ∗ (cid:80)M
i=1 |k(i)|)/(dh + d) in the multilingual
case, where k(i) is the number of labels in lan-
guage i.
The hierarchical models have Dense encoders
in all scenarios (Tables 3, 6, and 7), except
from the varying encoder experiment (Table 4).
For the low-resource scenario, the levels of data
availability are: tiny from 0.1% to 0.5%, small
from 1% to 5% and medium from 10% to 50%
of the original training set. For each level, the
average F1 across discrete increments of 0.1, 1
and 10 are reported respectively. The decision
thresholds, which were tuned on validation data
by Pappas and Popescu-Belis (2017), are set as
follows: for the full-resource scenario it is set to
0.4 for |Ys| < 400 and 0.2 for |Ys| ≥ 400, and
for the low-resource scenario it is set to 0.3 for
all sets.
The baselines are all
the monolingual and
multilingual neural networks from Pappas and
Popescu-Belis (2017),8 noted as [PB17], namely:
• NN: A neural network that feeds the av-
erage vector of the input words directly to
a classification layer, as the one used by
Klementiev et al. (2012).
• HNN: A hierarchical network with encoders
and average pooling at every level, followed
by a classification layer, as the one used by
Tang et al. (2015).
8For reference, in Table 4 we also compare to a logistic
regression trained with unigrams over the full vocabulary and
over the top-10% most frequent words by Mrini et al. (2017),
noted as [M17], which use the same settings and data.
147
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
9
1
9
2
3
3
6
8
/
/
t
l
a
c
_
a
_
0
0
2
5
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Models
abbrev.
LogReg-BOW-10%
[
] LogReg-BOW
7
1
M
] HAN-BIGRU
7
1
B
P
[
HAN-GRU
HAN-DENSE
GILE-HAN-BIGRU
GILE-HAN-GRU
GILE-HAN-DENSE
s
r
u
O
en
75.8
74.7
76.3
77.1
71.2
78.1
77.1
76.5
de
72.9
70.1
74.1
72.5
71.8
73.6
72.6
74.2
es
81.4
80.6
84.5
84.0
82.8
84.9
84.7
83.4
Languages
uk
pt
74.3
71.1
72.9
70.8
71.3
72.5
72.4
71.9
91.0
89.5
87.7
86.6
85.3
89.0
88.6
86.1
ru
79.2
76.5
82.9
83.0
79.8
82.4
83.6
82.7
ar
82.0
80.8
81.7
82.9
80.5
82.5
83.4
82.6
fa
77.0
75.5
75.3
76.0
76.6
75.8
76.0
77.2
Statistics
fl
nl
26M
5M
377K
138K
50K
377K
138K
50K
79.19
77.35
79.42
79.11
77.41
79.85
79.80
79.12
Table 4: Full-resource classification results on general (Yg) topic labels with DENSE and GRU encoders. Reported
are also the average number of parameters per language (nl) and the average F1 per language (fl).
• HAN: A hierarchical network with encoders
and attention, followed by a classification
layer, as the one used by Yang et al. (2016).
• MHAN: Three multilingual hierarchical net-
works with shared encoders, noted MHAN-
Enc, shared attention, noted MHAN-Att,
and shared attention and encoders, noted
MHAN-Both, as the ones used by Pappas
and Popescu-Belis (2017).
To ensure a controlled comparison to the
above baselines, for each model we evaluate
a version where their output layer is replaced
by our generalized input-label embedding output
layer using the same number of parameters; these
have the abbreviation ‘‘GILE’’ prepended in their
name (e.g., GILE-HAN). The scores of HAN and
MHAN models in Tables 3, 6, and 7 are the ones
reported by Pappas and Popescu-Belis (2017),
while for Table 4 we train them ourselves using
their code. Lastly, the best score for each pairwise
comparison between a joint input-label model and
its counterpart is marked in bold.
4.2.2 Results
Table 3 displays the results of full-resource docu-
ment classification using DENSE encoders for both
general and specific labels. On the left, we display
the performance of models on the English sub-
corpus when English and an auxiliary language are
used for training, and on the right, the performance
on the auxiliary language sub-corpus when that
language and English are used for training.
The results show that in 98% of comparisons
on general labels (top half of Table 3) the joint
input-label models improve consistently over the
corresponding models using a typical sigmoid
classification layer. This finding validates our
main hypothesis that the joint input-label models
successfully exploit the semantics of the labels,
which provide useful cues for classification, as
opposed to models which are agnostic to label
semantics. The results for specific labels (bottom
half of Table 3) demonstrate the same trend, with
the joint input-label models performing better in
87% of comparisons.
In Table 5, we also directly compare our embed-
ding to previous bilinear input-label embedding
formulations when using the best monolingual
configuration (HAN) from Table 3, exactly as
done in Section 4.1. The results on the general
labels show that GILE outperforms the previous
bilinear input-label models, BIL [YH15] and BIL
[N16], by +1.62 and +3.3 percentage points
on average, respectively. This difference is much
more pronounced on the specific labels, where
the label set is much larger, namely, +6.5 and
+13.5 percentage points, respectively. Similarly,
our model with constrained dimensionality is also
as good or better on average than the bilinear
input-label models, by +0.9 and +2.2 on general
labels and by −0.5 and +6.1 on specific labels
respectively, which highlights the importance of
learning nonlinear relationships across encoded
labels and documents. Among our ablated model
variants, as in the previous section, the best is
the one with only the label projection but it still
worse than our full model by −5.2 percentage
points. The improvements of GILE against each
baseline is significant and consistent on both data
sets. Hence, in the following experiments we will
only consider the best of these alternatives.
148
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
9
1
9
2
3
3
6
8
/
/
t
l
a
c
_
a
_
0
0
2
5
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
HAN
Yg output layer
Linear [PB17]
BIL [YH15]
BIL [N16]
GILE (Ours)
- constrained dj
- only label
- only input
Ys output layer
Linear[PB17]
BIL [YH15]
BIL [N16]
GILE (Ours)
- constrained dj
- only label
- only input
en
71.2
71.7
69.8
76.5
73.6
71.4
55.1
en
43.4
40.7
34.4
45.9
38.5
38.4
12.1
de
71.8
70.5
69.1
74.2
73.1
69.6
54.2
de
44.8
37.8
30.2
47.3
38.0
41.5
10.8
es
82.8
82.0
80.9
83.4
83.3
82.1
80.6
es
46.3
38.1
34.4
47.4
36.8
42.9
8.8
Languages
uk
pt
85.3
71.3
86.6
71.1
87.5
67.4
71.9
86.1
87.1
71.0
86.2
70.3
85.6
66.5
pt
41.9
33.5
33.6
42.6
35.1
38.3
20.5
uk
46.4
44.6
31.4
46.6
42.1
44.0
11.8
ru
79.8
80.6
79.9
82.7
81.6
80.6
60.8
ru
45.8
38.1
22.8
46.9
36.1
39.3
7.8
ar
80.5
80.4
78.4
82.6
80.4
81.1
78.9
ar
41.2
39.1
35.6
41.9
36.7
37.2
12.0
fa
76.6
76.0
75.1
77.2
76.4
76.2
74.0
fa
49.4
42.6
38.9
48.6
48.7
43.4
24.6
Table 5: Direct comparison with previous bilinear input-label models, namely, BIL [YH15] and BIL [N16], and
with our ablated model variants using the best monolingual configuration (HAN) from Table 3 on both general
(upper half) and specific (lower half) labels. Best scores among the competing models are marked in bold.
The best bilingual performance on average is
that of the GILE-MHAN-Att model, for both
general and specific labels. This improvement
can be attributed to the effective sharing between
label semantics across languages through the joint
multilingual input-label output layer. Effectively,
this model has the same multilingual sharing
scheme with the best model reported by Pappas
and Popescu-Belis (2017), MHAN-Att, namely,
sharing attention at each level of the hierarchy,
which agrees well with their main finding.
Interestingly,
the improvement holds when
using different types of hierarchical encoders,
namely, DENSE GRU, and biGRU, as shown in
Table 4, which demonstrate the generality of the
approach. In addition, our best models outperform
logistic regression trained either on top-10% most
frequent words or on the full vocabulary, even
though our models utilize many fewer parameters,
that is, 377K/138K vs. 26M/5M. Increasing the
capacity of our models should lead to even further
improvements.
Multilingual learning. So far, we have shown
that the proposed joint input-label models out-
perform typical neural models when training with
one and two languages. Does the improvement
remain when increasing the number of languages
even more? To answer the question we report in
Table 6 the average F1-score per language for
the best baselines from the previous experiment
(HAN and MHAN-Att) with the proposed joint
Models
General labelsSpecific labels
abbrev.
# lang. nl
fl
nl
fl
]HAN
7
1
B
P
[
MHAN
MHAN
sGILE-HAN
1
2
8
1
GILE-MHAN 2
GILE-MHAN 8
r
u
O
50K 77.41
40K 78.30
32K 77.91
50K 79.12
40K 79.68
32K 79.48
90K 44.90
80K 45.72
72K 45.82
90K 45.90
80K 46.49
72K 46.32
Table 6: Multilingual learning results. The columns
are the average number of parameters per language
(nl), average F1 per language (fl).
input-label versions of them (GILE-HAN and
GILE-MHAN-Att) when increasing the number
of languages (1, 2, and 8) that are used for train-
ing. Overall, we observe that the joint input-label
models outperform all the baselines independently
of the number of languages involved in the train-
ing, while having the same number of parameters.
We also replicate the previous result
that a
second language helps but beyond that there is
no improvement.
Low-resource transfer. We investigate here
whether joint input-label models are useful for
low-resource languages. Table 7 shows the low-
resource classification results from English to
seven other languages when varying the amount
of their training data. Our model with both shared
encoders and attention, GILE-MHAN, outper-
forms previous models in average, namely, HAN
149
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
9
1
9
2
3
3
6
8
/
/
t
l
a
c
_
a
_
0
0
2
5
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Levels
range
[PB17]
Ours
HAN MHAN GILE-MHAN
e
1-5%
10-50%
e 0.1-0.5% 29.9
d
51.3
1-5%
→
n
63.5
10-50%
e
s 0.1-0.5% 39.5
→
45.6
1-5%
n
74.2
10-50%
e
t 0.1-0.5% 30.9
p
→
44.6
n
60.9
e
k 0.1-0.5% 60.4
u
68.2
1-5%
→
n
76.4
10-50%
e
u 0.1-0.5% 27.6
→
39.3
1-5%
n
69.2
10-50%
e
r 0.1-0.5% 35.4
→
45.6
1-5%
n
48.9
10-50%
e
a 0.1-0.5% 36.0
→
55.0
n
69.2
e
1-5%
10-50%
a
r
f
39.4
52.6
63.8
41.5
50.1
75.2
33.8
47.3
62.1
60.9
69.0
76.7
29.1
40.2
69.4
36.6
46.6
47.8
41.3
55.5
70.0
42.9
51.6
65.9
39.0
50.9
76.4
39.6
48.9
62.3
61.1
69.4
76.5
27.9
40.2
70.4
46.1
49.5
61.8
42.5
55.4
69.7
Table 7: Low-resource classification results with
various sizes of training data using the general labels.
(Yang et al., 2016) and MHAN (Pappas and
Popescu-Belis, 2017), for low-resource classifi-
cation in the majority of the cases.
The shared input-label space appears to be
helpful especially when transferring from English
to German, Portuguese, and Arabic languages.
GILE-MHAN is significantly behind MHAN on
transferring knowledge from English to Spanish
and to Russian in the 0.1% to 0.5% resource
setting, but in the rest of the cases they have very
similar scores.
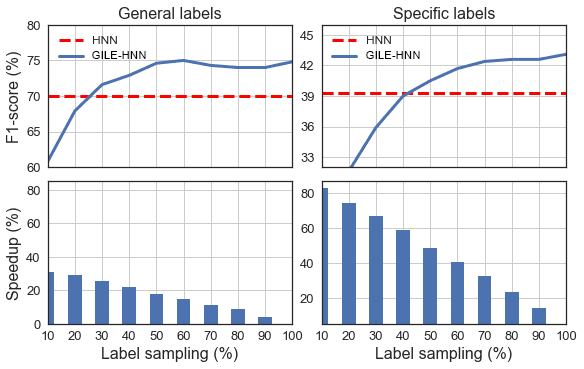
Label sampling. To speed up computation it is
possible to train our model by sampling labels,
instead of training over the whole label set. How
much speed-up can we achieve from this label
sampling approach and still retain good levels of
performance? In Figure 2, we attempt to answer
this question by reporting the performance of our
GILE-HNN model when varying the amount of
labels (%) that it uses for training over English
general and specific labels of the DW data set.
In both cases, the performance of GILE-HNN
tends to increase as the percentage of labels
sampled increases, but it levels off for the higher
percentages.
150
Figure 2: Varying sampling percentage for general and
specific English labels. (Top) GILE-HNN is compared
against HNN in terms of F1 (%). (Bottom) The runtime
speed-up over GILE-HNN trained on the full label set.
For general labels, top performance is reached
with a 40% to 50% sampling rate, which translates
to a 22% to 18% speed-up, whereas for the specific
labels, it is reached with a 60% to 70% sampling
rate, which translates to a 40% to 36% speed-up.
The speed-up is correlated to the size of the label
set, since there are many fewer general labels
than specific labels, namely, 327 vs. 1,058 here.
Hence, we expect even higher speedups for bigger
label sets. Interestingly, GILE-HNN with label
sampling reaches the performance of the baseline
with a 25% and 60% sample for general and
specific labels respectively. This translates to a
speed-up of 30% and 50%, respectively, compared
with a GILE-HNN trained over all labels. Overall,
these results show that our model is effective
and that it can also scale to large label sets.
The label sampling should also be useful in tasks
where the computation resources may be limited
or budgeted.
5 Related Work
5.1 Neural text Classification
Research in neural text classification was initially
based on feed-forward networks, which required
unsupervised pre-training (Collobert et al., 2011;
Mikolov et al., 2013; Le and Mikolov, 2014) and
later on they focused on networks with hierarchical
structure. Kim (2014) proposed a convolutional
neural network (CNN) for sentence classification.
Johnson and Zhang (2015) proposed a CNN for
high-dimensional data classification, while Zhang
et al. (2015) adopted a character-level CNN
for text classification. Lai et al. (2015) pro-
posed a recurrent CNN to capture sequential
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
9
1
9
2
3
3
6
8
/
/
t
l
a
c
_
a
_
0
0
2
5
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
information, which outperformed simpler CNNs.
Lin et al. (2015) and Tang et al. (2015) pro-
posed hierarchical
recurrent neural networks
and showed that they were superior to CNN-
based models. Yang et al. (2016) demonstrated
that a hierarchical attention network with bi-
directional gated encoders outperforms previous
alternatives. Pappas and Popescu-Belis (2017)
adapted such networks to learn hierarchical
document structures with shared components
across different languages.
The issue of scaling to large label sets has
been addressed previously by output layer approx-
imations (Morin and Bengio, 2005) and with
the use of sub-word units or character-level
modeling (Sennrich et al., 2016; Lee et al.,
2017) which is mainly applicable to structured
prediction problems. Despite the numerous stud-
ies, most of the existing neural text classification
models ignore label descriptions and semantics.
Moreover, they are based on typical output layer
parametrizations that are dependent on the label
set size, and thus are not able to scale well to
large label sets nor to generalize to unseen labels.
Our output layer parametrization addresses these
limitations and could potentially improve such
models.
5.2 Output Representation Learning
There exist studies that aim to learn output rep-
resentations directly from data without any seman-
tic grounding to word embeddings (Srikumar and
Manning, 2014; Yeh et al., 2018; Augenstein
et al., 2018). Such methods have a label-set-size
dependent parametrization, which makes them
data hungry, less scalable on large label sets, and
incapable of generalizing to unseen classes. Wang
et al. (2018) addressed the lack of semantic
grounding to word embeddings by proposing an
efficient method based on label-attentive text rep-
resentations which are helpful
text clas-
sification. However, in contrast to our study, their
parametrization is still label-set-size dependent
and thus their model is not able to scale well to
large label sets nor to generalize to unseen labels.
for
5.3 Zero-shot Text Classification
Several studies have focused on learning joint
input-label
representations grounded to word
semantics for unseen label prediction for images
(Weston et al., 2011; Socher et al., 2013; Norouzi
et al., 2014; Zhang et al., 2016; Fu et al., 2018),
called zero-shot classification. However, there are
fewer such studies for text classification. Dauphin
et al. (2014) predicted semantic utterances of text
by mapping them in the same semantic space with
the class labels using an unsupervised learn-
ing objective. Yazdani and Henderson (2015) pro-
posed a zero-shot spoken language understanding
model based on a bilinear input-label model able to
generalize to previously unseen labels. Nam et al.
(2016) proposed a bilinear joint document-label
embedding that learns shared word representations
between documents and labels. More recently, Shu
et al. (2017) proposed an approach for open-world
classification that aims to identify novel docu-
ments during testing but it is not able to generalize
to unseen classes. Perhaps the model most similar
to ours is from the recent study by Pappas et al.
(2018) on neural machine translation, with the
difference that they have single-word label des-
criptions and they use a label-set-dependent bias in
a softmax linear prediction unit, which is designed
for structured prediction. Hence,
their model
can neither handle unseen labels nor multi-label
classification, as we do here.
joint
Compared with previous
input-label
models, the proposed model has a more general
and flexible parametrization, which allows the
output layer capacity to be controlled. Moreover,
it is not restricted to linear mappings, which have
limited expressivity, but uses nonlinear mappings,
similar to energy-based learning networks (LeCun
et al., 2006; Belanger and McCallum, 2016). The
link to the latter can be made if we regard P (ij)
val
in Equation (11) as an energy function for the i-th
document and the j-th label, the calculation of
which uses a simple multiplicative transformation
(Equation (10)). Lastly,
the proposed model
performs well on both seen and unseen label sets
by leveraging the binary cross-entropy loss, which
is the standard loss for classification problems,
instead of a ranking loss.
6 Conclusion
We proposed a novel joint input-label embedding
model for neural text classification that gener-
alizes over existing input-label models and ad-
dresses their limitations while preserving high
performance on both seen and unseen labels. Com-
pared with baseline neural models with a typical
output layer, our model is more scalable and has
better performance on the seen labels. Compared
151
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
9
1
9
2
3
3
6
8
/
/
t
l
a
c
_
a
_
0
0
2
5
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
with previous joint input-label models, it performs
significantly better on unseen labels without
compromising performance on the seen labels.
These improvements can be attributed to the the
ability of our model to capture complex input-
label relationships, to its controllable capacity,
and to its training objective, which is based on
cross-entropy loss.
As future work, the label representation could
be learned by a more sophisticated encoder, and
the label sampling could benefit from importance
sampling to avoid revisiting uninformative labels.
Another interesting direction would be to find a
more scalable way of increasing the output layer
capacity—for instance, using a deep rather than a
wide classification network. Moreover, adapting
the proposed model to structured prediction, for
instance by using a softmax classification unit
instead of a sigmoid one, would benefit tasks such
as neural machine translation, language modeling,
and summarization in isolation but also when
trained jointly with multi-task learning.
Acknowledgments
We are grateful for the support from the European
Union through its Horizon 2020 program in
the SUMMA project n. 688139, see http://www.
summa-project.eu. We would also like to thank our
action editor, Eneko Agirre, and the anonymous
reviewers for their invaluable suggestions and
feedback.
References
Waleed Ammar, George Mulcaire, Yulia Tsvetkov,
Guillaume Lample, Chris Dyer, and Noah A.
Smith. 2016. Massively multilingual word em-
beddings. CoRR, abs/1602.01925.v2.
In Proceedings of
Isabelle Augenstein, Sebastian Ruder, and Anders
Søgaard. 2018. Multi-task learning of pairwise
sequence classification tasks over disparate
the 2018
label spaces.
Conference of the North American Chapter of
the Association for Computational Linguistics:
Human Language Technologies, Volume 1
(Long Papers), pages 1896–1906. New Orleans,
Louisiana.
Machine Learning, volume 48 of Proceedings
of Machine Learning Research, pages 983–992,
New York, New York, USA. PMLR.
Jianshu Chen, Ji He, Yelong Shen, Lin Xiao,
Xiaodong He, Jianfeng Gao, Xinying Song,
and Li Deng. 2015. End-to-end learning of LDA
by mirror-descent back propagation over a deep
architecture. In Advances in Neural Information
Processing Systems 28, pages 1765–1773.
Montreal, Canada.
Kyunghyun Cho, Bart van Merrienboer, Caglar
Gulcehre, Dzmitry Bahdanau, Fethi Bougares,
Holger Schwenk, and Yoshua Bengio. 2014.
Learning phrase representations using RNN
encoder–decoder for statistical machine trans-
lation. In Proceedings of the 2014 Conference
on Empirical Methods in Natural Language
Processing, pages 1724–1734, Doha, Qatar.
Ronan Collobert, Jason Weston, L´eon Bottou,
Michael Karlen, Koray Kavukcuoglu, and Pavel
Kuksa. 2011. Natural
language processing
(almost) from scratch. Journal of Machine
Learning Research, 12:2493–2537.
Yann N. Dauphin, G¨okhan T¨ur, Dilek Hakkani-
T¨ur, and Larry P. Heck. 2014. Zero-shot
learning and clustering for semantic utterance
classification. In International Conference on
Learning Representations. Banff, Canada.
Orhan Firat, Baskaran Sankaran, Yaser Al-
Onaizan, Fatos T. Yarman Vural,
and
Kyunghyun Cho. 2016. Zero-resource trans-
lation with multi-lingual neural machine trans-
lation. In Proceedings of the 2016 Conference
on Empirical Methods in Natural Language
Processing, pages 268–277, Austin, USA.
Andrea Frome, Greg S. Corrado, Jon Shlens, Samy
Bengio, Jeff Dean, Marc Aurelio Ranzato,
and Tomas Mikolov. 2013. DeViSE: A deep
visual-semantic embedding model, In C. J. C.
Burges, L. Bottou, M. Welling, Z. Ghahramani,
and K. Q. Weinberger, editors, Advances in
Neural Information Processing Systems 26,
pages 2121–2129. Curran Associates, Inc.
David Belanger and Andrew McCallum. 2016.
Structured prediction energy networks. In Pro-
ceedings of The 33rd International Conference on
Yanwei Fu, Tao Xiang, Yu-Gang
Jiang,
Xiangyang Xue, Leonid Sigal, and Shaogang
Gong. 2018. Recent advances in zero-shot
152
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
9
1
9
2
3
3
6
8
/
/
t
l
a
c
_
a
_
0
0
2
5
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
recognition: Toward data-efficient understand-
ing of visual content. IEEE Signal Processing
Magazine, 35(1):112–125.
Rie Johnson and Tong Zhang. 2015. Effective
use of word order for text categorization with
convolutional neural networks. In Proceedings
of the 2015 Conference of the North American
Chapter of the Association for Computational
Linguistics: Human Language Technologies,
pages 103–112, Denver, Colorado.
Yoon Kim. 2014. Convolutional neural networks
for sentence classification. In Proceedings of
the 2014 Conference on Empirical Methods in
Natural Language Processing, pages 1746–1751,
Doha, Qatar.
Alexandre Klementiev, Ivan Titov, and Binod
Inducing crosslingual dis-
Bhattarai. 2012.
In Pro-
tributed representations of words.
ceedings of COLING 2012, pages 1459–1474,
Mumbai, India.
Ankit Kumar, Ozan Irsoy, Jonathan Su, James
Bradbury, Robert English, Brian Pierce, Peter
Ondruska,
Ishaan Gulrajani, and Richard
Socher. 2015. Ask me anything: Dynamic mem-
ory networks for natural language processing.
In Proceedings of The 33rd International Con-
ference on Machine Learning, pages 334–343,
New York City, USA.
Siwei Lai, Liheng Xu, Kang Liu, and Jun
Zhao. 2015. Recurrent convolutional neural
networks for text classification. In Proceedings
the 29th AAAI Conference on Artificial
of
Intelligence, pages 2267–2273, Austin, USA.
Quoc V. Le and Tomas Mikolov. 2014. Distributed
representations of sentences and documents. In
Proceedings of The 31st International Confer-
ence on Machine Learning, pages 1188–1196,
Beijing, China.
Yann LeCun, Sumit Chopra, Raia Hadsell, Fu Jie
Huang, and et al. 2006. A tutorial on energy-
based learning. In Predicting Structured Data.
MIT Press.
Rui Lin, Shujie Liu, Muyun Yang, Mu Li, Ming
Zhou, and Sheng Li. 2015. Hierarchical re-
current neural network for document model-
ing. In Proceedings of the 2015 Conference
on Empirical Methods in Natural Language
Processing, pages 899–907. Lisbon, Portugal.
Thang Luong, Hieu Pham, and Christopher D.
Manning. 2015. Effective
to
attention-based neural machine translation. In
Proceedings of the 2015 Conference on Empir-
ical Methods in Natural Language Processing,
pages 1412–1421, Lisbon, Portugal.
approaches
Thomas Mensink,
Jakob Verbeek, Florent
Perronnin, and Gabriela Csurka. 2012. Metric
learning for large scale image classification:
Generalizing to new classes at near-zero cost. In
Computer Vision – ECCV 2012, pages 488–501,
Berlin, Heidelberg. Springer Berlin Heidelberg.
Tomas Mikolov, Ilya Sutskever, Kai Chen, Greg S
Corrado, and Jeff Dean. 2013. Distributed
representations of words and phrases and
their compositionality. In C. J. C. Burges,
L. Bottou, M. Welling, Z. Ghahramani,
and K. Q. Weinberger, editors, Advances in
Neural Information Processing Systems 26,
pages 3111–3119. Curran Associates, Inc.
Frederic Morin and Yoshua Bengio. 2005. Hier-
archical probabilistic neural network language
model. In Proceedings of the Tenth Interna-
tional Workshop on Artificial Intelligence and
Statistics, pages 246–252.
Khalil Mrini, Nikolaos Pappas, and Andrei
Popescu-Belis. 2017. Cross-lingual transfer for
news article labeling: Benchmarking statistical
and neural models. In Idiap Research Report,
Idiap-RR-26-2017.
Jinseok Nam, Eneldo Loza Menc´ıa, and Johannes
F¨urnkranz. 2016. All-in text: Learning docu-
ment, label, and word representations jointly.
the 13th AAAI Confer-
In Proceedings of
ence on Artificial
Intelligence, AAAI’16,
pages 1948–1954, Phoenix, Arizona.
Jason Lee, Kyunghyun Cho, and Thomas Hofmann.
2017. Fully character-level neural machine
translation without explicit segmentation. Tran-
sactions of the Association for Computational
Linguistics, 5:365–378.
Mohammad Norouzi, Tomas Mikolov, Samy
Bengio, Yoram Singer, Jonathon Shlens, Andrea
Frome, Greg Corrado, and Jeffrey Dean.
2014. Zero-shot learning by convex combina-
tion of semantic embeddings. In International
153
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
9
1
9
2
3
3
6
8
/
/
t
l
a
c
_
a
_
0
0
2
5
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Conference on Learning Representations, Banff,
Canada.
Bo Pang and Lillian Lee. 2005. Seeing stars:
Exploiting class relationships for sentiment
to rating scales.
categorization with respect
In Proceedings of the 43rd Annual Meeting
on Association for Computational Linguistics,
pages 115–124, Ann Arbor, Michigan.
Nikolaos Pappas, Lesly Miculicich, and James
Henderson. 2018. Beyond weight tying: Learn-
ing joint input-output embeddings for neural
machine translation. In Proceedings of the Third
Conference on Machine Translation: Research
Papers, pages 73–83, Belgium, Brussels.
Association for Computational Linguistics.
Nikolaos Pappas and Andrei Popescu-Belis. 2017.
Multilingual hierarchical attention networks
for document classification. In Proceedings of
the Eighth International Joint Conference on
Natural Language Processing (Volume 1: Long
Papers), pages 1015–1025.
Alexander M. Rush, Sumit Chopra, and Jason
Weston. 2015. A neural attention model for
abstractive sentence summarization. In Pro-
ceedings of the 2015 Conference on Empirical
Methods in Natural Language Processing,
pages 379–389. Lisbon, Portugal.
Rico Sennrich, Barry Haddow, and Alexandra
Birch. 2016. Neural machine translation of rare
words with subword units. In Proceedings of
the 54th Annual Meeting of the Association
for Computational Linguistics (Volume 1: Long
Papers), pages 1715–1725, Berlin, Germany.
Lei Shu, Hu Xu, and Bing Liu. 2017. DOC:
Deep open classification of text documents.
the 2017 Conference on
In Proceedings of
Empirical Methods
in Natural Language
Processing, pages 2911–2916, Copenhagen,
for Computational
Denmark. Association
Linguistics.
learning through cross-modal
Richard Socher, Milind Ganjoo, Christopher D.
Manning, and Andrew Y. Ng. 2013. Zero-
shot
transfer.
In Proceedings of
the 26th International
Conference on Neural Information Processing
Systems, NIPS’13, pages 935–943, Lake Tahoe,
Nevada.
Vivek Srikumar and Christopher D. Manning.
2014. Learning distributed representations for
structured output prediction. In Proceedings of
the 27th International Conference on Neural
Information Processing Systems - Volume 2,
NIPS’14, pages 3266–3274, Cambridge, MA,
USA. MIT Press.
Duyu Tang, Bing Qin, and Ting Liu. 2015.
Document modeling with gated recurrent
neural network for sentiment classification.
In Proceedings of
the 2015 Conference on
Empirical Methods in Natural Language Pro-
cessing, pages 1422–1432, Lisbon, Portugal.
Association for Computational Linguistics.
Guoyin Wang, Chunyuan Li, Wenlin Wang,
Yizhe Zhang, Dinghan Shen, Xinyuan Zhang,
Ricardo Henao, and Lawrence Carin. 2018.
Joint embedding of words and labels for
the
text classification.
56th Annual Meeting of the Association for
Computational Linguistics (Volume 1: Long
Papers), pages 2321–2331. Association for
Computational Linguistics.
In Proceedings of
Jason Weston, Samy Bengio, and Nicolas Usunier.
2010. Large scale image annotation: Learning to
rank with joint word-image embeddings. Mach.
Learn., 81(1):21–35.
Jason Weston, Samy Bengio, and Nicolas
Usunier. 2011. WSABIE: Scaling up to large
vocabulary image annotation. In Proceedings
of the Twenty-Second International Joint Con-
ference on Artificial Intelligence (Volume 3),
pages 2764–2770, Barcelona, Spain.
Zichao Yang, Diyi Yang, Chris Dyer, Xiaodong
He, Alex Smola, and Eduard Hovy. 2016.
Hierarchical attention networks for document
classification. In Proceedings of the 2016 Con-
ference of the North American Chapter of the-
Association for Computational Linguistics:
Human Language Technologies, pages 1480–1489,
San Diego, California.
Majid Yazdani and James Henderson. 2015. A
model of zero-shot learning of spoken language
understanding. In Proceedings of
the 2015
Conference on Empirical Methods in Natural
Language Processing, pages 244–249, Lisbon,
Portugal.
154
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
9
1
9
2
3
3
6
8
/
/
t
l
a
c
_
a
_
0
0
2
5
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Chih-Kuan Yeh, Wei-Chieh Wu, Wei-Jen Ko, and
Yu-Chiang Frank Wang. 2018. Learning deep
latent spaces for multi-label classification. In
Proceedings of the 32nd AAAI Conference on
Artificial Intelligence, New Orleans, USA.
Xiang Zhang, Junbo Zhao, and Yann LeCun. 2015.
Character-level convolutional networks for text
classification. In Advances in Neural Infor-
mation Processing Systems 28, pages 649–657,
Montreal, Canada.
Yang Zhang, Boqing Gong, and Mubarak Shah.
2016. Fast zero-shot image tagging. In Proceed-
ings of the IEEE Conference on Computer Vision
and Pattern Recognition, Las Vegas, USA.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
5
9
1
9
2
3
3
6
8
/
/
t
l
a
c
_
a
_
0
0
2
5
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
155