Gains and Losses Affect Learning Differentially at Low and
High Attentional Load
Kianoush Banaie Boroujeni1, Marcus Watson2, and Thilo Womelsdorf1
Abstract
■ Prospective gains and losses influence cognitive processing,
but it is unresolved how they modulate flexible learning in
changing environments. The prospect of gains might enhance
flexible learning through prioritized processing of reward-
predicting stimuli, but it is unclear how far this learning benefit
extends when task demands increase. Similarly, experiencing
losses might facilitate learning when they trigger attentional
reorienting away from loss-inducing stimuli, but losses may also
impair learning by increasing motivational costs or when nega-
tive outcomes are overgeneralized. To clarify these divergent
views, we tested how varying magnitudes of gains and losses
affect the flexible learning of feature values in environments
that varied attentional load by increasing the number of inter-
fering object features. With this task design, we found that
larger prospective gains improved learning efficacy and learning
speed, but only when attentional load was low. In contrast,
expecting losses impaired learning efficacy, and this impairment
was larger at higher attentional load. These findings functionally
dissociate the contributions of gains and losses on flexible
learning, suggesting they operate via separate control mecha-
nisms. One mechanism is triggered by experiencing loss and
reduces the ability to reduce distractor interference, impairs
assigning credit to specific loss-inducing features, and decreases
efficient exploration during learning. The second mechanism is
triggered by experiencing gains, which enhances prioritizing
reward-predicting stimulus features as long as the interference
of distracting features is limited. Taken together, these results
support a rational theory of cognitive control during learning,
suggesting that experiencing losses and experiencing distractor
interference impose costs for learning. ■
INTRODUCTION
Anticipating gains or losses have been shown to enhance
the motivational saliency of information (Failing &
Theeuwes, 2018; Berridge & Robinson, 2016; Yechiam &
Hochman, 2013b). Enhanced motivational saliency can be
beneficial when learning about the behavioral relevance of
visual objects. Learning which objects lead to higher gains
should enhance the likelihood in choosing those objects
in the future to maximize rewards, whereas learning which
objects lead to loss should enhance avoiding those objects
in the future to minimize loss (Collins & Frank, 2014; Maia,
2010). Although these scenarios are plausible from a ratio-
nal point of view, empirical evidence suggests more com-
plex consequences of gains and losses for adaptive
learning.
Prospective gains are generally believed to facilitate
learning and attention to reward predictive stimuli. But
most available evidence is based on tasks using simple
stimuli, leaving open whether the benefit of gains gener-
alizes to settings with more complex multidimensional
objects that have high demands on cognitive control.
With regard to losses, there is conflicting evidence with
some studies showing benefits and others showing dete-
rioration of performance when subjects experience or
1Vanderbilt University, Nashville, TN, 2York University, Toronto,
Canada
© 2022 Massachusetts Institute of Technology
anticipate losses (see below). It is not clear whether these
conflicting effects of loss are due to a U-shaped depen-
dence of loss effects on performance with only intermedi-
ate levels having positive effects ( Yechiam, Ashby, &
Hochman, 2019; Yechiam & Hochman, 2013a), or
whether experiencing loss might lead to a generalized
reorientation away from loss-inducing situations, which
in some task contexts impairs the encoding of the precise
features of the loss-inducing event (Barbaro, Peelen, &
Hickey, 2017; Laufer, Israeli, & Paz, 2016; McTeague, Gruss,
& Keil, 2015).
Distinguishing these possible effects of gains and losses
on flexible learning therefore requires experimental
designs that vary the complexity of the task, in addition
to varying the amount of gains and losses. Such an exper-
imental approach would allow to possibly discern an
inverted U-shaped effect of the magnitude of gains and
losses on learning, while also clarifying limitations of gains
and losses in supporting flexible learning at higher levels of
task complexity. Here, we propose such an experiment to
identify how gains and losses improve or impair flexible
learning at systematically increasing attentional demands.
It is widely believed that prospective gains improve
attention to reward predicting stimuli, which predicts that
learning about stimuli should be facilitated by increasing
their prospective gains. According to this view, anticipat-
ing gains acts as an independent top–down mechanism
Journal of Cognitive Neuroscience 34:10, pp. 1952–1971
https://doi.org/10.1162/jocn_a_01885
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
3
4
1
0
1
9
5
2
2
0
4
1
8
6
3
/
/
j
o
c
n
_
a
_
0
1
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
for attention, which has been variably described as “value-
based attentional guidance” (Anderson, 2019; Theeuwes,
2019; Wolfe & Horowitz, 2017; Bourgeois, Chelazzi, &
Vuilleumier, 2016), “attention for liking” (Gottlieb, 2012;
Hogarth, Dickinson, & Duka, 2010), or “attention for
reward” (San Martin, Appelbaum, Huettel, & Woldorff,
2016). These attention frameworks suggest that stimuli
are processed quicker and with higher accuracy when they
become associated with positive outcomes (Barbaro et al.,
2017; Hickey, Kaiser, & Peelen, 2015; Schacht, Adler,
Chen, Guo, & Sommer, 2012). The effect of anticipating
gains can be adaptive when the gain-associated stimulus
is a target for goal-directed behavior, but it can also dete-
riorate performance when the gain-associated stimulus is
distracting or task irrelevant, in which case it attracts
attentional resources away from more relevant stimuli
(Chelazzi, Marini, Pascucci, & Turatto, 2019; Noonan,
Crittenden, Jensen, & Stokes, 2018).
Compared with gains, the behavioral consequences of
experiencing or anticipating loss are often described in
affective and motivational terms rather than in terms of
attentional facilitation or impediment (Dunsmoor & Paz,
2015). An exception to this is the so-called loss attention
framework that describes how losses trigger shifts in atten-
tion to alternative options and thereby improve learning
outcomes ( Yechiam & Hochman, 2013a, 2014). The loss
attention framework is based on the finding that
experiencing loss causes a vigilance effect that triggers
enhanced exploration of alternative options (Lejarraga &
Hertwig, 2017; Yechiam & Hochman, 2013a, 2013b,
2014). The switching to alternative options following aver-
sive loss events can be observed even when the expected
values of the available alternatives are controlled for and
the switching away is not explained away by an affective
loss aversion response as subject with higher or lower loss
aversion both show loss-induced exploration (Lejarraga &
Hertwig, 2017). According to these insights, experiencing
loss should improve adaptive behavior by facilitating
avoidance of bad options. Consistent with this view,
humans and monkeys have been shown to avoid looking
at visual objects paired with unpleasant consequences
(such as a bitter taste or a monetary loss; Schomaker,
Walper, Wittmann, & Einhauser, 2017; Ghazizadeh,
Griggs, & Hikosaka, 2016; Raymond & O’Brien, 2009).
What is unclear, however, is whether loss-triggered
shifts of attention away from a stimulus reflects an unspe-
cific reorienting away from a loss-evoking situation or
whether it also affects the precise encoding of the loss-
inducing stimulus. The empirical evidence about this
question is contradictory with some studies reporting bet-
ter encoding and memory for loss-evoking stimuli and
other studies reporting poorer memory and insights about
the precise stimuli that triggered the aversive outcomes.
Evidence of a stronger memory representation of aversive
outcomes comes from studies reporting increased detec-
tion speed of stimuli linked to threat-related aversive out-
comes such as electric shocks (Ahs, Miller, Gordon, &
Lundstrom, 2013; Li, Howard, Parrish, & Gottfried,
2008), painful sounds (Rhodes, Ruiz, Rios, Nguyen, &
Miskovic, 2018; McTeague et al., 2015), threat-evoking
air puffs (Ghazizadeh et al., 2016), or fear-evoking images
(Ohman, Flykt, & Esteves, 2001). In these studies, subjects
were faster or more accurate in responding to stimuli that
were associated with aversive outcomes. The improved
responding to these threat-related, aversive stimuli indi-
cates that those stimuli are better represented than neutral
stimuli and hence can guide adaptive behavior away from
them. Notably, such a benefit is not restricted to threat-
related aversive stimuli but can also be seen in faster RTs
to stimuli associated with the loss of money, which is a
secondary “learned” reward (Suarez-Suarez, Holguin,
Cadaueira, Nobre, & Doallo, 2019; Bucker & Theeuwes,
2016; Small et al., 2005). For example, in an object-in-
scene learning task, attentional orienting to the incorrect
location was faster when subjects lost money for the
object at that location in prior encounters compared with
a neutral or positive outcome (Suarez-Suarez et al., 2019;
Doallo, Patai, & Nobre, 2013). Similarly, when subjects are
required to discriminate a peripherally presented target
object, they detect the stimulus faster following a short
(20 msec) spatial precue when the cued stimulus is linked
to monetary loss (Bucker & Theeuwes, 2016). This faster
detection was similar for monetary gains, indicating that
gains and losses can have near-symmetric, beneficial
effects on attentional capture. A similar benefit for loss-
as well as gain-associated stimuli has also been reported
when stimuli are presented briefly and subjects have to
judge whether the stimulus had been presented before
(O’Brien & Raymond, 2012). The discussed evidence
suggests that loss-inducing stimuli have a processing
advantage for rapid attentional orienting and fast per-
ceptual decisions even when the associated loss is a
secondary reward like money. However, whether this
processing advantage for loss-associated stimuli can be
used to improve flexible learning and adaptive behavior
is unresolved.
An alternate set of studies contradicts the assumption
that experiencing loss entails processing advantages by
investigating not the rapid orienting away from aversive
stimuli but the fine perceptual discrimination of stimuli
associated with negative outcomes (Shalev, Paz, & Avidan,
2018; Laufer et al., 2016; Laufer & Paz, 2012; Resnik, Laufer,
Schechtman, Sobel, & Paz, 2011; Schechtman, Laufer, &
Paz, 2010). In these studies, anticipating the loss of
money did not enhance but systematically reduced the
processing of loss-associated stimuli, causing impaired
perceptual discriminability and reduced accuracy, even
when this implied losing money during the experiment
(Shalev et al., 2018; Barbaro et al., 2017; Laufer et al.,
2016; Laufer & Paz, 2012). For example, losing money
for finding objects in natural scenes reduces the success
rate of human subjects to detect those objects compared
with searching for objects that promise gains (Barbaro
et al., 2017). One important observation in these studies
Boroujeni, Watson, and Womelsdorf
1953
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
3
4
1
0
1
9
5
2
2
0
4
1
8
6
3
/
/
j
o
c
n
_
a
_
0
1
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
is that the detrimental effect of losses is not simply
explained away by an overweighting of losses over gains,
which would be suggestive of an affective loss aversion
mechanism (Laufer & Paz, 2012). Rather, this literature
suggests that stimuli linked to monetary loss outcomes
are weaker attentional targets compared with neutral
stimuli or gain-associated stimuli. This weaker represen-
tation can be found with multiple types of aversive out-
comes, including when stimuli are associated with
monetary loss (Laufer et al., 2016; Laufer & Paz, 2012),
unpleasant odors (Resnik et al., 2011), or electric shock
(Shalev et al., 2018). One possible mechanism underlying
this weakening of stimulus representations following
aversive experience is that aversive outcomes are less
precisely linked to the stimulus causing the outcome.
According to this account, the credit assignment of an
aversive outcome might generalize to other stimuli that
share attributes with the actual stimulus whose choice
caused the negative outcome. Such a generalized assign-
ment of loss can have positive as well as negative conse-
quences for behavioral performance (Laufer et al., 2016;
Dunsmoor & Paz, 2015). It can lead to faster detection of
stimuli associated with loss, including monetary loss, in
situations that are similar to the original aversive situation
without requiring recognizing the precise object instance
that was causing the initial loss. This may lead to enhanced
learning in situations in which the precise stimulus features
are not critical. However, the wider generalization of
loss outcomes will be detrimental in situations that
require the precise encoding of the object instance that
gave rise to loss.
In summary, the surveyed empirical evidence suggests
a complex picture about how losses may influence adap-
tive behavior and flexible learning. On the one hand,
experiencing or anticipating loss may enhance learning
when it triggers attention shifts away from the loss-
inducing stimulus and when it enhances fast recognition
of loss-inducing stimuli to more effectively avoid them.
But on the other hand, evidence suggests that associating
loss with a stimulus can impair learning when the task
demands require precise insights about the loss-inducing
stimulus features, because these features may be less well
encoded after experiencing losses than gains, which will
reduce their influence on behavior or attentional guid-
ance in future encounters of the stimulus.
To understand which of these scenarios hold true, we
designed a learning task that varied two main factors. First,
we varied the magnitude of gains and losses to understand
whether the learning effects depend on the actual
gain/loss magnitudes. This factor was only rarely manipu-
lated in the discussed studies. To achieve this, we used a
token reward system in which subjects received tokens for
correct and lost tokens for incorrect choices. Second, we
varied the demands of attention (attentional load) by
requiring subjects to search for the target feature in
objects that varied nonrewarded, that is, distracting fea-
tures in either only one dimension (e.g., different colors),
or in two or three dimensions (e.g., different colors, body
shapes, and body pattern) when searching for the
rewarded feature. The variation of the object feature
dimensionality allows testing whether losses and gains dif-
ferentially facilitate or impair learning at varying atten-
tional processing load.
With this task design, we found across four rhesus mon-
keys, first, that expecting larger gains enhanced the effi-
cacy of learning targets at lower attentional loads, but
not at the highest attentional load. Second, we found
that experiencing loss generally decreased flexible learn-
ing, that larger losses exacerbate this effect, and that the
loss induced learning impairment is worse at high atten-
tional load.
Our study uses nonhuman primates as subjects to
establish a robust animal model for understanding the
influence of gains and losses on learning in cognitive
tasks with translational value for humans as well as other
species (e.g., see Yee, Leng, Shenhav, & Braver, 2022,
for a recent review). Establishing this animal model will
facilitate future studies about the underlying neurobio-
logical mechanisms. Leveraging this animal model is
possible because nonhuman primates readily under-
stand a token reward/punishment system similar to
humans and can track sequential gains and losses of
assets before cashing them out for primary (e.g., juice)
rewards (Taswell, Costa, Murray, & Averbeck, 2018; Rich
& Wallis, 2017; Seo & Lee, 2009; Shidara & Richmond,
2002).
METHODS
Experimental Procedures
All animal-related experimental procedures were in accor-
dance with the National Institutes of Health Guide for the
Care and Use of Laboratory Animals and the Society for
Neuroscience Guidelines and Policies and approved by
the Vanderbilt University Institutional Animal Care and
Use Committee.
Four pair-housed male macaque monkeys (8.5–14.4 kg,
6–9 years of age) were allowed separately to enter an apart-
ment cage with a custom-built, cage-mounted touch-
screen Kiosk-Cognitive-Engagement Station to engage
freely with the experimental task for 90–120 min per
day. The Kiosk-Cognitive-Engagement Station substituted
the front panel of an apartment cage with a 30-cm
recessed, 21-in. touchscreen and a sipper tube protruding
toward the monkey at a distance of ∼33 cm and a height
that allows animals sitting comfortably in front of the sip-
per tube with the touchscreen in reaching distance.
Details about the Kiosk Station and the training regime
are provided in Womelsdorf, Thomas, et al. ( 2021). In
brief, all animals underwent the same training regimes
involving learning to touch, hold, and release touch in a
controlled way at all touchscreen locations. Then animals
learned visual detection and discrimination of target
1954
Journal of Cognitive Neuroscience
Volume 34, Number 10
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
3
4
1
0
1
9
5
2
2
0
4
1
8
6
3
/
/
j
o
c
n
_
a
_
0
1
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
stimuli among increasingly complex nonrewarded dis-
tracting objects, with correct choices rewarded with fluid.
Objects were three-dimensionally rendered so-called
Quaddles that have a parametrically controllable feature
space, varying along four dimensions, including the color,
body shape, arm type, and surface pattern ( Watson,
Voloh, Naghizadeh, & Womelsdorf, 2019). Throughout
training, one combination of features was never rewarded
and hence termed “neutral,” which was the spherical, uni-
form, gray Quaddle with straight, blunt arms (Figure 1C).
Relative to the features of the neutral object, we could
then increase the feature space for different experimental
conditions by varying from trial-to-trial features from only
one, two, or three dimensions relative to the neutral object.
After monkeys completed the training for immediate fluid
reward upon a correct choice, a token history bar was
introduced and shown on the top of the monitor screen,
and animals performed the feature-learning task for
receiving tokens until they filled the token history bar with
5 tokens to cash out for fluid reward (Figure 1A). All
animals effortlessly transitioned from immediate fluid
reward delivery for correct choices to the token-based
reward schedules.
The visual display, stimulus timing, reward delivery, and
registering of behavioral responses was controlled by the
Unified Suite for Experiments, which integrates an IO-
controller board with a Unity3D video engine-based con-
trol for displaying visual stimuli, controlling behavioral
responses, and triggering reward delivery ( Watson, Voloh,
Thomas, Hasan, & Womelsdorf, 2019).
Task Paradigm
The task required monkeys to learn a target feature in
blocks of 35–60 trials by choosing one among three
objects, each composed of multiple features (Figure 1A–
C). At the beginning of each trial, a blue square with a
side length of 3.5 cm (3° radius wide) appeared on the
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
3
4
1
0
1
9
5
2
2
0
4
1
8
6
3
/
/
j
o
c
n
_
a
_
0
1
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
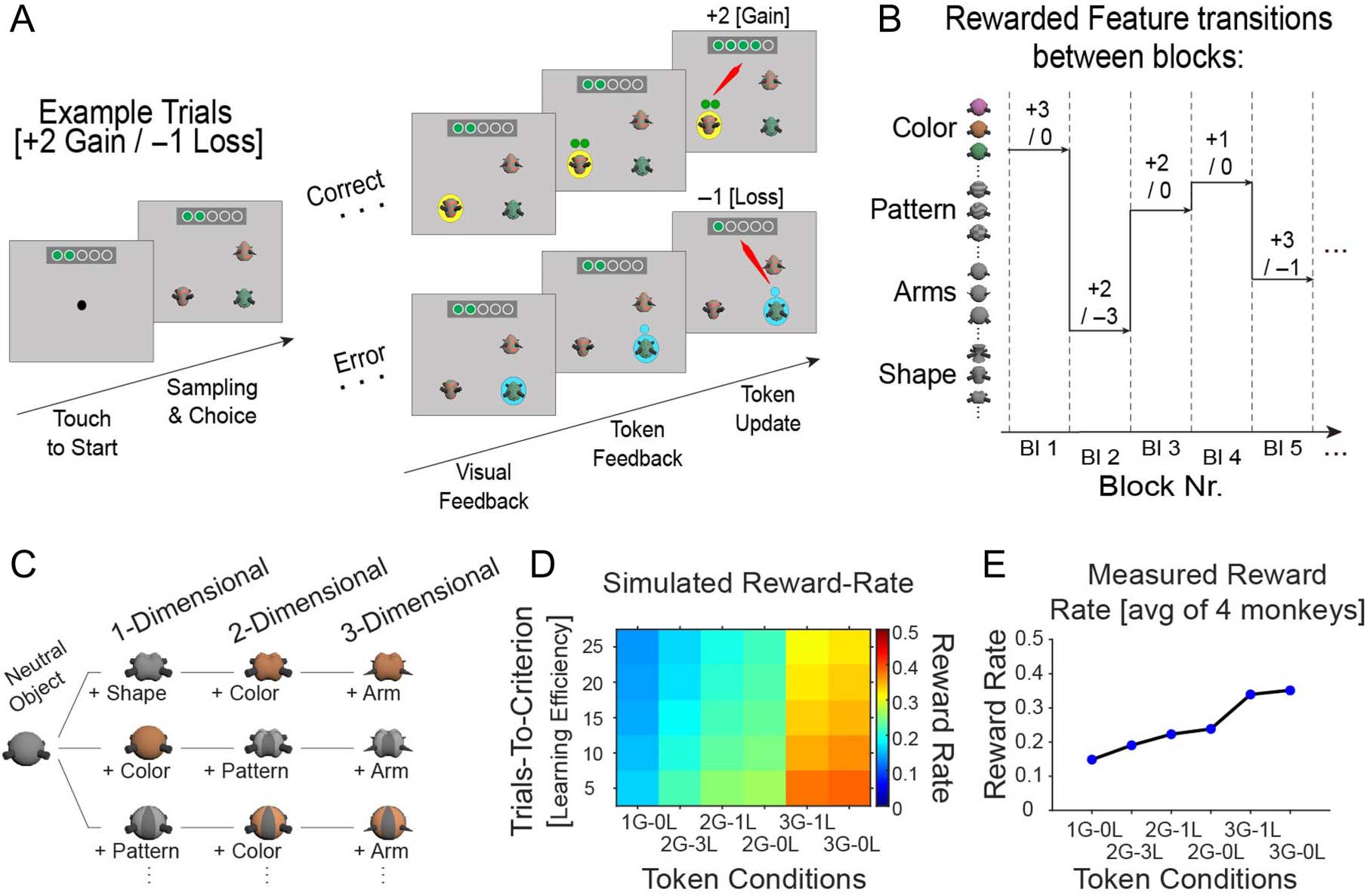
Figure 1. Task paradigm varying attentional load and token gains and losses. (A) The trial sequence starts with presenting three objects. The monkey
chooses one by touching it. Following a correct choice, a yellow halo provides visual feedback, then green tokens are presented above the stimulus
for 0.3 sec before they are animated to move upward toward the token bar where the gained tokens are added. Following an error trial visual
feedback is cyan, then empty token(s) indicate the amount of tokens that will be lost (here: −1 token). The token update moves the empty token to
the token bar where green tokens are removed from the token bar. When ≥5 tokens have been collected, the token bar blinks red/blue, three drops
of fluid are delivered, and the token bar reset. (B) Over blocks of 35–60 trials, one object feature (here: in rows) is associated with either 1, 2, or 3
token gains, whereas objects with other features are linked to either, 0, −1, or − 3 token loss. (C) Attentional load is varied by increasing the number
of features that define objects. The 1-D load condition presents objects that vary in only one feature dimension relative to a neutral object, the 2-D
load varies features of two feature dimensions, and the 3-D load condition varies three feature dimensions. For example, a 3-D object has different
shapes, colors, and arm types across trials (but the same neutral pattern). (D) Simulation of the expected reward rate animals receive with different
combinations of token gains and losses (x-axis) given different learning speed of the task ( y-axis). (E) Actual reward rates ( y-axis) for different token
conditions (x-axis) based on their learning speed across four monkeys.
Boroujeni, Watson, and Womelsdorf
1955
screen. To start a new trial, monkeys were required to
touch and hold the square for 500 msec. Within 500 msec
after touching the blue square, three stimuli appeared on
the screen at three out of four possible locations with an
equal distance from the screen center (10.5 cm, 17°
eccentricity). Each stimulus had a diameter of 3 cm
(∼2.5° radius wide) and was horizontally and vertically
separated from other stimuli by 15 cm (24°). To select
a stimulus, monkeys were required to touch the object
for a duration longer than 100 msec. If a touch was not
registered within 5 sec after the appearance of the stim-
uli, the trial was aborted and a new trial was started with
stimuli that differed from those of the aborted trial.
Each experimental session consisted of 36 learning
blocks. Four monkeys (B, F, I, and S) performed the task
and completed 33/1166, 30/1080, 30/1080, and 28/1008
sessions/blocks, respectively. We used a token-reward-
based multidimensional attention task in which monkeys
were required to explore the objects on the screen and
determine through trial and error a target feature while
learning to ignore irrelevant features and feature dimen-
sions. Stimuli were multidimensional 3-D rendered Quad-
dles, which varied in one to three features relative to a
neutral Quaddle objects (Figure 1C) ( Watson, Voloh,
Naghizadeh, et al., 2019). The objects were 2-D-viewed
and had the same 3-D view orientation across trials. Four
different object dimensions/features were used in the task
design (shape, color, arm, and pattern). For each session
features from 1, 2, or 3 feature dimensions were used as
potential target and distractor features. In each learning
block, one feature was selected to be the correct target.
Attentional load was varied by increasing the number of
features that varied from trial to trial to be either 1 (e.g.,
objects varied only in shape), 2 (e.g., objects varied in
shape and patterns), or 3 (e.g., objects varied in shape,
patterns and color). The target feature was uncued and
had to be searched for through trial and error in each
learning block. The target feature remained the same
throughout a learning block. After each block, the target
feature changed, and monkeys had to explore again to
find out the newly rewarded feature. The beginning of a
new block was not explicitly cued but was apparent as the
objects in the new block had different feature values than
the previous block. Block changes were triggered ran-
domly after 35–60 trials.
Each correct touch was followed by a yellow halo
around the stimulus as visual feedback (for 500 msec),
an auditory tone, and a fixed number of animated tokens
traveling from the chosen object location to the token
bar on top of the screen (Figure 1A). Erroneously touch-
ing a distractor object was followed by a blue halo
around the touched objects, a low-pitched auditory feed-
back, and in the loss conditions traveling of one or three
empty (gray) tokens to the token bar where the number
of lost tokens were removed from the already earned
tokens as an error penalty (feedback timing was the
same as for correct trials). To receive a fluid reward, that
is, to cash out the tokens, monkeys had to complete 5
tokens in the token bar. When 5 tokens were collected,
the token bar flashed red/blue three times, a high pitch
tone was played as auditory feedback, and fluid was
delivered. After cashing out, the token bar was reset to
five empty token placeholders. Monkeys could not go in
debt, that is, no token could be lost when there was no
token on the token bar or carry over tokens when gained
tokens were more than what they needed to complete a
token bar. Every block began with an empty token bar.
To make sure subjects did not carry over collected
tokens in the bar when there was a block change, the
block change only occurred when the token bar was
empty.
Experimental Design
In each learning block, one fixed token reward schedule
was used, randomly drawn from seven distinct schedules
(see below). We simulated the token schedules to reach a
nearly evenly spaced difference in reward rate while not
confounding the number of positive or negative tokens
with reward rate (Figure 1D, E). For simulating the
reward rate with different token gains and losses, we
used a tangent hyperbolic function to simulate a typical
learning curve by varying the number of trials needed to
reach ≥75% accuracy from 5 to 25 trials (the so called
“learning trials” in a block). This is the range of learning
trials the subjects showed for the different attentional
load conditions in 90% of blocks. We simulated 1000
blocks of learning for different combinations of gained
and lost tokens for correct and erroneous choices,
respectively. For each simulated token combination,
the reward rate was calculated by dividing the frequency
of the full token bar to the block length. The average
reward rate was then computed as the average reward
rate over all simulation runs for each token condition.
The reward rate showed on average what is the probabil-
ity of receiving reward per trial. Seven token conditions
were designed with a combination of varying gain (G; 1,
2, 3, and 5) and loss (L; 3, 1, and 0) conditions (1G-0L,
2G-3L, 2G-1L, 2G-0L, 3G-1L, 3G-0L, and 5G-0L). The 5G-
0L condition entailed providing 5 tokens for a correct
choice and no tokens lost for incorrect choices. This
condition was used to provide animals with more oppor-
tunity to earn fluid reward than would be possible with
the conditions that have lower reward rate. Because
gaining 5 tokens was immediately cashed out for fluid
delivery, we do not consider this condition for the token
gain and token loss analysis as it confounds secondary
and primary reinforcement in single trials. We also did
not consider for analysis those blocks in which there
could be a loss of tokens (conditions with 1L or 3L),
but the loss of tokens was not experienced because
the subjects did not make erroneous choices that would
have triggered the loss.
1956
Journal of Cognitive Neuroscience
Volume 34, Number 10
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
3
4
1
0
1
9
5
2
2
0
4
1
8
6
3
/
/
j
o
c
n
_
a
_
0
1
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Overall, the subjects’ engagement in the task was not
affected by token condition with monkeys performing all
∼36 blocks that were made available to them in each daily
session and requiring on average ∼90 min to complete
∼1200 trials. On rare occasions, a monkey took a break
from the task as evident in an intertrial interval of
>1 min., in which case we excluded the affected block
from the analysis. This happened in less than 1% of
learning blocks. There were no significant differences
between mean intertrial intervals across different token
conditions.
Analysis of Learning
The improvement of accuracy over successive trials at
the beginning of a learning block reflects the learning
curve, which we computed with a forward-looking 10-
trial averaging window in each block (Figure 3A, C, E).
We defined learning in a block as the number of trials
needed to reach criterion accuracy of ≥75% correct trials
over 10 successive trials. Monkeys on average reached
learning criterion in >75% of blocks (B = 67%, F =
75%, I = 83%, and S = 74%; see Figure 4). We computed
“postlearning accuracy” as the proportion of correct
choices in all trials after the learning criterion was
reached in a block (Figure 8).
Statistical Analysis
We first constructed linear mixed effect (LME) models
(Pinherio & Bates, 1996) that tested how learning speed
(indexed as the learning trial [LT] at which criterion per-
formance was reached) and accuracy after learning (LT/
Accuracy) over blocks are affected by three factors,
attentional load (AttLoad) with three levels (1, 2, and 3
distractor feature dimensions), the factor feedback gain
(FbGain) with three levels (gaining tokens for correct per-
formance: 1, 2, or 3), and the factor feedback loss
(FbLoss) with three levels (loss of tokens for erroneous
performance: 0, −1, or −3). All three AttLoad, FbGain,
and FbLoss factors were entered in the LMEs as continu-
ous measure (ratio data). We additionally considered as
random effects the factor monkeys (Monkey) with four
levels (B, F, I, and S) and the factor target features (Feat)
with four levels (color, pattern, arm, and shape). The
random effects control for individual variations of learn-
ing and for possible biases in learning features of some
dimensions better or worse than others. This LME had
the form:
LT or Accuracy ¼ AttLoad þ FbGain þ FbLoss
ð
þ 1 Monkey
Þ þ 1 Feat
j
ð
j
Þ þ b þ ε
(1)
The model showed significant main effects of all three
factors, and random effects were inside the 95% confi-
dence interval. To test for the interplay of motivational
variables and attentional load, we extended the model
with the interaction effects for AttLoad × FbGain and
AttLoad × FbLoss to
LT or Accuracy ¼ AttLoad þ FbGain þ FbLoss þ AttLoad
(cid:2) FbGain þ AttLoad (cid:2) FbLoss
Þ þ 1 Feat
þ 1 Monkey
j
ð
ð
j
Þ þ b þ ε
(2)
To compare the model with and without interaction
terms, we used Bayesian information criterion (BIC) as
well as the Theoretical Likelihood Ratio Test (Hox,
2002) to decide which model explains the data best.
We also tested two additional models that tested
whether the absolute difference of FbGain and FbLoss
played a significant role in accounting for accuracy and
learning speed using (DiffGain-Loss = FbGain − FbLoss) as
predictor. Second, we tested the role of reward rate
(RR) as a predictor. We calculated RR as the grand aver-
age of how many times a token bar was completed
(reward delivery across all trials for each monkey)
divided by the overall number of trials having the same
attentional load and token condition. As an alternative
estimation of RR, we used the reward rate from our
averaged simulation (Figure 1E). LMEs, as formulated
in Equation 2, better fitted the data than models that
included the absolute difference, or either of the two
estimations of RR, as was evident in lower Akaike infor-
mation criterion (AIC) and BIC when these variables
were not included in the models (all comparisons are
summarized in Table 1). We thus do not describe these
factors further.
In addition to the block-level analysis of learning
and accuracy (Equations 1 and 2), we also investigated
level to quantify how accuracy and RTs
the trial
(Accuracy/RT ) of the monkeys over trials are modu-
lated by four factors. The first factor was the learning
status (LearnState) with two levels (before and after
reaching the learning criterion). In addition, we used
the factor attentional load (AttLoad) with three levels (1,
2, and 3 distracting feature dimensions), the factor feed-
back gain (FbGain) on the previous trial with three levels
(gaining tokens for correct performance: 1/2/3), and the
factor feedback loss on the previous trial (FbLoss) with
three levels (loss of tokens for erroneous performance:
0/−1/−3).
Accuracy or RT ¼ LearnState þ AttLoad þ FbGains
þ FbLoss þ ð1 j MonkeyÞ
þ 1 Feat
j
Þ þ b þ ε
ð
(3)
Equation 3 was also further expanded to account for
interaction terms AttLoad × FbGain and AttLoad × FbLoss.
To quantify the effectiveness of the token bar to
modulate reward expectancy, we predicted accuracy or
RT of the animals by how many tokens were already
Boroujeni, Watson, and Womelsdorf
1957
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
3
4
1
0
1
9
5
2
2
0
4
1
8
6
3
/
/
j
o
c
n
_
a
_
0
1
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Table 1. Model Comparisons for Different Control Conditions
Model
Models on All Conditions
RRstimulation
RRExperienced
DiffGain-Loss
FBGain FBLoss
BIC
21,210
21,203
21,165
21,146
Models on Fixed Gain: 2, Variable Loss: 0, −1, −3
RR
FBLoss
Models on Fixed Loss: −1, Variable Gain: 2,3
RR
FBGain
7462
7404
5723
5722
Models on Fixed Gain: 3, Variable Loss: 0, −1
RR
FBLoss
10,384
10,377
Models on Fixed Loss: 0, Variable Gain: 1, 2, 3
RR
FBGain
15,356
11,975
AIC
21,174
21,167
21,130
210,801
7433
7375
5695
5694
10,353
10,346
15,323
11,943
LR-Stat
−49.69
−42.35
−58.84
p
<.001
<.001
<.001
−58.20
<.001
−1.04
.14
−7.29
<.001
−3380
<.001
The last row in each table is the model with gain and/or loss feedback, compared with the other models. LR-Stat = likelihood ratio stat.
earned and visible in the token bar, using the factor
TokenState defined as the number tokens visible in the
token bar as formalized in Equation 4.
Accuracy or RT ¼ TokenState þ LearnState
þ AttLoad þ ð1 j MonkeyÞ
þ 1 Feat
j
Þ þ b þ ε
ð
(4)
We compared models with and without including the
factor TokenState. We then ran 500 simulations of likeli-
hood ratio tests and found that the alternative model that
included the factor TokenState had a better performance
than the one without the factor TokenState ( p = .009,
LRstat = 1073, BICToken_state = 198669, BICwithout Token_state =
199730, AICToken_state = 198598, AICwithout Token_state =
199670).
In separate control analyses, we tested how learning var-
ied when only conditions were considered that either only
had variable gains at a fixed loss, or that had variable losses
at the same, fixed gain (Figure 5). Similar to the above-
described models, these analyses resulted in statistically
significant main effects of FbGain, FbLoss, and attention
load on learning speed and RT (see Results). Also,
models with separate gain and loss feedback variables
remained superior to the models with RR or DiffGain-Loss
(Table 1).
We also tested LMEs that excluded trials in which sub-
jects experienced only a partial loss, that is, when an error
was committed in an experimental condition that involved
the subtraction of 3 tokens (e.g., in the 2G-3L condition)
but the subjects had accumulated only 2 tokens. We
tested an LME model on trial-level performance accuracy
but did not find differences in performance accuracy on
trials following partial versus full loss.
Analyzing the Interactions of Motivation and
Attentional Load
To evaluate the influence of increasing gains and increas-
ing losses on attentional load, we calculated the motiva-
tional modulation index (MMI) as a ratio scale indicating
the difference in learning speed (the trials-to-criterion)
1958
Journal of Cognitive Neuroscience
Volume 34, Number 10
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
4
1
0
1
9
5
2
2
0
4
1
8
6
3
/
/
j
o
c
n
_
a
_
0
1
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
in the conditions with 3 versus 1 token gain (MMIGain) or
in conditions with 3 versus 0 token losses (MMILoss) rela-
tive to their sum as written in Equation 5:
MMIGain ¼ LTG3 − LTG1
LTG3 þ LTG1
MMILoss ¼ LTL3 − LTL0
LTL3 þ LTL0
(5)
Both MMILoss and MMIgain were controlled for variations
of attention load. For each monkey, we fitted a linear
regression model (least squares), with attention load
regressor, and regressed out attention load variations on
learning speed (trial-to-criterion). We then calculated
MMIGain and MMILoss separately for the low, medium,
and high attentional load condition. We statistically
tested these indices under the null hypothesis that
MMIGain or MMILoss is not different from zero by perform-
ing pairwise t tests on each gain or loss condition given
low, medium, and high attentional load. We used false
discovery rate (FDR) correction of p values for depen-
dent samples with a significance level of .05 (Benjamini
& Yekutieli, 2005).
To further test the load dependency of MMIs, we used
a permutation approach that tested the MMI across
attentional load conditions. To control for the number
of blocks, we first randomly subsampled 1000 times
100 blocks from each feedback gain/loss condition and
computed the MMI for each subsample separately for
the feedback gain and for the feedback loss conditions
in each attentional load condition (MMIs in gain condi-
tions for 3G and 1G and in loss conditions for 3L and
1L). In each attentional load condition and for the feed-
back gain and feedback loss conditions, we separately
formed the sampling distribution of the means (1000
sample means of randomly selected 100 subsamples).
We then repeated the same procedure, but this time
across all attentional load conditions and sampled 1000
times to form a distribution of means while controlling
for equal numbers of blocks per load condition. Using
bootstrapping (DiCicio & Efron, 1996), we computed
the confidence intervals on the sampling distributions
across all loads with an alpha level of p = .05 (Bonferroni
corrected for family-wise error rate) under the null
hypothesis that the MMI distribution for each load condi-
tion is not different from the population of all load condi-
tions. These statistics are used in Figures 6 and 7 for the
interaction analysis of load and MMI on learning and
accuracy, respectively.
Analyzing the Immediate and Prolonged Effects of
Outcomes on Accuracy
To analyze the effect of token income on accuracy in both
immediate and prolonged time windows, we calculated
the proportion of correct trials after a given token gained
or lost on the next nth upcoming trials. We computed that
for high/low gains (3G and 1G) and losses (−3L and 0 L).
For each nth trial, we used Wilcoxon tests to separately
test whether the difference of the proportion of correct
responses between high and low gains (green lines in
Figure 8F) and high and low losses (red lines in
Figure 8F) were significantly different from zero (sepa-
rately for low and high attentional load conditions). After
extracting the p values for all 40 trials (20 trials for each
load condition), we corrected the p values by FDR correc-
tion for dependent samples with an alpha level of .05.
Trials significantly different from zero are denoted by
red/green horizontal lines for gain/ loss conditions
(Figure 9F).
RESULTS
Four monkeys performed a feature-reward learning task
and collected tokens as secondary reinforcers to be cashed
out for fluid reward when 5 tokens were collected. The
task required learning a target feature in blocks of 35–60
trials through trial-and-error by choosing one among
three objects composed of multiple different object fea-
tures (Figure 1A, B). Attentional
load was varied by
increasing the number of distracting features of these
objects to be either only from the same feature dimen-
sion as the rewarded target feature (1-D load), or addi-
tionally from a second feature dimension (2-D load), or
from a second and third feature dimension (3-D load;
Figure 1C). Orthogonal to attentional load, we varied
between blocks the number of tokens that were gained
for correct responses (1, 2, or 3 tokens) or that could
be lost for erroneous responses (0, −1, −3 tokens). We
selected combinations of gains and losses so that losses
were used in a condition with relatively high reward rate
(e.g., the condition with 3 tokens gained and 1 loss
token), whereas other conditions had lower reward rate
despite the absence of loss tokens (e.g., the condition
with 1 gain and 0 loss tokens). This arrangement
allowed studying the effect of losses relatively indepen-
dent of overall reward rate (Figure 1D, E).
During learning, monkeys showed slower choice RTs
the more tokens were already earned (Figure 2A, C).
This suggests that they tracked the tokens they obtained
and were more careful responding the more they had
earned in those trials in which they were not yet certain
about the rewarded feature. After they reached the learn-
ing criterion (during plateau performance), monkeys
showed faster RTs the more tokens they had earned
(Figure 2B, D). LME models including the variable
TokenState explained the RTs better than those without
TokenState variable, p = .009, LRstat = 1073, BICToken_state =
198669, BICwithout Token_state = 199730, AICToken_state =
198598, AICwithout Token_state = 199670 (Figure 2E).
On average, subjects completed 1080 learning blocks
(SE = 32, range = 1008–1166) in 30 test sessions (SE =
1, range = 28–33). All monkeys showed slower learning
load
of the target feature with increased attentional
(Figure 3A, B) and when experiencing losing more
Boroujeni, Watson, and Womelsdorf
1959
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
4
1
0
1
9
5
2
2
0
4
1
8
6
3
/
/
j
o
c
n
_
a
_
0
1
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
4
1
0
1
9
5
2
2
0
4
1
8
6
3
/
/
j
o
c
n
_
a
_
0
1
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
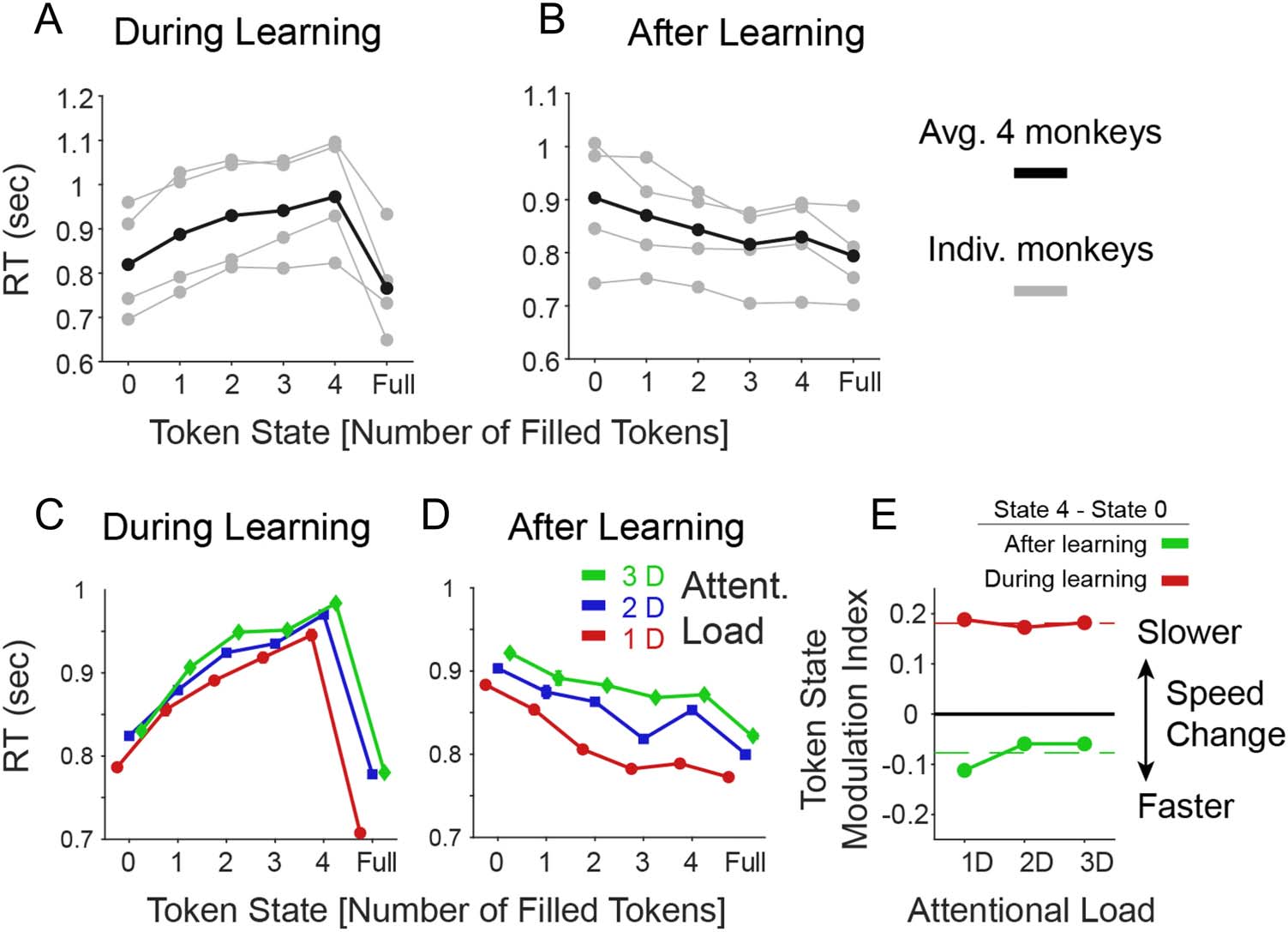
Figure 2. Effects of the number of earned tokens (“Token State”) on RTs. (A) Average RTs as a function of the number of earned tokens visible in
the token bar (x-axis) for individual monkeys (gray) and their average (in black). Included were only trials before reaching the learning criterion.
Over all trials, monkeys (B, F, I, and S) showed average RT of 785, 914, 938, and 733 msec, respectively. (B) Same as A, but including only trials after
the learning criterion was reached. (C–D) Same format as A–B, showing the average RTs across monkeys for the low, medium, and high attentional
load condition during learning (C) and after learning (E). (E) The Token State modulation index ( y-axis) shows the difference in RTs when the
animal had 4 tokens earned versus 1 token earned. During learning (red), RTs were slower with 4 than 1 earned tokens to similar degrees for
different attentional loads (x-axis). This pattern reversed after learning was achieved ( green). Dashed red lines show ground mean across all
attention loads.
tokens for incorrect responses (Figure 3E, F), and all
monkeys showed increased speed of learning the target
feature the more tokens they could earn for correct
responses (Figure 3C, D). The same result pattern was
evident for RTs (Figure 4A–C). The effects of load, loss,
and gains were evident in significant main effects of LME
models (see Methods, AttLoad: b = 4.37, p < .001; feed-
backLosses: b = 1.39, p ≤ .001; feedbackGains: b = −0.76,
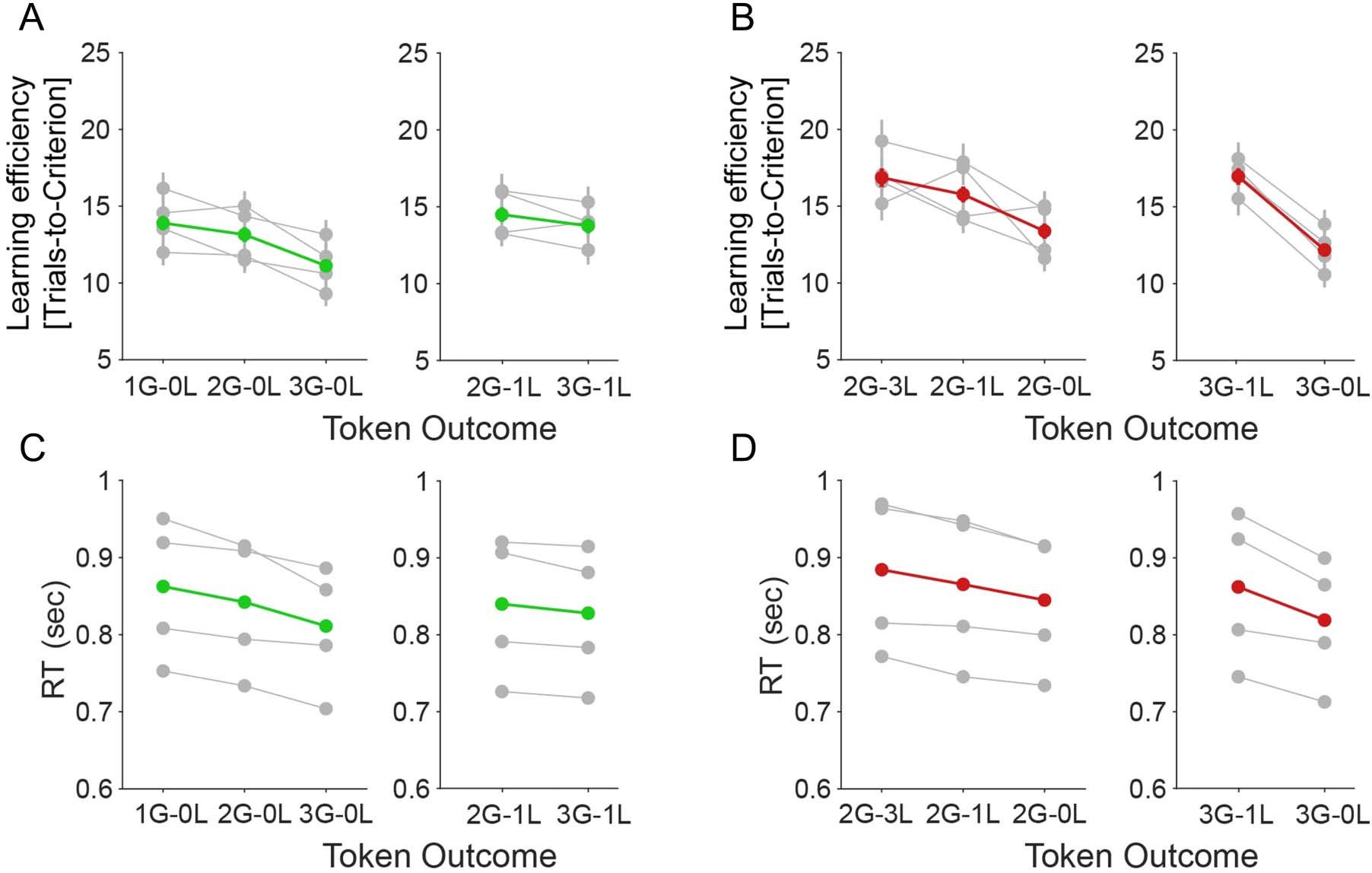
p = .008). As control analyses, we compared token con-
ditions with fixed losses (0 or − 1) and variable gains
(Figure 5B, D), and fixed gains (2G or 3G) and variable
losses (Figure 5A, C). We adjusted the LMEs for both RT
and learning speed. Similar to our previous observa-
tions, we found significant main effects of gain and loss
feedback on both RTs and learning speed (all feedback
variables had main effects at p < .001). We also tested
LMEs that included as factors the absolute differences of
gains and losses and the overall reward rate (estimated
as the received reward divided by the number of trials)
but found that models with these factors were inferior
to models without them (Table 1).
In all LME models, the factors monkeys (numbered 1–4)
and the target feature dimensions (arms, body shapes,
color, and surface pattern of objects) served as random
grouping effects. No significant random effects were
observed unless explicitly mentioned. We interpret the
main effects of attentional load, token gain, and token
loss as reflecting changes in the efficiency of learning
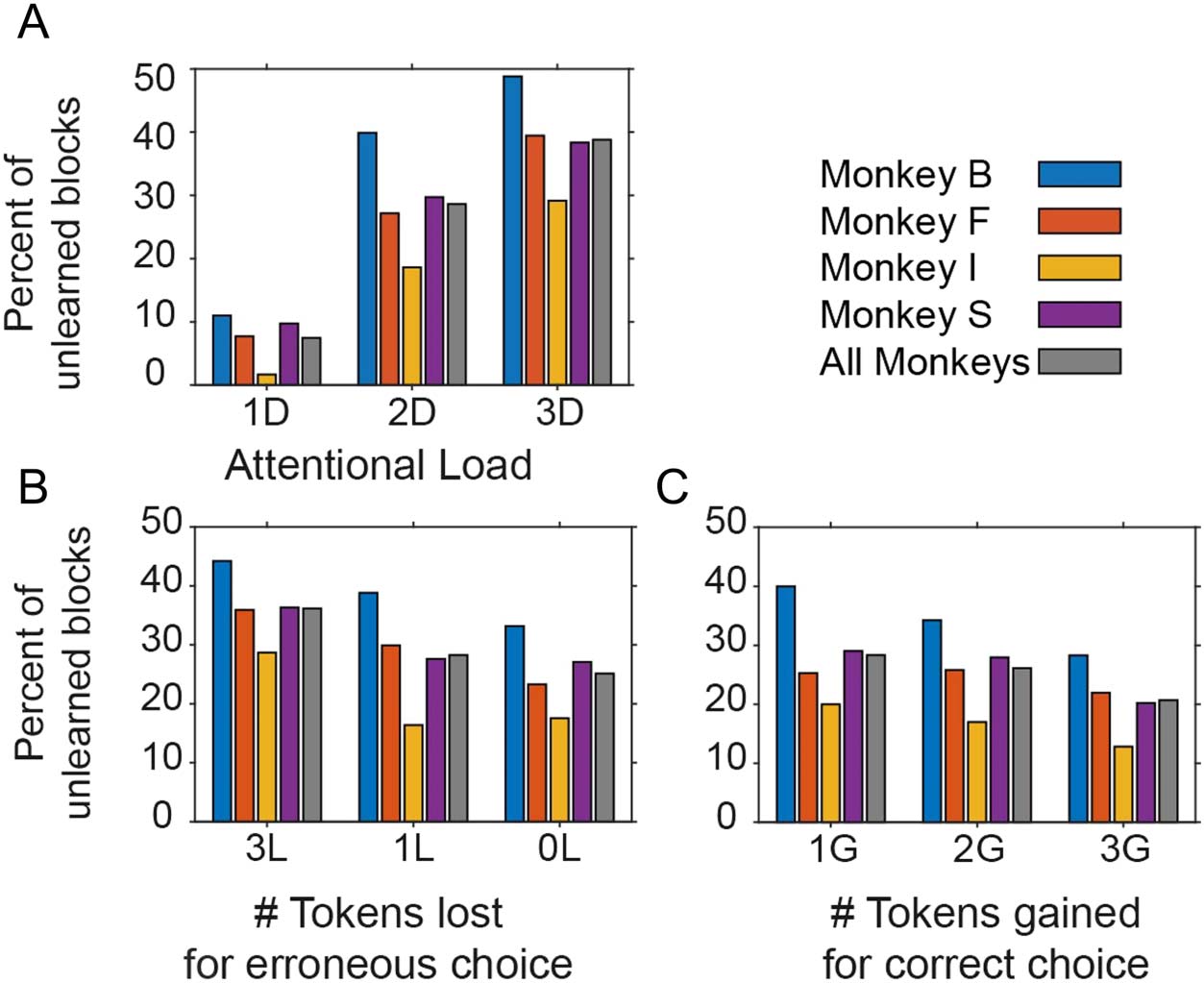
(Figure 3B, D, F and Figure 5A, B). Not only did mon-
keys learn faster at lower loads, when expecting less
losses, and when expecting higher gains, but they also
had fewer unlearned blocks under these same condi-
tions (Figure 6A–C).
The main effects of prospective gains and losses pro-
vide apparent support for a valence-specific effect of
motivational incentives and penalties on attentional effi-
cacy (Figure 7A). Because increasing losses impaired
rather than enhanced learning, they are not easily recon-
ciled with a “loss attention” framework that predicts that
both gains and losses should similarly enhance motiva-
tional saliency and performance (Figure 7A; Yechiam,
Retzer, Telpaz, & Hochman, 2015; Yechiam & Hochman,
2013b). However, the valence-specific effect was not
equally strong at low/medium/high attentional loads.
Although the effect of the loss magnitude interacted with
attentional load (b = −3.2, p = .012; Figure 7B), gain
magnitude and attentional load did not show a significant
interaction effect on learning (b = −0.13, p = .95, LMEs;
1960
Journal of Cognitive Neuroscience
Volume 34, Number 10
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
4
1
0
1
9
5
2
2
0
4
1
8
6
3
/
/
j
o
c
n
_
a
_
0
1
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
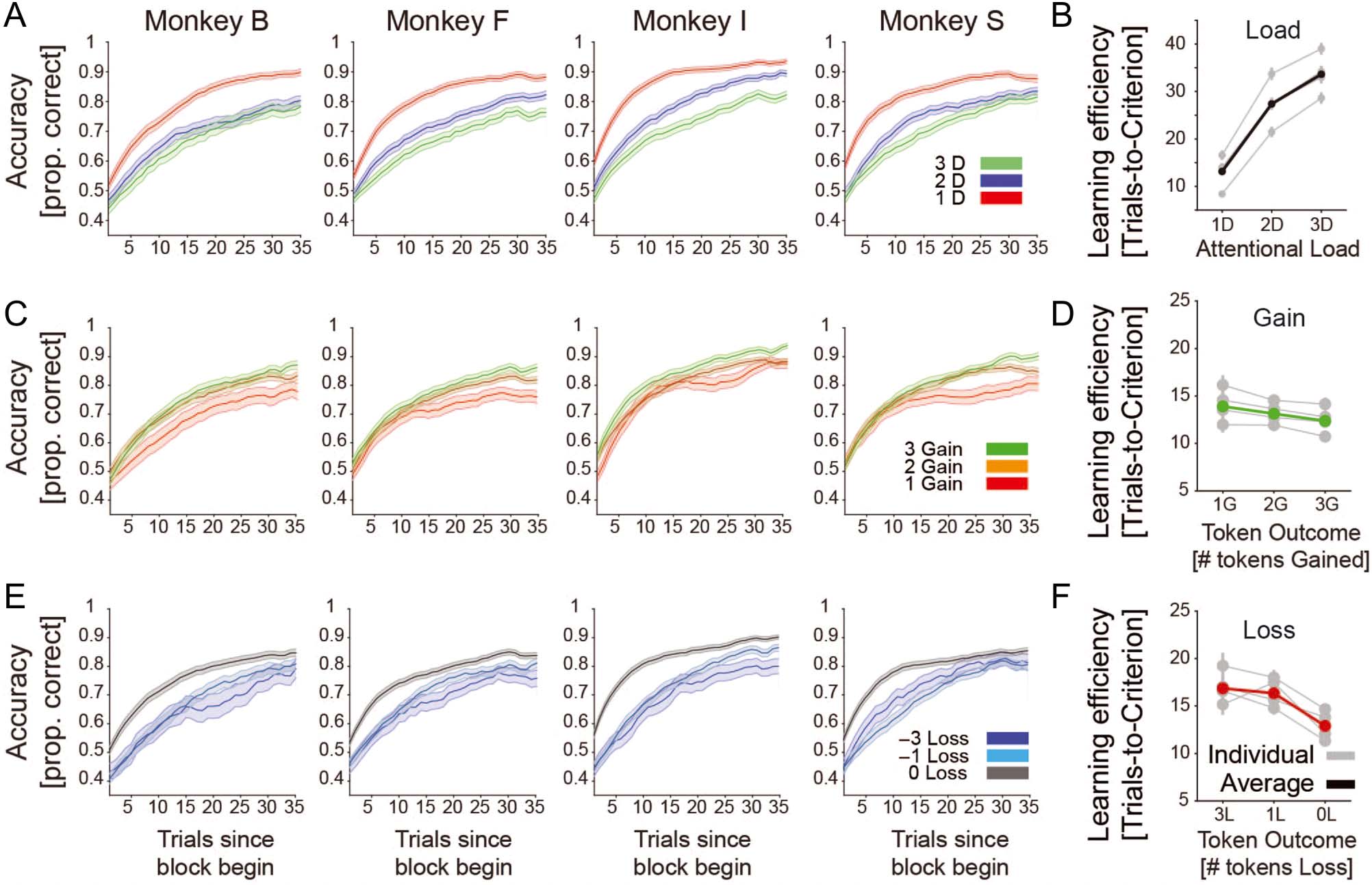
Figure 3. Average learning curves for each monkey and load, loss, and gain conditions. (A) The proportion correct performance ( y-axis) for
low/medium/high attentional load for each of four monkeys relative to the trial since the beginning of a learning block (x-axis). (B) The number of
trials-to-reach criterion ( y-axis) for low/medium/high attentional load (x-axis) for each monkey (in gray) and their average (in black). (C) Same as A
showing the learning for blocks in which 1, 2, or 3 tokens were gained for correct performance. Red line shows average across monkeys. (D) Same as
B for blocks where monkeys expected to lose 0, 1, or 3 tokens for incorrect choices. (E) Same as A and B, showing the learning for blocks in which 0,
1, or 3 tokens were lost for incorrect performance. Green line shows average across monkeys. Errors are SEs. (F) Same as B for blocks where
monkeys expected to win 1, 2, or 3 tokens for correct choices.
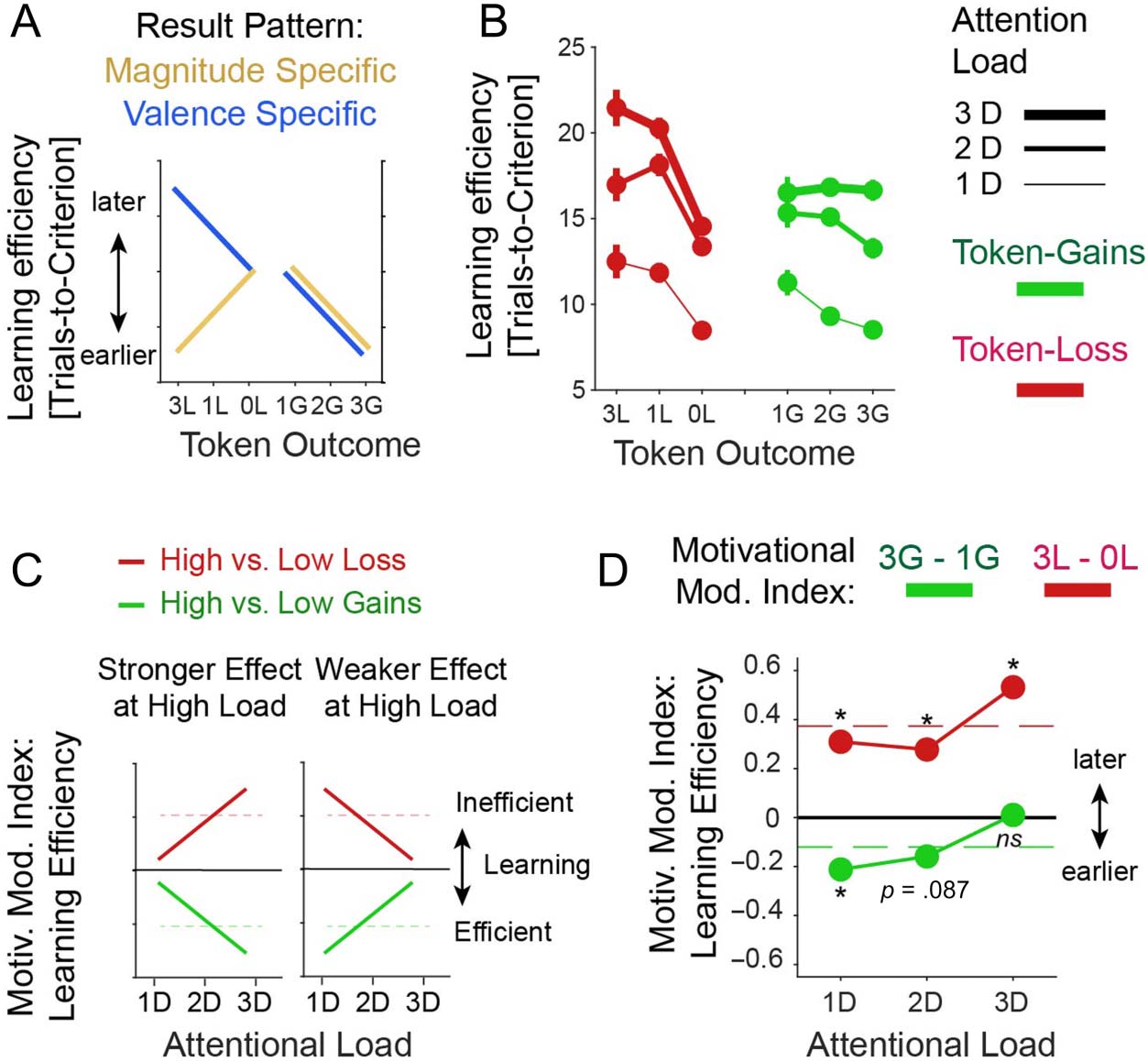
Figure 7B). We found that LME models with interaction
terms described the data better than without them
(likelihood ratio stat. = 60.2, p = .009, BIC = 21156
and 21184, and AIC = 21091 and 21143 for [AttLoad ×
( feedback L o ss e s + feedbackg a i n s)] and [AttL o a d +
feedbackLosses + feedbackgains], respectively). To visualize
these interactions, we calculated the MMI as the differ-
ence in learning efficacy (average number of trials-to-
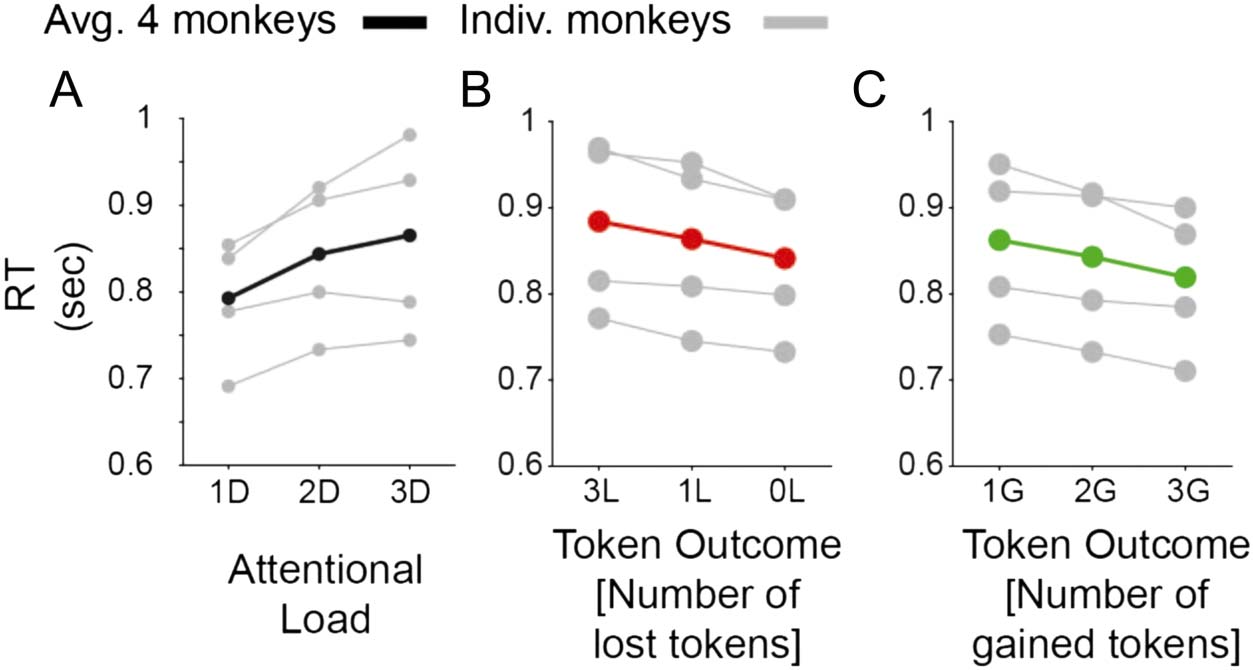
Figure 4. Main effects of
attentional load, number of
expected token-gains and
expected token-loss on and RT.
(A) The RTs ( y-axis) for
low/medium/high attentional
load (x-axis) for each monkey
(in gray) and their average (in
black). (B) Same as A for blocks
where monkeys expected to
lose 0, 1, or 3 tokens for
incorrect choices. (C) Same as B
for blocks where monkeys
expected to win 1, 2, or 3
tokens for correct choices.
Boroujeni, Watson, and Womelsdorf
1961
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
4
1
0
1
9
5
2
2
0
4
1
8
6
3
/
/
j
o
c
n
_
a
_
0
1
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5. Controlled analyses on main effects of expected token gains/loss when token loss/gain held fixed on learning speed and RT. (A) The
learning speed ( y-axis) for variable gains for fixed losses of 0 (left) and −1 (right). (B) The learning speed ( y-axis) for variable losses for fixed gains
of two (left) and three (right). low/medium/high attentional load (x-axis) for each monkey (in gray) and their average (in green). (C) The RT ( y-axis)
for variable gains for fixed losses of 0 (left) and −1 (right). (D) The RT ( y-axis) for variable losses for fixed gains of 2 (left) and 3 (right).
criterion) when expecting to gain 3 versus 1 token for
correct choices [MMIGains = Lefficacy3G − Lefficacy1G]
and when experiencing losing 3 versus 0 tokens for incor-
rect choices [MMILoss = Lefficacy3L − Lefficacy0L]. By
calculating the MMI for each attentional load condition,
we can visualize whether the motivation effect of
increased prospective gains and losses increased or
decreased with higher attentional load (Figure 7C). We
Figure 6. Proportion of
unlearned blocks across
conditions. (A) The number of
unlearned blocks ( y-axis) for
low/medium/high attentional
load (x-axis) for each monkey
(in color) and their average
(in gray). (B, C) Same as
(A) for loss (B) and for the gain
conditions (C).
1962
Journal of Cognitive Neuroscience
Volume 34, Number 10
Figure 7. The effect of
attentional load and expected
token gain/loss on learning
efficacy. (A) A magnitude-
specific hypothesis (orange)
predicts that learning efficacy is
high (learning criterion is
reached early) when the
absolute magnitude of expected
loss (to the left) and expected
gains (to the right) is high. A
valence-specific hypothesis
(blue) predicts that learning
efficacy is improved with high
expected gains (to the right)
and decreased with larger
penalties/losses. (B) Average
learning efficacy across four
monkeys at low/medium/high
attentional load (line thickness)
in blocks with increased
expected token-loss (to the left,
in red) and with increased
expected token gains (to the
right, green). (C) Hypothetical
interactions of expected
gains/losses and attentional
load. Larger incentives/penalties
might have a stronger
positive/negative effect at
higher load (left) or a weaker effect at higher load (right). The predictions can be quantified with the MMI, which is the difference of learning efficacy
for the high versus low gains conditions (or high vs. low loss conditions). (D) Average MMI shows that the slowing effect of larger penalties increased
with higher attentional load (red). In contrast, the enhanced learning efficacy with higher gain expectations are larger at lower attentional load and
absent at high attentional load (green). Dashed red lines show ground mean across all attention loads.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
4
1
0
1
9
5
2
2
0
4
1
8
6
3
/
/
j
o
c
n
_
a
_
0
1
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
found that the detrimental effect of larger prospective
losses on learning increased with attentional load,
causing a larger decrease in learning efficacy at high load
(Figure 7D; permutation test, p < .05). In contrast,
expecting higher gains improved learning most at
low attentional load and had no measurable effect at high
load (Figure 7D; permutation test, p < .05). Pairwise t-test
comparisons confirmed that MMILoss was significantly dif-
ferent from zero ( p < .001, df = 928, tstat = −3.83; p =
.007, df = 771, tstat = −2.70; and p < .001, df = 601,
tstat = −3.95 for low, medium, and high load), whereas
MMIGains was only significantly different from zero in the
low load gain condition ( p < .001, df = 579, tstat =
−3.39; p = .086, df = 450, tstat = −1.72; and p = .98,
df = 402, tstat = 0.02 for low, medium, and high load;
p values are FDR corrected for dependent samples with
an alpha level of .05).
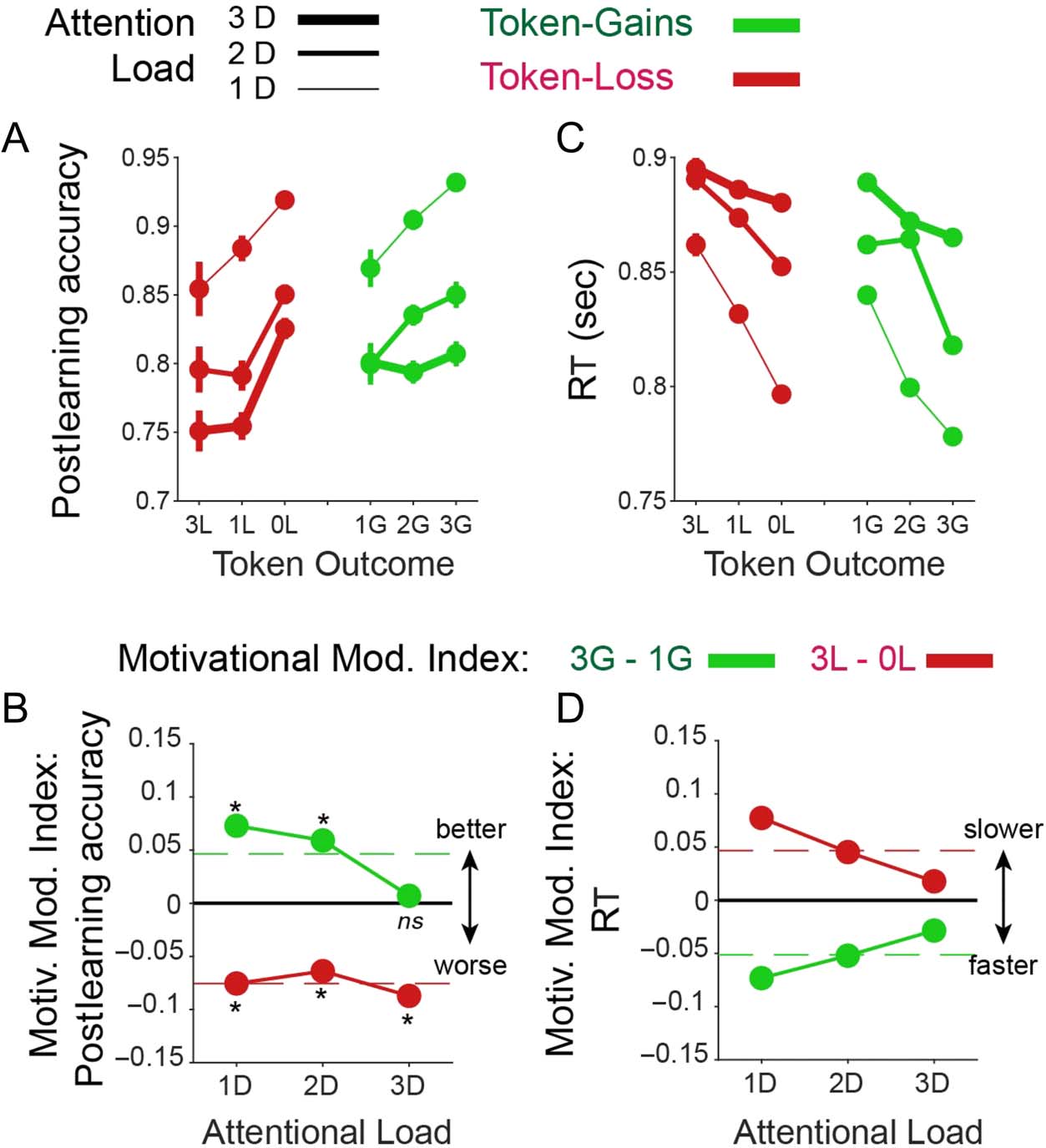
The contrasting effects of gains and losses on learning
efficiency were partly paralleled in postlearning accuracy
(Figure 8A, B). Accuracy was enhanced with larger
expected gains at lower but not at the highest attentional
load conditions (t-test pairwise comparison, p < .001, df =
579, tstat = 4.5; p = .011, df = 450, tstat = 2.56; and p =
.76, df = 402, tstat = 0.31 for low, medium, and high
load, respectively; FDR corrected for dependent samples
with an alpha level of .05) and accuracy was decreased
with larger expected losses at all loads (t-test pairwise com-
parison, p < .001, df = 928, tstat = 3.66; p = .013, df =
771, tstat = 2.48; and p = .005, df = 601, tstat = 2.78
for low, medium, and high load, respectively; FDR cor-
rected for dependent samples with an alpha level of .05).
This decrease was not modulated by load level (permuta-
tion test, p > .05; Figure 8A, B). In contrast to learning
speed and postlearning accuracy, RTs varied more
symmetrically across load conditions. At low attentional
load, choice times were fastest with larger expected
gains and with the smallest expected losses (Figure 8C,
D). At medium and higher attentional loads, these effects
were less pronounced. All MMIs were controlled for a
main effect of attentional load by regressing out attention
load variations on learning speed (trial-to-criterion; see
Methods).
To understand how prospective gains and losses
modulated learning efficiency on a trial-by-trial level,
we calculated the choice accuracy in trials immediately
after experiencing a loss of 3, 1, or 0 tokens and after
experiencing a gain of 1, 2, or 3 tokens. Experiencing
the loss of 3 tokens on average led to higher perfor-
mance in the subsequent trial when compared than
experiencing the loss of 0 or 1 token (Figure 9A). This
Boroujeni, Watson, and Womelsdorf
1963
Figure 8. The effect of
attentional load and token
gain/loss expectancy on
postlearning performance and
RTs. (A) Postlearning accuracy
( y-axis) when expecting varying
token loss (red) and gains
(green) at low/medium/high
attentional load (line
thickness). Overall, learning
efficiency decreased with larger
penalties and improved with
larger expected token-gains.
(B) The motivation modulation
index for low/medium/high
attentional load (x-axis) shows
that the improvement with
higher gains was absent at high
load, and the detrimental effect
of penalties on performance
was evident at all loads. (C, D)
Same format as A and B for RTs.
Subject slowed down when
expecting larger penalties and
speed up responses when
expecting larger gains (C).
These effects were largest at low
attentional load and decreased
at higher load (D). Dashed red
lines show ground mean across
all attention loads.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
3
4
1
0
1
9
5
2
2
0
4
1
8
6
3
/
/
j
o
c
n
_
a
_
0
1
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
behavioral improvement after having lost 3 tokens was
particularly apparent in the low attentional load condi-
tion and less in the medium and high attentional load
conditions (Figure 9B; LME model predicting the previous
trial effect on accuracy; [AttLoad × feedbackLosses], b =
0.01, p = .002). We quantified this effect by taking the
difference in performance for losing 3 versus 0 tokens,
which confirmed that there was on average a benefit of
larger penalties in the low load condition (Figure 9C).
Similar to losses, experiencing larger gains improved the
accuracy in the subsequent trial at low and medium atten-
tional load, but not at high attentional load (LME model
predicting previous trial effects on accuracy: for [AttLoad ×
feedbackGains], b = −0.03, p < .001; Figure 9B, C). Thus,
motivational improvements of posttoken feedback per-
formance adjustment were evident for token gains as
well as for losses, but primarily at lower and not at higher
attentional load.
Next, we analyzed how the on average improved
accuracy in trials after experiencing the loss of 3
tokens (Figure 9C) might relate to reduced learning
speed (Figure 7B) in the 3 loss conditions. To test this,
we selected trials from the block before the learning crite-
rion was reached and calculated accuracy in the nth trial
following the experience of the token outcome using a
running average window ranging from 1 to 20 trials. The
analysis showed that after losing 3 tokens, accuracy was
transiently increased compared with trials without losses
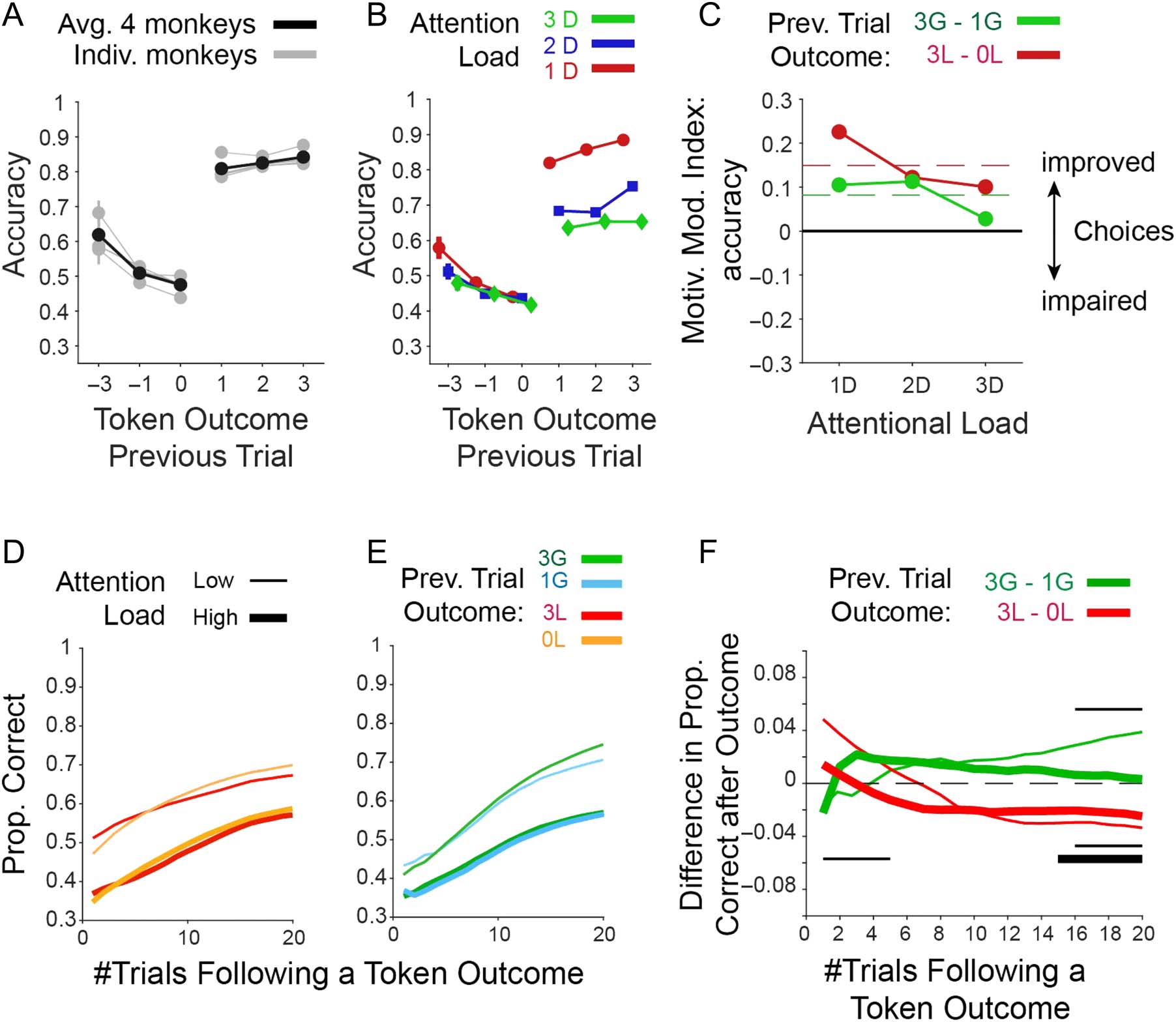
(Figure 9D, E), but this effect was transient and reversed
within two trials in the high load condition and within
five trials in the low load conditions (Figure 9F). For
the gain conditions, the results were different. Gaining
3 tokens led to a longer-lasting improvement of perfor-
mance when compared with gaining 1 token. This
improvement was more sustained in the low than in
the high attentional load condition (Figure 9E–F, the thin
black lines in the upper half of the panel mark trials for
which the accuracy difference of high vs. low gains was
significantly different from zero, Wilcoxon test, FDR cor-
rected for dependent samples across all trials and low
and high attentional load conditions with an alpha level
of .05). These longer-lasting effects on performance
closely resemble the main effects of losses and gains
on the learning efficacy (Figures 7 and 8) and suggest
that the block-level learning effects be traced back to
outcome-triggered performance changes at the single-
trial level with stronger negative effects after larger losses
and stronger positive effects after larger gains.
1964
Journal of Cognitive Neuroscience
Volume 34, Number 10
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
4
1
0
1
9
5
2
2
0
4
1
8
6
3
/
/
j
o
c
n
_
a
_
0
1
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 9. Effects of experienced token gains and losses on performance. (A) The effects of an experienced loss of 3, 1, or 0 tokens and of an
experienced gain of 1, 2, or 3 tokens (x-axis) on the subsequent trials’ accuracy ( y-axis). Gray lines are from individual monkeys, and black shows
their average. (B) Same format as A for the average previous trial outcome effects for low/medium/high attentional load. (C) MMI ( y-axis) quantifies
the improved accuracy after experiencing 3 versus 1 losses (red) and after experiencing 3 versus 1 token gains (green) for low/medium/high
attentional load. Dashed red lines show grand mean across attention load conditions. (D) The effect of an experienced loss of −3 or 0 token during
learning on the proportion of correct choices in the following nth trials (x-axis). (E) Same as D but for an experienced gain of 3 or 1 token. (F) The
difference in accuracy ( y-axis) after experiencing 3 versus 0 losses (red), and 3 versus 1 token gains (green) over n trials subsequent to the outcome
(x-axis). Thick and thin lines denote low and high attentional load conditions, respectively. Black thin and thick horizontal lines in the lower/upper
half of the panel show trials for which the difference of accuracy (high vs. low losses/gains) was significantly different than zero, Wilcoxon test, FDR
corrected for dependent samples across all trial points, and low and high attentional load conditions with an alpha level of .05.
DISCUSSION
We found that prospective gains and losses had opposite
effects on learning a relevant target feature. Experiencing
losing tokens slowed learning (increased the number of
trials to criterion), impaired retention (postlearning accu-
racy), and increased choice RTs, whereas experiencing
gaining tokens had the opposite effects. These effects var-
ied with attentional load in opposite ways. Larger penalties
for incorrect choices had maximally detrimental effects
when there were many distracting features (high load).
Conversely, higher gains for correct responses enhanced
flexible learning at lower attentional load but had no
beneficial effects at higher load. These findings were
paralleled on the trial level. Although there was a brief
improvement of accuracy following losses for two to five
trials following the experience of losses during learning,
accuracy declined following losses thereafter and on aver-
age prolonged learning. This posterror decline in learning
speed was stronger with larger (3 token) loss. In contrast
to losses, the experience of gains led to a more sustained
improvement of accuracy in subsequent trials, consistent
with better performance after gains, particularly when
attentional load was low.
Together, these results document apparent asymme-
tries of gains and losses on learning behavior. The nega-
tive effects of losing tokens and the positive effects of
gaining tokens were evident in all four monkeys. The
Boroujeni, Watson, and Womelsdorf
1965
intersubject consistency of the token and load effects sug-
gests that our results delineate a fundamental relationship
between the motivational influences of incentives (gains)
and disincentives (losses) on learning efficacy at varying
attentional loads.
Experiencing Loss Reduces Learning Efficacy with
Increased Distractor Loads
One key observation in our study is that rhesus monkeys
are sensitive to visual tokens as secondary reinforcers,
closely tracking their already obtained token assets
(Figure 2). This finding is consistent with prior studies in
rhesus monkeys showing that gaining tokens for correct
performance and losing tokens for incorrect performance
modulates performance in choice tasks (Taswell et al.,
2018; Rich & Wallis, 2017; Seo & Lee, 2009). This sensitivity
was essential in our study to functionally separate the influ-
ence of negative and positive valenced outcomes from the
influence of the overall saliency of outcomes. In our study,
the number of tokens for correct and incorrect perfor-
mance remained constant within blocks of ≥35 trials and
thus set a reward context for learning target features
among distractors (Sallet et al., 2007). When this reward
context entailed losing 3 tokens, monkeys learned the
rewarded target feature ∼5–7 trials later (slower) than
when incorrect choices led to no token change (depend-
ing on load; Figure 7B). At the trial level, experiencing los-
ing 3 tokens during the initial learning briefly enhanced
performance on immediately subsequent trials, suggest-
ing subjects successfully oriented away from the loss-
inducing stimulus features, but this effect reversed within
three trials after the loss experience, causing a sustained
decrease in performance and delayed learning when
experiencing losing 3 tokens (Figure 9C, F). This result
pattern suggests that experiencing losing 3 tokens led to
a short-lasting reorienting away from the loss-inducing
stimuli, but it does not enhance the processing, or the
remembering, of the chosen distractors. Experiencing loss
rather impairs using information from the erroneously
chosen objects to adjust behavior. This finding had a rela-
tively large effect size and was rather unexpected given var-
ious previous findings that would have predicted the
opposite effect. First, the loss attention framework sug-
gests that experiencing a loss causes an automatic vigi-
lance response that triggers subjects to explore alternative
options other than the chosen object ( Yechiam et al.,
2019; Yechiam & Hochman, 2013a, 2013b). Such an
enhanced exploration might have facilitated avoiding
objects with features that were associated with the loss
in the trials immediately following the loss experience
(Figure 9C, F). But our results suggest that the short-
lasting, loss-triggered reorienting to alternative objects
was not accompanied by a better encoding of the
loss-inducing stimuli but predicted a weaker encoding
or poorer credit assignment of the specific object fea-
tures of the loss-inducing object so that the animals
were less able to distinguish which objects in future tri-
als belonged to the loss-inducing objects. Such a weaker
encoding would lead to less informed exploration after
a loss, which would not facilitate but impair learning.
This account is consistent with human studies showing
poorer discrimination of stimuli when they are associ-
ated with monetary loss, aversive images or odors, or
electric shock (Shalev et al., 2018; Laufer et al., 2016;
Laufer & Paz, 2012; Resnik et al., 2011; Schechtman
et al., 2010).
A second reason why the overall decrement of perfor-
mance with loss was unexpected was that monkeys and
humans can clearly show nonzero (>0) learning rates for
negative outcomes when they are estimated separately
from learning rates for positive outcomes (Collins &
Frank, 2014; Caze & van der Meer, 2013; Seo & Lee,
2009; Frank, Moustafa, Haughey, Curran, & Hutchison,
2007; Frank, Seeberger, & O’Reilly, 2004), indicating that
negative outcomes in principle are useful for improving
the updating of value expectations. Although we found
improved performance immediately after incorrect
choices, this effect disappeared after ∼3 further trials
and overall caused slower learning. This finding suggests
that experiencing loss in a high attentional load context
reduced not the learning rates per se but impaired the
credit assignment process that updates the expected
values of object features based on token feedback. This
suggestion calls upon future investigations to clarify the
nature of the loss-induced impediment using computa-
tional modeling of the specific subcomponent processes
underlying the learning process ( Womelsdorf, Watson,
& Tiesinga, 2021).
A third reason why loss-induced impairments of learning
were unexpected are prior reports that monkeys success-
fully learn to avoid looking at objects that are paired with
negative reinforcers (such as a bitter taste; Ghazizadeh
et al., 2016). According to this prior finding, monkeys
should have effectively avoided choosing objects with
loss-inducing features when encountering them again.
Instead, anticipating token loss reduced their capability to
avoid the objects sharing features with the object that
caused token loss in previous trials, suggesting that losing
a token might attract attention (and gaze) similar to threat-
ening stimuli (like airpuffs; Ghazizadeh et al., 2016; White
et al., 2019) and thereby causing interference that impairs
avoiding the features of the loss-inducing stimuli in future
trials when there were multiple features in the higher
attentional load conditions.
The three discussed putative reasons for why loss might
not have improved but decreased performance points to
the complexity of the object space we used. When subjects
lost already attained tokens for erroneously choosing an
object with one, two, or three object features, they were
less able to assign negative credit to a specific feature of
the chosen object. Instead, they tend to overgeneralize
features of loss-induced objects to objects with shared fea-
tures that might also contain the rewarding feature.
1966
Journal of Cognitive Neuroscience
Volume 34, Number 10
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
3
4
1
0
1
9
5
2
2
0
4
1
8
6
3
/
/
j
o
c
n
_
a
_
0
1
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Consequently, they did not learn from erroneous choices
as efficiently as they would have learned with no or neutral
feedback after errors. This account is consistent with stud-
ies showing a wider generalization of aversive outcomes
and a concomitantly reduced sensitivity to the loss-
inducing stimuli (Shalev et al., 2018; Laufer et al., 2016;
Laufer & Paz, 2012; Resnik et al., 2011; Schechtman
et al., 2010). Consistent with such reduced encoding or
impaired credit assignment of the specific object fea-
tures, we found variable effects on posterror adjustment
(Figure 9B, D, E) and reduced longer-term performance
(i.e., over ∼5–20 trials) after experiencing loss (Figure 9F)
with the negative effects increasing with more distractors
in the higher attentional load condition (Figure 7B, D).
According to this interpretation, penalties such as losing
tokens are detrimental to performance when they do not
inform straightforwardly what type of features should be
avoided. This view is supported by additional evidence.
First, when tasks have simpler, binary choice options,
negative outcomes are more immediately informative
about which objects should be avoided, and learning
from negative outcomes can be more rapid than learning
from positive outcomes (Averbeck, 2017). We found a
similar improvement of performance in the low load con-
dition that lasted for one to three trials before perfor-
mance declined below average (Figure 9F). Second,
using aversive outcomes in a feature nonselective way
might incur a survival advantage in various evolutionary
meaningful settings. When a negative outcome promotes
generalizing from specific aversive cues (e.g., encounter-
ing a specific predator) to a larger family of aversive
events (all predator-like creatures), this can enhance fast
avoidance responses in future encounters (Barbaro et al.,
2017; Laufer et al., 2016; Dunsmoor & Paz, 2015; Krypotos,
Effting, Kindt, & Beckers, 2015). Such a generalized
response is also reminiscent of nonselective “escape”
responses that experimental animals show early during
aversive learning before they transition to more cue-
specific avoidance responses later in learning (Maia,
2010). The outlined reasoning helps in explaining why
we found that experiencing loss is not helpful to avoid
objects or object features when multiple, multidimen-
sional objects define the learning environment.
Experiencing Gains Enhance Learning Efficacy but
Cannot Compensate for Distractor Overload
We found that experiencing 3 tokens as opposed to 1
token for correct choices improved the efficacy of learn-
ing relevant target features by ∼4, ∼1.5, and ∼0 trials in
the low, medium, and high attentional load condition
(Figure 7). On the one hand, this finding provides fur-
ther quantitative support that incentives can improve
learning efficacy ( Walton & Bouret, 2019; Berridge &
Robinson, 2016; Ghazizadeh et al., 2016). In fact, across
conditions, learning was most efficient when the monkeys
expected 3 tokens and when objects varied in only one
feature dimension (1D, low attentional load condition).
However, this effect disappeared at high attentional load,
that is, when objects varied trial-by-trial in features of
three different dimensions (Figure 7). A reduced behav-
ioral efficiency of incentives in light of distracting informa-
tion is a known phenomenon in the problem-solving field
(Pink, 2009), but an unexpected finding in our task
because the complexity of the actual reward rule (the rule
was “find the feature that predicts token gains”) did not
vary from low to high attentional load. The only difference
between these conditions was the higher load of distract-
ing features, suggesting that the monkeys might have
reached a limitation in controlling distractor interference
that they could not compensate further by mobilizing
additional control resources.
But what is the source of this limitation to control dis-
tractor interference? One possibility is that when attention
demands increased in our task, monkeys are limited in
allocating sufficient control or “mental effort” to overcome
distractor interference (Shenhav et al., 2017; Klein-Flugge,
Kennerley, Friston, & Bestmann, 2016; Hosking, Cocker,
& Winstanley, 2014; Parvizi, Rangarajan, Shirer, Desai,
& Greicius, 2013; Walton, Rudebeck, Bannerman, &
Rushworth, 2007; Rudebeck, Walton, Smyth, Bannerman,
& Rushworth, 2006; Walton, Bannerman, Alterescu, &
Rushworth, 2003). Thus, subjects might perform poorer
at high attentional load partly because they are not allocat-
ing sufficient control of the task performance (Botvinick &
Braver, 2015). Rational theories of effort and control sug-
gest that subjects allocate control as long as the benefits of
doing so outweigh the costs of exerting more control.
Accordingly, subjects should perform poorer at higher
demand when the benefits (e.g., the reward rate for
correct performance) are not increased concomitantly
(Shenhav et al., 2017; Shenhav, Botvinick, & Cohen,
2013). One strength of such a rational theory of attentional
control is that it specifies the type of information that
limits control, which is assumed to be the degree of
cross-talk of conflicting information at high cognitive load
(Shenhav et al., 2017). According to this hypothesis, effort
and control demands rise concomitantly with the amount
of interfering information. This view provides a parsimoni-
ous explanation for our findings at high attentional load.
Although incentives can increase control allocation when
there is little cross-talk of the target feature with distractor
features (at low attentional load), the incentives are not
able to compensate for the increased cross-talk of distract-
ing features at the high attentional load condition. Our
results therefore provide quantitative support for a ratio-
nal theory of attentional control.
In our task, the critical transition from sufficient to insuf-
ficient control of interference was between the medium
and high attentional load condition, which corresponded
to an increase of distractor features that vary trial-by-trial
from 8 features (at medium attentional load) to 26 features
(at high attentional load). Thus, subjects were not able to
compensate for distractor interference when the number
Boroujeni, Watson, and Womelsdorf
1967
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
3
4
1
0
1
9
5
2
2
0
4
1
8
6
3
/
/
j
o
c
n
_
a
_
0
1
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
of interfering features were somewhere between 8 and 26,
suggesting that prospective gains—at least when using
tokens as reinforcement currency—hit a limit to enhance
attentional control within this range.
learning, which documents that expecting or anticipating
loss deteriorates flexible learning about the relevance of
objects in a multidimensional object space.
Acknowledgments
Impaired Learning in Loss Contexts and Economic
Decision Theory
The authors would like to thank Adam Neuman and Seyed-
Alireza Hassani for help collecting the data.
In economic decision theory, it is well documented that
making choices is suboptimal in contexts that frame out-
comes in terms of losses rather than gains (Tversky &
Kahneman, 1981, 1991). This view from behavioral eco-
nomics aims to explain which options individuals will
choose in a given context, which shares some resem-
blance with our task, where subjects learned to choose
one among three objects in learning contexts (blocks)
that were framed with variable token gains and losses.
In a context with higher potential losses, humans are less
likely to choose an equally valued option than in a gain
context. The reason for this irrational change in choice
preferences is believed to reside in an overweighting of
emotional content that devalues outcomes in loss con-
texts (Barbaro et al., 2017; Loewenstein, Weber, Hsee, &
Welch, 2001). Colloquial words for such emotional over-
weighting might be displeasure (Tversky & Kahneman,
1981), distress, annoyance, or frustration. Concepts
behind these words may relate to primary affective
responses of anger, disgust, or fear. However, these more
qualitative descriptors are not providing an explanatory
mechanism but rather tend to anthropomorphize the
observed deterioration of learning in loss contexts. More-
over, the economic view does not provide an explanation
why the learning would be stronger affected at higher
attentional load (Figure 7D).
Conclusion
Taken together, our results document the interplay of
motivational variables and attentional load during flexible
learning. We first showed that learning efficacy is reduced
when attentional load is increased despite the fact that the
complexity of the feature-reward target rule did not
change. This finding illustrates that cognitive control
processes cannot fully compensate for an increase in
distractors. The failure to fully compensate for enhanced
distraction was not absolute. Incentive motivation was able
to enhance learning efficacy when there were distracting
features of one or two feature dimensions but could not
help anymore to compensate for enhanced interference
when features of a third feature dimension intruded into
the learning of feature values. This limitation suggests that
crosstalk of distracting features represents a key process
involved in cognitive effort (Shenhav et al., 2017). More-
over, the negative effect of distractor interference was exac-
erbated by experiencing the loss of tokens for wrong
choices. This effect illustrates that negative feedback does
not help to avoid loss-inducing distractor objects during
Reprint requests should be sent to Thilo Womelsdorf, Depart-
ment of Psychology, Vanderbilt University, Nashville, TN 37240,
or via e-mail: thilo.womelsdorf@vanderbilt.edu.
Data Availability Statement
All data supporting this study and its findings, as well as
custom MATLAB code generated for analyses, are available
from the corresponding author upon reasonable request.
Author Contributions
Kianoush Banaie Boroujeni: Conceptualization; Data cura-
tion; Formal analysis; Investigation; Methodology;
Resources; Software; Validation; Visualization; Writing—
Original draft; Writing—Review & editing. Marcus Watson:
Conceptualization; Data curation; Formal analysis; Meth-
odology; Resources; Software; Writing—Review & editing.
Thilo Womelsdorf: Conceptualization; Formal analysis;
Funding acquisition; Investigation; Methodology; Project
administration; Writing—Original draft; Writing—Review
& editing.
Funding Information
National Institute of Mental Health (https://dx.doi.org/10
.13039/100000025), grant number: R01MH123687.
Diversity in Citation Practices
Retrospective analysis of the citations in every article pub-
lished in this journal from 2010 to 2021 reveals a persistent
pattern of gender imbalance: Although the proportions of
authorship teams (categorized by estimated gender iden-
tification of first author/ last author) publishing in the
Journal of Cognitive Neuroscience ( JoCN ) during this
period were M(an)/M = .407, W(oman)/M = .32, M/ W =
.115, and W/ W = .159, the comparable proportions
for the articles that these authorship teams cited were
M/M = .549, W/M = .257, M/ W = .109, and W/ W = .085
(Postle and Fulvio, JoCN, 34:1, pp. 1–3). Consequently,
JoCN encourages all authors to consider gender balance
explicitly when selecting which articles to cite and gives
them the opportunity to report their article’s gender cita-
tion balance.
REFERENCES
Ahs, F., Miller, S. S., Gordon, A. R., & Lundstrom, J. N. (2013).
Aversive learning increases sensory detection sensitivity.
Biological Psychology, 92, 135–141. https://doi.org/10.1016/j
.biopsycho.2012.11.004, PubMed: 23174695
1968
Journal of Cognitive Neuroscience
Volume 34, Number 10
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
3
4
1
0
1
9
5
2
2
0
4
1
8
6
3
/
/
j
o
c
n
_
a
_
0
1
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Anderson, B. A. (2019). Neurobiology of value-driven attention.
Current Opinion in Psychology, 29, 27–33. https://doi.org/10
.1016/j.copsyc.2018.11.004, PubMed: 30472540
Averbeck, B. B. (2017). Amygdala and ventral striatum
population codes implement multiple learning rates for
reinforcement learning. IEEE symposium series on
computational intelligence (SSCI), 1–5. https://doi.org/10
.1109/SSCI.2017.8285354
Barbaro, L., Peelen, M. V., & Hickey, C. (2017). Valence, not
utility, underlies reward-driven prioritization in human vision.
Journal of Neuroscience, 37, 10438–10450. https://doi.org/10
.1523/JNEUROSCI.1128-17.2017, PubMed: 28951452
Benjamini, Y., & Yekutieli, D. (2005). False discovery
rate-adjusted multiple confidence intervals for selected
parameters. Journal of the American Statistical Association,
100, 71–81. https://doi.org/10.1198/016214504000001907
Berridge, K. C., & Robinson, T. E. (2016). Liking, wanting, and
the incentive-sensitization theory of addiction. American
Psychologist, 71, 670–679. https://doi.org/10.1037
/amp0000059, PubMed: 27977239
Botvinick, M., & Braver, T. (2015). Motivation and cognitive
control: From behavior to neural mechanism. Annual
Review of Psychology, 66, 83–113. https://doi.org/10.1146
/annurev-psych-010814-015044, PubMed: 25251491
Bourgeois, A., Chelazzi, L., & Vuilleumier, P. (2016). How
motivation and reward learning modulate selective attention.
Progress in Brain Research, 229, 325–342. https://doi.org/10
.1016/bs.pbr.2016.06.004, PubMed: 27926446
Bucker, B., & Theeuwes, J. (2016). Appetitive and aversive
outcome associations modulate exogenous cueing. Attention,
Perception & Psychophysics, 78, 2253–2265. https://doi.org
/10.3758/s13414-016-1107-6, PubMed: 27146992
Caze, R. D., & van der Meer, M. A. (2013). Adaptive properties
of differential learning rates for positive and negative
outcomes. Biological Cybernetics, 107, 711–719. https://doi
.org/10.1007/s00422-013-0571-5, PubMed: 24085507
Chelazzi, L., Marini, F., Pascucci, D., & Turatto, M. (2019).
Getting rid of visual distractors: The why, when, how, and
where. Current Opinion in Psychology, 29, 135–147. https://
doi.org/10.1016/j.copsyc.2019.02.004, PubMed: 30856512
Collins, A. G., & Frank, M. J. (2014). Opponent actor learning
(OpAL): Modeling interactive effects of striatal dopamine on
reinforcement learning and choice incentive. Psychological
Review, 121, 337–366. https://doi.org/10.1037/a0037015,
PubMed: 25090423
DiCicio, T. J., & Efron, B. (1996). Bootstrap confidence
intervals. Statistical Science, 11, 189–228. https://doi.org/10
.1214/ss/1032280214
Doallo, S., Patai, E. Z., & Nobre, A. C. (2013). Reward
associations magnify memory-based biases on perception.
Journal of Cognitive Neuroscience, 25, 245–257. https://doi
.org/10.1162/jocn_a_00314, PubMed: 23066690
Dunsmoor, J. E., & Paz, R. (2015). Fear generalization and
anxiety: Behavioral and neural mechanisms. Biological
Psychiatry, 78, 336–343. https://doi.org/10.1016/j.biopsych
.2015.04.010, PubMed: 25981173
Failing, M., & Theeuwes, J. (2018). Selection history: How
reward modulates selectivity of visual attention.
Psychonomic Bulletin & Review, 25, 514–538. https://doi.org
/10.3758/s13423-017-1380-y, PubMed: 28986770
Frank, M. J., Moustafa, A. A., Haughey, H. M., Curran, T., &
Hutchison, K. E. (2007). Genetic triple dissociation reveals
multiple roles for dopamine in reinforcement learning.
Proceedings of the National Academy of Sciences, U.S.A.,
104, 16311–16316. https://doi.org/10.1073/pnas.0706111104,
PubMed: 17913879
Frank, M. J., Seeberger, L. C., & O’Reilly, R. C. (2004). By carrot
or by stick: Cognitive reinforcement learning in
parkinsonism. Science, 306, 1940–1943. https://doi.org/10
.1126/science.1102941, PubMed: 15528409
Ghazizadeh, A., Griggs, W., & Hikosaka, O. (2016). Ecological
origins of object salience: Reward, uncertainty, aversiveness,
and novelty. Frontiers in Neuroscience, 10, 378. https://doi
.org/10.3389/fnins.2016.00378, PubMed: 27594825
Gottlieb, J. (2012). Attention, learning, and the value of
information. Neuron, 76, 281–295. https://doi.org/10.1016/j
.neuron.2012.09.034, PubMed: 23083732
Hickey, C., Kaiser, D., & Peelen, M. V. (2015). Reward guides
attention to object categories in real-world scenes. Journal of
Experimental Psychology: General, 144, 264–273. https://doi
.org/10.1037/a0038627, PubMed: 25559653
Hogarth, L., Dickinson, A., & Duka, T. (2010). Selective
attention to conditioned stimuli in human discrimination
learning: Untangling the effects of outcome prediction,
valence, arousal, and uncertainty. In C. J. Mitchell & M. E.
Le Pelley (Eds.), Attention and associative learning: From
brain to behaviour (pp. 71–97). Oxford, United Kingdom:
Oxford University Press.
Hosking, J. G., Cocker, P. J., & Winstanley, C. A. (2014).
Dissociable contributions of anterior cingulate cortex and
basolateral amygdala on a rodent cost/benefit
decision-making task of cognitive effort.
Neuropsychopharmacology, 39, 1558–1567. https://doi.org
/10.1038/npp.2014.27, PubMed: 24496320
Hox, J. (2002). Multilevel analysis, techniques and
applications. Erlbaum. https://doi.org/10.4324
/9781410604118
Klein-Flugge, M. C., Kennerley, S. W., Friston, K., & Bestmann,
S. (2016). Neural signatures of value comparison in human
cingulate cortex during decisions requiring an effort–reward
trade-off. Journal of Neuroscience, 36, 10002–10015. https://
doi.org/10.1523/JNEUROSCI.0292-16.2016, PubMed:
27683898
Krypotos, A. M., Effting, M., Kindt, M., & Beckers, T. (2015).
Avoidance learning: A review of theoretical models and
recent developments. Frontiers in Behavioral Neuroscience,
9, 189. https://doi.org/10.3389/fnbeh.2015.00189, PubMed:
26257618
Laufer, O., Israeli, D., & Paz, R. (2016). Behavioral and neural
mechanisms of overgeneralization in anxiety. Current
Biology, 26, 713–722. https://doi.org/10.1016/j.cub.2016.01
.023, PubMed: 26948881
Laufer, O., & Paz, R. (2012). Monetary loss decreases perceptual
sensitivity. Journal of Molecular Neuroscience, 48, S64–S64.
Lejarraga, T., & Hertwig, R. (2017). How the threat of losses
makes people explore more than the promise of gains.
Psychonomic Bulletin & Review, 24, 708–720. https://doi.org
/10.3758/s13423-016-1158-7, PubMed: 27620178
Li, W., Howard, J. D., Parrish, T. B., & Gottfried, J. A. (2008).
Aversive learning enhances perceptual and cortical
discrimination of indiscriminable odor cues. Science, 319,
1842–1845. https://doi.org/10.1126/science.1152837,
PubMed: 18369149
Loewenstein, G. F., Weber, E. U., Hsee, C. K., & Welch, N.
(2001). Risk as feelings. Psychological Bulletin, 127, 267–286.
https://doi.org/10.1037/0033-2909.127.2.267, PubMed:
11316014
Maia, T. V. (2010). Two-factor theory, the actor-critic model,
and conditioned avoidance. Learning & Behavior, 38, 50–67.
https://doi.org/10.3758/LB.38.1.50, PubMed: 20065349
McTeague, L. M., Gruss, L. F., & Keil, A. (2015). Aversive
learning shapes neuronal orientation tuning in human
visual cortex. Nature Communications, 6, 7823. https://doi
.org/10.1038/ncomms8823, PubMed: 26215466
Noonan, M. P., Crittenden, B. M., Jensen, O., & Stokes, M. G.
(2018). Selective inhibition of distracting input. Behavioural
Boroujeni, Watson, and Womelsdorf
1969
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
3
4
1
0
1
9
5
2
2
0
4
1
8
6
3
/
/
j
o
c
n
_
a
_
0
1
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Brain Research, 355, 36–47. https://doi.org/10.1016/j.bbr
.2017.10.010, PubMed: 29042157
O’Brien, J. L., & Raymond, J. E. (2012). Learned Predictiveness
speeds visual processing. Psychological Science, 23, 359–363.
https://doi.org/10.1177/0956797611429800, PubMed:
22399415
Ohman, A., Flykt, A., & Esteves, F. (2001). Emotion drives
attention: Detecting the snake in the grass. Journal of
Experimental Psychology: General, 130, 466–478. https://doi
.org/10.1037/0096-3445.130.3.466, PubMed: 11561921
Parvizi, J., Rangarajan, V., Shirer, W. R., Desai, N., & Greicius,
M. D. (2013). The will to persevere induced by electrical
stimulation of the human cingulate gyrus. Neuron, 80,
1359–1367. https://doi.org/10.1016/j.neuron.2013.10.057,
PubMed: 24316296
Pinherio, J. C., & Bates, D. M. (1996). Unconstrained
parametrizations for variance-covariance matrices. Statistics
and Computing, 6, 289–296. https://doi.org/10.1007
/BF00140873
Pink, D. H. (2009). Drive: The surprising truth about what
motivates. New York: Riverhead Books.
Raymond, J. E., & O’Brien, J. L. (2009). Selective visual attention
and motivation: The consequences of value learning in an
attentional blink task. Psychological Science, 20, 981–988.
https://doi.org/10.1111/j.1467-9280.2009.02391.x, PubMed:
19549080
Resnik, J., Laufer, O., Schechtman, E., Sobel, N., & Paz, R.
(2011). Auditory aversive learning increases discrimination
thresholds. Journal of Molecular Neuroscience, 45(Suppl. 1),
S96–S97.
Rhodes, L. J., Ruiz, A., Rios, M., Nguyen, T., & Miskovic, V.
(2018). Differential aversive learning enhances orientation
discrimination. Cogniton & Emotion, 32, 885–891. https://doi
.org/10.1080/02699931.2017.1347084, PubMed: 28683593
Rich, E. L., & Wallis, J. D. (2017). Spatiotemporal dynamics
of information encoding revealed in orbitofrontal
high-gamma. Nature Communications, 8, 1139. https://doi
.org/10.1038/s41467-017-01253-5, PubMed: 29074960
Rudebeck, P. H., Walton, M. E., Smyth, A. N., Bannerman, D. M.,
& Rushworth, M. F. (2006). Separate neural pathways process
different decision costs. Nature Neuroscience, 9, 1161–1168.
https://doi.org/10.1038/nn1756, PubMed: 16921368
Sallet, J., Quilodran, R., Rothe, M., Vezoli, J., Joseph, J. P., &
Procyk, E. (2007). Expectations, gains, and losses in the
anterior cingulate cortex. Cognitive, Affective, & Behavioral
Neuroscience, 7, 327–336. https://doi.org/10.3758/cabn.7.4
.327, PubMed: 18189006
San Martin, R., Appelbaum, L. G., Huettel, S. A., & Woldorff, M. G.
(2016). Cortical brain activity reflecting attentional biasing
toward reward-predicting cues Covaries with economic
decision-making performance. Cerebral Cortex, 26, 1–11.
https://doi.org/10.1093/cercor/bhu160, PubMed: 25139941
Schacht, A., Adler, N., Chen, P., Guo, T., & Sommer, W. (2012).
Association with positive outcome induces early effects in
event-related brain potentials. Biological Psychology, 89,
130–136. https://doi.org/10.1016/j.biopsycho.2011.10.001,
PubMed: 22027086
Schechtman, E., Laufer, O., & Paz, R. (2010). Negative valence
widens generalization of learning. Journal of Neuroscience,
30, 10460–10464. https://doi.org/10.1523/JNEUROSCI.2377
-10.2010, PubMed: 20685988
Schomaker, J., Walper, D., Wittmann, B. C., & Einhauser, W.
(2017). Attention in natural scenes: Affective-motivational
factors guide gaze independently of visual salience. Vision
Research, 133, 161–175. https://doi.org/10.1016/j.visres.2017
.02.003, PubMed: 28279712
Seo, H., & Lee, D. (2009). Behavioral and neural changes after
gains and losses of conditioned reinforcers. Journal of
Neuroscience, 29, 3627–3641. https://doi.org/10.1523
/JNEUROSCI.4726-08.2009, PubMed: 19295166
Shalev, L., Paz, R., & Avidan, G. (2018). Visual aversive learning
compromises sensory discrimination. Journal of
Neuroscience, 38, 2766–2779. https://doi.org/10.1523
/JNEUROSCI.0889-17.2017, PubMed: 29439168
Shenhav, A., Botvinick, M. M., & Cohen, J. D. (2013). The
expected value of control: An integrative theory of
anterior cingulate cortex function. Neuron, 79, 217–240.
https://doi.org/10.1016/j.neuron.2013.07.007, PubMed:
23889930
Shenhav, A., Musslick, S., Lieder, F., Kool, W., Griffiths, T. L.,
Cohen, J. D., et al. (2017). Toward a rational and mechanistic
account of mental effort. Annual Review of Neuroscience,
40, 99–124. https://doi.org/10.1146/annurev-neuro-072116
-031526, PubMed: 28375769
Shidara, M., & Richmond, B. J. (2002). Anterior cingulate: Single
neuronal signals related to degree of reward expectancy.
Science, 296, 1709–1711. https://doi.org/10.1126/science
.1069504, PubMed: 12040201
Small, D. M., Gitelman, D., Simmons, K., Bloise, S. M., Parrish,
T., & Mesulam, M. M. (2005). Monetary incentives enhance
processing in brain regions mediating top–down control of
attention. Cerebral Cortex, 15, 1855–1865. https://doi.org/10
.1093/cercor/bhi063, PubMed: 15746002
Suarez-Suarez, S., Holguin, S. R., Cadaueira, F., Nobre, A. C.,
& Doallo, S. (2019). Punishment-related memory-guided
attention: Neural dynamics of perceptual modulation. Cortex,
115, 231–245. https://doi.org/10.1016/j.cortex.2019.01.029,
PubMed: 30852377
Taswell, C. A., Costa, V. D., Murray, E. A., & Averbeck, B. B.
(2018). Ventral striatum’s role in learning from gains and
losses. Proceedings of the National Academy of Sciences,
U.S.A., 115, E12398–E12406. https://doi.org/10.1073/pnas
.1809833115, PubMed: 30545910
Theeuwes, J. (2019). Goal-driven, stimulus-driven, and
history-driven selection. Current Opinion in Psychology, 29,
97–101. https://doi.org/10.1016/j.copsyc.2018.12.024,
PubMed: 30711911
Tversky, A., & Kahneman, D. (1981). The framing of decisions
and the psychology of choice. Science, 211, 453–458. https://
doi.org/10.1126/science.7455683, PubMed: 7455683
Tversky, A., & Kahneman, D. (1991). Loss aversion in riskless
choice: A reference-dependent model. Quarterly Journal
of Economics, 106, 1039–1061. https://doi.org/10.2307
/2937956
Walton, M. E., Bannerman, D. M., Alterescu, K., & Rushworth,
M. F. (2003). Functional specialization within medial frontal
cortex of the anterior cingulate for evaluating effort-related
decisions. Journal of Neuroscience, 23, 6475–6479. https://
doi.org/10.1523/JNEUROSCI.23-16-06475.2003, PubMed:
12878688
Walton, M. E., & Bouret, S. (2019). What is the relationship
between dopamine and effort? Trends in Neurosciences, 42,
79–91. https://doi.org/10.1016/j.tins.2018.10.001, PubMed:
30391016
Walton, M. E., Rudebeck, P. H., Bannerman, D. M., &
Rushworth, M. F. (2007). Calculating the cost of acting in
frontal cortex. Annals of the New York Academy of Sciences,
1104, 340–356. https://doi.org/10.1196/annals.1390.009,
PubMed: 17360802
Watson, M. R., Voloh, B., Naghizadeh, M., & Womelsdorf, T.
(2019). Quaddles: A multidimensional 3-D object set with
parametrically controlled and customizable features.
Behavior Research Methods, 51, 2522–2532. https://doi.org
/10.3758/s13428-018-1097-5, PubMed: 30088255
Watson, M. R., Voloh, B., Thomas, C., Hasan, A., & Womelsdorf,
T. (2019). USE: An integrative suite for temporally-precise
1970
Journal of Cognitive Neuroscience
Volume 34, Number 10
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
3
4
1
0
1
9
5
2
2
0
4
1
8
6
3
/
/
j
o
c
n
_
a
_
0
1
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
psychophysical experiments in virtual environments for
human, nonhuman, and artificially intelligent agents. Journal
of Neuroscience Methods, 326, 108374. https://doi.org/10
.1016/j.jneumeth.2019.108374, PubMed: 31351974
White, J. K., Bromberg-Martin, E. S., Heilbronner, S. R., Zhang,
K., Pai, J., Haber, S. N., et al. (2019). A neural network for
information seeking. Nature Communications, 10, 5168.
https://doi.org/10.1038/s41467-019-13135-z, PubMed:
31727893
Wolfe, J. M., & Horowitz, T. S. (2017). Five factors that guide
attention in visual search. Nature Human Behavior, 1, 1–8.
https://doi.org/10.1038/s41562-017-0058
Womelsdorf, T., Thomas, C., Neumann, A., Watson, M. R.,
Banaie Boroujeni, K., Hassani, S. A., et al. (2021). A Kiosk
Station for the assessment of multiple cognitive domains and
cognitive enrichment of monkeys. Frontiers in Behavioral
Neuroscience, 15, 721069. https://doi.org/10.3389/fnbeh
.2021.721069, PubMed: 34512289
Womelsdorf, T., Watson, M. R., & Tiesinga, P. (2021). Learning
at variable attentional load requires cooperation of working
memory, meta-learning and attention-augmented
reinforcement learning. Journal of Cognitive Neuroscience,
34, 79–107. https://doi.org/10.1162/jocn_a_01780, PubMed:
34813644
Yechiam, E., Ashby, N. J. S., & Hochman, G. (2019). Are we
attracted by losses? Boundary conditions for the approach
and avoidance effects of losses. Journal of Experimental
Psychology: Learning Memory and Cognition, 45, 591–605.
https://doi.org/10.1037/xlm0000607, PubMed: 29999403
Yechiam, E., & Hochman, G. (2013a). Loss-aversion or
loss-attention: The impact of losses on cognitive
performance. Cognitive Psychology, 66, 212–231. https://doi
.org/10.1016/j.cogpsych.2012.12.001, PubMed: 23334108
Yechiam, E., & Hochman, G. (2013b). Losses as modulators of
attention: Review and analysis of the unique effects of
losses over gains. Psychological Bulletin, 139, 497–518.
https://doi.org/10.1037/a0029383, PubMed: 22823738
Yechiam, E., & Hochman, G. (2014). Loss attention in a
dual-task setting. Psychological Science, 25, 494–502. https://
doi.org/10.1177/0956797613510725, PubMed: 24357614
Yechiam, E., Retzer, M., Telpaz, A., & Hochman, G. (2015). Losses
as ecological guides: Minor losses lead to maximization and
not to avoidance. Cognition, 139, 10–17. https://doi.org/10
.1016/j.cognition.2015.03.001, PubMed: 25797454
Yee, D. M., Leng, X., Shenhav, A., & Braver, T. S. (2022).
Aversive motivation and cognitive control. Neuroscience &
Biobehavioral Reviews, 133, 104493. https://doi.org/10.1016/j
.neubiorev.2021.12.016, PubMed: 34910931
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
3
4
1
0
1
9
5
2
2
0
4
1
8
6
3
/
/
j
o
c
n
_
a
_
0
1
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Boroujeni, Watson, and Womelsdorf
1971