FOCUS FEATURE:
Biomarkers in Network Neuroscience
Network-level permutation entropy of
resting-state MEG recordings: A novel biomarker
for early-stage Alzheimer’s disease?
Elliz P. Scheijbeler1,2, Anne M. van Nifterick1,2, Cornelis J. Stam2, Arjan Hillebrand2,
Alida A. Gouw1,2, and Willem de Haan1,2
1Alzheimer Center Amsterdam, Department of Neurology, Amsterdam Neuroscience,
Vrije Universiteit Amsterdam, Amsterdam, Netherlands
2Department of Clinical Neurophysiology and MEG Center, Department of Neurology,
Amsterdam Neuroscience, Vrije Universiteit Amsterdam, Amsterdam, Netherlands
a n o p e n a c c e s s
j o u r n a l
Keywords: Biomarker, Functional brain networks, Joint permutation entropy, Early-stage Alzheimer’s,
Magnetoencephalography
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
6
2
3
8
2
2
0
2
8
1
0
4
n
e
n
_
a
_
0
0
2
2
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
ABSTRACT
Increasing evidence suggests that measures of signal variability and complexity could present
promising biomarkers for Alzheimer’s disease (AD). Earlier studies have however been limited
to the characterization of local activity. Here, we investigate whether a network version of
permutation entropy could serve as a novel biomarker for early-stage AD. Resting-state source-
space magnetoencephalography was recorded in 18 subjects with subjective cognitive decline
(SCD) and 18 subjects with mild cognitive impairment (MCI). Local activity was characterized
by permutation entropy (PE). Network-level interactions were studied using the inverted joint
permutation entropy ( JPEinv), corrected for volume conduction. The JPEinv showed a reduction
of nonlinear connectivity in MCI subjects in the theta and alpha band. Local PE showed
increased theta band entropy. Between-group differences were widespread across brain
regions. Receiver operating characteristic (ROC) analysis of classification of MCI versus SCD
subjects revealed that a logistic regression model trained on JPEinv features (78.4% [62.5–93.3%])
slightly outperformed PE (76.9% [60.3–93.4%]) and relative theta power–based models (76.9%
[60.4–93.3%]). Classification performance of theta JPEinv was at least as good as the relative
theta power benchmark. The JPEinv is therefore a potential biomarker for early-stage AD that
should be explored in larger studies.
AUTHOR SUMMARY
Functional network disruption is a well-established finding in Alzheimer’s disease. Sensitive
network-based biomarkers are however not available. We aimed to detect neuronal
dysfunction at a predementia (mild cognitive impairment, MCI) stage of Alzheimer’s disease,
by applying a network-level neural variability measure to magnetoencephalography data: the
inverted joint permutation entropy ( JPEinv). This measure integrates information on local signal
variability/complexity and nonlinear coupling. We found significant differences in JPEinv
between subjects with subjective cognitive decline and MCI, primarily in the theta band. The
diagnostic ability of the JPEinv was reported to be similar to that of relative theta power, the
most potent neurophysiological biomarker of predementia Alzheimer’s disease to date.
Citation: Scheijbeler, E. P., van Nifterick,
A. M., Stam, C. J., Hillebrand, A., Gouw,
A. A., & de Haan, W. (2022). Network-level
permutation entropy of resting-state MEG
recordings: A novel biomarker for early-
stage Alzheimer’s disease? Network
Neuroscience, 6(2), 382–400. https://doi
.org/10.1162/netn_a_00224
DOI:
https://doi.org/10.1162/netn_a_00224
Supporting Information:
https://doi.org/10.1162/netn_a_00224
Received: 30 September 2021
Accepted: 15 December 2021
Competing Interests: The authors have
declared that no competing interests
exist.
Corresponding Authors:
Elliz P. Scheijbeler
e.p.scheijbeler@amsterdamumc.nl
Willem de Haan
w.dehaan@amsterdamumc.nl
Handling Editor:
Olaf Sporns
Copyright: © 2021
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license
The MIT Press
Network permutation entropy of MEG as a biomarker of early Alzheimer’s
INTRODUCTION
In the past decade, complex network approaches have increasingly been used to comprehend
the structure and function of brain networks, in healthy subjects as well as in patients with
neurological and psychiatric disorders (Bullmore & Sporns, 2009; Douw et al., 2019; Stam,
2014; van den Heuvel et al., 2019). Alzheimer’s disease (AD) is the major cause of dementia
in the aging Western population and has been a principal target for network studies (Babiloni
et al., 2020; Pievani et al., 2011). Abnormalities of structural and functional networks have
been demonstrated in AD, including its earliest stages (Pusil et al., 2019; M. Yu et al.,
2021). Initially, the focus was on the loss of the “small-world” organization that is seen in
healthy subjects, and the shift towards more random network topology (Stam et al., 2009; Stam
et al., 2007; Supekar et al., 2008). More recent studies have emphasized the selective vulner-
ability of highly connected hub regions (M. Yu et al., 2017). Complementary to clinical studies,
large-scale computational network models of AD have provided new analytical opportunities
and insights, for instance by suggesting the concept of “activity-dependent degeneration” as a
cause of synaptic failure and hub vulnerability, or by relating amyloid-driven neuronal
excitation/inhibition imbalance to the well-known large-scale oscillatory slowing in AD (de
Haan et al., 2012; Maestú et al., 2021; Stefanovski et al., 2021; Stefanovski et al., 2019).
Insights derived from such network-oriented models can be used to develop and test potential
new treatments in a simulated environment, and thereby guide future clinical studies (de Haan
et al., 2017).
While network approaches have helped to gain a better understanding of mechanisms
involved in the pathophysiology of AD, it is not clear whether measures derived from network
analysis could also serve as effective biomarkers—especially in the early stages of AD. Graph
theoretical analysis of brain networks is complex and has been hampered by methodological
problems. Reconstruction of functional networks from resting-state recordings of functional mag-
netic resonance imaging (fMRI), electroencephalography (EEG), or magnetoencephalography
(MEG), for instance, raises questions about the proper use of thresholds, error due to movement,
volume conduction, and state changes such as drowsiness and sleep (van Diessen et al., 2015; van
Wijk et al., 2010). These methodological issues may be responsible for the limited reproducibility
and reliability of connectivity and network measures, although recent studies do suggest improve-
ment in this respect (Briels et al., 2020; Colclough et al., 2016). In addition to robustness and good
reproducibility, clinically useful biomarkers need sensitivity and specificity of at least 80% or
higher (Babiloni et al., 2021; Colom-Cadena et al., 2020). Thus far, mainly conventional,
single-channel power spectral measures have proven their diagnostic and predictive value in
the predementia stages of AD (Gouw et al., 2017; Gouw et al., 2021; Horvath et al., 2018; Hughes
et al., 2019). While it is still entirely conceivable that the richness of brain network dynamics can
help to detect or distinguish early aberrant neuronal behavior, the question arises whether progress
can be made with a different type of approach, that somehow combines the best of both worlds.
Several research groups have emphasized the importance of studying the variability or
complexity of neural dynamics, at different spatial and temporal scales (Garrett et al., 2013;
McIntosh et al., 2010; Uddin, 2020; Waschke et al., 2021). A central idea is that a certain level
of variability in neural activity corresponds to a healthy state with flexible responses to internal
and external stimuli (Courtney & Hinault, 2021; Garrett et al., 2013; Waschke et al., 2021; D.
Yin & Kaiser, 2021). Neural variability has been shown to relate to age as well as cognitive and
behavioral performance (Angulo-Ruiz et al., 2021; Boylan et al., 2021; Dustman et al., 1999;
Gómez et al., 2013; Kumral et al., 2020). Neural variability may also reflect the activity of
modulating noradrenergic, dopaminergic, and cholinergic systems, and has been related to
the excitation/inhibition balance in neural networks (Bruining et al., 2020; Gao et al., 2017;
Magnetoencephalography (MEG):
Noninvasive, high-resolution
technique to detect fluctuations in
electromagnetic field strength around
the head, generated by the active
brain.
Volume conduction:
Propagation of neural activity
through surrounding brain tissue,
potentially picked up simultaneously
by multiple sensors, complicating
description of interregional coupling.
Spectral analysis:
Technique to quantitatively describe
properties of the oscillatory signal
generated by large groups of active
neurons, based on frequency and
amplitude.
Network Neuroscience
383
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
6
2
3
8
2
2
0
2
8
1
0
4
n
e
n
_
a
_
0
0
2
2
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Network permutation entropy of MEG as a biomarker of early Alzheimer’s
Garrett et al., 2015; Maestú et al., 2021; Pfeffer et al., 2021; Wang et al., 2018; Zheng et al.,
2012). It could therefore in theory relate AD pathophysiology at the cell/circuit level, such as
the amyloid-induced hyperexcitability mentioned above, to oscillatory changes at the larger
scale—a highly desired translational quality to develop a multiscale mechanistic description of
AD neurophysiology.
A wide range of measures can be used to quantify variability of time series of neural activity.
Of special interest is a large group of measures that are based on the concept of information
entropy (Bandt & Pompe, 2002; Costa et al., 2002, 2005; Courtiol et al., 2016; Dávalos et al.,
2019; Fadlallah et al., 2013; Inouye et al., 1991; Keshmiri, 2020; Kosciessa et al., 2020;
Richman & Moorman, 2000; Y. Yin et al., 2016). Entropy measures have been helpful in psycho-
physiological studies of healthy subjects (Fekete et al., 2021; Grady & Garrett, 2018; M. Liu
et al., 2019; Mahjoory et al., 2019; Miskovic et al., 2019; Waschke et al., 2019), and growing
evidence suggests that the measures can also be used to demonstrate a significant, progressive
loss of entropy of neural activity in AD patients (Ando et al., 2021; Echegoyen et al., 2020;
Gómez & Hornero, 2010; Maturana-Candelas et al., 2019; Shumbayawonda et al., 2020; Su
et al., 2021; W. Y. Yu et al., 2021). This suggests that measures of complexity or entropy could
have potential as biomarkers for AD. A limitation of previous studies is that they only consider
local activity and do not take into account interregional network communication, which is
known to be affected in AD (Babiloni et al., 2020; Engels et al., 2015; Engels et al., 2017;
Pievani et al., 2011). Recently developed measures apply concepts of variability or informa-
tion entropy to relations between multiple signals (Baracchini et al., 2021; Godfrey & Singh,
2021; Jamin & Humeau-Heurtier, 2020; King et al., 2013; Lee et al., 2017; L. Liu et al., 2010).
One example is the joint permutation entropy ( JPE), which makes it possible to analyze local
complexity and interregional nonlinear coupling in a single comprehensive analysis (Y. Yin
et al., 2019).
In the present study, we investigated whether the inverted JPE ( JPEinv) is a potential bio-
marker for early AD. The JPEinv was applied to resting-state source-space MEG recordings of
18 subjects with subjective cognitive decline and 18 subjects with predementia AD. The mea-
sure was computed in relevant frequency bands and was modified to prevent effects of volume
conduction/field spread (King et al. 2013). The magnitude of JPEinv group differences was com-
pared with a relative theta power benchmark and with local complexity findings, in order to
determine the added value of the network-level measure of entropy. The discriminative power
of theta JPEinv, local permutation entropy, and relative power were evaluated using logistic
regression models.
MATERIALS AND METHODS
Subjects
The study involved two age- and gender-matched groups totaling 36 subjects: 18 subjects with
subjective cognitive decline (SCD) and 18 subjects with amnestic mild cognitive impairment
(MCI). Data were obtained from the Amsterdam Dementia Cohort (van der Flier & Scheltens,
2018). All subjects visited the memory clinic of the VUmc Alzheimer Center in the period of
spring 2015–18 and provided written informed consent for the use of their data for research
purposes. Each subject received a standardized diagnostic workup including medical history
taking, neurological and neuropsychological examination, blood tests, 3T MRI of the brain,
routine MEG, and, when possible, a lumbar puncture to collect cerebrospinal fluid (van der
Flier & Scheltens, 2018). Diagnoses were generated during a multidisciplinary consensus
meeting according to the 2011 National Institute on Aging–Alzheimer’s Association (NIA-AA)
384
Joint permutation entropy:
Measure of both
complexity/variability and functional
connectivity, based on the temporal
similarity in permutation entropy
levels of different brain regions.
Nonlinear coupling:
Type of dynamic connectivity
between elements of a system in
which the changes in one element
are not proportional to the
simultaneous changes in the other
element.
Permutation entropy:
Measure of complexity/variability,
where the entropy is based on the
recurrence likelihood of short
temporal patterns of, for example,
local neuronal activity.
Relative power (spectral density):
Quantitative spectral analysis
measure that describes the
contribution of a specific frequency
range to an observed neural
oscillatory signal.
Mild cognitive impairment (MCI):
Condition in which a person
experiences cognitive decline,
objectively confirmed by cognitive
testing, but without substantial
interference in daily activities as seen
in dementia.
Network Neuroscience
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
6
2
3
8
2
2
0
2
8
1
0
4
n
e
n
_
a
_
0
0
2
2
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Network permutation entropy of MEG as a biomarker of early Alzheimer’s
criteria. Positive amyloid biomarkers (cerebrospinal fluid ptau/amyloid ratio > 0.020 and/or
abnormal amyloid PET) were available for all 18 (amnestic) MCI subjects. The SCD group
included 15 amyloid-negative subjects and three subjects with unknown biomarker status.
Demographic characteristics of the included subjects are presented in Table 1. Average
Mini–Mental State Examination (MMSE) scores were significantly lower in MCI than in SCD
subjects ( p < 0.01). Psychoactive medication use (not shown here) was incidental and did not
differ significantly between groups.
MEG Recordings
MEG recordings were obtained in a magnetically shielded room using a 306-channel whole-
head Vectorview MEG system (Elekta Neuromag Oy, Helsinki, Finland). The acquisition proto-
col consisted of at least two 5-min blocks of eyes-closed recording. Subjects were instructed
to relax but stay awake. Only data from the first eyes-closed session were analyzed here.
Recordings were sampled at 1,250 Hz with an online anti-aliasing filter (410 Hz) and high-pass
filter (0.1 Hz). A 3D-digitizer (Fastrak, Polhelmus, Colchester, VT, USA) was used to digitize the
locations of four or five head position indicator coils, which were used to continuously record
the subjects’ head position in relation to the MEG sensors. To provide an outline of the subjects’
scalp, ∼500 additional points were digitized. The scalp surface was used for coregistration with
the structural (MRI) template that produced the best fit.
MEG Source Reconstruction
The temporal extension of the signal space separation (tSSS) filter (implemented in MaxFilter
software, Elekta Neuromag Oy, version 2.2.15; Taulu & Simola, 2006) was used to suppress
correlated noise. Channels that contained excessive artefacts (i.e., flat, very noisy and squid-
jump channels) were discarded based on visual inspection of the raw data, before estimation
of the tSSS coefficients. The (denoised) signal was then reconstructed for all sensors (Taulu
et al., 2004; Taulu et al., 2005). In order to obtain source-localized activity for all regions,
an atlas-based beamforming approach was applied (Hillebrand et al., 2012). The broadband
MEG data (0.5–70 Hz) were projected through the beamformer spatial filters in order to recon-
struct time series of neuronal activity for 78 cortical regions of interest (ROIs) plus both hip-
pocampi, identified by means of automated anatomical labeling (AAL; Gong et al., 2009;
Tzourio-Mazoyer et al., 2002; Supplementary Table 1 in the Supporting Information). The cen-
troid voxel of each AAL region was used as representative for that ROI (Hillebrand et al.,
2016). The sphere that best fitted the scalp surface obtained from the coregistered MRI scan
was used as a volume conductor model. The volume conductor model, an equivalent current
dipole, and the MEG data covariance matrix were used to compute the broadband
Table 1. Demographic characteristics of the included subjects. MCI = Mild cognitive impairment.
M/F = male/female. MMSE = Mini–Mental State Examination. SCD = subjective cognitive decline.
SD = standard deviation. ** p < 0.01 (MCI versus SCD).
n
Age in years (mean ± SD)
M/F (n)
MMSE (mean ± SD)
SCD
18
64.2 ± 6.1
8/10
27.8 ± 2.1
MCI
18
64.1 ± 6.2
9/9
25.8 ± 1.9**
385
Network Neuroscience
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
2
3
8
2
2
0
2
8
1
0
4
n
e
n
_
a
_
0
0
2
2
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Network permutation entropy of MEG as a biomarker of early Alzheimer’s
beamformer weights. By projecting sensor-level MEG data through the normalized beamfor-
mer weights (Cheyne et al., 2007), time series of neuronal activity were obtained for each ROI.
Time Series Analysis
The source-reconstructed time series were converted to ASCII format. The first 20 epochs of
4,096 samples (3.2768 s) of the first eyes-closed recording were selected for analysis. Quan-
titative spectral as well as local and network-level entropy analyses were performed using
in-house developed software (BrainWave, version 0.9.163.26, available from home.kpn.nl
/stam7883/brainwave.html). The epochs were filtered in canonical frequency bands, i.e., theta
(4–8 Hz), alpha (8–13 Hz), beta (13–30 Hz), and broadband (0.5–45 Hz) using a discrete fast
Fourier transform. Relative theta power, permutation entropy, and inverted joint permutation
entropy measures were estimated for each epoch separately and averaged per person prior to
group statistics.
Permutation Entropy and Inverted Joint Permutation Entropy
Computation of the permutation entropy (PE) was based on the work by Bandt and Pompe
(2002). Consider a discrete time series X(t = 1, …, T ). In the present study, this time series cor-
responds to the local activity of a brain region, as reconstructed by an MEG beamformer. For
each time point t in the time series we can construct a vector with length n: (xt+1, …, xt+n).
Next, n rank values are assigned to each sample within the vector, such that the sample with
the highest amplitude gets rank 1, the sample with the second-highest amplitude gets rank 2,
and so on to the sample with the lowest value, which gets rank n. There are n! different pos-
sible permutations of a set of n ranks. Each different permutation can be considered a unique
symbol that can be designated with a letter. Physiologically, each letter reflects a sequence of n
data points of an MEG time series, recorded from a single brain region. The time series Xt has
now been converted to a sequence of n! different symbols. The probability for the occurrence
of a permutation is defined by the following:
# tjt≤T −n;
f
p πð Þ ¼
xtþ1; …; xtþn
ð
T −n þ 1
Þhas type π
g
:
(1)
(Shannon) entropy:
Measure of complexity/variability,
based on the occurrence likelihood
of specific distributions of
elements/states in a system (e.g.,
local neuronal activity levels in a
brain network).
From the probabilities we can construct a probability distribution with n! bins. The Shannon
information entropy of this distribution is given by the following:
X
H nð Þ ¼ −
p πð Þ logp πð Þ:
(2)
The maximum value of the entropy is log(n!). A normalized version of the permutation entropy
can be obtained as follows: PE(n) = H(n)/log(n!). Bandt and Pompe (2002) have shown that the
permutation entropy does not depend strongly upon the choice of n. They recommend choos-
ing n in the range 3–7, so that n! << T.
The PE is a robust measure of the complexity of a single time series. Recently, an extension
to multivariate time series, referred to as the joint permutation entropy ( JPE), was proposed by
Y. Yin et al. (2019). In this approach, a symbolic representation for each of two time series is
obtained as described above. Next, a matrix is constructed where each cell contains the prob-
ability of one of the (n! × n!)2 combinations of symbols in the two channels. This matrix forms a
probability distribution with (n! × n!)2 bins. From this, the JPE can be computed according to
Formula (2). In this study, the JPE was normalized between 0 and 1 by dividing it by its max-
imum value, that is, log(n! × n! − 2n!)2. The normalization factor reflects the number of bins in
the probability distribution matrix that was used to compute the JPE. Signal spread can cause
spurious correlations, also in the case of source-reconstructed MEG data (Hillebrand et al.,
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
2
3
8
2
2
0
2
8
1
0
4
n
e
n
_
a
_
0
0
2
2
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
386
Network permutation entropy of MEG as a biomarker of early Alzheimer’s
2012). To address this problem, all pairs of identical or mirrored symbols (i.e., the diagonals of
the probability distribution matrix; 2n! bins) were excluded from computation of the JPE. This
approach is similar to the suggestion by King et al. (2013).
Intuitively, we would expect a measure of nonlinear coupling to have higher values if cou-
pling is stronger. This is, by definition of the term, not true for the JPE. In order to facilitate
comparison to conventional connectivity measures, we introduce the inverted JPE, so that
higher JPEinv values correspond to stronger coupling:
JPEinv ¼ 1 − JPE:
(3)
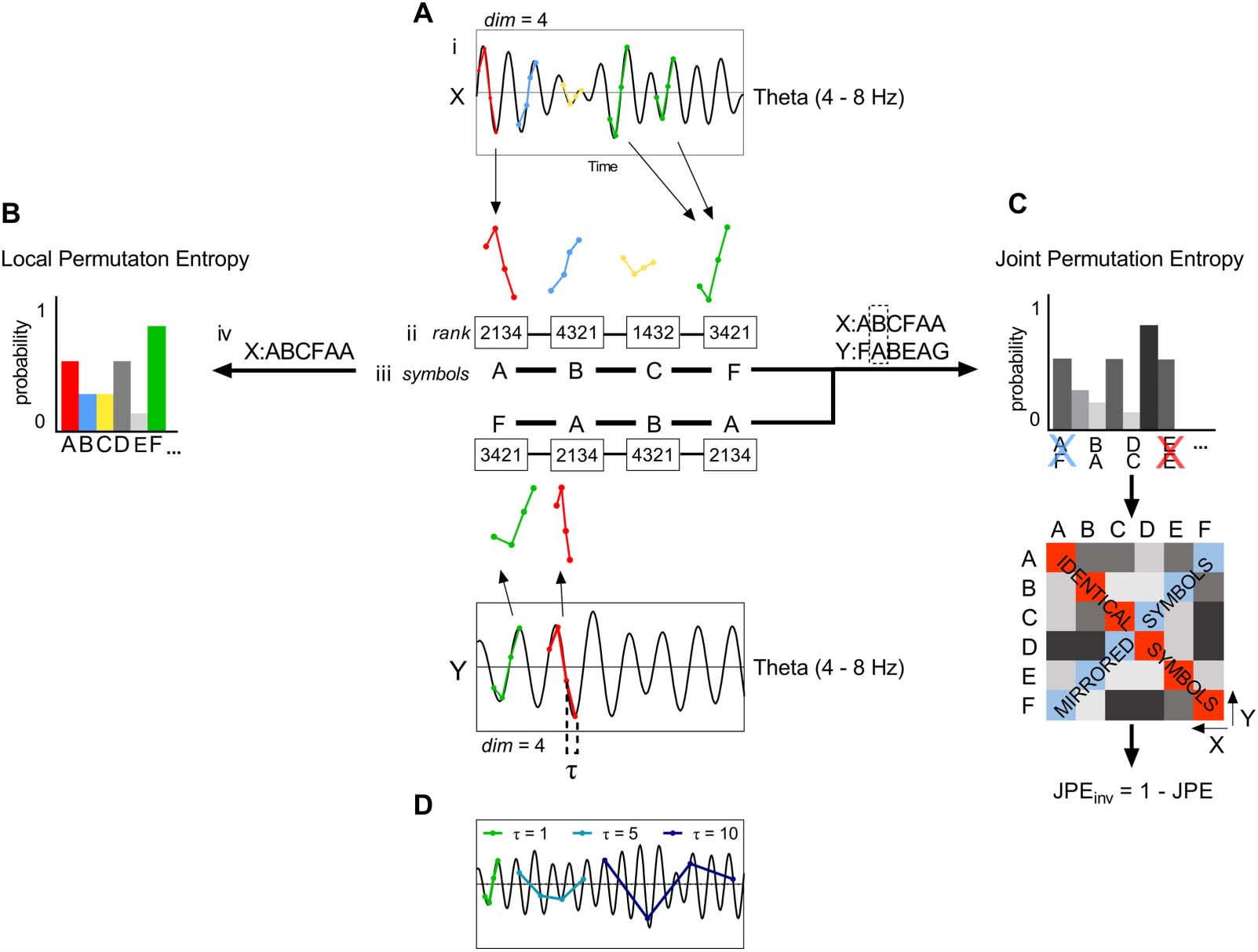
A schematic illustration of the method to obtain PE and JPEinv values is shown in Figure 1. Figure 2
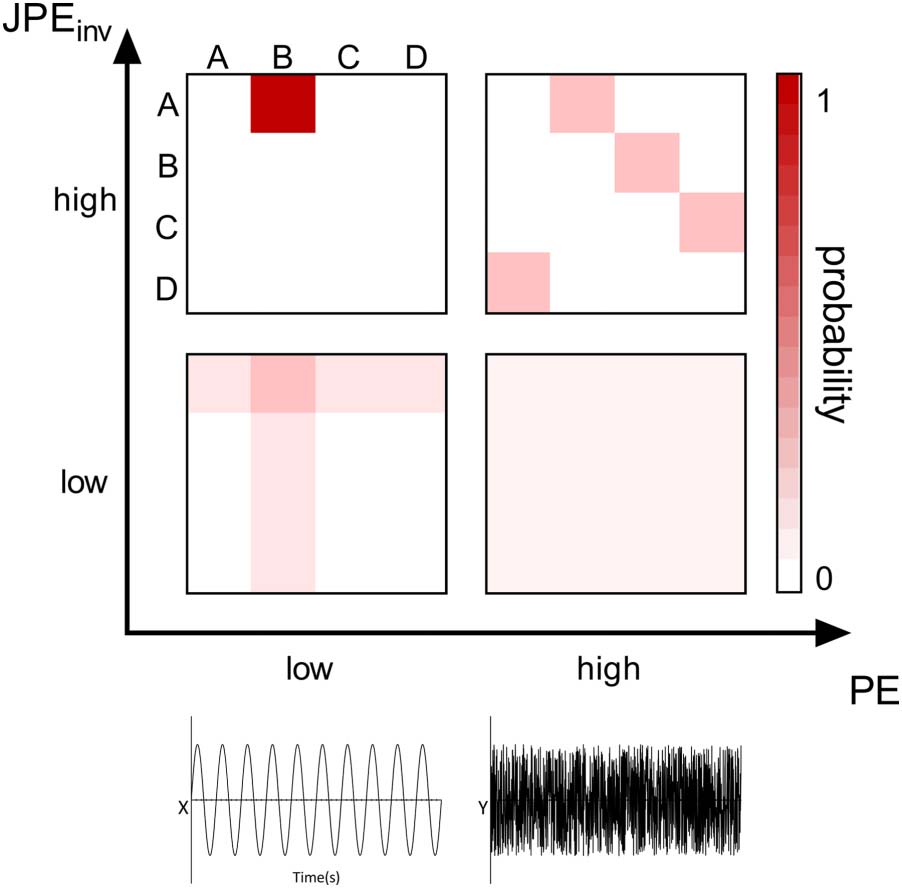
provides intuition on how the JPEinv integrates information on local complexity and
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
2
3
8
2
2
0
2
8
1
0
4
n
e
n
_
a
_
0
0
2
2
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Illustration of local permutation entropy and inverted joint permutation entropy analysis of multichannel recordings of brain activ-
Figure 1.
ity. (A) A single-channel recording of brain activity (e.g., MEG signal) is filtered in a frequency band of interest (i). Each sample in a specified
time window is assigned a rank (ii). This set of ranks, or ordinal pattern, is encoded as a symbol; in this case a letter (iii). A sequence of symbols
is obtained by repeating Step ii and iii for the whole time series (iv). For a length or embedding dimension n, there are n! possible different
patterns that can be assigned a unique symbol. Here, we make use of n = 4. (B) The frequency of occurrence of each symbol is used to obtain a
probability distribution. By computing the Shannon information entropy of this distribution, we obtain the local permutation entropy (PE),
allowing us to assess the complexity of a single time series. (C) A symbolic representation of a second time series is obtained as described
in panel A. The frequency of occurrence of each symbol pair is used to construct a probability distribution, and a symmetric matrix that reflects
the probability of occurrence of each possible symbol pair. To correct for the effect of volume conduction/field spread, symbol pairs made up
of identical or mirrored ordinal patterns (i.e., the diagonals of the matrix) are excluded from analysis (King et al., 2013). The joint permutation
entropy ( JPE) is derived from the probabilities of the remaining symbol pairs. The measure is normalized between 0 and 1 by dividing it by its
maximum value, that is, log(n! × n! − 2n!). Finally, the inverted JPE ( JPEinv) is obtained. (D) Lag or time delay τ describes the relation between n
samples of a time series, each separated by τ − 1 samples. Here, we made use of τ = 1. Larger time delays will result in permutations for
increasingly slower trends in the signal.
Network Neuroscience
387
Network permutation entropy of MEG as a biomarker of early Alzheimer’s
Figure 2. The JPEinv integrates information on local complexity and interregional coupling. Let us
imagine two time series, x and y, that can display varying values of PE and JPEinv. The symbol pair
probability distributions (derived from the time series as in Figure 1C) of four possible regimes are
plotted as a function of local complexity/variability (PE) and interregional coupling strength ( JPEinv).
Top left (high JPEinv/low PE): When both time series have low PE values, a few distinct ordinal
patterns—and their corresponding symbols (e.g., A and B)—make up most of the signal. If the time
series are strongly interconnected, symbol A in time series x will always be coupled to symbol B in
time series y and vice versa. Bottom left (low JPEinv/low PE): If simple (low entropy) signals are
weakly coupled, this results in coupling between symbol A in time series x and symbol B, as well
as less prevalent symbols C and D, in time series y. The same holds true for symbol B in time series
y: The symbol will be coupled to symbol A, as well as to less prevalent symbols C and D, in time
series x. Top right (high JPEinv/high PE): When both time series have high PE values, each symbol
(e.g., A, B, C, and D) has an equal probability of occurrence in the signal. If the time series are
strongly interconnected, this results in a high probability of occurrence for specific symbol pairs
(e.g., x = D & y = A, x = A & y = B, x = B & y = C, x = C & y = D). Bottom right (low JPEinv/high
PE): If the complex (high entropy) time series are weakly coupled, this results in a low probability of
occurrence of each symbol pair and a highly random signal.
interregional coupling. In the study of Y. Yin et al. (2019), the authors considered a coarse-
graining procedure to obtain entropy values for different timescales. However, how coarse-
graining affects the frequency content of the shortened signal is not obvious (Kosciessa et al.,
2020). To avoid this problem, and to relate our results to previous work, we applied different
band pass filters to the data and computed PE and JPEinv for the broadband or narrowband
filtered data.
Relative Theta Power
Relative theta power is the most potent neurophysiological biomarker of predementia AD to
date. The spectral measure is known to correlate with neuropsychological measures and total
tau, and has been related to clinical progression over time (Gouw et al., 2017; Musaeus et al.,
2018). Classifiers trained on spectral M/EEG features have achieved moderate to high accu-
racy rates for the classification of (early) AD and healthy control subjects. Gouw et al. (2021),
for instance, obtained an accuracy rate of 84.6% for the classification of AD and SCD subjects
using a random forest model—a finding that was replicated in an independent test set. The
Network Neuroscience
388
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
2
3
8
2
2
0
2
8
1
0
4
n
e
n
_
a
_
0
0
2
2
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Network permutation entropy of MEG as a biomarker of early Alzheimer’s
discriminative power and magnitude of group differences obtained using the proposed metrics
were therefore compared to conventional, single-channel power. The potential confounding
effect of oscillatory slowing on the JPEinv analysis was evaluated.
Statistical Analysis
Statistical analyses to compare the demographic characteristics of the diagnostic groups were
performed in SPSS for Mac ( Version 25.0. IBM Corp, Armonk, NY). Two-tailed independent
sample t tests were performed to test the equality of group means.
Nonparametric permutation tests were performed in order to compare JPEinv, PE, and spec-
tral measures between SCD and MCI subjects. The data were used to generate a probability
distribution for testing against the null hypothesis, rather than that a particular distribution was
assumed. The original configuration of subjects was randomly repartitioned (number of itera-
tions = 10,000), and the permutation p value represented the proportion of random partitions
that had a larger test statistic than the observed one. A q value < 0.05 (i.e., p value after false
discovery rate correction; Benjamini & Hochberg, 1995) was considered significant.
Logistic regression models with diagnosis (SCD-MCI) as dependent variable and JPEinv, PE,
or relative power features in the theta band as independent variables were used to assess the
diagnostic value of the MEG markers. Feature values were averaged over all 80 AAL regions
(i.e., 78 cortical regions and both hippocampi) before inclusion in the logistic regression
models. Receiver operating characteristic (ROC) curves were plotted to quantify between-
subject discrimination accuracy. Integrated area under the ROC curve (AUC) values were
reported with 95% confidence intervals. In order to evaluate the potential effect of oscillatory
slowing on the relationship between mean theta JPEinv and diagnostic group, one-way
ANCOVA with mean relative theta power as a covariate was performed.
RESULTS
JPEinv
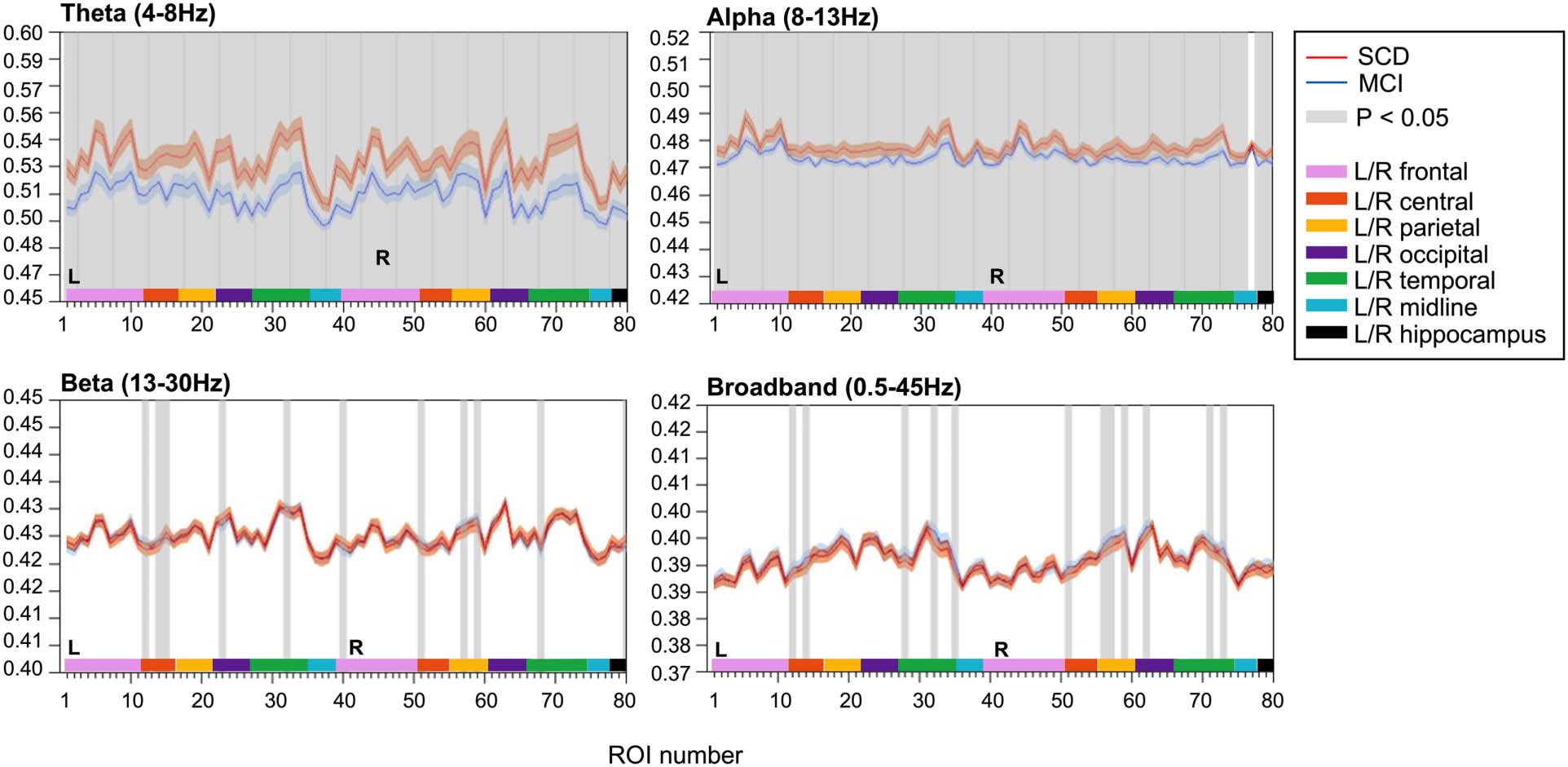
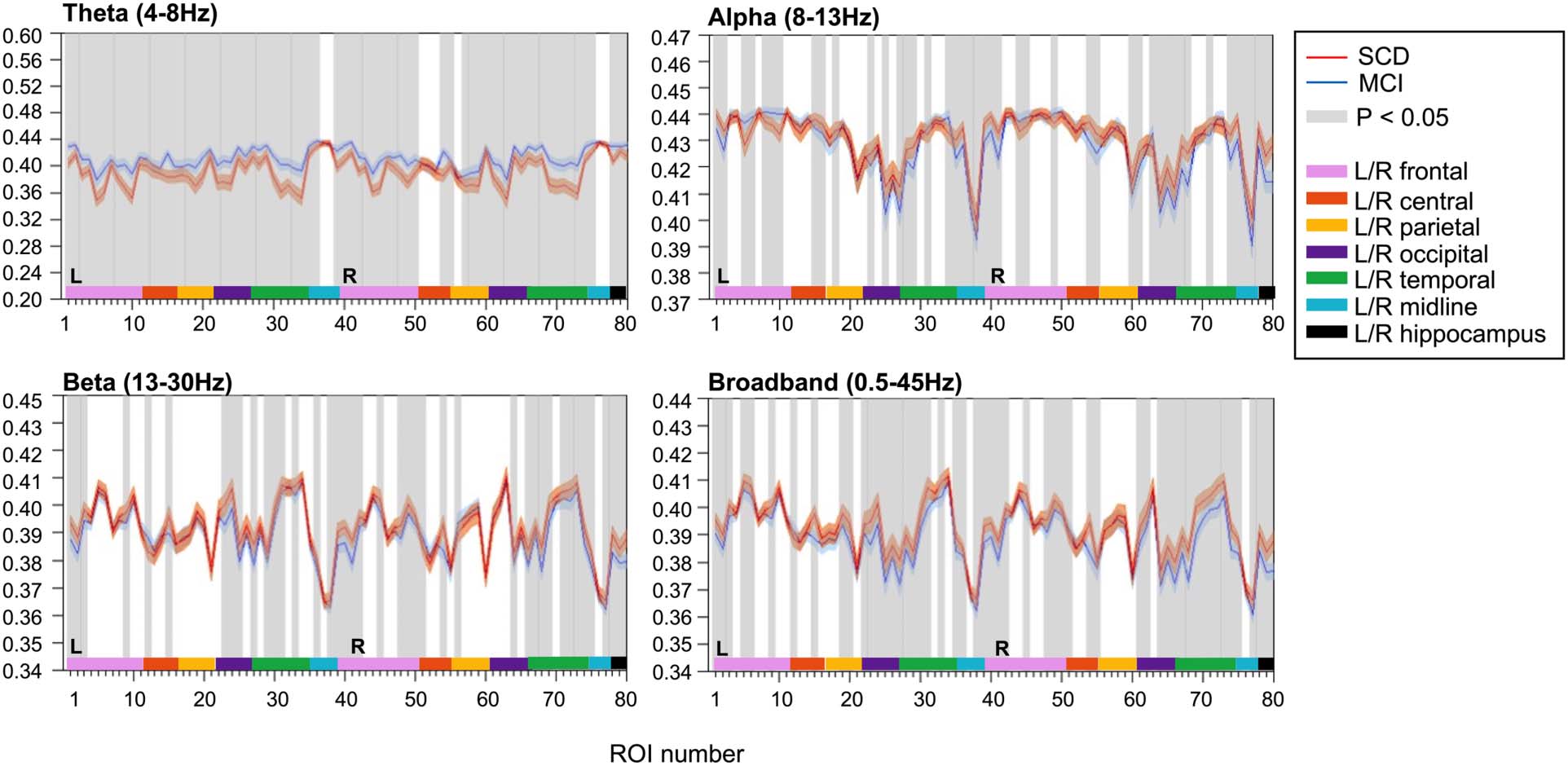
JPEinv analysis (τ = 1, n = 4) revealed disturbed functional network coupling in MCI. Average
JPEinv values were significantly lower in MCI than in SCD subjects in the theta and alpha band
(Figure 3). This was true for all cortical regions and both hippocampi, except for the right
insula in the alpha band. Each ROI number (1–80, order based upon Gong et al., 2009, Sup-
plementary Table 1) represents a brain region. Group differences were less distinct in beta and
broadband data, with only a few cortical regions (i.e., 10–12 regions) showing statistically sig-
nificant group differences in JPEinv-based functional connectivity (q < 0.05, FDR corrected).
JPEinv results obtained using different parameter (τ and n) settings are presented in the Support-
ing Information (Supplementary Figures 3 and 4).
PE
Local PE analysis (τ = 1, n = 4) revealed differences in local activity and complexity between
SCD and MCI subjects (Figure 4). Higher PE values were reported for MCI subjects in the theta
band, with increased signal complexity in 70 cortical regions and both hippocampi. Although
restricted to fewer regions of the brain, MCI subjects presented lower PE values than did SCD
subjects in the alpha, beta, and broadband data, suggesting reduced complexity in these fre-
quency bands. PE analysis was repeated for different values of τ and n (Supporting Information,
Supplementary Figures 1, 2, and 5). The role of these parameters in entropy computations is
addressed in the Discussion section.
Functional connectivity:
Large-scale, dynamic neuronal
communication between different
brain regions, assumed to be
estimated by the statistical
dependence between elements
(e.g., phase) of their signals.
Network Neuroscience
389
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
2
3
8
2
2
0
2
8
1
0
4
n
e
n
_
a
_
0
0
2
2
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Network permutation entropy of MEG as a biomarker of early Alzheimer’s
Inverted joint permutation entropy (τ = 1, n = 4). JPEinv values were calculated for narrowband, that is, theta (4–8 Hz), alpha (8–13 Hz),
Figure 3.
beta (13–30 Hz), and broadband (0.5–45 Hz) filtered MEG data. Each ROI number (1–80, order based upon Gong et al., 2009, Supplementary
Table 1) represents a brain region in the AAL atlas. Group means (±2 × SEM) are plotted in red for the SCD and in blue for the MCI group. ROIs
with significantly different JPEinv values (q < 0.05, FDR corrected) are presented in gray. The MCI group presented lower mean JPEinv values for
80 regions in the theta band and for 79 channels in the alpha band. Only a few regions showed significant between-group differences in the
beta (i.e., 10) and broadband (i.e., 12) data. AAL = automated anatomical labeling. FDR = false discovery rate. JPEinv = inverted joint permu-
tation entropy. MCI = mild cognitive impairment. SCD = subjective cognitive decline. SEM = standard error of the mean.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
2
3
8
2
2
0
2
8
1
0
4
n
e
n
_
a
_
0
0
2
2
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4. Local permutation entropy (τ = 1, n = 4). PE values were calculated for narrowband, that is, theta (4–8 Hz), alpha (8–13 Hz), beta (13–30 Hz),
and broadband (0.5–45 Hz) filtered MEG data. Each ROI number (1–80, order based upon Gong et al., 2009, Supplementary Table 1) represents a
brain region in the AAL atlas. Group means (±2 × SEM) are plotted in red for the SCD and in blue for the MCI group. ROIs with significantly
different PE values (q < 0.05, FDR corrected) are presented in gray. Group differences were most distinct in the theta band, with 72 channels
showing significantly higher PE values for MCI than for SCD subjects. AAL = automated anatomical labeling. FDR = false discovery rate. PE =
permutation entropy. MCI = mild cognitive impairment. SCD = subjective cognitive decline. SEM = standard error of the mean.
Network Neuroscience
390
Network permutation entropy of MEG as a biomarker of early Alzheimer’s
Relative Theta Power
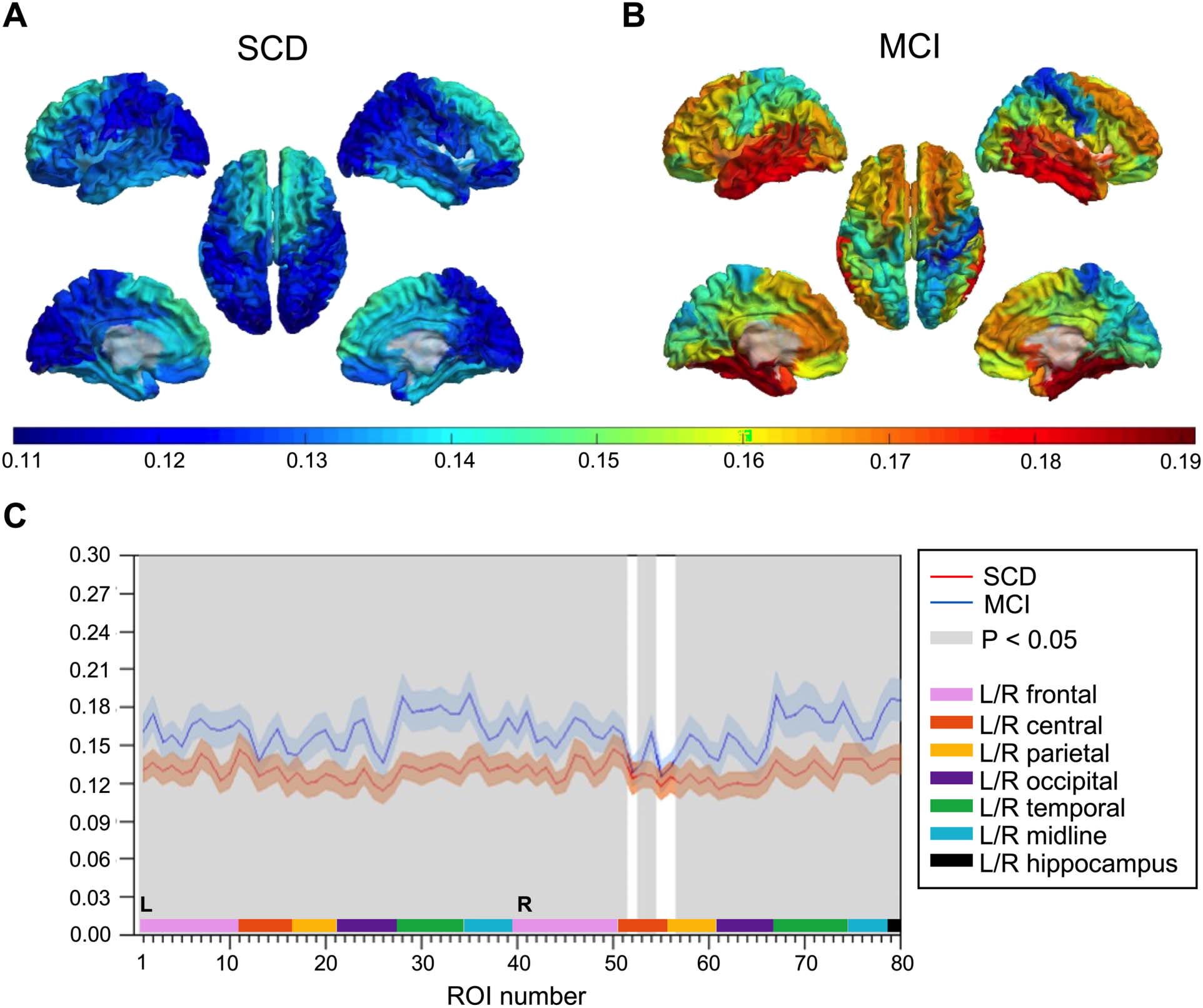
Spectral power analysis of local MEG activity revealed higher relative theta power in MCI than
in SCD subjects (Figure 5). Seventy-five cortical regions and both hippocampi showed statis-
tically significant group differences (q < 0.05, FDR corrected), with most prominent differences
in parietal and temporal regions.
Classification: ROC Analysis
As shown in previous sections, JPEinv and PE group differences were most pronounced in the
theta band. Average theta JPEinv, PE, and relative power values (i.e., averaged over all 80 ROIs)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
2
3
8
2
2
0
2
8
1
0
4
n
e
n
_
a
_
0
0
2
2
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5. Relative theta power. (A–B) Group-averaged relative theta power values for 78 cortical brain regions are displayed as color-coded
maps on a template brain, viewed from, in clockwise order, the left, top, right, right midline, and left midline. Hippocampi are not visualized.
Higher relative theta power is depicted in warmer and lower power in colder colors. (A) Average relative theta power in the SCD group. (B)
Average relative theta power in the MCI group. (C) Statistical analysis by permutation testing revealed higher relative theta power in MCI than
in SCD subjects. Each ROI number (1–80, order based upon Gong et al., 2009, Supplementary Table 1) represents a brain region in the AAL
atlas. Group means (±2 × SEM) are plotted in red for the SCD and in blue for the MCI group. ROIs with significantly different theta power
values (q < 0.05, FDR corrected) are presented in gray. AAL = automated anatomical labeling. FDR = false discovery rate. MCI = mild cognitive
impairment. SCD = subjective cognitive decline. SEM = standard error of the mean.
Network Neuroscience
391
Network permutation entropy of MEG as a biomarker of early Alzheimer’s
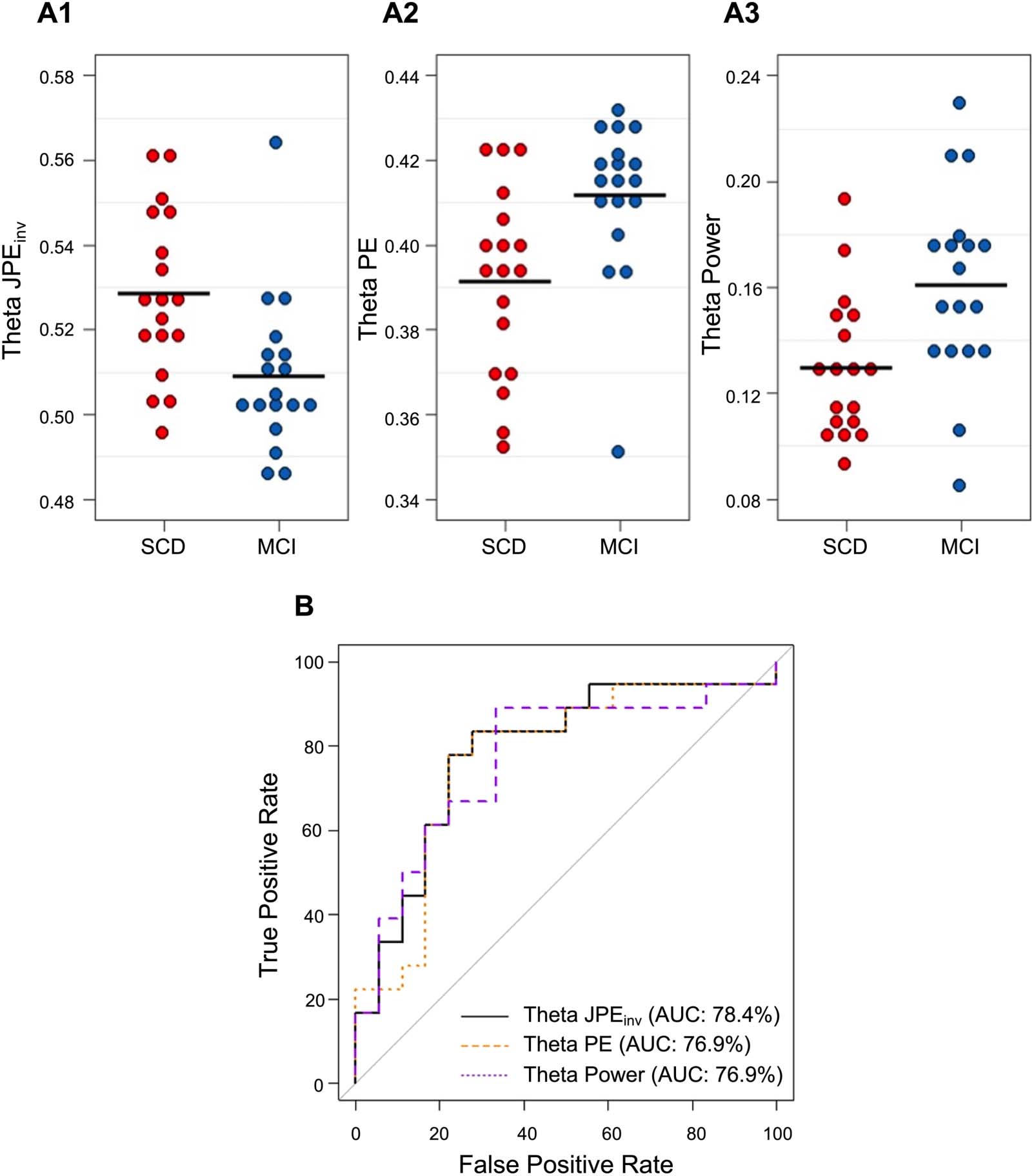
for the individual subjects are plotted in Figure 6A1–A3. Visual inspection of the data revealed
that the range of the MEG metrics partially overlapped between groups. The diagnostic value
of global theta JPEinv, PE, and relative power was therefore assessed with logistic regression
models. AUCs (and 95% confidence intervals) for SCD-MCI classification per MEG metric
are listed in Table 2. ROC curves for the individual predictors are plotted in Figure 6B. Highest
accuracy for differentiating between SCD and MCI subjects was achieved by the JPEinv-based
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
2
3
8
2
2
0
2
8
1
0
4
n
e
n
_
a
_
0
0
2
2
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6. Classification of SCD and MCI subjects based on global theta JPEinv, PE, and relative power. (A1–A3) Each dot depicts the whole-
brain average for a single subject. Black horizontal lines reflect the group means. JPEinv, PE, and relative power values are shown for the theta
band (4–8 Hz). Visual inspection revealed that MCI subjects (depicted in blue) generally had lower JPEinv, higher PE, and higher relative theta
power values than SCD subjects (depicted in red). (B) ROC curve analysis indicated that the highest diagnostic accuracy was achieved by
the JPEinv-based logistic regression model (AUC = 78.4%), followed by models trained on PE and relative theta power values (AUC = 76.9%).
AUC = area under the curve. JPEinv = inverted joint permutation entropy. PE = permutation entropy. MCI = mild cognitive impairment. SCD =
subjective cognitive decline.
Network Neuroscience
392
Network permutation entropy of MEG as a biomarker of early Alzheimer’s
Table 2. Classification of SCD and MCI subjects based on theta band JPEinv, PE, and relative
power. CI = confidence interval. JPEinv = inverted joint permutation entropy. PE = permutation
entropy.
MEG marker
Theta JPEinv
Theta PE
Relative theta power
AUC (95% CI)
78.4% (62.5–93.3%)
76.9% (60.3–93.4%)
76.9% (60.4–93.3%)
model (AUC = 78.4%), followed by the PE and relative theta power models (AUC = 76.9%).
One-way ANCOVA indicated that there was a significant effect of diagnostic group on mean
theta JPEinv after controlling for mean relative theta power (F(1, 33) = 5.27, p < 0.05, η2 =
0.14), suggesting that the entropy variance between groups can at least partially be explained
by nonlinear characteristics.
DISCUSSION
The aim of the present study was to explore the potential of a network version of permutation
entropy ( JPEinv) as a biomarker for early-stage AD. Substantially lower JPEinv values were
reported in MCI than in SCD subjects in the theta and alpha frequency bands, signifying
weaker network coupling in this predementia phase of AD. Local PE and relative power
were higher in MCI subjects in the theta band. The biomarker potential of all three measures
was evaluated using logistic regression models. The JPEinv-based model achieved the highest
accuracy when discriminating between subjects with SCD and MCI.
Lower Theta and Alpha JPEinv in MCI
The JPEinv showed significant differences between SCD and MCI subjects in the theta and
alpha band, in nearly all investigated brain regions (Figure 3). It is important to realize that
the joint entropy depends on both local entropy and the level of nonlinear coupling between
activity of different regions (Figure 2). Low levels of noninverted JPE typically reflect a combi-
nation of low local entropy and strong interregional coupling, while high levels of noninverted
JPE reflect the opposite pattern. To facilitate comparison with conventional functional connec-
tivity measures, we introduced the inverted JPE ( JPEinv). The lower JPEinv values reported here
reflect stronger local entropy in MCI (which is in line with the reported PE results) as well as
lower functional connectivity. Previous studies have reported a loss of functional connectivity
in AD, especially in the alpha and beta frequency bands (Babiloni et al., 2020; Engels et al.,
2015; Engels et al., 2017; Pievani et al., 2011). In predementia AD, however, both increased
(theta band) and decreased (alpha and beta band) functional connectivity have been reported
(Engels et al., 2017; Pusil et al., 2019). Phase- and amplitude-based connectivity measures
may have different sensitivities for changes in specific frequency bands (Briels et al., 2020).
Although the mixed local/interregional nature of the JPEinv complicates direct comparison with
conventional functional connectivity studies, this study shows that JPEinv can detect abnormal
communication between widely distributed brain regions in a predementia AD stage. Further-
more, the magnitude of the JPEinv differences between SCD and MCI subjects is much larger
than the effects reported in other functional connectivity studies. Connectivity measures have
so far shown inferior biomarker performance when compared with theta band power (Gouw
et al., 2017; Gouw et al., 2021; Scheltens et al., 2018).
Network Neuroscience
393
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
2
3
8
2
2
0
2
8
1
0
4
n
e
n
_
a
_
0
0
2
2
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Network permutation entropy of MEG as a biomarker of early Alzheimer’s
Higher Theta PE in MCI
To determine the added value of the JPEinv we compared the results with those obtained from
local PE analysis. We found a clear increase in theta band PE in MCI subjects, in almost
all brain regions. Several previous studies have suggested that entropy is actually decreased
in AD patients (Ando et al., 2021; Gómez & Hornero, 2010; Maturana-Candelas et al., 2019;
Shumbayawonda et al., 2020). In agreement with our present study, Maturana-Candelas et al.
(2019) have shown that local entropy can increase in the MCI stage, depending on the time-
scale at which entropy is calculated. Echegoyen et al. (2020) have also shown that the direc-
tion of PE changes may depend upon the frequency band. The increase in theta band PE that
was observed in MCI could reflect a transient phase of neuronal hyperactivity due to failure of
GABAergic inhibitory interneurons in the cortex (Maestú et al., 2021). Previous studies have
already suggested a relation between the excitation/inhibition balance and local measures of
signal variability/complexity (Waschke et al., 2021). Future model work will have to establish
more firmly whether a consistent relation exists between signal irregularity or entropy and the
excitation/inhibition balance. A link between micro- and macroscale neurophysiological phe-
nomena in AD is a highly desired translational feature (Maestú et al., 2021) and would
strengthen the basis for using entropy measures as biomarkers. The increase in local theta band
PE can also be related to the JPEinv findings: Higher local entropy and less interregional cou-
pling will produce lower JPEinv. By computing both PE and JPEinv, it may be possible to deter-
mine the relative contribution of local dynamics and interregional connectivity to the early
stages of AD.
The Role of Parameters in Entropy Computations
Computation of entropy measures such as the PE and JPEinv requires the choice of various
parameter settings. The pattern size n determines the total number of different patterns (n!).
In the original paper by Bandt and Pompe (2002), it was recommended to choose n such that
n! is much smaller than the length of the time series. This restriction is necessary to obtain
reliable statistics for the probability distributions. In the present study we choose a relatively
high value (n = 4), to compensate for the loss of patterns due to our correction method for the
effects of volume conduction/field spread (King et al., 2013). To demonstrate the validity of the
selected symbol size, we repeated the JPEinv and PE analysis for different settings of n (Support-
ing Information, Figures 1–3). Another important parameter is time-delay tau (τ). For an illus-
tration of the effect of using different values for tau, see Figure 1D in the present article, or
Figure 2 in Kottlarz et al. (2021). In agreement with Bandt and Pompe (2002), we used τ =
1 for our main analysis. To explore the possible effect of another choice for tau, we repeated
the analysis of JPEinv and PE for tau = sample frequency/ (3 × high-frequency filter) (Montez
et al., 2006); see the Supporting Information, Supplementary Figures 4 and 5. This choice of
tau was motivated by the argument that tau should be small enough to capture the highest
frequencies present in the signal after filtering. The results for different values of tau indicated
a shift of significant group differences from the theta and alpha bands to broadband data. For
the JPEinv, the direction of the difference between SCD and MCI subjects also changed. The
dependency of entropy results on the time delay parameter tau and frequency band is in line
with the notion of multiscale entropy as introduced by Costa et al. (2002). According to the
multiscale concept, the magnitude and direction of entropy differences depend upon the time-
scale. This can be explored by creating coarse-grained versions of the original time series and
plotting entropy as a function of these timescales. Although this coarse-graining procedure has
become very popular in entropy studies, its interpretation is not without problems (Courtiol
et al., 2016; Kosciessa et al., 2020). We therefore combined broadband and narrowband
Network Neuroscience
394
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
2
3
8
2
2
0
2
8
1
0
4
n
e
n
_
a
_
0
0
2
2
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Network permutation entropy of MEG as a biomarker of early Alzheimer’s
filtering with different settings of tau as an alternative procedure. Our results confirm the
importance of temporal scale for entropy measures.
Classification of Individuals
The diagnostic ability of the JPEinv and PE was compared with that of relative theta power, the
most potent neurophysiological biomarker of predementia AD to date (Babiloni et al., 2021;
Gouw et al., 2017; Gouw et al., 2021; Rossini et al., 2020). We restricted our analysis to mean
JPEinv, PE, and relative power of data filtered in the theta band. ROC analysis based upon logis-
tic regression showed that theta band JPEinv had the highest AUC. PE and theta power had
identical AUC, which was slightly lower than that obtained with JPEinv. One-way ANCOVA
with relative theta power as a covariate was performed to control for the potential confounding
effect of oscillatory slowing on the JPEinv analysis. A significant effect of diagnostic group on
mean theta JPEinv was still present after controlling for mean relative theta power, suggesting
that the entropy variance between groups can at least partially be explained by nonlinear
characteristics. The measure therefore has potential to outperform “pure” theta power as a
biomarker for early AD. Since the present study was rather small, and we did not have an
independent test set, we cannot yet conclude that the JPEinv performs significantly better than
PE or theta power. However, without any extensive optimization, the accuracy obtained with
the JPEinv and PE falls within the same range as the current “gold standard” in early AD:
relative theta power (Gouw et al., 2017; Gouw et al., 2021; Scheltens et al., 2018). Our results
are comparable to those obtained with the multiscale entropy in a study in advanced AD
patients (Ando et al., 2021). Further improvement of the JPEinv approach, for instance by opti-
mizing tau and n, or by making use of state-of-the-art machine learning techniques, holds
promise to deliver a highly sensitive biomarker.
Limitations
Weaknesses of the present study were its relatively small size and the lack of an independent
test set. For artifact removal we relied on our clinical pipeline, which included tSSS (Taulu &
Simola, 2006), but we did not use additional tools such as independent component analysis. It
should however be noted that the use of extensive preprocessing in combination with entropy
analysis has been questioned (Ando et al., 2021). During JPEinv analysis we corrected for vol-
ume conduction in a rigorous way, following the proposal by King et al. (2013). While this
conservative approach may have caused a certain amount of true functional connectivity to
be ignored, we still obtained striking group differences. The influence of volume conduction
correction rigidity should be addressed in follow-up studies. Although we did observe signif-
icant group differences in JPEinv and PE for frequency bands other than the theta band, we
refrained from (over)interpretation of these findings, since much fewer regions (except for
alpha band JPEinv) were involved and group differences were small. Future studies with larger
groups should confirm these findings. We furthermore only used mean values, averaged over
all ROIs, in the theta band as input for the classification analysis. Use of a larger range of input
features, including information from different ROIs and different frequency bands, in combi-
nation with sophisticated machine learning, will probably produce higher sensitivity and spec-
ificity values. This was not considered justified in the present study because of its small size
and exploratory character.
Conclusion
To conclude, we have shown that a multivariate version of the permutation entropy holds
promise as a biomarker for early-stage Alzheimer’s disease. The method could clearly separate
Network Neuroscience
395
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
2
3
8
2
2
0
2
8
1
0
4
n
e
n
_
a
_
0
0
2
2
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Network permutation entropy of MEG as a biomarker of early Alzheimer’s
subjects with MCI due to AD from control subjects with subjective cognitive complaints. Pre-
liminary analysis of classification results shows that performance of the JPEinv falls within the
same range as relative theta power—currently the most effective neurophysiological bio-
marker for early AD. Future studies will have to replicate and extend these results in larger
samples, preferably with longitudinal data. These samples should include individuals along
the entire AD continuum. The present findings could form the starting point for further
improvement of complexity-based measures and the use of advanced machine learning tech-
niques. Finally, computational (neural mass) modeling may help to relate measures of neural
variability and complexity such as the JPE to underlying neuronal excitation/inhibition
(im)balance, in order to gain a better mechanistic understanding of AD.
ACKNOWLEDGMENTS
The authors would like to thank the participants of the Amsterdam Dementia Cohort for their
contribution. Research of Amsterdam Alzheimer Center is part of the neurodegeneration pro-
gram of Amsterdam Neuroscience. The Amsterdam Alzheimer Center is supported by Alzhei-
mer Nederland and Stichting VUmc funds. The authors thank technicians P. J. Ris, C. H.
Plugge, N. Sijsma, N. C. Akemann, N. Zwagerman, and M.C. Alting Siberg for acquisition
of the MEG data.
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00224.
AUTHOR CONTRIBUTIONS
Elliz P. Scheijbeler: Formal analysis; Writing – original draft. Anne M. van Nifterick: Writing –
original draft. Cornelis J. Stam: Conceptualization; Formal analysis; Software; Writing – original
draft. Arjan Hillebrand: Conceptualization; Writing – review & editing. Alida A. Gouw:
Writing – review & editing. Willem de Haan: Data curation; Writing – review & editing.
REFERENCES
Ando, M., Nobukawa, S., Kikuchi, M., & Takahashi, T. (2021). Iden-
tification of electroencephalogram signals in Alzheimer’s disease
by multifractal and multiscale entropy analysis. Frontiers in Neu-
roscience, 15, 667614. https://doi.org/10.3389/fnins.2021
.667614, PubMed: 34262427
Angulo-Ruiz, B. Y., Muñoz, V., Rodríguez-Martínez, E. I., & Gómez,
C. M. (2021). Absolute and relative variability changes of the
resting state brain rhythms from childhood and adolescence to
young adulthood. Neuroscience Letters, 749, 135747. https://
doi.org/10.1016/j.neulet.2021.135747, PubMed: 33610662
Babiloni, C., Arakaki, X., Azami, H., Bennys, K., Blinowska, K.,
Bonanni, L., Bujan, A., Carrillo, M. C., Cichocki, A., de Frutos-
Lucas, J., Del Percio, C., Dubois, B., Edelmayer, R., Egan, G.,
Epelbaum, S., Escudero, J., Evans, A., Farina, F., Fargo, K., …
Guntekin B. (2021). Measures of resting state EEG rhythms for
clinical trials in Alzheimer’s disease: Recommendations of an
expert panel. Alzheimer’s and Dementia, 17(9), 1528–1553.
https://doi.org/10.1002/alz.12311, PubMed: 33860614
Babiloni, C., Blinowska, K., Bonanni, L., Cichocki, A., de Haan, W.,
Del Percio, C., Dubois, B., Escudero, J., Fernández, A., Frisoni, G.,
Guntekin, B., Hajos, M., Hampel, H., Ifeachor, E., Kilborn, K.,
Kumar, S., Johnsen, K., Johannsson, M., Jeong, J., … Randall F.
(2020). What electrophysiology tells us about Alzheimer’s
disease: A window into the synchronization and connectivity of
brain neurons. Neurobiology of Aging, 85, 58–73. https://doi.org
/10.1016/j.neurobiolaging.2019.09.008, PubMed: 31739167
Bandt, C., & Pompe, B. (2002). Permutation entropy: A natural
complexity measure for time series. Physical Review Letters,
88(17), 174102. https://doi.org/10.1103/ PhysRevLett.88
.174102, PubMed: 12005759
Baracchini, G., Mišić, B., Setton, R., Mwilambwe-Tshilobo, L.,
Girn, M., Nomi, J. S., Uddin, L. Q., Turner, G. R., & Spreng,
R. N. (2021). Inter-regional BOLD signal variability is an organi-
zational feature of functional brain networks. NeuroImage, 237,
118149. https://doi.org/10.1016/j.neuroimage.2021.118149,
PubMed: 33991695
Network Neuroscience
396
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
2
3
8
2
2
0
2
8
1
0
4
n
e
n
_
a
_
0
0
2
2
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Network permutation entropy of MEG as a biomarker of early Alzheimer’s
Benjamini, Y., & Hochberg, Y. (1995). Controlling the false discov-
ery rate: A practical and powerful approach to multiple testing.
Journal of the Royal Statistical Society: Series B (Methodological),
57(1), 289–300. https://doi.org/10.1111/j.2517-6161.1995
.tb02031.x
Boylan, M. A., Foster, C. M., Pongpipat, E. E., Webb, C. E.,
Rodrigue, K. M., & Kennedy, K. M. (2021). Greater BOLD vari-
ability is associated with poorer cognitive function in an adult
lifespan sample. Cerebral Cortex, 31(1), 562–574. https://doi
.org/10.1093/cercor/bhaa243, PubMed: 32915200
Briels, C. T., Schoonhoven, D. N., Stam, C. J., de Waal, H.,
Scheltens, P., & Gouw, A. A. (2020). Reproducibility of EEG func-
tional connectivity in Alzheimer’s disease. Alzheimer’s Research
and Therapy, 12(1), 68. https://doi.org/10.1186/s13195-020
-00632-3, PubMed: 32493476
Bruining, H., Hardstone, R., Juarez-Martinez, E. L., Sprengers, J.,
Avramiea, A. E., Simpraga, S., Houtman, S. J., Poil, S. S., Dallares,
E., Palva, S., Oranje, B., Matias Palva, J., Mansvelder, H. D., &
Linkenkaer-Hansen, K. (2020). Measurement of excitation-
inhibition ratio in autism spectrum disorder using critical brain
dynamics. Scientific Reports, 10(1), 9195. https://doi.org/10
.1038/s41598-020-65500-4, PubMed: 32513931
Bullmore, E., & Sporns, O. (2009). Complex brain networks: Graph
theoretical analysis of structural and functional systems. Nature
Reviews Neuroscience, 10(3), 186–198. https://doi.org/10.1038
/nrn2575, PubMed: 19190637
Cheyne, D., Bostan, A. C., Gaetz, W., & Pang, E. W. (2007). Event-
related beamforming: A robust method for presurgical functional
mapping using MEG. Clinical Neurophysiology, 118(8), 1691–1704.
https://doi.org/10.1016/j.clinph.2007.05.064, PubMed: 17587643
Colclough, G. L., Woolrich, M. W., Tewarie, P. K., Brookes, M. J.,
Quinn, A. J., & Smith, S. M. (2016). How reliable are MEG
resting-state connectivity metrics? NeuroImage, 138, 284–293.
https://doi.org/10.1016/j.neuroimage.2016.05.070, PubMed:
27262239
Colom-Cadena, M., Spires-Jones, T., Zetterberg, H., Blennow, K.,
Caggiano, A., DeKosky, S. T., Fillit, H., Harrison, J. E., Schneider,
L. S., Scheltens, P., de Haan, W., Grundman, M., van Dyck,
C. H., Izzo, N. J., Catalano, S. M., & Synaptic Health Endpoints
Working Group. (2020). The clinical promise of biomarkers of
synapse damage or loss in Alzheimer’s disease. Alzheimer’s
Research and Therapy, 12(1), 21. https://doi.org/10.1186
/s13195-020-00588-4, PubMed: 32122400
Costa, M., Goldberger, A. L., & Peng, C. K. (2002). Multiscale
entropy analysis of complex physiologic time series. Physical
Review Letters, 89(6), 068102. https://doi.org/10.1103
/PhysRevLett.89.068102, PubMed: 12190613
Costa, M., Goldberger, A. L., & Peng, C. K. (2005). Multiscale entropy
analysis of biological signals. Physical Review E, 71(2 Pt. 1),
021906. https://doi.org/10.1103/PhysRevE.71.021906, PubMed:
15783351
Courtiol, J., Perdikis, D., Petkoski, S., Müller, V., Huys, R., Sleimen-
Malkoun, R., & Jirsa, V. K. (2016). The multiscale entropy: Guide-
lines for use and interpretation in brain signal analysis. Journal of
Neuroscience Methods, 273, 175–190. https://doi.org/10.1016/j
.jneumeth.2016.09.004, PubMed: 27639660
Courtney, S. M., & Hinault, T. (2021). When the time is right: Tem-
poral dynamics of brain activity in healthy aging and dementia.
Progress in Neurobiology, 203, 102076. https://doi.org/10.1016/j
.pneurobio.2021.102076, PubMed: 34015374
Dávalos, A., Jabloun, M., Ravier, P., & Buttelli, O. (2019). On the
statistical properties of multiscale permutation entropy: Charac-
terization of the estimator’s variance. Entropy, 21(5), 450. https://
doi.org/10.3390/e21050450, PubMed: 33267164
de Haan, W., Mott, K., van Straaten, E. C., Scheltens, P., & Stam,
C. J. (2012). Activity dependent degeneration explains hub
vulnerability in Alzheimer’s disease. PLoS Computational Biology,
8(8), e1002582. https://doi.org/10.1371/journal.pcbi.1002582,
PubMed: 22915996
de Haan, W., van Straaten, E. C. W., Gouw, A. A., & Stam, C. J.
(2017). Altering neuronal excitability to preserve network con-
nectivity in a computational model of Alzheimer’s disease. PLoS
Computational Biology, 13(9), e1005707. https://doi.org/10.1371
/journal.pcbi.1005707, PubMed: 28938009
Douw, L., van Dellen, E., Gouw, A. A., Griffa, A., de Haan, W., van
den Heuvel, M., Hillebrand, A., Van Mieghem. P., Nissen, I. A.,
Otte, W. M., Reijmer, Y. D., Schoonheim, M. M., Senden, M., van
Straaten, E. C. W., Tijms, B. M., Tewarie, P., & Stam, C. J. (2019).
The road ahead in clinical network neuroscience. Network Neu-
roscience, 3(4), 969–993. https://doi.org/10.1162/netn_a_00103,
PubMed: 31637334
Dustman, R. E., Shearer, D. E., & Emmerson, R. Y. (1999). Life-span
changes in EEG spectral amplitude, amplitude variability and
mean frequency. Clinical Neurophysiology, 110(8), 1399–1409.
https://doi.org/10.1016/S1388-2457(99)00102-9, PubMed:
10454276
Echegoyen, I., López-Sanz, D., Martínez, J. H., Maestú, F., & Buldú,
J. M. (2020). Permutation entropy and statistical complexity in
mild cognitive impairment and Alzheimer’s disease: An analysis
based on frequency bands. Entropy, 22(1), 116. https://doi.org/10
.3390/e22010116, PubMed: 33285891
Engels, M. M. A., Stam, C. J., van der Flier, W. M., Scheltens, P., de
Waal, H., & van Straaten, E. C. (2015). Declining functional con-
nectivity and changing hub locations in Alzheimer’s disease: An
EEG study. BMC Neurology, 15, 145. https://doi.org/10.1186
/s12883-015-0400-7, PubMed: 26289045
Engels, M. M. A., van der Flier, W. M., Stam, C. J., Hillebrand, A.,
Scheltens, P., & van Straaten, E. C. W. (2017). Alzheimer’s
disease: The state of the art in resting-state magnetoencephalog-
raphy. Clinical Neurophysiology, 128(8), 1426–1437. https://doi
.org/10.1016/j.clinph.2017.05.012, PubMed: 28622527
Fadlallah, B., Chen, B., Keil, A., & Príncipe, J. (2013). Weighted-
permutation entropy: A complexity measure for time series incor-
porating amplitude information. Physical Review E, 87(2),
022911. https://doi.org/10.1103/PhysRevE.87.022911, PubMed:
23496595
Fekete, T., Hinrichs, H., Sitt, J. D., Heinze, H. J., & Shriki, O. (2021).
Multiscale criticality measures as general-purpose gauges of
proper brain function. Scientific Reports, 11(1), 14441. https://
doi.org/10.1038/s41598-021-93880-8, PubMed: 34262121
Gao, R., Peterson, E. J., & Voytek, B. (2017). Inferring synaptic
excitation/inhibition balance from field potentials. NeuroImage,
158, 70–78. https://doi.org/10.1016/j.neuroimage.2017.06.078,
PubMed: 28676297
Garrett, D. D., Nagel, I. E., Preuschhof, C., Burzynska, A. Z.,
Marchner, J., Wiegert, S., Jungehülsing, G. J., Nyberg, L.,
Network Neuroscience
397
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
2
3
8
2
2
0
2
8
1
0
4
n
e
n
_
a
_
0
0
2
2
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Network permutation entropy of MEG as a biomarker of early Alzheimer’s
Villringer, A., Li, S. C., Heekeren, H. R., Bäckman, L., &
Lindenberger, U. (2015). Amphetamine modulates brain signal
variability and working memory in younger and older adults.
Proceedings of the National Academy of Sciences, 112(24),
7593–7598. https://doi.org/10.1073/pnas.1504090112,
PubMed: 26034283
Garrett, D. D., Samanez-Larkin, G. R., MacDonald, S. W.,
Lindenberger, U., McIntosh, A. R., & Grady, C. L. (2013).
Moment-to-moment brain signal variability: A next frontier in
human brain mapping? Neuroscience and Biobehavioral
Reviews, 37(4), 610–624. https://doi.org/10.1016/j.neubiorev
.2013.02.015, PubMed: 23458776
Godfrey, M., & Singh, K. D. (2021). Measuring robust functional
connectivity from resting-state MEG using amplitude and entropy
correlation across frequency bands and temporal scales. Neuro-
Image, 226, 117551. https://doi.org/10.1016/j.neuroimage.2020
.117551, PubMed: 33186722
Gómez, C., & Hornero, R. (2010). Entropy and complexity analyses
in Alzheimer’s disease: An MEG study. Open Biomedical Engi-
n eering Jo urnal , 4, 2 23–235 . ht tps: // doi .org/10.217 4
/1874120701004010223, PubMed: 21625647
Gómez, C., Pérez-Macías, J. M., Poza, J., Fernández, A., & Hornero,
R. (2013). Spectral changes in spontaneous MEG activity across
the lifespan. Journal of Neural Engineering, 10(6), 066006.
https://doi.org/10.1088/1741-2560/10/6/066006, PubMed:
24100075
Gong, G., He, Y., Concha, L., Lebel, C., Gross, D. W., Evans, A. C.,
& Beaulieu, C. (2009). Mapping anatomical connectivity patterns
of human cerebral cortex using in vivo diffusion tensor imaging
tractography. Cerebral Cortex, 19(3), 524–536. https://doi.org/10
.1093/cercor/bhn102, PubMed: 18567609
Gouw, A. A., Alsema, A. M., Tijms, B. M., Borta, A., Scheltens, P.,
Stam, C. J., & van der Flier, W. M. (2017). EEG spectral analysis
as a putative early prognostic biomarker in nondemented,
amyloid positive subjects. Neurobiology of Aging, 57, 133–142.
https://doi.org/10.1016/j.neurobiolaging.2017.05.017, PubMed:
28646686
Gouw, A. A., Hillebrand, A., Schoonhoven, D. N., Demuru, M., Ris
Scheltens, P., & Stam, C. J. (2021). Routine magnetoencephalog-
raphy in memory clinic patients: A machine learning approach.
Alzheimer’s and Dementia, 13, e12227. https://doi.org/10.1002
/dad2.12227, PubMed: 34568539
Grady, C. L., & Garrett, D. D. (2018). Brain signal variability is
modulated as a function of internal and external demand in
younger and older adults. NeuroImage, 169, 510–523. https://
doi.org/10.1016/j.neuroimage.2017.12.031 , PubMed:
29253658
Hillebrand, A., Barnes, G. R., Bosboom, J. L., Berendse, H. W., &
Stam, C. J. (2012). Frequency-dependent functional connectivity
within resting-state networks: An atlas-based MEG beamformer
solution. NeuroImage, 59(4), 3909–3921. https://doi.org/10
.1016/j.neuroimage.2011.11.005, PubMed: 22122866
Hillebrand, A., Tewarie, P., van Dellen, E., Yu, M., Carbo, E. W. S,
Douw, L., Gouw, A. A., van Straaten, E. C. W., & Stam, C. J.
(2016). Direction of information flow in large-scale resting-state
networks is frequency-dependent. Proceedings of the National
Academy of Sciences, 113(14), 3867–3872. https://doi.org/10
.1073/pnas.1515657113, PubMed: 27001844
Horvath, A., Szucs, A., Csukly, G., Sakovics, A., Stefanics, G., &
Kamondi, A. (2018). EEG and ERP biomarkers of Alzheimer’s
disease: A critical review. Frontiers in Bioscience (Landmark),
23, 183–220. https://doi.org/10.2741/4587, PubMed: 28930543
Hughes, L. E., Henson, R. N., Pereda, E., Bruña, R., López-Sanz, D.,
Quinn, A. J., Woolrich, M. W., Nobre, A. C., Rowe, J. B., Maestú,
F., & BioFIND Working Group. (2019). Biomagnetic biomarkers
for dementia: A pilot multicentre study with a recommended
methodological framework for magnetoencephalography.
Alzheimer’s and Dementia, 11, 450–462. https://doi.org/10
.1016/j.dadm.2019.04.009, PubMed: 31431918
Inouye, T., Shinosaki, K., Sakamoto, H., Toi, S., Ukai, S., Iyama, A.,
Katsuda, Y., & Hirano, M. (1991). Quantification of EEG irregu-
larity by use of the entropy of the power spectrum. Electroen-
cephalography and Clinical Neurophysiology, 79(3), 204–210.
https://doi.org/10.1016/0013-4694(91)90138-T, PubMed:
1714811
Jamin, A., & Humeau-Heurtier, A. (2020). (Multiscale) cross-entropy
methods: A review. Entropy, 22(1), 45. https://doi.org/10.3390
/e22010045, PubMed: 33285820
Keshmiri, S. (2020). Entropy and the brain: An overview. Entropy,
22(9), 917. https://doi.org/10.3390/e22090917, PubMed:
33286686
King, J. R., Sitt, J. D., Faugeras, F., Rohaut, B., El Karoui, I., Cohen,
L., Naccache, L., & Dehaene, S. (2013). Information sharing in
the brain indexes consciousness in noncommunicative patients.
Current Biology, 23(19), 1914–1919. https://doi.org/10.1016/j
.cub.2013.07.075, PubMed: 24076243
Kosciessa, J. Q., Kloosterman, N. A., & Garrett D. D. (2020). Stan-
dard multiscale entropy reflects neural dynamics at mismatched
temporal scales: What’s signal irregularity got to do with it? PLoS
Computational Biology, 16(5), e1007885. https://doi.org/10.1371
/journal.pcbi.1007885, PubMed: 32392250
Kottlarz, I., Berg, S., Toscano-Tejeida, D., Steinmann, I., Bähr, M.,
Luther, S., Wilke, M., Parlitz, U., & Schlemmer, A. (2021).
Extracting robust biomarkers from multichannel EEG time series
using nonlinear dimensionality reduction applied to ordinal pat-
tern statistics and spectral quantities. Frontiers in Physiology, 11,
614565. https://doi.org/10.3389/fphys.2020.614565, PubMed:
33597891
Kumral, D., Şansal, F., Cesnaite, E., Mahjoory, K., Al, E., Gaebler,
M., Nikulin, V. V., & Villringer, A. (2020). BOLD and EEG signal
variability at rest differently relate to aging in the human brain.
N e u ro I m a g e , 2 0 7 , 11 6 3 7 3 . h t t p s : / / d o i . o r g / 1 0 . 1 0 1 6 / j
.neuroimage.2019.116373, PubMed: 31759114
Lee, H., Noh, G. J., Joo, P., Choi, B. M., Silverstein, B. H., Kim, M.,
Wang, J., Jung, W. S., & Kim, S. (2017). Diversity of functional
connectivity patterns is reduced in propofol-induced uncon-
sciousness. Human Brain Mapping, 38(10), 4980–4995. https://
doi.org/10.1002/hbm.23708, PubMed: 28670685
Liu, M., Song, C., Liang, Y., Knöpfel, T., & Zhou, C. (2019). Asses-
sing spatiotemporal variability of brain spontaneous activity by
multiscale entropy and functional connectivity. NeuroImage,
198, 198–220. https://doi.org/10.1016/j.neuroimage.2019.05
.022, PubMed: 31091474
Liu, L., Qian, X., & Lua, H. (2010). Cross-sample entropy of foreign
exchange time series. Physica A, 389(21), 4785–4792. https://doi
.org/10.1016/j.physa.2010.06.013
Network Neuroscience
398
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
2
3
8
2
2
0
2
8
1
0
4
n
e
n
_
a
_
0
0
2
2
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Network permutation entropy of MEG as a biomarker of early Alzheimer’s
Maestú, F., de Haan, W., Busche, M. A., & DeFelipe, J. (2021).
Neuronal excitation/inhibition imbalance: Core element of a
translational perspective on Alzheimer pathophysiology. Ageing
Research Reviews, 69, 101372. https://doi.org/10.1016/j.arr
.2021.101372, PubMed: 34029743
Mahjoory, K., Cesnaite, E., Hohlefeld, F. U., Villringer, A., &
Nikulin, V. V. (2019). Power and temporal dynamics of alpha
oscillations at rest differentiate cognitive performance involving
sustained and phasic cognitive control. NeuroImage, 188,
135–144. https://doi.org/10.1016/j.neuroimage.2018.12.001,
PubMed: 30517844
Maturana-Candelas, A., Gómez, C., Poza, J., Pinto, N., & Hornero,
R. (2019). EEG characterization of the Alzheimer’s disease con-
tinuum by means of multiscale entropies. Entropy, 21(6), 544.
https://doi.org/10.3390/e21060544, PubMed: 33267258
McIntosh, A. R., Kovacevic, N., Lippe, S., Garrett, D., Grady, C., &
Jirsa, V. (2010). The development of a noisy brain. Archives
Italiennes de Biologie, 148(3), 323–337. https://doi.org/10.4449
/aib.v148i3.1225, PubMed: 21175017
Miskovic, V., MacDonald, K. J., Rhodes, L. J., & Cote, K. A. (2019).
Changes in EEG multiscale entropy and power-law frequency
scaling during the human sleep cycle. Human Brain Mapping,
40(2), 538–551. https://doi.org/10.1002/hbm.24393, PubMed:
30259594
Montez, T., Linkenkaer-Hansen, K., van Dijk, B. W., & Stam, C. J.
(2006). Synchronization likelihood with explicit time-frequency
priors. NeuroImage, 33(4), 1117–1125. https://doi.org/10.1016/j
.neuroimage.2006.06.066, PubMed: 17023181
Musaeus, C. S., Engedal, K., Høgh, P., Jelic, V., Mørup, M., Naik,
M., Oeksengaard, A., Snaedal, J., Wahlund, L., Waldemar, G.,
& Andersen, B. B. (2018). EEG theta power is an early marker
of cognitive decline in dementia due to AD. Journal of Alzhei-
mer’s Disease, 64(4), 1359–1371. https://doi.org/10.3233/JAD
-180300, PubMed: 29991135
Pfeffer, T., Ponce-Alvarez, A., Tsetsos, K., Meindertsma, T.,
Gahnström, C. J., van den Brink, R. L., Nolte, G., Engel, A. K.,
Deco, G., & Donner, T. H. (2021). Circuit mechanisms for the
chemical modulation of cortex-wide network interactions and
behavioral variability. Science Advances, 7(29), eabf5620.
https://doi.org/10.1126/sciadv.abf5620, PubMed: 34272245
Pievani, M., de Haan, W., Wu, T., Seeley, W. W., & Frisoni, G. B.
(2011). Functional network disruption in the degenerative
dementias. Lancet Neurology, 10(9), 829–843. https://doi.org/10
.1016/S1474-4422(11)70158-2, PubMed: 21778116
Pusil, S., López, M. E., Cuesta, P., Bruña, R., Pereda, E., & Maestú, F.
(2019). Hypersynchronization in mild cognitive impairment: The
“X” model. Brain, 142(12), 3936–3950. https://doi.org/10.1093
/brain/awz320, PubMed: 31633176
Richman, J. S., & Moorman, J. R. (2000). Physiological time series
analysis using approximate entropy and sample entropy. Ameri-
can Journal of Physiology: Heart and Circulatory Physiology,
278(6), H2039–H2049. https://doi.org/10.1152/ajpheart.2000
.278.6.H2039, PubMed: 10843903
Rossini, P. M., Di Iorio, R., Vecchio, F., Anfossi, M., Babiloni, C.,
Bozzali, M., Bruni, A. C., Cappa, S. F., Escudero, J., Fraga, F. J.,
Giannakopoulos, P., Guntekin, B., Logroscino, G., Marra, C.,
Miraglia, F., Panza, F., Tecchio, F., Pascual-Leone, A., & Dubois,
B. (2020). Early diagnosis of Alzheimer’s disease: The role of
biomarkers including advanced EEG signal analysis. Report from
the IFCN-sponsored panel of experts. Clinical Neurophysiology,
131(6), 1287–1310. https://doi.org/10.1016/j.clinph.2020.03
.003, PubMed: 32302946
Scheltens, P., Hallikainen, M., Grimmer, T., Duning, T., Gouw,
A. A., Teunissen, C. E., Wink, A. M., Maruff, P., Harrison, J.,
van Baal, C. M., Bruins, S., Lues, I., & Prins, N. D. (2018). Safety,
tolerability and efficacy of the glutaminyl cyclase inhibitor
PQ912 in Alzheimer’s disease: Results of a randomized,
double-blind, placebo-controlled phase 2a study. Alzheimer’s
Research and Therapy, 10(1), 107. https://doi.org/10.1186
/s13195-018-0431-6, PubMed: 30309389
Shumbayawonda, E., López-Sanz, D., Bruña, R., Serrano, N.,
Fernández, A., Maestú, F., & Abasolo, D. (2020). Complexity
changes in preclinical Alzheimer’s disease: An MEG study of
subjective cognitive decline and mild cognitive impairment.
Clinical Neurophysiology, 131(2), 437–445. https://doi.org/10
.1016/j.clinph.2019.11.023, PubMed: 31884374
Stam, C. J. (2014). Modern network science of neurological disor-
ders. Nature Reviews Neuroscience, 15(10), 683–695. https://doi
.org/10.1038/nrn3801, PubMed: 25186238
Stam, C. J., de Haan, W., Daffertshofer, A., Jones, B. F., Manshanden,
I., van Cappellen van Walsum, A. M., Montez, T., Verbunt, J. P., de
Munck, J. C., van Dijk, B. W., Berendse, H. W., & Scheltens, P.
(2009). Graph theoretical analysis of magnetoencephalographic
functional connectivity in Alzheimer’s disease. Brain, 132(Pt. 1),
213–224. https://doi.org/10.1093/ brain/awn262, PubMed:
18952674
Stam, C. J., Jones, B. F., Nolte, G., Breakspear, M., & Scheltens, P.
(2007). Small-world networks and functional connectivity in
Alzheimer’s disease. Cerebral Cortex, 17(1), 92–99. https://doi
.org/10.1093/cercor/bhj127, PubMed: 16452642
Stefanovski, L., Meier, J. M., Pai, R. K., Triebkorn, P., Lett, T., Martin,
L., Bülau, K., Hofmann-Apitius, M., Solodkin, A., McIntosh,
A. R., & Ritter, P. (2021). Bridging scales in Alzheimer’s disease:
Biological framework for brain simulation with The Virtual Brain.
Frontiers in Neuroinformatics, 15, 630172. https://doi.org/10
.3389/fninf.2021.630172, PubMed: 33867964
Stefanovski, L., Triebkorn, P., Spiegler, A., Diaz-Cortes, M. A.,
Solodkin, A., Jirsa, V., McIntosh, A. R., Ritter, P., & Alzheimer’s
Disease Neuroimaging Initiative. (2019). Linking molecular
pathways and large-scale computational modeling to assess
candidate disease mechanisms and pharmacodynamics in
Alzheimer’s disease. Frontiers in Computational Neuroscience,
13, 54. https://doi.org/10.3389/fncom.2019.00054, PubMed:
31456676
Su, R., Li, X., Liu, Y., Cui, W., Xie, P., & Han, Y. (2021). Evaluation of
the brain function state during mild cognitive impairment based
on weighted multiple multiscale entropy. Frontiers in Aging
Neuroscience, 13, 625081. https://doi.org/10.3389/fnagi.2021
.625081, PubMed: 34393752
Supekar, K., Menon, V., Rubin, D., Musen, M., & Greicius, M. D.
(2008). Network analysis of intrinsic functional brain connectiv-
ity in Alzheimer’s disease. PLoS Computational Biology, 4(6),
e1000100. https://doi.org/10.1371/journal.pcbi.1000100,
PubMed: 18584043
Taulu, S., Kajola, M., & Simola, J. (2004). Suppression of interfer-
ence and artifacts by the signal space separation method. Brain
Network Neuroscience
399
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
2
3
8
2
2
0
2
8
1
0
4
n
e
n
_
a
_
0
0
2
2
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Network permutation entropy of MEG as a biomarker of early Alzheimer’s
Topography, 16(4), 269–275. https://doi.org/10.1023/ B:BRAT
.0000032864.93890.f9, PubMed: 15379226
Taulu, S., & Simola, J. (2006). Spatiotemporal signal space separa-
tion method for rejecting nearby interference in MEG measure-
ments. Physics in Medicine and Biology, 51(7), 1759. https://doi
.org/10.1088/0031-9155/51/7/008, PubMed: 16552102
Taulu, S., Simola, J., & Kajola, M. (2005). Applications of the signal
space separation method. IEEE Transactions on Signal Processing,
53(9), 3359–3372. https://doi.org/10.1109/TSP.2005.853302
Tzourio-Mazoyer, N., Landeau, B., Papathanassiou, D., Crivello, F.,
Etard, O., Delcroix, N., Mazoyer, B., & Joliot, M. (2002). Auto-
mated anatomical labeling of activations in SPM using a macro-
scopic anatomical parcellation of the MNI MRI single-subject
brain. NeuroImage, 15(1), 273–289. https://doi.org/10.1006
/nimg.2001.0978, PubMed: 11771995
Uddin, L. Q. (2020). Bring the noise: Reconceptualizing spontane-
ous neural activity. Trends in Cognitive Sciences, 24(9), 734–746.
https://doi.org/10.1016/j.tics.2020.06.003, PubMed: 32600967
van den Heuvel, M. P., Scholtens, L. H., & Kahn, R. S. (2019).
Multiscale neuroscience of psychiatric disorders. Biological Psy-
chiatry, 86(7), 512–522. https://doi.org/10.1016/j.biopsych.2019
.05.015, PubMed: 31320130
van der Flier, W. M., & Scheltens, P. (2018). Amsterdam Dementia
Cohort: Performing research to optimize care. Journal of Alzhei-
mer’s Disease, 62(3), 1091–1111. https://doi.org/10.3233/JAD
-170850, PubMed: 29562540
van Diessen, E., Numan, T., van Dellen, E., van der Kooi, A. W.,
Boersma, M., Hofman, D., van Lutterveld, R., van Dijk, B. W.,
van Straaten, E. C., Hillebrand, A, & Stam, C. J. (2015). Oppor-
tunities and methodological challenges in EEG and MEG resting
state functional brain network research. Clinical Neurophysiol-
ogy, 126(8), 1468–1481. https://doi.org/10.1016/j.clinph.2014
.11.018, PubMed: 25511636
van Wijk, B. C., Stam, C. J., & Daffertshofer, A. (2010). Comparing
brain networks of different size and connectivity density using
graph theory. PLoS ONE, 5(10), e13701. https://doi.org/10.1371
/journal.pone.0013701, PubMed: 21060892
Wang, D. J. J., Jann, K., Fan, C., Qiao, Y., Zang, Y. F., Lu, H., & Yang,
Y. (2018). Neurophysiological basis of multi-scale entropy
of brain complexity and its relationship with functional
connectivity. Frontiers in Neuroscience, 12, 352. https://doi.org
/10.3389/fnins.2018.00352, PubMed: 29896081
Waschke, L., Kloosterman, N. A., Obleser, J., & Garrett, D. D.
(2021). Behavior needs neural variability. Neuron, 109(5),
751–766. https://doi.org/10.1016/j.neuron.2021.01.023,
PubMed: 33596406
Waschke, L., Tune, S., & Obleser, J. (2019). Local cortical desyn-
chronization and pupil-linked arousal differentially shape brain
states for optimal sensory performance. eLife, 8, e51501.
https://doi.org/10.7554/eLife.51501, PubMed: 31820732
Yin, D., & Kaiser, M. (2021). Understanding neural flexibility from a
multifaceted definition. NeuroImage, 235, 118027. https://doi
.org/10.1016/j.neuroimage.2021.118027, PubMed: 33836274
Yin, Y., Shang, P., Ahn, A. C., & Peng, C. K. (2019). Multiscale joint
permutation entropy for complex time series. Physica A, 515(C),
388–402. https://doi.org/10.1016/j.physa.2018.09.179
Yin, Y., Shang, P., & Feng, G. (2016). Modified multiscale
cross-sample entropy for complex time series. Applied Mathe-
matics and Computation, 289, 98–110. https://doi.org/10.1016/j
.amc.2016.05.013
Yu, M., Engels, M. M. A., Hillebrand, A., van Straaten, E. C. W.,
Gouw, A. A., Teunissen, C., van der Flier, W. M., Scheltens, P.,
& Stam, C. J. (2017). Selective impairment of hippocampus and
posterior hub areas in Alzheimer’s disease: An MEG-based mul-
tiplex network study. Brain, 140(5), 1466–1485. https://doi.org
/10.1093/brain/awx050, PubMed: 28334883
Yu, M., Sporns, O., & Saykin, A. J. (2021). The human connectome
in Alzheimer disease: Relationship to biomarkers and genetics.
Nature Reviews Neurology, 17(9), 545–563. https://doi.org/10
.1038/s41582-021-00529-1, PubMed: 34285392
Yu, W. Y., Low, I., Chen, C., Fuh, J. L., & Chen, L. F. (2021). Brain
dynamics altered by photic stimulation in patients with
Alzheimer’s disease and mild cognitive impairment. Entropy,
23(4), 427. https://doi.org/10.3390/e23040427, PubMed:
33916588
Zheng, Y., Luo, J. J., Harris, S., Kennerley, A., Berwick, J., Billings,
S. A., & Mayhew, J. (2012). Balanced excitation and inhibition:
Model based analysis of local field potentials. NeuroImage,
63(1), 81–94. https://doi.org/10.1016/j.neuroimage.2012.06
.040, PubMed: 22759993
Network Neuroscience
400
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
2
3
8
2
2
0
2
8
1
0
4
n
e
n
_
a
_
0
0
2
2
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3