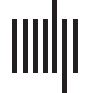FOCUS FEATURE: - Specialized Research AI at MIT

FOCUS FEATURE:
Network Communication in the Brain

Models of communication and control for
brain networks: distinctions, convergence,
and future outlook

Pragya Srivastava1, Erfan Nozari2, Jason Z. Kim1, Harang Ju3, Dale Zhou3, Cassiano Becker1,

Fabio Pasqualetti4, George J. Pappas2, and Danielle S. Bassett

1,2,5,6,7,8

1Department of Bioengineering, University of Pennsylvania, Philadelphia, PA USA
2Department of Electrical & Systems Engineering, University of Pennsylvania, Philadelphia, PA USA
3Neuroscience Graduate Group, Perelman School of Medicine, University of Pennsylvania, Philadelphia, PA USA
4Department of Mechanical Engineering, University of California, Riverside, CA USA
5Department of Physics & Astronomy, University of Pennsylvania, Philadelphia, PA USA
6Department of Neurology, University of Pennsylvania, Philadelphia, PA USA
7Department of Psychiatry, University of Pennsylvania, Philadelphia, PA USA
8Santa Fe Institute, Santa Fe, NM USA

Keywords: Communication models, Brain dynamics, Spatiotemporal scales in brain, Control models
for brain networks, Linear control, Time-varying control, Nonlinear control, Integrated models,
System identiﬁcation, Causality

ABSTRACT

Recent advances in computational models of signal propagation and routing in the
human brain have underscored the critical role of white-matter structure. A complementary
approach has utilized the framework of network control theory to better understand
how white matter constrains the manner in which a region or set of regions can direct or
control the activity of other regions. Despite the potential for both of these approaches to
enhance our understanding of the role of network structure in brain function, little work has
sought to understand the relations between them. Here, we seek to explicitly bridge
computational models of communication and principles of network control in a conceptual
review of the current literature. By drawing comparisons between communication and
control models in terms of the level of abstraction, the dynamical complexity, the
dependence on network attributes, and the interplay of multiple spatiotemporal scales, we
highlight the convergence of and distinctions between the two frameworks. Based on the
understanding of the intertwined nature of communication and control in human brain
networks, this work provides an integrative perspective for the ﬁeld and outlines exciting
directions for future work.

AUTHOR SUMMARY

Models of communication in brain networks have been essential in building a quantitative
understanding of the relationship between structure and function. More recently,
control-theoretic models have also been applied to brain networks to quantify the response
of brain networks to exogenous and endogenous perturbations. Mechanistically, both of
these frameworks investigate the role of interregional communication in determining the
behavior and response of the brain. Theoretically, both of these frameworks share common
features, indicating the possibility of combining the two approaches. Drawing on a large
body of past and ongoing works, this review presents a discussion of convergence and
distinctions between the two approaches, and argues for the development of integrated

a n o p e n a c c e s s

j o u r n a l

Citation: Srivastava, P., Nozari, E.,
Kim, J. Z., Ju, H., Zhou, D., Becker, C.,
Pasqualetti, F., Pappas, G. J., &
Bassett, D. S. (2020). Models of
communication and control for brain
networks: distinctions, convergence,
and future outlook. Network
Neuroscience, 4(4), 1122–1159.
https://doi.org/10.1162/netn_a_00158

DOI:
https://doi.org/10.1162/netn_a_00158

Received: 14 February 2020
Accepted: 21 July 2020

Competing Interests: The authors have
declared that no competing interests
exist.

Corresponding Author:
Danielle S. Bassett
dsb@seas.upenn.edu

Handling Editor:
Andrea Avena-Koenigsberger

Copyright: © 2020
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license

The MIT Press

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
4
1
1
2
2
1
8
6
6
9
2
7
n
e
n
_
a
_
0
0
1
5
8
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Models of communication and control for brain networks

models at the conﬂuence of the two frameworks, with potential applications to various topics
in neuroscience.

INTRODUCTION

The propagation and transformation of signals among neuronal units that interact via structural
connections can lead to emergent communication patterns at multiple spatial and temporal
scales. Collectively referred to as ‘communication dynamics,’ such patterns reﬂect and sup-
port the computations necessary for cognition (Avena-Koenigsberger, Misic, & Sporns, 2018;
Bargmann & Marder, 2013). Communication dynamics consist of two elements: (i) the dy-
namics that signals are subjected to, and (ii) the propagation or spread of signals from one
neural unit to another. Whereas the former is determined by the biophysical processes that act
on the signals, the latter is dictated by the structural connectivity of brain networks. Math-
ematical models of communication incorporate one or both of these elements to formal-
ize the study of how function arises from structure. Such models have been instrumental in
advancing our mechanistic understanding of observed neural dynamics in brain networks
(Avena-Koenigsberger et al., 2018; Bansal, Nakuci, & Muldoon, 2018; Bargmann & Marder,
2013; Bassett, Zurn, & Gold, 2018; Cabral et al., 2014; Hermundstad et al., 2013; N. J. Kopell,
Gritton, Whittington, & Kramer, 2014; Mišíc et al., 2015; Shen, Hutchison, Bezgin, Everling,
& McIntosh, 2015; Sporns, 2013a; Vázquez-Rodríguez et al., 2019).

Building on the descriptive models of neural dynamics, greater insight can be obtained if
one can perturb the system and accurately predict how the system will respond (Bassett et al.,
2018). The step from description to perturbation can be formalized by drawing on both histor-
ical and more recent advances in the ﬁeld of control theory. As a particularly well-developed
subﬁeld, the theory of linear systems offers ﬁrst principles of system analysis and design, both
to ensure stability and to inform control (Kailath, 1980). In recent years, this theory has been
applied to the human brain and to nonhuman neural circuits to ask how interregional con-
nectivity can be utilized to navigate the system’s state space (Gu et al., 2017; Tang & Bassett,
2018; Towlson et al., 2018), to explain the mechanisms of endogenous control processes (such
as cognitive control) (Cornblath et al., 2019; Gu et al., 2015), and to design exogenous inter-
vention strategies (such as stimulation) (Khambhati et al., 2019; Stiso et al., 2019). Applicable
across spatial and temporal scales of inquiry (Tang et al., 2019), the approach has proven use-
ful for probing the functional implications of structural variation in development (Tang et al.,
2017), heritability (W. H. Lee, Rodrigue, Glahn, Bassett, & Frangou, 2019; Wheelock et al.,
2019), psychiatric disorders (Fisher & Velasco, 2014; Jeganathan et al., 2018), neurological
conditions (Bernhardt et al., 2019), neuromodulatory systems (Shine et al., 2019), and detec-
tion of state transitions (Santanielloa et al., 2011; Santanielloa, Sherman, Thakor, Eskandar, &
Sarma, 2012). Further research in the area of application of network control theory to brain
networks can inform neuromodulation strategies (Fisher & Velasco, 2014; L. M. Li et al., 2019)
and stimulation therapies (Santanielloa, Gale, & Sarma, 2018).

Theoretical frameworks for communication and control share several common features. In
communication models, the observed neural activity is strongly inﬂuenced by the topology of
structural connections between brain regions (Avena-Koenigsberger et al., 2018; Bassett et al.,
2018). In control models, the energy injected through exogenous control signals is also con-
strained to ﬂow along the same structural connections. Thus, the metrics used to characterize
communication and control both show strong dependence on the topology of structural brain
networks. Interwoven with the topology, the dynamics of signal propagation in both the control
and communication models involve some level of abstraction of the underlying processes, and

Network Neuroscience

1123

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
4
1
1
2
2
1
8
6
6
9
2
7
n
e
n
_
a
_
0
0
1
5
8
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Models of communication and control for brain networks

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
4
1
1
2
2
1
8
6
6
9
2
7
n
e
n
_
a
_
0
0
1
5
8
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Figure 1. Goals of communication and control models share an inverse relationship. The propa-
gation of an initial stimulus is dictated by the underlying structural connections of the brain network
and results in the observed communication dynamics. Stimuli can be external (e.g., transcranial di-
rect current stimulation, sensory stimuli, behavioral therapy, drugs) or internal (e.g., endogenous
brain activity, cognitive control strategies). The primary goal of communication models is to capture
the evolution of communication dynamics by using dynamical models, and to characterize the pro-
cess of signal propagation, using graph-theoretic and statistical measures. In contrast, a fundamental
aim in the framework of control theory is to determine the control strategies that would navigate
the system from a given initial state to the desired ﬁnal state. Control signals (shown by the red
lightning bolt) move a controllable system along trajectories (shown as a red dotted curve on the
state plane) that connect the initial and ﬁnal states. Here, the cost of the trajectory is determined
by the energetics of the state transition. We show example trajectories T
1 and T2 on an example
energy landscape.

dictate the behavior of the system’s states. Despite these practical similarities, communication
and control models differ appreciably in their goals (Figure 1). Whereas communication mod-
els primarily seek to explain the patterns of neural signaling that can arise at rest or in response
to stimuli, control theory primarily seeks principles whereby inputs can be designed to elicit
desired patterns of neural signaling, under certain assumptions of system dynamics. In other
words, at a conceptual level, communication models seek to understand the state transitions
that arise from a given set of inputs (including the absence of inputs), whereas control models
seek to design the inputs to achieve desirable state transitions.

While relatively simple similarities and dissimilarities are apparent between the two ap-
proaches, the optimal integration of communication and control models requires more than a
superﬁcial comparison. Here, we provide a careful investigation of relevant distinctions and
a description of common ground. We aim to ﬁnd the points of convergence between the two
frameworks, identify outstanding challenges, and outline exciting research problems at their

Network Neuroscience

1124

Models of communication and control for brain networks

interface. The remainder of this review is structured as follows. First, we brieﬂy review the
fundamentals of communication models and network control theory in sections 2 and 3, re-
spectively. In both sections, we order our discussion of models from simpler to more complex,
and we place particular emphasis on each model’s spatiotemporal scale. Section 4 is devoted
to a comparison between the two approaches in terms of (i) the level of abstraction, (ii) the
complexity of the dynamics and observed behavior, (iii) the dependence on network attributes,
and (iv) the interplay of multiple spatiotemporal scales. In section 5, we discuss future areas
of research that could combine elements from the two avenues alongside outstanding chal-
lenges. Finally, we conclude by summarizing and elucidating the usefulness of combining the
two approaches and the implications of such work for understanding brain and behavior.

COMMUNICATION MODELS

In a network representation of the brain, neuronal units are represented as nodes, while in-
terunit connections are represented as edges. Such connections can be structural, in which
case they are estimated from diffusion imaging (Lazar, 2010), or can be functional (Morgan,
Achard, Termenon, Bullmore, & Vértes, 2018), in which case they are estimated by statistical
similarities in activity from functional neuroimaging. When the state of node j at a given time t
is inﬂuenced by the state of node i at previous time points, a communication channel is said
to exist between the two nodes, with node i being the sender and node j being the receiver
(Figure 2A). The set of all communication channels forms the substrate for communication pro-
cesses. A given communication process can be multiscale in nature: communication between
individual units of the network typically leads to the emergence of global patterns of commu-
nication thought to play important roles in computation and cognition (Avena-Koenigsberger
et al., 2018).

In brain networks, the state of a given node can inﬂuence the state of another node pre-
cisely because the two are connected by a structural or effective link. This structural constraint
on potential causal relations results in patterns of activity reﬂecting communication among
units. Such activity can be measured by techniques such as functional magnetic resonance
imaging (fMRI), electroencephalography (EEG), magnetoencephalography (MEG), and elec-
trocorticography (ECoG), among others (Beauchene, Roy, Moran, Leonessa, & Abaid, 2018;
Sporns, 2013b). In light of the complexity of observed activity patterns and in response to
questions regarding their generative mechanisms, investigators have developed mathematical
models of neuronal communication. Such models allow for inferring, relating, and predicting
the dependence of measured communication dynamics on the topology of brain networks.

Communication models can be roughly classiﬁed into three types: dynamical, topological,
and information theoretic. Dynamical models of communication are generative, and seek to
capture the biophysical mechanisms that transform signals and transmit them along structural
connections. Topological models of communication propose network attributes, such as mea-
sures of path and walk structure, to explain observed activity patterns. Information theoretic
models of communication deﬁne statistical measures to quantify the interdependence of nodal
activity, the direction of communication, and the causal relations between nodes. Several ex-
cellent reviews describe these three model types in great detail (Avena-Koenigsberger et al.,
2018; Bassett et al., 2018; Breakspear, 2017; Deco, Jirsa, Robinson, Breakspear, & Friston,
2008). Thus here we instead provide a rather brief description of the associated approaches
and measures, particularly focusing on aspects that will be relevant to our later comparisons
with the framework of control theory.

Dynamic Models and Measures

Dynamical models of communication aim to capture the biophysical mechanisms underlying
signal propagation between communicating neuronal units in brain networks. Such models

Network Neuroscience

1125

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

4
4
1
1
2
2
1
8
6
6
9
2
7
n
e
n
_
a
_
0
0
1
5
8
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Models of communication and control for brain networks

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
n
a
r
t
i
c
e
–
p
d

f
/

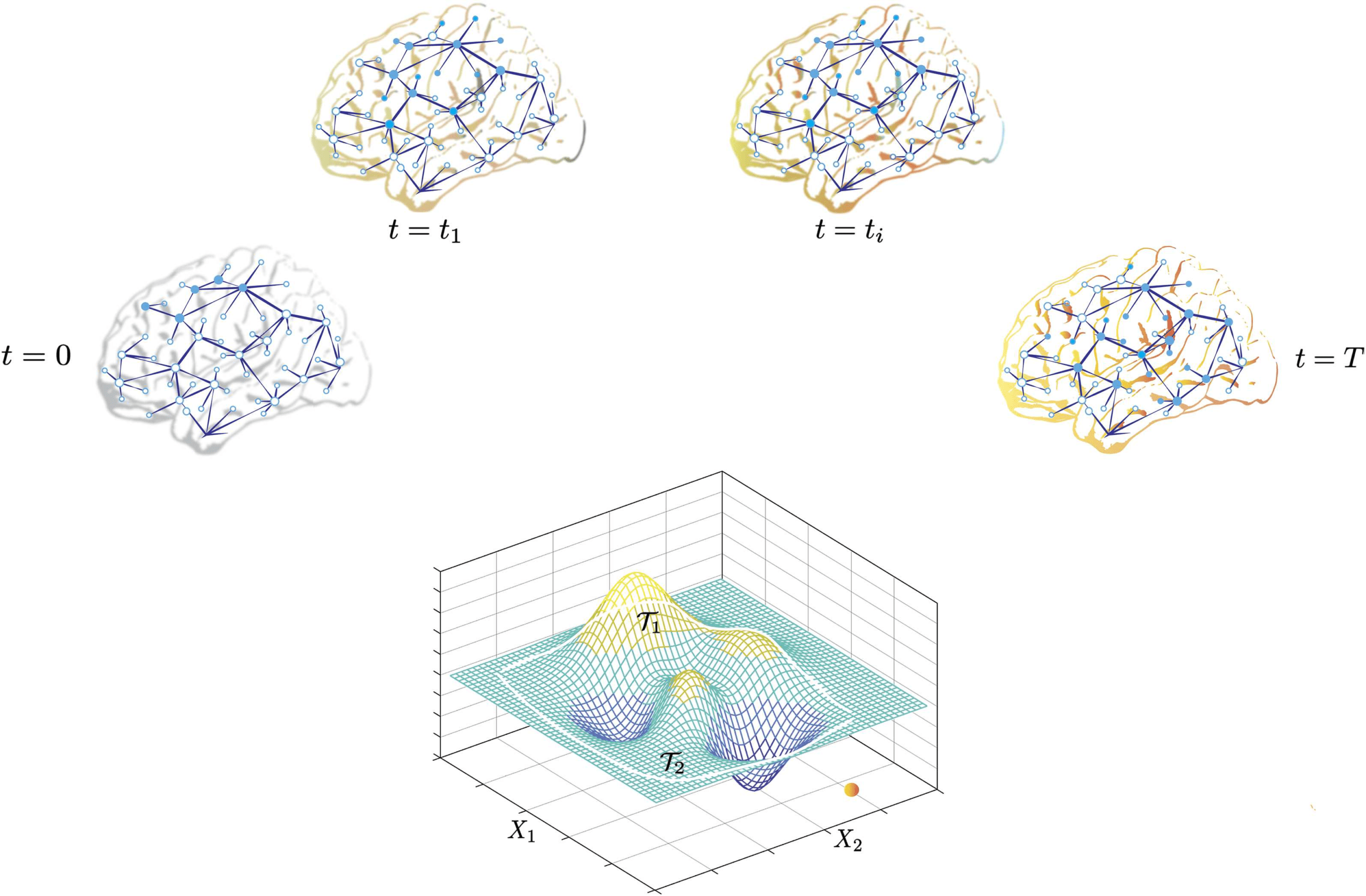
Figure 2. Models and measures of communication. (A) A communication event from sender node i to receiver node j causes dependencies
in the activity xj(t) of the j-th node on the activity xi(t) of the i-th node. (B) The three classes of mathematical approaches (empty triangles) to
understanding emergent communication dynamics, as well as potential areas of overlap (shaded triangles), shown along three axes. Topological
models (along caerulean axis) primarily construct measures based on paths or walks (red edges) between communicating nodes. Dynamical
models (along mauve axis) can be cast into differential equations (for continuous-time dynamics) or difference equations (for discrete time
dynamics) that capture dynamic processes governing the propagation of information at a given spatiotemporal scale. Information theoretic
models (along green axis) propose measures to compute the degree to which xj(t) statistically (and sometimes causally) depends on xi(t).

4
4
1
1
2
2
1
8
6
6
9
2
7
n
e
n
_
a
_
0
0
1
5
8
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

can be deﬁned at various levels of complexity, ranging from relatively simple linear diffusion
models to highly nonlinear ones. Dynamical models also differ in terms of the spatiotemporal
scales of phenomena that they seek to explain. The choice of explanatory scale impacts the
precise communication dynamics that the model produces, as well as the scale of collective
dynamics that can emerge.

The general form of a deterministic dynamical model at an arbitrary scale is given by

(Breakspear, 2017):

dx
dt

= f (x, A, u, β) .

(1)

Here, x encodes the state variables that are used to describe the state of the network, A encodes
the underlying connectivity matrix, and u encodes the input variables. The functional form of
f is set by the requirements (i.e., the expected utility) of the model. For example, at the level of
individual neurons communicating via synaptic connections, the conservation law for electric
charges (together with model ﬁtting for the gating variables) determines the functional form of
f in the Hodgkin-Huxley model (Hodgkin & Huxley, 1952). Similarly, at the scale of neuronal
ensembles, other biophysical mechanisms such as the interactions between excitatory and
inhibitory populations dictate f in the Wilson-Cowan model (Wilson & Cowan, 1972). Finally,
β encodes other parameters of the model, independent of the connectivity strength A. The

Network Neuroscience

1126

Models of communication and control for brain networks

β parameters can be phenomenological, thereby allowing for an exploration of the whole
phase space of possible behaviors; alternatively, the β parameters can be determined from
experiments in more data-driven models. In some limiting cases, it may also be possible to
derive β parameters in a given model at a particular spatiotemporal scale from complementary
models at a ﬁner scale via the procedure of coarse-graining (Breakspear, 2017).

Fundamentally, dynamical models seek to capture communication of the sort where one
unit causes a change in the activity of another unit or shares statistical features with another
unit. There is, however, little consensus on precisely how to measure these causal or statistical
relations. One of the most common measures is Granger causality (Granger, 1969), which
estimates the statistical relation of unit xi to unit xj by the amount of predictive power that the
“past” time series {xi(τ), τ < t} of xi has in predicting xj(t). While this prediction need not be linear, Granger causality has been historically measured via linear autoregression (Kami ´nski, Ding, Truccolo, & Bressler, 2001; Korzeniewska, Ma ´nczak, Kami ´nski, Blinowska, & Kasicki, 2003); see Bressler and Seth (2011) for a review in relation to brain networks. The use of temporal precedence and lead-lag relationships is also a basis for alternative def- initions of causality. In Nolte et al. (2008), for instance, the authors propose the phase-slope index, which measures the direction of causal inﬂuence between two time series based on the lead-lag relationship between the two signals in the frequency domain. Notably, this relation- ship can be used to measure the causal effect between neural masses coupled according to the structural connectome (Stam & van Straaten, 2012). Because not all states of a complex system can often be measured, several studies have opted to ﬁrst reconstruct (equivalent) state trajectories via time delay embedding (Shalizi, 2006; Takens, 1981) before measuring predic- tive causal effects (Harnack, Laminski, Schünemann, & Pawelzik, 2017; Sugihara et al., 2012). Finally, given the capacity to perturb the states or even parameters of the network (either exper- imentally or in simulations), one can observe the subsequent changes in other network states that occur, and thereby discover and measure causal effects (Smirnov, 2014, 2018). Topological Models and Measures The potential for communication between two brain regions, each represented as a network node, is dictated by the paths that connect them. It has been thought that long routes demand high metabolic costs and sustain marked delays in signal propagation (Bullmore & Sporns, 2012). Thus, the presence and nature of shortest paths through a network are commonly used to infer the efﬁciency of communication between two regions (Avena-Koenigsberger et al., 2018). If the shortest path length between node i and node j is denoted by d(i, j) (Latora & Marchiori, 2001) then the global efﬁciency through a network is deﬁned as the mean of the in- verse shortest path lengths ǫij = 1 d(i,j) (Ek, VerSchneider, & Narayan, 2016; Latora & Marchiori, 2001). Although measures based on shortest paths have been widely used, their relevance to the true system has been called into question for three reasons. First, systems that route infor- mation exclusively through shortest paths are vulnerable to targeted attack of the associated edges (Avena-Koenigsberger et al., 2018); yet, one might have expected brains to have evolved to circumvent this vulnerability, for example, by also using nonshortest paths for routing. Sec- ond, a sole reliance on shortest-path routing implies that brain networks have nonoptimally invested a large cost in building alternative routes that essentially are not used for commu- nication. Third, the ability to route a signal by the shortest path appears to require the signal or brain regions to have biologically implausible knowledge of the global network structure. These reasons have motivated the development of alternative measures, such as the number of parallel paths or edge-disjoint paths between two regions (Avena-Koenigsberger et al., 2018); Network Neuroscience 1127 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d t . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Models of communication and control for brain networks systems using such diverse routing strategies can attain greater resilience of communication processes (Avena-Koenigsberger et al., 2019). The resilience of interregional communication in brain networks is a particularly desired feature since fragile networks have been found to be associated with neurological disorders such as epilepsy (Ehrens, Sritharan, & Sarma, 2015; A. Li, Inati, Zaghloul, & Sarma, 2017; Sritharan & Sarma, 2014). The assumption of information ﬂow through all paths available between two regions leads to the notion of communicability. By denoting the adjacency matrix A, we can deﬁne the communicability between node i and node j as the weighted sum of all walks starting at node i and ending at node j (Estrada, Hatano, & Benzi, 2012): Gji = ∞ Σ k=0 ck(Ak)ji , (2) where Ak denotes the k-th power of A, and ck are appropriately selected coefﬁcients that both ensure that the series is convergent and assign smaller weights to longer paths. If the entries of A are all nonnegative (which is the context in which communicability is mainly used), then Gji is also real and nonnegative. Out of several choices that can be made, a particularly insightful one is ck = 1 k! . The resulting communicability, also known as the exponential communicability Gji = (eA)ji, allows for interesting analogies to be drawn with the thermal Green’s function and correlations in physical systems (Estrada et al., 2012). Additionally, since (Ak)ji directly encodes the weighted paths of length k from node i to node j, one can conveniently study the path length dependence of communication. Exponential communicability is also similar to the impulse response of the system, a familiar notion in control theory which we further explore in section 4. Another ﬂow-based measure of communication efﬁciency is the mean ﬁrst-passage time, which quantiﬁes the distance between two nodes when information is propagated by diffu- sion. Similar to the global efﬁciency, the diffusion efﬁciency is the average of the inverse of the mean ﬁrst-passage time between all pairs of network nodes. Interestingly, systems that evolve under competing constraints for diffusion efﬁciency and routing efﬁciency can display a di- verse range of network topologies (Avena-Koenigsberger et al., 2018). Note that these global measures of communication efﬁciency only provide an upper bound on the assumed commu- nicative capacity of the network; in networks with signiﬁcant community or modular structures (Schlesinger, Turner, Grafton, Miller, & Carlson, 2017), other architectural attributes such as the existence and interconnectivity of highly connected hubs are determinants of the integrative capacity of a network that global measures of communication efﬁciency fail to capture accu- rately (Sporns, 2013a). Network attributes that determine an efﬁcient propagation of externally induced or intrinsic signals may inform generative models of brain networks both in health and disease (Vértes et al., 2012). Moreover, such attributes can inform the choice of control inputs targeted to guide brain state transitions; we discuss this convergence in section 4. Further, quantifying communication channel capacity calls for the use of information theory, which we turn to now. Information Theoretic Models and Measures Information theory and statistical mechanics have been used to deﬁne several measures of information transfer such as transfer entropy and Granger causality. Such measures are built on the fact that the process of signal propagation through brain networks results in collective time-dependent activity patterns of brain regions that can be measured as time series. Entropic Network Neuroscience 1128 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d . / t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Models of communication and control for brain networks measures of communication aim to ﬁnd statistical dependencies between such time series to infer the amount and direction of information transfer. The processes underlying the observed time series are typically assumed to be Markovian, and measures of statistical dependence are calculated in a manner that reﬂects causal dependence. For this reason, the causal measures of communication proposed in the information theoretic approach share similarities with those used in dynamical causal inference (Valdes-Sosa, Roebroeck, Daunizeau, & Friston, 2011). A central quantity in information theory is the Shannon entropy, which measures the un- certainty in a discrete random variable I that follows the distribution p(i) and is given by H(I) = −Σ p(i) log(p(i)). One measure of statistical interdependency between two random i variables I and J is their mutual information, MI J = Σp(i, j) log p(i),log p(j) , where p(i, j) is their joint distribution and p(i) and p(j) are its marginals. Since mutual information is symmetric, it fails to capture the direction of information ﬂow between two processes (sequences of random variables) (Schreiber, 2000). log(p(i,j)) To address this limitation, the measure of transfer entropy was proposed to capture the di- rectionality of information exchange (Schreiber, 2000). Transfer entropy takes into account the transition probability between different states, which can be the result of a stochastic dynamic process (similar to Equation 1 but with a stochastic u) and obtained from the time series of activities of brain regions through imaging techniques. To measure the direction of informa- tion transfer between processes I and J, the notion of mutual information is generalized to the mutual information rate. The transfer entropy between processes I and J is given by (Schreiber, 2000): TJ→I = Σp(in+1, i (k) n , j (l) n ) log p(in+1|i p(in+1|i (l) n ) (k) n , j (k) n ) , (3) where processes I and J are assumed to be stationary Markov processes of order k and l, (k) n ) respectively. The quantity i denotes the transition probability to state in+1 at time n + 1, given knowledge of the previous (k) n ) if the process J does not k states. The quantity p(in+1|i inﬂuence the process I. (l) n ) denotes the state of process I(J) at time n while p((in+1|i (l) n ) is the same as p(in+1|i (k) n , j (k) n (j Similar to Granger causality, transfer entropy has been extensively used to compute the statistical interdependence of dynamic processes and to infer the directionality of information exchange. Later studies have sought to combine these two measures into a single framework by deﬁning the multi-information. This approach takes into account the statistical structure of the whole system and of each subsystem, as well as the structure of the interdependence between them (Chicharro & Ledberg, 2012). Such methods complement the topological and dynamical models to provide a unique perspective on communication, by quantifying information content and transformation. Communication Models Across Spatiotemporal Scales Whether considering models that are dynamical, topological, or information theoretic, we must choose the identity of the neural unit that is performing the communication. Individual neurons form basic units of computation in the brain, which communicate with other neu- rons via synapses. One particularly common model of communication at this cellular scale is the Hodgkin-Huxley model, which identiﬁes the membrane potential as the state variable whose evolution is determined by the conservation law for electric charge (Hodgkin & Huxley, 1952). Simpliﬁcations and dimensional reductions of the Hodgkin-Huxley model have led to related models such as the Fitzhugh-Nagumo model, which is particularly useful for studying Network Neuroscience 1129 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d t / . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Models of communication and control for brain networks the resulting phase space (Abbott & Kepler, 1990; Fitzhigh, 1961). Further simpliﬁcations of the neuronal states to binary variables have facilitated detailed accounts of network-based interactions such as those provided by the Hopﬁeld model (Abbott & Kepler, 1990; Bassett et al., 2018). Collectively, despite all capturing the state of an individual neuron, these mod- els differ from one another in the biophysical realism of the chosen state variables: the on/off states in the Hopﬁeld model are arguably less realistic than the membrane potential state in the Hodgkin-Huxley model. When considering a large population of neurons, a set of simpliﬁed dynamics can be de- rived from those of a single neuron by using the formalism and tools from statistical mechanics (Abbott & Kepler, 1990; Breakspear, 2017; Deco et al., 2008). The approximations prescribed by the laws of statistical mechanics—such as, for example, the diffusion approximation in the limit of uncorrelated spikes in neuronal ensembles—have led to the Fokker-Planck equations for the probability distribution of neuronal activities. From the evolution of such probability distributions, one can derive the dynamics of the moments, such as the mean ﬁring rate and variance (Breakspear, 2017; Deco et al., 2008). Several models of neuronal ensembles exist that exhibit rich collective behavior such as synchrony (Palmigiano, Geisel, Wolf, & Battaglia, 2017; Vuksanovi´c & Hövel, 2015), oscillations (Fries, 2005; N. Kopell, Börgers, Pervouchine, Malerba, & Tort, 2010), waves (Muller, Chavane, Reynolds, & Sejnowski, 2018; Roberts et al., 2019), and avalanches (J. M. Beggs & Plenz, 2003), each supporting different modes of commu- nication. In the limit where the variance of neuronal activity over the ensemble can be assumed to be constant (e.g., in the case of strong coherence), the Fokker-Planck equation leads to neu- ral mass models (Breakspear, 2017; Coombes & Byrne, 2019). Relatedly, the Wilson-Cowan model is a mean-ﬁeld model for interacting excitatory and inhibitory populations of neurons (Wilson & Cowan, 1972), and has signiﬁcantly inﬂuenced the subsequent development of theoretical models for brain regions (Destexhe & Sejnowski, 2009; Kameneva, Ying, Guo, & Freestone, 2017). At scales larger than that of neuronal ensembles, brain dynamics can be mod- eled by coupling neural masses, Wilson-Cowan oscillators, or Kuramato oscillators according to the topology of structural connectivity (Breakspear, 2017; Muller et al., 2018; Palmigiano et al., 2017; Roberts et al., 2019; Sanz-Leon, Knock, Spiegler, & Jirsa, 2015). Collectively, these models provide a powerful way to theoretically and computationally generate the large-scale temporal patterns of brain activity that can be explained by the theory of dynamical systems. When changing models to different spatiotemporal scales, we must also change how we think about communication. While communication might involve induced spiking at the neu- ronal scale, it may also involve phase lags at the population scale. Dynamical systems theory provides a powerful and ﬂexible framework to determine the emergent behavior in dynamic models of communication. As we saw in Equation 1, the evolution of the system is represented by a trajectory in the phase space constructed from the system’s state variables. A critical notion from this theory has been that of attractors, namely, stable patterns in this phase space to which phase trajectories converge. The range of emergent behavior exhibited by the dynamical system such as steady states, oscillations, and chaos is thus determined by the nature of its attractors that can be stable ﬁxed points, limit cycles, quasi-periodic, or chaotic. Oscillations, synchro- nization, and spiral or traveling wave solutions that result from dynamical models match with the patterns observed in brain networks, and have been proposed as the mechanisms con- tributing to cross-regional communication in brain (Buelhmann & Deco, 2010; Roberts et al., 2019; Rubino, Robbins, & Hatsopoulos, 2006). The class of communication models that generate oscillatory solutions holds an important place in models of brain dynamics (Breakspear, Heitmann, & Daffertshofer, 2010; Davison, Network Neuroscience 1130 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d . / t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Models of communication and control for brain networks Aminzare, Dey, & Ehrich Leonard, n.d.). Numerous classes of nonlinear models at both the micro- and macroscale exhibit oscillatory solutions, and they can be broadly classiﬁed into periodic (limit cycle), quasi-periodic (tori), and chaotic (Breakspear, 2017). Synchronization in the activity of spiking neurons is an emergent feature of neural systems that appears to be particularly important for a variety of cognitive functions (Bennett & Zukin, 2004). This fact has motivated efforts to model brain regions as interacting oscillatory units, whose dynamics are described by, for example, the Kuramoto model for phase oscillators. In its original form, the equation for the phase variable θi(t) of the i−th Kuramoto oscillator is given by (Acebrón, Bonilla, Vicente, Ritort, & Spigler, 2005; Kuramoto, 2003) ˙θi(t) = ωi + n ∑ j=1 Aij sin(θj(t) − θi(t)), (4) where ωi denotes the natural frequency of oscillator i, which depends on its local dynamics and parameters, and Aij denotes the net connection strength of oscillator j to oscillator i. Phase oscillators generally and the Kuramoto model speciﬁcally have been widely used to model neuronal dynamics (Breakspear et al., 2010). The representation of each oscillator by its phase (which critically depends on the weak coupling assumption Ermentrout & Kopell, 1990) makes it particularly tractable to study synchronization phenomena (Boccaletti, Latora, Moreno, Chavez, & Hwang, 2006; Börgers & Kopell, 2003; Chopra & Spong, 2009; Davison et al., n.d.; Vuksanovi´c & Hövel, 2015). Generalized variants of the Kuramoto model have also been proposed and studied in the context of neuronal networks (Cumin & Unsworth, 2007). CONTROL MODELS While the study of communication in the neural systems has developed hand-in-hand with our understanding of the brain, the study of control dynamics in (and on) the brain is rather young and still in early stages of development. In this section we review some of the basic elements of control theory that will allow us in later sections to elucidate the relationships between communication and control in brain networks. The Theory of Linear Systems The simplicity and tractability of linear time-invariant (LTI) models have sparked signiﬁcant interest in the application of linear control theory to neuroscience (Kailath, 1980; Tang & Bassett, 2018). LTI systems are most commonly studied in state space, and their simplest form is ﬁnite dimensional, deterministic, without delays, and without instantaneous effects of the input on the output. Such a continuous-time LTI system is described by the algebraic-differential equation d dt x(t) = Ax(t) + Bu(t) y(t) = Cx(t). (5a) (5b) Here, Equation 5a is a special case of Equation 1 (with the input matrix B corresponding to β), while the output vector y now allows for a distinction between the internal, latent state variables x and the external signals that can be measured, say, via neuroimaging. In the context of brain networks, the matrix A is most often chosen to be the structural connectivity matrix obtained from the imaging of white-matter tracts (Gu et al., 2015; Stiso et al., 2019). More recently effective connectivity matrices have also been encoded as A (Scheid et al., 2020; Stiso et al., 2020), as have functional connectivity matrices inferred from systems identiﬁcation Network Neuroscience 1131 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d . / t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Models of communication and control for brain networks l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d . 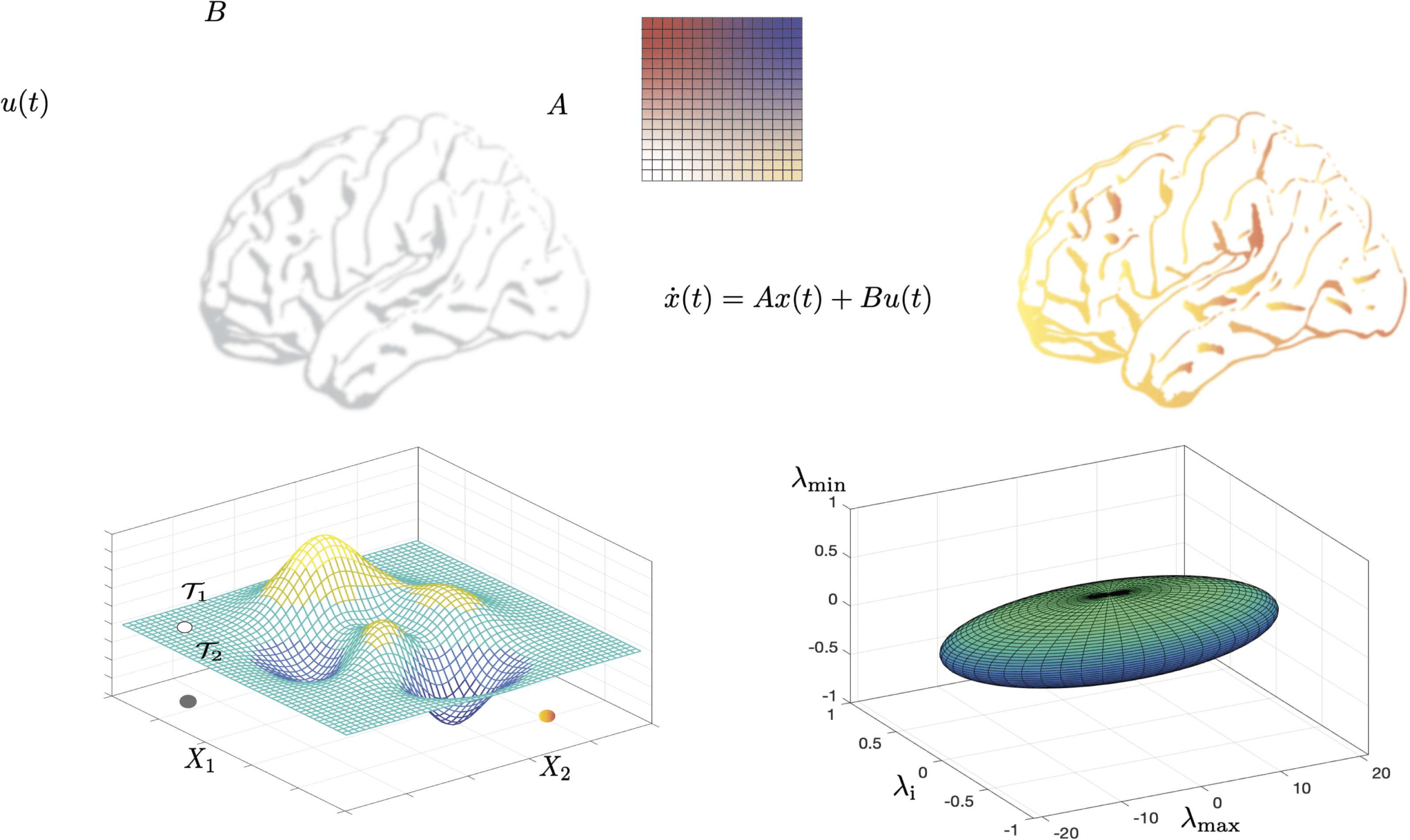/ t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 3. Control theory applied to brain networks. Control theory seeks to determine and quantify the controllability and observability properties of a given system. A system is controllable when a control input u(t) is guaranteed to exist to navigate the system from a given initial state to a desired ﬁnal state in a speciﬁed span of time. (A) We begin by encoding a brain network in the adjacency matrix denoted by A. Then, control signals u(t) act on the network via the input matrix B, leading to the evolution of the system’s state to a desired ﬁnal state according to some dynamics. The most common dynamics studied in this context is a linear time-invariant dynamics. Whether the system can be navigated between two arbitrary states in a given time period is determined by a full-rank condition on the controllability matrix. (B) The control energy landscape dictates the availability and difﬁculty of transitions between distinct system states. For a controllable system, several trajectories can exist which connect the initial and ﬁnal states. An optimum trajectory is then determined using the notion of optimal control. (C) The eigenvalues of the inverse Gramian matrix quantify the ease of moving the system along eigen directions that span the state space and form an N− ellipsoid whose surface reﬂects the control energy to make unit changes in the state of the system along the corresponding eigen direction. Here we show an ellipsoid constructed from the maximum, the minimum, and an intermediate eigenvalue of the Gramian for an example regular graph with N = 400 nodes and degree l = 40. The initial state has been taken to be at the origin, and the ﬁnal state is a random vector of length N with unit norm. Commonly used metrics of controllability such as the average controllability, can be constructed from the eigenvalues of the Gramian. methods (Deng & Gu, 2020). It is insightful to point out that in continuous-time LTI systems, the entries of matrix A have the unit of inverse time or a rate, implying that the eigenvalues of the matrix A represent the response rates of associated modes as they are excited by the stimuli u. The stimuli u represent exogenous control signals (e.g., strategies of neuromodulation such as deep brain stimulation, direct electrical stimulation and transcranial magnetic stimulation) or endogenous control (such as the mechanisms of cognitive control) and are injected into the brain networks via a control conﬁguration speciﬁed by the input matrix B (Figure 3). Then, Equation 5b speciﬁes the mapping between latent state variables x and the observable output vectors y measured via neuroimaging. Each element Cij of the matrix C thus describes the loading of the i-th measured signal on the activity level of the j-th brain region (or the j-th state in general, if states do not correspond to brain regions). Note that the number of states, inputs, and outputs need not be the same, in which case B and C are not square matrices. Network Neuroscience 1132 Models of communication and control for brain networks At the macroscale where linear models are most widely used, the state vector x often con- tains as many elements as the number of brain (sub)regions of interest with each element xi(t) representing the activity level of the corresponding region at time t, for example, correspond- ing to the mean ﬁring rate or local ﬁeld potential. The elements of the vector u are often more abstract and can model either internal or external sources. An example of an internal source would be a cognitive control signal from frontal cortex, whereas an example of an external source would be neurostimulation (Cornblath et al., 2019; Ehrens et al., 2015; Gu et al., 2015; Sritharan & Sarma, 2014). While a formal link between these internal or external sources and T 0 |u(t)|2dt represent the net en- the model vector u is currently lacking, it is standard to let ergy. The matrix B is often binary, with one nonzero entry per column, and encodes the spatial distribution of the input channels to brain regions. R Owing to the tractability of LTI systems, the state response of an LTI system (i.e., x(t)) to a given stimulus u(t) can be analytically obtained as: x(t) = eAtx(0) + eA(t−τ)Bu(τ)dτ. t 0 Z (6) In this expression, the matrix exponential eAt has a special signiﬁcance. If x(0) = 0, and if ui(t) is an impulse (i.e., a Dirac delta function) for some i, and if the remaining input channels are kept at zero, then Equation 6 simpliﬁes to the system’s impulse response x(t) = eAtbi , (7) where bi is the i-th column of B. Clearly, the impulse response has close ties to the commu- nicability property of the network introduced in section 4. We discuss this relation further in section 4, where we directly compare communication and control. Controllability and Observability in Principle One of the most successful applications of linear control theory to neuroscience lies in the evaluation of controllability. If the input-state dynamics (Equation 5a) is controllable, it is pos- sible to design a control signal u(t), t ≥ 0 such that x(0) = x0 and x(T) = x f for any initial state x0, ﬁnal state x f , and control horizon T > 0. In other words, a (continuous-time LTI)
system is controllable if it can be controlled from any initial state to any ﬁnal state in a given
amount of time; notice that controllability is independent of the system’s output. Using stan-
dard control-theoretic tools, it can be shown that the system Equation 5a is controllable if and
only if the controllability matrix C =
has full-rank n, where n denotes

B AB · · · An−1B

the dimension of the state (Kailath, 1980).

The notion of full-state controllability discussed above can at times be a strong requirement,
particularly as the size of the network (and therefore the dimension of the state space) grows.
If it happens that a system is not full-state controllable, the control input u(t) can still be
designed to steer the state in certain directions, despite the fact that not every state transition
is achievable. In fact, we can precisely determine the directions in which the state can and
cannot be steered using the input u(t). The former, called the controllable subspace, is given
by the range space of the controllability matrix C : all directions that can be written as a linear
combination of the columns of C . It can be shown that the state can be arbitrarily steered within
the controllable subspace, similar to a full-state controllable system (C.-T. Chen, 1998, §6.4).
Recall, however, that the rank of C is necessarily less than n for an uncontrollable system,
and so is the dimension of the controllable subspace. If this rank is r < n, we then have an Network Neuroscience 1133 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d / t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Models of communication and control for brain networks n − r dimensional subspace, called the uncontrollable subspace, which is orthogonal to the controllable one. In contrast to our full control over the controllable subspace, the evolution of the system is completely autonomous and independent of u(t) in the uncontrollable subspace (Kailath, 1980). Dual to the notion of controllability is that of observability, which has been explored to a lesser degree in the context of brain networks. Whereas an output can be directly computed when the input and initial state are speciﬁed (Equation 5), the converse is not necessarily true; it is not always possible to solve for the state from input-output measurements. The property that characterizes and quantiﬁes the possibility of determining the state from input-output measure- ments is termed observability, and can be understood as the possibility to invert the state-to- output map (Equation 5b), albeit over time. Interestingly, the input signal u(t) and matrix B are irrelevant for observability. Moreover, the system Equation 5 is observable if and only if its dual system dx(t)/dt = ATx(t) + CTu(t) is controllable (here, the superscript T denotes the trans- pose). This duality allows us to, for instance, easily determine the observability of Equation 5 by checking whether the observability matrix O = CT ATCT · · · (AT)n−1CT T has full rank. The notion of observability may be particularly relevant to the measurement of neural systems, and we discuss this topic further in sections 4 and 5. h i Controllability in Practice Once a system is determined to be controllable in principle, the next natural question is how to design a control signal u(t) that can move the system between two states. Although the existence of at least one such signal is guaranteed by controllability, this control signal and the resulting system trajectory may not be unique; for instance, an arbitrary intermediate point can be reached in T/2 time and then the ﬁnal state can be reached in the remaining time (both due to controllability). This nonuniqueness of control strategies leads to the problem of optimal control; that is, designing the best control signals that achieve a desired state transition, according to some criterion of optimality. The simplest and most commonly used criterion is the control energy deﬁned as ku(t)k2dt = T 0 Z T m ∑ j=1 0 Z uj(t)2dt , (8) where k · k denotes the Euclidean norm. The corresponding control signal that minimizes (8) is thus referred to as the minimum energy control. Owing to the tractability of LTI systems, this control signal and its total energy can be found analytically (Kirk, 2004). While certainly useful, the minimum energy criterion (Equation 8) has a number of limi- tations. In particular, the energy of all the control channels are weighted equally. Further, the state is allowed to become arbitrarily large between the initial and ﬁnal times. These limitations have motivated the more general linear-quadratic regulator (LQR) criterion T 0 Z m ∑ j=1 Rjuj(t)2 + n ∑ i=1 Qixi(t)2 dt = ! T 0 Z h u(t)TRu(t) + x(t)TQx(t) dt , (9) i where Rj and Qi are positive weights forming the diagonal entries of the matrices R and Q, respectively, and T denotes the transpose operator. Whereas the ﬁrst term in Equation 9 ex- presses the cost of control as in Equation 8, the second term introduces a cost on the trajectory Network Neuroscience 1134 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d t . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Models of communication and control for brain networks in state-space. This general form poses a trade-off between the two costs, and is particularly relevant in cases where some regions of state space are more preferred than others. By select- ing the entries of Q to be large relative to R, for instance, the resulting control will ensure that the state remains close to 0. The second term in Equation 9 can further be generalized to introduce a preferred trajectory in the state space by replacing x(t) by x(t) − x∗(t) where x∗(t) denotes the preferred trajectory. An analytical solution can also be found for the control signals minimizing the above generalized energy. Notably, the cost function Equation 9 has recently proven fruitful in the study of brain network architecture and development (Gu et al., 2017; Tang et al., 2017). Another central quantity of interest in characterizing the controllability properties of an LTI system is the Gramian matrix which, for continuous-time dynamics, is given as WT = T 0 Z eAtBBTeATtdt. (10) The invertibility of the Gramian matrix, equivalently to the full-rank condition of the controlla- bility matrix, ensures that the system is controllable. Further, the eigen-directions (eigenvectors) of the Gramian corresponding to its nonzero (positive) eigenvalues form a basis of the state sub- space that is reachable by the system (Figure 3C) (Lewis, Vrabie, & Syrmos, 2012; Y.-Y. Liu, Slotine, & Barabási, 2011), even when the Gramian is not invertible (note the relation with the controllable and uncontrollable subspaces discussed above). Intuitively then, the eigenvalues of the Gramian matrix quantify the ease of moving the system along corresponding eigen di- rections. Various efforts have thus been made to condense the n eigenvalues of the Gramian into a single, scalar controllability metric, such as the average controllability and control en- ergy (see below) (Gu et al., 2017; Kailath, 1980; Pasqualetti, Zampieri, & Bullo, 2014; Tang & Bassett, 2018). Using the controllability Gramian, it can in fact be shown that the energy (8) of the mininum- energy control is given by (assuming x(0) = 0 for simplicity) E = xT f W−1 T x f , (11) where x f denotes the ﬁnal state. The framework of minimum energy control and controllability metrics have recently been applied to brain networks, (see, e.g., Gu et al., 2017, 2015; Tang & Bassett, 2018; Tang et al., 2017). This framework further opens up interesting questions about its implications for control and the response of brain networks to stimuli; speciﬁcally, one might with to determine the physical interpretation of controllability metrics in brain networks and how they can inform optimal intervention strategies. We revisit this point while discussing the utility of communication models in addressing some of these questions in section 4-B. Generalizations to Time-Varying and Nonlinear Systems Used most often due to its simplicity and analytical tractability, the LTI model of system’s dynamics limits the temporal behavior that can be exhibited by the system to the following three types: exponential growth, exponential decay, and sinusoidal oscillations. In contrast, the brain exhibits a rich set of dynamics encompassing many other types of behaviors. Numer- ical simulation studies have sought to understand how such rich dynamics, occurring atop a complex network, respond to perturbative signals such as stimulation (Muldoon et al., 2016; Papadopoulos, Lynn, Battaglia, & Bassett, 2020). Yet, to more formally bring control-theoretic models closer to such dynamics and associated responses, the framework must be generalized Network Neuroscience 1135 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d . / t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Models of communication and control for brain networks to include non-linearity and/or time dependence. The ﬁrst step in such a generalization is the linear time-varying (LTV) system: d dt x(t) = A(t)x(t) + B(t)u(t) y(t) = C(t)x(t). (12a) (12b) Notably, a generalization of the optimal control problem (Equation 9) to LTV systems is fairly straightforward (Kirk, 2004). But, unlike LTI systems (Equation 6), it is generically not possible to solve for the state trajectory of an LTV system analytically. However, if the state trajectory can be found for n linearly independent initial states, then it can be found for any other initial state due to the property of linearity. In this case, moreover, many of the properties of LTI systems can be extended to LTV systems (C.-T. Chen, 1998), including the simple rank conditions of controllability and observability (Silverman & Meadows, 1967). Moving beyond the time dependence addressed in LTV systems, one can also consider the many nonlinearities present in real-world systems. In fact, the second common generalization of LTI systems (Equation 5) is to nonlinear control systems which, in continuous time, have the general state space representation: d dt x(t) = f (x(t), u(t), t) y(t) = h(x(t), t). (13a) (13b) The time dependence in f and h may be either explicit or implicit via the time dependence of x and u, resulting in a time-varying or time-invariant nonlinear system, respectively. Before proceeding to truly nonlinear aspects of Equation 13, it is instructive to consider the relationship between these dynamics and the linear models described above (Equations 5 and 12). Assume that for a given input signal u0(t), the solution to Equation 13 is given by x0(t) and y0(t). As long as the input u(t) to the system remains close to u0(t) for all time, then x(t) and y(t) also remain close to x0(t) and y(t), respectively. Therefore, one can study the dynamics of small perturbations δx(t) = x(t) − x0(t), δu(t) = u(t) − u0(t), and δy(t) = y(t) − y0(t) instead of the original state, input, and output. Using a ﬁrst-order Taylor expansion, it can immediately be seen that these signals approximately satisfy d dt δx(t) = A(t)δx(t) + B(t)δu(t) δy(t) = C(t)δx(t), (14a) (14b) ∂u0(t) , and C(t) = ∂h(x0(t),u0(t),t) which is an LTV system of the form given in Equation 12. In these equations, A(t) = ∂ f (x0(t),u0(t),t) B(t) = ∂ f (x0(t),u0(t),t) . Furthermore, A, B, and C are all known matrices that solely depend on the nominal trajectories u0(t), x0(t), y0(t). It is then clear that if the nonlinear system is time-invariant, and if u0(t) ≡ u0 is constant, and if x0(t) ≡ x0 is a ﬁxed point, then Equation 14 will take the LTI form (Equation 5). In either case, it is important to remember that this linearization is a valid approximation only locally (in the vicinity of the nominal system), and the original nonlinear system must be studied whenever the system leaves this vicinity. ∂x0(t) ∂x0(t) , Leaving the simplicity of linear systems signiﬁcantly complicates the controllability, ob- servability, and optimal control problems. Fortunately, if the linearization in Equation 14 is controllable (observable), then the nonlinear system is also locally controllable (observable) Network Neuroscience 1136 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d t / . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Models of communication and control for brain networks (Sontag, 2013) (see the topic of linearization validity discussed above). Notably, the converse is not true; the linearization of a controllable (observable) nonlinear system need not by con- trollable (observable). In such a case, one can take advantage of advanced generalizations of the linear rank condition for nonlinear systems (Sontag, 2013), although these tend to be too involved for practical use in large-scale neuronal network models. Interestingly, obtaining op- timality conditions for the optimal control of nonlinear systems is not signiﬁcantly more difﬁ- cult than that of linear systems. However, solving these optimality conditions (which can be done analytically for linear systems with quadratic cost functions, as mentioned above) leads to nonconvex optimization problems that lend themselves to no more than numerical solutions (Kirk, 2004). MODELS OF CONTROL AND COMMUNICATION: AREAS OF DISTINCTION, POINTS OF CONVERGENCE In this section, we build on the descriptions of communication and control provided in Sections 2 and 3 by seeking areas of distinction and points of convergence. We crystallize our discussion around four main topic areas: abstraction versus biophysical realism, linear versus nonlinear models, dependence on network attributes, and the interplay across different spatial or temporal scales. Our consideration of these topics will motivate a discussion of the outstanding challenges and directions for future research, which we provide in section 5. Abstraction Versus Biophysical Realism Across scientiﬁc cultures and domains of inquiry, the requirements of simplicity and tractability place strong constraints on the formulation of theoretical models. Depending on the behavior that the theory aims to capture, the models can capture detailed realistic elements of the sys- tem with the inputs from experiments (Bansal et al., 2019; Bansal, Medaglia, Bassett, Vettel, & Muldoon, 2018), or the models can be more phenomenological in nature with a pragmatic intent to make predictions and guide experimental designs. An example of a detailed realistic model in the context of neuronal dynamics is the Hodgkin-Huxley model, which takes into account the experimental results from detailed measurements of time-dependent voltage and membrane current (Abbott & Kepler, 1990). A corresponding example of a more phenomeno- logical model is the Hopﬁeld model, which encodes neuronal states in binary variables. Communication models similarly range from the biophysically real- Communication Models. istic to the highly phenomenological. Dynamical models informed by empirically measured natural frequencies, empirically measured time delays, and/or empirically measured strengths of structural connections place a premium on biophysical realism (Chaudhuri, Knoblauch, Gariel, Kennedy, & Wang, 2015a; Murphy, Bertolero, Papadopoulos, Lydon-Staley, & Bassett, 2020; Schirner, McIntosh, Jirsa, Deco, & Ritter, 2018). In contrast, Kuramoto oscillator models for communication through coherence can be viewed as less biophysically realistic and more phenomenological (Breakspear et al., 2010). Communication models also capture the state of a system differently, whether by discrete variables such as on/off states of units, or by continu- ous variables such as the phases of oscillating units. The diversity present in the current set of communication models allows theoreticians to make contact with experimental neuroscience at many levels (Bassett et al., 2018; N. J. Kopell et al., 2014; Ritter, Schirner, McIntosh, & Jirsa, 2013; Sanz-Leon et al., 2015). Alongside this diversity, communication models also share several common features. For instance, the state variables chosen to describe the dynamics of the system are motivated by neuronal observations and thus represent the system’s biological, chemical, or physical states. Network Neuroscience 1137 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d t . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Models of communication and control for brain networks The dynamics that state variables follow are also typically motivated by our understanding of the underlying processes, or approximations thereto. In building communication models, the experimental observations and intuition typically precede the mathematical formulation of the model, which in turn serves to generate predictions that help guide future experiments. A par- ticularly good example of this experiment-led theory is the Human Neocortical Neurosolver, whose core is a neocortical circuit model that accounts for biophysical origins of electrical currents generating MEG/EEG signals (Neymotin et al., 2020). Having been concurrently de- veloped with experimental neuroscience, theoretical models of communication are intricately tied to currently available measurements. The closeness to biophysical mechanisms is a feature that is also typically shown in other types of communication models. One might think that topological measures devoid of a dy- namical model tend to place a premium on phenomenology. But in fact, the cost functions that brain networks optimize typically reﬂect metabolic costs, routing efﬁciency, diffusion efﬁciency, or geometrical constraints (Avena-Koenigsberger et al., 2018, 2017; Laughlin & Sejnowski, 2003; Zhou, Lyn, et al., 2020). Minimization of metabolic costs has been shown to be a major factor determining the organization of brain networks (Laughlin & Sejnowski, 2003). Further, such constraints on metabolism also place limits on signal propagation and information processing. Are these features of communication models shared by control models? Con- Control Models. trol models have their origin in Maxwell’s analysis of the centrifugal governor that stabilized the velocity of windmills against disturbances caused by the motions of internal components (Maxwell, 1868). The ﬁeld of control theory was later further formalized for the stability of motion in linearized systems (Routh, 1877). Today, control theory is a framework in engineer- ing used to design systems and to develop strategies to inﬂuence the state of a system in a desired manner (Tang & Bassett, 2018). More recently, the framework of control theory has been applied to neural systems in order to quantify how controllable brain networks are, and to determine the optimal strategies or regions that are best to exert control on other regions (Gu et al., 2017; Tang & Bassett, 2018; Tang et al., 2017). Although initial efforts have proven quite successful, control theory and more generally, the theory of linear systems, has tradition- ally concerned itself with ﬁnding the mathematical principles behind the design and control of linear systems (Kailath, 1980), and is applicable to a wide variety of problems in many disci- plines of science and engineering. Because the application of control theory to brain networks has been a much more recent effort, identiﬁcation of appropriate state variables that are best posed to provide insights on control in brain networks is a potential area of future research. Applied to brain networks, control theoretical approaches have mostly utilized detailed knowledge of structural connections while assuming the linear dynamics formulated in Equation 5a. This simplifying abstraction implies that the inﬂuence of a system’s state at a given time propagates along the paths of the structural network encoded in A of Equation 5a to affect the system’s state at the next time point. The type of inﬂuence studied here is most consistent with the diffusion-based propagation of signals in communication models, and intuitively leads to the expected close relationship between diffusion-based communication measures and con- trol metrics. Indeed such a relationship exists between the impulse response (outlined in the previous section) and the network communicability. We elaborate further on this relationship in the next subsection. Some metrics that are commonly used to characterize the control properties of the brain are average controllability, modal controllability, and boundary controllability. These statistical Network Neuroscience 1138 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d t . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Models of communication and control for brain networks quantities can be calculated directly from the spectra of the controllability Gramian WT and the adjacency matrix A (Pasqualetti et al., 2014). A related and important quantity of interest here is the minimum control energy deﬁned as Equation 8 with u(t) denoting the control signals. While this quadratic dependence of ‘energy’ on input signals is appropriate for a linearized description of the system around a steady state, its actual dependence on the exogenous control signals must depend on several details such as the cost of generating control signals and the cost of coupling them to the system. In this sense, the control energy is a relatively abstract concept whose interpretation has yet to be linked to the physical costs of control in brain networks. This observation loops back to the fact that the development of control theory models has been more as an abstract mathematical framework which is then borrowed by several ﬁelds and thereafter modiﬁed by context. We discuss possible ways of reconciling the cost of control with actual biophysical costs known from communication models in section 5. Linear Versus Nonlinear Models In models of communication and dynamics, a reoccurring motif is the propagation of signal along connections. Graph measures such as small-worldness, global efﬁciency, and commu- nicability assume that strong and direct connections between two neural units facilitate com- munication (Avena-Koenigsberger et al., 2018; Estrada et al., 2012; Muldoon, Bridgeford, & Bassett, 2016; Watts & Strogatz, 1998). While these measures capture an intuitive concept and have been useful in predicting behavior, they themselves do not explicitly quantify the mechanism of communication or the form of the information. Dynamical models overcome the former limitation by quantitatively deﬁning the neural states of a system, and encoding the mechanism of communication in the differential or difference equations (Breakspear, 2017; Estrada et al., 2012). However, they only partially address the latter limitation, as it is unclear how a system might change its dynamics to communicate different information. There is, of course, no single spatial and temporal scale at which neural systems encode information. At the level of single neurons, neural spikes encode visual (Hubel & Wiesel, 1959) and spatial (Moser, Kropff, & Moser, 2008) features. At the level of neuronal populations in electroencephalography, changes in oscillation power and synchrony reﬂect cognitive and memory performance (Klimesch, 1999). At the level of the whole brain, abnormal spatiotempo- ral patterns in functional magnetic resonance imaging reﬂect neurological dysfunction (Broyd et al., 2009; Morgan, White, Bullmore, & Vertes, 2018; Thomason, n.d.). To accommodate this wide range of spatial and temporal scales of representation, we put forth control models as a rigorous yet ﬂexible framework to study how a neural system might modify its dynamics to communicate. The most immediate relationship between Linear Models: Level of Pairwise Nodal Interactions. dynamical models and information is through the system’s states. From this perspective, the activity or state of a single neural unit is the information to send, and communication occurs diffusively when the states of other neural units change as a result. There is an exact mathe- matical equivalence between communicability using factorial weights in Equation 2, and the impulse response of a linear dynamical system in Equation 7 through the matrix exponential. Speciﬁcally, we realize that the matrix exponential in the impulse response, eAt, can be written as communicability with factorial weights, such that eAt = ∞ ∑ k=0 ckAk, where ck = tk k! . Network Neuroscience 1139 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d . t / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Models of communication and control for brain networks This realization provides an explicit link between connectivity, dynamics, and communica- tion (Estrada et al., 2012). From the perspective of connectivity, the element in the i-th row and j-th column of the matrix exponential, [eA]ij is the total strength of connections from node j to node i through paths of all lengths. From a dynamic perspective, [eAt]ij is the change in the activity of node i after t time units as a direct result of node j having unit activity. Hence, the matrix exponential explicitly links a structural path-based feature to causal changes in activity under linear dynamics. Increasingly, the ﬁeld is realizing that the Linear Models: Level of Network-Wide Interactions. activity of neural systems is inherently distributed at both the neuronal (Steinmetz, Zatka-Haas, Carandini, & Harris, 2019; Yaffe et al., 2014) and areal (Tavor et al., 2016) levels. Hence, information is not represented as the activity of a single neural unit, but the pattern of activity, or state, of many neural units. As a result, we must broaden our concept of communication as the transfer of the system of neural units from an initial state x(0) to a ﬁnal state x(t). This perspective introduces a rich interplay between the underlying structural features of interunit interactions, and the dynamics supported by the structure to achieve a desired state transition. A crucial question in this distributed perspective of communication is the following: given that a subset of neural units are responsible for communication, what are the possible states that can be reached? For example, it seems extremely difﬁcult for a single neuron in the human brain to transition the whole brain to any desired state. This exact question has a clear and exact answer in the theory of dynamical systems and control through the controllability matrix. Speciﬁcally, given a subset of neural units K called the control set that are responsible for communication (either of their current state or the external stimuli applied to them) to the rest of the network, the space of possible state transitions is given by weighted sums of the columns of the controllability matrix, that is, the controllable subspace (cf. Section 8). Many studies in control theory are therefore directly relevant for communication, such as determining whether or not a particular control set can transition the system to any state given the underlying connectivity (Lin, 1974), or whether reducing the controllable subspace by removing neurons reduces the range of motion invivo (Yan et al., 2017). Linear Models: Accounting for Biophysical Costs. While determining the theoretical ability of performing a state transition is important, the neural units responsible for control may have to exert a biophysically infeasible amount of effort to perform the transition. Such a constraint is known to be present in many forms such as metabolic cost (Laughlin & Sejnowski, 2003; Liang, Zou, He, & Yang, 2013) and ﬁring rate capacity (Sengupta, Laughlin, & Niven, 2013). These constraints are explicitly taken into account in control theory through minimum energy control, and by extension, optimal control. As detailed in section 8, the minimum energy control places a homogeneous quadratic cost (control energy) on the amount of effort that the controlling neural units must exert to perform a state transition (Equation 8) while the general LQR optimal control additionally includes the level of activity of the neural units as a cost to penalize infeasibly large states (Equation 9). Within this framework of capturing distributed communication and biophysical constraints, there remains the outstanding question of how structural connectivity contributes to communi- cation. What features of connectivity enable a set of neural units to better transition the system than another set of units? To this end, many summary statistics have been put forth, mostly in terms of the controllability Gramian (Equation 10) due to its crucial role in determining the cost of control (Equation 11). Among them are the trace of the inverse of the Gramian, Network Neuroscience 1140 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d . / t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Models of communication and control for brain networks Tr(W−1 T ) that quantiﬁes the average energy needed to reach all states on the unit hypersphere det(WT) (or its logarithm), (Figure 3), and the square root of the determinant of the Gramian which is proportional to the volume of states that can be reached with unit input (Müller & Weber, 1972). Other studies summarize the contribution of connectivity from individual nodes (Gu et al., 2015; Simon & Mitter, 1968) or multiple nodes (Kim et al., 2018; Pasqualetti et al., 2014), leading to potential candidates for new measures of communication. p Nonlinear Models: Oscillators and Phases. When faced with the task of studying complex com- munication dynamics in neural systems, it is evident that the richness of neural behavior ex- tends beyond linear dynamics. Indeed, a typical analysis of neural data involves studying the power of the signals at various frequency bands for behaviors ranging from memory (Klimesch, 1999) to spatial representations (Moser et al., 2008), underscoring the importance of non- linear oscillations. To capture these oscillations, the earliest models of Hodgkin and Huxley (Hodgkin & Huxley, 1952), with subsequent simpliﬁcations of Izhikevich (Izhikevich, 2003) and FitzHugh-Nagumo (Fitzhigh, 1961), neurons, as well as population-averaged (Wilson & Cowan, 1972) systems, contain nonlinear interactions that can generate oscillatory behavior. In such systems, how do we quantify information and communication? Further, how would such a system change the ﬂow of communication? Some prior work has focused on lead-lag relationships between the signal phases (Nolte et al., 2008; Palmigiano et al., 2017; Stam & van Straaten, 2012), where the relation implies that communication occurs by the leading unit transmitting information to the lagging unit. A fundamental and ubiquitous equation to model this type of system is the Kuramoto equation (Equation 4), where each neural unit has a phase θi(t) that evolves forward in time according to the natural frequency ωi and a sinusoidal coupling with the phases of the other units θj, weighted by the coupling strength Aij (Acebrón et al., 2005; Kuramoto, 2003). This model has a vast theoretical and numerical foundation with myriad applications in control systems (Dörﬂer & Bullo, 2014). Given an oscillator system with ﬁxed parameters, how can the system establish and alter its lead-lag relationships? In the regime of frequency synchronization where the natural fre- quencies are not identical, the oscillators converge to a common synchronization frequency ωsync . As a result, the relative phases with respect to this frequency remain ﬁxed at θsync (Dörﬂer & Bullo, 2014), thereby establishing a lead-lag relationship. In this regime, the non- linear oscillator dynamics can be linearized about ωsync , to generate a new set of dynamics ˙θi ≈ ωi − N ∑ j=1 Lijθj, where L is the network Laplacian matrix of the coupling matrix A. In Skardal and Arenas (2015), the authors begin with an unstable general oscillator network that is not synchronized (i.e., does not have a true θsync) and perform state-feedback to stabilize an unstable set of phases θ∗, thereby inducing frequency synchronization with the corresponding lead-lag relationships. The core concept behind this state-feedback is to designate a subset of oscillators as “driven nodes,” and add an additional term that modulates the phases of these oscillators according to l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d . / t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Network Neuroscience 1141 ˙θi = ωi + N ∑ j=1 Aij sin(θj − θi) + Fi sin(θ∗ i − θi) . natural dynamics | {z } state-feedback | {z } Models of communication and control for brain networks Subsequent work focuses on expanding the form of the control input (Skardal & Arenas, 2016), and modiﬁcations to the coupling strength to a single node (Fan, Wang, Yang, & Wang, 2019). Hence, we observe that targeted modiﬁcation to the dynamics of subsets of oscillators can indeed set their lead-lag relationships. Generally, oscillator systems are not inherently phase oscillators. For example, the Wilson- Cowan (Wilson & Cowan, 1972), Izhikevich (Izhikevich, 2003), and FitzHugh-Nagumo (Fitzhigh, 1961) models are all oscillators with two state variables coupled through a set of nonlinear differential equations. The transformation of these state variables and equations into a phase oscillator form is the subject of weakly coupled oscillator theory (Dörﬂer & Bullo, 2014; Schuster & Wagner, 1990). In the event that the oscillators are not weakly coupled, then controlling the dynamics and phase relations begins to fall under the purview of linear time-varying systems (Equation 12) and nonlinear control (Khalil, 2002; Sontag, 2013). Dependence on Network Attributes In network neuroscience, recent studies have begun to characterize how network attributes inﬂuence communication and control in neuronal and regional circuits. In neuronal circuits, the spatiotemporal scale of communication has been studied from the perspective of statistical mechanics in the context of neuronal avalanches (J. M. Beggs & Plenz, 2003). Such studies show that activity propagates in a critical (J. Beggs & Timme, 2012), or at least slightly subcrit- ical (Priesemann et al., 2014; Wilting & Priesemann, 2018), regime. In a critical regime, the network connections are tuned to optimally propagate information throughout the network (J. M. Beggs & Plenz, 2003). Studies of microcircuits also show more explicitly that certain network topologies can play precise roles in communication. Hubs, which are neural units with many connections, often serve to transmit information within the network (Timme et al., n.d.). Groups of such hubs are called rich-clubs (Colizza, Flammini, Serrano, & Vespignani, 2006; Towlson, Vértes, Ahnert, Schafer, & Bullmore, 2013), which have been observed in a wide range of organisms (Faber, Timme, Beggs, & Newman, 2019; Shimono & Beggs, 2014), and they dominate information transmission and processing in networks (Faber et al., 2019). Cortical network topologies have highly nonrandom features (Song, Sjöström, Reigl, Nelson, & Chklovskii, 2005), which may support more complex routing of communication (Avena- Koenigsberger et al., 2019). In studies of neuronal gating, one group of neurons, such as the mediodorsal thalamus, can either facilitate or inhibit pathways of communication, such as that from the hippocampus to the prefrontal cortex (Floresco & Grace, 2003). Such complex routing of communication requires nonlinear dynamics, such as shunting inhibition (Borg- Graham, Monier, & Frégnac, 1998). Some models simulate inhibitory dynamics on cortical network topologies to study how those topologies may support the complex communication dynamics that occur in visual processing, such as visual attention (Olshausen, Anderson, & Van Essen,1993). Points of convergence between communication and control have been observed in regional brain networks. For example, hubs are studied in functional covariance networks and structural networks. Structural hubs are thought to act as sinks of early messaging accelerated by shortest- path structures and sources of transmission to the rest of the brain (Mišíc et al., 2015). The highly connected hub’s connections may support both the average controllability of the brain as well as the brain’s robustness to lesions of a fraction of the connections (B. Lee, Kang, Chang, & Cho, 2019). An area of distinction between control and communication in brain networks may depend on the hub topology. While communication may depend on the average controllability Network Neuroscience 1142 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d . t / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Models of communication and control for brain networks of hubs to steer the brain to new activity patterns, the brain regions that steer network dynamics to difﬁcult-to-reach states tend to not be hubs (Gu et al., 2015). In determining the full set of nodes that can confer full control of the network, hubs tend to not be in this set of driver nodes (Y.-Y. Liu et al., 2011). A point of convergence between communication and control is the consideration of how the brain network broadcasts control signals. Whereas the high degree of hubs may efﬁciently broadcast integrated control signals across the brain network in order to steer the brain to new patterns of activity, the brain regions with lower degree may receive a greater rate of control signals that are then transmitted to steer the brain to difﬁcult-to-reach patterns of activity (Zhou, Lyn, et al., 2020). To strike a balance between efﬁciency, robustness, and diverse dynamics, brain networks may have evolved toward optimizing brain network structures supporting and constraining the propagation of information. Brain networks reach a compromise between routing and diffu- sion of information compared to random networks optimized for either routing or diffusion (Avena-Koenigsberger et al., 2018). Brain networks also appear optimized for controllability and diverse dynamics compared to random networks (Tang et al., 2017). To understand how the brain can circumvent trade-offs between objectives like efﬁciency, robustness, and diverse dynamics, future studies could further investigate the network properties of the spectrum of random networks optimized toward these objectives. Existing studies focus on the trade-off between two objectives, such as network structure supporting information routing or diffu- sion, or average versus modal controllability. However, multiobjective optimization allows for further investigation of Pareto-optimal brain network evolution toward an arbitrarily large set of objective functions (Avena-Koenigsberger, Goni, Sole, & Sporns, 2015; Avena-Koenigsberger et al., 2014). The convergence between communication and control exists largely via the network topolo- gies with which they are related. Given the importance of ‘rich-club hubs’ and similar topo- logical attributes in integration and processing of information, it is natural to ask if similar properties also contribute to controllability or observability properties in brain networks. More speciﬁcally, given a region in the brain network with speciﬁc topological properties such as high degree, betweenness centrality, closeness centrality, or location between different mod- ules, what is the relationship between its role in information integration or processing and its role in controllability and observability? The tri-faceted interface of communication, control, and network topology holds great possibilities for future work, and some recent efforts have begun to relate the three (Ju, Kim, & Bassett, 2018). Interplay of Multiple Spatiotemporal Scales Most complex systems exhibit phenomena at one spatiotemporal scale that depend on phe- nomena occurring at another spatiotemporal scale. This interplay of scales is evident, for ex- ample, in the hierarchical energy cascade from lower modes (larger length scales) to higher modes (smaller length scales) in turbulent ﬂuids (Frisch, 1995), multiscaled models of mor- phogenesis (Manning, Foty, Steinberg, & Schoetz, 2010; Mao & Baum, 2015), and multiscaled models of cancer (Szyma ´nska, Cytowski, Mitchell, Macnamara, & Chaplain, 2018). A conve- nient way to study such an interplay is to transform the variables of mathematical models to their corresponding Fourier conjugate variables. This approach serves to map the larger length scales to Fourier modes of smaller wavelengths, and to map the longer timescales to smaller frequency bands. In most complex systems, current research efforts seek a quantitative under- standing of the interwoven nature of different spatiotemporal scales, which in turn can lead to an understanding of the system’s emergent behavior. Network Neuroscience 1143 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d / . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Models of communication and control for brain networks As one of the most complex systems, the brain naturally exhibits Communication Models. a rich cross-talk between different spatiotemporal scales. A key example of interplay among spatial scales is provided by recent evidence that activity propagates in a slightly subcritical regime, in which activity “reverberates” within smaller groups of neurons while still main- taining communication across those groups (Wilting & Priesemann, 2018). That cross-talk is structurally facilitated by topological features characteristic of each spatial scale: from neu- rons to neuronal ensembles to regions to circuits and systems (Bansal et al., 2019; N. J. Kopell et al., 2014; Shimono & Beggs, 2014). A key example of interplay among temporal scales is cross-frequency coupling (Canolty & Knight, 2010), which ﬁrst builds on the observation that the brain exhibits oscillations in different frequency bands thought to support informa- tion integration in cognitive processes from attention to learning and memory (Ba¸sar, 2004; Breakspear et al., 2010; Cannon et al., 2014; N. Kopell, Borgers, et al., 2010; N. Kopell, Kramer, Malerba, & Whittington, 2010). Cross-frequency coupling can occur between region i in one frequency band and region j in another frequency band, and be measure statistically (Tort, Komorowski, Eichenbaum, & Kopell, 2010). The phenomenon is thought to play a role in integrating information across multiple spatiotemporal scales (Aru et al., 2015). For example, directional coupling between hippocampal γ oscillations and the neocortical α/β oscillations occurs in the context of episodic memory (Grifﬁths et al., 2019). Interestingly, anomalies of oscillatory activity and cross-frequency coupling can serve as biomarkers of neuropsychiatric disease (Ba¸sar, 2013). While cross-scale interactions exist, most biophysical models have been developed to ad- dress the dynamics evident at a single scale. Despite that speciﬁc goal, such models can also sometimes be used to better understand the relations between scales. For example, the no- table complexity present at small scales often gives way to simplifying assumptions in some limits. That mathematical characteristic allows for coarse-grained models to be derived at the next larger spatiotemporal scale (Breakspear, 2017; Deco et al., 2008). Key examples of such coarse-graining include (i) the derivation of the Fokker-Planck equations for neuronal ensem- bles in the limit where the ﬁring activity of individual neurons are independent processes, and (ii) the derivation of neural mass models in the limit of strong coherence in neuronal ensembles. The procedure of coarse-graining is thus one theoretical tool that helps to bridge mathematical models of the system at different spatial scales, in at least some simplifying limits. Communication models also allow for an interplay between different length scales by two other mechanisms: (i) the inclusion of nonlinearities, which allow for coupling between dif- ferent modes, and (ii) the presence of global constraints. Regarding the former mechanism, a linearized description of dynamics can typically be transformed into the ‘normal’ modes of the system (i.e., the eigenvalues of the A matrix in Equation 5), and this description does not allow for the intermode coupling that would otherwise be permissible in a nonlinear communica- tion model. As an example of such nonlinear models, neural mass models and Wilson-Cowan oscillators can exhibit cross-frequency coupling via the mechanism of phase-amplitude cou- pling (Daffertshofer & van Wijk, 2011; Nozari & Cortés, 2019; Onslow, Jones, & Bogacz, 2014), where the amplitude of high-frequency oscillations are dependent on the phase of slowly vary- ing oscillations. Regarding the latter mechanism, interregional communication is constrained by the global design of brain networks that have evolved under constraints on transmission speed, spatial packing, metabolic cost, and communication efﬁciency (Laughlin & Sejnowski, 2003; Zhou, Lyn, et al., 2020). Are control models—like communication models—conducive to a careful Control Models. study of the rich interplay of multiple spatiotemporal scales in neural systems? This question Network Neuroscience 1144 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d / t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Models of communication and control for brain networks may be particularly relevant when control signals can only be injected at a given scale while the desired changes in brain activity lie at an altogether different scale. One way to interlink local and global scales in control models is to use global constraints, just as we discussed in the context of communication models. The application of control theory to a given system often requires ﬁnding control signals that minimize the overall cost of control and/or that constrain the system to follow an optimum trajectory. Both of these goals can be recast in terms of optimization problems where a suitable cost function is minimized (see section 3). In this sense, the global constraints dictate the control properties of the system. Given that linear models produce a limited number of behaviors in solution-space and do not allow for coupling between different modes (as discussed above and in section 3), the application of nonlinear control theory is highly warranted to bring an interesting interplay between different scales. Here, the theory of singular perturbations (Khalil, 2002) provides a natural and powerful tool to formally characterize the relationship between temporal scales in a multiple-timescale system (Nozari & Cortés, 2018). This theory formalizes the intuition that with respect to a subsystem at a ‘medium’ (or reference) temporal scale, the activity of subsystems at slower temporal scales is approximately constant while the activity of those at faster timescales can be approximated by their attractors (hence neglecting fast transients), and is particularly relevant for brain networks whereby timescale hierarchies have been robustly observed, both in vivo (Murray et al., 2014) and using computational modeling (Chaudhuri, Knoblauch, Gariel, Kennedy, & Wang, 2015b). Such extended control models thus form a natural approach toward a careful evaluation of cross-scale interactions. Another concrete way in which multiple scales can be incorporated into control models— while retaining simple linearized dynamics—is to build the complexity of the system into the network representation of the brain itself. The formalism of multilayered networks allows for the complexity of interacting spatiotemporal scales to be built into the structure where the layer identiﬁcation (and the deﬁnition of interlayer and intralayer edges) can be based on the inher- ent scales of the system (Muldoon, 2018; Schmidt, Bakker, Hilgetag, Diesmann, & van Albada, 2018). One concrete example of this architecture is a two-layer network in which each layer shares the same nodes (brain regions) but represents different types of connections. One such two-layer network could have nodes representing brain regions, edges in one layer representing slowly varying structural connections, and edges in the second layer representing functional connectivity with faster dynamics. Moreover, different frequency bands can be explicitly iden- tiﬁed as separate layers in a multiplex representation of brain networks (Buldú & Porter, 2017), allowing for a careful investigation of cross-frequency coupling. It would be of great interest in future to combine such a multilayer representation with the simple LTI dynamics in con- trol models to better understand how control signals can drive desired (multiscale) dynamics (Schmidt et al., 2018). The inbuilt complexity of structure can thus partially compensate for the requirement of dynamical complexity can be utilized to extend prior work seeking to un- derstand how multilayer architecture might support learning and memory in neural systems (Hermundstad, Brown, Bassett, & Carlson, 2011). OUTSTANDING CHALLENGES AND FUTURE DIRECTIONS Having discussed several areas of distinction and points of convergence, in this section we turn to a discussion of outstanding challenges and directions for future research. We focus our discussion around three primary topic areas: observability and information representation, sys- tem identiﬁcation and causal inference, and biophysical constraints. We will close in section 6 with a brief conclusion. Network Neuroscience 1145 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d / . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Models of communication and control for brain networks Observability and Information Representation In the theory of linear systems, observability is a notion that is dual to controllability and is con- sidered on an equal footing (Kailath, 1980) (cf. section 8). Interestingly, however, this equality has not been reﬂected in the use of these notions to study neural systems. The controllability properties of brain networks have comprised a large focus of the ﬁeld, whereas the concept of observability has not been applied to brain networks to an equivalent extent. The focus on the former over the latter is likely due in large part to historical inﬂuences over the processes of science, and not to any lack of utility of observability as an investigative notion. Indeed, observability may be crucial in experiments where the state variables differ from the variables that are being measured. A canonical example is situations where the state variables corre- spond to the average ﬁring rates of different neuronal populations, whereas the outputs being measured are behavioral responses. More precisely, speciﬁc stimuli (control signals) can be represented to have a more direct effect on neuronal activity patterns (state variables) that, in turn, produce behavioral responses such as eye movements (output variables) after undergo- ing cognitive processes in brain. In this example, observability refers to the ability of a system model to allow its underlying state (neuronal activity) to be uniquely determined based on the observation of samples of its output variables (behavioral responses) and an appropriate esti- mation method. Along similar direction, optimal control-based methods have been applied to detect the clinical and behavioral states and their transitions (Santanielloa et al., 2011, 2012). As discussed at length in section 3, the observability of state variables depends on the mapping between state variables and output variables encoded and determined by a state- to-output mapping (i.e., the matrix C in Equation 5). In this regard, the determination of state variables from measured output variables is a problem that, in spirit, bears resemblance to the well-studied problems of neural encoding and decoding of information. While the process of neural encoding involves representing the information about stimuli in the spiking patterns of neurons, the process of neural decoding is the inverse problem of determining the information contained in those spiking patterns to infer the stimuli (Churchland et al., 2012). Detailed statis- tical methods and computational approaches have been developed to address these problems (Kao, Stavisky, Sussillo, Nuyujukian, & Shenoy, 2014). The ﬁeld of neuronal encoding and de- coding stands at the interface of statistics, neuroscience, and computer science, but has not previously been strongly linked to control-theoretic models. Nevertheless, such a link seems intuitively fruitful, as the problem of determining state variables from a measured output and the problem of determining stimuli from the measured spiking activity of neurons are concep- tually quite similar to one another (Z. Chen, 2015). In the ﬁeld of control theory, analogous problems are generally referred to under the umbrella of state estimation and ﬁltering. For example, the Kalman ﬁlter in its simplest form consists of a recursive procedure to compute an optimal estimate of the state given the ob- servations of inputs and outputs of a linear dynamical system affected by normally distributed noise (Kailath, 1980). The conceptual similarity between neuronal decoding and the notion of observability promises to open an interface between control models and the ﬁeld of neu- ronal coding. For example, it will be interesting to ask if the tools and approaches from the well-established ﬁeld of neuronal decoding can be adapted to the framework of control theory and inform us about the observability of internal states of the brain. Framing and addressing such questions will be instrumental in providing insights to the nature of brain states and the dynamics of transitions between them. This intersection is also a potential area to integrate con- trol and communication models, with the goal of generating observed spiking patterns given a set of stimuli. Such an effort could provide a mechanistic understanding of the nature of Network Neuroscience 1146 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d / t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Models of communication and control for brain networks information propagated during various cognitive tasks, and of precisely how signals are trans- formed in that process. System Identiﬁcation and Causal Inference Network control theory promises to be an exciting ground to study and understand intrinsic human capacities such as cognitive control (Cornblath et al., 2019; Gu et al., 2015; Medaglia, 2018; Tang & Bassett, 2018). Cognitive control refers to the ability of the brain to inﬂuence its behavior in order to perform speciﬁc tasks. Common manifestations of cognitive control include monitoring the brain’s current state, calculating the difference from the expected be- havior for the speciﬁc task at hand, and deploying and dynamically adjusting itself according to the system’s performance (Miller & Cohen, 2001). While cognitive control shares some common features with the theory of network control, the outstanding problem in formalizing that relationship with greater biological plausibility falls primarily within the realm of system identiﬁcation (Ljung, 1987) (Figure 4). System identiﬁcation is a formal procedure which involves determining appropriate mod- els, variables, and parameters to describe system observations. The key ingredients of a system identiﬁcation scheme are (a) the input-output data, (b) a family of models, (c) an algorithm to estimate model parameters, and (d) a method to assess models against the data (Ljung, 1987). A successful system identiﬁcation scheme applied to a human capacity like cognitive con- trol can lead to a better identiﬁcation of state variables and controllers and help to bridge the gap between cognitive processes and network control theory. It is here, at the intersec- tion of cognitive control and network control theory, that communication models can again prove to be relevant. Since communication models have investigated state variables and dy- namics that are typically relatively close to the actual biophysical description of the system, system identiﬁcation can beneﬁt from communication models in supplying prior knowledge, assigning weights to plausible models, and setting the assessment criterion. Closely associated with the problem of system identiﬁcation is the topic of causal inference, which seeks to produce models that can predict the effects of external interventions on a system (Pearl, 2009). Such an association stems from the fact that dynamical models are intended to quantify how the system reacts to the application of external control inputs (i.e., interventions). In particular, as discussed in section 3, a controllable model implies the existence of a sequence of external inputs that is able to drive the system to any desired state. Therefore, appropriate control models are expected to express valid causal relationships between the external inputs and their inﬂuence on the system state. System identiﬁcation methods have been traditionally based on statistical inference method- ologies that are concerned with capturing statistical associations (i.e., correlations and depen- dencies) over time that do not necessarily imply cause-effect relationships (Koller & Friedman, 2009). Within that perspective, system identiﬁcation methods have been most successful in disciplinary areas where the fundamental mechanistic principles across variables (and hence their causal structure) are known, to a large extent, a priori (e.g., white and gray models). Con- sequently, when considering complex systems such as the brain, which are often associated with high-dimensional measurements potentially affected by hidden variables, the limitations of such methods become relevant, and the models thus produced may need to be further eval- uated for their causal validity. In this respect, the intersection of causal inference and (complex) system identiﬁcation is likely to become a promising area of future research. For example, it will be interesting to see how tools from system identiﬁcation may evolve to incorporate new Network Neuroscience 1147 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d / t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Models of communication and control for brain networks l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d . / t Figure 4. Intersection of control theory, communication models and system identiﬁcation. (A) Exogenous input applied to brain networks leads to the evolution of brain states (represented by vector x(t)) according to a speciﬁed dynamics (see Section 3). Given the observed vector y(t), the observability of brain states is determined by the invertibility of the state-to-output map (denoted by the matrix C ). (B) System identiﬁcation has been proposed as a key step in the application of network control theory to understand cognitive control and other cognitive processes. The key steps of the system identiﬁcation process can be further integrated with the insights from communication models, thus guiding future research on the formulation of theoretical frameworks to understand cognition. f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 methodologies from the theory of causal inference, and how the resulting tools might gen- erate additional requirements for experimental design and data collection in neuroscientiﬁc research. Biophysical Constraints In network control models, it is unknown how mathematical control energy relates to measure- ments of biophysical costs (also see section 4). Although predictions of control energy input have been experimentally supported by brain stimulation paradigms (Khambhati et al., 2019; Stiso et al., 2019), the control energy costs of the endogenous dynamics of brain activity are Network Neuroscience 1148 Models of communication and control for brain networks not straightforwardly described by external inputs. According to brain network communica- tion models of metabolically efﬁcient coding (Zhou, Lyn, et al., 2020), an intuitive hypothesis is that the average size of the control signals required to drive a brain network from an initial state to a target state correlates with the regional rates of metabolic expenditure (Hahn et al., 2020). Similar questions aiming to discover biophysical mechanisms of cognitive control have been tackled by ongoing investigations of cognitive effort, limited cognitive resources, motivation, and value-guided decision-making (Kool & Botvinick, 2018; Shenhav et al., 2017). However, there is limited evidence of metabolic cost operationalized as glucose consumption as a main contributor to cognitive control. Rather, the dynamics of the dopamine neurotransmitter, trans- porters, and receptors appear to be crucial (Cools, 2016; Westbrook & Braver, 2016). Recent work in network control theory has provided converging evidence for a relationship between dopamine and control in cognition and psychopathology (Braun et al., 2019). The subcorti- cal dopaminergic network and fronto-parietal cortical network may support the computation and communication of reward prediction errors in models of cost-beneﬁt decision-making, expected value of control, resource rational analysis, and bounded optimality (Westbrook & Braver, 2016). l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d / . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Cognitive control theories distinguish between the costs and allocation of control (Shenhav et al., 2017). Costs include behavioral costs, opportunity costs, and intrinsic implementation costs. Prevailing proposals of how the brain system allocates control include depletion of a resource, demand on a limited capacity, and interference by parallel goals and processes. Control allocation is then deﬁned as the expected value of control combined with the intrinsic costs of cognitive control. Broadly, a control process consists of monitoring control inputs and changes, specifying how and where to allocate control, and regulating the transmission of control signals (Nozari, Pasqualetti, & Cortés, 2019; Olshevsky, 2014; Summers & Lygeros, 2014). Notably, the implementation of how the brain regulates the transmission of control signals and accounts for the intrinsic costs of cognitive control require further development, providing promising avenues to apply mathematical models of brain network communication and control. Existing control models of brain dynamics, for instance, have mostly assumed noise-free dynamics (but also see Z. Chen & Sarma, 2017). Recent communication models can be applied to model noisy control by deﬁning how brain regions balance communication ﬁdelity and signal distortion in order to efﬁciently transmit control input messages at an optimal rate to receiver brain regions with a given ﬁdelity (Zhou, Lyn, et al., 2020). Such an approach may be particularly fruitful in ongoing efforts seeking to better understand the relations between cognitive function, network architecture, and brain age both in health and disease (Bunge & Whitaker, 2012; Morgan, White et al., 2018; Muldoon, Costantinia, Webber, Lesser, & Bassett, 2018). Potential Applications of the Integrated Framework In the previous sections, we have compared the theoretical frameworks and models of com- munication and control as applied to brain networks, and we have highlighted the convergent elements that can be utilized to integrate the two. We now focus on some examples where the development of an integrated model can indeed expand the range of questions that can be addressed. In augmenting communication models with control theory, From Communication to Control: the marked gain in utility is most evident in the potential development and understanding of Network Neuroscience 1149 Models of communication and control for brain networks therapeutic interventions. A successful intervention extends beyond an understanding of how different neural units communicate; neuromodulatory strategies must be designed to achieve the correct function(s). Hence, by building on the substantial insight provided by commu- nication models to characterize abnormal brain structure and function, control models pro- vide the tools to use these characterizations to design therapeutic stimuli (Yang, Connolly, & Shanechi, 2018). Beyond this rather direct practical utility, control models also enable falsi- ﬁable hypotheses to test existing communication models. For example, while one approach to validate a dynamical model of neural data is to see how well the model can predict future data (Yang, Sani, Chang, & Shanechi, 2019), another would be to perturb the system by using a stimulus and measure whether or not the neural activity changes in a way that is consistently predicted by the communication model (Bassett et al., 2018). Finally, control models enable the construction of empirical communication models of the brain through system identiﬁca- tion (Ljung, 1987). Such a scheme involves stimulating the brain with a diverse set of stimuli and constructing a communication model based on the observed responses. This approach would provide new insight about the brain, as the neural dependencies are derived from em- pirical perturbation as opposed to statistical dependencies. The system identiﬁcation approach is particularly promising given the brain’s consistent response to stimulation, as for example evidence by cortico-cortical evoked potentials (Keller et al., 2014). In extending control models to incorporate neural commu- From Control to Communication: nication, one of the primary areas of utility to the neuroscience community is the extension of local stimulation and perturbation experiments to a global, network-mediated understanding. From the study of neural circuits in songbirds (Fee & Scharff, 2010) to the targeted perturba- tion enacted by deep brain stimulation (Agarwal & Sarma, 2012; Santaniello et al., 2015), it is clear that neural units do not operate independently, but rather interact in complex ways. While a fully reductionist neural model may provide the most accurate prediction of neural activity, the neural substrates of behavior may rely on the coordinated behavior of millions of neurons across hundreds of brain regions. At this scale, a fully reductionist model for thera- peutic control and intervention is infeasible. Hence, the use of control models for designing biophysical interventions at the large scale can substantially beneﬁt from (simpliﬁed) commu- nication models that describe the propagation of activity across a coarse-grained network in a scalable manner. Whether through the use of dynamical synchronizability to virtually resect brain regions that may signiﬁcantly contribute to seizures (Khambhati, Davis, Lucas, Litt, & Bassett, 2016), or the use of whole-brain connectivity in C. elegans to identify neurons that reduce locomotion when ablated (Yan et al., 2017), communication models identify global substrates of behavior that can be used for controlled interventions. The mutually beneﬁcial interplay between control and Speciﬁc Areas Ripe for Integration: communication models suggests exciting opportunities for experimental and clinical appli- cations. Given a proposed integrated model that combines elements from both control and communication models, precise experimental or simulation designs can be constructed to test theoretical assumptions and predictions. Here we describe speciﬁc areas ripe for integration in the basic sciences (system identiﬁcation) and in the clinical sciences (neuromodulation). In the basic sciences, the broad area of system identiﬁcation, speciﬁcally the determination of appropriate state-space models Equation 1 and the corresponding connectivity matrices, has offered initial integration of communication and control (Friston, 2011; Yang et al., 2019). The classical bilinear form of dynamical causal models (Friston, Harrison, & Penny, 2003), for example, serves as one of the earliest steps in this regard. Aimed to capture the underlying Network Neuroscience 1150 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d t / . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Models of communication and control for brain networks biophysical processes, generative models of the form given in Equation 1 have degrees of complexity that preclude systematic control design. New approaches are thus required to ﬁnd simpler more analytically tractable state-space models, albeit supported by appropriate evi- dence using, for example, Bayesian analysis (Friston, 2011). Recent studies have ﬁtted linear and nonlinear dynamical models to explain neuroimaging activity in an attempt to arrive at the best dynamical models (Bakhtiari & Hossein-Zadeh, 2012; Becker, Bassett, & Preciado, 2018; Singh, Braver, Cole, & Ching, 2019; Yang et al., 2019). Identifying complete input-state-output control models such as those speciﬁed in Equation 13 are a natural next step, requiring novel strategies for the modeling of input (neurostimulation) and output (neuroimaging) mechanisms at different spatiotemporal scales. In the clinical sciences, neuromodulation techniques, often applied and analyzed at a local (region-wise) scale, provide a broad range of problems in which the rigorous integration of communication effects along brain networks can prove beneﬁcial (Johnson et al., 2013). Deep brain stimulation is often used to destabilize altered neuronal activity patterns in psychiatric or neurological disorders (Ramirez-Zamora et al., 2018) and is therefore a promising example for such integration. Here, computational models of communication capturing the interaction between neurons and their response to external inputs can augment the understanding of the local effects of stimulation (Andersson, Medvedev, & Cubo, 2018; Medvedev, Cubo, Olsson, Bro, & Andersson, 2019). In principle, such a deeper understanding can be used to build more effective control strategies (C. Liu, Zhou, Wang, & Loparo, 2018; Ramirez-Zamora et al., 2018; Santaniello et al., 2015). Similarly, direct electrical stimulation is a commonly used tech- nique in the treatment of epilepsy to (de)activate speciﬁc neuronal populations (Rolston, Desai, Laxpati, & E., 2011). However, deciphering the mapping between stimuli and the activated pattern has remained a challenging task (Rolston et al., 2011). Integrated communication and control models can again prove useful in this context and can be developed by ﬁrst building the communication models that accurately capture the neuronal interactions (internal net- works) and response to stimuli, and then utilizing those models to formulate accurate control models (Antal, Varga, Kincses, Nitsche, & Paulus, 2004; Stiso et al., 2019). A recent review discusses the possibility of combining direct electrical stimulation with ECoG recordings for possible advancements in the treatment of disorders such as epilepsy and Parkinson’s disease (Caldwell, Ojemann, & Rao, 2019). The integration of communication and control models can help more precisely implement and compare the efﬁcacy of clinical interventions by using di- rect electrical stimulation (Caldwell et al., 2019; Stiso et al., 2019; Yang et al., 2019). Integrated models that take into account the spatiotemporal scale of communication ex- plicitly can inform clinical intervention strategies that are typically applied locally to neuronal populations or brain regions. In theory, the formulation of control models and determination of optimal control signals typically requires systems-level information. In practice, the systems are modeled using structural or functional connectivity across several brain regions. In order to build system-level control models that can better inform intervention strategies, it will be important to combine communication models that accurately capture brain dynamics at large scales (Luft, Pereda, Banissy, & Bhattacharya, 2014; Witt et al., 2013). Integrated models will be crucial in building accurate control models that can in turn be used to design optimal stimuli. CONCLUSION The human brain is a complex dynamical system whose functions include both communi- cation and control. Understanding those functions requires careful experimental paradigms and thoughtful theoretical constructs with associated computational models. In recent years, Network Neuroscience 1151 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d / . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Models of communication and control for brain networks separate streams of literature have been developed to formalize the study of communication in brain networks, as well as to formalize the study of control in brain networks. Although the two ﬁelds have not yet been fully interdigitated, we posit that such an integration is neces- sary to understand the system that produces both functions. To support future efforts at their intersection, we brieﬂy review canonical types of communication models (dynamical, topo- logical, and information theoretic), as well as the formal mathematical framework of network control (controllability, observability, linear system control, linear time-varying system control, and nonlinear system control). We then turn to a discussion of areas of distinction between the two approaches, as well as points of convergence. That comparison motivates new di- rections in better understanding the representation of information in neural systems, in using such models to make causal inferences, and in experimentally probing the biophysical con- straints on communication and control. Our hope is that future studies of this ilk will provide fundamental, theoretically grounded advances in our understanding of the brain. CITATION DIVERSITY STATEMENT Recent work in neuroscience and other ﬁelds has identiﬁed a bias in citation practices such that papers from women and other minorities are under-cited relative to the number of such papers in the ﬁeld (Caplar, Tacchella, & Birrer, 2017; Chakravartty, Kuo, Grubbs, & McIlwain, 2018; Dion, Sumner, & Mitchell, 2018; Dworkin et al., 2020; Maliniak, Powers, & Walter, 2013; Thiem, Sealey, Ferrer, Trott, & Kennison, 2018). Here we sought to proactively consider choosing references that reﬂect the diversity of the ﬁeld in thought, race, geography, form of contribution, gender, and other factors. We used automatic classiﬁcation of gender based on the ﬁrst names of the ﬁrst and last authors (Dworkin et al., 2020), with possible combinations including male/male, male/female, female/male, and female/female. Excluding self-citations to the ﬁrst and senior author of our current paper, the references contain 56.4% male/male, 16.4% male/female, 18.5% female/male, 7.7% female/female, and 1% unknown categorization (codes in Zhou et al., 2020, were used to estimate these numbers). We look forward to future work that could help us to better understand how to support equitable practices in science. AUTHOR CONTRIBUTIONS P.S. and D.S.B. conceptulized the theme of paper. P.S., E.N., J.Z.K., H.J., and D.Z. ﬁnalized the structure and content. P.S., E.N., J.Z.K., H.J., D.Z., C.B., and D.S.B. wrote the paper. F.P. and G.J.P. provided useful edits and valuable feedback. D.S.B. ﬁnalized all the edits. FUNDING INFORMATION This work was primarily supported by the National Science Foundation (BCS-1631550), the Army Research Ofﬁce (W911NF-18-1-0244), and the Paul G. Allen Family Foundation. We would also like to acknowledge additional support from the John D. and Catherine T. MacArthur Foundation, the Alfred P. Sloan Foundation, the ISI Foundation, the Army Research Labora- tory (W911NF-10-2-0022), the Army Research Ofﬁce (Bassett-W911NF-14-1-0679, Grafton- W911NF-16-1-0474, DCIST-W911NF-17-2-0181), the Ofﬁce of Naval Research, the National Institute of Mental Health (2-R01-DC-009209-11, R01-MH112847, R01-MH107235, R21-M MH- 106799), the National Institute of Child Health and Human Development (1R01HD086888- 01), National Institute of Neurological Disorders and Stroke (R01 NS099348), and the National Science Foundation (BCS-1441502, BCS-1430087, and NSF PHY-1554488). The content is solely the responsibility of the authors and does not necessarily represent the ofﬁcial views of any of the funding agencies. Network Neuroscience 1152 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d / t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Models of communication and control for brain networks REFERENCES Abbott, L., & Kepler, T. B. (1990). Model neurons: From Hodgkin- Huxley to Hopﬁeld. Lecture Notes in Physics, 368. https://doi .org/10.1007/3540532676_37 Acebrón, J. A., Bonilla, L., Vicente, C. J. P., Ritort, F., & Spigler, R. (2005). The Kuramato model: A simple paradigm for synchroni- zation phenomena. Review of Modern Physics, 77. Agarwal, R., & Sarma, S. (2012). The effects of DBS patterns on basal ganglia activity and thalamic relay. Journal of Computational Neuroscience, 33, 151–167. Andersson, H., Medvedev, A., & Cubo, R. (2018). The impact of deep brain stimulation on a simulated neuron: inhibition, excita- tion, and partial recovery. In 2018 european control conference (ECC) (pp. 2034–2039). Antal, A., Varga, E. T., Kincses, T. Z., Nitsche, M. A., & Paulus, W. (2004). Oscillatory brain activity and transcranial direct cur- rent stimulation in humans. NeuroReport, 15(8). https://journals .lww.com/neuroreport/Fulltext/2004/06070/Oscillatory_brain _activity_and_transcranial_direct.18.aspx Aru, J., Aru, J., Priesemann, V., Wibral, M., Lana, L., Pipa, G., . . . Vicente, R. (2015). Untangling cross-frequency coupling in neu- roscience. Current Opinion in Neurobiology, 31, 51–61. Avena-Koenigsberger, A., Goni, J., Sole, R., & Sporns, O. (2015). Journal of the Royal Society Interface, Network morphospace. 12(103), 20140881. Avena-Koenigsberger, A., Goni, J., Betzel, R. F., van den Heuvel, M. P., Griffa, A., Hagmann, P., . . . Sporns, O. (2014). Using Pareto optimality to explore the topology and dynamics of the human connectome. Philosophical Transactions of the Royal So- ciety of London B, 369(1653). Avena-Koenigsberger, A., Misic, B., & Sporns, O. (2018). Commu- nication dynamics in complex brain networks. Nature Reviews Neuroscience, 19, 17–33. Avena-Koenigsberger, A., Miši´c, B., Hawkins, R. X., Griffa, A., Hagmann, P., Joaquin, G., et al. (2017). Path ensembles and a tradeoff between communication efﬁciency and resilience in the human connectome. Brain Structure and Function, 222(1). Avena-Koenigsberger, A., Yan, X., Kolchinsky, A., van den Heuvel, M. P., Hagmann, P., & Sporns, O. (2019). A spectrum of routing strategies for brain networks. PLoS Computational Biology, 15(3), e1006833. Ba¸sar, E. (2004). Memory and Brain Dynamics. CRC Press. Ba¸sar, E. (2013). Brain oscilaltions in neuropsychiatric disease. Dia- logues in Clinical Neuroscience, 15(3), 291–300. Bakhtiari, S. K., & Hossein-Zadeh, G.-A. (2012). Subspace-based identiﬁcation algorithm for characterizing causal networks in resting brain. NeuroImage, 60(2), 1236–1249. Bansal, K., Garcia, J. O., Tompson, S. H., Verstynen, T., Vettel, J. M., & Muldoon, S. F. (2019). Cognitive chimera states in human brain networks. Science Advances, 5(4). https://doi.org/10.1126/sciadv .aau8535 Bansal, K., Medaglia, J. D., Bassett, D. S., Vettel, J. M., & Muldoon, S. F. (2018). Data-driven brain network models differentiate vari- ability across language tasks. PLoS Computational Biology, 14(10), e1006487–e1006487. https://doi.org/10.1371/journal.pcbi.1006487 Bansal, K., Nakuci, J., & Muldoon, S. F. (2018). Personalized brain network models for assessing structure–function relationships. Current Opinion in Neurobiology, 52, 42–47. https://doi.org/10 .1016/j.conb.2018.04.014 Bargmann, C. I., & Marder, E. (2013). From the connectome to brain function. Nature Methods, 10(6), 483–490. https://doi.org/10 .1038/nmeth.2451 Bassett, D. S., Zurn, P., & Gold, J. I. (2018). On the nature and use of models in network neuroscience. Nature Review Neuroscience, 19(9), 566–578. https://doi.org/10.1038/s41583-018-0038-8 Beauchene, C., Roy, S., Moran, R., Leonessa, A., & Abaid, N. (2018). Comparing brain connectivity metrics: A didactic tutorial with a toy model and experimental data. Journal of Neural Engi- neering, 15(5), 056031. https://doi.org/10.1088/1741-2552/aad96e Becker, C. O., Bassett, D. S., & Preciado, V. M. (2018). Large-scale dynamic modeling of task-fMRI signals via subspace system iden- tiﬁcation. Journal of Neural Engineering, 15(6), 066016. Beggs, J., & Timme, N. (2012). Being critical of criticality in the brain. Frontiers in Physiology, 3, 163. https://doi.org/10.3389 /fphys.2012.00163 Beggs, J. M., & Plenz, D. (2003). Neuronal avalanchesin neocortical circuits . The Journal of Neuroscience, 23, 11167–11177. Bennett, M. V., & Zukin, S. R. (2004). Electrical coupling and neuronal synchronization in the mammalian brain. Neuron, 41, 495–511. Bernhardt, B. C., Fadaie, F., Liu, M., Caldairou, B., Gu, S., Jefferies, E., . . . Bemasconi, N. (2019). Temporal lobe epilepsy: Hippocam- pal pathology modulates connectome topology and controllabil- ity. Neurology, 92(19), e2209–e2220. Boccaletti, S., Latora, V., Moreno, Y., Chavez, M., & Hwang, D. U. (2006). Complex networks: Structure and dynamics. Physics Reports, 424(4), 175–308. Börgers, C., & Kopell, N. (2003). Synchronization in networks of excitatory and inhibitory neurons with sparse, random connec- tivity. Neural Computation, 15(3), 509–538. https://doi.org/10 .1162/089976603321192059 Borg-Graham, L. J., Monier, C., & Frégnac, Y. (1998). Visual input evokes transient and strong shunting inhibition in visual cortical neurons. Nature, 393(6683), 369–373. https://doi.org/10.1038 /30735 Braun, U., Harneit, A., Pergola, G., Menara, T., Schaefer, A., Betzel, R. F., . . . others (2019). Brain state stability during working memory is explained by network control theory, modulated function, and diminished in by dopamine d1/d2 receptor schizophrenia. arXiv preprint arXiv:1906.09290. Breakspear, M. (2017). Dynamic models of large-scale brain activity. Nature Neuroscience, 20(3). Breakspear, M., Heitmann, S., & Daffertshofer, A. (2010). Generative models of cortical oscillations: neurobiological implications of the Kuramoto model. Frontiers in Human Neuroscience, 4, 190. Bressler, S. L., & Seth, A. K. (2011). Wiener–Granger causality: A well established methodology. NeuroImage, 58(2), 323–329. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d / . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Network Neuroscience 1153 Models of communication and control for brain networks Broyd, S. J., Demanuele, C., Debener, S., Helps, S. K., James, C. J., & Sonuga-Barke, E. J. (2009). Default-mode brain dysfunction in mental disorders: A systematic review. Neuroscience & Bio behavioral Reviews, 33(3), 279–296. https://doi.org/10.1016/j .neubiorev.2008.09.002 Buelhmann, A., & Deco, G. (2010). Optimal information transfter in the cortex through synchronization. PLoS Computational Biol- ogy, 6. https://doi.org/10.1371/journal.pcbi.1000934 Buldú, J. M., & Porter, M. A. (2017). Frequency-based brain net- works: From a multiplex framework to a full multilayer descrip- tion. Network Neuroscience, 2(4), 418–441. https://doi.org/doi .org/10.1162/netn_a_00033 Bullmore, E., & Sporns, O. (2012). The economy of brain network organization. Nature Reviews Neuroscience, 13(5), 336–349. Bunge, S. A., & Whitaker, K. J. (2012). Brain imaging: Your brain scan doesn’t lie about your age. Current Biology, 22(18), R800-1. Cabral, J., Luckhoo, H., Woolrich, M., Joensson, M., Mohseni, H., Baker, A., . . . Deco, G. (2014). Exploring mechanisms of spon- taneous functional connectivity in MEG: How delayed network interactions lead to structured amplitude envelopes of band-pass ﬁltered oscillations. NeuroImage, 90, 423–435. https://doi.org /10.1016/j.neuroimage.2013.11.047 Cannon, J., McCarthy, M. M., Lee, S., Lee, Caldwell, D. J., Ojemann, J. G., & Rao, R. P. N. (2019). Direct elec- trical stimulation in electrocorticographic brain–computer inter- faces: Enabling technologies for input to cortex. Frontiers in Neuroscience, 13, 804. https://doi.org/10.3389/fnins.2019.00804 J., Börgers, C., Whittington, M. A., & Kopell, N. (2014). Neurosystems: Brain rhythms and cognitive processing. European Journal of Neuro- science, 39(5), 705–719. https://doi.org/10.1111/ejn.12453 Canolty, R. T., & Knight, R. T. (2010). The functional role of cross- frequency coupling. Trends in Cognitive Science, 506–515. https:// doi.org/10.1016/j.tics.2010.09.001 Caplar, N., Tacchella, S., & Birrer, S. (2017). Quantitative evalua- tion of gender bias in astronomical publications from citation counts. Nature Astronomy, 1(6), 0141. Chakravartty, P., Kuo, R., Grubbs, V., & McIlwain, C. (2018). #Com- municationSoWhite. Journal of Communication, 68(2), 254–266. Chaudhuri, R., Knoblauch, K., Gariel, M. A., Kennedy, H., & Wang, X.-J. (2015a). A large-scale circuit mechanism for hierarchical dy- namical processing in the primate cortex. Neuron, 88(2), 419–431. Chaudhuri, R., Knoblauch, K., Gariel, M.-A., Kennedy, H., & Wang, X.-J. (2015b). A large-scale circuit mechanism for hierarchical dy- namical processing in the primate cortex. Neuron, 88(2), 419–431. (1998). Linear system theory and design (3rd ed.). Chen, C.-T. Oxford University Press. Chen, Z. (2015). Advanced state space methods for neural and clin- ical data. Cambridge University Press. Chen, Z., & Sarma, S. V. (2017). Dynamic neuroscience: statistics, modeling, and control. Springer International Publishing. Chicharro, D., & Ledberg, A. (2012). Framework to study dynamic dependencies in networks of interacting processes. Physical Review E, 86, 041901. Chopra, N., & Spong, M. W. (2009). On exponential synchroniza- IEEE Transactions on Automatic tion of Kuramoto oscillators. Control, 54(2), 353–357. Churchland, M. M., Cunningham, J. P., Kaufman, M. T., Foster, J. D., Nuyujukian, P., Ryu, S. I., & Shenoy, K. V. (2012). Neural popu- lation dynamics during reaching. Nature, 487(7405), 51–56. Colizza, V., Flammini, A., Serrano, M. A., & Vespignani, A. (2006). Detecting rich-club ordering in complex networks. Nature Phys- ics, 2, 110–115. Cools, R. (2016). The costs and beneﬁts of brain dopamine for cogni- tive control. Wiley Interdisciplinary Reviews: Cognitive Science, 7(5), 317–329. Coombes, S., & Byrne, Á. (2019). Next generation neural mass mod- els. In F. Corinto & A. Torcini (Eds.), Nonlinear dynamics in com- putational neuroscience (pp. 1–16). Cham: Springer International Publishing. https://doi.org/10.1007/978-3-319-71048-8_1 Cornblath, E. J., Tang, E., Baum, G. L., Moore, T. M., Adebimpe, A., Roalf, D. R., . . . Bassett, D. S. (2019). Sex differences in net- work controllability as a predictor of executive function in youth. NeuroImage, 188, 122–134. Cumin, D., & Unsworth, C. P. (2007). Generalising the Kuramato model for the study of neuronal synchronization in the brain. Physica D, 226, 181–196. Daffertshofer, A., & van Wijk, B. C. M. (2011). On the inﬂuence of amplitude on the connectivity between phases. Frontiers in Neu- roinformatics, 5, 6. https://doi.org/10.3389/fninf.2011.00006 Davison, E. N., Aminzare, Z., Dey, B., & Ehrich Leonard, N. (n.d.). Mixed mode oscillations and phase locking in coupled ﬁtzhugh- nagumo model neurons. Chaos, 29. https://doi.org/10.1063/1 .5050178 Deco, G., Jirsa, V. K., Robinson, P. A., Breakspear, M., & Friston, K. (2008). The dynamic brain: From spiking neurons to neural masses and cortical ﬁelds. PLoS Computational Biology, 4, e1000092. Deng, S., & Gu, S. (2020). Controllability analysis of functional brain networks. arXiv:2003.08278. Destexhe, A., & Sejnowski, T. J. (2009). The Wilson-Cowan model, 36 years later. Biological Cybermetrics, 101, 1–2. https://doi.org /10.1007/s00422-009-0328-3 Dion, M. L., Sumner, J. L., & Mitchell, S. M. (2018). Gendered cita- tion patterns across political science and social science method- ology ﬁelds. Political Analysis, 26(3), 312–327. Dörﬂer, F., & Bullo, F. (2014). Synchronization in complex networks of phase oscillators: A survey. Automatica, 50(6), 1539–1564. https://doi.org/10.1016/j.automatica.2014.04.012 Dworkin, J. D., Linn, K. A., Teich, E. G., Zurn, P., Shinohara, R. T., & Bassett, D. S. (2020). The extent and drivers of gender im- balance in neuroscience reference lists. bioRxiv. https://doi.org /10.1101/2020.01.03.894378 Ehrens, D., Sritharan, D., & Sarma, S. V. (2015). Closed-loop con- trol of a fragile network: Application to seizure-like dynamics of an epilepsy model. Frontiers in Neuroscience, 9, 58. https://doi .org/10.3389/fnins.2015.00058 Ek, B., VerSchneider, C., & Narayan, D. A. (2016). Global efﬁciency of graphs. AKCE International Journal of Graphs and Combinator- ics. https://doi.org/10.1016/j.akcej.2015.06.001 Ermentrout, G. B., & Kopell, N. (1990). Oscillator death in systems of coupled neural oscillators. SIAM Journal on Applied Mathe- matics, 50(1), 125–146. Estrada, E., Hatano, N., & Benzi, M. (2012). The physics of commu- nicability in complex networks. Physics Reports, 514, 89–119. Network Neuroscience 1154 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d / . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Models of communication and control for brain networks Faber, S. P., Timme, N. M., Beggs, J. M., & Newman, E. L. (2019). Computation is concentrated in rich clubs of local cortical net- works. Network Neuroscience, 3(2), 384–404. https://doi.org /10.1162/netn_a_00069 Fan, H., Wang, Y., Yang, K., & Wang, X. (2019). Enhancing net- work synchronizability by strengthening a single node. Physical Review E, 99(4), 042305. https://doi.org/10.1103/PhysRevE.99 .042305 Fee, M. S., & Scharff, C. (2010). The songbird as a model for the generation and learning of complex sequential behaviors. ILAR Journal, 51(4), 362–377. https://doi.org/10.1093/ilar.51.4.362 Fisher, R. S., & Velasco, A. L. (2014). Electrical brain stimulation for epilepsy. Nature Reviews Neurology, 10(5), 261–270. https:// doi.org/10.1038/nrneurol.2014.59 Fitzhigh, R. (1961). Impluses and physiological states in theoretical models of nerve membrane. Biophysical Journal, 1, 446–466. Floresco, S. B., & Grace, A. A. (2003). Gating of hippocampal- evoked activity in prefrontal cortical neurons by inputs from the mediodorsal thalamus and ventral tegmental area. Journal of Neuroscience, 23(9), 3930–3943. https://doi.org/10.1523 /JNEUROSCI.23-09-03930.2003 Fries, P. (2005). A mechanism for cognitive dynamics: Neuronal com- munication through neuronal coherence. Trends in Cognitive Sciences, 9(10). Frisch, U. (1995). Turbulence. Cambridge University Press. Friston, K. J. (2011). Functional and effective connectivity: A review. Brain Connectivity. https://doi.org/10.1089/brain.2011.0008 Friston, K. J., Harrison, L., & Penny, W. (2003). Dynamic causal modelling. NeuroImage, 19(4), 1273–1302. Granger, C. W. J. (1969). Investigating causal relations by econo- metric models and cross-spectral methods. Econometrica: Jour- nal of the Econometric Society, 424–438. Grifﬁths, B. J., Parisha, G., Rouxa, F., Michelmanna, S., Plas, M. v. d., Kolibiusa, L. D., . . . Hanslmayr, S. (2019). Directional coupling of slow and fast hippocampal gamma with neocortical alpha/beta oscillations in human episodic memory. Proceedings of National Academy of Sciences, 116(43), 21834–21842. Gu, S., Betzel, R. F., Matter, M. G., Cieslak, M., Delio, P. R., Graftron, S. T., . . . Bassett, D. S. (2017). Optimal trajectories of brain state transitions. NeuroImage, 148, 305–317. Gu, S., Pasqualetti, F., Cieslak, M., Telesford, Q. K., Yu, A. B., Kahn, A. E., . . . Bassett, D. S. (2015). Controllability of structural brain networks. Nature Communications, 6(1), 8414. https://doi.org /10.1038/ncomms9414 Hahn, A., Breakspear, M., Rischka, L., Wadsak, W., Godbersen, G. M., Pichler, V., . . . Cocchi, L. (2020). Reconﬁguration of func- tional brain networks and metabolic cost converge during task performance. eLife. https://doi.org/10.1016/j.cub.2017.03.028 Harnack, D., Laminski, E., Schünemann, M., & Pawelzik, K. R. (2017). Topological causality in dynamical systems. Physical Review Letters, 119(9), 098301. Hermundstad, A. M., Bassett, D. S., Brown, K. S., Aminoff, E. M., (2013). Structural Clewett, D., Freeman, S., . . . Carlson, J. M. foundations of resting-state and task-based functional connectiv- ity in the human brain. Proceedings of the National Academy of Sciences, 110(15), 6169–6174. https://doi.org/10.1073/pnas .1219562110 Hermundstad, A. M., Brown, K. S., Bassett, D. S., & Carlson, J. M. (2011). Learning, memory, and the role of neural network archi- tecture. PLoS Computational Biology, 7, e1002063. Hodgkin, A., & Huxley, A. (1952). A quantitative description of membrane current and its application to conduction and excita- tion in nerve. Journal of Physiology, 117, 500–544. Hubel, D. H., & Wiesel, T. N. (1959). Receptive ﬁelds of single neu- rones in the cat’s striate cortex. The Journal of Physiology, 148(3), 574–591. https://doi.org/10.1113/jphysiol.1959.sp006308 Izhikevich, E. (2003). Simple model of spiking neurons. IEEE Trans- actions on Neural Networks, 14(6), 1569–1572. https://doi.org /10.1109/TNN.2003.820440 Jeganathan, J., Perry, A., Bassett, D. S., Roberts, G., Mitchell, P. B., & Breakspear, M. (2018). Fronto-limbic dysconnectivity leads to impaired brain network controllability in young people with bipolar disorder and those at high genetic risk. Neuroimage Clin- ical, 19, 71–81. Johnson, M. D., Lim, H. H., Netoff, T. I., Connolly, A. T., Johnson, N., Roy, A., . . . He, B. (2013). Neuromodulation for brain dis- orders: Challenges and opportunities. IEEE Transactions on Bio- medical Engineering, 60(3), 610–624. https://doi.org/10.1109 /TBME.2013.2244890 Ju, H., Kim, J. Z., & Bassett, D. S. (2018). Network structure of cascading neural systems predicts stimulus propagation and re- covery. arXiv:1812.09361. Kailath, T. (1980). Linear systems. Prentice-Hall. Kameneva, T., Ying, T., Guo, B., & Freestone, D. R. (2017). Neural mass models as a tool to investigate neural dynamics during sei- zures. Journal of Computational Neuroscience, 42(2), 203–215. https://doi.org/10.1007/s10827-017-0636-x Kami ´nski, M., Ding, M., Truccolo, W. A., & Bressler, S. L. (2001). Evaluating causal relations in neural systems: Granger causal- ity, directed transfer function and statistical assessment of signif- icance. Biological Cybernetics, 85(2), 145–157. Kao, J. C., Stavisky, S. D., Sussillo, D., Nuyujukian, P., & Shenoy, K. V. (2014). Information systems opportunities in brain–machine interface decoders. Proceedings of the IEEE, 102(5), 666–682. Keller, C. J., Honey, C. J., Mégevand, P., Entz, L., Ulbert, I., & Mehta, A. D. (2014). Mapping human brain networks with cortico- cortical evoked potentials. Philosophical Transactions of the Royal Society B: Biological Sciences, 369(1653), 20130528. https://doi .org/10.1098/rstb.2013.0528 Khalil, H. K. (2002). Nonlinear systems (3rd ed.). Prentice Hall. Khambhati, A. N., Davis, K. A., Lucas, T. H., Litt, B., & Bassett, D. S. (2016). Virtual cortical resection reveals push-pull network control preceding seizure evolution. Neuron, 91(5), 1170–1182. https://doi.org/10.1016/j.neuron.2016.07.039 Khambhati, A. N., Kahn, A. E., Costantini, J., Ezzyat, Y., Solomon, E. A., Gross, R. E., . . . Bassett, D. S. (2019). Functional control of electrophysiological network architecture using direct neuro- stimulation in humans. Network Neuroscience, 3(3), 848–877. Kim, J. Z., Soffer, J. M., Kahn, A. E., Vettel, J. M., Pasqualetti, F., & (2018). Role of graph architecture in controlling Bassett, D. S. dynamical networks with applications to neural systems. Nature Physics, 14, 91–98. Kirk, D. E. (2004). Optimal control theory: An introduction. Dover Publications. Network Neuroscience 1155 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d / . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Models of communication and control for brain networks Klimesch, W. (1999). EEG alpha and theta oscillations reﬂect cog- nitive and memory performance: A review and analysis. Brain Re- search Reviews, 29(2–3), 169–195. https://doi.org/10.1016/S0165 -0173(98)00056-3 Koller, D., & Friedman, N. (2009). Probabilistic graphical models: Principles and techniques. MIT press. Kool, W., & Botvinick, M. (2018). Mental labour. Nature Human Behaviour, 2(12), 899–908. Kopell, N., Börgers, C., Pervouchine, D., Malerba, P., & Tort, A. (2010). Gamma and theta rhythms in biophysical models of hip- pocampal circuits. In V. Cutsuridis, B. Graham, S. Cobb, & I. Vida (Eds.), Hippocampal microcircuits: A computational modeler’s resource book (pp. 423–457). New York, NY: Springer New York. https://doi.org/10.1007/978-1-4419-0996-1_15 Kopell, N., Kramer, M., Malerba, P., & Whittington, M. (2010). Are different rhythms good for different functions? Frontiers in Hu- man Neuroscience, 4, 187. https://doi.org/10.3389/fnhum.2010 .00187 Kopell, N. J., Gritton, H. J., Whittington, M. A., & Kramer, M. A. (2014). Beyond the connectome: The dynome. Neuron, 83(6), 1319–1328. https://doi.org/10.1016/j.neuron.2014.08.016 Korzeniewska, A., Ma ´nczak, M., Kami ´nski, M., Blinowska, K. J., & Kasicki, S. (2003). Determination of information ﬂow direc- tion among brain structures by a modiﬁed directed transfer func- tion (ddtf) method. Journal of Neuroscience Methods, 125(1–2), 195–207. Kuramoto, Y. (2003). Chemical oscillations, waves, and turbulence. Courier Corporation. Latora, V., & Marchiori, M. (2001). Efﬁcient behaviour of small- world networks. Physical Review Letters, 87, 198701. Laughlin, S. B., & Sejnowski, T. J. (2003). Communication in neu- ronal networks. Science, 301, 1870–1874. Lazar, M. (2010). Mapping brain anatomical connectivity using white matter tractography. NMR in Biomedicine, 23(7), 821–835. https:// doi.org/10.1002/nbm.1579 Lee, B., Kang, U., Chang, H., & Cho, K.-H. control architecture of complex brain networks. 154–162. https://doi.org/10.1016/j.isci.2019.02.017 (2019). The hidden iScience, 13, Lee, W. H., Rodrigue, A., Glahn, D. C., Bassett, D. S., & Frangou, S. (2019). Heritability and cognitive relevance of structural brain controllability. Cerebral Cortex, bhz293. Lewis, F. L., Vrabie, D. L., & Syrmos, V. L. (2012). Optimal control. John Wiley & Sons. Li, A., Inati, S., Zaghloul, K., & Sarma, S. (2017). Fragility in epileptic networks: The epileptic zone. 2017 American Control Confer- ence, 2817–2822. https://doi.org/10.23919/ACC.2017.7963378 Li, L. M., Violante, I. R., Leech, R., Ross, E., Hampshire, A., Opitz, A., . . . Sharp, D. J. (2019). Brain state and polarity dependent modulation of brain networks by transcranial direct current stim- ulation. Human Brain Mapping, 40(3), 904–915. https://doi.org /10.1002/hbm.24420 Liang, X., Zou, Q., He, Y., & Yang, Y. (2013). Coupling of functional connectivity and regional cerebral blood ﬂow reveals a physio- logical basis for network hubs of the human brain. Proceedings of the National Academy of Science of the United States of Amer- ica, 110(5), 1929–1934. Lin, C.-T. (1974). Structural controllability. IEEE Transaction on Automatic Control, AC-19(3). Liu, C., Zhou, C., Wang, J., & Loparo, K. A. (2018). Mathematical modeling for description of oscillation suppression induced by deep brain stimulation. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 26(9), 1649–1658. Liu, Y.-Y., Slotine, J.-J., & Barabási, A.-L. (2011). Controllability of complex networks. Nature, 473(7346), 167–173. https://doi.org /10.1038/nature10011 Ljung, L. (1987). System identiﬁcaion: Theory for the user. Prentice Hall. Luft, C. D. B., Pereda, E., Banissy, M. J., & Bhattacharya, J. (2014). Best of both worlds: Promise of combining brain stimulation and brain connectome. Frontiers in Systems Neuroscience, 8, 132. https://doi.org/10.3389/fnsys.2014.00132 Maliniak, D., Powers, R., & Walter, B. F. (2013). The gender citation gap in international relations. International Organization, 67(4), 889–922. Manning, M. L., Foty, R. A., Steinberg, M. S., & Schoetz, E.-M. (2010). Coaction of intercellular adhesion and cortical tension speciﬁes tissue surface tension. Proceedings of the National Acad- emy of Sciences, 107, 12517–12522. Mao, Y., & Baum, B. (2015). Tug of war - the inﬂuence of opposing physical forces on epithelial cell morphology. Developmental Biology, 401, 92–102. Maxwell, C. J. (1868). On governors. Proceedings of the Royal Society of London, 16, 270–283. Medaglia, J. D. (2018). Clarifying cognitive control and control- lable connectome. WIREs Cognitive Science. https://doi.org/10 .1002/wcs.1471 Medvedev, A., Cubo, R., Olsson, F., Bro, V., & Andersson, H. (2019). Control-engineering perspective on deep brain stimulation: Revi- sited. In 2019 American Control Conference (ACC) (pp. 860–865). (2001). An integrative theory of pre- frontal cortex function. Annual Review of Neuroscience, 24, 167–202. Miller, E. K., & Cohen, J. D. Mišíc, B., Betzel, R. F., Nematzadeh, A., ni, G., Griffa, A., Hagmann, P., . . . Sporns, O. (2015). Cooperative and competitive spreading dynamics on the human connectome. Neuron, 86, 1518–1529. Morgan, S. E., Achard, S., Termenon, M., Bullmore, E. T., & Vértes, P. E. (2018). Low-dimensional morphospace of topological mo- tifs in human fMRI brain networks. Network Neuroscience, 2, 285–302. https://doi.org/10.1162/netn_a_00038 Morgan, S. E., White, S. R., Bullmore, E. T., & Vertes, P. E. (2018). A network neuroscience approach to typical and atypical brain development. Biological Psychiatry: Cognitive Neuroscience and Neuroimaging, 3(9), 754–766. Moser, E. I., Kropff, E., & Moser, M.-B. (2008). Place cells, grid cells, and the brain’s spatial representation system. Annual Review of Neuroscience, 31(1), 69–89. https://doi.org/10.1146/annurev .neuro.31.061307.090723 Muldoon, S. F. (2018). Multilayer network modeling creates op- portunities for novel network statistics: Comment on "network science of biological sysetms at different scales: A review" by Gosak et al. Physics of Life Reviews, 24, 143–145. Muldoon, S. F., Bridgeford, E. W., & Bassett, D. S. (2016). Small- world propensity and weighted brain networks. Scientiﬁc Reports, 6, 22057. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d / t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Network Neuroscience 1156 Models of communication and control for brain networks Muldoon, S. F., Costantinia, J., Webber, W., Lesser, R., & Bassett, D. S. (2018). Locally stable brain states predict suppression of epileptic activity by enhanced cognitive effort. NeuroImage: Clin- ical, 18, 599–607. https://doi.org/10.1016/j.nicl.2018.02.027 Muldoon, S. F., Pasqualetti, F., Gu, S., Cieslak, M., Grafton, S. T., Vettel, J. M., & Bassett, D. S. (2016). Stimulation-based control of dynamic brain networks. PLoS Computational Biology, 12(9), e1005076. Muller, L., Chavane, F., Reynolds, J., & Sejnowski, T. J. (2018). Cortical travelling waves: Mechanisms and computational prin- ciples. Nature Review Neuroscience, 255–268. https://doi.org/10 .10138/nrn.2018.20 Müller, P., & Weber, H. (1972). Analysis and optimization of cer- tain qualities of controllability and observability for linear dy- namical systems. Automatica, 8(3), 237–246. https://doi.org/10 .1016/0005-1098(72)90044-1 Murphy, A. C., Bertolero, M. A., Papadopoulos, L., & Bassett, D. S. (2020). Multimodal network dynamics underpinning working memory. Nature Communications, 11, 3035. https://doi.org/10 .1038/s41467-020-15541-0 Murray, J. D., Bernacchia, A., Freedman, D. J., Romo, R., Wallis, (2014). A hierarchy of intrinsic J. D., Cai, X., . . . Wang, X.-J. timescales across primate cortex. Nature Neuroscience, 17(12), 1661. Neymotin, S. A., Daniels, D. S., Caldwell, B., McDougal, R. A., Carnevale, N. T., Jas, M., . . . Jones, S. R. (2020). Human Neo- cortical Neurosolver (HNN), a new software tool for interpreting the cellular and network origin of human MEG/EEG data. Elife, 9, e51214. Nolte, G., Ziehe, A., Nikulin, V. V., Schlögl, A., Krämer, N., Brismar, T., . . . Müller, K. (2008). Robustly estimating the ﬂow direction of information in complex physical systems. Physical Review Let- ters, 100(23), 234101. Nozari, E., & Cortés, J. (2018). Hierarchical selective recruitment in linear-threshold brain networks. Part II: Inter-layer dynamics and top-down recruitment. IEEE Transactions on Automatic Control. (Submitted) Nozari, E., & Cortés, J. (2019). Oscillations and coupling in inter- In American connections of two-dimensional brain networks. control conference (p. 193–198). Philadelphia, PA. Nozari, E., Pasqualetti, F., & Cortés, J. (2019). Heterogeneity of central nodes explains the beneﬁts of time-varying control sche- duling in complex dynamical networks. Journal of Complex Net- works, 7(5), 659–701. Olshausen, B., Anderson, C., & Van Essen, D. (1993). A neuro- biological model of visual attention and invariant pattern recog- Journal of nition based on dynamic routing of information. Neuroscience, 13(11), 4700–4719. https://doi.org/10.1523 /JNEUROSCI.13-11-04700.1993 Olshevsky, A. (2014). Minimal controllability problems. IEEE Trans- actions on Control of Network Systems, 1(3), 249–258. Onslow, A. C., Jones, M. W., & Bogacz, R. (2014). A canonical cir- cuit for generating phase-amplitude coupling. PLoS One, 9, e102591. Palmigiano, A., Geisel, T., Wolf, F., & Battaglia, D. (2017). Flexible information routin by transient synchrony. Nature Neuroscience, 1014–1022. https://doi.org/1038/nn.4569 Papadopoulos, L., Lynn, C. W., Battaglia, D., & Bassett, D. S. (2020). Relations between large scale brain connectivity and effects of regional stimulation depend on collective dynamical state. arXiv: 2002.00094. Pasqualetti, F., Zampieri, S., & Bullo, F. (2014). Controllability met- rics, limitations and algorithms for complex networks. IEEE Trans- actions on Control of Network Systems, 1(1), 40–52. https://doi .org/10.1109/TCNS.2014.2310254 Pearl, J. (2009). Causality. Cambridge University Press. Priesemann, V., Wibral, M., Valderrama, M., Pröpper, R., Le Van Quyen, M., Geisel, T., . . . Munk, M. H. J. (2014). Spike ava- lanches in vivo suggest a driven, slightly subcritical brain state. Frontiers in Systems Neuroscience, 8, 108. https://doi.org/10 .3389/fnsys.2014.00108 J. Ramirez-Zamora, A., Giordano, J., Gunduz, A., Brown, P., Sanchez, J. C., Foote, K. D., . . . Okun, M. S. (2018). Evolving applications, technological challenges and future opportunities in neuromodulation: Proceedings of the Fifth Annual Deep Brain Stimulation Think Tank. Frontiers in Neuroscience, 11, 734. Ritter, P., Schirner, M., McIntosh, A. R., & Jirsa, V. K. (2013). The virtual brain integrates computational modeling and multimodal neuroimaging. Brain Connectivity, 3(2), 121–145. https://doi .org/10.1089/brain.2012.0120 Roberts, J. A., Gollo, L. L., Abeysuriya, R. G., Roberts, G., Mitchell, (2019). Metastable P. B., Woolrich, M. W., & Breakspear, M. brain waves. Nature Communications, 10. Rolston, J. D., Desai, S. A., Laxpati, N. G., & Gross, R. E. (2011). Electrical stimulatiion for epilepsy: Experimental approaches. Nuerosurgery Clinics of North America, 425–442. https://doi.org /10.1016/j.nec.2011.07.010 Routh, E. (1877). A treatise on the stability of a given state of motion. Macmillan And Co. Rubino, D., Robbins, K. A., & Hatsopoulos, N. G. (2006). Propagat- ing waves mediate information transfer in the motor cortex. Na- ture Neuroscience, 9, 1549–1557. Santaniello, S., McCarthy, M. M., Montgomery, E. B., Gale, J. T., Kopell, N., & Sarma, S. V. (2015). Therapeutic mechanisms of high-frequency stimulation in parkinson’s disease and neu- ral restoration via loop-based reinforcement. Proceedings of the National Academy of Sciences, 112(6), E586–E595. Santanielloa, S., Burns, S. P., Golby, A. J., Singer, J. M., Anderson, W. S., & Sarma, S. (2011). Quickest detection of drug-resistant seizures: An optimal control approach. Epilepsy & Behavior, 22, S49–S60. Santanielloa, S., Gale, J. T., & Sarma, S. (2018). Systems approaches to optimizing deep brain stimulation therapies in Parkinson’s dis- ease. WIREs Systems Biology and Medicine. https://doi.org/10 .1002/wsbm.1421 Santanielloa, S., Sherman, D. L., Thakor, N. V., Eskandar, E. N., & Sarma, S. (2012). Optimal control-based bayesian detection of IEEE Transactions on clinical and behavioral state transitions. Neural Systems and Rehabilitation Engineering, 20. https://doi .org/10.1109/TNSRE.2012.2210246 Sanz-Leon, P., Knock, S. A., Spiegler, A., & Jirsa, V. K. (2015). Math- ematical framework for large-scale brain network modeling in the virtual brain. NeuroImage, 111, 385–430. https://doi.org/10 .1016/j.neuroimage.2015.01.002 Network Neuroscience 1157 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d / . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Models of communication and control for brain networks Scheid, B. H., Ashourvan, A., Stiso, J., Davis, K. A., Mikhail, F., Pasqualetti, F., . . . Bassett, D. S. (2020). Time-evolving con- trollability of effective connectivity networks during seizure pro- gression. arXiv:2004.03059. Schirner, M., McIntosh, A. R., Jirsa, V., Deco, G., & Ritter, P. (2018). Inferring multi-scale neural mechanisms with brain net- work modelling. Elife, 7, e28927. Schlesinger, K. J., Turner, O., Benjamin, Grafton, S., Miller, M. B., & Carlson, J. (2017). Improving resolution of dynamic communities in human brain networks through targeted node removal. PLoS One, e0187715. https://doi.org/10.1371/journal.pone.0187715 Schmidt, M., Bakker, R., Hilgetag, C. C., Diesmann, M., & van Albada, S. J. (2018). Multi-scale account of the network structure of macaque visual cortex. Brain Structure and Function, 223(3), 1409–1435. https://doi.org/10.1007/s00429-017-1554-4 Schreiber, T. (2000). Measuring information transfer. Physical Re- view Letters, 85(2), 461. Schuster, H. G., & Wagner, P. (1990). A model for neuronal oscil- lations in the visual cortex. 1. Mean-ﬁeld theory and derivation of the phase equations. Biological Cybernetics, 64(1), 77–82. Sengupta, B., Laughlin, S. B., & Niven, J. E. (2013). Balanced exci- tatory and inhibitory synaptic currents promote efﬁcient coding and metabolic efﬁciency. PLoS Computational Biology, 9(10), e1003263. Shalizi, C. R. (2006). Methods and techniques of complex systems In Complex systems science in biomedi- science: An overview. cine (p. 33–114). Springer. Shen, K., Hutchison, R. M., Bezgin, G., Everling, S., & McIntosh, A. R. (2015). Network structure shapes spontaneous functional connectivity dynamics. The Journal of Neuroscience, 35(14), 5579. https://doi.org/10.1523/JNEUROSCI.4903-14.2015 Shenhav, A., Musslick, S., Lieder, F., Kool, W., Grifﬁths, T. L., Cohen, J. D., & Botvinick, M. M. (2017). Toward a rational and mecha- nistic account of mental effort. Annual Review of Neuroscience, 40, 99–124. Shimono, M., & Beggs, J. M. (2014). Functional clusters, hubs, and communities in the cortical microconnectome. Cerebral Cortex, 25(10), 3743–3757. Shine, J. M., Breakspear, M., Bell, P. T., Ehgoetz Martens, K. A., Shine, R., Koyejo, O., . . . Poldrack, R. A. (2019). Human cogni- tion involves the dynamic integration of neural activity and neu- romodulatory systems. Natre Neuroscience, 22(2), 289–296. Silverman, L. M., & Meadows, H. (1967). Controllability and ob- servability in time-variable linear systems. SIAM Journal on Con- trol, 5(1), 64–73. Simon, J. D., & Mitter, S. K. (1968). A theory of modal control. In- formation and Control, 13(4), 316–353. https://doi.org/10.1016 /S0019-9958(68)90834-6 Singh, M., Braver, T., Cole, M., & Ching, S. (2019). Individualized dynamic brain models: Estimation and validation with resting- state fmri. bioRxiv, 678243. Skardal, P. S., & Arenas, A. (2015). Control of coupled oscillator networks with application to microgrid technologies. Science Ad- vances, 1(7), e1500339. https://doi.org/10.1126/sciadv.1500339 Skardal, P. S., & Arenas, A. (2016). On controlling networks of limit- cycle oscillators. Chaos: An Interdisciplinary Journal of Nonlinear Science, 26(9), 094812. https://doi.org/10.1063/1.4954273 Smirnov, D. A. (2014). Quantiﬁcation of causal couplings via dy- namical effects: A unifying perspective. Physical Review E, 90(6), 062921. Smirnov, D. A. (2018). Transient and equilibrium causal effects in coupled oscillators. Chaos: An Interdisciplinary Journal of Non- linear Science, 28(7), 075303. Song, S., Sjöström, P. J., Reigl, M., Nelson, S., & Chklovskii, D. B. (2005). Highly nonrandom features of synaptic connectivity in local cortical circuits. PLoS Biology, 3(3). https://doi.org/10 .1371/journal.pbio.0030068 Sontag, E. D. (2013). Mathematical control theory: deterministic ﬁnite dimensional systems. Springer New York. Sporns, O. (2013a). Network attributes for segregation and integra- tion in the human brain. Current Opinion in Neurobiology, 23, 162–171. Sporns, O. (2013b). Structure and function of complex brain net- works. Dialogues and Clinical Neuroscience, 15(3). Sritharan, D., & Sarma, S. V. (2014). Fragility in dynamic networks: Application to neural networks in the epileptic cortex. Neural Com- putational, 26(10), 2294–2327. Stam, C. J., & van Straaten, E. C. W. (2012). Go with the ﬂow: Use of a directed phase lag index (DPLI) to characterize patterns of phase relations in a large-scale model of brain dynamics. Neuro- Image, 62(3), 1415–1428. Steinmetz, N. A., Zatka-Haas, P., Carandini, M., & Harris, K. D. (2019). Distributed coding of choice, action and engagement across the mouse brain. Nature, 576(7786), 266–273. https://doi .org/10.1038/s41586-019-1787-x Stiso, J., Corsi, M.-C., Vettel, J. M., Garcia, J. O., Pasqualetti, F., De Vico Fallani, F., . . . Bassett, D. S. (2020). Learning in brain- computer interface control evidenced by joint decomposition of brain and behavior. Journal of Neural Engineering, Accepted in Principle, 17, 046018. Stiso, J., Khambhati, A. N., Menara, T., Kahn, A. E., Stein, J. M., Das, S. R., . . . Bassett, D. S. (2019). White matter network archi- tecture guides direct electrical stimulation through optimal state transitions. Cell Reports, 28(10), 2554–2566. Sugihara, G., May, R., Ye, H., Hsieh, C., Deyle, E., Fogarty, M., & Munch, S. (2012). Detecting causality in complex ecosystems. Science, 338(6106), 496–500. Summers, T. H., & Lygeros, J. (2014). Optimal sensor and actuator placement in complex dynamical networks. IFAC World Congress, 47(3), 3784–3789. Szyma ´nska, Z., Cytowski, M., Mitchell, E., Macnamara, C. K., & Chaplain, M. A. (2018). Computational modelling of cancer de- velopment and growth: Modelling at multiple scales and multi- scale modelling. Mathematical Oncology, 80, 1366–1403. Takens, F. (1981). Detecting strange attractors in turbulence. In Dynamical systems and turbulence, warwick 1980 (p. 366–381). Springer. Tang, E., & Bassett, D. S. (2018). Colloquium: Control of dynamics in brain networks. Review of Modern Physics, 90, 031003. Tang, E., Baum, G. L., Roalf, D. R., Satterthwaite, T. D., Pasqualetti, F., & Bassett, D. S. (2019). The control of brain network dynamics across diverse scales of space and time. arXiv:1901.07536. Network Neuroscience 1158 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d . / t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Models of communication and control for brain networks Tang, E., Giusti, C., Baum, G. L., Gu, S., Pollock, E., Kahn, A. E., . . . Bassett, D. S. (2017). Developmental increases in white mat- ter network controllability support a growind diversity of brain dynamics. Nature Communications, 1–16. Tavor, I., Jones, O. P., Mars, R. B., Smith, S. M., Behrens, T. E., & Jbabdi, S. (2016). Task-free MRI predicts individual differences in brain activity during task performance. Science, 352(6282), 216–220. https://doi.org/10.1126/science.aad8127 Thiem, Y., Sealey, K. F., Ferrer, A. E., Trott, A. M., & Kennison, R. (2018). Just Ideas? The Status and Future of Publication Ethics in Philosophy: A White Paper (Tech. Rep.). Thomason, M. E. (n.d.). Development of brain networks in utero: Relevance for common neural disorders. Biological Psychiatry. https://doi.org/10.1016/j.biopsych.2020.02.007 Timme, N. M., Ito, S., Myroshnychenko, M., Nigam, S., Shimono, M., Yeh, F.-C., . . . Beggs, J. M. (n.d.). High-degree neurons feed cortical computations.PLoS Computational Biology, 12, e1004858. https://doi.org/10.1371/journal.pcbi.1004858 Tort, A. B., Komorowski, R., Eichenbaum, H., & Kopell, N. (2010). Measuring phase-amplitude coupling between neuronal oscil- lations of different frequencies. Journal of Neurophysiology, 1195–1210. https://doi.org/10.1152/jn.00106.2010 Towlson, E. K., Vértes, P. E., Ahnert, S. E., Schafer, W. R., & Bullmore, E. T. (2013). The rich club of the C. elegans neuronal connectome. Journal of Neuroscience, 33(15), 6380–6387. Towlson, E. K., VÃ©rtes, P. E., Yan, G., Chew, Y. L., Walker, D. S., Schafer, W. R., & Barabási, A. L. (2018). Caenorhabditis elegans and the network control framework-FAQs. Philosophical Trans- action of Royal Society of London B, 373(1758). Valdes-Sosa, P. A., Roebroeck, A., Daunizeau, J., & Friston, K. (2011). Effective connectivity: Inﬂuence, causality and biophys- ical modelling. NeuroImage, 58, 339–361. Vázquez-Rodríguez, B., Suárez, L. E., Markello, R. D., Shaﬁei, G., (2019). Gradients of Paquola, C., Hagmann, P., . . . Misic, B. structure–function tethering across neocortex. Proceedings of the National Academy of Sciences, 116(42), 21219. https://doi.org /10.1073/pnas.1903403116 Vuksanovi´c, V., & Hövel, P. (2015). Dynamic changes in net- work synchrony reveal resting-state functional networks. Chaos: An Interdisciplinary Journal of Nonlinear Science, 25(2), 023116. https://doi.org/10.1063/1.4913526 Vértes, P. E., Alexander-Bloch, A. F., Gogtay, N., Giedd, J. N., Rapoport, J. L., & Bullmore, E. T. (2012). Simple models of human brain functional networks. Proceedings of the National Academy of Science of United States of America, 109(15), 5868–5873. Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of ‘small- world’ networks. Nature, 393(6684), 440–442. https://doi.org /10.1038/30918 Westbrook, A., & Braver, T. S. (2016). Dopamine does double duty in motivating cognitive effort. Neuron, 89(4), 695–710. Wheelock, M. D., Hect, J. L., Hernandez-Andrade, E., Hassan, S. S., Romero, R., Eggebrecht, A. T., Thomason, M. E. (2019). Sex differ- ences in functional connectivity during fetal brain development. Developmental Cognitive Neuroscience, 36, 100632. https://doi .org/10.1016/j.dcn.2019.100632 Wilson, H. R., & Cowan, J. D. (1972). Excitatory and inhibitory in- teractions in localised populations of model neurons. Biophysical Journal, 12. Wilting, J., & Priesemann, V. (2018). Inferring collective dynamical states from widely unobserved systems. Nature Communications, 9, 2325. Witt, A., Palmigiano, A., Neef, A., El Hady, A., Wolf, F., & Battaglia, (2013). Controlling the oscillation phase through precisely D. timed closed-loop optogenetic stimulation: A computational study. Frontiers in Neural Circuits, 7, 49. https://doi.org/10.3389 /fncir.2013.00049 Yaffe, R. B., Kerr, M. S. D., Damera, S., Sarma, S. V., Inati, S. K., & (2014). Reinstatement of distributed cortical Zaghloul, K. A. oscillations occurs with precise spatiotemporal dynamics dur- ing successful memory retrieval. Proceedings of the National Academy of Sciences, 111(52), 18727–18732. https://doi.org/10 .1073/pnas.1417017112 Yan, G., Vértes, P. E., Towlson, E. K., Chew, Y. L., Walker, D. S., Schafer, W. R., Barabasi, A.-L. (2017). Network control princi- ples predict neuron function in the Caenorhabditis elegans con- nectome. Nature, 550(7677), 519–523. https://doi.org/10.1038 /nature24056 Yang, Y., Connolly, A. T., & Shanechi, M. M. (2018). A control- theoretic system identiﬁcation framework and a real-time closed- loop clinical simulation testbed for electrical brain stimulation. Journal of Neural Engineering, 15(6), 066007. Yang, Y., Sani, O. G., Chang, E. F., & Shanechi, M. M. (2019). Dy- namic network modeling and dimensionality reduction for hu- man ECoG activity. Journal of Neural Engineering, 16(5), 056014. https://doi.org/10.1088/1741-2552/ab2214 Zhou, D., Cornblath, E. J., Stiso, J., Teich, E. G., Dworkin, J. D., (2020). Gender diversity state- Blevins, A. S., & Bassett, D. S. ment and code notebook v1.0. Zenodo. https://doi.org/10.5281 /zenodo.3672110 Zhou, D., Lynn, C. W., Cui, Z., Ciric, R., Baum, G. L., Moore, T. M., . . . Bassett, D. S. (2020). Efﬁcient coding in the economics of human brain connectomics. bioRxiv. https://doi.org/10.1101 /2020.01.14.906842 Network Neuroscience 1159 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / 4 4 1 1 2 2 1 8 6 6 9 2 7 n e n _ a _ 0 0 1 5 8 p d . t / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 FOCUS FEATURE: image

Download pdf