FOCUS FEATURE:
Network Communication in the Brain
Signal propagation via cortical hierarchies
Bertha Vázquez-Rodríguez
1,∗, Zhen-Qi Liu 1,∗, Patric Hagmann 2, and Bratislav Misic
1
1McConnell Brain Imaging Centre, Montréal Neurological Institute, McGill University, Montréal, Quebec, Canada
2Connectomics Lab, Department of Radiology, Lausanne University Hospital and University of Lausanne (CHUV-UNIL),
Lausanne, Switzerland
∗These authors contributed equally to this work.
Keywords: Connectome, Neural communication, Neural networks, Brain connectivity, Navigation
a n o p e n a c c e s s
j o u r n a l
ABSTRACT
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
4
4
1
0
7
2
1
8
6
6
9
3
9
n
e
n
_
a
_
0
0
1
5
3
p
d
/
.
t
The wiring of the brain is organized around a putative unimodal-transmodal hierarchy.
Here we investigate how this intrinsic hierarchical organization of the brain shapes the
transmission of information among regions. The hierarchical positioning of individual regions
was quantified by applying diffusion map embedding to resting-state functional MRI
networks. Structural networks were reconstructed from diffusion spectrum imaging and
topological shortest paths among all brain regions were computed. Sequences of nodes
encountered along a path were then labeled by their hierarchical position, tracing out path
motifs. We find that the cortical hierarchy guides communication in the network. Specifically,
nodes are more likely to forward signals to nodes closer in the hierarchy and cover a range of
unimodal and transmodal regions, potentially enriching or diversifying signals en route.
We also find evidence of systematic detours, particularly in attention networks, where
communication is rerouted. Altogether, the present work highlights how the cortical
hierarchy shapes signal exchange and imparts behaviorally relevant communication patterns
in brain networks.
AUTHOR SUMMARY
In the present report we asked how signals travel on brain networks and what types of nodes
they potentially visit en route. We traced individual path motifs to investigate the propensity
of communication paths to explore the putative unimodal-transmodal cortical hierarchy. We
find that the architecture of the network promotes signaling via the hierarchy, suggesting a
link between the structure and function of the network. Importantly, we also find instances
where detours are promoted, particularly as paths traverse attention-related networks. Finally,
information about hierarchical position aids navigation in some parts of the network, over
and above spatial location. Altogether, the present results touch on several emerging themes
in network neuroscience, including the nature of structure-function relationships, network
communication and the role of cortical hierarchies.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
INTRODUCTION
Adaptive behavior requires transmission of information between neuronal populations. The
architecture of white matter networks supports an array of signal propagation patterns, link-
ing sensation, cognition, and action (Avena-Koenigsberger, Misic, & Sporns, 2018). Brain
Citation: Vázquez-Rodríguez, B., Liu,
Z.-Q., Hagmann, P., & Misic, B. (2020).
Signal propagation via cortical
hierarchies. Network Neuroscience,
4(4), 1072–1090. https://doi.org/10.
1162/netn_a_00153
DOI:
https://doi.org/10.1162/netn_a_00153
Supporting Information:
https://doi.org/10.1162/netn_a_00153
https://doi.org/10.5281/zenodo.2872624
Received: 15 February 2020
Accepted: 15 June 2020
Competing Interests: The authors have
declared that no competing interests
exist.
Corresponding Author:
Bratislav Misic
bratislav.misic@mcgill.ca
Handling Editor:
Alex Fornito
Copyright: © 2020
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license
The MIT Press
Signal propagation via cortical hierarchies
networks, reconstructed from multiple species and at multiple spatial scales, possess multi-
ple nonrandom attributes that make such flexible communication possible, including near-
minimal path length and high clustering (Hilgetag & Kaiser, 2004; Kaiser & Hilgetag, 2006),
as well as assortative community structure (Betzel, Medaglia, & Bassett, 2018) and a densely
interconnected core (van den Heuvel, Kahn, Goñi, & Sporns, 2012).
How do signals traverse neural circuits and what types of neuronal populations do they
encounter along the way? The sequence of neurons and neuronal populations that a signal
passes through presumably transforms the nature of the signal itself and its downstream effect
(Amico et al., 2019; Avena-Koenigsberger et al., 2019; Graham & Rockmore, 2011; Miši´c,
Goñi, Betzel, Sporns, & McIntosh, 2014; Miši´c, Sporns, & McIntosh, 2014; Seguin, Razi, &
Zalesky, 2019; Worrell, Rumschlag, Betzel, Sporns, & Miši´c, 2017). For example, signals ex-
changed between closely clustered and functionally aligned populations may be relatively
unchanged, whereas signals exchanged between anatomically and functionally distant popu-
lations may be enriched or diversified (Bertolero, Yeo, & D’Esposito, 2017). A simple way to
infer potential signal trajectories in a network is the topological shortest path (hereafter sim-
ply referred to as a “path”; Avena-Koenigsberger et al., 2017; van den Heuvel et al., 2012).
For many classes of networks, including brain networks, decentralized communication mecha-
nisms may also take advantage of shortest paths without any knowledge of the global topology,
including diffusion (Goñi et al., 2014) and navigation (Seguin, van den Heuvel, & Zalesky,
2018). Thus, paths connecting pairs of nodes trace out unique motifs along their trajectory,
meaning that the nature of communication between any two regions is subject to the under-
lying structure (Avena-Koenigsberger et al., 2019; Graham & Rockmore, 2011; Miši´c et al.,
2015).
Signal propagation is likely to be constrained by the hierarchical organization of corti-
cal circuits. Evidence from classical anatomy and modern neuroimaging points to a continu-
ous sensory-transmodal hierarchy, spanning unimodal to transmodal cortex (Goulas, Zilles, &
Hilgetag, 2018; Hilgetag & Goulas, 2020; E. Jones & Powell, 1970; Mesulam, 1998). This con-
tinuous axis or gradient can be observed in the functional architecture of the cortex (Margulies
et al., 2016), running parallel to gradients in intracortical myelin (Huntenburg et al., 2017;
Paquola et al., 2019), cortical thickness (Wagstyl, Ronan, Goodyer, & Fletcher, 2015), gene
transcription (Burt et al., 2018; Fulcher, Murray, Zerbi, & Wang, 2019), excitation-inhibition
ratios (Wang, 2020), and intrinsic temporal timescales (Kiebel, Daunizeau, & Friston, 2008;
Murray et al., 2014). The influence of these multimodal gradients on signaling and communi-
cation in structural networks is a key question in systems neuroscience (Seguin et al., 2019;
Vázquez-Rodríguez et al., 2019).
Here we investigate how the functional hierarchy shapes the propagation of signals. We
reconstruct paths on structural networks and trace their trajectories through the unimodal-
transmodal gradient. We find that the hierarchical organization of the cerebral cortex con-
strains path trajectories, such that many paths follow a canonical bottom-up (ascending the
hierarchy) or top-down (descending the hierarchy) trajectory. Importantly, we find that paths
may potentially reverse direction in attention networks. Altogether, we find that the hierarchi-
cal organization of cortical circuits imposes a communication space on the structural network,
potentiating some types of signal propagation patterns while attenuating others.
RESULTS
The results are organized as follows. We first develop a methodology to trace signal trajec-
tories through the putative unimodal-transmodal hierarchy. We then investigate the extent to
1073
Shortest path:
The minimum contiguous set of
edges between two nodes.
Diffusion:
A decentralized communication
mechanism in which signals are
randomly forwarded among nodes in
a network.
Navigation:
A decentralized communication
mechanism in which signals are
forwarded to nodes that are closest to
the target node in some underlying
metric space, such as Euclidean
space or hierarchical space.
Unimodal-transmodal hierarchy:
A continuous axis separating
unimodal sensory-motor cortex from
transmodal association cortex.
Network Neuroscience
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
4
4
1
0
7
2
1
8
6
6
9
3
9
n
e
n
_
a
_
0
0
1
5
3
p
d
/
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Signal propagation via cortical hierarchies
which signal flows conform to the hierarchical organization of the cortex, and instances where
they diverge. Finally, we consider whether information about hierarchical position is sufficient
to sustain a decentralized navigation-like communication process. Data sources include the
following (see the Methods section for detailed procedures):
Structural connectivity. Structural and functional connectivity were derived from N = 66
healthy participants (source: Lausanne University Hospital). Structural connectivity was
reconstructed using diffusion spectrum imaging and deterministic streamline tractog-
raphy. A consistency- and length-based procedure was then used to assemble a group-
representative weighted structural connectivity matrix (Betzel, Griffa, Hagmann, & Miši´c,
2018; Miši´c et al., 2018; Miši´c et al., 2015).
Functional connectivity. Functional connectivity was estimated in the same individu-
als using resting-state functional MRI (rs-fMRI). A functional connectivity matrix was
constructed using pairwise Pearson correlations among regional time courses. A group-
average functional connectivity matrix was then estimated as the mean connectivity of
pairwise connections across individuals.
Path motif:
The sequence of node annotations
encountered on a shortest path
between two nodes.
We trace path motifs between all possible source-target node pairs on the weighted struc-
tural network (Figure 1; for a conceptually similar approach, see van den Heuvel et al., 2012).
We label nodes according to two different nomenclatures: hierarchical position and intrin-
sic network affiliation (Yeo et al., 2011). Hierarchical position is defined as the first principal
connectivity gradient of the diffusion map embedding over the FC matrix (Margulies et al.,
2016; see Methods). The continuous embedding vector spans a putative hierarchy, where lower
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
4
4
1
0
7
2
1
8
6
6
9
3
9
n
e
n
_
a
_
0
0
1
5
3
p
d
/
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
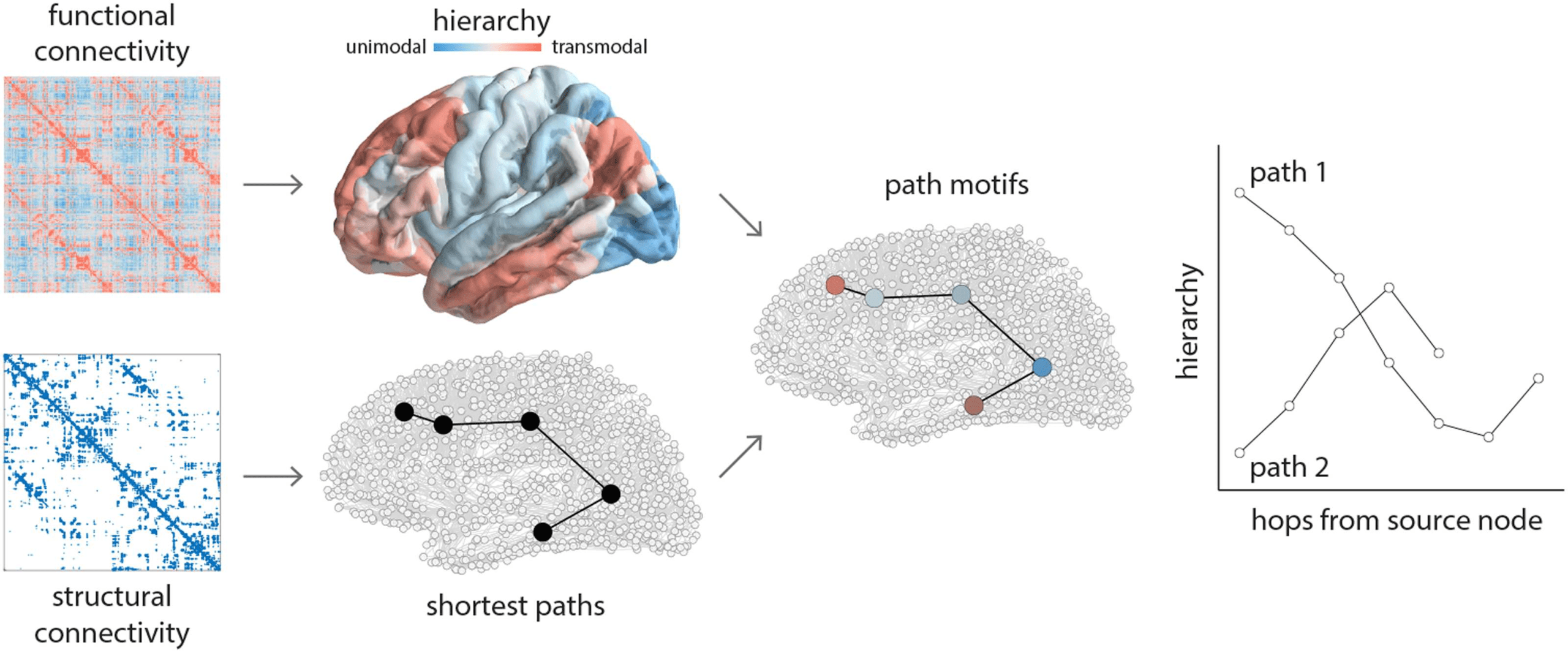
Figure 1. Tracing communication paths through cortical hierarchies. Structural and functional networks are reconstructed from diffusion-
weighted MRI and resting-state functional MRI, respectively. Shortest paths between all pairs of nodes are computed for structural networks
using the Floyd-Warshall algorithm (Floyd, 1962; Roy, 1959; Warshall, 1962). A cortical hierarchy is recovered from functional networks
using diffusion map embedding (Coifman et al., 2005). The first eigenvector is used to label nodes according to their position in the putative
unimodal-transmodal hierarchy (Margulies et al., 2016). Sequences of nodes encountered along a path are labeled by their hierarchical
position, tracing out path motifs. Note that some paths are longer and some are shorter, some paths ascend or descend through the hierarchy,
and some paths reverse their trajectory one or more times en route to the target node.
Network Neuroscience
1074
Signal propagation via cortical hierarchies
values correspond to unimodal regions and greater values correspond to transmodal regions.
We use the empirical cumulative distribution function of the first gradient to bin nodes into 10
classes of equal size. We enumerate the classes from 1 to 10, where 1 corresponds to unimodal
cortex and 10 to transmodal cortex.
Path Motifs Follow Hierarchies
We first investigate how path motifs map onto the putative unimodal-transmodal hierarchy. For
a given source and target class, we consider all possible paths between the constituent source
nodes and target nodes. We then compute the mean hierarchical position of every step encoun-
tered along the paths. Figure 2 shows the mean path motifs originating from a low-(class 2),
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
4
4
1
0
7
2
1
8
6
6
9
3
9
n
e
n
_
a
_
0
0
1
5
3
p
d
.
/
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
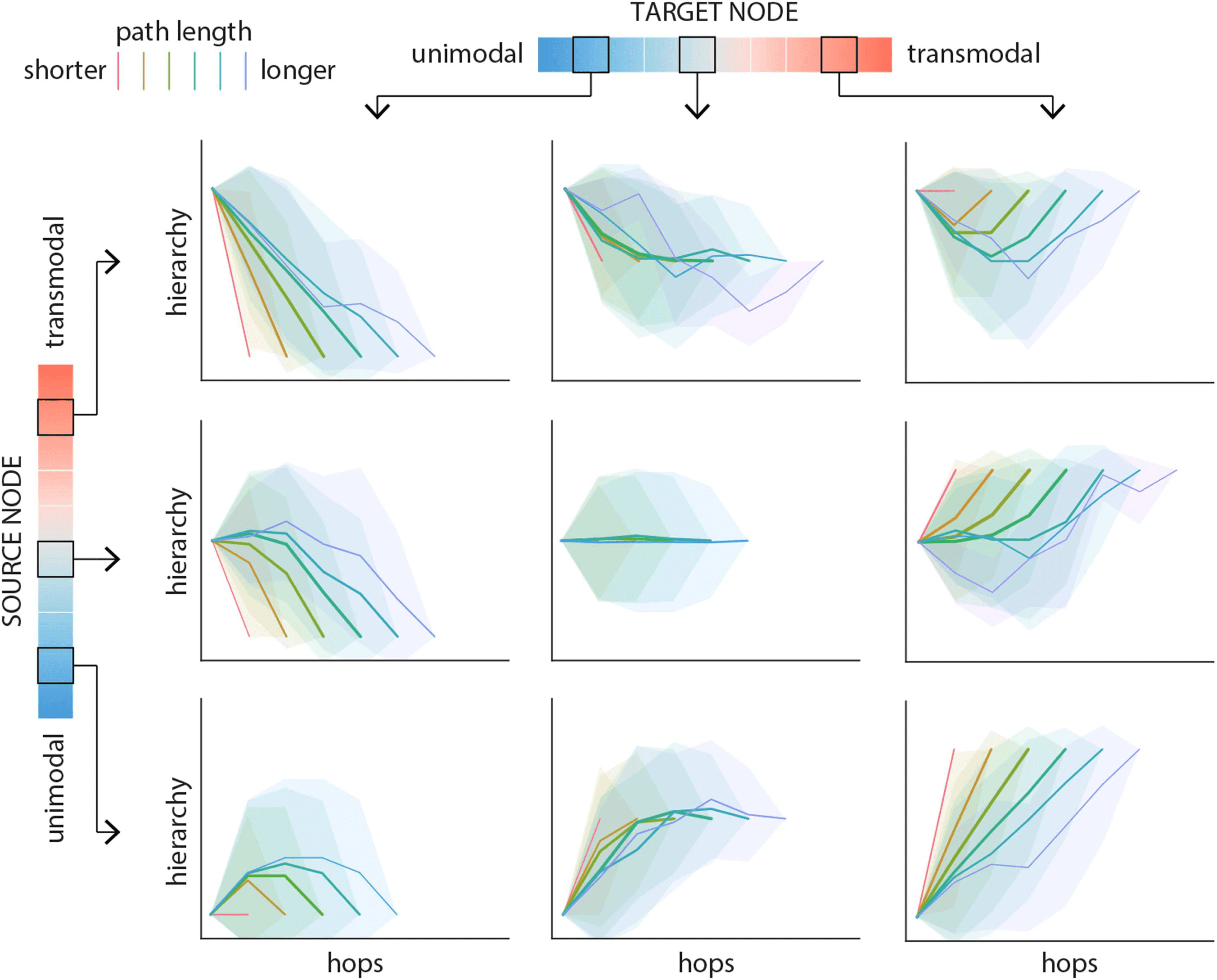
Figure 2. Path motifs. For each source-target pair, nodes along the corresponding path are labeled according to their position on the unimodal-
transmodal cortical hierarchy. Hierarchy values are binned into 10 equally sized levels, where level 1 corresponds to unimodal cortex and
level 10 corresponds to transmodal cortex. Path motifs are shown for three levels of source nodes (2, 6, and 9; rows) and three levels of target
nodes (2, 6, and 9; columns). Each plot shows the mean path motifs: path position (hop) is shown on the x-axis and the hierarchical level of the
node at each hop is shown on the y-axis. Paths are stratified according to their length, such that warmer colors indicate shorter paths and cooler
colors indicate longer paths. Shaded regions indicate 95% confidence intervals. Supporting Information Figure S1 shows the corresponding
results for a label-permuting null model.
Network Neuroscience
1075
Signal propagation via cortical hierarchies
Inflection point:
Points along a path where the path
motif changes slope, indicating a
change of direction, such as first
descending and then ascending
unimodal-transmodal hierarchy,
or vice versa.
intermediate-(class 6), and high-level (class 9) source region, to the same three regions as tar-
gets. Colors distinguish paths of different lengths.
In general, path motif shape depends on the relative hierarchical position of the source and
target nodes (Figure 2; rows and columns, respectively). For most paths, motifs sequentially
transition through the hierarchy, but there exist systematic differences in the nature of the tran-
sitions. Paths traversing a larger difference in the hierarchy (e.g., from class 2 to class 9) tend to
follow a more monotonic trajectory. Conversely, when the source and the target nodes occupy
the same or neighboring positions in the hierarchy, paths are more likely to follow a U-shape,
effectively taking detours to intermediate parts of the hierarchy (e.g., when source and target is
class 2). These trajectories are in contrast to trajectories recovered from null networks with
randomized topology (Supporting Information Figure S1) and randomized hierarchy labels
(Supporting Information Figure S2). It is noteworthy that the effect sizes for the latter are con-
siderably smaller, suggesting that path motifs are shaped both by the topology of the network,
and by the spatial structure of the unimodal-transmodal hierarchy.
Inflection Points in Communication Flow
In the previous section we observed that anatomical connectivity fundamentally shapes how
the unimodal-transmodal hierarchy is traversed, promoting some transitions while attenuating
others. To investigate how these “pushing” and “pulling” forces shape the communication
landscape, we next consider path trajectories at the nodal level. Specifically, we study how
the orientation of the flows changes along the course of the journey towards the target, which
we quantify by the slope of paths through the hierarchy.
For a given node, we calculate the mean slope of all paths as they pass through that node
(Figure 3A). If, on average, the slope of the paths when passing through a node is positive, this
suggests that the transmission is ascending through the hierarchy, from unimodal towards trans-
modal cortex. Conversely, nodes with negative slopes direct information flow towards areas
lower in the cortical hierarchy. Note that, in general, a node could participate in both ascend-
ing and descending paths, and this dependent measure reflects the mean flow of information
through that node.
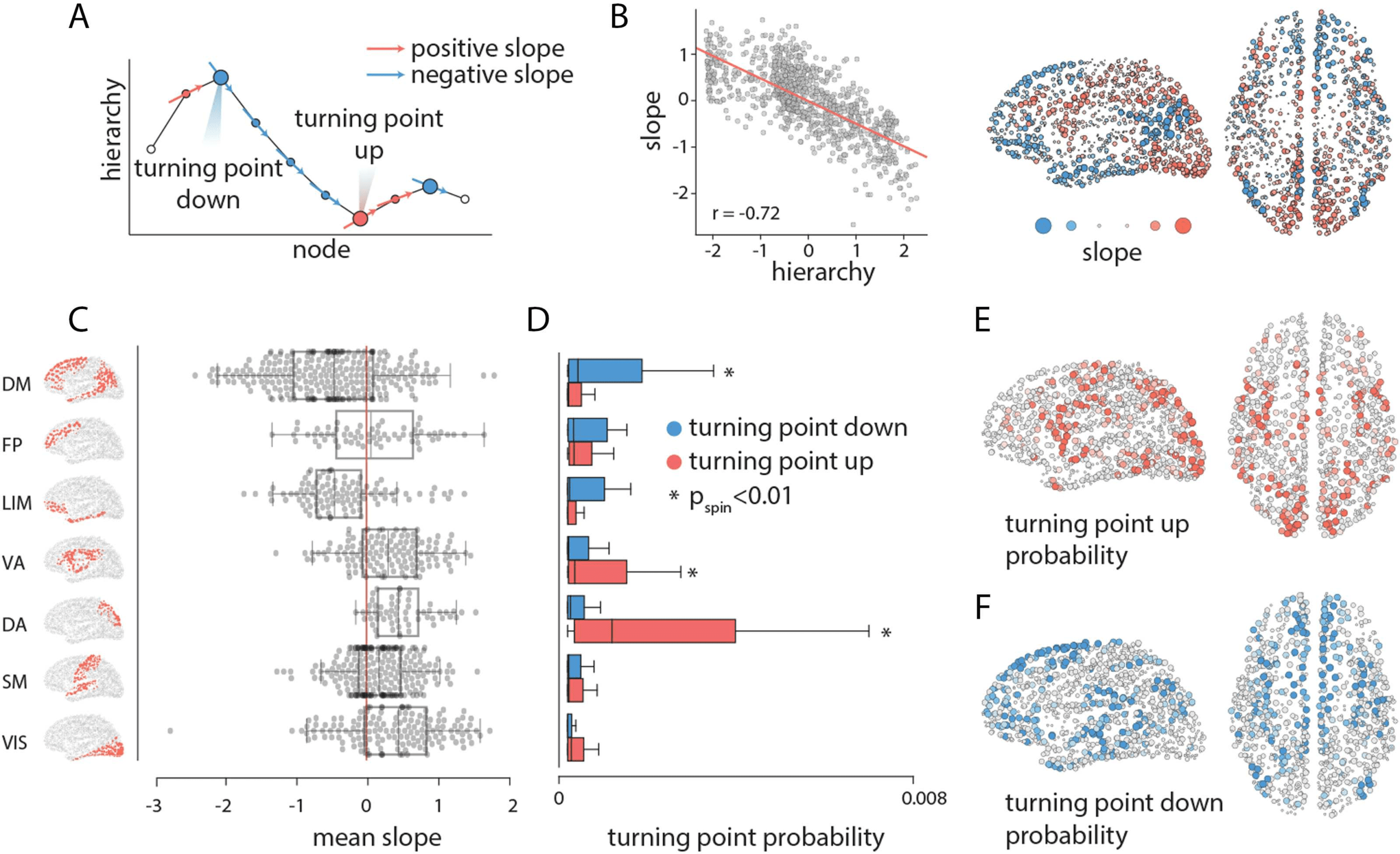
We first note that the mean slope for a given node is negatively correlated with the node’s
position in the unimodal-transmodal hierarchy (Figure 3B; r = −0.72, Pspin = 0.05). In other
words, nodes that occupy higher positions in the hierarchy tend to direct signal traffic towards
nodes lower in the hierarchy, and vice versa. This is consistent with the intuition developed in
the previous subsection. Figure 3B shows that areas that exhibit mainly positive mean slope
(i.e., direct information to ascend the hierarchy) are the supplementary motor area, somatomo-
tor cortex, and visual cortex. Areas with negative slope (i.e., directing information to descend
the hierarchy) are prefrontal cortex, posterior parietal cortex, auditory cortex, and inferotempo-
ral cortex. Stratifying these nodes by their membership in intrinsic networks (Yeo et al., 2011),
we find mean positive slopes for the visual, somatomotor, dorsal attention, ventral attention and
frontoparietal networks, and mean negative slopes for the limbic and default mode networks
(Figure 3C).
The slope of a path traversing a node also allows us to identify areas that redirect flow direc-
tion and promote detours. As we follow a path trajectory, we look for local extremum nodes
that reside between slopes with different signs, and tag them as turning points. Depending on
the type of extremum, we name the turning points as “turning up” points (local minima) or
“turning down” points (local maxima; Figure 3A). For example, a turning down point is a node
Network Neuroscience
1076
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
4
4
1
0
7
2
1
8
6
6
9
3
9
n
e
n
_
a
_
0
0
1
5
3
p
d
t
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Signal propagation via cortical hierarchies
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
4
4
1
0
7
2
1
8
6
6
9
3
9
n
e
n
_
a
_
0
0
1
5
3
p
d
/
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Inflection points in communication flow. As each path traverses the hierarchy, we can infer how individual brain regions direct
Figure 3.
communication flow. (A) Schematic showing a path motif, where the position along the x-axis indicates a node and the y-axis indicates the
hierarchical position of the node. The slope of the curve at each point tells whether the path is ascending or descending in the hierarchy. We
denote nodes where slope changes sign as turning points. Nodes where the slope changes from positive to negative are turning points down,
and nodes where the slope changes from negative to positive are turning points up. (B) The mean slope of each node (y-axis) is anticorrelated
with its position in the hierarchy. The mean slope of each node is shown for every brain region; warm colors indicate positive slopes, cool
colors indicate negative slopes. (C) The mean slope for seven intrinsic networks (Yeo et al., 2011). (D) Mean probability of turning points
up and down in seven intrinsic networks. Asterisks indicate values that are statistically significant according a label-permuting and spatial
autocorrelation-preserving null distribution (Pspin < 0.01, FDR-corrected). (E) Turning point up probability for individual regions. (F) Turning
point down probability for individual regions. Network assignments: DM = default mode, FP = frontoparietal, LIM = limbic, VA = ventral
attention, DA = dorsal attention, SM = somatomotor, VIS = visual.
Intrinsic networks:
Subnetworks of brain areas with
coherent time courses, identified by
clustering, independent component
analysis, or community detection.
that occupies a relatively higher position in the hierarchy and connects two lower level brain
areas (see Figure 3A). We first stratify nodes by their membership in intrinsic networks and
compute the mean turning point probability for each network. Figure 3D shows that networks
with the greatest probability of turning up paths (i.e., redirecting them to ascend the hierar-
chy) are the dorsal attention and ventral attention, whereas the default mode network has the
greatest turning down probability. At the regional level, regions with the greatest probability
of turning up the paths tend to be in attention-related networks, including the supplementary
motor area and posterior parietal cortex (Figure 3E). Conversely, superior and dorsolateral pre-
frontal, inferotemporal, and lateral temporal cortex are the most probable turning down points
(Figure 3F).
Network Neuroscience
1077
Signal propagation via cortical hierarchies
Temporal Evolution of Communication Flow
How does the hierarchical organization of the brain shape communication across time? Given
that most communication paths conform to the hierarchical organization of the network, we
next ask whether the hierarchy imparts memory on communication processes by exerting in-
fluence on the path trajectories. To address this question, we consider the temporal evolution
of communication patterns, envisioning the sequence of nodes traversed along a path as a time
series.
We explore how the position of a walker traversing the path depends on the positions it
occupied previously in its trajectory. Specifically, we compute the probability of going from
a node that belongs to the hierarchy level i to a node that belongs to hierarchy level j in one
step as a function of the position over the path (1-hop transitions; Figure 4A, left). To quantify
whether the hierarchical position of a walker depends on its previous hierarchical positions
(multi-hop transitions), we measure the transition probability of occupying hierarchy level i at
step t, given that the walker occupied hierarchy level j at step t − k, changing k from 1 to the
length of the path (multi-hop transitions; Figure 4A, right).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
4
1
0
7
2
1
8
6
6
9
3
9
n
e
n
_
a
_
0
0
1
5
3
p
d
.
t
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
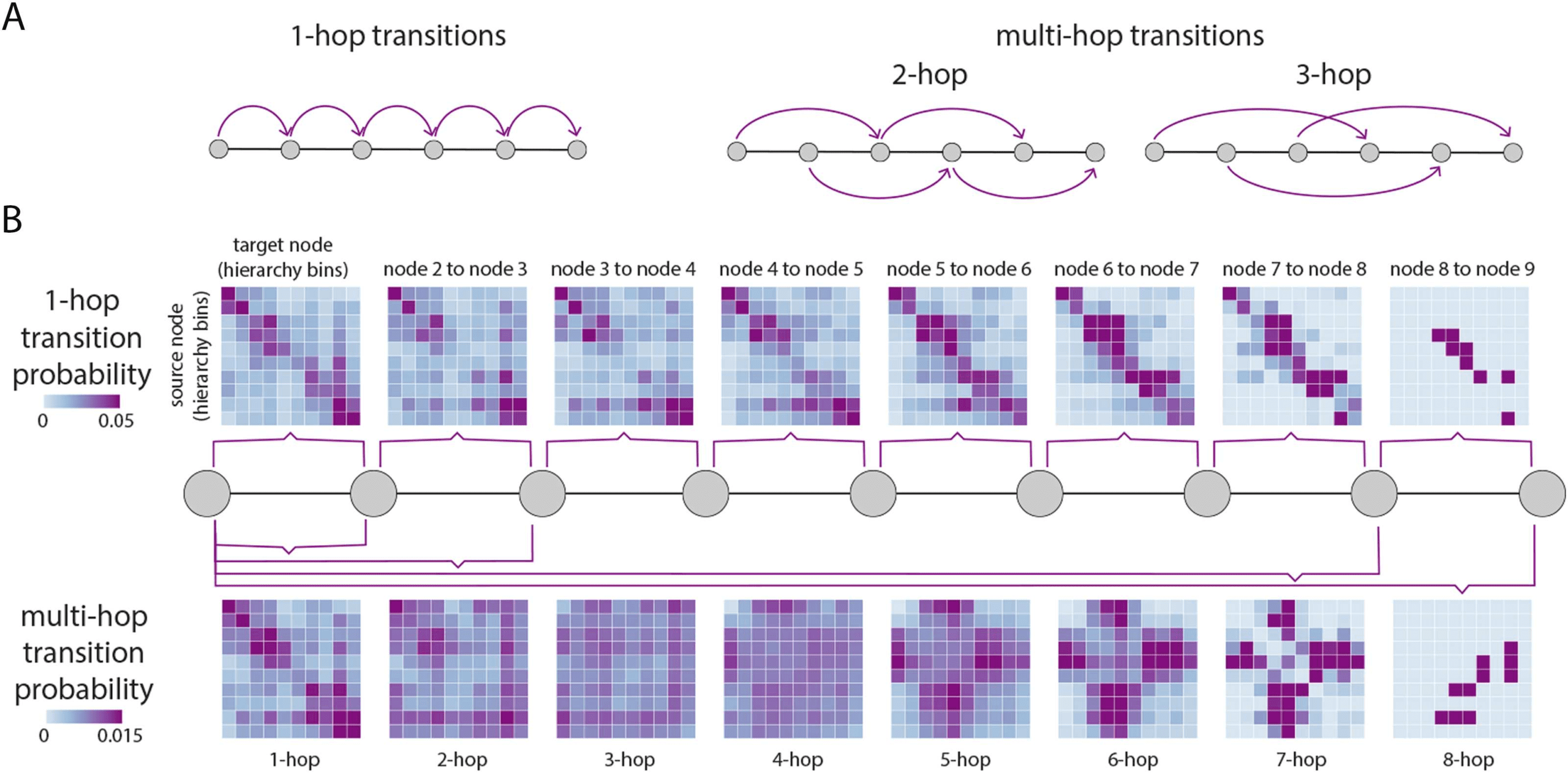
Figure 4. Transition probabilities in communication. As paths traverse the hierarchy, we quantify the probability that the current position of
a node in the unimodal-transmodal hierarchy depends on previous positions in the path. (A) With 1-hop transitions we quantify the transition
probability of a path going from hierarchy level i to level j in one step or hop. With multi-hop transitions we quantify the probability of a path
going from hierarchy level i to level j in k steps or hops. Thus, in a single path we consider multiple transitions. (B) Nodes are stratified by their
hierarchical position in 10 equally sized bins. Transition probability matrices are shown where source nodes (hierarchy bins) are in the rows,
and target nodes (hierarchy bins) are in the columns. The top row shows 1-hop transition probabilities and the bottom row shows multi-hop
transition probabilities. Transitions are shown for paths of up to length 9, corresponding to the diameter of the network. Note that the values
in the matrices display mean probabilities over multiple paths, hence the rows do not necessarily sum to 1 (see the Methods section for more
detail).
Network Neuroscience
1078
Signal propagation via cortical hierarchies
Figure 4B (top) shows 1-hop transition probabilities, as in a first-order Markov process.
Nodes are stratified according to their position in the hierarchy, with source nodes in the rows
and target nodes in the columns. Mean transition probabilities are greatest over the diagonal,
favoring the transmission of a walker to neighboring positions in the hierarchy, repeating the
theme from the previous two subsections. Figure 4 (bottom) shows average probabilities for
transitions (memories) over 2 steps or more. For memories 2, 3, and 4 steps away, transitions
become more uniform, meaning that the probability of occupying current position j does not
depend greatly on the position it occupied 2, 3, or 4 steps before. For greater memory values of
5, 6, and 7, there is an emergence of transitions between lower and intermediate, and higher
and intermediate hierarchy levels, with almost zero probability of a transition between lower
and higher levels. Altogether, we find that most 1-hop transitions follow the hierarchy, but that
communication over longer trajectories is biased towards some levels of the hierarchy and
away from others, particularly if the starting point is at intermediate levels. In other words, the
nodes visited by a walker earlier in the trajectory may exert influence on transition probabilities
later in the trajectory.
Navigation via Hierarchies
Given that communication paths closely align with the hierarchy of the network, we finally
ask whether it is possible to recapitulate the path architecture of the network by following the
hierarchy. We focus on navigation, a decentralized communication mechanism in which a
signal is forwarded to the connected neighbor that is closest in some distance to the target.
This distance is defined with respect to an underlying metric space, with the simplest such
space being the three-dimensional space that nodes are physically embedded in. For example,
previous work has demonstrated that it is possible to recapitulate the shortest path architecture
by forwarding signals to nodes that are physically closest to the target node (Seguin et al.,
2018). Decentralized mechanisms such as navigation are intuitively appealing as they do not
assume that signals or nodes possess knowledge of the global topology (Avena-Koenigsberger
et al., 2018; Seguin et al., 2018).
We therefore investigate whether signals could recapitulate the path structure of the network
if they are forwarded to the neighbor closest to the target node in the unimodal-transmodal hier-
archy. To quantify navigation as a communication process we measure the proportion of paths
that are successfully recovered (success ratio; SR). Given the importance of spatial embedding,
we identify regions for which navigation success improves when hierarchy information is taken
into account rather than only spatial factors. To operationalize a node’s proximity to the target
we use a linear combination of Euclidean distance in three-dimensional physical space and
distance in “hierarchy space” weighted by the parameter β as the following:
d(i, j) = βq(xi − xj)2 + (yi − yj)2 + (zi − zj)2+
(1 − β)(hi − hj),
where d(i, j) is the combined distance between nodes i and j, (xi, yi, zi) gives the position
of node i in three-dimensional Euclidean space, and hi gives the position of node i in one-
dimensional hierarchical space. For each pair of nodes we measure the success ratio as a
function of β, tuning β from 0 to 1, and find the β that maximizes the navigation success.
When β is valued close to 1, paths originating from the node are better recovered using spatial
proximity compared with hierarchical proximity; the opposite is true when β is valued close
to 0 (Figure 5A; see the Methods section for more detail).
Network Neuroscience
1079
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
4
1
0
7
2
1
8
6
6
9
3
9
n
e
n
_
a
_
0
0
1
5
3
p
d
t
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Signal propagation via cortical hierarchies
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
4
1
0
7
2
1
8
6
6
9
3
9
n
e
n
_
a
_
0
0
1
5
3
p
d
.
/
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
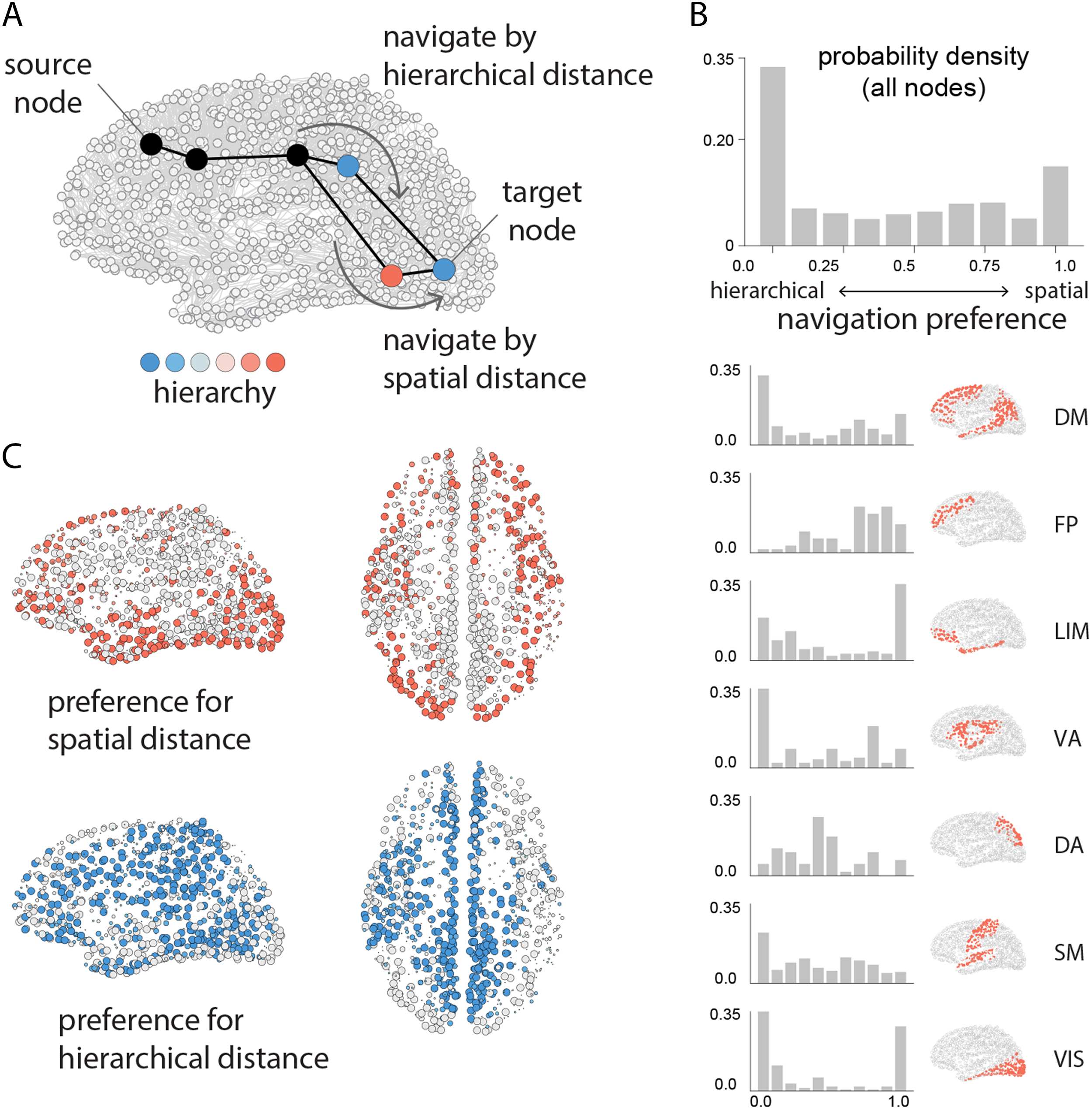
Figure 5. Navigation via hierarchical proximity. We evaluate the extent to which shortest paths can be recapitulated by an agent who is
aware of the three-dimensional spatial positions of the nodes (spatial navigation) and/or the hierarchical positions of the nodes (hierarchical
navigation), but not the topology of the network. (A) Schematic showing a putative path from source target, where an agent occupies the
third node in the path. Nodes are colored according to their position in the hierarchy. If the agent navigates using spatial information, it
will transition to the neighbor that is physically closest to the target (bottom). If the agent navigates using hierarchical information, it will
transition to the neighbor that is hierarchically closest to the target (top). We derive the navigation preference of each node (β parameter)
as the source of information that maximizes recapitulation of shortest paths (Muscoloni & Cannistraci, 2019; Muscoloni, Thomas, Ciucci,
Bianconi, & Cannistraci, 2017; Seguin et al., 2018). When β is valued close to 1, paths originating from the node are better recovered using
spatial proximity compared with hierarchical proximity; the opposite is true when β is valued close to 0. (B) Histogram of β values across all
nodes in the network. Histograms are also shown for seven intrinsic networks. (C) Individual brain regions are colored by their preference for
spatial navigation (warm colors) or hierarchical navigation (cool colors). Network assignments: DM = default mode, FP = frontoparietal, LIM =
limbic, VA = ventral attention, DA = dorsal attention, SM = somatomotor, VIS = visual.
Network Neuroscience
1080
Signal propagation via cortical hierarchies
Degree:
The number of edges or connections
in which a node participates.
Participation coefficient:
A measure of how evenly distributed
a node’s connections are among
the network’s communities
(1 = maximum, 0 = minimum).
Figure 5B shows the distribution of the β parameters that maximize navigation success for
each source-target pair. The distribution is bimodal, with prominent peaks at the extremes, sug-
gesting that most nodes have a strong preference for either hierarchical or spatial navigation.
Stratifying nodes by membership in intrinsic networks, we find that each network exhibits a
unique fingerprint, with some showing a preference for spatial navigation (frontoparietal), oth-
ers for hierarchical navigation (default), and others a mix between the two (dorsal attention).
Figure 5C shows that parts of the visual system, lateral temporal cortex, and dorsolateral pre-
frontal cortex exhibit a strong preference for spatial navigation (red; β > 0.8), while medial
parietal cortex, medial prefrontal cortex, and left temporo-parietal cortex exhibit a strong pref-
erence for hierarchical navigation (blue; β < 0.2).
Relation With Simple Measures
In this work we derived four dependent measures based on the concept of path motifs (slope,
tuning point up/down probability, and navigation preference). For completeness, we assess
the extent to which these node-level variables can be related to simpler measures. Supporting
Information Figure S4 shows linear regressions comparing each of the four path motif measures
(rows) with simpler network measures computed from structural and functional connectivity
matrices (columns). From the structural network we compute betweenness, closeness, cluster-
ing, degree, and mean edge length. All measures except degree are computed on the weighted
network. From the functional network we compute strength and participation coefficient (rel-
ative to the intrinsic network partition reported by Yeo et al., 2011). As expected, we find
weak to moderate correlations with path-based measures (betweenness, closeness) and with
degree, consistent with the notion that most centrality measures are correlated with each other
(Oldham et al., 2019). In addition, we find a positive correlation between participation and
mean slope (r = 0.52), suggesting that nodes with more diverse connection profiles are more
likely to direct communication towards the apex of the unimodal-transmodal hierarchy. In sum,
we find that the four path motif-derived measures are correlated with some simpler measures,
but cannot be wholly predicted from any one such measure.
DISCUSSION
In the present report we asked how signals travel on brain networks and what types of nodes
they potentially visit en route. We traced individual path motifs to investigate the propensity
of communication paths to explore the putative unimodal-transmodal cortical hierarchy. We
find that the architecture of the network promotes signaling via the hierarchy, suggesting a
link between the structure and function of the network. Importantly, we also find instances
where detours are promoted, particularly as paths traverse attention-related networks. Finally,
information about hierarchical position aids navigation in some parts of the network, over and
above spatial location. Altogether, the present results touch on a number of emerging themes in
network neuroscience, including the nature of structure-function relationships, network com-
munication, and the role of cortical hierarchies.
The most prominent observation is that most paths closely follow the cortical hierarchy,
traveling from unimodal to transmodal cortex and vice versa (Figure 2). This is reminiscent
of the notion that much of signal traffic follows a sequential bottom-up or top-down trajec-
tory, potentiating direct stimulus-response patterns (Worrell et al., 2017). At the same time,
the architecture of the network occasionally serves to redirect signal traffic and promote de-
tours. In particular, the default network appears to be the most likely mediator between areas
lower in the cortical hierarchy, while the dorsal attention and ventral attention networks act as
Network Neuroscience
1081
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
4
1
0
7
2
1
8
6
6
9
3
9
n
e
n
_
a
_
0
0
1
5
3
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Signal propagation via cortical hierarchies
mediators between areas higher in the hierarchy (Figure 3). The finding that attention net-
works are anatomically positioned to redirect signal traffic resonates with modern theories of
how attention and control networks shape fluid transitions between segregated and integrated
states, guiding adaptive reconfiguration during rest and task (de Pasquale et al., 2012; Fair
et al., 2007; Miši´c, Fatima et al., 2014; Mohr et al., 2016; Shine et al., 2016).
These results suggest that the architecture of the network promotes behaviorally relevant
communication patterns, and that the functional properties of individual areas are fundamen-
tally related to their anatomical network embedding. Indeed, multiple studies point to the
idea that the topology of brain networks endows individual regions with specific functional
attributes. For example, functional properties depend on local connectional profiles, includ-
ing motif composition (Gollo, Mirasso, Sporns, & Breakspear, 2014), asymmetry (Knock et al.,
2009), length (Vázquez-Rodríguez et al., 2019), and weight distribution (Melozzi et al., 2019).
At the global level, anatomical segregation, most prominently observed in the unimodal vi-
sual and somatosensory cortices, promotes specialized processing. Conversely, polysensory
association cortex is anatomically better integrated in the connectome, potentially allowing
information to be sampled from multiple parts of the network (Miši´c et al., 2015; Miši´c, Goñi,
et al., 2014; van den Heuvel et al., 2012). A recent report demonstrated that regions at the
top of the hierarchy are better positioned to act as “receivers” of information, while regions at
the bottom are better positioned to act as “senders” (Seguin et al., 2019). The present results
build on this literature, showing that the default and attentional networks present links between
parts of the cortical hierarchy. One prediction, to be tested in future studies, is that individual
differences in network architecture may potentiate some signaling patterns while attenuating
others. Wiring patterns in which the entire sensory-fugal hierarchy is more easily traversed may
promote integration between perception, cognition, and action. Thus, individual differences
in anatomical connectivity may allow signals to “ride” the hierarchy more easily, resulting in
better cognitive performance and more adaptive behavior.
In addition to network topology, we also highlight the contribution of spatial structure in
shaping path motifs. Comparison with rewired networks with geometric constraints yielded
large deviations from empirically derived path motifs (Supporting Information Figure S1), but
comparison with label-rotated null models yielded more modest effect sizes (Supporting
Information Figure S2). This suggests that path trajectories through the unimodal-transmodal
hierarchy are driven not only by network topology, but also by the strong spatial structure of
the hierarchy. Indeed, multiple studies have demonstrated that the probability and strength
of connectivity between areas is anticorrelated with their spatial proximity (Betzel & Bassett,
2018; Ercsey-Ravasz et al., 2013; Horvát et al., 2016; Miši´c, Fatima et al., 2014; Roberts et al.,
2016; Stiso & Bassett, 2018). As a result, the connectional fingerprint of a given area tends to
follow the distribution of spatial distances with its neighbors, such that hierarchical position
and spatial separation are closely intertwined (Oligschläger et al., 2017; Oligschläger et al.,
2019).
In shaping communication patterns, network architecture may also impart memory on sig-
nal traffic, such that transitions depend not only on the current position of the signal, but also
on positions they previously occupied in the hierarchy in their journey (Figure 4). We find
that most transitions between nodes that occupy neighboring positions in the hierarchy are
memoryless, but that transitions across disparate levels are not, with areas intermediate in the
hierarchy helping to mediate longer memory communication. The phenomenon of network
structure imposing non-Markovian network flows is also observed in other complex systems,
such as air passenger flows and journal citation flows (Rosvall, Esquivel, Lancichinetti, West,
& Lambiotte, 2014). In the brain, the functional consequences of this phenomenon may be the
Network Neuroscience
1082
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
4
1
0
7
2
1
8
6
6
9
3
9
n
e
n
_
a
_
0
0
1
5
3
p
d
t
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Signal propagation via cortical hierarchies
well-studied hierarchical organization of timescales and temporal receptive windows. Numer-
ous studies point to the idea that information accumulates over time across the cortical hier-
archy, such that the temporal dynamics of higher order regions unfold over slower timescales
(Kiebel et al., 2008; Murray et al., 2014), manifesting as a preference for long-range contextual
information (Honey et al., 2012). Understanding the precise link between network structure
and the hierarchy of intrinsic timescales remains a major question for future research (Demirta¸s
et al., 2019; Gollo, Roberts, & Cocchi, 2017).
More generally, these results open new questions about how broad spatial gradients in
synaptic connectivity, cytoarchitecture, and molecular composition interact with macroscale
network topology (Fulcher et al., 2019; Margulies et al., 2016; Vázquez-Rodríguez et al., 2019;
Wang, 2020). Current graph models of brain networks assume that all nodes are the same, but
as signals propagate through the network, they pass through a series of heterogeneous neu-
ral circuits and populations (Amico et al., 2019; Suarez, Markello, Betzel, & Misic, 2020).
Each stage in the trajectory may entail transformations that modern methods in network neu-
roscience do not consider. For example, the majority of path-based metrics consider the to-
tal lengths of paths between areas, but not the identity of nodes traversed during the path.
By drawing path motifs through maps annotated by molecular and cellular data, the present
methodology permits closer investigation into how local attributes of nodes may influence
communication in the network.
Note that the present method only traces out the shortest paths in the network, but this does
not preclude the possibility that communication takes place via mechanisms that are unaware
of the shortest paths in the network (Avena-Koenigsberger et al., 2018; Avena-Koenigsberger
et al., 2017; De Domenico, 2017; Suarez et al., 2020). Several recent reports point to diffusion-
like and navigation-like processes as potentially more biologically realistic alternatives (Goñi
et al., 2014; Gulyás, Bíró, K ˝orösi, Rétvári, & Krioukov, 2015; Miši´c, Sporns, & McIntosh, 2014;
Seguin et al., 2018), as they do not assume that signals possess knowledge of the global topol-
ogy. At the same time, multiple studies suggest that shortest paths in brain networks are read-
ily accessible by both diffusion (Goñi et al., 2014) and spatial navigation (greedy routing;
Seguin et al., 2018), without knowledge of the global topology. In other words, there are likely
to be some similarities between random walk motifs and path motifs, but this needs to be in-
vestigated in more detail. We envision that future studies will consider diffusion and navigation
trajectories, analogous to the approach we took with shortest paths.
We close by noting important methodological considerations. Although the present net-
works are derived from a consensus of 66 participants with high-quality imaging (Betzel, Griffa,
Hagmann, & Miši´c, 2018), there are several limitations. First, structural networks were recon-
structed using diffusion-weighted MRI and computational tractography, a technique that results
in systematic false positives and false negatives (de Reus & van den Heuvel, 2013; Maier-Hein
et al., 2017; Thomas et al., 2014). Second, the technique cannot be used to resolve the di-
rection of white matter projections, which means that some paths recovered from the network
may not exist. Third, the present reconstruction only includes cortical regions, leaving out
important topological contributions from the subcortex and cerebellum. Network communi-
cation is undoubtedly shaped by both sets of structures, and future studies should consider
subcortical-cortical and cerebellar-cortical signal traffic.
In summary, we develop a simple framework to trace communication patterns in brain
networks. We show that the putative unimodal-transmodal hierarchy shapes the propagation
of signals across the connectome. The present work highlights the importance of considering
Network Neuroscience
1083
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
4
1
0
7
2
1
8
6
6
9
3
9
n
e
n
_
a
_
0
0
1
5
3
p
d
t
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Signal propagation via cortical hierarchies
sequences of nodes encountered during signaling, and the role they might play in network-
wide communication.
METHODS
Data Acquisition
A total of N = 66 healthy young adults (16 females, 25.3 ± 4.9 years old) were scanned at the
Department of Radiology, University Hospital Center and University of Lausanne. The scans
were performed in 3-Tesla MRI scanner (Trio, Siemens Medical, Germany) using a 32-channel
head coil. The protocol included (a) a magnetization-prepared rapid acquisition gradient echo
(MPRAGE) sequence sensitive to white/gray matter contrast (1mm in-plane resolution, 1.2mm
slice thickness), (b) a diffusion spectrum imaging (DSI) sequence (128 diffusion-weighted vol-
umes and a single b0 volume, maximum b-value 8,000 s/mm2, 2.2 × 2.2 × 3.0 mm voxel size),
and (c) a gradient echo EPI sequence sensitive to BOLD contrast (3.3mm in-plane resolution
and slice thickness with a 0.3mm gap, TR 1,920 ms, resulting in 280 images per participant).
Participants were not subject to any overt task demands during the fMRI scan.
Structural Network Reconstruction
Gray matter was parcellated into 68 cortical nodes according to the Desikan-Killiany atlas
(Desikan et al., 2006). These regions of interest were then further divided into 1,000 approx-
imately equally sized nodes (Cammoun et al., 2012). Structural connectivity was estimated
for individual participants using deterministic streamline tractography. The procedure was im-
plemented in the Connectome Mapper Toolkit (Daducci et al., 2012), initiating 32 streamline
propagations per diffusion direction for each white matter voxel. Structural connectivity be-
tween pairs of regions was defined as the number of streamlines normalized by the mean length
of streamlines and mean surface area of the two regions, termed fiber density (Hagmann et al.,
2008). This normalization compensates for the bias towards longer fibers during streamline
reconstruction, as well as differences in region size.
To mitigate concerns about inconsistencies in reconstruction of individual participant con-
nectomes (D. Jones, Knösche, & Turner, 2013; Thomas et al., 2014), as well as the sensitive
dependence of network measures on false positives and false negatives (Zalesky et al., 2016),
we adopted a group-consensus approach (Betzel, Griffa, Hagmann, & Miši´c, 2018; de Reus &
van den Heuvel, 2013; Roberts, Perry, Roberts, Mitchell, & Breakspear, 2017). In constructing
a consensus adjacency matrix, we sought to preserve (a) the density and (b) the edge length dis-
tribution of the individual participant matrices (Betzel et al., 2016; Betzel, Griffa, Hagmann,
& Miši´c, 2018; Miši´c et al., 2015). We first collated the extant edges in the individual par-
ticipant matrices and binned them according to length. The number of bins was determined
heuristically, as the square root of the mean binary density across participants. The most fre-
quently occurring edges were then selected for each bin. If the mean number of edges across
participants in a particular bin is equal to k, we selected the k edges of that length that occur
most frequently across participants. To ensure that interhemispheric edges are not underrep-
resented, we carried out this procedure separately for inter- and intrahemispheric edges. The
binary density for the final whole-brain matrix was 2.17%. The weight associated with each
edge was then computed as the mean weight across all participants.
Functional Network Reconstruction
Functional MRI data were preprocessed using procedures designed to facilitate subsequent
network exploration (Power, Barnes, Snyder, Schlaggar, & Petersen, 2012). FMRI volumes were
Network Neuroscience
1084
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
4
1
0
7
2
1
8
6
6
9
3
9
n
e
n
_
a
_
0
0
1
5
3
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Signal propagation via cortical hierarchies
corrected for physiological variables, including regression of white matter, cerebrospinal fluid,
as well as motion (three translations and three rotations, estimated by rigid body coregistration).
BOLD time series were then subjected to a low-pass filter (temporal Gaussian filter with full
width half maximum equal to 1.92 s). The first four time points were excluded from subsequent
analysis to allow the time series to stabilize. Motion “scrubbing” was performed as described
by Power and colleagues (Power et al., 2012). The data were parcellated according to the same
atlas used for structural networks (Cammoun et al., 2012). Individual functional connectivity
matrices were defined as zero-lag Pearson correlation among the fMRI BOLD time series. A
group-consensus functional connectivity matrix was estimated as the mean connectivity of
pairwise connections across individuals.
Diffusion Map Embedding
Diffusion map embedding is a nonlinear dimensionality reduction algorithm (Coifman et al.,
2005). The algorithm seeks to project a set of embeddings into a lower dimensional Euclidean
space. Briefly, the similarity matrix among a set of points (in our case, the correlation matrix
representing functional connectivity) is treated as a graph, and the goal of the procedure is to
identify points that are proximal to one another on the graph. In other words, two points are
close together if there are many relatively short paths connecting them. A diffusion operator,
representing an ergodic Markov chain on the network, is formed by taking the normalized
graph Laplacian of the matrix. The new coordinate space is described by the eigenvectors of
the diffusion operator. We set the diffusion rate α = 1 and the variance of the Gaussian used
in affinity computation σ = 1. The procedure was implemented using the Dimensionality
Reduction Toolbox (https://lvdmaaten.github.io/drtoolbox/; van der Maaten, Postma, & van den
Herik, 2009).
Shortest Path Retrieval
Structural connectivity was encoded as an undirected weighted graph G ≡ {V, W} composed
of nodes V = {v1, v2, ... vn} and a matrix of fiber density values W = [wij], valued on the
interval [0,1]. To recover shortest paths, we first define a topological distance measure. The
weighted adjacency matrix was transformed from a connection weights to connection lengths
matrix using the transform L = −log(W), such that connections with greater weights are
mapped to shorter lengths (Goñi et al., 2014). Note that other transformations are also possible,
including L = 1/W. The drawback of this inverse transform is that it generates highly skewed
distributions of lengths L. As a result, a small number of connections are valued much more
than the rest, and they are disproportionately represented in shortest paths. The logarithmic
transform controls for this, yielding log-normal distributions of L (Avena-Koenigsberger et al.,
2017). Weighted shortest paths were recovered using the Floyd-Warshall algorithm (Floyd,
1962; Roy, 1959; Warshall, 1962; Brainconn Python Toolbox). Note that in many types of
networks there may exist multiple shortest paths between two nodes (edge-disjoint or not); in
our network this was not the case as we computed weighted shortest paths, yielding unique
paths between all source-target pairs.
Slopes and Inflection Points
A shortest path is defined as a sequence of nodes v1, v2, . . . , vn where vi is the node occupied
at the ith step of a path of length n. Each node has an associated hierarchical position value
h(vi), so the slope at node vi over one path is svi = h(vi+1) − h(vi). The average slope will be
the average of svi across all paths that node vi participates in, except in cases where the node
Network Neuroscience
1085
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
4
1
0
7
2
1
8
6
6
9
3
9
n
e
n
_
a
_
0
0
1
5
3
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Signal propagation via cortical hierarchies
Transition probability:
The probability that a signal is
forwarded from a source node
to a target node.
is the initial source or final target (i.e., the most extreme point in the path). As an example, let
us consider two paths, 1 : {A, B, C, D}, and 2 : {D, C, B, A}. The slope of the node C for the
C = h(D) − h(C), while for the second path it will be s2
first path will be s1
C = h(B) − h(C).
The average slope of the node C will be sC = (h(D) + h(B) − 2h(C))/2.
Transition Probabilities
We define the 1-hop transition probability matrix T as a function of the position t, where
t = 1, . . . , Diam(GSC) − 1. For each position there was one matrix T(t) defined as
Tij(t) =
#{sp : sp(t) = i, sp(t + 1) = j}
#{sp : length(sp) ≥ t + 1}
,
where i and j represent the hierarchy bins, thus (i, j) ∈ {h1, . . . , h10}. The expression
#{sp : ◦} represents the number of shortest paths, from the set of all shortest paths, that satisfy
the condition ◦.
For multi-hop transition probabilities, we define the transition matrix between hierarchy
bins as a function of hops k, denoted as M(k), where k = 1, . . . , Diam(GSC) − 1. For each hop
length k the matrix M(k) was defined as
Mij(k) =
Σθ
t=1(#{sp : sp(t) = i, sp(t + k) = j})
Σθ
t=1(#{sp : length(sp) ≥ t + k})
,
where i, j ∈ {h1, . . . , h10}, θ = length(sp) − k, θ ∈ [1, Diam(GSC) − 1].
Network Navigation
We measured navigation by simulating an agent or walker that traverses the network from
source node i to target node j. The agent has no knowledge of the global topology; instead,
they hop towards neighbors who are closest to the target node in some underlying metric
space. Across all source-target pairs, we measure the proportion of paths that are successfully
recovered (success ratio; SR; Seguin et al., 2018). To operationalize a node’s proximity to the
target we use a linear combination of the Euclidean distances in three-dimensional physical
space and in hierarchy space weighted by the parameter β as
d(i, j) =βq(xi − xj)2 + (yi − yj)2 + (zi − zj)2+
(1 − β)(hi − hj),
where di,j is the combined distance between nodes i and j, (xi, yi, zi) is a node’s position in
Euclidean space, and hi is a node’s position in hierarchy space. Both values were normalized
to lie in the interval [0,1]. In the context of neural communication, spatial navigation could
simply reflect a cost-minimization strategy, as signals are forwarded to the neighbor proximal
to the target. Since hierarchical position is estimated using diffusion map embedding applied
to functional connectivity, hierarchy distance can be interpreted as distance in functional simi-
larity. More generally, as the unimodal-transmodal hierarchy is observed for a number of local
properties, hierarchy distance could represent a mechanism where signals are forwarded to
populations with similar intrinsic electrophysiological rhythms, similar receptor distributions,
or similar molecular, or cytoarchitectonic properties.
Network Neuroscience
1086
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
4
1
0
7
2
1
8
6
6
9
3
9
n
e
n
_
a
_
0
0
1
5
3
p
d
t
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Signal propagation via cortical hierarchies
Given that navigation is a deterministic model, we calculated, for each node as a source,
the success ratio as a function of β. The resulting curves showed a global trend preferring Eu-
clidean distance, with optimal β values close to 0.8, consistent with previous reports (Seguin
et al., 2018). In each node, however, there exists substantial variance across β values, showing
a changing preference deviating from global trend. To better capture this preference for indi-
vidual nodes, we detrend the mean success ratio and select for each source node the β that
maximizes the detrended success ratio (Supporting Information Figure S5).
Null Models
The critical question underlying all reported analyses is the link between structural connectivity
and hierarchical position. To assess this question, we used two null models that systematically
disrupt the relationship between network topology and hierarchical labels. The first null model
rewires the structural network while preserving the edge lengths and hierarchical labels (Betzel
& Bassett, 2018; Gollo et al., 2018; Roberts et al., 2016). Edges were first binned according
to Euclidean distance. Within each length bin, pairs of edges were then selected at random
and swapped (Betzel & Bassett, 2018). The procedure was repeated 2,000 times, generating
a population of rewired structural networks that preserve the degree sequence of the original
network and approximately preserve the edge length distribution of the original network.
The second null model permutes hierarchical labels, but preserves their spatial autocorre-
lation (Alexander-Bloch et al., 2018). We first created a surface-based representation of the
Cammoun atlas on the FreeSurfer fsaverage surface using the Connectome Mapper Toolkit
(https://github.com/LTS5/cmp; Daducci et al., 2012). We used the spherical projection of the
fsaverage surface to define spatial coordinates for each parcel by selecting the vertex closest
to the center-of-mass of each parcel. The resulting spatial coordinates were used to generate
null models by applying randomly sampled rotations and reassigning node values based on
the closest resulting parcel (2,000 repetitions). The rotation was applied to one hemisphere
and then mirrored to the other hemisphere.
ACKNOWLEDGMENTS
The authors thank Dr. Alessandra Griffa for collecting, preprocessing, and sharing the neu-
roimaging dataset. We acknowledge the Department of Psychiatry of Lausanne University
Hospital and particularly Professor Philippe Conus, Professor Kim Do Cuenod, Raoul Jenni,
and Martine Cleusix for having helped with the recruitment process of the study volunteers.
The authors thank Ross Markello, Golia Shafiei, Vincent Bazinet, Laura Suarez, and Justine
Hansen for helpful comments on the manuscript. This research was undertaken thanks in part
to funding from the Canada First Research Excellence Fund, awarded to McGill University for
the Healthy Brains for Healthy Lives initiative.
AUTHOR CONTRIBUTIONS
Bertha Vázquez-Rodríguez: Methodology; Formal analysis; Writing - Original Draft. Zhen-Qi
Liu: Methodology; Formal analysis; Writing - Original Draft. Patric Hagmann Data: curation.
Bratislav Misic: Conceptualization; Supervision; Writing – Review & Editing.
FUNDING INFORMATION
Bratislav Misic, Natural Sciences and Engineering Research Council of Canada (NSERC Discov-
ery Grant), Award ID: 017-04265. Bratislav Misic, Canada Research Chairs Program. Bratislav
Misic, Fonds de recherche du Québec - Santé (Chercheur Boursier).
Network Neuroscience
1087
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
4
1
0
7
2
1
8
6
6
9
3
9
n
e
n
_
a
_
0
0
1
5
3
p
d
.
/
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Signal propagation via cortical hierarchies
DATA AVAILABILITY
The processed dataset (structural and functional matrices) is available at https://doi.org/10
.5281/zenodo.2872624 (Griffa, Alemán-Gómez, & Hagmann, 2019).
SUPPORTING INFORMATION
Supporting information is available at https://doi.org/10.1162/netn_a_00153.
REFERENCES
Alexander-Bloch, A. F., Shou, H., Liu, S., Satterthwaite, T. D., Glahn,
D. C., Shinohara, R. T., . . . Raznaha, A. (2018). On testing for
spatial correspondence between maps of human brain structure
and function. NeuroImage, 178, 540–551.
Amico, E., Abbas, K., Duong-Tran, D. A., Tipnis, U., Rajapandian,
(2019). Towards a mathematical
M., Chumin, E., . . . Goñi, J.
theory of communication for the human connectome. arXiv:1911.
02601.
Avena-Koenigsberger, A., Misic, B., & Sporns, O. (2018). Communi-
cation dynamics in complex brain networks. Nature Reviews Neu-
roscience, 19(1), 17–33. https://doi.org/10.1038/nrn.2017.149
Avena-Koenigsberger, A., Miši´c, B., Hawkins, R. X., Griffa, A.,
Hagmann, P., Goñi, J., & Sporns, O.
(2017). Path ensembles
and a tradeoff between communication efficiency and resilience
in the human connectome. Brain Structure and Function, 222(1),
603–618.
Avena-Koenigsberger, A., Yan, X., Kolchinsky, A., van den Heuvel,
M., Hagmann, P., & Sporns, O.
(2019). A spectrum of routing
strategies for brain networks. PLoS Computational Biology, 15(3),
e1006833.
Bertolero, M. A., Yeo, B. T., & D’Esposito, M. (2017). The diverse
club. Nature Communications, 8(1), 1–11.
Betzel, R. F., Avena-Koenigsberger, A., Goñi, J., He, Y., De Reus,
M. A., Griffa, A., . . . Sporns, O. (2016). Generative models of
the human connectome. NeuroImage, 124, 1054–1064.
Betzel, R. F., & Bassett, D. S. (2018). Specificity and robustness of
long-distance connections in weighted, interareal connectomes.
Proceedings of the National Academy of Sciences, 115(21),
E4880–E4889.
Betzel, R. F., Griffa, A., Hagmann, P., & Miši´c, B. (2018). Distance-
dependent consensus thresholds for generating group-representative
structural brain networks. Network Neuroscience, 3(2), 475–496.
Betzel, R. F., Medaglia, J. D., & Bassett, D. S. (2018). Diversity of
meso-scale architecture in human and non-human connectomes.
Nature Communications, 9(1), 346.
Burt, J. B., Demirta¸s, M., Eckner, W. J., Navejar, N. M., Ji, J. L.,
(2018). Hierarchy of transcrip-
Martin, W. J., . . . Murray, J. D.
tomic specialization across human cortex captured by structural
neuroimaging topography. Nature Neuroscience, 21(9), 1251.
Cammoun, L., Gigandet, X., Meskaldji, D., Thiran, J. P., Sporns, O.,
Do, K. Q., . . . Hagmann, P. (2012). Mapping the human con-
nectome at multiple scales with diffusion spectrum MRI. Journal
of Neuroscience Methods, 203(2), 386–397.
Coifman, R. R., Lafon, S., Lee, A. B., Maggioni, M., Nadler, B.,
(2005). Geometric diffusions as a
Warner, F., & Zucker, S. W.
tool for harmonic analysis and structure definition of data: Dif-
fusion maps. Proceedings of the National Academy of Sciences,
102(21), 7426–7431.
Daducci, A., Gerhard, S., Griffa, A., Lemkaddem, A., Cammoun, L.,
Gigandet, X., . . . Thiran, J.-P. (2012). The Connectome Mapper:
An open-source processing pipeline to map Connectomes with
MRI. PLoS ONE, 7(12), e48121.
De Domenico, M. (2017). Diffusion geometry unravels the emer-
gence of functional clusters in collective phenomena. Physical
Review Letters, 118(16), 168301.
Demirta¸s, M., Burt, J. B., Helmer, M., Ji, J. L., Adkinson, B. D.,
Glasser, M. F., . . . Murray, J. D.
(2019). Hierarchical hetero-
geneity across human cortex shapes large-scale neural dynamics.
Neuron, 101(6), 1181–1194.
de Pasquale, F., Della Penna, S., Snyder, A. Z., Marzetti, L., Pizzella,
V., Romani, G. L., & Corbetta, M. (2012). A cortical core for dy-
namic integration of functional networks in the resting human
brain. Neuron, 74(4), 753–764.
de Reus, M. A., & van den Heuvel, M. P. (2013). Estimating false
positives and negatives in brain networks. NeuroImage, 70,
402–409.
Desikan, R. S., Ségonne, F., Fischl, B., Quinn, B. T., Dickerson, B. C.,
Blacker, D., . . . Killiany, R. J. (2006). An automated labeling sys-
tem for subdividing the human cerebral cortex on MRI scans into
gyral based regions of interest. NeuroImage, 31(3), 968–980.
Ercsey-Ravasz, M., Markov, N. T., Lamy, C., Van Essen, D. C.,
Knoblauch, K., Toroczkai, Z., & Kennedy, H. (2013). A predic-
tive network model of cerebral cortical connectivity based on a
distance rule. Neuron, 80(1), 184–197.
Fair, D. A., Dosenbach, N. U., Church,
J. A., Cohen, A. L.,
Brahmbhatt, S., Miezin, F. M., . . . Schlaggar, B. L. (2007). De-
velopment of distinct control networks through segregation and
integration. Proceedings of the National Academy of Sciences,
104(33), 13507–13512.
Floyd, R. W. (1962). Algorithm 97: Shortest path. Communications
of the ACM, 5(6), 345.
Fulcher, B. D., Murray, J. D., Zerbi, V., & Wang, X.-J. (2019). Mul-
timodal gradients across mouse cortex. Proceedings of the Na-
tional Academy of Sciences, 116(10), 4689–4695.
Gollo, L. L., Mirasso, C., Sporns, O., & Breakspear, M.
(2014).
Mechanisms of zero-lag synchronization in cortical motifs. PLoS
Computational Biology, 10(4).
Gollo, L. L., Roberts, J. A., & Cocchi, L. (2017). Mapping how lo-
cal perturbations influence systems-level brain dynamics. Neuro-
Image, 160, 97–112.
Network Neuroscience
1088
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
4
1
0
7
2
1
8
6
6
9
3
9
n
e
n
_
a
_
0
0
1
5
3
p
d
.
/
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Signal propagation via cortical hierarchies
Gollo, L. L., Roberts, J. A., Cropley, V. L., Di Biase, M. A., Pantelis,
C., Zalesky, A., et al. (2018). Fragility and volatility of structural
hubs in the human connectome. Nature Neuroscience, 21(8),
1107.
Goñi, J., van den Heuvel, M. P., Avena-Koenigsberger, A., de
Mendizabal, N. V., Betzel, R. F., Griffa, A., . . . Sporns, O. (2014).
Resting-brain functional connectivity predicted by analytic mea-
sures of network communication. Proceedings of the National
Academy of Sciences, 111(2), 833–838.
Goulas, A., Zilles, K., & Hilgetag, C. C. (2018). Cortical gradients
and laminar projections in mammals. Trends in Neurosciences,
41(11), 775–788.
Graham, D., & Rockmore, D. (2011). The packet switching brain.
Maier-Hein, K. H., Neher, P. F., Houde, J.-C., Côté, M.-A., Garyfallidis,
E., Zhong, J., . . . Descoteaux, M. (2017). The challenge of map-
ping the human connectome based on diffusion tractography.
Nature Communications, 8(1), 1349.
Margulies, D. S., Ghosh, S. S., Goulas, A., Falkiewicz, M., Huntenburg,
J. M., Langs, G., . . . Smallwood, J. (2016). Situating the default-
mode network along a principal gradient of macroscale cortical
organization. Proceedings of the National Academy of Sciences,
113(44), 12574–12579. https://doi.org/10.1073/pnas.1608282113
Melozzi, F., Bergmann, E., Harris, J. A., Kahn, I., Jirsa, V., & Bernard,
C.
Individual structural features constrain the mouse
functional connectome. Proceedings of the National Academy
of Sciences, 116(52), 26961–26969.
(2019).
Journal of Cognitive Neuroscience, 23(2), 267–276.
Mesulam, M.-M. (1998). From sensation to cognition. Brain, 121(6),
Griffa, A., Alemán-Gómez, Y., & Hagmann, P. (2019). Structural and
functional connectome from 70 young healthy adults [dataset].
https://doi.org/10/5281/zenodo.2872624
Gulyás, A., Bíró, J. J., K ˝orösi, A., Rétvári, G., & Krioukov, D. (2015).
Navigable networks as nash equilibria of navigation games.
Nature Communications, 6, 7651.
Hagmann, P., Cammoun, L., Gigandet, X., Meuli, R., Honey, C. J.,
Wedeen, V. J., & Sporns, O. (2008). Mapping the structural core
of human cerebral cortex. PLoS Biology, 6(7).
Hilgetag, C. C., & Goulas, A.
(2020). “Hierarchy” in the organi-
zation of brain networks. Philosophical Transaction of the Royal
Society B, 375(1796), 20190319.
Hilgetag, C. C., & Kaiser, M.
(2004). Clustered organization of
cortical connectivity. Neuroinformatics, 2(3), 353–360.
Honey, C. J., Thesen, T., Donner, T. H., Silbert, L. J., Carlson, C. E.,
Devinsky, O., . . . Hasson, U. (2012). Slow cortical dynamics and
the accumulation of information over long timescales. Neuron,
76(2), 423–434.
Horvát, S., G˘am˘anut,, R., Ercsey-Ravasz, M., Magrou, L., G˘am˘anut,,
B., Van Essen, D. C., . . . Kennedy, H. (2016). Spatial embedding
and wiring cost constrain the functional layout of the cortical net-
work of rodents and primates. PLoS Biology, 14(7), e1002512.
Huntenburg, J. M., Bazin, P.-L., Goulas, A., Tardif, C. L., Villringer,
A., & Margulies, D. S.
(2017). A systematic relationship be-
tween functional connectivity and intracortical myelin in the
human cerebral cortex. Cerebral Cortex, 27(2), 981–997.
Jones, D., Knösche, T., & Turner, R. (2013). White matter integrity,
fiber count, and other fallacies: The do’s and don’ts of diffusion
MRI. NeuroImage, 73, 239–254.
Jones, E., & Powell, T.
(1970). An anatomical study of converg-
ing sensory pathways within the cerebral cortex of the monkey.
Brain, 93(4), 793–820.
Kaiser, M., & Hilgetag, C. C. (2006). Nonoptimal component place-
ment, but short processing paths, due to long-distance projec-
tions in neural systems. PLoS Computational Biology, 2(7), e95.
Kiebel, S. J., Daunizeau, J., & Friston, K. J. (2008). A hierarchy of
time-scales and the brain. PLoS Computational Biology, 4(11),
e1000209.
Knock, S., McIntosh, A., Sporns, O., Kötter, R., Hagmann, P., & Jirsa,
V.
(2009). The effects of physiologically plausible connectivity
structure on local and global dynamics in large scale brain mod-
els. Journal of Neuroscience Methods, 183(1), 86–94.
1013–1052.
Miši´c, B., Betzel, R. F., Griffa, A., De Reus, M. A., He, Y., Zuo, X.-N.,
. . . Zatorre, R. J. (2018). Network-based asymmetry of the human
auditory system. Cerebral Cortex, 28(7), 2655–2664.
Miši´c, B., Betzel, R. F., Nematzadeh, A., Goñi,
J., Griffa, A.,
Hagmann, P., . . . Sporns, O. (2015). Cooperative and compet-
itive spreading dynamics on the human connectome. Neuron,
86(6), 1518–1529.
Miši´c, B., Fatima, Z., Askren, M. K., Buschkuehl, M., Churchill, N.,
Cimprich, B., . . . Berman, M. G. (2014). The functional connec-
tivity landscape of the human brain. PLoS ONE, 9(10).
Miši´c, B., Goñi, J., Betzel, R. F., Sporns, O., & McIntosh, A. R.
(2014). A network convergence zone in the hippocampus. PLoS
Computational Biology, 10(12), e1003982.
Miši´c, B., Sporns, O., & McIntosh, A. R. (2014). Communication
efficiency and congestion of signal traffic in large-scale brain net-
works. PLoS Computational Biology, 10(1), e1003427.
Mohr, H., Wolfensteller, U., Betzel, R. F., Miši´c, B., Sporns, O.,
Richiardi, J., & Ruge, H.
Integration and segregation
(2016).
of large-scale brain networks during short-term task automatiza-
tion. Nature Communications, 7(1), 1–12.
Murray, J. D., Bernacchia, A., Freedman, D. J., Romo, R., Wallis,
J. D., Cai, X., . . . Wang, X. J.
(2014). A hierarchy of intrinsic
timescales across primate cortex. Nature Neuroscience, 17(12),
1661.
Muscoloni, A., & Cannistraci, C. V. (2019). Navigability evaluation
of complex networks by greedy routing efficiency. Proceedings
of the National Academy of Sciences, 116(5), 1468–1469.
Muscoloni, A., Thomas, J. M., Ciucci, S., Bianconi, G., & Cannistraci,
C. V. (2017). Machine learning meets complex networks via co-
alescent embedding in the hyperbolic space. Nature Communi-
cations, 8(1), 1–19.
Oldham, S., Fulcher, B., Parkes, L., Arnatkeviši ¯ut˙e, A., Suo, C., &
(2019). Consistency and differences between cen-
Fornito, A.
trality measures across distinct classes of networks. PLoS ONE,
14(7).
Oligschläger, S., Huntenburg, J. M., Golchert, J., Lauckner, M. E.,
Bonnen, T., & Margulies, D. S. (2017). Gradients of connectiv-
ity distance are anchored in primary cortex. Brain Structure and
Function, 222(5), 2173–2182.
Oligschläger, S., Xu, T., Baczkowski, B. M., Falkiewicz, M., Falchier,
A., Linn, G., & Margules, D. S. (2019). Gradients of connectivity
Network Neuroscience
1089
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
4
1
0
7
2
1
8
6
6
9
3
9
n
e
n
_
a
_
0
0
1
5
3
p
d
t
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Signal propagation via cortical hierarchies
distance in the cerebral cortex of the macaque monkey. Brain
Structure Function, 224(2), 925–935.
Paquola, C., Wael, R. V. D., Wagstyl, K., Bethlehem, R. A. I., Hong,
(2019). Microstructural
S.-J., Seidlitz, J., . . . Bernhardt, B. C.
and functionalgradients are increasingly dissociated in transmodal
cortices. PLoS Biology, 17(5), e3000284. https://doi.org/10.1371
/journal.pbio.3000284
Power, J. D., Barnes, K. A., Snyder, A. Z., Schlaggar, B. L., & Petersen,
S. E. (2012). Spurious but systematic correlations in functional
connectivity MRI networks arise from subject motion. Neuro-
Image, 59(3), 2142–2154.
Roberts, J. A., Perry, A., Lord, A. R., Roberts, G., Mitchell, P. B.,
Smith, R. E., . . . Breakspear, M. (2016). The contribution of ge-
ometry to the human connectome. NeuroImage, 124, 379–393.
Roberts, J. A., Perry, A., Roberts, G., Mitchell, P. B., & Breakspear,
(2017). Consistency-based thresholding of the human con-
M.
nectome. NeuroImage, 145, 118–129.
Rosvall, M., Esquivel, A. V., Lancichinetti, A., West,
J. D., &
Lambiotte, R.
(2014). Memory in network flows and its effects
on spreading dynamics and community detection. Nature Com-
munications, 5, 4630.
Roy, B.
(1959). Transitivité et connexité. Comptes Rendus Heb-
domadaires des Séances de l’ Académie des sciences, 249(2),
216–218.
Seguin, C., Razi, A., & Zalesky, A. (2019). Inferring neural signalling
directionality from undirected structural connectomes. Nature
Communications, 10(1), 1–13.
Seguin, C., van den Heuvel, M. P., & Zalesky, A. (2018). Naviga-
tion of brain networks. Proceedings of the National Academy of
Sciences, 115(24), 6297–6302.
Shine, J. M., Bissett, P. G., Bell, P. T., Koyejo, O., Balsters, J. H.,
Gorgolewski, K. J., . . . Poldrack, R. A. (2016). The dynamics of
functional brain networks: Integrated network states during cog-
nitive task performance. Neuron, 92(2), 544–554.
Stiso, J., & Bassett, D. S. (2018). Spatial embedding imposes con-
straints on neuronal network architectures. Trends in Cognitive
Sciences, 22(12), 1127–1142.
Suarez, L. E., Markello, R. D., Betzel, R. F., & Misic, B. (2020). Link-
ing structure and function in macroscale brain networks. Trends
in Cognitive of Sciences.
Thomas, C., Frank, Q. Y., Irfanoglu, M. O., Modi, P., Saleem, K. S.,
Leopold, D. A., & Pierpaoli, C.
(2014). Anatomical accuracy
of brain connections derived from diffusion MRI tractography is
inherently limited. Proceedings of the National Academy of Sci-
ences, 111(46), 16574–16579.
van den Heuvel, M. P., Kahn, R. S., Goñi, J., & Sporns, O. (2012).
High-cost, high-capacity backbone for global brain communica-
tion. Proceedings of the National Academy of Sciences, 109(28),
11372–11377.
van der Maaten, L., Postma, E., & van den Herik, J. (2009). Dimen-
sionality reduction: A comparative. Journal of Machine Learning
Research, 10, 66–71.
Vázquez-Rodríguez, B., Suárez, L. E., Markello, R. D., Shafiei, G.,
Paquola, C., Hagmann, P., . . . Misic, B. (2019). Gradients of struc-
ture–function tethering across neocortex. Proceedings of the
National Academy of Sciences, 116(42), 21219–21227. https://doi
.org.10.1073/pnas.1903403116
Wagstyl, K., Ronan, L., Goodyer, I. M., & Fletcher, P. C. (2015). Cor-
tical thickness gradients in structural hierarchies. NeuroImage,
111, 241–250.
Wang, X.-J.
(2020). Macroscopic gradients of synaptic excitation
and inhibition in the neocortex. Nature Reviews Neuroscience,
21, 169–178.
Warshall, S. (1962). A theorem on boolean matrices. Journal of the
ACM.
Worrell, J. C., Rumschlag, J., Betzel, R. F., Sporns, O., & Miši´c, B.
(2017). Optimized connectome architecture for sensory-motor
integration. Network Neuroscience, 1(4), 415–430.
Yeo, B., Krienen, F. M., Sepulcre, J., Sabuncu, M. R., Lashkari, D.,
Hollinshead, M., . . . Buckner, R. L.
(2011). The organization
of the human cerebral cortex estimated by intrinsic functional
connectivity. Journal of Neurophysiology, 106(3), 1125–1165.
Zalesky, A., Fornito, A., Cocchi, L., Gollo, L. L., van den Heuvel,
M. P., & Breakspear, M. (2016). Connectome sensitivity or speci-
ficity: Which is more important? NeuroImage, 142, 407–420.
Network Neuroscience
1090
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
4
4
1
0
7
2
1
8
6
6
9
3
9
n
e
n
_
a
_
0
0
1
5
3
p
d
t
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3