FOCUS FEATURE:
Linking Experimental and Computational Connectomics
Network remodeling induced by transcranial
brain stimulation: A computational model of
tDCS-triggered cell assembly formation
Han Lu
1,2
, Júlia V. Gallinaro
1
, and Stefan Rotter
1
1Bernstein Center Freiburg and Faculty of Biology, University of Freiburg, Freiburg, Germany
2Institute of Cellular and Integrative Neurosciences, University of Strasbourg, Strasbourg, France
a n o p e n a c c e s s
j o u r n a l
Keywords:
High-definition montage, Repetitive stimulation
tDCS, Homeostatic structural plasticity, Spiking neural network, Cell assembly,
ABSTRACT
Transcranial direct current stimulation (tDCS) is a variant of noninvasive neuromodulation,
which promises treatment for brain diseases like major depressive disorder. In experiments,
long-lasting aftereffects were observed, suggesting that persistent plastic changes are
induced. The mechanism underlying the emergence of lasting aftereffects, however, remains
elusive. Here we propose a model, which assumes that tDCS triggers a homeostatic response
of the network involving growth and decay of synapses. The cortical tissue exposed to tDCS
is conceived as a recurrent network of excitatory and inhibitory neurons, with synapses
subject to homeostatically regulated structural plasticity. We systematically tested various
aspects of stimulation, including electrode size and montage, as well as stimulation intensity
and duration. Our results suggest that transcranial stimulation perturbs the homeostatic
equilibrium and leads to a pronounced growth response of the network. The stimulated
population eventually eliminates excitatory synapses with the unstimulated population, and
new synapses among stimulated neurons are grown to form a cell assembly. Strong focal
stimulation tends to enhance the connectivity within new cell assemblies, and repetitive
stimulation with well-chosen duty cycles can increase the impact of stimulation even further.
One long-term goal of our work is to help in optimizing the use of tDCS in clinical
applications.
AUTHOR SUMMARY
Noninvasive brain stimulation techniques like tDCS have the potential to directly interfere
with neural activity, but may also trigger activity-dependent plasticity. We propose a model
to study the mechanism of tDCS and persistent aftereffects that may be induced as a
consequence of homeostatic structural plasticity. Based on the idea that tDCS perturbs
the ongoing activity of neurons, our model predicts that the stimulation also triggers a
rearrangement of synapses among stimulated and unstimulated neurons, eventually leading
to network remodeling and cell assembly formation. Focal and strong stimulation leads to
stronger cell assemblies, and so does repetitive stimulation with optimized stimulation
protocols. This is the first original work studying possible long-lasting aftereffects of
transcranial stimulation at the mesoscopic neuronal network level using a computational
model.
Citation: Lu, H., Gallinaro, J. V., &
Rotter, S. (2019). Network remodeling
induced by transcranial brain
stimulation: A computational model
of tDCS-triggered cell assembly
formation. Network Neuroscience,
3(4), 924–943. https://doi.org/10.1162/
netn_a_00097
DOI:
https://doi.org/10.1162/netn_a_00097
Supporting Information:
https://doi.org/10.1162/netn_a_00097
Received: 31 October 2018
Accepted: 14 May 2019
Competing Interests: The authors have
declared that no competing interests
exist.
Corresponding Author:
Stefan Rotter
stefan.rotter@bio.uni-freiburg.de
Handling Editor:
Sandra Diaz
Copyright: © 2019
Massachusetts Institute of Technology
Published under a Creative Commons
Attribution 4.0 International
(CC BY 4.0) license
The MIT Press
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
3
4
9
2
4
1
8
6
6
7
9
4
n
e
n
_
a
_
0
0
0
9
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A computational model of tDCS-triggered cell assembly formation
Somato-dendritic axis:
Imaginary axis linking the soma and
the distral dendrites of a pyramidal
neuron.
PET:
Positron-emission tomography, based
on a radioactive tracer that is
introduced into the body before the
induction of metabolic processes.
MEP/SEP:
The motor evoked potential or
sensory evoked potential is a signal
recorded from muscles or from the
surface of the brain, respectively, as a
result of a stimulus.
BDNF:
Growth factor that acts on certain
neurons. It supports survival of
neurons, growth, and differentiation
of new neurons and synapses.
INTRODUCTION
Transcranial direct current stimulation (tDCS) is a noninvasive brain stimulation technique,
where a weak constant current (1−2 mA) is applied to the brain via large electrodes attached
to the scalp (Edwards et al., 2013). It induces weak electric fields that are typically not sufficient
to trigger action potentials directly, but can polarize the membrane of neurons by fractions
of millivolts (Joucla & Yvert, 2009), depending on the orientation of the electric field vector
relative to the somato-dendritic axis of the neuron (Gluckman et al., 1996; Radman, Ramos,
Brumberg, & Bikson, 2009; Wiethoff, Hamada, & Rothwell, 2014). This membrane potential
deflection can influence spike timing and firing rates of neurons that are part of an active
network (Bikson, Radman, & Datta, 2006; Vöröslakos et al., 2018). Similar to other methods
of neuromodulation, tDCS is claimed to have a potential for alleviating symptoms of certain
brain diseases, such as major depressive disorder (Loo et al., 2012; Nitsche, Boggio, Fregni, &
Pascual-Leone, 2009) or chronic pain (Garcia-Larrea, 2016; Ngernyam et al., 2015).
Although there is a record of promising applications of tDCS, both positive and negative
outcomes have been reported in the literature (Horvath, Forte, & Carter, 2015). Typical issues
are due to insufficient sensitivity of measurements, or large intersubject and intrasubject vari-
ability (Wiethoff et al., 2014). Positive evidence includes immediate changes of neural activity
caused by tDCS, observed both in humans and in rodents. Positron emission tomography (PET)
in humans revealed that tDCS can influence the activity of neurons in different brain regions
(Lang et al., 2005), but the most affected region varies with electrode montage (Kuo et al.,
2013), skull thickness (Opitz, Paulus, Will, Antunes, & Thielscher, 2015), individual geometry
of cortex (Opitz et al., 2015), preexisting lesions (Minjoli et al., 2017), and other aspects. Sys-
tematic transcutaneous current stimulation experiments in rats (Vöröslakos et al., 2018) could
establish quantitative relations between the externally applied current, the induced electric
field, the associated membrane potential deflection, and the resulting firing rate change.
In addition to the instant impact on activity during stimulation, a sustained modulation of
neural activity was also observed in humans after stimulation was turned off. Lasting after-
effects of tDCS, measured as motor evoked potentials (MEP) triggered by transcranial mag-
netic stimulation (TMS), were first reported by Nitsche & Paulus (2000), and later confirmed in
motor cortex (Nitsche & Paulus, 2001) and somatosensory cortex as sensory evoked potentials
(SEP) (Matsunaga, Nitsche, Tsuji, & Rothwell, 2004). Animal studies suggested that the ele-
vated activity and excitability is not due to reverberating networks (Gartside, 1968a). Rather,
changes in synaptic protein synthesis (Gartside, 1968b) point towards increased synaptic plas-
ticity. In turn, blocking either brain-derived neurotrophic factor (BDNF; Fritsch et al., 2010),
NMDA receptors (Nitsche et al., 2003), or calcium channels (Monte-Silva et al., 2013) leads
to a reduction of the stimulation-induced increments of the field potential in mice, or MEP
in humans. Recent evidence suggests that multiple forms of plasticity are in fact contribut-
ing to tDCS aftereffects. Monte-Silva et al. (2013) observed that fast facilitation, or early-LTP
(e-LTP), was induced after a single tDCS session (13 min ) and lasted for at least 2 hr after
stimulation. In contrast, 26-min stimulation resulted in a reduced MEP amplitude. More inter-
estingly, repetitive tDCS with 20-min pauses interspersed (13 − 20 − 13 min ) resulted in late
facilitation, or late-LTP (l-LTP). An elevated MEP was observed one day after the second stim-
ulation, but not immediately after it. Functional LTP-like plastic changes of existing synapses
were observed in DCS (Ranieri et al., 2012). Given the timescales of l-LTP, structural plasticity
involving network remodeling also seems to play a role for the aftereffects. Structural changes
at a slower timescale, however, can easily be underestimated because of difficulties measuring
synapse turnover and changes in neuronal morphology in vivo. In summary, it is likely that both
Network Neuroscience
925
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
3
4
9
2
4
1
8
6
6
7
9
4
n
e
n
_
a
_
0
0
0
9
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A computational model of tDCS-triggered cell assembly formation
Hebbian and homeostatic as well as functional and structural forms of plasticity underlie tDCS
aftereffects.
Quantitative models of network remodeling have previously been described in the litera-
ture. Butz, Steenbuck, & van Ooyen (2014) first introduced the term homeostatic structural
plasticity with reference to previously published versions of the theory (Butz & van Ooyen,
2013; Butz, van Ooyen, & Wörgötter, 2009; van Ooyen, 2011), which was based on ample
experimental evidence that structural plasticity (Holtmaat & Svoboda, 2009; Oray, Majewska,
& Sur, 2004; Pfeiffer et al., 2018; Trachtenberg et al., 2002) as well as homeostatic regulation
of activity (Keck et al., 2013; Lee et al., 2013; Turrigiano & Nelson, 2004) are constantly taking
place in many brain areas. This homeostatic structural plasticity model was able to provide ex-
planations for cortical reorganization after stroke (Butz et al., 2009) and lesion (Butz-Ostendorf
& van Ooyen, 2017), and for the formation of certain global network features during devel-
opment (Butz et al., 2014; Gallinaro & Rotter, 2018). In this model, changing the number of
synaptic contacts between two neurons leads to an apparent facilitation or depression of this
specific connection, and the model may therefore also account for some cases of functional
plasticity. Based on these previous insights it seemed natural to explore the contribution of
homeostatic structural plasticity to the long-lasting aftereffects of transcranial brain stimulation.
In the present work, we hypothesize that employing proper stimulation protocols and
adequate current strengths, tDCS is potent enough to polarize single neurons in a network
(Vöröslakos et al., 2018). Based on this assumption, we assess the effect of such membrane
potential deflections on neuronal firing rates. In a neural network model with homeostatic
structural plasticity, we then systematically explore the influence of various stimulation param-
eters known from tDCS practice, such as electrode size and montage, stimulation strength, and
repetitive stimulation protocols. Our results suggest that tDCS can indeed induce substantial
network remodeling and cell assembly formation, and focused strong and/or repetitive stimu-
lation with well-chosen duty cycles can effectively boost the connectivity of the cell assemblies
formed. The enhanced cell assembly might contribute to the empirical finding of profound plas-
tic responses and enhanced therapeutic effects observed in current tDCS applications with a
high-definition montage (Kuo et al., 2013) and repetitive stimulation (Monte-Silva et al., 2013).
Our analysis also provides explanations for some of the negative results in tDCS practice.
METHODS
Neuron Model
All large-scale simulations of plastic neuronal networks of this study were performed with
the NEST simulator (Linssen et al., 2018). Most were simulated with NEST 2.14, while NEST
2.16 with MPI-based parallel computation was used in the long repetitive protocol to achieve
long simulation times. The linear, current-based leaky integrate-and-fire (LIF) neuron model
was used throughout. The dynamic behavior of this point neuron model is described by the
ordinary differential equation
τm
d
dt
Vi(t) =− Vi(t) + τm ∑
j
JijSj(t − d) + ΔV(t),
(1)
where τm is the membrane time constant. The variable Vi(t) is the membrane potential of
neuron i, with a resting value at 0 mV. ΔV(t) represents a polarization of the membrane
imposed by an external electric field. The spike train generated by neuron i is denoted by
Si(t) = ∑k δ(t − tk
i represents the individual spike times, and d is the synaptic
i ), where tk
Cell assembly:
A group of neurons with enhanced
mutual synaptic connectivity; arises
after repetitive activation.
High-definition montage:
Instead of using large sponge
electrodes, high-definition montage
employs smaller gel-based electrodes
to allow for more focal stimulation.
Point neuron:
A simplified neuron model that only
represents the somatic membrane
potential, disregarding the properties
of spatially extended dendrites and
axons.
Network Neuroscience
926
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
3
4
9
2
4
1
8
6
6
7
9
4
n
e
n
_
a
_
0
0
0
9
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A computational model of tDCS-triggered cell assembly formation
Table 1. Parameters of neuron model
V0
Vreset
0.0 mV 10.0 mV 20.0 mV
ref
2.0 ms
Vth
t
τm
10.0 ms
transmission delay. The entries of the matrix Jij denote the amplitude of the postsynaptic po-
tential that is induced in neuron i upon the arrival of a spike from neuron j. In our model, all
excitatory synapses have the amplitude JE = 0.1 mV, whereas all inhibitory synapses have an
amplitude of JI = −0.8 mV. When the membrane potential Vi(t) reaches the firing threshold,
Vth, an action potential is generated and the membrane potential is reset to Vreset = 10 mV.
All parameters are once more listed in Table 1.
Model of Transcranial DC Stimulation
The electric field (EF) induced by tDCS can directly affect the membrane potential of neurons.
Following Vöröslakos et al. (2018), we assumed that a strong enough EF will cause a small but
significant membrane potential depolarization or hyperpolarization on some neurons in the
network. The effective membrane potential deflection is determined by the orientation of the
electric field vector relative to the somato-dendritic axis of the neuron (Gluckman et al., 1996;
Radman et al., 2009; Wiethoff et al., 2014). When the electric field is properly aligned with the
axis (apical dendrite closer to anode than soma), the somatic membrane potential is depolar-
ized and the neuronal firing rate is increased. In contrast, if the electric field is perpendicular to
the axis, it cannot influence the activity of this particular neuron. As a consequence, cells with
extended and nonisotropic morphology, such as pyramidal neurons, should generally be more
influenced by tDCS than the more compact inhibitory interneurons, which is also confirmed by
Vöröslakos et al. (2018). Therefore, we assume only excitatory neurons to be sensitive to tDCS
because of their spatial extent and nonisotropic morphology. We then asked whether such
a polarization could also cause significant changes in the firing rate and, as a consequence,
trigger structural plasticity and network remodeling. As our model neurons are actually point
neurons with no spatial extent, we simply imposed an equivalent membrane potential bias ΔV
on the soma of the neuron (Gluckman et al., 1996; Kayyali & Durand, 1991); see Figure 1A.
This membrane potential bias also reflects the angle θ between the EF vector and somato-
dendritic axis of the neuron with a factor cos(θ); see Figure 1B. The smallest magnitude of a
membrane potential deflection reported in tDCS experiments to trigger physiological effects
was in the range of 0.1 mV (Jackson et al., 2016; Vöröslakos et al., 2018).
Relative Strength of Background Activity and tDCS
The effect of tDCS on a neuron with ongoing activity was assessed with single neuron sim-
ulations. The background input impinging onto the neuron was approximated by a spike
train with Poisson statistics and rate νext = 18.1 kHz, coupled to the neuron with synapses
of strength Jext = 0.1 mV. Given the parameters of our neuron model, this ongoing back-
ground activity leads to a fluctuating subthreshold membrane potential with a mean value
μ = νextτm Jext = 18.1 mV (Brunel, 2000). Different values of membrane polarization caused
by tDCS (from 0.1 mV to 1.2 mV) were considered in our study, as described above. The firing
rate of each condition was estimated from simulations of 100-s duration.
Network Model
Although there are a variety of EF distributions induced by different tDCS montages, we assume
simple uniform EF distributions in our model of the most affected area (Jackson et al., 2016).
Poisson process:
Simple statistical model to account
for a barrage of spikes, commonly
used to describe the synaptic inputs
driving a neuron.
Network Neuroscience
927
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
3
4
9
2
4
1
8
6
6
7
9
4
n
e
n
_
a
_
0
0
0
9
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A computational model of tDCS-triggered cell assembly formation
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
3
4
9
2
4
1
8
6
6
7
9
4
n
e
n
_
a
_
0
0
0
9
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
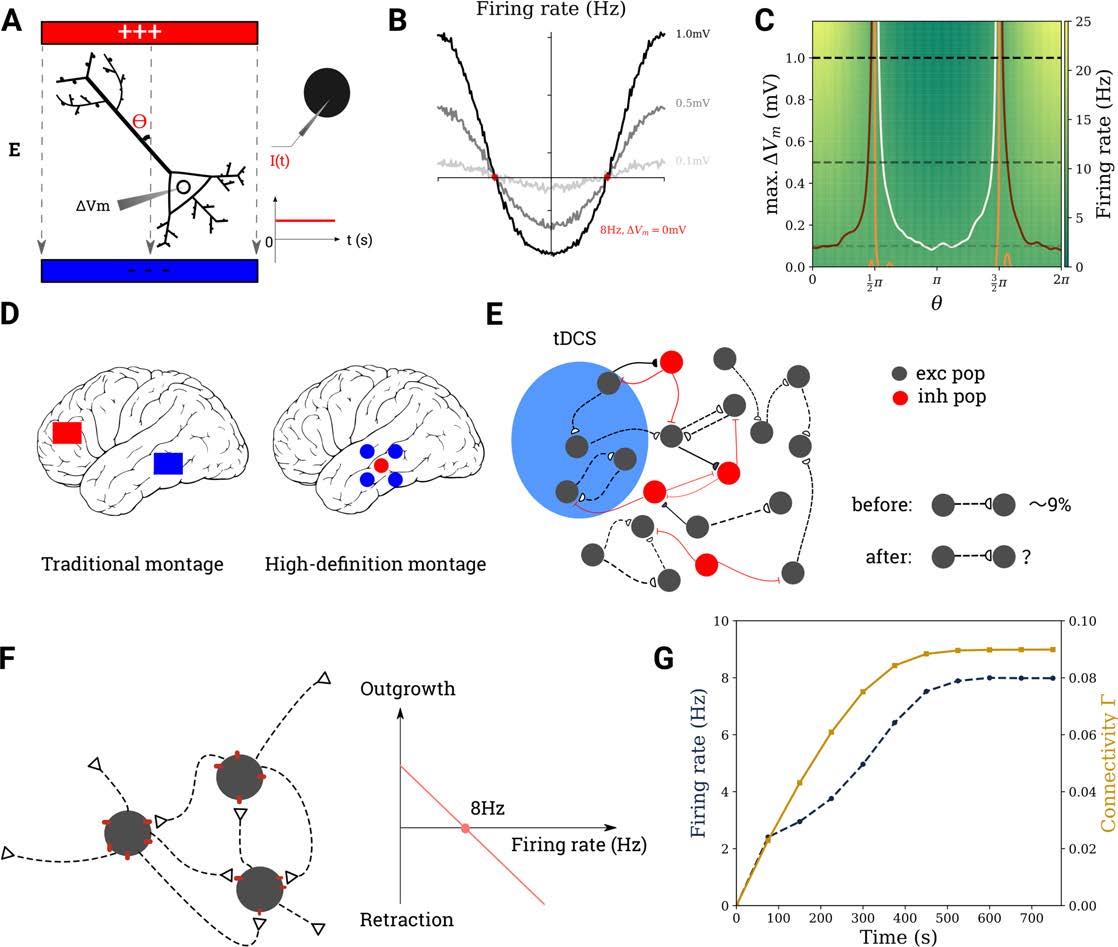
Figure 1. Modeling the effect of tDCS on cortical networks. (A) It is assumed that transcranial stimulation leads to a weak polarization of
the neuron’s membrane potential (left). For a point neuron, this is achieved by injecting a current of suitable strength into its soma (right). (B)
Firing rate modulation with the angle θ for three different values of ΔVm (dotted lines on C). (C) Firing rate of a neuron, the ongoing activity
of which is modulated by tDCS, for different values of θ and membrane polarization ΔVm. The contour lines correspond to 7 Hz, 8 Hz, and
9 Hz in white, orange, and maroon. (D) Electrode montages used in tDCS. (E) The region of interest subject to tDCS is modeled as a recurrent
network of excitatory and inhibitory neurons. (F) Excitatory-to-excitatory synapses require the combination of a bouton (empty triangle) and
a spine (red dot). The growth rate of both types of synaptic elements depends linearly on firing rate. (G) The network is grown from scratch
before each tDCS stimulation experiment.
This most affected area is modeled as an inhibition-dominated recurrent network (Brunel,
2000), comprising 10, 000 excitatory and 2, 500 inhibitory neurons. All connections involv-
ing inhibitory neurons were taken to be static. Excitatory and inhibitory synapses had fixed
synaptic weights of JE = 0.1 mV and JI = −0.8 mV, respectively. All these connections were
Network Neuroscience
928
A computational model of tDCS-triggered cell assembly formation
NE
10, 000
Table 2. Parameters of the network model
JI
ΓI−I
ΓE−I
JE
10% 10% 10% 0.1 mV −0.8 mV 30 kHz
ΓI−E
rext
NI
2, 500
Set-point hypothesis:
In the model of homeostatic
structural plasticity, neural firing rate
is actively maintained at a set-point
by adjusting synaptic input and
output.
randomly established, with 10% connection probability. In contrast, excitatory-to-excitatory
(E-E) connections were subject to a growth rule called homeostatic structural plasticity (Butz &
van Ooyen, 2013; Diaz-Pier, Naveau, Ostendorf, & Morrison, 2016; Gallinaro & Rotter, 2018).
The network had initially no E-E connections whatsoever, and they were grown according to
the specified rule during a growth period of 750 s for all simulations in the paper. Each neuron
in the network received Poissonian external input at a rate of rext = 30 kHz. For the parame-
ters chosen here, the network automatically entered an asynchronous-irregular state (Brunel,
2000). In all figures and simulations, transcranial DC stimulation was only applied after the
end of the growth period. All network parameters are once more listed in Table 2.
Homeostatic Structural Plasticity
Connections between excitatory neurons underwent continuous remodeling, governed by rate-
based homeostatic structural plasticity, as implemented in NEST (Diaz-Pier et al., 2016). Exci-
tatory synapses were formed by combining a presynaptic element (bouton) and a postsynaptic
element (spine). New synapses can form only if free synaptic elements are available. Pairs of
neurons can form multiple synapses between them, and each individual functional synapse
has the same weight JE = 0.1 mV. It has been observed in experiments that neurite growth
is governed by the concentration of intracellular calcium. It has been hypothesized that there
is a set-point of the calcium concentration, which the neuron strives to reach and stabilize
(Mattson & Kater, 1987; Ramakers et al., 2001). As a consequence, in the model of structural
plasticity we use in our work, growth and deletion of synaptic elements are linked to the time-
dependent intracellular calcium concentration C(t) = [Ca2+] of the neuron in question. In
fact, this variable has been shown to be a good indicator of the neuron’s firing rate (Grewe,
Langer, Kasper, Kampa, & Helmchen, 2010). Whenever the neuron emits a spike, the intracel-
lular calcium concentration experiences an increase by the amount βCa through calcium in-
flux. Between spikes, the calcium concentration decays exponentially with time constant τCa,
d
dt
C(t) =−
1
τCa
C(t) + βCaS(t).
(2)
The synaptic growth rule is as follows. When the firing rate (or calcium concentration) falls
below its set-point, the neuron will grow new synaptic elements and form functional synapses
to compensate for the lack of excitatory input. In contrast, if the firing rate rises above the
set-point, existing synapses are broken up and synaptic elements are removed. The respective
counterparts are added to the pool of free synaptic elements. We adopted a linear growth rule
applying to both presynaptic and postsynaptic elements alike (Gallinaro & Rotter, 2018):
d
dt
z(t) = ν
(cid:2)
1 −
(cid:3)
,
C(t)
1
(cid:7)
(3)
where z(t) is the total number of (presynaptic or postsynaptic) elements a neuron has available,
ν is the growth rate, and (cid:7) is the target level of calcium concentration. In any given moment,
free synaptic elements are randomly combined with matching free synaptic elements of other
neurons, forming new functional synapses. All the parameters defining the structural plasticity
rule are listed in Table 3.
Network Neuroscience
929
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
3
4
9
2
4
1
8
6
6
7
9
4
n
e
n
_
a
_
0
0
0
9
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A computational model of tDCS-triggered cell assembly formation
Table 3. Parameters of the structural plasticity model
(cid:7)
0.008
ν
0.004 s−1
τCa
10 s
βCa
0.0001
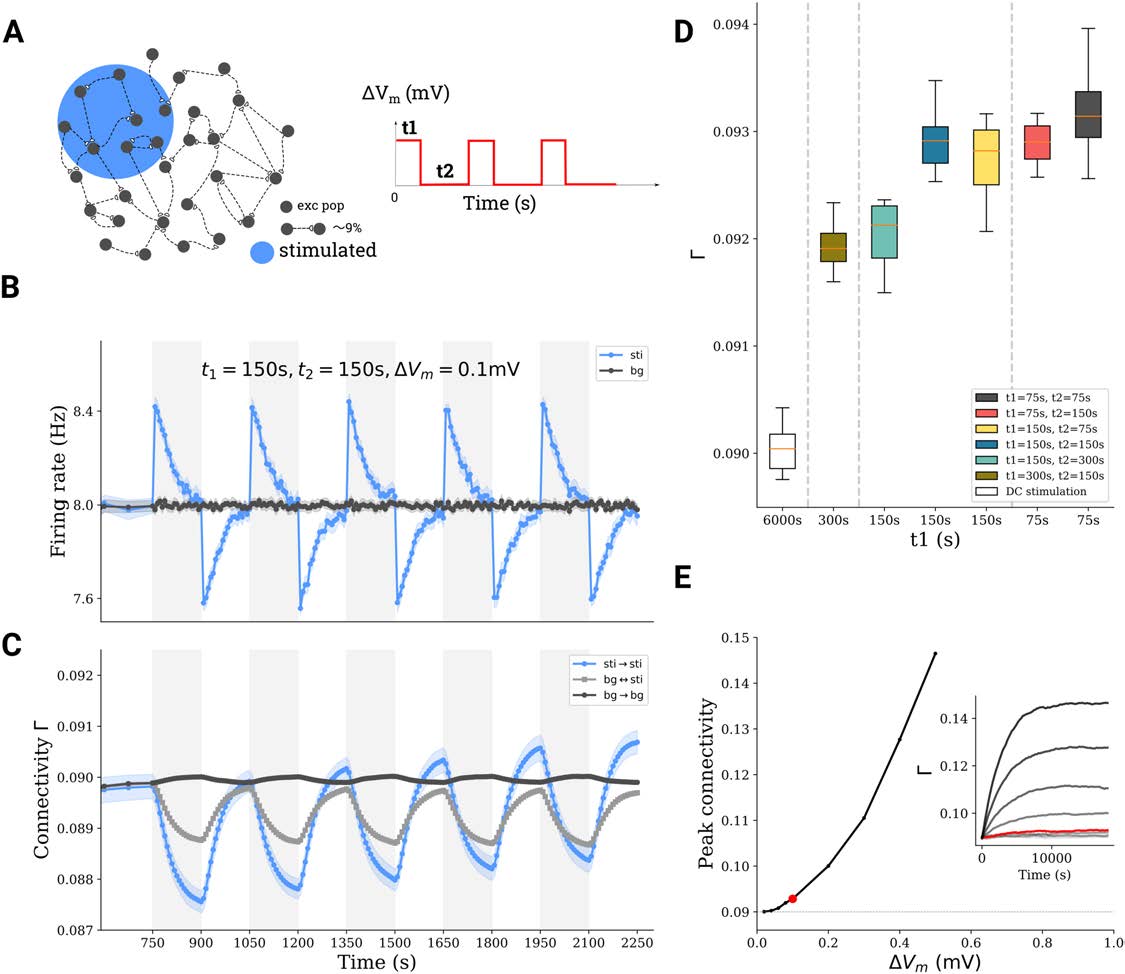
Protocols of Transcranial DC Stimulation
As suggested by current tDCS practice, many factors are essential to the outcome of a stimula-
tion. For example, the traditional montage of two large sponge electrodes of size 5 cm × 7 cm
induces a diffusive and weak EF. In contrast, high-definition montage using a small anodal elec-
trode surrounded by several small cathodal electrodes induces a focal and relatively strong EF
for the same stimulation current (Edwards et al., 2013). High-definition montage induces higher
current densities, affects smaller populations, and possibly opposite field polarity at the edge
of the cathodes. This method also exhibits better performance in tDCS practice, as compared
with conventional montage (Kuo et al., 2013). To test these factors in our model we employed
three different scenarios and systematically changed the size of the stimulated focus and the
intensity of the stimulation in all of them. A summary of the parameters used in the different
stimulation protocols described in this section can be found in Table 4.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
3
4
9
2
4
1
8
6
6
7
9
4
n
e
n
_
a
_
0
0
0
9
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
The first protocol we considered was a simplified scenario, in which only a sub-
Uni-group.
group of excitatory neurons in a large network was polarized by tDCS according to the above
described protocol, while the remaining neurons were not affected and received only baseline
external input. The focality of the stimulation is quantified by the percentage of excitatory neu-
rons stimulated fG1. The more focused a stimulation is, the smaller is the subgroup of neurons
affected by tDCS. The intensity of stimulation, on the other hand, is quantified by the amount
of polarization. A stronger EF would lead to stronger membrane polarization of the soma of
the model neurons. After a certain stimulation time t
stim, tDCS is turned off and the network is
allowed to relax for a period of t
and t
relax. Table 4 shows the values of fG1 and ΔV, as well as t
relax, used for the different figures.
stim
Bi-group. Neurons in biological brains may not be uniformly polarized by stimulation. This
is reflected in the bi-group scenario, in which a subgroup of neurons containing a fraction
fG1 of all excitatory neurons is polarized by ΔV1 (similarly to the uni-group scenario), while
the remaining excitatory neurons fG2 are stimulated with the same magnitude, but opposite
polarity ΔV2. Similarly to the uni-group scenario, after a certain stimulation time t
stim, tDCS is
turned off and the network is simulated for a relaxation period t
relax. The effect of stimulation
on connectivity IG was calculated as described below.
Tri-group. We designed yet another protocol, the tri-group scenario, to study the interaction
of two actively stimulated subgroups with an unstimulated background. Two subgroups of
excitatory neurons of the same size fG1 and fG2 are stimulated with the same magnitude, but
different polarity ΔV1 and ΔV2. The remaining excitatory neurons in the network fG3 remain
unstimulated. The resulting effect of stimulation on connectivity is measured as described
below.
To examine the effects of repetitive on-off stimulation, a certain fraction
Repetitive patterns.
fG1 of the excitatory neurons was stimulated in multiple cycles with the uni-group protocol.
Each cycle corresponds to a stimulation period of length t1 followed by a pause of length t2.
Network Neuroscience
930
A computational model of tDCS-triggered cell assembly formation
Table 4. Configurations of DC stimulation
−
−
ΔV1 [mV]
0.1
0.1
0.1
0.1
Protocol
uni-group
uni-group
tri-group
bi-group
bi-group
uni-group
tri-group
all
repetitive
repetitive
repetitive
repetitive
repetitive
fG1
10%
10%
30%
30%
10%, 30%, 50%, 70%
10%, 30%, 50%, 70%
10%, 20%, 30%, 40%
50%
10%
10%
10%
10%
10%
fG2
Figure
90%
2B
90%
2D
30%
3A
70%
3B
1 − fG1
4A
1 − fG1
4B
fG1
4C
50%
4I
90%
5D
90%
5E
90%
6-on-off
90%
6-alternating1
90%
6-alternating2
1
The stimulation intensities are −1.2, −0.8, −0.4, 0.4, 0.8,1.2 mV
The repetition round (n) were matched with n × t1 = 6, 000 s
The combinations used are (75, 75), (75, 150), (150, 75), (150, 150), (150, 300), (300, 150) s
The stimulation intensities are 0.02, 0.04, 0.06, 0.08, 0.1, 0.2, 0.3, 0.4, 0.5 mV
All results in this study except Figure 4I and Figure 5E are averages from 30 independent simulations.
fG3
−
−
40%
−
−
−
1 − fG1 − fG2
−
−
−
−
−
−
ΔV2 [mV]
0
0
−0.1
−0.1
−ΔV1
0
−ΔV1
−1.2, 1.2
0
0
0
0
0
−1.2, 1.2 1
−1.2, 1.2
−1.2, 1.2
−1.2, 1.2
0.1
multiple 4
0.1
±0.05
±0.1
0
−
−
−
−
−
−
0
−
−
−
4
3
2
ΔV3 [mV] Growth [s]
Repetition
no
no
no
no
no
no
no
no
yes2
80
3
3
3
tstim or t1[s]
150
150
150
150
150
150
150
150
multiple
75
150
150
150
3
trelax or t2[s]
300
300
300
300
5,850
5,850
5,850
5,850
150
150
150
150
750
750
750
750
750
750
750
750
750
750
750
750
750
The number of cycles nc in each scenario was arranged to achieve a total DC stimulation time
of nct1 = 6, 000 s.
Repetitive alternating stimulation is similar to the repetitive on-off protocol based on the
uni-group scenario. The difference is that, instead of pausing, neurons are stimulated with
opposite polarity and same magnitude. In Table 4 we compiled a summary of all parameters
for the stimulation protocols considered in our study.
Measurements and Calculations
The firing rate of a neuron was calculated from its spike count, in a 5-s activity
Firing rate.
recording, unless stated otherwise. The mean firing rate of a population was taken to be the
arithmetic mean of firing rates across neurons in the group.
Let (Aij) be the n × n connectivity matrix of a network with n neurons.
Synaptic connectivity.
Its columns correspond to the axons, and its rows correspond to the dendrites of the neurons
involved. The specific entry Aij of this matrix represents the total number of synapses from the
presynaptic neuron j to the postsynaptic neuron i. The mean connectivity of this network is
then given by Γ(t) = 1
n2 ∑ij Aij, where t is the observing time point.
Time integral of the connectivity. When comparing the effects of different stimulation scenar-
ios, one cannot simply consider the connectivity of the cell assembly at the end of simulation,
because connectivity typically decays with certain time constants. We used the integrated con-
nectivity change as a robust measure for the accumulated outcome of a stimulation. To account
for the integrals, we first fit the connectivity change during the relaxation phase by a sum of
three exponential decay functions:
Γ(t) = A1 exp−t/τ1 +A2exp−t/τ2 + A3 exp−t/τ3 .
(4)
The parameter Ak is the amplitude of a component that decays with time constant τk. We
then computed the total integral of the connectivity by integrating the sum of exponentials,
Network Neuroscience
931
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
3
4
9
2
4
1
8
6
6
7
9
4
n
e
n
_
a
_
0
0
0
9
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A computational model of tDCS-triggered cell assembly formation
amounting to IG = ∑k Akτk (see Figure S2 in the Supporting Information). This way we can
also account for connectivity transients that persist for a very long time, extrapolating beyond
the duration of our simulations.
RESULTS
Immediate Firing Rate Modulation by Transcranial DC Stimulation
We assume that the direct current applied to the brain during transcranial stimulation induces
small deflections of the somatic membrane potential of neurons (Vöröslakos et al., 2018) and
study the consequences of this deflection on neuronal firing rates. A polarization of the mem-
brane ΔVm in the range between −1.2 mV and 1.2 mV, which is not strong enough to elicit
spikes in a neuron at rest, can nevertheless induce appreciable firing rate changes in a neuron
with ongoing activity. Figures 1B and 1C show how the firing rate of a model neuron driven
by background input is modulated by both the strength of the depolarization and the angle θ
between the electric field (EF) and the somato-dendritic axis. Even for a polarization as weak
as ±0.1 mV, which is about the weakest depolarization known to cause observable physio-
logical effects in tDCS experiments (Vöröslakos et al., 2018), the firing rate change was found
to be larger than ±10% (Figure 1B, light gray curve). This suggests very clearly that tDCS can
have an appreciable impact on neuronal activity, even if the stimulation intensity is apparently
subthreshold. As neuronal spiking can affect synaptic connectivity via activity-dependent plas-
ticity, this raises the question whether transcranial stimulation can trigger plastic effects as well.
To find an answer to this question, we set up a plastic network representing the tissue most
affected by tDCS (Figures 1E–G) and study the effect of stimulation.
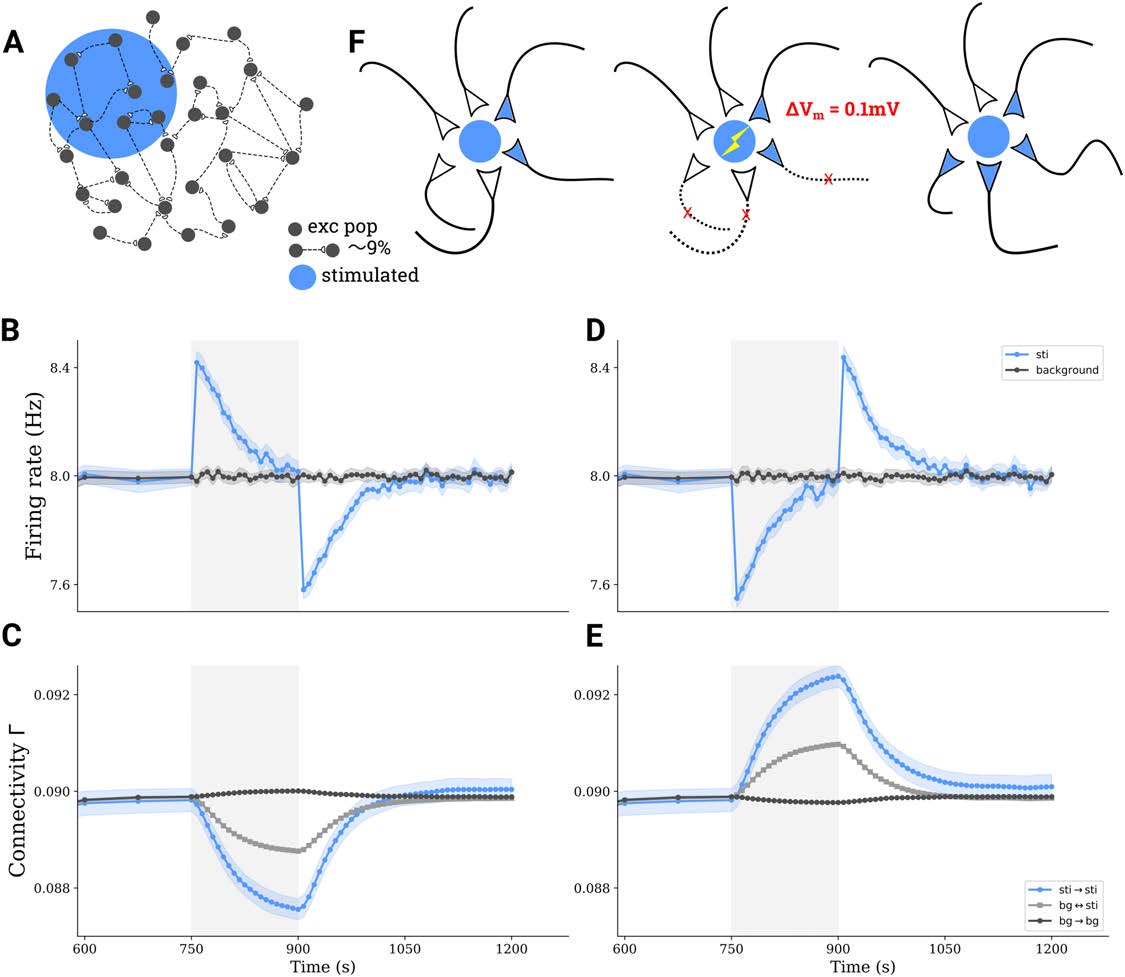
Network Remodeling Triggered by Transcranial DC Stimulation
Different electrode montages are used in tDCS (Figure 1D), and they are thought to trigger
different electric field distributions in the whole brain. We only modeled the most affected
region stimulated by the peak current intensity. To explore the homeostatic response of the
network, and the plastic processes associated with it, we first considered a simplified setting.
In the uni-group scenario, only a subset of excitatory neurons in a larger network is stimulated
(blue region in Figure 1E and Figure 2A). As shown in Figure 1F, tDCS disrupts the home-
ostatic equilibrium of the stimulated neurons by increasing their firing rate, initially leading
to a deletion of synapses between stimulated neurons (see Methods for details of the struc-
tural plasticity model). When the stimulation has ceased, the firing rate of stimulated neurons
drops because of a lack of recurrent input (Figure 2B), and the homeostatic process now trig-
gers the formation of new synapses, predominantly among the stimulated neurons (Figure 2C).
Figure 2F illustrates the process of cell assembly formation, similarly to what has been de-
scribed previously by Gallinaro & Rotter (2018). Before and after the stimulation, assuming
equilibrium in both cases, each neuron receives the same external input and fires at its target
rate (here, 8 Hz). Thus, the total number of input synapses from excitatory neurons will not have
changed through stimulation. What has changed, however, is the source of input synapses:
Before stimulation, input comes from both groups of neurons—to be stimulated (blue) and
background (empty)—without any bias. During stimulation, however, synapses are broken up,
and when stimulation is turned off, the stimulated neurons have more free synaptic elements
to offer. Background neurons, which are only indirectly affected by stimulation and deviate
less from their target rate, can only offer a few synaptic elements to form new connections.
Network Neuroscience
932
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
3
4
9
2
4
1
8
6
6
7
9
4
n
e
n
_
a
_
0
0
0
9
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A computational model of tDCS-triggered cell assembly formation
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
3
4
9
2
4
1
8
6
6
7
9
4
n
e
n
_
a
_
0
0
0
9
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
tDCS triggers the formation of cell assemblies. (A) A subgroup comprising 10% of all excitatory neurons in a larger network is
Figure 2.
stimulated by tDCS. (B) Average firing rate of directly stimulated (blue) and unstimulated (gray) excitatory neurons before, during, and after
applying a depolarizing stimulus. (C) Average connectivity among stimulated neurons (blue), among unstimulated neurons (dark gray), and
between neurons belonging to different groups (light gray) upon depolarizing stimulation. (D–E) Similar to (B–C), but for a hyperpolarizing
stimulus. Shaded areas on (B–E) indicate the stimulation period. (F) Illustration explaining the process of structural plasticity that happened
after a depolarizing tDCS. The stimulation triggers the removal of interpopulation synapses, and accelerates the growth of synapses among
stimulated neurons, leading to the formation of cell assemblies.
Since the formation of new synapses is based on the availability of free elements, this leads to
a bias for connections to be formed among stimulated neurons.
A similar process happens for hyperpolarizing DC (Figure 2D and 2E).
In this case,
however, the connectivity among stimulated neurons increases during tDCS because of
Network Neuroscience
933
A computational model of tDCS-triggered cell assembly formation
hyperpolarization and a resulting drop in firing rate. In summary, any perturbation to the
equilibrium of the network firing rate dynamics, no matter whether it is depolarizing or hy-
perpolarizing, will trigger an increased synaptic turnover and network remodeling by deleting
between-group synapses and forming new synapses within the stimulated group to form a cell
assembly.
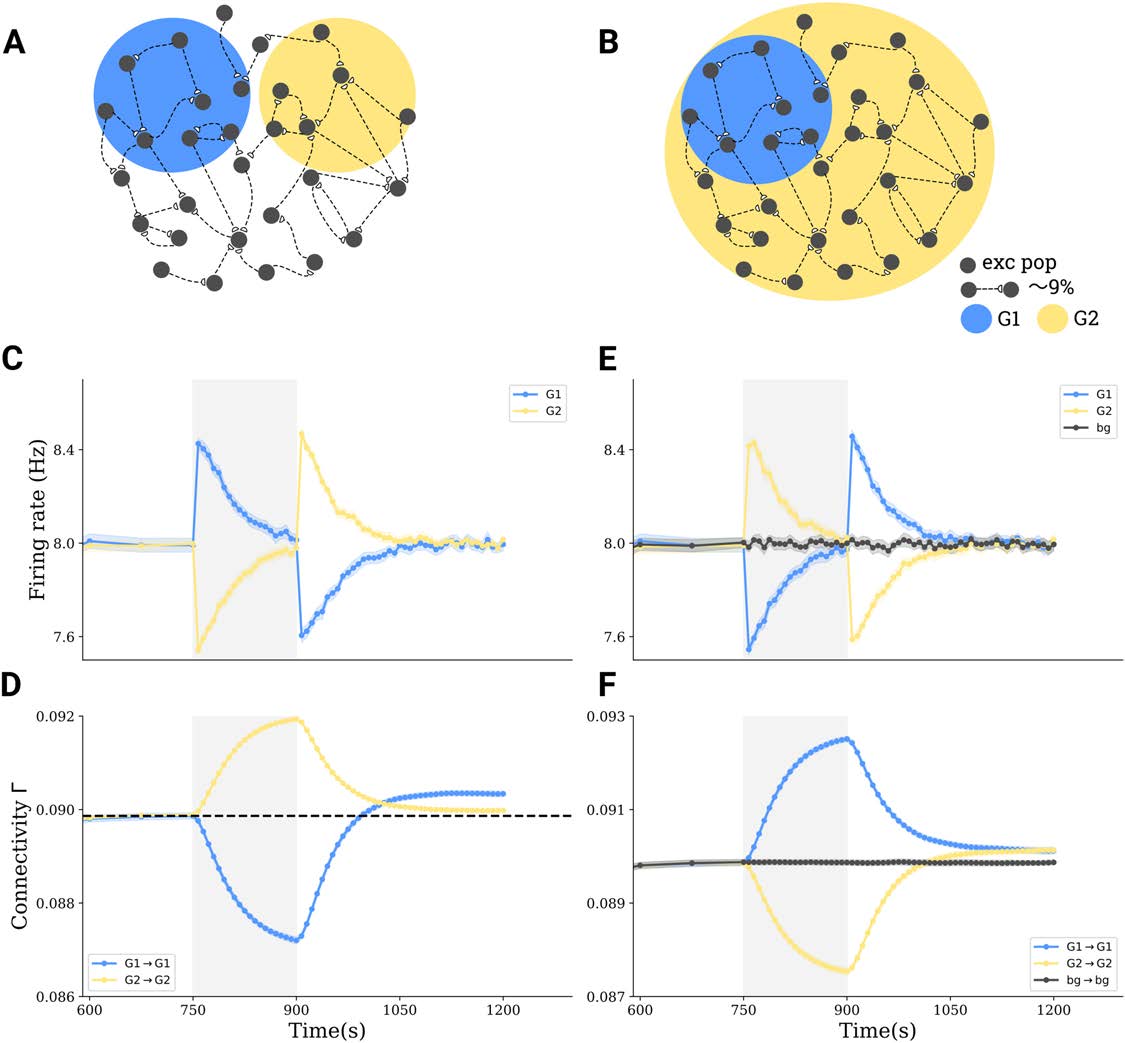
The Effect of Montage, Focality, and Intensity of Transcranial DC Stimulation
Stimulation is able to induce cell assembly formation in the uni-group scenario, as illustrated
in Figure 2. However, neurons affected by tDCS might not be uniformly depolarized or hy-
perpolarized. Parameters like stimulation montage, focality, or intensity certainly influence the
degree to which each neuron in the stimulated population is affected, and to what extent its
membrane potential is depolarized or hyperpolarized. Therefore, we investigated two alter-
native stimulation scenarios that capture some of the complexities of neuron polarization in
real tissue: tri-group stimulation (Figure 3A) and bi-group stimulation (Figure 3B), the details
of which are described in the Methods section. Similarly to the simplest scenario illustrated
in Figure 2, the stimulated neurons again form a cell assembly (Figures 3E and 3F) also under
more general conditions.
We performed a systematic study covering different degrees of stimulation focality and in-
tensity and compared the effects in all three scenarios: the bi-group (Figure 4A), uni-group
(Figure 4B), and tri-group (Figure 4C). Higher stimulus intensity is implemented as a stronger
membrane polarization, which results from a higher tDCS current density. Focality, quantified
as the percentage of neurons in the network affected by membrane polarization, describes how
focused stimulation is. More focused stimulation should have a polarizing effect on a smaller
percentage of neurons. In each scenario, the connectivity in a newly formed cell assembly
increases with absolute stimulation intensity and decreases with the size of the stimulated
population (Figures 4D–F). We conclude that strong and focused stimulation (like high-definition
stimulation) leads to stronger effects on the connectivity of the cell assembly. We further com-
pared the effects of bi-group, uni-group, and tri-group scenarios and found that the mon-
tage can greatly influence the outcome. When the polarization is very strong (above 0.8 mV)
and focused, the effect IG1 is much stronger in the uni-group scenario as compared with the
bi-group (Figure 4G) and tri-group (Figure 4H) scenario. But if the stimulus is weak, its effect
in the bi-group scenario is larger than in the uni-group scenario. Therefore, using opposite
polarities for stimulation could slightly boost cell assembly formation, provided the stimulus
is weak. However, for strong and/or focused stimulation, uni-group stimulation leads to more
pronounced cell assemblies.
The application of hyperpolarizing DC to all neurons in the background population can
either amplify or attenuate the effect of the actual depolarizing stimulus. Two aspects might
contribute to this phenomenon. Stimulating the background with reversed polarity increases
the discrepancy of the stimulated group compared with the background (from ΔVm to 2ΔVm),
but it may reduce the firing because of an activation of inhibitory neurons in the network.
To disentangle the situation, we fixed the sizes of both the stimulated and the unstimulated
group at 50% and then systematically changed the stimulus strength for both G1 and G2 in the
range between −1.2 mV and 1.2 mV. The effect on G1 connectivity for different polarizations
of G1 and G2 is displayed in Figure 4I. The values along the diagonal are very small, as there
is no cell assembly formation when both groups experience the same stimulation. When the
difference in stimulation of the two populations is large irrespective of its sign, the impact on G1
Network Neuroscience
934
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
3
4
9
2
4
1
8
6
6
7
9
4
n
e
n
_
a
_
0
0
0
9
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A computational model of tDCS-triggered cell assembly formation
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
3
4
9
2
4
1
8
6
6
7
9
4
n
e
n
_
a
_
0
0
0
9
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3.
Interactions between subpopulations and cell assembly formation in more complex stimulation paradigms. (A) Tri-group scenario:
30% of all neurons in a network (G1) are depolarized by 0.1 mV, another 30% (G2) are hyperpolarized by −0.1 mV, and the rest of 40% receives
no stimulus. (B) Bi-group scenario: 30% (G1) are hyperpolarized by −0.1 mV, and the remaining 70% (G2) are depolarized by 0.1 mV. (C,E)
Group averages of firing rates in G1 (blue) and in G2 (yellow) before, during, and after stimulation. (D,F) Group averages of the connectivity
within G1 (blue), within G2 (yellow), and between G1 and G2 (gray).
connectivity is also large (upper left and bottom right corners). We then checked whether the
relative difference between the polarization of G1 and G2 is sufficient to predict the stimulation
outcome. The white squares in Figure 4I indicate simulations in which the difference between
G1 and G2 polarization is the same (0.8 mV), but the actual connectivities for individual groups
Network Neuroscience
935
A computational model of tDCS-triggered cell assembly formation
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
3
4
9
2
4
1
8
6
6
7
9
4
n
e
n
_
a
_
0
0
0
9
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4. Comparison of tDCS effects with different electrode montage, as well as stimulus focality and intensity. (A) Bi-group stimulation
scenario. (B) Uni-group stimulation scenario. (C) Tri-group stimulation scenario. (D–F) Integrated G1 cell assembly connectivity (IG1) at different
focality and intensity levels for scenarios (A–C). (G,H) Difference between D and E, as well as F and E, respectively. (I) Integrated G1 cell
assembly connectivity integrals (IG1) for different stimulation intensity levels for a specialized bi-group scenario, where G1 and G2 comprise
half of the excitatory population, respectively. The white squares correspond to situations where the difference between stimulation intensities
of both groups amounts to 0.8 mV.
are different. The strongest effect was achieved when the polarization of one of the two groups
is 0 mV, which corresponds to the uni-group scenario. This supports the idea that network
effects might influence the interaction between two groups, and that uni-group stimulation
can achieve better outcomes than alterantive scenarios, provided stimulation is very strong.
Network Neuroscience
936
A computational model of tDCS-triggered cell assembly formation
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
3
4
9
2
4
1
8
6
6
7
9
4
n
e
n
_
a
_
0
0
0
9
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5. Repetitive stimulation boosts network remodeling. (A) A subnetwork of excitatory neurons (10%) is stimulated with a train of DC
stimuli. Stimulation time is t1, followed by a pause of duration t2. (B, C) Average firing rate and connectivity during a train of stimuli. (D) For
the same total stimulation time (6, 000 s), the boosting depends on the exact repetition protocol. (E) The peak connectivity reached depends
on the stimulation intensity; an asymmetric repetitive protocol (t1 = 75 s, t2 = 150 s) was used for all simulations here.
The Effect of Repetitive Transcranial DC Stimulation
Repetitive stimulation was simulated in our model by repeating stimulation of duration t1 in the
uni-group scenario (Figure 2) multiple times, with a pause of duration t2 between successive
stimulation periods (Figures 5A and 5B). The connectivity of the stimulated subpopulation gen-
erally increased upon repetition (Figure 5C). Figure 5D summarizes the outcome of different
combinations of t1 and t2. Compared with long uninterrupted DC stimulus (single stimulation
Network Neuroscience
937
A computational model of tDCS-triggered cell assembly formation
cycle with t1 = 6, 000 s), repetitive stimulation (total stimulation time of 6, 000 s distributed over
multiple cycles of shorter duration t1) led to higher final connectivity. We found that repetitive
stimulation generally potentiated the effect of tDCS on cell assembly connectivity. Figure 5E
demonstrates that after multiple repetitions, the connectivity appears to saturate at a level that
essentially depends on the imposed polarization. As a consequence, a single stimulation with
weak intensity for a very long time does not necessarily lead to high connectivity, while repet-
itive stimulation at high intensity may lead to (much) higher connectivity (see Figure S1 in the
Supporting Information). In our model we also tried very strong stimulation, repeated for sev-
eral rounds. This led to a very high assembly connectivity and eventually also to a very high
firing rate of the excitatory population. High firing rates, in turn, induced a strong homeostatic
response of the network and fast deletion of synapses, putting the network in an unfavorable
and somewhat pathological state (data not shown).
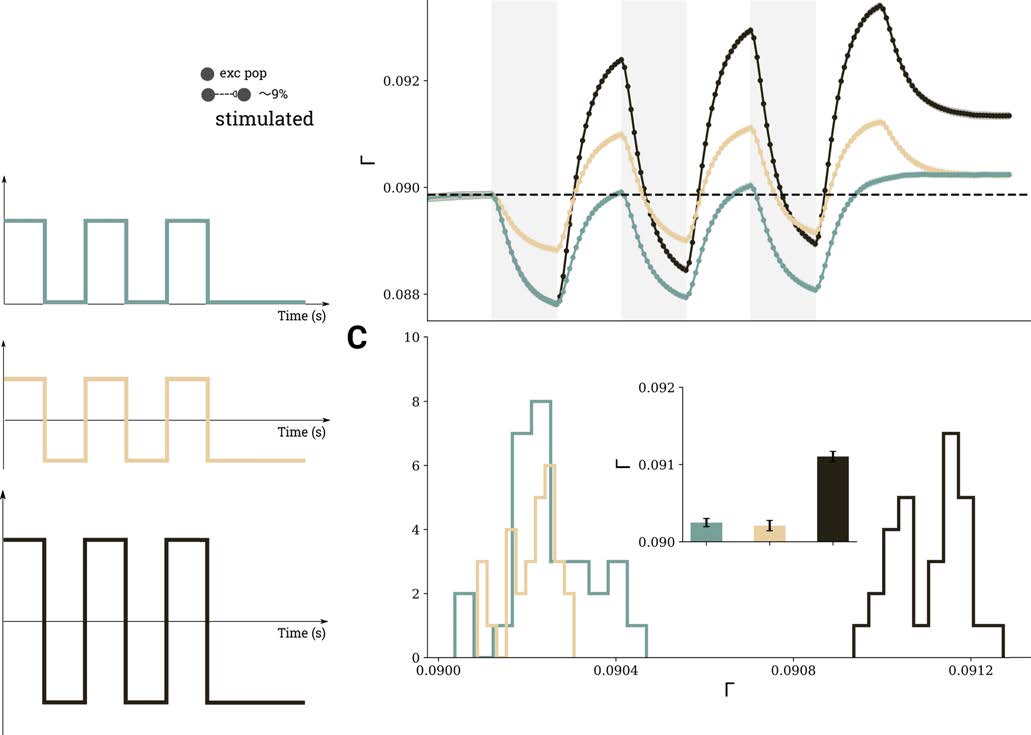
Repetitive stimulation can also be performed in cycles of alternating polarities, instead
of a simple on-off protocol. Figure 6 shows the connectivity changes for two stimulation
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
3
4
9
2
4
1
8
6
6
7
9
4
n
e
n
_
a
_
0
0
0
9
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6. Comparison of three different scenarios for repetitive DC stimulation. (A) 10% of excitatory neurons were stimulated, using the
same temporal protocol (t1 = 150 s, t2 = 150 s) in each case, but different amplitudes and polarities were employed, as indicated by the
three different curves. (B) Evolution of average connectivity for the different stimulation scenarios; color code matches the stimulus curves in
panel A. (C) Histograms of the connectivity reached after three cycles in the different scenarios extracted from 30 independent depolarizing
simulations; mean values and standard deviations are shown in the inset.
Network Neuroscience
938
A computational model of tDCS-triggered cell assembly formation
patterns: on-off, in which periods of depolarizing stimulation are followed by periods of no
stimulation, and alternating, in which periods of depolarization are followed by periods of
hyperpolarization. Simply substituting the off period by stimulation with different polarity
seems to boost cell assembly connectivity (compare light green and dark brown traces in
Figure 6B). However, if the alternating pattern has the same overall amplitude as the on-off
stimulation (compare light brown and green traces in Figure 6B), the effect on cell assembly
connectivity is the same as on the on-off pattern. Figure 6C depicts the final connectivity after
three repetitions in 30 independent trials (mean and standard deviation are indicated in the
inset).
DISCUSSION
We explored the plastic changes in network structure that can be induced by transcranial direct
current stimulation (tDCS), exploiting the homeostatic response of synaptic growth and decay.
We demonstrated that weak subthreshold DC stimulation induces changes of neuronal firing
rates and, thus, triggers network remodeling and cell assembly formation. Depolarized neu-
rons first reduce the number of excitatory input synapses during stimulation, but then create
new excitatory synapses predominantly with other stimulated neurons after stimulation is off.
Interestingly, hyperpolarization also causes new synapses being formed preferentially among
stimulated neurons. Stimulation triggers a profound and sustainable reorganization of network
connectivity and leads to the formation of cell assemblies. With the help of our model, we ex-
plored different parameters of tDCS stimulation and found that strong and focused stimulation
generally enhances the newly formed cell assemblies. We also observed that repetitive stimula-
tion with well-chosen duty cycles can boost the induction of structural changes, and repetitive
stimulation with alternating polarization may induce even higher connectivity changes.
We used network connectivity as a direct readout of stimulation effects, which is possible
in model simulations, but cannot easily be done in experiments. However, the factors that
we found to amplify the overall impact of stimulation are not unheard of in tDCS practice.
Strong and focused stimulation, for example, which results from a high-definition electrode
montage, does indeed lead to a stronger readout (MEP) and potentiates the therapeutic effects
as compared with a conventional montage (Kuo et al., 2013). While applying the same total
current, a high-definition montage induces stronger electric fields in smaller brain volumes
(Edwards et al., 2013). Moreover, a high-definition montage narrows down the most affected
brain region. We also found in our model that both factors indeed contribute to the induction
of higher connectivity. Moreover, repetitive stimulation can boost connectivity, provided the
duty cycles are chosen right. In fact, it has been demonstrated in experiments (Monte-Silva
et al., 2013) that two 13-min stimulations interrupted by a 20-min pause yields stronger MEP
aftereffects than a single, uninterrupted 26-min stimulation, while a repetition with a 24-h
pause in between could not accumulate the aftereffects at all. In our model, we likewise found
that multiple stimulation episodes with properly chosen pauses can achieve better effects than
a single, uninterrupted stimulation.
Other computational approaches have been employed previously to analyze the neuron-
scale mechanisms underlying tDCS or DCS. Most notably, Bikson et al. (2006) has explored
several aspects of this: extracellular potassium concentration, polarization of the axonal ter-
minal, action potential timing, and inhibitory neurons. Joucla & Yvert (2009) provided an esti-
mate of membrane potential changes for large axons exposed to an electric field, and Aspart,
Ladenbauer, & Obermayer (2016) conceived the influence of the electric field on neuronal
dendrites as external input to the soma. Another computational approach based on modern
neural imaging methods has shed light on the question of how strong the stimulation effects
Network Neuroscience
939
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
3
4
9
2
4
1
8
6
6
7
9
4
n
e
n
_
a
_
0
0
0
9
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A computational model of tDCS-triggered cell assembly formation
Spherical head model:
Standard three-shell head model,
which omits individual features, and
includes the brain, intermediate
skull, and outer-layer scalp.
actually are. Spherical head models were first used to estimate the 3-D current flow for any
given electrode montage (Miranda, Lomarev, & Hallett, 2006). Later, fMRI-based modeling
was employed to devise individualized treatment of stroke or depressive patients (Datta et al.,
2009; Ho et al., 2014; Huang et al., 2017). Our present work adopted insight and parameters
from both approaches. In addition, we developed a new and original computational model
to explore the impact of structural plasticity at the level of networks. This provides a bridge
between the level of single neurons and the level of large-scale networks. Although our model
contributes new explanations for some core observations in tDCS practice, there are still im-
portant issues left that cannot be appropriately addressed with our highly simplified model
lacking relevant features of brain geometry. Also, the exact rules of growth and the timescales
involved in homeostatic structural plasticity remain to be elucidated in experiments. To treat
the influence of tDCS on network dynamics and structural plasticity of multiple brain regions
would require a “network of networks” approach, which is, however, beyond the scope of our
current study.
What are the actual effects of tDCS on network activity and function? Although robust
and sustained effects of tDCS using relatively weak stimulation currents (1–2 mA) have been
demonstrated (Nitsche et al., 2009; Nitsche & Paulus, 2000), Horvath et al. (2015) pointed to
the difficulty reproducing positive results. Recently, Vöröslakos et al. (2018) have shown that
the amount of membrane polarization due to tDCS depends on the strength of the applied
current, and that there should be indeed no effect expected for very low intensities. Our sim-
ulation results suggest, however, that repetition could boost the impact on connectivity. The
peak connectivity reached after sufficiently many repetitions, however, depends on stimulus
intensity. Very weak stimulation cannot achieve high connectivity changes, even if repeated
ad infinitum. Strong stimulation within a safe range could achieve higher connectivity, but too
strong stimulation may lead to unfavorable network dynamics. Our model predicts very clearly
that the accumulated effect achieved by stimulation depends not only on the exact repetition
pattern, but also on stimulation intensity. On the other hand, a quantitative assessment of the
aftereffects is difficult. In our work, the effect of tDCS on the network is quantified by measur-
ing anatomical connectivity among stimulated and nonstimulated neurons. Such measurement
is currently not possible in experiments, neither in vivo nor in vitro. Transcranial stimulation
perturbs neuronal firing rates transiently and leads to the formation of cell assemblies, which
persist after tDCS has been switched off and neuronal activity is back to baseline. Therefore,
considering the homeostatic nature of structural plasticity, it is actually impossible to measure
the effect of tDCS using simple neuronal activity measures. The question is, what are the ef-
fects of altered connectivity on the activity and the function of neuronal networks, and how can
these effects be measured? This is a very interesting question, and the answer is complicated.
Even if newly formed cell assemblies do not affect spontaneous activity as the firing rate of
the neurons may be homeostatically regulated, they might still influence the evoked responses
of neurons. Interestingly, Horvath et al. (2015) reviewed many tDCS studies and found that
stimulation has a reliable effect only on the MEP amplitude, out of many potential biomarkers
that were tested. The debate about the effects of tDCS on network function should, therefore,
include the measures to quantify the outcome of a stimulation.
Another important issue raised by our work is that the total effect of stimulation might be
too weak for detection. The connectivity changes triggered by a single cycle of polarization
at ΔVm = 0.1mV can only be detected if the full connectome is available for quantification.
While possible in simulations, such a scenario is unrealistic in an experimental setting. Our
simulation results suggest, however, that the outcome should increase upon repetitive stimu-
lation and, therefore, possibly becomes easier to measure. The measurement time window of
Network Neuroscience
940
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
3
4
9
2
4
1
8
6
6
7
9
4
n
e
n
_
a
_
0
0
0
9
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A computational model of tDCS-triggered cell assembly formation
tDCS effects adds another puzzle to this question. The connectivity of the stimulated plastic
network undergoes constant changes. During and after stimulation, for instance, total con-
nectivity decreases and increases fast, constituting the homeostatic response. In contrast, the
newly formed cell assembly persists for much longer periods and decays only with a slower
time constant. It is not yet clear, however, which parameters influence this time constant, and
it might be that different current intensity and electrode size have an impact on it. In fact, Jamil
et al. (2017) recently observed in experiments that the current intensity might interact with
the duration of stimulation needed for the homeostatic reversal of plasticity. If the exact stim-
ulation protocol indeed influences the timescale of the aftereffect, naively comparing tDCS
effects under different stimulation conditions “before” and “after” does not provide sufficient
information regarding its outcome. In view of this, using a measure that takes the dynamics of
the changes triggered by stimulation into account, such as the IG measure introduced in this
work, could quantify the effects of stimulation much more reliably.
In general, one needs to interpret the results and predictions of our work on network re-
modeling induced by tDCS with due caution. Our current work, however, could be a first
step toward the goal of understanding and optimizing tDCS performance. More experiments
addressing the impact of tDCS in human and in animal brains are definitely needed, and the
results of our simulation study might indicate some new directions.
SUPPORTING INFORMATION
Supporting information for this article is available at http://doi.org/10.1162/netn_a_00097.
ACKNOWLEDGMENTS
The authors thank Claus Normann, Lukas Frase, Andre Russowsky Brunoni, Sandra Diaz-Pier,
and Benjamin Merkt for useful discussions. We also thank Uwe Grauer from the Bernstein
Center Freiburg as well as Bernd Wiebelt and Michael Janczyk from the Freiburg University
Computing Center for their assistance with HPC applications.
AUTHOR CONTRIBUTIONS
Investigation; Methodology;
Han Lu: Conceptualization; Data curation; Formal analysis;
Project administration; Resources; Visualization; Writing – Original Draft. Júlia V. Gallinaro:
Conceptualization; Formal analysis;
Investigation; Methodology; Project administration;
Resources; Software; Writing – Review & Editing. Stefan Rotter: Conceptualization; Funding
acquisition; Investigation; Methodology; Project administration; Resources; Supervision; Vali-
dation; Writing – Review & Editing.
FUNDING INFORMATION
Han Lu, Universitätsklinikum Freiburg. Han Lu, Neurex. Júlia V. Gallinaro, Erasmus Mundus/
EuroSPIN. Stefan Rotter, Carl Zeiss Stiftung. Stefan Rotter, Deutsche Forschungsgemeinschaft
(http://dx.doi.org/10.13039/501100001659), Award ID: INST 39/963-1 FUGG. Stefan Rotter,
Deutsche Forschungsgemeinschaft, Award ID: EXC 1086. Stefan Rotter, University of Freiburg,
Award ID: open access publication fund.
REFERENCES
Aspart, F., Ladenbauer,
J., & Obermayer, K.
(2016). Extending
integrate-and-fire model neurons to account for the effects of
weak electric fields and input filtering mediated by the dendrite.
PLoS Computational Biology, 12(11), e1005206.
Bikson, M., Radman, T., & Datta, A. (2006). Rational modulation of
neuronal processing with applied electric fields. In Engineering
in Medicine and Biology Society, 2006. EMBS’06. 28th Annual
International Conference of the IEEE (pp. 1616–1619).
Network Neuroscience
941
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
3
4
9
2
4
1
8
6
6
7
9
4
n
e
n
_
a
_
0
0
0
9
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A computational model of tDCS-triggered cell assembly formation
Brunel, N. (2000). Dynamics of sparsely connected networks of ex-
citatory and inhibitory spiking neurons. Journal of Computational
Neuroscience, 8(3), 183–208.
Butz, M., Steenbuck, I. D., & van Ooyen, A. (2014). Homeostatic
structural plasticity increases the efficiency of small-world net-
works. Frontiers in Synaptic Neuroscience, 6, 7.
Butz, M., & van Ooyen, A. (2013). A simple rule for dendritic spine
and axonal bouton formation can account for cortical reorga-
nization after focal retinal lesions. PLoS Computational Biology,
9(10), e1003259.
Butz, M., van Ooyen, A., & Wörgötter, F. (2009). A model for corti-
cal rewiring following deafferentation and focal stroke. Frontiers
in Computational Neuroscience, 3, 10.
Butz-Ostendorf, M., & van Ooyen, A.
Is lesion-induced
synaptic rewiring driven by activity homeostasis? In The rewiring
brain (pp. 71–92). London, United Kingdom: Elsevier.
(2017).
Datta, A., Bansal, V., Diaz, J., Patel, J., Reato, D., & Bikson, M.
(2009). Gyri-precise head model of transcranial direct current
stimulation: Improved spatial
focality using a ring electrode
versus conventional rectangular pad. Brain Stimulation: Basic,
Translational, and Clinical Research in Neuromodulation, 2(4),
201–207.
Diaz-Pier, S., Naveau, M., Ostendorf, M., & Morrison, A.
(2016).
Automatic generation of connectivity for large-scale neuronal
network models through structural plasticity. Frontiers in Neuro-
anatomy, 10, 57.
Edwards, D., Cortes, M., Datta, A., Minhas, P., Wassermann, E. M.,
& Bikson, M. (2013). Physiological and modeling evidence for
focal transcranial electrical brain stimulation in humans: A basis
for high-definition tDCS. NeuroImage, 74, 266–275.
Fritsch, B., Reis, J., Martinowich, K., Schambra, H. M., Ji, Y., Cohen,
L. G., & Lu, B. (2010). Direct current stimulation promotes
BDNF-dependent synaptic plasticity: Potential implications for
motor learning. Neuron, 66(2), 198–204.
Gallinaro, J. V., & Rotter, S. (2018). Associative properties of struc-
tural plasticity based on firing rate homeostasis in recurrent neu-
ronal networks. Scientific Reports, 8(1), 3754.
Garcia-Larrea, L. (2016). tDCS as a procedure for chronic pain re-
lief. Neurophysiologie Clinique/Clinical Neurophysiology, 46(3),
224.
Gartside, I. B. (1968a). Mechanisms of sustained increases of fir-
ing rate of neurones in the rat cerebral cortex after polarization:
Reverberating circuits or modification of synaptic conductance?
Nature, 220(5165), 382.
Gartside, I. B. (1968b). Mechanisms of sustained increases of firing
rate of neurones in the rat cerebral cortex after polarization: Role
of protein synthesis. Nature, 220(5165), 383.
Gluckman, B. J., Neel, E. J., Netoff, T. I., Ditto, W. L., Spano, M. L.,
& Schiff, S. J. (1996). Electric field suppression of epileptiform ac-
tivity in hippocampal slices. Journal of Neurophysiology, 76(6),
4202–4205.
Grewe, B. F., Langer, D., Kasper, H., Kampa, B. M., & Helmchen, F.
(2010). High-speed in vivo calcium imaging reveals neuronal
network activity with near-millisecond precision. Nature Methods,
7(5), 399.
Ho, K.-A., Bai, S., Martin, D., Alonzo, A., Dokos, S., Puras, P., & Loo,
C. K. (2014). A pilot study of alternative transcranial direct cur-
rent stimulation electrode montages for the treatment of major
depression. Journal of Affective Disorders, 167, 251–258.
Holtmaat, A., & Svoboda, K. (2009). Experience-dependent struc-
tural synaptic plasticity in the mammalian brain. Nature Reviews
Neuroscience, 10(9), 647.
Horvath, J. C., Forte, J. D., & Carter, O. (2015). Evidence that tran-
scranial direct current stimulation (tDCS) generates little-to-no
reliable neurophysiologic effect beyond MEP amplitude modula-
tion in healthy human subjects: A systematic review. Neuropsy-
chologia, 66, 213–236.
Huang, Y., Liu, A. A., Lafon, B., Friedman, D., Dayan, M., Wang,
X., . . . Parra, L. C. (2017). Measurements and models of elec-
tric fields in the in vivo human brain during transcranial electric
stimulation. eLife, 6, e18834.
Jackson, M. P., Rahman, A., Lafon, B., Kronberg, G., Ling, D., Parra,
L. C., & Biskon, M. (2016). Animal models of transcranial direct
current stimulation: Methods and mechanisms. Clinical Neuro-
physiology, 127(11), 3425–3454.
Jamil, A., Batsikadze, G., Kuo, H.-I., Labruna, L., Hasan, A., Paulus,
W., & Nitsche, M. A. (2017). Systematic evaluation of the im-
pact of stimulation intensity on neuroplastic after-effects induced
by transcranial direct current stimulation. Journal of Physiology,
595(4), 1273–1288.
Joucla, S., & Yvert, B. (2009). The mirror estimate: An intuitive pre-
dictor of membrane polarization during extracellular stimulation.
Biophysical Journal, 96(9), 3495–3508.
Kayyali, H., & Durand, D.
(1991). Effects of applied currents on
epileptiform bursts in vitro. Experimental Neurology, 113(2),
249–254.
Keck, T., Keller, G. B., Jacobsen, R. I., Eysel, U. T., Bonhoeffer, T., &
Hübener, M. (2013). Synaptic scaling and homeostatic plasticity
in the mouse visual cortex in vivo. Neuron, 80(2), 327–334.
Kuo, H.-I., Bikson, M., Datta, A., Minhas, P., Paulus, W., Kuo, M.-F.,
& Nitsche, M. A. (2013). Comparing cortical plasticity induced
by conventional and high-definition 4 × 1 ring tDCS: A neuro-
physiological study. Brain Stimulation: Basic, Translational, and
Clinical Research in Neuromodulation, 6(4), 644–648.
Lang, N., Siebner, H. R., Ward, N. S., Lee, L., Nitsche, M. A., Paulus,
W., . . . Frackowiak, R. S. (2005). How does transcranial DC stim-
ulation of the primary motor cortex alter regional neuronal activ-
ity in the human brain? European Journal of Neuroscience, 22(2),
495–504.
Lee, K. J., Queenan, B. N., Rozeboom, A. M., Bellmore, R., Lim,
S. T., Vicini, S., & Pak, D. T. (2013). Mossy fiber-CA3 synapses
mediate homeostatic plasticity in mature hippocampal neurons.
Neuron, 77(1), 99–114.
Linssen, C., Lepperd, M. E., Mitchell, J., Pronold, J., Eppler, J. M.,
Keup, C., . . . Plesser, H. E. (2018). NEST 2.16.0. https://doi.org/
10.5281/zenodo.1400175
Loo, C. K., Alonzo, A., Martin, D., Mitchell, P. B., Galvez, V., &
Sachdev, P.
(2012). Transcranial direct current stimulation for
depression: 3-week, randomised, sham-controlled trial. British
Journal of Psychiatry, 200(1), 52–59.
Matsunaga, K., Nitsche, M. A., Tsuji, S., & Rothwell, J. C. (2004).
Effect of transcranial DC sensorimotor cortex stimulation on so-
matosensory evoked potentials in humans. Clinical Neurophysi-
ology, 115(2), 456–460.
Network Neuroscience
942
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
3
4
9
2
4
1
8
6
6
7
9
4
n
e
n
_
a
_
0
0
0
9
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A computational model of tDCS-triggered cell assembly formation
Mattson, M. P., & Kater, S. B. (1987). Calcium regulation of neurite
Journal of Neuroscience,
elongation and growth cone motility.
7(12), 4034–4043.
Minjoli, S., Saturnino, G. B., Blicher, J. U., Stagg, C. J., Siebner,
H. R., Antunes, A., & Thielscher, A. (2017). The impact of large
structural brain changes in chronic stroke patients on the elec-
tric field caused by transcranial brain stimulation. NeuroImage:
Clinical, 15, 106–117.
Miranda, P. C., Lomarev, M., & Hallett, M. (2006). Modeling the
current distribution during transcranial direct current stimulation.
Clinical Neurophysiology, 117(7), 1623–1629.
Monte-Silva, K., Kuo, M. F., Hessenthaler, S., Fresnoza, S., Liebetanz, D.,
Paulus, W., & Nitsche, M. A. (2013). Induction of late LTP-like
plasticity in the human motor cortex by repeated non-invasive
brain stimulation. Brain Stimulation: Basic, Translational, and
Clinical Research in Neuromodulation, 6(3), 424–432.
Ngernyam, N., Jensen, M. P., Arayawichanon, P., Auvichayapat, N.,
Tiamkao, S., Janjarasjitt, S., . . . Auvichayapat, P. (2015). The ef-
fects of transcranial direct current stimulation in patients with
neuropathic pain from spinal cord injury. Clinical Neurophysi-
ology, 126(2), 382–390.
Nitsche, M. A., Boggio, P. S., Fregni, F., & Pascual-Leone, A. (2009).
Treatment of depression with transcranial direct current stimula-
tion (tDCS): A review. Experimental Neurology, 219(1), 14–19.
Nitsche, M. A., Fricke, K., Henschke, U., Schlitterlau, A., Liebetanz, D.,
Lang, N., . . . Paulus, W. (2003). Pharmacological modulation of
cortical excitability shifts induced by transcranial direct current
stimulation in humans. Journal of Physiology, 553(Pt. 1), 293–301.
Nitsche, M. A., & Paulus, W. (2000). Excitability changes induced
in the human motor cortex by weak transcranial direct current
stimulation. Journal of Physiology, 527(3), 633–639.
Nitsche, M. A., & Paulus, W.
(2001). Sustained excitability ele-
vations induced by transcranial DC motor cortex stimulation in
humans. Neurology, 57(10), 1899–1901.
Opitz, A., Paulus, W., Will, S., Antunes, A., & Thielscher, A. (2015).
Determinants of the electric field during transcranial direct cur-
rent stimulation. NeuroImage, 109, 140–150.
Oray, S., Majewska, A., & Sur, M. (2004). Dendritic spine dynamics
are regulated by monocular deprivation and extracellular matrix
degradation. Neuron, 44(6), 1021–1030.
Pfeiffer, T., Poll, S., Bancelin, S., Angibaud, J., Inavalli, V. K.,
Keppler, K., . . . Nägerl, U. V. (2018). Chronic 2p-STED imaging
reveals high turnover of dendritic spines in the hippocampus
in vivo. eLife, 7, e34700.
Radman, T., Ramos, R. L., Brumberg, J. C., & Bikson, M.
(2009).
Role of cortical cell type and morphology in subthreshold and
suprathreshold uniform electric field stimulation in vitro. Brain
Stimulation: Basic, Translational, and Clinical Research in Neuro-
modulation, 2(4), 215–228.
Ramakers, G., Avci, B., van Hulten, P., van Ooyen, A., van Pelt, J.,
Pool, C., & Lequin, M. (2001). The role of calcium signaling in
early axonal and dendritic morphogenesis of rat cerebral cortex
neurons under non-stimulated growth conditions. Developmen-
tal Brain Research, 126(2), 163–172.
Ranieri, F., Podda, M. V., Riccardi, E., Frisullo, G., Dileone, M.,
Profice, P., . . . Grassi, C. (2012). Modulation of LTP at rat hip-
pocampal ca3-ca1 synapses by direct current stimulation. Jour-
nal of Neurophysiology, 107(7), 1868–1880.
Trachtenberg, J. T., Chen, B. E., Knott, G. W., Feng, G., Sanes, J. R.,
Welker, E., & Svoboda, K. (2002). Long-term in vivo imaging of
experience-dependent synaptic plasticity in adult cortex. Nature,
420(6917), 788.
Turrigiano, G. G., & Nelson, S. B. (2004). Homeostatic plasticity in
the developing nervous system. Nature Reviews Neuroscience,
5(2), 97.
van Ooyen, A. (2011). Using theoretical models to analyse neural
development. Nature Reviews Neuroscience, 12(6), 311.
Vöröslakos, M., Takeuchi, Y., Brinyiczki, K., Zombori, T., Oliva, A.,
Fernández-Ruiz, A., . . . Berényi, A. (2018). Direct effects of tran-
scranial electric stimulation on brain circuits in rats and humans.
Nature Communications, 9(1), 483.
Wiethoff, S., Hamada, M., & Rothwell, J. C. (2014). Variability in
response to transcranial direct current stimulation of the motor
cortex. Brain Stimulation, 7(3), 468–475.
Network Neuroscience
943
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
/
3
4
9
2
4
1
8
6
6
7
9
4
n
e
n
_
a
_
0
0
0
9
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3