Excess Mutual Catalysis Is Required
for Effective Evolvability
Omer Markovitch**
Weizmann Institute of Science
Doron Lancet*,**
Weizmann Institute of Science
It is widely accepted that autocatalysis constitutes a
Abstract
crucial facet of effective replication and evolution (e.g., in Eigenʼs
hypercycle model). Other models for early evolution (e.g., by
Dyson, Gánti, Varela, and Kauffman) invoke catalytic networks,
where cross-catalysis is more apparent. A key question is how
the balance between auto- (self-) and cross- (mutual) catalysis
shapes the behavior of model evolving systems. This is
investigated using the graded autocatalysis replication domain
(GARD) model, previously shown to capture essential features
of reproduction, mutation, and evolution in compositional
molecular assemblies. We have performed numerical simulations
of an ensemble of GARD networks, each with a different set of
lognormally distributed catalytic values. We asked what is the
influence of the catalytic content of such networks on beneficial
evolution. Importantly, a clear trend was observed, wherein only
networks with high mutual catalysis propensity ( pmc) allowed
for an augmented diversity of composomes, quasi-stationary
compositions that exhibit high replication fidelity. We have
reexamined a recent analysis that showed meager selection in
a single GARD instance and for a few nonstationary target
compositions. In contrast, when we focused here on compotypes
(clusters of composomes) as targets for selection in populations
of compositional assemblies, appreciable selection response was
observed for a large portion of the networks simulated. Further,
stronger selection response was seen for high pmc values. Our
simulations thus demonstrate that GARD can help analyze
important facets of evolving systems, and indicate that excess
mutual catalysis over self-catalysis is likely to be important for the
emergence of molecular systems capable of evolutionlike behavior.
Keywords
Evolution, networks, selection,
composomes, metabolism
A version of this paper with color figures
is available online at http://dx.doi.org/10.1162/
artl_a_00064. Subscription required.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
8
3
2
4
3
1
6
6
3
2
8
4
a
r
t
l
/
_
a
_
0
0
0
6
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1 Introduction
The fundamental question of how primitive life emerged on the prebiotic Earth has drawn consider-
able scientific attention throughout the centuries [2, 5, 14, 15, 22, 42, 59, 64]. The path from organic
mixtures (i.e., the primeval soup) to reproducing lifelike protocells has traditionally been dominated by
two different views: the genetic, or replicator-first, approach, and the metabolism-first approach [2, 42]. Both
* Contact author.
** Department of Molecular Genetics, Weizmann Institute of Science, Rehovot 76100, Israel. E-mail: omermar@weizmann.ac.il (O.M.);
doron.lancet@weizmann.ac.il (D.L.)
© 2012 Massachusetts Institute of Technology
Artificial Life 18: 243–266 (2012)
O. Markovitch and D. Lancet
Excess Mutual Catalysis Is Required for Effective Evolvability
acknowledge the need for reliable information storage and transfer, assisted by self-replication. The
replicator-first approach suggests that life began with a single self-perpetuating biopolymer (e.g.,
RNA) [14, 15, 18, 19, 22, 37, 42, 64], which later evolved into multimolecular networks under the
replicatorʼs control. Orgel [41] has highlighted the relationship between molecular replication and
the concept of autocatalysis or self-catalysis. The metabolism-first approach suggests that the very first
life precursors must have been relatively complex molecular networks arising via spontaneous accre-
tion of simpler organic molecules [3, 9, 24, 25, 34, 48, 51, 53, 60]. In this scenario, it is further pro-
posed that faithful reproduction directly stems from certain network attributes. Therefore, one should
better understand the network properties of the implicated molecular assemblies [1, 47, 57, 66] if one
can merge the two seemingly conflicting scenarios for prebiotic evolution.
One embodiment of the metabolism-first view is the lipid world scenario, which considers non-
covalent assemblies of amphiphiles, such as micelles and vesicles formed by lipids [8, 39, 48, 50,
53, 69]. These are assumed to store information in the form of nonrandom molecular composi-
tions, and pass it to progeny via homeostatic growth accompanied by fission [49]. The graded auto-
catalysis replication domain (GARD) kinetic model for prebiotic evolution quantitatively describes
the details of such a process. It elaborates some of its evolution-related attributes [10–12, 27, 30,
44, 50, 58, 62, 67, 68], with an implied route to minimal protocells [8, 45, 49, 63, 65]. The model
is based on a catalytic network, usually presented in the form of a matrix h with autocatalysis (self-
catalysis) and cross (mutual) catalysis terms. Importantly, the system is kept away from thermo-
dynamic equilibrium by assembly fission [49]. Key in GARD dynamics are compotypes—clusters of
replication-prone quasi-stationary states (composomes, a term derived from the notion of composi-
tional genomes [49]), proposed to play a crucial role in the GARDʼs evolutionary behavior. Introducing
substantial inhibition in h is expected to result in net catalysis because an inhibitor of an inhibitor is
an activator [20].
Catalysis, the enhancement of reaction rate by an external chemical component, was recognized
as early as 1836 by Berzelius, and Ostwald applied the term autocatalysis in 1890 to reactions that gain
speed as they proceed [26, 44]. In the genetic approach to lifeʼs origin, researchers invoke one or
several autocatalytic molecules as the core of a prebiotic entity. This is exemplified by the hypercycle, a
set of self-replicating polynucleotides, coding for and acted upon by enzymes [10, 30, 58]. In the
metabolism-first domain, autopoiesis [67] and the chemoton model [12] are examples of collective
autocatalysis [25].
Collectively autocatalytic systems feature a central role not only for self-catalysis, but also for
mutual catalysis. In this, they arguably resemble present-day living cells, which harbor self-catalytic
polynucleotides as well as a plethora of mutual catalysts that constitute metabolic pathways. Here we
utilize a metabolism-first simulator to examine the relative importance of the two catalytic modes
(self- and mutual catalysis). Previously [11], an abstract chemistry model has been used to demon-
strate that self-maintaining organizations arise only once self-catalysis is completely inhibited [11, 62].
We attempt to extend such results in the realm of the GARD kinetic model, asking what features
of the h network contribute to the evolution of the ensuing compositional assemblies. It is shown
that excess mutual catalysis is a necessary, though not sufficient, condition for displaying several
evolutionlike characteristics, including a high number of composome types, higher evolvability scores,
and a significant response to selection.
Recently, it has been argued that collectively autocatalytic metabolic networks, such as the GARD,
do not allow for fitter compositional genomes to be maintained by selection. Vasas et al. [68] compared
the frequency ranking of random GARD compositional assemblies before and after selection, and
found that the relative ranks changed only slightly. This was taken as evidence for an inherent evolu-
tionary limitation of metabolism-first scenarios. Here it is demonstrated, based on a large number of
simulations, that when quasi-stationary composomes rather than arbitrary compositions serve as selec-
tion targets, GARD networks are capable of a significant response to selection. Importantly, this
can happen chiefly when a high proportion of mutual catalysis is present in a GARD network. The
results highlight the potentially important role of mutual catalysis, as compared to self-catalysis, in the
emergence of early lifelike systems.
244
Artificial Life Volume 18, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
8
3
2
4
3
1
6
6
3
2
8
4
a
r
t
l
/
_
a
_
0
0
0
6
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
O. Markovitch and D. Lancet
Excess Mutual Catalysis Is Required for Effective Evolvability
2 Model and Methods
2.1 GARD Formalism
The regular GARD formalism describes the time-dependent dynamics of a molecular assembly,
by following the fate of a compositional vector whose elements are the molecular counts ni within
the assembly:
r ¼ fn1; n2; … ; nNG g
ði ¼ 1; … ; NGÞ
ð1Þ
The vector dynamics is governed by mutually catalytic interactions among the invariable number of
constituent molecule types, NG. The assembly grows by accretion of environmental molecules, and
once a limiting size Nmax is attained, random fission is applied, producing two progeny of the same
size, Nmin = Nmax/2, one of which grows again, generating growth-fission cycles of consecutive
generations. GARD dynamics is described by a set of ordinary differential equations
dni
dt
¼ ðkf U
i N − kbni Þ 1 þ
!
;
XNG
j¼1
h
ij
nj
N
N ¼
XNG
i¼1
ni ;
ð2Þ
where dni/dt is in units of the individual reaction rates at which the counts of elements are chang-
ing [49], and kf and kb are respectively the basal forward and backward rate constants (joining and
≫ kb, reflecting a high equilibrium constant kf/kb for sponta-
leaving the assembly). Typically kf
neous amphiphile accretion (Table 1). Here Ui is the buffered concentration of molecule type i in
the environment (assumed here to be equal for all i values), N is the assembly current size, and hij is
Table 1. Simulation parameters. NG is the number of molecular types (repertoire size); Nmax is the assembly pre-fission size;
kf and kb are the respective basal forward and backward rate constants; Ui is the buffered environmental concentration of
molecule type i; A and j are the respective mean and standard deviation of the lognormal distribution of hij values (Appendix A.1,
Equation 12); GEN is the duration of a simulation; Lognormal random seeds is the range of random seeds used for simulations;
Lpop is the constant size of the population in the population GARD.
NG
Nmax
kf
kb
Ui
A
j
GEN
Lognormal random seeds
Lpop
100
NG
10-2
10-4
1/NG
−4.0
4.0
5,000
1–10,000
1,000
Artificial Life Volume 18, Number 3
245
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
8
3
2
4
3
1
6
6
3
2
8
4
a
r
t
l
/
_
a
_
0
0
0
6
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
O. Markovitch and D. Lancet
Excess Mutual Catalysis Is Required for Effective Evolvability
the non-negative matrix element signifying the rate enhancement exerted by an assembly molecule
of type j on an incoming or outgoing molecule of type i
kb(cid:1)ð1þh
iout þ jin ⇆
kf (cid:1)ð1þh
ij Þ
ij Þ
iin þ jin
ð3Þ
The chemical reaction in Equation 3 embodies the notion that molecular catalysis equally affects the
forward and the backward rates, obeying the constraint that a catalyst may not change the equilibrium
constant of the reaction it affects. This means that even under catalytic action, the relationship kf ≫ kb
prevails.
The matrix h represents a network of self-catalytic (diagonal elements) and mutually catalytic
(off-diagonal elements) catalytic interactions (Figure 1), with self-catalysis represented by the case
j = i (Appendix A.1, Equation 13). The matrix elements are randomly drawn from a lognormal
distribution (Appendix A.1 and Equation 12) [49].
2.2 GARD Simulations
The model is subjected to a kinetic Monte Carlo simulation based on Gillespieʼs algorithm [16, 17,
51] using parameter values similar to those employed in previous studies (Table 1). Simulations are
run using MATLAB versions 7.6–7.10 (the GARD10 code is available upon request). A set of
10,000 GARD simulations is generated, all with the same parameters, and each with a different
matrix h generated by the MATLAB pseudorandom number generator with seeds 1–10,000. The
validity of the conclusions drawn here is ascertained by repeating the simulations with smaller data
sets, with seeds 1–2,000 and 2,001–4,000, striving to verify that the entire 10,000-strong data set
adequately represents the GARD simulation space. The random sampling of h values may be per-
ceived as representing different possible GARD environmental chemistries.
The relative mutual catalysis power
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
8
3
2
4
3
1
6
6
3
2
8
4
a
r
t
l
/
pmc ¼
XNG
XNG
h
ij
j¼1
i¼1
XNG
h
q¼1
(cid:2)
NG
N 2
G
ð4Þ
_
a
_
0
0
0
6
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
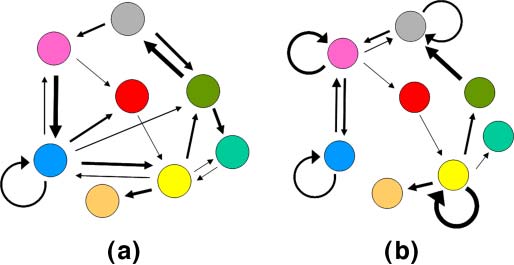
Figure 1. Network representation of GARDʼs h matrix. Two cartoon networks are shown, one with excess mutual catalysis
(a) and the other with excess self-catalysis (b). In the electronic version, colored circles represent different molecular
types, and arrow thickness represents catalysis strength (Equation 3). Self-catalysis is the shortest closed loop, containing
one molecular type (see Appendix A.1, Equation 13).
246
Artificial Life Volume 18, Number 3
O. Markovitch and D. Lancet
Excess Mutual Catalysis Is Required for Effective Evolvability
is defined as the sum of all rate enhancements divided by the sum of self-catalysis rates (diagonal h
2, an
elements). Because there are only NG diagonal elements and the total number of elements is NG
appropriate correction is introduced. Thus, the excess of mutual catalysis is represented by pmc > 1,
while the excess of self-catalysis (or autocatalysis) is portrayed by pmc < 1.
2.3 Compositional Similarity and Compotypes
The similarity between the compositions rm
of the respective assemblies at generations m and
y is defined as the dot product H (see Equation 5) of their composition vectors [49], typically cal-
culated at assembly size Nmax (end of the growth cycle).
and ry
Hðm; yÞ ¼ H rm; ry
(cid:1)
(cid:2)
¼
rm (cid:2) ry
jrmj (cid:2) jryj
ð5Þ
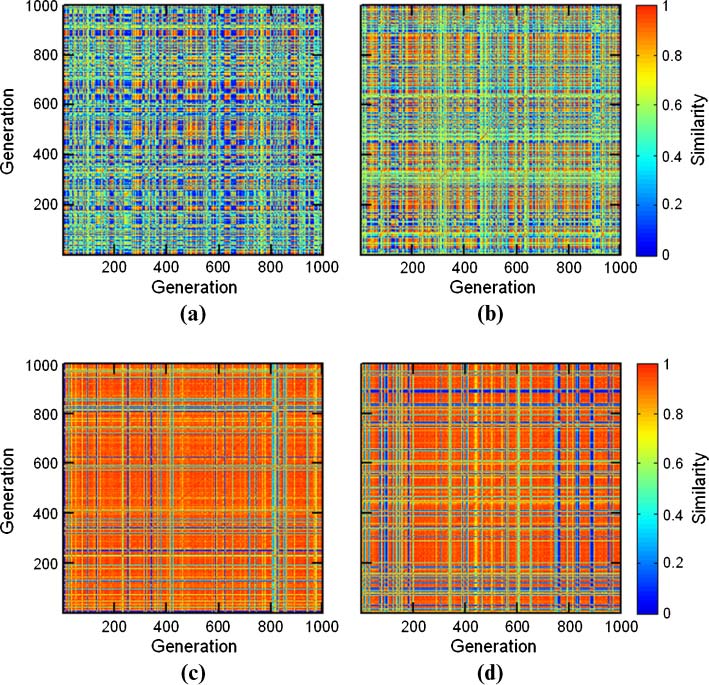
GARD dynamics is visually portrayed by a similarity carpet, showing H between any pair of parent
assemblies during a simulation (e.g., Figure 10 in Appendix A.4). Composomes, appearing as dense
areas with high similarity near the main diagonal, are defined as any two consecutive generations
where H(m, m + 1) ≥ 0.9 [56]. Inter-composome similarity is viewed by off-diagonal examination.
The time duration of different generations (Equation 2) is different due to different growth path-
ways; hence a certain level of selection is already achieved by the matrix h causing composomes to
appear more frequently than random compositions [49].
All the compositions belonging to composomes in the entire simulation undergo k-means cluster-
ing [56, 61], and the centers of mass of the resulting clusters are defined as compotypes.
2.4 Similarity Autocorrelation
The similarity autocorrelation function, c(Dt), akin to a Fourier transform of the compositional
similarity time series, is defined by
cðDtÞ ¼ 〈Hðm; mÞ (cid:2) Hðm; yÞ〉 ¼ 〈Hðm; yÞ〉
ð6Þ
where 〈…〉 denotes averaging over all generation pairs fulfilling y − m = Dt. This function is history
independent, that is, no conditions are imposed on the events occurring between generations m and y.
c(Dt) is fitted with a single exponential with parameters H and H0 using a least squares fit (see
Appendix A.2, and Figure 12 in Appendix A.4):
(cid:3)
cðDtÞ ¼ ð1 − H0Þ exp −
(cid:4)
Dt
H
þ H0
ð7Þ
The parameters H and H0 are used to define a measure of evolvability (Section 3).
2.5 Selection in GARD
For each simulation, the most frequent compotype is chosen as a target, T. A selection-GARD simulation
is then run, whereby the growth of an assembly at generation m is biased toward T via a growth bonus
parameter
Gb ¼ s (cid:2) H rm; T
ð
Þ
ð8Þ
manifested as a temporary enhancement of the corresponding hij values, as suggested [68], where s > 1 is
a fitness gain, embodying a selective advantage, and for consistency with previous work [68] H(rm
,T )
is calculated at assembly size Nmin, that is, the beginning of the growth cycle.
Artificial Life Volume 18, Number 3
247
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
8
3
2
4
3
1
6
6
3
2
8
4
a
r
t
l
/
_
a
_
0
0
0
6
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
O. Markovitch and D. Lancet
Excess Mutual Catalysis Is Required for Effective Evolvability
The modified matrix element hij′ is obtained at each generation according to
(cid:5)
h
′ ðmÞ ¼
ij
;
h
ij
Gb (cid:2) h
ij
;
i or j ∉ rm
i and j ∈ rm
ð9Þ
where i and j are molecular type indices, and hij modification is effected for all i, j (and j,i ) pairs
contained within the current assembly. Thus, the network will be perturbed only at edges present
within the current assembly according to how similar the current assembly is to the target. In the
selection-GARD simulation, a compotype T′ is identified as having the highest H value with respect
to T. An unambiguous identification of T′ is afforded by the fact that the mean similarity between T
and T′ in the entire data set is H = 0.9933 ± 0.0217. The selection excess is subsequently defined as
SE ¼
fT ′
fT
ð10Þ
where fT ′ and fT are the fractions of generations belonging the respective compotype (before and
after selection). Selection excesses ≥1.05 and ≤0.95 are respectively taken to represent positive and
negative target selection; the rest are taken to signify no selection.
2.6 Selection Dynamics in a Population of Compositional Assemblies
An initially random population of a fixed number of assemblies, Lpop, is allowed to simultaneously
grow according to Equations 1 and 2 and its idiosyncratic composition. When one of the assemblies
reaches the limiting size Nmax, it divides by random fission, and a randomly chosen assembly from
− 1 assemblies is removed, thus keeping the population size constant. This is
among the other Lpop
repeated for GEN splits (Table 1). This protocol is based on the classical Moran process [36, 68, 70],
and to some degree reflects an earlier attempt to simulate GARD populations [38].
The frequency of the target in each population is defined as the number of assemblies that are
highly similar (H ≥ 0.9) to the target compotype taken from regular GARD for the same h network
(Figure 13 in Appendix A.4). Selection is exerted by performing a simulation with the same parameters,
biasing the growth of assemblies toward a target compotype as for regular GARD (Equations 8 and 9).
The selection excess is defined as in Equation 10, where fT′ and fT are respectively the fractions of
assemblies within the population belonging to the target compotype before and after selection.
3 Results
3.1 Selection in GARD
We used GARD simulations to ask what is the selection response of compositional assemblies. A
value for the selection excess was obtained for each of 10,000 simulations, using a modest value of
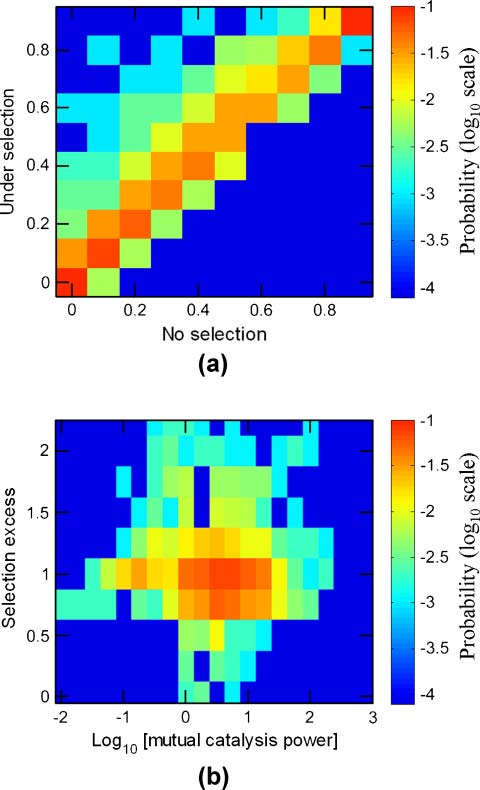
the fitness gain, s = 1.1, in line with previous work [68]. Figure 2a shows the correlation between the
frequencies of the target compotype with and without selection (examples of regular GARD carpets
before and after selection are given in Figure 14 in Appendix A.4). An overall skew is seen here
toward positive selection. The figure also demonstrates that significant positive selection, as well
as negative, occurs over most of the range of fT.
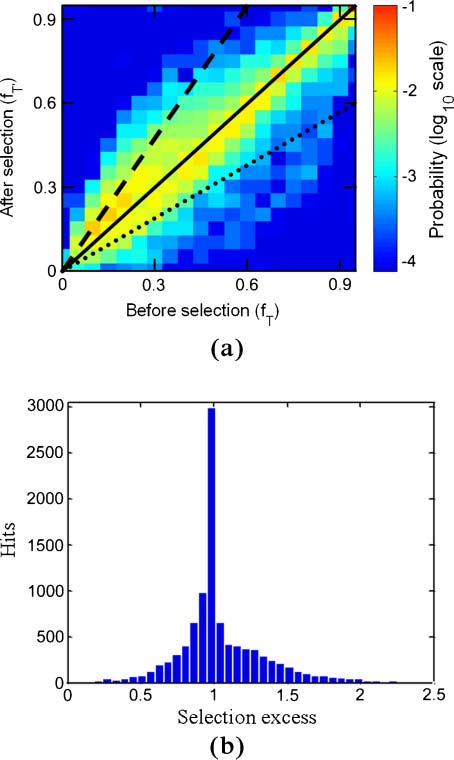
Figure 2b shows the distribution of selection excess values for the entire data set (Equation 10).
Importantly, a considerable percentage of the simulations (33%) show positive selection, with a mean
selection excess of 1.38 for selection excess >1.05, and as much as 10% shows selection excess >1.5.
Interestingly, 31% of the cases showed negative selection, with a mean selection excess of 0.775 for
selection excess <0.95, and about 36% were neutral to the selection pressure. Similar to the skewness in
Figure 2a, there is a slight bias in favor of positive selection, as indicated by an overall mean selection
248
Artificial Life Volume 18, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
8
3
2
4
3
1
6
6
3
2
8
4
a
r
t
l
/
_
a
_
0
0
0
6
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
O. Markovitch and D. Lancet
Excess Mutual Catalysis Is Required for Effective Evolvability
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
8
3
2
4
3
1
6
6
3
2
8
4
a
r
t
l
/
_
a
_
0
0
0
6
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 2. Selection in GARD. (a) The correlation between the frequencies of the target compotype in the basal simulation
(fT) and its frequency after applying selection (fT′). In the electronic version, color represents probability out of the entire
data set of 10,000 simulations, and positive and negative selection are respectively seen above and below the diagonal
(selection excess = 1.0, solid black line). The dashed and dotted lines respectively mark selection excesses of 3
2 and 1
2 .
(b) Selection excess histogram for the entire data set. Simulation parameters are given in Table 1.
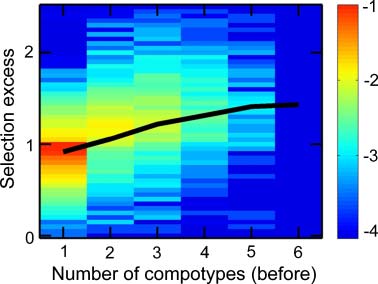
excess equal to 1.05. Notably, higher mean selection values positively correlate with the number of other
compotypes coexisting with the target compotype in a given system (Figure 15 in Appendix A.5).
GARD simulations are used to see how attributes of the catalytic network embodied in the matrix h
govern the evolution-related dynamics of compositional assemblies. It is asked how the mutually cata-
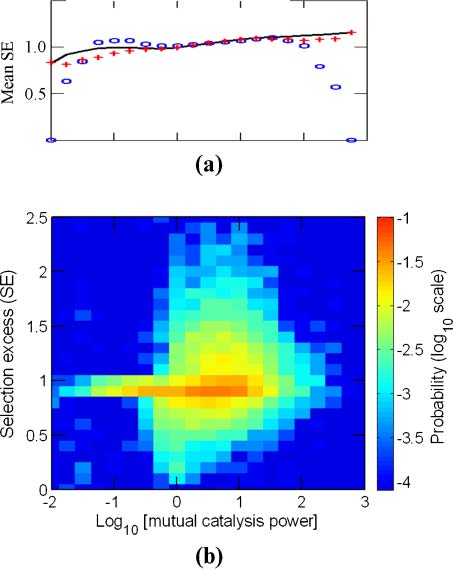
lytic power pmc (Equation 4) influences the selection response. A clear trend appears here, whereby
strong positive or negative selection is found almost entirely for pmc higher than 1 (Figure 3b).
The main trends appear also at lower simulation counts, barring small-number fluctuations at high
pmc (Figure 3a). For example, for the range of pmc > 100, a meaningful p-value with 5% significance
level is achieved only after performing more than 2,500 simulations (Table 3 in Appendix A.6). The
other two evolution-related parameters withstand similar scrutiny (below).
3.2 Populations of GARD Assemblies
The foregoing simulations of the regular GARD model addressed the case in which at each time
point only one GARD assembly is considered. To enhance the capacity to draw conclusions about
Artificial Life Volume 18, Number 3
249
O. Markovitch and D. Lancet
Excess Mutual Catalysis Is Required for Effective Evolvability
Figure 3. The dependence of selection excess (SE ) on mutual catalysis power (pmc). (a) Mean SE versus log10pmc, collected
from 10,000 GARD instances (solid black line, smoothed) or from two subsets of 2,000 instances, random seeds 1–2,000
(ovals) and 2,001–4,000 (crosses). (b) Density plot of SE versus log10pmc. In the electronic version, color represents prob-
ability of finding instances with specific (SE, pmc) values in all 10,000 GARD instances. Data is the same as in Figure 2.
selection in GARD, 1,000 simulations were performed, each for a population of 1,000 assemblies, under
the constant population conditions. Figure 4 shows an example of the dynamics for one of
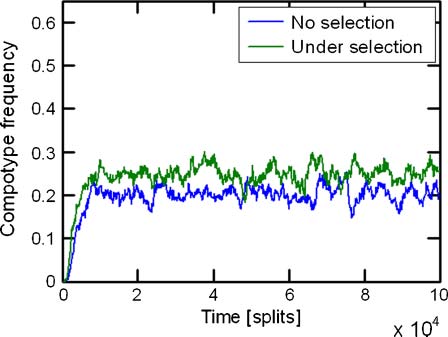
the networks. Starting from a population of random assemblies, the population frequency of the target
compotype gradually grows over the first 10,000 split events, reaching a plateau with fluctuations,
signifying the compositional preference imposed by the matrix h towards this compotype. When
selection toward this compotype is applied (Equation 9), this general behavior is retained, with a faster
Figure 4. An example of the development of a compotype in population dynamics, without and with selection. This figure shows the
fraction of assemblies in the population that are highly similar to a given compotype (see Section 2 and Figure 13 in Appendix A.4)
over a large number of splits. Simulation parameters are lognormal seed = 3, GEN = 100,000, and the rest are given in Table 1.
250
Artificial Life Volume 18, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
8
3
2
4
3
1
6
6
3
2
8
4
a
r
t
l
/
_
a
_
0
0
0
6
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
O. Markovitch and D. Lancet
Excess Mutual Catalysis Is Required for Effective Evolvability
growth and a higher plateau, that is, showing positive response to selection. Similar to Figure 3b, strong
positive or negative selection is much more prevalent for pmc values higher than 1 (Figure 5b).
The effect of selection pressure on the frequency of the target compotype for all 1,000 networks is
presented in Figure 5a. Similarly to Figure 2a, an overall skew toward positive selection is seen (about
50% of cases), with some cases of negative (about 15% of cases) or no response to selection, and with
a mean selection excess of 1.254 ± 0.804. Significantly, the ratio of the number of simulations showing
positive selection to that showing negative selection increased more than threefold, from 1.06 in the regular
GARD to 3.33 in the population-GARD. In line with previous work [68], the growth bonus was calculated
when the assembly size was Nmin (Equation 8). When the bonus was calculated for all time points between
Nmin and Nmax (for a smaller set of 100 population-GARD simulations), the overall selection response
seems to become even more positive (70% of cases), with a higher selection excess value of 1.399 ± 0.997.
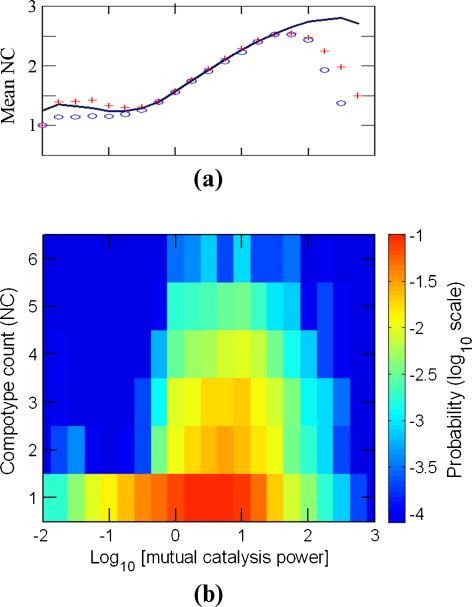
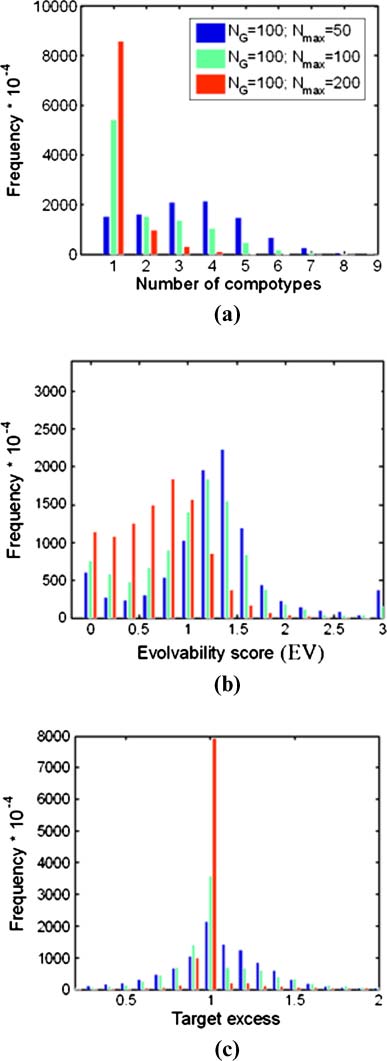
3.3 Compotype Diversity
The influence of pmc on one of the attributes of GARD diversity, the mean number of different com-
potypes appearing in a simulation, is now analyzed. It is found that as pmc increases, so does the mean
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
8
3
2
4
3
1
6
6
3
2
8
4
a
r
t
l
/
_
a
_
0
0
0
6
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5. Selection in population-GARD. Figure details for (a) and (b) are as in Figures 2a and 3b, respectively. Data set is
1,000 population-GARD simulations, whose parameters are collected in Table 1.
Artificial Life Volume 18, Number 3
251
O. Markovitch and D. Lancet
Excess Mutual Catalysis Is Required for Effective Evolvability
Figure 6. The dependence of compotype count (NC ) on pmc. Details are as in Figure 3.
= 100 (Figure 6a). Furthermore,
number of compotypes, reaching a maximal value of nearly 3 at pmc
in the realm of excess self-catalysis ( pmc < 0.5), one compotype appears in an overwhelming majority
of the cases (91%) (Figure 6b). In contrast, compotype counts between 2 and 6 are almost entirely
confined to the domain of excess mutual catalysis ( pmc > 2). Curiously, even among the ∼5,000
simulations that show only one compotype, a large majority have pmc > 2, suggesting that high mutual
catalysis is a necessary but not sufficient condition for a high number of compotypes.
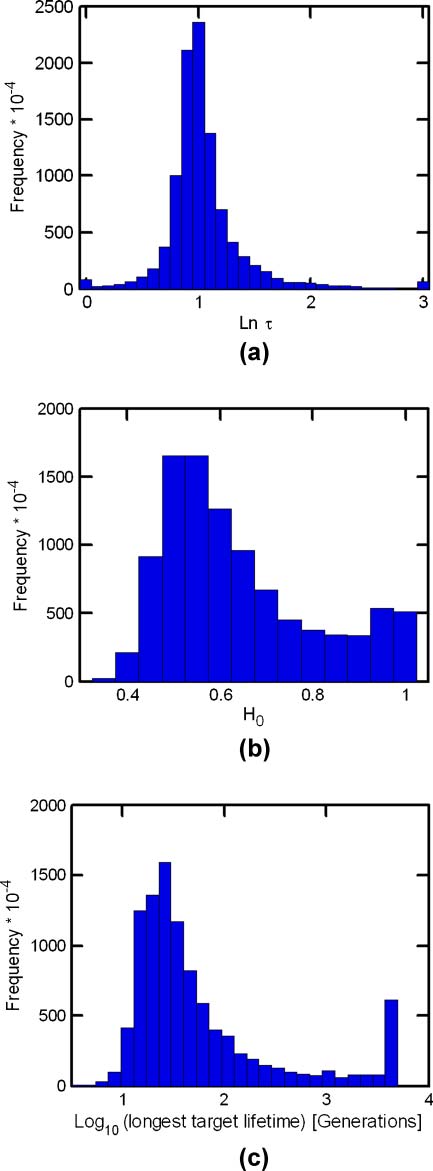
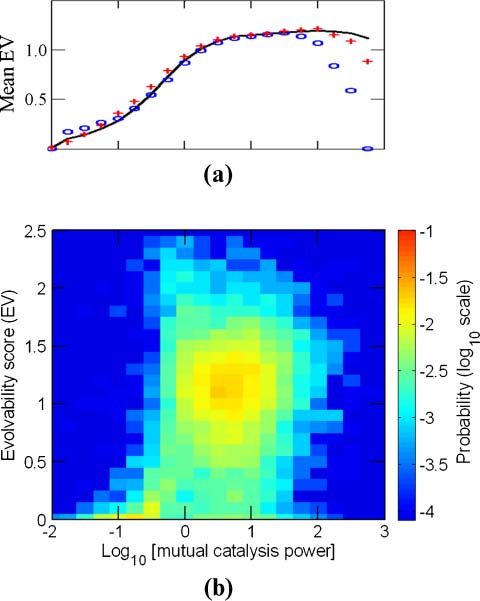
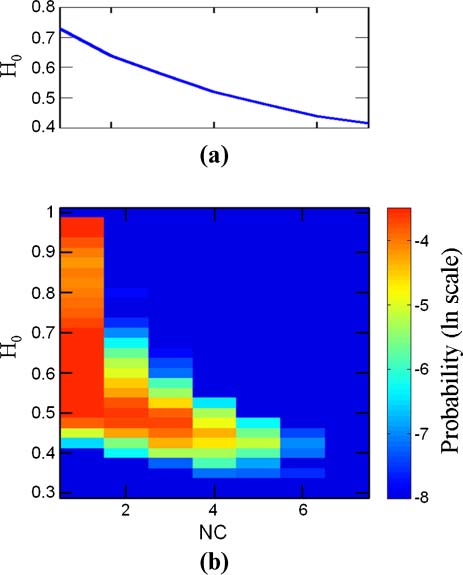
3.4 GARD Evolvability
The similarity autocorrelation function (Equation 6) and its derived parameters (Equation 7) are
employed to obtain information on the evolutionlike dynamics of GARD assemblies. One possible
interpretation of the value of H is a depiction of the whole-simulation average of the assembly composi-
tional lifetime. Longer H may be taken to represent better average maintenance of compositional similarity
between consecutive GARD generations, symbolizing better reproduction fidelity. Likewise, 1/H may be
thought of as related to the compositional mutation rate. Indeed, effective compositional preservation is
implicated by the most frequent number of generations, H ≈ 3, with a non-negligible probability for H ≥
10 (Figure 7a). Note that H does not represent the composomal lifetime. In fact, the most probable target
compotype lifetime (taking for simplicity the maximal time from each simulation) is 30, and the average is
434 generations (Figure 7c). The other similarity autocorrelation parameter, H0, is interpreted here as
showing the residual compositional similarity among assemblies along many generations in the entire
simulation. Thus, 1 − H0 is taken as proportional to the overall compositional diversity of assemblies
across the entire simulation. Note that H0 is not strongly correlated with the compotype count (Figure 16
in Appendix A.5, correlation coefficient −0.049, r2 = 0.89) and therefore constitutes a rather independent
diversity assessment attribute. The most probable H0 value is ∼0.5, with a smaller probability peak at
H0 ≈ 1. The latter stems from simulations in which a single compotype tends to dominate.
252
Artificial Life Volume 18, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
8
3
2
4
3
1
6
6
3
2
8
4
a
r
t
l
/
_
a
_
0
0
0
6
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
O. Markovitch and D. Lancet
Excess Mutual Catalysis Is Required for Effective Evolvability
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
8
3
2
4
3
1
6
6
3
2
8
4
a
r
t
l
/
_
a
_
0
0
0
6
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7. Distributions of H, H0, and composome duration. (a) A histogram of H: unit is number of generations, and the
rightmost bin represents all data with lnH > 3. (b) A histogram of H0, unitless. (c) Distribution of the longest appearance
of target compotypes. Data in panels is the same as in Figure 2.
Artificial Life Volume 18, Number 3
253
O. Markovitch and D. Lancet
Excess Mutual Catalysis Is Required for Effective Evolvability
Figure 8. The dependence of the evolvability score (EV ) on pmc. Details are as in Figure 3.
A score is defined, which could arguably assess a GARD systemʼs evolvability:
EV ¼ H ð1 − H0Þ
ð11Þ
A larger evolvability score will typically arise when the system concomitantly displays appreciable
trans-generation compositional preservation and higher overall compositional diversity. This compound
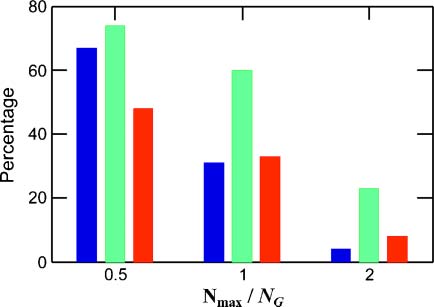
Figure 9. The percentage of regular-GARD instances exhibiting extreme evolution-related parameters as a function of
maximal assembly size (Nmax). In the electronic version, the values taken are: compotype count >2 (blue), evolvability
score >1 (green), and selection excess >1 (red). All parameters, except Nmax, are as in Figure 3b. Full histograms and
their related data are given in Appendix A.6 (Figure 17 and Table 3).
254
Artificial Life Volume 18, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
8
3
2
4
3
1
6
6
3
2
8
4
a
r
t
l
/
_
a
_
0
0
0
6
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
O. Markovitch and D. Lancet
Excess Mutual Catalysis Is Required for Effective Evolvability
measure reflects similar definitions of evolvability [7, 43]. Similar to the selection excess and number of
compotypes, a clear trend appears, whereby high evolvability scores are much more prevalent for pmc
values higher than 1 (Figure 8).
3.5 The Effect of Assembly Size
The effect of the assembly pre-fission size Nmax on GARDʼs evolutionlike behavior was studied by
performing two additional sets of 10,000 simulations, each with the same parameters as in Table 1 except
for Nmax = NG/2 and 2NG (Figure 9; Figure 17 and Table 3 in Appendix A.6). While for the smaller Nmax
value, the percentage of beneficial outcomes seems to be even higher than for the nominal Nmax = NG, a
larger Nmax value appears to have a disruptive effect because the system is nearing the equilibrium steady
state [23]. This is especially seen for the compotype count and the evolvability score.
4 Discussion
4.1 The Significance of Mutual Catalysis
One of the dominant concepts in prebiotic evolution research is the replicator-first scenario [10, 32,
40]. Based on the concept that molecular replication is related to self-catalysis [41], such views may be
perceived as related to the RNA-first scenario, positing that life began with a unique self-replicating
polyribonucleotide. In this realm, it is argued that more complex interaction networks have arisen
only at later stages, as when precursors for the autocatalytic molecule have been exhausted [31].
Our simulation results demonstrate an advantage for a network-first scenario, in which a large number
of molecular components mutually interact. While arising from a metabolism-related framework,
such results may be taken as relevant to the question of whether lifeʼs early precursors were a set
of replicators or a metabolic network. Note that the present work makes a direct comparison between
a metabolic network with frequent self-catalytic interactions and a metabolic network with frequent
mutually catalytic interactions, and therefore has only indirect relevance to the question of the validity
of replicator models. It is conceivable that future work incorporating templating biopolymers together
with mutually catalytic networks will better resolve this issue.
A widespread argument against metabolism-like entities being the first seed of life is the assertion
that metabolic networks cannot store and propagate information. The GARD model may be viewed
as a counterexample, as it is endowed with a (limited) capacity to store and propagate compositional
information. This has implications for a set of previously proposed models involving networks of
molecular interactions. Two of the earliest relevant concepts are Gántiʼs chemoton [12, 13, 63] and
Maturana and Varellaʼs autopoietic systems [35, 67]. Autopoiesis characterizes a spatially confined
network of molecular components, whose mutual interactions continuously regenerate the network
itself. The chemoton is described as a system of three subnetworks: metabolite generation, template
copying, and membrane synthesis. We prudently suggest that GARD may be viewed as a special case
of autopoietic-chemoton-like models, where template copying and compartmentation are embodied
in one entity, and a continuous supply of metabolites is afforded by the spontaneous accretion of
lipids from the buffered environment.
4.2 The Effect of Mutual Catalysis on GARD Diversity and Evolvability
An important result of this work is that networks within a certain range of kinetic parameters,
namely those that exhibit excess mutual catalysis, lead to enhanced diversity and evolvability of
GARD compotypes. The compotype count is a direct indication of the degree of composomal di-
versity. This result is related to an important aspect of early evolution: Self-catalysts tend to propa-
gate their own identity and suppress processes essential for the increasing complexity necessary for
transitions from early seeds of life toward systems resembling present-day life. The presently dem-
onstrated importance of mutual catalysis echoes the notion of systems prebiology [21, 57], whereby it
is suggested that life began its trajectory from complex chemical mixtures obeying network behavior
similar to that of metabolism in present-day cells.
Artificial Life Volume 18, Number 3
255
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
8
3
2
4
3
1
6
6
3
2
8
4
a
r
t
l
/
_
a
_
0
0
0
6
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
O. Markovitch and D. Lancet
Excess Mutual Catalysis Is Required for Effective Evolvability
4.3 Compotypes as Selection Targets
One of the unique corollaries of the GARD model is the emergence of composomes, dynamic states
of compositional assemblies that embody both metabolism-like characteristics and a rudimentary
capacity to store and propagate molecular information [49]. Composomes may be considered as
forming bridges between seemingly disparate views of the early seeds of life: metabolism first
and replicators first. Compotypes are further defined as centers of mass of composome clusters,
which may be regarded as analogous to species or quasi species [6]. This is due to the fact that
a compotype is a distinct entity, with distinct physical properties and hence fitness encoded in its
compositional information, different from those of other compotypes but still harboring consider-
able internal variability of constituents. Therefore, compotypes are considered as natural targets of
selection, as compared to randomly chosen compositions, as previously pursued [68]. Note that
here we have a measure of selection inherently present in the GARD model even in the absence
of external selective pressure, due to the fact that different composomes have different average
growth rates. This is seen in the present population GARD simulations, which are seeded with a random
population, but show a gradual increase of the population frequency of a specific compotype even in the
absence of externally imposed selection. This increase comes at the expense of other compositions be-
cause of the constant population condition.
4.4 Selection in a GARD
The present results show that GARD assemblies can exhibit positive or negative selection toward a
compotype target, as well as no selection at all. While in regular GARD the overall average selection
excess is merely 1.05, it is noteworthy that as many as 10% of the simulations show high selection
excess, >1.5. Importantly, these general results are borne out both in simulations of the regular
model and in simulations involving populations of assemblies. Previously, GARD population dy-
namics has been studied by addressing various emergent properties, including a comparison of finite
and infinite chemical environments [38]. Another study [70] showed that compositional inheritance
also emerges in the GARD model variants involving assembly populations and spatial proximity
interaction effects, and that it emerges in both a thermodynamic and a kinetic interaction regimen.
Analyzing GARD, both positive and negative selections can be observed in practice only when
the underlying network exhibits mutual catalysis excess. This conclusion is strengthened by its dem-
onstration in two different simulation modes: in the regular model and in populations. Notably, pos-
itive selection is observed appreciably more often in population GARD simulations, perhaps
reflecting the advantage of addressing populations of competing entities with different reproductive
rates. Furthermore, this selection response tends to be augmented as the number of coexisting com-
potypes increases in a given simulation, which may indicate a capacity of selective forces to provide an
edge to the target compotype in inter-compotype competition. Further in-depth analyses (currently
underway) of the ultrastructure of the h network, as well as subnetworks (quasi compartments [68]),
could lead to a better understanding of the influence of pmc and the compotype count on selection.
The present method for biasing the growth rate of a GARD target composition is in principle
similar to that used previously [68]. In both cases, modifications are in effect introduced to h matrix
elements. However, the previous analysis utilizes an interim formalism, the Eigen equation, for
replication-mutation dynamics [10], and the selection-related modification is exerted by multiplying
the growth rate by f H, defined in the same way as in Equation 8. The method utilized here involves
direct modification (Equation 9), a possible explanation for the discrepant results obtained by the
two reports. There are, however, additional significant differences between the two studies: (a) a pre-
fission value Nmax = 100 used here, as compared to Nmax = 6 used previously, an obligatory small
value required for the realistic application of Eigenʼs formalism with the available computing power;
(b) a large difference in repertoire size (NG = 100 here versus NG = 10 in the earlier study); (c) the
performance here of 10,000 random simulations, considered essential for proper statistical rigor, as
compared to only a single simulation done previously. Both points (b) and (c) provide a significant
edge to the present simulations in sampling the h interaction space, which allows drawing conclusions
256
Artificial Life Volume 18, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
8
3
2
4
3
1
6
6
3
2
8
4
a
r
t
l
/
_
a
_
0
0
0
6
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
O. Markovitch and D. Lancet
Excess Mutual Catalysis Is Required for Effective Evolvability
with higher certainty. In the future it will be interesting to consider additional methodologies to exert
external selection. One could be a variant of the presently used method, whereby the h network will be
biased by a constant factor and not employing target similarity-oriented bias. Another could be biasing
the environmental concentration Ui (Equation 2) by a constant factor based on the molecules that are
contained in the target compotype.
5 Conclusion
The GARD model embodies the inheritance of compositional information in the realm of a lipid
world scenario for early evolution [20, 21, 23, 27, 48, 49, 51, 55–57]. The GARD has recently been
pursued in several additional publications [20, 39, 68, 70] and has been chosen as an archetypal
metabolism-first realization [68]. This suggests that despite being a simulated toy model, the
GARD has sufficient complexity to shed light on some important questions in the field of prebiotic
origins. In the present work an attempt is made to shed further light on some of the GARDʼs
evolutionary features. It is expected that the present insights will become instrumental in further
efforts to extend the GARD beyond the monomer world [54], as has been preliminarily explored
[55]. This might be necessary to reveal the capacity of the GARD model to capture the much-
needed open-ended attributes of natural selection and evolution.
Acknowledgments
We thank Raphael Zidovetzki and Tsviya Olender for enlightening comments, Aron Inger for assistance
in coding, and Ágnes Tóth Petróczy, Azhar Ali Shah, Hugues Bersini, Leong Ting Lui, and Natalio
Krasnogor for discussions. This work is partly supported by EU-FP7 project MATCHIT and by the
Crown Human Genetics Center at the Weizmann Institute of Science.
References
1. Alon, U. (2007). Network motifs: Theory and experimental approaches. Nature Reviews Genetics, 8(6), 450–461.
2. Anet, F. A. (2004). The place of metabolism in the origin of life. Current Opinion in Chemical Biology, 8(6), 654–659.
3. Bachmann, P. A., Luisi, P. L., & Lang, J. (1992). Autocatalytic self-replicating micelles as models for
prebiotic structures. Nature, 357, 57–59.
4. Barabas, B., Toth, J., & Palyi, G. (2010). Stochastic aspects of asymmetric autocatalysis and absolute
asymmetric synthesis. Journal of Mathematical Chemistry, 48(2), 457–489.
5. Bedau, M. A. (2010). An Aristotelian account of minimal chemical life. Astrobiology, 10(10), 1011–1020.
6. Biebricher, C. K., & Eigen, M. (2006). What is a quasispecies? Current Topics in Microbiology and
Immunology, 299, 1–31.
7. Brookfield, J. F. Y. (2009). Evolution and evolvability: Celebrating Darwin 200. Biology Letters, 5(1), 44–46.
8. Chen, I. A., & Walde, P. (2010). From self-assembled vesicles to protocells. Cold Spring Harbor Perspectives
in Biology, 2/7/a002170.
9. Dyson, F. J. (1982). A model for the origin of life. Journal of Molecular Evolution, 18(5), 344–350.
10. Eigen, M., & Schuster, P. (1977). Hypercycle—Principle of natural self-organization. A. Emergence
of hypercycle. Naturwissenschaften, 64(11), 541–565.
11. Fontana, W., & Buss, L. W. (1994). What would be conserved if “the tape were played twice”? Proceedings
of the National Academy of Sciences of the U.S.A., 91(2), 757–761.
12. Gánti, T. (1975). Organization of chemical reactions into dividing and metabolizing units—Chemotons.
Biosystems, 7, 15–21.
13. Gánti, T. (1997). Biogenesis itself. Journal of Theoretical Biology, 187(4), 583–593.
14. Gesteland, F. R., Cech, R. T., & Atkins, F. J. (1999). The RNA world (p. 709). Cold Spring Harbor, MA:
Cold Spring Harbor Laboratory.
15. Gilbert, W. (1986). Origin of life—The RNA world. Nature, 319, 618–618.
Artificial Life Volume 18, Number 3
257
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
8
3
2
4
3
1
6
6
3
2
8
4
a
r
t
l
/
_
a
_
0
0
0
6
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
O. Markovitch and D. Lancet
Excess Mutual Catalysis Is Required for Effective Evolvability
16. Gillespie, D. T. (1976). General method for numerically simulating stochastic time evolution of coupled
chemical reactions. Journal of Computational Physics, 22(4), 403–434.
17. Gillespie, D. T. (1977). Master equations for random walks with arbitrary pausing time distributions.
Physics Letters A, 64(1), 22–24.
18. Hayden, E. J., von Kiedrowski, G., & Lehman, N. (2008). Systems chemistry on ribozyme self-construction: Evidence
for anabolic autocatalysis in a recombination network. Angewandte Chemie—International Edition, 47(44), 8424–8428.
19. Hughes, R. A., Robertson, M. P., Ellington, A. D., & Levy, M. (2004). The importance of prebiotic
chemistry in the RNA world. Current Opinion in Chemical Biology, 8(6), 629–633.
20. Hunding, A., Kepes, F., Lancet, D., Minsky, A., Norris, V., Raine, D., Sriram, K., & Root-Bernstein, R.
(2006). Compositional complementarity and prebiotic ecology in the origin of life. Bioessays, 28, 399–412.
21. Inger, A., Solomon, A., Shenhav, B., Olender, T., & Lancet, D. (2009). Mutations and lethality in
simulated prebiotic networks. Journal of Molecular Evolution, 69(5), 568–578.
22. Joyce, G. F. (2002). The antiquity of RNA-based evolution. Nature, 418, 214–221.
23. Kafri, R., Markovitch, O., & Lancet, D. (2010). Spontaneous chiral symmetry breaking in early
molecular networks. Biology Direct, 5(38). doi: 10.1186/1745-6150-5-38
24. Kaneko, K. (2002). Kinetic origin of heredity in a replicating system with a catalytic network. Journal
of Biological Physics, 28(4), 781–792.
25. Kauffman, S. A. (1993). The origins of order: Self organization and selection in evolution. Oxford, UK: Oxford
University Press.
26. Laidler, K. J. (1986). The development of theories of catalysis. Archive for History of Exact Sciences, 35(4), 345–374.
27. Lancet, D., Kafri, R., & Shenhav, B. (2002). Compositional genomes: Pre-RNA information transfer
in mutually catalytic assemblies. Geochimica et Cosmochimica Acta, 66(15A), A429–A429.
28. Lancet, D., Kedem, O., & Pilpel, Y. (1994). Emergence of order in small autocatalytic sets maintained
far from equilibrium—Application of a probabilistic receptor affinity distribution (RAD) model. Berichte
der Bunsen-Gesellschaft—Physical Chemistry Chemical Physics, 98(9), 1166–1169.
29. Lancet, D., Sadovsky, E., & Seidemann, E. (1993). Probability model for molecular recognition in
biological receptor repertoires—Significance to the olfactory system. Proceedings of the National Academy
of Sciences of the United States of America, 90(8), 3715–3719.
30. Lee, D. H., Severin, K., Yokobayashi, Y., & Ghadiri, M. R. (1997). Emergence of symbiosis in peptide
self-replication through a hypercyclic network. Nature, 390, 591–594.
31. Lifson, S. (1997). On the crucial stages in the origin of animate matter. Journal of Molecular Evolution, 44, 1–8.
32. Lifson, S., & Lifson, H. (1999). A model of prebiotic replication: Survival of the fittest versus extinction
of the unfittest. Journal of Theoretical Biology, 199(4), 425–433.
33. Limpert, E., Stahel, W. A., & Abbt, M. (2001). Log-normal distributions across the sciences: Keys and
clues. Bioscience, 51(5), 341–352.
34. Luisi, P. L., Walde, P., & Oberholzer, T. (1999). Lipid vesicles as possible intermediates in the origin of
life. Current Opinion in Colloid & Interface Science, 4(1), 33–39.
35. McMullin, B. (2000). Remarks on autocatalysis and autopoiesis. Annals of the New York Academy of Sciences,
901(1), 163–174.
36. Moran, P. A. P. (1958). Random processes in genetics. Mathematical Proceedings of the Cambridge Philosophical
Society, 54, 60–71.
37. Muller, U. F. (2006). Re-creating an RNA world. Cellular and Molecular Life Sciences, 63(11), 1278–1293.
38. Naveh, B., Sipper, M., Lancet, D., & Shenhav, B. (2004). Lipidia: An artificial chemistry of self-replicating
assemblies of lipid-like molecules. In 9th International Conference on the Simulation and Synthesis of Living
Systems (ALIFE9) (pp. 466–471).
39. Norris, V., Hunding, A., Kepes, F., Lancet, D., Minsky, A., Raine, D., Root-Bernstein, R., & Sriram, K. (2007). The
first units of life were not simple cells. Origins of Life and Evolution of Biospheres, 37(4–5), 429–432.
40. Orgel, L. (2000). Origin of life—A simpler nucleic acid. Science, 290, 1306–1307.
258
Artificial Life Volume 18, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
8
3
2
4
3
1
6
6
3
2
8
4
a
r
t
l
/
_
a
_
0
0
0
6
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
O. Markovitch and D. Lancet
Excess Mutual Catalysis Is Required for Effective Evolvability
41. Orgel, L. E. (1992). Molecular replication. Nature, 358, 203–209.
42. Orgel, L. E. (2004). Prebiotic chemistry and the origin of the RNA world. Critical Reviews in Biochemistry
and Molecular Biology, 39(2), 99–123.
43. Pigliucci, M. (2008). Opinion—Is evolvability evolvable? Nature Reviews Genetics, 9(1), 75–82.
44. Plasson, R., Brandenburg, A., Jullien, L., & Bersini, H. (2010). Autocatalyses. In H. Fellermann,
M. Dorr, M. Hanczyc, L. Laursen, S. Maurer, D. Merkle, P. Monnard, K. Stoy, & S. Rasmussen
(Eds.), Twelfth International Conference on the Synthesis and Simulation of Living Systems (pp. 4–11).
Cambridge, MA: MIT Press.
45. Rasmussen, S., Bedau, M. A., Chen, L., Deamer, D., Krakauer, D. C., Packard, N. H., & Stadler, P. F.
(Eds.). (2009). Protocells: Bridging nonliving and living matter (p. 684). Cambridge, MA: MIT Press.
46. Rosenwald, S., Kafri, R., & Lancet, D. (2002). Test of a statistical model for molecular recognition in
biological repertoires. Journal of Theoretical Biology, 216(3), 327–336.
47. Schuster, P., & Stadler, F. (2003). Networks in molecular evolution. Complexity, 8(1), 34–42.
48. Segre, D., Ben-Eli, D., Deamer, D. W., & Lancet, D. (2001). The lipid world. Origins of Life and Evolution
of the Biosphere, 31(1–2), 119–145.
49. Segre, D., Ben-Eli, D., & Lancet, D. (2000). Compositional genomes: Prebiotic information transfer in
mutually catalytic noncovalent assemblies. Proceedings of the National Academy of Sciences of the United States
of America, 97(8), 4112–4117.
50. Segre, D., & Lancet, D. (2000). Composing life. Embo Reports, 1(3), 217–222.
51. Segre, D., Lancet, D., Kedem, O., & Pilpel, Y. (1998). Graded autocatalysis replication domain (GARD):
Kinetic analysis of self-replication in mutually catalytic sets. Origins of Life and Evolution of the Biosphere,
28(4–6), 501–514.
52. Segre, D., Shenhav, B., Kafri, R., & Lancet, D. (2001). The molecular roots of compositional inheritance.
Journal of Theoretical Biology, 213(3), 481–491.
53. Shapiro, R. (2006). Small molecule interactions were central to the origin of life. Quarterly Review of
Biology, 81(2), 105–125.
54. Shapiro, R. (2007). A simpler origin for life. Scientific American, 296(4), 46–53.
55. Shenhav, B., Bar-Even, A., Kafri, R., & Lancet, D. (2005). Polymer GARD: Computer simulation of covalent
bond formation in reproducing molecular assemblies. Origins of Life and Evolution of the Biosphere, 35(2), 111–133.
56. Shenhav, B., Oz, A., & Lancet, D. (2007). Coevolution of compositional protocells and their environment.
Philosophical Transactions of the Royal Society B—Biological Sciences, 362, 1813–1819.
57. Shenhav, B., Solomon, A., Lancet, D., & Kafri, R. (2005). Early systems biology and prebiotic networks.
Transactions on Computational Systems Biology, 1, 14–27.
58. Silvestre, D. A. M. M., & Fontanari, J. F. (2008). The information capacity of hypercycles. Journal of
Theoretical Biology, 254(4), 804–806.
59. Sole, R. V., Rasmussen, S., & Bedau, M. (2007). Introduction. Artificial protocells. Philosophical Transactions
of the Royal Society B—Biological Sciences, 362, 1725–1725.
60. Stadler, P. F. (1991). Dynamics of autocatalytic reaction networks. 4. Inhomogeneous replicator networks.
Biosystems, 26(1), 1–19.
61. Steinley, D. (2006). K-means clustering: A half-century synthesis. British Journal of Mathematical &
Statistical Psychology, 59, 1–34.
62. Szathmáry, E. (1995). A classification of replicators and lambda-calculus models of biological organization.
Proceedings of the Royal Society B—Biological Sciences, 260(1359), 279–286.
63. Szathmáry, E., Santos, M., & Fernando, C. (2005). Evolutionary potential and requirements for minimal
protocells. Topics in Current Chemistry, 259, 167–211.
64. Szathmáry, E., & Smith, J. M. (1997). From replicators to reproducers: The first major transitions leading
to life. Journal of Theoretical Biology, 187(4), 555–571.
65. Thomas, J. A., & Rana, F. R. (2007). The influence of environmental conditions, lipid composition, and
phase behavior on the origin of cell membranes. Origins of Life and Evolution of Biospheres, 37(3), 267–285.
Artificial Life Volume 18, Number 3
259
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
8
3
2
4
3
1
6
6
3
2
8
4
a
r
t
l
/
_
a
_
0
0
0
6
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
O. Markovitch and D. Lancet
Excess Mutual Catalysis Is Required for Effective Evolvability
66. Ullrich, A., Rohrschneider, M., Scheuermann, G., Stadler, P. F., & Flamm, C. (2011). In silico evolution
of early metabolism. Artificial Life, 17(2), 87–108.
67. Varela, F. G., Maturana, H. R., & Uribe, R. (1974). Autopoiesis: The organization of living systems,
its characterization and a model. Biosystems, 5(4), 187–196.
68. Vasas, V., Szathmáry, E., & Santos, M. (2010). Lack of evolvability in self-sustaining autocatalytic
networks constrains metabolism—First scenarios for the origin of life. Proceedings of the National
Academy of Sciences of the United States of America, 107(4), 1470–1475.
69. Weber, A. L. (2000). Sugars as the optimal biosynthetic carbon substrate of aqueous life throughout
the universe. Origins of Life and Evolution of the Biosphere, 30(1), 33–43.
70. Wu, M., & Higgs, P. G. (2008). Compositional inheritance: Comparison of self-assembly and catalysis.
Origins of Life and Evolution of Biospheres, 38(5), 399–418.
Appendix
A.1 Distribution and Sampling of the GARD Matrix B
While not much is known about the values of the rate enhancement between prebiotic molecules,
there is a need to consider such values by a physically reasonable method. hij values are randomly
generated based on a lognormal distribution
Pðh
ij Þ ¼
1
p exp −
j
ffiffiffiffiffiffi
2k
h
ij
− AÞ2
ðln h
ij
2j2
!
ð12Þ
where A and j are the mean and standard deviation, respectively, which can be considered as a
“natural” distribution [33], in accordance with the receptor affinity distribution formalism [28, 29,
46], and it was also shown that a lognormal h increases the reproduction fidelity over the normal h
in GARD [52]. Each randomization of the h network may be thought of as representing the relative
rates of the NG molecules as they might ensue from different possible GARD environments.
Self-catalysis in GARD is represented by
h
iout þ iin →
ii iin þ iin
Often self-catalysis is written as [4]
X þ Y →
h
XY Y þ Y
ð13Þ
ð14Þ
The seeming dichotomy between the notations hii and hXY is clarified on noting that in the GARD,
molecules have two states, in and out, which behave as distinct chemical species. While it is possible
that more complex pathways would also be autocatalytic [44], this work refers to self-catalysis as the
simplest closed subnetwork of the h network, containing one element (Figure 1).
A.2 Fitting the Similarity Autocorrelation Function
The fitting procedure is as follows: (1) Calculate H0 as the mean of c(Dt) in the interval [GEN/4,
GEN/2]. (2) Guess H‡
as the first instance c(Dt) drops below H0. (3) Smooth the c(Dt) tail by forcing:
c(Dt > H‡
) = H0. (4) Fit an exponential (Equation 7) to the smoothed c(Dt), using nonlinear least
squares with a tolerance of 10-5.
Examples are given in Figure 12 in Appendix A.4.
260
Artificial Life Volume 18, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
8
3
2
4
3
1
6
6
3
2
8
4
a
r
t
l
/
_
a
_
0
0
0
6
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
O. Markovitch and D. Lancet
Excess Mutual Catalysis Is Required for Effective Evolvability
A.3 p-Values
See Table 2.
Table 2. Studentʼs t-test statistical analysis for the selection excess of h networks exhibiting pmc > 100 (Equations 4 and
10). Test was run using MATLAB function ttest, against the null hypothesis that the data are a random sample from a
normal distribution with mean 1.0, per specific ranges of lognormal random seeds.
Random-seed range
pmc > 100*
†
Selection excess
p-Value
50–300
300–800
1,000–3,500
5,000–10,000
3
5
40
70
0.973 ± 0.0395
3.57 (cid:1) 10-1
1.311 ± 0.389
1.49 (cid:1) 10-1
1.100 ± 0.325
5.95 (cid:1) 10-2
1.119 ± 0.248
1.45 (cid:1) 10-4
1–10,000
143
1.105 ± 0.272
8.03 (cid:1) 10-6
*The number of networks exhibiting high pmc value.
†
Mean and standard deviation of the selection excess of these networks
(under regular GARD simulations).
A.4 Examples
See Figures 10–14.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
8
3
2
4
3
1
6
6
3
2
8
4
a
r
t
l
/
_
a
_
0
0
0
6
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
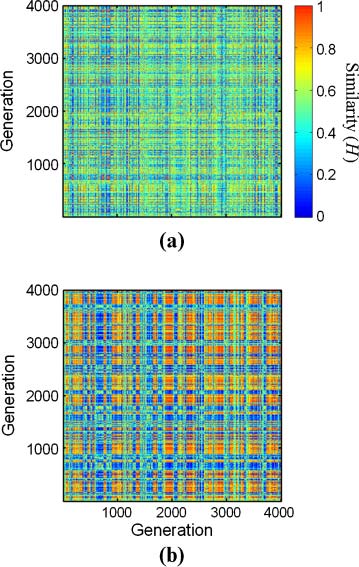
Figure 10. Example of carpets from two regular-GARD simulations with lognormal seeds 42 and 41 (a and b, respectively)
and the rest of the parameters as in Table 2. Compotype counts are 4 and 2, respectively. h matrices are presented in
Figure 11, and functions c(Dt) in Figure 12.
Artificial Life Volume 18, Number 3
261
O. Markovitch and D. Lancet
Excess Mutual Catalysis Is Required for Effective Evolvability
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
8
3
2
4
3
1
6
6
3
2
8
4
a
r
t
l
/
_
a
_
0
0
0
6
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
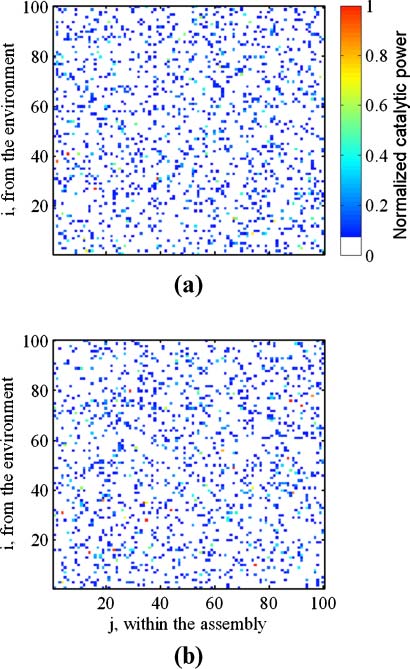
Figure 11. h matrices for the two simulations in Figure 10. pmc values are 1.98 and 0.81, respectively. To better express the
richness of the h matrix, catalytic values are scaled according to hij = 2 log10 hij
0 are generated according to
Equation 12).
0 – 4 (values of hij
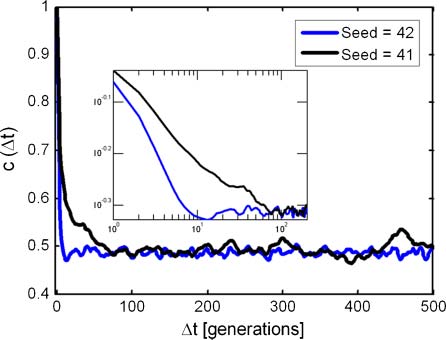
Figure 12. Functions c(Dt) for the two simulations in Figure 10. Insert shows initial decay on a log-log scale. Fitted parameters
for Equation 7 are H = 2.57, H0 = 0.49 (seed = 41), and H = 6.32, H0 = 0.50 (seed = 42).
262
Artificial Life Volume 18, Number 3
O. Markovitch and D. Lancet
Excess Mutual Catalysis Is Required for Effective Evolvability
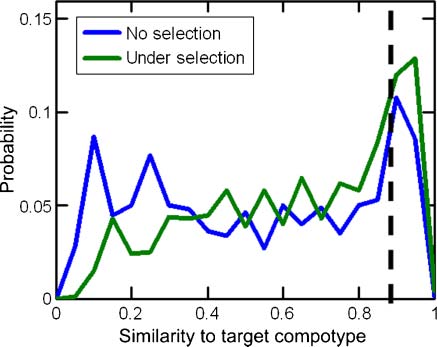
Figure 13. Example histograms of similarity between the target compotype from a regular GARD simulation, for a popula-
tion of 1,000 assemblies, with and without selection. A cutoff of H ≥ 0.9 (dashed line) is imposed to identify the frequency of
the compotype in the GARD population. Simulation details are lognormal seed = 3, GEN = 5,000, and the rest as in Table 2.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
8
3
2
4
3
1
6
6
3
2
8
4
a
r
t
l
/
_
a
_
0
0
0
6
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 14. Regular-GARD similarity carpets before and after selection. (a) Similarity carpet of the GARD instance gen-
erated with lognormal seed 114. The frequency of the target compotype is fT = 0.27. (b) The same carpet as (a), after
applying selection pressure, whereby the new frequency of the target is fT′ = 0.34. (c) Similarity carpet of the GARD
instance generated with lognormal seed 168. Here fT = 0.82. (d) The results after applying selection pressure. Here
fT′ = 0.74. Simulation parameters are in Table 1.
Artificial Life Volume 18, Number 3
263
O. Markovitch and D. Lancet
Excess Mutual Catalysis Is Required for Effective Evolvability
A.5 Selection Excess and the Number of Compotypes
See Figures 15–16.
Figure 15. The dependence of selection excess on the number of compotypes (before selection). Black solid line plots
the average selection excess per compotype count. Figure details are as in Figure 2a.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
8
3
2
4
3
1
6
6
3
2
8
4
a
r
t
l
/
_
a
_
0
0
0
6
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 16. The weak dependence of H0 on the number of compotypes (NC ). (a) Average H0 versus NC after 5-point
moving-average smoothing. Fitting the smoothed data to a linear curve gives a slope of −0.0485 with r 2 = 0.89. (b)
Density plot of the probability to have a simulation with a pair of H0 and NC values. In the electronic version, the color
represents the normalized probability to find a network with such a pair (in scale; red means that about 300 simulations
fall in this bin). Simulation parameters are as in Figure 15.
264
Artificial Life Volume 18, Number 3
O. Markovitch and D. Lancet
Excess Mutual Catalysis Is Required for Effective Evolvability
A.6 Assembly Size
See Figures 17 and Table 3.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
8
3
2
4
3
1
6
6
3
2
8
4
a
r
t
l
/
_
a
_
0
0
0
6
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 17. Histograms of the three evolution-related parameters, per Nmax values. (a) Number of compotypes (NC ). In
the electronic version, blue bars are with Nmax = NG/2, green bars are with Nmax = NG, and red bars are with Nmax = 2NG.
The rest of parameters are as in Figure 15. (b) Evolvability score (EV ). (c) Selection excess (SE ).
Artificial Life Volume 18, Number 3
265
O. Markovitch and D. Lancet
Excess Mutual Catalysis Is Required for Effective Evolvability
Table 3. Mean values collected from Figure 17. Number in parenthesis refers to the percentage of simulations that show
positive or negative selection.
Number
Nmax = 2NG
Mean value
Nmax = NG
Nmax = NG/2
NC
EV
SE
SE > 1.05
SE < 0.95
1.20
0.72
1.01
2.03
1.11
1.05
3.38
1.35
1.04
1.36 (8%)
1.38 (33%)
1.28 (48%)
0.85 (13%)
0.77 (31%)
0.71 (30%)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
8
3
2
4
3
1
6
6
3
2
8
4
a
r
t
l
/
_
a
_
0
0
0
6
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
266
Artificial Life Volume 18, Number 3