Evolving Homogeneous
Neurocontrollers for a
Group of Heterogeneous
Robots: Coordinated
Motion, Cooperation, and
Acoustic Communication
Abstract This article describes a simulation model in which artificial
evolution is used to design homogeneous control structures and
adaptive communication protocols for a group of three autonomous
simulated robots. The agents are required to cooperate in order to
approach a light source while avoiding collisions. The robots are
morphologically different: Two of them are equipped with infrared
sensors, one with light sensors. Thus, the two morphologically
identical robots should take care of obstacle avoidance; the other
one should take care of phototaxis. Since all of the agents can emit
and perceive sound, the group’s coordination of actions is based
on acoustic communication. The results of this study are a proof
of concept: They show that dynamic artificial neural networks
can be successfully synthesized by artificial evolution to design the
neural mechanisms required to underpin the behavioral strategies
and adaptive communication capabilities demanded by this task.
Postevaluation analyses unveil operational aspects of the best
evolved behavior. Our results suggest that the building blocks
and the evolutionary machinery detailed in the article should be
considered in future research work dealing with the design of
homogeneous controllers for groups of heterogeneous cooperating
and communicating robots.
Elio Tuci*,**
Universite´ Libre de Bruxelles (ULB)
Christos Ampatzis**
Universite´ Libre de Bruxelles (ULB)
Federico Vicentiniy
Politecnico di Milano
Marco Dorigo**
Universite´ Libre de Bruxelles (ULB)
Keywords
Collective robotics, evolutionary robotics,
dynamic neural networks, social behavior,
coordinated motion, signaling
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
4
2
1
5
7
1
6
6
2
4
7
0
a
r
t
l
.
/
.
.
2
0
0
8
1
4
2
1
5
7
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1 Introduction and Motivation
This article describes a set of simulations in which evolutionary robotics methods are used to auto-
matically design, through artificial evolution, adaptive communication mechanisms for a swarm of
autonomous robots.
* Corresponding author.
** IRIDIA, CoDE, Universite´ Libre de Bruxelles (ULB), 50 Avenue F. Roosevelt, CP 194/6, 1050 Bruxelles, Belgium. E-mail: etuci@ulb.ac.be
(E.T.); campatzi@ulb.ac.be (C.A.); mdorigo@ulb.ac.be (M.D.)
y Robotics Laboratory, Mechanics Department, Politecnico di Milano, P.zza Leonardo da Vinci 32, 20133 Milan, Italy. E-mail: federico.vicentini@
polimi.it
n 2008 Massachusetts Institute of Technology
Artificial Life 14: 157 – 178 (2008)
E. Tuci et al.
Evolving Homogeneous Neurocontrollers for a Group of Heterogeneous Robots
Communication is particularly important in any type of multirobot system, because it allows the
coordination of actions in scenarios that require cooperation among the agents. Several types of
communication protocols have been employed by roboticists to improve the effectiveness of the
collective behavior of a group of robots. Among them, situated communication protocols are be-
coming increasingly popular owing to their relevance in the domain of swarm robotics — a research
field dedicated to the study of how relatively simple physically embodied agents can be designed
such that a desired collective behavior emerges from the local interactions among agents, and be-
tween the agents and the environment [8, 9]. ‘‘Situated communication’’ refers to social interactions
in which the physical instantiation of the message contributes to defining its semantics (see [6] for
more details). In other words, the semantics of a signal is grounded in the perceptual experience of
the receiver.1 A classic example of situated communication in nature is stigmergy in social insects
[12, 15]. Stigmergy is a method whereby individuals communicate with each other by modifying their
local environment. For instance, ants, by laying down pheromone along their trail, influence each
other’s behavior.
Swarm robotics represents a novel way of doing collective robotics in which autonomous
cooperating agents are controlled by distributed and local rules. That is, each agent uses individual
mechanisms and local perception to decide what action to take. In a multirobot system with these
characteristics, (situated) communication refers to those circumstances in which the individual ac-
tions carried out by an agent, by perturbing the perceptual state of one or more observers, make
possible various forms of social coordination among the members of the group [4]. Swarm robotic
systems are of particular interest for roboticists because (i) the failure of individual components does
not significantly hinder the performance of the group (robustness); (ii) cooperative behavior makes it
possible to reduce the complexity of the individuals (simplicity of single units), and (iii) the control
mechanisms used are not dependent on the number of agents in the swarm (scalability).
Ongoing research work in swarm robotics is focusing on the development of design methods to
obtain effective group-level behaviors from the definition of individual mechanisms and ground
the semantics of communication in the perceptual experience of single agents [17, 26, 28]. The re-
search presented in this article aims to contribute to the development of swarm robotic systems
through the study of a particular scenario that requires a swarm of robots to use communication in
order to perform a collective navigation task. In particular, our objective is to prove that evolutionary
robotics methods can be successfully applied to the design of homogeneous controllers for a mor-
phologically different swarm of robots.
Evolutionary robotics is a methodological tool to automate the design of robots’ controllers [21].
Evolutionary robotics is based on the use of artificial evolution to find sets of parameters for
artificial neural networks that guide the robots to the accomplishment of their objectives, avoiding
dangers. In this study, the evolutionary robotics methods allow us to develop adaptive communi-
cation mechanisms that are grounded in the perceptual experience of the receiver and fully integrated
with all of the other underlying structures that underpin the behavioral repertoire of each robot.
Unlike other design methods, evolutionary robotics does not require the designer to make strong
assumptions concerning what behavioral and communication mechanisms are needed by the robots.
The experimenter specifies the characteristics of a social context in which robots are required to
cooperate. The agent’s mechanisms for communicative and noncommunicative behavior are deter-
mined by an evolutionary process which favors (through selection) those solutions that improve the
fitness (i.e., a measure of an agent’s or group’s ability to accomplish its task) of an agent and/or of a
group of agents.
In evolutionary robotics, the homogeneous approach (i.e., where a controller is cloned in each
robot of a group) is extensively used to deal with morphologically identical robots. This approach
is preferred because it facilitates the design process. For example, the evaluation of the collective
1 An alternative to situated communication is abstract communication protocols,
in which the physical signal (the medium) that
transports the message does not have any semantic properties. Only the content of the message has meaning. Examples of abstract
communication are protocols in which messages are exchanged by robots through wireless Ethernet [25].
158
Artificial Life Volume 14, Number 2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
4
2
1
5
7
1
6
6
2
4
7
0
a
r
t
l
.
/
.
.
2
0
0
8
1
4
2
1
5
7
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
E. Tuci et al.
Evolving Homogeneous Neurocontrollers for a Group of Heterogeneous Robots
behavior of different homogeneous groups can be directly used to quantitatively estimate the ef-
fectiveness of their control structures and, subsequently, to compare them. If the robots of a group
do not share the same controller, it becomes less intuitive to define the criteria for estimating, from
the observation of the collective behavior, the effectiveness of each control structure within a group
and to compare different controllers associated with different groups [22]. Moreover, the homo-
geneity of control structures does not preclude the emergence of behavioral specializations. For
example, the work of Quinn et al. [24] shows that leader-follower specialization can be obtained in
a homogeneous group of robots by using dynamic neural network controllers. However, to the
best of our knowledge, the homogeneous approach has never been employed in the context of
morphologically different robots. In this context, neural plasticity may be required (a) to deal with
specialization or role assignment among morphologically similar robots, as well as (b) to take
account of the morphological differences in the sensory-motor apparatus of the agents. In this
article, the process by which a single controller adapts to morphologically different robots is referred
to as dynamic speciation. Given the nature of the adaptive task described in this article, we decided to
use it as a test bed to explore the potential of the homogeneous approach to design controllers for
morphologically different robots.
The results of this study are a proof of concept: They show that dynamic artificial neural net-
works can be successfully synthesized by artificial evolution to design the neural mechanisms re-
quired to underpin the behavioral strategies and adaptive communication capabilities demanded by
the task. In particular, we have developed a sound signaling system that allows a group of mor-
phologically heterogeneous agents that differ in their sensory capabilities to coordinate their ac-
tions in order to approach a lightbulb without collisions. Postevaluation analyses unveil operational
aspects of the best-evolved behavior. For example, we show that adaptive group behavior can be
achieved without the need of (i) individual built-in mechanisms for distinguishing between self- and
non-self-produced signals, or of (ii) complex neural structures that regulate the turn-taking during
communication.
1.1 Structure of the Article
In what follows, we first present a review of previous work in which control mechanisms for
communicative and noncommunicative behavior in swarm robotic systems have been designed by
using evolutionary robotic methods (Section 2). In Section 3, we describe the simulation scenario
investigated in this research work. In Sections 4, 5, 6, and 7 we describe methodological issues of our
study. In Section 8, we illustrate the results and postevaluation analysis of our simulations. Dis-
cussion and conclusions are presented in Sections 9 and 10.
2 State of the Art
In this section we review research work focused on the issue of designing, through artificial evo-
lution, neural mechanisms for communicative and noncommunicative behavior in swarms of auto-
nomous robots. In particular, we describe those works in which, as in ours, the structure of the
communication (i.e., the syntax and semantics) is automatically designed by the evolutionary pro-
cess. Consequently, we do not consider those interesting works on communication in multirobot
interactions are designed by using methods other
systems in which the mechanisms for social
than evolutionary robotics. For a survey of work in those fields, we refer the reader to the articles
[2, 5, 11, 25].
A number of experiments have been carried out in the recent past in which agents asked to solve
rather simple tasks that require cooperation and coordination, develop simple forms of ritualized
social interactions and/or signaling capabilities. In the work described in [23, 24], a team of robots
is required to move in an arbitrarily chosen direction by remaining at a distance from each other
inside the range of their infrared sensors. This work is particularly important in that it shows that
it is possible to design, through artificial evolution, neural mechanisms that, by simply using the
Artificial Life Volume 14, Number 2
159
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
4
2
1
5
7
1
6
6
2
4
7
0
a
r
t
l
.
/
.
.
2
0
0
8
1
4
2
1
5
7
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
E. Tuci et al.
Evolving Homogeneous Neurocontrollers for a Group of Heterogeneous Robots
infrared sensors’ readings, allow a group of homogeneous robots to engage in social interactions that
result in the emergence of roles such as leader and follower. The authors also describe the evolution
of communication among the robots by showing that behavior for social coordination first evolves
in a noncommunicative context, and only subsequently acquires its adaptive function. Still in the
domain of social interactions for collective navigation tasks, Baldassarre et al. [3] evolved neuro-
controllers for a group of homogeneous robots required to move together towards a target. Contrary
to the work described in [24], Baldassarre et al. made use of a dedicated communication channel in
the form of a loudspeaker continuously emitting a tone and directional microphones.
In the work described in [18, 19], the authors illustrate the evolution of communicative behavior
based on a simple vocabulary consisting of four signals. This communication protocol is used by a
group of four robots to halt in two target areas so that, at any given time, each target area does not
host more than half of the team. In [7], the author describes an experiment in which two autono-
mous agents, equipped with sound sensors and effectors, have to remain close to each other as long
as possible. An operational description of the best-evolved solutions reveals that the sound signaling
system is used by the agents both for self-stimulation and for social interaction. This evidence seems
to go against a shared perspective in biology and psychology that tends to distinguish the behavior of
natural organisms as socially relevant and non-socially-relevant. The author uses the counterintuitive
result of his analysis to point out the importance of grounding the functional description of the
behavior of natural organisms in ‘‘what we know about the operation (at different levels) of the
system concerned’’ [7, p. 43].
The work of Trianni and Dorigo [26] points to the advantages of evolved versus hand-coded
acoustic communication protocols in a task in which a group of physically-linked robots is required
to move while avoiding holes in the ground. The work shows that the behavior of swarms exploiting
an evolved acoustic communication protocol is more robust than the behavior of swarms using a
hand-designed protocol. Similarly, Ampatzis et al. [1] show that a categorization task can be more
efficiently performed by a pair of robots when the social interactions are mediated by a simple
evolved acoustic communication protocol.
Our experiment is strongly based on some of the research described in this section. For example,
we draw inspiration from [7] for modeling the sound signaling system of our robots (see Section 5).
Furthermore, we draw inspiration from [24] in designing the fitness function described in Section 4.
Other aspects of our work, such as the nature of the cooperative scenario used to investigate issues
concerning the evolution of acoustic communication (i.e., social
interactions in morphologically
heterogeneous robots) and other methodological choices, are original and innovative. In Section 9,
we point the reader to similarities and differences between our work and those described in this
section, and we highlight the novel and interesting parts of our research work.
3 Experimental Setup
We consider the following experiment: Three simulated robots—referred to as robots or agents
hereafter—are required to navigate towards a light source, while remaining close to each other.
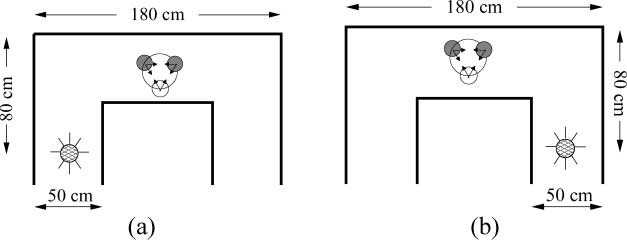
The robots are placed in an arena, as shown in Figure 1. The arena is composed of walls and a light
that is always turned on. The light can be situated in the bottom left corridor (Env. L) or in the bottom
right corridor (Env. R). The robots are initialized with their centers anywhere on an imaginary circle of
radius 12 cm centered in the top corridor, at a minimum distance of 3 cm from each other. The initial
orientation of each robot is determined by applying an angular displacement randomly chosen in the
interval [(cid:2)30j, 30j] with respect to a vector originating from the center of the robot and pointing
towards the centroid of the group. The goal of the robots is (i) to navigate towards the light, whose
position changes according to the type of environment they are situated in, and (ii) to avoid collisions.
The peculiarity of the task lies in the fact that the robots are equipped with different sets of
sensors. In particular, two robots are equipped with infrared and sound sensors but they have no
ambient light sensors. These robots are referred to as RIR (see Figure 2a). The other robot is
160
Artificial Life Volume 14, Number 2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
4
2
1
5
7
1
6
6
2
4
7
0
a
r
t
l
.
/
.
.
2
0
0
8
1
4
2
1
5
7
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
E. Tuci et al.
Evolving Homogeneous Neurocontrollers for a Group of Heterogeneous Robots
Figure 1. (a) Env. L; (b) Env. R. In both pictures, the thick lines represent the arena walls, the two small filled circles represent
robots RIR, the small white circle represents robot RAL, and the light is represented by the filled circles at the bottom left and
right. For each robot, the black arrows indicate the region within which the robot’s heading is randomly chosen.
equipped with ambient light and sound sensors, but it has no infrared sensors. We refer to this robot
as RAL (see Figure 2b). Robots RIR can perceive the walls and other agents through infrared sensors,
while the robot RAL can perceive the light. Therefore, given the nature of the task, the robots are
forced to cooperate in order to accomplish their goal. In fact, it would be very hard for each of them
to solve the task solely based on their own perception of the world. RAL can hardly avoid collisions;
RIR can hardly find the light source. Thus, the task requires cooperation and coordination of actions
between the different types of robots.
Although the robots differ with respect to their sensory capabilities, they are homogeneous with
respect to their controllers. That is, the same controller, synthesized by artificial evolution, is cloned
in each member of the group. Both types of robots are equipped with a sound signaling system
(more details in Section 5). However, contrary to other studies [see 3, 18, 19], we do not assume that
the agents are capable of distinguishing their own sound from that of the other agents. The sound
broadcast into the environment is perceived by the agent through omnidirectional microphones.
Therefore, acoustic signaling is subject to problems such as the need to distinguish one’s own sound
from those of others and mutual interference due to lack of turn-taking [7].
The reason why we chose the group to be composed of two RIR and one RAL robots is that this
intuitively seems to be the smallest group capable of spatially arranging itself adaptively in order to suc-
cessfully navigate the considered world. Preliminary studies have shown that with two-robot groups,
evolution tends to favor solutions in which, during navigation, RIR remains in front of RAL. This type of
Figure 2. (a) The robots RIR; (b) the robots RAL; (c) the network architecture. Only the connections for one neuron of
each layer are drawn. The input layer of RIR takes readings as follows: Neuron N1 takes input from the infrared sensors
(IR0 + IR1 + IR2)/3, N2 from (IR 4 + IR5 + IR6)/3, N3 from (IR8 + IR9 + IR10)/3, N4 from (IR12 + IR13 + IR14)/3, N5 from the
sound sensor S2, and N6 from the sound sensor S1. The input layer of RAL takes readings as follows: N1 and N2 take input
from ambient light sensors AL1, N3 and N4 take input from AL2, N5 from S2, and N6 from S1. Here M1 and M2 are the left
and the right motors, respectively. L is the loudspeaker.
Artificial Life Volume 14, Number 2
161
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
4
2
1
5
7
1
6
6
2
4
7
0
a
r
t
l
.
/
.
.
2
0
0
8
1
4
2
1
5
7
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
E. Tuci et al.
Evolving Homogeneous Neurocontrollers for a Group of Heterogeneous Robots
group has trouble in making left and right turns. As we will show in the next sections of this article, a
three-robot group in which the RAL tends to remain behind the two RIR companions employs safer and
more robust navigation strategies, which allow the robots to make left and right turns successfully.
4 The Fitness Function
During evolution, each genotype is translated into a robot controller and cloned into each agent.
Then, the group is evaluated twelve times: six trials in Env. L, and six trials in Env. R. The sequence
order of environments within the twelve trials has no bearing on the overall performance of the
group, since each robot controller is reset at the beginning of each trial. Each trial (e) differs from the
others in the initialization of the random number generator, which influences the robots’ starting
position and orientation, and in the noise added to motors and sensors. Within a trial, the robot life
span is 400 simulated seconds (4,000 simulation cycles). In each trial, the group is rewarded by an
evaluation function fe, which seeks to assess the ability of the team to approach the lightbulb, while
avoiding collisions and staying within the range of the robots’ infrared sensors:2
fe ¼ KP
XT
ðdt (cid:2) Dt(cid:2)1Þ tanhðSt =qÞ:
t¼i
As in [24], the simulation time steps are indexed by t, and T is the index of the final time step of
the trial; dt is the Euclidean distance between the group’s location at time step t and its location at
time step 0, and Dt(cid:2)1 is the largest value that dt has attained prior to time step t. Therefore, the factor
dt (cid:2) Dt(cid:2)1 measures any gain that the team has made on its previous best distance from its initial
location, which is taken to be the centroid of the group.
The factor tanh(St/U) reduces any fitness increment given by dt (cid:2) Dt(cid:2)1 when one or more robots
are outside of the infrared sensor range: St is a measure of the team’s dispersal beyond the infrared
sensor range U ¼ 24.6 cm at time step t. Recall that the robot RAL has no infrared sensors.
Therefore, it does not have a direct feedback at each time step of its distance from its groupmates.
Nevertheless, the sound can be used indirectly by this robot to adjust its position within the group. If
each robot is within range U of at least one other, then St ¼ 0. Otherwise, the shortest two lines that
connect all three robots are found, and St is the distance by which the longer of these exceeds U. The
function tanh(x) ensures that, as the robots begin to disperse, the team’s score increment falls sharply.
i¼1 ci V cmax reduces the score in proportion to the number
of collisions that have occurred during the trial, where ci is the number of collisions of the robot i and
cmax ¼ 4 is the maximum number of collisions allowed. P ¼ 0 if S3
i¼1 ci > cmax. The team’s
accumulated score is multiplied by K ¼ 3.0 if the group moved towards the lightbulb; otherwise K ¼
1.0. A trial is terminated early if (a) the team reached the lightbulb, ( b) the team’s distance from the
lightbulb exceeds an arbitrary limit, set to 150 cm, or (c) the team exceeds the maximum number of
allowed collisions, cmax.
The factor P ¼ 1 (cid:2) (S3
i¼1 ci/cmax) if S3
5 The Robots
The controllers are evolved in a two-dimensional simulation environment, which models the kine-
matics of simple geometries and the functional properties of three types of sensors: infrared, ambient
light, and sound sensors (see [27] for a detailed description of the simulator). As illustrated in Figure 2a, b,
2 This fitness function is very similar to the one used in [24], from which it differs mainly in the parameter K. This parameter has been
introduced to give a selective advantage to those groups that move towards the lightbulb. In order to facilitate comparisons between our work
and that detailed in [24], we provide a description of the fitness function that uses a similar mathematical notation to that employed in [24].
162
Artificial Life Volume 14, Number 2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
4
2
1
5
7
1
6
6
2
4
7
0
a
r
t
l
.
/
.
.
2
0
0
8
1
4
2
1
5
7
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
E. Tuci et al.
Evolving Homogeneous Neurocontrollers for a Group of Heterogeneous Robots
Figure 3. This picture has been adapted from [7]. It shows the working principles of the shadowing mechanism.
our robots are modeled as circular objects of 5.8-cm radius. Differential-drive kinematic equations, as
presented in [10], are used to update the position of the robots within the environment.
Each robot RIR has 12 infrared sensors (IRi) placed on the perimeter of its circular body (see
Figure 2a). Robot RAL has two ambient light sensors (AL1) and (AL2) positioned at F67.5j with
respect to its facing direction (see Figure 2b). The signals of both infrared sensors and ambient light
sensors are a function of the distance between the robot and the obstacle.3
Both RIR and RAL robots are equipped with a loudspeaker (L) that is situated at the center of the
body of each robot, and with two omnidirectional microphones (S1 and S2), placed at F45j with
respect to the robot’s heading. Sound is modeled as an instantaneous, additive field of single
frequency with time-varying intensity (Di a [0.0, 1.0]) which decreases as the inverse square of the
distance from the source, as previously modeled in [7]. Robots can perceive signals emitted by
themselves and by other agents. The modeling of the perception of sound is inspired by what is
described in [7]. There is no attenuation of intensity for self-produced signal. The perception of
sound emitted by others is affected by a shadowing mechanism, which is modeled as a linear atten-
uation without refraction, proportional to the distance ysh traveled by the signal within the body of
the receiver (see [7] for details). This distance is computed as follows:
ysh ¼ ysenð1 (cid:2) AÞ;
0 V A < 1; A ¼ y2 (cid:2) R2 y2 sen ; ð1Þ where ysen is the distance between the sound source and the sensor, y is the distance between the sound source and the center of the body of the receiver, and R is the robot’s radius (see also Figure 3). The self- component of the sound signal is simply equal to Di. In order to calculate the non-self-component, first we scale the intensity of sound emitted by the sender (D j) by applying the inverse square law with respect to the distance between the sound source and the microphones of the receiver. Subsequently, we 3 The morphological structure and sensory apparatus of our robots model some of the characteristics of the s-bots. The s-bots are small wheeled cylindrical robots, 5.8 cm in radius, equipped with a variety of sensors, and whose mobility is ensured by a differential drive system (see [20] for details). Artificial Life Volume 14, Number 2 163 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u a r t l / / l a r t i c e - p d f / / / / 1 4 2 1 5 7 1 6 6 2 4 7 0 a r t l . / . . 2 0 0 8 1 4 2 1 5 7 p d . . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 E. Tuci et al. Evolving Homogeneous Neurocontrollers for a Group of Heterogeneous Robots multiply the scaled intensity by an attenuation factor c, which ranges linearly from 1 when ysh ¼ 0 to 0.1 when ysh ¼ 2R. To summarize, the reading Sˆ is of each sound sensor s of robot i is computed as follows: ˆSis ¼ self þ non-self; self ¼ Di ; non-self ¼ R2 y2 sen c: X Dj ja½1;3(cid:8) j p i ð2Þ The auditory receptive field of each microphone is bounded within the interval [0.0, 1.0]. Therefore, the sound sensor can be saturated by the self-emitted sound if a robot emits at its highest intensity (Di ¼ 1.0). Ten percent uniform noise is added to all sensor readings, motor outputs, and position of the robot. 6 The Robots’ Neural Controller The agent controller is composed of a network of five interneurons and an arrangement of six sensory neurons and three output neurons (see Figure 2c). The sensory neurons receive input from the agent’s sensory apparatus. Thus, for robots RIR, the network receives the readings from the infrared and sound sensors. For robots RAL, the network receives the readings from the ambient- light and sound sensors. The interneuron network (from N7 to N11) is fully connected. Additionally, each interneuron receives one incoming synapse from each sensory neuron. Each output neuron (from N12 to N14) receives one incoming synapse from each interneuron. There are no direct connections between sensory and output neurons. The network neurons are governed by the following state equation: dyi dt ¼ 8 >>>< >>>:
1
Hi
1
H i
ð(cid:2)yi þ gIiÞ;
(cid:2)yi þ
Xk
j¼h
i a ½1; 6(cid:8);
Nji jð yj þ hj Þ þ gIi
!
;
i a ½7; 14(cid:8);
jðxÞ ¼ 1
1þe(cid:2)x ;
ð3Þ
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
4
2
1
5
7
1
6
6
2
4
7
0
a
r
t
l
.
/
.
.
2
0
0
8
1
4
2
1
5
7
p
d
.
.
where, using terms derived from an analogy with real neurons, yi represents the cell potential, Hi the
decay constant, g a gain factor, Ii the intensity of the sensory perturbation on sensory neuron i, Nji the
strength of the synaptic connection from neuron j to neuron i, hj the bias term, and j ( yj + hj)
the firing rate. For each i, the indices h and k are set by taking into account the network architecture.
The cell potentials yi of the 12th and 13th neurons, mapped into [0.0,1.0] by a sigmoid function j
and then linearly scaled into [(cid:2)6.5, 6.5], set the robot motor’s output. The cell potential yi of the 14th
neuron, mapped into [0.0, 1.0] by a sigmoid function j, is used by robot r to control the intensity of
the sound emitted, Dr. The following parameters are genetically encoded: (i) the strength of synaptic
connections Nji; (ii) the decay constant Hi of the interneurons and of the neuron N14; (iii) the bias
term hi of the sensory neurons, of the interneurons, and of the neuron N14. The decay constant Hi of
the sensory neurons and of the output neurons N12 and N13 is set to 0.1. Cell potentials are set to 0
at any time the network is initialized or reset, and circuits are integrated using the forward Euler
method with an integration step size dt ¼ 0.1.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
7 The Evolutionary Algorithm
A simple generational genetic algorithm is employed to set the parameters of the networks [14]. The
population contains 80 genotypes. Generations following the first one are produced by a combination
164
Artificial Life Volume 14, Number 2
E. Tuci et al.
Evolving Homogeneous Neurocontrollers for a Group of Heterogeneous Robots
of selection with elitism, recombination, and mutation. For each new generation, the three highest-
scoring individuals (the elite) from the previous generation are retained unchanged. The remainder of
the new population is generated by fitness-proportional selection (also known as roulette wheel
selection) from the individuals of the old population. Each genotype is a vector composed of 84 real
values (70 connection weights, 6 decay constants, 7 bias terms, and a gain factor). Initially, a random
population of vectors is generated by initializing each component of each genotype to values chosen
uniformly random from the range [0,1]. New genotypes, except the elite, are produced by applying
recombination with a probability of 0.3 and mutation. Mutation entails that a random Gaussian offset
is applied to each real-valued vector component encoded in the genotype, with a probability of 0.15.
The mean of the Gaussian is 0, and its standard deviation is 0.1. During evolution, all vector
component values are constrained to remain within the range [0,1]. Genotype parameters are linearly
mapped to produce network parameters with the following ranges: biases hi a [(cid:2)4, (cid:2)2] with i a [1,
6]; biases hi a [(cid:2)5, 5] with i a [7, 14]; weights Nij a [(cid:2)6, 6] with i a [1, 6] and j a [7, 11]; weights Nij
a [(cid:2)10, 10] with i a [7, 11] and j a [7, 14]; gain factor g a [1, 13]. Decay constants are firstly linearly
mapped into the range [(cid:2)1.0, 1.3] and then exponentially mapped into Hi a [10(cid:2)1.0, 101.3]. The lower
bound of Hi corresponds to the integration step size used to update the controller; the upper bound,
arbitrarily chosen, corresponds to about 1/20 of the maximum length of a trial (i.e., 400 s).
8 Results
Ten evolutionary simulations, each using a different random initialization, were run for between
2,500 and 3,600 generations of the evolutionary algorithm. In particular, the termination criterion for
each run was set to a time corresponding to 86,400 s of CPU time. The variation in the number of
generations among differently seeded evolutionary runs is related to the performance of the robots
in each trial. For example, the evolutionary runs with more generations are those in which trials
tended to last for a shorter duration than the given time limits (i.e., 400 simulated seconds; see also
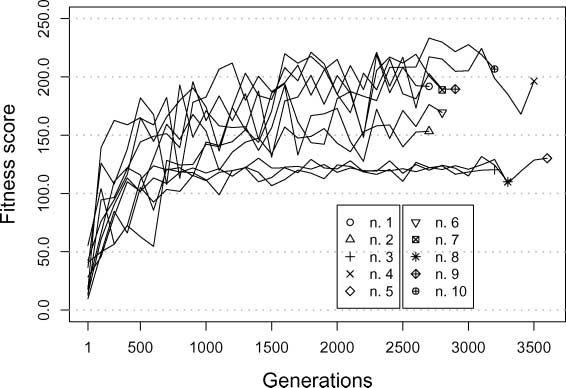
Section 4). Figure 4 shows the fitness of the best group at each generation of ten evolutionary runs.
Given the way in which the fitness is computed, and given the dimensions of the world, scores
higher than 200 refer to groups that manage to repeatedly get very close to the light in both types of
environment. The graph indicates that several runs produced successful groups. However, the graph
also indicates that the fitness of the best groups of the most successful evolutionary runs oscillates
Figure 4. Average fitness (12 trials) of the best groups at each generation of ten evolutionary runs. The key indicates the
correspondence between evolutionary runs and postevaluated groups (see Section 8.1 for details).
Artificial Life Volume 14, Number 2
165
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
4
2
1
5
7
1
6
6
2
4
7
0
a
r
t
l
.
/
.
.
2
0
0
8
1
4
2
1
5
7
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
E. Tuci et al.
Evolving Homogeneous Neurocontrollers for a Group of Heterogeneous Robots
quite a lot throughout the evolution. These oscillations may be related to overestimation of the fitness
of the best groups. It may have happened that, during evolution, the best groups took advantage of
favorable conditions, which are determined by the existence of between-generation variation in the
starting positions and relative orientation of the robots and other simulation parameters. Thus, in
the next section, we show the results of a first series of postevaluation tests aimed to estimate the
effectiveness of the best-evolved navigation strategies of each run, under circumstances in which the
effect of favorable conditions linked to the initialization of the robots is ruled out.
8.1 First Postevaluation Tests
In order to have a better estimate of the behavioral capabilities of the evolved controllers, we post-
evaluated, for each evolutionary simulation, the genotype with the highest fitness. The groups of robots
controlled by neural networks built from these genotypes are referred to as n. 1 to n. 10, respectively.
During postevaluation, each group is subject to a set of 1,200 trials in each of the two environments.
The number 1,200 arises from systematically varying the initial positions of the three robots according to
the following criteria: (i) we defined four different types of spatial arrangements in which the robots are
placed at the vertices of an imaginary equilateral triangle inscribed in a circle of radius 12 cm centered in
the top corridor (see Figure 5); (ii) for each spatial arrangement, we identified three possible relative
positions of the robot RAL with respect to the walls of the corridor (see white circle in Figure 5); (iii) for
each of these 12 (four times three) initial positions, the postevaluation was performed 100 times. The
initial orientation of each robot was determined by applying an angular displacement randomly chosen
in the interval [(cid:2)30j, 30j] with respect to a vector originating from the center of the robot and pointing
towards the centroid of the group. The 12 different arrangements take into account a set of relative
positions among the robots, and between the robots and the walls so that the success rate of the group
is not biased by these elements.
For the sake of clarity, we decided to estimate the effectiveness of the robots’ behavioral capa-
bilities during postevaluation by employing a binary criterion (successful vs. unsuccessful), instead of
the fitness function as during evolution. In particular, a group is considered successful if its centroid
is less than 10 cm away from the lightbulb. However, preliminary tests revealed this criterion to be
too demanding for the robots in the 400 s trials. Many of the initial positions resulting from the sys-
tematic variation explained above require the robots to spend a lot of the time at their disposal in
rearranging themselves to be able to safely progress towards the light, leaving little time for naviga-
tion. It appeared that some of the evolutionary conditions (e.g., the random initialization of the
robots’ initial position and the few evaluation trials) did not favor groups capable of quickly arrang-
ing themselves for phototaxis regardless of their initial positions. Consequently, even groups capable
of moving towards the light without colliding were nonetheless often unsuccessful due to a lack of
time for fulfilling the 10 cm criterion of success. Since our interest here is in collision-free navigation
strategies and not on other characteristics of the phototactic movement, such as the speed (i.e., how
quickly the robots get to the lightbulb), we decided to make the postevaluation trials 2.5 times longer
than the trials during evolution (i.e., 1,000 s, or 10,000 simulation cycles). This should (i) give the
Figure 5. The robots’ initial positions (from P1 to P12) during the postevaluation phase. White circles refer to robot RAL;
gray circles refer to robot RIR. For each robot, the black arrows indicate the region within which the robot’s heading is
randomly chosen. See text in Section 8 for details.
166
Artificial Life Volume 14, Number 2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
4
2
1
5
7
1
6
6
2
4
7
0
a
r
t
l
.
/
.
.
2
0
0
8
1
4
2
1
5
7
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
E. Tuci et al.
Evolving Homogeneous Neurocontrollers for a Group of Heterogeneous Robots
Figure 6. Results of postevaluation showing the success rate with confidence interval (computed with the binomial test)
over 1,200 trials per type of environment (black bars refer to Env. L, and white bars to Env. R) of the groups of robots
(n. 1 to n. 10) whose controllers are built from the genotype with the highest fitness of each evolutionary simulation.
robots enough time to compensate for possible disruptive effects induced by initial positions never
or very rarely experienced during evolution,4 and (ii) provide us with a fair estimation of the naviga-
tion capabilities of each of the groups selected for postevaluation. At the beginning of each post-
evaluation trial, the controllers are reset (see Section 6 for details).
The results of the postevaluation phase are shown in Figure 6. We notice that the best groups are
n. 9 and n. 10, which achieve performance above 90% in both environments. Groups n. 4 and n. 7
display performance above 80% in both environments. The performance of all the other groups is
clearly unsatisfactory. Groups n. 2, 3, 5, and 8 proved to be capable of accomplishing the task only
when located in Env. R, and group n. 1 was particularly effective in Env. L. This phenomenon can
be explained by considering that the two environments require two different types of turn— a left
turn in Env. L, and a right turn in Env. R. By looking at the behavior of the groups through a simple
graphical interface, we observed that the successful groups employ two different navigation strategies
to make the two types of turn (see Section 8.2). We also observed that those groups that systemati-
cally fail in either of the two environments lack the capability to make either turn.
Note that when looking at the performance of the best-evolved groups, as shown in Figure 6, one
has to take into account the arbitrary criteria we chose to determine whether or not a group of robots is
successful in any given trial: No robot may collide with the walls or with the other robots. This is a very
strict condition, which, given the nature of the task, requires each agent to be very accurate in coor-
dinating its movement. Further postevaluation tests proved that if we allow the group to make a
certain number (viz., four) of collisions before calling a trial a failure, then several groups would come
out almost always successful in both types of environment (data not shown). Whether or not the
robots should be allowed to collide and the extent to which a single collision invalidates the perfor-
mance of the group are issues that go beyond the scope of this article and will not be discussed further.
Instead, we focus on other performance measures, which tell us more about the characteristics of the
best-evolved groups. For instance, by looking at the data shown in Table 1, we notice that, except for
group n. 2, the majority of the failures in Env. L are due to collisions. In Env. R the performance of all
the groups is sensibly better than in Env. L (see columns 4 and 5 of Table 1). If we look at the average
distances to the light (see columns 6 and 7 of Table 1) and the relative standard deviations (see columns 8
4 The set of starting conditions during postevaluation is a subset of the set of starting conditions experienced by the robots during
evolution (see Section 3 for details). However, whereas during evolution each group is evaluated on 12 randomly chosen starting
conditions, during postevaluation the best-evolved groups are evaluated on a larger set of starting conditions, of size 1,200.
Artificial Life Volume 14, Number 2
167
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
4
2
1
5
7
1
6
6
2
4
7
0
a
r
t
l
.
/
.
.
2
0
0
8
1
4
2
1
5
7
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
E. Tuci et al.
Evolving Homogeneous Neurocontrollers for a Group of Heterogeneous Robots
Table 1. Further results of the postevaluation test, showing for the best evolved groups: (i) the percentage of unsuccessful
trials due to exceeded time limit without the group having reached the target (columns 2 and 3); (ii) the percentage of
unsuccessful trials that terminated due to collisions (columns 4 and 5); (iii) the average and standard deviation of the final
distance of the centroid of the group to the light during the unsuccessful trials (respectively, columns 6 and 8 for Env. L,
and columns 7 and 9 for Env. R). Note that in all trials, the initial distance between the centroid of the group and the light
is equal to 85.14 cm.
Failure due to time limit (%)
Failure due to collisions (%)
Avg.
Std. dev.
Distance to the light (cm)
Group
n. 1
n. 2
n. 3
n. 4
n. 5
n. 6
n. 7
n. 8
n. 9
n. 10
Env. L
0.00
85.33
0.00
0.67
0.00
0.00
0.58
0.00
0.00
0.00
Env. R
52.75
1.83
1.00
0.50
0.00
31.00
10.00
0.00
0.83
2.17
Env. L
10.92
14.67
100.00
14.00
100.00
23.42
10.92
100.00
1.08
1.75
Env. R
Env. L
Env. R
Env. L
Env. R
9.92
3.17
0.42
4.50
1.00
82.19
52.17
6.63
32.74
66.30
46.17
4.36
18.22
81.02
36.38
4.049
12.02
57.83
69.30
13.50
15.32
79.05
41.13
2.94
12.93
17.08
77.50
64.27
11.89
29.92
6.00
1.92
1.00
1.50
50.98
40.80
30.18
14.18
80.94
53.03
2.34
11.59
77.71
50.22
11.44
21.08
82.28
90.37
13.19
31.81
and 9), we can see that in Env. L failures happen rather far away from the light. For example, for groups
n. 3, 5, and 8—100% unsuccessful in Env. L—the final distance to the light is almost equal to the initial
distance. This reveals a lack of coordination of movement during the initial phase, when the robots have
to assume a configuration that favors group phototaxis. In Env. R, the smaller final distances to the light
seem to imply a problem, possibly common to several groups, in making the right turn.
In the rest of this section, we concentrate on the analysis of the group n. 9, which proved to be the
most effective in the first postevaluation test. The tests we are going to describe have been carried out
for all the best-evolved groups. It turned out that the successful navigation strategies of all the best-
evolved groups are very similar both in behavior and in the communication mechanisms exploited to
obtain the coordination of actions. Therefore, the reader should consider the operational description of
the behavior of the group n. 9 to be representative of all the successful navigation strategies of any
best-evolved group. These groups seem to differ in the robustness of the mechanisms that underpin
their behavior rather than in the nature of these mechanisms.
8.2 Group n. 9: A Description of the Behavioral Strategies
In this subsection we provide a qualitative description of the individual motion of the robot group
n. 9 as observed through a simple graphical interface.
First of all, we noticed that the systematic variation of the initial positions of the robots during
postevaluation brings about contingencies in which the coordination of movement of the group to-
ward the target requires an initial effort of the robots in rearranging their relative positions.5 During
5 Movies of the performance of the group in both environments are available at http://iridia.ulb.ac.be/supp/IridiaSupp2006-006/.
168
Artificial Life Volume 14, Number 2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
4
2
1
5
7
1
6
6
2
4
7
0
a
r
t
l
.
/
.
.
2
0
0
8
1
4
2
1
5
7
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
E. Tuci et al.
Evolving Homogeneous Neurocontrollers for a Group of Heterogeneous Robots
this initial phase of a trial, a dynamic process guided by the nature of the flow of sensations induces
the specialization of the controllers with respect to the physical characteristics of the robots and to
the roles that they play in the group. This phase is followed by the navigation phase, in which the
group maintains a rather regular spatial configuration; namely, the two robots RIR place themselves
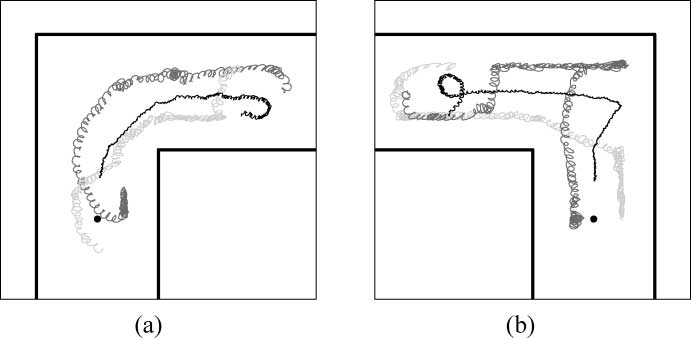
between the target and the robot RAL. Note, however, that while Env. L requires the group to make a
left turn, Env. R requires the group to make a right turn. This asymmetry in the environmental
structures corresponds to differences in behavioral strategies employed by the group to reach the
target, as shown in Figure 7. While in Env. L the robots simply turn towards the light, keeping their
relative positions in the group, in Env. R, we first observe an alignment of the agents along the far
right wall (see Figure 7b). Subsequently, the agent close to the corner (see the dark gray line) over-
comes the other two, and the group starts moving towards the target once the classical configuration
of the two robots RIR between the target and the robot RAL is reestablished.
Another important qualitative element is that each of the members of the group is characterized by
a movement with a strong angular component (counterclockwise). In other words, the robots proceed
toward the light by rotating on the spot. Within a trial, pure linear movement replaces the rotational
behavior only sporadically and for very short intervals (see movies available at http://iridia.ulb.ac.be/
supp/IridiaSupp2006-006/). This can happen in order to avoid an imminent danger of collision or if
required by the navigational strategy of the group. The evolution of the rotational movement is not
particularly surprising if we think about its effect on the perception of sound. In particular, the rota-
tional movement may introduce rhythm in perception. The oscillations of perceived sound, produced
by the rotational movement and/or by the oscillations manifested in signaling behavior, may provide
the robots the cues to adjust their positions relative to each other. Further and deeper investigations
into the nature of sound signals and its relationship with the robots’ motion will be carried out in the
next sections.
The starting position and the rotational movement have a strong effect on the time it takes the
group to reach the target. Indeed, according to postevaluation tests, most of the successful trials of
group n. 9 last longer than the 400 s given to the groups to complete the task during the evolutionary
phase (data not shown).
8.3 Group n. 9: A Description of the Signaling Behavior
Each robot of the group is required to coordinate its actions in order (i) to remain close to the other
two agents without incurring collisions, and (ii) to take actions that bring the group closer to the
Figure 7. Trajectories of the agents of group n. 9 during a successful trial (a) in Env. L and (b) in Env. R. The black lines
are the trajectories of a robot RAL, and the gray lines are the trajectories of robots RIR. The thick horizontal and ver-
tical segments represent the walls. In each part, we depict only the side of the corridor where the light (the small black
dot) is located.
Artificial Life Volume 14, Number 2
169
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
4
2
1
5
7
1
6
6
2
4
7
0
a
r
t
l
.
/
.
.
2
0
0
8
1
4
2
1
5
7
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
E. Tuci et al.
Evolving Homogeneous Neurocontrollers for a Group of Heterogeneous Robots
target. What is the role of signaling in the achievement of these goals? Is signaling used by the robot
RAL to communicate to the robots RIR information concerning the relative position of the target?
Similarly, is signaling used by the robots RIR to inform the robot RAL on the position of obstacles
against which it may collide? In order to provide an answer to this type of question, we carried out
a series of tests that look at the properties of the sound signals perceived by each robot during a
successful trial in each environment.
In particular, for robot group n. 9, we proceeded by separately recording the self and the non-
self components of the sound perceived by each microphone, and the heading at each time step of each
robot during a successful trial in each environment. Subsequently, with a fast Fourier transform (FFT)
analysis, we looked at these signals in order to identify oscillatory phenomena or other distinctive
features in sound production and perception whose properties can be exploited by the robots to
coordinate their actions. The reader can find all the details of this analysis at http://iridia.ulb.ac.be/
supp/IridiaSupp2006-006/. In the remainder of this section, we summarize and discuss the results of
our tests.
Before proceeding further, we should remind the reader that the intensity of sound received by
each microphone results from the summation of two components — the self and the non-self— and
the noise. The self component (i.e., the agent’s own signal) is determined only by the intensity of the
sound emitted by the robot itself. The non-self component is determined by the intensity at which
the sound is emitted from the loudspeaker of a sender as well as by the relative distance and orien-
tation of the loudspeaker with respect to the receiver’s microphones (see Section 5). Although the
agents have no means to distinguish between the self and the non-self components of the perceived
sound, they can act in a way to determine patterns in the flow of sensations that are informative
about their spatial relationships.
The results of our analysis show that there are no oscillatory phenomena in sound production for
either robot. Oscillations are instead observed in the perceived sound. The results also indicate that the
oscillations of the perceived sound are produced by the rotational movement of each robot through the
effect that the movement has on the nature of the non-self components. Further tests on the sound
signals reveal that: (a) the mean value of the self components contributes more than 90% of the
perceived sound; (b) the non-self components are very weak, possibly due to the relatively long robot-
robot distances. However, we notice that, if not attenuated by the shadowing effect, the nonself plus
the self component may be sufficient to saturate the sensors’ receptive field.
This evidence suggests that during navigation, the readings of the sound sensors of each robot
may go through oscillations constrained between an upper and a lower bound. The upper bound is
reached when the sum of the self and the non-self component is equal to or bigger than the satura-
tion value of the sound sensors (i.e., 1.0). The lower bound is close to the intensity of the self
component that is reached when the non-self components are strongly attenuated by the shadowing
effect. These oscillations are very small, since they concern less than 10% of the auditory receptive
field, and they are certainly not very regular, since the random noise applied to the sensor readings
may disrupt the regularity of the oscillations determined by the contingencies (i.e., rotational move-
ments and robots’ relative distances). However, in spite of being small and noisy, these oscillations
seem to be the only phenomenon related to the perception of sound that plays a significant role in
the coordination of action of the group. In fact, given a controller sufficiently sensitive to capture
them, they may represent a valuable perceptive cue for the receiver to spatially discriminate sound
sources and consequently, the relative position and orientation of the emitter(s). For example, low
intensity of sound corresponds to conditions in which the body of the receiver is placed between its
sound receptor and the sound source; high intensity of sound corresponds to conditions in which
the sound receptor is between the body of the receiver and the sound source. Robots capable of
detecting these spatial relationships can use them to make movements towards or away from a sound
source. Moreover, the oscillations of perceived sound produced by the rotational movement might
emphasize the intensity differences between the two sound receptors. These differences, known as
interaural intensity differences (hereafter referred to as IIDs; see [16]), may provide the robots the cues to
adjust their positions relative to each other. These cues might be exploited by the robots to remain
170
Artificial Life Volume 14, Number 2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
4
2
1
5
7
1
6
6
2
4
7
0
a
r
t
l
.
/
.
.
2
0
0
8
1
4
2
1
5
7
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
E. Tuci et al.
Evolving Homogeneous Neurocontrollers for a Group of Heterogeneous Robots
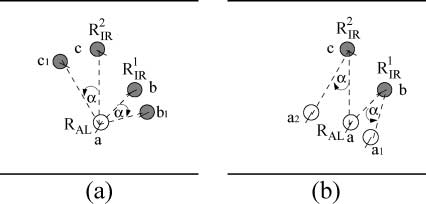
Figure 8. (a) Test A: Robots RIR (the gray circles) are displaced by an angle a with respect to robot RAL (empty circle).
This picture represents a hypothetical state in which the readings of the sound sensors of robot RAL are computed
considering R1
IR located in position c1 instead of c. (b) Test B: Robot RAL is
displaced by an angle a with respect to robots RIR. This picture represents a hypothetical state in which the readings of
the sound sensors of robot R1
IR are computed considering RAL located in position a1 instead of a. The sound sensors of
robot R2
IR are computed considering RAL located in position a2 instead of a.
IR located in position b1 instead of b, and R2
close to each other while avoiding collisions and moving towards the target. Given the lack of com-
plexity in the robots’ sound production, we tend to exclude the idea that signaling behavior concerns
more articulated forms of communication.
8.4 Group n. 9: Signaling Behavior and the Group’s Coordination of Actions
The results of postevaluation tests described in the previous section led us to formulate a series of
hypotheses concerning the mechanisms the robots may use to cooperate and coordinate their ac-
tions. In particular, we identified oscillatory phenomena in sound perception that may represent the
structures that underpin the successful navigational strategies described in Section 8.2.
In this subsection, we describe further postevaluation tests, which are meant to gather empirical
evidence in support of our hypotheses. This is because the observation of the phenomena described
in previous sections is not sufficient to rule out the possibility that sound signaling is partially or
totally operationally irrelevant to the achievement of successful navigational strategies. In fact, the
use of sound may be limited to the robot RAL. The robots RIR may ignore the sound and base their
movements on the readings of the infrared sensors. This would be sufficient to keep both robots RIR
close to RAL. The latter, by moving towards the target, would inevitably bring the group to the light.
Another possibility is that none of the robots use sound. In this case, the group might employ
unchanging phototactic movement, which may work as well, given that the dimensions of the cor-
ridors and the positions of the lights in the two environments do not vary. For example, the robot
RAL may move for about 65 cm east or west according to the characteristics of the environment and
then south; the robots RIR have simply to follow RAL avoiding collisions.
The tests we describe in the remainder of this section provide us further evidence (a) to strengthen
our hypothesis concerning the functional meaning of oscillations in robots’ perceived sound, and (b) to
rule out the hypothesis that sound is operationally irrelevant. In particular, our goal is to demonstrate
that sound is really essential for the robots to coordinate their movements and that the oscillations of
perceived sound produced by the robots’ rotational movement are indeed the perceptual phenomenon
the agents exploit to mutually coordinate their actions.
We run two postevaluation tests, test A and test B. In both tests, we interfere with the propagation
of sound in the environment by disrupting the orientation of the robot emitter with respect to the
heading of the receiver (see Figure 8). In particular, in each test the robots undergo sets of 1,200 trials
in each type of environment. For all the simulation cycles following the first6 10 s of each trial of
a set, the sound-sensor readings of a type of robot (RAL or RIR) are computed with respect to a
hypothetical state of the system in which each robot of the other type is supposed to be reoriented by
6 Applying any disruptions after 10 s (i.e., 100 simulation cycles) gives time to the controllers to reach a functional state different from
the initial one, arbitrarily chosen by the experimenter, in which the cell potential of the neurons is set to 0 (see Section 6).
Artificial Life Volume 14, Number 2
171
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
4
2
1
5
7
1
6
6
2
4
7
0
a
r
t
l
.
/
.
.
2
0
0
8
1
4
2
1
5
7
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
E. Tuci et al.
Evolving Homogeneous Neurocontrollers for a Group of Heterogeneous Robots
a fixed angular displacement, ranging from a minimum of 18j to a maximum of 180j, with a ran-
domly chosen direction (clockwise or counterclockwise) with respect to the heading of the receiver.
The magnitude of the angular displacement does not vary in each set of 1,200 trials in a given
environment. Note that the updating of the infrared sensors of robots RIR and of the ambient light
sensors of RAL do not undergo any disruption during these tests. The hypothetical states are taken
into account only for updating the sound-sensor readings of one type of robot at a time. In par-
ticular, in test A, the sound perceived by the robot RAL is computed with reference to a hypothetical
state in which the orientations of both robots RIR with respect to RAL’s heading are changed in order
to meet the angular displacement requirements (see Figure 8a). No disruptions are applied to update
the sound perceived by robots RIR. In test B, the sound perceived by the robots RIR is computed
with reference to a hypothetical state in which the orientation of the robot RAL with respect to the
RIRs’ heading is changed in order to meet the angular displacement requirements (see Figure 8b). In
this type of test, no disruptions are applied to update the sound perceived by RAL.
From what is said above, we can infer that test A and test B disrupt any kind of regularities in the
perception of sound that are linked to the sender-receiver relative orientation. In particular, by
varying the sender-receiver orientation, we indirectly increase or decrease the magnitude of the non-
self component. In Section 8.3, we have seen that oscillations of the perceived sound and IIDs
are the only two phenomena of signaling behavior that might be used by the robots to coordinate
their actions. In test A and test B, spatial cues provided by these two phenomena no longer refer to
the current status of the system, but to hypothetical states artificially introduced. Consequently, a
drop in the group performance in test A is a sign that these cues are exploited by the robot RAL to
successfully carry out its task. Similarly, a drop in the group performance in test B is a sign that these
cues are exploited by the robots RIR to successfully carry out their task. If both types of test show a
drop in group performance, we say that sound signaling is a common means of communication
exploited by both types of robots to mutually coordinate their actions.
The results of test A are shown in Figure 9a, b. The results of test B are shown in Figure 9c, d.
From these graphs we notice that the performance of the group is significantly disrupted by al-
terations of the orientation of one type of robot with respect to the heading of the other type of
robot. In particular, the bigger the magnitude of the angular displacement, the bigger the percentage
of failure of the system. The majority of failures are due to robot-wall collision. Observing the
behavior of the group in these conditions, we noticed that under the effects induced by the dis-
ruptions, the robots are not capable of remaining close to each other, that is, within the infrared
sensors’ range. When the distances becomes too large, the robots start wandering around the arena,
and the trial terminates due to a collision of the robot RAL with the arena walls. Only in a few
circumstances do the robots not lose contact with each other, and even then they are not capable of
reaching the target within the time limits (see Figure 9, black area of the bars).
These results prove that the group performance is severely disrupted when the hypothetical status
of the system used to update the sound-sensor readings of either type of robot is significantly dif-
ferent from the current circumstances. If the oscillations of the sound sensors’ readings and IIDs of
either type of robot do not reflect the environmental contingencies, the group performance in both
environments is disrupted. We conclude that, for both types of robot, spatial cues provided by the
oscillations of perceived sound and possibly by IIDs have a bearing on the development of effective
navigational strategies. Sound signaling seems to be a common means of communication exploited
by both types of robot to mutually coordinate their actions.
8.5 Group n. 9: The Significance of the Interaural Intensity Differences
The results of the tests reported in the previous section back up our claim concerning the oper-
ational value of sound for the robots’ coordination of actions. We now turn our attention to the
phenomena of IIDs, to establish whether the latter are cues used by the robots to coordinate their
actions. Alternatively, oscillations of perceived sound may be sufficiently informative on the con-
tingencies to allow the robots to successfully accomplish their goal.
172
Artificial Life Volume 14, Number 2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
4
2
1
5
7
1
6
6
2
4
7
0
a
r
t
l
.
/
.
.
2
0
0
8
1
4
2
1
5
7
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
E. Tuci et al.
Evolving Homogeneous Neurocontrollers for a Group of Heterogeneous Robots
Figure 9. Percentage of failure during 1,200 trials in each type of environment in postevaluation tests with disruptions
applied to the relative orientation of the robots during the computation of the perceived sound. (a) and (b) refer to test A.
The robots RIR, during all the simulation cycles following the first 10 s of any trial, are considered to be reoriented with
respect to the heading of the robot RAL by applying the angular displacement indicated on the horizontal axis and randomly
choosing its direction (clockwise or counterclockwise). (c) and (d) refer to test B. The robot RAL is reoriented with respect
to the heading of each robot RIR as explained above. (a) and (c) refer to tests in Env. L; (b) and (d) refer to tests in Env. R.
The black areas of the bars refer to the percentage of trials terminated without collisions and with the group not having
reached the target. The light gray areas of the bars refer to the percentage of trials terminated due to robot-robot
collisions. The dark gray areas of the bars refer to the percentage of trials terminated due to robot-wall collisions.
In these tests we progressively reduce the IIDs to the point at which the two sound receptors (S1
and S2) of a type of robot are impinged on by the same stimulus. Consequently, these disruptions
hinder the ability of the robots to use IIDs as cues for localization of sound sources and for their
coordination of actions. At the same time, we preserve the role of oscillations of perceived sound as
cues for spatial discrimination and localization of sound sources.
In each test, the robots undergo sets of 1,200 trials in each type of environment. For all the
simulation cycles following the first 10 s of each trial of a set, the reading of one sound sensor (S1 or
S2) of a type of robot (RAL or RIR) is modified in order to reduce the IID of a given percentage,
ranging from a minimum of 10% to a maximum of 100% (i.e., both sensors return the same
reading). The magnitude of the decrease of the IIDs does not vary in each set of 1,200 trials in a
given environment. Disruptions that reduce the IIDs of a given percentage are independently applied
to (i) the robot RAL and robots RIR, (ii) sound sensors S1 and S2, and (iii) Env. L and Env. R, for a
total of eight different types of tests — two types of robots times two types of sound sensors times
two types of environments. If we observe a sensible drop of the percentage of success of the group
for disruptions applied to either of the two types of robot in either of the two types of environment,
regardless of the sound sensor disrupted (S1 or S2), then we conclude that, for that type of robot,
IIDs are cues used to coordinate its actions during the navigation towards the light. In any other
Artificial Life Volume 14, Number 2
173
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
4
2
1
5
7
1
6
6
2
4
7
0
a
r
t
l
.
/
.
.
2
0
0
8
1
4
2
1
5
7
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
E. Tuci et al.
Evolving Homogeneous Neurocontrollers for a Group of Heterogeneous Robots
circumstances, we conclude that the oscillations of perceived sound, without IIDs, are sufficiently
informative on the contingencies to allow the robots to successfully accomplish their goal.
The results of the full series of tests, available at http://iridia.ulb.ac.be/supp/IridiaSupp2006-
006/, show that for both types of robot and for both sound sensors, the progressive reduction
of the IIDs is associated with a drop in performance of the group. Figure 10 shows only the results
of tests in which, regardless the sound sensor disrupted, the rate of failure of the group in a type of
environment is above 90% when the IIDs are made unavailable to a type of robot (see Figure 10, last
bar of each graph). These are the tests in which disruptions are applied to sound sensors S1 and S2
of a robot RAL in Env. L (see Figure 10a, b) and of robots RIR in Env. R (see Figure 10c, d). In these
cases, we conclude that IIDs are cues strictly necessary for a specific type of robot to be able to
coordinate its actions.
In all the other cases (robot RAL in Env. R, and robots RIR in Env. L), although a progressive
reduction of the IIDs corresponds to a drop in performance of the group, the disruptions applied to
either of the two sound sensors do not equally affect the performance of the group. With the IIDs
completely removed, the rate of failure of the group ranges between 40% and 60% in the cases in
which disruptions concern (i) robot RAL and sound sensor S2 in Env. R; and (ii) robots RIR in Env. R
(see graphs at http://iridia.ulb.ac.be/supp/IridiaSupp2006-006/). Further analyses of the behavior
of the group under these circumstances are required in order to provide an explanation of these
results. These analyses will be carried out in future works. However, we believe that the group might
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
4
2
1
5
7
1
6
6
2
4
7
0
a
r
t
l
.
/
.
.
2
0
0
8
1
4
2
1
5
7
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 10. (a) and (b) show the percentage of failure during 1,200 trials with disruptions applied to RAL sound sensors S1 in
Env. L and S2 in Env. R. (c) and (d) show the percentage of failure during 1,200 trials with disruptions applied to RIR sound
sensors S1 and S2 in Env. L. The disruptions concern the decrease of the IIDs by the percentage indicated on the horizontal
axis. The black areas of the bars refer to the percentage of trials terminated without collisions and with the group not
having reached the target. The light gray areas of the bars refer to the percentage of trials terminated due to robot-robot
collisions. The dark gray areas of the bars refer to the percentage of trials terminated due to robot-wall collisions.
174
Artificial Life Volume 14, Number 2
E. Tuci et al.
Evolving Homogeneous Neurocontrollers for a Group of Heterogeneous Robots
be able to assume spatial configurations that facilitate navigation in spite of the absence of IIDs for
either type of robot.
9 Discussion
The results reported in Section 8 have shown that dynamic neural networks, shaped by artificial
evolution, can be successfully used to design homogeneous control structures for a group of mor-
phologically heterogeneous cooperating and communicating robots. Postevaluation analyses unveiled
the mechanisms that underpin the cooperation and coordination of actions of the group. In partic-
ular, we focused on the study of the evolved acoustic communication protocol of the best-evolved
group. First we showed that: (i) all the robots emit sound at a very high intensity; (ii) signaling
behavior is not characterized by oscillatory phenomena; (iii) periodic phenomena, generated by the
receiver through a rotational movement associated with phototaxis, characterize the perception of
sound. Then, we proved that oscillations of perceived sound and interaural intensity differences
(IIDs) are cues largely exploited by the robots to generate adaptive actions to navigate safely (i.e.,
without collisions) towards the target. In particular, the robots exploit these cues to regulate their
individual actions with respect to the relative position of the sound source(s).
It is reasonable to consider that the evolved behavioral and communication strategies treated in
Section 8 are limited to the peculiarities of our simulations. However, our successful results point to
the relevance, for the robotics community, of features of our methodological approach that are of
more general applicability and that may be used in future research work dealing with the design of
homogeneous controllers for groups of heterogeneous cooperating and communicating robots. In
particular, we draw the attention of the reader to the following distinctive features of our work: (i) the
model of the sound; (ii) the way in which the controllers are wired up with the sensory apparatus of
the robots; (iii) the dynamic speciation of the homogeneous controller, whose mechanisms underpin
sensory-motor coordination and social interactions in structurally different agents. In the remainder
of this section, we further discuss these issues, whose significance, in our opinion, goes beyond the
research reported in this paper.
The model of sound, although inspired by the work of Di Paolo [7], presents peculiarities of
particular interest. As in Di Paolo [7], and contrary to other experimental work in evolutionary
robotics, we did not make use of directional microphones, or any other form of hard-wired or hand-
coded mechanisms, to discriminate between different sound sources or between self- and non-self-
produced sound. For example, in the work of Marocco and Nolfi [19], four directional microphones
capture the sound of the nearest robot located within F45.0j left or right of each microphone. As
well as being barely portable in a physical system, these types of models preclude the possibility of
investigating the principles underlying behavioral coordination through sound signaling in a team
of autonomous agents. This follows from the fact that, in these models, the problem of synchroniza-
tion or turn-taking to avoid mutual interference, and of spatial discrimination of sound sources, are
circumvented thanks to the implementation details. With respect to what is described in [7], we
strongly simplified the characteristics of the robot’s controller. In particular, we did not implement
the neural structures that provide to the agents in Di Paolo’s work the means to further regulate the
intensity of the emission of sound (regulation of a sound effector [7]) and the receptiveness of
the sound sensory neurons (sensory gain regulation [7]). We simplified the mechanisms to constrain
the production of sound by fixing a limit to the intensity of the signal, which also corresponds to the
saturation level of the sound sensors. That is, the self-produced sound can completely saturate the
sound sensors of the emitter. Although arbitrarily implemented by the authors, these simplifications
were introduced to compensate for an increase in structural complexity in the controller due to the
nature of the agents’ sensory apparatuses. In particular, while the agents in the work described in [7] the
agents are equipped only with sound sensors, in this work, the agents are equipped with light or infrared
sensors as well. Moreover, we investigated teams of three robots instead of two robots. Possibly due to
these differences, the evolved solutions in Di Paolo’s work and the evolved solutions in ours diverge
Artificial Life Volume 14, Number 2
175
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
4
2
1
5
7
1
6
6
2
4
7
0
a
r
t
l
.
/
.
.
2
0
0
8
1
4
2
1
5
7
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
E. Tuci et al.
Evolving Homogeneous Neurocontrollers for a Group of Heterogeneous Robots
significantly. Whereas in Di Paolo’s 2000 model, oscillations and synchronization in sound production
underpin behavioral coordination, in our model, there is no oscillation in sound production.
From an engineering point of view, it is worth mentioning that, although extremely effective in
preventing collisions, the best evolved navigation strategies are not characterized by fast phototactic
movement. On the one hand, the strong rotational movement allows for behavioral coordination
through sound signaling, as explained above. On the other hand, it slows down the movement
towards the light. We believe that alternative navigation strategies can potentially be achieved by
reintroducing some of the mechanisms originally proposed in [7]. These mechanisms facilitate the
evolution of oscillatory behavior in sound production and the distinction between self and non-self
components, without having to model phenomena such as time-varying frequencies and the Doppler
effect. A group of robots in which each agent is capable of differentiating between self and nonself
and of associating the intensity of the sound perceived in each ear with the distance to the sound
source may favor linear over rotational movements. Other hardware specifications, such as the
position of the microphones on the robot body, might facilitate the evolution of faster phototactic
movement. These issues will be the subject of future investigations.
With regard to the way in which the controllers are wired up with the sensory apparatus of the
robots, we would like to provide further justifications for our implementation choices. Our goal was
to generate, through artificial evolution, a controller capable of guiding both types of robot. For this
reason, we chose to keep the group homogeneous with respect to the controllers. That is, at time 0
of each trial, each robot is equipped with exactly the same control structure. However, the properties
of the controllers allow for dynamic speciation, that is, differentiation of the functionality of each con-
troller. Evidence for this emerged from the FFT analysis as described in Section 8.3. In particular, we
noticed that the robot RAL rotates slightly faster than the other two robots. This suggests that the
controllers of RAL adjust to its physical properties. This adjustment, or differentiation, is determined
by the attainment, by each controller, of different stable oscillatory dynamics due to the oscillatory
pattern experienced through the robot’s sensory apparatus.
We also wanted to reduce to a minimum the number of parameters that define the search space of
the evolutionary algorithm. For this reason, we decided to use neural structures in which the same
input neurons in different networks are linked to different types of sensors (see Section 6 for details).
Our results suggest that implementation details make it possible to generate, through artificial evolu-
tion, homogeneous controllers that can efficiently guide morphologically identical as well as morpholog-
ically different groups of robots. In our case, the differences in the flow of sensation coming from
different sensory channels (viz., the infrared, ambient light, and sound sensors) contribute to induce
the specialization of the controllers with respect to the physical characteristics of the robots, and to
the relative role that they play in the group (dynamic speciation). This latter mechanism can also be
exploited in case of hardware failure, in which an online reassignment of the association between an
agent’s sensors and the network’s input neurons might provide a robust mechanism to preserve the
functionality of multirobot systems. However,
in order to efficiently exploit our methodological
choices in the latter context, further investigations are required to determine the plasticity of con-
trollers in those circumstances in which they have already undertaken a process of dynamic specia-
tion. That is, it is an open question whether a neurocontroller already specialized to receive as input
the reading of a particular set of sensors is capable of redefining its functionality to guide a robot
with a different set of sensors.
10 Conclusions
In a context in which robots differ in their sensory capabilities, cooperation and coordination of actions
of the group are achieved by using an acoustic communication protocol controlled by evolved neural
mechanisms. Acoustic signals, determined by the individual emission of a single-frequency tone, pro-
vide the perceptual cues used by the robots to go beyond the limits of their sensory apparatus in order
to obtain robust phototactic strategies as well as obstacle avoidance behavior. The results of a series of
176
Artificial Life Volume 14, Number 2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
4
2
1
5
7
1
6
6
2
4
7
0
a
r
t
l
.
/
.
.
2
0
0
8
1
4
2
1
5
7
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
E. Tuci et al.
Evolving Homogeneous Neurocontrollers for a Group of Heterogeneous Robots
postevaluation tests carried out on the behavioral strategies of the best-evolved group of robots show
interesting operational aspects of the system (see Sections 8.3, 8.4, and 8.5). In particular, our analyses
highlight fundamental relationships between the motion of the agents and the appearance of wave-
forms in sound perception (affordances [13]), which are exploited by the robots to mutually coordinate
their actions. We have also provided evidence that the agents’ motion is guided by mechanisms that
exploit interaural intensity differences, that is, cues used by natural organisms to localize sound sources.
To conclude, from the results of this research we learn something about how evolution gets to
exploit the physics of our system to develop group navigational strategies based on the mutual
coordination of actions and cooperation among the agents. The results of this work are a proof of
concept: they show that dynamic artificial neural networks can be successfully synthesized by
artificial evolution to design the neural mechanisms required to underpin the behavioral strategies
and adaptive communication capabilities demanded by this task. The analysis of evolved individual
and social skills gives us an estimation of the potential of our implementation choices at various
levels, from the model of sound to the characteristics of the robots’ controller. Although the evolved
behavioral and communication strategies may be limited to the peculiarities of this case study, our
methodological approach is of more general applicability. In particular, the dynamic speciation of the
robots’ controllers, as well as the elements of the models that bring forth the causal relationships
between the physics of the system and the nature of the best-evolved collective strategies, can be
employed by roboticists for the design of more complex forms of social interactions and commu-
nication in groups of autonomous robots.
Acknowledgments
E. Tuci and M. Dorigo acknowledge European Commission support via the ECAgents project,
funded by the Future and Emerging Technologies program (grant IST-1940). The authors thank
their colleagues at IRIDIA for stimulating discussions and feedback during the preparation of this
article. M. Dorigo acknowledges support from the Belgian F.R.S.-FNRS, of which he is a research
director, and from the ANTS project, an Action de Recherche Concerte´e funded by the Scientific
Research Directorate of the French Community of Belgium. The information provided is the sole
responsibility of the authors and does not reflect the Community’s opinion. The Community is not
responsible for any use that might be made of data appearing in this publication.
References
1. Ampatzis, C., Tuci, E., Trianni, V., & Dorigo, M. (in press). Evolution of signaling in a multi-robot
system: Categorization and communication. Adaptive Behavior.
2. Balch, T., & Arkin, R. C. (1994). Communication in reactive multiagent robotic systems. Autonomous
Robots, 1(1), 27 – 52.
3. Baldassarre, G., Nolfi, S., & Parisi, D. (2003). Evolving mobile robots able to display collective behavior.
Artificial Life, 9, 255 – 267.
4. Bonabeau, E., Dorigo, M., & Theraulaz, G. (1999). Swarm intelligence: From natural to artificial systems.
New York: Oxford University Press.
5. Cao, Y. U., Fukunaga, A. S., & Kahng, A. (1997). Cooperative mobile robotics: Antecedents and directions.
Autonomous Robots, 4(1), 7 – 27.
6. Clancey, W. J. (1997). Situated cognition: On human knowledge and computer representations. Cambridge, UK:
Cambridge University Press.
7. Di Paolo, E. (2000). Behavioral coordination, structural congruence and entrainment in a simulation of
acoustically coupled agents. Adaptive Behavior, 8(1), 27 – 48.
8. Dorigo, M., & S¸ahin, E. (2004). Swarm robotics — Special issue editorial. Autonomous Robots, 17(2 – 3),
111 – 113.
9. Dorigo, M., & S¸ahin, E. (2007). Swarm robotics. Scholarpedia. http://scholarpedia.org/articles/
Swarm_Robotics. Accessed November 2007.
Artificial Life Volume 14, Number 2
177
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
4
2
1
5
7
1
6
6
2
4
7
0
a
r
t
l
.
/
.
.
2
0
0
8
1
4
2
1
5
7
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
E. Tuci et al.
Evolving Homogeneous Neurocontrollers for a Group of Heterogeneous Robots
10. Dudek, G., & Jenkin, M. (2000). Computational principles of mobile robotics. Cambridge, UK: Cambridge
University Press.
11. Fong, T., Nourbakhsh, I., & Dautenhahn, K. (2002). A survey of socially interactive robots. Robotics
and Autonomous Systems, 42(3 – 4), 143 – 166.
12. Garnier, S., Gautrais, J., & Theraulaz, G. (2007). The biological principles of swarm intelligence.
Swarm Intelligence, 1(1), 3 – 31.
13. Gibson, J. J. (1977). The theory of affordances. In R. Shaw & J. Bransford (Eds.), Perceiving, acting and
knowing. Toward an ecological psychology (pp. 67 – 82). Hillsdale, NJ: Lawrence Erlbaum Associates.
14. Goldberg, D. E. (1989). Genetic algorithms in search, optimization and machine learning. Reading, MA:
Addison-Wesley.
15. Grasse´, P. P. (1959). La reconstruction du nid et les coordinations inter-individuelles chez Bellicositermes
natalensis et Cubitermes sp. La the´orie de la stigmergie: Essai d’interpre´tation du comportement des termites
constructeurs. Insectes Sociaux, 6, 41 – 81.
16. Kandel, E., Schwartz, J., & Jessell, T. (Eds.) (2000). Principles of neural science (4th ed.). New York:
McGraw-Hill.
17. Kube, C. R., & Zhang, H. (1993). Collective robotics: From social insects to robots. Adaptive Behaviour,
2(2), 189 – 218.
18. Marocco, D., & Nolfi, S. (2005). Emergence of communication in embodied agents: Co-adapting
communicative and non-communicative behaviours. In A. Cangelosi, G. Bugmann, & R. Borisyuk
(Eds.), Modeling Language, Cognition and Action: 9th Neural Computation and Psychology Workshop. Singapore:
World Scientific.
19. Marocco, D., & Nolfi, S. (2006). Self-organization of communication in evolving robots. In L. Rocha,
L. Yaeger, M. Bedau, D. Floreano, R. Goldstone, & A. Vespignani (Eds.), Proceedings of the 10th International
Conference on the Simulation and Synthesis of Living Systems (Artificial Life X) (pp. 178 – 184). Cambridge, MA:
MIT Press.
20. Mondada, F., Pettinaro, G. C., Guignard, A., Kwee, I. W., Floreano, D., Deneubourg, J.-L., Nolfi, S.,
Gambardella, L. M., & Dorigo, M. (2004). SWARM-BOT: A new distributed robotic concept. Autonomous
Robots, 17(2 – 3), 193 – 221.
21. Nolfi, S., & Floreano, D. (2000). Evolutionary robotics: The biology, intelligence, and technology of self-organizing
machines. Cambridge, MA: MIT Press.
22. Quinn, M. (2001a). A comparison of approaches to the evolution of homogeneous multi-robot
teams. In Proceedings of the 2001 Congress on Evolutionary Computation (pp. 128 – 135). Piscataway, NJ:
IEEE Press.
23. Quinn, M. (2001b). Evolving communication without dedicated communication channels. In J. Kelemen &
P. Sosik (Eds.), Advances in Artificial Life: 6th European Conference on Artificial Life (pp. 357 – 366). Berlin:
Springer Verlag.
24. Quinn, M., Smith, L., Mayley, G., & Husbands, P. (2003). Evolving controllers for a homogeneous system
of physical robots: Structured cooperation with minimal sensors. Philosophical Transactions of the Royal Society
of London, Series A, 361, 2321 – 2344.
25. Støy, K. (2001). Using situated communication in distributed autonomous mobile robots. In Proceedings
of the 7th Scandinavian Conference on Artificial Intelligence (pp. 44 – 52). Amsterdam: IOS Press.
26. Trianni, V., & Dorigo, M. (2006). Self-organisation and communication in groups of simulated and
physical robots. Biological Cybernetics, 95, 213 – 231.
27. Vicentini, F., & Tuci, E. (2006). Swarmod: A 2D s-bot’s simulator. Technical Report TR/IRIDIA/2006-005,
IRIDIA, CoDE, Universite´ Libre de Bruxelles. This report is available at http://iridia.ulb.ac.be/
IridiaTrSeries.html (accessed March 2006).
28. Winfield, A. F. T., Sa, J., Gago, M. C., Dixon, C., & Fisher, M. (2005). On formal specification of emergent
behaviours in swarm robotic systems. International Journal of Advanced Robotic Systems, 2(3), 363 – 370.
178
Artificial Life Volume 14, Number 2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
4
2
1
5
7
1
6
6
2
4
7
0
a
r
t
l
.
/
.
.
2
0
0
8
1
4
2
1
5
7
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3