Efficient Content-Based Sparse Attention with Routing Transformers
Aurko Roy Mohammad Saffar Ashish Vaswani David Grangier
Google Research
{aurkor,msaffar,avaswani,grangier}@google.com
Abstract
Self-attention has recently been adopted for
a wide range of sequence modeling problems.
Despite its effectiveness, self-attention suffers
from quadratic computation and memory re-
quirements with respect to sequence length.
Successful approaches to reduce this complex-
ity focused on attending to local sliding win-
dows or a small set of locations independent
of content. Our work proposes to learn dy-
namic sparse attention patterns that avoid
allocating computation and memory to attend
to content unrelated to the query of interest.
This work builds upon two lines of research:
It combines the modeling flexibility of prior
work on content-based sparse attention with
the efficiency gains from approaches based on
local, temporal sparse attention. Our model,
the Routing Transformer, endows self-attention
with a sparse routing module based on on-
line k-means while reducing the overall com-
plexity of attention to O(n1.5d) from O(n2d)
for sequence length n and hidden dimension
d. We show that our model outperforms com-
parable sparse attention models on language
modeling on Wikitext-103 (15.8 vs 18.3
perplexity), as well as on image generation on
ImageNet-64 (3.43 vs 3.44 bits/dim) while
using fewer self-attention layers. Additionally,
we set a new state-of-the-art on the newly
released PG-19 data-set, obtaining a test
perplexity of 33.2 with a 22 layer Routing
Transformer model trained on sequences of
length 8192. We open-source the code for
Routing Transformer in Tensorflow.1
1
Introduction
Generative models of sequences have witnessed
rapid progress driven by the application of atten-
1https://github.com/google-research
/google-research/tree/master/routing
transformer.
53
tion to neural networks. In particular, Bahdanau
et al. (2015), Cho et al. (2014), and Vaswani et al.
(2017) relied on attention to drastically improve
the state-of-the art in machine translation. Subse-
quent research (Radford et al., 2018; Devlin et al.,
2019; Liu et al., 2019; Yang et al., 2019) demon-
strated the power of self-attention in learning
powerful representations of language to address
several natural language processing tasks. Self-
attention also brought impressive progress for
generative modeling outside of language, for
example, image (Parmar et al., 2018; Menick and
Kalchbrenner, 2018; Child et al., 2019) and music
generation (Huang et al., 2018; Child et al., 2019).
Self-attention operates over sequences in a
step-wise manner: At every time-step, attention
assigns an attention weight to each previous input
element (representation of past time-steps) and
uses these weights to compute the representation
of the current time-step as a weighted sum of the
past input elements (Vaswani et al., 2017). Self-
attention (Shaw et al., 2018) is a particular case
of attention (Bahdanau et al., 2015; Chorowski
et al., 2015; Luong et al., 2015).
Self-attention is commonly used in auto-
regressive generative models. These models gen-
erate observations step-by-step, modeling the
probability of the next symbol given the previously
generated ones. At every time step, self-attentive
generative models can directly focus on any part
of the previous context. In contrast, recurrent
neural networks (RNNs) and convolutional neural
networks (CNNs) have direct interactions with
only a local neighborhood of context around the
current time step.
This advantage, however, comes at a price:
Unlike recurrent networks or convolution net-
works, the time and space complexity of self-
attention is quadratic in n,
the length of the
sequence. Specifically, for every position i ≤ n,
self-attention computes weights for its whole
context of length i, which induces a complexity
i≤n i = n(n − 1)/2. This makes it difficult
of
(cid:2)
Transactions of the Association for Computational Linguistics, vol. 9, pp. 53–68, 2021. https://doi.org/10.1162/tacl a 00353
Action Editor: Xavier Carreras. Submission batch: 6/2020; Revision batch: 8/2020; Published 02/2021.
c(cid:3) 2021 Association for Computational Linguistics. Distributed under a CC-BY 4.0 license.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
3
1
9
2
3
9
3
2
/
/
t
l
a
c
_
a
_
0
0
3
5
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
to scale attention-based models to modeling long
sequences. However, long sequences are the norm
in many domains, including music, image, speech,
video generation, and document-level machine
translation.
Therefore, an important research direction is
to investigate sparse and memory efficient forms
of attention in order to scale to tasks with large
sequence lengths. Previous work has proposed
data independent or fixed sparsity patterns bound-
ing temporal dependencies, such as local or strided
attention. At each time step, the model attends
only to a fixed number of time steps in the past
(Child et al., 2019). Extensions to local attention
have suggested learning the length of the tem-
poral sparsity for each attention module in the
network (Sukhbaatar et al., 2019). These strat-
egies draw their inspiration from RNNs and
CNNs and bound their complexity by attend-
ing only to representations summarizing a local
neighborhood of the current
time step. Their
attention matrices (matrices containing the atten-
tion weights for every pair of previous, current
time-step) are natively sparse and require instan-
tiating only non-zero entries. While these ap-
proaches have achieved good results, fixing the
sparsity pattern of a content based mechanism
such as self-attention can limit its ability to pool
in information from large contexts.
As an alternative to local attention, Correia
et al. (2019) consider content-based sparsity, an
approach allowing for arbitrary sparsity patterns.
This formulation, however, does require instan-
tiating a full dense attention matrix prior to spar-
sification through variants of L0-sparsity or
sparsemax approximations (Blondel et al., 2019).
The present work builds upon these two lines
of research and proposes to retain the modeling
flexibility of content-based sparse attention while
leveraging the efficiency of natively sparse at-
tention matrices. Our formulation avoids sparse-
max variants and relies on clustering of attention
instead. Each attention module considers a
clustering of the space: The current time-step only
attends to context belonging to the same cluster.
In other words, the current time-step query is
routed to a limited number of context elements
through its cluster assignment. This strategy draws
inspiration from the application of spherical k-
means clustering to the Maximum Inner Product
Search (MIPS) problem.
Our proposed model, Routing Transformer,
combines our efficient clustering-based sparse
attention with classical local attention to reach
excellent performance both for language and
image generation. These results are obtained with-
out the need to maintain attention matrices larger
than batch length which is the case with the seg-
ment level recurrence mechanism used in Dai et al.
(2019) and Sukhbaatar et al. (2019). We pres-
ent experimental results on language modeling
(enwik-8, Wikitext-103, and PG-19) and
unconditional image generation (CIFAR-10 and
ImageNet-64). Routing Transformer sets new
state-of-the-art, while having comparable or
fewer number of self-attention layers and heads,
on Wikitext-103 (15.8 vs 18.3 perplexity),
PG-19 (33.2 vs 33.6 perplexity), and on
ImageNet-64 (3.43 vs 3.44 bits/dim). We also
report competitive results on enwik-8 (0.99
vs 0.98 perplexity) and present ablations on
CIFAR-10.
2 Related Work
Attention with Temporal Sparsity: Research on
efficient attention neural models parallels the
advent of attention-based architectures. In the
context of
Jaitly et al.
speech recognition,
(2016) proposed the Neural Transducer, which
segments sequences in non-overlapping chunks
and attention is performed in each chunk inde-
pendently. Limiting attention to a fixed temporal
context around the current prediction has also
been explored in Chorowski et al. (2015), while
Chiu and Raffel (2018) dynamically segment the
sequence into variable sized-chunks.
Hierarchical attention strategies have also been
explored: The model first considers which part of
the inputs should be attended to before computing
full attention in a contiguous neighborhood of the
selected area (Gregor et al., 2015; Xu et al., 2015;
Luong et al., 2015). Later, hierarchical attention,
simplified by Liu et al. (2018), alternates coarse
layers (attending to the whole sequence at a lower
temporal resolution) with local layers (attending
to a neighborhood of the current prediction).
This alternating strategy is also employed by
Child et al. (2019), who introduce bounded and
strided attention, namely, attending to a fixed
context in the past at a sub-sampled temporal
resolution. This work formalizes such a strategy
54
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
3
1
9
2
3
9
3
2
/
/
t
l
a
c
_
a
_
0
0
3
5
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
using a sparse attention formalism, showing how
it relates to full attention with a specific sparsity
pattern in the attention matrix. It shows that
sparse attention is sufficient to get state-of-the-art
results in modeling long sequences over language
modeling, image generation and music generation.
Sukhbaatar et al. (2019) build upon this work and
show that it is possible to obtain further sparsity by
letting the model learn the length of the temporal
context for each attention module. This work also
makes use of the attention cache introduced in Dai
et al. (2019), a memory mechanism to train models
over temporal contexts which extend beyond the
length of the training batches.
Attention with Content-Based Sparsity: The
above work mainly relies on two efficient ideas:
attending to less elements by only considering
a fixed bounded local context in the past, and
attending to less elements by decreasing the
temporal resolution of context. These ideas do
not allow arbitrary sparsity patterns in attention
matrices. Content-based sparse attention has been
introduced to allow for richer patterns and more
expressive models. (Martins and Kreutzer (2017)
and Malaviya et al. (2018)) propose to compute
attention weights with variants of sparsemax.
Correia et al. (2019) generalize this approach
to every layer in a Transformer using entmax
which allows for more efficient inference. This
line of work allows for learning arbitrary sparsity
attention patterns from data, based on the content
of the current query and past context. However,
sparsity here cannot be leveraged to improve space
and time complexity because sparsemax/entmax
formulations require instantiating the full attention
matrix prior to sparsification. This is a drawback
compared with temporal sparsity approaches. Our
work is motivated by bridging this gap and allows
for arbitrary sparsity patterns while avoiding
having to instantiate non-zero entries of attention
matrices.
Contemporaneous to our work, Kitaev et al.
(2020) proposed to use Locality Sensitive Hashing
(LSH) using random hyperplanes to infer content
based sparsity patterns for attention: tokens that
to attend
into the same hash bucket, get
fall
to each other. While similar in spirit
to our
approach, the approach of Kitaev et al. (2020)
keeps the randomly initialized hyperplanes fixed
throughout, while we use mini-batch spherical k-
means to learn the space-partitioning centroids.
The motivation in both approaches is to approx-
imate MIPS in the context of dot product
attention, for which both LSH and spherical k-
means have been used in literature. However,
typically spherical k-means is known to out-
perform LSH for MIPS (see, e.g., Auvolat et al.,
2015). This is borne out in the common task of
Imagenet-64 generation, where Reformer gets
around 3.65 bits/dim (Figure 3), while the Routing
Transformer gets 3.43 bits/dim (see Table 4 for a
comparison).
Sparse Computation beyond Attention:
Learning models with sparse representations/
activations for saving time and computation has
been addressed in the past in various contexts.
Previous work often refers to this goal as gating
for conditional computation. Gating techniques
relying on sampling and straight-through gradient
estimators are common (Bengio et al., 2013; Eigen
et al., 2013; Cho and Bengio, 2014). Conditional
computation can also be addressed with rein-
forcement learning (Denoyer and Gallinari, 2014;
Indurthi et al., 2019). Memory augmented neural
networks with sparse reads and writes have also
been proposed in Rae et al. (2016) as a way to scale
Neural Turing Machines (Graves et al., 2014). In
the domain of language modeling, a related work
is the sparsely gated Mixture-of-experts (MOE)
(Shazeer et al., 2017), where sparsity is induced
by experts and a trainable gating network controls
the routing strategy to each sub-network. Another
related work is Lample et al. (2019) who use
product quantization based key-value lookups to
replace the feed forward network in the Trans-
former. Our work differs from theirs in that we
make use of dynamic key-value pairs to infer spar-
sity patterns, while their key-value pairs are the
same across examples.
3 Self-Attentive Auto-regressive
Sequence Modeling
Auto-regressive sequence models decompose the
probability of a sequence x = (x1, . . . , xn) as
p(x) = pθ(x1)
n(cid:3)
i=2
pθ(xi|x
follows that
(cid:8)Qi − μ(cid:8) , (cid:8)Kj − μ(cid:8) < ε. This implies via
triangle inequality that:
(13)
Thus, from Equation 12 it follows that, Q(cid:4)
i Kj >
1 − 2ε2. Therefore, when two time steps i > j
are assigned the same cluster due to a small
(cid:8)Qi − μ(cid:8) , (cid:8)Kj − μ(cid:8) distance, it also means that
their attention weight Q(cid:4)
i Kj is high, namely, Kj
is an approximate solution to the MIPS objective
of Equation 9 for query Qi. This analysis shows
that our clustering routing strategy preserves large
attention weights as non-zero entries.
Because we route attention via spherical
k-means clustering, we dub our model Routing
Transformer. We give a detailed pseudo-code
implementation for the routing attention compu-
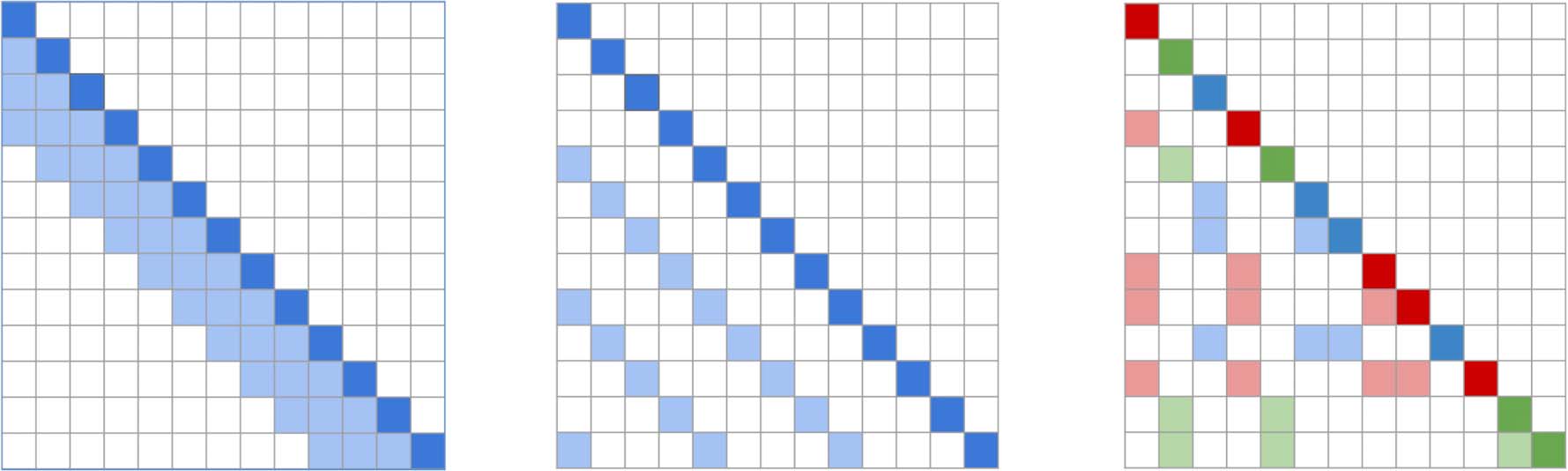
tation in Algorithm 1. A visualization of the at-
tention scheme and its comparison to local and
strided attention is given in Figure 1. The com-
putational complexity of this variant of sparse
attention is O(nkd + n2d/k). Cluster assignments
correspond to the first term, that is, it compares
n routing vectors to all k centroids in a space of
size d. Query/key dot products corresponds to the
second term, that is, assuming balanced clusters,
each of the n queries is compared to n/k in
its cluster through a dot product of dimension d.
n as in Child
Therefore the optimal choice of k is
et al. (2019), thereby reducing overall memory
(cid:5)
and computational cost to O
instead of
O(n2d) (Vaswani et al., 2017).
n1.5d
√
(cid:4)
In practice, we apply mini-batch k-means to
train the cluster centroids. However, in order to
58
K ← Q
Algorithm 1 Routing Attention
1: Queries, Keys and Values: Q, K, V ∈ Rn×d
2: Centroid: μ ∈ Rk×d
3: decay: λ
4: if left to right mask then
5:
6: (cid:6) Normalize to unit ball
7: Q ← LayerNorm(Q) (cid:6) scale, bias disabled
8: K ← LayerNorm(K) (cid:6) scale, bias disabled
9: Qprod ← μQ(cid:4)
(cid:6) k × n
10: if not left to right mask then
11:
12: w ← n/k
13: Qidx ← top-k(Qprod, w)
14: Qidx ← sort(Qidx)
15: Kidx ← Qidx
16: if not left to right mask then
17:
(cid:6) k × n
(cid:6) attention window
(cid:6) k × w
(cid:6) sort to preserve order
(cid:6) k × w
Kprod ← μK (cid:4)
Kidx ← top-k(Kprod, w)
Kidx ← sort(Kidx)
(cid:6) k × w
(cid:6) sort to preserve
A ← ltr(A)
(cid:6) k × w × d
(cid:6) k × w × d
(cid:6) k × w × d
(cid:6) k × w × w
19: Q(cid:5) ← gather(Q, Qidx)
20: K (cid:5) ← gather(K, Kidx)
21: V (cid:5) ← gather(V, Kidx)
22: A ← Q(cid:5)(K (cid:5))(cid:4)
23: if left to right mask then
24:
25: A ← softmax(A).
26: V (cid:5) ← einsum(kww, kwd → kwd, A, V (cid:5))
27: X ← scatter(Kidx, V (cid:5))
28: Qm ← one-hot(arg max(Qprod))
29: Km ← one-hot(arg max(Kprod))
30: (cid:6) Update centroids
31: μ ← λμ + (1 − λ)QmQ/2 + (1 − λ)KmK/2
32: return X
(cid:6) k × n
(cid:6) k × n
(cid:6) k × w × w
√
infer balanced routing patterns, we define the
sets Si to be of equal size roughly n/k ∼
n,
is, for every centroid μi we sort
tokens
that
by distance to μi and cluster membership is
determined by this threshold (top-k). This adds an
additional O(n log n) term to the cost, however
note that this is eclipsed by the dominating term of
O(n1.5d). This strategy is simple and efficient. In
particular, it guarantees that all clusters have the
same size, which is extremely important in terms
of computational efficiency on parallel hardware
like graphic cards. As a downside, this assignment
does not guarantee that each point belongs to a
single cluster. In the future, we want to investigate
using balanced variants of k-means (Banerjee and
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
3
1
9
2
3
9
3
2
/
/
t
l
a
c
_
a
_
0
0
3
5
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
3
1
9
2
3
9
3
2
/
/
t
l
a
c
_
a
_
0
0
3
5
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Figure 1: Figures showing 2-D attention schemes for the Routing Transformer compared to local attention and
strided attention of (Child et al., 2019). The rows represent the outputs while the columns represent the inputs. For
local and strided attention, the colored squares represent the elements every output row attends to. For attention
routed as in Section 4.1, the different colors represent cluster memberships for the output token.
Ghosh, 2004; Malinen and Fr¨anti, 2014) which is
not common in an online setting.
During training, we update each cluster centroid
μ by an exponentially moving average of all the
keys and queries assigned to it:
μ ← λμ +
(1−λ)
2
(cid:6)
Qi +
(1−λ)
2
(cid:6)
Kj,
i:μ(Qi)=μ
j:μ(Kj )=μ
where λ is a decay parameter that we usually set
to 0.999. Additionally, we also exclude padding
tokens from affecting the centroids.
There is an additional nuance regarding
clustering queries and keys that comes into
left
play when using causal attention (i.e.,
to right masking), as is usually the case in
language models. When grouping queries and
keys belonging to a certain cluster centroid μ,
we may get as members queries Qi for keys
Kj where time-step i ≤ j. This therefore re-
quires an additional masking strategy in addition
to the lower triangular mask used for causal at-
tention. One solution that avoids having to use
an additional mask, is to simply share keys and
queries. Empirically, we have found that
this
works at par or better than separate keys and que-
ries together with an additional masking strategy
in the causal attention setting. For encoder self
attention and encoder-decoder cross-attention, ad-
ditional masking or sharing queries and keys is
not necessary.
5 Experiments
We evaluate our sparse attention model on
various generative modeling tasks including text
59
and image generation. The following sections
report our results on CIFAR-10, Wikitext-
103 (Merity et al., 2017), enwik-8 (Mahoney,
2011), ImageNet-64, as well as PG-19 (Rae
et al., 2020). We find that a scaled up version
of local attention is a surprisingly strong baseline
and that our Routing Transformer outperforms
Transformer-XL (Dai et al., 2019) and the Sparse
Transformer model of Child et al. (2019) on all
tasks. On the recently released PG-19 data-set, we
find that local attention again is a strong baseline,
with a slightly worse performance compared to
Transformer-XL (Dai et al., 2019). We also
find that the Routing Transformer model out-
performs both Transformer-XL (Dai et al., 2019)
and Compressive Transformer (Rae et al., 2020),
setting a new state-of-the-art result.
In all our models except
the one used for
PG-19, we allocate half the heads to do local
attention and the other half to route attention as
in Equation 8. For all our experiments except
for PG-19, we use the Adam optimizer (Kingma
and Ba, 2015) with learning rate 2 × 10−4 with
β1 = 0.9 and β2 = 0.98 following the learning
rate schedule described in Vaswani et al. (2017).
We train all models on 128 TPUv3 cores. The
setup used for PG-19 is described in Section 5.5.
5.1 CIFAR-10
CIFAR-10 is a widely used image data-set
that consists of 60,000 colored images of size
32 × 32. Since the sequence lengths in this case
are relatively short (3072), we use this as a toy
data-set
to perform various ablations to tease
apart the effect of various hyperparameter choices
Model
Transformer
Local Transformer
Random Transformer
Routing Transformer
Routing Transformer
Routing Transformer
Routing Transformer
Routing Transformer
Routing Transformer
Routing Transformer
Routing Transformer
Routing Transformer
Routing Transformer
Routing Transformer
Routing Transformer
Routing Transformer
Routing Transformer
Routing Transformer
Routing Transformer
Routing Transformer
Routing Transformer
Routing Transformer
Routing Transformer
Routing Transformer
Routing Transformer
Routing Transformer
Routing Transformer
Routing heads Routing Layers Attention window Bits/dim Steps/sec
0
0
4 (random)
2
4
8
2
4
8
2
4
8
2
4
8
2
4
8
2
4
8
2
4
8
2
4
8
0
0
8 (random)
2
2
2
4
4
4
8
8
8
12
12
12
2
2
2
4
4
4
8
8
8
12
12
12
3072
512
512
512
512
512
512
512
512
512
512
512
512
512
512
1024
1024
1024
1024
1024
1024
1024
1024
1024
1024
1024
1024
2.983
3.009
3.076
3.005
2.986
2.992
2.995
2.975
2.991
2.995
2.971
3.190
2.978
2.994
3.400
2.975
2.950
2.982
2.990
2.958
3.003
2.991
2.983
3.131
2.973
3.005
3.291
5.608
9.023
5.448
7.968
7.409
6.682
7.379
6.492
5.385
6.442
5.140
3.897
5.685
4.349
3.062
7.344
6.440
5.192
6.389
5.112
3.674
5.057
3.597
2.329
4.151
2.788
1.711
Table 1: Ablation studies of the Routing Transformer model on the CIFAR-10 data-set. All the models
have a total of 12 attention layers and 8 heads. Routing layers when present are always added at the
top of the model. A Routing Transformer model with less than 12 routing attention layers and less than
8 routing heads, has the remaining layers and heads of type local attention. A Random Transformer
model has a random attention head in place of the routing attention head. We report the performance in
bits/dim on the test set and step times are reported on a TPUv3.
on the model performance. We train 12 layer
models with a total of 8 attention heads, and
report a comparison of the effect of various hyper-
parameter choices on the performance and speed
on this data-set. In particular, the following hyper-
parameters are varied 1) the number of routing
attention heads, 2) the number of routing attention
layers, and 3) the size of the attention window.
For routing attention we use k = 6 while varying
the attention window, to see the effect on speed
and performance. All the CIFAR-10 models are
trained with a batch size of 32 and for a total of
200,000 steps. In addition, we also compare the
Routing Transformer to a Random Transformer,
where Kidx is randomly chosen rather than being
drawn from nearest neighbor search. For a fair
comparison, we take the best model from Table 1,
with an attention window of 512 and replace all
routing heads with random heads. We present the
ablation results in Table 1 and discuss it in more
detail in Section 6.
5.2 Wikitext-103
Wikitext-103 (Merity et al., 2017) is a large
public benchmark data-set for testing long term
dependencies in word-level language models. It
contains over 100 million tokens from 28K articles
extracted from Wikipedia with an average of 3.6K
tokens per article, which makes it a reference data-
set to model long-term textual dependencies. We
60
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
3
1
9
2
3
9
3
2
/
/
t
l
a
c
_
a
_
0
0
3
5
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
train a 10 layer Routing Transformer with 16 heads
using the relative position encoding of Shaw et al.
(2018) and with attention and ReLU dropout rate
of 0.3 each. For routing attention as in Section 4.1
we choose k = 16 and attention window to be 256
during both training and evaluation. We describe
our results in Table 2 and compare it to other
recent work on sparse or recurrent attention such
as Adaptive Inputs (Baevski and Auli, 2019) and
TransformerXL (Dai et al., 2019) as well as a local
attention with relative position encoding baseline
(Huang et al., 2018). We find that local attention
is a great inductive bias for sparse attention and
is better than the adaptive methods proposed in
Baevski and Auli (2019); Sukhbaatar et al. (2019).
Moreover, our Routing Transformer model is able
to get a test perplexity of 15.8 improving on
the 18.3 obtained by TransformerXL (Dai et al.,
2019) while having fewer self-attention layers, and
without the need for segment level recurrence.
5.3 enwik-8
The enwik-8 (Mahoney, 2011) is a data-set to
benchmark text compression algorithms in the
context of the Hutter prize. This data-set consists
of the first 100M bytes of unprocessed Wikipedia.
It is typically used to evaluate character-level
language models. Similar to the prior work of
Dai et al. (2019) and Child et al. (2019) we use a
sequence length n = 8192 and benchmark our
results against various baselines including local
attention. We train a 24 layer model with 8
attention heads with an attention and ReLU
dropout rate of 0.4 each and using the relative
position encoding of Shaw et al. (2018). For
routing attention as in Section 4.1 we set k = 32
and attention window 256. We report perplexity of
0.99 like TransformerXL and Sparse Transformer,
slightly under 0.98 from Adaptive Transformer.
5.4 ImageNet 64×64
than text, we report
In order to evaluate the ability of our model to
capture long term dependencies on a modality
other
results on the
ImageNet 64 × 64 data-set as used in Child et al.
(2019). For auto-regressive image generation, this
data-set consists of images of 64 × 64 × 3 bytes
represented as long sequences of length 12,288
presented in raster scan, red-green-blue order. We
train a 24 layer model with 16 attention heads, with
half the heads performing local attention, and the
other half routing attention as in Section 3. For
routing attention we set k = 8, attention window
2048, batch size 1, and train our model for roughly
70 epochs as in Child et al. (2019). We compare
our model to a scaled-up ImageTransformer model
with local attention (Parmar et al., 2018) and the
SparseTransformer model of Child et al. (2019).
We find that local attention (Parmar et al.,
2018) is a strong baseline for image generation,
obtaining 3.48 bits/dim when scaled up to 24
layers and 16 heads, compared to later work like
Sub-scale Pixel Networks (SPN) (Menick and
Kalchbrenner, 2018). Our Routing Transformer
model achieves a performance of 3.425 bits/dim
(see Table 4) compared to the previous state-
of-the-art of 3.437 bits/dim (Child et al., 2019),
thereby showing the advantage of the content
based sparsity formulation of Section 4.1.
5.5 PG-19
PG-19 is a new data-set released by Rae et al.
(2020) which is larger and longer than previous
language modeling data-sets. The data-set
is
created from approximately 28,000 Project
Gutenberg books published before 1919, con-
sisting of 1.9 billion tokens and comprises an
average context size of roughly 69,000 words.
This is text that is 10× longer in context than
all prior data-sets such as Wikitext-103, with
minimal pre-processing and an open vocabulary
that makes it extremely challenging for long text
modeling tasks. We use a subword vocabulary of
size approximately 98,000 and report perplexities
normalized by the token counts reported in Rae
et al. (2020). On this data-set we train a 22 layer
Routing Transformer model with 8 heads with a
sequence length of 8192 and set a new state-of-
the-art result on this data-set, improving on both
Compressive Transformers (Rae et al., 2020), as
well as Transformer-XL (Dai et al., 2019). For
this data-set we change our training setup in three
ways. Firstly, we use only 2 routing heads instead
of sharing it equally with local heads. Secondly,
we use routing heads only in the last two layers
of the model instead of having them present in
every layer. This is motivated by our empirical
finding that long range attention is only needed
in the last few layers – see also Rae and Razavi
(2020). Finally, we use the Adafactor optimizer
(Shazeer and Stern, 2018) which is more memory
efficient than Adam in training larger models.
We use a learning rate constant of 0.01 with a
61
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
3
1
9
2
3
9
3
2
/
/
t
l
a
c
_
a
_
0
0
3
5
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Model
Layers Heads Perplexity
LSTMs (Grave et al., 2017)
QRNNs (Merity et al., 2018)
Adaptive Transformer (Sukhbaatar et al., 2019)
Local Transformer
Adaptive Input (Baevski and Auli, 2019)
TransformerXL (Dai et al., 2019)
Routing Transformer
−
−
36
16
16
18
10
−
−
8
16
16
16
16
40.8
33.0
20.6
19.8
18.7
18.3
15.8
Table 2: Results on language modeling on Wikitext-103 data-set. Local
Transformer refers to Transformer (Vaswani et al., 2017) with relative position
encoding (Shaw et al., 2018) together with local attention. Perplexity is reported
on the test set.
Model
Layers
Heads
Bits per byte
T64 (Al-Rfou et al., 2019)
Local Transformer
TransformerXL (Dai et al., 2019)
Sparse Transformer (Child et al., 2019)
Adaptive Transformer (Sukhbaatar et al., 2019)
Routing Transformer
64
24
24
30
24
12
2
8
8
8
8
8
1.13
1.10
0.99
0.99
0.98
0.99
Table 3: Results on language modeling on enwik-8 data-set. Local Transformer refers to
Transformer (Vaswani et al., 2017) with relative position encoding (Shaw et al., 2018) together
with local attention. Bits per byte (bpc) is reported on the test set.
Model
Layers Heads Bits/dim
Glow (Kingma and Dhariwal, 2018)
PixelCNN (Van den Oord et al., 2016)
PixelSNAIL (Chen et al., 2018)
SPN (Menick and Kalchbrenner, 2018)
ImageTransformer (Parmar et al., 2018)
Sparse Transformer (Child et al., 2019)
Reformer (Kitaev et al., 2020)
Routing Transformer
−
−
−
−
24
48
−
24
−
−
−
−
16
16
−
16
3.81
3.57
3.52
3.52
3.48
3.44
3.65
3.43
Table 4: Results on image generation on ImageNet- 64 in bits/dim.
linear warmup over 10,000 steps followed by a
rsqrt normalized decay. We do not make use
of any dropout, or weight decay. The hidden
dimension of our model is 1032 and the batch size
is 8192 tokens.
From Table 5, we see that Local Transformer
again sets a very strong baseline, with a 24-layer
local attention model obtaining a test set perplexity
of 39.3, while a 36-layer Transformer-XL gets
36.3. Moreover, a 22-layer Routing Transformer
improves on the 36-layer Compressive
model
Transformer, obtaining a test set perplexity of
33.2 compared to 33.6, while being able to gen-
erate sequences of length 8192.
6 Analysis
6.1 Local vs Global
As reported in Section 5, a scaled up version of
local attention is a strong baseline for efficient
attention over long sequences. From Table 1 we
see that local attention is slightly worse than full
attention – 3.009 vs 2.983 bits per dim. Adding 2
62
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
3
1
9
2
3
9
3
2
/
/
t
l
a
c
_
a
_
0
0
3
5
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Model
Layers
Heads
Perplexity
Local Transformer
TransformerXL (Dai et al., 2019)
Compressive Transformer (Rae et al., 2020)
Routing Transformer
24
36
36
22
8
−
−
8
39.3
36.3
33.6
33.2
Table 5: Results on language modeling on PG-19 data-set. Local Transformer refers to
Transformer (Vaswani et al., 2017) with relative position encoding (Shaw et al., 2018)
together with local attention. Perplexity is normalized by the number of tokens reported
in (Rae et al., 2020) and is reported on the test set.
layer 0
layer 1
layer 2
layer 3
layer 4
layer 5
layer 6
layer 7
layer 8
layer 9
JSD(local(cid:8)local)
0.0038 ± 0.0018
0.3071 ± 0.1217
0.2164 ± 0.0803
0.1163 ± 0.0336
0.1840 ± 0.0562
0.2284 ± 0.0225
0.1901 ± 0.0525
0.1566 ± 0.0685
0.1638 ± 0.0739
0.2095 ± 0.0560
JSD(local(cid:8)routing)
0.4706 ± 0.0319
0.6674 ± 0.0153
0.5896 ± 0.0249
0.6047 ± 0.0181
0.6266 ± 0.0062
0.6463 ± 0.0155
0.6471 ± 0.0040
0.5798 ± 0.0235
0.5993 ± 0.0148
0.6127 ± 0.0053
JSD(routing(cid:8)routing)
0.1579 ± 0.0576
0.5820 ± 0.0104
0.4015 ± 0.0121
0.4144 ± 0.0264
0.4191 ± 0.0879
0.4687 ± 0.0449
0.5175 ± 0.0469
0.4350 ± 0.0139
0.4268 ± 0.0291
0.3581 ± 0.0019
Table 6: Jensen-Shannon divergence between the attention distributions of a random local
attention head and a random head that routes attention as in Section 4.1 per layer on the
Wikitext-103 data-set. We report means and standard deviations computed over 10 runs
and use the natural logarithm so that divergences are upper-bounded by 0.6931.
routing layers with 4 heads almost closes the gap
with the performance of full attention, achieving
2.986 bits per dim. Adding more routing layers
and heads improves performance up to a point,
with the best performing model with an attention
window of 512 having 4 routing layers and 4
routing heads, and achieving 2.975 bits per dim.
Increasing the attention window from 512 to 1024
uniformly results in improvement in every setting.
The best model on CIFAR-10 has an attention
window of 1024 with 4 routing layers and 4 routing
heads. Interestingly, the best Routing Transformer
models perform better than full attention, but not
by a large enough amount to rule out noise. More
importantly, Table 1 shows the importance of
local attention in building intermediate represen-
tations, with a model with only routing attention
layers and heads with attention windows of 512
and 1024 achieving 3.400 and 3.291 bits per dim
respectively.
Thus Table 1 shows us the importance of local
representations, as well as the benefit of adding
a few routing layers and heads to enforce a more
global representation. Because attention weights
are a probability distribution on the entire set of
tokens, we evaluate the difference in attention
patterns between local and routing attention by
computing the Jensen-Shannon divergence bet-
ween the two kinds of attention distributions for a
random subset of heads in our network on the
Wikitext-103 data-set. The divergence is
computed over the entire sequence length of 4096.
We average over 10 runs and report means and
standard deviations of the JSD in Table 6. Note
that the JSD is always non-negative and is upper-
bounded by 0.6931 when computed using the
natural logarithm. We observe that the divergence
between the different local heads is always very
low compared to the divergence between local
and routing attention heads, which is almost
always very close to the upper-bound of 0.6931.
Divergence between different routing attention
heads falls somewhere in between, being closer
to the upper-bound. This shows that the attention
distribution inferred by the routing attention of
Section 4.1 is highly non-local in nature and
different heads specialize in attending to very
different parts of the input.
63
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
3
1
9
2
3
9
3
2
/
/
t
l
a
c
_
a
_
0
0
3
5
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Model
Dataset Seq. length Layers Heads Attention window Steps/sec
PG-19
Local Transformer
Routing Transformer PG-19
8192
8192
24
22
8
8
512
512
1.231
0.7236
Table 7: Step time comparison between Local Transformer and Routing Transformer on a TPUv3
for the PG-19 data-set.
that
Qualitatively, from the ablations in Table 1,
we hypothesize that the reason for the strong
performance of the Routing Transformer is due
to the fact
it combines building local
representations over several layers, together with
enforcing global consistency for every token.
This is achieved via an approximate MIPS over
the entire set of tokens (see Section 4.1), and
selecting pairs that have a high dot product for
attention. This allows various entities such as
gender, nouns, dates and names of places to be
consistent throughout the entire sequence, since
on expectation the dot product similarity between
similar entities are high, while for differing enti-
ties they are expected to be low. Essentially, we
conjecture that for every time step, the prediction
depends on a small support of high value tokens:
Local attention facilitates local consistency and
fluency, while a full dot product attention would
facilitate global consistency. However, for long
sequences, since full attention is infeasible, we
believe that using spherical k-means to perform
a MIPS search over the global set of tokens
and performing attention between these high dot
product items is a good approximation to full
dot product attention. The importance of the
MIPS search to select high dot product items is
highlighted from the ablation in Table 1, where we
see that a Random Transformer performs worse
compared to a Local Transformer and a Routing
Transformer with the same configuration (3.076
vs 3.009 vs 2.971 bits/dim).
6.2 Recurrence vs Sparse Attention
sparse attention is an
We also note that
orthogonal approach to that of Transformer-
XL and Compressive Transformer, which train
on small sequences and by performing careful
cross attention over cached previous chunks
hope to generalize to longer sequences. By
contrast, we directly train on long sequences from
the Compressive
the beginning—for example,
Transformer trains on chunks of size 512 for
PG-19, while we train on sequences of length
8192. The benefit of the Transformer-XL like
approach is that it is less memory consuming
and thus is able to scale to 36 layers. Sparse
attention (including local attention) on the other
hand is more memory expensive since it trains
directly on long sequences and therefore can scale
to fewer layers for the same problem. However,
as we demonstrate, it is competitive with the
Transformer-XL like approaches even when using
fewer layers and is guaranteed to generalize to the
long sequence length that it was trained on.
6.3 Wall-Clock Time
We compare the step times for training the various
sparse attention models on the CIFAR-10 data-
set in Table 1 as well as on the PG-19 data-set in
Table 7. For PG-19 we report only a comparison
between the Local Transformer and the Routing
Transformer, since sequence lengths are 8192 and
performing full attention is infeasible. All the
step time comparisons are made on a TPUv3,
with the same number of cores and batch sizes
to facilitate a fair comparison. As we see from
local attention is much faster than
Table 1,
full attention, training at 9.023 steps per second
compared to 5.608 steps per second. The Routing
Transformer models on CIFAR-10 have step
times that depend on the number of routing heads,
with the best performing model with the same
attention budget as local attention (i.e., an attention
window of 512), which has 8 routing layers and 4
routing heads, training at 5.140 steps per second.
Other Routing Transformer models are faster
while still matching full attention, for example, 2
routing layers with 4 routing heads trains at 7.409
steps per second. Therefore, Local Transformer is
roughly between 1.22 − 1.76× faster than the best
performing Routing Transformers. On the other
hand Transformer is between 0.76 − 1.09× faster
than the best Routing Transformers.
On PG-19, we see from Table 7 that the Local
Transformer is roughly 1.7× faster compared to
the Routing Transformer, similar to the trend on
CIFAR-10. This trade-off with respect to speed
64
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
3
1
9
2
3
9
3
2
/
/
t
l
a
c
_
a
_
0
0
3
5
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
compared to the Local Transformer is due to the
lack of support for sparse operations on the TPU;
on the GPU various sparse kernels have been pro-
posed which promise to significantly speed up
training of these models (Gale et al., 2020). Note
that our goal in this work is a memory efficient
version of sparse attention that can well approx-
imate full attention for long sequences; wall-clock
time efficiency is only a secondary goal.
7 Conclusion
Transformer models constitute the state-of-the-
art
in auto-regressive generative models for
sequential data. Their space-time complexity is,
however, quadratic in sequence length, due to their
attention modules. Our work proposes a sparse
attention model,
the Routing Transformer. It
relies on content-based sparse attention motivated
by non-negative matrix factorization. Compared
with local attention models, it does not require
fixed attention patterns but enjoys similar space-
time complexity. In contrast with prior work on
content-based sparse attention, it does not require
computing a full attention matrix but still selects
sparsity patterns based on content similarity.
Our experiments over text and image generation
draw two main conclusions. First, we show that
a scaled up version of local attention establishes
a strong baseline on modern benchmark, even
compared to recent
state-of-the-art models.
Second, we show that the Routing Transformer re-
defines the state-of-the-art in large long sequence
benchmarks of Wikitext-103, PG-19 and
ImageNet-64, while being very close to do so
on enwik-8 as well. Our analysis also shows that
routing attention modules offer complementary at-
tention patterns when compared to local attention.
Overall, our work contributes an efficient
attention mechanism that applies to the modeling
of long sequences and redefines the state of the
art for auto-regressive generative modeling. Our
approach could prove useful in domains where
the inputs are naturally sparse, such as 3D point
clouds, social networks, or protein interactions.
Acknowledgments
The authors would like to thank Phillip Wang and
Aran Komatsuzaki for a Pytorch implementation
of Routing Transformer. The authors would also
like to thank Yonghui Wu, Weikang Zhou, and
Dehao Chen for helpful feedback in improving the
implementation of this work. The authors would
also like to thank anonymous reviewers and the
Action Editor of TACL for their constructive
comments, which helped improve the exposition
of this work.
References
Rami Al-Rfou, Dokook Choe, Noah Constant,
Mandy Guo, and Llion Jones. 2019. Character-
level
deeper
language modeling with
self-attention. In Proceedings of the AAAI Con-
ference on Artificial Intelligence, volume 33,
pages 3159–3166. DOI: https://doi.org
/10.1609/aaai.v33i01.33013159
Alex Auvolat, Sarath Chandar, Pascal Vincent,
Hugo Larochelle, and Yoshua Bengio. 2015.
Clustering is efficient for approximate max-
imum inner product search. arXiv preprint
arXiv:1507.05910.
Jimmy Lei Ba, Jamie Ryan Kiros, and Geoffrey
E. Hinton. 2016. Layer normalization. arXiv
preprint arXiv:1607.06450.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
3
1
9
2
3
9
3
2
/
/
t
l
a
c
_
a
_
0
0
3
5
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Alexei Baevski and Michael Auli. 2019. Adaptive
language
for neural
In International Conference on
input
modeling.
Learning Representations.
representations
Dzmitry Bahdanau, Kyunghyun Cho, and Yoshua
Bengio. 2015. Neural machine translation by
jointly learning to align and translate.
In
3rd International Conference on Learning
Representations, ICLR 2015.
Arindam Banerjee
Joydeep Ghosh.
and
2004. Frequency-sensitive competitive learn-
ing for scalable balanced clustering on high-
dimensional hyperspheres. IEEE Transactions
on Neural Networks, 15(3):702–719. DOI:
https://doi.org/10.1109/TNN.2004
.824416, PMID: 15384557
Yoshua Bengio, Nicholas L´eonard, and Aaron
Courville. 2013. Estimating or propagating
gradients through stochastic neurons for con-
ditional computation. arXiv preprint arXiv:
1308.3432.
Mathieu Blondel, Andr´e F. T. Martins, and
Vlad Niculae. 2019. Learning classifiers with
65
fenchel-young losses: Generalized entropies,
margins, and algorithms. In The 22nd Inter-
national Conference on Artificial Intelligence
and Statistics, AISTATS 2019, 16–18 April
2019, Naha, Okinawa, Japan, pages 606–615.
Leon Bottou and Yoshua Bengio. 1995. Conver-
gence properties of the k-means algorithms.
In Advances in Neural Information Processing
Systems, pages 585–592.
Xi Chen, Nikhil Mishra, Mostafa Rohaninejad,
and Pieter Abbeel. 2018. Pixelsnail: An im-
proved autoregressive generative model. In
International Conference on Machine Learn-
ing, pages 864–872.
Rewon Child, Scott Gray, Alec Radford, and Ilya
Sutskever. 2019. Generating long sequences
transformers. arXiv preprint
with sparse
arXiv:1904.10509.
Chung-Cheng Chiu and Colin Raffel. 2018.
Monotonic chunkwise attention. In 6th Inter-
national Conference on Learning Representa-
tions, ICLR 2018, Vancouver, BC, Canada,
April 30 – May 3, 2018, Conference Track
Proceedings. OpenReview.net.
Kyunghyun Cho and Yoshua Bengio. 2014. Expo-
nentially increasing the capacity-to-computa-
tion ratio for conditional computation in deep
learning. arXiv preprint arXiv:1406.7362.
Kyunghyun Cho, Bart van Merri¨enboer, Caglar
Gulcehre, Dzmitry Bahdanau, Fethi Bougares,
Holger Schwenk, and Yoshua Bengio. 2014.
Learning phrase representations using rnn
encoder–decoder for statistical machine trans-
lation. In Proceedings of the 2014 Conference
on Empirical Methods in Natural Language
Processing (EMNLP), pages 1724–1734.
Jan K. Chorowski, Dzmitry Bahdanau, Dmitriy
Serdyuk, Kyunghyun Cho, and Yoshua Bengio.
2015. Attention-based models
speech
recognition. In Advances in Neural Information
Processing Systems, pages 577–585.
for
Gonc¸alo M. Correia, Vlad Niculae,
and
Andr´e F. T. Martins. 2019. Adaptively sparse
the 2019
transformers.
Conference on Empirical Methods in Natural
Language Processing and the 9th Internatio-
In Proceedings of
nal Joint Conference on Natural Language Pro-
cessing (EMNLP-IJCNLP), pages 2174–2184.
DOI: https://doi.org/10.18653/v1
/D19-1223
Zihang Dai, Zhilin Yang, Yiming Yang, Jaime G.
Carbonell, Quoc Le, and Ruslan Salakhutdinov.
language
2019. Transformer-xl: Attentive
models beyond a fixed-length context.
In
Proceedings of the 57th Annual Meeting of
the Association for Computational Linguistics,
pages 2978–2988.
Ludovic Denoyer and Patrick Gallinari. 2014.
Deep sequential neural network. arXiv preprint
arXiv:1410.0510.
Jacob Devlin, Ming-Wei Chang, Kenton Lee, and
Kristina Toutanova. 2019. BERT: Pre-training
of deep bidirectional transformers for language
understanding. In NAACL-HLT (1).
David Eigen, Marc’Aurelio Ranzato, and Ilya
Sutskever. 2013. Learning factored represen-
tations in a deep mixture of experts. arXiv
preprint arXiv:1312.4314.
Trevor Gale, Matei Zaharia, Cliff Young, and
Erich Elsen. 2020. Sparse GPU kernels for deep
learning. arXiv preprint arXiv:2006.10901.
Improving neural
Edouard Grave, Armand Joulin, and Nicolas
Usunier. 2017.
language
models with a continuous cache. In 5th Inter-
national Conference on Learning Represen-
tations, ICLR 2017, Toulon, France, April
24-26, 2017, Conference Track Proceedings.
OpenReview.net.
Alex Graves, Greg Wayne, and Ivo Danihelka.
2014. Neural turing machines. arXiv preprint
arXiv:1410.5401.
Karol Gregor,
Ivo Danihelka, Alex Graves,
Danilo Jimenez Rezende, and Daan Wierstra.
2015. DRAW: A recurrent neural network
for image generation. Francis R. Bach and
David M. Blei, editors, In Proceedings of
the 32nd International Conference on Machine
Learning, ICML 2015, Lille, France, 6-11 July
2015, volume 37 of JMLR Workshop and
Conference Proceedings, pages 1462–1471.
JMLR.org.
66
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
3
1
9
2
3
9
3
2
/
/
t
l
a
c
_
a
_
0
0
3
5
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Ari Holtzman, Jan Buys, Li Du, Maxwell Forbes,
and Yejin Choi. 2020. The curious case
of neural text degeneration. In International
Conference on Learning Representations.
Cheng-Zhi Anna Huang, Ashish Vaswani, Jakob
Uszkoreit, Ian Simon, Curtis Hawthorne, Noam
Shazeer, Andrew M. Dai, Matthew D. Hoffman,
Monica Dinculescu, and Douglas Eck. 2018.
Music transformer: Generating music with
long-term structure. In International Confer-
ence on Learning Representations.
Sathish Reddy Indurthi,
Insoo Chung, and
Sangha Kim. 2019. Look harder: A neural
machine translation model with hard attention.
the 57th Conference of
In Proceedings of
the Association for Computational Linguistics,
pages 3037–3043. DOI: https://doi.org
/10.18653/v1/P19-1290
Navdeep Jaitly, Quoc V. Le, Oriol Vinyals,
Ilya Sutskever, David Sussillo, and Samy
Bengio. 2016. An online sequence-to-sequence
model using partial conditioning. In Advances
in Neural Information Processing Systems,
pages 5067–5075.
Diederik P. Kingma and Jimmy Ba. 2015.
Adam: A method for stochastic optimization.
Yoshua Bengio and Yann LeCun, editors,
In 3rd International Conference on Learning
Representations, ICLR 2015, San Diego, CA,
USA, May 7-9, 2015, Conference Track
Proceedings.
Durk P. Kingma and Prafulla Dhariwal. 2018.
Glow: Generative flow with invertible 1×1 con-
volutions. In Advances in Neural Information
Processing Systems, pages 10215–10224.
Nikita Kitaev, Lukasz Kaiser, and Anselm
Levskaya. 2020. Reformer: The efficient
transformer. In International Conference on
Learning Representations.
Guillaume Lample, Alexandre Sablayrolles,
Marc’Aurelio Ranzato, Ludovic Denoyer, and
Herv´e J´egou. 2019. Large memory layers with
product keys. In Advances in Neural Informa-
tion Processing Systems, pages 8548–8559.
Peter J. Liu, Mohammad Saleh, Etienne Pot, Ben
Goodrich, Ryan Sepassi, Lukasz Kaiser, and
Noam Shazeer. 2018. Generating wikipedia by
summarizing long sequences. In International
Conference on Learning Representations.
Xiaodong Liu, Pengcheng He, Weizhu Chen, and
Jianfeng Gao. 2019. Multi-task deep neural
networks for natural language understanding.
In Proceedings of the 57th Annual Meeting of
the Association for Computational Linguistics,
pages 4487–4496.
Minh-Thang Luong, Hieu Pham, and Christopher
D. Manning. 2015. Effective approaches to
attention-based neural machine translation. In
Proceedings of the 2015 Conference on Empir-
ical Methods in Natural Language Processing,
pages 1412–1421. DOI: https://doi.org
/10.18653/v1/D15-1166
Matt Mahoney. 2011. Large text compression
benchmark. URL: http://www.mattmahoney
.net/text/text.html
Chaitanya Malaviya, Pedro Ferreira, and Andr´e
F. T. Martins. 2018. Sparse and constrained
attention for neural machine translation. In
Proceedings of the 56th Annual Meeting of
the Association for Computational Linguistics
(Volume 2: Short Papers), pages 370–376, Mel-
bourne, Australia. Association for Computa-
tional Linguistics. DOI: https://doi.org
/10.18653/v1/P18-2059
Mikko I. Malinen and Pasi Fr¨anti. 2014. Balanced
k-means for clustering. In Joint IAPR Inter-
national Workshops on Statistical Techniques
in Pattern Recognition (SPR) and Structural
and Syntactic Pattern Recognition (SSPR),
pages 32–41. Springer. DOI: https://doi
.org/10.1007/978-3-662-44415-3 4
Andr´e F. T. Martins and Julia Kreutzer. 2017.
Learning what’s easy: Fully differentiable neu-
ral easy-first taggers. In Proceedings of the 2017
Conference on Empirical Methods in Natural
Language Processing, pages 349–362, Copen-
hagen, Denmark. Association for Computa-
tional Linguistics. DOI: https://doi.org
/10.18653/v1/D17-1036
Jacob Menick and Nal Kalchbrenner. 2018.
Generating high fidelity images with subscale
pixel networks and multidimensional upscaling.
In International Conference on Learning
Representations.
67
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
3
1
9
2
3
9
3
2
/
/
t
l
a
c
_
a
_
0
0
3
5
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
Stephen Merity, Nitish Shirish Keskar, and
Richard Socher. 2018. An analysis of neural
language modeling at multiple scales. arXiv
preprint arXiv:1803.08240.
Stephen Merity, Caiming Xiong, James Bradbury,
and Richard Socher. 2017. Pointer sentinel
mixture models. In 5th International Confer-
ence on Learning Representations, ICLR 2017,
Toulon, France, April 24-26, 2017, Conference
Track Proceedings. OpenReview.net.
Niki Parmar, Ashish Vaswani, Jakob Uszkoreit,
Lukasz Kaiser, Noam Shazeer, Alexander Ku,
and Dustin Tran. 2018. Image transformer.
In International Conference on Machine
Learning, pages 4055–4064.
Alec Radford, Karthik Narasimhan, Tim
Salimans, and Ilya Sutskever. 2018. Improv-
ing language understanding by generative
pre-training. URL https://s3-us-west
-2.amazonaws.com/openai-assets
/research-covers/languageunsupervised
/languageunderstandingpaper.pdf
Jack Rae, Jonathan J. Hunt,
Ivo Danihelka,
Timothy Harley, Andrew W. Senior, Gregory
Wayne, Alex Graves, and Timothy Lillicrap.
2016. Scaling memory-augmented neural net-
works with sparse reads and writes. In Advances
in Neural Information Processing Systems,
pages 3621–3629.
Jack Rae and Ali Razavi. 2020. Do transfor-
mers need deep long-range memory? In Pro-
ceedings of the 58th Annual Meeting of the
Association for Computational Linguistics,
pages 7524–7529. Association for Computa-
tional Linguistics. Online. DOI: https://
doi.org/10.18653/v1/2020.acl-main
.672
Jack W. Rae, Anna Potapenko, Siddhant M.
Jayakumar, Chloe Hillier, and Timothy P.
Lillicrap. 2020. Compressive transformers for
long-range sequence modelling. In Internatio-
nal Conference on Learning Representations.
Peter Shaw,
and Ashish
Jakob Uszkoreit,
Vaswani. 2018. Self-attention with relative
position representations. In Proceedings of the
2018 Conference of
the North American
Chapter of the Association for Computational
Linguistics: Human Language Technologies,
Volume 2 (Short Papers), pages 464–468.
DOI: https://doi.org/10.18653/v1
/N18-2074
Noam Shazeer, Azalia Mirhoseini, Krzysztof
Maziarz, Andy Davis, Quoc V. Le, Geoffrey E.
Hinton, and Jeff Dean. 2017. Outrageously
large neural networks: The sparsely-gated
mixture-of-experts layer. In 5th International
Conference on Learning Representations, ICLR
2017, Toulon, France, April 24-26, 2017, Con-
ference Track Proceedings. OpenReview.net.
Noam Shazeer and Mitchell Stern. 2018. Adafac-
tor: Adaptive learning rates with sublinear
memory cost. In International Conference on
Machine Learning, pages 4596–4604.
Sainbayar Sukhbaatar,
´Edouard Grave, Piotr
Bojanowski, and Armand Joulin. 2019. Adap-
tive attention span in transformers. In Pro-
ceedings of
the 57th Annual Meeting of
the Association for Computational Linguistics,
pages 331–335. DOI: https://doi.org
/10.18653/v1/P19-1032
Aaron Van den Oord, Nal Kalchbrenner, Lasse
Espeholt, Oriol Vinyals, Alex Graves, and
image generation
others. 2016. Conditional
In Advances in
with PixelCNN decoders.
Neural
Systems,
pages 4790–4798.
Information Processing
Ashish Vaswani, Noam Shazeer, Niki Parmar,
Jakob Uszkoreit, Llion Jones, Aidan N. Gomez,
Łukasz Kaiser, and Illia Polosukhin. 2017.
In Advances
Attention is all you need.
in Neural Information Processing Systems,
pages 5998–6008.
Kelvin Xu,
Ba,
Jimmy
Ryan Kiros,
Kyunghyun Cho, Aaron C. Courville, Ruslan
Salakhutdinov, Richard S. Zemel, and Yoshua
Bengio. 2015. Show, attend and tell: Neural
image caption generation with visual attention.
Francis R. Bach and David M. Blei, editors, In
Proceedings of the 32nd International Con-
ference on Machine Learning, ICML 2015,
Lille, France, 6-11 July 2015, volume 37 of
JMLR Workshop and Conference Proceedings,
pages 2048–2057. JMLR.org.
Zhilin Yang, Zihang Dai, Yiming Yang, Jaime
Carbonell, Russ R Salakhutdinov, and Quoc V.
Le. 2019. XLNet: Generalized autoregressive
In
pretraining for
Advances in Neural Information Processing
Systems, pages 5753–5763.
language understanding.
68
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
5
3
1
9
2
3
9
3
2
/
/
t
l
a
c
_
a
_
0
0
3
5
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3