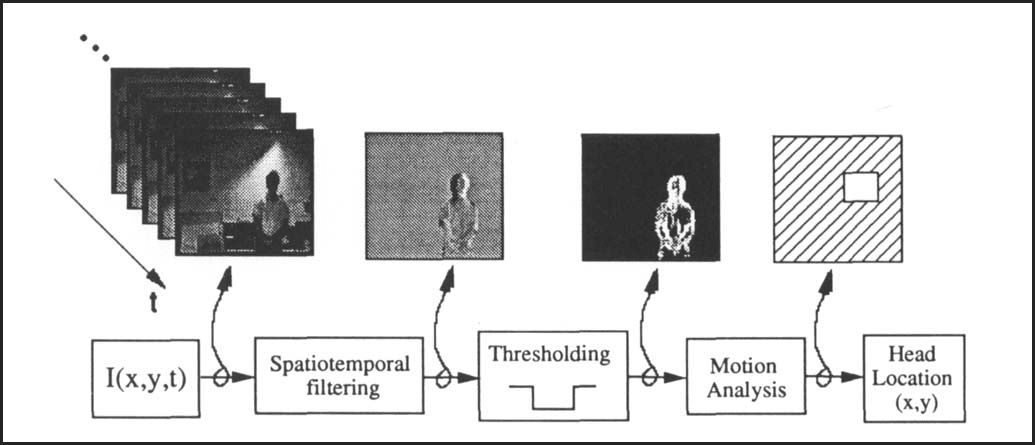
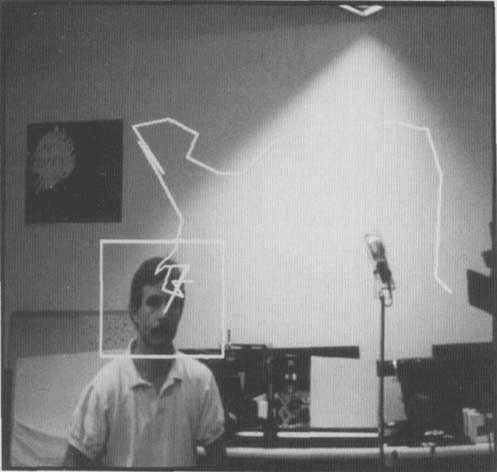
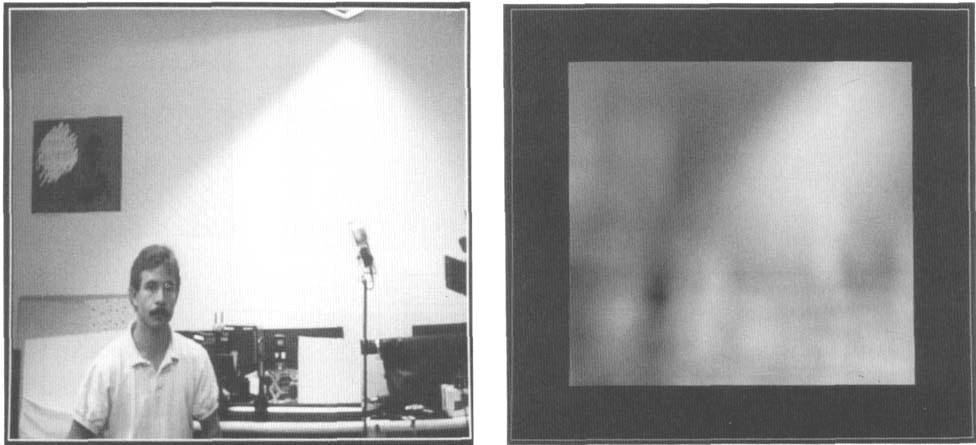
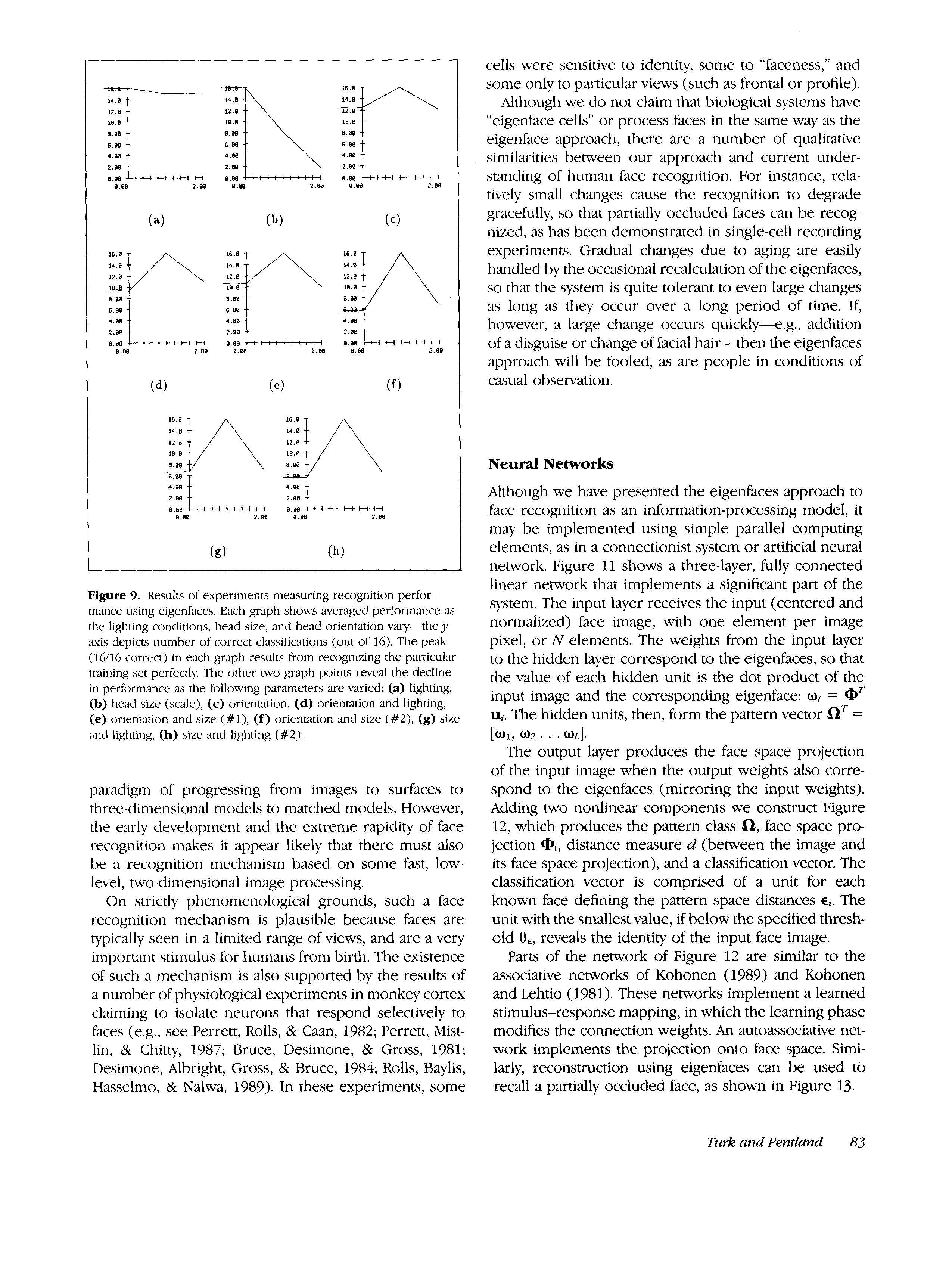
E i g e d c e s for Recognition
Matthew Turk and Alex Pentland
Vision and Modeling Group
The Media Laboratory
Massachusetts Institute of Technology
Abstract
We have developed a near-real-time computer system that
can locate and track a subject’s head, and then recognize the
person by comparing characteristics of the face to those of
known individuals. The computational approach taken in this
system is motivated by both physiology and information theory,
as well as by the practical requirements of near-real-time per-
formance and accuracy. Our approach treats the face recog-
nition problem as an intrinsically two-dimensional (2-D)
recognition problem rather than requiring recovery of three-
dimensional geometry, taking advantage of the fact that faces
are normally upright and thus may be described by a small set
of 2-D characteristic views. The system functions by projecting
face images onto a feature space that spans the significant
variations among known face images. The significant features
are known as “eigenfaces,” because they are the eigenvectors
(principal components) of the set of faces; they do not neces-
sarily correspond to features such as eyes, ears, and noses. The
projection operation characterizes an individual face by a
weighted sum of the eigenface features, and so to recognize a
particular face it is necessary only to compare these weights to
those of known individuals. Some particular advantages of our
approach are that it provides for the ability to learn and later
recognize new faces in an unsupervised manner, and that it is
easy to implement using a neural network architecture.
INTRODUCTION
The face is our primary focus of attention in social in-
tercourse, playing a major role in conveying identity and
emotion. Although the ability to infer intelligence or
character from facial appearance is suspect, the human
ability to recognize faces is remarkable. We can recog-
nize thousands of faces learned throughout our lifetime
and identify familiar faces at a glance even after years of
separation. This skill is quite robust, despite large
changes in the visual stimulus due to viewing conditions,
expression, aging, and distractions such as glasses or
changes in hairstyle or facial hair. As a consequence the
visual processing of human faces has fascinated philos-
ophers and scientists for centuries, including figures such
as Aristotle and Darwin.
Computational models of face recognition, in partic-
ular, are interesting because they can contribute not only
to theoretical insights but also to practical applications.
Computers that recognize faces could be applied to a
wide variety of problems, including criminal identifica-
tion, security systems, image and film processing, and
human-computer interaction. For example, the ability to
model a particular face and distinguish it from a large
number of stored face models would make it possible
to vastly improve criminal identification. Even the ability
to merely detect faces, as opposed to recognizing them,
can be important. Detecting faces in photographs, for
instance, is an important problem in automating color
film development, since the effect of many enhancement
and noise reduction techniques depends on the picture
content (e.g., faces should not be tinted green, while
perhaps grass should).
Unfortunately, developing a computational model of
face recognition is quite difficult, because faces are com-
plex, multidimensional, and meaningful visual stimuli.
They are a natural class of objects, and stand in stark
contrast to sine wave gratings, the “blocks world,” and
other artificial stimuli used in human and computer vi-
sion research (Davies, Ellis, & Shepherd, 1981). Thus
unlike most early visual functions, for which we may
construct detailed models of retinal o r striate activity,
face recognition is a very high level task for which com-
putational approaches can currently only suggest broad
constraints on the corresponding neural activity.
We therefore focused our research toward developing
a sort of early, preattentive pattern recognition capability
that does not depend on having three-dimensional in-
formation or detailed geometry. Our goal, which we
believe we have reached, was to develop a computational
model of face recognition that is fast, reasonably simple,
and accurate in constrained environments such as an
office o r a household. In addition the approach is bio-
logically implementable and is in concert with prelimi-
0 1991 Massachusetts Institute of Technology
Journal of Cognitive Neuroscience Volume 3, Number 1
D
o
w
n
l
o
a
d
e
d
f
r
o
m
l
l
/
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
D
h
o
t
w
t
n
p
:
o
/
a
/
d
m
e
d
i
t
f
r
p
o
r
m
c
.
h
s
i
p
l
v
d
e
i
r
r
e
c
c
t
h
.
m
a
i
r
e
.
d
c
u
o
m
o
/
c
n
j
o
a
c
r
t
n
i
c
/
e
a
–
r
p
t
d
i
c
3
l
1
e
7
–
1
p
d
1
f
9
/
3
2
3
0
/
1
1
8
/
7
o
1
c
/
n
1
1
7
9
5
9
5
1
7
3
2
7
1
/
7
j
1
o
p
c
d
n
.
b
1
y
9
g
9
u
1
e
.
s
3
t
.
o
1
n
.
0
7
8
1
.
S
p
e
d
p
f
e
m
b
b
y
e
r
g
2
u
0
e
2
s
3
t
/
j
.
t
.
.
.
f
.
o
n
1
8
M
a
y
2
0
2
1
nary findings in the physiology and psychology of face
recognition.
The scheme is based on an information theory ap-
proach that decomposes face images into a small set of
characteristic feature images called “eigenfaces,” which
may be thought of as the principal components of the
initial training set of face images. Recognition is per-
formed by projecting a new image into the subspace
spanned by the eigenfaces (“face space”) and then clas-
sifying the face by comparing its position in face space
with the positions of known individuals.
Automatically learning and later recognizing new faces
is practical within this framework. Recognition under
widely varying conditions is achieved by training on a
limited number of characteristic views (e.g., a “straight
on” view, a 45” view, and a profile view). The approach
has advantages over other face recognition schemes in
its speed and simplicity, learning capacity, and insensitiv-
ity to small or gradual changes in the face image.
Background and Related Work
Much of the work in computer recognition of faces has
focused on detecting individual features such as the eyes,
nose, mouth, and head outline, and defining a face model
by the position, size, and relationships among these fea-
tures. Such approaches have proven difficult to extend
to multiple views, and have often been quite fragile,
requiring a good initial guess to guide them. Research
in human strategies of face recognition, moreover, has
shown that individual features and their immediate re-
lationships comprise an insufficient representation to ac-
the performance of adult human face
count for
identification (Carey & Diamond, 1977). Nonetheless,
this approach to face recognition remains the most pop-
ular one in the computer vision literature.
Bledsoe (1966a,b) was the first to attempt semiauto-
mated face recognition with a hybrid human-computer
system that classified faces on the basis of fiducial marks
entered on photographs by hand. Parameters for the
classification were normalized distances and ratios
among points such as eye corners, mouth corners, nose
tip, and chin point. Later work at Bell Labs (Goldstein,
Harmon, & Lesk, 1971; Harmon, 1971) developed a vec-
tor of up to 21 features, and recognized faces using
standard pattern classification techniques. The chosen
features were largely subjective evaluations (e.g., shade
of hair, length of ears, lip thickness) made by human
subjects, each of which would be quite difficult to
automate.
An early paper by Fischler and Elschlager (1973) at-
tempted to measure similar features automatically. They
described a linear embedding algorithm that used local
feature template matching and a global measure of fit to
find and measure facial features. This template matching
approach has been continued and improved by the re-
cent work of Yuille, Cohen, and Hallinan (1989) (see
Yuille, this volume). Their strategy is based on “deform-
able templates,” which are parameterized models of the
face and its features in which the parameter values are
determined by interactions with the image.
Connectionist approaches to face identification seek to
capture the configurational, or gestalt-like nature of the
task. Kohonen (1989) and Kohonen and Lahtio (1981)
describe an associative network with a simple learning
algorithm that can recognize (classify) face images and
recall a face image from an incomplete or noisy version
input to the network. Fleming and Cottrell(l990) extend
these ideas using nonlinear units, training the system by
backpropagation. Stonham’s WSARD system (1986) is a
general-purpose pattern recognition device based on
neural net principles. It has been applied with some
success to binary face images, recognizing both identity
and expression. Most connectionist systems dealing with
faces (see also Midorikawa, 1988; O’Toole, Millward, &
Anderson, 1988) treat the input image as a general 2-D
pattern, and can make no explicit use of the configura-
tional properties of a face. Moreover, some of these
systems require an inordinate number of training ex-
amples to achieve a reasonable level of performance.
Only very simple systems have been explored to date,
and it is unclear how they will scale to larger problems.
Others have approached automated face recognition
by characterizing a face by a set of geometric parameters
and performing pattern recognition based on the param-
eters (e.g., Kaya & Kobayashi, 1972; Cannon, Jones,
Campbell, & Morgan, 1986; Craw, Ellis, & Lishman, 1987;
Wong, Law, & Tsaug, 1989). Kanade’s (1973) face identi-
fication system was the first (and still one of the few)
systems in which all steps of the recognition process
were automated, using a top-down control strategy di-
rected by a generic model of expected feature charac-
teristics. His system calculated a set of facial parameters
from a single face image and used a pattern classification
technique to match the face from a known set, a purely
statistical approach depending primarily on local histo-
gram analysis and absolute gray-scale values.
Recent work by Burt (1988a,b) uses a “smart sensing”
approach based on multiresolution template matching.
This coarse-to-fine strategy uses a special-purpose com-
puter built to calculate multiresolution pyramid images
quickly, and has been demonstrated identifying people
in near-real-time. This system works well under limited
circumstances, but should suffer from the typical prob-
lems of correlation-based matching, including sensitivity
to image size and noise. The face models are built by
hand from face images.
THE EIGENFACE APPROACH
Much of the previous work on automated face recogni-
tion has ignored the issue of just what aspects of the face
stimulus are important for identification. This suggested
to us that an information theory approach of coding and
72
Journal of Cognitive Neuroscience
Volume 3, Number 1
D
o
w
n
l
o
a
d
e
d
f
r
o
m
l
l
/
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
D
h
o
t
w
t
n
p
:
o
/
a
/
d
m
e
d
i
t
f
r
p
o
r
m
c
.
h
s
i
p
l
v
d
e
i
r
r
e
c
c
t
h
.
m
a
i
r
e
.
d
c
u
o
m
o
/
c
n
j
o
a
c
r
t
n
i
c
/
e
a
–
r
p
t
d
i
c
3
l
1
e
7
–
1
p
d
1
f
9
/
3
2
3
0
/
1
1
8
/
7
o
1
c
/
n
1
1
7
9
5
9
5
1
7
3
2
7
1
/
7
j
1
o
p
c
d
n
.
b
1
y
9
g
9
u
1
e
.
s
3
t
.
o
1
n
.
0
7
8
1
.
S
p
e
d
p
f
e
m
b
b
y
e
r
g
2
u
0
e
2
s
3
t
/
j
.
.
.
.
t
.
f
o
n
1
8
M
a
y
2
0
2
1
decoding face images may give insight into the infor-
mation content of face images, emphasizing the signifi-
cant local and global “features.” Such features may or
may not be directly related to our intuitive notion of face
features such as the eyes, nose, lips, and hair. This may
have important implications for the use of identification
tools such as Identikit and Photofit (Bruce, 1988).
In the language of information theory, we want to
extract the relevant information in a face image, encode
it as efficiently as possible, and compare one face encod-
ing with a database of models encoded similarly. A simple
approach to extracting the information contained in an
image of a face is to somehow capture the variation in a
collection of face images, independent of any judgment
of features, and use this information to encode and com-
pare individual face images.
In mathematical terms, we wish to find the principal
components of the distribution of faces, or the eigenvec-
tors of the covariance matrix of the set of face images,
treating an image as a point (or vector) in a very high
dimensional space. The eigenvectors are ordered, each
one accounting for a different amount of the variation
among the face images.
These eigenvectors can be thought of as a set of fea-
tures that together characterize the variation between
face images. Each image location contributes more or
less to each eigenvector, so that we can display the ei-
genvector as a sort of ghostly face which we call an
eigenface. Some of the faces we studied are illustrated
in Figure 1, and the corresponding eigenfaces are shown
in Figure 2. Each eigenface deviates from uniform gray
where some facial feature differs among the set of train-
ing faces; they are a sort of map of the variations between
faces.
Each individual face can be represented exactly in
terms of a linear combination of the eigenfaces. Each
face can also be approximated using only the “best”
eigenfaces-those
that have the largest eigenvalues, and
which therefore account for the most variance within
the set of face images. The best M eigenfaces span an
all possible
M-dimensional subspace-“face
images.
space”-of
The idea of using eigenfaces was motivated by a tech-
nique developed by Sirovich and Kirby (1987) and Kirby
and Sirovich (1990) for efficiently representing pictures
of faces using principal component analysis. Starting with
an ensemble of original face images, they calculated a
best coordinate system for image compression, where
each coordinate is actually an image that they termed an
eigenpicture. They argued that, at least in principle, any
collection of face images can be approximately recon-
structed by storing a small collection of weights for each
face and’s small set of standard pictures (the eigenpic-
tures). The weights describing each face are found by
projecting the face image onto each eigenpicture.
It occurred to us that if a multitude of face images can
be reconstructed by weighted sums of a small collection
of characteristic features or eigenpictures, perhaps an
efficient way to learn and recognize faces would be to
build up the characteristic features by experience over
time and recognize particular faces by comparing the
feature weights needed to (approximately) reconstruct
them with the weights associated with known individuals.
Each individual, therefore, would be characterized by
the small set of feature or eigenpicture weights needed
to describe and reconstruct them-an
extremely com-
pact representation when compared with the images
themselves.
This approach to face recognition involves the follow-
ing initialization operations:
1. Acquire an initial set of face images (the training
set).
2. Calculate the eigenfaces from the training set, keep-
ing only the M images that correspond to the highest
eigenvalues. These M images define the face space. As
new faces are experienced, the eigenfaces can be up-
dated or recalculated.
3. Calculate the corresponding distribution in M-di-
mensional weight space for each known individual, by
projecting their face images onto the “face space.”
These operations can also be performed from time
to time whenever there is free excess computational
capacity.
Having initialized the system, the following steps are
then used to recognize new face images:
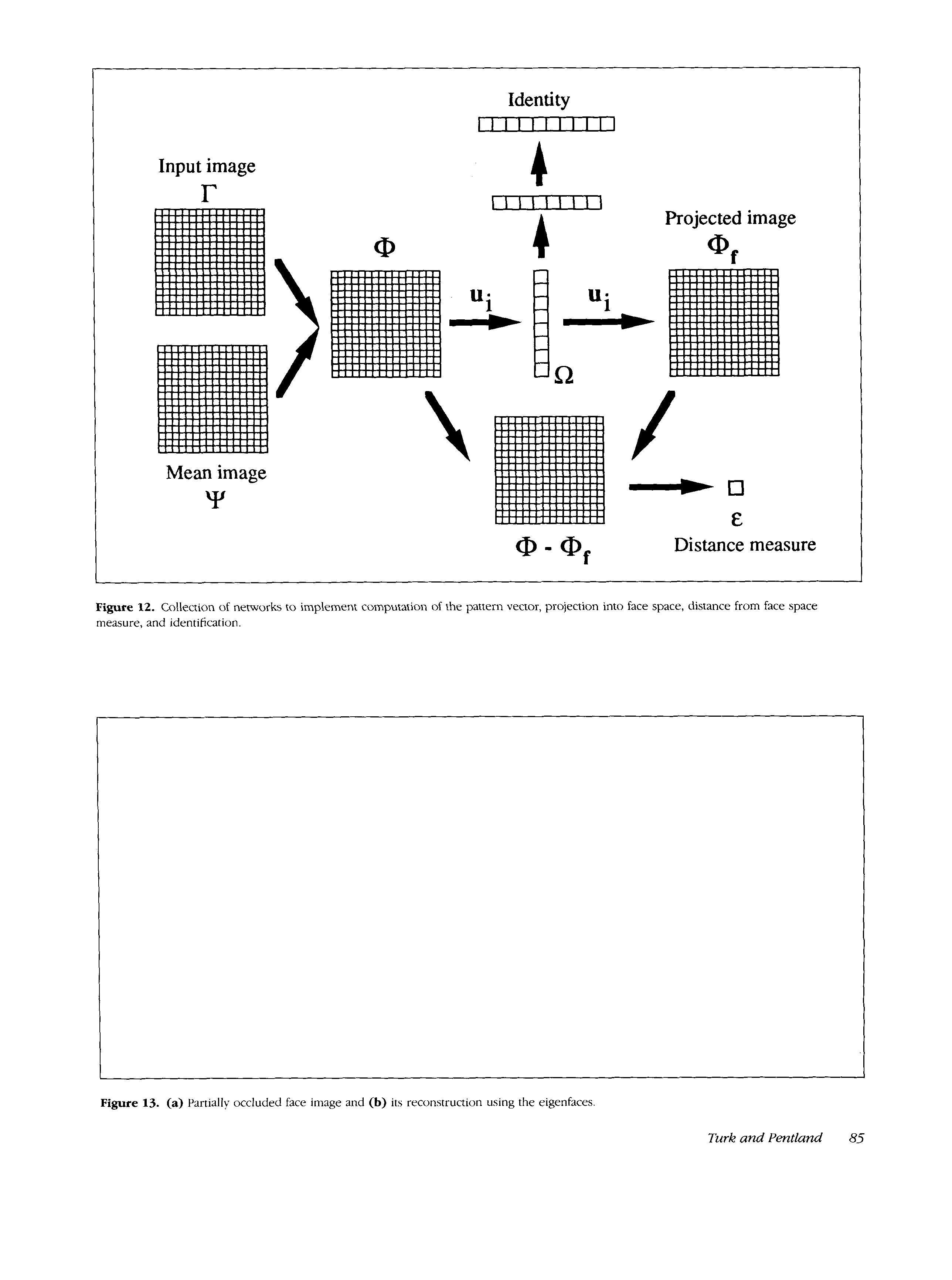
1. Calculate a set of weights based on the input image
and the M eigenfaces by projecting the input image onto
each of the eigenfaces.
2. Determine if the image is a face at all (whether
known or unknown) by checking to see if the image is
sufficiently close to “face space.”
3. If it is a face, classify the weight pattern as either a
known person or as unknown.
4. (Optional) Update the eigenfaces and/or weight
patterns.
5. (Optional) If the same unknown face is seen several
times, calculate its characteristic weight pattern and in-
corporate into the known faces.
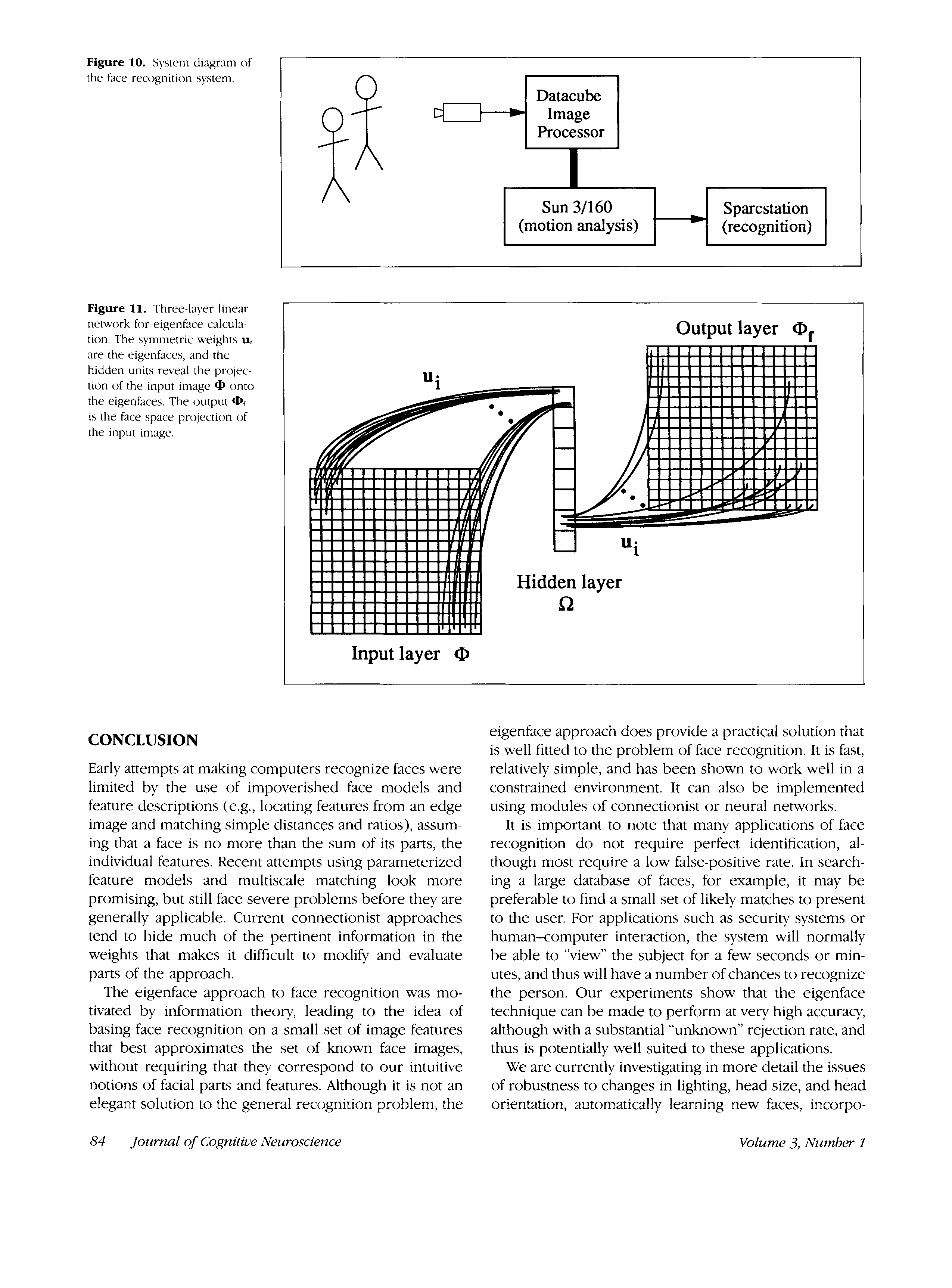
Calculating Eigenfaces
Let a face image Z(x,y) be a two-dimensional N by N array
of (8-bit) intensity values. An image may also be consid-
ered as a vector of dimension N2, so that a typical image
of size 256 by 256 becomes a vector of dimension 65,536,
or, equivalently, a point in 65,536-dimensional space. An
ensemble of images, then, maps to a collection of points
in this huge space.
Images of faces, being similar in overall configuration,
will not be randomly distributed in this huge image space
and thus can be described by a relatively low dimen-
sional subspace. The main idea of the principal compo-
Turk and Pentland
73
D
o
w
n
l
o
a
d
e
d
f
r
o
m
l
l
/
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
D
h
o
t
w
t
n
p
:
o
/
a
/
d
m
e
d
i
t
f
r
p
o
r
m
c
.
h
s
i
p
l
v
d
e
i
r
r
e
c
c
t
h
.
m
a
i
r
e
.
d
c
u
o
m
o
/
c
n
j
o
a
c
r
t
n
i
c
/
e
a
–
r
p
t
d
i
c
3
l
1
e
7
–
1
p
d
1
f
9
/
3
2
3
0
/
1
1
8
/
7
o
1
c
/
n
1
1
7
9
5
9
5
1
7
3
2
7
1
/
7
j
1
o
p
c
d
n
.
b
1
y
9
g
9
u
1
e
.
s
3
t
.
o
1
n
.
0
7
8
1
.
S
p
e
d
p
f
e
m
b
b
y
e
r
g
2
u
0
e
2
s
3
t
/
j
.
.
.
.
t
.
f
o
n
1
8
M
a
y
2
0
2
1
Figure 1. (a)Face images
used as the training set.
D
o
w
n
l
o
a
d
e
d
f
r
o
m
l
l
/
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
D
h
o
t
w
t
n
p
:
o
/
a
/
d
m
e
d
i
t
f
r
p
o
r
m
c
.
h
s
i
p
l
v
d
e
i
r
r
e
c
c
t
h
.
m
a
i
r
e
.
d
c
u
o
m
o
/
c
n
j
o
a
c
r
t
n
i
c
/
e
a
–
r
p
t
d
i
c
3
l
1
e
7
–
1
p
d
1
f
9
/
3
2
3
0
/
1
1
8
/
7
o
1
c
/
n
1
1
7
9
5
9
5
1
7
3
2
7
1
/
7
j
1
o
p
c
d
n
.
b
1
y
9
g
9
u
1
e
.
s
3
t
.
o
1
n
.
0
7
8
1
.
S
p
e
d
p
f
e
m
b
b
y
e
r
g
2
u
0
e
2
s
3
t
/
j
.
.
f
.
t
.
.
o
n
1
8
M
a
y
2
0
2
1
nent analysis (or Karhunen-Loeve expansion) is to find
the vectors that best account for the distribution of face
images within the entire image space. These vectors de-
fine the subspace of face images, which we call “face
space.” Each vector is of length N‘, describes an N by N
image, and is a linear combination of the original face
images. Because these vectors are the eigenvectors of
the covariance matrix corresponding to the original face
images, and because they are face-like in appearance, we
refer to them as “eigenfaces.” Some examples of eigen-
faces are shown in Figure 2 .
Let the training set of face images be rl, r2, r3, . . . ,
r,,, The average face of the set is defined by * =
+Z:=:=, r,. Each face differs from the average by the
= I?, – W , An example training set is shown
vector
in Figure la, with the average face
shown in Figure
l b . This set of very large vectors is then subject to prin-
cipal component analysis, which seeks a set of M ortho-
normal vectors, un, which best describes the distribution
of the data. The kth vector, u k , is chosen such that
l M
A k = – (Uz@n)2
M n=1
( 1 )
is a maximum, subject to
74
Journal of Cognitive Neuroscience
The vectors w and scalars Xk are the eigenvectors and
eigenvalues, respectively, of the covariance matrix
c = – c
1
M n = ~
= A T
( 3 )
where the matrix A = [al cP2 . . . @MI.
The matrix C,
however, is N’ by N’, and determining the N’ eigenvec-
tors and eigenvalues is an intractable task for typical
image sizes. Me need a computationally feasible method
to find these eigenvectors.
If the number of data points in the image space is less
than the dimension of the space ( M < N’), there will be
only M - 1, rather than N2, meaningful eigenvectors.
(The remaining eigenvectors will have associated eigen-
values of zero.) Fortunately we can solve for the N2-
dimensional eigenvectors in this case by first solving for
the eigenvectors of an M by M matrix--e.g., solving a
16 X 16 matrix rather than a 16,384 X 16,384 matrix-
Volume 3, Number 1
Following this analysis, we construct the M by M matrix
L = ATA, where L,, =
and find the M eigenvec-
tors, VL, of L . These vectors determine linear combina-
tions of the M training set face images to form the
eigenfaces UI.
M
Ul = x v [ k @ k ,
k = 1
t! = 1 , . . . ,M
( 6 )
With this analysis the calculations are greatly reduced,
from the order of the number of pixels in the images
( N 2 ) to the order of the number of images in the training
set (M). In practice, the training set of face images will
be relatively small (M G N’), and the calculations become
quite manageable. The associated eigenvalues allow us
to rank the eigenvectors according to their usefulness in
characterizing the variation among the images. Figure 2
shows the top seven eigenfaces derived from the input
images of Figure 1.
Using Eigenfaces to Classify a Face Image
The eigenface images calculated from the eigenvectors
of L span a basis set with which to describe face images.
Sirovich and Kirby (1987) evaluated a limited version of
this framework on an ensemble of M = 115 images of
Caucasian males, digitized in a controlled manner, and
found that about 40 eigenfaces were sufficient for a very
good description of the set of face images. With M‘ =
40 eigenfaces, RMS pixel-by-pixel errors in representing
cropped versions of face images were about 2%.
Since the eigenfaces seem adequate for describing face
images under very controlled conditions, we decided to
investigate their usefulness as a tool for face identifica-
tion. In practice, a smaller M’ is sufficient for identifica-
tion, since accurate reconstruction of the image is not a
requirement. In this framework, identification becomes
a pattern recognition task. The eigenfaces span an M’-
dimensional subspace of the original N’
image space.
The M’ significant eigenvectors of the L matrix are chosen
as those with the largest associated eigenvalues. In many
of our test cases, based o n M = 16 face images, M’ = 7
eigenfaces were used.
A new face image (I?) is transformed into its eigenface
components (projected into “face space”) by a simple
operation,
wk = U,’