Droplets As Liquid Robots
Abstract Liquid droplets are very simple objects present in our
everyday life. They are extremely important for many natural
phenomena as well as for a broad variety of industrial processes. The
conventional research areas in which the droplets are studied include
physical chemistry, fluid mechanics, chemical engineering, materials
science, and micro- and nanotechnology. Typical studies include
phenomena such as condensation and droplet formation, evaporation
of droplets, or wetting of surfaces. The present article reviews the
recent literature that employs droplets as animated soft matter. It
is argued that droplets can be considered as liquid robots possessing
some characteristics of living systems, and such properties can
be applied to unconventional computing through maze solving or
operation in logic gates. In particular, the lifelike properties and
behavior of liquid robots, namely (i) movement, (ii) self-division,
and (iii) group dynamics, will be discussed.
Jitka Čejková*,**
University of Chemistry and
Technology Prague
†
Taisuke Banno
Keio University
‡
Martin M. Hanczyc
University of Trento
University of New Mexico
František Štěpánek**
University of Chemistry and
Technology Prague
Keywords
Robot, droplet, movement, self-division,
group dynamics
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
3
4
5
2
8
1
6
6
6
9
1
7
a
r
t
l
/
_
a
_
0
0
2
4
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1 Introduction
The word “robot” was first introduced in 1920 in a famous Czech play R.U.R. (Rossumʼs Universal
Robots) [22], where robots are not clanking metal constructions, but humanlike beings made of soft
matter. The author of the play, Karel Čapek, describes them as being made of a protoplasm—a
substantive essence of living matter. It is described by Domin in the first act as “a blob of some
kind of colloidal jelly that even a dog wouldnʼt eat.” At the time the similarities between colloidal
materials and the living protoplasm inside cells was already being investigated [27, 37].
Today robots are typically thought of as dynamic electromechanical objects. In contrast, Čapekʼs
robots did not have wheels, electric power, or computer systems to control them. They were based
only on chemical principles and consisted of fluidic colloidal substances. Thus we can consider a
droplet based on chemical principles and activated through fluid dynamics to be an embodiment of
robotics more sympathetic to Čapekʼs original conception. Such soft-bodied robots might be made
from a variety of substances, including liquid droplets [56] and gels [68]. Such chemical and liquid
robots could perform autonomous movement through the exploitation of chemical potential
without using predefined mechanical parts, but rather using self-organized fluid dynamics.
* Contact author.
** Chemical Robotics Laboratory, University of Chemistry and Technology Prague, Technická 3, Prague 6, 166 28, Czech Republic.
E-mail: Jitka.Cejkova@vscht.cz ( J.Č.); Franktisek.Stepanek@vscht.cz (F.Š.)
† Department of Applied Chemistry, Keio University, Yokohama, Japan. E-mail: banno@applc.keio.ac.jp
‡ Laboratory for Artificial Biology, Centre for Integrative Biology (CIBIO), University of Trento, Trento, Italy; Chemical and Biological
Engineering, University of New Mexico, USA. E-mail: martin.hanczyc@unitn.it
© 2017 by the Massachusetts Institute of Technology. Published under a Creative Commons Attribution 3.0
Artificial Life 23: 528–549 (2017) doi:10.1162/ARTL_a_00243
Unported (CC BY 3.0) license.
J. Čejková et al.
Droplets As Liquid Robots
The play R.U.R. is famous not only because of the invention of the word “robot”; it was a con-
troversial play that was ahead of its time. Briefly, it was about a mad scientist, Rossum, who dis-
covers how to create artificial life and starts creating artificial human beings. What follows is a
factory for making robots, a robot rebellion, and the extinction of the human race. Although the
play is almost one hundred years old, it provokes many contemporary questions. In a way, R.U.R.
also predicted biological engineering, which is now taking halting steps toward creating artificial life.
In addition the play used the term “robotka” for female robot, even without gender equality require-
ments in its time. Only the masculine form “robot” found its way into many languages; the word
“robotka” is not used, even in Czech.
The term “robot” derives from the Czech word “robota,” which means forced labor. In the context
of robots in general this meaning still holds. In the context of droplets as liquid robots, we can argue
that any force acting on the droplet would induce a response such as movement, division, or release
of content. In this article we will develop the idea that forces shape the dynamics of droplets in many
different liquid robot contexts.
In another view, droplet-based liquid robots can be considered as a physical embodiment of
Braitenbergʼs vehicles [18]. These motile vehicles possess simple environmental sensors linked to ac-
tuators at the wheels for movement. In this way Braitenbergʼs vehicles were capable not only of
motion and directed taxis, but also of complex behaviors. It can be argued that mobile droplets
possess the basic attributes of vehicles (e.g., sensors, actuators, body), including sensory-motor cou-
pling [46, 51, 57].
The present article is structured as follows. First we introduce droplets in general. Then a literature
overview is given to summarize the context of droplet behavior: (i) movement, (ii) self-division,
and (iii) group dynamics. This is followed by some examples of droplets moving in mazes or
manipulated in logic gates. Finally, liquid marbles are presented as another potential embodiment
of liquid-based robotics.
2 Droplets and Vesicles
Droplets are liquid entities for which a degree of immiscibility is required between at least two
phases (gas-liquid or liquid-liquid), and the attractive and repulsive interactions between molecules
at the interface can give rise to a surface tension, which defines among other things the shape of a
droplet. Standard examples include water droplets in air [95], water droplets in oil [5], and oil drop-
lets in water [24]. In addition, molecules can partition preferentially into the water or the oil phase,
depending on their hydrophilic or hydrophobic properties. For example, oil-soluble dyes (e.g., Oil
Red O, Sudan Black) are used for better visualization of oil phases, while inorganic salts (e.g., NaCl)
dissolve preferentially in aqueous phases. However, surfactants, which are amphiphilic molecules
containing both hydrophilic and hydrophobic groups, self-assemble on the phase boundary
(Figure 1). Surfactants are surface-active compounds that can lower the interfacial tension between
the two phases. Droplets can of course form also in the absence of surfactants, but surface-active
molecules that self-assemble at the droplet boundary are useful in modulating the interfacial tension
of the interface and therefore the properties and behavior of droplets. Another purpose of surfactants
is to stabilize droplets by lowering in general the interfacial tension and suppressing droplet
coalescence.
When an aqueous droplet is covered by a continuous lipid bilayer in a bulk aqueous phase, it is
called a vesicle [11]. The self-assembled amphiphilic molecules on the vesicle surface define the ves-
icle. In principle a vesicle is a water-in-oil-in-water droplet with an aqueous core that can contain
water-soluble molecules and a lipid bilayer membrane where oil-soluble molecules can be incorpo-
rated. Vesicles are dispersed in the continuous water phase and range in size from tens of nanome-
ters to hundreds of micrometers. For artificially made vesicles using phospholipids or lipids derived
from biomembranes, the term liposomes is often used, and applications for liposomes range from
artificial cells [60] to drug delivery to microcontainers [98].
Artificial Life Volume 23, Number 4
529
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
3
4
5
2
8
1
6
6
6
9
1
7
a
r
t
l
/
_
a
_
0
0
2
4
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
J. Čejková et al.
Droplets As Liquid Robots
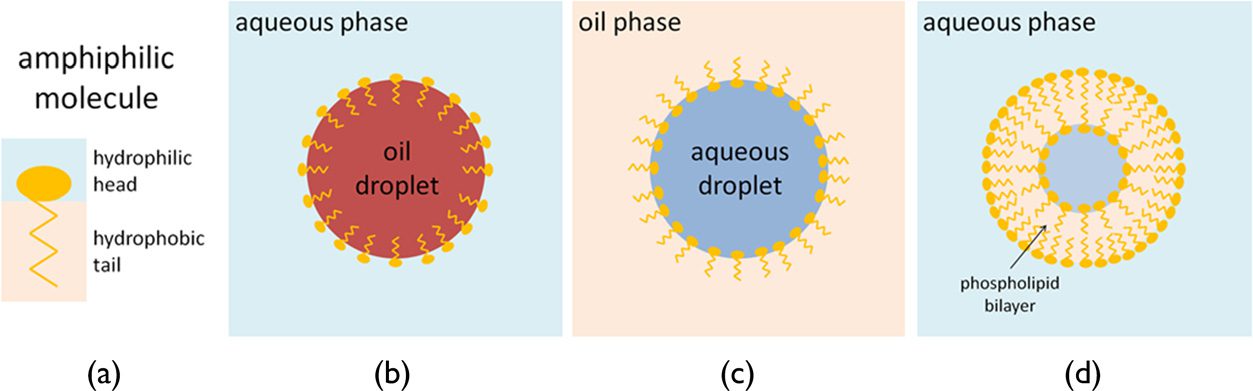
Figure 1. (a) A representation of an amphiphilic surfactant molecule consisting of a hydrophilic head that preferentially
partitions in the aqueous phase and a hydrophobic tail that preferentially partitions in the oil phase. Different architec-
tures of surfactants in differently arranged multiphase systems: (b) oil droplet in water phase, (c) aqueous droplet in oil
phase, (d) vesicle consisting of a phospholipid bilayer.
Droplets can be produced in various ways. To produce a single droplet or a few droplets, simply
dropping liquid from a micropipette or a syringe can be sufficient. Large quantities of droplets can
be produced by a wide range of techniques including, for example, atomizers, nebulizers, and
homogenizers of various designs. These techniques will produce thousands to millions of droplets
dispersed in the continuous phase as emulsions. Typical architectures include oil in water (Figure 1b)
or water in oil (Figure 1c) emulsions, but more complex organizations such as double emulsions also
exist [36]. The implementation of robotic platforms and microfluidics for the generation and analysis
of droplets has been demonstrated [43, 47, 49, 59, 74]. In general, droplets can be produced easily.
However, long-term stability is typically achieved through the presence of surfactants, which
increase the kinetic stability of the system.
3 Moving Droplets
Droplets can be designed to move and can be controlled by various external forces, and thus the
droplets can mimic both the behavior of nonliving objects, such as rocks rolling down a hill, and also
the behavior of living cells or small organisms that can move purposefully in response to various
stimuli. There are several examples of motion due to applied forces or perceived stimuli: Gravita-
tional force induces gravitaxis (geotaxis), a gradient of chemicals that are soluble in the fluid induces
chemotaxis, movement in the gradient of cellular adhesion sites or substrate-bound chemoattrac-
tants is called haptotaxis, electrotaxis (or galvanotaxis) is directional movement in response to an
electric field, magnetotaxis is movement in a magnetic field, phototaxis is the ability to respond
to light, and thermotaxis is migration along a gradient of temperature. These kinds of natural move-
ments are well known for biological objects that have locomotion organelles [23], and in the same
way the movement of synthetic objects can be studied for orthologous dynamics. If droplets can
become animated and follow one or more of these types of motion, then it would be justified to
argue that they are liquid robots, as one of the primary characteristics of robotics is programmed
movement. Although it is not common to term moving droplets as robots [56, 92], in the case of
solid particles we commonly encounter terms such as swimming micro- or nano-robots [16, 65, 70,
78]. The different types of motion will be presented in the following subsections: Section 3.1 will
describe artificial haptotaxis, Section 3.2 will summarize the movement of droplets mimicking
chemotaxis, and Section 3.3 will present other examples of oriented movement (such as magneto-
taxis or galvanotaxis of droplets).
Figure 2 shows several contexts in which a droplet can be placed and tasked for movement,
viewed in vertical cross section. Droplets have been shown to move when placed on a solid surface
in air [21] (a), surrounded fully by another liquid (b), or placed in a thin layer of a liquid in contact
with both substrate and air [24] (c). When there is an interaction of droplet with solid substrate, the
shape of the droplet can change as a result of change in contact angle. Another type of droplet
530
Artificial Life Volume 23, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
3
4
5
2
8
1
6
6
6
9
1
7
a
r
t
l
/
_
a
_
0
0
2
4
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
J. Čejková et al.
Droplets As Liquid Robots
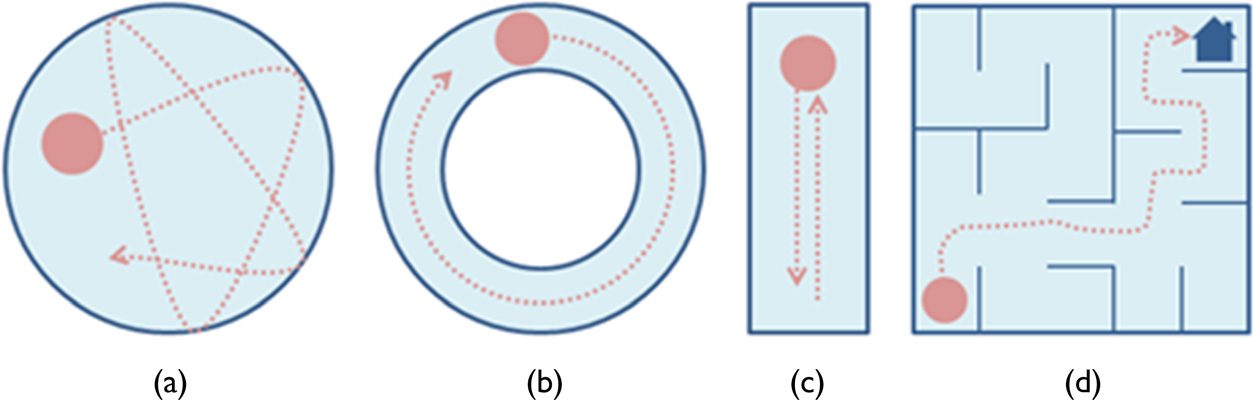
Figure 2. Configuration of droplet movement experiments in a side view: (a) droplet on a solid substrate surrounded by
air, (b) droplet on a solid substrate surrounded fully by another liquid, (c) droplet on a solid substrate placed in a thin
layer of another liquid, (d) droplet freely swimming in another liquid, (e) droplet floating on the surface of an another
liquid, (f) droplet in a channel.
motion is swimming (d), in the case when the droplet and surrounding liquid have similar densities.
This will require that viscosity dominate and the droplet move by creating friction with the sur-
rounding fluid. The floating of a droplet on the surface of another liquid (e) happens if the droplet
has a lower density than the continuous phase. Both internal droplet dynamics and proximal fluid
dynamics in the surrounding fluid may govern droplet movement. Finally, in microfluidics the drop-
lets can move within channels (f ). The width of channels and the droplet diameters have similar
magnitudes, and the channels are not open to the air. However there can be a configuration where
the droplet moves in a channel that is open to the air [62]. Some atypical experimental setups have
been used; for example, Sumino et al. have shown rotational motion within a circle normal to the
horizontal plane and climbing motion on a stairlike substrate [90].
Studies on oil droplet movement can be performed in various geometrical configurations.
Various arenas, shown from the top, are presented in Figure 3. Commonly a round petri dish is
used with various depths of the continuous phase [94], where 2D trajectories of droplets are
observed and recorded (a). Circular channels can be created, for example, by two rings attached
to the glass substrate [76] (b). The space between the inner and outer rings (walls) forms in principle
an endless channel ideal for self-propelled droplet experiments. Simple architectures are based on
rectangular cells or wide channels (c). Some works deal with droplet movement in more complex
systems such as mazes [24, 62] (d).
Figure 3. Configuration of droplet movement experiments in a top view: (a) round dish, (b) circular channel, (c) straight
channel, and (d) maze.
Artificial Life Volume 23, Number 4
531
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
3
4
5
2
8
1
6
6
6
9
1
7
a
r
t
l
/
_
a
_
0
0
2
4
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
J. Čejková et al.
Droplets As Liquid Robots
The droplet movement can be characterized by various parameters; the most common ones are
directionality and velocity. Other parameters include acceleration, pause duration, and turning angle
[46, 51, 57]. In our article [24] on chemotactic decanol droplets we evaluated also the induction time,
that is, the time needed for the response to the chemical signal. In the following text, we will
summarize experiments according to the designed experimental setup.
3.1 Droplet Movement on Solid Surfaces
In nature, motion induced by an adhesion gradient is called haptotaxis. Droplets can move on solid
surfaces without an additional continuous liquid phase if there is any difference in surface properties
between the front and the rear of the droplet. This usually results in a difference in contact angle
between different parts of the droplet and produces artificial haptotaxis. We present examples below
that might be used for various targeted outcomes, such as reversible or irreversible movement.
The classic experiment by the Whitesides group showed how droplets of water can in fact move
“uphill” against gravity if the solid surface is patterned with areas that affect the contact angle of the
droplet [53]. Droplets consisting of n-alkanes and silane molecules behave as self-runners on hydro-
philic glass or silicon substrates [32]. The mechanism is based on leaving a hydrophobic coating on
the hydrophilic substrate, which shifts the center of mass and pushes the droplets towards the ex-
posed hydrophilic area. The movement stops due to depletion of free hydrophilic substrate. It is
noted that the droplet trajectories never cross. In another study, reversible self-propelled droplet
movements of long-chain alkanes at solid-gas interfaces have been shown [63], with reversibility
of movement modulated by temperature changes near the alkane bulk melting temperature.
Cira et al. [21] have shown that miscible liquids such as propylene glycol and water deposited on
clean glass cause the motion of neighboring droplets over a distance, because these droplets are
stabilized by evaporation-induced surface tension gradients. The droplets move in response to
the vapor emitted by neighboring droplets. This kind of movement enables the crossing of droplet
trajectories, and no permanent change of substrate surface occurs.
Sumino et al. [90] described oil droplet movement on a glass substrate that is based on a differ-
ence in surface tension between the front and the rear of the droplet. This mechanism also
allows reversible movement. They have also studied self-running motion of an oil droplet on an
acid-treated glass substrate [89]. Similarly, squalene droplets move on a hydrophobic solid substrate
[44]. Thus, when using specific substrates and chemical droplets, haptotaxis can be artificially created
and studied as long as the system can maintain a differential in surface energy along the droplet with
the underlying substrate. This creation and maintenance of a differential in surface energy also un-
derlies the mechanisms of droplet movement presented in the following subsections.
3.2 Chemotactic Droplet Movement
In nature, if a motile cell senses soluble molecules and follows a concentration gradient to the
source, or if it moves away from a source of undesirable chemicals (e.g., repellent, toxin), it is dis-
playing a directional movement called positive or negative chemotaxis, respectively [23]. This phe-
nomenon is well known to biologists and intensively studied in living systems. Recently a few
laboratories have started to focus on the movement properties of artificial constructs, including
the directional movement of nonliving objects in chemical gradients, and such movement is usually
called artificial chemotaxis.
Almost all observed movements of droplets in chemical gradients are in fact movements due to
gradients of surface tension that are induced by chemical signals. These systems usually involve two
immiscible liquids, with one liquid forming the droplet and the other forming the continuous phase
(Figure 2b–f ). When a surfactant is placed in an aqueous system, it self-assembles at the air-liquid or
liquid-liquid interface and lowers the surface tension of the system. Kurup and Basu [35, 61] have
used the term tensiophoresis for droplet movement due to a gradient of surface tension. When the
surface tension of a liquid is altered, liquid and surfactants flow from areas of low surface tension
532
Artificial Life Volume 23, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
3
4
5
2
8
1
6
6
6
9
1
7
a
r
t
l
/
_
a
_
0
0
2
4
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
J. Čejková et al.
Droplets As Liquid Robots
to areas of high surface tension along an interface. This flow continues until the differential in in-
terfacial tension is null, and this phenomenon is known as Marangoni flow.
The Marangoni-type oil droplet movements are driven by thermal or chemical concentration
gradients that affect the local interfacial tension. The properties of the movement are dependent
on the size and shape of the droplets. Nagai et al. [73] have found that a pentanol droplet with a
volume of less than 0.1 Al shows irregular translational motion, whereas intermediate-sized droplets
of 0.1–200 Al show vectorial motion. This mode selection is interpreted in terms of competition
between the droplet size and the critical wave number in the instability due to the Marangoni effect.
In addition, Horibe et al. [51] showed mode-switching for oleic-anhydride-fueled oil droplets that
again depended directly on the size (volume) of the droplets. For this system it was also argued that
the self-moving oleic-anhydride-fueled oil droplets are an embodiment of homeostasis and therefore
contain the basis for sensory-motor coupling. Later, possible memory effects in these self-moving
droplets were reported, implying perhaps a limited degree of autonomy [46, 57].
We have studied the movement of 1-decanol droplets in the presence of sodium decanoate so-
lution [24] (Figure 4a). Decanol droplets were able to follow salt additions and mimic the chemo-
tactic behavior of living organisms [23]. This droplet system has also the ability to reverse the
direction of movement repeatedly, to carry and release a chemically reactive cargo, to select a stron-
ger concentration gradient from two options, and to initiate chemotaxis by an external temperature
stimulus. Again here the interfacial tension between the decanol droplets and the surrounding aque-
ous solution is governed by the interaction of the decanoate surfactant with the added salt gradients.
A system of oil droplet movement based on fatty acid chemistry has been proposed by Hanczyc
et al. [45, 48, 97] (Figure 4b). An oil phase containing oleic anhydride precursor was introduced into
an aqueous environment that contained oleate micelles. The products of the precursor hydrolysis
were coupled to the movement of the oil droplet and the production of waste vesicles. The oil
droplet successfully moved away from this waste product into fresh unmodified solution, displaying
a form of chemotaxis. It has been also shown how droplets can move in a pH gradient. In this case
the droplets move as they consume the on-board fuel. The droplets move as they generate a local
pH gradient through the chemical hydrolysis of the precursor. The self-generated pH gradient then
affects the interfacial tension between the droplet and the aqueous environment. As verification of
the mechanism, the autonomous motion can be overridden by large external pH gradients imposed
on the aqueous environment, resulting in directed chemotaxis. The same chemistry was used by
Suzuki et al. [92], who prepared an alginate gel capsule robot with an embedded droplet.
Ban and Nakata [8] have studied nitrobenzene droplets containing di-(2-ethylhexyl)phosphoric
acid (DEHPA) in a phosphate buffer solution. In this system, gels containing various alkaline-earth
metal ions induced movement of oriented droplets, mimicking chemotaxis. The directional move-
ment was due to the metal ions creating asymmetric convection due to interfacial surface tension
differences. In addition the same droplets are responsive to pH gradients [10]. pH-sensitive move-
ment was shown also by Banno et al. [13]. They used n-heptyloxybenzaldehyde oil droplets that were
self-propelled in the presence of ester-containing cationic surfactant. Later they studied the differ-
ences in droplet behavior dependent on surfactant concentration and type and also the phosphate
concentration [14]. This group [72] also demonstrated the underwater self-propelled motion of
micrometer-sized oil droplets controlled by using chemical reactions, namely pH-induced motion
of 4-heptyloxybenzaldehyde droplets using a hydrolyzable gemini cationic surfactant. In this study
the droplets moved towards higher pH, where the rate of hydrolysis was increased (Figure 4c).
In the previous examples, the importance of a chemical gradient, either self-generated or exter-
nally imposed, is noted for producing an imbalance in the interfacial tension around a droplet,
resulting in chemotactic droplet movement. The formation of a chemical gradient that triggers drop-
let movement can also be controlled by light and is then termed photo-driven chemopropulsion
( photo-chemopropulsion) [33]. Photoirradiation in the close proximity of a dichloromethane
(DCM) droplet containing 2-hexyldecanoic acid (HDA) and chromoionophore I (CI) (molar ratio
HDA : CI ≈ 170 : 1) initiates a rapid pH change in the aqueous channel fluid. This leads to a cascade
of events involving, for example, protonation of the 2-hexyldecanoate ion and a change in surface
Artificial Life Volume 23, Number 4
533
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
3
4
5
2
8
1
6
6
6
9
1
7
a
r
t
l
/
_
a
_
0
0
2
4
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
J. Čejková et al.
Droplets As Liquid Robots
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
3
4
5
2
8
1
6
6
6
9
1
7
a
r
t
l
/
_
a
_
0
0
2
4
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
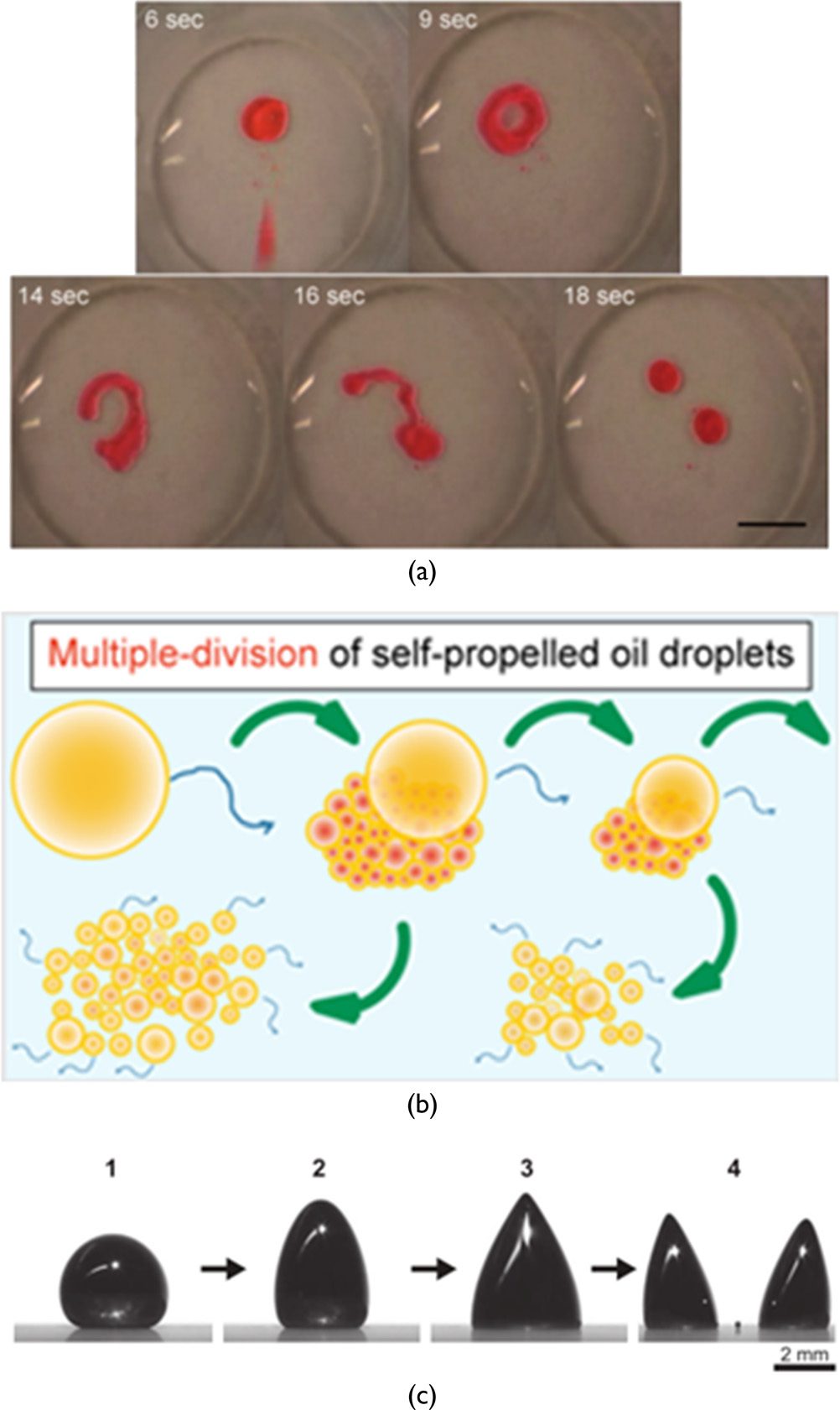
Figure 4. Examples of moving droplets. (a) Schematic representation of repeatable chemotactic decanol droplet move-
ment in a salt gradient (reprinted with permission from [24]; © 2014 American Chemical Society). (b) Nitrobenzene
droplet containing oleic anhydride and Oil Red O as colorant moving in a dish containing both oleate micelles and a pH
indicator thymolphthalein (reprinted with permission from [45]; © 2011 The Royal Society). (c) pH-induced self-propelled
motion of micrometer-sized oil droplets controlled by using chemical reactions (reprinted with permission from [72];
© 2014, American Chemical Society).
tension of the fluid surrounding the droplet, resulting in a fast movement of the droplet away from
the light source.
Directed motion of a nitrobenzene droplet floating in an aqueous solution can be generated by
using a laser beam, which causes a local increase of temperature leading to temperature-induced
Marangoni convection [82]. With these laser-induced flows the droplet is able to move backward
534
Artificial Life Volume 23, Number 4
J. Čejková et al.
Droplets As Liquid Robots
or forward, depending on whether the laser beam is focused on the top or the bottom part of the
droplet. Dixit et al. [30] have shown that water droplets covered by a surfactant or a lipid monolayer
immersed in an organic liquid (decanol or mineral oil) can be controlled using infrared light via both
the thermocapillary effect and convection. Hu and Ohta [52] have shown the manipulation of aque-
ous droplets by optically induced Marangoni circulation. For more details about Marangoni-driven
swimmers we recommend the recent review article of Maass et al. [67]. Table 1 in [67] summarizes
the properties of different droplet systems, namely droplet size, droplet velocity, and active
swimming period.
In these experimental systems, it is clear that when the physical mechanism of droplet motion is
known, the droplets can be manipulated, resulting in various forms of directional taxis. The systems
are typically compositionally very simple, and therefore external control is relatively easy to imple-
ment. Precise control may be exerted more efficiently using light/thermal gradients rather than
purely dissipative chemical gradients. This type of artificial chemotaxis of droplets should be con-
trasted with biological systems, which are vastly more complex, and whose taxis mechanisms are
complicated. Living cells responding to and then decoupling from external stimuli are common
and result in a kind of autonomy. The liquid robots presented here are far less autonomous and
perhaps more easily controlled. It is possible that as the degree of complexity in droplets is increased,
so will their autonomy. The degree of external control necessary for directed motion can then be
experimentally tested.
3.3 Other Types of Droplet Movement
A fully functioning electromagnetic actuation (EMA) system for the manipulation of liquid robots
was proposed and fabricated by Zadražil et al. [100]. The system consisted of a custom-made ex-
perimental setup using a set of four solenoids and a control algorithm written in LabVIEW software
with micro-droplets moving with two degrees of freedom on an air-water interface. The magnetic
liquid robots were made from kerosene droplets (stabilized by Tween 65) containing iron oxide
nanoparticles (size approximately 10 nm). The EMA system proved to be a robust system for ma-
nipulation and navigation of droplets of variable size (diameter 100 Am–1 mm). Furthermore, the
LabVIEW-based algorithm was effective in performance and manipulation tasks. Using a video
feedback loop to obtain information about the instantaneous droplet position and velocity, the al-
gorithm calculates the currents required in each of the four solenoids such that the resulting mag-
netic force acting on the droplet drives it in the desired direction. The algorithm is optimized to
achieve a “soft landing,” that is, to smoothly decelerate the droplet as it approaches the target
setpoint without overshooting it. The system allows the user to freely switch between locomotion
tasks (user-defined target position, user-defined trajectory, or gamepad control), and so it provides
the basis for a wide range of potential future applications involving the use of such liquid robots.
There are additional systems for the two-dimensional magnetic manipulation of droplets, such as
manipulation of aqueous droplets suspended in silicone oil [64]. For example, water droplets can be
coated with magnetic porous Si nanoparticles in dichloromethane [31] and manipulated with external
control. The ability to control the magnetic droplets by external magnetic fields shares some simi-
larities with remote control of traditional mechanoelectrical robots in that no contact between the
robot and the operator is necessary.
Overall, most studies of droplet movement analyze lateral motion. There are only a few works
that describe vertical motion. As an example, Phan [79] has demonstrated the vertical oscillation of a
water droplet between two stationary water-oil interfaces. This mechanism of oscillatory motion is
not due to magnetism, but rather to the electrostatic interaction of the droplet with either interface.
When in proximity to one interface, the electrostatic potential of the droplet changes and the droplet
then travels to the other interface, where the electostatic potential again changes, resulting in repeat-
able oscillations in the vertical dimension.
Velev et al. [99] have shown a liquid-liquid microfluidic system for manipulating freely suspended
water or hydrocarbon droplets, which float on a denser perfluorinated oil and are driven by an
Artificial Life Volume 23, Number 4
535
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
3
4
5
2
8
1
6
6
6
9
1
7
a
r
t
l
/
_
a
_
0
0
2
4
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
J. Čejková et al.
Droplets As Liquid Robots
alternating or constant applied electric field. Apart from the influence of applied magnetic or electric
fields, the motion of droplets has been observed on a horizontal air-water interface purely due to
surface tension effects. For example, it was recently shown how an oil droplet is repelled by a me-
niscus in pure water but shows the opposite behavior and is attracted to the wall when surfactant is
added to the water [66]. The addition of surfactant changes the interfacial energy and therefore the
macroscopic behavior of the system. That article also presented a very simple system consisting of
drinking water, plant oil, and dishwashing detergent as surfactant. This is a good example of the fact
that liquid robots are in principle already easily accessible and exploitable.
Motile droplets as in the examples above can be quite simple in composition. A more intricate
system was developed by Sanchez et al. [84]. They observed self-sustained flows in active gels in the
absence of external forces. Their active gel consisted of substances extracted from living cells;
namely, the protein streptavidin served as a scaffold where clusters of kinesin motor proteins were
assembled and mediated the bundling of microtubules. Such an active gel was introduced into water,
forming water-in-oil emulsions, and autonomous droplet motility was observed due to self-sustained
active flows of microtubule bundles at the inner surfaces of droplets. The dynamic properties of this
material stemmed from the higher-order assembly of active molecules into emulsion droplets.
4 Droplet Division
The field of robotics continues to develop robots from new materials and with new functionalities.
For example, stretchable and deformable electronic devices have been introduced, showing distinct
advantages over standard rigid wafer-based systems [81]. Some target functionalities of new types of
robots include self-healing, shape change (morphing), reconfiguration, and self-replication. For ex-
ample, several studies in robotics demonstrate how a robot can replicate by moving, collecting, and
assembling another copy of itself from provided parts [91].
With regard to liquid robots, Grzybowskiʼs group has studied the self-division of macroscopic
droplets [19]. A droplet of dichloromethane that contained 45–50% 2-hexyldecanoic acid (2-HDA)
was placed in a solution of KOH (pH 12). The interfacial reaction between 2-HDA and the base led
to the accumulation of the deprotonated 2-HDA at the interface and to the increase of the interfacial
area (elongation of the droplet). The droplet divided into two smaller droplets, and they divided
further in the same way, until nanometer size was reached. The droplets could divide indefinitely
and thus dissolve, or division could be limited under the control of the pH.
Later, Caschera et al. [20] showed that nitrobenzene droplets loaded with cationic surfactant and
added to anionic surfactant formed tori, followed by breaking into two or more smaller droplets
(Figure 5a). The division event occurs through a temporary minimum in interfacial tension coupled
with fluid dynamics as the catanionic system approaches equilibrium. Conditions that support spon-
taneous droplet fission were tested for several different surfactant pairs. Also, salt-induced droplet
fusion in cationic surfactant has been shown, demonstrating a rudimentary fission-fusion cycle
capable of the addition of new chemistries or refueling of the droplets.
In addition, Derenyi and Lagzi [28] have shown a self-division of millimeter-sized fatty acid drop-
lets, again governed by surface tension effects. The division was controlled by an autonomous chem-
ical reaction (a pH clock reaction). The pH change affected the protonation state of the fatty acid
head groups; the change in fatty acids led to a change of surface tension followed by destabilization
and expansion of the droplet. The resulting ringlike structure became unstable (Plateau–Rayleigh
instability) followed by the coalescence of some connected protrusions and the division of the un-
stable droplet. Statistically, the most frequent outcome is the self-division of a droplet into two
daughter droplets of the same size.
Both self-propelled motion and division of micrometer-sized oil droplets induced by chemical
conversion of the oil components was studied by Banno and Toyota (Figure 5b [12]). Hydrolysis
of the surfactant in the system produced a hydrophobic product that added to the mass of the oil
droplet, and eventually this resulted in droplet division [15]. From a theoretical and modeling
536
Artificial Life Volume 23, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
3
4
5
2
8
1
6
6
6
9
1
7
a
r
t
l
/
_
a
_
0
0
2
4
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
J. Čejková et al.
Droplets As Liquid Robots
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
3
4
5
2
8
1
6
6
6
9
1
7
a
r
t
l
/
_
a
_
0
0
2
4
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5. Examples of dividing droplets. (a) Spontaneous droplet division (reprinted with permission from [20]; © 2013
WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim). (b) Schematic illustration of the proposed mechanism for multiple
division of self-propelled oil droplets (from [12]; © The Royal Society of Chemistry 2015). (c) Magnetically triggered
ferrofluid droplet division on a superhydrophobic surface (reprinted with permission from [95]; © 2013 American
Association for the Advancement of Science).
perspective, Schwartz et al. discussed the analogy between cell division (and propulsion) and the
division of droplets in the presence of surfactants and determined that the energies required to drive
both motion and division are quite small [86]. Their hypotheses are based on the work of Greenspan
[40, 41], who studied this problem in the 1970s.
Another self-dividing system was introduced by Sato et al., testing the influence of surface area
on the state of the system [85]. Their assumption is that a synthetic cell will divide if the ratio of the
surface area to volume increases. Their droplets (formed by a mixture of sorbitan monooleate (Span 80)
and polyoxyethylene sorbitan monooleate (Tween 80) with alkaline phosphate buffer solution)
were placed in a hydrophobic oil (mineral oil or liquid paraffin with p-nitrophenyl palmitate (pNPP)).
The aqueous droplets increased their surface area through a hydrolysis reaction. Division occurred
Artificial Life Volume 23, Number 4
537
J. Čejková et al.
Droplets As Liquid Robots
through the increase in surface area, and it was shown that the temperature and viscosity of the
microenvironment influenced the division types (e.g., equal versus unequal divisions, and multiple
buddings).
Armstrong and Hanczyc [5] revisited a dynamic water-in-oil system first described by Bütschli in
1892. In their experiments, sodium hydroxide was added to olive oil in a Petri dish, and lifelike be-
havior of aqueous droplets was observed, including droplet group dynamics. Various kinds of droplet
division and other behavior modes (explosion, vibration, stardust, galaxies) were observed by
Croninʼs group when searching the compositional space of the droplets placed in an aqueous phase
[43]. Song et al. [87] have shown the splitting of droplets by laser irradiation. It is notable that in [43]
the behaviors of droplets were selected over time, resulting in the evolution of droplet composition.
This demonstrates that the behavior of droplets is tied to their individual composition. From a
robotics perspective, the chemical content of a droplet could be considered as its programming.
On the other hand, droplet division can be manipulated by externally imposed forces. Timonen
et al. [95] have shown manipulation and division of magnetic aqueous ferrofluid droplets on a low-
friction lotus-leaf–like superhydrophobic surface with an external magnetic field (Figure 5c). A
ferrofluid droplet was subjected to increasing magnetic field from a cylindrical permanent magnet. This
resulted in a division into numerous daughter droplets that formed different static self-assembled
patterns to minimize their total energy. When the magnetic field decreased, the relaxation of conical
daughter droplets into spherical ones occurred.
Recently, we have found that decanol droplets surrounded by a decanoate solution containing salt
perform intriguing shape changes [26]. Depending on the initial system composition, interesting
patterns (e.g., stars, tentacular structures) are observable during the evaporation of the aqueous
phase. In addition, the division of droplets can occur. The interesting point is that when the evap-
oration is completed, the droplets usually return more or less to the original spherical shape. Such
reproducible morphological changes in simple droplets, dependent on the initial state of the system,
can be used to produce predictable temporal state changes in liquid robotics.
Much like the mechanisms of self-motion, droplet division appears to be achievable if the inter-
facial tension is reduced. This is often governed by the addition or production of surfactants. Under
these conditions a small amount of energy in the form of internal or external fluid dynamics appears
to be enough to trigger division events. The division may be noisy, producing several droplets of
various dimensions, or well-controlled, transforming one droplet into two daughter droplets of the
same size. In all examples provided here we can see the propensity for liquid droplets, either pushed
from equilibrium or created far from equilibrium, to produce such dynamics. Such soft-material
properties of droplets make them ideal for key aspects of soft robotics, namely self-healing, shape
change (morphing), reconfiguration, and self-replication. Consider a robot tasked to pass through a
small hole. The droplet can divide, go through in the form of smaller objects, and then coalesce to
form the original liquid robot.
Although we have highlighted a few examples from the literature in which the controlled fusion
and division of droplets was studied, the development of a functional liquid robot remains a
challenging task.
5 Problem Solving by Droplets
5.1 Droplets in Mazes
Above we summarized diverse approaches to animating droplets for both motion and division.
Several groups have applied such dynamic liquid robots to solve rudimentary tasks. For example,
could a self-moving droplet solve a maze? Maze solving, and finding the shortest path or all paths in
mazes, are computational problems that could be solved by using algorithms. There are several types
of mazes that could be treated. Here we will consider only 2D perfect mazes (called also simply
connected mazes), mazes without any loops or closed circuits and without any inaccessible areas.
From each point, there is exactly one path to any other point, and the maze has exactly one solution.
538
Artificial Life Volume 23, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
3
4
5
2
8
1
6
6
6
9
1
7
a
r
t
l
/
_
a
_
0
0
2
4
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
J. Čejková et al.
Droplets As Liquid Robots
There are several approaches a human might take toward maze solving [7]. Imagine a human
being standing at the starting point of a huge perfect maze. Here we will introduce just three sim-
plest options. First, the human can use the algorithm called random mouse, meaning to run randomly
in the corridors and hope to find the way out. A disadvantage of this algorithm is that it is extremely
slow and there is a probability that the human will never reach the exit. A better approach is to use
the wall-follower algorithm, which is based on keeping one hand in contact with one wall of the maze
and following that wall. The solver is guaranteed not to get lost and will eventually reach the exit.
The time spent in the maze may depend on the choice of hands; sometimes a left-hand path may be
much shorter than a right-hand path or vice versa. If the solver has a chalk, a Trémauxʼs algorithm
can be implemented. In this method the solver makes a random decision where to go from the start
point and draws lines on the floor to mark his path. If the solver reaches the endpoint of any cor-
ridor, he goes back to the closest crossroad where he chooses any corridor that he has not visited
yet. The paths are either unlabeled (which means unvisited yet), marked once, or marked twice
(meaning leading to the dead end). These approaches work also for traditional robots, programmed
to behave similarly to people.
It is also possible for self-propelled droplets to solve mazes. The self-propelled droplets can im-
plement the random mouse algorithm, with a low probability that the droplet will reach the exit; the
time for solving the maze may be long. The wall-follower and Trémauxʼs algorithms are not appli-
cable to liquid droplets without some further signal that could prompt the liquid robot towards the
exit [38].
In all articles where it was shown how chemotactic droplets can solve a maze, the droplets have
in fact followed the shortest path predefined by a concentration gradient in the channels of the
maze. Therefore diffusion and Marangoni flows are the physical solvers of the maze in principle,
and the droplet follows the gradients in order to minimize its free energy [2]. The chemoattractant
(i.e., the chemical substance placed at the exit) diffuses and causes a surface tension gradient that a
droplet can sense. If the liquid robot is placed anywhere in a perfect maze and follows the steepest
gradient, it reaches the source of the chemical signal. The intelligence of liquid robots is not in the
ability to find the target, but in the ability to follow the track leading to the target. Note that not all
droplets have this ability and not all kinds of droplets can follow the gradient chemotactically.
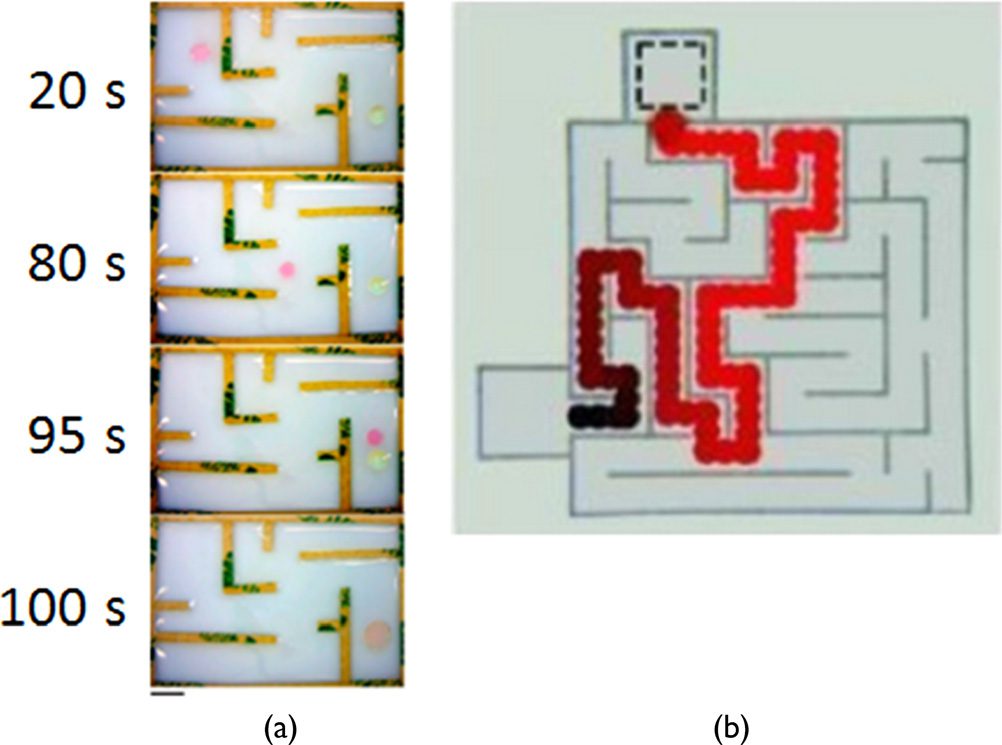
We have shown that decanol droplets are able to solve a maze containing a thin layer of sodium
decanoate solution and locomote to the position with the highest concentration of salt (Figure 6a
Figure 6. Examples of droplets in topologically complex systems. (a) Chemotactic decanol droplet following salt in a maze
(reprinted with permission from [24]; © 2014, American Chemical Society). (b) Maze-solving HDA droplet following
HCl gradient (reprinted with permission from [62]; © 2010, American Chemical Society).
Artificial Life Volume 23, Number 4
539
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
3
4
5
2
8
1
6
6
6
9
1
7
a
r
t
l
/
_
a
_
0
0
2
4
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
J. Čejková et al.
Droplets As Liquid Robots
[24]). In principle the path was indicated in advance as the salt spread from the source point by dif-
fusion and Marangoni-induced flow along the liquid surface. The decanol droplet representing the
liquid robot demonstrates the ability to follow this path without mistake and without exploring alter-
native paths. In the absence of the gradient of surface tension and determination of the shortest path,
the droplet remains at the start point without any long-distance motion or exploratory behavior.
Lagzi et al. [62] have shown maze solving by chemotactic droplets, where oil droplets (mineral oil
or dichlormethane) containing 2-hexyldecanoic acid (HDA) were able to move to the area with
lowest pH (Figure 6b). As in the case described above, the pH gradient predefined the proper path,
and the oil droplets with HDA followed this path. As a control, droplets without HDA have not
shown chemotactic ability and have not followed the gradient. In principle, the H+ ions from the
target of the maze were the physical solvers of the maze, while the droplets enabled visualization of
the shortest path [2].
Francis et al. [34] presented self-propelled chemotactic ionic liquid droplets that spontaneously
travel along the liquid-air interface by release of surfactant-type ions when following HCl, similarly to
Lagziʼs system. The droplets were placed in any position within the fluidic network, and in every
case they spontaneously traveled towards the chemoattractant source.
A further example of solving mazes by droplets is a recent article by Jin et al. [54]. They present
self-propelling artificial swimmers in the form of oil droplets in an aqueous surfactant solution
driven by interfacial Marangoni flows induced by micellar solubilization of the oil phase. The authors
demonstrated that chemotaxis along micellar surfactant gradients can guide these swimmers through
a microfluidic maze.
The intelligence of droplets consists in their ability to follow environmental signals; they are not
able to solve the maze by themselves. This is not trivial, in that a droplet is able to sense its imme-
diate environment and then link the environmental patterning to self-motion. Using ionic liquids for
liquid robots instead of organic compounds will have advantages due to their negligible vapor pres-
sure, low combustibility, and high thermal stability. Further, they are suitable solvents for numerous
chemical species and can be used in a wide range of harsh reactions.
5.2 Droplets in Logic Gates
Research in unconventional computing includes analyzing new types of systems for their ability to
perform basic logical operations. In some ways these unconventional systems mimic their electronic
counterparts, but there are striking differences, including slow processing and high parallelism. It has
been already shown that logical arguments could be performed by unconventional systems such as
the slime mould Physarum [1, 3] or swarms of crabs [42]. A number of articles describe logic gates in
chemical media, namely, those based on chemical wave propagation in excitable media (e.g., the
Belousov-Zhabotinsky reaction) [88]. In past decades the research on logic gates has also focused
on using droplets or bubbles.
Microfluidic computing elements, such as logic gates for logic operations, adders for arithmetic
operations, and memory to store information, have been created [69]. Microfluidic chips with logic
have been designed, where the presence or state of one droplet was influenced by the state of other
droplets, or by the state of the chip. For example, pneumatic membrane valves have been used to
open and close different channels and force droplets to execute a certain protocol depending on
which valves were activated [29]. This allowed the creation of NOT, NAND, and NOR gates, flip-flops,
oscillators, self-driven peristaltic pumps, and a 12-bit shift register. Cheow et al. [55] have demon-
strated droplet-based microfluidic AND/OR and NOT logic gates. Logic operations were based on the
nonlinear change in hydrodynamic resistance for channels containing droplets. Digital microfluidic
logic gates were also shown, for example, by Toepke [96] and Zhao and Chakrabarty [105]. A uni-
versal microfluidic logic gate that is capable of conducting all 16 logic operations in one chip was
presented by Zhang et al. [101].
The team of Prakash [80] has shown bubble logic processors implemented with nitrogen bubbles
in water (with added surfactant 2%(w/w) Tween 20 to stabilize the interfaces) flowing through
540
Artificial Life Volume 23, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
3
4
5
2
8
1
6
6
6
9
1
7
a
r
t
l
/
_
a
_
0
0
2
4
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
J. Čejková et al.
Droplets As Liquid Robots
PDMS microfluidic chips. Computational models related to bubble logic circuits were presented also
by Anandan et al. [4]. Recently Prakashʼs group demonstrated synchronous water-based ferrofluid
droplet generation and propagation in an oil-based carrier fluid between two parallel Teflon-coated
glass surfaces [58]. A rotating magnetic field enables parallel manipulation of arbitrary numbers of
ferrofluid droplets on permalloy tracks. The limits of synchronization were defined in dependence
on frequency and droplet diameter.
Mertaniemi et al. [71] have demonstrated water droplets in air on superhydrophobic substrates,
either coalescing or rebounding, depending on the Weber number and impact parameter. Under
conditions when droplets rebound (not coalesce), experiments were performed on droplet logic
gates (NOT/FANOUT and AND/OR). A toggle flip-flop memory based on controlled droplet collisions
was successfully demonstrated, as well as a basis for programmable encapsulated chemistry.
Therefore certain logical operations, also associated with traditional programmed robots, can be
implemented with droplet-based liquid robots. So far a substantial amount of external structure—for
example, in the construction and architecture of microfluidic channels—is necessary for computing
with input and output droplets, with the operations performed by droplets playing a key role in
much larger systems. It has not yet been shown that individual droplets regardless of context can
execute logical operations of note. Thus we consider the collective behavior and potential interac-
tions of multiple droplets in the next section.
6 Multi-droplet Interactions
Since single droplets are able to demonstrate dynamic properties from self-motion to self-division to
maze solving, it is intriguing to ask what types of behaviors can be demonstrated by multiple drop-
lets, including swarms. Some works focus on the behavior of two or more droplets that either touch
each other (and form a matrix of “artificial tissue”) or are distributed in the environment indepen-
dently and are able to mimic intracellular communication by means of chemical signals. In the same
way as in the populations of living objects or robots, the collective behavior and swarming of liquid
robots can be investigated. As Aristotle pointed out, “the whole is more than the sum of its parts”1—
in terms of droplet behavior a swarm of liquid robots may display more useful properties than indi-
vidual droplets; a swarm could perhaps perform targeted tasks better, faster, more robustly, or more
efficiently.
For a start, we can ask whether two or more droplets influence each other in a measurable way.
In [51], we studied in detail the motion of single and multiple self-propelled droplets over the course
of minutes. In our experiments we studied the behavior of two droplets placed in one petri dish, and
as a control experiment we observed two droplets separately in two petri dishes. We found that in
the early part of the experiment (the first 20 minutes) two droplets tended to move close to one
another, resulting in a circling effect. Compared to controls, we found that the two droplets influ-
ence each other and this influence depended on droplet size (volume).
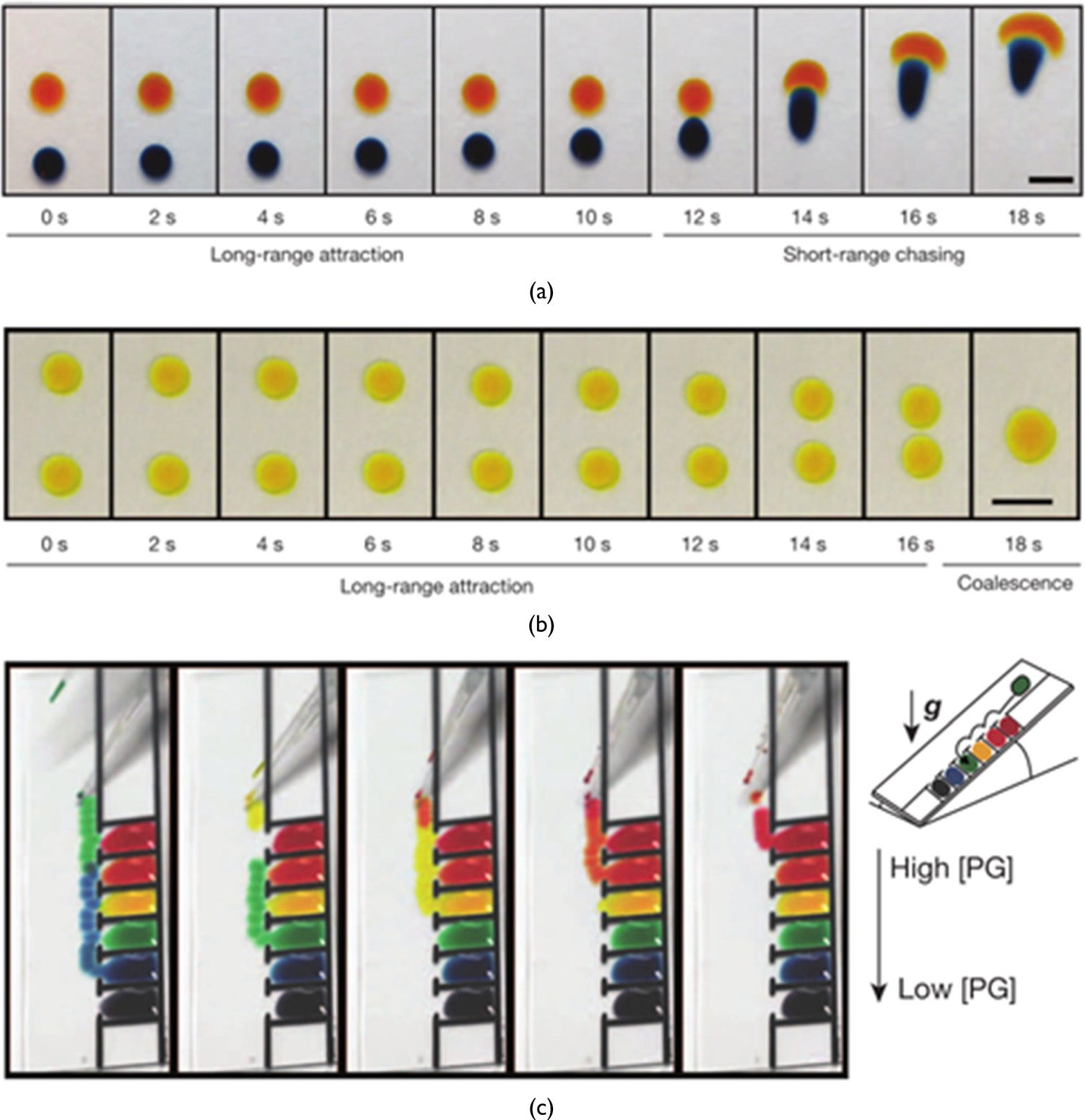
Multiple droplet behavior may be influenced by attraction or repulsion, but a droplet may change
its state through coalescence. Cira et al. [21] have shown that droplets consisting of propylene glycol
and water mixtures fuse only if they have the same composition; otherwise they repel each other. In
their device, droplets moved down a ramp by gravity. Along the way, a droplet merged only with a
container of matched composition (and thus surface tension); otherwise the droplet moved along
until it met a container with the appropriate mixture. In such a way the droplets sort themselves
through surface tension (Figure 7).
These are examples where the behavior of the systems changes due to the presence of more than
one droplet. Perhaps the droplets show some kind of “intelligence,” or at least selectivity based on
composition. Such purely intrinsic behavior of multiple droplets has great potential for applications
1 “In the case of all things which have several parts and in which the totality is not, as it were, a mere heap, but the whole is something
beside the parts,….” (Aristotle, Metaphysics, Book 8, part 6).
Artificial Life Volume 23, Number 4
541
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
3
4
5
2
8
1
6
6
6
9
1
7
a
r
t
l
/
_
a
_
0
0
2
4
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
J. Čejková et al.
Droplets As Liquid Robots
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
3
4
5
2
8
1
6
6
6
9
1
7
a
r
t
l
/
_
a
_
0
0
2
4
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7. Interaction of two-component droplets consisting of water and propylene glycol mixture. (a) Repulsion of
droplets with different compositions. (b) Coalescence of droplets with the same composition. (c) Surface tension
sorter. (Reprinted from [21] by permission of Nature Publishing Group.)
of liquid robots where identical droplets may be tasked to work together or specialized droplets may
form a working consortium. In this way the system may become more robust and also suitable for
diverse targeted outcomes.
7 Liquid Marbles
A special category of droplets, distinct from the liquid-liquid systems depicted in Figure 2, are so-
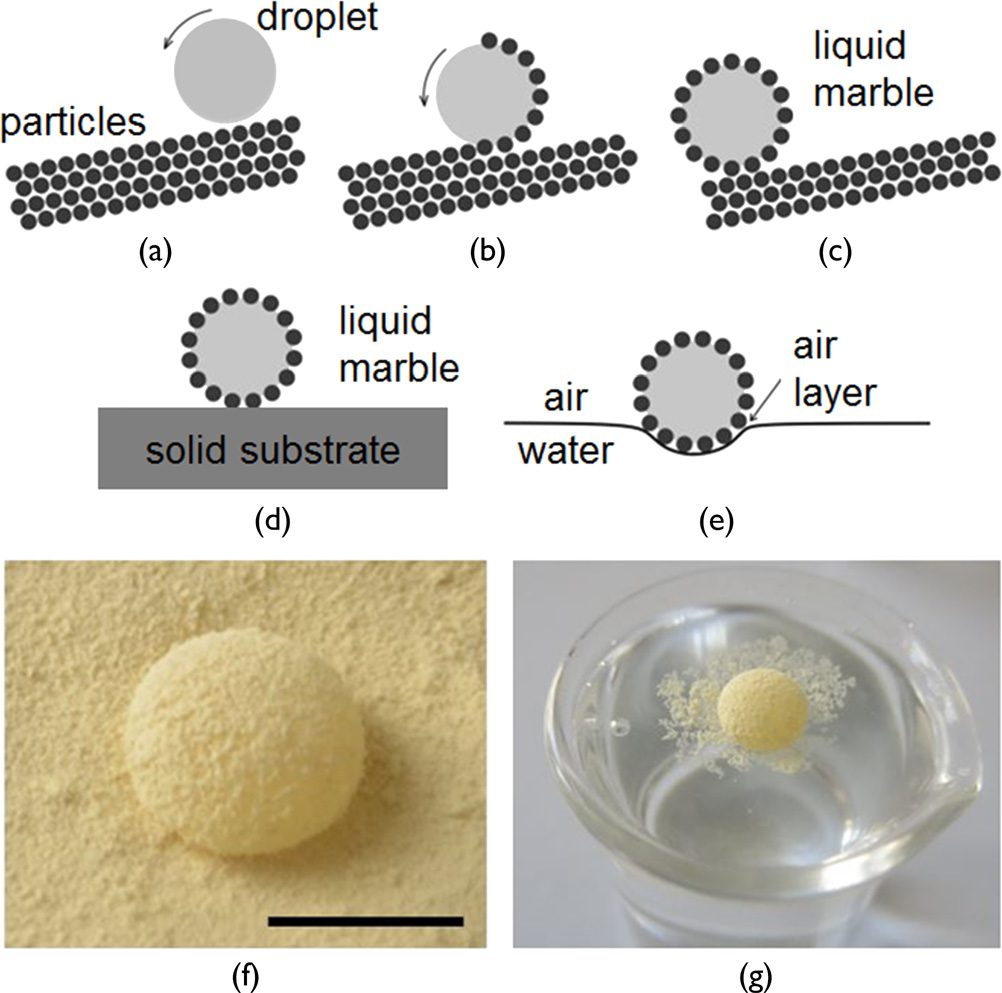
called liquid marbles as defined by Aussillous and Quéré in 2001 [6]. A liquid marble is a liquid
droplet encapsulated in a hydrophobic powder that adheres to its surface (Figure 8). Preparation
of liquid marbles is a very simple operation—a small amount of liquid is rolled on a layer of
hydrophobic powder consisting of nano- or microparticles, which spread spontaneously at the
liquid-air interface. This process results in a liquid marble that has some of the properties of a
liquid droplet and at the same time behaves as a soft solid. Liquid marbles are an alternative to
superhydrophobic surfaces, because particles at the interface prevent the liquid in the marble from
542
Artificial Life Volume 23, Number 4
J. Čejková et al.
Droplets As Liquid Robots
Figure 8. Liquid marbles. (a)–(c) Scheme of liquid-marble preparation process. (d) Scheme of liquid marble on a solid
substrate. (e) Scheme of liquid marble floating on the water surface. (f) Photograph of liquid marble (100 Al of water
covered by Lycopodium). Scale bar corresponds to 5 mm. (g) Photograph of liquid marble from (f) floating on water
surface (reprinted with permission from [25]).
wetting the carrier surface. The substrate on which the liquid marble moves can be a solid or even a
liquid surface. Liquid marbles can serve, for example, to transport of small volumes of liquids or
powders [25, 83].
Like with simple droplets, liquid marbles can be moved using external forces. Ooi [75] summa-
rized methods for manipulation of liquid marbles, mainly by electrostatic and magnetic forces, with
other options mentioned (e.g., mechanical, gravitational, irradiation, changes in temperature or pH).
Magnetic force could be used for both the manipulation [103] and also for controlled fusion of two
liquid marbles [104]. Bormashenko et al. have shown self-propulsion of liquid marbles filled with
aqueous alcohol solutions and placed on a water surface [17]. Recently Paven et al. introduced a
system whereby laser-driven liquid marbles can push 150 times their own weight [77]. This type
of droplet thus also shows potential to be used as a liquid robot and is attracting further interest.
8 Conclusions and Outlook
It is widely accepted that robots are artificial objects that can in some contexts make human life
easier. However, the idea of electromechanical robots dominates. In the present review we have
described how simple droplets can be an embodiment of liquid robots. These droplet-based robots
have the ability to sense gradients and even each other, resulting in directional chemotactic motion
and also group dynamics. The composition of individual robots also influences their behavior. Even
with such rudimentary abilities, the droplets are able to sense chemical gradients in complex envi-
ronments and thereby to solve mazes. In addition, droplet-based liquid robots are soft and can de-
form [9], sometimes to such an extent that the droplets divide into daughter droplets. Moreover,
they can change their own shape [26]. Along with fusion, this forms the basis of self-replication and
perhaps even evolution. Although multiple droplets in an experiment can perform logical operations,
it remains to be seen how individual droplets can also perform logic based on their chemistry.
Artificial Life Volume 23, Number 4
543
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
3
4
5
2
8
1
6
6
6
9
1
7
a
r
t
l
/
_
a
_
0
0
2
4
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
J. Čejková et al.
Droplets As Liquid Robots
Like Braitenbergʼs vehicles, droplet-based liquid robots can be semi-autonomous and self-
propelled. And like billiard balls, droplet-based robots can be deterministically controlled by external
forces. It is this potential for both external and embedded control that makes liquid robots intriguing
and useful as a branch of robotics.
Due to the ability of droplets to change state (e.g., by fission or fusion), the link between chemical
composition and function, and the link between environmental information and self-movement, it is
possible to design liquid robots that not only perform targeted delivery but also process complex
input information—for example, to distinguish the inside from the outside of a tumor and provide
controlled doses of therapeutic substances in a manner not available with current theranostics. Be-
yond medicine, liquid robots as smart materials may allow for the prolonged proper function of
machines, organisms, and infrastructure [46, 57].
With regard to potential engineering applications, the area of environmental sensing and reme-
diation is one where droplet-based devices could prove to be valuable and technically feasible. For
example, it has been recently demonstrated that droplets can encapsulate chemical species and per-
form oriented motion in microchip channels, where they can induce phenomena such as the floc-
culation of a dispersed model pollutant [102]. At the same time, it has to be kept in mind that droplet
movement in an actual real-world environment without well-defined channels, in a fluid of uncon-
trolled composition, and in the presence of macroscopic convective transport is a rather different
task.
Although droplets as liquid robots are promising tools for performing various tasks, there is still a
long way to go before we can use them in real life. All droplet studies presented in this article were
performed in well-defined laboratory conditions, and nobody has yet focused on robustness of
droplet systems. For practical application of liquid droplets in biological or environmental use,
one must consider the influence of ambient noise on the dynamics of droplets. To transfer liquid
robots in the form of droplets from laboratories to real-world conditions is a challenging task in the
area of liquid robotics.
A possible way of increasing the robustness of robotic devices in a real-world environment is to
proceed from individual robots to robotic swarms [39]. In nature, this is a successful survival strat-
egy used by collective organisms such as swarms of insects, schools of fish, and flocks of birds.
Collective phenomena are observable also in cells, as in the multicellular development of Dictyostelium
cells [50, 93]. The main benefit is that even if a number of individuals are lost, the majority can still
complete the mission, thanks to a combination of the statistics of large numbers and mutual com-
munication that leads to the so-called swarm intelligence. Thus, the collective motion of interacting
droplet swarms is an area of research that can improve the practical application potential of droplet-
based liquid robots.
Acknowledgment
J.Č. was financially supported by the Czech Science Foundation (Grant No. 17-21696Y). M.M.H.
was financially supported by the European Commission FP7 Future and Emerging Technologies
Proactive (EVOBLISS 611640).
References
1. Adamatzky, A. (2015). Slime mould processors, logic gates and sensors. Philosophical Transactions of the Royal
Society A, 373(2046), 20140216.
2. Adamatzky, A. (2017). Physical maze solvers. All twelve prototypes implement 1961 Lee algorithm. In
A. Adamatzky (Ed.), Emergent computation: A festschrift for Selim G. Akl (pp. 489–504). Cham: Springer
International Publishing.
3. Adamatzky, A., & Schubert, T. (2014). Slime mold microfluidic logical gates. Materials Today, 17(2), 86–91.
4. Anandan, P., Gagliano, S., & Bucolo, M. (2015). Computational models in microfluidic bubble logic.
Microfluidics and Nanofluidics, 18(2), 305–321.
5. Armstrong, R., & Hanczyc, M. (2013). Bütschli dynamic droplet system. Artificial Life, 19(3–4), 331–346.
544
Artificial Life Volume 23, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
3
4
5
2
8
1
6
6
6
9
1
7
a
r
t
l
/
_
a
_
0
0
2
4
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
J. Čejková et al.
Droplets As Liquid Robots
6. Aussillous, P., & Quéré, D. (2006). Properties of liquid marbles. Proceedings of the Royal Society A:
Mathematical, Physical and Engineering Science, 462(2067), 973–999.
7. Babula, M. (2009). Simulated maze solving algorithms through unknown mazes. In L. Czaja (Ed.),
Proceedings of XVIIIth Concurrency, Specification and Programming Workshop (pp. 13–22). Krakow.
8. Ban, T., & Nakata, H. (2015). Metal-ion-dependent motion of self-propelled droplets due to the
Marangoni effect. The Journal of Physical Chemistry B, 119(23), 7100–7105.
9. Ban, T., Yamada, T., Aoyama, A., Takagi, Y., & Okano, Y. (2012). Composition-dependent shape changes
of self-propelled droplets in a phase-separating system. Soft Matter, 8(14), 3908–3916.
10. Ban, T., Yamagami, T., Nakata, H., & Okano, Y. (2013). pH-dependent motion of self-propelled droplets
due to Marangoni effect at neutral pH. Langmuir, 29(8), 2554–2561.
11. Banno, T., Kazayama, Y. & Toyota, T. (2014). Giant vesicle formation of novel polymerizable amphiphile
associated with its polymerization and hydrolysis in water. Chemistry Letters, 43(11), 1707–1709.
12. Banno, T., Kuroha, R., Miura, S., & Toyota, T. (2015). Multiple-division of self-propelled oil droplets
through acetal formation. Soft Matter, 11(8), 1459–1463.
13. Banno, T., Kuroha, R., & Toyota, T. (2012). pH-sensitive self-propelled motion of oil droplets in the
presence of cationic surfactants containing hydrolyzable ester linkages. Langmuir, 28(2), 1190–1195.
14. Banno, T., Miura, S., Kuroha, R., & Toyota, T. (2013). Mode changes associated with oil droplet
movement in solutions of gemini cationic surfactants. Langmuir, 29(25), 7689–7696.
15. Banno, T., & Toyota, T. (2015). Molecular system for the division of self-propelled oil droplets by
component feeding. Langmuir, 31(25), 6943–6947.
16. Behkam, B., & Sitti, M. (2006). Towards hybrid swimming microrobots: Bacteria assisted propulsion of
polystyrene beads. In Proceedings of the 28th Annual International Conference of the IEEE Engineering in Medicine
and Biology Society (pp. 2421–2424). doi:10.1109/IEMBS.2006.259841
17. Bormashenko, E., Bormashenko, Y., Grynyov, R., Aharoni, H., Whyman, G., & Binks, B. P. (2015). Self-
propulsion of liquid marbles: Leidenfrost-like levitation driven by Marangoni flow. The Journal of Physical
Chemistry C, 119(18), 9910–9915.
18. Braitenberg, V. (1986). Vehicles: Experiments in synthetic psychology. Cambridge, MA: MIT Press.
19. Browne, K. P., Walker, D. A., Bishop, K. J. M., & Grzybowski, B. A. (2010). Self-division of macroscopic
droplets: Partitioning of nanosized cargo into nanoscale micelles. Angewandte Chemie, 122(38), 6908–6911.
20. Caschera, F., Rasmussen, S., & Hanczyc, M. M. (2013). An oil droplet division–fusion cycle.
ChemPlusChem, 78(1), 52–54.
21. Cira, N. J., Benusiglio, A., & Prakash, M. (2015). Vapour-mediated sensing and motility in two-
component droplets. Nature, 519(7544), 446–450.
22. Čapek, K. (1920). R.U.R. – Rossumovi Univerzálni Roboti [Rossumʼs Universal Robots]. Prague: Aventinum.
23. Čejková, J., Holler, S., Quyen, N. T., Kerrigan, C., Štěpánek, F., & Hanczyc, M. M. (2017). Chemotaxis
and chemokinesis of living and non-living objects. In A. Adamatzky (Ed.), Advances in unconventional
computing (pp. 245–260). Cham, Switzerland: Springer International Publishing.
24. Čejková, J., Novák, M., Štěpánek, F., & Hanczyc, M. M. (2014). Dynamics of Chemotactic droplets in salt
concentration gradients. Langmuir, 30(40), 11937–11944.
25. Čejková, J., & Rychecký, O. (2017). Tekuté kuličky. Chemické Listy, 111, 109–114.
26. Čejková, J., Štěpánek, F., & Hanczyc, M. M. (2016). Evaporation-induced pattern formation of decanol
droplets. Langmuir, 32(19), 4800–4805.
27. de Jong, H. B. (1932). Die Koazervation und ihre Bedeutung für die Biologie. Protoplasma, 15(1), 110–173.
28. Derenyi, I., & Lagzi, I. (2014). Fatty acid droplet self-division driven by a chemical reaction. Physical
Chemistry Chemical Physics, 16(10), 4639–4641.
29. Devaraju, N. S. G. K., & Unger, M. A. (2012). Pressure driven digital logic in PDMS based microfluidic
devices fabricated by multilayer soft lithography. Lab on a Chip, 12(22), 4809–4815.
30. Dixit, S. S., Kim, H., Vasilyev, A., Eid, A., & Faris, G. W. (2010). Light-driven formation and rupture of
droplet bilayers. Langmuir, 26(9), 6193–6200.
Artificial Life Volume 23, Number 4
545
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
3
4
5
2
8
1
6
6
6
9
1
7
a
r
t
l
/
_
a
_
0
0
2
4
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
J. Čejková et al.
Droplets As Liquid Robots
31. Dorvee, J. R., Derfus, A. M., Bhatia, S. N., & Sailor, M. J. (2004). Manipulation of liquid droplets using
amphiphilic, magnetic one-dimensional photonic crystal chaperones. Nature Materials, 3(12), 896–899.
32. Dos Santos, F. D., & Ondarçuhu, T. (1995). Free-running droplets. Physical Review Letters, 75(16), 2972–2975.
33. Florea, L., Wagner, K., Wagner, P., Wallace, G. G., Benito-Lopez, F., Officer, D. L., & Diamond, D.
(2014). Photo-chemopropulsion—light-stimulated movement of microdroplets. Advanced Materials, 26(43),
7339–7345.
34. Francis, W., Fay, C., Florea, L., & Diamond, D. (2015). Self-propelled chemotactic ionic liquid droplets.
Chemical Communications, 51(12), 2342–2344.
35. Kurup, G. K., & Basu, A. S. (2012). Passive, label-free droplet sorting based on chemical composition
using tensiophoresis. In 16th International Conference on Miniaturized Systems for Chemistry and Life Sciences (pp. 76–78).
36. Giri, T. K., Choudhary, C., Ajazuddin, Alexander A., Badwaik, H., & Tripathi, D. K. (2013). Prospects of
pharmaceuticals and biopharmaceuticals loaded microparticles prepared by double emulsion technique for
controlled delivery. Saudi Pharmaceutical Journal, 21(2), 125–141.
37. Graham, T. (1861). Liquid diffusion applied to analysis. Philosophical Transactions of the Royal Society of London,
151, 183–224.
38. Grančič, P., & Štěpánek, F. (2013). Swarming behavior of gradient-responsive colloids with chemical
signaling. The Journal of Physical Chemistry B, 117(26), 8031–8038.
39. Grančič, P., & Štĕpánek, F. (2013). Chemical swarm robots. In S. Kernbach (Ed.), Handbook of collective
robotics: Fundamentals and challenges (pp. 745–771). Stanford, CA: PAN.
40. Greenspan, H. P. (1977). On the dynamics of cell cleavage. Journal of Theoretical Biology, 65(1), 79–99.
41. Greenspan, H. P. (1978). On fluid-mechanical simulations of cell division and movement. Journal of Theoretical
Biology, 70(1), 125–134.
42. Gunji, Y.-P., Nishiyama, Y., Adamatzky, A., Simos, T. E., Psihoyios, G., Tsitouras, C., & Anastassi, Z.
(2011). Robust soldier crab ball gate. Complex Systems, 20(2), 93.
43. Gutierrez, J. M. P., Hinkley, T., Taylor, J. W., Yanev, K., & Cronin, L. (2014). Evolution of oil droplets in
a chemorobotic platform. Nature Communications, 5, 5571.
44. Haidara, H., Vonna, L., & Schultz, J. (1997). Surfactant induced Marangoni motion of a droplet into an
external liquid medium. Journal of Chemical Physics, 107(2), 630–637.
45. Hanczyc, M. M. (2011). Metabolism and motility in prebiotic structures. Philosophical Transactions of the Royal
Society B: Biological Sciences, 366(1580), 2885–2893.
46. Hanczyc, M. M., & Ikegami, T. (2010). Chemical basis for minimal cognition. Artificial Life, 16(3), 233–243.
47. Hanczyc, M. M., Parrilla, J. M., Nicholson, A., Yanev, K., & Stoy, K. (2014). Creating and maintaining
chemical artificial life by robotic symbiosis. Artificial Life, 21(1), 47–54.
48. Hanczyc, M. M., Toyota, T., Ikegami, T., Packard, N., & Sugawara, T. (2007). Fatty acid chemistry at the
oil-water interface: Self-propelled oil droplets. Journal of the American Chemical Society, 129(30), 9386–9391.
49. Henson, A., Gutierrez, J. M. P., Hinkley, T., Tsuda, S., & Cronin, L. (2015). Towards heterotic computing
with droplets in a fully automated droplet-maker platform. Philosophical Transactions of the Royal Society A,
373(2046), 20140221.
50. Hilgardt, C., Cejkova, J., Hauser, M. J. B., & Sevcikova, H. (2008). Streamless aggregation of Dictyostelium
in the presence of isopropylidenadenosin. Biophysical Chemistry, 132(1), 9–18.
51. Horibe, N., Hanczyc, M. M., & Ikegami, T. (2011). Mode switching and collective behavior in chemical oil
droplets. Entropy, 13(3), 709–719.
52. Hu, W., & Ohta, A. (2011). Aqueous droplet manipulation by optically induced Marangoni circulation.
Microfluidics and Nanofluidics, 11(3), 307–316.
53. Chaudhury, M. K., & Whitesides, G. M. (1992). How to make water run uphill. Science, 256(5063), 1539–1541.
54. Chenyu, J., Krüger, C., & Maass, C. C. (2017). Chemotaxis and auto-chemotaxis of self-propelling droplet
swimmers. Proceedings of the National Academy of Sciences of the U.S.A., 114(20), 5089–5094.
55. Cheow, L. F., Yobas, L., & Kwong, D.-L. (2007). Digital microfluidics: Droplet based logic gates. Applied
Physics Letters, 90(5), 054107.
546
Artificial Life Volume 23, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
3
4
5
2
8
1
6
6
6
9
1
7
a
r
t
l
/
_
a
_
0
0
2
4
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
J. Čejková et al.
Droplets As Liquid Robots
56. Ikegami, T. (2010). Chemical robot: Self-organizing self-moving oil droplet. Journal of the Robotics Society of
Japan, 28(4), 435–444.
57. Ikegami, T., Horibe, N., & Hanczyc, M. M. (2015). Potential memory effects in self-moving oil droplets.
International Journal of Unconventional Computing, 11(5–6), 345–355.
58. Katsikis, G., Cybulski, J. S., & Prakash, M. (2015). Synchronous universal droplet logic and control. Nature
Physics, 11(7), 588–596.
59. Kunstmann-Olsen, C., Hanczyc, M. M., Hoyland, J., Rasmussen, S., & Rubahn, H.-G. (2016). Uniform
droplet splitting and detection using lab-on-chip flow cytometry on a microfluidic PDMS device. Sensors
and Actuators B: Chemical, 229, 7–13.
60. Kurihara, K., Tamura, M., Shohda, K.-i., Toyota, T., Suzuki, K., & Sugawara, T. (2011). Self-reproduction
of supramolecular giant vesicles combined with the amplification of encapsulated DNA. Nature Chemistry,
3(10), 775–781.
61. Kurup, G. K., & Basu, A. S. (2011). Tensiophoresis: Migration and sorting of droplets in an interfacial
tension gradient. In 15th International Conference on Miniaturized Systems for Chemistry and Life Sciences
(pp. 1367–1369).
62. Lagzi, I., Soh, S., Wesson, P. J., Browne, K. P., & Grzybowski, B. A. (2010). Maze solving by chemotactic
droplets. Journal of the American Chemical Society, 132(4), 1198–1199.
63. Lazar, P., & Riegler, H. (2005). Reversible self-propelled droplet movement: A new driving mechanism.
Physical Review Letters, 95(13), 136103.
64. Lehmann, U., Hadjidj, S., Parashar, V. K., Vandevyver, C., Rida, A., & Gijs, M. A. M. (2006). Two-
dimensional magnetic manipulation of microdroplets on a chip as a platform for bioanalytical applications.
Sensors and Actuators B: Chemical, 117(2), 457–463.
65. Li, D., Choi, H., Cho, S., Jeong, S., Jin, Z., Lee, C., Ko, S. Y., Park, J.-O., & Park, S. (2015). A hybrid
actuated microrobot using an electromagnetic field and flagellated bacteria for tumor-targeting therapy.
Biotechnology and Bioengineering, 112(8), 1623–1631.
66. Li, S., Liu, J., Hou, J., & Zhang, G. (2015). Meniscus-induced motion of oil droplets. Colloids and Surfaces
A: Physicochemical and Engineering Aspects, 469, 252–255.
67. Maass, C. C., Krüger, C., Herminghaus, S., & Bahr, C. (2016). Swimming droplets. Annual Review of Condensed
Matter Physics, 7(1), 171–193.
68. Maeda, S., Hara, Y., Yoshida, R., & Hashimoto, S. (2007). Chemical robot—design of self-walking gel.
In Proceedings of 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems. doi:10.1109/
IROS.2007.4399392
69. Marr, D. W., & Munakata, T. (2007). Micro/nanofluidic computing. Communications of the ACM, 50(9),
64–68.
70. Martel, S., & Mohammadi, M. (2010). Using a swarm of self-propelled natural microrobots in the form of
flagellated bacteria to perform complex micro-assembly tasks. In 2010 IEEE International Conference on
Robotics and Automation. doi:10.1109/ROBOT.2010.5509752
71. Mertaniemi, H., Forchheimer, R., Ikkala, O., & Ras, R. H. (2012). Rebounding droplet–droplet collisions
on superhydrophobic surfaces: From the phenomenon to droplet logic. Advanced Materials, 24(42),
5738–5743.
72. Miura, S., Banno, T., Tonooka, T., Osaki, T., Takeuchi, S., & Toyota, T. (2014). pH-induced motion control
of self-propelled oil droplets using a hydrolyzable gemini cationic surfactant. Langmuir, 30(27), 7977–7985.
73. Nagai, K., Sumino, Y., Kitahata, H., & Yoshikawa, K. (2005). Mode selection in the spontaneous motion
of an alcohol droplet. Physical Review E, 71(6), 065301.
74. Nejatimoharrami, F., Faina, A., Cejkova, J., Hanczyc, M. M., & Stoy, K. (2016). Robotic automation to
augment quality of artificial chemical life experiments. In C. Gershenson et al. (Eds.), Proceedings of the
Artificial Life Conference 2016 (pp. 634–635). Cambridge, MA: MIT Press.
75. Ooi, C. H., & Nguyen, N.-T. (2015). Manipulation of liquid marbles. Microfluidics and Nanofluidics, 19(3),
483–495.
76. Oshima, S., Nomoto, T., Toyota, T., & Fujinami, M. (2014). Surface tension gradient around an alcohol
droplet moving spontaneously on a water surface. Analytical Sciences, 30(4), 441–444.
Artificial Life Volume 23, Number 4
547
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
3
4
5
2
8
1
6
6
6
9
1
7
a
r
t
l
/
_
a
_
0
0
2
4
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
J. Čejková et al.
Droplets As Liquid Robots
77. Paven, M., Mayama, H., Sekido, T., Butt, H.-J., Nakamura, Y., & Fujii, S. (2016). Light-driven delivery and
release of materials using liquid marbles. Advanced Functional Materials, 26(19), 3199–3206.
78. Peyer, K. E., Zhang, L., & Nelson, B. J. (2013). Bio-inspired magnetic swimming microrobots for
biomedical applications. Nanoscale, 5(4), 1259–1272.
79. Phan, C. M. (2014). Rechargeable aqueous microdroplet. The Journal of Physical Chemistry Letters, 5(8), 1463–1466.
80. Prakash, M., & Gershenfeld, N. (2007). Microfluidic bubble logic. Science, 315(5813), 832–835.
81. Rogers, J. A., Someya, T., & Huang, Y. (2010). Materials and mechanics for stretchable electronics. Science,
327(5973), 1603–1607.
82. Rybalko, S., Magome, N., & Yoshikawa, K. (2004). Forward and backward laser-guided motion of an oil
droplet. Physical Review E, 70(4), 046301.
83. Rychecký, O., Majerská, M., Král, V., Štěpánek, F., & Čejková, J. (2017). Spheroid cultivation of HT-29
carcinoma cell line in liquid marbles. Chemical Papers, 71(6), 1055–1063.
84. Sanchez, T., Chen, D. T. N., DeCamp, S. J., Heymann, M., & Dogic, Z. (2012). Spontaneous motion in
hierarchically assembled active matter. Nature, 491(7424), 431–434.
85. Sato, Y., Yasuhara, K., Kikuchi, J.-i., & Sato, T. N. (2013). Synthetic cell division system: Controlling equal
vs. unequal divisions by design. Scientific Reports, 3, 3475.
86. Schwartz, L. W., Roy, R. V., Eley, R. R., & Princen, H. M. (2004). Surfactant-driven motion and splitting
of droplets on a substrate. Journal of Engineering Mathematics, 50(2–3), 157–175.
87. Song, C., Moon, J. K., Lee, K., Kim, K., & Pak, H. K. (2014). Breathing, crawling, budding, and splitting
of a liquid droplet under laser heating. Soft Matter, 10(15), 2679–2684.
88. Steinbock, O., Kettunen, P., & Showalter, K. (1996). Chemical wave logic gates. The Journal of Physical
Chemistry, 100(49), 18970–18975.
89. Sumino, Y., Kitahata, H., Yoshikawa, K., Nagayama, M., Nomura, S.-i. M., Magome, N., & Mori, Y.
(2005). Chemosensitive running droplet. Physical Review E, 72(4), 041603.
90. Sumino, Y., Magome, N., Hamada, T., & Yoshikawa, K. (2005). Self-running droplet: emergence of
regular motion from nonequilibrium noise. Physical Review Letters, 94(6), 068301.
91. Suthakorn, J., Cushing, A. B., & Chirikjian, G. S. (2003). An autonomous self-replicating robotic system.
In Proceedings 2003 IEEE/ASME International Conference on Advanced Intelligent Mechatronics. doi:10.1109/
AIM.2003.1225085
92. Suzuki, A., Maeda, S., Hara, Y., & Hashimoto, S. (2012). Capsule gel robot driven by self-propelled oil
droplet. In IEEE International Conference on Intelligent Robots and Systems (pp. 2180–2185). doi:10.1109/
IROS.2012.6385738
93. Ševčíková, H., Čejková, J., Krausová, L., Přibyl, M., Štěpánek, F., & Marek, M. (2010). A new traveling wave
phenomenon of Dictyostelium in the presence of cAMP. Physica D: Nonlinear Phenomena, 239(11), 879–888.
94. Tanaka, S., Sogabe, Y., & Nakata, S. (2015). Spontaneous change in trajectory patterns of a self-propelled
oil droplet at the air-surfactant solution interface. Physical Review E, 91(3), 032406.
95. Timonen, J. V. I., Latikka, M., Leibler, L., Ras, R. H. A., & Ikkala, O. (2013). Switchable static and
dynamic self-assembly of magnetic droplets on superhydrophobic surfaces. Science, 341(6143), 253–257.
96. Toepke, M. W., Abhyankar, V. V., & Beebe, D. J. (2007). Microfluidic logic gates and timers. Lab on a
Chip, 7(11), 1449–1453.
97. Toyota, T., Maru, N., Hanczyc, M. M., Ikegami, T., & Sugawara, T. (2009). Self-propelled oil droplets
consuming “fuel” surfactant. Journal of the American Chemical Society, 131(14), 5012–5013.
98. Ullrich, M., Hanuš, J., Dohnal, J., & Štěpánek, F. (2013). Encapsulation stability and temperature-dependent
release kinetics from hydrogel-immobilised liposomes. Journal of Colloid and Interface Science, 394, 380–385.
99. Velev, O. D., Prevo, B. G., & Bhatt, K. H. (2003). On-chip manipulation of free droplets. Nature, 426(6966),
515–516.
100. Zadražil, A., Čermochová, V., Ullrich, M., Hanuš, J., Štěpánek, F., & McCaskill, J. (2016). Remote
manipulation with microlablets and control of enzymatic reaction. In Design and Manufacture of Functional
Microcapsules and Engineered Products. Engineering Conferences International.
548
Artificial Life Volume 23, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
3
4
5
2
8
1
6
6
6
9
1
7
a
r
t
l
/
_
a
_
0
0
2
4
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
J. Čejková et al.
Droplets As Liquid Robots
101. Zhang, M., Wang, L., Wang, X., Wu, J., Li, J., Gong, X., Qin, J., Li, W., & Wen, W. (2011). Microdroplet-
based universal logic gates by electrorheological fluid. Soft Matter, 7(16), 7493–7497.
102. Zhao, G., & Pumera, M. (2014). Marangoni self-propelled capsules in a maze: Pollutants ‘sense and act’ in
complex channel environments. Lab on a Chip, 14(15), 2818–2823.
103. Zhao, Y., Fang, J., Wang, H., Wang, X., & Lin, T. (2010). Magnetic liquid marbles: Manipulation of liquid
droplets using highly hydrophobic Fe3O4 nanoparticles. Advanced Materials, 22(6), 707–710.
104. Zhao, Y., Gu, H., Xie, Z., Shum, H. C., Wang, B., & Gu, Z. (2012). Bioinspired multifunctional Janus
particles for droplet manipulation. Journal of the American Chemical Society, 135(1), 54–57.
105. Zhao, Y., & Chakrabarty, K. (2010). Digital microfluidic logic gates and their application to built-in
self-test of lab-on-chip. IEEE Transactions on Biomedical Circuits and Systems, 4(4), 250–262.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
3
4
5
2
8
1
6
6
6
9
1
7
a
r
t
l
/
_
a
_
0
0
2
4
3
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Artificial Life Volume 23, Number 4
549