David H. Ackley*,**
University of New Mexico
†
Elena S. Ackley
Ackleyshack LLC
Keywords
Robust first computing, best effort
computing, movable feast machine,
asynchronous cellular automata
The ulam Programming Language
for Artificial Life
Abstract Traditional digital computing demands perfectly reliable
memory and processing, so programs can build structures once then
use them forever—but such deterministic execution is becoming
ever more costly in large-scale systems. By contrast, living systems,
viewed as computations, naturally tolerate fallible hardware by
repairing and rebuilding structures even while in use—and suggest
ways to compute using massive amounts of unreliable, merely
best-effort hardware. However, we currently know little about
programming without deterministic execution, in architectures
where traditional models of computation—and deterministic
ALife models such as the Game of Life—need not apply. This
expanded article presents ulam, a language designed to balance
concurrency and programmability upon best-effort hardware,
using lifelike strategies to achieve robust and scalable computations.
The article reviews challenges for traditional architecture, introduces
the active-media computational model for which ulam is designed,
and then presents the language itself, touching on its nomenclature
and surface appearance as well as some broader aspects of robust
software engineering. Several ulam examples are presented; then
the article concludes with a brief consideration of the couplings
between a computational model and its physical implementation.
1 A Language for Soft Strong Artificial Life
We present ulam, a new programming language for the research and development of indefinitely
scalable soft strong artificial life—software creatures, embodied within some sort of digital machinery,
that produce benefits for society. The language—mostly named after Stanislaw Ulam for his pio-
neering contributions especially in cellular automata [37]—is designed to work on best-effort computing
hardware [4], where deterministic execution is not guaranteed. As a result, ulam programs—including
the examples shown herein—are typically organized less like traditional algorithms than like living
processes, employing mechanisms like reproduction, swarming, and growth and healing.
Why does the world need a new programming language, when it already has so many? Although
ulam presumes an unreliable, distributed computational model, one could certainly imagine imple-
menting such a model using, say, a Python script duplicated across a networked array of Raspberry
Pi computers—no new language needed. Indeed, if the main goal were to get output from some
particular computation, such a direct approach could make a lot of sense. However, as with most
programming languages, ulamʼs primary purpose is less to implement any given task than to provide
* Contact author.
** Department of Computer Science, University of New Mexico, Albuquerque, NM 87131, USA. E-mail: ackley@cs.unm.edu
† Ackleyshack LLC, P.O. Box 993, Placitas, NM 87043, USA. E-mail: esa@ackleyshack.com
© 2016 Massachusetts Institute of Technology Artificial Life 22: 431–450 (2016) doi:10.1162/ARTL_a_00212
Published under a Creative Commons Attribution
3.0 Unported (CC BY ) license.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
2
4
4
3
1
1
6
6
6
0
9
5
a
r
t
l
/
_
a
_
0
0
2
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. H. Ackley and E. S. Ackley
The ulam Programming Language for Artificial Life
a framework for envisioning, expressing, and reasoning about—as well as executing—a particular
style of physically realizable dynamical behavior. ulam provides significant gains in conciseness
and expressiveness for its targeted best-effort computations, and that has enabled us to achieve
greater levels of composability and complexity than we dared to attempt with our prior C++
and Java implementations.
Bedau [12] distinguished hard, soft, and wet varieties of artificial life research as those that employ
hardware such as robots, or just software running inside computers, or actual chemical preparations
and reactions. There are also varied weak and strong philosophical positions (e.g., [35]) about how best
to understand the purpose and results of artificial life work. The goal of weak ALife we take to be
living system models—abstract conceptual entities assessed primarily by their scientific, pedagogical, or
artistic values. We take the goal of strong ALife, by contrast, to be living system instances—embodied
physical entities assessed primarily by the value of the work they perform—judged as living, ulti-
mately, by their ability to make a living.
This article is an expansion of [5], with updates throughout and primary new material including
a fuller treatment of the ulam language; a new section connecting the ulam design to robust soft-
ware engineering; and a new example and discussion about an unexpected consequence of indefinite
scalability. Section 2 motivates computer architecture based on living systems design, with program-
ming used to shape the dynamics of active-media systems—unbounded but unreliable systems where
energy costs are prepaid to encourage parallelism. Section 3 presents a few best-effort slogans both as
antidotes to determinism and as prototype design patterns for living computation. Then Section 4
introduces ulam in the context of robust software engineering, and Section 5 presents several ex-
amples. Finally, Section 6 stresses the links between the computational and the physical, and Section 7
offers some concluding thoughts.
2 Beyond Determinism
As the hegemony of CPU and RAM declines, for the first time in decades significantly new
computer architectures are appearing, such as the nothing-but-net neural architecture of IBMʼs
TrueNorth [29]. With the potential on the horizon for a major evolutionary transition in computer
architecture, it is an opportune time to reconnect with first principles before shortlisting successors.
The result of such a process, we believe, will be the recognition of artificial life as a (perhaps the)
major force driving future architectural innovation.
2.1 Escape from the SDA
Serial deterministic computing based on CPU and RAM is a vast attractor, a valley deep and wide, in
a notional space of all possible models of computation, including parallel, probabilistic, and analogue
methods. This serial deterministic attractor (SDA) is laced with interlocking design decisions—such as
binary number representations and the general exaltation of software efficiency—surrounding its
core demand for logical correctness. The inherent fragility of extremely efficient software can be
masked by extremely reliable hardware [3]—but only until a fault, or a bug, or an attacker, appears.
Although the SDAʼs robustness and security properties are dubious, and its scalability is rapidly
dwindling [19], the assumption of deterministic execution has been so dominant for so long that
alternatives may seem unthinkable. One might imagine that fields like fault tolerance (e.g., [25]) or
probabilistic algorithms [26] fall outside the SDA, but by “virtually guaranteeing” deterministic
execution, they actually entrench it. The same is true of many other nontraditional but still determin-
istic models, such as synchronous cellular automata (e.g., [38, 37, 36]), data-flow machines and systolic
arrays (e.g., [16, 17]), and asynchronous circuit-level techniques such as GALS and RALA [27, 21].
Probabilistic cellular automata (PCAs) (e.g., [22, 11]) do go decisively beyond determinism, and
they are general enough to embrace the kind of models we explore—but their motivations and
methods are sharply divergent from the present effort. PCA work often presumes simple and styl-
ized noise models, and proceeds—preferably by formal analysis—to derive insights into equilibrium
432
Artificial Life Volume 22, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
2
4
4
3
1
1
6
6
6
0
9
5
a
r
t
l
/
_
a
_
0
0
2
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. H. Ackley and E. S. Ackley
The ulam Programming Language for Artificial Life
distributions and other system properties. But when such research begins by postulating a state
transition matrix, the small matter of actual PCA programming is silently assumed away. Yes, the
transition matrix is a powerfully general device; no, you donʼt want to program in it.
In addition, PCA models generally assume quite simple and low-order departures from determin-
ism, such as i.i.d. update probabilities or random permutations—but as we shall see in Section 6,
when moving beyond deterministic hardware to achieve indefinite scalability, the interactions be-
tween physical and computational levels can be sufficiently complex that the applicability of simple
PCA models is far from certain.
Recently, there have been some serious programming research efforts that, while remaining
mostly traditional, do explicitly abandon determinism and accept some small output errors—often
with the motivation of increased parallel efficiency (e.g., [19, 20, 30, 32]). We cheer all such efforts,
but worry they may fail to gain traction because their incremental practicality leaves them struggling
up the sides of the SDA valley, with all the downhill directions behind them.
2.2 Colonize the RFA
There is at least one fundamental alternative to the SDA, which we here call the robust-first attractor
(RFA), in the space of all possible models of computation. We have been breaking trail in the RFA
for some time [6, 3, 7, 2, 8] and can report it is strikingly unlike the SDA, but at least as vast: It is a
natural way to understand the computational properties of living systems, which have always made do
without the luxury of deterministic execution.
Life fills space, as long as suitable resources are available; every RFA architecture must do the
same, and that core demand for indefinite scalability is surrounded by interacting design decisions often
deeply complementary to the SDAʼs. A von Neumann machine by itself simply isnʼt an RFA archi-
tecture; it is incomplete, and thus unevaluable, until a method is defined for tiling unbounded space
with it ([2] has further discussion).
Most software-based artificial life models are designed to run on single von Neumann machines.1
Unsurprisingly, therefore, the properties of such models typically depend critically on deterministic
execution, as typified by the utter collapse of constructs in Conwayʼs Game of Life when facing even
mild asynchrony ([14]; see also [13]).
Determinism is a property of the small and the fragile; it is fundamentally misaligned with living
systems. It warps our expectations; it is time to move on.
2.3 Programmable Active Media
SDA models are well suited to implementation in passive, “cold” materials, where uniformity rules,
change is rare, and free energy is expensive—conditions where, indeed, living systems may survive
but will rarely thrive. However, some environments are diverse in space, dynamic in time, and
energetically rich, bountiful, like a rain forest or a sunny day at the shore. We abstract such cir-
cumstances into active-media computational models—unbounded spatial architectures in which
each discretized location performs logical state transitions based on its local neighborhood, but
with uncertain and variable frequencies and only limited reliability.
An active medium can change spontaneously and is inherently nondeterministic. In a programmable
active medium we get to pick its state transition function—to specify, up to reliability limits, that
certain neighborhood patterns shall stay constant (like memory, say) while others produce transitions
like a processor or a data transport, or, indeed, act like different types of hardware at different
moments. The state transition function we supply is executed asynchronously in parallel across
the medium, avoiding overlapping state transitions, again, with good but not guaranteed reliability.
It may become possible to implement programmable active media in, say, DNA (e.g., [18, 34]); it is
already possible in electronics [7, 34].
1 Though there have certainly been exceptions, both proposed [31] and implemented [1]. Additionally, powerful modeling systems like
Ready [23], though still fundamentally deterministic, now exploit many-core parallelism.
Artificial Life Volume 22, Number 4
433
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
2
4
4
3
1
1
6
6
6
0
9
5
a
r
t
l
/
_
a
_
0
0
2
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. H. Ackley and E. S. Ackley
The ulam Programming Language for Artificial Life
2.4 A New Deal for Hardware and Software
Clearly, compared to SDA architectures, the active-media model presents a very different division of
labor, as traditional hardware components like “processor” and “memory” and “bus”—and their
floorplanning—are placed largely under software control. This refactoring will presumably incur a
hardware price–complexity penalty something like FPGA versus ASIC or worse—but that, in turn,
may be more than offset by enabling new optimizations akin to RISC versus CISC, combined with
the hair-down liberation of merely best-effort hardware determinism.
So, while the programmable active-media framework is likely a splendid deal for hardware, it may
seem a brutal one–two punch for software, stunned by nondeterminism from below and then flat-
tened by expanded mission responsibilities from above. But hereʼs the thing: On the one hand, the
software engineering job should be harder, because its relative simplicity was purchased with precisely
those von Neumann machine features—a single processing locus, uniform passive memory, reliabil-
ity all on hardware—that led to its Achillesʼ heels of unscalability and unsecurability. Serial deter-
minism was a simple, sensible starting point, but software engineering and many related fields have
emerged since von Neumannʼs time, and we now know quite a bit about constructing, managing,
and evolving complex systems. From the RFA looking back, for software still to be demanding
general pointers and flat RAM and cache-coherent global determinism seems like clutching a blankie.
The future will arrive anyway.
That said, and on the other hand, softwareʼs big promotion becomes less terrifying as we get down
to work, because, like hope from Pandoraʼs box, “best effort” wafts upwards from the nondetermin-
istic hardware into the software as well. As a system component, weʼll do our best with what weʼve
got and what we get, but if things go really wrong, we can simply delete ourselves and let our kin cover
for us. Correctness and robustness are measured by degrees and circumstances in living systems; in
the RFA they are highly respected qualities rather than merely purported necessities.
3 Principles of Active-Media Programming
To help make the RFA more concrete and clearly distinct from the SDA, in this section we offer
some RFA slogans or design principles, with brief ALife motivations or implications. The end of
Section 2.4 above concerns a principle that might be called Thereʼs always dying; here are five more:
(cid:129) Happy and you know it: Make the goals obvious.
(cid:129) Space is the place : Space is the core data structure.
(cid:129) Embrace the race : Just help the better answer win.
(cid:129) Chance it: Replace state with statistics.
(cid:129) Use it or lose it: A cycle saved is a cycle wasted.
Happy and you know it: The key to robustness is effective redundancy, and one excellent ap-
proach is to give subcomponents not just tasks to do but also ways to measure their own success.
Unit tests are a simple SDA example; in the RFA, geometric goals (“Bigger should be lower”) and
local consistency rules (“If Iʼm linked to you, you should be linked to me”) allow the execution of
external productive computations to be combined with ongoing internal processes like machine con-
struction and maintenance.
Space is the place: The SDA tries to obliterate space using random-access memory, then acts all
surprised by buffer overflows; the RFA uses space as the backbone organizing principle for both
access control and computation, like the cat thatʼs picky about whoʼs allowed near, but then grooms
everything in reach. The ALife community is largely in good shape here: A great strength of typical
ALife models is their fundamentally spatial organization, unlike, say, typical genetic algorithms.
434
Artificial Life Volume 22, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
2
4
4
3
1
1
6
6
6
0
9
5
a
r
t
l
/
_
a
_
0
0
2
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. H. Ackley and E. S. Ackley
The ulam Programming Language for Artificial Life
Embrace the race: The SDA generally abhors race conditions,2 but in the RFA, with many
components interacting and making things better locally, a race can be, not a regrettable shame
to be hidden, but a fine tool for making a larger-scale decision, which may then be amplified by
spectators for subsequent processing. ALife models also do well with this—often identifying their
race conditions with names involving “selection.”
Chance it: The SDA is typically deterministic even when itʼs not supposed to matter, as in break-
ing ties or sizing a supposedly ample buffer or time delay. But with determinism off the table, many
RFA tasks can be dramatically simplified by replacing state with probabilities, and rather complex
dynamics can be implemented using remarkably little per-object state, as demonstrated in Section 5.3
below. Alife models are mixed on this, but the field faces some hard unlearning.
Use it or lose it: The active-media abstraction is a programmable space in which energy is a
nonrefundable sunk cost, and even though actual power is limited, this idealization shifts the dis-
cussion from the stultifying task of minimizing the cost of energy consumed to the galvanizing task
of maximizing the value of energy provided. Parallel computing involves many values changing fre-
quently; other things being equal, the RFA programmer seeks to minimize the average change age per site
in some productive way.
4 The Ulam Programming Language
Such slogans help to establish goals and shared context but are no substitute for executable code.
For several years, we have been exploring a tile-based indefinitely scalable architecture called the
movable feast machine (MFM) [6, 7, 2]. Over the last two years we have been developing an open-
source C++ MFM engine [9], which is currently deployed in mfms, a Linux-based thread-per-tile
simulator running on conventional multicores, but is designed and written for eventual cross-
compilation onto indefinitely scalable tile-per-tile physical hardware.
We have also been developing an open-source compiler for a new language we call ulam [10]
that generates code to run on the MFM. We give only a few bullet points for flavor to get started
here—thereʼs runnable code in the next section—but ulam deliberately looks and works much like
a conventional object-oriented procedural language:
(cid:129) The command-line driver, ulam, is a Perl script. The ulam compiler itself, culam, is
written in C++, and its output is heavily templated C++, so that despite weird data sizes
and packing (see below), the g++ compiler downstream can sometimes find quite delicious
assembly code sequences. The key compilation output is a .so shared library, which can
be dynamically linked into the mfms simulator from the command line, or packed into a
cryptographically signed runnable container (.mfz file, “movable-feast zip”) along with
sources, simulator starting configurations, and arbitrary files.
(cid:129) Groups of 1 to 32 bits can be declared as primitive values, using a variety of semantics (see
Table 1). Note that ulam is quite strict about what operators apply to what types, largely to
support language robustness features (see Section 4.5). One-dimensional arrays of zero
or more items are provided, bit-packed up to 32 total bits.
(cid:129) The ulam analogue to an object instance is called an Atom, but an Atom is also analogous
to a word of memory in a tagged architecture, so every object is the same size—96 bits in the
current design, with 25 reserved for the object type and error correction. The analogue to a
class is called an element, which may define constants, parameters, nonstatic methods,
and up to (96 − 25 =) 71 bits of data members.
2 And even those rare authors who accept nondeterminism usually see races as no more than tolerable [30, 15], although there are
exceptions (e.g., [28]).
Artificial Life Volume 22, Number 4
435
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
2
4
4
3
1
1
6
6
6
0
9
5
a
r
t
l
/
_
a
_
0
0
2
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. H. Ackley and E. S. Ackley
The ulam Programming Language for Artificial Life
Table 1. ulam primitive types, available in all bit widths from k = 1 to the default of 32, except that Bool defaults to 1 bit,
and rounds down to odd widths to avoid ties.
ulam type
Unary(k)
Interpretation
Base 1 (population count)
Unsigned(k)
Base 2
Operators
− + * / == != < > <= >=
− + * / == != < > <= >=
Int(k)
Bool(k)
Bits(k)
Twoʼs complement
− + * / == != < > <= >=
Boolean (unary majority)
! == != && ||
Uninterpreted bit values
== != << >> & |^
(cid:129) There is composition but at present no inheritance; the analogue to a struct is called a
quark, which may be any size from 0 to 32 bits, and which may be templated with
compile-time numeric constants. There is also union with the typical meaning. An as
keyword introduces a conditional declaration akin to a Java “instanceof” plus a cast, to access
specific class members inside Atom instances.
Overall, an ulam program consists of a compiled set of class definitions, plus a finite initial
layout of Atoms. There is no main(), and by default the initial layout is empty, so in the simplest
case no computation occurs at all, unless and until some external influence causes one or more
Atoms to be created.
4.1 Language Design Decisions for Robust Software Engineering
The term “robustness” can seem frustratingly vague, compared to the crystalline purity—at least in
principle—of the term “correctness.” Compared to most machines, living systems are famously
robust—but thatʼs when theyʼre in environments where they evolved.
In the general case, there are just too many ways for systems to fail—due to latent defects, to
unexpected conditions or interactions, to age or attack or accident. Nothing can survive forever,
so—without referring to some actual device in some actual environment—how should failures
be prioritized?
In lieu of a strong formal theory of robust programming, in the rest of this section we illustrate
our qualitative approach to abstract robustness in the ulam language design, touching on its memory
and processing model, and its data and operator semantics.
4.2 Reduce Deterministic Memory
Computer working memory has a tough job: It must reliably store values indefinitely, yet also reliably
alter those values at a momentʼs notice. Unlike typical procedural languages, ulam provides no direct
language support for persistent memory—there is a function-call stack, but that only lasts for a single
event, and there is no dedicated heap or general-purpose main memory. “RAM” support, such as it is,
is provided by the EventWindow quark in the standard library, which provides read/write access to
a small, two-dimensional patch of sites (Figure 1), each of which can contain one atom, perhaps with a
constant amount of additional state (for example, associated with I/O in the “third dimension”).
Event window accessing is relative to the atom having the event, which is, by definition, located
in the center site at (0,0). During a single event, no assurances are given about the contents (or even
the existence) of any sites outside the event window—forcing the ulam element programmer to stop
hoarding data and make hard choices up front about what to represent explicitly within the atom, and
what to build up stigmergically instead.
436
Artificial Life Volume 22, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
2
4
4
3
1
1
6
6
6
0
9
5
a
r
t
l
/
_
a
_
0
0
2
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. H. Ackley and E. S. Ackley
The ulam Programming Language for Artificial Life
Figure 1. The neighborhood for a state transition, provided by the EventWindow quark in the standard library, com-
prises the 41 sites within Manhattan distance 4 of the event center at site index 0.
4.3 Reduce Deterministic Processing
The MFM provides best-effort deterministic computation for the duration of a single state transition
that updates a single event window. Since there is no privileged main( ) method, from the point of
view of an element, execution occurs during a call to a handful of special methods (see Table 2),
especially the behave( ) method implementing that elementʼs state transition function.
Note the MFMʼs commitment to best-effort single-event determinism—though weak compared
to traditional serial determinism—is just one possible engineering tradeoff between programmability
and performance for an indefinitely scalable system. With this approach, for example, while one
given site has an event, its forty nearest neighbors cannot. There is also significant locking overhead
to provide best-effort site consistency when an event window crosses tile boundaries ([7] has details).
In a more aggressive design, by contrast, overlapping event windows could be permitted, and
their site accesses would race against each other in the memory system and intertile communications,
much as poorly written thread-based code does in multicore systems today. As we have gained ex-
perience programming robust ulam elements, such a prospect is becoming less utterly terrifying
than it was during the original movable-feast design—but we leave any serious consideration of such
possibilities to future work.
Table 2. ulam privileged methods for elements (E) and/or quarks and unions (Q).
Special method
Void behave( )
Int test( )
Int toInt( )
T aref(Int)
Void aset(Int, T)
On
E
EQ
Q
EQ
EQ
Purpose
Perform event
Run unit tests
Custom cast to Int
Custom array read
Custom array write
Artificial Life Volume 22, Number 4
437
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
2
4
4
3
1
1
6
6
6
0
9
5
a
r
t
l
/
_
a
_
0
0
2
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. H. Ackley and E. S. Ackley
The ulam Programming Language for Artificial Life
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
2
4
4
3
1
1
6
6
6
0
9
5
a
r
t
l
/
_
a
_
0
0
2
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 2. Four separate simulations. Top left: Sixteen-atom self-constructed Line segment. Top right: Self-constructed
Box. Bottom left: Example of catastrophic Box failure mode. Bottom right: Example of bounded Box2 failure mode. See
text.
4.4 Reduce Primitive Sizes
One blindingly obvious robustness principle took us embarrassingly long to see: Nonexistent bits cannot
fail. As discussed above, we designed ulam to support variable-width primitives because the Atom
is so small that down-to-the-bit space management is often inevitable—but eliminating unneeded
bits also helps mitigate bit failures. A single bit flip in an Unsigned(32) could change the stored
value by billions; if the programmerʼs actual intent was to store an integer percentage, then, say, an
Unsigned(7) wins in space efficiency and robustness.
A fundamental robustness goal is to avoid creating leverage the program doesnʼt need—and ex-
cess high-order bits are just one example. As a concrete example, our experience developing a self-
constructing Box element illustrates how easy-to-overlook software engineering concerns can have
significant robustness consequences.
The Box element exploits the fact that the EventWindow quark supports neighborhood access
under any of the eight square symmetries—expressed in code by type Symmetry, which is a typedef
for Unsigned(3). Starting from a Line element that constructs a horizontal line segment (Figure 2,
top left), we made a reusable abstraction called a QLine, and created a Box element3 composed of a
QLine plus an additional symmetry data member, indicating which way this particular line segment
should grow. When one side of the box was complete, it would copy itself to seed another line
3 See the Appendix for commented ulam source code of Line (and its underlying quark QLine) as well as Box2, which, aside from
naming, differs from Box only at line 12 of Appendix A.2.
438
Artificial Life Volume 22, Number 4
D. H. Ackley and E. S. Ackley
The ulam Programming Language for Artificial Life
segment if there was an empty site beyond—but with the next rotational symmetry in the copyʼs data
member. After four such line segments, the Box would be complete (Figure 2, top right).
The use of QLine inside Box shows one way that composability can work in ulam, providing
reasonably clean modular code and good separation of concerns between creating a line segment on
the one hand, and placing and orienting it on the other, to create a more complex structure. For
typical programming languages the example could easily end there, but here we are also interested
in the robustness of the solution, and to that end the simulator provides a variety of mechanisms to
damage computations deliberately, either via ongoing automatic processes or manually operated tools.
While investigating the dynamics of Box using the xray simulator tool to induce random atomic
bit flips, we were surprised by the virulent, nearly spacing-filling failure modes that sometimes
occurred (Figure 2, bottom left.) Debugging revealed that a bit flip in the symmetry data member
was selecting the flipped EventWindow symmetries, causing the next rotation to turn the wrong
way, so the confused Box spreads rather than closing. That led us to write element Box2, which
stores only the two bits needed for the rotational symmetries, and we found that while xray probing
triggered construction of misaligned Box2 atoms, no runaway metastases were observed (Figure 2,
bottom right).
The robustness lesson is: Bits that arenʼt stored cannot be corrupted in storage. By using just two
bits, to represent only the four rotations of the box sides, and then expanding those bits to the full
three-bit EventWindow.Symmetry as needed, the third symmetry bit is always a freshly gen-
erated zero, rather than a copy of an ever-aging bit from memory. Though in principle that new zero
could also fail, during its brief existence the damage would be limited because the Box “germline”
remains unaffected.
Beyond that, a software design lesson may also be gleaned here about specificity versus gener-
ality. It is inelegant for Box2 to define a custom symmetry type directly in terms of primitives
(Appendix A.2, line 12). It would be cleaner to use a type provided by EventWindow like Box
did (as suggested by Appendix A.2, line 11). Without disrupting backward compatibility, a future
EventWindow redesign may recognize that the existing general EventWindow.Symmetry
can be decomposed into a more specific two-bit rotation and a one-bit flip, and expose those types
separately as well, allowing simultaneously improved space efficiency and robustness without
violating modularity.
4.5 Offer Robust Semantics
ulam is a strongly typed language, which we view as a robustness and efficiency feature both; and
for parsing convenience as well as clarity, type names are distinguished lexically by an initial upper-
case letter. Here we touch on some aspects of the ulam type system that involve robustness.
A major decision in the design of ulam is that arithmetic operations and casts saturate in the
destination type. So after a = 5; and a += a;, for example, then a will be 7—if a was declared
as Unsigned(3).
Traditionally, arithmetic operations simply overflow when the result bit width exceeds the storage
width. Thatʼs cheap to implement, and—according to the traditional thinking—if the answer is incor-
rect anyway, who cares how incorrect it is? But in best-effort computing, even though saturation and
overflow both yield incorrect answers, saturation is often less wrong, and that matters for robustness.
Given that numeric types saturate, bitwise operations like shifts are defined to produce type
Bits—an ordered collection with no aggregate numeric interpretation. If programmers really want
to shift an Int to the left, say, and thereby possibly change the sign of the result, they must ex-
plicitly cast the Bits result back to an Int, and accept the consequences.
As a more obvious robustness feature, Unary, the overlooked black sheep of number formats,
is a first-class type in ulam. Though unary is only suitable for small values, small values are surpris-
ingly common in programs—and for such values, unary numbers are as inherently robust as binary
numbers are pointlessly efficient. The bit flip that can cause a huge error in binary causes an error of
one in unary. Why take the risk if you donʼt have to?
Artificial Life Volume 22, Number 4
439
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
2
4
4
3
1
1
6
6
6
0
9
5
a
r
t
l
/
_
a
_
0
0
2
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. H. Ackley and E. S. Ackley
The ulam Programming Language for Artificial Life
Closely related to Unary is the ulam Bool type, which uses only odd bit widths and has value
true if and only if its storage contains more ones than zeros. It is symmetric with respect to bit
flips, unlike the traditional nonzero-is-true “bool,” in which an accidental false→true transition
is much more likely than the reverse.
For all of these design decisions, there is no guarantee they will help in any particular case. But,
again, in best-effort computing, providing a guarantee is not required, and—more to the point—the
inability to provide a guarantee is no excuse to give up and collapse into chaos.
5 Small ulam Examples
Here we present several examples of ulam code that we have created recently, embodying living
principles like reproduction (uncontrolled and controlled) and group formation and action.
5.1 Fork Bomb
In Unix-derived operating systems [24], the fork system call initiates a new process, copied from the
one that issued the fork call. Known colloquially as a fork bomb, a trivial program built around a loop
like while (true) { fork( ); } will rapidly swamp the machine with processes doing nothing
but attempting to reproduce.
Figure 3 presents complete ulam code for an analogous runaway-reproducing fork bomb. Line 1
declares the language version in use. Line 7 declares an instance of the Event-Window quark as a
data member. EventWindow, which conveniently consumes only zero bits of atomic state, offers
the expected 2D neighborhood access methods, as well as a one-dimensional mechanism that often
suffices, as here: The self—the atom having the event—is by definition at ew[0], with increas-
ing 1D array indices spreading outwards in 2D breadth-first as shown in Figure 1.
With up as “north,” ew[1] is the adjacent site west, so one might expect ForkBomb to pro-
duce a westward-growing line. But the element metadata (inside the structured comment, at line 4)
declares that all eight square rotations and reflections are valid for ForkBomb, so a random trans-
form is chosen for each of its events. It quickly explodes into a ragged mass (Figure 4) that will
eventually fill space, as each randomly sited event—and randomly chosen symmetry for that
event—does or does not happen to convert a remaining empty site into another ForkBomb atom.
Running ulam on ForkBomb.ulam compiles it into C++ intermediate code, which is then
processed by the standard GCC tools, yielding a custom ulam element library (libcue.so) that
can be dynamically loaded into the MFM simulator—and, hopefully soon, into actual hardware tiles.
Loaded into the simulator, the library adds the FB element to the available element palette, allowing
computations like Figure 4 to be run immediately.
Figure 3. A complete ulam element. Copies itself from the event window center (ew[0]) to ew[1], which in this case
might be any adjacent site. See text.
440
Artificial Life Volume 22, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
2
4
4
3
1
1
6
6
6
0
9
5
a
r
t
l
/
_
a
_
0
0
2
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. H. Ackley and E. S. Ackley
The ulam Programming Language for Artificial Life
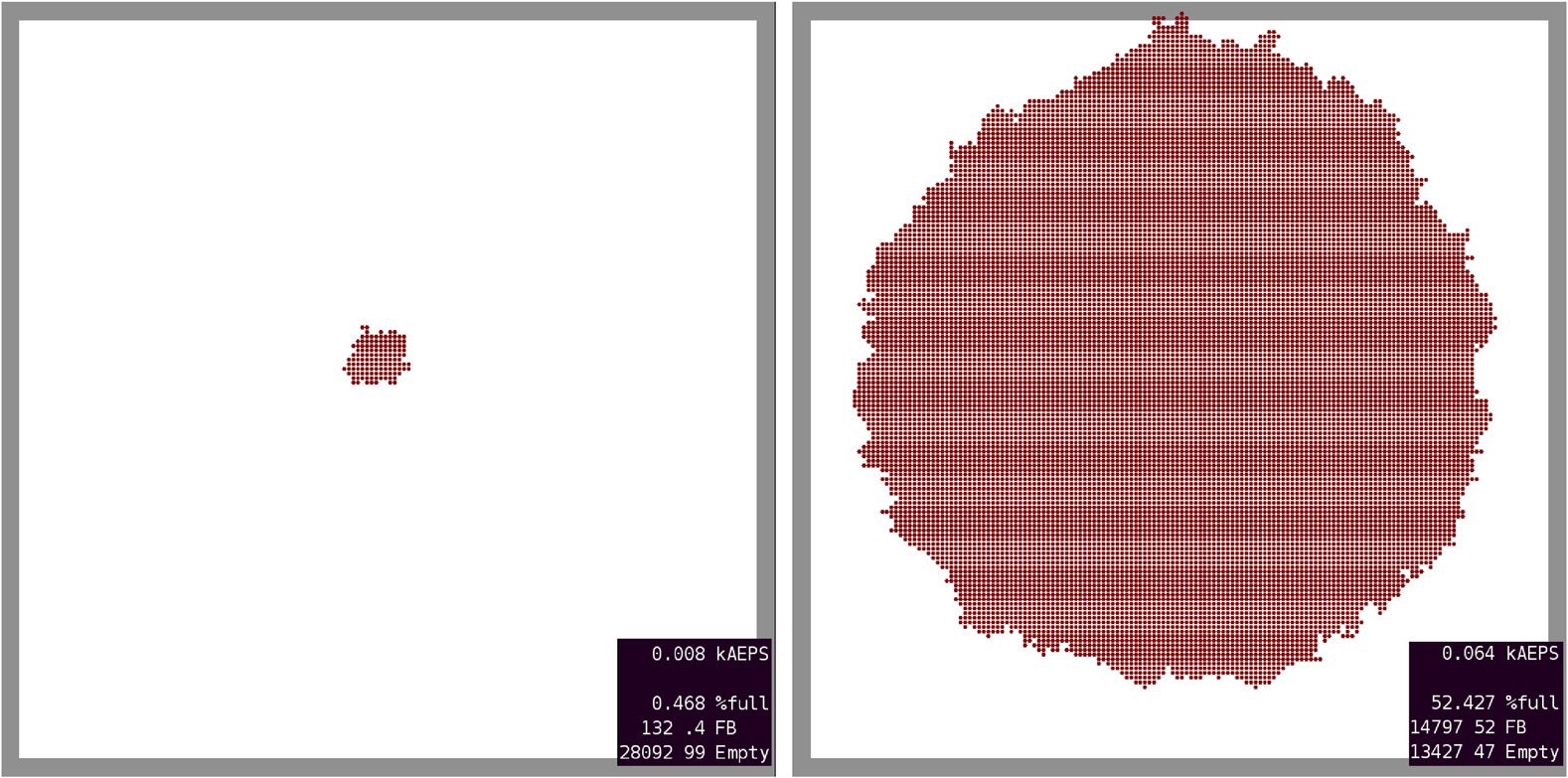
Figure 4. Uncontrolled (and uncontested) growth of a single initial ForkBomb. Left: After an average of 8 events per site
(8 AEPS). Right: After 64 AEPS.
5.2 Telomere
The forkbomb is so simple and obvious that itʼs sort of a “Hello world!” for active media, but its cancerous
rampage is a poor example of ALife programming. Inspired by the telomere DNA sequences that shrink
during reproduction, Figure 5 illustrates a reusable ulam software component that provides controlled
reproduction of a single starting atom into a clonal population of 2(2width − 1) atoms, assuming all clones
survive and spread out sufficiently. The group-forming “mob” in Section 5.4 below uses this strategy.
5.3 Stochastic Timer
In embedded systems, a watchdog timer is often used as a last-ditch backstop to monitor critical pro-
cesses that should complete in a timely fashion, but might fail to do so—for any reason, including a
Figure 5. The Telomere quark dup( ) method offers controlled growth to elements containing it.
Artificial Life Volume 22, Number 4
441
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
2
4
4
3
1
1
6
6
6
0
9
5
a
r
t
l
/
_
a
_
0
0
2
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. H. Ackley and E. S. Ackley
The ulam Programming Language for Artificial Life
Figure 6. A stochastic timer. A four-bit Timexp(4,1) separates time scales over four orders of magnitude, combining
fine-grained initial resolution with overall long duration.
software bug or a hardware fault. A watchdog timerʼs timeout value is usually set very generously to
avoid interfering with normal operations. In ulam, using a normal binary number big enough to
count to thousands or millions of events would consume ten or twenty bits of the scarce atomic bit
budget—which seems especially profligate in that the exact moment of a watchdog timeout is all but
irrelevant anyway.
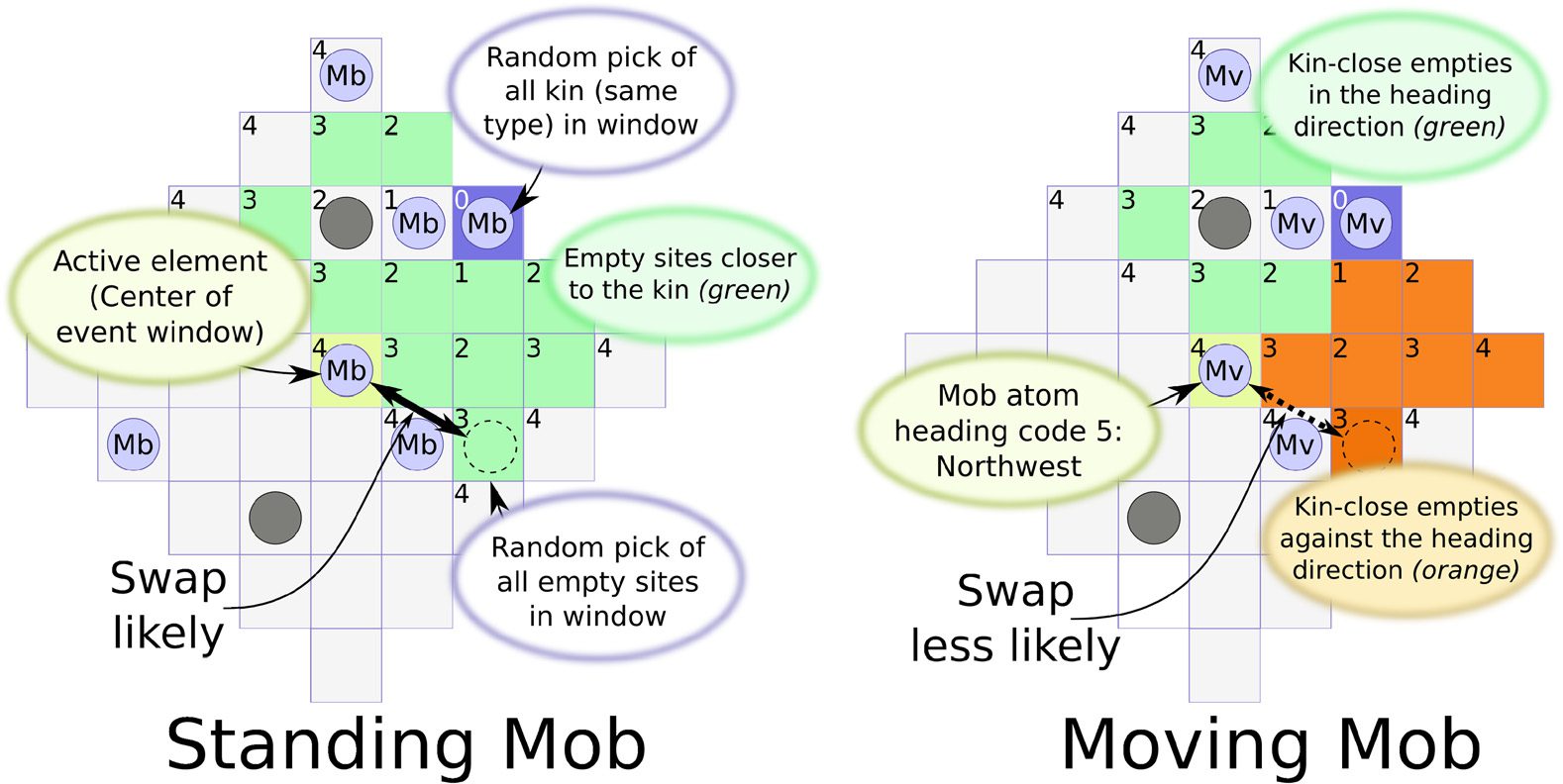
Figure 7. Two mob atom types evaluate their options, having picked at random from the empty sites (green or light gray)
and a random other mob atom. Left: The basic mob rule: Swap if the empty is closer to the kin. Right : Mobs induce drift
by discouraging moves against a heading direction (orange or dark gray). See text and Figure 8.
442
Artificial Life Volume 22, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
2
4
4
3
1
1
6
6
6
0
9
5
a
r
t
l
/
_
a
_
0
0
2
1
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. H. Ackley and E. S. Ackley
The ulam Programming Language for Artificial Life
Figure 8. (Left) At 10 kAEPS a mob using just the basic mob rule (Figure 7, left) has broken up, but (right) adding statistical
gravity and a directional bias (Figure 7, right) yields a long-lived, slowly moving mob. Mobs began as single centered atoms.
Figure 6a shows an alternate approach, saving most of those bits by using statistics instead of
state, as mentioned with the “chance it” principle in Section 3. Timexp is a quark template taking a
bit size parameter (exp), and a multiplier (k). Here exp specifies both its range of counting ability,
and how much it consumes from the atomic bit budget; k scales the entire curve.
So a Timexp(4,1) quark, for example, can be dropped into any element with four bits to spare, and
its count() method can be called thousands of times, with very high probability (Figure 6b), before
its alarm() method returns true. When its t data member is 0, k<