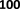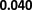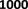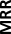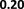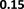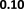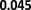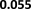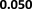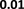Data Intelligence Just Accepted MS.
https://doi.org/10.1162/dint_a_00200
Research Paper
Citation: Tsai, H.C., Chi, H.W., Shen, J.J. et al.: Source-aware embedding training on
heterogeneous information networks. Data Intelligence 5(2023) doi:
https://doi.org/10.1162/dint_a_00200
Source-Aware Embedding Training on
Heterogeneous Information Networks
Tsai Hor Chan1
1. Department of Statistics and Actuarial
Science The University of Hong Kong
Hong Kong, China
hchanth@connect.hku.hk
Chi Ho Wong2
2. Department of Computer Science and Engineering
The Hong Kong University of Science and Technology
Hong Kong, China
chwongcc@connect.ust.hk
Jiajun Shen3
3TCL Corporate Research (Hong
Kong) Hong Kong, China
shenjiajun90@gmail.com
Guosheng Yin1
Department of Statistics and Actuarial Science
The University of Hong Kong
Hong Kong, China
gyin@hku.hk
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
d
n
/
i
Keywords: Heterogeneous information network, Graph representation learning, Distribution alignment, Recommendation
system, Adversarial learning, Graph neural network
t
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
i
t
/
.
/
1
0
1
1
6
2
d
n
_
a
_
0
0
2
0
0
2
0
7
0
9
2
3
d
n
_
a
_
0
0
2
0
0
p
d
/
.
t
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
multi-entity characteristics introduce heterogeneity to HINs and
feature different distributions among different types of entities
and relations, state-of-the-art (SOTA) methods mostly focus on
developing transformation techniques to bring feature
tasks,
to real-world
Abstract: Heterogeneous information networks (HINs) have
been extensively applied
such as
recommendation systems, social networks, and citation networks.
While existing HIN representation
learning methods can
effectively learn the semantic and structural features in the
network, little awareness was given to the distribution discrepancy
of subgraphs within a single HIN. However, we find that ignoring
such distribution discrepancy among subgraphs from multiple
sources would hinder the effectiveness of graph embedding
learning algorithms. This motivates us to propose SUMSHINE
(Scalable Unsupervised Multi-Source Heterogeneous Information
Network Embedding) — a scalable unsupervised framework to
align the embedding distributions among multiple sources of an
HIN. Experimental results on real-world datasets in a variety of
downstream tasks validate the performance of our method over
information network
the
embedding algorithms.
state-of-the-art heterogeneous
I. INTRODUCTION
Heterogeneous information network (HIN), also known as
heterogeneous graph, is an advanced graph data structure which
contains enriched structural and semantic
information.
Learning the representations of HINs has recently drawn
to
significant attention for
industrial applications and machine learning research.
its outstanding contribution
HINs have a variety of real-world applications including
recommendation systems [1], citation networks [2], natural
language processing [3, 4], and social media [5, 6]. An HIN
is a multi-relation and multi-entity graph summarizing the
relations between entities, which represents a key abstraction
for organizing information in diverse domains and modelling
real-world problems in a graphical manner.
Heterogeneous information network embedding methods
aim to encode each of the entities and relations in the HIN to a
low-dimensional vector, which give feature representations to
entities and relations in the HIN. Since the multi-relation and
© 2023 Chinese Academy of Sciences. Published under a Creative Commons Attribution 4.0 International (CC BY 4.0) license.
Data Intelligence Just Accepted MS.
https://doi.org/10.1162/dint_a_00200
distributions of different entity types and relation types to the
same embedding space [3, 7, 8].
However, as of today, SOTA methods often operate on an
HIN constructed by subgraphs from multiple sources, and
most research has been based on the often implicit assumption
that the effect of distribution discrepancies among different
subgraphs on embedding learning is negligible. The major
contribution of this work is to raise awareness to the graph
learning community that this assumption does not hold in
many cases. For instance, graph-based recommendation sys-
tem often takes advantage of the information embedded in
HINs, where an HIN often contains a user-content interaction
graph with high-degree content entity nodes as well as a
knowledge graph with low-degree content entity nodes. The
difference in graph structures (i.e., average node degrees,
graph sizes, sparsity of connections) leads to distribution
discrepancies among subgraphs sources in the HIN. As we
will show in this paper, simply ignoring such distribution
discrepancies when training HIN embeddings would lead to
sub-optimal embedding learning performance.
Although none of the existing heterogeneous graph embed-
ding approaches attempt to solve the aforementioned problem,
there are several attempts in heterogeneous graph neural
networks (GNNs) that try to transfer a GNN model trained on
one graph to another [9, 10]. They often apply domain transfer
techniques to graph neural networks so that the knowledge
learned from one graph can be better transferred to another.
Note that these approaches differ from our approach in the
following important aspects: 1) Unlike the supervised learning
nature of GNN models, we are tackling the graph embedding
learning task which aims to infer node representations from
graph structures in an unsupervised manner. 2) These domain
adaption approaches often focus on adapting the learned model
of one graph to another, while we focus on how to learn one
model from a graph merged from sources.
In this work, we study the distribution discrepancy is-
sue in heterogeneous graph embedding learning. We sur-
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
d
n
/
i
t
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
i
/
/
t
.
1
0
1
1
6
2
d
n
_
a
_
0
0
2
0
0
2
0
7
0
9
2
3
d
n
_
a
_
0
0
2
0
0
p
d
/
t
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Data Intelligence Just Accepted MS.
https://doi.org/10.1162/dint_a_00200
learning framework
mise that simply merging sub-graphs from different sources
when training graph embeddings may negatively impact the
effectiveness, which unfortunately is de facto the only known
approach to leverage data from multiple graphs. Motivated by
this limitation, we develop a scalable unsupervised multi-
source representation
learning
information network embeddings, named
heterogeneous
SUMSHINE
Unsupervised Multi-Source
(Scalable
Heterogeneous Information Network Embedding). It allows to
train
network
embeddings from different sources into a distribution-aligned
latent embedding space, and we confirmed that the embedding
learning performance can be significantly improved as our
framework
the distribution
discrepancy issue in learning heterogeneous information
network embeddings.
to cope with
heterogeneous
is designed
information
large-scale
for
Our contributions can be summarized as follows:
• We study the distribution misalignment problem in HIN
embeddings and conclude that the HIN embeddings
should be trained with distribution alignment performed
on the subgraph sources of the HIN to achieve optimal
downstream task performance. To the best of our
knowledge, we are the first to introduce source-level
information
distribution alignment
network embedding.
to heterogeneous
• We propose source-aware negative sampling to balance
the training samples by source, while preserving the
scalability advantage of negative sampling. This design
overcomes the scalability constraints of existing HIN
embedding methods using GNNs.
• We validate our proposed method empirically on both link
prediction and node classification downstream tasks,
using a variety of real-world datasets. We also highlight a
practical application of our method on recommendation
systems with extensive experiments.
II. RELATED WORKS
A. Heterogeneous Information Network Embedding
Heterogeneous information network embedding has shown
significant successes in learning the feature representations of
an HIN. Existing HIN embedding methods aim to learn a
low dimensional feature representation of an HIN. They apply
different transformation techniques to bring the embeddings
into the same latent embedding space [7, 8]. Most of the HIN
embedding methods focus on leveraging the multi-relation
characteristic in the HIN, which are known as similarity- based
methods [3, 4, 11, 12, 13]. Similarity-based methods are widely
adopted to learn the HIN representations by encoding the
similarity between the source and destination entities in an
edge. Within this class, there are translational methods, such as
TransE [3], TransR [4] and TransD [11]. They take relations as
translations of the head and tail entity embeddings. An- other
class of similarity-based HIN embedding methods uses bilinear
methods, such as RESCAL [14], CompleX [13], and DistMult
[12]. These methods represent relation embeddings
as a transformation of the head and tail entity embeddings [15].
There are also meta-path-based methods [16], and meta- graph-
based methods [17], utilizing the structural features in an HIN
as attempts to align the path-based or subgraph-based
distributions.
Despite their success, these works assume only one source in
the HIN and do not consider the distributional difference
among sources of subgraphs. And there is a need to align the
distributions of feature embeddings from different sources of
the HIN to improve downstream task performance. Without
loss of generality, we focus on similarity-based embedding
methods to illustrate our distribution alignment approach. Our
method can be easily applied to all HIN embedding methods on
multi-source HINs in general as the alignment is performed on
samples of node and relation type embeddings.
Recently there are methods using GNNs to learn the
representations of an HIN [7, 9, 18, 19, 20, 21]. Although
GNNs can extract the enriched semantic information contained
in
the HIN, the embeddings of these models are often
trained on a supervised or semi-supervised basis with respect to
a specific task. Label information on nodes and edges needs to
be provided for satisfactory embedding learning. And they can
hardly be generalized when the embeddings need to be applied
to another task. Additionally, most GNN-based methods work
with the adjacency matrix of the HIN, e.g., graph convolutional
neural network (GCN) [18] and its variants [1] on HIN perform
node aggregation based on the transformed adjacency matrix.
These matrices cannot be processed by the memory. Therefore,
it is difficult to apply GNN-based HIN embedding methods for
large-scale tasks such as recommendation systems which
contain networks with billions of user nodes and millions of
movies.
In contrast,
the aforementioned similarity-based HIN
embedding methods perform embedding learning on edge
samples, which allows parallelism and therefore scalability.
Since the trained embeddings learn HIN representations by
encoding the similarity, the similarity features of the HIN are
not associated with a specific task. These properties motivate us
to propose a multi-source HIN representation
learning
framework which is not only applicable to any downstream task
but also is scalable to large HINs.
B. Distribution Alignment
Distribution alignment, also known as domain adaptation in
transfer learning, has been a key topic in HIN representation
learning, as the heterogeneity in entities and relations intro-
duces misalignments in their respective distributions. There are
many attempts in existing work to align the distributions of key
features in an HIN. Transformation approaches aim to learn
a
transformation matrix or an attention mechanism to
translate the feature embeddings of different types (nodes or
edges) into the same embedding space [7, 8]. Most of the
similarity-based methods mentioned above also attempt to
align the feature embeddings between entities and relations in
an HIN [3, 4, 11, 12]. For example, TransE [3] approximates
distribution of the tail node embedding in an edge by the
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
d
n
/
i
t
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
i
/
/
t
.
1
0
1
1
6
2
d
n
_
a
_
0
0
2
0
0
2
0
7
0
9
2
3
d
n
_
a
_
0
0
2
0
0
p
d
/
t
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Data Intelligence Just Accepted MS.
https://doi.org/10.1162/dint_a_00200
sum of head and relation embeddings. Heterogeneous graph
attention network (HAN) [8] adopts a learnable transformation
layer to each node type to transform the node embeddings into
a space invariant to node types.
Adversarial learning approaches introduce discriminator
networks as a domain classifier whose losses are used to
measure high-dimensional distribution differences [10, 19, 22,
23]. Moreover, several works applied distance measures such as
the maximum mean discrepancy
to perform
distribution alignment [9], these works aim to minimize the
distances between distributions to align the distributions of
feature embeddings. These alignment methods have been
extensively applied to domain adaptation to improve transfer
learning performance among multiple graphs. However, these
methods are never introduced to align the feature distributions
within an HIN.
(MMD)
Inspired by the above works in distribution alignment, we
include both the distance measure approach and the adversarial
approach in our proposed framework. We use these alignment
methods to align the distributions of HIN embeddings with
respect to sources, in addition to their original attempts to align
the distributions of nodes or edge types. We assess the
performance of these distribution alignment methods in
aligning the embedding distributions by experiments on
different downstream tasks, such as node classification and link
prediction.
III. PROBLEM STATEMENT
A. Definitions
Heterogeneous Information Network: A heterogeneous in-
formation network is defined by a graph 𝒢 = (𝒱, ℰ, 𝒜, ℛ) where
𝒱, ℰ, 𝒜, ℛ represent the set of entities (nodes), relations (edges),
entity types, and relation types, respectively. A triple in E is
defined by e = (h, r, t), where h, t ∈ 𝒱 are the heads and tails
nodes representing the entities in 𝒢, and 𝑟 ∈ ℛ represents the
type of relation connecting the entities. For 𝑣 ∈ 𝒱, 𝑣 is mapped
to an entity type by a function 𝜏(𝑣) ∈ 𝒜, and 𝑟 is mapped to a
relation type by a function 𝜙(𝑟) ∈ ℛ.
Heterogeneous Information Network Embeddings: We
encode the similarity of each node in the HIN to a 𝑑-
dimensional vector with a similarity function 𝑓(𝑒). The node
and edge type embeddings can be used as input features for
training an arbitrary downstream task model.
IV. Methodology
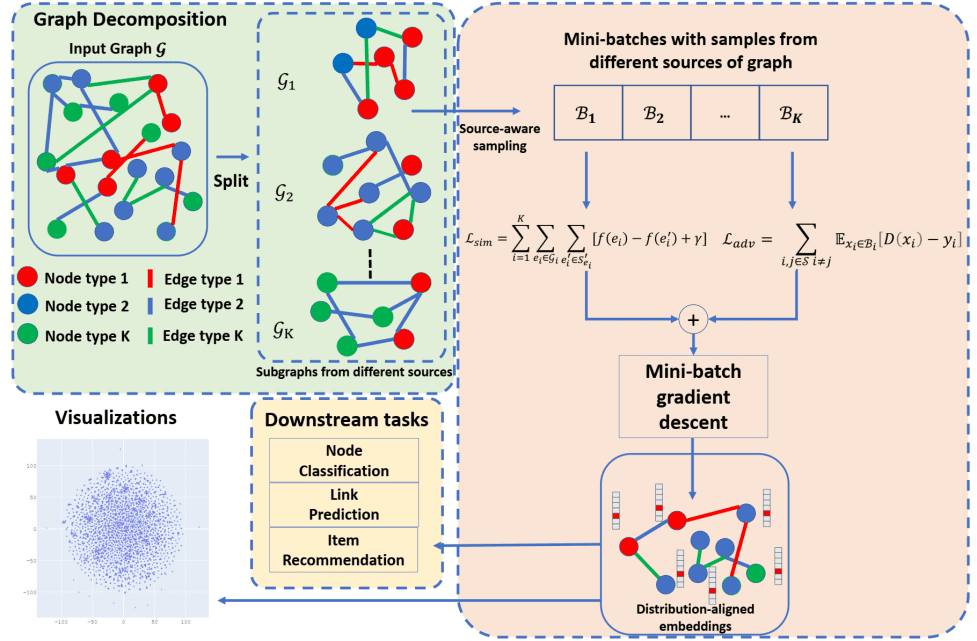
We introduce SUMSHINE in this section. The major com-
ponent of SUMSHINE consists of a source-aware negative
sampling strategy and a loss function designed to regularize
distribution discrepancies across subgraphs. Conceptual
visualization of the training paradigm of SUMSHINE is shown
in Figure 1.
A. Source-Aware Negative Sampling
Given a positive edge e = (h, r, t), negative sampling re-
places either a head or a tail (but not both) by another arbitrary
node in the HIN to produce negative edges which do not exist
in the original graph [3, 5]. The embeddings can be learned by
maximizing the distance between the positive samples (i.e.,
ground truth edges) and the negative samples. However,
sampling from imbalanced subgraphs leads to data imbalance
problem between subgraph sources. Edges in larger subgraphs
(such as a user interaction graph) are sampled more often than
the smaller subgraphs (such as an album knowledge graph). To
rebalance the data with respect to sources, we introduce source-
aware negative sampling to sample edges uniformly from each
subgraph source. By source-aware sampling we can balance the
number of edges sampled by sources, and reduce the bias on
embeddings from data imbalance. For each subgraph source 𝒢7
in 𝒢, we sample a fixed-size batch of edges from it to match the
dimensions of sample embedding matrices. Given and edge
𝑒7 = (ℎ7, 𝑟7, 𝑡7) from a source 𝒢7 , we select a set of negative
G or a tail node
samples 𝑆EF
G within the
G or 𝑡7
by 𝑡7
subgraph. We denote the set of negative samples as
G by replacing either a head node by ℎ7
G are entities other than ℎ7
G , where ℎ7
G and 𝑡7
G = {(ℎ7
𝑆EF
G, 𝑟7, 𝑡7)| ℎ7
G ∈ 𝒱>} ∪ {(ℎ7, 𝑟7, 𝑡7
G)| 𝑡7
G ∈ 𝒱>}.
The negative samples are combined with a batch of positive
edges to compute the similarity on a mini-batch basis. The
similarity-based loss function is given by
;
ℒJ7K = L L L [𝑓(𝑒7) − 𝑓(𝑒7
S∈TUF
EF
EF∈𝒢F
79:
S
G) + 𝛾]R
,
where 𝛾 is the margin and [𝑥]R = max (x, 0). The scoring
function 𝑓(𝑒) is uniquely defined by the HINE method. We
assume the embeddings of the edge samples are independent
and identically distributed (IID). We use mini-batch gradient
descent [5] to back-propagate the similarity loss to the
embeddings to learn the HIN representation.
B. Problem: Multi-Source Heterogeneous Information Net-
B. Aligning Sources with Regularization
work Embeddings
Consider a heterogeneous information network 𝒢 =
(𝒱, ℰ, 𝒜, ℛ), let 𝒮 represents the set of sources in 𝒢. We have
;
; = {(𝒱=, ℰ=, 𝒜=, ℛ>)}79:
a series of 𝐾 = |𝒮| subgraphs {𝒢7}79:
as the predefined sources of 𝒢. Let 𝒳 be the embeddings
space of nodes and edge types in 𝒢, and let 𝒳7denote the
embedding space of nodes and edge types in each subgraph
𝒢7.
We wish to assign an embedding x ∈ X to each node and edge
;
type in 𝒢. We also wish to align the distributions of {𝒳7}79:
such that for a model ℳ trained on graph 𝒢, on a given
downstream task 𝒯, the model ℳ can perform accurately.
As mentioned above, one of the key issues we want to ad- dress
here is to alleviate the distribution discrepancies among different
subgraphs. More specifically, given an arbitrary pair of
; , we define the distribution functions 𝑃 and
subgraphs in {𝒢7}79:
𝑄 on the embedding space to be the embedding distributions on
the two subgraphs, and we aim to encourage less distribution
discrepancy between 𝑃 and 𝑄 despite their domain differences.
To achieve this, we introduce two regularization methods —
adversarial
distance-measure-based
regularization.
regularization
and
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
d
n
/
i
t
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
i
/
t
/
.
1
0
1
1
6
2
d
n
_
a
_
0
0
2
0
0
2
0
7
0
9
2
3
d
n
_
a
_
0
0
2
0
0
p
d
/
t
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Data Intelligence Just Accepted MS.
https://doi.org/10.1162/dint_a_00200
Fig. 1: Training paradigm of our proposed SUMSHINE HIN Embedding method.
We first introduce distance-measure-based regularization. In
this paper, we adopt the distance measures MMD [24], the
Kullback–Leiber (KL) divergence, and the Jensen–Shannon
(JS) divergence [25] in our experiments, while our framework
can be generalized to incorporate any distance measures. We
use ∆ to denote the distribution distance between P and Q.
The KL divergence on P and Q is defined as
Δ;Z(𝑃 ∥ 𝑄) = L 𝑃(𝑥) log _
a∈𝒳
𝑃(𝑥)
𝑄(𝑥)
,
‘
and the JS divergence is the symmetric and smoothed version
of the KL divergence defined by
ΔbT(𝑃 ∥ 𝑄) =
1
2
eΔ;Z(𝑃 ∥ 𝑄) + Δ;Z(𝑄 ∥ 𝑃)f.
The MMD loss is a widely used approach to alleviate the
marginal distribution disparity [26]. Given a reproducing kernel
Hilbert space (RKHS)
[24], MMD is a distance measure
between P and Q which is defined as
𝑀𝑀𝐷(𝑃 ∥ 𝑄) = i𝜇k − 𝜇li
ℋ
,
where 𝜇k and 𝜇lare respectively the kernel means computed
on 𝑃 and 𝑄 by a kernel function 𝑘(∙) (e.g., a Gaussian kernel).
We perform distribution alignment between pairs of subgraphs.
For each batch sampled by source-aware sampling and each
pair of sources, we compute the distribution differences of
embeddings for both relation types and entities, using one of
the distance measures introduced above. The regularization loss
ℒp7Jq is the sum of distribution distances for both entity and
relation type embeddings over each pair of sources. The total
loss can be obtained by combining ℒp7Jq with the similarity loss
to propagate both the similarity and the distribution discrepancy
into HIN embedding training,
ℒqrq = ℒp7Jq + 𝜆ℒJ7K (1)
where λ is a tuning parameter.
Alignment methods based on distance measures heavily
relies on the measure chosen, and the high dimensional
distribution difference such as the geodesic difference may not
be incorporated by the measure. R Connor et. al [27] suggested
that the high dimensionality of data in the metric space may
cause metrics of distribution differences
to be biased.
Adversarial Regularization, on the contrary, uses a feedforward
network as a discriminative classifier
the
distributional differences in high dimension to avoid comparing
high-dimensional data
the metric space directly and
ameliorate the bias compared to the aforementioned distance
measures [28].
to capture
in
With the recent development of adversarial distribution
alignment [10, 23, 28, 29], we
introduce adversarial
regularization to HIN embedding training. We consider the
embed- dings from different subgraphs trained by an HIN
embedding method as the generated information, and use an
adversarial discriminator D as a domain classifier to classify the
source of the embeddings. As a result, we consider the loss from
the discriminator a measure of distribution discrepancy
between the sources and use it to align the embeddings
distributions from different sources [10, 28].
Let ℬ7 ⊆ 𝒳7be the node and edge type embeddings in a sampled
batch from a subgraph source 𝒢7. The discriminator receives the
batch of embeddings ℬ7 , and generates the probability that
which source these embeddings are from. The predictions are
compared with the ground truth one-hot label 𝑦7, where its i-th
entry is 1 with the rest being zeros. The loss of the discriminator
is given by
ℒw = L 𝔼yF∈ℬF
>∈𝒮
[𝐷(𝑥7) − 𝑦7].
We then compute the adversarial loss and combine it together
with the similarity loss. We compute the distribution distance
by inverting the true label 𝑦7 to 𝑦z where 𝑖 ≠ 𝑗. The adversarial
loss is then given by
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
d
n
/
i
t
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
i
/
t
/
.
1
0
1
1
6
2
d
n
_
a
_
0
0
2
0
0
2
0
7
0
9
2
3
d
n
_
a
_
0
0
2
0
0
p
d
/
t
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Data Intelligence Just Accepted MS.
https://doi.org/10.1162/dint_a_00200
ℒ~p(cid:127) = L 𝔼yF∈ℬF
>∈𝒮
(cid:128)𝐷(𝑥7) − 𝑦z(cid:129).
given node from source 𝑖 with embedding 𝑧 in the shared-
semantic embedding space 𝑍 and ℳ7 be the downstream
task model trained to make prediction 𝑦(cid:156) = ℳ7(𝑧) [10],
The loss 𝐷(𝑥7) − 𝑦z for each pair of sources 𝑖 and 𝑗 indicates
the distributional difference between them. We aim to include
this adversarial loss to the embeddings such that the
embeddings can be more similar in distribution to fool the
discriminator. We then multiply the adversarial loss by the
tuning parameter 𝜆 and compute the aggregated loss using
equation (1) with ℒp7Jq replaced by ℒ~p(cid:127).
ℒ7 = (cid:157) 𝑝7(𝑧)Δ(𝑃(cid:151)7(𝑦|𝑧), 𝑃(𝑦|𝑧))𝑑𝑧
,
(cid:158)
where Δ is the divergence function to determine the loss of
predicted labels to ground truth labels. We have the following
theorem:
Theorem 1 If the following conditions are satisfied:
V. THEORETICAL ANALYSIS
(cid:135)𝑃(cid:151)7(𝑦|𝑧) − 𝑃(cid:151)z(𝑦|𝑧)(cid:135) < 𝑐7z, ∀𝑖, 𝑗 ∈ 𝒮 We provide theoretical analysis to show why aligning the distribution of embeddings from different sources of sub- graphs in a heterogeneous graph can improve the downstream task performance, where the error of generalization will be bounded by probability with an optimized bound. Settings We first define the loss of generalization. When generalizing the model from a origin environment to the target environment on the same task 𝒯 , we want to minimize the generalization bound 𝜖 such that the error of generalization is bounded by 𝜖 in probability, which is for any 𝛿 > 0,
ℙe(cid:135)ℒr(cid:136)(cid:137) − ℒpEJq(cid:135) ≤ 𝜖f ≤ 1 − 𝛿,
where ℒr(cid:136)(cid:137), ℒpEJq are the losses of the origin and destination
respectively for the downstream task 𝒯and (cid:135)ℒr(cid:136)(cid:137) − ℒpEJq(cid:135) is
the error of transferal. We further assume that the source
discrepancy leads to the largest generalization error than any
pairs of subgraphs in 𝒢, which is formulated in assumption 1.
Assumption 1 Suppose {𝒢}79:
subgraph sources of 𝒢, let 𝒢J(cid:139)
{𝒢}79:
; which has the largest generalization error,
; is the set of 𝐾 pre-defined
∗, 𝒢J(cid:141)
∗be the pair of subgraphs in
(cid:142)ℒ𝒢(cid:143)(cid:139)
∗ − ℒ𝒢(cid:143)(cid:141)
∗ (cid:142) ≥ (cid:142)ℒ𝒢(cid:145)(cid:139) − ℒ𝒢(cid:145)(cid:141)
(cid:142) ∀𝑠:, 𝑠(cid:148) ∈ 𝒮,
(cid:135)𝑝7(𝑧) − 𝑝z(𝑧)(cid:135)
𝑝7(𝑧)
< 𝜖7z, ∀𝑖, 𝑗 ∈ 𝒮
Then we have
;
;
L L(ℒ7 − ℒz)
79: 7¡z
z9:
;
;
≤ L L(ℒ7𝜖7z − 𝑐7z + 𝑐7z + 𝜖7z)
.
79: 7¡z
z9:
Theorem 1 states that if we want to control the
generalization loss from each source i to any other sources,
we need to align both the semantic meaning and the distributions
𝑝7(𝑧) of the embeddings by controlling every pairwise distance.
The proof of theorem 1 is given by Zhang et al. [10]. Since all
the subgraphs are trained jointly and the subgraph embeddings
are essentially having the same semantic meaning, we further
assume 𝑐7z → 0 in theorem 1 as the embeddings having very
close semantic meanings (i.e., ground truth labels will be the
same for a given 𝑧). Then we have the following corollary:
Corollary 1 If 𝑐7z → 0, we have the following reduced version of
theorem 1:
;
;
L L(ℒ7 − ℒz)
79: 7¡z
z9:
;
;
≤ L L ℒ7𝜖7z
.
(2)
79: 7¡z
z9:
∗ − ℒ𝒢(cid:143)(cid:141)
∗ (cid:142). This assumption is
where ℒ(cid:137) is the downstream task loss using a graph 𝑔, then we
assume that for any pair of subgraph in 𝒢, the generalization
loss is less than or equal to (cid:142)ℒ𝒢(cid:143)(cid:139)
reasonable since the sources of subgraphs are mostly having
the largest semantic difference and least overlaps. We can
focus on minimizing the source-level embedding distribution
discrepancy with this assumption.
To obtain a theoretical bound of source-level
generalization error, we generalize the current pairwise
analysis from Zhang et al. [10] to multiple sources. Given a
specific downstream 𝒯 and a series of true labels
;
(cid:150)𝑃(cid:151)7(𝑦|𝑧)(cid:153)
task loss for source 𝑖, and 𝑝7(𝑧) is the density function of a
for each source 𝑖 in 𝒮. ℒ7 is the downstream
79:
Equation (2) indicates that in order to reduce the
generalization error between any pairwise environments, we
only need to minimize the distribution difference of all pairs
of environments. In other words, we want to minimize
which can be achieved by minimizing the adversarial loss
ℒ~p(cid:127). On the other hand, the similarity loss ℒJ7K can highlight
the node and edge features in the graph, thus ℒ7 can still be
minimized.
VI. THEORETICAL ANALYSIS
A. Datasets
We collect public datasets for benchmarking HIN embedding
methods that contain multiple sources: WordNet18 (WN18)
[3] and DBPedia (DBP). Table II provides a summary of the
datasets used for experiments. We also compose a real
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
d
n
/
i
t
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
t
.
/
1
0
1
1
6
2
d
n
_
a
_
0
0
2
0
0
2
0
7
0
9
2
3
d
n
_
a
_
0
0
2
0
0
p
d
.
t
/
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Data Intelligence Just Accepted MS.
https://doi.org/10.1162/dint_a_00200
TABLE I: Example heterogeneous graph embedding methods and their scoring functions
Model
Embedding Space
Relation Embeddings
Scoring Function
Space Complexity
TransE [3]
TransR [4]
TransD [11]
RESCAL [14]
DistMult [12]
ComplEx [13]
h, t ∈ Rd
h, t ∈ Rd
h, t, Mh, Mt ∈ Rd
h, t ∈ Rd
h, t ∈ Rd
h, t ∈ Cd
r ∈ Rd
r ∈ Rd, Mrt ∈ Rk×d
r, Mr ∈ Rd
Mrt ∈ Rd×d
r ∈ Rd
r ∈ Cd
−∥ e𝑴(cid:136)𝑴𝒉
𝑻 + 𝑰f𝒕 ∥“
∥h + r – t∥𝒑
∥ 𝑴𝒓𝒉 + 𝒓− 𝑴𝒓𝒕 ∥𝒑
𝑻 + 𝑰f𝒉 + 𝒓 − e𝑴(cid:136)𝑴𝒉
𝒉𝑻𝑴𝒓𝒕
𝒉« 𝒅𝒊𝒂𝒈(𝒓)𝒕
𝒉« Ree𝒅𝒊𝒂𝒈(𝒓)f𝒕
O(d)
O(d2)
O(d2)
O(d2)
O(d)
O(d)
h, r, t: embeddings of head, relation, and tail; d: dimension of the embedding vector; Re(z): real part of complex number z; diag(x): diagonal entries of
matrix x; Cd: complex space of dimension d; Mr, Mt: learnable matrices to transform the relation or tail embeddings.
TABLE II: Datasets Summary
A. Benchmarking Methods
Dataset
DBP-Total1
DBP-WD2
DBP-YG3
MRec-Total
MRec-Album
MRec-User
WN18-Total
WN18-A
WN18-B
WN18-C
|𝒱|
118,907
42,201
37,805
284,908
57,203
235,693
40,943
39,398
20,179
7,516
|ℛ|
305
259
236
8
5
3
18
6
7
5
|ℰ|
118,907
60,000
60,000
307,029
62,915
246,629
151,442
96,598
41,836
13,008
|𝒜|
1
1
1
1
1
1
1
1
1
1
1 Total: The whole graph constructed by merging the sub-
graph sources
2 WD: Wikidata source of DBPedia
3 YG: WordNet source of DBPedia
dataset, namely MRec (Movie Recommendation), based on real
user movie watching data from a practical recommendation
system. MRec has two sources — one is representing the
user-movie interaction graph, containing the users’ movie-
watch histories, and another one is simulating the knowledge
graph of the album of movies with ground truth entities related
to the movies such as tags, directors, and actors. We use the
MRec dataset to model the distribution difference caused by
graph sizes in HINs. To validate the performance when our
method is applied to more than two sources, we perform
experiments on the WN18 dataset which contains three sources
of subgraphs — namely A, B, and C. The subgraphs are created
by categorizing the relations according to their semantic
meanings so that different subgraphs will correspond to
different sets of relations, incurring different average node
degree per relation type. Details on the sources can be found in
the Appendix.
For node classification, we collect channel labels from
the MRec dataset for 7000 movie nodes where these nodes are
present in both the user interaction graph and album knowledge
graph. Each movie node is labelled by one of the following
six classes: “not movie”, channel 1 to 4, or “other movie” (i.e.
channel information not available). We additionally sample
3000 “not movie” (i.e., negative) entities from the MRec data
for training in order to produce class-wise balanced data. We
randomly choose 7000 movie entities and 3000 non-movie
entities from the testing graph as the testing data.
We compare our method against the baseline HIN embed-
ding learning methods, including TransE [3], TransR [4], and
DistMult [12], and validate the improvements provided by our
method. We also show the performance of GNN-based
approaches [18, 20, 21], of which the main goal is to learn node
embeddings for a specific downstream task, as a reference. For
simplicity, we use the scoring function of TransE [3] in our
proposed framework, while the performance of our method
with other scoring functions is presented by ablation studies in
Section VII-A. To validate the effectiveness of our approach,
we apply the node and edge type embeddings produced by each
approach as the feature input to downstream tasks. Table I
presents a summary of the embedding methods and their
scoring functions
Descriptions of each method are listed below:
• TransE [3]: Learning the relations in a multi-relation
graph by translating the source and destination node
embeddings of the relation.
• TransD [11]: In addition to TransR translating the relation
space, TransD also maps the entity space to a
common latent space.
• TransR [4]: Building entities and relations in separate
embedding spaces, and project entities to relation space
then building translation between the projected entities.
• RESCAL [14]: RESCAL is a bilinear model that captures
latent semantics of a knowledge graph through associate
entities with vectors and represents each relation as a
matrix that models pairwise interaction between entities.
Entities and relations are represented as a multi-
dimensional tensor to factorize the feature vectors to rank
r.
• DistMult [12]: Improving
the
time complexity of
RESCAL to linear time by restricting the relationship to
only symmetric relations.
B. Experiment Settings
We perform inductive link prediction [30] as the down-
stream task to validate our framework. After we obtain the node
and edge type embeddings produced by different HIN
embedding approaches, we use a multiple layer perceptron
(MLP) matcher model to perform the downstream task. A
matcher model is a binary classifier that output the probability
of having a link given the edge embedding (i.e., concatenated
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
d
n
/
i
t
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
.
t
/
/
1
0
1
1
6
2
d
n
_
a
_
0
0
2
0
0
2
0
7
0
9
2
3
d
n
_
a
_
0
0
2
0
0
p
d
t
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Data Intelligence Just Accepted MS.
https://doi.org/10.1162/dint_a_00200
embedding of head, tail and relation) as the input. For GNN
baselines, we directly train a GNN to perform link prediction
instead of MLP. A matcher model can perform inductive link
prediction across subgraphs rather than transductive [30] link
prediction which can only predict linkage with the observed
data (i.e., the subgraph used for training).
To highlight the advantage of combining subgraphs and
learning embeddings in distribution-aligned latent embedding
space, we design an experiment setting for inductive link
prediction as follows: When training for the downstream tasks,
we only take the training data that contain edges from one
subgraph while keeping the data which contain edges from
other graphs as evaluation data. Note that we borrow this setting
from the literature on GNN transfer learning [9, 10], where the
goal of these works is to transfer the GNN model from one
graph to another. However in our setting, rather than showing
how transferrable the downstream task models are, we show
how a distribution-aligned embedding training mechanism can
benefit the downstream task performance, especially when
subgraphs. For
there are distribution
demonstration of results, we denote the training-testing split in
each link prediction experiment with an arrow “Training →
Testing” for notational convenience.
shifts among
For each testing edge, we replace the head and then the
tail to each of the 1000 negative entities sampled from the
testing entities. We rank the true edge together with its negative
samples according to the probability that an edge exists be-
tween the head and tail output from the MLP matcher model.
We sample 1000 negative entities to corrupt the ground truth
edge instead of all the testing entities in the subgraph because
scaling the metrics can enhance the comparability among
datasets. Since each testing entity has an equal probability to be
replaced, the downstream task performance is not affected by
the choice of the sample size of negatives.
We use node classification as another downstream task. We
first train an MLP node classification model on one source
of subgraph and then test the model on another source. The
classification model takes an HIN node embedding as the input,
and classify the node to one of the six classes according to its
embedding.
We evaluate the link prediction performance using Hits@n
and mean reciprocal rank (MRR) and the node classification
performance using classification accuracy. More details on
evaluation metrics and model configurations are presented in
the appendix.
C. Link Prediction
We validate our framework by inductive link prediction.
Table III provides a summary of the prediction performance of
our method to various baselines. We choose the JS divergence
to be the distance measure for alignment. More discussions on
the effects of different distance measures will be included in
section VII-B. The experiments are performed on MRec and
DBPedia datasets with two sources. We observe that the link
prediction results after distribution alignment, with either
or
regularization
adversarial
distance-measure-based
regularization, are uniformly better among the benchmarks for
all evaluation metrics. The performance of adversarial
regularization is superior to the JS divergence, which supports
the superiority of adversarial alignment over distance-
measured-based alignment. The results show that inductive link
prediction is optimized for multi-source graphs if we align the
distributions of the embeddings.
We also observe that GNN models underperform our method
in most of the inductive link prediction tasks. GNN link
prediction models can extract global features by aggregating
node features from the whole graph (e.g., through the
transformed adjacency matrix), which is more capable than
similarity-based method focusing on local similarity features.
However, the misalignment in subgraph sources still decrease
the performance of GNN-based link prediction models, which
make them underperform our model in general. Additionally,
out-of-memory errors were reported for GNN models when the
size of user graph is doubled in the User→Album experiment.
This highlights the scalability constraints of GNN models.
We further validate our framework on datasets with more
than two sources. Table IV presents the results of inductive link
prediction performance for each of the six training-testing splits
on the WN18 dataset. We observe that in most of the tasks the
performances are
improved with distribution aligned
embeddings. This validate the consistency of our framework
when K is generalized to be larger than 2 (i.e., multiple sources).
The MRec dataset is simulated to have a significant
imbalance of data with respect to sources. Hence the data
without source-aware sampling are mostly sampled from the
user interaction graph and only a few of them are from the
album knowledge graph. It is noteworthy that since the user-
interaction graph is sparse (i.e. as users have diverged
interests), the link prediction model trained on the album
knowledge graph, is heavily biased and less transferrable to the
user-interaction graph, leading to a performance which
occasionally worse than a random guess.
With source-aware sampling, smaller subgraphs can be
sampled equal times to larger subgraphs. Therefore, the
information in the smaller subgraphs can be leveraged
especially when there is a large degree of data imbalance among
the sub- graphs. Hence source-aware sampling significantly
increases the awareness to small subgraphs, which resolves the
data imbalance problem in existing methods.
D. Node Classification
Table V presents the node classification performance with or
without distribution alignment respectively. We observe that
there are improvements in accuracy for both user to album and
album to user transferal tasks. Note that the MRec dataset
contains subgraphs with significant different average node
degrees. Therefore, without taking into account the imbalance
issue, the node and edge type embeddings will be dominated
by the semantic information contained in the user interaction
graph. With the help of distribution alignment
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
d
n
/
i
t
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
/
t
.
1
0
1
1
6
2
d
n
_
a
_
0
0
2
0
0
2
0
7
0
9
2
3
d
n
_
a
_
0
0
2
0
0
p
d
/
t
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Data Intelligence Just Accepted MS.
https://doi.org/10.1162/dint_a_00200
TABLE III: Link prediction performance of SUMSHINE to baseline methods on DBPedia and MRec datasets (JS: Regularization
loss is the JS Divergence; ADV: Regularization loss is the adversarial loss).
DBP
MRec
Model
TransE [3]
TransR [4]
GIN [20]
GCN [18]
GAT [21]
SUMSHINE-JS
SUMSHINE-ADV
YG→WD
User→Album
WD→YG
Album→User
MRR ↑ Hit@10↑ MRR Hit@10 MRR Hit@10 MRR Hit@10
0.0067
0.0130
0.0044
0.0295
0.1290
0.0293
0.0981
0.0276
0.0674
0.0368
0.1040
0.0474
0.3386
0.0487
0.0055
0.1100
0.0559
0.1643
0.0834
0.0262
0.1549
0.0060
0.0670
0.0275
0.1337
0.0414
0.0149
0.1232
0.0232
0.0632
0.0498
0.0435
0.0553
0.0653
0.1022
0.0117
0.0302
0.0259
0.0244
0.0288
0.0320
0.0536
0.0232
0.0638
0.0607
0.0511
0.0653
0.1236
0.1257
0.0059
0.0051
0.0587
0.0608
0.0305
0.0380
0.1954
TABLE IV: Link prediction performance of our method to
TransE on the WordNet18 dataset which has three sources. The
similarity loss used for SUMSHINE is the same as TransE.
TransE
SUMSHINE
Data Split MRR↑ Hit@10↑ MRR Hit@10
0.0089
0.0079
0.0103
0.0100
0.0092
0.0072
0.0080
0.0087
0.0075
0.0099
0.0073
0.0069
0.0064
0.0061
0.0067
0.0104
0.0126
0.0115
0.0136
0.0138
A → B
B → A
B → C
C → B
A → C
C → A
0.0081
0.0134
0.0086
0.0123
during embedding training, the structure information in the
movie-knowledge graph can be leveraged and ameliorate the
domination of the user-interaction graph, hence the recall may
be higher while the precision is sacrificed to adjust the bias
caused by a large difference in average node degrees.
respectively, which is shown in Table VI. We observe that the
is decreased significantly after
distribution discrepancy
adversarial alignment. According to the flat-minima hypothesis
[31], smooth regions are the key for smooth transferal of the
features between distributions, which allow better alignments
in features from the subgraphs. The downstream task models
can hence make use of the aligned features to improve their
performances.
TABLE VI: JS Divergences of the trained embeddings of DBP
and MRec with respect to their sources (User and Album for
MRec; WD and YG for DBP). The comparison is performed
between distribution-aligned embeddings (SUMSHINE) and
the original embeddings (TransE).
Data Split
TransE
SUMSHINE
User — Album
WD — YG
8.7493
0.5870
0.0831
0.1522
TABLE V: Node classification performance (in classification
accuracy) of TransE with or without distribution alignment
respectively.
— ABLATION STUDIES
Data Split
TransE
SUMSHINE
User → Album
Album → User
0.5392
0.5497
0.5548
0.6249
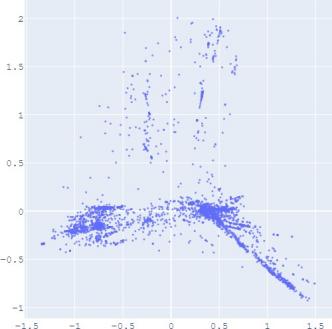
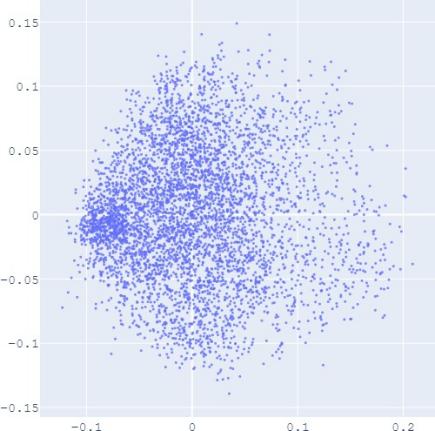
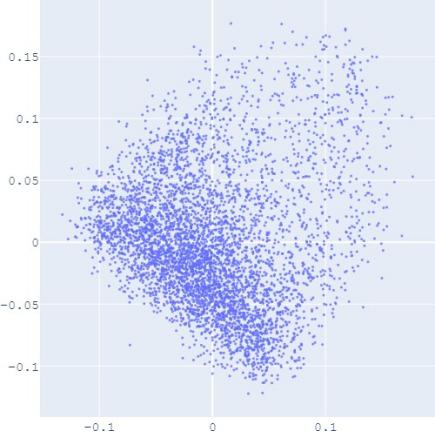
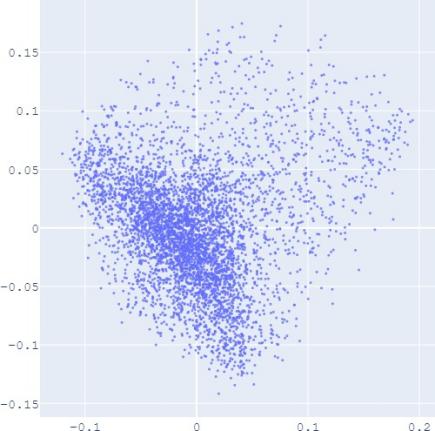
E. Visualization
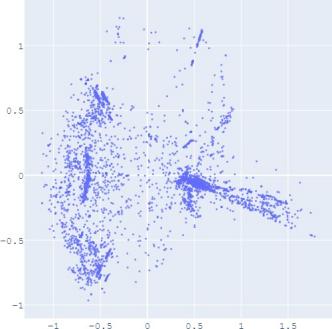
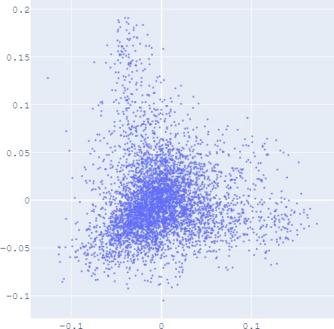
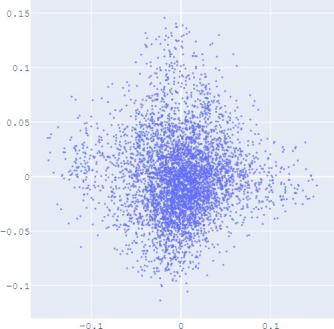
To validate the performance of our alignment method, we
use Isomap plots to visualize the trained embeddings with
or without distribution alignment, respectively. The high-
dimensional information such as geodesic distance can be
preserved by Isomap when reducing the dimension of the
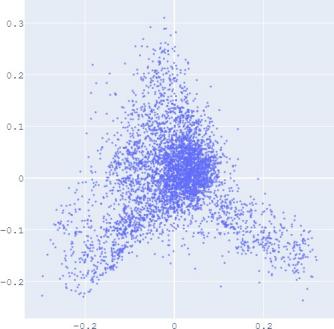
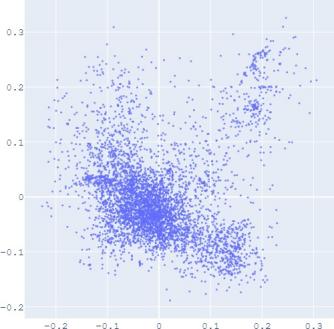
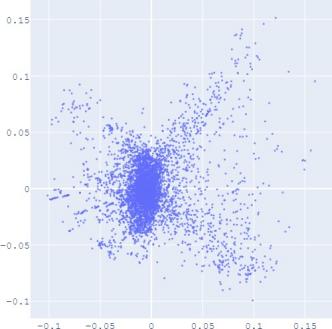
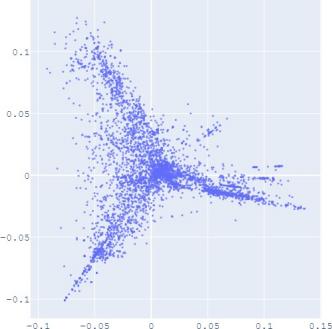
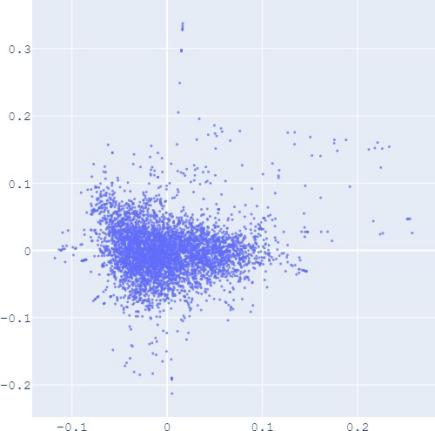
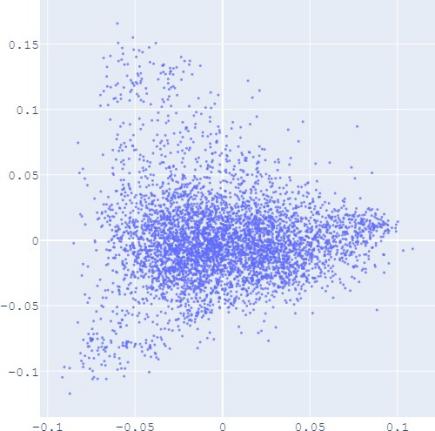
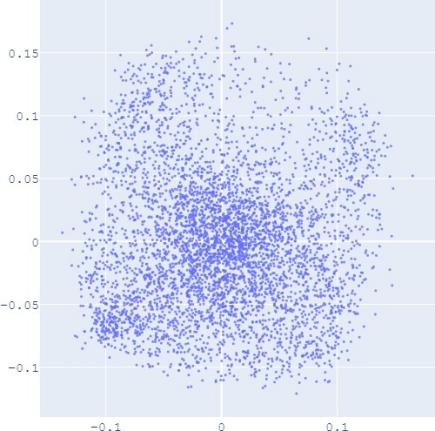
embedding distribution. Figure 2 shows the Isomap plot of the
embedding trained by TransE and SUMSHINE on the DBPedia
dataset and the MRec dataset. More visualizations are shown in
the appendix.
It
is observed
that with distribution alignment,
the
distributions of embeddings in YG and WD are smoother (i.e.
having fewer random clusters and more flat regions), while the
source-invariant features such as modes of distributions are
still preserved by similarity learning. The alignment in
distributions can also be validated quantitatively by computing
the JS divergences without and with adversarial regularization
A. Impact of Scoring Functions
We experiment with other HIN embedding methods by
exploring different scoring functions. Table VII demonstrates
the performance on link prediction using the embeddings with
or without distribution alignment respectively. Similar to that
of TransE, we observe that distribution alignment can still
improve inference performance when the scoring function is
altered. We can verify that the performance of our framework
is invariant to the changes in scoring functions, which indicates
that by training distribution-aligned HIN embeddings the
downstream tasks can perform more accurately with any
chosen scoring function. This ensures the extensibility of our
framework when new HIN embedding methods are developed.
B. Impact of Distance Measures
We further evaluate the performance of our model when the
distance measure is changed to another one, e.g., the KL
divergence or MMD. Table VIII presents the performance of
our framework on link prediction on the DBPedia dataset when
using different distance measures. We observe that both
distance measures can align the distributions of embeddings
and improve the downstream task performance. Since MMD
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
d
n
/
i
t
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
.
/
t
/
1
0
1
1
6
2
d
n
_
a
_
0
0
2
0
0
2
0
7
0
9
2
3
d
n
_
a
_
0
0
2
0
0
p
d
.
t
/
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Data Intelligence Just Accepted MS.
https://doi.org/10.1162/dint_a_00200
(a) WD No DA
(b) YG No DA
(c) WD With DA
(d) YG With DA
(e) User No DA
(f) Album No DA
(g) User With DA
(h) Album With DA
Fig. 2: Isomap plots of the embeddings of DBP by sources WD and YG, and MRec by sources User and Album, with or
without distribution alignment (DA) respectively. The alignment method used is adversarial regularization.
TABLE VII: Link prediction performances of different
similarity functions. The alignment method is adversarial
regularization.
TABLE VIII: Link prediction performances of alignment using
different distance measures on the DBPedia dataset. The
similarity loss for SUMSHINE the same as TransE.
Model
User → Album
Hit@3
MRR
Album → User
MRR Hit@3
Model
WD
→
YG
YG WD
→
MRR Hit@3 MRR Hit@3
TransE
SUMSHINE-TransE
TransR
SUMSHINE-TransR
TransD
SUMSHINE-TransD
DistMult
SUMSHINE-DistMult
RESCAL
SUMSHINE-RESCAL
0.0064
0.1232
0.0670
0.1904
0.0059
0.1381
0.0206
0.0238
0.0053
0.0428
0.0024
0.1421
0.0758
0.2297
0.0023
0.1703
0.0169
0.0245
0.0022
0.0495
0.0084
0.1954
0.0051
0.2208
0.0088
0.1144
0.0448
0.0688
0.0326
0.1109
0.0030
0.2358
0.0020
0.2850
0.0047
0.1567
0.0555
0.0704
0.0350
0.1300
features
computes the distribution distance in a Hilbert space [24], it can
incorporate higher-dimensional
the KL
divergence, the link prediction performance with MMD is
better than that with the KL divergence, while the time
complexity of MMD is higher. We conclude that using distance
measures can align
the
embedding quality, with small variations to the distance
measure selected.
the distributions and
improve
than
C. Impact of Subgraph Sizes
The difference in sizes among the subgraphs highlights the
distribution discrepancies. The aforementioned size difference
between the user-interaction graph and album knowledge graph
is a typical example of the size difference. We further study
how SUMSHINE performs as the ratio of sizes (in the number
of edges) changes. We compose different variants of the MRec
dataset with different ratios of the total number of
TransE
SUMSHINE-KL
SUMSHINE-MMD
SUMSHINE-JS
0.0130
0.0283
0.0471
0.0474
0.0117
0.0221
0.0534
0.0518
0.0064
0.0251
0.0280
0.0320
0.0056
0.0235
0.0204
0.0330
edges — from an approximately equal number of edges to large
differences in the total number of edges. We compare link
prediction performance with the original TransE and the
distribution-aligned version with adversarial regularization and
use MRR as the evaluation metric.
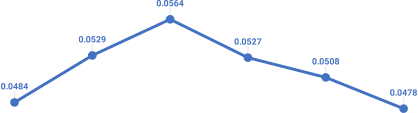
Figure 3 demonstrates a decreasing trend of MRR as the ratio
(album: user) of the number of edges changes from 1:4 to 1:1,
which indicates that our framework has better performance
when the size between subgraphs has larger differences. On the
other hand, TransE is having improving performance as the
number of edges of the subgraphs are close to each other.
However, the link prediction performance of TransE is still
lower without distribution alignment. The reason is that the user
interaction graph has diverged features where the features
cannot be smoothly transferred without distribution alignment.
For application on graph-based recommendation systems
where the user interaction graph and album graph typically
have a large difference in graph size, our framework performs
better to resolve the information misalignment problem for
better recommendation performance. This is a practical
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
d
n
/
i
t
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
t
.
/
1
0
1
1
6
2
d
n
_
a
_
0
0
2
0
0
2
0
7
0
9
2
3
d
n
_
a
_
0
0
2
0
0
p
d
t
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Data Intelligence Just Accepted MS.
https://doi.org/10.1162/dint_a_00200
— CONCLUSION AND FUTURE WORK
We propose SUMSHINE — a scalable unsupervised multi-
source graph embedding framework on HINs, which is shown
to improve the downstream task performance on the HIN.
Extensive experiments have been performed on real datasets
and different downstream tasks. Our results demonstrate that
the embedding distributions in the subgraph sources of the HIN
can be successfully aligned by our method. We also show by
ablation studies that the our framework is robust when the
distance measure or
is altered.
the scoring
Additionally, we show that our framework performs better
when the sources are having a larger difference in the graph
size.
function
Our framework can be further generalized to integrate
multimodal HIN embeddings by aligning the distributions
of the side information embeddings such as image or text
embeddings. Incorporating multimodality opens the possibility
of practical application of our framework to common-sense
knowledge graphs where the graph is constructed by merging
numerous knowledge bases, including text and image features.
ACKNOWLEDGMENT
We thank the anonymous reviewers and Dr. Pan Yi Teng for
their insights and advice on this research. This work was
partially supported by the Research Grants Council of Hong
Kong (17308321) and the HKU-TCL Joint Research Center for
Artificial Intelligence sponsored by TCL Corporate Research
(Hong Kong).
REFERENCES
[1] Kojima, R., Ishida,S. Ohta, M. et al.: KGCN: A graph-
based deep learning framework for chemical structures.
Journal of Cheminformatics 12, 1–10 (2020).
[2] Hu,W., Fey, M., Zitnik, M. et al.: Open graph benchmark:
Datasets for machine learning on graphs. arXiv preprint
arXiv:2005.00687 (2020).
[3] Bordes, A., Usunier, N., Garcia-Duran, A. et al.: Translating
embeddings for modeling multi-relational data. Advances in
Neural Information Processing Systems 26, (2013).
[4] Lin, Y., Liu, Z., Sun, M. et al.: Learning entity and relation
embeddings for knowledge graph completion. In: Twenty-
ninth AAAI Conference on Arti- Ficial Intelligence, (2015).
[5] Lerer, A., Wu, L., Shen, J. et al.: PyTorch-BigGraph:
A large-scale graph embedding system. In: Proceedings of
the 2nd SysML Conference, (2019).
[6] Gottschalk, S., Demidova, E. A multilin- gual event-
centric temporal knowledge graph. In: European Semantic
Web Conference. pp. 272–287 (2018).
[7] Hu, Z., Dong, Y., Wang, K. et al.: Heterogeneous graph
transformer. In: Proceedings of The Web Conference, pp.
2704–2710 (2020).
Fig. 3: Performance (in MRR) of album→user link prediction
task of SUMSHINE-ADV with respect to different ratios of the
number of edges (A:U) between the album knowledge graph
(A) and the user interaction graph (U).
Fig. 4: Link prediction performance (in MRR) of SUMSHINE-
ADV on DBPedia dataset with respect to different values of λ.
Here the YG source is the training set and the WD source is
the testing set.
insight of the above results on the industrial application of our
framework.
D. Impact of Tuning Parameter λ
We study the impact of tuning parameter λ in equation (1)
on the performance of our method. We explore a grid of values
of λ: [0.01, 0.1, 1, 10, 100, 1000] and perform adversarial
distribution alignment with each λ value. Figure 4 shows
how our methods perform on DBPedia datasets with different
values of λ. We observe that the optimal performance is
obtained when λ is 1. We also observe that the link prediction
performance is worse when λ is too small or too large. When
λ is too large, the regularization on the embeddings is too
heavy such that the similarity feature is not preserved by the
embeddings, and the lack of similarity features will decrease
the link prediction performance. On the other hand, when λ is
too small, the misalignment in distribution is not penalized
by the alignment loss, the distribution misalignment will also
decrease the link prediction performance. Hence λ should
carefully be tuned to achieve optimal downstream task
performance.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
d
n
/
i
t
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
/
.
t
1
0
1
1
6
2
d
n
_
a
_
0
0
2
0
0
2
0
7
0
9
2
3
d
n
_
a
_
0
0
2
0
0
p
d
t
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Data Intelligence Just Accepted MS.
https://doi.org/10.1162/dint_a_00200
[8] Wang, X., Ji, H., Shi, C.B. et al.: Heterogeneous
graph attention network. I n: The World Wide Web
Conference, pp. 2022–2032 (2019).
[9] Yang, S., Song, G., Jin, Y. et al.: Domain adaptive
classification on heterogeneous information networks. In:
International Joint Conference on Artificial Intelligence,
pp. 1410–1416 (2020).
[10] Zhang, Y., Song, G., Du, L. et al.: Dane: Domain adaptive
network embedding. In: International Joint Conference on
Artificial Intelligence, pp. 4362–4368 (2019).
[11] Ji, G., He, S., Xu, L. et al.: Knowledge graph embedding
via dynamic mapping matrix. In: Proceedings of the 53rd
Annual Meeting of the Association for Computational
Linguistics and the 7th International Joint Conference on
Natural Language Processing (Volume 1, Long Papers) pp.
687–696 (2015).
[12] Yang, B. Yih, W. He, X. et al.: Embedding entities and
relations for learning and inference in knowledge bases. In:
The 3rd
on Learning
Representations, (2015).
International Conference
[13] Trouillon, T., Welbl, J.,
Riedel, S. et al.: Complex
embeddings for simple link prediction. In: International
conference on machine learning, pp. 2071–2080 (2016).
[14] Nickel, M., Tresp, V., Kriegel, H.-P. A three-way model
for collective learning on multi-relational data.
In:
Proceedings of the 28th International Conference on
International Conference on Machine Learning, pp. 809–
816 (2011).
[15] Balazevic, I., Allen, C., Hospedales, T. Multi-relational
in Neural
poincare graph
Information Processing Systems, 32, 4463– 4473 (2019).
embeddings. Advances
representation
[16] Dong, Y., Chawla,N. V., Swami, A. Metapath2vec:
Scalable
for heterogeneous
networks. In: Proceedings of the 23rd ACM SIGKDD
International Conference on Knowledge Discovery and
Data Mining, pp. 135–144 (2017).
learning
[17] Zhang, D., Yin, J., Zhu, X. et al.: Meta-graph2vec:
Complex semantic path augmented heterogeneous network
embedding. In: Pacific-Asia Conference on Knowledge
Discovery and Data Mining. pp.196–208 (2018).
[18] Kipf, T. N., Welling, M. Semi-supervised classification
with graph convolutional networks. In: International
Conference on Learning Representations (ICLR), (2017).
[19] Wu, M., Pan, S., Zhou, C. et al.: Unsupervised domain
adaptive graph convolutional networks. In: Proceedings of
The Web Conference 2020, pp. 1457–1467 (2020).
[20] Xu, K., Hu,W., Leskovec, J. et al.: How powerful are graph
International Conference on
In:
neural networks?”
Learning Representations, (2018).
[21]
Velicˇkovic´, P., Cucurull, G., Casanova, A. e t al . :
Graph
preprint
networks.
arXiv:1710.10903 (2017).
attention
arXiv
[22] Huang, T., Xu, K., Wang, D. Da-hgt: Domain adaptive
preprint
transformer.
arXiv
heterogeneous
arXiv:2012.05688 (2020).
graph
[23] Tzeng, E., Hoffman, J., Saenko, K. et al.: Adversarial
discriminative domain adaptation. In: Proceedings of the
IEEE Conference on Computer Vision and Pattern
Recognition, pp. 7167–7176 (2017).
[24] Tolstikhin, I.O., Sriperumbudur, B. K., Scho¨lkopf, B.
Minimax estimation of maximum mean discrepancy with
radial kernels. Advances in Neural Information Processing
Systems, 29 pp. 1930–1938 (2016).
[25] Fuglede, B.,Topsoe, F. Jensen-shannon divergence and
hilbert space embedding. In: International Symposium on
Information Theory, ISIT 2004, Proceedings. p. 31 (2004)
.
[26] Ding, Z., Li, S., Shao, M. et al.: Graph adaptive knowledge
transfer for unsupervised domain adaptation.
In:
Proceedings of the European Conference on Computer
Vision (ECCV), pp. 37–52 (2018).
[27] Connor, R., Cardillo, F. A., Moss, R. et al.: Evaluation of
Jensen-shannon distance over sparse data. In: International
Conference on Similarity Search and Applications, pp.
163–168 (2013).
[28] Ganin, Y., Ustinova, E., Ajakan, H. et al.: Domain-
adversarial training of neural networks. The Journal of
Machine Learning Research, 17(1), 2096–2030 (2016).
[29] Goodfellow, I., Pouget-Abadie, J., Mirza, M. Generative
adversarial networks. Communications of the ACM, 63(11),
139–144 (2020).
[30] Hao, Y., Cao, X., Fang, Y. et al.: Inductive link prediction
for nodes having only attribute information. arXiv preprint
arXiv:2007.08053 (2020).
[31] Dziugaite, G.K., Roy, D.M. Computing nonvacuous
generalization bounds for deep (stochastic) neural networks
with many more parameters than training data. arXiv
preprint arXiv:1703.11008 (2017).
[32] Han, X., Cao, S., Lv, X. et al.: Openke: An open toolkit for
knowledge embedding.
In: Proceedings of the 2018
Conference on Empirical Methods in Natural Language
Processing: System Demonstrations, pp. 139–144 (2018).
[33] Wang, M., Yu, L., Zheng, D. et al.: Deep graph library:
Towards efficient and scalable deep learning on graphs. In:
ICLR Workshop on Representation Learning on Graphs
and Manifolds. 2019.
APPENDIX
A. Relation Decomposition of WN18
The sources A, B, and C of WN18 are decomposed by
relations according to their semantic meaning, where the names
of the relations for each source can be found below:
• A: instance hyponym, hyponym, hypernym, member
holonym, instance hypernym, member meronym
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
d
n
/
i
t
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
.
t
/
1
0
1
1
6
2
d
n
_
a
_
0
0
2
0
0
2
0
7
0
9
2
3
d
n
_
a
_
0
0
2
0
0
p
d
.
/
t
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Data Intelligence Just Accepted MS.
https://doi.org/10.1162/dint_a_00200
• B: member of domain topic, synset domain usage of,
synset domain region of, member of domain region,
derivationally related form, member of domain usage,
synset domain topic of
• C: part of, verb group, similar to, also see, has part
B. Model Configurations
We use adagrad as the optimizer with a learning rate of
0.005 and a weight decay of 0.001 for all models. Each positive
edge is trained with four negative edges to compute the margin-
based loss. The size of the minibatch is 1024. The embeddings
of each experiment are trained with 2000 epochs and all the
methods converged at this level.
For link prediction, we train a matcher model for each
experiment to be an MLP with two hidden layers of hidden
dimension 200. The matcher model takes the concatenated
head, relation and tail embeddings as the input and has output
the softmax probability of having a link. For GNN matcher
models (GCN/GAT/GIN), the number of layers is set to be 2
with the final dropout ratio to be 0.4. We train each of the
matcher models for 200 epochs in each experiment.
For node classification, we train an MLP classifier with 1
hidden layer of hidden dimension 200 and a softmax output
layer for the probability of the six classes. We train the
classifier in each experiment for 200 epochs.
C. Implementation Details
We implement our methods in Python. We utilize OpenKE
[32] as the backend for loading triples to training and perform-
ing link prediction evaluation using the trained embeddings.
We also use the dgl library [33] to perform graph-related
computations and PyTorch to perform neural network com-
putations. The models are trained on a server equipped with
four NVIDIA TESLA V100 GPUs. The codes and data for the
paper are available and will be made public after this paper is
published.
D. Metrics
• Link prediction metrics:
– Mean reciprocal rank (MRR): Mean of reciprocal
ranks of first relevant edge. Given a series of query
testing edges 𝑄, and rank7 be the rank of a true
edge over 1000 negative entities chosen, the MRR is
computed by
MRR =
1
|𝑄|
|l|
L
79:
1
rank7
– Mean rank (MR): Mean rank of the first relevant
edge, subject to larger variance as the high-rank edges
which contain diverged features dominate the mean
of ranks. MR is computed by
MR =
1
|𝑄|
|l|
L rank7
79:
– Hit rate @ n: the fraction of positives that rank in
the top n rankings among their negative samples.
• Classification metrics:
– Accuracy: The fraction of correct predictions to the
total number of ground truth labels.
E. Additional Visualizations
Figure 5 presents the visualization results of the embeddings
of entities from WN18 dataset, with and without distribution
alignment, respectively.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
d
n
/
i
t
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
.
/
/
t
1
0
1
1
6
2
d
n
_
a
_
0
0
2
0
0
2
0
7
0
9
2
3
d
n
_
a
_
0
0
2
0
0
p
d
t
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Data Intelligence Just Accepted MS.
https://doi.org/10.1162/dint_a_00200
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
(a) Source A No DA
(b) Source B No DA
(c) Source C No DA
e
d
u
d
n
/
i
t
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
t
/
/
.
1
0
1
1
6
2
d
n
_
a
_
0
0
2
0
0
2
0
7
0
9
2
3
d
n
_
a
_
0
0
2
0
0
p
d
t
.
/
i
(d) Source A With DA
(e) Source B With DA
(f) Source C With DA
Fig. 5: Isomap plots of the embeddings of WN18 by sources A, B, and C, with and without distribution alignment (DA)
respectively. The alignment method used is adversarial regularization.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3