Cortical Transformation of Stimulus Space in Order

Cortical Transformation of Stimulus Space in Order
to Linearize a Linearly Inseparable Task

Meng-Huan Wu1*, David Kleinschmidt2*, Lauren Emberson3, Donias Doko4,
Shimon Edelman5, Robert Jacobs1, and Rajeev Raizada1

Abstract

■ The human brain is able to learn difficult categorization tasks,
even ones that have linearly inseparable boundaries; however, it
is currently unknown how it achieves this computational feat. We
investigated this by training participants on an animal categori-
zation task with a linearly inseparable prototype structure in a
morph shape space. Participants underwent fMRI scans before
and after 4 days of behavioral training. Widespread representa-
tional changes were found throughout the brain, including an
untangling of the categories’ neural patterns that made them

more linearly separable after behavioral training. These neural
changes were task dependent, as they were only observed while
participants were performing the categorization task, not during
passive viewing. Moreover, they were found to occur in frontal
and parietal areas, rather than ventral temporal cortices, suggest-
ing that they reflected attentional and decisional reweighting,
rather than changes in object recognition templates. These re-
sults illustrate how the brain can flexibly transform neural repre-
sentational space to solve computationally challenging tasks. ■

INTRODUCTION

Just by a quick glance at a photograph of an animal, peo-
ple can say with reasonably good accuracy whether the
photo was of a cat or a dog. The apparent ease with
which this is accomplished belies the computational
complexity of this process. If we think of each image as
a point in a “pixel space” (where each dimension is the
brightness of one pixel), categories such as “dog” and
“cat” correspond to parts of this image space that are
highly tangled, like two pieces of paper crumpled to-
gether (DiCarlo & Cox, 2007). Somehow, the brain trans-
forms these tangled, linearly inseparable representations
to linearly separable representations that are computa-
tionally simple to read out.

How does the brain achieve this feat? To study how the
brain transforms its representation of a linearly insepa-
rable task, three key ingredients must be combined to-
gether. First, we need to study representational change.
To observe a change, at least two fMRI scanning sessions
are required, so that they can be directly compared: one
before participants have learned the task, and the other
after they have been trained on it. Second, we need to
use a linearly inseparable task, that is, one that cannot
be solved using a linear category boundary. Although lin-
early separable tasks are simpler and easier for partici-
pants to learn, the real world is rarely so cooperative.

1University of Rochester, 2Rutgers University, 3Princeton
University, 4Quinnipiac University, 5Cornell University
*These authors contributed equally to this work.

Very few real-world tasks are linearly separable. We there-
fore chose to study an inseparable one. The third key ingre-
dient is to use a task that allows lower-level pixel space
aspects to be clearly distinguishable from higher level
shape space properties. Human beings can recognize a
cat as being a cat rather than a dog, regardless of whether
it is seen from the front, side, above, or below. Each of those
different viewpoints produces a vastly different visual pro-
jection on the retina (the eye’s version of pixel space), but
in all cases, the same 3-D cat-shaped body is giving rise to
them. In this study, we therefore chose to present 3-D
shapes in a variety of different viewpoints and to require
participants to categorize the 3-D shapes themselves, dis-
counting irrelevant viewpoint information.

The most important difference between this study and
much of the earlier work is the fact that our study scanned
the participants twice: once before training and then a sec-
ond fMRI scan after several days of behavioral training.
Without pre- and postscans of this sort, it is not possible
to measure representational change. One might argue that
the pretraining scan is unnecessary, as one can plausibly
assume that an untrained brain will not contain any pre-
existing representations of the task that is about to be
learned. Several studies using only posttraining scans have
been carried out and have provided very valuable insights
(e.g., Seger, Braunlich, Wehe, & Liu, 2015; Folstein,
Palmeri, & Gauthier, 2013; Reber, Stark, & Squire, 1998).
Despite the plausibility of this assumption, we wish to ar-
gue that actually collecting pretraining fMRI data is neces-
sary to truly study representational change. Even a “naive”
participant will already have seen and categorized literally

Journal of Cognitive Neuroscience 32:12, pp. 2342–2355
https://doi.org/10.1162/jocn_a_01533

D
o
w
n
l
o
a
d
e
d

/
j

t
t

f
/

i
t
.

:
/
/

f
r
o
m
D
o
h
w
t
t
n
p
o
:
a
/
d
/
e
m
d
i
f
r
t
o
p
m
r
c
h
.
s
p
i
l
d
v
i
r
e
e
r
c
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
m
c
n
/
j
a
o
r
t
c
i
c
n
e
/
–
a
p
r
d
t
i
3
c
2
l
1
e
2
–
2
p
3
d
4
f
2
/
2
3
0
2
1
/
4
1
1
2
4
/
2
2
3
o
4
c
2
n
_
/
a
1
_
8
0
6
1
2
5
2
3
2
3
3
p
/
d
j
o
b
c
y
n
g
_
u
a
e
_
s
0
t
1
o
5
n
3
0
3
7
.
S
p
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3

/
j

o
n

0
5

M
a
y

2
0
2
1

millions of visual stimuli, so the experimental stimulus ma-
terials may very possibly trigger some sort of indirect visual
recognition memory, even if they are just patterns of dots.
In many fMRI studies, the question of interest is not
only whether some neural representation exists in the
brain (if a person can perform a task, then logically their
brain must contain some sort of information about it, in
some form), but more specifically whether we are able to
detect that representation and measure its properties.
Thus, even though one can logically deduce that training
has changed the representational content of the par-
ticipants’ brains, it is scientifically of great interest to test
whether information about those representational changes
can actually be measured using our existing experimental
techniques.

The second crucial aspect of this study is our use of a
linearly inseparable task. Again, this is not unprecedented
in the literature. However, existing studies of linearly in-
separable tasks lacked one or more of our set of three
crucial ingredients, thereby allowing our study to ask
questions that have not been addressed. Specifically,
using a prototype distortion paradigm, Braunlich, Liu,
and Seger (2017) demonstrated that support vector re-
gression can be used to predict each stimuli’s distance
from the category boundary and from the prototype.
Using an XOR stimulus space, Li, Ostwald, Giese, and
Kourtzi (2007) demonstrated that a support vector ma-
chine (SVM) can be used to decode which category each
stimulus belonged to. A key difference between those
studies and the one presented here is that they used flat
2-D stimuli, whereas we presented 3-D shapes from mul-
tiple viewing angles. This allowed us to show that cate-
gory learning mechanisms operated beyond recognizing
stimuli differences in the pixel space and that such mech-
anisms can be generalized to more naturalistic category
learning settings in shape space. Moreover, our proto-
type category structure is arguably more natural than
the XOR task. The XOR task has an elegant logical form,
but tasks with that structure rarely arise in everyday life.
In contrast, many tasks have the prototype structure, for
example: Is this person in my tribe or a stranger? Am I
close to home or far away?

The third crucial aspect of this study is that we used a
category structure that was defined in shape space, not
pixel space. Critically, each exemplar in our study was
presented from multiple viewing angles. In previous ex-
periments, each exemplar was presented only in one
canonical angle, meaning that two exemplars could be
perfectly discriminated based solely on differences in
pixel values (Braunlich et al., 2017; Mack, Love, & Preston,
2016; Folstein, Gauthier, & Palmeri, 2012). Such discrim-
inations can presumably be accomplished by recruiting
low-level visual cortices and frontal regions (Reber
et al., 1998) without involving shape-selective regions
such as lateral occipital complex. In contrast, because
we presented each exemplar from multiple viewing an-
gles, our experimental task forced participants to map

stimuli that are vastly different in pixel space to the same
exemplar in shape space. This manipulation made it less
likely that low-level visual regions would underlie cate-
gory learning and much more likely that higher level re-
gions sensitive to object shape would play an important
role in the acquisition of category structures.

In summary, to address our question of interest, we
needed pre- and posttraining scans, a linearly inseparable
task, and 3-D shapes presented from different view-
points. All three of these aspects of the study needed
to be combined together at once to be able to attack this
goal. Although some experiments have already been per-
formed that individually include some subset of these
three necessary ingredients, to the best of our knowl-
edge, no existing study has combined all three at once,
until the one presented here. Therefore, our study is able
to investigate how the brain transforms its representation
of a linearly inseparable task in a new way. Our experi-
mental design allows us, for the first time, to test the
following three claims at once: that observed representa-
tional changes are indeed changes, that these changes
are in response to trying to solve a linearly inseparable
task, and that these changes reflect shape-level rather
than pixel-level stimulus properties.

METHODS

Participants

Eighteen University of Rochester students participated in
the study. They all gave written consent in accordance
with University of Rochester research subjects review
board. One participant was run before the paradigm
was finalized, and two participants failed to learn the task
(posttest categorization accuracy lower than 0.5); there-
fore, only 15 participants are included for further fMRI
analysis.

Stimuli and Design

Stimuli were 3-D animal shapes, and the generation pro-
cedure is described in https://github.com/kleinschmidt/
animorph (Edelman, Bülthoff, & Bülthoff, 1999). Many
aspects of the animal shapes could be parametrically al-
tered to change their appearance, for example, length
and girth of the torso, ear size and position, angles of
the legs, and so on. There were 55 such parameters in
all. We wanted to create shape categories that were de-
fined not just by one or two salient features but which in-
stead involved changes to the overall animal appearance
resulting from many features all changing together. We
therefore created two approximately orthogonal vectors
that cut obliquely through the 55-dimensional parameter
space, with those two vectors producing a 2-D shape space
that involved changes in many different features together.
These two vectors will be referred to as the x- and y-axes.

Wu et al.

2343

D
o
w
n
l
o
a
d
e
d

/
j

t
t

f
/

i
t
.

:
/
/

/
j

o
n

0
5

M
a
y

2
0
2
1

ruled out the hypothesis that the brain merely picked up
stimuli differences in the pixel space and provided
evidence that the brain did indeed learn the shape dif-
ference between animals. Stimuli could vary in seven
possible pitches and five possible orientations (several ex-
treme orientation and pitch angles are shown in Figure 2).

Procedure

Participants came in for six separate sessions: a pretrain-
ing scanning session, four behavioral training sessions,
and a posttraining scanning session, all on separate days.
Each of the four training sessions consisted of 320 trials
in four 80-trial blocks. Participants were told they were go-
ing to learn to tell the difference between two varieties of
animals called “Daxes”: the ones that lived on the island of
Didoop and the ones that did not. On each trial, the par-
ticipant saw a picture of one of the animals and had to
press one of the two buttons to report whether it was a
“Didoop Dax” or a “non-Didoop Dax.” Participants were
told whether they were correct or incorrect by a thumbs
up or thumbs down icon, with additional positive feed-
back on correctly identified “Didoop Dax” trials in the
form of a picture of a tropical island. The tropical island
was shown for additional feedback when participants cor-
rectly identified a Didoop Dax animal, as the task context
described that Dax animals lived on the island of Didoop.1
On the first day of training, participants saw only the
canonical view of the animals until they exceeded 60%
accuracy for one 80-trial block. In all subsequent blocks,
variation in the orientation was introduced, and animals
would be sampled from all five orientations. On the sec-
ond day, after participants again achieved 60% accuracy
on one block, additional variation in the pitch angle was
added until the end of all training sessions, and animals
will be sampled from all viewing angles. Note that the
number of trials and blocks remained identical regard-
less of the learning curve of each participant.

The pre- and posttraining scanning sessions were iden-
tical. Participants performed three different tasks, each on
the exact same stimuli sequence presented in the same
order. First, they passively viewed the stimuli. Next, the
participants performed the same classification task they
were trained on (the Dax task) and a pitch angle

Figure 2. Each animal was displayed in various orientations and
pitches. In this figure, the animals are displayed at the extremes of the
ranges of orientation and pitch angles to illustrate the wide range of
viewpoints that were included in the categorization task. In the pitch
discrimination task, the participants’ task was to identify the two
rightmost animals as “standing on a steep hill” and to identify the two
leftmost animals as “not standing on a steep hill.”

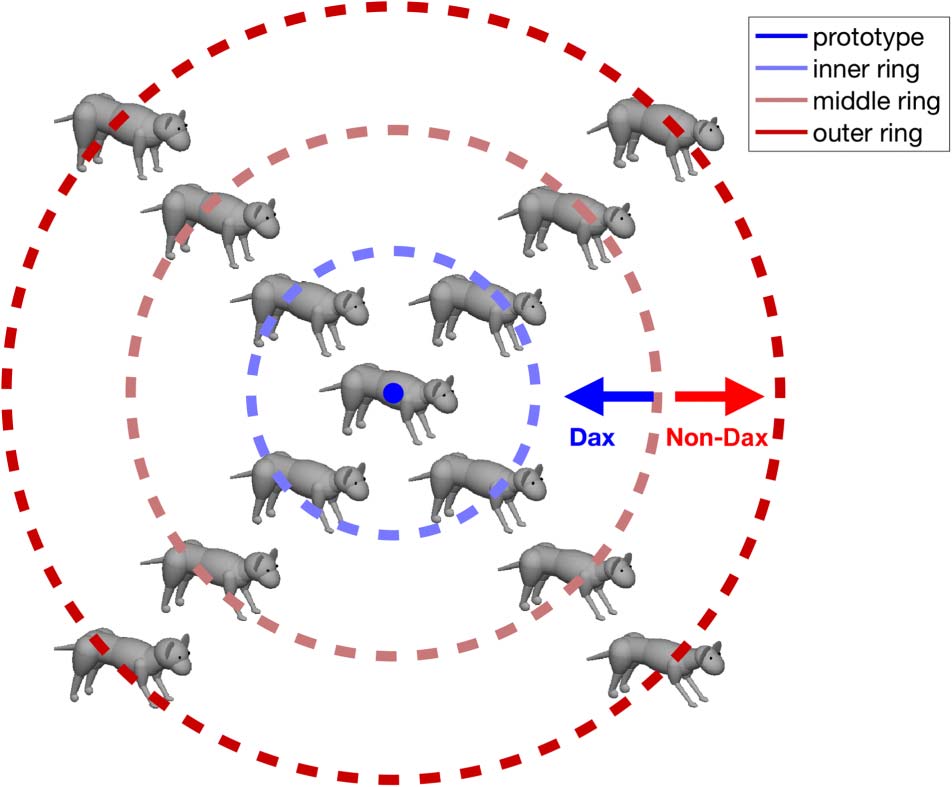
Figure 1. 2-D morph space of novel animals used in the fMRI sessions.
During behavioral training, only animals in the inner and outer ring
were shown to the participants; therefore, middle ring animals were not
preassigned to either of the two categories.

The resulting shape space is shown in Figure 1. Al-
though many individual features varied, some are par-
ticularly noticeable, for example, how fat or thin the
animals’ bodies were, their front knee angle, and the dis-
tances between ears and between eyes. To define the
Dax and non-Dax categories in this shape space, we defined
a central region as the Dax category, and the outer regions
of the space as non-Dax, as can also be seen from that
figure. All of the animals used in the experiment were
formed by a linear combination of these two basis vectors.
In this space, we defined a linearly inseparable prototype
category structure (Figure 1). We first picked a point in the
x, y space to serve as the central prototype. Animal shapes
closer than a critical distance to this prototype were de-
fined to be “Didoop Daxes,” and shapes farther than the
critical distance were “non-Didoop Daxes” (for brevity,
we refer to the categories as “Dax” and “non-Dax”).

This prototype stimulus design has two important prop-
erties. First, the Daxes and non-Daxes were completely
tangled in the current stimulus space: No linear transfor-
mation of this parameter x, y space can make the catego-
ries linearly separable. Second, these stimuli are drawn
from a continuously and parametrically varying space,
which differs from previous fMRI studies of linearly insep-
arable category tasks (Mack, Preston, & Love, 2013). The
current methods of stimulus construction make it possible
to formulate explicit models of stimuli representations
and the corresponding pairwise similarity structure of
the stimulus parameters that can be compared against
the similarity structure of the neural representations.

We also varied the viewing angle of the stimuli, such
that several stimuli vastly different in pixel space were
in fact the same animal. Unlike previous studies (e.g.,
Reber et al., 1998), this critical experiment design feature

2344

Journal of Cognitive Neuroscience

Volume 32, Number 12

D
o
w
n
l
o
a
d
e
d

/
j

t
t

f
/

i
t
.

:
/
/

/
j

o
n

0
5

M
a
y

2
0
2
1

discrimination task where they had to determine whether the
animal was standing on a steep hill or not (the slant task). For
all the tasks performed in the scanner, the stimulus appeared on
the screen for 2 sec from the onset of each trial, and participants
had 3 sec to respond. During the Dax task, the participant saw a
picture of one of the animals and had to press one of the two
buttons to report whether it was a “Didoop Dax” or a “non-
Didoop Dax.” In the pitch discrimination task, participants were
asked, “Is the animal standing on a steep hill or not?”. The par-
ticipants were informed that they should respond solely based
on animals’ pitch angle and not their shape. Examples of the
stimuli shown at different pitch angles and orientations, along
with labels indicating which ones were to be classed as on a
steep hill or not, are shown in Figure 2. Before beginning the
pitch task, participants had two practice trials, one at the stee-
pest pitch and one at the shallowest pitch, which were repeated
until both were responded to correctly. The order of these
two tasks was counterbalanced across participants, whereas
the passive task always occurred first. In the pretraining scan-
ning session, participants were asked to categorize animals
without any knowledge about the category; they were
instructed to pay close attention to the animals and take their
best guess.

We wished to test whether participants could learn the
linearly inseparable boundary and generalize it to novel
animals, instead of merely learning individual associa-
tions between each animal shape and its category label.
To test for generalization, the stimuli that we presented
during the fMRI scanning sessions consisted not only of
animal shapes that had been shown during the behavioral
training sessions but also some novel stimuli drawn from
previously unsampled parts of the 2-D shape space.

Thus, the stimuli that the participants saw in the scan-
ning sessions were a variant of the stimuli that were used
during the behavioral training, forming an “X” in the x, y
space (Figure 1). Among these stimuli, four non-Dax stim-
uli (referred to as outer ring) were also shown to the par-
ticipants during the behavioral training sessions, and all
the other stimuli were shown only during the fMRI scans.
The fMRI-only stimuli were the prototype, four Dax stimuli
(inner ring) that were generated by rotating the four Dax
stimuli seen during training by 45° in the morph space,
and four intermediate stimuli (middle ring) that were equi-
distant from the Dax and non-Dax stimuli (on the category
boundary shown in Figure 1).

Jitters of 0, 2, and 4 sec were added after the response
phase ended. Each of these 13 animal shapes was shown four
times each for four runs, for 52 trials each per block and 208
trials in total, 16 per unique animal shape. Animal shape, ori-
entations, pitches, and trial order for the 208 trials were iden-
tical in all three tasks, for all participants and sessions.

Image Acquisition

Whole-brain images were acquired with a 3-T Siemens
MAGNETOM Trio scanner with a 32-channel head coil
located at the Rochester Center for Brain Imaging. At

the start of each participant’s scanning session, a high-
resolution structural T1 contrast image was acquired using
a magnetization-prepared rapid gradient-echo pulse se-
quence (repetition time = 2530, echo time = 3.44 msec,
flip angle = 7°, field of view = 256 mm, matrix = 256 ×
256, 1 × 1 × 1 mm sagittal left-to-right slices). An in-
terleaved EPI pulse sequence was used for T2* contrast
(repetition time = 2000 msec, echo time = 30 msec, flip
angle = 90°, field of view = 256 × 256 mm, matrix = 64 ×
64, 30 sagittal left-to-right slices, voxel size = 4 × 4 × 4 mm).
The first six volumes of each run were discarded to allow
for signal equilibration.

fMRI Data Preprocessing

Functional images were processed using SPM8. Prepro-
cessing stages included motion correction, slice time
correction, and spatial normalization. Beta estimates for
each voxel were obtained by fitting a general linear model
to the time series signal, where we convolved each stimulus
onset with a standard hemodynamic response function. As is
standard, the general linear model also included constant
term columns, one for each of the 12 runs, to allow it to
account for run-to-run variations in baseline BOLD signal.

Candidate Models and Construction of Model
Representational Dissimilarity Matrices

We constructed a high-level prototype distance model
and a low-level pose-only model to compare their effec-
tiveness in explaining neural representational dissimilar-
ity matrices (RDMs). The former aimed to capture the
task-relevant information between animals in the animal
morph space; its RDM was a 13 × 13 matrix, where each
entry was calculated as the difference in Euclidean dis-
tances between the animals and the center (e.g., two an-
imals on the same ring will have a zero in the RDM entry).
The latter aimed to capture the voxel activation responses
of early visual cortex for each viewing angle, and its RDM
was a 35 × 35 matrix (five orientations and seven pitch an-
gles). We first constructed a set of Gabor filter banks vary-
ing in four spatial scales (scaling factor = 1.7 and minimum
wavelength = 3) and six orientations (Field, 1987). For
each animal in each viewing angle, a 1444-dimensional
Gabor feature vector was computed by convolving the
image stimulus with the Gabor filter banks. Finally, the
pose-only model features were calculated by averaging
Gabor feature vectors for each viewing angle across dif-
ferent animals, and each entry in this model was calculated
as the Pearson correlation between the pose-only model
features of viewing angle pairs.

The prototype distance model contained all and only
information about the Dax versus non-Dax categoriza-
tion task, whereas the pose-only model pooled Gabor
features across animal shapes and were completely irrel-
evant to that task. Note that the dimension of the two
model RDMs are different, one is the number of different

Wu et al.

2345

D
o
w
n
l
o
a
d
e
d

/
j

f
/

t
t

i
t
.

:
/
/

/
j

o
n

0
5

M
a
y

2
0
2
1

animal shapes (13 × 13) and the other is the number of dif-
ferent viewing angles for each animal shape (35 × 35). In
theory, a 13 × 35 = 455-dimensional RDM matrix could
be constructed such that each dimension represents one an-
imal in one viewing angle. However, this number would ex-
ceed the total number of stimulus presentations, so it would
be impossible to make accurate fMRI activation estimates
to fill this RDM. Fortunately, our aim is not to compare the
fit of the 13 × 13 prototype distance model against the fit
of the 35 × 35 pose-only Gabor model, so there is no
need to model both factors simultaneously. Our main hy-
pothesis is to test how representations of animal shape
space change before and after training.

Finally, to investigate whether neural representations
are encoding pitch angle information, we constructed a
7 × 7 pitch model where each entry was calculated as
the pitch angle differences for each of the seven different
pitch angles.

Representational Similarity Analysis

The RDMs for the candidate models were described in the
preceding subsection. Here, we describe the construction of
the neural RDMs. We applied representational similarity anal-
ysis (RSA; Kriegeskorte, Mur, & Bandettini, 2008; Edelman,
Grill-Spector, Kushnir, & Malach, 1998) to each of the 48 bilat-
eral Harvard-Oxford Atlas (Desikan et al., 2006) ROIs. To cre-
ate the neural RDM for the prototype distance model, the
features of each animal was calculated by averaging the beta
values across trials of the same animal shape, and each entry
(i, j) in this RDM was calculated as 1 minus Pearson correla-
tion between features from animal i and animal j. The neural
RDM for the pose-only Gabor model was created in a similar
fashion, whereas features of each viewing angle were calculat-
ed by averaging beta values from trials with the same viewing
angle instead. Finally, the neural RDM for the pitch model was
similarly created by averaging beta values from trials with the
same pitch angle together. To investigate how well each
model fit the neural RDM, Kendall’s τa correlation is calcu-
lated between the entries in upper triangular part of mod-
el and neural RDM for each ROI in each participant.
Kendall’s τa correlation is selected because the two model
RDMs (described in previous section) contained multiple
ties (Nili et al., 2014). For each ROI, a Student’s t test was
applied on the Fisher Z-transformed correlation values
across participants. p Values across all 48 bilateral ROIs
and two scanning sessions were corrected with false dis-
covery rate (FDR; Benjamini & Hochberg, 1995).

Visualizing Representation Using
Multidimensional Scaling

To visualize the representational organization of animal
shapes in each ROI, we applied classical metric multi-
dimensional scaling (MDS; Torgerson, 1952) to the group
average RDM.2 After a double-centering operation, we

decomposed the group average RDM (termed Savg here)
into eigenvectors and eigenvalues:

Savg ¼ VDV T ; where V T V ¼ I

(1)

The low-dimensional coordinates of each animal shape
can then be computed by

Pavg ¼ VD

2 ¼ Savg (cid:2) VD−1

D
o
w
n
l
o
a
d
e
d

(2)

/
j

t
t

f
/

i
t
.

:
/
/

/
j

o
n

0
5

M
a
y

2
0
2
1

To compute confidence intervals for each animal shape,
we generated 500 group average RDMs by bootstrap re-
sampling participants with replacement and calculated
their coordinates as

Pbootstap;avg ¼ VD

2 ¼ Sbootsrap;avg (cid:2) VD−1

(3)

We visualized the bootstrap sample coordinates by fitting
a 2-D ellipse that contains 95% of the points (details are
described in the Appendix of Abdi, Dunlop, & Williams,
2009).

Previous studies have applied the DISTATIS algorithm
(Abdi et al., 2009) to the RDMs of individual participants.
Instead of calculating the group average RDM, DISTATIS
calculates a weight for each participant based on the sim-
ilarities between individual participant’s RDM and out-
puts a compromise matrix, which weights and averages
each participant’s RDM accordingly. We obtained qual-
itatively similar figures by applying this algorithm, so to
save space in the present paper we show only the figures
that were generated by applying MDS to group average
RDMs.

Cross-task Linear SVM Classifier

During the categorization task, participants pressed the
same button to indicate animal categories. To identify brain
regions that were sensitive to button responses but not cat-
egory information, for each ROI in each participant we
trained a linear SVM classifier (MATLAB fitcsvm function)
in one task to distinguish between Button 1 and Button 2
presses and tested it on another task. A Student’s t test was
performed on the accuracy for each ROI to determine
whether the accuracy was higher than 0.5. Cross-task SVM
classifier was applied here instead of RSA because there
were only two conditions (Button 1 and Button 2 presses),
and the resulting dissimilarity matrix would only contain
one unique correlation value.

2346

Journal of Cognitive Neuroscience

Volume 32, Number 12

RESULTS

Participants Successfully Learned the Linearly
Inseparable Category Boundary

We trained participants to categorize novel animals with
various orientations and pitches as “Dax” or “non-Dax.”
The task was fairly challenging, in large part due to the
fact that the different presentations of each animal
spanned a wide range of different viewing angles. To learn
which animals were Dax or non-Dax, the participants
needed to categorize the intrinsic shape of each animal,
abstracted away from the viewing angle that it happened
to be seen from.

The challenging nature of the task can be seen from
the fact that, over the course of training, the participants’
performance did not reach plateau even after 4 days of
training. However, the 92% mean accuracy in the final
training session shows that participants did indeed suc-
ceed at learning the task.

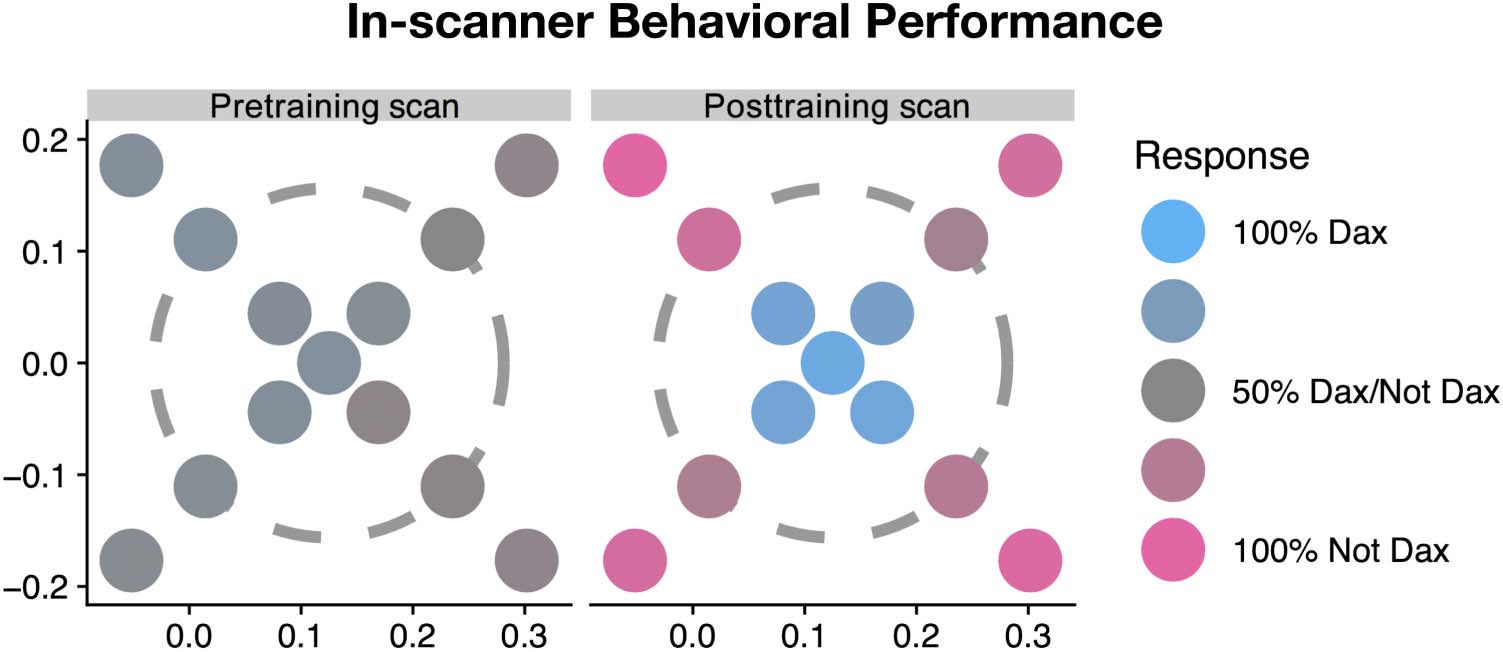
After behavioral training, participants performed a
similar Dax categorization task in the scanner without
feedback. For statistical tests of whether the participants
categorized particular stimuli as Dax or non-Dax, the
proportion of category label responses for each animal
stimulus were calculated for each of the 15 participants,
and then those 15 values were subjected to a group-
level random effects t test against the chance level of
50%. Four outer ring animals were classified as non-
Dax (t(14) = 37, p < 1e−14, 95% non-Dax responses averaged across animals and participants, chance = 50%), whereas the novel inner ring (t(14) = 9.5, p < 1e−7) and prototype animals (t(14) = 10.9, p < 1e−7) are classified as Dax (Figure 3). Furthermore, proportion of Dax responses was significantly higher for prototype than that for inner ring animals (t(14) = 4.56, p< .001); this prototype effect corroborated with previous studies (Knowlton & Squire, 1993). Overall, this suggested that participants accurately learned the linearly inseparable category boundary and were able to generalize it on novel animals. Representational Distances in Intraparietal Sulcus and Inferior Frontal Gyrus Were Ranked According to Distances to Prototype If participants could indeed learn the linearly inseparable category boundary, then how did their brains manage to untangle this category information from complex and linearly inseparable low-level visual representations? Ac- cording to prototype theory (Cutzu & Edelman, 1998; Posner & Keele, 1968), novel stimuli were assigned to the category with the closest prototype. We therefore constructed a prototype distance model where the dis- similarity between each animal pair was calculated as their Euclidean distance differences between the proto- type animal in the morph space. 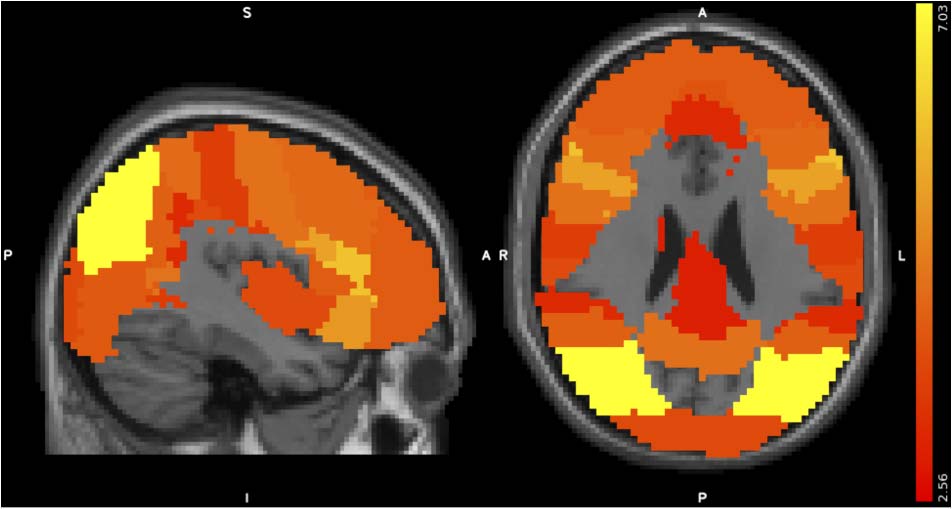We then correlated this model RDM with that of all bilateral Harvard-Oxford ROIs using RSA. Twenty-five of 48 Harvard-Oxford Atlas regions were significantly correlated with prototype distance model when participants were performing the Dax clas- sification task after behavioral training (t > 2.56, FDR-
corrected across all ROIs and pre/post sessions); no ROIs
are significantly correlated with the model before training
(Figure 4). Among these regions, intraparietal sulcus3 and
inferior frontal gyrus had the highest t values. This was
consistent with previous studies demonstrating that in-
traparietal and frontal areas were differentially activated
during visual category learning tasks (Seger et al., 2000).
Although the participants were performing the Dax
categorization task in the scanner, they pressed one of
two buttons to indicate which category they judged each
stimulus to be. When interpreting the resulting fMRI ac-
tivation, we must therefore be careful to distinguish be-
tween genuinely categorization-related activation and
purely motor-related activation. The very design of the
task can make these two types of activation difficult to
pull apart, as every categorization decision is accom-
panied by its corresponding button press. Fortunately, our
experimental design avoids this problem, as the internal
state of the participants before training as opposed to after
training are very different. Specifically, in the pretraining

D
o
w
n
l
o
a
d
e
d

/
j

f
/

t
t

i
t
.

:
/
/

/
j

Figure 3. Group-averaged
proportion of Dax responses
during the category
discrimination task performed
in the MRI scanner. Left:
pretraining scans. Right:
posttraining scans.

o
n

0
5

M
a
y

2
0
2
1

Wu et al.

2347

ROI with significant above-chance accuracy was the post-
central gyrus (somatosensory cortex), and even that region
fails to reach significance after correcting for multiple com-
parisons (t(14) = 2.46, p < .04 uncorrected, p = .97 cor- rected). Although it is not unexpected to find that somatosensory cortex contained button press information, it is nonetheless reassuring to see that such information was present only in sensorimotor areas. In contrast, the frontal and parietal areas that our RSAs found to contain in- formation about the structure of the Dax category did not show significant results in this button press cross-decoding task (inferior frontal gyrus ROI: t(14) = −1.48, p > .9 un-
corrected; intraparietal sulcus: t(14) = −2.24, p > .95 un-
corrected), suggesting that the information that they
encoded did indeed reflect the Dax category structure, rath-
er than merely the button presses that the participants used
for giving their responses while performing the categoriza-
tion task. Moreover, the fact that the button press cross-
decoding performed somewhat worse than chance in those
frontal and parietal regions suggests that their neural in-
formation content had changed markedly between the
pretraining and posttraining scans, even though the partici-
pants were engaging in the same sorts of button presses in
both cases. This is precisely what would be expected if, as
we suggest, those regions encoded Dax category informa-
tion in a manner that was distinct from merely encoding
button press responses.

A common finding in cross-decoding analyses is that
the results are different, depending on which condition
is used for training the classifier and which for testing.
Specifically, if the two different conditions differ in how
noisy they are, the cross-decoding classifiers typically
perform best when trained on the less noisy condition
(Kaplan et al., 2015). Our present analyses also follow
this pattern. The results described in the preceding par-
agraph were obtained when training the SVM on the
post-behavioral training fMRI scans, during which the
participants were successfully able to perform the Dax
category task. During the pre-behavioral training fMRI
scans, the participants had to try to perform the Dax
task even though they had not yet had an opportunity
to learn which animals were Daxes and which were not.
It is therefore to be expected that their neural responses
during this scan would be noisy and highly variable and
that training an SVM on this pre-behavioral training fMRI
data would yield little cross-decoding transfer when tested
on the post-behavioral training scans. This is indeed what
we found. When the SVM was trained on the pretraining
scans and tested on the posttraining scans, no regions
reached statistical significance, even without any multiple
comparison correction.

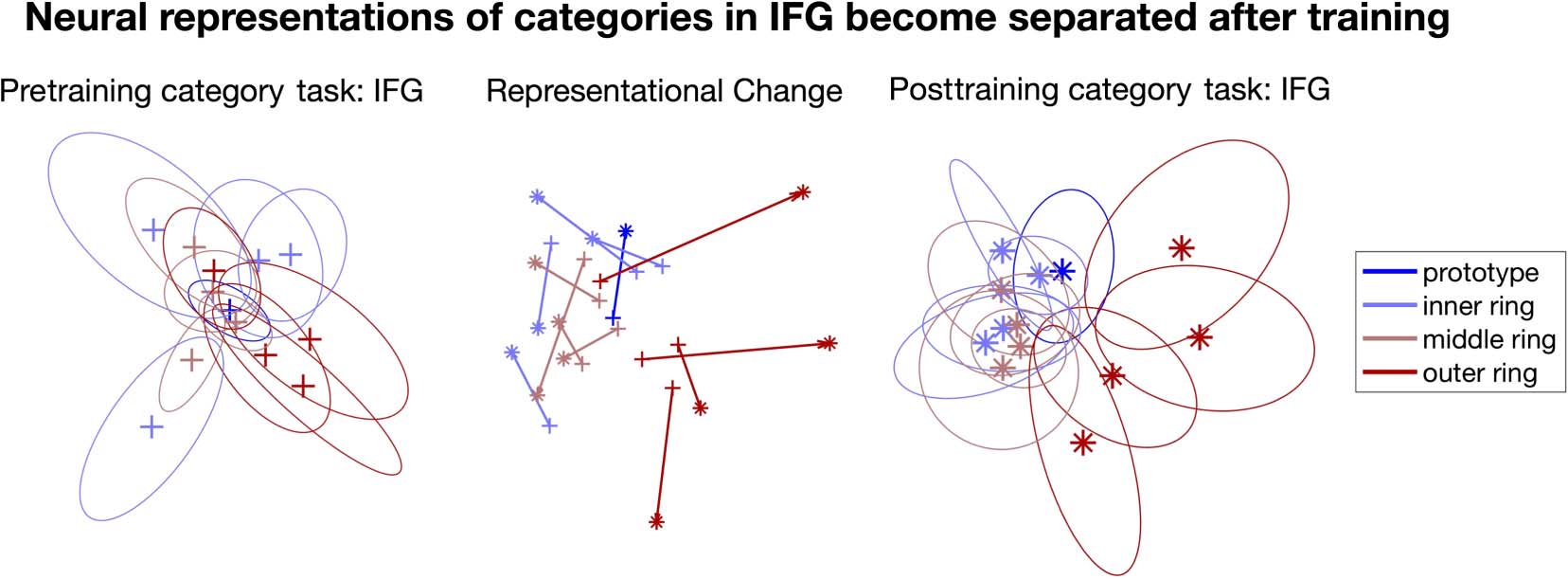
To visualize how the representational structure chang-
es after behavioral training, we applied MDS on inferior
frontal gyrus. Qualitatively, the outer ring animals was
clearly separated from other stimuli after behavioral train-
ing (Figure 5, right), but not before training (Figure 5,
left).

Figure 4. t Value maps for Kendall’s τa correlation between RDMs of
the prototype distance model and the activation patterns within each
ROI (collected during the categorization task, in the post-behavioral
training MRI scan). The t value of t = 2.56 corresponds to an
FDR-corrected p value of .05.

fMRI scan, the participants were pressing Dax and non-Dax
buttons, using the same buttons as they would later use in
the posttraining fMRI scan. However, before behavioral
training, they do not yet have any category structure infor-
mation encoded in their brains. Thus, during this pretrain-
ing scan, their motoric and category-related activations were
dissociated.

Therefore, to distinguish between motor output and
Dax category neural information, we performed a cross-
decoding analysis (see, e.g., Kaplan, Man, & Greening,
2015, for a review; note that we used a classifier cross-
decoding analysis instead of similarity-based analysis be-
cause there were only two button press categories, and
similarity matrices made from only two conditions are un-
informative because they contain only one unique off-
diagonal data point). Specifically, we trained a linear
SVM classifier to distinguish between fMRI data elicited
by the two different button press responses during the
posttraining Dax task and tested that same trained SVM
on fMRI data from the pretraining Dax task. Following
the logic laid out above, the rationale is as follows: If the
SVM succeeds in classifying pre-behavioral training fMRI
test data from a given brain area, then the activation in
that area must be representing motor output button press
responses rather than actual Dax category information,
because the pretraining fMRI data cannot contain any
Dax category information, due to the participants not
yet knowing what the Dax category is. In contrast, if the
SVM fails to classify the pre-behavioral training fMRI test
data, then the information that the SVM had extracted
from its post-behavioral training Dax task fMRI data must
have been about the Dax category itself.

We carried out precisely this test, training the SVM
with Matlab’s built-in fitcsvm function. The classifier’s de-
coding performance was calculated for each participant
in each ROI, and the average of the participants’ accu-
racies was tested against the 50% chance-level using a
t test, in the standard manner. We found that the only

2348

Journal of Cognitive Neuroscience

Volume 32, Number 12

D
o
w
n
l
o
a
d
e
d

/
j

t
t

f
/

i
t
.

:
/
/

/
j

o
n

0
5

M
a
y

2
0
2
1

Figure 5. Left and right: MDS plot of inferior frontal gyrus during Dax discrimination task before (left) and after (right) the behavioral training. It can
be seen that the outer ring of animals (shown in saturated red) became markedly separated from the others after behavioral training. Middle:
Representational change of each animal shape, showing the pre- versus posttraining differences in MDS position. Note that the coordinates in the left
figure were aligned to the right one via Procrustes analysis.

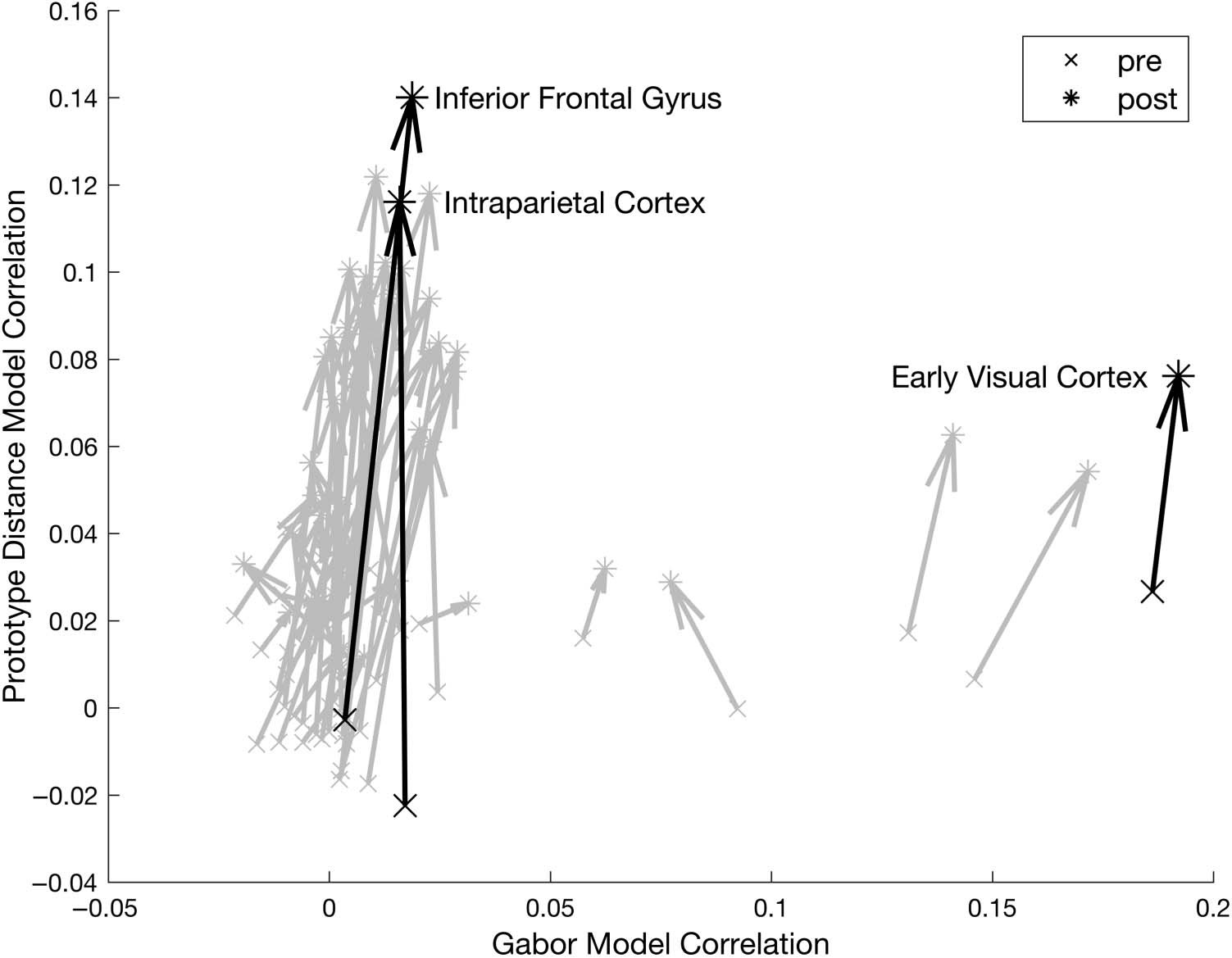
As a comparison, we also performed RSA with the
pose-only model, that captured low-level visual model
features like pitch and orientation (averaged across all an-
imal shapes) to see whether there were low-level brain
representation changes before and after behavioral train-
ing. Confirming that the pose model reflects low-level vi-
sual processing, in both fMRI sessions, the correlations
with the pose model were significant in early visual cor-
tices only. Moreover, we find no differences in the fit of
the pose model for pre- and posttraining, indicating that
there is no effect of categorization training on low-level
visual cortex representations (Figure 6). Overall, this

suggested that widespread representational change was
only observed in the task-relevant shape dimension,
not the irrelevant viewing angle one.

Previous studies (Mack et al., 2016) had demonstrated
that hippocampus representations can adapt and reflect
learned category structure of the current task. However,
in our study, the hippocampus RDM (extracted with
Harvard-Oxford subcortical atlas) was not significantly
correlated with our prototype distance model. A search-
light analysis with spherical radius of three voxels also
vealed no such clusters around previously reported MNI
coordinates. Future studies with higher voxel precision

Figure 6. RSA correlation with
the task-irrelevant Gabor filter
model and the task-relevant
prototype distance model.
Each arrow shows an ROI’s
representational change elicited
by behavioral training. Some
named ROIs of particular
interest are highlighted in black.

D
o
w
n
l
o
a
d
e
d

/
j

f
/

t
t

i
t
.

:
/
/

/
j

o
n

0
5

M
a
y

2
0
2
1

Wu et al.

2349

and a better hippocampus mask are needed to test
whether the medial-temporal lobe regions can represent
category structure in a similar manner as the cortical
regions reported here.

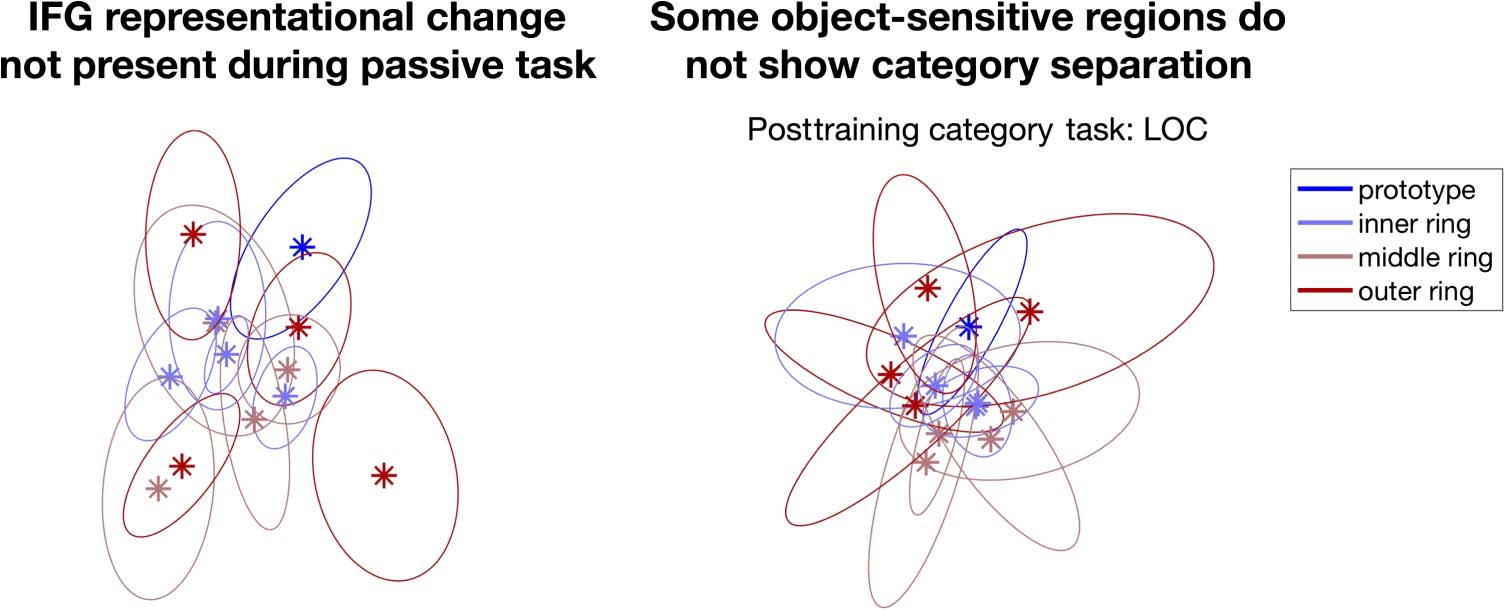
Representational Change Is Task Dependent

Was the representational change widespread across the
brain observed only when participants were performing
the Dax categorization task? In other words, was atten-
tion on the task-relevant dimension necessary to sepa-
rate Dax and non-Dax animals? To test this hypothesis,
we applied the same RSA pipeline on beta activation
images while participants were performing the passive
viewing and pitch discrimination task. None of the ROIs
were significantly correlated with the prototype distance
model in either task (Figure 7). This suggested that un-
tangling of linearly inseparable category information
might be an attentional or decisional effect, rather than
a task-independent retuning of low-level visual cortex
representations.

Task-dependent Dynamic Switching between
Different Representations in Multiple Frontal
and Parietal Regions

Recent studies have shown that dorsal pathway regions
dynamically switch between different representations de-
pending on the current task, with neural representational
structures reconfiguring themselves to more strongly
represent the information relevant to the task that is
being performed at the time (Bracci, Daniels, & Op de
Beeck, 2017; Vaziri-Pashkam & Xu, 2017). Although the
primary question of interest in this study was to investi-
gate training-induced representational changes in the
Dax task, the fact that our participants also performed a
slant discrimination task provides us with an opportunity
to ask whether our data also show this task-dependent
representational switching effect.

To test this, we created a 7 × 7 pitch angle model
where each entry in this RDM represents the difference

between pitch angles. To construct the neural RDM for
each ROI, for each animal pitch angle, we averaged the
activation patterns across viewpoints and animal shapes.
We then correlated this model RDM with that of all bilat-
eral Harvard-Oxford ROIs using RSA to see how these
model correlations changed depending on which task
the participants were performing. Specifically, for each
participant and each ROI, we carried out a paired t test,
comparing the Fisher z-transformed pitch task and Dax
task correlations across different task conditions. This
comparison was performed only for the posttraining
scans, because the categorization task model fit was triv-
ially poor during the pretraining scans simply because the
participants had not yet learned how to perform that task.
Dynamic task-dependent representational switching
would manifest itself as the pitch model fitting better
while the participants were performing the pitch task
and the prototype distance model fitting better during
the Dax task. We found precisely this effect in several
multiple frontal and parietal regions (t > 3.084, paired t
test, FDR-corrected across all ROIs). The intersection of
these regions (Table 2) and those containing category-
relevant representational changes (Table 1) were as fol-
lows: middle frontal gyrus, inferior frontal gyrus, superior
parietal lobe, posterior supramarginal gyrus, and intra-
parietal sulcus.

Existing Theories of How Category Learning Affects
Dimensions of the Stimulus Space and Their
Relations to Our Current Findings

In this study, we investigated how learning a categoriza-
tion task resulted in the transformation of a stimulus
space. This question has previously been explored by
classical theories of category learning, most notably the
generalized context model (Nosofsky, 1986). That model
predicted that categorization training should induce an
expansion of category-relevant dimensions. Augmented
with the dimensional modulation theory (Goldstone,
1994), the theories also predicted that such expansion
might be greater across category boundaries than within

Figure 7. Left: MDS plot of the
inferior frontal gyrus during the
passive viewing task after
behavioral training. Right: MDS
plot of the lateral occipital
complex during the Dax
discrimination task after
behavioral training. In contrast
to the category separation that
was shown in Figure 5, the plots
here show no category
separation.

2350

Journal of Cognitive Neuroscience

Volume 32, Number 12

D
o
w
n
l
o
a
d
e
d

/
j

t
t

f
/

i
t
.

:
/
/

/
j

o
n

0
5

M
a
y

2
0
2
1

Table 1. Harvard-Oxford Atlas Regions Significantly Correlating
with the Prototype Distance Model during the Categorization
Task in the Posttraining Session

Table 2. Harvard-Oxford Atlas Regions Significantly Correlating
with the Pitch Model More during the Pitch Task than
Categorization Task in the Posttraining Session

t Values
(dof = 14)

Corrected
p Values

Regions

t Values
(dof = 14)

Corrected
p Values

Regions

Frontal pole

Insular cortex

Superior frontal gyrus

Middle frontal gyrus

Inferior frontal gyrus,
pars triangularis

Inferior frontal gyrus,
pars opercularis

Precentral gyrus

Middle temporal gyrus,
anterior division

Middle temporal gyrus,
posterior division

Middle temporal gyrus,
temporooccipital part

Inferior temporal gyrus,
temporooccipital part

Postcentral gyrus

Superior parietal lobule

Supramarginal gyrus,
anterior division

Supramarginal gyrus,
posterior division

Angular gyrus

Intraparietal sulcus

Lateral occipital cortex,

inferior division

Paracingulate gyrus

Cingulate gyrus,

posterior division

Precuneous cortex

Frontal orbital cortex

Occipital fusiform gyrus

Frontal operculum

cortex

Occipital pole

4.177

3.868

4.019

4.384

6.008

5.426

4.563

2.980

3.248

4.581

3.566

3.619

4.451

3.863

3.243

4.231

7.031

4.119

3.204

3.004

4.553

5.229

2.780

4.193

3.844

.004

.005

.004

.003

.001

.003

.020

.013

.003

.008

.007

.003

.005

.013

.004

<.001 .004 .014 .020 .003 .002 .028 .004 .005 The regions showing the statistically strongest effects are highlighted in bold font. categories, leading to a classical categorical perception ef- fect. Some compelling examples of such effects were found by Folstein and colleagues (e.g., Folstein et al., 2013), who found behavioral and fMRI evidence of dimensional D o w n l o a d e d l l / / / / j f / t t i t . : / / f r o m D o h w t t n p o : a / d / e m d i f r t o p m r c h . s p i l d v i r e e r c t c . m h a i e r d . u c o o m c n / j a o r t c i c n e / - a p r d t i 3 c 2 l 1 e 2 - 2 p 3 d 4 f 2 / 2 3 0 2 1 / 4 1 1 2 4 / 2 2 3 o 4 c 2 n _ / a 1 _ 8 0 6 1 2 5 2 3 2 3 3 p / d j o b c y n g _ u a e _ s 0 t 1 o 5 n 3 0 3 7 . S p d e f p e b m y b e g r u 2 e 0 s 2 t 3 / j t . / f o n 0 5 M a y 2 0 2 1 Middle frontal gyrus Inferior frontal gyrus, pars triangularis Precentral gyrus Superior parietal lobule Supramarginal gyrus, posterior division Lateral occipital cortex, superior division Supracalcarine cortex 3.808 3.587 3.084 4.835 3.320 3.940 3.249 .015 .018 .028 .006 .023 .015 .023 modulation: an expansion of stimulus space across the cat- egory boundary, along the task-relevant dimension. In contrast, this study investigated a different hypothe- sis: In our prototype task design, a computationally efficient way to transform the linearly inseparable space into a separable one would be to represent all stimuli in terms only of their distance from the central prototype Dax animal. In such a transformation, which would be analogous to how kernel algorithms in machine learning can solve this sort of task, the stimulus space would not be radically warped. Recall that the animals were arranged in concentric rings around the center of the stimulus space, as shown in Figure 1. If the distance-from-the-center trans- formation were applied to this space, then all the animals within a given ring would become more similar to each other, even if they started off on opposite sides of the stim- ulus space. It would be as if the space started off like a stretched out Chinese fan, which then gets transformed by being folded back into a narrow strip. In contrast, dimen- sional expansion could stretch or compress the circular rings into ovals, but diametrically opposite sides of the stim- ulus space would always remain opposite to each other. As Figure 6 shows, almost all brain areas showed an increased fit with this prototype distance model after train- ing, compared with before. Some areas, most notably the inferior frontal gyrus and intraparietal cortex, showed very marked increases in fit. Nonetheless, the prototype model was far from capturing everything in the data. As the MDS plots in Figure 5 of neural representational space in the inferior frontal gyrus show, the stimuli in the outermost ring did indeed move further away from the central proto- type after training, and to some extent the outer ring stim- uli may even have slightly bunched together. However, if the representations had perfectly matched the prototype model’s predictions, then all of these outer ring stimuli would have collapsed together into a single point (and, Wu et al. 2351 moreover, the stimuli on the other rings would have col- lapsed together to their own separate points too). Clearly, no such collapse took place. So, although the de- gree of fit of the prototype model increased markedly from pre- to posttraining, it remained a very incomplete description of how the neural representational space ac- tually behaved. Although the inferior frontal gyrus exhibited the non- linear warping illustrated in Figure 5, this does not rule out the possibility that other brain regions might have shown more classical dimensional modulation effects. In our 2-D stimulus space, all of the stimulus dimensions were relevant, so the prediction of the generalized con- text model would be of an expansion in all directions. Our RSA methods would be unable to reveal a uniform expansion of this sort, as any uniform scaling leaves the relative similarities between different stimuli unchanged. To rectify this problem, we carried out an exploratory analysis, suggested by a reviewer, to examine (1) whether categorization training resulted in an overall expansion of our stimulus space and (2) whether categorization train- ing differentially expanded representational distances across the category boundary more the within the boundary. In short, we did not find statistically significant evi- dence for uniform expansion of this sort. That is not to say that such expansion was entirely absent: Several ROIs, listed below, did indeed show weak evidence of ex- pansion. However, as with all of the tests involving the 48 Harvard-Oxford ROIs in this study, multiple comparisons correction (using FDR) was carried out. After applying this correction, none of the ROIs survived as significantly showing the expansion effect. The details of this additional analysis were as follows: for each ROI and each participant, we extracted distance entries from the 13 × 13 animal shape neural RDM. Entries were grouped by whether (1) both animals were inner ring animals (inner–inner), (2) both animals were non-Daxes (outer–outer), and (3) one animal was Dax and the other was not (inner–outer). A two-way ANOVA was performed on the averaged entries in each of the 48 ROIs, where one factor was whether two animals were within or between the categories, and the other factor was before/after behavioral training. Even without multi- ple correction for the 48 ROIs, we found no main effect of animal category on representational distances in any ROI. Before multiple correction, a main effect of training on representational distances was observed in the frontal pole, frontal medial cortex, frontal orbital cortex, frontal operculum cortex, anterior middle temporal gyrus, and inferior temporal gyrus. We found no significant inter- action effect between animal category and training on rep- resentational distances, and no effects were significant in the Tukey post hoc tests between pairs of animal category relations. In summary, this additional analysis did not definitively rule out the hypothesis that representational space was expanded in all directions. Indeed, some regions showed a weak tendency toward this, but not, in our data at least, to a degree that reached statistical significance. Similarly, we did not find significant evidence that representational distances were expanded more across the category bound- ary compared to within each category. Although these results might at first sight seem inconsistent with the di- mensional modulation theory, we believe that they are not so much inconsistent as simply inconclusive, for this particular question. Our stimuli and task were not de- signed to test for dimensional modulation of this sort, and indeed, a study that seeks to be a sensitive probe of such questions would probably end up being structured very differently. The question of how dimensional modu- lation, that is, expansion along task-relevant dimensions, might relate to more nonlinear warping of stimulus space is an interesting one and seems likely to be a fruitful area of investigation for future work. DISCUSSION In this study, we examined how learning a linearly insep- arable category boundary affected neural representations across the brain. Our results suggested several findings. First, we found that after participants successfully learned this category boundary, the representations of Dax and non-Dax animals became linearly separated in a low- dimensional space. Second, this separation reflected a task-dependent attentional mechanism; it was only pres- ent when participants were performing the Dax categori- zation task and appeared most prominently in regions like the inferior frontal gyrus and the intraparietal sulcus. Previous fMRI studies suggested that learning-dependent changes during visual category learning paradigms can be observed in parietal cortex (Hebart, Schriever, Donner, & Haynes, 2016; Mack et al., 2013; Hebart, Donner, & Haynes, 2012; Freedman & Assad, 2006) and pFC (Hebart et al., 2012, 2016; Jiang et al., 2007). Furthermore, it was hypothesized that these regions in the frontoparietal network represented abstract category or rule information independent of motor responses (Hebart et al., 2012) and stimulus types. Our results further suggest that linearly inseparable category boundaries could also be represented in similar frontoparietal network regions. Recently, increasing evidence demonstrated that object representations were present in both the ventral and dor- sal visual pathways (Bracci et al., 2017; Vaziri-Pashkam & Xu, 2017; Jeong & Xu, 2016; Li, Mayhew, & Kourtzi, 2009; Konen & Kastner, 2008). It was hypothesized that, although visual representations in ventral pathway were largely task independent, those in dorsal pathway were shaped by the current task to reflect the most diagnostic feature dimension (Bracci et al., 2017; Vaziri-Pashkam & Xu, 2017). The current study offers additional evidence that the posterior parietal cortex represents linearly insep- arable category information only when this information is task relevant. 2352 Journal of Cognitive Neuroscience Volume 32, Number 12 D o w n l o a d e d l l / / / / j t t f / i t . : / / f r o m D o h w t t n p o : a / d / e m d i f r t o p m r c h . s p i l d v i r e e r c t c . m h a i e r d . u c o o m c n / j a o r t c i c n e / - a p r d t i 3 c 2 l 1 e 2 - 2 p 3 d 4 f 2 / 2 3 0 2 1 / 4 1 1 2 4 / 2 2 3 o 4 c 2 n _ / a 1 _ 8 0 6 1 2 5 2 3 2 3 3 p / d j o b c y n g _ u a e _ s 0 t 1 o 5 n 3 0 3 7 . S p d e f p e b m y b e g r u 2 e 0 s 2 t 3 / j / t f . o n 0 5 M a y 2 0 2 1 Previous studies have hypothesized that whether rep- resentational changes in visual cortices were task- independent (i.e., persisted in passive viewing tasks) de- pended on how the stimulus morph space was formed (Folstein, Palmeri, Van Gulick, & Gauthier, 2015; Folstein et al., 2012). Accord- ing to that hypothesis, complex stim- uli generated from a factorial space (select an origin and two orthogonal axes and generate the stimuli by picking [x, y] values on this plane) should yield task-independent representational changes in ventral visual pathway re- gions. Although the stimuli used in the current study were also generated factorially, we did not observe significant representational changes in all ROIs during the passive viewing and pitch discrimination task. This difference might be due to our usage of a linearly inseparable cate- gory boundary, as opposed to the separable boundary used by Folstein and colleagues. Furthermore, these pre- vious studies used fMRI rapid adaptation paradigms to demonstrate these modulation effects (Folstein et al., 2013; Jiang et al., 2007), so future studies are needed to investigate whether or not experimental paradigm differ- ences also played an interactive role in it. Two initial motivations for the prototype design of this study were as follows: First, this type of linearly insepara- ble task structure is simpler and perhaps more ecologi- cally valid than the XOR task that is often thought of as the canonically inseparable task. Second, studies using non- linear kernels in machine learning (Schölkopf, Smola, & Bach, 2002) have used a similar task structure to demonstrate how a transformation of stimulus space can turn a linearly inseparable task into a separable one. The fact that we observed similar transformations in the posttraining neural representational spaces does not, of course, imply that the brain actually implements this sort of kernel algorithm. However, both the machine learning work and our neural data suggest that transform- ing an inseparable stimulus space into a linearly insepara- ble form is a computationally useful step for a system to take. The question of how the brain implements this step at the level of neural circuits remains unaddressed and could be a fruitful area for future work. Another advantage of the prototype structure over the XOR task is that it could potentially be better suited for future studies of internal cat- egory structure, a topic that is somewhat underinvestigated. Previous studies (Nosofsky, 1986) have suggested that categorization training can expand category-relevant di- mensions. Because all dimensions in our stimulus space were relevant to the categorization task, the generalized context model would predict an overall expansion in our stimulus space. However, the prototype category struc- ture of our stimulus space would not be learnable simply by expanding the overall space, as no such expansion would be able to move the inner “island” of Dax animals outside its enclosing ring of non-Dax animals. Instead, some sort of nonlinear transformation is required, and the kernel transformation mentioned in the previous par- agraph can be a plausible mechanism. Clearly, this study involves the learning of only one task, so from this study alone, it is impossible to know whether these findings will generalize to the learning of other computationally challenging tasks that require the transformation of stimulus space. We do not see any rea- son why the particular task and stimuli here should be nonrepresentative, but only further studies can tell. In summary, our study investigated how the neural representation of a stimulus space becomes reshaped by the learning of a task. Specifically, we investigated a task with a linearly inseparable prototype structure, going beyond the linearly separable tasks that have typically been used in previous studies. By visualizing neural representational structure with MDS, we found that some regions (notably, the inferior frontal gyrus and the in- traparietal sulcus) showed a marked untangling of the categories’ neural patterns that made them more linearly separable after behavioral training. However, these neu- ral changes did not appear to reflect permanent changes in representation but instead were dynamically task de- pendent, being observed only while participants were performing the categorization task, but not during pas- sive viewing. The task-dependent nature of these chang- es, together with the fact that they were found to occur in frontal and parietal areas rather than ventral temporal cortices, suggests that they reflected attentional and de- cisional reweighting, rather than changes in object recog- nition templates. Although classical theories of category learning (Nosofsky, 1986) did a good job of explaining how linearly separable tasks might be learned, they were less able to account for linearly inseparable tasks such as the one used in this study. Our results provide new in- sights into the nonlinear warping of neural representation- al space and how the brain uses such transformations to solve computationally challenging tasks. Reprint requests should be sent to Meng-Huan Wu, University of Rochester, 500 Joseph C. Wilson Blvd., Rochester, NY 14627-0001, or via e-mail: menghuanwu@rochester.edu; mhjasonwu@gmail.com. Notes 1. The picture increased participants’ task engagement over multiple days of training. 2. Pearson correlations were used to calculate fMRI RDMs, so we were aware that this violated classical MDS’s assumption of Euclidean distance matrix. However, because all eigenvalues we obtained were positive and this was used mainly as a visual- ization technique, we left the development of rigorous resam- pling and projection techniques for future work. 3. Throughout the paper, we used the term “intraparietal sul- cus” instead of the name that happens to be used in the text files that accompany the Harvard-Oxford atlas downloads, which is “lateral occipital cortex, superior division.” This is because this ROI is indeed in the parietal cortex, so in referring to it as the intraparietal sulcus we thereby avoid creating any unnecessary confusion. Moreover, recent papers in the goal-relevant visual Wu et al. 2353 D o w n l o a d e d l l / / / / j f / t t i t . : / / f r o m D o h w t t n p o : a / d / e m d i f r t o p m r c h . s p i l d v i r e e r c t c . m h a i e r d . u c o o m c n / j a o r t c i c n e / - a p r d t i 3 c 2 l 1 e 2 - 2 p 3 d 4 f 2 / 2 3 0 2 1 / 4 1 1 2 4 / 2 2 3 o 4 c 2 n _ / a 1 _ 8 0 6 1 2 5 2 3 2 3 3 p / d j o b c y n g _ u a e _ s 0 t 1 o 5 n 3 0 3 7 . S p d e f p e b m y b e g r u 2 e 0 s 2 t 3 / j f / t . o n 0 5 M a y 2 0 2 1 processing literature that discuss the intraparietal sulcus provide coordinates for that region that fall into this Harvard-Oxford ROI (Henderson & Serences, 2019; Swisher, Halko, Merabet, McMains, & Somers, 2007). REFERENCES Abdi, H., Dunlop, J. P., & Williams, L. J. (2009). How to compute reliability estimates and display confidence and tolerance intervals for pattern classifiers using the Bootstrap and 3-way multidimensional scaling (DISTATIS). Neuroimage, 45, 89–95. DOI: https://doi.org/10.1016/j.neuroimage.2008.11.008, PMID: 19084072 Benjamini, Y., & Hochberg, Y. (1995). Controlling the false discovery rate: A practical and powerful approach to multiple testing. Journal of the Royal Statistical Society: Series B: Methodological, 57, 289–300. DOI: https://doi.org/10.1111/ j.2517-6161.1995.tb02031.x Bracci, S., Daniels, N., & Op de Beeck, H. (2017). Task context overrules object- and category-related representational content in the human parietal cortex. Cerebral Cortex, 27, 310–321. DOI: https://doi.org/10.1093/cercor/bhw419, PMID: 28108492, PMCID: PMC5939221 Braunlich, K., Liu, Z., & Seger, C. A. (2017). Occipitotemporal category representations are sensitive to abstract category boundaries defined by generalization demands. Journal of Neuroscience, 37, 7631–7642. DOI: https://doi.org/10.1523/ JNEUROSCI.3825-16.2017, PMID: 28674173, PMCID: PMC6596645 Cutzu, F., & Edelman, S. (1998). Representation of object similarity in human vision: Psychophysics and a computational model. Vision Research, 38, 2229–2257. DOI: https://doi.org/ 10.1016/S0042-6989(97)00186-7 Desikan, R. S., Ségonne, F., Fischl, B., Quinn, B. T., Dickerson, B. C., Blacker, D., et al. (2006). An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. Neuroimage, 31, 968–980. DOI: https://doi.org/10.1016/j.neuroimage.2006. 01.021, PMID: 16530430 DiCarlo, J. J., & Cox, D. D. (2007). Untangling invariant object recognition. Trends in Cognitive Sciences, 11, 333–341. DOI: https://doi.org/10.1016/j.tics.2007.06.010, PMID: 17631409 Edelman, S., Bülthoff, H. H., & Bülthoff, I. (1999). Effects of parametric manipulation of inter-stimulus similarity on 3D object recognition. Spatial Vision, 12, 107–123. DOI: https://doi.org/10.1163/156856899X00067, PMID: 10195391 Edelman, S., Grill-Spector, K., Kushnir, T., & Malach, R. (1998). Toward direct visualization of the internal shape representation space by fMRI. Psychobiology, 26, 309–321. Field, D. J. (1987). Relations between the statistics of natural images and the response properties of cortical cells. Journal of the Optical Society of America A, 4, 2379–2394. DOI: https://doi.org/10.1364/JOSAA.4.002379, PMID: 3430225 Folstein, J. R., Gauthier, I., & Palmeri, T. J. (2012). How category learning affects object representations: Not all morphspaces stretch alike. Journal of Experimental Psychology: Learning, Memory, and Cognition, 38, 807–820. DOI: https://doi.org/ 10.1037/a0025836, PMID: 22746950, PMCID: PMC3390763 Folstein, J. R., Palmeri, T. J., & Gauthier, I. (2013). Category learning increases discriminability of relevant object dimensions in visual cortex. Cerebral Cortex, 23, 814–823. DOI: https://doi.org/10.1093/cercor/bhs067, PMID: 22490547, PMCID: PMC3593573 Folstein, J. R., Palmeri, T. J., Van Gulick, A. E., & Gauthier, I. (2015). Category learning stretches neural representations in visual cortex. Current Directions in Psychological Science, 24, 17–23. DOI: https://doi.org/10.1177/0963721414550707, PMID: 25745280, PMCID: PMC4346144 Freedman, D. J., & Assad, J. A. (2006). Experience-dependent representation of visual categories in parietal cortex. Nature, 443, 85–88. DOI: https://doi.org/10.1038/nature05078, PMID: 16936716 Goldstone, R. L. (1994). Influences of categorization on perceptual discrimination. Journal of Experimental Psychology: General, 123, 178–200. DOI: https://doi.org/10.1037/0096-3445.123.2.178, PMID: 8014612 Hebart, M. N., Donner, T. H., & Haynes, J.-D. (2012). Human visual and parietal cortex encode visual choices independent of motor plans. Neuroimage, 63, 1393–1403. DOI: https:// doi.org/10.1016/j.neuroimage.2012.08.027, PMID: 22922368 Hebart, M. N., Schriever, Y., Donner, T. H., & Haynes, J.-D. (2016). The relationship between perceptual decision variables and confidence in the human brain. Cerebral Cortex, 26, 118–130. DOI: https://doi.org/10.1093/cercor/bhu181, PMID: 25112281 Henderson, M., & Serences, J. T. (2019). Human frontoparietal cortex represents behaviorally relevant target status based on abstract object features. Journal of Neurophysiology, 121, 1410–1427. DOI: https://doi.org/10.1152/jn.00015.2019, PMID: 30759040, PMCID: PMC6485745 Jeong, S. K., & Xu, Y. (2016). Behaviorally relevant abstract object identity representation in the human parietal cortex. Journal of Neuroscience, 36, 1607–1619. DOI: https://doi. org/10.1523/JNEUROSCI.1016-15.2016, PMID: 26843642, PMCID: PMC4737772 Jiang, X., Bradley, E., Rini, R. A., Zeffiro, T., Vanmeter, J., & Riesenhuber, M. (2007). Categorization training results in shape- and category-selective human neural plasticity. Neuron, 53, 891–903. DOI: https://doi.org/10.1016/j.neuron.2007.02.015, PMID: 17359923, PMCID: PMC1989663 Kaplan, J. T., Man, K., & Greening, S. G. (2015). Multivariate cross-classification: Applying machine learning techniques to characterize abstraction in neural representations. Frontiers in Human Neuroscience, 9, 151. DOI: https://doi.org/ 10.3389/fnhum.2015.00151, PMID: 25859202, PMCID: PMC4373279 Knowlton, B. J., & Squire, L. R. (1993). The learning of categories: Parallel brain systems for item memory and category knowledge. Science, 262, 1747–1749. DOI: https:// doi.org/10.1126/science.8259522, PMID: 8259522 Konen, C. S., & Kastner, S. (2008). Two hierarchically organized neural systems for object information in human visual cortex. Nature Neuroscience, 11, 224–231. DOI: https://doi.org/10.1038/nn2036, PMID: 18193041 Kriegeskorte, N., Mur, M., & Bandettini, P. A. (2008). Representational similarity analysis—Connecting the branches of systems neuroscience. Frontiers in Systems Neuroscience, 2, 4. DOI: https://doi.org/10.3389/neuro.06.004.2008, PMID: 19104670, PMCID: PMC2605405 Li, S., Mayhew, S. D., & Kourtzi, Z. (2009). Learning shapes the representation of behavioral choice in the human brain. Neuron, 62, 441–452. DOI: https://doi.org/10.1016/j.neuron. 2009.03.016, PMID: 19447098 Li, S., Ostwald, D., Giese, M., & Kourtzi, Z. (2007). Flexible coding for categorical decisions in the human brain. Journal of Neuroscience, 27, 12321–12330. DOI: https://doi.org/ 10.1523/JNEUROSCI.3795-07.2007, PMID: 17989296, PMCID: PMC6673243 Mack, M. L., Love, B. C., & Preston, A. R. (2016). Dynamic updating of hippocampal object representations reflects new conceptual knowledge. Proceedings of the National Academy of Sciences, U.S.A., 113, 13203–13208. DOI: https://doi.org/ 10.1073/pnas.1614048113, PMID: 27803320, PMCID: PMC5135299 2354 Journal of Cognitive Neuroscience Volume 32, Number 12 D o w n l o a d e d l l / / / / j t t f / i t . : / / f r o m D o h w t t n p o : a / d / e m d i f r t o p m r c h . s p i l d v i r e e r c t c . m h a i e r d . u c o o m c n / j a o r t c i c n e / - a p r d t i 3 c 2 l 1 e 2 - 2 p 3 d 4 f 2 / 2 3 0 2 1 / 4 1 1 2 4 / 2 2 3 o 4 c 2 n _ / a 1 _ 8 0 6 1 2 5 2 3 2 3 3 p / d j o b c y n g _ u a e _ s 0 t 1 o 5 n 3 0 3 7 . S p d e f p e b m y b e g r u 2 e 0 s 2 t 3 / j / f t . o n 0 5 M a y 2 0 2 1 Mack, M. L., Preston, A. R., & Love, B. C. (2013). Decoding the brain’s algorithm for categorization from its neural implementation. Current Biology, 23, 2023–2027. DOI: https://doi.org/10.1016/j.cub.2013.08.035, PMID: 24094852, PMCID: PMC3874407 Nili, H., Wingfield, C., Walther, A., Su, L., Marslen-Wilson, W., & Kriegeskorte, N. (2014). A toolbox for representational similarity analysis. PLoS Computational Biology, 10, e1003553. DOI: https://doi.org/10.1371/journal.pcbi.1003553, PMID: 24743308, PMCID: PMC3990488 Nosofsky, R. M. (1986). Attention, similarity, and the identification– categorization relationship. Journal of Experimental Psychology: General, 115, 39–61. DOI: https://doi.org/10.1037/0096-3445. 115.1.39, PMID: 2937873 Posner, M. I., & Keele, S. W. (1968). On the genesis of abstract ideas. Journal of Experimental Psychology, 77, 353–363. DOI: https://doi.org/10.1037/h0025953, PMID: 5665566 Reber, P. J., Stark, C. E. L., & Squire, L. R. (1998). Cortical areas supporting category learning identified using functional MRI. Proceedings of the National Academy of Sciences, U.S.A., 95, 747–750. DOI: https://doi.org/10.1073/pnas.95.2.747, PMID: 9435264, PMCID: PMC18492 Seger, C. A., Poldrack, R. A., Prabhakaran, V., Zhao, M., Glover, G. H., & Gabrieli, J. D. (2000). Hemispheric asymmetries and individual differences in visual concept learning as measured by functional MRI. Neuropsychologia, 38, 1316–1324. DOI: https://doi.org/10.1016/S0028-3932(00) 00014-2 Seger, C. A., Braunlich, K., Wehe, H. S., & Liu, Z. (2015). Generalization in category learning: The roles of representational and decisional uncertainty. Journal of Neuroscience, 35, 8802–8812. DOI: https://doi.org/10.1523/ JNEUROSCI.0654-15.2015, PMID: 26063914, PMCID: PMC4461686 Swisher, J. D., Halko, M. A., Merabet, L. B., McMains, S. A., & Somers, D. C. (2007). Visual topography of human intraparietal sulcus. Journal of Neuroscience, 27, 5326–5337. DOI: https://doi.org/10.1523/JNEUROSCI.0991-07.2007, PMID: 17507555, PMCID: PMC6672354 Schölkopf, B., Smola, A. J., & Bach, F. (2002). Learning with kernels: Support vector machines, regularization, optimization, and beyond. Cambridge, MA: MIT Press. Torgerson, W. S. (1952). Multidimensional scaling: I. Theory and method. Psychometrika, 17, 401–419. DOI: https://doi. org/10.1007/BF02288916 Vaziri-Pashkam, M., & Xu, Y. (2017). Goal-directed visual processing differentially impacts human ventral and dorsal visual representations. Journal of Neuroscience, 37, 8767–8782. DOI: https://doi.org/10.1523/JNEUROSCI.3392-16.2017, PMID: 28821655, PMCID: PMC5588467 D o w n l o a d e d l l / / / / j f / t t i t . : / / f r o m D o h w t t n p o : a / d / e m d i f r t o p m r c h . s p i l d v i r e e r c t c . m h a i e r d . u c o o m c n / j a o r t c i c n e / - a p r d t i 3 c 2 l 1 e 2 - 2 p 3 d 4 f 2 / 2 3 0 2 1 / 4 1 1 2 4 / 2 2 3 o 4 c 2 n _ / a 1 _ 8 0 6 1 2 5 2 3 2 3 3 p / d j o b c y n g _ u a e _ s 0 t 1 o 5 n 3 0 3 7 . S p d e f p e b m y b e g r u 2 e 0 s 2 t 3 / j f / t . o n 0 5 M a y 2 0 2 1 Wu et al. 2355 Cortical Transformation of Stimulus Space in Order image

Download pdf