Complex Program Induction for Querying Knowledge
Bases in the Absence of Gold Programs
Amrita Saha1 Ghulam Ahmed Ansari1 Abhishek Laddha∗ 1
Karthik Sankaranarayanan1 Soumen Chakrabarti2
1IBM Research India, 2Indian Institute of Technology Bombay
amrsaha4@in.ibm.com, ansarigh@in.ibm.com, laddhaabhishek11@gmail.com,
kartsank@in.ibm.com, soumen@cse.iitb.ac.in
Abstract
1 Introduction
Recent years have seen increasingly com-
plex question-answering on knowledge bases
(KBQA) involving logical, quantitative, and
comparative reasoning over KB subgraphs.
Neural Program Induction (NPI) is a pragmatic
approach toward modularizing the reasoning
process by translating a complex natural lan-
guage query into a multi-step executable pro-
gram. While NPI has been commonly trained
with the ‘‘gold’’ program or its sketch, for
realistic KBQA applications such gold pro-
grams are expensive to obtain. There, prac-
tically only natural language queries and the
corresponding answers can be provided for
training. The resulting combinatorial explo-
sion in program space, along with extremely
sparse rewards, makes NPI for KBQA ambi-
tious and challenging. We present Complex
Imperative Program Induction from Terminal
Rewards (CIPITR), an advanced neural pro-
grammer that mitigates reward sparsity with
auxiliary rewards, and restricts the program
space to semantically correct programs using
high-level constraints, KB schema, and in-
ferred answer type. CIPITR solves complex
KBQA considerably more accurately than
key-value memory networks and neural sym-
bolic machines (NSM). For moderately com-
plex queries requiring 2- to 5-step programs,
CIPITR scores at least 3× higher F1 than the
competing systems. On one of the hardest class
of programs (comparative reasoning) with
5–10 steps, CIPITR outperforms NSM by a
factor of 89 and memory networks by 9 times.1
∗Now at Hike Messenger
1The NSM baseline in this work is a re-implemented
version, as the original code was not available.
185
Structured knowledge bases (KB) like Wikidata
and Freebase can support answering questions
(KBQA) over a diverse spectrum of structural
complexity. This includes queries with single-hop
(Obama’s birthplace) (Yao, 2015; Berant et al.,
2013), or multi-hop (who voiced Meg in Family
Guy) (Bast and Haußmann, 2015; Yih et al., 2015;
Xu et al., 2016; Guu et al., 2015; McCallum et al.,
2017; Das et al., 2017), or complex queries such
as ‘‘how many countries have more rivers and
lakes than Brazil?’’ (Saha et al., 2018). Complex
queries require a proper assembly of selected
operators from a library of graph, set, logical, and
arithmetic operations into a complex procedure,
and is the subject of this paper.
Relatively simple query classes, in particular,
in which answers are KB entities, can be served
with feed-forward (Yih et al., 2015) and seq2seq
(McCallum et al., 2017; Das et al., 2017) networks.
However, such systems show copying or rote
learning behavior when Boolean or open numeric
domains are involved. More complex queries
need to be evaluated as an acyclic expression
graph over nodes representing KB access, set,
logical, and arithmetic operators (Andreas et al.,
2016a). A practical alternative to inferring a state-
less expression graph is to generate an imperative
sequential program to solve the query. Each step
of the program selects an atomic operator and
a set of previously defined variables as argu-
ments and writes the result to scratch memory,
which can then be used in subsequent steps. Such
imperative programs are preferable to opaque,
monolithic networks for
interpretability
and generalization to diverse domains. Another
their
Transactions of the Association for Computational Linguistics, vol. 7, pp. 185–200, 2019. Action Editor: Scott Wen-tau Yih.
Submission batch: 8/2018; Revision batch: 11/2018; Final submission: 1/2019; Published 4/2019.
c(cid:3) 2019 Association for Computational Linguistics. Distributed under a CC-BY 4.0 license.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
6
2
1
9
2
4
3
5
6
/
/
t
l
a
c
_
a
_
0
0
2
6
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
motivation behind opting for the program induc-
tion paradigm for solving complex tasks, such as
complex question answering, is modularizing the
end-to-end complex reasoning process. With this
approach it is now possible to first train separate
modules for each of the atomic operations in-
volved and then train a program induction model
that learns to use these separately trained models
and invoke the sub-modules in the correct fashion
to solve the task. These sub-modules can even
be task-agnostic generic models that can be pre-
trained with much more extensive training data,
while the program induction model learns from
examples pertaining to the specific task. This par-
adigm of program induction has been used for
decades, with rule induction and probabilistic pro-
gram induction techniques in Lake et al. (2015)
and by constructing algorithms utilizing formal
theorem-proving techniques in Waldinger and
Lee (1969). These traditional approaches (e.g.,
Muggleton and Raedt, 1994) incorporated domain
specific knowledge about programming languages
instead of applying learning techniques. More
recently, to promote generalizability and reduce
dependecy on domain specific knowledge, neu-
ral approaches have been applied to problems
like addition, sorting, and word algebra problems
(Reed and de Freitas, 2016; Bosnjak et al., 2017)
as well as for manipulating a physical environment
(Bunel et al., 2018).
Program Induction has also seen initial prom-
ise in translating simple natural language queries
into programs executable in one or two hops
over a KB to obtain answers (Liang et al.,
2017). In contrast, many of the complex queries
from Saha et al. (2018), such as the one in
Figure 1, require up to 10-step programs involving
multiple relations and several arithmetic and
logical operations. Sample operations include
gen−set: collecting {t : (h, r, t) ∈ KB}, comput-
ing set−union, counting set sizes (set−count),
comparing numbers or sets, and so forth. These
operations need to be executed in the correct order,
with correct parameters, sharing information via
intermediate results to arrive at the correct answer.
Note also that the actual gold program is not
available for supervision and therefore the large
space of possible translation actions at each step,
coupled with a large number of steps needed to get
any payoff, makes the reward very sparse. This
renders complex KBQA in the absence of gold
programs extremely challenging.
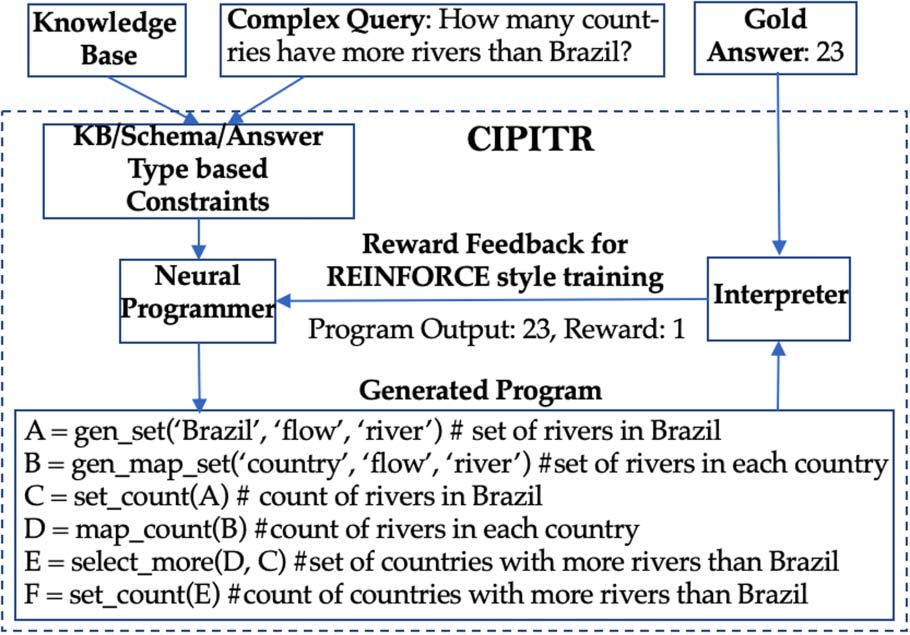
Figure 1: The CIPITR framework reads a natural lang-
uage query and writes a program as a sequence of
actions, guided at every step by constraints posed by
the KB and the answer-type. Because the space of actions
is discrete, REINFORCE is used to learn the action
selection by computing the reward from the output
answer obtained by executing the program and the
target answer, which is the only source of supervision.
Main Contributions
• We present ‘‘Complex Imperative Program
Induction from Terminal Rewards’’ (CIPITR),2
an advanced Neural Program Induction
(NPI) system that is able to answer complex
logical, quantitative, and comparative queries
by inducing programs of length up to 7, using
20 atomic operators and 9 variable types.
This, to our knowledge, is the first NPI sys-
tem to be trained with only the gold answer
as (very distant) supervision for inducing
such complex programs.
• CIPITR reduces the combinatorial program
space to only semantically correct programs
by (i) incorporating symbolic constraints
guided by KB schema and inferred an-
swer type, and (ii) adopting pragmatic pro-
gramming techniques by decomposing the
final goal
into a hierarchy of sub-goals,
thereby mitigating the sparse reward problem
by considering additional auxiliary rewards
in a generic, task-independent way.
We evaluate CIPITR on the following two
challenging tasks: (i) complex KBQA posed by
the recently-published CSQA data set (Saha et al.,
2018) and (ii) multi-hop KBQA in one of the more
2The code and reinforcement learning environment of
CIPITR is made public in https://github.com/CIPITR/
CIPITR.
186
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
6
2
1
9
2
4
3
5
6
/
/
t
l
a
c
_
a
_
0
0
2
6
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
popularly used KBQA data sets WebQuestionsSP
(Yih et al., 2016). WebQuestionsSP involves
complex multi-hop inferencing, sometimes with
additional constraints, as we will describe later.
However, CSQA poses a much greater challenge,
with its more diverse classes of complex que-
ries and almost 20-times larger scale. On a data
set such as CSQA, contemporary models like
neural symbolic machines (NSM) fail to handle
exponential growth of the program search space
caused by a large number of operator choices
at every step of a lengthy program. Key-value
memory networks (KVMnet) (Miller et al., 2016)
are also unable to perform the necessary complex
multi-step inference. CIPITR outperforms them
both by a significant margin while avoiding
exploration of unwanted program space or mem-
orization of low-entropy answer distributions. On
even moderately complex programs of length
2–5, CIPITR scored at least 3× higher F1 than
both. On one of the hardest class of programs of
around 5–10 steps (i.e., comparative reasoning),
CIPITR outperformed NSM by a factor of 89 and
KVMnet by a factor of 9. Further, we empirically
observe that among all the competing models,
CIPITR shows the best generalization across
diverse program classes.
2 Related Work
Whereas most of the earlier efforts to handle
complex KBQA did not involve writable mem-
ory, some recent systems (Miller et al., 2016;
Neelakantan et al., 2015, 2016; Andreas et al.,
2016b; Dong and Lapata, 2016) used end-to-
end differentiable neural networks. One of the
state-of-the-art neural models for KBQA, the key-
value memory network KVMnet (Miller et al.,
2016) learns to answer questions by attending on
the relevant KB subgraph stored in its memory.
Neelakantan et al. (2016) and Pasupat and Liang
(2015) support simple queries over tables, for
example, of the form ‘‘find the sum of a specified
column’’ or ‘‘list elements in a column more
than a given value.’’ The query is read by a re-
current neural network (RNN), and then, in each
translation step,
the column and operator are
selected using the query representation and history
of operators and columns selected in the past.
Andreas et al. (2016b) use a ‘‘stateless’’ model
where neural network based subroutines are
assembled using syntactic parsing.
Recently, Reed and de Freitas (2016) took an
early influential step with the NPI compositional
framework that learns to decompose high level
tasks like addition and sorting into program steps
(carry, comparison) aided by persistent memory.
It is trained by high-level task input and output
as well as all the program steps. Li et al. (2016)
and Bosnjak et al. (2017) took another important
step forward by replacing NPI’s expensive strong
supervision with supervision of the program-
sketch. This form of supervision at every inter-
mediate step still keeps the problem simple, by
arresting the program space to a tractable size.
Although such data are easy to generate for sim-
pler problems such as arithmetic and sorting,
it is expensive for KBQA. Liang et al. (2017)
proposed the NSM framework in absence of the
gold program, which translates the KB query
to a structured program token-by-token. While
being a natural approach for program induction,
NSM has several inherent limitations preventing
generalization towards longer programs that are
critical for complex KBQA. Subsequently, it was
evaluated only on WebQuestionsSP (Yih et al.,
2016), that requires relatively simpler programs.
We consider NSM as the primary and KVMnet
as an additional baseline and show that CIPITR
significantly outperforms both, especially on the
more complex query types.
3 Complex KBQA Problem Set-up
3.1 CSQA Data Set
The CSQA data set (Saha et al., 2018) contains
1.15M natural language questions and its corre-
sponding gold answer from WikiData Knowledge
Base. Figure 1 shows a sample query from the
data set along with its true program-decomposed
form, the latter not provided by CSQA. CSQA is
particularly suited to study the Complex Program
Induction (CPI) challenge over other KBQA data
sets because:
• It contains
large-scale training data of
question-answer pairs across diverse classes
of complex queries, each requiring different
inference tools over large KB sub-graphs.
• Poor state-of-the-art performance of mem-
ory networks on it motivates the need for
sweeping changes to the NPI’s learning
strategy.
187
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
6
2
1
9
2
4
3
5
6
/
/
t
l
a
c
_
a
_
0
0
2
6
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
• The massive size of the KB involved (13 mil-
lion entities and 50 million tuples) poses a
scalability challenge for prior NPI techniques.
• Availability of KB metadata helps standard-
ize comparisons across techniques (explained
subsequently).
We adapt CSQA in two ways for the CPI problem.
Removal of extended conversations: To be
consistent with the NSM work on KBQA, we
discard QA pairs that depend on the previous
dialogue context. This is possible as every query
is annotated with information on whether it is
self-contained or depends on the previous con-
text. Relevant statistics of the resulting data set
are presented in Table 3.
Use of gold entity, type, and relation anno-
tations to standardize comparisons: Our focus
being on the reasoning aspect of the KBQA
problem, we use the gold annotations of canonical
KB entities, types, and relations available in the
in order
data set along with the the queries,
to remove a prominent source of confusion in
comparing KBQA systems (i.e., all systems take
as inputs the natural language query, with spans
identified with KB IDs of entities, types, relations,
and integers). Although annotation accuracy af-
fects a complete KBQA system, our focus here is
on complex, multi-step program generation with
only final answer as the distant supervision, and
not entity/type/relation linking.
3.2 WebQuestionsSP Data Set
In Figure 2 we illustrate one of the most com-
plex questions from the the WebQuestionsSP data
set and its semantic parsed version provided by hu-
man annotator. Questions in the WebQuestionsSP
data set are answerable from the Freebase KB and
tyically require up to 2-hop inference chains,
sometimes with additional requirements of satis-
fying specific constraints. These constraints can
be temporal (e.g., governing−position−held−from)
or non-temporal (e.g., government−office−position−
or−title). The human-annotated semantic parse of
the questions provide the exact structure of the
subgraph and the inference process on it to reach
the final answer. As in this work, we are focusing
on inducing programs where the gold entity rela-
tion annotations are known; for this data set as
well, we use the human-annotations to collect all
188
Figure 2: Semantic parsed form of a sample Question
from WebQuestionsSP, along with the depiction of the
reasoning over the subgraph to reach the answer.
the entities and relations in the oracle subgraph
associated with the query. The NPI model has
to understand the role of these gold program
inputs in question-answering and learn to induce
a program to reflect the same inferencing.
4 Complex Imperative Program
Induction from Terminal Rewards
4.1 Notation
This subsection introduces the different notations
commonly used by our model.
Nine variable-types:
(distinct from KB types)
• KB artifacts: ent(entity), rel(relation), type
• Base data types: int, bool, N one (empty
argument type used for padding)
• Composite data types: set (i.e., set of KB
entities) or map−set and map−int (i.e., a
mapping function from an entity to a set of
KB entities or an integer)
Twenty Operators:
• gen−set(ent, rel, type) → set
• verif y(ent, rel, ent) → bool
• gen−map set(type, rel, type) → map−set
• map−count(map−set) → map−int
• set {union/ints/dif f }(set, set) → set
• map−{union/ints/dif f }(map−set,
map−set) → map−set
• set−count(set) → int
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
6
2
1
9
2
4
3
5
6
/
/
t
l
a
c
_
a
_
0
0
2
6
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
• select−{atleast/atmost/more/less/
equal/approx}(map int, int) → set
• select−{max/min}(map int) → ent
• no−op() (i.e., no action taken)
Symbols and Hyperparameters:
(typical values)
• num−op: Number of operators (20)
• num−var−types: Number of variable types (9)
• max−var: Maximum number of variables
accommodated in memory for each type (3)
• m: Maximum number of arguments for an
operator (N one padding for fewer argu-
ments) (3)
• dkey & dval: Dimension of the key and value
embeddings (dkey (cid:6) dval) (100, 300)
• np & nv: Number of operators and argument
variables sampled per operator each time
(4, 10)
• f with subscript: some feed-forward network
Embedding Matrices: The model is trained with
a vocabulary of operators and variable-types.
In order to sample operators, two matrices M op key
∈ Rnum op×dkey and M op val ∈ Rnum op×dval are
needed for encoding the operator’s key and
value embedding. The key embedding is used
for looking up and retrieving an entry from the
operator vocabulary and the corresponding value
embedding encodes the operator information. The
variable type has only the value embedding
M vtype val ∈ Rnum op×dval as no lookup is needed
on it.
Operator Prototype Matrices: These matrices
store the argument variable type information
the m arguments of every operator
in
for
M op arg ∈ {0, 1, . . . , num−var−types}num op×m
and the output variable type created by it
in
M op out ∈ {0, 1, . . . , num−var−types}num op.
Memory Matrices: This is the query-specific
scratch memory for storing new program variables
as they get created by CIPITR. For each variable
type, we have separate key and value embedding
matrices M var key ∈ Rnum var type×max var×dkey
and M var val ∈ Rnum var type×max var×dval, re-
spectively for looking up a variable in memory
and accessing the information in it. In addition, we
also have a variable attention matrix M var att ∈
Rnum var type×max var which stores the attention
vector over the variables declared of each type.
CIPITR consists of three components:
The preprocessor takes the input query and the
KB and performs the task of entity, relation,
and type linking which acts as input to the
program induction. It also pre-populates the
variable memory matrices with any entity,
relation, type, or integer variable directly
extracted from the query.
language question,
The programmer model takes as input the nat-
ural
the KB, and the
pre-populated variable memory tables to gen-
erate a program (i.e., a sequence of operators
invoked with past instantiated variables as
their arguments and generating new variables
in memory).
The interpreter executes the generated program
with the help of the KB and scratch memory
and outputs the system answer.
During training, the predicted answer is com-
pared with the gold to obtain a reward, which is
sent back to CIPITR to update its model pa-
rameters through a REINFORCE (Williams,
1992) objective. In the current version of CIPITR,
the preprocessor consults an oracle to link enti-
ties, types and relations in the query to the KB.
This is to isolate the programming performance
of CIPITR from the effect of imperfect linkage.
Extending earlier studies (Karimi et al., 2012;
Khalid et al., 2008) to investigate robustness of
CIPITR to linkage errors may be of future interest.
4.2 Basic Memory Operations in CIPITR
We describe some of the foundational modules
invoked by the rest of CIPITR.
Memory Lookup: The memory lookup looks
up scratch memory with a given probe, say x (of
arbitrary dimension), and retrieves the memory
entry having closest key embedding to x. It first
passes x through a feed-forward layer to transform
its dimension to key embedding dimension x−key.
Then, by computing softmax over the matrix
multiplication of M x key and xkey, the distribution
over the memory variables for lookup is obtained.
xkey = f (x), xdist = sof tmax(M x keyxkey)
189
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
6
2
1
9
2
4
3
5
6
/
/
t
l
a
c
_
a
_
0
0
2
6
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
6
2
1
9
2
4
3
5
6
/
/
t
l
a
c
_
a
_
0
0
2
6
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
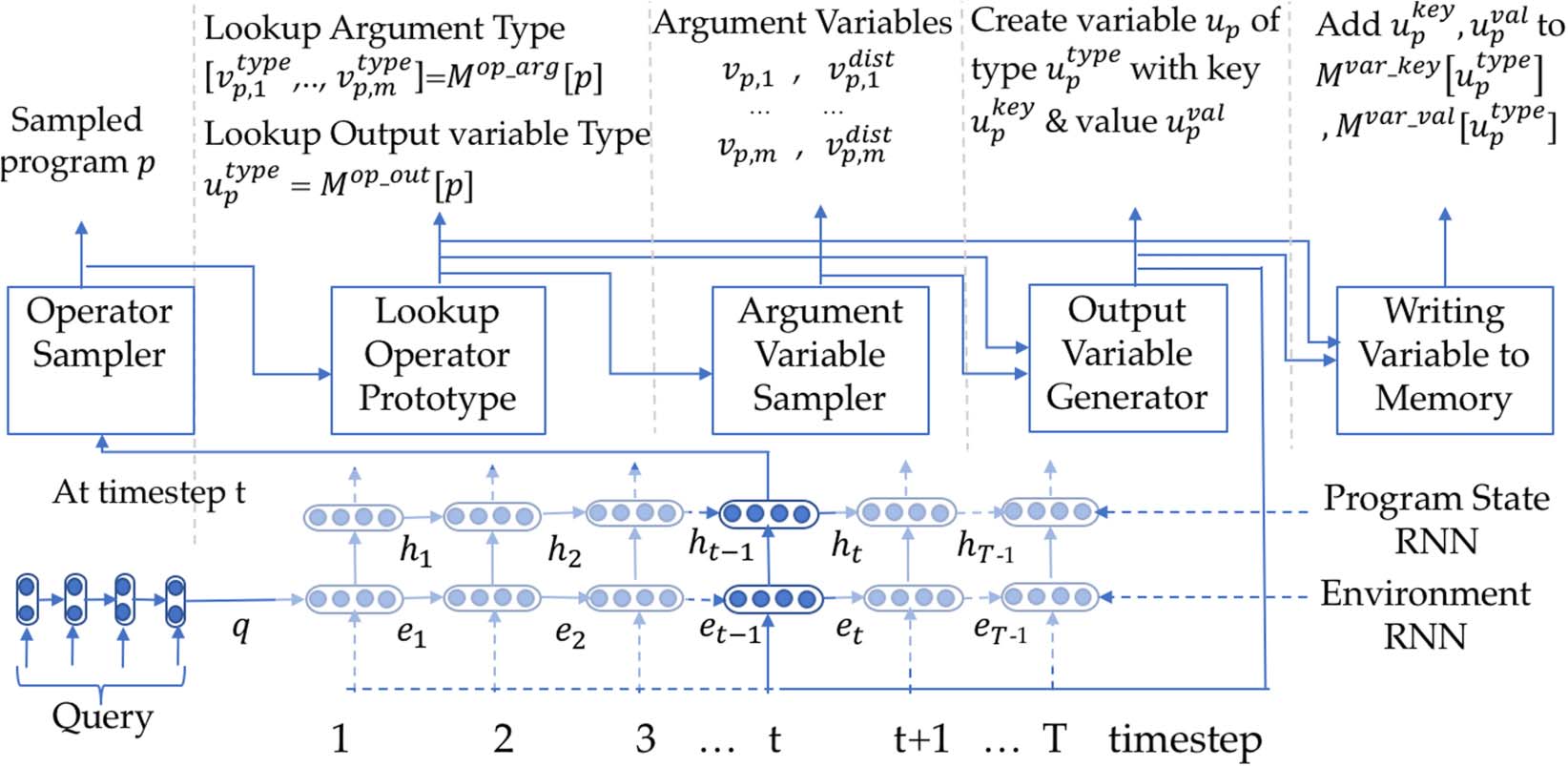
Figure 3: CIPITR Control Flow (with np=1 & nv=1 for simplicity) depicting the order in which different modules
(see Section 4) are invoked. A corresponding example execution trace of the CIPITR algorithm is given in
Figure 4.
Feasibility Sampling: To restrict the search space
to meaningful programs, CIPITR incorporates
both high-level generic or task-specific constraints
when sampling any action. The generic constraints
can help it adopt more pragmatic programming
styles like not repeating lines of code or avoiding
syntactical errors. The task specific constraints
ensure that the generated program is consistent
as per the KB schema or on execution gives an
answer of the desired variable type. To sample
from the feasible subset using these constraints,
the input sampling distribution, xdist, is element-
wise transformed by a feasibility vector xf eas
followed by a L1-normalization. Along with
the top-k entries
the transformed distribution,
xsampled is also returned.
Algorithm 1 Feasibility Sampling
Input:
• xdist ∈ RN (where N is the size of the population
set over which lookup needs to be done)
• xf eas ∈ {0, 1}N (boolean feasibility vector)
• k (top-k sampled)
Procedure: FeasSampling (xdist, xf eas, k)
xdist = xdist (cid:7) xf eas (elementwise multiply)
xdist = L1-Normalized(xdist)
xsampled = k-argmax(xdist)
Output: xdist, xsampled
Writing a new variable to memory: This oper-
ation takes a newly generated variable, say x, of
type xtype and adds its key and value embedding
to the row corresponding to xtype in the memory
matrices. Further, it updates the attention vector
for xtype to provide maximum weight to the newest
variable generated, thus, emulating a stack like
behavior.
Algorithm 2 Write a new variable to memory
Input:
• xkey, xval the key and value embedding of x
• xtype is a scalar denoting type of variable x
Procedure: WriteVarToMem(xkey, xval, xtype)
i is the 1st empty slot in the row M x key[xtype, :]
M var key[xtype, i] = xkey
M var val[xtype, i] = xval
M var att[xtype, :] = L1-Normalized(M var att[xtype, :]
+ One-Hot(i))
4.3 CIPITR Architecture
In Figure 3, we sketch the CIPITR components;
in this section we describe them in the order they
appear in the model.
Query Encoder: The query is first parsed into
a sequence of KB-entities and non-KB words.
KB entities e are embedded with the concatenated
vector [TransE(e), 0] using Bordes et al. (2013),
and non-KB words ω with [0, GloVe(ω)]. The
final query representation is obtained from a GRU
encoder as q.
NPI Core: The query representation q is fed at
the initial timestep to an environment encoding
190
RNN, which gives out the environment state et
at every timestep. This, along with the value
embedding uval
t−1 of the last output variable gen-
erated by the NPI engine, is fed at every timestep
into another RNN that finally outputs the pro-
gram state ht. ht is then fed into the successive
modules of the program induction engine as
described below. The ‘OutVarGen’ algorithm des-
cribes how to obtain uval
t−1.
Procedure: NPI Core(et−1, ht−1, uval
t−1)
et = GRU (et−1, uval
t−1)
ht = GRU (et, uval
t−1, ht−1)
Output: et, ht
Operator Sampler:
It takes the program state
ht, a Boolean vector pf eas
denoting operator
t
feasibility, and the number of operators to sample
np. It passes ht through the Lookup operation
followed by Feasibility Sampling to obtain the
top-np operations (Pt).
p
Argument Variable Sampler: For each sam-
pled operator p, it takes: (i) program state ht, (ii)
the list of variable types V type
of the m arguments
p
obtained by looking up the operator prototype
matrix M op arg, and (iii) a Boolean vector V f eas
that indicates the valid variable configurations for
the m-tuple arguments of the operator p. For each
of the m arguments, a feed-forward network fvtype
first transforms the program state ht to a vector in
Rmax var. It is then element-wise multiplied with
the current attention state over the variables in
memory of that type. This provides the program-
state-specific attention over variables vatt
p,j which is
then passed through the Lookup function to obtain
the distribution over the variables in memory.
Next, feasibility sampling is applied over the joint
distribution of its argument variables, comprised
of the m individual distributions. This provides
the top-nv tuples of m-variable instantiations Vp.
· · · vtype
Output Variable Generator: The new variable
up of type utype
p = M op out[p] is generated by the
procedure OutVarGen by invoking a sampled
operator p with m variables vp,1 · · · vp,m of type
vtype
p,m as arguments. This also requires
p,1
generating the key and value embedding, which
are both obtained by applying different feed-
forward layers over the concatenated represen-
tation of the value embedding of the operator
M op val[p], argument types (M vtype val[vtype
p,1 ] · · ·
M vtype val[vtype
p,m ]) and the instantiated variables
· · · M var val[vtype
(M var val[vtype
p,m , vp,m]).
p,1 , vp,1]
The newly generated variable is then written to
memory using Algorithm WriteVarToMem.
, V f eas
p
, nv)
])(cid:7)fvtype(ht)
Procedure: ArgVarSampler(ht, V type
p
forj ∈ 1, 2, · · · , m do
p,j = sof tmax(M var att[V type
vatt
p,j = Lookup(vatt
vdist
V dist
p = vdist
p,0
V dist
p
Output: Vp
× vdist
p,1
, Vp = FeasSampling(V dist
p,j
p
p,j , fvar, M var key[V type
· · · × vdist
p,m , (cid:2) Joint Distribution
p,j
])
, V f eas
p
, nv)
End-to-End CIPITR training: CIPITR takes a
natural language query and generates an output
program in a number of steps. A program is
composed of actions, which are operators applied
over variables (as in Figure 3). In each step, it
selects an operator and a set of previously defined
variables as its arguments, and writes the operator
output to a dynamic memory, to be subsequently
used for further search of next actions. To reduce
exposure bias (Ranzato et al., 2015), CIPITR
uses a beam search to obtain multiple candidate
programs to provide feedback to the model from
a single training instance. Algorithm 3 shows the
pseudocode of the program induction algorithm
(with beam size b as 1 for simplicity), which goes
over T time steps, each time sampling np feasible
operators conditional to the program state. Then,
for each of the np operators, it samples nv feasible
Algorithm 3 CIPITR pseudo-code (beam size=1)
Query Encoding: q = GRU (Query)
Initialization: e1, h1 = f (q), A = [ ]
for t ∈ 1, · · · , T do
p,m ] = M op arg[p]
t
, np)
= FeasibleOp()
pf eas
t
Pt = OperatorSampler(ht, pf eas
C = {}
for p ∈ Pt do
= [vtype
p,1 , · · · , vtype
V type
p
V f eas
= FeasibleVar(p)
p
Vp = ArgVarSampler(ht, V type
for V ∈ Vp do
C = C
(p, V, V type
) = arg max(C)
p
p = OutVarGen(p, V type
ukey
p , utype
, uval
p
WriteVarToMem(ukey
, uval
et+1, ht+1 = NPICore(et, ht)
A.append((p, V ))
(p, V, V type
p , utype
p
(cid:2)
)
)
p
p
p
p
, V )
, V f eas
p
, nv)
Output: A
191
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
6
2
1
9
2
4
3
5
6
/
/
t
l
a
c
_
a
_
0
0
2
6
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
variable instantiations, resulting in a total of np ∗ nv
candidates out of which b most-likely actions are
sampled for the b beams and the corresponding
newly generated variables written into memory.
This way the algorithm progresses to finally output
b candidate programs, each of which will feed the
model back with some reward. Finally, in order
to learn from the discrete action samples, the
REINFORCE objective (Williams, 1992) is used.
Because of lack of space, we do not provide
the equation for REINFORCE, but our objective
formulation remains very similar to that in Liang
et al. (2017). We next describe several learning
challenges that arise in the context of this overall
architecture.
5 Mitigating Large Program Space and
Sparse Reward
Handling complex queries by expanding the oper-
ator set and generating longer programs blows up
the program space to a huge size of (num−op ∗
(max−var)m)T . This, in absence of gold pro-
grams, poses serious training challenges for the
programmer. Additionally, whereas the relatively
simple NSM architecture could explore a large
beam size (50–100),
the complex architecture
of CIPITR entailed by the CPI problem could
only afford to operate with a smaller beam size
(≤ 20), which further exacerbates the sparsity of
the reward space. For example, for integer an-
swers, only a single point in the integer space
returns a positive reward, without any notion of
partial reward. Such a delayed—indeed, terminal—
reward causes high variance, instability, and local
minima issues. A problem as complex as ours
requires not only generic constraints for produc-
ing semantically correct programs, but also in-
corporation of prior knowledge,
if the model
permits. We now describe how to guide CIPITR
more efficiently through such a challenging en-
vironment using both generic and task-specific
constraints.
Phase change network: For complex real-word
problems, the reinforcement learning community
has proposed various task-abstractions (Parr and
Russell, 1998; Dietterich, 2000; Bakker and
Schmidhuber, 2004; Barto and Mahadevan, 2003;
Sutton et al., 1999) to address the curse of dimen-
sionality in exponential action spaces. HAMs,
proposed by Parr and Russell (1998), is one such
important form of abstraction aimed at restricting
Figure 4: An example of a CIPITR execution trace
depicting the internals of memory and action sampling
to generate the program: (A = gen−set(Brazil, f low,
river), B = set−count(A)).
the realizable action sequences.
Inspired by
HAMs, we decompose the program synthesis into
phases having restricted action spaces. The first
phase (retrieval phase) constitutes gathering the
information from the preprocessed input variables
only (i.e., KB entities, relations, types, integers).
This restricts the feasible operator set to gen−set,
gen−map−set, and verif y. In the second phase
(algorithm phase) the model is allowed to operate
on all the generated variables in order to reach
the answer. The programmer learns whether to
switch from the first phase to the second at any
timestep t, based on parameter φt (φt = 1 indicating
192
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
6
2
1
9
2
4
3
5
6
/
/
t
l
a
c
_
a
_
0
0
2
6
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
change of phase, where φ0 = 0) which is ob-
tained as φt = 11{max(sigmoid(f (ht)), φt−1) ≥
φthresh} if t < T /2, else 1 (T being total time-
steps and φthresh is set to 0.8 in our experi-
ments). The motivation behind this is similar
to the multi-staged techniques that have been
adopted in order to make QA tasks more tractable,
as in Yih et al. (2015) and Iyyer et al. (2017).
In contrast, here we further allow the model to
learn when to switch from one stage to the next.
Note that this is a generic characteristic, as for
every task, this kind of phase division is possible.
Generating semantically correct programs: Other
than the generic syntactical and semantic rules,
the NPI paradigm also allows us to leverage
prior knowledge and to incorporate task-specific
symbolic constraints in the program representation
learning in an end-to-end differentiable way.
• Enforcing KB consistency: Operators used
in the retrieval phase (described above) must
honor the KB-imposed constraints, so as not
to initialize variables that are inconsistent
with respect to the KB. For example, a set
variable assigned from gen−set is considered
valid only when the ent, rel, type arguments
to gen−set are consistent with the KB.
• Biasing the last operator using answer
type predictor: Answer type prediction is
a standard preprocessing step in question
answering (Li and Roth, 2002). For this
we use a rule-based predictor that has 98%
accuracy. The predicted answer type helps
in directing the program search toward the
correct answer type by biasing the sampling
towards feasible operators that can produce
the desired answer type.
• Auxiliary reward strategy: Jaccard scores
of the executed program’s output and the
gold answer set is used as reward. An in-
valid program gets a reward of −1. Further,
to mitigate the sparsity of the extrinsic
rewards, an additional auxiliary feedback is
designed to reward the model on generating
an answer of the predicted answer-type. A
linear decay makes the effect of auxiliary
reward vanish eventually. Such a curriculum
learning mechanism, while being particularly
useful for the more complex queries, is still
quite generic as it does not require any
additional task-specific prior knowledge.
Beam Management and Action Sampling
• Pruning beams by target answer type:
Penalize beams that terminate with an answer
type not matching the predicted answer type.
• Length-based normalization of beam scores:
To counteract the characteristic of beam search
favoring shorter beams as more probable and
to ensure the scoring is fair to the longer
beams, we normalize the beam scores with
respect to their length.
• Penalizing beams for no−op operators:
Another way of biasing the beams toward
generating longer sequences, is by penalizing
for the number of times a beam takes no−op
as the action. Specifically, we reduce the
beam score by a hyperparameter-controlled
logarithmic factor of the number of no−op
actions taken till now.
• Stochastic beam exploration with entropy
annealing: To avoid early local minima
where the model severely biases towards
specific actions, we added techniques like (i)
a stochastic version of beam search to sample
operators in an (cid:4)-greedy fashion (ii) dropout,
and (iii) entropy-based regularization of
action distribution.
Sampling only feasible actions: Sampling a
feasible action requires first sampling a feasible
operator and then its feasible variable arguments:
• The operator must be allowed in the current
phase of the model’s program induction.
• Valid Variable instantiation: A feasible
operator should be having at least one valid
instantiation of its formal arguments with
non-empty variable values that are also
consistent with the KB.
• Action Repetition: An action (i.e., an oper-
ator invoked with a specific argument in-
stantiation) should not be repeated at any
time step.
• Some operators disallow some arguments;
for example, union or intersection of a set
with itself.
193
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
6
2
1
9
2
4
3
5
6
/
/
t
l
a
c
_
a
_
0
0
2
6
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Timesteps
Entropy-Loss Wt.
Feasible Program
after iterations
Beam Pruning after
iterations
Auxillary Reward
till iterations
Learning Rate
Simple
2
5e−4
Logical
4
5e−4
Verify
5
5e−6
Quanti
7
5e−3
Quant
Count
7
5e−3
Comp
7
5e−2
Comp WebQSP
Count
7
5e−2
All
3 to 5
5e−3
1000
2000
100
0
1e−5
100
0
1e−5
500
100
0
1e−5
1300
1300
1500
1500
1300
1300
1300
1000
800
1e−5
800
1e−5
800
1e−5
800
1e−5
50
100
200
1e−4
Table 1: Critical hyperparameters.
6 Experiments
We compare CIPITR against baselines (Miller
et al., 2016; Liang et al., 2017) on complex KBQA
and further identify the contributions of the ideas
presented in Section 5 via ablation studies. For
this work, we limit our effort on KBQA to the
setting where the query is annotated with the gold
KB-artifacts, which standardizes the input to the
program induction for the competing models.
6.1 Hyperparameters Settings
We trained our model using the Adam Optimizer
and tuned all hyperparameters on the validation
set. Some parameters are selectively turned on/
off after few training iterations, which is itself a
hyperparameter (see Table 1). We combined reward/
loss such as entropy annealing and auxiliary re-
wards using different weights detailed in Table 1.
The key, value embedding dimensions are set to
100, 300.
6.2 WebQuestionsSP Data Set
We first evaluate our model on the more popularly
used WebQuestionsSP data set.
6.2.1 Rule-Based Model on WebQuestionsSP
Though quite a few recent works on KBQA have
evaluated their model on WebQuestionsSP, the
reported performance is always in a setting where
the gold entities/relations are not known. They
either internally handle the entity and relation-
linking problem or outsource it to some external
or in-house model, which itself might have been
trained with additional data. Additionally,
the
entity/relation linker outputs used by these models
are also not made public, making it difficult to set
up a fair ground for evaluating the program induc-
tion model, especially because we are interested
in the program induction given the program inputs
and handling the entity/relation linking is beyond
the scope of this work. To avoid these issues, we
use the human-annotated entity/relation linking
data available along with the questions as input
to the program induction model. Consequently
the performance reported here is not comparable
to the previous works evaluated on this data set,
as the query annotation is obtained here from an
oracle linker.
Further, to gauge the proficiency of the pro-
posed program induction model, we construct a
rule-based model which is aware of the human
annotated semantic parsed form of the query—that
is, the inference chain of relations and the exact
constraints that need to be additionally applied
to reach the answer. The pseudocode below
elaborates how the rule based model works on the
human-annotated parse of the given query, taking
as input the central entity, the inference chain,
and associated constraints and their type. This
Procedure: RuleBasedModel(parse, KB)
ent1 ← parse[‘T opicEntityM id’]
rel1 ← parse[‘Inf erentialChain’][0]
ans ← {x | (ent1, rel1, x) ∈ KB}
for c ∈ parse[‘Constraints’]
c−rel ← c[‘N odeP redicate’]
c−op ← c[‘Operator’]
c−arg ← c[‘Argument’]
if c[‘ArgumentT ype’] == ‘Entity’
ans ← ans ∩ {x | (c−arg, c−rel, x) ∈ KB}
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
6
2
1
9
2
4
3
5
6
/
/
t
l
a
c
_
a
_
0
0
2
6
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
else
(cid:2)
ans ←
{x | (x, c rel, y) ∈ KB,
x∈ans
c−arg (cid:2)c−op y}
if len(parse[‘Inf erentialChain’]) > 1
rel2 ← parse[‘Inf erentialChain’][1]
ans ←
{y | (x, rel2, y) ∈ KB}
(cid:2)
x∈ans
Output: ans
194
Question Type
Inference-chain-len-1, no constraint
Inference-chain-len-1 with constraint
Inference-chain-len-2, no constraint
Inference-chain-len-2, with nontemporal constraint
Inference-chain-len-2, with temporal constraint
All
Rule
Based
87.34
93.64
82.85
61.26
35.63
81.19
CIPITR
89.09
79.94
88.69
63.07
48.86
82.85
Table 2: F1 scores(%) of CIPITR and rule-based model(as in Sec.6.2.1) on WebQuestionsSP test set having
1,639 queries.
inference rule, manually derived, can be written
out in a program form, which on execution will
give the final answer. On the other hand, the task
of CIPITR is to actually learn the program by
looking at training examples of the query and
corresponding answer. Both the models need to
induce the program using the gold entity/relation
data. Subsequently, the rule-based model is indeed
a very strong competitor as it is generated by
annotators having detailed knowledge about the
KB.
6.2.2 Results on WebQuestionsSP
A comparative performance analysis of
the
proposed CIPITR model, the rule-based model
and the SparQL executor is tabulated in Table 2.
The main take-away from these results is that
CIPITR is indeed able to learn the rules behind
the multi-step inference process simply from the
distance supervision provided by the question-
answer pairs and even perform slightly better in
some of the query classes.
6.3 CSQA Data Set
We now showcase the performance of the pro-
posed models and related baselines on the CSQA
data set.
6.3.1 Baselines on CSQA
KVMnet with decoder (2016), which performed
best on CSQA data set (Saha et al., 2018) (as
discussed in Section 2), learns to attend on a KB
subgraph in memory and decode the attention
over memory-entries as their likelihood of being
in the answer. Further, it can also decode a vocab-
ulary of non-KB words like integers or booleans.
However, because of the inherent architectural
constraints, it is not possible to incorporate most
of the symbolic constraints presented in Section 5
in this model, other than KB-guided consistency
and biasing towards answer-type. More impor-
tantly, recently the usage of these models have
been criticized for numerical and boolean question
answering as these deep networks can easily mem-
orize answers without ‘‘understanding’’ the logic
behind the queries simply because of the skew
in the answer distribution. In our case this effect
is more pronounced as CSQA evinces a curi-
ous skew in integer answers to ‘‘count’’ queries.
Fifty-six percent of training and 52% of test
count-queries have single digit answers. Ninety
percent of training and 81% of test count-queries
have answers less than 200. Though this makes it
unfair to compare NPI models (that are oblivious
to the answer vocabulary) with KVMnet on such
queries, we still train a KVMnet version on a
balanced resample of CSQA, where, for only
the count queries, the answer distribution over
integers has been made uniform.
NSM (2017) uses a key-variable memory and
decodes the program as a sequence of operators
and memory variables. As the NSM code was not
available, we implemented it and further incor-
porated most of the six techniques presented in
Table 4. However, constraints like action repe-
tition, biasing last operator selection, and phase
change cannot be incorporated in NSM while
keeping the model generic, as it decodes the
program token by token.
6.3.2 Results on CSQA
In Table 3 we compare the F1 scores obtained
by our system, CIPITR, against
the KVMnet
and NSM baselines. For NSM and CIPITR, we
train seven models with different hyperparameters
tuned on each of the seven question types. For the
train and valid splits, a rule-based query type
classifier with 97% accuracy was used to bucket
queries into the classes listed in Table 3. For each
of these three systems, we also train and evaluate
195
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
6
2
1
9
2
4
3
5
6
/
/
t
l
a
c
_
a
_
0
0
2
6
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Quant
Comp
↓ Run name \ Question type → Simple Logical Verify Quanti. Count Compar. Count
42K
Training Size Stats.
7K
Test Size Stats.
9.60
KVMnet
0.00
NSM, best at top beam
0.00
NSM best over top 2 beams
0.00
NSM, best over top 5 beams
0.00
NSM, best over top 10 beams
0.33
CIPITR, best at top beam
0.41
CIPITR, best over top 2 beams
1.01
CIPITR, best over top 5 beams
1.54
CIPITR, best over top 10 beams
122K
18K
17.80
12.38
15.34
29.18
30.71
51.33
51.72
52.01
52.71
43K
9K
27.28
28.70
35.67
50.80
60.18
89.43
90.48
90.97
90.98
93K
18K
37.56
35.40
41.23
64.70
69.86
87.72
87.78
87.96
88.92
462K
81K
41.40
78.38
80.12
86.46
96.78
96.52
96.55
97.18
97.18
99K
9K
0.89
4.31
4.65
6.98
10.69
23.91
25.85
27.19
28.92
41K
7K
1.63
0.17
0.21
0.48
2.09
15.12
19.85
29.45
32.98
All
904K
150K
26.67
10.63
11.02
12.07
14.36
58.92
62.52
69.25
73.71
Table 3: F1 score (%) of KVMnet and NSM, and CIPITR. Bold numbers indicate the best among KVMnet and
top beam score of NSM and CIPITR.
one single model over all question types. KVMnet
does not have any beam search, the NSM model
uses a beam size of 50, and CIPITR uses only 20
beams for exploring the program space.
Our manual inspection of these seven query
categories show that simple and verify are simplest
in nature requiring 1-line programs while logical
is moderately difficult, with around 3 lines of code.
The query categories next in order of complexity
are quantitative and quantitative count, needing
a sequence of 2–5 operations. The hardest types
are comparative and comparative count, which
translate to an average of 5–10 lined programs.
Analysis: The experiments show that on the
simple to moderately difficult (i.e., first three)
query classes, CIPITR’s performance at the top
beam is up to 3 times better than both the base-
lines. The superiority of CIPITR over NSM is
showcased better on the more complex classes
where it outperforms the latter by 5–10 times,
with the biggest impact (by a factor of 89 times)
being on the ‘‘comparative’’ questions. Also, the
5× better performance of CIPITR over NSM over
All category evinces the better generalizability
of the abstract high-level program decomposition
approach of the former.
On the other hand,
training the KVMnet
model on the balanced data helps showcase the
real performance of the model, where CIPITR
outperforms KVMnet significantly on most of
the harder query classes. The only exception is
the hardest class (Comp, Count with numerical
answers) where the abrupt ‘‘best performance’’
of KVMnet can be attributed to its rote learning
Feature
Action Repetition
Phase Change
Valid Variable
Instantiation
Biasing last operator
Auxiliary Reward
Beam Pruning
F1 (%)
1.68
2.41
3.08
7.52
9.85
10.34
Table 4: Ablation testing on comparative questions:
Top beam’s F1 score obtained by omitting each of the
above features from CIPITR, originally having F1 of
15.123%.
abilities simply because of its knowledge of the
answer vocabulary, which the program induction
models are oblivious to, as they never see the
actual answer.
Lastly,
in our experimental configurations,
whereas CIPITR and NSM’s parameter-size is
almost comparable, KVMnet’s is approximately
6× larger.
Ablation Study: To quantitatively analyze the
utility of the features mentioned in Section 5,
we experiment with various ablations in Table 4
by turning off each feature, one at a time. We
show the effect on the hardest question category
(‘‘comparative’’) on which our proposed model
achieved reasonable performance. We see in
the table that each of the 6 techniques helped
the model significantly. Some of them boosted
F1 by 1.5–4 times, while others proved to be
instrumental to obtained large improvements in
F1 score of over 6–9 times.
To summarize, CIPITR has the following
advantages, inducing programs more efficiently
196
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
6
2
1
9
2
4
3
5
6
/
/
t
l
a
c
_
a
_
0
0
2
6
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Input
Ques
Type
Query
Simple
Who is associated with
Robert Emmett O’Malley ?
Verify
Is Sergio Mattarella the
chief of state of Italy ?
Logical
Which cities were
Animal Kingdom filmed on or
share border with Pedralba ?
Quant
Count
Quant
Comp
How many nucleic acid sequences
encodes Calreticulin or
Neurotensin/neuromedin-N ?
What municipal councils are
the legislative bodies for
max US administrative territories ?
Which works did less number of
people do the dubbing for
than Herculesy el rey de Tesalia ?
( E,R,T)
E0: Robert Emmett O’Malley
R0: associated with
T0: person
E0: Sergio Mattarella,
E1: Italy,
R0: chief of state
E0: Animal Kingdom,
E1: Pedralba,
R0: filmed on,
R1: Share border,
T0: cities
E0: Calreticulin,
E1: Neurotensin/neuromedin-N,
R0: encoded by,
T0: nucleic acid
T0: muncipal council,
T1: US administrative territories
R0: legislative body of
E0: Herculesy el rey de Tesalia,
R0: dubbed by,
T0: works,
T1: people
CIPITR Program
NSM program
A = gen set(E0, R0, T0)
A = gen set(E0, R0, T0)
A = verify(E0, R0, E1)
A = verify(E0, R0, E1)
A = gen set(E0, R0, T0);
B = gen set(E1, R1, T0);
C = set union(A,B)
A = gen set(E1, R1, T0);
B = gen set(E1, R1, None);
C = set union(A,B)
A = gen set(E0, R0, T0);
B = gen set(E1, R0, T0);
C = set union(A,B);
D = set count(C)
A = gen map set(T0, R0, T1);
B = map count(A);
C = select max(B)
A = gen map set(T0, R0, T1);
B = gen set(E0, R0, T1);
C = set count(B);
D= map count(A);
E = select less(D,C)
A = gen set(E0, R0, T0);
B = set count(A);
C = set union(A,B)
A = gen map set(T0, R0, T1);
B = gen map set(T0, R0, T1);
C = map count(A)
A = gen set(E0, R0, T1);
B= gen set(E0, R0, T1);
C= gen map set(T0, R0, T1);
D= set diff(A,B)
Table 5: Qualitative analysis of programs for different type of question for CIPITR and NSM.
and pragmatically, as illustrated by the sample
outputs in Table 5:
• Generating syntactically correct programs:
Because of the token-by-token decoding of
the program, NSM cannot restrict its search
to only syntactically correct programs, but
rather only resorts to a post-filtering step
during training. However, at test time, it
could still generate programs with wrong
syntax, as shown in Table 5. For example,
for the Logical question, it invokes a gen−set
with a wrong argument type None and for the
Quantitative count question, it invokes the
set−union operator on a non-set argument.
On the other hand, CIPITR, by design,
can never generate a syntactically incorrect
program because at every step it implicitly
samples only feasible actions.
• Generating semantically correct programs:
CIPITR is capable of incorporating different
generic programming styles as well as problem-
specific constraints, restricting its search
space to only semantically correct programs.
As shown in Table 5, CIPITR is able to gen-
erate at least meaningful programs having
the desired answer-type or without repeating
lines of code. On the other hand the NSM-
generated programs are often semantically
wrong, for instance, both in the Quantitative
and Quantitative Count based questions, the
type of the answer is itself wrong, rendering
the program meaningless. This arises once
again, owing to the token-by-token decoding
of the program by NSM which makes it hard
to incorporate high level rules to guide or
constrain the search.
• Efficient search-space exploration: Owing
to the different strategies used to explore the
program space more intelligently, CIPITR
scales better to a wide variety of complex
queries by using less than half of NSM’s
beam size. We experimentally established
that for programs of length 7 these various
techniques reduced the average program
space from 1.33 × 1019 to 2,998 programs.
7 Conclusion
We presented CIPITR, an advanced NPI frame-
work that significantly pushes the frontier of
complex program induction in absence of gold
programs. CIPITR uses auxiliary rewarding tech-
niques to mitigate the extreme reward sparsity
and incorporates generic pragmatic programming
styles to constrain the combinatorial program
space to only semantically correct programs. As
future directions of work, CIPITR can be further
improved to handle the hardest question types
by making the search more strategic, and can
be further generalized to a diverse set of goals
when training on all question categories together.
197
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
6
2
1
9
2
4
3
5
6
/
/
t
l
a
c
_
a
_
0
0
2
6
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Other potential directions of research could be
toward learning to discover sub-goals to further
decompose the most complex classes beyond just
the two-level phase transition proposed here.
Additionally, further improvements are required
to induce complex programs without availability
of gold program input variables.
References
Jacob Andreas, Marcus Rohrbach, Trevor Darrell,
and Dan Klein. 2016a. Learning to compose
neural networks for question answering. In
NAACL HLT 2016, The 2016 Conference of the
North American Chapter of the Association for
Computational Linguistics: Human Language
Technologies, pages 1545–1554.
Jacob Andreas, Marcus Rohrbach, Trevor Darrell,
and Dan Klein. 2016b. Learning to compose
neural networks for question answering. In
NAACL-HLT, pages 1545–1554.
B. Bakker and J. Schmidhuber. 2004. Hierarchi-
cal reinforcement learning based on subgoal
discovery and subpolicy specialization. In Pro-
ceedings of the 8th Conference on Intelligent
Autonomous Systems IAS-8, pages 438–445.
Andrew G. Barto and Sridhar Mahadevan. 2003.
Recent advances in hierarchical reinforcement
learning. Discrete Event Dynamic Systems,
13(1-2):41–77.
Hannah Bast and Elmar Haußmann. 2015. More
accurate question answering on freebase. In
CIKM, pages 1431–1440.
J. Berant, A. Chou, R. Frostig, and P. Liang.
2013. Semantic parsing on Freebase from
question-answer pairs. In EMNLP Conference,
pages 1533–1544.
Antoine Bordes, Nicolas Usunier, Alberto Garcia-
Duran, Jason Weston, and Oksana Yakhnenko.
2013. Translating embeddings for modeling
In NIPS Conference,
multi-relational data.
pages 2787–2795.
Matko Bosnjak, Tim Rockt¨aschel,
Jason
Naradowsky, and Sebastian Riedel. 2017. Pro-
gramming with a differentiable forth interpreter.
In Proceedings of the 34th International Con-
ference on Machine Learning, ICML 2017,
pages 547–556.
Rudy Bunel, Matthew J. Hausknecht, Jacob
Devlin, Rishabh Singh, and Pushmeet Kohli.
2018. Leveraging grammar and reinforcement
learning for neural program synthesis. In Inter-
national Conference on Learning Representa-
tions (ICLR).
Rajarshi Das, Manzil Zaheer, Siva Reddy, and
Andrew McCallum. 2017. Question answering
on knowledge bases and text using universal
schema and memory networks. In ACL (2),
pages 358–365.
Peter Dayan and Geoffrey E. Hinton. 1993.
learning. In Advances
Feudal reinforcement
in Neural Information Processing Systems 5,
[NIPS Conference], pages 271–278.
Thomas G. Dietterich. 2000. Hierarchical re-
inforcement
learning with the maxq value
function decomposition. Journal of Artificial
Intelligence Research, 13(1):227–303.
Li Dong and Mirella Lapata. 2016. Language
to logical form with neural attention. In ACL,
volume 1, pages 33–43.
Kelvin Guu, John Miller, and Percy Liang. 2015.
Traversing knowledge graphs in vector space.
In EMNLP Conference.
Mohit Iyyer, Wen-tau Yih, and Ming-Wei Chang.
2017. Search-based neural structured learning
for sequential question answering. In ACL,
volume 1, pages 1821–1831.
Sarvnaz Karimi, Justin Zobel, and Falk Scholer.
2012. Quantifying the impact of concept rec-
ognition on biomedical information retrieval.
Information Processing & Management, 48(1):
94–106.
Mahboob Alam Khalid, Valentin Jijkoun, and
Maarten De Rijke. 2008. The impact of named
entity normalization on information retrieval
for question answering. In Proceedings of the
IR Research, 30th European Conference on
Advances in Information Retrieval, ECIR’08,
pages 705–710.
Brenden M. Lake, Ruslan Salakhutdinov, and
Joshua B. Tenenbaum. 2015. Human-level con-
cept
learning through probabilistic program
induction. Science, 350(6266):1332–1338.
198
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
6
2
1
9
2
4
3
5
6
/
/
t
l
a
c
_
a
_
0
0
2
6
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chengtao Li, Daniel Tarlow, Alexander L. Gaunt,
Marc Brockschmidt, and Nate Kushman. 2016.
Neural program lattices. In International Con-
ference on Learning Representations (ICLR).
Marc’Aurelio Ranzato, Sumit Chopra, Michael
Auli, and Wojciech Zaremba. 2015. Sequence
level training with recurrent neural networks.
CoRR, abs/1511.06732.
X. Li and D. Roth. 2002. Learning question clas-
sifiers. In COLING, pages 556–562.
Chen Liang, Jonathan Berant, Quoc Le, Kenneth
D. Forbus, and Ni Lao. 2017. Neural symbolic
machines: Learning semantic parsers on free-
base with weak supervision. In Proceedings of
the 55th Annual Meeting of the Association for
Computational Linguistics, pages 23–33.
Andrew McCallum, Arvind Neelakantan, Rajarshi
Das, and David Belanger. 2017. Chains of rea-
soning over entities, relations, and text using
In Proceedings
recurrent neural networks.
of
the European
Chapter of the Association for Computational
Linguistics, EACL 2017, Volume 1: Long
Papers, pages 132–141.
the 15th Conference of
Alexander H. Miller, Adam Fisch, Jesse Dodge,
Amir-Hossein Karimi, Antoine Bordes, and
Jason Weston. 2016. Key-value memory net-
works for directly reading documents.
In
EMNLP, pages 1400–1409.
Stephen Muggleton and Luc De Raedt. 1994.
Inductive logic programming: Theory and meth-
ods. Journal of Logic Programming, 19/20:
629–679.
Arvind Neelakantan, Quoc V. Le, Martin Abadi,
Andrew McCallum, and Dario Amodei. 2016.
Learning a natural
language interface with
neural programmer. arXiv preprint, arXiv:
1611.08945.
Arvind Neelakantan, Quoc V. Le, and Ilya
Sutskever. 2015. Neural programmer: Inducing
latent programs with gradient descent. CoRR,
abs/1511.04834.
Ronald Parr and Stuart Russell. 1998. Reinforce-
ment learning with hierarchies of machines.
the 1997 Conference on
In Proceedings of
Advances in Neural Information Processing
Systems 10, NIPS ’97, pages 1043–1049.
Scott Reed and Nando de Freitas. 2016. Neural
programmer-interpreters. In International Con-
ference on Learning Representations (ICLR).
Amrita Saha, Vardaan Pahuja, Mitesh M. Khapra,
Karthik Sankaranarayanan, and Sarath Chandar.
2018. Complex sequential question answering:
Towards learning to converse over
linked
question answer pairs with a knowledge graph.
In AAAI.
Richard S. Sutton, Doina Precup, and Satinder
Singh. 1999. Between mdps and semi-mdps:
A framework for
temporal abstraction in
reinforcement learning. Artificial Intelligence,
112(1-2):181–211.
Reut Tsarfaty, Ilia Pogrebezky, Guy Weiss, Yaarit
Natan, Smadar Szekely, and David Harel. 2014.
Semantic parsing using content and context:
A case study from requirements elicitation.
the 2014 Conference on
In Proceedings of
Empirical Methods
in Natural Language
Processing (EMNLP), pages 1296–1307.
Richard J. Waldinger and Richard C. T. Lee.
1969. PROW: A step toward automatic program
writing. In Proceedings of the 1st International
Joint Conference on Artificial Intelligence,
pages 241–252.
Ronald J Williams. 1992. Simple statistical gradient-
following algorithms for connectionist
re-
inforcement learning. In Reinforcement Learning,
Springer, pages 5–32.
Kun Xu, Siva Reddy, Yansong Feng, Songfang
Huang, and Dongyan Zhao. 2016. Question
answering on Freebase via relation extraction
and textual evidence. arXiv preprint, arXiv:
1603.00957.
Xuchen Yao. 2015. Lean question answering over
Freebase from scratch. In NAACL Conference,
pages 66–70.
Panupong Pasupat and Percy Liang. 2015. Com-
positional semantic parsing on semi-structured
tables. arXiv preprint arXiv:1508.00305.
Scott Wen-tau Yih, Ming-Wei Chang, Xiaodong
He, and Jianfeng Gao. 2015. Semantic parsing
via staged query graph generation: Question
199
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
6
2
1
9
2
4
3
5
6
/
/
t
l
a
c
_
a
_
0
0
2
6
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
answering with knowledge base. In ACL Con-
ference, pages 1321–1331.
Wen-tau Yih, Matthew Richardson, Chris Meek,
Ming-Wei Chang, and Jina Suh. 2016. The
value of semantic parse labeling for knowledge
base question answering. In Proceedings of the
54th Annual Meeting of the Association for
Computational Linguistics (Volume 2: Short
Papers), volume 2, pages 201–206.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
2
6
2
1
9
2
4
3
5
6
/
/
t
l
a
c
_
a
_
0
0
2
6
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
200