Common and Distinct Roles of Frontal Midline Theta and
Occipital Alpha Oscillations in Coding Temporal
Intervals and Spatial Distances
Mingli Liang1
, Jingyi Zheng2, Eve Isham1, and Arne Ekstrom1
Abstract
■ Judging how far away something is and how long it takes to
get there is critical to memory and navigation. Yet, the neural
codes for spatial and temporal information remain unclear, par-
ticularly the involvement of neural oscillations in maintaining
such codes. To address these issues, we designed an immersive
virtual reality environment containing teleporters that displace
participants to a different location after entry. Upon exiting the
teleporters, participants made judgments from two given
options regarding either the distance they had traveled (spatial
distance condition) or the duration they had spent inside the
teleporters (temporal duration condition). We wirelessly recorded
scalp EEG while participants navigated in the virtual environ-
ment by physically walking on an omnidirectional treadmill and
traveling through teleporters. An exploratory analysis revealed
significantly higher alpha and beta power for short-distance
versus long-distance traversals, whereas the contrast also re-
vealed significantly higher frontal midline delta–theta–alpha
power and global beta power increases for short versus long
temporal duration teleportation. Analyses of occipital alpha in-
stantaneous frequencies revealed their sensitivity for both spa-
tial distances and temporal durations, suggesting a novel and
common mechanism for both spatial and temporal coding. We
further examined the resolution of distance and temporal cod-
ing by classifying discretized distance bins and 250-msec time
bins based on multivariate patterns of 2- to 30-Hz power spectra,
finding evidence that oscillations code fine-scale time and dis-
tance information. Together, these findings support partially
independent coding schemes for spatial and temporal informa-
tion, suggesting that low-frequency oscillations play important
roles in coding both space and time. ■
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
3
3
1
1
2
3
1
1
1
9
6
5
6
8
2
/
/
j
o
c
n
_
a
_
0
1
7
6
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
INTRODUCTION
Background
Tracking where we are in space and time is important for
both navigation and episodic memory (Ekstrom & Isham,
2017; Eichenbaum & Cohen, 2014; Robin & Moscovitch,
2014; Tulving, 2002). However, it is not clear what neural
mechanisms are recruited for spatial and temporal coding
in humans and whether they share similar coding principles
(Ekstrom & Isham, 2017; Frassinetti, Magnani, & Oliveri,
2009; Walsh, 2003). Movement, either physical or imagined,
is a core part of both our sense of space and time and
induces robust hippocampal low-frequency oscillations
(3–12 Hz) in both rats ( Vanderwolf, 1969) and humans
(Goyal et al., 2020; Bohbot, Copara, Gotman, & Ekstrom,
2017; Jacobs, 2013; Watrous, Fried, & Ekstrom, 2011;
Ekstrom et al., 2005). Because movement typically involves
changes in both space and time, one possibility is that low-
frequency oscillations play a role in coding both variables.
Past investigations have established an important role
for hippocampal theta oscillations in coding spatial
distance in humans, but evidence is lacking for the role
1University of Arizona, 2Auburn University
© 2021 Massachusetts Institute of Technology
of neocortical theta oscillations in distance coding. For ex-
ample, hippocampal theta power increases linearly with
the amount of distance traveled in virtual reality (Bush
et al., 2017; Vass et al., 2016), cross-regional theta connec-
tivity plays a critical role in judgments of relative spatial dis-
tance (Kim et al., 2018), and theta network connectivity
differentiates distance from temporal contextual retrieval
( Watrous, Tandon, Conner, Pieters, & Ekstrom, 2013).
However, it is not clear whether neocortical theta oscilla-
tions can code spatial distance in a similar fashion and if
scalp EEG can reveal such a cortical theta distance code.
In addition, although past studies have established a role
for low-frequency oscillations in spatial distance coding,
their role in representing temporal durations remains less
clear. The medial temporal lobes of rodents are capable
of internally generating representations that track time pas-
sage (Wang, Romani, Lustig, Leonardo, & Pastalkova, 2015;
Itskov, Curto, Pastalkova, & Buzsáki, 2011; MacDonald,
Lepage, Eden, & Eichenbaum, 2011; Pastalkova, Itskov,
Amarasingham, & Buzsáki, 2008). Given the strong pres-
ence of delta and theta oscillations in medial temporal
lobes, it is possible that low-frequency oscillations contrib-
ute to temporal duration coding and that such a time code
can manifest in neocortical low-frequency oscillations as
well. Past studies have also revealed a role for cortical beta
Journal of Cognitive Neuroscience 33:11, pp. 2311–2327
https://doi.org/10.1162/jocn_a_01765
oscillations in supporting duration reproduction in
humans, such as the finding that increased alpha–beta cou-
pling strengths yield better time reproduction precision
(Grabot et al., 2019), and higher beta power recorded
with scalp EEG predicts longer reproduced durations
(Kononowicz & van Rijn, 2015). Therefore, both delta–
theta and beta band oscillations are strong potential
candidates specifically dedicated to temporal duration
coding, or both spatio-temporal coding, an issue we
seek to resolve here. Beside low-frequency power
changes, another possible oscillatory timing mechanism
is alpha frequency modulation. Alpha frequency varia-
tions manifest independently of changes in alpha power
(Samuel, Wang, Hu, & Ding, 2018), and alpha frequency
modulation has been implicated in the temporal resolu-
tion of visual perception (Cecere, Rees, & Romei, 2015;
Samaha & Postle, 2015). Nonetheless, how alpha
frequency fluctuations relate to duration timing remains
unclear and unresolved.
Objectives
In this current study, we aim at experimentally dissociating
the spatial distance and temporal duration information
available to participants. Then, we examine whether and
how low-frequency oscillations support spatial distance
and temporal duration coding as well as whether such
spatio-temporal processing shares similar coding
schemes. To address these research questions, we devel-
oped a teleportation task in an immersive and ecologically
enriched virtual environment (Figure 1), largely similar to
the experimental design in Vass et al. (2016) and capable
of disentangling spatial and temporal information. In this
task, participants entered a virtual teleporter, were pre-
sented with a black screen for a couple of seconds, and
then exited at a different location in the virtual environ-
ment. After exiting, participants were prompted to make
a binary-choice judgment regarding the distance they
were transported inside the teleporter (the spatial dis-
tance task) or how long the duration was they spent inside
the teleporter. By manipulating the distance and duration
information independently, we disentangled participants’
memory for spatial distance from that of temporal dura-
tion. This in turn allowed us to examine their neural cor-
relates separately. In addition, participants navigated
around the virtual reality by physically walking on an
omnidirectional treadmill while wearing a head-mounted
display, allowing us to study the relationship between
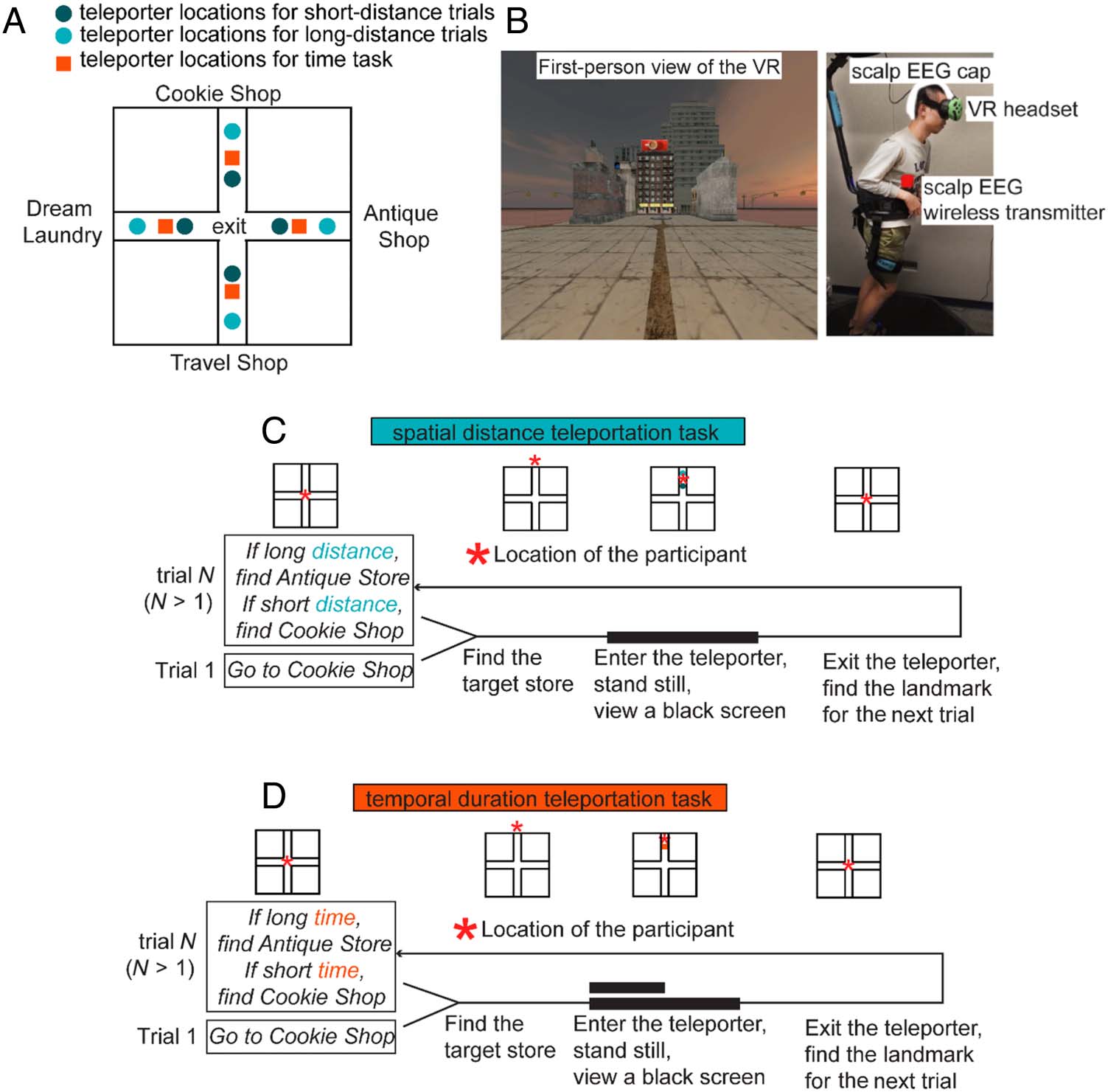
Figure 1. Spatial and temporal
teleportation tasks as well as
virtual reality ( VR) setup. (A)
Layout of the VR and the
possible entry locations of
teleporters. (B) A view of the
virtual environment and the
VR-scalp EEG setup. (C) Task
flow in the spatial task.
Participants were teleported
either a short or long distance
inside teleporters while
standing still. (D) Task
flow in the temporal task.
Participants either experienced
a short (4 sec) or long (8 sec)
duration inside teleporters
while standing still.
2312
Journal of Cognitive Neuroscience
Volume 33, Number 11
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
3
3
1
1
2
3
1
1
1
9
6
5
6
8
2
/
/
j
o
c
n
_
a
_
0
1
7
6
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
cortical oscillations and spatio-temporal processing under
more ecologically enriched conditions.
Hypotheses
We tested two primary hypotheses. First, for the within-
task difference hypothesis, we tested whether cortical
oscillatory power (2–30 Hz) and occipital alpha frequen-
cies responded differently within tasks, that is, judging
short versus long spatial distance, or short versus long
temporal durations. Second, for the between-task differ-
ence hypothesis, we tested whether such oscillatory codes
differed between tasks, that is, for spatial distance versus
temporal duration judgments, which might further
support the ideas of independent codes ( Watrous et al.,
2013) versus a common magnitude estimation mechanism
(Walsh, 2003) for spatio-temporal coding. Together, these
analyses allowed us to address to what extent the coding
for spatial distance and temporal durations involves
common versus distinct neural mechanisms.
METHODS
This study was approved by the institutional review board
at the University of Arizona, and all participants provided
informed consent. The data analyzed in this study are
available at osf.io/3vxkn/.
Participants
We tested 19 adults (7 women, 12 men) from the Tucson
community. Because this is the first investigation of its type
(scalp-recorded oscillatory correlates of spatio-temporal
processing), it is difficult to estimate exact effect sizes
needed to determine the sample size. Therefore, we
based our sample size on a previous study in which we
observed movement-related changes in low-frequency
oscillations during navigation (Liang, Starrett, & Ekstrom,
2018). Participants received monetary ($20/hr) and/or
class credit for compensation. Before testing, participants
received a virtual reality training session, which involved
30 min of walking on the omnidirectional treadmill with
a head-mounted display on. We implemented the train-
ing to screen out participants with potential susceptibility
to cybersickness.
Stimuli, Apparatus, and Virtual Reality
The virtual environment was constructed with the Unity
Engine and rendered with an HTC Vive headset. Immersive
walking experiences were simulated with an omnidirec-
tional treadmill (KAT VR Gaming Pro, KAT VR). Physical
walking motions on the omnidirectional treadmill were
translated into movements in the virtual reality.
The size of the virtual environment was 560 × 560 vir-
tual square meters. The layout of the virtual environment
was a plus (+) sign (Figure 1A), with four arms extending
from the center. Four target stores were placed at the end
of each arm (Cookie Shop, Dream Laundry, Antique Store,
and Travel Shop). Identical filler buildings were placed
along each arm.
The entry point to the teleporters was rendered as a
purple circle. When participants “collided” with teleporters
in the virtual reality, they initiated a teleportation event.
During teleportation, they stood still for a few seconds
while viewing a black screen on the head-mounted display
and eventually exited at the center of the plus maze.
Behavioral Tasks
Participants completed two tasks: a spatial distance task
and a temporal duration task. In the spatial task, the tele-
porters displaced the participants with one of the two
possible spatial distances while the teleportation duration
was kept constant. In the temporal task, the teleportation
process could last a short (4 sec) or long (8 sec) duration,
while the teleporters transported the participants a fixed
distance. Each task involved 48 trials. Both tasks involved
a navigation phase, a teleportation phase, and a judg-
ment phase.
Navigation Phase
At the beginning of a trial, participants started at the center
of the plus maze and navigated to a target store. The target
store was either specified for the first trial, or it needed to
be determined for the following trials. When arriving at the
target store, participants entered a dummy teleporter in
front of the target store. This involved showing a black
screen for 4 sec and rotating participant’s camera angle
by 180°. This dummy teleporter was set up to timestamp
participants’ arrival times on the EEG and was not used in
any subsequent analyses. If participants arrived at the
wrong store, the dummy teleporters sent participants back
to the center of the plus maze and they searched for the
store again. During the navigation phase, no teleporters
were visible except for four dummy teleporters in front
of four target stores to detect arrivals at the correct store.
Teleportation Phase
After navigating to the target store, participants then
walked up to and entered a new teleporter spawned in
front of the target store. In the spatial distance task, for
long-distance trials, the teleporters spawned 200 virtual
meters away from the center of the plus maze, and for
short-distance trials, the teleporters spawned 100 virtual
meters away from the center. In the temporal duration
task, the teleporters spawned 144 meters away from the
center. Upon entering the teleporter, participants stood
still, with the camera fading to a completely black screen
in 200 msec. They viewed the black screen for a specific
duration (spatial task: 5.656 sec, temporal task: 4 or
8 sec). Then, participants reemerged at the center of the
Liang et al.
2313
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
3
3
1
1
2
3
1
1
1
9
6
5
6
8
2
/
/
j
o
c
n
_
a
_
0
1
7
6
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
plus maze, with their camera fading from pure black to
the view standing at the center of plus maze, in 200 msec.
Judgment Phase
After exiting the teleporter, written instructions were pro-
vided to the participants by showing a billboard message
overlaid on top of the virtual reality view. The instructions
were used to decide which target store to visit for the
current trial. For the spatial task, instructions were as
follows: “If far distance, go find store A. If short distance,
go find store B.” For the temporal task, instructions were
as follows: “If long time, go find store A. If short time, go
find store B.” The instructions in the virtual reality disap-
peared when participants walked further than 55 m away
from the center of the plus maze. By asking participants to
judge spatial distance and temporal durations, we ensured
that they maintained these two task-relevant variables.
Parameters for the Behavioral Tasks
For the spatial task, the duration of viewing the black
screen was 5.656 sec for both long-distance and short-
distance trials. Short distance was defined as teleporting
100 m, and long distance was defined as teleporting
200 m (Figure 1C). For the temporal task, the distance tel-
eported was kept constant, at 141.4 m. For short-duration
trials, participants viewed 4 sec of a black screen during
teleportation, whereas for long-duration trials, they
viewed 8 sec of a black screen (Figure 1D). We selected
these parameters for our spatial and temporal tasks to
ensure the average teleportation speeds were the same
between spatial and temporal tasks: The average telepor-
tation speed for the spatial task was 1
2× (200 m/5.656 sec +
100 m/5.656 sec) ≈ 26.52 m/sec, and the average speed for
2 × (141.4 m/8 sec + 141.4 m/4 sec) ≈
the temporal task was 1
26.51 m/sec. This is because movement speed has been
shown to affect low-frequency oscillations (Caplan et al.,
2003), and thus, we attempted to control for movement
speed during teleportation.
The order of short/long trials was pseudorandomized
across the 48 trials. Short and long teleportation each
had 24 trials, with each target store visited 12 times. Two
sets of short/long orders were generated so that spatial
and temporal tasks did not use the same set of short/long
sequences. The order of task types, and the short/long
sequence sets, was counterbalanced across participants.
Before starting the main experiment, participants were
shown three examples each: short-distance teleportation,
long-distance teleportation, short temporal duration
teleportation, and long temporal duration teleportation.
Some participants repeated this practice procedure until
they reported understanding the differences between
short/long trials.
After each block of 12 trials, participants had the option
to take a short break of 3 min. When participants took a
break, we first asked participants to stand still and relax
for 90 sec on the omnidirectional treadmill while wearing
the head-mounted display and viewing a black screen.
Then, we recorded the 90-sec EEG data as the baseline.
Pooling across the spatial and temporal tasks, we
recorded, on average, 364.74 sec (SD = 183.64 sec) of
EEG baseline data.
EEG Acquisition and Preprocessing
The continuous EEG was recorded with a 64-channel
BrainVision ActiCAP system, which included a wireless
transmission MOVE module and two BrainAmp amplifiers
(BrainVision LLC). We recorded from 64 active electrodes,
placed on the scalp according to the International 10–20
system. The reference electrode was located at FCz, and
no online filter was applied to the recordings. Before the
experimenter proceeded to start the recordings, imped-
ances of all 64 electrodes were confirmed below 5 kΩ.
Preprocessing and analyses were performed with
EEGLAB (Makeig, Debener, Onton, & Delorme, 2004)
and customized codes in MATLAB (The MathWorks). No
offline rereferencing or interpolation of electrodes was
performed on the continuous data. A 1650th-order
Hamming windowed sinc finite impulse response filter
was performed for 1- to 50-Hz bandpass filtering on the
continuous data using the EEGLAB pop_newfilt() func-
tion, with a transition bandwidth of 1 Hz, the passband
edges of 1 and 50 Hz, and cutoff frequencies (−6 dB) of
0.5 and 50.5 Hz. Artifact subspace reconstruction was then
applied to the filtered continuous data, with the EEGLAB
clean_asr() function, to repair large amplitude spikes that
were 5 SDs away from the clean segments of the continuous
data.
EEG Epoching and Segmentation
The continuous EEG data were segmented using a time
window aligned with the start and end of teleportation
(not including the fade-to-black or fade-to-clear 200-msec
windows). This segmentation procedure yielded 48
epochs with a length of 5.656 sec for the spatial task and
48 epochs with a length of either 4 or 8 sec for the tempo-
ral task. No baseline correction was applied. To keep the
number of trials constant across participants, we did not
reject trials based on incorrect behavioral responses. We
did not reject trials based on a voltage threshold because
we mainly used independent component analysis (ICA) to
correct artifacts, as described below.
Artifact Correction with ICA
ICA with the infomax algorithm was performed in EEGLAB
to correct artifacts. Note that we ran ICA on the artificial
“continuous data structure” by concatenating all the data
in the distance task, time task, and resting baseline task.
Our motivation was data in those three tasks should
2314
Journal of Cognitive Neuroscience
Volume 33, Number 11
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
–
p
d
l
f
/
/
/
3
3
1
1
2
3
1
1
1
9
6
5
6
8
2
/
/
j
o
c
n
_
a
_
0
1
7
6
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
receive identical ICA correction procedure. We used an
automatic component selection procedure, ICLabel
(Pion-Tonachini, Kreutz-Delgado, & Makeig, 2019), to
avoid experimenter bias in identifying noisy components.
Components were rejected automatically if they had
labels of “Muscle,” “Eye,” “Heart,” “Line Noise,” or
“Channel Noise” if their probability was higher than 90%
for being one of those labels. On average, 8.84 (13.81%
of all components, SD = 3.91) components were rejected.
Time–Frequency Analysis
Power Measures for Delta, Theta, Alpha, and
Beta Bands
We estimated the instantaneous power during the telepor-
tation windows with 6-cycle Morlet wavelets using code
from Hughes, Whitten, Caplan, and Dickson (2012). We
sampled frequencies from 2 to 30 Hz in 20 logarithmic fre-
quency steps, that is, 2, 2.31, 2.66, 3.07, and 3.54 Hz for
delta band; 4.08, 4.70, 5.42, 6.25, and 7.21 Hz for theta
band; 8.32, 9.59, and 11.06 Hz for alpha band; and 12.76,
14.71, 16.96, 19.56, 22.56, 26.01, and 30 Hz for beta band.
Zero paddings were added to both ends of the signal. No
baseline correction was applied to the power estimates.
Logarithmic transform with a base of 10 was applied to
the obtained power values before averaging. Mean power
for each band was measured as log power averaged across
time points within the teleportation window, across fre-
quencies within a band, and across trials of interest.
Cluster-based Permutation Tests for Multiple
Comparison Correction
Cluster-based permutation tests (Maris & Oostenveld,
2007) were used to determine the statistical significance
between the mean power values for short versus long
trials. Correction for multiple comparisons was imple-
mented in Fieldtrip. First, to identify uncorrected signifi-
cant power contrasts, 64 (electrodes) × 4 (frequency
bands) = 256 Wilcoxon signed rank two-tailed tests were
performed, alpha = .05. Clusters were found by connect-
ing significant sample pairs (Electrode × Frequency
Bands) with spatiospectral adjacency (minimum neigh-
bor of channels was set to 0), and cluster-level statistics
were computed using a weighted sum (Hayasaka &
Nichols, 2004) of all the z values returned by Wilcoxon
signed rank tests within a cluster. Second, a surrogate dis-
tribution of cluster-level statistics was generated by ran-
domly shuffling condition labels 1000 times on the
subject level and retrieving the maximum cluster-level
test statistic for each permutation. Third, p values of
the observed cluster statistics were obtained by bench-
marking to the surrogate distribution. Empirical clusters
with a p value smaller than .025 (either left tail or right
tail) were reported.
We chose the nonparametric Wilcoxon signed rank tests
over the parametric paired t tests because the normality
assumption for t tests was violated. For all the power spectra
contrast we conducted, all the power spectra differences
showed a distribution different from normal distributions
(one-sample Kolmogorov–Smirnov test, alpha = .05, all
ps < .01). In the results reported in which we employed
the Wilcoxon signed rank tests, medians instead of means
were reported.
Effect Size Calculation
Cohen’s d was used as an estimate for effect sizes. For a
within-participant paired comparisons between Condition 1
and Condition 2, we estimated the effect sizes using the
following formula:
ð
d ¼ mean Condition 1
Þ
std Condition 1 − Condition 2
ð
Þ
Þ − mean Condition 2
ð
Frequency Measures for Alpha (8–12 Hz) Band
To estimate alpha frequency, we used a frequency sliding
technique (Cohen, 2014) to estimate the alpha frequency
fluctuations. We first used a 125th-order finite impulse re-
sponse 8- to 12-Hz bandpass filter (using MATLAB firls()
function) on the segmented EEG data, with a transition
bandwidth of 1.2 and 1.8 Hz, the passband edges of 8
and 12 Hz, and cutoff frequencies (−6 dB) of 7.12 and
12.98 Hz. We then employed the Hilbert transform on
the filtered segmented EEG data to obtain the instanta-
neous phase estimates of alpha oscillations during tele-
portation windows. Instantaneous frequencies at time
point t were estimated as
φ
t
− φ
2π
where f is the estimated instantaneous alpha frequency, φ
is the estimated phase, and s is the EEG sampling rate.
Here, we defined and estimated the instantaneous
frequencies based on how many cycles the phase of alpha
oscillations could go through in 1 sec. Then, to smooth
the frequency estimates, we applied a 10th-order median
filter. We dropped the frequency estimates for the first
100 msec and last 100 msec for every trial because of
potential inaccurate estimates of frequencies at the
edges of signal.
ft ¼
(cid:2) s
(1)
t−1
We selected the following occipital electrodes to ana-
lyze their alpha frequency based on two criteria: visible
alpha prevalence in the raw traces and an identical cluster
of occipital electrodes to what we used in our past study
(Liang et al., 2018). These 18 electrodes corresponded to
Pz, P3, P7, O1, Oz, O2, P4, P8, P1, P5, PO7, PO3, POz,
PO4, PO8, P6, P2, and Iz.
Alpha frequency for each behavioral task is measured
as alpha frequency estimates averaged across time points
during the windows of interest, averaged across elec-
trodes of interest, and averaged across trials of interest.
To compare the alpha frequency variations between
Liang et al.
2315
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
3
1
1
2
3
1
1
1
9
6
5
6
8
2
/
/
j
o
c
n
_
a
_
0
1
7
6
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
two conditions, we submitted the averaged alpha fre-
quencies of 19 participants to two-tailed Wilcoxon signed
rank tests (alpha = .05). Six Wilcoxon signed rank tests
were conducted, and the p values reported in the
Results section were false discovery rate (FDR) corrected
(Groppe, 2021; Benjamini & Yekutieli, 2001), with the
FDR set to 0.05.
Classification Analyses
Binary Classification of the Duration/Distance Types
To further confirm the role of frontal midline delta–theta
oscillations in spatial and temporal judgments, a binary
support vector machine (SVM) classifier was used to de-
code the types of teleportation using power of delta,
theta, alpha, and beta bands, averaged at specific elec-
trodes. For delta power, theta power, and alpha power,
four electrodes around the frontal midline region were se-
lected (Fz, FC1, Cz, and FC2). For beta power, all available
electrodes (64 electrodes) were chosen. Binary SVM clas-
sifiers were implemented in MATLAB, with the function
fitcsvm(), with the kernel function set up as linear.
Three decoding tasks on a within-participant level were
implemented: (1) decoding whether the trial was from
teleportation trials involving short or long distance, (2) de-
coding whether the trial was from short-duration trials or
the 4- to 8-sec portions of long-duration trials in the time
task, and (3) decoding whether the trial was from short-
duration trials or the 0- to 4-sec portions of long-duration
trials. The ratio of train–test split for each iteration was 67–
33%. The training–testing sampling procedure was reiter-
ated 1000 times for each participant and for each decoding
task. An accuracy percentage score was calculated using
the predicted and actual labels of the testing data. The final
decoding accuracy scores for 19 participants were submit-
ted to two-tailed Wilcoxon signed rank tests, against the
null hypothesis that the decoding accuracy was 50%. In to-
tal, 12 tests were conducted in the binary classification
analysis, and the p values were FDR corrected (Groppe,
2021; Benjamini & Yekutieli, 2001), with the FDR set to
0.05.
In addition, we implemented a between-task classifier
(space vs. time tasks) on a between-subject level. We com-
bined trials from the space task and the time task across
19 participants, resulting in a data set of 19 × 2 × 48 =
1824 trials. Then, we tested whether we could successfully
decode the task labels using the 912-trial data set. By per-
forming the classification on an between-subject level
(with the task orders counterbalanced), we avoided the
possible confound of systematic drift over the course of
experiment, which could have affected our decoding ac-
curacy because of the blocked nature of the spatial versus
temporal judgments in our design (Benwell et al., 2019).
For features used for training classifiers, we employed the
2- to 30-Hz power spectra from 64 electrodes averaged
within each trial, resulting in 20 × 64 = 1280 features.
The ratio of train–test split for each iteration was 67–33%.
The train–test split was repeated 100 times. To determine
the statistical significance of decoding accuracy, we submit-
ted the accuracies from 100 iterations to a two-tailed
Wilcoxon signed rank test against the null hypothesis
of 50%.
Fine-Scale Time Decoding Analyses
To examine whether continuous time codes were pres-
ent in the scalp EEG signal, SVM classifier was trained
to decode times beginning at the onset of teleportation
using the 2- to 30-Hz power spectra from 64 electrodes.
The SVM algorithm was implemented in MATLAB using
the fitcecoc() function, with coding style as onevsall
and other parameters as default.
Time bins of 250 msec were extracted by discretizing 2-
to 30-Hz power estimates. The size of time bins was cho-
sen as the same one used by Bright et al.(2020). Therefore,
short/long-distance teleportation trials (5.656 sec) yielded
22 bins (22 × 250 msec = 5.5 sec, the last 156 msec of data
were dropped), short temporal duration trials (4 sec)
yielded 16 bins, and long temporal duration trials (8 sec)
yielded 32 bins. For the resting baseline data (90 sec long
for each resting session), we broke 90 sec into continuous
segments of 4 sec, and from there, each 4 sec of baseline
data were segmented into 16 bins.
Power estimates within each time bin were averaged
over time, and the resulting power spectra within each
bin were used to trained classifiers. The number of fea-
tures was 20 frequencies × 64 electrodes = 1280 fea-
tures. For each classification iteration, train–test split
ratio was 75–25%. To increase the independence be-
tween training sets and testing sets, a consecutive block
of trials was reserved as the testing data, and the rest of
data was used for training. Given our way of splitting the
data, we were able to reiterate the classification proce-
dure for a limited number of times: For the distance task,
the procedure was repeated 37 times; for the short-
interval and long-interval trials, 19 times; and for the
baseline task, 16 times.
We calculated the accuracy score by summing how many
correct predictions were made in 100 iterations for each
time-bin label. The accuracy scores were then averaged
across all iterations, yielding a final accuracy score for each
participant. Given that number of time bins was different
across the distance task, time task, and baseline task,
comparisons between them would be difficult. We stan-
dardized the accuracy scores as the accuracy ratios by divid-
ing them against the chance-level performance (ratios =
classification accuracy
). For the distance task time decoder,
chance level
the chance level was 1/22 = ∼4.55%; for decoding time
in short temporal duration trials, the chancel level was
1/16 = 6.25%; for decoding time in long-duration trials,
the chance level was 1/32 = 3.125%; and for decoding time
in the baseline data, the chance level was 1/16 = 6.25%.
To test whether we successfully decoded fine-scale
temporal information above chance, we submitted the
2316
Journal of Cognitive Neuroscience
Volume 33, Number 11
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
3
1
1
2
3
1
1
1
9
6
5
6
8
2
/
/
j
o
c
n
_
a
_
0
1
7
6
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
standardized accuracy ratios for 19 participants to a two-
tailed Wilcoxon signed rank test against the null hypoth-
esis that the accuracy ratios were different from 1. Ten
signed rank tests were performed for this hypothesis,
and the p values were FDR corrected (Groppe, 2021;
Benjamini & Yekutieli, 2001), with the FDR set to 0.05.
To visualize the time decoder performance and the
posterior probability distribution, we calculated a n × n
(n = the number of time bins) matrix to summarize the
time decoder prediction outputs. For element (i, j) in the
matrix, the value represented the probability of a Time
Bin #i was predicted as Time Bin #j.
Calculation of Absolute Decoding Errors in the
Fine-scale Time Analysis
n
P
1 pi (cid:2) i−j
j
After retrieving the posterior probability distribution of
decoding responses (the n × n matrix, where n is the
number of bins), we calculated the absolute decoding
errors for each time bin, using the following equation:
j (cid:2) binSize, where n is the number
errors ¼
of bins, i are the possible decoder responses, pi is the
posterior probability for response i, the ground-truth
bin index is j, and binSize is the size of time bin. After
obtaining the decoding error curve (as a function of
the ground-truth bin labels), we fitted the error curve
with linear regression. The p values of the slope were re-
ported in the Results section.
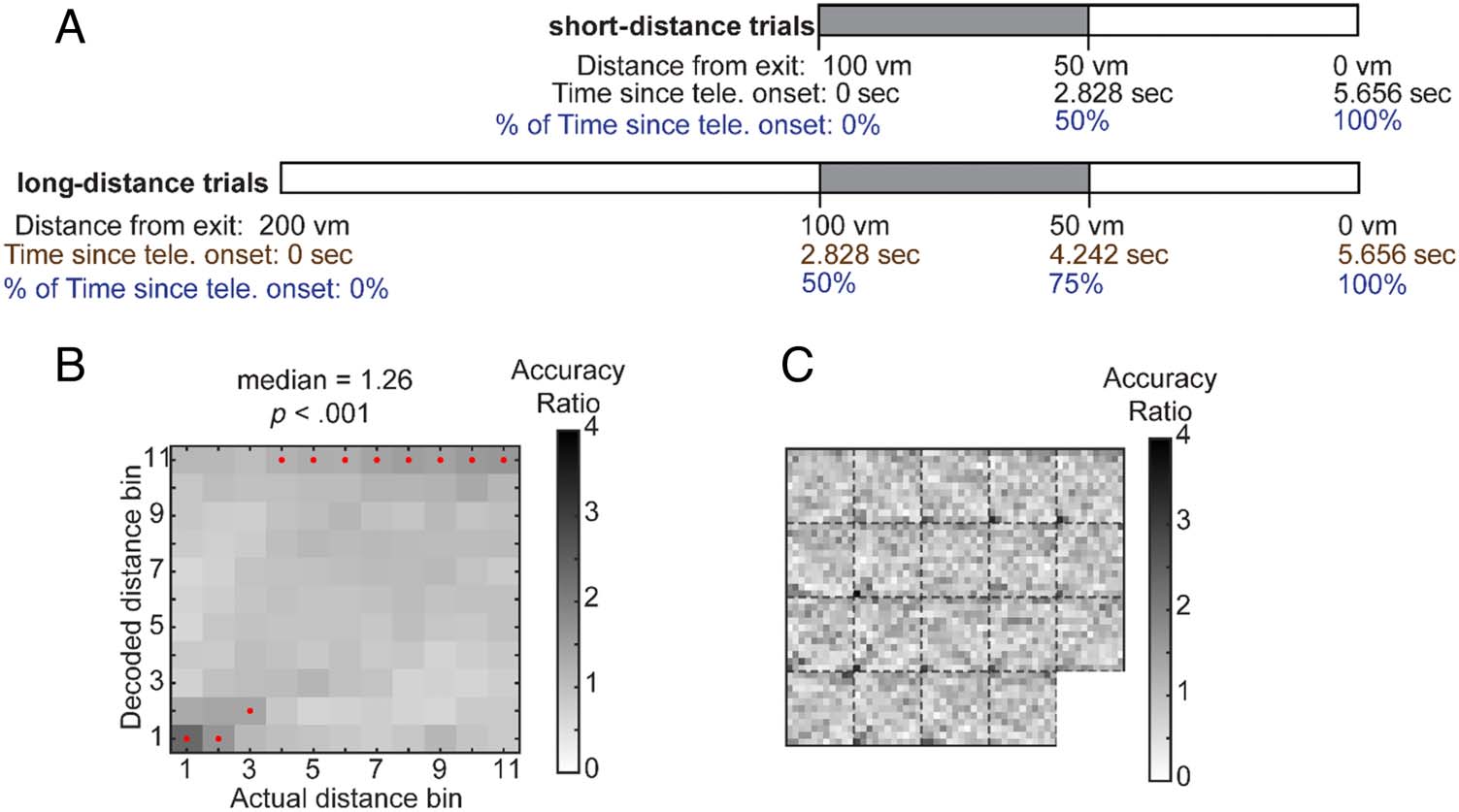
Fine-Scale Distance Decoding Analyses
To examine whether continuous distance codes were also
present in the scalp EEG power, we discretized data from
spatial distance teleportation trials into multiple small
“distance” bins and trained SVM classifiers with 2- to
30-Hz power spectra averaged within each distance bin.
To avoid the confounded decoding of fine-scale
distance and time, we selected data with only maximal
overlap in conceptual distance updating but with zero
overlap in the temporal dimension. We selected the
0- to 2.828-sec portions of short-distance trials and the
2.828- to 4.242-sec portions of long-distance trials. Although
they did not overlap in time ranges, they conceptually cov-
ered the same range of spatial distance (see Figure 6A).
After the data selection, the 2- to 30-Hz power series of both
short- and long-distance trials were discretized into 11 dis-
tance bins, with each distance bin covering 4.42 m of dis-
tance. For short-distance trials, each distance bin occupied
248 msec (with a sample rate of 500 Hz, 248 msec = 124
sampling points), and for long-distance trials, each distance
bin occupied 248/2 = 124 msec (124 msec = 62 sampling
points). Power estimates within each time bin were
averaged. We trained multiclass SVM classifiers with 1280
power spectra features (64 electrodes × 20 frequency).
For each classification iteration, 75% of the trials were
selected as the training data and 25% of the trials were
reserved as the testing data. To increase the independence
between training sets and testing sets, a consecutive block
of trials was reserved as the testing data, and the rest of
data was used for training. We were able to reiterate the
classification procedure 37 times. The resulting classifica-
tion accuracy ratios were averaged across the 37 iterations
for each participant, and the 19 participant scores were
submitted to two-tailed Wilcoxon signed rank tests, testing
whether they were significantly different than 1.
RESULTS
Participants Correctly Judged Spatial and Temporal
Teleportation Durations with High Accuracy
Participants performed well above chance in both the
spatial and temporal teleportation tasks. For the spatial
task, of 48 trials, participants on average made 0.68 errors
(SD = 0.89) in judging how far the distance they traveled
at the first attempt. For the temporal task, of 48 trials,
participants on average made 1.79 errors (SD = 2.51)
in judging how long they spent inside teleporters. On av-
erage, participants finished the spatial task within 53.46
(SD = 12.73) min and the temporal teleportation task
within 52.35 (SD = 9.24) min.
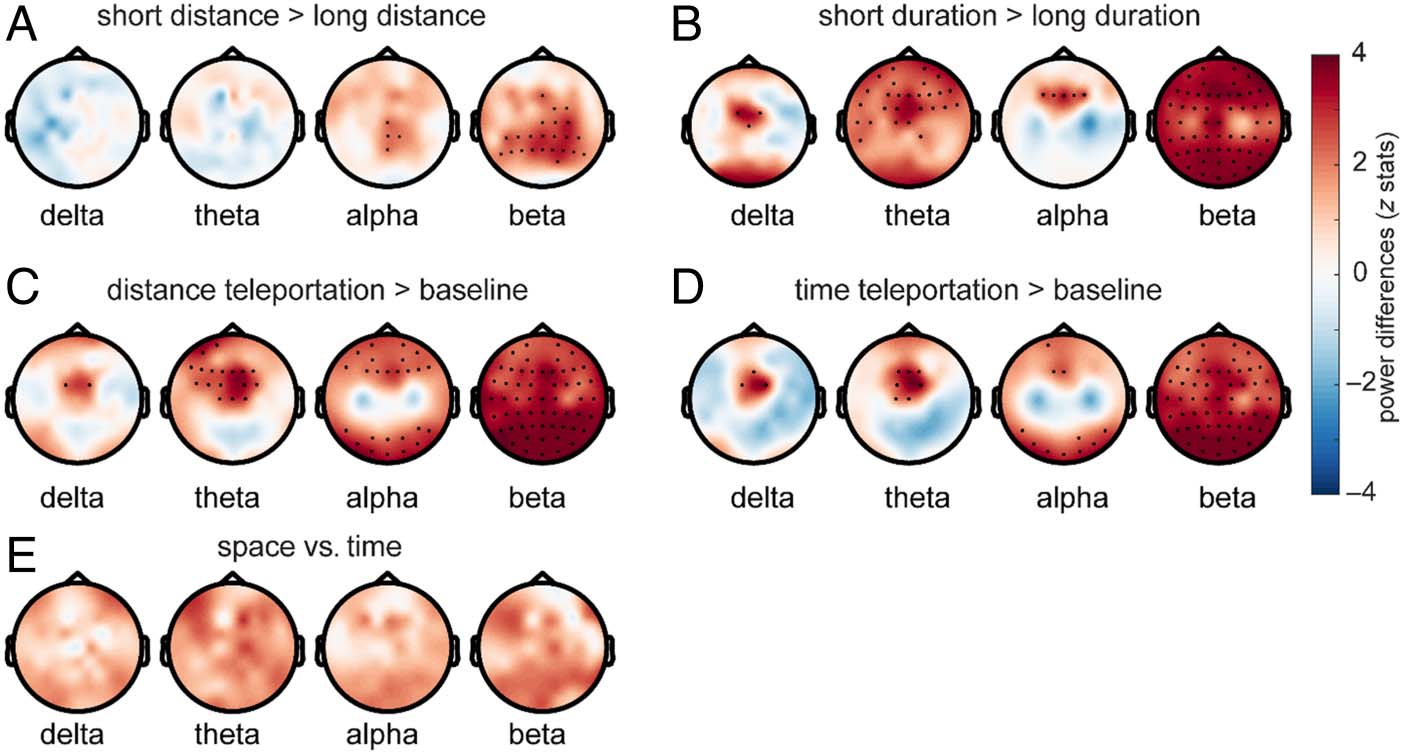
Within-Task Comparisons: Longer Distances
Traveled Associated with Decreases in Alpha and
Beta Power Compared to Shorter
Distance Traversals
We first tested the within-task difference hypothesis in
the spatial distance task. We compared delta, theta,
alpha, and beta power between short-distance and long-
distance teleportation trials and used a cluster-based per-
mutation test for multiple comparison correction. When
comparing short-distance versus long-distance trials, the
permutation test returned a cluster with a p value of .015.
For short-distance trials, we found higher alpha power
at central electrodes (Pz, CP2, Cz, and CPz; Figure 2A;
Cohen’s d = 0.55; averaged log10 alpha power for short
distance: median ± SD = 4.99 ± 0.34, averaged log10
alpha power for long distance: median ± SD = 4.91 ±
0.32) and higher beta power over central–posterior elec-
trodes (Cohen’s d = 0.91; averaged beta power for short
distance: median ± SD = 4.51 ± 0.26, averaged beta
power for long distance: median ± SD = 4.50 ± 0.26).
These findings support a possible role for alpha and beta
power changes in spatial distance coding.
Within-Task Comparisons: Longer Temporal
Durations Were Associated with Frontal
Delta–Theta–Alpha Power and Global Beta
Power Decreases Compared to Shorter
Temporal Durations
We then tested the within-task difference hypothesis for
temporal duration teleportation by comparing the power
Liang et al.
2317
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
3
1
1
2
3
1
1
1
9
6
5
6
8
2
/
/
j
o
c
n
_
a
_
0
1
7
6
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 2. Oscillatory
fluctuations present during
spatial distance and temporal
duration teleportation. (A)
Short-distance teleportation
trials resulted in increased
alpha and beta power compared
to long-distance trials. (B)
Short-duration teleportation
trials resulted in increased
frontal midline delta–theta–
alpha power increases and
global beta power increases
compared to long-duration
trials. (C, D) Spatio-temporal
coding was associated with
frontal delta–theta, frontal and
posterior alpha, and global beta
power increases compared to
resting baseline. (E) No power
differences were observed
within the canonical frequency bands between the distance task and the time task. Black dots are electrodes considered significant after multiple
comparison correction. Colors represent the Wilcoxon signed rank tests’ z statistics.
spectra between short-duration and long-duration trials
(Figure 2B). The cluster-based permutation test returned
a positive cluster ( p < .001). This effect was most pro-
nounced over frontal midline electrodes for delta power
(Cohen’s d = 1.03; short duration: median ± SD = 4.47 ±
0.22, long duration: median ± SD = 4.42 ± 0.23), over
frontal electrodes for theta power (Cohen’s d = 0.97;
short duration: median ± SD = 4.86 ± 0.19, long dura-
tion: median ± SD = 4.83 ± 0.20), and over frontal elec-
trodes for alpha power (Cohen’s d = 0.98; short duration:
median ± SD = 4.35 ± 0.24, long duration: median ±
SD = 4.32 ± 0.25). We also found global beta power
changes (Cohen’s d = 1.63; short duration: median ± SD =
4.59 ± 0.25, long duration: median ± SD = 4.55 ± 0.26).
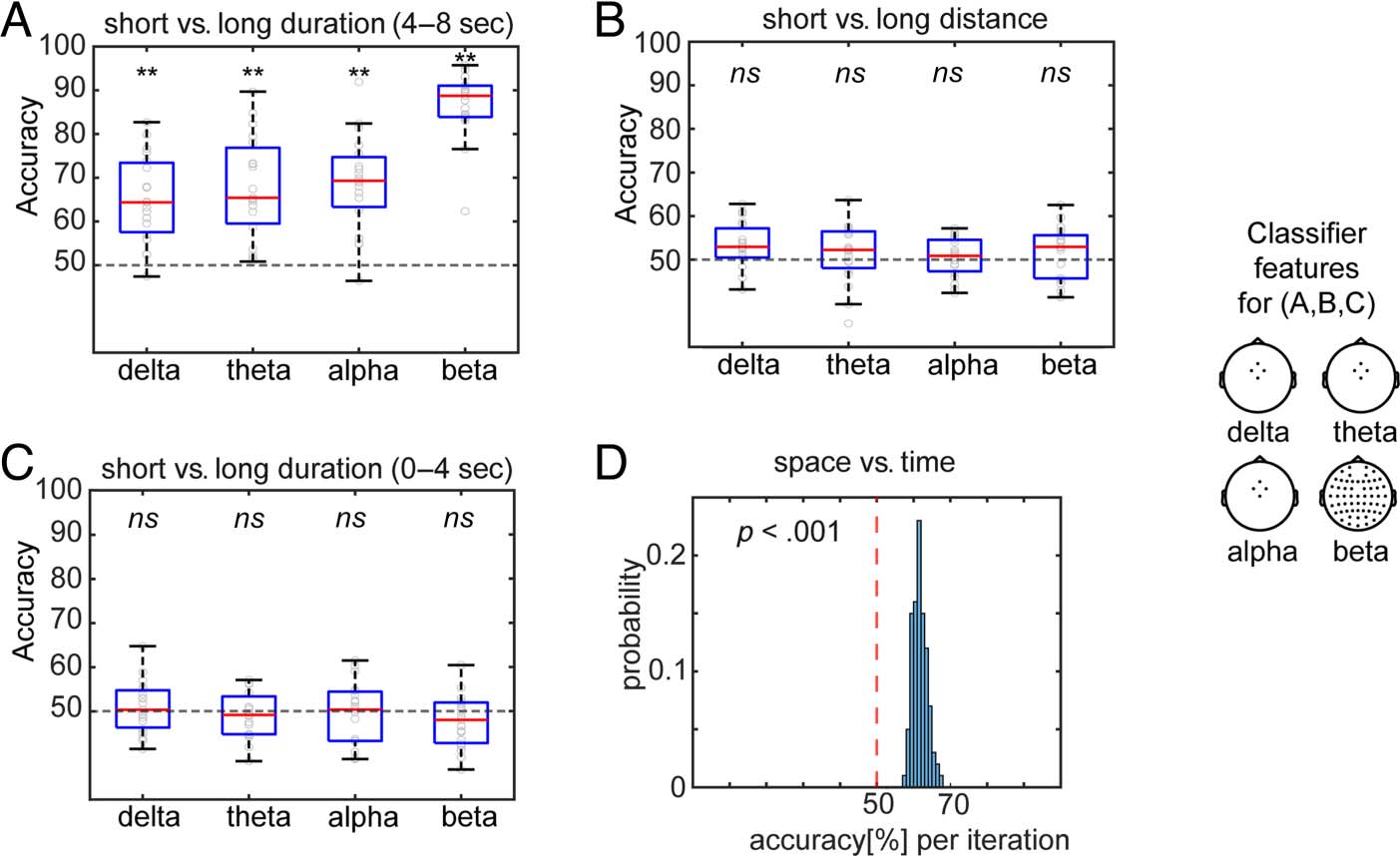
To further confirm the role of frontal midline theta os-
cillations in duration timing, we trained a binary classifier
to decode types of temporal durations in the teleporter
(Figure 3). We successfully decoded whether a trial was a
short duration trial or the 4- to 8-sec portion of a long-
duration trial (Figure 3A; classifiers trained with frontal
midline delta power: median ± SD = 64.40 ± 9.89%,
frontal midline theta: median ± SD = 65.42 ± 11.68%,
frontal midline alpha: median ± SD = 69.34 ± 10.89%,
global beta: median ± SD = 88.76 ± 7.51%; all pcorrected =
.002). However, we could not decode the distance traveled
in the teleporter significantly above chance (Figure 3B;
classifiers trained with frontal midline delta power:
median ± SD = 52.93 ± 5.09%, pcorrected = .06; theta:
Figure 3. Within-task (A–C) and
between-task (D) decoding using
power as features. (A) Different
durations (short vs. long) could
be decoded from frontal delta,
theta, alpha, and global beta
power separately. (B) Different
distances (short vs. long) could
not be decoded from frontal
midline delta–theta, alpha, or
global beta power. (C) As a
control analysis, decoders were
not able to differentiate whether a
trial was from short-duration trials
or from the 0- to 4-sec segments
of long-duration trials. (D) When
aggregating trials across
participants, we were able to
decode whether a trial was in the
space or time condition based on
the single-trial multivariate
patterns of power. The histogram
of classification accuracies based
on 100 iterations is shown.
**All pFDR = .002. Each circle
represents a participant in A–C.
2318
Journal of Cognitive Neuroscience
Volume 33, Number 11
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
3
1
1
2
3
1
1
1
9
6
5
6
8
2
/
/
j
o
c
n
_
a
_
0
1
7
6
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
median ± SD = 52.26 ± 6.77%, pcorrected = 1; alpha:
median ± SD = 50.88 ± 4.47%, pcorrected = 1; beta: median ±
SD = 52.94 ± 5.95%, pcorrected = 1), suggesting frontal
midline delta–theta–alpha power and global beta power
alone contained sufficient information regarding the tem-
poral duration being coded but not the distance traveled.
As an additional control analysis, we trained the same
classifier with frontal midline delta–theta–alpha power
and global beta power to discriminate the 0- to 4-sec
portion of the long-duration trials from the short-duration
trials. This served as a control because participants could
not have known what types of durations they experienced
until they crossed the 4-sec threshold within the telepor-
ter. Indeed, the classifier was not able to decode whether
the trials were short-duration trials (4 sec) or the 0- to 4-sec
portion of long-duration trials (Figure 3C; delta: 50.33 ±
5.88%, theta: 49.16 ± 5.33%, alpha: 50.34 ± 7.25%, beta:
48.04 ± 5.94%; all pcorrected > .05). Together, these find-
ings support a general role for global beta power changes
in spatio-temporal processing, and a unique role of frontal
midline delta–theta–alpha oscillations, in coding temporal
durations.
Between-Task Comparisons: Spatial and Temporal
Teleportation Did Not Induce Focal Differences in
Delta, Theta, Alpha, or Beta Power
To test our between-task hypothesis regarding differ-
ences in oscillatory codes between spatial and temporal
tasks, we compared the power spectra among spatial,
temporal, and baseline tasks (Figure 2C and D).
For both contrasts (distance task > baseline, time task >
baseline), the cluster-based permutation tests returned sig-
nificant positive cluster with p values < .001. The effect was
most pronounced over frontal midline electrodes for delta
power (Cohen’s d for distance vs. baseline: 0.60, distance–
baseline: median ± SD = 0.12 ± 0.27; Cohen’s d for time
vs. baseline: 0.77, time–baseline: median ± SD = 0.12 ±
0.15), over frontal electrodes for theta power (Cohen’s
d for distance vs. baseline: 1.04, distance–baseline: medi-
an ± SD = 0.07 ± 0.07; Cohen’s d for time vs. baseline:
1.01, time–baseline: median ± SD = 0.05 ± 0.08), and
over frontal and occipital electrodes for alpha power
(Cohen’s d for distance vs. baseline: 0.82, distance–
baseline: median ± SD = 0.20 ± 0.18; Cohen’s d for time
vs. baseline: 0.76, time–baseline: median ± SD = 0.10 ±
0.21). We also found widespread increases in beta power
(Cohen’s d for distance vs. baseline: 1.81, distance–
baseline: median ± SD = 0.16 ± 0.08; Cohen’s d for time
vs. baseline: 1.80, time–baseline: median ± SD = 0.14 ±
0.07). These findings suggest that, compared to a passive
baseline, participants showed distinct oscillatory profiles
while maintaining spatio-temporal information during
the teleportation tasks, which was consistent with their
high performance in the behavioral tasks.
task (Figure 2E). The cluster-based permutation test did
not reveal any clusters with a p value lower than threshold.
This suggests that the spatial and temporal teleportation
tasks did not differ in overall power when compared
within each of the canonical frequency bands (delta,
theta, alpha, and beta bands).
Between-Task Comparison: Successful Decoding of
Spatial and Temporal Trials Based on Single-Trial
Multivariate Patterns of Power
It could be possible that spatial and temporal coding did
not differ in terms of power changes in focal frequency
bands; instead, spatio-temporal coding might differ in
the multivariate patterns across electrodes and frequen-
cies in a manner that generalized across participants.
To test this possibility, we used multivariate power fea-
tures to classify whether trials were from the spatial or
temporal task. The classifier revealed above-chance clas-
sification of task labels (Figure 3D; median = 61.46%, SD
over 100 iterations = 1.97%; Wilcoxon signed-rank test,
z = 8.68, p < .001). These findings suggest the single-
trial multivariate patterns significantly differed between
spatial and temporal tasks in a manner that generalized
across participants. The findings together support the no-
tion of a partially independent space–time code.
Alpha Frequency Modulation: A Common
Mechanism for Spatial and Temporal Judgments
We hypothesized that occipital alpha frequency modula-
tion could be an additional form of distance and duration
coding in our teleportation task, as suggested by Cao and
Händel (2019) and Samaha and Postle (2015). To test this
idea, we first assayed whether there were differences in
occipital alpha frequencies during the teleportation tasks
compared to the task-irrelevant resting baseline. Both
spatial and temporal teleportation tasks showed faster oc-
cipital alpha frequencies than the baseline (Figure 4A;
spatial task: median ± SD = 10.23 ± 0.30 Hz, temporal
task: 10.13 ± 0.25 Hz, baseline: 10.00 ± 0.26 Hz; spatial
task vs. baseline: Wilcoxon signed rank test, z = 3.74,
pcorrected = .001; temporal task vs. baseline: z = 3.78,
pcorrected = .001). These findings suggest that occipital
alpha frequencies were significantly altered during
spatio-temporal coding compared to a resting baseline.
Second, we asked whether occipital alpha frequency
differed between the spatial and temporal tasks.
Comparing across all participants, the spatial distance
task showed significantly faster occipital alpha compared
to the temporal teleportation task (Figure 4A; z = 2.62,
pcorrected = .026). The findings of differences in alpha fre-
quencies between spatial and temporal teleportation
tasks might reflect another distinction in oscillatory codes
for spatio-temporal information.
Next, we asked whether the power spectra profiles dif-
fered between the spatial distance and temporal duration
Therefore, we asked whether the observed occipital
alpha frequencies were sensitive to distance and duration
Liang et al.
2319
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
3
1
1
2
3
1
1
1
9
6
5
6
8
2
/
/
j
o
c
n
_
a
_
0
1
7
6
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4. Occipital alpha
frequency modulation as a
shared mechanism for both
spatial and temporal coding.
Medians across participants
are shown under the box
plots. (A) The spatial and
temporal tasks showed faster
alpha frequency than baseline,
and the distance task showed
faster alpha frequency than
the time task. (B) In the
distance task, traveling a
short distance resulted in
faster alpha than traveling
a long distance. (C) In the
time task, short-duration
trials resulted in faster alpha
than long-duration trials.
(D) No differences were
found between short-duration
trials and the 0- to 4-sec
portion of long-duration
trials. (E) Histograms of alpha frequencies at 18 occipital electrodes during the distance task. Data from three example
participants were shown. **pFDR < .01, *pFDR < .05. ns = not significant.
information. We first compared the averaged alpha fre-
quency at occipital electrode sites for short- versus
long-distance trials. When comparing across participants,
results revealed that occipital alpha oscillations were of
higher frequency for short-distance trials compared to
long-distance trials (Figure 4B; short distance: median ±
SD = 10.26 ± 0.29 Hz, long distance: 10.20 ± 0.30 Hz;
z = 3.38, pcorrected = .003). Occipital alpha frequency also
varied between short and long temporal duration trials.
Occipital alpha frequency was faster for short-duration
trials than the 4- to 8-sec portion of long-duration trials
(Figure 4C; short temporal duration: median ± SD = 10.28 ±
0.24 Hz, long temporal duration (4–8 sec): 10.00 ± 0.31 Hz;
z = 3.58, pcorrected = .002).
As a control analysis, we tested whether there were dif-
ferences in occipital alpha frequencies for short-duration
trials versus the 0- to 4-sec portion of long-duration trials.
The alpha frequencies did not differ (Figure 4D; short
temporal duration: median ± SD = 10.28 ± 0.24 Hz, long
temporal duration (0–4 sec): 10.24 ± 0.23 Hz; z = 0.76,
pcorrected = .1). Together, these findings support alpha
frequency modulation as a shared mechanism for coding
spatial distance and temporal durations.
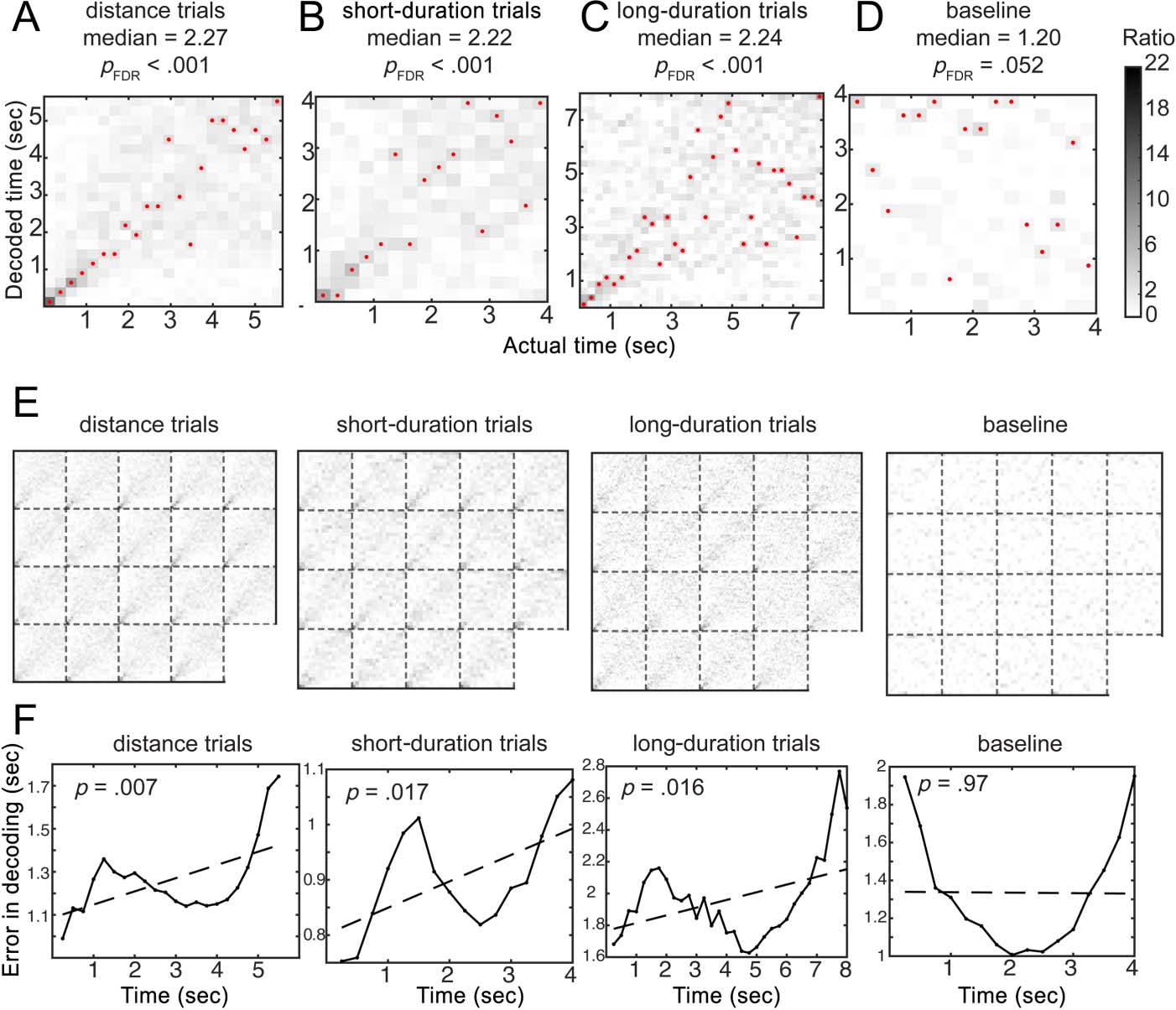
Fine-Scale Temporal Information Was Decoded
From Multivariate Patterns of 2- to 30-Hz
Power Spectra
We next tested whether temporal duration codes might
be present in the EEG data at a finer scale, inspired by
Bright et al. (2020), for example, at the level of 250 msec.
Therefore, we trained classifiers on 2- to 30-Hz power to
decode times since onset of teleportation. We were able
to decode fine-scale temporal information from the dis-
tance teleportation trials significantly above chance
(Figure 5A; accuracy: median ± SD = 10.34 ± 1.32%, ac-
curacy ratios: median ± SD = 2.27 ± 0.29; Wilcoxon
signed rank test, z = 3.82, pcorrected < .001), from the
short-duration trials (Figure 5B; accuracy: median ±
SD = 13.87 ± 1.67%, accuracy ratios: median ± SD =
2.22 ± 0.27; z = 3.82, pcorrected < .001), and from the
long-duration trials as well (Figure 5C; accuracy: median ±
SD = 6.99 ± 0.95%, accuracy ratios: median ± SD = 2.24 ±
0.30; z = 3.82, pcorrected < .001). As a control analysis, we
applied the fine-scale time decoder for data obtained in
the baseline task. The decoder was able to decode time
from the baseline data marginally better than chance after
multiple comparison correction (accuracy: median ± SD =
7.50 ± 1.87%, accuracy ratios: median ± SD = 1.20 ± 0.30;
z = 2.37, pcorrected = .052). However, time decoding
performance for the baseline task was significantly worse
than those in the temporal and distance tasks (baseline <
distance task, baseline < short duration trials, baseline <
long duration trials: all zs = −3.82, ps < .001). These
findings suggest the intriguing possibility that fine-
scaled temporal codes are embedded in low-frequency
oscillations.
We note that, after entry into the teleporter, partici-
pants exhibited a P300-like ERP response (Polich, 2007)
at the Cz electrode. Therefore, we repeated the fine-
scaled time classification analyses, with the grand-
averaged EEG traces subtracted from every trial. After
removing the grand ERP responses, we were still able
to successfully decode fine-scale temporal information
from the distance teleportation trials (accuracy: median ±
SD = 11.08 ± 1.29%, accuracy ratios: median ± SD =
2.44 ± 0.28; Wilcoxon signed rank test, z = 3.82,
pcorrected < .001), from the short-duration trials (accuracy:
median ± SD = 15.52 ± 1.93%, accuracy ratios: median ±
SD = 2.48 ± 0.31; z = 3.82, pcorrected < .001), and from
2320
Journal of Cognitive Neuroscience
Volume 33, Number 11
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
3
1
1
2
3
1
1
1
9
6
5
6
8
2
/
/
j
o
c
n
_
a
_
0
1
7
6
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
the long-duration trials (accuracy: median ± SD = 8.22 ±
1.08%, accuracy ratios: median ± SD = 2.63 ± 0.35; z =
3.82, pcorrected < .001).
Furthermore, to exclude the possible contribution of
movement-related artifact in early onsets of a trial, we
removed the first second of teleportation epochs and
repeated the fine-scale time decoding analyses. We were
again able to successfully decode fine-scale time informa-
tion from the distance teleportation trials above chance
(accuracy: median ± SD = 8.80 ± 1.05%, accuracy ratios:
median ± SD = 1.58 ± 0.19; z = 3.82, pcorrected < .001),
from the short-duration trials (accuracy: median ± SD =
12.65 ± 1.97%, accuracy ratios: median ± SD = 1.52 ±
0.24; z = 3.82, pcorrected < .001), and from the long-duration
trials above chance as well (accuracy: median ± SD =
5.67 ± 0.89%, accuracy ratios: median ± SD = 1.59 ± 0.25;
z = 3.82, pcorrected < .001).
absolute decoding errors for each time bin and fitted the
error curves with a linear regression model (Figure 5F).
Results of the linear regression fitting indicated that the
decoding errors were significantly larger for later time bins;
this effect was found in the distance trials, short-duration
trials, and long-duration trials, but not in the baseline task
(for distance trials: slope [estimate, standard error (SE)] =
[0.06, 0.02], t = 3.03, p = .007; for short-duration trials:
slope [estimate, SE] = [0.05, 0.02], t = 2.70, p = .017; for
long-duration trials: slope [estimate, SE] = [0.05, 0.02],
t = 2.56, p = .016; for the baseline task: slope [estimate,
SE] = [−0.003, 0.07], t = −0.04, p = .97). The results
suggest that the fine-scale temporal information revealed
by the decoders are aligned with the human behavioral
findings of increased variability for longer reproduced
durations (Rakitin et al., 1998; Ivry & Hazeltine, 1995).
We discuss the implications in the Discussion section.
Decoding Errors Linearly Increased as Time
Progressed Forward
Fine-Scale Distance Information Was Also Present
in Multivariate Patterns of 2- to 30-Hz Power
We noticed a qualitative pattern that the decoding re-
sponses were less precise as time progressed forward in
the posterior probability distribution of time decoding
responses. To quantitatively test this, we calculated the
Given our findings with fine-scale temporal information,
we also tested whether fine-scale distances could be de-
coded using the same approach. Indeed, we found that
the classifiers were able to decode fine-scale distance
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
Figure 5. Fine-scale temporal
information during the
teleportation can be decoded
from scalp EEG 2- to 30-Hz power
spectra. Heat maps visualize the
posterior probability
distributions of the decoder
responses. High classification
accuracy is indicated by dark
colors on the diagonal. (A–D)
Fine-scale timing information can
be decoded from 2- to 30-Hz
power in the distance task and
time task, with accuracies
significantly higher than chance
level and higher than the baseline
task. Medians of accuracy ratios
across 19 participants were
reported. Units of the color bar
are accuracy ratios. Red dots
mark the highest posterior
probability in decoder responses.
(E) Decoder response
probability distributions from
19 participants. Each subsquare
displays the time decoding heat
map from one participant.
(F) Decoding errors linearly
increased as time progressed in
the spatial and temporal tasks,
but not in the baseline task.
Dashed lines indicate the linear
regression fitting models of
the decoding errors.
/
/
3
3
1
1
2
3
1
1
1
9
6
5
6
8
2
/
/
j
o
c
n
_
a
_
0
1
7
6
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Liang et al.
2321
Figure 6. Fine-scale
distance information during
teleportation (tele.) can be
decoded from multivariate
power patterns. (A) Decoding
fine-scale distance information
while taking care of the
temporal confound. To
minimize the dependence
between temporal and distance
information, we selected data
(the shaded portions) from
both short-distance trials and
long-distance trials that had
zero overlaps in the temporal
dimension. Red dots mark the
highest posterior probability in
decoder responses. (B)
Fine-scale distance information
could be decoded in the
distance task. Heat maps
visualize the posterior
probability distribution of the
decoder responses. (C) Posterior probability distributions plotted for each participant.
Each subsquare displays the distance decoding heat map from a participant.
information from the spatial task (Figure 6A; accuracy:
median ± SD = 11.45 ± 1.60%, accuracy ratios: median ±
SD = 1.26 ± 0.18; Wilcoxon signed rank test, z = 3.70, p <
.001). The findings of the fine-scale distance code support
the possibility that participants linearly updated their
spatial position inside teleporters. The demonstrations of
both fine-scale distance and temporal codes in the multi-
variate power spectra patterns reveal another common
aspect that exists in spatio-temporal coding.
DISCUSSION
In the current study, we tested whether neural oscilla-
tions recorded at the scalp supported maintenance of
spatial distance and temporal duration information.
Decades of research support a role for low-frequency
oscillations, in both cortex and hippocampus, in coding spa-
tial information during navigation (Kropff, Carmichael,
Moser, & Moser, 2021; McFarland, Teitelbaum, & Hedges,
1975; Vanderwolf, 1969; for reviews, see Jacobs, 2013;
Watrous et al., 2011). To attempt to disentangle space
and time, whose changes are strongly intertwined in
movement speed, participants experienced teleportation
of different spatial distance and temporal durations in the
absence of any optic flow or other sensory input to provide
cues about speed, similar to the design in Vass et al. (2016).
Results from power spectra analyses suggested the sensi-
tivity of central–posterior alpha power and global beta
power for spatial distances as well as a role of frontal theta
and global beta power changes for temporal duration.
Furthermore, the analysis of instantaneous alpha
frequencies revealed a robust association between alpha
frequency and magnitudes of distances and durations,
suggesting alpha frequency modulation as a potential
common mechanism for spatial and temporal coding.
Classifiers trained on power spectra further support the
hypothesis that both distance and temporal information
could be decoded from scalp EEG signals at a fine-scale
resolution.
Given that hippocampal delta–theta power displays a
distance code (Bush et al., 2017; Vass et al., 2016), as well
as a connectivity between rodent’s prefrontal and hippo-
campal theta during mobility ( Young & McNaughton,
2009; Siapas, Lubenov, & Wilson, 2005), we were sur-
prised to find that the cortical delta–theta power did
not exhibit significant differences between short-distance
and long-distance trials. This null finding cannot be ex-
plained by the failure of task design or the absence of
spatial coding during the teleportation period. This is be-
cause participants demonstrated high accuracy in identi-
fying distances traveled upon exiting the teleporters, and
power spectra analyses revealed significantly different os-
cillatory profiles for the distance task compared to base-
line (Figure 2C). What could lead to such a disconnect?
Here, we offer three speculations on the null findings
linking cortical theta and spatial distance coding. One
possibility is that prefrontal theta oscillations are phase
locked but not amplitude locked to hippocampal theta
( Young & McNaughton, 2009), and therefore, phase in-
formation in frontal theta but not power changes code
spatial distance duration (see Watrous et al., 2013, for
an example of this). This is an issue we cannot address
in the current study because scalp EEG does not give re-
liable access to hippocampal signals. A second possibility
is that frontal midline theta may be locked to the
temporal-processing or memory-related components,
but not the movement-related components, of hippo-
campal theta oscillations (Goyal et al., 2020; Watrous
2322
Journal of Cognitive Neuroscience
Volume 33, Number 11
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
3
1
1
2
3
1
1
1
9
6
5
6
8
2
/
/
j
o
c
n
_
a
_
0
1
7
6
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
et al., 2013). A third possibility is that hippocampal
movement-related theta oscillations manifest in the cor-
tex within the traditional alpha band (8–12 Hz) consistent
with the alpha frequency modulation we observed for
both spatial and temporal judgments. The third interpre-
tation is consistent with recent reports (Goyal et al.,
2020; Aghajan et al., 2017; Bohbot et al., 2017) that hip-
pocampal movement-related theta oscillations, particularly
during real-world movements, manifest most prominently
above 8 Hz, which would align with the frequency range of
traditional alpha band (8–12 Hz) rather than theta band
(4–8 Hz).
Our results supporting a role for frontal delta–theta
power but not distance coding have important implica-
tions. In the power spectra analysis, we found frontal
midline delta–theta and frontal alpha power sensitive to
the temporal durations, whereas central–posterior alpha
power was sensitive to the distance information. The re-
sults provide further evidence for partially independent
codes for space and time in the human brain. Our findings
demonstrating cortical beta oscillations sensitive to tem-
poral duration align with previous reports of timing-
related beta power in the time production domain
(Grabot et al., 2019; Kononowicz & van Rijn, 2015) and
movement-related frontal midline delta–theta increases
(Liang et al., 2018). On the other hand, our findings re-
garding central–occipital alpha oscillations related to dis-
tance are consistent with notions that human navigation
is enriched with regarding to visual input (Ekstrom,
2015), with occipital alpha oscillations particularly sensi-
tive to visual-related changes (such as optic flow; Cao &
Händel, 2019). As proposed by Goyal et al. (2020), a theo-
retical link might therefore exist between hippocampal
movement-related theta and occipital alpha oscillations.
For example, eye closure induces alpha power increases
both at occipital sites and in the hippocampus (Geller
et al., 2014). Our current results would suggest differing
roles in navigation for frontal midline theta (4–8 Hz)
and occipital alpha (8–12 Hz), which were both found
relevant to movement (Liang et al., 2018), and frontal
midline theta and occipital alpha oscillations could
possibly cooperate to support task-dependent spatial
or temporal processing. Therefore, a helpful next step
would be to determine how these signals coordinate
between the hippocampus and cortex in our task using
human intracranial recordings.
We note that, when we compared the power spectra of
the spatial and temporal teleportation task, we did not find
significant differences. Yet, we were able to classify whether
a trial was from the spatial or temporal task with an accuracy
better than chance in a manner that was generalizable
across participants. This suggests the classifiers captured
higher-order differences (perhaps the underlying connec-
tivity patterns) between the oscillatory coding of space
and time, other than the mean of power fluctuations. One
future direction is to examine the affinity of connectivity
patterns for spatial coding and temporal coding, using a
similar behavioral task used in this study. We predict that
the networks for spatio-temporal coding should diverge,
both measured using scalp EEG data and using intracranial
EEG data (as suggested by Watrous et al., 2013).
In addition to our findings that spatial distance and tem-
poral duration involve differences in oscillatory codes,
both for short versus long teleportation durations and in
their multivariate patterns, we also found a common role
for alpha frequency modulation in supporting spatio-
temporal coding. Specifically, we found faster occipital
alpha for smaller magnitudes of durations/distances.
What roles could endogenous alpha frequency modulation
possibly play here? One explanation is the processing-speed
theory, whereby occipital alpha frequency indexes the
processing speed of incoming sensory information
(Klimesch, Doppelmayr, Schimke, & Pachinger, 1996).
We speculate that the sensory processing speed differed
between short- and long-duration trials because of their
different cognitive demands. To complete the temporal
task, participants only needed to track time passage in the
teleporter up to 4 sec, and not beyond 4 sec, and therefore,
the cognitive demands differed between the 0- to 4-sec and
4- to 8-sec portions of the temporal task.
In contrast to the processing-speed account, another
possibility, however, relates to a perceptual resolution
account. For example, it could be that occipital alpha
frequency is linked to the perceptual resolution of
duration timing. For example, individuals with 10-Hz
resting occipital alpha oscillations might discriminate
two temporal durations with a minimum of 100-msec
(1/10) differences, and those with 12-Hz resting alpha
could discriminate two durations with 83.33-msec mini-
mal differences (1/12). This perceptual resolution ac-
count is also supported by Samaha and Postle (2015),
showing that occipital alpha frequency reflects the
“refresh rate” of visual perception and occipital alpha
represents the perceptual unit of temporal processing
(Cecere et al., 2015). Future studies should investigate
the potential causal links between occipital alpha frequency
and spatio-temporal processing, given recent findings
that transcranial alternating current stimulation–induced
alpha frequency shifts led to shifts in subjective time ex-
periences (Mioni et al., 2020) and that clinical popula-
tions with Alzheimer’s show irregularities in parietal
alpha oscillations (Montez et al., 2009).
Given that we found alpha frequency modulation and
beta power fluctuations related to both spatial and tem-
poral judgments, our results also provide evidence for a
common mechanism for spatial and temporal coding in-
volving magnitude estimation. Although distance-related
beta power has rarely been studied in a scalp EEG setting,
the timing-related beta power we observed has been
noted in predicting the accuracy and precision of time
production (Grabot et al., 2019; Kononowicz & van
Rijn, 2015). Our findings suggest that beta oscillations
may reflect a common magnitude representation under-
lying both spatial and temporal processing and that such
Liang et al.
2323
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
3
1
1
2
3
1
1
1
9
6
5
6
8
2
/
/
j
o
c
n
_
a
_
0
1
7
6
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
distance and fine-scale temporal information could be
widely accessible in neocortical regions, including early
sensory and motor cortices. Future studies can bridge
the gap of research between spatial and temporal pro-
cessing and further elaborate the roles of beta oscillations
in spatial coding versus temporal coding, with a variety of
tasks such as estimating and reproducing spatial distance
with a path integration task (Harootonian, Wilson,
Hejtmánek, Ziskin, & Ekstrom, 2020).
Another important finding from our study is the ability
to decode fine-scale distance and temporal information
from cortical low-frequency power spectra. Interestingly,
when attempting to decode temporal information, we
showed that the decoding error linearly increased as the
time bins progressed forward. These findings are closely
aligned with the behavioral findings in which humans
show larger variability in time reproduction responses
for longer intervals (Rakitin et al., 1998; Ivry & Hazeltine,
1995). One intriguing possibility is that the cortical low-
frequency oscillations support a fine-scale representation
of temporal intervals. Future studies can test this possi-
bility by linking the decodability of fine-scale time infor-
mation and the accuracy/precision of time reproduction
in human participants.
Notably, our findings of decodable fine-scale temporal
information are qualitatively similar to the findings based
on recordings from entorhinal temporal context cells
(Bright et al., 2020). The tenet of a unified math model
of space and time (Howard et al., 2014) is that the neural
representations are the Laplace transform of space and
time, coded through the exponentially decayed firing
rates of neurons. However, the theory does not directly
predict or rule out the involvement of neural oscillations
in coding space and time. Here, we demonstrated that
neural oscillations could yield a similar time representa-
tion possibly with scale invariance, and we suggest that
neural oscillations could be a synergistic component on
top of single neuron firing rates for spatio-temporal cod-
ing. Another question that should be clarified through fu-
ture studies is whether the neural representations of
spatial distance also possess scale invariance like the rep-
resentations of time (i.e., reproducing longer distances is
associated with greater variability in responses).
Behavioral findings suggest path integration errors sys-
tematically scaled with path lengths (Harootonian et al.,
2020), which will predict linearly increases in decoding
errors as distances increase. Future studies should fur-
ther test the links between oscillatory representations
of fine-scale space and time, and the behavioral phenom-
ena of spatio-temporal reproduction, using a reproduc-
tion paradigm, such as reproducing space and time in
virtual reality (Robinson & Wiener, 2021).
Limitations
It is worth considering some potential limitations with
our paradigm, which we nonetheless believe do not
undermine or challenge our findings. One concern could
be that, because participants knew how far they would
travel before entering the teleporter, distance coding
was therefore transient and completed before entering
the teleporters, thus nullifying the existence of distance
coding during the teleportation. We note, however, that
maintenance of distance information during the telepor-
tation was still necessary for accurate performance in the
spatial teleportation task. When participants entered the
teleporter, although they knew beforehand whether it
was a short or long distance, they had to maintain this
information during teleportation to make the correct de-
cision upon exiting the teleporter. Our interpretation of
perceiving spatial distance before decisions about move-
ment is consistent with a rich literature in human spatial
navigation, suggesting that humans first estimate dis-
tance based on perceptual cues and then attempt to
maintain this in working memory as they actively navigate
to different goals (Knapp & Loomis, 2004; Philbeck &
Loomis, 1997; Philbeck, Loomis, & Beall, 1997). Using a
similar spatial distance teleportation design, Vass et al.
(2016) showed that the spatial distance teleportation task
resulted in different oscillatory profiles from those during
the resting state (viewing a black screen outside the ex-
perimental context). We similarly found a clear difference
between teleportation and a resting baseline task. These
findings suggest that the spatial teleportation task trig-
gered distance information processing absent in a resting
state condition.
Another concern could be that movement-related noise
from the navigation phase permeated into the EEG data
during the teleportation, thus confounding the findings
we presented here. Note that the amount of noise, if
any, should be identical between short and long trials,
and between the spatial and temporal tasks, given that
participants stood still after they entered the teleporter.
Therefore, noise should not confound the findings regard-
ing the contrasts of EEG responses between short and
long trials or between the spatial and temporal tasks.
Conclusions
Our study addressed an important issue regarding whether
spatial and temporal processing share common or distinct
mechanisms (Gauthier, Prabhu, Kotegar, & van
Wassenhove, 2020; Gauthier, Pestke, & Van Wassenhove,
2019; Eichenbaum & Cohen, 2014; Watrous et al., 2013;
Ekstrom, Copara, Isham, Wang, & Yonelinas, 2011;
Frassinetti et al., 2009). Our findings suggest that spatial
and temporal judgments during navigation differ as a func-
tion of power changes within specific frequency bands:
Whereas spatial judgments resulted in changes in cortical
alpha and beta power, different temporal durations were
linked to changes in frontal midline delta–theta, frontal
and posterior alpha, and global beta power. Consistent with
the idea of separable representations for space and time,
spatial and temporal discounting are behaviorally distinctive
2324
Journal of Cognitive Neuroscience
Volume 33, Number 11
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
3
1
1
2
3
1
1
1
9
6
5
6
8
2
/
/
j
o
c
n
_
a
_
0
1
7
6
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
from each other (Robinson, Michaelis, Thompson, &
Wiener, 2019), estimating spatial distance is subject to large
errors (Zhao, 2018) while estimating suprasecond durations
can be performed with high accuracy (Grabot et al., 2019),
and spatial and temporal estimation errors distort in oppos-
ing manners (Brunec, Javadi, Zisch, & Spiers, 2017).
Previous reports have also hinted at a dissociation between
space and time at the neural level, although using different
paradigms in which temporal information, in particular, in-
volved order and not duration ( Watrous et al., 2013;
Ekstrom et al., 2011). More generally, evidence exists for
and against the notion that space and time processing are
of the same nature, and we also found evidence for alpha
frequency modulation as a common mechanism for spatial
and temporal coding. Thus, one implication of our study is
that there are both distinct and common mechanisms
related to how we process spatial distance and temporal
durations.
Acknowledgments
This research was supported by the National Science Foundation
(NSF BCS-1630296, A. D. E.). We thank Stephanie Doner for the
assistance in scalp EEG data collection, Eva Robinson for feedback
on the article, and the participants for being part of this study.
Reprint requests should be sent to Arne Ekstrom, Department of
Psychology, University of Arizona, 1503 E. University Blvd.,
Tucson, AZ 85721, or via e-mail: adekstrom@email.arizona.edu.
Funding Information
Arne Ekstrom: National Science Foundation (https://dx.doi
.org/10.13039/100000001), grant number: NSF BCS-
1630296.
Diversity in Citation Practices
A retrospective analysis of the citations in every article pub-
lished in this journal from 2010 to 2020 has revealed a per-
sistent pattern of gender imbalance: Although the
proportions of authorship teams (categorized by estimated
gender identification of first author/last author) publishing
in the Journal of Cognitive Neuroscience ( JoCN) during
this period were M(an)/M = .408, W(oman)/M = .335,
M/ W = .108, and W/ W = .149, the comparable proportions
for the articles that these authorship teams cited were
M/M = .579, W/M = .243, M/ W = .102, and W/ W = .076
(Fulvio et al., JoCN, 33:1, pp. 3–7). Consequently, JoCN en-
courages all authors to consider gender balance explicitly
when selecting which articles to cite and gives them the op-
portunity to report their article’s gender citation balance.
REFERENCES
Aghajan, Z. M., Schuette, P., Fields, T. A., Tran, M. E., Siddiqui,
S. M., Hasulak, N. R., et al. (2017). Theta oscillations in the
human medial temporal lobe during real-world ambulatory
movement. Current Biology, 27, 3743–3751. https://doi.org
/10.1016/j.cub.2017.10.062, PubMed: 29199073
Benjamini, Y., & Yekutieli, D. (2001). The control of the false
discovery rate in multiple testing under dependency. Annals
of Statistics, 29, 1165–1188.
Benwell, C. S. Y., London, R. E., Tagliabue, C. F., Veniero, D.,
Gross, J., Keitel, C., et al. (2019). Frequency and power of
human alpha oscillations drift systematically with time-on-task.
Neuroimage, 192, 101–114. https://doi.org/10.1016/j
.neuroimage.2019.02.067, PubMed: 30844505
Bohbot, V. D., Copara, M. S., Gotman, J., & Ekstrom, A. D.
(2017). Low-frequency theta oscillations in the human
hippocampus during real-world and virtual navigation.
Nature Communications, 8, 14415. https://doi.org/10.1038
/ncomms14415, PubMed: 28195129
Bright, I. M., Meister, M. L. R., Cruzado, N. A., Tiganj, Z., Buffalo,
E. A., & Howard, M. W. (2020). A temporal record of the past
with a spectrum of time constants in the monkey entorhinal
cortex. Proceedings of the National Academy of Sciences,
U.S.A., 117, 20274–20283. https://doi.org/10.1073/pnas
.1917197117, PubMed: 32747574
Brunec, I. K., Javadi, A.-H., Zisch, F. E. L., & Spiers, H. J. (2017).
Contracted time and expanded space: The impact of
circumnavigation on judgements of space and time.
Cognition, 166, 425–432. https://doi.org/10.1016/j.cognition
.2017.06.004, PubMed: 28624709
Bush, D., Bisby, J. A., Bird, C. M., Gollwitzer, S., Rodionov, R.,
Diehl, B., et al. (2017). Human hippocampal theta power
indicates movement onset and distance travelled. Proceedings
of the National Academy of Sciences, U.S.A., 114, 12297–12302.
https://doi.org/10.1073/pnas.1708716114, PubMed: 29078334
Cao, L., & Händel, B. (2019). Walking enhances peripheral
visual processing in humans. PLoS Biology, 17, 1–23. https://
doi.org/10.1371/journal.pbio.3000511, PubMed: 31603894
Caplan, J. B., Madsen, J. R., Schulze-Bonhage, A.,
Aschenbrenner-Scheibe, R., Newman, E. L., & Kahana, M. J.
(2003). Human theta oscillations related to sensorimotor
integration and spatial learning. Journal of Neuroscience, 23,
4726–4736. https://doi.org/10.1523/JNEUROSCI.23-11-04726
.2003, PubMed: 12805312
Cecere, R., Rees, G., & Romei, V. (2015). Individual differences
in alpha frequency drive crossmodal illusory perception.
Current Biology, 25, 231–235. https://doi.org/10.1016/j.cub
.2014.11.034, PubMed: 25544613
Cohen, M. X. (2014). Fluctuations in oscillation frequency
control spike timing and coordinate neural networks.
Journal of Neuroscience, 34, 8988–8998. https://doi.org/10
.1523/JNEUROSCI.0261-14.2014, PubMed: 24990919
Eichenbaum, H., & Cohen, N. J. (2014). Can we reconcile
the declarative memory and spatial navigation views on
hippocampal function? Neuron, 83, 764–770. https://doi.org
/10.1016/j.neuron.2014.07.032, PubMed: 25144874
Ekstrom, A. D. (2015). Why vision is important to how we
navigate. Hippocampus, 25, 731–735. https://doi.org/10.1002
/hipo.22449, PubMed: 25800632
Ekstrom, A. D., Caplan, J. B., Ho, E., Shattuck, K., Fried, I., &
Kahana, M. J. (2005). Human hippocampal theta activity
during virtual navigation. Hippocampus, 15, 881–889. https://
doi.org/10.1002/hipo.20109, PubMed: 16114040
Ekstrom, A. D., Copara, M. S., Isham, E. A., Wang, W., &
Yonelinas, A. P. (2011). Dissociable networks involved in
spatial and temporal order source retrieval. Neuroimage, 56,
1803–1813. https://doi.org/10.1016/j.neuroimage.2011.02
.033, PubMed: 21334445
Ekstrom, A. D., & Isham, E. A. (2017). Human spatial navigation:
Representations across dimensions and scales. Current
Opinion in Behavioral Sciences, 17, 84–89. https://doi.org
/10.1016/j.cobeha.2017.06.005, PubMed: 29130062
Frassinetti, F., Magnani, B., & Oliveri, M. (2009). Prismatic
lenses shift time perception. Psychological Science, 20,
Liang et al.
2325
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
3
1
1
2
3
1
1
1
9
6
5
6
8
2
/
/
j
o
c
n
_
a
_
0
1
7
6
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
949–954. https://doi.org/10.1111/j.1467-9280.2009.02390.x,
PubMed: 19549081
Gauthier, B., Pestke, K., & Van Wassenhove, V. (2019). Building
the arrow of time... Over time: A sequence of brain activity
mapping imagined events in time and space. Cerebral
Cortex, 29, 4398–4414. https://doi.org/10.1093/cercor
/bhy320, PubMed: 30566689
Gauthier, B., Prabhu, P., Kotegar, K. A., & van Wassenhove, V.
(2020). Hippocampal contribution to ordinal psychological
time in the human brain. Journal of Cognitive Neuroscience,
32, 2071–2086. https://doi.org/10.1162/jocn_a_01586,
PubMed: 32459130
Geller, A. S., Burke, J. F., Sperling, M. R., Sharan, A. D., Litt, B.,
Baltuch, G. H., et al. (2014). Eye closure causes widespread
low-frequency power increase and focal gamma attenuation
in the human electrocorticogram. Clinical Neurophysiology,
125, 1764–1773. https://doi.org/10.1016/j.clinph.2014.01.021,
PubMed: 24631141
Goyal, A., Miller, J., Qasim, S. E., Watrous, A. J., Zhang, H., Stein,
J. M., et al. (2020). Functionally distinct high and low
theta oscillations in the human hippocampus. Nature
Communications, 11, 2469. https://doi.org/10.1038/s41467
-020-15670-6, PubMed: 32424312
Grabot, L., Kononowicz, T. W., la Tour, T. D., Gramfort, A.,
Doyère, V., & van Wassenhove, V. (2019). The strength of
alpha–beta oscillatory coupling predicts motor timing
precision. Journal of Neuroscience, 39, 3277–3291. https://
doi.org/10.1523/JNEUROSCI.2473-18.2018, PubMed:
30792271
Groppe, D. (2021). Fdr_bh, Benjamini & Hochberg/Yekutieli
false discovery rate control procedure for a set of statistical
tests, MATLAB Central File Exchange. https://www
.mathworks.com/matlabcentral/fileexchange/27418-fdr_bh.
Retrieved June 10, 2021.
Harootonian, S. K., Wilson, R. C., Hejtmánek, L., Ziskin, E. M., &
Ekstrom, A. D. (2020). Path integration in large-scale space
and with novel geometries: Comparing vector addition and
encoding-error models. PLoS Computational Biology, 16,
1–27. https://doi.org/10.1371/journal.pcbi.1007489, PubMed:
32379824
Hayasaka, S., & Nichols, T. E. (2004). Combining voxel intensity
and cluster extent with permutation test framework.
Neuroimage, 23, 54–63. https://doi.org/10.1016/j.neuroimage
.2004.04.035, PubMed: 15325352
Howard, M. W., MacDonald, C. J., Tiganj, Z., Shankar, K. H., Du,
Q., Hasselmo, M. E., et al. (2014). A unified mathematical
framework for coding time, space, and sequences in the
hippocampal region. Journal of Neuroscience, 34,
4692–4707. https://doi.org/10.1523/JNEUROSCI.5808-12
.2014, PubMed: 24672015
Hughes, A. M., Whitten, T. A., Caplan, J. B., & Dickson, C. T.
(2012). BOSC: A better oscillation detection method, extracts
both sustained and transient rhythms from rat hippocampal
recordings. Hippocampus, 22, 1417–1428.
Itskov, V., Curto, C., Pastalkova, E., & Buzsáki, G. (2011). Cell
assembly sequences arising from spike threshold adaptation
keep track of time in the hippocampus. Journal of
Neuroscience, 31, 2828–2834. https://doi.org/10.1523
/JNEUROSCI.3773-10.2011, PubMed: 21414904
Ivry, R. B., & Hazeltine, R. E. (1995). Perception and
production of temporal intervals across a range of
durations: Evidence for a common timing mechanism.
Journal of Experimental Psychology: Human Perception
and Performance, 21, 3–18. https://doi.org/10.1037/0096
-1523.21.1.3, PubMed: 7707031
Jacobs, J. (2013). Hippocampal theta oscillations are slower in
humans than in rodents: Implications for models of spatial
navigation and memory. Philosophical Transactions of the
Royal Society of London, Series B: Biological Sciences, 369,
20130304. https://doi.org/10.1098/rstb.2013.0304, PubMed:
24366145
Kim, K., Schedlbauer, A., Rollo, M., Karunakaran, S., Ekstrom,
A. D., & Tandon, N. (2018). Network-based brain stimulation
selectively impairs spatial retrieval. Brain Stimulation, 11,
213–221. https://doi.org/10.1016/j.brs.2017.09.016, PubMed:
29042188
Klimesch, W., Doppelmayr, M., Schimke, H., & Pachinger, T.
(1996). Alpha frequency, reaction time, and the speed of
processing information. Journal of Clinical Neurophysiology,
13, 511–518. https://doi.org/10.1097/00004691-199611000
-00006, PubMed: 8978623
Knapp, J. M., & Loomis, J. M. (2004). Limited field of view
of head-mounted displays is not the cause of distance
underestimation in virtual environments. Presence:
Teleoperators and Virtual Environments, 13, 572–577.
https://doi.org/10.1162/1054746042545238
Kononowicz, T. W., & van Rijn, H. (2015). Single trial beta
oscillations index time estimation. Neuropsychologia, 75,
381–389. https://doi.org/10.1016/j.neuropsychologia.2015.06
.014, PubMed: 26102187
Kropff, E., Carmichael, J. E., Moser, E. I., & Moser, M.-B. (2021).
Frequency of theta rhythm is controlled by acceleration,
but not speed, in running rats. Neuron, 109, 1029–1039.
https://doi.org/10.1016/j.neuron.2021.01.017, PubMed:
33567253
Liang, M., Starrett, M. J., & Ekstrom, A. D. (2018). Dissociation
of frontal–midline delta–theta and posterior alpha
oscillations: A mobile EEG study. Psychophysiology, 55,
e13090. https://doi.org/10.1111/psyp.13090, PubMed:
29682758
MacDonald, C. J., Lepage, K. Q., Eden, U. T., & Eichenbaum, H.
(2011). Hippocampal “time cells” bridge the gap in
memory for discontiguous events. Neuron, 71, 737–749.
https://doi.org/10.1016/j.neuron.2011.07.012, PubMed:
21867888
Makeig, S., Debener, S., Onton, J., & Delorme, A. (2004).
Mining event-related brain dynamics. Trends in Cognitive
Sciences, 8, 204–210. https://doi.org/10.1016/j.tics.2004.03
.008, PubMed: 15120678
Maris, E., & Oostenveld, R. (2007). Nonparametric statistical
testing of EEG- and MEG-data. Journal of Neuroscience
Methods, 164, 177–190. https://doi.org/10.1016/j.jneumeth
.2007.03.024, PubMed: 17517438
McFarland, W. L., Teitelbaum, H., & Hedges, E. K. (1975).
Relationship between hippocampal theta activity and running
speed in the rat. Journal of Comparative and Physiological
Psychology, 88, 324–328. https://doi.org/10.1037/h0076177,
PubMed: 1120805
Mioni, G., Shelp, A., Stanfield-Wiswell, C. T., Gladhill, K. A.,
Bader, F., & Wiener, M. (2020). Modulation of individual
alpha frequency with tACS shifts time perception. Cerebral
Cortex Communications. 1, tgaa064.
Montez, T., Poil, S.-S., Jones, B. F., Manshanden, I., Verbunt,
J. P. A., van Dijk, B. W., et al. (2009). Altered temporal
correlations in parietal alpha and prefrontal theta oscillations
in early-stage Alzheimer disease. Proceedings of the National
Academy of Sciences, U.S.A., 106, 1614–1619. https://doi.org
/10.1073/pnas.0811699106, PubMed: 19164579
Pastalkova, E., Itskov, V., Amarasingham, A., & Buzsáki, G.
(2008). Internally generated cell assembly sequences in the
rat hippocampus. Science, 321, 1322–1327. https://doi.org/10
.1126/science.1159775, PubMed: 18772431
Philbeck, J. W., & Loomis, J. M. (1997). Comparison of two
indicators of perceived egocentric distance under full-cue
and reduced-cue conditions. Journal of Experimental
Psychology: Human Perception and Performance, 23,
2326
Journal of Cognitive Neuroscience
Volume 33, Number 11
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
3
1
1
2
3
1
1
1
9
6
5
6
8
2
/
/
j
o
c
n
_
a
_
0
1
7
6
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
72–85. https://doi.org/10.1037/0096-1523.23.1.72, PubMed:
9090147
Philbeck, J. W., Loomis, J. M., & Beall, A. C. (1997). Visually
perceived location is an invariant in the control of action.
Perception & Psychophysics, 59, 601–612. https://doi.org/10
.3758/BF03211868, PubMed: 9158334
Pion-Tonachini, L., Kreutz-Delgado, K., & Makeig, S. (2019).
ICLabel: An automated electroencephalographic
independent component classifier, dataset, and website.
Neuroimage, 198, 181–197. https://doi.org/10.1016/j
.neuroimage.2019.05.026, PubMed: 31103785
Polich, J. (2007). Updating P300: An integrative theory of
P3a and P3b. Clinical Neurophysiology, 118, 2128–2148.
https://doi.org/10.1016/j.clinph.2007.04.019, PubMed:
17573239
Rakitin, B. C., Gibbon, J., Penney, T. B., Malapani, C., Hinton, S. C.,
& Meck, W. H. (1998). Scalar expectancy theory and
peak-interval timing in humans. Journal of Experimental
Psychology: Animal Behavior Processes, 24, 15–33. https://doi
.org/10.1037/0097-7403.24.1.15, PubMed: 9438963
Robin, J., & Moscovitch, M. (2014). The effects of spatial
contextual familiarity on remembered scenes, episodic
memories, and imagined future events. Journal of
Experimental Psychology: Learning, Memory, and
Cognition, 40, 459–475. https://doi.org/10.1037/a0034886,
PubMed: 24219084
Robinson, E., Michaelis, K., Thompson, J. C., & Wiener, M.
(2019). Temporal and spatial discounting are distinct in
humans. Cognition, 190, 212–220. https://doi.org/10.1016/j
.cognition.2019.04.030, PubMed: 33290808
Robinson, E. M., & Wiener, M. (2021). Dissociable neural
indices for time and space estimates during virtual distance
reproduction. Neuroimage, 226, 117607. https://doi.org/10
.1016/j.neuroimage.2020.117607, PubMed: 33290808
Samaha, J., & Postle, B. R. (2015). The speed of alpha-band
oscillations predicts the temporal resolution of visual
perception. Current Biology, 25, 2985–2990. https://doi.org
/10.1016/j.cub.2015.10.007, PubMed: 26526370
Samuel, I. B. H., Wang, C., Hu, Z., & Ding, M. (2018). The
frequency of alpha oscillations: Task-dependent modulation
and its functional significance. Neuroimage, 183, 897–906.
https://doi.org/10.1016/j.neuroimage.2018.08.063, PubMed:
30176369
Siapas, A. G., Lubenov, E. V., & Wilson, M. A. (2005). Prefrontal
phase locking to hippocampal theta oscillations. Neuron,
46, 141–151. https://doi.org/10.1016/j.neuron.2005.02.028,
PubMed: 15820700
Tulving, E. (2002). Episodic memory: From mind to brain.
Annual Review of Psychology, 53, 1–25. https://doi.org/10
.1146/annurev.psych.53.100901.135114, PubMed: 11752477
Vanderwolf, C. H. (1969). Hippocampal electrical activity and
voluntary movement in the rat. Electroencephalography and
Clinical Neurophysiology, 26, 407–418. https://doi.org/10
.1016/0013-4694(69)90092-3, PubMed: 4183562
Vass, L. K., Copara, M. S., Seyal, M., Shahlaie, K., Farias, S. T.,
Shen, P. Y., et al. (2016). Oscillations go the distance: Low-
frequency human hippocampal oscillations code spatial
distance in the absence of sensory cues during teleportation.
Neuron, 89, 1180–1186. https://doi.org/10.1016/j.neuron
.2016.01.045, PubMed: 26924436
Walsh, V. (2003). A theory of magnitude: Common cortical
metrics of time, space and quantity. Trends in Cognitive
Sciences, 7, 483–488. https://doi.org/10.1016/j.tics.2003.09
.002, PubMed: 14585444
Wang, Y., Romani, S., Lustig, B., Leonardo, A., & Pastalkova, E.
(2015). Theta sequences are essential for internally generated
hippocampal firing fields. Nature Neuroscience, 18, 282–288.
https://doi.org/10.1038/nn.3904, PubMed: 25531571
Watrous, A. J., Fried, I., & Ekstrom, A. D. (2011). Behavioral
correlates of human hippocampal delta and theta oscillations
during navigation. Journal of Neurophysiology, 1747–1755.
https://doi.org/10.1152/jn.00921.2010, PubMed: 21289136
Watrous, A. J., Tandon, N., Conner, C. R., Pieters, T., & Ekstrom,
A. D. (2013). Frequency-specific network connectivity
increases underlie accurate spatiotemporal memory retrieval.
Nature Neuroscience, 3, 349–356. https://doi.org/10.1038/nn
.3315, PubMed: 23354333
Young, C. K., & McNaughton, N. (2009). Coupling of theta
oscillations between anterior and posterior midline cortex
and with the hippocampus in freely behaving rats. Cerebral
Cortex, 19, 24–40. https://doi.org/10.1093/cercor/bhn055,
PubMed: 18453538
Zhao, M. (2018). Human spatial representation: What we
cannot learn from the studies of rodent navigation. Journal
of Neurophysiology, 120, 2453–2465. https://doi.org/10.1152
/jn.00781.2017, PubMed: 30133384
Liang et al.
2327
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
3
1
1
2
3
1
1
1
9
6
5
6
8
2
/
/
j
o
c
n
_
a
_
0
1
7
6
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3