COLLEGE MAJOR CHOICE AND

NEIGHBORHOOD EFFECTS IN A

HISTORICALLY SEGREGATED SOCIETY:

EVIDENCE FROM SOUTH AFRICA

Biniam E. Bedasso

Collaborative Africa Budget

Reform Initiative

Centurion, 0062 South Africa

biniam.bedasso@cabri-sbo.org

Abstract
This paper explores factors aﬀecting the choice of investment in
speciﬁc human capital in the presence of signiﬁcant inter-group
and spatial inequalities. I use four years of admissions application
data at an elite university in South Africa in conjunction with quar-
terly labor force data to trace the link between aptitude-adjusted
expected earnings, neighborhood eﬀects, and the choice of college
major. The paper relies on the availability of a rich set of academic
and geographical information in the admissions database to make
causal inference. The results show that expected earnings have
a positive impact on major choice independently of high school
background when the ex ante distribution of earnings captures
the full range of between-major and within-major income diﬀer-
entials. White applicants are more responsive to diﬀerentials in
expected earnings than black applicants. Neighborhood eﬀects in-
ﬂuence college major choice through near-peer role models and
relative achievement at the high school level.

https://doi.org/10.1162/edfp_a_00249

472

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
4
3
4
7
2
1
6
9
3
0
1
4
e
d
p
_
a
_
0
0
2
4
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Biniam E. Bedasso

I N T RO D U C T I O N

1 .
In an era of increasing specializations and rising wage diﬀerentials, not all diplomas are
created equal. There are a number of studies in the existing literature that show the link
between the distribution of college majors and income inequality (Grogger and Eide
1995; Arcidiacono 2004). Gender and racial income gaps are also partly explained by
the heterogeneity of human capital (Daymont and Andrisani 1984; Weinberger 1998).
As one goes up the education ladder, diﬀerences in income will be as much about the
type of training acquired as about the number of years spent in school. Hence, under-
standing inequality, especially in the middle part of the income distribution, requires
having a good grasp of factors inﬂuencing the allocation of heterogeneous human cap-
ital. The impact of the allocation of specialized training is likely to be pronounced in
developing countries where it has more power to shape the composition of elites and
the nature of the middle class. The allocation of talent across various ﬁelds of specializa-
tion with diﬀerential impact on innovation and technological change will aﬀect growth
in the long run (Murphy, Shleifer, and Vishny 1991). The eﬀect of the allocation of spe-
cialized human capital could be far-reaching enough to inﬂuence institutional quality
to the extent that it shapes the preferences of elites (Bedasso 2015).

This paper examines the determinants of college major choice in South Africa in
the context of signiﬁcant inter-group and spatial inequalities that have continued to
characterize South African society.1 By investigating factors inﬂuencing college major
choice, I seek to shed light on the role of heterogeneous human capital in the repro-
duction of inequality in South Africa. Speciﬁcally, the paper attempts to answer two
questions: (1) How do various groups respond to diﬀerentials in major-speciﬁc expected
earnings against the backdrop of sizeable inequality in economic and sociopolitical en-
dowments? and (2) How do peer eﬀects and relative achievement inﬂuence college
major choice at the levels of speciﬁc neighborhoods and high schools? I exploit the
extensive information contained in the admissions database of the University of Cape
Town (UCT) between 2010 and 2013, jointly with the Quarterly Labor Force Survey con-
ducted at a national level. The novelty of the dataset lies in the amount of information
it provides about the high school education and area of residence of college applicants.
Moreover, the status of UCT as the best ranked institution of higher education on the
African continent allows me to put the analysis in the context of elite formation in a
society that has been undergoing social and political transformation.2

In standard theoretical frameworks, college major choice is analyzed as part of a
lifecycle model of stochastic career choice (Altonji, Blom, and Meghir 2012). This ap-
proach helps establish a link between educational choices at earlier stages in life and
the choice of college major. Therefore, to the extent that pre-college educational oppor-
tunities are determined by space, it is possible to draw a connection between spatial
inequality and major choice. There are a number of channels through which spatial

1. The educational inequalities of the Apartheid era continue to persist in South Africa, as manifested in disparities
in schooling outcomes between historically black and historically white schools (Van der Berg 2007). Regional
inequality is rife in the schooling system in South Africa. As of 2013, less than 44 percent of public schools in
one of the poorest provinces oﬀer math in grades 10 through 12. The corresponding ﬁgure for the best served
province is 91 percent.

2. Two of the most widely cited university rankings—the Times Higher Education Ranking and the QS World

University Ranking—consistently rank the University of Cape Town as the best university in Africa.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
4
3
4
7
2
1
6
9
3
0
1
4
e
d
p
_
a
_
0
0
2
4
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

473

College Major Choice

inequality may inﬂuence individual decisions in college. This includes the quality of
schools in a given geographical area, the inﬂuence of near-peer role models, and the ef-
fect of relative achievement in diﬀerent schools. Essentially, individuals are constrained
by all or some of these background factors as they optimize expected lifetime earnings
from each major.

I estimate a random utility model of the determinants of choice between ﬁve fac-
ulties (or departments) at UCT with nesting structure elicited from the data. I exploit
the availability of two sets of national test scores with varying emphasis on measur-
ing overall ability and college adaptability to identify the eﬀect of aptitude-adjusted ex-
pected earnings while controlling for academic ability directly. I use two speciﬁcations
of expected earnings based on alternative assumptions regarding the information set
applicants face about future income. The results show that aptitude-adjusted expected
earnings exert a positive impact on major choice. However, the eﬀect of expected earn-
ings is absorbed by the antecedent eﬀect of high school curriculum choice when the
ex ante distribution of earnings is assumed to be egalitarian. On the contrary, when
the ex ante distribution of earnings accounts for merit-based diﬀerentials in income,
expected earnings continue to hold a positive eﬀect on major choice independently of
high school curriculum. As far as racial disparities are concerned, white applicants are
shown to be, on average, 1.8 times more responsive to major-speciﬁc earnings diﬀeren-
tials than black applicants.

With regard to neighborhood eﬀects, I exploit the variation in past admission trends
to UCT across 3,773 postcodes represented in the database to capture the inﬂuence of
near-peer role models. Correcting for possible clustering of unobserved preferences
along postcodes, a one standard deviation increase in the ratio of near-peers who were
admitted to a certain faculty during the last three years is shown to increase by around 9
percent the probability of choosing the same faculty. I also endeavor to explore whether
there is a bright side to spatial inequality. Based on the assumption that applicants who
belong to the high end of the grade distribution in a less competitive high school have
better self-esteem than academically similar students who have gone to more competi-
tive high schools, I test whether being a “big frog in a small pond” induces applicants to
choose high return majors. The results show that top ranking applicants from a bottom
quartile high school are consistently more likely to choose health and other sciences
over humanities than applicants with higher average grades who nevertheless belong
to a lower rung of the grade distribution in a top quartile high school.

This paper belongs in a long vein of literature on career choice under uncertainty
(see for example, Altonji 1993; Keane and Wolpin 1999; Arcidiacono 2004; Montmar-
quette, Cannings, and Mahseredjian 2002; Wiswall and Zafar 2015). For that matter,
much of the theoretical framework I formulate in the next section is based on these
papers. Most studies have, either implicitly or explicitly, dealt with the impact of major
choice on income inequality. However, there has been little focus on the implications of
overall inequality, let alone group and spatial inequality, for the pattern of major choice.
To be sure, there have been notable theoretical contributions linking segregation and
human capital investment to overall inequality (see, for example, Bénabou 1996). The
economics and sociology literatures are rich in empirical evidence on the impact of ge-
ographical segregation on educational outcomes (Braddock 1980; Card and Rothstein
2007; Goldsmith 2009). But there is still little evidence on the eﬀect of neighborhood

474

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
4
3
4
7
2
1
6
9
3
0
1
4
e
d
p
_
a
_
0
0
2
4
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Biniam E. Bedasso

characteristics on educational outcomes in the context of heterogeneous human cap-
ital. This paper contributes to the literature in three ways. First, it takes advantage of
extensive geographical variation in the data to analyze the determinants of college ma-
jor choice in perspective with spatial inequality. Second, it enriches the empirical mea-
surement of expected earnings by using alternative assumptions regarding the ex ante
distribution of future income. Third, it exploits big administrative data to estimate the
determinants of major choice in a developing country, which would otherwise have
been impossible due to the absence relevant survey data.3

The remainder of the paper is organized as follows. Section 2 outlines the theoretical
framework and the empirical strategy I apply to answer the questions raised in this
paper. Section 3 provides an overview of the data and summary statistics. Section 4 is
devoted to presentation of results. Section 5 concludes.

2 . T H E O R E T I C A L F R A M E WO R K A N D E M P I R I C A L S T R AT E G Y
The choice of college major is part of a dynamic lifecycle decision-making process.
In most cases, the sequence of choices starts as early as high school, where students
and their parents may have to choose the type of curriculum to be pursued. This will
then be followed by a series of choices on whether to go to college or join the labor
market, which college to attend, and what major to choose. The last stage of decision-
making often consists of the choice of occupation conditional on education. Because I
am dealing with the choice of college major at the point of admission, I will start with
specifying the value function of individual i who has already chosen to go to college and
picked out major j from a set of available alternatives j = 1, 2, . . . , J,

(cid:2)

v1i j = E1(u1i j | a, θ ) + β

E1(v2i j | a)da,

(1)

where u1i j is the ﬂow utility in period 1 (i.e., college) conditional on ability, a, and pref-
erence, θ , both of which might not be directly observable. The second term in equation
1 comprises the terminal value of lifetime earnings expected in period 2 (i.e., work)
conditional on ability. β is the discount rate. The utility received by the student while
attending college in major j is determined by the psychic and pecuniary costs of major
j, as well as individual preference for that particular major. This can be written as

u1i j = α1Ci j + α2Xi + ε1i j,

(2)

where Xi is a vector of individual, school, and neighborhood characteristics that may
inﬂuence the inclination of student i towards major j. ε1i j is the unobserved preference
of the individual. Ci j is a combination of psychic and pecuniary costs speciﬁc to the
individual. The individualized cost function is given by

Ci j = γ1Ai j(h) + γ2Zi j,

(3)

where Ai j(h) is the observed academic ability of the individual for major j that is as-
sumed to aﬀect the psychic cost of major j through the intensity of eﬀort required to

3. Most of the existing studies of college major choice are based on the National Longitudinal Surveys of Youth in

the United States.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
4
3
4
7
2
1
6
9
3
0
1
4
e
d
p
_
a
_
0
0
2
4
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

475

College Major Choice

complete college. At the point of college admission, observed ability is a function of high
school preparation, h, and, therefore, conditional on choices made earlier in life. Zi j is
the pecuniary cost of major j, which is assumed to be speciﬁc to individual i because
the relative cost of college varies across socioeconomic backgrounds. This is because
credit markets are imperfect. Substituting equation 3 in equation 2, the ﬂow utility of
attending college in major j can be parameterized as follows,

u1i j = α1γ1Ai j(h) + α1γ2Zi j + α2Xi + ε1i j.

(4)

The measure of expected lifetime earnings—that is, the second term of the value
function in equation 1—depends on the type of information applicants have, ex ante,
about earnings diﬀerentials across and within college majors. Accordingly, I formu-
late two discrete form speciﬁcations of expected earnings based on alternative assump-
tions regarding the information set applicants face. First, assuming that applicants have
generic information about the returns to major j, the expected earnings of individual i
in major j can be written as

E1(v2i j ) = pi j(a)eg
j

+ (1 − pi j(a))ed
j

(5)

j and ed

where pi j(a) is the probability of successfully completing college, which is assumed to
be a function of ability (a), and eg
j represent, respectively, median income after
graduating in major j and median income after dropping out of college. Because ap-
plicants are assumed to have generic information about earnings diﬀerentials, ability
aﬀects expected earnings, ex ante, only through the probability of successfully com-
pleting college. In a way, this speciﬁcation can be considered to be based on egalitarian
distribution of expected earnings.

Second, assuming that applicants have full information, ex ante, about where they
are likely to fall in the earnings distribution based on their ability, the expected earnings
of individual i with ability a in major j is given as

E1(v2i j ) = eg
j,a

(6)

In contrast to the egalitarian measure of expected earnings in equation 5, this spec-
iﬁcation can be considered to be predicated on meritocratic distribution of expected
earnings.

I can now combine equations 4 and 5 or 6 to arrive at a reduced form equation
that can be estimated empirically. This means the indirect utility for individual i from
majoring in j can be written as a linear function of observed academic ability, individual
and neighborhood characteristics, and expected earnings:

v1i j = α1γ1Ai(h) + α1γ2Zi j + α2Xi + μβ[E1(v2i j )] + ε1i j,

(7)

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
4
3
4
7
2
1
6
9
3
0
1
4
e
d
p
_
a
_
0
0
2
4
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

where E1(v2i j ) = pi j(a)(eg
i j

− ed

i j ) + pi jed

i j or E1(v2i j ) = eg

j,a.

Generally, the choices made in high school, which are expected to inﬂuence ma-
jor choice through Ai j, are constrained by geographical space. In countries such as
South Africa that are characterized by signiﬁcant spatial inequality, neighborhood char-
acteristics aﬀect major choice both directly through shaping preferences and indirectly
through Ai j(h). Hence, provided there are appropriate constructs to measure regional

476

Biniam E. Bedasso

distribution of resources and neighborhood characteristics, the model speciﬁed in
equation 7 can be estimated to explain the choice of college major in South Africa.

The parameters in equation 7 can be estimated using standard techniques as long
as certain assumptions are made regarding the distribution of unobservables. First, I
assume that ε1i j is independently distributed across individuals once relevant neighbor-
hood characteristics are controlled for. Second, I assume ε1i j is correlated across majors
sharing certain characteristics. For example, the unobserved preference of a student for
a physics degree is likely to be correlated with the unobserved preference for a chem-
istry degree. The same might not hold between physics and history. Formally, suppose
there are N groups of academic streams across which the J majors are distributed. This
means a student will have to choose an academic stream n = 1, . . . , N before deciding
on which speciﬁc major to pursue. This implies that the ﬁnal choice set can be written
as follows:

j ∈ {( j11, . . . , jJ11), ( j12, . . . , jJ22), . . . , ( j1N, . . . , jJN N )}.

This type of structure leads to nested logit probabilities with J alternatives and N
nests. Suppose the full set of explanatory variables can be split into explanatory variables
of nest choice, Wn, and explanatory variables of the choice of speciﬁc alternatives, Sn j.
Note that I have dropped the individual index i and the period index 1 for simplicity.
This means equation 7 can be rewritten as

(cid:3)
v j = W
n

(cid:3)
κn + S
n j

λ j + εn j.

(8)

Provided that εn j is drawn from a generalized extreme value distribution, the prob-

ability of choosing the jth alternative belonging to the nth nest is given by

Pr( j) = Pr( j | n) Pr(n)

(cid:3)

λ j/τn)

exp(S(cid:3)
n j
exp(S(cid:3)
n j

j∈Jn

λ j/τn)

(cid:4)

(cid:3)

exp[W (cid:3)
n
n∈N exp[W (cid:3)

κn + τnIVn)]

(cid:5)

(9)

(cid:3)

where IVn = ln(
nest.

j=1 exp(S(cid:3)

n j

λ j )) and τn measures the correlation of εn j within a given

The coeﬃcients in equation 9, including the dissimilarity coeﬃcient τn, can be es-
timated using the full information maximum likelihood method. I will return to the
issue of identiﬁcation once I have presented the data in the next section.

3 . DATA
I use the admissions application database of the UCT to estimate the model of major
choice speciﬁed in the previous section. The data are available for the entire popula-
tion of applicants, which ranges between 13,897 and 16,077 applicants per year, for the
four years from 2010 to 2013. In addition to basic demographic information and aca-
demic record, as of 2013, UCT has started collecting data on family background and
high school characteristics from all applicants. Therefore, I use the population of ap-
plicants in 2013 to estimate the model. Moreover, information from previous years is
utilized to identify neighborhood trends based on patterns of admission of applicants

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
4
3
4
7
2
1
6
9
3
0
1
4
e
d
p
_
a
_
0
0
2
4
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

477

College Major Choice

from a given neighborhood over the four years. The application database is rich in geo-
graphical information as applicants could be traced to the level of residential postcode.
Moreover, the names of the high schools of the applicants are given in the dataset. This
means I can exploit spatial variations across 3,773 postcodes and 1,577 high schools.

Much of the analysis is based on the entire population of applicants, regardless of
admission status. This is done in the interest of minimizing the selection bias that
may arise due to the university admission process, as well as the decision of applicants
whether or not to accept oﬀers. Prospective students apply for majors in one or two of
UCT’s faculties as their ﬁrst and second choices. Applications to individual faculties
are evaluated independently and admission is oﬀered or denied by the respective fac-
ulty. Therefore, the ﬁrst choices of prospective students at the point of application are
supposed to reﬂect the revealed preferences of individuals before supply constraints
are imposed. Second choices, by contrast, are less informative because applicants may
act strategically by listing a less popular major as a second choice in order to minimize
potential loss.4

Estimation of the model speciﬁed in the previous section requires data on expected
earnings. The combination of earnings and college major data are available for the third
and fourth quarters of the Quarterly Labor Force Survey in 2012. Ideally, the expected
lifetime earnings of applicants in each ﬁeld of study are estimated using a sample of cur-
rent workers of various age groups who share similar characteristics as the applicant.
However, this approach can be problematic in the case of South Africa because the earn-
ings trajectories of mature workers in 2012 are likely to have been shaped by a distorted
system during apartheid. This dynamic is unlikely to hold in the postapartheid period.
Therefore, I have restricted the age limit of the sample of workers that are used to cal-
culate expected earnings to thirty years.5 Another challenge in this case is that there are
not enough observations of college educated, under-thirty-years-olds in the Quarterly
Labor Force Survey data to estimate earnings on a full range of personal and group
characteristics. Therefore, I have chosen to use the earnings of the under-thirty-year-
olds sample for each major to approximate expected earnings of college applicants. The
fact that the earnings of current workers are based on realized choices of college ma-
jor might introduce selection bias in the sense that current workers are already sorted
by aptitude. This means the expected earnings of high-scoring applicants in less se-
lective majors could be biased downwards. The bias is upward in case of low-scoring
applicants in more selective majors. However, I expect the eﬀect of such biases to be
minimal since the earnings diﬀerential among majors is more likely to emanate from
systematic diﬀerences in the occupations in which they lead than from individual abil-
ity. I will return to the calculation of individualized aptitude-adjusted expected earnings
later in this section.

Table 1 presents a summary of variables that are used to estimate the model of major
choice. The categories of choice are organized in terms of oﬃcial faculties at UCT. I have
combined the faculties of humanities and law to simplify the choice set into ﬁve facul-
ties: three in science and technology (health sciences, engineering, science) and two in

I would like to thank one of the anonymous referees for pointing out this scenario.

4.
5. This choice makes more practical sense particularly if one assumes that college students are able to observe

more closely the incomes of those who are the in same generation as they are than that of older people.

478

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
4
3
4
7
2
1
6
9
3
0
1
4
e
d
p
_
a
_
0
0
2
4
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Biniam E. Bedasso

Table 1. Summary Statistics of College Applications and Labor Market Data

Commerce

Engineering

3,359

0.22

2,600

0.12

Number of applicants

Ratio of admitted

Academic record

NSC Math

NSC English

NSC Life orientation

NBT Math

NBT Academic literacy

Number of high school science courses

Socioeconomic background

Ratio of public school

Ratio of private school

Ratio of first-generation college

Demographic variables

Male

Female

Black

White

Colored and Asian

Labor market variables

67.8
(17.2)

70.5
(9.9)

79.6
(9.3)

46.9
(17.3)

63.5
(12.7)

1.5
(1.1)

0.27

0.73

0.42

0.48

0.52

0.50

0.24

0.25

Health
Sciences

3,738

0.08

65.9
(17.5)

71.2
(10.2)

80.8
(8.9)

43.6
(16.8)

60.2
(13.9)

Science

1,263

0.21

64.1
(17.1)

68.8
(9.8)

77.9
(9.2)

43.5
(16.4)

61.1
(14.1)

Humanities
and Law

3,257

0.20

59.5
(18.1)

66.6
(10.5)

75.1
(10.0)

36.0
(12.7)

60.9
(13.7)

69.0
(16.4)

68.5
(9.8)

78.3
(9.3)

48.2
(17.2)

60.2
(14.3)

2.4
(0.81)

2.3
(0.71)

2.3
(0.78)

1.1
(0.90)

0.33

0.67

0.47

0.70

0.30

0.55

0.22

0.21

0.31

0.69

0.48

0.31

0.69

0.53

0.17

0.28

0.31

0.69

0.51

0.47

0.53

0.51

0.26

0.22

0.27

0.73

0.47

0.34

0.66

0.48

0.25

Total

14,217

0.15

65.4
(17.7)

69.3
(10.3)

78.4
(9.6)

44.7
(17.0)

61.2
(13.8)

1.8
(1.0)

0.29

0.71

0.47

0.44

0.56

0.51

0.24

0.25

Undergraduate median earnings:

16,000

20,000

18,000

16,000

15,000

Under 30 years old (in rand)

Technical school median earnings:

10,200

11,000

10,000

9,000

10,500

Under 30 years old (in rand)

Expected earnings 1: Egalitarian

distribution (in rand)

Expected earnings 2: Meritocratic

distribution (in rand)

11,939
(738)

19,399
(13,831)

13,195
(1,978)

21,760
(13,311)

12,582
(1,364)

20,023
(12,015)

10,545
(1,375)

17,912
(12,269)

9,449
(555)

16,662
(11,746)

11,487
(1,879)

19,079
(12,791)

Notes: Standard deviation is given in parentheses in case of mean. NBT = National Benchmark Test; NSC = National Senior Certificate.

social sciences (commerce, humanities and law). The admission rates show that health
sciences and engineering are by far the most selective faculties. Academic preparation
is measured by six variables displayed in the second panel of table 1. First, scores in
the three compulsory subjects of the National Senior Certiﬁcate (NSC) examination—
English, mathematics, and life orientation—are applied to measure basic academic
ability. Second, scores in the National Benchmark Test (NBT), which is used as an ad-
ditional requirement for admission into major universities in South Africa, is utilized
to measure the probability of success in college and in a professional environment.
The NBT is speciﬁcally designed to gauge the adaptability of students to college cur-
riculum. The test is given in three modules: academic literacy, quantitative literacy,
and mathematics. Third, the number of science courses a student has taken in high
school is used as a proxy for the level of preparation in science and technology. The high

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
4
3
4
7
2
1
6
9
3
0
1
4
e
d
p
_
a
_
0
0
2
4
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

479

College Major Choice

standard deviation, relative to the mean of the number of science courses, indicates that
high school graduates vary signiﬁcantly in terms of their preparation in science.

Table 1 also presents variables that are used to measure socioeconomic background.
A majority of the applicants attended private high schools, signifying the middle-class
status of most applicants. In terms of the educational background of families, over 47
percent of applicants would be the ﬁrst ones in three generations to have earned a col-
lege degree. Demographic characteristics of applicants show that women constitute the
majority of applicants. Black applicants form 51 percent of the applicant pool. White ap-
plicants constitute 24 percent and Colored applicants (people of mixed ancestry, which
has become a distinctive group through the lines drawn by the Apartheid regime) and
Indians make up 25 percent.

The bottom panel in table 1 presents summary of expected earnings for each faculty.
The ﬁrst row contains the median monthly earnings of workers under thirty years of
age with a three- or four-year college degree in each ﬁeld. The second row presents the
median income of workers in the same age group who have completed only a technical
school diploma in one of the ﬁve ﬁelds. The incomes of technical school graduates are
utilized to approximate the expected earnings of applicants in case they drop out of
college.

I use the two alternative speciﬁcations that are laid out in equations 5 and 6 to
calculate aptitude-adjusted expected earnings for every applicant. To compute the ﬁrst
measure, I apply the formula in equation 5 to individualize the median income of each
major by adjusting it with the probability of each applicant’s success in college. I use
the NBT scores to predict the probability of success. It is to be expected that each faculty
has a speciﬁc requirement of skill sets determining success in that particular ﬁeld. In
order to determine which NBT module to use as a weight to calculate expected earnings
in a given ﬁeld, I run a probit regression of admission probability on the three types of
NBT scores for the years prior to 2013. This is done under the assumption that university
oﬃcials know the skill sets that are required to succeed in a given ﬁeld and have already
incorporated that information in the admission process. Based on the results of the
probit regression (reported in Appendix A), math scores are used to adjust expected
earnings in engineering, health sciences, and science, whereas academic literacy scores
are used to adjust expected earnings in commerce and humanities and law.

In computing the second measure, I simply calculate the decile distribution of
monthly income of each major and assign individuals to diﬀerent deciles based on their
aptitude. I assume the distribution of income for a certain major is aligned with the dis-
tribution of aptitude for that particular major. Accordingly, a person with a median NBT
score can expect to earn the median income, whereas a person with a 95th-percentile
NBT score can expect to fall in the top decile of the income distribution for that ma-
jor. This is a simplistic measure that is intended to emphasize the potential impact of
ability on labor market returns and inequality within the same major. As in the ﬁrst
measure, math scores are used to determine aptitude for engineering, health sciences,
and science, whereas academic literacy scores are used in the cases of commerce and
humanities and law. The last two rows in table 1 present descriptive statistics for the
alternative measures of aptitude-adjusted expected earnings.

The next step concerns identiﬁcation of the nesting structure that is supposed to
govern the choice process of applicants. Intuitively, one can assume that applicants

480

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
4
3
4
7
2
1
6
9
3
0
1
4
e
d
p
_
a
_
0
0
2
4
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Biniam E. Bedasso

Table 2. Correlation Between First and Second Choice Faculties

Second Choice

First Choice

Commerce

Engineering

Health Sciences

Science

Humanities and Law

Commerce

Engineering

Health sciences

Science

Humanities and law

0.22
−0.04
−0.11
−0.03
−0.04

−0.09
0.32
−0.02
0.08
−0.23

−0.12
−0.06
0.27

0.03
−0.12

−0.08
0.10

0.21
−0.11
0.44

0.02
−0.22
−0.22
−0.05
−0.15

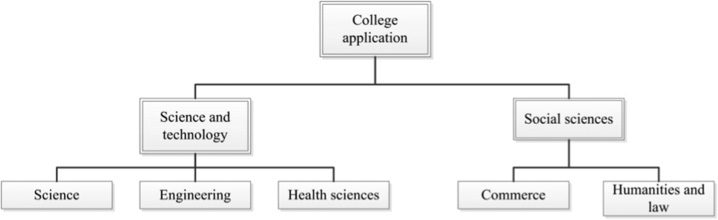
Figure 1. Nesting structure

diﬀerentiate between the broad categories of science and technology on the one hand
and social sciences on the other hand before picking speciﬁc faculties and departments
within those categories. This assumption is corroborated by the clustering of skill sets
required for admission along the science and technology versus social sciences divide.
On top of all this, I am able to explicitly show the correlation of choices across facul-
ties because there are data on the ﬁrst and second choices of most applicants. Table 2
shows that an overwhelming number of applicants choose two majors in the same fac-
ulty as ﬁrst and second choices. When applicants decide to choose a second major in
another faculty, they mostly choose within the nests of social sciences and science and
technology. These results justify the assumption that unobserved preference for spe-
ciﬁc majors is correlated within nests. Figure 1 displays the nesting structure that will
be used to implement the nested logit estimation in the next section.

At this point, I can turn to the model speciﬁed in equation 8 to discuss the sources
of empirical identiﬁcation. Note that the main coeﬃcients of interest in the vectors
of parameters Wn and Sn j relate to the eﬀects of expected earnings and neighborhood
characteristics. The fact that expected earnings are measured by the quantile income
of contemporary workers can be used as an exclusion restriction to identify the eﬀect
of expected earnings on the choices of college applicants. However, the eﬀect of quan-
tile income is conditional on the probability of success or aptitude, which is measured
by NBT results. The test scores of applicants in relevant modules are likely to inﬂu-
ence major choice through channels other than the probability of success. Therefore,
μβ in equation 6 may not be identiﬁed independently of pi j unless there is exogenous
variation in test results. The strategy I follow to identify μβ involves using the NSC
scores in math, English, and life orientation to control for unobserved preference that

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
4
3
4
7
2
1
6
9
3
0
1
4
e
d
p
_
a
_
0
0
2
4
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

481

College Major Choice

would otherwise be attributed to NBT results. For instance, a high score in NSC math
is suﬃcient to predict whether an applicant would enjoy attending college in engineer-
ing. Once that eﬀect is controlled for, the residual eﬀect of NBT, which is designed to
measure adaptability of prior knowledge to college curriculum, can be assumed to be
aﬀecting major choice through expected future earnings.

The coeﬃcients of neighborhood eﬀects are identiﬁed because they are estimated
based on geographical variations. There is a valid concern that unobserved preference
for educational outcomes could be correlated with the choice of residence. In other
words, parents choose decent neighborhoods and good schools in the interest of bet-
ter educational outcomes for their children. However, it is unlikely that parents would
choose one neighborhood over the other because they want their children to study, say,
engineering, in college. Even if they do, all they can consider, at high school level, is
curriculum and quality, which are directly controlled for through high school science
preparation and NSC grades for core subjects.

4 . R E S U LT S
Determinants of High School Curriculum Choice
Both theory and existing empirical evidence suggest that the choice of college major
is conditional on high school preparation. More accurately, the choice of high school
curriculum is often made in an anticipation of a certain college major and career path.
This means an important part of the decision is already made in high school. How-
ever, individuals make two more nontrivial decisions at the point of college application.
First, they can choose whether or not to switch the broad ﬁeld they pursued in high
school based on the information they have discovered about their own aptitude dur-
ing high school. Second, whether or not they are switching ﬁelds, college applicants
need to choose majors that are more speciﬁc than high school curriculums. I begin the
presentation of results with the determinants of the choice of high school curriculum.
Table 3 presents the determinants of the number of high school science electives
students take. I consider both individual-level and municipality-level correlates of cur-
riculum choice. In column 1, all the explanatory variables are basic demographic and
socioeconomic variables that are also included in the college major choice estimations
(to be presented later). Both black and white students are found to take fewer science
courses than Colored and Indians. The dummies for female and ﬁrst-generation col-
lege are also negative, and public high schools are associated with more science courses.
The positive coeﬃcient of public high school is probably because those students from
public high schools who apply to an elite university, such as UCT, self-select themselves
on their inclination for technical subjects.

Considering that geographical location may have an impact on school quality and
availability of some electives in such a historically segregated country as South Africa, I
account for municipality-level eﬀects by introducing 240 municipality dummies in col-
umn 1. Subsequently, in column 2, I examine what might be driving the municipality-
level eﬀects by estimating the correlation between key socioeconomic and political
variables at the municipality level, and the municipality ﬁxed-eﬀects calculated based
on column 1. Finally, column 3 controls for the municipality-level socioeconomic and
political variables directly in estimating the determinants of high school curriculum.

482

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
4
3
4
7
2
1
6
9
3
0
1
4
e
d
p
_
a
_
0
0
2
4
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Biniam E. Bedasso

Table 3. Determinants of Science Curriculum in High School

Number of
Science Electives

Municipality
Fixed Effect

Number of
Science Electives

(1)

(2)

(3)

Dependent Variable

Individual-level correlates

Female dummy

Public school dummy

First-generation college dummy

Black dummy

White dummy

−0.215***
(0.008)
0.070***
(0.009)
−0.064***
(0.008)
−0.359***
(0.012)
−0.086***
(0.012)

Municipality-level correlates

Ratio of households above poverty line

Ratio of individuals with high school certificate

Percentage of ANC votes

Municipality fixed effect (240 municipality dummies)
R2

Number observations

Yes

0.08

11,644

−2.28***
(0.047)
1.21***
(0.032)

.792***

(0.011)

0.70

234

Notes: Standard errors are given in parentheses. ANC = African National Congress.
***Statistically significant at the 99% confidence level.

−0.219***
(0.008)
0.061***
(0.009)
−0.076***
(0.008)
−0.338***
(0.011)
−0.080***
(0.011)

−2.18***
(0.137)
1.14***
(0.100)

.788***

(0.035)

0.07

11,644

The results in columns 2 and 3 show that students applying from municipalities with
higher levels of secondary school attainment are more prepared in science subjects. To
the extent that high school completion is linked to availability of schooling resources,
this result suggests that students from municipalities with better schooling resources
come better prepared in science subjects. However, once educational attainment is con-
trolled for, the coeﬃcient of households above poverty line becomes strongly negative.
This indicates that students from poorer municipalities apply to UCT probably because
they are well prepared in high school science curriculum. Coupled with the positive
coeﬃcients of the public school variable in column 1, this ﬁnding points to the likeli-
hood that students from poorer backgrounds self-select themselves to applying to UCT
based on their preparation in high school science subjects. This result may have impli-
cations for the possibility of using improvements in high school science education in
poorer areas as a means to reduce inequality through equitable access to elite higher
education.

The Effects of Expected Labor Market Returns
This section focuses on the role of expected labor market earnings in the choice of
college major. The choice between science and technology on the one hand and social
sciences on the other hand, which represents the ﬁrst-level decision according to the
nesting structure in ﬁgure 1, is speciﬁed as a function of high school curriculum or, al-
ternatively, municipality-level variables inﬂuencing high school curriculum choice. The

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
4
3
4
7
2
1
6
9
3
0
1
4
e
d
p
_
a
_
0
0
2
4
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

483

College Major Choice

choice of speciﬁc faculties, which is modeled as a second-level decision, is a function
of major-speciﬁc expected earnings, family background, and demographic variables.

Table 4 presents the coeﬃcient estimates of the random utility model of major
choice. Because the magnitude of the coeﬃcients in table 4 is not directly interpretable,
average marginal eﬀects of selected variables are presented in table 5 to provide an in-
tuitive interpretation of the estimates. Columns 1 and 2 show that expected earnings,
measured under alternative assumptions about ex ante distribution of earnings after
graduation, exert a positive eﬀect on the probability of choosing a given major. At the
very least, the comparison between columns 1 and 2 demonstrates that the role of ex-
pected earnings is robust to alternative speciﬁcations with fundamentally diﬀerent as-
sumptions about the impact of ability on income distribution.

The eﬀect of expected earnings, as measured by the more egalitarian indicator, dis-
appears once high school curriculum is controlled for in column 4. In contrast, the
meritocratic measure of expected earnings, which captures more information about
post-college income diﬀerentials, continues to hold a strong eﬀect on major choice
independently of high school curriculum, as shown in column 5. It may be that the
coeﬃcient of the egalitarian measure is picking up the correlation between expected
earnings and unobserved preferences, which is removed once high school curriculum
is controlled for. The fact that this is not the case with the meritocratic measure sug-
gests that expected earnings need to capture long-term income diﬀerentials to predict
major choice net of unobserved preferences.

As columns 3 to 5 show, the number of science electives applicants took in high
school increases the probability of choosing a major in college in science and technol-
ogy. The choice of high school curriculum contains so much information about the
aptitude of individuals for alternative ﬁelds with varying levels of ﬁnancial desirability
that it absorbs the explanatory power of major-speciﬁc median income. In other words,
as far as median income can predict, applicants have already incorporated information
on potential earnings when they decided on high school curriculum a few years earlier.
Column 7 in table 5 displays that a one standard deviation increase in the number of
high school science subjects raises the probability of choosing a major in science and
technology by 0.22, on average. In order to account for the indirect eﬀects of geograph-
ical factors on major choice, I control for municipality-level variables that are shown
in the previous section to be correlated with the number of high school science elec-
tives applicants took. Accordingly, columns 6 and 7 show that applicants coming from
poorer municipalities tend to choose majors in science and technology over majors in
social sciences. This result indicates that prospective students from poorer areas apply
to UCT mainly because they aspire to major in areas of science and technology.

The responsiveness of individuals to expected earnings might depend on the
amount and quality of information they have about a number of factors, including the
academic requirements of—and labor market returns to—diﬀerent majors. As with
many other things in South Africa, the information young people have about college
and the labor market may be inﬂuenced signiﬁcantly by their ethnic or racial back-
ground. In an attempt to disentangle the potential eﬀect of race on shaping the respon-
siveness of applicants, the ﬁrst two speciﬁcations in table 4 are repeated for the black
and white subpopulations in columns 8 to 11. The results show that both measures
of major-speciﬁc expected earnings have positive and statistically signiﬁcant eﬀects on

484

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
4
3
4
7
2
1
6
9
3
0
1
4
e
d
p
_
a
_
0
0
2
4
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Biniam E. Bedasso

*
*
*
8
9
4
0

)
3
8
0
0
(

*
*
*
3
5
3
0

)
8
4
0
0
(

*
*
*
7
9
2
0

)
7
3
0
0
(

*
*
*
8
1
2
0

)
2
4
0
0
(

*
*
*
5
7
3
0

)
5
3
0
0
(

e
t
i
h
W

)
1
1
(

e
t
i
h
W

)
0
1
(

*
*
*
7
1
1
4

)
5
7
5
0
(

k
c
a
B

)
9
(

k
c
a
B

)
8
(

*
*
*
2
0
5
2

)
8
4
4
0
(

l
l

u
F

)
7
(

l
l

u
F

)
6
(

*
*
*
3
9
8
1

)
2
1
3
0
(

l
l

u
F

)
5
(

l
l

u
F

)
4
(

3
0
2
0

)
8
0
3
0
(

l
l

u
F

)
3
(

l
l

u
F

)
2
(

l
l

u
F

)
1
(

*
*
*
9
6
6
2

)
6
8
2
0
(

*
*
*
3
4
2
1

)
2
3
0
0
(

*
*
*
2
5
2
1

)
2
3
0
0
(

*
*
*
9
2
4
1

)
9
2
0
0
(

)
s
e
c
n
e
c
S

a
c
o
S

n
o
i
t
u
b
i
r
t
s
i
d

n
a
i
r
a
t
i
l

a
g
e

1
s
g
n
n
r
a
e

d
e
t
c
e
p
x
e

n
o
i
t
a
u
p
o
P

n
o
i
t
u
b
i
r
t
s
i
d

c
i
t
a
r
c
o
t
i
r
e
m

2
s
g
n
n
r
a
e

d
e
t
c
e
p
x
e

:
e
c
n
e
r
e
f
e
R
(

y
g
o
o
n
h
c
e
T

d
n
a

e
c
n
e
c
S

:
e
c
o
h
C
1

e
v
e
L

s
e
v
i
t
c
e
e

e
c
n
e
c
s

o
o
h
c
s

h
g
h

f
o

r
e
b
m
u
N

s
n
r
u
t
e
R

t
e
k
r
a
m
n
o
N
d
n
a

t
e
k
r
a
M
h
t
i

w
e
c
o
h
C

r
o
a
M

f
o

e
d
o
M
y
t
i
l
i
t

U
m
o
d
n
a
R

f
o

s
e
t
a
m

i
t
s
E

4
e
l
b
a
T

*
*
*
0
4
4
2
−

*
*
*
1
9
5
2
−

)
7
0
7
0
(

)
2
4
5
0
(

1
6
7
0
−

*
*
0
7
4
0

)
5
8
1
0
(

)
7
1
7
0
(

)
3
4
5
0
(

7
5
8
0
−

*
*
*
4
0
5
0

)
6
8
1
0
(

y
t
i
l

a
p
c
n
u
m
n

e
t
a
c
fi
i
t
r
e
c

o
o
h
c
s

h
g
h

h
t
i

w
s
l
a
u
d
i
v
i
d
n

f
o

o
i
t
a
R

y
t
i
l

a
p
c
n
u
m
n

e
n

i
l

y
t
r
e
v
o
p

e
v
o
b
a

s
d
o
h
e
s
u
o
h

f
o

o
i
t
a
R

y
t
i
l

a
p
c
n
u
m
n

s
e
t
o
v
C
N
A

f
o

e
g
a
t
n
e
c
r
e
P

*
*
2
6
0
0

)
6
0
0
0
(

*
*
*
2
7
0
0

)
7
0
0
0
(

*
*
5
4
0
0

)
7
0
0
0
(

*
*
4
4
0
0

)
8
0
0
0
(

*
*
*
4
6
0
0

)
6
0
0
0
(

*
*
*
4
5
0
0

)
8
0
0
0
(

*
*
*
5
3
0
0

)
7
0
0
0
(

*
*
*
3
3
0
0

)
8
0
0
0
(

*
*
*
7
4
0
0

)
4
0
0
0
(

*
*
*
2
5
0
0

)
4
0
0
0
(

*
*
*
4
3
0
0

)
4
0
0
0
(

*
*
*
0
3
0
0

)
5
0
0
0
(

*
*
*
8
4
0
0

)
4
0
0
0
(

*
*
*
9
4
0
0

)
5
0
0
0
(

*
*
*
4
3
0
0

)
4
0
0
0
(

*
*
*
1
3
0
0

)
5
0
0
0
(

*
*
*
4
5
0
0

)
2
1
0
0
(

*
*
*
6
6
0
0

)
2
1
0
0
(

*
*
*
6
3
0
0

)
8
0
0
0
(

*
*
*
2
3
0
0

)
8
0
0
0
(

*
*
*
4
7
0
0

)
5
1
0
0
(

*
*
*
3
8
0
0

)
4
1
0
0
(

*
*
*
6
4
0
0

)
9
0
0
0
(

*
*
*
2
4
0
0

)
0
1
0
0
(

*
*
*
7
9
0
0

)
7
1
0
0
(

*
*
*
7
6
0
0

)
3
1
0
0
(

*
*
*
6
5
0
0

)
1
1
0
0
(

*
*
*
4
5
0
0

)
1
1
0
0
(

)
1
0
0
0
(

0
0
0
0
−

*
*
*
3
2
0
0
−

)
4
0
0
0
(

)
3
0
0
0
(

1
0
0
0
−

0
0
0
0

)
4
0
0
0
(

*
*
*
9
0
6
0

)
8
8
0
0
(

*
*
*
5
6
5
0

)
7
8
0
0
(

*
*
*
2
0
2
0

)
3
3
0
0
(

*
*
*
6
8
1
0

)
5
3
0
0
(

*
*
*
1
5
0
0

)
3
0
0
0
(

*
*
*
4
5
0
0

)
3
0
0
0
(

*
*
*
4
3
0
0

)
3
0
0
0
(

*
*
*
2
3
0
0

)
3
0
0
0
(

*
*
*
2
5
0
0

)
2
0
0
0
(

*
*
*
8
4
0
0

)
3
0
0
0
(

*
*
*
3
3
0
0

)
2
0
0
0
(

*
*
*
1
3
0
0

)
3
0
0
0
(

)
w
a
L

d
n
a

s
e
i
t
i
n
a
m
u
H

:
e
c
n
e
r
e
f
e
R
(

s
e
i
t
l
u
c
a
F

c
fi
c
e
p
S

:
e
c
o
h
C
2

e
v
e
L

e
c
r
e
m
m
o
C

h
t
a
m
C
S
N

g
n
i
r
e
e
n
g
n
E

s
e
c
n
e
c
s

h
t
l
a
e
H

e
c
n
e
c
S

3
9
4
3
−

5
8
4
3
−

7
5
0
6
−

8
6
0
6
−

4
1
1
3
1
−

9
2
1
3
1
−

6
4
2
2
1
−

2
2
2
2
1
−

5
8
3
5
1
−

5
5
1
3
1
−

9
6
1
3
1
−

1
5
6
1

7
0
0
1

1
5
1
2

1
9
3
1

1
9
5
0

1
0
9
1

6
6
1
1
−

7
6
1
0
−

5
5
2
2

6
2
8
3

y
m
m
u
d

e
a
m
e
F
,
y
m
m
u
d

k
c
a
B

,
y
m
m
u
d

e
g
e

l
l

o
c

n
o
i
t
a
r
e
n
e
g
–
t
s
r
i

F
,
y
m
m
u
d

o
o
h
c
s

i
l

b
u
P
,
n
o
i
t
a
t
n
e
i
r
o

e
f
i
l

C
S
N

,
h
s
i
l

g
n
E
C
S
N

,
h
t
a
m
C
S
N

:
s
l
o
r
t
n
o
c

c
fi
c
e
p
s
–
e
s
a
c

r
e
h
t
O

y
g
o
o
n
h
c
e
t

d
n
a

e
c
n
e
c
s

s
e
c
n
e
c
s

a
c
o
s

d
o
o
h

i
l

e
k

i
l
–
g
o
L

7
6
4
2

2
1
3
4

9
3
2
9

7
6
2
9

2
1
5
1
1

7
6
2
9

s
e
s
a
c

f
o

r
e
b
m
u
N

.
s
s
e
r
g
n
o
C

a
n
o
i
t
a
N
n
a
c
i
r
f
A
=
C
N
A

.
e
r
e
h

d
e
t
r
o
p
e
r

t
o
n

e
r
a

e
b
a
t

e
h
t

d
e
t
s
i
l

s
l
o
r
t
n
o
c

a
n
o
i
t
i
d
d
a

n
e
v
e
s

r
o
f

s
t
n
e
c
fi
f
e
o
C

.
s
e
s
e
h
t
n
e
r
a
p

n
e
v
i
g

e
r
a

s
r
o
r
r
e

d
r
a
d
n
a
t
S

:
s
e
t
o
N

.
l
e
v
e

e
c
n
e
d
fi
n
o
c
%
9
9
e
h
t

t
a

t
n
a
c
fi
n
g
i
s

y
l
l

a
c
i
t
s
i
t
a
t
s
*
*
*

;
l
e
v
e

e
c
n
e
d
fi
n
o
c
%
5
9
e
h
t

t
a

t
n
a
c
fi
n
g
i
s

y
l
l

a
c
i
t
s
i
t
a
t
S
*
*

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
4
3
4
7
2
1
6
9
3
0
1
4
e
d
p
_
a
_
0
0
2
4
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

485

College Major Choice

Table 5. Average Marginal Effectsa

Expected Earnings 1:
Egalitarian Distribution
(Own Effect)

Expected Earnings 2:
Meritocratic Distribution
(Own Effect)

Number of High
School Science
Electivesf

(1)

(2)

(3)

(4)

(5)

(6)

(7)

Choice

Blackb

Whitec

White to
Black ratio

Blackd

Whitee

White to
Black Ratio

Science and technology

Commerce

Engineering

Health sciences

Science

Humanities and law

0.504***
(0.090)
0.426***
(0.077)
0.561***
(0.101)
0.229***
(0.042)
0.141***
(0.026)

0.913***
(0.128)
0.617***
(0.089)
0.713***
(0.103)
0.470***
(0.069)
0.465***
(0.068)

1.81

1.45

1.27

2.05

3.29

0.071***
(0.009)
0.060***
(0.008)
0.079***
(0.011)

0.032
(0.004)
0.019***
(0.003)

0.110***
(0.018)
0.074***
(0.013)
0.086***
(0.015)
0.056***
(0.009)
0.056***
(0.009)

1.55

1.23

1.09

1.75

2.94

0.222***
(0.090)

Notes: aStandard deviations of the mean are given in parentheses. bCalculation based on column 8 in table 4. cCalculation based on
column 10 in table 4. dCalculation based on column 9 in table 4. eCalculation based on column 11 in table 4. fCalculation based on
column 3 in table 4.
***Statistically significant at the 99% confidence level.

the probability of choosing a given major in both subpopulations. More importantly,
columns 1 to 6 in table 5 present the average marginal eﬀects of a one standard de-
viation increase in the natural logarithm of expected earnings in a certain major on
the probability of choosing that major for the black and white subpopulations. Notably,
white applicants are more responsive to changes in expected earnings across all majors
and speciﬁcations of expected earnings. However, the gap in responsiveness between
black and white applicants is the smallest for the more selective and ﬁnancially reward-
ing majors, such as health sciences and engineering. In general, the meritocratic mea-
sure of expected earnings is shown to result in smaller gaps in responsiveness between
black and white applicants. In other words, when we account for ﬁner distinctions in
potential income after graduation, black applicants appear more responsive to expected
earnings than when we only take median income.

Spatial Inequality and Neighborhood Effects
I have begun to account for the eﬀect of spatial inequality on major choice through
the use of municipality-level controls in the previous section. Nevertheless, spatial in-
equality in South Africa is much ﬁner than diﬀerences at the municipality level. This
section focuses on neighborhood eﬀects down to the postcode and speciﬁc high school
levels. First, I construct a measure of neighborhood-level admission trends for each of
the 3,773 postcodes. This variable measures the ratio of students admitted to UCT to
a given program from a single postcode out of the total number of students admitted
from the same geographical area in the same year. This is calculated using admissions
data between 2010 and 2012. I expect this variable to capture the inﬂuence of near-peer
role models in a given neighborhood on the career decisions of college applicants. The
notion of nearness in this context has both generational and spatial dimensions. The

486

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
4
3
4
7
2
1
6
9
3
0
1
4
e
d
p
_
a
_
0
0
2
4
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Biniam E. Bedasso

Table 6. Average National Senior Certificate Scores in Student-School Quartiles

Quartiles of Students Within a School

1st

2nd

3rd

4th

54.5

63.6

71.1
78.3b

Quartiles of Schools

2nd

59.5

68.4

75.3

82.9

3rd

62.2

70.9

77.8

85.5

4th

65.2

73.8
80.2a

87.1

Notes: aThis cell represents a group of applicants from a highly competitive high
school: Small Frog in a Big Pond. bThis cell represents a group of applicants from
a less competitive high school: Big Frog in a Small Pond.

neighborhood-level admission variable might be picking up a correlation between the
unobserved preferences of applicants in the same neighborhood. Hence, in order to
isolate the temporal near-peer eﬀect, I correct for clustered errors at the postcode level.
In addition to inﬂuencing current decisions through past role models, the neighbor-
hood eﬀect might impact major choice by shaping the beliefs of individuals about their
own ability. This hypothesis draws on established arguments about the “frog-pond” ef-
fect in the sociology of education literature (Davis 1966; Espenshade, Hale, and Chung
2005). The hypothesis predicts that a high-achieving student from a relatively less
competitive school, that is, a big frog in a small pond (BFSP), tends to choose a more
demanding major in college than a relatively low-achieving student from a more com-
petitive school, that is, a small frog in a big pond (SFBP). In order to assign frog–pond
identiﬁcation to the population of applicants in the data, I create a pool of 1,557 high
schools with at least ﬁve applicants to UCT between 2010 and 2013. Then I calculate a
three-subject average NSC score for each school based on average scores in math, En-
glish, and life orientation. This makes it possible to allocate schools across a distribution
of average grades divided into four quartiles. The next step is creating school-level quar-
tiles of students using the same measurement as above. Table 6 displays the average
grades for the sixteen student–school quartile combinations. The tightness of the dis-
tribution indicates that applicants to UCT already self-select themselves on their high
school grades. I have identiﬁed one pair of BFSP and SFBP based on the criteria that
the “big frogs” belong to the top quartile in their school even if their grades on average
are lower than the “small frogs” in a more competitive school. The average score in the
SFBP cell in table 6 is statistically greater than the average grade in the BFSP cell. I
compare the eﬀect of belonging to the BFSP cell as opposed to belonging to the SFBP
cell on major choice, controlling for all other cell categories.

Table 7 presents the estimated coeﬃcients of the random utility model with neigh-
borhood and school eﬀects described above. The results show that the impact of
neighborhood-level admission trend on the choice for the respective major is highly
signiﬁcant under all speciﬁcations. The higher the number of students admitted to a
certain ﬁeld in the previous three years, the more likely it is for current applicants to
choose the same ﬁeld. The marginal eﬀects obtained in table 8 show that the highest
impact of near-peer role models is manifested in the choice of health sciences. A one
standard deviation increase in the ratio of near-peers who were admitted to a health

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
4
3
4
7
2
1
6
9
3
0
1
4
e
d
p
_
a
_
0
0
2
4
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

487

College Major Choice

Table 7. Estimates of Random Utility Model of Major Choice with Neighborhood and School Effects

Population

ln Expected earnings 1: Egalitarian distribution

ln Expected earnings 2: Meritocratic distribution

Ratio of near-peers admitted to the same faculty

Full

(1)

0.386
(0.374)

0.703***
(0.195)

Full

(2)

0.230***
(0.038)
0.724***
(0.172)

Full

(3)

0.798
(0.417)

Full

(4)

0.234***
(0.044)

Full

(5)

1.231***
(0.374)

0.435**
(0.220)

Full

(6)

0.233***
(0.043)
0.568***
(0.129)

Level 1 Choice: Science and Technology (Reference: Social Sciences)

Number of high school science electives

1.244***
(0.041)

1.235***
(0.041)

1.249***
(0.042)

1.243***
(0.042)

1.238***
(0.042)

1.237***
(0.042)

Level 2 Choice: Specific Faculties (Reference: Humanities and Law)

Dummy of Top-quartile NSC Score in a Bottom-quartile School (Reference: Dummy of 3rd Quartile NSC score in a Top-quartile School)

Commerce

Engineering

Health sciences

Science

0.937**
(0.490)
0.987**
(0.487)
1.059**
(0.492)
1.056**
(0.492)

1.108**
(0.542)
0.972*
(0.538)
1.284**
(0.538)
1.243**
(0.548)

0.656
(0.439)

0.494
(0.413)
0.862*
(0.480)
0.813*
(0.477)

0.852**
(0.428)

0.553
(0.454)
1.078**
(0.450)
0.998**
(0.474)

Other Case-specific Controls: NSC math, NSC English, NSC life orientation, Public school dummy, First-generation college dummy,

Black dummy, Female dummy, 14 school-student quartile combinations
τn Science and technology
τn Social sciences

0.907

0.986

1.613
−12,243
9,267

1.847
−12,227
9,267

0.116

0.487

0.596

0.851

0.855
−10,894
8,334

1.032
−10,893
8,334

0.556
−10,884
8,334

0.727
−10,875
8,334

Log-likelihood

Number of cases

Notes: Standard errors are given in parentheses. Coefficients for 21 additional controls listed in the table are not reported here. NSC = National
Senior Certificate.
*Statistically significant at the 90% confidence level; **statistically significant at the 95% confidence level; ***statistically significant at the
99% confidence level.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
4
3
4
7
2
1
6
9
3
0
1
4
e
d
p
_
a
_
0
0
2
4
9
p
d

Table 8. Average Marginal Effects of Ratio of Near-Peers
Admitted to the Same Facultya

Choice

Commerce

Engineering

Health sciences

Science

Humanities and law

(1)b

0.104***
(0.037)
0.115***
(0.052)
0.147***
(0.041)
0.071***
(0.026)
0.040***
(0.032)

(2)c

0.104***
(0.037)
0.110***
(0.049)
0.143***
(0.040
0.067***
(0.025)
0.037***
(0.030)

Notes: aStandard deviations of the mean are given in paren-
thesis. bCalculation based on column 1 in table 7. cCalculation
based on column 2 in table 7.
***Statistically significant at the 99% confidence level.

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

488

Biniam E. Bedasso

sciences faculty during the last three years increases the probability of choosing health
sciences by over 14 percent. On the contrary, the same increase in the case of humani-
ties and law results in no more than a 4 percent rise in the probability of choosing the
same ﬁeld.

Columns 3 to 6 in table 7 include the frog–pond indicators generated based on table
6. The frog–pond eﬀect is mainly about the self-evaluation of students in high school in
comparison with their schoolmates. Therefore, the eﬀect is more accurately measured
after controlling for choices in high school, such as high school curriculum. The results
show that there is an indication of a frog–pond eﬀect in the choice of commerce, health
sciences, and science under most speciﬁcations. For engineering, the eﬀect is limited
to speciﬁcations excluding admission trends of near-peer role models. These results
are unlikely to be spurious because, out of twelve student–school quartile combinations
that are characterized by average NSC scores lower than the SFBP cell, the only category
that has a positive and signiﬁcant eﬀect on any choice is the BFSP cell. It might be
interesting to put these results in perspective with the eﬀect of near-peer role models.
The path-dependent eﬀect of neighborhood-level admission trends may suggest that
applicants from less competitive schools might end up choosing low return majors. The
frog–pond eﬀect adds a twist to that story. After all, the career destiny of some students
from less competitive and, presumably, underresourced schools might be improved by
the fact that they have maintained relatively high self-esteem coming out of high school.

5 . C O N C L U S I O N
This paper has set out to examine the determinants of college major choice against
the backdrop of inter-group and spatial inequalities. I have used the extensive set of
academic, geographical, and socioeconomic information contained in the admissions
application database of the University of Cape Town to estimate random utility models
of major choice. In line with the predictions of the lifecycle model of career choice,
the choice of high school curriculum is shown to be crucial for the choice of college
major. However, expected earnings maintain a positive impact on major choice inde-
pendently of high school background when the ex ante distribution of earnings captures
the full range of between-major and within-major income diﬀerentials. At a neighbor-
hood level, the inﬂuence of near-peer role models on the choices of college applicants
is found to be large and signiﬁcant.

The dynamics of major choice at a selective institution such as UCT is likely to
have signiﬁcant implications in the long run for social and economic transformation.
Potential ineﬃciencies in the allocation of talent that might be caused by persistent in-
equalities will hamper innovation and mass ﬂourishing à la Edmund Phelps (Phelps
2014). Although the gap between white and black students in response to potential
diﬀerentials in expected earnings remains, it is encouraging that the magnitude is sig-
niﬁcantly smaller in the case of high-return majors, such as health sciences. Moreover,
good preparation in high school science electives seems to embolden applicants from
poorer and far-oﬀ municipalities to apply to UCT, hoping to major in science and tech-
nology ﬁelds. Considering the importance of high school curriculum and neighbor-
hood eﬀects, policy measures that will improve the availability of science education at

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
4
3
4
7
2
1
6
9
3
0
1
4
e
d
p
_
a
_
0
0
2
4
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

489

College Major Choice

the high school level or account for the eﬀect of near-peer role models in college admis-
sions may go a long way in terms of moderating income inequality in South Africa.

ACKNOWLEDGMENTS
I would like to thank the Information and Communication Technology Services of the University
of Cape Town for allowing me access to the admissions database. I am grateful to Kende Kefale
for facilitating access to the database. I thank Max Price and two anonymous referees for com-
ments and suggestions. I thank Chris Rooney and Callee Davis for excellent research assistance.
Financial support for this research has been provided by Economic Research Southern Africa.
This paper was completed during my time at Princeton University.

REFERENCES
Altonji, Joseph G. 1993. The demand for and return to education when education outcomes are
uncertain. Journal of Labor Economics 11(1): 48–83.

Altonji, Joseph G., Erica Blom, and Costas Meghir. 2012. Heterogeneity in human capital in-
vestments: High school curriculum, college major, and careers. Annual Review of Economics 4(1):
185–223.

Arcidiacono, Peter. 2004. Ability sorting and the returns to college major. Journal of Econometrics
121(1–2): 343–375.

Bedasso, Biniam E. 2015. Educated bandits: Endogenous property rights and intra-elite distribu-
tion of human capital. Economics & Politics 27(3): 404–432.

Bénabou, Roland. 1996. Equity and eﬃciency in human capital investment: The local connection.
Review of Economic Studies 63(2): 237–264.

Braddock II, Jomills Henry. 1980. The perpetuation of segregation across levels of education.
Sociology of Education 53(3): 178–186.

Card, David, and Jesse Rothstein. 2007. Racial segregation and the black-white test score gap.
Journal of Public Economics 91(11–12): 2158–2184.

Davis, James A. 1966. The campus as a frog pond: An application of the theory of relative depri-
vation to career decisions of college men. American Journal of Sociology 72(1): 17–31.

Daymont, Thomas N., and Paul J. Andrisani. 1984. Job preferences, college major, and the gender
gap in earnings. Journal of Human Resources 19(3): 408–428.

Espenshade, Thomas J., Lauren E. Hale, and Chang Y. Chung. 2005. The frog pond revisited:
High school academic context, class rank, and elite college admission. Sociology of Education
78(4): 269–293.

Goldsmith, Pat Rubio. 2009. Schools or neighborhoods or both? Race and ethnic segregation
and educational attainment. Social Forces 87(4): 1913–1941.

Grogger, Jeﬀ, and Eric Eide. 1995. Changes in college skills and the rise in the college wage
premium. Journal of Human Resources 30(2): 280–310.

Keane, Michael P., and Kenneth I. Wolpin. 1999. The career decisions of young men. Journal of
Political Economy 105(3): 473–522.

Montmarquette, Claude, Kathy Cannings, and Sophie Mahseredjian. 2002. How do young peo-
ple choose college majors? Economics of Education Review 21(6): 543–556.

490

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/

1
4
3
4
7
2
1
6
9
3
0
1
4
e
d
p
_
a
_
0
0
2
4
9
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Biniam E. Bedasso

Murphy, Kevin M., Andrei Shleifer, and Robert W. Vishny. 1991. The allocation talent: Implica-
tions for growth. Quarterly Journal of Economics 106(2): 503–530.

Phelps, Edmund. 2014. Mass ﬂourishing: How grassroots innovation created jobs, challenge and
change. Princeton, NJ: Princeton University Press.

Van der Berg, Servaas. 2007. Apartheid’s enduring legacy: Inequalities in education. Journal of
African Economies 16(5): 849–880.

Weinberger, Catherine. 1998. Race and gender wage gaps in the market for recent college grad-
uates. Industrial Relations 37(1): 67–84.

Wiswall, Matthew, and Basit Zafar. 2015. Determinants of college major choice: Identiﬁcation
using an information experiment. Review of Economic Studies 82(2): 791–824.

A P P E N D I X A : P RO B I T R E G R E S S I O N R E S U LT S

Table A.1. Probit Estimates of Admission Probability as a Function of National Benchmark Test Scores (Pooled Population
of Applicants from 2010 to 2012)

Commerce

Engineering

Health Sciences

Science

Humanities and Law

Academic Literacy score

Quantitative Literacy score

Mathematics Score

Pseudo R2

Log likelihood

Number of observations

0.026***
(0.002)
0.004**
(.002)
0.024***
(0.002)

0.14
−3,516
6,452

0.010***
(0.002)
−0.001
(0.002)
0.040***
(0.001)

0.20
−2,174
5,050

0.017***
(0.003)
−0.003
(0.002)
0.020***
(0.002)

0.10
−1,732
5,970

0.002
(0.003)

0.004
(0.003)
0.028***
(0.002)

0.11
−1,161
2,144

0.023***
(0.003)
−0.001
(0.003)

0.013
(0.003)

0.08
−1,094
2,008

Notes: Standard errors are given in parentheses.
**Statistically significant at the 95% confidence level; ***statistically significant at the 99% confidence level.

A P P E N D I X B : DATA S O U R C E S

(1) Admission application data: The database of the Information and Communication

Technology Services of the University of Cape Town.

(2) Earnings Data: Quarterly labor force survey, Statistics South Africa.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
e
d
p
a
r
t
i
c
e
–
p
d

f
/