Cognitive Control as a Multivariate
Optimization Problem

Harrison Ritz, Xiamin Leng, and Amitai Shenhav

Abstract

■ A hallmark of adaptation in humans and other animals is our
ability to control how we think and behave across different set-
tings. Research has characterized the various forms cognitive
control can take—including enhancement of goal-relevant
information, suppression of goal-irrelevant information, and
overall inhibition of potential responses—and has identified
computations and neural circuits that underpin this multitude
of control types. Studies have also identified a wide range of
situations that elicit adjustments in control allocation (e.g.,
those eliciting signals indicating an error or increased process-
ing conflict), but the rules governing when a given situation will
give rise to a given control adjustment remain poorly under-
stood. Significant progress has recently been made on this
front by casting the allocation of control as a decision-making
problem. This approach has developed unifying and normative
models that prescribe when and how a change in incentives

and task demands will result in changes in a given form of con-
trol. Despite their successes, these models, and the experi-
ments that have been developed to test them, have yet to face
their greatest challenge: deciding how to select among the mul-
tiplicity of configurations that control can take at any given
time. Here, we will lay out the complexities of the inverse prob-
lem inherent to cognitive control allocation, and their close
parallels to inverse problems within motor control (e.g., choos-
ing between redundant limb movements). We discuss existing
solutions to motor control’s inverse problems drawn from opti-
mal control theory, which have proposed that effort costs act to
regularize actions and transform motor planning into a
well-posed problem. These same principles may help shed light
on how our brains optimize over complex control configura-
tion, while providing a new normative perspective on the ori-
gins of mental effort. ■

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

3
4
4
5
6
9
1
9
9
6
6
5
8

/
j

o
c
n
_
a
_
0
1
8
2
2
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

“There are many paths up the mountain, but the view
from the top is always the same”
— Chinese Proverb

INTRODUCTION

Over the past half-century, our understanding of the
human brain’s capacity for cognitive control has grown
tremendously (Menon & D’Esposito, 2022; Friedman &
Robbins, 2022; von Bastian et al., 2020; Koch, Poljac,
Müller, & Kiesel, 2018; Fortenbaugh, DeGutis, &
Esterman, 2017; Abrahamse, Braem, Notebaert, & Verguts,
2016; Westbrook & Braver, 2015; Botvinick & Cohen,
2014). The field has developed consistent ways of defining
and operationalizing control, such as in terms of its func-
tions and what distinguishes different degrees of automa-
ticity (Cohen, Servan-Schreiber, & McClelland, 1992;
Shiffrin & Schneider, 1977; Posner & Snyder, 1975). It

This article is part of a Special Focus entitled, Perspectives from
the 2021 recipients of the Cognitive Neuroscience Society’s
Young Investigator Award, Dr. Anne Collins and Dr. Amitai
Shenhav.

Brown University

© 2022 Massachusetts Institute of Technology

has developed consistent methods for eliciting control
and measuring the extent to which control is engaged by
a given task (von Bastian et al., 2020; Weichart, Turner, &
Sederberg, 2020; Koch et al., 2018; Gonthier, Braver, &
Bugg, 2016; Danielmeier & Ullsperger, 2011; Egner,
2007). It has demonstrated how such control engagement
varies across individuals (von Bastian et al., 2020;
Friedman & Miyake, 2017) and over the life span (Luna,
2009; Braver & Barch, 2002). Finally, research in this area
has made substantial progress toward mapping the neural
circuitry that underpins the execution of different forms of
cognitive control (Menon & D’Esposito, 2022; Friedman &
Robbins, 2022; Parro, Dixon, & Christoff, 2018; Shenhav,
Botvinick, & Cohen, 2013). The factors that determine
how cognitive control is configured have, on the other
hand, remained mysterious and heavily debated (Shenhav
et al., 2017).

Studies have uncovered reliable antecedents for control
adjustments, including the commission of an error
(Danielmeier & Ullsperger, 2011; Rabbitt, 1966) or
changes in task demands (Gratton, Coles, & Donchin,
1992; Logan & Zbrodoff, 1979). However, it has been a
longstanding goal for the field to develop a comprehen-
sive model of how people use the broader array of infor-
mation they monitor to configure the broader array of
control signals they can deploy. To address this question,

Journal of Cognitive Neuroscience 34:4, pp. 569–591
https://doi.org/10.1162/jocn_a_01822

models have proposed that the problem of determining
control allocation can be solved through a general
decision-making process that involves weighing the costs
and benefits of potential control allocations (Lieder,
Shenhav, Musslick, & Griffiths, 2018; Verguts, Vassena, &
Silvetti, 2015; Westbrook & Braver, 2015; Shenhav et al.,
2013). These models have already shown promise in
accounting for how people adjust individual control sig-
nals (e.g., how much to adjust attention toward a particular
task) based on the incentives and demands of a given task
environment (Bustamante, Lieder, Musslick, Shenhav, &
Cohen, 2021; Lieder et al., 2018; Musslick, Shenhav,
Botvinick, & Cohen, 2015; Verguts et al., 2015). Here, we
focus on a different aspect of this problem: How is it that
people navigate the multitude of solutions that can match
the demands of their environment? How can cognitive
control scale to configuring the complex information
processing we deploy throughout our daily life? What is
the relationship of mental effort to the multiplicity
of options for configuring control? Building off well-
characterized computational models from motor
planning, we examine how multiplicity presents a critical
challenge to cognitive control configuration, and how
algorithmic principles from motor control can help to
overcome these challenges and refine our understanding
of goal-directed cognition.

THE MULTIPLICITY OF COGNITIVE CONTROL

To study the mechanisms that govern the allocation of
cognitive control, researchers have sought to identify reli-
able predictors of changes in control allocation within and
across experiments. These triggers for control adjustment
have in turn provided insight into signals—such as errors
and processing conflict—that the brain could monitor to
increase or decrease control. Research has shown that
control adjustments induced by these signals, even within
the same setting, vary not only in degree but also kind
(see Table 1).

Error-related Control Adjustments

In common cognitive control tasks such as the Stroop,
Simon, and Eriksen flanker task (von Bastian et al., 2020;
Egner, 2007), participants have prepotent biases that often
lead to incorrect responses (e.g., responding based on the
salient flanking arrows rather than the goal-relevant cen-
tral arrow). Errors thus serve a useful indicator that the
participant was likely underexerting control and should
adjust their control accordingly (Yeung, Botvinick, &
Cohen, 2004). The best-studied instantiation of error-
related control adjustments manifests in a participant’s
tendency to respond more slowly and more accurately
after an error (Danielmeier & Ullsperger, 2011; Laming,
1979; Rabbitt, 1966), which can be understood as together
reflecting post-error adjustments in caution. Indeed, work
using models like the drift diffusion model1 (DDM; Ratcliff

& McKoon, 2008; Ratcliff, 1978; see Figure 1A), post-error
slowing, and post-error increases in accuracy can be jointly
accounted for by an increase in one’s response threshold,
the criterion they set for how much evidence to accumu-
late about the task stimuli before deciding how to respond
(Fischer, Nigbur, Klein, Danielmeier, & Ullsperger, 2018;
Dutilh et al., 2012).

Experiments investigating the neural implementation of
these post-error adjustments have found that threshold
adjustments are associated with the suppression of
motor-related activity (Fischer et al., 2018; Danielmeier,
Eichele, Forstmann, Tittgemeyer, & Ullsperger, 2011).
For instance, Danielmeier et al. (2011) had participants
perform a Simon-like task that required them to respond
based on the color of an array of dots that were moving in a
direction compatible or incompatible with the correct
color response. When participants responded incorrectly,
they tended to be slower and more accurate on the follow-
ing trial. This increased caution was coupled with
decreased BOLD activity in motor cortex on that subse-
quent trial, consistent with the possibility that errors led
to controlled adjustments of decision threshold (in this
case by putatively lowering the baseline activity to require
more evidence before responding).

In addition to changing overall caution, errors can also
influence how specific stimuli are processed. Studies have
shown that error trials can be followed by selective
enhancement of task-relevant (target) processing
(Steinhauser & Andersen, 2019; Danielmeier et al., 2011,
2015; Maier, Yeung, & Steinhauser, 2011; King, Korb, von
Cramon, & Ullsperger, 2010) and/or suppression of task-
irrelevant (distractor) processing (Fischer et al., 2018;
Danielmeier et al., 2011, 2015). For instance, in the same
study by Danielmeier et al. (2011), errors tended to be
followed by increased activity in regions encoding the tar-
get stimulus dimension and decreased activity in regions
encoding the distractor dimension (see also the works of
Fischer et al., 2018; King et al., 2010). Thus, whereas post-
error slowing effects reflect control over one’s decision
threshold, such post-error reductions of interference
likely reflect a different form of control, one that adjusts
the influence of target- and distractor-related information
on the evidence that is accumulated before reaching that
threshold (target and distraction contributions to the drift
rate in the DDM).

Conflict-related Control Adjustments

In addition to error commission, another potential indica-
tor of insufficient control is the presence of processing
conflict (Botvinick, Braver, Barch, Carter, & Cohen,
2001; Berlyne, 1957), such as when a person feels simul-
taneously drawn to respond left (e.g., based on target
information) and right (e.g., based on a distractor). One of
the best-studied forms of conflict-related control adjust-
ment is the conflict adaptation or congruency sequence
effect, which manifests as reduced sensitivity to response

570

Journal of Cognitive Neuroscience

Volume 34, Number 4

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

3
4
4
5
6
9
1
9
9
6
6
5
8

/
j

o
c
n
_
a
_
0
1
8
2
2
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Table 1. Multiplicity of Control Adaptations in Response to Errors, Conflict, and Incentives

Errors

RT h

Threshold h

Motor cortex activation i

Behavior

Cognitive Process (DDM)

Neuroscience

(Fischer et al., 2018;
Dutilh et al., 2012)

(Danielmeier et al., 2011;

King et al., 2010)

(Danielmeier et al., 2011; King et al.,
2010; Jentzsch & Dudschig, 2009;
Debener et al., 2005; Gehring &
Fencsik, 2001; Rabbitt, 1966)

Error Rate i

(Danielmeier et al., 2011; Maier et al.,

2011; Marco-Pallarés, Camara,
Münte, & Rodríguez-Fornells, 2008;
Laming, 1968, 1979)

Interference h

Distractor drift rate i

Target-related activation h

(Steinhauser & Andersen, 2019;

(Fischer et al., 2018)

(Steinhauser & Andersen, 2019;

Maier et al., 2011; King et al., 2010;
Ridderinkhof, 2002)

Danielmeier et al., 2011;
Maier et al., 2011; King et al., 2010)

Distractor-related activation i

(Fischer et al., 2018;

Danielmeier et al., 2011;
King et al., 2010)

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

3
4
4
5
6
9
1
9
9
6
6
5
8

/
j

o
c
n
_
a
_
0
1
8
2
2
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Conflict

RT h

Threshold h

STN activation h

(Herz, Zavala, Bogacz, & Brown, 2016;

Verguts et al., 2011)

(Fontanesi et al., 2019;
Herz et al., 2016)

(Frank et al., 2015; Wiecki & Frank,

2013; Ratcliff & Frank, 2012;
Cavanagh et al., 2011; Aron, 2007)

Interference i

Distractor drift rate i

Target-related activation h

(Braem, Verguts, Roggeman, &

(Ritz & Shenhav, 2021)

(Egner et al., 2007;

Notebaert, 2012; Danielmeier et al.,
2011; Funes et al., 2010; Kerns,
2006; Ullsperger et al., 2005; Kerns
et al., 2004; Gratton et al., 1992)

Egner & Hirsch, 2005)

Incentives

RT i Accuracy h

Threshold h

(Frömer et al., 2021; Chiew & Braver,
2016; Ličen et al., 2016; Yee, Krug,
Allen, & Braver, 2016; Fröber &
Dreisbach, 2014; Soutschek et al., 2014)

(Leng et al., 2021;
Dix & Li, 2020;
Thurm, Zink, & Li, 2018)

Target effect h

(Adkins & Lee, 2021;
Krebs et al., 2010)

Threshold i

(Leng et al., 2021)

Drift rate h

( Jang et al., 2021;

Leng et al., 2021;
Dix & Li, 2020)

Target-related activation h

(Grahek et al., 2021;
Etzel et al., 2016;
Soutschek et al., 2015)

Distractor effect i

Target drift rate h

Distractor-related activation i

(Chiew & Braver, 2016; Soutschek

(Ritz & Shenhav, 2021)

(Padmala & Pessoa, 2011)

et al., 2014; Padmala & Pessoa, 2011)

RT variability i

Accumulation noise i

Sustained task-relevant activation h

(Esterman et al., 2014, 2016)

(Ritz et al., 2020;

(Esterman et al., 2017)

Manohar et al., 2015)

Ritz, Leng, and Shenhav

571

(in)congruency after a person has previously performed
one or more high-conflict (e.g., incongruent) trials ( Jiang
& Egner, 2014; Funes, Lupiáñez, & Humphreys, 2010;
Egner, Delano, & Hirsch, 2007; Egner & Hirsch, 2005;
Gratton et al., 1992). These adaptations are analogous
to examples of post-error reductions of interference
described above and have the same candidate computa-
tional underpinnings in adjustments to the rate of evi-
dence accumulation (Musslick, Cohen, & Shenhav,
2019; Musslick et al., 2015; Kerns et al., 2004). These con-
trol adjustments have likewise been found to be associ-
ated with changes in task-specific processing pathways
(Egner, 2008; Egner, Delano, & Hirsch, 2007). For exam-
ple, Egner and Hirsch (2005) showed that participants
were less sensitive to Stroop incongruence after higher-
conflict trials, and that this was coupled with increased
activity in the target-associated cortical areas (fusiform
face area for face targets).

Another body of work has shown that conflict can trigger
changes to response threshold, particularly within a trial, for
instance when selecting between two similarly valued
options (Fontanesi, Gluth, Spektor, & Rieskamp, 2019; Frank
et al., 2015; Wiecki & Frank, 2013; Ratcliff & Frank, 2012;
Cavanagh et al., 2011; Verguts, Notebaert, Kunde, & Wühr,
2011; Aron, 2007). These adjustments have been linked to
interactions between dorsal anterior cingulate cortex and
the subthalamic nucleus ( Wessel, Waller, & Greenlee,
2019; Frank et al., 2015; Brittain et al., 2012; Cavanagh
et al., 2011; Schroeder et al., 2002). For instance, simulta-
neous EEG-fMRI has revealed that BOLD in dorsal anterior
cingulate cortex and mediofrontal EEG theta power moder-
ates the relationship between decision conflict and adjust-
ments to response threshold (Frank et al., 2015).

Incentive-related Control Adjustments

In addition to signals like error and conflict that reflect dips
in performance, the need for control can also be signaled
by the presence of performance-based incentives (e.g.,
monetary rewards for good performance). Incentives can
influence overall performance—for instance, often leading
participants to perform tasks faster and more accurately
across trials (Parro et al., 2018; Yee & Braver, 2018). Incen-
tives can also trigger task-specific adjustments of cognitive
control, enhancing the processing of goal-relevant informa-
tion (Etzel, Cole, Zacks, Kay, & Braver, 2016; Soutschek,
Strobach, & Schubert, 2014; Krebs, Boehler, & Woldorff,
2010) and/or suppressing the processing of distractor infor-
mation (Padmala & Pessoa, 2011), likely reflecting changes
in associated drift rates similar to error-related adjustments
discussed above (cf. Ritz & Shenhav, 2021, discussed fur-
ther below). Also similar to error-related findings, there is
evidence that incentive-related control adjustments are
mediated by changes in processing within stimulus-selective
circuits (Hall-McMaster, Muhle-Karbe, Myers, & Stokes,
2019; Esterman, Poole, Liu, & DeGutis, 2017; Etzel et al.,
2016; Soutschek, Stelzel, Paschke, Walter, & Schubert,

2015; Padmala & Pessoa, 2011). For example, Padmala and
Pessoa (2011) used a Stroop task to show that participants
are less sensitive to distractor information when under
performance-contingent rewards. They found that this
distractor inhibition was mediated by reduced activation
in cortical areas sensitive to the distracting stimuli (visual
word form area for text distractors).

Performance incentives have been shown to influence not
only how well one performs on a given trial but also how con-
sistently they perform within and across trials. When per-
forming sustained attention tasks that require participants
to repeat the same response on most trials (e.g., frequent
go trials) but respond differently on rare occurrences of a dif-
ferent trial type (e.g., infrequent no-go trials), attentional
lapses can manifest as increased variability in response times
across trials (Fortenbaugh et al., 2017). When performance is
incentivized, participants demonstrate both higher accuracy
and lower response time variability (Esterman et al., 2014,
2016, 2017). These performance improvements can be
accounted for by assuming that incentives influence control
over how noisily evidence is accumulated within each trial
(e.g., because of mind-wandering; Ritz, DeGutis, Frank,
Esterman, & Shenhav, 2020; Manohar et al., 2015). Neuroim-
aging studies suggest that enacting the control required to
achieve more consistent (less variable) performance is asso-
ciated with increases in both sustained and evoked
responses in domain-general attentional networks and
stimulus-specific regions (Esterman et al., 2017).

Multidimensional Configuration of
Cognitive Control

Previous research has uncovered a multiplicity of adjust-
ments that occur in response to changes in the demands
or incentives for control. Importantly, they show that a
monitored signal2 (e.g., an error) can produce several dif-
ferent control adjustments and that a control adjustment
(e.g., increased caution) can be elicited by several different
monitored signals. Rather than a strict one-to-one relation-
ship between monitored signals and control adjustments,
this diversity suggests that participants make simulta-
neous decisions across multiple control effectors.

This control multiplicity is evident in studies of post-
error adjustments discussed above (Danielmeier &
Ullsperger, 2011), in which errors can result in both
increased caution (i.e., more conservative response
thresholds) and a change in attentional focus to favor
target over distractor information (putatively underpinned
by adjustments in drift rate). Experiments have found
that both adjustments appear to occur simultaneously
(Fischer et al., 2018; Danielmeier et al., 2011, 2015; King
et al., 2010), reflecting a multifaceted response to the
error event.

In a recent experiment, we showed that people can also
exert independent control over their processing of targets
and distractors (Ritz & Shenhav, 2021). Like Danielmeier
et al. (2011), participants responded to a random dot

572

Journal of Cognitive Neuroscience

Volume 34, Number 4

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

3
4
4
5
6
9
1
9
9
6
6
5
8

/
j

o
c
n
_
a
_
0
1
8
2
2
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

kinematogram based on dot color, while ignoring dot
motion. Across trials, we parametrically varied both the
target coherence (how easily the correct color could be
identified) and distractor interference (how coherently
dots were moving in the same or opposite direction as
the target response). We found that participants exerted
control over their processing of both target and distractor
information, but that they did so independently and
differentially depending on the relevant task demands.
Under performance incentives, participants preferentially
enhanced their target sensitivity, whereas after high-
conflict trials, participants preferentially suppressed
their distractor sensitivity (and, to a lesser extent, also
enhanced target sensitivity). A similar pattern has been
observed at the neural level while participants perform a
Stroop task (Soutschek et al., 2015). Whereas perfor-
mance incentives preferentially enhanced sensitivity in
target-related areas (visual word form area for text
targets), conflict expectations preferentially suppressed
sensitivity in distractor-related areas (fusiform face area
for face distractors). These findings demonstrate that con-
trol can be flexibly reconfigured across multiple inde-
pendent control signals to address relevant incentives
and task demands.

There is also evidence that different people prioritize
different control strategies within the same setting. For
instance, Boksem, Meijman, and Lorist (2006) had partic-
ipants perform the Simon task over an extended experi-
mental session and observed performance fatigue in the
form of slower and less accurate responding over time.
Toward the end of the session, the experimenters intro-
duced monetary incentives and found that this counter-
acted the effects of fatigue, but did so heterogeneously
across the group. When making an error during this incen-
tivized period, some participants responded by focusing
more on responding quickly, while others focused on
responding accurately. The engagement of these differen-
tial control strategies was associated with changes in dis-
tinct ERPs (error-related negativity vs. contingent negative
variation). Similar variability in reliance on different con-
trol strategies has been seen across the life span (Ritz
et al., 2020; Fortenbaugh et al., 2015; Luna, 2009; Braver
& Barch, 2002) and between clinical and healthy popula-
tions (Grahek, Shenhav, Musslick, Krebs, & Koster, 2019;
Lesh, Niendam, Minzenberg, & Carter, 2011; Casey et al.,
2007).

Collectively, previous research suggests that there is a
many-to-many mapping between the information that par-
ticipants monitor related to task demands, performance,
and incentives, and the multitude of control signals that
participants can deploy. Recent theoretical models have
explained this heterogeneity in terms of the flexible
deployment of control, proposing that there is an inter-
vening decision process that integrates monitored infor-
mation, determining which strategies to engage, and to
what extent, based on the current situation (Lieder et al.,
2018; Verguts et al., 2015; Shenhav et al., 2013).

SELECTION AND CONFIGURATION OF
MULTIVARIATE CONTROL

Casting control allocation as a decision process provides a
path toward addressing how people integrate information
from their environment to select the optimal control allo-
cation. This process of optimization entails finding the
best solution for an objective function and set of con-
straints. Objective functions define the costs and benefits
of different solutions, whereas soft constraints (e.g., costs)
and hard constraints (e.g., boundary conditions) limit the
space of possible solutions. Optimization has long played
a central and productive role in building computational
accounts of multivariate planning in the domain of motor
control (Shadmehr & Ahmed, 2020; Wolpert & Landy,
2012; Todorov & Jordan, 2002; Uno, Kawato, & Suzuki,
1989; Flash & Hogan, 1985), suggesting that this research
into how the brain coordinates actions may offer general
principles for how the brain coordinates cognition.

The starting point for solving any optimization problem
is identifying the objective function. Researchers in
decision-making and motor control have suggested that
participants maximize the amount of reward harvested
per unit time (reward rate; Manohar et al., 2015;
Shadmehr, Orban de Xivry, Xu-Wilson, & Shih, 2010;
Niv, Daw, Joel, & Dayan, 2007; Harris & Wolpert, 2006).
Studies have found that people’s motor actions are sensi-
tive to incentives, with faster and/or more accurate move-
ment during periods when they can earn more rewards
(Adkins, Lewis, & Lee, 2022; Codol, Forgaard, Galea, &
Gribble, 2021; Sukumar, Shadmehr, & Ahmed, 2021;
Codol, Holland, Manohar, & Galea, 2020; Yoon, Jaleel,
Ahmed, & Shadmehr, 2020; Manohar, Muhammed, Fallon,
& Husain, 2019; Manohar, Finzi, Drew, & Husain, 2017;
Manohar et al., 2015; Pekny, Izawa, & Shadmehr, 2015;
Trommershäuser, Maloney, & Landy, 2003a, 2003b). For
example, participants will saccade toward a target location
more quickly and more precisely on trials that are worth
more money (Manohar et al., 2015, 2017, 2019). Responding
faster and more accurately breaks the traditional speed-
accuracy trade-off (Manohar et al., 2015; Bogacz, Brown,
Moehlis, Holmes, & Cohen, 2006) and is thought to
reflect the use of control to optimize both reward and
duration (Shadmehr & Ahmed, 2020).

It has been similarly proposed that a core objective of cog-
nitive control allocation is also the maximization of reward
rate (Lieder et al., 2018; Boureau, Sokol-Hessner, & Daw,
2015; Manohar et al., 2015; Shenhav et al., 2013; Bogacz
et al., 2006). That is, that people select how much and what
kinds of control to engage at a given time based on how con-
trol will maximize expected payoff (e.g., performance-based
incentives like money or social capital) while minimizing the
time it takes to achieve that payoff. Consistent with this
proposal, studies have shown that people configure infor-
mation processing (e.g., adjust their response thresholds)
in ways that maximize reward rate (Balci et al., 2011; Starns
& Ratcliff, 2010; Simen et al., 2009) and that they adjust

Ritz, Leng, and Shenhav

573

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

3
4
4
5
6
9
1
9
9
6
6
5
8

/
j

o
c
n
_
a
_
0
1
8
2
2
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

3
4
4
5
6
9
1
9
9
6
6
5
8

/
j

o
c
n
_
a
_
0
1
8
2
2
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

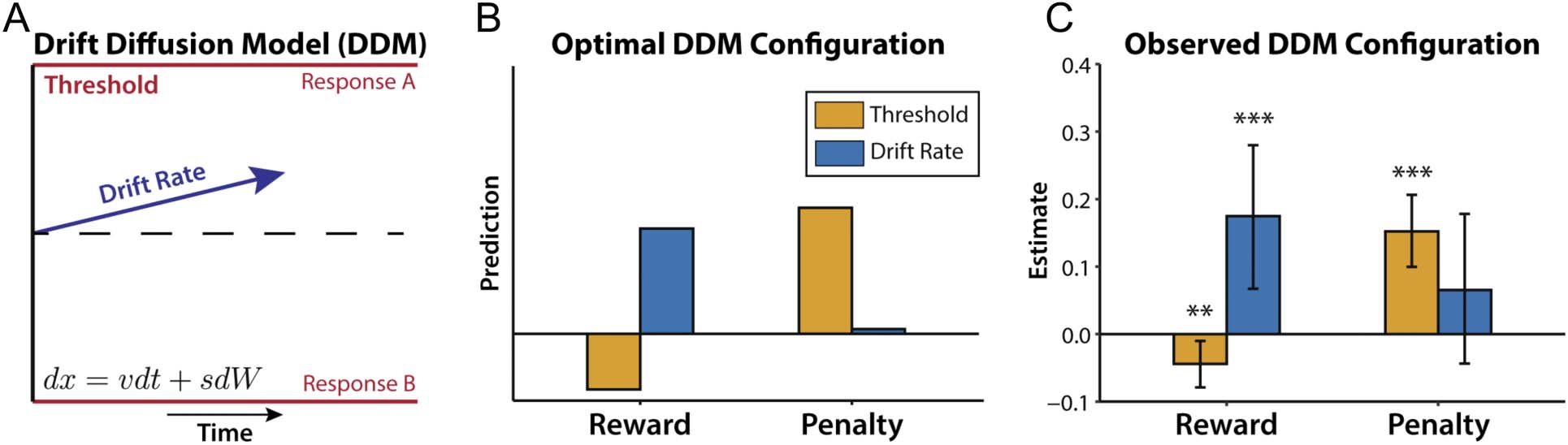
Figure 1. Multivariate control configurations optimize reward rate. (A) In the DDM, the speed and accuracy of a decision are largely determined by
the rate of evidence accumulation (drift rate; blue) and how much evidence the decision mechanism requires to make a choice (threshold; red).
Evidence accumulates according to both the drift rate (v) and Gaussian diffusion noise (s). (B) Leng et al. (2021) had participants perform a
self-paced Stroop task, and examined how they adjusted their drift rate and threshold with varying levels of reward for correct responses and
penalties for errors. A reward-rate optimal model predicted that higher rewards should bias their control configuration toward higher drift rates
and lower thresholds, whereas larger penalties should bias these configurations toward higher thresholds and have little impact on drift. (C) DDM
fits to task performance confirmed these predictions, demonstrating that participants adjusted their control configuration in a multivariate and
reward-rate-optimal manner.

this configuration over time based on local fluctuations in
reward rate (Otto & Daw, 2019; Guitart-Masip, Beierholm,
Dolan, Duzel, & Dayan, 2011).

We recently used a reward-rate optimization framework
to make model-based predictions for how people coordi-
nate multiple types of control (Leng, Yee, Ritz, & Shenhav,
2021). Participants performed a Stroop task that was self-
paced, enabling them to dynamically adjust at least two
forms of control: their overall drift rate (governing both
how fast and accurate they are) and their response thresh-
old (governing the extent to which they trade off speed for
accuracy; Figure 1A). We varied the amount of money par-
ticipants could gain with each correct response and the
amount they could lose with each incorrect response.
Participants could increase their response threshold to
guarantee that every response was correct, but this came
at the cost of completing fewer trials and therefore earning
fewer rewards over the course of the experiment. Increasing
their drift rate can achieve higher reward rates, but is sub-
ject to effort costs, which we will return to later. The reward-
rate optimal configuration across both drift and threshold
would be to increase drift rate and decrease threshold for
larger rewards and increase thresholds for larger penalties
(Figure 1B). Critically, we found that participants’ DDM
configuration matched the predictions of this optimal
model (Figure 1C). These results provide evidence that
participants’ performance can align with the optimal joint
configuration across multiple control parameters.

These studies validate the proposal that control alloca-
tion can be framed as decision-making over multidimen-
sional configurations of control (i.e., combination of
different control types engaged to different degrees)
and that these decisions seek to optimize an objective
function such as expected reward rate. DDM is useful for
studying these configuration processes, as it provides a
well-defined cognitive process model with criteria for good

performance. Similar optimality analyses have also been
performed in domains like working memory (Sims, 2015;
Sims, Jacobs, & Knill, 2012), demonstrating the generality
of this approach. However, for all the algorithmic tools it
provides, this decision-making framework also presents
an entirely new set of challenges. Most notably, the many pos-
sible control configurations to choose from often means that
there will be multiple equivalent solutions to this decision.
Here, again, valuable insights can be gained from research
on motor control, where these challenges and their potential
solutions have been extensively explored.

INVERSE PROBLEMS IN MOTOR AND
COGNITIVE CONTROL

Inverse Problems in Motor Control

Some of the most influential computational modeling of
motor planning was founded at the Central Labor Institute
in Moscow in the early 20th century. This group formalized
for the first time a fundamental problem for motor control:
How does the motor system choose among the many
similar actions that could be taken to achieve a goal
( Whiting, 1983; Bernstein, 1935/1967)? This problem is
centered around the fact that motor control is inherently
ill-posed, with more degrees of freedom in the body (e.g.,
joints) than in the task space, increasing the inherent chal-
lenge of selecting the best motor action among many
equivalent options.

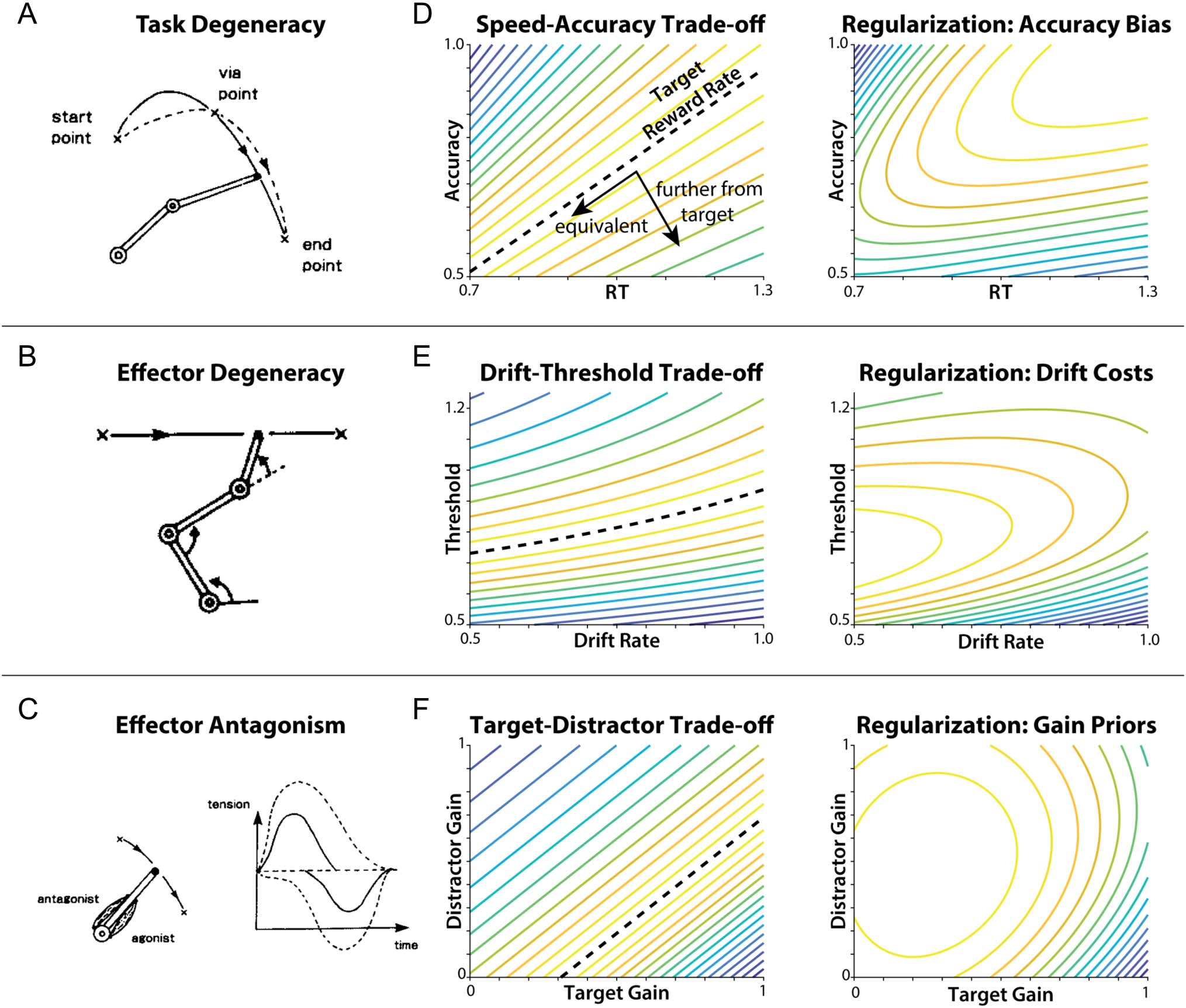
These motor redundancies can occur in several
domains of motor planning (Kawato, Maeda, Uno, &
Suzuki, 1990). At the task level, there may be many trajec-
tories through the task space that achieve the same goals,
such as the paths a hand could take on its way to picking
up a cup (Task Degeneracy; Figure 2A). At the effector
level, there are often more degrees of freedom in the

574

Journal of Cognitive Neuroscience

Volume 34, Number 4

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

3
4
4
5
6
9
1
9
9
6
6
5
8

/
j

o
c
n
_
a
_
0
1
8
2
2
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 2. Degeneracies in motor and cognitive control. (A) There are many trajectories can achieve the goal of moving from a start point to an endpoint
during motor control results in task degeneracy. (B) There are more degrees of freedom in the effectors (arm joints) than in the task (1D movement)
and that there are many configurations that can produce the same movement, resulting in effector degeneracy. (C) Some effectors have opposite
influences over actions (e.g., agonist and antagonist muscles), resulting in effector antagonism. (D–F) Analogous forms of degeneracy arise in relatively
simple examples of cognitive control (left side of each panel), such as when optimizing parameters of a DDM to achieve a target reward rate. Each of
these forms of degeneracy can be solved in an analogous way to motor control using different forms of regularization (right side of each panel). (D) The
target reward rate can be achieved with an infinite number of speed-accuracy trade-offs (points along dashed line), resulting in task degeneracy. A
solution to this degeneracy is to include an additional preference for high accuracy, creating a globally optimal solution. (E) Equivalent reward rates can
also be achieved with various trade-offs between different model parameters being controlled (e.g., levels of drift rate and threshold), resulting in a form
of “effector” degeneracy. A solution to effector degeneracy is to place a cost on higher drift rates, biasing parameter configurations toward lower drift
rates and creating a globally optimal solution. (F) “Effector” antagonism in cognitive control can result from opposing contributions of target gains
(positive effect on drift rate) and distractor gains (negative effect on drift rate) on reward rate. A solution to effector antagonism is to set a prior on
control gains, biasing these gains toward the prior configuration (e.g., high distractor sensitivity and low target sensitivity) and creating a globally optimal
solution. (A–C) Reprinted by permission from Springer Nature: Biological Cybernetics, Kawato et al. (1990), copyright (1990).

skeletomotor system than in the task space, creating an
“inverse kinematics” problem for mapping from goals on
to actions (Effector Degeneracy; Figure 2B). For example,
there are many ways you could move your arm to trace a
line with the tip of your finger. A related problem arises
when there is redundancy across effectors, such as in ago-
nist and antagonistic muscles (Effector Antagonism;

Figure 2C). Because of their opponency, the same action
can occur by trading off the contraction of one muscle
against the relaxation of the other. These inverse problems
have been a major challenge for theoretical motor control
and to the extent that a similar problem occurs in cognitive
control, solutions from the motor domain may help guide
our understanding of ill-posed cognitive control.

Ritz, Leng, and Shenhav

575

Inverse Problems in Cognitive Control:
The Algorithmic Level

Considering the massive degrees of freedom that exist in
neural information processing systems, cognitive control
is a prime candidate for inverse problems of its own.
To illustrate this, we can return to the example of how
people decide to allocate control across parameters of the
DDM (Figure 2D–F). As reviewed above, participants can
separately control individual parameters of evidence accu-
mulation, specifically drift rate (Bond, Dunovan, Porter,
Rubin, & Verstynen, 2021; Ritz & Shenhav, 2021), threshold
(Fischer et al., 2018; Cavanagh & Frank, 2014), and accu-
mulation noise (Mukherjee, Lam, Wimmer, & Halassa, 2021;
Ritz et al., 2020; Nakajima, Schmitt, & Halassa, 2019). This
test case of finding a reward-rate optimal configuration of
DDM parameters faces the same set of challenges as those
outlined above from motor control.

First, just as there are many hand trajectories that can
produce a desired outcome, there are also many ways to
produce good decision-making performance (Figure 2D).
Different combinations of accuracy (numerator) and RT
(denominator) can trade off to produce the same reward
rate. This creates an equivalence in the task space between
different performance outcomes with regard to the goals
of the system.

Second, just as there are more degrees of freedom in
the arm than in many motor tasks, there is more flexibility
in information processing than in many cognitive tasks.
For example, the same patterns of behavior (and there-
fore expected reward rates) can result from different con-
figurations of DDM parameters (Bogacz et al., 2006;
Figure 2E). From a model-fitting perspective, this forces
researchers to limit the parameters they attempt to infer
from behavior, fixing at least one parameter value (often
accumulation noise), while estimating the others (Bogacz
et al., 2006; Ratcliff & Rouder, 1998). This degeneracy sim-
ilarly limits a person’s ability to perform the “mental
model-fitting” required to optimize across all these control
configurations when deciding how to allocate control.
These difficulties are exacerbated in more biologically
plausible models of evidence accumulation like the leaky
competing accumulator (Usher & McClelland, 2001),
which introduce additional parameters (e.g., related to
memory decay and levels of inhibition across competing
response units), resulting in even greater parameter
degeneracy (Miletić, Turner, Forstmann, & van Maanen,
2017). A similar trade-off exists in the classic debate
between early and late attentional selection, namely,
whether attention operates closer to sensation or closer
to response selection (Driver, 2001). Given that attention
appears to operate at multiple processing stages (Lavie,
Hirst, de Fockert, & Viding, 2004), degeneracies will arise
in conditions under which early and late attentional con-
trol produce similar changes in task performance.

Third, just as there is antagonism across motor effec-
tors, there is also antagonism across cognitive processes.

That is, even when the algorithmic goal is clear, there are
degenerate control signals that can achieve this goal. For
instance, in typical interference-based paradigms (e.g.,
flanker or Stroop), participants must respond to one
element of a stimulus while ignoring information that is
irrelevant and/or distracting. To increase the overall rate
of accumulation of goal-related information, a person
can engage two different forms of attentional control:
enhance targets or suppress distractors. Utilizing either
of these strategies will improve performance, meaning
that the cognitive controller could trade off enhancing tar-
gets or suppressing distractors to reach the same level of
performance (Figure 2F). Recent work has shown that tar-
get and distractor processing can be controlled indepen-
dently in conflict tasks (Adkins et al., 2022; Ritz & Shenhav,
2021; Evans & Servant, 2020), creating an ill-posed problem
of coordinating across these strategies.

Inverse Problems in Cognitive Control:
The Implementational Level

Optimally configuring a decision processes is difficult, fac-
ing several challenges that are similar to those that occur
when planning a motor action. In the case of algorithmic
cognitive models, parameter degeneracy (e.g., DDM) and
process degeneracy (e.g., target-distractor trade-off )
make it difficult to optimally configure information pro-
cessing. However, problems at this level of analysis reflect
the best-case scenario, as these cognitive models are
themselves often intended to be lower-dimensional repre-
sentations of the underlying neural processes (Bogacz,
2007). At the implementational level, cognitive control
occurs over the complex neural instantiation of these
algorithms, further exacerbating the ill-posed nature of
the control problem.

One domain in which there can be redundancy in neural
control is at the stage of processing at which control is
applied, mirroring debates about early and late attentional
selection highlighted above. Previous work has suggested
that control can influence “early” sensory processing
(Adam & Serences, 2021; Egner & Hirsch, 2005) and “late”
processing in PFC (Mante, Sussillo, Shenoy, & Newsome,
2013; Stokes et al., 2013). To the extent that interven-
tions along processing pathways have a similar influence
on performance for a given task, there is a dilemma of
where to allocate control.

The difficulty in deciding “where” to allocate control is
magnified as the control targets move from macroscale
processing pathways to local configurations of neural pop-
ulations. For example, a controller could need to configure
a small neural network to produce a specific spiking profile
in response to inputs. Confounding this goal, it has been
shown that a broad range of cellular and synaptic parame-
ters produce very similar neuron- and network-level
dynamics at the scale of only a few units (Goaillard &
Marder, 2021; Alonso & Marder, 2019; Marder & Goaillard,
2006; Prinz, Bucher, & Marder, 2004). For example, very

576

Journal of Cognitive Neuroscience

Volume 34, Number 4

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

3
4
4
5
6
9
1
9
9
6
6
5
8

/
j

o
c
n
_
a
_
0
1
8
2
2
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

different configuration of sodium and potassium con-
ductance can produce very similar bursting profiles
(Golowasch, Goldman, Abbott, & Marder, 2002), analo-
gously to the redundancy of antagonistic muscles. These
findings demonstrate that even simple neural networks
face an ill-posed configuration problem, highlighting
additional challenges to the biological implementation
of cognitive control. Despite this degeneracy, research on
brain–computer interfaces has shown that animals can exert
fine-grained control over neural populations. Animals are
capable of evoking arbitrary activity patterns to maximize
reward (Athalye, Carmena, & Costa, 2019), even at the level
of controlling single neurons (Patel, Katz, Kalia, Popovic, &
Valiante, 2021; Prsa, Galiñanes, & Huber, 2017).

Across these different scales of implementation, the
optimization of neural systems faces a core set of inverse
problems: There are many macroscale configurations that
map similarly onto task goals, and there are many micro-
scale configurations that map similarly on to local dynam-
ics. This problem is closely related to the long-debated
issue of multiple realizability in philosophy of science,
which, in its applications to neuroscience, has explored
the lack of one-to-one mapping between neural and men-
tal phenomena (e.g., whether pain is identical to “C fiber”
activity; Putnam, 1967). The lack of one-to-one mappings
between structure and function poses not only an inferen-
tial problem to scientists and philosophers but also an
optimization problem to a brain’s control system.

The Problem with Inversion
As we’ve outlined above, the core difficulty in specifying
cognitive control signals comes from situations in which
the brain needs to map a higher-dimensional control con-
figuration on to a lower-dimensional task space, particu-
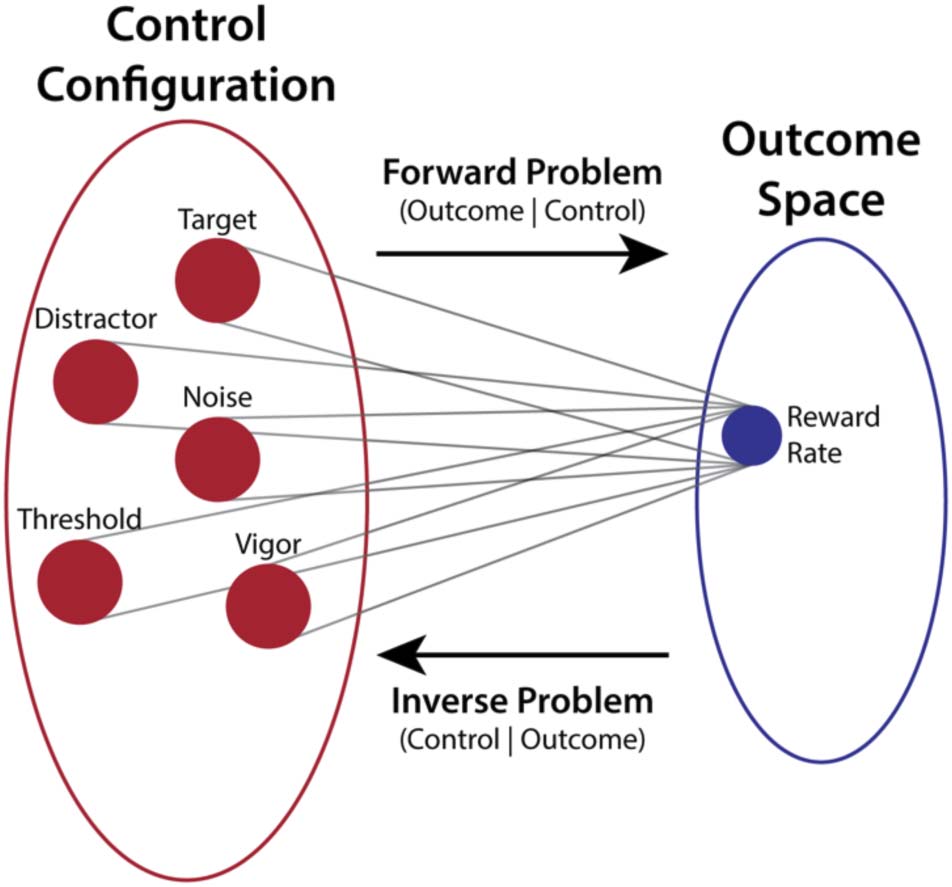
larly when there is redundancy in this mapping (Figure 3).
This class of problems has been extensively explored in
applied mathematics ( Willcox, Ghattas, & Heimbach,
2021; Calvetti & Somersalo, 2018; Evans & Stark, 2002;
Engl, Hanke, & Neubauer, 1996), and this field has devel-
oped helpful formalisms and solutions to the problems
faced by the brain. We can first consider the forward prob-
lem, where a brain forecasts what would happen if it
adopted a specific control configuration. For example,
the controller may predict how performance will change
if it raises its decision threshold. This problem generally
has a unique solution, as a specific configuration will usu-
ally produce a specific result even if there is redundancy.
Furthermore, projecting from a higher-dimensional con-
figuration to a lower-dimensional outcome will compress
the output, resulting in a stable solution.

However, the goal in optimization is to solve the inverse
problem, in this case inferring which control configurations
will produce a desired task state. As discussed earlier, this
problem is generally ill-posed (Hadamard, 1902) because
there are multiple redundant solutions for implementing
cognitive control. Another reason this is an ill-posed

Figure 3. Forward and inverse problems in cognitive control. The
forward problem in cognitive control entails predicting how a control
configuration (left) would lead to a task state (right). This problem
is stable because it maps from a high-dimensional control space onto
a lower-dimensional task space. Specification of cognitive control
requires solving the inverse problem, however, inferring the optimal
control configuration to achieve a goal. This problem is unstable
because it (redundantly) maps from a lower-dimensional task space into
a higher-dimensional control space.

problem is that this projects a lower-dimensional outcome
into a higher-dimensional configuration (Calvetti & Somer-
salo, 2018; Engl et al., 1996). For example, the controller may
optimize reward rate, but to do so must configure many
potential neural targets. Because outcomes are noisy (e.g.,
noisy estimates of values due to sampling error or imper-
fect forecasting), projection into a higher dimensional
control space will amplify this noise. In this regime, small
changes in values or goals can produce dramatically differ-
ent control configurations, leading to an unstable optimi-
zation process. Without compensatory measures, these
features of ill-posed cognitive control would impede the
brain’s ability to effectively achieve goals.

This fundamental challenge of inferring the actions that
will achieve goals has long been a central one within
research on computational motor control (McNamee &
Wolpert, 2019). Thankfully, these inverse problems can
be made tractable although well-established modifications
to the optimization process (Engl et al., 1996; Tikhonov,
1963). Motor theorists have leveraged these solutions to
help explain action planning, and in doing so providing
insight into the nature of effort costs.

SOLVING THE INVERSE PROBLEM

Motor Solutions to the Inverse Problem

A major innovation in theoretical motor control was to
reframe the motor control problem as an optimization

Ritz, Leng, and Shenhav

577

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

3
4
4
5
6
9
1
9
9
6
6
5
8

/
j

o
c
n
_
a
_
0
1
8
2
2
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

problem. Under this perspective, actions optimize an
objective function over the duration of the motor action
(similarly to the reward rate used for decision optimiza-
tion). For scientists who took this approach, a primary
focus was to understand people’s objective functions
and, in particular, the costs that constrain people’s actions.
Researchers proposed that people place a cost on jerky
movements (Flash & Hogan, 1985), muscle force (Uno
et al., 1989; Nelson, 1983; Chow & Jacobson, 1971), or
action-dependent noise (Harris & Wolpert, 1998), and
therefore try to minimize one or more of these while pur-
suing their goals. A core difference between these
accounts was whether costs depended on movement tra-
jectories (Flash & Hogan, 1985) or muscle force (Uno
et al., 1989), with the latter better explaining bodily con-
straints on actions (e.g., because of range of movement).
It now appears that actions are constrained by a muscle-
force-dependent cost (Morel, Ulbrich, & Gail, 2017;
Diedrichsen, Shadmehr, & Ivry, 2010; O’Sullivan, Burdet,
& Diedrichsen, 2009; Uno et al., 1989) and likely also
endpoint noise (O’Sullivan et al., 2009; Todorov, 2005;
Harris & Wolpert, 1998). However, it remains unclear
whether these effort costs are because of physiological
factors like metabolism, or whether they reflect a more
general property of the decision process. Although
metabolism would be an obvious candidate for these
effort costs, researchers have found that subjective effort
appraisals are largely uncorrelated with information being
signaled by bodily afferents (Marcora, 2009). Further-
more, whereas metabolic demands should increase line-
arly with muscle force (Szentesi, Zaremba, van Mechelen,
& Stienen, 2001), effort costs are better accounted for
by a quadratic relationship (Shadmehr & Ahmed, 2020;
Diedrichsen, Shadmehr, & Ivry, 2010).

These discrepancies suggest that motor effort may not
depend solely on energy expenditure but also on proper-
ties of the optimization process (e.g., related to the antic-
ipated control investment). A promising explanation for
these effort costs may arise from the solution to motor
control’s ill-posed inverse problem. A central method for
solving ill-posed problems is to constrain the solution
space through regularization (i.e., placing costs on higher
intensities of muscle force), a role that motor control
theorists have proposed for effort costs (Kawato et al.,
1990; Jordan, 1989). For example, across all motor plans
that would produce equivalent performance outcomes,
there is only one solution that also expends the least
effort. From this perspective, motor effort enables better
planning by creating global solutions to degenerate plan-
ning problems.

Regularization as a Solution to Ill-posed Cognitive
Control Selection

Much like motor control, cognitive control must also solve
a degenerate inverse problem. Like motor control, cogni-
tive control is subjectively costly (McGuire & Botvinick,

2010; Kahneman, 1973). For example, participants will
forego money ( Westbrook, Kester, & Braver, 2013) and
even accept pain (Vogel, Savelson, Otto, & Roy, 2020) to
avoid more cognitively demanding tasks. If physical effort
regularizes degenerate motor planning, then it is plausible
that cognitive effort similarly regularizes degenerate cogni-
tive planning. Recasting physical and mental effort as a reg-
ularization cost brings these domains in line with a wide
range of related psychological phenomena. For example,
inferring depth from visual inputs is also an ill-posed
problem, and this inference has been argued to depend
on regularization (Bertero, Poggio, & Torre, 1988; Poggio,
Koch, & Brenner, 1985; Poggio, Torre, & Koch, 1985).

Recent proposals have drawn connections between
cognitive effort and regularization under a variety of
theoretical motivations. For instance, it has been pro-
posed that cognitive effort enhances multitask learning
(Musslick, Saxe, Hoskin, Reichman, & Cohen, 2020; Kool
& Botvinick, 2018), where effort costs regularize toward
task-general policies (“habits”) that enable better transfer
learning. It has been also been proposed, based on princi-
ples of efficient coding (Zénon, Solopchuk, & Pezzulo,
2019), that effort costs enable compressed and more
metabolically efficient stimulus-action representations.
Finally, effort costs have been motivated from the perspec-
tive of model-based control (Piray & Daw, 2021), where
regularization toward a default policy allows for more effi-
cient long-range planning. These accounts offer different
perspectives on the benefits of regularized control, com-
plementing motor control’s emphasis on solving ill-posed
inverse problems.

Regularization in inverse problems has a normative
Bayesian interpretation, in which constraints come from
prior knowledge about the solution space (Calvetti &
Somersalo, 2018). This Bayesian perspective has been
influential in modeling ill-posed problems like inferring
knowledge from limited exemplars (Tenenbaum, Kemp,
Griffiths, & Goodman, 2011, Tenenbaum, Griffiths, &
Kemp, 2006) and planning sequential actions (Botvinick
& Toussaint, 2012; Friston, Samothrakis, & Montague,
2012; Solway & Botvinick, 2012). Regularization and
Bayesian inference have been a productive approach for
understanding how people solve ill-posed problems in
cognition and action. Within the Bayesian frameworks,
effort costs can be recast in terms of shrinkage toward a
prior, providing further insight into how a regularization
perspective could inform cognitive control. If there are
priors on cognitive or neural configurations, such as auto-
matic processes like habits, then regularized control
would penalize deviations from those defaults.

A Bayesian perspective on the relationship between
automaticity and control costs makes an interesting and
counterintuitive prediction: When people’s priors are to
exert high levels of control, they will find it difficult to relax
their control intensity. Research on control learning sup-
ports these predictions. A large body of work has found
that participants learn to exert more control when they

578

Journal of Cognitive Neuroscience

Volume 34, Number 4

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

3
4
4
5
6
9
1
9
9
6
6
5
8

/
j

o
c
n
_
a
_
0
1
8
2
2
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

expect a task to be difficult ( Jiang, Beck, Heller, & Egner,
2015; Bugg & Chanani, 2011; Yu, Dayan, & Cohen, 2009;
Logan & Zbrodoff, 1979) or when stimuli are associated
with conflict (Bugg & Hutchison, 2013; Bugg & Crump,
2012). This results in an allocation of excessive and mal-
adaptive levels of control when a trial turns out to be easy
(Logan & Zbrodoff, 1979). A recent experiment by
Bustamante et al. (2021) extended these findings by show-
ing how biases in control exertion can emerge through
feature-specific reward learning. Participants performed
a color-word Stroop task where they could choose to
either name the color (more control-demanding) or read
the word (less control-demanding). They learned that
certain stimulus features would yield greater reward for
color-naming and other features would yield greater
reward for word-reading. Critically, during a subsequent
transfer phase, participants had trouble learning to adap-
tively disengage control when faced with a combination of
stimulus features that had each previously predicted
greater reward for greater effort. That is, they had learned
to overexert control. It remains to be determined whether
this overexertion is because of effort mobilization, or
control priors that make color-naming less effortful
(Athalye et al., 2019; Yu et al., 2009).

This work highlights connections between control the-
ory and forms of reinforcement learning that have been
well-characterized within the cognitive sciences, whereby
an agent is presumed to select actions (or sequences of
actions) that maximize their expected long-term reward
(Collins, 2019; Neftci & Averbeck, 2019; Sutton & Barto,
2018). Indeed, the parallels between these two modeling
frameworks are rich, most notably in that both seek to
optimize goal-directed behavior by optimizing the
Bellman equation (a formula for estimating an action’s
expected future payoff; Anderson & Moore, 2007; Kalman,
1960). Ways in which these traditions often differ is that
control theory traditionally emphasizes prospective
model-based planning of a feedback policy over a contin-
uous state space, whereas reinforcement learning usually
focuses on gradually learning an action policy over a dis-
crete state space (Recht, 2018). Reinforcement learning
could speculatively intersect with cognitive control by
learning the control priors highlighted above (comple-
menting use-based automaticity; Miller, Shenhav, &
Ludvig, 2019) and evolutionary priors; Cisek, 2019; Zador,
2019), or could be involved in learning higher-level con-
trol policies (e.g., learning a sequence of subgoals; Frank
& Badre, 2012).

ALGORITHMS FOR MOTOR AND
COGNITIVE CONTROL

Motor and cognitive control appear to solve similar prob-
lems (action-outcome inversion) and plausibly through
similar computational principles (regularized optimiza-
tion). The next logical step is to ask whether cognitive

control has developed similar algorithmic solutions to this
inversion as the motor control system. A longstanding
gold-standard algorithm for modeling motor actions is
the linear quadratic regulator (LQR), which plays a central
role in the optimal feedback control theory of motor plan-
ning (Haar & Donchin, 2020; Shadmehr & Krakauer, 2008;
Todorov & Jordan, 2002). Building off the success of opti-
mal feedback control in the motor domain, this algorithm
provides a promising candidate for understanding the
planning and execution of cognitive actions.

LQR can provide the optimal solution to sequential con-
trol problems when two specific criteria are met. First, the
system under control must have linear dynamics, such as a
cruise controller that adjusts the speed of a car. Second,
the control process must be optimizing a quadratic objec-
tive function. This usually involves minimizing both the
squared goal error (e.g., the squared deviation from
desired speed) and the squared control intensity (e.g.,
the squared motor torque). Under these conditions,
LQR provides an analytic (i.e., closed-form) solution to
the optimal policy,3 avoiding the curse of dimensionality
( Van Rooij, 2008). LQR is equivalent to the Kalman
filtering method for optimal inference (Todorov, 2008;
Kalman & Bucy, 1961), and the linear quadratic Gaussian
algorithm combines inference and control for computa-
tionally tractable optimal behavior under state uncertainty
(Yeo, Franklin, & Wolpert, 2016; Todorov, 2005).

In the domain of motor control, LQR empirically
captures participants’ motor trajectories (Yeo et al., 2016;
Stevenson, Fernandes, Vilares, Wei, & Kording, 2009;
Todorov & Jordan, 2002), particularly in the case where
there are mid-trajectory perturbations to goals or effectors
(Takei, Lomber, Cook, & Scott, 2021; Nashed, Crevecoeur, &
Scott, 2012; Knill, Bondada, & Chhabra, 2011; Diedrichsen,
2007; Liu & Todorov, 2007). A striking example of the
power of this model to capture behavior was observed
in an experiment on motor coordination (Diedrichsen,
2007). Participants performed a reaching task in which
the goal either depended on both arms (e.g., rowing),
or where each arm had a separate goal (e.g., juggling).
During the reach, the experimenters perturbed one of
the arms and found that participants compensated with
both arms only when they were both involved in the same
goal. In LQR, this goal-dependent coordination arises
because of the algorithm’s model-based feedback control,
with squared effort costs favoring distributing the work
across goal-relevant effectors. Accordingly, this study
found that LQR simulations accurately captured partici-
pants’ reach trajectories. Furthermore, participants’
behavior also confirmed a key prediction of LQR, namely,
that noise correlations between arms will be task-specific,
constraining control to the goal-relevant dimensions of
the task manifold (the “minimal intervention principle”;
Todorov & Jordan, 2002).

A starting point for developing algorithmic links
between cognitive and motor control is to consider
whether cognitive control is a problem that is well-suited

Ritz, Leng, and Shenhav

579

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

3
4
4
5
6
9
1
9
9
6
6
5
8

/
j

o
c
n
_
a
_
0
1
8
2
2
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

for LQR. The first prediction from LQR is that the dynamics
between cognitive states are approximately linear. One
measure of these dynamics comes from task switching,
in which participants switch between multiple stimulus-
response rules (“task sets”; Monsell, 2003). Researchers
have found that these transitions between task sets are
well-captured by linear dynamics (Musslick & Cohen,
2021; Musslick, Bizyaeva, Agaron, Leonard, & Cohen,
2019; Steyvers, Hawkins, Karayanidis, & Brown, 2019).
For example, when participants are given a variable

amount of time to prepare for a transition between two
tasks (e.g., responding based on letters vs digits), the ste-
reotypical switch cost of slower responding after a task
switch compared to a task repetition decreases with
greater preparation time (Rogers & Monsell, 1995). A sim-
ple re-analysis of this pattern shows that switch costs can
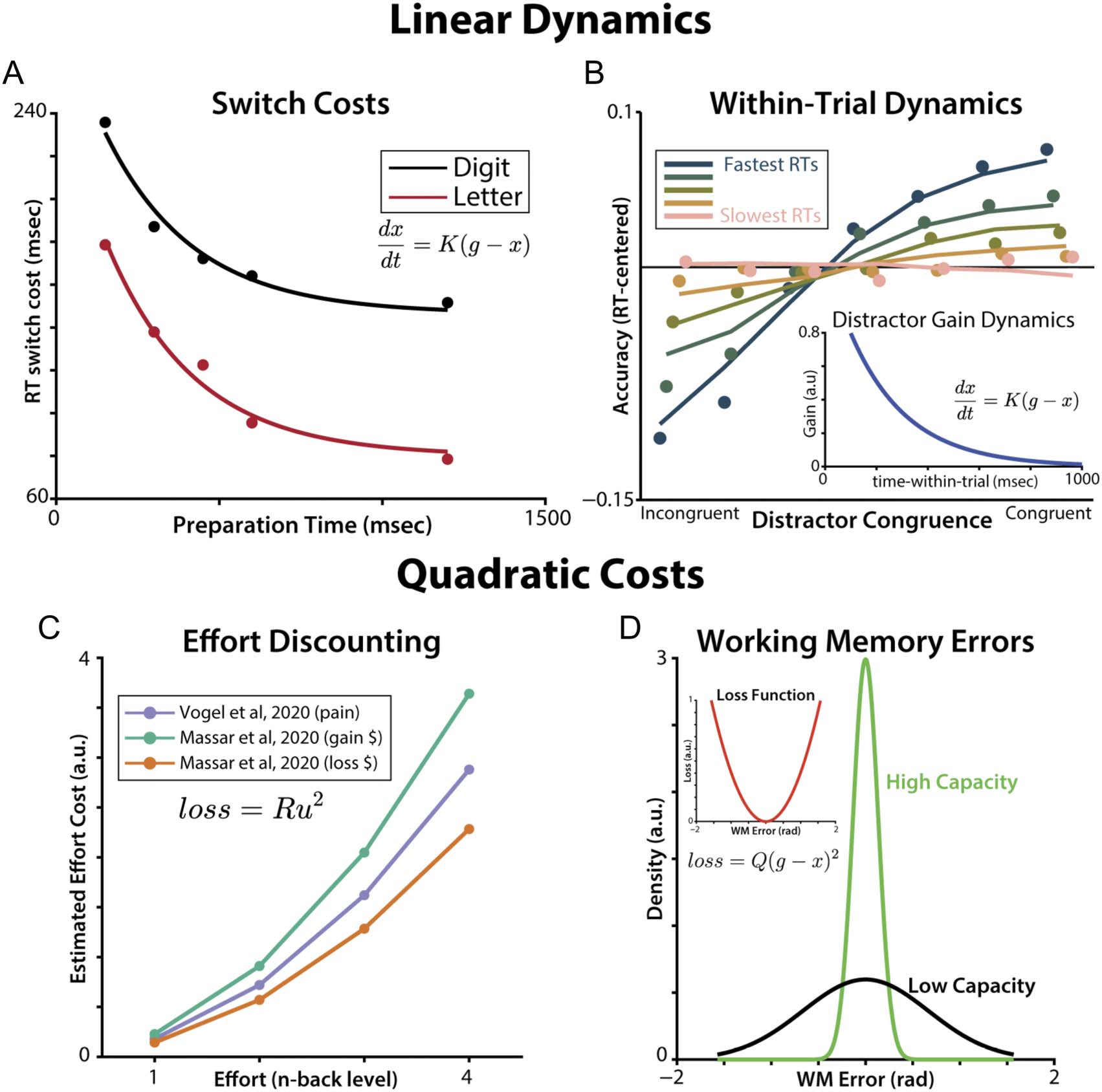
be well-captured by a linear dynamical model (Figure 4A).
Whereas switching to the “letter” or “digit” task had
different initial and asymptotic performance costs, they
appear to exhibit a similar rate of change.

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

3
4
4
5
6
9
1
9
9
6
6
5
8

/
j

o
c
n
_
a
_
0
1
8
2
2
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 4. Linear-quadratic properties of cognitive control. (A–B) There is evidence of linear cognitive control reconfiguration dynamics both
between trials and within a given trial. (A) In task-switching experiments, participants’ switch costs (slower and less accurate performance when
performing a different task than on the previous trial) exponentially decay with longer preparation time (time between the end of one trial and
the start of the next), consistent with linear dynamics. Lines show a maximum likelihood fit to data from Rogers and Monsell (1995) in which
participants switched between letter and digit tasks at predictable intervals. We estimated a shared decay rate (K) across tasks, with separate initial
conditions and asymptote fit to average switch costs in each task. (B) In a response conflict task, participants were less sensitive to distractor conflict
(parametrically varying stimulus-response congruence) at later response times (Ritz & Shenhav, 2021). This experiment modeled participants’
distractor sensitivity dynamics as exponentially decaying over time within each trial (inset), consistent with linear dynamics ( Weichart et al., 2020;
White et al., 2011). (C–D) Quadratic cost functions are evident in studies of effort discounting and working memory. (C) In effort-discounting tasks,
participants’ subjective cost of n-back tasks quadratically increases with their working memory load. Estimated cost functions are plotted from
the works of Massar et al. (2020) and Vogel et al. (2020). (D) Errors on working memory tasks are approximately Gaussian, consistent with a quadratic
loss function on accuracy (Sims et al., 2012).

580

Journal of Cognitive Neuroscience

Volume 34, Number 4

Linear dynamics have also been observed in attentional
adjustments that occur within a trial of a given task. For
instance, recent work has shown that performance on an
Eriksen flanker task can be accounted for by a DDM variant
in which initially broad attention narrows within a trial to
primarily focus only the central target, resulting in a shift
from the drift rate being initially dominated by the flankers
to being primarily dominated by the target ( Weichart
et al., 2020; Servant, Montagnini, & Burle, 2014; White,
Ratcliff, & Starns, 2011). Using the dot motion task
described earlier, we recently showed that these within-trial
dynamics can be further teased apart into target-enhancing
and distractor-suppressing elements of feature-based
attention, each with its own independent dynamics (Ritz
& Shenhav, 2021). These dynamics were well-captured by
an accumulation model that regulated feature gains with a
linear feedback control law (Figure 4B).

A second prediction from LQR is that cognitive effort
costs are quadratic. There are two lines of evidence that
support this prediction. One line of evidence comes from
studies of cognitive effort discounting, which examine
how people explicitly trade off different amounts of reward
(e.g., money) against different levels of cognitive effort
(e.g., n-back load). These studies quantify the extent to
which different levels of effort are treated as a cost when
making those decisions (i.e., how much reward is dis-
counted by this effort), and many of them find that
quadratic effort discounting captures choice the best
among their tested models4 (Figure 4C; Petitet, Attaallah,
Manohar, & Husain, 2021; Massar, Pu, Chen, & Chee, 2020;
Vogel et al., 2020; Białaszek, Marcowski, & Ostaszewski,
2017; Soutschek et al., 2014; although see also the works
of Chong et al., 2017; Hess, Lothary, O’Brien, Growney, &
DeLaRosa, 2021; McGuigan, Zhou, Brosnan, & Thyagarajan,
2019). A second line of evidence supporting quadratic
costs is found in tasks that require participants to hold a
stimulus in working memory (e.g., a Gabor patch of a
given orientation) and then reproduce that stimulus after
a delay period. Errors on this task tend to be approxi-
mately Gaussian (Sprague, Ester, & Serences, 2016; Ma,
Husain, & Bays, 2014; van den Berg, Shin, Chou, George,
& Ma, 2012; Bays & Husain, 2008; Wilken & Ma, 2004),
consistent with the predictions of ideal observer models
that incorporate quadratic loss function (Sims, 2015; Sims
et al., 2012; Figure 4D).

Recent work has begun to make explicit links between
LQR and the neural implementation of cognitive control.
Most notably, Bassett and colleagues have used LQR to
model the large-scale control of brain networks (e.g., Tang
& Bassett, 2018). This approach uses LQR modeling of
whole-brain network dynamics to understand the ability
of subnetworks to reconfigure macroscale brain states
(Braun et al., 2021; Gu et al., 2015, 2021; Betzel, Gu,
Medaglia, Pasqualetti, & Bassett, 2016; see also Yan et al.,
2017). For instance, in an fMRI experiment using the
n-back task, Braun et al. (2021) used an LQR model to
infer inferred that the brain requires more control to

maintain a stable 2-back state than a 0-back state, as well
as more control to transition from a 0-back state into a
2-back state than vice versa. Interestingly, individual
differences in these model-derived estimates of stability
and flexibility were associated with differences in dopa-
mine genotype, dopaminergic receptor blockade, and
schizophrenia diagnosis (Braun et al., 2021). An LQR
mo de lin g approach has be e n si m ila rl y use d to
model dynamics in directly recorded neural activity to
understand how local connectivity influences control
demands (Athalye et al., 2021; Stiso et al., 2019), with
accompanying theories of how these configuration pro-
cesses are learned through reinforcement learning
(Athalye et al., 2019).

Conclusions and Future Directions

The second half of the 20th century saw a wave of progress
on mathematical models for optimal control problems in
applied mathematics. A second wave of computational
motor control followed closely, combining rigorous mea-
surement of motor actions with normative models from
this new optimal control theory (Todorov & Jordan,
2002; Uno et al., 1989; Flash & Hogan, 1985; Nelson,
1983; Chow & Jacobson, 1971). Recently, a third wave of
cognitive control research has extended optimal control
principles to goal-directed cognition (Musslick & Cohen,
2021; Piray & Daw, 2021; Lieder et al., 2018; Tang &
Bassett, 2018; Shenhav et al., 2013, 2017; Yu et al., 2009;
Bogacz et al., 2006). This work tries to formalize the prin-
ciples that tie these different frameworks together, high-
lighting how cognitive control can learn from decades of
computational motor control research. These principles
have the potential to inform the theoretical development
and focused empirical investigation into the architecture
of goal-directed cognition. As behavioral tasks, statistical
techniques, and neuroimaging methods improve our
measurements of how the brain configures information
processing, theoretical constraints will be essential for
asking the right questions.

One insight that arises from casting cognitive control as
regularized optimization is that the sources of the control
costs that can enable “failures” of control are not neces-
sarily because of cognitive limitations (e.g., limited capac-
ity to engage multiple control signals). Instead, these
costs can arise because of the flexibility of cognition,
enabling a complex brain to optimize over degenerate
control actions. Under this framework, effort costs help
solve the decision problem of how to configure control.
One productive application of this perspective may be to
help shed light on why people differ in how they config-
ure these multivariate signals, for instance prioritizing
some forms of control over others. A regularization per-
spective would emphasize understanding different
people’s priors (e.g., perceptions of their own abilities;
Shenhav, Fahey, & Grahek, 2021; Bandura, 1977) and

Ritz, Leng, and Shenhav

581

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

3
4
4
5
6
9
1
9
9
6
6
5
8

/
j

o
c
n
_
a
_
0
1
8
2
2
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

configural redundancy when accounting for people’s
mental effort costs.

There are several important avenues for building further
on the promising theoretical and empirical foundations
that have been recently established in the study of multi-
variate control optimization. For instance, it will be impor-
tant to understand how effort’s role in solving the inverse
problem trades off against other proposed benefits like
generalization (Musslick et al., 2020; Kool & Botvinick,
2018) and efficiency (Zénon et al., 2019). It will also be
important to develop finer-grained connections between
computational theories of regularized cognitive control
and the algorithmic and implementational theories of
how the brain performs control optimization and execu-
tion. For instance, to what extent can specific regularized
control algorithms such as LQR explain the dynamics of
cognitive control optimization and deployment? How
does the cognitive control system integrate across multi-
ple monitored signals of goal progress and achievement
(Haar & Donchin, 2020), including different forms of
errors and conflict (Ebitz & Platt, 2015; Shen et al.,
2015)? While LQR modeling has been a powerful approach
for understanding the role of neural connectivity in goal-
driven brain dynamics, more work is needed to bridge
these findings to cognitive models of control optimization
and specification.

In addition to understanding the computational goals of
cognitive control optimization, it will be equally important
to understand how biological control algorithms deviate
from optimality. A substantial body of research has charac-
terized apparent deviations from optimality during judg-
ment and decision-making in the form of heuristics and
biases (Kahneman, 2003; Tversky & Kahneman, 1974).
Such seemingly irrational behaviors have been accounted
for within decision frameworks by formalizing the rational
bounds on optimality (Bhui & Xiang, 2021; Gershman &
Bhui, 2020; Lieder & Griffiths, 2019; Parpart, Jones, &
Love, 2018; Lieder, Hsu, & Griffiths, 2014; Lieder, Griffiths,
& Goodman, 2012; Simon, 1955). The LQR algorithm may
similarly reflect bounded optimality, as LQR is suboptimal
when its linear-quadratic assumptions are a poor match to
a task. A cognitive control system that uses LQR could
reflect a trade-off between better computational tracta-
bility and poorer worst-case performance. Future research
should incorporate the heuristics, biases, and approxima-
tions that influence cognitive control into models of con-
trol planning.

Progress on these questions will in turn require more
precise estimates of the underlying control processes.
The study of motor control has benefited immensely from
high-resolution measurements of motor effectors, for
instance tracking hand position during reaching. Analo-
gous measures of cognitive control are much more diffi-
cult to acquire, in part because they require inference from
motor movements (e.g., response time) and/or patterns of
activity within neural populations whose properties are
still poorly understood and are typically measured with

limited spatiotemporal resolution. Future experiments
should combine computational modeling with spatiotem-
porally resolved neuroimaging to understand the imple-
mentation of different types of control. In addition to
addressing core questions at the heart of multivariate con-
trol optimization, such methodological improvements will
also help us better understand the heterogeneity of multi-
variate effort. For instance, an untested assumption
implied by existing theoretical frameworks is that all forms
of cognitive control will incur subjective costs in a similar
fashion, for instance that higher levels of drift rate and
higher levels of threshold will both be experienced as
effortful (cf. Shenhav et al., 2013). Although there is con-
sistent evidence that enhancements to drift rate incur a
cost, it remains less clear whether adjustments to response
threshold incur a cost over and above the reductions to
reward rate they can cause (cf. Leng et al., 2021). Further
research is needed to examine this question and to
explore both the magnitude and functional form of these
cost functions across a wider array of control signals, espe-
cially with respect to deviations from participants’ default
configurations.

Our cognitive control is extremely complex and flexi-
ble and primarily operates over latent processes like
decision-making, all features that make studying cogni-
tive control a challenge. Thankfully, we can gain better
traction on this inference by drawing from the rich
empirical and theoretical traditions in better-constrained
fields like motor control (Broadbent, 1977). The norma-
tive principles of optimal control theory, which have
proven so fruitful in motor control, can similarly help
inform our theories and investigations into cognitive con-
trol. Although our cognition will certainly diverge from
these normative theories, these approaches can provide
a core foundation for understanding how we control our
thoughts and actions.

Acknowledgments

Special thanks to Laura Bustamante, Romy Frömer, and the rest
of the Shenhav Lab for helpful discussions on these topics.

Reprint requests should be sent to Harrison Ritz, Cognitive,
Linguistic, and Psychological Sciences, Carney Institute for
Brain Science, Brown University, Providence, RI, or via e-mail:
harrison.ritz@gmail.com.

Funding Information

This work was supported by the Training Program for
Interactionist Cognitive Neuroscience.

Xiamin Leng, National Institutes of Health (https://dx.doi
.org/10.13039/100000002), grant number: T32-MH115895.
Amitai Shenhav, National Institutes of Health (https://dx.doi
.org/10.13039/100000002), grant number: R01MH124849.
Amitai Shenhav, National Science Foundation (https://dx
.doi.org/10.13039/100000001), grant number: 2046111.

582

Journal of Cognitive Neuroscience

Volume 34, Number 4

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

3
4
4
5
6
9
1
9
9
6
6
5
8

/
j

o
c
n
_
a
_
0
1
8
2
2
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Diversity in Citation Practices

Retrospective analysis of the citations in every article pub-
lished in this journal from 2010 to 2021 reveals a persistent
pattern of gender imbalance: Although the proportions of
authorship teams (categorized by estimated gender iden-
tification of first author/last author) publishing in the Jour-
nal of Cognitive Neuroscience ( JoCN) during this period
were M(an)/M = .407, W(oman)/M = .32, M/W = .115, and
W/W = .159, the comparable proportions for the articles
that these authorship teams cited were M/M = .549,
W/M = .257, M/W = .109, and W/W = .085 (Postle and
Fulvio, JoCN, 34:1, pp. 1–3). Consequently, JoCN encour-
ages all authors to consider gender balance explicitly
when selecting which articles to cite and gives them the
opportunity to report their article’s gender citation bal-
ance. The authors of this article report its proportions of
citations by gender category to be M/M = .716, W/M =
.142, M/ W = .066, W/ W = .077.

Notes

1. Note that the DDM shares properties with several other evi-
dence accumulation models that enable similar behavioral pre-
dictions and, in some cases, finer-grained predictions for neural
implementation (Bogacz, 2007). We focus on the DDM as a ref-
erence point through much of this article because its properties
have been closely studied from the theoretical and empirical
perspective and it lends itself well to mechanistic hypotheses,
but our attributions to this model and its parameters should be
seen as potentially generalizable to related models.
2. We will use the term “monitored signal” to refer to signals
that act as inputs to decisions about control allocation. In con-
trast, we use “control signals” to refer to the control that is allo-
cated as a result of this decision process (analogous to “motor
commands”; Shenhav et al., 2013).
3. The analytic solutions to these algorithms rely on ordinary
least squares solutions for optimizing quadratic loss functions
and Gaussian identities describing how quadratic loss functions
change under linear dynamics. For in-depth mathematical
treatments, see Recht (2018), Shadmehr and Krakauer (2008),
and Anderson and Moore (2007).
4. A concern about effort discounting is that it ought to be
estimated based on cognitive demands rather than task
demands. Notably, participants consistently show quadratic
effort discounting in the n-back task, one domain where there
is at least a well-characterized linear relationship between these
levels of task load and PFC activity (Braver et al., 1997).

REFERENCES

Abrahamse, E., Braem, S., Notebaert, W., & Verguts, T. (2016).

Grounding cognitive control in associative learning.
Psychological Bulletin, 142, 693–728. https://doi.org/10.1037
/bul0000047, PubMed: 27148628

Adam, K. C. S., & Serences, J. T. (2021). History modulates
early sensory processing of salient distractors. Journal of
Neuroscience, 41, 8007–8022. https://doi.org/10.1523
/JNEUROSCI.3099-20.2021, PubMed: 34330776

Adkins, T. J., & Lee, T. (2021). Reward reduces habitual errors

by enhancing the preparation of goal-directed actions.
https://doi.org/10.31234/osf.io/hv9mz

Adkins, T., Lewis, R., & Lee, T. (2022). Heuristics contribute
to sensorimotor decision-making under risk. Psychonomic

Bulletin & Review, 29, 145–158. https://doi.org/10.3758/s13423
-021-01986-x, PubMed: 34508307

Alonso, L. M., & Marder, E. (2019). Visualization of currents

in neural models with similar behavior and different
conductance densities. eLife, 8, e42722. https://doi.org/10
.7554/eLife.42722, PubMed: 30702427

Anderson, B. D. O., & Moore, J. B. (2007). Optimal control:

Linear quadratic methods. Courier Corporation.

Aron, A. R. (2007). The neural basis of inhibition in cognitive
control. Neuroscientist, 13, 214–228. https://doi.org/10.1177
/1073858407299288, PubMed: 17519365

Athalye, V. R., Carmena, J. M., & Costa, R. M. (2019). Neural
reinforcement: Re-entering and refining neural dynamics
leading to desirable outcomes. Current Opinion in
Neurobiology, 60, 145–154. https://doi.org/10.1016/j.conb
.2019.11.023, PubMed: 31877493

Athalye, V. R., Khanna, P., Gowda, S., Orsborn, A. L., Costa, R. M.,
& Carmena, J. M. (2021). The brain uses invariant dynamics to
generalize outputs across movements. bioRxiv. https://doi.org
/10.1101/2021.08.27.457931

Balci, F., Simen, P., Niyogi, R., Saxe, A., Hughes, J. A., Holmes,
P., et al. (2011). Acquisition of decision making criteria:
Reward rate ultimately beats accuracy. Attention, Perception
& Psychophysics, 73, 640–657. https://doi.org/10.3758/s13414
-010-0049-7, PubMed: 21264716

Bandura, A. (1977). Self-efficacy: Toward a unifying theory of
behavioral change. Psychological Review, 84, 191–215.
https://doi.org/10.1037/0033-295X.84.2.191, PubMed: 847061

Bays, P. M., & Husain, M. (2008). Dynamic shifts of limited

working memory resources in human vision. Science, 321,
851–854. https://doi.org/10.1126/science.1158023, PubMed:
18687968

Berlyne, D. E. (1957). Uncertainty and conflict: A point of

contact between information-theory and behavior-theory
concepts. Psychological Review, 64, 329–339. https://doi.org
/10.1037/h0041135, PubMed: 13505970

Bernstein, N. A. (1935/1967). The problem of the interrelation
of coordination and localization. In N. A. Bemstein (Ed.), The
co-ordination and regulation of movements (pp. 15–59).
Oxford: Pergamon Press. (Original work published 1935).
Bertero, M., Poggio, T. A., & Torre, V. (1988). Ill-posed problems
in early vision. Proceedings of the IEEE, 76, 869–889. https://
doi.org/10.1109/5.5962

Betzel, R. F., Gu, S., Medaglia, J. D., Pasqualetti, F., & Bassett,
D. S. (2016). Optimally controlling the human connectome:
The role of network topology. Scientific Reports, 6, 30770.
https://doi.org/10.1038/srep30770, PubMed: 27468904

Bhui, R., & Xiang, Y. (2021). A rational account of the repulsion

effect. https://doi.org/10.31234/osf.io/hxjqv

Białaszek, W., Marcowski, P., & Ostaszewski, P. (2017). Physical
and cognitive effort discounting across different reward
magnitudes: Tests of discounting models. PLoS One, 12,
e0182353. https://doi.org/10.1371/journal.pone.0182353,
PubMed: 28759631

Bogacz, R. (2007). Optimal decision-making theories: Linking
neurobiology with behaviour. Trends in Cognitive Sciences,
11, 118–125. https://doi.org/10.1016/j.tics.2006.12.006,
PubMed: 17276130

Bogacz, R., Brown, E., Moehlis, J., Holmes, P., & Cohen, J. D.
(2006). The physics of optimal decision making: A formal
analysis of models of performance in two-alternative
forced-choice tasks. Psychological Review, 113, 700–765.
https://doi.org/10.1037/0033-295X.113.4.700, PubMed:
17014301

Boksem, M. A., Meijman, T. F., & Lorist, M. M. (2006). Mental

fatigue, motivation and action monitoring. Biological
Psychology, 72, 123–132. https://doi.org/10.1016/j.biopsycho
.2005.08.007, PubMed: 16288951

Ritz, Leng, and Shenhav

583

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

3
4
4
5
6
9
1
9
9
6
6
5
8

/
j

o
c
n
_
a
_
0
1
8
2
2
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Bond, K., Dunovan, K., Porter, A., Rubin, J. E., & Verstynen, T.

(2021). Dynamic decision policy reconfiguration under
outcome uncertainty. eLife, 10, e65540. https://doi.org/10
.7554/eLife.65540, PubMed: 34951589

Botvinick, M. M., Braver, T. S., Barch, D. M., Carter, C. S., &
Cohen, J. D. (2001). Conflict monitoring and cognitive
control. Psychological Review, 108, 624–652. https://doi.org
/10.1037/0033-295x.108.3.624, PubMed: 11488380

Botvinick, M. M., & Cohen, J. D. (2014). The computational and
neural basis of cognitive control: Charted territory and new
frontiers. Cognitive Science, 38, 1249–1285. https://doi.org/10
.1111/cogs.12126, PubMed: 25079472

Botvinick, M., & Toussaint, M. (2012). Planning as inference.

Trends in Cognitive Sciences, 16, 485–488. https://doi.org/10
.1016/j.tics.2012.08.006, PubMed: 22940577

Casey, B. J., Epstein, J. N., Buhle, J., Liston, C., Davidson, M. C.,
Tonev, S. T., et al. (2007). Frontostriatal connectivity and
its role in cognitive control in parent–child dyads with
ADHD. American Journal of Psychiatry, 164, 1729–1736.
https://doi.org/10.1176/appi.ajp.2007.06101754, PubMed:
17974939

Cavanagh, J. F., & Frank, M. J. (2014). Frontal theta as a
mechanism for cognitive control. Trends in Cognitive
Sciences, 18, 414–421. https://doi.org/10.1016/j.tics.2014.04
.012, PubMed: 24835663

Cavanagh, J. F., Wiecki, T. V., Cohen, M. X., Figueroa, C. M.,

Samanta, J., Sherman, S. J., et al. (2011). Subthalamic nucleus
stimulation reverses mediofrontal influence over decision
threshold. Nature Neuroscience, 14, 1462–1467. https://doi
.org/10.1038/nn.2925, PubMed: 21946325

Boureau, Y.-L., Sokol-Hessner, P., & Daw, N. D. (2015).

Chiew, K. S., & Braver, T. S. (2016). Reward favors the prepared:

Deciding how to decide: Self-control and meta-decision
making. Trends in Cognitive Sciences, 19, 700–710. https://
doi.org/10.1016/j.tics.2015.08.013, PubMed: 26483151

Braem, S., Verguts, T., Roggeman, C., & Notebaert, W. (2012).
Reward modulates adaptations to conflict. Cognition, 125,
324–332. https://doi.org/10.1016/j.cognition.2012.07.015,
PubMed: 22892279

Braun, U., Harneit, A., Pergola, G., Menara, T., Schäfer, A.,

Betzel, R. F., et al. (2021). Brain network dynamics during
working memory are modulated by dopamine and
diminished in schizophrenia. Nature Communications, 12,
3478. https://doi.org/10.1038/s41467-021-23694-9, PubMed:
34108456

Braver, T. S., & Barch, D. M. (2002). A theory of cognitive control,
aging cognition, and neuromodulation. Neuroscience and
Biobehavioral Reviews, 26, 809–817. https://doi.org/10.1016
/S0149-7634(02)00067-2, PubMed: 12470692

Braver, T. S., Cohen, J. D., Nystrom, L. E., Jonides, J., Smith, E. E.,
& Noll, D. C. (1997). A parametric study of prefrontal cortex
involvement in human working memory. Neuroimage, 5,
49–62. https://doi.org/10.1006/nimg.1996.0247, PubMed:
9038284

Brittain, J. S., Watkins, K. E., Joundi, R. A., Ray, N. J., Holland, P.,
Green, A. L., et al. (2012). A role for the subthalamic nucleus in
response inhibition during conflict. Journal of Neuroscience,
32, 13396–13401. https://doi.org/10.1523/JNEUROSCI.2259
-12.2012, PubMed: 23015430

Broadbent, D. E. (1977). Levels, hierarchies, and the locus of
control. Quarterly Journal of Experimental Psychology, 29,
181–201. https://doi.org/10.1080/14640747708400596
Bugg, J. M., & Chanani, S. (2011). List-wide control is not
entirely elusive: Evidence from picture-word Stroop.
Psychonomic Bulletin & Review, 18, 930–936. https://doi.org
/10.3758/s13423-011-0112-y, PubMed: 21638107

Bugg, J. M., & Crump, M. J. (2012). In support of a distinction
between voluntary and stimulus-driven control: A review of
the literature on proportion congruent effects. Frontiers in
Psychology, 3, 367. https://doi.org/10.3389/fpsyg.2012.00367,
PubMed: 23060836

Bugg, J. M., & Hutchison, K. A. (2013). Converging evidence for
control of color–word Stroop interference at the item level.
Journal of Experimental Psychology: Human Perception
and Performance, 39, 433–449. https://doi.org/10.1037
/a0029145, PubMed: 22845037

Bustamante, L., Lieder, F., Musslick, S., Shenhav, A., & Cohen, J.
(2021). Learning to overexert cognitive control in a Stroop
task. Cognitive, Affective, & Behavioral Neuroscience, 21,
453–471. https://doi.org/10.3758/s13415-020-00845-x,
PubMed: 33409959

Calvetti, D., & Somersalo, E. (2018). Inverse problems: From
regularization to Bayesian inference. WIRES Computational
Statistics, 10, e1427. https://doi.org/10.1002/wics.1427

Incentive and task-informative cues interact to enhance
attentional control. Journal of Experimental Psychology:
Human Perception and Performance, 42, 52–66. https://doi
.org/10.1037/xhp0000129, PubMed: 26322689

Chong, T. T.-J., Apps, M., Giehl, K., Sillence, A., Grima, L. L., &

Husain, M. (2017). Neurocomputational mechanisms
underlying subjective valuation of effort costs. PLoS Biology,
15, e1002598. https://doi.org/10.1371/journal.pbio.1002598,
PubMed: 28234892

Chow, C. K., & Jacobson, D. H. (1971). Studies of human
locomotion via optimal programming. Mathematical
Biosciences, 10, 239–306. https://doi.org/10.1016/0025-5564
(71)90062-9

Cisek, P. (2019). Resynthesizing behavior through phylogenetic

refinement. Attention, Perception & Psychophysics, 81,
2265–2287. https://doi.org/10.3758/s13414-019-01760-1,
PubMed: 31161495

Codol, O., Forgaard, C. J., Galea, J. M., & Gribble, P. L. (2021).
Sensorimotor feedback loops are selectively sensitive to
reward. bioRxiv. https://doi.org/10.1101/2021.09.16.460659
Codol, O., Holland, P. J., Manohar, S. G., & Galea, J. M. (2020).
Reward-based improvements in motor control are driven by
multiple error-reducing mechanisms. Journal of Neuroscience,
40, 3604–3620. https://doi.org/10.1523/JNEUROSCI.2646-19
.2020, PubMed: 32234779

Cohen, J. D., Servan-Schreiber, D., & McClelland, J. L. (1992).
A parallel distributed processing approach to automaticity.
American Journal of Psychology, 105, 239–269. https://doi
.org/10.2307/1423029, PubMed: 1621882

Collins, A. G. E. (2019). Reinforcement learning: Bringing

together computation and cognition. Current Opinion in
Behavioral Sciences, 29, 63–68. https://doi.org/10.1016/j
.cobeha.2019.04.011

Danielmeier, C., Allen, E. A., Jocham, G., Onur, O. A., Eichele,

T., & Ullsperger, M. (2015). Acetylcholine mediates
behavioral and neural post-error control. Current Biology,
25, 1461–1468. https://doi.org/10.1016/j.cub.2015.04.022,
PubMed: 25959965

Danielmeier, C., Eichele, T., Forstmann, B. U., Tittgemeyer, M.,

& Ullsperger, M. (2011). Posterior medial frontal cortex
activity predicts post-error adaptations in task-related visual
and motor areas. Journal of Neuroscience, 31, 1780–1789.
https://doi.org/10.1523/JNEUROSCI.4299-10.2011, PubMed:
21289188

Danielmeier, C., & Ullsperger, M. (2011). Post-error adjustments.
Frontiers in Psychology, 2, 233. https://doi.org/10.3389/fpsyg
.2011.00233, PubMed: 21954390

Debener, S., Ullsperger, M., Siegel, M., Fiehler, K., von Cramon,

D. Y., & Engel, A. K. (2005). Trial-by-trial coupling of
concurrent electroencephalogram and functional magnetic
resonance imaging identifies the dynamics of performance
monitoring. Journal of Neuroscience, 25, 11730–11737.

584

Journal of Cognitive Neuroscience

Volume 34, Number 4

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

3
4
4
5
6
9
1
9
9
6
6
5
8

/
j

o
c
n
_
a
_
0
1
8
2
2
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

https://doi.org/10.1523/JNEUROSCI.3286-05.2005, PubMed:
16354931

Diedrichsen, J. (2007). Optimal task-dependent changes of

bimanual feedback control and adaptation. Current Biology,
17, 1675–1679. https://doi.org/10.1016/j.cub.2007.08.051,
PubMed: 17900901

Diedrichsen, J., Shadmehr, R., & Ivry, R. B. (2010). The

coordination of movement: Optimal feedback control and
beyond. Trends in Cognitive Sciences, 14, 31–39. https://doi
.org/10.1016/j.tics.2009.11.004, PubMed: 20005767

Dix, A., & Li, S.-C. (2020). Incentive motivation improves
numerosity discrimination: Insights from pupillometry
combined with drift-diffusion modelling. Scientific Reports,
10, 2608. https://doi.org/10.1038/s41598-020-59415-3,
PubMed: 32054923

Driver, J. (2001). A selective review of selective attention
research from the past century. British Journal of
Psychology, 92, 53–78. https://doi.org/10.1348
/000712601162103, PubMed: 11802865

Dutilh, G., Vandekerckhove, J., Forstmann, B. U., Keuleers, E.,
Brysbaert, M., & Wagenmakers, E. J. (2012). Testing theories
of post-error slowing. Attention, Perception & Psychophysics,
74, 454–465. https://doi.org/10.3758/s13414-011-0243-2,
PubMed: 22105857

Ebitz, R. B., & Platt, M. L. (2015). Neuronal activity in primate
dorsal anterior cingulate cortex signals task conflict and
predicts adjustments in pupil-linked arousal. Neuron, 85,
628–640. https://doi.org/10.1016/j.neuron.2014.12.053,
PubMed: 25654259

Egner, T. (2007). Congruency sequence effects and cognitive
control. Cognitive, Affective & Behavioral Neuroscience, 7,
380–390. https://doi.org/10.3758/cabn.7.4.380, PubMed: 18189011
Egner, T. (2008). Multiple conflict-driven control mechanisms in
the human brain. Trends in Cognitive Sciences, 12, 374–380.
https://doi.org/10.1016/j.tics.2008.07.001, PubMed: 18760657

Egner, T., Delano, M., & Hirsch, J. (2007). Separate

conflict-specific cognitive control mechanisms in the human
brain. Neuroimage, 35, 940–948. https://doi.org/10.1016/j
.neuroimage.2006.11.061, PubMed: 17276088

Egner, T., & Hirsch, J. (2005). Cognitive control mechanisms

resolve conflict through cortical amplification of task-relevant
information. Nature Neuroscience, 8, 1784–1790. https://doi
.org/10.1038/nn1594, PubMed: 16286928

Engl, H. W., Hanke, M., & Neubauer, A. (1996). Regularization
of inverse problems. The Netherlands: Springer Science &
Business Media. https://doi.org/10.1007/978-94-009-1740-8

Esterman, M., Grosso, M., Liu, G., Mitko, A., Morris, R., &
DeGutis, J. (2016). Anticipation of monetary reward can
attenuate the vigilance decrement. PLoS One, 11, e0159741.
https://doi.org/10.1371/journal.pone.0159741, PubMed:
27472785

Esterman, M., Poole, V., Liu, G., & DeGutis, J. (2017).

Modulating reward induces differential neurocognitive
approaches to sustained attention. Cerebral Cortex, 27,
4022–4032. https://doi.org/10.1093/cercor/bhw214, PubMed:
27473320

Esterman, M., Reagan, A., Liu, G., Turner, C., & DeGutis, J.
(2014). Reward reveals dissociable aspects of sustained
attention. Journal of Experimental Psychology: General,
143, 2287–2295. https://doi.org/10.1037/xge0000019,
PubMed: 25313950

Etzel, J. A., Cole, M. W., Zacks, J. M., Kay, K. N., & Braver,
T. S. (2016). Reward motivation enhances task coding in
frontoparietal cortex. Cerebral Cortex, 26, 1647–1659.
https://doi.org/10.1093/cercor/bhu327, PubMed: 25601237
Evans, N. J., & Servant, M. (2020). A model-based approach to
disentangling facilitation and interference effects in conflict
tasks. https://doi.org/10.31234/osf.io/tu8ym

Evans, S. N., & Stark, P. B. (2002). Inverse problems as statistics.
Inverse Problems, 18, R55. https://doi.org/10.1088/0266-5611
/18/4/201

Fischer, A. G., Nigbur, R., Klein, T. A., Danielmeier, C., &

Ullsperger, M. (2018). Cortical beta power reflects decision
dynamics and uncovers multiple facets of post-error
adaptation. Nature Communications, 9, 5038.
https://doi.org/10.1038/s41467-018-07456-8, PubMed:
30487572

Flash, T., & Hogan, N. (1985). The coordination of arm

movements: An experimentally confirmed mathematical
model. Journal of Neuroscience, 5, 1688–1703. https://doi
.org/10.1523/JNEUROSCI.05-07-01688.1985, PubMed:
4020415

Fontanesi, L., Gluth, S., Spektor, M. S., & Rieskamp, J. (2019).

A reinforcement learning diffusion decision model for
value-based decisions. Psychonomic Bulletin & Review, 26,
1099–1121. https://doi.org/10.3758/s13423-018-1554-2,
PubMed: 30924057

Fortenbaugh, F. C., DeGutis, J., & Esterman, M. (2017). Recent

theoretical, neural, and clinical advances in sustained
attention research. Annals of the New York Academy of
Sciences, 1396, 70–91. https://doi.org/10.1111/nyas.13318,
PubMed: 28260249

Fortenbaugh, F. C., DeGutis, J., Germine, L., Wilmer, J. B.,
Grosso, M., Russo, K., et al. (2015). Sustained attention
across the life span in a sample of 10,000: Dissociating
ability and strategy. Psychological Science, 26, 1497–1510.
https://doi.org/10.1177/0956797615594896, PubMed:
26253551

Frank, M. J., & Badre, D. (2012). Mechanisms of hierarchical

reinforcement learning in corticostriatal circuits 1:
Computational analysis. Cerebral Cortex, 22, 509–526.
https://doi.org/10.1093/cercor/bhr114, PubMed: 21693490
Frank, M. J., Gagne, C., Nyhus, E., Masters, S., Wiecki, T. V.,
Cavanagh, J. F., et al. (2015). fMRI and EEG predictors
of dynamic decision parameters during human
reinforcement learning. Journal of Neuroscience, 35,
485–494. https://doi.org/10.1523/JNEUROSCI.2036-14.2015,
PubMed: 25589744

Friedman, N. P., & Miyake, A. (2017). Unity and diversity of

executive functions: Individual differences as a window on
cognitive structure. Cortex, 86, 186–204. https://doi.org/10
.1016/j.cortex.2016.04.023, PubMed: 27251123

Friedman, N. P., & Robbins, T. W. (2022). The role of prefrontal

cortex in cognitive control and executive function.
Neuropsychopharmacology, 47, 72–89. https://doi.org/10
.1038/s41386-021-01132-0, PubMed: 34408280

Friston, K., Samothrakis, S., & Montague, R. (2012). Active

inference and agency: optimal control without cost functions.
Biological Cybernetics, 106, 523–541. https://doi.org/10.1007
/s00422-012-0512-8, PubMed: 22864468

Fröber, K., & Dreisbach, G. (2014). The differential influences of
positive affect, random reward, and performance-contingent
reward on cognitive control. Cognitive, Affective & Behavioral
Neuroscience, 14, 530–547. https://doi.org/10.3758/s13415
-014-0259-x, PubMed: 24659000

Frömer, R., Lin, H., Dean Wolf, C. K., Inzlicht, M., & Shenhav, A.
(2021). Expectations of reward and efficacy guide cognitive
control allocation. Nature Communications, 12, 1–11.
https://doi.org/10.1038/s41467-021-21315-z, PubMed:
33589626

Funes, M. J., Lupiáñez, J., & Humphreys, G. (2010). Sustained
vs. transient cognitive control: Evidence of a behavioral
dissociation. Cognition, 114, 338–347. https://doi.org/10.1016
/j.cognition.2009.10.007, PubMed: 19962136

Gehring, W. J., & Fencsik, D. E. (2001). Functions of the medial

frontal cortex in the processing of conflict and errors.

Ritz, Leng, and Shenhav

585

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

3
4
4
5
6
9
1
9
9
6
6
5
8

/
j

o
c
n
_
a
_
0
1
8
2
2
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Journal of Neuroscience, 21, 9430–9437. https://doi.org/10
.1523/JNEUROSCI.21-23-09430.2001, PubMed: 11717376

Gershman, S. J., & Bhui, R. (2020). Rationally inattentive

intertemporal choice. Nature Communications, 11, 3365.
https://doi.org/10.1038/s41467-020-16852-y, PubMed:
32620804

Goaillard, J. M., & Marder, E. (2021). Ion channel degeneracy,
variability, and covariation in neuron and circuit resilience.
Annual Review of Neuroscience, 44, 335–357. https://doi
.org/10.1146/annurev-neuro-092920-121538, PubMed:
33770451

Golowasch, J., Goldman, M. S., Abbott, L. F., & Marder, E.
(2002). Failure of averaging in the construction of a
conductance-based neuron model. Journal of
Neurophysiology, 87, 1129–1131. https://doi.org/10.1152/jn
.00412.2001, PubMed: 11826077

Gonthier, C., Braver, T. S., & Bugg, J. M. (2016). Dissociating

proactive and reactive control in the Stroop task. Memory &
Cognition, 44, 778–788. https://doi.org/10.3758/s13421-016
-0591-1, PubMed: 26861210

Grahek, I., Schettino, A., Koster, E., & Andersen, S. K. (2021).
Dynamic interplay between reward and voluntary attention
determines stimulus processing in visual cortex. Journal of
Cognitive Neuroscience, 33, 2357–2371. https://doi.org/10
.1162/jocn_a_01762, PubMed: 34272951

Grahek, I., Shenhav, A., Musslick, S., Krebs, R. M., & Koster, E.

(2019). Motivation and cognitive control in depression.
Neuroscience and Biobehavioral Reviews, 102, 371–381.
https://doi.org/10.1016/j.neubiorev.2019.04.011, PubMed:
31047891

Gratton, G., Coles, M. G., & Donchin, E. (1992). Optimizing the

use of information: Strategic control of activation of
responses. Journal of Experimental Psychology: General,
121, 480–506. https://doi.org/10.1037/0096-3445.121.4.480,
PubMed: 1431740

Herz, D. M., Zavala, B. A., Bogacz, R., & Brown, P. (2016).

Neural correlates of decision thresholds in the
human subthalamic nucleus. Current Biology,
26, 916–920. https://doi.org/10.1016/j.cub.2016.01.051,
PubMed: 26996501

Hess, T. M., Lothary, A. F., O’Brien, E. L., Growney, C. M., &

DeLaRosa, J. (2021). Predictors of engagement in young and
older adults: The role of specific activity experience.
Psychology and Aging, 36, 131–142. https://doi.org/10.1037
/pag0000561, PubMed: 32686945

Jang, H., Lewis, R., & Lustig, C. (2021). Opposite reactions to
loss incentive by young and older adults: Insights from
diffusion modeling. PsyArXiv. https://doi.org/10.31234/osf.io
/4a3rc

Jentzsch, I., & Dudschig, C. (2009). Why do we slow down after
an error? Mechanisms underlying the effects of posterror
slowing. Quarterly Journal of Experimental Psychology,
62, 209–218. https://doi.org/10.1080/17470210802240655,
PubMed: 18720281

Jiang, J., Beck, J., Heller, K., & Egner, T. (2015). An

insula-frontostriatal network mediates flexible cognitive
control by adaptively predicting changing control demands.
Nature Communications, 6, 8165. https://doi.org/10.1038
/ncomms9165, PubMed: 26391305

Jiang, J., & Egner, T. (2014). Using neural pattern classifiers to
quantify the modularity of conflict-control mechanisms in the
human brain. Cerebral Cortex, 24, 1793–1805. https://doi.org
/10.1093/cercor/bht029, PubMed: 23402762

Jordan, M. I. (1989). Indeterminate motor skill learning
problems. Attention and Performance XIII: Motor
Representation and Control. London: Taylor & Francis.
Kahneman, D. (2003). A perspective on judgment and choice:
Mapping bounded rationality. American Psychologist, 58,
697–720. https://doi.org/10.1037/0003-066X.58.9.697,
PubMed: 14584987

Gu, S., Fotiadis, P., Parkes, L., Xia, C. H., Gur, R. C., Gur, R. E.,

Kahneman, D. (1973). Attention and effort. Englewood Cliffs,

et al. (2021). Network controllability mediates the
relationship between rigid structure and flexible dynamics.
bioRxiv. https://doi.org/10.1101/2021.04.23.441156
Gu, S., Pasqualetti, F., Cieslak, M., Telesford, Q. K.,

Yu, A. B., Kahn, A. E., et al. (2015). Controllability of
structural brain networks. Nature Communications,
6, 8414. https://doi.org/10.1038/ncomms9414, PubMed:
26423222

Guitart-Masip, M., Beierholm, U. R., Dolan, R., Duzel, E., &
Dayan, P. (2011). Vigor in the face of fluctuating rates of
reward: An experimental examination. Journal of Cognitive
Neuroscience, 23, 3933–3938. https://doi.org/10.1162/jocn_a
_00090, PubMed: 21736459

Haar, S., & Donchin, O. (2020). A revised computational
neuroanatomy for motor control. Journal of Cognitive
Neuroscience, 32, 1823–1836. https://doi.org/10.1162/jocn_a
_01602, PubMed: 32644882

Hadamard, J. (1902). Sur les problèmes aux dérivées partielles

et leur signification physique (pp. 49–52). Princeton
University Bulletin.

Hall-McMaster, S., Muhle-Karbe, P. S., Myers, N. E., & Stokes, M. G.
(2019). Reward boosts neural coding of task rules to optimize
cognitive flexibility. Journal of Neuroscience, 39, 8549–8561.
https://doi.org/10.1523/JNEUROSCI.0631-19.2019, PubMed:
31519820

Harris, C. M., & Wolpert, D. M. (1998). Signal-dependent noise
determines motor planning. Nature, 394, 780–784. https://
doi.org/10.1038/29528, PubMed: 9723616

Harris, C. M., & Wolpert, D. M. (2006). The main sequence of
saccades optimizes speed-accuracy trade-off. Biological
Cybernetics, 95, 21–29. https://doi.org/10.1007/s00422-006
-0064-x, PubMed: 16555070

NJ: Prentice-Hall.

Kalman, R. E. (1960). On the general theory of control systems.
IFAC Proceedings Volumes, 1, 491–502. https://doi.org/10
.1016/S1474-6670(17)70094-8

Kalman, R. E., & Bucy, R. S. (1961). New results in linear filtering
and prediction theory. Journal of Fluids Engineering, 83,
95–108. https://doi.org/10.1115/1.3658902

Kawato, M., Maeda, Y., Uno, Y., & Suzuki, R. (1990). Trajectory
formation of arm movement by cascade neural network
model based on minimum torque-change criterion.
Biological Cybernetics, 62, 275–288. https://doi.org/10.1007
/BF00201442, PubMed: 2310782

Kerns, J. G. (2006). Anterior cingulate and prefrontal cortex

activity in an FMRI study of trial-to-trial adjustments on the
Simon task. Neuroimage, 33, 399–405. https://doi.org/10
.1016/j.neuroimage.2006.06.012, PubMed: 16876434

Kerns, J. G., Cohen, J. D., MacDonald, A. W., III, Cho, R. Y.,
Stenger, V. A., & Carter, C. S. (2004). Anterior cingulate
conflict monitoring and adjustments in control. Science,
303, 1023–1026. https://doi.org/10.1126/science.1089910,
PubMed: 14963333

King, J. A., Korb, F. M., von Cramon, D. Y., & Ullsperger, M.
(2010). Post-error behavioral adjustments are facilitated by
activation and suppression of task-relevant and task-irrelevant
information processing. Journal of Neuroscience, 30,
12759–12769. https://doi.org/10.1523/JNEUROSCI.3274-10
.2010, PubMed: 20861380

Knill, D. C., Bondada, A., & Chhabra, M. (2011). Flexible,

task-dependent use of sensory feedback to control hand
movements. Journal of Neuroscience, 31, 1219–1237.
https://doi.org/10.1523/JNEUROSCI.3522-09.2011, PubMed:
21273407

586

Journal of Cognitive Neuroscience

Volume 34, Number 4

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

3
4
4
5
6
9
1
9
9
6
6
5
8

/
j

o
c
n
_
a
_
0
1
8
2
2
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Koch, I., Poljac, E., Müller, H., & Kiesel, A. (2018). Cognitive

structure, flexibility, and plasticity in human multitasking: An
integrative review of dual-task and task-switching research.
Psychological Bulletin, 144, 557–583. https://doi.org/10.1037
/bul0000144, PubMed: 29517261

Kool, W., & Botvinick, M. (2018). Mental labour. Nature

Human Behavior, 2, 899–908. https://doi.org/10.1038/s41562
-018-0401-9, PubMed: 30988433

Krakauer, J. W., Ghazanfar, A. A., Gomez-Marin, A., MacIver, M. A.,

& Poeppel, D. (2017). Neuroscience needs behavior:
Correcting a reductionist bias. Neuron, 93, 480–490.
https://doi.org/10.1016/j.neuron.2016.12.041, PubMed:
28182904

Krebs, R. M., Boehler, C. N., & Woldorff, M. G. (2010). The

influence of reward associations on conflict processing in the
Stroop task. Cognition, 117, 341–347. https://doi.org/10.1016
/j.cognition.2010.08.018, PubMed: 20864094

Behavior, 37, 233–278. https://doi.org/10.1016/S0065-2407
(09)03706-9

Ma, W. J., Husain, M., & Bays, P. M. (2014). Changing concepts
of working memory. Nature Neuroscience, 17, 347–356.
https://doi.org/10.1038/nn.3655, PubMed: 24569831

Maier, M. E., Yeung, N., & Steinhauser, M. (2011). Error-related
brain activity and adjustments of selective attention following
errors. Neuroimage, 56, 2339–2347. https://doi.org/10.1016/j
.neuroimage.2011.03.083, PubMed: 21511043

Manohar, S. G., Chong, T. T., Apps, M. A., Batla, A., Stamelou, M.,

Jarman, P. R., et al. (2015). Reward pays the cost of noise reduction
in motor and cognitive control. Current Biology, 25, 1707–1716.
https://doi.org/10.1016/j.cub.2015.05.038, PubMed: 26096975
Manohar, S. G., Finzi, R. D., Drew, D., & Husain, M. (2017).

Distinct motivational effects of contingent and noncontingent
rewards. Psychological Science, 28, 1016–1026. https://doi.org
/10.1177/0956797617693326, PubMed: 28488927

Laming, D. R. J. (1968). Information theory of choice-reaction

Manohar, S. G., Muhammed, K., Fallon, S. J., & Husain, M.

times. Academic Press.

Laming, D. (1979). Choice reaction performance following an
error. Acta Psychologica, 43, 199–224. https://doi.org/10
.1016/0001-6918(79)90026-X

Lavie, N., Hirst, A., de Fockert, J. W., & Viding, E. (2004). Load
theory of selective attention and cognitive control. Journal of
Experimental Psychology: General, 133, 339–354. https://doi
.org/10.1037/0096-3445.133.3.339, PubMed: 15355143

Leng, X., Yee, D., Ritz, H., & Shenhav, A. (2021). Dissociable
influences of reward and punishment on adaptive cognitive
control. PLoS Computational Biology, 17, e1009737.
https://doi.org/10.1371/journal.pcbi.1009737, PubMed:
34962931

Lesh, T. A., Niendam, T. A., Minzenberg, M. J., & Carter, C. S.

(2011). Cognitive control deficits in schizophrenia:
Mechanisms and meaning. Neuropsychopharmacology, 36,
316–338. https://doi.org/10.1038/npp.2010.156, PubMed:
20844478

Ličen, M., Hartmann, F., Repovš, G., & Slapničar, S. (2016). The

impact of social pressure and monetary incentive on
cognitive control. Frontiers in Psychology, 7, 93. https://doi
.org/10.3389/fpsyg.2016.00093, PubMed: 26903901

Lieder, F., & Griffiths, T. L. (2019). Resource-rational analysis:
Understanding human cognition as the optimal use of limited
computational resources. Behavioral and Brain Sciences,
43, e1. https://doi.org/10.1017/S0140525X1900061X,
PubMed: 30714890

Lieder, F., Griffiths, T. L., & Goodman, N. D. (2012). Burn-in,
bias, and the rationality of anchoring NIPS (pp. 2699–2707).
Stanford.

Lieder, F., Hsu, M., & Griffiths, T. L. (2014). The high availability
of extreme events serves resource-rational decision-making.
Proceedings of the Annual Meeting of the Cognitive Science
Society. escholarship.org

Lieder, F., Shenhav, A., Musslick, S., & Griffiths, T. L. (2018).

Rational metareasoning and the plasticity of cognitive
control. PLoS Computational Biology, 14, e1006043.
https://doi.org/10.1371/journal.pcbi.1006043, PubMed:
29694347

Liu, D., & Todorov, E. (2007). Evidence for the flexible

sensorimotor strategies predicted by optimal feedback
control. Journal of Neuroscience, 27, 9354–9368. https://
doi.org/10.1523/JNEUROSCI.1110-06.2007, PubMed:
17728449

Logan, G. D., & Zbrodoff, N. J. (1979). When it helps to be
misled: Facilitative effects of increasing the frequency of
conflicting stimuli in a Stroop-like task. Memory & Cognition,
7, 166–174. https://doi.org/10.3758/BF03197535

Luna, B. (2009). Developmental changes in cognitive control
through adolescence. Advances in Child Development and

(2019). Motivation dynamically increases noise resistance by
internal feedback during movement. Neuropsychologia, 123,
19–29. https://doi.org/10.1016/j.neuropsychologia.2018.07
.011, PubMed: 30005926

Mante, V., Sussillo, D., Shenoy, K. V., & Newsome, W. T. (2013).
Context-dependent computation by recurrent dynamics in
prefrontal cortex. Nature, 503, 78–84. https://doi.org/10.1038
/nature12742, PubMed: 24201281

Marco-Pallarés, J., Camara, E., Münte, T. F., & Rodríguez-Fornells,
A. (2008). Neural mechanisms underlying adaptive actions
after slips. Journal of Cognitive Neuroscience, 20, 1595–1610.
https://doi.org/10.1162/jocn.2008.20117, PubMed: 18345985

Marcora, S. (2009). Perception of effort during exercise is
independent of afferent feedback from skeletal muscles,
heart, and lungs. Journal of Applied Physiology, 106,
2060–2062. https://doi.org/10.1152/japplphysiol.90378.2008,
PubMed: 18345985

Marder, E., & Goaillard, J.-M. (2006). Variability, compensation
and homeostasis in neuron and network function. Nature
Reviews Neuroscience, 7, 563–574. https://doi.org/10.1038
/nrn1949, PubMed: 16791145

Massar, S., Pu, Z., Chen, C., & Chee, M. (2020). Losses motivate
cognitive effort more than gains in effort-based decision
making and performance. Frontiers in Human
Neuroscience, 14, 287. https://doi.org/10.3389/fnhum.2020
.00287, PubMed: 32765247

McGuigan, S., Zhou, S. H., Brosnan, M. B., & Thyagarajan, D.
(2019). Dopamine restores cognitive motivation in Parkinson’s
disease. Brain, 142, 719–732. https://doi.org/10.1093/brain
/awy341, PubMed: 30689734

McGuire, J. T., & Botvinick, M. M. (2010). Prefrontal cortex,
cognitive control, and the registration of decision costs.
Proceedings of the National Academy of Sciences, U.S.A.,
107, 7922–7926. https://doi.org/10.1073/pnas.0910662107,
PubMed: 20385798

McNamee, D., & Wolpert, D. M. (2019). Internal models in

biological control. Annual Review of Control, Robotics, and
Autonomous Systems, 2, 339–364. https://doi.org/10.1146
/annurev-control-060117-105206, PubMed: 31106294
Menon, V., & D’Esposito, M. (2022). The role of PFC

networks in cognitive control and executive function.
Neuropsychopharmacology, 47, 90–103. https://doi.org/10
.1038/s41386-021-01152-w, PubMed: 34408276

Miletić, S., Turner, B. M., Forstmann, B. U., & van Maanen, L.

(2017). Parameter recovery for the leaky competing
accumulator model. Journal of Mathematical Psychology,
76, 25–50. https://doi.org/10.1016/j.jmp.2016.12.001

Miller, K. J., Shenhav, A., & Ludvig, E. A. (2019). Habits without
values. Psychological Review, 126, 292–311. https://doi.org
/10.1037/rev0000120, PubMed: 30676040

Ritz, Leng, and Shenhav

587

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

3
4
4
5
6
9
1
9
9
6
6
5
8

/
j

o
c
n
_
a
_
0
1
8
2
2
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Monsell, S. (2003). Task switching. Trends in Cognitive Sciences,
7, 134–140. https://doi.org/10.1016/S1364-6613(03)00028-7,
PubMed: 12639695

Morel, P., Ulbrich, P., & Gail, A. (2017). What makes a

reach movement effortful? Physical effort discounting
supports common minimization principles in decision making
and motor control. PLoS Biology, 15, e2001323. https://doi.org
/10.1371/journal.pbio.2001323, PubMed: 28586347

Mukherjee, A., Lam, N. H., Wimmer, R. D., & Halassa, M. M.

(2021). Thalamic circuits for independent control of
prefrontal signal and noise. Nature, 600, 100–104. https://doi
.org/10.1038/s41586-021-04056-3, PubMed: 34614503

Musslick, S., Bizyaeva, A., Agaron, S., Leonard, N., & Cohen, J. D.
(2019). Stability–flexibility dilemma in cognitive control: A
dynamical system perspective. Proceedings of the 41st
Annual Meeting of the Cognitive Science Society.

Musslick, S., & Cohen, J. D. (2021). Rationalizing constraints
on the capacity for cognitive control. Trends in Cognitive
Sciences, 25, 757–775. https://doi.org/10.1016/j.tics.2021.06
.001, PubMed: 34332856

Musslick, S., Cohen, J. D., & Shenhav, A. (2019). Decomposing
individual differences in cognitive control: A model-based
approach. Proceedings of the 41st Annual Meeting of the
Cognitive Science Society.

Musslick, S., Saxe, A., Hoskin, A. N., Reichman, D., & Cohen, J. D.
(2020). On the rational boundedness of cognitive control:
Shared versus separated representations. https://doi.org/10
.31234/osf.io/jkhdf

Musslick, S., Shenhav, A., Botvinick, M., & Cohen, J. (2015). A
computational model of control allocation based on the
expected value of control. 2nd Multidisciplinary Conference
on Reinforcement Learning and Decision Making.
Presented at the Multidisciplinary Conference on
Reinforcement Learning and Decision Making.

Nakajima, M., Schmitt, L. I., & Halassa, M. M. (2019). Prefrontal
cortex regulates sensory filtering through a basal ganglia-to-
thalamus pathway. Neuron, 103, 445–458. https://doi.org/10
.1016/j.neuron.2019.05.026, PubMed: 31202541

Nashed, J. Y., Crevecoeur, F., & Scott, S. H. (2012). Influence of
the behavioral goal and environmental obstacles on rapid
feedback responses. Journal of Neurophysiology, 108,
999–1009. https://doi.org/10.1152/jn.01089.2011, PubMed:
22623483

Neftci, E. O., & Averbeck, B. B. (2019). Reinforcement learning

in artificial and biological systems. Nature Machine
Intelligence, 1, 133–143. https://doi.org/10.1038/s42256-019
-0025-4

Nelson, W. L. (1983). Physical principles for economies of
skilled movements. Biological Cybernetics, 46, 135–147.
https://doi.org/10.1007/BF00339982, PubMed: 6838914

Niv, Y., Daw, N. D., Joel, D., & Dayan, P. (2007). Tonic

dopamine: Opportunity costs and the control of response
vigor. Psychopharmacology, 191, 507–520. https://doi.org/10
.1007/s00213-006-0502-4, PubMed: 17031711

O’Sullivan, I., Burdet, E., & Diedrichsen, J. (2009). Dissociating
variability and effort as determinants of coordination. PLoS
Computational Biology, 5, e1000345. https://doi.org/10.1371
/journal.pcbi.1000345, PubMed: 19360132

Otto, A. R., & Daw, N. D. (2019). The opportunity cost of time
modulates cognitive effort. Neuropsychologia, 123, 92–105.
https://doi.org/10.1016/j.neuropsychologia.2018.05.006,
PubMed: 29750987

Padmala, S., & Pessoa, L. (2011). Reward reduces conflict by
enhancing attentional control and biasing visual cortical
processing. Journal of Cognitive Neuroscience, 23, 3419–3432.
https://doi.org/10.1162/jocn_a_00011, PubMed: 21452938
Parpart, P., Jones, M., & Love, B. C. (2018). Heuristics as

Bayesian inference under extreme priors. Cognitive Psychology,

102, 127–144. https://doi.org/10.1016/j.cogpsych.2017.11.006,
PubMed: 29500961

Parro, C., Dixon, M. L., & Christoff, K. (2018). The neural basis
of motivational influences on cognitive control. Human
Brain Mapping, 39, 5097–5111. https://doi.org/10.1002/hbm
.24348, PubMed: 30120846

Patel, K., Katz, C. N., Kalia, S. K., Popovic, M. R., & Valiante, T. A.
(2021). Volitional control of individual neurons in the human
brain. Brain, 144, 3651–3663. https://doi.org/10.1093/brain
/awab370, PubMed: 34623400

Pekny, S. E., Izawa, J., & Shadmehr, R. (2015). Reward-dependent
modulation of movement variability. Journal of Neuroscience,
35, 4015–4024. https://doi.org/10.1523/JNEUROSCI.3244-14
.2015, PubMed: 25740529

Petitet, P., Attaallah, B., Manohar, S. G., & Husain, M. (2021).
The computational cost of active information sampling
before decision-making under uncertainty. Nature Human
Behaviour, 5, 935–946. https://doi.org/10.1038/s41562-021
-01116-6, PubMed: 34045719

Piray, P., & Daw, N. D. (2021). Linear reinforcement learning

in planning, grid fields, and cognitive control. Nature
Communications, 12, 4942. https://doi.org/10.1038/s41467
-021-25123-3, PubMed: 34400622

Poggio, T., Koch, C., & Brenner, S. (1985). III-Posed problems

early vision: From computational theory to analogue
networks. Proceedings of the Royal Society of London, Series
B: Biological Sciences, 226, 303–323. https://doi.org/10.1098
/rspb.1985.0097

Poggio, T., Torre, V., & Koch, C. (1985). Computational vision
and regularization theory. Nature, 317, 314–319. https://doi
.org/10.1038/317314a0, PubMed: 2413361

Posner, M., & Snyder, C. (1975). Attention and cognitive

control. Reprinted in Cognitive Psychology: Key Readings
(2004). London: Psychology Press.

Prinz, A. A., Bucher, D., & Marder, E. (2004). Similar network

activity from disparate circuit parameters. Nature
Neuroscience, 7, 1345–1352. https://doi.org/10.1038/nn1352,
PubMed: 15558066

Prsa, M., Galiñanes, G. L., & Huber, D. (2017). Rapid

integration of artificial sensory feedback during operant
conditioning of motor cortex neurons. Neuron, 93,
929–939. https://doi.org/10.1016/j.neuron.2017.01.023,
PubMed: 28231470

Putnam, H. (1967). Psychological predicates. Art, Mind, and

Religion, 1, 37–48.

Rabbitt, P. M. (1966). Errors and error correction in

choice-response tasks. Journal of Experimental Psychology,
71, 264–272. https://doi.org/10.1037/h0022853, PubMed:
5948188

Ratcliff, R. (1978). A theory of memory retrieval.

Psychological Review, 85, 59–108. https://doi.org/10.1037
/0033-295X.85.2.59

Ratcliff, R., & Frank, M. J. (2012). Reinforcement-based decision

making in corticostriatal circuits: mutual constraints by
neurocomputational and diffusion models. Neural
Computation, 24, 1186–1229. https://doi.org/10.1162/NECO
_a_00270, PubMed: 22295983

Ratcliff, R., & McKoon, G. (2008). The diffusion decision model:

Theory and data for two-choice decision tasks. Neural
Computation, 20, 873–922. https://doi.org/10.1162/neco
.2008.12-06-420, PubMed: 18085991

Ratcliff, R., & Rouder, J. N. (1998). Modeling response times for
two-choice decisions. Psychological Science, 9, 347–356.
https://doi.org/10.1111/1467-9280.00067

Recht, B. (2018). A tour of reinforcement learning: The view

from continuous control. arXiv [mathOC].

Ridderinkhof, K. R. (2002). Micro- and macro-adjustments
of task set: Activation and suppression in conflict tasks.

588

Journal of Cognitive Neuroscience

Volume 34, Number 4

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

3
4
4
5
6
9
1
9
9
6
6
5
8

/
j

o
c
n
_
a
_
0
1
8
2
2
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Psychological Research, 66, 312–323. https://doi.org/10.1007
/s00426-002-0104-7, PubMed: 12466928

Ritz, H., DeGutis, J., Frank, M. J., Esterman, M., &

Shenhav, A. (2020). An evidence accumulation model of
motivational and developmental influences over sustained
attention. 42nd Annual Meeting of the Cognitive Science
Society.

Ritz, H., & Shenhav, A. (2021). Humans reconfigure

target and distractor processing to address
distinct task demands. bioRxiv. https://doi.org/10.1101/2021
.09.08.459546

Rogers, R. D., & Monsell, S. (1995). Costs of a predictible switch
between simple cognitive tasks. Journal of Experimental
Psychology: General, 124, 207–231. https://doi.org/10.1037
/0096-3445.124.2.207

Schroeder, U., Kuehler, A., Haslinger, B., Erhard, P., Fogel, W.,

Tronnier, V. M., et al. (2002). Subthalamic nucleus
stimulation affects striato-anterior cingulate cortex circuit
in a response conflict task: A PET study. Brain, 125,
1995–2004. https://doi.org/10.1093/brain/awf199, PubMed:
12183345

Servant, M., Montagnini, A., & Burle, B. (2014). Conflict tasks
and the diffusion framework: Insight in model constraints
based on psychological laws. Cognitive Psychology, 72,
162–195. https://doi.org/10.1016/j.cogpsych.2014.03.002,
PubMed: 24762975

Shadmehr, R., & Ahmed, A. A. (2020). Vigor: Neuroeconomics
of movement control. Cambridge, MA: MIT Press. https://doi
.org/10.7551/mitpress/12940.001.0001

Shadmehr, R., & Krakauer, J. W. (2008). A computational
neuroanatomy for motor control. Experimental Brain
Research, 185, 359–381. https://doi.org/10.1007/s00221-008
-1280-5, PubMed: 18251019

Shadmehr, R., Orban de Xivry, J. J., Xu-Wilson, M., & Shih, T. Y.
(2010). Temporal discounting of reward and the cost of time
in motor control. Journal of Neuroscience, 30, 10507–10516.
https://doi.org/10.1523/JNEUROSCI.1343-10.2010, PubMed:
20685993

Shen, C., Ardid, S., Kaping, D., Westendorff, S., Everling, S., &
Womelsdorf, T. (2015). Anterior cingulate cortex cells identify
process-specific errors of attentional control prior to
transient prefrontal-cingulate inhibition. Cerebral Cortex, 25,
2213–2228. https://doi.org/10.1093/cercor/bhu028, PubMed:
24591526

Shenhav, A., Botvinick, M. M., & Cohen, J. D. (2013). The

expected value of control: An integrative theory of anterior
cingulate cortex function. Neuron, 79, 217–240. https://doi
.org/10.1016/j.neuron.2013.07.007, PubMed: 23889930

Shenhav, A., Musslick, S., Lieder, F., Kool, W., Griffiths, T. L.,

Cohen, J. D., et al. (2017). Toward a rational and mechanistic
account of mental effort. Annual Review of Neuroscience,
40, 99–124. https://doi.org/10.1146/annurev-neuro-072116
-031526, PubMed: 28375769

Shenhav, A., Fahey, M. P., & Grahek, I. (2021). Decomposing
the motivation to exert mental effort. Current Directions in
Psychological Science, 30, 307–314. https://doi.org/10.1177
/09637214211009510, PubMed: 34675454

Shiffrin, R. M., & Schneider, W. (1977). Controlled and

automatic human information processing: II. Perceptual
learning, automatic attending and a general theory.
Psychological Review, 84, 127–190. https://doi.org/10.1037
/0033-295X.84.2.127

Simen, P., Contreras, D., Buck, C., Hu, P., Holmes, P., & Cohen,
J. D. (2009). Reward rate optimization in two-alternative
decision making: Empirical tests of theoretical predictions.
Journal of Experimental Psychology: Human Perception
and Performance, 35, 1865–1897. https://doi.org/10.1037
/a0016926, PubMed: 19968441

Simon, H. A. (1955). A behavioral model of rational choice.

Quarterly Journal of Economics, 69, 99–118. https://doi.org
/10.2307/1884852

Sims, C. R. (2015). The cost of misremembering: Inferring the
loss function in visual working memory. Journal of Vision,
15, 2. https://doi.org/10.1167/15.3.2, PubMed: 25740875

Sims, C. R., Jacobs, R. A., & Knill, D. C. (2012). An ideal observer
analysis of visual working memory. Psychological Review,
119, 807–830. https://doi.org/10.1037/a0029856, PubMed:
22946744

Solway, A., & Botvinick, M. M. (2012). Goal-directed decision

making as probabilistic inference: A computational
framework and potential neural correlates. Psychological
Review, 119, 120–154. https://doi.org/10.1037/a0026435,
PubMed: 22229491

Soutschek, A., Stelzel, C., Paschke, L., Walter, H., & Schubert, T.
(2015). Dissociable effects of motivation and expectancy on
conflict processing: An fMRI study. Journal of Cognitive
Neuroscience, 27, 409–423. https://doi.org/10.1162/jocn_a
_00712, PubMed: 25203271

Soutschek, A., Strobach, T., & Schubert, T. (2014). Motivational

and cognitive determinants of control during conflict
processing. Cognition & Emotion, 28, 1076–1089. https://doi
.org/10.1080/02699931.2013.870134, PubMed: 24344784
Sprague, T. C., Ester, E. F., & Serences, J. T. (2016). Restoring
latent visual working memory representations in human
cortex. Neuron, 91, 694–707. https://doi.org/10.1016/j.neuron
.2016.07.006, PubMed: 27497224

Starns, J. J., & Ratcliff, R. (2010). The effects of aging on the
speed-accuracy compromise: Boundary optimality in the
diffusion model. Psychology and Aging, 25, 377–390. https://
doi.org/10.1037/a0018022, PubMed: 20545422

Steinhauser, M., & Andersen, S. K. (2019). Rapid adaptive

adjustments of selective attention following errors revealed
by the time course of steady-state visual evoked potentials.
Neuroimage, 186, 83–92. https://doi.org/10.1016/j
.neuroimage.2018.10.059, PubMed: 30366075

Stevenson, I. H., Fernandes, H. L., Vilares, I., Wei, K., & Kording,
K. P. (2009). Bayesian integration and non-linear feedback
control in a full-body motor task. PLoS Computational
Biology, 5, e1000629. https://doi.org/10.1371/journal.pcbi
.1000629, PubMed: 20041205

Steyvers, M., Hawkins, G. E., Karayanidis, F., & Brown, S. D.

(2019). A large-scale analysis of task switching practice effects
across the lifespan. Proceedings of the National Academy of
Sciences, U.S.A., 116, 17735–17740. https://doi.org/10.1073
/pnas.1906788116, PubMed: 31427513

Stiso, J., Khambhati, A. N., Menara, T., Kahn, A. E., Stein,
J. M., Das, S. R., et al. (2019). White matter network
architecture guides direct electrical stimulation through
optimal state transitions. Cell Reports, 28, 2554–2566.
https://doi.org/10.1016/j.celrep.2019.08.008, PubMed:
31484068

Stokes, M. G., Kusunoki, M., Sigala, N., Nili, H., Gaffan, D., &
Duncan, J. (2013). Dynamic coding for cognitive control in
prefrontal cortex. Neuron, 78, 364–375. https://doi.org/10
.1016/j.neuron.2013.01.039, PubMed: 23562541
Sukumar, S., Shadmehr, R., & Ahmed, A. A. (2021).
Effects of reward history on decision-making and
movement vigor. bioRxiv. https://doi.org/10.1101/2021.07.22
.453376

Sutton, R. S., & Barto, A. G. (2018). Reinforcement learning: An

introduction (2nd ed.). Cambridge, MA: MIT Press.

Szentesi, P., Zaremba, R., van Mechelen, W., & Stienen, G. J.

(2001). ATP utilization for calcium uptake and force
production in different types of human skeletal muscle fibres.
Journal of Physiology, 531, 393–403. https://doi.org/10.1111/j
.1469-7793.2001.0393i.x, PubMed: 11230512

Ritz, Leng, and Shenhav

589

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

3
4
4
5
6
9
1
9
9
6
6
5
8

/
j

o
c
n
_
a
_
0
1
8
2
2
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Takei, T., Lomber, S. G., Cook, D. J., & Scott, S. H. (2021).

Transient deactivation of dorsal premotor cortex or parietal
area 5 impairs feedback control of the limb in macaques.
Current Biology, 31, 1476–1487. https://doi.org/10.1016/j.cub
.2021.01.049, PubMed: 33592191

Tang, E., & Bassett, D. S. (2018). Colloquium: Control of

dynamics in brain networks. Reviews of Modern Physics, 90,
031003. https://doi.org/10.1103/RevModPhys.90.031003

Tenenbaum, J. B., Griffiths, T. L., & Kemp, C. (2006). Theory-
based Bayesian models of inductive learning and reasoning.
Trends in Cognitive Sciences, 10, 309–318. https://doi.org/10
.1016/j.tics.2006.05.009, PubMed: 16797219

Tenenbaum, J. B., Kemp, C., Griffiths, T. L., & Goodman, N. D.

(2011). How to grow a mind: Statistics, structure, and
abstraction. Science, 331, 1279–1285. https://doi.org/10.1126
/science.1192788, PubMed: 21393536

Thurm, F., Zink, N., & Li, S. C. (2018). Comparing effects of
reward anticipation on working memory in younger and
older adults. Frontiers in Psychology, 9, 2318. https://doi.org
/10.3389/fpsyg.2018.02318, PubMed: 30546333
Tikhonov, A. N. (1963). On the solution of ill-posed

problems and the method of regularization [Doklady
Akademii Nauk] (pp. 501–504). Russian Academy of
Sciences.

Todorov, E. (2005). Stochastic optimal control and estimation

methods adapted to the noise characteristics of the
sensorimotor system. Neural Computation, 17, 1084–1108.
https://doi.org/10.1162/0899766053491887, PubMed:
15829101

Todorov, E. (2008). General duality between optimal control
and estimation. 47th IEEE Conference on Decision and
Control, 4286–4292. ieeexplore.ieee.org. https://doi.org/10
.1109/CDC.2008.4739438

Todorov, E., & Jordan, M. I. (2002). Optimal feedback
control as a theory of motor coordination. Nature
Neuroscience, 5, 1226–1235. https://doi.org/10.1038/nn963,
PubMed: 12404008

Trommershäuser, J., Maloney, L. T., & Landy, M. S. (2003a).
Statistical decision theory and trade-offs in the control of
motor response. Spatial Vision, 16, 255–275. https://doi.org
/10.1163/156856803322467527, PubMed: 12858951

Trommershäuser, J., Maloney, L. T., & Landy, M. S. (2003b).

Statistical decision theory and the selection of rapid,
goal-directed movements. Journal of the Optical Society
of America A, 20, 1419–1433. https://doi.org/10.1364/josaa.20
.001419, PubMed: 12868646

Tversky, A., & Kahneman, D. (1974). Judgment under

uncertainty: Heuristics and biases. Science, 185, 1124–1131.
https://doi.org/10.1126/science.185.4157.1124, PubMed:
17835457

Ullsperger, M., Bylsma, L. M., & Botvinick, M. M. (2005). The
conflict adaptation effect: it’s not just priming. Cognitive,
Affective & Behavioral Neuroscience, 5, 467–472. https://doi
.org/10.3758/cabn.5.4.467, PubMed: 16541815

Uno, Y., Kawato, M., & Suzuki, R. (1989). Formation and control
of optimal trajectory in human multijoint arm movement.
Minimum torque-change model. Biological Cybernetics, 61,
89–101. https://doi.org/10.1007/BF00204593, PubMed:
2742921

Usher, M., & McClelland, J. L. (2001). The time course of

perceptual choice: The leaky, competing accumulator model.
Psychological Review, 108, 550–592. https://doi.org/10.1037
/0033-295x.108.3.550, PubMed: 11488378

van den Berg, R., Shin, H., Chou, W.-C., George, R., & Ma, W. J.
(2012). Variability in encoding precision accounts for visual
short-term memory limitations. Proceedings of the National
Academy of Sciences, U.S.A., 109, 8780–8785. https://doi.org
/10.1073/pnas.1117465109, PubMed: 22582168

Van Rooij, I. (2008). The tractable cognition thesis. Cognitive

Science, 32, 939–984. https://doi.org/10.1080
/03640210801897856, PubMed: 21585437

Verguts, T., Notebaert, W., Kunde, W., & Wühr, P. (2011).
Post-conflict slowing: Cognitive adaptation after conflict
processing. Psychonomic Bulletin & Review, 18, 76–82.
https://doi.org/10.3758/s13423-010-0016-2, PubMed:
21327366

Verguts, T., Vassena, E., & Silvetti, M. (2015). Adaptive
effort investment in cognitive and physical tasks: A
neurocomputational model. Frontiers in Behavioral
Neuroscience, 9, 57. https://doi.org/10.3389/fnbeh.2015
.00057, PubMed: 25805978

Vogel, T. A., Savelson, Z. M., Otto, A. R., & Roy, M. (2020).
Forced choices reveal a trade-off between cognitive effort
and physical pain. eLife, 9, e59410. https://doi.org/10.7554
/eLife.59410, PubMed: 33200988

von Bastian, C. C., Blais, C., Brewer, G. A., Gyurkovics, M.,
Hedge, C., Kałamała, P., et al. (2020). Advancing the
understanding of individual differences in attentional control:
Theoretical, methodological, and analytical considerations.
https://doi.org/10.31234/osf.io/x3b9k

Weichart, E. R., Turner, B. M., & Sederberg, P. B. (2020). A

model of dynamic, within-trial conflict resolution for decision
making. Psychological Review, 127, 749–777. https://doi.org
/10.1037/rev0000191, PubMed: 32212764

Wessel, J. R., Waller, D. A., & Greenlee, J. D. (2019). Non-

selective inhibition of inappropriate motor-tendencies during
response-conflict by a fronto-subthalamic mechanism. eLife,
8, e42959. https://doi.org/10.7554/eLife.42959, PubMed:
31063130

Westbrook, A., & Braver, T. S. (2015). Cognitive effort: A

neuroeconomic approach. Cognitive, Affective & Behavioral
Neuroscience, 15, 395–415. https://doi.org/10.3758/s13415
-015-0334-y, PubMed: 25673005

Westbrook, A., Kester, D., & Braver, T. S. (2013). What is the
subjective cost of cognitive effort? Load, trait, and aging
effects revealed by economic preference. PLoS One, 8,
e68210. https://doi.org/10.1371/journal.pone.0068210,
PubMed: 23894295

White, C. N., Ratcliff, R., & Starns, J. J. (2011). Diffusion models

of the flanker task: Discrete versus gradual attentional
selection. Cognitive Psychology, 63, 210–238. https://doi.org
/10.1016/j.cogpsych.2011.08.001, PubMed: 21964663

Whiting, H. T. A. (1983). Human motor actions: Bernstein

Reassessed. Elsevier.

Wiecki, T. V., & Frank, M. J. (2013). A computational model of

inhibitory control in frontal cortex and basal ganglia.
Psychological Review, 120, 329–355. https://doi.org/10.1037
/a0031542, PubMed: 23586447

Wilken, P., & Ma, W. J. (2004). A detection theory account of
change detection. Journal of Vision, 4, 1120–1135. https://
doi.org/10.1167/4.12.11, PubMed: 15669916

Willcox, K. E., Ghattas, O., & Heimbach, P. (2021). The

imperative of physics-based modeling and inverse theory in
computational science. Nature Computational Science, 1,
166–168. https://doi.org/10.1038/s43588-021-00040-z
Wolpert, D. M., & Landy, M. S. (2012). Motor control is

decision-making. Current Opinion in Neurobiology, 22,
996–1003. https://doi.org/10.1016/j.conb.2012.05.003,
PubMed: 22647641

Yan, G., Vértes, P. E., Towlson, E. K., Chew, Y. L., Walker, D. S.,

Schafer, W. R., et al. (2017). Network control principles
predict neuron function in the Caenorhabditis elegans
connectome. Nature, 550, 519–523. https://doi.org/10.1038
/nature24056, PubMed: 29045391

Yee, D. M., & Braver, T. S. (2018). Interactions of motivation
and cognitive control. Current Opinion in Behavioral

590

Journal of Cognitive Neuroscience

Volume 34, Number 4

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

3
4
4
5
6
9
1
9
9
6
6
5
8

/
j

o
c
n
_
a
_
0
1
8
2
2
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Sciences, 19, 83–90. https://doi.org/10.1016/j.cobeha.2017.11
.009, PubMed: 30035206

Yee, D. M., Krug, M. K., Allen, A. Z., & Braver, T. S. (2016).

Humans integrate monetary and liquid incentives to motivate
cognitive task performance. Frontiers in Psychology, 6,
2037. https://doi.org/10.3389/fpsyg.2015.02037, PubMed:
26834668

Yeo, S. H., Franklin, D. W., & Wolpert, D. M. (2016). When
optimal feedback control is not enough: Feedforward
strategies are required for optimal control with active
sensing. PLoS Computational Biology, 12, e1005190.
https://doi.org/10.1371/journal.pcbi.1005190, PubMed:
27973566

Yeung, N., Botvinick, M. M., & Cohen, J. D. (2004). The neural

basis of error detection: Conflict monitoring and the
error-related negativity. Psychological Review, 111, 931–959.
https://doi.org/10.1037/0033-295X.111.4.931, PubMed:
15482068

Yoon, T., Jaleel, A., Ahmed, A. A., & Shadmehr, R. (2020).

Saccade vigor and the subjective economic value
of visual stimuli. Journal of Neurophysiology, 123,
2161–2172. https://doi.org/10.1152/jn.00700.2019,
PubMed: 32374201

Yu, A. J., Dayan, P., & Cohen, J. D. (2009). Dynamics of
attentional selection under conflict: toward a rational
Bayesian account. Journal of Experimental Psychology:
Human Perception and Performance, 35, 700–717. https://
doi.org/10.1037/a0013553, PubMed: 19485686

Zador, A. M. (2019). A critique of pure learning and what
artificial neural networks can learn from animal brains.
Nature Communications, 10, 3770. https://doi.org/10.1038
/s41467-019-11786-6, PubMed: 31434893

Zénon, A., Solopchuk, O., & Pezzulo, G. (2019). An

information-theoretic perspective on the costs of cognition.
Neuropsychologia, 123, 5–18. https://doi.org/10.1016/j
.neuropsychologia.2018.09.013, PubMed: 30268880

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

/

3
4
4
5
6
9
1
9
9
6
6
5
8

/
j

o
c
n
_
a
_
0
1
8
2
2
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Ritz, Leng, and Shenhav

591

Download pdf