Can Signal Delay be Functional?
Including Delay in Evolved
Robot Controllers
Abstract Engineers, control theorists, and neuroscientists often
view the delay imposed by finite signal propagation velocities as a
problem that needs to be compensated for or avoided. In this article,
we consider the alternative possibility that in some cases, signal delay
can be used functionally, that is, as an essential component of a
cognitive system. To investigate this idea, we evolve a minimal robot
controller to solve a basic stimulus-distinction task. The controller is
constrained so that the solution must utilize a delayed recurrent
signal. Different from previous evolutionary robotics studies, our
controller is modeled using delay differential equations, which (unlike
the ordinary differential equations of conventional continuous-time
recurrent neural networks) can accurately capture delays in signal
propagation. We analyze the evolved controller and its interaction
with its environment using classical dynamical systems techniques.
The analysis shows what kinds of invariant sets underlie the various
successful and unsuccessful performances of the robot, and what
kinds of bifurcations produce these invariant sets. In the second
phase of our analysis, we turn our attention to the parameter h, which
describes the amount of signal delay included in the model. We show
how the delay destabilizes certain attractors that would exist if there
were no delay and creates other stable attractors, resulting in an agent
that performs well at the target task.
Matthew Egbert*
University of Auckland
School of Computer Science
Te Ao Mārama–Centre for
Fundamental Inquiry
mde@matthewegbert.com
Andrew Keane
University of Auckland
Department of Mathematics
Claire Postlethwaite*
University of Auckland
Department of Mathematics
c.postlethwaite@auckland.ac.nz
Nelson Wong
University of Auckland
Department of Mathematics
Keywords
Evolutionary robotics, delay, delay
differential equations, lag, dynamical
systems, finite signal conduction velocity
1 Introduction
After NASAʼs New Horizons flew past Pluto, it turned its antenna toward Earth and began transmit-
ting the data that it had gathered. The distance between the probe and Earth was so vast that even
though the radio signals traveled at the speed of light, there was a five-hour delay between the start
of the transmission and the receipt of the first bit of data. Electrical signals moving through copper
wires travel almost as fast as those radio waves, moving at roughly 95% of the speed of light. When
the wire is short, as is the case in a robotʼs control circuitry, the delay between the emission of a
signal and its receipt at the other end of the wire is so brief that it can often be approximated as
nonexistent—an instantaneous transfer of information. The situation in your nervous system is dif-
ferent: The signals that travel along the neurons in your body and brain travel at a comparative snailʼs
* Corresponding authors.
© 2019 Massachusetts Institute of Technology
Artificial Life 25: 315–333 (2019) https://doi.org/10.1162/artl_a_00299
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
5
4
3
1
5
1
8
9
6
2
9
0
a
r
t
l
/
_
a
_
0
0
2
9
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
M. Egbert et al.
Can Signal Delay be Functional?
pace, with some types of signals taking three seconds to travel a mere meter, a difference of nine
orders of magnitude.
Slow signal propagation implies working with information that is old and sending instructions
that get to their destination too late, and robots can become remarkably difficult to control when
signal delay is significant. Even relatively short delays in signal propagation can be problematic when
the signals are involved in a feedback loop, and feedback loops are commonplace in both biological
organisms and robotics.1 For these reasons, roboticists tend to see delay as a problem to be over-
come. They embrace the biologically unrealistic conduction velocity of copper, and build robots out
of rigid materials that go quickly and precisely to where theyʼre told and stay where theyʼve been put.
By doing these things, these engineers can stay in control, working with accurate information and
simplified models of their systems that allow them to apply calculus and other mathematical formal-
isms, not just to predict or describe or control their creations, but even to prove that their systems
will perform as desired.
What, if anything, is lost in this approach? Certain modern efforts in robotics, psychology, and
philosophy of mind have returned to biology for inspiration, wondering how it is that floppy and
squishy biological bodies can be controlled with nervous tissues that are extremely complex, hetero-
geneous, asynchronous, and seemingly disordered. These researchers are interested not in how
brains are similar to computers, but instead in how they are different, and how by coming to un-
derstand these differences we might develop a better understanding of natural and artificial forms of
agency, cognition, and intelligence.
One emphasis in this perspective is upon the dynamical (i.e., time-related) differences between
brains and computers [4, 28]. Nervous tissues have their own autonomous and temporal dynamics.
For example, small neural circuits known as central pattern generators produce rhythmic or chaotic
activity, and the brainʼs various rhythms, with their own intrinsic natural frequencies, are famous (if
not well understood). Instead of viewing cognition as a kind of computation, the dynamical perspec-
tive sees it more generally as the result of an interaction between the autonomous dynamics of the
nervous tissues (and other parts of the body) and the world.
The classic, computationalist “brains are like computers” perspective can be made to fit within
this approach, but the emphasis is rather different. Computation generally is divided into three dis-
tinct and sequential phases: First data is acquired, then it is processed, and then an output is pro-
duced. Early efforts in AI such as Shakey the Robot [19] worked this way, and it remains common in
modern AI efforts such as image classification, where the data describing an image is entered, then
processed so as to produce an output that categorizes the image. In the computationalistʼs perspec-
tive, the important part of the system is how an AI can best build a model from the data and use that
model to make intelligent cognition-like decisions. The dynamical perspective is different. It blends
data input, processing, and output into one ongoing interaction, less easy to untangle, between
coupled dynamical systems. The important part in this perspective is the ongoing interaction be-
tween the brain, body, and world [2]. Instead of trying to figure out how a computer program could
generate the best possible internal representation of its environment, the question becomes (more
broadly) how to create a dynamical system that results in intelligent behavior when coupled to a
body in an environment [5]. In this latter approach, the use of manifest internal representations
becomes optional, and the set of possible brain architectures grows, as it is no longer committed
to notions of computation or internal model creation.
The field of evolutionary robotics has established itself as a popular method for investigating this
dynamical perspective. The method consists essentially of using an evolutionary algorithm to tune
the parameters of a dynamical system so that when it is coupled to the sensors and motors of a
robot, the system performs a target behavior. Once a solution is identified by the genetic algorithm,
the dynamics of the whole brain + body + environment system are analyzed to understand how the
desired behavior is accomplished. One of the reasons evolutionary robotics is appealing is that it
1 For example, sensors that indicate the position of a robot’s arm may be used to determine how next to move that arm, which
influences the state of the sensor, and so on.
316
Artificial Life Volume 25, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
5
4
3
1
5
1
8
9
6
2
9
0
a
r
t
l
/
_
a
_
0
0
2
9
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
M. Egbert et al.
Can Signal Delay be Functional?
allows us to generate examples of an interesting cognitive behavior that is not as complicated as
those found in nature and that thus might be more easily studied and understood. The hope is that
an understanding of these artificial systems will inform our understanding of their natural counter-
parts. A second appealing aspect of this approach is that it does not assume that the brain (i.e., the
neural network) is the locus of the systemʼs intelligence, but instead shows how intelligent behavior
can emerge from, and in a sense be fundamentally built out of, interaction between brains, bodies,
and the environments in which they are situated. A third appealing aspect of evolutionary robotics is
that studies often involve simulated bodies and environments, where the entire system is formulated
as a set of differential equations, allowing researchers to employ dynamical systems analysis on the
entire system (and/or parts of it), providing a formal language (attractors, separatrices, bifurcations,
etc.) that can be used to describe how the intelligent behavior takes place.
Some of the best examples of work in this area have examined cognitive abilities such as categorical
perception [3], associative learning [14], and behaviors performed by the nematode Caenorhabditis elegans
[15]. In these and most other evolutionary robotics investigations, the neural networks used are
continuous-time recurrent neural networks (CTRNNs) [1]. These are described by a set of coupled
ordinary differential equations (ODEs), where each equation describes the dynamics of a single node in
the network (conceptualized as a neuron or group of neurons) and takes the following form:
s dyi
dt
¼ −yi þ
X
(cid:3)
(cid:2)
wji r yj −b
j
þ I;
j
(1)
where yi is the excitation of node i; b and s are bias and time constants; r is the logistic sigmoidal
function; wji is the weight of the connection from node j to node i; and I is an input signal into the
node, such as the state of a light sensor on the robot.
CTRNNs are universal dynamical approximators [2], but this does not mean that all dynamical
systems are easily or simply approximated by CTRNNs. Of particular interest here, CTRNNs do not
easily capture the delayed influence that we discussed at the start of this article, where the change in
a variable is directly influenced by the state of a variable at some time in the past. To be clear, this is not
to say that CTRNNs are ahistorical or that the effects of a perturbation are all immediate. Conven-
tional CTRNNs are recurrent stateful systems, and signals can propagate through these networks in
historical ways (i.e., where the current state is the result of its history). But this is qualitatively dif-
ferent than delayed influence, and this difference is demonstrated by the fact that delayed systems
cannot in general be described by ODEs, requiring a different mathematical formulation known as
delayed differential equations (DDEs).
To elaborate, ODEs take the form _y(t ) = f(t, y(t )), where the state of the system at time t is the
finite vector y(t) and f is the evolution function. The simplest DDE systems extend ODEs to
include one or more historical terms, thus:
_y tð Þ ¼ f
ð
ð
t; y tð Þ; y t − s1
ð
Þ; y t −s2
Þ; …
Þ;
(2)
where each sj is a fixed parameter. Other forms of DDEs are possible, where for instance a delayed
derivative of a variable appears on the right-hand side, or where the amount of delay (the sj in the
equation above) is itself a dynamic variable, or depends on the current state of the system ( i.e., sj =
sj( y)). The inclusion of delay means that unlike an ODE, where the state is completely captured by
the finite vector y, the state of a DDE system includes the continuous history of the variables as far
back as the longest delay (s = maxj (sj )) in the system. The phase space of the DDE is thus no
longer finite, but is the infinite-dimensional space C ( [−s, 0]; ℝn ) × ℝ. Here, C ( [−s, 0]; ℝn ) is
the infinite-dimensional space of continuous functions over the interval [−s, 0], and s 2 ℝ represents
time. This infinite dimensionality often entails more complex dynamics and makes DDE systems more
difficult to investigate than ODEs. As a case in point: To specify an initial-value problem, one must
specify an initial history (a function segment) over the time interval [−s, 0]. An often-used choice of
Artificial Life Volume 25, Number 4
317
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
5
4
3
1
5
1
8
9
6
2
9
0
a
r
t
l
/
_
a
_
0
0
2
9
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
M. Egbert et al.
Can Signal Delay be Functional?
initial history in numerical solutions of DDEs (and the method employed below) is a constant value, but
this is only a one-dimensional subspace of the infinite-dimensional possible space of initial histories.
Despite the increase in complexity, provided certain constraints are met (e.g., the delay is not very
short), these delayed systems are often numerically tractable. In fact, many physical or biological
phenomena have been modeled using delayed differential equations. Examples include climate
models, where delay times model, for instance, the time taken for an oceanic wave to travel across
the Pacific Ocean [11], and lasers, where the delay times model the transit time for the light to cross
an optical cavity [18]. These models can often be simpler to analyze than large systems of ODEs or
PDEs, which would be required to otherwise incorporate the modeled delayed effect.
A number of tools exist for Python and Matlab designed for analyzing DDE systems. In the
work presented below, the Python package pydelay [10] was used for the numerical integration dur-
ing evolution, plotting, and analysis, and DDE-Biftool [8, 21], a Matlab package for continuation of
solutions to DDEs, was used as part of the bifurcation analysis.
The dynamical approach argues that we should take seriously the time-related properties of nervous
and other bodily tissues when trying to understand natural cognition, but a primary methodology used to
investigate these ideas (CTRNN-based evolutionary robotics) precludes a dynamical phenomenon known
to operate in nervous tissues: delayed influence due to the finite conduction velocity of nervous tissues.
Why have the effects of time delays been omitted so far in evolutionary robotics? The most
straightforward explanation is that ordinary differential equations are easier to analyze than delay
differential equations. But there may also be a conceptual hangover from the classical computation-
alist and engineering perspectives, where delay is generally seen as a problem to be overcome rather
than as a feature that might contribute to a functional cognitive system. This might cause researchers
to think, “Letʼs first figure out the easier case, where delay is omitted and from there move on to the
more difficult and more complicated case where delay is included.” “Furthermore,” they might ar-
gue, “delay may not play an important or interesting role in the generation of intelligent, adaptive
functional behaviors.” This perspective both props up and is itself supported by the common as-
sumption that neurons are as fast as they can possibly be given the other constraints that they must
satisfy. But in the following subsection (a lightly edited version of the review in [7]) we present
evidence from neuroscience research that argues against this dismissal of delay; evidence that sup-
ports the notion that delay plays an important role in the generation of functional intelligent behav-
ior. Some of this evidence is circumstantial, but in one case that we describe, the finite conduction
velocity of certain neurons in octopuses clearly plays an essential role in the production of one of its
coordinated activities. This evidence sets the scene for the remainder of the article, which presents
our evolutionary-robotics-based investigation of how delay can underlie good performance in a
simple cognitive task.
1.1 Delay in Natural and Artificial Systems
Delay is well recognized in neuroscience, where the finite conduction velocity of neurons is known
to cause delayed effects. In this context, as in engineering, delay is often characterized as a problem
to be compensated for or avoided. For instance, Swadlow and Waxman [24] and Chklovskii et al. [6]
suggest that evolution has acted to maximize conduction velocity to the point that any further in-
crease would come at too great a cost in terms of increased neuronal volume, additional metabolic
costs, reliability, and so on.
When nervous tissues are involved in reflexive responses to damage caused by cuts, heat, or the
like, it makes good sense that they would evolve to conduct as fast as they possibly can. But it is
interesting to note that neuronal conduction velocities vary over three orders of magnitude from 0.3
to 120 meters per second [24]. This wide range of conduction velocities is largely the result of two
ways that neurons vary: mylenation and axon diameter—thicker, mylenated axons conduct more
quickly than those that are thinner or less mylenated [29]. In the peripheral nervous system, neurons
associated with pain and temperature conduct more slowly than those associated with muscle acti-
vation, and within the central nervous system there exist a wide variety of conduction velocities with
318
Artificial Life Volume 25, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
5
4
3
1
5
1
8
9
6
2
9
0
a
r
t
l
/
_
a
_
0
0
2
9
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
M. Egbert et al.
Can Signal Delay be Functional?
“some axonal systems [that] are nearly exclusively fast-conducting (corticospinal, corticotectal, and
sensory thalamocortical axons), some [that] are exclusively slowly conducting, with impulses taking
many 10s of ms to reach their terminals (cortically projecting neurons of the locus coeruleus and
substantia nigra), and some [that] consist of a broad spectrum of axons (corpus callosum, some
corticocortical populations, corticothalamic neurons of layer 6)” [24].
The presence of different conduction velocities does not eliminate the possibility that neurons
have evolved to be as fast as possible. Constraints upon different neural systems may vary, in some
cases enabling the growth of faster, but more costly neurons. Such constraints, however, do not
explain another common feature of neural conduction velocities: They change over time. This
change takes place over both long and short time scales. To give examples: Callosal axons can
change progressively (1–2%/day) over periods of months [23], while bursts in neuron activity
can increase the conduction velocity for seconds afterwards [24].
In many cases, it remains unclear what the function is of this variation and how it is accom-
plished. What is clear is that such variation in conduction velocity will undoubtedly influence the
relative times at which signals arrive at particular neurons, which we would expect to seriously in-
fluence neural dynamics. As a case in point, Hebbian learning and other synaptic plasticity rules
describe how synapses change as a function of the timing of the firing of downstream and upstream
neurons [12, 13, 25]. These mechanisms rely upon signals arriving more or less synchronously,
which suggests very precise timing, as the voltage change produced when a synapse fires lasts only
2–4 ms. In some cases the conduction velocity of neurons appears to be tuned so as to synchronize
the arrival of stimuli along different-length axons. One such case occurs in peripheral cephalopod
nerve fibers. The conduction velocities of these fibers is structured so as to synchronize the arrival
time of stimuli that occur at different distances from the organismʼs central nervous systems [20, 24]
(essentially, the shorter fibers conduct at a lower velocity than the longer fibers). Other examples of
conduction velocity being modulated so as to synchronize the arrival have also been found—a num-
ber of examples can be found in [9].
Here we see the first clear examples of delay playing a functional role. The conduction velocity of
these neurons is not just something to be maximized, but should instead (or in addition) be tuned so
as to enable synchronous activation of the muscles along an octopusʼs arm.
The synchronization of signals along axons of different lengths is a straightforward example of
delay playing a functional role. It is almost an anti-temporal mechanism—a mechanism that erases
temporal differences between signals. This kind of mechanism is easy for us to understand—are
there also less easily understood functions that delay might perform? Evolutionary robotics, and
more broadly the field of artificial life, involves the creation of artificial systems that can be used
to aid in the investigation of complex biological phenomena. In the next section, we develop an
artificial system that uses delay in signal propagation in part of its sensorimotor feedback loop to
solve a simple discrimination task. By understanding how the artificial system takes advantage of
signal delay, we hope to expand our understanding of the ways that delay can be used as part of
sensorimotor feedback systems or cognitive architectures. Such knowledge would hopefully prove
useful in the study of delay in natural systems.
2 Model
To evaluate how delay can contribute to solving a task, we consider a minimal model (first presented
in [7]) that consists of a robot situated in a one-dimensional periodic environment of length 1. The
robotʼs “brain” is modeled as a single neuron with one recurrent, delayed, and weighted synaptic
connection. The velocity of the robot is determined by the following ODE:
dx
dt
¼
2
1 þ exp −4y
ð
Þ
− 1:0;
Artificial Life Volume 25, Number 4
(3)
319
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
5
4
3
1
5
1
8
9
6
2
9
0
a
r
t
l
/
_
a
_
0
0
2
9
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
M. Egbert et al.
Can Signal Delay be Functional?
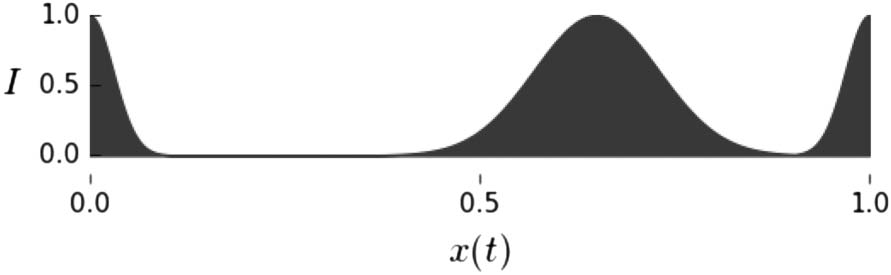
Figure 1. The state of the sensor (I) is a function of the current position of the robot, x(t). In each trial the location of the
peaks is different. This figure shows one example environment.
where x is the robotʼs position and y is the excitation of its neuron, which is governed by the
following DDE:
s dy tð Þ
dt
¼ − cy tð Þ3 þ ωy t − h
ð
Þ þ wI þ b:
(4)
In this equation, s is a time-scale parameter and −cy(t )3 formalizes a tendency of the neuron to
return to a base level of excitation (the cubic is included so that this tendency grows increasingly
strong as the system moves farther away from the base level of excitation, which prevents the sys-
tem from exploding). The second term describes the influence of the delayed recurrent connection,
where ω expresses the weight of the connection and h describes the delay associated with it. The
third term, wI, indicates a scaled sensory input (described below), and b is a constant bias term.
The input to the neuron (I ) is a function of the robotʼs current position:
I ¼ exp
(cid:5)
Þ2
(cid:4)
− x tð Þjpn
ð
0:0018
þ exp
(cid:4)
− x tð Þjpw
ð
0:0128
Þ2
(cid:5)
;
(5)
where A|B = min{|A − B|, |1.0 − |A − B||} represents the distance between points A and B (in
accordance with the minimum image convention followed for periodic boundary conditions). The
input (I ) has been plotted as a function of the robotʼs current position, x(t ), in Figure 1, with the
position of the narrow peak ( pn = 0) and the position of the wide peak ( pw = 0.75). Informally, one
can think of there being two hills in the agentʼs environment, of equal height, but with one narrower
and steeper than the other. In this description, I corresponds to the altitude of the robot.
A simple genetic algorithm was used to tune the parameters described by the Greek letters in the
equations above, so that after approximately 50s (s being the time unit), the robot is located near the
narrow peak. To evaluate the fitness of a parameterization, 120 initial-value problems of duration d 2
[45, 55] were solved numerically, where the initial starting position of the robot (x0) and the position
2 {0, 0.05, …, 1} and
of the wide peak ( pw ) were taken from the Cartesian product {(x0, pw )|x0
pw 2 {0.25, 0.35, …, 0.75}}. In all evaluations, the narrow-peak position is pn = 0. The excitation
preceding the trial was set to a constant value, yt≤0 = 0. Each of these 120 initial-value problems
were given a score, S = 0.5 + 0.5((cid:2)xt >d −10|pn ) − 0.5((cid:2)xt >d −10|pw ), which is higher when the average
distance of the robot during the last 10s of the trial ((cid:2)xt >d−10) is close to the narrow peak and far
away from the wide peak. The fitness is then given by f =
4), the product of all of the 120
scores after they have been scaled to lie within [0.75, 1].
4 + 3
S( S
Q
3 Analysis
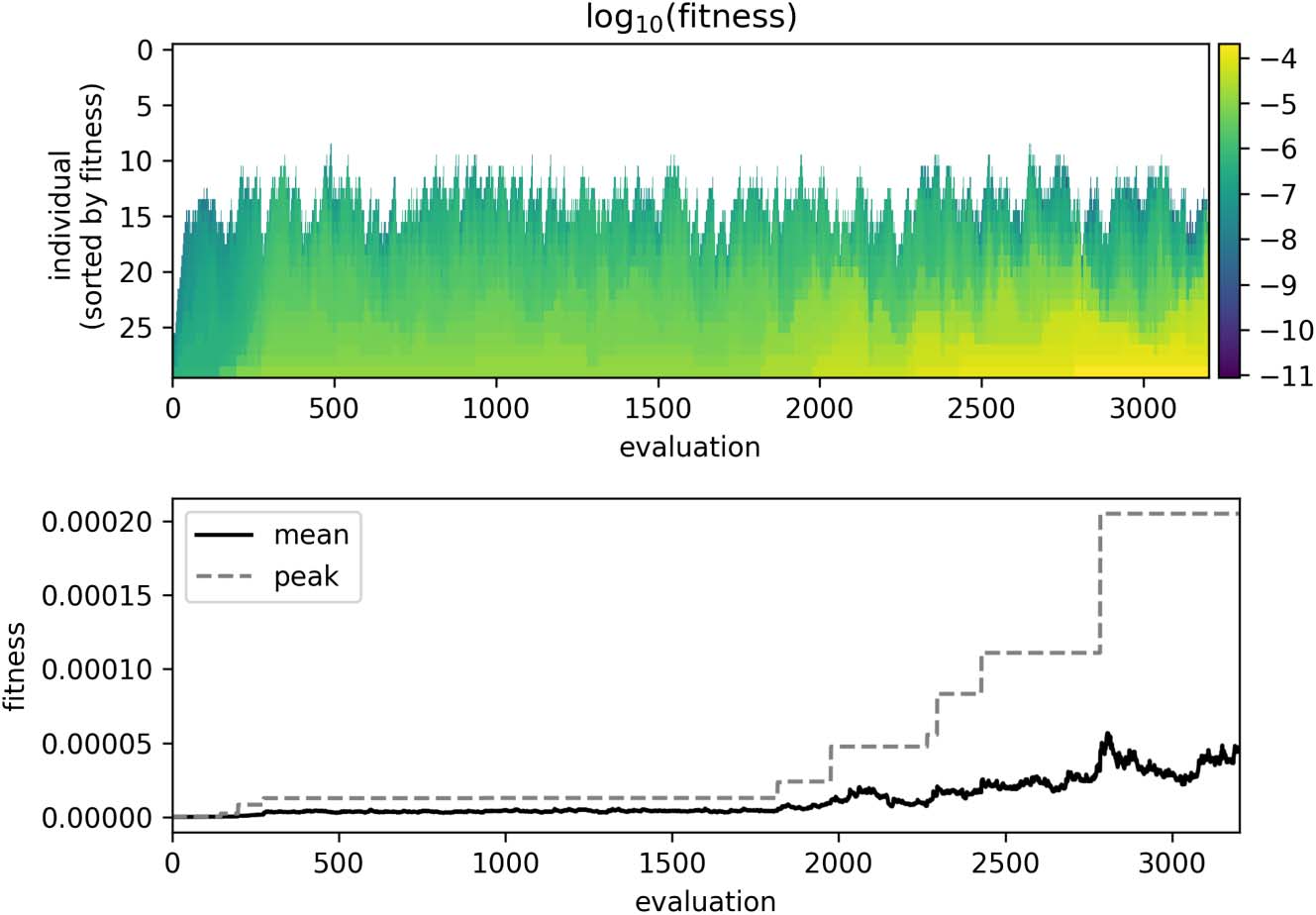
We performed 32 evolutionary runs, each lasting approximately 3500 tournaments. The parameters
of the best-performing individual can be found in Table 1, and the evolutionary change in pop-
ulation fitness in the run that produced this agent is presented in Figure 2. The remainder of this
section presents our analysis of this system.
320
Artificial Life Volume 25, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
5
4
3
1
5
1
8
9
6
2
9
0
a
r
t
l
/
_
a
_
0
0
2
9
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
M. Egbert et al.
Can Signal Delay be Functional?
Table 1. Evolved parameters. Parameters specified to three digits of precision. Simulation was conducted with an
absolute tolerance of 10−6 and a relative tolerance of 10−3.
s:
w:
ω:
0.563
1.794
−1.297
c:
b:
h:
9.595
−0.272
1.140
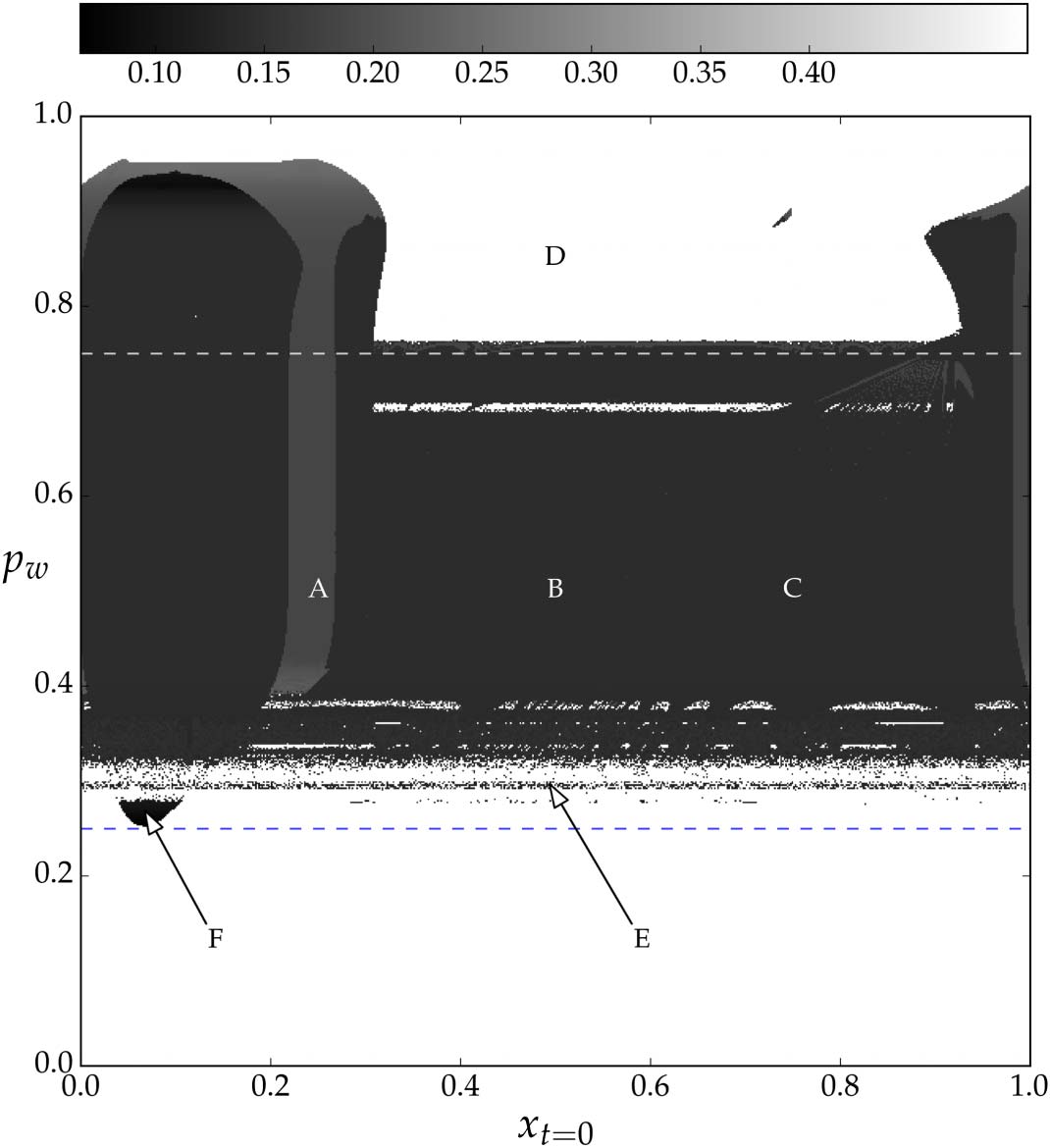
An overall summary of performance can be seen in Figure 3, which indicates the maximum dis-
tance between the robot and the narrow peak in the last 10s of a 100s trial for different initial robot
starting positions (horizontal axis) and different placements of the wide peak (vertical axis). The
controller performs well in the majority of initial conditions, especially those initial conditions that
were evaluated during the evolution, where pw 2 [0.25, 0.75].
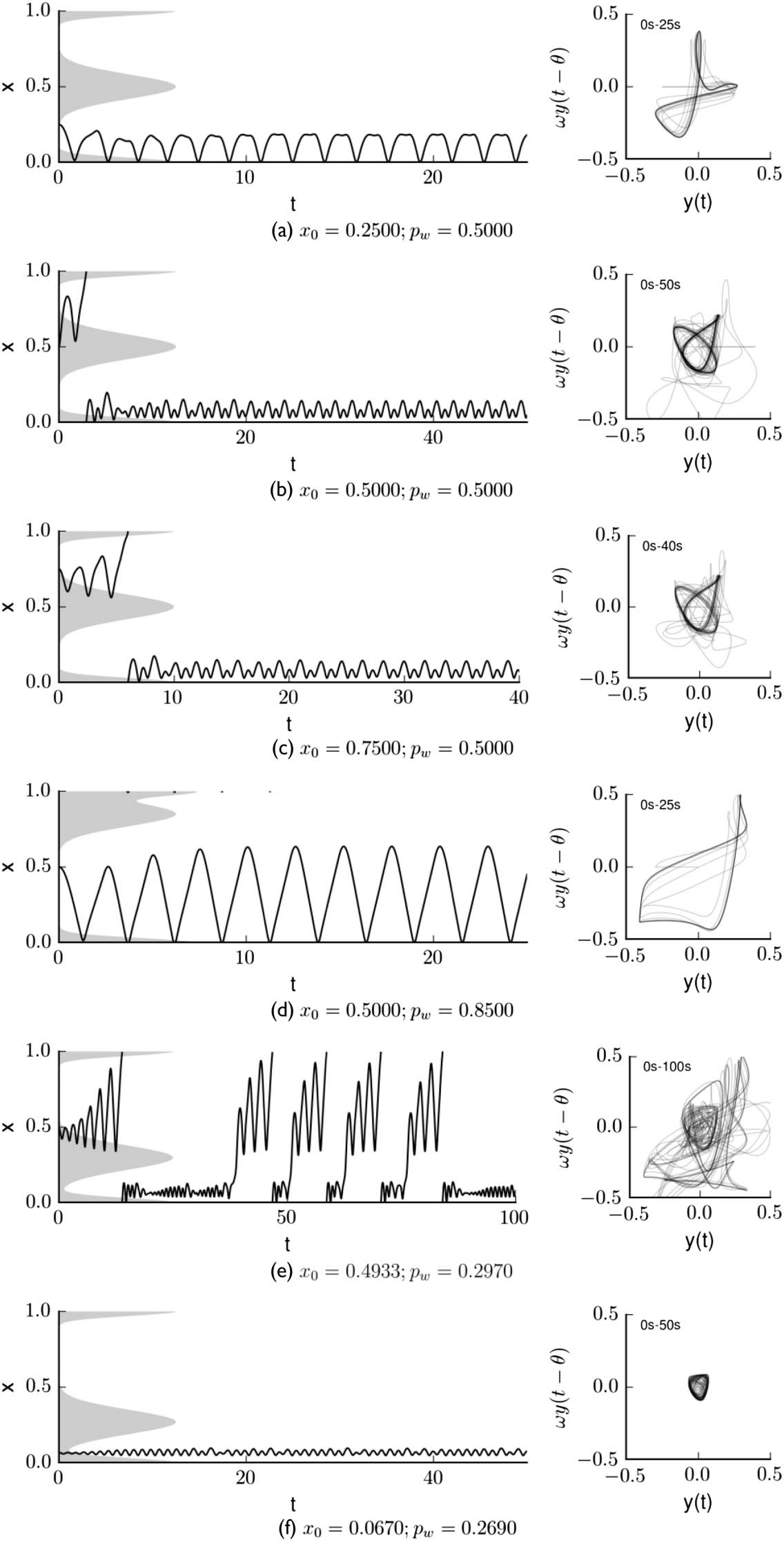
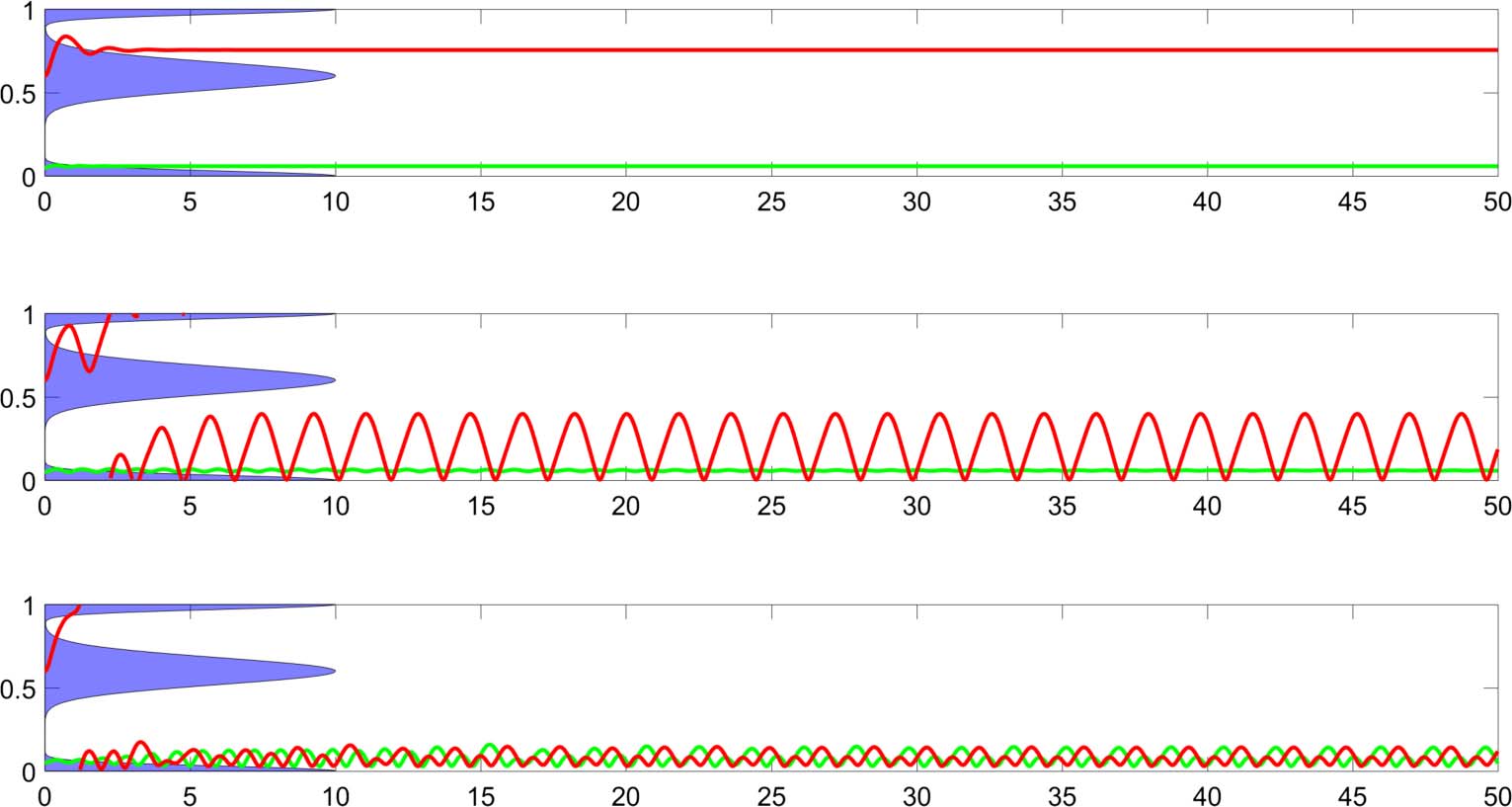
The plots in Figure 4 show trajectories taken in various successful and unsuccessful trials, pro-
viding a first glimpse of some of the qualitative variety demonstrated in this system. The only things
differing in these trials are the placement of the distractor wide peak and the initial position of the
robot. These conditions are indicated above each set of plots. The plots on the left show how the
robotʼs position changes over time, and those on the right indicate the state of the robotʼs neuron
excitation ( y) plotted against its weighted delayed value, ωy(t − h ) (the second term in the RHS of
Equation 4). Note that the trajectories in the right column appear to self-intersect only because the
phase space is infinite-dimensional and the figure presents a two-dimensional projection of that
space.
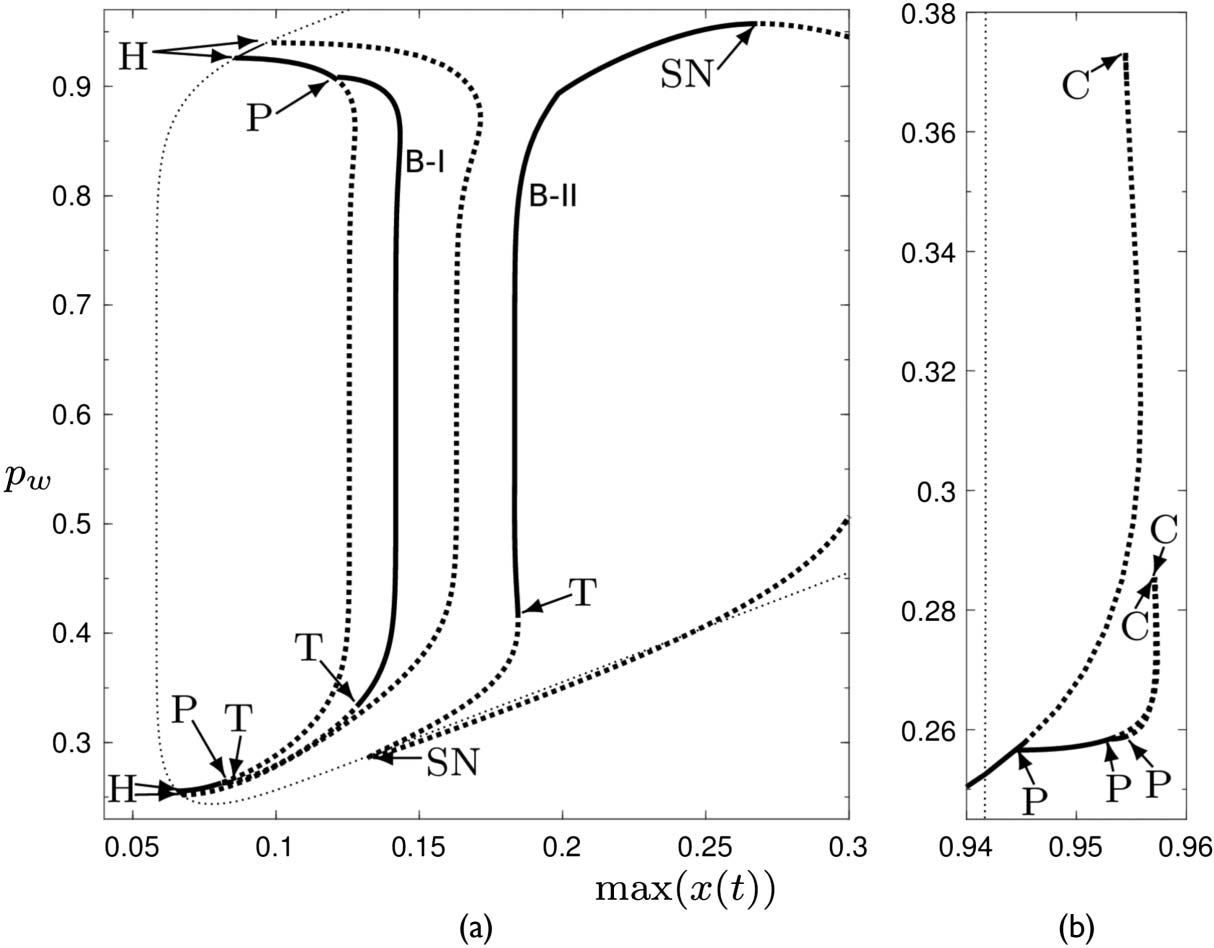
The diverse dynamics seen in Figure 4 can be explained in terms of the attractors that exist for
different values of the parameter pw . We find the attractors by conducting a bifurcation analysis,
using the continuation software DDE-Biftool, to numerically continue (i.e., track) branches of equi-
libria and periodic orbits while varying pw. In contrast to simulations, this reveals both stable and
unstable solutions. The software can calculate the stability properties of the solutions and identify
different types of bifurcations. Understanding how the different solution types are organized in
Figure 2. Progression of fitness evaluations during evolution. The top plot shows the distribution of fitness across the
population as it evolved. In this figure, each column indicates the fitness of the population (sorted by fitness).
Artificial Life Volume 25, Number 4
321
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
5
4
3
1
5
1
8
9
6
2
9
0
a
r
t
l
/
_
a
_
0
0
2
9
9
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
M. Egbert et al.
Can Signal Delay be Functional?
Figure 3. Initial condition survey. Values in this image indicate the maximum distance of the agent from the narrow peak
in the last 10s of 100s simulation 100, max(x90