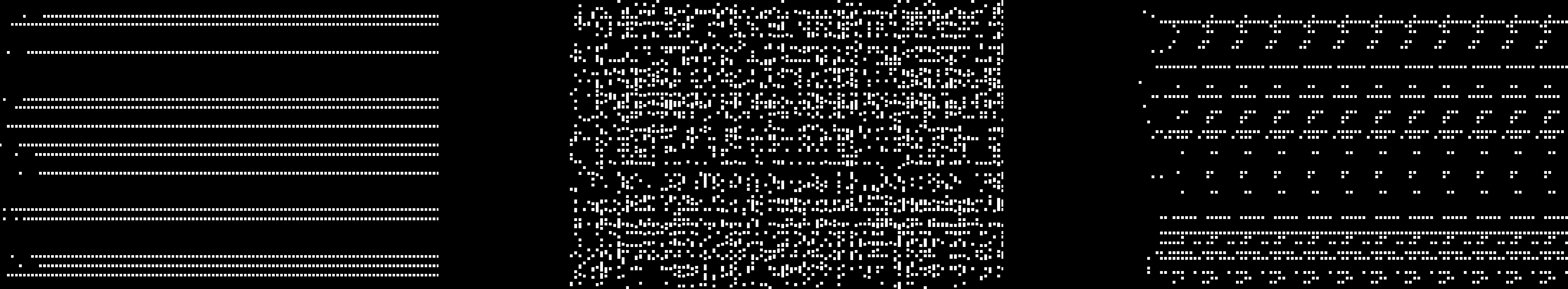Artificial Gene Regulatory
Networks—A Review
In nature, gene regulatory networks are a key mediator
Abstract
between the information stored in the DNA of living organisms
(their genotype) and the structural and behavioral expression this
finds in their bodies, surviving in the world (their phenotype).
They integrate environmental signals, steer development, buffer
stochasticity, and allow evolution to proceed. In engineering,
modeling and implementations of artificial gene regulatory
networks have been an expanding field of research and
development over the past few decades. This review discusses
the concept of gene regulation, describes the current state of
the art in gene regulatory networks, including modeling and
simulation, and reviews their use in artificial evolutionary settings.
We provide evidence for the benefits of this concept in natural
and the engineering domains.
Sylvain Cussat-Blanc*
University of Toulouse
IRIT – CNRS – UMR5505
sylvain.cussat-blanc@ut-capitole.fr
Kyle Harrington
University of Idaho
Computational and Physical
Systems Group
Virtual Technology and Design
kharrington@uidaho.edu
Wolfgang Banzhaf
Michigan State University
BEACON Center for the Study of
Evolution in Action
Department of Computer Science
and Engineering
banzhafw@msu.edu
Keywords
Gene regulatory networks, evolutionary
algorithms, morphogenesis, control
dynamics, neuromodulation
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1 Introduction
Ever since the seminal 1975 article by King and Wilson [88], the biological community has been aware
that there is more to the genome than nucleic acid sequences translated into amino acid sequences.
However, the apparatus for transcription and translation of DNA information into protein function
has been studied since the 1950s, leading to the “Central Dogma” of Molecular Biology [25, 26]. By
that time Schroedinger in his famous 1944 work on life [128] had already alluded to the possibility of
an executing role (i.e., more than an information template role) for his “aperiodic crystal” at the
foundation of life. With the development of the operon model in 1961, Jacob and Monod [71] firmly
established the idea of regulation in our understanding of the life-organizing functions of DNA.
The central challenge that gene regulatory networks address is the translation between spatial
patterns of information, as provided by different types of macromolecules such as oligomers and
polymers—that is, the configuration of matter in space—and the dynamical processes in time neces-
sarily underlying any type of behavior. With regulation, the study of objects in biology is enlarged by
the study of processes. Spatial arrangements of objects (the material of life) are replaced by temporal
* Corresponding author.
© 2019 Massachusetts Institute of Technology
Artificial Life 24: 296–328 (2018) doi:10.1162/artl_a_00267
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
arrangements of processes as the core principles of living systems. While space remains an important
aspect of life (natural life without spatial embodiment is unthinkable), it is the dynamic aspects of
entities that play the dominant role. With regulation, the notion of time, dynamics, transients, and
steady states becomes of utmost importance in our understanding of organisms.
The simplest self-contained genetic regulatory element (or motif ) is a feedback loop. A com-
pletely new phenomenon (oscillations in time) can emerge in such an otherwise dull behavioral
landscape; for as soon as there is a mixture of positive and negative feedback connections in the
loop, the tiniest amount of noise can cause oscillations to emerge, bringing about a new behavior of
this system with an intrinsic time scale. Thus, it is to be expected that larger gene regulatory
networks, consisting of many genes, contain a variety of network motifs with both positive and
negative feedback connections [111]. Between these motifs, weaker connections can accumulate
causes and distribute effects.
Additionally, we can immediately see that many different behaviors should be expected to emerge
from such networks. While the details of these behaviors are the result of possibly delicate network
interactions and therefore difficult to predict, the fact that networks allow a richness of behaviors to
emerge is important for adaptivity of living organisms. For example, the growth of the body of an
organism and the behavior of its parts in different phases of its development do not obey strict rules
directly able to generate these elements. Rather, we have to assume a set of processes that obey their
own internal logic of regulation and develop in phases, influenced by the environment and
controlled by different subsets of the genetic regulatory network. In multicellular organisms,
there are many precursor cell phases until a final cell state is reached, and development can be seen
as a process of gradual approach to the state of maturity of a body, rather than its immediate
instantiation.
We can finally see that noise and stochastic events are likely playing a key role in promoting
variety [122]. First off, regulation is sensitive to single molecule activities, bringing about the
possibility of stochastic quantum effects influencing the outcome. However, the Brownian motion
underlying diffusion that we are used to averaging out from underlying cause-effect relationships
brings another type of stochasticity into these systems, providing additional time scales that corre-
spond to the spatial organization of the organisms and their environment.
This article is aimed at providing a brief overview of the phenomena and models of gene regu-
latory networks and delving into the applicability of these concepts in man-made artefacts. Thus,
Section 2 discusses some of the most important phenomena in biological gene regulatory systems,
and Section 3 provides an overview of the modeling efforts that have been made over the years to
describe and understand these phenomena. Section 4 is then dedicated to a discussion of the internal
dynamics of artificial regulatory network models, and Section 5 reviews the current applications of
these approaches. The article concludes in Section 6 with a discussion of the future of artificial gene
regulatory network research.
2 Gene Regulation in Nature
Regulation in general refers to the control of the flow of certain quantities by signals from another
entity. If we consider the multitude of flows that have to be arranged for a living organism to func-
tion properly, it becomes clear that the first target of gene regulation has to be the control of met-
abolic fluxes. From the intake of nutrients to the expulsion of waste, the energy household of cells
needs to be organized and controlled. Enzymes and their expression levels are the material patterns
that have to be arranged in time to make this possible.
However, this is just the most basic regulatory need of organisms. The sophisticated weaving
together of behaviors to produce the life cycle of a cell or organism, or to allow it to survive under
adverse circumstances, stand to gain as much from regulation as energy fluxes do [57].
All of this leads to the conclusion that the control of gene expression levels, which in turn control
the interaction of the organism with its environment, is the most basic function one can imagine for
Artificial Life Volume 24, Number 4
297
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
a gene. But in addition, gene products can interact with other genes and their products, thus forming
a network that allows intrinsic time scales and autonomy (self-regulation) to emerge [32]. The
following subsections discuss these topics more in detail.
2.1 Gene Expression, Cell Function, and Differentiation
The behavior and type of a cell are characterized by its gene expression patterns. This is because the
gene expression patterns describe the components of the cell that have been constructed. By
construction we mean the transcription of DNA into RNA, and its possible subsequent translation
into protein. RNA expression levels therefore can be used to identify specific cell types. One speaks
of the fingerprint of a cell, revealed in its expression pattern [2, 53] through RNA sequencing
techniques.
However, as always in biology, individual cells vary a lot. Therefore, while the characterization of
cell types is a convenient way of clustering cell behaviors into classes, there is nevertheless substantial
variation between different cells even in the same cell class (or type). Historically, this was difficult to
examine in the laboratory, since most techniques could only be used to analyze cell mixtures. With
the advent of single-cell transcriptomics, however, the situation has changed and differences down
to the individual cell level can be resolved [45, 136].
It is also becoming clear that not only do individual cells of the same type have differences in
their expression profile, but cells vary their expression levels depending on circumstances and age
[87]. No wonder: Cells are open systems, best characterized at any time as in steady state or in
transition. This confirms the intuitive ideas first proposed by Waddington in 1957 [144], as depicted
in Figure 1.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
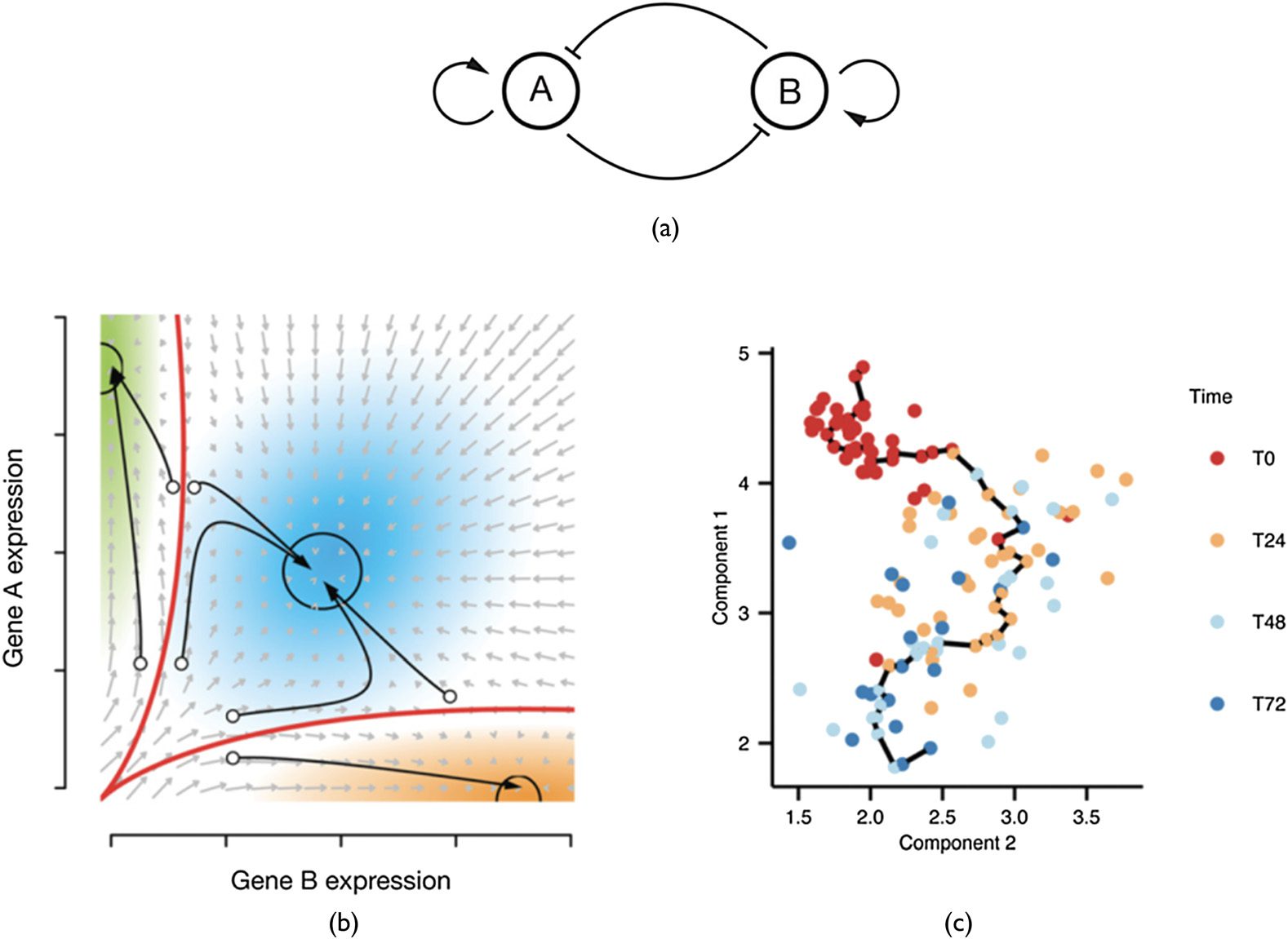
Figure 1. The trajectory of a cell, after [136]. (a) Idealized regulatory network with two genes inhibiting each other. (b) Three
resulting distinct stable states (attractors) with their attractor basins indicated by arrows. (c) Gene expression levels of the
components over time can be considered as trajectories through expression space. Time quantified in arbitrary units and
indicated in colors. © 2015 Trapnell; Published by Cold Spring Harbor Laboratory Press under a CC BY-NC 4.0 license. [136].
298
Artificial Life Volume 24, Number 4
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
2.2 Genomic and Protein Aspects
Gene expression happens through a process of gene activation and subsequent generation of protein
and/or RNA products. The activation and control of gene expression is the focus of genetic reg-
ulation, where multiple mechanisms influence the rate of gene expression. While the machinery of
gene expression is complex and varies across organisms, some features are consistent. Gene expres-
sion requires the recruitment of a RNA polymerase to a geneʼs region of the DNA sequence, which
will then transcribe the gene into mRNA by forming RNA polymers from nucleotides. Promoter
sequences are used to initiate transcription of a gene by recruiting the polymerase. Transcription
factors modulate the rate of expression by inhibiting or enhancing the rate of transcription of genes.
Transcription factors are themselves the products of gene expression, serving as a source of feed-
back for the regulation of genetic networks. While the transcription of genes yields mRNA, in the
case of protein products an additional step of translation must be performed to produce a protein
product from a given mRNA molecule. However, mRNA itself can spawn other types of RNA
(iRNA, etc.), which take on their own regulatory or interaction role in the processes leading to
protein production.
As mentioned above, the products of gene expression are protein and RNA molecules, some of
which are transcription factors while others directly contribute to the metabolism and behavior of
cells. The behavior and function of a cell are the result of the gene expression that has contributed to
the current state of the cell. That is to say, the size, membrane composition, and structure of a cell
are defined by, among other things, the gene products that reside within the cell. As a consequence,
the state and function of a cell are determined by the composition of the cell, which is the result of
gene expression, degradation, and so on. Readers interested in these mechanisms can find an
extended review in [67].
2.3 Significance of GRNs in Cellular Physiology
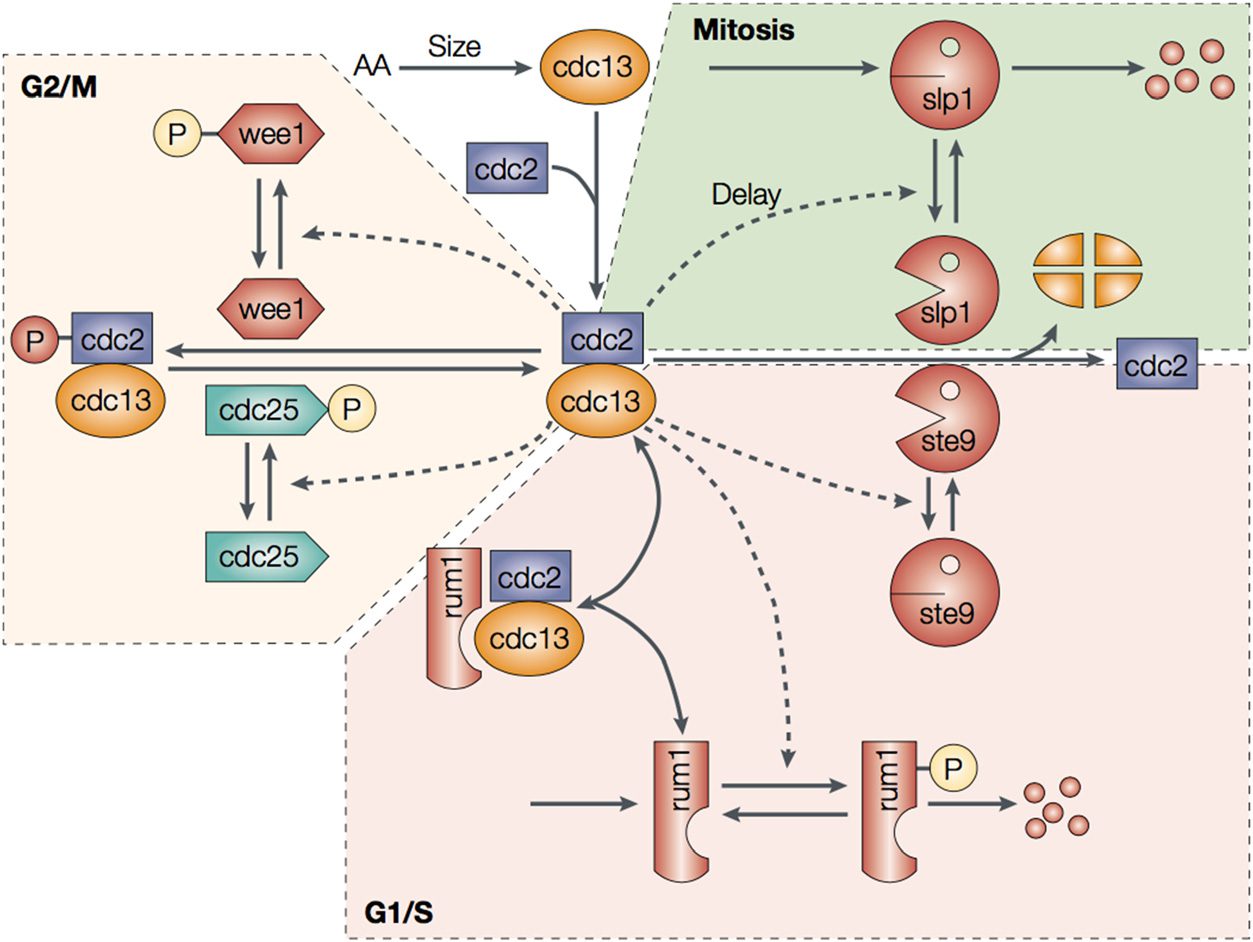
The cell cycle is fundamental to biological organisms, as it governs the process of cell division and
therefore of replication. One of the classic model organisms for studying the cell cycle is fission
yeast. Regulation of the cell cycle in fission yeast has been well characterized [140]. The cell cycle
is controlled by three modules of its gene regulatory network that operate at different phases of the
cycle: G1/S, G2/M, and mitosis. In the G1/S phase, cells grow and replicate DNA. There are four
key control elements involved in this process (see Figure 2): cdc2 and cdc13, which are two proteins
shared throughout all three phases of the cell cycle, pair to form complexes that activate key path-
ways; and ste9 and rum1, which maintain bottlenecks via degradation and inhibition of cdc13 and
the cdc2-cdc13 complex. In turn, cdc2-cdc13 acts to reduce the activity of ste9 and rum1. As the
cycle proceeds through G2/M and mitosis, other players take part in the control of the cell cycle
through similar feedback mechanisms. In the cell cycle of yeast and mammalian cells, a number of
these interactions involve the explicit control of transcription factors, such as e2f and p53 [46],
where p53 is well known for its role as a tumor suppressor [120]. The interested reader will find
ample literature to review on the intricate details of the regulation of the cell cycle, starting from
[140]. The key feature that we hope to convey to the reader is that the dynamic feedback between
the activity of regulatory elements (as manifested by their concentration and localization within the
cell) allows the gene regulatory network to transition between different modes of activity. In the case
of fission yeast, this interplay manifests itself as distinct modules that operate at different phases of
the cell cycle.
2.4 Significance of GRNs in Developmental Biology
We now consider the evolutionarily conserved Delta-Notch signaling pathway present in metazoans
[3]. Delta-Notch signaling was initially studied because of its role in neurogenesis (growth of the
nervous system). The intercellular signaling of this system exhibits a lateral inhibition dynamic, where
a cell that commits to neural differentiation inhibits its neighbors from doing so. This increases the
sparseness of cells that commit to a neural fate. The Delta-Notch signaling pathway is regulated by a
Artificial Life Volume 24, Number 4
299
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
Figure 2. Cell cycle network of fission yeast from [140].
suite of achaete-scute genes that produce transcription factors that both control and are themselves
controlled by lateral inhibition [98]. Again, we see that feedback loops are involved in the control of
genetically regulated networks. The Delta-Notch pathway not only is evolutionarily conserved, but
plays many roles beyond neurogenesis in development, such as embryonic segmentation in Drosophila
[99], wing patterning in Drosophila [70], and blood vessel formation in mice [12] and zebrafish [142].
While the Delta-Notch pathway is a well-studied case, genetic regulation is fundamental through-
out developmental biology. The patterning of positional cues in Drosophila development, such as
Bcd, a key determinant of anterior-posterior polarity, is regulated by multiple transcription factor
binding sites with various binding strengths [114]. Eight key transcription factors are involved in
providing positional information during Drosophila development (including Bcd), and recent work
has shown that it is possible to predict the resultant patterning by modeling the interactions of reg-
ulatory elements on the basis of the underlying regulatory sequences [129]. The role of transcription
factors in the patterning of Drosophila even transcends the individual organism itself, where maternal
inclusion of localized transcription factors in the embryo expedites segmental patterning.
2.5 Significance of GRNs in Evolution
The two primary forms of genetic regulation that have evolved are transcription factors and micro-
RNAs (miRNAs). While transcription factors are proteins with variable binding affinities to partic-
ular regulatory sequences, miRNAs are simpler. They are short RNA sequences that can bind to
regulatory sequences and repress gene products [9]. Both miRNAs and transcription factors are
known to be highly conserved throughout evolution; however, a key difference between the two
regulatory mechanisms is their binding affinity. Transcription factors can generally bind to a range
of sequence patterns with variable binding strength, while miRNAs have almost exact binding spec-
ificity due to nucleotide complementarity. As a result, the rates of evolution of miRNA (slow due to
exact binding) and transcription factors (fast due to reduced specificity) have been predicted to differ
by approximately 4 orders of magnitude [21].
A fascinating evolutionary mechanism that has played a significant role in the evolution of GRNs
is the occurrence of transposable elements. Transposable elements (TEs) are sequences that move
300
Artificial Life Volume 24, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
and replicate throughout the genome, and are commonly described as genomic parasites [17]. TEs
have been clearly shown to be beneficial to hosts in some cases, such as the upregulation of factors
leading to pesticide resistance [23]. The dynamics of replicating TEs contributes to the establishment
of sequence motifs that have related sequence patterns. TEs serve as a source of novel and deriv-
ative genetic material that can be recycled into regulatory sequences and binding elements [50]. The
molecular mechanisms underlying the evolution of gene regulatory networks are diverse, ranging
from proteins to RNA-binding elements, and effectively form a genomic ecosystem.
2.6 Significance of GRNs in Epigenetics
The expression of genes relies not only upon genetic sequences, but also upon the accessibility of
the genes. Epigenetics is concerned with heritable traits that are not encoded within the sequence
of the genome. Most forms of epigenetics involve altering the physical structure of the sequence,
such as wrapping DNA around histones and methylation of nucleotides. Chromatin is a collection of
DNA, RNA, and protein that condenses the structure of these molecules, which allows for
increased stability, density, and organization. Within chromatin, DNA is wrapped around histones
to form nucleosomes. The accessibility of DNA sequences in these nucleosomes has a significant
influence on the expression of genes located within the nucleosome [62]. Furthermore, modification
of histones further alters gene expression to the extent that gene expression can be predicted from
the known modifications [82].
DNA methylation is another form of epigenetic regulation that involves structural modification
of nucleotides in the sequence itself. One of the key mechanisms of DNA methylation is physically
blocking enhancer and/or promoter regions, thus altering the expression of a gene [80]. Methylation
itself is the addition of one carbon with three hydrogens to an existing structure; in the case of DNA
methylation the existing structures are nucleotides. This additional structure is sufficient to modify
binding sites to the point of prohibiting interactions with regular binders of a regulatory sequence.
Methylation can be induced by environmental factors [72]. The methylated state of a DNA sequence
can be transmitted through multiple cell divisions, as well as across generations [56]. In this way the
evolution of GRNs can be affected by epigenetic modifications, which may be derived from envi-
ronmental factors that were experienced as a result of genetically regulated behaviors.
In summary, gene regulation has emerged as a key player in translating the information provided
by an organismʼs inherited DNA into the structure (via growth and development) and behavior of
that organism. Time scales range from seconds (in the case of the regulation of metabolism in neu-
rons [102]) to thousands of years (in the case of evolutionary processes). Gene regulatory networks
have been compared to the compilers of computer languages that translate code into behavior of the
underlying machine. However, there is much more to the computational modeling of gene regula-
tion, and this brings us to our next topic.
3 Computational Gene Regulatory Networks
Artificial gene regulatory networks are a complex example of systems biology [89]. Comprehensive
models of the gene regulatory process would require a large range of complexity, from molecular
dynamics to morphogenetic coupling, making complete and exact models prohibitively expensive.
As a result, GRN models generally focus on particular aspects of genetic regulation; for example, the
Gillespie algorithm [58] attempts to capture the stochasticity of genetic regulation without modeling
stochastic molecular dynamics. While we primarily focus on computational and evolutionary models
of gene regulatory networks in this review, we will also touch on mathematical studies and analyses
of the dynamics of GRNs.
3.1 Biological Models
There are a number of approaches that are used for modeling gene regulatory networks [16, 35].
These approaches include differential equations, stochastic simulations, Petri nets, flux balance
Artificial Life Volume 24, Number 4
301
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
analysis, graphical models, and more. A number of reviews modeling genetic regulation have been
written, many of which primarily focus on biological modeling [81]. We begin our discussion of
biological models by introducing the steps of gene regulation and how they are modeled, but
ultimately focus on how these models are subjected to evolution.
Gene regulatory networks are commonly modeled with Hill kinetics, which models the cooper-
ative binding of two or more proteins to promoters, enhancers, silencers, and other regulatory re-
gions of a gene. These kinetics are formulated using reaction rules that describe the rates of
association/dissociation of a gene and regulatory proteins to form a complex as functions of the
cooperativity of multiple binding proteins. The complexes formed by the binding of regulatory pro-
teins are used in conjunction with additional reactions to either directly produce protein products or,
more realistically, model the transcription of mRNA, which is later translated into protein products.
While the initial approaches to analyzing gene regulatory networks focused on deterministic
models, such as ordinary-differential-equation-based mean-field approximations, the use of stochas-
tic models has been increasing in recent research. Heightened attention to stochastic gene expression
has been strongly supported by observations of stochasticity-driven differences between cells with
identical genetic background, and by single-molecule experiments [49, 123, 124]. The cornerstone of
stochastic simulation of chemical kinetics is the Gillespie algorithm [58] and its extensions for
adaptive time steps [59].
It is well known that GRNs are stochastic systems where noise can have a significant effect on
resulting cellular behaviors [49]. The occurrence of noise is generally discussed in conjunction with
the common observation of small numbers of some molecular species acting in a GRN, where fluc-
tuations in the concentration of such species can lead to significant changes in network dynamics.
However, biological mechanisms have evolved not only to control and eliminate such effects of
molecular noise, but also to amplify and exploit it [116]. In a more detailed study of noise cascading
through a GRN, the authors of [115] show that even in networks that do not involve small con-
centrations of some molecular species it is possible for noise to have significant effects due to global
network modulation and upstream effects.
Biophysical models focus on capturing aspects of genetic regulation that extend beyond the
scope of simulating chemical kinetics. This has been heavily utilized in computational models of
Drosophila segmentation [69, 104], neural development of zebrafish [150], and vascular biology
[12], where GRNs tuned to biological networks interact with cytoskeletal and chemotactic behaviors
to predict the temporal behavior of vascular dynamics [94]. The same model has also been utilized to
show how the bistable dynamics of a GRN can be used to regulate pattern formation for healthy
angiogenesis [11, 141].
3.2 Dynamics and Analysis
Mathematical studies of genetic regulation have been driven primarily by the dynamical systems
community. As a result, the majority of analytical work has focused on the stability and attractor
dynamics of gene regulatory networks. It is important to address these mathematical foundations of
gene regulatory dynamics, as they inform researchers of the capabilities of GRN representations. For
example, in the Delta-Notch signaling system discussed in Section 2.4 the previous belief had been
that cells would decide on an environmental preference and then move to favor that preference.
Through a dynamical systems study focusing on the bistable nature of a genetically regulated model,
it was shown that the decisions for motion and for location preference operate in parallel [11]. This
conclusion was reached by evaluating the dynamic stability of cellular behaviors as a function of
cellular phenotype and environmental inputs to the cellʼs gene regulatory network. Similarly, the
synthetic biology community has begun to use models of GRNs to develop hypotheses for exper-
imental validation [67].
The theoretical biology community has been studying the dynamics of GRNs for many years,
beginning with Boolean networks, where genes are defined by on-off states [83, 85]. Mathematical
methods have extended this class of models with tools for the analytical discovery of steady states,
302
Artificial Life Volume 24, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
attractors that the GRNs will tend towards without external stimuli [110]. Such analysis led to the
prediction that evolution will drive single-cell genetic network dynamics toward greater dynamic
stability [84]. In a detailed analysis of a Boolean GRN derived from the biology of the cell cycle,
Deritei et al. [37] show that this ubiquitous GRN is inherently modular with a switch that triggers the
completion of the cell cycle after passing a restriction point. These analytical and dynamical studies
of Boolean GRNs have led to concrete predictions that can be experimentally verified.
Information-theoretic approaches to the analysis of gene regulatory networks often draw upon
techniques from statistical mechanics that describe the state space for molecular arrangements, and
allow one to relate distributions of biophysical states to information in terms of the entropic cost of
molecular configurations. Tkačik et al. [135] use information theory to show that, given biologically
observed noise levels in gene expression, it is possible for genes to encode more than one bit of
information (“on” or “off ” ), a point that becomes particularly pertinent when addressing the rep-
resentation of GRNs. Through a combined experimental and analytical study Cheong et al. [22]
show how negative feedback of signaling and transcription can suppress noise, thus facilitating com-
munication between collections of cells. By drawing upon methodologies from information theory,
these studies have shown how cells can regulate the otherwise confounding noise of the biological
environment to store and transmit meaningful information.
3.3 Representations
Boolean models of GRNs capture the on-off nature of genes, switching when concentration of
proteins crosses threshold values that represent the transition between on and off states [83]. Early
studies of this Boolean model investigate the stability and oscillatory dynamics of random Boolean
GRNs [85], and later studies show support for the validity of the Boolean GRN model [131].
Arguments for the use of Boolean GRN models often draw upon the quantity of information avail-
able from biological experiments, suggesting that the amount of information made available by gene
expression profiling is only adequate for training Boolean GRN models [95]. Furthermore, the
simplicity of Boolean models makes it easier to map out the state space of a GRN, thus facilitating
analysis.
Petri nets (PNs) are a formalism commonly used in modeling distributed systems [118]. PNs are
graphical models that use nodes and edges to represent places and transitions, where places can
contain variable numbers of tokens. When used to model GRNs, places represent molecules (pro-
teins, mRNA, complexes), transitions represent possible reactions (excitation and inhibition, includ-
ing reversibility), and tokens represent concentrations. There is a wide range of PN models that
incorporate features such as stochasticity; as a result, PNs have direct relations to Boolean GRNs
and the Gillespie algorithm. Matsuno et al. [108] present an application of PNs to modeling E-phage
gene expression that readily incorporates key relevant molecular species and transition types. The
interested reader is directed to [19] for an extensive review of PNs for biochemical models.
To study the network structure effects of a GRN, Banzhaf (2003) developed in [5] a model that
uses a sequence of bits to represent a genome, with mobile protein elements that bind according to
bit patterns, similar to transcriptional footprints [14]. The features of the model are demonstrated
by showing a wide variety of dynamic characteristics, the effects of genetic perturbations, and the
evolution of the model with an evolutionary strategy. This bit-string matching representation was
simplified to an integer-based representation [30], which has been shown to be effective in numer-
ous applications discussed in Section 5.
3.4 Evolution
Although we have focused our discussion on features of gene regulatory networks that are being
modeled and analytical approaches to modeling, one of the most powerful approaches to under-
standing gene regulatory networks is the use of evolutionary methods. Gene regulatory networks
are evolved reaction networks, and the existence of a naturally observed GRN is prefaced by an
process that transformed the GRN into its observed state. An understanding of the evolvability
Artificial Life Volume 24, Number 4
303
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
Figure 3. Graphical representation of gene activation with Reilʼs artificial regulatory network. Each line represents one gene
activation level: Dot means that the gene is activated; white space means it is disabled. Reprinted from Reil, T. (1999). [117].
of GRNs serves as a basis for understanding why particular gene regulatory mechanisms have
emerged.
The ability to evolve the simplified bit-string-based GRN model of [5] to fit multiple mathemat-
ical expressions was explored in [93], where oscillatory, sigmoid, and exponential decay functions
were successfully matched.
In a stochastic simulation model using the Gillespie algorithm, Leier et al. [96] show that a com-
prehensive GRN model with first-order and second-order reactions and homodimer formations can
be evolved to obtain oscillatory dynamics. A particular challenge of this evolutionary problem is
compensating for the noisy dynamics, which can shift the period and amplitude of observed oscil-
lations; this leads to a need for evaluating each simulation trajectory and aggregating over the results,
as opposed to observations.
It has been shown that in Boolean GRNs evolving under a gene duplication/divergence model,
functionality can be well conserved even under extreme evolutionary conditions [1]. Long term evo-
lution of biologically plausible GRNs using agent-based models shows the emergence of evolution-
ary sensors—genes that sense evolutionary pressures—that allow for rapid evolutionary change in
response to environmental variation [27]. In a related study it was shown that under variations in
fitness, such as environmental variation, the ability of GRNs to adapt to new environments can be
enhanced [44]. In Section 5 we discuss a number of evolutionary methods and genetic representa-
tions that have been used in applications of GRNs.
4 Internal Dynamics of GRNs
Before applying gene regulation to agent control, researchers focused on understanding internal
dynamics of gene regulation. In 1999, Reil was one of the first to present a biologically plausible
model used in an artificial life context [117]. In his work, he randomly generated a set of variable-size
binary genomes in which each gene started with the particular sequence 0101, named the promoter.
Promoters exist in living systems: A very specific sequence of nucleotides, the TATA1 box, is
known to identify a geneʼs starting position. As presented in Figure 3, Reil used a simple visualiza-
tion technique to observe gene activation and inhibition over time with randomly generated net-
works. He obtained several activation patterns such as stable, chaotic, or oscillatory patterns. Reil
also pointed out that after random genome deteriorations, the system was able to rebuild the same
pattern through an oscillation period.
The artificial gene regulatory network proposed in [5] is strongly inspired by real gene regulation.
In this work, the genome is coded as a set of 32-bit integers (in other words, a bit string). Each gene
of a genome starts with a promoter coded by the sequence “XYZ01010101,” where XYZ is any bit
−8 in a bit
sequence to complete a 32-bit integer. The combination “01010101” has a probability of 2
string equivalent to a TATA box from a real DNA sequence. The gene coded after a promoter has a
1 T = thymine and A = adenine.
304
Artificial Life Volume 24, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
Figure 4. Examples of protein concentration dynamics obtained with the artificial gene regulatory network of [5].
Reprinted from Banzhaf, (2003).
Figure 5. Example of heterochronic control in gene regulatory networks: By mutating one bit of a protein, the regulation
dynamics is only slightly changed. Reprinted from Banzhaf, (2003). [5].
fixed size of five integers (160 bits, each integer having 32 bits). Upstream from the promoter, two
integers code for an enhancing site and for an inhibiting site, thus regulating gene expression activity.
In this model, all DNA transcription mechanisms are omitted to focus on gene regulation dynamics
itself. This kind of genome can produce various activation dynamics, as presented in Figure 4.
Randomly generated genomes were used in these experiments.
A key property observed in these networks is heterochrony [6]. As depicted by Figure 5, small
changes in the network structure or concentration only imply small changes in network dynamics.
This behavior is crucial when the network is evolved for artificial life applications: Heterochrony
smooths the fitness landscape, making it more evolvable. This model has also been used in
[18] to analyze the inner temporal dynamics of gene regulatory networks using pole-balancing
and signal-processing benchmarks and its capacity to reproduce input signals within a delayed
time frame.
Pictures and videos have been employed to visualize the dynamics of GRNs and observe the
complexity of the behaviors generated. In research by Cussat-Blanc and Pollack (2012), the
GRN, cloned to every pixel of the picture, computed the RGB components of each pixel of
the picture [31]. Each GRN used the pixel coordinates (input proteins) to compute the color com-
ponent (output proteins). GRNs were evolved using interactive evolution: Users were tasked with
selecting the most beautiful images, and GRNs were mutated and recombined based on this selec-
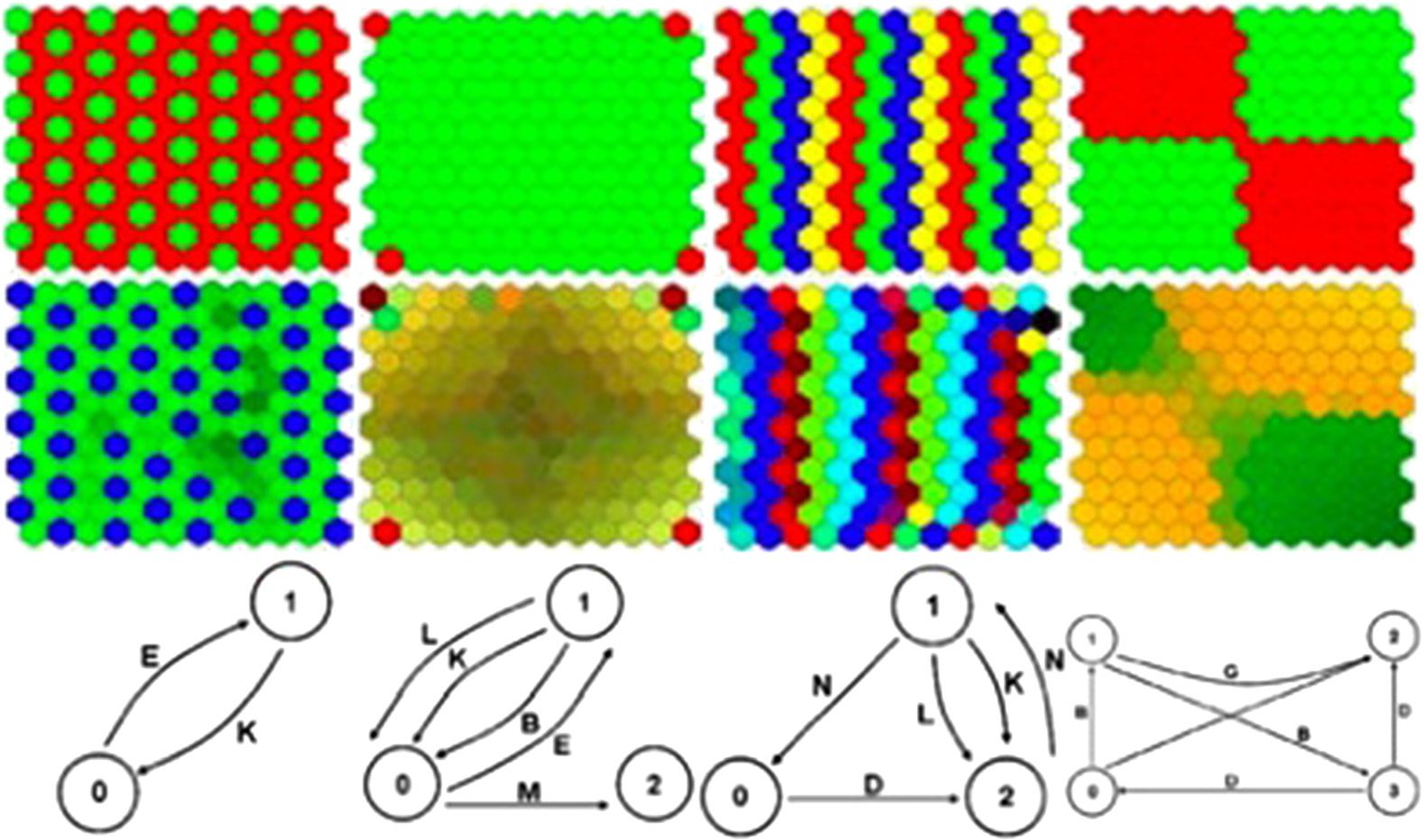
tion mechanism. Some of the generated pictures, representing snapshots of the network dynamics,
are presented in Figure 6, while Figure 7 presents screenshots of videos.2 This work allowed the
exploration of possible behavioral structures generated by gene regulatory networks. For example, in
picture (b) of Figure 6, repetitive patterns can be observed with some modifications. That shows the
2 More examples and the software to generate pictures and videos can be found online: http://www.irit.fr/∼Sylvain.Cussat-Blanc/
ColorfulRegulation/index_en.php.
Artificial Life Volume 24, Number 4
305
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
Figure 6. Examples of pictures generated with a gene regulatory network. Image from [31]. Reprinted from Cussat-Blanc,
S., & Pollack, J. (2012).
capacity of gene regulatory networks to produce modular patterns. Pictures (b–d) also show the ability
of the GRN to produce both smooth and abrupt variations, as codified here in color transitions.
Finally, picture (e) depicts the GRNʼs capacity to produce extremely complex behavior, with very
different outputs for close input values. More details about properties highlighted in these pictures
can be found in [31].
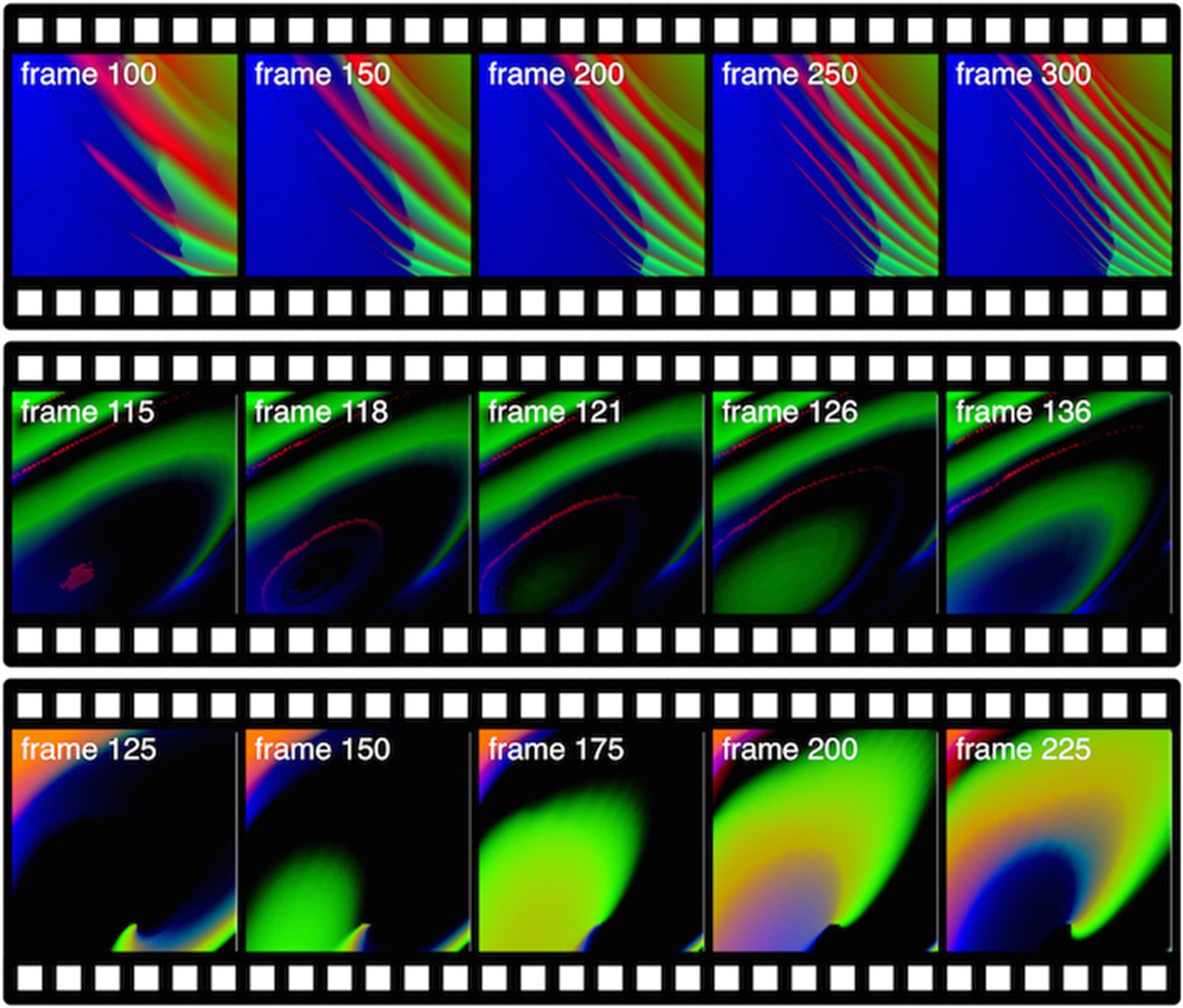
Videos can capture the temporal aspect of gene regulation. As presented in Figure 7, oscillatory
behaviors can be easily visualized. Other videos show chaotic and steady-state behaviors, which are
the two other main behaviors of gene regulatory networks in addition to oscillations.
The computability of gene regulatory networks has been been studied extensively over the past
years. A full review of computability in GRNs can be found in [103]. Artificial GRNs have also been
used to investigate a number of questions in the context of evolution. Using Reilʼs DNA-like model,
Rohlf and Winkler studied the evolvability of GRNs and showed a strong relationship between their
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7. Examples of videos generated with a gene regulatory network.
306
Artificial Life Volume 24, Number 4
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
robustness against noise and their robustness against genetic material deletions due to the evolutionary
process [119], which are key properties in real-world applications. Schramm et al. investigated the role of
redundancy in artificial gene regulatory networks [127], showing that genetic redundancy can enhance
evolvability up to a point, after which greater redundancy becomes deleterious. Genetic networks were
able to evolve modular genotypes when subjected to dynamic fitness landscapes [100]. Recent work
has shown that evolved GRNs can achieve greater hierarchical modularity than neural networks [107].
Numerous studies remain to be performed regarding the evolution of GRNs, and some of those
can be approached from the perspective of artificial life, which is our next topic.
5 Gene Regulatory Networks and Artificial Life
As in nature, the role of (artificial) gene regulatory networks in artificial life and evolutionary com-
puting systems is manifold. In general terms, GRNs promote our understanding and implementa-
tion of the genotype-phenotype map in those systems, notably the nonlinearity between those
representations. In this section, we shall discuss some of the most important applications.
The phenomena produced by GRNs can be classified into (i) interactions between genes through
their expression products, (ii) spatial patterning of expression, and (iii) temporal structuring of ex-
pression. There is a close connection between those phenomena and applications, where spatial
structuring enables embryogenesis and design, temporal structuring allows for development and dy-
namic control of agents, and interaction among genes (and their products) allows for neuromodula-
tion and indirect encoding of various structures.
This section presents the main application work using artificial gene regulatory networks. Their use
started in artificial embryogenesis, described in Section 5.1, which aims at reproducing the devel-
opment of multicellular organisms. These models are perfect theoretical frameworks to develop, im-
prove, and understand gene regulation in a setup comparable to or inspired by biological examples.
Following this period, researchers started to use these models to solve real-world problems. Due to
their intrinsic ability to control behaviors of cells, artificial gene regulatory networks were first trans-
ferred to agent-based systems, discussed in Section 5.2 in more detail. In this case artificial GRNs are
used to produce agent behavior by using an agentʼs sensors as input proteins to an AGRN and using
an agentʼs actuators to be controlled by the AGRNʼs output proteins. First real-world applications were
taken from evolutionary robotics. Successful applications in virtual agents then led to more recent work
using AGRNs as neuromodulators in neural-network-based learning systems (see Section 5.3) or as
indirect encoders for neural networks or genetic programming trees (see Section 5.4).
5.1 Artificial GRNs in Artificial Embryogenesis
The previous section provided an explanation of the dynamics and properties emerging from gene
regulation. In this section we discuss applications of artificial gene regulatory networks. One of the
most obvious ones is artificial embryogenesis. Artificial embryogenesis draws inspiration from bio-
logical mechanisms involved in the growth of a living organism, from the initial single-cell zygote to
a whole mature organism. In this process, gene regulation is a central mechanism that controls a
wide range of interactions between the cells and their micro environment. Therefore, artificial gene
regulatory networks have frequently been used in artificial embryogenesis. They have been employed
to control cells, their cell cycle regulation (when to divide), their migration strategy, and their
specialization (color or function). This section provides an overview of existing models of embryo-
genesis that are based on artificial gene regulatory networks.
5.1.1 Background on Pattern Generation
Turing produced the first work on modeling morphogenetic development in 1952. He suggested
that a reaction-diffusion model could capture cell development from a chemical point of view
[138]. In his model, a set of differential equations governs the dynamics of morphogen concentra-
tions in an environment. Even though this seminal work did not include any discrete form of cells or
Artificial Life Volume 24, Number 4
307
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
Figure 8. Example of a dappled system obtained with Turingʼs reaction-diffusion system. Image reprinted from Turing
[138].
genetic regulation, Turingʼs model has served as the basis for most of the past and current models of
artificial embryogenesis and patterning [109].
Turingʼs model was mainly used to describe lower-level phenomena such as chemical substance
diffusion in the environment (see Figure 8). Bio-inspired mechanisms have been used to add cells
interacting with this environment, mainly for the diffusion of morphogens produced by organisms,
as in [5, 30, 47, 52, 75, 90, 92, 117, 133].
At the cellular level, cellular automata, proposed by von Neumann in the 1950s, are considered a
key contribution. At the time, von Neumann was working on self-replicating machines. He stated
the hypothesis that a system able to manipulate elementary components could be capable of con-
structing a copy of itself. Due to the technical complexity of building such a machine, he imagined a
universal automaton able to pick up and to assemble arbitrary components. During the same period
of time, the mathematician Ulam was working on recursively defined objects. Recursive objects are
cells in an infinite matrix, which can have two states: active or passive. Cells evolve over time fol-
lowing rules based on their neighborhood. Ulam suggested von Neumann use this kind of environ-
ment to avoid technical problems with his universal constructors. Von Neumann was successful
with a proof for such a constructor, and in 1966 the theory of von Neumannʼs self-replicating
machines, implemented as cellular automata, was posthumously published [143].
In 1970, Conway defined the famous game-of-Life cellular automaton [55], in which cells have
only two states (dead or alive) and two simple rules using a Moore neighborhood. Depending on the
initial environment configuration (repartition of living and dead cells at the beginning of the simu-
lation), several shapes emerged and were able to move, to reproduce, or to merge (see Figure 9). In
1999, de Garis encoded the transition rules of a cellular automaton into a genome evolved with a
genetic algorithm [34]. He observed that, using a von Neumann neighborhood, only 14 states were
possible for a cell in a 2D environment at each time step. This allowed a simple coding of the rules in
a genome, enabling evolution with a standard genetic algorithm. With this setup, de Garis was able
to produce several simple shapes (e.g., triangles and squares) or more complex shapes (e.g., letters,
turtles, and snowmen), as illustrated in Figure 10.
Figure 9. Example of shape produced by Conwayʼs game of Life. Shown here is a glider, able to move in its environment
across the grid, time step after time step. Courtesy of Gthcommon, https://commons.wikimedia.org/wiki/File:SimuCA.gif.
308
Artificial Life Volume 24, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
Figure 10. Examples of shapes produced with cellular automata. Reprinted from de Garis, H. (1999). [34].
5.1.2 Simulating Cell Differentiation
Whereas the previous work was focused on developing shapes, cell differentiation is one of the key
aspects for simulating artificial embryogenesis. In a natural developmental process, cell differentia-
tion dictates the specialization of a cell type. Starting from a unique cell, it allows the creation of
various cell types, such as neurons, muscle cells and liver cells, which will have very different func-
tions in organisms. In 1969, Kauffman introduced random Boolean networks (RBNs) [85] to sim-
ulate this feature. The interpretation of this regulatory network was simple: Each node controls a
gene, and the node state represents the gene activity (activated or inhibited). The genome transcrip-
tion produced the cellʼs final function.
In 1994, Dellaert and Beer proposed a developmental model using this network [36]. In his
model, a Boolean network represented an artificial regulatory network for cell differentiation
control Boolean networks were at the time (and still are) classical approaches in computational
biology to simulate gene regulatory networks of real living systems. In this work, the authors used
a 2D matrix that allowed simple cell divisions: The initial organism was made of only one cell that
was covering the entire grid; during the first division, the grid was split into two, horizontally or
vertically (the division plane orientation was controlled by the genome), and the new cell could
differentiate. The aim was to visually observe cell differentiation by a modification of the cell color
and explore the capacity of Boolean networks to produce various shapes with the help of genetic
algorithm. Dellaert obtained several shapes, such as presented in Figure 11.
In 1997, Eggenberger Hotz explored asymmetric division and division plan control with a model
able to produce a simple creature with a user-defined shape. This creature was able to move in the
environment, actuated by an artificial gene regulatory network [47]. With this design, the model was
able to simulate natural mechanisms of asymmetric cell division [68]. This kind of division allowed
Figure 11. Illustration of Dellaertʼs developmental model. A random Boolean network was used as an artificial gene
regulatory network in order to produce user-defined shapes and cell differentiations (colors). Reprinted from Dellaert,
F., & Beer, R. (1994). [36].
Artificial Life Volume 24, Number 4
309
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
cell differentiation by producing daughter cells with different proteins. The regulatory network
produced a specific protein used to adjust the orientation of the cell division plane and the division
timing. The regulatory network also controlled cell physical dynamics and its own gene regulation,
which corresponded to adhesion coefficients between cells. Cells periodically emitted molecules that
modified adhesion parameters between cells and the environment. With this setup, Eggenberger
Hotz produced a growing creature with a T shape. It was able to move in the environment by mod-
ifying its morphology [48].
In 2004, Bentley used fractal AGRNs, in which genes are expressed as fractal protein subsets of
the Mandelbrot set, with the proteins interacting through a fractal chemistry, to show that this struc-
ture can produce complex growing shapes with a very small amount of genetic material [13]. The
system demonstrated the capacity of GRNs—when associated with a developmental process—to
compress the data necessary to generate shapes and behaviors. Krohn studied the dynamics involved
in this process and applied a fractal AGRN to classical control problems such as mountain car
driving and pole balancing [91].
In 2005, Flann et al. used a graph implementation of an artificial regulatory network to develop
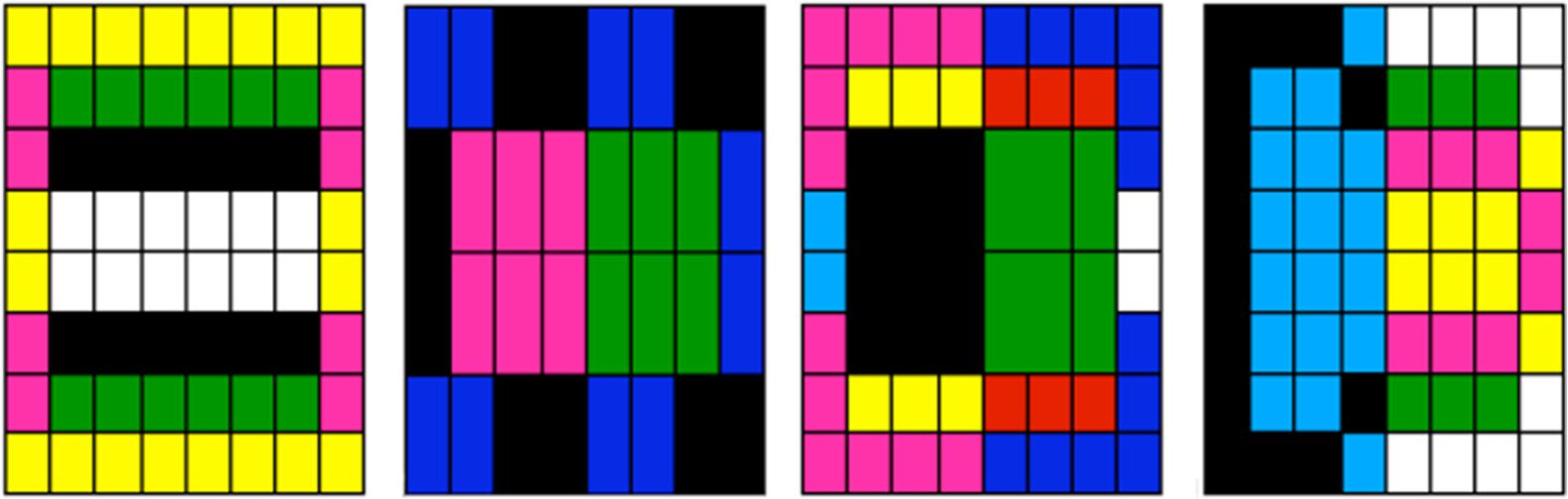
pictures composed of differentiated cells (illustrated by Figure 12 [51]). Similarly to Dellaert, the aim
was to explore differentiation mechanisms in cells, but here with an increased level of complexity in
terms of shapes produced. In the graph in the lowest panel of the figure, each node represents the
expression level of a distinct protein, and each edge represents the interaction between proteins. In
this model, cell coloration (see upper panels of the figure) revealed the cellular differentiation.
Whereas simple shapes were easily produced with this kind of network, the use of multiple networks
in parallel was necessary to produce more complex shapes. In this case, protein concentration levels
had to be combined to determine the global gene activity.
Chavoya and Duthen developed an artificial gene regulatory network model in 2008 to solve the
French flag problem [20]. It was inspired by the model in [5]. The goal was to explore the coevo-
lution of shape and color (i.e., cell differentiation), both controlled by the same AGRN. Illustrative
results are presented in Figure 13. The authors used a cellular automaton to generate the shape,
Figure 12. Examples of shapes produced by Flannʼs regulation network. The first line of images shows desired patterns; the
second line shows the best obtained patterns after genetic evolution. The lowest panel shows the corresponding regulation
networks. Reprinted from Flann, N., Hu, J., Bansal, M., Patel, V., & Podgorski, G. (2005). [51].
310
Artificial Life Volume 24, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
Figure 13. Chavoya and Duthenʼs French flag and its protein concentration curves. This problem puts to the test the cell
differentiation capacities of developmental models. Here, differentiation is indicated by color shifts. Reprinted from
Chavoya, A., & Duthen, Y. (2008). [20].
based on de Garisʼ work, where rules were enabled or disabled by the artificial gene regulatory
network. Moreover, morphogen gradients, pre-positioned in the environment, gave localization
information to cells and generated further information for the artificial gene regulatory network.
The authors obtained perfectly scalable flags and furthermore several shapes such as multicolor
squares, triangles, and polyhedrons (3D).
Also in 2008, Knabe et al. proposed a model close to Chavoyaʼs. Their approach employed an
artificial regulatory network in which Chavoyaʼs cellular automaton was replaced by a cellular growth
system [90] using cellular Potts models [61], which were en vogue at that time in biological simu-
lations of cell proliferation. Cells acted in a pixel matrix. They grew by absorbing free pixels and
following a development axis controlled by an artificial gene regulatory network. The latter mech-
anism indicated its growth direction to the cell with its height/width ratio and its current shape.
When a cell was composed of 24 pixels, it started its mitosis by dividing according to an axis or-
thogonal to the last division axis. This division axis could also be modified by the regulatory net-
work. Here, two morphogens were used to determine cell color. However, in this model,
morphogens were not pre-positioned, but produced by the cells. Therefore, cells had to regulate
the morphogen production to obtain the appropriate concentration according to the final shape
given by the user. Knabe et al. tested his model with the French flag problem and used a genetic
algorithm with a fitness function that evaluates the difference d between the tested individual T
and the expected pattern Ri of size w × h :
(cid:3)
(cid:1)
d Ri ; T
¼ 1
wh
Xh−1
x¼0
(cid:6)
(cid:4)
Xh−1
(cid:6)
(cid:6)
sgn R i
xy
y¼0
(cid:5)
(cid:6)
(cid:6)
(cid:6):
− Txy
The results obtained were close to the expected pattern in 75% of cases.
Artificial Life Volume 24, Number 4
311
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
In his study of complex systems, Doursat used a model based on gene expression levels to
simulate the developmental process of complex shapes [41, 42]. An artificial regulatory network
composed of three layers was used:
(cid:129) A first layer used positioning data given by morphogens.
(cid:129) A central layer contained boundary nodes, which allowed horizontal and vertical
segmentation of the embryo. Gene regulation was also managed with this layer, thanks to
the production of activator and inhibitor proteins.
(cid:129) A third layer determined the regulatory protein production thanks to the concentrations of
activator and inhibitor proteins produced by the second layer.
This regulatory network depended on a developmental model built with two simple rules:
1. Cell division allowed each cell of the organism to divide with a particular probability,
2.
Intercellular adhesion forces, based on a mass and spring, kept the global consistency of
the organism.
In this developmental system, a 2D environment contained two kinds of morphogens that allow
cell positioning. Starting from an initial cell cluster, Doursat produced an organism in which several
differentiated areas appeared due to cell differentiation. Many shapes were produced, such as the
salamander presented in Figure 14a. In the salamander morphology, several differentiated areas,
highlighted with different cell colors, are observable: legs, abdomen (divided into six pieces), and
head (divided into ten pieces). Doursat was able to manipulate an organismʼs morphology simply by
modifying experimental parameters (especially weights and functions implicated in the regulatory
network). The same initial cell cluster was used with different parameters to produce an eight-legged
organism at the end of the developmental process (Figure 14b).
Also in 2008, Joachimczak and Wróbel proposed stepping up to the third dimension and into
continuous space, substantially increasing the complexity of the models [75]. Every cell had an
Figure 14. Developed shapes and an overview of corresponding artificial gene regulatory network of Doursatʼs devel-
opmental model. Images reprinted from Doursat [41].
312
Artificial Life Volume 24, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
Figure 15. Example of organisms produced with Joachimczakʼs model: On the left, a dumbbell; on the right, a 3D French
flag. Reprinted from Joachimczak, M., & Wróbel, B. (2008). [75]. And Joachimczak, M., & Wróbel, B. (2009). [76].
artificial gene regulatory network and regulated a quantity of morphogens produced on its own.
These morphogens guided the development of daughter cells in the environment. Cells had various
sizes, depending on their stage of evolution. The organismʼs genome was one of the strengths of this
model because of its capacity for complexification over generations. It was composed of a list of
genetic elements where each element has a specific type with different functions during the genome
parsing stage. The main types were:
(cid:129) Regulatory elements: (also called promoters), regulated the activation of genes.
(cid:129) Genes: products or substrates produced by the cell that were used to give pieces of
information to the regulatory elements. They could be internal (intracellular ), external
(extracellular; also called morphogens), or receptors (interacted with external products and
influenced the cell division axis).
(cid:129) Special elements: coded the outputs of the regulatory network.
Affinities (the concentration values of the morphogens) were computed between promoters and
products. They created connections between the regulatory elements that finally built a regulatory
network. Simple shapes such as a screw, nut, or dumbbell could be produced with this model. In
their most recent work, the same authors showed the differentiation capacity of cells by extending
the French flag problem to the third dimension [76]. Figure 15 illustrates these experiments. Self-
repairing was a further property of this model: When a certain number of cells were killed at the
beginning of the development, the organism was able to regenerate a shape to the desired pattern.
In 2011, Cussat-Blanc et al. used a discrete developmental model in which cells were controlled
by an artificial gene regulatory network in order to produce 2D colored shapes [28]. In contrast to
the previous model, the growing organism was required to develop a metabolism based on an ar-
tificial chemistry defined in the environment. The model was based on the coevolution of a bit-
string artificial gene regulatory network that controlled the cell specialization into different colors,
and a rule set that controlled the proliferation of the cells. Both were evolved using an evolutionary
algorithm: the rule set to produce a shape and the necessary metabolism to survive, and the artificial
gene regulatory network to specialize the cells as targeted by the user. The authors showed how mor-
phogen gradients guided the AGRN to the regionalization of the cells. Figure 16 illustrates this model.
The models described in this section inspired many researchers to develop their own artificial
regulatory networks or to apply such systems to specific problems. As one of many possible exam-
ples, Bongard and Pfeifer used a model close to Reilʼs model to develop modular robots [15]. These
robots had a neural network that controlled each module (for rotation, elongation, etc.). The genetic
expression of the artificial gene regulatory network allowed the activation or the inhibition of 23
phenotypically predefined transformations, such as module size growth, module division, parameter
modifications, and neural network topology.
5.1.3 Morphology and Controllers
Based on their previous work, Schramm et al. used an artificial gene regulatory network to evolve
both the morphology and the controller of virtual animats [73, 74, 78, 126]. The morphology was
Artificial Life Volume 24, Number 4
313
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
Figure 16. Multicellular organism with metabolism growing in a chemical environment with specialization skills. On the
right, the artificial gene regulatory network obtained and interaction between its genes. Reprinted from Cussat-Blanc,
S. et al. (2011). [28].
grown from a single cell using a developmental model comparable to the one presented above.
The artificial gene regulatory network was then used to control the cell behavior (cell division,
division-plane orientation, etc.). After a given developmental time, the morphology was frozen.
The cells were transferred to a simulated aquatic environment, and the cell aggregate was trans-
formed using Delaunay triangulation to a set of masses (centers of the cells) and springs (cell con-
nections). The artificial gene regulatory network previously used to control the growth of cells was
now used to control the spring stiffness in order to move the animat in the environment. AGRNs
were evolved to reach the maximum distance. Figure 17 presents one of the animats obtained with
such a method.
Such approaches brought artificial creatures closer to resembling living systems. Living systems
learn locomotion and everything else during their entire life, from the very few first cells to the end
of their lives; however, most previous work did not take this into consideration and used a fixed
morphology. In this domain, AGRNs paired with a developmental model could exhibit powerful
solutions, given their capacity of adaptation to changing environments. The oscillatory behavior
of AGRNs was used to control the ATRON modular robot [149]: The robot, possessing a snakelike
structure, was successfully controlled by an artificial gene regulatory network with the fractal
representation [13].
In all previous work, artificial gene regulatory networks and developmental models were used
with a specific objective described by a fitness function of the evolutionary algorithm. However,
living beings do not act in the environment with an explicit lifelong objective function. While using
a fitness function helps to quickly obtain interesting results and simplify the analysis of the creatures
obtained, it can trap the system in a local optimum due to the engineering of the fitness function
itself.
Figure 17. Animats first grown with AGRNs controlling cells in a developmental model and then moving in their
simulated environment. Reprinted from Joachimczak, M. et al. (2014). Published under a CC BY 4.0 license. [74].
314
Artificial Life Volume 24, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
Figure 18. Example of a robot “grown” using MapDevo3D: (a) the robotʼs morphology; (b) its modular organization;
(c–g) the robot immersed in a physics engine. Reprinted from Doursat, R., & Sánchez, C. (2014). [43].
In 2014, Doursat and Sánchez gave an overview on how coevolution of morphology and con-
troller using evolution and development can help to generate multicellular soft robots [43]. After
classifying existing approaches in modular/soft robotics into four different categories of morpho-
genetic engineering,3 from human assembly (constructing) to rewriting/inserting (generating), passing
through syncing/swarming (coalescing), and growing/aggregating (developing), they presented the
three key components of their system, MapDevo3D, a multicellular soft-robot-growing platform:
(cid:129) Cells (represented as a swarm) can adhere through elastic forces.
(cid:129) Positional information (morphogenes) can diffuse in the environment for cell-cell
communication.
(cid:129) An artificial gene regulatory network can control cells.
With this system, the authors grew a 3D multicellular organism composed of hundreds of cells of
27 different types, organized in “tissues” (i.e., modules) able to walk across the environment and
climb stairs. Figure 18 illustrates this experiment.
Disset et al. (2014) proposed simplifying this fitness function and building a virtual envi-
ronment complex enough to allow creatures with complex behaviors to emerge [38]. The fitness
function was extremely simple: The artificial creature (and thus the artificial gene regulatory
network that controls its cells) was evaluated based on its survival duration. The evolutionary
algorithm, which evolves the AGRN, could explore all the possible strategies to reach this aim.
In these first experiments, the authors proposed evolving 2D creatures fighting against harmful
particles. Cells could, in addition to classical division and communication with morphogens, spe-
cialize into two different types: nutritive (capacity to extract energy from the environment) and
protective (capacity to resist the particles). Cells had to self-organize in order to survive as long
as possible.
In 2016, this work was extended to the third dimension and explored the developmental strat-
egies in a more realistic environment in which cells must proliferate both in soil which contains
nutritive resources, and in the air, where sunlight transforms the nutriment into energy [39]. Once
3 The science of engineering growing systems.
Artificial Life Volume 24, Number 4
315
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
Figure 19. Example of creatures obtained with an AGRN controlling growing animats without an explicit fitness function
in the evolutionary algorithm. Image reprinted from Disset et al. [39].
again, the fitness function consisted of only the survival duration of the organism. In this experi-
ment, the results were at first deceptive: Evolution was stuck in a local optimum. The authors ex-
plored novelty search strategies in order to surpass this deceptive result. (Novelty search had already
been used in previous work on artificial embryogenesis [79]). The authors obtained complex growth
strategies such as, for instance, the one presented in Figure 19, with simple diversity measures
balancing the survival duration objective.
5.1.4 Bridging the Gap to Reality
While up to this point computational simulations of GRNs have advanced beyond the reach of
synthetic biology, biological engineering has been rapidly catching up, with applications from record-
ing images [97] and basic image processing [134] using engineered microbes, to quorum-sensing
regulated drug delivery [151]. A number of computational elements have been developed using syn-
thetic biology [66], and the development of BioBricks [130] has stimulated a movement in synthetic
biology akin to the early days of electronic engineering. The limits of phenomena that can be un-
derstood from the perspective of biological circuit engineering have yet to be discovered [65]. The
field and future of synthetic biology are well beyond the scope of this review, and so we direct the
interested reader to some of the extensive reviews of the field [24, 54, 86].
5.2 Agent Control
Artificial embryogenesis was one of the first applications of artificial gene regulatory networks. Be-
cause AGRNs serve as the central controller of living cells, artificial embryogenesis was a perfect and
natural framework to develop the models and explore their capabilities. Once they reached a satis-
factory level of quality, researchers started to evaluate possible use of these controllers in different
types of applications, more oriented towards real-world problems. This subsection presents the use
of artificial gene regulatory networks of different kinds in the control of virtual agents.
One of the first applications of artificial embryogenesis was to use an artificial gene regulatory
network to control a pole cart [91, 113]. This experiment, a typical benchmark in the evolutionary
computation community, consists of balancing a pole on top of a cart. The cartʼs motion (left or
right, with no possibility to stay put) is in a one-dimensional continuous environment of limited
space. The controller senses the position of the cart, the pole angle, the cart velocity, and the angular
velocity of the pole. This benchmark has been solved with multiple machine learning approaches
[10, 146].
316
Artificial Life Volume 24, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
In 2010, Nicolau et al. used a bit-string artificial gene regulatory network based on the model in
[6]. The model included input and output proteins connected to the sensors and the effectors of the
cart. These proteins had specific hand-designed signatures, and their concentrations were updated
differently than regulatory proteins: Input protein concentrations were not regulated by the network
but fed by the cart sensors, and output proteins were regulated but did not regulate other proteins.
In order to evolve the GRN to find the optimal controller, a (250+250) evolution strategy (ES) with
up to 50 generations was used with a mutation consisting of mutating 1% of the genome bits with a
1/5 adaptation rule. The authors showed rapid convergence of the ES-evolved GRN with very good
generalization capability of the network. Using the generalization test from [146], the evolved
AGRNs showed close to optimum generalization behavior. With the same model, Nicolau et al.
demonstrated later a decision-making system for index trading. The system decides to buy, sell,
or do nothing according to the fluctuations of trading indices provided [112].
A similar experiment was developed by Trefzer et al. in 2010, in which an artificial gene regula-
tory network was used to solve various obstacle-avoidance tasks (cave, maze, distributed obstacles)
[137]. Interestingly, the problem was implemented on an E-Puck robot, which shows the capacity of
AGRNs to bridge the gap to reality. This work was recently extended with artificial epigenetic
networks, in which artificial gene regulatory networks are used as the central system to dynamically
distribute control tasks [139].
AGRN models have been employed to control agents in ecosystems for foraging tasks.
Joachimczak and Wróbel [77] presented AGRNs expressing rich dynamics and motion patterns.
Harrington and Magbunduku (2017) presented evidence suggesting that competitive dynamics
in an ecology of genetically regulated agents can stimulate the evolution of complex behavior [63].
In 2014, in a complex environment, Sanchez and Cussat-Blanc used an artificial gene regulatory
network to control a virtual car in TORCS, a simulated car environment [125]. In this work, an artificial
gene regulatory networkʼs input proteins were connected to the car sensors (distance to the track
border and longitudinal and lateral speeds; see Figure 20), and the output proteins to the actuators
(wheel, accelerator, and brake). After evolution on asphalt tracks only, the best network obtained
was able to drive on any kind of track (turn shapes, etc.) and on other surfaces (asphalt, ice, rocks,
Figure 20. Gene-regulated car driving. Left: Inputs of the artificial gene regulatory network from the car sensors. Right:
Evolved artificial gene regulatory network. Reprinted from Sanchez, S., & Cussat-Blanc, S. (2014). [125].
Artificial Life Volume 24, Number 4
317
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
etc.). Figure 20 shows the best AGRN obtained after evolution. This approach was extremely com-
petitive with other approaches from the literature: It was able to win the Simulated Car Racing
Championship4 in 2015 against eight other competitors of various kinds (neural networks, optimized
scripts, etc.).
5.3 Neuromodulation
Recent work has begun to make a connection between learning and genetic regulation. In 2013,
Harrington, et al. studied a robot navigation problem with a robot controlled by a temporal-difference
reinforcement learning agent [64]. By introducing a neuromodulatory system governed by a GRN to
control the agentʼs learning and memory, the robot was able to outperform traditional reinforcement
learning. In a follow-up study, the ability of the genetically regulated neuromodulation system was
utilized in a multi-task setting, where agents had to solve an array of different problems with both
discrete and continuous state spaces, as well as one-shot and continuous rewards [29]. Agents were
required to learn to solve a series of problems, while the same AGRN was used to regulate the learn-
ing parameters for each problem. It was shown that an evolved GRN could accelerate the learning of
multiple tasks, and general problem-solving GRNs could improve learning beyond traditional rein-
forcement learning.
5.4 AGRN as Indirect Encoders
By exploiting previously developed algorithms for the genetic programming of register machines,
Banzhaf and Lasarezyk (2005) realized an artificial-chemistry implementation of genetic program-
ming [7]. The asynchronous evaluation of the evolved program represented an alternative approach
to genetic programming, based on the parallel nature of chemical systems.
In 2012, Lopes and Costa implemented a similar idea of using a bit-string AGRN to indirectly
encode a GP tree [105]. The AGRN was evolved using an evolution strategy. Before evaluation,
genes following promoter sites expressed operators of the GP tree, and the inhibitor and enhancer
sites were used to connect the operators. Lopes (2015) used this indirect encoding to evolve programs
in symbolic regression problems (n-bit parity, squares, Fibonacci series, etc.), with promising results
with respect to the quality of solutions and the very small programs generated [106].
In the same period, Wróbel and colleagues proposed using artificial gene regulatory networks to
encode artificial neural networks [147, 148]. They used a leaky integrate-and-fire model of a spiking
neural network (SNN) [33], in which regulatory units (equivalent to regulatory proteins) encoded the
neurons of the regulatory network, connections between neurons were given by protein connections
through inhibiting and enhancing sites, and the protein concentrations provided the potential of
each neuronal membrane. With this encoding, the authors showed the capacity of the produced
SNN, after evolution of the AGRN, to reproduce spikes when input stimuli were of high enough
frequencies. Recently, indirect encoding of recurrent neural networks into genetic networks was
used to solve dynamic problems such as state space targeting in a numerical dynamical system, the
inverted pendulum, and orbit transfer control in a gravitational system [139].
The approaches introduced here are still in the early stages of their development, yet they are
growing in complexity. Their main objective is to use an AGRNʼs very compact encoding to evolve
large networks: An AGRN possesses a small genome in comparison to the millions or billions of
parameters needed to optimize a deep neural network, for example. This compact encoding is
expected to reduce the computation cost of optimization, as in nature.
5.5 Summary of the Applications
Artificial gene regulatory networks have been studied in a variety of contexts and applications, from
dynamical systems to circuit design. In Table 1 we have listed key references for applications of
AGRNs of which we are aware. Early research on AGRNs focused on the study of dynamic
4 http://cs.adelaide.edu.au/∼optlog/SCR2015/index.html.
318
Artificial Life Volume 24, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
Table 1. Summary of references for applications of AGRNs.
Problem
Dynamics analysis
Morphogenesis
Agent control
ODEs
[30] [31] [91]
[100] [107] [127]
[13] [15] [28] [38]
[39] [41] [42] [47]
[48] [51] [73] [74]
[75] [76] [126] [138]
[4] [63] [73] [74]
[77] [91] [125] [149]
AGRN representations
RBN
[1] [27] [37]
[44] [83] [84]
[85] [110] [131]
Bit strings
[5] [6] [18] [93]
[96] [117] [119]
[20] [36]
[90]
[112] [113]
[137] [139]
Neuromodulation
[29] [64]
Indirect encoding
[147] [148]
[7] [105] [139]
behaviors of networks using a wide range of representations. Recently, advanced applications of
AGRNs have favored the use of bit strings and ODE-based models. As research on AGRNs
continues, we expect that applications will continue to utilize and extend such models.
Figure 21 presents the references from Table 1 partitioned into the different categories of dy-
namics study, evo-devo (i.e., artificial embryogenesis), agent control, neuromodulation, and indirect
encoding over the years. We take this as an indicator of research interest in each topic. The pub-
lication year of an article is calculated backward from 2017 in 5-year bins. Interestingly, we can
observe a massive increase in publications at the beginning of the 21st century and the appearance
of first applications. Evo-devo was a dominant benchmark to support the theoretical development
of artificial gene regulatory networks (certainly because it is a very natural use of these networks) up
Figure 21. Partitioned references of artificial gene regulatory network approaches over the years.
Artificial Life Volume 24, Number 4
319
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
until very recently (2012). Since 2012, however, Evo-devo topics seem to be decreasing in frequency,5
and the field appears to be transitioning to more real-world applications of gene regulation (agent
control, neuromodulation, and indirect encoding). This seems due to a certain maturity of the tech-
nology and a better understanding of AGRN functioning. It also has to be noted that theoretical
publications are still necessary to further develop artificial gene regulatory networks, since knowledge
of their biological counterpart is still expanding very quickly and transfer between the two
communities (ALife and genetics/bioinformatics) is recurrent due to the strong links existing
between the models.
6 Conclusion
In this article we have reviewed existing work on the use of gene regulatory networks for compu-
tational purposes. We first introduced how genetic regulation works in living systems, followed by a
discussion of existing computational models. This shows the diversity of encodings and dynamics
that are currently being used; however, a rigorous comparison of models has yet to be performed.
Recently, an initial study has been conducted in order to compare various encodings and dynamics
[40]. Without doubt, the community would benefit from standardized benchmarks to facilitate the
comparison of various models of gene regulation as well as other optimizable models, such as
artificial neural networks, genetic programming, and handwritten scripts. The increasing frequency
of competitions organized at conferences is one step in this direction, and serves as a good basis of
comparison.
In our past experience of presenting artificial gene regulatory networks and applications to var-
ious real-world control problems, we are often asked about the difference between artificial gene
regulatory networks and artificial neural networks (ANNs). While artificial gene regulatory networks
and artificial neural networks can be used for similar purposes, AGRNs utilize a compact genetic
representation: For instance, instead of encoding connection weights between neurons, which can
mean the need to optimize millions of variables in recent deep neural networks, artificial gene reg-
ulatory networks only encode the 3D structure of proteins that codes for the dynamic interaction
between them. This drastically reduces the number of variables, to a few hundred. This has wide-
spread consequences, especially in the age of deep learning (DL) [60]. While applications of evolu-
tionary algorithms to DL have just started to appear [101, 121], we expect that evolving DL neural
networks with AGRNs will be a major application area in the future.
For a direct comparison between AGRNs and ANNs, however, the recurrent connectivity of
AGRNs allows them to be best compared to recurrent neural networks. While there is significant
work to be done in relating artificial gene regulatory networks to artificial neural networks, initial
steps have been taken in [145]. There, Watson et al. show that evolving simple artificial gene reg-
ulatory networks is equivalent to the associative learning of weights in a Hopfield network. How-
ever, this observation has not been extended to artificial gene regulatory networks with more
complex genetic representations. Also, Baran et al. recently proposed the use of AGRNs to study
the evolution of social behavior and, more precisely, the underlying development of the brainʼs
neural circuitry [8]. This opens new perspectives for studies of the connection between artificial
neural networks and artificial gene regulatory networks.
Two other properties of AGRNs that are, in our opinion, particularly interesting and not yet
fully used and understood are temporal dynamics and heterochrony. The first, temporal dy-
namics, allows a certain memory to emerge in the network: Concentrations can be updated con-
stantly, at every time step of the simulation or problem resolution, while actions are executed
once in a while. This provides the network with all the history of a given state of the environ-
ment, which is naturally kept by protein concentrations and provides a memory system of the
5 The evo-devo community is now also moving to application domains such as computational biology and soft robotics.
320
Artificial Life Volume 24, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
GRN. Not yet mathematically studied or fully understood, these dynamics could be beneficial
for long-term decision making.
The second, heterochrony, is a crucial property of these networks. As described previously in this
article, this mechanism allows a slow modification of the network dynamics when mutation occurs.
This mechanism is not yet sufficiently employed in current mutation operators of genetic algorithms.
While crossover operators have been recently improved in [29], mutation is still crucial in AGRN
optimization, since most approaches use very high mutation rates (∼75%), if not exclusively muta-
tion. Whereas the NEAT algorithm has strongly impacted the evolution of neural networks [132],
improving the evolutionary algorithm is a central question in order to find the best possible network
for a given problem. More work is necessary in this domain in order to generate better results with
artificial gene regulatory networks.
Finally, one domain in which artificial gene regulatory networks could excel but have not been
well tested is online learning. Thanks to their easy-to-modify structure based on protein affinities,
slight changes of proteinsʼ tags while the agent is acting in the environment should be possible. A
mechanism, comparable to backpropagation in artificial neural networks, will have to be designed in
order to intelligently change these values according to the rewards obtained by the agent. The ar-
chitecture of artificial gene regulatory networks should be helpful here, due to the small number of
parameters one needs to modify in order to change entire networks. One could easily imagine
particle-swarm-optimization-like motion, in which the AGRNʼs proteins would move in a 3D space
(for a model based on three tags such as Cussat-Blanc et al.ʼs [39, 40, 125] model), attracted and
repelled by other proteins according to the efficacy of the networks for a given task.
Possibilities opened by gene regulatory networks are numerous. Whereas biologists have made
significant progress in understanding the inner mechanisms of gene regulation in living systems,
much remains to be discovered and understood. These mechanisms produce extremely complex
behaviors in living organisms, from embryogenesis to the regulation of everyday life. Computer
science and more specifically artificial intelligence will benefit from these discoveries and, with gene
regulatory networks, could produce more intelligent behaviors for artificial agents in the near future.
Acknowledgments
K.H. thanks the NSF Idaho EPSCoR Program and the National Science Foundation under award
number IIA-1301792. W.B. thanks the Canadian NSERC for funding under discovery grant
numbers RGPIN 283304-2012 and 2018-05365, and Michigan State University for providing JR
Koza Endowment funding.
References
1. Aldana, M., Balleza, E., Kauffman, S., & Resendiz, O. (2007). Robustness and evolvability in genetic
regulatory networks. Journal of Theoretical Biology, 245(3), 433–448.
2. Andersson, N., Skrtic, S. M., Håkanson, R., & Ohlsson, C. (2005). A gene expression fingerprint of mouse
stomach ECL cells. Biochemical and Biophysical Research Communications, 332(2), 404–410.
3. Artavanis-Tsakonas, S., Rand, M. D., & Lake, R. J. (1999). Notch signaling: Cell fate control and signal
integration in development. Science, 284(5415), 770–776.
4. Asr, N. R., & Majd, V. J. (2013). A new artificial genetic regulatory network model and its application in
two dimensional robot control. International Journal of Information and Electronics Engineering, 3(5), 461–465.
5. Banzhaf, W. (2003). Artificial regulatory networks and genetic programming. In R. Riolo & B. Worzel
(Eds.), Genetic programming theory and practice (pp. 43–61). New York: Springer.
6. Banzhaf, W. (2003). On the dynamics of an artificial regulatory network. In W. Banzhaf, T. Christaller,
P. Dittrich, J. Kim, & J. Ziegler (Eds.), European Conference on Artificial Life (pp. 217–227). New York: Springer.
7. Banzhaf, W., & Lasarczyk, C. (2005). Genetic programming of an algorithmic chemistry. In U.-M. OʼReilly, T.
Yu, R. Riolo, & B. Worzel (Eds.), Genetic programming theory and practice II (pp. 175–190). New York: Springer.
8. Baran, N. M., McGrath, P. T., & Streelman, J. T. (2017). Applying gene regulatory network logic to the
evolution of social behavior. Proceedings of the National Academy of Sciences of the U.S.A., 114, 5886–5893.
Artificial Life Volume 24, Number 4
321
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
9. Bartel, D. P. (2004). MicroRNAs: Genomics, biogenesis, mechanism, and function. Cell, 116, 281–297.
10. Barto, A. G., Sutton, R. S., & Anderson, C. W. (1983). Neuronlike adaptive elements that can solve
difficult learning control problems. IEEE Transactions on Systems, Man, and Cybernetics, 5, 834–846.
11. Bentley, K., Harrington, K., & Regan, E. R. (2014). Can active perception generate bistability?
Heterogeneous collective dynamics and vascular patterning. In H. Sayama, J. Rieffel, S. Risi, R. Doursat,
& H. Lipson (Eds.), Proceedings of ALIFE XIV: The Fourteenth International Conference on the Synthesis and
Simulation of Living Systems (pp. 328–335). Cambridge, MA: MIT Press.
12. Bentley, K., Mariggi, G., Gerhardt, H., & Bates, P. A. (2009). Tipping the balance: Robustness of tip cell
selection, migration and fusion in angiogenesis. PLOS Computational Biology, 5(10), e1000549.
13. Bentley, P. J. (2004). Evolving beyond perfection: An investigation of the effects of long-term evolution
on fractal gene regulatory networks. Biosystems, 76(1), 291–301.
14. Berg, O. G., & von Hippel, P. H. (1988). Selection of DNA binding sites by regulatory proteins: II. The
binding specificity of cyclic AMP receptor protein to recognition sites. Journal of Molecular Biology, 200(4),
709–723.
15. Bongard, J., & Pfeifer, R. (2003). Evolving complete agents using artificial ontogeny. In F. Hara & R.
Pfeifer (Eds.), Morpho-functional machines: The new species (pp. 237–258). New York: Springer.
16. Bower, J. M., & Bolouri, H. (2001). Computational modeling of genetic and biochemical networks. Cambridge, MA:
MIT Press.
17. Brookfield, J. F. Y. (2005). The ecology of the genome-mobile DNA elements and their hosts. Nature
Reviews Genetics, 6, 128–136.
18. Byrne, J., Nicolau, M., Brabazon, A., & OʼNeill, M. (2014). An examination of synchronisation in artificial
gene regulatory networks. In IEEE Congress on Evolutionary Computation (CEC) (pp. 2764–2769).
Piscataway, NJ: IEEE.
19. Chaouiya, C. (2007). Petri net modelling of biological networks. Briefings in Bioinformatics, 8(4), 210–219.
20. Chavoya, A., & Duthen, Y. (2008). A cell pattern generation model based on an extended artificial
regulatory network. BioSystems, 94(1–2), 95–101.
21. Chen, K., & Rajewsky, N. (2007). The evolution of gene regulation by transcription factors and
microRNAs. Nature Reviews Genetics, 8(2), 93–103.
22. Cheong, R., Rhee, A., Wang, C. J., Nemenman, I., & Levchenko, A. (2011). Information transduction
capacity of noisy biochemical signaling networks. Science, 334(6054), 354–358.
23. Chung, H., Bogwitz, M. R., McCart, C., Andrianopoulos, A., ffrench-Constant, R. H., Batterham, P., &
Daborn, P. J. (2007). Cis-regulatory elements in the accord retrotransposon result in tissue-specific
expression of the Drosophila melanogaster insecticide resistance gene Cyp6g1. Genetics, 175, 1071–1077.
24. Church, G. M., Elowitz, M. B., Smolke, C. D., Voigt, C. A., & Weiss, R. (2014). Realizing the potential of
synthetic biology. Nature Reviews Molecular Cell Biology, 15(4), 289–294.
25. Crick, F. (1958). On protein synthesis. In F. Sanders (Ed.), Symposia of the Society for Experimental Biology,
number XII: The biological replication of macromolecules (pp. 138–163). Cambridge, UK: Cambridge University Press.
26. Crick, F. (1970). Central dogma of molecular biology. Nature, 227, 561–563.
27. Crombach, A., & Hogeweg, P. (2008). Evolution of evolvability in gene regulatory networks. PLoS
Computational Biology, 4(7), e1000112.
28. Cussat-Blanc, S., Bredeche, N., Luga, H., Duthen, Y., & Schoenauer, M. (2011). Artificial gene regulatory
network and spatial computation: A case study. In T. Lenaerts, M. Giacobini, H. Bersini, P. Bourgine,
M. Dorigo, & R. Doursat (Eds.), European Conference on Artificial Life (pp. 192–199). Cambridge, MA:
MIT Press.
29. Cussat-Blanc, S., & Harrington, K. (2015). Genetically-regulated neuromodulation facilitates multi-task
reinforcement learning. In S. Silva (Ed.), Proceedings of the 2015 Annual Conference on Genetic and Evolutionary
Computation (pp. 551–558). New York: ACM.
30. Cussat-Blanc, S., Luga, H., & Duthen, Y. (2008). From single cell to simple creature morphology and metabolism.
In S. Bullock, J. Noble, R. Watson, & M. Bedau (Eds.), Artificial Life XI: Proceedings of the Eleventh International
Conference on the Simulation and Synthesis of Living Systems (pp. 134–141). Cambridge, MA: MIT Press.
322
Artificial Life Volume 24, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
31. Cussat-Blanc, S., & Pollack, J. (2012). Using pictures to visualize the complexity of gene regulatory
networks. In C. Ofria et al. (Eds.), The 13th International Conference on the Simulation and Synthesis of Living
Systems (pp. 491–498). Cambridge, MA: MIT Press.
32. Davidson, E. H. (2006). The regulatory genome: Gene regulatory networks in development and evolution. San Diego, CA:
Academic Press.
33. Dayan, P., & Abbott, L. (2001). Theoretical neuroscience: Computational and mathematical modeling of neural systems.
Cambridge, MA: MIT Press.
34. de Garis, H. (1999). Artificial embryology and cellular differentiation. In P. Bentley (Ed.), Evolutionary
Design by Computers (pp. 281–295). San Francisco: Morgan Kaufmann.
35. De Jong, H. (2002). Modeling and simulation of genetic regulatory systems: A literature review. Journal
of Computational Biology, 9, 67–103.
36. Dellaert, F., & Beer, R. (1994). Toward an evolvable model of development for autonomous agent
synthesis. In R. Brooks & P. Maes (Eds.), Artificial Life IV: Proceedings of the Fourth International Workshop on
the Synthesis and Simulation of Living Systems. Cambridge, MA: MIT Press.
37. Deritei, D., Aird, W. C., Ercsey-Ravasz, M., & Regan, E. R. (2016). Principles of dynamical modularity in
biological regulatory networks. Scientific Reports, 6, 21957.
38. Disset, J., Cussat-Blanc, S., & Duthen, Y. (2014). Self-organization of symbiotic multicellular structures.
In H. Sayama, J. Reiffel, S. Risi, R. Doursat, & H. Lipson (Eds.), Artificial Life XIV: Proceedings of the
Fourteenth International Conference on the Synthesis and Simulation of Living Systems (pp. 541–548). Cambridge,
MA: MIT Press.
39. Disset, J., Cussat-Blanc, S., & Duthen, Y. (2016). Evolved developmental strategies of artificial
multicellular organisms. In C. Gershenson, T. Froese, et al. (Eds.), Artificial Life XV: Proceedings of the
Fifteenth International Symposium on the Synthesis and Simulation of Living Systems (pp. 360–367). Cambridge, MA:
MIT Press.
40. Disset, J., Wilson, D. G., Cussat-Blanc, S., Sanchez, S., Luga, H., & Duthen, Y. (2017). A comparison
of genetic regulatory network dynamics and encoding. In G. Ochoa (Ed.), Proceedings of the Genetic and
Evolutionary Computation Conference (pp. 91–98). New York: ACM.
41. Doursat, R. (2008). Organically grown architectures: Creating decentralized, autonomous systems by
embryomorphic engineering. In R. Wuertz (Ed.), Organic computing (pp. 167–200). New York: Springer.
42. Doursat, R. (2009). Facilitating evolutionary innovation by developmental modularity and variability.
In F. Rothlauf et al. (Eds.), Proceedings of the 11th Annual Conference on Genetic and Evolutionary Computation
(pp. 683–690). New York: ACM.
43. Doursat, R., & Sánchez, C. (2014). Growing fine-grained multicellular robots. Soft Robotics, 1(2),
110–121.
44. Draghi, J., & Wagner, G. P. (2009). The evolutionary dynamics of evolvability in a gene network model.
Journal of Evolutionary Biology, 22(3), 599–611.
45. Dueck, H., Khaladkar, M., Kim, T. K., Spaethling, J. M., Francis, C., Surosh, S., Fisher, S. A., Seale, P.,
Beck, S. G., Bartfai, T., Kuhn, B., Eberwine, J., & Kim, J. (2015). Deep sequencing reveals cell-type-
specific patterns of single-cell transcriptome variation. Genome Biology, 16(122).
46. Dynlacht, B. D. (1997). Regulation of transcription by proteins that control the cell cycle. Nature,
389(6647), 149–152.
47. Eggenberger, P. (1997). Evolving morphologies of simulated 3D organisms based on differential gene
expression. In P. Husbands & I. Harvey (Eds.), Fourth European Conference on Artificial Life (pp. 205–213).
Cambridge, MA: MIT Press.
48. Eggenberger Hotz, P. (2004). Asymmetric cell division and its integration with other developmental
processes for artificial evolutionary systems. In J. Pollack, M. Bedau, P. Husbands, T. Ikegami, & R. A.
Watson (Eds.), Artificial Life IX: Proceedings of the Ninth International Conference on the Simulation and Synthesis of
Living Systems (pp. 387–392). Cambridge, MA: MIT Press.
49. Elowitz, M. B., Levine, A. J., Siggia, E. D., & Swain, P. S. (2002). Stochastic gene expression in a single
cell. Science, 297(5584), 1183–1186.
50. Feschotte, C. (2008). Transposable elements and the evolution of regulatory networks. Nature Reviews
Genetics, 9(5), 397–405.
Artificial Life Volume 24, Number 4
323
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
51. Flann, N., Hu, J., Bansal, M., Patel, V., & Podgorski, G. (2005). Biological development of cell patterns:
Characterizing the space of cell chemistry genetic regulatory networks. In M. Capcarrere et al. (Eds.),
European Conference on Artificial Life (pp. 57–66). New York: Springer.
52. Fleischer, K., & Barr, A. (1992). A simulation testbed for the study of multicellular development: The
multiple mechanisms of morphogenesis. In C. Langton (Ed.), Artificial life III: Proceedings of the Workshop on
Artificial Life (p. 389–416). Reading, MA: Addison-Wesley.
53. Fox, R. M., Von Stetina, S. E., Barlow, S. J., Shaffer, C., Olszewski, K. L., Moore, J. H., Dupuy, D., Vidal,
M., & Miller, D. M. (2005). A gene expression fingerprint of C. elegans embryonic motor neurons.
BMC Genomics, 6(42).
54. Gao, X. J., & Elowitz, M. B. (2016). Synthetic biology: Precision timing in a cell. Nature, 538(7626),
462–463.
55. Gardner, M. (1970). Mathematical games: The fantastic combinations of John Cowayʼs new solitaire game
“life”. Scientific American, 223(4), 120–123.
56. Gaydos, L. J., Wang, W., & Strome, S. (2014). H3K27me and PRC2 transmit a memory of repression
across generations and during development. Science, 345(6203), 1515–1518.
57. Gerhart, J., & Kirschner, M. (2006). The plausibility of life. New Haven, CT: Yale University Press.
58. Gillespie, D. T. (1975). An exact method for numerically simulating the stochastic coalescence process in
a cloud. Journal of the Atmospheric Sciences, 32(10), 1977–1989.
59. Gillespie, D. T., & Petzold, L. R. (2003). Improved leap-size selection for accelerated stochastic
simulation. The Journal of Chemical Physics, 119(16), 8229–8234.
60. Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep learning. Cambridge, MA: MIT Press.
61. Graner, F., & Glazier, J. A. (1992). Simulation of biological cell sorting using a two-dimensional extended
Potts model. Physical Review Letters, 69(13), 2013.
62. Grewal, S. I., & Moazed, D. (2003). Heterochromatin and epigenetic control of gene expression. Science,
301(5634), 798–802.
63. Harrington, K., & Magbunduku, L. (2017). Competitive dynamics in eco-evolutionary genetically-
regulated swarms. In C. Knibe et al. (Eds.), ECAL 2017: The Fourteenth European Conference on Artificial
Life (pp. 190–197). Cambridge, MA: MIT Press.
64. Harrington, K. I., Awa, E., Cussat-Blanc, S., & Pollack, J. (2013). Robot coverage control by evolved
neuromodulation. In P. Angelov, D. Levine, & P. Erdi (Eds.), The 2013 International Joint Conference on
Neural Networks (pp. 1–8). Piscataway, NJ: IEEE.
65. Harrington, K. I. S. (2016). A circuit basis for morphogenesis. Theoretical Computer Science, 633, 28–36.
66. Hasty, J., McMillen, D., & Collins, J. J. (2002). Engineered gene circuits. Nature, 420(6912), 224–230.
67. Hasty, J., McMillen, D., Isaacs, F., & Collins, J. J. (2001). Computational studies of gene regulatory
networks: In numero molecular biology. Nature Reviews Genetics, 2(4), 268–279.
68. Horvitz, H., & Herskowitz, I. (1992). Mechanisms of asymmetric cell division: Two Bs or not two Bs, that
is the question. Cell, 68(2), 237.
69. Hunding, A., Kauffman, S. A., & Goodwin, B. C. (1990). Drosophila segmentation: Supercomputer
simulation of prepattern hierarchy. Journal of Theoretical Biology, 145(3), 369–384.
70. Huppert, S. S., Jacobsen, T. L., & Muskavitch, M. A. (1997). Feedback regulation is central to Delta-Notch
signalling required for Drosophila wing vein morphogenesis. Development, 124(17), 3283–3291.
71. Jacob, F., & Monod, J. (1961). Genetic regulatory mechanisms in the synthesis of proteins. Journal of
Molecular Biology, 3, 318–356.
72. Jaenisch, R., & Bird, A. (2003). Epigenetic regulation of gene expression: How the genome integrates
intrinsic and environmental signals. Nature Genetics, 33, 245–254.
73. Joachimczak, M., Kowaliw, T., Doursat, R., & Wróbel, B. (2013). Controlling development and
chemotaxis of soft-bodied multicellular animats with the same gene regulatory network. In P. Lio,
O. Miglino, G. Nicosia, S. Nolfi, & M. Pavone (Eds.), Proceedings of the European Conference on Artificial Life
(pp. 454–461). Cambridge, MA: MIT Press.
324
Artificial Life Volume 24, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
74. Joachimczak, M., Suzuki, R., & Arita, T. (2014). Fine grained artificial development for body-controller
coevolution of soft-bodied animats. Artificial Life, 14, 239–246.
75. Joachimczak, M., & Wróbel, B. (2008). Evo-devo in silico: A model of a gene network regulating
multicellular development in 3D space with artificial physics. In S. Bullock, J. Noble, R. Watson, &
M. Bedau (Eds.), Artificial Life XI: Proceedings of the Eleventh International Conference on the Simulation and
Synthesis of Living Systems (pp. 297–304). Cambridge, MA: MIT Press.
76. Joachimczak, M., & Wróbel, B. (2009). Evolution of the morphology and patterning of artificial embryos:
Scaling the tricolour problem to the third dimension. In G. Kampis, I. Karsai, & E. Szathmáry (Eds.),
Proceedings of the 10th European Conference on Artificial Life (pp. 35–43). Cambridge, MA: MIT Press.
77. Joachimczak, M., & Wróbel, B. (2010). Evolving gene regulatory networks for real time control of
foraging behaviours. In H. Fellerman et al. (Eds.), Artificial Life XII: Proceedings of the 12th International
Conference on the Synthesis and Simulation of Living Systems (pp. 348–358). Cambridge, MA: MIT Press.
78. Joachimczak, M., & Wróbel, B. (2012). Co-evolution of morphology and control of soft-bodied
multicellular animats. In T. Soule et al. (Eds.), Proceedings of the 14th Annual Conference on Genetic and
Evolutionary Computation (pp. 561–568). New York: ACM.
79. Joachimczak, M., & Wróbel, B. (2012). Open ended evolution of 3D multicellular development controlled
by gene regulatory networks. In C. Adami, D. M. Bryson, C. Ofri, & R. T. Pennock (Eds.), Artificial Life
XIII: Proceedings of the 13th International Conference on the Simulation and Synthesis of Living Systems (pp. 67–74).
Cambridge, MA: MIT Press.
80. Jones, P. A., & Takai, D. (2001). The Role of DNA methylation in mammalian epigenetics. Science,
293(5532), 1068–1070.
81. Karlebach, G., & Shamir, R. (2008). Modelling and analysis of gene regulatory networks. Nature Reviews
Molecular Cell Biology, 9(10), 770–780.
82. Karli, R., Chung, H.-R., Lasserre, J., Vlahoviek, K., & Vingron, M. (2010). Histone modification levels are
predictive for gene expression. Proceedings of the National Academy of Sciences of the U.S.A., 107(7), 2926–2931.
83. Kauffman, S. (1969). Homeostasis and differentiation in random genetic control networks. Nature,
224(5215), 177–178.
84. Kauffman, S., Peterson, C., Samuelsson, B., & Troein, C. (2004). Genetic networks with canalyzing Boolean
rules are always stable. Proceedings of the National Academy of Sciences of the U.S.A., 101(49), 17102–17107.
85. Kauffman, S. A. (1969). Metabolic stability and epigenesis in randomly constructed genetic nets. Journal
of Theoretical Biology, 22(3), 437–467.
86. Khalil, A. S., & Collins, J. J. (2010). Synthetic biology: Applications come of age. Nature Reviews Genetics, 11(5), 367.
87. Kim, J., & Eberwine, J. (2010). RNA: State memory and mediator of cellular phenotype. Trends in Cell
Biology, 20(6), 311–318.
88. King, M., & Wilson, A. (1975). Evolution at two levels in humans and chimpanzees. Science, 188, 107–116.
89. Kitano, H. (2002). Systems biology: A brief overview. Science, 295(5560), 1662–1664.
90. Knabe, J., Schilstra, M., & Nehaniv, C. (2008). Evolution and morphogenesis of differentiated
multicellular organisms: Autonomously generated diffusion gradients for positional information.
In S. Bullock, J. Noble, R. Watson, & M. Bedau (Eds.), Artificial Life XI: Proceedings of the Eleventh
International Conference on the Simulation and Synthesis of Living Systems. Cambridge, MA: MIT Press.
91. Krohn, J. P. (2013). A Gene regulatory network model for control. Ph.D. thesis, University College London.
92. Kumar, S., & Bentley, P. (2003). Biologically inspired evolutionary development. In A. Tyrrell, P.
Haddow, & J. Torresen (Eds.), Proceedings of the 5th International Conference on Evolvable Systems: From biology
to hardware (pp. 57–68). New York: Springer.
93. Kuo, P. D., Leier, A., & Banzhaf, W. (2004). Evolving dynamics in an artificial regulatory network model.
In X. Yao et al. (Eds.), International Conference on Parallel Problem Solving from Nature VIII (pp. 571–580).
New York: Springer.
94. Kur, E., Kim, J., Tata, A., Comin, C. H., Harrington, K. I., da F. Costa, L., Bentley, K., & Gu, C. (2016).
Temporal modulation of collective cell behavior controls vascular network topology. eLife, 5, e13212.
95. Lähdesmäki, H., Shmulevich, I., & Yli-Harja, O. (2003). On learning gene regulatory networks under the
Boolean network model. Machine Learning, 52(1–2), 147–167.
Artificial Life Volume 24, Number 4
325
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
96. Leier, A., Kuo, P. D., Banzhaf, W., & Burrage, K. (2006). Evolving noisy oscillatory dynamics in genetic
regulatory networks. In P. Collet et al. (Eds.), European Conference on Genetic Programming EuroGP-2006
(pp. 290–299). New York: Springer.
97. Levskaya, A., Chevalier, A. A., Tabor, J. J., Simpson, Z. B., et al. (2005). Engineering Escherichia coli to see
light. Nature, 438(7067), 441.
98. Lewis, J. (1996). Neurogenic genes and vertebrate neurogenesis. Current Opinion in Neurobiology, 6(1), 3–10.
99. Liao, B.-K., Jrg, D. J., & Oates, A. C. (2016). Faster embryonic segmentation through elevated Delta-
Notch signalling. Nature Communications, 7, 11861.
100. Lipson, H., Pollack, J. B., & Suh, N. P. (2002). On the origin of modular variation. Evolution, 56(8), 1549–1556.
101. Liu, H., Simonyan, K., Vinyals, O., Fernando, C., & Kavukcuoglu, K. (2017). Hierarchical representations
for efficient architecture search. ArXiv, 171100436v1, 1–13.
102. Loaiza, A., Porras, O. H., & Barros, L. F. (2003). Glutamate triggers rapid glucose transport stimulation in
astrocytes as evidenced by real-time confocal microscopy. Journal of Neuroscience, 23(19), 7337–7342.
103. Lones, M. A. (2016). Computing with artificial gene regulatory networks. In H. Iba & N. Noman (Eds.),
Evolutionary Computation in Gene Regulatory Network Research (pp. 398–424). Hoboken: NJ: Wiley.
104. Lopes, F. J., Vieira, F. M., Holloway, D. M., Bisch, P. M., & Spirov, A. V. (2008). Spatial bistability
generates hunchback expression sharpness in the Drosophila embryo. PLoS Computational Biology, 4(9).
105. Lopes, R. L., & Costa, E. (2012). The regulatory network computational device. Genetic Programming and
Evolvable Machines, 13(3), 339–375.
106. Lopes, R. M. L. (2015). A computational model inspired by gene regulatory networks. Ph.D. thesis, Universidade de
Coimbra, Coimbra, Portugal.
107. Lowell, J., & Pollack, J. (2016). Developmental encodings promote the emergence of hierarchical
modularity. In C. Gershenson, T. Froese, et al. (Eds.), Artificial Life XV: The 15th International Conference
on the Synthesis and Simulation of Living Systems (pp. 344–351). Cambridge, MA: MIT Press.
108. Matsuno, H., Doi, A., Nagasaki, M., & Miyano, S. (2000). Hybrid Petri net representation of gene regulatory
network. In Pacific Symposium on Biocomputing, Vol. 5 (p. 87). Singapore: World Scientific Press Singapore.
109. Meinhardt, H. (2009). The algorithmic beauty of sea shells (4th ed.). New York: Springer.
110. Mestl, T., Plahte, E., & Omholt, S. W. (1995). A mathematical framework for describing and analysing
gene regulatory networks. Journal of Theoretical Biology, 176(2), 291–300.
111. Milo, R., Shen-Orr, S., Itzkovitz, S., Kashtan, N., Chklovskii, D., & Alon, U. (2002). Network motifs:
Simple building blocks of complex networks. Science, 298(5594), 824–827.
112. Nicolau, M., OʼNeill, M., & Brabazon, A. (2014). Dynamic index trading using a gene regulatory network
model. In A. I. Esparcia-Alczar & A. M. Mora (Eds.), European Conference on the Applications of Evolutionary
Computation (pp. 251–263). New York: Springer.
113. Nicolau, M., Schoenauer, M., & Banzhaf, W. (2010). Evolving genes to balance a pole. In A. Esparcia-Alcazar
et al. (Eds.), European Conference on Genetic Programming EuroGP 2010 (pp. 196–207). New York: Springer.
114. Ochoa-Espinosa, A., Yucel, G., Kaplan, L., Pare, A., Pura, N., Oberstein, A., Papatsenko, D., & Small, S.
(2005). The role of binding site cluster strength in bicoid-dependent patterning in Drosophila. Proceedings
of the National Academy of Sciences of the U.S.A., 102(14), 4960–4965.
115. Pedraza, J. M., & van Oudenaarden, A. (2005). Noise propagation in gene networks. Science, 307(5717),
1965–1969.
116. Rao, C. V., Wolf, D. M., & Arkin, A. P. (2002). Control, exploitation and tolerance of intracellular noise.
Nature, 420(6912), 231–237.
117. Reil, T. (1999). Dynamics of gene expression in an artificial genome—implications for biological and
artificial ontogeny. In D. Floreano, J.-D. Nicoud, & F. Mondada (Eds.), European Conference on Artificial
Life (pp. 457–466). New York: Springer.
118. Reisig, W. (2012). Petri nets: An introduction (Vol. 4). Berlin, Hiedelberg: Springer Science & Business Media.
119. Rohlf, T., & Winkler, C. R. (2009). Emergent network structure, evolvable robustness, and nonlinear
effects of point mutations in an artificial genome model. Advances in Complex Systems, 12, 293–310.
326
Artificial Life Volume 24, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
120. Ryan, K. M., Phillips, A. C., & Vousden, K. H. (2001). Regulation and function of the p53 tumor
suppressor protein. Current Opinion in Cell Biology, 13, 332–337.
121. Salismans, T., Ho, J., Chen, X., Sidor, S., & Sutskever, I. (2017). Evolution strategies as a scalable
alternative to reinforcement learning. ArXiv, 170303864v2, 1–13.
122. Samoilov, M. S., Price, G., & Arkin, A. P. (2006). From fluctuations to phenotypes: The physiology
of noise. Scienceʼs STKE, 2006(366), re17.
123. Sanchez, A., & Golding, I. (2013). Genetic determinants and cellular constraints in noisy gene expression.
Science, 342(6163), 1188–1193.
124. Sánchez, Á., & Kondev, J. (2008). Transcriptional control of noise in gene expression. Proceedings of the
National Academy of Sciences of the U.S.A., 105(13), 5081–5086.
125. Sanchez, S., & Cussat-Blanc, S. (2014). Gene regulated car driving: Using a gene regulatory network to
drive a virtual car. Genetic Programming and Evolvable Machines, 15(4), 477–511.
126. Schramm, L., Jin, Y., & Sendhoff, B. (2009). Emerged coupling of motor control and morphological
development in evolution of multi-cellular animats. In G. Kampis, I. Karsai, & E. Szathmáry (Eds.),
European Conference on Artificial Life (pp. 27–34). Cambridge, MA: MIT Press.
127. Schramm, L., Jin, Y., & Sendhoff, B. (2012). Redundancy in the evolution of artificial gene regulatory
networks for morphological development. In Y. Jin et al. (Eds.), IEEE Symposium on Computational
Intelligence in Bioinformatics and Computational Biology. Piscataway, NJ: IEEE.
128. Schroedinger, E. (1944). What is life? Cambridge, UK: Cambridge University Press.
129. Segal, E., Raveh-Sadka, T., Schroeder, M., Unnerstall, U., & Gaul, U. (2008). Predicting expression
patterns from regulatory sequence in Drosophila segmentation. Nature, 451(7178), 535–540.
130. Shetty, R. P., Endy, D., & Knight, T. F. (2008). Engineering BioBrick vectors from BioBrick parts.
Journal of Biological Engineering, 2(1), 5.
131. Shmulevich, I., Dougherty, E. R., & Zhang, W. (2002). From Boolean to probabilistic Boolean networks
as models of genetic regulatory networks. Proceedings of the IEEE, 90(11), 1778–1792.
132. Stanley, K. (2004). Efficient evolution of neural networks through complexification. Ph.D. thesis, The University of
Texas at Austin.
133. Stewart, F., Taylor, T., & Konidaris, G. (2005). METAmorph: Experimenting with genetic regulatory
networks for artificial development. In M. Capcarrere, A. Freitas, P. Bentley, C. Johnson, & J. Timmis
(Eds.), European Conference on Artificial Life (pp. 108–117). New York: Springer.
134. Tabor, J. J., Salis, H. M., Simpson, Z. B., Chevalier, A. A., Levskaya, A., Marcotte, E. M., Voigt, C. A., &
Ellington, A. D. (2009). A synthetic genetic edge detection program. Cell, 137(7), 1272–1281.
135. Tkačik, G., Callan, C. G., & Bialek, W. (2008). Information flow and optimization in transcriptional
regulation. Proceedings of the National Academy of Sciences of the U.S.A., 105(34), 12265–12270.
136. Trapnell, C. (2015). Defining cell types and states with single-cell genomics. Genome Research, 25(10),
1491–1498.
137. Trefzer, M. A., Kuyucu, T., Miller, J. F., & Tyrrell, A. M. (2010). Evolution and analysis of a robot
controller based on a gene regulatory network. In G. Tempesti, A. M. Tyrrell, & J. F. Miller (Eds.),
International Conference on Evolvable Systems (pp. 61–72). New York: Springer.
138. Turing, A. (1952). The chemical basis of morphogenesis. Philosophical Transactions of the Royal Society of
London. Series B, Biological Sciences, 237(641), 37–72.
139. Turner, A. P., Caves, L. S. D., Stepney, S., Tyrrell, A. M., & Lones, M. A. (2017). Artificial epigenetic
networks: Automatic decomposition of dynamical control tasks using topological self-modification.
IEEE Transactions on Neural Networks and Learning Systems, 28, 218–230.
140. Tyson, J. J., Chen, K., & Novak, B. (2001). Network dynamics and cell physiology. Nature Reviews Molecular
Cell Biology, 2(12), 908–916.
141. Venkatraman, L., Regan, E. R., & Bentley, K. (2016). Time to decide? Dynamical analysis predicts partial
tip/stalk patterning states arise during angiogenesis. PLOS ONE, 11(11), e0166489.
142. Villefranc, J. A., Nicoli, S., Bentley, K., Jeltsch, M., Zarkada, G., Moore, J. C., Gerhardt, H., Alitalo, K., &
Lawson, N. D. (2013). A truncation allele in vascular endothelial growth factor c reveals distinct modes of
signaling during lymphatic and vascular development. Development, 140(7), 1497–1506.
Artificial Life Volume 24, Number 4
327
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Cussat-Blanc, K. Harrington, and W. Banzhaf
Artificial Gene Regulatory Networks
143. von Neumann, J. (1966). Theory of self-reproducing automata. (Edited and completed by A. Burks.) Urbana:
University of Illinois Press.
144. Waddington, C. H. (2014). The strategy of the genes, Vol. 20. New York: Routledge.
145. Watson, R. A., Wagner, G. P., Pavlicev, M., Weinreich, D. M., & Mills, R. (2014). The Evolution of
Phenotypic Correlations and “Developmental Memory.” Evolution, 68(4), 1124–1138.
146. Whitley, D., Dominic, S., Das, R., & Anderson, C. W. (1993). Genetic reinforcement learning for
neurocontrol problems. In Genetic algorithms for machine learning (pp. 103–128). New York: Springer.
147. Wróbel, B., Abdelmotaleb, A., & Joachimczak, M. (2012). Evolving spiking neural networks in the
GReaNs (gene regulatory evolving artificial networks) platform. In EvoNet2012: Evolving Networks, from
Systems/Synthetic Biology to Computational Neuroscience Workshop at Artificial Life XIII (pp. 19–22).
148. Wróbel, B., & Joachimczak, M. (2014). Using the genetic regulatory evolving artificial networks (GReaNs)
platform for signal processing, animat control, and artificial multicellular development. In Growing adaptive
machines (pp. 187–200). New York: Springer.
149. Zahadat, P., Christensen, D., Katebi, S., & Stoy, K. (2013). Sensor-coupled fractal gene regulatory
networks for locomotion control of a modular snake robot. In A. Martinoli, F. Mondada, N. Correll,
G. Mermoud, M. Egerstedt, M. Hsieh, L. Parker, & K. Sty (Eds.), Distributed autonomous robotic systems
(pp. 517–530). New York: Springer.
150. Zhang, L., Radtke, K., Zheng, L., Cai, A. Q., Schilling, T. F., & Nie, Q. (2012). Noise drives sharpening
of gene expression boundaries in the zebrafish hindbrain. Molecular Systems Biology, 8(1), 613.
151. Zhou, S. (2016). Synthetic biology: Bacteria synchronized for drug delivery. Nature, 536(7614), 33–34.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
2
4
4
2
9
6
1
6
6
7
1
8
7
a
r
t
l
/
_
a
_
0
0
2
6
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
328
Artificial Life Volume 24, Number 4