ARTICLE
Communicated by Oleksandr Popovych
Mean-Field Approximations With Adaptive Coupling
for Networks With Spike-Timing-Dependent Plasticity
Benoit Duchet
benoit.duchet@ndcn.ox.ac.uk
Nuffield Department of Clinical Neuroscience, University of Oxford, Oxford
X3 9DU, U.K., and MRC Brain Network Dynamics Unit, University of Oxford,
Oxford X1 3TH, U.K.
Christian Bick
c.bick@vu.nl
Department of Mathematics, Vrije Universiteit Amsterdam, Amsterdam 1081 HV,
the Netherlands; Amsterdam Neuroscience—Systems and Network Neuroscience,
Amsterdam 1081 HV, the Netherlands; and Mathematical Institute, University
of Oxford, Oxford X2 6GG, U.K.
Áine Byrne
aine.byrne@ucd.ie
School of Mathematics and Statistics, University College Dublin,
Dublin D04 V1W8, Ireland
Understanding the effect of spike-timing-dependent plasticity (STDP) is
key to elucidating how neural networks change over long timescales and
to design interventions aimed at modulating such networks in neuro-
logical disorders. However, progress is restricted by the significant com-
putational cost associated with simulating neural network models with
STDP and by the lack of low-dimensional description that could provide
analytical insights. Phase-difference-dependent plasticity (PDDP) rules
approximate STDP in phase oscillator networks, which prescribe synap-
tic changes based on phase differences of neuron pairs rather than dif-
ferences in spike timing. Here we construct mean-field approximations
for phase oscillator networks with STDP to describe part of the phase
space for this very high-dimensional system. We first show that single-
harmonic PDDP rules can approximate a simple form of symmetric STDP,
while multiharmonic rules are required to accurately approximate causal
STDP. We then derive exact expressions for the evolution of the average
PDDP coupling weight in terms of network synchrony. For adaptive net-
works of Kuramoto oscillators that form clusters, we formulate a fam-
ily of low-dimensional descriptions based on the mean-field dynamics
of each cluster and average coupling weights between and within clus-
ters. Finally, we show that such a two-cluster mean-field model can be
Neural Computation 35, 1481–1528 (2023)
https://doi.org/10.1162/neco_a_01601
© 2023 Massachusetts Institute of Technology
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1482
B. Duchet, C. Bick, and Á. Byrne
fitted to synthetic data to provide a low-dimensional approximation of a
full adaptive network with symmetric STDP. Our framework represents
a step toward a low-dimensional description of adaptive networks with
STDP, and could for example inform the development of new therapies
aimed at maximizing the long-lasting effects of brain stimulation.
1 Introduction
Synaptic plasticity is considered the primary mechanism for learning and
memory consolidation. Neurons with similar activity patterns strengthen
their synaptic connections, while others connections may weaken. Spike-
timing-dependent plasticity (STDP) has been suggested as an unsuper-
vised, local learning rule in neural networks (Gerstner et al., 1996; Song
et al., 2000) motivated by experimental findings (Markram et al., 1997; Bi &
Poo, 1998; Feldman, 2000; Froemke & Dan, 2002; Cassenaer & Laurent, 2007;
Sgritta et al., 2017). These experimental studies reported synaptic strength-
ening or weakening depending on the order and timing of pre- and postsy-
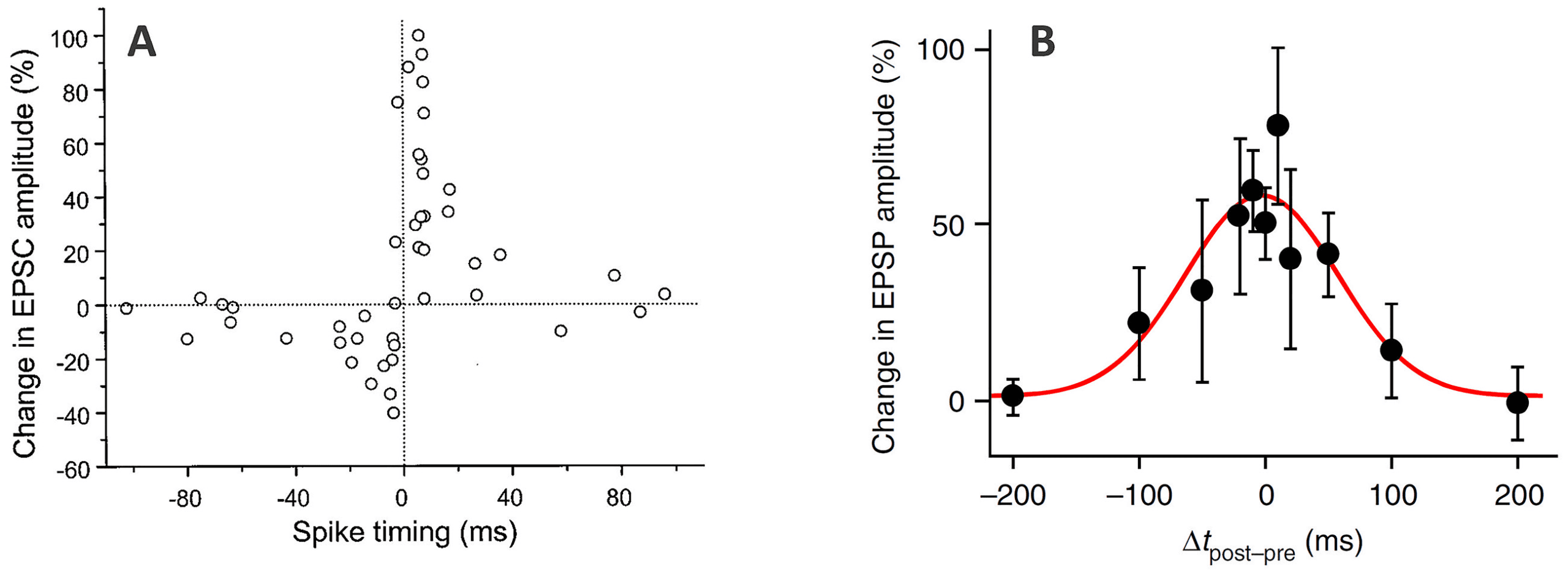
naptic spikes. In causal STDP (see Figure 1A), long-term potentiation (LTP)
occurs when the postsynaptic neuron fires shortly after the presynaptic
neuron. Conversely, long-term depression (LTD) occurs when the postsy-
naptic neuron fires shortly before the presynaptic neuron. The closer the
spike times are, the larger the effect. Noncausal, symmetric STDP has also
been reported in the hippocampus (Abbott & Nelson, 2000; Mishra et al.,
2016; see Figure 1B). Although Donald Hebb emphasized the importance
of causality in his theory of adaptive synaptic connections in 1949 (Hebb,
2005), such noncausal rules, which neglect temporal precedence, are some-
times referred to as Hebbian plasticity rules.1
As a major contributor to long-term plasticity (timescale of 1 s or longer),
STDP is key to long-term neural processes in the healthy brain, such as
memory (Litwin-Kumar & Doiron, 2014) and sensory encoding (Coulon
et al., 2011), but also to modulate networks affected by neurological dis-
orders (Madadi Asl et al., 2022). In particular, long-term plasticity is critical
to the design of effective therapies for neurological disorders based on in-
vasive and noninvasive brain stimulation. Paired associative stimulation
using transcranial magnetic stimulation (TMS) has been shown to trigger
STDP-like changes (Müller-Dahlhaus et al., 2010; Johnen et al., 2015; Wirat-
man et al., 2022), and STDP models have been used to design electrical
stimulation for stroke rehabilitation (Kim et al., 2021). Coordinated reset
deep brain stimulation (DBS) for Parkinson’s disease was designed to in-
duce long-term plastic changes outlasting stimulation using STDP models
1
In this work, we call plasticity rules causal when temporal precedence is enforced (as
in “classical” STDP rules; Bi & Poo, 1998), and symmetric when inverting spike timings and
phase differences leads to the same type of adaptation. We stay clear of the ambiguous
term Hebbian STDP, which is also sometimes used to refer to causal STDP in the experi-
mental literature (Cassenaer & Laurent, 2007; Sgritta et al., 2017).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Mean-Field Approximations for Networks With STDP
1483
Figure 1: Examples of STDP observed in pairing experiments. In typical STDP
pairing experiments, the presynaptic neuron is stimulated shortly before or after
forcing the postsynaptic neuron to fire by injecting a brief current pulse (with
a controlled delay). The pairing is repeated many times for each value of the
delay. (A) Causal STDP in synapses on glutamatergic neurons in rat hippocam-
pal culture. Adapted from Bi and Poo (1998). (B) Symmetric STDP in CA3-CA3
synapses in the hippocampus (slices in the rat). Adapted from Mishra et al.
(2016). In both panels, the horizontal axes represent the difference in spike tim-
ing (postsynaptic minus presynaptic), and the vertical axes represent measures
of the change in synaptic strength, either involving excitatory postsynaptic cur-
rents (EPSC, panel A) or excitatory postsynaptic potentials (EPSP, panel B).
(Tass & Majtanik, 2006) and was later validated in nonhuman primates (Tass
et al., 2012; Wang et al., 2016) and patients (Adamchic et al., 2014).
However, progress in these areas is restricted by the significant compu-
tational cost associated with simulating neural network models with STDP
and by the lack of low-dimensional description of such networks. Indeed,
simulating networks with STDP of even moderate size for more than a
couple of minutes of biological time can be impractical because the num-
ber of weight updates scales with the square of the network size. Low-
dimensional mean-field approximations have been developed for networks
with short-term plasticity (Tsodyks et al., 1998; Taher et al., 2020; Gast et al.,
2020; Schmutz et al., 2020; Gast et al., 2021), but reductions for STDP have
assumed that plasticity does not change firing rates and spike covariances
(Ocker et al., 2015) or that the network is in a balanced state at every point
in time (Akil et al., 2021). Even if node dynamics are given by a simple
Kuramoto-type model, it is a challenge to understand the dynamics of large
networks with adaptivity. While the continuum limit of Kuramoto-type net-
works with STDP-like adaptivity can be described by integro-differential
equations from a theoretical perspective (Gkogkas et al., 2021), these do not
necessarily elucidate the resulting network dynamics or yield a computa-
tional advantage. Approaches like the Ott-Antonsen reduction (Ott & An-
tonsen, 2008), which have been instrumental to deriving low-dimensional
descriptions of phase oscillators (see Bick et al., 2020) are not directly
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1484
B. Duchet, C. Bick, and Á. Byrne
applicable to adaptive networks where all connection weights evolve in-
dependently of one another. Indeed, one would not expect an exact mean-
field description with only a few degrees of freedom to be possible (as for
the Kuramoto model with static connectivity) without making further as-
sumptions, as any exact low-dimensional description would have to reflect
the high, adaptivity-induced multistability (Berner et al., 2019).
Models of causal, additive STDP based on differences in spike timing
are exemplified by the work of Song et al. (2000). They assumed that the
synaptic strength κ
kl from presynaptic neuron l to postsynaptic neuron k is
updated only when either neurons spike and the corresponding change in
synaptic strength from l to k is given by
⎧
⎪⎨
⎪⎩
(cid:3)κ
kl
=
−(cid:3)tkl
/τ+
−|(cid:3)tkl
|/τ−
A+e
−A−e
0
− tl
> 0,
for (cid:3)tkl
for (cid:3)tkl
for (cid:3)tkl
= tk
< 0,
= 0,
(1.1)
where the most recent spike times of neurons k and l are tk and tl, the pa-
rameters A+ and A− determine the magnitude of LTP and LTD, and τ+ and
τ− determine the timescale of LTP and LTD, respectively (see Figure 4A).
Conversely, symmetric STDP with both LTP and LTD can be modeled by
asserting that synaptic strengths are updated when either neuron spikes,
with a change in synaptic strength from l to k given by the Mexican hat
function (Ricker wavelet),
(cid:3)κ
kl
=
2a√
3bπ 1/4
(cid:9)
(cid:8)
2
(cid:6)
(cid:7)
1 −
(cid:3)tkl
b
−(cid:3)t2
e
kl
/(2b2 ),
(1.2)
where a scales the magnitude of STDP, and b scales the temporal width of
the Mexican hat (see Figure 2A).
k
To approximate STDP in phase oscillator networks, simpler phase-
dependent plasticity (PDDP) rules have been developed that prescribe
synaptic changes based on differences in phase of neuron pairs rather than
differences in spike timing. If the state of oscillator k is given by a phase vari-
able θ
∈ [0, 2π ) on the circle, the change of coupling weight between oscil-
lators k and l according to PDDP depends on their phase difference θ
− θ
k.
l
While symmetric STDP can be approximated by the symmetric PDDP rule
originally proposed by Seliger et al. (2002), several authors added a phase-
shift parameter ϕ in order to approximate causal STDP-like learning (Aoki
& Aoyagi, 2009; Berner et al., 2019), as well as other types of plasticity. With
this single-harmonic PDDP rule, the weight κ
kl from oscillator l to oscillator
k evolves according to
dκ
kl
dt
= (cid:8) [λ cos(θ
l
− θ
+ ϕ) − κ
kl] ,
k
(1.3)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Mean-Field Approximations for Networks With STDP
1485
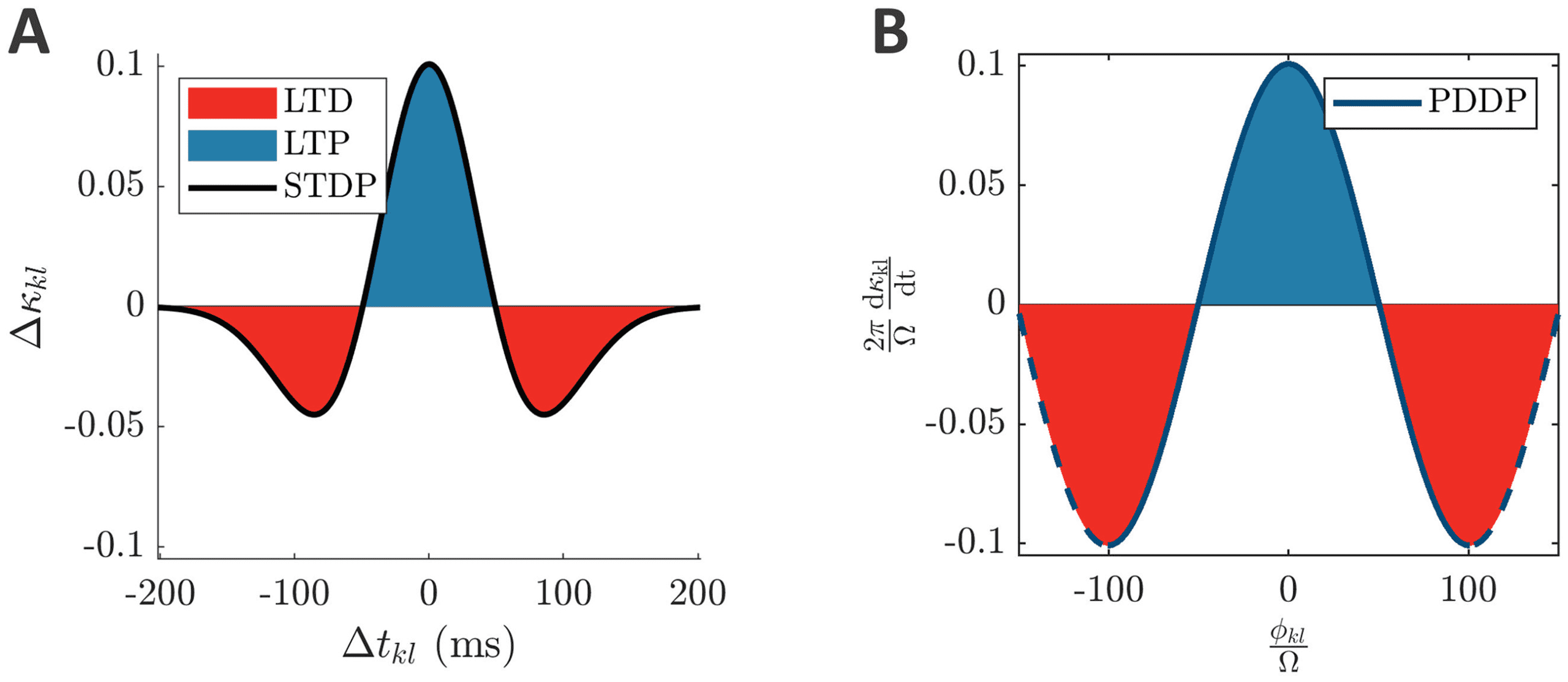
Figure 2: From symmetric STDP to single-harmonic PDDP. (A) Symmetric
STDP function (Mexican hat, equation 1.2) describing the change in weight (cid:3)κ
kl
as a function of the difference between spike times (cid:3)tkl. (B) Considering the
kl mod 2π instead of the difference between spike times, the
phase difference φ
STDP function in panel A can be approximated by the PDDP function in panel
φ
B (equation 1.3 with ϕ = 0). The horizontal axis is
kl
(cid:11) , and the vertical axis is
2π
to enable comparison with panel A. The solid blue line corresponds to
(cid:11)
= 0; the dashed blue line
one oscillatory period at frequency (cid:11) centered on φ
kl
extends beyond one period. The parameters used in panel A are a = 0.025822,
b = 0.049415, corresponding to λ = 1, (cid:8) = 0.5, (cid:11) = 10π in panel B. LTP is high-
lighted in blue and LTD in red.
dκ
kl
dt
where λ controls the strength of PDDP relative to the decay of the synaptic
strength and (cid:8) sets the relative timescale between the plasticity mechanism
and the phase dynamics. When ϕ = 0, we recover the learning rule intro-
duced by Seliger et al., which is symmetric around a phase difference of
zero. For ϕ = π/2, the cosine term is antisymmetric around zero, which pro-
vides a first level of approximation of additive, causal STDP (in the absence
of the decay term). However, this is a coarse approximation. A PDDP rule
directly based on causal STDP exponential kernels (Maistrenko et al., 2007)
could be more closely related to causal STDP. Lücken et al. (2016) proposed
such a rule and determined the correspondence between the parameters of
the causal STDP rule, the parameters of the PDDP rule, and the parameters
of the underlying network of coupled oscillators (see Figure 4B). Impor-
tantly, the synaptic strengths are continuously updated based on the evolv-
ing phase differences, while standard models of neural plasticity assume
updates as discrete events when a neuron spikes.
Here, we construct mean-field approximations for coupled Kuramoto
phase oscillators subject to PDDP and compare these approximations to
fully adaptive networks where every edge evolves according to STDP.
Specifically, we consider two types of PDDP rules: rules that update
connection weights continuously, as was done in previous studies, and
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1486
B. Duchet, C. Bick, and Á. Byrne
event-based rules, where weights are updated according to phase differ-
ences at a particular phase corresponding to spiking. In section 2, we show
that single-harmonic PDDP rules can indeed approximate symmetric STDP
in adaptively coupled networks of Kuramoto oscillators, while a multihar-
monic rule is required to accurately approximate causal STDP. For PDDP
rules, we derive exact equations describing the evolution of the mean cou-
pling strength in terms of the Kuramoto/Daido order parameters that en-
code synchrony of the oscillators’ phases (see section 3). We then focus
on networks with symmetric adaptive coupling that naturally form clus-
ters (see section 2). For such networks, we construct mean-field approxi-
mations (see section 4) for the emergent coupling topologies, where each
cluster corresponds to a coupled population. If we assume that coupling
between clusters is through the mean coupling strength—rather than by
individual weights between oscillators—we obtain low-dimensional Ott-
Antonsen equations for the mean-field limit. We explicitly analyze the dy-
namics of the reduced equations for adaptive networks for one and two
clusters. Note that these mean-field descriptions are not valid globally (i.e.,
there is no single reduced equation that is valid on all of state space) but
rather aim to capture the dynamics on part of overall phase space deter-
mined by the initial conditions. In other words, we have a family of low-
dimensional dynamics that can describe part of the phase space for this
very high-dimensional system. Finally, we show that the dynamics of the
full network can be approximated by such a family of low-dimensional dy-
namics by extracting the mean field description from the emergent cluster-
ing (see section 5). Since brain activity is transient, we focus on transients
and consider additive plasticity without bounds on individual weights for
causal STDP. In line with previous studies, however, we include a weight
decay term when considering symmetric STDP (Seliger et al., 2002; Berner
et al., 2019).
2 PDDP Can Approximate STDP in Kuramoto Networks
Adaptation of network connections through STDP rely—as the name
suggests—on the timing of action potentials of the coupled neurons. If the
state of each neuron can be described by a single phase variable (e.g., if the
coupling is weak; Ashwin et al., 2016), then it may be possible to approx-
imate STDP by an adaptation rule that depends on the phase differences
between oscillators such as equation 1.3. In this section, we now consider
general PDDP rules, which can update weights continuously (as in equa-
tion 1.3) or update at discrete time points (spiking events). We show that
for a network of phase oscillators, these PDDP rules can approximate both
symmetric and causal STDP. For causal STPD, the accuracy increases sub-
stantially as the number of harmonics in the PDDP rule is increased.
To illustrate this, we focus on the Kuramoto model (Kuramoto, 1975),
which is widely used to understand synchronization phenomena in
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Mean-Field Approximations for Networks With STDP
1487
neuroscience and beyond, subject to plasticity. Specifically, we consider N
coupled Kuramoto oscillators where oscillators represent coupled neurons
(Weerasinghe et al., 2019; Nguyen et al., 2020; Weerasinghe et al., 2021). The
phase θ
k of oscillator k evolves according to
dθ
k
dt
= ω
k
+ 1
N
N(cid:10)
l=1
kl sin(θ
κ
l
− θ
k)
(2.1)
with intrinsic frequency ω
kl of the synaptic connections
from oscillator l to oscillator k (subject to plasticity). The (complex-valued)
Kuramoto-Daido order parameters,
k and strength κ
Z(m) = 1
N
N(cid:10)
k=1
eimθ
k ,
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
for m ∈ Z capture the (cluster) synchrony of the oscillator phases. The mag-
nitude of the first-order parameter Z := Z(1)—simply called the Kuramoto
order parameter—captures global synchrony, that is, for Z = ρei(cid:14)
, we have
|Z| = ρ = 1 if all oscillators have the same phase θ
= · · · = θN. Similarly,
1
|Z(2)| = 1 if the oscillators form two antiphase clusters where θ
k or
θ
j
+ π, and so on.
= θ
= θ
k
j
2.1 Principles to Convert STDP to PDDP. PDDP rules prescribe synap-
tic changes based on differences in phase of neuron pairs rather than differ-
ences in spike timing and can be used to approximate both symmetric and
causal STDP in phase oscillator networks. In particular, the approximation
is expected to hold under the assumption that the evolution of phase dif-
ferences is slower than the phase dynamics (Lücken et al., 2016). Under this
assumption, spike time differences are approximated by dividing phase dif-
ferences by the mean angular frequency of the network (cid:11) = 1
N
N
k=1
As the phase difference is continuous in time, the discrete weight up-
dates, based on spike-time differences in the case of STDP, can be converted
to a continuous-time differential equation in terms of the phase differences.
As a result, the coupling weight between each pair of neurons updates con-
tinuously based on the phase difference between the pre- and postsynap-
tic oscillators; we refer to this as continuously updating PDDP or simply
PDDP when there is no ambiguity. STDP updates occur every time a neu-
ron spikes, while PDDP updates occur continuously at every point in time.
To ensure that STDP and continuously updating PDDP scale similarly, we
scale the discrete STDP updates by the average number of spikes per unit
time (cid:11)/2π.
(cid:11)
k.
ω
Rather than updating weights continuously, we can restrict weight up-
dates to occur only at spiking events. We say that oscillator k spikes if its
phase increases through θ
k be the qth firing time of neuron k.
= 0, and let tq
k
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1488
B. Duchet, C. Bick, and Á. Byrne
At each spiking event, we update the coupling weight between each pair of
neurons based on their phase difference; we give explicit examples of the
functional form of the updates below. We refer to this type of PDDP rule as
event-based PDDP (ebPDDP). While there is an explicit phase dependence
through the events, the actual change only depends on the phase difference.
To ensure appropriate scaling, we again multiply by the average number of
spikes per unit time and introduce an additional factor that is only nonzero
when either the pre- or postsynaptic neuron spikes. This factor is de-
(cid:13)
δ(t − tq
fined as C =
/2, where δ denotes the Dirac delta
l )
function.2
δ(t − tq
k ) +
(cid:12) (cid:11)
(cid:11)
q
q
kl
dt
= −(cid:8)κ
2.2 Symmetric STDP and Single-Harmonic PDDP. In this section, we
show that symmetric, noncausal STDP modeled by equation 1.2 together
with the weight decay dκ
kl can be approximated by the single-
harmonic PDDP learning rule introduced by Seliger et al. (2002; see equa-
tion 1.3 with ϕ = 0). We refer to this rule in what follows as the Seliger rule.
As detailed in the previous section, discrete STDP updates should be scaled
by (cid:11)/2π to obtain continuous PDDP updates. Therefore, by matching the
scaled maximum of equation 1.2 with the maximum of equation 1.3, we
have [(cid:11)/(2π )]
= (cid:8)λ, which determines the value of λ for a
given (cid:8) (see the example in Figure 2). Moreover, to ensure that the scale
of spike timing differences in the STDP rule and the scale of phase differ-
ences in the PDDP rule match without modifying the Seliger rule, we choose
b ≈ π/(2(cid:11)) (see Figure 2). Arbitrary values of b could be accommodated by
scaling the phase difference term in the Seliger rule as detailed in the pre-
vious section. The corresponding event-based PDDP rule reads
(cid:9)
(cid:13)
3bπ 1/4)
(cid:12)
2a/(
√
(cid:6)
(cid:11)
(cid:11)
dκ
kl
dt
= (cid:8)
λ
eb
q
δ(t − tq
k ) +
2
δ(t − tq
l )
q
cos(θ
l
− θ
k) − κ
kl
,
(2.2)
= λ 2π
with λ
ever the pre- or postsynaptic neuron spikes.
eb
(cid:11) . Note that updates to the coupling strengths happen when-
As shown in Figure 3, both single-harmonic PDDP rules (the Seliger
rule and equation 2.2) can approximate symmetric STDP (equation 1.2) in
networks of Kuramoto oscillators. Simulation details can be found in ap-
pendix A.1. The time evolution of the weight distribution (panel A), the
coupling matrix at the last simulation time point (panel B), as well as the
the time evolution of the average coupling (panel C1) and network syn-
chrony (panels C2–C3) are comparable across learning rules. In particu-
lar, the Pearson’s correlation between the STDP coupling matrix and the
2
The division by 2 ensures that this rule scales similarly to the STDP rule and the PDDP
rule with continuous updates.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Mean-Field Approximations for Networks With STDP
1489
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
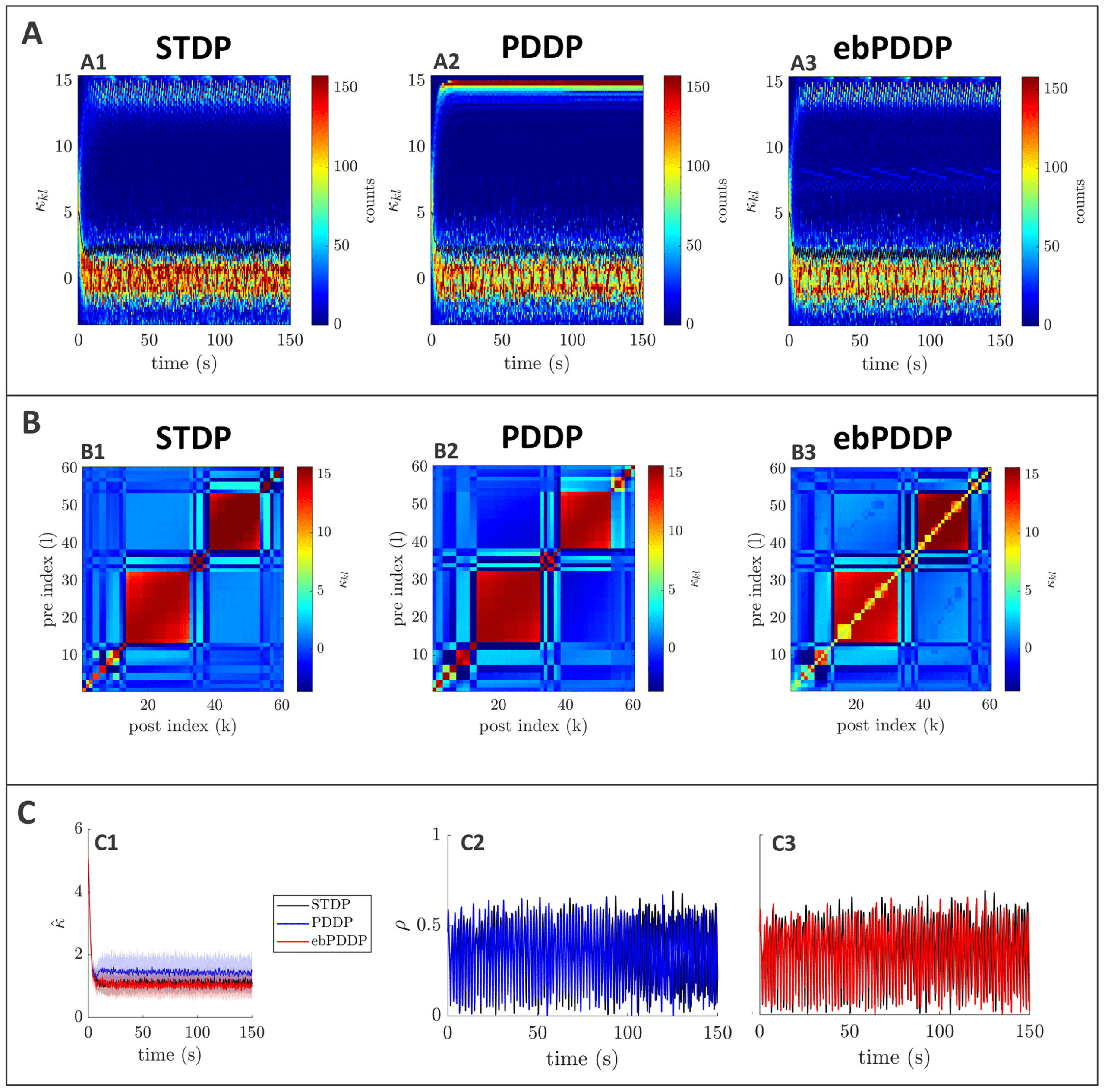
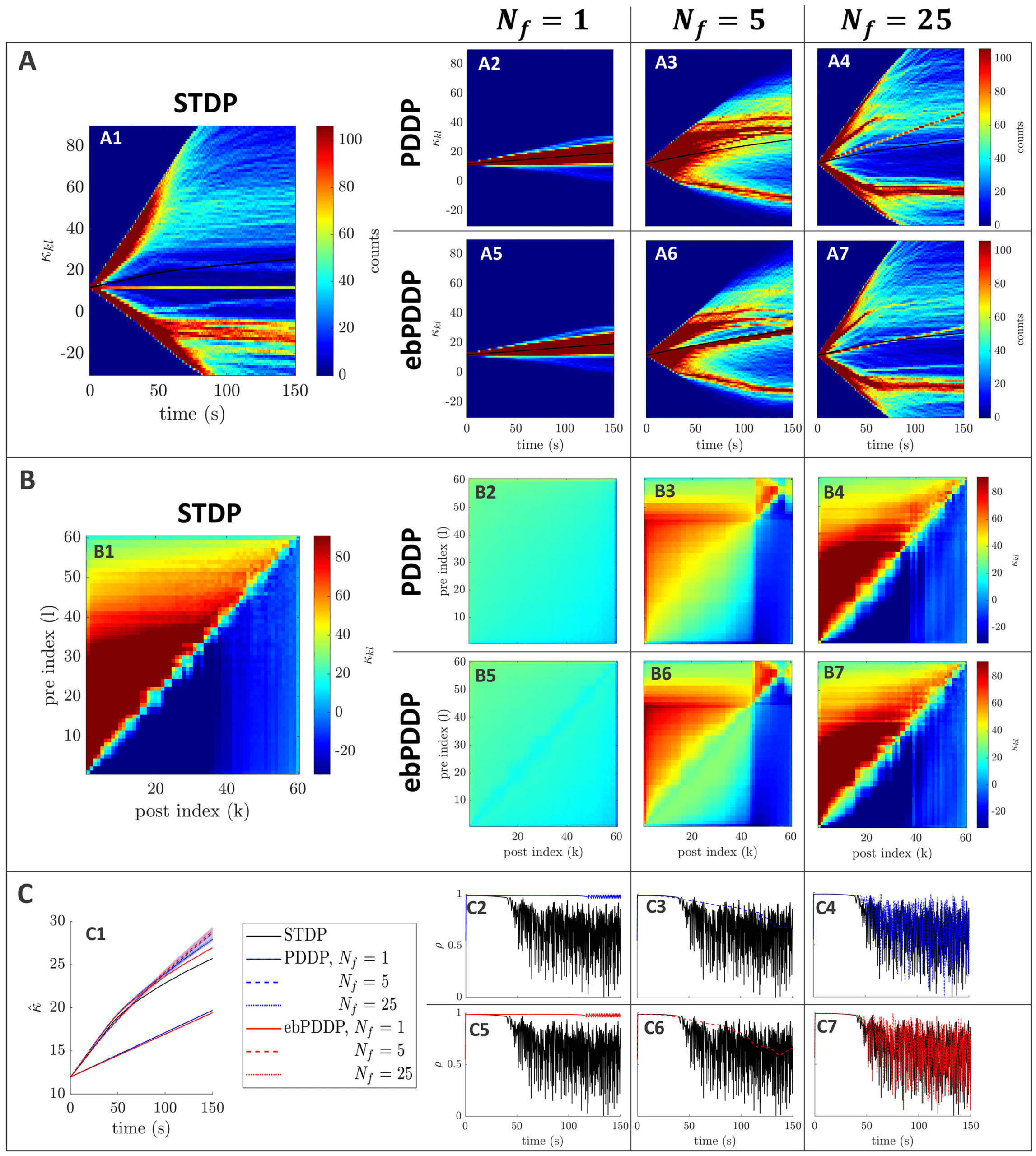
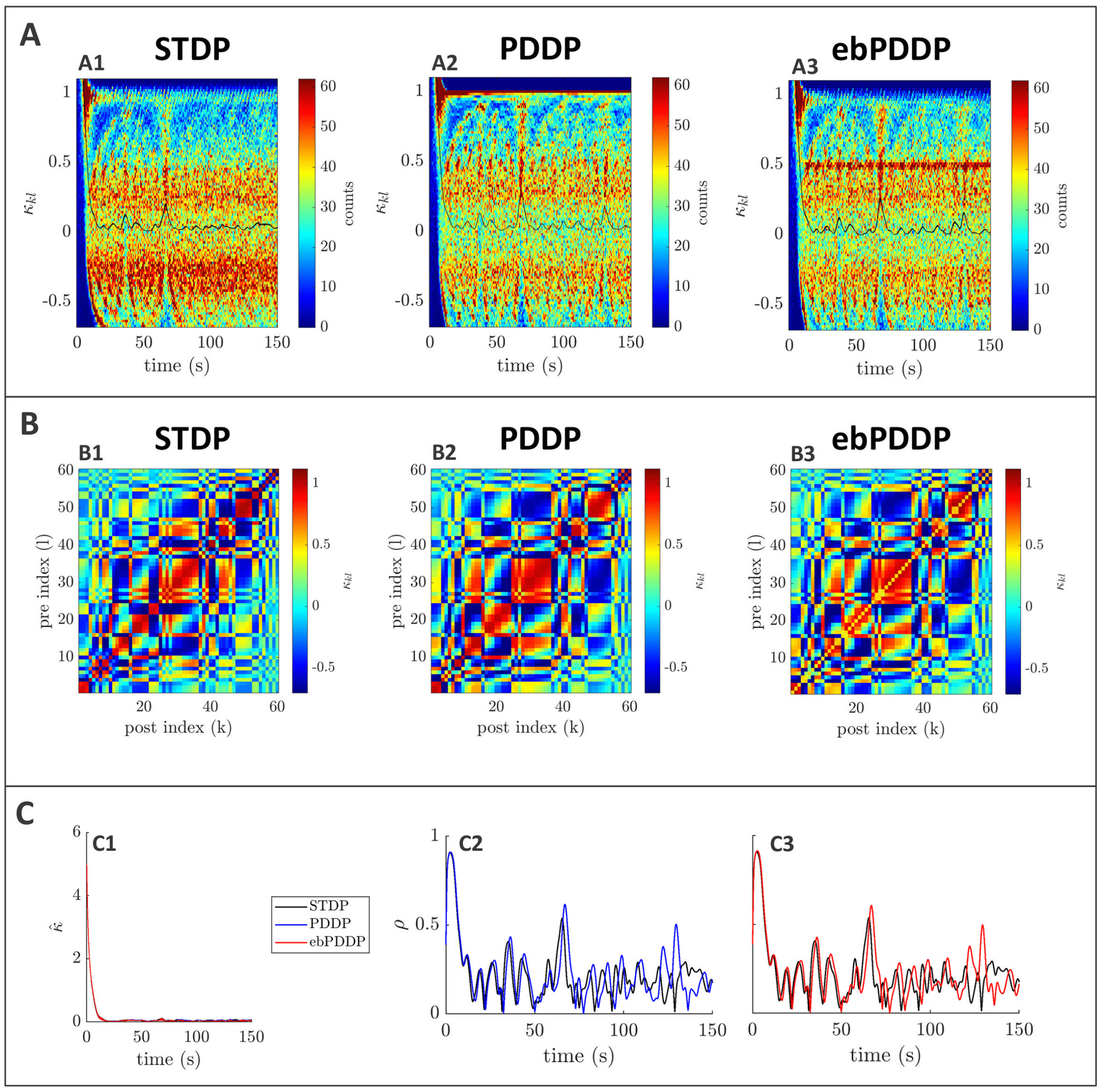
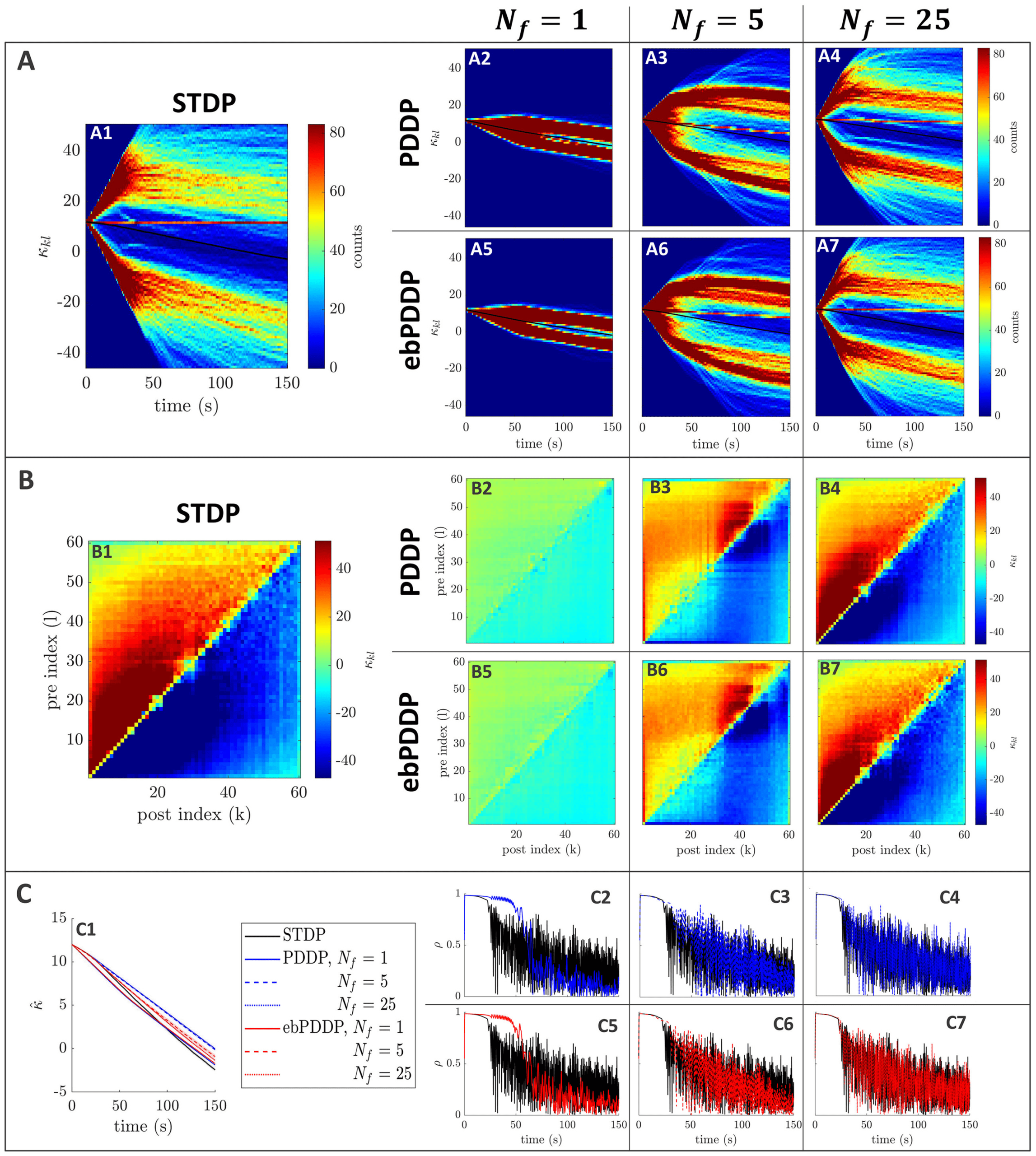
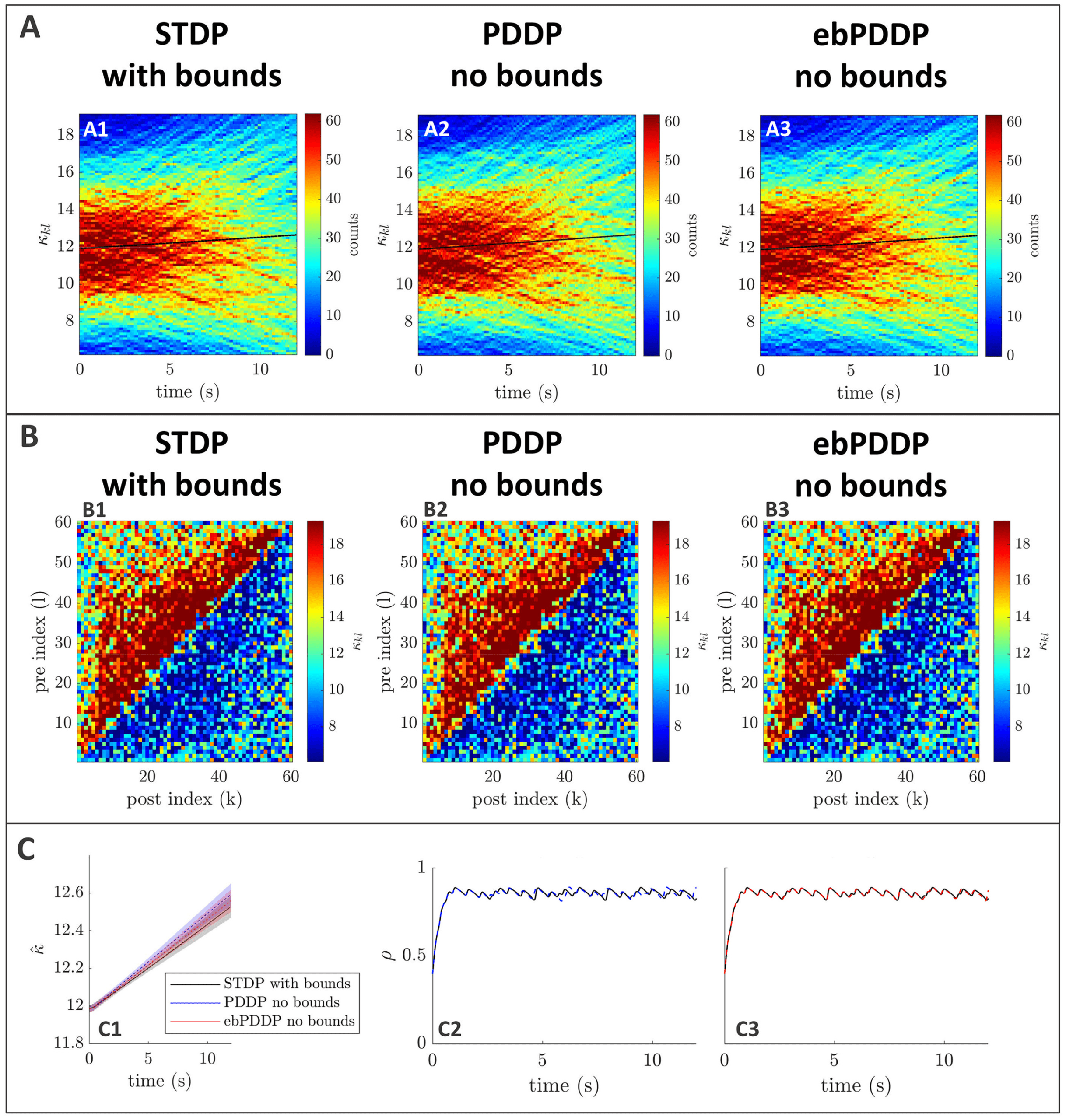
Figure 3: Comparison between symmetric STDP and PDDP in a Kuramoto
network (two synchronized cluster state). (A) Evolution of the distribution of
coupling weights with time (100 bins at each time point). The average weight is
represented by a thin black line. STDP is shown in A1, PDDP in A2, and ebPDDP
in A3. (B) Coupling matrix at t = 150 s, with oscillators sorted by natural fre-
quency. STDP is shown in panel B1, PDDP in panel B2, and ebPDDP in panel
B3. (C) Time evolution of average coupling (see panel C1, where error bars rep-
resent the standard error of the mean over five repeats; the high variability is due
to sensitivity to initial conditions) and network synchrony (see panels C2 and
C3). STDP is shown in black, PDDP in blue, and ebPDDP in red. (a = 0.38733,
b = 0.049415, σκ = 3, (cid:3) = 1.2π, (cid:11) = 10π (5 Hz)).
PDDP coupling matrix is 0.88, while the correlation between the STDP cou-
pling matrix and the ebPDDP coupling matrix is 0.90. For the parameter
set shown in Figure 3, we see the emergence of two synchronized clusters.
For this type of dynamics, the average coupling as a function of time may be
1490
B. Duchet, C. Bick, and Á. Byrne
better captured by ebPDDP than PDDP (panel C1). However, for the desyn-
chronized state (shown in Figure 11 in appendix C), there is little difference
between continuous PDDP and ebPDDP. In both states, the accuracy of the
approximation could be improved by considering a Fourier expansion of
the Mexican hat function rather than a single cosine term. We explore this
for causal, nonsymmetric STDP in the next section, as we found that a single
sine term is generally a poor approximation of the causal STDP kernel.
2.3 Causal STDP and Multiharmonic PDDP. In the previous section,
we considered PDDP rules with a single harmonic in the phase difference.
To get a better approximation of causal STDP, one can take more harmonics
into account.
2.3.1 Obtaining Multiharmonic PDDP Rules from Causal STDP. To approx-
imate causal STDP, we consider the PDDP rule proposed by Lücken et al.
(2016) as
dκ
kl
dt
=
(cid:11)
2π
(cid:7)
A+e
−φ
kl
(cid:11)τ+ − A−e
φ
−2π
kl
(cid:11)τ−
(cid:8)
= F(φ
kl ),
(2.3)
l
kl
− θ
= (θ
kl is small and positive, which will lead to a potentiation of κ
where φ
k) mod 2π, (cid:11) is the mean (angular) frequency of the
network, and other parameters have been defined in equation 1.1. In
equation 2.3, both synaptic potentiation (first term) and synaptic depres-
sion (second term) are described without requiring a piecewise definition
thanks to the fast-decaying exponentials. The correspondence of this PDDP
rule with additive STDP is illustrated in Figure 4B. If the postsynaptic neu-
ron k spikes (i.e., its phase increases through 0) shortly after the presynaptic
neuron l, φ
kl.
Conversely, if the postsynaptic neuron spikes shortly before the presynap-
tic neuron, φ
− 2π is small and negative, which will lead to a depression
of κ
kl. As laid out in section 2.1, spike time differences are approximated in
equation 2.3 by dividing phase differences by the network mean angular
frequency. Moreover, the scaling factor (cid:11)/2π (average number of spikes
per unit time) accounts for the conversion of discrete weight updates to
a continuous-time differential equation. The corresponding event-based
PDDP rule can be obtained as
(cid:11)
(cid:11)
kl
(cid:8)
dκ
kl
dt
=
q
δ(t − tq
k ) +
2
(cid:7)
δ(t − tq
l )
q
−φ
kl
(cid:11)τ+ − A−e
φ
−2π
kl
(cid:11)τ−
A+e
⎞
=
π
(cid:11)
⎛
(cid:10)
⎝
q
δ(t − tq
k ) +
(cid:10)
q
δ(t − tq
l )
⎠ F(φ
kl ),
,
(2.4)
where F is given by equation 2.3.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Mean-Field Approximations for Networks With STDP
1491
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
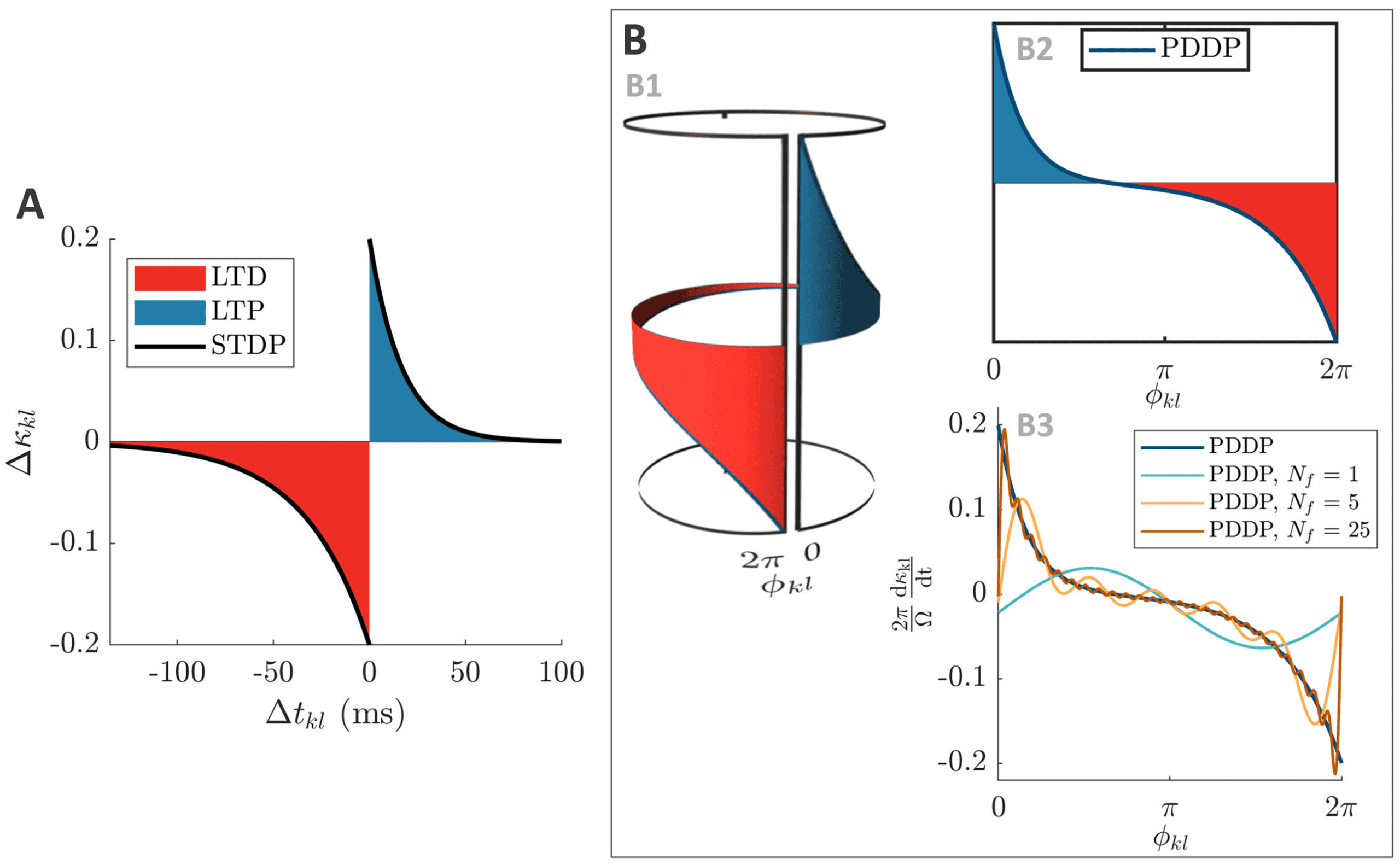
Figure 4: From causal STDP to multiharmonic PDDP. (A) STDP function (equa-
tion 1.1) describing the change in weight (cid:3)κ
kl as a function of the difference
between spikes times (cid:3)tkl. (B) Considering the phase difference φ
kl mod 2π in-
stead of the difference between spike times, the STDP function in panel A can
be approximated by the PDDP function in panel B2 (equation 2.3). As shown
= 0 and
in panel B1, wrapping the PDDP function around a cylinder to join φ
kl
= 2π illustrates the correspondence with the STDP function. In panel B3, the
φ
kl
PDDP function is approximated using truncated Fourier series with 1, 5, and
25 Fourier components. The vertical axis is 2π
to enable comparison with
panel A. The parameters used in all panels are τ+ = 16.8 ms and τ− = 33.7 ms,
A+ = A− = 0.2. LTP is highlighted in blue and LTD in red.
dκ
kl
dt
(cid:11)
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
In both cases, we can expand F(φ
kl ) as a Fourier series of the phase dif-
ference since φ
kl ) a 2π-periodic
kl is defined modulo 2π, which makes F(φ
function. The Fourier expansion will be key to deriving the evolution of
the average coupling strength in section 3 and can be truncated to include
only N f components for simulations (see the examples in Figure 4C). We
note that the PDDP rule by Berner et al. (2019) with ϕ ≈ π/2 is a single-
harmonic version of the rule by Lücken et al. (2016, with a vertical shift),
> 1
and call truncated Fourier expansions of equations 2.3 and 2.4 with N f
“multiharmonic PDDP.” We express the Fourier series of F as
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
F(φ
kl ) =
∞(cid:10)
m=−∞
cmemi(θ
l
−θ
k )
= a0
2
+
∞(cid:10)
m=1
[am cos{m(θ
l
− θ
k)} + bm sin{m(θ
l
− θ
k)}] ,
(2.5)
1492
B. Duchet, C. Bick, and Á. Byrne
where (cm)m∈Z are the complex-valued Fourier coefficients, or equivalently
(am)m∈N, and (bm)m∈N∗ are the real-valued Fourier coefficients. The Fourier
coefficients only depend on the parameters of the STDP rule, equation 1.1,
and (cid:11), and the real-valued coefficients can be obtained analytically as
(cid:18)
2π
F(x) cos(mx)dx
(cid:19)
A+τ+
1 + m2τ 2
+
2π
(cid:21)
(cid:20)
1 − e
− 2π
τ+
+ A−τ−
1 + m2τ 2
−
(cid:20)
− 2π
e
τ− − 1
(cid:21)(cid:22)
,
F(x) sin(mx)dx
am = 1
π
=
0
(cid:11)
2π 2
(cid:18)
bm = 1
π
0
(cid:6)
=
(cid:11)
2π 2
mA+τ 2
+
1 + m2τ 2
+
(cid:21)
(cid:20)
1 − e
− 2π
τ+
+ mA−τ 2
−
1 + m2τ 2
−
(cid:20)
1 − e
− 2π
τ−
(cid:9)
(cid:21)
.
(2.6)
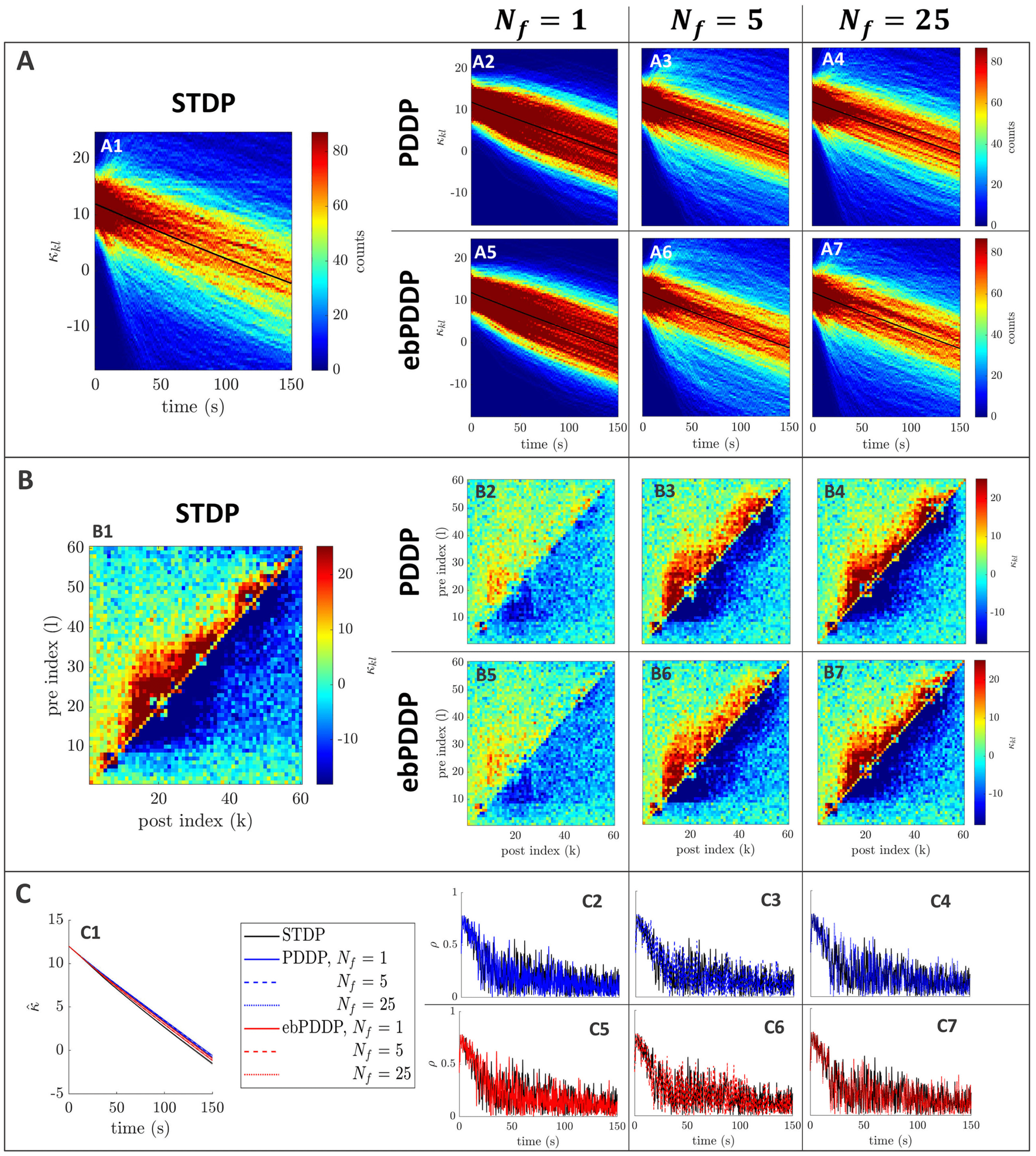
2.3.2 Comparison of Learning Rules. Multiharmonic PDDP can approxi-
mate causal STDP in Kuramoto networks (simulation details can be found
in appendix A.2). As the number of harmonics included in the PDDP rules
is increased, the dynamics for the networks with PDDP begin to match
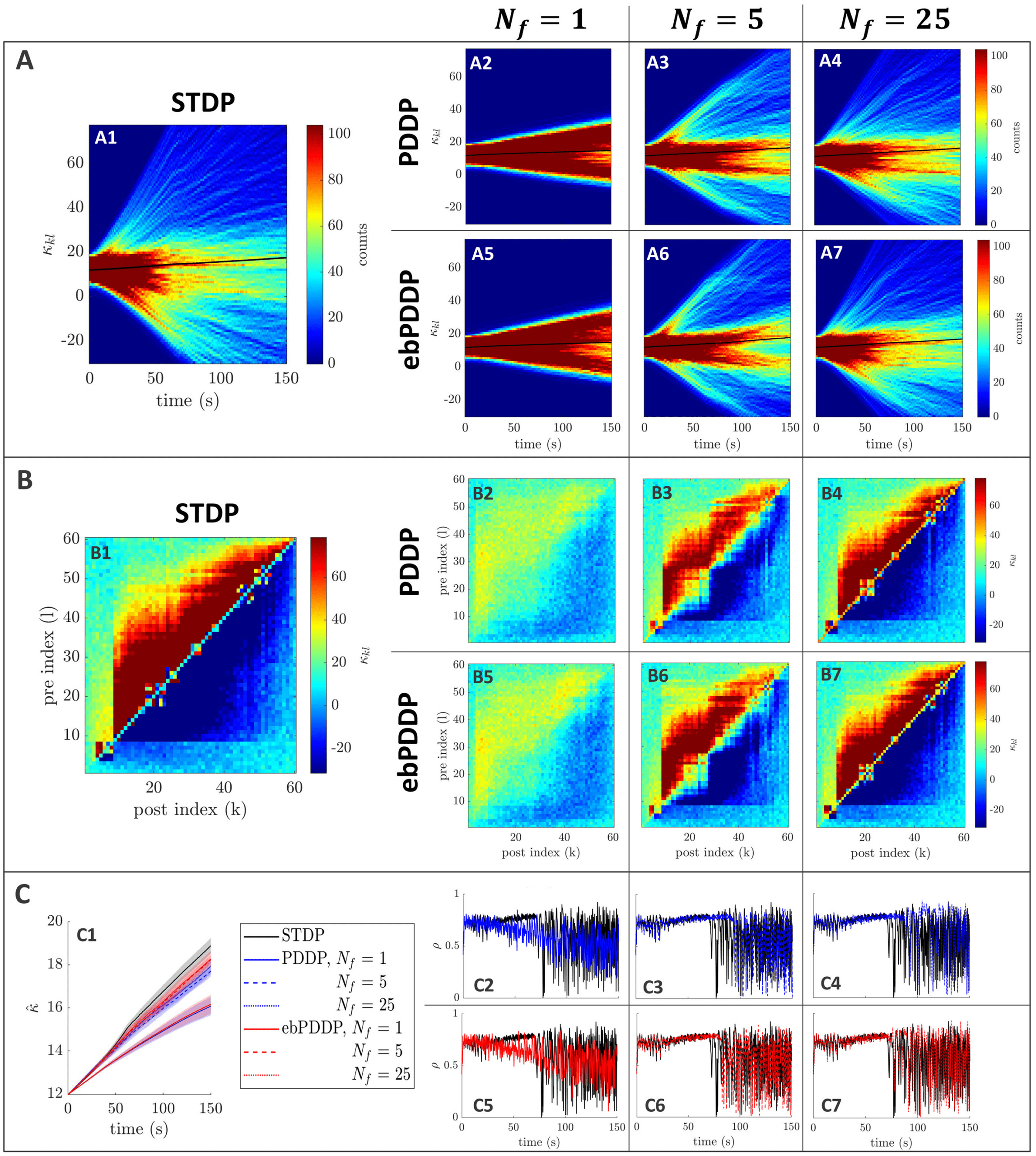
those of the STDP network (see Figure 5). The time evolution of the weight
distribution (panel A), the coupling matrix at the last simulation time
point (panel B), as well as the the time evolution of the average coupling
(panel C1) and network synchrony (panels C2 to C7) are closely matched for
causal STDP and multiharmonic PDDP or ebPDDP when enough Fourier
= 25). Simulations were also performed for
components are included (N f
a range of parameter values, and the findings were similar (see Figures 12
= 1) can pro-
to 15 in appendix C). Single-harmonic PDDP or ebPDDP (N f
vide a first level of approximation of causal STDP in certain cases when the
time evolution of the weight distribution is simple (see Figure 14). How-
ever, single-harmonic rules are unable to describe more complex cases, even
qualitatively (as seen in Figure 5). In all cases studied for a network fre-
quency of 5 Hz, 25 Fourier components are deemed sufficient to approxi-
mate the dynamics of the network with causal STDP. While the performance
of ebPDDP is similar to PDDP, ebPDDP is slightly more accurate than PDDP.
To quantitatively compare STDP to PDDP and ebPDDP, we construct error
metrics for the time evolution of the weight distribution ehist(κ
kl ), the aver-
age coupling e ˆκ , and the network synchrony eρ, and consider the Pearson’s
correlation between coupling matrices at the last simulation time point rκ ∞
kl .
These metrics are defined in appendix A.2. In general, these metrics im-
prove with increasing N f (see Figure 6A), although stagnation or a slight
worsening can be seen when the error is already low. Though it is of no con-
sequence in Kuramoto networks with sine coupling, self-coupling weights
are consistently different between causal STDP and multiharmonic PDDP
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Mean-Field Approximations for Networks With STDP
1493
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5: Comparison between STDP and PDDP in a Kuramoto network
(β = 0.5, σκ = 0.2, (cid:3) = 0.6π , (cid:11) = 10π (5 Hz)). Results for PDDP and ebPDDP
are shown for 1, 5, and 25 Fourier components N f (first, second, and third
columns on the right-hand side of the figure, respectively). (A) Evolution of the
distribution of coupling weights with time (100 bins at each time point). The
average weight is represented by a thin black line. STDP is shown in panel A1,
PDDP in panels A2 to A4, and ebPDDP in panels A5 to A7. (B) Coupling ma-
trix at t = 150 s, with oscillators sorted by natural frequency. STDP is shown in
panel B1, PDDP in panels B2 to B4, and ebPDDP in panels B5 to B7. (C) Time
evolution of average coupling (in panel C1, error bars represent the standard
error of the mean over five repeats) and network synchrony (panels C2 to C7).
STDP is shown in black, PDDP in blue, and ebPDDP in red. In all panels, the
approximation becomes better as N f is increased.
1494
B. Duchet, C. Bick, and Á. Byrne
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
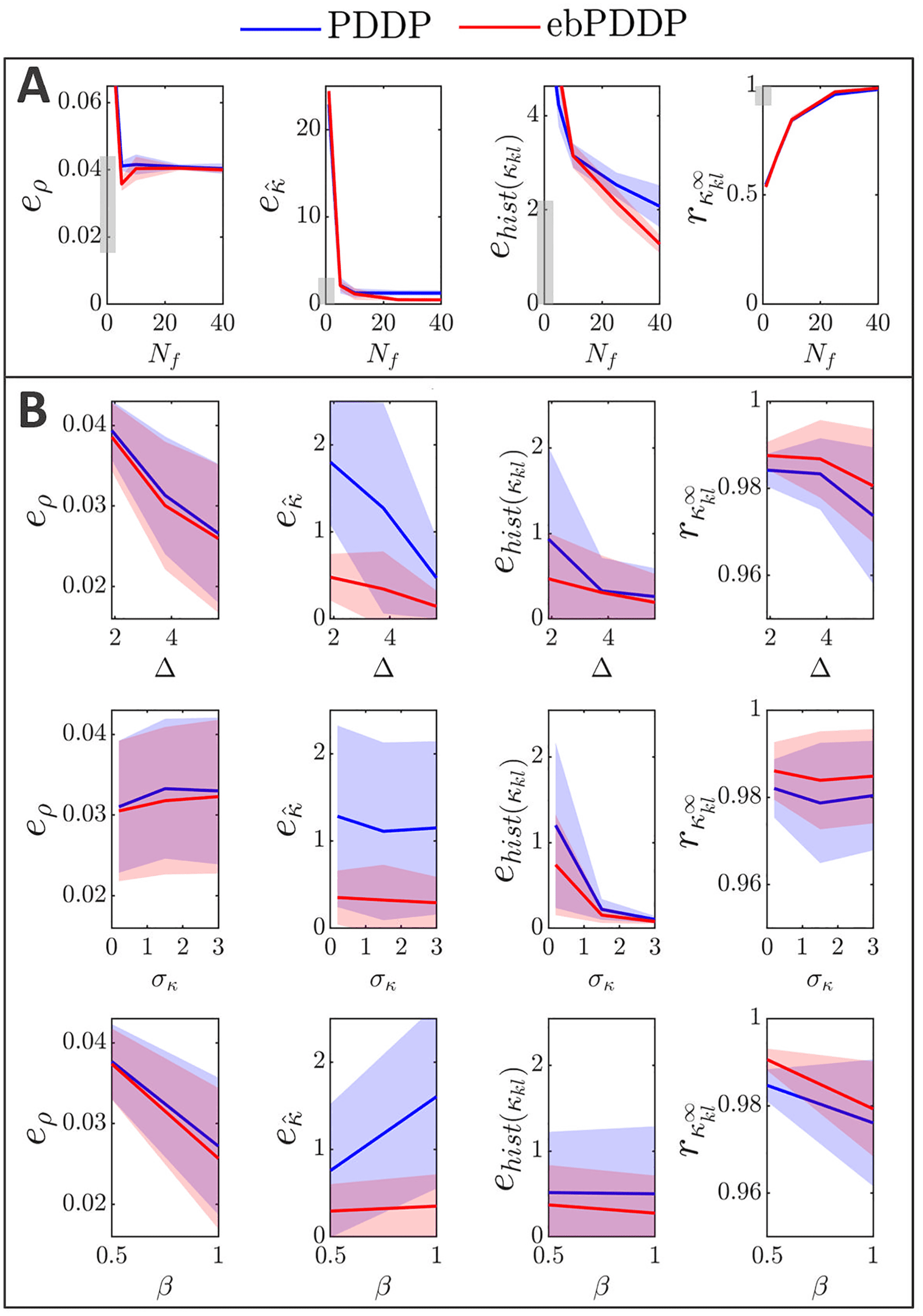
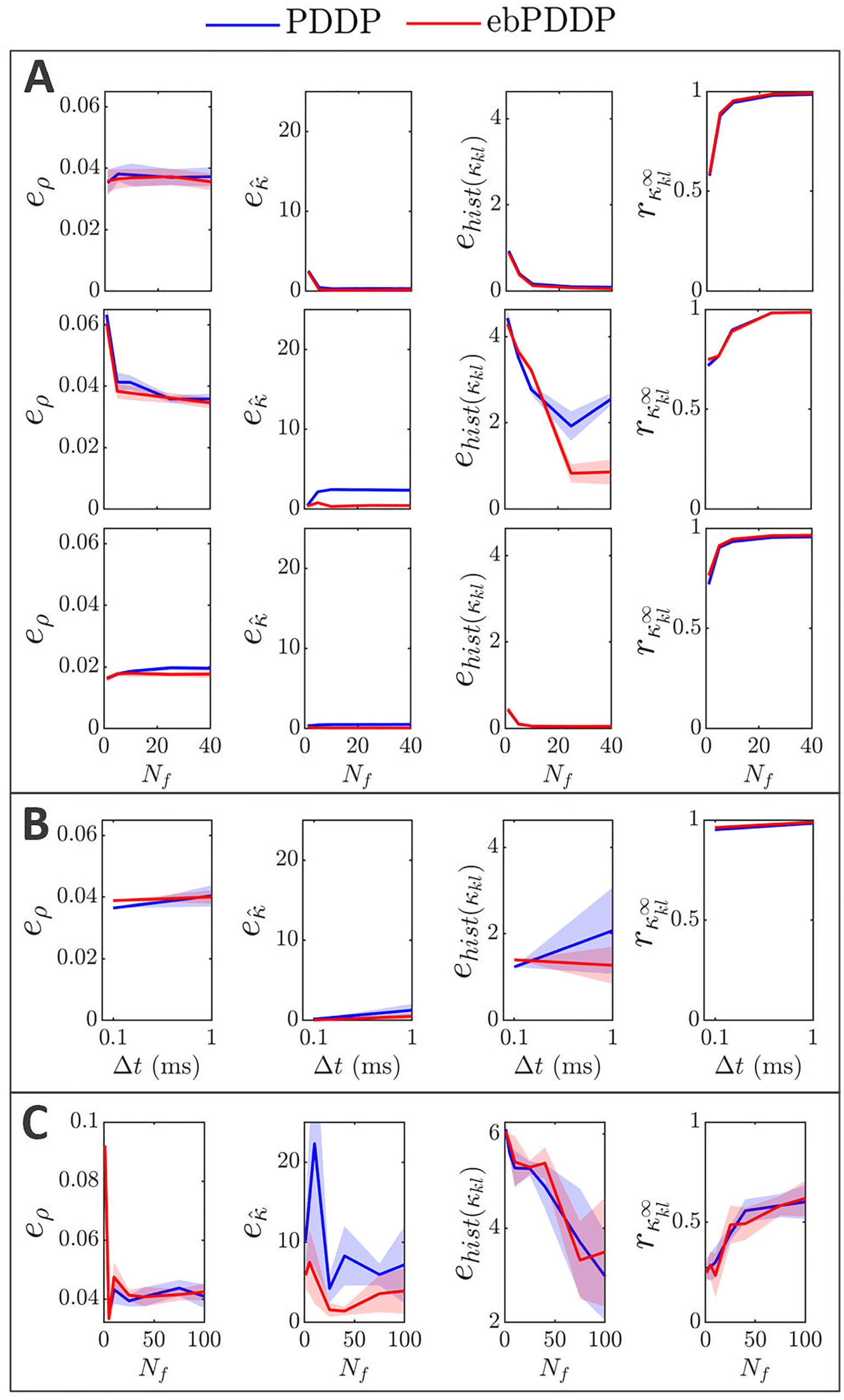
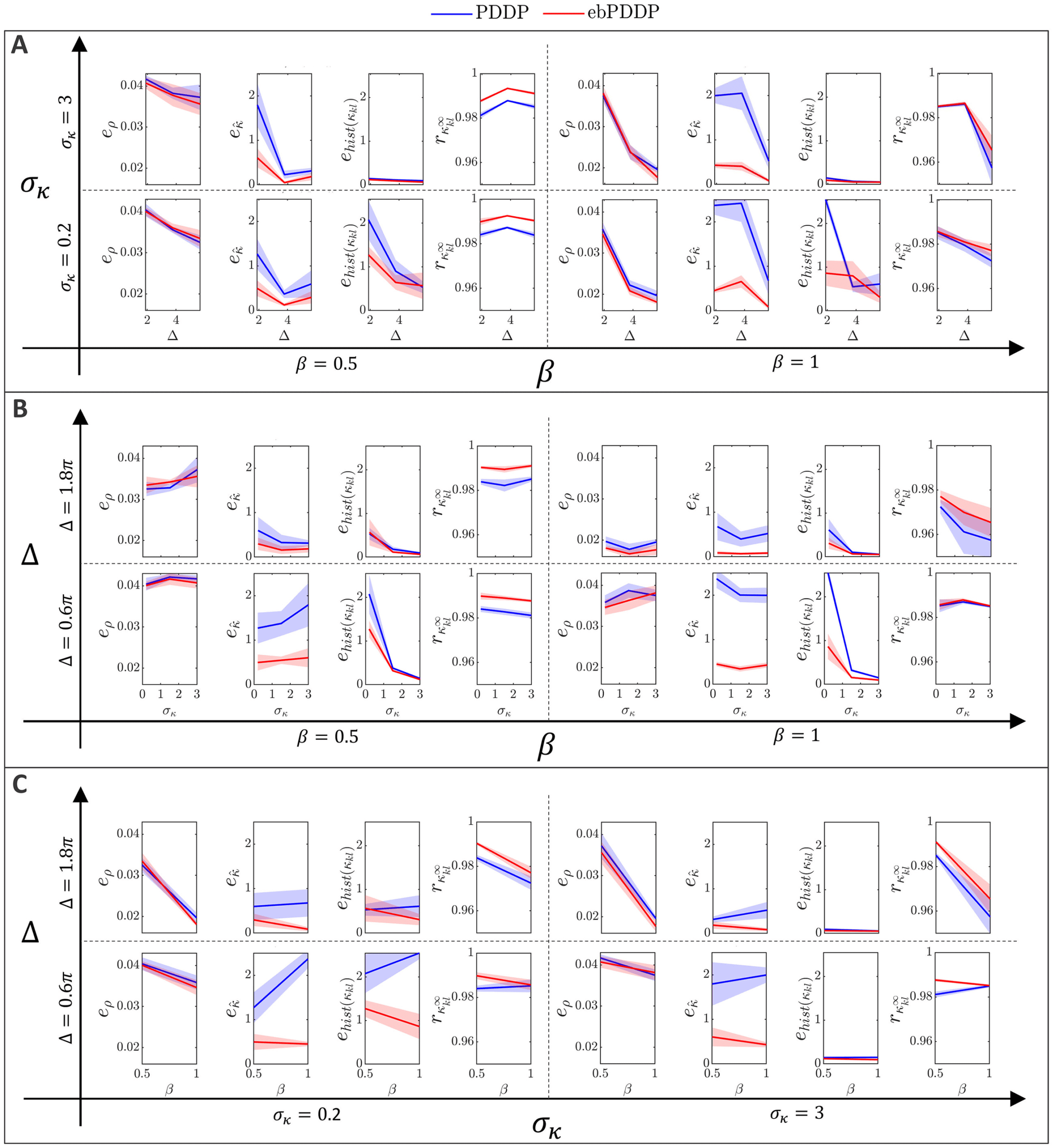
, (cid:3), σκ , and β on error metrics. Error metrics for PDDP
Figure 6: Influence of N f
compared to STDP for the time evolution of network synchrony eρ, average
coupling e ˆκ and distribution of weights ehist(κ
kl ), and for the coupling matrix at
the last stimulation point rκ∞
are shown in the first, second, third, and fourth
kl
columns, respectively. Results for PDDP are in blue and for ebPDDP in red.
(A) Influence of the number of Fourier coefficients N f on the error metrics for
the parameters used in Figure 5 (β = 0.5, σκ = 0.2, (cid:3) = 0.6π, (cid:11) = 10π). Error
bars show the standard error of the mean (sem) over five repeats. (B) Influence
= 40. The standard de-
of the network parameters on the error metrics for N f
viation of the oscillator frequency distribution (cid:3) is shown in the first row, the
standard deviation of the initial weight distribution σκ is given in the second
row, and the ratio for the LTP to LTD scaling factors β is depicted in the third
row. All combinations of parameters (cid:3) = {0.6π , 1.2π , 1.8π }, σκ = {0.2, 1.5, 3},
β = {0.5, 1} are included with five repeats for each combination. In each row,
averaging is performed over the parameters that do not correspond to the hor-
izontal axis (standard deviation error bars). Note that the scale of the vertical
axes is 2 to 10 times smaller than in panel A for readability (range indicated by
gray bars). See Figure 19 for detailed slices in parameter space.
Mean-Field Approximations for Networks With STDP
1495
or ebPDDP in our simulations. This is due to the truncated Fourier expan-
sions of F not being zero when the phase difference is zero (see Figure 4B3).
kl
2.3.3 Parameter Dependence. Model parameters influence the four met-
rics described in the previous section (see Figure 6B), although the impact
is minor (always stays > 0.96). Increasing the standard deviation
on rκ ∞
of the frequency distribution ((cid:3)) tends to improve the error metrics, except
kl , which gets slightly lower. This is expected since a larger (cid:3) reduces syn-
rκ ∞
chrony and makes the weight distribution more unimodal. The impact of
the standard deviation of the initial coupling distribution (σκ ) on the met-
rics is smaller, except for the time evolution of the weight distribution. The
effect of the ratio of the scales of LTD to LTP (β = A−/A+) depends on the
metric considered. The largest effect is a lowering of eρ when LTD domi-
nates (β = 1) compared to the balanced situation (β = 0.5). This is due to
the fact that the time evolution of ρ is closely approximated with N f
= 1
when LTD dominates, whereas in the balanced state, more Fourier compo-
nents are required to obtain a good approximation. Since dominant LTD
leads to lower synchrony, this matches the previous observation that lower
synchrony is associated with lower error metrics. Time courses of ρ for both
states can be found in appendix C; Figure 12 shows the balanced state, and
Figure 14 shows the LTD dominant regime.
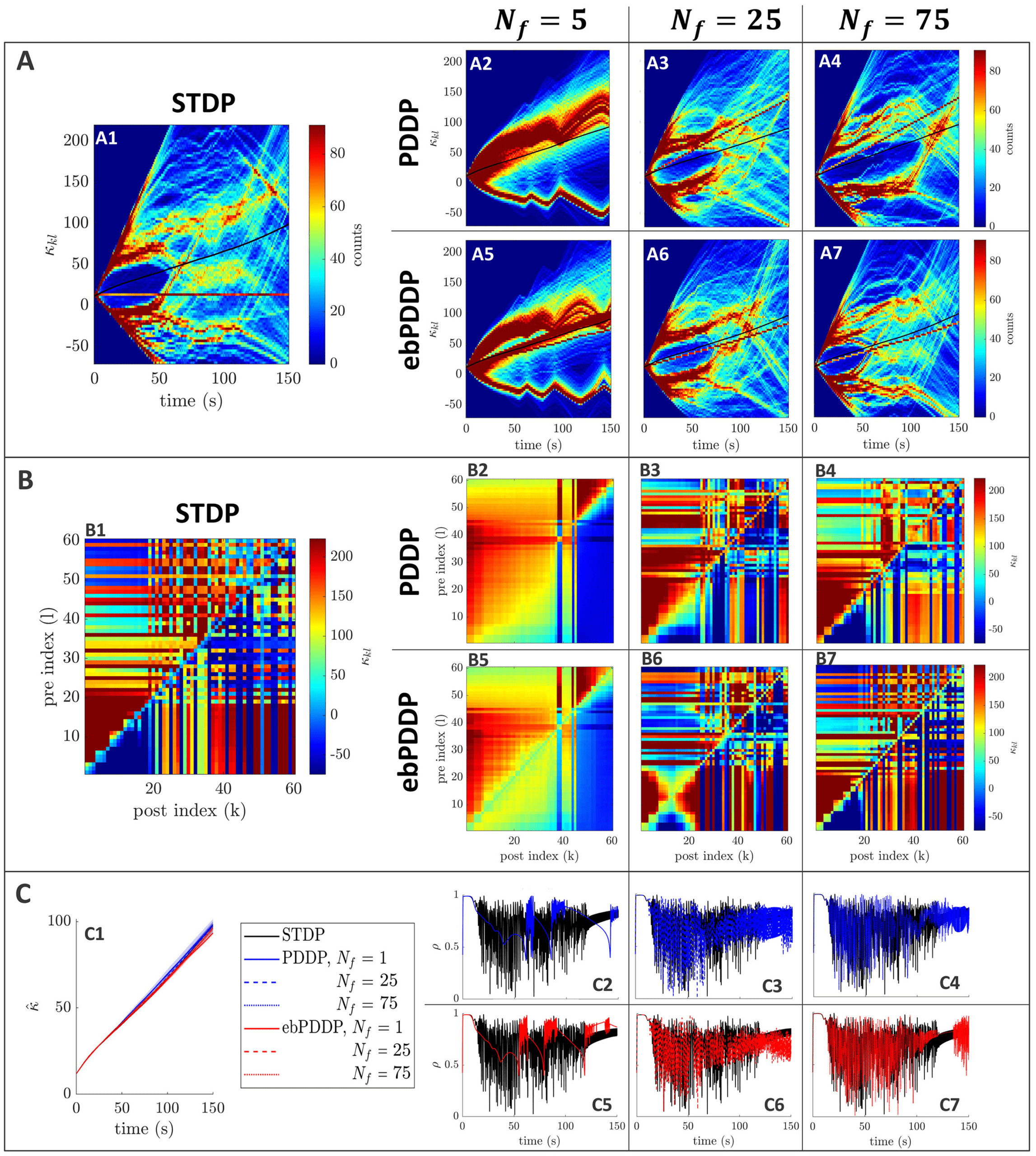
To test the robustness of our findings, we studied a network with a mean
frequency four times higher (20 Hz) and considered the least favorable part
of parameter space (lowest (cid:3), lowest σκ , and β = 0.5) (see Figure 15 in ap-
pendix C). The order of magnitude of the error metrics is the same as for
5 Hz, except for rκ ∞
kl (see Figure 18C in appendix C). The lower value for
rκ ∞
kl may be explained by the greater complexity and finer structures in the
coupling matrix. However, the coupling matrix obtained at the last stim-
= 75 (see Figure 15 in
ulation point with multiharmonic ebPDDP for N f
appendix C, panel B7) is qualitatively very similar to the coupling matrix
obtained with STDP (ses panel B1). At 20 Hz, the period of the oscillators
is comparable to the STDP time constants; hence, the weight distribution
patterns unfolding in time are more highly multimodal than at 5 Hz. These
patterns are still well approximated by multiharmonic PDDP and ebPDDP,
but a larger number of Fourier components than at 5 Hz is warranted for ac-
curate results. Simulating this higher-frequency network required a smaller
simulation time step ((cid:3)t = 0.1 ms). However, the time step has overall little
impact on the error metrics at lower frequencies (see Figure 18 in appendix
C, panel B).
Additional explorations of the parameter dependencies can be found in
Figures 18 and 19 in appendix C.
3 Evolution of the Average Coupling Strength in Networks with PDDP
While each coupling weight κ
now derive evolution equations for the average coupling weight
kl evolves independent of one another, we
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1496
B. Duchet, C. Bick, and Á. Byrne
ˆκ = 1
N2
N(cid:10)
N(cid:10)
k=1
l=1
κ
kl
(3.1)
for both continuously updating and event-based PDDP. Obtaining the
mean coupling weight dynamics is necessary for constructing our mean-
field approximations, which are based on the average coupling weights
within and between populations.
3.1 Average Coupling for General PDDP. Suppose that each weight
kl evolves according to a general, continuously updating PDDP rule dκ
κ
=
kl
dt
F(φ
kl ), where F is a 2π-periodic function of the phase difference φ
kl. The
PDDP rule in section 2.3 with F approximating causal STDP (see equa-
tion 2.3) is a particular example. Writing F(φ
kl ) =
k ) as in
equation 2.5 and differentiating equation 3.1 yields
m=−∞ cmemi(θ
(cid:11)∞
−θ
l
d ˆκ
dt
=
∞(cid:10)
m=−∞
cm
N2
N(cid:10)
N(cid:10)
k=1
l=1
emiθ
−miθ
l e
k .
(3.2)
This expression can be written in terms of the Kuramoto-Daido order pa-
rameters Z(m). We have Z(−m) = ¯Z(m) and consequently equation 3.2 reads
d ˆκ
dt
=
∞(cid:10)
m=−∞
cmZ(m) ¯Z(m) =
∞(cid:10)
(cid:23)
(cid:23)
Z(m)
(cid:23)
(cid:23)2.
cm
m=−∞
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
The series converges as |Z(m)| ≤ 1 and the Fourier series of F is assumed
to converge. Since cm + c−m = am and 2c0
= a0, the evolution equation for ˆκ
can be simplified to
d ˆκ
dt
= a0
2
+
∞(cid:10)
m=1
am|Z(m)|2.
(3.3)
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
In the case of F approximating causal STDP, the coefficients (am)m∈N are
given by equation 2.6. In the absence of bounds on the coupling weights,
equation 3.3 exactly describes the average coupling strength in a phase os-
cillator network with PDDP, as illustrated in Figure 7.
If the PDDP rule contains a decay term, the evolution of the mean cou-
pling strength will reflect this as well. More concretely, consider an evolu-
tion of individual coupling weights dκ
kl] as in the PDDP
= (cid:8) [λF(φ
kl ) − κ
kl
dt
Mean-Field Approximations for Networks With STDP
1497
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
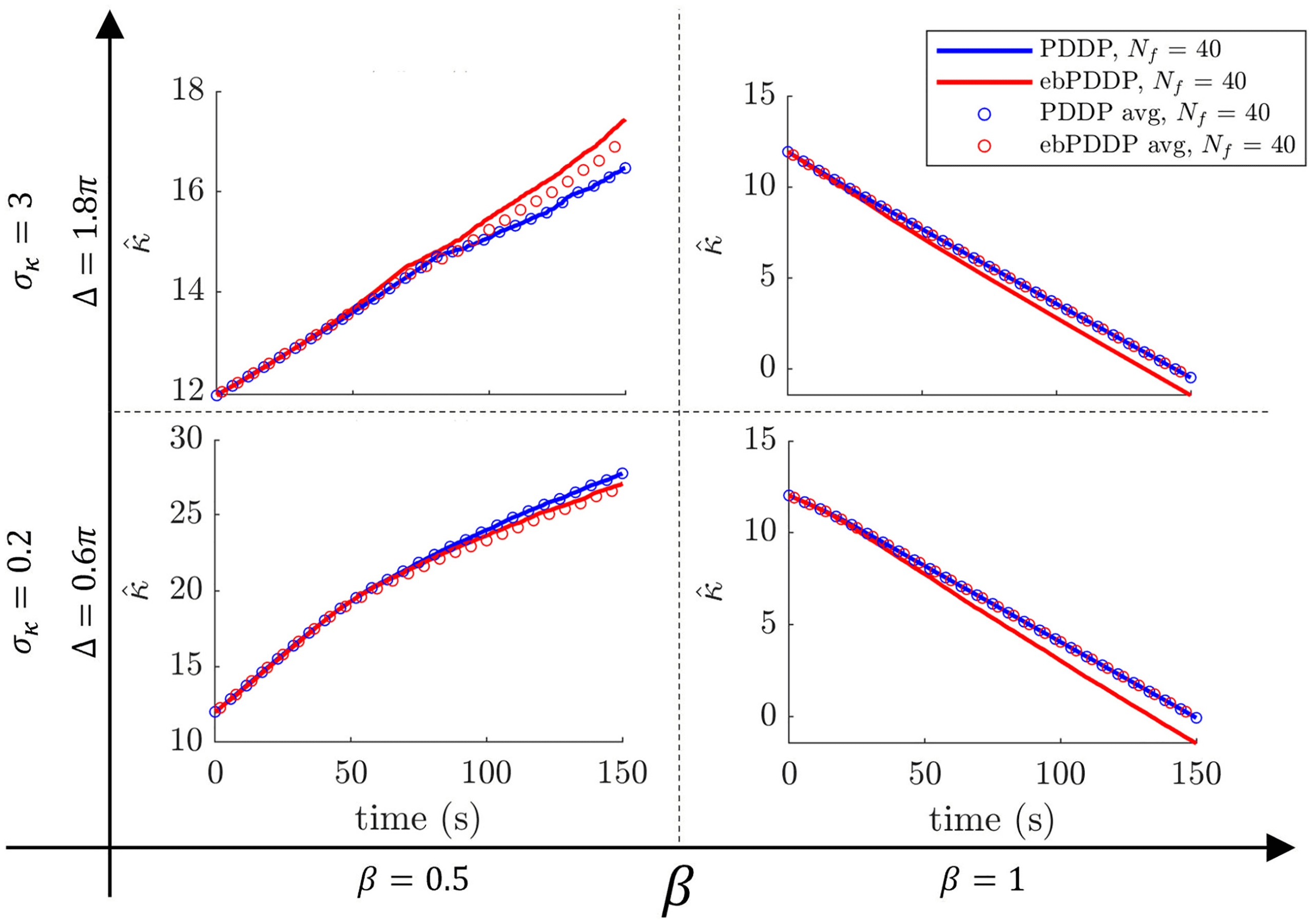
Figure 7: Simulation of average coupling rules in Kuramoto networks. Equa-
tion 3.3 (blue circles) describes exactly the average coupling weight in
Kuramoto networks with PDDP (blue lines). The correspondence between
equation 3.6 (red circles) and the average coupling weight in Kuramoto net-
works with ebPDDP (equation 2.4, red lines) is not exact, as explained in the
main text. The same numbers of Fourier components are used in all cases
= 40). The four sets of parameters used for the simulations are indicated
(N f
by the bold axes and correspond to those used in Figure 5, as well as Figures 12,
13, and 14 in appendix C.
rule by Seliger et al. (2002) where λ and (cid:8) are parameters. Then the evolution
of the average coupling is
(cid:6)
(cid:24)
= (cid:8)
λ
d ˆκ
dt
+
a0
2
∞(cid:10)
m=1
(cid:25)
(cid:9)
am|Z(m)|2
− ˆκ
.
(3.4)
= cos(ϕ) and all other Fourier coefficients equal to zero,
In particular, for a1
this equation exactly describes the evolution of the average coupling for the
PDDP rule given by equation 1.3.
3.2 Average Coupling for General Event-Based PDDP. We consider
the general ebPDDP rule represented by equation 2.4 where F is any
2π-periodic function of the phase difference that can be expanded as a
Fourier series according to equation 2.5. To obtain the corresponding aver-
age coupling strength, the Dirac deltas indicating spiking events need to be
1498
B. Duchet, C. Bick, and Á. Byrne
q
(cid:11)
δ(t − tq
k ) ≈ (cid:11)δ(θ
expressed as functions of a neuron’s phases. Since θ
k is defined mod 2π, we
have
k) as in Coombes & Byrne (2019). We use this ap-
proximation to define an ebPDDP rule that depends only on the phases of
the oscillators:
dκ
kl
dt
= π (δ(θ
k) + δ(θ
l )) F(φ
(3.5)
kl ).
Using the Fourier expansion of F as before, the corresponding average
coupling ˆκ can be obtained as
d ˆκ
dt
= π
∞(cid:10)
m=−∞
cm
N2
N(cid:10)
N(cid:10)
(cid:26)
k=1
l=1
emiθ
l δ(θ
−miθ
k)e
k + e
−miθ
k δ(θ
l )emiθ
l
(cid:27)
.
(cid:11)
With θ defined mod 2π, δ(θ ) can also be Fourier-expanded as δ(θ ) =
1
2π
p∈Z epiθ (Coombes & Byrne, 2019). Since
1
N
N(cid:10)
k=1
δ(θ
±miθ
k)e
k = 1
2πN
N(cid:10)
(cid:10)
k=1
p∈Z
e(p±m)iθ
k
= 1
2π
(cid:10)
p∈Z
1
N
N(cid:10)
k=1
epiθ
k = 1
2π
(cid:10)
p∈Z
Z(p),
⎞
⎠
Z(p)
∞(cid:10)
(cid:20)
Z(m) + ¯Z(m)
(cid:21)
cm
m=−∞
(cid:20)
Z(p)
Re
∞(cid:10)
p=1
(cid:21)
⎞
⎠
∞(cid:10)
(cid:21)
(cid:20)
Z(m)
.
cmRe
m=−∞
we obtain
d ˆκ
dt
=
⎛
⎝ 1
2
⎛
(cid:10)
p∈Z
=
⎝1 + 2
Using the real-valued Fourier coefficients defined in equation 2.6, this ex-
pression becomes
⎛
d ˆκ
dt
=
⎝1 + 2
(cid:20)
Z(p)
Re
∞(cid:10)
p=1
(cid:21)
⎞
⎠
(cid:24)
+
a0
2
∞(cid:10)
m=1
(cid:25)
(cid:21)
.
(cid:20)
Z(m)
amRe
(3.6)
As in section 3.1, this result can be extended to include a decay term.
Simulations show that average weights obtained from equation 3.6 are
similar to average weights obtained from equation 2.4 as shown in Fig-
ure 7. Although equation 3.6 is an exact description of the average weight
in phase oscillator networks with adaptivity given by equation 3.5 (where
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Mean-Field Approximations for Networks With STDP
1499
the Dirac deltas are functions of phase), our simulations are based on equa-
tion 2.4 (where the Dirac deltas are functions of time). The approximation
(cid:11)
k) used to derive equation 3.5 from equation 2.4 gives
δ(t − tq
k ) ≈ (cid:11)δ(θ
q
rise to the discrepancies visible in Figure 7.
4 Mean-Field Dynamics of Oscillator Populations with Adaptive
Coupling
Symmetric or nearly symmetric STDP rules can lead to the formation of
densely connected clusters with homogeneous coupling strength (see sec-
tion 2.2 and, for example, Popovych et al., 2015; Berner et al., 2019; Röhr
et al., 2019). Specifically, Figure 3 shows the emergence of multiple clus-
ters of distinct mean intrinsic frequencies. For the remainder we will focus
on such plasticity rules and interpret each cluster as an emergent popula-
tion of phase oscillators. Suppose that there are M emergent clusters and
the corresponding populations μ ∈ {1, . . . , M} have Nμ oscillators. Rewrit-
ing equation 2.1 with the cluster labeling, the evolution of θμ,k, the phase of
oscillator k ∈ {1, . . . , Nμ} in cluster μ is given by
˙θμ,k
= ωμ,k
+ 1
N
M(cid:10)
Nν(cid:10)
ν=1
l=1
κμν,kl sin(θν,l
− θμ,k),
(4.1)
where κμν,kl is the coupling strength from oscillator l in population ν to os-
cillator k in population μ. We now suggest a low-dimensional description of
the resulting dynamics for populations corresponding to emergent clusters
in the fully adaptive network in terms of the population Kuramoto-order
parameters Zμ := 1
Nμ
k=1 eiθ
(cid:11)
Nμ
k .
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
4.1 Low-Dimensional Dynamics for Homogeneous Coupling. Using
the assumption that the emergent coupling within and between clusters is
homogeneous, we replace individual coupling strengths κμν,kl from oscil-
lators in population ν to oscillators in population μ by the mean coupling
strength from population ν to population μ:
ˆκμν = 1
NμNν
Nμ(cid:10)
Nν(cid:10)
k=1
l=1
κμν,kl
.
Writing qμ = Nμ
N for the relative population size, we obtain
˙θμ,k
= ωμ,k
+
M(cid:10)
ν=1
qν
Nν
ˆκμν
Nμ(cid:10)
l=1
sin(θν,l
− θμ,k),
which describes homogeneously coupled populations.
(4.2)
(4.3)
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1500
B. Duchet, C. Bick, and Á. Byrne
Such networks of Kuramoto oscillators admit an exact low-dimensional
description in terms of the dynamics of the population order parameter Zμ
due to the Ott-Antonsen reduction (Ott & Antonsen, 2008, 2009; see also
Bick et al., 2020). In the mean-field limit of infinitely large networks, the
Kuramoto-Daido order parameters Z(m)
μ for each population μ describe the
distribution of oscillators. The key observation for this reduction is that
for networks of the form equation 4.3 the mth Kuramoto-Daido order pa-
rameter can be expressed as a power of the Kuramoto-order parameter
Zμ := Z(1)
μ . If we assume that the intrinsic fre-
quencies ωμ,k are distributed according to a Lorentzian with mean (cid:11)μ and
width (cid:3)μ, then the dynamics of equation 4.3 are determined by
μ , that is, Z(m)
μ )m = Zm
μ = (Z(1)
dZμ
dt
= (−(cid:3)μ + i(cid:11)μ)Zμ + 1
2
M(cid:10)
ν=1
qν ˆκμν (Zν − ¯ZνZ2
μ).
(4.4)
The dynamical equations for the evolving coupling weights can be
derived as in section 3 and then taking the limit N → ∞. Now the Ott-
Antonsen reduction allows us to simplify the expressions through Z(m)
μ =
dκνμ, jk
=
Zm
μ . If individual weights evolve according to the general PDDP rule
dt
F(θν, j
− θμ,k), then
d ˆκμν
dt
=
∞(cid:10)
m=−∞
cmZm
ν .
μ ¯Zm
(4.5)
Similarly,
(cid:26) (cid:11)
p∈Z Z(p)
μ
for the event-based rule (see equation 3.5) we note that
(cid:27)
=
1−|Zμ|2
1−Zμ− ¯Zμ+|Zμ|2
=: f (Zμ) and thus
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
d ˆκμν
dt
=
∞(cid:10)
(cid:26)
cm
m=−∞
f (Zμ)Zm
ν + f (Zν ) ¯Zm
μ
(cid:27)
.
(4.6)
Decay terms can be incorporated in the same way as above.
Note that equation 4.4 together with either equation 4.5 or 4.6 form a
closed set of equations. In the following, we analyze the dynamics of the
reduced equations explicitly. Here, we focus on the symmetric STDP rule
approximated by a single harmonic PPDP rule, equation 1.3, with ϕ = 0
such that
(cid:26)
= (cid:8)
d ˆκμν
dt
λ Re(Zμ ¯Zν ) − ˆκμν
(cid:27)
.
(4.7)
Equations 4.4 and 4.7 now form a closed low-dimensional system of cou-
pled adaptive oscillator populations. While these equations can be analyzed
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Mean-Field Approximations for Networks With STDP
1501
explicitly—as we will do in the following sections—some insights have
been obtained using geometric singular perturbation theory for a very small
time-scale separation parameter (cid:8) (https://arxiv.org/pdf/2301.07071.pdf).
4.2 Single Harmonic PDDP, One Population. We begin by considering
a one-population model to illustrate the types of behavior possible for a
one-cluster state. For a one-population model, the learning rule equation 4.7
does not depend on the mean phase. Thus, the phase dynamics decouple,
leading to two-dimensional effective dynamics3 determined by
d ˆκ
dt
dρ
dt
(cid:12)
= (cid:8)
λρ2 − ˆκ
(cid:13)
,
(cid:7)
−(cid:3) + 1
2
ˆκ − 1
2
=
(cid:8)
ˆκρ2
ρ,
(4.8)
(4.9)
where ρ := |Z|. Note that in contrast to mean-field descriptions of Ku-
ramoto oscillators with an adaptive global coupling parameter that depend
linearly on the mean field Z (Ciszak et al., 2020), we here have a quadratic
dependency.
(cid:28)
There is a trivial fixed point at ˆκ = 0, ρ = 0. While ˆκ = λρ2, ρ =
1 − 2(cid:3)
ˆκ
defines a pair of nontrivial fixed points, which exist for λ > 8(cid:3). Comput-
ing the Jacobian, we find that the trivial solution is stable for all physical
parameter values ((cid:3) > 0, (cid:8) > 0), and for the nontrivial fixed points, one is
stable and the other unstable.
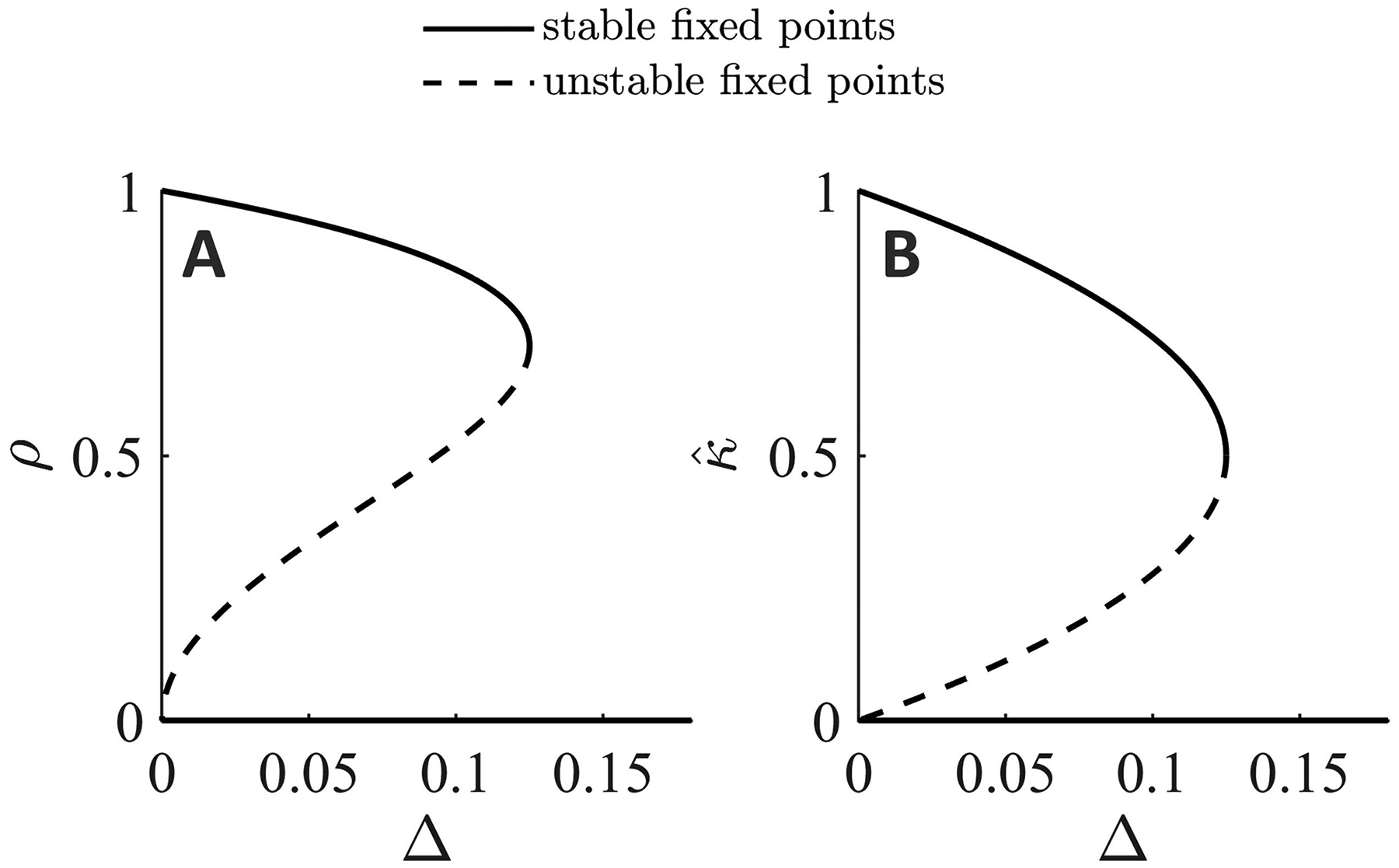
Using XPPAUT (Ermentrout, 2002), we performed a one-parameter
continuation in the heterogeneity parameter (cid:3) (see Figure 8). When the
heterogeneity is low, there exists a nontrivial stable fixed point, where the
mean coupling does not decay to zero, whereas after the saddle-node bi-
furcation at (cid:3) = 0.125, the mean coupling will always decay to zero and
the oscillators will be asynchronous (ρ = 0). As the strength of the plastic-
ity rule λ is increased, the saddle node moves to the right, and the region of
bistability (where the trivial and non-trivial fixed points coexist) increases.
These results agree with analytical results outlined above.
4.3 Single Harmonic PDDP, Two Populations. Next consider two
adaptively coupled populations evolving according to
dZ1
dt
= (−(cid:3) + i(cid:11))Z1
+ 1
2
q ˆκ
11Z1(1 − |Z1
|2)
+ 1
2
(1 − q) ˆκ
12(Z2
− ¯Z2Z2
1),
(4.10)
3
Note that equilibrium points of the effective dynamics correspond to periodic solu-
tions of the full system.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1502
B. Duchet, C. Bick, and Á. Byrne
Figure 8: Bifurcation analysis of the mean-field equations for a single popula-
tion. One parameter continuation in the heterogeneity parameter (cid:3) for equa-
tions 4.8 and 4.9 with λ = 1 and (cid:8) = 0.5. A saddle-node bifurcation occurs at
(cid:3) = 0.125, which corresponds to the analytical value λ/8.
dZ2
dt
= (−(cid:3) + i[(cid:11) + (cid:3)(cid:11)])Z2
+ 1
2
q ˆκ
21(Z1
− ¯Z1Z2
2)
+ 1
2
(1 − q) ˆκ
22Z2(1 − |Z2
|2),
(4.11)
where q is the fraction of oscillators in population 1 and (cid:3)(cid:11) is the difference
in mean intrinsic frequency between oscillators in each population. The dy-
namics for the intrapopulation coupling are as in the one-population model,
d ˆκμμ
dt
= (cid:8)
(cid:12)
λ|Zμ|2 − ˆκμμ
(cid:13)
,
(4.12)
for μ ∈ [1, 2], while the interpopulation coupling is given by equation 4.7.
Setting q = 0.5 (two equally sized populations), we perform a one-
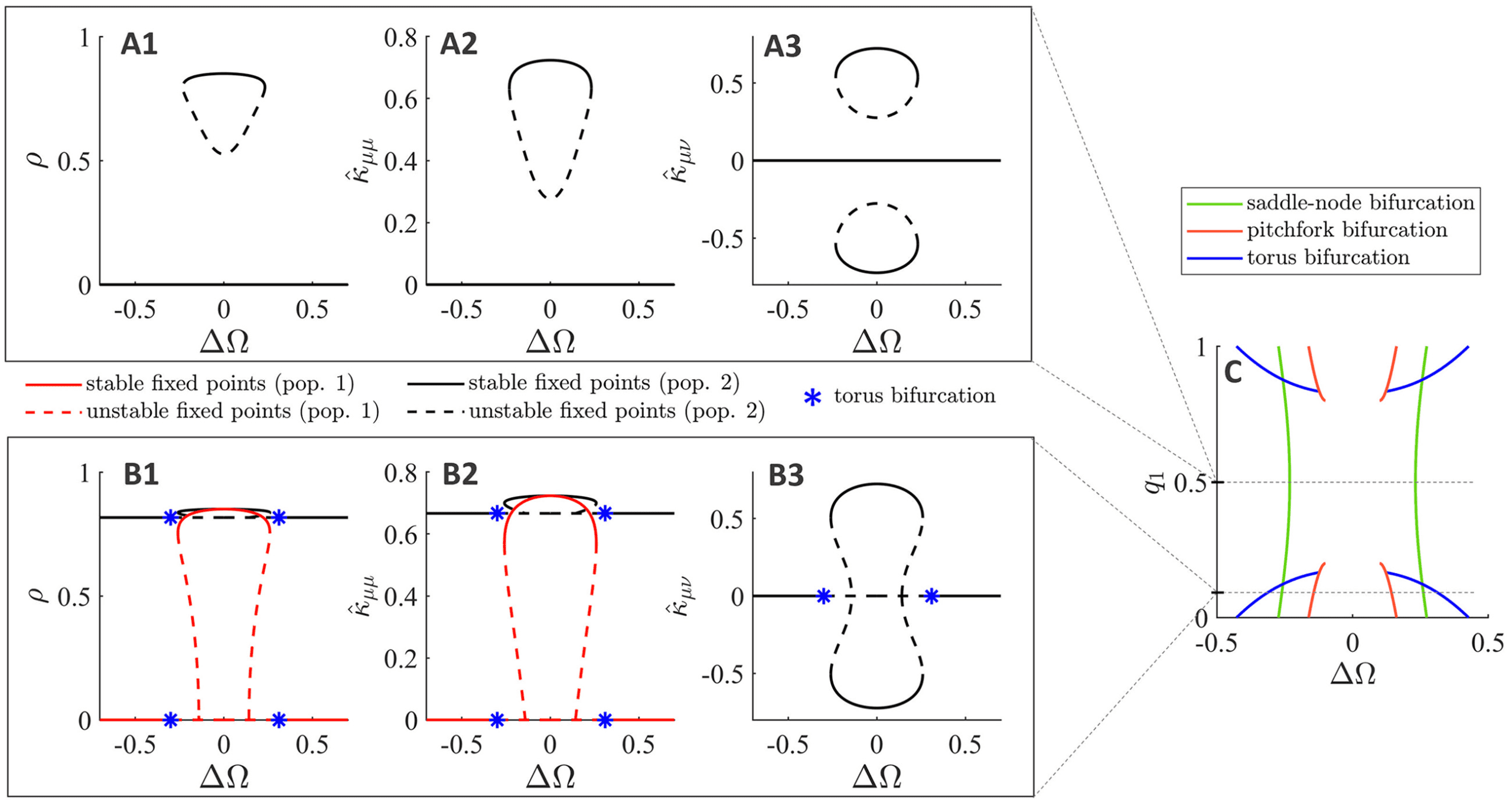
parameter continuation in the intrinsic frequency difference (cid:3)(cid:11) (see Fig-
ure 9A). We find that for a small range of (cid:3)(cid:11) values ((cid:3)(cid:11) ∈ [−0.23, 0.23])
the two populations synchronize in frequency. This frequency-locked so-
lution lies on an invariant set, where the level of synchrony of each pop-
ulation is identical (ρ
2) and the coupling strengths are symmetric
1
( ˆκ
21). The system itself, however, is generally not symmet-
12
ric (unless (cid:3)(cid:11) = 0) due to distinct intrinsic frequencies resulting in dis-
tinct mean phases of the two populations. The two nontrivial equilibrium
branches in the interpopulation coupling strength (see Figure 9, panel
A3), correspond to the in-phase/symmetric solution (positive ˆκμν) and the
antiphase/asymmetric solution (negative ˆκμν).
22, ˆκ
= ˆκ
= ˆκ
= ρ
11
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Mean-Field Approximations for Networks With STDP
1503
Figure 9: Bifurcation analysis of the mean-field equations for a two-population
model. One- and two-parameter continuations for the system of equations given
by equations 4.10 to 4.12 and 4.7. (A) One-parameter continuation in intrin-
sic frequency difference (cid:3)(cid:11) for equally sized populations (q = 0.5). Given the
symmetry in the system, both populations have the same within-population
synchrony and intra-/interpopulation coupling strengths. Black solid (dashed)
lines correspond to the stable (unstable) fixed-point values for both popula-
tions/sets of coupling strengths. (B) Continuation in (cid:3)(cid:11) for q = 0.1. As the
mean interpopulation coupling strengths are equal, the curve in panel B3
corresponds to both ˆκ
21. (C) Two-parameter continuation in the in-
trinsic frequency difference (cid:3)(cid:11) and the relative size of population 1 q, show-
ing the saddle-node, pitchfork, and torus bifurcation curves. Parameter values:
(cid:3) = 0.1, (cid:11) = 30, (cid:8) = 0.5, λ = 1.
12 and ˆκ
12
12
= ˆκ
= ˆκ
= 0, ρ
2
For general population sizes q, an additional branch of solution can
emerge, where one population is fully asynchronous and the other is par-
tially synchronized with nontrivial dynamics (e.g., ρ
(cid:9)= 0); we call
1
this the decoupled solution. More specifically, the structure of the equations
implies that ρ
= 0 defines a dynamically invariant set. On this
1
set, the coupling strength ˆκ
11 decays exponentially, and the second popu-
lation evolves independent of the first one (as the network is decoupled)
according to the equations of motion for a single population with adaptive
coupling. The decoupled solution now corresponds to the nontrivial solu-
tion branch for a single population (see Figure 8), which exists for λ > 8(cid:3).
The only difference here is that the coupling ˆκ is replaced by an effective
coupling qμ ˆκμμ scaled with the (relative) population size. Hence, decoupled
solutions exist only for q < 2(cid:3)/λ (population 2 has nontrivial dynamics
ρ
(cid:9)= 0). Note
2
that these are equilibrium points for the effective dynamics but periodic
solutions in the full system.
(cid:9)= 0) and q > 8(cid:3)/λ (population 1 has nontrivial dynamics ρ
1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1504
B. Duchet, C. Bick, and Á. Byrne
(cid:9)= ρ
(cid:9)= ˆκ
12 and ˆκ
Letting q = 0.1, we find and continue the decoupled solution where pop-
ulation 1 is asynchronous and population 2 has nontrivial dynamics (ρ
= 0,
1
ρ
(cid:9)= 0) (see Figure 9B). The dynamics of population 1 (population 2) is
2
shown in red (black). The interpopulation coupling strengths are equal
for all values of (cid:3)(cid:11). Hence, the curve in Figure 9, panel B3 corresponds
to ˆκ
21. The decoupled solution goes unstable at a torus bifurca-
tion (blue stars) (cid:3)(cid:11) ≈ −0.3 and restabilizes at a second torus bifurcation
at (cid:3)(cid:11) ≈ 0.3. The frequency-locked solution branches off the decoupled so-
lution at a pitchfork bifurcation at (cid:3)(cid:11) ≈ −0.15 and (cid:3)(cid:11) ≈ 0.15. As in the
q = 0.5 case, for the frequency-locked solution, the two populations have
nonzero within-population synchrony and intra-/interpopulation coupling
strengths. However, the within-population synchrony and the intrapopula-
tion coupling strength are no longer equal (ρ
22). We note that
1
the trivial solution (ρμ = 0, ˆκμν = 0), which is stable for all values of (cid:3)(cid:11), is
not shown in Figure 9B, as it would have obscured the unstable region of
the decoupled solution.
2, ˆκ
11
Finally, we performed a two-parameter continuation in (cid:3)(cid:11) and q (see
Figure 9C). The saddle-node curves, which demarcate the region of exis-
tence for the coupled solution, are shown in green. The coupled solution
exists between the two green curves. The orange curve corresponds to the
pitchfork bifurcation, where the frequency-locked solution branches off the
decoupled solution. There is a global bifurcation at q = 0.2 = 2(cid:3)/λ and
q = 0.8 = 8(cid:3)/λ, when the decoupled solution ceases to exist, and so there
is no longer a pitchfork bifurcation. The torus bifurcation curve, where the
decoupled solution changes stability, is plotted in blue. In the region be-
tween the torus bifurcation curve and the saddle-node bifurcation curve,
the two populations have nontrivial dynamics. The interpopulation cou-
pling is weak enough that the populations do not entrain. Hence, the mean
phases precess at different rates, and as such, the phase difference oscillates
in time. As a result, the coupling strengths oscillate as the populations move
in- and out-of-phase with each other. Given that the coupling strengths and
the synchrony are interdependent, the synchrony variables also oscillate in
time.
5 Describing the Full Adaptive Network Using Coupled Populations
Evolving according to Mean-Field Dynamics
In this section, we aim to approximate a network of Kuramoto oscillators
(see equation 2.1) with adaptivity given by symmetric PDDP (see equa-
tion 1.3 with ϕ = 0) using two coupled populations evolving according to
the mean-field dynamics. As shown in section 2.2, the full adaptive network
with symmetric PDDP is itself a good approximation of the full adaptive
network with symmetric STDP. Here, we optimize parameters of the cou-
pled mean-field equations to best approximate the full network.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Mean-Field Approximations for Networks With STDP
1505
5.1 Optimizing the Parameters of the Two-Population Mean-Field to
Approximate the Full Adaptive Network. To approximate the full adap-
tive network, we consider the two-population mean-field model,
⎧
⎨
⎩
dZμ
dt
d ˆκμν
dt
= (−(cid:3)μ + i(cid:11)μ)Zμ + 1
2
(cid:12)
(cid:26)
= (cid:8)μ(cid:8)ν
λμλν Re
Zμ ¯Zν
− ˆκμν
,
(cid:11)
(cid:27)
2
ν=1 qν ˆκμν
(cid:13)
(cid:26)
Zν − ¯ZνZ2
μ
(cid:27)
,
(5.1)
where μ, ν ∈ {1, 2} are population indices, Zμ is the order parameter of pop-
ulation μ, and ˆκμν is the average weight from population ν to population μ.
Synthetic data from the full adaptive network are generated by simulating
a network of N = 100 Kuramoto oscillators (see equation 2.1) with adaptiv-
ity given by symmetric PDDP (see equation 1.3 with ϕ = 0). Further details
on the generation of synthetic data, as well as descriptions of the test and
training sets are in appendix B.
(cid:11)
1, (cid:8)
To describe the full adaptive network using the two-population mean-
field approximation, equation 5.1, we optimize (cid:8)μ and λμ with μ ∈ {1, 2}, as
well as the proportion of oscillators allocated to the first population denoted
by q1. Note that adaptivity parameters within and between populations (λ
1,
λ
2, (cid:8)
2) are not the same as adaptivity parameters between oscillators in
the full network (λ and (cid:8)). The optimal proportion of oscillators to allocate
to each population is also unclear; we therefore optimize the allocation of
oscillators as follows. We sort oscillators by the average value of their mean
/N) and allocate the first 100 × q1% to the
κ
outgoing coupling (i.e.,
kl
= 1 − q1). This
first population and the rest to the second population (q2
results in populations of size N1 and N2, and initial conditions for equa-
tion 5.1 can be obtained from the initial conditions used to simulate the full
adaptive network. For each initial condition, the parameters (cid:11)μ and (cid:3)μ are
obtained as the median frequency and half of the interquartile range of the
frequency of oscillators in each population, respectively. The optimization
= {0.1, 0.2, 0.3, . . . , 0.9}, and for each value
is performed as a sweep over q1
of q1, 36 local optimizations over the remaining parameters are carried out.
Each local optimization starts from a random set of parameters and con-
sists of successive optimizations using patternsearch and fminsearch (Mat-
labR2021a) over all initial conditions in the training set.
N
k=1
The cost function minimized by the optimization is the average over ini-
tial conditions in the training set of
(cid:10)
c = wρ
[ρ
mod(tn) − ρ
dat(tn)]2 + wψ
n
+ w ˆκ
(cid:10)
n
[ ˆκ
mod(tn) − ˆκ
dat(tn)]2 ,
(cid:10)
n
[ψ
mod(tn) − ψ
dat(tn)]2
where tn are all the time points corresponding to the second half of the sim-
ulation (to limit the influence of transients), ρ is the modulus of the order
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1506
B. Duchet, C. Bick, and Á. Byrne
Figure 10: Performance of the two-population mean-field approximation. Each
panel compares the sum of squared differences over time between model and
synthetic data for ρ or ˆκ, averaged over the training or test set. The two-
population mean-field approximation with optimized plasticity parameters is
shown in dark blue, the two-population mean-field approximation with plas-
ticity parameters obtained from the full system is shown in light blue, the
two-population model without adaptivity is shown in dark orange, and the
constant model is shown in orange. Training and test sets are composed of 13
and 20 trajectories, respectively, with varied initial conditions (more details in
appendix B).
parameter of the entire system, ψ is the (unwrapped) phase of the order
parameter of the entire system, ˆκ is the mean coupling weight of the entire
system, and subscripts “mod” and “dat” refer to equation 5.1 and synthetic
data from the full adaptive network, respectively. The coefficients wρ, wψ ,
w ˆκ are chosen to ensure that the costs corresponding to ρ, ψ, and ˆκ are on
a similar scale. Compared to fitting only to the end point, our approach
can capture nonconstant behaviors in ρ or ˆκ, as well as frequency through
phase evolution. For the two-population mean-field approximation, the or-
der parameter of the whole system is obtained as Z = q1Z1
+ q2Z2, and
similarly the average coupling is obtained as ˆκ = q2
+
+ q1q2 ˆκ
2 ˆκ
+ q2
1 ˆκ
22
q1q2 ˆκ
21.
12
11
5.2 Performance on Training and Test Sets. The optimized two-
population mean-field approximation with the lowest cost was found for
= 0.6 (dark blue in Figure 10), and its parameters are given in Table 1.
q1
To test the model performance, we construct three control models; (1) a
constant model defined from initial conditions by ρ = ρ
0 and ˆκ = ˆκ
0, (2) a
= 0.6 as in the fully opti-
two-population mean-field approximation with q1
mized model but without adaptivity ((cid:8)
= 0), and (3) a two-population
mean-field approximation where λ
= 0.5 are chosen to
λ
2
1
match λ and (cid:8), respectively. For the third control model, we performed a
sweep over q1 and found the best fit for q1
= (cid:8)
= 25 and (cid:8)
= 0.95.
(cid:8)
2
1
2
1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Mean-Field Approximations for Networks With STDP
1507
The fully optimized two-population mean-field approximation with the
lowest cost on the training set is better at describing the dynamics of ρ and ˆκ
on both the training set and the test set than the controls shown in Figure 10
in appendix C. This shows that to best reproduce synthetic data from the full
adaptive model, it is necessary to consider both the evolution of the or-
der parameter and of the average weights and to optimize the within-
and between-population adaptivity parameters. The constant model is
shown in light orange, the two-population mean-field approximation with
no adaptivity is shown in dark orange, and the two-population mean-
field approximation where the plasticity parameters are not optimized is
in light blue. In the test set, the greatest improvement of the optimized
two-population mean-field approximation over the controls is for ˆκ (Fig-
ure 10D). With the exception of the constant model, the controls already
approximate ρ well in the test set, see Figure 10C. Representative trajecto-
ries of the two-population mean-field approximation obtained from initial
conditions in the test set approximate the network synchrony, phase, and
average coupling of synthetic data from the full adaptive network (see Fig-
ure 20 in appendix C). The approximation of ˆκ is overall better when (cid:8)μ and
λμ are optimized. We note that while transients were not included in the cost
function used to fit to synthetic data, they are relatively well described by
the model when starting from random connectivity with different means in
the test set (see Figure 20).
6 Discussion
Using simulations, we showed that PDDP and ebPDDP can provide use-
ful approximations of STDP. In particular, single-harmonic rules can ap-
proximate simple forms of symmetric STDP, while multiharmonic rules
are required to accurately approximate causal STDP. In the latter case, the
accuracy of the approximation increases with the number of Fourier coeffi-
cients before reaching a plateau. The Fourier coefficients can be easily com-
puted using analytical expressions only involving causal STDP parameters
(see equation 2.6). We found ebPDDP to be a slightly better approximation
than PDDP in the case of both symmetric STDP and causal STDP. This is ex-
pected since contrary to PDDP, ebPDDP restricts synaptic weight updates
to spiking events, which is conceptually closer to STDP. One limitation of
approximating STDP using plasticity rules based on phase difference is that
the evolution of phase differences is required to be slower than the phase
dynamics (Lücken et al., 2016). Under this assumption, the intricate evolu-
tion of coupling weights can be well approximated by PDDP and ebPDDP
(see Figures 11 and 15 in appendix C). For best results, the STDP function
should also decay to zero faster than the network mean frequency for both
positive and negative spike-timing differences (in the case of causal STDP,
to avoid both components in equation 2.3 strongly overlapping).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1508
B. Duchet, C. Bick, and Á. Byrne
We derived exact expressions for the evolution of the average coupling
weight in networks of phase oscillators with PDDP and ebPDDP. These
expressions make no assumption about the underlying network (in particu-
lar, no assumption about the strength and type of coupling between oscilla-
tors), and are compatible with any plasticity rule based on phase difference
as long as it can be expanded as a Fourier series of the phase difference.
As a proof of principle, we focused on mean-field approximations based
on the average coupling evolution for two-cluster states in a population
of adaptive Kuramoto oscillators and performed a bifurcation analysis to
highlight the different possible behaviors. Here we have focused predomi-
nantly on the Kuramoto model with adaptivity rules that mimic the adap-
tation between individual neural cells. However, as a prototypical model to
study synchronization in neuroscience, the Kuramoto model has also found
application on different scales including whole-brain modeling, epilepsy,
and Parkinson’s disease (Cumin & Unsworth, 2007; Breakspear et al., 2010;
Cabral et al., 2014; Schmidt et al., 2015; Ponce-Alvarez et al., 2015; Finger
et al., 2016; Asllani et al., 2018; Weerasinghe et al., 2019, 2021; Bick et al.,
2020; Duchet et al., 2022). While here each Kuramoto oscillator typically
represents neural populations rather than individual cells, our results may
still help understand the role of adaptivity in such networks—albeit with
potentially different adaptivity rules on different timescales.
Our framework could easily be adapted to consider more biologically re-
alistic oscillator models, such as the θ -neuron model or the formally equiv-
alent quadratic integrate-and-fire (QIF) neuron model. Like the Kuramoto
model, the θ -neuron model is amenable to the Ott-Antonsen ansatz and as
such, is amenable to exact mean-field description (Luke et al., 2013). For
the QIF model, the equivalent Lorentzian ansatz should be used (Montbrió
et al., 2015). The model analysis would be identical, but given the explicit
phase dependency in the coupling, we can expect a richer set of dynam-
ics for a network of θ -neurons than observed here for Kuramoto oscillators.
We could also include explicit synaptic variables, as in Byrne et al. (2020), to
more accurately model synaptic processing. More generally, under the as-
sumption of weak coupling, even more detailed neuron models, such as the
Hodgkin-Huxley model, can be approximated by networks of phase oscil-
lators through phase reduction (Brown et al., 2004; Pietras & Daffertshofer,
2019). While the resulting phase equations will generically contain higher-
order terms that affect the global dynamics, a truncation to first order (i.e.,
Kuramoto-type coupling) can still provide suitable approximation where
the first harmonics are dominant and shape the dynamics. While generic
higher-order terms may break the Ott-Antonsen ansatz, its extensions (see,
e.g., Vlasov et al., 2016; Tyulkina et al., 2018) or more general moment clo-
sure approaches (Kuehn, 2016) can provide suitable approximations that do
not rely on a single order parameter to capture clustering; the dynamics of
the mean coupling strength may then depend on more than a single order
parameter. Indeed, previous studies of adaptive oscillators (Berner et al.,
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Mean-Field Approximations for Networks With STDP
1509
2019) and our full network simulations point to the existence of three-, four-,
and five-cluster states that motivate extending the results presented here.
Although computationally expensive and, perhaps, numerically challeng-
ing, both the bifurcation analysis and model fitting could be extended to
consider more than two clusters.
Combining theoretical insight and data-driven inference, we fitted a two-
cluster mean-field approximation to a full adaptive network of Kuramoto
oscillators in order to obtain a low-dimensional representation of the full
system. The goal here is not to find a relationship between model param-
eters and (microscopic) parameters that could be measured in the brain
(which is hardly ever possible with limited data), but to find a mean-field
model with plasticity that can be used to describe population-level record-
ings, such as local field potentials. While the two-cluster mean-field model
can approximate the full adaptive network on the test set, the accuracy of
the approximation could be improved in several ways. First, a richer train-
ing set could be used. Second, the mean-field description of the order pa-
rameter is not exact, and a moment or cumulant approach may capture
more of the full system dynamics (Tyulkina et al., 2018). Third, consider-
ing more than two populations may provide a more accurate approxima-
tion. Fourth, rather than allocating oscillators to clusters by thresholding
their mean outgoing coupling, a finer partition could be learned (Snyder
et al., 2020). Nevertheless, data-driven inference of low-dimensional rep-
resentations of phase-oscillator networks (Thiem et al., 2020; Snyder et al.,
2020; Fialkowski et al., 2022) is a promising approach to approximate the
behavior of networks with STDP. Once clusters have been identified, a very
recent mean-field technique based on the collective coordinate method can
be used (Fialkowski et al., 2022).
More general types of STDP call for extensions of our framework. First,
one would naturally expect that the strength of plastic connections is
bounded. We included soft bounds in our investigation of symmetric STDP
through a damping term (see equation 1.3), which is conserved in the aver-
age coupling (see equation 3.4), and is therefore present in the mean-field
analyses carried out in sections 4 and 5. While neither soft nor hard bounds
can easily be included in the average coupling derivation for causal STDP,
we show that short transients of causal STDP with hard bounds are well
captured by causal PPDP/ebPPD without bounds (see Figures 16 and 17 in
appendix C). Second, we primarily focused on symmetric STDP rules, that
is, interchanging the order of spikes will have little to no effect on the change
of connection strength. For such adaptation, the network naturally forms
clusters of strongly connected units (see Figure 3). By contrast, the causal-
ity of traditional asymmetric STDP rules will be reflected in the network
structure as shown in Figure 5 and highlighted very recently in Thiele et al.
(2023). To analyze the mean-field dynamics of such networks, a natural ap-
proach would be to computationally identify emerging feedforward struc-
tures in such networks instead of looking for clusters. In this case, finding a
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1510
B. Duchet, C. Bick, and Á. Byrne
corresponding low-dimensional description as in section 4 is more chal-
lenging. Third, we consider STDP adaptation rules that depend on pairs of
oscillator states. More elaborate, spike-based rules such as triplet interac-
tions have recently attracted attention (Pfister & Gerstner, 2006; Montangie
et al., 2020). It would be interesting to have such adaptation reflected in the
STDP model as these could be interpreted as “higher-order” network effects
(see Bick et al., 2021).
As a step toward low-dimensional description of adaptive networks
with STDP, our framework has implications for the study of long-term neu-
ral processes. In particular, the effects of clinically available DBS quickly
disappear when stimulation is turned off; thus, stimulation needs to be
provided continuously. To spare physiological activity as much as pos-
sible, it would therefore be highly desirable to design stimuli aimed at
eliciting long-lasting effects. Continuous stimulation can also lead to habit-
uation, where stimulation benefits diminish considerably over the years in
some patients with essential tremor (Fasano & Helmich, 2019). Optimizing
brain stimulation to have long-lasting effects so far has relied on computa-
tional studies (Tass & Majtanik, 2006; Popovych & Tass, 2012; Ebert et al.,
2014; Popovych et al., 2015; Manos et al., 2018) or on analytical insights
under the simplifying assumption that spiking is triggered only by stim-
ulation pulses (Kromer & Tass, 2020). Other analytical approaches based
on mean-field models are focused on short-term changes due to stimula-
tion and do not consider plastic changes (Duchet et al., 2020; Weerasinghe
et al., 2019, 2021). Our framework offers an alternative, where exact evolu-
tion equations for the average coupling within and between neural popula-
tions could inform the development of new therapies aimed at maximizing
the long-term effects of brain stimulation. Although microscopic connectiv-
ity is unknown, stimulation can be designed to change average connectivity
and impact synchrony as beneficial.
Appendix A: Simulation Methods Used to Compare STDP to PDDP
Using simulations, we compare networks of Kuramoto oscillators with
adaptivity given by symmetric or causal STDP, to the same networks with
adaptivity given by the corresponding single- or multiharmonic PDDP and
ebPDDP rules.
A.1 Symmetric Learning Rules. We simulate networks of N = 60 Ku-
ramoto oscillators evolving according to equation 2.1, where the natural
frequencies ω
k are sampled from a normal distribution of mean (cid:11) = 10π
(5 Hz) unless otherwise stated and standard deviation (cid:3). A normal distri-
bution was chosen over a Lorentzian distribution to avoid extreme natural
frequencies, which lead to increased variability in simulation repeats. Ini-
tial conditions are also sampled from normal distributions. Phases θ
k(t =
0 s) are sampled from the circular equivalent of N
and couplings
0, π 2/9
(cid:27)
(cid:26)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Mean-Field Approximations for Networks With STDP
1511
(cid:26)
(cid:27)
kl
dt
5, σ 2
κ
= −(cid:8)κ
. The evolution of the coupling weights κ
κ
kl (t = 0 s) from N
kl is
simulated according to equation 1.2 (symmetric STDP), together with the
weight decay dκ
kl, equation 1.3, with ϕ = 0 (symmetric PDDP), or
equation 2.2 (symmetric ebPDDP). For ebPDDP, we use δ(t − tq
(t)/(cid:3)t
is the indicator function of Iq
+ (cid:3)t) and (cid:3)t is the simula-
where 1Iq
k
tion time step. The network is simulated for 150 s, using the Euler method
with (cid:3)t = 1 ms unless otherwise stated. We use (cid:8) = 0.5, and the values of
other parameters are detailed in Figures 3 and 11.
k ) ≈ 1Iq
= [tq
k
, tq
k
k
k
A.2 Causal Learning Rules. Error metrics (described below) are com-
puted between multiharmonic PDDP or ebPDDP and causal STDP for se-
lected regions of parameter space. To limit computational cost, we constrain
causal STDP parameters based on data and biological motivations. We use
τ+ = 16.8 ms and τ− = 33.7 ms, which were obtained by fitting equation 1.1
to experimental data (data published in Bi & Poo, 1998, and fit in Bi & Poo,
2001). Several experimental studies have reported the LTD time constant
τ− to be larger than the LTP time constant τ+, for example, in the rat hip-
pocampus (Bi & Poo, 1998), somatosensory cortex (Feldman, 2000), and
visual cortex (Froemke & Dan, 2002). We take A+ = 0.2 and A−/A+ = β.
Since the time window for LTD is twice as long as the time window for
LTP, we choose β = 0.5 to study a balanced situation where LTP domi-
nates for shorter spike-timing differences and LTD dominates for longer
spike-timing differences, and β = 1 to study a situation where LTD always
dominates.
(cid:27)
(cid:26)
12, σ 2
κ
We simulate networks of Kuramoto oscillators as for symmetric STDP
(see section A.2) with the following differences. Initial couplings κ
kl (t = 0 s)
are sampled from N
kl is
simulated according to equation 1.1 (causal STDP), equation 2.3 (causal
PDDP), or equation 2.4 (causal ebPDDP). For PDDP and ebPDDP, the
Fourier expansion of F is truncated after N f coefficients. No weight decay
term is included.
. The evolution of the coupling weights κ
The comparison of multiharmonic PDDP or ebPDDP to causal STDP re-
lies on four error metrics. In the following error metric definitions, we use
the subscript or superscript X to refer to quantities corresponding to mul-
tiharmonic PDDP or ebPDDP. To compare the time evolution of network
synchrony, we define
(cid:29)
eρ =
[ρ
X(t) − ρ
STDP(t)]2
(cid:30)
,
(A.1)
where (cid:10).(cid:11) denotes time averaging over the duration of the simulation
[0, tmax] and ρ(t) = |Z(t)| is the network synchrony. To compare the time
evolution of the network average coupling, we compute
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1512
(cid:29)
e ˆκ =
[ ˆκ
X(t) − ˆκ
STDP(t)]2
(cid:30)
,
B. Duchet, C. Bick, and Á. Byrne
(A.2)
where the average coupling is given by equation 3.1. The time evolution of
the weight distribution is compared using
ehist(κ
kl )
= n2
bins
N4
”
,
!
2
(t)
j (t) − hSTDP
hX
j
(cid:31)
nbins(cid:10)
j=1
(A.3)
where h j(t) is the count of couplings weights falling into the jth bin in the
histogram of coupling weights at time t (bin boundaries are identical across
rules and time for a given set of parameters). The fourth error metric rκ ∞
is
the Pearson’s correlation coefficient between the STDP coupling matrix and
the PDDP/ebPDDP coupling matrix at the last stimulation time point. The
scaling factors in equation A.3 and the choice of a correlation measure for
the fourth metric ensure that the corresponding metrics are independent
of the size of the network and the number of bins. For each set of param-
eters, the four metrics are averaged across five repeats. For a given repeat
and a given set of parameters, the same random samples are used as initial
conditions to compare the network evolution between plasticity rules.
kl
Appendix B: Methodological Details Pertaining to the Optimization
of the Two-Population Mean-Field Approximation
Synthetic data are generated by stimulating N = 100 Kuramoto oscillators
evolving according to equation 2.1, with adaptivity given by symmetric
PDDP (equation 1.3 with ϕ = 0, λ = 25, and (cid:8) = 0.5). Oscillator natural fre-
quencies ω
k are sampled from a Lorentzian distribution of center (cid:11) = 10π
(5 Hz) and width (cid:3) = 0.6π. Initial phases are sampled from a Von Mises dis-
tribution of standard deviation π/4. Initial couplings κ
kl (t = 0 s) are sam-
pled from N
. The network is simulated for 20 s, using the Euler
method with (cid:3)t = 0.1 ms.
, 0.52
ˆκ
0
(cid:26)
(cid:27)
We create a training set and a test set based on different initial conditions
and in particular various ˆκ
= {2, 2, 2, 3,
0. The training set corresponds to ˆκ
0
4, 5, 5, 10, 10, 15, 15, 15, 20} and the test set to ˆκ
= {3.5, 3.5, 3.5, 3.5, 7, 7, 7, 7,
0
12, 12, 12, 12, 17, 17, 17, 17, 22, 22, 22, 22}. For each trajectory in the training
and test sets, natural frequencies, initial phases, and initial couplings are
sampled from their respective distributions. Repeated ˆκ
0 values therefore
correspond to different systems with different initial synchrony.
For optimization speed and accuracy, the two-population mean-field ap-
proximation is simulated using the variable order solver ode113 in Matlab
(variable-step, variable-order Adams-Bashforth-Moulton solver of orders 1
to 13).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Mean-Field Approximations for Networks With STDP
1513
Appendix C: Supplementary Figures and Tables
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
Figure 11: Comparison between symmetric STDP and PDDP in a Kuramoto
network (desynchronized state). (A) Evolution of the distribution of coupling
weights with time (100 bins at each time point). The average weight is repre-
sented by a thin black line. STDP is shown in panel A1, PDDP in panel A2, and
ebPDDP in panel A3. (B) Coupling matrix at t = 150 s, with oscillators sorted by
natural frequency. STDP is shown in panel B1, PDDP in panel B2, and ebPDDP
in panel B3. (C) Time evolution of average coupling (panel C1: error bars rep-
resent the standard error of the mean over five repeats, too small to see) and
network synchrony (C2 and C3). STDP is shown in black, PDDP in blue, and
ebPDDP in red. a = 0.025822, b = 0.049415, σκ = 3, (cid:3) = 0.2π , (cid:11) = 10π (5 Hz).
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1514
B. Duchet, C. Bick, and Á. Byrne
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
Figure 12: Comparison between STDP and PDDP in a Kuramoto network,
[β = 0.5, σκ = 3, (cid:3) = 1.8π , (cid:11) = 10π (5 Hz)]. Results for PDDP and ebPDDP are
shown for 1, 5, and 25 Fourier components N f (first, second, and third columns
on the right hand-side of the figure, respectively). (A) Evolution of the distribu-
tion of coupling weights with time (100 bins at each time point). The average
weight is represented by a thin black line. STDP is shown in panel A1, PDDP
in panels A2 to A4, and ebPDDP in panels A5 to A7. (B) Coupling matrix at
t = 150 s, with oscillators sorted by natural frequency. STDP is shown in panel
B1, PDDP in panels B2 to B4, and ebPDDP in panels B5 to B7. (C) Time evolu-
tion of average coupling (panel C1: error bars represent the standard error of
the mean over five repeats) and network synchrony (panels C2 to C7). STDP is
shown in black, PDDP in blue, and ebPDDP in red.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Mean-Field Approximations for Networks With STDP
1515
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
Figure 13: Comparison between STDP and PDDP in a Kuramoto network,
[β = 1, σκ = 0.2, (cid:3) = 0.6π, (cid:11) = 10π (5 Hz)]. Results for PDDP and ebPDDP are
shown for 1, 5, and 25 Fourier components N f (first, second, and third columns
on the right-hand side of the figure, respectively). (A) Evolution of the distribu-
tion of coupling weights with time (100 bins at each time point). The average
weight is represented by a thin black line. STDP is shown in panel A1, PDDP
in panels A2 to A4, and ebPDDP in panels A5 to A7. (B) Coupling matrix at
t = 150 s, with oscillators sorted by natural frequency. STDP is shown in panel
B1, PDDP in panels B2 to B4, and ebPDDP in panels B5 to B7. (C) Time evolu-
tion of average coupling (panel C1: error bars represent the standard error of
the mean over five repeats) and network synchrony (panels C2 to C7). STDP is
shown in black, PDDP in blue, and ebPDDP in red.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1516
B. Duchet, C. Bick, and Á. Byrne
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
Figure 14: Comparison between STDP and PDDP in a Kuramoto network,
[β = 1, σκ = 3, (cid:3) = 1.8π , (cid:11) = 10π (5 Hz)]. Results for PDDP and ebPDDP are
shown for 1, 5, and 25 Fourier components N f (first, second, and third columns
on the right-hand side of the figure, respectively). (A) Evolution of the distribu-
tion of coupling weights with time (100 bins at each time point). The average
weight is represented by a thin black line. STDP is shown in panel A1, PDDP
in panels A2 to A4, and ebPDDP in panel A5 to A7. (B) Coupling matrix at
t = 150 s, with oscillators sorted by natural frequency. STDP is shown in panel
B1, PDDP in panels B2 to B4, and ebPDDP in panels B5 to B7. (C) Time evolu-
tion of average coupling (panel C1: error bars represent the standard error of
the mean over five repeats) and network synchrony (panels C2 to C7). STDP is
shown in black, PDDP in blue, and ebPDDP in red.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Mean-Field Approximations for Networks With STDP
1517
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
Figure 15: Comparison between STDP and PDDP in a Kuramoto network,
[β = 0.5, σκ = 0.2, (cid:3) = 0.6π , (cid:11) = 40π (20 Hz), (cid:3)t = 0.1 ms]. Results for PDDP
and ebPDDP are shown for 5, 25, and 75 Fourier components N f (first, second,
and third columns on the right-hand side of the figure, respectively). (A) Evo-
lution of the distribution of coupling weights with time (100 bins at each time
point). The average weight is represented by a thin black line. STDP is shown in
panel A1, PDDP in panels A2 to A4, and ebPDDP in panels A5 to A7. (B) Cou-
pling matrix at t = 150 s, with oscillators sorted by natural frequency. STDP is
shown in panel B1, PDDP in panels B2 to B4, and ebPDDP in panels B5 to B7.
(C) Time evolution of average coupling (panel C1: error bars represent the stan-
dard error of the mean over five repeats) and network synchrony (panels C2 to
C7). STDP is shown in black, PDDP in blue, and ebPDDP in red.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1518
B. Duchet, C. Bick, and Á. Byrne
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
Figure 16: Comparison between STDP with hard bounds and PDDP without
bounds in a Kuramoto network, [β = 1, σκ = 0.2, (cid:3) = 0.6π , (cid:11) = 10π (5 Hz)].
= 40 Fourier components. For
Results for PDDP and ebPDDP are shown for N f
STDP, hard bounds are enforced such that no individual weight can go below 0
or above 30. (A) Evolution of the distribution of coupling weights with time (100
bins at each time point). The average weight is represented by a thin black line.
STDP with hard bounds is shown in panel A1, PDDP without bounds in panel
A2, and ebPDDP without bounds in panel A3. (B) Coupling matrix at t = 12 s,
with oscillators sorted by natural frequency. STDP with hard bounds is shown
in panel B1, PDDP without bounds in panel B2, and ebPDDP without bounds in
panel B3. (C) Time evolution of average coupling (panel C1: error bars represent
the standard error of the mean over five repeats) and network synchrony (panels
C2 and C3). STDP with hard bounds is shown in black, PDDP without bounds
in blue, and ebPDDP without bounds in red.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Mean-Field Approximations for Networks With STDP
1519
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
Figure 17: Comparison between STDP with hard bounds and PDDP without
bounds in a Kuramoto network, [β = 0.5, σκ = 3, (cid:3) = 1.8π , (cid:11) = 10π (5 Hz)].
= 40 Fourier components. For
Results for PDDP and ebPDDP are shown for N f
STDP, hard bounds are enforced such that no individual weight can go below 0
or above 30. (A) Evolution of the distribution of coupling weights with time (100
bins at each time point). The average weight is represented by a thin black line.
STDP with hard bounds is shown in panel A1, PDDP without bounds in panel
A2, and ebPDDP without bounds in panel A3. (B) Coupling matrix at t = 12 s,
with oscillators sorted by natural frequency. STDP with hard bounds is shown
in panel B1, PDDP without bounds in panel B2, and ebPDDP without bounds in
panel B3. (C) Time evolution of average coupling (panel C1: error bars represent
the standard error of the mean over five repeats) and network synchrony (panels
C2 and C3). STDP with hard bounds is shown in black, PDDP without bounds
in blue, and ebPDDP without bounds in red.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1520
B. Duchet, C. Bick, and Á. Byrne
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 18: Influence of N f , (cid:3)t, and network frequency on error metrics. Error
metrics for PDDP compared to STDP for the time evolution of network syn-
chrony eρ, average coupling e ˆκ and distribution of weights ehist(κ
kl ), and for the
coupling matrix at the last stimulation point rκ∞
are shown in the first, second,
kl
third, and fourth columns, respectively. Results for PDDP are in blue and for
ebPDDP in red. Showing SEM error bars over five repeats. (A) Influence of the
number of Fourier coefficients N f on the error metrics for the parameters used
in Figure 12 (β = 0.5, σκ = 3, (cid:3) = 1.8π, (cid:11) = 10π ) in the first row; in Figure 13
(β = 1, σκ = 0.2, (cid:3) = 0.6π , (cid:11) = 10π) in the second row; and in Figure 14 (β = 1,
σκ = 3, (cid:3) = 1.8π , (cid:11) = 10π ) in the third row. (B) Influence of the time step (cid:3)t
for the parameters used in Figure 5 (β = 0.5, σκ = 0.2, (cid:3) = 0.6π , (cid:11) = 10π ) and
= 40. (C) Influence of the number of Fourier coefficients N f on error metrics
N f
for the parameters used in the 20 Hz example, see Figure 15 (β = 0.5, σκ = 0.2,
(cid:3) = 0.6π , (cid:11) = 40π , (cid:3)t = 0.1 ms).
Mean-Field Approximations for Networks With STDP
1521
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
Figure 19: Influence of σκ , (cid:3), and β on error metrics (slices through parameter
space). Error metrics for PDDP compared to STDP for the time evolution of
network synchrony eρ (first and fifth columns), average coupling e ˆκ (second and
sixth columns), and distribution of weights ehist(κ
kl ) (third and seventh columns),
and for the coupling matrix at the last stimulation point rκ∞
(fourth and eighth
kl
columns). Results for PDDP are in blue and for ebPDDP in red. Each of the
panels represents a different slice through parameter space as indicated by the
= 40 Fourier components, with sem
axes. The error metrics are shown for N f
error bars over five repeats.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1522
B. Duchet, C. Bick, and Á. Byrne
Figure 20: Representative trajectories from initial conditions in the test set. The
two-population mean-field approximation with optimized plasticity parame-
ters is shown in dark blue, the two-population mean-field approximation with
plasticity parameters obtained from the full system is shown in light blue, and
synthetic data from the full adaptive Kuramoto network are shown in black.
The first row shows the network synchrony, the second row the network phase,
and the third row the network average coupling.
Table 1: Best Parameters of Two-Population Mean-Field Approximation.
Parameter
(cid:8)
1
(cid:8)
2
λ
1
λ
2
Value
0.0263
3.0262
5.2985
5.4759
Notes: Parameters correspond to equation 5.1. Full
network parameters used to generate synthetic data
for the optimization are given in appendix B.
Acknowledgments
We are grateful to Rafal Bogacz and Alessandro Torcini for helpful dis-
cussions. We acknowledge the use of the University of Oxford Advanced
Research Computing facility in carrying out this work http://dx.doi.org/
10.5281/zenodo.22558
Funding Information
B.D. was supported by Medical Research Council grant MC_UU_00003/1.
C.B. acknowledges support from the Engineering and Physical Sciences Re-
search Council through grant EP/T013613/1.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Mean-Field Approximations for Networks With STDP
1523
Data Availability Statement
No new data were created or analyzed in this study. We are sharing code
at https://github.com/benoit-du/STDPvsPDDP to compare the evolution
of a Kuramoto network with STDP to the evolution of a Kuramoto network
with PDDP and ebPDDP.
References
Abbott, L. F., & Nelson, S. B. (2000). Synaptic plasticity: Taming the beast. Nature
Neuroscience, 3(11), 1178–1183. 10.1038/81453, PubMed: 11127835
Adamchic, I., Hauptmann, C., Barnikol, U. B., Pawelczyk, N., Popovych, O.,
Barnikol, T. T., . . . Tass, P. A. (2014). Coordinated reset neuromodulation for
Parkinson’s disease: Proof-of-concept study. Movement Disorders, 2(13), 1679–
1684. 10.1002/mds.25923
Akil, A. E., Rosenbaum, R., & Josi´c, K. (2021). Balanced networks under spike-
time dependent plasticity. PLOS Computational Biology 17(5), e1008958. 10.1371/
journal.pcbi.1008958
Aoki, T., & Aoyagi, T. (2009). Co-evolution of phases and connection strengths
in a network of phase oscillators. Physical Review Letters 102(3). 10.1103/
PhysRevLett.102.034101
Ashwin, P., Coombes, S., & Nicks, R. (2016). Mathematical frameworks for oscillatory
network dynamics in neuroscience. Journal of Mathematical Neuroscience 6(1), 2.
10.1186/s13408-015-0033-6
Asllani, M., Expert, P., & Carletti, T. (2018). A minimally invasive neurostimulation
method for controlling abnormal synchronisation in the neuronal activity. PLOS
Computational Biology, 14(7), e1006296. 10.1371/journal.pcbi.1006296
Berner, R., Schöll, E., & Yanchuk, S. (2019). Multiclusters in networks of adaptively
coupled phase oscillators. SIAM Journal on Applied Dynamical Systems, 18(4), 2227–
2266. 10.1137/18M1210150
Bi, G. Q., & Poo, M. M. (1998). Synaptic modifications in cultured hippocampal neu-
rons: Dependence on spike timing, synaptic strength, and postsynaptic cell type.
Journal of Neuroscience, 18(24), 10464–10472. 10.1523/jneurosci.18-24-10464.1998,
PubMed: 9852584
Bi, G. Q., & Poo, M. M. (2001). Synaptic modification by correlated activity:
Hebb’s postulate revisited. Annual Review of Neuroscience 24, 139–166. 10.1146/
annurev.neuro.24.1.139, PubMed: 11283308
Bick, C., Goodfellow, M., Laing, C. R., & Martens, E. A. (2020). Understanding
the dynamics of biological and neural oscillator networks through exact mean-
field reductions: A review. Journal of Mathematical Neuroscience, 10(1), 10. 10.1186/
s13408-020-00086-9
Bick, C., Gross, E., Harrington, H. A., & Schaub, M. T. (2021). What are higher-order
networks? arXiv:2104.11329.
Breakspear, M., Heitmann, S., & Daffertshofer, A. (2010). Generative models of cor-
tical oscillations: Neurobiological implications of the Kuramoto model. Frontiers
in Human Neuroscience, 4, 190. 10.3389/fnhum.2010.00190
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1524
B. Duchet, C. Bick, and Á. Byrne
Brown, E., Moehlis, J., & Holmes, P. (2004). On the phase reduction and response dy-
namics of neural oscillator populations. Neural Computation, 16, 673–715. 10.1162/
089976604322860668
Byrne, Á., O’Dea, R. D., Forrester, M., Ross, J., & Coombes, S. (2020). Next-generation
neural mass and field modeling. Journal of Neurophysiology, 123(2), 726–742.
10.1152/jn.00406.2019, PubMed: 31774370
Cabral, J., Luckhoo, H., Woolrich, M., Joensson, M., Mohseni, H., Baker, A., . . .
Deco, G. (2014). Exploring mechanisms of spontaneous functional connectiv-
ity in MEG: How delayed network interactions lead to structured amplitude
envelopes of band-pass filtered oscillations. NeuroImage, 90, 423–435. 10.1016/
j.neuroimage.2013.11.047, PubMed: 24321555
Cassenaer, S., & Laurent, G. (2007). Hebbian STDP in mushroom bodies facilitates
the synchronous flow of olfactory information in locusts. Nature, 448(7154), 709–
713. 10.1038/nature05973, PubMed: 17581587
Ciszak, M., Marino, F., Torcini, A., & Olmi, S.
(2020). Emergent excitabil-
ity in populations of nonexcitable units. Physical Review E, 102(5), 050201.
10.1103/PhysRevE.102.050201
Coombes, S., & Byrne, Á. (2019). Next generation neural mass models. In F. Corinto
& A. Torcini (Eds.), Nonlinear dynamics in computational neuroscience (pp. 1–16).
Springer. 10.1007/978-3-319-71048-8_1
Coulon, A., Beslon, G., & Soula, H. A. (2011). Enhanced stimulus encoding capabil-
ities with spectral selectivity in inhibitory circuits by STDP. Neural Computation,
23(4), 882–908. 10.1162/NECO_a_00100, PubMed: 21222530
Cumin, D., & Unsworth, C. (2007). Generalising the Kuramoto model for the study
of neuronal synchronisation in the brain. Physica D: Nonlinear Phenomena, 226(2),
181–196. 10.1016/j.physd.2006.12.004
Duchet, B., Sermon, J. J., Weerasinghe, G., Denison, T., & Bogacz, R. (2022). How to
entrain a selected neuronal rhythm but not others: Open-loop dithered brain stimulation
for selective entrainment. bioRxiv:2022.07.06.499051. 10.1101/2022.07.06.499051
Duchet, B., Weerasinghe, G., Cagnan, H., Brown, P., Bick, C., & Bogacz, R. (2020).
Phase-dependence of response curves to deep brain stimulation and their rela-
tionship: From essential tremor patient data to a Wilson–Cowan model. Journal
of Mathematical Neuroscience, 10(1), 10. 10.1186/s13408-020-00081-0
Ebert, M., Hauptmann, C., & Tass, P. A. (2014). Coordinated reset stimulation in a
large-scale model of the STN-GPE circuit. Frontiers in Computational Neuroscience,
8, 154. 10.3389/fncom.2014.00154
Ermentrout, B. (2002). Simulating, analyzing, and animating dynamical systems. Society
for Industrial and Applied Mathematics. 10.1137/1.9780898718195
Fasano, A., & Helmich, R. C. (2019). Tremor habituation to deep brain stimulation:
Underlying mechanisms and solutions. Movement Disorders, 34(12), 1761–1773.
10.1002/mds.27821, PubMed: 31433906
Feldman, D. E. (2000). Timing-based LTP and LTD at vertical inputs to layer II/III
pyramidal cells in rat barrel cortex. Neuron, 27(1), 45–56. 10.1016/S0896-6273(00)
00008-8, PubMed: 10939330
Fialkowski, J., Yanchuk, S., Sokolov, I. M., Schöll, E., Gottwald, G. A., & Berner,
R. (2022). Heterogeneous nucleation in finite size adaptive dynamical networks.
arXiv:2207.02939.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Mean-Field Approximations for Networks With STDP
1525
Finger, H., Bönstrup, M., Cheng, B., Messé, A., Hilgetag, C., Thomalla, G., . . . König,
P. (2016). Modeling of large-scale functional brain networks based on structural
connectivity from DTI: Comparison with EEG derived phase coupling networks
and evaluation of alternative methods along the modeling Path. PLOS Computa-
tional Biology, 12(8), e1005025. 10.1371/journal.pcbi.1005025
Froemke, R. C., & Dan, Y. (2002). Spike-timing-dependent synaptic modification
induced by natural spike trains. Nature, 416(6879), 433–438. 10.1038/416433a,
PubMed: 11919633
Gast, R., Knösche, T. R., & Schmidt, H. (2021). Mean-field approximations of net-
works of spiking neurons with short-term synaptic plasticity. Physical Review E,
10, 44310. 10.1103/physreve.104.044310
Gast, R., Schmidt, H., & Knösche, T. R. (2020). A mean-field description of bursting
dynamics in spiking neural networks with short-term adaptation. Neural Compu-
tation, 32(9), 1615–1634. 10.1162/neco_a_01300, PubMed: 32687770
Gerstner, W., Kempter, R., Van Hemmen, J. L., & Wagner, H. (1996). A neuronal learn-
ing rule for sub-millisecond temporal coding. Nature, 383(6595), 76–78. 10.1038/
383076a0, PubMed: 8779718
Gkogkas, M. A., Kuehn, C., & Xu, C. (2021). Continuum limits for adaptive network
dynamics. arXiv:2109.05898.
Hebb, D. (2005). The organization of behavior: A neuropsychological theory. Psychology
Press. 10.4324/9781410612403
Johnen, V. M., Neubert, F. X., Buch, E. R., Verhagen, L. M., O’Reilly, J., Mars, R. B.,
& Rushworth, M. F. (2015). Causal manipulation of functional connectivity in
a specific neural pathway during behaviour and at rest. eLife, 2015(4). 10.7554/
eLife.04585
Kim, K., Yoo, S. J., Kim, S. Y., Lee, T., Lim, S. H., Jang, J. E., . . . Choi, J. W. (2021).
Subthreshold electrical stimulation as a low power electrical treatment for stroke
rehabilitation. Scientific Reports, 11(1), 11. 10.1038/s41598-021-93354-x
Kromer, J. A., & Tass, P. A. (2020). Long-lasting desynchronization by decoupling
stimulation. Physical Review Research, 2(3), 2. 10.1103/physrevresearch.2.033101
Kuehn, C. (2016). Moment closure—A brief review. In E. Schöll, S. Klapp, & P. Hövel
(Eds.), Control of self-organizing nonlinear systems (pp. 253–271). Springer. 10.1007/
978-3-319-28028-8_13
Kuramoto, Y. (1975). Self-entrainment of a population of coupled non-linear oscil-
lators. In International Symposium on Mathematical Problems in Theoretical Physics
(pp. 420–422).
Litwin-Kumar, A., & Doiron, B. (2014). Formation and maintenance of neuronal as-
semblies through synaptic plasticity. Nature Communications, 5(1), 1–12. 10.1038/
ncomms6319
Lücken, L., Popovych, O. V., Tass, P. A., & Yanchuk, S. (2016). Noise-enhanced cou-
pling between two oscillators with long-term plasticity. Physical Review E, 93(3).
10.1103/PhysRevE.93.032210
Luke, T. B., Barreto, E., & So, P. (2013). Complete classification of the macroscopic
behaviour of a heterogeneous network of theta neurons. Neural Computation, 25,
3207-3234. 10.1162/NECO_a_00525
Madadi Asl, M., Vahabie, A.-H., Valizadeh, A., & Tass, P. A. (2022, Mar). Spike-
timing-dependent plasticity mediated by dopamine and its role in Parkinson’s
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1526
B. Duchet, C. Bick, and Á. Byrne
disease pathophysiology. Frontiers in Network Physiology, 10. 10.3389/FNETP.2022
.817524
Maistrenko, Y. L., Lysyansky, B., Hauptmann, C., Burylko, O., & Tass, P. A. (2007).
Multistability in the Kuramoto model with synaptic plasticity. Physical Review E—
Statistical, Nonlinear, and Soft Matter Physics, 75(6). 10.1103/PhysRevE.75.066207
Manos, T., Zeitler, M., & Tass, P. A. (2018). How stimulation frequency and intensity
impact on the long-lasting effects of coordinated reset stimulation. PLOS Compu-
tational Biology, 14(5). 10.1371/journal.pcbi.1006113
Markram, H., Lübke, J., Frotscher, M., & Sakmann, B. (1997). Regulation of synaptic
efficacy by coincidence of postsynaptic APs and EPSPs. Science, 275(5297), 213–
215. 10.1126/science.275.5297.213, PubMed: 8985014
Mishra, R. K., Kim, S., Guzman, S. J., & Jonas, P. (2016). Symmetric spike timing-
dependent plasticity at CA3-CA3 synapses optimizes storage and recall in au-
toassociative networks. Nature Communications, 7. 10.1038/ncomms11552
Montangie, L., Miehl, C., & Gjorgjieva, J. (2020). Autonomous emergence of connec-
tivity assemblies via spike triplet interactions. PLOS Computational Biology, 16(5),
e1007835. 10.1371/journal.pcbi.1007835
Montbrió, E., Pazó, D., & Roxin, A. (2015). Macroscopic description for networks of
spiking neurons. Physical Review, 10(5), 021028. 10.1103/PhysRevX.5.021028
Müller-Dahlhaus, F., Ziemann, U., & Classen, J. (2010). Plasticity resembling spike-
timing dependent synaptic plasticity: The evidence in human cortex. Frontiers in
Synaptic Neuroscience, 2. 10.3389/fnsyn.2010.00034
Nguyen, P. T. M., Hayashi, Y., Baptista, M. D. S., & Kondo, T. (2020). Collective al-
most synchronization-based model to extract and predict features of EEG signals.
Scientific Reports, 10(1), 10. 10.1038/s41598-020-73346-z
Ocker, G. K. Litwin-Kumar, A., & Doiron, B. (2015). Self-organization of microcir-
cuits in networks of spiking neurons with plastic synapses. PLOS Computational
Biology, 11(8), 11. 10.1371/journal.pcbi.1004458
Ott, E., & Antonsen, T. M. (2008). Low dimensional behavior of large systems of
globally coupled oscillators. Chaos: An Interdisciplinary Journal of Nonlinear Science,
18(3), 18. 10.1063/1.2930766
Ott, E., & Antonsen, T. M. (2009). Long time evolution of phase oscillator systems.
Chaos, 19(2), 19. 10.1063/1.3136851
Pfister, J. P., & Gerstner, W. (2006). Triplets of spikes in a model of spike
timing-dependent plasticity. Journal of Neuroscience, 26(38), 9673–9682. 10.1523/
JNEUROSCI.1425-06.2006, PubMed: 16988038
Pietras, B., & Daffertshofer, A. (2019). Network dynamics of coupled oscillators and
phase reduction techniques. Physics Reports, 819, 1–105. 10.1016/j.physrep.2019
.06.001
Ponce-Alvarez, A., Deco, G., Hagmann, P., Romani, G. L., Mantini, D., & Corbetta,
M. (2015). Resting-state temporal synchronization networks emerge from connec-
tivity topology and heterogeneity. PLOS Computational Biology, 11(2), e1004100.
10.1371/journal.pcbi.1004100
Popovych, O. V., & Tass, P. A. (2012). Desynchronizing electrical and sensory coor-
dinated reset neuromodulation. Frontiers in Human Neuroscience, 6(2012), 1–14.
10.3389/fnhum.2012.00058, PubMed: 22279433
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Mean-Field Approximations for Networks With STDP
1527
Popovych, O. V., Xenakis, M. N., & Tass, P. A. (2015). The spacing principle for
unlearning abnormal neuronal synchrony. PLOS One, 10(2), e0117205. 10.1371/
journal.pone.0117205
Röhr, V., Berner, R., Lameu, E. L., Popovych, O. V., & Yanchuk, S. (2019). Frequency
cluster formation and slow oscillations in neural populations with plasticity.
PLOS One, 14(11), e0225094. 10.1371/journal.pone.0225094
Schmidt, R., LaFleur, K. J., de Reus, M. A., van den Berg, L. H., & van den Heuvel,
M. P. (2015). Kuramoto model simulation of neural hubs and dynamic syn-
chrony in the human cerebral connectome. BMC Neuroscience, 16(1), 16. 10.1186/
s12868-015-0193-z
Schmutz, V., Gerstner, W., & Schwalger, T. (2020). Mesoscopic population equations
for spiking neural networks with synaptic short-term plasticity. Journal of Mathe-
matical Neuroscience, 10(1), 10. 10.1186/s13408-020-00082-z
Seliger, P., Young, S. C., & Tsimring, L. S. (2002). Plasticity and learning in a network
of coupled phase oscillators. Physical Review E—Statistical Physics, Plasmas, Fluids,
and Related Interdisciplinary Topics, 65(4), 7. 10.1103/PhysRevE.65.041906
Sgritta, M., Locatelli, F., Soda, T., Prestori, F., & D’Angelo, E. U. (2017). Hebbian spike-
timing dependent plasticity at the cerebellar input stage. Journal of Neuroscience,
37(11), 2809–2823. 10.1523/JNEUROSCI.2079-16.2016, PubMed: 28188217
Snyder, J., Zlotnik, A., & Lokhov, A. Y. (2020). Data-driven selection of coarse-
grained models of coupled oscillators. Physical Review Research, 2(4), 2. 10.1103/
PhysRevResearch.2.043402
Song, S., Miller, K. D., & Abbott, L. F. (2000). Competitive Hebbian learning through
spike-timing-dependent synaptic plasticity. Nature Neuroscience 3(9), 919–926.
10.1038/78829, PubMed: 10966623
Taher, H., Torcini, A., & Olmi, S. (2020). Exact neural mass model for synaptic-
based working memory. PLOS Computational Biology, 16(12), e1008533. 10.1371/
journal.pcbi.1008533
Tass, P. A., & Majtanik, M. (2006). Long-term anti-kindling effects of desynchronizing
brain stimulation: A theoretical study. Biological Cybernetics, 94(1), 58–66. 10.1007/
s00422-005-0028-6, PubMed: 16284784
Tass, P. A., Qin, L., Hauptmann, C., Dovero, S., Bezard, E., Boraud, T., & Meissner, W.
G. (2012). Coordinated reset has sustained aftereffects in Parkinsonian monkeys.
Annals of Neurology, 7(5), 816–820. 10.1002/ana.23663
Thiele, M., Berner, R., Tass, P. A., Schöll, E., & Yanchuk, S. (2023). Asymmetric adap-
tivity induces recurrent synchronization in complex networks. Chaos, 33(2), 33.
10.1063/5.0128102
Thiem, T. N., Kooshkbaghi, M., Bertalan, T., Laing, C. R., & Kevrekidis, I. G. (2020).
Emergent spaces for coupled oscillators. Frontiers in Computational Neuroscience,
14, 36. 10.3389/fncom.2020.00036
Tsodyks, M., Pawelzik, K., & Markram, H. (1998). Neural networks with dynamic
synapses. Neural Computation, 10(4), 821–835. 10.1162/089976698300017502,
PubMed: 9573407
Tyulkina, I. V., Goldobin, D. S., Klimenko, L. S., & Pikovsky, A. (2018). Dynamics
of noisy oscillator populations beyond the Ott-Antonsen ansatz. Physical Review
Letters, 120(26). 10.1103/PhysRevLett.120.264101
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1528
B. Duchet, C. Bick, and Á. Byrne
Vlasov, V., Rosenblum, M., & Pikovsky, A. (2016). Dynamics of weakly inhomoge-
neous oscillator populations: Perturbation theory on top of Watanabe-Strogatz
integrability. Journal of Physics A: Mathematical and Theoretical, 49(31), 49LT02.
10.1088/1751-8113/49/31/31LT02
Wang, J., Nebeck, S., Muralidharan, A., Johnson, M. D., Vitek, J. L., & Baker,
K. B. (2016). Coordinated reset deep brain stimulation of subthalamic nucleus
produces long-lasting, dose-dependent motor improvements in the 1-methyl-4-
phenyl-1,2,3,6-tetrahydropyridine non-human primate model of Parkinsonism.
Brain Stimulation, 9(4), 609–617. 10.1016/j.brs.2016.03.014, PubMed: 27151601
Weerasinghe, G., Duchet, B., Bick, C., & Bogacz, R. (2021). Optimal closed-loop deep
brain stimulation using multiple independently controlled contacts. PLOS Com-
putational Biology, 17(8), e1009281. 10.1371/journal.pcbi.1009281
Weerasinghe, G., Duchet, B., Cagnan, H., Brown, P., Bick, C., & Bogacz, R.
(2019). Predicting the effects of deep brain stimulation using a reduced cou-
pled oscillator model. PLOS Computational Biology, 15(8), e1006575. 10.1371/
journal.pcbi.1006575
Wiratman, W., Murakami, T., Tiksnadi, A., Kobayashi, S., Hanajima, R., & Ugawa, Y.
(2022). Enhancement of LTD-like plasticity by associative pairing of quadripulse
magnetic stimulation with peripheral nerve stimulation. Clinical Neurophysiology,
138, 9–17. 10.1016/j.clinph.2022.03.009, PubMed: 35358770
Received July 17, 2022; accepted April 26, 2023.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
5
9
1
4
8
1
2
1
5
2
7
7
3
n
e
c
o
_
a
_
0
1
6
0
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3