ARTICLE - Specialized Research AI at MIT

ARTICLE

Communicated by Richard Zemel

How to Represent Part-Whole Hierarchies
in a Neural Network

Geoffrey Hinton
hinton@cs.toronto.edu
Google Research; and Vector Institute, Toronto, Ontario M5G 1M1, Canada;
and Department of Computer Science, University of Toronto,
Toronto, ON M5S 2E4, Canada

This article does not describe a working system. Instead, it presents a sin-
gle idea about representation that allows advances made by several dif-
ferent groups to be combined into an imaginary system called GLOM.1
The advances include transformers, neural fields, contrastive represen-
tation learning, distillation, and capsules. GLOM answers the question:
How can a neural network with a fixed architecture parse an image into
a part-whole hierarchy that has a different structure for each image?
The idea is simply to use islands of identical vectors to represent the
nodes in the parse tree. If GLOM can be made to work, it should signif-
icantly improve the interpretability of the representations produced by
transformer-like systems when applied to vision or language.

1 Overview of the Idea

There is strong psychological evidence that people parse visual scenes into
part-whole hierarchies and model the viewpoint-invariant spatial relation-
ship between a part and a whole as the coordinate transformation between
intrinsic coordinate frames that they assign to the part and the whole (Hin-
ton, 1979). If we want to make neural networks that understand images in
the same way as people do, we need to figure out how neural networks
can represent part-whole hierarchies. This is difficult because a real neu-
ral network cannot dynamically allocate a group of neurons to represent
a node in a parse tree.2 The inability of neural nets to dynamically allo-
cate neurons was the motivation for a series of models that used “capsules”
(Sabour, Frosst, & Hinton, 2017; Hinton, Sabour, & Frosst, 2018; Kosiorek,
Sabour, Teh, & Hinton, 2019). These models made the assumption that
a group of neurons called a capsule would be permanently dedicated to

GLOM is derived from the slang “glom together,” which may derive from the word

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

agglomerate.

What neurons do is determined by their incoming and outgoing weights, and real

neurons cannot completely change these weights rapidly.

Neural Computation 35, 413–452 (2023)
https://doi.org/10.1162/neco_a_01557

414

G. Hinton

a part of a particular type occurring in a particular region of the image.
A parse tree could then be created by activating a small subset of these
preexisting, type-specific capsules and the appropriate connections be-
tween them. This article describes a very different way of using capsules
to represent the part-whole hierarchy in a neural net.

Although this article is primarily concerned with the perception of a sin-
gle static image, GLOM is most easily understood as a pipeline for process-
ing a sequence of frames, so a static image will be treated as a sequence of
identical frames.

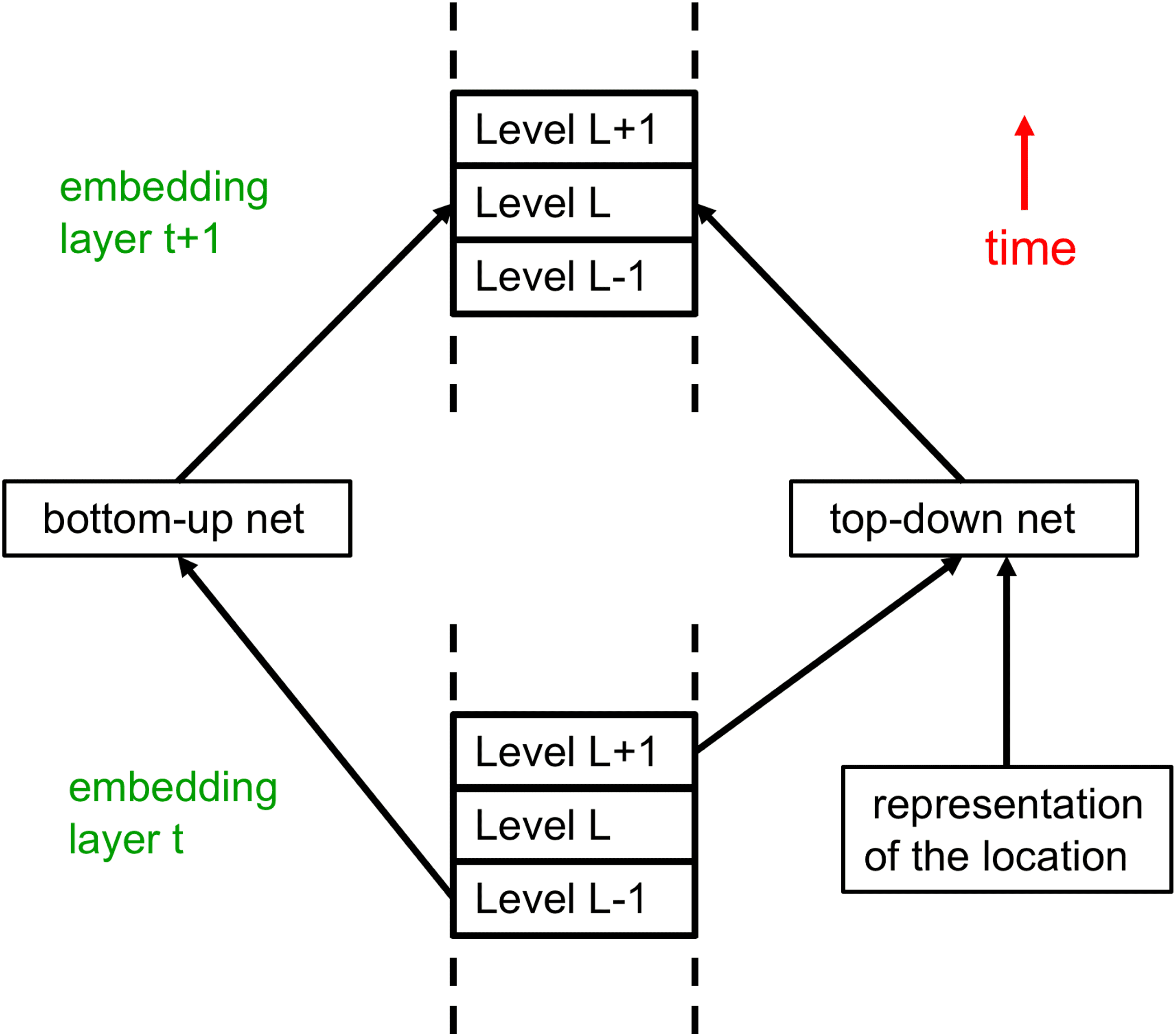
The GLOM architecture3 is composed of a large number of columns4
that all use exactly the same weights. Each column is a stack of spatially
local autoencoders. Each autoencoder in the stack learns a different level
of representation for what is happening in the same small image patch by
transforming the embedding at one level into the embedding at an adjacent
level using a multilayer bottom-up encoder and a multilayer top-down de-
coder. These levels correspond to the levels in a part-whole hierarchy. When
shown an image of a face, for example, a single column might converge
on embedding vectors5 representing a nostril, a nose, a face, and a person.
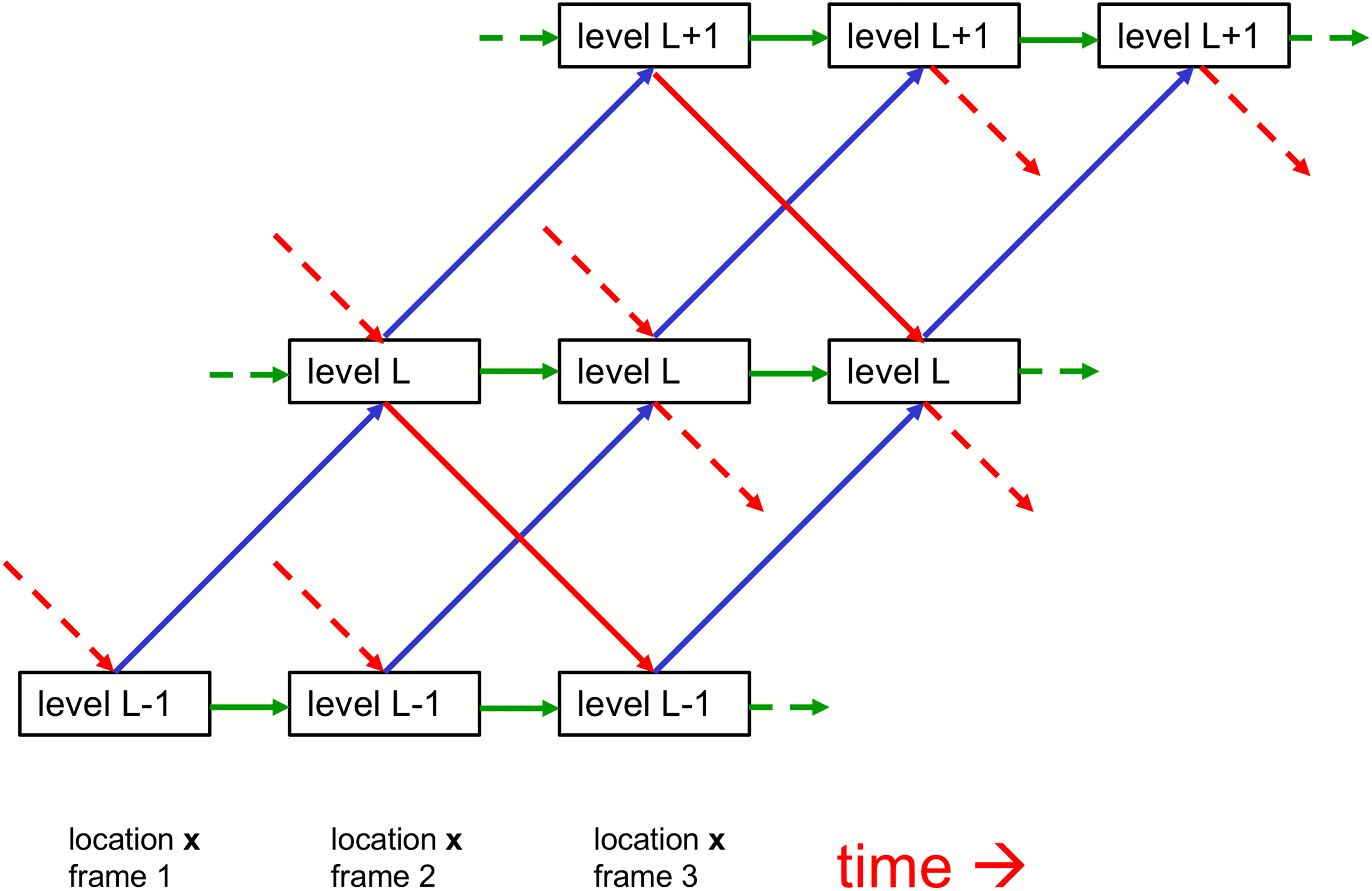
Figure 1 shows how the embeddings at different levels interact in a single
column.

Figure 1 does not show the interactions between embeddings at the
same level in different columns. These are much simpler than the interac-
tions within a column because they do not need to implement part-whole
coordinate transforms. They are like the attention-weighted interactions be-
tween columns representing different word fragments in a multiheaded
transformer (Devlin, Chang, Lee, & Toutanova, 2018), but they are simpler
because the query, key and value vectors are all identical to the embedding
vector. The role of the intercolumn interactions is to produce islands of iden-
tical embeddings at a level by making each embedding vector at that level
regress toward other similar vectors at nearby locations.6 This creates mul-
tiple local “echo chambers” in which embeddings at a level attend mainly to
other like-minded embeddings. It may seem wasteful to replicate the same
embedding vector across many locations, but it facilitates iterative segmen-
tation as the network settles.

The GLOM architecture has some similarity to models that use the errors in top-down
predictions as their bottom-up signals (Rao & Ballard, 1999), but in a nonlinear system,
the bottom-up signals cannot just carry the prediction error because the full activity vector
is required to select the right operating regime for the nonlinear units.

Each level in a column bears some resemblance to a hypercolumn as described by

neuroscientists.

An embedding vector is the activity vector of a “universal” capsule that is capable of

representing many different types of entity.

In cortex, this type of intercolumn interaction would be implemented by long-range,
excitatory lateral connections and the shorter-range inhibitory connections would imple-
ment the competition between alternative embeddings within a capsule.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

How to Represent Part-Whole Hierarchies in a Neural Network

415

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 1: Showing the bottom-up, top-down, and same-level interactions
among three adjacent levels of the proposed GLOM architecture for a single
column. The blue and red arrows representing bottom-up and top-down in-
teractions are implemented by two different neural networks that have several
hidden layers. These networks can differ between pairs of levels, but they are
shared across columns and across time steps. The top-down net should prob-
ably use sinusoidal units (Sitzmann, Martel, Bergman, Lindell, & Wetzstein,
2020). For a static image, the green arrows could simply be scaled residual con-
nections that implement temporal smoothing of the embedding at each level.
For video, the green connections could be neural networks that learn tem-
poral dynamics based on several previous states of the capsule. Interactions
between the embedding vectors at the same level in different columns are im-
plemented by a nonadaptive, attention-weighted, local smoother, which is not
shown.

At each discrete time and in each column separately, the embedding at a

level is updated to be the weighted average of four contributions:

1. The prediction produced by the bottom-up neural net acting on the

embedding at the level below at the previous time

2. The prediction produced by the top-down neural net acting on the

embedding at the level above at the previous time

3. The embedding vector at the previous time step
4. The attention-weighted average of the embeddings at the same level

in nearby columns at the previous time

416

G. Hinton

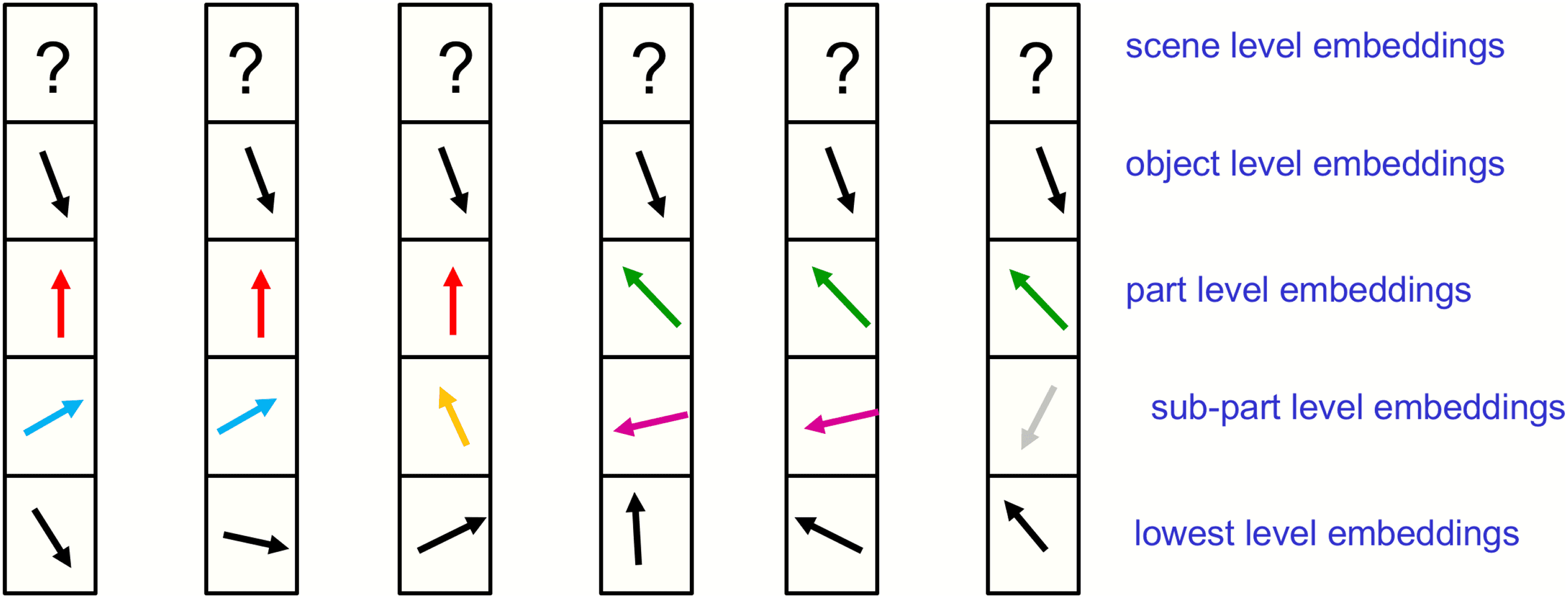
Figure 2: A picture of the embeddings at a particular time in six nearby
columns. All of the locations shown belong to the same object, and the scene
level has not yet settled on a shared vector. The complete embedding vector
for each location is shown by dividing the vector into a separate section for
each level in the part-whole hierarchy and then showing the high-dimensional
embedding vector for a level as a 2D vector. This makes it easy to illustrate
alignment of the embedding vectors of different locations. The islands of iden-
tical vectors at the various levels shown in the figure represent a parse tree. But
islands of identity are considerably more powerful than phrase structure gram-
mars. They have no difficulty representing disconnected objects as in, “Will this
slow phrase structure grammarians down?”

For a static image, the embeddings at a level should settle down over
time to produce distinct islands of nearly identical vectors.7 These islands
should be larger at higher levels as shown in Figure 2. Using the islands
of similarity to represent the parse of an image avoids the need to allocate
groups of neurons to represent nodes of the parse tree on the fly or to set
aside groups of neurons for all possible nodes in advance. Instead of allocat-
ing neural hardware to represent a node in a parse tree and giving the node
pointers to its ancestor and descendants, GLOM allocates an appropriate ac-
tivity vector to represent the node and uses the same activity vector for all
the locations belonging to the node.8 The ability to access the ancestor and
descendants of the node is implemented by the bottom-up and top-down
neural nets rather than by using RAM to do table look-up.

Like BERT (Devlin et al., 2018), the whole system can be trained end-
to-end to reconstruct images at the final time step from input images with

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

If an object is moving relative to the point of fixation, the capsules at the edge of the
object will need to radically change their embeddings. Capsules representing locations
that stay within the same object will only need to change their object-level embedding
vectors slightly to represent the change in the pose of the object relative to the camera.

The idea of using similarity of vectors to do segmentation has been used in earlier

work on directional unit Boltzmann machines (Zemel, Williams, & Mozer, 1995).

How to Represent Part-Whole Hierarchies in a Neural Network

417

missing regions, but the objective function also includes two regularizers
that encourage islands of near-identical vectors at each level. The regular-
izers are simply the agreement between the new embedding at a level and
the bottom-up and top-down predictions. Increasing this agreement facili-
tates the formation of local islands.

2 Introduction

This article proposes the idea of using islands of similar vectors to represent
the parse tree of an image and then explores some of the many ramifications
of this idea by describing an imaginary system called GLOM that imple-
ments it. It concludes with some speculations about how the brain might
implement some aspects of GLOM. But first some disclaimers:

Disclaimer 1: Human vision is a sampling process in which intelligently
chosen fixation points are used to acquire the information required to
perform a task using retinas that have much higher resolution around
the fixation point. The same neural circuitry is reused for each new
fixation. For the purposes of this article, I assume a single retina or
camera with uniform resolution and consider what happens only on
the first fixation.

Disclaimer 2: To avoid cumbersome terms like “sub-sub-parts,” I often
talk about parts and wholes as if there were only two levels in the part-
whole hierarchy. But a section of the complete embedding vector that
is called a whole when considering levels L-1 and L is also called a
part when considering levels L and L+1.

In a computer that has general-purpose, random-access memory, the ob-
vious way to represent the part-whole hierarchy for a specific image is to
create a graph structure for that particular image by dynamically allocat-
ing pieces of the memory to the nodes in the graph and giving each node
pointers to the nodes it is connected to. Combining this type of dynami-
cally created graph with neural network learning techniques has recently
shown great promise (Bear et al., 2020), but if the whole computer is a neu-
ral network, it is far less obvious how to represent part-whole hierarchies
that are different for every image if we want the structure of the neural net
to be identical for all images. If we allow three-way interactions in which
the activity of one neuron gates the connection between two other neurons
(Hinton, 1981c), it is easy to make the connections dynamic, but it is still
unclear how to dynamically create a graph structure without the ability to
allocate neurons on the fly. It is especially difficult in a real neural net where
the knowledge is in the connection weights, which cannot easily be copied.
One rather cumbersome solution to this problem is to set aside a group
of neurons, called a capsule, for each possible type of object or part in each

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

418

G. Hinton

region of the image9 and to use a routing algorithm to dynamically connect
a small subset of active capsules into a graph that represents the parse of the
image at hand. The activities of neurons within a capsule can then represent
properties of a part such as the pose or deformation of a particular mouth
or face.

With considerable effort, models that use capsules have achieved some
successes in supervised and unsupervised learning on small data sets
(Sabour et al., 2017; Hinton et al., 2018; Kosiorek et al., 2019), but they have
not scaled well to larger data sets (Barham & Isard, 2019). Capsules do not
have the signature of really practical ideas like stochastic gradient descent
or transformers, which just want to work. The fundamental weakness of
capsules is that they use a mixture to model the set of possible parts. This
forces a hard decision about whether a car headlight and an eye are really
different parts. If they are modeled by the same capsule, the capsule cannot
predict the identity of the whole. If they are modeled by different capsules,
the similarity in their relationship to their whole cannot be captured.

One way to avoid using a mixture for modeling the different types of
part is to have a set of identical, universal capsules, each of which contains
enough knowledge to model any type of part (Locatello et al., 2020; Sri-
vastava, Goh, & Salakhutdinov, 2019; Sun, Tagliasacchi et al., 2020). This al-
lows part identities to have distributed representations, which allows better
sharing of knowledge between similar parts. In neuroscience terminology,
identities are value coded rather than place coded. However, it creates a
symmetry breaking problem in deciding which universal object-level cap-
sule each part should be routed to.10

A more radical version of universal capsules, which avoids both sym-
metry breaking and routing, is to preassign a universal capsule to every
location in the image. These ubiquitous universal capsules can be used to
represent whatever happens to be at that location. An even more profli-
gate version is to dedicate several different levels of ubiquitous universal
capsule to each location so that a location can belong to a scene, an object,
a part, and a subpart simultaneously. This article explores this profligate
way of representing the part-whole hierarchy. It was inspired by a biologi-
cal analogy, a mathematical analogy, and recent work on neural scene rep-
resentations (Ha, 2016; Sitzmann, Zollhoefer, & Wetzstein, 2019).

2.1 The Biological Analogy. All the cells in the body have a copy of the
whole genome. It seems wasteful for brain cells to contain the instructions
for behaving like liver cells, but it is convenient because it gives every cell its
own private access to whatever DNA it might choose to express. Each cell

These regions can be larger for higher-level parts that are more diverse but occur

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

more sparsely in any one image.

Adam Kosoriek suggested using universal capsules in 2019, but I was put off by the

symmetry-breaking issue and failed to realize the importance of this approach.

How to Represent Part-Whole Hierarchies in a Neural Network

419

has an expression intensity11 for each gene, and the vector of expression
intensities is similar for cells that form part of the same organ.

The analogy with neural nets goes like this: Each location in the image
corresponds to a biological cell. The complete embedding vector for a loca-
tion is like the vector of gene expression intensities for a cell. The forward
pass is like the developmental process that allows a new vector of gene ex-
pression intensities to be determined by the previous vectors of expression
intensities. Objects are like organs: they are a collection of locations whose
embedding vectors are all very similar at a high level. Within an object, the
embedding vectors may differ at lower levels that correspond to the parts
of the object (see Figure 2).

2.2 The Mathematical Analogy. The Kolmogorov-Arnold superposi-
tion theorem states that every multivariate continuous function can be rep-
resented as a superposition of continuous functions of one variable.12 For
example, multiplication can be represented as the sum of the logs of the
individual arguments followed by exponentiation. In machine learning ter-
minology, when it comes to multi-argument functions, addition is all you
need. This assumes, of course, that you can find the right single-argument
functions to encode the arguments of the multivariate function you want to
represent and then find the right function to decode the sum. Kolmogorov
proved this can always be done, but the encoder functions used for the proof
are so bizarre that they are of no practical relevance to neural networks.

The theorem does, however, suggest an interesting approach to com-
bining information coming from many different locations. Perhaps we can
learn how to encode the information at each location in such a way that
simply averaging the encodings from different locations is the only form
of interaction we need.13 This idea is already used in set transformers (Lee
et al., 2019) for combining information from different members of a set. If
we modify this suggestion slightly to use an attention-weighted local av-
erage, we get a particularly simple form of transformer in which the key,
the query, and the value are all the same as the embedding itself, and the
only interaction between locations is attention-weighted smoothing at each
level. All of the adaptation occurs in the bottom-up and top-down neural
networks at each location, which are depicted by the blue and red arrows in
Figure 1. These networks are shared across all locations and all time steps,
but possibly not across all levels of the part-whole hierarchy.

I use the word intensity rather than the word level so as not to confuse scalar intensi-

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

ties with discrete levels in a part-whole hierarchy.

This solves a version of Hilbert’s 13th problem.
This has a resemblance to variational learning (Neal & Hinton, 1997), where we start
by assuming that the log posterior distribution over the whole set of latent variables is
determined by the sum of their individual log posterior distributions and then we try to
learn a model for which this additive approximation works well.

420

G. Hinton

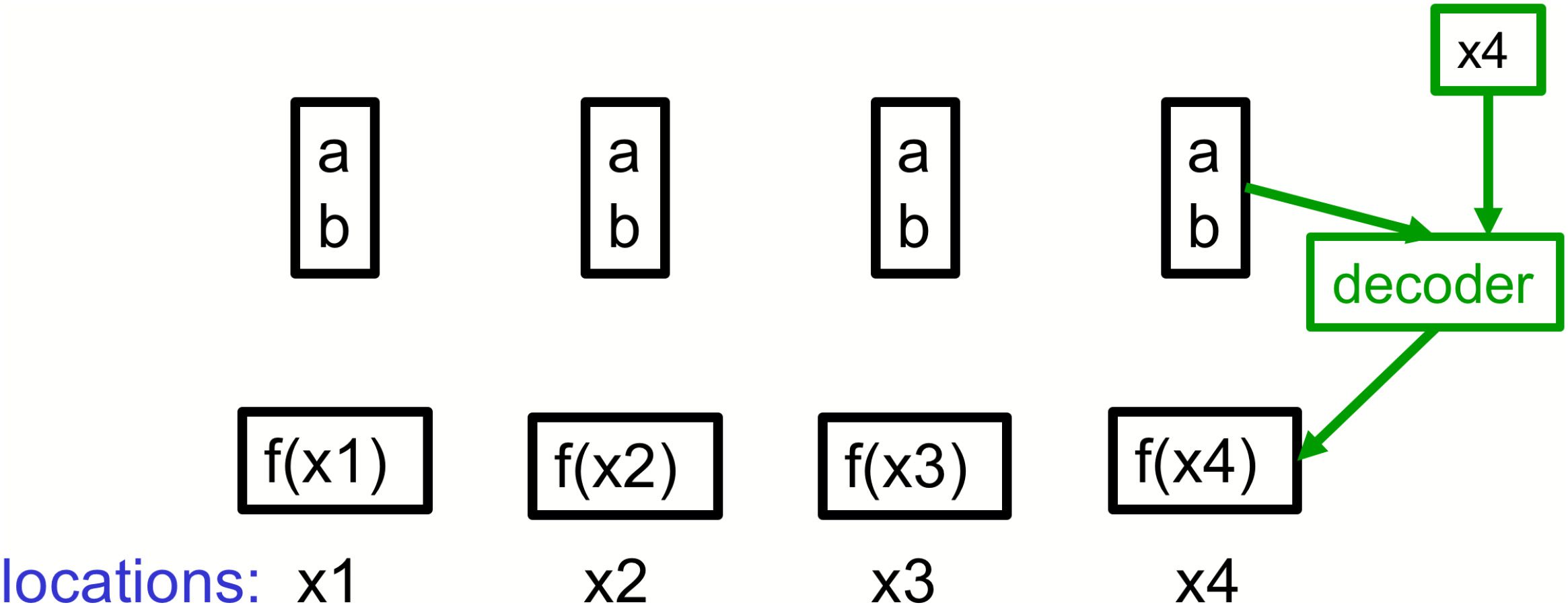
Figure 3: A very simple example of a neural field using individual pixels as the
locations. The intensities of four pixels can all be represented by the same code
(a, b) even though their intensities vary according to the function f (x) = ax + b.
The decoder has an extra input that specifies the location.

2.3 Neural Fields. Suppose we want to represent the value of a scalar
variable, such as the depth or intensity, at every point in an image. A sim-
ple way to do this is to quantize the image locations into pixels and use an
array that specifies the scalar variable at each pixel. If the values of differ-
ent pixels are related, it may be more efficient to use a neural network that
takes as input a code vector representing the image and outputs an array of
pixel values. This is what the decoder of an autoencoder does. Alternatively
we could use a neural network that takes as input a code vector represent-
ing the image plus an additional input representing an image location and
outputs the predicted value at that location. This is called a neural field,14
and this way of using neural networks has recently become very popular
(Ha, 2016; Sitzmann et al., 2020; Mildenhall et al., 2020). Figure 3 shows a
very simple example in which the intensities at a set of locations can all be
reconstructed from the same code, even though the intensities vary.

For a complicated image, the neural net could transform a code vector
representing the whole image plus a vector representing an image location
into the value at that location. But if images are composed of familiar objects
and objects are composed of familiar parts it is much more efficient to use a
hierarchy of neural fields.15 In GLOM, the scene-level top-down neural net-
work converts the scene vector plus an image location into the appropriate

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

An early example of using neural fields is described in Oore, Hinton, and Dudek
(1997). The image is always the same, so only the location input is needed. The 12 channels
at each image location are the depths returned by 12 sonar detectors pointing in different
directions. The match between the neural net’s prediction for each location and the actual
data at the robot’s current location is used to perform a Bayesian update of the mobile
robot’s probability distribution over locations.

A small step in this direction is simply to have a separate neural field for each type
of object. This makes it easy to represent scenes composed of familiar objects in novel
arrangements (Niemeyer & Geiger, 2020).

How to Represent Part-Whole Hierarchies in a Neural Network

421

object vector for that location. This vector includes information about the
3-D pose of the object relative to the camera. All of the locations that be-
long to the same object are given exactly the same object-level vector. The
object-level top-down neural network then converts an object vector plus
a location into the part vector that is appropriate for that location and so
on. For example, exactly the same top-down network acting on exactly the
same face vector is able to predict the nose vector in some locations and the
mouth vector in other locations.

2.4 Explicit versus Emergent Representations of the Part-Whole Hier-
archy. In the symbolic AI representation of the part-whole hierarchy, each
node has a unique symbol or memory address, and this symbol or address
has an arbitrary relationship to the content. In GLOM, the embedding vec-
tor at a particular level that is shared by all the locations in an island at that
level plays the same role as the address of a node in a graph, but this vector
is not arbitrary. The top-down neural network must predict the embedding
vector of a part at level L from the embedding vector of an object at level
L+1. This involves using the pose relative to the camera encoded at level
L+1 and a representation of the image location to compute where the loca-
tion is within the intrinsic coordinate frame of the object. This determines
which level L part the location belongs to.

There is a very important difference between using an address bus to
follow a pointer to the representation of a part of a known object and using
a top-down neural network to compute the part vector. Unlike table lookup,
the top-down neural net finds it much easier to deal with shapes in which
there are symmetries between the parts. Replicated parts, like the legs of
a centipede, for example, add very little complexity to the neural net, and
this remains true even if the legs change along the centipede, so long as
they change in a predictable way. Bilateral symmetries that align with the
intrinsic coordinate frame of an object reduce the required capacity of the
top-down neural net by almost a factor of two.

It is much harder, however, for the neural net to make use of symmetries
that do not align with the coordinate frame,16 and people are generally un-
aware of such symmetries. Most people, for example, are totally unaware of
the threefold rotational symmetry of a cube, despite its name, until they are
forced to use a body diagonal through the center of the cube as its intrinsic
top-bottom axis (Hinton, 1979). They then cease to be aware of any of the
right angles in the cube because these angles no longer align with the new
intrinsic coordinate frame.17

This is why Canonical Capsules (Sun, Tagliasacchi et al., 2020) discover the natural

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

intrinsic coordinate frames.

Most people have enormous difficulty imagining a cube when they are forced to use
a body diagonal as the top-bottom axis. When asked to point out the corners that are not at
the two ends of this axis, they typically point out four corners arranged in a square about

422

G. Hinton

3 Some Design Decisions

This section discusses some decisions that need to be made when specifying
the GLOM architecture.

3.1 How Many Levels Are There? GLOM assumes that the part-whole
hierarchy has a fixed depth. People can deal with very deep hierarchies
that have stars near the top and atomic nuclei near the bottom. The way to
handle such an enormous range is to have a flexible mapping between en-
tities in the world and the levels of GLOM (Hinton, 1990). This allows the
very same neurons to be used for stars at one time and for atomic nuclei at
another, which has the added advantage of facilitating analogies between
structures at very different scales like solar systems and atoms. The recur-
sive reuse of the neural hardware raises many interesting issues about tem-
porary storage and control flow (Ba, Hinton, Mnih, Leibo, & Ionescu, 2016)
that will only be fleetingly addressed here.

A reasonable number of embedding levels would be about five. This
allows for the pupil and the white of an eye to be the lowest-level sub-
subparts in a scene composed of objects that are people with parts that are
faces and subparts that are eyes. If finer details such as the dilation of the iris
are required, people probably need to remap the world onto their hardware
so that, for example, the face becomes the scene.18

One interesting question is whether the bottom-up and top-down neural
nets can be shared across levels as well as across locations. This would not
work for the lower levels of language processing where entities at different
levels, like phonemes or words, have very different properties, but vision
is far more fractal. A big advantage of sharing across levels is that the vec-
tor representation used for a particular face when it was at the object level
would then be forced to be consistent with its representation when it was
at the part level. This would make it much easier to remap the visual world
onto the hardware by simply copying all of the vectors up or down a few
levels. After having used fine details of an eye to extract a highly informed
vector representation of the eye when it was at the object level, this same
vector could then be used to represent the eye when it was at the subpart

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

halfway up the axis. This structure (two square-based pyramids stuck together base-to-
base) is actually an octahedron. An octahedron is the dual of a cube with vertices for
faces and faces for vertices. So people preserve the fourfold rotational symmetry of a cube
relative to its familiar coordinate system. This suggests that the symmetry structure is one
of the most important properties encoded in the embedding vector of an object.

The levels in the part-whole hierarchy that are represented in the inferotemporal
pathway are probably not the brain’s only representation of space. The inferotemporal
pathway is used for object recognition, and there may well be other representations of the
world that are used for other purposes such as detecting ego motion or visually maintain-
ing balance.

How to Represent Part-Whole Hierarchies in a Neural Network

423

level.19 In this article, however, I assume that the representations are not
shared across levels, so the bottom-up and top-down neural nets are differ-
ent at each level.

3.2 How Fine-Grained Are the Locations? Locations could be as
fine-grained as pixels, or they could correspond to larger image patches
(Dosovitskiy et al., 2020). To avoid additional complexity when explaining
the basic idea of the article, I assume that the grid of locations remains the
same at all levels, but this is probably not the best choice.

The granularity could change at different embedding levels. If higher
levels in the part-whole hierarchy use a larger stride, the top-down neural
net would need to output multiple different predictions for the multiple
lower-level locations that fall within one higher-level location. Similarly, the
bottom-up neural net would need to look at all the lower-level locations that
get combined at the next level up.

One convenient way to be sensitive to a large spatial context while also
being able to see fine detail is to have images at several different spatial
resolutions, all of which have the same number of pixels. The coarsest image
conveys a large spatial context but lacks fine detail and the finest image
conveys the fine details but only for a small region. If the visual input is
structured into multiple images in this way, it would make sense to make
peripheral locations cover larger regions, but this article will ignore that
issue because it makes everything more complicated.

3.3 Does the Bottom-Up Net Look at Nearby Locations? Even if the
granularity at different levels remains unchanged, the bottom-up neural
net could look at the embedding vectors at nearby locations. This is a less
pure version of GLOM, which allows the interactions between locations
to be more complex than just averaging. The purely bottom-up pathway
then resembles a convolutional neural net but with the predictions for the
next level up being made by a multilayer neural net that implements a far
more complicated function than just a matrix multiply followed by a scalar
nonlinearity.

The disadvantage of allowing the bottom-up net to look at other loca-
tions is that two locations with identical representations at the part level
may have different spatial contexts. We would then lose a very nice prop-
erty of the pure version of GLOM: locations that have identical representa-
tions at the part level make exactly the same bottom-up predictions at the
object level.

By looking at other locations, the bottom-up net can reduce the uncer-
tainty before it predicts a distribution at the next level up, and this seems

This assumes that the vector can be transported to a different column if the fixation

point changes when the face becomes the object of attention rather than the eye.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

424

G. Hinton

like a good thing to do. But it should be possible to get a similar reduction
in uncertainty after making the prediction when the attention-weighted
smoothing combines an uncertain bottom-up prediction from one location
with the uncertain bottom-up predictions from nearby locations. Of course,
this assumes that the bottom-up net can represent the uncertainty in its pre-
dictions and that the uncertainties in different locations can be combined
correctly by the attention-weighted smoothing. This issue is addressed in
section 9.

3.4 How Does the Attention Work? One of the contributors to the up-
date of the embedding of level L at location x is the attention-weighted av-
erage of the embeddings of level L at nearby locations at the previous time
step. GLOM assumes the simplest form of attention weighting in which the
weight wxy that location x gives to the embedding at location y is given by

wxy = eβLx.Ly
z eβLx.Lz

(cid:2)

(3.1)

where . is the scalar product of the two embedding vectors, z indexes all the
locations that location x attends to at level L, and β is an “inverse temper-
ature” parameter that determines the sharpness of the attention. β could
increase as GLOM settles to a firm interpretation of the image. The way at-
tention is intended to work in GLOM has already been used successfully in
a system called ACNe (Sun, Jiang, Trulls, Tagliasacchi, & Yi, 2020).

Pioneering work on using Markov random fields for image segmenta-
tion (Geman & Geman, 1984) used the presence of a boundary between
pixel x and pixel y to prevent x from attending to y. A boundary is more
than just a big intensity difference between x and y because its existence de-
pends on the intensities at other locations. Similarly, early work on learning
spatially coherent properties of images used the presence of boundaries to
select which expert interpolator to use (Becker & Hinton, 1993). Like the
seashore, boundaries have a rich life of their own, and much more work
needs to be done to integrate them into GLOM, especially into its attention
mechanism.

3.5 The Visual Input. In most neural networks, the visual input arrives
at the bottom layer. In GLOM, a patch of the raw visual input could define
the bottom-level embedding at a location by vectorizing the intensities in
the image patch, but it is probably more sensible to first apply a convolu-
tional neural net that can see a larger region of the image. The output of
this convolutional net would then be the primary, lowest-level embedding
at each location.

The convolutional net is an open loop way to solve the following in-
ference problem: what lowest-level embedding for that location would be

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

How to Represent Part-Whole Hierarchies in a Neural Network

425

able to reconstruct the pixel intensities using the learned neural field shared
by all locations. Once the lowest-level embedding has been initialized, it
can be refined in a closed loop by backpropagating the reconstruction error
through the neural field (Williams, Revow, & Hinton, 1995).

There is no need to confine the direct visual input to the primary
embedding layer. A coarser scale convolutional net operating on a
lower-resolution image could provide useful hints about the higher-level
embeddings. For example, a pale vertical oval with a darker horizontal
band slightly more than halfway up suggests one kind of face (Viola &
Jones, 2004), so a convolutional net operating on coarse pixels can provide
useful information to directly initialize the higher-level embeddings.20

4 Color and Texture

Consider an object whose individual parts are either entirely pale green or
entirely mauve. The color of a part is straightforward, but what color is the
whole object? One of the motivations for GLOM was the idea that the whole
object has a compound color that might be called “pale-green-or-mauve,”
and at the object level every location belonging to the object has exactly the
same compound color. The object is pale-green-and-mauve all over. When
deciding which other locations at the object level to attend to, preference
would be given to locations with a similar compound color.21

A similar idea applies to textures. The individual texture elements have
their own shapes and poses and spatial relationships, but an object with a
textured surface has exactly the same texture everywhere at the object level.
GLOM extends this idea to shapes. An object may have parts that are very
different from one another, but at the object level, it has exactly the same
compound shape in all of the locations that it occupies.

5 Cluster Discovery versus Cluster Formation

The EM capsule model (Hinton et al., 2018) attempts to activate capsules
that represent wholes (e.g., a face) by looking for clusters of similar vec-
tor votes for the pose of the whole. These vector votes come from already
identified parts (e.g., a nose or mouth), and although the weights on these
votes can be modified by an iterative routing procedure, the vector votes
themselves remain fixed. This is quite problematic if one of the parts has
an underdetermined pose. For example, a circle representing an eye has no

The visual part of the thalamus has direct connections to multiple different levels in

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

the hierarchy of visual areas.

The information that the whole object is pale-green-or-mauve does not specify
whether a particular part is pale green or mauve or the compound color pale-green-or-
mauve. So the top-down neural net that predicts a part from the whole object needs to
restrict the color of the part to this limited palette without specifying it precisely.

426

G. Hinton

specific orientation, and its position in a face depends on whether it is a left
or right eye. It does, however, provide some information about the scale of
the face, and it makes a unimodal prediction for the location of the face in
the direction orthogonal to the unknown line between the two eyes.22

In GLOM, the embedding vector of a location at level L-1 does not cast
an immutable vector vote for the embedding at level L. Instead, it provides
a bottom-up vector contribution to this embedding that is combined with
the vector contribution coming from level L+1 and the attention-weighted
contributions coming from the level L embeddings of other locations to de-
termine the updated level L embedding vector. The bottom-up contribu-
tion can start off being quite vague, and it can become sharper from time
step to time step as top-down and lateral contextual information progres-
sively refines the level L-1 embedding of the location. The islands of similar
embedding vectors at a level can be viewed as clusters, but these clus-
ters are not discovered in immutable data. They are formed by the inter-
action between an intralevel process that favors islands of similarity and
dynamically changing suggestions coming from the location’s embeddings
at adjacent levels.

Unlike earlier capsule models, GLOM has no difficulty representing mul-
tiple copies of the same type of object. The object-level embedding vector
for a location encodes fine-grain information about the 3D pose of the object
relative to the camera as well as the type. So islands that are each composed
of identical object-level vectors representing that particular object can form
archipelagos in which the islands differ only in their pose information.

6 Replicating Embedding Vectors over Locations

At first sight, it seems very inefficient to give a copy of the object-level em-
bedding vector to every location that belongs to an object. Compelling intu-
itions that stem from programming computers with random access memory
suggest that it would be much better to have a single copy of a data struc-
ture for the object. These intuitions are probably misleading for neural nets
that do not have RAM, and even if RAM is available, there are two good
reasons for replicating the embedding vectors over an island.

The island growing process at each level may eventually settle down to
several islands of nearly identical vectors, but the search for these islands
needs to be able to consider alternative clusterings of locations into islands,
and it also needs to allow for negotiations between locations within an is-
land about what identical vector to settle on at each level. These negotia-
tions are nontrivial because each location is also trying to satisfy interlevel

The Stacked Capsule Autoencoder model (Kosiorek et al., 2019) deals with this issue
by using a set transformer (Lee et al., 2019) to allow the parts to interact. This should allow
the poses and identities of the parts to be disambiguated before they attempt to activate
capsules at the next level up.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

How to Represent Part-Whole Hierarchies in a Neural Network

427

constraints that come from its own embedding vectors at the level above
and the level below, and these embeddings are also being refined at every
time step. During the search, it is very helpful for every location to have
its own version of the embedding vector at each level. Uncertainty in the
clustering can be represented by making the embedding vector at a loca-
tion be a blend of the vectors for the different clusters that it might decide
to join. This blend can be refined over time, and the fact that it lives in a
high-dimensional continuous space should make optimization easier.

Intuitively, a blend of two rather different embedding vectors is not
similar to either vector. This is true in a low-dimensional vector space,
but intuitions derived from low-dimensional spaces cannot be trusted
when dealing with high-dimensional spaces. The average of two high-
dimensional vectors is much closer to each of those vectors than it is to a
random vector. This can be understood by thinking about the correlation
between the components of a vector and the components of its average with
some other random vector. If the vectors are high-dimensional, this corre-
lation will be significant.23

A further advantage of islands of near identity is that it allows long-range
interactions within a level to be sparse. If there is more sparsity at higher lev-
els, the interactions can be longer range without increasing the amount of
computation. For locations that belong to an island far away, all the object-
level information about that island is contained in each of its locations, so
it is only necessary to sample one of those locations for that distant island
to compete with other closer islands for a location’s attention. Of course,
this means that distant islands contribute fewer logits to the attention soft-
max than closer islands, but the exponential used in the attentional softmax
means that one logit from a highly relevant distant island can outcompete
multiple logits from a closer but much less relevant island.

A simple way to choose which other locations are allowed to compete for
the attention of location x is to sample, without replacement, from a gaus-
sian centered at x. Higher-level embeddings can sample the same number
of other locations but from a larger gaussian. The sampling could be done
only once so it was part of the architecture of the net. Alternatively, lacu-
nae in the sampling could be greatly reduced by sampling independently
at each time step.

7 Learning Islands

Let us assume that GLOM is trained to reconstruct at its output the uncor-
rupted version of an image from which some regions have been removed.

This explains why the first stage of a language model can convert a word like bank
into a single high-dimensional embedding vector rather than needing separate vectors
for the “river” and the “money” senses.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

428

G. Hinton

This objective should ensure that information about the input is preserved
during the forward pass, and if the regions are sufficiently large, it should
also ensure that identifying familiar objects will be helpful for filling in the
missing regions. To encourage islands of near identity, we need to add a
regularizer, and experience shows that a regularizer that simply encourages
similarity between the embeddings of nearby locations can cause the repre-
sentations to collapse. All the embedding vectors may become very small so
that they are all very similar and the reconstruction will then use very large
weights to deal with the very small scale. To prevent collapse, contrastive
learning (Becker & Hinton, 1992; Paccanaro & Hinton, 2001; van den Oord,
Li, & Vinyals, 2018) uses negative examples and tries to make represen-
tations that should agree be close while maintaining separation between
representations which should not agree.24

Contrastive learning has been applied successfully to learn representa-
tions of image crops (Chen, Kornblith, Norouzi, & Hinton, 2020; Bachman,
Hjelm, & Buchwalter, 2019; He, Fan, Wu, Xie, & Girshick, 2020; Chen, Ko-
rnblith, Swersky, Norouzi, & Hinton, 2020; Tejankar, Koohpayegani, Pillai,
Favaro, & Pirsiavash, 2020) It learns to make the representations of two dif-
ferent crops of the same image agree and the representations of two crops
from different images disagree. But this is not a sensible thing to do if our
aim is to recognize objects. If crop 1 contains objects A and B and crop 2 from
the same image contains objects B and C, it does not make sense to demand
that the representations of the two crops be the same at the object level.
It does make sense at the scene level, however. For scenes containing one
prominent object, it may be possible to recognize objects using representa-
tions that are designed to recognize scenes, but as soon as we distinguish
different levels of embedding, it becomes clear that it would be better to
use a contrastive loss function that encourages similar representations for
two locations at level L only if they belong to the same entity at level L. If
they belong to different level L entities, their level L embeddings should be
significantly different.

From the point of view of a location, at all but the top level, it needs to
decide which other locations its level L embedding should be similar to. It
can then learn to resemble those embeddings and be repelled from the em-
beddings of locations that belong to different objects in the same or other
images. Recent work that uses the similarity of patches along a possible ob-
ject trajectory to influence whether contrastive learning should try to make
them more similar has shown impressive performance at finding correspon-
dences between patches in video sequences (Jabri, Owens, & Efros, 2020).
The obvious solution is to regularize the bottom-up and top-down
neural networks by encouraging each of them to predict the consensus

Maintaining separation is quite different from asking representations that should be
separate to be far apart. Once two representations are sufficiently different, there is no
further pressure to push them even further apart.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

How to Represent Part-Whole Hierarchies in a Neural Network

429

opinion. This is the weighted geometric mean of the predictions coming
from the top-down and bottom-up networks, the attention-weighted aver-
age of the embeddings at nearby locations at the previous time step and
the previous state of the embedding. Training the inter level predictions to
agree with the consensus will clearly make the islands found during feed-
forward inference be more coherent.

An important question is whether this type of training will necessarily
cause collapse if it is not accompanied by training the interlevel predictions
to be different for negative examples that use the consensus opinions for
unrelated spatial contexts. Using layer or batch normalization should re-
duce the tendency to collapse, but a more important consideration may be
the achievability of the goal.

When the positive examples in contrastive learning are used to try to ex-
tract very similar representations for different patches of the same image,
the goal is generally not achievable and the large residual errors will always
be trying to make the representations collapse. If, however, an embedding at
one location is free to choose which embeddings at other locations it should
resemble, the goal can be achieved almost perfectly by learning to form is-
lands of identical vectors and attending almost entirely to other locations
that are in the same island. This should greatly reduce the tendency toward
collapse, and when combined with the deep denoising autoencoder objec-
tive function and other recent tricks (Grill et al., 2020; Chen & He, 2020) it
may eliminate the need for negative examples.

8 Representing Coordinate Transformations

When neural networks are used to represent shape, they generally work
much better if they represent the details of a shape relative to its intrinsic
coordinate frame rather than relative to a frame based on the camera or the
world (Taylor, Hinton, & Roweis, 2007; Deng et al., 2020).

Work on the use of neural fields for generating images has established
that there are much better ways to represent the location than using two
scalars for its x and y coordinates (Sitzmann et al., 2020; Mildenhall et al.,
2020). The product of a delta function at the location with both horizontal
and vertical sine and cosine waves of various frequencies works well. A
similar representation is used in transformers for the position of a word
fragment in a sentence.

The success of highly redundant representations of location suggests that
there may also be highly redundant representations of the nontranslational
degrees of freedom of a coordinate transform that work much better in a
neural net than the matrices or quaternions commonly used in computer
graphics.25 Let us suppose that we would like the pose of a part (e.g., the

The standard matrix representation uses the scale of the matrix to represent the
change in scale caused by the coordinate transform. Using the scale of the weights to
represent scale in this analog way is a particularly bad idea for neural nets.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

430

G. Hinton

coordinate transform between the retina and the intrinsic frame of reference
of a part) to be represented by a vector that is a subsection of the embedding
vector representing the part. A multilayer neural network whose weights
capture the viewpoint-invariant coordinate transform between a part and
a whole can then operate on the pose vector of the part to predict the pose
vector of the whole. If we simply flatten the 4×4 matrix representation of
a pose into a vector, it is easy to hand-design a multilayer neural net that
takes this vector as input and produces as output a vector that corresponds
to the flattened result of a matrix-matrix multiply, provided we know what
matrix to multiply by, which depends on the identity of the part. This de-
pendence on the part identity was the reason for allocating a separate cap-
sule to each type of part in earlier capsule models. Unfortunately, the vector
space of flattened 4×4 matrices does not make it easy to represent uncer-
tainty about some aspects of the pose and certainty about others. This may
require a much higher-dimensional representation of pose. Designing this
representation by hand is probably inferior to using end-to-end learning
with stochastic gradient descent. Nevertheless, section 9 discusses one ap-
proach to representing uncertainty in a neural net to demonstrate that it is
not a major problem.

In a universal capsule the part identity is represented by an activity vec-
tor rather than by the choice of which capsule to activate, so the neural net
that implements the appropriate part-whole coordinate transform needs to
condition its weights on the part-identity vector.26 Consequently, the en-
tire part-level vector of a location needs to be provided as input to the
bottom-up neural net that computes the part-whole coordinate transform.
This makes the computation much more complicated, but it greatly simpli-
fies the design of the architecture. It means that we do not need to designate
one part of the embedding vector at a level to represent the pose and the
rest to represent other aspects of the entity at that level. All we need to do
is to make sure that the neural net that predicts the embedding at one level
from the embedding below (or above) has sufficient expressive power to ap-
ply a coordinate transform to those components of the embedding vector
that represent pose and to make this coordinate transform be contingent on
those components of the vector that represent the identity of the part. Since
this neural net is going to be learned by stochastic gradient descent, we do
not even need to keep components of the embedding vector that represent
the pose separate from the components that represent other properties of
the entity at that level; for example, individual components can be tuned to
combinations of pose, identity, deformation, texture and so on.

Entangling the representations of identity and pose may seem like a bad
idea, but how else can a bottom-up prediction from a diagonal line express

In stacked capsule autoencoders (Kosiorek et al., 2019) the capsule identity deter-
mines the default object-part coordinate transform, but the transform can be modulated
by a vector that represents the deformation of the object.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

How to Represent Part-Whole Hierarchies in a Neural Network

431

the opinion that the whole is either a tilted square or an upright diamond?
To express this distribution using activities of basis functions, we need basis
functions that are tuned to combinations of identity and pose.

Using a small matrix or quaternion to represent pose makes it easy to
model the effects of viewpoint changes using linear operations. At first
sight, abandoning these explicit representations of pose seems likely to
compromise the ability of a capsule to generalize across viewpoints. This
would be true if each capsule dealt with only one type of object, but uni-
versal capsules will have seen many different types of object from many
different viewpoints, and any new type of object will be well approximated
by a weighted average of familiar types, all of which have learned to model
the effects of viewpoint. Moreover, the weights in this average will be the
same for all viewpoints. So if a novel object is only seen from a single view-
point, a universal capsule may well be able to recognize it from radically
different viewpoints.

The same argument about generalization can be applied to CNNs, but
there is a subtle difference: GLOM is forced to model the coordinate trans-
forms between parts and wholes correctly in order to be able to make use of
the spatial relationship between one part and another by using a simple av-
eraging operation at the level of the whole. It is the viewpoint invariance of
these part-whole spatial relationships that makes it possible to generalize
to radically new viewpoints.

9 Representing Uncertainty

It is tempting to imagine that the individual components of an embedding
vector correspond to meaningful variables such as the six degrees of free-
dom of the pose of an object relative to the camera or the class of an ob-
ject. This would make it easy to understand the representation, but there
is a good reason for making the relationship between physically meaning-
ful variables and neural activities a little less direct. To combine multiple
sources of information correctly, it is essential to take the uncertainty of each
source into account.

Suppose we want to represent M-dimensional entities in such a way
that different sources of information can contribute probability distribu-
tions over the M-dimensional space rather than just point estimates. We
could use a population of N (cid:2) M neurons, each of which is tuned to a gaus-
sian in the M-dimensional space (Williams & Agakov, 2002). If we take logs,
a neuron then corresponds to a parabolic bump in the log probability. This
bump could be very wide in some directions and very narrow in others. It
could even be a horizontal ridge that is infinitely wide in some of the direc-
tions. We treat the activity of a neuron as a vertical scaling of its parabolic
bump and simply add up all the scaled bumps to get a parabolic bump that
represents the log of the unnormalized gaussian distribution represented
by the population of N neurons.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

432

G. Hinton

Sources of information can now contribute probability distributions,
which will be multiplied together by simply contributing additively to the
activities of the N neurons. If we want to keep N relatively small, there will
be limitations on the probability distributions that can be represented, but
given a budget of N neurons, learning should be able to make good use
of them to approximate the predictive distributions that are justified by the
data. If, for example, it is possible for a part to predict the horizontal location
of a whole without making this prediction contingent on other aspects of the
pose or identity of the whole, it would be helpful to tune a handful of the N
neurons to well-spaced values on the dimension representing the horizon-
tal location of the whole in the underlying M-dimensional space. The part
can then contribute a gaussian distribution along this horizontal dimension
by making appropriate contributions to this handful of neurons. The rela-
tive magnitudes of the contributions determine the mean of the gaussian,
and their overall scale determines the inverse variance of the gaussian.

The assumption that the neurons have gaussian tuning in the underlying
M-dimensional space of possible entities was just a simplification to show
that neural networks have no problem in representing gaussian probabil-
ity distributions and combining them appropriately. A much more flexible
way to tune the neurons would be to use a mixture of a gaussian and a uni-
form (Hinton, 2002). The log of this distribution is a localized bump, which
will be called a unibump. The sides of a unibump splay out and eventually
become horizontal when we are far enough from the mean that the uniform
completely dominates the gaussian. Unlike a parabolic bump, which has a
quadratically large gradient far from its maximum, a unibump has zero gra-
dient far from its maximum so it makes no contribution to the shape of the
unnormalized distribution far from its mean. This allows unibumps to rep-
resent multimodal probability distributions. The sum of one set of nearby
unibumps can represent one mode, and the sum of another set of unibumps
that are close to one another but far from the first set can represent another
mode. Using neural activities that correspond to vertical scalings of the
unibumps, it is possible to control both the location and the sharpness of
each mode separately.

The assumption that individual neurons are tuned to a mixture of a gaus-
sian and a uniform was just a simplification to show that neural networks
can represent multimodal distributions. The basis functions that neurons
actually learn for representing multimodal log probability distributions in
an underlying latent space do not need to be local in that space.

The need to represent uncertainty prevents the simplest kind of repre-
sentation in which activity in a single neuron represents one dimension of
an M-dimensional entity, but it still allows neurons to have tuning curves
in the M-dimensional space. Whether it is possible for someone trying to
understand the representations to jointly infer both the underlying latent
space and the tuning curves of the neurons in that space is an interesting
open problem. But even when it is hard to figure out what the individual

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

How to Represent Part-Whole Hierarchies in a Neural Network

433

neurons are doing, it should still be trivial to find islands of nearly identical
vectors, so it should be easy to see how GLOM is parsing an image or how
a similar model applied to language is parsing a sentence.

When considering how to represent uncertainty about the pose or iden-
tity of a part, it is important to realize that each location assumes that it
is only occupied by at most one part at each level of the hierarchy.27 This
means that all the neural activities in the embedding vector at a level re-
fer to the same part: there is no binding problem because the binding is
done via the location. So a location can use two different neurons whose
tuning curves in the underlying M-dimensional space overlap by a lot
without causing any confusion. If we do not start by allocating different
subsets of the neurons to different locations, the broad tuning curves in the
M-dimensional underlying space that are needed for representing uncer-
tainty will cause confusion for the properties of different objects. That is
why coarse coding, which uses a single population of broadly tuned neu-
rons to model several different entities at the same time (Hinton, 1981a)
cannot model uncertainty efficiently.

9.1 Combining Different Sources of Information When Updating the
Embeddings. The embedding at each level is updated using information
from the previous time step at adjacent levels and also at other locations on
the same level. These sources are far from independent, especially when
the image is static so that the visual input is identical at multiple time
steps. The higher-level embeddings obviously depend on the earlier lower-
level embeddings. Also, the same-level embeddings that contribute to the
attention-weighted local average will have been influenced by early states
of the very embedding that the attention-weighted average is trying to up-
date. To avoid becoming overconfident, it is better to treat the different
sources of information as alternative paths for computing the embedding
vector from the visual input. This justifies taking a weighted geometric
mean of the distributions28 predicted by the individual sources rather than
a simple product of these distributions, which would be appropriate if they
were independent. For interpreting a static image with no temporal con-
text, the weights used for this weighted geometric mean need to change
during the iterations that occur after a new fixation. Initially the bottom-
up source should be by far the most reliable, but later, the top-down and
lateral sources will improve. Experiments with deep belief nets (Hinton,
2006) show that gradually increasing the weighting of top-down relative to

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

We assume the visual world is opaque. Transparency, like reflections in a window of
an indoor scene superimposed on an outdoor scene would need to be handled by switch-
ing attention between the two different scenes.

When taking the geometric mean of some distributions, we assume that the product

of the distributions is renormalized to have a probability mass of 1.

434

G. Hinton

bottom-up leads to more plausible reconstructions at later times, suggest-
ing that this will be important when GLOM is trained as an end-to-end deep
denoising autoencoder.

10 Comparisons with Other Neural Net Models

This section compares GLOM to some of the neural net models that influ-
enced its design.

10.1 Comparison with Capsule Models. The main advantage of
GLOM, compared with capsule models,29 is that it avoids the need to preal-
locate neurons to a discrete set of possible parts at each level. The identity of
a part becomes a vector in a continuous space of feature activities. This al-
lows for much more sharing of knowledge between similar parts, like arms
and legs, and much more flexibility in the number and type of parts belong-
ing to an object of a particular type.

A second advantage of GLOM is that it does not require dynamic rout-
ing. Instead of routing information from a part capsule to a specific cap-
sule that contains knowledge about the relevant type of whole, every
location that the part occupies constructs its own vector representation of
the whole. The constraint that a part at one location only belongs to one
whole is a necessary consequence of the the fact that the alternative wholes
at that location are alternative activity vectors on the same set of neurons.
Uncertainty about which of several wholes is the correct parent of a part
can still be captured by using blends of activity vectors.

A third advantage of GLOM is that the cluster formation procedure for
forming islands is much better than the clustering procedure used in cap-
sule models. To make methods like EM work well when the number of clus-
ters is unknown, it is helpful to introduce split and merge operations (Ueda,
Nakano, Ghahramani, & Hinton, 2000) but these operations happen auto-
matically during island formation. Hierarchical Bayesian concerns about
finding the correct number of clusters at an embedding level are addressed
by starting with one island per location and then reducing the number of
distinctly different islands by making embedding vectors agree. This reduc-
tion occurs in a continuous space with no need for discrete changes in the
number of clusters.

The main disadvantage of GLOM, compared to most capsule models, is
that knowledge about the shape of a specific type of object is not localized
to a small group of neurons (possibly replicated across quite large regions).
Instead, the bottom-up and top-down neural nets (which may be different

Some capsule models already use universal capsules in which vectors of activity
rather than groups of neurons are used to represent the part identity, but they do not
replicate these vectors across all locations within the object (Srivastava et al., 2019).

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

How to Represent Part-Whole Hierarchies in a Neural Network

435

for every pair of adjacent levels) have to be replicated at every location.
For computer implementations, the replication across locations is a big ad-
vantage because it allows a weight to be used many times each time it is
retrieved from memory, but for biological neural nets, it seems very waste-
ful of synapses. The point of the analogy with genes is that biology can
afford to be wasteful so this objection may not be as serious as it seems.
There is, however, a more serious issue for a biological version of GLOM:
the ubiquitous universal capsules would need to learn the same knowledge
separately at every different location, and this is statistically very inefficient.
Fortunately, section 12 shows how locations can share what their bottom-up
and top-down models have learned without sharing any of their weights.
By allocating neurons to locations rather than to types of object or a part,
GLOM eliminates a major weakness of capsule models, but it preserves
most of the good aspects of those models:

• Handling the effects of viewpoint properly: The weights of the
bottom-up and top-down neural networks capture the viewpoint-
invariant spatial relationships between parts and wholes, and the
neural activities capture the viewpoint equivariant information about
the pose of an object or part.

• Coincidence filtering: Objects are recognized by using agreement be-
tween high-dimensional predictions from their parts. In GLOM, the
idea of using agreement is taken even further because it is also used
to represent objects and parts as islands of identity.

• No dynamic allocation of neurons: The part-whole hierarchy can be
represented without dynamically allocating neurons to nodes in the
parse tree.

10.2 Comparison with Transformer Models. The GLOM architecture
shown in Figure 1 can be rearranged by viewing the vertical time-slices in
Figure 1 as layers in Figure 4. This rearrangement of GLOM is then equiv-
alent to a standard version of a transformer (Vaswani et al., 2017) but with
the following changes:

• The weights are the same at every layer because GLOM is a recurrent

net and we have converted the time slices into layers.

• The attention mechanism is greatly simplified by using the embed-
ding vector at a level as the query, the key, and also the value. The
complex interactions between different locations that are normally
implemented by attention are thus reduced to a simple, attention-
weighted, smoothing operation.

• The multiple heads used to provide more expressive power in most
transformers are repurposed to implement the multiple levels of a
part-whole hierarchy, and the interactions between the heads at a lo-
cation are highly structured so that a level only interacts with the ad-
jacent levels.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

436

G. Hinton

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 4: This is a different way of visualizing the architecture shown in Figure
1, which makes the relationship of that architecture to transformers more obvi-
ous. The horizontal dimension, which represents time in Figure 1, becomes the
vertical dimension, which represents layers in this figure. At each location, ev-
ery layer now has embeddings for all of the levels in the part-whole hierarchy.
This corresponds to vertically compressing the depiction of the levels within a
single time slice in Figure 1. A single forward pass through this architecture is
all that is required to interpret a static image. All of the level-specific bottom-up
and top-down neural nets are shown here as a single neural net. Figure 5 shows
the individual bottom-up and top-down neural nets for this alternative way of
viewing the GLOM architecture.

• The bottom-up and top-down neural networks that compute the in-
teractions between adjacent levels perform coordinate transforma-
tions between the distributed representations of the poses of parts
and wholes, and these coordinate transformations depend on the dis-
tributed representations of the types of the part and the whole.

The justification for eliminating the distinction among the query, the key,
the value, and the embedding itself is as follows: Consider trying to get a
potential mouth to be corroborated by a potential nose in a transformer.
The mouth needs to ask, “Is there anyone in the right spatial relationship

How to Represent Part-Whole Hierarchies in a Neural Network

437

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 5: A picture of two adjacent layers of GLOM for a single location (i.e.,
part of a single column). During the forward pass, the embedding vector at level
L receives input from the level L-1 embedding vector in the previous layer via
a multilayer, bottom-up neural net. It also receives input from the level L+1
embedding in the previous layer via a multilayer, top-down neural net. The
dependence on level L+1 in the previous layer implements top-down effects
during the forward pass. The level L embedding in layer t + 1 also depends on
the level L embedding in layer t and an attention-weighted sum of the level L
embeddings at other nearby locations in layer t. These within-level interactions
are not shown.

to me who could be a nose? If so, please tell me to be more mouth-like.”
This seems to require the mouth to send out a nose query (that includes
the appropriate pose relative to the mouth) that will match the key of the
nose. The nose then needs to send back a mouth-like value (that includes
the appropriate pose relative to the nose).

But the mouth could also be corroborated by an eye, so it needs to send
out a different query that will match the key of an eye. This could be han-
dled by using separate heads for a mouth-looking-for-a-nose and a mouth-
looking-for-an-eye (as in categorial grammar), but that seems clumsy.

A more elegant solution (inherited from capsule models) is to use a
form of the Hough transform. The potential mouth predicts a vector for
the face it might be part of. The potential nose and eye do the same.

438

G. Hinton

All you need now is agreement of the predictions at the face level so
query=key=value=embedding. The face level can then give top-down
support to its parts instead of the support coming from a value vector sent
by one part to another using a coordinate transform specific to the identities
of the two parts.

10.3 Comparison with Convolutional Neural Networks. Capsules

were originally motivated by three perceived deficiencies of CNNs:

1. The pooling operation in a CNN was designed to achieve local in-
variance to translation in the activity vector at the next level up. It
seems better to ask for invariance in the weights but equivariance in
the activities.

2. CNNs attempt to generalize across viewpoints by using a lot of exam-
ples of different viewpoints, which may be produced by augmenting
the data set with transformed images. Computer graphics general-
izes across viewpoints by having explicit representations of the poses
of objects or parts relative to the camera. A change in viewpoint, even
a very big one, can be modeled perfectly by linear operations on these
explicit poses. Using the viewpoint-invariant relationship between
the pose of a part and the pose of the whole seems like a highly ef-
ficient way to generalize to radically new viewpoints. CNNs do not
appear to be doing this, but appearances can be deceptive.

3. In CNNs, the activity of a neuron is determined by the scalar product
of a weight vector with an activity vector. This is not a good way
to model covariance structure, which is important in vision. Taking
the scalar product of an activity vector with another activity vector
makes powerful operations like coincidence detection and attention
much easier. Coincidences in a high-dimensional embedding space
are a good way to filter out noise caused by occlusion or missing parts
because, unlike sums, they are robust to the absence of some of the
coinciding predictions.

The first deficiency is only apparent. It depends on a common misun-
derstanding of how CNNs represent the positions of parts. The vector of
channel activities at a gridpoint can have a rate-coded representation of the
position of a part that is far more accurate than the stride between grid-
points. So when the stride is increased at the next level by pooling, it does
not mean that the position of a part is encoded less accurately. A bigger
stride does not produce representations that are more translationally in-
variant. Gridpoints are used to allocate neural hardware not to represent
positions. Their spacing is limited by the fact that the neural hardware at
a gridpoint assumes it will never be representing more than one of what-
ever it represents, not by the accuracy with which position needs to be
represented.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

How to Represent Part-Whole Hierarchies in a Neural Network

439

Attempts to deal with the second perceived deficiency led to some in-
teresting models. The transforming autoencoder (Hinton, Krizhevsky, &
Wang, 2011) forced an encoder to extract an explicit representation of pose
in each capsule by insisting that the reconstructed image should be a trans-
formed version of the original image and specifying this transformation as
a matrix that multiplied whatever matrix elements were extracted by the
encoder. Similarly, the EM capsule model extrapolated much better to new
viewpoints when it was forced to use a matrix to represent the relationship
of a part to a whole.

Unfortunately, perception has to deal with uncertainties that are not
present in computer graphics,30 and it needs to be able to represent cor-
related uncertainties in its pose predictions so that multiple sources of
information can be combined properly. This rules out a simple matrix repre-
sentation of pose. Once we accept that distributions over the possible poses
of an entity will be represented by the scales assigned to basis functions in
the log probability space, it is quite possible that CNNs actually learn to do
something like this. This might allow them to approximate Hough trans-
forms, though this is hard to do without taking scalar products of activity
vectors.

The third deficiency can be rectified by moving to a transformer-like
architecture that uses scalar products of activity vectors to modulate
attention.

If you like CNNs, GLOM can be viewed as a special type of CNN that

differs from a standard CNN in the following ways:

• It only uses 1×1 convolutions (except at the front end).
• Interactions between locations are done by parameter-free averaging
that implements a coincidence filter that allows it to use a Hough
transform to activate units rather than using only matched filters.
• Rather than using a single feedforward pass through the levels of
representation, it iterates to allow top-down influences that are im-
plemented by neural fields.

• It includes contrastive, self-supervised learning and performs hierar-
chical segmentation as a part of recognition rather than as a separate
task. No more boxes.

10.4 Representing the ISA Hierarchy. An important idea in Good Old-
Fashioned Artificial Intelligence (GOFAI) is property inheritance. It is not

Even if a generative model is stochastic, it may still be certain about which stochastic
choices it made. In some more complex generative models, however, a level only specifies
the probability distributions of poses for parts at the level below, and an iterative process
then reconciles these distributions (Osindero & Hinton, 2008). This kind of generative
model may be needed for modeling very precise relationships between highly variable
parts, such as two praying hands, and it does need to be able to represent probability
distributions over poses.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

440

G. Hinton

necessary to explicitly represent that elephants suckle their young because
an elephant ISA mammal and, unless otherwise stated, an elephant inher-
its this property from its more general type. A simple way to implement
property inheritance in a neural network is to make different entities cor-
respond to different vectors of activity on the same set of neurons. Imag-
ine that the components of the vector that represents a concept are ordered
from very general to very specific. Mammals all have similar values for the
more general components and differ on less general components. Indian
and African elephants differ on only fairly specific components. When a
neural net learns to make the vectors for concepts have causal effects on
other vectors, effects that should be the same for all mammals but not the
same for all vertebrates, will naturally be implemented by the outgoing
weights of the neurons that are active for all mammals but not for all verte-
brates. This way of implementing property inheritance makes it easy to add
exceptions. The components of a vector that are common to birds will learn
weights that capture the knowledge that birds fly, and the more specific
components that differentiate penguins from other birds will learn stronger
weights that overrule the general case (Hinton, 1981b).

This way of implementing property inheritance has the added advan-
tage that types do not need to form a tree. Dogs inherit many properties
from being canines (like wolves), but they also inherit many properties
from being pets (like cats). There is no guarantee that properties inherited
from these more general, partially overlapping classes will be consistent,
but unlike logic, neural networks have no difficulty dealing with conflicting
evidence.

At first sight, the idea of using different sections of the vector represen-
tation of a concept to capture different levels in the ISA hierarchy conflicts
with the idea of using different sections to capture different levels in the
part-whole hierarchy. This seems problematic because hooked beak is a part
of a bird but it also defines a type of bird. The two ideas can be reconciled
by first dividing the embedding vector for a location into sections that rep-
resent different levels in the part-whole hierarchy and then dividing each
section into subsections that represent different levels in the type hierarchy.

10.5 The Relationship to 2D Ising Models. For each location sepa-
rately, the embedding vectors at levels L-1 and L+1 on the previous time
step provide input to the neurons that represent the current embedding vec-
tor at level L. This acts like the conditioning input in a conditional Markov
random field: it influences the current step of the iterative, island-forming
process that tries to make the embedding of the location at level L agree
with the embeddings of other locations at level L.

In a 2D Ising model, a two-dimensional array of binary-valued spins set-
tles into a state in which nearby spins tend to agree so as to minimize an en-
ergy function that favors agreement between neighboring spins. The model
proposed here resembles the 2D Ising model because it uses a 2D grid of im-
age locations, but it generalizes the model in the following ways:

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

How to Represent Part-Whole Hierarchies in a Neural Network

441

1. It replaces binary spins with high-dimensional real-valued vectors.
The fact that these lie in a continuous space should facilitate the
search for islands of agreement.
it replaces a single field of spins with fields at multiple levels and al-
lows adjacent level embeddings of the same location to interact (He,
Zemel, & Carreira-Perpinan, 2004; Saremi & Sejnowski, 2013). The
interactions between levels are quite complicated because they in-
volve coordinate transformations between parts and wholes. So for
each pair of adjacent embedding levels, the top-down and bottom-
up interactions at each location must be computed by a multilayer
neural net rather than a simple weight matrix.

10.6 Comparison with Other Methods for Removing Redundancy.
Methods like principal components analysis remove redundancy in the
data by limiting the number of available dimensions in the representation.
By contrast, a restricted Boltzmann machine with a large number of hidden
units squeezes out redundancy by making nearly all of the exponentially
many possible binary configurations of the hidden units have such high
energy that they are effectively unavailable. This is a much more flexible
way of eliminating redundancy (Shi & Zhu, 2007). It can model multiple fat
manifolds31 that have different intrinsic dimensionalities, and even within
a fat manifold, it can model variations in the effective dimensionality in
different parts of the manifold. The island-forming objective belongs to the
second class of methods. At each level, it allows for a large number of small
islands if that is what the data require but strives to use a small number of
large islands if that is possible.

11 Video

This article focuses on using the GLOM architecture to process a single fix-
ation of a static image, but the architecture is motivated by the need to deal
with video, and learning from video is often much easier than learning from
static images (Sabour, Tagliasacchi, Yazdani, Hinton, & Fleet, 2021), so I will
briefly discuss the simplest temporal extension which is to a single fixation
of a time-varying image.

To avoid confusion it may be helpful to distinguish three types of time:
• Event time: This is the actual time at which an event occurs.
• Representation time: This is the actual time at which a particular rep-
resentation of an event occurs in the neural network. If the bottom-
up neural network uses a predictive model, representations of events

A manifold is a subset of the points in a space that have lower intrinsic dimension-
ality than the full space. If we take the points on a manifold and add a small amount of
noise that has full dimensionality, the points no longer form a strict manifold, but they
will all be close to the manifold. Such a set of points will be said to lie on a fat manifold.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

442

G. Hinton

could be in synchrony with the events themselves, or they could even
precede the events, which would make catching a ball a lot easier.
• Reference time: This is the actual time that an internal representation
refers to. When a memory is retrieved, for example, the reference time
of the constructed representation is usually long before the represen-
tation time. The reference time can also differ by a lot from the event
time if the memory is not veridical.

For a sequence of frames representing a static image, multiple time steps
can be used to settle on an appropriate set of islands at each level. But in a
dynamic image, the very same time steps must also be used to deal with the
fact that the occupants of a location at each level can change with time.32

An advantage of using islands of identical vectors to represent an object
is that motions between successive frames that are small compared to the
size of the object only require large changes to a small subset of the locations
at the object level. All of the locations that remain within the object need
to change only sightly to represent the slight change in pose of the object
relative to the camera.

If the changes in an image are small and predictable, the time steps im-
mediately following a change of fixation point can be used to allow the em-
beddings at all levels to settle on slowly changing islands of agreement that
track the changes in the dynamic image. The lowest-level embeddings may
change quite rapidly, but they should receive good top-down predictions
from the more stable embeddings at the level above. Once the embeddings
have formed sensible islands, there is then no problem in using the very
same time step for improving the interpretation of each frame and for keep-
ing the embeddings locked on to the dynamic image.

If the changes are rapid, there is no time available to iteratively settle
on a good set of embedding vectors for interpreting a specific frame. This
means that the GLOM architecture cannot correctly interpret complicated
shapes if the images are changing rapidly. Try taking an irregularly shaped
potato and throwing it up in the air in such a way that it rotates at one or
two cycles per second. Even if you smoothly track the potato, you cannot
see what shape it is.

12 Is GLOM Biologically Plausible?

Although GLOM is biologically inspired, it has several features that appear
to make it implausible as a biological model. Three of these features are
addressed here.

• The weight sharing between the bottom-up or top-down models in

different columns

This creates a problem for the idea of progressively putting more weight on the top-

down predictions as the network settles.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

How to Represent Part-Whole Hierarchies in a Neural Network

443

• The need to process negative pairs of examples for contrastive learn-

ing without interrupting the video pipeline

• The use of backpropagation to learn the hidden layers of the top-

down and bottom-up models

12.1 Is the Neocortex a Giant Distillery? The replication of DNA in
every cell is unproblematic: that is what DNA is good at. But biologists of-
ten object to models that use weight sharing claiming that there is no ob-
vious way to replicate the weights (Lillicrap, Santoro, Marris, Akerman, &
Hinton, 2020). GLOM, however, suggests a fairly simple way to solve this
problem by using contextual supervision. In a real brain, what we want
is an efficient way of training the bottom-up and top-down nets at a lo-
cation so that they compute the same function as the corresponding nets
at other locations. There is no need for the weights to be identical as long
as corresponding nets are functionally identical. We can achieve this using
knowledge distillation (Buciluˇa, Caruana, & Niculescu-Mizil, 2006; Hinton,
Vinyals, & Dean, 2014). For each level separately, the two students at each
location are the bottom-up and top-down neural nets. The teacher is the
consensus opinion that is a weighted geometric mean of the opinions of
the two students, the previous state of the embedding, and the attention-
weighted embeddings at other locations.33

Regressing a student’s prediction toward the consensus, allows knowl-
edge in the neural nets at other locations to be transferred to the student via
the attention-weighted averaging. It is not as effective as sharing weights
with those other neural nets, but it works quite well (Hinton et al., 2014),
and in the long run, all of the networks will converge to similar functions
if the data distribution is translation invariant. In the long run, however,
we are all dead.34 So it is interesting to consider what happens long before
convergence when the local models are all fairly different.

Suppose all of the locations that form a nose have the same embedding
vector at the part level. If they all had exactly the same bottom-up model,
they would all make exactly the same prediction for the face at the object
level. But if the bottom-up models at different locations are somewhat dif-
ferent, we will get a strong ensemble effect at the object level: the average of
all the simultaneous bottom-up predictions for the same object in different
locations will be much better than the individual predictions.

Strictly speaking, this is an example of co-distillation where the ensemble of all the
students is used as the teacher. Co-distillation was initially based on an analogy with how
scientists in a community learn from each other (Hinton, 2014), but the same mechanism
could be used in a community of columns. In both cases, it would help to explain how
a system can win by just replicating a lot of people or columns without requiring any
significant architectural innovation.
There are alternative facts.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

444

G. Hinton

One advantage of sharing knowledge between locations via distillation
rather than by copying weights is that the inputs to the bottom-up models
at different locations do not need to have the same structure. This makes it
easy to have a retina whose receptive fields get progressively larger farther
from the fovea, which is hard to handle using weight sharing in a convolu-
tional net. Many other aspects, such as the increase in chromatic aberration
farther from the fovea, are also easily handled. Two corresponding nets at
different locations should learn to compute the same function of the optic
array even though this array is preprocessed differently by the imaging pro-
cess before being presented to the two nets. Co-distillation also means that
the top-down models do not need to receive their location as an input since
it is always the same for any given model.

Finally, using distillation to share knowledge between location-specific
neural networks solves a puzzle about the discrepancy between the number
of synapses in the visual system (about 1013) compared to the number of fix-
ations we make in our first 10 years (about 109). Conservative statisticians,
concerned about overfitting, would prefer these numbers to be the other
way around.35 If we use, say, 104 columns in different locations, the bottom-
up and top-down models at one location only have about 109 synapses be-
tween them. Conversely, the number of training examples used to learn the
knowledge that is shared across an ensemble of 104 locations is about 1013,
though many of these examples are highly correlated.

Neural networks that have more training cases than parameters are less
magical than some of the highly overparameterized networks in current
use, but they may generalize in more predictable ways when presented with
data that lie outside their training distribution because the function they
compute has been much more highly constrained by the data.

12.2 A Role for Sleep in Contrastive Learning? If negative examples
are required, GLOM might appear less plausible as a biological model be-
cause of the added complexity of finding and processing pairs of images
that are similar when they should not be. There is, however, one intriguing
possibility that emerged from conversations with Terry Sejnowski in 1983
and 2020.

When using contrastive learning to get representations that are simi-
lar for neighboring video frames, the most effective negative examples are
frames in the same video that are nearby but not immediately adjacent. We
could avoid compromising the real-time performance of GLOM by taking it
offline at night to do the negative learning that prevents the representations
from collapsing. If the highest-level embeddings have the ability to gener-
ate sequences at the highest level, the top-down networks could be used to

It should help that each example allows contrastive learning at several different lev-
els and the target vectors for contrastive learning are much richer than a single one-of-N
label.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

How to Represent Part-Whole Hierarchies in a Neural Network

445

generate sequences of embeddings at every level in each column. This pro-
cess does not require any attention between columns because it does not
need to perform perceptual inference, so it might be able to generate plau-
sible sequences at a much faster rate than the normal speed. Then we simply
do the negative learning for the bottom-up models using the same length
of real-time window as is used when awake. There is evidence that high-
speed, top-down sequence generation occurs during the spindle stage of
sleep (Lee & Wilson, 2002; Nádasdy, Hirase, Czurkó, Csicsvari, & Buzsáki,
1999).

The idea that sleep is used to keep apart representations that should not
be confused is not new (Crick & Mitchison, 1983). Hinton and Sejnowski
(1986) even suggested that sleep could be used for following the deriva-
tives of the normalizing term in the negative phase of Boltzmann machine
learning. But this reincarnation of the idea has two big advantages over
Boltzmann machines. First, contrastive unsupervised learning scales much
better than Boltzmann machine learning, and second, it is far more tolerant
of a temporal separation between the positive and negative phases.

Preliminary experiments using contrastive learning for MNIST digits
show that the learning still works if a large number of positive updates
are followed by a large number of negative updates. Representation col-
lapse is fairly slow during the positive-only learning, and the representa-
tions can shrink by a significant factor without much affecting performance.
So maybe some pairs of embeddings that ought to be well separated get too
close together during the day and are then pushed apart again at night. This
would explain why complete sleep deprivation for a few days causes such
serious mental confusion.36 The experiments with MNIST also show that
after a lot of positive-only learning, performance degrades but is rapidly
restored by a small amount of negative learning.

To avoid very long periods of negative-only learning, it might be advis-
able to start with a negative phase of sleep to push representations apart,
and then alternate with a positive phase using input sequences that were
generated from the top level or even from a recurrent network close to
the sensory input. This conflicts with the Crick-Mitchison theory that REM
sleep is for unlearning, but it would still be compatible with our failure to
remember almost all of our dreams if episodic memory retrieval depends
on the top-level, and the top-level simply does not learn during REM sleep
because those episodes did not happen.

12.3 Communicating Error Derivatives in the Brain. The straightfor-
ward way to train GLOM is to ask it to fill in missing regions of images

If sleep is just for doing extra rehearsal or for integrating the day’s experiences with
older experiences, it is not clear why complete lack of sleep for a few days has such dev-
astating effects.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

446

G. Hinton

and to backpropagate the reconstruction error through the entire tempo-
ral settling process using backpropagation through time. The contrastive
representation learning at each level can then be viewed as an additional
regularizer. Unfortunately, it is hard to see how a brain could backprop-
agate through multiple time steps. If, however, the consensus opinion at
every level can provide a sufficient teaching signal for the bottom-up and
top-down models that predict the embedding vector at that level, imple-
mentation in a brain becomes a lot more feasible.

If we could ensure that the representations improved over time, the tem-
poral derivatives of neural activities could represent error derivatives, and
the local learning procedure would then be spike-time-dependent plasticity
in which the increase in a synapse strength is proportional to the product
of the presynaptic activity with the postsynaptic rate of increase of activ-
ity.37 Assuming spikes are caused by an underlying rate variable, we can
get a noisy but unbiased estimate38 of the rate of change of this underlying
rate variable by applying a derivative filter to the postsynaptic spike train,
which is exactly what STDP does.

A recent review paper (Lillicrap et al., 2020) discusses at great length
how temporal derivatives can be used as error derivatives in order to ap-
proximate backpropagation in a feedforward network.39 The review paper
assumes a separate phase in which derivatives, in the form of activity per-
turbations, are allowed to flow back from the higher levels to the lower
levels. This process does not seem plausible for a video pipeline. By con-
trast, the settling process of GLOM propagates the derivatives required for
learning as the temporal derivatives of activity at all levels, and the time
steps required for this propagation can be the same time steps as are used
for video frames.

For dynamic images, it may seem paradoxical that the representations
just keep getting better, but it is no more paradoxical than a surfer who just
keeps going downhill without ever changing her elevation. The surface on
which the surfer is going downhill is not the same surface. Similarly the
time slice of reality for which the representations are forever improving is
not the same time slice. The brain surfs reality.

Unfortunately, this does not explain how to get the derivatives required
for learning the hidden layers of the bottom-up and top-down neural net-
works. Nor does it explain how the derivatives of the error signals at each

This fits very well with the strongly held beliefs of Jeff Hawkins and others that the

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

brain learns by predicting what comes next.

so long as they are unbiased.

Stochastic gradient descent is extremely tolerant of noise in the gradient estimates

This paper summarizes the results of simulations that show that this proposal can
be made to work quite well, but not as well as vanilla CNNs. A significant contributor
to the performance gap is the statistical inefficiency caused by the lack of weight sharing
and co-distillation should help to fix this.

How to Represent Part-Whole Hierarchies in a Neural Network

447

level are backpropagated through the bottom-up or top-down networks to
make the appropriate contributions to the derivatives at adjacent levels.
Those thorny issues are addressed in a paper in preparation.

13 Discussion

This article started life as a design document for an implementation, but it
was quickly hijacked by the need to justify the design decisions. I have used
the imaginary GLOM architecture as a vehicle for conveying a set of inter-
connected ideas about how a neural network vision system might be orga-
nized. The absence of a working implementation makes it easier to focus
on expressing the ideas clearly, and it avoids the problem of confounding
the quality of the ideas with the quality of the implementation, but it also
creates serious credibility concerns. The difference between science and phi-
losophy is that experiments can show that extremely plausible ideas are just
wrong and extremely implausible ones, like learning a entire complicated
system by end-to-end gradient descent, are just right. I am currently col-
laborating on a project to test out the ability of the GLOM architecture to
generalize shape recognition to radically new viewpoints, and I am hoping
that other groups will also test out the ideas presented here. This article has
gone on long enough already, so I conclude by making some brief philo-
sophical comments.

The idea that nodes in a parse tree are represented by islands of similar
vectors unifies two very different approaches to understanding perception.
The first approach is classical Gestalt psychology, which tried to model per-
ception by appealing to fields and was obsessed by the idea that the whole
is different from the sum of the parts.40 In GLOM, a percept really is a field
and the shared embedding vector that represents a whole really is very dif-
ferent from the shared embedding vectors that represent the parts. The sec-
ond approach is classical artificial intelligence, which models perception by
appealing to structural descriptions. GLOM really does have structural de-
scriptions, and each node in the parse tree has its own “address,” but the
addresses live in the continuous space of possible embeddings, not in the
discrete space of hardware locations.

Some critics of deep learning argue that neural nets cannot deal with
compositional hierarchies and that there needs to be a “neurosymbolic” in-
terface that allows neural network front and back ends to hand over the
higher-level reasoning to a more symbolic system.41 I believe that our pri-
mary mode of reasoning is by using analogies that are made possible by the
similarities between learned high-dimensional vectors, and a good analogy

Thanks to George Mandler for this more accurate translation.
This is reminiscent of Cartesian dualism which postulated an interface between the

body and the mind.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

448

G. Hinton

for the neurosymbolic interface is a car manufacturer who spends 50 years
expounding the deficiencies of electric motors but is eventually willing to
use them to inject the gasoline into the engine.

The phenomenal success of BERT (Devlin et al., 2018), combined with
earlier work that demonstrates that neural networks can output parse trees
if that is what the task requires (Vinyals et al., 2014), clearly demonstrates
that neural networks can parse sentences if they want to. By structuring the
interactions between the multiple heads in BERT so that they correspond to
levels of representation and by adding a contrastively learned regularizer
to encourage local islands of agreement over multiple word fragments at
each level, it may be possible to show that GLOMBERT actually does parse
sentences.

Acknowledgments

Many people helped me arrive at the set of ideas described in this arti-
cle: Terry Sejnowski, Ilya Sutskever, Andrea Tagliasacchi, Jay McClelland,
Chris Williams, Rich Zemel, Sue Becker, Ruslan Salakhutdinov, Nitish Sri-
vastava, Tijmen Tieleman, Taco Cohen, Vincent Sitzmann, Adam Kosoriek,
Sara Sabour, Simon Kornblith, Ting Chen, Boyang Deng, and Lala Li were
particularly helpful. People who helped me to improve the presentation of
the ideas include David Fleet, David Ha, Michael Isard, Keith Oatley, Si-
mon Kornblith, Lawrence Saul, Tim Shallice, Jon Shlens, Andrea Tagliasac-
chi, Ashish Vaswani, and several others. I especially l thank Jeff Dean and
David Fleet for creating the environment at Google that made this research
possible.

References

Ba, J., Hinton, G. E., Mnih, V., Leibo, J. Z., & Ionescu, C. (2016). Using fast weights
to attend to the recent past. In D. Lee, M. Sugiyama, U. Luxburg, I. Guyon, &
R. Garnett (Eds.), Advances in neural information processing systems, 29 (pp. 4331–
4339). Curran.

Bachman, P., Hjelm, R. D., & Buchwalter, W. (2019). Learning representations by
maximizing mutual information across views. In H. Wallach, H. Larochelle, A.
Beygelzimer, F. d’Alché-Buc, E. Fox, & R. Garnett (Eds.), Advances in neural infor-
mation processing systems, 32 (pp. 15535–15545). Curran.

Barham, P., & Isard, M. (2019). Machine learning systems are stuck in a rut. In HotOS
’19: Proceedings of the Workshop on Hot Topics in Operating Systems (pp. 177–183).
Bear, D. M., Fan, C., Mrowca, D., Li, Y., Alter, S., Nayebi, A., Schwartz, J., Fei-Fei,
L., Wu, J., Tenenbaum, J. B., & Yamins, D. L. K. (2020). Learning physical graph
representations from visual scenes. arXiv:2006.12373.

Becker, S., & Hinton, G. E. (1992). A self-organizing neural network that discov-
ers surfaces in random-dot stereograms. Nature, 355 (6356), 161–163. 10.1038/
355161a0

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

How to Represent Part-Whole Hierarchies in a Neural Network

449

Becker, S., & Hinton, G. (1993). Learning mixture models of spatial coherence. Neural

Computation, 5(2), 267–277. 10.1162/neco.1993.5.2.267

Buciluˇa, C., Caruana, R., & Niculescu-Mizil, A. (2006). Model compression. In KDD
’06: Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Dis-
covery and Data Mining (pp. 535–541).

Chen, T., Kornblith, S., Norouzi, M., & Hinton, G. (2020). A simple framework for
contrastive learning of visual representations. In Proceedings of the 37th Interna-
tional Conference on Machine Learning (pp. 1597–1607).

Chen, T., Kornblith, S., Swersky, K., Norouzi, M., & Hinton, G. (2020). Big self-

supervised models are strong semi-supervised learners. arXiv:2006.10029.

Chen, X., & He, K.
arXiv:2011.10566v1.

(2020). Exploring simple Siamese representation learning.

Crick, F., & Mitchison, G. (1983). The function of dream sleep. Nature, 304, 111–114.

10.1038/304111a0

Deng, B., Lewis, J. P., Jeruzalski, T., Pons-Moll, G., Hinton, G., Norouzi, M., &
Tagliasacchi, A. (2020). NASA: Neural articulated shape approximation. In Pro-
ceedings of the European Conference on Computer Vision.

Devlin, J., Chang, M., Lee, K., & Toutanova, K. (2018). BERT: Pretraining of deep
bidirectional transformers for language under standing. In Proceedings of the
NAACL-HLT.

Dosovitskiy, A., Beyer, L., Kolesnikov, A., Weissenborn, D., Zhai, X., Unterthiner, T.,
Dehghani, M., Minderer, M., Heigold, G., Gelly, S., Uszkoreit, J., & Houlsby, N.
(2020). An image is worth 16 × 16 words: Transformers for image recognition at scale.
arXiv:2010.11929.

Geman, S., & Geman, D. (1984). Stochastic relaxation, Gibbs distributions, and the
Bayesian restoration of images. IEEE Transactions on Pattern Analysis and Machine
Intelligence, 6(6), 721–741. 10.1109/TPAMI.1984.4767596

Grill, J.-B., Strub, F., Altché, F., Tallec, C., Richemond, P. H., Buchatskaya, E., Doersch,
C., Pires, B. A., Guo, Z. D., Azar, M. G., Piot, B., Kavukcuoglu, K., Munos, R., &
Valko, M. (2020). Bootstrap your own latent: A new approach to self-supervised learning.
arXiv:2006.07733.

Ha, D. (2016). Generating large images from latent vectors. blog.otoro.net.
He, K., Fan, H., Wu, Y., Xie, S., & Girshick, R. (2020). Momentum contrast for unsu-
pervised visual representation learning. In Proceedings of the IEEE/CVF Conference
on Computer Vision and Pattern Recognition.

He, X., Zemel, R. S., & Carreira-Perpinan, M. (2004). Multiscale conditional random
fields for image labeling. In Proceedings of the 2004 IEEE Computer Society Confer-
ence on Computer Vision and Pattern Recognition.

Hinton, G. (1979). Some demonstrations of the effects of structural descriptions in
mental imagery. Cognitive Science, 3(3), 231–250. 10.1207/s15516709cog0303_3
Hinton, G. (1981a). Shape representation in parallel systems. In Proceedings of the
Seventh International Joint Conference on Artificial Intelligence (vol. 2, pp. 1088–
1096).

Hinton, G. E. (1981b). Implementing semantic networks in parallel hardware. In G.
E. Hinton & J. A. Anderson (Eds.), Parallel models of associative memory. Erlbaum.
Hinton, G. E. (1981c). A parallel computation that assigns canonical object-based
frames of reference. In Proceedings of the 7th International Joint Conference on Artifi-
cial Intelligence (vol. 2, pp. 683–685).

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

450

G. Hinton

Hinton, G. (1990). Mapping part-whole hierarchies into connectionist networks. Ar-

tificial Intelligence, 46, 47–75. 10.1016/0004-3702(90)90004-J

Hinton, G. E. (2002). Training products of experts by minimizing contrastive diver-

gence. Neural Computation, 14(8), 1771–1800. 10.1162/089976602760128018

Hinton, G. (2006). Grant proposal to the natural sciences and engineering research council.

https://www.cs.toronto.edu/hinton/absps/NSERC06.pdf.
Hinton, G. (2014). Dark knowledge. Talk at Toyota Technical Institute.
Hinton, G., Krizhevsky, A., & Wang, S. (2011). Transforming auto-encoders. In T.
Honkela (Ed.), ICANN 2011: Artificial Neural Networks and Machine Learning (pp.
44–51). Springer-Verlag.

Hinton, G. E., Sabour, S., & Frosst, N. (2018). Matrix capsules with EM routing. In

Proceedings of the International Conference on Learning Representations.

Hinton, G., & Sejnowski, T. (1986). Learning and relearning in Boltzmann machines.
In D. E. Rumelhart & J. L. McClelland (Eds.), Parallel distributed processing: Ex-
plorations in the microstructure of cognition, vol. 1: Foundations (pp. 282–317). MIT
Press.

Hinton, G., Vinyals, O., & Dean, J. (2014). Distilling the knowledge in a neural net-

work. In NIPS 2014 Deep Learning Workshop. Curran.

Jabri, A., Owens, A., & Efros, A. A. (2020). Space-time correspondence as a contrastive

random walk. arXiv:2006.14613.

Kosiorek, A., Sabour, S., Teh, Y. W., & Hinton, G. E. (2019). Stacked capsule autoen-
coders. In H. Wallach, H. Larochelle, A. Beygelzimer, F. d’Alché-Buc, E. Fox, &
R. Garnett (Eds.), Advances in neural information processing systems, 32 (pp. 15512–
15522). Curran.

Lee, A. K., & Wilson, M. A. (2002). Memory of sequential experience in the hippocam-
pus during slow wave sleep. Neuron, 36(6), 1183–1194. 10.1016/S0896-6273(02)
01096-6

Lee, J., Lee, Y., Kim, J., Kosiorek, A., Choi, S., & Teh, Y. W. (2019). Set transformer:
A framework for attention-based permutation-invariant neural networks. In K.
Chaudhuri & R. Salakhutdinov (Eds.), Proceedings of the 36th International Confer-
ence on Machine Learning, vol. 97 (pp. 3744–3753).

Lillicrap, T., Santoro, A., Marris, L., Akerman, C., & Hinton, G. E. (2020). Back-
propagation and the brain. Nature Reviews Neuroscience, 21, 335–346. 10.1038/
s41583-020-0277-3

Locatello, F., Weissenborn, D., Unterthiner, T., Mahendran, A., Heigold, G., Uszkor-
eit, J., Dosovitskiy, A., & Kipf, T. (2020). Object-centric learning with slot attention.
arXiv:2006.15055.

Mildenhall, B., Srinivasan, P. P., Tancik, M., Barron, J. T., Ramamoorthi, R., & Ng, R.
(2020). NeRF: Representing scenes as neural radiance fields for view synthesis.
In Proceedings of the European Conference on Computer Vision (pp. 405–421).

Nádasdy, Z., Hirase, H., Czurkó, A., Csicsvari, J., & Buzsáki, G. (1999). Replay and
time compression of recurring spike sequences in the hippocampus. Journal of
Neuroscience, 19(21), 9497–9507.

Neal, R., & Hinton, G. (1997). A view of the EM algorithm that justifies incremental,
sparse, and other variants. In M. I. Jordomn (Ed.), Learning in graphical models (pp.
355–368). Springer.

Niemeyer, M., & Geiger, A. (2020). GIRAFFE: Representing scenes as compositional gen-

erative neural feature fields. arXiv:2011.12100.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

How to Represent Part-Whole Hierarchies in a Neural Network

451

Oore, S., Hinton, G. E., & Dudek, G. (1997). A mobile robot that learns its place. Neural

Computation, 9(3), 683–699. 10.1162/neco.1997.9.3.683

Osindero, S., & Hinton, G. (2008). Modeling im-age patches with a directed hierar-
chy of Markov random fields. In J. Platt, D. Koller, Y. Singer, & S. Roweis (Eds.),
Advances in neural information processing systems, 20. Curran.

Paccanaro, A., & Hinton, G. E. (2001). Learning distributed representations of con-
cepts using linear relational embedding. IEEE Transactions on Knowledge and Data
Engineering, 13(2), 232–244. 10.1109/69.917563

Rao, R., & Ballard, D. (1999). Predictive coding in the visual cortex: A functional
interpretation of some extra-classical receptive-field effects. Nature Neuroscience,
2. 79–87. 10.1038/4580

Sabour, S., Frosst, N., & Hinton, G. E. (2017). Dynamic routing between capsules.
In I. Guyon, Y. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, &
R. Garnett (Eds.), Advances in neural information processing systems, 30 (pp. 3856–
3866). Curran.

Sabour, S., Tagliasacchi, A., Yazdani, S., Hinton, G., & Fleet, D. (2021). Unsupervised

part representation by flow capsules. arXiv:2011.13920v2.

Saremi, S., & Sejnowski, T. J. (2013). Hierarchical model of natural images and the
origin of scale invariance. In Proceedings of the National Academy of Sciences, 110(8),
3071–3076. 10.1073/pnas.1222618110

Shi, K., & Zhu, S. (2007). Mapping natural image patches by explicit and implicit
manifolds. In 2007 IEEE Conference on Computer Vision and Pattern Recognition (pp.
1–7).

Sitzmann, V., Martel, J., Bergman, A., Lindell, D., & Wetzstein, G. (2020). Implicit
neural representations with periodic activation functions. In H. Larochelle, M.
Ranzato, R. Hadsell, M. F. Balcan, & H. Lin (Eds.), Advances in neural information
processing systems, 33. Curran.

Sitzmann, V., Zollhoefer, M., & Wetzstein, G. (2019). Scene representation networks:
Continuous 3D-structure-aware neural scene representations. In H. Larochelle,
M. Ranzato, R. Hadsell, M. F. Balcan, & H. Lin (Eds.), Advances in neural informa-
tion processing systems, 32 (pp. 1121–1132). Curran.

Srivastava, N., Goh, H., & Salakhutdinov, R. (2019). Geometric capsule autoencoders for

3D point clouds. arXiv:1912.03310.

Sun, W., Tagliasacchi, A., Deng, B., Sabour, S., Yazdani, S., Hinton, G., & Yi, K. M.
(2020). Canonical capsules: Unsupervised capsules in canonical pose. arXiv:2012.04718.
Sun, W., Jiang, W., Trulls, E., Tagliasacchi, A., & Yi, K. M. (2020). ACNe: Attentive
context normalization for robust permutation-equivariant learning. In Proceed-
ings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (pp.
11286–11295).

Taylor, G. W., Hinton, G. E., & Roweis, S. (2007). Modeling human motion using
binary latent variables. In B. Schölkopf, J. Platt, & T. Hoffman (Eds.), Advances in
neural information processing systems, 19. MIT Press.

Tejankar, A., Koohpayegani, S. A., Pillai, V., Favaro, P., & Pirsiavash, H. (2020). ISD:

Self-supervised learning by iterative similarity distillation. arXiv:2012.09259.

Ueda, N., Nakano, R., Ghahramani, Z., & Hinton, G. E. (2000). SMEM al-
gorithm for mixture models. Neural Computation, 12(9). 2109–2128. 10.1162/
089976600300015088

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
3
4
1
3
2
0
7
2
2
2
1
n
e
c
o
_
a
_
0
1
5
5
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

452

G. Hinton

van den Oord, A., Li, Y., & Vinyals, O. (2018). Representation learning with contrastive

predictive coding. arXiv:1807.03748.

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, L.
U., & Polosukhin, I. (2017). Attention is all you need. In I. Guyon, Y. V. Luxburg,
S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, & R. Garnett (Eds.), Advances
in neural information processing systems, 30 (pp. 5998–6008). Curran.

Vinyals, O., Kaiser, L., Koo, T., Petrov, S., Sutskever, I., & Hinton, G. E. (2014). Gram-
mar as a foreign language. In Z. Ghahramani, M. Welling, C. Cortes, N. Lawrence,
& K.Q. Weinberger (Eds.), Advances in neural information processing systems, 27.
Curran.

Viola, P., & Jones, M. J. (2004). Robust real-time face detection. International Journal of

Computer Vision, 57, 137–154. 10.1023/B:VISI.0000013087.49260.fb

Williams, C. K. I., & Agakov, F. V. (2002). Products of gaussians and probabilis-
tic minor component analysis. Neural Computation, 14(5), 1169–1182. 10.1162/
089976602753633439

Williams, C., Revow, M., & Hinton, G. (1995). Using a neural net to instantiate a
deformable model. In G. Tesauro, D. Toretsky, & T. Leen (Eds.), Advances in neural
information processing systems, 7 (pp. 965–972). MIT Press.

Zemel, R. S., Williams, C. K. I., & Mozer, M. C. (1995). Lending direction to neural

networks. Neural Networks, 8(4), 503–512. 10.1016/0893-6080(94)00094-3

Received February 23, 2022; accepted July 24, 2022.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d