ARTICLE - Specialized Research AI at MIT

ARTICLE

Communicated by Simon Du

On the Explainability of Graph Convolutional Network
With GCN Tangent Kernel

Xianchen Zhou
zhouxianchen13@nudt.edu.cn
Hongxia Wang
wanghongxia@nudt.edu.cn
National University of Defense Technology, Changsha 410073, P.R.C.

Graph convolutional network (GCN) is a powerful deep model in dealing
with graph data. However, the explainability of GCN remains a difficult
problem since the training behaviors for graph neural networks are hard
to describe. In this work, we show that for GCN with wide hidden fea-
ture dimension, the output for semisupervised problem can be described
by a simple differential equation. In addition, the dynamics of the behav-
ior of output is decided by the graph convolutional neural tangent kernel
(GCNTK), which is stable when the width of hidden feature tends to be
infinite. And the solution of node classification can be explained directly
by the differential equation for a semisupervised problem. The experi-
ments on some toy models speak to the consistency of the GCNTK model
and GCN.

1 Introduction

Graph neural networks (GNNs) are widely used in dealing with non-Euclid
data (Wu et al., 2021). A typical kind of GNN, the graph convolutional net-
work (GCN; Kipf & Welling, 2016; Wu et al., 2019), achieves great perfor-
mance in several fields, including society and transportation (Zhou et al.,
2020; Wu et al., 2021). Therefore, many researchers focus on the theoreti-
cal aspects of GNN, especially GCN, including expressive power (Xu, Hu,
Leskovec, & Jegelka, 2018; Loukas, 2020; Chen, Villar, Chen, & Bruna, 2019)
and generalization capability (Garg, Jegelka, & Jaakkola, 2020; Scarselli,
Tsoi, & Hagenbuchner, 2018; Xu et al., 2020). The explainability of GNN,
which often studies the underlying relationship behind predictions, has
also gotten the broad attention of numerous experts and scholars (Yuan,
Yu, Gui, & Ji, 2020). Since many GNNs are proposed without explaining
them, they are treated as a black box and cannot be trusted in critical appli-
cations concerning privacy and safety. Therefore, it is necessary to develop

Hongxia Wang is the corresponding author.

Neural Computation 35, 1–26 (2023)
https://doi.org/10.1162/neco_a_01548

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
1
1
2
0
7
5
4
2
1
n
e
c
o
_
a
_
0
1
5
4
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

H. Wang and X. Zhou

explanation techniques to study the causal relationship behind GNN
predictions.

Some methods explore GNNs’ explainability by identifying important
nodes related to their prediction. Gradients and features-based methods
(Baldassarre & Azizpour, 2019; Pope, Kolouri, Rostami, Martin, & Hoff-
mann, 2019) and perturbation-based methods (Ying, Bourgeois, You, Zit-
nik, & Leskovec, 2019; Luo et al., 2020; Schlichtkrull et al., 2020; Funke et al.,
2021) employ different model metrics, including gradients or antiperturba-
tion ability, to indicate the importance of different nodes, while decompo-
sition methods (Schwarzenberg, Hübner, Harbecke, Alt, & Hennig, 2019;
Schnake et al., 2020) and surrogate methods (Huang et al., 2020; Vu & Thai,
2020; Zhang et al., 2021) decomposing GNNs or finding a surrogate model
to simplify and explain the GNNs. However, most of this work seeks to
understand GNN predictions by post hoc explanation, which means the
explanations cannot be used to predict GNN output before training.

In this article, we focus on GCN behaviors in dealing with the node clas-
sification problem (Kipf & Welling, 2016) and try to interpret GCN, which
can be applied to predict its output before training. Since the objective func-
tion for training GCN is often nonconvex, it is hard to analyze GCN be-
havior directly. Recently neural tangent kernel (NTK; Bartlett, Helmbold,
& Long, 2018; Arora et al., 2019; Jacot, Gabriel, & Hongler, 2018) has been
proposed to analyze deep neural networks including GNNs in different
perspectives. Du, Hou, et al. (2019) use the aggregation and combination
formulation of infinitely wide GNNs to define the graph NTK (GNTK) at
graph level, which can predict the results of graph-level classification prob-
lems. Following the definition of GNTK, Huang et al. (2021) defines an NTK
of GCN in node level and focus on the trainability of ultrawide GCNs. How-
ever, neither of the two works can be applied for analyzing node classifica-
tion problems directly based on GNTK.

Here, we establish a GCN tangent kernel (GCNTK) in matrix form and
use it to analyze the learning dynamics of wide GCN under gradient de-
scent for node classification problems. GCNTK can also predict test nodes’
label and help to explain the importance of different training nodes for
prediction.

We summarize our contributions as follows:

• The convergence of GCNTK. Since the input and output of GCN are in
matrix form, the formula of a gaussian process for GCN (GCNGP) is
complex. We first give the explicit formula for GCNGP and GCNTK
and demonstrate that GCNTK can converge to a fixed form as the
GCN’s layer width tends to be infinite.

• The convergence of training loss and stability of GCNTK. We prove that
the loss constrained on the training data set tends to zero, as the width
of parameter matrix tends to be infinite. And the GCNTK remains
fixed during the training procedure.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
1
1
2
0
7
5
4
2
1
n
e
c
o
_
a
_
0
1
5
4
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Explainability of GCN With GCNTK

• Predictions for the test nodes’ label based on linear dynamics. We formally
obtain the predictions of test nodes’ label with infinite-width GCN.
We first find that the solution of semisupervised problems mainly de-
pends on the ratio of kernel restricting on the training and test data
set. The prediction on the test nodes and the impact of training nodes
can be interpreted well by the GCNTK.

2 Related Work

2.1 GNNs and GCNs. GNNs learn task-specific node/edge/graph rep-
resentations via hierarchical iterative operators and obtain great success in
graph learning tasks. A classical GNN consists of aggregation and combina-
tion operators, which gather information from neighbors iteratively. GCN,
as a typical GNN, defines the convolution on the spectral domain and ap-
plies a filter operator on the feature components. Its aggregation function
can be treated as a weighted summation of neighbors’ feature. Among this,
a specific GCN proposed in Kipf and Welling (2016) uses a 1-localized Cheb-
Net to define convolution and obtain the model in equation 3.1 with the bias
term, which obtains significant advantages in dealing with node classifica-
tion problems.

2.2 Explainability of GNNs. The explainability of GNNs can be ex-
plored by identifying important nodes related to GNN’s prediction. For
example, SA and guided BP (Baldassarre & Azizpour, 2019) use gradi-
ent square values as the importance and contributions of different nodes,
while Grad-CAM (Pope et al., 2019) maps the final layer to the input nodes
space to generate the importance. GNN perturbation methods including
GNNExplainer (Ying et al., 2019), PGExplainer (Luo et al., 2020), Graph-
Mask (Schlichtkrull, De Cao, & Titov, 2020), and ZORRO (Funke, Khosla, &
Anand, 2021) consider the influence of node perturbations on predictions.
Surrogate and decomposition models, including GraphLime (Huang et al.,
2020), PGM-explainer (Vu & Thai, 2020), Relex (Zhang, Defazio, & Ramesh,
2021), LRP (Baldassarre & Azizpour, 2019), and GNN-LRP (Schnake et al.,
2020), explain GNN by employing a simple and interpretable surrogate
model to approximate the predictions. However, most of these models ex-
plain the GNN afterward and GNN is still a black box to some extent. It
means these models can provide an explanation of GNN’s output but can-
not predict the results before training.

Starting from a spectral GCN, a classical and special GNN, this article ad-
dresses GCN’s interpretability and analyzes its causal relationship between
the predictions and training nodes, which help to predict GCN’s output
beforehand.

2.3 Neural Tangent Kernel. Based on the gaussian process (GP;
Neal, 1995; Lee et al., 2018; de G. Matthews, Rowland, Hron, Turner, &

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
1
1
2
0
7
5
4
2
1
n
e
c
o
_
a
_
0
1
5
4
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

H. Wang and X. Zhou

Ghahramani, 2018) property of deep neural networks, Jacot et al. (2018) in-
troduce the neural tangent kernel and describe the exact dynamics of a fully
connected network’s output through gradient flow training in an overpa-
rameterized situation. This initial work has been followed by a series of
studies, including the exacter description (Arora et al., 2019; Lee et al., 2019),
generalization for different initialization (Liu, Zhu, & Belkin, 2020; Sohl-
Dickstein, Novak, Schoenholz, & Lee, 2020), and NTK for different struc-
tures of neural networks (Arora et al., 2019; Li et al., 2021; Luo, Xu, Ma, &
Zhang, 2021).

As for graph deep learning, Du, Hou, et al. (2019) considered graph-
supervised problems and defined graph NTK (GNTK) in graph level based
on GNN’s aggregation function, which can be used to predict an unlabeled
graph. Immediately after Du, Hou, et al. (2019), Huang et al. (2021) defined
GNTK for GCN and conducted research on how to deepen GCN. Since
the GNTK formulation in Huang et al. (2021) is based on training nodes,
the predictions of testing nodes cannot be obtained directly. In this article,
we derive a matrix form of GCN tangent kernel (GCNTK) and provide an
explicit form to predict the behavior of testing nodes directly.

3 Preliminaries

, v

Let G = (V, E, X ) be a graph with N vertices, where V = {v
, . . . , vN} rep-
resents N vertices or nodes. The adjacency matrix A = (ai j )N×N represents
the link relation. X ∈ RN×d0 is the node feature matrix. A typical semisuper-
vised problem defined on graph is node classification. Assume that there
exist k classes of nodes, and each node v
i in graph G has an associated
∈ Rk. However, only some of the nodes in
one-hot representation label yi
V denoted by V
train are annotated. The task of node classification is to pre-
dict the labels for the unlabeled nodes in Vtest.

train

= {i|v

} and Itest = {i|v

First, we give some notations in matrix form. Assume that the index of a
training and a test set is I
∈ Vtest}, respec-
∈ V
tively. For an arbitrary matrix X = (Xi j )N×d, denote the ith row of matrix
∈ RN×N be a diagonal matrix
X by Xi and the jth column by X;, j. Let Itrain
where the training index is 1 and the other index set is 0, with a similar def-
= ItrainX ∈ RN×d represents the X constraining on the
inition for Itest. Xtrain
training set by rows, with a similar definition for Xtest. For an arbitrary ma-
trix A ∈ RN×N, Atrain,test
= ItrainAItest represents A constraining on the train-
ing index by rows and test index by columns.

A GCN f : RN×d0 −→ RN×dL+1 is a nonlinear transform defined by HL+1 =

f (X0), which can be expressed in the recurrent form,

(cid:2)

Hl+1 = AXlW l+1 + Bl+1
Xl+1 = φ(Hl+1)

l = 0, . . . , L,

(3.1)

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
1
1
2
0
7
5
4
2
1
n
e
c
o
_
a
_
0
1
5
4
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Explainability of GCN With GCNTK

with parameters

⎧
⎨

⎩

= σω√

W l
i, j

dl−1
β l
i, j

= σ

Bl
i, j

ωl

i, j

(3.2)

, β l

×dl+1 , Bl+1 ∈ RN×dl+1 . ωl
i j

where φ represents the activation function. Xl ∈ RN×dl is the l layer out-
put, and X0 = X ∈ RN×d0 is the initial node feature matrix of G. W l+1 ∈
Rdl
i, j are trainable variables drawn independent
∼
and identically distributed (i.i.d.) from a standard gaussian with ωl
i j
N(0, 1) at initialization. The weight and bias variance σω and σ
b are prede-
fined constant variances. The parameterization, equation 3.2, is nonstan-
dard, and we refer to it as “NTK parameterization” (Jacot et al., 2018; Arora
et al., 2019; Liu et al., 2020; Littwin, Galanti, Wolf, & Yang, 2020). Unlike
the standard parameterization (Sohl-Dickstein, Novak, Schoenholz, & Lee,
2020; Franceschi et al., 2021) that leads to a divergent NTK, the NTK pa-
rameterization has a width-dependent scaling factor
in each layer and

, β l
i, j

1√

dl−1

thus can normalize the backward dynamics by a convergent NTK.

, β l
i j

Define θ l ≡ vec({ωl
i j

}), which is a column-wise stacked (N + dl−1) dl
× 1 vector of all parameters in layer l. Let θ = vec(∪L+1
θ l ) denote all the
l=1
θ l ), with similar definitions for θ ≥l0 .
network parameters, θ ≤l0 = vec(∪l0
Let θt denote the network parameters at time t, and θ
0 represents the ini-
tial values. Combined with the current parameter θt, the output of GCN
is denoted by the function f (X, θt ) = HL+1(X, θt ) ∈ RN×dL+1 , where dL+1
= k
represents the number of classes of nodes. To simplify the representation,
we use f (X ) = f (X, θ ), ft (X ) = f (X, θt ).

We use the loss L on the labeled nodes for learning the θ by the gradient

l=1

descent (GD),

L = 1/2

(cid:6)

(cid:7)

i∈I

train

(cid:8)

f (X )i,:

, yi

(3.3)

where f (X )i,: represents the i row of GCN output.

Then the square loss function equation 3.3, can be written as

L = 1/2(cid:10) f (X )train

− Ytrain

(cid:10)2
2

= 1/2(cid:10)Itrain( f (X ) − Y)(cid:10)2
2

(3.4)

Here Y ∈ RN×k is the matrix of N labels in one-hot representation. Although
the label of the test nodes, Ytext cannot obtained, the loss on the training set
slice can be represented directly.

Next, since the gradient flow of GCNs involves the gradient of the ma-

trix, we give its definition as follows. The vectorization of a matrix X is

vec(X ) = [X11

, . . . , Xm1

, X12

, . . . , Xm2

, . . . , X1n, . . . , Xmn]

(cid:11)

(mn × 1).

(3.5)

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
1
1
2
0
7
5
4
2
1
n
e
c
o
_
a
_
0
1
5
4
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

H. Wang and X. Zhou

We define the derivative of matrix F ∈ Rp×q with respect to matrix X ∈ Rm×n
by vector representation as

∇XF =

∂F
∂X

∂ vec(F)
∂ vec(X )

∈ Rpq×mn.

(3.6)

Let η be the learning rate of GD. Applying the gradient flow on the GCN,

the optimization procedure can be written as

˙θt = −η∇θ L = −η∇θ ft (X )T ∇

ft (X )

(3.7)

Let ˙ft (X ) = ˙ft (vec(X )) ∈ RNdL+1

×1 be a vector representation; then

˙ft (X ) = ∇θ ft (X ) ˙θt = −η∇θ ft (X )∇θ ft (X )

(cid:11)∇

ft (X )

L ∈ RNdL+1

×1.

(3.8)

Definition 1. Similar to the definition of NTK in Jacot et al. (2018), the GCNTK
(cid:10)t is defined by

(cid:10)t = (cid:10)t (X, X ) = ∇θ ft (X )∇θ ft (X )

(cid:11)

= (cid:11)L+1
l=1

∇θ l ft (X )∇θ l ft (X )

(cid:11) ∈ RNdL+1

×NdL+1 .

(3.9)

Then equation 3.8 can be written as

˙ft (X ) = −η(cid:10)t (X, X )∇

ft (X )

(3.10)

ft (X )

L ∈ RNdL+1

×1 is the gradient of the loss with respect to the output
Here ∇
matrix, and ∇θ ft (X )(cid:11) ∈ R|θ |×NdL+1 is the gradient of the output with respect
to θ at time t.

Equations 3.7 and 3.8 are two differential equations that describe the
evolution of parameters and output, respectively. The behavior of output
depends on the time-dependent GCNTK (cid:10)t. However, (cid:10)t depends on the
random draw of θt, which makes the differential equations hard to solve.
This article assumes that the width tends to infinity to obtain the conver-
gence of (cid:10)t.

4 Main Results

4.1 Convergence of GCNTK with Respect to Width d. GNTK (Du,
Hou, et al., 2019; Huang et al., 2021) gives an NTK formula on GNNs
based on the distinct node and the dynamics behavior on the training set.
However, for the semisupervised problem on the graph, the convergence
of GCNTK in matrix form has not been researched. Since the formula of

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
1
1
2
0
7
5
4
2
1
n
e
c
o
_
a
_
0
1
5
4
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Explainability of GCN With GCNTK

GCNTK involves the complex gradient computation of matrix, it has not
been given exactly. Therefore, we first focus on the convergence of GCNTK.

Theorem 1. For a GCN defined by equation 3.1 under the NTK parameterization,
the GCNTK at (cid:10)
0 defined by equation 3.9 converges in probability to a determin-
istic limiting kernel

(cid:10)
0

−→ (cid:10),

(4.1)

as the layers width d1

, d2

, . . . , dL+1

−→ ∞.

The proof details of multi-output GPs and NTK are in appendix A. We

give the proof sketch as follows.

In order to prove theorem 1, denote A ⊗ B as a Kronecker product of
A and B. We first show that the output of GCNs at each layer is also in
correspondence with a certain class of multioutput GPs defined by

Hl ∼ GP

⎛

⎡

⎜
⎝

⎢
⎣

0
…
0

⎤

⎞

⎥
⎦ , Kl (X, X

(cid:15)

) ⊗ Idl

⎟
⎠ , l = 1, . . . , L + 1,

(4.2)

where

Kl (X, X

(cid:15)

∗ I + σ 2
∗ I + σ 2

wE(AXl−1)(AX
wE

) = σ 2
b
= σ 2
b
× (Aφ(Hl−1(X )))(Aφ(Hl−1(X

Hl−1∼GP((cid:2)0,Kl−1 (X,X(cid:15) )⊗Idl )

(cid:15)(l−1))

(cid:11)

(cid:15)

(cid:11),

)))

(4.3)

with base case

K1(X, X

(cid:15)

) = σ 2
b

∗ I + σ 2
w

1
d0

AX(AX

(cid:15)

(cid:11), l = 1, 2, . . . , L + 1.
)

(4.4)

According to equation 4.2, we have the convergence of GCNTK:

(cid:10)
0

−→ (cid:10)L(X, X )

(cid:11) (cid:12)= (cid:10),

as dl

−→ ∞, l = 1 · · · , L + 1.

(4.5)

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
1
1
2
0
7
5
4
2
1
n
e
c
o
_
a
_
0
1
5
4
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Here

(cid:10)l (X, X

(cid:15)

(cid:11) = Idl
)

(cid:15)

⊗ Kl (X, X
l = 2, . . . , L + 1,

) + Idl

⊗ diag( ˙(cid:11)l−1(X, X

(cid:15)

)A ˜(cid:10)l−1(X, X

(cid:15)

(cid:11)
)

(cid:11),

(4.6)

where

˙(cid:11)l−1(X, X

(cid:15)

with

) = E( ˙φ(Hl−1

:,1 (X )) ◦ ˙φ(Hl−1

:,1 (X

(cid:10)1(X, X

(cid:15)

(cid:11) = Idl
)

⊗ K1(X, X

(cid:15)

H. Wang and X. Zhou

(cid:15)

))),

(4.7)

(4.8)

◦ is the Hadamard product and ˙φ is the derivative of φ.

Remark 1. Jacot et al. (2018) and Yang (2019) show that the NTK of fully
connected networks at initialization (cid:10)
0 converges to a deterministic kernel
(cid:10) based on the GP property. Theorem 1 shows that the GCNTK also con-
verges at initialization. Compared with the results in Du, Hou, et al. (2019),
which define the GNTK from a single node perspective, this article defines
the GCNTK in matrix form first and is suitable for further analysis of node
classification problems.

4.2 The Behavior of GCNTK with Respect to Time t. Furthermore, we
focus on the behavior of GCN and GCNTK during the training procedure.
We use GCNTK to provide a simple proof of the convergence of GCN un-
der gradient descent on the training nodes. The stability of GCNTK and
parameters during the training procedure is guaranteed in our proof. Since
Lee et al. (2019) show that both the convergence of NTK and standard pa-
rameterization can be obtained by similar proof procedure, we prove the
convergence under standard parameterization. Compared with NTK pa-
rameterization, standard parameterization is common in the realization of
GCN (Kipf & Welling, 2016; Wu et al., 2019), which is defined as

(cid:2)

⎧
⎨

⎩

and

Hl+1 = AXlW l+1 + Bl+1
Xl+1 = φ(Hl+1)

l = 0, . . . , L

W l
i, j

= ωl
i j

∼ N
(cid:7)

bl
i j

= β l
i j

∼ N

(cid:22)

(cid:21)
0, σ 2
ω
dl
(cid:8)

0, σ 2
b

(4.9)

(4.10)

Different from the NTK parameterization, the standard NTK kernel (Sohl-
Dickstein et al., 2020; Park, Sohl-Dickstein, Le, & Smith, 2019) is defined as

(cid:2)

(cid:10)t := (cid:10)t (X, X ) = 1
d
(cid:10) := limd→∞ (cid:10)
0

∇θ f (X, θt )∇θ f (X, θt )T
in probability

(4.11)

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
1
1
2
0
7
5
4
2
1
n
e
c
o
_
a
_
0
1
5
4
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Explainability of GCN With GCNTK

Theorem 1 has proven that (cid:10) exists. Next, we prove that (cid:10)t is invariant
with respect to t as the width tends to infinity. Before that, we give some
assumptions.

1. For the GCN model defined in equations 4.9 and 4.10, the widths in

each layers are identical: d1

= d2

= · · · = dL = d.

2. The analytic GCNTK kernel (cid:10) in equation 4.11 is of full rank and

positive.

3. The activation function φ is Lipschitz continuous and smooth,

satisfying

(cid:23)
(cid:23)φ(cid:15)

(cid:23)
(cid:23)

∞

|φ(0)|,
(cid:24)
(cid:24)
(cid:24) /|x − ˜x| = C1
(cid:24)φ(x) − φ( ˜x)

sup
x(cid:18)= ˜x

(cid:24)
(cid:24)φ(cid:15)

(x) − φ(cid:15)

(cid:24)
(cid:24) /|x − ˜x| = C2
( ˜x)

< ∞, (4.12) < ∞. (4.13) Assumption 1 is easy to satisfy in the limit condition. Assumption 2 holds since the NTK kernel is a multiplication of the derivative. Common activa- tion functions like Relu, and sigmoid satisfy assumption 3. Under the setting of node classification problem, we have the parameter update formula, θt+1 = θt − η∇θ ft (X )T ∇ L, ft (X ) and the gradient flow equation is ˙θt = −η∇θ ft (X )T ∇ L. ft (X ) Using the following shorthand, f (θt ) g (θt ) gtrain(θt ) J(θt ) (cid:12)= vec( f (X, θt )) ∈ RNk×1, (cid:12)= vec( f (X, θt ) − Y) ∈ RNk×1, (cid:12)= vec(Itrain( f (X, θt ) − Y)) = I ⊗ Itraing (θt ) ∈ RNk×1, (cid:12)= ∇θ f (θt ) ∈ RNk×|θ |, we have θt+1 = θt − ηJ (cid:11) (θt )gtrain (θt ) or ˙θt = −ηJ (cid:11) (θt )gtrain (θt ) . (4.14) (4.15) (4.16) (4.17) (4.18) l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / / 3 5 1 1 2 0 7 5 4 2 1 n e c o _ a _ 0 1 5 4 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 10 H. Wang and X. Zhou Then the behavior of GCN satisfies ˙f (θt ) = −ηJ(θt )J (cid:11) (θt )I ⊗ Itraing (θt ) . (4.19) Note that J(θt )J(cid:11) Itrain). It is easy to prove that the eigenvalues of (cid:10) except for some zeros. Define (θt ) is connected tightly with (cid:10). Denote (cid:10) = (cid:10) · (I ⊗ train train are equal to that of (cid:10) λ min λ max λ((cid:10) = min λ>0
= max λ((cid:10)

train) > λ

min((cid:10))

train) = λ

max((cid:10))

critical

2
+ λ

max

min

(4.20)

We first show that the Jacobian is local Lipschitz, where the Lipschitzness
constant K is related to parameters A, L, C1
Lemma 1. There exist a K > 0, and N, for every d ≥ N; the following holds with
high probability over random initialization:

, C2, and d.

⎧
⎨

⎩

1√
d

(cid:10)J(θ ) − J( ˜θ )(cid:10)F ≤ K(cid:10)θ − ˜θ (cid:10)

(cid:10)J(θ )(cid:10)F ≤ K

∀θ , ˜θ ∈ B

(cid:21)
θ

− 1
2

, d

(cid:22)

(4.21)

where

B (θ

, R) := {θ : (cid:10)θ − θ

(cid:10)

< R} . (4.22) The proof of lemma 1 is in section B.3 in online appendix B. It shows 0, the Jacobian J(θ ) is Lipschitz that in the neighborbood of initialization θ continuous when d is large enough. Then for the gradient descent and gradient flow, we have the following main results: Theorem 2. Assume assumptions 1, 2, and 3 hold. For δ 0 there exist R0 holds with probability at least 1 − δ gradient descent with learning rate η = η d , critical, > 0, N ∈ N, and K > 1, such that for every d ≥ N, the following
0 over random initialization when applying

> 0 and η

< η 0 0 (cid:21) ≤ 2 ⎧ ⎪⎨ ⎪⎩ (cid:23) (cid:23) (cid:23) (cid:23) gtrain (θt ) (cid:23) (cid:26) (cid:23)θ t j=1 j 1 − η (cid:23) (cid:23) 2 − θ j−1 ≤ 3KR0 λ min d− 1 2 (cid:22) t R0 0 λ min 3 (4.23) l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / / 3 5 1 1 2 0 7 5 4 2 1 n e c o _ a _ 0 1 5 4 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Explainability of GCN With GCNTK and (cid:10)(cid:10) 0 − (cid:10)t (cid:10) F sup t ≤ 6K3R0 λ min − 1 2 . d 11 (4.24) Theorem 3. Assume assumptions 1, 2, and 3 hold. For δ critical, 0 > 0, N ∈ N, and K > 1, such that for every d ≥ N, the following
there exist R0
holds with probability at least 1 − δ
0 over random initialization when applying
gradient flow with learning rate η = η
d ,

> 0 and η
0

< η 0 (cid:23) (cid:23) (cid:23) (cid:23) gtrain (θt ) 2 (cid:10)θt − θ 0 (cid:10) 2 0 λ mintR0 ≤ e− 1 η 3 (cid:21) 1 − e− 1 3 ≤ 3KR0 λ min (cid:22) λ η 0 mint d− 1 2 ⎧ ⎨ ⎩ and (cid:10)(cid:10) 0 − (cid:10)t (cid:10) F sup t ≤ 6K3R0 λ min − 1 2 . d (4.25) (4.26) Remark 2. Lee et al. (2019), Du, Lee, Li, Wang, and Zhai (2019), and Allen- Zhu, Li, and Song (2019) show the convergence of an overparameterized, fully connected network and the stability of NTK, while theorems 2 and 3 extend the convergence and stability of GCNTK for a semisupervised prob- lem. As the GCNTK converges at initialization time when the width tends to be infinite, it also remains fixed during training. Different from the su- pervised problem, the convergence rate of GCN for a semisupervised prob- lem depends on the smallest eigenvalues of the GCNTK constrained on the training nodes. Therefore for the same graph, training GCN with fewer training nodes is faster in general. The proof is in appendix B. 4.3 GCN Explanation Based on Training Dynamics Equation. Under the infinite width assumption, GCNTK remains fixed, and the training dy- namics can be computed by the evolution equation 3.8. We can obtain the explanation of GCN with infinite width based on the solution of the training dynamics equation. Theorem 4. For a graph convolutional network defined by equation 3.1 in the limits as the layers width d1 −→ ∞, the output of GCN is , . . . , dL+1 , d2 d vec( ft (X )) dt = −η(cid:10) train · vec(( ft (X ) − Y))), (4.27) where (cid:10) train = (cid:10) · I ⊗ Itrain. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / / 3 5 1 1 2 0 7 5 4 2 1 n e c o _ a _ 0 1 5 4 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 12 H. Wang and X. Zhou The solution of equation 3.4 vec( ft (X ) − Y) = e traintvec( f0(X ) − Y). −η(cid:10) (4.28) The slice of (cid:10) the training set is (cid:10) test,train. Then we have train constraining on the rows of the testing set and the columns of vec( ft (X ) − Y)train Similarly, from −η(cid:10) = e train,traint (vec( f0(X ) − Y))train . (4.29) dvec( ft (X ))test dt = −η(cid:10) test,trainvec( ft (X ) − Y)train = −η(cid:10) test,traine −η(cid:10) train,traint (vec( f0(X ) − Y))train , (4.30) we have vec( ft (X ))test = −(cid:10) (cid:10)−1 train,train(I − e −η(cid:10) train,traint )(vec( f0(X ) − Y))train test,train + vec( f0(X ))test. (4.31) Theorem 4 shows that the output label of the test nodes is influenced by train,train. As t −→ ∞, the output label two factors of GCNTK, (cid:10) is a linear combination of the label of training nodes. Define test,train and (cid:10) M = (cid:10) test,train (cid:10)−1 train,train ; (4.32) then M describes the contribution of labeled nodes. Therefore, according to equation 4.31, the influence of training nodes on the testing nodes can be obtained easily. 5 Experiments Little previous work has provided beforehand explanations of GNN. And to our knowledge, there is no beforehand explanation model investigating the node classification problem. In this article, we compare only the output of GCN and GCNTK and verify the consistency of their predictions. We use synthetic data sets to obtain some conclusions which are implicit in the classical GCN. Synthetic data sets: In order to verify the prediction correctness in theorem 4, we build some subgraphs with a few nodes that have common pat- terns in various graph data sets. All the nodes in these graphs except one are labeled with red or green. We use the GCN and GCNTK to l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / / 3 5 1 1 2 0 7 5 4 2 1 n e c o _ a _ 0 1 5 4 8 p d . 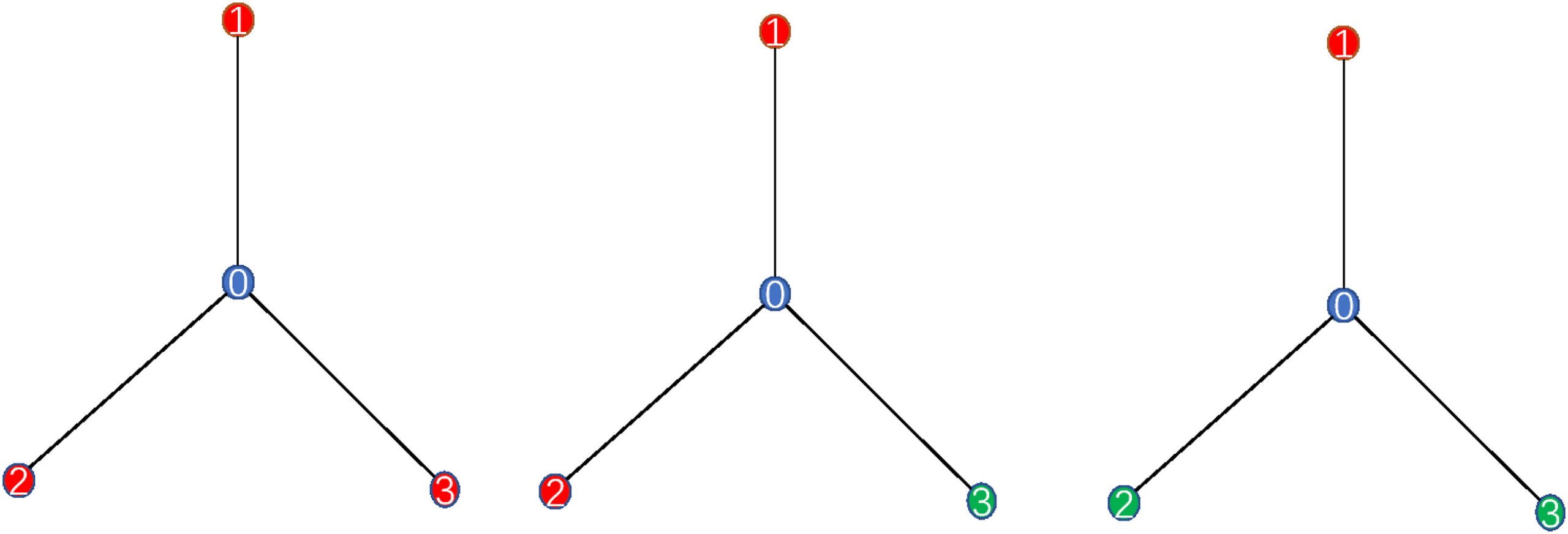f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Explainability of GCN With GCNTK 13 Figure 1: Using GCNTK to predict the color of node 0, the GCNTK ratio M = (0.33, 0.33, 0.33). Then node 0 in the left, the middle, and the right is predicted using equation 4.31 as red, red, and green, respectively, which is completely consistent with the result of GCN. predict the label (red or green) of the unlabeled (blue) node, respec- tively based on labeled nodes, and obtain the contribution of those labeled nodes. GCN model: We train the node classification model using different types of graphs by the classical GCN in Kipf and Welling (2016) where the feature matrix X is set by the identity matrix. And we only predict the label of one node (in blue). 5.1 Experiments on the Star Graph. Theorem 4 shows that the pre- dicted label is only influenced by the contribution of unlabeled nodes, where the contribution ratio is M defined by equation 4.32. For instance, if there is no link between the test nodes and training nodes, then (cid:10) = 0. As a result, no node has an effect on the training nodes. 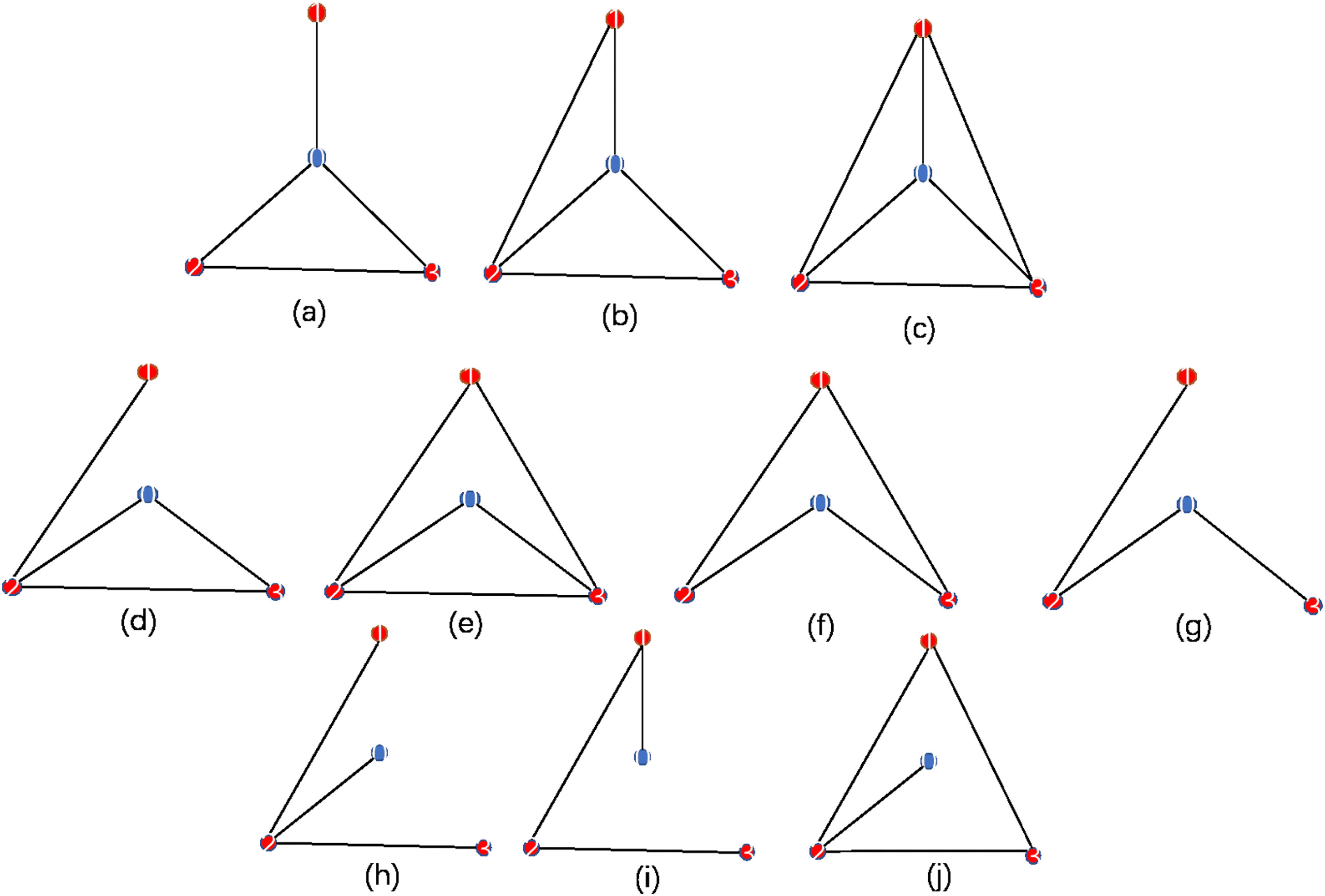test,train 5.2 Common Patterns with Four Nodes. In this section, we compute the contribution ratio M of all the patterns with four nodes in Figures 1 and 2. As is shown in Table 1, the labeled nodes make different predictions of 0. The ratio displays the importance of the node related to the predicted node. The positive or negative ratio of one training node means that predicted node tends to be the same as or different from that node. And the absolute value of the ratio means the importance of different nodes. In Figures 2c and 2f, all the labeled nodes make the same positive contri- bution to the predicted nodes. Therefore, the largest number of those nodes with the same color decide the color of node 0. In addition, in Figures 2g, 2e, and 2h, different nodes make different positive contribution to node 0. And in Figures 2g, 2i, and 2j, some nodes even make negative contribution to node 0. We can find that node 2 in Figure 2g, 1 in Figure 2i, and 2 in Figure 2j make the greatest contribution to the predicted node 0. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / / 3 5 1 1 2 0 7 5 4 2 1 n e c o _ a _ 0 1 5 4 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 14 H. Wang and X. Zhou l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / / 3 5 1 1 2 0 7 5 4 2 1 n e c o _ a _ 0 1 5 4 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 2: Different patterns with four nodes. Red nodes are training nodes with labels, and the blue node is the unlabeled node to be predicted. Table 1: The Contribution Ratio M of Different Graphs. 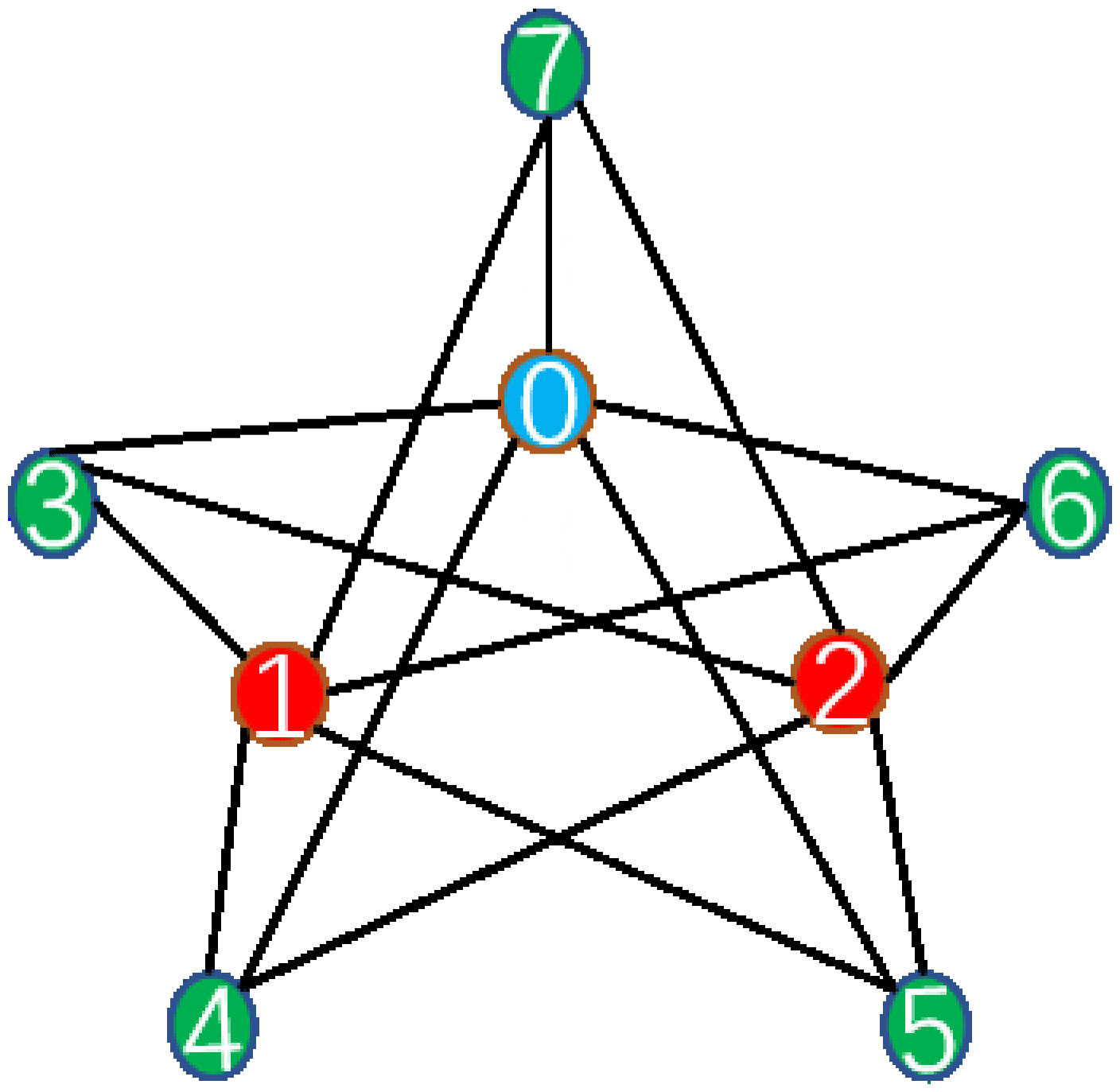Number M Number M a c e g i (0.38, 0.31, 0.31) (0.33, 0.33, 0.33) (0.10, 0.45, 0.45) (−0.34, 0.74, 0.60) (1.5, −0.85, 0.35) b d f h j (0, 1, 0) (0, 0, 1) (0.33, 0.33, 0.33) (0.29, 0.42, 0.29) (−0.16, 1.32, −0.16) 5.3 A Special Case. In this section, we display an interesting experiment that is inconsistent with the intuition that similar neighbors should have the same labels. The graph in Figure 3 shows that different colored nodes connect with each other, but the node with the same color is separate. Then we use the labeled node 1 to 7 to predict the unlabeled node 0. 6 Conclusion Graph convolutional networks (GCNs) are widely studied and perform well for node classification problems. However, the causal relationship un- der the predictions is unknown and thus restricts their applications in the areas of security and privacy. To interpret GCN, we assume that the GCN Explainability of GCN With GCNTK 15 Figure 3: Node 0 is connected with all the green nodes, but GCN still predicts node 0 as red. GCNTK can be used to explain the results. Since the contribution ratio of training nodes is M = (0, 0, 0, 0, 0, 0.5, 0.5), only red nodes contribute to node 0’s label. has an infinite width. We define the GCNTK to analyze the GCN training procedure and predict its output. Firstly, we prove that the GCNTK con- verges and is stable as the width tends to infinite. Then we find for GCN, with an infinite width, that the output value of unlabeled nodes can be pre- dicted by a linear combination of the training nodes’ label. The coefficients of training nodes can be computed by GCNTK and imply the importance of training nodes to the unlabeled nodes. Finally, we conduct experiments on synthetic data sets including common patterns in small model graphs to demonstrate the effectiveness of GCNTK. Appendix A: Computing GCNGP and GCNTK Similar to Lee et al. (2018) and Arora et al. (2019), GCNGP can be written as a recursive formula. Let the activation function φ be a differentiable function. Let X and X(cid:15) ], where be two inputs in RN×d1 . Denote Hl = [Hl 1 , . . . , Hl dl , Hl 2 = Hl j ⎞ ⎟ ⎟ ⎠ ⎛ ⎜ ⎜ ⎝ hl 1 j ... hl N j is a column vector. We have ⎞ ⎛ ⎟ ⎟ ⎠ = ⎜ ⎜ ⎝ ⎛ ⎜ ⎜ ⎝ hl+1 1 j ... hl+1 N j (cid:11)dl m=1(AXl )1mWm j ... + b1 j (cid:11)dl m=1(AXl )NmWm j + bN j ⎞ ⎛ ⎟ ⎟ ⎠ = ⎜ ⎜ ⎝ (cid:20)(AXl )1,: (cid:20)(AXl )N,: ⎞ ⎟ ⎟ ⎠. , W:, j ... , W:, j (cid:21) + B1 j (cid:21) + BN j (A.1) (A.2) l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / / 3 5 1 1 2 0 7 5 4 2 1 n e c o _ a _ 0 1 5 4 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 16 H. Wang and X. Zhou Based on the central limit theorem, Lee et al. (2018) show that for each hl+1 , i j i = 1, . . . N, j = 1, . . . dl+1, hl+1 ∼ GP(0, Ki). Note that the gaussian process hl+1 i j has the same and independent Ki with respect to j. We need to establish the relation of Hl+1 j with respect to column element. i j According to the intrinsic coregionalization model for the multioutput gaussian process theory, we have Hl j ∼ GP H ∼ GP ⎛ ⎡ ⎜ ⎝ ⎢ ⎣ ⎛ ⎡ ⎜ ⎝ ⎢ ⎣ 0 ... 0 0 ... 0 ⎤ ⎞ ⎥ ⎦ , Kl (X, X (cid:15) ⎟ ⎠, ) ⎤ ⎥ ⎦ , Kl (X, X (cid:15) ) ⊗ Idl ⎞ ⎟ ⎠, where Kl (X, X(cid:15) j(X(cid:15) ance of different dimension. For H j, ) = cov(Hl j(X ), Hl )) is a matrix that represents the covari- Kl (X, X (cid:15) )mn = E(hl (cid:15) )) n j(X m j(X )hl δ(m − n) + σ 2 = σ 2 b wE((AXl−1)m, : (AX (cid:15)l−1)n, : (cid:11) ). (A.4) Then we write Kl (X, X(cid:15) ) in matrix form based on equation A.4. Kl (X, X (cid:15) ∗ I + σ 2 ∗ I + σ 2 wE(AXl−1)(AX wE ) = σ 2 b = σ 2 b × (Aφ(Hl−1(X )))(Aφ(Hl−1(X Hl−1∼GP((cid:2)0,Kl−1(X,X(cid:15) )⊗Idl ) (cid:11) (cid:15)(l−1)) (cid:15) (cid:11), ))) with base case Kl (X, X (cid:15) ) = σ 2 b ∗ I + σ 2 w AX(AX (cid:15) (cid:11). ) 1 d0 Let then Jl (X ) = ∇θ ≤l Hl (X ) = [∇θ l Hl (X ), ∇θ n0, with
probability at (1 − δ
/10) over random initialization,
0

(cid:10)gtrain(θ

0)(cid:10) < R0 . (B.1) λ min Let C = 3 KR0 > n0 such that for every
in lemma 1. There exists a large n1
d > n1, equations 4.21 and B.1 hold with probability at least (1 − δ
/5) over
0
random initialization. The case that t = 0 holds obviously, and we assume
equation 4.21 holds for t = t. By induction, we can obtain the second for-
mula in equation 4.23,

(cid:10)θt+1

− θt

(cid:10)

≤ η

(cid:23)
(cid:23)

(cid:23)
(cid:23)
J (θt )

(cid:23)
(cid:23)

(cid:23)
(cid:23)
gtrain (θt )
2

(cid:10)θt+1

− θt

(cid:10)

+ · · · + (cid:10)θ

− θ

(cid:10)
2

(cid:28)
t

(cid:27)

1 −

min
3

(B.2)

(cid:27)

Kη
0R0√
d

1 −

min
3

(cid:28)

j−1

≤ Kη
0√
d
t+1(cid:6)

≤

j=1

= Kη

0R0√
d

(cid:22)

t+1

(cid:22)

(cid:21)
1 − η
(cid:21)
1 − η

λ
min
3

1 −

(cid:22)

t+1

λ
min
3

(cid:21)
1 − η
λ
η

min

3
λ

min

− 1
2 .

(B.3)

= Kη

≤ Kη

0R0√
d
0R0√
d
= 3KR0
λ

min

Therefore, the second formula of equation 4.23 at t = t + 1 can be satisfied.
Since

(cid:10)θt+1

− θ

(cid:10)

≤ (cid:10)θt+1

− θt

(cid:10)

+ · · · + (cid:10)θ

− θ

(cid:10)

≤ 3KR0
λ

min

− 1

2 ,

(B.4)

θt+1

∈ B

(cid:21)
θ

, Cd− 1

(cid:22)

(cid:23)
(cid:23)
(cid:23)
(cid:23)
gtrain(θt+1)
2
(cid:23)
(cid:23)
(cid:23)
(cid:23)
I ⊗ Itraing (θt+1) − I ⊗ Itraing (θt ) + I ⊗ Itraing (θt )
2

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
1
1
2
0
7
5
4
2
1
n
e
c
o
_
a
_
0
1
5
4
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Explainability of GCN With GCNTK

I ⊗ ItrainJ( ˜θt ) (θt+1

(cid:23)
(cid:23)
− θt ) + I ⊗ Itraing (θt )

(cid:23)
(cid:23)
(cid:23)
(cid:23)
(cid:23)
(cid:23)
(cid:23)−ηI ⊗ ItrainJ( ˜θt )J (θt )T I ⊗ Itraing (θt ) + I ⊗ Itraing (θt )
(cid:23)
(cid:23)
(cid:21)
(cid:22)
(cid:23)
I ⊗ ItrainI ⊗ Itrain
(cid:23)
(cid:23)
(cid:23)
(cid:23)I ⊗ Itrain
(cid:23)
(cid:23)
(cid:23)
(cid:23)
(cid:23)I ⊗ Itrain(I − ηJ( ˜θt )J (θt )T )
(cid:23)

− ηI ⊗ ItrainJ( ˜θt )J (θt )T I ⊗ Itrain
(cid:23)
(cid:23)
(cid:23)
(cid:23)
gtrain (θt )
2
(cid:28)
t

− ηI ⊗ ItrainJ( ˜θt )J (θt )T
(cid:27)

1 −

(cid:23)
(cid:23)
(cid:23)

≤

min
3

(cid:23)
(cid:23)
g (θt )
(cid:23)

(B.5)

where ˜θt ∈ B

(cid:21)
θ

(cid:22)

, Cd− 1

is a linear interpolation between θt and θt+1.

0) J (θ

(cid:23)
(cid:23)
(cid:23)
(cid:23)
(cid:23)I − ηJ( ˜θt )J (θt )T )
(cid:23)
(cid:23)
(cid:23)
(cid:23)I − ηJ (θ
(cid:23)
(cid:23)
(cid:23)I − η
(cid:23)
(cid:23)
(cid:23)I − η

+ ηJ (θ

(cid:10) + η

(cid:10)
0

0)T + ηJ (θ

0) J (θ

0)T − ηJ( ˜θt )J (θt )T

0) J (θ

0)T − ηJ( ˜θt )J (θt )T

(cid:23)
(cid:23)
(cid:23)

(cid:10) − η

(cid:10)
0

+ ηJ (θ

0)T − ηJ( ˜θt )J (θt )T

≤ (cid:10)I − η

(cid:10)(cid:10)

+ η

(cid:10)(cid:10) − (cid:10)
0

(cid:10)

+ η

0) J (θ

0)T − J( ˜θt )J (θt )T

0) J (θ
(cid:23)
(cid:23)
(cid:23)J (θ

(cid:23)
(cid:23)
(cid:23)
2

;

(B.6)

then

≤

(cid:23)
(cid:23)
(cid:23)
(cid:23)
(cid:23)I ⊗ Itrain(I − ηJ( ˜θt )J (θt )T )
(cid:23)
2
(cid:23)
(cid:23)
(cid:23)
(cid:23)
I ⊗ Itrain(I − η
I ⊗ Itrain((cid:10) − (cid:10)

(cid:23)
(cid:23)
0)(cid:10)

+ η

(cid:23)
(cid:23)
(cid:23)I ⊗ Itrain(J (θ

0) J (θ

+ η

(cid:23)
(cid:23)
0)T − J( ˜θt )J (θt )T )
(cid:23)
2

(cid:23)
(cid:23)

(B.7)

Since η

< 2 +λmax λ min , we have (cid:23) (cid:23) I ⊗ Itrain(I − η 0 (cid:23) (cid:23) (cid:10)) 2 = σ max (I ⊗ Itrain(I − η 0 (cid:10))) ≤ 1 − η 0 λ min . (B.8) Because (cid:10) 0 → (cid:10), there exists n3 such that d > n3,

I ⊗ Itrain((cid:10) − (cid:10)

(cid:23)
(cid:23)
0
(cid:23)
(cid:23)
(cid:23)I ⊗ Itrain(J (θ
(cid:23)
(cid:23)
(cid:23)J (θ

0) J (θ

(cid:23)
(cid:23)
2

(cid:23)
(cid:23)

≤ η

I ⊗ Itrain((cid:10) − (cid:10)
(cid:23)
(cid:23)
0)T − J( ˜θt )J (θt )T )
(cid:23)
2

0)T − J (θ

0) J (θt )T + J (θ

0) J (θt )T − J( ˜θt )J (θt )T

(cid:23)
(cid:23)
F

≤

min
3

(B.9)

(cid:23)
(cid:23)
(cid:23)

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
1
1
2
0
7
5
4
2
1
n
e
c
o
_
a
_
0
1
5
4
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

H. Wang and X. Zhou

≤

(cid:23)
(cid:23)
(cid:23)J (θ
(cid:23)
(cid:23)
J (θ
(cid:23)
(cid:23)
J (θ
√

(cid:29)

(cid:30)

(cid:23)
(cid:23)

J (θ
(cid:23)
(cid:23)
(cid:23)J (θ
(cid:23)
(cid:23)
(cid:23)J (θ

0)T − J (θt )T

+
(cid:23)
(cid:23)
(cid:23)
2
(cid:23)
(cid:23)
0)T − J (θt )T
(cid:23)
√

(cid:23)
(cid:23)

F
√

≤ K

d (cid:10)θ

= K2d (cid:10)θt − θ

(cid:10)
2

− θt

(cid:10)

2
+ K2d

+ K
dK
(cid:23)
(cid:23)
(cid:23)
(cid:23) ˜θt − θ

(cid:23)
(cid:23)
J (θt )T
(cid:23)
(cid:23)
(cid:23)
(cid:23)
(cid:23)
0) − J( ˜θt )
(cid:23)J (θt )T
(cid:23)
(cid:23)
(cid:23)J (θt )T

2
(cid:23)
(cid:23)
0) − J( ˜θt )

(cid:31)
0) − J( ˜θt )
J (θ
(cid:23)
(cid:23)
J (θ
(cid:23)
(cid:23)
J (θ
(cid:23)
(cid:23)θ

√

− ˜θt

(cid:23)
(cid:23)
2

(cid:23)
(cid:23)
(cid:23)
2
(cid:23)
(cid:23)
(cid:23)

≤ 2K2d

3KR0
λ

min

− 1
2 .

Choose d ≥ ( 18K3R0

min

)2:

(cid:23)
(cid:23)
(cid:23)
(cid:23)
(cid:23)I ⊗ Itrain(1 − ηJ( ˜θ )tJ (θt )T )
(cid:23)

≤ 1 − η

min

≤ 1 −

min
3

Therefore,

(cid:23)
(cid:23)

gtrain (θt+1)

(cid:27)

≤

1 −

(cid:23)
(cid:23)
2

(cid:28)

t+1

min
3

We obtain the convergence of (cid:10)t:

min
3

+ 2η

0K2 3KR0
λ

min

− 1
2

0) J (θ

0)T − J (θt ) J (θt )T

(cid:23)
(cid:23)
(cid:23)
F

− (cid:10)t

(cid:10)

(cid:10)(cid:10)
0
(cid:23)
(cid:23)
(cid:23)J (θ
(cid:23)
(cid:23)
(cid:23)J (θ
(cid:23)
(cid:23)
(cid:23)J (θ

= 1
d
= 1
d
= 1
d
≤ 1
d

0) J (θ
(cid:29)

J (θ
(cid:23)
(cid:23)
(cid:23)J (θ

(cid:23)
(cid:23)
J (θ

(cid:23)
(cid:23)

0)T − J (θ

0) J (θt )T + J (θ

0) J (θt )T − J (θt ) J (θt )T

(cid:30)

0)T − J (θt )T

(cid:23)
(cid:23)
(cid:23)

+ [J (θ
(cid:23)
(cid:23)
(cid:23)

+ 1
d

0) − J (θt )] J (θt )T
(cid:23)
(cid:23)
0) − J (θt )
F

J (θ

(cid:23)
(cid:23)

F
(cid:23)
(cid:23)
(cid:23)J (θt )T

(cid:10)
2

+ K2 (cid:10)θt − θ

(cid:10)

≤ K2 (cid:10)θt − θ
≤ 6K3R0
λ

min

− 1
2 .

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

3
5
1
1
2
0
7
5
4
2
1
n
e
c
o
_
a
_
0
1
5
4
8
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

(B.10)

(B.11)

(B.12)

(cid:23)
(cid:23)
(cid:23)

(cid:23)
(cid:23)
(cid:23)
F

(B.13)

(cid:2)

Explainability of GCN With GCNTK

B.2 Proof of Theorem 4. There exist R0 and d0 such that d > d0 with

probability at (1 − δ
0

/10) over random initialization,

(cid:10)gtrain(θ

0)(cid:10)

≤ R0

(B.14)

Let C = 3KR0
such that d > n2, with probability at least (1 − δ
0

min

. Using the same arguments, one can show that there exists n2

/10),

1
d

J(θ )J(θ )T (cid:22) 1
3

λ
minId ∀θ ∈ B

(cid:21)
θ

, Cd

− 1
2

(cid:22)

Let

!
t : (cid:10)θt − θ

(cid:10)

= inf

”

− 1
2

≥ 3KR0
λ

min

We claim that t1

= ∞. If not, then for all t < t1, θt ∈ B(θ 0 , Cd− 1 2 ) and (cid:10)t = 1 d J(θt )J(θt )T (cid:22) 1 3 minId; λ thus, (cid:7) d dt (cid:8) (cid:10)gtrain(t)(cid:10)2 2 = −2I ⊗ Itrain η 0g(t)T (cid:10)tI ⊗ Itraing(t) ≤ − 2 3 − 2 3 ≤ e (cid:10)gtrain(t)(cid:10)2 2 η 0 λ min (cid:10)gtrain(t)(cid:10)2 2 . λ η 0 mint(cid:10)gtrain(0)(cid:10)2 2 ≤ e − 2 3 λ η 0 mintR2 0 . Note that d dt (cid:10)θt − θ 0 (cid:10) 2 ≤ (cid:23) (cid:23) (cid:23) (cid:23) (cid:23) (cid:23) (cid:23) (cid:23) 2 d dt θt = η 0 d (cid:23) (cid:23) (cid:23) (cid:23) J (θt ) gtrain(t) 2 (B.15) (B.16) (B.17) (B.18) l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / / 3 5 1 1 2 0 7 5 4 2 1 n e c o _ a _ 0 1 5 4 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 ≤ η η λ − 1 3 0 0KR0e (cid:21) 1 − e mintd −1/2. (cid:22) − 1 3 λ η 0 mint d ≤ 3KR0 λ min − 1 2 ≤ 3KR0 λ min (cid:21) 1 − e − 1 3 λ η 0 (B.19) (cid:22) mint1 d − 1 2 (cid:10)θt − θ 0 (cid:10) 2 < 3KR0 λ min − 1 2 . d This contradicts the definition of t1 and thus t1 = ∞. (B.20) (cid:2) 22 H. Wang and X. Zhou B.3 Proof of Lemma 1. Theorem 5 (Corollary 5.35 in Vershynin, 2010). Let P = PN,n be an N × n random matrix whose entries are independent standard normal random variables. Then for every t ≥ 0, with probability at least 1 − 2 exp , one has −t2/2 (cid:7) (cid:8) √ √ N − n − t ≤ λ min(P) ≤ λ max(P) ≤ √ N + √ n + t. Let θ = {W, B} and ˜θ = { ˜W, ˜B}, θ }. Therefore, choose a suit- 0 able t and a large d; with high probability over random initialization, we have = {W0 , B0 (cid:23) (cid:23) , (cid:23) (cid:23) W 1 (cid:23) (cid:23) (cid:23) (cid:23) , W l 0 √ (cid:23) (cid:23) ≤ (cid:10)W 1 (cid:23) (cid:23) ˜W 1 (cid:23) (cid:23) ≤ 3σω for 2 ≤ l ≤ L + 1. (cid:10) + C√ d ≤ σω 0 (cid:23) (cid:23) ˜W l 0 d + √ √ d0 d0 + t + C√ d ≤ 3σω √ d√ d0 , (B.21) For l ≥ 1, denote δl (X, θ ) = ∂ f L+1(X, θ ) ∂Hl (X ) = L# k=l diag(σ (cid:15) (Hl (X )))(W l+1(cid:11) ⊗ A) ∈ RNk×Nd. (B.22) (cid:21)$ (cid:21)$ Assume that σω and σ definition of GCN and assumption of φ, (cid:10)φ(Hl (X, θ ))(cid:10) trolled by the O (cid:10)W i(cid:10) O b are the same level. Then according to the 2 can be con- 2 can be controlled by , where C1 and C2 are the Lipschitz continuous and smoothness constants. Therefore, there exists a constant K1, depending on σ 2 ω, σ 2 b , N, and L such that for l = 1, . . . , L, , and (cid:10)δl (X, θ )(cid:10) l i=1 C1 (cid:22) L i=l C2 (cid:10)W i(cid:10) (cid:10)A(cid:10) (cid:10)A(cid:10) (cid:22) 2 2 2 2 (cid:10)φ(Hl (X, θ ))(cid:10) 2 ≤ K1d1/2, (cid:23) (cid:23) (cid:23) (cid:23)δl (X, θ ) 2 ≤ K1 (cid:10)φ(Hl (X, θ )) − φ(Hl (X, ˜θ ))(cid:10) (cid:23) (cid:23) (cid:23)δl (X, θ ) − δl (X, ˜θ ) (cid:23) ≤ K1 ≤ K1d1/2(θ − ˜θ )(cid:10) . 2 (cid:10)(θ − ˜θ )(cid:10) 2 2 2 (B.23) With high probability over random initialization, we have (cid:10)J(θ )(cid:10)2 F = = ≤ (cid:6) l (cid:6) l (cid:6) l (cid:23) (cid:23) J (cid:7) W l (cid:8)(cid:23) (cid:23)2 F + (cid:7) (cid:23) (cid:23) J Bl (cid:8)(cid:23) (cid:23)2 F (cid:23) (cid:23) (cid:23) (cid:23)2 I ⊗ Aφ(Hl (X, θ ))δl (X, θ ) F + (cid:23) (cid:23) (cid:23)2 (cid:23) I ⊗ Iδl (X, θ ) F (1 + (cid:10)A(cid:10)2 2K2 1d) (cid:23) (cid:23) (cid:23)2 (cid:23)δl (X, θ ) F l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / / 3 5 1 1 2 0 7 5 4 2 1 n e c o _ a _ 0 1 5 4 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Explainability of GCN With GCNTK 23 ≤ ≤ (cid:6) l (cid:6) l (1 + (cid:10)A(cid:10)2 2K2 1d)Nk(cid:10)δl (X, θ )(cid:10)2 2 (1 + (cid:10)A(cid:10)2 2K2 1d)K2 1Nk(cid:10)θ − ˜θ (cid:10)2 2 ≤ 2(L + 1)((cid:10)A(cid:10)2 2K2 1d)K2 1Nk. (cid:6) (B.24) (cid:10)J(θ ) − J( ˜θ )(cid:10)2 F = ≤ ≤ (cid:10)I ⊗ Aφ(Hl (X, θ ))δl (X, θ ) − I ⊗ Aφ((Hl (X, ˜θ )))δl (X, ˜θ )(cid:10)2 F l + (cid:10)δl (X, θ ) − δl (X, ˜θ )(cid:10)2 F (cid:6) ((cid:10)I ⊗ Aφ(Hl (X, θ ))δl (X, θ ) − I ⊗ Aφ(Hl (X, θ ))δl (X, ˜θ )(cid:10)2 F l + (cid:10)I ⊗ Aφ(Hl (X, θ ))δl (X, ˜θ ) − I ⊗ Aφ((Hl (X, ˜θ )))δl (X, ˜θ )(cid:10)2 F + (cid:10)δl (X, θ ) − δl (X, ˜θ )(cid:10)2 F ) (cid:6) 1d + K2 1 )Nk(cid:10)θ − ˜θ (cid:10)2 1d + (cid:10)A(cid:10)K4 ((cid:10)A(cid:10)K4 2 l ≤ 3(L + 1)(cid:10)A(cid:10)K4 1dNk(cid:10)θ − ˜θ (cid:10)2 2 . (B.25) Set K2 = max(2(L + 1)((cid:10)A(cid:10)2 2K2 1 )K2 1Nk, 3(L + 1)(cid:10)A(cid:10)K4 1Nk); then 1√ d (cid:10)J(θ )(cid:10)F ≤ K 1√ d (cid:10)J(θ ) − J( ˜θ )(cid:10)F ≤ K(cid:10)θ − ˜θ (cid:10) 2 . (B.26) (cid:2) Acknowledgments This work was supported by the National Natural Science Foundation of China (grant 61977065) and the National Key Basic Research Program (grant 2020YFA0713504). References Allen-Zhu, Z., Li, Y., & Song, Z. (2019). A convergence theory for deep learning via over-parameterization. In Proceedings of the International Conference on Machine Learning (pp. 242–252). Arora, S., Du, S. S., Hu, W., Li, Z., Salakhutdinov, R., & Wang, R. (2019). On exact computation with an infinitely wide neural net. In H. Wallach, H. Larochelle, A. Beygelzimer, F. d’Alché-Buc, E. Fox, & R. Garnett (Eds.), Advances in neural information processing systems, 32 (pp. 8139–8148). Red Hook, NY: Curran. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / / 3 5 1 1 2 0 7 5 4 2 1 n e c o _ a _ 0 1 5 4 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 24 H. Wang and X. Zhou Baldassarre, F., & Azizpour, H. (2019). Explainability techniques for graph convolutional networks. arXiv:1905.13686. Bartlett, P., Helmbold, D., & Long, P. (2018). Gradient descent with identity initial- ization efficiently learns positive definite linear transformations by deep resid- ual networks. In Proceedings of theInternational Conference on Machine Learning (pp. 521–530). Chen, Z., Villar, S., Chen, L., & Bruna, J. (2019). On the equivalence between graph iso- morphism testing and function approximation with GNNs. arXiv:1905.12560. de G. Matthews, A. G., Rowland, M., Hron, J., Turner, R. E., & Ghahramani, Z. (2018). Gaussian process behaviour in wide deep neural networks. In Proceedings of the International Conference on Learning Representations. Du, S., Lee, J., Li, H., Wang, L., & Zhai, X. (2019). Gradient descent finds global min- ima of deep neural networks. In Proceedings of the International Conference on Ma- chine Learning (pp. 1675–1685). Du, S. S., Hou, K., Salakhutdinov, R. R., Poczos, B., Wang, R., & Xu, K. (2019). Graph neural tangent kernel: Fusing graph neural networks with graph kernels. In H. Wallach, H. Larochelle, A. Beygelzimer, F. d’Alché-Buc, E. Fox, & R. Garnett (Eds.), Advances in neural information processing systems, 32 (pp. 5723–5733). Red Hook, NY: Curran. Franceschi, J.-Y., de Bézenac, E., Ayed, I., Chen, M., Lamprier, S., & Gallinari, P. (2021). A neural tangent kernel perspective of GANs. arXiv:2016.05566v4. Funke, T., Khosla, M., & Anand, A. (2021). Hard masking for explaining graph neural networks. https://openreview.net/forum?id=uDN8pRAdsoC Garg, V., Jegelka, S., & Jaakkola, T. (2020). Generalization and representational limits of graph neural networks. In Proceedings of the International Conference on Machine Learning (pp. 3419–3430). Huang, Q., Yamada, M., Tian, Y., Singh, D., Yin, D., & Chang, Y. (2020). Graphlime: Local interpretable model explanations for graph neural networks. arXiv:2001.06216. Huang, W., Li, Y., Du, W., Da Xu, R. Y., Yin, J., Chen, L., & Zhang, M. (2021). Towards deepening graph neural networks: A GNTK-based optimization perspective. arXiv:2103.03113. Jacot, A., Gabriel, F., & Hongler, C. (2018). Neural tangent kernel: Convergence and generalization in neural networks. In H. Wallach, H. Larochelle, A. Beygelzimer, F. d’Alché-Buc, E. Fox, & R. Garnett (Eds.), Advances in neural information process- ing systems, 32 (pp. 8580–8589). Red Hook, NY: Curran. Kipf, T. N., & Welling, M. (2016). Semi-supervised classification with graph convolutional networks. arXiv:1609.02907. Lee, J., Bahri, Y., Novak, R., Schoenholz, S. S., Pennington, J., & Sohl-Dickstein, J. (2018). Deep neural networks as gaussian processes. In Proceedings of the Interna- tional Conference on Learning Representations. Lee, J., Xiao, L., Schoenholz, S., Bahri, Y., Novak, R., Sohl-Dickstein, J., & Penning- ton, J. (2019). Wide neural networks of any depth evolve as linear models under gradient descent. In H. Wallach, H. Larochelle, A. Beygelzimer, F. d’Alché-Buc, E. Fox, & R. Garnett (Eds.), Advances in neural information processing systems, 32 (pp. 8572–8583). Red Hook, NY: Curran. Li, M. B., Nica, M., & Roy, D. M. (2021). The future is log-gaussian: ReNets and their infinite-depth-and-width limit at initialization. arXiv:2106.04013. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / / 3 5 1 1 2 0 7 5 4 2 1 n e c o _ a _ 0 1 5 4 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Explainability of GCN With GCNTK 25 Littwin, E., Galanti, T., Wolf, L., & Yang, G. (2020). On infinite-width hypernetworks. In H. Larochelle, M. Ranzato, R. Hadsell, M. F. Balcan, & H. Lin (Eds.), Advances in neural information processing systems, 33. Red Hook. NY: Curran. Liu, C., Zhu, L., & Belkin, M. (2020). On the linearity of large non-linear models: When and why the tangent kernel is constant. In H. Larochelle, M. Ranzato, R. Hadsell, M. F. Balcan, & H. Lin (Eds.), Advances in neural information processing systems, 33. Red Hook. NY: Curran. Loukas, A. (2020). How hard is to distinguish graphs with graph neural networks? arXiv:2005.06649. Luo, D., Cheng, W., Xu, D., Yu, W., Zong, B., Chen, H., & Zhang, X. (2020). Parame- terized explainer for graph neural network. arXiv:2011.04573. Luo, T., Xu, Z.-Q. J., Ma, Z., & Zhang, Y. (2021). Phase diagram for two-layer ReLU neural networks at infinite-width limit. Journal of Machine Learning Research, 22(71), 1–47. Neal, R. M. (1995). Bayesian learning for neural networks. Lecture Notes in Computer Science 118. Berlin: Springer. Park, D., Sohl-Dickstein, J., Le, Q., & Smith, S. (2019). The effect of network width on stochastic gradient descent and generalization: an empirical study. In Proceedings of the International Conference on Machine Learning (pp. 5042–5051). Pope, P. E., Kolouri, S., Rostami, M., Martin, C. E., & Hoffmann, H. (2019). Explain- ability methods for graph convolutional neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (pp. 10772–10781). Piscataway, NJ: IEEE. Scarselli, F., Tsoi, A. C., & Hagenbuchner, M. (2018). The Vapnik–Chervonenkis di- mension of graph and recursive neural networks. Neural Networks, 108, 248–259. 10.1016/j.neunet.2018.08.010 Schlichtkrull, M. S., De Cao, N., & Titov, I. (2020). Interpreting graph neural networks for NLP with differentiable edge masking. arXiv:2010.00577. Schnake, T., Eberle, O., Lederer, J., Nakajima, S., Schütt, K. T., Müller, K.-R., & Mon- tavon, G. (2020). Higher-order explanations of graph neural networks via relevant walks. arXiv:2006.03589. Schwarzenberg, R., Hübner, M., Harbecke, D., Alt, C., & Hennig, L. (2019). Layer-wise relevance visualization in convolutional text graph classifiers. arXiv:1909.10911. Sohl-Dickstein, J., Novak, R., Schoenholz, S. S., & Lee, J. (2020). On the infinite width limit of neural networks with a standard parameterization. arXiv:2001.07301. Vershynin, R. (2010). Introduction to the non-asymptotic analysis of random matrices. arXiv preprint arXiv:1011.3027. Vu, M. N., & Thai, M. T. (2020). PGM-explainer: Probabilistic graphical model explana- tions for graph neural networks. arXiv:2010.05788. Wu, F., Souza, A., Zhang, T., Fifty, C., Yu, T., & Weinberger, K. (2019). Simplifying graph convolutional networks. In Proceedings of the International Conference on Ma- chine Learning (pp. 6861–6871). Wu, Z., Pan, S., Chen, F., Long, G., Zhang, C., & Yu, P. S. (2021). A comprehensive sur- vey on graph neural networks. IEEE Transactions on Neural Networks and Learning Systems, 32(1), 4–24. 10.1109/Tnnls.2020.2978386 Xu, K., Hu, W., Leskovec, J., & Jegelka, S. (2018). How powerful are graph neural net- works? arXiv:1810.0026. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / / 3 5 1 1 2 0 7 5 4 2 1 n e c o _ a _ 0 1 5 4 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 26 H. Wang and X. Zhou Xu, K., Zhang, M., Li, J., Du, S. S., Kawarabayashi, K.-i., & Jegelka, S. (2020). How neu- ral networks extrapolate: From feedforward to graph neural networks. arXiv:2009.11848. Yang, G. (2019). Scaling limits of wide neural networks with weight sharing: Gaus- sian process behavior, gradient independence, and neural tangent kernel derivation. arXiv:1902.04760. Ying, R., Bourgeois, D., You, J., Zitnik, M., & Leskovec, J. (2019). GNNExplainer: Generating explanations for graph neural networks. In H. Wallach, H. Larochelle, A. Beygelzimer, F. d’Alché-Buc, E. Fox, & R. Garnett (Eds.), Advances in neural information processing systems, 32, 9240. Red Hook, NY: Curran. Yuan, H., Yu, H., Gui, S., & Ji, S. (2020). Explainability in graph neural networks: A tax- onomic survey. arXiv:2012.15445. Zhang, Y., Defazio, D., & Ramesh, A. (2021). RelEx: A model-agnostic relational model explainer. In Proceedings of the 2021 AAAI/ACM Conference on AI, Ethics, and Society (pp. 1042–1049). New York: ACM. Zhou, J., Cui, G., Hu, S., Zhang, Z., Yang, C., Liu, Z., . . . Sun, M. (2020). Graph neural networks: A review of methods and applications. AI Open, 1, 57–81. https ://www.sciencedirect.com/science/article/pii/S2666651021000012. 10.1016/j .aiopen.2021.01.001 Received March 22, 2022; accepted July 21, 2022. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / / 3 5 1 1 2 0 7 5 4 2 1 n e c o _ a _ 0 1 5 4 8 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3

Download pdf