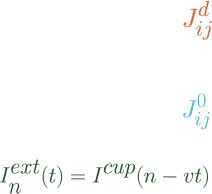ARTICLE
Communicated by Luca Mazzucato
Nonequilibrium Statistical Mechanics
of Continuous Attractors
Weishun Zhong
wszhong@mit.edu
James Franck Institute, University of Chicago, Chicago, IL 60637,
and Department of Physics, MIT, Cambridge, MA 02139, U.S.A.
Zhiyue Lu
zhiyuelu@unc.edu
James Franck Institute, University of Chicago, Chicago, IL 60637, U.S.A.
David J. Schwab
dschwab@gc.cuny.edu
Initiative for the Theoretical Sciences, CUNY Graduate Center, New York, NY 10016,
and Center for the Physics of Biological Function, Princeton University and City
University of New York, Princeton, NJ 08544, and New York, NY, 10016
Arvind Murugan
amurugan@uchicago.edu
Department of Physics and the James Franck Institute, University of Chicago,
Chicago, IL 60637, U.S.A.
Continuous attractors have been used to understand recent neuroscience
experiments where persistent activity patterns encode internal represen-
tations of external attributes like head direction or spatial location. How-
ever, the conditions under which the emergent bump of neural activity in
such networks can be manipulated by space and time-dependent external
sensory or motor signals are not understood. Here, we find fundamental
limits on how rapidly internal representations encoded along continuous
attractors can be updated by an external signal. We apply these results to
place cell networks to derive a velocity-dependent nonequilibrium mem-
ory capacity in neural networks.
1 Introduction
Dynamical attractors have found much use in neuroscience as models for
carrying out computation and signal processing (Poucet & Save, 2005).
D.S. and A.M. contributed equally to this work.
Neural Computation 32, 1033–1068 (2020) © 2020 Massachusetts Institute of Technology
https://doi.org/10.1162/neco_a_01280
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
6
1
0
3
3
1
8
6
4
8
5
8
n
e
c
o
_
a
_
0
1
2
8
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1034
W. Zhong, Z. Lu, D. Schwab, and A. Murugan
While point-like neural attractors and analogies to spin glasses have been
widely explored (Hopfield, 1982; Amit, Gutfreund, & Sompolinsky, 1985b),
an important class of experiments is explained by continuous attractors,
where the collective dynamics of strongly interacting neurons stabilizes
a low-dimensional family of activity patterns. Such continuous attractors
have been invoked to explain experiments on motor control based on path
integration (Seung, 1996; Seung, Lee, Reis, & Tank, 2000), head direction
(Kim, Rouault, Druckmann, & Jayaraman, 2017) control, spatial represen-
tation in grid or place cells (Yoon et al., 2013; O’Keefe & Dostrovsky, 1971;
Colgin et al., 2010; Wills, Lever, Cacucci, Burgess, & O’Keefe, 2005; Wimmer,
Nykamp, Constantinidis, & Compte, 2014; Pfeiffer & Foster, 2013), among
other information processing tasks (Hopfield, 2015; Roudi & Latham, 2007;
Latham, Deneve, & Pouget, 2003; Burak & Fiete, 2012).
These continuous attractor models are at the fascinating intersection of
dynamical systems and neural information processing. The neural activity
in these models of strongly interacting neurons is described by an emer-
gent collective coordinate (Yoon et al., 2013; Wu, Hamaguchi, & Amari,
2008; Amari, 1977). This collective coordinate stores an internal represen-
tation (Sontag, 2003; Erdem & Hasselmo, 2012) of the organism’s state in
its external environment, such as position in space (Pfeiffer & Foster, 2013;
McNaughton et al., 2006) or head direction (Seelig & Jayaraman, 2015).
However, such internal representations are useful only if they can be
driven and updated by external signals that provide crucial motor and
sensory input (Hopfield, 2015; Pfeiffer & Foster, 2013; Erdem & Hasselmo,
2012; Hardcastle, Ganguli, & Giocomo, 2015; Ocko, Hardcastle, Giocomo,
& Ganguli, 2018). Driving and updating the collective coordinate using ex-
ternal sensory signals opens up a variety of capabilities, such as path plan-
ning (Ponulak & Hopfield, 2013; Pfeiffer & Foster, 2013), correcting errors
in the internal representation or in sensory signals (Erdem & Hasselmo,
2012; Ocko et al., 2018), and the ability to resolve ambiguities in the external
sensory and motor input (Hardcastle et al., 2015; Evans, Bicanski, Bush, &
Burgess, 2016; Fyhn, Hafting, Treves, Moser, & Moser, 2007).
In all of these examples, the functional use of attractors requires interac-
tion between external signals and the internal recurrent network dynamics.
However, with a few significant exceptions (Fung, Wong, Mao, & Wu, 2015;
Mi, Fung, Wong, & Wu, 2014; Wu et al., 2008; Wu & Amari, 2005; Monasson
& Rosay, 2014; Burak & Fiete, 2012), most theoretical work has either been
in the limit of no external forces and strong internal recurrent dynamics, or
in the limit of strong external forces where the internal recurrent dynamics
can be ignored (Moser, Moser, & McNaughton, 2017; Tsodyks, 1999).
Here, we study continuous attractors in neural networks subject to ex-
ternal driving forces that are neither small relative to internal dynamics nor
adiabatic. We show that the physics of the emergent collective coordinate
sets limits on the maximum speed at which internal representations can be
updated by external signals.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
6
1
0
3
3
1
8
6
4
8
5
8
n
e
c
o
_
a
_
0
1
2
8
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Nonequilibrium Statistical Mechanics of Continuous Attractors
1035
Our approach begins by deriving simple classical and statistical laws sat-
isfied by the collective coordinate of many neurons with strong, structured
interactions that are subject to time-varying external signals, Langevin
noise, and quenched disorder. Exploiting these equations, we demonstrate
two simple principles: (1) an equivalence principle that predicts how much
the internal representation lags a rapidly moving external signal, and (2) un-
der externally driven conditions, quenched disorder in network connec-
tivity that can be modeled as a state-dependent effective temperature.
Finally, we apply these results to place cell networks and derive a nonequi-
librium driving-dependent memory capacity, complementing numerous
earlier works on memory capacity in the absence of external driving.
2 Collective Coordinates in Continuous Attractors
We study N interacting neurons following the formalism presented in Hop-
field (2015),
din
dt
= − in
τ
+
N(cid:2)
k=1
Jnk f (ik) + Iext
n (t) + η
int (t),
(2.1)
/i0 )
where f (ik) = (1 + e−ik
−1 is the neural activation function that represents
the firing rate of neuron k, and in is an internal excitation level of neuron n
akin to the membrane potential. We consider synaptic connectivity matrices
with two distinct components:
Ji j
= J0
i j
+ Jd
i j
.
(2.2)
As shown in Figure 1, J0
i j encodes the continuous attractor. We will
focus on 1D networks with p-nearest neighbor excitatory interactions
= J(1 − (cid:4)) if neurons |i − j| ≤ p,
to keep bookkeeping to a minimum: J0
i j
= −J(cid:4) otherwise. The latter term, −J(cid:4), with 0 ≤ (cid:4) ≤ 1, represents
and J0
i j
long-range, nonspecific inhibitory connections as frequently assumed in
models of place cells (Monasson & Rosay, 2014; Hopfield, 2010), head
direction cells (Chaudhuri & Fiete, 2016), and other continuous attractors
(Seung et al., 2000; Burak & Fiete, 2012).
The disorder matrix Jd
i j represents random long-range connections, a
form of quenched disorder (Seung, 1998; Kilpatrick, Ermentrout, & Doiron,
2013). Finally, Iext
n (t) represents external driving currents from, for example,
sensory and motor input possibly routed through other regions of the brain.
The Langevin noise η
int (t) represents private noise internal to each neuron
(Lim & Goldman, 2012; Burak & Fiete, 2012).
A neural network like equation 2.1 qualitatively resembles a similarly
connected network of Ising spins at fixed magnetization (Monasson &
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
6
1
0
3
3
1
8
6
4
8
5
8
n
e
c
o
_
a
_
0
1
2
8
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1036
W. Zhong, Z. Lu, D. Schwab, and A. Murugan
Figure 1: The effective dynamics of neural networks implicated in head direc-
tion and spatial memory is described by a continuous attractor. Consider N neu-
rons connected in a 1D topology, with local excitatory connections between p
nearest neighbors (blue), global inhibitory connections (not shown), and ran-
dom long-range disorder (orange). Any activity pattern quickly condenses into
a droplet of contiguous firing neurons (red) of characteristic size; the droplet
center of mass ¯x is a collective coordinate parameterizing a continuous attrac-
tor. The droplet can be driven by space and time-varying external currents Iext
n (t)
(green).
Rosay, 2014). At low noise, the activity in such a system will condense
(Monasson & Rosay, 2014; Hopfield, 2010) to a localized droplet, since inter-
faces between firing and nonfiring neurons are penalized by J(1 − (cid:4)). The
(cid:3)
n n f (in )
center of mass of such a droplet, ¯x ≡
(cid:3)
n f (in ) is an emergent collective coor-
dinate that approximately describes the stable low-dimensional neural ac-
tivity patterns of these N neurons. Fluctuations about this coordinate have
been extensively studied (Wu et al., 2008; Burak & Fiete, 2012; Hopfield,
2015; Monasson & Rosay, 2014).
3 Space and Time-Dependent External Signals
We focus on how space and time-varying external signals, modeled here as
external currents Iext
n (t), can drive and reposition the droplet along the at-
tractor. We will be primarily interested in a cup-shaped current profile that
moves at a constant velocity v, Iext
n (t) = Icup(n − vt), where Icup(n) = d(w −
|n|), n ∈ [−w, w], Icup(n) = 0 otherwise. Such a localized time-dependent
drive could represent landmark-related sensory signals (Hardcastle et al.,
2015).
The effective dynamics of the collective coordinate ¯x in the presence
n (t) can be obtained by computing the effective force on the
of currents Iext
droplet of finite size. We find that (see appendix A)
γ ˙¯x = −∂ ¯xV ext ( ¯x, t),
(3.1)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
6
1
0
3
3
1
8
6
4
8
5
8
n
e
c
o
_
a
_
0
1
2
8
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Nonequilibrium Statistical Mechanics of Continuous Attractors
1037
where V ext ( ¯x, t) is a piecewise quadratic potential V cup( ¯x − vt) for currents
n (t) = Icup(n − vt), and γ is the effective drag coefficient of the droplet.
Iext
(Here, we neglect rapid transients of timescale τ (Wu et al., 2008).)
The strength of the external signal is set by the depth d of the cup Icup(n).
Previous studies have explored the d = 0 case—undriven diffusive dynam-
ics of the droplet (Burak & Fiete, 2012; Monasson & Rosay, 2013, 2014, 2015)
or the large d limit (Hopfield, 2015) when the internal dynamics can be ig-
nored. Here we focus on an intermediate regime, d < dmax, where internal
representations are updated continuously by the external currents, with-
out any jumps (Ponulak & Hopfield, 2013; Pfeiffer & Foster, 2013; Erdem &
Hasselmo, 2012).
In fact, as shown in the section C.2 we find a threshold signal strength
dmax beyond which the external signal destabilizes the droplet, instantly
“teleporting” the droplet from any distant location to the cup without con-
tinuity along the attractor, erasing any prior positional information held in
the internal representation.
We focus here on d < dmax, a regime with continuity of internal repre-
sentations. Such continuity is critical for many applications, such as path
planning (Ponulak & Hopfield, 2013; Pfeiffer & Foster, 2013; Erdem & Has-
selmo, 2012) and resolving local ambiguities in position within the global
context (Hardcastle et al., 2015; Evans et al., 2016; Fyhn et al., 2007). In this
regime, the external signal updates the internal representation with finite
gain (Fyhn et al., 2007) and can thus fruitfully combine information in both
the internal representation and the external signal. Other applications that
simply require short-term memory storage of a strongly fluctuating vari-
able may not require this continuity restriction.
3.1 Equivalence Principle. We first consider driving the droplet in a
network at constant velocity v using an external current Iext
= Icup(n − vt).
n
We allow for Langevin noise but no disorder in the couplings Jd = 0 in this
section. For very slow driving (v → 0), the droplet will settle into and track
the bottom of the cup. When driven at a finite velocity v, the droplet cannot
stay at the bottom since there is no net force exerted by the currents Iext
n at
that point.
Instead, the droplet must lag the bottom of the moving external drive by
an amount (cid:7)xv = ¯x − vt such that the slope of the potential V cup provides an
≡ γ v needed to keep the droplet in motion at velocity
effective force Fmotion
v, that is,
v
−∂ ¯xV cup((cid:6)(cid:7)xv (cid:7)) = Fmotion
v
≡ γ v.
(3.2)
This equation, which we call an equivalence principle in analogy with iner-
tial particles in an accelerated frame, is verified by simulations in Figure 2b.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
6
1
0
3
3
1
8
6
4
8
5
8
n
e
c
o
_
a
_
0
1
2
8
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1038
W. Zhong, Z. Lu, D. Schwab, and A. Murugan
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
6
1
0
3
3
1
8
6
4
8
5
8
n
e
c
o
_
a
_
0
1
2
8
0
p
d
.
/
n
(t) with velocity v, we simply add an effective force Fmotion
Figure 2: (a) The mean position and fluctuations of the droplet driven by cur-
= Icup(n − vt) are described by an “equivalence” principle; in a frame
rents Iext
n
co-moving with Icup
=
γ v where γ is a drag coefficient. (b) This prescription correctly predicts that the
droplet lags the external driving force by an amount linearly proportional to
velocity v, as seen in simulations. (c) Fluctuations of the driven droplet’s po-
sition, due to internal noise in neurons, are also captured by the equivalence
principle. If p((cid:7)xv ) is the probability of finding the droplet at a lag (cid:7)xv , we find
(cid:7)xv is independent of velocity and can be collapsed
that kBT log p((cid:7)xv ) − Fmotion
onto each other (with fitting parameter T). (Inset: log p((cid:7)xv ) before subtracting
Fmotion
v
(cid:7)xv .)
v
v
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Nonequilibrium Statistical Mechanics of Continuous Attractors
1039
Similar results on a lag between driving forces and the response were ob-
tained in earlier works (Fung et al., 2015; Mi et al., 2014).
In fact, we find that the the above equivalence principle predicts the en-
tire distribution p((cid:7)xv ) of fluctuations of the lag (cid:7)xv due to Langevin noise
(see Figure 2c). By binning the lag (cid:7)xv (t) for trajectories of the droplet ob-
tained from repeated numerical simulations, we determined p((cid:7)xv ), the oc-
cupancy of the droplet in the moving frame of the drive. As detailed in
appendix C, data for different velocities collapse using an effective temper-
ature scale T, verifying that
kBT log p((cid:7)xv ) = −(V cup((cid:7)xv ) − Fmotion
v
(cid:7)xv ),
(3.3)
Our results here are consistent with the fluctuation-dissipation result
obtained in Monasson and Rosay (2014) for driven droplets. In summary,
in the co-moving frame of the driving signal, the droplet’s position (cid:7)xv
fluctuates as if it were in thermal equilibrium in the modified potential
V e f f = V cup − Fmotion
(cid:7)xv .
v
4 Speed Limits on Updates of Internal Representation
The simple equivalence principle implies a striking bound on the update
speed of internal representations. A driving signal cannot drive the droplet
at velocities greater than some v
crit is larger
than the cup. In the appendix, we find v
= 2d(w + R)/3γ , where 2R is the
droplet size.
crit if the predicted lag for v > v
Larger driving strength d increases v
crit, but as was previously discussed,
we require d < dmax in order to retain continuity and stability of the inter-
nal representation. Hence, we find an absolute upper bound on the fastest
external signal that can be tracked by the internal representation,
crit
v ∗ = κ pJγ −1,
(4.1)
where p is the range of interactions, J is the synaptic strength, γ −1 is the
mobility or inverse drag coefficient of the droplet, and κ is a dimensionless
O(1) number.
5 Disordered Connections and Effective Temperature
We now consider the effect of long-range quenched disorder Jd
i j in the
synaptic matrix (Seung, 1998; Kilpatrick et al., 2013), which breaks the
exact degeneracy of the continuous attractor, creating an effectively rugged
landscape, V d( ¯x), as shown schematically in Figure 3 and computed in
sections E.1 and E.2. When driven by a time-varying external signal, Iext
(t),
the droplet now experiences a net potential V ext ( ¯x, t) + V d( ¯x). The first
i
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
6
1
0
3
3
1
8
6
4
8
5
8
n
e
c
o
_
a
_
0
1
2
8
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1040
W. Zhong, Z. Lu, D. Schwab, and A. Murugan
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
6
1
0
3
3
1
8
6
4
8
5
8
n
e
c
o
_
a
_
0
1
2
8
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3: Disorder in neural connectivity is well approximated by an effective
temperature Td for a moving droplet. (a) Long-range disorder breaks the degen-
eracy of the continuous attractor, creating a rough landscape. A droplet mov-
ing at velocity v in this rough landscape experiences random forces. (b) The
fluctuations of a moving droplet’s position, relative to the cup’s bottom, can
be described by an effective temperature Td. We define a potential V ((cid:7)xv ) =
−kBTd log p((cid:7)xv ) where p((cid:7)xv ) is the probability of the droplet’s position fluc-
tuating to a distance (cid:7)xv from the peak external current. We find that V ((cid:7)xv )
corresponding to different amounts of disorder ˜σ 2 (where ˜σ 2 is the average
number of long-range disordered connections per neuron in units of 2p), can
be collapsed by the one fitting parameter Td. Inset: Td is linearly proportional to
the strength of disorder ˜σ .
term causes motion with velocity v and a lag predicted by the equivalence
principle, and for sufficiently large velocities v, the effect of the second term
can be modeled as effective Langevin white noise. To see this, note that
V d( ¯x) is uncorrelated on length scales larger than the droplet size; hence,
for large enough droplet velocity v, the forces Fd(t) ≡ −∂ ¯xV d|
¯x= ¯x(t) due to
disorder are effectively random and uncorrelated in time. More precisely,
let σ 2 = Var(V d( ¯x)). In section E.3, we compute Fd(t) and show that Fd(t)
has an autocorrelation time, τcor = 2R/v, due to the finite size of the droplet.
Thus, on longer timescales, Fd(t) is uncorrelated and can be viewed
as Langevin noise for the droplet center of mass ¯x, associated with a
Nonequilibrium Statistical Mechanics of Continuous Attractors
1041
disordered-induced temperature Td. Through repeated simulations with
different amounts of disorder σ 2, we inferred the distribution p((cid:7)xv ) of the
droplet position in the presence of such disorder-induced fluctuations (see
Figure 3). The data collapse in Figure 3b confirms that the effect of disorder
(of size σ 2) on a rapidly moving droplet can indeed be modeled by an ef-
∼ σ τcor. (For simplicity, we assume
fective disorder-induced temperature Td
that internal noise η
int in equation 2.1 is absent here. Note that in general,
η
int will also contribute to Td. Here we focus on the contribution of disorder
to an effective temperature Td since internal noise η
int has been considered
in prior work (Fung et al., 2015).)
Thus, the disorder Jd
i j effectively creates thermal fluctuations about the
lag predicted by the equivalence principle; such fluctuations may carry the
droplet out of the driving cup Icup(n − vt) and prevent successful update of
the internal representation. We found that this effect can be quantified by a
simple Arrhenius-like law,
r ∼ exp(−(cid:7)E(v, d)/kBTd ),
(5.1)
where (cid:7)E(v, d) is the energy gap between where the droplet sits in the drive
and the escape point, predicted by the equivalence principle, and Td is the
disorder-induced temperature. Thus, given a network of N neurons, the
probability of an external drive moving the droplet successfully across the
network is proportional to exp(−rN). (Note that r depends on N in a way
such that exp(−rN) becomes a step function as N → ∞: always successful
below a critical amount of disorder (capacity) and always failing beyond
this capacity.)
6 Implications: Memory Capacity of Driven Place Cell Networks
The capacity of a neural network to encode multiple memories has been
studied in numerous contexts since Hopfield’s original work (Hopfield,
1982). While specifics differ (Amit, Gutfreund, & Sompolinsky, 1985a;
Battaglia & Treves, 1998; Monasson & Rosay, 2014; Hopfield, 2010), the ca-
pacity is generally set by the failure to retrieve a specific memory because of
the effective disorder in neural connectivity due to other stored memories.
However, these works on capacity do not account for nonadiabatic exter-
nal driving. Here, we use our results to determine the capacity of a place cell
network (O’Keefe & Dostrovsky, 1971; Battaglia & Treves, 1998; Monasson
& Rosay, 2014) to both encode and manipulate memories of multiple spa-
tial environments at a finite velocity. Place cell networks (Tsodyks, 1999;
Monasson & Rosay, 2013, 2014, 2015) encode memories of multiple spatial
environments as multiple continuous attractors in one network. Such net-
works have been used to describe recent experiments on place cells and grid
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
6
1
0
3
3
1
8
6
4
8
5
8
n
e
c
o
_
a
_
0
1
2
8
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1042
W. Zhong, Z. Lu, D. Schwab, and A. Murugan
cells in the hippocampus (Yoon et al., 2013; Hardcastle et al., 2015; Moser,
Moser, & Roudi, 2014).
(i) as seen in Figure 4a, where π μ
In experiments that expose a rodent to different spatial environments
μ = 1, . . . M (Alme et al., 2014; Moser, Moser, & McNaughton, 2017; Moser,
Moser, & Roudi, 2014; Kubie & Muller, 1991), the same place cells i =
1, . . . , N are seen having “place fields” in different spatial arrangements
π μ
is a permutation specific to environ-
ment μ. Consequently, Hebbian plasticity suggests that each environment μ
μ
would induce a set of synaptic connections J
i j that corresponds to the place
μ
( j)| < p.
field arrangement in that environment: J
i j
That is, each environment corresponds to a 1D network when the neurons
are laid out in a specific permutation π μ. The actual network has the sum
μ
of all these connections Ji j
i j over the M environments the rodent
is exposed to.
= J(1 − (cid:4)) if |π μ
(i) − π μ
M
μ=1 J
(cid:3)
=
i j, the remaining J
While Ji j above is obtained by summing over M structured environ-
μ
ments, from the perspective of, say, J1
i j look like long-range
disordered connections. We will assume that the permutations π μ
(i) cor-
responding to different environments are random and uncorrelated, a
common modeling choice with experimental support (Hopfield, 2010;
Monasson & Rosay, 2014, 2015; Alme et al., 2014; Moser et al., 2017).
Without loss of generality, we assume that π 0(i) = i (blue environment
=
i j. The disordered matrix Jd
in Figure 4.) Thus, Ji j
i j
then has an effective variance σ 2 ∼ (M − 1)/N. Hence, we can apply our
previous results to this system. Now consider driving the droplet with
velocity v in environment 1 using external currents. The probability of
successfully updating the internal representation over a distance L is given
by Pretrieval
, where r is given by equation 5.1.
In the thermodynamic limit N → ∞, with w, p, L/N held fixed, Pretrieval
becomes a Heaviside step function (cid:11)(Mc − M) at some critical value Mc
given by
= e−rL/v
M−1
μ=1 J
= J0
i j
+ Jd
i j
, Jd
i j
(cid:3)
μ
Mc ∼ [v(cid:7)E(v, d)]2 N
(log N)2
(6.1)
for the largest number of memories that can be stored and retrieved at veloc-
ity v. (cid:7)E(v, d) = (4dw − 3γ v − 2dR)(−vγ + 2dR)/4d. Figure 4 shows that
our numerics agree well with this formula, showing a novel dependence of
the capacity of a neural network on the speed of retrieval and the strength
of the external drive. Note that the fact that equation 6.1 scales sublinearly
in N reflects our choice of “perfect” retrieval in the definition of success-
ful events. As in earlier works, Hopfield (1982), Hertz, Krogh, Palmer, and
Horner (1991), and Amit et al. (1985a, 1985b), the precise definition of ca-
pacity can change capacity by log factors.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
6
1
0
3
3
1
8
6
4
8
5
8
n
e
c
o
_
a
_
0
1
2
8
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Nonequilibrium Statistical Mechanics of Continuous Attractors
1043
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
6
1
0
3
3
1
8
6
4
8
5
8
n
e
c
o
_
a
_
0
1
2
8
0
p
d
.
/
Figure 4: Nonequilibrium capacity of place cell networks limits retrieval of spa-
tial memories at finite velocity. (a) Place cell networks model the storage of
multiple spatial memories in parts of the hippocampus by coding multiple con-
tinuous attractors in the same set of neurons. Neural connections encoding spa-
tial memory 2, 3, . . . act like long-range disorder for spatial memory 1. Such
disorder, through an increased effective temperature, reduces the probability
of tracking a finite velocity driving signal. (b) The probability of successful re-
trieval, Pretrieval, decreases with the number of simultaneous memories M and
velocity v (with N = 4000, p = 10, (cid:4) = 0.35, τ = 1, J = 100, d = 10, w = 30 held
fixed). (c) Pretrieval simulation data collapse when plotted against M/(N/(log N)2)
(parameters same as panel b with v = 0.8 held fixed and N varies). (d) The
nonequilibrium capacity Mc as a function of retrieval velocity v.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1044
W. Zhong, Z. Lu, D. Schwab, and A. Murugan
7 Conclusion
We have considered continuous attractors in neural networks driven by lo-
calized time-dependent currents Icup(n − vt). In recent experiments, such
currents can represent landmark-related sensory signals (Hardcastle et al.,
2015) when a rodent is traversing a spatial environment at velocity v or
signals that update the internal representation of head direction (Seelig &
Jayaraman, 2015). Several recent experiments have controlled the effective
speed of visual stimuli in virtual reality environments (Meshulam, Gau-
thier, Brody, Tank, & Bialek, 2017; Aronov, Nevers, & Tank, 2017; Kim et al.,
2017; Turner-Evans et al., 2017). Other experiments have probed cross-talk
between memories of multiple spatial environments (Alme et al., 2014). Our
results predict an error rate that rises with speed and with the number of
environments.
While our analysis used specific functional forms for, among others, the
current profile Icup(n − vt), our bound simply reflects the finite response
time in moving emergent objects, much like moving a magnetic domain
in a ferromagnet using space and time-varying fields. Thus, we expect our
bound to hold qualitatively for other related forms (Hopfield, 2015).
In addition to positional information considered here, continuous attrac-
tors are known to also receive velocity information (Major, Baker, Aksay, Se-
ung, & Tank, 2004; McNaughton et al., 2006; Seelig & Jayaraman, 2015; Ocko
et al., 2018). We do not consider such input in the main text but extend our
analysis to velocity integration in appendix D.
In summary, we found that the nonequilibrium statistical mechanics of
a strongly interacting neural network can be captured by a simple equiv-
alence principle and a disorder-induced temperature for the network’s
collective coordinate. Consequently, we were able to derive a velocity-
dependent bound on the number of simultaneous memories that can be
stored and retrieved from a network. We discussed how these results, based
on general theoretical principles on driven neural networks, allow us to
connect robustly to recent time-resolved experiments in neuroscience (Kim
et al., 2017; Turner-Evans et al., 2017; Hardcastle et al., 2015; Hardcastle, Ma-
heswaranathan, Ganguli, & Giocomo, 2017; Campbell et al., 2018) on the
response of neural networks to dynamic perturbations.
Appendix A: Equations for the Collective Coordinate
As in the main text, we model N interacting neurons as
din
dt
= − in
τ
+
N(cid:2)
k=1
Jnk f (ik) + Iext
n (t) + ηint
n (t),
where f (i) =
1
1 + e−i/i0
.
(A.1)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
6
1
0
3
3
1
8
6
4
8
5
8
n
e
c
o
_
a
_
0
1
2
8
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Nonequilibrium Statistical Mechanics of Continuous Attractors
1045
The synaptic connection between two different neurons i, j is Ji j
= J(1 − (cid:4))
if neurons i and j are separated by a distance of at most p neurons and
= −J(cid:4) otherwise; note that we set the self-interaction to zero. The internal
Ji j
noise is a white noise, (cid:6)ηint
n (t)
are external driving currents, discussed below.
δ(t) with an amplitude Cint. Iext
n (0)(cid:7) = Cint
n (t)ηint
Such a quasi-1D network with p-nearest neighbor interactions resembles
a similarly connected network of Ising spins at fixed magnetization in its be-
havior; the strength of inhibitory connections (cid:4) constrains the total number
of neurons 2R firing at any given time to 2R ∼ p(cid:4)−1. It was shown (Hopfield,
2010; Monasson & Rosay, 2013, 2014) that below a critical temperature T,
the w firing neurons condense into a contiguous droplet of neural activity,
minimizing the total interface between firing and nonfiring neurons. Such
a droplet was shown to behave like an emergent quasi-particle that can dif-
fuse or be driven around the continuous attractor. We define the center of
mass of the droplet as
(cid:2)
¯x ≡
n f (in).
(A.2)
n
The description of neural activity in terms of such a collective coordinate ¯x
greatly simplifies the problem, reducing the configuration space from the
2N states for the N neurons to N-state, and consists of the center of mass of
the droplet along the continuous attractor (Wu et al., 2008). The computa-
tional abilities of these place cell networks, such as spatial memory storage,
path planning, and pattern recognition, are limited to parameter regimes in
which such a collective coordinate approximation holds (e.g., noise levels
less than a critical value T < Tc) .
The droplet can be driven by external signals such as sensory or motor
input or input from other parts of the brain. We model such external input
by the currents Iext
in equation A.1—for example, sensory landmark-based
n
input (Hardcastle et al., 2015). When an animal is physically in a region
covered by place fields of neurons i, i + 1, . . . , i + z, currents Iext
through Iext
i+z
i
can be expected to be high compared to all other currents Iext
. Other models
of driving in the literature include adding an antisymmetric component Ai j
to synaptic connectivities Ji j (Ponulak & Hopfield, 2013); we consider such
a model in appendix D.
Let {i ¯x
k
} denote the current configuration such that the droplet is centered
at location ¯x. The Lyapunov function of the neural network is given by Hop-
field (2015):
j
L[ ¯x] ≡ L[ f (i ¯x
k )]
(cid:4)
(cid:2)
= 1
τ
0
k
f (i ¯x
k )
f
−1(x)dx − 1
2
(cid:2)
n,k
Jnk f (i ¯x
k ) f (i ¯x
n) −
(cid:2)
k
f (i ¯x
k )Iext
k
(t).
(A.3)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
6
1
0
3
3
1
8
6
4
8
5
8
n
e
c
o
_
a
_
0
1
2
8
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1046
W. Zhong, Z. Lu, D. Schwab, and A. Murugan
(cid:3)
In a minor abuse of terminology, we will refer to terms in the Lya-
punov function as energies, even though energy is not conserved in
this system. For future reference, we denote the second term VJ( ¯x) =
−1/2
n), which captures the effect of network synaptic con-
nectivities. Under the rigid bump approximation used in Hopfield (2015),
that is, ignoring fluctuations of the droplet, we find
nk Jnk f (i ¯x
k ) f (i ¯x
VJ( ¯x) = − 1
2
≈ − 1
2
(cid:2)
f (i ¯x
n)Jnk f (i ¯x
k )
n,k
(cid:2)
|n− ¯x|≤R,
|k− ¯x|≤R
f (i ¯x
k ).
n)Jnk f (i ¯x
(A.4)
(A.5)
For a quasi 1D network with p-nearest neighbor interactions and no dis-
order, VJ( ¯x) is constant, giving a smooth, continuous attractor. However, as
discussed later, in the presence of disorder, VJ( ¯x) has bumps (i.e., quenched
disorder) and is no longer a smooth, continuous attractor.
To quantify the effect of the external driving, we write the third term in
equation A.3:
V ext ( ¯x, t) = −
(cid:2)
Iext
k
(t) f (i ¯x
k )
≈ −
k
(cid:2)
|k− ¯x|
where
V1( ¯x) = −d
(cid:6)
(R − ¯x)(w − R − ¯x
2
) + (R + ¯x)(w −
(cid:7)
,
)
w + ¯x
2
V2( ¯x) = − d
2
(R + w − ¯x)2.
(B.1)
(B.2)
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
We plot V ext given by equation B.1 versus the c.o.m. position of droplet
in Figure 6a.
B.1 A Thermal Equivalence Principle. The equivalence principle we
introduced in the main text allows us to compute the steady-state position
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
6
1
0
3
3
1
8
6
4
8
5
8
n
e
c
o
_
a
_
0
1
2
8
0
p
d
.
/
Nonequilibrium Statistical Mechanics of Continuous Attractors
1049
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
Figure 6: (a) V ext for external driving signal Icup(x, t) with v = 0, plotted from
equation B.1 with d = 20, R = 15, w = 30. (b) Effective potential Ve f f experi-
enced by the droplet for a moving cup-shaped external driving signal, plot-
ted from equation C.1 with d = 10, R = 15, w = 30, γ v = 140. (c) Schematic
illustrating the idea of the equivalence principle (see equation 3.2). The dif-
≡ −kBT log p((cid:7)xv ), experienced by
ference between the effective potential, Ve f f
a moving droplet, and that of a stationary droplet, V cup, is a linear potential,
(cid:7)xv is pro-
Vlin
portional to velocity as Fmotion
(cid:7)xv . The slope θ of the linear potential Vlin
= −Fmotion
v
= −Fmotion
v
= γ v.
v
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
6
1
0
3
3
1
8
6
4
8
5
8
n
e
c
o
_
a
_
0
1
2
8
0
p
d
.
/
and the effective new potential seen in the co-moving frame. Crucially, the
fluctuations of the collective coordinate are described by the potential ob-
tained through the equivalence principle. The principle correctly predicts
both the mean (see equation 3.2) and the fluctuation (see equation 3.3) of
the lag (cid:7)xv . Therefore, it is actually a statement about the equivalence of ef-
fective dynamics in the rest frame and in the co-moving frame. Specializing
to the drive Icup(x, t), the equivalence principle predicts that the effective po-
tential felt by the droplet (moving at constant velocity v) in the co-moving
frame equals the effective potential in the stationary frame shifted by a lin-
v (cid:7)xv , that accounts for the fictitious forces due to
= −Fmot
ear potential, Vlin
the change of coordinates (see Figure 6c).
Since we used equation B.1 for the cup shape and the lag (cid:7)xv depends
linearly on v, we expect that the slope of the linear potential Vlin also de-
pends linearly on v. Here the sign convention is chosen such that Vlin
< 0
corresponds to the droplet moving to the right.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1050
W. Zhong, Z. Lu, D. Schwab, and A. Murugan
Appendix C: Speed Limit for External Driving Signals
In the following, we work in the co-moving frame with velocity v at which
the driving signal is moving. We denote the steady-state c.o.m. position in
this frame to be (cid:7)x∗
v and a generic position to be (cid:7)xv .
When v > 0, the droplet will sit at a steady-state position (cid:7)x∗
v < 0. The
equivalence principle says we should subtract a velocity-dependent linear
v (cid:7)xv = γ v(cid:7)xv from V ext to account for the motion:
potential Fmot
Ve f f ((cid:7)xv ) = V cup((cid:7)xv ) − γ v(cid:7)xv .
(C.1)
We plot Ve f f vs (cid:7)xv in Figure 6b. Notice that there are two extremal
v , and
points of the potential, corresponding to the steady-state position, (cid:7)x∗
the escape position, (cid:7)xesc
v :
(cid:7)x
(cid:7)xesc
∗
v = γ v/2d,
v = (dw − γ v + dR)/d.
(C.2)
We are now in position to derive v
crit presented in the main text. We ob-
serve that as the driving velocity v increases, (cid:7)x∗
v will get closer
to each other, and there will be a critical velocity such that the two coincide.
and solving for v, we
By simply equating the expression for xesc and x∗
v and (cid:7)xesc
found that
v
crit
= 2d(w + R)
3γ
.
(C.3)
C.1 Steady-State Droplet Size. Recall that the Lyapunov function of
the neural network is given by equatin A.3:
L[ ¯x] = 1
τ
(cid:4)
(cid:2)
f (i ¯x
k )
0
k
−1(x)dx + VJ( ¯x) + V ext ( ¯x, t).
f
(C.4)
Compared to the equation of motion (e.o.m.), equaiton A.1, we see that
the first term corresponds to the decay of neurons in the absence of interac-
tion from neighbors (decay from the on state to the off state), and the second
term corresponds to the interaction Jnk term in the e.o.m, and the third term
corresponds to the Iext
in the e.o.m. Since we are interested in the steady-
n
state droplet size, and thus only in the neurons that are on, the effect of
the first term can be neglected (also note that 1/τ (cid:13) Ji j; when using the
Lyapunov function to compute steady-state properties, the first term can
be ignored).
To obtain general results, we also account for long-range disordered con-
i j consists of random connections among all
i j here. We assume Jd
nections Jd
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
6
1
0
3
3
1
8
6
4
8
5
8
n
e
c
o
_
a
_
0
1
2
8
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Nonequilibrium Statistical Mechanics of Continuous Attractors
1051
the neurons. We can approximate these random connections as random per-
i j, and the full Ji j is the sum over M − 1 such permutations
mutations of J0
plus J0
i j.
For the cup-shaped driving and its corresponding effective potential,
equation C.1, we are interested in the steady-state droplet size under this
driving, so we first evaluate Ve f f at the steady-state position (cid:7)x∗
v in equa-
tion C.2. To make the R-dependence explicit in the Lyapunov function, we
evaluate L( ¯x) under the rigid bump approximation used in Hopfield (2015),
assuming f (i ¯x
k ) = 1 for |k − ¯x| ≤ R, and = 0 otherwise.
We find that for M − 1 sets of disorder interactions, the Lyapunov func-
tion is
(cid:6)
L[ f (i ¯x
k )] = J
((cid:4)R2 − ((cid:4) + 2p)R + p(p + 1)
(cid:7)
2
+ (γ v )2
4d
− pm(2R − p)2
+ Rd(R − 2w),
(C.5)
where we have defined the reduced disorder parameter m = (M − 1)/N and
have used the equivalence principle in equation 3.2 to add an effective linear
potential to take into account the motion of the droplet.
Next, we note that the steady-state droplet size corresponds to a local ex-
tremum of the Lyapunov function. Extremizing equation C.5 with respect
to droplet radius R, we obtain the steady-state droplet radius as a function
of the external driving parameters d, w, and the reduced disorder parame-
ter m,
R(d, w, m) = 2p − 4p2m + 2wd/J + (cid:4)
2d/J − 8pm + 4(cid:4)
,
(C.6)
where we observe that in the formula, the only dimensionful parameters
d and J appear together to ensure the overall result is dimensionless. Our
result for R reduces to R0
4 by setting M = 1 and d = w = 0.
= p
2(cid:4)
+ 1
C.2 Upper Limit on External Signal Strength. Here we present the cal-
culation for maximal driving strength Iext beyond which the activity droplet
will “teleport”—that is, disappear at the original location and recondense
at the location of the drive, even if these two locations are widely separated.
We now refer to this maximal signal strength as the teleportation limit. We
can determine this limit by finding out the critical point where the energy
barrier of breaking up the droplet at the original location is zero.
For simplicity, we assume that initially, the cup-shaped driving signal is
some distance x0 from the droplet and not moving (the moving case can
be solved in exactly the same way by using the equivalence principle and
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
6
1
0
3
3
1
8
6
4
8
5
8
n
e
c
o
_
a
_
0
1
2
8
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1052
W. Zhong, Z. Lu, D. Schwab, and A. Murugan
Figure 7: Schematics of three scenarios during a teleportation process. In the
initial configuration, the droplet is outside the cup. An energetically unfavor-
able intermediate configuration is penalized by (cid:7)E: the droplet breaks apart
into two droplets—one outside the cup and one inside it. In the final configura-
tion, with the lowest energy, the droplet inside the cup grows to a full droplet
while the droplet outside shrinks to zero size. Above each droplet is its corre-
sponding radius R.
going to the co-moving frame of the droplet). We consider three scenarios
during the teleportation process. (1) In the initial configuration, the droplet
has not yet teleported and stays at the original location with radius
R(0, 0, m). (2) In the intermediate configuration, the activity is no longer
contiguous, giving a droplet with radius δ(d, w, m) at the center of the cup,
and another droplet with radius R(d, w, m) − δ(d, w, m) at the original lo-
cation (when teleportation happens, the total firing neurons changes from
R(0, 0, m) to R(d, w, m)). (3) In the final configuration, the droplet has suc-
cessfully teleported to the center of the cup, with radius R(d, w, m). The
three scenarios are depicted schematically in Figure 7.
The global minimum of the Lyapunov function corresponds to scenario
3. However, there is an energy barrier between configuration 1 and con-
figuration 3, corresponding to the Ve f f difference between configuration 1
and 2. We would like to find the critical split size δc(d, w, m) that maximizes
the difference in Ve f f , which corresponds to the largest energy barrier the
network has to overcome in order to teleport from configuration 1 to 3. For
the purpose of derivation, in the following we rename L[ f (im
k )] in equa-
tion C.5 as E0(d, w, m)(cid:14)
R(d,w,m) to emphasize its dependence on the external
driving parameters and disordered interactions. The subscript 0 stands for
the default one-droplet configuration, and it is understood that E0(d, w, m)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
6
1
0
3
3
1
8
6
4
8
5
8
n
e
c
o
_
a
_
0
1
2
8
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Nonequilibrium Statistical Mechanics of Continuous Attractors
1053
is evaluated at the network configuration of a single droplet at location m
with radius R(d, w, m).
The energy for configuration 1 is simply E0(0, 0, m), and the energy for
configuration 3 is E0(d, w, m). However, the energy for configuration 2 is
not just the sum of E0 from the two droplets. Due to global inhibitions pre-
sented in the network, when there are two droplets, there will be an extra
interaction term when we evaluate the Lyapunov function with respect to
this configuration. The interaction energy between two droplets in Figure 7
is
Eint (m)|R,δ = 4JRδ((cid:4) − 2pm).
(C.7)
Therefore, the energy barrier for split size δ is
(cid:7)E(d, w, m)(cid:14)δ = E0(0, 0, m)(cid:14)
+ Eint (m)(cid:14)
R(d,w,m)−δ + E0(d, w, m)(cid:14)δ
R(d,w,m),δ − E0(0, 0, m)(cid:14)
R(0,0,m)
Therefore, maximizing (cid:7)E with respect to δ, we find
δc =
dw
d − 8J pm + 4J(cid:4)
.
.
(C.8)
(C.9)
Now we have obtained the maximum energy barrier during a telepor-
tation process, (cid:7)E(cid:14)δc . A spontaneous teleportation will occur if (cid:7)E(cid:14)δc
≤
0, and this in turn gives an upper bound on the external driving sig-
nal strength d ≤ dmax one can have without any teleportation spontaneous
occurring.
We plot the numerical solution of dmax obtained from the solving
(cid:7)E(dc, w, m)(cid:14)δc = 0, compared with results obtained from the simulation
in Figure 8, and find perfect agreement.
We also obtain an approximate solution by observing that the only rele-
vant scale for the critical split size δc is the radius of the droplet, R. We set
δc = cR for some constant 0 ≤ c ≤ 1. In general, c can depend on dimension-
less parameters like p and (cid:4). Empirically we found the constant to be about
0.29 in our simulation.
The droplet radius R is a function of d, w, m as we see in equation C.6,
for some steady-state
but to first-order approximation, we can set R = R∗
radius R∗
. Then we can solve
dmax(M) = 4J((cid:4) − 2pm)
w/cR∗ − 1
.
(C.10)
Note that the denominator is positive because w > R and 0 ≤ c ≤ 1.
The simulation result also confirms that the critical split size δc stays
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
6
1
0
3
3
1
8
6
4
8
5
8
n
e
c
o
_
a
_
0
1
2
8
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1054
W. Zhong, Z. Lu, D. Schwab, and A. Murugan
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
6
1
0
3
3
1
8
6
4
8
5
8
n
e
c
o
_
a
_
0
1
2
8
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 8: Teleportation depth dmax plotted against disorder parameter m. The
dots are data obtained from simulations for different N but with p = 10, (cid:4) =
0.35, τ = 1, J = 100, and w = 30 held fixed. The dotted line is the theoretical
curve plotted from solving (cid:7)E(dc
= 0 for dc numerically.
, w, m)(cid:14)δ
c
approximately constant. We have checked that the dependence on param-
eters J, w, m in equation C.10 agrees with the numerical solution obtained
from solving Ebar(dc, w, m)(cid:14)δc = 0, up to the undetermined constant c.
C.3 Speed Limit on External Driving. Recall that given a certain signal
strength d, there is an upper bound on how fast the driving can be (see
equation C.3). Then in particular, for dmax, we obtain an upper bound on
how fast an external signal can drive the network:
vmax = 8J(w + R∗)((cid:4) − 2pm)
3γ (w/cR∗ − 1)
.
For w (cid:15) R∗
, we can approximate
≈ 16JcR∗
v
max
((cid:4)/2 − pm)
3γ
.
(C.11)
(C.12)
In the absence of disorder, m = 0, the maximum velocity is bounded by
v
max
≤ 8c
3
(cid:4)JR∗
γ
≤ 8c
3
(cid:4)JRmax
γ
.
(C.13)
Nonequilibrium Statistical Mechanics of Continuous Attractors
1055
Recall that in equation C.10, we have
R(d, w (cid:15) R, 0) ≤ R(dmax
+ 1
4
, w (cid:15) R, 0)
+ 2cR
∗ + O
(cid:9)
(cid:8)
R
w
= p
2(cid:4)
(cid:2) p
2(cid:4)
+ 2cRmax
,
(C.14)
where in the second line we have used equation C.6 for d = dmax, m = 0,
and w (cid:15) R. Upon rearranging, we have
Rmax
(cid:2) 1
1 − 2c
.
p
2(cid:4)
Plugging in equation C.13, we have
v
max
≤ 8c
3
(cid:4)JRmax
γ
(cid:2)
8
3(c−1 − 2)
J p
γ
.
(C.15)
(C.16)
Therefore, we have obtained a fundamental limit on how fast the droplet
can move under the influence of external signal, namely,
v
f und
= κJ pγ −1,
(C.17)
where κ = 8/3(c−1 − 2) is a dimensionless O(1) number.
Appendix D: Path Integration and Velocity Input
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
6
1
0
3
3
1
8
6
4
8
5
8
n
e
c
o
_
a
_
0
1
2
8
0
p
d
.
/
Place cell networks (Ocko et al., 2018) and head direction networks (Kim
et al., 2017) are known to receive information about both velocity and land-
mark information. Velocity input can be modeled by adding an antisym-
metric part Ai j to the connectivity matrix Ji j, which effectively tilts the
continuous attractor.
Consider now
Ji j
= J0
i j
+ Jd
i j
+ A0
i j
,
(D.1)
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
where A0
i j
= A, if 0 < i − j ≤ p; −A, if 0 < j − i ≤ p; and 0 otherwise. The antisymmetric part A0 i j will provide a velocity v that is proportional to the size A of A0 i j for the droplet (see Figure 9). In the presence of disorder, we can simply go to the co-moving frame of velocity v, and the droplet experiences an extra disorder-induced noise η A in addition to the disorder- induced temperature Td. 1056 W. Zhong, Z. Lu, D. Schwab, and A. Murugan Figure 9: Velocity of droplet v plotted against the size A of the antisymmetric matrix. We hold all other parameters fixed with the same value as in Figure 8. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 2 6 1 0 3 3 1 8 6 4 8 5 8 n e c o _ a _ 0 1 2 8 0 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 10: Left: At fixed A = 5, a collection of 500 diffusive trajectories in the co- moving frame at velocity v, where v is taken to be the average velocity of all the trajectories. We can infer the diffusion coefficient D from the variance of these trajectories as Var(x) = 2Dt. Right: logD plotted against log ˜σ 2. The straight line has slope 1/2, corresponding to D ∝ ˜σ . We found that (cid:6)η A(t)η A(0)(cid:7) ∝ ˜σ δ(t) (see Figure 10), where ˜σ 2 is the aver- age number of disordered connection per neuron in units of 2p. Therefore, all our results in the main text apply to the case when both the external drive Iext (x, t) and the antisymmetric part A0 i j exist. Specifically, we can just replace the velocity v used in the main text as the sum of the two velocities corresponding to Iext (x, t) and A0 i j. Nonequilibrium Statistical Mechanics of Continuous Attractors 1057 Appendix E: Quenched Disorder: Driving and Disorder-Induced Temperature i j in addition to ordered connections J0 E.1 Disordered Connections and Disordered Forces. From now on, we include disorder connections Jd i j that correspond to the nearest p-neighbor interactions. We assume Jd i j consists of random connections among all the neurons. These random connections can be approximated as random permutations of J0 i j, such that the full Ji j is the sum over M − 1 such permutations plus J0 i j. We clip the Ji j matrix according to the following rule for each entry when summing over J0 i j and Jd i j: J(1 − (cid:4)) + J(1 − (cid:4)) → J(1 − (cid:4)), J(1 − (cid:4)) + J(−(cid:4)) → J(1 − (cid:4)), J(−(cid:4)) + J(−(cid:4)) → J(−(cid:4)). (E.1) Therefore, adding more disorder connections to Ji j amounts to changing the inhibitory −J(cid:4) entries to the exitory J(1 − (cid:4)). We would like to characterize the effect of disorder on the system. Un- i j, we can define a (quenched) disorder = J0 der the decomposition Ji j i j potential that captures all the disorder effects on the network: + Jd V d( ¯x) ≡ V d[ f (i ¯x k )] = − 1 2 (cid:2) nk nk f (i ¯x Jd k ) f (i ¯x n). Its corresponding disorder-induced force is then given by Fd( ¯x) = −∂ ¯xV d( ¯x). (E.2) (E.3) E.2 Variance of Disorder Forces. We compute the distribution of V d( ¯x) using a combinatorial argument as follows. Under the rigid droplet approximation, calculating V d( ¯x) amounts to summing all the entries within an R-by-R diagonal block submatrix J( ¯x) i j n )Jnk f (i( ¯x) nk f (i( ¯x) within the full synaptic matrix Ji j (recall that V d( ¯x) ∝ k )). Each set of disorder connections is a random permutation of J0 i j, and thus has the same number of excitatory entries as J0 i j, namely, 2pN. Since the inhibitory connections do not play a role in the summation by virtue of equation E.1, it suffices to consider only the effect of adding excitatory con- nections in Jd (cid:3) i j to J0 i j. There are M − 1 sets of disordered connections in Jd i j, and each has 2pN excitatory connections. Suppose we add these 2pN(M − 1) excitatory l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 2 6 1 0 3 3 1 8 6 4 8 5 8 n e c o _ a _ 0 1 2 8 0 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 1058 W. Zhong, Z. Lu, D. Schwab, and A. Murugan connections one by one to J0 i j. Each time an excitatory entry is added to an entry y in the R-by-R block J( ¯x) i j , there are two possible situations depending on the value of y before addition: if y = J(1 − (cid:4)) (excitatory), the addition of an excitatory connection does not change the value of y because of the clipping rule in equation E.1; if y = −J(cid:4) (inhibitory), the addition of an ex- citatory connection to y changes y to J(1 − (cid:4)). In the latter case, the value of V d( ¯x) is changed because the summation of entries within J( ¯x) i j has changed, while in the former case, V d( ¯x) stays the same. (Note that if the excitatory connection is added outside J( ¯x) i j , it does not change V d( ¯x) and thus can be neglected.) We have in total 2pN(M − 1) excitatory connections to be added, and in total (2R − p)2 potential inhibitory connections in the R-by-R block J( ¯x) to be i j flipped to an excitatory connection. We are interested in, after adding all the 2pN(M − 1) excitatory connections, how many inhibitory connections are changed to excitatory connections and the corresponding change in V d( ¯x). We can get an approximate solution if we assume that the probabil- ity of flipping an inhibitory connection does not change after the subse- quent addition of excitatory connections and stays constant throughout the addition of all the 2pN(M − 1) excitatory connections. This requires 2pN(M − 1) (cid:13) N2, that is, M (cid:13) N, which is a reasonable assumption since the capacity cannot be O(N). For a single addition of exitatory connection, the probability of success- is proportional to the frac- i j over the total number of entires fully flipping an inhibitory connection within J( ¯x) i j tion of the inhibitory connections within J( ¯x) in J0 i j: l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 2 6 1 0 3 3 1 8 6 4 8 5 8 n e c o _ a _ 0 1 2 8 0 p d . / q(flip) = (2R − p)2 N2 . So the probability of getting n inhibitory connections flipped is P(n) = (cid:8) (cid:9) 2pN(M − 1) n qn(1 − q)2pN(M−1)−n. (E.4) (E.5) f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 In other words, the distribution of flipping n inhibitory connections to ex- i j obeys n ∼ B(2pN(M − 1), q). The i j to J0 citatory connections after adding Jd mean is then (cid:6)n(cid:7) = 2pN(M − 1)q = 2p(2R − p)2 (cid:8) (cid:9) M − 1 N = (2R − p)22pm, (E.6) Nonequilibrium Statistical Mechanics of Continuous Attractors 1059 where we have defined the reduced disorder parameter m ≡ (M − 1)/N. The variance is (cid:6)n2(cid:7) = 2pN(M − 1)q(1 − q) = 2pN(M − 1) (2R − p)2 N2 ≈ (2R − p)22pm, (cid:9) (cid:8) 1 − (2R − p)2 N2 (E.7) where in the last line we have used N (cid:15) 2R − p. Since changing n inhibitory connections to n excitory connections amounts to changing V d( ¯x) by −1/2(J(1 − (cid:4)) − J(−(cid:4))) = −J/2, we have Var(V d( ¯x)) ≡ σ 2 = J2(R − p/2)2 pm. (E.8) E.3 Disorder Temperature from Disorder-Induced Force. We focus n gives rise to a constant velocity v for the droplet here on the case where Iext (as in the main text). In the co-moving frame, the disorder-induced force Fd( ¯x) acts on the c.o.m. like random kicks with correlation within the droplet size. For fast enough velocity, those random kicks are sufficiently decorre- lated and become white noise at temperature Td. To extract this disorder-induced temperature Td, we consider the auto- correlation of Fd[ ¯x(t)] between two different c.o.m. locations ¯x(t) and ¯x(cid:16)(t(cid:16)) (and thus different times t and t(cid:16)), (cid:16) C(t, t ) ≡ (cid:6)Fd[ ¯x(t)]Fd[ ¯x(t (cid:16) )](cid:7), (E.9) where the expectation value is averaging over different realizations of the quenched disorder. Using equation E.3, we have (cid:16) C(t, t ) = (cid:6)∂ ¯xV d( ¯x)∂ ¯x(cid:16)V d( ¯x = ∂ ¯x∂ ¯x(cid:16) (cid:6)V d( ¯x)V d( ¯x (cid:16) (cid:16) )(cid:7) )(cid:7). (E.10) (E.11) Within time t − t(cid:16) , if the droplet moves a distance less than its size 2R, k ) and f (i ¯x(cid:16) then V d computed at t and t(cid:16) will be correlated because f (i ¯x k ) have nonzero overlap. Therefore, we expect that the autocorrelation func- tion (cid:6)V d( ¯x)V d( ¯x(cid:16) )(cid:7) behaves like the 1D Ising model with finite correlation length ξ = 2R (up to a prefactor to be fixed later): (cid:6)V d( ¯x)V d( ¯x (cid:16) )(cid:7) ∼ exp (cid:8) − | ¯x − ¯x(cid:16)| ξ (cid:9) . (E.12) l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 2 6 1 0 3 3 1 8 6 4 8 5 8 n e c o _ a _ 0 1 2 8 0 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 1060 W. Zhong, Z. Lu, D. Schwab, and A. Murugan (cid:10) (cid:11) Hence, C(t, t(cid:16) ) ∼ exp . Going to the co-moving frame, we can write the c.o.m. location as before, (cid:7)xv = ¯x − vt, so the autocorrelation func- tion becomes (cid:16)| − | ¯x− ¯x ξ (cid:16) C(t, t ) ∼ exp = exp − − (cid:8) (cid:8) (cid:8) ≈ exp − |((cid:7)xv + vt) − ((cid:7)x(cid:16) v + vt(cid:16) )| (cid:9) ξ |v (t − t(cid:16) ) + ((cid:7)xv − (cid:7)x(cid:16) v )| (cid:9) ξ (cid:9) , v|t − t(cid:16)| ξ (E.13) where in the last line, we have used that the droplet moves much faster in the stationary frame than the c.o.m. position fluctuates in the co-moving frame, so v (t − t(cid:16) ) (cid:15) (cid:7)xv − (cid:7)x(cid:16) v . Now let us define the correlation time to be τcor = ξ /v = 2R/v. Then (cid:8) (cid:16) C(t, t ) ∼ exp − (cid:9) . |t − t(cid:16)| τcor (E.14) For T ≡ |t − t(cid:16)| (cid:15) τcor, we want to consider the limiting behavior of C(t, t(cid:16) ) under an integral. Note that (cid:9) (cid:8) (cid:4) (cid:4) T T dt 0 0 (cid:16) dt exp − |t − t(cid:16)| τcor Therefore, we have for T (cid:15) τcor, (cid:9) (cid:8) (cid:4) (cid:4) (cid:16) dt exp − |t − t(cid:16)| τcor T T dt 0 0 so we can write = τcor[2(T − τcor) + 2τcore −T/τcor ] ≈ 2τcorT (if T (cid:15) τcor). (E.15) = 2τcor (cid:4) T (cid:4) T dt 0 0 (cid:16)δ(t − t (cid:16) ), dt (E.16) (cid:8) exp − (cid:9) |t − t(cid:16)| τcor → 2τcorδ(t − t (cid:16) ), (E.17) and it is understood that this holds in the integral sense. Therefore, for T (cid:15) τcor, we expect Fd(x) to act like uncorrelated white noise, and we can write (cid:16) C(t, t ) = Td δ(t − t (cid:16) ) ∝ τcorδ(t − t (cid:16) ), (E.18) where Td is a measure of this disorder-induced white noise. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 2 6 1 0 3 3 1 8 6 4 8 5 8 n e c o _ a _ 0 1 2 8 0 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Nonequilibrium Statistical Mechanics of Continuous Attractors 1061 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / Figure 11: Uncollapsed data for the occupancies − log p((cid:7)xv ) for different amounts of long-range disordered connections. Parameters are the same as in Figure 3 (see section of F.1 for further details). To deduce the form of disorder temperature Td, we present the uncol- lapsed occupancies − log p((cid:7)xv ) = V ((cid:7)xv )/kBTd (described in the caption of Figure 3) in Figure 11. In a comparison with Figure 3, we can see that Td successfully captures the effect of disorder on the statistics of the emergent droplet if Td = ˜kτcorσ, (E.19) where σ is given in equation E.8 and ˜k is a fitting constant. Appendix F: Derivation of the Memory Capacity for Driven Place Cell Network In this section, we derive the memory capacity for driven place cell network described equation 6.1. Our continuous attractor network can be applied to study the place cell network. We assume a 1D physical region of length L. We study a network with N place cell neurons and assume each neuron has a place field of size d = 2pL/N that covers the region [0, L] as a regular tiling. The N neurons are assumed to interact as in the leaky integrate-and-fire model of neurons. The / / / 3 2 6 1 0 3 3 1 8 6 4 8 5 8 n e c o _ a _ 0 1 2 8 0 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 1062 W. Zhong, Z. Lu, D. Schwab, and A. Murugan external driving currents Iext (x, t) can model sensory input when the mouse is physically in a region covered by place fields of neurons i, i + 1, . . . , i + z; through Iext currents Iext i+z can be expected to be high compared to all other currents Iext , which corresponds to the cup-shape drive we used throughout the main text. j i It has been shown that the collective coordinate in the continuous attrac- tor survives to multiple environments provided the number of stored mem- ories m < mc is below the capacity mc of the network. Below the capacity, the neural activity droplet is multistable; that is, neural activity forms a stable contiguous droplet as seen in the place field arrangement corresponding to any one of the m environments. Note that such a contiguous droplet will not appear contiguous in the place field arrangement of any other environ- ment. Capacity was shown to scale as mc = α(p/N, R)N, where α is an O(1) number that depends on the size of the droplet R and the range of interac- tions p. However, this capacity is about the intrinsic stability of the droplet and does not consider the effect of rapid driving forces. When the droplet escapes from the driving signal, it has to overcome a certain energy barrier. This is the difference in Ve f f between the two ex- tremal points (cid:7)x∗ v . Therefore, we define the barrier energy to be (cid:7)E = Ve f f (xesc v ), and we evaluate it using equations C.1 and C.2: v and (cid:7)xesc v ) − Ve f f ((cid:7)x∗ (cid:7)E(v, d) = (4dw − 3γ v − 2dR)(−γ v + 2dR) 4d . (F.1) Note this is the result we used in equation 6.1. As in the main text, the escape rate r is given by the Arrhenius law: (cid:8) r ∼ exp − (cid:9) . (cid:7)E(v, d) kBTd (F.2) The total period of time of an external drive moving the droplet across a distance L (L ≤ N, but without loss of generality, we can set L = N) is T = L/v. We can imagine chopping T into infinitesimal intervals (cid:7)t s.t. the probability of successfully moving the droplet across L without escaping is l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 2 6 1 0 3 3 1 8 6 4 8 5 8 n e c o _ a _ 0 1 2 8 0 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Pretrieval (1 − r(cid:7)t) T (cid:7)t = lim (cid:7)t→0 −rT = e = e = exp(− N v e −rN/v −(cid:7)E(v,d)/kBTd ). (F.3) Nonequilibrium Statistical Mechanics of Continuous Attractors 1063 Td is given by equation E.19: Td √ = 2˜kRJ(R − p/2) v √ ≡ k mv −1, pm (F.4) where in the last step, we have absorbed all the constants (assuming R is constant over different m’s) into the definition of k. Now we want to find the scaling behavior of m s.t. In the thermodynamic limit (N → ∞), Pretrieval becomes a Heaviside step function (cid:11)(mc − m) at some critical memory mc. With the aid of some hindsight, we try m = α2 (log N)2 . Then in the thermodynamic limit, (F.5) lim N→∞ Pretrieval = lim N→∞ = lim N→∞ exp(− N v e exp(− N v N − log Nv(cid:7)E(v,d)/αkBk) −v(cid:7)E(v,d)/αkBk) = lim N→∞ (cid:5) = exp(− 1 v N1−v(cid:7)E(v,d)/αkBk) 1, α < v(cid:7)E(v, d)/kBk 0, α > v(cid:7)E(v, d)/kBk
.
(F.6)
Therefore, we have arrived at the expression for capacity mc or, in terms
of M = mcN + 1 ≈ mcN(N (cid:15) 1),
(cid:7)2 N
(cid:6)
Mc =
v(cid:7)E(v, d)
kBk
(log N)2
or
Mc ∼
(cid:6)
v(cid:7)E(v, d)
(cid:7)2 N
(log N)2
.
(F.7)
(F.8)
F.1 Numerics of the Place Cell Network Simulations. In this section,
we explain our simulations in Fig. 4 in detail.
Recall that we only determine the Arrhenius-like escape rate r up to an
overall constant. We can absorb it into the definition of (cid:7)E(v, d) (given by
equation F.1) as an additive constant a,
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
6
1
0
3
3
1
8
6
4
8
5
8
n
e
c
o
_
a
_
0
1
2
8
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1064
W. Zhong, Z. Lu, D. Schwab, and A. Murugan
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
6
1
0
3
3
1
8
6
4
8
5
8
n
e
c
o
_
a
_
0
1
2
8
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
v = log{v −1 log r/[(cid:7)E(v, d) + a]} against log(M −
Figure 12: Top: Plotting −1/Td
1). Different solid lines correspond to data with different v, and the dashed
line corresponds to the (M − 1)−1/2 curve. Bottom: Plotting v −1 log r
M − 1 ∝
(cid:7)E(v, d) against v. Different solid lines correspond to data with different M,
and the dashed line corresponds to the (cid:7)E(v, d) + a curve.
√
(cid:12)
r = exp
−
(cid:7)E(v, d) + a
(cid:13)
kBkv
(M − 1)/N
(cid:14)
.
Then the theoretical curve corresponds to
Pretrieval
= e
−Nr/v .
(F.9)
(F.10)
Therefore, our model, equation F.10, has three parameters to determine:
γ , k, and a. In Figure 12 we determine the parameters by collapsing data
−1
and see that the best fit is found provided γ = 240.30, k = 5255.0k
, a =
B
−0.35445. Henceforth, we fix these three parameters to these values.
Nonequilibrium Statistical Mechanics of Continuous Attractors
1065
√
√
In the bottom plot of Figure 12, we offset the effect of M by multiply-
ing v −1 log r by
M − 1, and we see that curves corresponding to different
M − 1 dependence in Td. The
M collapse to each other, confirming the
collapsed line we are left with is just the v-dependence of (cid:7)E(v, d), up to
overall constant.
In the top panel of Figure 12, we offset the effect of v in Td by multiplying
v −1 to log r/[(cid:7)E(v, d) + a]. We see that different curves corresponding to
different v’s collapse to each other, confirming the v −1 dependence in Td.
The curve we are left with is the M dependence in Td, which we see fits
nicely with the predicted
M − 1.
√
In Figure 4b, we run our simulation with the following parameters held
fixed: N = 4000, p = 10, (cid:4) = 0.35, τ = 1, J = 100, d = 10, and w = 30. Along
the same curve, we vary M from 6 to 30, and the series of curves corresponds
to different v from 0.6 to 1.2.
In Figure 4c, we hold the following parameters fixed: p = 10, (cid:4) =
0.35, τ = 1, J = 100, d = 10, w = 30, and v = 0.8. Along the same curve, we
vary M/ N
(log N)2 from 0.1 to 0.6, and the series of curves corresponds to dif-
ferent N from 1000 to 8000.
In Figures 4b and 4c, the theoretical model we used is equation F.10 with
the same parameters given above.
In Figure 4d, we replotted the theory and data from Figure 4b. For the
= 0.5, and call the cor-
theoretical curve, we find the location where Pretrieval
responding M value “theoretical capacity.” For the simulation curve, we
= 0.5, and call the corresponding M value the
extrapolate to where Pretrieval
“simulation capacity.”
For all simulation curves above, we drag the droplet from one end of the
continuous attractor to the other end of the attractor and run the simulation
300 times. We then measure the fraction of successful events (defined as
the droplet survived in the cup throughout the entire trajectory of moving)
and failed events (defined as the droplet escape from the cup at some point
before reaching the other end of the continuous attractor). We define the
simulation Pretreival as the fraction of successful events.
Acknowledgments
We thank Jeremy England, Ila Fiete, John Hopfield, and Dmitry Krotov
for discussions. A.M. and D.S. are grateful for support from the Simons
Foundation MMLS investigator program. We acknowledge the University
of Chicago Research Computing Center for support of this work.
References
Alme, C. B., Miao, C., Jezek, K., Treves, A., Moser, E. I., & Moser, M.-B. (2014). Place
cells in the hippocampus: Eleven maps for eleven rooms. Proc. Natl. Acad. Sci.
U.S.A., 111(52), 18428–18435.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
6
1
0
3
3
1
8
6
4
8
5
8
n
e
c
o
_
a
_
0
1
2
8
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1066
W. Zhong, Z. Lu, D. Schwab, and A. Murugan
Amari, S. (1977). Dynamics of pattern formation in lateral-inhibition type neural
fields. Biol. Cybern., 27(2), 77–87.
Amit, D., Gutfreund, H., & Sompolinsky, H. (1985a). Storing infinite numbers of pat-
terns in a spin-glass model of neural networks. Phys. Rev. Lett., 55(14), 1530–1533.
Amit, D. J., Gutfreund, H., & Sompolinsky, H. (1985b). Spin-glass models of neural
networks. Phys. Rev. A, 32(2), 1007.
Aronov, D., Nevers, R., & Tank, D. W. (2017). Mapping of a non-spatial dimension
by the hippocampal-entorhinal circuit. Nature, 543(7647), 719–722.
Battaglia, F., & Treves, A. (1998). Attractor neural networks storing multiple space
representations: A model for hippocampal place fields. Physical Review E, 58(6),
7738–7753.
Burak, Y., & Fiete, I. R. (2012). Fundamental limits on persistent activity in networks
of noisy neurons. Proc. Natl. Acad. Sci. U.S.A., 109(43), 17645–17650.
Campbell, M. G., Ocko, S. A., Mallory, C. S., Low, I. I., Ganguli, S., & Giocomo, L. M.
(2018). Principles governing the integration of landmark and self-motion cues in
entorhinal cortical codes for navigation. Nature Neuroscience, 21(8), 1096.
Chaudhuri, R., & Fiete, I. (2016). Computational principles of memory. Nat. Neurosci.,
19(3), 394–403.
Colgin, L. L., Leutgeb, S., Jezek, K., Leutgeb, J. K., Moser, E. I., McNaughton, B. L.,
& Moser, M.-B. (2010). Attractor-map versus autoassociation based attractor dy-
namics in the hippocampal network. J. Neurophysiol., 104(1), 35–50.
Erdem, U. M., & Hasselmo, M. (2012). A goal-directed spatial navigation model us-
ing forward trajectory planning based on grid cells. Eur. J. Neurosci., 35(6), 916–
931.
Evans, T., Bicanski, A., Bush, D., & Burgess, N. (2016). How environment and self-
motion combine in neural representations of space. J. Physiol., 594(22), 6535–6546.
Fung, C. A., Wong, K. M., Mao, H., & Wu, S. (2015). Fluctuation-response relation
unifies dynamical behaviors in neural fields. Physical Review E, 92(2), 022801.
Fyhn, M., Hafting, T., Treves, A., Moser, M.-B., & Moser, E. I. (2007). Hippocampal
remapping and grid realignment in entorhinal cortex. Nature, 446(7132), 190–194.
Hardcastle, K., Ganguli, S., & Giocomo, L. M. (2015). Environmental boundaries as
an error correction mechanism for grid cells. Neuron, 86(3), 827–839.
Hardcastle, K., Maheswaranathan, N., Ganguli, S., & Giocomo, L. M. (2017). A mul-
tiplexed, heterogeneous, and adaptive code for navigation in medial entorhinal
cortex. Neuron, 94(2), 375–387.
Hertz, J., Krogh, A., Palmer, R. G., & Horner, H. (1991). Introduction to the theory of
neural computation. Physics Today, 44, 70.
Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective
computational abilities. In PNAS, 79, 2554–2558.
Hopfield, J. J. (2010). Neurodynamics of mental exploration. Proceedings of the Na-
tional Academy of Sciences, 107(4), 1648–1653.
Hopfield, J. J. (2015). Understanding emergent dynamics: Using a collective activity
coordinate of a neural network to recognize time-varying patterns. Neural Com-
put., 27(10), 2011–2038.
Kilpatrick, Z. P., Ermentrout, B., & Doiron, B. (2013). Optimizing working mem-
ory with heterogeneity of recurrent cortical excitation. J. Neurosci., 33(48), 18999–
19011.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
6
1
0
3
3
1
8
6
4
8
5
8
n
e
c
o
_
a
_
0
1
2
8
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Nonequilibrium Statistical Mechanics of Continuous Attractors
1067
Kim, S. S., Rouault, H., Druckmann, S., & Jayaraman, V. (2017). Ring attractor dy-
namics in the drosophila central brain. Science, 356(6340), 849–853.
Kubie, J. L., & Muller, R. U. (1991). Multiple representations in the hippocampus.
Hippocampus, 1(3), 240–242.
Latham, P. E., Deneve, S., & Pouget, A. (2003). Optimal computation with attractor
networks. J. Physiol. Paris, 97(4–6), 683–694.
Lim, S., & Goldman, M. S. (2012). Noise tolerance of attractor and feedforward mem-
ory models. Neural Comput., 24(2), 332–390.
Major, G., Baker, R., Aksay, E., Seung, H. S., & Tank, D. W. (2004). Plasticity and
tuning of the time course of analog persistent firing in a neural integrator. Proc.
Natl. Acad. Sci. U.S.A., 101(20), 7745–7750.
McNaughton, B. L., Battaglia, F. P., Jensen, O., Moser, E. I., & Moser, M.-B. (2006).
Path integration and the neural basis of the “cognitive map.” Nat. Rev. Neurosci.,
7(8), 663–678.
Meshulam, L., Gauthier, J. L., Brody, C. D., Tank, D. W., & Bialek, W. (2017). Col-
lective behavior of place and non-place neurons in the hippocampal network.
Neuron, 96(5), 1178–1191.
Mi, Y., Fung, C. A., Wong, K. M., & Wu, S. (2014). Spike frequency adaptation im-
plements anticipative tracking in continuous attractor neural networks. In Z.
Ghahramani, M. Welling, C. Cortes, N. D. Lawrence, & K. Q. Weinberger (Eds.),
Advances in neural information processing systems, 27 (pp. 505–513). Red Hook, NY:
Curran.
Monasson, R., & Rosay, S. (2013). Crosstalk and transitions between multiple spatial
maps in an attractor neural network model of the hippocampus: Phase diagram.
Physical Review E, 87(6), 062813.
Monasson, R., & Rosay, S. (2014). Crosstalk and transitions between multiple spa-
tial maps in an attractor neural network model of the hippocampus: Collective
motion of the activity. Physical Review E, 89(3).
Monasson, R., & Rosay, S. (2015). Transitions between spatial attractors in place-cell
models. Phys. Rev. Lett., 115(9), 098101.
Moser, E. I., Moser, M.-B., & McNaughton, B. L. (2017). Spatial representation in the
hippocampal formation: A history. Nat. Neurosci., 20(11), 1448–1464.
Moser, E. I., Moser, M.-B., & Roudi, Y. (2014). Network mechanisms of grid cells.
Philos. Trans. R. Soc. Lond. B Biol. Sci., 369(1635), 20120511.
Ocko, S. A., Hardcastle, K., Giocomo, L. M., & Ganguli, S. (2018). Emergent elas-
ticity in the neural code for space. Proc. Natl. Acad. Sci. U.S.A., 115(50), E11798–
E11806.
O’Keefe, J., & Dostrovsky, J. (1971). The hippocampus as a spatial map: Preliminary
evidence from unit activity in the freely-moving rat. Brain Res., 34(1), 171–175.
Pfeiffer, B. E., & Foster, D. J. (2013). Hippocampal place-cell sequences depict future
paths to remembered goals. Nature, 497(7447), 74–79.
Ponulak, F., & Hopfield, J. J. (2013). Rapid, parallel path planning by propagating
wavefronts of spiking neural activity. Front. Comput. Neurosci., 7.
Poucet, B., & Save, E. (2005). Neuroscience: Attractors in memory. Science, 308(5723),
799–800.
Roudi, Y., & Latham, P. E. (2007). A balanced memory network. PLOS Comput. Biol.,
3(9), 1679–1700.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
6
1
0
3
3
1
8
6
4
8
5
8
n
e
c
o
_
a
_
0
1
2
8
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1068
W. Zhong, Z. Lu, D. Schwab, and A. Murugan
Seelig, J. D., & Jayaraman, V. (2015). Neural dynamics for landmark orientation and
angular path integration. Nature, 521(7551), 186–191.
Seung, H. S. (1996). How the brain keeps the eyes still. Proceedings of the National
Academy of Sciences, 93(23), 13339–13344.
Seung, H. S. (1998). Continuous attractors and oculomotor control. Neural Netw.,
11(7–8), 1253–1258.
Seung, H. S., Lee, D. D., Reis, B. Y., & Tank, D. W. (2000). Stability of the memory of
eye position in a recurrent network of conductance-based model neurons. Neuron,
26(1), 259–271.
Sontag, E. D. (2003). Adaptation and regulation with signal detection implies internal
model. Syst. Control Lett., 50(2), 119–126.
Tsodyks, M. (1999). Attractor neural network models of spatial maps in hippocam-
pus. Hippocampus, 9(4), 481–489.
Turner-Evans, D., Wegener, S., Rouault, H., Franconville, R., Wolff, T., Seelig, J. D., . .
. Jayaraman, V. (2017). Angular velocity integration in a fly heading circuit. Elife,
6.
Wills, T. J., Lever, C., Cacucci, F., Burgess, N., & O’Keefe, J. (2005). Attractor dynamics
in the hippocampal representation of the local environment. Science, 308(5723),
873–876.
Wimmer, K., Nykamp, D. Q., Constantinidis, C., & Compte, A. (2014). Bump attrac-
tor dynamics in prefrontal cortex explains behavioral precision in spatial working
memory. Nat. Neurosci., 17(3), 431–439.
Wu, S., & Amari, S.-I. (2005). Computing with continuous attractors: Stability and
online aspects. Neural Comput., 17(10), 2215–2239.
Wu, S., Hamaguchi, K., & Amari, S.-I. (2008). Dynamics and computation of contin-
uous attractors. Neural Comput., 20(4), 994–1025.
Yoon, K., Buice, M. A., Barry, C., Hayman, R., Burgess, N., & Fiete, I. R. (2013). Spe-
cific evidence of low-dimensional continuous attractor dynamics in grid cells.
Nat. Neurosci., 16(8), 1077–1084.
Received September 21, 2019; accepted January 29, 2020.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
2
6
1
0
3
3
1
8
6
4
8
5
8
n
e
c
o
_
a
_
0
1
2
8
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3