An Investigation into the - Specialized Research AI at MIT

An Investigation into the
Origin of Autopoiesis

Abstract Using a glider in the Game of Life cellular automaton as
a toy model of minimal persistent individuals, this article explores
how questions regarding the origin of life might be approached
from the perspective of autopoiesis. Specifically, I examine how
the density of gliders evolves over time from random initial
conditions and then develop a statistical mechanics of gliders that
explains this time evolution in terms of the processes of glider
creation, persistence, and destruction that underlie it.

Randall D. Beer*
Indiana University

Cognitive Science Program
rdbeer@indiana.edu

Keywords
Autopoiesis, origin of life, statistical
mechanics, cellular automata

1 Introduction

The origin of life remains one of the most fascinating and frustrating puzzles in science [23, 29, 36].
Not only is it a singular event in our own history, but it engages some of the most fundamental and
potentially universal questions in biology. For example, any discussion of the origins of life neces-
sarily involves taking a stance, either explicitly or implicitly, on the difficult problem of what life is in
the first place. If one equates a living system with its molecular components, then the question of
origins becomes one of biochemistry: What reactions gave rise to the particular set of biomolecules
that underlie terrestrial life? In contrast, if one identifies life with its potential for evolution, then
concern shifts to the origin of replication. From an energetic perspective, the problem is how met-
abolic cycles arose to harness energy flows. If one conceives of the essence of living systems as
informational, then the origin of the genetic code becomes a central focus. And so on.

Terrestrial life consists of a complicated set of intertwined biochemical processes of metabolism,
compartmentalization, and replication. Unfortunately, its modern form provides little direct evidence
for the historical pathway by which life emerged from its abiotic precursors. In origin-of-life debates,
the main battle lines are usually drawn between replication-first and metabolism-first scenarios, al-
though compartmentalization is also frequently mentioned [22]. In the replication-first scenario, life
began as a self-copying molecule. By far the most common version of this idea is currently the RNA
world hypothesis, in which it is argued that because RNA molecules can play both informational and
catalytic roles, they preceded and enabled the later adoption of DNA for template-based replication
and proteins for catalysis [18]. In contrast, in the metabolism-first scenario, life began with autocatalytic
networks of chemical reactions that were able to sustain their organization under far-from-equilibrium
conditions by dissipating available flows of energy [15, 19]. Finally, compartmentalization emphasizes
the need for any biochemical machinery to be contained within membranes that maintain their cohe-
sion, protect them from disruptive external influences, and regulate the necessary exchange of waste
and nutrients with the external environment [28, 30].

* Corresponding author.

Artificial Life 26: 5–22 (2020) https://doi.org/10.1162/artl_a_00307

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
6
1
5
1
8
9
6
3
4
7
a
r
t
l

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

R. D. Beer

An Investigation into the Origin of Autopoiesis

One conception of life that has played little direct role in investigations into its origins is Maturana
and Varelaʼs notion of autopoiesis [25, 34]. Broadly speaking, autopoiesis falls into the general class
of contained metabolism conceptions of life. However, it is formulated at a much more abstract
level of description. Autopoiesis attempts to characterize living systems in a way that abstracts away
the specific biochemical details of terrestrial life and the many secondary features it exhibits that are
often taken as definitional. Instead, Maturana and Varela sought to highlight only universal princi-
ples, which they conceived as fundamentally organizational in nature. Specifically, an autopoietic (lit.
self-creating) system is a network of processes that have the dual properties of self-production and
self-individuation. Self-production means that the network of processes produces components
whose interactions generate and maintain the very same network of processes that produced them.
Self-individuation means that the system constructs and maintains its own boundary as an essential
part of its operation. In Maturana and Varelaʼs terms, a living system is an autopioetic system op-
erating in the physical world (i.e., a molecular autopoietic system).

What might an analysis of the origin of life look like from the perspective of autopoiesis? Given
its abstract character, autopoiesis obviously has nothing specific to say about the energetic favorabil-
ity of one biochemical pathway over another. Likewise, it has little to say about the origin of rep-
lication, since autopoiesis is more concerned with the problem of persistence of the individual and
views reproduction as an additional complication. On an autopoietic account, life begins when au-
topoiesis begins, by whatever process. Thus, questions about the origin of life in some particular
universe become questions about the origin of autopoiesis in that universe. As a first step in the
investigation of such questions, we adopt a statistical treatment. Since a given autopoietic organiza-
tion defines a set of possible structural instantiations, we can examine the statistical mechanics of
those configurations by coarse-graining over individual components and processes. Of particular
interest are the processes that create, preserve, and destroy those configurations.

Previous work has utilized Conwayʼs Game-of-Life (GoL) cellular automaton as a simple model
within which to carry out a systematic theoretical exploration of the concept of autopoiesis and its con-
sequences [4]. The basic idea was to treat GoL as a kind of physics from which we can derive an artificial
chemistry. Bounded persistent spatiotemporal entities such as gliders were then analyzed in terms of the
network of reactions that underlie them, and these networks were shown to satisfy an interpretation of
the self-production and self-individuation conditions [6]. The interaction between such individuals and
their environments was also characterized [5]. The only specific result from this previous work that I
needed for the present article was that the resulting glider organization admits, at each grid location, the
16 structural instantiations shown in Figure 1 (2 forms × 2 chiralities × 4 orientations). My inves-
tigation was formulated entirely in terms of the statistical mechanics of sets of these configurations.
The goal of this article was to extend this research program to an exploration of questions on the origin
of life from an autopoietic perspective, using a glider in the Game of Life as a toy model. Specifically, I
developed a statistical mechanics of gliders and used it to study their origin, proliferation, and extinction. It
is important to be as clear as possible about the purpose and limitations of this investigation. GoL pro-
vides a simple model universe in which we can study in detail the transition to autopoietic entities. Such
models can help to hone our intuitions and to develop the conceptual, mathematical, and computational
tools necessary to move forward. A consideration of the possible implications of this investigation for the
origin of life in the physical universe will be left for the discussion section at the end of the article.

The article is organized as follows. I begin with a brief review of the general statistical properties
of GoL. This is followed by a large simulation experiment examining how the density of gliders
evolves over time from random initial conditions parameterized by the initial 1-density (the number
of ones per site). I then develop a theoretical framework for studying the statistical mechanics of
gliders and the processes of creation, persistence, and destruction that underlie their time evolution.
This framework is then used to explain the main features of the simulation experiment. After
showing how the basic theoretical framework can be extended to calculate more refined properties,
the article concludes with a discussion of some possible implications for thinking about the origin of
biological life and directions for future work.

An earlier version of this article appeared previously [8].

Artificial Life Volume 26, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
6
1
5
1
8
9
6
3
4
7
a
r
t
l

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

R. D. Beer

An Investigation into the Origin of Autopoiesis

Figure 1. The 16 possible configurations of a glider in the Game of Life. The horizontal black line separates the wedge
(top) and rocket (bottom) forms. The dashed vertical gray line separates the left- and right-handed configurations. Each
quadrant contains the four possible orientations of a configuration with a given form and chirality.

2 Some Facts of Life

The general statistical evolution of the GoL universe provides the background against which the
emergence, proliferation, and extinction of gliders occur. Gliders both contribute to and are influ-
enced by that evolution. Accordingly, I begin with a brief review of the mean density evolution of
GoL from random initial conditions [3, 27].

Consider a 100 × 100 grid with periodic boundary conditions. At time t = 0, we randomly
initialize the grid by setting each site to 1 with a probability p (0 with a probability 1 − p). The initial
1-density in a grid whose states are chosen in this way will be binomially distributed, with a mean of
p and a variance of p(1 − p). We then evolve the grid forward in time using GoL physics, and track
its density. Repeating this experiment many times gives an estimate of the mean density evolution of
GoL, (cid:2)q

t ( p).

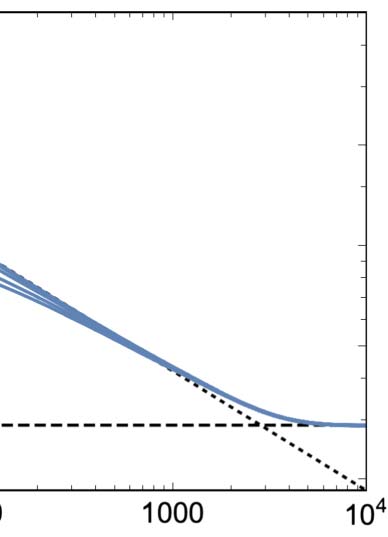
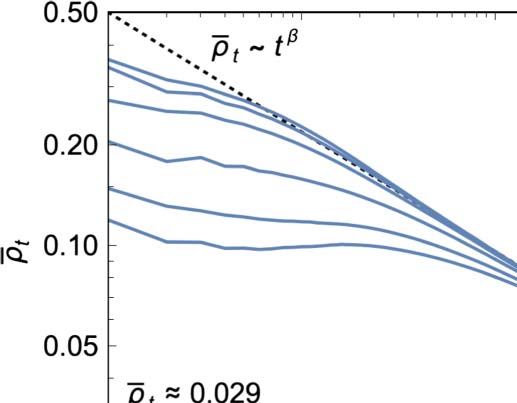
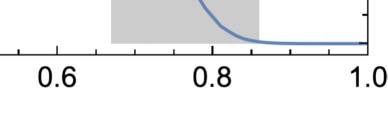
There is a strong general tendency for the mean 1-density to decay toward 0 over time regardless
of its initial value. For a wide range of initial densities 0.15 ≤ p ≤ 0.6, this decay exhibits a universal
form divided into three epochs (Figure 2(a)). First, there is an initial transient whose shape and du-
ration depend on p. Second, there is a power law decay with a scaling exponent of b ≈ −0.36 (dotted
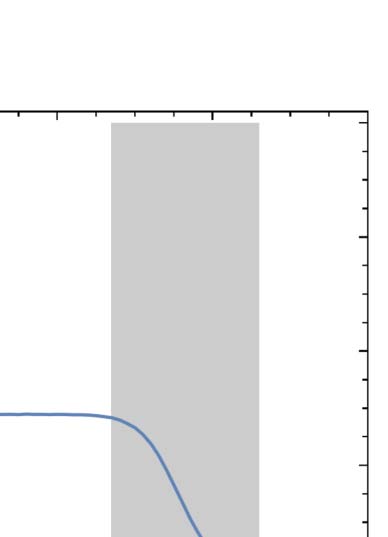
line). Finally, the power law decay flattens out to a common asymptotic density of (cid:2)q∞ ≈ 0.029
(dashed horizontal line).

The general long-term behavior of GoL is perhaps best illustrated by plotting an estimate of its
asymptotic 1-density as a function of p (Figure 2(b)). In this plot, the behavior described above
shows up as a large flat region of nonzero (cid:2)q∞. Sufficiently far outside of this range, we observe very
different behavior, with the 1-density falling all the way to 0. Between these two regions of distinct
(cid:2)q∞ values are transition regions in which (cid:2)q∞ varies smoothly with p. Thus, gliders exist in a universe
in which the mean 1-density is generally falling over time and whose long-term fate depends only
weakly on p except for two transition regions centered around p ≈ 0.065 and p ≈ 0.757.

Artificial Life Volume 26, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
6
1
5
1
8
9
6
3
4
7
a
r
t
l

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

R. D. Beer

An Investigation into the Origin of Autopoiesis

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
6
1
5
1
8
9
6
3
4
7
a
r
t
l

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Figure 2. The time evolution of mean density in GoL. (a) A log-log plot of the time evolution of mean 1-density (cid:2)q
t(p) for
different initial 1-probabilities p = 0.15, 0.2, 0.3, 0.4, 0.5, 0.6. (b) The asymptotic mean 1-density (cid:2)q∞(p) as a function of
1-probability p, with transition regions marked in gray. All curves represent the mean of 105 samples.

3 Mean Glider Density Evolution

We now turn our attention to the time evolution of the mean glider density. Let us begin with some
data. We duplicate the experiment described in the previous section, except now we track mean
glider density rather than 1-density. Repeating this experiment many times over a fine grid of
1-probabilities gives us a map of the time evolution of the mean glider density as a function of
p (Figure 3(a)).

This map reveals several interesting features. Gliders generally exist over only a limited range of
initial 1-probabilities and time, which we might call the glider era. For 0.2 ≤ p ≤ 0.6, the mean glider
density rises very quickly to a peak at t ≈ 60 and then begins a slow fall toward 0. However, as we
approach the lower value of p ≈ 0.04 or the upper value of p ≈ 0.85, the pattern changes. Now there
is a delay before the increase begins and a much slower rise toward a lower peak. Interestingly, near
these transition regions, the population of gliders never quite decays to 0 (dim horizontal bands in
Figure 3(a)). At still more extreme values of p, gliders never arise.

Some of this structure can be seen more clearly in high-resolution slices at constant p or t (Figure 3(b),
3(c)). At t = 0, the mean glider density has a single peak at p ≈ 0.23. By t = 5, a burst of glider creation at
larger p values has produced a second peak at p ≈ 0.64. Subsequent glider creation at intermediate
p values then lifts the valley between these two peaks until, by t = 60, a broad mesa appears. This
mesa then begins to slowly decrease in height over the next several thousand time steps until its
center collapses by t = 5000, leaving behind two small peaks at its edges corresponding to the two
faint bands of glider persistence mentioned earlier.

Artificial Life Volume 26, Number 1

R. D. Beer

An Investigation into the Origin of Autopoiesis

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
6
1
5
1
8
9
6
3
4
7
a
r
t
l

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Figure 3. An experimental study of the time evolution of gliders. (a) Mean glider density (cid:2)gt(p) as a function of time t and
initial 1-probability p. For each value of p (resolution Dp = 0.01), the corresponding strip of time (resolution Dt = 1)
represents the time evolution of the mean glider density for 104 random initial conditions on a 100 × 100 grid with
periodic boundary conditions. The portion of the plot for which t > 4000 has been scaled by a factor of 5 in order to
bring out two faint bands of asymptotic glider persistence. Shown below are selected larger-sample-size (105 samples)
slices at constant t (b) and constant p (c).

Artificial Life Volume 26, Number 1

R. D. Beer

An Investigation into the Origin of Autopoiesis

Thus, gliders arise quite robustly from random initial conditions and proliferate for hundreds
of time steps before slowly falling to extinction (except for two small ranges of p, for which
gliders persist indefinitely). These results set an agenda for the analysis to be performed in
the rest of this article. What are the processes by which gliders are created and destroyed?
Can we quantify them? How does the balance between these processes change over time?
How does it vary with p? How does the interplay between creation and destruction give rise
to all of the features described above? In order to answer such questions, we will first need
to develop the necessary theoretical tools.

4 A Statistical Mechanics of Gliders

Let (cid:2)gt( p) be the mean density of gliders in the grid at time t, given a random initial state characterized
by a 1-probability p. When advancing in time, existing gliders can either persist or be destroyed and
t ( p), and (cid:2)G−
new gliders can be created. Let (cid:2)Gþ
t ( p) denote the corresponding mean glider
density creation, persistence, and destruction operators, respectively. Then the mean glider density at
time t can be expressed as

t ( p), (cid:2)G0

(cid:2)gt pð Þ ¼ (cid:2)gt−1 pð Þ þ (cid:2)Gþ

t−1 pð Þ− (cid:2)G−

t−1 pð Þ

¼ (cid:2)G0

t−1 pð Þ þ (cid:2)Gþ

t−1 pð Þ:

Note that the definitions of creation, persistence, and destruction are grounded in our previous
analysis of what it means for a glider to persist [5]. Specifically, a glider at time t is considered
to be the same as a glider at time t + 1 if the latter falls entirely within the light cone of the
former.

Calculating these operators is an exercise in combinatorics (see the Appendix for full details). Let
G5×5 and G7×7 respectively denote the sets of 5 × 5 and 7 × 7 configurations that contain a glider.
Let ℬ1(G5×5) be the 1-basin of a glider, that is, the set of 7 × 7 configurations that evolve into 5 × 5
configurations containing a glider in one step. In addition, let ℬ1(G5×5)\G7×7 be the set of 7 × 7
configurations that are 1-precursors of gliders but that do not themselves contain a glider, and
denote its cardinality by |ℬ1(G
7×7|k denote the Hamming weight
5×5)\G
5×5)\G
decomposition of |ℬ1(G
7×7 that con-
tain exactly k 1s.

5×5)\G
7×7|, that is, the number of configurations in ℬ1(G

With these definitions in place, the creation operator (cid:2)Gþ

0 ( p) can be expressed as just the expected
increase in mean glider density due to glider precursors in the 1-basin evolving into gliders in the
next step. Since setting each site to 1 with probability p in a 7 × 7 = 49 site grid induces a binomial
distribution over the number of 1s in the grid, we have

7×7|. Finally, let |ℬ1(G

5×5)\G

”

(cid:2)
(cid:2)

pð Þ ¼ E

(cid:2)Gþ
0

(cid:2)
(cid:2)

;

ℬ1 G5(cid:2)5
ð
ð 49
k

Þ∖G7(cid:2)7
Þ

ð
k∼B 49; p

Þ:

Expanding this expectation using the probability mass function of the binomial distribution ð N
k
(1 − p)N−k and canceling the normalization factor, we obtain

Þpk

(cid:2)Gþ
0

pð Þ ¼

X49

(cid:2)
(cid:2)

k ¼ 0

ð
ℬ1 G5(cid:2)5

Þ∖G7(cid:2)7

(cid:2)
(cid:2)

ð
k pk 1− p

Þ49−k:

Artificial Life Volume 26, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
6
1
5
1
8
9
6
3
4
7
a
r
t
l

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

R. D. Beer

An Investigation into the Origin of Autopoiesis

A similar approach can be taken with the persistence operator (cid:2)G0

5×5) that contains preexisting gliders. If we denote by ~G

0( p), except that now our con-
7×7 the set of

cern is with the subset of ℬ1(G
7 × 7 configurations that do not contain a glider, then

(cid:2)G0
0 pð Þ ¼

X49

(cid:2)
(cid:2)

k ¼ 0

ð
ℬ1 G5(cid:2)5

Þ∖~G7(cid:2)7

(cid:2)
(cid:2)

ð
k pk 1− p

Þ49−k:

Finally, the destruction operator (cid:2)G−

0 ( p) concerns the subset of glider-containing 7 × 7 configu-
rations that evolve into 5 × 5 configurations without gliders. This is most easily computed from the
persistence operator as

0 pð Þ ¼ (cid:2)g0 pð Þ − (cid:2)G0
(cid:2)G−

0 pð Þ:

If we generalize the glider 1-basin ℬ1(G5×5) to the t-basin ℬt(G) (the set of configurations that evolve

to G in t steps), then it is straightforward to express the glider density operators for arbitrary time:

X2tþ5
Þ2

(cid:2)
(cid:2)

k ¼ 0

X2tþ5
Þ2

(cid:2)
(cid:2)

(cid:2)Gþ
t

pð Þ ¼

ℬtþ1 G5(cid:2)5
ð

ð
Þ∖ℬt G7(cid:2)7

(cid:2)
(cid:2)

ð
k pk 1− p

ð
Þ 2tþ5

Þ2−k;

(cid:2)G0
t pð Þ ¼

ℬtþ1 G5(cid:2)5
ð

Þ∖ℬ~t G7(cid:2)7
ð

(cid:2)
(cid:2)

ð
k pk 1 − p

ð
Þ 2tþ5

Þ2−k;

k ¼ 0
pð Þ ¼ (cid:2)gt pð Þ− (cid:2)G0

(cid:2)G−
t

t pð Þ:

For example, the basic idea of the generalized creation density operator expression is to remove from the
(t + 1)-basin of a glider those configurations that would evolve to a glider in t steps. Note that these
expressions assume that the size of the grid is large relative to (2t + 5) × (2t + 5). Once the two sizes
become comparable, the boundary conditions of the grid must be taken into account.

Several different methods for computing the coefficients in these expressions are possible. Con-
sider the creation operator coefficients |ℬ1(G5×5)\G7×7|k. In the forward algorithm, we scan each pos-
sible 7 × 7 configuration, filter out those in G7×7, and then evolve it one step forward in time and
truncate to 5 × 5. If the resulting configuration contains a glider, then we increment the coefficient
corresponding to the number of 1s in the original 7 × 7 precursor. In the backward algorithm, we work
backward from each 5 × 5 glider configuration, doing a depth-first search through possible inver-
sions of the constituent cells and then filtering and counting as before. The incremental aggregation
algorithm, which avoids individually visiting each possible precursor, can be used to calculate mean
glider density operator coefficients in a way similar to its use for calculating GoL mean-field-theory
coefficients [7]. Finally, considerable success has been achieved applying Boolean satisfiability
solvers to a variety of problems in GoL [17, 21]. Details of the approach we take in this article
to calculate glider density operator coefficients are given in the Appendix.

Plots of the t = 1 coefficients are shown in Figure 4. Note that the creation, persistence, and
destruction coefficients have very different magnitudes and peak at different values of k. Unfortu-
nately, the density operator coefficients quickly become very expensive to compute exactly. Indeed,
the total glider 1-basin ℬ1(G5×5) already contains over 40 billion configurations. Thus, we will resort
to Monte Carlo estimates of glider density and density operators for larger t.

5 Glider Origin and Proliferation

Using the above theory, we will analyze the time evolution of gliders in two stages (Figure 5). During
stage 1, which will be the focus of this section, the glider density quickly rises to its peak. The following

Artificial Life Volume 26, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
6
1
5
1
8
9
6
3
4
7
a
r
t
l

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

R. D. Beer

An Investigation into the Origin of Autopoiesis

Figure 4. Glider creation (cid:2)Gþ
Note that each set of coefficients has a different scale (indicated on the left).

0 (p) (green), persistence (cid:2)G0

0(p) (blue), and destruction (cid:2)G−

0 (p) (red) operator coefficients.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
6
1
5
1
8
9
6
3
4
7
a
r
t
l

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Figure 5. A decomposition of the mean glider density over p at selected times on a 100 × 100 grid. In each plot, the
current mean glider density (cid:2)gt(p) is black, the previous mean glider density (cid:2)gt−1(p) is gray, and the mean creation (cid:2)Gþ
t−1(p),
persistence (cid:2)G0
t−1(p) densities are green, blue, and red, respectively. The inset of the t = 200 plot shows
an expanded view of the boxed area. The gray boxes in the t = 5000 plot mark the GoL asymptotic 1-density transition regions
shown in Figure 2. The t = 0 and t = 1 plots were calculated exactly, whereas the remaining plots were based on Monte Carlo
estimates (105 samples per value of p).

t−1(p), and destruction (cid:2)G−

Artificial Life Volume 26, Number 1

R. D. Beer

An Investigation into the Origin of Autopoiesis

section will study stage 2, during which the glider density slowly falls to its asymptotic value. The boundary
between the two stages is somewhat p-dependent, but occurs at roughly t ≈ 60. The analysis in these two
sections decomposes and explains the family of plots in Figure 3(b).

The following relations are all trivial consequences of the definitions above, but can be useful for

interpreting the correspondingly colored plots in Figure 5:
t−1 pð Þ þ (cid:2)Gþ
t−1 pð Þ þ (cid:2)G−
t−1 pð Þ − (cid:2)G−

(cid:2)gt pð Þ ¼ (cid:2)G0
(cid:2)gt−1 pð Þ ¼ (cid:2)G0
(cid:2)gt pð Þ − (cid:2)gt−1 pð Þ ¼ (cid:2)Gþ

t−1 pð Þ;
t−1 pð Þ;
t−1 pð Þ:

Our story begins on a random grid with 1-probability p. What is the density of gliders occurring
completely by chance in a such a grid, before any time evolution has taken place? This density is
given by (cid:2)g0( p). Since there are 16 possible glider configurations and each glider contains five 1-cells
and seventeen 0-cells, we have (cid:2)g0( p) = 16p5(1 − p)17 (Figure 5, t = 0). This function has a single
maximum at p * = 5/22 ≈ 0.23, where the density of the grid coincides with that of a glider and the
probability of gliders occurring randomly is thus maximized. As we move away from this value, the
chances of randomly creating a glider fall smoothly to zero.

Advancing one time step, the processes of glider creation, persistence, and destruction begin. The
mean glider density at t = 1, (cid:2)g1( p) (black curve in Figure 5, t = 1), now has two peaks. What causes
these peaks? One might suspect that the left one is a holdover from the previous peak in (cid:2)g0( p), but
this turns out to be incorrect. Almost all random initial gliders are immediately destroyed by under-
going destructive interactions with their environment (red curve). Only a small fraction of them
persist (blue curve), and they do so at a smaller value of p than the earlier peak. In fact, almost
all of the glider density observed at t = 1 is due to the creation of new gliders (green curve).

Comparing the green creation density plot for t = 1 in Figure 5 with the green creation coeffi-
cient plot in Figure 4 from which it is derived, we note an apparent discrepancy. Although (cid:2)Gþ
0 ( p) has
two peaks, |ℬ1\G7×7|k appears to have only one. Where does the second peak come from? Given
the scale of the coefficient plot, it may seem as if the creation coefficients are zero below about k =
15, but in fact they are nonzero until k = 4. For example, the k = 10 creation coefficient is 509,208.
These coefficients are differentially multiplied by the polynomial terms from the probability mass
function of the binomial distribution, resulting in nonlinear amplification or attenuation at different
values of p. Thus, the overall shape of operator density curves can only be understood in terms of
the interaction between the coefficient and polynomial factors.

As time continues to advance, the interplay between creation and destruction becomes more com-
plicated before eventually settling down to a simpler pattern that carries the mean glider density to its
maximum around t ≈ 60. At t = 2, the balance between creation and destruction at smaller p holds the
left peak relatively constant, but the dominance of destruction at larger p pulls the right peak down and
moves it to the right. Over the next several time steps, this balance shifts back and forth, alternately
raising each peak until, by t = 6, both have reached their maximum height. Then the two peaks drop
slightly and stabilize. Simultaneously, the valley between the two peaks begins to rise.

For the remainder of stage 1, changes in mean glider density occur only for values of p that fall within
the valley between the two peaks. The floor of this valley slowly rises to become a mesa by the end of stage
1. The rise is fueled by a slight dominance of creation over destruction that can be seen clearly in the t = 15
plot. As the glider density approaches its maximum around t ≈ 60, the magnitude of this creation bias
steadily drops until creation and destruction temporarily balance and change in glider density pauses.

6 Glider Extinction and Asymptotics

Beyond the maximum glider density at t ≈ 60, stage 2 begins. This stage is mainly characterized by a
long slow collapse of the mesa observed at the end of stage 1. The drop in glider density is driven by

Artificial Life Volume 26, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
6
1
5
1
8
9
6
3
4
7
a
r
t
l

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

R. D. Beer

An Investigation into the Origin of Autopoiesis

the dominance of destruction over creation in stage 2. The fall is slow because the imbalance is very
small, as can be seen in the zoomed inset at t = 200, and it only decreases further as time passes.
During the collapse of the mesa, there is also quite a bit of transient activity around its edges. Initially,
the mesa widens. Then its edges rise and flatten several times (e.g., Figure 5, t = 200). As the mesa
continues to drop, the earlier valley eventually reappears (Figure 5, t = 2500). The bottom of the valley
then slowly falls toward zero density as both creation and destruction cease. Asymptotically, only two
small peaks of glider density at the edges of the former mesa or valley remain (Figure 5, t = 5000).

What is so special about these edges? Why do these narrow ranges of p values behave so differ-
ently, both transiently and asymptotically, from all of the others? At least part of the answer can be
found in the statistical physics of the GoL universe. Recall that transition regions separate values of p
for which (cid:2)q∞( p) = 0 and (cid:2)q∞( p) = 0.029 (gray boxes in Figure 2(b)). If we superimpose the locations
of these transition regions in asymptotic 1-density on the plot of the asymptotic glider density (cid:2)g∞( p),
the connection becomes clear (gray boxes in Figure 5, t = 5000). The transition regions in asymp-
totic 1-density align with the asymptotic glider density peaks, and thus with the peaks in the early
parts of stage 1 and the mesa edges in stage 2.

What appears to be happening is the following. On the one hand, as in any nontrivial pattern, the
only environments in which gliders can come into being are those of intermediate density; extreme
densities quickly decay to the all-0 quiescent state. On the other hand, the only environments that
gliders can survive in the long term are those that are fairly sparse; denser environments quickly lead
to destructive interactions. The transition regions represent a tradeoff between these two extremes.
Note that the asymptotic glider density peaks are shifted toward the outer edges of the 1-density
transition regions, suggesting that the balance is not a trivial one.

Finally, in order to highlight the trends in glider density dynamics, it is useful to decompose it over time at
a fixed value of p rather than as a function of p at fixed times as in Figure 5. This amounts to decomposing
plots such as the one shown in Figure 3(c). Such a decomposition is shown in Figure 6 for p = 0.4 and t ≤
100. We see that, after a brief initial transient, all five curves climb to their peaks before slowly falling toward
0. Creation peaks first (green), followed quickly by destruction (red) and then later by (cid:2)gt−1( p) (gray) and (cid:2)gt( p)
(black), and finally by persistence (blue). Note that, although creation dominates destruction at first,
they quickly become almost perfectly balanced, so that extremely small differences between the two
processes drive first the proliferation and eventually the extinction of gliders. Indeed, the two curves
are almost tangent at their crossing point, so that the actual peak of glider density is quite subtle.

7 Refinements and Extensions

Applying the same general approach described above, we can also calculate more refined properties
of the time evolution of gliders. We briefly consider two examples here.

Figure 6. A decomposition of the mean glider density over time for p = 0.4. Color conventions are the same as in Figure 5.
The curves represent means of 105 samples.

Artificial Life Volume 26, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
6
1
5
1
8
9
6
3
4
7
a
r
t
l

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

R. D. Beer

An Investigation into the Origin of Autopoiesis

The first refinement we will examine is decomposing creation density by glider form. Consider
(cid:2)Gþ
0 ( p) (green curve in the t =1 plot in Figure 5). In order to split this into its wedge and rocket
components (Figure 1), we need to separate the |ℬ1(G
7×7|k coefficients into wedge and
rocket contributions. The result is shown in Figure 7(a). Interestingly, we find that the rocket form
dominates creation at lower values of p and the wedge form dominates at higher values. This is due
to the fact that the rocket 1-basin is larger around the left peak and the wedge 1-basin is larger
around the right peak. Decomposition by glider form can easily be applied to the other glider density
operators to examine how the contribution of glider form varies with time.

5×5)\G

A second possible refinement is to decompose the persistence density by perturbation class. Con-
sider (cid:2)G0
0( p) (blue curve in the t = 1 plot in Figure 5). We know from previous work that the set of
nondestructive glider perturbations can be divided into six classes depending on the state of the
glider after the perturbation occurs [5]. These classes were assigned the arbitrary color names GRAY,
BLACK, BLUE, BROWN, ORANGE, and GREEN. Of the gliders that persist from t = 0 to t = 1, what
fraction arises from each class? Splitting the coefficients |ℬ1(G5×5)\~G7×7|k by perturbation class,
we can calculate the contributions from each class. The result is shown in Figure 7(b). We see that
this persistence is dominated by the so-called null perturbations (GRAY and BLACK), which have no
effect on the natural time evolution of rockets and wedges, respectively [5]. Although their peak
contribution is almost two orders of magnitude smaller, BLUE perturbations begin to dominate for
p > 0.45. BROWN, ORANGE, and GREEN perturbations are extremely small for all p. Once again, this
decomposition can be extended to later times.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
6
1
5
1
8
9
6
3
4
7
a
r
t
l

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Figure 7. More refined decompositions of glider density operators. (a) A decomposition of glider creation (cid:2)Gþ
0 (p) (solid curve)
into its wedge (dashed) and rocket (dotted) contributions. (b) A decomposition of glider persistence (cid:2)G0
0(p) (upper blue curve)
into its perturbation class contributions (GRAY, BLACK, BLUE, BROWN, ORANGE, and GREEN). The inset shows a vertical expansion of
the plot. All of the curves in these plots result from exact calculations.

Artificial Life Volume 26, Number 1

R. D. Beer

An Investigation into the Origin of Autopoiesis

Finally, I present preliminary results from three extensions of the present work, each of which is
mentioned in the discussion section. The first extension involves moving beyond a focus on gliders
alone. As an initial step toward a broader analysis of the origin of autopoiesis in GoL, Figure 8(a) shows
a statistical study of a dozen of the most common persistent bounded entities in GoL [9]. At left, the

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
6
1
5
1
8
9
6
3
4
7
a
r
t
l

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Figure 8. Preliminary results from several extensions of the present work. (a) Mean density of twelve of the most com-
mon patterns in GoL for random initial grids with a 1-probability of p (left) and over time from an initially random grid
with 1-probability p = 0.4 (right). Data represent the mean of 105 samples on a 100 × 100 grid with periodic boundary
conditions. Images of these and many other GoL patterns can be found at http://www.conwaylife.com/wiki. (b) Examples
of the ways in which an overlapping pair of gliders can be created from nonglider configurations (top left), split from an
existing glider (top right), persist over time (bottom left ), and annihilate one another (bottom right). (c) Examples of
new persistent bounded entities that are stabilized by a single cell externally held on (red) or off (pink), including a static
configuration (top left), an oscillating configuration (top right), and a moving configuration (bottom).

Artificial Life Volume 26, Number 1

R. D. Beer

An Investigation into the Origin of Autopoiesis

mean density of each class of entity in random grids with a 1-probability of p is shown. Note that one
entity (Blinker) dominates all the others. Note also that the densities of all twelve entities peak over
roughly the same range of p. At right, the initial time evolution of these densities is shown for p = 0.4.
Note that the initial density of an entity is not necessarily predictive of its subsequent time evolution. For
example, the entity with the lowest initial density (Pond) eventually surpasses four others whose den-
sities were initially much higher. It is also interesting that two pairs of entities with very different initial
densities evolve to almost the same density (Block + Blinker and Loaf + Boat).

The second extension concerns multiple gliders. The theory developed in this article accounts for
the independent creation, persistence, and destruction of individual gliders. However, multiple gliders
that share portions of their boundaries can also occur (Figure 8(b)). For example, overlapping glider
pairs can appear spontaneously from nonglider precursors (Figure 8(b), top left), split from a single
glider precursor (top right), persist from one time step to the next (bottom left), or destroy one an-
other (bottom right). It would be interesting to extend the theory developed in this article to explicitly
account for such multiglider interactions. For example, one could imagine defining a splitting operator
for characterizing the mean glider density changes induced by one glider dividing into two.

The third extension concerns the nature of the Conway physics. In GoL, entities can persist indef-
initely in an otherwise empty grid. In a more realistic physics, autopoietic systems would require non-
equilibrium conditions supported by a flow of low-entropy energy and material. As a first step toward
such nonequilibrium conditions, we can consider a version of GoL in which particular cells are held off
or on in particular patterns. Under such driven conditions, new GoL entities can appear that feed off
this external source of order. Three examples are shown in Figure 8(c). In the first (top left), a new static
pattern that would collapse in standard GoL is stabilized by a single cell that is externally held on (red
cell). In the second (top right), a new oscillating pattern is driven by alternately switching a single cell on
(red) and off (pink). In the third example (bottom), a standard GoL block follows an externally held cell
(red) that moves diagonally by one grid location every fifth time step.

8 Discussion

Employing a glider in the Game of Life as a toy model of autopoiesis, this article has taken some
initial steps toward an investigation into the origin and proliferation of life from an autopoietic per-
spective. First, I presented the results of a large simulation experiment examining how the density of
gliders evolves over time from random initial conditions parameterized by initial 1-density. Then I
developed a glider statistical mechanics grounded in the dynamics of glider configurations and the
combinatorics of their basins of attraction. This theory was then used to calculate the probability of
gliders appearing in random grids and to decompose the time evolution of glider density into its
creation, persistence, and destruction components. Finally, I showed how this theory could be
extended to calculate more refined properties such as decomposing creation by glider form and
persistence by perturbation class.

What can we conclude about the origin of gliders from this analysis? The glider era is certainly a
well-delineated region in time and initial 1-density, suggesting that statistically robust processes are at
work. However, this analysis has revealed a remarkably rich and, at times, rather delicate interplay
between the processes of glider creation, persistence, and destruction underlying this era. Given this
extended interplay, is it even correct to ask about the origin of gliders, as if it were a unique event?
Although we can exactly calculate the probability that gliders appear in random grids, we saw that
almost all such gliders are immediately destroyed and it is gliders that are subsequently created that
fuel the proliferation. Perhaps we should focus instead on the overall dynamics of the underlying
processes, with a particular emphasis on the conditions in which glider creation and persistence
dominate glider destruction.

Because these processes are highly density-dependent, it is difficult to separate their dynamics
from the broader statistical evolution of the GoL universe itself. This has an interesting resonance
with the perspective put forward in a recent book [29]. The authors argue that the origin of life

Artificial Life Volume 26, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
6
1
5
1
8
9
6
3
4
7
a
r
t
l

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

R. D. Beer

An Investigation into the Origin of Autopoiesis

involves not some isolated local event, but rather a series of planetary phase transitions in which the
emergence of structure at one stage provides the foundation for the emergence of the next. Although
highly simplified, GoL might be a useful toy model in which to investigate in some detail how such a
global scenario might play out. For example, the analysis carried out for gliders in this article could
easily be repeated for the dozen or so most common forms of persistent localized entities that typically
arise from random initial conditions over roughly the same time scale in GoL. It would be interesting
to study the co-emergence of this “ecosystem” as a collective phenomenon in the time evolution of
GoL, toward which the preliminary work shown in Figure 8(a) is a first step.

In the short term, there are several other avenues for future work. There is still much to be done
in fully understanding how the delicate interplay between the density operators and their various
decompositions gives rise to all of the observed features of glider density evolution. This would
be facilitated by improved algorithms for computing density operator coefficients, as well as better
mathematical formulations. Finally, how might reproduction fit into this picture? Although nothing
like a genome is present in a glider, a small number of “splitting” perturbations exist that produce
two gliders from one, with the properties of the new gliders depending in a systematic way on the
properties of the original one (Figure 8(c), top right).

More broadly, investigations into the origin of life have typically focused on specific prebiotic
chemical interactions that could lead to a form of replication, metabolism, or compartmentalization
[26]. Autopoiesis can be thought of as providing a kind of organizational backbone for the molecular
and energetic considerations of operating in the physical world, as every living system must do.
Perhaps the most interesting implication of adopting an autopoietic perspective on questions of
origins is the shift it induces to what might be called an “organization-first” approach. The basic
idea is to change the focus from specific molecular components and reaction pathways to the sim-
plest possible autopoietic organizations relative to a given physics. Cellular automata offer a rich
variety of simple physics in which we can investigate the emergence, degradation, stabilization,
and complexification of organizations. However, carrying such a program forward will require mov-
ing beyond the kind of purely statistical treatment undertaken in this article to a direct investigation
of the dynamics that underlie these configuration statistics. How do sets of interacting processes
spontaneously organize into closed networks with a self-generated boundary? How are we to char-
acterize the dynamics of process dependence networks themselves? Despite the fact that an under-
standing of the dynamics of organizations has barely begun, both in general [13, 14, 16] and for GoL
specifically [6], this is the direction in which we must push.

Of course, the study of abstract toy models can only take us so far. Ultimately, it will be necessary
to take the physical reality into account. The best way to conceive of these physical details is as a
source of material constraint on the formation of autopoietic systems. Very simple autopoietic sys-
tems are common in GoL owing to its intrinsically dissipative (state space volumes contract onto
limit sets) and therefore pattern-forming nature. In the physical world, much more work (both fig-
uratively and literally) needs to be done to produce and maintain autopoietic organizations, signif-
icantly raising their minimal complexity. As is well known, properly harnessing energy flows is
essential to the physical instantiation of autopoiesis, making nonequilibrium thermodynamics a cen-
tral concern.

One possible path toward such physical concerns is to explore the application of autopoietic
concepts to more realistic protocell models [2]. However, the path that I prefer is an incremental
one, endowing simple cellular automata models such as GoL with increasingly more physically re-
alistic characteristics. This way we can systematically explore how each additional physical constraint
influences the networks of processes that can form. Because cellular automata have been seriously
pursued as a modeling methodology for physical systems for many years, there is a wide literature to
draw upon for this endeavor [11, 12, 32, 33]. For example, reversibility [24, 35], temperature depen-
dence [1, 27], conserved quantities [10, 31], driven/nonequilibrium conditions (Figure 8(c)), and so
on, can all be incorporated, and cellular automata have even been used to model various aspects of
biochemistry [20]. In any case, we need to identify the simplest physical settings in which generic
features of the origin of life can be explored so that we can place the specific historical contingencies

Artificial Life Volume 26, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
6
1
5
1
8
9
6
3
4
7
a
r
t
l

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

R. D. Beer

An Investigation into the Origin of Autopoiesis

underlying the emergence of terrestrial life into its proper position within the broader space of possible
scenarios by which autopoiesis more broadly can arise within an initially nonautopoietic universe.

Acknowledgments
I would like to thank Eran Agmon and the anonymous reviewers for their feedback on an earlier
draft of this article. Portions of this work were presented at the workshop on “The Biological Foun-
dations of Enactivism” held at the 2016 Artificial Life XV Conference in Cancún, Mexico, and I
thank the participants for discussion. Computation performed for this research was supported in
part by Lilly Endowment, Inc., through its support for the Indiana University Pervasive Technology
Institute, and in part by the Indiana METACyt Initiative. The Indiana METACyt Initiative at IU is
also supported in part by Lilly Endowment, Inc.

References
1. Adachi, S., Peper, F., & Lee, J. (2004). The Game of Life at finite temperature. Physica D, 198(3–4), 182–196.

2. Agmon, E., Gates, A. J., Churavy, V., & Beer, R. D. (2016). Exploring the space of viable configurations in

a model of metabolism-boundary co-construction. Artificial Life, 22, 153–171.

3. Bagnoli, F., Rechtman, R., & Ruffo, S. (1991). Some facts of Life. Physica A, 171, 249–264.
4. Beer, R. D. (2004). Autopoiesis and cognition in the Game of Life. Artificial Life, 10, 309–326.
5. Beer, R. D. (2014). The cognitive domain of a glider in the Game of Life. Artificial Life, 20, 183–206.
6. Beer, R. D. (2015). Characterizing autopoiesis in the Game of Life. Artificial Life, 21, 1–19.

7. Beer, R. D. (2017). Computing aggregate properties of preimages for 2D cellular automata. Chaos, 27, 111104.

8. Beer, R. D. (2018). On the origin of gliders. In T. Ikegami, N. Virgo, O. Witkowski, M. Oka, R. Suzuki, &
H. Iizuka (Eds.), Proceedings of the 2018 Conference on Artificial Life (pp. 67–74). Cambridge, MA: MIT Press.

9. Berlekamp, E. R., Conway, J. H., & Guy, R. K. (1982). What is Life? In E. R. Berlekamp, J. H. Conway, &
R. K. Guy (Eds.), Winning ways for your mathematical plays, Vol. 2 (Chapter 25, pp. 817–850). New York:
Academic Press.

10. Capobioanco, S., & Toffoli, T. (2012). Conserved quantities in discrete dynamics: What can be recovered

from Noetherʼs theorem, how, and why? Natural Computing, 11, 565–577.

11. Chopard, B., & Droz, M. (1998). Cellular automata modeling of physical systems. Cambridge, UK: Cambridge

University Press.

12. Chopard, B. (2009). Cellular automata modeling of physical systems. In R. A. Meyers (Ed.), Encyclopedia of

complexity and systems science (pp. 865–892). New York: Springer-Verlag.

13. Crutchfield, J. P., & Görnerup, O. (2006). Objects that make objects: The population dynamics of

structural complexity. Journal of the Royal Society Interface, 3, 345–349.

14. Dittrich, P., & Speroni di Fenizio, P. (2007). Chemical organisation theory. Bulletin of Mathematical Biology, 69,

1199–1231.

15. Dyson, F. (1999). Origins of life. Cambridge, UK: Cambridge University Press.

16. Fontanna, W., & Buss, L. W. (1994). The arrival of the fittest: Toward a theory of biological organization.

Bulletin of Mathematical Biology, 56, 1–64.

17. Hartman, C., Heule, M. H., Kwekkeboom, K., & Noels, A. (2013). Symmetry in Gardens of Eden. The

Electronic Journal of Combinatorics, 20(3), 16.

18. Joyce, G. F., & Orgel, L. E. (2006). Progress toward understanding the origin of the RNA world. In R. F.

Gesteland (Ed.), The RNA world (3rd ed.), (pp. 23–56). Boca Roton, FL: CRC Press.

19. Kaufmann, S. A. (2000). Investigations. Oxford, UK: Oxford University Press.

20. Kier, L. B., & Seybold, P. G. (2009). Cellular automata modeling of complex biochemical systems. In R. A.
Meyers (Ed.), Encyclopedia of complexity and systems science (pp. 848–865). New York: Springer-Verlag.

21. Knuth, D. E. (2015). The art of computer programming, Vol. 4, Fascicle 6: Satisfiability. Boston: Addison-Wesley.

Artificial Life Volume 26, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
6
1
5
1
8
9
6
3
4
7
a
r
t
l

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

R. D. Beer

An Investigation into the Origin of Autopoiesis

22. Lanier, K. A., & Williams, L. D. (2017). The origin of life: Models and data. Journal of Molecular Evolution, 84,

85–92.

23. Luisi, P. L. (2006). The emergence of life: From chemical origins to synthetic biology. Cambridge, UK: Cambridge

University Press.

24. Margolus, N. (1984). Physics-like models of computation. Physica D, 10, 81–95.

25. Maturana, H. R., & Varela, F. J. (1973/1980). Autopoiesis: The organization of the living. In H. R.
Maturana & F. J. Varela (Eds.), Autopoiesis and Cognition. Dordrecht, The Netherlands: D. Reidel.

26. Ruiz-Mirazo, K., Briones, C., & de la Escosura, A. (2014). Prebiotic systems chemistry: New perspectives

for the origins of life. Chemical Reviews, 114, 285–366.

27. Schulman, L. S., & Seiden, P. (1978). Statistical mechanics of a dynamical system based on Conwayʼs Game

of Life. Journal of Statistical Physics, 19, 293–314.

28. Segré, D., Ben-Eli, D., Deamer, D. W., & Lancet, D. (2001). The lipid world. Origins of Life and Evolution of

the Biosphere, 31, 119–145.

29. Smith, E., & Morowitz, H. J. (2016). The origin and nature of life on earth: The emergence of the fourth geosphere.

Cambridge, UK: Cambridge University Press.

30. Szostak, J. W., Bartel, D. P., & Luisi, P. L. (2001). Synthesizing life. Nature, 409, 387–390.

31. Taati, S. (2012). Conservation laws in cellular automata. In G. Rozenberg, T. Bäck, & J. N. Kok. (Eds.),

Handbook of natural computing (pp. 259–286). New York: Springer-Verlag.

32. Toffoli, T. (1984). Cellular automata as an alternative to (rather than an approximation of) differential

equations in modeling physics. Physica D, 10(1–2), 117–127.

33. Toffoli, T., & Margolus, N. (1987). Cellular automata machines: A new environment for modeling. Cambridge, MA:

MIT Press.

34. Varela, F. J. (1979). Principles of biological autonomy. New York: North-Holland.
35. Vichniac, G. Y. (1984). Simulating physics with cellular automata. Physica D, 10(1–2), 96–116.

36. Walker, S. I., Packard, N., & Cody, G. D. (2018). Re-conceptualizing the origins of life. Philosophical

Transactions of the Royal Society A, 375, 20160337.

Appendix

This appendix gives the details underlying the calculation of the t = 0 glider density operator
coefficients described in the main text. In principle, one could compute coefficients such as
|ℬ1(G5×5)\G7×7|k by explicitly generating the set ℬ1(G5×5), removing all elements that contain
gliders, and then counting the number of 1s in each remaining element. However, the sizes of
these sets make such a direct approach untenable in practice. Instead, we directly compute the
Hamming weight decompositions of only relatively small sets and then calculate the coefficients
of interest by appropriately combining these “atomic” weights.

The basic idea of the calculation is illustrated in Figure 9. In radius-1 cellular automata such as GoL,
the configuration of an n × n lattice at time t is influenced by the configuration of the enclosing (n − 2) ×
(n − 2) lattice at time t − 1. Let ℒ n×n denote the set of all configurations of an n × n lattice, let Gn×n
denote the subset of ℒn×n that contains a glider, and let ℬ1(G
5×5) denote the subset of ℒ
7×7 that evolves
5×5 in one step (i.e., its 1-basin). Recall from the main text that, for any given subset of interest S, we
to G
need to compute the Hamming weight decomposition |S|k in order to compute (cid:2)GS

0 ( p) from

”

X49

(cid:2)GS
0 pð Þ ¼ E

j
k
Þ
For the persistence operator (cid:2)G0

ð 49
k

k ¼ 0

ð
k pk 1 − p

Þ49−k:

0( p), the subset of interest is ℬ1(G
7×7 (indicated in blue in
Figure 9). This subset is composed of all the ways that a glider can persist from one time step to the
next. Previous work demonstrated that there are exactly six ways that this can happen, arbitrarily

5×5)\~G

Artificial Life Volume 26, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
6
1
5
1
8
9
6
3
4
7
a
r
t
l

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

R. D. Beer

An Investigation into the Origin of Autopoiesis

Figure 9. An illustration of the various subsets of configurations relevant for the calculations given in the Appendix. ℒn×n
denotes the set of n × n lattices in GoL, Gn×n denotes the subset of n × n lattices containing gliders, and ℬ1(G5×5) denotes
the 1-basin of G5×5 (that is, the set of 7 × 7 precursors of G5×5). The subsets of ℒ 7×7 related to glider creation, persis-
tence, and destruction are colored green, blue, and red, respectively.

labeled by colors [4]. With W indicating the wedge form and R indicating the rocket form, we can
write these possibilities as W —→
W, and
BLACK
R —→
GREEN

R. Then we have that the Hamming weight decompositions of the subset of gliders that

R, W—→
ORANGE

W, W —→
BROWN

R, W —→
BLUE

R, R —→
GRAY

persist to the wedge form and the subset of gliders that persist to the rocket form are given by

(cid:2)
(cid:2)
(cid:2)

G →W
j

j
k

¼ W —→
BLUE

G →R
j

(cid:2)
(cid:2)
(cid:2)

¼ W —→
BLACK

(cid:2)
(cid:2)
(cid:2)

;

(cid:2)
(cid:2)
(cid:2)

þ R —→
GRAY

(cid:2)
(cid:2)
(cid:2)

þ W —→
BROWN

k
(cid:2)
(cid:2)
(cid:2)

(cid:2)
(cid:2)
(cid:2)

þ W —→
ORANGE

(cid:2)
(cid:2)
(cid:2)

þ R —→
GREEN

(cid:2)
(cid:2)
(cid:2)

;

respectively. From these we can compute the required persistence operator coefficients using

ð
jℬ1 G5(cid:2)5

Þ∖~G7(cid:2)7j

¼ G →W

j
k

Finally, a term such as W —→
BROWN

þ G →R
(cid:2)
(cid:2)
(cid:2)

; R

B
B
B
B
B
B
B
B
B
@

B
B
B
B
B
B
B
B
@

x1
x5
x8
x10
x12
x14
x21

x2
x6
x9
x11
x13
x15
x22

x3
0
0
0
0
x16
x23

0
0
1
1
0
x17
x24

0
1
0
1
0
x18
x25

0
0
0
1
0
x19
x26

x4
x7
0
0
0
x20
x27

can be computed from the solutions of

B
B
B
B
@

C
C
C
C
C
C
C
C
A

C
C
C
C
C
C
C
C
C
A

⋅
⋅
0
0
0

0
0
0
1
0

0
1
1
0
0

0
0
1
1
0

C
C
C
;
C
A

⋅
0
0
0
0

(cid:2)
(cid:2)
(cid:2)

where f is the GoL update function and dots denote locations whose values are irrelevant. As men-
tioned in the main text, there are many different ways to solve such equations. For the computations
underlying the results in this article, we extract a set of relations among the xi from this equation,
simplify them symbolically, and compile a specialized iterative solver that counts the number of
solutions in each Hamming weight class without having to store those solutions. The resulting
weights must then be multiplied by 8 to take account of the fact that the rocket form on the
right-hand side of this equation can appear in four different orientations and two different chiralities.
The other five terms can be computed in the same manner.

Artificial Life Volume 26, Number 1

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
a
r
t
l
/

a
r
t
i
c
e
–
p
d

f
/

2
6
1
5
1
8
9
6
3
4
7
a
r
t
l

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

R. D. Beer

An Investigation into the Origin of Autopoiesis

For the creation operator (cid:2)Gþ
Figure 9). We can express this as
(cid:2)
(cid:2)
(cid:2)
(cid:2)
(cid:2)
(cid:2)

(cid:2)
(cid:2)

ℬ1 G5(cid:2)5
ð

Þ∖G7(cid:2)7

ð
¼ ℬ1 W5(cid:2)5

(cid:2)
(cid:2)

ð
þ ℬ1 R5(cid:2)5

(cid:2)
(cid:2)

(cid:3)

− G →W

þ G →R

(cid:4)

;

0 ( p), the subset of interest is ℬ1(G5×5)\G7×7 (indicated in green in

where ℬ1(W
5×5) and ℬ1(R
5 × 5, respectively. For example, |ℬ1(W
0

5×5) are the 7 × 7 configurations that evolve to wedges or rockets in
5×5)|k can be computed from solutions to

B
B
B
B
B
B
B
B
B
@

B
B
B
B
B
B
B
B
@

x1
x8
x15
x22
x29
x36
x43

x2
x9
x16
x23
x30
x37
x44

x3
x10
x17
x24
x31
x38
x45

x4
x11
x18
x25
x32
x39
x46

x5
x12
x19
x26
x33
x40
x47

x6
x13
x20
x27
x34
x41
x48

x7
x14
x21
x28
x35
x42
x49

B
B
B
B
@

C
C
C
C
C
C
C
C
A

C
C
C
C
C
C
C
C
C
A

⋅
⋅
0
0
0

0
0
0
1
0

0
1
0
1
0

0
0
1
1
0

C
C
C
C
A

⋅
0
0
0
0

and similarly for |ℬ1(R5×5)|k. Once again, the resulting coefficients need to be multiplied by 8.

For the destruction operator (cid:2)G−

0( p), the subset of interest is G7×7\ℬ1(G5×5) (indicated in red in
Figure 9). Since, as explained in the main text, the destruction operator can be written in terms of
other known quantities, a direct calculation of the destruction operator coefficients is unnecessary.
However, to derive the destruction coefficients plotted in Figure 4, we use
(cid:2)
(cid:2)

(cid:2)
(cid:2)

(cid:4)

G7(cid:2)7∖ℬ1 G5(cid:2)5

¼ G7(cid:2)7
j

0 →W

þ G
j

0 →R

;

(cid:3)
− G
j

where the terms in the parentheses are calculated in the same way as the analogous unprimed terms
above except that we use a past-centered formulation of the individual wedge and rocket transfor-
mation terms rather than the future-centered formulation employed above. For example, the equa-
tion from which the term W 0 —→
BROWN
0

(cid:2)
(cid:2)
(cid:2) is derived becomes

R 0

(cid:2)
(cid:2)
(cid:2)

B
B
B
B
B
B
B
B
B
@

B
B
B
B
B
B
B
B
@

x1
x8
x12
x15
x17
x19
x21

x2
x9
x13
0
0
0
x22

x3
0
0
0
1
0
x23

x4
0
1
0
1
0
x24

x5
0
0
1
1
0
x25

x6
x10
0
0
0
0
x26

x7
x11
x14
x16
x18
x20
x27

C
C
C
C
C
C
C
C
A

C
C
C
C
C
C
C
C
C
A

B
B
B
B
B
B
B
B
@

⋅
⋅
⋅
⋅
⋅
⋅
⋅

⋅
⋅
⋅
0
0
0
0

⋅
⋅
0
0
1
1
0

⋅
⋅
0
1
1
0
0

⋅
⋅
0
0
0
1
0

⋅
⋅
⋅
⋅
0
0
0

C
C
C
C
C
C
C
C
A

;

and |G7×7|k is given by decomposing all the ways that a glider can be centered in a 7 × 7 lattice:

(cid:5)

8
< ¼ 16 : 0 (cid:6) ; 27 k −5 j G7(cid:2)7 j k 5 ≤ k ≤ 32; otherwise: Finally, we have the plots in Figure 7. The coefficients of the wedge and rocket decompositions of (cid:2)Gþ 5×5)|k − |G → R|k , 0 ( p) (Figure 7(a)) are given by |ℬ1(W respectively. The perturbation class decomposition coefficients in Figure 7b are given by the six unprimed glider transformation terms W —→ BLACK 5×5)|k − |G → W|k and |ℬ1(W (cid:2) (cid:2) , …, R —→ (cid:2) GRAY ; W ; R (cid:2) (cid:2) (cid:2) (cid:2) (cid:2) (cid:2) (cid:2) (cid:2) (cid:2) . k k 22 Artificial Life Volume 26, Number 1 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u a r t l / / l a r t i c e - p d f / / / / 2 6 1 5 1 8 9 6 3 4 7 a r t l / _ a _ 0 0 3 0 7 p d . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 An Investigation into the image

Download pdf