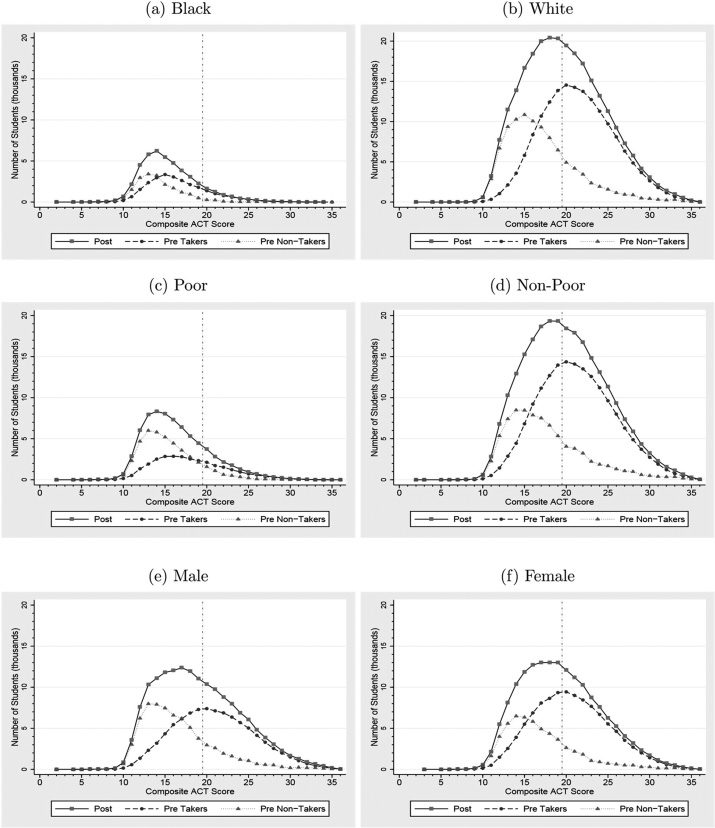
ACT FOR ALL: THE EFFECT OF MANDATORY
COLLEGE ENTRANCE EXAMS ON
POSTSECONDARY ATTAINMENT AND CHOICE
Joshua Hyman
Department of Public Policy
University of Connecticut
West Hartford, CT 06117
joshua.hyman@uconn.edu
Abstract
This paper examines the effects of requiring and paying for all
public high school students to take a college entrance exam, a
policy adopted by eleven states since 2001. I show that prior to
the policy, for every ten poor students who score college-ready
on the ACT or SAT, there are an additional five poor students
who would score college-ready but who take neither exam. I use
a difference-in-differences strategy to estimate the effects of the
policy on postsecondary attainment and find small increases in
enrollment at four-year institutions. The effects are concentrated
among students less likely to take a college entrance exam in the
absence of the policy and students in the poorest high schools.
The students induced by the policy to enroll persist through col-
lege at approximately the same rate as their inframarginal peers.
I calculate that the policy is more cost-effective than traditional
student aid at boosting postsecondary attainment.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
2
3
2
8
1
1
6
9
1
8
7
1
e
d
p
_
a
_
0
0
2
0
6
p
d
f
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
281
doi:10.1162/EDFP_a_00206
© 2017 Association for Education Finance and Policy
The Effects of Mandatory ACT-Taking
I N T RO D U C T I O N
1 .
Inequality in educational attainment has widened substantially during recent decades.
Not only do minority and low-income students enroll in postsecondary education in
lower proportions than their majority and higher-income counterparts, but conditional
on enrolling, these students are less likely to persist through college and complete a de-
gree (Bailey and Dynarski 2011). Although certainly not every low-income and minority
student would benefit from postsecondary education, recent research suggests that a
nontrivial number of high-achieving, disadvantaged students either do not attend col-
lege or attend a less selective school than they could (Pallais and Turner 2006; Bowen,
Chingos, and McPherson 2009; Hoxby and Avery 2013; Dillon and Smith 2017). Poli-
cies that induce low-income students to attend and persist at appropriately selective
institutions could have substantial implications for reducing educational inequality.
Many policies and interventions aim to increase the educational attainment of dis-
advantaged students. Policies such as Head Start, class size reduction, and school fi-
nance reform, which aim to increase the human capital of students, as well as policies
such as student aid that reduce the cost of college, have all been shown to success-
fully increase postsecondary attainment (Deming 2009; Deming and Dynarski 2010;
Dynarski, Hyman, and Schanzenbach 2013; Hyman, forthcoming). These policies are
all quite expensive, however, costing tens of thousands of dollars to induce one ad-
ditional student to enroll in college (Dynarski, Hyman, and Schanzenbach 2013). Re-
cently, interventions aimed at reducing informational and administrative barriers to
college enrollment have found large effects at a fraction of the cost of the more tradi-
tional tools mentioned above (Bettinger et al. 2012; Hoxby and Turner 2012; Carrell and
Sacerdote forthcoming). It remains to be seen whether these low-cost policies can be
implemented effectively at scale.
In this paper, I examine the impacts of an inexpensive policy aimed at boosting post-
secondary attainment that is currently operating at scale. Eleven states require and pay
for college entrance exams (i.e., the ACT or SAT) for all public school eleventh graders.
Given that it costs less than $50 per student for states to implement this policy, very small effects on college-going would suffice for the policy to be as cost effective as tra- ditional student aid. In this paper, I examine the effect of mandatory college entrance exams on postsecondary enrollment, persistence, and choice. I use an original student- level dataset containing six complete cohorts of eleventh-grade public high school stu- dents in Michigan, a state that implemented a mandatory ACT policy in 2007. The data include demographics, eighth- and eleventh-grade statewide assessment scores, infor- mation on postsecondary enrollment, and ACT and SAT scores for all test-takers during the sample period. To begin my analysis, I use the post-policy ACT score distribution to deduce what fraction of pre-policy non-takers would score at a college-ready level if they took the exam.1 I show that for every ten poor students taking a college entrance exam and scoring college-ready, there are an additional five poor students who do not take the test but who would score college-ready if they did. This represents a contribution to 1. The basic intuition for how I calculate the pre-policy number of students who did not take the exam, but would have scored college-ready, is by subtracting the number of test-takers who score college-ready in the pre-period from the number who do so in the post-period. 282 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / f / e d u e d p a r t i c e – p d l f / / / / 1 2 3 2 8 1 1 6 9 1 8 7 1 e d p _ a _ 0 0 2 0 6 p d f / . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Joshua Hyman the emerging literature on “undermatch.” Hoxby and Avery (2013) focus on the sup- ply of disadvantaged students who take a college entrance exam and score in the top 10 percent of takers but do not apply to selective colleges. I use a lower threshold of “high-achieving,” and look back further in the college application process, finding a large supply of disadvantaged students who would score well enough to enroll in a se- lective four-year college but who are dropping out of the application process prior to even taking a college-entrance exam. To examine the effects of the mandatory ACT policy on postsecondary outcomes, I use a difference-in-differences (DID) style approach that compares changes in college- going from before to after the implementation of the policy for students in schools without a test center in the pre-policy period relative to students in schools that had a test center. In doing so, I exploit the fact that schools without a test center pre-policy had lower test-taking rates and thus experience a larger treatment dosage. I use propensity score matching to restrict my analysis to a sample of test center and non–test center schools that have similar observed characteristics. I estimate a 0.6 percentage point (2 percent) effect of the policy on the probability that a student enrolls in a four-year college. This overall effect masks important het- erogeneity, with larger effects (1.3 points, 5 percent) for students with a low-to-mid-level probability of taking the ACT in the absence of the policy. Effects are also larger among males (0.9 points, 3 percent), poor students (1.0 points, 6 percent), and students at schools with a high poverty share (1.3 points, 6 percent). Two recent studies estimate the effects of the mandatory ACT policy using aggregate state-level data, and thus can- not estimate heterogeneity by student or school characteristics (Klasik 2013; Goodman 2016). By using microdata, I am able to show that this policy is in fact effective at re- ducing inequality, with effects on college enrollment concentrated among economically disadvantaged students and poor schools. Finally, I find suggestive evidence that the marginal student induced into college by the policy persists through college at the same rate as the inframarginal student. Because my data follow students over time, my study can estimate persistence through college as a result of the policy. Given the extent of inequality in postsecondary persis- tence (Bailey and Dynarski 2011), this is a necessary parameter for understanding the policy’s full welfare effects. The most similar study to my own is that by Hurwitz et al. (2015), which uses Col- lege Board microdata and a DID approach to estimate the four-year college enrollment effects of Maine’s mandatory SAT policy.2 The present paper makes two primary contri- butions beyond Hurwitz et al. The first is external validity: Maine is a small and unique state, whereas Michigan is a large and more representative state. Further, most state- mandated college entrance exam policies require the ACT and are offered during nor- mal school hours. The Maine policy requires the SAT and is offered only on Saturday. To the extent that these policy features alter the policy’s effects, the Michigan case may be more generalizable. The second contribution is that because of data limitations, Hur- witz et al. are unable to estimate effects on two-year college enrollment. I show that the policy’s effect on four-year college enrollment is not primarily due to displacing two-year enrollments. 2. I compare the results of that study with my own in section 6. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / f e d u e d p a r t i c e – p d l f / / / / 1 2 3 2 8 1 1 6 9 1 8 7 1 e d p _ a _ 0 0 2 0 6 p d . f / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 283 The Effects of Mandatory ACT-Taking The DID estimator used in this paper yields an effect that is arguably causal but is a lower bound of the true policy impact because some portion of the effect is likely experienced equally by students at both test center and non–test center schools, and is thus not captured by this methodology. Using this lower bound, however, I calculate that the mandatory college entrance exam policy is more cost-effective than traditional student aid at boosting postsecondary attainment. The remainder of this paper is structured as follows: Section 2 discusses the manda- tory college entrance exam policy. Section 3 describes the data. Section 4 examines the population of college-ready students not taking a college entrance exam pre-policy. Sec- tion 5 examines the policy’s effects on postsecondary outcomes. Section 6 discusses the interpretation of my DID estimates and possible supply-side capacity constraints. Finally, section 7 concludes with a comparison of the costs and benefits of mandatory college entrance exams to other education policies. 2 . C O S T S, I N F O R M AT I O N , A N D M A N DATO RY C O L L E G E E N T R A N C E E X A M S The ACT and SAT are college admission exams required for admission to nearly all four-year institutions across the country.3 Historically, these exams have been taken ex- clusively by students considering applying to a four-year institution. Since 2001, how- ever, eleven states have implemented free and mandatory college entrance exams for all high school juniors, and several more are planning to implement the reform in the near future.4 These states tend to cite increasing college access as the motivation for the policy. Most of the mandatory ACT-adopting states are centrally located within the United States in the Central and Mountain census divisions. After Illinois, Michigan is the most populous state to have adopted the policy. The state-mandated ACT and SAT are the official exams used for college admis- sion purposes. Traditionally, the ACT and SAT are offered on Saturday mornings, cost students between $30 and $50, and require students to travel to the nearest test center. Fee waivers are available for low-income students but take-up is low, perhaps because it requires paperwork on the part of the student and coordination with high school coun- selors. State-mandated exams are typically given during the school day, at no financial cost to the student, and at the student’s high school. As with the standard ACT and SAT, students can select colleges to which they send their scores. Students are mailed an of- ficial score report several weeks after they take the exam. Mandatory college entrance exams provide a substantial change to the structure of the four-year college application process that reduces the monetary, psychic, and time cost of applying to college.5 While spending $30 to $50 and five hours on a Saturday represents a small share of the overall 3. Exceptions are primarily for-profit institutions, specialty or religious institutions, and institutions that admit all or nearly all applicants. All four-year public universities in Michigan require the ACT or SAT for admission. 4. Appendix table A.1 (which can be found on the Education Finance and Policy Web site at www.mitpressjournals .org/doi/suppl/10.1162/EDFP_a_00206) lists the states that have adopted this policy, which exam they use (nearly all use the ACT rather than the SAT), and the year that the first eleventh grade cohort was exposed to the policy. In order of adoption, the states are: Colorado, Illinois, Maine, Michigan, Kentucky, Tennessee, Delaware, North Carolina, Louisiana, Wyoming, and Alabama. 5. Recent research has shown that small changes to the structure of choice-making, such as changes in the default choice, can have large behavioral effects in various policy domains like retirement savings plans (Madrian and Shea 2001; Beshears et al. 2009). Similarly, a small change to the structure of the college entrance exam score report sending process was shown to have large effects on the number of score reports students sent (Pallais 2015). 284 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / f e d u e d p a r t i c e – p d l f / / / / 1 2 3 2 8 1 1 6 9 1 8 7 1 e d p _ a _ 0 0 2 0 6 p d f . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Joshua Hyman cost of applying to and attending college, these monetary and time costs can represent a real hurdle to low-income students, particularly if taking the test requires seeking time off from employment. Further, approximately half of public school students do not at- tend a high school with a test center in the school, so they would have to find and travel to the nearest test center.6 Offering the exam for free during school all but eliminates these costs to the student. Mandatory college entrance exams could also alleviate information constraints in the college application process. Students taking the ACT or SAT may learn about col- lege accessibility because after the test they may receive mailings from postsecondary institutions. Test-takers may also learn about their college-going ability. The score on these tests provides students with a signal of their likelihood of being admitted to, and succeeding at, a four-year college or university. Finally, mandatory college entrance exams may increase information about the col- lege application process by altering school-level behavior. In Michigan, most schools have at least some resources available to help students prepare for the tests, and some schools with greater resources offer entire classes devoted to preparing for the exams.7 More broadly, this policy has the potential to increase the college-going culture at a school, which has been shown to be an important instrument in increasing the post- secondary attainment of disadvantaged students (Jackson 2010). 3 . DATA This paper uses an original dataset containing all students attending Michigan public high schools in six recent eleventh grade cohorts (2003–04 through 2008–09). The data contain time-invariant demographics such as sex, race, and date of birth, as well as time-varying characteristics such as free and reduced-price lunch status, limited- English-proficiency (LEP) status, special education (SPED) status, and student’s home address. The data also contain eighth and eleventh grade state assessment results. For the cohorts of students exposed to the mandatory ACT exam, the eleventh-grade assessment results include ACT scores. Student-level postsecondary enrollment in- formation is obtained by matching students to the National Student Clearinghouse (NSC).8 School- and district-year level characteristics from the Common Core of Data are merged to the dataset based on where and when students are enrolled in high school. I acquired and merged in several other key pieces of information. Using student name, date of birth, sex, race, and eleventh grade home zip code, I matched the Michi- gan data to microdata from ACT, Inc., and The College Board on every ACT- and SAT-taker in Michigan over the sample period. This allows me to observe ACT-takers pre-policy, as well as students who took the SAT instead of the ACT pre-policy. I also 6. Bulman (2015) finds that the opening of an SAT test center in a high school has large effects on SAT-taking, and on educational attainment. That paper also examines the effects in three school districts (Stockton, CA; Palm Beach, FL; and Irving, TX) of offering a free SAT. He finds four-year enrollment effects of the policies on the order of 15 percent. Although these effects are larger than those I estimate, a single district in the state offering the SAT for free is quite a different policy than a statewide implementation of a mandatory exam. 7. From author’s discussions with guidance counselors and state departments of education. 8. The NSC is a nonprofit organization that houses postsecondary enrollment information on over 90 percent of undergraduate enrollment nationwide. See Dynarski, Hemelt, and Hyman (2015) for a detailed discussion of the NSC matching process and coverage rates. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / f e d u e d p a r t i c e – p d l f / / / / 1 2 3 2 8 1 1 6 9 1 8 7 1 e d p _ a _ 0 0 2 0 6 p d . f / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 285 The Effects of Mandatory ACT-Taking Table 1. Sample Means of Michigan Eleventh Grade Student Cohorts All Cohorts (2004–09) (1) Pre-ACT Cohorts (2004–06) (2) Post-ACT Cohorts (2007–09) (3) Difference: (3) – (2) (4) p-Value: (4) = 0 (5) Demographics Female White Black Hispanic Other race Free or reduced lunch Special education Limited English Local unemployment Driving miles to nearest ACT test center Educational attainment Reaches twelfth grade Graduates high school Enrolls in any college Enrolls in four-yr college ACT score ACT-taking rate All students Males Females Blacks Whites Free or reduced lunch Non-free lunch
post-policy cohorts. Preliminary findings suggest little to no impact of the policy on college-going (Dynarski
et al. 2013). The Michigan Merit Curriculum, also implemented around this time, increased the course require-
ments necessary to graduate high school. The first cohort exposed to the policy was in eleventh grade in 2010,
however, and thus not in my sample.
294
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
2
3
2
8
1
1
6
9
1
8
7
1
e
d
p
_
a
_
0
0
2
0
6
p
d
.
/
f
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Joshua Hyman
school pre-policy, to those that did. I estimate the following equation using OLS:
Yisdt = β0 + β1Postt + β2NoCenterisd + β3(Postt ∗ NoCenterisd ) + β4Xisdt + αs + εisdt,
(2)
where Yisdt is a postsecondary outcome for student i in school s in district d in cohort
t. Post is a dummy for attending eleventh grade post-policy, NoCenter is a dummy for
attending a school without a pre-policy ACT test center (which drops out when I include
school fixed effects), X is a vector of student-level and school- and district-year level
covariates, and α is a full set of school fixed effects.20 ɛ is the error term clustered at the
school level. β3, the coefficient of interest, is the effect of the policy in schools with no
pre-policy test center relative to those with a center.
The intuition behind the above strategy is that schools without a test center will
experience a slightly larger increase in ACT-taking because of the mandatory ACT policy
than will schools with a pre-existing test center. The identifying assumption behind
my estimation strategy is that any differential changes in college enrollment after the
mandatory ACT policy between the students in these two groups of schools are due to
the effects of the policy. Other similarly timed statewide education reforms or factors
that are changing over time, and could affect college-going, are assumed to affect the
two types of schools equally.
Columns 1 and 2 of table 3 show student-weighted sample means of schools with
and without a test center before the mandatory ACT policy. Slightly over half of students
attend a school with a test center, even though there are double the number of schools
without a center. Not only are schools with test centers much larger, but they tend to
enroll students with higher academic achievement, higher ACT-taking rates, and higher
educational attainment. Schools with a test center are more likely to be in an urban or
suburban area, and less likely to be in a rural area.21
Given the DID design, the threat to validity is not if the two types of schools are
different but rather if they are changing differentially over time. In columns 4 and 5
of table 3, I show means at the two types of schools in the post period, and the DID
estimate in column 7. There is some evidence that the populations of these schools are
changing differentially over time. There is an increase in free lunch status for schools
without a center over time, relative to schools with a center, and a decrease in eleventh
grade enrollment.
To ensure that the schools with and without a test center are similar except for
their test center status, I use propensity score matching on a series of school- and
district-year level observed characteristics to create a sample of matched test center and
20. Unless otherwise noted, X includes student-level sex, race, free lunch status, LEP, SPED, and eighth grade
test score; school-year level fraction black, fraction free-lunch eligible, number of eleventh graders and mean
eighth grade scores; and the same district-year level covariates plus guidance counselor–pupil ratio, dummies
indicating urban/rural status, and the local unemployment rate.
It is not surprising that schools with a center are quite different than those without, as becoming a test center is
primarily a demand-driven phenomenon. To become a test center, a teacher, counselor, or administrator from
the school fills out an online form. They agree to be open on at least one testing day per year, must expect
at least 35 students on the testing day, and must have the proper room conditions and seating arrangements,
which are then verified by an ACT official.
21.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
2
3
2
8
1
1
6
9
1
8
7
1
e
d
p
_
a
_
0
0
2
0
6
p
d
f
/
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
295
The Effects of Mandatory ACT-Taking
Table 3.
Sample Means Pre- and Post-Policy by Pre-Policy Test Center Status
Before Mandatory ACT Policy
After Mandatory ACT Policy
No Center
(1)
Center
(2)
Difference
(3)
No Center
(4)
Center
(5)
Difference
(6)
Diff-in-Diff Matched Sample
(6) – (3)
(7)
Diff-in-Diff
(8)
Demographics
Black
Hispanic
Free lunch
Eighth grade scores
Pupil–Teacher ratio
0.124
0.032
0.248
−0.009
20.6
Grade 11 enrollment
216.6
Local unemployment
Urban area
Rural area
Educational attainment
Take ACT or SAT
Graduate high school
Enroll in any college
Enroll in four–year college
Enroll in two–year college
7.57
0.543
0.457
0.540
0.847
0.554
0.292
0.262
0.166
0.029
0.220
0.071
21.8
345.1
7.11
0.711
0.289
0.607
0.876
0.611
0.343
0.268
−0.043*
0.003
0.028*
−0.080**
−1.2
−128.5***
0.45*
−0.167***
0.167***
−0.067***
−0.029***
−0.056***
−0.050***
−0.006
0.145
0.037
0.331
−0.025
19.8
223.3
0.180
0.032
0.292
0.056
20.1
360.1
9.26
0.551
0.449
0.927
0.847
0.576
0.306
0.270
8.83
0.714
0.286
0.932
0.879
0.631
0.352
0.279
Number of schools
523
251
Number of students
165,009 181,463
518
251
168,825 186,468
0.008
0.002
0.012*
0.000
−0.035
0.005
0.040**
−0.080**
−0.3
−136.8***
0.43
−0.163***
0.9
−8.3*
−0.024
0.004
0.163*** −0.004
0.061***
−0.005
−0.032*** −0.003
−0.055***
0.001
−0.046***
−0.009
0.004
−0.003
0.003
0.000
−0.006
−0.010
1.5
−6.7
−0.057
0.005
−0.005
0.039***
−0.001
0.005
0.008*
−0.003
Notes: The sample is all first-time, public school Michigan eleventh graders in years 2004–09, conditional on reaching spring of eleventh grade.
“No Center” and “Center” refer to whether or not a high school was an ACT test center before the mandatory ACT policy. The sample for column
8 is restricted to the 226 schools without a pre-policy ACT test center and the 226 schools with a pre-policy test center matched using nearest
neighbor matching.
*Significant at the 10% level; **significant at the 5% level; ***significant at the 1% level.
non-test-center schools.22 I use nearest neighbor matching (without replacement), be-
cause it tends to produce the best balance of covariates in my sample. I show that my
results are not sensitive to either propensity score reweighting, or to other methods of
matching such as kernel or caliper matching, that have been shown to produce supe-
rior results in some contexts (Heckman, Ichimura, and Todd 1997; Busso, DiNardo,
and McCrary 2013). Because some of the schools with a test center have extremely high
propensity scores where there are few similar non-test center schools, I trim the ten per-
cent of schools with the highest propensity scores—these tend to be very large schools
in suburban areas. Trimming fewer of the center-schools produces similar results but
inferior covariate balance.23
I find that after the propensity score matching, there is no evidence that schools with
and without a test center are trending differentially with respect to their composition
22. The following covariates are included in the propensity score regression: (1) school- and district-level pupil–
teacher ratio, percent free-lunch eligible, grade eleven enrollment, and fraction black; (2) average school-level
eighth and eleventh grade test scores; (3) dummies for school urban/rural status; (4) the growth rate in the
school’s eleventh grade enrollment; (5) the district-year level guidance counselor-pupil ratio; and (6) the local
unemployment rate.
If I trim the sample by 20 percent, my college enrollment results display the same pattern of heterogeneity and
are slightly larger in magnitude. If I do not trim any of the test center schools with the highest propensity scores,
the balance of covariates across the two types of schools is substantially worse and the pattern of heterogeneity
is again the same, but slightly smaller in magnitude.
23.
296
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
2
3
2
8
1
1
6
9
1
8
7
1
e
d
p
_
a
_
0
0
2
0
6
p
d
.
f
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Joshua Hyman
(see column 8, table 3). None of the covariates has a statistically significant DID esti-
mate. Rates of ACT-taking at schools without a pre-policy center nonetheless increase
by 4 percentage points after the policy relative to schools with a pre-policy center. This
4-percentage-point gap arguably captures the effect on test-taking of having a test center
in one’s high school. There is no DID effect on high school graduation or overall col-
lege enrollment, but a marginally statistically significant 0.8 percentage point increase
in four-year enrollment.
It is important to note that most stories involving differences in unobservables bi-
asing the effects would provide a downward bias on the results. For example, if particu-
larly active or motivated teachers, counselors, or administrators are those who initiate a
test center at a school, it seems likely that such staff would more effectively implement
the mandatory ACT policy or engage in other practices aimed at boosting enrollment
than staff at non-test-center schools.
To further test the validity of the DID methodology, I plot college attendance rates
of schools in the matched sample by cohort and test center status. Trends in college en-
rollment are nearly identical across the two types of schools prior to the mandatory ACT
policy (figure 3). This suggests that college enrollment would have continued to trend
in parallel in the absence of the policy, satisfying one of the key identifying assump-
tions of my estimation strategy. The pre-policy level of four-year college enrollment is
higher in the matched sample of schools with a test center, presumably reflecting that
some of the students induced into taking the ACT by having a center in their school
subsequently enroll in a four-year college.
The regression-adjusted DID results estimated using equation 2 show little effect of
the policy on overall enrollment regardless of covariates, school fixed effects, or match-
ing method (table 4, row 1, columns 1–5). The point estimate is between 0.3 and 0.5
percentage points, is statistically insignificant, and is fairly stable across the columns.
The effect on the probability that a student enrolls at a four-year institution is 0.8 per-
centage points (standard error of 0.4 percentage points—column 6).24 Panel B of figure
3 depicts this DID effect visually. Adding covariates does not alter the estimate but the
inclusion of school fixed effects lowers the coefficient to 0.6 percentage points. This
represents a 1.9 percent increase in the four-year enrollment rate, off of the pre-policy
mean of 32.1 percent. There is a smaller corresponding negative (and statistically in-
significant) point estimate for two-year enrollment.25
The coefficient on the Post dummy in column 8 of table 4 indicates a 1.1 percentage
point increase in four-year enrollment post policy among students at schools with a test
center pre-policy. The 0.6 percentage point increase for the non-test center schools is
above and beyond this increase. Although the 1.1-point increase may in part be driven
by the policy change, I cannot disentangle the effects of the policy for schools with a
pre-policy center from other factors changing over time. In this sense, the DID effect
that I estimate likely represents a lower bound of the policy’s impact.
24. Note that the standard errors do not account for the propensity score matching. Eichler and Lechner (2002)
show that in their sample the standard errors that ignore the matching are similar to bootstrapped standard
errors that take the matching into account.
I define two-year enrollment as enrolling in a two-year school and not a four-year school, so that two- and four-
year enrollment are mutually exclusive. Estimates of the effect of the policy on enrollment at selective four-year
or out-of-state colleges were statistically imprecise.
25.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
2
3
2
8
1
1
6
9
1
8
7
1
e
d
p
_
a
_
0
0
2
0
6
p
d
/
f
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
297
The Effects of Mandatory ACT-Taking
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
2
3
2
8
1
1
6
9
1
8
7
1
e
d
p
_
a
_
0
0
2
0
6
p
d
/
f
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Notes: Figure shows college enrollment pre- and post-mandatory ACT by whether or not a student attends a school with an ACT test
center pre-mandatory ACT. The sample is restricted to the propensity score matched sample of high schools. Panel A includes any
college enrollment, Panel B includes four-year enrollment only, and Panel C includes two-year enrollment.
Figure 3. College Enrollment by Cohort and Pre-Policy Test Center Status.
298
Joshua Hyman
t
n
e
m
l
l
o
r
n
E
e
r
o
c
S
–
P
g
n
i
t
h
g
i
e
W
)
5
1
(
)
4
0
0
0
(
.
2
0
0
0
−
.
4
0
0
0
.
)
3
0
0
0
(
.
l
e
n
r
e
K
i
g
n
h
c
t
a
M
)
4
1
(
)
4
0
0
0
(
.
2
0
0
0
−
.
4
0
0
0
.
)
3
0
0
0
(
.
)
4
0
0
0
(
.
3
0
0
0
−
.
5
0
0
0
.
)
3
0
0
0
(
.
1
7
2
0
.
0
7
2
0
.
5
6
7
1
0
7
,
4
7
9
4
1
6
,
Y
Y
Y
Y
Y
Y
*
*
*
3
1
0
0
.
)
5
0
0
0
(
.
0
0
0
0
.
)
1
1
0
0
(
.
)
5
0
0
0
(
.
5
0
0
0
−
.
Y
N
6
6
2
0
.
3
1
8
6
3
5
,
)
4
0
0
0
(
.
3
0
0
0
−
.
*
*
*
2
1
0
0
.
)
3
0
0
0
(
.
)
2
1
0
0
(
.
7
0
0
0
−
.
N
N
r
a
e
Y
–
o
w
T
=
.
r
a
V
.
p
e
D
)
3
1
(
)
2
1
(
)
1
1
(
i
g
n
h
c
t
a
M
r
o
b
h
g
i
e
N
t
s
e
r
a
e
N
e
r
o
c
S
–
P
g
n
i
t
h
g
i
e
W
)
0
1
(
*
7
0
0
0
.
)
4
0
0
0
(
.
*
*
*
1
1
0
0
.
)
3
0
0
0
(
.
l
e
n
r
e
K
i
g
n
h
c
t
a
M
)
9
(
i
g
n
h
c
t
a
M
r
o
b
h
g
i
e
N
t
s
e
r
a
e
N
)
8
(
)
7
(
)
6
(
6
0
0
0
.
)
4
0
0
0
(
.
6
0
0
0
.
)
4
0
0
0
(
.
*
8
0
0
0
.
)
4
0
0
0
(
.
*
*
*
1
1
0
0
.
)
3
0
0
0
(
.
*
*
*
1
1
0
0
.
)
3
0
0
0
(
.
*
*
*
6
1
0
0
.
)
4
0
0
0
(
.
*
8
0
0
0
.
)
4
0
0
0
(
.
*
*
8
0
0
0
.
)
3
0
0
0
(
.
e
r
o
c
S
–
P
g
n
i
t
h
g
i
e
W
)
5
(
4
0
0
0
.
)
4
0
0
0
(
.
*
*
*
4
1
0
0
.
)
3
0
0
0
(
.
l
e
n
r
e
K
i
g
n
h
c
t
a
M
)
4
(
i
g
n
h
c
t
a
M
r
o
b
h
g
i
e
N
t
s
e
r
a
e
N
)
3
(
)
2
(
)
1
(
3
0
0
0
.
)
4
0
0
0
(
.
3
0
0
0
.
)
4
0
0
0
(
.
3
0
0
0
.
)
4
0
0
0
(
.
*
*
*
5
1
0
0
.
)
3
0
0
0
(
.
*
*
*
6
1
0
0
.
)
3
0
0
0
(
.
*
*
*
9
2
0
0
.
)
5
0
0
0
(
.
5
0
0
0
.
)
5
0
0
0
(
.
*
*
*
9
1
0
0
.
)
3
0
0
0
(
.
5
6
7
1
0
7
,
4
7
9
4
1
6
,
7
1
3
0
.
0
2
3
0
.
Y
Y
Y
Y
Y
Y
Y
N
1
2
3
0
.
3
1
8
6
3
5
,
N
N
Y
Y
Y
Y
Y
Y
5
6
7
1
0
7
,
4
7
9
4
1
6
,
8
8
5
0
.
0
9
5
0
.
*
4
1
0
0
−
.
)
8
0
0
0
(
.
)
5
1
0
0
(
.
5
1
0
0
−
.
Y
N
7
8
5
0
.
3
1
8
6
3
5
,
N
N
)
1
1
0
0
(
.
4
1
0
0
−
.
)
5
1
0
0
(
.
2
2
0
0
−
.
l
o
o
h
c
s
n
i
r
e
t
n
e
c
t
s
e
t
o
N
*
t
s
o
P
t
s
o
P
n
i
r
e
t
n
e
c
t
s
e
t
o
N
l
o
o
h
c
s
s
e
t
a
i
r
a
v
o
C
s
t
c
e
f
f
e
d
e
x
fi
l
o
o
h
c
S
n
a
e
m
y
c
i
l
o
p
–
e
r
P
e
z
i
s
l
e
p
m
a
S
t
n
e
m
l
l
o
r
n
E
r
a
e
Y
–
r
u
o
F
=
.
r
a
V
.
p
e
D
t
n
e
m
l
l
o
r
n
E
y
n
A
=
.
r
a
V
.
p
e
D
t
n
e
m
l
l
o
r
n
E
y
r
a
d
n
o
c
e
s
t
s
o
P
n
o
T
C
A
y
r
o
t
a
d
n
a
M
e
h
t
f
o
t
c
e
f
f
E
e
h
T
.
4
e
l
b
a
T
t
u
o
h
t
i
w
s
l
o
o
h
c
s
6
2
2
e
h
t
o
t
d
e
t
c
i
r
t
s
e
r
s
i
l
e
p
m
a
s
e
h
t
,
3
1
–
1
1
d
n
a
,
8
–
6
,
3
–
1
s
n
m
u
o
c
l
r
o
F
.
e
d
a
r
g
h
t
n
e
v
e
e
l
f
o
g
n
i
r
p
s
i
g
n
h
c
a
e
r
n
o
l
a
n
o
i
t
i
d
n
o
c
,
9
0
–
4
0
0
2
s
r
a
e
y
n
i
s
r
e
d
a
r
g
h
t
n
e
v
e
e
l
i
n
a
g
h
c
M
i
l
o
o
h
c
s
c
i
l
b
u
p
,
e
m
i
t
–
t
s
r
fi
l
l
a
s
i
l
e
p
m
a
s
e
h
T
:
s
e
t
o
N
.
4
1
d
n
a
,
9
,
4
s
n
m
u
o
c
l
n
i
d
e
s
u
s
i
6
0
0
.
f
o
i
h
t
d
w
d
n
a
b
d
n
a
l
e
n
r
e
k
i
v
o
k
n
h
c
e
n
a
p
E
n
A
.
t
n
e
m
e
c
a
p
e
r
l
t
u
o
h
t
i
i
w
g
n
h
c
t
a
m
r
o
b
h
g
e
n
i
t
s
e
r
a
e
n
l
e
g
n
i
s
g
n
i
s
u
d
e
h
c
t
a
m
r
e
t
n
e
c
t
s
e
t
y
c
i
l
o
p
–
e
r
p
a
h
t
i
w
s
l
o
o
h
c
s
6
2
2
e
h
t
d
n
a
r
e
t
n
e
c
t
s
e
t
T
C
A
y
c
i
l
o
p
–
e
r
p
a
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
2
3
2
8
1
1
6
9
1
8
7
1
e
d
p
_
a
_
0
0
2
0
6
p
d
/
f
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
299
.
l
e
v
e
l
%
1
e
h
t
t
a
i
t
n
a
c
fi
n
g
i
s
*
*
*
;
l
e
v
e
l
%
5
e
h
t
t
a
i
t
n
a
c
fi
n
g
i
s
*
*
;
l
e
v
e
l
%
0
1
e
h
t
t
a
t
n
a
c
fi
n
g
S
*
i
i
.
l
e
v
e
l
l
o
o
h
c
s
e
h
t
t
a
d
e
r
e
t
s
u
c
l
e
r
a
s
e
s
e
h
t
n
e
r
a
p
n
i
s
r
o
r
r
e
d
r
a
d
n
a
t
S
.
n
o
i
s
s
e
r
g
e
r
l
e
d
o
m
y
t
i
l
i
b
a
b
o
r
p
r
a
e
n
i
l
e
t
a
r
a
p
e
s
a
s
i
n
m
u
o
c
l
h
c
a
E
The Effects of Mandatory ACT-Taking
Heterogeneity of Impacts
It seems unlikely that all students would be equally impacted by the mandatory ACT
policy. Many students would take the ACT regardless of the policy. Other students are
forced to take the ACT, but are so academically unprepared—or otherwise off the path
of application to college—that being forced to take the exam will have no impact on
their educational plans. In this section I estimate heterogeneity in the effects of the
policy on college-going. This heterogeneity captures differences across groups both in
treatment dosage (i.e., some groups will experience larger effects on ACT-taking) and
in sensitivity of college-going to a given dosage.
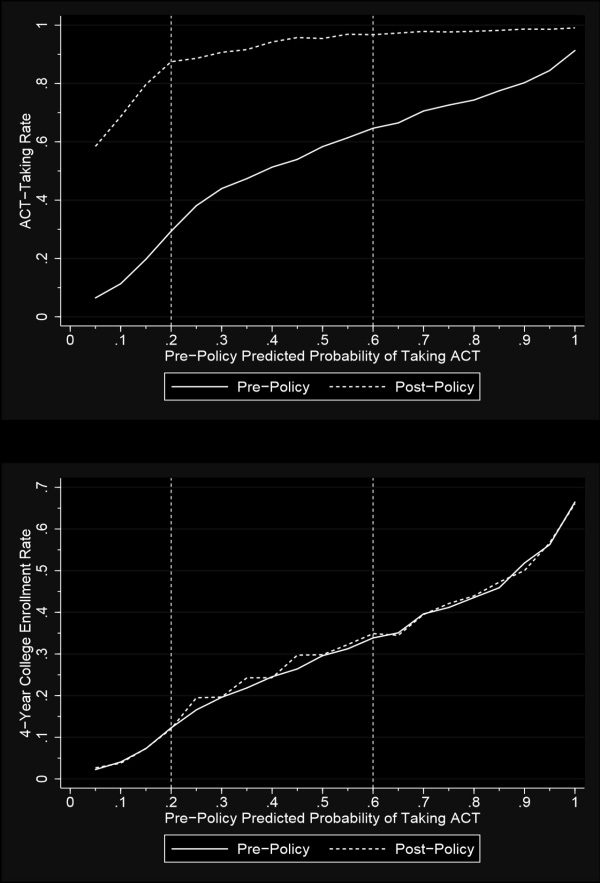
To home in on the marginal student most impacted by this policy, I create an index
measuring the predicted probability that a student would take the ACT based on the
pre-policy relationship between ACT-taking and student-level observed demographic
characteristics. Specifically, I estimate the following equation using OLS:
TAKEisdt = β0 + β1Xisdt + αs + εisdt,
(3)
where X includes all main effects and interactions of sex, race, free and reduced-price
lunch status, and LEP and SPED status. α is again a full set of school fixed effects.26
I estimate this equation using only pre-policy students, then predict (cid:2)TAKE for all stu-
dents pre- and post-policy, thus creating for all students a predicted probability of taking
the ACT in the absence of the policy.27
I show that the mandatory ACT policy increases ACT-taking most for students with
the lowest predicted probability. Panel A of figure 4 breaks students into vigintiles
(twenty quantiles) based on this index, and plots mean ACT-taking rates of students
in pre-policy cohorts (solid line) and of students in post-policy cohorts (dashed line).
The distance between the two lines in this figure represents the treatment dosage, in
the sense that it gives the change in the ACT-taking rate for students with a given prob-
ability of taking the ACT pre-policy. Table 5 reports the DID effects of the policy on
ACT-taking and college enrollment for all students, and by quintiles of this predicted
probability index. Among all students, there is a 3.4 percentage point effect of the policy
on ACT-taking in non-test center high schools, relative to test center schools (column 1,
row 1). The increases are largest for students with the lowest pre-policy probability (row
1, columns 2–6), with no change for high-probability students.
The remaining rows of the first column in table 5 replicate the preferred specifi-
cation from Table 4. Despite the large impact on ACT-taking among students with a
very low pre-policy probability, the effects on four-year enrollment are near zero for this
group, as they are for students in the top two quintiles of the probability index. Effects
are largest on four-year college enrollment for students with a low or mid-level probabil-
ity.28 In Panel B of figure 4, I plot the pre-policy raw four-year college enrollment rates
for each vigintile of the predicted probability of ACT-taking (solid line). I then estimate
26. Appendix table B.2 (available online) reports the results from this regression. The results are nearly identical
when using probit or logit.
27. Abadie, Chingos, and West (2012) show that forming subgroups based on a predicted outcome fitted within the
control group can cause biases. This is not the case here due to my use of the difference-in-differences estimator
as opposed to a simple comparison of the outcome in the pre-versus post-policy period. The difference in the
fit of the prediction between the pre- and post-policy students will not vary differentially across schools with
and without a pre-policy test center.
28. Results are similar when dividing the predicted probability index by tercile or quartile.
300
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
2
3
2
8
1
1
6
9
1
8
7
1
e
d
p
_
a
_
0
0
2
0
6
p
d
.
/
f
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Joshua Hyman
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
2
3
2
8
1
1
6
9
1
8
7
1
e
d
p
_
a
_
0
0
2
0
6
p
d
f
.
/
Notes: Panel A plots the ACT-taking rate pre- and post-mandatory ACT at twenty quantiles of the predicted probability that a student
would take the ACT based on the pre-policy relationship between observed characteristics and ACT-taking. Panel B plots the raw, pre-
policy four-year enrollment rate among students in the matched sample of high schools (solid line) at these same twenty quantiles.
It then adds to this line the difference-in-difference four-year enrollment effect of the policy (dashed line). Note the smaller scale of
the y-axis in Panel B to more clearly show the difference between the two lines.
Figure 4. ACT-Taking and College Enrollment by Predicted Probability of ACT-Taking.
equation 2 separately for each vigintile and add the DID coefficient to the pre-policy
rate (dashed line). As seen in table 5, the enrollment effects are entirely concentrated
within the second and third quintiles of the predicted probability index.
To increase precision and collapse students into a group that seems marginal, and
a group whose college enrollment behavior seems relatively unaffected by the policy, I
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
301
The Effects of Mandatory ACT-Taking
Table 5.
Using Students’ Predicted Probability of ACT-Taking Pre-Policy to Narrow in on the Marginal Student
All
(1)
0.034***
(0.013)
0.580
Very Low
(2)
0.044***
(0.012)
0.199
0.003
(0.004)
0.587
0.006
(0.004)
0.321
−0.003
(0.004)
0.266
−0.001
(0.008)
0.305
−0.002
(0.005)
0.077
0.001
(0.007)
0.227
Y
Y
Pre-Policy Probability (Take ACT)
Low
(3)
Middle
(4)
High
(5)
Very High
(6)
Low/Middle
(7)
Tails
(8)
0.038***
(0.010)
0.028***
(0.006)
0.457
0.600
0.013
(0.008)
0.497
0.013**
(0.007)
0.207
−0.000
(0.007)
0.290
Y
Y
0.014**
(0.007)
0.616
0.012**
(0.006)
0.305
0.001
(0.007)
0.311
Y
Y
0.007
(0.007)
0.710
−0.008
(0.007)
0.676
0.001
(0.008)
0.398
−0.010
(0.007)
0.277
Y
Y
0.007
(0.012)
0.835
0.003
(0.007)
0.765
0.001
(0.008)
0.553
0.002
(0.007)
0.212
Y
Y
0.032***
(0.006)
0.531
0.036**
(0.018)
0.618
0.014**
(0.006)
0.559
0.013**
(0.005)
0.259
0.001
(0.005)
0.301
Y
Y
−0.003
(0.004)
0.608
0.000
(0.004)
0.369
−0.003
(0.004)
0.239
Y
Y
Dependent Variable
Take ACT
Enroll in:
Any college
Four-year college
Two-year college
Covariates
School fixed effects
Y
Y
Sample size
536,813
86,136
117,944
117,381
104,082
111,270
235,325
301,488
Notes: The sample is all first-time, public school Michigan eleventh graders in years 2004–09, conditional on reaching spring of eleventh grade.
The sample is restricted to the 226 schools without a pre-policy ACT test center and the 226 schools with a pre-policy test center matched
using nearest neighbor matching. Each point estimate is from a separate linear probability model, difference-in-difference regression. Standard
errors in parentheses are clustered at the school level. Pre-policy dependent variable means are in italics below the standard errors.
**Significant at the 5% level; ***significant at the 1% level.
combine the low and middle students together, and the very low, high, and very high
students together. I call this latter group the “tails” of the distribution, capturing stu-
dents who either would have taken the ACT regardless or who are so off the college track
that taking it makes no difference for their college-going behavior. Among students in
the low to middle range of the predicted probability index (between the two vertical
lines in figure 4), there is a 1.3 percentage point, or 5 percent, increase in enrollment
at four-year colleges. There is no effect among students in the tails of the distribution,
and the difference across groups is statistically significant (p-value = 0.05).
To guide policy, it would also be helpful to examine which types of students along
specific observed dimensions have college enrollment behavior that is most influenced
by the mandatory ACT. Table 6 presents results separately by race, sex, and poverty
status. Although the effects among black students are imprecisely estimated, boys and
poor students (those eligible for free lunch) appear to experience relatively large gains
of approximately 1 percentage point. These gains represent a near 3.5 percent increase
for boys and a 6 percent increase for poor students relative to their pre-policy mean, and
both point estimates are statistically significant at the 5 percent level. Unfortunately, the
estimates are not precise enough to reject equality across groups.
Finally, I examine the effects by school poverty share. This is a particularly policy-
relevant dimension, as education policies are easier to implement at the school level
than only to students with particular characteristics. I split students into terciles based
on the share of students in their school who qualify for free or reduced-price lunch.
I then combine students in the low- and middle-poverty schools, and compare the
302
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
2
3
2
8
1
1
6
9
1
8
7
1
e
d
p
_
a
_
0
0
2
0
6
p
d
.
/
f
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Joshua Hyman
Table 6.
Heterogeneity in the Effect of the Mandatory ACT by Student Demographics and School Poverty Share
Dependent Variable
Enroll in:
Any college
Four-year college
Two-year college
All
(1)
White
(2)
Black
(3)
Female
(4)
Male
(5)
Non-Poor
(6)
Poor
(7)
Low/Middle
(8)
High
(9)
School Poverty Share
0.003
(0.004)
0.587
0.006
(0.004)
0.003
(0.004)
0.605
0.005
(0.004)
0.003
(0.011)
0.515
0.009
(0.009)
0.321
−0.003
(0.004)
0.334
−0.002
(0.004)
0.256
−0.006
(0.009)
−0.000
(0.005)
0.622
0.002
(0.005)
0.350
−0.002
(0.005)
0.005
(0.005)
0.552
0.009**
(0.004)
0.291
−0.004
(0.004)
−0.001
(0.004)
0.640
0.004
(0.004)
0.370
−0.005
(0.004)
0.016**
(0.007)
0.415
0.010**
(0.005)
0.164
0.006
(0.006)
−0.000
(0.004)
0.634
0.001
(0.004)
0.368
−0.001
(0.004)
0.009
(0.007)
0.494
0.013**
(0.006)
0.228
−0.004
(0.006)
0.266
0.271
0.259
0.272
0.261
0.271
0.251
0.266
0.267
Covariates
School fixed effects
Y
Y
Y
Y
Y
Y
Y
Y
Y
Y
Y
Y
Y
Y
Y
Y
Y
Y
Sample size
536,813
417,851
83,061
268,573
268,240
384,331
148,147
358,113
178,700
Notes: The sample is as in Table 5. Each point estimate is from a separate linear probability model, difference-in-difference regression. Free
lunch is measured as of eleventh grade. Standard errors in parentheses are clustered at the school level. Pre-policy dependent variable means
are in italics below the standard errors.
**Significant at the 5% level.
effects on those in high-poverty schools. Students in high-poverty schools experience a
statistically significant increase in four-year enrollment of 1.3 percentage points or 5.7
percent (table 6, column 9). There is no impact among students at schools with low to
middle levels of poverty, and the p-value for the test of equality across the two groups
is 0.11.29
Do Marginal Enrollees Drop Out?
Although college entry has been rising in recent decades, college completion has re-
mained flat (Bound, Lovenheim, and Turner 2010). A key concern with a policy such
as the mandatory ACT is that it may induce marginal students to attend but not persist
through college. If this is the case, then the effects on four-year enrollment rates would
overstate the benefits of the program.
In table 7, I present the effects of the policy on the share of students who enroll in
a four-year college and persist to the second, third, and fourth years. If all students in-
duced into college by the policy subsequently dropped out, then these point estimates
would equal zero. As a reminder, the definition of enrollment is whether a student en-
rolls by the second fall following on-time high school graduation. Given that my data
capture enrollment through summer 2013, students in the most recent cohort who en-
rolled in college during the second fall after on-time high school graduation have only
had time to progress through their second year of college. Consequently, this exercise
requires dropping one or more post-policy cohorts from the sample. Row 1, column 1,
29. To further explore effect heterogeneity, in Appendix table A.3 (available online), I present results by eighth-
grade test score, which proxies for student ability. I find that the effects are driven by both low- and high-ability
students.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
2
3
2
8
1
1
6
9
1
8
7
1
e
d
p
_
a
_
0
0
2
0
6
p
d
f
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
303
The Effects of Mandatory ACT-Taking
Table 7.
Examining Whether Four-Year Enrollment Effects Persist
Dependent Variable
Enroll within two years
and persist to year 2
and persist to year 3
and persist to year 4
and graduate in four years
Enroll within one year
and persist to year 2
and persist to year 3
and persist to year 4
and graduate in four years
and graduate in five years
Three Pre-Policy Cohorts Plus:
All 3 Post
Cohorts
(1)
First 2 Post
Cohorts
(2)
First Post
Cohort Only
(3)
Pre-Policy
Dep. Var. Mn.
(4)
0.006
(0.004)
0.004
(0.003)
0.006*
(0.003)
0.005
(0.003)
0.004
(0.003)
0.007*
(0.004)
0.005
(0.004)
0.004
(0.003)
0.006*
(0.004)
0.005
(0.003)
0.005
(0.003)
0.005
(0.003)
0.002
(0.002)
0.007
(0.005)
0.006
(0.004)
0.006
(0.004)
0.007*
(0.004)
0.005*
(0.003)
0.006
(0.004)
0.006
(0.004)
0.006
(0.004)
0.006*
(0.004)
0.004
(0.003)
0.004
(0.003)
0.321
0.278
0.259
0.244
0.096
0.291
0.256
0.240
0.228
0.091
0.169
Sample size
Covariates
School fixed effects
536,813
448,234
357,181
Y
Y
Y
Y
Y
Y
Notes: The sample is as in tables 5 and 6. Each point estimate is from a separate linear proba-
bility model, difference-in-difference regression. Standard errors in parentheses are clustered at
the school level.
*Significant at the 10% level.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
2
3
2
8
1
1
6
9
1
8
7
1
e
d
p
_
a
_
0
0
2
0
6
p
d
f
/
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
reports the previously estimated four-year enrollment result for the full sample.
Columns 2 and 3 show the effect of dropping the most recent and two most recent
post-policy cohorts, respectively, each yielding a point estimate of 0.07.
The second row shows the effect on enrolling and persisting to the second year.
Among the full sample, the effect is somewhat attenuated to 0.4 percentage points.
The effect in percent terms shrinks from 1.9 percent to 1.4 percent given the smaller
pre-policy fraction of students enrolling and persisting to the second year (column 4).
Examining the effect of the mandatory ACT policy on persisting to the third and fourth
years of college requires dropping post-policy cohorts from the sample. The effect on
enrolling and persisting to the third year is again 0.4 percentage points (row 3, column
2), but on persisting to the fourth year is 0.7 percentage points (row 4, column 3; sig-
nificant at the 10 percent level), and the same as the effect on enrolling for that sample.
Although the results are imprecise and vary by sample and persistence measure, it ap-
pears that students induced to enroll by the policy persist through college at a similar
rate as inframarginal students. At the very least, I can reject with 90 percent confidence
that all students induced to enroll drop out by their fourth year of college.
304
Joshua Hyman
The implementation of the policy is too recent to accurately assess if there are in-
creases in degree completion, but I attempt to take a first glimpse at this important
measure. The effect on enrolling and then earning a bachelor’s degree within four years
is a statistically significant 0.5 percentage points (row 5, column 3), or 5.2 percent. I also
examine effects on degree receipt within five years. Doing so, however, requires that I
redefine the enrollment measure to include only those enrolling by the first fall fol-
lowing on-time high school graduation. The enrollment effect using this measure (0.6
percentage points) is the same as before and marginally statistically significant. The
bottom row of table 7 shows that the effect on five-year degree receipt is 0.4 percentage
points, or 2.4 percent compared to the 2.1 percent effect on enrollment. The results are
imprecisely estimated, but suggest that students induced to enroll by the policy earn
a degree at a similar rate as inframarginal students. These results are consistent with
other recent studies showing that students induced into colleges by dismantling barri-
ers to the college application process persist at high rates (Bettinger et al. 2012; Carrell
and Sacerdote forthcoming).
Robustness Checks
In this section, I briefly describe and summarize results from several robustness checks
that examine the sensitivity of my estimates. In the online Appendix B, I discuss the de-
tails of these analyses and present complete results (see Appendix table B.1). The first
check estimates the DID equation controlling for pre-trending of the outcome vari-
able. Given the relatively few data points (three) before the policy change over which
to estimate the pre-trend, this is not my preferred specification. Nevertheless, the re-
sults controlling for the pre-trends are slightly attenuated, but very similar to the main
results.
The second robustness check uses a different method of constructing the treatment
and comparison groups. Instead of grouping students by their high schools’ pre-policy
test center status, I use a student’s home address during the eleventh grade, and the
address of the nearest pre-policy test center, to group students by whether they live
far from (treatment) or close to (comparison) the nearest pre-policy center. This strat-
egy serves as a test of the external validity of the matched sample to the entire Michi-
gan sample, as well as a test of the sensitivity of the results to the different method of
constructing the treatment/comparison group.30 Among the propensity score matched
sample of schools, the effects of the policy on postsecondary outcomes are similar using
the distance measure and show the same pattern of heterogeneity, with coefficients that
are generally greater in magnitude and more precisely estimated. The results and pat-
tern of heterogeneity are still similar when not restricting the analysis to the matched
sample of schools, suggesting the effects of the policy can be extrapolated to the entire
population of Michigan.
30.
I prefer the school-level test center method as my main strategy, and the distance method as a robustness check
for two reasons: (1) separating students by distance into treatment and comparison groups is arbitrary because
distance is a continuous measure, and (2) it is easier to understand the selection process of schools becoming
test centers than of students living close to or far from a test center. Thus, I can more convincingly sign any
possible bias due to selection on unobserved characteristics when using the test center strategy than when
using the distance strategy.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
2
3
2
8
1
1
6
9
1
8
7
1
e
d
p
_
a
_
0
0
2
0
6
p
d
/
f
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
305
The Effects of Mandatory ACT-Taking
6 . D I S C U S S I O N
Interpretation of Effects
The effects estimated in this paper using the DID design may represent a lower bound
of the statewide policy impact. There is likely some portion of the effect that is not
captured by this methodology because it is experienced equally by students at schools
with a pre-policy test center and those without. Another way to characterize the effects
is that they are local average treatment effects (LATEs) estimated for a specific and
marginal group of students. The LATE is the expected outcome gain for those induced
to receive treatment through a change in the instrument (Imbens and Angrist 1994).
In this context, these are post-policy ACT-takers who were enrolled in a high school
without a pre-policy center and would not have taken a college entrance exam pre-policy
in their high school, but would have if enrolled at a high school with a center.
To obtain a treatment on the treated estimate for this group of students, I scale the
effects on four-year enrollment by the first-stage DID increase in ACT-taking. Doing so
yields a treatment on the treated estimate suggesting that 18 percent of this marginal
group of students would subsequently enroll in a four-year college (= 0.6 / 3.4).31 This
result is consistent with the large treatment effects often realized by marginal students
picked up by LATEs in the context of education policies (Card 1995). If the results were
scalable, however, we would expect to see statewide increases in four-year enrollment
rates of 18 percent as a result of the policy.
This number represents one possible upper bound of the policy’s impact, yet it
seems extraordinarily high. Hurwitz et al. (2015) estimate the effect of a mandatory
SAT policy in Maine using a DID approach. They estimate that the policy increased the
four-year enrollment rate from 4 to 6 percent. This magnitude of effects is far closer to
the main effect of the policy that I estimate (2 percent) than the 18 percent upper bound
calculated above.
Capacity Constraints
Another issue regarding the interpretation of my results involves supply-side capacity
constraints on the side of colleges. For example, Bound and Turner (2007) find that a 10
percent increase in a state’s cohort size leads to a 4 percent decrease in the fraction of
students earning a BA from that state. In the present context, if there are a fixed number
of slots in the short run, the statewide effect of the policy should be weakly larger in
the long run once supply can expand to meet demand and all new college-aspirants can
attend.
It is also possible, however, given the DID design, that in the face of short-run ca-
pacity constraints, colleges could accept more applications from students in schools
with no pre-policy center, displacing students enrolled at high schools with a pre-policy
center. In this scenario, my estimated effect would reflect a short-run compositional ef-
fect, whereas the long-run DID estimate may be smaller as colleges expand and admit
all students regardless of pre-policy test center status. Although I cannot conclusively
rule out this story, there is little reason to think that in the matched sample of schools,
31. Results are the same for a more formal two-stage-least-squares analysis of the effect of taking the ACT on
enrollment, where the excluded instrument is the interaction of a dummy for being in the post-policy period,
with a dummy for being enrolled in a school without a pre-policy center.
306
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
2
3
2
8
1
1
6
9
1
8
7
1
e
d
p
_
a
_
0
0
2
0
6
p
d
/
f
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Joshua Hyman
students would be displaced at a higher rate from schools with a pre-policy test center
than from schools without one. The two types of schools are similar across observed
characteristics and have similarly sized supplies of college-goers pre-policy who could
be potentially displaced by the new enrollees.
7 . C O N C L U S I O N
Nearly a dozen states have incorporated the ACT or SAT into their eleventh grade
statewide assessment, requiring that all public school students take a college entrance
exam. In this paper, I exploit the implementation of this policy to show that for every
ten poor students who take a college entrance exam pre-policy and score college-ready,
there are an additional five poor students who do not take the test but would score
college-ready.
I compare changes in college-going rates pre- and post-policy among students at
schools that did not have an ACT test center pre-policy to those that did, finding an
increase in four-year enrollment by 0.6 percentage points or 2 percent. The effect was
larger among boys (0.9 points), poor students (1.0 point), students in the poorest high
schools (1.3 points), and students less likely to take a college entrance exam in the ab-
sence of the policy (1.3 points). The effect on enrolling in a four-year college for up to
four years is similar, implying that students induced to attend college by the policy per-
sist at the same rate as inframarginal college-goers.
Although these increases in the four-year college enrollment rate might not appear
to be dramatically large, relative to other educational interventions this policy is inex-
pensive and currently being implemented on a large scale. The direct costs to states
of a mandatory ACT policy include: (1) the per-student test fee, which for spring 2012
was $32 (a $2 discount off the price a student would pay privately);32 (2) a statewide
administration management fee, which is approximately $1 per student; and (3) the costs associated with trainings, meetings, and other logistical issues, which comes to less than $1 per student.33 Whereas (2) and (3) vary by state, the total cost is substantially
less than $50 per student in all mandatory ACT states, especially because the actual cost to a state is the direct cost of the policy minus the cost to design, administer, and grade the portions of the eleventh grade exam displaced by the ACT. Further, this cost calcula- tion ignores savings to families who no longer have to pay for a college entrance exam. Thus, the “social cost” is even lower, given that much of the cost can be considered a transfer. To show the relative cost-effectiveness of the mandatory ACT policy at increasing postsecondary attainment, I compare the policy to other educational interventions that increase college-going. I create an index of cost-effectiveness by dividing a policy’s cost by the proportion of students it induces into college. For example, assuming a $50 per
student cost and an increase in the four-year college enrollment rate of 0.6 percentage
points, the amount spent by the mandatory ACT policy to induce a single child into
32. States can include the writing portion of the ACT for an additional $15 per test. 33. All mandatory ACT costs come from communications between the author and staff at state departments of education. All costs of other policies are in 2007 dollars and come from Levine and Zimmerman (2010) unless otherwise noted. The costs of the early childhood programs and STAR have been discounted back to age zero using a 3 percent discount rate. Costs of mandatory ACT and other high school and college interventions have not been discounted. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / f e d u e d p a r t i c e – p d l f / / / / 1 2 3 2 8 1 1 6 9 1 8 7 1 e d p _ a _ 0 0 2 0 6 p d / . f f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 307 The Effects of Mandatory ACT-Taking college is $8,333 (= $50 / 0.006).34 This figure is an upper bound, given that the true cost is substantially less than $50 and the 0.6 percentage point effect is a likely lower
bound. Also, targeting the policy at students in the poorest schools would reduce this
figure to under $4,000. More traditional education policies are far more expensive than the mandatory ACT policy. Given the effects on college enrollment estimated in Deming (2009), Head Start has a cost per student induced into college of $133,000 (= $8,000 / 0.06). The cost per student induced into college from the class size decrease in the Tennessee STAR exper- iment is even larger: $400,000 (= $12,000 / 0.03) (Dynarski, Hyman, and Schanzen- bach 2013). Dynarski (2003) showed that it takes approximately $21,000 of traditional
student aid to induce a single student into college, including the aid spent on students
who would have enrolled regardless.
Other policies aim specifically to boost college enrollment by dismantling admin-
istrative barriers to enrollment. For example, Bettinger et al. (2012) randomly offered
families at H&R Block assistance filling out the Free Application for Federal Student
Aid, finding a cost per student induced into college of $1,100 (= $88 / 0.08). This policy
is extremely cost effective, although it is unclear whether this policy could be success-
fully operated on a scale as large as the mandatory ACT policy.
Given that these estimated costs per student induced into college do not reflect the
statistical precision of the enrollment effects, and that the interventions earlier in stu-
dents’ lives may have impacts beyond those on postsecondary attainment, these com-
parisons are best viewed as rough approximations. Nonetheless, they suggest that rela-
tive to other interventions operating on a large scale such as traditional student aid, the
mandatory ACT policy is very cost effective.
Still, the mandatory ACT is far from a cure-all. The results in section 3 suggest
that requiring all students to take a college entrance exam increases the supply of poor
students scoring at a college-ready level by nearly 50 percent. Yet the policy increases
the number of poor students enrolling at a four-year institution by only 6 percent. In
spite of the policy, there remains a large supply of disadvantaged students who are high-
achieving and not on the path to enrolling at a four-year college. Researchers and policy
makers are still faced with the important question of which policies can further stem
the tide of rising inequality in educational attainment.
ACKNOWLEDGMENTS
I thank Susan Dynarski, John Bound, Brian Jacob, and Jeff Smith for their advice and support. I
am grateful for helpful conversations with Charlie Brown, Eric Brunner, Steve DesJardins, John
DiNardo, Tom Downes, Rob Garlick, Michael Gideon, Andrew Goodman-Bacon, Steve Hemelt,
Kevin Stange, Caroline Theoharides, Elias Walsh, and seminar participants at the University of
Michigan and Association for Education Finance and Policy. Thanks for helpful comments from
Amy Schwartz and two anonymous referees. I am grateful to ACT, Inc., and the College Board
for the data used in this paper. In particular, I thank Ty Cruce, John Carrol, and Julie Noble at
ACT, Inc., and Sherby Jean-Leger at the College Board. Thanks to the Institute of Education Sci-
ences, U.S. Department of Education, for providing support through grant R305E100008 to the
34. One way to think of this calculation is as follows: if 1,000 students are treated with the policy at a cost of $50 per student, six will be induced to attend college (= 1,000 × 0.006) at a total cost of $50,000 (= $50 × 1,000). Thus, the cost per student induced into college is $8,333 (= $50,000 / 6).
308
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
2
3
2
8
1
1
6
9
1
8
7
1
e
d
p
_
a
_
0
0
2
0
6
p
d
.
/
f
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Joshua Hyman
University of Michigan. Thanks to my partners at the Michigan Department of Education (MDE)
and Michigan’s Center for Educational Performance and Information (CEPI). This research used
data structured and maintained by the Michigan Consortium for Education Research (MCER).
MCER data are modified for analysis purposes using rules governed by MCER and are not iden-
tical to those data collected and maintained by MDE and CEPI. Results, information, opinions,
and any errors are my own and are not endorsed by or reflect the views or positions of MDE or
CEPI.
REFERENCES
Abadie, Alberto, Matthew M. Chingos, and Martin R. West. 2012. Endogenous stratification in
randomized experiments. NBER Working Paper No. 19742.
ACT, Inc. 2002. Understanding your ACT assessment scores. Available www.act.org/content
/act/en/products-and-services/the-act/your-scores/understanding-your-scores.html. Accessed
9 November 2016.
Bailey, Martha J., and Susan M. Dynarski. 2011. Gains and gaps: A historical perspective on in-
equality in college entry and completion. In Whither opportunity: Rising inequality, schools, and
children’s life chances, edited by Greg Duncan and Richard Murnane, pp. 117–133. New York: The
Russel Sage Foundation.
Beshears, John, James J. Choi, David Laibson, and Bridgette C. Madrian. 2009. The impor-
tance of default options for retirement saving outcomes: Evidence from the United States.
In Social Security policy in a changing environment, edited by Jeffrey Brown, Jeffrey Liebman,
and David A. Wise, pp. 167–195. Chicago: University of Chicago Press. doi:10.7208/chicago
/9780226076508.003.0006.
Bettinger, Eric P., Bridget Terry Long, Philip Oreopoulos, and Lisa Sanbonmatsu. 2012. The
role of application assistance and information in college decisions: Results from the H&R Block
FAFSA experiment. Quarterly Journal of Economics 127(3):1205–1242. doi:10.1093/qje/qjs017.
Bound, John, and Sarah E. Turner. 2007. Cohort crowding: How resources affect collegiate at-
tainment. Journal of Public Economics 91(5):877–899. doi:10.1016/j.jpubeco.2006.07.006.
Bound, John, Michael Lovenheim, and Sarah E. Turner. 2010. Why have college completion rates
declined? An analysis of changing student preparation and collegiate resources. American Eco-
nomic Journal. Applied Economics 2(3):1–31. doi:10.1257/app.2.3.129.
Bowen, William G., Matthew M. Chingos, and Michael S. McPherson. 2009. Crossing the finish
line: Completing college at America’s public universities. Princeton, NJ: Princeton University Press.
Bulman, George. 2015. The effect of access to college assessments on enrollment and attainment.
American Economic Journal. Applied Economics 7(4):1–36. doi:10.1257/app.20140062.
Busso, Matias, John DiNardo, and Justin McCrary. 2013. Finite sample properties of semipara-
metric estimators of average treatment effects. Unpublished paper, University of Michigan.
Card, David. 1995. Earnings, schooling, and ability revisited. In Research in labor economics, vol. 14,
edited by Solomon Polachek, pp. 23–48. Greenwich, CT: JAI Press.
Carrell, Scott, and Bruce Sacerdote. (forthcoming). Why Do College Going Interventions Work?
American Economic Journal: Applied Economics.
Deming, David. 2009. Early childhood intervention and life-cycle skill development: Evidence
from Head Start. American Economic Journal. Applied Economics 1(3):111–134. doi:10.1257/app.1.3.111.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
2
3
2
8
1
1
6
9
1
8
7
1
e
d
p
_
a
_
0
0
2
0
6
p
d
f
/
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
309
The Effects of Mandatory ACT-Taking
Deming, David, and Susan M. Dynarski. 2010. Into college, out of poverty? Policies to increase
the postsecondary attainment of the poor. In Targeting investments in children: Fighting poverty
when resources are limited, edited by Philip Levine and David Zimmerman, pp. 283–302. Chicago:
University of Chicago Press. doi:10.7208/chicago/9780226475837.003.0011.
Dillon, Eleanor, and Jeffrey Smith. 2017. The determinants of mismatch between students and
colleges. Journal of Labor Economics 35(1):45–66.
DiNardo, John. 2002. Propensity score reweighting and changes in wage distributions. Unpub-
lished paper, University of Michigan.
DiNardo, John, Nicole Fortin, and Thomas Lemieux. 1996. Labor market institutions and the
distribution of wages, 1973–1992: A semiparametric approach. Econometrica 64(5):1001–1044.
doi:10.2307/2171954.
Dynarski, Susan M. 2003. Does aid matter? Measuring the effect of student aid on
college attendance and completion. American Economic Review 93(1):279–288. doi:10.1257
/000282803321455287.
Dynarski, Susan M., Joshua M. Hyman, and Diane Whitmore Schanzenbach. 2013. Experimental
evidence on the effect of childhood investments on postsecondary attainment and degree com-
pletion. Journal of Policy Analysis and Management 32(4):692–717. doi:10.1002/pam.21715.
Dynarski, Susan M., Ken Frank, Brian Jacob, and Barbara Schneider. 2013. The effect of the
Michigan Promise Scholarship on educational outcomes. Unpublished paper, University of
Michigan.
Dynarski, Susan M., Steven W. Hemelt, and Joshua M. Hyman. 2015. The missing manual: Using
National Student Clearinghouse data to track postsecondary outcomes. Educational Evaluation
and Policy Analysis 37(1S):53S–79S. doi:10.3102/0162373715576078.
Efron, Bradley, and Robert Tibshirani. 1993. An introduction to the bootstrap: Monographs on statis-
tics and applied probability, vol. 57. New York: Chapman Hall. doi:10.1007/978-1-4899-4541-9.
Eichler, Martin, and Michael Lechner. 2002. An evaluation of public employment pro-
grammes in the East German state of Sachsen-Anhalt. Labour Economics 9(2):143–186.
doi:10.1016/S0927-5371(02)00039-8.
Goodman, Sarena. 2016. Learning from the test: Raising selective college enrollment by provid-
ing information. Review of Economics and Statistics 98(4):671–684. doi:10.1162/REST_a_00600.
Heckman, James J., Hidehiko Ichimura, and Petra E. Todd. 1997. Matching as an econometric
evaluation estimator: Evidence from evaluating a job training programme. Review of Economic
Studies 64(4):605–654. doi:10.2307/2971733.
Hoxby, Caroline, and Christopher Avery. 2013. The “missing one-offs”: The hidden sup-
ply of high-achieving, low-income students. Brookings Papers on Economic Activity 46(1):1–65.
doi:10.1353/eca.2013.0000.
Hoxby, Caroline, and Sarah Turner. 2012. Expanding college opportunities for high-achieving,
low income students. Stanford Institute for Economic Policy Research Discussion Paper No. 12–
014.
Hurwitz, Michael, Jonathan Smith, Sunny Niu, and Jessica Howell. 2015. The Maine question:
How is 4-year college enrollment affected by mandatory college entrance exams? Educational
Evaluation and Policy Analysis 37(1):138–159. doi:10.3102/0162373714521866.
310
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
2
3
2
8
1
1
6
9
1
8
7
1
e
d
p
_
a
_
0
0
2
0
6
p
d
/
.
f
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Joshua Hyman
Hyman, Joshua M. (forthcoming). Does money matter in the long run? Effects of school spending
on educational attainment. [In press] American Economic Journal: Economic Policy.
Imbens, Guido W., and Joshua Angrist. 1994. Identification and estimation of local average treat-
ment effects. Econometrica 62(2):467–475. doi:10.2307/2951620.
Jackson, C. Kirabo. 2010. A little now for a lot later: A look at a Texas Advanced Placement Incen-
tive Program. Journal of Human Resources 45(3):591–639.
Klasik, Daniel. 2013. The ACT of enrollment: The college enrollment effects of state-required col-
lege entrance exam testing. Educational Researcher 42(3):151–160. doi:10.3102/0013189×12474065.
Levine, Phillip B., and David J. Zimmerman. 2010. Targeting investments in children: Fighting
poverty when resources are limited. Chicago: University of Chicago Press. doi:10.7208/chicago
/9780226475837.001.0001.
Madrian, Brigette C., and Dennis F. Shea. 2001. The power of suggestion: Inertia in 401(k)
participation and savings behavior. Quarterly Journal of Economics 116(4):1149–1187. doi:10.1162
/003355301753265543.
Pallais, Amanda. 2015. Small differences that matter: Mistakes in applying to college. Journal of
Labor Economics 33(2):493–520. doi:10.1086/678520.
Pallais, Amanda, and Sarah Turner. 2006. Opportunities for low income students at top col-
leges and universities: Policy initiatives and the distribution of students. National Tax Journal
59(2):357–386. doi:10.17310/ntj.2006.2.08.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
–
p
d
l
f
/
/
/
/
1
2
3
2
8
1
1
6
9
1
8
7
1
e
d
p
_
a
_
0
0
2
0
6
p
d
.
f
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
311