Abstract Neural Representations of Category Membership
beyond Information Coding Stimulus or Response

Robert M. Mok1,2

and Bradley C. Love1,3

Abstract

■ For decades, researchers have debated whether mental rep-
resentations are symbolic or grounded in sensory inputs and
motor programs. Certainly, aspects of mental representations
are grounded. However, does the brain also contain abstract
concept representations that mediate between perception and
action in a flexible manner not tied to the details of sensory
inputs and motor programs? Such conceptual pointers would
be useful when concepts remain constant despite changes in
appearance and associated actions. We evaluated whether
human participants acquire such representations using fMRI.
Participants completed a probabilistic concept learning task in
which sensory, motor, and category variables were not perfectly
coupled or entirely independent, making it possible to observe
evidence for abstract representations or purely grounded repre-
sentations. To assess how the learned concept structure is

represented in the brain, we examined brain regions implicated
in flexible cognition (e.g., pFC and parietal cortex) that are most
likely to encode an abstract representation removed from
sensory–motor details. We also examined sensory–motor re-
gions that might encode grounded sensory–motor-based repre-
sentations tuned for categorization. Using a cognitive model to
estimate participants’ category rule and multivariate pattern anal-
ysis of fMRI data, we found the left pFC and human middle tem-
poral visual area (MT)/V5 coded for category in the absence of
information coding for stimulus or response. Because category
was based on the stimulus, finding an abstract representation
of category was not inevitable. Our results suggest that certain
brain areas support categorization behavior by constructing
concept representations in a format akin to a symbol that differs
from stimulus–motor codes. ■

INTRODUCTION

Concepts organize our experiences into representations
that can be applied across domains to support higher-order
cognition. How does the brain organize sensory input into
an appropriate representation for categorization? Are
concepts simply a combination of sensory signals and motor
plans, or does the brain construct a separate concept repre-
sentation, abstracted away from sensory–motor codes?
Despite much research on how people organize sensory in-
formation into a format suited for categorization (e.g., Love,
Medin, & Gureckis, 2004; Kruschke, 1992; Nosofsky, 1986)
and its neural basis (e.g., Zeithamova et al., 2019; Bowman &
Zeithamova, 2018; Mack, Love, & Preston, 2016; Folstein,
Palmeri, & Gauthier, 2013; Mack, Preston, & Love, 2013;
Davis, Love, & Preston, 2012a, 2012b; Cromer, Roy, &
Miller, 2010; Seger & Miller, 2010; Freedman & Assad,
2006; Sigala & Logothetis, 2002), few have explicitly exam-
ined whether category representations exist indepen-
dently of sensory–motor information (Figure 1A).

Some concepts seem to be “grounded” in sensory or
motor experiences (Barsalou, 2008). For instance, the idea

This article is part of a Special Focus entitled Integrating Theory
and Data: Using Computational Models to Understand
Neuroimaging Data; deriving from a symposium at the 2020
Annual Meeting of the Cognitive Neuroscience Society.
1University College London, 2University of Cambridge, 3The
Alan Turing Institute, London, UK

of “pain” is based on experiences of pain, and the meta-
phorical use of the word is presumably linked to those
bodily experiences. Certain aspects of concepts are more
abstracted from first-hand experience and act more like
symbols or pointers, which can support flexible cognition.
For example, we know water can be used to clean the
dishes, but when we are thirsty, we drink it. The same ob-
ject can also appear entirely different in some contexts,
such as a camouflaging stick insect appearing as a leaf or
when a caterpillar changes into a butterfly. In such cases
where sensory information is unreliable or exhibits changes,
an amodal symbol working as an abstract pointer may aid
reasoning and understanding. Cognitive science and ar-
tificial intelligence researchers discuss the use of amodal
symbols—abstracted away from specific input patterns—
for solving complex tasks, arguing they provide a founda-
tion to support higher cognition (Marcus, 2001; Pylyshyn,
1984; Fodor, 1975; also see Markman & Dietrich, 2000).
In contrast, theories of grounded cognition suggest that all
“abstract” representations are grounded in, and therefore
fully explained by, sensory–motor representations
(Barsalou, 1999; Harnad, 1990). Indeed, sensory–motor var-
iables and categories are often correlated in the real world,
and the brain may never need to represent “category” in a
way that can be disentangled from perception and action.
Here, we consider several competing accounts. Closely
related to “grounded cognition,” some researchers empha-
size a central role of action for cognition ( Wolpert &

© 2020 Massachusetts Institute of Technology. Published under a
Creative Commons Attribution 4.0 International (CC BY 4.0) license.

Journal of Cognitive Neuroscience 34:10, pp. 1719–1735
https://doi.org/10.1162/jocn_a_01651

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

3
4
1
0
1
7
1
9
2
0
4
1
8
3
0

/

/
j

o
c
n
_
a
_
0
1
6
5
1
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Witkowski, 2014; Wolpert & Ghahramani, 2000; Rizzolatti,
Riggio, Dascola, & Umiltá, 1987), such that category repre-
sentations could simply consist of the appropriate
stimulus–motor representations and associations
(Figure 1B). An alternative view holds that category-
modulated stimulus representations are key for categori-
zation, where stimulus information is transformed into a
representation suited for categorization (as in cognitive
models: e.g., Love et al., 2004; Kruschke, 1992). In these
models, an attention mechanism gives more weight to
relevant features so that within-category stimuli become
closer and across-category stimuli are pushed apart in
representational space (Figure 1C). Finally, the brain may
recruit an additional amodal, symbol-like concept represen-
tation (Marcus, 2001; Pylyshyn, 1984; Newell, 1980; Fodor,
1975) to explicitly code for category, separate from
sensory–motor representations. For instance, sensory infor-
mation is processed (e.g., modulated by category structure)
and then transformed into an abstract category representa-
tion before turning into a response (Figure 1D). This repre-
sentation resembles an amodal symbol in that it has its own
representational format (e.g., orthogonal to sensory–motor
codes) and acts as a pointer between the relevant sensory
signals (input) and motor responses (output). The advan-
tage of such a representation is that it can play a role in solv-
ing the task and can persist across superficial changes in
appearance and changes in motor commands. People’s
ability to reason and generalize in an abstract fashion sug-
gests the brain is a type of symbol processor (Marcus, 2001).
Here, we aimed to test whether the brain constructs an
abstract concept representation separate from stimulus
and motor signals, if the “category” code consists of
category-modulated stimulus representations and motor

codes, or if it simply consists of stimulus–motor mappings.
We designed a probabilistic concept learning task where
the stimulus, category, and motor variables were not per-
fectly coupled nor entirely independent, to allow partici-
pants to naturally form the mental representations
required to solve the task, and used multivariate pattern
analysis (MVPA) on fMRI data to examine how these vari-
ables were encoded across the brain. For evidence sup-
porting the amodal account (Figure 1D), some brain
regions should encode category information but not the
stimulus or response. For the category-modulated sensory
account (Figure 1C), regions should encode both stimulus
and category information, with no regions that encode
category without stimulus information. Finally, for the
sensory–motor account (Figure 1B), regions should code
for category, stimulus, and motor response (separately or
concurrently), with no regions encoding category without
sensory or motor information.

We recruited participants to an initial behavioral session
where they first learned the task and invited a subset of par-
ticipants who performed relatively well to partake in an
fMRI study. To assess how the learned concept structure
is represented in the brain, we focused on brain regions
implicated in flexible cognition, including pFC and parietal
cortex, which are strong candidates for representing the
abstract concept structure without being tied to sensory–
motor variables, and sensory–motor regions that are in-
volved in stimulus processing and may encode grounded
representations such as category-modulated stimulus
representations as the basis of concept knowledge. We
focused on these regions to test for category representa-
tions after learning rather than testing regions that might
be involved in learning (e.g., hippocampus, medial pFC),

Figure 1. How the brain transforms stimulus into a concept representation for categorization. Stimuli are 12 motion dot patterns (100% coherent),
from 0° to 330° in 30° steps. Blue and green colors denote the two categories. (A) An observer must transform the percept into intermediate
representations for accurate categorization behavior. (B–D) Possible representations the brain might use for categorization. (B) Each stimulus is
associated with a motor response, where the category representation is grounded in sensory–motor codes. (C) Stimulus-modulated representations
as category representation. The stimulus representation is modulated by the category structure, which is turned into a motor representation for the
response. (D) The category-modulated stimulus representation is associated with an abstract representation of each category with a different
representational format to the sensory motor codes (blue and green circles), which is then turned into a response.

1720

Journal of Cognitive Neuroscience

Volume 34, Number 10

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

3
4
1
0
1
7
1
9
2
0
4
1
8
3
0

/

/
j

o
c
n
_
a
_
0
1
6
5
1
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

because participants spent a significant amount of time
learning the category structure in a prior behavioral ses-
sion (see Methods).

METHODS

Participant Recruitment and Behavioral Session

We recruited participants to partake in a behavioral session
to assess their ability to learning the probabilistic concept
learning task. One hundred thirty-one participants com-
pleted the behavioral session, and we invited a subset of
higher performing participants who were MRI compatible
to participate in the fMRI study. We set the threshold for
being invited to no lower than 60% accuracy over two
blocks of the task (50% chance). Only two participants in
the behavioral session performed below 60% accuracy.

Participants (fMRI Study)

Thirty-nine participants took part in the fMRI study (most
returned ∼2–4 weeks after the behavioral session). Six
participants were excluded because of lower-than-chance
performance, misunderstanding the task, or falling asleep
during the experiment. The remaining 33 participants
(23 women) were aged 19–34 years (mean = 24.04 years,
SEM = 0.61 years). The study was approved by the University
College London Research Ethics Committee (reference:
1825/003).

Stimuli and Apparatus

Stimuli consisted of coherently moving dots produced in
PsychoPy (Peirce et al., 2019), images of faces and buildings
(main task), and images of flowers and cars (practice). In
each dot-motion stimulus, there were 1000 dots, and dots
were 2 pixels in size and moved at a velocity of ∼0.8° per
second. The dot-motion stimuli and images were 12° in
diameter (or on longest axis). The fixation point was a black
circle with 0.2° diameter. A gray circle (1° diameter) was
placed in front of the dot stimulus but behind the fixation
point to discourage smooth pursuit. The natural images
were provided by members of Cognitive Brain Mapping
Lab at RIKEN BSI. The task was programmed and run in
PsychoPy in Python 2.7. The task was presented on an
LCD projector (1024 × 768 resolution), which was viewed
through a tilted mirror in the fMRI scanner. We monitored
fixation with an eye tracker (Eyelink 1000 Plus, SR Research)
and reminded participants to maintain fixation between
runs as necessary.

Behavioral Task

To examine how the brain constructs an appropriate
mental representation for categorization, we designed a
probabilistic concept learning task to be first performed
in a behavioral session and then the same probabilistic
categorization task in the fMRI session. Specifically, we

set out to test whether any brain regions coded for an
abstract category signal separate from stimulus and motor
signals, if the category signal mainly consisted of category-
modulated sensory signals, or if the category signal was
simply a combination or coexistence of sensory–motor
signals. To this end, we designed a probabilistic categoriza-
tion task where the task variables (category, stimulus, and
motor response) were not perfectly coupled or entirely
independent.

On each trial, participants were presented with a set of
moving dots moving coherently in one direction and were
required to judge whether it belonged to one category
(“Face”) or another (“Building”) with a corresponding left
or right button press. The motion stimulus was presented
for 1 sec, followed by an ISI ranging from 1.8 to 7.4 sec
( jittered), then the category feedback (Face or Building
stimulus) for 1 sec. The intertrial interval was 1.8 sec.
Naturalistic images were used to encourage task engage-
ment and to produce a strong stimulus signal.

The moving-dot stimuli spanned 12 directions from 0° to
330° in 30° steps, with half the motion directions assigned
to one of two categories determined by a category bound.
For half of the participants, the category bound was placed
at 15°, so that directions from 30° to 180° were in one
category, and directions from 210° to 330° and 0° were in
the other category. For the other half of the participants,
the objective category bound was placed at 105°, so that
directions from 120° to 270° were in one category, and
directions from 0° to 90° and 300° to 330° were in the
other category.

The corrective category feedback consisted of a face or
building stimulus, which informed the participant which
category the motion stimulus was most likely part of. The
feedback was probabilistic such that the closer to the
bound a stimulus was, the more probabilistic the feedback
was (see Figure 2A). In the practice sessions, participants
were introduced to a deterministic version of the task
before the probabilistic task (see Experimental Procedure:
Behavioral Session section below).

Behavioral Task Rationale

Probabilistic category feedback was used to decouple the
stimulus from the category to a certain extent. Most previ-
ous concept learning studies used deterministic feedback,
such that each stimulus was always associated with the
same (correct) category feedback. In terms of conditional
probability, the probability of a stimulus belonging to a
given category (Pr(category A | stimulus x)) with deter-
ministic category feedback is 1. With probabilistic category
feedback, the conditional probability is less than 1, and as
the stimulus–feedback association becomes weaker (more
probabilistic), it approaches 0.5 (not predictive). In this
way, the stimulus and category are weakly coupled and
may lead participants to form a category representation
abstracted from the more concrete experimental variables
(such as stimulus and motor response). On the other hand,

Mok and Love

1721

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

3
4
1
0
1
7
1
9
2
0
4
1
8
3
0

/

/
j

o
c
n
_
a
_
0
1
6
5
1
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

3
4
1
0
1
7
1
9
2
0
4
1
8
3
0

/

/
j

o
c
n
_
a
_
0
1
6
5
1
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 2. Behavioral task. (A) On each trial, a dot-motion stimulus was presented and participants judged whether it was in Category A or B. At the
end of each trial, probabilistic category feedback (a face or building stimulus) informed the participant which category the motion stimulus most
likely belonged to. (B) Probabilistic category structure. For motion stimuli to the left of the category bound (dotted line), the feedback will most
likely be a face (Category A), and stimuli to the right will most likely be a building (Category B). For example, for the motion direction where the blue
section is 4/7, the participant will see a face four out of seven times and a building three out of seven times (corresponding to the 3/7 green section).
The closer the motion direction to the category bound, the more probabilistic the feedback.

participants could still perform the task at greater accuracy
than chance if they relied heavily on the stimulus,
grounding the category in the stimulus representations.

Furthermore, the category–response association was
flipped after each block (e.g., left button press for
Category A in the first block, right button press for
Category A in the second block), to discourage participants
simply associating each category with a motor response
across the experiment. Of course, it was still possible for
participants to associate the category with a motor plan
and change this association across blocks, leading to a
category representation based on motor planning.

In summary, the task required participants to learn the
category that each motion-dot stimulus belonged to by its
probabilistic association to an unrelated stimulus (face
or building as category feedback), whereby the probabi-
listic feedback could lead participants to form an abstract
or grounded category representation. In addition, the
category–motor association was flipped across blocks.
Together, the category, stimulus, and motor variables were
weakly coupled, allowing us to assess whether there are
brain regions that code for these variables together or
independently of one another.

Experimental Procedure: Behavioral Session
(Practice and Main Experiment)

To ensure participants understood the main experimental
task, they were given four practice task runs with each
version gradually increasing in task complexity. In the first
three runs, the task was the same as described above
except that the images used for feedback were pictures
of flowers and cars. In the fourth run, it was a practice
run of the main task described above. Before each run,
the experimenter explained the task to the participant.

Participants were instructed to learn which motion direc-
tions led to the appearance of Flower images and which led
to the Car images. Specifically, they were told that, when

the moving dot stimulus appears, they should press the left
(or right) button if they think a Flower will appear or the
right (or left) button if they think a Car will appear. In the
first run, the category boundary was at 90° (up–down rule),
and motion directions were presented in sequential order
around the circle. The category (“Flower” or “Car”) feed-
back was deterministic such that each dot-motion stimulus
was always followed by the same category stimulus feed-
back. For feedback, participants were presented with the
image in addition to a color change in the fixation point
(correct: green, incorrect: red, too slow: yellow). In the
second run, the task was the same except the motion
directions were presented in a random order. In the third
run, participants were told that the feedback is probabi-
listic, meaning that the feedback resembles the weather
report: It is usually correct, but sometimes it is not. For
example, of the five times you see that motion direction,
you will be shown a flower stimulus as feedback four times,
but you will be shown a car once. So the feedback is helpful
on average, but sometimes it can be misleading. In the
fourth run, participants were introduced to a new task to
be used in the main experiment, with a new probabilistic
category boundary (15° or 105°) and with face and building
images as feedback.

Once participants completed the practice runs and were
comfortable with the task, they proceeded to the main
experimental session where they learnt the category rule
from trial and error. In each block, participants completed
seven trials per direction condition, giving 84 trials per
block. The experimenter informed participants that the
category–response association flipped after each block.
Participants completed three or four experimental runs.

Experimental Procedure: fMRI Session

A subset of participants was invited to attend an fMRI ses-
sion. Participants were given one practice block run as a
reminder of the task and then proceeded to complete

1722

Journal of Cognitive Neuroscience

Volume 34, Number 10

the main experiment in the scanner. Participants learned
through trial and error. They were not informed about
the location of the category boundary in either the behav-
ioral or fMRI session, which partially explains why their
performance was not at ceiling. A cognitive model fit to
individuals’ behavior indicates that participants’ category
boundaries differed from the optimal boundary (see
below).

Participants completed three or four blocks of the
probabilistic category learning task (four participants
performed an extra block because of low performance on
early block runs), then a motion localizer block, and a
face–scene localizer block (block order for localizer runs
was counterbalanced across participants). After the scan
session, participants completed a postscan questionnaire
to assess their understanding of the task and to report
their subjective category rule.

Each task block took approximately 12 min, and the
whole scan session (main task, localizers, and structural
scans) took slightly over an hour. Including preparation,
practice, and postexperiment debriefing, the whole
session took approximately 2 hr.

Localizer Tasks

To localize the face-selective fusiform face area (FFA;
Allison, Puce, Spencer, & McCarthy, 1999; Kanwisher,
McDermott, & Chun, 1997) and place-sensitive parahippo-
campal place area (PPA; Epstein & Kanwisher, 1998) in
individuals, participants completed an event-related locali-
zer scan where they were presented with faces and build-
ings and made a response when they saw an image repeat
(1-back task), which was followed by feedback (the fixation
point changed to green for correct and red for incorrect).
On each trial, an image of a face or building was presented
for 1 sec with ISIs between stimulus and feedback (green/
red fixation color change) ranging from 1.8 to 7.4 sec
( jittered), with an intertrial interval of 1.8 sec. A total of
42 faces and 42 buildings were presented in a random
order. Participants also completed a motion localizer run
that was not used here.

MRI Data Acquisition

Functional and structural MRI data were acquired on a 3-T
TrioTim scanner (Siemens) using a 32-channel head coil at
the Wellcome Trust Centre for Neuroimaging at University
College London. An EPI-BOLD contrast image with 40 slices
was acquired in 3-mm3 voxel size, repetition time (TR) =
2800 msec, and echo time (TE) = 30 msec, and the flip angle
was set to 90°. A whole-brain field map with 3-mm3 voxel
size was obtained with a first TE = 10 msec, second TE =
12.46 msec, and TR = 1020 msec, and the flip angle was
set to 90°. A T1-weighted (T1w) structural image was
acquired with 1-mm3 voxel size, TR = 2.2 msec, and TE =
2.2 msec, and the flip angle was set to 13°.

Behavioral Model and Data Analysis

The probabilistic nature of the feedback meant that partic-
ipants did not perform exactly according to the objective
category rule determined by the experimenter, and in-
spection of behavioral performance curves suggested
that most participants formed a category rule slightly differ-
ent to the objective rule. To get a handle on the category
rule participants formed, we applied a behavioral model
to estimate each participant’s subjective category boundary
from their responses.

The model contains a decision bound defined by two
points, b1 and b2, on a circle (0°–359°). Category A proceeds
clockwise from point b1, whereas Category B proceeds
clockwise from b2. Therefore, the positions of b1 and b2
define the deterministic category boundary between
Categories A and B. To illustrate, if b1 = 15° and b2 =
175°, stimulus directions from 15° to 175° would be in one
category, and stimulus directions from 175° to 359° and from
0° to 15° would be in the other category. Note that the
number of stimulus directions is not constrained to be equal
across categories, as illustrated in this example (five and
seven directions in each category). Despite this, there were six
stimulus directions in each category for most participants.
The only source of noise in this model are the positions
of b1 and b2, which are normally distributed as N (0, σ). As
the σ parameter—the standard deviation of the positions
of b1 and b2—increases, the position of the boundary for a
given trial becomes noisier, and therefore it becomes more
likely that an item may be classified contrary to the position
of the boundary. In practice, no matter the value of σ, it is
always more likely that an item will be classified according
to the positions of b1 and b2. The standard deviation param-
eter provides an estimate of how uncertain participants
were of the category boundary. If a participant responded
perfectly consistently according to a set of bounds (deter-
ministically), σ would be low, whereas if the participant was
more uncertain of the bound locations and responded
more probabilistically, σ would be higher.

The probability a stimulus x is an A or B is calculated
according to whichever boundary b1 or b2 is closer. This
is a numerical simplification as it is possible for the further
boundary to come into play and even for boundary noise to
lead to b1 or b2 to traverse the entire circle. However, for
the values of σ we consider, both of these possibilities are
highly unlikely. The probability that stimulus x is labeled
according to the mean positions of b1 and b2 is
(cid:1)

(cid:3)

1 − p z > x − bx
σ

j

j

where z is distributed according to the standard normal
distribution and bx is b1 or b2, whichever is closer to x.
Intuitively, the further the item is from the boundary posi-
tion, the more likely it is to be classified according to the
boundary position as noise (i.e., σ) is unlikely to lead to
sufficient boundary movement in that trial. The probabi-
lity an item is labeled in the alternative category (i.e.,

Mok and Love

1723

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

3
4
1
0
1
7
1
9
2
0
4
1
8
3
0

/

/
j

o
c
n
_
a
_
0
1
6
5
1
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

“incorrect” responses against the bound defined by the
mean positions of b1 and b2) is simply 1 minus the above
quantity.

In other words, the probability a stimulus is in a certain
category is a Gaussian function of the distance to the
closest bound, where the further away the stimulus is
from the bound, the more likely it is to be a part of that
category (see Figure 3A for an illustration of the model).

Maximum likelihood estimation was used to obtain es-
timates for each participant (using the optimize function
in SciPy). Model estimates of the subjective category
bound fit participant behavior as expected. Specifically,
there was high accuracy (concordance) with respect to
the estimated subjective category bound (mean propor-
tion correct = 0.82, SEM = 0.01; see Figure 3B).

Modeling and analyses were performed in Python 3.7.

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

3
4
1
0
1
7
1
9
2
0
4
1
8
3
0

/

/
j

o
c
n
_
a
_
0
1
6
5
1
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 3. Task model, behavioral results, and model-based fMRI analysis procedure. (A) The model takes individual participant behavior as input and
estimates their subjective category bound (b1 and b2) and standard deviation (σ). (B) Categorization behavior. Proportion Category A responses
plotted as a function of motion directions ordered by individual participants’ estimated category boundary. Blue curve represents the mean, and
error bars represent SEM. Translucent lines represent individual participants. (C) Model-based fMRI analysis procedure illustration. Voxel activity
patterns are extracted from each ROI for each motion direction condition (top), and a classifier was trained (SVM) to decode the category based on
the model-based estimation of the category boundary for each participant (bottom). The data in the scatterplot were generated to illustrate example
patterns of voxel activity evoked by the motion direction stimuli (two voxels shown here) belonging to each category (blue for Category A, green for
Category B). The line is a possible support vector plane that reliably discriminates voxel patterns elicited by stimuli in Category A from stimuli in
Category B. To test for an abstract category signal, we subtracted the classification accuracy for the category SVM by an SVM trained to discriminate
orthogonal (90° rotated) directions (see Methods for details).

1724

Journal of Cognitive Neuroscience

Volume 34, Number 10

fMRI Preprocessing

Results included in this article come from preprocessing
performed using fMRIprep 1.2.3 (Esteban et al., 2019;
RRID:SCR_016216), which is based on Nipype 1.1.6-dev
(Gorgolewski et al., 2011; RRID:SCR_002502).

Anatomical Data Preprocessing

The T1w image was corrected for intensity nonuniformity
using N4BiasFieldCorrection (Avants, Tustison, & Song,
2009; ANTs 2.2.0) and used as T1w reference throughout
the workflow. The T1w reference was then skull-stripped
using antsBrainExtraction.sh (ANTs 2.2.0), using OASIS as
the target template. Spatial normalization to the ICBM
152 Nonlinear Asymmetrical template version 2009c
(Fonov, Evans, McKinstry, Almli, & Collins, 2009; RRID:
SCR_008796) was performed through nonlinear registra-
tion with antsRegistration (ANTs 2.2.0, RRID:SCR_004757;
Avants, Epstein, Grossman, & Gee, 2008), using brain-
extracted versions of both T1w volume and template.
Brain tissue segmentation of cerebrospinal fluid (CSF),
white matter (WM), and gray matter (GM) was performed
on the brain-extracted T1w using fast (FSL 5.0.9, RRID:
SCR_002823; Zhang, Brady, & Smith, 2001).

Functional Data Preprocessing

For each of the five or six BOLD runs found per subject
(three or four task runs plus two localizer runs), the
following preprocessing was performed. First, a reference
volume and its skull-stripped version were generated using
a custom methodology of fMRIPrep. A deformation field to
correct for susceptibility distortions was estimated based
on a field map that was coregistered to the BOLD refer-
ence, using a custom workflow of fMRIPrep derived from
D. Greve’s epidewarp.fsl script and further improvements
of HCP Pipelines (Glasser et al., 2013). On the basis of the
estimated susceptibility distortion, an unwarped BOLD ref-
erence was calculated for a more accurate coregistration
with the anatomical reference. The BOLD reference was
then coregistered to the T1w reference using flirt (FSL
5.0.9; Jenkinson & Smith, 2001) with the boundary-based
registration (Greve & Fischl, 2009) cost-function.
Coregistration was configured with 9 degrees of freedom
to account for distortions remaining in the BOLD refer-
ence. Head-motion parameters with respect to the BOLD
reference (transformation matrices, and six corresponding
rotation and translation parameters) are estimated before
any spatiotemporal filtering using mcflirt (FSL 5.0.9;
Jenkinson, Bannister, Brady, & Smith, 2002). BOLD runs
were slice-time corrected using 3dTshift from AFNI
20160207 (Cox & Hyde, 1997; RRID:SCR_005927). The
BOLD time series (including slice-timing correction
when applied) were resampled onto their original, native
space by applying a single, composite transform to correct
for head-motion and susceptibility distortions. These

resampled BOLD time series will be referred to as pre-
processed BOLD in original space or just preprocessed
BOLD. The BOLD time series were resampled to
MNI152NLin2009cAsym standard space, generating a pre-
processed BOLD run in MNI152NLin2009cAsym space.
First, a reference volume and its skull-stripped version
were generated using a custom methodology of
fMRIPrep. Several confounding time series were calculated
based on the preprocessed BOLD: framewise displace-
ment, DVARS, and three region-wise global signals.
Framewise displacement and DVARS are calculated for
each functional run, both using their implementations
in Nipype (following the definitions by Power, Barnes,
Snyder, Schlaggar, & Petersen, 2012). The three global
signals are extracted within the CSF, the WM, and the
whole-brain masks. In addition, a set of physiological
regressors were extracted to allow for component-based
noise correction (CompCor; Behzadi, Restom, Liau, &
Liu, 2007). Principal components are estimated after
high-pass filtering the preprocessed BOLD time series
(using a discrete cosine filter with 128-sec cutoff ) for the
two CompCor variants: temporal (tCompCor) and anatom-
ical (aCompCor). Six tCompCor components are then cal-
culated from the top 5% variable voxels within a mask
covering the subcortical regions. This subcortical mask is
obtained by heavily eroding the brain mask, which ensures
it does not include cortical GM regions. For aCompCor, six
components are calculated within the intersection of the
aforementioned mask and the union of CSF and WM masks
calculated in T1w space, after their projection to the native
space of each functional run (using the inverse BOLD-
to-T1w transformation). The head-motion estimates calcu-
lated in the correction step were also placed within the
corresponding confounds file. All resamplings can be per-
formed with a single interpolation step by composing all
the pertinent transformations (i.e., head-motion transform
matrices, susceptibility distortion correction when avail-
able, and coregistrations to anatomical and template
spaces). Gridded (volumetric) resamplings were performed
using antsApplyTransforms (Advanced Normalization
Tools), configured with Lanczos interpolation to minimize
the smoothing effects of other kernels (Lanczos, 1964).
Nongridded (surface) resamplings were performed using
mri_vol2surf (FreeSurfer).

Many internal operations of fMRIPrep use Nilearn 0.4.2
(Abraham et al., 2014; RRID:SCR_001362), mostly within
the functional processing workflow. For more details of the
pipeline, see the section corresponding to workflows in
fMRIPrep’s documentation.

ROIs

To study how the brain represented category, stimulus,
and response variables in the probabilistic categorization
task, we focused on a set of visual, parietal, and prefrontal
brain ROIs hypothesized to be involved in coding these
variables after learning.

Mok and Love

1725

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

3
4
1
0
1
7
1
9
2
0
4
1
8
3
0

/

/
j

o
c
n
_
a
_
0
1
6
5
1
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

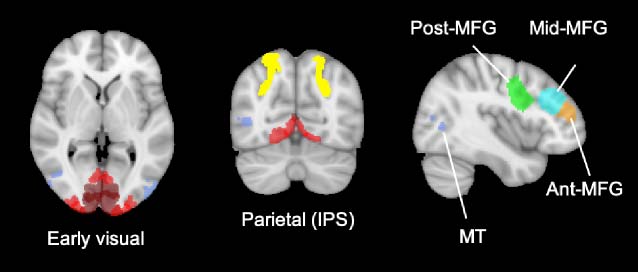
We selected anatomical masks from Wang et al. (2014;
scholar.princeton.edu/napl/resources) to examine areas
involved in early visual processing, motion processing,
and attention, including early visual cortex (EVC; V1, V2,
and V3 merged), motion-sensitive human middle temporal
visual area (MT)/ V5 (Dubner & Zeki, 1971), and the intrapar-
ietal sulcus (IPS). We included EVC to assess stimulus-
related representations including orientation and direction.
The IPS is implicated in both attention (Kastner &
Ungerleider, 2000; Corbetta, Miezin, Shulman, & Petersen,
1993; Mesulam, 1981) and category learning (Freedman &
Assad, 2016; Seger & Miller, 2010). However, we did not
have strong reasons to focus on specific parts of the IPS,
so we merged IPS1 to IPS5 to make a large IPS ROI.

Because these masks are provided in T1 structural MRI
space (1-mm3), when they were transformed into individual
participant functional space (3 mm3), several masks did not
cover GM accurately (too conservative, thereby excluding
some GM voxels). Therefore, we applied a small amount of
smoothing to the mask (with a Gaussian kernel of 0.25 mm,
using fslmaths) for a more liberal inclusion of neighboring
voxels, before transforming it to individual-participant space.
In addition, several potential ROIs were too small to be
mapped onto our functional scans. Specifically, there were
several participants with zero voxels in those masks after
transforming to functional space, even with smoothing.
This included the motion-sensitive area MST and the supe-
rior parietal lobule (SPL1), which were not included.

pFC is strongly implicated representing abstract task
variables (Duncan, 2001; Miller & Cohen, 2001) and task-
relevant sensory signals (e.g., Jackson, Rich, Williams, &
Woolgar, 2017; Erez & Duncan, 2015; Roy, Riesenhuber,
Poggio, & Miller, 2010; Meyers, Freedman, Kreiman,
Miller, & Poggio, 2008; Goldman-Rakic, 1995). We selected
prefrontal regions implicated in cognitive control and task
representations (Fedorenko, Duncan, & Kanwisher, 2013;
Duncan, 2010; imaging.mrc-cbu.cam.ac.uk/imaging
/MDsystem) including the posterior, middle (approximately
Area 8), and anterior (approximately Area 9) portion of the
middle frontal gyrus.

Primary motor cortex was selected to examine represen-
tations related to the motor response and to test for any
stimulus or category signals. Primary motor cortex masks
were taken from the Harvard-Oxford atlas.

We also localized and examined brain responses in the
FFA and PPA, to assess whether face and place regions,
involved in processing stimuli at the feedback phase, were
involved in representing the learned category (see proce-
dure below). For example, if participants learnt that a set of
motion directions belonged to Category A, which was asso-
ciated with face stimuli as feedback, the FFA might show
information about the learnt category during the motion
direction stimulus phase (i.e., not to the face but according
to the learnt category bound). It is worth noting that we are
interested in assessing the information coding the learnt
category (Category A vs. B), not the probabilistically pre-
sented face versus building feedback stimulus.

Apart from the FFA and PPA (where bilateral ROIs were
used; see below), we included both left and right ROIs.
Masks were transformed from standard Montreal
Neurological Institute space to each participant’s native
space using Advanced Normalization Tools (Avants et al.,
2009).

fMRI General Linear Model

We used the general linear model (GLM) in FMRI Expert
Analysis Tool ( Woolrich, Ripley, Brady, & Smith, 2001;
FMRIB Software Library Version 6.00; fsl.fmrib.ox.ac.uk/fsl/)
to obtain estimates of the task-evoked brain signals for each
stimulus, which was used for subsequent MVPAs.

For the main GLM, we included one explanatory variable
(EV) to model each motion stimulus trial (estimating trial-
wise betas for subsequent MVPA) and an EV for each cate-
gory feedback stimulus linked to each motion stimulus
condition (12 EVs, not used in subsequent analyses; see
trial-wise GLM examining the feedback response below).
No spatial smoothing was applied. Stimulus EVs were
1 sec with ISIs between stimulus and feedback ranging
from 1.8 to 7.4 sec ( jittered), and the intertrial interval
was 1.8 sec. Each block run was modeled separately for
leave-one-run-out cross-validation for MVPA.

To examine motor-related brain responses, we per-
formed an additional GLM using the same number of EVs
except the EVs were time-locked to the response rather
than the motion stimulus (stimulus time plus RT) and
modeled as an event lasting 0.5 sec, with the assumption
that the motor events were shorter than the stimulus
(although this made little difference to the results). For
trials without a response, the stimulus was modeled from
stimulus onset as done in the main GLM and then excluded
in subsequent motor-related analyses. Feedback stimuli
were modeled with a single EV as above.

To localize the face-selective FFA and place-sensitive
PPA, we performed an additional GLM in SPM12 (www.fil
.ion.ucl.ac.uk/spm/software/spm12/). We applied spatial
smoothing using a Gaussian kernel of FWHM 6 mm and
included one EV for faces and one EV for building stimuli,
as well as polynomials of degrees 0:6 to model drift in the
data. Stimulus EVs were 1 sec with ISIs between stimulus
and feedback (green/red fixation point color change)
ranging from 1.8 to 7.4 sec ( jittered), with an intertrial
interval of 1.8 sec. We included three contrasts Faces >
Buildings, Buildings > Faces, and overall Visual Activation
(Faces and Buildings). To define individual participant
ROIs, we used minimum statistic conjunctions with visual
activations. To localize the FFA, the conjunction was (Face >
Building) & Visual. For the PPA, the conjunction was
(Building > Face) & Visual. The rationale behind this
conjunction is that functional ROIs should be not only
simply selective but also visually responsive (all voxels that
were deactivated by visual stimulation were not included).
The conjunction was thresholded liberally at p < .01 uncorrected. The peaks for each functional ROI were 1726 Journal of Cognitive Neuroscience Volume 34, Number 10 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / j / o c n a r t i c e - p d l f / / / 3 4 1 0 1 7 1 9 2 0 4 1 8 3 0 / / j o c n _ a _ 0 1 6 5 1 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 detected visually in the SPM results viewer, and we ex- tracted the top 100 contiguous voxels around that peak. There were four participants for which we could not find clear peaks and clusters for the left FFA, five participants for the right FFA, seven participants for the left PPA, and six participants for the right PPA. Because we were unable to reliably localize these areas for all participants in both hemispheres, we used unilateral ROIs for participants with unilateral FFA/PPA ROIs and excluded participants for that ROI if they did not have either a left or right FFA or PPA ROI. The difficultly in localizing these areas for a subset of participants might have been because of our relatively short (two runs) event-related localizer design. In sum- mary, when testing the FFA, we excluded two participants (no left or right FFA), and when testing the PPA, we ex- cluded four participants (no left or right PPA). We also performed a motion localizer, but likely because of the short localizer and the event-related design, it was not possible to reliably localize participant-specific motion- sensitive regions. To examine information during the category feedback, we performed an additional GLM modeling the same events as the main GLM (locked to motion stimuli and feedback stimuli), except that one EV was used to model each feedback trial (estimating trial-wise betas for subse- quent MVPA) and one EV for each motion stimulus condi- tion (12 EVs). This additional GLM was used to estimate the trial-wise feedback mainly for practical reasons. If modeling all cue and feedback trials, it becomes a substan- tially larger model for FMRIB Software Library. By model- ing the cue period trials in a separate GLM to the feedback trials, we were able to reduce the number of EVs per model (96 rather than 168). MVPA To examine brain representations of category, stimulus, and motor response, we used MVPA across our selected ROIs. Specifically, we trained linear support vector ma- chines (SVMs; cf. Kamitani & Tong, 2005) to assess which brain regions contained information about the category (“Face” or “Building”), stimulus (direction, orientation, and 12-way classifier), and motor response (left or right button press). Decoding analyses were performed using linear sup- port vector classifiers (C = 0.1) using Scikit-learn Python package (Pedregosa et al., 2011) with a leave-one-run-out cross-validation procedure. To test for abstract category coding, we first trained a classifier to discriminate between motion directions belonging to the two categories for each participant’s subjective category bound. To ensure that this was a pure category signal unrelated to stimulus differences (e.g., simply decoding opposite motion directions), we trained a classifier based on the participant’s subjective category bound, rotated 90°. For a strict test of an abstract category signal, we subtracted the classification accuracy of the first classifier from accuracy of the second classifier. The rea- soning behind this is that, if a brain region contains infor- mation about the stimulus direction but no information about category, it is still possible to obtain significant clas- sification accuracy for the category classifier (Category A vs. Category B). However, if the brain region primarily encoded stimulus information, there should be as much information for the orthogonal directions in the voxel activity patterns within an ROI (assuming sensory biases across voxels are equal). Therefore, if a brain region carries information about the category and sensory con- tent, there would be greater classification accuracy when decoding across directions across the category boundary (with category and sensory information) than classification accuracy for the directions across the rotated boundary (sensory but no category information). The subtraction allows us to test whether the brain regions carry abstract category information over and above the sensory informa- tion. If there is only sensory information and no category information, the subtracted classification accuracies should be centered around zero. Negative values would suggest more information across directions across the boundary orthogonal to the category bound. This would most likely reflect unequal perceptual biases across voxels in that brain region, where that brain region contained more information about the motion directions across the rotated boundary compared to those across the category boundary (by chance, i.e., stimulus based, unrelated to the learned category). Different participants were randomly assigned to different objective category boundaries, which makes a systematic bias unlikely. Previous studies have tested whether a brain region contains information that can discriminate members of different categories. However, these studies could not rule out the contributions of the stimulus features to the category decoder. In our study, stimulus feature differences are matched when comparing stimuli across the category boundary versus stimuli across the orthogonal boundary. This subtraction method ensures that the sensory signal is not the main contributor to any category code found. To ensure this category signal was not related to motor preparation or the response, we also subtracted the former category classifier accuracy from a motor response classifier accuracy (discriminating between left and right button presses). For stimulus direction coding, we trained classifiers to discriminate between all six pairs of opposite motion direc- tions (0° vs. 180°, 30° vs. 210°, etc.) and averaged across the classification accuracies. To examine motor response coding, we trained classifiers to discriminate between left and right button presses on the GLM where we locked the EVs to the motor responses (RTs). As a control analysis, we tested whether a classifier trained on the objective category structure (i.e., defined by the experimenter) produced similar results to the sub- jective category analysis. The procedure was the same as Mok and Love 1727 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / j / o c n a r t i c e - p d l f / / / 3 4 1 0 1 7 1 9 2 0 4 1 8 3 0 / / j o c n _ a _ 0 1 6 5 1 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 the abstract category classifier above, except that the direc- tions in each category were determined by the experi- menter. In another set of control analyses, we assessed if there was any information about the stimulus. We tested for orientation coding by training a classifier on all 12 pairs of orthogonal orientations irrespective of the motion direction (0° vs. 90° and 0° vs. 270°, 30° vs. 120°, 30° vs. 300°) and averaged across the classification accuracies. Finally, for a more general measure of stimulus coding, we trained a 12-way classifier to assess stimulus coding for each motion direction. We used one-sample t tests (one-tailed) against chance- level performance of the classifier (using SciPy; Virtanen et al., 2020). Multiple comparisons across ROIs were cor- rected by controlling the expected false discovery rate (FDR) at 0.05 (Seabold & Perktold, 2010). For decoding category, we corrected across 12 ROIs (all apart from bilateral EVC and bilateral motor cortex), and for the direction and 12-way classifier, we corrected across 14 ROIs (excluding bilateral motor cortex). Bonferroni correction was used for tests with two ROIs (correcting for visual and motor hemispheres for orientation and motor decoding, respectively). For others, we report the uncorrected p values because none survived even without correction. MVPA and statistical analyses were performed in Python 3.7. Brain–Behavior Correlations To assess whether the brain’s representation of the abstract category signal contributed to categorization per- formance, we performed robust regression (Seabold & Perktold, 2010) to assess the relationship between catego- rization performance (concordance to the estimated subjective category structure) with classifier accuracy for the category for the ROIs with greater-than-chance classifi- cation accuracy for category. Matplotlib (Hunter, 2007) and Seaborn ( Waskom, 2020) were used for plotting and creating figures in this article. Data and Code Availability Statement The code for the behavioral model and data analysis is available at github.com/robmok/memsampCode. The behavioral and fMRI data will be made publicly available at openneuro.org/. RESULTS To assess how learned concept structure is represented in the brain, 33 participants learned a probabilistic concept structure in an initial behavioral session and returned on a separate day to perform the probabilistic categorization task (the same task in the behavioral session) while they underwent an fMRI scan. We used a model to estimate individual participants’ subjective category bound (see Methods and Figure 3A and B). Briefly, the model assumes that participants form a mental decision boundary in the (circular) stimulus space to separate the categories, and there is some uncer- tainty of the placement of this bound. Formally, the model has three parameters: The first two determines bound placement (b1 and b2), and the third is a standard deviation parameter (σ) that models the (normally distributed) noise in this bound. σ provides an estimate of how certain (lower σ) participants are of their boundary placement. The model-estimated category bounds corresponded to participants’ categorization behavior. To compute a mea- sure of behavioral accuracy, we computed the proportion of categorization responses consistent with individual participants’ estimated category bound. There was a strong correlation between the standard deviation pa- rameter of the model σ and behavioral accuracy (r = −.90, p = 9.00e−13), suggesting the standard deviation parameter characterizes an aspect of the categorization behavior well. To evaluate the three main accounts of how the brain organizes information for categorization, we performed MVPA across visual, parietal, and prefrontal ROIs hypothe- sized to be involved in representing the learned concept structure (Figure 3). Specifically, we trained linear SVMs to assess which brain regions contained information about category (A or B), stimulus (directions), and response (left or right). For a strict test of an abstract category signal unrelated to stimulus features, we trained a classifier to discriminate between motion directions in Category A versus directions in Category B and subtracted this from a control classifier trained to discriminate between direc- tions in Category A rotated 90° versus directions in Category B rotated 90°. This ensured that the classifier was not simply picking up information discriminating opposite stimulus directions (see Methods for details). Our findings most strongly align with the hypothesis that the brain constructs an amodal symbol for representing category, independent of sensory–motor variables. Specifically, we found an abstract category signal over and above stimulus information in the middle portion of the left middle frontal gyrus (mMFG: p = .0025, q(FDR) = 0.029) and left motion-sensitive area MT ( p = .0086, q(FDR) = 0.048; Figures 4A and 5A and B). This is particularly striking because the category is based on the stimulus direction, and there was no hint of a direction signal in these regions ( ps > .41; Figures 4B and 5A and B).

Consistent with the idea that abstract category repre-
sentations can aid performance, we found that the strength
of category decoding was positively correlated with catego-
rization accuracy (responses consistent with the model-
estimated category bound) in the left MT (robust regression;
β = 0.74, p < .05; Figure 5D) with a similar trend for the left mMFG (β = 0.73, p = .067; Figure 5C). We also confirmed that the category signal was stronger than the motor code in the left mMFG by subtracting the classifier 1728 Journal of Cognitive Neuroscience Volume 34, Number 10 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / j / o c n a r t i c e - p d l f / / / 3 4 1 0 1 7 1 9 2 0 4 1 8 3 0 / / j o c n _ a _ 0 1 6 5 1 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / j / o c n a r t i c e - p d l f / / / 3 4 1 0 1 7 1 9 2 0 4 1 8 3 0 / / j o c n _ a _ 0 1 6 5 1 p d . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 4. fMRI MVPA results. (A) Abstract category coding in the left mMFG cortex and left MT. Abstract category coding over and above sensory coding was computed by the category classifier accuracy minus the classifier accuracy trained on orthogonal (90° rotated) directions. (B) No strong effects showing stimulus motion direction information. (C) The right motor cortex showed significant information coding response. (D) The right EVC showed significant information coding orientation. (E) The right MT contained sensory information as shown by the 12-way stimulus classifier, with the right EVC showing a similar trend. Normalized decoding accuracy measures are normalized by subtracting chance values (direction = 1/2, 12-way = 1/12, motor = 1/2, orientation = 1/2), apart from abstract category that subtracts from a control classifier (chance = 0). ***p = .0025; *p < .05; +p < .06. trained to discriminate motion directions across categories from the motor classifier ( p = .015). Bonferroni-corrected p = .19; Figure 4C) but no informa- tion about category or direction ( ps > .42).

As expected, we found information coding motor re-
sponse in the motor cortex (right: p = .006; Bonferroni-
corrected for hemisphere, p = .011; left: p = .095;

Notably, abstract category coding was only present for
the participant-specific subjective category structure
(“objective” category bound classifiers across all ROIs:

Mok and Love

1729

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

3
4
1
0
1
7
1
9
2
0
4
1
8
3
0

/

/
j

o
c
n
_
a
_
0
1
6
5
1
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 5. Abstract category coding and correlations with categorization behavior. (A–B) Univariate scatterplots showing significant abstract category
coding in the left mMFG (A) and left MT (B), with no evidence of stimulus and motor coding. Gray dots are individual participants. (C–D) The
strength of abstract category coding in MT (D) was correlated with categorization accuracy, that is, consistent responses with subjective category
bound. There was a trend in the same direction in the left mMFG (C). In D and E, beta coefficients are from a robust regression analysis, and the
shaded area represents 95% confidence intervals for the slope. ***p = .0025, *p < .05. Error bars represent SEM. Normalized decoding accuracy measures are normalized by subtracting chance values, apart from abstract category that subtracts from a control classifier (chance = 0). ps > .06). Furthermore, we found no evidence of category
coding in the FFA or in the PPA ( ps > .31).

Although we did not find category and stimulus repre-
sentations intertwined, this was not because stimulus rep-
resentations were not decodable in our data. We trained a
classifier on orientation in the EVC and found activity
coding orientation (Figure 4D, p < .05, Bonferroni- corrected for hemisphere). We also trained a 12-way clas- sifier to assess if there was any information about the stimulus that would not be found simply by examining orientation or direction responses and found that the right MT encoded information on the stimulus ( p = .005, q(FDR) = 0.03) and a trend for right EVC ( p = .06, q(FDR) = 0.18; Figure 4E). Notably, there was no evidence for this in the left mMFG or left MT, which encoded ab- stract category ( ps > .74).

DISCUSSION

We examined the neural representations underlying cate-
gorization and found that the brain constructs an abstract

category signal with a different representational format to
sensory and motor codes. Specifically, the left pFC and MT
encoded category in the absence of stimulus information,
despite category structure being based on those stimulus
features. Furthermore, the strength of this representation
was correlated with categorization performance based on
participants’ subjective category bound estimated by our
model.

Although some representations may be grounded in
bodily sensations, for tasks that require flexibility and repre-
sentations to support abstract operations, an amodal symbol
of a different representational format to that of sensory–
motor representations may prove useful (Marcus, 2001;
Pylyshyn, 1984; Newell, 1980; Fodor, 1975). Indeed, a cate-
gory representation tied to a motor plan or stimulus feature
would facilitate stimulus–motor representations effectively
in specific circumstances but become unusable given slight
changes in context. In this study, it was possible to solve
the task in multiple ways, such as a combination of the
sensory–motor variables, using a category-modulated
sensory representation or additionally recruiting an amodal

1730

Journal of Cognitive Neuroscience

Volume 34, Number 10

representation (Figure 1B–D). Despite this, we found the
brain produces an additional abstract representation to
support categorization (Figure 1D). Specifically, by apply-
ing a decoding approach to test for a category signal over
and above a sensory code, we showed that the left mMFG
and MT encoded a category signal abstracted from the sen-
sory information. Furthermore, these areas did not carry
any information about stimulus or response (evidenced
by the motor, direction, orientation, and 12-way stimulus
classifier), and the category code was significantly stronger
than the motor code. In contrast, we did not find any
regions that encoded both the category and stimulus, as
predicted by the account where category information is
grounded in category-modulated stimulus representa-
tions (Figure 1C). We also did not find any regions that
encoded both the category and the motor response, as
predicted by the account where category is grounded in
stimulus–motor associations (Figure 1B). Therefore, our
findings suggest that brain constructs an amodal symbol
for representing category, independent of sensory–motor
variables. It is worth noting that our results do not suggest
that the brain does not use sensory information or that
there are no grounded neural representations but, rather,
that the brain constructs an additional category represen-
tation abstracted from the sensory–motor information
for categorization.

In addition to the left pFC, we found that the left MT
encoded a category signal in the absence of sensory infor-
mation, whereas the right MT was only driven by sensory
information. One possible explanation is that the category
signal originated from the left pFC, which was sent back to
modulate the left MT. This may have resulted in competi-
tion between the category and sensory signals, and the
task-relevant category signal won out over the bottom–
up sensory signal. Because there was no category signal
in the right pFC, the right MT was not affected by the task
and coded the bottom–up stimulus signal. Alternatively,
the left MT may simply be more affected by top–down
modulation from pFC. For instance, task-relevant atten-
tional modulation in the left PPA (when attending to
scenes vs. faces) seems to be stronger and more reliable
than the right PPA (Chadick, Zanto, & Gazzaley, 2014;
Gazzaley, Cooney, McEvoy, Knight, & D’Esposito, 2005).
Unfortunately, most fMRI studies of perceptual or category
learning using motion-dot stimuli did not examine the left
and right MT hemispheres separately and did not report
differential effects of category and stimulus across hemi-
spheres. Future studies or meta-analytic studies could ex-
amine whether or not the left or right MT is more strongly
modulated by task demands or if the lateralized modula-
tion of sensory cortices depends on the relative lateralized
recruitment of control regions such as pFC.

Previous studies have found strong stimulus coding and
category-related modulation stimulus representations
during concept or perceptual learning (Ester, Sprague, &
Serences, 2020; Braunlich & Love, 2019; Kuai, Levi, &
Kourtzi, 2013; Mack et al., 2013; Zhang & Kourtzi, 2010;

Freedman & Assad, 2006; Kourtzi, Betts, Sarkheil, &
Welchman, 2005). For example, concept learning studies
that used object stimuli have shown strong modulation
of sensory signals in the lateral occipital cortex after
learning (Braunlich & Love, 2019; Kuai et al., 2013;
Mack et al., 2013).

One major difference between prior work and the
current study is the probabilistic relationship between
stimulus and feedback. In the world outside the laboratory,
the relationship between stimulus and feedback is not
always deterministic and people must make decisions
and learn in the presence of this uncertainty. For example,
after viewing dark clouds and the weather forecast, a
person with picnic plans is faced with the decision of
whether to continue. After deciding, they update their
knowledge based on whether it rained, which is a probabi-
listic function of what was known at the time of decision.
Another key difference between our study with many
studies of concept learning is that the response mapping
was switched after each block so that we could observe
possible differences between category representations
and stimulus–response mappings. Some researchers sug-
gest that changing the response mapping should disrupt
procedural learning processes involved in concept learning
(Maddox & Ashby, 2004), which is one reason why
response mappings are often held constant within a
participant.

These two differences with previous studies made it pos-
sible for us to observe a strong category signal that was not
strictly modulated by stimulus representations, nor motor
response. This category signal was of a different format
than information related to stimulus or response. We need
not have observed this finding. It would have been possible
for the brain to solve this task using a stimulus-modulated
category representation (i.e., stimulus and category repre-
sented in related formats) in which the response mapping
varied across blocks. Instead, it appears that an intermedi-
ate category signal was used by participants. Although our
design did not necessitate our main finding, it is possible
that the relatively loose coupling between stimulus, cate-
gory, and response encouraged forming a category repre-
sentation of a different format than either stimulus or
response. Many real-world categories may place related
demands on learners. For example, relational categories,
such as thief, are not closely tied to sensory representa-
tions (Jones & Love, 2007).

It may be argued that, because participants had to flip
the category–motor mapping across blocks, we encour-
aged participants to use the stimulus or the category infor-
mation and discouraged a motor-based strategy. However,
it was still possible to ground category information into
motor representations by associating sensory representa-
tions to the motor plan within a block and reprogram the
association across blocks. Because there were relatively
few blocks, this would have been possible—and a viable
strategy. If the brain primarily relies on the sensory–motor
association for the category representation and behavior,

Mok and Love

1731

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

3
4
1
0
1
7
1
9
2
0
4
1
8
3
0

/

/
j

o
c
n
_
a
_
0
1
6
5
1
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

we would find representation of motor plans without an
abstract category code (i.e., not tied to motor plans), which
is not in line with our results. Furthermore, we showed
evidence for an amodal category signal using a decoding
approach that tested for a category signal over and above
stimulus coding and also showed that the category signal
was stronger than the motor code. To test the hypothesis
that our design might have discouraged participants to use
motor-based representations, future studies could com-
pare groups that had to switch the motor responses
versus those that did not and whether the latter group
would form a grounded, motor-based neural representa-
tion for categorization in the absence of abstract category
representations.

Some of our analyses yielded negative classification
accuracy values, including in the abstract category and
the direction classifier accuracies (Figure 4A and B). As
noted in the Methods, the purpose of subtracting the
category classifier from the classifier trained on the orthog-
onal bound was to find category signal over and above any
sensory information contained in the voxels. Negative
values would simply reflect no category information, in ad-
dition to more information across directions across the
boundary orthogonal to the category bound (i.e., sensory
biases in the voxels unrelated to the task). For the direction
classifier, there were some regions that showed negative
classification accuracy values. In this analysis, the theoreti-
cally lowest possible value is zero, and values around zero
would reflect the absence of any direction information. We
were unable to find anything systematic that contributed to
the negative values and suggest that these effects were
most likely attributable to reasons unrelated to the task,
such as some nonstationarity across blocks.

There are similarities between our probabilistic concep-
tual learning paradigm and tasks learning the transition
probability structure of object-to-object sequences. In
those tasks, the probability that an Object A is most likely
followed by an Object B (e.g., with a probability of .75) but
could also be followed by another Object C (probability
of .25)—that is, participants learn the statistical depen-
dencies between objects, like how our participants learn
the probabilistic dependencies between stimuli and cate-
gories. Interestingly, one study by Schapiro, Rogers,
Cordova, Turk-Browne, and Botvinick (2013) showed
participants learnt and accurately represent object–object
associations with a structured community structure in
several brain regions including the left pFC. Specifically,
pattern similarity analysis showed that the left pFC, anterior
temporal lobe, and superior temporal gyrus encoded the
statistical, relational structure across the objects. Other
studies found that the regions in the medial temporal lobe
including the hippocampus and entorhinal cortex are
involved in the learning and retrieval of associations and
prediction of object–object transitions (e.g., Garvert,
Dolan, & Behrens, 2017; Schapiro, Turk-Browne,
Norman, & Botvinick, 2016). Because our current study
focused on category representations after learning, it

would be interesting for future studies to test whether
medial temporal lobe structures are involved in learning
probabilistic conceptual structures in a similar way.

There are several open questions to be explored in the
future. Our study was not optimized to study to role of
the hippocampus in category learning, as we examined
category representations after learning. Future studies
could examine the neural representations involved in
probabilistic concept learning early in learning and com-
pare them to representations during categorization after
learning is complete, to explore whether how the neural
representations change as concept information is consol-
idated into long-term memory.

Future work could also assess the causal involvement of
these abstract category representations in mMFG and MT.
One idea would be to use TMS to disrupt the left mMFG
and left MT to assess whether these areas act causally to
support categorization behavior. It would be interesting
to test whether mMFG or MT plays a more important role,
by observing the fMRI signal after disruption. It could be
that the mMFG is the origin of the category signal, but it
is its influence on MT that leads to effective categorization
behavior (e.g., TMS to mMFG leads to disruption of the
MT category representation but not vice versa, where
stimulation at both sites disrupts behavior).

What is the use of an abstract, symbol-like concept rep-
resentation? In real-world scenarios, there are often no
explicit rules and reliable feedback is rare. Building an ab-
stract representation that can be mapped onto different
contexts can be useful in real-world tasks, where the
meaning of a situation can remain constant while the
contextually appropriate stimulus or response changes.
As we find here, the brain constructs an amodal, abstract
representation with a different representational format
separate from sensory–motor codes, well suited for flex-
ible cognition in a complex world.

Acknowledgments

We thank Johan Carlin for his help on experimental design and
data collection and Amna Ali for her help on data collection. We
thank Kurt Braunlich for his advice on analysis tools. We thank
the Love Lab for the helpful discussions on the project. We are
grateful to the members of Cognitive Brain Mapping Lab at
RIKEN BSI for sharing natural images used in this study.

Reprint requests should be sent to Robert M. Mok or Bradley C.
Love, Department of Experimental Psychology, University
College London, 26 Bedford Way, London, WC1H 0AP, UK, or
via e-mails: robert.mok@ucl.ac.uk; b.love@ucl.ac.uk.

Data Availability Statement

Scripts will be available on GitHub, data will be available
on openneuro.

Funding Information

Royal Society (http://dx.doi.org/10.13039/501100000288),
grant number: 18302. Wellcome Trust (http://dx.doi.org

1732

Journal of Cognitive Neuroscience

Volume 34, Number 10

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

3
4
1
0
1
7
1
9
2
0
4
1
8
3
0

/

/
j

o
c
n
_
a
_
0
1
6
5
1
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

/10/13039/100004440), grant number: WT106931MA.
National Institutes of Health (http://dx.doi.org/10.13039
/100000002), grant number: 1P01HD080679.

REFERENCES

Abraham, A., Pedregosa, F., Eickenberg, M., Gervais, P., Mueller,
A., Kossaifi, J., et al. (2014). Machine learning for neuroimaging
with scikit-learn. Frontiers in Neuroinformatics, 8, 14.
https://doi.org/10.3389/fninf.2014.00014, PubMed: 24600388
Allison, T., Puce, A., Spencer, D. D., & McCarthy, G. (1999).
Electrophysiological studies of human face perception. I:
Potentials generated in occipitotemporal cortex by face and
non-face stimuli. Cerebral Cortex, 9, 415–430. https://doi.org
/10.1093/cercor/9.5.415, PubMed: 10450888

Avants, B. B., Epstein, C. L., Grossman, M., & Gee, J. C. (2008).

Symmetric diffeomorphic image registration with cross-
correlation: Evaluating automated labeling of elderly and
neurodegenerative brain. Medical Image Analysis, 12, 26–41.
https://doi.org/10.1016/j.media.2007.06.004, PubMed:
17659998

Avants, B. B., Tustison, N., & Song, G. (2009). Advanced
normalization tools (ANTS). Insight Journal, 2, 1–35.

Barsalou, L. W. (1999). Perceptual symbol systems. Behavioral
and Brain Sciences, 22, 577–609. https://doi.org/10.1017
/S0140525X99002149, PubMed: 11301525

Barsalou, L. W. (2008). Grounded cognition. Annual Review
of Psychology, 59, 617–645. https://doi.org/10.1146/annurev
.psych.59.103006.093639, PubMed: 17705682

Behzadi, Y., Restom, K., Liau, J., & Liu, T. T. (2007). A

component based noise correction method (CompCor) for
BOLD and perfusion based fMRI. Neuroimage, 37, 90–101.
https://doi.org/10.1016/j.neuroimage.2007.04.042, PubMed:
17560126

Bowman, C. R., & Zeithamova, D. (2018). Abstract memory
representations in the ventromedial prefrontal cortex and
hippocampus support concept generalization. Journal of
Neuroscience, 38, 2605–2614. https://doi.org/10.1523
/JNEUROSCI.2811-17.2018, PubMed: 29437891

Braunlich, K., & Love, B. C. (2019). Occipitotemporal

representations reflect individual differences in conceptual
knowledge. Journal of Experimental Psychology: General,
148, 1192–1203. https://doi.org/10.1037/xge0000501,
PubMed: 30382719

Chadick, J. Z., Zanto, T. P., & Gazzaley, A. (2014). Structural and
functional differences in medial prefrontal cortex underlies
distractibility and suppression deficits in aging. Nature
Communications, 5, 4223. https://doi.org/10.1038
/ncomms5223, PubMed: 24979364

Corbetta, M., Miezin, F. M., Shulman, G. L., & Petersen, S. E.
(1993). A PET study of visuospatial attention. Journal of
Neuroscience, 13, 1202–1226. https://doi.org/10.1523
/JNEUROSCI.13-03-01202.1993, PubMed: 8441008

Cox, R. W., & Hyde, J. S. (1997). Software tools for analysis and
visualization of fMRI data. NMR in Biomedicine, 10, 171–78.
https://doi.org/10.1002/(SICI)1099-1492(199706/08)10:4
/5<171::AID-NBM453>3.0.CO;2-L, PubMed: 9430344

Cromer, J. A., Roy, J. E., & Miller, E. K. (2010). Representation of
multiple, independent categories in the primate prefrontal
cortex. Neuron, 66, 796–807. https://doi.org/10.1016/j
.neuron.2010.05.005, PubMed: 20547135

Davis, T., Love, B. C., & Preston, A. R. (2012a). Learning the

exception to the rule: Model-based fMRI reveals specialized
representations for surprising category members. Cerebral
Cortex, 22, 260–273. https://doi.org/10.1093/cercor/bhr036,
PubMed: 21666132

Davis, T., Love, B. C., & Preston, A. R. (2012b). Striatal and
hippocampal entropy and recognition signals in category
learning: Simultaneous processes revealed by model-based
fMRI. Journal of Experimental Psychology: Learning,
Memory, and Cognition, 38, 821–839. https://doi.org
/10.1037/a0027865, PubMed: 22746951

Dubner, R., & Zeki, S. M. (1971). Response properties and

receptive fields of cells in an anatomically defined region of
the superior temporal sulcus in the monkey. Brain Research,
35, 528–532. https://doi.org/10.1016/0006-8993(71)90494-X,
PubMed: 5002708

Duncan, J. (2001). An adaptive coding model of neural function in
prefrontal cortex. Nature Reviews Neuroscience, 2, 820–829.
https://doi.org/10.1038/35097575, PubMed: 11715058

Duncan, J. (2010). The multiple-demand (MD) system of the
primate brain: Mental programs for intelligent behaviour.
Trends in Cognitive Sciences, 14, 172–179. https://doi
.org/10.1016/j.tics.2010.01.004, PubMed: 20171926

Epstein, R., & Kanwisher, N. (1998). A cortical representation of
the local visual environment. Nature, 392, 598–601. https://
doi.org/10.1038/33402, PubMed: 9560155

Erez, Y., & Duncan, J. (2015). Discrimination of visual

categories based on behavioral relevance in widespread
regions of frontoparietal cortex. Journal of Neuroscience,
35, 12383–12393. https://doi.org/10.1523/JNEUROSCI
.1134-15.2015, PubMed: 26354907

Esteban, O., Markiewicz, C. J., Blair, R. W., Moodie, C. A., Isik, A. I.,
Erramuzpe, A., et al. (2019). fMRIPrep: A robust preprocessing
pipeline for functional MRI. Nature Methods, 16, 111–116.
https://doi.org/10.1038/s41592-018-0235-4, PubMed: 30532080
Ester, E. F., Sprague, T. C., & Serences, J. T. (2020). Categorical

biases in human occipitoparietal cortex. Journal of
Neuroscience, 40, 917–931. https://doi.org/10.1523
/JNEUROSCI.2700-19.2019, PubMed: 31862856

Fedorenko, E., Duncan, J., & Kanwisher, N. (2013). Broad
domain generality in focal regions of frontal and parietal
cortex. Proceedings of the National Academy of Sciences,
U.S.A., 110, 16616–16621. https://doi.org/10.1073/pnas
.1315235110, PubMed: 24062451

Fodor, J. A. (1975). The language of thought. Cambridge, MA:

Harvard University Press.

Folstein, J. R., Palmeri, T. J., & Gauthier, I. (2013). Category learning
increases discriminability of relevant object dimensions in
visual cortex. Cerebral Cortex, 23, 814–823. https://doi
.org/10.1093/cercor/bhs067, PubMed: 22490547

Fonov, V. S., Evans, A. C., McKinstry, R. C., Almli, C. R., & Collins,
D. L. (2009). Unbiased nonlinear average age-appropriate
brain templates from birth to adulthood. Neuroimage,
47(Suppl. 1), S102. https://doi.org/10.1016/s1053-8119
(09)70884-5

Freedman, D. J., & Assad, J. A. (2006). Experience-dependent
representation of visual categories in parietal cortex. Nature,
443, 85–88. https://doi.org/10.1038/nature05078, PubMed:
16936716

Freedman, D. J., & Assad, J. A. (2016). Neuronal mechanisms of
visual categorization: An abstract view on decision making.
Annual Review of Neuroscience, 39, 129–147. https://doi
.org/10.1146/annurev-neuro-071714-033919, PubMed:
27070552

Garvert, M. M., Dolan, R. J., & Behrens, T. E. J. (2017). A map of
abstract relational knowledge in the human hippocampal–
entorhinal cortex. eLife, 6, e17086. https://doi.org/10.7554
/eLife.17086, PubMed: 28448253

Gazzaley, A., Cooney, J. W., McEvoy, K., Knight, R. T., &
D’Esposito, M. (2005). Top–down enhancement and
suppression of the magnitude and speed of neural activity.
Journal of Cognitive Neuroscience, 17, 507–517. https://doi
.org/10.1162/0898929053279522, PubMed: 15814009

Mok and Love

1733

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

3
4
1
0
1
7
1
9
2
0
4
1
8
3
0

/

/
j

o
c
n
_
a
_
0
1
6
5
1
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Glasser, M. F., Sotiropoulos, S. N., Wilson, J. A., Coalson, T. S.,

Fischl, B., Andersson, J. L., et al. (2013). The minimal
preprocessing pipelines for the Human Connectome Project.
Neuroimage, 80, 105–124. https://doi.org/10.1016
/j.neuroimage.2013.04.127, PubMed: 23668970

Goldman-Rakic, P. S. (1995). Cellular basis of working memory.

Neuron, 14, 477–485. https://doi.org/10.1016/0896
-6273(95)90304-6, PubMed: 7695894

Gorgolewski, K., Burns, C. D., Madison, C., Clark, D., Halchenko,

Y. O., Waskom, M. L., et al. (2011). Nipype: A flexible,
lightweight and extensible neuroimaging data processing
framework in Python. Frontiers in Neuroinformatics, 5,
13. https://doi.org/10.3389/fninf.2011.00013, PubMed:
21897815

Greve, D. N., & Fischl, B. (2009). Accurate and robust brain

image alignment using boundary-based registration.
Neuroimage, 48, 63–72. https://doi.org/10.1016/j.neuroimage
.2009.06.060, PubMed: 19573611

Harnad, S. (1990). The symbol grounding problem. Physica D:
Nonlinear Phenomena, 42, 335–346. https://doi.org/10.1016
/0167-2789(90)90087-6

Hunter, J. D. (2007). Matplotlib: A 2D graphics environment.
Computing in Science and Engineering, 9, 90–95. https://
doi.org/10.1109/MCSE.2007.55

Jackson, J., Rich, A. N., Williams, M. A., & Woolgar, A. (2017).
Feature-selective attention in frontoparietal cortex: Multivoxel
codes adjust to prioritize task-relevant information. Journal
of Cognitive Neuroscience, 29, 310–321. https://doi.org/10
.1162/jocn_a_01039, PubMed: 27626230

Jenkinson, M., Bannister, P., Brady, M., & Smith, S. (2002).
Improved optimisation for the robust and accurate linear
registration and motion correction of brain images.
Neuroimage, 17, 825–841. https://doi.org/10.1016
/S1053-8119(02)91132-8, PubMed: 12377157

Jenkinson, M., & Smith, S. (2001). A global optimisation method
for robust affine registration of brain images. Medical Image
Analysis, 5, 143–156. https://doi.org/10.1016/S1361-8415(01)
00036-6, PubMed: 11516708

Jones, M., & Love, B. C. (2007). Beyond common features: The
role of roles in determining similarity. Cognitive Psychology,
55, 196–231. https://doi.org/10.1016/j.cogpsych.2006
.09.004, PubMed: 17094958

Kamitani, Y., & Tong, F. (2005). Decoding the visual and

subjective contents of the human brain. Nature Neuroscience,
8, 679–685. https://doi.org/10.1038/nn1444, PubMed:
15852014

Kanwisher, N., McDermott, J., & Chun, M. M. (1997). The

fusiform face area: A module in human extrastriate cortex
specialized for face perception. Journal of Neuroscience,
17, 4302–4311. https://doi.org/10.1523/JNEUROSCI.17-11
-04302.1997, PubMed: 9151747

Kastner, S., & Ungerleider, L. G. (2000). Mechanisms of visual
attention in the human cortex. Annual Review of Neuroscience,
23, 315–341. https://doi.org/10.1146/annurev.neuro.23.1.315,
PubMed: 10845067

Kourtzi, Z., Betts, L. R., Sarkheil, P., & Welchman, A. E. (2005).
Distributed neural plasticity for shape learning in the human
visual cortex. PLoS Biology, 3, e204. https://doi.org/10.1371
/journal.pbio.0030204, PubMed: 15934786

Kruschke, J. K. (1992). ALCOVE: An exemplar-based connectionist
model of category learning. Psychological Review, 99, 22–44.
https://doi.org/10.1037/0033-295X.99.1.22, PubMed: 1546117
Kuai, S.-G., Levi, D., & Kourtzi, Z. (2013). Learning optimizes
decision templates in the human visual cortex. Current
Biology, 23, 1799–1804. https://doi.org/10.1016/j.cub.2013
.07.052, PubMed: 24012311

Lanczos, C. (1964). Evaluation of noisy data. Journal of the

Society for Industrial and Applied Mathematics, Series B:

Numerical Analysis, 1, 76–85. https://doi.org/10.1137
/0701007

Love, B. C., Medin, D. L., & Gureckis, T. M. (2004). SUSTAIN: A
network model of category learning. Psychological Review,
111, 309–332. https://doi.org/10.1037/0033-295X.111.2.309,
PubMed: 15065912

Mack, M. L., Love, B. C., & Preston, A. R. (2016). Dynamic

updating of hippocampal object representations reflects new
conceptual knowledge. Proceedings of the National
Academy of Sciences, U.S.A., 113, 13203–13208. https://doi
.org/10.1073/pnas.1614048113, PubMed: 27803320

Mack, M. L., Preston, A. R., & Love, B. C. (2013). Decoding
the brain’s algorithm for categorization from its neural
implementation. Current Biology, 23, 2023–2027. https://doi
.org/10.1016/j.cub.2013.08.035, PubMed: 24094852

Maddox, W. T., & Ashby, F. G. (2004). Dissociating explicit and
procedural-learning based systems of perceptual category
learning. Behavioural Processes, 66, 309–332. https://doi.org
/10.1016/j.beproc.2004.03.011, PubMed: 15157979
Marcus, G. F. (2001). The algebraic mind: Integrating

connectionism and cognitive science. Cambridge, MA: MIT
Press. https://doi.org/10.7551/mitpress/1187.001.0001

Markman, A. B., & Dietrich, E. (2000). Extending the classical
view of representation. Trends in Cognitive Sciences, 4,
470–475. https://doi.org/10.1016/S1364-6613(00)01559-X,
PubMed: 11115761

Mesulam, M. M. (1981). A cortical network for directed attention
and unilateral neglect. Annals of Neurology, 10, 309–325.
https://doi.org/10.1002/ana.410100402, PubMed: 7032417
Meyers, E. M., Freedman, D. J., Kreiman, G., Miller, E. K., &
Poggio, T. (2008). Dynamic population coding of category
information in inferior temporal and prefrontal cortex.
Journal of Neurophysiology, 100, 1407–1419. https://doi.org
/10.1152/jn.90248.2008, PubMed: 18562555

Miller, E. K., & Cohen, J. D. (2001). An integrative theory of

prefrontal cortex function. Annual Review of Neuroscience,
24, 167–202. https://doi.org/10.1146/annurev.neuro.24.1.167,
PubMed: 11283309

Newell, A. (1980). Physical symbol systems. Cognitive Science,
4, 135–183. https://doi.org/10.1016/S0364-0213(80)80015-2
Nosofsky, R. M. (1986). Attention, similarity, and the identification–

categorization relationship. Journal of Experimental
Psychology: General, 115, 39–61. https://doi.org/10.1037/0096
-3445.115.1.39, PubMed: 2937873

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B.,
Grisel, O., et al. (2011). Scikit-learn: Machine learning in Python.
Journal of Machine Learning Research, 12, 2825–2830.

Peirce, J., Gray, J. R., Simpson, S., MacAskill, M., Höchenberger,

R., Sogo, H., et al. (2019). PsychoPy2: Experiments in
behavior made easy. Behavior Research Methods, 51,
195–203. https://doi.org/10.3758/s13428-018-01193-y,
PubMed: 30734206

Power, J. D., Barnes, K. A., Snyder, A. Z., Schlaggar, B. L., &

Petersen, S. E. (2012). Spurious but systematic correlations
in functional connectivity MRI networks arise from subject
motion. Neuroimage, 59, 2142–2154. https://doi.org/10.1016
/j.neuroimage.2011.10.018, PubMed: 22019881

Pylyshyn, Z. W. (1984). Computation and cognition: Toward a
foundation for cognitive science. Cambrige, MA: MIT Press.

Rizzolatti, G., Riggio, L., Dascola, I., & Umiltá, C. (1987).
Reorienting attention across the horizontal and vertical
meridians: Evidence in favor of a premotor theory of
attention. Neuropsychologia, 25, 31–40. https://doi.org/10
.1016/0028-3932(87)90041-8, PubMed: 3574648

Roy, J. E., Riesenhuber, M., Poggio, T., & Miller, E. K. (2010).
Prefrontal cortex activity during flexible categorization.
Journal of Neuroscience, 30, 8519–8528. https://doi.org/10
.1523/JNEUROSCI.4837-09.2010, PubMed: 20573899

1734

Journal of Cognitive Neuroscience

Volume 34, Number 10

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

3
4
1
0
1
7
1
9
2
0
4
1
8
3
0

/

/
j

o
c
n
_
a
_
0
1
6
5
1
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Schapiro, A. C., Rogers, T. T., Cordova, N. I., Turk-Browne, N. B.,
& Botvinick, M. M. (2013). Neural representations of events
arise from temporal community structure. Nature
Neuroscience, 16, 486–492. https://doi.org/10.1038/nn.3331,
PubMed: 23416451

Schapiro, A. C., Turk-Browne, N. B., Norman, K. A., & Botvinick,
M. M. (2016). Statistical learning of temporal community
structure in the hippocampus. Hippocampus, 26, 3–8.
https://doi.org/10.1002/hipo.22523, PubMed: 26332666
Seabold, S., & Perktold, J. (2010). Statsmodels: Econometric
and statistical modeling with Python. In Proceedings of the
9th Python in Science Conference (pp. 92–96). https://doi
.org/10.25080/Majora-92bf1922-011

Seger, C. A., & Miller, E. K. (2010). Category learning in the

brain. Annual Review of Neuroscience, 33, 203–219. https://
doi.org/10.1146/annurev.neuro.051508.135546, PubMed:
20572771

Sigala, N., & Logothetis, N. K. (2002). Visual categorization
shapes feature selectivity in the primate temporal cortex.
Nature, 415, 318–320. https://doi.org/10.1038/415318a,
PubMed: 11797008

Virtanen, P., Gommers, R., Oliphant, T. E., Haberland, M., Reddy,

T., Cournapeau, D., et al. (2020). SciPy 1.0: Fundamental
algorithms for scientific computing in Python. Nature Methods,
17, 261–272. https://doi.org/10.1038/s41592-019-0686-2,
PubMed: 32015543

Wang, J. X., Rogers, L. M., Gross, E. Z., Ryals, A. J., Dokucu, M. E.,

Brandstatt, K. L., et al. (2014). Targeted enhancement of
cortical–hippocampal brain networks and associative memory.

Science, 345, 1054–1057. https://doi.org/10.1126/science
.1252900, PubMed: 25170153

Waskom, M. (2020). An introduction to Seaborn—Seaborn
0.10.1 documentation. Statistical Data Visualization.

Wolpert, D. M., & Ghahramani, Z. (2000). Computational principles
of movement neuroscience. Nature Neuroscience, 3, 1212–1217.
https://doi.org/10.1038/81497, PubMed: 11127840

Wolpert, D. M., & Witkowski, J. (2014). A conversation with

Daniel Wolpert. Cold Spring Harbor Symposia on Quantitative
Biology, 79, 297–298. https://doi.org/10.1101/sqb.2014.79.19,
PubMed: 26092903

Woolrich, M. W., Ripley, B. D., Brady, M., & Smith, S. M. (2001).
Temporal autocorrelation in univariate linear modeling of
fMRI data. Neuroimage, 14, 1370–1386. https://doi.org/10
.1006/nimg.2001.0931, PubMed: 11707093

Zeithamova, D., Mack, M. L., Braunlich, K., Davis, T., Seger, C. A.,
van Kesteren, M. T. R., et al. (2019). Brain mechanisms of
concept learning. Journal of Neuroscience, 39, 8259–8266.
https://doi.org/10.1523/JNEUROSCI.1166-19.2019, PubMed:
31619495

Zhang, Y., Brady, M., & Smith, S. (2001). Segmentation of brain
MR images through a hidden Markov random field model and
the expectation–maximization algorithm. IEEE Transactions
on Medical Imaging, 20, 45–57. https://doi.org/10.1109/42
.906424, PubMed: 11293691

Zhang, J., & Kourtzi, Z. (2010). Learning-dependent plasticity

with and without training in the human brain. Proceedings of
the National Academy of Sciences, U.S.A., 107, 13503–13508.
https://doi.org/10.1073/pnas.1002506107, PubMed: 20628009

l

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

p

:
/
/

d
i
r
e
c
t
.

m

i
t
.

e
d
u

/
j

/

o
c
n
a
r
t
i
c
e
–
p
d

l

f
/

/

/

3
4
1
0
1
7
1
9
2
0
4
1
8
3
0

/

/
j

o
c
n
_
a
_
0
1
6
5
1
p
d

.

f

b
y
g
u
e
s
t

t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Mok and Love

1735

Download pdf