About This Issue - Specialized Research AI at MIT

About This Issue

As we are reminded by the contents of
Gareth Loy’s two-volume Musimath-
ics (MIT Press, 2006–2007), computer
music can be viewed as one of the lat-
est developments in the centuries—
indeed, millennia—of intellectual
endeavor connecting mathematics
and music. In particular, the ancient
expression of musical intervals as in-
teger ratios has, throughout history
and to this day, fascinated musically
inclined scientists and scientiﬁcally
inclined musicians. Towering over
most of these was the nineteenth-
century physicist Hermann
Helmholtz, who ﬁnally found, in the
interference patterns of overtones in
the cochlea, a scientiﬁcally satisfac-
tory explanation for consonance and
tonal harmony, connected to the
integer ratios of just intonation.
Twentieth-century modernism,
however, largely viewed tuning the-
ory, and particularly the concerns of
just intonation, as anachronistic: a
movement proclaiming the liberation
of dissonance had no need for purer
consonances. It remained for digital
sound synthesis to give composers a
means of transferring Helmholtz’s in-
sights to thoroughly nontraditional
pitch worlds. At Bell Laboratories,
John Pierce and Max Mathews exper-
imented with synthetic spectra hav-
ing corresponding, nonstandard
tuning systems—a line of thinking
that led to John Chowning’s 1977
composition Stria (documented com-
prehensively in the preceding issue of
this journal and on the present issue’s
DVD). William Sethares’s book Tun-

ing,Timbre, Spectrum, Scale (Springer,
1999) has further explored this ter-
rain. Besides composition with syn-
thetic timbres, though, there are
other areas of computer music where
tuning theory can crop up—which
brings us to the ﬁrst two articles in
the present issue of Computer Music
Journal. Each article treats a visible
manifestation of tuning: microtonal
controllers in the ﬁrst case, and mi-
crotonal notation in the second.
The article by Andrew Milne,

William Sethares, and James Plamon-
don explains, in considerable depth,
the mathematics underlying certain
principles of microtonal keyboard
layout. One of these principles is
transpositional invariance. On in-
struments having this property, geo-
metrical shapes (e.g., chords) can be
transposed intact, much like sliding a
barre chord along a guitar fretboard.
Such keyboards are termed isomor-
phic. (Non-microtonal examples in-
clude the chromatic button accordion
and the Janko piano; the most inﬂu-
ential microtonal example was the
groundbreaking “generalized key-
board” of R. H. M. Bosanquet, whose
design is described in appendices to
Helmholtz’s On the Sensations of
Tone as a Physiological Basis for the
Theory of Music.) Another, related
principle is tuning invariance. This
term, introduced here by Milne et al.,
describes the ability, on an isomor-
phic keyboard, to preserve geometri-
cal shapes across a continuum of
related tuning systems. The authors
explain what it means for an interval

to be “the same” as its tuning
changes, and they provide examples
of related tuning systems across
which musical patterns can be
tuning-invariant. Many historically
(and even ethnomusicologically) rele-
vant tuning systems can be generated
from a single interval (plus the oc-
tave), as in the cycle of ﬁfths. As the
interval’s tuning changes, so does the
tuning of all the pitch classes in the
tuning system. This means that an
isomorphic instrument can feature a
continuous controller for dynami-
cally retuning all the instrument’s
pitches along the continuum that in-
cludes these tuning systems, without
requiring the performer to learn new
ﬁngerings for different systems (or
different keys). Although their article
is chieﬂy a mathematical exposition,
the authors brieﬂy consider the edu-
cational and creative ramiﬁcations of
such an instrument. Mr. Plamon-
don’s forthcoming controller, the
“Thummer,” embodies these design
principles.

Microtonality presents interesting

challenges, not only for the design
of new instruments (and, of course,
for performers of traditional instru-
ments), but also for notation. Com-
posers have adopted different, often
idiosyncratic, conventions for nam-
ing the pitches of nonstandard tuning
systems and displaying them on the
page. For example, Ben Johnston’s
music, like that of his mentor Harry
Partch, employs a microtonal just in-
tonation for which the composer de-
veloped his own notation system,

Front cover. The top illustration
shows the Thummer, a portable, mi-
crotonal controller that embodies the
principles described in the article by
Andrew Milne et al. By default, the
Thummer uses a key layout invented

by Kaspar Wicki in the late 1800s. At
the bottom is a screen image from
the article by Andreas Steﬁk et al.,
showing Ben Johnston’s microtonal
accidentals.

Back cover. This illustration, from

the article by Andrew Milne et al.,
shows how an isomorphic layout
(here, the Wicki design) exhibits tun-
ing invariance as the perfect ﬁfth, F,
changes in size from 4/7 of an octave
to 3/5 of an octave.

About This Issue

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o
m

j
/

a
r
t
i
c
e
–
p
d

f
/

3
1
4
1
1
8
5
4
9
6
6
/
c
o
m

j
.

2
0
0
7
3
1
4
1
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

which in Mr. Johnston’s case is com-
mon Western music notation with
added accidentals. Not only the un-
usual accidentals, but also the non-
standard intonation of normally
notated notes, pose difﬁculties for
performers. It comes as no surprise
that computer technology can help.
In “An Automatic Translator for
Semantically Encoded Musical Lan-
guages,” Andreas Steﬁk, Melissa
Steﬁk, and Mark Curtiss describe
software they developed to convert
between various music representa-
tions, such as Mr. Johnston’s nota-
tion and “performance notation,” in
which notes are annotated with their
deviation in cents from equal tem-
perament. (The Kepler Quartet has
used parts of this technology for ear-
training in preparation for recording
Mr. Johnston’s string quartets.) The
authors describe their software as
providing a general-purpose frame-
work for translating between arbi-
trary music representations, not just
notations related to tuning. As an ex-
ample, they demonstrate its ability to
easily incorporate a staff based on the
chromatic scale. Yet encoding and de-
coding the semantics of microtonal
systems, such as Ben Johnston’s, is a
substantially more difﬁcult task to
implement in translation software,
according to the authors.

Software representations of music
often reﬂect the programming para-
digm of the environment in which
they are implemented. Paradigms
used in constructing software for
music composition include object-
oriented, functional, and data-ﬂow
programming, among others. The ar-
ticle by Patrick Hill, Simon Holland,
and Robin Laney serves as an intro-
duction to a paradigm that is new for

music software, aspect-oriented pro-
gramming (AOP). The authors argue
that aspect-oriented music represen-
tation is well suited to compositional
idioms in which musical raw materi-
als are combined and reused in a man-
ner that creates tangled, polyarchic
relationships. After brieﬂy explaining
the concepts of aspect-oriented pro-
gramming, they describe their soft-
ware, called AspectMusic. Written in
Smalltalk, AspectMusic consists of
two parts: HyperMusic, which imple-
ments what is known in AOP as a
symmetric approach, and Music-
Space, which implements an asym-
metric approach.

Paul Nauert’s article investigates
complexities of rhythm, which are
somewhat analogous to the complex-
ities of intonation described in the
ﬁrst article, but he focuses on compo-
sitional techniques rather than math-
ematical details. He explores two
models of rhythm familiar to ethno-
musicologists—the additive and the
divisive—and shows how he employs
these models in algorithmically com-
posing music for human performers
that is conventionally notated but
nontraditional and rhythmically so-
phisticated. The additive model builds
up rhythms by concatenating units of
possibly different sizes, whereas the
divisive model divides a longer unit
(e.g., a measure) into equal parts. (It
might be stretching the point to ﬁnd
here an analogy with the contrast be-
tween just intonation and equal divi-
sions of the octave. One could also
draw a comparison between ﬂexible
intonation, which underlies the no-
tion of tuning invariance, and the
rhythmic quantization that Mr.
Nauert applies to make his music
more practical for performers.) The

author describes a series of additive
and divisive algorithms that he imple-
mented in OpenMusic, a Lisp-based
visual programming environment.
He also discusses a hybrid approach
with both addition- and division-
based features.

The reviews in this issue cover,
among other items, a “visual music
marathon,” the ﬁrst volume of the
Gareth Loy book mentioned earlier,
a book on new digital instruments
(focusing on controllers, sensors,
biosignal acquisition, and intelli-
gent systems), and a ﬁve-CD histori-
cal anthology from the archives of
the Groupe de Recherches Musi-
cales (GRM).

For the two-disc DVD set attached

to this issue, this year’s curators—
Tae Hong Park, Robert Gluck, and
Lonce Wyse—have assembled an in-
teresting collection of recordings
(some with video tracks) by com-
posers having a wide variety of na-
tionalities and cultural backgrounds.
As usual, the DVD also includes
sound and video examples to accom-
pany recent articles. However, this
year the examples are all by com-
posers: Natasha Barrett, David Cope,
and John Chowning. This year’s DVD
initiates an annual studio report pre-
sented in video, the ﬁrst being by the
Center for the Performing Arts and
Technology at the University of
Michigan. Finally, the DVD-ROM
portions of the discs include, among
other ﬁles, the complete quadra-
phonic audio for the original and
newly reconstructed versions of
Stria, optical scans of Mr. Chown-
ing’s notes and extant source code,
and Kevin Dahan’s source code for re-
constructing the piece.

Computer Music Journal

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o
m

j
/

a
r
t
i
c
e
–
p
d

f
/

3
1
4
1
1
8
5
4
9
6
6
/
c
o
m

j
.

2
0
0
7
3
1
4
1
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computer Music Journal

Volume 31, Number 4

Winter 2007

Contents

About This Issue

Letters

News

Performance Interfaces and
Tuning Theory

Isomorphic Controllers and Dynamic Tuning: Invariant Fingering over
a Tuning Continuum Andrew Milne, William Sethares,
and James Plamondon

Music Representation

An Automatic Translator for Semantically Encoded Musical
Languages Andreas Steﬁk, Melissa Steﬁk, and Mark Curtiss

An Introduction to Aspect-Oriented Music Representation
Patrick Hill, Simon Holland, and Robin Laney

Compositional Algorithms

Division- and Addition-Based Models of Rhythm in a Computer-
Assisted Composition System Paul Nauert

Reviews

Events

Boston Cyberarts Festival: Visual Music Marathon/The Puppet Master
by Eric Chasalow Peter McMurray
71

Publications

Eduardo R. Miranda and Marcelo M. Wanderley: New Digital Musical
Instruments: Control and Interaction Beyond the Keyboard
Victor Lazzarini

Gareth Loy: Musimathics: The Mathematical Foundations of Music,
Volume One Mark Ballora

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o
m

j
/

a
r
t
i
c
e
–
p
d

f
/

3
1
4
1
1
8
5
4
9
6
6
/
c
o
m

j
.

2
0
0
7
3
1
4
1
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Recordings

Various: GRM Archives

James Harley

Irwin Chusid, Curator: Interesting Results: Music by a Committee
of One Andrew Fletcher

Products

Primera Bravo SE Disc Publisher

James Harley

Products of Interest

DVD Program Notes

Instructions to Contributors

102

113

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o
m

j
/

a
r
t
i
c
e
–
p
d

f
/

3
1
4
1
1
8
5
4
9
6
6
/
c
o
m

j
.

2
0
0
7
3
1
4
1
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Letters

Proof of the Equivalence of the
Spiral Array and the Line of
Fifths in Chew and Chen’s Pitch-
Spelling Algorithm

In a recent article published in this
journal (Meredith 2007), I presented
the results of a study in which Chew
and Chen’s (2003a, 2003b, 2005)
pitch-spelling algorithm was re-
implemented and then optimized by
running it with 1,296 different pa-
rameter-value combinations on a test
corpus containing 195,972 notes and
consisting of 216 movements from
baroque and classical works.

One of the parameters of the
tested implementation of the algo-
rithm allows the line of ﬁfths to be
used instead of the spiral array
(Chew 2000) when calculating the
center of effect. I reported that, in
99.54 percent of the parameter-value
combinations (including the best-
performing ones), the results gener-
ated by the algorithm using the line
of ﬁfths were identical to those pro-
duced using the spiral array. There
were only 2 (poorly performing) cases
out of 432 parameter-value combina-
tion classes where the output of the
tested implementation of the algo-
rithm using the line of ﬁfths was dif-
ferent from that using the spiral array
(Meredith 2007, p. 65).

However, further study has revealed

that it can be proved that changing
from using the spiral array to using
the line of ﬁfths while keeping all
other parameter values constant
should never make any difference to
the output generated by Chew and
Chen’s algorithm. I shall now present
a proof of this result.

Let P be a set of notes, let CES be
the center of effect of P in the spiral
array and let CEL be the center of ef-
fect of P on the line of ﬁfths. CES is a
three-dimensional position vector,
given by the following equation:

CE
S

(
)
d n p n
( )
( )

∑

∈
n P

d n
( )

∑

∈
n P

(1)

where d(n) is the duration of the
note n and p(n) is the position vector
within the spiral array of the pitch
name class assigned to n. CEL is a
real number given by the following
equation:

∑

∈
n P

CE
L

(
)
d n k n
( )
( )
∑

d n
( )

(2)

∈
n P

where k(n) is the index of the pitch
name class assigned to the note n.

Let’s suppose that we wish to use
Chew and Chen’s algorithm to as-
sign to a note N, whose pitch class is
c, the pitch name class that is closest
to the center of effect of P. Let KS(N)
be the set that contains the indices of
the pitch name classes that can be as-
signed to N that are closest to CES in
the spiral array; and let KL(N) be the
set that contains the indices of the
pitch name classes that can be as-
signed to N that are closest to CEL on
the line of ﬁfths. I shall now prove
the following theorem.

Theorem 1 For a given set of notes
P and a given note N, the set KL(N) is
always equal to KS(N).

Proof For any note, n, whose pitch

name class has been assigned,

p n
( )

(
k n
sin ( ) /

(cid:2)

)
2
,

(
k n

(cid:2)
( ) /

)
2
,

k n
( )

cos

r
h

Equations 1 and 3 imply that

∑

∈
n P

d n
( )

CE
S

(
k n
sin ( )

(cid:2)

r
h
∑

∈
n P

d n
( )

)
2

(
k n
( )

(cid:2)

)
2

cos

d n
( )

r
h
∑
(
)
d n k n
( )
( )

∈
n P

∑

∈
n P

∑

∈
n P

d n
( )

(5)

∑

∈
n P

d n
( )

Equations 2 and 5 together imply

that

CE
S

∑

∈
n P

d n
( )

∑

∈
n P

d n
( )

(
k n
sin ( ) /

(cid:2)

r
h
∑

∈
n P

d n
( )

)
2

cos

r
h
∑

∈
n P

(
k n

(cid:2)
( ) /

)
2

(6)

d n
( )

CE
L

In other words, the z component of
the position vector of CES in the spi-
ral array is CEL, the center of effect of
P on the line of ﬁfths. It can readily
be shown that
{

(
k k
|

mod

)
)

c
7
(

)

K N
(
L

is an integer

)

and

i
(
(
and Abs

−
k CE
)
(
L

is a minimum

(7)

)}

(3)

where Abs(x) is x if x ≥ 0 and –x
otherwise. Similarly, it is clear that

K N
(
S

)

{

(
k k
|

c
7
(

mod

)
12
)

where r/h is the aspect ratio of the
spiral array and k(n) is the index of
the pitch name class of n. Let’s fur-
ther deﬁne that p(k) denotes the spi-
ral array position vector associated
with the index k and that therefore
(
k

)
2
,

p k
( )

sin

(cid:2)

r
h

(4)

(
k

(cid:2)

)
2
,

cos

r
h

Letters

is an integer

)

and

i
(
(
|

p k
( )

−

CE
S

is a minimum

(8)

)}

where |x| is the length of the vector
x and p(k) is as deﬁned in Equation 4.
From Equations 7 and 8, it follows
that KL(N) is always equal to KS(N) if
and only if
(
(

)
12
) −
)
12

Abs
(
12

is a minimum

) ⇔

mod

(
12

c
(
7

)

−

(9)

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o
m

j
/

a
r
t
i
c
e
–
p
d

f
/

3
1
4
1
1
8
5
4
9
6
6
/
c
o
m

j
.

2
0
0
7
3
1
4
1
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟

Let’s define that CES,x and CES,y
denote the x and y components of
CES, respectively. That is, from
Equation 5,

∑

∈
n P

d n
( )

∑

∈
n P

d n
( )

S x
,

and

S y
,

(
k n
sin ( )

)
(cid:2) 2
/

d n
( )

(10)

r
h
∑

∈
n P

cos

r
h
∑

(
k n
( )

)
(cid:2) 2
/

d n
( )

(11)

∈
n P

From Equations 4, 6, 10, and 11, it

follows that

(
12

c
(
7

mod

) −
)
12

CE
S

c
(
7

mod

(
(
12
(
(
12

sin

cos

r
h
r
h
(
12

c
(
7

mod
) −
)
12

CE
L

c
(
7

mod

)
(cid:2)
)
12
)
(cid:2)
)
12

) −
) −

S x
,

S y
,

and therefore

(
12

c
7
(

mod

) −
12
)

CE
S

sin

cos

r
h
r
h
(
12

(
(cid:2)
i
6
(
(cid:2)
i
6
+

c
7
(

mod

(cid:2)
12
)

c
7
(

mod
) −
12
)

(cid:2)
12
)

CE
L

mod

) −
2
) −
2

S x
,

S y
,

(12)

But sin(2πj + x) =sin x and cos(2πj +
x) = cos x for all integers j. Therefore
) −
)
12

mod

(
12

c
(
7

mod

(cid:2)
)
12

(
c
sin (
7
(
c
cos (
7

r
h
r
h
(
12

mod

(cid:2)
)
/
12
2
) −
)
12

c
(
7

mod

) −
) −

S x
,

S y
,

(13)

This implies that the x and y com-
ponents of p(12i + (7c mod 12)) – CES
are constant for all values of i. This
corresponds to the geometrical fact
that all the possible spellings of a
given note N lie on a straight line par-
allel with the central axis of the spi-

ral array. Therefore, for a given note
N with a pitch class c and a given
context set of notes P, |p(12i + (7c
mod 12)) – CES| is a minimum if and
only if the absolute value of its z
component is a minimum. That is,
) ⇔
(
(

)
12
) −
)
12

Abs
(
12

is a minimum

mod

(
12

c
(
7

)

−

which, as stated above (see Equa-
tion 9), implies that KL(N) is always
equal to KS(N).

[End of proof.]

Theorem 1 implies that, for a given

note N and a given context set of
notes P, the set of pitch name classes
that can be assigned to N that are
closest to the center of effect of P in
the spiral array is always the same as
the set of pitch name classes assign-
able to N that are closest to the cen-
ter of effect of P on the line of ﬁfths.
Note that KL(N) has cardinality 2 if
the minimum value of Abs(12i + (7c
mod 12) – CEL) is 6; otherwise, KL(N)
contains a single value.

It remains for me to explain why
changing from the line of ﬁfths to the
spiral array (while keeping all other
parameter values constant) in the
implementation of Chew and Chen’s
algorithm used by Meredith (2007)
caused the algorithm to generate dif-
ferent results in two of the 432 pa-
rameter-value combination classes
tested. Table 1 shows the details for
these two classes of parameter-value
combinations.

classes, the three note error counts
should have been equal.

Unfortunately, I have so far been

unable to reproduce the results in
Table 1. I re-compiled and ran the
code used by Meredith (2007) using
two different versions of Lisp (MCL
on Mac OS 9.2 and SBCL on open-
Suse Linux 10.2). For both versions,
the note error count was 10,403 for
all the parameter value combinations
in class 1 in Table 1 and 12,457 for all
the parameter value combinations in
class 2 in Table 1. These new results
are consistent with Theorem 1,
which suggests that the discrepancies
in Table 1 were the result of an error
whose source I have, unfortunately,
not yet been able to identify. If fur-
ther investigation does not provide
an explanation for the discrepancies
in Table 1, then, clearly, the complete
experiment reported in my recent ar-
ticle (Meredith, 2007) will have to be
re-run and the statistics recomputed
in order to conﬁrm the conclusions
drawn. The results of these further
investigations will be reported in a
future letter to the editor.

David Meredith
London, UK

References

Chew, E. 2000. “Towards a Mathe-
matical Model of Tonality.” PhD
thesis, Massachusetts Institute of
Technology, Cambridge, Massa-
chusetts.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o
m

j
/

a
r
t
i
c
e
–
p
d

f
/

3
1
4
1
1
8
5
4
9
6
6
/
c
o
m

j
.

2
0
0
7
3
1
4
1
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

As can be seen in Table 1, for the

Chew, E., and Y.-C. Chen. 2003a.

parameter-value combinations in
these two classes, the note error count
achieved using the spiral array with
an aspect ratio of √⎯
than that when the line of ﬁfths was
used and lower than that when the
spiral array was used with an aspect
⎯ 2/15. However, according to
ratio of √⎯
Theorem 1, within each of these two

⎯ 15/2 was lower

“Determining Context-Deﬁning
Windows: Pitch Spelling Using the
Spiral Array.” Proceedings of the
Fourth International Conference
on Music Information Retrieval.
Baltimore, Maryland.

Chew, E., and Y.-C. Chen. 2003b.
“Mapping MIDI to the Spiral
Array: Disambiguating Pitch

Computer Music Journal

⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟
⎯
⎯
⎯
⎯
⎯
⎯

Table 1. Parameter-Value Combinations in Two Classes in Which Changing from SA to LOF Made a Differ-
ence in the Experiment Reported by Meredith (2007).

Class ws wr

4
4
4
4
4
4

1
1
1
1
1
1

AspectRatio ChunkSize

StartOrSound

SAOrLOF MaxSAIndex) Note error count

(MinSAIndex

√⎯
⎯ 2/15
⎯ 2/15
√⎯
√⎯
⎯ 15/2
√⎯
⎯ 2/15
√⎯
⎯ 2/15
⎯ 15/2
√⎯

500
500
500
500
500
500

Starting
Starting
Starting
Starting
Starting
Starting

LOF
SA
SA
LOF
SA
SA

(–15 19)
(–15 19)
(–15 19)
(–22 26)
(–22 26)
(–22 26)

10,403
10,403
9,760
12,457
12,457
12,031

Spellings.” Proceedings of the 8th
INFORMS Computer Society Con-
ference. Norwell, Massachusetts:
Kluwer, pp. 259–275.

Chew, E., and Y.-C. Chen. 2005.

“Real-Time Pitch Spelling Using
the Spiral Array.” Computer Music
Journal 29(2):61–76.

Meredith, D. 2007. “Optimizing

Chew and Chen’s Pitch-Spelling
Algorithm.” Computer Music Jour-
nal 31(2):54–72.

Elaine Chew responds:

I have followed with interest the
evaluations of the Chew and Chen
(2003a, 2003b, 2005) pitch-spelling
algorithm in Meredith and Wiggins
(2005) and Meredith (2007), as well as
Meredith’s recent letter regarding the
equivalence of the use of the pitch-
class helix in the spiral array and the
line-of-ﬁfths representation in the
Chew and Chen pitch-spelling algo-
rithm. The purpose of my response
here is not to verify the correctness of
Meredith’s algebraic proof; I write to
provide some context for the use of
the spiral array, and geometric inter-
pretations of the equivalence of the
pitch-class helix in the spiral array
and the line of ﬁfths, and the situa-
tions under which this holds true.
For the beneﬁt of the reader who
may not be familiar with the spiral

array, I make a clear distinction be-
tween the pitch-class helix, a compo-
nent of the spiral array model, and
the spiral array, a model consisting of
a number of nested helices and an
interior-point approach to a traditional
representation (Chew, forthcoming). I
shall place the spiral array in the con-
text of pitch representations in West-
ern tonal music, provide reasons for
the selection of the aspect ratio in the
spiral array model, and present evi-
dence of the beneﬁts of higher- (than
one) dimensional representations of
pitch classes for chord and key recogni-
tion. I present the motivations for, and
advantages of, the spiral array represen-
tation for pitch spelling in the context
of a system for tonal analysis. Finally,
I give geometric interpretations for
why the line of ﬁfths is sufﬁcient for
the particular task of pitch spelling.
Meredith has evaluated the Chew

and Chen pitch-spelling algorithm
with admirable thoroughness on a
large corpus of baroque and classical
works. In Chew and Chen, we pro-
posed a pitch-spelling algorithm de-
signed to handle the pitch-spelling
challenges (key changes, particularly
abrupt ones) posed by a late Beethoven
sonata, Op. 109, and tested it with 19
parameter-value combinations. The
parameter values consist of the local
window sizes for phase one and two
of the algorithm, and the relative
weight on local versus global infor-

mation in phase two. Meredith re-
implemented and tested the Chew
and Chen algorithm with 1,296 pa-
rameter-value settings. In addition
to these parameter values, he also
varied the aspect ratio (r/h) for the
pitch-class helix in the spiral array,
including setting it to the limit value
as h→∞ or r→0, which results in the
line of ﬁfths.

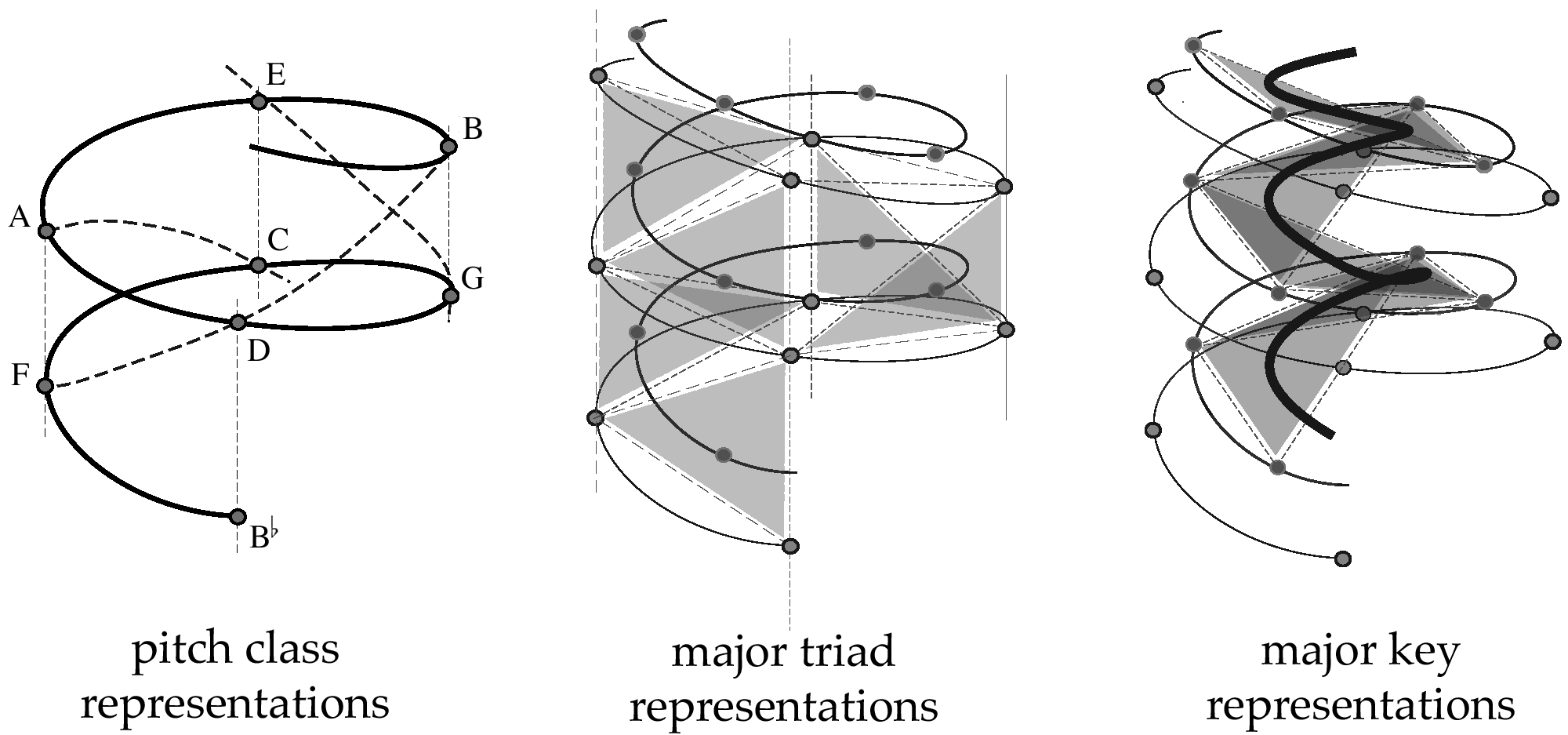
The spiral array (Chew 2000) is a
geometric representation for tonality.
It consists of an array of nested he-
lices, representing tonal elements at
different hierarchical levels (pitch
classes, major and minor triads, ma-
jor and minor keys, etc.) in the same
space (see Figure 1). The representa-
tions on each inner spiral are derived
mathematically as convex combina-
tions of their lower level constituents.
Each interior point thus deﬁned is
called a center of effect of its con-
stituents. The aspect ratio of the
pitch-class helix, and the weights for
deﬁning higher-level representations,
are determined so that the spatial or-
ganization of the objects reﬂects their
perceived closeness. The Chew and
Chen algorithm uses only the pitch-
class helix in the spiral array, and the
general concept of the center of ef-
fect. The aspect ratio in the spiral ar-
ray is selected to satisfy the perceived
relative closeness among the pitch
classes represented—for example,
pitches related by intervals of perfect

Letters

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o
m

j
/

a
r
t
i
c
e
–
p
d

f
/

3
1
4
1
1
8
5
4
9
6
6
/
c
o
m

j
.

2
0
0
7
3
1
4
1
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

⎯
⎯
⎯
⎯
⎯
⎯
⎯
⎯
⎯
⎯
⎯
⎯
⎯
⎯
⎯
⎯
⎯
⎯

Figure 1. Pitch class, major
triad, and major key repre-
sentations in the spiral ar-
ray, an example of an array
of nested helices. (Repro-
duced from Chew 2005.)

Figure 2. The line of ﬁfths
with C-major triad pitch
classes highlighted, and a
possible C-major triad cen-
ter of effect indicated.
(c.e. = center of effect.)

ﬁfths and fourths are considered to be
as close as, or closer than, those re-
lated by major thirds and minor sixths,
modeled as mathematical constraints
(Chew 2000, pp. 61–97). Hence, we
chose not to modify this parameter.
The pitch-class representations in
the spiral array model can be thought
of as the line of ﬁfths wrapped in an
ascending helix on a cylinder of ra-
dius r, one pitch class per quarter
turn, so that pitches related by an
interval of a major third line up verti-
cally one above another. The pitch-
class helix is a three-dimensional
conﬁguration of Longuet-Higgins’s
(1962a, 1962b) Harmonic Network.
The Harmonic Network is, in turn,
related to the Tonnetz, which has
been attributed to Euler, and which
researchers have used for charting tri-
adic movements in Western tonal
music (Cohn 1997, 1998). Both the
Harmonic Network and the Tonnetz
have, embedded in their representa-
tions, lines of ﬁfths in one dimension;
in addition, they also include lines of
thirds (major or minor) in another di-
mension to emphasize the other in-
terval fundamental to the triad.

The concept of the center of effect

was inspired by Longuet-Higgins’s
and Steedman’s (1971) key ﬁnding al-
gorithm, which is based on the fact
that pitches in a key form compact
clusters in the Harmonic Network.
Like the interior-point approach to
solving linear programming problems
in operations research, the center-of-
effect method uses the interior space,
rather than the discrete points on the
lattice, to identify the closest key by
a nearest-neighbor search (Chew
2000, 2001). The closest triad is lo-
cated in a similar fashion (Chew 2000).
The advantage of the added major/

minor third dimension in both 2D
and 3D allows the center of effect of
subsets of pitch classes in a triad to be
located inside the convex hull of its

Figure 1

Figure 2

constituents for easy recognition. Sim-
ilarly, the 2D and 3D conﬁgurations of
the Harmonic Network allow the cen-
ter of effect of subsets of pitch classes
in a key to be located within the con-
vex hull of the constituent pitches of
that key for robust identiﬁcation.

Consider the same center-of-effect
method applied to chord recognition
on a line of ﬁfths, shown in Figure 2.
The pitches of the C-major triad are
C, E, and G, shown as gray discs,
with a possible center of effect near
D. If only C and G are sounded, then
the closest major-triad center of ef-
fect is likely to be F, instead of the
more appropriate C. Thus, the line of
ﬁfths does not possess sufﬁcient
depth of representation for chord
recognition using the center-of-effect
method. In a higher-dimensional rep-
resentation where the pitch-class rep-
resentations of a triad form a compact
set, any subset of the pitches would
result in a center of effect inside the
convex hull of the triad components,

thus enabling chord identiﬁcation by
nearest neighbor searches. The same
concept extends to key ﬁnding.

The Chew and Chen pitch-spelling
algorithm came about when we real-
ized that, to create a real-time system
for analyzing music from live perfor-
mance, we need a robust way to con-
vert numeric pitch representations to
pitch names for mapping to the spiral
array, so as to perform tonal analysis
on the pitch information using the
spiral array key-ﬁnding and chord-
tracking algorithms. The system for
which the Chew and Chen pitch-
spelling algorithm was originally de-
signed, MuSA, evolved into MuSA.RT
(Chew and François 2003, 2005), an in-
teractive, real-time tonal analysis and
visualization system, which has been
demonstrated in live performance.

The Chew and Chen algorithm is

motivated by the fact that pitch
spellings, for the most part, follow
the assignment of accidentals in a
key: If one knows the key, one can

Computer Music Journal

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o
m

j
/

a
r
t
i
c
e
–
p
d

f
/

3
1
4
1
1
8
5
4
9
6
6
/
c
o
m

j
.

2
0
0
7
3
1
4
1
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

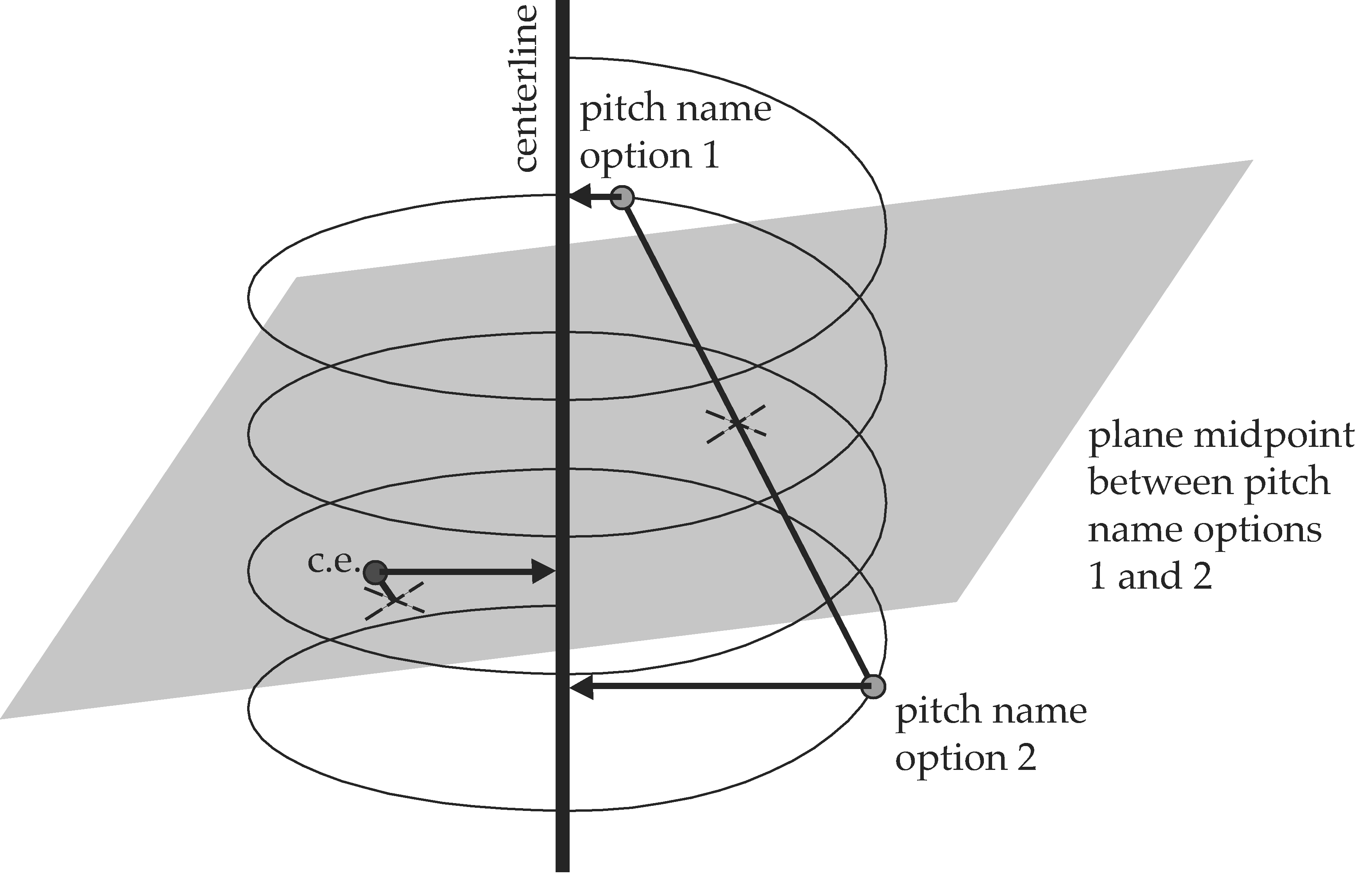
Figure 3. Hypothetical sit-
uation in which represen-
tations of pitch-name
options do not fall on a
vertical line. (c.e. = center
of effect.)

then spell the pitches correctly. Con-
versely, if one knows the correct
pitch spellings, one can then have
better information with which to de-
termine the key. Thus, pitch spelling
is very much related to key ﬁnding.
Because the key can be identiﬁed, in
the spiral array, by a nearest neighbor
search for the key representation
closest to the present center of effect,
we use the current center of effect as
a proxy for key, and determine the
best pitch spelling using a nearest
neighbor search among the candidate
pitch-class representations. This ap-
proach has two advantages: it is par-
allel to the music theoretic and a
musician’s conceptual process for
pitch spelling, and the consistency of
use of representation among the anal-
ysis (pitch spelling, chord recogni-
tion, key ﬁnding) and visualization
modules in the MuSA.RT system.
Given the theoretical underpin-
nings of the Chew and Chen algo-
rithm, the links between key ﬁnding
and pitch spelling, and the proven ad-
vantage of using a higher-dimensional
representation of the tonal system for
music analysis, why would a line of
ﬁfths be sufﬁcient for the pitch-
spelling algorithm? Meredith’s re-
sult can be understood as a particular
outcome of the geometric structure
of the options for spelling any pitch
in the Western tonal system: The
multiple options are aligned verti-
cally in the pitch-class helix, parallel
to its centerline. For example, the op-
tions for spelling MIDI note 61 are
{ . . . , B##, C#, D(cid:2), . . . }. On the pitch-
class helix, the pitches { B##, C# } and
{ C#, D(cid:2) } are separated by three
cycles of the spiral each, to line up
vertically above each other. Thus,
given a center of effect, the spelling
of the note closest to that center of
effect can be found by a nearest
neighbor search after projecting the
center of effect and all pitch classes

onto the centerline; the projected
pitch class representations would
then form the line of ﬁfths.

The same result would not hold if
the pitch-name options do not fall on
a vertical line. Consider the hypo-
thetical situation shown in Figure 3,
where two pitch-name options are
not vertically aligned. These two
pitch name options are shown as gray
discs, and the present center of effect
is given by the black disc. The plane
represents all points equidistant from
the two pitch-name options. When
considering the center of effect in the
three-dimensional space, it resides
above the plane, and thus is closer to
the pitch-class representation that is
higher up on the pitch-class spiral
(option 1). After projecting the center
of effect and the representations of
the two pitch names to the center-
line, the pitch class that is lower on
the helix (option 2) is the one closer
to the center of effect.

When the pitch-name options are
aligned vertically, the equidistant hy-
perplane is perpendicular to the cen-
terline, and ﬁnding the closest pitch
name in the three-dimensional space
is equivalent to ﬁnding the closest
pitch name on the line of ﬁfths. It
would seem that it is this property of
pitch spelling in the Western tonal

system, the vertical alignment of
pitch-name options, that makes the
line of ﬁfths representation sufﬁcient
for pitch spelling in the Chew and
Chen algorithm. Once the process of
spelling is started with the same cen-
ter of effect, and the pitch-class helix
and line-of-ﬁfths representations
have been established to be equiva-
lent for pitch spelling, the subsequent
center-of-effect determination and
spelling assignments should continue
on the same track. Any discrepancies
should be due only to the way the
processes are initialized.

Elaine Chew
Cambridge, Massachusetts, USA

References

Chew, E. 2000. “Towards a Mathe-
matical Model of Tonality.” PhD
thesis, Massachusetts Institute of
Technology, Cambridge, Massa-
chusetts.

Chew, E. 2001. “Modeling Tonality:

Applications to Music Cognition.”
Proceedings of the 23rd Annual
Meeting of the Cognitive Science
Society. Edinburgh, Scotland, UK,
pp. 206–211.

Chew, E. 2005. “Regards on Two Re-
gards by Messiaen: Post-tonal Mu-

Letters

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o
m

j
/

a
r
t
i
c
e
–
p
d

f
/

3
1
4
1
1
8
5
4
9
6
6
/
c
o
m

j
.

2
0
0
7
3
1
4
1
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

sic Segmentation Using Pitch
Context Distances in the Spiral
Array.” Journal of New Music Re-
search 34(4):341–354.

Chew, E. Forthcoming. “Thinking
Out of the Grid and Inside the
Spiral—Geometric Interpretations
of and Comparisons with the Spiral
Array Model.” Computing in Mu-
sicology 15.

Chew, E., and Y.-C. Chen. 2003a.

“Determining Context-Deﬁning
Windows: Pitch Spelling Using the
Spiral Array.” Proceedings of the
Fourth International Conference
on Music Information Retrieval.
Baltimore, Maryland.

Chew, E., and Y.-C. Chen. 2003b.
“Mapping MIDI to the Spiral
Array: Disambiguating Pitch
Spellings.” Proceedings of the
Eighth INFORMS Computing So-
ciety Conference. Kluwer Acade-

mic Publishers, OR/CS Interfaces
Series 21, pp. 259–275.

a Historical Perspective.” Journal
of Music Theory 42:167–180.

Chew, E., and Y.-C. Chen. 2005.

Longuet-Higgins, H. C. 1962a. “Let-

“Real-Time Pitch Spelling Using
the Spiral Array.” Computer Music
Journal 29(2):61–76.

Chew, E. and François, A. R. J. 2003.

“MuSA.RT: Music on the Spiral Ar-
ray. Real-Time.” Proceedings of the
ACM Multimedia ’03 Conference.
Berkeley, California, pp. 448–449.
Chew, E. and François, A. R. J. 2005.
“Interactive multi-scale visualiza-
tions of tonal evolution in
MuSA.RT Opus 2.” ACM Comput-
ers in Entertainment 3(4):1–16.
Cohn, R. 1997. “Neo-Riemannian
Operations, Parsimonious Tri-
chords, and their Tonnetz Repre-
sentations.” Journal of Music
Theory 41(1):1–66.

Cohn, R. 1998. “Introduction to Neo-
Riemannian Theory: A Survey and

ter to a Musical Friend.” Music Re-
view 23:244–248.

Longuet-Higgins, H. C. 1962b. “Sec-
ond Letter to a Musical Friend.”
Music Review 23:271–280.

Longuet-Higgins, H. C. and Steed-

man, M. J. 1971. “On Interpreting
Bach.” Machine Intelligence
6:221–241.

Meredith, D. 2007. “Optimizing

Chew and Chen’s Pitch-Spelling
Algorithm.” Computer Music Jour-
nal 31(2):54–72.

Meredith, D. and Wiggins, G. A.

(2005). “Comparing Pitch Spelling
Algorithms.” Proceedings of the
Sixth International Conference on
Music Information Retrieval. Lon-
don, UK.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o
m

j
/

a
r
t
i
c
e
–
p
d

f
/

3
1
4
1
1
8
5
4
9
6
6
/
c
o
m

j
.

2
0
0
7
3
1
4
1
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computer Music Journal

News

Mathematics and Computation
in Music

The newly founded Society for Math-
ematics and Computation in Music
presented its ﬁrst international con-
ference in conjunction with the Na-
tional Institute for Music Research in
Berlin, Germany, 18–20 May 2007.
Sessions included “Metalanguages
and Representation,” “Computa-
tional Models in Music Psychology,”
“Computational Models of Musical
Instruments,” “Comparative Com-
putational Analysis,” and “Mathe-
matical Approaches to Composition.”
The conference was also the occasion
for the presentation of the ﬁrst issue
of the Journal of Mathematics and
Music.

Audio Mostly

Audio Mostly 2007, the Second Con-
ference on Interaction with Sound,
was hosted by the Fraunhofer Insti-
tute for Digital Media Technology in
Ilmenau, Germany, 27–28 September
2007. The conference targets content
creators, interaction designers, and
behavioral researchers interested in
furthering the interactive potential of
applications such as games and mu-
sic through the use of sound. The
keynote speakers include Raymond
MacDonald, professor of music psy-
chology at Glasgow Caledonian Uni-
versity, and Juergen Herra of the
Fraunhofer Institute, a key contribu-
tor in the development of MP3 per-
ceptual coding.

Web: www.mcm2007.info

Web: www.audiomostly.com

Society for Music Perception
and Cognition

Bergen Interactive Music
Conference

The Society for Music Perception and
Cognition held its annual conference
at Concordia University in Quebec,
Canada, 30 July–3 August 2007. Al
Bregman (McGill University) deliv-
ered the keynote address on auditory
scene analysis. Symposia were or-
ganized around music as a multi-
modal experience, motion capture
approaches to studying music per-
formance, probabilistic models and
music cognition, music in multime-
dia, beats and metrical processing,
and performance preparation. A
satellite workshop, “Motion Capture
Data Exchange and the Establish-
ment of a Preliminary Database of
Music Performance,” was organized
at the Centre for Interdisciplinary
Research in Music Media and Tech-
nology (CIRMMT) at McGill
University.

Web: alcor.concordia.ca/~smpc2007

The ﬁrst Bergen International Music
Conference (BIMUC) was held in
Bergen, Norway, 25–29 April 2007.
The conference hosted teachers, per-
formers, and researchers discussing
and presenting work on music learn-
ing and on the creative and artistic
development of young people. Pre-
sentations included “Evaluating
Creative Work in Digital Musics”
by Ian Stevenson and “MusicDelta –
an Interactive, Internet-based Learn-
ing Resource for Music Education”
by Yrjan Tangenes and Gesle
Johnsen.

Web: www.bimuc.no

Victorian Music Machines

The 41st annual Association for
Recorded Sound Collections Confer-

ence took place in Milwaukee, Wis-
consin, 2–5 May 2007. Presentation
topics ranged from the study of auto-
matic musical instruments to an au-
dio necrology of musical ﬁgures lost
during the year 1957. There were sev-
eral sessions on special collections
and a pre-conference workshop on
the preservation of audio in the digi-
tal domain.

Web: www.arsc-audio.org/

conference2007.html

Signal Processing and Audio

The 2007 IEEE Workshop on Applica-
tions of Signal Processing to Audio
and Acoustics was scheduled to be
held 21–24 October 2007 in New
Paltz, New York. In addition to topics
on spatial coding, Internet audio, mu-
sical signal analysis, synthesis tools,
and the creation of musical sounds,
the focal area for this year’s work-
shop was acoustic scene analysis. Si-
mon Haykin (McMaster University)
was scheduled to deliver a keynote
address on a cognitive cocktail party
processor based on “cognitive dy-
namic systems.” The other scheduled
keynote speaker was Al Bregman
(McGill University) with a talk on
progress in the study of auditory
scene analysis.

Web: www.kecl.ntt.co.jp/icl/

signal/waspaa2007

Computational Models and
Flamenco Music

The Fourth International Workshop
on Computational Music Theory,
“Computational Models for Music
Similarity applied to Flamenco Mu-
sic,” was held 16–20 July 2007 in
Barcelona, Spain. The conference was

News

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o
m

j
/

a
r
t
i
c
e
–
p
d

f
/

3
1
4
1
1
8
5
4
9
6
6
/
c
o
m

j
.

2
0
0
7
3
1
4
1
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Figure 1. A jam session at
electro-music 2007. (Photo:
Hong Waltzer.)

hosted by Escola Superior de Música
de Catalunya in collaboration with
the Music Technology Group of the
Pompeu Fabra University. The inten-
tion of the conference was to facili-
tate collaborative problem-solving on
musical similarity, with special at-
tention to ﬂamenco music.

Web: www.esmuc.net/sonologia/

iwcmt07/index.html

electro-music in Philadelphia

The electro-music 2007 festival took
place at the Cheltenham Art Center
in Philadelphia, Pennsylvania, 1–3
June. The festival consisted of con-
certs, jam sessions, lectures, demos,
and workshops. The scope of the
event includes experimental music,
circuit bending, computer music,
musique concrète, improvisation,
and algorithmic music. Seminar,
demonstration, and workshop pre-
senters included Rebecca Mercuri,
Doctor T (Emile Tobenfeld), Howard
Muscovitz, and Ge Wang. The confer-
ence is an extension of the activity of
a community built around the electro-
music Web site.

for the festival and served as mentors
for the creation of new works by
emerging local artists. Trevor
Wishart premiered his work Angel,
commissioned by the festival host,
New Adventures in Sound Art.
Barry Truax performed a set of solo
and collaborative works with instru-
mentalist Randy Raine-Reusch com-
bining Asian instruments and
electroacoustics.

tion competition. The festival pre-
sented 80 musical works, including
13 world premieres, and 37 pieces
from Portuguese composers. Among
the featured events were perfor-
mances by Electroacoustic Theatre,
Electric Voice Theatre, Sond’Ar-te
Electric Ensemble, and the Loud-
speaker Orchestra.

Web: www.misomusic.com/ingl/

circul/mviva/2007.html

Web: electro-music.com

Web: www.naisa.ca/

Sound Travels

The ninth edition of the Sound
Travels Festival of Sound Art was
scheduled for 1 July–1 October 2007
at venues in and around Toronto
Island, Canada. Sound Travels in-
cludes the Sign Waves series of sound
sculptures and installations, outdoor
and indoor concerts, site-speciﬁc per-
formances, soundwalks, artist talks,
and workshops. Featured artists in-
cluded Kristi Allik and Tony Ka Tung
Leung. Trevor Wishart and Barry
Truax were composers-in-residence

soundtravels

Música Viva

The Música Viva Festival 2007 ex-
panded its venue this year to include
Lisbon and Porto, Portugal, and was
scheduled to be held 11–22 Septem-
ber. This year’s festival was entitled
“Perception and Aesthetics within
Musical Creation; Transmutations
of Sound and New Technologies.”
The conference included concerts and
lectures, presentations for children,
and the presentation of prizewinners
of the annual Música Viva composi-

Sound in Space at ZKM

The next_generation festival was
held 21–24 June 2007 at the Zentrum
für Kunst und Medientechnologie
(ZKM, Center for Art and Media) in
Karlsruhe, Germany. The theme of
this year’s festival was “Music in
Space.” Concerts and symposia on
new aesthetic directions and techni-
cal developments were presented,
along with new works by young com-
posers that were analyzed and dis-
cussed. A focal point of the festival
was the Klandom instrument with
over 50 channels of sound and cus-

Computer Music Journal

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o
m

j
/

a
r
t
i
c
e
–
p
d

f
/

3
1
4
1
1
8
5
4
9
6
6
/
c
o
m

j
.

2
0
0
7
3
1
4
1
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

tom “room-control” software for
spatialization.

Web: on1.zkm.de/zkm/stories/

storyReader$5704

Synthèse in Bourges

The Institut International de
Musique Electroacoustique de
Bourges presented the 37th annual
Synthèse festival 1–10 June 2007 in
Bourges, France. Some concert ses-
sions were devoted to themes such as
video music, young composers, or a
particular instrument, whereas others
were devoted to music from speciﬁc
countries including China, Poland,
and Canada. The winners of the 34th
International Competition of Electro-
acoustic Music and Sound Art were
announced (see the accompanying
news item), and the winning compo-
sitions were performed. Composers
whose work was presented included
Jon Appleton, Francis Dhomont,
Louis Dufort, Denis Dufour, Beatriz
Ferreyra, Max Mathews, Barry Truax,
and Hans Tutschku. Francis Dhomont
presented his work Premières traces
du Choucas.

Web: www.imeb.net

Bourges Competition Winners

The winners of the 34th Interna-
tional Competition of Electroacous-
tic Music and Sound Art have been
announced. In the Residence section
for composers between 18 and 25
years of age, the prizewinners in-
cluded Bryan Jacobs for Within
Scenes of Hurt, Damian Ryan for
Conﬁgurational energy landscape #3,
Yukari Uto for Nigero, Oliver Car-
man for Amorphous Materials, Peng
Guan for Extremer, and Gregory Cor-
nelius for Earth and Green.

The Trivium/Quadrivium section
for composers over 25 years of age is
broken down in to different cate-
gories. The prize for abstract music
went to Antonino Chiaramonte for
Riﬂessioni and Krzysztof Wolek for
Mobile Variations. The prize for pro-
gram music went to John Young for
Ricordiamo Forli. For electroacoustic
music with instruments, the prize
was given to João Pedro Oliveira for
Beyond. Two prizes for works for
dance and theater were given, one
to Costa Simao for Subterrâneos C
Corpo, and the other to Todor Todor-
off for The familiar ones of the
labyrinth. The prize for multimedia
went to Bérangère Maximin for
Black ink.

The Magisterium prize for com-
posers with over 25 years of profes-
sional experience was given to Roger
Doyle for his work, The Ninth Set –
Sector 4. Honorable mentions for the
categories can also be found on the
Web site of Institut International de
Musique Electroacoustique de
Bourges.

Web: www.imeb.net

JTTP 2007 Competition Winners

The winners of the composition com-
petition Jeu de temps (Time Play, or
JTTP), organized by the Canadian
Electroacoustic Community, have
been announced. The competition
encourages and promotes Canadian
sound artists. The top ﬁve winners
for 2007 are Dominic Thibault for
Nuit noire, Nuit grise (2006), Georges
Forget for Orages D’acier (2007),
Thierry Gauthier for Cycles (2007),
Olivier Girouard for Le pont du sou-
venir (2007), and Félix Lebrun-Paré
for La volonté du périscope (2007).
Winners will have their works per-
formed in the ÉuCuE concert series
and broadcast over several Internet

radio stations. An online issue of
eContact! dedicated to the competi-
tion contains more information
about the music as well as download-
able sound ﬁles of each piece.

Web: eContact.ca

Prix Ars Electronica 2007

Prix Ars Electronica has announced
the 2007 winners of its International
Competition for CyberArts. Cate-
gories include computer animation,
hybrid art, interactive art, digital
communities, freestyle computing,
and digital musics. The Golden Nica
for digital musics this year went to
Masahiro Miwa for the work Reverse
Simulation Music. A discussion
about the work on Mr. Miwa’s Web
site (aloalo.co.jp/nakazawa/method/
method020_e.html) says that his ex-
periments seek “to reverse the usual
conception of computer simulations.
Rather than modeling within a com-
puter space the various phenomena
of the world based on the laws of
physics, phenomena that have been
veriﬁed within a computer space are
modeled in the real world.”

Awards of distinction in digital
musics were given to Israel Martínez
for Mi Vida, and to Drumcorps for
Grist. There were an additional
twelve honorary mentions for the
digital musics category, the details of
which can be found on the Ars Elec-
tronica Web site.

Web: www.aec.at/en/prix/

winners.asp

Giga-Hertz Composition Award

The winner of the Giga-Hertz award
for electronic music for 2007 is
Jonathan Harvey for his extensive
oeuvre at the crossroads between

News

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o
m

j
/

a
r
t
i
c
e
–
p
d

f
/

3
1
4
1
1
8
5
4
9
6
6
/
c
o
m

j
.

2
0
0
7
3
1
4
1
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

electronic and instrumental music.
The award is sponsored by ZKM, the
EXPERIMENTALSTUDIO for acous-
tic art, the Association of the SWR
(Southwest Broadcasting), and the
city of Karlsruhe, Germany. The to-
tal prize money for the awards is
€48,000, currently the largest such
prize for electronic music composi-
tion. Four special prizes went to
Mark Andre, Daniel Mayer, Flo
Menezes, and Vassos Nicolaou,
each of whom will receive support
for the realization and production of
artistic projects either at the ZKM

Institute for Music and Acoustics or
at the EXPERIMENTALSTUDIO for
acoustic art.

Web: www.giga-hertz-preis.de/

preistraeger07_e.html

Gaudeamus Music Week and
Competition

The International Gaudeamus Music
Week took place in Amsterdam
3–9 September 2007. The festival is
designed to provide young composers

with opportunity and exposure. As
part of the festival, compositions
nominated for the Gaudeamus Prize
are premiered. The categories of
music for the prize include chamber
orchestra, chamber music, and elec-
tronic music. The nominees in elec-
tronic music at this year’s event were
Hugo Morales Murguia for Top your
buffer, Stelios Manousakis for Do
Digital Monkeys Inhabit Virtual
Trees?, and Juan Andrés Verdaguer
for Embryen.

Web: www.gaudeamus.nl

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o
m

j
/

a
r
t
i
c
e
–
p
d

f
/

3
1
4
1
1
8
5
4
9
6
6
/
c
o
m