A Statistical Analysis of Summarization Evaluation Metrics Using
Resampling Methods
Daniel Deutsch, Rotem Dror, and Dan Roth
Department of Computer and Information Science
University of Pennsylvania, USA
{ddeutsch,rtmdrr,danroth}@seas.upenn.edu
Abstract
The quality of a summarization evaluation
metric is quantified by calculating the correla-
tion between its scores and human annotations
across a large number of summaries. Currently,
it is unclear how precise these correlation es-
timates are, nor whether differences between
two metrics’ correlations reflect a true differ-
ence or if it is due to mere chance. In this work,
we address these two problems by proposing
methods for calculating confidence intervals
and running hypothesis tests for correlations
using two resampling methods, bootstrapping
and permutation. After evaluating which of
the proposed methods is most appropriate for
summarization through two simulation exper-
iments, we analyze the results of applying
these methods to several different automatic
evaluation metrics across three sets of human
annotations. We find that the confidence in-
tervals are rather wide, demonstrating high
uncertainty in the reliability of automatic met-
rics. Further, although many metrics fail to
show statistical improvements over ROUGE,
two recent works, QAEval and BERTScore,
do so in some evaluation settings.1
1
Introduction
Accurately estimating the quality of a summary
is critical for understanding whether one summa-
rization model produces better summaries than
another. Because manually annotating summary
quality is costly and time consuming, researchers
have developed automatic metrics that approx-
imate human judgments (Lin, 2004; Tratz and
Hovy, 2008; Giannakopoulos et al., 2008; Zhao
et al., 2019; Deutsch et al., 2021, among others).
Currently, automatic metrics themselves are
evaluated by calculating the correlations between
1Our code is available at https://github.com
/CogComp/stat-analysis-experiments.
their scores and human-annotated quality scores.
The value of a metric’s correlation represents how
similar its scores are to humans’, and one metric
is said to be a better approximation of human
judgments than another if its correlation is higher.
However, there is no standard practice in sum-
marization for calculating confidence intervals
(CIs) for the correlation values or running hypoth-
esis tests on the difference between two metrics’
correlations. This leaves the community in doubt
about how effective automatic metrics really are
at replicating human judgments as well as whether
the difference between two metrics’ correlations
is truly reflective of one metric being better than
the other or if it is an artifact of random chance.
In this work, we propose methods for cal-
culating CIs and running hypothesis tests for
summarization metrics. After demonstrating the
usefulness of our methods through a pair of sim-
ulation experiments, we then analyze the results
of applying the statistical analyses to a set of
summarization metrics and three datasets.
The methods we propose are based on the re-
sampling techniques of bootstrapping (Efron and
Tibshirani, 1993) and permutation (Noreen, 1989).
Resampling techniques are advantageous because,
unlike parametric methods, they do not make
assumptions which are invalid in the case of sum-
marization (§3.1; §4.1). Bootstrapping and permu-
tation techniques use a subroutine that samples a
new dataset from the original set of observations.
Since the correlation of an evaluation metric to
human judgments is a function of matrices of
values (namely the metric’s scores and human
annotations for multiple systems across multiple
input texts; §2), this subroutine must sample new
matrices in order to generate a new instance, in
contrast to standard applications of bootstrapping
and permutation that sample vectors of numbers.
To that end, we propose three different bootstrap-
ping (§3.2) and permutation (§4.2) techniques for
1132
Transactions of the Association for Computational Linguistics, vol. 9, pp. 1132–1146, 2021. https://doi.org/10.1162/tacl a 00417
Action Editor: Mark Johnson. Submission batch: 4/2021; Revision batch: 7/2021; Published 10/2021.
c(cid:2) 2021 Association for Computational Linguistics. Distributed under a CC-BY 4.0 license.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
1
7
1
9
7
0
9
4
8
/
/
t
l
a
c
_
a
_
0
0
4
1
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
resampling matrices, each of which makes dif-
ferent assumptions about whether the systems or
inputs are constant or variable in the calculation.
In order to evaluate which resampling methods
are most appropriate for summarization, we per-
form two simulations. The first demonstrates that
the bootstrapping resampling technique which as-
sumes both the systems and inputs are variable
produces CIs that generalize best to held-out data
(§5.1). The second shows that the permutation
test which makes the same assumption has more
statistical power than the equivalent bootstrap-
ping method and Williams’ test (Williams, 1959),
a parametric hypothesis test that is popular in
machine translation (§5.2).
Finally, we analyze the results of estimating CIs
and applying hypothesis testing to a set of sum-
marization metrics using annotations on English
single- and multi-document datasets (Dang and
Owczarzak, 2008; Fabbri et al., 2021; Bhandari
et al., 2020). We find that the CIs for the metrics’
correlations are all rather wide, indicating that
the summarization community has relatively low
certainty in how similarly automatic metrics rank
summaries with respect to humans (§6.1). Addi-
tionally, the hypothesis tests reveal that QAEval
(Deutsch et al., 2021) and BERTScore (Zhang
et al., 2020) emerge as the best metrics in several
of the experimental settings, whereas no other
metric consistently achieves statistically better
performance than ROUGE (§6.2; Lin, 2004).
Although we focus on summarization, the tech-
niques we propose can be applied to evaluate
automatic evaluation metrics in other text gen-
eration tasks, such as machine translation or
structure-to-text. The contributions of this work
include (1) a proposal of methods for calculating
CIs and running hypothesis tests for summa-
rization metrics, (2) simulation experiments that
provide evidence for which methods are most
appropriate for summarization, and (3) an anal-
ysis of the results of the statistical analyses
applied to various summarization metrics on three
datasets.
2 Preliminaries: Evaluating Metrics
Summarization evaluation metrics are typically
used to either argue that a summarization system
generates better summaries than another or that an
individual summary is better than another for the
same input. How similarly an automatic metric
does these two tasks with respect to humans is
quantified as follows.
Let X be an evaluation metric that is used
to approximate some ground-truth metric Z. For
example, X could be ROUGE and Z could be
a human-annotated summary quality score. The
similarity of X and Z is evaluated by calcu-
lating two different correlation terms on a set
of summaries. First, the summaries from sum-
marization systems S = {S1, . . . , SN } on input
document(s) D = {D1, . . . , DM } are scored us-
ing X and Z. We refer to these scores as matrices
X, Z ∈ RN ×M in which xj
i are the scores
of X and Z on the summary output by system Si
on input Dj. Then, the correlation between X and
Z is calculated at one of the following levels:
(cid:7)(cid:8)
(cid:4)(cid:5)
i and zj
⎛
⎞
(cid:6)
(cid:6)
N
rSYS(X, Z) = CORR
⎝
1
M
xj
i ,
1
M
zj
i
(cid:16)
⎠
i=1
rSUM(X, Z) =
1
M
(cid:6)
j
j
(cid:11)(cid:12)(cid:13)
CORR
i , zj
xj
i
j
(cid:14)(cid:15)
N
i=1
where CORR(·) typically calculates the Pearson,
Spearman, or Kendall correlation coefficients.2
These two correlations quantify how similarly
X and Z score systems and individual sum-
maries per-input for systems S and documents
D. The system-level correlation rSYS calculates the
correlation between the scores for each system
(equal to the average score across inputs), and
the summary-level correlation rSUM calculates an
average of the correlations between the scores
per-input.3
The correlations rSYS and rSUM are also used to
reason about whether X is a better approximate of
Z than another metric Y is, typically by showing
that r(X, Z) > r(Y, Z) for either r.
3 Correlation Confidence Intervals
Although the strength of the relationship between
X and Z on one dataset is quantified by the cor-
relation levels rSYS and rSUM, each r is only a point
2For clarity, we will refer to rSUM and rSYS as correlation
levels and Pearson, Spearman, and Kendall as correlation
coefficients.
3Other definitions for the summary-level correlation have
been proposed, including directly calculating the correlation
between the scores for all summaries without grouping them
by input document (Owczarzak and Dang, 2011). However,
the definition we use is consistent with recent work on
evaluation metrics (Peyrard et al., 2017; Zhao et al., 2019;
Bhandari et al., 2020; Deutsch et al., 2021). Our work can be
directly applied to other definitions as well.
1133
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
1
7
1
9
7
0
9
4
8
/
/
t
l
a
c
_
a
_
0
0
4
1
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
estimate of the true correlation of the metrics,
denoted ρ, on inputs and systems distributed sim-
ilarly to those in D and in S. Although we cannot
directly calculate ρ, it is possible to estimate it
through a CI.
3.1 The Fisher Transformation
The standard method for calculating a CI for a
correlation is the Fisher transformation (Fisher,
1992). The transformation maps a correlation co-
efficient to a normal distribution, calculates the CI
on the normal curve, and applies the reverse trans-
formation to obtain the upper and lower bounds:
zr = arctanh(r)
(cid:13)
ru, r(cid:2) = tanh
zr ± zα/2 · c /
√
(cid:14)
n − b
where r is the correlation coefficient, n is the
number of observations, zα/2 is the critical value
of a normal distribution, and b and c are constants.4
Applying the Fisher transformation to calculate
CIs for ρSYS and ρSUM is potentially problematic.
First, it assumes that the input variables are nor-
mally distributed (Bonett and Wright, 2000). The
metrics’ scores and human annotations on the
datasets that we experiment with are, in general,
not normally distributed (see Appendix A). Thus,
this assumption is violated, and we expect this
is the case for other summarization datasets as
well. Second, it is not clear whether the transfor-
mation should be applied to the summary-level
correlation since its final value is an average of
correlations, which is not strictly a correlation.5
3.2 Bootstrapping
A popular nonparametric method of calculating a
CI is bootstrapping (Efron and Tibshirani, 1993).
Bootstrapping is a procedure that estimates the
distribution of a test statistic by repeatedly sam-
pling with replacement from the original dataset
and calculating the test statistic on each sample.
Unlike the Fisher transformation, bootstrapping is
a very flexible procedure that does not assume
the data are normally distributed nor that the test
statistic is a correlation, making it appropriate for
summarization.
(cid:2)
√
4b = 3, 3, 4 and c = 1,
.437 for Pearson,
Spearman, and Kendall, respectively (Bonett and Wright,
2000).
1 + r2/2,
5Correlation coefficients cannot be averaged because they
are not additive in the arithmetic sense, however it is standard
practice in summarization.
Figure 1: An illustration of the three methods for
sampling matrices during bootstrapping. The dark blue
color marks values selected by the sample. Only 3
system and input samples are shown here, when N and
M are actually sampled with replacement.
However, it is not clear how to perform boot-
strap sampling for correlation levels. Consider a
more standard bootstrapped CI calculation for the
mean accuracy of a question-answering model on a
dataset with k instances. Since the mean accuracy
is a function of the k individual correct/incorrect
labels, each bootstrap sample can be constructed
by sampling with replacement from the original
k instances k times. In contrast, the correlation
levels are functions of the matrices X and Z, so
each bootstrap sample should also be a pair of
matrices of the same size that are sampled from
the original data.
There are at least three potential methods for
sampling the matrices:
1. BOOT-SYSTEMS: Randomly sample with re-
placement N systems from S, then select the
sampled system scores for all of the inputs.
2. BOOT-INPUTS: Randomly sample with replace-
ment M inputs from D, then select all of the
system scores for the sampled inputs.
3. BOOT-BOTH: Randomly sample with replace-
ment M inputs from D and N systems from
S, then select the sampled system scores for
the sampled inputs.
Once the samples are taken, the corresponding
values from X and Z are selected to create the
sampled matrices. An illustration of each method
is shown in Figure 1.
Each sampling method makes its own assump-
tions about the degrees of freedom in the sampling
process that results in different interpretations of
the corresponding CIs. BOOT-INPUTS assumes that
there is only uncertainty on the inputs while the
systems are held constant. CIs derived from this
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
1
7
1
9
7
0
9
4
8
/
/
t
l
a
c
_
a
_
0
0
4
1
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1134
Algorithm 1 BOOT-BOTH Confidence Interval
Input: X, Z ∈ RN ×M , k ∈ N, α ∈ [0, 1]
Output: (1 − α) × 100%-confidence interval
for (i, j) ∈ {1, . . . , N } × {1, . . . M } do
S ← samp. {1, . . . , N } w/ repl. N times
D ← samp. {1, . . . , M } w/ repl. M times
1: samples ← an empty list
2: for k iterations do
3:
4:
5: Xs, Zs ← empty N × M matrices
6:
7:
8:
9:
10: Append r(Xs, Zs) to samples
11: end for
12: (cid:4), u ← (α/2) × 100 and (1 − α/2) × 100
Xs[i, j] ← X[S[i], D[j]]
Zs[i, j] ← Z[S[i], D[j]]
end for
percentiles of samples
12: return (cid:4), u
sampling technique would express a range of val-
ues for the true correlation ρ between X and Z for
the specific set of systems S and inputs from the
same distribution as those in D. The opposite as-
sumption is made for BOOT-SYSTEMS (uncertainty
in systems, inputs are fixed). BOOT-BOTH, which
can be viewed as sampling systems followed by
sampling inputs, assumes uncertainty on both
the systems and the inputs. Therefore the cor-
responding CI estimates ρ for systems and inputs
distributed the same as those in S and D.
Algorithm 1 contains the pseudocode for calcu-
lating a CI via bootstrapping using the BOOT-BOTH
sampling method. In §5.1 we experimentally
evaluate the Fisher transformation and the three
bootstrap sampling methods, then analyze the CIs
of several different metrics in §6.1.
4 Significance Testing
Although CIs express the strength of the corre-
lation between two metrics, they do not directly
express whether one metric X correlates to an-
other Z better than Y does due to their shared
dependence on Z. This statistical analysis is per-
formed by hypothesis testing. The specific one-
tailed hypothesis test we are interested in is:
H0 : ρ(X , Z) − ρ(Y, Z) ≤ 0
H1 : ρ(X , Z) − ρ(Y, Z) > 0
4.1 Williams’ Test
One method for hypothesis testing the difference
between two correlations with a dependent vari-
able that is used frequently to compare machine
translation metrics is Williams’ test (Williams,
1959). It uses the pairwise correlations between
X, Y , and Z to calculate a t-statistic and a cor-
responding p-value.6 Williams’ test is frequently
used to compare machine translation metrics’ per-
formances at the system-level (Mathur et al., 2020,
among others).
However, the test faces the same issues as the
Fisher transformation: It assumes the input vari-
ables are normally distributed (Dunn and Clark,
1971), and it is not clear whether the test should
be applied at the summary-level.
4.2 Permutation Tests
Bootstrapping can be used to calculate a p-value
in the form of a paired bootstrap test in which
the sampling methods described in §3.2 can be
used to resample new matrices from X, Y , and Z
in parallel (details omitted for space). However,
an alternative and closely related nonparametric
hypothesis test is the permutation test (Noreen,
1989). Permutation tests tend to be used more
frequently than paired bootstrap tests for hypoth-
esis testing because they directly test whether any
observed difference between two values is due
to random chance. In contrast, paired bootstrap
tests indirectly reason about this difference by
estimating the variance of the test statistic.
Similarly to bootstrapping, a permutation test
applied to two paired samples estimates the distri-
bution of the test statistic under H0 by calculating
its value on new resampled datasets. In contrast
to bootstrapping, the resampled datasets are con-
structed by randomly permuting which sample
each observation in a pair belongs to (i.e., re-
sampling without replacement). This relies on
assuming the pair is exchangeable under H0,
which means H0 is true for either sample assign-
ment for the pair. Then, the p-value is calculated
as the proportion of times the test statistic across
all possible permutations is greater than the ob-
served value. A significant p-value implies the
observed test statistic is very unlikely to occur if
H0 were true, resulting in its rejection. In practice,
calculating the distribution of H0 across all pos-
sible permutations is intractable, so it is instead
estimated on a large number of randomly sampled
permutations.7
6The full equation is omitted for space. See Graham and
Baldwin (2014) for details.
7This is known as an approximate randomization test.
1135
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
1
7
1
9
7
0
9
4
8
/
/
t
l
a
c
_
a
_
0
0
4
1
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 2: An illustration of the three permutation methods which swap system scores, document scores, or scores
for individual summaries between X and Y .
Algorithm 2 PERM-BOTH Hypothesis Test
Xs[i, j] ← Y [i, j]
Ys[i, j] ← X[i, j]
for (i, j) ∈ {1, . . . , N } × {1, . . . , M } do
if random Boolean is true then
Input: X, Y, Z ∈ RN ×M , k ∈ N, α ∈ [0, 1]
Output: p-value
1: Standardize X and Y
2: c ← 0
3: δ ← r(X, Z) − r(Y, Z)
4: for k iterations do
5: Xs, Ys ← empty N × M matrices
6:
7:
8:
9:
10:
11:
12:
13:
14:
15:
16:
17:
18:
19: end for
20: return c/k
end for
δs ← r(Xs, Z) − r(Ys, Z)
if δs > δ then
c ← c + 1
Xs[i, j] ← X[i, j]
Ys[i, j] ← Y [i, j]
end if
end if
else
(cid:6) swap
(cid:6) do not swap
For example, a permutation test applied to test-
ing the difference between two QA models’ mean
accuracies on the same dataset would sample a
permutation by swapping the models’ outputs for
the same input. Under H0, the models’ mean ac-
curacies are equal, so randomly exchanging the
outputs is not expected to change their means. In
the case of evaluation metrics, each permutation
sample can be taken by randomly swapping the
scores in X and Y . There are at least three ways
of doing so:
1. PERM-SYSTEMS: For each system, swap its
scores for all inputs with probability 0.5.
2. PERM-INPUTS: For each input, swap its scores
for all systems with probability 0.5.
3. PERM-BOTH: For each summary, swap its
scores with probability 0.5.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
1
7
1
9
7
0
9
4
8
/
/
t
l
a
c
_
a
_
0
0
4
1
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
To account for differences in scale, we standard-
ize X and Y before performing the permutation.
Figure 2 contains an illustration of each method,
and the pseudocode for a permutation test using
the PERM-BOTH method is provided in Algorithm 2.
Similarly to the bootstrap sampling methods,
each of
the permutation methods makes as-
sumptions about the system and input document
underlying distribution. This results in different
interpretations of how the tests’ conclusions will
generalize. Since PERM-SYSTEMS randomly assigns
system scores for all documents in D to either
sample, we only expect the test’s conclusion to
generalize to a system distributed similarly to
those in S evaluated on the specific set of docu-
ments D. The opposite is true for PERM-INPUTS. The
results for PERM-BOTH (which can be viewed as
first swapping systems followed by swapping in-
puts) are expected to generalize for both systems
and documents distributed similarly to those in
S and D.
In §5.2 we run a simulation to compare the
different hypothesis testing approaches, then an-
alyze the results of hypothesis tests applied to
summarization metrics in §6.2.
5 Simulation Experiments
We run two sets of simulation experiments in
order to determine which CI (§5.1) and hypoth-
esis test (§5.2) methods are most appropriate for
summarization metrics.
The datasets used in the simulations are the
multi-document summarization dataset TAC’08
(Dang and Owczarzak, 2008) and two subsets
of the single-document summarization CNN/DM
dataset (Nallapati et al., 2016) annotated by Fabbri
et al. (2021) and Bhandari et al. (2020). These
datasets have N = 58/16/25 summarization
models and M = 48/100/100 inputs, respec-
tively. The summaries were assigned overall
1136
responsiveness, relevance, or Lightweight Pyra-
mid (Shapira et al., 2019) scores, respectively, by
human annotators. The scores of the automatic
metrics are correlated to these human annotations.
5.1 Confidence Interval Simulation
In practice, evaluation metrics are almost always
used to score summaries produced by systems S (cid:7)
on inputs D(cid:7) which are disjoint (or nearly disjoint)
from and assumed to be distributed similarly to
the data that was used to calculate the CI, S,
and D. It is still desirable to use the CI as an
estimate of the correlation of a metric on S (cid:7) and D(cid:7),
however this scenario violates assumptions made
by some of the bootstraping sampling methods
(e.g., BOOT-SYSTEMS assumes that D is fixed).
This simulation aims to demonstrate the effect of
violating these assumptions on the accuracy of
the CIs.
Setup. The simulation works as follows. The
systems S and inputs D are each randomly par-
titioned into two equally sized disjoint sets SA,
SB, DA, and DB. Then the submatrices XA, ZA,
XB, and ZB are selected from X and Z based
on the system and input partitions. Matrices XA
and ZA are used to calculate a 95% CI using one
of the methods described in §3, and then it is
checked whether sample correlation r(XB, ZB)
is contained by the CI. The entire procedure is re-
peated 1000 times, and the proportion of times the
CI contains the sample correlation is calculated.
It is expected that a CI which generalizes well
to the held-out data should contain the sample
correlation 95% of the time under the assumption
that the data in A and B is distributed similarly.
The larger the difference from 95%, the worse the
CI is at estimating the correlation on the held-out
data.
The results of the simulation calculated on
TAC’08 and CNN/DM using both the Fisher trans-
formation and the different bootstrap sampling
methods to CIs for QAEval-F1 (Deutsch et al.,
2021) are shown in Table 1.8
BOOT-BOTH Generalizes the Best. Among the
bootstrap methods, BOOT-BOTH produces CIs that
come closest to the ideal 95% rate. Any devia-
tions from this number reflect that the assumption
that all of the inputs and systems are distributed
8The Fisher transformation was directly applied to the
averaged summary-level correlation.
CI Method
TAC’08
Fabbri et al. Bhandari et al.
ρSYS ρSUM
ρSYS
Fisher
0.72 1.00
BOOT-SYSTEMS 0.76 0.72
BOOT-INPUTS
0.58 0.70
0.82 0.92
BOOT-BOTH
0.87
0.81
0.70
0.98
ρSUM
1.00
0.73
0.73
0.93
ρSYS
0.85
0.80
0.68
0.94
ρSUM
1.00
0.72
0.62
0.88
Table 1: The proportion of times the 95% con-
fidence interval for the true correlations ρ of
QAEval-F1 calculated using Pearson contains the
sample correlation of a held-out set of systems
and inputs for the different methods of calculating
confidence intervals. Values in bold are closest to
0.95 (and less than 1.0) and significantly different
under a one-tailed difference of proportions z-test
at α = 0.05.
similarly is not true, but overall violating this
assumption does not have a major impact.
The other bootstrap methods, which sample
only systems or inputs, captures the correlation on
the held-out data far less than 95% of the time. For
instance, the CIs for ρSYS on Bhandari et al. (2020)
only successfully estimate the held-out correlation
on 80% and 68% of trials. This means that a 95%
CI calculated using BOOT-INPUTS is actually only
a 68% CI on the held-out data. This pattern is
the same across the different correlation levels
and datasets. The lower values for only sampling
inputs indicates that more variance comes from
the systems rather than the inputs.
Fisher Analysis. The Fisher transformation at
the system-level creates CIs that generalize worse
than BOOT-BOTH. The summary-level CI captures
the held-out sample correlation 100% of the time,
implying that the CI width is too large to be use-
ful. We believe this is due to the fact that as the
absolute value of r(X, Z) decreases, the width of
the Fisher CI increases. Summary-level correla-
tions are lower than system-level correlations (see
§6.1), and therefore Fisher transformation results
in a worse CI estimate at the summary-level.
Conclusion. This experiment presents strong
evidence that violating the assumptions that ei-
ther the systems/inputs are fixed or that the data
is normally distributed does result in worse CIs.
Hence, the BOOT-BOTH method provides the most
accurate CIs for scenarios in which summarization
metrics are frequently used.
1137
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
1
7
1
9
7
0
9
4
8
/
/
t
l
a
c
_
a
_
0
0
4
1
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
5.2 Power Analysis
The power of a hypothesis test is the probability of
accepting the alternative hypothesis given that it is
actually true (equal to 1.0 –the type-II error rate). It
is desirable to have as high of a power as possible
in order to avoid missing a significant difference
between metrics. This simulation estimates the
power of each of the hypothesis tests.
Setup. Measuring power requires a scenario in
which it is known that ρ is greater for one met-
ric than another (i.e., H1 is true). Since this is
not known to be true for any pair of proposed
evaluation metrics, we artificially create such a
scenario by adding randomness to the calculation
of ROUGE-1.9 We define Rk to be ROUGE-1
calculated using a random k% of the candidate
summary’s tokens. We assume that since Rk only
evaluates a summary with k% of its tokens, it is
quite likely that it is a worse metric than standard
ROUGE-1 for k < 100.
To estimate the power, we score summaries
with ROUGE-1 and Rk for different k values and
count how frequently each hypothesis test rejects
H0 in favor of identifying ROUGE-1 as a superior
metric. This trial is repeated 1000 times, and the
proportion of significant results is the estimate of
the power.
Since the various hypothesis tests make differ-
ent assumptions about whether the systems and
inputs are fixed or variable, it is not necessarily
fair to directly compare their powers. Because the
assumptions of BOOT-BOTH and PERM-BOTH most
closely align with the typical use case of summa-
rization, we compare their powers. We addition-
ally include Williams’ test because it
is fre-
quently used for machine translation metrics and
it produces interesting results, discussed below.
PERM-BOTH Has the Highest Power. Figure 3
plots the power curves for various values of k on
the CNN/DM annotations by Fabbri et al. (2021).
We find that PERM-BOTH has the highest power
among the three tests for all values of k. As k ap-
proaches 100%, the difference between ROUGE-1
and Rk becomes smaller and harder to detect, thus
the power for all methods approaches 0.
BOOT-BOTH has lower power than PERM-BOTH
both at the summary-level and system-level, in
9We use the recall variant of ROUGE for experiments
on TAC’08 and Bhandari et al. (2020) and the F1 variant on
Fabbri et al. (2021) throughout the paper.
Figure 3: The system- and summary-level Pearson
estimates of the power of the BOOT-BOTH, PERM-BOTH,
and Williams hypothesis test methods calculated on the
annotations from Fabbri et al. (2021). The power for
BOOT-BOTH and Williams at the system-level is ≈ 0 for
all values.
which it is near 0. This result is consistent with
permutation tests being more useful for hypothesis
testing than their bootstrapping counterparts. We
believe the power differences in both levels are
due to the variance of the two correlation levels.
As we observe in §6.1, the system-level CIs have
significantly larger variance than at the summary-
level, making it harder for the paired bootstrap to
reject the system-level H0.
Williams’ test has low power.
Interestingly, the
power of Williams’ test for all k is ≈ 0, implying
the test never rejects H0 in this simulation. This
is surprising because Williams’ test is frequently
used to compare machine translation metrics at the
system-level and does find differences between
metrics. We believe this is due to the strength of
the correlations of ROUGE-1 to the ground-truth
judgments as follows.
The p-value calculated by Williams is a func-
tion of the pairwise correlations of X, Y , and
Z and the number of observations. The closer
both r(X, Z) and r(Y, Z) are to 0, the higher the
p-value. The correlation of ROUGE-1 in this sim-
ulation is around 0.6 and 0.3 at the system- and
summary-levels.
the system-level
In contrast,
correlations for the metrics submitted to the Work-
shop on Machine Translation (WMT) 2019’s me-
trics shared task for de-en are on average 0.9
(Ma et al., 2019). Among the 231 possible pair-
wise metric comparisons in WMT’19 for de-en,
Williams’ test yields 81 significant results. If the
correlations are shifted to have an average value of
0.6, only 3 significant results are found. Thus we
conclude that Williams’ test’s power is worse for
detecting differences between lower correlation
values.
1138
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
1
7
1
9
7
0
9
4
8
/
/
t
l
a
c
_
a
_
0
0
4
1
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
1
7
1
9
7
0
9
4
8
/
/
t
l
a
c
_
a
_
0
0
4
1
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
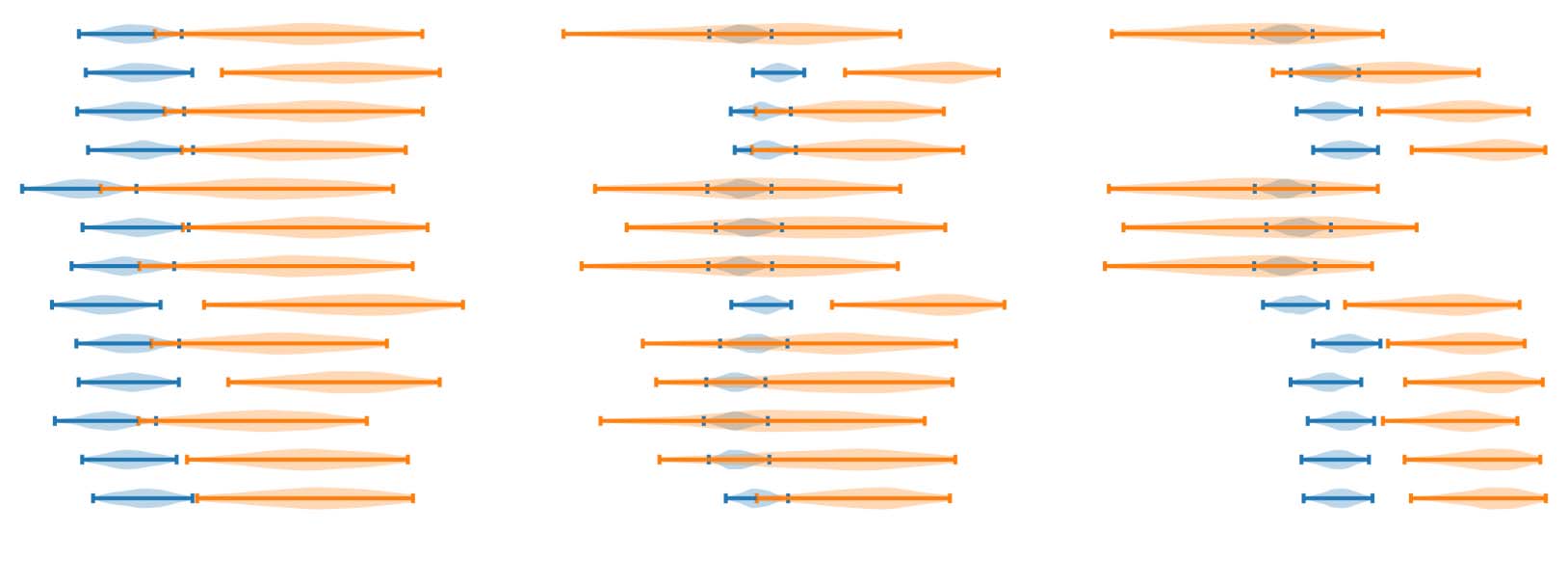
Figure 4: The 95% confidence intervals for ρSUM (blue) and ρSYS (orange) calculated using Kendall’s correlation
coefficient on TAC’08 (left) and CNN/DM summaries (middle, Fabbri et al. (2021); right, Bhandari et al. (2020))
are rather large, reflecting the uncertainty about how well these metrics agree with human judgments of summary
quality.
Because this simulation is performed with
summarization metrics on a real summarization
dataset, we believe it is faithful enough to a real-
istic scenario to conclude that Williams’ test does
indeed have low power when applied to sum-
marization metrics. However, we do not expect
Williams’ test to have 0 power when used to detect
differences between machine translation metrics.
Conclusion. Since PERM-BOTH has the best sta-
tistical power at both the system- and summary-
levels, we recommend it for hypothesis testing the
difference between summarization metrics.
6 Summarization Analysis
We run two experiments that calculate CIs (§6.1)
and run hypothesis tests (§6.2) for many different
summarization metrics on the TAC’08 and CNN/
DM datasets (§5). Each experiment also includes
an analysis which discusses the implications of
the results for the summarization community.
The metrics used for experimentation are the
following: AutoSummENG (Giannakopoulos et al.,
2008), BERTScore (Zhang et al., 2020), BEwT-E
(Tratz and Hovy, 2008), METEOR (Denkowski
and Lavie, 2014), MeMoG (Giannakopoulos and
Karkaletsis, 2010), MoverScore (Zhao et al.,
2019),NPowER (Giannakopoulos and Karkaletsis,
2013), QAEval (Deutsch et al., 2021), ROUGE
(Lin, 2004), and S3 (Peyrard et al., 2017). We use
the metrics’ implementations in the SacreROUGE
library (Deutsch and Roth, 2020).
6.1 Confidence Intervals
Figure 4 shows the 95% CIs calculated via
BOOT-BOTH for ρSUM and ρSYS for each metric calcu-
lated using Kendall’s τ . Since ROUGE is the most
commonly used metric, the following discussion
will mostly focus on its results, however the con-
clusions largely apply to other metrics as well.
Confidence Intervals are Large. The most ap-
parent observation is that the CIs are rather large,
especially for ρSYS. The ROUGE-2 ρSYS CIs are
[.49, .74] for TAC’08 and [−.09, .84] on CNN/DM
using the annotations from Fabbri et al. (2021).
The wide range of values demonstrates that there is
a large amount of uncertainty around how precise
the correlations reported in the literature truly are.
The size of the CIs has serious implications
for how trustable existing automatic evaluations
are. Since Kendall’s τ is a function of the num-
ber of pairs of systems in which the automatic
metric and ground-truth agree on their rankings,
the metrics’ CIs can be translated to upper- and
lower-bounds on the number of incorrect rank-
ings. Specifically, ROUGE-2’s system-level CI
on Fabbri et al. (2021) implies it incorrectly ranks
systems with respect to humans 9% to 54% of
the time. This means that potentially more than
half of the time ROUGE ranks one summariza-
tion model higher than another on CNN/DM, it
is wrong according to humans, a rather surprising
result. However, it is consistent with similar find-
ings by Rankel et al. (2013), who estimated the
same result to be around 37% for top-performing
systems on TAC 2008-2011.
1139
We suspect that the true ranking accuracy of
ROUGE (as well as the other metrics) is not likely
to be at the extremes of the confidence interval
due to the distribution of the bootstrapping sam-
ples shown in Figure 4. However, this experiment
highlights the uncertainty around how well au-
tomatic metrics replicate human annotations of
summary quality. An improved ROUGE score
does not necessarily mean a model produces bet-
ter summaries. Likewise, not improving ROUGE
should not disqualify a model from further consid-
eration. Consequently, researchers should rely less
heavily on automatic metrics for determining the
quality of summarization models than they cur-
rently do. Instead, the community needs to develop
more robust evaluation methodologies, whether it
be task-specific downstream evaluations or faster
and cheaper human evaluation.
Comparing CNN/DM annotations. The CIs
calculated on the annotations by Bhandari et al.
(2020) are in general higher and more narrow than
on Fabbri et al. (2021). We believe this is due to the
method of selecting the summaries to be annotated
for each of the datasets. Bhandari et al. (2020)
selected summaries based on a stratified sample
of automatic metric scores, whereas Fabbri et al.
(2021) selected summaries uniformly at random.
Therefore, the summaries in Bhandari et al. (2020)
are likely easier to score (due to a mix of high- and
low-quality summaries) and are less representative
of the real data distribution than those in Fabbri
et al. (2021).
6.2 Hypothesis Testing
Although nearly all of the CIs for the metrics are
overlapping, this does not necessarily mean that
no metric is statistically better than another since
the differences between two metrics’ correlations
could be significant.
In Figure 5, we report the p-values for test-
ing H0 : ρ(X , Z) − ρ(Y, Z) ≤ 0 using the
PERM-BOTH permutation test at the system- and
summary-levels on TAC’08 and CNN/DM for
all possible metric combinations (see Azer et al.
[2020] for a discussion about how to interpret
p-values). The Bonferroni correction (which low-
ers the significance level for rejecting each indi-
vidual null hypothesis such that the probability
of making one or more type-I errors is bounded
by α; Bonferroni, 1936; Dror et al., 2017) was
applied to test suites grouped by the X metric at
α = 0.05.10 A significant result means that we
conclude that ρ(X , Z) > ρ(Y, Z).
The metrics that are identified as being sta-
tistically superior to others at the system-level on
TAC’08 and CNN/DM using the annotations from
Fabbri et al. (2021) are QAEval and BERTScore.
Although they are statistically indistinguishable
from each other, QAEval does improve over more
metrics than BERTScore does on TAC’08. At the
summary-level, BERTScore has significantly bet-
ter results than all other metrics. Overall, none of
the other metrics consistently outperform all vari-
ants of ROUGE. Results using either the Spearman
or Kendall correlation coefficients are largely con-
sistent with Figure 5, although QAEval no longer
improves over some metrics, such as ROUGE-2,
at the system-level on TAC’08.
The results on the CNN/DM annotations pro-
vided by Bhandari et al. (2020) are less clear. The
ROUGE variants appear to perform well, a con-
clusion also reached by Bhandari et al. (2020). The
hypothesis tests also find that S3 is statistically
better than most other metrics. S3 scores systems
using a learned combination of features which
includes ROUGE scores, likely explaining this re-
sult. Similarly to the CI experiment, the results on
the annotations provided by Bhandari et al. (2020)
and Fabbri et al. (2021) are rather different, poten-
tially due to differences in how the datasets were
sampled. Fabbri et al. (2021) uniformly sampled
summaries to annotate, whereas Bhandari et al.
(2020) sampled them based on their approximate
quality scores, so we believe the dataset of Fabbri
et al. (2021) is more likely to reflect the real data
distribution.
7 Limitations
The large widths of the CIs in §6.1 and the lack of
some statistically significant differences between
metrics in §6.2 are directly tied to the size of the
datasets that were used in our analyses. However,
to the best of our knowledge, the datasets we used
are some of the largest available with annotations
of summary quality. Therefore, the results pre-
sented here are our best efforts at accurately mea-
suring the metrics’ performances with the data
available. If we had access to larger datasets with
more summaries labeled across more systems, we
10A version of the results when the correction is applied to
p-values grouped by the dataset and correlation level pair is
included in Appendix B.
1140
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
1
7
1
9
7
0
9
4
8
/
/
t
l
a
c
_
a
_
0
0
4
1
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
1
7
1
9
7
0
9
4
8
/
/
t
l
a
c
_
a
_
0
0
4
1
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5: The results of running the PERM-BOTH hypothesis test to find a significant difference between metrics’
Pearson correlations. A blue square means the test returned a significant p-value at α = 0.05, indicating the row
metric has a higher correlation than the column metric. An orange outline means the result remained significant
after applying the Bonferroni correction.
suspect that the scores of the human annotators
and automatic metrics would stabilize to the point
where the CI widths would narrow and it would
be easier to find significant differences between
metrics.
Although it is desirable to have larger datasets,
collecting them is difficult because obtaining hu-
man annotations of summary quality is expensive
and prone to noise. Some studies report having
difficulty obtaining high-quality judgments from
crowdworkers (Gillick and Liu, 2010; Fabbri et al.,
2021), whereas others have been successful us-
ing the crowdsourced Lightweight Pyramid Score
(Shapira et al., 2019), which was used in Bhandari
et al. (2020).
Then, it is unclear how well our experiments’
conclusions will generalize to other datasets with
different properties, such as documents coming
from different domains or different length sum-
maries. The experiments in Bhandari et al. (2020)
show that metric performance depends on which
dataset you use to evaluate, whether it be TAC
or CNN/DM, which is supported by our results.
However, our experiments also show variability in
performance within the same dataset when using
different quality annotations (see the differences in
results between Fabbri et al. [2021] and Bhandari
et al. [2020]). Clearly, more research needs to be
done to understand how much of these changes in
performance is due to differences in the properties
of the input documents and summaries versus how
the summaries were annotated.
8 Related Work
Summarization CIs and hypothesis
testing
were applied for summarization evaluation met-
rics over the years in a relatively inconsistent
manner—if at all. To the best of our knowledge,
the only instances of calculating CIs for summa-
rization metrics is at the system-level using a boot-
strapping procedure equivalent to BOOT-SYSTEMS
(Rankel et al., 2012; Davis et al., 2012). Some
works do perform hypothesis testing, but it is not
clear which statistical test was run (Tratz and Hovy,
2008; Giannakopoulos et al., 2008). Others report
whether or not the correlation itself is significantly
different from 0 (Lin, 2004), which does not quan-
tify the strength of the correlation nor allow for
comparisons. Some studies apply Williams’ test
to compare summarization metrics. For instance,
Graham (2015) use it to compare BLEU (Papineni
et al., 2002) and several variants of ROUGE, and
Bhandari et al. (2020) compares several different
1141
metrics at the system-level. However, our exper-
iments demonstrated in §5.2 that Williams’ test
has lower power than the suggested methods due
to the lower correlation values.
As an alternative to comparing metrics’ corre-
lations, Owczarzak et al. (2012) argue for compar-
ison based on the number of system pairs in which
both human judgments and metrics agree on sta-
tistically significant differences between the sys-
tems, a metric also used in the TAC shared-task for
summarization metrics (Dang and Owczarzak,
2009, among the others). This can be viewed simi-
larly to Kendall’s τ in which only statistically sig-
nificant differences between systems are counted
as concordant. However, the differences in dis-
criminative power across metrics was not statisti-
cally tested itself.
More broadly in evaluating summarization sys-
tems, Rankel et al. (2011) argue for comparing the
performance of summarization models via paired
t-tests or Wilcoxon signed-rank tests (Wilcoxon,
1992). They demonstrate these tests have more
power than the equivalent unpaired test when used
to separate human and model summarizers.
Machine Translation The summarization and
machine translation (MT) communities face the
same problem of developing and evaluating auto-
matic metrics to evaluate the outputs of models.
Since 2008, the Workshop on Machine Transla-
tion (WMT) has run a shared-task for developing
evaluation metrics (Mathur et al., 2020, among
others). Although the methodology has changed
over the years, they have converged on comparing
metrics’ system-level correlations using Williams’
test (Graham and Baldwin, 2014). Since Williams’
test assumes the input data is normally distributed
and our experiments show it has low power for
summarization, we do not recommend it for com-
paring summarization metrics. However, human
annotations for MT are standardized to be nor-
mally distributed, and the metrics have higher
correlations to human judgments, thus Williams’
test will probably have higher power when applied
to MT metrics. Nevertheless, the methods pro-
posed in this work can be directly applied to MT
metrics as well.
9 Conclusion
In this work, we proposed several different meth-
ods for estimating CIs and hypothesis testing
for summarization evaluation metrics using re-
sampling methods. Our simulation experiments
demonstrate that assuming variability in both the
systems and input documents leads to the best
generalization for CIs and that permutation-based
hypothesis testing has the highest statistical
power. Experiments on several different evalua-
tion metrics across three datasets demonstrate high
uncertainty in how well metrics correlate to hu-
man judgments and that QAEval and BERTScore
do achieve higher correlations than ROUGE in
some settings.
Acknowledgments
The authors would like to thank Lyle Ungar,
Daniel Khashabi, Eyal Ben David, and the anony-
mous reviewers for their valuable feedback on
our work.
This work was partly supported by a Focused
Award from Google, by contracts FA8750-19-2-
1004 and FA8750-19-2-0201 with the US Defense
Advanced Research Projects Agency (DARPA),
and by the Office of the Director of National Intel-
ligence (ODNI), Intelligence Advanced Research
Projects Activity (IARPA), via IARPA contract no.
2019-19051600006 under the BETTER Program.
The views and conclusions contained herein are
those of the authors and should not be interpreted
as necessarily representing the official policies,
either expressed or implied, of ODNI, IARPA,
DARPA, the Department of Defense, or the U.S.
Government. The U.S. Government is authorized
to reproduce and distribute reprints for govern-
mental purposes notwithstanding any copyright
annotation therein.
References
Erfan Sadeqi Azer, Daniel Khashabi, Ashish
Sabharwal, and Dan Roth. 2020. Not all
claims are created equal: Choosing the right
statistical approach to assess hypotheses. In
Proceedings of the 58th Annual Meeting of
the Association for Computational Linguistics,
pages 5715–5725, Online. Association for
Computational Linguistics. https://doi.org
/10.18653/v1/2020.acl-main.506
Manik Bhandari, Pranav Narayan Gour, Atabak
Ashfaq, Pengfei Liu, and Graham Neubig. 2020.
Re-evaluating evaluation in text summariza-
tion. In Proceedings of the 2020 Conference on
1142
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
1
7
1
9
7
0
9
4
8
/
/
t
l
a
c
_
a
_
0
0
4
1
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Empirical Methods in Natural Language Pro-
cessing (EMNLP), pages 9347–9359, Online.
Association for Computational Linguistics.
https://doi.org/10.18653/v1/2020
.emnlp-main.751
D. Bonett and T. A. Wright. 2000. Sample size
requirements for estimating Pearson, Kendall
and Spearman correlations. Psychometrika,
65:23–28. https://doi.org/10.1007
/BF02294183
Carlo E. Bonferroni. 1936. Teoria Statistica Delle
Classi e Calcolo Delle Probabilita, Libreria
internazionale Seeber.
Hoa Trang Dang and Karolina Owczarzak. 2008.
Overview of the TAC 2008 Update Summa-
rization Task. In Proc. of the Text Analysis
Conference (TAC).
H. T. Dang and K. Owczarzak. 2009. Overview
of the TAC 2009 Summarization track. In Text
Analysis Conference (TAC).
Sashka T. Davis, John M. Conroy, and Judith
D. Schlesinger. 2012. OCCAMS–An optimal
combinatorial covering algorithm for multi-
document summarization. In 2012 IEEE 12th
International Conference on Data Mining
Workshops, pages 454–463. IEEE.
Michael J. Denkowski and Alon Lavie. 2014.
Meteor universal: Language specific transla-
tion evaluation for any target
language. In
Proceedings of the Ninth Workshop on Statis-
tical Machine Translation, WMT@ACL 2014,
June 26–27, 2014, Baltimore, Maryland, USA,
pages 376–380. The Association for Computer
Linguistics. https://doi.org/10.3115
/v1/w14-3348.
Daniel Deutsch, Tania Bedrax-Weiss, and Dan
Roth. 2021. Towards question-answering as
an automatic metric for evaluating the con-
tent quality of a summary. Transactions of the
Association for Computational Linguistics, 9.
Daniel Deutsch
and Dan Roth.
2020.
SacreROUGE: An open-source library for us-
ing and developing summarization evaluation
metrics. In Proceedings of Second Workshop
for NLP Open Source Software (NLP-OSS),
pages 120–125, Online. Association for Com-
putational Linguistics. https://doi.org
/10.18653/v1/2020.nlposs-1.17
Rotem Dror, Gili Baumer, Marina Bogomolov,
and Roi Reichart. 2017. Replicability analysis
for natural language processing: Testing signif-
icance with multiple datasets. Transactions of
the Association for Computational Linguistics,
5:471–486. https://doi.org/10.1162
/tacl_a_00074
Rotem Dror, Gili Baumer, Segev Shlomov, and
Roi Reichart. 2018. The hitchhiker’s guide to
testing statistical significance in natural lan-
guage processing. In Proceedings of the 56th
Annual Meeting of the Association for Compu-
tational Linguistics (Volume 1: Long Papers),
pages 1383–1392. https://doi.org/10
.18653/v1/P18-1128
Rotem Dror, Lotem Peled-Cohen,
Segev
Shlomov, and Roi Reichart. 2020. Statistical
significance testing for natural language pro-
cessing. Synthesis Lectures on Human Language
Technologies, 13(2):1–116. https://doi.org
/10.2200/S00994ED1V01Y202002HLT045
Olive Jean Dunn and Virginia Clark. 1971. Com-
parison of tests of the equality of dependent
correlation coefficients. Journal of the Ameri-
can Statistical Association, 66(336):904–908.
Bradley Efron and Robert Tibshirani. 1993.
An Introduction to the Bootstrap. Springer.
https://doi.org/10.1080/01621459
.1971.10482369
A. R. Fabbri, Wojciech Kryscinski, Bryan
McCann, R. Socher, and Dragomir Radev.
2021. SummEval: Re-evaluating summariza-
tion evaluation. Transactions of the Associa-
tion for Computational Linguistics, 9:391–409.
https://doi.org/10.1162/tacl a 00373
Ronald Aylmer Fisher. 1992. Statistical methods
for research workers, Breakthroughs in Sta-
tistics, Springer, pages 66–70. https://doi
.org/10.1007/978-1-4612-4380-9 6
George Giannakopoulos and Vangelis Karkaletsis.
2010. Summarization system evaluation varia-
tions based on n-gram graphs. In Proceedings
of the Third Text Analysis Conference, TAC
2010, Gaithersburg, Maryland, USA, Novem-
ber 15–16, 2010. NIST.
1143
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
1
7
1
9
7
0
9
4
8
/
/
t
l
a
c
_
a
_
0
0
4
1
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
George Giannakopoulos and Vangelis Karkaletsis.
2013. Summary evaluation: Together we stand
In Computational Linguistics
NPowER-ed.
and Intelligent Text Processing – 14th Inter-
national Conference, CICLing 2013, Samos,
Greece, March 24-30, 2013, Proceedings,
Part II, volume 7817 of Lecture Notes in
Computer Science, pages 436–450. Springer.
https://doi.org/10.1007/978-3-642
-37256-8 36
A.
and
George Giannakopoulos, Vangelis Karkaletsis,
Panagiotis
Vouros,
George
Stamatopoulos. 2008. Summarization system
evaluation revisited: N-gram graphs. ACM
Transactions on Audio, Speech, and Language
Processing, 5(3):5:1–5:39. https://doi
.org/10.1145/1410358.1410359
Dan Gillick and Yang Liu. 2010. Non-expert eval-
uation of summarization systems is risky. In
Proceedings of the 2010 Workshop on Creat-
ing Speech and Language Data with Amazon’s
Mechanical Turk, Los Angeles, USA, June 6,
2010, pages 148–151. Association for Com-
putational Linguistics.
Yvette Graham. 2015. Re-evaluating automatic
summarization with BLEU and 192 shades of
ROUGE. In Proceedings of the 2015 Con-
ference on Empirical Methods in Natural
Language Processing, pages 128–137, Lisbon,
Portugal, Association for Computational Lin-
guistics. https://doi.org/10.18653
/v1/D15-1013
Yvette Graham and Timothy Baldwin. 2014.
Testing for significance of increased corre-
lation with human judgment. In Proceedings
of the 2014 Conference on Empirical Meth-
ods in Natural Language Processing (EMNLP),
pages 172–176.
Chin-Yew Lin. 2004. ROUGE: A package for
automatic evaluation of summaries. In Text
Summarization Branches Out, pages 74–81,
Barcelona, Spain. Association for Computa-
tional Linguistics. https://doi.org/10
.3115/v1/D14-1020
Qingsong Ma, Johnny Wei, Ondˇrej Bojar, and
Yvette Graham. 2019. Results of the WMT19
Metrics Shared Task: Segment-level and strong
MT systems pose big challenges. In Proceed-
ings of the Fourth Conference on Machine
Translation (Volume 2: Shared Task Papers,
Day 1), pages 62–90.
Nitika Mathur, Johnny Wei, Markus Freitag,
Qingsong Ma, and Ondˇrej Bojar. 2020. Results
of the WMT20 Metrics Shared Task. In Pro-
ceedings of the Fifth Conference on Machine
Translation, pages 688–725.
Ramesh Nallapati, Bowen Zhou, Cicero Nogueira
dos Santos, Caglar Gulcehre, and Bing Xiang.
2016. Abstractive text summarization using
sequence-to-sequence RNNs and beyond. In
Proceedings of CoNLL, pages 280–290.
Eric W. Noreen. 1989. Computer Intensive Meth-
ods for Hypothesis Testing: An Introduction.
Wiley, New York, 19:21. https://doi.org
/10.18653/v1/K16-1028
Karolina Owczarzak, John M. Conroy, Hoa Trang
Dang, and Ani Nenkova. 2012. An assessment
of the accuracy of automatic evaluation in sum-
marization. In Proceedings of Workshop on
Evaluation Metrics and System Comparison
for Automatic Summarization@NACCL-HLT
2012, Montr`eal, Canada, June 2012, 2012,
pages 1–9. Association for Computational
Linguistics.
Karolina Owczarzak and Hoa Trang Dang. 2011.
Overview of the TAC 2011 Summarization
Track: Guided task and AESOP task.
In
Proceedings of the Text Analysis Conference
(TAC 2011), Gaithersburg, Maryland, USA,
November.
Kishore Papineni, Salim Roukos, Todd Ward,
and Wj Zhu. 2011. BLEU: A method for au-
tomatic evaluation of machine translation. In
ACL, July, pages 311–318. https://doi
.org/10.3115/1073083.1073135
Maxime Peyrard, Teresa Botschen, and Iryna
Gurevych. 2017. Learning to score system
summaries for better content selection evalu-
ation. In Proceedings of the Workshop on New
Frontiers in Summarization, NFiS@EMNLP
2017, Copenhagen, Denmark, September 7,
2017, pages 74–84. Association for Compu-
tational Linguistics, https://doi.org/10
.18653/v1/w17-4510
1144
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
1
7
1
9
7
0
9
4
8
/
/
t
l
a
c
_
a
_
0
0
4
1
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Peter Rankel, John Conroy, Eric Slud, and Dianne
O’Leary. 2011. Ranking human and machine
summarization systems. In Proceedings of the
2011 Conference on Empirical Methods in Nat-
ural Language Processing, pages 467–473,
Edinburgh, Scotland, UK. Association for
Computational Linguistics.
Peter A. Rankel, John M. Conroy, Hoa Trang
Dang, and Ani Nenkova. 2013. A decade of
automatic content evaluation of news sum-
maries: Reassessing the state of the art. In
Proceedings of the 51st Annual Meeting of
the Association for Computational Linguis-
tics (Volume 2: Short Papers), pages 131–136,
Sofia, Bulgaria. Association for Computational
Linguistics.
Peter A. Rankel, John M. Conroy, and Judith D.
Schlesinger. 2012. Better metrics to automat-
ically predict the quality of a text summary.
Algorithms, 5(4):398–420. https://doi
.org/10.3390/a5040398
Nornadiah Mohd Razali and Yap Bee Wah.
2011. Power comparisons of Shapiro-Wilk,
Kolmogorov-Smirnov, Lilliefors and Anderson-
Darling Tests. Journal of Statistical Modeling
and Analytics, 2(1):21–33.
Ori Shapira, David Gabay, Yang Gao, Hadar
Ronen, Ramakanth Pasunuru, Mohit Bansal,
Yael Amsterdamer, and Ido Dagan. 2019.
Crowdsourcing lightweight pyramids for man-
ual summary evaluation. In Proceedings of
the 2019 Conference of the North American
Chapter of the Association for Computational
Linguistics: Human Language Technologies,
NAACL-HLT 2019, Minneapolis, MN, USA,
June 2–7, 2019, Volume 1 (Long and Short
Papers), pages 682–687. Association for Com-
putational Linguistics. https://doi.org
/10.18653/v1/n19-1072
Samuel Sanford Shapiro and Martin B. Wilk.
1965. An Analysis of variance test
for
normality (complete samples). Biometrika,
52(3/4):591–611.
Stephen Tratz and Eduard H. Hovy. 2008. Sum-
marization evaluation using transformed basic
elements. In Proceedings of
the First Text
Analysis Conference, TAC 2008, Gaithersburg,
Maryland, USA, November 17–19, 2008. NIST.
Frank Wilcoxon. 1992. Individual comparisons by
ranking methods. In Breakthroughs in Statis-
tics, pages 196–202, Springer. https://doi
.org/10.1093/biomet/52.3-4.591
Evan James Williams. 1959. Regression Analysis,
volume 14, Wiley.
Tianyi Zhang, Varsha Kishore, Felix Wu,
Kilian Q. Weinberger, and Yoav Artzi. 2020.
BERTScore: Evaluating text generation with
BERT. In 8th International Conference on
Learning Representations, ICLR 2020, Addis
Ababa, Ethiopia, April 26-30, 2020. OpenRe-
view.net.
Wei Zhao, Maxime Peyrard, Fei Liu, Yang
Gao, Christian M. Meyer, and Steffen Eger.
2019. MoverScore: Text generation evaluating
with contextualized embeddings and earth
mover distance. In Proceedings of the 2019
Conference on Empirical Methods in Natural
Language Processing and the 9th International
Joint Conference on Natural Language Pro-
cessing, EMNLP-IJCNLP 2019, Hong Kong,
China, November 3–7, 2019, pages 563–578.
Association for Computational Linguistics.
https://doi.org/10.18653/v1/D19
-1053
1145
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
1
7
1
9
7
0
9
4
8
/
/
t
l
a
c
_
a
_
0
0
4
1
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A Normality Testing
To understand if the normality assumption holds
for summarization data we ran the Shapiro-Wilk
test for normality (Shapiro and Wilk, 1965), which
was reported to have the highest power out of
several alternatives (Razali and Wah, 2011; Dror
et al., 2018, 2020). The results of the tests for the
ground-truth responsiveness scores and automatic
metrics are in Table 2. Most of the p-values are
significant, i.e., applying a statistical test which
assumes normality is incorrect in general.
B Extended Bonferroni Correction
Figure 6 contains the results from the pairwise hy-
pothesis tests (§6.2) when then Bonferroni correc-
tion is applied to set of p-values grouped by the
dataset and correlation level pair instead of each da-
taset, correlation level, and metric shown in Figure 5.
The results are overall very similar with only a
handful of results now becoming not significant.
Metric
TAC’08
Fabbri et al.
Bhandari et al.
rSUM
rSYS
rSUM
rSYS
Resp/Rel/Pyr
100.0 0.00
AutoSummENG 18.8 0.26
37.5 0.53
MeMoG
29.2 0.36
NPowER
35.4 0.00
BERTScore
22.9 0.06
BEwTE
27.1 0.15
METEOR
47.9 0.25
MoverScore
QAEval-F1
58.3 0.00
33.3 0.06
ROUGE-1
31.2 0.71
ROUGE-2
25.0 0.13
ROUGE-L
29.2 0.44
ROUGE-SU4
20.8 0.32
S3
32.0
33.0
33.0
33.0
26.0
37.0
27.0
35.0
40.0
32.0
34.0
26.0
32.0
26.0
0.52
0.01
0.01
0.01
0.15
0.00
0.00
0.00
0.01
0.00
0.00
0.13
0.00
0.00
rSUM
75.0
28.0
28.0
28.0
28.0
33.0
30.0
31.0
45.0
30.0
61.0
37.0
44.0
47.0
rSYS
0.84
0.55
0.55
0.55
0.18
0.68
0.61
0.50
0.21
0.91
0.62
0.12
0.84
0.66
Table 2: For rSYS the p-value of the Shapiro-Wilk
test. For rSUM, the percent of the per-input doc-
ument
tests which had a significant result at
α = 0.05. A significant p-value means H0 (the
data is distributed normally) is rejected. For rSUM,
the larger the percentage the more the data appears
to be not normally distributed.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
–
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
4
1
7
1
9
7
0
9
4
8
/
/
t
l
a
c
_
a
_
0
0
4
1
7
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6: The results of running the PERM-BOTH hypothesis test to find a significant difference between metrics’
Pearson correlations with the Bonferroni correction applied per dataset and correlation level pair instead of per
metric (as in Figure 5). A blue square means the test returned a significant p-value at α = 0.05, indicating the row
metric has a higher correlation than the column metric. An orange outline means the result remained significant
after applying the Bonferroni correction.
1146