A New Model for Investigating
the Evolution of Transcription
Control Networks
Dafyd J. Jenkins**
University of Birmingham
Dov J. Stekel*,**
University of Birmingham
Keywords
Transcription network, artificial evolution,
in silico genetics, stochastic simulation,
systems biology
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
Abstract Biological systems show unbounded capacity for complex
behaviors and responses to their environments. This principally arises
from their genetic networks. The processes governing transcription,
translation, and gene regulation are well understood, as are the
mechanisms of network evolution, such as gene duplication and
horizontal gene transfer. However, the evolved networks arising from
these simple processes are much more difficult to understand, and
it is difficult to perform experiments on the evolution of these
networks in living organisms because of the timescales involved.
We propose a new framework for modeling and investigating the
evolution of transcription networks in realistic, varied environments.
The model we introduce contains novel, important, and lifelike
features that allow the evolution of arbitrarily complex transcription
networks. Molecular interactions are not specified; instead they are
determined dynamically based on shape, allowing protein function
to freely evolve. Transcriptional logic provides a flexible mechanism
for defining genetic regulatory activity. Simulations demonstrate a
realistic life cycle as an emergent property, and that even in simple
environments lifelike and complex regulation mechanisms are
evolved, including stable proteins, unstable mRNA, and repressor
activity. This study also highlights the importance of using in silico
genetics techniques to investigate evolved model robustness.
1 Introduction
Transcription regulatory networks provide essential and complex functionality for any cell. Under-
standing the mechanisms behind the interactions forming these networks, their behavior, and also
their evolution and development, is essential for increasing our knowledge of this core process of
life. However, as it has taken many millions of years of evolution for this complexity to arise,
laboratory experiments in evolving transcription networks can only provide a fraction of this time
frame. In this study, we introduce a new in silico model including several novel features for inves-
tigating the function, behavior, and evolution of transcription networks.
The availability of large-scale computational power has allowed the development of realistic
in silico and quantitative modeling of many biological systems [49]. While long-term laboratory-based
* Contact author.
** Centre for Systems Biology, School of Biosciences, University of Birmingham, Edgbaston, Birmingham, B15 2TT, UK. E-mail: djj134@
bham.ac.uk (D.J.J.); d.j.stekel@bham.ac.uk (D.J.S.)
n 2009 Massachusetts Institute of Technology
Artificial Life 15: 259 – 291 (2009)
/
/
/
1
5
3
2
5
9
1
6
6
2
5
8
1
a
r
t
l
.
/
2
0
0
9
.
s
t
e
k
e
l
.
0
0
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. J. Jenkins and D. J. Stekel
Investigating the Evolution of Transcription Control Networks
evolutionary experiments are possible [27, 52], computational methods allow the simulation of much
longer periods of evolution in a practical timescale. This is because the life span of a simulated
individual can take a fraction of the time of its real-life equivalent. Computational models allow
selection of mutants and phenotypes at a much more specific level than laboratory experiments, as
much more detail about specific pathways, interactions, genotypes, and behaviors can be more easily
obtained. Indeed, the use of in silico genetics provides more than just a way of selecting or viewing
molecules and organisms; it provides a new and powerful tool for investigating a model molecular
system —allowing knockouts to be instantly generated, accurate and specific mutations to be applied
to any molecule, and any kinetic rate to be modified.
Many models and methods have been developed to approach the question of transcription net-
work evolution. Such models include the artificial genome (AG) [53], artificial regulatory network
(ARN) [39], the contributions by Franc¸ois and Hakim [23] evolving networks with specific functions
such as bistability or oscillatory dynamics, and those by Deckard and Sauro [19] evolving networks to
perform specific computational functions, such as square-root and cube-root calculators. Also, a
comprehensive review of early gene regulatory systems modeling is given by de Jong [18]. While
these studies use the biological regulatory network paradigm, the models are often taken out of
biological context. Alternatively, many other studies investigate networks to perform specific func-
tions, typically logic functions analogous to electrical circuits. For example, many studies of tran-
scription network models investigate global properties of the networks, such as whether the network
is distributed as a power law, or is of a scale-free topology [1, 3, 7]. These studies are very valuable, as
biological transcription regulatory networks share many attributes with the designed electrical circuits
we use day to day, and indeed, analysis of the motifs within sequenced organisms (most notably
Escherichia coli and Saccharomyces cerevisiae) show many similarities to traditional electrical components,
such as the feed-forward loop motif, which can function as a low-pass filter [6, 42, 44].
Moreover, these previous studies treat the evolving transcription regulatory network as a
standalone entity, whereas in reality the transcription regulatory network is just one of many systems
interacting together within a biological cell. Also, the fitness functions used to evaluate the per-
formance of the evolving networks are typically nonbiological, in that they have only a single, ar-
tificial goal, such as to produce a desired output from a given input. Indeed it has been suggested
that this single, focused goal approach to evolving such networks produces non-modularity, which is
in contrast to the highly modular structure we see in real transcription networks [34].
Another approach to modeling evolution of cells often used within the ALife literature is
individual-based models (IbMs). In the IbM approach, each model is treated as an individual, or agent,
with its own set of specific components. These individuals then compete within an environment for
resources, much like any biological organism. The most biologically focused IbM to date is the
COSMIC model [50], which aims to evolve bacterial function from the genetic level (transcription
networks) up to the environment level (population dynamics). Other IbM approaches include the
artificial chemistry model [29] and Avida [48].
The model presented in this study aims to more accurately model not only a transcription
regulatory network and its processes and components (biological approach), but also the encapsu-
lating cell and associated functions and systems within it (systems biology and ALife approaches).
The sole objective of this cell is that of all organisms: to survive in its environment and propagate.
While this single-objective approach may seem to contrast with the arguments presented by Kashtan
and Alon [34], the objective is in fact a complex combination of many smaller, possibly conflicting
objectives. Unlike many other models presented previously, the model is simulated stochastically, as
previous studies have shown the stochastic nature of intrinsic and extrinsic noise found within any
biological system [33, 43].
The model also introduces a method for incorporating transcriptional logic, which enables complex
Boolean logic to be performed at the transcriptional regulation level and allows phenomena such as
cooperativity between transcription factors similar to that found in biological cells.
In addition to this, the model also introduces a new method for determining molecule interaction
strengths through binding affinities that are based on molecular shape. The introduction of such a
260
Artificial Life Volume 15, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
5
3
2
5
9
1
6
6
2
5
8
1
a
r
t
l
.
/
2
0
0
9
.
s
t
e
k
e
l
.
0
0
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. J. Jenkins and D. J. Stekel
Investigating the Evolution of Transcription Control Networks
method means that proteins are not assigned a designated function, except in the case of the specialized
function of RNA polymerase. This allows proteins to evolve their own functions, as, for instance,
transcription factors, enzymes in metabolism, signaling, or indeed a combination of these functions.
This study presents the new model and methods in depth, along with results of comprehensive
analysis of the model over parameter ranges and the behaviors observed. An introduction to the
evolution methodology is also presented, supported by an analysis of the resultant evolution in an
idealistic environment.
The study highlights the power and importance of using in silico genetics tools to investigate
models and analyze their behavior, and we make hypotheses about the model’s behavior in more
complex environments.
2 Processes of Biological Cells
Biological cells have many interacting processes governing cell growth and division, metabolism of
food releasing energy, transcription of genes, and translation of the resultant product into protein.
The interaction between these processes and the cell’s environment produce the complex behaviors
we observe. One process in particular, transcription regulation, has an enormous influence on a cell’s
ability to respond to changes in environment, including food availability and starvation, or shock
such as heat or acid, by the use of positive and negative feedback.
2.1 Transcription and Translation
Transcription and translation are the two main processes involved in the production of protein from
a gene. Transcription involves a protein, known as RNA polymerase (RNAP), binding to the DNA
at a specific place, known as a promoter site. Once the RNAP has bound to the promoter site for a
gene, transcription initiates, causing the DNA helix to unwind immediately in front of the RNAP.
The RNAP molecule then, using one of the strands of DNA as a template, produces a molecule of
messenger RNA (mRNA). This mRNA transcript is then translated into one or more identical
proteins by ribosomes. We have based our model on the simple processes involved in prokaryotic
transcription and translation, and have not included more complicated processes found in eukary-
otes, such as splicing.
2.2 Transcription Regulation
As transcription and translation require energy, it is favorable to only use these processes when
necessary. Some gene products are required under many or all conditions, and so their production
may be less strongly regulated. However, other products may only be required in specific conditions,
such as shock, meaning that much stronger and complex regulation is required. Transcription can be
regulated in a number of ways, one of which is via transcription factors (TFs). A gene may need to
be turned on (activated) or turned off (repressed) by one or more TFs to affect when it is tran-
scribed. TFs bind to specific sequences on the DNA, which act as regulatory sites for the associated
genes, either helping the RNAP to bind to the promoter site in the case of activator TFs, or blocking
the promoter site, preventing RNAP binding.
Networks of transcription regulation for responding to the environment can be both simple and
complex. Many of the particularly well-studied networks, at both biological and theoretical levels, are
in the model bacterium Escherichia coli. These include the lac operon, which enables response to
glucose or lactose in the environment [32, 65], the tryptophan operon, which controls production of
the amino acid tryptophan using a repressor [2, 56], and the heat shock system [22, 40].
3 Models and Methods
The model we present in this study is a novel transcription regulation network and cellular model for
evolving bacteria within a range of environments. Like other models such as COSMIC, AG, and
Artificial Life Volume 15, Number 3
261
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
5
3
2
5
9
1
6
6
2
5
8
1
a
r
t
l
.
/
2
0
0
9
.
s
t
e
k
e
l
.
0
0
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. J. Jenkins and D. J. Stekel
Investigating the Evolution of Transcription Control Networks
ARN, our model can be viewed on a number of different levels: (i) molecular, (ii) interaction
networks, and (iii) cellular and population.
Each level provides different challenges that must be met through evolution and natural selection.
3.1 Molecular Level
At the lowest level, the model consists purely of molecules. Molecules can be divided into two
types: mobile molecules, such as proteins, which can move freely within the cell cytoplasm, and DNA-
based molecules, which are portions of the DNA that perform specific functions, such as gene
regulation.
3.1.1 Mobile Molecules
In a single cell there are thousands of different types of molecules, ranging from individual ions to
sugars to larger macromolecules such as proteins [2]. Our model substantially reduces the types of
molecules into five broad classes:
1. Protein. Proteins are the workhorses of the model, as they can potentially perform a
number of functions: as transcription factors, as metabolic enzymes, or for signaling.
Proteins are not assigned any function; instead, their binding affinity with other molecules
determines their functions.
2. RNA polymerase. This is a protein that performs the specific function of initiating
transcription when bound to a gene promoter site, and transcribes the gene, forming a
molecule of messenger RNA. The level of RNA polymerase is determined at the start
of simulation, and no more of it can be created, nor can any be degraded (it is assumed
that this intrinsic machinery would be managed elsewhere by the model). This is the only
protein with a prespecified function.
3. mRNA. Messenger RNA molecules act as templates for proteins.
4. Energy. Energy is the global term used for any molecule that is used up to perform or
fuel a function (such as in transcription or translation) and is thus analogous to ATP.
Energy is used to determine cell states. The model has the capacity to include further
types of energy that could be used in specific reactions.
5. Food. Food provides energy to the model cell. Food molecules are broken down by a
protein binding to them. Each food type has a number of parameters:
(a) Time to be broken down
(b) Molecule type yielded (either a different type of food, or energy)
(c) Amount of molecules yielded.
While the model abstracts an actual cell considerably, it still has an enormous and varying amount of
complexity. For instance, a pathway such as the glycolytic cycle could be modeled completely,
introducing numerous types of food, as each individual metabolite is included, also requiring many
different protein enzymes; alternatively, a single food type could represent the entire pathway.
3.1.2 DNA-Based Molecules
In prokaryotic cells, the DNA typically has the following four types of region: encoding genes, which
contain the genetic information used to produce mRNA molecules, cis-activating elements and cis-repressing
elements, which when occupied by a transcription factor upregulate or downregulate transcription of
262
Artificial Life Volume 15, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
5
3
2
5
9
1
6
6
2
5
8
1
a
r
t
l
.
/
2
0
0
9
.
s
t
e
k
e
l
.
0
0
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. J. Jenkins and D. J. Stekel
Investigating the Evolution of Transcription Control Networks
its associated gene, and promoter elements, which are used by RNAP molecules as an indicator for
the beginning of an encoding gene, which can then be transcribed. Our model implements these
types of regions by assigning a regulatory region consisting of a number of cis-activating, cis-repressing,
and promoter elements to an encoding gene; and also associated with the gene are an mRNA and
a protein. The encoding gene itself does not have a representation other than the transcribed product.
3.2 Molecule Shape and Binding Domains
Each molecule within the model has a specific shape, which is used to determine its binding affinity
with other molecules. Molecule shape is represented by a number of binding domains, or sites; there-
fore, the number of binding sites a molecule has determines the number of molecules to which it can
bind at any time, and also determines dynamically what functions it can perform. The shape of real
molecules depends on their atomic and charge configuration, which would require a very high-
dimensional space to be accurately represented. In our model, we represent the shape of a binding
domain with just two dimensions, so that the shape is modeled by a point on the surface of a unit
sphere. The two spherical polar coordinates (u, f) corresponding to the point on the sphere are the
genetic information of the binding domain, and thus are free to mutate. The polar coordinates,
transformed into the Cartesian coordinate system (x, y, z ), are then used in the function to determine
the binding affinity with another shape, and thus the corresponding phenotype.
3.2.1 Binding Affinity
The binding affinity between two binding sites is a function of the Euclidean distance between one
site and the antipode of the other site (denoted as D). In this way the strongest binding would be
from two complementary, opposite shapes. Because association is diffusion limited, different binding
strengths are implemented as dissociation rates, which are given by
Koff ¼
jD
1 (cid:2) ðD=2r Þa
ð1Þ
where j is a scaling factor, r is the radius of the sphere (in this case 1), and a is a Hill-like coefficient
for modifying the affinity curve saturation.
This binding affinity function is used to calculate the stability of all complexes. An exception to
implementation uses a fixed
this is the RNAP-promoter complex. For that, our current model
complex dissociation rate that is dependent only on the occupancy of the associated activator and
repressor sites, and not on the shape of the promoter or RNAP molecule. This is to ensure that
regardless of mutation to the promoter site, the RNAP is still able to function.
3.2.2 Allosteric Effects
In the cases where a molecule has multiple binding domains, it is possible for it to be bound to several
other molecules simultaneously. The occupation of a binding domain has been shown to be able to
cause conformational changes to other domains of the molecule [2]. Our model introduces such a
concept, so that each binding domain has two shapes: the natural shape in which the domain exists when
the parent molecule is a monomer, and the allosteric shape in which the domain exists when it and
another domain of the parent molecule are part of a larger, multi-molecule complex.
3.3 Molecule Interaction
The molecules are assumed to exist in a well-stirred system. This means that all molecules will
have the same interaction rate. The diffusion-limited interaction rate of mobile-mobile molecule
Artificial Life Volume 15, Number 3
263
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
5
3
2
5
9
1
6
6
2
5
8
1
a
r
t
l
.
/
2
0
0
9
.
s
t
e
k
e
l
.
0
0
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. J. Jenkins and D. J. Stekel
Investigating the Evolution of Transcription Control Networks
interactions is slower than that of DNA-mobile molecule interactions [16, 36], and so interactions
between two molecules depends on their molecular type.
3.4 Polymerization
Polymerization between molecules to form large complexes is an integral component of many
cellular processes, such as in signaling networks, increasing molecular stability, or the formation of
physical structures in a cell, such as the actin cytoskeleton or a flagellum. Our model allows polymer
chains to form and break dynamically. This allows signaling mechanisms and transfer of information,
and prevents protein and mRNA molecules from being degraded. Due to computational constraints,
complexes are only permitted to consist of up to three molecules. Because we do not model physical
structures, this constraint does not weaken the model.
3.5 Metabolism
Metabolism is a core function of any cell. Metabolic pathways within the model are any reactions
involving a food molecule and any protein. Pathways can be implemented with various levels of
realism. For instance, glycolysis could be included in a model by adding each metabolite from the
cycle, each with its own catabolism time and product, or a single food could be used to represent the
entire pathway.
3.6 Degradation
Molecule degradation can occur actively or passively. Active degradation involves another molecule
binding to the molecule and changing its structure, causing it to degrade, whereas passive degra-
dation does not require any interaction from other molecules, a single molecule breaking down either
spontaneously or due to environmental conditions. The model currently only implements passive
degradation, and so molecules will break down spontaneously according to a stability parameter, or
rate. Only those that are produced by genes within the cell (i.e., generic proteins and mRNAs) de-
grade; other molecules are treated as stable.
3.7 Transcription and Translation
Transcription and translation are two of the fundamental processes represented within the model.
Transcription initiation occurs after a promoter site has been bound by an RNA polymerase for a given
period of time. Once transcription initiation has occurred, and the cell has enough free energy, the
polymerase transcribes the gene in a single reaction. Each gene will have a specific length of nucleo-
tides, which is used, together with a rate of elongation, to generate the reaction rates for transcribing a
gene. The following equation shows the generic transcription reactions within the model:
RNAP þ promoter W RNAP promoter þ energy
! promoter þ RNAP transcribing
! RNAP þ mRNA
ð2Þ
Translation is modeled in a similar way to transcription, in that the process is reduced to a single
reaction. If the cell has enough free energy, translation of an mRNA molecule can occur. Each
mRNA molecule will have a length that is once again used, together with the abundance of
ribosomes, to generate a reaction time for the translation process. The following equation shows the
generic translation reactions within the model:
mRNA þ energy ! mRNA þ translating mRNA ! protein
ð3Þ
264
Artificial Life Volume 15, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
5
3
2
5
9
1
6
6
2
5
8
1
a
r
t
l
.
/
2
0
0
9
.
s
t
e
k
e
l
.
0
0
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. J. Jenkins and D. J. Stekel
Investigating the Evolution of Transcription Control Networks
Table 1. Expression states and descriptions.
0
1
2
Repressed
No possible expression
Unactivated
Basal or leaky expression
Activated
Full possible expression
3.7.1 Transcription Regulation
Regulation of transcription is performed by transcription factors binding to the cis-activator, cis-
repressor, or promoter sites in the regulatory region of a gene. The effect of an activated regulatory
region is that the promoter site and RNA polymerase molecule will bind more strongly, increasing
the chance of transcription initiation. Conversely, the effect of a repressed regulatory region is that
binding is prevented between the promoter site and RNA polymerase, turning off any transcription.
To determine the state of a regulatory region (activated, repressed, or neutral) we employ a novel
method that we term transcription logic. Transcription logic consists of a Boolean logic table and a cor-
responding function called the expression state. A column, or Boolean variable, is added to the logic table
for each cis-activator and cis-repressor element in the regulatory region. All possible Boolean com-
binations of these variables are then generated in the table. For each row in the table an expression level is
given as shown in Table 1 to reflect whether transcription is possible and how likely it is to initiate.
Using this method, any possible function can be applied to the regulatory region, giving the model
its complexity and flexibility. For instance, to simulate the expression of the lac operon, the regulatory
region would consist of a single cis-activator, a single cis-repressor, and a single promoter site. The
transcription logic function for the lac operon is given in Table 2.
3.8 Model Simulation
The model is simulated using a modified Gibson-Bruck stochastic algorithm [24] (code available on
request). Therefore, on using a stochastic framework, time is continuous, molecule abundances are
discrete values rather than concentrations, and intrinsic noise is introduced. Due to the incorporation
of realistic reaction rates for transcription, translation, and molecular interactions, accurate timescales
for these processes are produced, providing a realistic timescale for model output.
Modifications to the algorithm include static reactions, which are non-Markov, fixed-time reactions
that allow species abundances or reaction rates to be changed, for example due to environmental
changes. Also, logic-based termination criteria have been introduced for ending each model simulation.
Models are simulated until one of the following termination criteria is met:
(cid:7) The model has reached the appropriate replication threshold of free energy:
ðbase replication thresholdÞ þ ðgenome sizeÞ (cid:8) ðadditional energy per geneÞ
Table 2. Example of transcription logic for lac regulation, where + is bound and (cid:2) is unbound.
Activator
Repressor
Expression state
(cid:2)
(cid:2)
+
+
(cid:2)
+
(cid:2)
+
1
0
2
0
Artificial Life Volume 15, Number 3
265
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
5
3
2
5
9
1
6
6
2
5
8
1
a
r
t
l
.
/
2
0
0
9
.
s
t
e
k
e
l
.
0
0
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. J. Jenkins and D. J. Stekel
Investigating the Evolution of Transcription Control Networks
(cid:7) The model has reached a maximum simulation time threshold (simulation wall time).
(cid:7) The model does not have enough free energy to produce either an mRNA or a protein,
and no protein or mRNA exists; then the model is classed as dead.
3.9 Model Parameters
The model consists of a number of free parameters, which are able to evolve, and fixed parameters.
Free parameters include all molecule and DNA element shape parameters (u, f), with the exception
of energy, food, and RNAP, which are fixed during evolution. Protein and mRNA degradation rates
are also free to evolve. The fixed parameters, such as transcription and translation rates, food uptake
and metabolism rates, and diffusion-limited molecule interaction rates, are all derived where possible
from Escherichia coli experiments. In the simulations we present, all proteins have two domains (with
allosteric effects) with a simplified metabolism of a single food molecule that is broken down to yield
energy. The fixed parameters used in the model are given in Table 3.
3.10 Evolutionary Framework
The evolutionary framework used in this work is based on a standard genetic algorithm, in which a
population size is fixed, and random models are initialized to fill this population. Each model in the
initial population is then simulated sequentially. Upon termination of the simulation, the simulated
time and energy level are recorded. As the fitness function for the model is the time taken for
replication, models with a small fitness value (quicker replication) are therefore fitter than models
with a larger fitness (slower replication). Model fitness is determined as follows:
(cid:7) If the model reached the replication threshold before the simulation time was exceeded,
then the fitness is the simulated time for the model to replicate.
(cid:7) If the model did not replicate, but still had some free energy, then the fitness is
max simulation time (cid:8) ðmax simulation time=final energy levelÞ
Using this fitness function, models that were terminated with higher levels of energy will be treated
more favorably than those with lower levels.
(cid:7) If the model died, then its fitness is infinity.
Once the initial population has been created and initially simulated, the evolution process begins. The
use of a fixed-size population structure provides a source of competition between organisms. Each
model in the population (regardless of its previous simulation) replicates to produce an identical
model. If the cell survived (replicated or hit the simulated time threshold), then the mobile molecules
within the parent cell (proteins, mRNAs, and food), excluding RNA polymerase, are randomly
divided between the two cells using a random normal (A = 0.5, j = 0.1) for each molecular species.
Dead models receive no molecules. Evolutionary operators are then applied to each model in turn,
and each copy of the model is simulated. Once again the simulated time and energy are recorded.
The population must then be reduced to its original size using an elitism strategy: models are se-
lected (without replacement) according to their fitness. In this, and subsequent generations, models
that did not replicate but did not die are allowed to be selected; if not enough surviving models exist,
new random models are introduced. The resulting new population is then carried forward to the
next generation, where the process starts again. Each parameter setting is run three times.
The structural parameters for the evolutions (the binding affinity parameters a and j) were
determined from analysis of simulation results over a wide range of parameters. This analysis can be
found in Appendix 2.
266
Artificial Life Volume 15, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
5
3
2
5
9
1
6
6
2
5
8
1
a
r
t
l
.
/
2
0
0
9
.
s
t
e
k
e
l
.
0
0
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. J. Jenkins and D. J. Stekel
Investigating the Evolution of Transcription Control Networks
Table 3. Parameters that are fixed during evolution in the current model implementation.
Parameter
Food species
Initial genome size (number
of genes)
Mobile-mobile molecule
interaction rate
DNA-mobile molecule
interaction rate
Value(s)
Notes
1
1
10-4 s-1
10-2 s-1
Represents glucose (1 food molecule c14 glucose)
[41, 16]
[36]
Regulatory region
Lac operon regulation
RNA polymerase per gene
3
Each cell has f2000 active RNAP [26] and up
to 700 operons [55]
Gene length
1,080 nt
E. coli K-12 genome length 4,639,221 bp with
4,289 genes [14]
Transcription rate
50 nt/s
[4, 12]
Transcription cost
8 energy molecules
f2000 ATP to transcribe 1,080 nucleotides [47]
Transcription initiation rate
Activated RNAP-promoter
complex off rate
1 s-1
0.1 s-1
Gives 90% chance of transcription starting
Unactivated RNAP-promoter
1 s-1
Gives 50% chance of transcription starting
complex off rate
Protein size
Translation rate
Translation cost
360 aa
15 aa/s
Each amino acid is three nucleotides
[65, 2]
6 energy molecules
f1,500 ATP to translate 360 aa [47]
Ribosome abundance
4.5 ribosomes/mRNA
18,000 ribosomes per cell; up to 4,000 mRNA
molecules per cell [12]
Food uptake rate
1.5 s-1
Loosely calculated from actual glucose uptake rates
Food metabolism rate
3.5 s-1 per enzyme
Loosely calculated from glycolytic cycle rates
Energy released from metabolism
2 molecules
Glycolysis yields 36 ATP molecules (1 energy
molecule = 252 ATP)
Initial energy amount (and after
100
replication)
Initial protein amount
10
Artificial Life Volume 15, Number 3
267
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
5
3
2
5
9
1
6
6
2
5
8
1
a
r
t
l
.
/
2
0
0
9
.
s
t
e
k
e
l
.
0
0
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. J. Jenkins and D. J. Stekel
Investigating the Evolution of Transcription Control Networks
Value(s)
Notes
Table 3. (continued)
Parameter
Initial food amount
10
Replication base energy threshold
1,000
Additional energy per gene
Population size
Number of generations
Maximum simulation time
100
100
50
1 h
Mutation rate P(m)
0.1, 0.3, 0.5
Varied rates used for sensitivity analysis
Gene duplication rate P(d)
0.1, 0.3, 0.5
Varied rates used for sensitivity analysis
Gene loss rate P(l )
0.1, 0.3, 0.5
Varied rates used for sensitivity analysis
Binding affinity j
1, 10, 20, 30, 40, 50
Approximate range determined from model
dynamics analysis
Binding affinity a
1
Fixed value determined from model
dynamics analysis
Mutation shape, random normal,
0.2
std. dev.
Initial protein degradation rate
10random normal (-2.5,0.5)
Average time 612 s
Initial mRNA degradation rate
10random normal (-2.5,0.1)
Average time 324 s
Mutation protein degradation rate,
0.2
std. dev.
Mutation mRNA degradation rate,
0.05
std. dev.
3.11 Evolutionary Operators
The evolution framework currently supports three evolutionary operators, gene duplication, gene loss,
and mutation. These operators are applied to each parameter within each gene with a given prob-
ability. The evolutionary results presented in the results section are obtained using low gene dupli-
cation, gene loss, and mutation rates ( P(d ) = P(l ) = P(m) = 0.1).
3.11.1 Gene Duplication
Gene duplication has been shown to have had a significant influence on the evolution of genomes
[60, 30], and has been used in previous models such as ARN [5, 39] and the mathematical model by
Wagner [63]. Therefore, it is important for this process to be included within our model. However, in
view of real evolutionary timescales and the timescale that can be feasibly simulated computationally,
the duplication and loss events are simulated at a much higher rate than has been estimated over
the course of millions of years of evolution.
268
Artificial Life Volume 15, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
5
3
2
5
9
1
6
6
2
5
8
1
a
r
t
l
.
/
2
0
0
9
.
s
t
e
k
e
l
.
0
0
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. J. Jenkins and D. J. Stekel
Investigating the Evolution of Transcription Control Networks
Gene duplication is implemented using the following algorithm: For each gene in the genome, the
gene and its regulatory region are duplicated, with the specified probability P(d ). The products of the
original and duplicated gene are considered to be different molecular species.
3.11.2 Gene Loss
While the genome can increase in size using gene duplication, it can also decrease in size by gene
loss. Gene loss is also an important process in the evolution of genomes, as it allows the genome to
remove useless (nonfunctional) junk genes. This is preferable in that junk genes would still be rep-
licated or transcribed, and so waste energy.
Gene loss is implemented using the following algorithm: For each gene in the genome (while
there are still at least two genes), the gene, its mRNA and protein products, and its regulatory region
are removed from the model, with the specified probability P(l ).
3.11.3 Mutation
Mutation (or divergence) is the primary operator for increasing diversity within bacteria that are re-
producing asexually. Any shape (including natural and allosteric forms of domains, and cis-regulatory
DNA elements) or degradation rate in the model is available to mutate. The mutation operator used is
a random normal noise added to the shape, or a lognormal random noise to the degradation rate. More
technical details of this mutation operator are described in Appendix 1.
3.12 In Silico Genetics
In silico genetics is the equivalent of performing genetic experiments in vitro, except the cells are
simulated on a computer. To allow similar experiments to be performed on our model, a custom
in silico genetics tool was developed, allowing modification of any free or fixed parameter within
lines to be created, with changes such as gene or regulatory
the cell. This enables mutant cell
site knockout, novel genes, increased or decreased molecule stability, or change in molecular shape.
Using this technique, it is possible to examine the effects of perturbations in a cell, similarly to the
techniques used in the laboratory.
4 Results and Discussion
4.1 Model Dynamics
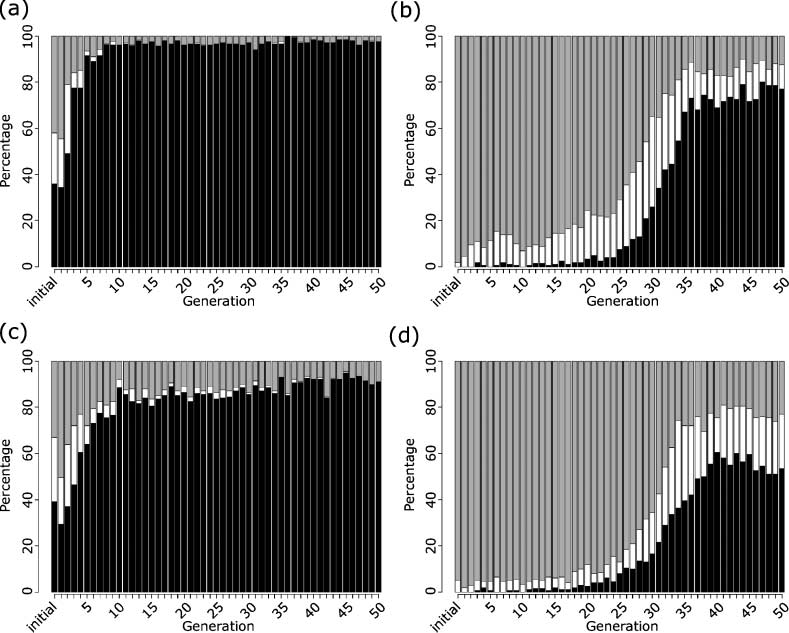
Models consisting of a single gene exhibited four different classes of behaviors, as seen in Figure 1.
The first behavior is growth (Figure 1a), where the energy gradually increases up to the replication
threshold; this behavior may indicate a linear cell volume increase, which is consistent with observed
volume growth in E. coli [38]. The second behavior is death (Figure 1b), where the energy hits 0 (or
some other death criterion level), due to over expression of the genes and unsustainable usage of
energy. These two behaviors are primary behaviors, of which only one is observed over the course of
a simulation (the cell either replicates or dies). The second set of behaviors are secondary, in that there
can be many instances of them observed throughout the simulation. Peaking behavior can be seen in
Figure 1c. This behavior consists of a growth phase, followed immediately by a substantial decrease
in energy (this can be seen from the figure at around 600 and 1050 s into the simulation). Coinciding
with the drop in energy is an immediate increase in protein, indicating that the peaking of energy is
due to transcription and translation. The sudden decrease in energy over a matter of minutes would
be expected with the current parameters, as the approximate time to initiate transcription is 1 s, the
time to transcribe the gene is 21.6 s, and a further 24 s for a fully translated protein to be produced
(with 4.5 ribosomes per mRNA), meaning that in a matter of minutes multiple mRNA molecules
can be produced and many more proteins can be produced from them. Plateauing behavior can be
seen in Figure 1d. This behavior consists of the energy level remaining static for a period of time.
Artificial Life Volume 15, Number 3
269
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
5
3
2
5
9
1
6
6
2
5
8
1
a
r
t
l
.
/
2
0
0
9
.
s
t
e
k
e
l
.
0
0
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. J. Jenkins and D. J. Stekel
Investigating the Evolution of Transcription Control Networks
Figure 1. Examples of model behaviors. All models have the same structural parameters j = 1 and a = 1, and randomly
initialized evolvable parameters. (a) is an example of growth, where the protein level stays constant and the energy level
rises steadily, reaching the replication threshold of 1,100 free-energy molecules in around 900 s. (b) is an example of
death, where the protein level slowly increases up to around 150 molecules after 500 s, whereas the energy rapidly falls
to around 20 molecules and stays close to this amount before it eventually runs out. (c) is an example of peaking, where
the protein level slowly rises to around 200 molecules, before a large rapid increase in energy around 500 s; the protein
level then rises again, followed by an even faster drop in energy, causing a peak in the energy. This behavior is repeated
several more times before the energy threshold is reached. (d) is an example of plateauing, where, after an initial drop
followed by increase in energy, the energy and protein levels appear to reach a steady state around 1500 s, causing a
plateau in both protein and energy levels. Black lines plot the energy; gray lines plot the protein level.
This indicates a period of transcriptional and translational inactivity, as the figure shows there is
enough energy for producing an mRNA transcript, but no transcription takes place, meaning either
the gene is repressed, or the limited RNA polymerase molecules are bound to other molecules. This
behavior may be observed in real cells undergoing a stress, such as heat or acid shock. The stress
response often leads to large changes in gene expression, as unimportant genes are switched off and
only essential response genes (such as those encoding chaperon or helper proteins) are switched on
to conserve energy [47]. Laboratory evolution of E. coli has shown that mutations reducing the tran-
scription of flagella synthesis genes in the stringent response regulatory network offer a significant
fitness advantage [52].
The behaviors and dynamics of the model described above were investigated using random
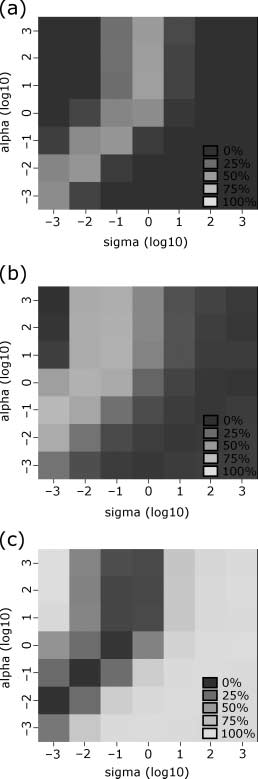
initializations with the structural parameters j = 1 and a = 1. Investigation of the sensitivity of the
model to these structural parameters is detailed in Appendix 2.
4.2 Parameters Essential for Model Replication
An investigation was conducted into which evolvable parameters are most important for model
replication. 1,000 models were randomly initialized and simulated in a constant-external-food
environment, and the evolvable parameters were recorded. To compensate for stochasticity, each
initialization was simulated 20 times, recording if the model replicated. Each model was classified
270
Artificial Life Volume 15, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
5
3
2
5
9
1
6
6
2
5
8
1
a
r
t
l
.
/
2
0
0
9
.
s
t
e
k
e
l
.
0
0
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. J. Jenkins and D. J. Stekel
Investigating the Evolution of Transcription Control Networks
either as replicating (class 1) or not (class 0), depending on the majority results from the 20 sim-
ulations. Both univariate and multivariate methods were used to determine important parameters for
replication.
4.2.1 Univariate Analysis
Logistic regression [15] with a controlled false-discovery rate [10] was used to determine the sig-
nificance of each parameter as a predictor for model replication. Table 4 shows the eight significant
parameters (q < 0.05). The most significant and accurate predictor for class membership was the
protein degradation rate, with an accuracy of over 81%. Other significant parameters included the
mRNA degradation rate and various repressor- and promoter-complex minimum dissociation rates,
although their classification accuracy is only slightly higher than for classifying all models as class 0
(nonreplicating, 55.4%). These results indicate that the optimal network topology for replication in
this simplistic environment would require specific interaction between various molecules and the
repressor and promoter sites, and is also very sensitive to the degradation rates of gene products.
The sensitivity to the protein degradation rate is likely to be due to the protein molecule’s role as a
metabolic enzyme. As the model can only gain energy by breaking down food molecules and only
protein molecules have this functionality, the interaction of protein and food molecules is very
important. The advantage of a stable protein is that there is an increased probability that the protein
will interact with food molecules before it degrades, allowing more metabolic reactions to take place.
Interestingly, the stability of the protein-food complex does not appear to be a significant parameter.
This indicates that only the rates of food-protein bindings are important, as stochastic effects mean
that sufficient numbers of weakly active proteins may be sufficient to allow replication. Stable
proteins also need to be replaced less frequently than unstable proteins, requiring less transcription
and translation activity and therefore saving energy.
4.2.2 Multivariate Analysis
Multivariate analysis was performed with GALGO [61], using the diagonal
linear discriminant
analysis (DLDA) classifier, 200 solutions, and a goal fitness of 0.85. All other options were set to
default. Models consisting of two to five parameters were generated, and each model size was used
Table 4. Univariate analysis of significant evolvable parameters. For each parameter its ID number, original p-value from
a logistic regression, adjusted q-value from controlling the false discovery rate, classification accuracy, sensitivity,
and specificity are shown.
p
q
Classification accuracy (%)
Sensitivity
Specificity
Parameter
Protein degradation rate
Protein-repressor complex koff
Protein-promoter complex koff
All-promoter complex koff
mRNA degradation rate
Energy-promoter complex koff
ID
22
5
6
26
23
14
< 2e-16
5.2e-15
1.38e-10
1.794e-9
1.29e-8
1.118e-7
1.06e-7
6.89e-7
6.05e-7
3.146e-6
8.1e-5
3.51e-4
Food-repressor complex koff
10
0.00273
0.01014
Protein-protein complex koff
8
0.00346
0.011245
81.7
54.7
60.4
57.6
58.1
58.3
55.3
56
0.77803
0.84838
0.32287
0.77617
0.34978
0.80866
0.28027
0.81408
0.32287
0.78881
0.23318
0.86462
0.12556
0.89711
0.12108
0.91336
Artificial Life Volume 15, Number 3
271
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
5
3
2
5
9
1
6
6
2
5
8
1
a
r
t
l
.
/
2
0
0
9
.
s
t
e
k
e
l
.
0
0
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. J. Jenkins and D. J. Stekel
Investigating the Evolution of Transcription Control Networks
five times. Multivariate solutions were able to improve the classification accuracy by more than 5%
over univariate solutions. Table 5 shows the optimal solutions generated during each GALGO run
on each model size, and Table 6 shows the proportion of parameters selected in the optimal
solutions. A model size of 2 generates a solution that includes the two most significant parameters
from the univariate analysis, which again indicates a network topology dependent on repressor inter-
action and protein degradation rate. This solution only improves the classification by 2% over the
single most significant single parameter, therefore highlighting the major contribution this parameter
makes to model replication. Increasing the model size further only yields slight improvements in
classification. A five-parameter classifier achieves only 5% improvement, and a 10-parameter clas-
sifier only improves by around 0.5% on that. This result indicates that very few parameters have any
significant effect on classification, though most of them were found to be significant from the
univariate analysis. The parameters that appeared most frequently in the multivariate solutions were
again protein and mRNA degradation rate, indicating the model’s sensitivity to molecule stability and
interactions with the repressor and promoter sites on the DNA.
4.3 Evolution: Constant, Single-Food Environment
4.3.1 Realistic Replication Time is an Emergent Property
The cell cycle, or time to replicate, appeared to reach a minimum of around 300 s, with typical
replication times for the evolved population between 400 and 1000 s. The replication time of E. coli
K-12 depends on the growth medium, ranging from 20 min up to an hour or more [47]. The
replication time of our most efficient evolved cells ranged from around 6 to 15 min (the average time
for one final generation was 11.5 min); therefore it is fair to claim realistic cell replication times as an
emergent property, as our cells only model regulatory, metabolic, and signaling genes, while
processes such as cell growth and DNA replication are not explicitly included in the model. Models
consisting of two or more genes evolved similar cell replication times to models consisting of only
a single gene,
indicating that having multiple genes may not always be prohibitive of efficient
replication times. Figure 2a shows an example simulation of an evolved model that replicates in
13.4 min and has a protein steady state level of around 200 molecules.
Replication times and chance of replication were also evolved to be more consistent. 1000 sim-
ulations of an evolved model and of its ancestor model and were examined. The evolved model
replicated in 96.7% of the simulations, and the ancestor model achieved only 94.9% replication.
100 replication events were selected from each model for comparison, and the results are shown in
Table 7. The maximum speed of replication was similar between the ancestor and evolved models;
however, the mean replication time and standard deviation were reduced in the evolved model. This
indicates that the model has evolved not to maximize the speed of replication, but rather to replicate
as consistently as possible.
4.3.2 Evolution of Stable Proteins and Unstable mRNA
Investigating other aspects of the evolved model also shows some interesting and lifelike trends and
principles. The degradation rates of mRNA and protein species within a range of models from dif-
ferent evolutionary environments displayed similar behavior, selecting for unstable mRNA molecules
with typical mean half-life of under 3 min and stable proteins with typical mean half-life of several
hours (see Table 8).
These are remarkably close to turnover rates in biological cells. The average turnover time for an
mRNA molecule in E. coli is around 5 min [11], and protein stabilities in E. coli and Saccharomyces
cerevisiae, although wide ranging, are often an order of magnitude higher than those of mRNA [9,
46, 64]. Table 8 shows the evolved changes in mean mRNA and protein turnover rates. Although the
two start at similar levels, the mRNA half-life decreases from 5.53 to 2.8 min, whereas the protein
half-life increases from 10.46 to around 360 min. The increased stability of the protein would allow
272
Artificial Life Volume 15, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
5
3
2
5
9
1
6
6
2
5
8
1
a
r
t
l
.
/
2
0
0
9
.
s
t
e
k
e
l
.
0
0
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. J. Jenkins and D. J. Stekel
Investigating the Evolution of Transcription Control Networks
Table 5. Multivariate solutions generated by GALGO. For each model size and run, the best solution, and its
classification accuracy (using logistic regression), sensitivity and specificity are shown. All five runs with a model size
of 2 generated the same optimal solution. All optimal solutions included parameters 5 (protein-repressor complex koff )
and 22 (protein degradation rate), which were also the two most significant parameters identified from the
univariate analysis. All parameters in the optimal solutions, with the exception of 3 (protein-RNAP complex koff ),
13 (energy-repressor complex koff ), 16 (RNAP-repressor complex koff ), 19 (mRNA-promoter complex koff ) and
25 (all repressor complex koff ), were identified as significant from the univariate analysis. The only significant univariate
parameter not included in the multivariate solutions was 10 (food-repressor complex koff ).
Model
size
Run no.
Optimal
solution
Classification
accuracy (%)
Sensitivity
Specificity
2
3
4
5
5, 22
83.8
0.80493
0.86462
5, 14, 22
84
0.81839
0.85740
5, 6, 22
5, 22, 26
5, 6, 22
5, 22, 23
85.5
84.5
85.5
84.8
0.82511
0.87906
0.81839
0.86643
0.82511
0.87906
0.82287
0.86823
5, 6, 13, 22
86.2
0.84081
0.87906
5, 22, 23, 26
86
0.84081
0.87545
5, 6, 14, 22
5, 6, 14, 22
3, 5, 6, 22
86.3
86.3
85.1
0.83632
0.88448
0.83632
0.88448
0.82287
0.87365
5, 6, 14, 22, 23
86.8
0.85650
0.87726
5, 16, 22, 23, 26
86
0.84081
0.87545
5, 6, 8, 14, 22
5, 6, 14, 19, 22
86.3
86.3
0.83632
0.88448
0.83632
0.88448
5, 14, 22, 25, 26
84.5
0.82511
0.86101
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
the same protein to metabolize more food molecules, and so decrease the need for further protein
production. However, the large standard deviation of the mean protein degradation rate indicates a
very large variation between individual models.
We use in silico genetics to investigate the response of the model to changes in the degradation
rates. Decreasing the mRNA degradation rate (mRNA stability increased to 35 min from 3.1 min)
Artificial Life Volume 15, Number 3
273
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
5
3
2
5
9
1
6
6
2
5
8
1
a
r
t
l
.
/
2
0
0
9
.
s
t
e
k
e
l
.
0
0
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. J. Jenkins and D. J. Stekel
Investigating the Evolution of Transcription Control Networks
Table 6. Evolvable parameters selected in optimal solutions generated by GALGO. For each parameter, its ID number
and its percentage in solutions of different model sizes are shown. Parameter proportion in model solutions is
averaged over five runs.
Percentage in model size
Parameter
Protein-RNAP complex koff
Protein-repressor complex koff
Protein-promoter complex koff
Protein-protein complex koff
Energy-repressor complex koff
Energy-promoter complex koff
RNAP-repressor complex koff
mRNA-promoter complex koff
Protein degradation rate
mRNA degradation rate
All-repressor complex koff
All-promoter complex koff
ID
3
5
6
8
13
14
16
19
22
23
25
26
2
0.3
88.7
7.5
0
0
0
0
0
3
2.4
81.5
29.4
0.1
0.8
13.6
0.2
1.6
4
11.3
74.4
66.1
6
9.2
23.3
3.1
2.8
5
4.2
97.8
65.4
6.3
19.4
31.8
7.1
11.8
100
100
100
100
0.5
0
2.9
36.7
7.1
6.7
31.2
2.7
17.3
23.4
9.6
21.9
has the effect of increasing steady state protein levels from around 200 molecules in the evolved
model to around 850 molecules in the mutated model and increasing the replication time from 13.4
to 38 min (Figure 2c). This is because the mRNA molecules exist within the system for a longer
period of time, therefore allowing more transcription. In this example the model is still capable of
replication, but with a longer replication time. Increasing the protein degradation rate (protein
stability is decreased to 6 min from 246.2 min) leads to a decreased protein steady state level after the
initial transcription activity of around 150 molecules, which rapidly decreases, leading to an increased
replication time of 18.8 min, up from 13.4 min. Figure 2d shows how the initial protein level is
reached and then transcription is repressed, as expected. However, the protein level then quickly
decreases, rather than staying constant. Once again,
in this example the protein level was high
enough to support replication, but with decreased efficiency.
The evolution of very stable protein molecules for metabolism is paralleled in real organisms.
In general, however, the stability of proteins is highly dependent on their function. Signaling pro-
teins are often very unstable, allowing rapid response to stimuli; proteins that harm the cell under
stressed conditions may be unstable, or actively degraded, to deal with this. Therefore, the
environmental conditions and functions required by the cell are likely to strongly influence the
evolution of the stability of proteins. It is important to note that even though the protein is very
stable, it is being diluted as a result of cell division, and so the cells need to replenish the protein to be
able to function.
Rapid mRNA turnover has previously been suggested as a mechanism to enable rapid response
to environmental changes [22]. Here, however, we find that mRNA is rapidly turned over on realistic
timescales, even in an unchanging environment. Thus it would seem that this turnover is an
274
Artificial Life Volume 15, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
5
3
2
5
9
1
6
6
2
5
8
1
a
r
t
l
.
/
2
0
0
9
.
s
t
e
k
e
l
.
0
0
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. J. Jenkins and D. J. Stekel
Investigating the Evolution of Transcription Control Networks
emergent property associated with two-step gene product synthesis that enables protein production
for minimum energy cost. It is, more than anything else, an adaptation for efficiency.
4.3.3 Evolution of Basic Repressor Activity
Models evolved for effective growth in a constant food environment all developed a single-gene
repressor regulatory network, where the single gene was repressed either by a product of the gene
(mRNA or protein) or by energy or food molecules. This structure was seen in all model lineages.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
5
3
2
5
9
1
6
6
2
5
8
1
a
r
t
l
.
/
2
0
0
9
.
s
t
e
k
e
l
.
0
0
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
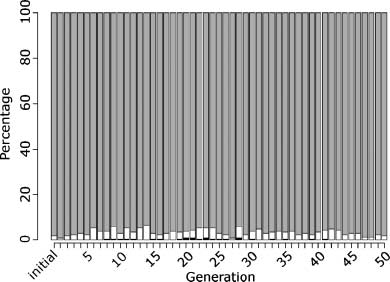
Figure 2. Example simulations of evolved model. (a) shows the wild-type model, where, following the usual lag phase of
the energy level dropping to below 20 molecules due to initiation of transcription and subsequent increase in protein, the
energy level rapidly increases at around 500 s, with the protein reaching a steady state of 200 molecules. The energy
threshold is reached by 800 s. (b) shows the repressor knockout mutant, in which peaking has been introduced, as the
protein level does not enter steady state due to the increased transcription. After several peaks, the energy threshold is
reached after 1,500 s. (c) shows the increased mRNA stability mutant, in which the lag phase is significantly increased, due
to increased translation. Wild-type growth occurs around 2,000 s, however, with a protein steady state of 850 molecules.
(d) shows the decreased protein stability mutant, in which wild-type growth occurs after 550 s; however, a protein
steady state is not reached. (e) shows the 0-protein mutant, in which the lag phase continues for around 500 s, after
which transcription and translation occur, causing wild-type growth after 650 s with a protein steady state of 300
molecules. (f ) shows the 500-protein mutant, in which no lag phase is evident and wild-type growth occurs immediately,
the energy threshold being reached in around 500 s, with a protein steady state of 500 molecules. Black lines plot energy;
gray lines plot protein level. All plots are shown on the same scale.
Artificial Life Volume 15, Number 3
275
D. J. Jenkins and D. J. Stekel
Investigating the Evolution of Transcription Control Networks
Table 7. Mean replication times and standard deviations and minimum replication times for 100 replication simulations of
the ancestor and the evolved model.
Model
Ancestor
Evolved
Mean replication
time (min)
Std. dev. (min)
Minimum replication
time (min)
15.48
14.14
5.19
3.73
9.27
9.38
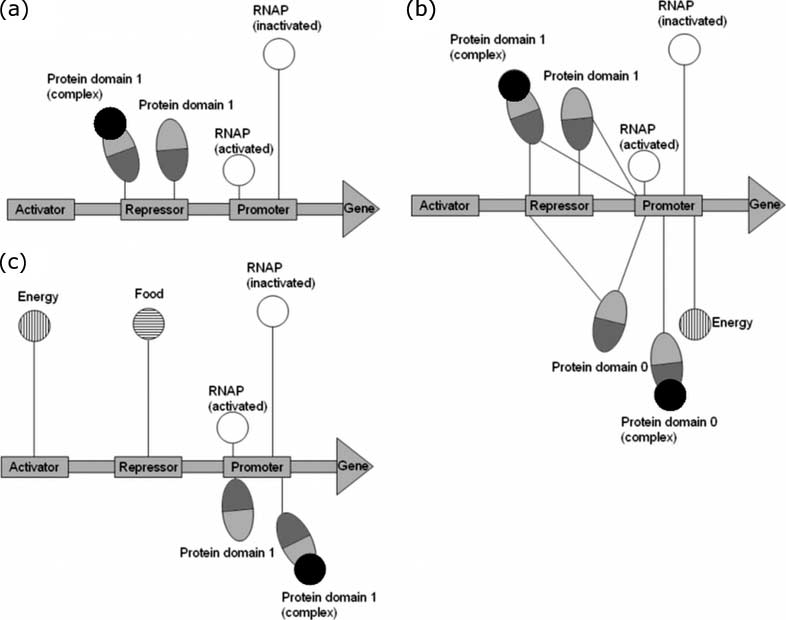
Figure 3a shows a typical ancestor-model gene regulatory network (a connection between DNA and
molecules is shown only if the Kd of the binding between them is less than 100 nM). We can see that
the ancestor model already has a simple repressor system, with the protein product negatively self-
regulating its own production.
Figure 3b shows an evolved model from the ancestor model in Figure 3a. Here we can see that
the repressor still exists, but the network has grown to include the protein’s second binding domain
as a TF, with the repressor shape remaining relatively fixed during the course of the evolution. We
can also see that the model has evolved to use the promoter site as a secondary repressor, with fairly
large changes in the promoter site’s shape. The large changes to the promoter site do not affect
the RNAP binding (see Section 3.2.1). Figure 2a shows the cell initially producing protein up to
a required threshold and then repressing any more production, saving energy for replication, where-
as Figure 2b shows a simulation of the knockout mutant. Without repression, peaking has been
introduced into the model dynamics. As shown previously, peaking is the result of mass transcriptional
and translational activity. Instead of the model repressing protein production when a required level was
reached, in the mutant there is no evidence of repression, and proteins are produced in several bursts
of transcription and translation activity, which uses large amounts of energy. This causes the model to
make several false starts before finally reaching its required energy threshold, thereby doubling the
replication time from 13.4 to 27.7 min.
Therefore the optimal regulatory system for the single-constant, abundant food environment is a
single-gene repressor. This allows the model to metabolize food successfully and efficiently to ensure
that enough energy is saved to reach the replication threshold. This behavior is fundamentally
realistic, as there are more than 2,000 known negative regulation interactions in E. coli [35], such as
the tryptophan operon [2, 56], and many of these are autoregulated. Negative feedback performs
several functions: it (i) turns off potential transcription of the gene, if not currently required (for
example, for stress-response proteins), thereby saving energy, (ii) helps to maintain a specific concen-
tration of the protein (homeostasis), (iii) increases the speed of response within a transcription
network [54], and (iv) minimizes mRNA usage [58].
Other network topologies were also evolved. Figure 3c shows an evolved network where both an
activator and a repressor exist. However, the transcription factors in this example are food and energy
molecules, rather than gene products. Energy or food molecules binding directly to the DNA is per-
mitted in this model, although for steric reasons it does not appear to happen in life. Real cells have
evolved to use energy, food, or other types of molecules as signals in regulation by using their binding to
Table 8. Mean protein and mRNA half-lives and standard deviations for initial and evolved generations.
Generation Mean half-life (min) Std. dev. (min)
Range (min) Mean half-life (min) Std. dev. (min) Range (min)
Protein
mRNA
1
50
276
10.46
14.21
0.13 – 75.36
359.59
384.14
25.5 – 1833.27
5.53
2.8
1.44
3.002 – 10.72
0.505
1.41 – 3.95
Artificial Life Volume 15, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
5
3
2
5
9
1
6
6
2
5
8
1
a
r
t
l
.
/
2
0
0
9
.
s
t
e
k
e
l
.
0
0
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. J. Jenkins and D. J. Stekel
Investigating the Evolution of Transcription Control Networks
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
5
3
2
5
9
1
6
6
2
5
8
1
a
r
t
l
.
/
2
0
0
9
.
s
t
e
k
e
l
.
0
0
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3. Example of transcription regulation networks. Two cell lineages were observed, each originating from the initial
generation. The final population consisted of 95% of models from the major cell lineage, and the remaining 5% from the
minor lineage. Specific bindings of Kd < 100 nM are shown. (a) shows the ancestor network of the major cell lineage from
the population. Very strong repressor binding by a single binding domain of the protein is evident. (b) shows an example
evolved network from the major cell lineage. The ancestor repressor connections are still present, although slightly
weakened. However, the same protein domain has evolved a specific binding to the promoter site as well. Other evolved
specific bindings are the other binding domain of the protein to both the repressor and promoter sites, and energy
binding to the promoter site. (c) shows an evolved network from the minor cell lineage from the same population. Specific
binding to the repressor site again exists, although using the food molecule, as does specific binding to the promoter site by
a single binding domain of the protein. A specific binding to the activator site using the energy molecule also exists, which
was not present in the major cell lineage. Binding strength is approximated by molecules’ distance from DNA.
transcription factors, causing allosteric changes and affecting the function of the transcription factor.
An example is allolactose in the lac regulatory mechanism, in which the lactose metabolite binds to
the LacI repressor and prevents it from binding to the DNA, potentially allowing the transcription of
the lacZ gene. A simple solution would be to restrict the domain shapes that the DNA regulatory
elements can take. On limiting the shape space, the food or energy molecules will be unable to bind
sufficiently well to the DNA regulatory elements, therefore forcing the model to use a protein as a
transcription factor.
The emergence of such a fundamental and lifelike network structure indicates the potential
power and complexity of the new model as a tool for investigating the evolution of transcription
networks.
4.3.4 Protein Is Regulated to a Realistically Small Copy Number
The protein copy numbers observed within evolved models are typically between 50 and 400 mole-
cules, and in the majority of simulations a stable level was reached within this range. The protein copy
Artificial Life Volume 15, Number 3
277
D. J. Jenkins and D. J. Stekel
Investigating the Evolution of Transcription Control Networks
numbers per E. coli cell of enzymes within the glycolytic pathway range from only 100 copies up to
several thousand, each varying in the course of the cell cycle [59], although the numbers for many
enzymes are unknown. Although our simulations appear to be at least an order of magnitude different,
an enzyme copy number is likely to be a function of its substrate copy number, and so we should
observe different levels of protein under different conditions. Each food molecule in our model
is equivalent to 14 glucose molecules (see Table 3), and therefore, once we have taken the scaling of
food molecules within the model into consideration, the levels of our simulated cell’s enzymes are
similar to those observed in biological cells. For example, the enzyme phosphoglycerate kinase has
a copy number of around 3,000 molecules in the growth phase [59], and assuming each molecule
can metabolize only a single 1,3-bisphosphoglycerate molecule at a time, our model would require
around 200 proteins to metabolize the equivalent food molecules. This enzyme copy number is well
within the observed simulated copy number of many evolved cells; however, it must be noted that our
model approximates the glycolytic pathway into a single reaction and so is a much simplified, inexact
pathway.
Using the in silico genetics tool, we investigated the effect on the cell’s ability to replicate by
changing the starting protein level to simulate biased cell replication, which leaves the cell with an
extreme amount of protein (very small or large). It is important for biological cells to cope with
extremes of protein level, as the replication process may create these situations. Figure 2 shows an
example of each extreme case: no protein (Figure 2e) and 500 proteins (Figure 2f ). The behavior for
no protein is similar to that in the wild-type cell, with the exception of a longer lag period at the
beginning of the simulation, as there are no proteins to metabolize the food, nor any transcription
taking place. Once the cell has started to transcribe the gene and proteins are produced, the growth
of the cell is very similar to wild-type growth. In the opposite case, where there is a large number of
proteins at the beginning of the simulation, we see a different dynamic. Due to the large number of
free proteins in the cell, the food molecules entering the cell are immediately consumed, producing
large amounts of energy. For the same reason, the gene is immediately repressed, preventing any
transcription, and so the protein level remains constant.
4.4 Further Discussions
4.4.1 Environments with Increasing Complexity
The results presented previously indicate that even in the simplest of evolutionary environments, we
observe nontrivial and realistic behaviors and mechanisms, such as the evolution of rapidly turned-
over mRNA and repressor activity. However, the evolved network structures are relatively sim-
ple, which is an indication of the simplicity of a chemostatlike environment (an environment that
free-living bacteria such as E. coli would not normally encounter, nor be adapted to). We predict that
in increasingly complex environments, that would be more representative of evolutionary conditions
in nature, the model would produce even more complex network structures and solutions. Due to
the flexibility of the model, it will be straightforward to create more complex environments, each
presenting different problems to be solved.
An example complex environment to investigate would consist of multiple food sources. E. coli is
able to grow on a number of sugars; in the presence of multiple sugars it is able to selectively me-
tabolize the most energy-efficient food first, using regulatory mechanisms such as the lac operon. As
the model already implements the lac operon’s transcription logic, it is fair to assume that a similar
switching mechanism requiring both activation and repression activity may evolve within an envi-
ronment with two or more different food sources.
Another environment may consist of a food source that is varying in a predictable way, analogous
to a day-night cycle. Organisms have evolved mechanisms for responding to these cycles, known as
circadian rhythms, by developing circadian biological clocks. Prokaryotic circadian clocks, found
within cyanobacteria such as Synechococcus, consist of only three genes, kaiA, kaiB, and kaiC, which are
able to exhibit rhythmic behavior [21]. The proposed regulation of the circadian clock is a feedback
278
Artificial Life Volume 15, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
5
3
2
5
9
1
6
6
2
5
8
1
a
r
t
l
.
/
2
0
0
9
.
s
t
e
k
e
l
.
0
0
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. J. Jenkins and D. J. Stekel
Investigating the Evolution of Transcription Control Networks
loop involving all three proteins, with unknown interactions between them, and both activation and
repression of the genes [31]. Eukaryotes, including mammals and plants, have evolved more com-
plex clocks that include multiple oscillating loops that are thought to provide robustness to noise and
seasonal effects [20, 28]. This proposed feedback loop could be represented within our model and
could produce a circadian clock that is tuned to the availability of food.
Many organisms live in an environment in which food or other resources are limited and their
availability to the organism may fluctuate. The organism therefore requires mechanisms to optimally
use these limited resources, for example, the starvation response in E. coli governed by RpoS (js,
j38 ) [51]. It is predicted that our model will behave in a similar, albeit simpler, way to that of E. coli
cells when faced with starvation. Upon detection of carbon starvation, RpoS upregulates the tran-
scription of hundreds of genes that help to protect the cell against stresses, while downregulating
hundreds of other genes. The cell enters a stationary phase in which it has an increased chance for
survival. Although RpoS is in fact a j factor that binds to RNAP, helping it to recognize specific
promoter sequences, our model could still simulate a similar mechanism. For instance,
if the
starvation TF could bind strongly to the enzyme’s repressor site as an unbound monomer, but when
in a complex (with food) were unable to bind, then the same response would be observed: When
food is available, the repressor site is unbound, allowing production of the enzyme, whereas if no
food is detected by the starvation TF, then enzyme production is prevented. While the current model
does not support j factors, they can easily be incorporated by removing the specific RNAP molecule
and allowing any protein with appropriate shape to function as an RNA polymerase.
The current formulation of the model, with its constant environment and generational population
structure, is in some ways analogous to a chemostat. Further developments could include an explicit
spatial structure, which could potentially lead to coexistence of different species [37]. In the current
formulation, replication time is a fair measure of fitness, since in a chemostat the fastest-growing
bacteria will dominate the population; in a spatially explicit environment, this is not necessarily the
case, and an alternative approach to fitness may be necessary.
4.4.2 Molecule Shape Dimensionality
Our scalable 2D continuous shape space is a substantial simplification of the high-dimensional
protein shapes in real cells. Other models, such as the model proposed by van Noort et al. [62] and
extended by Cordero and Hogeweg [17], use an even greater simplification, with a 1D discretized
shape space, and yet are still able to produce complex and realistic networks. This indicates that a
high-dimensional shape space is not essential for the evolution of complex networks; however, an
adequately large shape space is required. Future work could investigate the effect of shape space
dimensionality on the evolution of complex networks.
4.4.3 Recombination
Recombination is essential for higher-order eukaryotes, and is also thought to be a major source of
genetic variation in primeval genomes [57]. While modern day bacteria such as Escherichia coli and
Campylobacter jejuni do not use sexual recombination, they do have other mechanisms for DNA
exchange, such as DNA uptake, horizontal gene transfer via plasmids and phages (HGT), and
internal genome recombination [47]. In the current model formulation, genes can only be transferred
vertically (VGT), that is, they are passed from parent cell to daughter cell only. Future model
formulations may include processes of DNA exchange between organisms, such as HGT.
4.4.4 Limitations of the Model
The maximum genome size of the models is currently limited to six genes. This is due to com-
putational requirements of the simulation algorithm (Gibson-Bruck) when simulating large genomes.
Use of an alternative simulation algorithm such as the Gillespie algorithm [25] may reduce the
computational requirements of larger genomes.
Artificial Life Volume 15, Number 3
279
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
5
3
2
5
9
1
6
6
2
5
8
1
a
r
t
l
.
/
2
0
0
9
.
s
t
e
k
e
l
.
0
0
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. J. Jenkins and D. J. Stekel
Investigating the Evolution of Transcription Control Networks
Due to the modeling approach and the necessity for efficient simulation of the model, polymerization
is limited to generating complexes of up to three molecules. However, as previously noted, physical
structures of the cell, for instance, long polymers, are not modeled, and so this limitation does not harm
the model.
A further limitation is the simulation of the environment and evolution. A generational approach,
using a genetic algorithm, does not accurately model a growing bacterial culture, in which cells would
be dividing at different times. This could lead to some cells dividing several times while others divide
only once. This, as well as spatial structure, may be included in future model formulations.
4.4.5 Potential Network Analysis Techniques
The analysis of both the final networks and the dynamics of the evolution of these networks is likely
to become increasingly difficult as the complexity of the environment and hence networks increases.
The analysis of biological networks currently suffers from a number of problems, such as obtaining
networks from data and determining the functionality of particular sections of the network, due to
the size of the whole-genome networks and noise in the data collected [45]. The concept of network
motifs has been introduced to analyze the building blocks of complex networks as a way to elucidate
function in the networks, and has been applied to several genomes, including artificial networks [6,
42, 44]. Such an approach may be required to analyze the structure and function of the evolved
networks from the model. Applying such a technique across several generations and large simulated
evolutionary timescales may help to identify how and why specific network structures are evolved,
which is currently not possible with laboratory experiments.
Analyzing the evolutionary dynamics using techniques such as evolutionary activity statistics [8,
13] may provide valuable information and details about the evolutionary process, and may also high-
light specific and important components of the system. Once these components have been iden-
tified, this information can be used along with traditional network analysis, such as network motifs,
to help identify and separate functional modules within the networks.
5 Summary and Conclusion
In this study a new model of evolving transcription control networks in prokaryotic cells has been
introduced. The model incorporates several novel mechanisms, realistic and evolvable parameters,
and a scalable level of complexity. The models are simulated using a stochastic framework, from
which the dynamics of the model were investigated over a range of parameters. Several key realistic
network structures and model behaviors were observed, and important parameters determining
whether a model would replicate are presented and discussed.
Evolutionary runs of the models were performed using a standard genetic algorithm incorpo-
rating realistic evolutionary operators, in an idealized constant-food environment. The initial and
evolved networks are presented, as well as overall population dynamics. The results of these evo-
lutions show that over the short evolutionary time frame used, the models optimize their initial
network configurations to produce a more robust and shorter replication time, and a few novel
network interactions were introduced. Several realistic behaviors emerged during the simulated
evolution. A realistic cell replication time emerged, and the most efficiently replicating models
consisted of a single gene, which controlled its own expression through a repressor mechanism,
indicating a necessity to remove nonessential genes. This network structure (or motif ) is prevalent in
many instances in all organisms, and typically one of its purposes is maintaining protein levels.
Realistic mRNA and protein degradation rates evolved that also follow the general principles found
in E. coli and S. cerevisiae in typically displaying differences up to several orders of magnitude between
the stabilities of mRNA and proteins.
The robustness of the evolved models was investigated using in silico genetics to produce mutant
models consisting of various knockouts and perturbations to the stability of molecules and com-
280
Artificial Life Volume 15, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
5
3
2
5
9
1
6
6
2
5
8
1
a
r
t
l
.
/
2
0
0
9
.
s
t
e
k
e
l
.
0
0
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. J. Jenkins and D. J. Stekel
Investigating the Evolution of Transcription Control Networks
plexes. Many models were shown to be resilient against fairly large perturbations; however, the
dynamics of the models after certain mutations (such as regulatory site knockouts) were substantially
changed, as would be expected from real cells.
The exploratory results presented in this study indicate that the model allows reasonably realistic
modeling and evolution of transcription control networks in an abstracted prokaryotic cell, allowing
complex behaviors in simple environments, and provides the functionality to easily simulate more
complex and biologically interesting environments.
Acknowledgments
The authors would like to thank Alastair Channon, Charles Penn, Chrisantha Fernando, Francesco
Falciani, Helen Parsons, Jan-Ulrich Kreft, Jon Rowe, Lewis Bingle, Patricia Welham, and Pete Lund for
helpful discussions and comments on the manuscript. D.J.J. is funded by BBSRC Strategic Research
Studentship BBS/S/S/2005/12006. Computer simulations were carried out using the Birmingham
Biosciences High Performance Computer Cluster, funded by BBSRC REI grant BB/D524624/1.
References
1. Albert, R. (2005). Scale-free networks in cell biology. Journal of Cell Science, 118, 4947 – 4957.
2. Alberts, B., Johnson, A., Lewis, J., Raff, M., Roberts, K., & Walter, P. (2002). Molecular Biology of the Cell
(4th ed.). New York: Garland Science.
3. Babu, M. M., Aravind, L., Luscombe, N. M., Gerstein, M., & Teichmann, S. A. (2004). Structure
and evolution of transcriptional regulatory networks. Current Opinion in Structural Biology, 14,
283 – 291.
4. Bai, L., Santangelo, T. J., & Wang, M. D. (2006). Single-molecule analysis of RNA polymerase
transcription. Annual Review of Biophysics and Biomolecular Structure, 35, 343 – 360.
5. Banzhaf, W. (2003). On the dynamics of an artificial regulatory network. In Proceedings of the 7th
European Conference on Artificial Life.
6. Banzhaf, W., & Kuo, P. D. (2004). Network motifs in natural and artificial transcriptional regulatory
networks. Journal of Biological Physics and Chemistry, 4(2), 85 – 92.
7. Baraba´si, A.-L., & Albert, R. (1999). Emergence of scaling in random networks. Science, 286,
509 – 512.
8. Bedau, M. A., Synder, E., & Packard, N. H. (1998). A classification of long-term evolutionary
dynamics. In Proceedings of the 6th International Conference on Artifical Life. Cambridge, MA: MIT Press.
9. Belle, A., Tanay, A., Shamir, R., & O’Shea, E. K. (2006). Quantification of protein half-lives in
the budding yeast proteome. Proceedings of the National Academy of Sciences of the U.S.A., 103(35),
13004 – 13009.
10. Benjamini, Y., & Hochberg, Y. (1995). Controlling the false discovery rate: A practical and powerful
approach to multiple testing. Journal of the Royal Statistical Society: Series B, 57(1), 289 – 300.
11. Bernstein, J. A., Khodursky, A. B., Lin, P.-H., Lin-Chao, S., & Cohen, S. N. (2002). Global analysis
of mRNA decay and abundance in Escherichia coli at single-gene resolution using two-color fluorescent
DNA microarrays. Proceedings of the National Academy of Sciences of the U.S.A., 99(15), 9697 – 9702.
12. Bremer, H., & Dennis, P. P. (1996). Escherichia coli and Salmonella: Cellular and molecular biology (2nd ed.),
Volume 2, pp. 1553 – 1569. Washington, DC: ASM Press.
13. Channon, A. (2001). Passing the ALife test: Activity statistics classify evolution in Geb as unbounded.
In Advances in Artificial Life: Proceedings of the 6th European Conference on Artificial Life (ECAL2001).
Heidelburg: Springer Verlag.
14. Chaudhuri, R. R., & Pallen, M. J. (2006). xBASE, a collection of online databases for bacterial
comparative genomics. Nucleic Acids Research, 34 (Database issue), D335 – D337.
15. Christensen, R. (1997). Log-linear models and logistic regression (2nd ed.). Berlin: Springer Verlag.
16. Clarkson, J., Shu, J.-C., Harris, D. A., Campbell, I. D., & Yudkin, M. D. (2004). Fluorescence and
kinetic analysis of the SpoIIAB phosphorylation reaction, a key regulator of sporulation in Bacillus subtilis.
Biochemistry, 43(11), 3120 – 3128.
Artificial Life Volume 15, Number 3
281
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
5
3
2
5
9
1
6
6
2
5
8
1
a
r
t
l
.
/
2
0
0
9
.
s
t
e
k
e
l
.
0
0
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. J. Jenkins and D. J. Stekel
Investigating the Evolution of Transcription Control Networks
17. Cordero, O. X., & Hogeweg, P. (2006). Feed-forward loop circuits as a side effect of genome
evolution. Molecular Biology and Evolution, 23(10), 1931 – 1936.
18. de Jong, H. (2000). Modeling and simulation of genetic regulatory systems: A literature review (Research report 4032).
Institut National de Recherche en Informatique et en Automatique.
19. Deckard, A., & Sauro, H. M. (2004). Preliminary studies on the in silico evolution of biochemical
networks. ChemBioChem, 5, 1423 – 1431.
20. Dodd, A. N., Salathia, N., Hall, A., Ke´vei, E., To´th, R., Nagy, F., Hibberd, J. M., Millar, A. J., & Webb,
A. A. R. (2005). Plant circadian clocks increase photosynthesis, growth, survival, and competitive
advantage. Science, 309, 630 – 633.
21. Dvornyk, V., Vinofradova, O., & Nevo, E. (2003). Origin and evolution of circadian clock genes
in prokaryotes. Proceedings of the National Academy of Sciences of the U.S.A., 100(5), 2495 – 2500.
22. El-Samad, H., Kurata, H., Doyle, J. C., Gross, C. A., & Khammash, M. (2005). Surviving heat
shock: Control strategies for robustness and performance. Proceedings of the National Academy of Sciences
of the U.S.A., 102(8), 2736 – 2741.
23. Franc¸ois, P., & Hakim, V. (2004). Design of genetic networks with specified functions by evolution
in silico. Proceedings of the National Academy of Sciences of the U.S.A., 101(2), 580 – 585.
24. Gibson, M. A., & Bruck, J. (2000). Efficient exact stochastic simulation of chemical systems with
many species and many channels. Journal of Physical Chemistry A, 104, 1876 – 1889.
25. Gillespie, D. T. (1976). A general method for numerically simulating the stochastic time evolution
of coupled chemical reactions. Journal of Computational Physics, 22, 403 – 434.
26. Grainger, D. C., Hurd, D., Harrison, M., Holdstock, J., & Busby, S. J. W. (2005). Studies of the
distribution of Escherichia coli cAMP-receptor protein and RNA polymerase along the E. coli
chromosome. Proceedings of the National Academy of Sciences of the U.S.A., 102(49), 17693 – 17698.
27. Herring, C. D., Raghunathan, A., Honisch, C., Applebee, T. P. M. K., Joyce, A. R., Albert, T. J., Blattner, F. R.,
van den Boom, D., Cantor, C. R., & Palsson, B. O. (2006). Comparative genome sequencing of Escherichia coli
allows observation of bacterial evolution on a laboratory timescale. Nature, 38(12), 1406– 1412.
28. Hirota, T., & Fukada, Y. (2004). Resetting mechanism of central and peripheral circadian clocks in
mammals. Zoological Science, 21, 359 – 368.
29. Hoar, R. M., Penner, J. K., & Jacob, C. (2003). Transcription and evolution of a virtual bacteria culture.
In Proceedings of the 2003 Congress on Evolutionary Computation.
30. Hughes, A. L. (2005). Gene duplication and the origin of novel proteins. Proceedings of the National
Academy of Sciences of the U.S.A., 102(25), 8791 – 8792.
31. Ishiura, M., Kutsuna, S., Aoki, S., Iwasaki, H., Andersson, C. R., Tanabe, A., Golden, S. S., Johnson,
C. H., & Kondo, T. (1998). Expression of a gene cluster kaiABC as a circadian feedback process
in cyanobacteria. Science, 281, 1519 – 1523.
32. Jacob, F., & Monod, J. (1961). Genetic regulatory mechanisms in the synthesis of proteins. Journal
of Molecular Biology, 3, 318 – 356.
33. Kærn, M., Elston, T. C., Blake, W. J., & Collins, J. J. (2005). Stochasticity in gene expression: From
theories to phenotypes. Nature Reviews Genetics, 6, 451 – 462.
34. Kashtan, N., & Alon, U. (2005). Spontaneous evolution of modularity and network motifs. Proceedings
of the National Academy of Sciences of the U.S.A., 102(39), 13771 – 13778.
35. Keseler, I. M., Collado-Vides, J., Gama-Castro, S., Ingraham, J., Paley, S., Paulsen, I. T., Peralta-Gil, M.,
& Karp, P. D. (2005). EcoCyc: A comprehensive database resource for Escherichia coli. Nucleic Acids Research,
33 (Database issue), D334 – D337.
36. Koch, S. J., & Wang, M. D. (2003). Dynamic force spectroscopy of protein-DNA interactions by
unzipping DNA. Physical Review Letters, 91(2), 028103.
37. Kreft, J.-U. (2004). Biofilms promote altruism. Microbiology, 150, 2751 – 2760.
38. Kubitschek, H. E. (1990). Cell volume increase in Escherichia coli after shifts to richer media. Journal
of Bacteriology, 172(1), 94 – 101.
39. Kuo, P. D., Banzhaf, W., & Leier, A. (2006). Network topology and the evolution of dynamics in an
artificial genetic regulatory network model created by whole genome duplication and divergence. Biosystems,
85(3), 177 – 200.
282
Artificial Life Volume 15, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
5
3
2
5
9
1
6
6
2
5
8
1
a
r
t
l
.
/
2
0
0
9
.
s
t
e
k
e
l
.
0
0
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. J. Jenkins and D. J. Stekel
Investigating the Evolution of Transcription Control Networks
40. Kurata, H., El-Samad, H., Iwasaki, R., Ohtake, H., Doyle, J. C., Grigorova, I., Gross, C. A., & Khammash,
M. (2006). Module-based analysis of robustness tradeoffs in the heat shock reponse system. PLoS
Computational Biology, 2(7), e59.
41. Magnin, T., Lord, M., & Yudkin, M. D. (1997). Contribution of partner switching and SpoIIAA
cycling to regulation of jF activity in sporulating Bacillus subtilis. Journal of Bacteriology, 179(12),
3922 – 3927.
42. Mangan, S., & Alon, U. (2003). Structure and function of the feed-forward loop network motif. Proceedings
of the National Academy of Sciences of the U.S.A., 100(21), 11980 – 11985.
43. McAdams, H. H., & Arkin, A. (1997). Stochastic mechanisms in gene expression. Proceedings of the National
Academy of Sciences of the U.S.A., 94, 814 – 819.
44. Milo, R., Shen-Orr, S., Itzkovikz, S., Kashtan, N., Chklovskii, D., & Alon, U. (2002). Network motifs:
Simple building blocks of complex networks. Science, 298, 824 – 827.
45. Myers, C. L., Robson, D., Wible, A., Hibbs, M. A., Chiriac, C., Theesfeld, C. L., Dolinski, K., &
Troyanskaya, O. G. (2005). Discovery of biological networks from diverse functional genomic data. Genome
Biology, 6(13), R114.
46. Nath, K., & Koch, A. L. (1970). Protein degradation in Escherichia coli: 1. Measurement of rapidly and
slowly decaying components. The Journal of Biological Chemistry, 245(11), 2889 – 2900.
47. Neidhardt, F. C., Ingraham, J. L., & Schaechter, M. (1990). Physiology of the bacterial cell: A molecular
approach. Sunderland, MA: Sinauer Associates Inc.
48. Ofria, C., & Wilke, C. O. (2004). Avida: A software platform for research in computational evolutionary
biology. Artificial Life, 10(2), 191 – 229.
49. Palsson, B. O. (2006). Systems biology: Properties of reconstructed networks. Cambridge, UK: Cambridge
University Press.
50. Paton, R., Gregory, R., Vlachos, C., Saunders, J., & Wu, H. (2004). Evolvable social agents for
bacterial systems modeling. IEEE Transaction on Nanobioscience, 3(3), 208 – 216.
51. Peterson, C. N., Mandel, M. J., & Silhavy, T. J. (2005). Escherichia coli starvation diets: Essential
nutrients weigh in distinctly. Journal of Bacteriology, 187(22), 7549 – 7553.
52. Phillipe, N., Crozat, E., Lenski, R. E., & Schneider, D. (2007). Evolution of global regulatory
networks during a long-term experiment with Escherichia coli. BioEssays, 29(9), 846 – 860.
53. Quayle, A. P., & Bullock, S. (2006). Modelling the evolution of genetic regulatory networks. Journal of
Theoretical Biology, 238(4), 737 – 753.
54. Rosenfeld, N., Elowitz, M. B., & Alon, U. (2002). Negative autoregulation speeds the response times of
transcription networks. Journal of Molecular Biology, 323, 785 – 793.
55. Salgado, H., Moreno-Hagelsieb, G., Smith, T. F., & Collado-Vides, J. (2000). Operons in
Escherichia coli: Genomic analyses and predictions. Proceedings of the National Academy of Sciences of the
U.S.A., 97(12), 6652 – 6657.
56. Santilla´n, M., & Mackey, M. C. (2001). Dynamic regulation of the tryptophan operon: A modeling study
and comparison with experimental data. Proceedings of the National Academy of Sciences of the U.S.A., 98(4),
1364 – 1369.
57. Santos, M., Zintzaras, E., & Szathma´ry, E. (2004). Recombination in primeval genomes: A step
forward but still a long leap from maintaining a sizeable genome. Journal of Molecular Evolution, 59,
507 – 519.
58. Stekel, D. J., & Jenkins, D. J. (2008). Strong negative self regulation of prokaryotic transcription factors
increases the intrinsic noise of protein expression. BMC Systems Biology, 2(6).
59. Sundararaj, S., Guo, A., Habibi-Nazhad, B., Rouani, M., Stothard, P., Ellison, M., & Wishart, D. S.
(2004). The CyberCell Database (ccdb): A comprehensive, self-updating, relational database to
coordinate and facilitate in silico modeling of Escherichia coli. Nucleic Acids Research, 32 (Database issue),
D293 – D295.
60. Teichmann, S. A., & Babu, M. M. (2004). Gene regulatory network growth by duplication. Nature Genetics,
36(5), 492 – 496.
61. Trevino, V., & Falciani, F. (2006). GALGO: An R package for multivariate variable selection using
genetic algorithms. Bioinformatics, 22(9), 1154 – 1156.
Artificial Life Volume 15, Number 3
283
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
5
3
2
5
9
1
6
6
2
5
8
1
a
r
t
l
.
/
2
0
0
9
.
s
t
e
k
e
l
.
0
0
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. J. Jenkins and D. J. Stekel
Investigating the Evolution of Transcription Control Networks
62. van Noort, V., Snel, B., & Huynen, M. A. (2004). The yeast coexpression network has a small-world,
scale-free architecture and can be explained by a simple model. EMBO Reports, 5(3), 280 – 284.
63. Wagner, A. (1994). Evolution of gene networks by gene duplications: A mathematical model and its
implication on genome organization. Proceedings of the National Academy of Sciences of the U.S.A., 91,
4387 – 4391.
64. Wang, Y., Liu, C. L., Storey, J. D., Tibshirani, R. J., Herschlag, D., & Brown, P. O. (2002). Precision and
functional specificity in mRNA decay. Proceedings of the National Academy of Sciences of the U.S.A., 99(9),
5860 – 5865.
65. Yildirim, N., & Mackey, M. C. (2003). Feedback regulation in the lactose operon: A mathematical
modeling study and comparison with experimental data. Biophysical Journal, 84, 2841 – 2851.
Appendix 1: Mutation Operator
For each gene in the genome, the binding sites of its regulatory region elements, its mRNA product,
and its protein product can mutate with a specified probability. The mutation operator on shape is as
follows:
(cid:7) Random noise is generated at the pole of the shape sphere
D ¼ random normal ðmean ¼ 0; std : dev: ¼ SHAPE NOISE SDEV Þ
ðin the u directionÞ
ð4Þ
c ¼ random ½0; 2kÞ
ðin the f directionÞ
(cid:7) The generated noise is then rotated to the current coordinates (u, f) using Cartesian
algebra:
x ¼ cosu cosf sinD cosc (cid:2) sinf sinD sinc þ sinu cosf cosD
y ¼ cosu sinf sinD cosc þ cosf sinD sinc þ sinu sinf cosD
z ¼ (cid:2)sinu sinD cosc þ cosu cosD
ð5Þ
ð6Þ
ð7Þ
ð8Þ
The Cartesian coordinates can then be transformed back into polar coordinates in the standard way.
As well as the shape mutation, the mRNA and protein product can mutate their degradation rate
with lognormal noise:
degradation ratenew ¼ degradation rateold (cid:8) 10random normal ðmean¼0;std : dev:¼DEG RATE NOISE SDEV Þ
ð9Þ
Appendix 2: Structural Parameter Analysis
The distribution of random models meeting the three termination criteria (replicate, stationary, and
death) was investigated over a large range of the binding affinity parameters, j and a. The results
of 1000 randomly initialized models for each parameter setting (10-3 up to 103), simulated in a
constant and abundant food environment (meaning that the model will always be able to take up
food at the specified rate), are shown in Figure 4. Figure 4a shows the replicating models for each
284
Artificial Life Volume 15, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
5
3
2
5
9
1
6
6
2
5
8
1
a
r
t
l
.
/
2
0
0
9
.
s
t
e
k
e
l
.
0
0
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. J. Jenkins and D. J. Stekel
Investigating the Evolution of Transcription Control Networks
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
5
3
2
5
9
1
6
6
2
5
8
1
a
r
t
l
.
/
2
0
0
9
.
s
t
e
k
e
l
.
0
0
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4. Random model simulations over structural parameters. (a) shows the proportion of models replicating in each
of the environments. A clear light band can be seen passing through from bottom left to top middle,
indicating
environments that are easier to survive in. (b) shows the proportion of models that are stationary. A darker band is seen,
indicating fewer stationary models following the same pattern as in (a), although skewed to the left. (c) shows the
proportion of models that died in each environment. A light band can again be seen, and follows the same pattern as the
dark band in (b). Black is 0%, white is 100%.
parameter, where a clear band of livable parameters can be seen. We see in Figure 4b that it is highly
likely for a random model to be simulated for an hour without replicating; from Figure 4c we have
the inverse of (a), and we see a band of non-dying parameters and the majority of parameters giving
a large percentage of dying models. It is useful to see the parameter ranges in which random models
struggle to replicate, as parameters in those ranges will provide good starting points for evolution,
and will encourage more searching of the solution space. The parameter ranges used for subsequent
evolutionary experiments were j = 1 to 50 and a = 1.
Appendix 3: Parameter Analysis
Table 9 shows the full univariate analysis results for all 26 parameters, and Table 10 shows
the proportions of all 26 parameters in the optimal solutions generated from the multivariate
analysis.
Artificial Life Volume 15, Number 3
285
D. J. Jenkins and D. J. Stekel
Investigating the Evolution of Transcription Control Networks
Appendix 4: Evolution Results: Population Dynamics
A4.1 Affects of S and Mutation Rate on Population Dynamics
Results from the experiments indicate that the binding affinity parameter j has a substantial effect
on the potential for evolving models. In Figure 5a we can see a low-mutation environment with a
very small j. The population is very quickly (within five generations) dominated by models that are
replicating, and by the end of the short evolution of 50 generations we can see that the final
population had around 95% replicating models, with no models being in the stationary phase after
1 h. In comparison with the initial population, less than 40% of models were replicating, and around
20% were in the stationary phase, leaving the remaining 40% of models dying. However, we see a
very different population dynamic if we have a larger j value. Figure 5b shows a low-mutation
environment, but with a large binding affinity value j = 50. Here 95% of the initial population die,
with no models replicating at all. In the early stages of the evolution we see a slight increase in the
number of models that do not die, but do not replicate either, and we start to see models that are
persistently capable of replicating, but do not quickly take over the population as was seen in Fig-
ure 5a. Around halfway through the evolution by generation 25, we start to see a monotonic increase
in replicating models, and by generation 40 up to 75% of the population consists of replicating mod-
els. However, the proportion of stationary models each generation remains fairly constant between
10% and 20%, as do those of replicating and dying models after generation 40.
In a high-mutation environment we see a similar population dynamic (Figure 5c). The small value
of j once again quickly reaches a large number of models, which replicate, albeit slightly slower than
in the low-mutation environment. Also, the replicating models only consist of around 90% of the
population, less than in the low-mutation environment. In a high-mutation environment with a larger
j we can also see a similar behavior to that in a low-mutation environment. Figure 5d shows j = 30,
where the same initial lag period before the models capable of replicating begin to fill the population
occurs as in the low-mutation environment. Once again the maximum number of replicating models
is lower than in the low-mutation environment. In some cases of larger j, no replicating models are
able to establish themselves within the population, as shown in Figure 6.
This change in behavior can be explained in two ways. Firstly, the size of the binding affinity
parameter j determines the shape space’s complexity. In a low-value shape space, there are effectively
fewer shapes that each molecule can take, and so it is more likely to have an initial population with a
number of models that have similar enough shapes to provide the required interactions and dynamics.
With a larger value, the shape space increases in size; therefore molecule shapes have to be more
accurate to achieve the same interactions and dynamics required. As we can see from the figures, low-j
environments start with a larger number of replicating models, up to 40% of the population, whereas
in a higher-j environment it takes many generations of searching the shape space for a random model
to survive and replicate well enough to start propagating through the population. Secondly, the
mutation rate affects the rate of evolution within the population. In the low-mutation environment, the
population quickly reaches equilibrium, where around 95% of the population are replicating models.
The low mutation rate also means that once a model has achieved the required interactions and
dynamics to replicate, it is unlikely to mutate away from this state, and so we see only 5% of the
population dies each generation. This death rate will also be due to stochastic affects, as there is a small
probability that even the most highly optimized model will die. In the high-mutation environment, we
can see that the mutation rate of 50% is having a detrimental affect on the evolution. While the initial
population has a similar distribution of models to that in the low-mutation environment, it takes several
generations longer to reach equilibrium, and once it has reached it there is a larger proportion of dying
models, as it is more likely that a model will mutate and lose required interactions.
A4.2 Genome Size in the Population
Genome size was also recorded during evolution. In a low-mutation environment, the average genome
size is no larger than 1.3 genes per model, larger models are quickly selected out, and a low equilibrium
286
Artificial Life Volume 15, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
5
3
2
5
9
1
6
6
2
5
8
1
a
r
t
l
.
/
2
0
0
9
.
s
t
e
k
e
l
.
0
0
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
D. J. Jenkins and D. J. Stekel
Investigating the Evolution of Transcription Control Networks
genome size is achieved within the population. In contrast, in the high-mutation environment the
average genome size quickly reaches around 1.7 genes per model, and again stays around this size. A
small genome size is expected, due to the simple environmental challenges requiring little complex
regulation and also due to the selection pressure implicitly imposed by the replication criteria. Each gene
requires an extra 10% energy of the replication threshold, which means that junk genes will be
detrimental to reaching its replication threshold. Results of evolutionary runs where the genome size
was initially larger than 1 gene also show an average final gene size slightly larger than 1, indicating that
the extra genes are not likely to be required for efficient and fast replication.
A4.3 Cell Lineages in the Population
Examining the final population of each evolution shows that the majority of all models in the popula-
tion come from a single common ancestor. In the low-mutation, low-j environment the final popula-
tion usually consisted of two lineages; in one case the population was split approximately equally between
them, but in another case 95% of the models had the same initial ancestor. In all cases in this envi-
ronment, all the lineages could be traced back to the initial population. In a high-j environment we see
a different pattern. Instead of multiple lineages competing for space in the population, we see the
dominance of a single model. In two cases 100% of the final population consisted of models derived
from a single model (emerging in generations 1 and 3), and the third case consisted of two lineages with
offspring from one model from generation 19 contributing to 98% of the population; the other 2%
were from a model from the initial population. In a high-mutation environment we see different
population distributions. In a low-j environment there is a mixture between complete dominance of a
single model and partial dominance of one model against either one or two other models. In all cases,
however, all the models trace back to the initial population. In the high-j environment a different
population distribution is dominant. In each case the final population consists of over 50 lineages, each
occupying only 1–10% of the population, but tracing back up to 20 generations.
Table 9. Univariate analysis of all evolvable parameters. For each parameter its ID number, original p-value from a
logistic regression, adjusted q-value from controlling the false-discovery rate, its classification accuracy, and its sensitivity
and specificity are shown.
p
q
Classification accuracy (%)
Sensitivity
Specificity
Parameter
Protein degradation rate
Protein-repressor complex koff
Protein-promoter complex koff
All-promoter complex koff
mRNA degradation rate
Energy-promoter complex koff
ID
22
5
6
26
23
14
<2e-16
5.2e-15
1.38e-10
1.794e-9
1.29e-8
1.118e-7
1.06e-7
6.89e-7
6.05e-7
3.146e-6
8.1e-5
3.51e-4
Food-repressor complex koff
10
0.00273
0.01014
Protein-protein koff
Protein-RNAP koff
8
3
0.00346
0.011245
0.0233
0.06731
Energy-repressor koff
13
0.0375
0.0975
81.7
54.7
60.4
57.6
58.1
58.3
55.3
56
56.8
55.1
0.77803
0.84838
0.32287
0.77617
0.34978
0.80866
0.28027
0.81408
0.32287
0.78881
0.23318
0.86462
0.12556
0.89711
0.12108
0.91336
0.08969
0.95307
0.03587
0.96570
Artificial Life Volume 15, Number 3
287
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
>