A Geometric Characterization of Population Coding
in the Prefrontal Cortex and Hippocampus during
a Paired-Associate Learning Task
Yue Liu1, Scott L. Brincat2, Earl K. Miller2, and Michael E. Hasselmo1
Abstract
■ Large-scale neuronal recording techniques have enabled dis-
coveries of population-level mechanisms for neural computa-
tion. However, it is not clear how these mechanisms form by
trial-and-error learning. In this article, we present an initial ef-
fort to characterize the population activity in monkey prefrontal
cortex (PFC) and hippocampus (HPC) during the learning
phase of a paired-associate task. To analyze the population data,
we introduce the normalized distance, a dimensionless metric
that describes the encoding of cognitive variables from the geo-
metrical relationship among neural trajectories in state space. It
is found that PFC exhibits a more sustained encoding of the
visual stimuli, whereas HPC only transiently encodes the identity
of the associate stimuli. Surprisingly, after learning, the neural
activity is not reorganized to reflect the task structure, raising
the possibility that learning is accompanied by some “silent”
mechanism that does not explicitly change the neural represen-
tations. We did find partial evidence on the learning-dependent
changes for some of the task variables. This study shows the feasi-
bility of using normalized distance as a metric to characterize and
compare population-level encoding of task variables and suggests
further directions to explore learning-dependent changes in the
neural circuits. ■
INTRODUCTION
With the development of experimental techniques for re-
cording the activity of a large number of neurons, re-
searchers have started exploring the possibility that the
collective dynamics of interacting populations of neurons
form basic units for some neural computations (Sussillo,
2014). The collective dynamics are usually described by
neural trajectories in state space, which represent firing
rates evolving through time. By looking at the collective
neural dynamics through the lens of dynamical systems,
several studies have identified cognitive functions with fa-
miliar concepts in dynamical systems. For example, in
Mante, Sussillo, Shenoy, and Newsome (2013), it was
shown that the monkey prefrontal network performed
a context-dependent decision-making task by forming a
pair of line attractors for the two contexts (Mante et al.,
2013). In Remington, Narain, Hosseini, and Jazayeri
(2018), the authors showed that, in an interval produc-
tion task, monkey frontal cortex circuits encoded the in-
formation about the time interval to be reproduced in
the initial condition of the neural population dynamics,
and the neural dynamics for different reproduced time
intervals were represented by parallel neural trajectories
with different speeds (Remington et al., 2018).
Despite great progress in revealing collective functional
features in neural computation, it remains unclear how
1Boston University, 2Massachusetts Institute of Technology
© 2020 Massachusetts Institute of Technology
these collective features are formed during training.
Although it has been shown that similar features are pres-
ent in recurrent neural networks trained on the same task
by backpropagation, the learning dynamics of these recur-
rent neural networks are likely to differ from real neural
circuits. To elucidate the solutions to this problem, one
should look at how population dynamics change during
the learning phase of a task. There exist studies that look
at population-level changes during motor learning (Golub
et al., 2018; Vyas et al., 2018; Sadtler et al., 2014), but sim-
ilar work for cognitive learning has been scarce (although
see Durstewitz, Vittoz, Floresco, & Seamans, 2010). In
this article, we present an initial effort to characterize
population-level dynamics during the learning phase of
a cognitive task.
The task we analyzed is a paired-associate task where a
monkey learned associations between a pair of randomly
chosen visual stimuli (cues) and a third visual stimulus
(associate). We are interested in the type of changes in
the population activity that correlate with learning in this
task. For analysis of the neural recording data, we intro-
duced a dimensionless metric, which we called normalized
distance (ND), that describes the geometric relationships
among neural trajectories for different experimental condi-
tions. Unlike decoding methods, ND characterizes the en-
coding of all task variables in the population based directly
on the geometry of the neural code. The dimensionless
property of ND also enables comparisons of information
in population codes between different learning stages as
Journal of Cognitive Neuroscience 32:8, pp. 1455–1465
https://doi.org/10.1162/jocn_a_01569
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
t
n
p
o
:
a
/
d
/
e
m
d
i
f
r
t
o
p
m
r
c
h
.
s
p
i
l
d
v
i
r
e
e
r
c
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
m
c
n
/
j
a
o
r
t
c
i
c
n
e
/
–
a
p
r
d
t
i
3
c
2
l
8
e
1
–
4
p
5
d
5
f
2
/
0
3
1
2
3
/
6
8
5
/
5
1
4
o
5
c
5
n
_
/
a
1
_
8
0
6
1
1
5
9
6
5
9
4
p
/
d
j
o
b
c
y
n
g
_
u
a
e
_
s
0
t
1
o
5
n
6
0
9
8
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
/
j
f
t
.
/
o
n
0
5
M
a
y
2
0
2
1
well as different brain areas. Using this metric, we then
compared population-level dynamics between PFC and
hippocampus (HPC) as well as across learning stages
in terms of the information content in the population
codes. Our results reveal a series of differences in the
dynamics of the information content between PFC and
HPC. Differences in population coding across learning
stages are also present, albeit in one of the two animals.
These results demonstrate that ND is a robust way of
measuring information content in population codes with
high temporal resolution in the face of noisy neural data.
METHODS
Task and Recording
We analyzed neural recording data from a previous study
on a paired-associate learning task (Brincat & Miller,
2015). In that study, two macaque monkeys were trained
to perform an object paired-associate learning task that re-
quired them to learn arbitrary associations between pairs
of visual images of objects. On each day, six novel images
were chosen. Four of them were randomly assigned as
the cue objects, and the other two were assigned as the
associate objects. Two random cue objects were then
paired with a random associate object, forming a 4:2 map-
ping from cues to associates (Figure 1A).
The structure of a trial is illustrated in Figure 1B.
During each trial, after a 500-msec fixation period, the
monkeys were first presented with one of the cue stimuli
for 500 msec. Then, after a delay of 750 msec, the mon-
keys were presented with one of the associate objects for
another 500 msec. The monkeys should indicate whether
the previous two stimuli are associated with each other
by making a saccade to the indicated position on the
screen if they match. If the two previous stimuli do not
match, the monkeys were required to hold the fixation.
After a 250-msec delay, the match stimulus will appear on
the screen for 500 msec, after which the monkeys were
required to make the saccade to the same position as in
the match trial. The monkeys were rewarded with water
if the response was correct (Figure 1B).
During each recording session, the monkey must learn
novel associations from trial and error. The monkeys
were able to learn the associations above chance in all
recording sessions (Figure 1C). Microelectrodes were
lowered into the lateral PFC and HPC and recorded spikes
and local field potential (LFP) signals while the monkeys
were performing the paired-associate learning task.
Across all sessions, 353 neurons in PFC and 128 neurons
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
t
n
p
o
:
a
/
d
/
e
m
d
i
f
r
t
o
p
m
r
c
h
.
s
p
i
l
d
v
i
r
e
e
r
c
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
m
c
n
/
j
a
o
r
t
c
i
c
n
e
/
–
a
p
r
d
t
i
3
c
2
l
8
e
1
–
4
p
5
d
5
f
2
/
0
3
1
2
3
/
6
8
5
/
5
1
4
o
5
c
5
n
_
/
a
1
_
8
0
6
1
1
5
9
6
5
9
4
p
/
d
j
o
b
c
y
n
g
_
u
a
e
_
s
0
t
1
o
5
n
6
0
9
8
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
/
j
.
/
f
t
o
n
0
5
M
a
y
2
0
2
1
Figure 1. Overview of the task and two potential neural circuit mechanisms for learning the task. During each session, six random stimuli are
arranged into two-to-one mappings (A), and the monkey is required to learn the mappings via trial and error. On each trial, the monkey receives a
cue and a choice stimuli separated by a 750-msec delay, after which it has to make a decision of whether the two stimuli match by a saccade response
for match. For nonmatch trials, the match stimulus is shown after 250 msec, after which the monkey is required to make the same saccade as in
match trials (B). During each session, the monkey’s performance gradually increases (C). To solve this task, the underlying neural circuit could
employ two computational strategies (D). It could learn to develop more similar representations for cue stimuli that correspond to the same
associate (Scenario 1), or it could learn to change the landscape of its dynamics such that at the end of the delay period, the neural states
corresponding to different associate stimuli are separated by an energy barrier (Scenario 2). Panels A, B, and C are adapted from Brincat et al. (2015).
1456
Journal of Cognitive Neuroscience
Volume 32, Number 8
in HPC were recorded. During each session, 5–25 neurons
were simultaneously recorded in PFC and 5–16 in HPC.
The ways the underlying neural circuit can learn to
solve this task can be broadly divided into two categories.
It could be that the network develops more similar rep-
resentations for the cues that belong to the same associ-
ate (Figure 1D, Scenario 1), as previously suggested by a
single-cell analysis (Brincat & Miller, 2016) as well as re-
sults showing categorical representation in PFC (e.g.,
Roy, Riesenhuber, Poggio, & Miller, 2010; Freedman,
Riesenhuber, Poggio, & Miller, 2001). Another possibility
is that the landscape of the network dynamics changes
with learning, whereas the network responses to cues re-
main unchanged. In particular, the landscape changes in
such a way that, after learning, the network states at the
end of the delay corresponding to different associate
stimuli are separated by an energy barrier (Figure 1D,
Scenario 2). Because of this, subsequent input driven
by the associate stimulus is more likely to take them to
different final decision states. In this scenario, learning
could be facilitated by “silent” mechanisms such as synaptic
plasticity (Stokes, 2015; Mongillo, Barak, & Tsodyks, 2008;
Bi & Poo, 1998). As will be shown by the analysis using the
ND metric, the neural trajectories are not clustered by cue
category during the delay interval even after learning,
thereby lending support to the second possibility.
Normalized Distance
In this section, we introduce the metric we used to charac-
terize the information content in a neural population. This
metric is computed from distance between neural trajecto-
ries in state space but normalized properly to account for
the true neural information about task variables. Hence,
we named it normalized distance (ND). This metric is sim-
ilar to the one used to characterize the community struc-
ture in fMRI data (Schapiro, Turk-Browne, Norman, &
Botvinick, 2016), as well as the “abstraction index” used
in analyzing electrophysiological data (Bernardi et al.,
2019). Both of these metrics and ND describe the commu-
nity structure of neural states organized by task variables.
The metrics used in Schapiro et al. (2016) and Bernardi
et al. (2019) are computed by dividing the across-group
correlation coefficient or Euclidean distance by the
same quantity within a group. The difference between
ND and the previous two metrics is that ND is computed
on a moment-by-moment basis. Therefore, it reveals the
dynamics of the neural information.
When analyzing recordings from a population of neu-
rons, it is often convenient to represent the simultaneous
activity of all neurons as a point in a “state space.” A state
space is a high-dimensional space where each axis repre-
sents the activity (in our case, binned spike counts) of
one neuron. Over time, the population dynamics can
be represented by a trajectory through the state space.
The ND for two task conditions A and B is a function of
time ND(A, B, t). At each point in time, it is defined to be
the average Euclidean distance between pairs of neural
trajectories that represent different task conditions divided
by the average Euclidean distance between pairs of neural
trajectories that represent the same task condition (see
Figure 2 for a graphical illustration).
(cid:1)
Þ ¼ Dij
(cid:1)
dij
xi tð Þ − xj tð Þ
(cid:3)
xi tð Þ − xj tð Þ
ð
ND A; B; t
(cid:3)
(cid:3) ¼
i2A; j2B
(cid:4)
(cid:1)
(cid:4)
(1)
(cid:4)
(cid:4)
(cid:4)
(cid:4)
(cid:4)
(cid:4)
(cid:3)
(cid:1)
i; j2A or
i; j2B
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
t
n
p
o
:
a
/
d
/
e
m
d
i
f
r
t
o
p
m
r
c
h
.
s
p
i
l
d
v
i
r
e
e
r
c
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
m
c
n
/
j
a
o
r
t
c
i
c
n
e
/
–
a
p
r
d
t
i
3
c
2
l
8
e
1
–
4
p
5
d
5
f
2
/
0
3
1
2
3
/
6
8
5
/
5
1
4
o
5
c
5
n
_
/
a
1
_
8
0
6
1
1
5
9
6
5
9
4
p
/
d
j
o
b
c
y
n
g
_
u
a
e
_
s
0
t
1
o
5
n
6
0
9
8
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
/
j
t
/
f
.
o
n
0
5
M
a
y
2
0
2
1
In the equation above, i and j are indices for neural
trajectories and Dij and dij represent the Euclidean dis-
tance between neural trajectories i and j when they belong
to the same or different task conditions, respectively. xi(t)
and xj(t) are population vectors at time t for neural trajec-
tories i and j. Brackets denote averaging, and vertical lines
denote the magnitude of a vector.
ND provides a way of computing the information ex-
plicitly encoded in the population from the geometry
of the neural data. In Equation 1, the numerator is the
average variability in the population code induced by
the task condition of interest (here, A and B). The de-
nominator is the average variability induced by all the
other factors when the task condition of interest is fixed.
The variability in the denominator could come from
nested task conditions within A and B, trial history, or
simply intrinsic neuronal noise. An ND(A, B) greater than
1 indicates that the population code carries information
about task condition A versus B, because there is extra
variability in the population code caused by the differ-
ence between A and B beyond the variability caused by
all the other factors. Geometrically, it means that the neu-
ral states at time t are clustered according to task condi-
tions A and B. On the other hand, an ND(A, B) close to 1
indicates that the population code does not carry infor-
mation about A versus B, because the neural states are
randomly distributed in the state space.
It is worth emphasizing again that the normalizing part
in ND (the denominator in Equation 1) is crucial. A large
Euclidean distance between two neural trajectories (the
numerator of Equation 1) does not necessarily indicate
that the neural population encodes information about
the experimental variable. To illustrate this, we simulated
two populations of neurons that respond to one of the
four cues A1, A2, B1, and B2 (Figure 2) on a given trial.
In this case, the four cues are organized by two higher-
level “categories” A and B. The first population only has
selectivity for the identity of the cues (Figure 2A, cue-
selective population). The second population of neurons
has selectivity for both the higher-order categories (whether
a cue belongs to Category A or B) and the lower-order cue
identity (Figure 2B, category-selective population). The
firing rate at each time point was simulated as a Gaussian
random variable with a time-varying mean. There are equal
numbers of neurons with any given selectivity in both pop-
ulations. We computed the ND between the two categories
ND(A, B, t) as well as the raw distance between the neural
trajectories for A and B (intergroup distance, the numerator
Liu et al.
1457
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
t
n
p
o
:
a
/
d
/
e
m
d
i
f
r
t
o
p
m
r
c
h
.
s
p
i
l
d
v
i
r
e
e
r
c
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
m
c
n
/
j
a
o
r
t
c
i
c
n
e
/
–
a
p
r
d
t
i
3
c
2
l
8
e
1
–
4
p
5
d
5
f
2
/
0
3
1
2
3
/
6
8
5
/
5
1
4
o
5
c
5
n
_
/
a
1
_
8
0
6
1
1
5
9
6
5
9
4
p
/
d
j
o
b
c
y
n
g
_
u
a
e
_
s
0
t
1
o
5
n
6
0
9
8
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
/
j
/
t
.
f
o
n
0
5
M
a
y
2
0
2
1
Figure 2. ND characterizes the geometry of neural trajectories in the state space. We simulated an experiment where a neural population responds to
one of the four cues during each trial. We compared different metrics for extracting information about stimulus category in two simulated neural
populations. One population contains sets of neurons that are purely selective for one of the four cues (A1, A2, B1, or B2; cue-selective population, A).
The other population contains sets of neurons with selectivity for both the cue category (A, B) and the cue identity (A1, A2, B1, B2; category-selective
population, B). (Left) Low-dimensional representation of the neural trajectories for both populations in the top 3 principal component space. Each
trajectory represents the trial-averaged population activity under one condition. Darker color means later in time. (Center left) The condition-averaged
firing rates for an example neuron in the population. The example neuron in the cue-selective population fires most for A1 and remains at baseline firing
for all the other conditions (top). The example neuron in the category-selective population fires most for A1, less for A2, and remains at a baseline firing
rate for B1 and B2 (bottom). (Center) ND for the category-selective population goes above 1 and falls back when the single-cell selectivity returns to
baseline. On the other hand, ND for the cue-selective population fluctuates around 1. (Center right) The intergroup distance (the numerator of ND) for
both the cue-selective and category-selective populations goes up because of the increased overall firing rate with time in both populations. Therefore,
the intergroup distance alone, without proper normalization, does not accurately reflect the neural information. (Right) The decoding accuracy for cue
category (A vs. B) quickly grows above chance in both populations because of the larger raw distances between all pairs of neural trajectories. Therefore,
although category information is only explicitly encoded in the category-selective population, the decoding accuracy does not reflect this distinction.
of ND(A, B, t) in Equation 1). As a result, the ND(A, B, t) for
the two populations have distinctively different time
courses that correlate with their single-cell selectivity for
the higher-order variables (Figure 2, center). On the other
hand, the intergroup distance between A and B has a similar
time course for both populations, showing that the raw dis-
tance is not enough to capture the information content in
the population (Figure 2, center right).
The neural trajectories used in the computation of ND
could be the population activity during a single trial or trial-
averaged activity for one task condition. This is largely a
practical choice and does not affect the rationale above.
For this data set, the neural trajectories represent the trial-
averaged neural activity over time for a given task condition.
Comparison with Decoding Accuracy and
Single-Cell Percentage of Explained Variance
An alternative way of quantifying the information in the
population code is by constructing a pattern classifier to
separate neural activity vectors in the state space accord-
ing to task conditions. However, decoding may miss
important geometric properties of the neural states. To
show this, we trained a linear discriminant analysis classi-
fier to distinguish between cue category A and B using
the two simulated neural populations above. The decoder
was trained on 67% of randomly selected trials and tested
on the held-out trials. This procedure was repeated 10
times, and the decoding accuracy was averaged. As shown
in Figure 2 (rightmost), the decoders for the two popula-
tions behave almost identically. They can both decode the
cue category perfectly after a certain point in time.
Therefore, decoding accuracy can be blind to important
geometric characteristics in the neural data.
The form of the ND (Equation 1) also reminds one of
single-cell measures such as percentage of explained var-
iance (PEV ). However, computing PEV in the case of
nested task conditions can be tricky. In the example
above, one cannot compute PEV by simply constructing
a linear model for the firing rate of individual neurons
using all stimuli and category conditions (A1, A2, B1, B2,
A, B) as regressors, as these regressors will be correlated.
Another way would be to use only the cue category (A, B)
as regressors, but in this way, the purely cue-selective
1458
Journal of Cognitive Neuroscience
Volume 32, Number 8
neurons would also have nonzero PEV for cue category.
One can construct auxiliary regressors as in Brincat and
Miller (2016) to balance out the PEVs for different regres-
sors, which is reminiscent of the normalizing term in the
computation of ND. However, this technique is hard to
generalize to situations when there are unequal numbers
of cues that belong to each category, whereas ND is gener-
alizable to any situation involving nested task conditions.
RESULTS
We applied the ND metric introduced above to compute the
time evolution of the information encoded in the neural
population. We started out by computing the ND for cate-
gory information (if the cue belongs to Associate A or B) and
found that neither PFC nor HPC exhibits sustained above-
chance ND for category for all learning stages. This indicates
that the neural representations for cues corresponding to
the same associate do not become more similar with learn-
ing, contrary to what is suggested by one of the hypotheses
proposed (Figure 1D, Scenario 1). Therefore, the neural cir-
cuit may be employing the learning mechanism where the
landscape of the network dynamics is modified with learn-
ing (Figure 1D, Scenario 2). Next, the same ND metric is
deployed to calculate the information content of other
task variables including cue identity, associate identity,
decision/movement, and trial outcome.
To look at learning-dependent changes in the neural
activity, we divided each learning session into three stages
(early, mid, and late) by evenly dividing all trials within a
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
t
n
p
o
:
a
/
d
/
e
m
d
i
f
r
t
o
p
m
r
c
h
.
s
p
i
l
d
v
i
r
e
e
r
c
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
m
c
n
/
j
a
o
r
t
c
i
c
n
e
/
–
a
p
r
d
t
i
3
c
2
l
8
e
1
–
4
p
5
d
5
f
2
/
0
3
1
2
3
/
6
8
5
/
5
1
4
o
5
c
5
n
_
/
a
1
_
8
0
6
1
1
5
9
6
5
9
4
p
/
d
j
o
b
c
y
n
g
_
u
a
e
_
s
0
t
1
o
5
n
6
0
9
8
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
/
j
f
t
/
.
o
n
0
5
M
a
y
2
0
2
1
Figure 3. Normalized distance for categories. The ND for cue category was calculated by grouping the neural trajectories according to the cue
category (A). PFC has intermittent information about the category information (that A1 and A2 both predict A1, and B1 and B2 predict B1; B, red
lines), whereas HPC in Monkey J also has intermittent information (B, blue lines). But neither regions show a sustained increase in ND for cue
category throughout learning. The shaded areas show 68% confidence interval computed from 10000 iterations of bootstrap resampling across
sessions. Dots on top represent time points when the ND is significantly larger than 1 ( p < .05, cluster-based permutation test). Gray-shaded areas
indicate periods when the cue and associate are presented and response is made.
Liu et al.
1459
session. Neural trajectories were obtained from condition-
averaged firing rates. Firing rates were computed every
1 msec using a box-car moving window with a width of
50 msec. Therefore, there are four neural trajectories
during the cue period (four cues) and eight neural trajecto-
ries after the associate stimulus is presented (4 cues × 2
associates). A given ND was computed by partitioning all
neural trajectories into groups that correspond to each
task condition, and then the average across-group dis-
tance was divided by the average within-group distance,
as detailed in the Normalized Distance section. For all
the population analysis, except for the one on trial out-
come (see Trial Outcome Encoding section), only ses-
sions where five or more neurons were simultaneously
recorded were used in computing ND, and for a given ses-
sion, only correct trials were included in calculating the
condition-averaged response. For the trial outcome analy-
sis, both correct and incorrect trials in all sessions are
used. All the analyses were performed using simulta-
neously recorded neurons. To test which part of the trial
the ND is significantly larger than 1, we used a cluster-
based permutation test (Maris & Oostenveld, 2007). To
perform this test, we first created a data set representing
ND at chance level, which is 1 across all time points. The
sample size of the chance data set is the same as the ac-
tual data. As a first-order test, we computed for each time
point a one-sided t test against the chance. The cluster-
based permutation test then stipulates a cluster of time
points as having an ND significantly larger than chance
when the sum of the t statistic within that cluster is larger
than 95% of the random shuffles.
Neural Trajectories during the Delay Interval Are
Not Clustered by Cue Category
The two hypotheses in the Task and Recording section on
how the neural circuits can learn to solve this task make
different predictions about the clustering of neural states
during the delay interval before and after learning
(Figure 1D). Therefore, we started out by investigating
whether the information about the cue category was en-
coded in PFC and HPC. By cue category, we mean whether
the cue was paired with associate A0 or B0. We define Cues
A1 and A2 to be in Cue Category A and Cues B1 and B2
to be in Cue Category B. The ND between cue categories
(denoted by ND(A, B)) was computed according to
Equation 1. Different neural trajectories were grouped
according to the category of their cues (Figure 3A).
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
t
n
p
o
:
a
/
d
/
e
m
d
i
f
r
t
o
p
m
r
c
h
.
s
p
i
l
d
v
i
r
e
e
r
c
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
m
c
n
/
j
a
o
r
t
c
i
c
n
e
/
-
a
p
r
d
t
i
3
c
2
l
8
e
1
-
4
p
5
d
5
f
2
/
0
3
1
2
3
/
6
8
5
/
5
1
4
o
5
c
5
n
_
/
a
1
_
8
0
6
1
1
5
9
6
5
9
4
p
/
d
j
o
b
c
y
n
g
_
u
a
e
_
s
0
t
1
o
5
n
6
0
9
8
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
/
j
/
.
t
f
o
n
0
5
M
a
y
2
0
2
1
Figure 4. Normalized distance for cues. To calculate the ND for cues, trial-averaged neural trajectories were grouped according to the cue identity
(A, different colors correspond to different groups). ND (cues) is the ratio of the average Euclidean distance between neural trajectories across
groups to that of neural trajectories within groups. PFC (B, left) and, in one of the two animals, HPC (B, right) significantly encode cue information.
The information in PFC persists longer, potentially reflecting the longer timescale of the neuronal activity in PFC compared to HPC. The average ND
during the cue presentation does not change with learning in both brain regions. The shaded areas show 68% confidence interval computed from
10000 iterations of bootstrap resampling across sessions. Dots on top represent time points when the ND is significantly larger than 1 ( p < .05,
cluster-based permutation test). Gray-shaded areas indicate periods when the cue and associate are presented and response is made.
1460
Journal of Cognitive Neuroscience
Volume 32, Number 8
Importantly, because there are four task conditions before
the associate was presented and eight task conditions
after, the grouping of neural trajectories was different
before and after the associate was presented as well.
Therefore, ND(A, B) was calculated in different ways for
the two stages (Figure 3A). According to the discussion
above, an ND larger than 1 implies that the population
contains information about the category of the cues. On
the other hand, an ND close to 1 implies that the popula-
tion does not carry information about the cue category.
As shown in Figure 3, in PFC, there is intermittent in-
formation about the cue category during the cue and de-
lay periods (Figure 3B, left). This might reflect some
representation for the cue category. However, this signal
is much weaker than the information about cues (com-
pare Figure 4B). Similarly, ND(A, B) for HPC is intermit-
tent for one of the two animals (Figure 3B). These results
indicate that the neural representations for cues are not
clustered according to the associates they are paired
with, even after learning. According to the discussions
in the Task and Recording section, this suggests that
learning in this task is not reflected in the changes of neu-
ral representation for cues (Figure 1D, Scenario 1) but
might be facilitated by the changes in the synaptic
weights of the neural network (Stokes, 2015; Mongillo
et al., 2008; Bi & Poo, 1998) such that the landscape of
the network dynamics is gradually reshaped during learn-
ing (Figure 1D, Scenario 2).
Normalized Distance for Other Task Variables
We next looked at the encoding of other task variables
using the same ND metric (see ND section), including
the identity of the cues (A1 vs. A2 vs. B1 vs. B2), associ-
ates (A0 vs. B0), decision/movement preparation (match
vs. nonmatch),1 and trial outcome. We found that PFC
populations encode the identity of the cue and associate
stimuli in a sustained fashion, whereas HPC has a more
transient encoding of the cue and the associate. Only the
HPC population in one of the two animals shows a signif-
icant encoding of the cues. In one of the two monkeys,
the PFC population also shows a slowly ramping
decision/movement information at the end of the trial.
Moreover, the outcome of the previous trial is encoded
by both PFC and HPC populations for seconds during the
intertrial interval. In the subsequent sections, the time
evolution of ND for each task variable across learning
stages and brain areas will be presented in turn.
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
t
n
p
o
:
a
/
d
/
e
m
d
i
f
r
t
o
p
m
r
c
h
.
s
p
i
l
d
v
i
r
e
e
r
c
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
m
c
n
/
j
a
o
r
t
c
i
c
n
e
/
-
a
p
r
d
t
i
3
c
2
l
8
e
1
-
4
p
5
d
5
f
2
/
0
3
1
2
3
/
6
8
5
/
5
1
4
o
5
c
5
n
_
/
a
1
_
8
0
6
1
1
5
9
6
5
9
4
p
/
d
j
o
b
c
y
n
g
_
u
a
e
_
s
0
t
1
o
5
n
6
0
9
8
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
/
j
t
/
.
f
o
n
0
5
M
a
y
2
0
2
1
Figure 5. Normalized distance for associates. The ND for associates was computed during the period after the associate has been presented. Neural
trajectories were grouped according to the identity of the associate stimuli (A). Both PFC (B, left) and HPC (B, right) encode information about the
identity of the associate stimulus. The information in PFC sustains longer than that in HPC (the shaded areas show 68% confidence interval computed
from 10000 iterations of bootstrap resampling across sessions). Dots on top represent time points when the ND is significantly larger than 1 ( p < .05,
cluster-based permutation test). Gray-shaded areas indicate periods when the cue and associate are presented and response is made. In the HPC of
Monkey J, the information about the associate stimulus is stronger later in learning (rightmost of B, ND averaged across the associate presentation
period). Asterisks indicate statistical significance using Mann–Whitney U test.
Liu et al.
1461
Cue Encoding
The ND between the four cue stimuli was computed as a
function of time. The normalization factor in Equation 1
was calculated from the distances between trajectories
encoding the same cue but different associate stimuli
(Figure 4A). Figure 4 shows the ND among cues as a
function of time. In PFC for both monkeys and HPC for
Monkey J, ND (cues) rapidly goes up when the cue is pre-
sented at t = 500 msec, reflecting the encoding of the
cue information at stimulus presentation. The informa-
tion about the cues then gradually decays to baseline
and rapidly decreases after the subsequent stimulus (as-
sociate) is presented. Notably, the ND for PFC has a more
sustained dynamics than HPC. This implies that the net-
work timescale in PFC may be longer than that in HPC.
There are no significant learning-dependent changes in
ND for both PFC and HPC during the cue period
(Figure 4B, Mann–Whitney U test). Overall, the results
show that the PFC population carries sustained informa-
tion about the cues. The HPC population in one of the
two animals shows significant but more transient en-
coding of the cues.
Associate Encoding
0
, B
0
) was
The ND between the two associate stimuli, ND (A
computed as in Equation 1, where the denominator is the
average distance between neural trajectories encoding
the same associate stimulus but different cue stimuli
(Figure 5A). The ND was only computed after the associ-
ate was presented. As shown in Figure 5, the ND between
0
) rapidly increases when the as-
the two associates (A
sociate is presented (t = 1750 msec). Similar to cue encod-
ing, the ND in PFC shows sustained information for a longer
period than that in HPC (compare Figure 5B, red and blue
lines). In addition, we observed an interesting learning-
dependent change in the HPC of one of the monkeys: The
average ND during the associate presentation period is sig-
nificantly smaller during the early learning period (the first
one third of the session) than the mid (the middle one
0
vs. B
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
t
n
p
o
:
a
/
d
/
e
m
d
i
f
r
t
o
p
m
r
c
h
.
s
p
i
l
d
v
i
r
e
e
r
c
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
m
c
n
/
j
a
o
r
t
c
i
c
n
e
/
-
a
p
r
d
t
i
3
c
2
l
8
e
1
-
4
p
5
d
5
f
2
/
0
3
1
2
3
/
6
8
5
/
5
1
4
o
5
c
5
n
_
/
a
1
_
8
0
6
1
1
5
9
6
5
9
4
p
/
d
j
o
b
c
y
n
g
_
u
a
e
_
s
0
t
1
o
5
n
6
0
9
8
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
/
j
f
/
t
.
o
n
0
5
M
a
y
2
0
2
1
Figure 6. Normalized distance for decision/movement. The ND for decision/movement was calculated by grouping the neural trajectories according to
whether it is a match or a nonmatch trial (A). In the PFC of Monkey J, information about the match versus nonmatch trial type starts to ramp up halfway
through the second stimulus interval (B, left). The ND for HPC fluctuates around 1 for both monkeys (B, right). The shaded area shows 68% confidence
interval computed from 10000 iterations of bootstrap resampling across sessions. Dots on top represent time points when the ND is significantly larger
than 1 ( p < .05, cluster-based permutation test). Gray-shaded areas indicate periods when the associate is presented and response is made.
1462
Journal of Cognitive Neuroscience
Volume 32, Number 8
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
t
n
p
o
:
a
/
d
/
e
m
d
i
f
r
t
o
p
m
r
c
h
.
s
p
i
l
d
v
i
r
e
e
r
c
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
m
c
n
/
j
a
o
r
t
c
i
c
n
e
/
-
a
p
r
d
t
i
3
c
2
l
8
e
1
-
4
p
5
d
5
f
2
/
0
3
1
2
3
/
6
8
5
/
5
1
4
o
5
c
5
n
_
/
a
1
_
8
0
6
1
1
5
9
6
5
9
4
p
/
d
j
o
b
c
y
n
g
_
u
a
e
_
s
0
t
1
o
5
n
6
0
9
8
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
/
j
t
f
.
/
o
n
0
5
M
a
y
2
0
2
1
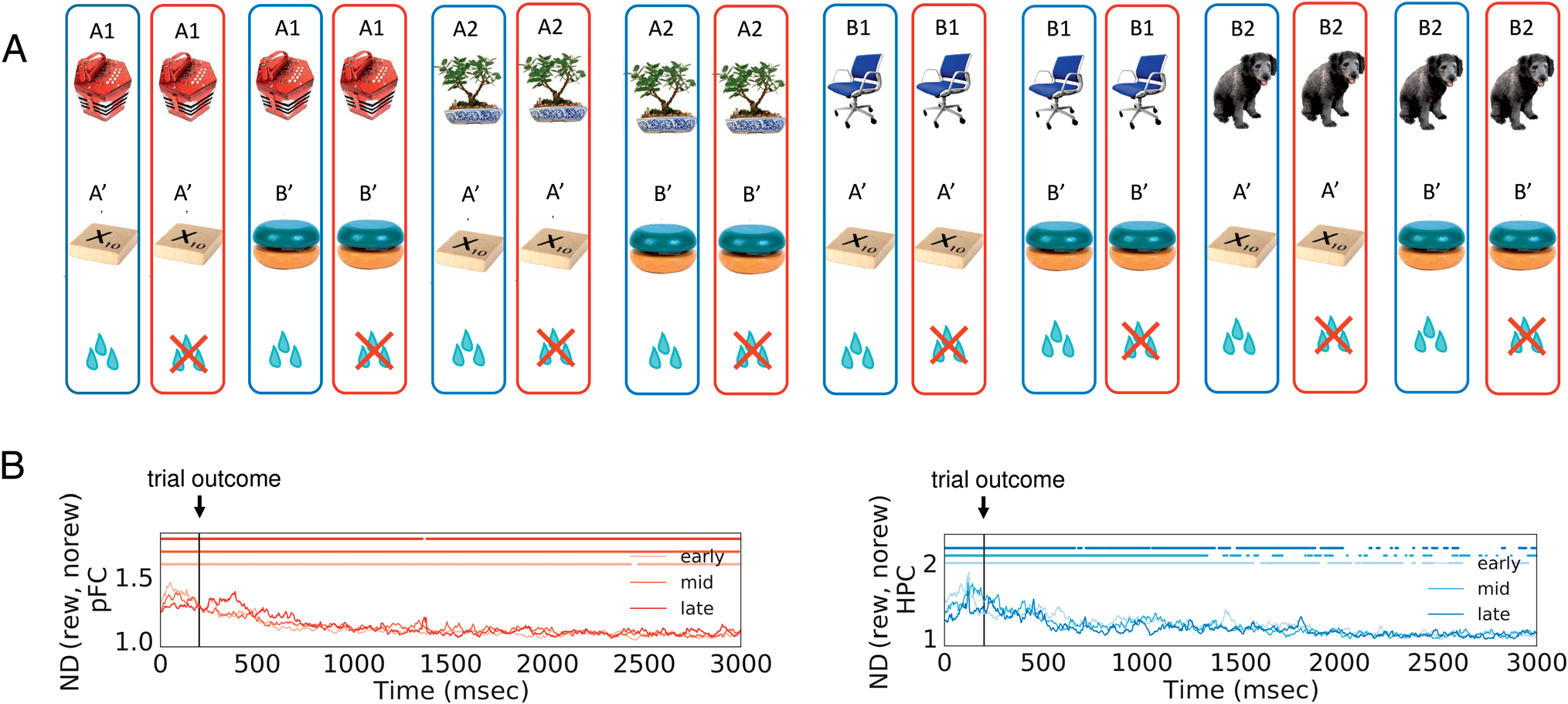
Figure 7. Normalized distance for trial outcome. The ND for trial outcome was calculated by grouping the neural trajectories according to if the
animal was rewarded (A). In PFC (B, red lines), the information for trial outcome persists throughout the 2.8-sec intertrial interval, as reflected by an
ND significantly greater than 1 (dots on the top part of the figure). In HPC, the information about trial outcome also persists for over a second
(B, blue lines). The shaded area shows 68% confidence interval computed from 10000 iterations of bootstrap resampling across sessions. Dots on top
represent time points when the ND is significantly larger than 1 ( p < .05, cluster-based permutation test).
third) and late (the last one third) learning periods
(Figure 5B, rightmost column, Mann–Whitney U test: p =
.003 between early and late, p = .01 between early and
mid). This possibly reflects some reconfigurations within
the HPC circuit that enable it to represent the associate
stimulus more strongly with learning.
Decision Variable/Movement Encoding
To investigate the neural signals about the upcoming
decision/movement after the monkeys received the se-
quence of stimuli, we computed the ND between match
and nonmatch trials. Because we only looked at correct
trials, the decision about match versus nonmatch trials is
perfectly confounded with movement preparation. In
this experiment, there is no way to look at one of them
without the influence of the other.
The ND between match and nonmatch trials is shown
in Figure 6. It was calculated by grouping the neural
trajectories according to whether it is a match or a non-
match trial (Figure 6A). In the PFC of one of the monkeys,
the ND between match and nonmatch trials starts to
ramp up halfway during the second stimulus presentation
period when all the information needed to form the de-
cision is present. There is a latency of about 150 msec
between the appearance of the associate information in
PFC and that of the decision information (Figure 6B).
This potentially indicates the time that the monkey took
to compare the incoming associate stimulus with the cue
stimulus in the working memory. In contrast, in HPC, the
ND between match and nonmatch trials fluctuates
around 1 until the time of the response saccade
(Figure 6B, blue lines). Therefore, HPC does not encode
the decision variable during the time when the
match/nonmatch decision is presumably being made.
Trial Outcome Encoding
In Brincat and Miller (2015), it was shown that the syn-
chrony between PFC and HPC increases after the trial out-
come, potentially serving as the communication signal
between the two brain regions to facilitate associative
learning. In this section, we computed the ND between
the rewarded and nonrewarded trials after the trial out-
come (Figure 7A). The information of trial outcome per-
sists for seconds in both PFC and HPC, as measured by an
ND that is significantly greater than 1. In PFC, the ND is
significantly greater than 1 throughout the 2.8-sec interval
we looked at after the trial outcome (Figure 7B, red lines).
In HPC, the ND falls back to 1 more quickly, but the infor-
mation on trial outcome still persists for more than 1 sec
(Figure 7B, blue lines). These results show that, aside
from the synchronous LFPs between PFC and HPC
(Brincat & Miller, 2015), the spiking activity in both
regions also carries information about the outcome of
the previous trial for seconds after the reward feedback.2
DISCUSSION
In this article, we developed a new metric called normalized
distance (ND) that characterizes neural information in the
population code based on the geometric organization of
Liu et al.
1463
neural trajectories in the state space. We then applied this
metric to recordings from a paired-associate learning task
(Brincat & Miller, 2015, 2016) to compare the dynamics of
the coding of different task variables across learning stages
and brain areas (PFC and HPC). We found the following:
(1) The PFC population carries information about the
identity of both the cue and the associate stimuli. (2) The
HPC population carries information about the identity of
the associate stimuli. The encoding of the cue stimuli is sta-
tistically significant in one of the two monkeys. (3) The PFC
population exhibits a longer network timescale for stimulus
coding (Figures 4 and 5). (4) The information about the cue
category is only intermittent in PFC and in one of the animals
in HPC (Figure 3). (5) The information about the previous
trial’s outcome persists for seconds in both PFC and HPC
(Figure 7). We also found other interesting neural signals,
albeit only in one of the two monkeys. These include the
following: (6) Coding for the associate object increases
with learning in HPC but not PFC (Figure 5), and (7) infor-
mation for decision/movement slowly ramps up in PFC but
not HPC (Figure 6).
The results of (3), (6), and (7) above were not reported
in the original article (Brincat & Miller, 2015, 2016). In
particular, the network timescale for object coding was
found to be longer in PFC than HPC, potentially provid-
ing suitable temporal dynamics for PFC to integrate in-
coming information from other cortices. It was indeed
reported that single neurons in PFC have, on average,
longer time constants than motor areas (Murray et al.,
2014).
In the original papers (Brincat & Miller, 2015, 2016),
the authors used another metric, bias-corrected PEV, to
calculate neural information across learning. They discov-
ered that the object category coding was present in PFC
but not HPC (Brincat & Miller, 2015, 2016). We found
some evidence that corroborates this finding (Figure 3).
However, they also found that the object category coding
increased with learning, which we did not find using the
ND metric (Figure 3). It could be that the different met-
rics used caused different results, but it should be noted
that learning effects are subtle in this experiment.
There are other studies that reported single-cell activ-
ity during associative learning (Suzuki, 2007; Sakai &
Miyashita, 1991). These earlier studies used metrics
based on single-cell firing rates to correlate with learning
performance and experimental conditions. In contrast, in
this article, the ND metric we used characterizes the dis-
tributed information in the population code.
The ND metric developed in this article serves a similar
role as decoding accuracy commonly adopted in analyz-
ing population-level data. In decoding analysis, hyper-
planes are constructed that separate training data from
different categories as much as possible according to
some objective function, and the decoding accuracy re-
flects how well these hyperplanes separate the held-out
test data. It is noted, however, that, in high-dimensional
cases where the number of neurons is comparable with
the number of data points (as in our case here as well as
data obtained by modern large-scale recording tech-
niques), the decoding accuracy can be generically high
(Buonomano & Maass, 2009) and thus does not necessar-
ily reflect the underlying geometry of the neural code. It
is therefore difficult to interpret results obtained by di-
rectly comparing decoding accuracies across different re-
cording sessions. On the other hand, ND is directly
computed from the geometrical configuration of the data
and therefore can be used regardless of the number of
data points compared with the number of dimensions.
Thus, ND provides a clear geometrical picture of the un-
derlying neural code, as illustrated using the simulated
data in Figure 2.
In this data set, HPC does not encode the category
information of the cues that would help predict the up-
coming stimuli even after learning. This seems contra-
dictory with the study by Stachenfeld et al. showing
that HPC contains a predictive map of the environment
(Stachenfeld, Botvinick, & Gershman, 2017), and the
study by McKenzie et al. showing rodent HPC popula-
tion encodes the hierarchical structure of the task
(McKenzie et al., 2014). However, the scenario studied
by Stachenfeld et al. is a reinforcement learning task in
a spatial setting where sensory experience is almost con-
tinuous. The task studied by McKenzie et al. also has a
spatial component, and the population activity was ob-
served to be largely organized by spatial context. On
the other hand, the task we analyzed here is a simple se-
quential associative learning task. It could be that, in this
simple setting, the HPC is not utilized to form more so-
phisticated relational representations (Eichenbaum,
2017).
The ND is directly calculated from the geometry of
neuronal population responses in the state space.
Therefore, it provides a characterization of the degree
of “tangling” of the underlying neuronal manifolds.
Disentangled neuronal manifolds were argued to be cru-
cial in forming a good neuronal representation for
higher-level processing (DiCarlo & Cox, 2007). An ND
larger than 1 indicates that the neuronal manifolds repre-
senting different variables are somewhat disentangled.
However, we do note that other geometric properties
such as curvature and topology (Bernardi et al., 2019;
Chaudhuri, Gerçek, Pandey, Peyrache, & Fiete, 2019)
are needed to provide a complete characterization of
the neuronal manifold.
Acknowledgments
Y. L. would like to thank John D. Murray for useful discussions.
All authors would like to thank the two anonymous reviewers
for helpful comments. This work was supported by U.S. Office
of Naval Research (ONR) MURI Award N00014-16-1-2832 ( Y. L.,
M. E. H., and E. K. M.), ONR DURIP Award N00014-17-1-2304
( Y. L., M. E. H., and E. K. M.), and NIMH R37MH087027 (S. L. B.
and E. K. M.).
1464
Journal of Cognitive Neuroscience
Volume 32, Number 8
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
t
n
p
o
:
a
/
d
/
e
m
d
i
f
r
t
o
p
m
r
c
h
.
s
p
i
l
d
v
i
r
e
e
r
c
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
m
c
n
/
j
a
o
r
t
c
i
c
n
e
/
-
a
p
r
d
t
i
3
c
2
l
8
e
1
-
4
p
5
d
5
f
2
/
0
3
1
2
3
/
6
8
5
/
5
1
4
o
5
c
5
n
_
/
a
1
_
8
0
6
1
1
5
9
6
5
9
4
p
/
d
j
o
b
c
y
n
g
_
u
a
e
_
s
0
t
1
o
5
n
6
0
9
8
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
/
j
f
/
t
.
o
n
0
5
M
a
y
2
0
2
1
Reprint requests should be sent to Yue Liu, Department of
Physics, Boston University, Boston, MA 02215, or via e-mail:
liuyue@bu.edu.
Notes
1.
In this experiment, we cannot tease apart the neural infor-
mation for decision variable versus general preparation of an
upcoming movement.
2.
In this analysis, we did not look at each monkey individ-
ually because there are not enough usable data for one of the
monkeys.
REFERENCES
Bernardi, S., Benna, M. K., Rigotti, M., Munuera, J., Fusi, S., &
Salzman, C. D. (2019). The geometry of abstraction in
hippocampus and pre-frontal cortex. bioRxiv. https://doi.org/
10.1101/408633.
Bi, G. Q., & Poo, M. M. (1998). Synaptic modifications in
cultured hippocampal neurons: Dependence on spike
timing, synaptic strength, and postsynaptic cell type. Journal
of Neuroscience, 18, 10464–10472.
Brincat, S. L., & Miller, E. K. (2015). Frequency-specific
hippocampal–prefrontal interactions during associative
learning. Nature Neuroscience, 18, 576–581.
Brincat, S. L., & Miller, E. K. (2016). Prefrontal cortex networks
shift from external to internal modes during learning.
Journal of Neuroscience, 36, 9739–9754.
Buonomano, D. V., & Maass, W. (2009). State-dependent
computations: Spatiotemporal processing in cortical
networks. Nature Reviews Neuroscience, 10, 113–125.
Chaudhuri, R., Gerçek, B., Pandey, B., Peyrache, A., & Fiete, I.
(2019). The intrinsic attractor manifold and population
dynamics of a canonical cognitive circuit across waking and
sleep. Nature Neuroscience, 22, 1512–1520.
DiCarlo, J. J., & Cox, D. D. (2007). Untangling invariant object
recognition. Trends in Cognitive Sciences, 11, 333–341.
Durstewitz, D., Vittoz, N. M., Floresco, S. B., & Seamans, J. K.
(2010). Abrupt transitions between prefrontal neural
ensemble states accompany behavioral transitions during
rule learning. Neuron, 66, 438–448.
Eichenbaum, H. (2017). On the integration of space, time, and
memory. Neuron, 95, 1007–1018.
Freedman, D. J., Riesenhuber, M., Poggio, T., & Miller, E. K.
(2001). Categorical representation of visual stimuli in the
primate prefrontal cortex. Science, 291, 312–316.
Golub, M. D., Sadtler, P. T., Oby, E. R., Quick, K. M., Ryu, S. I.,
Tyler-Kabara, E. C., et al. (2018). Learning by neural
reassociation. Nature Neuroscience, 21, 607–616.
Mante, V., Sussillo, D., Shenoy, K. V., & Newsome, W. T. (2013).
Context-dependent computation by recurrent dynamics in
prefrontal cortex. Nature, 503, 78–84.
Maris, E., & Oostenveld, R. (2007). Nonparametric statistical
testing of EEG- and MEG-data. Journal of Neuroscience
Methods, 164, 177–190.
McKenzie, S., Frank, A. J., Kinsky, N. R., Porter, B., Rivière, P. D.,
& Eichenbaum, H. (2014). Hippocampal representation of
related and opposing memories develop within distinct,
hierarchically organized neural schemas. Neuron, 83,
202–215.
Mongillo, G., Barak, O., & Tsodyks, M. (2008). Synaptic theory
of working memory. Science, 319, 1543–1546.
Murray, J. D., Bernacchia, A., Freedman, D. J., Romo, R.,
Wallis, J. D., Cai, X., et al. (2014). A hierarchy of intrinsic
timescales across primate cortex. Nature Neuroscience, 17,
1661–1663.
Remington, E. D., Narain, D., Hosseini, E. A., & Jazayeri, M.
(2018). Flexible sensorimotor computations through rapid
reconfiguration of cortical dynamics. Neuron, 98,
1005–1019.
Roy, J. E., Riesenhuber, M., Poggio, T., & Miller, E. K. (2010).
Prefrontal cortex activity during flexible categorization.
Journal of Neuroscience, 30, 519–8528.
Sadtler, P. T., Quick, K. M., Golub, M. D., Chase, S. M., Ryu, S. I.,
Tyler-Kabara, E. C., et al. (2014). Neural constraints on
learning. Nature, 512, 423–426.
Sakai, K., & Miyashita, Y. (1991). Neural organization for the
long-term memory of paired associates. Nature, 354,
152–155.
Schapiro, A. C., Turk-Browne, N. B., Norman, K. A., & Botvinick,
M. M. (2016). Statistical learning of temporal community
structure in the hippocampus. Hippocampus, 26, 3–8.
Stachenfeld, K. L., Botvinick, M. M., & Gershman, S. J. (2017).
The hippocampus as a predictive map. Nature Neuroscience,
20, 1643–1653.
Stokes, M. G. (2015). ‘Activity-silent’ working memory in
prefrontal cortex: A dynamic coding framework. Trends in
Cognitive Sciences, 19, 394–405.
Sussillo, D. (2014). Neural circuits as computational dynamical
systems. Current Opinion in Neurobiology, 25, 156–163.
Suzuki, W. (2007). Integrating associative learning signals across
the brain. Hippocampus, 17, 842–850.
Vyas, S., Even-Chen, N., Stavisky, S. D., Ryu, S. I., Nuyujukian, P.,
& Shenoy, K. V. (2018). Neural population dynamics
underlying motor learning transfer. Neuron, 97,
1177–1186.
D
o
w
n
l
o
a
d
e
d
l
l
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
f
r
o
m
D
o
h
w
t
t
n
p
o
:
a
/
d
/
e
m
d
i
f
r
t
o
p
m
r
c
h
.
s
p
i
l
d
v
i
r
e
e
r
c
t
c
.
m
h
a
i
e
r
d
.
u
c
o
o
m
c
n
/
j
a
o
r
t
c
i
c
n
e
/
-
a
p
r
d
t
i
3
c
2
l
8
e
1
-
4
p
5
d
5
f
2
/
0
3
1
2
3
/
6
8
5
/
5
1
4
o
5
c
5
n
_
/
a
1
_
8
0
6
1
1
5
9
6
5
9
4
p
/
d
j
o
b
c
y
n
g
_
u
a
e
_
s
0
t
1
o
5
n
6
0
9
8
.
p
S
d
e
f
p
e
b
m
y
b
e
g
r
u
2
e
0
s
2
t
3
/
j
f
.
/
t
o
n
0
5
M
a
y
2
0
2
1
Liu et al.
1465